上海市闵行区2006—2007学年初二年级上学期期末考试数学试卷
闵行区2007学年度第一学期期末试卷及答案

2007学年第一学期闵行区八年级期终考试数 学 试 卷(考试时间90分钟,满分100分)一、填空题(本题共14小题,每小题2分,满分28分) 1______________. 2.计算:2(2-= _____________.3.函数 y _______________.4.已知()f x 1()2f =______________.5.在实数范围内分解因式:221x x --=__________________________.6.已知关于x 的一元二次方程2340x x m ++-=的一个实数根是1,那么m =_______. 7.已知关于x 的一元二次方程24(4)0x x m --+=有两个不相等的实数根,那么m 的取值范围是_____________.8.已知直角坐标平面内两点 A (3,-1)和B (-1,2),那么A 、B 两点间的距离等 于_______.9.已知直角三角形的两边长分别为5,12,那么第三边的长为 . 10.底边为定长的等腰三角形的顶点的轨迹是 . 11.如果正比例函数的图像经过点(2,-3),那么它的函数解析式为 . 12.已知反比例函数1k y x-=的图像在每个象限内,y 的值 随x 的值增大而减小,那么k 的取值范围是_______. 13.如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30︒夹角,这棵树在折断前的高度为 米.学校_______________________ 班级__________ 学号_________ 姓名______________…………………………密○………………………………………封○………………………………………○线…………………………(第13题图)14.如图,在△ABC 中,AB = AC ,边AC 的垂直平分线分别交边AB 、AC 于点E 、F ,如果75B ∠=︒,那么∠BCE = ______度.二、选择题(本大题共4题,每题2分,满分8分)15.下列二次根式中,与8是同类二次根式的是 ………………………………( ) (A )12; (B )2.0; (C )43; (D )98. 160m n ⋅<),那么化简结果正确的是…………………………( ) (A) (B)-(C)-(D)17.在Rt △ABC 中,90A ∠=︒,∠B 与∠C 的平分线相交于点O ,那么∠BOC 等于…………………………………………………………………………………( ) (A )100°; (B )120°; (C )135°; (D )150°.18.下列命题中,其逆命题是真命题的命题个数有………………………………( ) (1)全等三角形的对应角相等;(2)对顶角相等;(3)等角对等边. (4)两直线平行,同位角相等;(5)全等三角形的面积相等; (A )1个;(B )2个;(C )3个; (D )4个.三、简答题(本大题共5题,每题6分,满分30分) 192(第14题图)ABCE F20.解方程:(1)(2)70x x -+=.21.在直角坐标平面内,已知点C 在x 轴上,它到点A (2,1)和点B (3,4)的距离相等,求点C 的坐标.22.已知正比例函数1y k x =(10k ≠)的图像经过A (2,-4)、B (m ,2)两点. (1)求m 的值;(2)如果点B 在反比例函数2k y x=(20k ≠)的图像经过,求反比例函数的解析式.23.已知:如图,E 是四边形ABCD 的边AD 上一点,且△ABC 和△CDE 都是等边三角形. 求证:BE = AD .四、(本大题共3题,每题8分,满分24分) 24.如图,在甲、乙两同学进行400米跑步比赛中,路程s (米)与时间t (秒)之间的函数关系的图像分别为折线OAB 和线段OC ,请根据图上信息回答下列问题:(1)_________________先到达终点; (2)第______秒时,_____追上_____; (3)比赛全程中,_____的速度始终保持不变;(4)写出优胜者在比赛过程中所跑的路程s (米)与时间t (秒)之间的函数关系式:_________________________.(第23题图)(第24题图)秒)25.如图,某小区在一个长为40米,宽为26米的长方形ABCD 场地上修建三条同样宽度的道路,其中两条道路与AB 平行,另一条道路与AD 平行,其余部分铺设草坪.如果每一块草坪的面积都是144平方米,求道路的宽度.26.如图,在四边形ABCD 中,︒=∠=∠90ADC ABC ,对角线AC 与BD 相交于点O ,M 、N 分别是边AC 、BD 的中点. (1)求证:MN ⊥BD ;(2)当︒=∠15BCA ,AC = 10 cm ,OB = OM 时,求MN 的长..(第26题图)ABCDMNOCD(第25题图)五、(本题满分10分)27.如图,在Rt △ABC 中,90BAC ∠=︒,AB = AC ,点M 、N 在边BC 上. (1)如图1,如果AM = AN ,求证:BM = CN ; (2)如图2,如果M 、N 是边BC 上任意两点,并满足45MAN ∠=︒,那么线段BM 、MN 、 NC 是否有可能使等式222MN BM NC =+ 成立?如果成立,请证明;如果不成立, 请说明理由.………………………………………………………………………………………………………………………………………………………密 封 线 内 不准 答 题ABCN(第27题图2)ABC(第27题图1)2007学年第一学期闵行区八年级期末考试数学试卷参考答案及评分意见一、填空题(本题共14小题,每小题2分,满分28分)1. 2. 21222-; 3.2x ≤; 4.22; 5.(11x x --;6.0;7.8m >-; 8.5; 9.13或119; 10.底边的垂直平分线(底边的中点除外); 11.32y x =-; 12.1k >; 13.12;14.︒45. 二、选择题(本大题共4题,每题2分,满分8分) 15..D ; 16.B ; 17.C ; 18.B ..三、简答题(本大题共5题,每题6分,满分30分)19.解:原式=4分)= ……………………………………………………………………(2分)20.解:原方程可变形为0722=-+x x ,……………………………………………………(2分)(9)(8)0x x +-=.……………………………………………………(2分)解得 19x =-,28x =.………………………………………………………(2分)所以,原方程的根是19x =-,28x =.21.解:设点C 坐标为(x ,0).…………………………………………………………(1分)利用两点间的距离公式,得 AC =BC = …(1分)根据题意,得AC = BC ,∴22AC BC =.即 22(2)1(3)16x x -+=-+.…………………………………………………(2分)解得 x = 10.……………………………………………………………(1分)所以,点C 的坐标是(10,0).………………………………………………(1分)22.解:(1)因为函数图像经过点A (2,-4),所以2 k 1 = -4,得k 1 = -2.………………………………………………………(2分)所以,正比例函数解析式:2y x =-.…………………………………………(1分)(2)根据题意,当 y = 2 时,-2 m = 2, 得m = -1.…………………………(1分)于是,由点B 在反比例函数2k y x =的图像上,得221k=-,解得 22k =-. 所以,反比例函数的解析式是2y x=-.………………………………………(2分)23.证明:∵△ABC 和△CDE 都是等边三角形,∴BC = AC ,CE = CD ,∠ACB = ∠ECD = 60º.……………………………(2分)∴∠ACB + ∠ACE = ∠ECD + ∠ACE .即得∠BCE = ∠ACD .…………(1分)在△BCE 和△ACD 中,,,,BC AC BCE ACD CE CD =⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△ACD (S .A .S ).……………………………………………(2分)∴BE = AD .……………………………………………………………………(1分)四、(本大题共3题,每题8分,满分24分)24.(1)乙;…………………………………………………………………………………(1分)(2)40,乙、甲;………………………………………………………………………(3分)(3)乙;…………………………………………………………………………………(1分)(4)S = 8 t (050t ≤≤).……………………………………………………………(3分)25.解:设道路的宽度为x 米. …………………………………………………………(1分)根据题意,得 (402)(26)6144x x --=⨯. …………………………………(3分)整理后,得 246880x x -+=.…………………………………………………(1分)解得 12x =,244x =(不合题意,舍去).…………………………………(2分)答:道路的宽度为2米. ………………………………………………………(1分)26.(1)证明:联结BM 、DM .∵︒=∠=∠90ADC ABC ,点M 、点N 分别是边AC 、BD 的中点,∴12BM DM AC ==.…………………………………………………(1分)∵N 是BD 的中点,∴MN ⊥BD . ……………………………………………………………(2分)(2)解:∵︒=∠15BCA ,12BM CM AC ==, ∴︒=∠=∠15CBM BCA .∴︒=∠30BMA .……………………………………………………………(2分)∵OB = OM ,∴︒=∠=∠30BMA OBM .…………………………………(1分)∵AC = 10,12BM AC =,∴BM = 5.……………………………………(1分)在Rt △BMN 中,90BNM ∠=︒,︒=∠30NBM , ∴12.52MN BM ==.………………………………………………………(1分)五、(本题满分10分)27.(1)证明:∵AB = AC ,∴∠B = ∠C .∵AM = AN ,∴∠AMN = ∠ANM .即得∠AMB = ∠ANC .…………………………………………………(1分)在△ABM 和△CAN 中,,,,AMB ANC B C AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△CAN (A .A .S ).………………………………………(2分)∴BM = CN .………………………………………………………………(1分)另证:过点A 作AD ⊥BC ,垂足为点D .∵AB = AC ,AD ⊥BC ,∴BD = CD .………………………………………(1分)同理,证得MD = ND .………………………………………………………(1分)∴BD MD CD ND -=-.即得 BM = CN .………………………………………………………………(2分)(2)222MN BM NC =+成立.证明:过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE = BM .联结AE 、EN . ∵AB = AC ,90BAC ∠=︒,∴45B C ∠=∠=︒.∵CE ⊥BC ,∴45ACE B ∠=∠=︒.………………………………………(1分)在△ABM 和△ACE 中,,,,AB AC B ACE BM CE =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△ACE (S .A .S ).∴AM = AE ,∠BAM = ∠CAE .…………………………………………(2分)∵90BAC ∠=︒,45MAN ∠=︒,∴45BAM CAN ∠+∠=︒.于是,由∠BAM = ∠CAE ,得45MAN EAN ∠=∠=︒.…………………(1分)在△MAN 和△EAN 中,,,,AM AE MAN EAN AN AN =⎧⎪∠=∠⎨⎪=⎩∴△MAN ≌△EAN (S .A .S ).∴MN = EN .…………………………………………………………………(1分)在Rt △ENC 中,由勾股定理,得222EN EC NC =+.即得222MN BM NC =+.…………………………………………………(1分)另证:由90BAC ∠=︒,AB = AC ,可知,把△ABM 绕点A 逆时针旋转90︒后,AB与AC 重合,设点M 的对应点是点E .于是,由图形旋转的性质,得AM =AE ,∠BAM = ∠EAN .…………………………………………………………(3分)以下证明同上.。
2022-2023学年上海市闵行区高二年级上册学期期末数学试题【含答案】

2022-2023学年上海市闵行区高二上学期期末数学试题一、填空题1.直线4350x y +-=的一个法向量为____________. 【答案】()4,3 (答案不唯一)【分析】根据直线的法向量的求法写出一个即可.【详解】解:由题知直线4350x y +-=的一个方向向量为()3,4-, 故该直线的一个法向量可为()4,3. 故答案为:()4,3 (答案不唯一)2.若a 是4m +,4m -的等差中项,则=a _________. 【答案】4【分析】根据等差中项的性质得到方程,解得即可. 【详解】解:因为a 是4m +,4m -的等差中项, 所以244a m m =++-,所以4a =. 故答案为:43.以点()3,4为圆心,且经过原点的圆的方程为________. 【答案】()()223425x y -+-=【分析】设圆的方程为()()22234x y r -+-=,再把原点坐标代入求出2r 可得答案. 【详解】由题设圆的标准方程为()()()222340x y r r -+-=>, 因为原点在圆上,所以()()222304025=-+-=r , 所以圆的标准方程为()()223425x y -+-=. 故答案为:()()223425x y -+-=. 4.双曲线221416y x -=的离心率为______.【分析】根据双曲线方程求出a 、c ,即可得解. 【详解】解:双曲线221416y x -=,则24a =,216b =,所以2a =,c =所以离心率ce a==5.过点()0,4作直线与抛物线2y x =有且仅有一个交点,这样的直线可以作出_______条. 【答案】3【分析】讨论三种情况:当直线的斜率不存在时符合题意;当直线的斜率k 存在,当0k =时符合题意;当0k ≠时,过点()0,4的直线l 与抛物线2y x =相切符合题意.【详解】解:(1)当过点()0,4的直线斜率不存在时,显然0x =与抛物线2y x =有且只有一个交点, (2)①当过点()0,4且直线与抛物线2y x =的对称轴平行,即斜率为0时,显然4y =与抛物线2y x =有且只有一个交点,②当直线过点()0,4且斜率存在,且与抛物线相切时,直线与抛物线只有一个交点,设直线方程为4y kx =+,代入到抛物线方程2y x =,消y 得:()2281160k x k x +-+=,由已知有0k ≠,则()2281640k k ∆=--= ,解得116k =,即直线方程为6411y x =+,综上可得:过点()0,4的直线l 与抛物线2y x =有且只有一个交点的直线l 共有3条 故答案为:36.直线1:330l x y -+=与直线2:0l x y +=的夹角记为θ,则cos θ=___________.【分析】根据直线方程可确定两直线倾斜角的正切值,由()12tan tan θθθ=-,结合两角和差正切公式可求得tan θ,进而由同角三角函数关系求得cos θ.【详解】设直线12,l l 的倾斜角分别为12,θθ,则11tan 3θ=,2tan 1θ=-,()1212124tan tan 3tan tan 221tan tan 3θθθθθθθ-∴=-===+, 又π0,2θ⎡⎤∈⎢⎥⎣⎦,cos θ∴=.7.已知集合(){}22,4M x y xy =+≤与()()(){}222,|11,0N x y x y r r =-+-≤>满足M N N ⋂=,则r 的取值范围是_______【答案】(0,2【分析】分别求出两圆的圆心坐标与半径,由M N N ⋂=,可得N M ⊆,即两圆内切或内含,通过半径关系即可求得答案.【详解】解:方程224x y +=表示以()0,0O 为圆心,12r =的圆,()()22211x y r -+-=表示以()1,1A 为圆心,2r r =的圆,则集合(){}22,4M x y xy =+≤表示以()0,0O 为圆心,12r =的圆形区域内点的集合(包含边界),集合()()(){}222,|11,0N x y x y r r =-+-≤>表示以()1,1A 为圆心,2r r =的圆形区域内点的集合(包含边界),因为M N N ⋂=,所以圆A 与圆O 内切或内含,所以2OA r -且0r >,解得02r <≤(0,2r ∈.故答案为:(0,28.若点P ,Q 在双曲线222023x y -=的渐近线上,且OPQ △的面积为1(O 为坐标原点),则PQ 长度的最小值为_______. 【答案】2【分析】先求出渐近线方程,发现两渐近线垂直,设出P ,Q 两点坐标,根据OPQ △面积为1,得出坐标之间关系,用坐标表示PQ ,再用基本不等式即可. 【详解】解:由题知双曲线方程为222023x y -=, 所以双曲线渐近线为y x =±, 故两条渐近线斜率之积为-1, 即两渐近线垂直, 故OPQ △为直角三角形, 记()()1122,,,P x x Q x x -,所以12,OP OQ ==, 因为三角形OPQ 的面积为1,所以112OP OQ ⋅=,122=, 解得121x x ⋅=,因为P Q ==≥=2=,当且仅当121x x ==时取等, 故PQ 长度的最小值为2. 故答案为:29.若直线()12y k x -=-与椭圆22116x y m+=恒有两个不同的公共点,则m 的取值范围是______.【答案】()4,1616,3⎛⎫+∞ ⎪⎝⎭【分析】首先求出直线过定点及方程表示椭圆时参数m 的取值范围,依题意定点()2,1在椭圆内部,即可得到不等式,解得即可.【详解】解:因为22116x y m+=表示椭圆,0m ∴>且16m ≠, 对于直线()12y k x -=-,令2010x y -=⎧⎨-=⎩,解得21x y =⎧⎨=⎩,即直线恒过定点()2,1,因为直线()12y k x -=-与椭圆22116x y m+=恒有两个不同的公共点, 所以点()2,1在椭圆内部,所以2221116m +<,解得43m >或0m <,综上可得()4,1616,3m ⎛⎫∈+∞ ⎪⎝⎭.故答案为:()4,1616,3⎛⎫+∞ ⎪⎝⎭10.若点(),P x y 在曲线()22314x y +-=上,且不等式20x y t +-<恒成立,则t 的取值范围是______.【答案】6t >【分析】不等式20x y t +-<恒成立,即()max 2t x y >+恒成立,取2cos ,3sin x y αα==+,[)0,2πα∈可知(),x y 在曲线上,代入2x y +,利用辅助角公式即可求得最大值,求出范围. 【详解】解:由题知不等式20x y t +-<恒成立, 即2t x y >+恒成立, 只需()max 2t x y >+即可,因为(),P x y 在曲线()22314x y +-=上,取2cos ,3sin x y αα==+,[)0,2πα∈, 即()2cos ,3sin P αα+, 所以2co 2s 2sin 6x y αα+=++()6αϕ=++6≤, 当π2αϕ+=时等式成立,故()max 62x y +=,即6t >.故答案为: 6t >11.设直线l :0ax by c ,其中a ,2b ,c 成等差数列.过原点O 作直线l 的垂线,垂足为P ,则P 到直线4370x y -+=距离的最大值为________. 【答案】235##4.6 【分析】根据等差中项的性质得到4a c b +=,即可得到直线l 恒过定点()1,4A -,求出点A 到直线4370x y -+=的距离,即可得解.【详解】解:因为a ,2b ,c 成等差数列,所以4a c b +=, 直线l :0ax by c ,则直线恒过点()1,4A -,则点()1,4A -到直线4370x y -+=的距离235d ==, 过原点O 作直线l 的垂线,垂足为P ,所以P 到直线4370x y -+=距离的最大值235. 故答案为:23512.如图,设曲线C 是由1C :()2168044y x y =-+-≤≤和2C :()2444y x y =-≤≤组成,对于点(),0B b ,若在曲线C 上恰好存在6个不同的点1P ,2P ,1Q ,2Q ,1M ,2M ,使得1P 和2P ,1Q 和2Q ,1M 和2M 都关于点B 对称,则b 的取值范围是_____________.【答案】5,42⎛⎫⎪⎝⎭【分析】首先判断这三对点中必有两组对称点,每一组对称点有一点在曲线()2444y x y =-<<上,而另一点在曲线()2168044y x y =-+-<<上,设()11,x y ,()22,x y 关于(),0B b 对称,即可得到方程组,从而得此式到2133280y b =-,再根据此式有两个不同解,求出b 的取值范围,即可得解.【详解】解:若()00R ,x y 是曲线()2444y x y =-≤≤上一点,即2004y x =,如果它关于(),0B b 的对称点()00,R x y '''也在此段曲线上,即2004y x ''=, 而()00102y y +=',即00y y '=-,所以22000044y y x x ''===,所以RR '垂直于x 轴, 同理,若曲线()2168044y x y =-+-≤≤上一点,如果它关于(),0B b 的对称点也在此段曲线上,则它们的连线垂直于x 轴,结合抛物线的对称性,可知,对于任意的(0,5)之间的b ,有且只有一对不同的点关于点(),0B b 对称. 为了在曲线上有三对不同的点关于(),0B b 对称,则必须有两组对称点,每一组对称点中必须有一点在曲线()2444y x y =-<<上,而另一点在曲线()2168044y x y =-+-<<上,设()11,x y ,()22,x y 关于(),0B b 对称,则()()21122212124801612102y x y x x x b y y ⎧=⎪=-⎪⎪⎨+=⎪⎪+=⎪⎩,()124,4y y <<-,从而()22111241680y y x x -=+-,即2133280y b =-,此式要在(-4,4)之间有两个不同解,即0328048b <-<,解得542b <<,即5,42b ⎛⎫∈ ⎪⎝⎭. 故答案为:5,42⎛⎫⎪⎝⎭二、单选题13.“35m -<<”是“方程22153x y m m +=-+表示椭圆”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】B【分析】先根据椭圆知识求出方程22153x y m m +=-+表示椭圆的充要条件,再根据必要不充分条件的概念可得结果.【详解】因为方程22153x ym m +=-+表示椭圆的充要条件是503053m m m m ->⎧⎪+>⎨⎪-≠+⎩,即35m -<<且1m ≠,故“35m -<<”是“方程22153x y m m +=-+表示椭圆”的必要而不充分条件.故选:B.【点睛】本题考查了椭圆的标准方程,考查了必要不充分条件,属于基础题. 14.A 是定直线外的一定点,则过点A 且与定直线相切的圆的圆心轨迹是( ) A .圆 B .椭圆C .双曲线的一支D .抛物线【答案】D【分析】设动圆的圆心为C ,因为圆C 是过定点A 与定直线l 相切的,所以CA d =,由抛物线的定义,即可判断轨迹.【详解】解:设动圆的圆心为C ,定直线为l , 因为圆C 是过定点A 与定直线l 相切的, 所以||CA d =,即圆心C 到定点A 和定直线l 的距离相等.且A 在l 外, 由抛物线的定义可知,C 的轨迹是以A 为焦点,l 为准线的抛物线.故选:D .15.已知三角形中三边长为a ,b ,c ,若lg a ,lg b ,lg c 成等差数列,则直线ax by a +=与直线bx cy b +=的位置关系为( )A .平行B .相交但不垂直C .垂直D .重合【答案】D【分析】根据等差中项的性质及对数的运算可得2ac b =,再根据两直线的位置关系判断即可. 【详解】解:因为lg a ,lg b ,lg c 成等差数列,所以lg lg 2lg a c b +=,即2ac b =, 对于直线ax by a +=与直线bx cy b +=,满足a b a b c b==, 所以直线ax by a +=与直线bx cy b +=重合. 故选:D16.设双曲线()22210y x b b-=>的左右焦点分别为1F ,2F ,双曲线上的点P 满足OP b =,且213PF PF =,则b =( ).A .2B .3C .22D .32【答案】A【分析】根据双曲线方程求出a ,再根据双曲线的定义及213PF PF =,求出1PF 、2PF ,再分别在2POF 、1POF △中利用余弦定理,即可得到225c b +=,从而求出2b ,即可得解. 【详解】解:双曲线()22210y x b b-=>,则1a =,因为213PF PF =且1222PF PF a -==,所以13PF =,21PF =,设2POF α∠=,则1πPOF α∠=-,在2POF 中2222222cos PF OF OP OF OP α=+-⋅,即2212cos c b bc α=+-①, 在1POF △中()2221112cos πPF OF OP OF OP α=+-⋅-,即2292cos c b bc α=++②,所以①+②得()22102c b =+,则225c b +=,又221c b =+,解得22b =,所以b =故选:A三、解答题17.已知圆C :()2221x y -+=.(1)判断直线y x =与圆的位置关系并说明理由; (2)过点()3,2向圆作切线,求切线的方程. 【答案】(1)相离 (2)3x =和3410x y --=【分析】(1)根据圆心到直线的距离即可判断直线y x =与圆的位置关系.(2)分别讨论切线的斜率存在和不存在的情况,根据圆心到切线的距离等于半径求解即可. 【详解】(1)圆C :()2221x y -+=,圆心()2,0C ,半径1r =,圆心()2,0C 到直线y x =的距离1d =,所以直线与圆的位置关系为相离.(2)当切线的斜率不存在时,设切线为3x =,则圆心()2,0C 到直线3x =的距离231d r =-==,符合条件.当切线的斜率存在时,设切线为:()23y k x -=-,即230kx y k -+-=,圆心()2,0C 到直线230kx y k -+-=的距离1d ==,解得34k =,即切线为:3410x y --=. 综上切线为:3x =和3410x y --= 18.在等差数列{}n a 中,已知45a =. (1)若21a =,求数列{}n a 的通项公式;(2)若数列的前5项和510S >,求公差的取值范围. 【答案】(1)23n a n =-(2)3d <【分析】(1)首先根据4242a a d -=-求出公差,即可求出通项公式; (2)设数列{}n a 的公差为d ,依题意可得153a d =-,再根据等差数列求和公式得到5255S d =-,从而得到不等式,解得即可.【详解】(1)解:因为45a =,21a =,所以公差42242a a d -==-,所以()2223n a a n d n =+-=-. (2)解:设数列{}n a 的公差为d ,因为45a =,所以135a d +=,则153a d =-, 所以()515454552552325S a d d d d -⨯⨯=+=+=-,因为510S >, 所以25510d ->,解得3d <.19.如图所示,一种建筑由外部的等腰梯形PQRS 、内部的抛物线以及水平的杠杆AB 组成,其中PS 和QR 分别与抛物线相切于A ,B ,A ,B 分别是PS 和QR 的中点.梯形的高和CD 的长度都是4米.(1)求杠杆AB 的长度; (2)求等腰梯形的周长. 【答案】(1)22 (2)102【分析】(1)以PQ 所在的直线为x 轴,O 为原点,PQ 的垂直平分线为y 轴建立平面直角坐标系,设AB CD 、分别与y 轴的交点为M N 、点,根据已知条件求出C D ,坐标,设抛物线的解析式为()20y ax a =<,代入D 求出抛物线方程,令=2y -解得x 可得答案;(2)由(1)242+==PQ SR AB ()(),00->P p p ,直线AP 的解析式为()0y kx b k =+≠,把A P 、代入解得,k b ,利用直线AP 的解析式与抛物线方程联立,再由Δ0=解得122==p p 得AP , A ,B 分别是PS 和QR 的中点得2==QR PS AP ,从而得出答案.【详解】(1)以PQ 所在的直线为x 轴,O 为原点,PQ 的垂直平分线为y 轴建立平面直角坐标系, 设AB CD 、分别与y 轴的交点为M N 、点,则y 轴为图象的对称轴, 且12AM MB AB ==,12==CN ND CD ,2==MN OM 米,2+=PQ SR AB ,所以()()2424,-,,--C D ,设抛物线的解析式为()20y ax a =<, 代入()24,-D 得()20y ax a =<解得1a =-,所以()222=--<<y x x , 当=2y -时22x -=-,解得x =())22-,-A B ,所以(==AB , 所以杠杆AB的长度为(2)由(1)2+==PQ SR AB()2-A ,设()(),00->P p p,且≠p 直线AP 的解析式为()0y kx b k =+≠,把A P 、代入得20b pk b ⎧+=-⎪⎨+=⎪⎩,解得k b ⎧=⎪⎪⎨⎪=⎪⎩所以直线AP的解析式为=+y x,与抛物线方程联立得20=x , 因为PS 和QR 分别与抛物线相切于A ,B ,所以20⎛⎫∆=-=40⎫=⎪⎭p ,40-=p,解得p ,经检验,p =是分式方程的根,符合题意,所以0⎛⎫ ⎪ ⎪⎝⎭P,由勾股定理得=AP 因为A ,B 分别是PS 和QR的中点,所以2===QR PS AP所以+++==QR PS PQ SR即等腰梯形的周长为.20.已知双曲线C :()222210,0x y a b a b-=>>的左、右焦点分别为1F 、2F ,直线l 过右焦点2F 且与双曲线C 交于A 、B 两点.(1)若双曲线C 322C 的焦点坐标; (2)设1a =,3b =l 的斜率存在,且()110F A F B AB +⋅=,求l 的斜率; (3)设l 35OA OB OA OB +=-,求双曲线C 的离心率. 【答案】(1)(3,0),(3,0) (2)15(3)2【分析】(1)由离心率公式和,,a b c 的关系,即可得到结果;(2)求出右焦点的坐标,设出直线方程,与双曲线方程联立,由韦达定理结合已知条件,即可求出直线的斜率.(3)设直线l 的方程为()y k x c =-,与双曲线方程联立,消元,运用韦达定理,结合由题意得出的0OA OB ⋅=,即可得到a 、c 的关系,从而求出离心率. 【详解】(1)解:由题意得222222,3,cb ec a b a====+, 解得1,2,3a b c ===故双曲线C 的焦点坐标为(3,0),(3,0)-.(2)解:双曲线2213y x -=,可得2(2,0)F , 设()()1122,,,A x y B x y ,直线l 的斜率为:2121y y k x x -=-,设直线l 的方程为(2)y k x =-,联立直线与双曲线的方程22213y kx k y x =-⎧⎪⎨-=⎪⎩,消去y 得()222234430kxk x k -+--=,由直线与双曲线有两个交点,则230k -≠且()23610k ∆=+>,即k ≠可得212243k x x k +=-,则()21212224124433k k y y k x x k k k ⎛⎫+=+-=-= ⎪--⎝⎭, 又()1112,F A x y =+,()1222,F B x y =+()110F A F B AB +⋅=,可得()()112221124,,0x x y y x x yy +++⋅--=,即()()()()1121222140x x x x y y y y ++-++-=, 将2121y y k x x -=-代入上式,可得()121240x x y y k ++++=, 得2224124033k k k k k ++⋅=--,可得235k =,解得k =l的斜率为. (3)解:右焦点为2(,0)F c ,设直线l 的方程为()y k x c =-,()()1122,,,A x y B x y ,联立直线与双曲线的方程2222()1y k x c x y a b =-⎧⎪⎨-=⎪⎩,消去y 得:()2222222222220b a k x ca k x a k c a b -+--=,()()24422222222 440c a k b a k a k c a b ∆=+-+>,222222212122222222,ca k a k c a b x x x x b a k b a k ---+==--,则()2222222212121212222()()a b b c y y k x c x c k x x c c x x k a k b -⎡⎤=--=+-+=⋅⎣⎦-,由OA OB OA OB +=-,得()()22OA OBOA OB +=-,整理得0OA OB ⋅=,则12120x x y y +=,即()22222222220a b a k c k a b b c ++-=,则()()2222222222220a b a k a b k a b b a b +⎡+++⎤⎣⎦-=,整理得2224422a b k b a a b=--,因为l 的斜率35k =,所以22442235a b b a a b=--,整理得223b a =, 则2223c a a -=,224c a =,2c a =, 所以离心率2ce a==. 21.已知椭圆方程为223144x y +=,左右焦点分别为1F ,2F ,()2,0A 是长轴的右端点.点C 在椭圆上,C 关于原点的对称点为B .过C 作直线l 垂直于x 轴,与x 轴相交于M .(1)当C 为椭圆的上顶点时,求三角形12F F C 的周长(直接写出结果); (2)若C 在第一象限,且直线BM 与直线AC 的斜率乘积为12-,求tan BAC ∠;(3)在(2)的条件下,设PQ 是椭圆上位于第四象限的两点(Q 在P 的右边),直线l 与线段PQ 相交于N ,且满足PN QC PC QN ⋅=⋅.判断四边形AQPB 的形状,并说明理由. 【答案】(1)464 (2)2;(3)四边形AQPB 是梯形,理由见解析.【分析】(1)由椭圆方程求出,,a b c ,结合椭圆性质即可得;(2)设00(,)C x y ,由已知斜率之积为12-和点C 在椭圆上,求得C 点坐标后,判断出AC BC ⊥,在直角三角形中计算;(3)由PN QC PC QN ⋅=⋅得PN PCQN QC=,由三角形面积公式得出PCN QCN ∠=∠,则PC CQ k k =-,设QC 的斜率为k ,直线QC 的方程为1(x 1)y k -=-,则直线PC 的方程为1(1)y k x -=--,直线方程与椭圆方程联立后求得,Q P 坐标,计算出PQ k 后即可得.【详解】(1)2a =,23b =42643c =-=,C 为椭圆的上顶点时,122CF CF a ===,12462F F c ==,∴12CF F △的周长为224a c += (2)设00(,)C x y ,(000,0x y >>),则00(,)B x y --,00(),M x ,又(2,0)A , 00001222BM ACy y k k x x =⋅=--,2000(2)y x x =--,代入22003144x y +=,得200320x x -+=,解得01x =或02x =(与A 重合,舍去),∴01y =,即(1,1)C , 由10112AC k -==--,1BC k =,得AC BC ⊥,又AC ==BC ==∴tan 2BCBAC AC∠==; (3)设1122(,),(,P x y Q x y ), 由PN QC PC QN ⋅=⋅得PN PCQN QC=, 1sin 21sin 2PCN QCNPC CN PCN PN PC S QNSQC QC CN QCN ∠===∠,∴sin sin PCN QCN ∠=∠, PCN ∠与∠QCN 均为锐角,所以PCN QCN ∠=∠,则PC CQ k k =-,设QC 的斜率为k ,直线QC 的方程为1(x 1)y k -=-,则直线PC 的方程为1(1)y k x -=--,由22341(1)x y y k x ⎧+=⎨-=-⎩,得222(13)6(1)3610k x k k x k k ++-+--=, 1x =是此方程的一根,∴22236113k k x k --=+,同理21236113k k x k +-=+,22(1)1y k x =-+,11(1)1y k x =--+,所以2222211222212122361361(2)(2)1131336136131313PQk k k k k y y k x x k k k k k k k x x x x k k +---+--+-++====--+----++, 又101123AB k --==--,即AB PQ k k =,所以//AB PQ ,由椭圆的对称性BP AQ ≠, 所以四边形AQPB 是梯形.【点睛】关键点点睛:本题考查直线与椭圆相交问题,解题关键在于由PN QC PC QN ⋅=⋅判断出直线PC 与QC 的斜率相反,因此引入直线QC 的斜率k 为参数,求出,Q P 点坐标,然后通过计算出得平行的结论.。
2022-2023学年上海市闵行区闵行中学、文绮中学高二年级下册学期3月月考数学试题【含答案】

2022-2023学年上海市闵行区闵行中学、文绮中学高二下学期3月月考数学试题一、填空题1.小张同学计划从6本历史类读本、5本军事类读本和3本哲学类读本中任选1本阅读,则不同的选法共有______种.【答案】14【分析】根据分类加法计数原理可得答案.【详解】解:根据分类加法计数原理可知,共有种不同的选法.65314++=故答案为:14.2.五名旅客在三家旅店投宿的不同方法有______种.【答案】53【分析】每名旅客都有种选择,根据分步乘法计数原理可得出五名旅客投宿的方法种数.3【详解】由于每名旅客都有种选择,因此,五名旅客在三家旅店投宿的不同方法有种.353故答案为:.53【点睛】本题考查分步乘法计数原理的应用,考查计算能力,属于基础题.3.计算:__________.01220232023202320232023C C C C ++++= 【答案】20232【分析】由二项式定理性质可知所有二项式系数和为,即可得出结果.()1nx +2n【详解】由题意可知,()1202C 1C C C nn nn n n n x x x x+=⋅⋅+++⋅+ 当时,令,即可得.2023n =1x =012202320232023202320232023C C C C 2++++= 故答案为:202324.在5名男生和4名女生中选出3人,至少有一名男生的选法有________种(填写数值).【答案】80【分析】先由题意,分别确定从5名男生和4名女生中选出3人,和选出的3人全部都是女生对应的选法种数,进而可求出结果.【详解】从5名男生和4名女生中选出3人,共有种选法;3998784321C ⨯⨯==⨯⨯选出的3人全部都是女生,共有种选法;344C =因此,至少有一名男生的选法有种.84480-=故答案为80【点睛】本题主要考查组合问题,熟记组合的概念,以及组合数的计算公式即可,属于常考题型.5.若,则______.()()34222141214112x x x a a x a x a x +-⋅-=++++ 12314a a a a ++++= 【答案】0【分析】赋值法求二项展开式部分项的系数之和.【详解】令,()()()342221401214112f x x x x a a x a x a x =+-⋅-=++++ 则,,()001f a ==()12310411a a a f a a +++=+=+ 所以.()()12314100a a a a f f ++++=-= 故答案为:0.6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中能被5整除的数共有______个.【答案】216【分析】分个位是0或者5两种情况利用排列知识讨论得解.【详解】当个位是0时,前面四位有种排法,此时共有120个五位数满足题意;45120A =当个位是5时,首位不能是0,所以首位有4种排法,中间三位有种排法,所以此时共有4424A =个五位数满足题意.424=96⨯所以满足题意的五位数共有个.120+96=216故答案为216【点睛】本题主要考查排列组合的应用,意在考查学生对该知识的理解掌握水平.7.在的展开式中,项的系数为_____________.(用数字作答)()9a b c ++432a b c 【答案】1260【分析】由,然后利用二项式定理得出含项为,然后利用()()99a b c a b c ++=++⎡⎤⎣⎦4a ()5549C a b c +二项式展开式通项求出中项的系数,与相乘即可得出结果.()5b c +32b c 59C 【详解】,展开式中含的项为,()()99a b c a b c ++=++⎡⎤⎣⎦ 4a ()5549C a b c +中含项为,()5b c +32b c 2325C b c 因此,的展开式中项的系数为.()9a b c ++432a b c 52951260C C =故答案为.1260【点睛】本题考查二项展开式的应用,在处理含三项的问题时,可将其转化为两项的和来处理,考查运算求解能力,属于中等题.8.今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有_____种不同的方法(用数字作答)【答案】1260【详解】同色球不加以区分,共有(种)排法.【解析】排列与组合.9.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的两张参观券连号,那么不同的分法种数是________.【答案】96【详解】试题分析:5张参观券全部分给4人,分给同一人的2张参观券连号,方法数为:1和2,2和3,3和4,4和5,四种连号,其它号码各为一组,分给4人,共有4×=96种44A 【解析】排列、组合及简单计数问题10.“赛龙舟”是端午节的习俗之一,也是端午节最重要的节日民俗活动之一,某单位龙舟队欲参加端午节龙舟赛,参加训练的8名队员中有3人只会划左桨,3人只会划右桨,2人既会划左桨又会划右桨.现要选派3人划左桨、3人划右桨共6人去参加比赛,则不同的选派方法共有__________种.【答案】37【分析】按照所选得6人中所含会划左右桨的人数进行分类,即可得到答案.【详解】第一类:参加比赛的6人中没有会划左右桨的,共有种,3333C C 1=第二类:参加比赛的6人中有1人会划左右桨的,共有种,1322332C C C 12=第三类:参加比赛的6人中有2人会划左右桨的,共有种,132233332C C 2C C 24+=则共有种.1122437++=故答案为:3711.一个口袋内有4个不同的红球,6个不同的白球,若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种__________.【答案】186【详解】试题分析:设取红球个,白球个,则x y 5(04){27(06)x y x x y y +=≤≤+≥≤≤,取法为.234{,{,{321x x x y y y ===∴===233241464646186C C C C C C ++=【解析】古典概型.12.定义域为集合上的函数满足:{1,2,3,,12}⋅⋅⋅()f x ①;②();③、、成等比数列;这样的不同(1)1f =|(1)()|1f x f x +-=1,2,,11x =⋅⋅⋅(1)f (6)f (12)f 函数的个数为________()f x 【答案】155【分析】分析出f (x )的所有可能的取值,得到使f (x )中f (1)、f (6)、f (12)成等比数列时对应的项,再运用计数原理求出这样的不同函数f (x )的个数即可.【详解】解:经分析,f (x )的取值的最大值为x ,最小值为2﹣x ,并且成以2为公差的等差数列,故f (6)的取值为6,4,2,0,﹣2,﹣4.f (12)的取值为12,10,8,6,4,2,0,﹣2,﹣4,﹣6,﹣8,﹣10,所以能使f (x )中的f (1)、f (6)、f (12)成等比数列时,f (1)、f (6)、f (12)的取值只有两种情况:①f (1)=1、f (6)=2、f (12)=4;②f (1)=1、f (6)=﹣2、f (12)=4.|f (x +1)﹣f (x )|=1(x =1,2,…,11),f (x +1)=f (x )+1,或者f (x +1)=f (x )﹣1,即得到后项时,把前项加1或者把前项减1.(1)当f (1)=1、f (6)=2、f (12)=4时;将要构造满足条件的等比数列分为两步,第一步:从f (1)变化到f (6),第二步:从f (6)变化的f (12).从f (1)变化到f (6)时有5次变化,函数值从1变化到2,故应从5次中选择3步加1,剩余的两次减1.对应的方法数为10种.35C =从f (6)变化到f (12)时有6次变化,函数值从2变化到4,故应从6次变化中选择4次增加1,剩余两次减少1,对应的方法数为15种.46C =根据分步乘法原理,共有10×15=150种方法.(2)当f (1)=1、f (6)=﹣2、f (12)=4时,将要构造满足条件的等比数列分为两步,第一步:从f (1)变化到f (6),第二步:从f (6)变化的f (12).从f (1)变化到f (6)时有5次变化,函数值从1变化到﹣2,故应从5次中选择1步加1,剩余的4次减1.对应的方法数为5种.15C =从f (6)变化到f (12)时有6次变化,函数值从﹣2变化到4,故应从6次变化中选择6次增加1,对应的方法数为1种.66C =根据分步乘法原理,共有5×1=5种方法.综上,满足条件的f (x )共有:150+5=155种.故填:155.【点睛】解决本题的难点在于发现 f (x )的取值规律,并找到使f (1)、f (6)、f (12)成等比数列所对应的三项.然后用计数原理计算种类.本题属于难题.二、单选题13.的二项展开式中,二项式系数最大的项是第( )项.10(1)x -A .6B .5C .4和6D .5和7【答案】A【分析】由二项展开的中间项或中间两项二项式系数最大可得解.【详解】因为二项式展开式一共11项,其中中间项的二项式系数最大,10(1)x -易知当r =5时,最大,即二项展开式中,二项式系数最大的为第6项.10rC 故选:A14.将4名新老师安排到三所学校去任教,每所学校至少一人,则不同的安排方案的种数是,,A B C ( )A .54B .36C .24D .18【答案】B【分析】分类讨论分别有两名新教师的情况,进而计算出4名新教师安排到三所学校,,A B C ,,A B C 去任教每所学校至少一人的所有情况,【详解】将4名新教师安排到三所学校去任教,每所学校至少一人,分配方案是:,,,A B C 1,1,2学校有两名新老师:;A 2142C C 12=学校有两名新老师:;B 2142C C 12=学校有两名新老师:C 2142C C 12=所以共有种情况,2142363C C =故选:B.15.已知,则被10除所得的余数为( )122332020202020201C 2C 2C 2C 2a =+++++ a A .0B .1C .2D .3【答案】B【分析】根据题意得到,再利用二项式定理展开即可得到答案.()10201039101a ===-【详解】,()201223320202010202020201C 2C 2C 2C 21239a =+++++=+== 又因为,()()()()10290101928910101010101C 10C 101C 101C 1011a =-=+-+-++-+ 又因为都是10的倍数,()()()290101928910101010C 10,C 101,C 101,,C 101--- 所以被除所得的余数为.a 101故选:B16.已知r ,s ,t 为整数,集合A ={a |a =2r +2s +2t ,0≤r <s <t }中的数从小到大排列,组成数列{an },如a 1=7,a 2=11,a 121=( )A .515B .896C .1027D .1792【答案】C【解析】(1)由于为整数且,下面对进行分类讨论:最小取2时,符合条件 r s t 、、0,r s t ≤<<t t 同理可得,,……,时符合条件的的个数,最后利用加法原理计算即127,11,a a ==3t =4t =10t =a 得.【详解】为整数且最小取,此时符合条件的数有,当时,可 r s t 、、0,r s t t ≤<<∴2a 221C =3t =,s r 在0,1,2中取,符合条件有的数有所以a 233C =,同理0120130231232227,22211,22213a a a =++==++==++= 时,符合条件有的数有,……,时,符合条件有的数有4t =a 246C =t n =a 2nC ,且,是的最小值,即时,.222234123++++n n C C C C C += (3)10=120C 121a 111n +=10t =01101212221027a =++=故选:.C 【点睛】本题考查组合及组合数公式,有理数指数幂的运算性质,数列的概念及简单表示法,难度较难.三、解答题17.解方程(1);421010x C C +=(2).4321126n n P P +=【答案】(1)或;(2)2x =4x =4n =【分析】(1)根据得到或,计算得到答案;421010x C C +=24x +=26x +=(2)根据排列公式计算得到答案.4321126n n P P +=【详解】(1)则或,解得或 421010x C C +=24x +=26x +=2x =4x =(2),即4321126n n P P +=(21)(2)(21)(22)126(1)(2)n n n n n n n +--=--化简得到:,解得或(舍去)28631240n n -+=4n =318n =【点睛】本题考查了解关于排列的方程,漏解是容易发生的错误,意在考查学生的计算能力.18.晚会上有5个不同的歌唱节目和3个不同的舞蹈节目,分别按以下要求各可以排出多少种不同的节目单:(1)3个舞蹈节目排在一起;(2)3个舞蹈节目彼此分开;(3)3个舞蹈节目先后顺序一定;(4)前4个节目中既要有歌唱节目,又要有舞蹈节目.【答案】(1)4320;(2)14400;(3)6720;(4)37440.【分析】(1)要把个舞蹈节目要排在一起,则可以采用捆绑法,把三个舞蹈节目看做一个元素和另3外个元素进行全排列,不要忽略三个舞蹈节目本身也有一个排列.5(2)个舞蹈节目彼此要隔开,可以用插空法来解,即先把个唱歌节目排列,形成个位置,选三个356把舞蹈节目排列.(3)使用倍分法分析:先求出个节目全排列的排法数目,分析三个舞蹈节目本身的顺序,由倍分法计8算可得答案.(4)先不考虑限制条件,个节目全排列有种方法前 个节目中要有舞蹈的否定是前四个节目全是888P 唱歌有用所有的排列减去不符合条件的排列,得到结果.4454P P 【详解】(1),33664320P P =(2),535614400P P =(3),33886720P P =(4).84485437440P P P -=【点睛】本题主要考查的是排列组合公式的应用,以及捆绑法、插空法、倍分法的应用,是基础题.19.(1)已知的展开式中的“二项式系数之和”比“各项系数之和”大255,求的值;nn (2)求展开式所有的有理项;8(3)求展开式中系数最大的项.8【答案】(1);(2);(3)84112,256x x -731792x-【分析】(1)先求各项系数和,再求二项式系数和计算求解即可;(2)先写出展开式的通项公式,按照有理项求解即可;(3)根据通项公式求出系数,计算系数最大可得,再应用通项公式求解即得.6r =【详解】(1)令可得,展开式中各项系数之和为,而展开式中的二项式系数之和为,1x =(1)n-2n,2(1)255,8n n n ∴--=∴=(2);883322188C (2)(2)C r r rr r rrr r T x xx----+=-=- 当为整数时,为有理项,则或832r r--1r T +2r =8r =所以展开式所有的有理项为:;4112,256x x -(3)设第项最大,且为偶数1r +r 则,解得:,22882288(2)C (2)C (2)C (2)C r r r r r r r r ++--⎧-≥-⎨-≥-⎩6r =所以展开式中系数最大的项为:.8667663238(2)C 1792xx----=20.设函数,其中.()223ln 1f x a x ax x =+-+0a >(1)当时,求函数在处的切线方程;1a =()y f x =()1,3(2)讨论的单调性;()y f x =(3)若的图象与轴没有公共点,求的取值范围.()y f x =x a【答案】(1)3y =(2)函数在上单调递减,在上单调递增()f x 10,a ⎛⎫⎪⎝⎭1,a ⎛⎫+∞ ⎪⎝⎭(3)1,e⎛⎫+∞ ⎪⎝⎭【分析】(1)利用导数求出切线的斜率,得切线方程;(2)求出函数导数,解关于导函数的不等式即可得出单调区间;(3)根据函数有最小值,只需满足最小值大于0即可得解.【详解】(1)当时,,故,1a =()()233ln 1,21f x x x x f x x x =+-+=+-'()10f '=此时函数在处的切线方程为:.()y f x =()1,33y =(2)由题意,的定义域为,()f x ()0,∞+,()()()2221233232ax ax a x ax f x a x a x x x -++-='=+-=则当时,单调递增;当时,单调递减.1x a >()()0,f x f x '>10x a <<()()0,f x f x '<故函数在上单调递减,在上单调递增.()f x 10,a ⎛⎫⎪⎝⎭1,a ⎛⎫+∞ ⎪⎝⎭(3)由(2)知函数的最小值为, ()f x 1f a ⎛⎫ ⎪⎝⎭又,且的图象与轴没有公共点,()2110f a a =++>()y f x =x 只需的最小值恒大于0,即恒成立,()f x 10f a ⎛⎫> ⎪⎝⎭故,得,221113ln 10a a a a a ⎛⎫⋅-+> ⎪⎝⎭+1e >a 所以的取值范围为.a 1,e ⎛⎫+∞ ⎪⎝⎭21.我们称元有序实数组为维向量,为该向量的范数,()*n n ∈N ()12,,,nx x x n 12nxx x +++ 已知维向量,其中,记范数为奇数的维向量的个数为n ()12,,,n a x x x ={}1,0,1,1,2,i x i n∈-= n a,这个向量的范数之和为.nA nA nB(1)求和的值;2A 2B (2)求的值;2023A (3)当为偶数时,证明:.n ()131n n B n -=⋅-【答案】(1)224,4A B ==(2)2023312+(3)证明见解析【分析】(1)根据新定义计算即可;(2)类比(1),结合排列组合的知识,二项式定理,求解即可;2023A (3)类比(2)的考虑方法,可得,0221C 2C 2C 2n n n n n n n A --=⋅+⋅++⋅ ,由二项式定理可得,根据组合数的运()()113311C 23C 2C2n n n n nnnB n n ---=-⋅⋅+-⋅⋅++⋅ 312n nA -=算性质化简得解.nB 【详解】(1)范数为奇数的二元有序实数对有:,()()()()1,0,1,0,0,1,0,1--它们的范数依次为,1,1,1,1;224,4A B ∴==(2)当为奇数时,在向量的个坐标中,n ()12,,n a x x x =n要使得范数为奇数,则0的个数一定是偶数,可按照含0个数为进行讨论:∴0,2,4,,1n - 的个坐标中含0个0,其余坐标为1或-1,an 共有个,每个的范数为;0C 2n n ⋅a n 的个坐标中含2个0,其余坐标为1或-1,an 共有个,每个的范数为;22C 2n n -⋅a 2n -的个坐标中含个0,其余坐标为1或-1,an n 1-共有个,每个的范数为1;1C 2n n -⋅a ,0221C 2C 2C 2n n n n n n n A --∴=⋅+⋅++⋅ ,0221(21)C 2C 2C 2C n n n n n n n n n --+=⋅+⋅++⋅+,022(21)22C C C (1)n n n n n n n n --=⋅-⋅++- 两式相加除以2得:022131C 2C 2C 22n n n n n n n n A --+=⋅+⋅++⋅= .20232023312A +∴=(3)当为偶数时,在向量的个坐标中,要使得范数为奇数,则0的个数一n ()123,,,,n a x x x x =n 定是奇数,所以可按照含0个数为:进行讨论:的个坐标中含1个0,其余坐标为11,3,,1n ⋯-a n 或-1,共有个,每个的范数为;11C 2n n -⋅a n 1-的个坐标中含3个0,其余坐标为1或-1,共有个,每个的范数为;a n 33C 2n n -⋅a 3n -的个坐标中含个0,其余坐标为1或-1,a n n 1-共有个,每个的范数为1;所以,1C 2n n -⋅a 11331C 2C 2C 2n n n n n n n A ---=⋅+⋅++⋅ .()()113311232C 2n n nn n n n B n C n C ---=-⋅⋅+-⋅⋅++⋅ 因为,①01122(21)C 2C 2C 2C n n n n nn n n n --+=⋅+⋅+⋅++ ,②01122(21)C 2C 2C 2(1)C n n n n n nn n n n ---=⋅-⋅+⋅-+- 得,,2-①②113331C 2C 22n n n n n ---⋅+⋅+= 所以.312n n A -=思路一:因为,()()()()()11!!C C !!!1!kk n n n n n k n k n n k n k k n k --⇒-=-⋅=⋅=---所以.()()113311C 23C 2C 2n n nn n n n B n n ---=-⋅⋅+-⋅⋅++⋅ ()11331111C 2C 2C 2n n nn n n n ------=⋅+⋅++⋅ ()123411112C 2C 2C n n nn n n n ------=⋅+⋅++ .()11312312n n n n --⎛⎫-=⋅=⋅- ⎪⎝⎭思路二:得,.2+①②02231C 2C 22n n n n n -+⋅+⋅+= 又因为,()()()()111!!C C !!1!!k k n n n n k k n n k n k k n k ---=⋅=⋅=---所以()()()()111!!C C !!1!!k kn n n n k k n n k n k k n k ---=⋅=⋅=---()()()1133111331C 2C 2C 2C 23C 21C 2n n n n n nn n n n n n n n ------=⋅+⋅++⋅-⋅+⋅⋅++-⋅⋅()()10123211113131C 2C 2C 23122n n n n n n n n n n nA n n n --------⎛⎫-+=-⋅+⋅++⋅=⋅-=⋅- ⎪⎝⎭【点睛】关键点点睛:本题的难点在于理解新定义,学会类比的方法从特殊到一般,其次对组合数,二项式式定理的的灵活运用,化简变形要求较高,属于难题.。
上海市闵行区上海师范大学附属中学闵行分校2023-2024学年高一下学期6月期末考试数学试题

2023-2024学年上海师大附中闵行分校高一(下)期末数学试卷一、填空题(本大题共有12小题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,1-6题每个空格填对得4分,7-12题每个空格填对得5分,否则一律得0分。
1.(4分)若复数z=(m2﹣m﹣2)+i(m2﹣4)是纯虚数,则实数m= .2.(4分)已知向量=(x,1),=(﹣2,2),若,则实数x= .3.(4分)函数f(x)=sin2x的最小正周期为 .4.(4分)若角α的终边过点P(4,﹣3),则= .5.(4分)在等差数列{a n}中,a1940=1940,a102+a1922=2024,则a84= .6.(4分)设k∈R,向量=(3,4),=(k,﹣1).若在方向上的数量投影为1,则k= .7.(5分)方程cos2x﹣sin x=0在区间[0,2π]上的所有解的和为 .8.(5分)关于x的实系数一元二次方程x2+kx+3=0有两个虚根x 1和x2,若,则实数k = .9.(5分)已知函数f(x)=sin(ωx)(ω>0)在[0,3π]有且仅有5个零点,则实数ω的取值范围是 .10.(5分)设无穷数列{a n}的前n项和为S n.若S n=2n+1+n﹣2,则= .11.(5分)疫情期间,为保障市民安全,要对所有街道进行消毒处理,某消毒装备的设计如图所示,PQ为路面,AB为消毒设备的高,BC为喷杆,AB⊥PQ,∠ABC=,C处是喷洒消毒水的喷头,且喷射角∠DCE=,已知AB=2,BC=1.则消毒水喷洒在路面上的宽度DE的最小值为 .12.(5分)设{a n}是由正整数组成且项数为m的增数列,已知a1=1,a m=100,数列{a n}任意相邻两项的差的绝对值不超过1,若对于{a n}中任意序数不同的两项a s和a t,在剩下的项中总存在序数不同的两项a p和a q,使得a s+a t=a p+a q,则的最小值为 .二、选择题(本大题共有4题,满分18分,第13、14题每题4分,第15、16题每题5分)每题有且只有一个正确选项。
2023-2024学年上海市闵行区九年级(上)期末数学试卷(一模)+答案解析

2023-2024学年上海市闵行区九年级(上)期末数学试卷(一模)一、选择题:本题共6小题,每小题4分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列命题中,真命题是()A.两个直角三角形一定相似B.两个等腰三角形一定相似C.两个钝角三角形一定相似D.两个等边三角形一定相似2.在中,,,,那么的值是()A. B. C. D.3.下列说法错误的是()A.如果与都是单位向量,那么B.如果,那么或C.如果为非零向量,那么D.如果,为非零向量,那么与平行4.如图,已知,直线,,分别交直线于点A、B、C,交直线于点D、E、F,那么下列比例式正确的是()A.B.C.D.5.已知二次函数的解析式为,下列关于函数图象的说法正确的是()A.对称轴是直线B.图象经过原点C.开口向上D.图象有最低点6.如图,在平面直角坐标系xOy中,二次函数的图象经过,,如果实数P表示的值,实数Q表示的值,那么P、Q的大小关系为()A.B.C.D.无法确定二、填空题:本题共12小题,每小题4分,共48分。
7.计算:______.8.已知,那么______.9.计算:______.10.在中,,如果,,那么______.11.如图,在中,点D在边AC上,点E在边BC上,,AD::3,那么的值为______.12.将抛物线向上平移2个单位,平移后的抛物线的顶点坐标是______.13.抛物线的对称轴是直线,如果点、在此抛物线上,那么______填“>”、“=”或“<”14.小明沿斜坡坡面向上前进了5米,垂直高度上升了1米,那么这个斜坡的坡比是______.15.已知反比例函数,如果,,那么k______填“>”或“<”16.“二鸟饮泉”问题中记载:“两塔高分别为30步和20步.两塔之间有喷泉,两鸟从两塔顶同时出发,以相同速度沿直线飞往喷泉中心,同时抵达.喷泉与两塔在同一平面内,求两塔之间的距离.”如图,已知,,M是AB上一点,,在C处测得点M的俯角为,,,那么______.17.新定义:如果等腰三角形腰上的中线与腰的比值为黄金分割数黄金数,那么称这个等腰三角形为“精准三角形”.如图,是“精准三角形”,,,垂足为点D,那么BD的长度为______.18.如图,在中,,,点D为边BC上的点,联结AD,将沿AD翻折,点B落在平面内点E处,边AE交边BC于点F,联结CE,如果,那么的值为______.三、解答题:本题共7小题,共78分。
2024年上海市闵行区中考三模数学试卷(含解析)

2023学年第二学期初三年级学业质量调研数学试卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.4.本次考试不能用计算器.一、选择题:(本大题共6题,每题4分,满分24分)1. 下列说法正确的是( )A. 无限小数都是无理数B. 没有立方根C. 正数的两个平方根互为相反数D. 没有平方根2. 已知,,而且和的方向相反,那么下列结论中正确的是( )A. B. C. D. 3. 下列成语所反映的事件中,是确定事件的是( )A. 十拿九稳B. 守株待兔C. 水中捞月D. 一箭双雕4. 方差是刻画数据波动程度的量.对于一组数据,,,…,,可用如下算式计算方差:,其中“5”是这组数据的( )A 最小值 B. 平均数 C. 中位数 D. 众数5. “利用描点法画函数图象,进而探究函数的一些简单性质”是初中阶段研究函数的主要方式,请试着研究函数,其图象位于( )A. 第一、二象限B. 第三、四象限C. 第一、三象限D. 第二、四象限6. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( ).1125-(13)--3a →=2b →=b →a →32a b →→=23a b →→=32a b →→=-23a b →→=-1x 2x 3x n x ()()()()2222212315555n s x x x x n ⎡⎤=-+-+-+⋅⋅⋅-⎣⎦21y x=ABCD O BD 60ABD ∠=︒E OB F OD ,E F O ,B D OE OF =E ,AD AB 12,E E F ,BC CD 12,F F 1212E E F FA. 菱形→平行四边形→矩形→平行四边形→菱形B. 菱形→正方形→平行四边形→菱形→平行四边形C. 平行四边形→矩形→平行四边形→菱形→平行四边形D. 平行四边形→菱形→正方形→平行四边形→菱形二、填空题:(本大题共12题,每题4分,满分48分)7. 若函数是反比例函数,则的值是__.8. 为了考察闵行区15000名九年级学生数学知识与能力测试的成绩,从中抽取50本试卷,每本试卷25份,那么样本容量是__.9. 如果关于的多项式在实数范围内因式分解,那么实数的取值范围是________.10. 某班共有6名学生干部,其中4名是男生,2名是女生,任意抽一名学生干部去参加一项活动,其中是女生的概率为_____.11. 如果二次函数图象的一部分是下降的,那么的取值范围是__.12. 一个多边形的内角和是,这个多边形的边数是______.13. 若点P 到上的所有点的距离中,最大距离为8,最小距离为2,那么的半径为__.14. 如图,在平行四边形ABCD 中,点M 是边CD 中点,点N 是边BC 中点,设,,那么可用,表示为_____________.15. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线的长为________.的的2m y x =-m x 22x x m -+m 241y x x =-+x 1080︒A A AB a = BC b = MN a bA B A B C A B a 60︒ 1.5km OA = AB km16. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P ,Q ,M 均为正六边形的顶点.若点P ,Q 的坐标分别为,,则点M 的坐标为__.17. 如图,为等腰直角三角形,为的重心,E 为线段上任意一动点,以为斜边作等腰(点D 在直线的上方),为的重心,设两点的距离为d ,那么在点E 运动过程中d 的取值范围是_________.18. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形,则________.()-()0,3-ABC 1906A AB G ∠=︒=,,ABC AB CE Rt CDE △BC 2G Rt CDE △12G G 、xOy x ()2(2)03y x x =-≤≤OABC ()21034y x bx c x =++≤≤OABC b =三、解答题:(本大题共7题,满分78分)19. 计算:.20. 解方程组:21. 如图,一次函数y 1=﹣x ﹣1的图象与x 轴交于点A ,与y 轴交于点B ,与反比例函数图象的一个交点为M (﹣2,m ).(1)求反比例函数解析式;(2)求点B 到直线OM 的距离.22. 如图,某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口.温水的温度为30℃,流速为;开水的温度为100℃,流速为.某学生先接了一会儿温水,又接了一会儿开水,得到一杯温度为60℃的水(不计热损失),求该学生分别接温水和开水的时间.23. 如图,在梯形ABCD 中,AD //BC ,AC 与BD 相交于点O ,点E 在线段OB 上,AE 的延长线与BC 相交于点F ,OD 2 = OB ·OE .(1)求证:四边形AFCD 是平行四边形;(2)如果BC =BD ,AE ·AF =AD ·BF ,求证:△ABE ∽△ACD .的(10383π++2256012x xy y x y ⎧-+=⎨+=⎩2k y x=20ml /s 15ml /s 280ml24. 蔬菜大棚是一种具有出色保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间,如图,某个温室大棚的横截面可以看作矩形和抛物线构成,其中E 点为抛物线的拱顶且高,,,取中点O ,过点O 作线段的垂直平分线交抛物线于点E ,若以O 点为原点,所在直线为x 轴,为y 轴建立如图所示平面直角坐标系.解决下列问题:(1)如图,求抛物线的解析式;(2)如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置,,若,求两个正方形装置的间距的长;(3)如图,在某一时刻,太阳光线(太阳光线为平行线)透过A 点恰好照射到C 点,此时大棚截面的阴影为,求的长.25. 如图,已知在中,射线 ,P 是边上一动点,,交射线于点D ,连接.,,.的ABCD AED 4m 3m AB =4m BC =BC BC OE AED BC OE LFGT SMNR 0.75m FL NR ==GM BK ABC AM BC ∥BC APD B ∠=∠PD AM CD 4AB =6BC ==60B ∠︒(1)求证:;(2)如果以为半径的圆A 与以为半径的圆B 相切,求线段的长度;(3)将绕点A 旋转,如果点D 恰好与点B 重合,点C 落在点E 的位置上,求此时的余切值.2AP AD BP =⋅AD BP BP ACD BEP ∠2023学年第二学期初三年级学业质量调研数学试卷(考试时间100分钟,满分150分)一、选择题:(本大题共6题,每题4分,满分24分)1. 下列说法正确的是( )A. 无限小数都是无理数B. 没有立方根C. 正数的两个平方根互为相反数D. 没有平方根【答案】C【分析】根据无理数、立方根、平方根的定义解答即可.【详解】A 、无限循环小数是有理数,故不符合题意;B 、有立方根是,故不符合题意;C 、正数的两个平方根互为相反数,正确,故符合题意;D 、﹣(﹣13)=13有平方根,故不符合题意,故选:C .【点睛】本题考查了无理数、立方根、平方根,掌握无理数、立方根、平方根的定义是解题的关键.2. 已知,,而且和的方向相反,那么下列结论中正确的是( )A. B. C. D. 【答案】D 【分析】根据,而且和的方向相反,可得两者的关系,即可求解.【详解】∵,而且和的方向相反∴故选D.【点睛】本题考查的是向量,熟练掌握向量的定义是解题的关键.3. 下列成语所反映的事件中,是确定事件的是( )A. 十拿九稳B. 守株待兔C. 水中捞月D. 一箭双雕【答案】C【分析】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事1125-(13)--1125-15-3a →=2b →=b →a →32a b→→=23a b →→=32a b →→=-23a b →→=-3,2a b == b a 3,2a b == b a 32a b =-件.根据必然事件、不可能事件、随机事件的概念进行解答即可.【详解】解:A. 十拿九稳是随机事件,不符合题意;B.守株待兔是随机事件,不符合题意;C.水中捞月是不可能事件,是确定事件,符合题意;D. 一箭双雕是随机事件,不符合题意;故选:C .4. 方差是刻画数据波动程度的量.对于一组数据,,,…,,可用如下算式计算方差:,其中“5”是这组数据的( )A. 最小值B. 平均数C. 中位数D. 众数【答案】B【分析】根据方差公式的定义即可求解.【详解】方差中“5”是这组数据的平均数.故选B .【点睛】此题主要考查平均数与方差的关系,解题的关键是熟知方差公式的性质.5. “利用描点法画函数图象,进而探究函数的一些简单性质”是初中阶段研究函数的主要方式,请试着研究函数,其图象位于( )A. 第一、二象限B. 第三、四象限C. 第一、三象限D. 第二、四象限【答案】A【分析】根据的取值,判断的范围即可求解.【详解】解:当时,,此时点第一象限,当时,,此时点在第二象限,故选:A .【点睛】本题主要考查函数的图像、描点法等知识点,掌握分类讨论思想是解答本题的关键.6. 如图,在矩形中,为对角线的中点,.动点在线段上,动点在线段上,点同时从点出发,分别向终点运动,且始终保持.点关于的对称点为;点关于的对称点为.在整个过程中,四边形形状的变化依次是( )在1x 2x 3x n x ()()()()2222212315555n s x x x x n ⎡⎤=-+-+-+⋅⋅⋅-⎣⎦()()()()2222212315555n s x x x x n ⎡⎤=-+-+-+⋅⋅⋅-⎣⎦21y x =x y 0x >0y >0x <0y >ABCD O BD 60ABD ∠=︒E OB F OD ,E F O ,B D OE OF =E ,AD AB 12,E E F ,BC CD 12,F F 1212E E F FA. 菱形→平行四边形→矩形→平行四边形→菱形B. 菱形→正方形→平行四边形→菱形→平行四边形C. 平行四边形→矩形→平行四边形→菱形→平行四边形D. 平行四边形→菱形→正方形→平行四边形→菱形【答案】A【分析】根据题意,分别证明四边形是菱形,平行四边形,矩形,即可求解.【详解】∵四边形是矩形,∴,,∴,,∵、,∴∵对称,∴,∴∵对称,∴,∴,同理,∴∴∴四边形是平行四边形,如图所示,1212E E F F ABCD AB CD ∥90BAD ABC ∠=∠=︒60BDC ABD ∠=∠=︒906030ADB CBD ∠=∠=︒-︒=︒OE OF =OB OD =DF EB=21DF DF BF BF ==,21,BE BE DE DE ==1221E F E F =260F DC CDF ∠=∠=︒130EDA E DA ∠=∠=︒160E DB ∠=︒160F BD ∠=︒11DE BF ∥1221E F E F ∥1212E E F F当三点重合时,,∴即∴四边形是菱形,如图所示,当分别为的中点时,设,则,,在中,,连接,,∵,∴是等边三角形,∵为中点,∴,,∴,根据对称性可得,∴,∴,∴是直角三角形,且,∴四边形是矩形,,,E F O DO BO =1212DE DF AE AE ===1212E E EF =1212E E F F ,E F ,OD OB 4DB =21DF DF ==13DE DE ==Rt △ABD 2,AB AD ==AE AO 602ABO BO AB ,∠=︒==ABO E OB AE OB ⊥1BE=AE ==1AE AE ==2221112,9,3AD DE AE ===22211AD AE DE =+1DE A 190E ∠=︒1212E E F F当分别与重合时,都是等边三角形,则四边形是菱形∴在整个过程中,四边形形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形,故选:A .【点睛】本题考查了菱形的性质与判定,平行四边形的性质与判定,矩形的性质与判定,勾股定理与勾股定理的逆定理,轴对称的性质,含30度角的直角三角形的性质,熟练掌握以上知识是解题的关键.二、填空题:(本大题共12题,每题4分,满分48分)7. 若函数是反比例函数,则的值是__.【答案】【分析】本题考查反比例函数定义.根据反比例函数的定义:,列式计算即可.【详解】解:∵函数是反比例函数,∴,故答案为:8. 为了考察闵行区15000名九年级学生数学知识与能力测试的成绩,从中抽取50本试卷,每本试卷25份,那么样本容量是__.【答案】1250【分析】本题主要考查样本容量,掌握样本容量的概念是解题的关键.根据抽取的试卷的本数每本试卷的份数即可得出答案.【详解】样本容量是1250.故答案:1250.为,F E ,D B 11,BE D BDF 1212E E F F 1212E E F F 2m y x =-m 1-()10-=≠y kxk 2m y x =-1m =-1-⨯50251250⨯=∴9. 如果关于的多项式在实数范围内因式分解,那么实数的取值范围是________.【答案】【分析】原多项式在实数范围内能因式分解,说明方程=0有实数根,即转换为 不小于0,再代入求值即可.【详解】由题意知:∵关于的多项式在实数范围内因式分解,∴=0有实数根,∴a=1,b=-2,c=m ,则,解得:;故答案:.【点睛】本题考查因式分解,其实是考查一元二次方程根与判别式的关系,能够转换思维解题是关键.10. 某班共有6名学生干部,其中4名是男生,2名是女生,任意抽一名学生干部去参加一项活动,其中是女生的概率为_____.【答案】【详解】分析:根据概率公式用女生人数除以总人数即可得结论.详解:所有等可能结果共有6种,其中女生有2种,∴恰好是女生的概率为. 故答案为.点睛:本题考查了概率公式:随机事件A 的概率P (A )=事件A 可能出现的结果数除以所有可能出现的结果数.11. 如果二次函数的图象的一部分是下降的,那么的取值范围是__.【答案】【分析】本题主要考查二次函数的性质,掌握二次函数的性质是解题的关键.根据函数解析式可得抛物线开口向上,则当在对称轴左侧时,函数图象下降,所以求出函数的对称轴即可求解.【详解】解:,又抛物线开口向上,当时,随的增大而减小,图像下降;当时,随的增大而增大,图像上升;二次函数的图像的一部分是下降的,,故答案为:.12. 一个多边形的内角和是,这个多边形的边数是______.【答案】8为x 22x x m -+m 1m £22x x m -+24b ac ∆=-x 22x x m -+22x x m -+224(2)41440b ac m m ∆=-=--⨯⨯=-≥1m £1m £132163=13241y x x =-+x 2x ≤x ()224123y x x x =-+=--∴2x ≤y x 2x ≥y x 241y x x =-+∴2x ≤2x ≤1080︒【分析】本题主要考查多边形内角和,熟练掌握多边形内角和公式是解题的关键;因此此题可根据多边形内角和公式进行求解即可.【详解】解:由题意得:,∴;故答案为8.13. 若点P 到上的所有点的距离中,最大距离为8,最小距离为2,那么的半径为__.【答案】或者【分析】本题考查了点与圆的位置关系,分点P 在外和内两种情况讨论,当点P 在外时,最大距离与最小距离之差等于直径;当点P 在内时,最大距离与最小距离之和等于直径,即可得.【详解】解:点P 在外时,外一点到上所有的点的距离中,最大距离是,最小距离是,的半径长等于;点P 在内时,内一点到上所有的点的距离中,最大距离是,最小距离是,的半径长等于,故答案为:或者.14. 如图,在平行四边形ABCD 中,点M 是边CD 中点,点N 是边BC 的中点,设,,那么可用,表示为_____________.【答案】【分析】根据平行四边形的性质和线段的中点,可用表示出,用表示出,再根据,即可用和表示出.【详解】∵,∴.∵四边形ABCD 是平行四边形,∴,()2180n -⨯︒()21801080n -⨯︒=︒8n =A A 35A A A A A O P O 82O ∴ 8232-=A O P O 82O ∴ 8252+=35AB a = BC b = MN a b1122a b - a MC b CN MN MC CN =+ a b MN BC b = CB b =-u u r r CD AB a ==∵点M 是边CD 中点,点N 是边BC 的中点,∴,,∴.故答案为:.【点睛】本题考查平行四边形的性质,线段的中点和向量的线性运算.利用数形结合的思想是解答本题的关键.15. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线的长为________.【答案】##【分析】本题考查了切线的性质,求弧长,根据题意得出,将已知数据代入弧长公式,即可求解.【详解】解:∵过点,两条切线相交于点,列车在从到行驶的过程中转角为.∴,∴,∴圆曲线的长为故答案:.16. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P ,Q ,M 均为正六边形的顶点.若点P ,Q 的坐标分别为,,则点M 的坐标为__.的为1122MC AB a == 1122CN CB b ==- 1111()2222MN MC CN a b a b =+=+-=- 1122a b - A B A B C A B a 60︒ 1.5km OA = AB km 2π12π60AOB ∠=︒A B C A B a 60︒90CAO CBO ∠=∠=︒18060AOB ACB α∠=︒-∠==︒ AB ()603ππ18022km ⨯⨯=π2()-()0,3-【答案】【分析】设中间正六边形的中心为,连接.判断出,的长,可得结论.本题考查正多边形与圆,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.【详解】解:设中间正六边形的中心为,连接.点,的坐标分别为,,图中是7个全等的正六边形,,,,,,,故答案为:17. 如图,为等腰直角三角形,为的重心,E 为线段上任意一动点,以为斜边作等腰(点D 在直线的上方),为的重心,设两点的距离为d ,那么在点E 运动过程中d 的取值范围是_________.()2-D DB OCCM D DB P Q (-(0,3)-AB BC ∴==3OQ =OA OB ∴==OC ∴=2DQ DB OD == 1OD ∴=2QD DB CM ===()2M ∴-()2-ABC 1906A AB G ∠=︒=,,ABC AB CE Rt CDE △BC 2G Rt CDE △12G G 、【答案】【分析】当点E 与点B 重合时,,当点E 与点A 重合时,的值最大,利用重心的性质以及勾股定理求得,,证明,推出是等腰直角三角形,据此求解即可.【详解】解:当点E 与点B 重合时,,当点E 与点A 重合时,的值最大,如图,点分别为的中点,∵为等腰直角三角形,为的重心,∴,∴,同理,∴,,,,,即,∴,∴是等腰直角三角形,∴∴故答案为:【点睛】本题考查了相似三角形的判定和性质,重心的性质,勾股定理,等腰直角三角形的判定和性质,解答本题的关键是明确题意,找出所求问题需要的条件.18. 在平面直角坐标系中,一个图形上的点都在一边平行于轴的矩形内部(包括边界),这些矩形中面积最0d ≤≤0d =d 1CG =2CG =12CG G BCA ∽△△12CG G △0d =d FH BC AC 、ABC 1906A AB G ∠=︒=,,ABC 12AF BF FC BC =====113G F AF ==1CG ==11322DH AH HC AC AB =====2113G H DH ==2CG ==1245BAC G CG ∠=∠=︒AC BC ==21CG CG ==21CG AC CG BC =12CG G BCA ∽△△12CG G △122G G CG ==0d ≤≤0d ≤≤xOy x小的矩形称为该图形的关联矩形.例如:如图,函数的图象(抛物线中的实线部分),它的关联矩形为矩形.若二次函数图象的关联矩形恰好也是矩形,则________.【答案】或【分析】根据题意求得点,,,根据题意分两种情况,待定系数法求解析式即可求解.【详解】由,当时,,∴,∵,四边形是矩形,∴,①当抛物线经过时,将点,代入,∴解得:②当抛物线经过点时,将点,代入,∴解得:综上所述,或,故答案为:或.【点睛】本题考查了待定系数法求抛物线解析式,理解新定义,最小矩形的限制条件是解题的关键.()2(2)03y x x =-≤≤OABC ()21034y x bx c x =++≤≤OABC b =7122512-()3,0A ()3,4B ()0,4C ()2(2)03y x x =-≤≤0x =4y =()0,4C ()3,0A ABCO ()3,4B O B ,()0,0()3,4B ()21034y x bx c x =++≤≤019344c b c =⎧⎪⎨⨯++=⎪⎩712b =,A C ()3,0A ()0,4C ()21034y x bx c x =++≤≤419304c b c =⎧⎪⎨⨯++=⎪⎩2512b =-712b =2512b =-7122512-三、解答题:(本大题共7题,满分78分)19. 计算:.【答案】【分析】本题考查了实数的运算,熟练掌握运算法则是解题的关键;原式第一项利用立方根的定义化简,第二项利用绝对值的代数意义化简,第三项分母有理化,最后一项利用零指数幂法则计算即可得到结果.【详解】.20. 解方程组:【答案】或【分析】利用因式分解法求,得到或,然后得到两个二元一次方程组,分别求出方程组的解即可.【详解】解:由(1)得或,或,解方程组得:, ,则原方程组的解为 和 .【点睛】本题主要考查解二元二次方程组,解此题的关键在于利用因式分解法将第一个方程求解,然后得到新的方程组.也可以利用代入消元法进行求解.21. 如图,一次函数y 1=﹣x ﹣1的图象与x 轴交于点A ,与y 轴交于点B ,与反比例函数图象的一个交点为M (﹣2,m ).(1)求反比例函数的解析式;(2)求点B 到直线OM 的距离.(10383π++4-(1383π+-+2321=+--+4=-2256012x xy y x y ⎧-+=⎨+=⎩1184x y =⎧⎨=⎩2293x y =⎧⎨=⎩22560x xy y -+=20x y -=30x y -=20x y -=30x y -=2012x y x y -=⎧⎨+=⎩3012x y x y -=⎧⎨+=⎩1184x y =⎧⎨=⎩2293x y =⎧⎨=⎩1184x y =⎧⎨=⎩2293x y =⎧⎨=⎩2k y x=【答案】(1)(2.【分析】(1)根据一次函数解析式求出M 点的坐标,再把M 点的坐标代入反比例函数解析式即可;(2)设点B 到直线OM 的距离为h ,过M 点作MC ⊥y 轴,垂足为C ,根据一次函数解析式表示出B 点坐标,利用△OMB 的面积=×BO×MC 算出面积,利用勾股定理算出MO 的长,再次利用三角形的面积公式可得OM•h,根据前面算的三角形面积可算出h 的值.【详解】解:(1)∵一次函数y1=﹣x ﹣1过M (﹣2,m ),∴m=1.∴M(﹣2,1).把M (﹣2,1)代入得:k=﹣2.∴反比列函数为.(2)设点B 到直线OM的距离为h ,过M 点作MC ⊥y 轴,垂足为C .∵一次函数y 1=﹣x ﹣1与y 轴交于点B ,∴点B 的坐标是(0,﹣1).∴.在Rt △OMC 中,,∵,∴.∴点B 到直线OM .22. 如图,某校的饮水机有温水、开水两个按钮,温水和开水共用一个出水口.温水的温度为30℃,流速为;开水的温度为100℃,流速为.某学生先接了一会儿温水,又接了一会儿开水,得到一杯22y x =-12122k y x =22y x=-OMB 1S 1212∆=⨯⨯===OMB 1S OM h 2∆=⋅⋅==20ml /s 15ml /s温度为60℃的水(不计热损失),求该学生分别接温水和开水的时间.【答案】该学生接温水的时间为,接开水的时间为【分析】本题考查一元一次方程的实际应用, 设该学生接温水的时间为,则接温水,开水,由物理常识的公式可得方程,解方程即可.【详解】解:设该学生接温水的时间为,根据题意可得:,解得,∴,∵,∴,∴该学生接温水的时间为,接开水的时间为.23. 如图,在梯形ABCD 中,AD //BC ,AC 与BD 相交于点O ,点E 在线段OB 上,AE 的延长线与BC 相交于点F ,OD 2 = OB ·OE .(1)求证:四边形AFCD 是平行四边形;(2)如果BC =BD ,AE ·AF =AD ·BF ,求证:△ABE ∽△ACD .【答案】(1)证明见解析;(2)证明见解析【分析】(1)由题意,得到,然后由AD ∥BC ,得到,则,即可得到AF//CD ,即可得到结论;(2)先证明∠AED=∠BCD ,得到∠AEB=∠ADC ,然后证明得到,即可得到△ABE ∽△ADC.【详解】证明:(1)∵OD 2 =OE · OB ,∴.∵AD//BC ,280ml 8s 8ss x 20ml x ()28020ml x -s x ()()()2060302802010060x x ⨯-=-⨯-8x =208160ml ⨯=()280160120ml -=()120158s ÷=()8s 8s OE OD OD OB =OA OD OC OB =OA OE OC OD =AE AD BE DC =OE OD OD OB=∴.∴. ∴ AF//CD .∴四边形AFCD 是平行四边形.(2)∵AF//CD ,∴∠AED=∠BDC ,.∵BC=BD ,∴BE=BF ,∠BDC=∠BCD∴∠AED=∠BCD .∵∠AEB=180°∠AED ,∠ADC=180°∠BCD ,∴∠AEB=∠ADC .∵AE·AF=AD·BF ,∴.∵四边形AFCD 是平行四边形,∴AF=CD .∴. ∴△ABE ∽△ADC .【点睛】本题考查了相似三角形的判定和性质,平行线分线段成比例,平行四边形的判定和性质,以及平行线的性质,解题的关键是熟练掌握相似三角形的判定方法,正确找到证明三角形相似的条件.24. 蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间,如图,某个温室大棚的横截面可以看作矩形和抛物线构成,其中E 点为抛物线的拱顶且高,,,取中点O ,过点O 作线段的垂直平分线交抛物线于点E ,若以O 点为原点,所在直线为x 轴,为y 轴建立如图所示平面直角坐标系.解决下列问题:(1)如图,求抛物线的解析式;OA OD OC OB =OA OE OC OD=BE BF BD BC =--AE AD BF AF=AE AD BE DC=ABCD AED 4m 3m AB =4m BC =BC BC OE AED BC OE(2)如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置,,若,求两个正方形装置的间距的长;(3)如图,在某一时刻,太阳光线(太阳光线为平行线)透过A 点恰好照射到C 点,此时大棚截面的阴影为,求的长.【答案】(1); (2);(3)【分析】(1)根据题意得到的坐标,设函数解析式为,求出点坐标,待定系数法求出函数解析式即可;(2)根据正方形性质得到,求出时,对应的自变量的值,得到的长,再减去两个正方形的边长即可得解;(3)设直线的解析式为,根据题意求出直线的解析式,进而设出过点的光线解析式为,利用光线与抛物线相切,求出的值,进而求出点坐标,即可得出的长.【小问1详解】解:由题知,E 点为抛物线顶点坐标为,LFGT SMNR 0.75m FL NR ==GM BK 2144y x =-+0.5m 97m 12E 24y ax =+A 3.75m HL HF FL =+= 3.75y =FN AC y kx b =+AC 34y x m =-+m K BK ()0,4设抛物线的解析式为,四边形为矩形,为的中垂线, ,,,,,将其代入中,有,,抛物线的解析式为;【小问2详解】解:四边形和为正方形,,,延长交于点,延长交于点,易知四边形和为矩形,,,,,当时,,解得,,,,;【小问3详解】解:为的中垂线, ,,,,24y ax =+ ABCD OE BC 4m BC =∴4m AD BC ==2m OB = 3m AB =∴()2,3A -24y ax =+344a =+14a ∴=-∴2144y x =-+ LFGT SMNR 0.75m FL NR ==∴0.75m MN FG FL NR ====LF BC H RN BC J FHJN ABFH ∴3m FH AB ==FN HJ =3.75m HL HF FL ∴=+= 2144y x =-+3.75y =214 3.754x -+=1x =±()1,0H ∴-()1,0J 2m FN HJ ∴==0.5m GM FN FG MN ∴=--= OE BC 4m BC =2m OB OC ==∴()2,0B -()2,0C设直线的解析式为,则,解得,直线的解析式为,太阳光为平行线,设过点且平行于直线的解析式为,由题意得与抛物线相切,即只有一个交点,联立,整理得,则,解得,,当时,,,,.【点睛】本题考查二次函数的实际应用,坐标与图形,中垂线性质,待定系数法求出函数解析式,正方形的性质,矩形的性质和判定.读懂题意,正确的求出二次函数解析式,利用数形结合的思想进行求解,是解题的关键.25. 如图,已知在中,射线 ,P 是边上一动点,,交射线于点D ,连接.,,.(1)求证:;AC y kx b =+2023k b k b +=⎧⎨-+=⎩3432k b ⎧=-⎪⎪⎨⎪=⎪⎩∴AC 3342y x =-+ K AC 34y x m =-+34y x m =-+234144y x m y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩234160x x m -+-=()()224344160b ac m -=---=7316m =∴373416y x =-+0y =7312x =73,012K ⎛⎫∴ ⎪⎝⎭()2,0B - 73972m 1212BK ∴=+=ABC AM BC ∥BC APD B ∠=∠PD AM CD 4AB =6BC ==60B ∠︒2AP AD BP =⋅(2)如果以为半径的圆A 与以为半径的圆B 相切,求线段的长度;(3)将绕点A 旋转,如果点D 恰好与点B 重合,点C 落在点E 的位置上,求此时的余切值.【答案】(1)证明见解析(2)2 (3)【分析】(1)先由平行线证明,再由已知条件,证明,得出对应边成比例,即可得出结论;(2)设,作于H ,,先根据勾股定理求出,再由勾股定理得出,由两圆外切时,,得出方程,解方程即可;(3)作于G ;先根据题意得出,解方程求出,再证明为等边三角形求出,然后证明四边形为矩形得出,,求出,即可求的余切值,【小问1详解】,,,,,;【小问2详解】设,作于H ,如图所示∶,,,,根据勾股定理得∶,AD BP BP ACD BEP ∠APBDAP ∠=∠APD B ∠=∠ABP DPA ∽AP BP DA AP=BP x =AH BC ⊥AH 222AP PH AH =+AB AD BP =±PG AB ⊥2416 4.x x AD AB x-+===BP ABP PG ADCH BE CD AH ===90ABE ADC ∠=∠=︒BF BEP ∠ AM BC ∥APB DAP =∴∠∠ APD B ∠=∠ABP DPA ∴∽△△AP BP DA AP∴=∴2AP AD BP =⋅BP x =AH BC ⊥ =60B ∠︒4AB =30BAH ∴∠=︒122BH AB ∴==A H ==()(2222222416AP PH AH x x x =+=-+=-+,两圆相切时,,即,解得:,的长度为2;【小问3详解】根据题意得:,解得:,,,为等边三角形,,,,,∴四边形为矩形,,,作于G ,如图所示:则,,,.【点睛】本题是相似形综合题,考查了相似三角形的判定与性质、勾股定理、两圆外切的条件、等边三角形的判定与性质、三角函数等知识;通过作辅助线运用勾股定理和证明等边三角形、矩形是解题的关键.22416AP x x AD BP x-+∴==AB AD BP =±24164x x x x-+=±2x =∴BP 2416 4.x x AD AB x-+===4x =4BP ∴=60ABP ∠=︒4AB BP ==ABP ∴ 4AD AB ==4CH BC BH =-=AD CH ∥90AHC ∠=︒ADCH BE CD AH ∴===90ABE ADC ∠=∠=︒PG AB ⊥PG BE ∥PG =PG BE ∴=∴112BF FG BG ===cot BE EBP BF ∴∠==。
2023-2024学年上海市闵行区七年级下学期期末数学试题及答案

2023学年第二学期期末七年级学业质量调研数学试卷(考试时间90分钟,满分100分)考生注意:1.本试卷含四个大题,共27题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出解答的主要步骤.4.考试可以使用科学计算器.一、选择题:(本大题共6题,每题2分,满分12分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.在,73, 3.14,2π-,中,有理数的个数有()A.1个B.2个C.3个D.4个2.下列等式中,正确的是()A.5= B.(25= C.5=± D.132=3.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),那么棋子“炮”的坐标为()A.(3,0)B.(3,1)C.(3,2)D.(2,2)4.下列判断正确的是()A.等腰三角形任意两角相等B.等腰三角形底边上中线垂直底边C.任意两个等腰三角形全等D.等腰三角形三边上的中线都相等5.下面是“作AOB∠的平分线”的尺规作图过程:①在OA 、OB 上分别截取OD 、OE ,使OD OE =;②分别以点D 、E 为圆心,以大于12DE 的同一长度为半径作弧,两弧交于AOB ∠内的一点C ;③作射线OC .OC 就是所求作的角的平分线.该尺规作图可直接利用三角形全等说明,其中三角形全等的依据是()A.三边对应相等的两个三角形全等B.两边及它们的夹角对应相等的两个三角形全等C.两角及它们的夹边对应相等的两个三角形全等D.两角及其中一个角的对边对应相等的两个三角形全等6.将一副直角三角板作如图所示摆放,6045GEF MNP ∠=︒∠=︒,,AB CD ,则下列结论不正确的是()A.GE MP ∥B.150EFN ∠=︒C.60BEF ∠=︒D.AEG PMN∠=∠二、填空题:(本大题共12题,每题2分,满分24分)7.4的算术平方根是________.8._______.9.方程5243x -=的解是_______.10.数轴上,已知点A 表示的数是a =点B 表示的数是b ,且实数b 满足b a <,那么点B 表示的正整数是_______.11.据第一财经报道:“2024年第一季度,上海 G DP 总量11098.46亿元,同比增速5%,拔得全国头筹.”将数字11098.46保留三个有效数字后,近似数为_______.12.伞兵在高空跳离飞机往下降落,在打开降落伞前,下降的高度h (米)与下降的时间t (秒)的关系可以近似地表示为24.9h t =(不计空气阻力),一个伞兵在打开降落伞前的一段时间内下降了920米,这段时间大约有_______秒(精确到1秒).13.将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则12∠+∠=______.14.若点P (3,m ﹣2)在x 轴上,则点Q (m ﹣3,m +1)在第__象限.15.在ABC 中,如果25AB BC AC ==,,的长为素数,那么AC 的长是_______.16.如图,在ABC 中,BD 平分4ABC DE BC AD AED ∠=,,,△∥的周长为11,那么AB 的长是_______.17.如图,在△ABC 和△DEF 中,点B 、F 、C 、E 在同一直线上,BF =CE ,AC ∥DF ,请添加一个条件,使△ABC ≌△DEF ,这个添加的条件可以是________.(只需写一个,不添加辅助线)18.如图,已知AB AC =,AD 平分BAC ∠,60DEB EBC ∠=∠=︒,若7BE =,3DE =,则BC =________.三、解答题(本大题共8题,满分64分)19.不用计算器,计算:2+-20.不用计算器,计算:))22+⨯+21.计算(结果表示为含幂的形式):1112223-⎛⎫+ ⎪⎝⎭22.在ABC 中,已知60A ∠=︒,:1:2B C ∠∠=,求B ∠,C ∠的度数.23.如图,已知在ABC 中,点D 、G 分别在边BC AC 、上,且B GDC ∠=∠,点F 在线段DG 的延长线上,点E 在边GC 上,如果13∠=∠,说明AD EF 的理由.解:因为B GDC ∠=∠(已知),所以AB ∥ ().所以1∠=().因为13∠=∠(已知),所以3∠=(等量代换).所以AD EF ().24.如图,在直角坐标平面内,已知点(31)A ,.(1)已知点B 与点A 关于原点对称,那么点B 的坐标是;把点B 向右平移4个单位,得到点C ,那么点C 的坐标是;(2)顺次联结线段AB BC 、和AC ,那么ABC 的面积等于;(3)已知点D 在y 轴上,如果BCD △的面积与ABC 的面积相等,那么点D 的坐标是.25.如图,已知在ABD △中,AB AD =,射线AF 交BD 于点O ,BAC DAC ∠<∠,点E 、F 在射线AF 上,且BCF DEF BAD ∠=∠=∠.试判断AC 与ED 的数量关系,并说明理由.26.如图,在直角坐标平面内,已知面积为10的正方形ABCD 的顶点A 在x 轴上,且点A 的坐标为(1,0),点B 的坐标为(2,3).分别过点B 、点D 作x 轴的垂线BM 和DN ,垂足分别为M 、N .(1)利用ADN BAM ≌,可求得点D 的坐标为,用类似的方法可求出点C 的坐标为;(2)如果正方形ABCD 绕着顶点顺时针方向在x 轴上连续翻转.翻转1次(即以点A 为旋转中心,沿着x 轴的正方向顺时针旋转正方形ABCD ),点B 落在x 轴上(记作1B 那么点1B 的坐标为.继续沿着x 轴的正方向翻转正方形ABCD ,它在x 轴上的落点分别是23456C D A B C 、、、、按此规律翻转下去,当2024次翻转后,在x 轴上落点的坐标为.27.如图,已知在ABC 中,(060)AB BC ABC αα=∠=<<︒,,,射线AM AB ⊥,点P 为射线AM 上的动点(点P 不与点A 重合),连接BP ,将线段BP 绕点B 顺时针旋转角度α后,得到线段BQ ,连接PQ 、QC .(1)试说明PAB QCB ≌的理由;(2)延长QC 交射线AM 于点D ,在点P 的移动过程中,QDM ∠的大小是否发生变化?若改变请说明理由,若不改变,请求出QDM ∠的大小(用含α的代数式表示);(3)当BQ AC ∥时,AB m AP n ==,,过点Q 作QE 垂直射线AB ,垂足为E ,那么AEQ S = (用m 、n 的代数式表示).2023学年第二学期期末七年级学业质量调研数学试卷(考试时间90分钟,满分100分)考生注意:1.本试卷含四个大题,共27题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出解答的主要步骤.4.考试可以使用科学计算器.一、选择题:(本大题共6题,每题2分,满分12分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.在,73, 3.14,2π-,中,有理数的个数有()A.1个B.2个C.3个D.4个【答案】B【解析】【分析】本题主要考查了有理数的概念,有理数可分为整数和分数,其中分数可化为有限小数或无限循环小数,根据分类对题目中的实数进行化简判断即可.=73是分数,为有理数;3.14是有限小数,为有理数;π为无理数,故2π-是无理数;=,为无理数;∴73和 3.14是有理数,故选:B.2.下列等式中,正确的是()A.5= B.(25= C.5=±D.132=【答案】B【解析】【分析】本题考查了二次根式的性质,正确化简各数是解题关键,直接利用二次根式的性质化简,进而得出答案.=-,故选项A错误;【详解】解:A:5B:(25=,故选项B正确;C5=,故选项C错误;D==,故选项D错误;2故选:B.3.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),那么棋子“炮”的坐标为()A.(3,0)B.(3,1)C.(3,2)D.(2,2)【答案】C【解析】【分析】根据“车”的位置,向右平移2个单位,再向下平移3个单位得到坐标原点,建立平面直角坐标系,再根据“炮”的位置解答.【详解】解:由棋子“车”的坐标为(﹣2,3)、棋子“马”的坐标为(1,3),建立如图平面直角坐标系,原点为底边正中间的点,以底边为x轴,向右为正方向,以左右正中间的线为y 轴,向上为正方向;根据建立的坐标系可知,棋子“炮”的坐标为(3,2).故选:C.【点睛】本题考查坐标确定位置,是基础考点,掌握相关知识是解题关键.4.下列判断正确的是()A.等腰三角形任意两角相等B.等腰三角形底边上中线垂直底边C.任意两个等腰三角形全等D.等腰三角形三边上的中线都相等【答案】B【解析】【分析】根据等腰三角形的性质和全等三角形的判定即可得解.【详解】解:A、等腰三角形任意两底角相等,故错误,不合题意;B、等腰三角形底边上中线垂直底边,故正确,符合题意;C、任意两个等腰三角形不一定全等,故错误,不合题意;D、等腰三角形三边上的中线不一定相等,若为等边三角形,则满足,故错误,不合题意;故选:B.【点睛】本题考查了等腰三角形的性质,还涉及了全等三角形的判定,属于基础知识.5.下面是“作AOB∠的平分线”的尺规作图过程:①在OA、OB上分别截取OD、OE,使OD OE=;②分别以点D、E为圆心,以大于12DE的同一长度为半径作弧,两弧交于AOB∠内的一点C;③作射线OC.OC就是所求作的角的平分线.该尺规作图可直接利用三角形全等说明,其中三角形全等的依据是()A.三边对应相等的两个三角形全等B.两边及它们的夹角对应相等的两个三角形全等C.两角及它们的夹边对应相等的两个三角形全等D.两角及其中一个角的对边对应相等的两个三角形全等【答案】A【解析】【分析】由作图可得EO DO =,EC DC =,根据三角形全等的判定方法“SSS ”解答.【详解】解∶连接EC ,DC ,由作图可得EO DO =,EC DC =,EO DO =,在OEC 和ODC 中EC DC CO CO OD OE =⎧⎪=⎨⎪=⎩∴()SSS OEC ODC ≌,∴AOC BOC ∠∠=,∴OC 平分AOB ∠.故选:A .【点睛】本题考查了全等三角形的应用,以及基本作图,熟练掌握三角形全等的判定方法并读懂题目信息是解题的关键.6.将一副直角三角板作如图所示摆放,6045GEF MNP ∠=︒∠=︒,,AB CD ,则下列结论不正确的是()A.GE MP∥ B.150EFN ∠=︒ C.60BEF ∠=︒ D.AEG PMN ∠=∠【答案】C【解析】【分析】本题主要考查了平行线的性质与判定,三角板中角度的计算,由三角板中角度的特点可得90EGF MPN MPG ==︒=∠∠∠,则GE MP ∥,即可判断A ;由平角的定义即可判断B ;过点F 作FH AB ∥,则FH AB CD ∥∥,由平行线的性质得到45180HFN MNP BEF HFE ==︒+=︒∠∠,∠∠,进而求出75BEF ∠=︒,即可判断C ;再由平角的定义即可得到AEG PMN ∠=∠,即可判断D .【详解】解:∵90EGF MPN MPG ==︒=∠∠∠,∴GE MP ∥,故A 结论正确,不符合题意;∵30EFG ∠=︒,∴180150EFN EFG =︒-=︒∠∠,故B 结论正确,不符合题意;如图所示,过点F 作FH AB ∥,∵AB CD ,∴FH AB CD ∥∥,∴45180HFN MNP BEF HFE ==︒+=︒∠∠,∠∠,∴105EFH EFN HFN =-=︒∠∠∠,∴75BEF ∠=︒,故C 结论错误,符合题意;∴18045AEG FEG BEF =︒--=︒∠∠,∴AEG PMN ∠=∠,故D 结论正确,不符合题意;故选:C .二、填空题:(本大题共12题,每题2分,满分24分)7.4的算术平方根是________.【答案】2【解析】【分析】本题考查了算术平方根的定义,熟练掌握算术平方根的概念是解题的关键;根据算术平方根的概念即可求出结果.【详解】解:224= ,∴4的算术平方根是2,故答案为:2.8._______.【答案】473【解析】【分析】本题主要考查分数指数幂.根据分数指数幂的定义求解可得.473=,故答案为:473.9.方程5243x -=的解是_______.【答案】3-【解析】【分析】本题考查了高次方程.由53243=,可得结果.【详解】解:53243= ,5243x -=,3x ∴=-;∴方程5243x -=的解是3-.故答案为:3-.10.数轴上,已知点A 表示的数是a =点B 表示的数是b ,且实数b 满足b a <,那么点B 表示的正整数是_______.【答案】1【解析】【分析】本题考查了在数轴上表示实数,绝对值的知识,先求出a 的绝对值,即可求得答案.【详解】解:∵a =∴a =,∵b a <,∴b <∴点B 表示的正整数是1,故答案为:1.11.据第一财经报道:“2024年第一季度,上海 G DP 总量11098.46亿元,同比增速5%,拔得全国头筹.”将数字11098.46保留三个有效数字后,近似数为_______.【答案】41.1110⨯【解析】【分析】本题主要考查了科学记数法,四舍五入求近似数,把一个数表示成a 与10的n 次幂相乘的形式(110a ≤<,a 不为分数形式,n 为整数),这种记数法叫做科学记数法,确定n 的方法是,将原数变为a 时,小数点移动的位数,当小数点向右移动时,n 的值为移动位数的相反数,当小数点向左移动时,n 的值为小数点移动位数的值,根据科学记数法进行计算即可.【详解】解:411098.46 1.10984610=⨯,保留三个有效数字后41.1110⨯,故答案为:41.1110⨯.12.伞兵在高空跳离飞机往下降落,在打开降落伞前,下降的高度h (米)与下降的时间t (秒)的关系可以近似地表示为24.9h t =(不计空气阻力),一个伞兵在打开降落伞前的一段时间内下降了920米,这段时间大约有_______秒(精确到1秒).【答案】14【解析】【分析】本题考查实数运算,理解算术平方根的意义是解答关键,将920h =代入24.9h t =进行计算即可.【详解】解:当920h =时,2920 4.9t =,∵0t ≥,解得14t =≈秒,故答案为:14.13.将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则12∠+∠=______.【答案】90︒##90度【解析】【分析】作CD AB ∥,根据平行线的性质得出13∠=∠,24∠=∠,又3490∠+∠=︒,即可求解.【详解】解:如图所示,作CD AB ∥,13∴∠=∠,又AB EF ∥,∴CD EF ∥,24∴∠=∠,又3490∠+∠=︒ ,1290∴∠+∠=︒.故答案为:90︒.【点睛】本题考查了平行线的性质与判定,掌握平行线的性质与判定是解题的关键.14.若点P (3,m ﹣2)在x 轴上,则点Q (m ﹣3,m +1)在第__象限.【答案】二【解析】【分析】根据x 轴上的点的纵坐标为0,列出方程m-2=0,求出m 的值,再求出点Q 的坐标,即可得出答案.【详解】由题意,得m ﹣2=0,∴m =2.∴m ﹣3=﹣1<0,m +1=3>0,∴点Q (-1,3)在二象限,故答案为:二.【点睛】本题考查了点的坐标,明确各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).15.在ABC 中,如果25AB BC AC ==,,的长为素数,那么AC 的长是_______.【分析】本题考查三角形三边的关系和素数的概念,先根据三角形两边之和大于第三边,三角形两边只差小于第三边求出AC 的取值范围,再根据AC 的长是素数得到AC 的值.【详解】解:∵AC AB BC <+,AC BC AB >-,∴37AC <<,∵AC 的长是素数,∴5AC =,故答案为:5.16.如图,在ABC 中,BD 平分4ABC DE BC AD AED ∠=,,,△∥的周长为11,那么AB 的长是_______.【答案】7【解析】【分析】本题考查平行直线的性质和等腰三角形的性质,先根据角平分线和平行直线的性质证明EBD EDB ∠=∠,从而到EB ED =,再根据AED △的周长进行换算,即可得到答案.【详解】解:∵BD 平分ABC ∠,∴EBD DBC ∠=∠,∵DE BC ∥,∴EDB DBC ∠=∠,∴EBD EDB ∠=∠,∴EB ED =,∵AED △的周长等于11,∴11AE ED AD ++=,∴11AE EB AD ++=,∴11AB AD +=,故答案为:7.17.如图,在△ABC 和△DEF 中,点B 、F 、C 、E 在同一直线上,BF =CE ,AC ∥DF ,请添加一个条件,使△ABC ≌△DEF ,这个添加的条件可以是________.(只需写一个,不添加辅助线)【答案】AC =DF (答案不唯一)【解析】【详解】∵BF =CE ,∴BF +FC =CE +FC ,即BC =EF ;∵AC ∥DF ,∴∠ACB =∠DFE ,△ABC 和△DEF 中有一角一边对应相等,∴根据全等三角形的判定,添加AC =DF ,可由SAS 得△ABC ≌△DEF ;添加∠B =∠E ,可由ASA 得△ABC ≌△DEF ;添加∠A =∠D ,可由AAS 得△ABC ≌△DEF .故答案为:AC=DF .(答案不唯一)18.如图,已知AB AC =,AD 平分BAC ∠,60DEB EBC ∠=∠=︒,若7BE =,3DE =,则BC =________.【答案】10【解析】【分析】如图,延长ED 交BC 于M ,延长AD 交BC 于N ,结合题意根据等腰三角形“三线合一”的性质,可得,AN BC BN CN ⊥=,易证BEM △为等边三角形,结合已知求出4DM =,在DNM 中运用30︒角所对的直角边等于斜边的一半解三角形可求解.【详解】解:延长ED 交BC 于M ,延长AD 交BC 于N ,如图,∵,AB AC AD =平分BAC ∠,∴1,2AN BC BN CN BC ⊥==,∵60EBC DEB ∠=∠=︒,∴BEM △为等边三角形,∴7,60BM EM BE EMB ===∠=︒,∵3DE =,∴4DM =,∵AN BC ⊥,∴90DNM ∠=︒,∴30NDM ∠=︒,∴122NM DM ==,∴725BN BM MN =-=-=,∴210BC BN ==,故答案为:10.【点睛】本题考查了等腰三角形的性质、等边三角形的判定和性质;解含30︒角的直角三角形;解题的关键是灵活运用相关性质进行计算.三、解答题(本大题共8题,满分64分)19.不用计算器,计算:2+-【解析】【分析】本题考查了二次根式的乘法、立方根等知识点,熟练掌握各运算法则是解题关键.先计算二次根式的乘法、立方根,再计算加减法即可得.【详解】解:原式55=+-=20.不用计算器,计算:))22+⨯+【答案】1【解析】【分析】本题考查二次根式的混合运算,先去括号,再合并同类项即可.【详解】解:))22+⨯+222=-+342=-+-1=-.21.计算(结果表示为含幂的形式):1112223-⎛⎫+ ⎪⎝⎭【答案】112232-【解析】【分析】本题主要考查了分数指数幂和负指数幂,先运算负指数幂,再通过平方差公式进行变形,化解即可得到答案.【详解】解:1112223-⎛⎫+ ⎪⎝⎭1122123=+112211112222232323-=⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭11222211222323-=⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭11222323-=-112232=-.22.在ABC 中,已知60A ∠=︒,:1:2B C ∠∠=,求B ∠,C ∠的度数.【答案】40B ∠=︒,80C ∠=︒【解析】【分析】先根据∠B :∠C =1:2,设∠B =x °,∠C =2x °,再根据三角形内角和为180°可得方程260180x x ++︒=︒,算出x 的值即可.【详解】解:由:1:2B C ∠∠=,设B x ∠=,2C x ∠=,则有:260180x x ++︒=︒,解得:40x =︒,40B ∴∠=︒,80C ∠=︒.【点睛】本题主要考查了三角形内角和定理,关键是掌握三角形内角和为180°.23.如图,已知在ABC 中,点D 、G 分别在边BC AC 、上,且B GDC ∠=∠,点F 在线段DG 的延长线上,点E 在边GC 上,如果13∠=∠,说明AD EF的理由.解:因为B GDC ∠=∠(已知),所以AB ∥ ().所以1∠=().因为13∠=∠(已知),所以3∠=(等量代换).所以AD EF ().【答案】DF ,同位角相等,两直线平行,2∠,两直线平行,内错角相等,2∠,内错角相等,两直线平行【解析】【分析】本题主要考查了平行线的性质与判定,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.根据平行线的判定与性质解答即可.【详解】解:∵B GDC ∠=∠(已知),∴AB DF ∥(同位角相等,两直线平行),∴12∠=∠(两直线平行,内错角相等),∵13∠=∠(已知),∴32∠=∠(等量代换),∴AD EF (内错角相等,两直线平行),故答案为:DF ,同位角相等,两直线平行,2∠,两直线平行,内错角相等,2∠,内错角相等,两直线平行.24.如图,在直角坐标平面内,已知点(31)A ,.(1)已知点B 与点A 关于原点对称,那么点B 的坐标是;把点B 向右平移4个单位,得到点C ,那么点C 的坐标是;(2)顺次联结线段AB BC 、和AC ,那么ABC 的面积等于;(3)已知点D 在y 轴上,如果BCD △的面积与ABC 的面积相等,那么点D 的坐标是.【答案】(1)(3,1)--,(1,1)-(2)4(3)(3,1)--,(1,1)-【解析】【分析】(1)直角坐标系上一点(),x y 关于原点对称的点为(),x y --,向右平移后,纵坐标不变,横坐标加上平移的值;(2)根据三角形的面积公式直接进行计算即可;(3)BCD △与ABC 有相同的边BC ,根据面积相等,得到边BC 上的高相等,再根据点D 在y 轴上即可得到答案.【小问1详解】解:∵(31)A ,,点B 与点A 关于原点对称,∴点B 坐标为的(3,1)--,把点B 向右平移4个单位,得到点C ,∴点C 坐标为的)34(,1+--,即(1,1)-故答案为:(3,1)--,(1,1)-;【小问2详解】解:ABC 如下图所示,1142422ABC S BC h =⋅=⨯⨯=△,故答案为:4;【小问3详解】解:∵BCD △与ABC 有相同的边BC ,∴当BC 边上的高相等时,两个三角形的面积相等,∵在ABC 中,BC 边上的高为2,∴点D 到BC 的垂线长为2,∵点D 在y 轴上,∴点D 如下图所示,∴点D 的坐标是()0,1或()0,3-,故答案为:()0,1或()0,3-.【点睛】本题考查了直角坐标系中点的坐标、点的平移和原点对称的性质,以及三角形的面积公式,解题的关键是正确求出点的坐标.25.如图,已知在ABD △中,AB AD =,射线AF 交BD 于点O ,BAC DAC ∠<∠,点E 、F 在射线AF 上,且BCF DEF BAD ∠=∠=∠.试判断AC 与ED 的数量关系,并说明理由.【答案】AC ED =,理由见解析【解析】【分析】本题考查全等三角形的判断和性质、等腰三角形的性质,解题的关键是添加正确的辅助线,在射线AF 作点M ,EM ED =,先根据等腰三角形的性质和已知条件证明EDA BAO ∠=∠和BCA AED ∠=∠,从而证明()AAS BCA AED ≌,即可得到AC ED =.【详解】解:AC ED =,理由如下,如下图所示,在射线AF 作点M ,EM ED =,∵EM ED =,∴EMD EDM ∠=∠,∵AB AD =,∴ABD ADB ∠=∠,∵BCF BAD ∠=∠,∴ADB A EDM AB MD D =∠==∠∠∠,∴M EDA BD =∠∠,∵BOA MOD =∠,D ABO AM =∠∠,∴M BAO BD =∠∠,∴EDA BAO ∠=∠,∵BCF DEF ∠=∠,∴BCA AED ∠=∠,∵BCA AED EDA BAO AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS BCA AED ≌,∴AC ED =.26.如图,在直角坐标平面内,已知面积为10的正方形ABCD 的顶点A 在x 轴上,且点A 的坐标为(1,0),点B 的坐标为(2,3).分别过点B 、点D 作x 轴的垂线BM 和DN ,垂足分别为M 、N.(1)利用ADN BAM ≌,可求得点D 的坐标为,用类似的方法可求出点C 的坐标为;(2)如果正方形ABCD 绕着顶点顺时针方向在x 轴上连续翻转.翻转1次(即以点A 为旋转中心,沿着x 轴的正方向顺时针旋转正方形ABCD ),点B 落在x 轴上(记作1B 那么点1B 的坐标为.继续沿着x 轴的正方向翻转正方形ABCD ,它在x 轴上的落点分别是23456C D A B C 、、、、按此规律翻转下去,当2024次翻转后,在x 轴上落点的坐标为.【答案】(1)()2,1-,()1,4-(2)()20241A +【解析】【分析】本题考查坐标与图形、正方行的性质、全等三角形的判定与性质和图形的翻转,(1)通过正方形和直角三角形的性质证明两个角和一条边相等即可证明三角形全等;(2)先求出正方行的边长,再根据翻转的性质得到每次翻转后横坐标的增加量,找出落在x 轴上的点的变化规律,即可得到答案.【小问1详解】解:∵四边形ABCD 是正方形,∴AB AD =,90BAD ∠=︒,∵90DAN BAM ∠+∠=︒,90DAN NDA ∠+∠=︒,∴BAM NDA ∠=∠,∵BAM NDA DNA AMB AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADN BAM ≌,∴3AN BM ==,1DN AM ==,∴点D 的坐标为()2,1-如下图所示,过点C 作x 轴的垂线,垂足为F ,过点D 作y 轴的垂线,垂足为E ,两条垂线交于点P,∵90CDP EDA ∠+∠=︒,90NDA EDA ∠+∠=︒,∴CDP NDA ∠=∠,∵CDP NDA CPD DNA DC AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADN CDP ≌,∴1DP DN ==,3CP AN ==,∴四边形DNFP 正方形,∴1DP NF PF ===∴1PE DE DP =-=,4CF CP PF =+=,∴点C 的坐标为()1,4-,故答案为:()2,1-,()1,4-【小问2详解】解:根据旋转的性质得到1AB AB =,∵正方形ABCD 的面积为10,∴AB =,∴点1B 的坐标为()1+,∵每次翻转后,点的横坐标增加量为正方形的边长,即,∴第二次翻转后2C 的坐标为()1++,即()1+∴第三次翻转后3D 的坐标为()1+,即()1+,∴第四次翻转后4A 的坐标为()1+,∴第五次翻转后4B 的坐标为()1+,∴落在x 轴上的点以A 、B 、C 、D 周期变化,∵20244506÷=,∴第2024次翻转后的点坐标为()20241A +,故答案为:()1+,()20241A +.27.如图,已知在ABC 中,(060)AB BC ABC αα=∠=<<︒,,,射线AM AB ⊥,点P 为射线AM 上的动点(点P 不与点A 重合),连接BP ,将线段BP 绕点B 顺时针旋转角度α后,得到线段BQ ,连接PQ 、QC .(1)试说明PAB QCB ≌的理由;(2)延长QC 交射线AM 于点D ,在点P 的移动过程中,QDM ∠的大小是否发生变化?若改变请说明理由,若不改变,请求出QDM ∠的大小(用含α的代数式表示);(3)当BQ AC ∥时,AB m AP n ==,,过点Q 作QE 垂直射线AB ,垂足为E ,那么AEQ S = (用m 、n 的代数式表示).【答案】(1)理由见解析(2)不改变,QDM α∠=(3)mn【解析】【分析】(1)先证明PBA QBC ∠=∠,再根据两条边相等,即可证得两个三角形全等;(2)先证明()SAS DAB DCB ≌,得到DA DC =,DBA DBC ∠=∠,再计算出DBA ∠的值,再证明DAC DBA ∠=∠,最后根据三角形外角定理即可求得QDM ∠的大小;(3)证明QB 是ABE ∠的角平分线,根据角平分线定理得到BC BE =,QE QC =,再根据BC AB m ==,QC PA n ==,即可得到BE 和QE ,根据三角形面积公式进行计算即可.【小问1详解】证明:根据旋转的性质得到PN QB =,PBQ α∠=,∴PBQ ABC ∠=∠,∴PBA QBC ∠=∠,∵PB QB PBA QBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS PAB QCB ≌;【小问2详解】解:如下图所示,连接BD ,∵()SAS PAB QCB ≌,∴90QCB PAB ∠=∠=︒,∴90DCB DAB ∠=∠=︒,∵BC AB DCB DAB DB DB =⎧⎪∠=∠⎨⎪=⎩,∴()SAS DAB DCB ≌,∴DA DC =,1122DBA DBC ABC α∠=∠=∠=∴DAC DCA ∠=∠,∵90DAC CAB DBA CAB ∠+∠=∠+∠=︒,∴12DAC DBA α∠=∠=,∵QDM DAC DCA DAC α∠=∠+∠=∠=,∴QDM ∠大小不改变,且QDM α∠=;【小问3详解】解:如下图所示,∵BQ AC ∥,∴ACB CBQ CAB QBE ∠=∠∠=∠,,∵ACB CAB ∠=∠,∴QBE CBQ ∠=∠,∴QB 是ABE ∠的角平分线,∵90QCB ∠=︒,∴CB QC ⊥,∵⊥QE AB ,∴BC BE =,QE QC =,∵BC AB m ==,QC PA n ==,∴BE m =,QE n =,∴()1122AQE S AE QE AB BE QE mn =⋅=+⋅= ,故答案为:mn .【点睛】本题考查全等三角形的判断和性质、三角形外角定理、直角三角形的性质和角平分线定理,解题的关键是熟练掌握三角形全等的判定条件.。
上海市闵行区2006—207学年初二年级上学期期末考试数学试卷

上海市闵行区2006— 207学年初二年级上学期期末考试数学试卷数学试卷(考试时间90分钟,满分100分)一、填空题(本大题共 14题,每题2分,满分28分)1签 ^一 ______________ . 4.若 2a 3b 4c ,那么 a : b : c = ____________ 知3、4、5、a 成比例,那么 a = ________________ . 6 .正比例函数 y ___________ 象限.7.函数y ________________ .x 2,那么f= _________________11 2k9•反比例函数$的图象在每个象限内 y 的值随着x 的逐渐增大而增大, x &已知 )那么k 的取值范围是 _____________2.已知 =2.236,=7.071,那么 0.05 = 3 .如果x____ . 5.已2x 的图象经过10.命题等腰三角形的两个底角相等”的逆命题是_________________________________________ . 11.如图,在Rt A ABC中,斜边AB的垂直平分线交边AB于点E,交边BC于点D,如果,那么度.12.已知,在Rt △ ABC中,上的中线,CD = 5 cm ,,CD是边AB ,那么BC = _________________ c m .x13.已知等腰直角三角形ABC的斜边BC = 16 , BD是的平分线,DE丄BC ,垂足为点E,那么△ DEC的周长是___________ .14.如图,在△ ABC 中,AB = AC ,是边BC的中点,DE丄AB,垂足为点C(第11题图)C,点DE,如果AE = 2,那么AB = ____________2 D(第14题图)、选择题(本大题共4题,每题3分,满分12分)15.下列图象中,是函数图象的是()(A ) ( B) ( C)( D)x16.已知某等腰三角形的周长为36,腰长为x, 底边长为y,那么y与x之间的函数关系式及定义^域是- /^J—r5555555555555555555555555()(A) (B)V362x(0曇:⑹;(C) y(D) 362x(9:18i.17.下列各组中的两个三角形一■定全等的是 5 5 5 5 55!)55555555()(A )以100度为) (A)12;(B) AD12;(C) Q AD6;(D )丨.AD 6・三、简答题:(本大题共6题,每题6分,满分36 分)1920.计算:2. 3 訂??1.21•正比例函数丫賦和反比例函数丫&的图象交于M、N两点,且点M的横坐标为,x请求出正比例函数的解析式和两交点M、N的坐标.22. 已知V只昭,其中y1与x成正比例,y2与x成反比例,且当X 1时,V七当x 2时,丫求y与x的函数解析式.23. 已知:如图,点P是等边△ ABC 内一点,,如果把厶APB绕点A旋转,使点B与点C重合,此时点P落在点处,求的度数.AP B (第23题图)C24. 已知:如图,在Rt△ ABC中,C 90 , A 30 , E是边BC的中点,BF // AC , EF// AB , EF = 4 cm .求(1)F 的度数;(2)AB 的长.四、解答题:(本大题共2题,每题7分,满分14分)25. 如图,直线I经过原点和点A(3,5),点B在x轴的正半轴上,且ABO 45 , AH丄OB,垂足为点H .(1)求直线I所对应的函数解析式;(2)求线段AH、OB的长度之比;(3)如果点P是线段OB上一点,设BP = x ,△ APB的面积为S,写出S与x的函数关系式,并指出自变量x的取值范围.当x取何值时,/ APB为钝角.(第25题图)B (第24题图)26. 如图,已知CD // AB , D 90 , AB = 2 CD , AE 丄BC , CE = BE , 1、?、 3 是否相等?如果相等,请证明;如果不相等,请说明理由.五、(本题共1题,满分10分)27. 如图1, OP是的平分线,请你利用该图形画一对以OP所在直线为对称轴的非直角三角形的全等三角形.完成要求,并将所画的全等三角形用符号语言表示为:S请你参考这个画全等三角形的方法,解答下列问题:(1)如图2,在△ ABC中,是直角, B 60 , AD、CE分别是RAC、BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(2)如图3, 在厶ABC 中,如图ACR不是直角,而(1)中的其他条件不变,请问,你在(1)中得到的结论是否仍然成立?如果成立,请证明;如果不成立,请说明理由.M(第 26题图) E B F A 图2 D C2006学年第一学期八年级期末考试数学试卷 参考答案及评分标准一、填空题(本大题共 14题,每题2分,满分28分) 1.兀 2. 0.2236;3.4. 6:4:3;5.&9; .k 20; 6. 二、四;7. a 5 ;31 ;10.有两个V rX • 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 52 ,,门,分2可由对称性得出 .,,,,,,,,,,,,,,,,,,2分 22•解:由题意可设、心0).,,,,,,,,,,,1 分x因为当 时 ;当£ 2时,ykl k2 4, 所以,,2 分 I2k k 5.12kl 解得分k J2 所以y 2x i 分x23.解:•••△ APB ◎△. ,,,,,,,,1 分,又,•CAP PAC 60 ,即PAP 60 , • △ PAP是等边三角形.35 5 5 5 5 5 5^ 分p C AP CAP P 112 60 >2 2,,分24.解:(1): C 90 , 別,ABC 60•55 5 5 5 5 5 5 5 5 5 5 5 51 5 5 5 5 5 5 1分EF//ABBEF ABC . 5 5 5 5 5 5 5 5 55!,,1 分•-BF//AC , EBF C 郭,• r5 5 5 5 5 5 5 5 5 5 5 5 5 5 1)))))))1分(2) •/ :BF, F 30 ,EF 4 •BE 1EFif • 55 55 5 5 5 5 5 5 5 5 5 5 5 51))5 1分2•/ E 是边BC 的中点, •RC .5 5 5 5 5 5 5 5 5 5 ,,1C 90?,AB.,1 )))))))1分25•解:(1)根据题意,设直线I的函数解析式是y賦山0).5 •••点A(3,5)在直线I 上,••• k • 3X• 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 52,门门分3(2) •- A(3,5) , AH, •AH,OH1•ABO 45且AHB, • RH AH 5 OB OH BH 8 5 5 5 5 5 5 5 5 5 5 5!2分(3) S 5x (0 x琦,5 5 5 5 5 5 5 5 55'2,,门J分当3 x S时* APB为钝角•,,“ 1))5) ))))))) 1分26•解: 1 2」• ,,, 5 5 5 5 5 5 5 5 55 51))))))))1分证明:•址BC , CE BE,•- AC AB,即得2 5 5 55 5 5215 5 5 5 5 5 5 5 5^分•,•••乂又••• D 90 , ••,,,,,,,,,,,,,,,2 分•••CD//AB ,•,即得BAD 90 .于是,由,,?3,得• ,,,,,,,,,,,,,,,,,,2 分说明:学生如果利用全等三角形证得,得2分.27•解:(1)图略(用边角边”的方法截得)•,,,,,,,,,,,,1 分符号的表示要对应顶点写在对应位置. ,,,,,,,,,,1 分(2)数量关系为FE FD •,,,,,,,,,,,,,,,,,1 分(3)结论仍然成立.,,,,,,,,,,,,,,,,,,,,1 分证明:如图,在AC上截取AG A匚连结FG • ,,,,,,1 分因为为公共边,可证也•,,,,,1 分AFE AFG,FE FG由B 60 h AD> CE分别是RAC1、的平分线,可得2 3 60,所以/所以由3 耳及FC为公共边•可得△ CFG BA CFD. ,,,,,,,,,,,,,,,,,3 分所以FG FD.所以FE FD,…分。
闵行2007学年第二学期八年级数学期终测试卷
闵行区2007学年第二学期八年级期末考试数学试卷参考答案以及评分标准一、填空题(本大题共14题,每题2分,满分28分)1.-3; 2.(2,0); 3.x > -12; 4.24y x =-;5.三;6.10x =,21x =-,32x =;7.1x a =;8.12;9.30;10.540;11.13;12.120;13.AD ;14.90A ∠=︒. 二、选择题(本大题共4题,每题2分,满分8分)15.B ;16.D ;17.D ;18.C .三、(本大题共4题,每题6分,满分24分) 19.解:原方程化为2x -+, ………………………………………(1分) 两边平方,得 222144x x x -=-+,………………………………………(1分) 整理后,得 2450x x +-=,……………………………………………(1分) 解得 11x =,25x =-. ……………………………………………(1分) 经检验:11x =,25x =-是原方程的根. …………………………………(1分) 所以,原方程的根是11x =,25x =-. ……………………………………(1分)20.解:由 ① 得0x y -=,20x y -=.……………………………………………(1分)原方程组化为 220,5,x y x y -=⎧⎨+=⎩ 2220,5.x y x y -=⎧⎨+=⎩………………………………(1分) 分别解这两个方程组,得原方程组的解是11,x y ⎧=⎪⎪⎨⎪=⎪⎩22,x y ⎧=⎪⎪⎨⎪=⎪⎩ 332,1,x y =⎧⎨=⎩ 442,1.x y =-⎧⎨=-⎩ ………………………(4分) 21.(1)CE ;(1分) AC .(1分)(2)作图正确,(3分),结论.(1分)22.解:(1)根据题意,得A (-1,0)在一次函数2y x m =+的图像上,∴20m -+=,解得m = 2.……………………………………………………………(2分)(2)由m = 2,得一次函数的解析式是22y x =+.当y = 0时,得220x +=,解得x = -1.∴点A 的坐标是A (-1,0).当x = 0时,得y = 2.∴点B 的坐标是B (0,2).于是根据题意,得点C 、D 的坐标分别是C (0,1)、D (2,0). (2分)设所求一次函数的解析式是y k x b =+.根据题意,得方程组1,20,b k b =⎧⎨+=⎩ 解得1,21.k b ⎧=-⎪⎨⎪=⎩ ∴所求一次函数的解析式是112y x =-+.……………………………(2分)四、(本大题共4题,第(23)、(24)题每题7分,第(25)、(26)题每题8分,满分30分)23.解:(1)∵四边形ABCD 是平行四边形,∴AD // BC ,∠B =∠D .∴180B BAD ∠+∠=︒.…………………………………………………(1分)于是由60B ∠=︒,得60B D ∠=∠=︒,120BAD ∠=︒.………………(1分)∵AE ⊥BC ,AF ⊥CD ,∴90AEB AFD ∠=∠=︒.∴30BAE DAF ∠=∠=︒.………………………………………………(1分)于是由EAF BAD BAE DAF ∠=∠-∠-∠,得60EAF ∠=︒. ………(1分)另解:∵四边形ABCD 是平行四边形,∴AB // CD .∴180B C ∠+∠=︒. (1分)于是由60B ∠=︒,得120C ∠=︒. ……………………………………(1分)∵AE ⊥BC ,AF ⊥CD ,∴90AEC AFDC ∠=∠=︒.在四边形AECF 中,360EAF AEC C AFC ∠+∠+∠+∠=︒,…………(1分)∴60EAF ∠=︒. ………………………………………………………(1分)(2)在Rt △ABE 中,90AEB ∠=︒,AB = 6,由60B ∠=︒,得30BAE ∠=︒,∴13BE AB ==.…………………(2分) 由勾股定理,得AE =即得AE =1分)24.解:(1)设函数1()y f x =的解析式为1y k x b =+.根据题意,函数1()y f x =的图像经过点(1500,200)、(0,100),(1分)所以,得方程组1500200,100.k b b +=⎧⎨=⎩……………………………………(1分) 解得 1,15100.k b ⎧=⎪⎨⎪=⎩ ………………………………………………………(1分)所以,所求函数解析式为1110015y x =+.……………………………(1分) (2)设函数2()y g x =的解析式为21y k x =. 根据题意,得函数2()y g x =的图像经过点(1500,200),所以,21500200k =.解得 2215k =.………………………………(1分) 当x = 2300时,117602300100153y =⨯+=, 229202300153y =⨯=. 所以,12y y <.…………………………………………………………(1分) 所以,如果每月用车的行驶路程为2300千米,应租用甲出租车公司. ……………………………………………………………………………(1分)25.解:设甲店进了x 箱饮料,则乙店进了(25 - x )箱饮料.…………………(1分)根据题意,得100010003501025x x+-=-.……………………………………(2分) 两边同是乘以x (25 - x ),并整理,得226025000x x -+=.解得 110x =,2250x =.…………………………………………(2分) 经检验,110x =,2250x =是原方程的解.但当x = 250时,25 –x = -225 < 0,不合题意,所以,取x = 10.………………………………………………(1分) 于是,25 –x = 15.…………………………………………………………(1分) 答:甲、乙两店分别进了10箱和15箱饮料.……………………………(1分)26.证明:(1)∵CD // BE ,∴∠CDE =∠DEB .…………………………………(1分)∵O 是边BC 的中点,∴CO = BO .………………………………(1分)在△COD 和△BOE 中,,,,C D O B E OC OD B O EC O B O ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△COD ≌△BOE (A .A .S ).∴CD = BE .…………………………………………………………(2分)(2)∵CD // BE ,CD = BE ,∴四边形BECD 是平行四边形.………(1分)∵∠ABD = 2∠BED ,且∠ABD =∠BED +∠BDE ,∴∠BED =∠BDE .∴BD = BE .…………………………………………………………(2分) ∴四边形BECD 是菱形.……………………………………………(1分)五、(本大题只有1题,第(1)小题4分,第(2)(3)小题每题3分,满分10分)27.证明:(1)过点M 分别作MG ⊥AB ,MH ⊥CD ,垂足为点G 、H .∵点M 是边BC 的中点,∴BM = CM .∵在梯形ABCD 中,AD // BC ,AB = CD ,∴60B C ∠=∠=︒.又∵MG ⊥AB ,MH ⊥CD ,∴90BGM CHM ∠=∠=︒.∴△BGM ≌△CHM .得MG = MH ,且30BMG CMH ∠=∠=︒,即得120GMH EMF ∠=∠=︒.………………………………………(2分) 又∵∠EMF =∠EMG +∠GMF ,且∠GMH =∠GMF +∠FMH ,∴∠EMG =∠FMH .于是,由90BGM CHM ∠=∠=︒,MG = MH ,得△EGM ≌△FHM .∴ME = MF .…………………………………………………………(2分)(2)当点E 、F 在边AB 、CD 上移动时,五边形AEMFD 的面积的大小不会改变.…………………………………………………………………(1分)∵△EGM ≌△FHM ,∴EMG FMH S S ∆∆=.即得五边形五边形AEMFD AGMHD S S =.……………………………………(2分)(3)联结AM (在备用图中1).当点E 、F 恰好是边AB 、CD 的中点,且AB = CD ,得BE = CF .又∵ME = MF ,BM = CM ,∴△BEM ≌△CFM .∴∠BME =∠CMF .∵120EMF ∠=︒,∴1(180)302BME EMF ∠=︒-∠=︒.…………(1分) 于是,由60B ∠=︒,得90BEM ∠=︒.∵点E 是边AB 的中点,∴ME 是边AB 的垂直平分线.∴MA = MB .于是,由60B ∠=︒,得△ABM 是等边三角形.……………………(1分) ∴60AMB ∠=︒.即得∠AMB =∠C .∴AM // CD .又∵AD // MC ,∴四边形AMCD 是平行四边形.∴AD = CM .于是,由BC = 8,BM = CM ,得CM = 4.即得AD = 4.…………………………………………………………(1分)说明:如果学生在证得△BEM 是直角三角形,且30BEM ∠=︒. ………………(1分)利用直角三角形的性质求得BE = 2,进而求得AB = 4.分别过点A 、D 作AK ⊥BC ,DL ⊥BC ,垂足为点K 、L (在备用图2中).利用直角三角形的性质求得BN = 4,CL = 4.………………………………(1分) 求得KL = 4,并说明四边形AKLD 是矩形,进而求得AD = 4.……………(1分)A B C D M E F (第26题图) G H A B C D M E F (备用图1) A B C D M E F (备用图2) K L。
上海市闵行区2009学年预备年级上期末考试数学试卷

闵行区学校班级学号姓名……………………………………密○…………………………………………封○…………………………………○线……………………………………2021学年第一学期六年级质量调研考试数学试卷〔考试时间90分钟,总分值100分〕1.本试卷含四个大题,共27题;2.除第一、二大题外,其余各题如无特别说明,都必须写出计算的主要步骤;3.本次考试答题时可使用计算器.试卷中,π.一、选择题(本大题共6小题,每题3分,总分值18分)1.以下说法中错误的选项是……………………………………………………………〔〕〔A〕如果整数a是整数b的倍数,那么b是a的因数;第- 1 - 页第 - 2 - 页〔B 〕一个合数至少有3个因数;〔C 〕在正整数中,除2外所有的偶数都是合数; 〔D 〕在正整数中,除了素数都是合数.2.以下分数中不能化成有限小数的是……………………………………………〔 〕 〔A 〕169; 〔B 〕38; 〔C 〕185; 〔D 〕507. 3.三个数为2、4、8,假设再添加一个数,使这四个数能组成一个比例,那么这个数可以是…………………………………………………………………………〔 〕〔A 〕2; 〔B 〕4; 〔C 〕6; 〔D 〕8. 4.六〔1〕班男生人数是女生人数的54,那么女生人数是全班人数的…………〔 〕〔A 〕51; 〔B 〕45; 〔C 〕94; 〔D 〕95.5.扇形的半径扩大为原来的2倍,圆心角缩小为原来的21,那么扇形的面积〔 〕〔A 〕不变; 〔B 〕扩大为原来的2倍; 〔C 〕缩小为原来的21; 〔D 〕扩大为原来的4倍.6.如图,点A 表示的数是21,那么点B 表示的数第 - 3 - 页是………………………〔 〕〔A 〕113; 〔B 〕114;〔C 〕115; 〔D 〕116. 二、填空题〔本大题共12题,每题2分,总分值24分〕 7.写出16的所有因数:.8.既能被2整除,又能被5整除的两位数共有个. 9.分解素因数:84 . 10.652的倒数是.11.在括号内填上适当的数,使等式成立:412)(92415)(5++==.12.比拟大小:74116. 13.将分数1141化成循环小数:=1141.︰18秒 .15.3:2:=b a ,5:4:=c b ,那么=c b a ::.16.从1~20这20个数中任意抽取一个数,抽到的数为素数的可能性的大小为.17.一段弧所在的圆的半径为12厘米,弧所对的圆心角为60°,那么这段弧的长 为厘米.18.如果圆的周长是62.8厘米,那么这个圆的面积是平方厘米. 三、〔本大题共4小题,总分值24分〕B1 A O第 - 4 - 页19.〔此题总分值6分〕 计算:1586553-+. 20.〔此题总分值6分〕 计算:4332112512⨯÷.21.〔此题总分值6分〕计算:3223.75(21)85%3535⨯-+÷.22.〔此题总分值6分〕 15:31:54x = ,求x 的值.四、〔本大题共5题,总分值34分〕 23.〔此题总分值6分〕某班级共有学生36人,其中31的同学报名参加乒乓球课外活动班,92的同学报名参加了羽毛球课外活动班.问:参加乒乓球课外活动班的同学比参加羽毛球课外活 动班的同学多几人? 24.〔此题总分值7分〕5公斤甘蔗可榨出甘蔗汁3公斤,问: 〔1〕120公斤甘蔗可榨出甘蔗汁多少公斤? 〔2〕要想得到60公斤甘蔗汁,需要甘蔗多少公斤? 25.〔此题总分值7分〕第 - 5 - 页 某商店以每件200元的价格购进一批服装,加价40%后作为定价出售.〔1〕求该服装的售价是每件多少元?〔2〕促销活动期间,商店对该服装打八折出售,这时每件服装还可盈利多少元? 26.〔此题总分值7分〕如图,一只羊被4米长的绳子拴在长为3米,宽为2米的长方形水泥台的一个顶点上,水泥台的周围都是草地,问这头羊能吃到草的草地面积是多少?〔结果准确到0.01平方米〕 27.〔此题总分值7分〕在抗震救灾的捐款活动中,六〔2〕班同学的捐款人数情况如右图所示,其中捐款10元的人数为10人.请根据图像答复以下问题:〔1〕六〔2〕班共有多少名学生?〔2〕捐款5元的人数是多少? 〔3〕全班平均每人捐款多少元? 闵行区2021学年第一学期六年级质量调研考试数学试卷参考答案以及评分标准 一、选择题(本大题共6小题,每题3分,总分值18分)1.D ;2.C ;3.B ;4.D ;5.B ;6.D .二、填空题〔本大题共12题,每题2分,总分值24分〕 …………………………………………………………………………密 封 线 内 不 准捐款捐款50捐款5捐款捐款209081 15135第 - 6 - 页7.1,2,4,8,16 ; 8.9; 9.2×2×3×7; 10.176; 11.8、1. 12.>;13.27.3 ; 14.8; 15.8∶12∶15; 16.52; 17.12.56;18.314.三、〔本大题4小题,每题6分,总分值24分〕 19.解:原式301630253018-+=………………………………………………………〔2分〕3027=……………………………………………………………………〔2分〕109=.……………………………………………………………………〔2分〕 20.解:原式415232512⨯÷=…………………………………………………………〔2分〕415322512⨯⨯=…………………………………………………………〔2分〕第 - 7 - 页56=〔或511〕.…………………………………………………………〔2分〕 21.解:原式517100851514415÷+⨯=…………………………………………………〔2分〕1751008527⨯+=…………………………………………………………〔1分〕4127+=…………………………………………………………………〔1分〕415=〔或433〕.………………………………………………………〔2分〕22.解:因为15:31:54x =,所以341155⨯=⨯x .………………………………〔2分〕所以41525=x .……………………………………………………………〔2分〕所以第 - 8 - 页203=x .………………………………………………………………〔2分〕四、〔本大题共5题,总分值34分〕23.解:参加乒乓球课外活动班的人数为123136=⨯〔人〕. ……………………〔2分〕参加羽毛球课外活动班的人数为89236=⨯〔人〕.………………………〔2分〕 所以 4812=-〔人〕.………………………………………………………〔1分〕答:参加乒乓球课外活动班的同学比参加羽毛球课外活动班的同学多4人.〔1分〕24.解:〔1〕根据题意 1公斤甘蔗可榨甘蔗汁53公斤.……………………………〔1分〕7253120=⨯〔公斤〕.…………………………………………………〔2分〕〔2〕榨1公斤甘蔗汁需要甘蔗35公斤.……………………………………〔1分〕1003560=⨯〔公斤〕.…………………………………………………〔2分〕答:〔1〕120公斤甘蔗可榨出甘蔗汁72公斤.第 - 9 - 页〔2〕要想得到60公斤甘蔗汁,需要甘蔗100公斤.………………〔1分〕〔其它方法参照评分〕25.解:〔1〕200+200×40%=280〔元〕.…………………………………………〔3分〕〔2〕280×0.8-200 = 24〔元〕.……………………………………………〔3分〕 答:〔1〕该服装的售价是每件280元. 〔2〕这时每件服装还可盈利24元.…………………………………〔1分〕 26.解:3602903601903604270222⨯π⨯+⨯π⨯+⨯π⨯………………………………………〔3分〕453π=…………………………………………………………………………〔1分〕61.41≈〔平方米〕.…………………………………………………………〔2分〕 答:这头羊能吃到草的草地面积约为.…………………………〔1分〕 27.解:〔1〕4136090=,第 - 10 - 页404110=÷.………………………………………………〔2分〕〔2〕10181%15360135360901=----,410140=⨯.………………………〔2分〕〔3〕捐5元的人数为4人;捐10元的人数为10人;捐20元的人数为1536013540=⨯人; 捐50元的人数为61001540=⨯人;捐100元的人数为58140=⨯人; 捐款总额为:122051006501520101045=⨯+⨯+⨯+⨯+⨯〔元〕. 5.30401220=÷〔元〕.…………………………………………………〔2分〕 答:〔1〕六〔2〕班共有40名学生;〔2〕捐款5元的人数是4人;〔3〕全班平均每人捐款30.5元.……………………………………〔1分〕。
2024—-2025学年上海市闵行区航华中学九年级上学期数学期中考试试卷

2024—-2025学年上海市闵行区航华中学九年级上学期数学期中考试试卷1.下列命题正确的是()A.等腰三角形都是相似图形B.矩形都是相似图形C.菱形都是相似图形D.圆都是相似图形2.某一时刻,身高的小丽在阳光下地面上的影长是,同一时刻同一地点测得某旗杆地面上的影长是,那么该旗杆的高是()A.5B.20C.40D.83.四边形的对角线交于点,下列比例式中能判定的是()A.B.C.D.4.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,下边各组边的比不能表示sinB的()A.B.C.D.5.如果||=2,=-,那么下列说法正确的是()A.||=2||B.是与方向相同的单位向量C.2-=D.∥6.如图,点A(1,7),B(1,1),C(4,1),D(6,1),若△CDE与△ABC相似,那么在下列选项中,点E的坐标不可能...是().A.(6,2)B.(6,3)C.(6,5)D.(4,2).7.已知,则=_____.8.已知点是线段的黄金分割点,如果,那么线段______.9.在比例尺是的地图上测得地铁9号线七宝站到虹桥火车站的直线距离约是2.5厘米,那么9号线七宝站到虹桥火车站的实际直线距离约是______千米.10.如果两个相似三角形周长的比是,那么它们面积的比是______.11.若与的方向相反,且长度为5,用表示,则=__________.12.如图,已知点在射线上,点在射线上,,.则______.(含的式子表示)13.如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)14.如图,点G是的重心,,,那么的长为____________15.如图,已知在中,边,高,正方形的顶点、在边上,顶点、分别在边和上,那么这个正方形的边长等于___________.16.已知梯形中,,点分别是边上的点,,如果,那么______.17.根据三角形外心的概念,我们可引入下一个新定义:定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在中,,,,如果准外心P在边上,那么的长为_____.18.已知矩形中,是边上一点,将绕点旋转得到,使得点的对应点落在线段上,如果的延长线恰好经过点,那么的长度等于______.19.计算:.20.\如图,已知两个不平行的向量.先化简,再求作:.21.如图,在中,,,过点作,垂足为点.(1)求的值.(2)点是延长线上一点,连结,当时,求线段的长.22.某体育看台侧面的示意图如图所示,观众区的坡度为,顶端离水平地面的高度为10m,从顶棚的处看处的仰角,竖直的立杆上、两点间的距离为处到观众区底端处的水平距离为3m,求:顶棚的处离地面的高度.(,结果精确到0.1m)23.如图,已知是中的角平分线,是上的一点,且.(1)求证:;(2)求证:;(3)求的长.24.已知在直角坐标系内的位置如图所示,,双曲线与边交于点,与边交于点.(1)求的值;(2)当的正切值为时,连接,求的面积与直线的表达式;(3)在(2)的条件下,设直线与轴交于点,点在射线上,连接,如果与相似,试求点的坐标.25.在中,,点为边上一点,且,点分别为边上的动点(点在点的右边),且.设,.(1)如图1,当时,求的长;(2)如图2,当点在边上时,求关于的函数解析式,并写出函数的定义域;(3)连接,当是以边为腰的等腰三角形时,直接写出的长.。
2024-2025学年上海市闵行区六校联考高一(上)期中数学试卷(含答案)
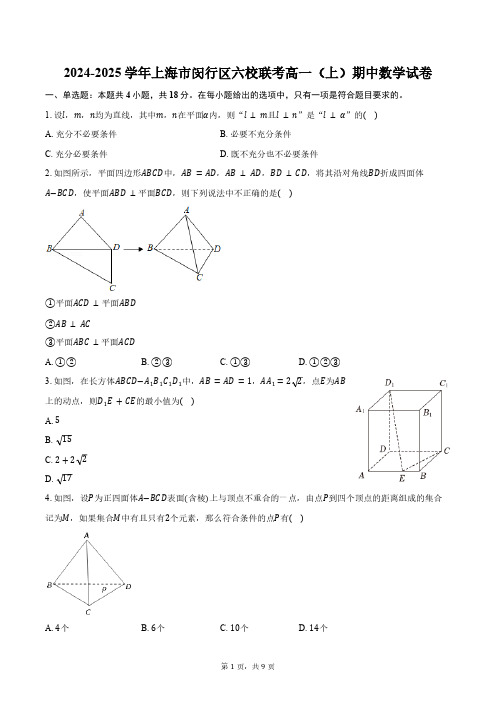
2024-2025学年上海市闵行区六校联考高一(上)期中数学试卷一、单选题:本题共4小题,共18分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.设l,m,n均为直线,其中m,n在平面α内,则“l⊥m且l⊥n”是“l⊥α”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件2.如图所示,平面四边形ABCD中,AB=AD,AB⊥AD,BD⊥CD,将其沿对角线BD折成四面体A−BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )①平面ACD⊥平面ABD②AB⊥AC③平面ABC⊥平面ACDA. ①②B. ②③C. ①③D. ①②③3.如图,在长方体ABCD−A1B1C1D1中,AB=AD=1,AA1=22,点E为AB上的动点,则D1E+CE的最小值为( )A. 5B. 15C. 2+22D. 174.如图,设P为正四面体A−BCD表面(含棱)上与顶点不重合的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )A. 4个B. 6个C. 10个D. 14个二、填空题:本题共12小题,共54分。
5.如果一条直线和两条异面直线中的一条平行,那么它和另一条直线的位置关系是______.6.若平面α⋂β=l,直线a⊂α,直线b⊂β,a∩b=M,则点M与l的位置关系为______.7.正方体ABCD−A1B1C1D1中,异面直线AB与DC1所成角的大小为______.8.在正方体ABCD−A1B1C1D1中,AA1=2,则直线AB到平面CDD1C1的距离为______.9.△AOB的斜二测直观图△A′O′B′如图所示,则△AOB的面积是______.10.以下四个命题中,真命题是______(只填真命题的序号).①若a,b是两条直线,且a//b,则a平行于经过b的任何平面;②若直线a和平面α满足a//α,则a与α内的任何直线平行;③若直线a,b和平面α满足a//α,b//α,则a//b;④若直线a,b和平面α满足a//b,a//α,b⊄α,则b//α.11.一个圆台的两个底面半径分别为1和2,高为1,则该圆台的体积为______.12.已知圆锥的表面积为12π,其侧面展开图是一个半圆.则圆锥的高为______.13.正方体ABCD−A1B1C1D1的棱长为2,E是棱DD1的中点,则平面AC1E截该正方体所得的截面面积为______.14.如图所示,求一个棱长为2的正四面体的体积,可以看成一个棱长为1的正方体切去四个角后得到,类比这种分法,一个相对棱长都相等的四面体A−BCD,其三组棱长分别为AB=CD=5,AD=BC= 13,AC=BD=10,则此四面体的体积为______.15.某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为63的正方体的六个面所截后剩余的部分,(球心与正方体的中心重合),若其中一个截面圆的周长为6π,则该球的表面积是______.16.在《九章算术》中,将四个面都是直角三角形的四面体称之为鳖臑,在鳖臑A−BCD中,AB⊥平面BCD,且有BD⊥CD,AB=BD=2,CD=1,点P是AC上的一个动点,则三角形PBD的面积的最小值为.三、解答题:本题共5小题,共78分。
2024-2025学年上海市闵行区九年级上学期数学期中试卷

2024学年第一学期期中考试九年级数学试卷(考试时间:100分钟 满分150分)1.本试卷含三个大题,共25题,答题时,考生务必按答题要求在答题纸规定的位置上作答在草稿纸,本试卷上答题一律无效.2.除第一,二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.3.本次考试不可以使用科学计算器.一,选择题(本大题共6题,每小题4分,满分24分)1.如果两个相似三角形对应边之比是1:4,那么它们的对应边上的中线之比是( )A.1:2B.1:16C.1:8D.1:42.在ABC △中,已知90C ∠=︒,5AB =,4BC =,那么cos B 的值为( ) A.34 B.35 C.45 D.433.在ABC △中,D ,E 分别是边AB ,AC 上的点,在下列已知条件中,不能判定//DE BC 的是( ) A.CE BD EA DA = B.DE AE BC AC = C.AC AE AB AD = D.CE BD CA BA =4.下列命题中,假命题的是( )A.如果0k =或0a =,那么0ka =B.如果m ,n 为实数,那么()()m na mn a =C.如果a kb =(k 为实数),那么//a bD.如果||3a =,那么3a b =或3a b =-5.如图,传送带和地面所成斜坡的坡度为1:3,它把物体从地面点A 处送到离地面3米高的B 处,则物体从A 到B 所经过的路程为( )A. B. 米 D.9米6.如图,在正方形ABCD 中,点E ,M 是边AD ,CD 上的点,BE ,BM 与AC 交于点F ,G .如果45EBM ∠=︒,那么下列结论中,错误的是( )A.AEF CBF △∽△B.CMG BFG △∽△C.ABG CFB △∽△D.ABF CBG △∽△ 二,填空题(本大题共12题,每题4分,满分48分)7.已知43x y =,那么2x x y=+________. 8.上海与杭州的实际距离约200千米,在比例尺为1:5000000的地图上,上海与杭州的图上距离约________厘米.9.已知e 为单位向量,向量a 与e 的方向相反,且长度为6,那么a =________.(用e 表示)10.已知P 是线段AB 上的一点,且2AP AB BP =⋅,如果2AB =,那么AP 的长是________.11.已知两个相似三角形的周长之比是2:3,面积之差是50,那么这两个三角形中较小三角形的面积是________.12.已知D ,E 分别是ABC △的边AB ,AC 上的点(不与端点重合),且DE 与BC 不平行,要使得ADE △与ABC △相似,那么添加一个条件可以为________(只填一个).13.在ABC △中,已知13AB AC ==,12tan 5B =,点G 是ABC △的重心,那么AG 的长是________. 14.如图,已知////AD BE CF ,如果32AB BC =,4AD =,9CF =,那么BE 的长是________.15.如图,某兴趣小组用无人机进行航拍测高,无人机从相距1号楼和2号楼的地面正中间点B 垂直起飞到点A 处,测得1号楼顶部E 的俯角为60︒,测得2号楼顶部F 的俯角为45︒.已知1号楼的高度为20米,那么2号楼的高度为________米(结果保留根号).16.已知在梯形ABCD 中,//AD BC ,90ABC ∠=︒,对角线AC ,BD 相交于点O ,且AC BD ⊥,如果:2:3AD BC =,那么:DB AC =________.17.如图,在Rt ABC △中,90ACB ∠=︒,9AB =,cot 2A =,点D ,E 在边AB ,AC 上,将ADE △沿着DE 翻折后,点A 的对应点在线段BC 的延长线上的点P 处,如果BPD A ∠=∠,那么DE 的长为________.18.Rt ABC △中,90C ∠=︒,3AC =,2BC =,将此三角形绕点A 旋转,当点B 的对应点D 在直线BC 上,点C 的对应点在点E 处,那么BDE △的面积是________.三,解答题(第19-22题,每题10分,第23-24题,每题12分,第25题14分,共78分)19.(本题满分10分) 2.20.(本题满分10分,第(1)小题6分,第(2)小题4分)如图,点E 在平行四边形ABCD 边BC 上一点,对角线AC ,BD 相交于点O ,AE ,AC 交BD 于点G ,O ,已知:3:1AG GE =.(1)求:EC BC 的值.(2)设BA a =,AO b =,那么EC =_______,GB =_______(用向量a ,b 表示).21.(本题满分10分,其中每小题各5分)已知:如图,在ABC △中,6AB AC ==,4BC =,AB 的垂直平分线交AB 于点E ,交BC 的延长线于点D .(1)求CD 的长度.(2)过C 作CH DE ⊥于点H ,求CH 的长度.22.(本题满分10分)图1是一款平板电脑支架,由托板,支撑板和底座构成.工作时,可将平板电脑吸附在托板上,底座放置在桌面上.图2是其侧面结构示意图,已知托板AB 长200mm,支撑板CB 长80mm,当130ABC ︒∠=,70BCD ∠=︒时,求托板顶点A 到底座CD 所在平面的距离(结果精确到1mm ).(参考数据:sin700.94≈︒,cos700.34≈︒,tan70 2.75≈︒, 1.41≈ 1.73≈)图1 图223.(本题满分10分,其中每小题各6分)如图在Rt ABC △中,90ACB ∠=︒,D ,E 分别位于边AB ,BC 上.且CD CA =,DE AB ⊥.(1)求证:2CA CE CB =⋅.(2)联结AE ,取AE 的中点M ,联结CM 并延长交AB 于点H .求证:CH AB ⊥.24.(本题满分12分,第(1)小题2分第(2,3)小题各5分)如图在平面直角坐标系xOy 内,已知点(1,0)A ,(5,0)B ,(3,4)C -,(0,3)D ,点P 在x 轴的负半轴上,且AP AB =.(1)求直线PD 的表达式.(2)点M 是直线PD 在第三象限上的点,联结AM ,且2MP PA PB =⋅,求tan PMA ∠的值.(3)在(2)的条件下,联结AC ,BC ,在直线CM 上是否存在点E ,使得AEC ACB ∠=∠.若存在,求出点E 的坐标,若不存在,请说明理由.25.(本题满分14分,其中第(1)小题4分,第(2)小题4分,第(3)小题6分)已知,在梯形ABCD 中,//AB CD ,90ABC ∠=︒,6AB =,8BC =,tan 2D =,点E 是射线CD 上一动点(不与点C 重合),将BCE △沿着BE 进行翻折,点C 的对应点记为点F .图1 图2 图3 图4(1)如图1,当点F 位于梯形ABCD 的中位线MN 上时,求CE 的长.(2)如图2,当点E 在线段CD 上时,设CE x =,BFC EFCS y S =△△,求y 与x 之间的函数关系式,并写出定义域. (3)如图3,联结AC ,线段BF 与射线CA 交于点G ,当CBG △是等腰三角形时,求CE 的长.。
2024上海初三二模数学试卷分类《23题几何证明题》

第23题图上海市2024届初三二模数学试卷分类汇编——23题几何证明题【2024届·宝山区·初三二模·第23题】1.(本题满分12分,第(1)小题6分,第(2)小题6分)如图10,在⊙O 中,直径AB 垂直于弦CD ,垂足为点E ,联结AC 、DO ,延长DO 交AC 于点F .(1)求证:2AF OF DF =⋅;(2)如果8CD =,2BE =,求OF 的长.【2024届·崇明区·初三二模·第23题】2.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知在四边形ABCD 中,//AB CD ,对角线AC 平分DAB ∠,点O 是AC 上一点,以OA 为半径的⊙O 过B 、D 两点.(1)求证:四边形ABCD 是菱形;(2)设⊙O 与AC 交于点E ,联结DE 并延长,交AB 的延长线于点F ,若2AB AC EC =⋅,求证:AE EF =.图10图8图9【2024届·奉贤区·初三二模·第23题】3.(本题满分12分,第(1)小题6分,第(2)小题6分)如图8,在四边形ABCD 中,//AB DC ,B ADC ∠=∠,点E 、F 分别在边AB 、BC 上,且ADE ∠=CDF ∠.(1)求证:CF CB AE AB ⋅=⋅;(2)联结AC 、EF ,如果//EF AC ,求证:四边形ABCD 是菱形.【2024届·虹口区·初三二模·第23题】4.(本题满分12分,第(1)小题6分,第(2)小题6分)如图9,在Rt ABC ∆中,90C ∠=︒,延长CB 至点D ,使得DB CB =,过点A 、D 分别作//AE BC ,//DE BA ,AE 与DE 相交于点E ,联结BE .(1)求证:BE CD ⊥;(2)联结AD 交BE 于点F ,联结CE 交AD 于点G .如果FBA ADB ∠=∠,求证:23AG AB =.图8图7【2024届·黄浦区·初三二模·第23题】5.(本题满分12分)如图8,M 、N 分别是平行四边形ABCD 边AD 、BC 的中点,对角线BD 交AN 、CM 分别于点P 、Q .(1)求证:13PQ BD =;(2)当四边形ANCM 是正方形时,试从内角大小和邻边的数量关系的角度探究平行四边形ABCD 的形状特征.【2024届·嘉定区·初三二模·第23题】6.(本题满分12分,第(1)小题6分,第(2)小题6分)如图7,在梯形ABCD 中,//AD BC ,AB DC =,点P 在四边形ABCD 内部,PB PC =,联结PA 、PD .(1)求证:APD ∆是等腰三角形;(2)已知点Q 在AB 上,联结PQ ,如果//AP CD ,AQ AP =,求证:四边形AQPD 是平行四边形.第23题图第23题图【2024届·金山区·初三二模·第23题】7.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知:D 是ABC ∆的边BC 上一点,点E 在ABC ∆外部,且BAE CAD ∠=∠,ACD ADC∠=∠ADE =∠,DE 交AB 于点F .(1)求证:AB AE =;(2)如果AD AF =,求证:2EF BF AB =⋅.【2024届·静安区·初三二模·第23题】8.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,直线EF 经过矩形ABCD 顶点D ,分别过顶点A 、C 作EF 的垂线,垂足分别为点E 和点F ,且DE DF =,联结AC .(1)求证:2AD AE AC =⋅;(2)联结BE 和BF ,求证:BE BF =.【2024届·闵行区·初三二模·第23题】9.(本题满分12分,第(1)小题4分,第(2)小题8分)沪教版九年级第二学期的教材给出了正多边形的定义.......:各边相等、各角也相等的多边形叫做正多边形.同时还提到了一种用直尺和圆规作圆的内接正六边形和圆的内接正五边形的方法,但课本上并未证明.我们现开展下列探究活动.活动一:如图1,展示了一种用尺规作⊙O 的内接正六边形的方法.①在⊙O 上任取一点A ,以A 为圆心、AO 为半径作弧,在⊙O 上截得一点B ;②以B 为圆心,AO 为半径作弧,在⊙O 上截得一点C ;再如此从点C 逐次截得点D 、E 、F ;③顺次联结AB 、BC 、CD 、DE 、EF 、FA .(1)根据正多边形的定义.........,我们只需要证明,.(请用符号语言表示,不需要说明理由),就可证明六边形ABCDEF 是正六边形.活动二:如图2,展示了一种用尺规作⊙O 的内接正五边形的方法.①作⊙O 的两条互相垂直的直径PQ 和AF ;②取半径OP 的中点M ;再以M 为圆心、MA 为半径作弧,和半径OQ 相交于点N ;③以点A 为圆心,以AN 的长为半径作弧,与⊙O 相截,得交点B .如此连续截取3次,依次得分点C 、D 、E ,顺次联结AB 、BC 、CD 、DE 、EA ,那么五边形ABCDE 是正五边形.(2)已知⊙O 的半径为2,求边AB 的长,并证明五边形ABCDE 是正五边形.(参考数据:22sin 22.52-︒=,21cos 22.52+︒=,1025sin 364-︒=,51cos364+︒=,1025sin 724+︒=.)第23题图2第23题图1第23题图【2024届·浦东新区·初三二模·第23题】10.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在菱形ABCD 中,点E 是边DC 上的任意一点(不与点D 、C 重合),AE 交对角线BD 于F ,过点E 作//EG BC 交BD 于点G .(1)求证:2DF FG BF =⋅;(2)当2BD DF AD DE ⋅=⋅时,求证:AE DC ⊥.【2024届·普陀区·初三二模·第23题】11.(本题满分12分)已知:如图7,四边形ABCD 中,//AB CD ,点E 在边AD 上,CE 与BA 的延长线交于点F ,FA AEAB ED=.(1)求证:四边形ABCD 为平行四边形;(2)联结FD ,分别延长FD 、BC 交于点G ,如果2FC FD FG =⋅,求证:AD CG BF CD ⋅=⋅.图7第23题图图7已知:如图,在四边形ABCD 中,//AD BC ,点E 是对角线AC 上一点,EA ED =,且DAB DEC ∠=∠=DCB ∠.(1)求证:四边形ABCD 是菱形;(2)延长DE 分别交线段AB 、CB 的延长线于点F 、G ,如果GB BC =,求证:22AD EF GD =⋅.【2024届·松江区·初三二模·第23题】13.(本题满分12分,第(1)小题6分,第(2)小题6分)如图7,已知AB 是⊙1O 与⊙2O 的公共弦,12O O 与AB 交于点C ,12O O 的延长线与⊙2O 交于点P ,联结PA 并延长,交⊙1O 于点D .(1)联结1O A 、2O A ,如果AB AD AP ==,求证:12O A O A ⊥;(2)如果123PO PO =,求证:PA AD =.第23题图第23题图如图,在菱形ABCD 中,点E 、G 、H 、F 分别在边AB 、BC 、CD 、DA 上,AE AF =,CG CH =,CG AE ≠.(1)求证://EF GH ;(2)分别联结EG 、FH ,求证:四边形EGHF 是等腰梯形.【2024届·杨浦区·初三二模·第23题】15.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在梯形ABCD 中,//AD BC ,AB CD =,BD BC =,DBC ∠的平分线交AD 延长线于点E ,交CD 于点F .(1)求证:四边形BCED 是菱形;(2)联结AC 交BF 于点G ,如果AC CE ⊥,求证:2AB AG AC =⋅.第23题图已知:在梯形ABCD 中,//AD BC ,BD AD ⊥,点E 在边AD 上(点E 不与点A 、D 重合),点F 在边CD 上,且ABD EBF C ∠=∠=∠.(1)求证:AB BEBD BF=;(2)联结EF ,与BD 交于点G ,如果BG EG =,求证:四边形BEDF 为等腰梯形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006学年第一学期八年级期末考试数 学 试 卷(考试时间90分钟,满分100分)题号 一 二 三 四 五 总分 得分一、填空题(本大题共14题,每题2分,满分28分) 19=__________.2.已知5 = 2.236,50 = 7.071,那么05.0 = _________________. 3.如果x 27x x =______________. 4.若234a b c == ,那么a ∶b ∶c = _________________. 5.已知3、4、5、a 成比例,那么a = _____________. 6.正比例函数2y x =-的图象经过___________象限. 7.函数5y x =-______________.8.已知2()1x f x x -=-,那么2f =__________________.9.反比例函数12k y x-=的图象在每个象限内y 的值随着x 的逐渐增大而增大,那么k 的取值范围是___________.10.命题“等腰三角形的两个底角相等”的逆命题是______________________________________. 11.如图,在Rt △ABC 中,斜边AB 的垂直平分线交边AB 于点E ,交边BC 于点D ,如果28B ∠=︒, 那么=∠CAD ___________度.12.已知,在Rt △ABC 中,90C ∠=︒,CD 是边AB上的中线,CD = 5 cm ,30A ∠=︒,那么BC = ________ cm .13.已知等腰直角三角形ABC 的斜边BC = 16,BD 是B ∠的平分线,DE ⊥BC ,垂足为点E ,那么△DEC 的周长是___________.学校_______________________ 班级__________ 学号_________ 姓名______________ …………………………密○………………………………………封○………………………………………○线…………………………ACED(第11题图)x oxo o xoxxx x xy y y o o(A )(B )(C )oo(D )y 14.如图,在△ABC 中,AB = AC ,120A ∠=︒,点D是边BC 的中点,DE ⊥AB ,垂足为点E ,如果AE = 2,那么AB = ____________.二、选择题(本大题共4题,每题3分,满分12分)15.下列图象中,是函数图象的是…………………………………………………( )16. 已知某等腰三角形的周长为36,腰长为x ,底边长为y ,那么y 与x 之间的函数关系式及定义域是…………………………………………………………………( ) (A )218(09)y x x =+<<; (B )362(018)y x x =-<≤; (C )362(018)y x x =-<<; (D )362(918)y x x =-<<.17.下列各组中的两个三角形一定全等的是………………………………………( ) (A )以100度为内角,10厘米为一边长的两个等腰三角形; (B )斜边相等的两个直角三角形; (C )有一边相等的两个等腰直角三角形; (D )以4、9为边的两个等腰三角形.18.在△ABC 中,7=AB ,5=AC ,AD 是边BC 的中线,那么AD 的取值范围是…………………………………………………………………………………( ) (A )120<<AD ; (B )122<<AD ;(C )60<<AD ; (D )61<<AD .三、简答题:(本大题共6题,每题6分,满分36分) 19321142a a a a a.A(第14题图)BCE2 D20.计算:13223323323---+-.21.正比例函数y k x =和反比例函数xy 6-=的图象交于M 、N 两点,且点M 的横坐标为2-,请求出正比例函数的解析式和两交点M 、N 的坐标.22.已知21y y y +=,其中1y 与x 成正比例,2y 与x 成反比例,且当1=x 时,4=y ;当2=x 时,5=y ;求y 与x 的函数解析式.23.已知:如图,点P 是等边△ABC 内一点,112APB ∠=︒,如果把△APB 绕点A 旋转,使点B 与点C 重合,此时点P 落在点P '处,求PP C '∠的度数.24.已知:如图,在Rt △ABC 中,90C ∠=︒,30A ∠=︒,E 是边BC 的中点,BF // AC ,EF// AB ,EF = 4 cm .求(1)F ∠的度数;(2)AB 的长.CBAPP '(第23题图)ACBE F(第24题图)321 ED CBA (第26题图)四、解答题:(本大题共2题,每题7分,满分14分)25.如图,直线l 经过原点和点(3,5)A ,点B 在x 轴的正半轴上,且45ABO ∠=︒,AH ⊥OB ,垂足为点H .(1)求直线l 所对应的函数解析式; (2)求线段AH 、OB 的长度之比;(3)如果点P 是线段OB 上一点,设BP = x ,△APB 的面积为S ,写出S 与x 的函数关 系式,并指出自变量x 的取值范围.当x 取何值时,∠APB 为钝角.26.如图,已知CD // AB ,90D ∠=︒,AB = 2 CD ,AE ⊥BC ,CE = BE ,1∠、2∠、3∠是否相等?如果相等,请证明;如果不相等,请说明理由.(第25题图)五、(本题共1题,满分10分)27.如图1,OP 是MON ∠的平分线,请你利用该图形画一对以OP 所在直线为对称轴的非直角三角形的全等三角形.完成要求,并将所画的全等三角形用符号语言表示为: ≌ .请你参考这个画全等三角形的方法,解答下列问题:(1) 如图2,在△ABC 中,ACB ∠是直角,60B ∠=︒,AD 、CE 分别是BAC ∠、BCA ∠ 的平分线,AD 、CE 相交于点F .请你判断并写出FE 与FD 之间的数量关系; (2)如图3,在△ABC 中,如图ACB ∠不是直角,而(1)中的其他条件不变,请问,你在(1)中得到的结论是否仍然成立?如果成立,请证明;如果不成立,请说明理由.M O P N 图1┌ F E D C A 图3 B A BC DE F 图2………………………………………………………………………………………………………………………………………………………密 封 线 内不 准 答题2006学年第一学期八年级期末考试数学试卷参考答案及评分标准一、填空题(本大题共14题,每题2分,满分28分) 1.3; 2.0.2236; 3.2; 4.6:4:3; 5.203; 6. 二、四; 7. 5a ≤; 8. 2- ; 9.12k >; 10.有两个内角相等的三角形是等腰三角形; 11.34;12.5; 13.16; 14. 8.二、选择题(本大题共4题,每题3分,满分12分) 15.C ; 16.D ; 17.D ; 18.D .三、简答题(本大题共6题,每题6分,满分36分)19.解:原式412a a a a a a 3分 3a a……………………………………………………………3分 20.解:原式3(233)23(32)31)1293431+=+---- ………………………2分 2364331=- …………………………………………2分 435=-. ………………………………………………………2分 21.解:(2,3)M -. ……………………………………………………………2分 x y 23-=. ………………………………………………………………2分 可由对称性得出)3,2(-N .………………………………………………2分 22.解:由题意可设2112(00)k y k x k k x =+≠≠、. ……………………………1分 因为当1=x 时,4=y ;当2=x 时,5=y所以12124,12 5.2k k k k +=⎧⎪⎨+=⎪⎩ ……………………………………………………2分解得122,2.k k =⎧⎨=⎩ ……………………………………………………………2分所以xx y 22+=.…………………………………………………………1分23.解:∵△APB ≌△AP C ',∴112AP C APB '∠=∠=︒. ……………………1分且,AP AP BAP CAP ''=∠=∠,又60BAP PAC ∠+∠=︒,∴60CAP PAC '∠+∠=︒ ,即60PAP '∠=︒,∴△PAP '是等边三角形. …………………………3分 ∴1126052PP C AP C AP P '''∠=∠-∠=︒-︒=︒.………………………2分24.解:(1)∵90C ∠=︒,30A ∠=︒,∴60ABC ∠=︒.……………………………………………………1分 ∵EF //AB ,60BEF ABC ∠=∠=︒. ………………………………1分 ∵BF //AC ,90EBF C ∠=∠=︒,∴30F ∠=︒. ………………………………………………………1分(2)∵90EBF ∠=︒,30F ∠=︒,4EF =∴122BE EF ==.…………………………………………………1分 ∵E 是边BC 的中点,∴4BC =. ………………………………1分 ∵90C ∠=︒,30A ∠=︒,∴28AB BC ==.……………………1分25.解:(1)根据题意,设直线l 的函数解析式是y k x =(0k ≠). ∵点(3,5)A 在直线l 上,∴53k =.∴x y 35=.…………………………………………………………2分 (2)∵(3,5)A ,AH OB ⊥,∴5AH =,3OH =.∵45ABO ∠=︒,且90AHB ∠=︒,∴5BH AH ==.∴8OB OH BH =+=. ……………………………………………2分(3)x S 5= (08x <≤).………………………………………………2分 当38x <<时, APB ∠为钝角.……………………………………1分26.解:123∠=∠=∠. …………………………………………………………1分 证明:∵AE BC ⊥,CE BE =,∴AC AB =,即得23∠=∠. ………………………………………2分 ∵2AB CD =,∴2AC CD =.又∵90D ∠=︒,∴130∠=︒. ………………………………………2分 ∵CD //AB ,∴180BAD D ∠+∠=︒,即得90BAD ∠=︒. 于是,由12390BAD ∠+∠+∠=∠=︒,130∠=︒,23∠=∠, 得12330∠=∠=∠=︒.………………………………………………2分说明:学生如果利用全等三角形证得23∠=∠,得2分.27.解:(1)图略(用“边角边”的方法截得). ………………………………1分 符号的表示要对应顶点写在对应位置. …………………………1分 (2)数量关系为FD FE =. ……………………………………………1分 (3)结论仍然成立. ……………………………………………………1分证明:如图,在AC 上截取AE AG =,连结FG .………………1分 因为21∠=∠,AF 为公共边,可证AEF ∆≌AGF ∆.……………1分 所以FG FE AFG AFE =∠=∠,.由60B ∠=︒,AD 、CE 分别是BCA BAC ∠∠、的平分线,可得2360∠+∠=︒. 所以60AFE CFD AFD ∠=∠=∠=︒.所以60CFG ∠=︒.由43∠=∠及FC 为公共边.可得△CFG ≌△CFD . ……………………………………………3分 所以FD FG =.所以FD FE =. ……………………………………………………1分FED CAB1y34G。
