二次函数综合(1)
二次函数综合试题及答案

二次函数综合试题及答案一、选择题1. 若二次函数y=ax^2+bx+c的图象开口向下,则a的取值范围是()。
A. a > 0B. a < 0C. a = 0D. a ≠ 0答案:B2. 已知二次函数y=2x^2-4x+3,其顶点坐标为()。
A. (1, 1)B. (2, -1)C. (1, 3)D. (2, 3)答案:A二、填空题3. 写出二次函数y=-2x^2+4x-1的顶点坐标为______。
答案:(1, 1)4. 若二次函数y=x^2-6x+k的图象与x轴有两个交点,则k的取值范围是______。
答案:k < 9三、解答题5. 已知二次函数y=ax^2+bx+c(a≠0),且该函数图象与x轴有两个交点,求证:b^2-4ac>0。
证明:已知二次函数y=ax^2+bx+c(a≠0)的图象与x轴有两个交点,即方程ax^2+bx+c=0有两个实数根。
根据判别式的性质,当Δ=b^2-4ac>0时,方程有两个不相等的实数根。
因此,b^2-4ac>0。
6. 已知二次函数y=-x^2+6x-5,求该函数的对称轴方程。
解:二次函数y=-x^2+6x-5的对称轴方程为x=-b/2a=-6/(2*(-1))=3。
四、计算题7. 已知抛物线y=-2x^2+4x+1与x轴交于点A、B,求A、B两点的坐标。
解:令y=0,得-2x^2+4x+1=0。
解得x1=-1/2,x2=3/2。
因此,A点坐标为(-1/2, 0),B点坐标为(3/2, 0)。
8. 已知二次函数y=2x^2-4x+3的顶点坐标为(1, 1),求该函数的对称轴方程。
解:已知二次函数y=2x^2-4x+3的顶点坐标为(1, 1),根据顶点式y=a(x-h)^2+k,对称轴方程为x=h。
因此,对称轴方程为x=1。
二次函数综合练习一(含答案)

2013年-----二次函数综合练习一一.选择题(共17小题)1.(2013•重庆)一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是()2.C D.3.(2013•雅安)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为().C D.2.C D.5.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x 2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数6.(2013•深圳)已知二次函数y=a (x ﹣1)2﹣c 的图象如图所示,则一次函数y=ax+c 的大致图象可能是( ).CD .7.(2013•齐齐哈尔)数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x 2+1与y=的交点的横8.(2013•攀枝花)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数y=与y=bx+c 在同一直角坐标系内的大致图象是().CD .9.(2013•聊城)二次函数y=ax 2+bx 的图象如图所示,那么一次函数y=ax+b 的图象大致是( ).CD .10.(2013•呼和浩特)在同一直角坐标系中,函数y=mx+m 和y=﹣mx +2x+2(m 是常数,且m ≠0)的图象可能是.CD .11.(2013•达州)二次函数y=ax 2+bx+c 的图象如图所示,反比例函数与一次函数y=cx+a 在同一平面直角坐标系中的大致图象是( ).CD .12.(2012•西宁)如图,二次函数y=ax 2+bx+c 的图象过(﹣1,1)、(2,﹣1)两点,下列关于这个二次函数的叙述正确的是( )13.(2012•泰安)二次函数y=a (x+m )2+n 的图象如图,则一次函数y=mx+n 的图象经过( )14.(2013•舟山)若一次函数y=ax+b (a ≠0)的图象与x 轴的交点坐标为(﹣2,0),则抛物线y=ax 2+bx 的对称轴216.(2013•泰安)对于抛物线y=﹣(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小,17.(2013•日照)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有()二.填空题(共10小题)18.(2013•南通)已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于_________.19.(2013•荆州)若根式有意义,则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第_________象限.20.(2013•营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第_________象限.21.(2013•绵阳)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣;④3|a|+|c|<2|b|.其中正确的结论是_________(写出你认为正确的所有结论序号).22.(2013•贺州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是_________.(填正确结论的序号)23.(2013•德阳)已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c >0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有_________.24.(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=于点B、C,则BC的长值为_________.25.(2013•本溪)在平面直角坐标系中,把抛物线y=﹣x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是_________.26.(2012•南京)已知下列函数①y=x2;②y=﹣x2;③y=(x﹣1)2+2.其中,图象通过平移可以得到函数y=x2+2x﹣3的图象的有_________(填写所有正确选项的序号).27.(2012•自贡)正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM= _________cm时,四边形ABCN的面积最大,最大面积为_________cm2.三.解答题(共3小题)28.(2013•宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).(1)求抛物线的解析式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.29.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.30.(2013•牡丹江)如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.2013年-----二次函数综合练习一参考答案与试题解析一.选择题(共17小题)1.(2013•重庆)一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是()y=﹣﹣>﹣2.C D.3.(2013•雅安)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为().C D.﹣图象在第一三象限,2.C D.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数5.y=的函数图象,既是轴对称图形,又是中心对称图形;6.(2013•深圳)已知二次函数y=a(x﹣1)2﹣c的图象如图所示,则一次函数y=ax+c的大致图象可能是().C D.7.(2013•齐齐哈尔)数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=的交点的横的图象,即可得解.y=8.(2013•攀枝花)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数y=与y=bx+c 在同一直角坐标系内的大致图象是( ).CD .,9.(2013•聊城)二次函数y=ax 2+bx 的图象如图所示,那么一次函数y=ax+b 的图象大致是( ).C D.﹣10.(2013•呼和浩特)在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是.C D.,与x=11.(2013•达州)二次函数y=ax2+bx+c的图象如图所示,反比例函数与一次函数y=cx+a在同一平面直角坐标系中的大致图象是().C D.的图象在第一、三象限,12.(2012•西宁)如图,二次函数y=ax2+bx+c的图象过(﹣1,1)、(2,﹣1)两点,下列关于这个二次函数的叙述正确的是()13.(2012•泰安)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过()14.(2013•舟山)若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(﹣2,0),则抛物线y=ax2+bx的对称轴即可求解.=﹣216.(2013•泰安)对于抛物线y=﹣(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小,﹣17.(2013•日照)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有(),(舍去),二.填空题(共10小题)18.(2013•南通)已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于3.x=x==∴19.(2013•荆州)若根式有意义,则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第二象限.的图象位于第二、四象限,=y=20.(2013•营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第四象限.21.(2013•绵阳)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣;④3|a|+|c|<2|b|.其中正确的结论是①③④(写出你认为正确的所有结论序号).>x﹣轴交点的横坐标分别为﹣b=x﹣>>m+n22.(2013•贺州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是①②⑤.(填正确结论的序号)=1=123.(2013•德阳)已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c >0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有①③④.=1,代入得(﹣24.(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=于点B、C,则BC的长值为6.y=时,25.(2013•本溪)在平面直角坐标系中,把抛物线y=﹣x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是y=﹣(x+1)2+4.x﹣(26.(2012•南京)已知下列函数①y=x2;②y=﹣x2;③y=(x﹣1)2+2.其中,图象通过平移可以得到函数y=x2+2x﹣3的图象的有①③(填写所有正确选项的序号).27.(2012•自贡)正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM=cm时,四边形ABCN的面积最大,最大面积为cm2.,即=x×﹣x+,﹣=最大,最大值是﹣×(+×+=cm 故答案是:,三.解答题(共3小题)28.(2013•宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).(1)求抛物线的解析式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.29.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.∴,∴30.(2013•牡丹江)如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.﹣×。
2021年中考数学《二次函数综合压轴题》模拟训练题集(一)

2021年中考数学《二次函数综合压轴题》模拟训练题集(一)1.已知二次函数y=+bx+c(b、c为常数)的图象经过点(0,﹣1)和点A(4,1).(1)求b、c的值;(2)如图1,点C(10,m)在抛物线上,点M是y轴上的一个动点,过点M平行于x轴的直线l平分∠AMC,求点M的坐标;(3)如图2,在(2)的条件下,点P是抛物线上的一动点,以P为圆心、PM为半径的圆与x轴相交于E、F 两点,若△PEF的面积为2,请直接写出点P的坐标.2.如图,抛物线y=ax2+6x﹣5交x轴于A,B两点,交y轴于C点,点B的坐标为(5,0),直线y=x﹣5经过点B,C.(1)求抛物线的函数表达式;(2)点P是直线BC上方抛物线上的一动点,求△BCP面积S的最大值并求出此时点P的坐标;(3)过点A的直线交直线BC于点M,连接AC当直线AM与直线BC的一个夹角等于∠ACB的3倍时,请直接写出点M的坐标.3.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的解析式,并直接写出当x满足什么值时y<0?(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP面积最大?若存在,求出点P的坐标;若不存在,请说明理由;(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.4.如图,矩形OABC中,O为原点,点A在y轴上,点C在x轴上,点B的坐标为(4,3),抛物线y=﹣x2+bx+c 与y轴交于点A,与直线AB交于点D,与x轴交于C,E两点.(1)求抛物线的表达式;(2)点P从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,与此同时,点Q从点A出发,在线段AC上以每秒个单位长度的速度向点C运动,当其中一点到达终点时,另一点也停止运动.连接DP、DQ、PQ,设运动时间为t(秒).①当t为何值时,△DPQ的面积最小?②是否存在某一时刻t,使△DPQ为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.5.在平面直角坐标系中,已知抛物线y=﹣x2+4x.(1)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线y=﹣x2+4x的“方点”的坐标;(2)如图,若将该抛物线向左平移1个单位长度,新抛物线与x轴相交于A、B两点(A在B左侧),与y轴相交于点C,连接BC.若点P是直线BC上方抛物线上的一点,求△PBC的面积的最大值;(3)第(2)问中平移后的抛物线上是否存在点Q,使△QBC是以BC为直角边的直角三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,说明理由.6.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.(1)求抛物线的函数解析式;(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.7.如图,在矩形OABC中,点O为原点,点A的坐标为(0,4),点C的坐标为(4,0),抛物线y=﹣x2+bx+c 经过点A、C,与AB交于点D.(1)求抛物线的函数解析式;(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.求S关于m的函数表达式;(3)抛物线y=﹣x2+bx+c的顶点为F,对称轴为直线l,当S最大时,在直线l上,是否存在点M,使以M、Q、D、F为顶点的四边形是平行四边形,若存在,请写出符合条件的点M的坐标;若不存在,请说明理由.8.如图1,抛物线y=ax2+bx﹣3经过A、B、C三点,己知点A(﹣3,0)、C(1,0).(1)求此抛物线的解析式.(2)点P是直线AB下方的抛物线上一动点(不与A、B重合),①过点F作x轴的垂线,垂足为D,交直线AB于点E,动点P在什么位置时,PE最大,求出此时P点的坐标.②如图2,连接AP.以AP为边作图示一侧的正方形APMN,当它恰好有一个顶点落在抛物线对称轴上时,求出对应的P点的坐标.9.如图a,已知抛物线y=﹣x2+bx+c经过点A(4,0)、C(0,2),与x轴的另一个交点为B.(1)求出抛物线的解析式.(2)如图b,将△ABC绕AB的中点M旋转180°得到△BAC′,试判断四边形BC′AC的形状.并证明你的结论.(3)如图a,在抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC全等?若存在,请直接写出点D的坐标;若不存在请说明理由.10.如图,已知二次函数y=x2﹣2x+m的图象与x轴交于点A、B,与y轴交于点C,直线AC交二次函数图象的对称轴于点D,若点C为AD的中点.(1)求m的值;(2)若二次函数图象上有一点Q,使得tan∠ABQ=3,求点Q的坐标;(3)对于(2)中的Q点,在二次函数图象上是否存在点P,使得△QBP∽△COA?若存在,求出点P的坐标;若不存在,请说明理由.11.在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.(1)直接写出:b的值为;c的值为;点A的坐标为;(2)点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.①如图1,过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;②若△CDM为等腰直角三角形,直接写出点M的坐标.12.如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A,B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.(1)求线段OC的长度;(2)设直线BC与y轴交于点D,点C是BD的中点时,求直线BD和抛物线的解析式,(3)在(2)的条件下,点P是直线BC下方抛物线上的一点,过P作PE⊥BC于点E,作PF∥AB交BD于点F,是否存在一点P,使得PE+PF最大,若存在,请求出该最大值;若不存在,请说明理由.13.已知抛物线y=ax2+bx+c经过点A(﹣2,0),B(3,0),与y轴负半轴交于点C,且OC=OB.(1)求抛物线的解析式;(2)在y轴负半轴上存在一点D,使∠CBD=∠ADC,求点D的坐标;(3)点D关于直线BC的对称点为D′,将抛物线y=ax2+bx+c向下平移h个单位,与线段DD′只有一个交点,直接写出h的取值范围.14.如图①,在平面直角坐标系中,抛物线y=x2的对称轴为直线l,将直线l绕着点P(0,2)顺时针旋转∠α的度数后与该抛物线交于AB两点(点A在点B的左侧),点Q是该抛物线上一点(1)若∠α=45°,求直线AB的函数表达式;(2)若点p将线段分成2:3的两部分,求点A的坐标(3)如图②,在(1)的条件下,若点Q在y轴左侧,过点p作直线l∥x轴,点M是直线l上一点,且位于y 轴左侧,当以P,B,Q为顶点的三角形与△P AM相似时,求M的坐标.15.如图,Rt△FHG中,∠H=90°,FH∥x轴,=0.6,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数y1=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点E(0,﹣3),顶点为C(1,﹣4),点D为二次函数y2=a(x﹣1﹣m)2+0.6m﹣4(m>0)图象的顶点.(1)求二次函数y1的函数关系式;(2)若准黄金直角三角形的顶点F与点A重合、G落在二次函数y1的图象上,求点G的坐标及△FHG的面积;(3)设一次函数y=mx+m与函数y1、y2的图象对称轴右侧曲线分别交于点P、Q.且P、Q两点分别与准黄金直角三角形的顶点F、G重合,求m的值,并判断以C、D、Q、P为顶点的四边形形状,请说明理由.16.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(﹣1,0),B(3,0)两点,与y 轴交于点C,连接BC.(1)求该抛物线的函数表达式;(2)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由;(3)点P是直线BC上方抛物线上的点,若∠PCB=∠BCO,求出P点的到y轴的距离.17.如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.(1)求直线OA及抛物线的解析式;(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为,如果存在,求出P的坐标;如果不存在,请说明理由.18.如图,抛物线y=ax2﹣x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.(1)求该抛物线的解析式;(2)当△PDE是以DE为底边的等腰三角形时,求点P的坐标;(3)当四边形ACPB的面积最大时,求点P的坐标并求出最大值.19.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.(1)求抛物线的解析式;(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;(3)点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;20.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.①求点P的坐标和PE的最大值.②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.21.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx与x轴交于点A(10,0),点B(1,2)是抛物线上点,点M为射线OB上点(不含O,B两点),且MH⊥x轴于点H.(1)求直线OB及抛物线解析式;(2)如图1,过点M作MC∥x轴,且与抛物线交于C,D两点(D位于C左边),若MC=MH,点Q为直线BC上方的抛物线上点,求△BCQ面积的最大值,并求出此时点Q的坐标;(3)如图2,过点B作BE∥x轴,且与抛物线交于E,在线段OA上有点P,在点H从左向右运动时始终有AP =2OH,过点P作PN⊥x轴,且PN与直线OB交于点N,当M与N重合时停止运动,试判断在此运动过程中△MNE与△BME能否全等,若能请求出全等时的HP长度,若不能请说明理由.22.如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)交x轴于A(﹣4,0),B(2,0),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)点D是第二象限内的抛物线上一动点.①求△ADE面积最大值并写出此时点D的坐标;②若tan∠AED=,求此时点D坐标;(3)连接AC,点P是线段CA上的动点,连接OP,把线段PO绕着点P顺时针旋转90°至PQ,点Q是点O 的对应点.当动点P从点C运动到点A,则动点Q所经过的路径长等于(直接写出答案)23.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).(1)求该抛物线的表达式及顶点坐标;(2)点P为抛物线上一点(不与点A重合),联结PC.当∠PCB=∠ACB时,求点P的坐标;(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.24.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为A(﹣2,0),且经过点B(﹣5,9),与y 轴交于点C,连接AB,AC,BC.(1)求该抛物线对应的函数表达式;(2)点P为该抛物线上点A与点B之间的一动点.①若S△P AB=S△ABC,求点P的坐标.②如图②,过点B作x轴的垂线,垂足为D,连接AP并延长,交BD于点M.连接BP并延长,交AD于点N.试说明DN(DM+DB)为定值.25.如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.(1)请直接写出这条抛物线和直线AE、直线AC的解析式;(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;②在①的条件下,判断CG与AE的数量关系,并直接写出结论.26.如图,在平面直角坐标系中,直线y=﹣x+n与x轴,y轴分别交于点B,点C,抛物线y=ax2+bx+(a≠0)过B,C两点,且交x轴于另一点A(﹣2,0),连接AC.(1)求抛物线的表达式;(2)已知点P为第一象限内抛物线上一点,且点P的横坐标为m,请用含m的代数式表示点P到直线BC的距离;(3)抛物线上是否存在一点Q(点C除外),使以点Q,A,B为顶点的三角形与△ABC相似?若存在,直接写出点Q的坐标;若不存在,请说明理由.27.已知抛物线y=ax2﹣2ax+3与x轴交于点A、B(A左B右),且AB=4,与y轴交于C点.(1)求抛物线的解析式;(2)如图,证明:对于任意给定的一点P(0,b)(b>3),存在过点P的一条直线交抛物线于M、N两点,使得PM=MN成立;(3)将该抛物线在0≤x≤4间的部分记为图象G,将图象G在直线y=t上方的部分沿y=t翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为m,最小值为n,若m﹣n≤6,求t的取值范围.28.如图,抛物线y=﹣x﹣1与y轴交于点A,点B是抛物线上的一点,过点B作BC⊥x轴于点C,且点C的坐标为(9,0).(1)求直线AB的表达式;(2)若直线MN∥y轴,分别与抛物线,直线AB,x轴交于点M、N、Q,且点Q位于线段OC之间,求线段MN长度的最大值;(3)在(2)的条件下,当四边形MNCB是平行四边形时,求点Q的坐标.29.如图,对称轴为x=1的抛物线经过A(﹣1,0),B(2,﹣3)两点.(1)求抛物线的解析式;(2)P是抛物线上的动点,连接PO交直线AB于点Q,当Q是OP中点时,求点P的坐标;(3)C在直线AB上,D在抛物线上,E在坐标平面内,以B,C,D,E为顶点的四边形为正方形,直接写出点E的坐标.30.如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M 以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.(1)求经过B、C、D三点的抛物线解析式;(2)点P在(1)中的抛物线上,当M为AC中点时,若△P AM≌△PDM,求点P的坐标;(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.31.已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.(1)求抛物线的解析式;(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD 平分四边形ABCD的面积,求点D的坐标;(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P 作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.32.如图,已知抛物线y=﹣x2+bx+c经过点A(3,0),点B(0,3).点M(m,0)在线段OA上(与点A,O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.(1)求抛物线表达式;(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;(3)当△PBQ为等腰三角形时,求m的值.33.如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.(1)求抛物线的表达式及点A的坐标;(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠P AB=45°.求证:△PQA∽△ACB;(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.34.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+(a+)x+c(a≠0)经过点A(﹣3,﹣2),与y轴交于点B(0,﹣2),抛物线的顶点为点C,对称轴与x轴交于点D.(1)求抛物线的表达式及点C的坐标;(2)点E是x轴正半轴上的一点,如果∠AED=∠BCD,求点E的坐标;(3)在(2)的条件下,点P是位于y轴左侧抛物线上的一点,如果△P AE是以AE为直角边的直角三角形,求点P的坐标.35.如图,若m是正数,直线l:y=﹣m与y轴交于点A;直线a:y=x+m与y轴交于点B;抛物线L:y=x2+mx 的顶点为C,且L与x轴左交点为D.(1)若AB=12,求m的值,此时在抛物线的对称轴上存在一点P使得△OBP的周长最小,求点P坐标;(2)当点C在直线l上方时,求点C与直线l距离的最大值;(3)在抛物线L和直线a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出m=2020和m=2020.5时“美点”的个数.36.如图1,抛物线W:y=ax2﹣2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).(1)求直线AB的解析式;(2)过点C作CE⊥x轴,交x轴于点E,若AC平分∠DCE,求抛物线W的解析式;(3)若a=,将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.37.在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.(1)如图1,取点M(1,0),则点M到直线l:y=x﹣1的距离为多少?(2)如图2,点P是反比例函数y=在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=?若存在,求出点P的坐标,若不存在,请说明理由.(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.38.如图,直线y=﹣x+m与抛物线y=ax2+bx都经过点A(6,0),点B,过B作BH垂直x轴于H,OA=3OH.直线OC与抛物线AB段交于点C.(1)求抛物线的解析式;(2)当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.39.如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=﹣x+2经过点B,C.(1)求抛物线的解析式;(2)点P是直线BC上方抛物线上一动点,设点P的横坐标为m.求△PBC面积最大值和此时m的值;(3)Q是抛物线上一点,若∠ABC=∠CBQ,直线BQ与y轴的交点M,请直接写出M的坐标.40.如图1,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC,∠ABC=90°,AB与y轴交于点E,连接CE.(1)求项点B的坐标并求出这条抛物线的解析式;(2)点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系武,并求出S的最大值;(3)如图2,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.41.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+ax+a(a≠0)交x轴于点A和点B(点A在点B左边),交y轴于点C,连接AC,tan∠CAO=3.(1)如图1,求抛物线的解析式;(2)如图2,D是第一象限的抛物线上一点,连接DB,将线段DB绕点D顺时针旋转90°,得到线段DE(点B与点E为对应点),点E恰好落在y轴上,求点D的坐标;(3)如图3,在(2)的条件下,过点D作x轴的垂线,垂足为H,点F在第二象限的抛物线上,连接DF交y 轴于点G,连接GH,sin∠DGH=,以DF为边作正方形DFMN,P为FM上一点,连接PN,将△MPN沿PN 翻折得到△TPN(点M与点T为对应点),连接DT并延长与NP的延长线交于点K,连接FK,若FK=,求cos∠KDN的值.42.定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C1与抛物线C2组成一个开口向上的“月牙线”,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx ﹣12m,(m>0).(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的解析式;(2)求M,N两点的坐标;(3)在第三象限内的抛物线C1上是否存在一点P,使得△P AM的面积最大?若存在,求出△P AM的面积的最大值;若不存在,说明理由.43.如图,抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y=﹣+2经过点A,C.(1)求抛物线的解析式;(2)点P在抛物线在第一象限内的图象上,过点P作x轴的垂线,垂足为D,交直线AC于点E,连接PC,设点P的横坐标为m.①当△PCE是等腰三角形时,求m的值;②过点C作直线PD的垂线,垂足为F.点F关于直线PC的对称点为F′,当点F′落在坐标轴上时,请直接写出点P的坐标.44.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.①试用含m的代数式表示线段PN的长;②求线段PN的最大值.45.如图,在平面直角坐标系中,线段AB的端点坐标分别为A(0,6)、B(6,6).点Q在线段AB上,以Q为项点的抛物线y=﹣x2+bx+c与y轴交于点D,与x轴的一个交点为C.设点Q的横坐标为m,点C的横坐标为n(n>m).(1)当m=0时,求n的值.(2)求线段AD的长(用含m的式子表示);(3)点P(2,0)在x轴上,设△BPD的面积为S,求S与m的关系式;(4)当△DCQ是以QC为直角边的直角三角形时,直接写出m的值.46.如图,已知二次函数的图象经过点A(4,4),B(5,0)和原点O,P为二次函数图象上的一个动点,过点P 作x轴的垂线,垂足为D(m,0),并与直线OA相较于点C.(1)求出二次函数的解析式;(2)当点P在直线OA的上方时,求线段PC的最大值;(3)当点P在直线OA的上方时,是否存在一点P,使射线OP平分∠AOy,若存在,请求出P点坐标;若不存在.请说明理由;(4)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,若存在,求出P点的坐标;若不存在,请说明理由.47.如图:抛物线y=x2+bx+c与直线y=﹣x﹣1交于点A,B.其中点B的横坐标为2.点P(m,n)是线段AB 上的动点.(1)求抛物线的表达式;(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?(3)在平角直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形,在(2)的情况下,在平面内找出所有符合要求的整点R,使P、Q、B、R为整点平行四边形,请直接写出整点R的坐标.48.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B,C,已知A(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D,是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.49.如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.(1)求抛物线的解析式;(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;(3)若点P在第四象限,连结P A、PE及AE,当t为何值时,△P AE的面积最大?最大面积是多少?(4)是否存在点P,使△P AE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.50.如图,抛物线y=(x+2)(x﹣2k)交x轴于点A、B,(A左B右),与y轴交于点C,把射线BC沿x轴翻折交抛物线于点D,交y轴于点F,点D纵坐标为6.(1)求抛物线的解析式;(2)点P为第四象限抛物线上一点,连接PB、PC,设点P横坐标为m,△PBC的面积为S,求S与m的函数解析式(不要求写出自变量取值范围);(3)在(2)的条件下,PD交y轴于点E,交BC于点M,过点P作y轴平行线交BD、BC于点G、H,若△MEF与△MGH面积的和为6,求△PBC的面积.。
专题二 二次函数的综合——2023届中考数学热点题型突破(含答案)

专题二二次函数的综合——2023届中考数学热点题型突破题型1 二次函数与线段最值问题1.在平面直角坐标系中, 点B 的坐标为, 将抛物线向左平移 2 个单位长度后的顶点记为A. 若点P是x 轴上一动点, 则的最小值是( )A. 8B.C. 9D.2.如图, 抛物线与x轴正半轴交于点A, 与y 轴交于点B.(1)求直线AB的解析式及抛物线顶点坐标;(2)点P为第四象限内且在对称轴右侧抛物线上一动点, 过点 P作轴, 垂足为C,PC交AB于点D, 求的最大值, 并求出此时点P的坐标;(3)将抛物线向左平移n个单位长度得到抛物线, 若抛物线与直线AB 只有一个交点, 求n的值.3.已知:如图,二次函数与x轴交于点A,B,点A在点B左侧,交y 轴于点C,.(1)求抛物线的解析式;(2)在第一象限的抛物线上有一点D,连接AD,若,求点D坐标;(3)点P在第一象限的抛物线上,于点Q,求PQ的最大值?题型2 二次函数与图形面积问题4.如图,抛物线与x轴的两个交点坐标为、.(1)求抛物线的函数表达式;(2)矩形的顶点P,Q在x轴上(P,Q不与A,B重合),另两个顶点M,N在抛物线上(如图).①当点P在什么位置时,矩形周长最大?求这个最大值并写出点P的坐标;②判断命题“当矩形周长最大时,其面积最大”的真假,并说明理由.5.在平面直角坐标系xOy 中, 已知抛物线经过,两点. P是抛物线上一点, 且在直线AB的上方.(1)请直接写出抛物线的解析式.(2)若面积是面积的 2 倍, 求点P的坐标.(3)如图, OP交AB于点C,交AB于点D. 记,,的面积分别为,,. 判断是否存在最大值. 若存在, 求出最大值; 若不存在, 请说明理由.6.已知抛物线与x轴相交于A、B两点,与y轴交于C点,且,.(1)求抛物线的解析式;(2)点P为抛物线上位于直线BC上方的一点,连结PB、PC.①如图1,过点P作轴交BC于点D,交x轴于点E,连结OD.设的面积为,的面积为,若,求S的最大值;②如图2,已知,Q为平面内一点,若以点A、C、P、Q为顶点的四边形是以CP为边的平行四边形,求点Q的坐标.题型3 二次函数与图形判定问题7.如图,已知二次函数(b,c为常数)的图象经过点,点,顶点为点M,过点A作轴,交y轴于点D,交该二次函数图象于点B,连接BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m()个单位,使平移后得到的二次函数图象的顶点落在的内部(不包括的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).8.如图, 已知点, 以点D为顶点的抛物线经过点A, 且与直线交于点B,.(1)求抛物线的表达式和点D的坐标.(2)在对称轴上存在一点M, 使得, 求出点M 的坐标.(3)已知点P 为抛物线对称轴上一点, 点Q 为平面内一点, 是否存在以P,B,C,Q为顶点的四边形是菱形的情形? 若存在, 直接写出点P 的坐标; 若不存在, 请说明理由.9.如图,已知抛物线与x轴交于点,,与y轴交于点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为,过点P作x轴的垂线l交抛物线于点Q.(1)求抛物线的解析式;(2)当点P在线段OB上运动时,直线l交直线BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)点P在线段AB上运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与相似?若存在,求出点Q的坐标;若不存在,请说明理由.答案以及解析1.答案:D解析:,平移后抛物线的解析式为,点A的坐标为.如图, 作点A关于 x轴对称的点连接交x轴于点P则此时有最小值,最小值为的长,易知,,的最小值是.2.答案: (1)(2)(3)解析: (1)对于,令, 则, 解得,,.令, 则,.设直线AB的解析式为,则解得直线AB的解析式为.抛物线顶点坐标为.(2)如图, 过点D作轴于点E, 则.,,.设点P的坐标为,则点D的坐标为,.,又,当时, 的值最大, 最大值为,此时,此时点P 的坐标为.(3)设抛物线的解析式为. 令,整理, 得,3.答案:(1)(2)(3)解析:(1)当时,,解得,,,.,,,抛物线的解析式为;(2)如图,作于E,,,设,则,,,解得,,,;(3)如图,作轴,交BC于F,则,,,,,由,可知,直线BC的解析式为,设,则,,,时,PF的最大值为,的最大值为.4.答案:(1)(2)①Р在时,矩形的周长最大,最大值为10;②命题是假命题解析:(1)解:将、代入中得,解得,抛物线的函数表达式为,(2)解:抛物线的对称轴为,设点,则,①P,Q关于对称,,则,矩形的周长为,当时,l的值最大,最大值为10,即Р在时,矩形的周长最大,最大值为10.②假命题.由①可知,当矩形周长最大时,长为3,宽为2,面积为6,当为正方形时,,解得,点Р的坐标为,点Q的坐标为,,正方形的面积;故命题是假命题.5.答案: (1)(2) 或(3) 存在,解析:(1)将,分别代入, 得解得所以抛物线的解析式为.(2)设直线AB的解析式为,将,分别代入, 得解得所以直线AB的解析式为.如图 (1), 过点P 作轴, 垂足为M,PM交AB于点N, 过点B 作, 垂足为E,所以因为,,所以.因为的面积是面积的 2 倍,所以, 所以.设,则,所以, 即,解得,,所以点P的坐标为或.(3) 存在.因为, 所以,, 所以,所以.因为,,所以.设直线AB交y轴于点F, 则.如图 (2), 过点P作轴, 垂足为H,PH交 AB于点G.因为, 所以.因为, 所以,所以,所以.设.由 (2) 可得,所以.又,所以当时, 的值最大, 最大值为.6.答案:(1)(2)见解析①6②或解析:(1)由题意,得,,此抛物线的解析式为:.(2)①由可得:设直线BC的解析式为:,则,,直线BC的解析式为:,设,则,,,当时,S的最大值为6.②在OB上截取,则,,又,,,,,运用待定系数法法可求:直线CF的解析式为:,直线BP的解析式为:,,解得或4,,,轴,ACPQ是以CP为边构成平行四边形,,点Q在x轴上,或.7.答案:(1)二次函数解析式为;点M的坐标为(2)(3),,,解析:(1)把点,点代入二次函数得,,解得,二次函数解析式为,配方得,点M的坐标为;(2)设直线AC解析式为,把点,代入得,,解得,直线AC的解析式为,如图所示,对称轴直线与两边分别交于点E、点F.把代入直线AC解析式解得,则点E坐标为,点F坐标为,,解得;(3)连接MC,作轴并延长交AC于点N,则点G坐标为,,,,把代入解得,则点N坐标为,,,,,由此可知,若点P在AC上,则,则点D与点C必为相似三角形对应点①若有,则有,,,,,,若点P在y轴右侧,作轴,,,,把代入,解得,;同理可得,若点P在y轴左侧,则把代入,解得,;②若有,则有,,,若点P在y轴右侧,把代入,解得;若点P在y轴左侧,把代入,解得;;.所有符合题意得点P坐标有4个,分别为,,,.8.答案: (1)(2)(3)存在, 点P的坐标为,, ,或解析: (1) 将代入, 得,将,分别代入, 得解得故抛物线的表达式为.抛物线的顶点D的坐标为.(2)易知抛物线的对称轴为直线, 且点A,C 关于对称轴对称.作直线AB, 交直线于点M, 则点M即为所求.令,解得,,故.设直线AB 的表达式为,将,分别代入, 得解得故直线AB 的表达式为,当时, , 故.(3)设,易得,①当时,该四边形是以BC为对角线的菱形, 则, 即, 解得,点P 的坐标为.②当时,该四边形是以PC 为对角线的菱形, 则, 即,解得, 故点P的坐标为或.③当时,该四边形是以PB为对角线的菱形, 则, 即, 解得,故点P 的坐标为或.综上可知, 点P的坐标为,,,或9.答案:(1)(2)当时,四边形CQMD是平行四边形(3)点Q的坐标为或解析:(1)设抛物线的解析式为,把点的坐标代入,得,解得抛物线的解析式为,即.(2)点D与点C关于x轴对称,点,,设直线BD的表达式为,把,代入得,,解得,直线BD的关系表达式为,设,,,,当时,四边形CQMD为平行四边形,,解得,(不合舍去),故当时,四边形CQMD是平行四边形;(3)在中,,,,当以点B、M为顶点的三角形与相似时,分三种情况:①若时,,如图1所示,当时,,即,,,,,,解得,,(不合舍去),,,,,点Q的坐标为;②若时,如图2所示,此时点P、Q与点A重合,,③由于点M在直线BD上,因此,这种情况不存在,综上所述,点Q的坐标为或.。
2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(一)

2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(一)1.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.(1)求抛物线的解析式;(2)求点P在运动的过程中线段PD长度的最大值;(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.2.如图1,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点B坐标为(3,0),点C坐标为(0,3).(1)求抛物线的表达式;(2)点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)如图2,点M为该抛物线的顶点,直线MD⊥x轴于点D,在直线MD上是否存在点N,使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.3.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.已知点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,连接AP、PC、CD.(1)求这个抛物线的表达式.(2)当四边形ADCP面积等于4时,求点P的坐标.(3)①点M在平面内,当△CDM是以CM为斜边的等腰直角三角形时,直接写出满足条件的所有点M的坐标;②在①的条件下,点N在抛物线对称轴上,当∠MNC=45°时,直接写出满足条件的所有点N的坐标.4.如图,抛物线y=x2+bx+c与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为C,D,BC=CD.(1)求b,c的值;(2)求直线BD的函数解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.5.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).(1)求抛物线的解析式;(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.①求S与m之间的函数关系式,并写出自变量m的取值范围;②当S取得最值时,求点P的坐标.(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.6.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C(0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.7.如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数解析式;(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.8.已知二次函数图象过点A(﹣2,0),B(4,0),C(0,4).(1)求二次函数的解析式.(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标;若不存在,请说明理由.(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角θ,且tanθ=,求点K的坐标.9.如图,在平面直角坐标系中,抛物线y=x2+bx+c与y轴交于点A(0,2),与x轴交于B(﹣3,0)、C两点(点B在点C的左侧),抛物线的顶点为D.(1)求抛物线的表达式;(2)用配方法求点D的坐标;(3)点P是线段OB上的动点.①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;③若点Q是射线OA上的动点,且始终满足OQ=OP,连接AP,DQ,请直接写出AP+DQ的最小值.10.如图1,已知:抛物线y=a(x+1)(x﹣3)交x轴于A,C两点,交y轴于点B,且OB =2CO.(1)求二次函数解析式;(2)在二次函数图象(如图2)位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;(3)抛物线对称轴上是否存在点P,使得△ABP为直角三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.参考答案1.解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴,解得,∴抛物线解析式为y=x2﹣4x+3;(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3),∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,∵a=﹣1<0,∴当x=时,线段PD的长度有最大值;(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1),综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.2.解:(1)∵点B(3,0),点C(0,3)在抛物线y=﹣x2+bx+c图象上,∴,解得:,∴抛物线解析式为:y=﹣x2+2x+3;(2)∵点B(3,0),点C(0,3),∴直线BC解析式为:y=﹣x+3,如图,过点P作PH⊥x轴于H,交BC于点G,设点P(m,﹣m2+2m+3),则点G(m,﹣m+3),∴PG=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m,=×PG×OB=×3×(﹣m2+3m)=﹣(m﹣)2+,∵S△PBC有最大值,∴当m=时,S△PBC∴点P(,);(3)存在N满足条件,理由如下:∵抛物线y=﹣x2+2x+3与x轴交于A、B两点,∴点A(﹣1,0),∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点M为(1,4),∵点M为(1,4),点C(0,3),∴直线MC的解析式为:y=x+3,如图,设直线MC与x轴交于点E,过点N作NQ⊥MC于Q,∴DE=4=MD,∴∠NMQ=45°,∵NQ⊥MC,∴∠NMQ=∠MNQ=45°,∴MQ=NQ,∴MQ=NQ=MN,设点N(1,n),∵点N到直线MC的距离等于点N到点A的距离,∴NQ=AN,∴NQ2=AN2,∴(MN)2=AN2,∴(|4﹣n|)2=4+n2,∴n2+8n﹣8=0,∴n=﹣4±2,∴存在点N满足要求,点N坐标为(1,﹣4+2)或(1,﹣4﹣2).3.解:(1)∵抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),∴抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,即﹣3a=2,解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+2;(2)连接OP,设点P(x,﹣x2﹣x+2),∵抛物线y=﹣x2﹣x+2交y轴于点C,∵S =S 四边形ADCP =S △APO +S △CPO ﹣S △ODC =×AO ×y P +×OC ×|x P |﹣×CO ×OD =4,∴×3×(﹣x 2﹣x +2)+×2×(﹣x )﹣×1×2=4,∴x 1=﹣1,x 2=﹣2, ∴点P (﹣1,)或(﹣2,2);(3)①如图2,若点M 在CD 左侧,连接AM ,∵∠MDC =90°,∴∠MDA +∠CDO =90°,且∠CDO +∠DCO =90°, ∴∠MDA =∠DCO ,且AD =CO =2,MD =CD , ∴△MAD ≌△DOC (SAS )∴AM =DO ,∠MAD =∠DOC =90°, ∴点M 坐标(﹣3,1),若点M 在CD 右侧,同理可求点M '(1,﹣1); ②如图3,∵抛物线的表达式为:y =﹣x 2﹣x +2=﹣(x +1)2+;∴对称轴为:直线x =﹣1,∴点D在对称轴上,∵MD=CD=M'D,∠MDC=∠M'DC=90°,∴点D是MM'的中点,∵∠MCD=∠M'CD=45°,∴∠MCM'=90°,∴点M,点C,点M'在以MM'为直径的圆上,当点N在以MM'为直径的圆上时,∠M'NC=∠M'MC=45°,符合题意,∵点C(0,2),点D(﹣1,0)∴DC=,∴DN=DN'=,且点N在抛物线对称轴上,∴点N(﹣1,),点N'(﹣1,﹣)延长M'C交对称轴与N'',∵点M'(1,﹣1),点C(0,2),∴直线M'C解析式为:y=﹣3x+2,∴当x=﹣1时,y=5,∴点N''的坐标(﹣1,5),∵点N''的坐标(﹣1,5),点M'(1,﹣1),点C(0,2),∴N''C==M'C,且∠MCM'=90°,∴MM'=MN'',∴∠MM'C=∠MN''C=45°∴点N''(﹣1,5)符合题意,综上所述:点N的坐标为:(﹣1,)或(﹣1,﹣)或(﹣1,5).4.解:(1)∵BO=3AO=3,∴点B(3,0),点A(﹣1,0),∴抛物线解析式为:y=(x+1)(x﹣3)=x2﹣x﹣,∴b=﹣,c=﹣;(2)如图1,过点D作DE⊥AB于E,∴CO∥DE,∴,∵BC=CD,BO=3,∴=,∴OE=,∴点D横坐标为﹣,∴点D坐标为(﹣,+1),设直线BD的函数解析式为:y=kx+b,由题意可得:,解得:,∴直线BD的函数解析式为y=﹣x+;(3)∵点B(3,0),点A(﹣1,0),点D(﹣,+1),∴AB=4,AD=2,BD=2+2,对称轴为直线x=1,∵直线BD:y=﹣x+与y轴交于点C,∴点C(0,),∴OC=,∵tan∠CBO==,∴∠CBO=30°,如图2,过点A作AK⊥BD于K,∴AK=AB=2,∴DK===2,∴DK=AK,∴∠ADB=45°,如图,设对称轴与x轴的交点为N,即点N(1,0),若∠CBO=∠PBO=30°,∴BN=PN=2,BP=2PN,∴PN=,BP=,当△BAD∽△BPQ,∴,∴BQ==2+,∴点Q(1﹣,0);当△BAD∽△BQP,∴,∴BQ==4﹣,∴点Q(﹣1+,0);若∠PBO=∠ADB=45°,∴BN=PN=2,BP=BN=2,当△DAB∽△BPQ,∴,∴,∴BQ=2+2∴点Q(1﹣2,0);当△BAD∽△PQB,∴,∴BQ==2﹣2,∴点Q(5﹣2,0);综上所述:满足条件的点Q的坐标为(1﹣,0)或(﹣1+,0)或(1﹣2,0)或(5﹣2,0).5.解:(1)∵直线x=1是抛物线的对称轴,且点C的坐标为(0,3),∴c=3,﹣=1,∴b=2,∴抛物线的解析式为:y=﹣x2+2x+3;(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点M(1,4),∵抛物线的解析式为:y=﹣x2+2x+3与x轴相交于A,B两点(点A位于点B的左侧),∴0=﹣x2+2x+3∴x1=3,x2=﹣1,∴点A(﹣1,0),点B(3,0),∵点M(1,4),点B(3,0)∴直线BM解析式为y=﹣2x+6,∵点P在直线BM上,且PD⊥x轴于点D,PD=m,∴点P(3﹣,m),∴S△PCD=×PD×OD=m×(3﹣)=﹣m2+m,∵点P在线段BM上,且点M(1,4),点B(3,0),∴0<m≤4∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4)②∵S=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,S有最大值为,∴点P(,3)∵0<m≤4时,S没有最小值,综上所述:当m=3时,S有最大值为,此时点P(,3);(3)存在,若PC=PD=m时,∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6);若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,∴m3=﹣2﹣2(舍去),m4=﹣2+2,∴点P(4﹣,﹣2+2);若DC=PC时,∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,∴m5=0(舍去),m6=6(舍去)综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.6.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,∴直线AC的解析式为y=﹣3x+3,又∵抛物线对称轴为直线x=﹣=2,∴x=2时,y=﹣3×2+3=﹣3,故,点M的坐标为(2,﹣3);(3))∵OB=OC=3,OB⊥OC,∴△BOC是等腰直角三角形,∵EF∥y轴,直线BC的解析式为y=﹣x+3,∴△DEF只要是直角三角形即可与△BOC相似,∵D(2,1),A(1,0),B(3,0),∴点D垂直平分AB且到点AB的距离等于AB,∴△ABD是等腰直角三角形,∴∠ADB =90°,如图,①点F 是直角顶点时,点F 的纵坐标与点D 的纵坐标相同,是1,∴x 2﹣4x +3=1,整理得x 2﹣4x +2=0,解得x =2±, 当x =2﹣时,y =﹣(2﹣)+3=1+, 当x =2+时,y =﹣(2+)+3=1﹣, ∴点E 1(2﹣,1+)E 2(2+,1﹣), ②点D 是直角顶点时,易求直线AD 的解析式为y =x ﹣1,联立,解得,,当x =1时,y =﹣1+3=2,当x =4时,y =﹣4+3=﹣1,∴点E 3(1,2),E 4(4,﹣1),综上所述,存在点E 1(2﹣,1+)或E 2(2+,1﹣)或E 3(1,2)或E 4(4,﹣1),使以D 、E 、F 为顶点的三角形与△BCO 相似.7.解:(1)∵抛物线y =x 2+bx +c 交x 轴于点A (1,0),与y 轴交于点C (0,﹣3),∴,解得:,∴抛物线解析式为:y=x2+2x﹣3;(2)∵抛物线y=x2+2x﹣3与x轴于A,B两点,∴点B(﹣3,0),∵点B(﹣3,0),点C(0,﹣3),∴OB=OC=3,∴∠OBC=∠OCB=45°,如图1,当点D在点C上方时,∵∠DBC=15°,∴∠OBD=30°,∴tan∠DBO==,∴OD=×3=,∴CD=3﹣;若点D在点C下方时,∵∠DBC=15°,∴∠OBD=60°,∴tan∠DBO==,∴OD=3,∴DC=3﹣3,综上所述:线段CD的长度为3﹣或3﹣3;(3)如图2,在BO上截取OE=OA,连接CE,过点E作EF⊥AC,∵点A(1,0),点C(0,﹣3),∴OA=1,OC=3,∴AC===,∵OE=OA,∠COE=∠COA=90°,OC=OC,∴△OCE≌△OCA(SAS),∴∠ACO=∠ECO,CE=AC=,∴∠ECA=2∠ACO,∵∠PAB=2∠ACO,∴∠PAB=∠ECA,=AE×OC=AC×EF,∵S△AEC∴EF==,∴CF===,∴tan∠ECA==,如图2,当点P在AB的下方时,设AP与y轴交于点N,∵∠PAB=∠ECA,∴tan∠ECA=tan∠PAB==,∴ON=,∴点N(0,﹣),又∵点A(1,0),∴直线AP解析式为:y=x﹣,联立方程组得:,解得:或,∴点P坐标为:(﹣,﹣),当点P在AB的上方时,同理可求直线AP解析式为:y=﹣x+,联立方程组得:,解得:或,∴点P坐标为:(﹣,),综上所述:点P的坐标为(﹣,),(﹣,﹣).8.解:(1)∵二次函数图象过点B(4,0),点A(﹣2,0),∴设二次函数的解析式为y=a(x+2)(x﹣4),∵二次函数图象过点C(0,4),∴4=a(0+2)(0﹣4),∴a=﹣,∴二次函数的解析式为y=﹣(x+2)(x﹣4)=﹣x2+x+4;(2)存在,理由如下:如图1,取BC中点Q,连接MQ,∵点A(﹣2,0),B(4,0),C(0,4),点P是AC中点,点Q是BC中点,∴P(﹣1,2),点Q(2,2),BC==4,设直线BP解析式为:y=kx+b,由题意可得:,解得:∴直线BP的解析式为:y=﹣x+,∵∠BMC=90°∴点M在以BC为直径的圆上,∴设点M(c,﹣c+),∵点Q是Rt△BCM的中点,∴MQ=BC=2,∴MQ2=8,∴(c﹣2)2+(﹣c+﹣2)2=8,∴c=4或﹣,当c=4时,点B,点M重合,即c=4,不合题意舍去,∴c=﹣,则点M坐标(﹣,),故线段PB上存在点M(﹣,),使得∠BMC=90°;(3)如图2,过点D作DE⊥BC于点E,设直线DK与BC交于点N,∵点A(﹣2,0),B(4,0),C(0,4),点D是AB中点,∴点D(1,0),OB=OC=4,AB=6,BD=3,∴∠OBC=45°,∵DE⊥BC,∴∠EDB=∠EBD=45°,∴DE=BE==,∵点B(4,0),C(0,4),∴直线BC解析式为:y=﹣x+4,设点E(n,﹣n+4),∴﹣n+4=,∴n=,∴点E(,),在Rt△DNE中,NE===,①若DK与射线EC交于点N(m,4﹣m),∵NE=BN﹣BE,∴=(4﹣m)﹣,∴m=,∴点N(,),∴直线DK解析式为:y=4x﹣4,联立方程组可得:,解得:或,∴点K坐标为(2,4)或(﹣8,﹣36);②若DK与射线EB交于N(m,4﹣m),∵NE=BE﹣BN,∴=﹣(4﹣m),∴m=,∴点N(,),∴直线DK解析式为:y=x﹣,联立方程组可得:,解得:或,∴点K坐标为(,)或(,),综上所述:点K的坐标为(2,4)或(﹣8,﹣36)或(,)或(,).9.解:(1)∵抛物线y=x2+bx+c与y轴交于点A(0,2),与x轴交于B(﹣3,0),∴∴∴抛物线解析式为:y=x2﹣x+2;(2)∵y=x2﹣x+2=﹣(x+1)2+,∴顶点D坐标(﹣1,);(3)①∵抛物线y=x2﹣x+2与x轴交于B(﹣3,0)、C两点,∴点C(1,0)设点E(m,m2﹣m+2),则点P(m,0),∵PE=PC,∴m2﹣m+2=1﹣m,∴m=1(舍去),m=﹣,∴点E(﹣,)②如图,连接AE交对称轴于点N,连接DE,作EH⊥DN于H,交y轴于点F,∵点A(0,2),点E(﹣,),∴直线AE解析式为y=﹣x+2,∴点N坐标(﹣1,)∴DH==,HN==,∴DH=NH,且EH⊥DN,∴∠DEH=∠NEH,∴点F到AE,DE的距离相等,∴DN∥y轴,EH⊥DN,∴EH⊥y轴,∴EF=;③在x轴正半轴取点H,使OH=OA=2,∵OH=OA,∠AOP=∠QOH=90°,OP=OQ,∴△AOP≌△HOQ(SAS)∴AP=QH,∴AP+DQ=DQ+QH≥DH,∴点Q在DH上时,DQ+AP有最小值,最小值为DH的长,∴AP+DQ的最小值==.10.解:(1)对于抛物线y=a(x+1)(x﹣3),令y=0,得到a(x+1)(x﹣3)=0,解得x=﹣1或3,∴C(﹣1,0),A(3,0),∴OC=1,∵OB=2OC=2,∴B(0,2),把B(0,2)代入y=a(x+1)(x﹣3)中得:2=﹣3a,a=﹣∴二次函数解析式为=;(2)设点M的坐标为(m,),则点N的坐标为(2﹣m,),MN=m﹣2+m=2m﹣2,GM=矩形MNHG的周长C=2MN+2GM=2(2m﹣2)+2()==∴当时,C有最大值,最大值为;(3)∵A(3,0),B(0,2),∴OA=3,OB=2,由对称得:抛物线的对称轴是:x=1,∴AE=3﹣1=2,设抛物线的对称轴与x轴相交于点E,当△ABP为直角三角形时,存在以下三种情况:①如图1,当∠BAP=90°时,点P在AB的下方,∵∠PAE+∠BAO=∠BAO+∠ABO=90°,∴∠PAE=∠ABO,∵∠AOB=∠AEP,∴△ABO∽△PAE,∴,即,∴PE=3,∴P(1,﹣3);②如图2,当∠PBA=90°时,点P在AB的上方,过P作PF⊥y轴于F,同理得:△PFB∽△BOA,∴,即,∴BF=,∴OF=2+=,∴P(1,);③如图3,以AB为直径作圆与对称轴交于P1、P2,则∠AP1B=∠AP2B=90°,设P1(1,y),∵AB2=22+32=13,由勾股定理得:AB2=P1B2+P1A2,∴12+(y﹣2)2+(3﹣1)2+y2=13,解得:y=1±,∴P(1,1+)或(1,1﹣),综上所述,点P的坐标为(1,﹣3)或(1,)或(1,1+)或(1,1﹣)。
二次函数中常见的几种综合题型

二次函数中常见的几种综合题型二次函数常见的几类综合题型一、求线段最大值及根据面积求点坐标问题1.已知抛物线 $y=x^2+bx+c$ 的图象与 $x$ 轴的一个交点为 $B(5,0)$,另一个交点为 $A$,且与 $y$ 轴交于点 $C(0,5)$。
1) 求直线 $BC$ 与抛物线的解析式;2) 若点 $M$ 是抛物线在 $x$ 轴下方图象上的一个动点,过点 $M$ 作 $MN\parallel y$ 轴交直线 $BC$ 于点 $N$,求$MN$ 的最大值;3) 在 (2) 的条件下,$MN$ 取得最大值时,若点 $P$ 是抛物线在 $x$ 轴下方图象上任意一点,以 $BC$ 为边作平行四边形 $CBPQ$,设平行四边形 $CBPQ$ 的面积为 $S_1$,$\triangle ABN$ 的面积为 $S_2$,且 $S_1=6S_2$,求点$P$ 的坐标。
2.对称轴为直线 $x=-1$ 的抛物线$y=ax^2+bx+c(a\neq0)$ 与 $x$ 轴相交于 $A$、$B$ 两点,其中点 $A$ 的坐标为 $(-3,0)$。
1) 求点 $B$ 的坐标;2) 已知 $a=1$,$C$ 为抛物线与 $y$ 轴的交点。
①若点 $P$ 在抛物线上,且 $S_{\trianglePOC}=4S_{\triangle BOC}$,求点 $P$ 的坐标;②设点 $Q$ 是线段 $AC$ 上的动点,作 $QD\perp x$ 轴交抛物线于点 $D$,求线段 $QD$ 长度的最大值。
二、求三角形周长及面积的最值问题3.已知抛物线 $y=ax^2+bx+c$ 经过 $A(-3,a-b+c)$,$B(1,a+b+c)$,$C(c,a+3c-b)$ 三点,其顶点为 $D$,对称轴是直线 $l$,$l$ 与 $x$ 轴交于点 $H$。
1) 求该抛物线的解析式;2) 若点 $P$ 是该抛物线对称轴 $l$ 上的一个动点,求$\triangle PBC$ 周长的最小值;3) 如图 (2),若 $E$ 是线段 $AD$ 上的一个动点($E$ 与$A$、$D$ 不重合),过点 $E$ 作平行于 $y$ 轴的直线交抛物线于点 $F$,交 $x$ 轴于点 $G$,设点 $E$ 的横坐标为 $m$,$\triangle ADF$ 的面积为 $S$。
二次函数综合试题及答案

二次函数综合试题及答案一、选择题1. 下列哪个选项不是二次函数的一般形式?A. y = ax^2 + bx + cB. y = 3x^2 + 5C. y = 2x + 1D. y = -x^2 + 3答案:C2. 二次函数y = ax^2 + bx + c的顶点坐标为:A. (-b, c)B. (-b/2a, c)C. (-b/2a, 4ac - b^2 / 4a)D. (b, -c)答案:C二、填空题1. 若二次函数y = ax^2 + bx + c的图象开口向上,且顶点坐标为(-1, -4),则a的值为______。
答案:a > 02. 二次函数y = x^2 - 2x + 3的最小值为______。
答案:2三、解答题1. 已知二次函数y = 2x^2 - 4x + 3,求该函数与x轴的交点。
解:令y = 0,得到方程2x^2 - 4x + 3 = 0。
使用求根公式,得到x1 = (2 + √10) / 2,x2 = (2 - √10) / 2。
因此,与x轴的交点坐标为((2 + √10) / 2, 0)和((2 - √10) / 2, 0)。
2. 某抛物线经过点(1, 1)和(2, 4),且对称轴为直线x = 2。
求该抛物线的解析式。
解:设抛物线解析式为y = a(x - 2)^2 + k。
将点(1, 1)代入,得到a(1 - 2)^2 + k = 1,即a + k = 1。
将点(2, 4)代入,得到a(2 - 2)^2 + k = 4,即k = 4。
解得a = -3,k = 4。
因此,抛物线的解析式为y = -3(x - 2)^2 + 4。
四、应用题1. 某工厂生产一种产品,其成本函数为C(x) = 0.5x^2 - 100x + 5000,其中x为生产数量。
求该工厂生产多少件产品时,成本最低。
解:成本函数C(x) = 0.5x^2 - 100x + 5000是一个开口向上的二次函数,其顶点即为成本最低点。
二次函数与几何综合(1)

二次函数与几何综合1.已知关于x 的一元二次方程a x 2+bx +1=0,中,b+m +1; (1)若a =4,求b 的值;(2)若方程a x 2+bx +1=0有两个相等的实数根,求方程的根.2.如图,利用一面增(墙EF 最长可利用28米),围成一个矩形花园ABCD .与培平行的一边 BC 上要预留2米宽的入口(如图中AN 所示,不用砌墙)用60米长的墙的材料,当矩形 的长BC 为多少米时,矩形花园的面积为30平方米:能否围成430平方米的矩形花为 什么?3.如图,直线AB :y =kx +3过点(-2,4)与抛物线y =交于A 、B 两点; (1)直接写出点A 、点B 的坐标;(2)在直线AB 的下方的抛物线上求点P ,使△ABP 的面积等于5.N4.如图,抛物线y=(x-1) 2+m的图象与x轴交于A、B两点与y轴交于点C,且AB=4;(1)求抛物线的解析式;(2)将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D、E两个不同的点,求k 的取值范围;(3)M为线段QB上一点(不含O、B两点)过点M作y轴的平行线交抛物线于点M,交线段BC于点P,若△PCN为等腰三角形,求M点的坐标.图1图2图35.利用一面长为22米的墙和46米的篱笆围成如图所示的矩形菜地菜地有2个2米宽的门,门用其它材料.(1)如何搭建使矩形菜地的面积方200平方米?(2)如何搭建使矩形菜地的面积最大,最大为多少平方米?6.如图1,边长为4的正方形ABCD 中,点E 在AB 边上(不与点A ,B 重合),点F 在BC 边上(不与点B 、C 重合).第一次操作:将线段EF 绕点F 断时针旋转,当点E 落在正方形上时,记为点G ;第二次操作:将线段FG 绕点G 顺时针旋转,当点F 落在正方形上时,记为点H ;依此橾作下去…(1)图2中的△EFD 是经过两次操作后得到的,其形状为 ,求此时线段EF 的长; (2)若经过三次操作可得到四边形EFGH .①请判断四边形EFGH 的形状为 ,此时AE 与BF 的数蜇关系是 ;②以①中的结论为前提,设AE 的长为x ,四边形EFGH 的面积为y ,求y 与x 的函数关系式及面积y 的取值范围.图1 图2 备用图EF A B CDEFA B C DHF A BC DEG7.如图,一次函数122y x=+分别交y轴、x轴于A、B两点,抛物线2y x bx c=-++过A、B两点.(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)在(2)的情况下,以A,M、N、D为项点作平行四边形,求第四个项点D的坐标.8.某商场在1月至12月份经销某种品牌的服装,由于受到时令的影明,该种服装的销售情況 如下:销售价格1y (元/件)与销售月份x (月)的关系大致满足如图的函数,销售成本2y (元/件)与销售月份x (月)满足2y =10100(16)14(612)3x x x x x x -+⎧⎪⎨⎪⎩≤<且为整数≤<且为整数,月销售量3y (件)与销售月份x (月)満足3y =1Ox -20.(1)根据图象求出销售价格1y (元/件)与销售月份x (月)之间的函数关系式:(6≤x ≤12且x 为整数)(2)求出该服装月销售利润W (元)与月份x (月)之向的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤x ≤12且x 为整数)9.如图,等边△ABC 和等边△DEC ,CE 和AC 重合.CEB .(1)求证:AD =BE ;(2)若CE 绕点C 顺时针旋转30°,连BD 交AC 于点G ,取AB 的中点F 连FG ,求证:BE =2FG ; (3)在(2)的条件下AB =2,则AG =________.(直接写出结果)备用AB C DEFG G FEDCBAEDCBA10..如图开口向下的抛物线y=a2x+bx+c交x轴于A(−1,0)、B(5,0)两点,交y轴于点C(0,5)(1)求抛物线的解析式;(2)设抛物线的顶点为D,求△BCD的面积;(3)在(2)的条件下,P、Q为线段BC上两点(P左Q右,且P、Q不与B、C重合),PQ=,在第一象限的抛物线上是否存在这样的点R,使△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.备用图2备用图1。
二次函数(十二大题型综合归纳 )(学生版)--新九年级数学

二次函数(十二大题型综合归纳)题型1:二次函数的概念1以下函数式二次函数的是()A.y=ax2+bx+cB.y=2x-12-4x2C.y=ax2+bx+c a≠0D.y=x-1x-22二次函数y=2x x−3的二次项系数与一次项系数的和为()A.2B.-2C.-1D.-4题型2:二次函数的值3已知二次函数y=x2+2x-5,当x=3时,y=.4已知二次函数y=ax2+2c,当x=2时,函数值等于8,则下列关于a,c的关系式中,正确的是()A.a+2c=8B.2a+c=4C.a-2c=8D.2a-c=45二次函数y=ax2+bx-3a≠0的图象经过点2,-2,则代数式2a+b的值为.题型3:二次函数的条件6已知y=mx m-2+2mx+1是y关于x的二次函数,则m的值为()A.0B.1C.4D.0或47关于x的函数y=a-bx2+1是二次函数的条件是()A.a≠bB.a=bC.b=0D.a=0题型4:列二次函数关系式8已知有n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数为m,则m关于n的函数解析式为.题型5:特殊二次函数的图像和性质9关于二次函数y =-34x 2-1的图像,下列说法错误的是()A.抛物线开口向下B.对称轴为直线x =0C.顶点坐标为0,-1D.当x <0时,y 随x 的增大而减小,当x >0时,y 随x 的增大而增大10抛物线y =34x 2与抛物线y =-34x 2+3的相同点是()A.顶点相同B.对称轴不相同C.开口方向一样D.顶点都在y 轴上11如果二次函数y =ax 2+m 的值恒大于0,那么必有()A.a >0,m 取任意实数B.a >0,m >0C.a <0,m >0D.a ,m 均可取任意实数12对于二次函数y =-3(x -2)2的图象,下列说法正确的是()A.开口向上B.对称轴是直线x =-2C.当x >-2时,y 随x 的增大而减小D.顶点坐标为2,013二次函数:①y =-13x 2+1;②y =12(x +1)2-2;③y =-12(x +1)2+2;④y =12x 2;⑤y =-12(x -1)2;⑥y =12(x -1)2.(1)以上二次函数的图象的对称轴为直线x =-1的是(只填序号);(2)以上二次函数有最大值的是(只填序号)﹔(3)以上二次函数的图象中关于x 轴对称的是(只填序号).14设函数y 1=x -a 12,y 2=x -a 22,y 3=x -a 3 2.直线x =b 的图象与函数y 1,y 2,y 3的图象分别交于点A b ,c 1,B b ,c 2 ,C b ,c 3,()A.若b <a 1<a 2<a 3,则c 2<c 3<c1B.若a 1<b <a 2<a 3,则c 1<c 2<c 3C.若a 1<a 2<b <a 3,则c 3<c 2<c 1 D.若a 1<a 2<a 3<b ,则c 3<c 2<c 115已知二次函数y =(x -m )2,当x ≤1时,y 随x 的增大而减小,则m 的取值范围是.16已知关于x 的一元二次方程x 2-(2m +1)x +m 2-1=0有实数根a ,b ,则代数式a 2-ab +b 2的最小值为.题型6:与特殊二次函数有关的几何知识17在平面直角坐标系中,点A是抛物线y=a x-42+k与y轴的交点,点B是这条抛物线上的另一点,且AB⎳x轴,则以AB为边的等边三角形ABC的周长为.18在平面直角坐标系内有线段PQ,已知P(3,1)、Q(9,1),若抛物线y=(x-a)2与线段PQ有交点,则a的取值范围是.19二次函数y=-x+3的图象上任意二点连线不与x轴平行,则t的取值范围2+h t≤x≤t+2为.题型7:二次函数y=ax2+bx+c的图像和性质20下列抛物线中,与抛物线y=x2-2x+8具有相同对称轴的是()A.y=4x2+2x+4B.y=x2-4xC.y=2x2-x+4D.y=-2x2+4x21若抛物线y=x2+ax+1的顶点在y轴上,则a的值为()A.2B.1C.0D.-222抛物线y=x-1x+5图象的开口方向是(填“向上”或“向下”).23当二次函数y=ax2+bx+c有最大值时,a可能是()A.1B.2C.-2D.324已知抛物线y=x2-2bx+b2-2b+1(b为常数)的顶点不在抛物线y=x2+c(c为常数)上,则c应满足()A.c≤2B.c<2C.c≥2D.c>225已知二次函数y=x2-2mx+m的图象经过A1,y1,B5,y2两个点,下列选项正确的是()A.若m<1,则y1>y2B.若1<m<3,则y1<y2C.若1<m<5,则y1>y2D.若m>5,则y1<y2题型8:二次函数y=ax2+bx+c的最值与求参数范围问题26已知直线y=2x+t与抛物线y=ax2+bx+c a≠0,且点B、B m,n有两个不同的交点A3,5是抛物线的顶点,当-2≤a≤2时,m的取值范围是.27已知抛物线y=x2+bx+c经过点(1,-2),(-2,13).(1)求抛物线解析式及对称轴.(2)关于该函数在0≤x<m的取值范围内,有最小值-3,有最大值1,求m的取值范围.28已知二次函数y=mx2-4m2x-3(m为常数,m>0).(1)若点(-2,9)在该二次函数的图象上.①求m的值:②当0≤x≤a时,该二次函数值y取得的最大值为18,求a的值;(2)若点P(x,y)是该函数图象上一点,当0≤x p≤4时,y p≤-3,求m的取值范围.题型9:根据二次函数y=ax2+bx+c的图像判断有关信息29函数y=ax2+bx+c a≠0与y=kx的图象如图所示,现有以下结论:①c=3;②k=3;③3b+c+6=0;④当1<x<3时,x2+b-1x+c<0.其中正确的为.(填写序号即可)30如图,已知二次函数y=ax2+bx+c a≠0的图象与x轴交于点A-1,0,与y轴的交点在0,-2和0,-1之间(不包括这两点),对称轴为直线x=1,下列结论:①4a+2b+c>0;②4ac-b2<8a;③13<a<23;④b>c;⑤直线y=k i(k i>0,i=1,2,3,⋯,2023)与抛物线所有交点的横坐标之和为4046;其中正确结论的个数有()A.2个B.3个C.4个D.5个题型10:二次函数的应用31如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为8m ,两侧距地面4m 高处各有一盏灯,两灯间的水平距离为6m ,则这个门洞内部顶端离地面的距离为()A.7.5B.8C.649D.64732某炮兵部队实弹演习发射一枚炮弹,经x 秒后的高度为y 米,且时间x 与高度y 的关系为y =ax 2+bx .若此炮弹在第5秒与第16秒时的高度相等,则在下列哪一个时间段炮弹的高度达到最高.()A.第8秒B.第10秒C.第12秒D.第15秒33在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y (单位:米)与飞行的水平距离x (单位:米)之间具有函数关系y =-116x 2+58x +32,则小康这次实心球训练的成绩为()A.14米B.12米C.11米D.10米34某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m ).有下列结论:①AB =30m ;②池底所在抛物线的解析式为y =145x 2-5;③池塘最深处到水面CD 的距离为3.2m ;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为1.2m .其中结论错误的是()A.①B.②C.③D.④35某建筑工程队借助一段废弃的墙体CD,CD长为18米,用76米长的铁栅栏围成两个相连的长方形仓库,为了方便取物,在两个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,现有如下两份图纸(图纸1点A在线段DC的延长线上,图纸2点A在线段DC上),设AB =x米,图纸1,图纸2的仓库总面积分别为y1平方米,y2平方米.(1)分别写出y1,y2与x的函数关系式;(2)小红说:“y1的最大值为384.y2的最大值为507.”你同意吗?请说明理由.题型11:二次函数的解答证明题36已知二次函数y=-x2+bx+c.(1)当b=4,c=3时,①求该函数图象的顶点坐标.②当-1≤x≤3时,求y的取值范围.(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.37如图,已知二次函数y=-12x2+bx+c的图象与x轴交于A1,0,B,与y轴交于点C0,-52.CD∥x轴交抛物线于点D.(1)求b,c的值.(2)已知点E在抛物线上且位于x轴上方,过E作y轴的平行线分别交AB,CD于点F,G,且GE= 2GD,求点E的坐标.38在直角坐标系中,设函数y=ax2+bx+c(a,b,c是常数,a≠0).(1)已知a=1.①若函数的图象经过0,3和-1,0两点,求函数的表达式;②若将函数图象向下平移两个单位后与x轴恰好有一个交点,求b+c的最小值.(2)若函数图象经过-2,m,-3,n和x0,c,且c<n<m,求x0的取值范围.题型12:二次函数压轴题39在平面直角坐标系中,抛物线y=-x2-4x+c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为-5,0.(1)求点C的坐标;(2)如图1,若点P是第二象限内抛物线上一动点,求三角形ACP面积的最大值;(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.。
中考数学 二次函数综合试题及详细答案

中考数学 二次函数综合试题及详细答案一、二次函数1.已知二次函数223y ax ax =-+的最大值为4,且该抛物线与y 轴的交点为C ,顶点为D .(1)求该二次函数的解析式及点C ,D 的坐标;(2)点(,0)P t 是x 轴上的动点,①求PC PD -的最大值及对应的点P 的坐标;②设(0,2)Q t 是y 轴上的动点,若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点,求t 的取值范围.【答案】(1)2y x 2x 3=-++,C 点坐标为(0,3),顶点D 的坐标为(1,4);(2)①最,P 的坐标为(3,0)-,②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】(1)先利用对称轴公式x=2a 12a--=,计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;(2)根据三角形的三边关系:可知P 、C 、D 三点共线时|PC-PD|取得最大值,求出直线CD 与x 轴的交点坐标,就是此时点P 的坐标;(3)先把函数中的绝对值化去,可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ 过点(0,3),即点Q 与点C 重合时,两图象有一个公共点,当线段PQ 过点(3,0),即点P 与点(3,0)重合时,两函数有两个公共点,写出t 的取值;②线段PQ 与当函数y=a|x|2-2a|x|+c (x≥0)时有一个公共点时,求t 的值;③当线段PQ 过点(-3,0),即点P 与点(-3,0)重合时,线段PQ 与当函数y=a|x|2-2a|x|+c (x <0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t 的取值.【详解】解:(1)∵2a x 12a-=-=, ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4,∴抛物线过点()1,4.得a 2a 34-+=,解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3,顶点D 的坐标为()1,4.(2)①∵PC PD CD -≤,∴当P,C,D 三点在一条直线上时,PC PD -取得最大值.连接DC 并延长交y 轴于点P ,PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入,得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+,将()P t,0,()Q 0,2t 的坐标代入,可得线段PQ 所在直线的方程为y 2x 2t =-+.(1)当线段PQ 过点()3,0-,即点P 与点()3,0-重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时t 3=-. ∴当t 3≤-时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (2)当线段PQ 过点()0,3,即点Q 与点C 重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时3t 2=. 当线段PQ 过点()3,0,即点P 与点()3,0重合时,t 3=,此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (3)将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥,并整理,得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=,解得7t 2=. ∴当7t 2=时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述,t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】 本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.2.如图:在平面直角坐标系中,直线l :y=13x ﹣43与x 轴交于点A ,经过点A 的抛物线y=ax 2﹣3x+c 的对称轴是x=32. (1)求抛物线的解析式;(2)平移直线l 经过原点O ,得到直线m ,点P 是直线m 上任意一点,PB ⊥x 轴于点B ,PC ⊥y 轴于点C ,若点E 在线段OB 上,点F 在线段OC 的延长线上,连接PE ,PF ,且PE=3PF .求证:PE ⊥PF ;(3)若(2)中的点P 坐标为(6,2),点E 是x 轴上的点,点F 是y 轴上的点,当PE ⊥PF 时,抛物线上是否存在点Q ,使四边形PEQF 是矩形?如果存在,请求出点Q 的坐标,如果不存在,请说明理由.【答案】(1)抛物线的解析式为y=x 2﹣3x ﹣4;(2)证明见解析;(3)点Q 的坐标为(﹣2,6)或(2,﹣6).【解析】【分析】(1)先求得点A 的坐标,然后依据抛物线过点A ,对称轴是x=32列出关于a 、c 的方程组求解即可;(2)设P (3a ,a ),则PC=3a ,PB=a ,然后再证明∠FPC=∠EPB ,最后通过等量代换进行证明即可;(3)设E (a ,0),然后用含a 的式子表示BE 的长,从而可得到CF 的长,于是可得到点F 的坐标,然后依据中点坐标公式可得到22x x x x Q P F E ++=,22y y y y Q P F E ++=,从而可求得点Q 的坐标(用含a 的式子表示),最后,将点Q 的坐标代入抛物线的解析式求得a 的值即可.【详解】(1)当y=0时,14033x -=,解得x=4,即A (4,0),抛物线过点A ,对称轴是x=32,得161203322a c a -+=⎧⎪-⎨-=⎪⎩, 解得14a c =⎧⎨=-⎩,抛物线的解析式为y=x 2﹣3x ﹣4; (2)∵平移直线l 经过原点O ,得到直线m ,∴直线m 的解析式为y=13x . ∵点P 是直线1上任意一点, ∴设P (3a ,a ),则PC=3a ,PB=a .又∵PE=3PF ,∴PC PB PF PE=. ∴∠FPC=∠EPB .∵∠CPE+∠EPB=90°,∴∠FPC+∠CPE=90°,∴FP ⊥PE .(3)如图所示,点E 在点B 的左侧时,设E (a ,0),则BE=6﹣a .∵CF=3BE=18﹣3a ,∴OF=20﹣3a .∴F (0,20﹣3a ).∵PEQF 为矩形,∴22x x x x Q P F E ++=,22y y y y Q P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0,∴Q x =a ﹣6,Q y =18﹣3a .将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=4或a=8(舍去).∴Q (﹣2,6).如下图所示:当点E 在点B 的右侧时,设E (a ,0),则BE=a ﹣6.∵CF=3BE=3a ﹣18,∴OF=3a ﹣20.∴F (0,20﹣3a ).∵PEQF 为矩形, ∴22x x x x Q P F E ++=,22y y y y Q P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0,∴Q x =a ﹣6,Q y =18﹣3a . 将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=8或a=4(舍去).∴Q (2,﹣6).综上所述,点Q 的坐标为(﹣2,6)或(2,﹣6).【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式,用含a 的式子表示点Q 的坐标是解题的关键.3.如图,已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ,B 两点,且点A (1,-4)为抛物线的顶点,点B 在x 轴上。
二次函数综合(一)——面积问题
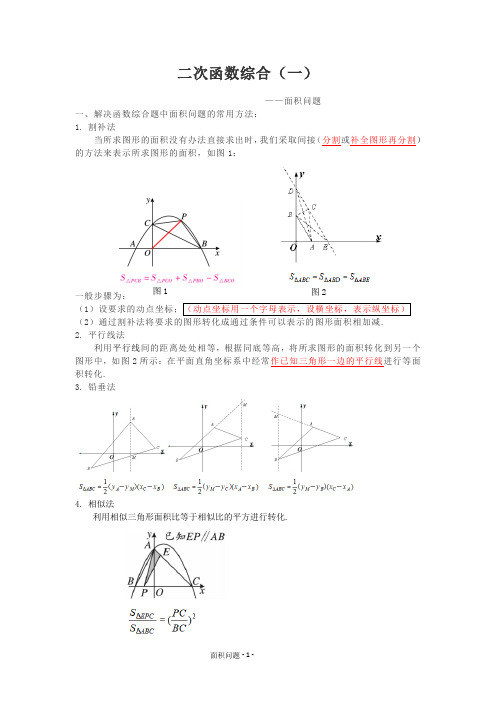
二次函数综合(一) ——面积问题
一、解决函数综合题中面积问题的常用方法:
1. 割补法
当所求图形的面积没有办法直接求出时,我们采取间接(分割或补全图形再分割)的方法来表示所求图形的面积,如图1:
4. 相似法
利用相似三角形面积比等于相似比的平方进行转化.
二、基本题型
1.如图,在平面直角坐标系中,△AOB的顶点O为原点,已知点A(3,6),B(5,2),求△AOB的面积.
2.已知二次函数的图像y=-x2+3x+4与x轴交于A、B两点(点A在点B的左端),与y轴交于点C,抛物线的顶点为D。
求△ACD的面积。
3已知二次函数的图像y=-x2+3x+4与x轴交于A、B两点(点A在点B的左端),与y轴交于点C,抛物线的顶点为D。
求△BCD的面积。
2023年中考数学重难点专题复习-特殊三角形问题(二次函数综合)【有答案】

2023年中考数学重难点专题复习-特殊三角形问题(二次函数综合)1.综合与探究如图,抛物线2y ax bx c =++经过()1,0A -,()3,0B ,()0,3C 三点,与y 轴交于点C ,作直线BC .(1)求抛物线和直线BC 的函数解析式.(2)D 是直线BC 上方抛物线上一点,求BDC 面积的最大值及此时点D 的坐标.(3)在抛物线对称轴上是否存在一点P ,使得以点P ,B ,C 为顶点的三角形是等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系中,抛物线2y ax x m =++(a ≠0)的图象与x 轴交于A 、C 两点,与y 轴交于点B ,其中点B 坐标为(0,-4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D 是直线AB 下方抛物线上一个动点,连接AD 、BD ,探究是否存在点D ,使得△ABD 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点P 为该抛物线对称轴上的动点,使得△P AB 为直角三角形,请求出点P 的坐标.3.已知,如图,抛物线2y x bx c =-++经过直线3y x =-+与坐标轴的两个交点A ,B ,此抛物线与x 轴的另一个交点为C ,抛物线的顶点为D .(1)求此抛物线的解析式;(2)设点Q 是线段AB 上的动点,作QM x ⊥轴交抛物线于点M ,求线段QM 长度的最大值;(3)在x 轴上是否存在点N 使ADN △为直角三角形?若存在,确定点N 的坐标;若不存在,请说明理由.4.已知抛物线2y ax bx c =++与x 轴交于()2,0A -、()6,0B 两点,与y 轴交于点()0,3C -.(1)求抛物线的表达式;(2)点P 在直线BC 下方的抛物线上,连接AP 交BC 于点M ,过点P 作x 轴的垂线l ,垂线l 交BC 于点E ,AD ∥垂线l ,求证ADM PEM ∽;当PM AM 最大时,求点P 的坐标及PM AM的最大值; (3)在(2)的条件下,在l 上是否存在点D ,使BCD 是直角三角形,若存在,请直接写出点D 的坐标;若不存在,请说明理由.5.如图,已知抛物线2y x bx c =++与x 轴交于点1,0A 和点()3,0B -.(1)求此抛物线的解析式;(2)点M 在抛物线的对称轴上,点Q 在x 轴下方的抛物线上,当MAQ 是以AQ 为斜边的等腰直角三角形时,求点M 的坐标.6.如图,抛物线223y ax x =++与x 轴的一个交点是()3,0A ,与y 轴交于B 点,点P 在拋物线上.(1)求a 的值;(2)过点P 作x 轴的垂线交直线AB 于点E ,设点P 的横坐标为(03)m m <<,PE l =,求l 关于m 的函数关系式;(3)当PAB 是直角三角形时,求点P 的坐标.7.如图1,在平面直角坐标系中,抛物线2143y x bx =-++经过()13A -,,与y 轴交于点C ,经过点C 的直线与抛物线交于另一点()6,E m ,点M 为抛物线的顶点,抛物线的对称轴与x 轴交于点D .(1)求直线CE的解析式;(2)如图2,点P为直线CE上方抛物线上一动点,连接PC,PE,当PCE的面积最大时,求点P的坐标以及PCE 面积的最大值;(3)如图3,将点D右移一个单位到点N,连接AN,将(1)中抛物线沿射线NA平移得到新抛物线y',y'经过点N,y'的顶点为点G,在新抛物线y'的对称轴上是否存在点H,使得MGH是等腰三角形?若存在,请直接写出点H 的坐标:若不存在,请说明理由.30,,8.如图,在平面直角坐标系中,二次函数2=-++的图象与坐标轴相交于A、B、C三点,其中A点坐标为()y x bx cB 点坐标为10,,连接AC、BC.动点P从点A出发,在线段AC个单位长度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.(1)求b、c的值.(2)在P、Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?(3)在线段AC上方的抛物线上是否存在点M,使MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点9.如图,已知直线y =x +3与x 轴交于点A ,与y 轴交于点B ,抛物线2y x bx c =-++经过A 、B 两点,与x 轴交于另一个点C ,对称轴与直线AB 交于点E ,抛物线顶点为D .(1)点A 的坐标为 ,点B 的坐标为 .(2)①求抛物线的解析式;② 点M 是抛物线在第二象限图象上的动点,是否存在点M ,使得△MAB 的面积最大?若存在,请求这个最大值并求出点M 的坐标;若不存在,请说明理由;(3)点P 从点D 出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t 秒,当t 为何值时,以P 、B 、C 为顶点的三角形是等腰三角形?直接写出所有符合条件的t 值.10.如图,抛物线1C :()2120y ax ax a =+>与x 轴交于点A ,顶点为点P .(1)直接写出抛物线1C 的对称轴是______,用含a 的代数式表示顶点P 的坐标______;(2)把抛物线1C 绕点(),0M m 旋转180°得到抛物线2C (其中0m >),抛物线2C 与x 轴右侧的交点为点B ,顶点为点Q .②在①的条件下,是否存在ABP 为等腰三角形,若存在请求出a 的值,若不存在,请说明理由.11.如图,关于x 的二次函数y =x 2+bx +c 的图象与x 轴交于点A (1,0)和点B ,与y 轴交于点C (0,3),抛物线的对称轴与x 轴交于点D .(1)求二次函数的解析式.(2)有一个点M 从点A 出发,以每秒1个单位的速度在AB 上向点B 运动,另一个点N 从点D 与点M 同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M 到达点B 时,点M 、N 同时停止运动,问点M 、N 运动到何处时,△MNB 面积最大,试求出最大面积.(3)在y 轴上是否存在一点P ,使△PBC 为等腰三角形?若存在,请直接写出点P 的坐标,若不存在请说明理由.12.如图,抛物线212y ax x c =-+的图象与x 轴交点为A 和B ,与y 轴交点为()0,3D ,与直线23y x =--交点为A 和C .(1)求抛物线的解析式;(2)在直线23y x =--上是否存在一点M ,使得ABM 是等腰直角三角形,如果存在,求出点M 的坐标,如果不存在请说明理由.(3)若点E 是x 轴上一个动点,把点E 向下平移4个单位长度得到点F ,点F 向右平移4个单位长度得到点G ,点G 向上平移4个单位长度得到点H ,若四边形EFGH 与抛物线有公共点,请直接写出点E 的横坐标E x 的取值范围.。
二次函数综合试题及答案

二次函数综合试题及答案一、选择题1.下列四个函数中,不是二次函数的是()A. y = 2x^2 + 3x - 1B. y = -x^2 + 5x + 2C. y = 3x + 4D. y = x^2 + 2x - 3答案:C2.若二次函数y = ax^2 + bx + c的图象开口朝上,且在x = -1处有最小值0,则a,b,c的值应满足的关系是()A. a < 0,b < 0,c > 0B. a > 0,b > 0,c < 0C. a > 0,b < 0,c > 0D. a < 0,b > 0,c < 0答案:C3.已知二次函数y = ax^2 + bx + c的图象过点(1, 4),且在x = 2处有最大值5,那么a,b,c的值应满足的关系是()A. a = 1,b = 2,c = 3B. a = -1,b = -2,c = -3C. a = 1,b = -2,c = 3D. a = -1,b = 2,c = -3答案:C二、计算题1.求函数y = 2x^2 - 3x + 1的对称轴和顶点坐标。
解答:对称轴的公式为x = -b / (2a),代入a = 2,b = -3,得x = 3/4。
将x = 3/4代入原方程得y = 2(3/4)^2 - 3(3/4) + 1 = 1/8。
所以对称轴为x = 3/4,顶点坐标为(3/4, 1/8)。
2.求函数y = x^2 + 4x - 5的零点。
解答:函数的零点即为方程x^2 + 4x - 5 = 0的解。
使用求根公式,得x = (-4 ± √(4^2 - 4 * 1 * -5)) / (2 * 1)= (-4 ± √(16 + 20)) / 2= (-4 ± √36) / 2= (-4 ± 6) / 2解得x1 = -5,x2 = 1。
所以函数的零点为-5和1。
二次函数基础知识综合练(2)

二次函数综合练习(1)一、填空题 1.抛物线22-=x y 的顶点坐标为( ) 2.二次函数y=(x -3)(x +2)的图象的对称轴是( ) 3.已知抛物线y=x 2-8x +c 的顶点在x 轴上,则c 的值是( )4.童装专卖店销售一种童装,若这种童装每天获利y (元)与销售单价x (元)满足关系 y=-x 2+50x -500,则要想获得最大利润每天必须卖出( ) 5.二次函数y =x 2-2x+1与x 轴的交点个数是( ) 6.若A(-134,y 1)、B(-1,y 2)、C(53,y 3)为二次函数y=-x 2-4x+5的图象上的三点,则y 1、y 2、y 3的大小关系是( )7.把抛物线y =2x 2先向左平移3个单位,向上平移4个单位,所得抛物线的函数表达式为( ) 8.某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8m ,两侧距地 面4米高处各有一个挂校名匾用的铁环,两铁环的水平距离为6 m ,则校门的高为(精 确到0.1 m ,水泥建筑物的厚度忽略不计)( )9.二次函数c bx ax y ++=2的图象如图所示,则abc ,ac b 42-,b a +2,c b a ++这四个式子中,值为正数的有( ) 10.已知函数y=x 2-2x -2的图象如图2示,根据其中提供的信息,可求得使y ≥1成立的x的取值范围是( )第8题) (第9第11.抛物线2)3(94-=x y 与x 轴的交点为A ,与y 轴的交点为B ,则△AOB 的面积为 。
12.某二次函数的图象与x 轴交于点(-1,0),(4,0),且它的形状与抛物线y =-x 2形状相同。
则这个二次函数的解析式为 。
13.二次函数的图象经过三个定点(2,0),(3,0),(•0,-•1),则它的解析式为________,该图象的顶点坐标为__________.对称轴 14.当k=________时,直线x+2y+k+1=0和2x+y+2k=0的交点在抛物线y=-x 2上.15.已知二次函数y=x 2-2(k+1)x+k 2+2的图象与x 轴交点的横坐标分别为x 1,x 2,且(x 1+1)(x 2+1)=8,则k 的值为__________. 16.如果y 与x 2成正比例,并且它的图象上一点P 的横坐标a 和纵坐标b 分别是方程x 2-x-6=0的两根,那么这个函数的解析式为_________. 17.抛物线y=x 2-4x+11的对称轴是直线________,顶点坐标为________. 18.如果抛物线y=-23x 2+(m+2)x+27m 的对称轴为直线x=32,则m 的值为_________.19.把函数y=5x 2+10mx+n 的图象向左平移2个单位,向上平移3个单位,•所得图象的函数解析式为y=5x 2+30x+44,则m=_______,n=_______. 20.开口向下的抛物线y=a (x+1)(x-4)与x 轴交于A 、B 两点,与y•轴交于点C .•若∠ACB=90°,则a 的值为________. 21.如图,二次函数y=x 2-ax+a-5的图象交x 轴于点A 和B ,交y 轴于点C ,当线段AB•的长度最短时,点C 的坐标为________. 22.在同一直角坐标系内,二次函数y 1=ax 2+bx+c 与y 2=cx 2+bx+a 的图象大致为( )23.在同一直角坐标系内,函数y=ax 2+bx 与y=b x(b ≠0)的图象大致为( )25.给出下列四个函数:y=-2x ,y=2x-1,y=3x (x>0),y=-x 2+3(x>0),其中y 随x•的增大而减小的函数有( )26.当m 取任何实数时,抛物线y=-2(x-m )2-m 的顶点所在的直线为( ) A .x 轴 B .y 轴 C .y=x D .y=-x27.当m 取任何实数时,抛物线y=-2(x+m )2-m 2的顶点所在的曲线为( ) A .y=x 2 B .y=-x 2 C .y=x 2(x>0) D .y=-x 2(x>0)28.已知抛物线y=ax 2+bx+c (a ≠0)与抛物线y=x 2-4x+3关于x 轴对称,则a 、b 、c•的值分别是( ) A .-1,4,-3 B .-1,-4,-3 C .-1,4,3 D .-1,-4,3 29、.已知二次函数y =x 2+(2k +1)x +k 2-1的最小值是0,则k 的值是( )A.43 B.-43 C.45 D.-45二次函数综合练习(2)30.如果抛物线y=-23x 2+(m+2)x+27m 的对称轴为直线x=32,则m 的值为_________.31、如果抛物线y=x 2-6x+c-2的顶点到x 轴的距离是3,那么c 的值等于( )32、直线y=3x-3与抛物线y=x 2-x+1的交点的个数是( ).33.抛物线y=4x 2-1与y 轴的交点坐标是_________,与x 轴的交点坐标是_____. 34.在同一坐标系中,二次函数y=-21x 2,y=x 2,y=-3x 2的开口由大到小的顺序是______.35.已知抛物线y=-2(x+1)2-3,如果y 随x 的增大而减小,那么x 的取值范围是______ 36.函数y=34x -2-3x 2有最_ _值为___.37.函数y=21x 2+2x+1写成y=a(x -h)2+k 的形式是( )38.抛物线y=-2x 2-x+1的顶点在第_____象限( )39.不论m 取任何实数,抛物线y=a(x+m)2+m(a ≠0)的顶点都( )A.在y=x 直线上;B.在直线y=-x 上;C.在x 轴上;D.在y 轴上40、函数y=ax 2+bx+c(a ≠0)的图象经过原点和第一、三、四象限,则函数有最______值,且a________0,b________0,c__________0。
专题七 二次函数综合问题

质求解.确定函数最值时,函数自变量的取值范围应确定正确.
(2)已知两个定点和一条定直线,要求在定直线上确定一点,使得这个点到两定点距离和最小,其变形问题有三角
形周长最小或四边形周长最小等.这类问题的解决方法是:作其中一个定点关于已知直线的对称点,连接对称点
与另一个定点,所得直线与已知直线的交点即为所求的点,然后通过求直线的表达式及其与定直线的交点坐标,
顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.
2
解:(3)存在.设点 P 的坐标为(m,- m +m+4),点 Q 的坐标为(t,-t+4),
由已知得 tan∠OCA=
= = .
①当点 Q 在点 P 的左侧时,如图②所示,分别过点 P,Q 作 x 轴的垂线,垂足分别为 N,M.
小值时,求点M的坐标及这个最小值.
思路分析:(3)可求MQ=OB=1,则求MC+MQ+BQ的最小值,只需确定MC+BQ的最小值,这可利
用
点
点O关于抛物线对称轴的对称点进行求解.
C
或
解:(3)如图②所示,过点 C 作 CF∥x 轴,交 y 轴于点 G,交抛物线于点 F,连接 OF,交抛物线的对称轴
x=-1 于点 M,过点 M 作 MQ⊥y 轴于点 Q,连接 MC,BQ,由对称性可知 MC=MF.
直线 BC 的表达式为 y=-x+4.
(2)点F是抛物线对称轴上一点,当FA+FC的值最小时,求出点F的坐标及FA+FC的最小值.
解:(2)如图①所示,∵点 A,B 关于抛物线的对称轴 x=1 对称,
二次函数综合题

二次函数综合题类型一㊀对称性㊁增减性问题1.已知二次函数y =ax 2-2ax.(1)二次函数图象的对称轴是直线x =㊀;(2)当0ɤx ɤ3时,y 的最大值与最小值的差为4,求该二次函数的表达式;(3)若a <0,对于二次函数图象上的两点P (x 1,y 1),Q (x 2,y 2),当t ɤx 1ɤt +1,x 2ȡ3时,均满足y 1ȡy 2,请结合函数图象,直接写出t 的取值范围.(2)当=解:(1)a 1>;0时,ȵ该函数图象的对称轴为直线x 1,ʑ当x =1时,y 有最小值为-a ,当x =3时,y 有最大值为3a ,ʑ3a -(-a )=4,ʑa =1,ʑ二次函数的表达式为y =x 2-2x.当a <0时,同理可得,y 有最大值为-a ;y 有最小值为3a ,ʑ-a -3a =4,ʑa =-1,ʑ二次函数的表达式为y=-x2+2x,综上所述,该二次函数的表达式为y=x2-2x或y=-x2+2x;(3)-1ɤtɤ2.ʌ解法提示ɔȵa<0,该函数图象的对称轴为直线x=1,ʑx<1时,y随x的增大而增大,x>1时,y随x的增大而减小,x=-1和x=3时的函数值相等.ȵtɤx1ɤt+1,x2ȡ3时,均满足y1ȡy2,ʑtȡ-1,t+1ɤ3,ʑ-1ɤtɤ2.2.在平面直角坐标系xOy中,点(m-2,y1),(m, y2),(2-m,y3)在抛物线y=x2-2ax+1上,其中mʂ1且mʂ2.(1)求出该抛物线的对称轴(用含a的式子表示);(2)当m=0时,若y1=y3,比较y1与y2的大小关系,并说明理由;(3)若存在大于1的实数m,使y1>y2>y3,求a的取值范围.解:(1)ȵy=x2-2ax+1,ʑ抛物线对称轴为直线x=--2a2=a; (2)y1>y2.理由如下:ȵm=0,y1=y3,ʑ点(-2,y1)与点(2,y3)关于抛物线对称轴对称,ʑ抛物线对称轴为直线x=-2+22=0,即a=0,ʑy=x2+1,ʑ抛物线开口向上,顶点坐标为(0,1),ʑy2=1为函数最小值,ʑy1>y2;(3)将(m-2,y1),(m,y2),(2-m,y3)分别代入y=x2-2ax+1,得y1=m2-4m-2am+4a+5,y2=m2-2am+1,y3= m2-4m+2am-4a+5,ȵy1>y2>y3,ʑm2-4m-2am+4a+5>m2-2am+1>m2-4m+ 2am-4a+5,解得m-1<a<1.ȵm>1,ʑ0<a<1.3.已知抛物线y=2x2-4mx+2m2-1.(1)求该抛物线的顶点坐标;(2)若直线y =n 与该抛物线交于点A ,B ,且AB=2,求n 的值;(3)若抛物线y =2x 2-4mx +2m 2-1经过点P (t ,y 1),Q (t +1,y 2),y 1y 2<0,求y 1的取值范围.解:(1)ȵy =2x 2-4mx +2m 2-1=2(x -m )2-1,ʑ该抛物线顶点坐标为(m ,-1);(2)ȵAB =2,抛物线对称轴为直线x =m ,1,n ),(m +1,n )ʑ抛物线与直线y =n 的两个交点坐标为(m -,将(m +1,n )代入y =2(x -m )2-1得n =2-1=1;(3)ȵ抛物线y =2(x -m )2-1,a =2>0,ʑ抛物线开口向上,对称轴为直线x =m ,令2(x -m )2-1=0,解得x 1=m -22,x 2=m +22,ʑx 2-x 1=2>1.ȵy 1y 2<0,ʑy 1<0,y 2>0或y 1>0,y 2<0,如解图①,当y 1<0,y 2>0时,t <m +22<t +1,ʑm+22-1<t<m+22,第3题解图①当t=m时,y1取最小值为-1,ʑ-1ɤy1<0,如解图②,当y第3题解图②t<m-22<t+1,ʑm-22-1<t<m-22,将t=m-22-1代入y=2(x-m)2-1得y=2(m-22-1-m)2-1=2+22,ʑ0<y1<2+22,综上所述,-1ɤy1<0或0<y1<2+22.类型二㊀公共点问题考向一㊀定抛物线与动线段1.如图,已知直线y =2x +1与抛物线y =2x 2+bx +c 交于点A (0,1),B (3,7),点C (4,m )在该直线上.(1)求该抛物线的顶点坐标;(2)将线段AC 沿着y 轴向上或向下平移,使平移后的线段AᶄCᶄ(点Aᶄ,Cᶄ分别为点A ,C 的对应点)与该抛物线只有一个公共点,设点Aᶄ的纵坐标为n ,求n 的取值范围.解:(1)将点A (0,1),B (3,7)代入y =2x 2+bx +c ,得c =1,2ˑ32+3b +c =7,{解得b =-4,c =1,{ʑy =2x 2-4x +1=2(x -1)2-1,ʑ该抛物线的顶点坐标为(1,-1);(2)将C(4,m)代入y=2x+1得,m=2ˑ4+1=9,ʑC(4,9),当x=4时,y=2x2-4x+1=2ˑ42-4ˑ4+1=17.①若线段AC向上平移,当线段AC向上平移17 -9=8个单位时,线段AᶄCᶄ与抛物线有一个交点Cᶄ(4,17),此时点Aᶄ的坐标为(0,9).若向上平移超过8个单位,则抛物线与线段AᶄCᶄ没有交点,ʑ1<nɤ9;②若线段AC向下平移,设线段AC向下平移a个单位,令2x+1-a=2x2-4x+1,整理得2x2-6x+a=0,令(-6)2-4ˑ2a=0,解得a=92,ʑn=1-92=-72,综上所述,n的取值范围为1<nɤ9或n=-72.2.在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a ʂ0)经过点A (3,-4)和B (0,2).(1)求抛物线的表达式和顶点坐标;(2)将抛物线在A ,B 之间的部分记为图象M (含A ,B 两点).将图象M 沿直线x =3翻折,得到图象N.若过点C (9,4)的直线y =kx +b 与图象M ㊁图象N 都相交,且只有两个交点,求b 的取值范围.解:(1)将点A (3,-4)和B (0,2)代入抛物线y =ax 2+4x +c (a ʂ0),可得9a +12+c =-4,c =2,{解得a =-2,c =2,{ʑ抛物线的表达式为y =-2x 2+4x +2.ȵy =-2x 2+4x +2=-2(x -1)2+4,ʑ抛物线的顶点坐标为(1,4);(2)设点B (0,2)关于x =3的对称点为Bᶄ,则点Bᶄ(6,2).如解图,若直线y =kx +b 经过点C (9,4)和Bᶄ(6,2),可得b =-2.若直线y =kx +b 经过点C (9,4)和A (3,-4),可得b =-8.当直线y =kx +b 平行x 轴时,b =4,综上所述,第2题解图考向二㊀动抛物线与定线段(直线) 1.已知:抛物线y=x2-2x+3a+1(a为常数).(1)当a=1时,求该抛物线的顶点坐标;(2)抛物线上有两点M(-1,yM ),N(2,yN),请比较y M与y N的大小;(3)在平面直角坐标系中,若该抛物线在xɤ3的部分与直线y=2x-3有两个交点,求a的取值范围.解:(1)当a=1时,抛物线为y=x2-2x+4=(x-1)2+3,则该抛物线的顶点坐标为(1,3);(2)由题意易知抛物线的对称轴为直线x= --22ˑ1=1,ȵ抛物线开口向上,且1-(-1)=2,2-1=1,2>1,ʑy M>y N;(3)ȵ二次函数的图象在xɤ3的部分与一次函数y=2x-3的图象有两个交点,令x2-2x+3a+1=2x-3,整理得x2-4x+3a+4=0,由根的判别式得16-4(3a+4)>0,解得a<0,把x=3代入y=2x-3,得y=3ˑ2-3=3,把(3,3)代入y=x2-2x+3a+1得3=9-6+3a+1,解得a=-13,ʑa的取值范围为-13ɤa<0.2.(2021燕山区二模)在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(aʂ0).(1)求抛物线的对称轴及抛物线与y轴交点坐标;(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.解:(1)ȵ抛物线y=ax2-2ax-3a,ʑ抛物线的对称轴是直线x=--2a2a=1,令x=0,则y=-3a,ʑ抛物线与y轴交点坐标为(0,-3a); (2)y=ax2-2ax-3a=a(x2-2x-3)=a(x+1)(x-3),ʑ抛物线与x轴交于点A(-1,0),D(3,0),与y 轴交于点E(0,-3a),顶点坐标是(1,-4a).由题意得点C(0,4),B(3,4),①当a>0时,如解图①,显然抛物线与线段BC 无公共点;②当a<0时,若抛物线顶点在线段BC上,如解图②,则顶点坐标为(1,4),ʑ-4a=4,ʑa=-1;③当a<0时,若抛物线的顶点不在线段BC上,如解图③,ȵ抛物线与线段BC恰有一个公共点,ʑ-3a>4,ʑa<-43,综上所述,a的取值范围是a<-43第2题解图考向三㊀动抛物线与动直线1.(2021西城区一模)在平面直角坐标系xOy中,抛物线y=ax2-2a2x+1(aʂ0)与y轴交于点A,过点A作x轴的平行线与抛物线交于点B.(1)直接写出抛物线的对称轴;(2)若AB=4,求抛物线所对应的函数解析式;(3)已知点P(a+4,1),Q(0,a+1),如果抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.解:(1)抛物线的对称轴为直线x=a;ʌ解法提示ɔȵ抛物线y=ax2-2a2x+1(aʂ0),ʑ抛物线的对称轴为直线x=--2a22a=a. (2)由题意可知抛物线的对称轴为直线x=ʃ2,ʑa=ʃ2,ʑ抛物线所对应的函数解析式为y=2x2-8x+1或y=-2x2-8x+1;(3)当a>0时,如解图①,抛物线过点P(a+4, 1)时,则a+42=a,解得a=4,ʑQ(0,5),此时,抛物线与线段PQ有一个公共点.当a<0时,如解图②,抛物线过点P(a+4,1)时,a+4=0,解得a=-4,㊀图②第1题解图此时,Q(0,-3),抛物线与线段PQ有一个公共点;综上所述,当0<aɤ4或-4ɤa<0时,抛物线与线段PQ恰有一个公共点.类型三㊀整点问题1.(2021顺义区一模)在平面直角坐标系xOy中,抛物线y=ax2-4ax+3a(a>0)与y轴交于点A.(1)求点A和抛物线顶点的坐标(用含a的式子表示);(2)直线y=-ax+3a与抛物线y=ax2-4ax+3a围成的区域(不包括边界)记作G.横㊁纵坐标都为整数的点叫做整点.①当a=1时,结合函数图象,求区域G中整点的个数;②当区域G中恰有6个整点时,直接写出a的取值范围.解:(1)ȵy=ax2-4ax+3a=a(x-2)2-a,ʑ抛物线的顶点的坐标为(2,-a).ȵ抛物线y=ax2-4ax+3a(a>0)与y轴交于点A,ʑA(0,3a);(2)①当a=1时,直线y=-x+3,抛物线y=x2-4x+3,可得直线y=-x+3与抛物线y=x2-4x+3的交点为(3,0),(0,3);则(1,1),(2,0)是区域G中的两个整点,即区域G中整点的个数为2个;②32<aɤ2.ʌ解法提示ɔ联立直线y=-ax+3a与抛物线y= ax2-4ax+3a,可得交点为(0,3a),(3,0),ʑ区域G由0ɤxɤ3,-aɤyɤ3a组成;当x=1时,与直线的交点为(1,2a),与抛物线的交点为(1,0),同理可得,当x=2时,与直线的交点为(2,a),与抛物线的交点为(2,-a),区域G中的整点不包括边界,整点有6个,如解图,当0<a< 1时,G中最多有1个整点;当a=1时,G中有2个整点;当1<aɤ1.5时,G中最多有5个整点;当1.5<aɤ2时,G中最多有6个整点;当2<aɤ3.5时,G中最多有13个整点;ʑ当32<aɤ2时,区域G中恰有6个整点.第1题解图2.在平面直角坐标系xOy中,抛物线y=ax2-2ax+ a-1(其中a是常数,a>0)与y轴交于点A.我们将横㊁纵坐标都是整数的点叫做 整点 .(1)求该抛物线的顶点坐标;(2)如果线段OA(包含端点)上的 整点 个数大于3个且小于8个,求a的取值范围;(3)若抛物线与x轴围成的区域(含边界)内有6个整点,求a的取值范围.解:(1)ȵy=ax2-2ax+a-1=a(x-1)2-1,ʑ该抛物线的顶点坐标为(1,-1);(2)ȵ点A为抛物线与y轴的交点,ʑ点A的坐标为(0,a-1).ȵa>0,线段OA(包含端点)上的整点个数大于3个且小于8个,则a-1>2,且a-1<7,ʑa的取值范围为3<a<8;(3)当a=1时,抛物线的解析式为y=x2-2x,如解图,此时抛物线与x轴围成的区域(含边界)内有4个整点,第2题解图当a=14时,抛物线与x轴围成的区域(含边界)内有6个整点,当a=19时,抛物线与x轴围成的区域(含边界)内有8个整点,ȵ抛物线的顶点坐标为(1,-1),ʑ要使抛物线与x轴围成的区域(含边界)内有6个整点,则x=-2所对应的y值要大于0,且x =-1所对应的y值小于等于0,ʑ4a+4a+a-1>0,a+2a+a-1ɤ0,解得a>19,且aɤ14,ʑ当抛物线与x轴围成的区域(含边界)内有6个整点时,a的取值范围为19<aɤ14.。
二次函数代几综合专题
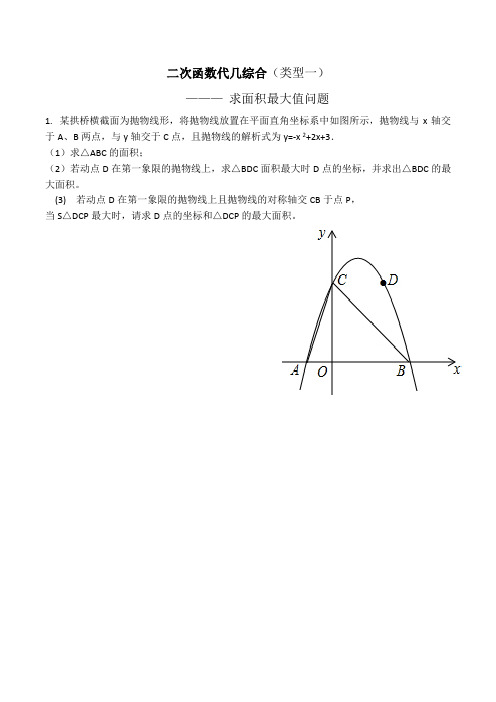
二次函数代几综合(类型一)
———求面积最大值问题
1. 某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x 2+2x+3.
(1)求△ABC的面积;
(2)若动点D在第一象限的抛物线上,求△BDC面积最大时D点的坐标,并求出△BDC的最大面积。
(3) 若动点D在第一象限的抛物线上且抛物线的对称轴交CB于点P,
当S△DCP最大时,请求D点的坐标和△DCP的最大面积。
2、如图,二次函数y=x 2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
(3)在二次函数上有一动点P,过点P作PM⊥x轴交线段BD于点M,判断PM有最大值还是有最小值,如有,求出线段PM长度的最大值或最小值并求出此时S △BDP的面积.。
二次函数综合题解题方法

二次函数综合题解题方法二次函数是高中数学中一个重要的内容,也是学生们比较头疼的一个部分。
在解题过程中,很多学生常常会感到困惑和无从下手。
今天我们就来系统地总结一下二次函数综合题的解题方法,希望能够帮助大家更好地掌握这一部分知识。
首先,我们需要明确二次函数的一般形式:y=ax^2+bx+c,其中a、b、c为常数且a≠0。
在解二次函数综合题时,我们通常会遇到以下几种情况:1. 求二次函数的顶点坐标和对称轴,对于y=ax^2+bx+c,其顶点坐标为(-b/2a, c-b^2/4a),对称轴为x=-b/2a。
我们可以利用这些公式来求解顶点坐标和对称轴。
2. 求二次函数的图像和特征,通过顶点坐标和对称轴,我们可以画出二次函数的图像,并且根据a的正负来判断抛物线的开口方向。
这对于理解二次函数的形状和特征非常重要。
3. 求二次函数与坐标轴的交点,当我们需要求二次函数与x轴和y轴的交点时,可以将y=0或x=0代入二次函数的表达式中,从而求得交点的坐标。
4. 求二次函数的零点和解二次方程,通过因式分解、配方法或者求根公式,我们可以求得二次函数的零点,也就是方程y=ax^2+bx+c=0的解。
以上就是二次函数综合题的解题方法总结,希望能够帮助大家更好地理解和掌握二次函数的相关知识。
在解题过程中,我们需要注意以下几点:1. 仔细分析题目,理清思路,确定解题的步骤和方法。
2. 熟练掌握二次函数的基本形式和相关公式,灵活运用。
3. 注意细节,避免计算错误和漏解。
4. 多做练习,加深对二次函数的理解和掌握。
通过不断的练习和总结,相信大家一定能够掌握好二次函数综合题的解题方法,取得更好的成绩。
希望本文的内容能够对大家有所帮助,谢谢大家的阅读!。
初中数学-动点在二次函数中的综合(1)

动点在二次函数中的综合(1)1.如图,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C.(1)求该抛物线的函数解析式;(2)点D(4,m)在抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出P点的坐标;如果不存在,请说明理由.2.如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.(1)求抛物线的解析式;(2)点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;(3)在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.3.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x+1)(x﹣3)交x轴于A、B两点,交y 轴于点C,∠ABC=45°,(1)求抛物线的解析式;(2)如图2,P为第一象限内抛物线上一点,△BCP的面积为3时,且∠BCP>45°,求P点坐标;(3)如图3,在(2)的条件下,D、E为抛物线上的点,且两点关于抛物线对称轴对称,过D作x轴垂线交过点P且平行于x轴的直线于Q,EQ交抛物线于R,延长QD至H,连接RH,tan∠ERH=,当线段DH=4时,求点D的坐标.4.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣3与x轴交于A、B两点,与y轴交于点C.(1)请直接写出A、B、C三点的坐标:A B C(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.设运动的时间为t(秒),①当t为何值时,BP=BQ?②是否存在某一时刻t,使△BPQ是直角三角形?若存在,请求出所有符合条件的t的值,若不存在,请说明理由.5.如图,在平面直角坐标系xOy中,一次函数y=x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B(1)求m的值及抛物线的函数表达式;(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q 的横坐标;若存在,请说明理由;(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问是否为定值,如果是,请求出结果,如果不是请说明理由.(参考公式:在平面直角坐标之中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=)6.如图,在平面直角坐标系中,直线y=kx﹣7与y轴交于点C,与x轴交于点B,抛物线y=ax2+bx+14a 经过B、C两点,与x轴的正半轴交于另一点A,且OA:OC=2:7.(1)求抛物线的解析式;(2)点D在线段CB上,点P在对称轴的左侧抛物线上,PD=PB,当tan∠PDB=2,求点P的坐标;(3)在(2)的条件下,点Q(7,n)在第四象限,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.7.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.(1)试求抛物线的解析式;(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m的最大值及此时点P的坐标;(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.8.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.(1)求抛物线的函数表达式;(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.9.如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.10.如图,已知抛物线y=﹣x2+bx+c经过点A(5,)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;(1)求抛物线对应的函数解析式;(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.①求点P和点F的坐标;②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.。
