ABAQUS单元类型及特点汇总
abaqus单元命名规则

Abaqus单元命名规则Abaqus是一款功能强大的工程仿真软件,广泛应用于各种领域,包括机械、材料、土木工程等。
在Abaqus中,单元类型、维度、特殊选项、节点数目以及单元名称等方面都有一定的命名规则。
本文将对这些规则进行简要介绍。
1. 单元类型Abaqus中的单元类型非常丰富,包括一维单元、二维单元和三维单元等。
在定义单元类型时,一般采用以下方式:* 一维单元:1D* 二维单元:2D* 三维单元:3D此外,还可以通过在数字后面添加字母来进一步描述单元的类型。
例如,1D-M表示一维质量单元,2D-B表示二维弯曲单元等。
2. 单元维度Abaqus中的单元分为一维、二维和三维三种类型,每种类型的单元都有相应的维度。
一般来说,一维单元的维度为长度,二维单元的维度为面积,三维单元的维度为体积。
在定义单元维度时,一般采用以下方式:* 一维单元:L* 二维单元:A* 三维单元:V3. 特殊选项Abaqus中的一些特殊选项也有相应的命名规则。
例如,在定义接触单元时,需要使用特定的关键字来描述接触类型、接触面以及目标面等。
此外,对于一些具有特殊属性的单元,例如热传导单元、流体流动单元等,也需要使用特定的关键字来描述其属性。
4. 节点数目Abaqus中的每个单元都由一定数量的节点组成。
一般来说,每个节点的编号都是唯一的,并且按照一定的顺序进行编号。
在定义节点数目时,一般采用以下方式:* 对于一维单元:节点数目为2或4。
* 对于二维单元:节点数目为3或6。
* 对于三维单元:节点数目为4或8或12等。
需要注意的是,对于一些具有特殊属性的单元,例如接触单元、弹簧单元等,节点数目可能会不同。
因此,在定义这些单元时需要特别注意节点数目的问题。
5. 单元名称在Abaqus中,每个单元都需要一个唯一的名称。
一般来说,单元名称应该能够清晰地表达出该单元的类型、属性以及一些特殊选项等信息。
例如,对于一个一维质量单元,可以使用“mass1d”作为名称;对于一个二维弹簧-阻尼器单元,可以使用“spring2d”作为名称等。
abaqus c3d8p单元类型

Abaqus软件是一款广泛应用于工程实践中的有限元分析软件,因其强大的功能和稳定的性能而备受工程师和研究人员的青睐。
在Abaqus中,有许多不同的单元类型可供用户选择,每种单元类型都有其特定的适用范围和优缺点。
其中,c3d8p单元类型是Abaqus中常用的一种典型的八节点有限元单元类型,本文将对其进行详细介绍。
1. c3d8p单元类型概述c3d8p单元是Abaqus中的八节点有限元单元类型,它具有平行六面体的形状,适用于对复杂的结构进行分析。
该单元类型在模拟物体的各向同性材料时表现出色,能够准确地描述结构的应力、应变和变形等力学特性。
2. c3d8p单元类型的特点(1)高精度:c3d8p单元类型具有八个节点,可以更准确地刻画结构的变形情况,提高了分析的精度和准确度。
(2)适用范围广:该单元类型适用于各种各样的结构分析,包括金属结构、混凝土结构和复合材料等。
(3)对称性好:c3d8p单元类型具有较好的对称性,可以在分析中减小误差,保证分析结果的准确性。
3. c3d8p单元类型的应用场景c3d8p单元类型广泛应用于工程领域的结构分析和设计中,包括但不限于:(1)航空航天领域:用于飞机、航天器等复杂结构的应力、疲劳和损伤分析。
(2)土木工程领域:用于桥梁、隧道等土木结构的承载能力和稳定性分析。
(3)机械制造领域:用于汽车、机器设备等的零部件强度和刚度分析。
(4)材料科学领域:用于纤维增强复合材料的强度和疲劳性能分析。
4. c3d8p单元类型的优缺点(1)优点:a. 高精度:能够准确描述结构的应力、应变和变形特性;b. 适用范围广:可用于各种结构的分析;c. 对称性好:分析结果更加准确。
(2)缺点:a. 计算成本高:由于节点数较多,计算成本较高;b. 不适用于屈曲分析:在一些特定情况下,c3d8p单元类型不适用于屈曲分析。
5. c3d8p单元类型的使用注意事项在使用c3d8p单元类型进行分析时,需要注意以下几点:(1)合理网格划分:合理的网格划分是保证分析精度和效率的关键,需要根据分析对象的实际情况进行网格划分。
(完整版)ABAQUS实体单元类型总结

在ABAQUS中,基于应力/位移的实体单元类型最为丰富:(1)在ABAQUS/Sandard中,实体单元包括二维和三维的线性单元和二次单元,均可以采用完全积分或缩减积分,另外还有修正的二次Tri单元(三角形单元)和Tet单元(四面体单元),以及非协调模式单元和杂交单元。
(2)ABAQUS/Explicit中,实体单元包括二维和三维的线性缩减积分单元,以及修正的二次二次Tri单元(三角形单元)和Tet单元(四面体单元),没有二次完全积分实体单元。
------------------------------------------------------------------------------------------------------------按照节点位移插值的阶数,ABAQUS里的实体单元可以分为以下三类:线性单元(即一阶单元):仅在单元的角点处布置节点,在各个方向都采用线性插值。
二次单元(即二阶单元):在每条边上有中间节点,采用二次插值。
修正的二次单元(只有Tri 或Tet 才有此类型):在每条边上有中间节点,并采用修正的二次插值。
******************************************************************************* ***************1、线性完全积分单元:当单元具有规则形状时,所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。
缺点:承受弯曲载荷时,会出现剪切自锁,造成单元过于刚硬,即使划分很细的网格,计算精度仍然很差。
2、二次完全积分单元:优点:(1)应力计算结果很精确,适合模拟应力集中问题;(2)一般情况下,没有剪切自锁问题(shear locking)。
但使用这种单元时要注意:(1)不能用于接触分析;(2)对于弹塑性分析,如果材料不可压缩(例如金属材料),则容易产生体积自锁(volumetric locking);(3)当单元发生扭曲或弯曲应力有梯度时,有可能出现某种程度的自锁。
abaqus单元属性大总结
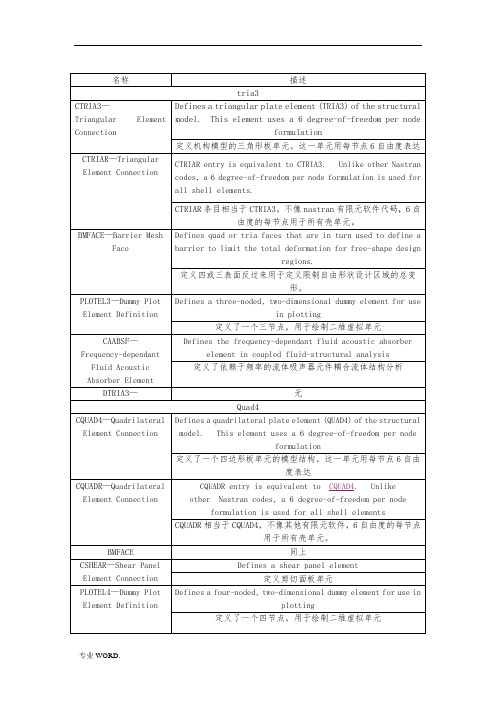
S3/S3R 单元可以作为通用壳单元使用。
由于单元中的常应变近似,需要划分较细的网格来模拟弯曲变形或高应变梯度。
S4R 单元性能稳定,适用围很广对于复合材料,为模拟剪切变形的影响,应使用适于厚壳的单元(例如S4、S4R、S3、S3R、S8R),并要注意检查截面是否保持平面。
对于几何非线性分析,在ABAQUS/Standard中的小应变壳单元(S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65)使用总体拉格朗日应变算法,应力应变可以相对于参考构型的材料方向改定。
垫片单元是小应变小位移单元,默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。
对于有限膜应变单元(所有的膜单元以及S3/S3R, S4, S4R, SAX,和 SAXA单元)和在ABAQUS/Explicit中的小应变单元,其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。
此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。
(更详细地说明可以参考ABAQUS相关手册)。
用户可以决定与*section print和*section file相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。
C3D20RP 20-node brick, triquadratic displacement, trilinear pore pressure, reducedintegration20节点实体,三重二次位移,三线孔隙压力,缩减积分C3D20R PH 20-node brick, triquadratic displacement, trilinear pore pressure, hybrid, linearpressure, reduced integration20节点实体,三重二次位移,三线孔隙压力,混合动力,线压力,缩减积分。
abaqus六面体单元类型

abaqus六面体单元类型1、单元族群,如下图所示为力学分析中常用的单元族群,这些族群的主要区别在于几何特征的差异,适合于研究不同的结构类型,选择合适的族群可以在不降低计算精度条件下,减少计算量,比如:一座高楼大厦如果全用实体单元建模,可能需要千万甚至上亿个实体单元,但如果将大厦的梁柱简化为梁单元,墙和楼板简化为壳单元模拟,单元数量将急剧减少。
单元编号法则1:它们的首字母或前几位字符通常会作为单元编号的起始字符。
比如:‘C3D8’中首字母'C’为Continuum elements 的首字母。
2、自由度,是分析过程中计算的基本变量,比如力学分析中的自由度是节点的平移和旋转自由度;传热分析中需要考虑的自由度是节点温度;渗流分析则是孔隙压力自由度。
单元编号法则2:单元自由度通常由单元族群和尾部字符确定,比如尾部字符包含T,则表示包含温度自由度,包含P,则表示包含孔压自由度。
3、节点数,自由度仅在节点位置上计算,而其他位置上的数值则通过内部公式插值获得,而插值方法由单元节点数确定,比如8节点六面体单元,采用线性插值方式,称为一阶单元;而20节点六面体单元,也就是在每条单元边中间增加一个节点,采用二次方程插值,因此被称为二阶单元。
单元编号法则3:节点数量会在单元编号中直接体现,比如C3D8中的‘8’表示8节点;而其中的‘3’或‘2’后面跟着D字符,则需要和‘3D'/‘2D’一起辨识为三维/二维单元。
4、单元架构,自由度和节点就像是零件,要把这些零件有机的组合起来,就需要装配说明,而单元架构就是这样的一套装配说明,装配好之后才能称为单元。
比如对于拉格朗日架构的单元,材料是跟随单元同步移动;而欧拉架构的单元,材料则可以在单元中流动。
其次,为了满足一些特殊的计算需求,会对一些基本构架进行修改,比如壳体单元分薄壳和厚壳,主要区别是否考虑壳体法向应力分量。
另外,不同自由度之间的耦合也是需要特殊的架构去描述。
abaqus壳单元类型与介绍

abaqus壳单元类型与介绍
Abaqus提供了多种壳单元类型,用于建模薄壳结构。
以下是几种常用的壳单元类型及其介绍:
1. S4R:四边形单元,适用于规则四边形薄壳结构。
单元的变形模态是平面应变模态。
2. S4RS:四边形单元,与S4R类似,但包含了剪切应变模态。
适用于需要考虑剪切效应的薄壳结构。
3. S4: 与S4R类似,但可以用于非规则四边形薄壳结构。
4. S4RSW:S4RS单元的扩展版本,增加了自由转动刚度。
适用于需要考虑薄壳结构的弯曲刚度和自由扭转刚度的情况。
5. S3: 三角形薄壳单元,适用于规则或非规则三角形薄壳结构。
与S4单元相比,S3单元具有更高的变形计算效率。
以上只是几种常见的壳单元类型,Abaqus还提供了其他类型的壳单元,如S8R、S9R、S8、S9等。
选择合适的壳单元类型需要根据具体的模型以及需要考虑的变形模态和计算效率来决定。
(完整版)Abaqus单元类型选择

构尺寸的1/10,比如: – 支撑或点载荷之间的距离 – 尺寸变化很大的横截面之间的距离 – 最高振动模态的波长
A1.14
结构单元(壳和梁) vs. 连续体单元
• 壳单元 – 使用表面模型构成的壳单元近似 模拟三维实体连续体单元。
A1.4
ABAQUS中的单元
族
• 有限元族是一种广泛的分类 方法。
• 同族的单元共享许多基本特 征。
• 在同一族单元中又有许多变 异。
连续体(实体单元)
刚体单元
ABAQUS/analysis_单元选择标准
壳单元
梁单元
薄膜单元
无限单元
特殊单元,如弹簧、 阻尼器和质量单元
桁架单元
A1.5
ABAQUS中的单元
ABAQUS/analysis_单元选择标准
Element type
单元类型选择标准
概述
• ABAQUS中的单元 • 结构单元(壳和梁) vs. 连续体单元 • 使用连续体单元模拟弯曲 • 应力集中 • 接触 • 不可压材料 • 网格生成 • 选择实体单元总结
ABAQUS/analysis_单元选择标准
节点个数 (插值) • 节点的单元编号决定了单元域内
节点自由度的插值方式。 • ABAQUS包含一阶和二阶插值方
式的单元。
ABAQUS/analysis_单元选择标准
一次插值
二次插值
A1.6
ABAQUS/analysis_单元选择标准
ABAQUS中的单元
自由度 • 在有限元分析过程中,单元节点的自由度是基本变量。 • 自由度的例子:
ABAQUS实体单元类型总结教学内容

在ABAQUS中,基于应力/位移的实体单元类型最为丰富:(1)在ABAQUS/Sandard中,实体单元包括二维和三维的线性单元和二次单元,均可以采用完全积分或缩减积分,另外还有修正的二次Tri 单元(三角形单元)和Tet 单元(四面体单元),以及非协调模式单元和杂交单元。
(2)ABAQUS/Explicit 中,实体单元包括二维和三维的线性缩减积分单元,以及修正的二次二次Tri单元(三角形单元)和Tet单元(四面体单元),没有二次完全积分实体单元。
按照节点位移插值的阶数,ABAQUS里的实体单元可以分为以下三类:线性单元(即一阶单元) :仅在单元的角点处布置节点,在各个方向都采用线性插值。
二次单元(即二阶单元) :在每条边上有中间节点,采用二次插值。
修正的二次单元(只有Tri 或Tet 才有此类型) :在每条边上有中间节点,并采用修正的二次插值。
******************************************************************************* ***************1 、线性完全积分单元:当单元具有规则形状时,所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。
缺点:承受弯曲载荷时,会出现剪切自锁,造成单元过于刚硬,即使划分很细的网格,计算精度仍然很差。
2、二次完全积分单元:优点:(1)应力计算结果很精确,适合模拟应力集中问题;( 2)一般情况下,没有剪切自锁问题( shear locking)。
但使用这种单元时要注意:( 1 )不能用于接触分析;( 2)对于弹塑性分析,如果材料不可压缩 (例如金属材料) ,则容易产生体积自锁 ( volumetric locking);(3)当单元发生扭曲或弯曲应力有梯度时,有可能出现某种程度的自锁。
3、线性减缩积分单元:减缩积分单元,比普通的完全积分单元在每个方向少用一个积分点;线性缩减积分单元:只在单元的中心有一个积分点,由于存在沙漏数值问题(hourglass)而过于柔软。
ABAQUS中单元特点总结
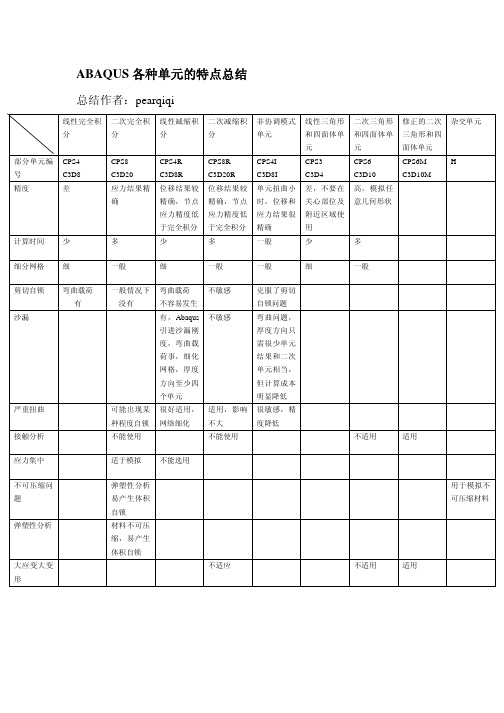
�
ABAQUS 各种单元完全积 分 二次完全积 分 线性减缩积 分 二次减缩积 分 非协调模式 单元 线性三角形 和四面体单 元 部分单元编 号 精度 CPS4 C3D8 差 CPS8 C3D20 应力结果精 确 CPS4R C3D8R 位移结果较 精确,节点 应力精度低 于完全积分 计算时间 细分网格 剪切自锁 少 细 弯曲载荷 有 沙漏 多 一般 一般情况下 没有 少 细 弯曲载荷 不容易发生 有,Abaqus 引进沙漏刚 度,弯曲载 荷事,细化 网格,厚度 方向至少四 个单元 严重扭曲 可能出现某 种程度自锁 接触分析 应力集中 不可压缩问 题 不能使用 适于模拟 弹塑性分析 易产生体积 自锁 弹塑性分析 材料不可压 缩,易产生 体积自锁 大应变大变 形 不适应 不适用 适用 不能选用 用于模拟不 可压缩材料 很好适用, 网络细化 适用,影响 不大 不能使用 不敏感 CPS8R C3D20R 位移结果较 精确,节点 应力精度低 于完全积分 多 一般 不敏感 CPS4I C3D8I 单元扭曲小 时,位移和 应力结果很 精确 一般 一般 克服了剪切 自锁问题 弯曲问题, 厚度方向只 需很少单元 结果和二次 单元相当, 但计算成本 明显降低 很敏感,精 度降低 不适用 适用 CPS3 C3D4 差,不要在 关心部位及 附近区域使 用 少 细 多 一般 二次三角形 和四面体单 元 CPS6 C3D10 高,模拟任 意几何形状 修正的二次 三角形和四 面体单元 CPS6M C3D10M H 杂交单元
ABAQUS中单元特点总结

ABAQUS中单元特点总结ABAQUS中的单元是指用于建模和分析几何结构中的离散要素。
每个单元代表结构中的一个局部区域,可以包含几何形状、材料属性和物理特性等信息。
在ABAQUS中,有多种类型的单元可供选择,每种类型的单元都有其独特的特点和适用范围。
以下是对ABAQUS中单元的几个特点的总结。
1.单元的几何特点:每个单元都可以具有不同的几何形状,如线性、面状或体状。
在ABAQUS中,目前支持的几何形状包括点、线、三角形、四边形和六面体等。
这些几何形状的选择取决于模型的复杂性和所需的准确程度。
2.单元的类型:ABAQUS提供了广泛的单元类型,以适应不同类型的分析。
常用的单元类型包括点单元(节点)、线单元、壳单元和体单元。
每个单元类型都有自己的应用领域和限制。
例如,点单元适用于仅在节点处施加负载或约束的情况,而壳单元适用于描述薄壁结构。
3.单元的连接性:单元的连接性指单元之间的关系,包括节点之间的连接和边界条件的施加。
在ABAQUS中,可以定义节点之间的连接关系,如线节点、面节点或体节点。
通过连接节点,可以构建更大的单元或复杂的结构。
此外,还可以在单元上应用约束和负载,以模拟真实的加载情况。
4.单元的材料特性:每个单元都可以具有不同的材料属性,如弹性模量、泊松比、屈服强度等。
这些材料属性可以用于模拟不同类型的材料行为,如弹性、塑性、粘弹性等。
通过在单元上应用适当的材料属性,可以模拟出材料的真实行为,进而对结构的响应进行分析。
5.单元的计算精度:在进行结构分析时,计算精度对结果的准确性和可靠性至关重要。
在ABAQUS中,不同类型的单元具有不同的计算精度。
例如,线性单元通常用于近似线性材料,而高阶单元可以更好地描述非线性材料。
选择适当的单元类型和计算精度对于获取准确和可靠的分析结果非常重要。
总之,ABAQUS中的单元具有不同的几何特点、类型、材料特性、连接性和计算精度,可以灵活地模拟和分析各种结构的行为。
abaqus热力耦合单元类型

abaqus热力耦合单元类型摘要:一、Abaqus 热力耦合单元概述二、Abaqus 热力耦合单元的类型三、各类型热力耦合单元的特点及应用四、总结正文:一、Abaqus 热力耦合单元概述Abaqus 是一款广泛应用于各种工程领域中的有限元分析软件,其热力耦合单元是用于模拟热传导和热膨胀等热力学现象的子程序。
通过热力耦合单元,可以实现对材料在不同温度下的力学性能进行准确的分析,从而优化设计和提高产品的性能。
二、Abaqus 热力耦合单元的类型在Abaqus 中,热力耦合单元主要分为以下几种类型:1.热传导单元(Thermal Conductivity Element):这种单元主要用于模拟材料在一维或二维空间中的热传导现象,适用于分析稳态或瞬态热传导问题。
2.热膨胀单元(Thermal Expansion Element):这种单元主要用于模拟材料在温度变化时的线性或非线性热膨胀现象,适用于分析材料在不同温度下的尺寸变化。
3.热应变单元(Thermal Strain Element):这种单元主要用于模拟材料在温度变化时的热应变现象,适用于分析材料在不同温度下的应变和应力分布。
4.热力耦合单元(Coupled Thermal-Mechanical Element):这种单元综合了热传导、热膨胀和热应变等多种热力学现象,适用于分析材料在复杂温度场下的热力耦合问题。
三、各类型热力耦合单元的特点及应用1.热传导单元:特点是可以模拟材料在一维或二维空间中的热传导现象,适用于分析稳态或瞬态热传导问题。
应用领域包括建筑、机械、电子等工程领域中的热传导问题。
2.热膨胀单元:特点是可以模拟材料在温度变化时的线性或非线性热膨胀现象,适用于分析材料在不同温度下的尺寸变化。
应用领域包括金属、陶瓷、塑料等材料在温度变化时的尺寸稳定性问题。
3.热应变单元:特点是可以模拟材料在温度变化时的热应变现象,适用于分析材料在不同温度下的应变和应力分布。
abaqus单元形状

abaqus单元形状Abaqus是一种常用的有限元分析软件,它提供了多种不同形状的单元用于建模和分析结构。
下面我将从几个常见的角度介绍一些Abaqus中可用的单元形状。
1. 线性单元(Linear Elements):一维线性单元(1D Linear Elements),例如节点单元(Node Element)和梁单元(Beam Element),用于模拟结构中的线性行为。
二维线性单元(2D Linear Elements),例如三角形单元(Triangle Element)和四边形单元(Quadrilateral Element),用于模拟平面结构。
三维线性单元(3D Linear Elements),例如四面体单元(Tetrahedron Element)和六面体单元(Hexahedron Element),用于模拟立体结构。
2. 非线性单元(Nonlinear Elements):二维非线性单元(2D Nonlinear Elements),例如平面应变单元(Plane Strain Element)和平面应力单元(Plane Stress Element),用于模拟结构的非线性行为。
三维非线性单元(3D Nonlinear Elements),例如几何非线性单元(Geometric Nonlinear Element)和材料非线性单元(Material Nonlinear Element),用于模拟非线性结构。
3. 特殊单元(Special Elements):壳单元(Shell Element),用于模拟薄壳结构,如板和薄膜。
拉索单元(Truss Element),用于模拟绳索或索条等拉伸元件。
接触单元(Contact Element),用于模拟结构之间的接触和摩擦。
除了上述常见的单元形状,Abaqus还提供了其他一些特殊的单元形状,如混凝土单元、岩石单元等,用于特定的工程应用。
总之,Abaqus提供了广泛的单元形状选项,可以根据具体的分析需求选择适当的单元形状进行建模和分析。
abaqus一次单元和完全积分单元

abaqus是一个用于有限元分析的强大软件。
在使用abaqus进行有限元分析时,用户需要选择合适的单元进行建模和求解。
abaqus中包含了多种类型的单元,其中一次单元和完全积分单元是比较常见且重要的两种类型。
本文将对这两种单元进行介绍和比较,以帮助用户更好地理解它们的特点和适用范围。
一次单元(C3D8)是abaqus中常用的一种典型六面体单元,其具有以下特点:1.1. 六面体单元:一次单元是一个六面体单元,具有8个节点和27个自由度。
它可以用于模拟各种三维结构的应力、应变分布和变形情况。
1.2. 简单高效:一次单元具有结构简单、计算高效的特点,适用于大多数情况下的有限元分析。
1.3. 局限性:但是,一次单元并不适用于所有情况。
在模拟高梯度场、弯曲效应或者非常规加载条件下,一次单元可能无法提供准确的结果。
相对而言,完全积分单元(C3D8I)是对一次单元的改进和扩展,其特点如下:2.1. 对弯曲效应和非线性材料有更好的适用性:完全积分单元具有更好的适用性,尤其是在模拟高梯度场、弯曲效应或者非线性材料的情况下更能提供准确的结果。
2.2. 全积分:完全积分单元是指在有限元积分时采用全积分法,这意味着对于单元内部的应力和应变的计算更加准确。
2.3. 计算量大:由于采用全积分法,完全积分单元的计算量较大,因此在处理大型模型或者需要高精度结果的情况下,需要考虑计算成本和时间。
一次单元和完全积分单元各有其特点和适用范围。
在实际应用中,用户需要根据具体的分析对象和需求来选择合适的单元类型。
对于结构简单、加载条件不太复杂的情况下,一次单元是一个非常合适的选择,它能够在保证计算效率的同时提供较为准确的结果;而对于复杂的加载条件或者非线性材料的模拟,完全积分单元则更能满足精度的要求。
对于有限元分析工程师来说,熟练掌握并灵活运用这两种单元类型是非常重要的。
3. 适用范围的具体案例在工程实践中,一次单元和完全积分单元的选择取决于具体的分析对象和需求。
如何选择ABAQUS单元类型

1、按照节点位移插值的阶数,可以将ABAQUS单元分为线性单元、二次单元和修正的二次单元2、线性完全积分单元在承受弯曲载荷时会出现剪切自锁,造成单元过于刚硬,即使划分很细的网格,计算精度仍然很差3、二次完全积分单元适于模拟应力集中问题,一般情况下不会出现剪切自锁,但不能在接触分析和弹塑性分析中使用4、线性减缩积分单元对位移的求解结果较精确,在弯曲载荷下不容易发生剪切自锁,网格的扭曲变形(例如Quad单元的角度远远大于或小于90°)对其分析精度影响不大,但这种单元需要划分较细的网格来克服沙漏问题,且不适于求解应力集中部位的节点应力5、二次减缩积分单元不但支持了线性减缩积分单元的优点,而且不划分很细的网格也不会出现严重的沙漏问题,即使在复杂应力状态下,对自锁问题也不敏感,但它不适于接触分析和大应变问题6、非协调模式单元克服了剪切自锁问题,在单元扭曲比较小的情况下得到的位移和应力结果很精确,但如果所关心部位的单元扭曲比较大,其分析精度会降低7、线性Tri单元和Tet单元的精度很差,二次Tet单元(C3D10)适于ABAQUS/Standand中的小位移无接触问题,修正的二次Tet单元(C3D10M)适于ABAQUS/Explicit,以及ABAQUS/Standand中的大变形和接触问题8、ABAQUS的壳单元可以有多种分类方法,按照薄壳和厚壳来划分,可以分为通用目的(general-purpose)壳单元和特殊用途(special-purpose)壳单元;按照单元的定义方式,可以分为常规(conventional)壳单元和连续体(continuum)壳单元9、ABAQUS中的所有梁单元都可以产生轴向变形、弯曲变形和扭转变形,B21和B31单元(线性梁单元)以及B22和B32单元(二次梁单元)即适用于模拟剪切变形引起重要作用的深梁,又适用于模拟剪切变形不太重要的细长梁,三次单元B23和B33只需划分很少的单元就可以得到较精确的结果1、对于应力集中问题,尽量不要使用线性减缩积分单元,可使用二次单元来提高精度。
ABAQUS不同单元种类的解析精度对比

ABAQUS不同单元种类的解析精度对比
ABAQUS中提供了丰富的单元类型,根据单元位移函数(形函数)的不同,可以分为一次单元和二次单元,这两种单元分别具有不同的特征。
对于一次单元,它存在以下特点:
1. 解析负荷小,计算占用资源少;
2. 在沿着变形的方向,如果网格数量少,精度会很差,网格质量差的话,精度也会降低。
3. 一次四面体单元,在结构分析中的精度太差,一般不推荐使用。
对于二次单元,它存在以下特点:
1. 解析负荷大,计算占用资源多;
2. 与一次单元相比,很少的二次单元就可以得到精度高的结果;
3. 中间节点的位置,对精度影响很显著。
一般来说,不建议一次单元和二次单元的混合使用(除特殊场合外)。
下面就通过ABAQUS对不同阶次类型的单元进行受力比较:
首先是Shell单元,如图为不同Shell单元受剪力的情况。
对不同Shell单元进行求解计算,得到其位移和Von-Mises应力分布云图:
位移云图 Von-Mises应力云图
可以看到,求解结果及精度存在着很大的影响。
这与单元的形状和阶次有很大的关系,二次四边形单元得到的求解结果最精确,一次三角形最差。
然后再对不同的Shell单元施加弯曲载荷,如图:
通过ABAQUS求解计算,分别得到其位移和Von-Mises分布图,如下:
位移云图 Von-Mises应力云图
可以看到,在承受弯曲载荷时,各单元求解所得到的结果相差不
大。
再对Solid单元进行剪力求解对比:
结果如下:
位移云图 Von-Mises应力云图
可见,二次四面体和二次六面体单元得到的结果最为精确,一次四面体单元表现出明显的剪切自锁现象。
ABAQUS单元介绍

以C为开头的单元为实体CONTINUUM单元,如:C3D4,CPE4,C3D20R,CPS2E;
以S为开头的单元为壳SHELL单元,如:S4R,S8R5,SAX2,SC8R;
以B为开头的单元为梁BEAM单元,如:B21,B22H,B31,B31H;
以T为开头的单元为桁架TRUSS单元,如:T2D2,T2D2E,T2D3T;
以R为开头的单元为刚性RIGID单元,如:R2D2,R3D3,R3D4,RAX2;
以M为开头的单元为膜MEMBRANE单元,如:M3D3,M3D4R,MAX2;
以F为开头的单元为流体FLUID单元,如:F2D2,F3D4,FAX2;
以AC为开头的单元为声学ACOUSTIC单元,如:AC1D3,AC3D20,ACAX6;
以GK为开头的单元为衬垫GASKET单元,如:GK2D2,GK3D18N,GKAX4;
另外,ABAQUS还提供了点质量单元MASS,管单元PIPE,积分单元IT,连接单元JOINT,线弹性单元LS,无限元CIN,等以适应不同模型的需要.
2D,3D表示二维,三维
PE表示平面应变单元,PS表示平面应力单元
AX表示轴对称单元
2D,3D,PE,PS,AX后面的数字一般指单元所具有的节点个数(梁单元,轴对称膜单元和轴对称壳单元除外,这些单元名称中标明了插值的阶数,如B31表示一阶三维梁单元,B32表示二阶三维梁单元,MAX2表示3节点二次轴对称膜单元,SAX1表示2节点线性轴对称壳单元)
以R结尾的单元为缩减积分单元
以H结尾的单元为杂交单元
以E结尾的单元为考虑压电效应的单元
以T结尾的单元为考虑热效应的耦合单元。
(完整版)ABAQUS实体单元类型总结

在ABAQUS中,基于应力/位移的实体单元类型最为丰富:(1)在ABAQUS/Sandard中,实体单元包括二维和三维的线性单元和二次单元,均可以采用完全积分或缩减积分,另外还有修正的二次Tri单元(三角形单元)和Tet单元(四面体单元),以及非协调模式单元和杂交单元。
(2)ABAQUS/Explicit中,实体单元包括二维和三维的线性缩减积分单元,以及修正的二次二次Tri单元(三角形单元)和Tet单元(四面体单元),没有二次完全积分实体单元。
------------------------------------------------------------------------------------------------------------按照节点位移插值的阶数,ABAQUS里的实体单元可以分为以下三类:线性单元(即一阶单元):仅在单元的角点处布置节点,在各个方向都采用线性插值。
二次单元(即二阶单元):在每条边上有中间节点,采用二次插值。
修正的二次单元(只有Tri 或Tet 才有此类型):在每条边上有中间节点,并采用修正的二次插值。
******************************************************************************* ***************1、线性完全积分单元:当单元具有规则形状时,所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。
缺点:承受弯曲载荷时,会出现剪切自锁,造成单元过于刚硬,即使划分很细的网格,计算精度仍然很差。
2、二次完全积分单元:优点:(1)应力计算结果很精确,适合模拟应力集中问题;(2)一般情况下,没有剪切自锁问题(shear locking)。
但使用这种单元时要注意:(1)不能用于接触分析;(2)对于弹塑性分析,如果材料不可压缩(例如金属材料),则容易产生体积自锁(volumetric locking);(3)当单元发生扭曲或弯曲应力有梯度时,有可能出现某种程度的自锁。
abaqus受剪板单元类型

abaqus受剪板单元类型
在Abaqus中,对于受剪板单元类型,有几种常见的选择。
这些选择通常基于你正在模拟的具体问题和所需的精度。
以下是几种常见的受剪板单元类型:
四边形(Quadrilateral):四边形是二维元素,通常用于模拟平面应变或平面应力问题。
如果你正在处理的是薄板或薄膜,并且剪切应变是主要的关注点,那么四边形是一个很好的选择。
六面体(Hexahedron):六面体元素是三维元素,通常用于模拟三维问题。
当涉及到较大的剪切应变或三维效应时,可能需要使用六面体元素。
八面体(Octahedron):八面体元素类似于六面体元素,但它们具有八个角点而不是六个。
这使得它们在某些情况下更适合模拟剪切行为,特别是当涉及到较大的剪切应变或需要更高的精度时。
二十面体(Icosahedron):二十面体元素是一种非常灵活的元素类型,通常用于模拟复杂的几何形状和应变状态。
它们可以很好地处理剪切行为,特别是当涉及到复杂的应力分布和较高的剪切应变时。
选择哪种受剪板单元类型取决于你的具体问题和需求。
你可能需要根据你的模型的具体几何形状、应力和应变状态以及所需的精度来选择最适合的元素类型。
在进行模拟之前,进行一些试验和误差分析也是非常重要的,以确保所选的元素类型能够提供准确的模拟结果。
abaqus单元形状

abaqus单元形状Abaqus软件是一种用于模拟和分析实体的有限元分析软件,使用者可以选择不同的单元类型来描述物体的形状和行为。
Abaqus提供了多种不同的单元类型,以适应不同类型的问题和目标。
下面我将介绍几种常见的Abaqus单元形状。
1. 线单元(Beam elements): 线单元用于描述长而细的结构物,如梁和柱。
它们是一维元素,沿着长度方向进行分割,并通过节点连接。
这些单元可以模拟结构物的弯曲和扭转行为。
线单元通常使用于考虑结构物细长性质的工程问题。
2. 平面单元(Plane elements): 平面单元用于描述平面或轴对称物体。
它们是二维元素,通常用于平面应力和平面应变问题的分析。
平面单元可以分为三角形单元和四边形单元。
三角形单元更适用于不规则形状,而四边形单元更适用于规则形状。
3. 壳单元(Shell elements): 壳单元用于描述薄壁结构,如板、壳和薄膜等。
它们是二维元素,具有厚度。
壳单元可以包括模拟薄壁结构的平面应力、平面应变和轴对称问题。
壳单元分为四边形壳单元和三角形壳单元。
4. 体单元(Solid elements): 体单元用于描述实体结构,如块体或立方体。
它们是三维元素,用于分析三维应力和应变问题。
体单元可以分为四面体单元和六面体单元。
四面体单元适用于非规则形状,而六面体单元适用于规则形状。
5. 结合单元(Combined elements): 结合单元是使用不同类型单元进行组合的元素。
结合单元可以用于描述复杂的几何形状和行为。
例如,可以组合使用线单元、壳单元和体单元来模拟不同部分的结构。
6. 其他单元类型:除了上述常见的单元类型外,Abaqus还提供了许多其他单元类型,如弹簧单元、等效固体单元和连接单元等。
总之,Abaqus提供了丰富的单元形状选择,以满足不同类型的工程和科学问题的分析需求。
根据问题的性质和特点,使用者可以选择适合的单元类型来模拟和分析结构的形状和行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABAQUS单元类型及特点汇总1、单元表征单元族:单元名字里开始的字母标志着这种单元属于哪一个单元族。
C3D8I是实体单元;S4R是壳单元;CINPE4是无限元;梁单元;刚体单元;膜单元;特殊目的单元,例如弹簧,粘壶和质量;桁架单元。
自由度dof(和单元族直接相关):每一节点处的平动和转动1 1方向的平动2 2方向的平动3 3方向的平动4 绕1轴的转动5 绕2轴的转动6 绕3轴的转动7 开口截面梁单元的翘曲8 声压或孔隙压力9 电势11 度(或物质扩散分析中归一化浓度)12+梁和壳厚度上其它点的温度轴对称单元1 r方向的平动2 z方向的平动6 r-z方向的转动节点数:决定单元插值的阶数数学描述:定义单元行为的数学理论积分:应用数值方法在每一单元的体积上对不同的变量进行积分。
大部分单元采用高斯积分方法计算单元内每一高斯点处的材料响应。
单元末尾用字母“R”识别减缩积分单元,否则是全积分单元。
ABAQUS拥有广泛适用于结构应用的庞大单元库。
单元类型的选择对模拟计算的精度和效率有重大的影响;节点的有效自由度依赖于此节点所在的单元类型;单元的名字完整地标明了单元族、单元的数学描述、节点数及积分类型;所用的单元都必须指定单元性质选项。
单元性质选项不仅用来提供定义单元几何形状的附加数据,而且用来识别相关的材料性质定义;对于实体单元,ABAQUS参考整体笛卡尔坐标系来定义单元的输出变量,如应力和应变。
可以用*ORIENTATION选项将整体坐标系改为局部坐标系;对于三维壳单元,ABAQUS参考建立在壳表面上的一个坐标系来定义单元的输出变量。
可以用*ORIENTATION选项更改这个参考坐标系。
2.实体单元(C)实体单元可在其任何表面与其他单元连接起来。
C3D:三维单元CAX:无扭曲轴对称单元,模拟3600的环,用于分析受轴对称载荷作用,具有轴对称几何形状的结构;CPE:平面应变单元,假定离面应变ε33为零,用力模拟厚结构;CPS:平面应力单元,假定离面应力σ33为零,用力模拟薄结构;广义平面应变单元包括附加的推广:离面应变可以随着模型平面内的位置线性变化。
这种数学描述特别适合于厚截面的热应力分析。
可以扭曲的轴对称单元:用来模拟初始时为轴对称的几何形状,且能沿对称轴发生扭曲。
这些单元对于模拟圆柱形结构,例如轴对称橡胶套管的扭转很有用。
反对称单元的轴对称单元:用来模拟初始为轴对称几何形状的反对称变形。
适合于模拟像承受剪切载荷作用的轴对称橡胶支座一类的问题。
如果不需要模拟非常大的应变或进行一个复杂的,改变接触条件的问题,则应采用二次减缩积分单元(CAX8R,CPE8R,CPS8R,C3D20R)如果存在应力集中,则应在局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20等)。
对含有非常大的网格扭曲模拟(大应变分析),采用细网格划分的线性减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R等)对接触问题采用线性减缩积分单元或非协调元(CAX4I,CPE4I,CPS4I,C3D8I)的细网格划分。
如果在模型中采用非协调元应使网格扭曲减至最小。
三维情况应尽可能采用块状单元(六面体)。
当几何形状复杂时,完全采用块体单元构造网格会很困难,因此可能有必要采用稧形和四面体单元,但尽量少用,并远离需要精确求解的区域。
一些前处理程序包括网格划分方法,它们可用四面体单元构造任意形状的网格。
只要采用二次四面体单元(C3D10),其结果对小位移问题应该是合理的。
小结:在实体单元中所用的数学公式和积分阶数对分析的精度和花费有显著的影响;使用完全积分单元,尤其是一阶(线性)单元,容易形成自锁现象,正常情况不用;一阶减缩积分单元容易出现沙漏现象;充分的单元细化可减小这种问题;在分析中如有弯曲位移,且采用一阶减缩积分单元时,应在厚度方向至少用4个单元;沙漏现象在二阶减缩积分单元中较少见,一般问题应考虑应用这些单元;非协调单元的精度依赖于单元扭曲的量值;结果的数值精度依赖于所用的网格,应进行网格细化研究以确保该网格对问题提供了唯一的解答。
但是应记住使用一个收敛网格不能保证计算结果与问题的实际行为相匹配:它还依赖于模型其他方面的近似化和理想化程度;通常只在想要得到精确结果的区域细划网格;ABAQUS具有一些先进特点如子模型,它可以帮助对复杂模拟得到有用的结果。
3.壳单元(S)可以模拟有一维尺寸(厚度)远小于另外两维尺寸,且垂直于厚度方向的应力可以忽略的结构。
一般壳单元:S4R,S3R,SAX1,SAX2,SAX2T。
对于薄壳和厚壳问题的应用均有效,且考虑了有限薄膜应变;薄壳单元:STRI3,STRI35,STRI65,S4R5,S8R5,S9R5,SAXA。
强化了基尔霍夫条件,即:垂直于壳中截面的平面保持垂直于中截面;厚壳单元:S8R,S8RT。
二阶四边形单元,在小应变和载荷使计算结果沿壳的跨度方向上平缓变化的情况下,比普通单元产生的结果更精确;对于给定的应用,判断是属于薄壳还是厚壳问题,一般:如果单一材料制造的各向同性壳体的厚度和跨度之比在1/20-1/10之间,认为是厚壳问题;如果比值小于1/30,则认为是薄壳问题;若介于1/30-1/20之间,则不能明确划分。
由于横向剪切柔度在复合材料层合壳结构中作用显著,故比值(厚跨比)将远小于“薄”壳理论中采用的比值。
具有高柔韧中间层的复合材料(“三明治”复合材料)有很低的横向剪切刚度并且几乎总是被用来模拟“厚”壳;横向剪切力和剪切应变存在于普通壳单元和厚壳单元中。
对于三维单元,提供了可估计的横向剪切应力。
计算这些应力时忽略了弯曲和扭转变形的耦合作用,并假定材料性质和弯曲力矩的空间梯度很小;壳单元可以使用每个单元的局部材料方向,各项异型材料的数据,如纤维增强复合材料,以及单元输出变量,如应力和应变,都按局部材料方向而定义。
在大位移分析中,壳单元上的局部材料轴随着材料各积分点上的平均运动而转动;线性、有限薄膜应变、四边形壳单元(S4R)是较完备的而且适合于普通范围的应用;线性、有限薄膜应变、三角形壳单元(S3R)可作为通用的壳单元来应用。
由于在单元内部近似为应变场,精细的网格划分可用于求解弯曲变形和高应变梯度;考虑到在复合材料层合壳模型中剪切柔度的影响,将采用“厚”壳单元(S4R,S3R,S8R)四边形或三角形的二次壳单元,用于一般的小变形薄壳是很有效的。
它们对剪力自锁和薄膜锁死是不敏感的;在接触模拟中不用选用二阶三角形壳单元(STRI65),要采用9节点的四边形壳单元(S9R5);对于仅经历几何线性行为的非常大的模型,线性、薄壳单元(S4R5)一般将比通用壳单元花费更少;小结:壳单元的横截面特性可以由沿厚度方向的数值积分确定(*SHELL SECTION),或在分析开始时应用计算的横截面刚度(*SHELL GENERAL SECTION);*SHELL GENERAL SECTION是非常有效的,但仅用于线性材料,*SHELL SECTION可用于线性和非线性材料;数值积分在沿壳厚度方向的一系列积分点上进行。
这些积分点就是单元变量可以被输出的位置。
最外层的积分点位于壳单元的表面。
壳单元法线方向决定了单元的正和负表面,为了正确地定义接触和解释输出数据,必须知道其对应的是哪个面。
壳法线还定义了施加在单元上正压力载荷的方向,并可以在ABAQUS/Post中画出;壳单元利用材料方向局部化到每个单元。
在大位移分析中,局部材料轴随单元而转动。
*ORIENTATION被用来定义非默认的局部坐标系统。
单元的变量,如应力和应变,在局部方向输出;*TRANSFORM定义节点的局部坐标系,集中载荷和边界条件被应用在局部坐标系中。
所用节点的输出,如位移,也默认为基于局部的坐标系;矢量图可以使模拟结果可视化,特别是用来观察结构的运动和载荷路径。
4.梁单元(B)模拟一维尺寸(长度)远大于另外二维尺寸的构件,且只有长度方向上的应力比较显著。
对于包含接触的任何模拟,应使用一阶、剪切变形的梁单元(B21,B31)如果结构刚度非常大或者非常柔软,在几何非线性模拟中应当使用杂交梁单元(B21H,B32H,等)使用欧拉-伯努利(三次)梁单元(B23,B33)精度很高,可模拟承受分布载荷作用的梁,例如动态振动分析。
如果横向剪切变形也很重要,要使用铁摩辛柯(二次型)梁单元(B22,B32)模拟有开口薄壁横截面的结构,应当使用考虑了开口截面翘曲理论的梁单元(B31OS,B32OS)小结:梁单元的性质由截面(*BEAM SECTION或*BEAM GENERAL SECTION)的数值积分决定,或直接给出截面积、惯性矩和扭转常数(*BEAM GENERAL SECTION);当使用*BEAM GENERAL SECTION选项时,模拟开始时进行一次数值积分,并且假定材料是弹性的;ABAQUS包括大量的标准横截面形状。
其它形状可以通过定义SECTION=ARBITRARY来模拟;必须定义横截面取向,方法是通过给出第三个节点,或者在单元性质定义中定义一个矢量。
截面取向在ABAQUS后处理中可以画出;当梁作为壳的加强构件使用时,梁的横截面可能偏离节点;线性和二次型包含剪切变形的影响,三次型梁不考虑剪切柔度。
开口截面梁准确地模拟了扭转和薄壁开口截面翘曲(包括翘曲约束)的影响;多点约束和约束方程可以用来连接模型中铰接、刚性连接等节点的自由度;“弯矩”型图使得像梁这样的一维单元的结果很清楚地表示出来;ABAQUS后处理图的硬拷贝可以得到PostScript和HPGL的格式。
5.桁架单元(T)只能承受拉伸和压缩载荷的杆,不能承受弯曲,模拟铰接框架结构,近似模拟线缆和弹簧。
6.刚体单元(R)没有独立的自由度。
7.非线性分析结构问题中存在着三种非线性来源:材料、几何和边界(接触)。
这些因素的任意组合都可以出现在ABAQUS的分析中;几何非线性发生在位移量值影响结构响应的情况下。
这包括大位移和转动效应、突然翻转和载荷硬化;非线性问题是利用牛顿-拉弗森方法来进行迭代求解的。
非线性问题比线性问题所需要的计算机资源要高许多倍;非线性分析步被分为许多增量步。
ABAQUS通过迭代,在新的载荷增量结束时近似地达到静力学平衡。
ABAQUS在整个模拟计算中完全控制载荷的增量和收敛性;状态文件允许在分析运行时监控分析过程的进展。
信息文件包含了载荷增量和迭代过程的详细信息;在每个增量步结束时可以保存计算结果,这样结构响应的演化就可以用ABAQUS/Post显示出来。
计算结果也可以用x-y图的形式绘出。
8.材料ABAQUS包含一个广泛的材料库,可模拟各种工程材料的性质。
其中包括金属塑性和橡胶弹性模型;金属塑性模型的应力-应变数据必须用真实应变定义;金属塑性模型假定材料具有一旦屈服即不可压缩的性质。
