正方体展开图的11种情况

正方体11种平面展开图口诀

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”“7”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

口诀：中间没有面，三三连一线（1种摆法-33）。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

正方体展开全图11种情况

圆柱圆锥
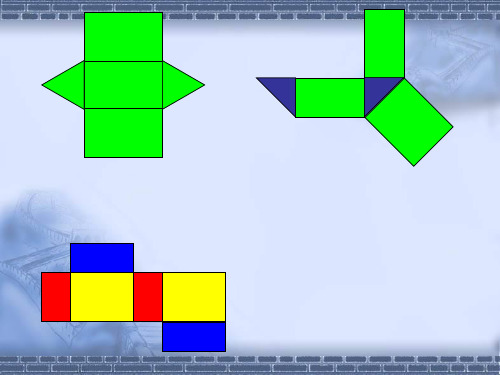
三棱锥
四棱锥
五棱锥
正方体展开图
“一四一” 型
“二三一” 型
“三三” 型
“二二二” 型
第一类（6种）：中间四连方，两侧各有一个。
展开1
第一类（6种）：中间四连方，两侧各有一个。
展开2
第一类（6种）：中间四连方，两侧各有一个。
展开3
第一类（6种）：中间四连方，两侧各有一各有一个。
展开5
第一类（6种）：中间四连方，两侧各有一个。
展开6
第二类（3种）：中间三连方，两侧各有一、二个。
展开7
第二类（3种）：中间三连方，两侧各有一、二个。
展开8
第二类（3种）：中间三连方，两侧各有一、二个。
展开9
展开10
第三类（1种）：中间二连方，两侧各有二个。
相间的两个小正方形（中间隔着一个小正方形）是正方体的两个对面，如图6中的A面和B面；“Z”字两端处的小正方形是正方体的对面，如图7、图8的A面和B面．
A
A
B
A
B
图6
图7
B
图8
图9
例3．（2005河南）如图9，一个正方体的每个面上都写有一个汉字，其平面展开图如图9所示，那么在该正方体中，和“超”相对的字是．
A
B
变形：如图有一长方体房间，在房间内一角A 处有一只小虫，它想到房间的另一角 B处去吃食物，它采取怎样的行走路线最近？
A
B
一、一线不过四
是指在正方体展开图中，一条直线上的小正方形不会超过四个，如图1、图2都不是正方体的展开图．
图1
图2
例1．（2004连云港）下面每个图片都是由6个大小相同的正方形组成，其中不能折成正方体的是（）

正方体11种折叠方法

探究正方体的展开图
将一个正方体的表面沿某些棱剪开，展成一个平面，共有哪些不同的图形呢？只从本质上讲，有以下三类共11种。

一、“141型”（共6种）
特点：这类展开图中，最长的一行（或一列）有4个正方形（图1～图6）。

理解：有4个面直线相连，其余2个面分别在“直线”两旁，位置任意。

二、“231型”与“33型”（共4种）
特点：这类展开图中，最长的一行（或一列）有3个正方形（如图7～图10）。

理解：在“231型”中，“3”所在的行（列）必须在中间，“2”、“1”所在行（列）分属两边（前后不分），且“2”与“3”同向，“1”可以放在“3”的任意一个正方形格旁边，这种情况共有3种，而“33型”只有1种。

三、“222型”（只有1种）
特点：展开图中，最多只有2个面直线相连（图11）。

评注：⑴将上面11个图中的任意一个，旋转一定角度或翻过来，看上去都与原图似有不同，但这只是图形放置的位置或方式不同。

实际上，它与原图能够完全重合，不能算作一个独立的新图，而从上面11个图中任取两个，不论怎样操作（旋转、翻折、平移等），它们都不可能完全重合，即彼此是独立的、不同的图形。

⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图，如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型，就一定不能折成正方体。

概括地说，只要不符合上述“141”、“231”和“33”、“222”的特点，就不能折成正方体。

如图12，如果将其看作“231”型，那么，无论怎么看，“2”和“3”都不是同向，故不能折成正方体。

其实，它属于“123”（或“321”）型。

正方体的11种展开图

正方体的11种展开图
正方体有11种平面展开图，不可谓不多，那么，我们该如何理解掌握这11种正方体的平面展
开图呢？正方体的平面展开图有11种之多，不容易记牢记全．为了更好的记忆掌握，我们可以把这11种展开图分成4类，只要把握各类的特征，就容易记忆了．
第一类：中间四连方，两侧各一个，共6种。

第二类：中间三连方，两侧各一、二个，共3种。

第三类：中间二连方，两侧各两个，只有1种。

第四类：两排各3个，也只有1种。

对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀：
一四一呈6种，一三二有3种，二二二与三三各1种，展开图共有11种．
1．“141型”，中间一行4个作侧面，上下两个各作为上下底面，•共有6种基本图形。

2．“132型”，中间3个作侧面，共3种基本图形。

3．“222型”，两行只能有1个正方形相连。

4．“33型”，两行只能有1个正方形相连。

（当132型、 222型时要注意不能出现田字形）。