Kaiser滤波器的参数设计方法
滤波器设计步骤

滤波器设计步骤:1、确定滤波器阶数n;2、电路实现形式选择,传递函数的确定;3、电路中元器件的选择,包括运算放大器的选择、阻容值设置等,最后形成电路原理图;4、仿真结果(幅频特性图)及优化设计;5、调试注意事项,确定影响滤波器参数实现的关键元件。
每一种电路按照以上步骤完成设计,本周内完成!1、有源低通滤波器f c =50kHz一、最低阶数的选取主要功能参数为: 1) 带内不平坦度α1=0.5dB2) 阻带衰减α2≥40dB ,这里取45dB 3) 增益G=10 4) 通带范围50kHz使用滤波器设计软件,计算得出:若选取巴特沃斯滤波器,最低阶数为n=9;若选取切比雪夫滤波器,得到同样满足要求的切比雪夫滤波器的最低阶数为n=6。
由于高阶滤波器电路复杂,造价较高,所以在同样满足技术指标的情况下,选取滤波器的最低阶数,即n=6。
二、电路实现形式选择及传递函数的确定实现切比雪夫低通滤波器的电路有许多种,这里选择无限增益多端反馈电路(MFB ),见图1。
MFB 滤波器是一种常用的反相增益滤波器,它具有稳定好和输出阻抗低等优点。
图1 二阶MFB 低通滤波电路图2滤波器的级联如图2所示,电路由三个二阶MFB 低通滤波电路串联实现,在图1所示电路中,当f=0时,C 1和C 2均开路,所以M 点的电压为121R RU U M -= M 点的电流方程 C I I I I ++=321MI 2I 3I 1I CV 2V 1N42322111sC U R U R U U R U U MM M M ++-=- (式1)其中 M U R sCU 3121-= (式2)解式1和式2组成的联立方程,得到每个二阶MFB 低通滤波器的传递函数为3221232132112121111R R C C s R R R R R sC R R U U +⎪⎪⎭⎫ ⎝⎛+++-=最后得出六阶切比雪夫低通滤波器的传递函数为⨯+⎪⎪⎭⎫ ⎝⎛+++-⨯+⎪⎪⎭⎫ ⎝⎛+++-=654326546534532212321321121411111111R R C C s R R R R R sC R R R R C C s R R R R R sC R R U U98652987985781111R R C C s R R R R R sC R R +⎪⎪⎭⎫ ⎝⎛+++-三、电路中元器件的选择使用滤波器设计软件,计算得出每节电路的阻值容值,如图2所示。
滤波器设计中的滤波器参数和滤波器系数的计算

滤波器设计中的滤波器参数和滤波器系数的计算在信号处理中,滤波器的设计起着至关重要的作用。
滤波器可以帮助我们去除信号中的噪声,并突出所需的频率成分。
滤波器的设计通常涉及到计算滤波器参数和滤波器系数的过程。
本文将介绍滤波器设计中的滤波器参数和滤波器系数的计算方法。
一. 滤波器参数的计算在开始计算滤波器参数之前,我们首先需要确定滤波器的类型和规格。
常见的滤波器类型有低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
每种滤波器类型都有其特定的参数,如截止频率、通带衰减、阻带衰减等。
1. 截止频率截止频率是指滤波器对信号进行截断的频率。
对于低通滤波器来说,截止频率是指滤波器能够传递的最高频率;对于高通滤波器来说,截止频率是指滤波器所能通过的最低频率。
带通滤波器和带阻滤波器则有两个截止频率。
截止频率的计算通常涉及到滤波器的阶数和滤波器类型。
具体的计算方法可参考相关的滤波器设计工具或算法。
2. 通带衰减和阻带衰减通带衰减是指滤波器在通带内对信号的衰减程度,通常以分贝(dB)为单位表示。
阻带衰减是指滤波器在阻带内对信号的抑制程度。
通带衰减和阻带衰减通常与滤波器的设计规格和要求有关。
一般来说,通带衰减越小,阻带衰减越大,滤波器的设计难度也就越大。
通过合理的滤波器设计算法,可以计算得到满足特定通带和阻带要求的滤波器参数。
二. 滤波器系数的计算滤波器系数是滤波器的输出值与输入值之间的系数关系。
根据滤波器的类型和设计方法的不同,滤波器系数的计算方式也各异。
下面介绍两种常见的滤波器系数计算方法:FIR滤波器和IIR滤波器。
1. FIR滤波器FIR(Finite Impulse Response)滤波器的特点是冲激响应为有限序列。
FIR滤波器系数的计算通常基于窗函数法、最小二乘法或均匀频率抽取法等。
窗函数法是一种常见的FIR滤波器设计方法。
它通过在频域上将理想滤波器与窗函数进行卷积,从而实现对滤波器系数的计算。
常见的窗函数包括矩形窗、汉宁窗、海明窗等。
基于kaiser窗的电力系统谐波和间谐波参数估计

基于Kaiser窗的插值FFT谐波与间谐波的参数估计摘要:随着精密仪器在电网中的应用日益增多,由间谐波引起的如感应电动机的振动与噪声、电压闪变等问题也日益突出。
间谐波的精确检测是解决这些问题的前提,因此研究间谐波的检测方法具有重要的现实意义。
基于凯泽窗优良的窗函数特性,提出了加凯泽窗的分段逼近参数估计方法,分析了该方法的可行性和优点,在时域与频域对凯泽窗和其他窗函数的间谐波检测性能进行了详细比较,并通过仿真验证了凯泽窗的设计灵活性,以及该方法的正确性和有效性。
关键词:间谐波;加窗插值;频谱泄露;栅栏效应;凯泽窗The Detection and Realization of Power-harmonics andinterharmonics based on LabviewABSTRACT:With the widespread of sophisticated equipments in power system, problems that are associated with interharmonics, such as the noise and vibration of induction-motor, voltage flicker and so on, has been increasingly prominent. To detect interharmonics precisly is the prerequisite of solving such problems, therefore, the research on interharmonics detection is of practical significance.Based on the excellent window function performance of the Kaiser window, the method of segmentation approximation is proposed to estimate the parameters of interharmonics, and the feasibility and merits of this method is analyzed. In addition, the comparison of interharmonics detection performances between the Kaiser window and other windowed interpolation algorithms in both the time and frequency domain are given to verity the flexibility of the Kaiser window method. The validity of the method is proved through simulation results, and their precision in interharmonic detection are also analysized according to the corresponding national standard.Key words: Interharmonics; Windowed Interpolation algorithm; frequency spectrum leakage; picket fence effects; Kaiser window0引言随着经济和社会的发展,各种基于电力电子技术的波动性负荷如变频调速设备、整流供电装置、循环变流器件等的应用日益广泛,这些设备运行时电流中包含大量的间谐波。
基于 Kaiser-Hamming锐化法的CIC滤波器性能改进
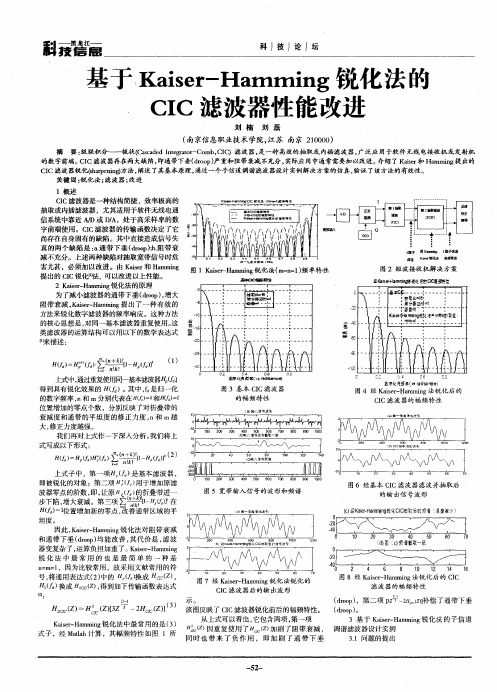
1概 述
Kh ̄ t n n ̄ a c 瞄 i &lmrl r c m n 1 t # -豫 CC I 滤波器是一种结构简捷 ,效率极 高的 抽取或 内插滤波器 ,尤其适用于软 件无线 电通 信系统 中靠近 MD或 DA, 于高采样率 的数 / 处 营 字前端使用 。C C I 滤波器 的传输 函数决定 了它 星. 30 尚存在 自身固有 的缺陷 。其中直接造成信号失 真 的两个 缺陷是 __ 带下垂 (r p ; 阻带衰 a 通 ao ) . o b 儿L 减不充分。上述两种缺陷对抽取宽带信号时危 自 一 {盎 蠹 章 ( t n 害尤甚 ,必须加 以改进 。由 K i r Ha ig as 和 mm n e 图 1Ka e- a mig 化 法 ( n 1频 率特 性 i rH m n 锐 s m= = ) 提出的 CC锐化【 , 以改进以上性能。 ! 可 弦 盔肆0蘑寄酶嬲 c 2 K i rHa mig锐化法的原理 as — m n e 为了减小滤波器的通带下垂( ro )增大 dop , 阻带衰减 , a e H m i 提 出了一种有效 的 K s - a mn i r g 方法来锐化数字滤波器的频率 响应 。这种方法 的核心思想是 , 对同一基本滤波器重复使用。 这 类 滤波器 的ቤተ መጻሕፍቲ ባይዱ算结构 可以用 以下的数学表达式
() 1
攒 : 垃蔫赣 蓐E j | 确 叼: 镬 {
上式中, 通过重复使用同—基本滤波器 ) 得到具有锐化效果 的 ( )。其 中, 是归一化 f d 的数字频率, n和 m分别代表在 日 = 和Hf= )o ( 1 2 位置增加的零点个数 ,分别反 映了对折叠带 的 衰减度和通带 的平坦度 的修 正力度 , m越 n和 大, 修正力度越强 。 我们再对上式作一下深入分析 。 我们将上 式写成 以下形式 :
滤波器设置原则及相关计算

滤波器设置原则及相关计算滤波器是一种常见的信号处理工具,通过对输入信号进行滤波以提取所需信息或去除干扰噪声。
在实际的应用中,滤波器的设置原则和相关计算十分重要,正确的设置可以有效地提高滤波器的性能,进而提高系统的整体性能。
滤波器的设置原则:1.确定滤波器类型:根据所需的滤波效果,选择合适的滤波器类型,如低通、高通、带通、带阻等。
2.选择滤波器参数:根据信号的频率、幅度等特征选择滤波器参数,如截止频率、带宽、阻带范围等,以满足所需的滤波效果。
3.确定滤波器阶数:滤波器的阶数是指滤波器中反馈环和前向通路的数量,阶数越高,滤波器的效果越好,但同时也会带来更多的计算复杂度和延迟。
4.根据系统实际情况确定滤波器的输入和输出阻抗:滤波器的输入输出阻抗需要匹配系统的实际情况,在滤波器与其他部分连接时,应该将阻抗进行匹配以提高系统的整体性能。
滤波器的相关计算:1.计算滤波器的理论传递函数:滤波器的理论传递函数可通过计算系统的差分方程得到,根据系统的阶数、截止频率等参数进行计算,得到滤波器的理论传递函数。
2.计算滤波器的实际传递函数:实际上,制造和设计的滤波器在实际应用中存在着误差和偏差,因此需要通过实验或仿真等方式,得到滤波器的实际传递函数,以验证滤波器是否满足预期效果。
3.计算滤波器的群延迟:滤波器引入的群延迟会导致信号的相位变化,影响系统的整体性能,因此需要计算滤波器的群延迟,并尽可能地减小群延迟。
4.根据设计要求计算滤波器的阻抗、带宽等参数:根据所需的滤波效果,计算合适的阻抗、带宽、截止频率等参数,以满足设计要求。
总之,滤波器的设置原则和相关计算需要综合考虑滤波器的类型、参数、阶数、输入输出阻抗以及实际应用情况,经过合理的设计和计算,可以有效地提高滤波器的性能,从而提高系统的整体性能。
在使用滤波器的过程中,除了设置原则和相关计算以外,还需要进行一系列的优化和调试,以满足应用实际需求。
滤波器的优化和调试:1.选择合适的滤波器结构:滤波器的结构会影响滤波器的效果和计算复杂度,可以根据实际需求选择合适的结构,如IIR(无限冲激响应)滤波器、FIR(有限冲激响应)滤波器、卷积神经网络滤波器等。
Kaiser滤波器的参数设计方法

数字信号技术 目前 已经在各行各业得到了充分 的利用 , 随 着信息时代 的发展 , 该技术也得到了更大的关注 , 尤其是在信 息通讯, 信 号处理 ,自动控制, 军事 国防 , 医疗及家 电等领域 , 已经 逐 步 取 代 了传 统 模 数 转 换 处 理 系统 。F I R滤 波 器 中 的 K a i s e r滤波器 的设计与研究,常用设计方法有窗函数法,频率采 样法 ,切 比需夫逼近法等,但 由于 窗函数能够进行截断处理 , 还可 以对信号进行平滑操作 , 因此窗 函数法在数字滤波器 的设 计 中具有很大 的优势,可以更加有 效地保持信号信息 。k a i s e r窗是窗函数中的最 优化 窗, 它 的主瓣集 中了大部分的频带 内 能 ,同时可 以对旁瓣起到最大 的抑制作用 。本文将通 过选用 k a i s e r窗 ( 最优化 窗)进行 k a i s e r滤波器的参数 设计 ,并对 设计参数值 进行调整与分析选择最 优的主瓣 宽度和 旁瓣衰减 以得到设计所需要滤波标准数字滤波器。 窗函数的种类有矩形 窗、汉明窗、布 莱克曼 窗、凯塞窗。如果进行 设计 时使用 了矩 形窗 , 那么必然会 出现 以下不足 之处:首先,它不 能改变最小 阻带衰减 , 从而使起在很多应用 中得不到满足 ; 其 次,矩形窗 是对无 限长度 的序列 的直接截取 , 存在着跳变 点,因此会增大 序 列长度 M ,即使每个旁瓣的宽度减小 ,但瓣下的面积不变 , 则最 小阻带衰减仍 为 2 1 d B保持不变 。 狄 拉 克 函数 , 在 频 域 内窗 函数 与狄 拉 克 函数 越 靠 近 ,则信 号越 准确 。实 际上 不可能在 时域和频域都 不会是失真 的窗 函 数 , 因此 应 合 理 选 择 可 以满 足 设 计 要求 的 窗 函数 。k a i s e r 窗 ( 最优化窗 )进行 k a i s e r滤波器 的参数设计更为有效 ,操作 更为简化 , 对设计参数值进行调整与分析选择 最优 的主瓣宽度 和旁瓣衰减 以得到设计所 需要滤波标准数字滤波器。 凯塞窗可 以通过改变参数 B和 M 的值来实现 改变 阻带衰 减和过度宽带 。 其 目的是将频率响应 的主 瓣与 旁瓣 的能量谱 的 比值 达 到 最 大 。 具 体 设 计 步骤 : 1 . 根据 过度 带宽度及衰减要求 , 选择 窗函数 的类型并估计 窗 口长度 N 。待求滤波器的过渡 带宽与窗口长度近似成反比 。
基于Kaiser窗函数的FIR数字滤波器设计

输 入模 块 的 主要 功 能 是 完 成 对 输 入数 据 的处 理 , 窗 函数 在 设 计 FR数 字 滤 波 器 中 起 很 重 要 的作 为后续 电路 作准 备 。它主 要 由并 串转 换单 元 ( 1 a 、 I 图 - ) 图 _) 图 一 用 .正 确 的选 择 窗 函数可 以提 高所 设计 的数 字滤 波器 移位 寄存 器 单元 ( l b 和 数据 的预 相加 单 元 ( 1 的性能 . 者在 满足设 计要 求 的情 况下 , 小 FR数字 c  ̄ 成 。 或 减 I )t f (1 2 乘累 加模块 滤 波器 的阶数 调整 窗 口长度 N可 以有 效地 控 制过渡
阐述 了 FR 数 字 滤波 器 的原理 、 I 线性 相位 条 件 , 论 了窗 函数 设 计方 法 , 利 用 V 讨 并 HDL语 言基 于 K i r窗 ae s
函数进 行 FR 滤波 器的仿 真设 计 。仿真 表 明 : 助软件 设 计 实现数 字 滤波 器简便 易行 , I 借 滤波性 能指 标 能较
o ‘7 .. -】
o I E CL K
() 3 锁存模 块 锁 存模 块 ( 3 的 主要 功 能是 将 乘 累加模 块 的输 图 )
再用 8 二进 制补 码表示 为 : 位
ho= 0 ) 00 01 () h 5= 00 1 0 h2= ( ) 11 11 () h1 = l1 0 3 1 h1 h1) 11 1 ( = ( = 11 0 ) 4 10 h3= ( ) 0010 () h1 = 0000 2
图 2 累加 模 块 乘
选 择 低 通 滤 波 器 , asr 设 计 方 法 ,s 5 MH , Ki 窗 e F = z F = . MHz 阶数 为 1 e1 5 , 6位 , 线性相 位 。 计 出符合 设计 设
Kaiser窗设计低通滤波器

实验五FIR滤波器设计方法一、实验目的:1、掌握不同窗函数的性能指标;2、根据指标选择窗函数设计FIR滤波器。
3、掌握频率采样法设计FIR滤波器二、实验内容:自定滤波器的类型(低通,高通或带通)、设计指标(通带截止频率、通带波纹、阻带截止频率、阻带衰减)1、根据指标选择合适的窗函数,用窗口设计法设计符合指标的FIR滤波器;并验证其性能是否满足预定指标。
参考书上例题2、根据指标选择合适的采样点数,用频率采样法设计符合指标的FIR滤波器;并验证其性能是否满足预定指标。
参考书上例题求出通带内的Rp和阻带内的As,或者用两行两列的子图分别将结果列出来。
3、求输入x(n)=[cos(w1n)+cos(w2n)]u(n)经过系统后的输出y(n)。
其中w1位于通带内,w2位于阻带内,要求做一个两行两列的子图,第一个做x的时域波形,第二个做x的幅度谱,第三个做y的时域波形,第四个做y的幅度谱。
三、实验平台:MATLAB集成系统四、设计流程:用Kaiser窗设计符合要求的低通滤波器;五、程序清单:Wp=0.2pi,Rp=0.25Ws=0.3pi,As=50dB1>> wp=0.2*pi;ws=0.3*pi;As=50;tr_width=ws-wp;>> M=ceil((As-7.95)/(2.285*tr_width)+1)+1M =61>> n=[0:1:M-1];beta=0.1102*(As-8.7)beta =4.5513>> wc=(ws+wp)/2;hd=ideal_lp(wc,M);>> w_kai=(kaiser(M,beta))';h=hd.*w_kai;>> [db,mag,pha,gra,w]=freqz_m(h,[1]);delta_w=2*pi/1000;>> As=-round(max(db(ws/delta_w+1:1:501)))As =52>> subplot(2,2,1);stem(n,hd);title('Ideal Impulse Response')>> axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('hd(n)')>> subplot(2,2,2);stem(n,w_kai);title('kaiser window')>> axis([0 M-1 0 1.1]);xlabel('n');ylabel('w(n)')>> subplot(2,2,3);stem(n,h);title('Actual Impulse Response')>> axis([0 M-1 -0.1 0.3]);xlabel('n');ylabel('h(n)')>> subplot(2,2,4);plot(w/pi,db);title('Magnitude Respone in dB')>> grid;>> axis([0 1 -100 10]);xlabel('freayency in pi units');ylabel('Decibels')2> M=60;alpha=(M-1)/2;l=0:M-1;w1=(2*pi/M)*l;>> Hrs=[ones(1,7),0.5925,0.1099,zeros(1,43),0.1099,0.5925,ones(1,6)];>> Hdr=[1,1,0,0];wd1=[0,0.2,0.3,1];>> k1=0:floor((M-1)/2);k2=floor((M-1)/2)+1:M-1;>> angH=[-alpha*(2*pi)/M*k1,alpha*(2*pi)/M*(M-k2)];>> H=Hrs.*exp(j*angH);h=real(ifft(H,M));>> [db,mag,pha,grd,w]=freqz_m(h,1);[Hr,ww,a,l]=Hr_Type2(h);>> subplot(2,2,1);plot(w1(1:31)/pi,Hrs(1:31),'o',wd1,Hdr);>> axis([0,1,-0.1,1.1]);title('Frequency Sampoles:M=60');>> xlabel('frequency in pi units');>> ylabel('Hr(k)');>> subplot(2,2,2);stem(l:h);>> subplot(2,2,2);stem(l,h);>> axis([-1,M,-0.1,0.3])>> title('Impulse Response');xlabel('n');ylabel('h(n)');>> subplot(2,2,3);plot(ww/pi,Hr,w1(1:31)/pi,Hrs(1:31),'o');>> axis([0,1,-0.2,1.2]);title('Amplitude Response')>> xlabel('ferquency in pi units');ylabel('Hrs(w)')>> subplot(2,2,4);plot(w/pi,db);axis([0,1,-60,10]);grid>> subplot(2,2,4);plot(w/pi,db);axis([0,1,-100,10]);grid>> title('Magnitude Response');xlabel('ferquency in pi units');ylabel('Decibels') >>六、调试和测试结果:所得Kaiser窗的图形及相应参数如下:由图知最小的阻带衰减已经大于50dB,符合要求。
kaiser窗函数公式

kaiser窗函数公式Kaiser窗函数公式是一种常用的数字信号处理技术,它在信号处理领域有着广泛的应用。
本文将介绍Kaiser窗函数的公式及其在信号处理中的应用。
Kaiser窗函数是一种窗函数,用于在时域上对信号进行加窗处理。
其公式为:w(n) = I0 [α·√(1-(n/N)^2)] / I0 (α)其中,w(n)表示窗函数在n时刻的取值,I0表示第一类修正贝塞尔函数,α是控制窗函数的参数,N是窗函数的长度。
Kaiser窗函数的特点是具有较窄的主瓣宽度和较低的旁瓣衰减。
通过调整参数α的值,可以控制主瓣宽度和旁瓣衰减的程度。
当α的值越大,主瓣宽度越窄,旁瓣衰减越好。
在信号处理中,Kaiser窗函数常用于频谱分析、滤波器设计和信号重建等领域。
下面将分别介绍其在这些领域中的应用。
首先是频谱分析。
频谱分析是对信号在频域上进行分析的过程,可以用来研究信号的频率成分。
Kaiser窗函数可以用于对信号进行加窗处理,使得信号在频域上呈现出较好的主瓣宽度和旁瓣衰减效果,从而提高频谱分析的准确性。
其次是滤波器设计。
滤波器是一种能够对信号进行频率选择性处理的系统,常用于去除噪声或者滤波信号。
Kaiser窗函数可以用于设计滤波器的窗函数,通过调整窗函数的参数α,可以得到满足滤波器设计要求的滤波器。
最后是信号重建。
信号重建是指通过采样和插值等技术,将离散信号恢复为连续信号的过程。
Kaiser窗函数可以用于对离散信号进行加窗处理,从而减小重建误差,并提高信号重建的质量。
除了上述应用外,Kaiser窗函数还可以用于调制解调、图像处理、音频处理等领域。
在实际应用中,根据具体的需求,可以选择合适的窗函数及其参数,来实现对信号的处理和分析。
Kaiser窗函数是一种常用的数字信号处理技术,通过对信号进行加窗处理,可以改善信号的频谱特性,并实现对信号的精确处理和分析。
在频谱分析、滤波器设计和信号重建等领域,Kaiser窗函数都有着重要的应用。
滤波器的设计方法

滤波器的设计方法滤波器是一种用于信号处理的重要工具,可以用于去除信号中的噪声、调整信号的频率响应等。
滤波器的设计方法可以分为两类:基于时间域的设计方法和基于频域的设计方法。
基于时间域的设计方法主要是通过改变滤波器的时间响应来实现滤波的效果。
最常用的时间域设计方法是窗函数法和直接设计法。
窗函数法是一种简单而直观的设计方法。
它的基本思想是将滤波器的频率响应乘以一个窗函数,从而限制滤波器的时域响应范围,达到滤波的效果。
常用的窗函数有矩形窗、汉宁窗、汉明窗等。
直接设计法是一种根据滤波器的设计要求直接得到其传递函数的方法。
这种方法主要用于设计IIR滤波器,其基本步骤是:首先,选择合适的滤波器类型(如低通、高通、带通、带阻等)和滤波器阶数;然后,确定滤波器的零极点位置;最后,根据零极点位置计算滤波器的传递函数。
基于频域的设计方法主要是通过改变滤波器的频率响应来实现滤波的效果。
最常用的频域设计方法是理想滤波器法和频率抽样法。
理想滤波器法是一种以理想滤波器的频率响应为目标,通过变换到时域来设计滤波器的方法。
它的基本思想是,将理想滤波器的频率响应作为目标函数,通过傅里叶变换将其转换到时域,得到滤波器的冲激响应,再通过采样和巴特沃斯窗函数处理得到最终的滤波器。
频率抽样法是一种根据滤波器的频率响应来设计滤波器的方法。
它的基本思想是,在频率域上对目标频率响应进行采样,通过多项式插值得到频率抽样函数,再通过傅里叶变换将其转换到时域,得到滤波器的冲激响应。
除了以上介绍的常见的设计方法外,还有一些基于遗传算法、粒子群优化算法等优化算法的设计方法。
这些方法通过优化算法来搜索设计空间,找到满足设计要求的滤波器参数。
这些方法通常能得到更好的设计结果,但计算量较大,适用于一些对设计结果精度要求较高的场合。
总之,滤波器的设计方法有多种,每种设计方法都有其适用范围和优缺点。
根据实际需求和设计要求选择合适的设计方法,可以得到满足要求的优质滤波器。
kaiser 标准化四分法

kaiser 标准化四分法
Kaiser四分法(Kaiser Normalization)是一种基于信息论的方法,用于特征选择。
在信号处理中,信号通过快速傅里叶变换(FFT)进行频谱分析,得到频谱图。
Kaiser四分法可以用于频谱图中的特征提取,它根据信号的频谱图,将频谱分为四个部分,并计算每个部分的熵值。
熵值越大,表示该部分包含的信息量越大,越有可能成为信号的特征。
具体来说,Kaiser四分法将频谱图分为四个部分:低频部分、中频部分、中高频部分和高频部分。
这些部分的选择标准如下:
●低频部分:包含信号中最低频率的成分,通常是信号的主要能量分布区域。
●中频部分:包含信号中中等频率的成分,通常是信号的细节和结构信息。
●中高频部分:包含信号中较高频率的成分,通常是信号中的噪声和干扰成
分。
●高频部分:包含信号中最高频率的成分,通常是信号中的噪声和干扰成分。
在计算每个部分的熵值时,可以使用不同的方法,例如直方图法、小波变换法等。
熵值越大,表示该部分包含的信息量越大,越有可能成为信号的特征。
因此,可以根据熵值的大小,选择出信号中的重要特征,并进行进一步的特征提取和分析。
基于.凯塞窗高通滤波器设计说明书

安康学院学年论文﹙设计﹚题目基于凯瑟窗高通滤波器设计学生姓名刘玲学号 0828024057 所在院(系) 电子与信息工程系专业班级 08电子信息工程指导教师余顺园2011年8月13 日基于凯瑟窗高通滤波器设计作者:刘玲(安康学院电子与信息工程系电子信息工程专业08级.陕西 安康 725000)指导教师:余顺园【摘要】数字滤波器是一种具有频率选择性的离散线性系统.在信号数字处理中有着广泛的应用。
设数字滤波器的传输函数为()()n h e h d jw d ,是与其对应的单位脉冲响应()n h d 是无限长的. 需要求对()jw d e h 的一个逼近。
采用窗函数设计法时. 可以通过对理想滤波器的单位采样响应加窗来设计滤波器。
本文就是引入MATLAB 设计FIR 数字滤波器.利用凯瑟窗函数设计高通滤波器。
高通滤波器就是从频率s f ~∞.其幅频特性平直。
它使信号中高于s f 的频率成分几乎不受衰减的通过.而低于s f 的频率成分将受到极大地衰减。
凯瑟窗方法是一种应用广泛的可调窗.它可以通过改变窗函数的形状来控制窗函数旁瓣的大小.而在设计中可根据滤波器的衰减指标来确定窗函数的形状。
【关键词】数字滤波器 高通滤波器 凯瑟窗 MATLABDesign of high-pass filter Based on the Kaiser windowAuthor: Liu Ling(Grade08,Class1,Major Electronic and information engineering.Electronic andinformation engineering Dept..Ankang University.Ankang 725000.Shaanxi )Directed: by Yu ShunyuanAbstract :Digital filter is one kind has the frequency selective discrete linear system, digital signal processing in a wide range of applications. Set the transfer function ofa digital filter is expressed as ()jw d e h ,and its unit impulse response is ()n h d , thedemand of the long, to a approximation ()jw d e h . The window function design method, can through to the ideal of the filter sampling response unit with window to come design filter.This paper is introducing MATLAB design FIR digital filters, using the Kaiser window function design high-pass filter. High-pass filter is from the frequency, the ~ ∞ amplitude frequency characteristics flat. It makes signal in frequency components of the higher than almost from the attenuation, and through the lower than frequency components will be greatly decrease. Kaiser window method is used widely adjustable window, it can change the shape of the window function to control the size of the window function sidelobes, and in the design of the filter according to index to determine the attenuation of the shape of the window functionKey words :Digital filter , High-pass filter, Kaiser window, MATLAB0 引言随着科学技术的发展.数字滤波器在数字信号处理领域中已经得到广泛应用。
用凯泽窗设计线性相位带通FIR滤波

中国地质大学(北京)本科课程报告课程名称数字信号处理实验名称用凯泽窗设计线性相位带通FIR滤波学生姓名衡星院(系)地球物理与信息技术学院专业测控技术与仪器学号1010152213指导教师陈玉东2018年1月10日中国地质大学(北京)目录1实验目的 (1)2实验环境 (1)3实验原理及设计流程图 (1)4实验内容及程序源代码 (2)5实验结果 (5)6实验思考 (6)7心得与体会 (7)1实验目的基于MATLAB 环境,熟悉窗函数法设计线性相位FIR 滤波器的原理和方法。
2实验环境硬件环境:计算机,软件环境:MATLAB 平台。
3实验原理及设计流程图(1)利用凯泽窗原理求解滤波器长度N 和形状参数β:凯泽窗是对于给定的阻带衰减,使主瓣具有最大能量意义下的最佳窗函数,因此具有最陡的过渡带。
窗函数的形式为:10 )(] )121(1 [)(020-≤≤---=N n I N n I n w k ,ββ,其中β为形状参数,I 0[x ]是第一类修正零阶贝塞尔函数,其幂函数展开式为:∑∞=+=120])(1[1][k k xx I .若给定滤波器的过渡带宽度∆ω(rad)和阻带衰减A s (dB),则滤波器的长度和形状参数β可由下列经验公式给出:ωΔ286.295.7-≈s A N ,0.40.1102(8.7)50dB 0.5842(21)0.07886(21)2150dB 021dB s s s s s s A A A A A A β-≥⎧⎪=-+-≤≤⎨⎪≤⎩,,,,代入11110.15s p s p ωωωωπω∆=-==-,As =60dB 得N =50,β=5.65.(2)理想带通滤波器单位抽样响应h d (n )的计算:若H d (e jw )为理想带通线性相位滤波器,12(e )0j c c j d e H ωαωωωω-⎧≤≤⎪=⎨⎪⎩,,其它,那么,该理想带通滤波器可以根据两个幅值相等而截止频率不同的理想低通滤波器形成,截止频率分别近似为:11122211();()22c p s c p s ωωωωωω=+=+,故2121()()21sin[()]sin[()]11()d d 22()()c c c c j n j n c cd n n h ne e n n ωωωαωαωωωαωαωωπππαπα++------=-=--⎰⎰,其中α为线性相位所必须的移位,应满足α=(N-1)/2.(3)设计流程图:计算h(n)=h d(n)·w k(n)用stem(w k)显示w k(n)输入带通指标:ωp1、ωp2、ωs1、ωs2、A s、编写函数dbpfilter_FIR.m用以计算带通滤波器单位抽样响应h(n)计算N(N为奇数)及β编写函数kaiser_WF.m计算凯泽窗函数w k(n)计算滤波器的幅频及对数幅频特性并画图打印结果、验证指标要求调用ideal_LP计算h d(n)4实验内容及程序源代码(1)凯泽窗函数文件kaiser_WF.m:function wk=kaiser_WF(N,beta)%N---凯泽窗序列的长度%beta---凯泽窗参数%wk---凯泽窗序列n=[0:1:N-1];for i=1:1:Ntemp=1-(1-2*n(i)/(N-1))^2;if temp<-eps;disp('负数开方');endbessel_w(i)=bessel_IM(beta*sqrt(temp));endwk=bessel_w/bessel_IM(beta);(2)贝塞尔函数bessel_IM.m:function s=bessel_IM(x)eps=10^(-12);k=1;s=1;D=1;while D>(eps*s)T=x/(2*k);D=D*T^2;s=s+D;k=k+1;end所用的公式为:∑∞=+=120]2(!1[1][k k xk x I .(3)理想低通滤波器单位抽样响应函数ideal_LP.m :function [hd]=ideal_LP(wc,N)%hd ---理想低通滤波器单位冲激响应(0<=n<=(n-1))%wc ---截至频率(单位弧度/秒)%N ---理想低通滤波器的长度alpha=(N-1)/2;n=[0:(N-1)];m=n-alpha+eps;hd=sin(wc*m)./(pi*m);(4)dbpfilter.m 主程序文件:通带截止频率ωp 1=0.3π,ωp 2=0.5π;ωs 1=0.15π,ωs 2=0.65π,阻带衰减大于60dB.%d_omega ---输入数字频率数组(向量);%d_omega(1)---阻带下边缘截止频率%d_omega(2)---通带下边缘截止频率%d_omega(3)---通带上边缘截止频率%d_omega(4)---阻带上边缘截止频率%N ---数字带通滤波器的长度%hd ---理想数字带通滤波器单位冲激响应%h ---实际数字带通滤波器单位冲激响应(所设计的)%wk ---凯泽窗序列%beta ---凯泽窗参数As=60;d_omega=[0.15,0.3,0.5,0.65]*pi delta_w=d_omega(2)-d_omega(1);N=(As-7.95)/(2.286*delta_w)N=ceil(N);M=N;while M>0M=M/2;if M==ceil(N/2);N=N+1;end end N=Nn=[0:1:N-1];beta=0.1102*(As-8.7)wk=kaiser_WF(N,beta)wc_lower=(d_omega(1)+d_omega(2))/2;wc_upper=(d_omega(3)+d_omega(4))/2;hd=ideal_LP(wc_upper,N)-ideal_LP(wc_lower,N) h=hd.*wk;[H,w]=freqz(h,1,1000,'whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));figure(1);clf;subplot(221);stem(n,hd);title('理想带通滤波器单位冲激响应');axis([-1,N,-0.4,0.6]);ylabel('h_d(n)');subplot(222);stem(n,wk);title('凯泽窗(Kaiser)');axis([-1,N,0,1.3]);ylabel('w_k(n)');subplot(223);stem(n,h);axis([-1,N,-0.4,0.6]);ylabel('h(n)');title('实际带通滤波器单位冲激响应');subplot(224);plot(w/pi,db);axis([0,1,-100,10]);ylabel('分贝');title('实际带通滤波器频率响应(dB)');xlabel('单位为弧度(\pi)');axis([01-8010]);set(gca,'XTickMode','manual','XTick',d_omega/pi);set(gca,'YTickMode','manual','YTick',[-500]);grid;fileID=fopen('FIR_KAISER_W_h.txt','w');fprintf(fileID,'有限长单位冲激响应滤波器长度N=%d\n\n',N);fprintf(fileID,'%12s\n','h');fprintf(fileID,'%12.8f\n',h);fclose(fileID);5实验结果运行结果如下:d_omega=0.47120.9425 1.5708 2.0420N=48.3174N=49beta=5.6533wk=1至13列0.02040.03600.05600.08060.11020.1447 0.18420.22850.27740.33020.38640.44540.506114至26列0.56770.62900.68910.74670.80070.8501 0.89380.93090.96060.98230.9956 1.00000.995627至39列0.98230.96060.93090.89380.85010.8007 0.74670.68910.62900.56770.50610.44540.386440至49列0.33020.27740.22850.18420.14470.1102 0.08060.05600.03600.0204wc_lower=0.7069wc_upper=1.8064hd=1至13列0.0048-0.00180.0106-0.0080-0.0318-0.00880.0130 -0.00240.00720.03920.0139-0.0301-0.013314至26列-0.0042-0.0450-0.02130.06120.0478-0.00510.0487 0.0398-0.1711-0.22950.10280.35000.102827至39列-0.2295-0.17110.03980.0487-0.00510.04780.0612 -0.0213-0.0450-0.0042-0.0133-0.03010.013940至49列0.03920.0072-0.00240.0130-0.0088-0.0318-0.0080 0.0106-0.00180.0048图用凯泽窗设计出的线性相位带通滤波器6实验思考(1)窗函数有哪些指标要求?窗函数有截短和平滑的作用,窗函数选择的好,可以在相同阶次的情况下,提高滤波器的性能,或是在满足设计要求的情况下,减少滤波器阶数。
利用kaiser窗设计低通滤波器程序

%--------------------------------------------------------------------------%利用kaiser窗设计低通滤波器m文件%默认输入参数:N=64% beta=5.568% wc=0.5pi%输出参数:通带边界(wp)% 阻带边界(ws)% 通带波纹% 阻带衰减%--------------------------------------------------------------------------function varargout = lpfilter(varargin)% LPFILTER M-file for lpfilter.fig% LPFILTER, by itself, creates a new LPFILTER or raises the existing% singleton*.%% H = LPFIL TER returns the handle to a new LPFILTER or the handle to% the existing singleton*.%% LPFILTER('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in LPFILTER.M with the given input arguments. %% LPFILTER('Property','V alue',...) creates a new LPFIL TER or raises the% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before lpfilter_OpeningFunction gets called. An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to lpfilter_OpeningFcn via varargin.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)".%% See also: GUIDE, GUIDA TA, GUIHANDLES% Edit the above text to modify the response to help lpfilter% Last Modified by GUIDE v2.5 29-Jun-2007 13:21:40% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @lpfilter_OpeningFcn, ...'gui_OutputFcn', @lpfilter_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin & isstr(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before lpfilter is made visible.function lpfilter_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MA TLAB % handles structure with handles and user data (see GUIDA TA) % varargin command line arguments to lpfilter (see V ARARGIN)% Choose default command line output for lpfilterhandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes lpfilter wait for user response (see UIRESUME)% uiwait(handles.figure1);%--------------------------------------------------------------------------%设置滤波器长度,beta和截止频率编辑框的初始值%设置窗体的标题set(handles.figure1,'name','FIR低通滤波器');set(handles.edit_N,'string','64');set(handles.edit_beta,'string','5.568');set(handles.edit_fc,'string','0.5');%--------------------------------------------------------------------------%由设置的初始值求取滤波器的理想单位脉冲响应handles.wc=0.5*pi;handles.M=64;handles.hd=ideal_lp(handles.wc,handles.M);%--------------------------------------------------------------------------%绘制滤波器的理想单位脉冲响应axes(handles.axes_hd);n=[0:1:handles.M-1];plot(n,handles.hd); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%55title('滤波器理想脉冲响应');axis([0 handles.M-1 min(handles.hd) max(handles.hd)+0.01]);xlabel('n');ylabel('hd(n)');grid on;guidata(hObject,handles);% --- Executes on button press in plot.function plot_Callback(hObject, eventdata, handles)% hObject handle to plot (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)%--------------------------------------------------------------------------%从编辑框获取滤波器长度,beta和截止频率的值handles.M = str2double(get(handles.edit_N,'String'));handles.beta = str2double(get(handles.edit_beta,'String'));handles.wc = str2double(get(handles.edit_fc,'String'))*pi;%求取滤波器的理想单位脉冲响应handles.hd=ideal_lp(handles.wc,handles.M);%绘制滤波器的理想单位脉冲响应axes(handles.axes_hd);plot(0,0);n=[0:1:handles.M-1];plot(n,handles.hd);title('滤波器理想脉冲响应');axis([0 handles.M-1 min(handles.hd) max(handles.hd)]);xlabel('n');ylabel('hd(n)');grid on;%--------------------------------------------------------------------------%求取kaiser窗函数handles.w_kai=(kaiser(handles.M,handles.beta))';%绘制kaiser窗函数axes(handles.axes_wkaiser);plot(n,handles.w_kai);title('kaiser窗');axis([0 handles.M-1 min(handles.w_kai) max(handles.w_kai)]);xlabel('n');ylabel('w(n)');grid on;%--------------------------------------------------------------------------%求取滤波器的实际单位脉冲响应handles.h=handles.hd.*handles.w_kai;%绘制滤波器的实际单位脉冲响应axes(handles.axes_h);plot(n,handles.h);title('滤波器实际脉冲响应');axis([0 handles.M-1 min(handles.h) max(handles.h)]);xlabel('n');ylabel('h(n)');grid on;%--------------------------------------------------------------------------%求取滤波器的频率特性,并绘制幅频特性(转换到0—pi)[H,w] = freqz(handles.h,[1],handles.M*6,'whole');% freqz(handles.h,[1],handles.M*6);H=(H(1:1:handles.M*3))';w=(w(1:1:handles.M*3))';mag=abs(H);db=20*log10((mag+eps)/max(mag));% pha=angle(H);%绘制幅频特性(转换到0—pi)axes(handles.axes_lp);plot(w/pi,db);title('FIR滤波器的幅频特性(0-pi)');axis([0 1 min(db) max(db)]);xlabel('Frequency in pi units');ylabel('Decibels');grid on;guidata(hObject,handles);%--------------------------------------------------------------------------%由求得幅频特性计算通带边界,阻带边界,通带纹波和阻带衰减%由beta值计算阻带衰减Asif handles.beta<4.5513As=fzero(@myfun,20,[],handles.beta)+21;elseAs=handles.beta/0.1102+8.7;end%计算通带边界wp,阻带边界wsw_w=(As-7.95)/((handles.M-1)*14.36)*2;ws=0.5*(w_w+2*handles.wc/pi);wp=0.5*(2*handles.wc/pi-w_w);% mag=(mag+eps)/max(mag);%计算通带纹波rp% deta_w=2*pi/(handles.M*6);% w_temp=mag(floor(ws/deta_w));% mag_temp=abs(mag(1:floor(ws/deta_w))-w_temp);rp=20*log10(max(mag));%--------------------------------------------------------------------------%在相应的编辑框中显示通带边界,阻带边界,通带纹波和阻带衰减str=sprintf('%.2f',wp);set(handles.edit_wp,'string',str);str=sprintf('%.2f',ws);set(handles.edit_ws,'string',str);str=sprintf('%.4f',rp);set(handles.edit_rp,'string',str);str=sprintf('%.2f',-As);set(handles.edit_As,'string',str);%--------------------------------------------------------------------------%退出程序function exit_Callback(hObject, eventdata, handles)% hObject handle to exit (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA) close(handles.figure1);%--------------------------------------------------------------------------%自定义函数,计算理想低通滤波器的单位脉冲响应function hd=ideal_lp(wc,M);alpha=(M-1)/2;n = [0:1:(M-1)];m=n-alpha+eps;hd=sin(wc*m)./(pi*m);% --- Outputs from this function are returned to the command line. function varargout = lpfilter_OutputFcn(hObject, eventdata, handles)% varargout cell array for returning output args (see V ARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Get default command line output from handles structurevarargout{1} = handles.output;% --- Executes during object creation, after setting all properties. function edit_N_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_N (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_N_Callback(hObject, eventdata, handles)% hObject handle to edit_N (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_N as text% str2double(get(hObject,'String')) returns contents of edit_N as a double% --- Executes during object creation, after setting all properties.function edit_beta_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_beta (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_beta_Callback(hObject, eventdata, handles)% hObject handle to edit_beta (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_beta as text% str2double(get(hObject,'String')) returns contents of edit_beta as a double% --- Executes during object creation, after setting all properties.function edit_fc_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_fc (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_fc_Callback(hObject, eventdata, handles)% hObject handle to edit_fc (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_fc as text% str2double(get(hObject,'String')) returns contents of edit_fc as a double% --- Executes during object creation, after setting all properties.function edit_ws_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_ws (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_ws_Callback(hObject, eventdata, handles)% hObject handle to edit_ws (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_ws as text% str2double(get(hObject,'String')) returns contents of edit_ws as a double% --- Executes during object creation, after setting all properties.function edit_wp_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_wp (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_wp_Callback(hObject, eventdata, handles)% hObject handle to edit_wp (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_wp as text% str2double(get(hObject,'String')) returns contents of edit_wp as a double% --- Executes during object creation, after setting all properties.function edit_rp_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_rp (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_rp_Callback(hObject, eventdata, handles)% hObject handle to edit_rp (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_rp as text% str2double(get(hObject,'String')) returns contents of edit_rp as a double% --- Executes during object creation, after setting all properties.function edit_As_CreateFcn(hObject, eventdata, handles)% hObject handle to edit_As (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispcset(hObject,'BackgroundColor','white');elseset(hObject,'BackgroundColor',get(0,'defaultUicontrolBackgroundColor')); endfunction edit_As_Callback(hObject, eventdata, handles)% hObject handle to edit_As (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hints: get(hObject,'String') returns contents of edit_As as text% str2double(get(hObject,'String')) returns contents of edit_As as a double% --- Executes on button press in lp_radiobutton.function lp_radiobutton_Callback(hObject, eventdata, handles)% hObject handle to lp_radiobutton (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB% handles structure with handles and user data (see GUIDA TA)% Hint: get(hObject,'V alue') returns toggle state of lp_radiobutton% --- Executes on button press in hp_lradiobutton.function hp_lradiobutton_Callback(hObject, eventdata, handles)% hObject handle to hp_lradiobutton (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB % handles structure with handles and user data (see GUIDA TA)% Hint: get(hObject,'V alue') returns toggle state of hp_lradiobutton close(handles.figure1);hpfilter% --- Executes on button press in bp_lradiobutton.function bp_lradiobutton_Callback(hObject, eventdata, handles)% hObject handle to bp_lradiobutton (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB % handles structure with handles and user data (see GUIDA TA)% Hint: get(hObject,'V alue') returns toggle state of bp_lradiobutton close(handles.figure1);bpfilter% --- Executes on button press in bb_lradiobutton.function bb_lradiobutton_Callback(hObject, eventdata, handles)% hObject handle to bb_lradiobutton (see GCBO)% eventdata reserved - to be defined in a future version of MA TLAB % handles structure with handles and user data (see GUIDA TA)% Hint: get(hObject,'V alue') returns toggle state of bb_lradiobuttonclose(handles.figure1);bbfilter。
基于Kaiser的FIR数字滤波器设计报告书

课程设计课程设计名称:基于Kaiser窗的FIR数字低通滤波器设计专业班级:电信1003班学生姓名:董成成学号: 201046830509指导教师:李相国课程设计时间:2013年6月电子信息工程专业课程设计任务书学生姓名董成成专业班级电信1003班学号201046830509题目基于Kaiser窗的FIR数字低通滤波器设计课题性质工程技术研究课题来源自拟课题指导教师李相国同组姓名主要内容设计一个具有如下性能指标的FIR数字低通滤波器:pω=0.25π,sω=0.4π,pδ=0.01,sδ=0.001;窗函数为Kaiser窗;分析最后设计结果性能。
任务要求1.温习窗函数法设计数字FIR滤波器的原理和设计方法;2.求出最后所设计出的滤波器冲激响应系数;3.绘制所设计滤波器的增益响应曲线。
参考文献[1] 胡广书. 数字信号处理—理论、算法与实现[M]. 北京: 清华大学出版社, 1997.[2] R. Lyons. Understanding Digital Signal Processing [M]. 2nd ed.Prentice Hall PTR., 2004.[3] A.V.奥本海姆, R.W.谢弗and J.R.巴克. 离散时间信号处理[M].第二版. 西安交通大学出版社, 2001.[4] S. K. Mitra. Digital Signal Processing: A Computer-BasedApproach[M]. 3rd ed. McGraw-Hill, 2005.审查意见指导教师签字:教研室主任签字:年月日说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计(论文)首页1 需求分析基于Kaiser 窗的FIR 低通滤波器是利用Kaiser 函数截取无限冲击响应h(n),最后利用函数freqz 得到加窗后的滤波器的幅频响应和相频响应。
2 概要设计(1)代入参数值,计算ω∆、c ω、As 、β、M 的值: omegap=0.25*pi;omegas=0.4*pi;deltap=0.01;deltas=0.001; omegac=(omegap+omegas)/2; deltaomega=omegas-omegap; As=-20*log10(deltas); beta=0.1102*(As-8.7);M=ceil((As-8)/(2.285*deltaomega));(2)定义定义域,Kaiser 函数求得)(t k ω,截取冲击响应h(n)得出滤波器时域值h,并求其频域特性:开始读入窗口长度M计算h d (n)用Kaiser 窗函数求w(n)计算H(k)=frez[h(n)]绘图子(函数)绘制H(k)幅度相位曲线结束图6-1 主程序框图计算h(n)= h d (n) w(n)n=0:M;p=M/2;wk=kaiser(M+1,beta);h=(sin(omegac*(n-p))./(pi*(n-p+eps))).*wk';[H,w]=freqz(h,1);(3)定义定义域,画滤波特性Nc=fix(omegac/(pi/length(w)));>> Hd=[ones(1,Nc),zeros(1,length(w)-Nc)];>> N=length(h);L=N/2;>> b=2*(h(L:-1:1));k=[1:1:L];k=k-0.5;w1=[0:1:511]'*pi/512; >> A2=cos(w1*k)*b';>> E=Hd-A2';>> subplot(3,1,1)>> stem(n,h,'fill','MarkerSize',2)>> axis([0,N,-0.1,0.5])>> subplot(3,1,2)>> plot(w,20*log10(abs(H)))>> axis([0 pi -100 10])>> subplot(3,1,3)>> plot(w,E)>> axis([0 pi -0.001 0.001])3 运行环境Window2003系统和Win7系统4 开发工具和编程语言Matlab软件、Matlab语言5 详细设计>> clear;----【清除变量】----------------------------------omegap=0.25*pi;omegas=0.4*pi;deltap=0.01;deltas=0.001; omegac=(omegap+omegas)/2; deltaomega=omegas-omegap;-----【利用p s ωωω-=∆ 2/)(s p c ωωω+=计算得出ω∆和c ω】----------As=-20*log10(deltas); beta=0.1102*(As-8.7);M=ceil((As-8)/(2.285*deltaomega));----【利用s As δlg 20-= )7.8(1102.0-⨯=As β ω∆-=285.295.7As M 算得As 、β和阶数M 】------------------------------------------------ n=0:M; p=M/2;wk=kaiser(M+1,beta);h=(sin(omegac*(n-p))./(pi*(n-p+eps))).*wk';--------【根据Kaiser 函数求得)(t k ω,截取冲击响应)()](sin[)(p n p n c n h --=πω得到滤波器时域表达式】-----------------------------------------[H,w]=freqz(h,1); -------【利用frez函数求出滤波器频域的表达式】----------------------------------------Nc=fix(omegac/(pi/length(w)));>> Hd=[ones(1,Nc),zeros(1,length(w)-Nc)]; >> N=length(h);L=N/2;>> b=2*(h(L:-1:1));k=[1:1:L];k=k-0.5;w1=[0:1:511]'*pi/512;>> A2=cos(w1*k)*b';>> E=Hd-A2';>> subplot(3,1,1)>> stem(n,h,'fill','MarkerSize',2)>> axis([0,N,-0.1,0.5])>> subplot(3,1,2)>> plot(w,20*log10(abs(H)))>> axis([0 pi -100 10])>> subplot(3,1,3)>> plot(w,E)>> axis([0 pi -0.001 0.001])----------【定义定义域,画滤波特性,所利用的函数有:fix取整函数,ones 生成全1矩阵,zeros生成全零矩阵,subplot画子图,plot画图函数,axis 函数规定横纵坐标范围】---------------------------------6 调试分析此次课程设计没有调用子函数,整个程序实现得出基于Kaiser窗函数的滤波特性,在编写的过程中,通过查阅Matlab书籍和数字信号处理教科书,不断完善,不断修改,得到理想的实验结果。
切比雪夫(kaiser窗)滤波器

目录1 绪论 (1)1.1 课题背景 (1)1.2 课题目的 (2)2 课程设计预习与原理 (3)2.1 课程设计预习 (3)2.1.1 卷积运算的演示 (3)2.2.2 采样定理的演示 (9)2.2 课程设计原理 (11)2.2.1 频谱分析原理 (11)2.2.2 IIR设计原理 (12)2.2.3 FIR设计原理 (12)3 课程设计步骤和过程 (15)3.1 IIR设计步骤和过程 (15)3.2 FIR设计步骤和过程 (15)4 设计程序的调试和运行结果 (17)4.1 切比雪夫低通滤波器程序的调试和运行结果 (17)4.2 切比雪夫高通滤波器程序的调试和运行结果 (19)4.3 切比雪夫带通滤波器程序的调试和运行结果 (21)4.4 Kaiser低通滤波器程序的调试和运行结果 (23)4.5 Kaiser高通滤波器程序的调试和运行结果 (25)4.6 Kaiser带通滤波器程序的调试和运行结果 (27)5 总结 (29)参考文献 (32)附录 (33)附录 A (33)附录 B (45)1 绪论1.1 课题背景数字滤波器是数字信号处理的基础,用来对信号进行过滤、检测与参数估计等处理,在通信、图像、语音、雷达等许多领域都有着十分广泛的应用。
尤其在图像处理、数据压缩等方面取得了令人瞩目的进展和成就。
数字滤波器的设计有许多现成的高级语言设计程序,但他们都存在设计效率较低,不具有可视图形,不便于修改参数等缺点,而Matlab为数字滤波的研究和应用提供了一个直观、高效、便捷的利器。
他以矩阵运算为基础,把计算、可视化、程序设计融合到了一个交互式的工作环境中。
尤其是Matlab工具箱使各个领域的研究人员可以直观方便地进行科学研究与工程应用。
其中的信号处理工具箱、图像处理工具箱、小波工具箱等更是为数字滤波研究的蓬勃发展提供了可能。
MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
用凯泽窗设计线性相位带通fir滤波器

用凯泽窗设计线性相位带通fir滤波器
设计线性相位带通FIR滤波器可以采用凯泽窗(Kaiser Window)方法,该方法可以实现对滤波器的频率响应和相位特性的精确控制。
下面是设计线性相位带通FIR滤波器的步骤:
1.确定设计参数:确定带通滤波器的通带截止频率(如f1
和f2)、阻带截止频率(如f3和f4)、通带最大衰减要求
(如Ap),以及阻带最小衰减要求(如As)。
2.计算滤波器阶数:根据设计参数,使用巴特沃斯
(Butterworth)滤波器近似公式或其他设计方法计算出滤
波器的理想阶数N。
3.计算窗函数参数:根据设计参数和所选窗函数,计算出窗
函数的β参数。
凯泽窗的β参数可以通过下面的公式计算
得到:β = 0.1102 * (Ap - 8.7)
4.计算窗函数长度:根据设计参数、所选窗函数和已计算出
的β参数,计算出所需的窗函数长度M。
可以使用下面的
公式计算得到: M = (N - 1) / 2 + 1 + 2 * ceil((As - 8) / (2.285
* 2 * π / (f4 - f3)))
5.生成滤波器的频率响应:使用窗函数和所选窗函数长度,
生成理想的频率响应h[i]。
6.频率响应补偿:根据滤波器的频率响应h[i],进行线性相
位处理,即将h[i]对称地补偿,使得滤波器具有线性相位
特性。
7.输出滤波器系数:对补偿后的频率响应进行逆FFT变换得
到滤波器的时域系数h[n],即滤波器的单位脉冲响应。
根据上述步骤设计得到的滤波器是线性相位的带通FIR滤波器,并可以根据设计参数和窗函数的选择进行精确的频率和相位特性控制。
凯塞窗的FIR滤波器设计

3.基于凯塞窗的FIR 滤波器设计1. 设计思路设欲设计的滤波器的理想频率响应为)(d ωj e H ,单位脉冲响应为)(n h d ,)(n h d 与)(d ωj e H 是一对傅式变换,因此有ωωjn n d j d e n h e H -∞-∞→∑=)()(ωπωωππd e e H n jn j d d )(21)(h ⎰-=根据给定的)(d ωj e H 求得的)(n h d 一般是无限长的且是非因果的。
为了得到一个因果的有限长的滤波器h(n),最直接的方法是截断)(n h d ,或者说用一个窗口函数)(n ω对)(n h d 进行加窗处理h(n)= )(n h d )(n ωh(n)成为实际设计FIR 滤波器的单位脉冲响应,其频率响应为)(ωj e H 为: ωωj N n j e n h e H ∑-==10)()( 其中N 为窗口)(n ω的长度。
窗口函数的形状和窗口长度N 决定了窗函数法设计出的FIR 滤波器的性能。
2. 设计要求及方案设计一凯塞窗的低通FIR 滤波器,要求如下:通带截止频率 wp=0.4π;阻带截止频率ws=0.7π;阻带最小衰减Rs=45dB ;3.用MTALAB 算法设计凯塞窗的低通FIR 滤波器>> wp=0.4*pi;>> ws=0.7*pi;>> DB=ws-wp; %计算过渡带宽度>> Rs=45;>> beta=0.5842*(Rs-21)^0.4+0.07886*(Rs-21); %计算凯塞窗的控制参数>> M=ceil((Rs-8)/2.285/DB); %计算凯塞窗所需阶数M>> wc=(wp+ws)/2/pi; %计算理想低通滤波器通带截止频率>> hn=fir1(M,wc,kaiser(M+1,beta)); %调用firl函数计算低通FIRDF的h(n) >> figure(1);>> plot(hn);>> xlabel('频率/Hz');ylabel('幅值');>> title('数字滤波器幅频响应|H(ejOmega)| ');>> figure(2);>> freqz(hn,1,512);仿真出的频率响应曲线如图3.1所示:图3.1:频率响应曲线相频特性及幅度特性曲线如下图3.2所示:图3.2:相频特性及幅度特性曲线。
kaiser函数用法

kaiser函数用法一、什么是kaiser函数Kaiser函数是一种用于数字信号处理中的窗函数,它被广泛应用于信号谱分析、滤波器设计、傅里叶变换等领域。
由于Kaiser函数具有较好的频谱特性和抑制副瓣的能力,因此在实际应用中得到了广泛的使用。
二、Kaiser函数的数学表达式Kaiser函数的数学表达式如下所示:w(n)=I0(β√1−(nN)2)I0(β)其中,w(n)表示n时刻处的Kaiser窗函数值,I0表示零阶修正的第一类贝塞尔函数,N表示窗函数的长度,β表示Kaiser窗函数的形状参数。
三、Kaiser函数的参数解释1.窗函数的长度N:表示Kaiser窗函数的采样点个数,通常取偶数。
2.Kaiser窗函数的形状参数β:影响Kaiser窗函数频域特性的重要参数,决定了主瓣宽度和副瓣抑制能力。
β的取值范围一般是0~10之间,其中0表示矩形窗,10表示理想的低通滤波器。
四、Kaiser函数的特性Kaiser函数具有以下几个特性:1.主瓣宽度可调:通过调整Kaiser窗函数的形状参数β,可以控制主瓣的宽度。
当β增大时,主瓣会变得更宽,相应地副瓣抑制能力也会增强。
2.副瓣抑制能力强:Kaiser函数在频域上具有较好的抑制副瓣的能力,可以在不损失频域分辨率的情况下实现有效的滤波。
3.相位失真较小:Kaiser函数对信号的相位响应变化较小,可以有效地维持信号的相位特性。
4.窗函数衰减较慢:相比于其他窗函数,Kaiser函数的衰减速度较慢,能够较好地保留信号的频率分量。
五、Kaiser函数的应用Kaiser函数在信号处理领域具有广泛的应用,其中包括以下几个方面:1. 信号谱分析Kaiser函数可以用于信号的频谱分析,通过选择合适的形状参数β,可以实现对不同频率成分的有效分析。
2. 滤波器设计Kaiser函数可以用于滤波器的设计,特别是需要灵活调节主瓣宽度和副瓣抑制能力的情况。
通过选择合适的形状参数β,可以设计出具有良好频率响应的滤波器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Kaiser滤波器的参数设计方法
摘要:matlab是一种数值计算效率高和可视化的科学计算的软件,它可以快速的进行复杂的数值计算、算法原型并且通过矩阵公式解决一些特殊问题。
本文利用matlab中kaiser窗进行滤波器的设计,设计了fir数字低通滤波器,得到的实验结果符合确定的性能指标,通过结果可以看出kaiser窗进行滤波器的设计的优点。
关键词:fir滤波器;matlab;kaiser窗
中图分类号:tm46 文献标识码:a 文章编号:1674-7712 (2013)04-0076-01
数字信号技术目前已经在各行各业得到了充分的利用,随着信息时代的发展,该技术也得到了更大的关注,尤其是在信息通讯,信号处理,自动控制,军事国防,医疗及家电等领域,已经逐步取代了传统模数转换处理系统。
fir滤波器中的kaiser滤波器的设计与研究,常用设计方法有窗函数法,频率采样法,切比需夫逼近法等,但由于窗函数能够进行截断处理,还可以对信号进行平滑操作,因此窗函数法在数字滤波器的设计中具有很大的优势,可以更加有效地保持信号信息。
kaiser窗是窗函数中的最优化窗,它的主瓣集中了大部分的频带内能,同时可以对旁瓣起到最大的抑制作用。
本文将通过选用kaiser窗(最优化窗)进行kaiser滤波器的参数设计,并对设计参数值进行调整与分析选择最优的主瓣宽度和旁瓣衰减
以得到设计所需要滤波标准数字滤波器。
窗函数的种类有矩形窗、汉明窗、布莱克曼窗、凯塞窗。
如果进行设计时使用了矩形窗,那
么必然会出现以下不足之处:首先,它不能改变最小阻带衰减,从而使起在很多应用中得不到满足;其次,矩形窗是对无限长度的序列的直接截取,存在着跳变点,因此会增大序列长度m,即使每个旁瓣的宽度减小,但瓣下的面积不变,则最小阻带衰减仍为21db 保持不变。
狄拉克函数,在频域内窗函数与狄拉克函数越靠近,则信号越准确。
实际上不可能在时域和频域都不会是失真的窗函数,因此应合理选择可以满足设计要求的窗函数。
kaiser窗(最优化窗)进行kaiser滤波器的参数设计更为有效,操作更为简化,对设计参数值进行调整与分析选择最优的主瓣宽度和旁瓣衰减以得到设计所需要滤波标准数字滤波器。
凯塞窗可以通过改变参数β和m的值来实现改变阻带衰减和过度宽带。
其目的是将频率响应的主瓣与旁瓣的能量谱的比值达到最大。
具体设计步骤:
1.根据过度带宽度及衰减要求,选择窗函数的类型并估计窗口长度n。
待求滤波器的过渡带宽与窗口长度近似成反比。
根据待求滤波器理想频率响应求出单位脉冲响应。
在一般情况下,是不能用封闭公式表示的,需要采用数值方法表示。
从到采样n,采用离散傅里叶反变换(dft)即可求出。
2.计算滤波器单位脉冲响应。
该值可以通过式求出,其中为单位脉冲响应,为窗函数。
3.验算技术指标是否满足要求。
为了计算数字滤波器在频域中的特性,可调freqz子程序。
滤波器的主要特性指标有,特征频率:
(1)通带截频为通带频率下降的最小值。
(2)阻带截频为阻带频率衰耗下降到的最小值。
(3)转折频率为信号功率衰减到1/2时的频率。
(4)固有频率滤波器的谐振频率。
(5)带通宽度:需要通过的频谱宽度。
(6)纹波:1或3db宽度范围内波动的峰--峰值。
(7)阻尼系数的倒数称为品质因数:
(8)灵敏度:
确定技术指标为:通带截止频率;阻带截止频率;实际通带波动;最小阻带衰减。
分析:
滤波器的长度为33;线性相位斜率为2.3473;实际通带波动为31.1735;最小阻带衰减为1,最小阻带衰减为1。
不符合要求,需要进行优化。
改变,所得结果:滤波器的长度为47;线性相位斜率为3.4493;实际通带波动为43.8289;最小阻带衰减为0。
改变凯塞窗函数中,所得结果:
(1)当不变,改变,其他程序不变。
实验结果:滤波器的长度为33;线性相位斜率为2.3047;实际通带波动为31.9292;最小
阻带衰减为1。
(2)时,改变其他程序不变。
结果:滤波器的长度为47;线性相位斜率为3.4768;实际通带波动为42.8806;最小阻带衰减为0。
通过以上几组仿真可以看出,用kaiser窗函数设计数字滤波器时,如果不能达到要求,可以通过改变参数来改变滤波器的性能,当设值不变时,可以通过改变值来调整滤波器的性能,当值不变时,可以通过改变值来调整来满足设计要求。
参考文献:
[1]张亚妮.基于matlab数字滤波器的设计[j].陕西师范大学,2005,24,5:717-719.
[2]阎毅,黄联芬.数字信号处理[m].北京:北京大学出版社,2006:162-193.
[3]楼顺天,李博菡.基于matlab的系统分析与设计-信号处理[m].西安:西安电子科技大学出版社,1998.
[4]optimaldesignstudyofhighorderfirdigitalfiltersbasedo nneuralnetworkalgorithm[j].journalofsystemsengineeringand electronics,2004(2).
[5]digitalimagingreconstructionfrommultipleanglediversi tyusingdigitalfilteringtechnique[j].chinesejournalofsyste msengineeringandelectronics,1991(1).
[作者简介]邵国军(1964.11.15-),男,浙江余姚,大专,实验
师,电子通信、电子测量的实验教学和科研开发;陈国龙,男,浙江宁波,大专,实验师,电子电路、电子工程、电子声像的实验教学和科研开发。
