第十一章全等三角形测试题(B)新人教版八年级上

合集下载

八年级数学上册《第十一章三角形》单元测试卷及答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷及答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、选择题1．下列长度的三条线段能组成三角形的是（）A．3，3，7 B．3，4，8 C．5，6，11 D．5，6，102．如图，一扇窗户打开后，用窗钩BC可将其固定，这里所运用的数学原理是（）A．三角形具有稳定性B．两点确定一条直线C．两点之间线段最短D．三角形的两边之和大于第三边3．一个正多边形，它的每一个内角都等于140°，则该正多边形是（）A．正六边形B．正七边形C．正八边形D．正九边形4．把一块直角三角板和一把直尺如图放置，若∠1=35°，则∠2的度数等于（）A．65°B．55°C．45°D．60°5．如图，AD是△ABC的边BC上的高，若BC=3，AB=6，AD=4则AB边上的高为（）A．1 B．2 C．3 D．无法计算6．如图1是我国古建筑墙上采用的八角形空窗，其轮廓是一个正八边形，窗外之境如同镶嵌于一个画框之中．如图2是八角形空窗的示意图，它的一个外角∠1=（）A．45°B．60°C．110°D．135°7．如图，在△ABC中，点I到△ABC的三边距离相等，连接AI､BI，若∠ACB=70∘，则∠AIB的大小为（）A．160∘B．140∘C．130∘D．125∘8．如图AB∥CD，点E在线段BC上（不与点B，C重合），连接DE，若∠D=40°，∠BED=60°则∠B=（）A．10°B．20°C．40°D．60°二、填空题9．一个不等边三角形的两边分别为5cm和7cm，第三边的长度为奇数，则满足条件的三角形共有个．10．正十边形的每个内角是度.11．如图，在△ABC中，AD是BC边上的中线，若S△ABC=12，AC=3则点D到AC的距离为．12．如图，在△ABC中，点O是△ABC角平分线的交点，若∠A=70°，∠BOC=．13．如图，在△ABC中AB=AC，点D、E分别在边BC、AB上AD=DE，如果∠CAD=60°，∠BDE=15°那么∠C=°．14．如图，AB//CD，∠BED=110°，BF平分∠ABE，DF平分∠CDE，则∠BFD=．三、解答题15．AD、BE为△ABC的高，AD、BE相交于H点∠C=50°，求∠BHD．16．如图，△ABC中∠ACB=90°，CD为AB边上的高，BE平分∠ABC，且分别交CD，AC于点F，E求证：CE=CF．17．如图，在△ABC中，BD是∠ABC的平分线，CE是AB边上的高，且∠ACB＝60°，∠ADB＝100°，求∠A和∠ACE的度数．18．如图，在Rt△ABC中，∠ACB＝90°，∠A＝40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E，点F为AC延长线上的一点，连接DF.（1）求∠CBE的度数；（2）若∠F＝25°，求证：BE∥DF.19．（本题满分10分）如图AC∥EF，∠1+∠3=180°．（1）求证AF∥CD；（2）若AC平分∠FAB，AC⊥EB于点C，∠4=78°求∠BCD的度数．参考答案1．D2．A3．D4．B5．B6．A7．D8．B9．510．14411．412．125°13．3514．125°15．解：∵AD是△ABC的高∴∠BHD+∠HBD=90°∵BE是△ABC的高∴∠HBD+∠C=90°∴∠BHD=∠C∵∠C=50°∴∠BHD=50°．16．证明：∵∠ACB=90°∴∠ACD+∠BCD=90°∵CD为AB边上的高∴∠ADC=90°∴∠A+∠ACD=90°∴∠A=∠BCD∵BE是∠ABC的平分线∴∠ABE=∠CBE∴∠CFE=∠BCD+∠CBE=∠A+∠ABE∵∠CEF=∠A+∠ABE∴∠CEF=∠CFE∴CE=CF．17．解：∵∠ADB＝∠DBC+∠ACB∴∠DBC＝∠ADB﹣∠ACB＝100°﹣60°＝40°．∵BD是角平分线∴∠ABC＝80°∴∠A＝180°﹣∠ABC﹣∠ACB＝40°；∵CE是高∴∠AEC＝90°∴∠ACE＝90°﹣∠A＝50°18．（1）解：∵∠ACB＝90°，∠A＝40°∴∠CBD=∠A+∠ACB=130°∵BE平分∠CBD∠CBD=65°∴∠CBE=12（2）证明：∵∠ACB＝90°∴∠BCE=90°∵∠CBE=65°∴∠BEC=90°－65°=25°∵∠F＝25°∴∠F=∠BEC∴BE∥DF19．（1）证明：∵AC∥EF∴∠1+∠2=180°．又∵∠1+∠3=180°∴∠2=∠3．∴AF∥CD．（2）解：∵AC平分∠FAB∴∠2=∠CAD．∵∠2=∠3∴∠CAD=∠3．∵∠4+∠ADC=180°且∠4=78°∴∠ADC=180°−78°=102°．∴∠CAD=∠3=180°−102°2=39°∵AC⊥EB ∴∠ACB=90°．∴∠BCD=90°−∠3=90°−39°=51°．。

八年级(上)第十一章全等三角形(参考答案及评分标准)

八年级（上）第十一章全等三角形章测试题参考答案及评分标准一、选择题1～ 5 题：C 、C 、A 、B 、D 6～10 题：C 、B 、C 、D 、B 二、填空题11、AC=AE ，12、95°，13、6.5cm ，14、∠D AB=CO ，AD=CD ，BD=OD ，AO=CB ，15、12，16、3 ，△ABO ≌△CDO ，17、115O ，18、30O ，19、AC 的中点，20、375 三、解答题21、（1）BE=CF ……2分（2）证明：∵BE=CF∴BE+EC=CF+EC ，即BC=EF ……3分 ∵AB//DE，∴∠B =∠DEF ……4分在△ABC 和DEF 中⎪⎩⎪⎨⎧=∠=∠=DE AB DEF B EF BC∴△ABC ≌△DEF ……8分 22、证明：在△ABC 和DCB 中⎪⎩⎪⎨⎧===DB AC BC BC DC AB ∴ △ABC ≌△DCB ∴ ∠A= ∠D ， ……4分在△ABO 和DCO 中⎪⎩⎪⎨⎧=∠=∠∠=∠DC AB DOC AOB D A ∴ △ABO ≌ △DCO ……7分∴∠1=∠2 ……8分 23、（1）答：共2对，△DEG ≌ △BFH 和△AEH ≌ △CFG ……2分（2）证明： △DEG ≌ △BFH ∵四边形ABCD 是平行四边形 ∴AD ∥CB ， AB ∥CD∴∠E=∠F ，∠HGC=∠GHA ……4分又∵∠DGE=∠HGC ，∠FHB=∠GHA∴∠DGE=∠FHB ， ……6分在△DGE 和BFH 中⎪⎩⎪⎨⎧=∠=∠∠=∠BF DE FHB DGE BFH DEG ∴△DEG ≌△BFH ……10分 24、（1）证明：∵AD 是高 ∴∠ADB =∠ADC=90° 在Rt△ABD 和Rt△ACD 中⎩⎨⎧==ADAD AC AB∴Rt△ABD ≌Rt△ACD ……2分 ∴BD=CD 即 2BD=BC在Rt△ACD 中 ∠DA C+∠C=90°∴∠EBC=∠DAC ……3分在△AEH 和△BEC 中⎪⎩⎪⎨⎧=∠=∠=∠=∠O BEC AEB BE AE DAC EBC 90∴△AEH ≌△BEC(ASA) ……6分 ∴AH=BC 又∵2BD=BC∴AH=2BD ……7分（2）成立（提示：在Rt△AHE 和Rt△ACD 中，先证∠ACD =∠AHE ，再证Rt△AHE ≌Rt△BCE ，得到AH=BC,得出AH=2BD ） ……10分 25、解：（1）已知：⑤，③，④ 求证：①，②证明：在AB 上截取一点F ，使AF=AD在△ADE 和△AFE 中⎪⎩⎪⎨⎧=∠=∠=AE AE EAB EAD AD AF ∴△ADE ≌△AFE ……3分 ∴ED=EF ，∠AFE=∠D∵AD+BC=AB ，∴BF=BC ……4分在△BEF 和△BEC 中⎪⎩⎪⎨⎧=∠=∠=BE BE CBE ABE BC BF ∴△BEF ≌△BEC ，∴∠BFE=∠C ，EF=EC∴ED=EC ……7分 ∵∠BFE+∠AFE=180O ，∴∠C+∠D=180O ，∴AD ∥BC ……8分AB CDEF（2）命题一，已知：①，③，④求证：②，⑤ ……10分命题二，已知：①，②，③求证：④，⑤ ……12分26、解：（1）EF 与FD 之间的数量关系为FE=FD ……2分（2）（1）中的结论FE=FD 仍然成立。

人教版数学八年级上册第十一章全等三角形测试卷

A B D C A E B C D第23章全等三角形测试题班级姓名成绩一、选择题（每小题3分，共15分）、1、某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）A 、带①去B 、带②去C 、带③去D 、①②③都带去2、通过下列变换能得到全等形的是（）A 、平移B 、平移、旋转C 、平移、翻转D 、平移、旋转、翻转 3、根据下列条件，不能画出唯一△ABC 的是（）A 、AB=6 BC=4，AC=8；B 、AB=4，BC=3，∠A=30°；C 、∠C=60°，∠B=45°，AB=4；D 、∠C=90°，AB=5，AC=44、/如图，Rt ΔABC 沿直角边BC 所在的直线向右平移得到ΔDEF ，下列结论中错误的是（） A 、ΔABC ≌ΔDEF B 、∠DEF ＝90° C 、AC ＝DF D 、EC ＝CF 5、在△ABC 内部取一点P ，使得点P 到△ABC 的三边距离相等，则点P 应是 △ABC 的（）的交点A 、高B 、角平分线C 、中线D 、垂直平分线二、填空题（每题4分，共20分）6、如图，⊿ABC ≌⊿DEC ，AB=8,AC=7,则DE=7、如图，已知AD ＝BC ，要证明ΔABC ≌ΔBAD,还需要一个条件 .8、已知，如图，AD=AC ，BD=BC ，O 为AB 上一点，那么，图中共有对全等三角形 9、已知：如图，△ABC ≌△ADE ，∠BAD=50°，∠DAC=20°,∠CAE= °．10、如图:在△ABC 中，∠C=90°，AD 平分∠BAC ，BC=10cm ，BD=6cm ，则D 到AB 的距离为． (第2题图)③①②FDC A （第3题图）A B CD E D C B A （第6题图）（第7题图）（第8题图）（第9题图）（第10题图）C A OB DAC OB AB C三、尺规作图，并保留作图痕迹（5分） 11、先作出∠ABC 的角平分线。

新人教版八年级数学第11章全等三角形单元试卷及参考答案.docx

新人教版八年级数学第—章单元考试试卷一、选择题（每小题3分，共30分）1.在ZV1BC 中，ZB=ZC,与AABC 全等的三角形有一个角是100。

，那么在△ABC 中与这100。

角对应相等的角是（）4•如图，L1^AB = DC, AD = BC, E, F 在 DB 上两点J=L BF=DE,若ZAEB=120。

，ZADB = 30°,则 ZBCF=() A.15O 0 B.40° C.80°D.90°5. 如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的关系是（）A.相等B.不相等C.互余或相等D.互补或相等6. 如图，丄BC, BE±AC t Z1 = Z2, AD=AB f 贝U （）A.Z1 = ZEFDB.BE=EC C ・BF=DF=CD D.FD//BC7.如图所示，BE 丄AC 于点且 =BD = ED,若ZABC=54°,则ZE=()A.25°B.27。

C.30°D.45°8. 如图所示，亮亮书上的三角形被黒迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A.ZAB.ZBC.ZCD.ZB 或ZC 2. 如图，在CD 上求一点P, 使它到O 久OB 的距离和等，则P 点是（ A.线段CD 的中点C.OA 与CD 的中乖线的交点B.OA 与OB 的中垂线的交点 D.CZ ）与ZAOB 的平分线的交点3.如图所示，竺△CDB,A.AABD 和△CDS 的面积和等卜•面四个结论屮，不正确的是（）B.AABD 和△CDB 的周长和等C.ZA+ZABD= ZC+ZCBDD.AD//BC, HAD=BCA. SSSB.SASC. AASD.ASA第3题图A第4题图第7题图9. 如图，在厶ABC 中，4Q 平分ABAC,过B 作BE 丄AQ 于& 过E 作EF 〃AC 交AB 10•将一张长方形纸片按如图所示的方式折叠，BC 、BQ 为折痕，则ZCBD 的度数为（）A. 60°B. 75°C. 90°D. 95°二、填空题（每题3分，共15分）11・能够 ___________________ 的两个图形叫做全等图形.12.已知，如图，AD=AC, BD=BC, O 为AB h 一点，那么，图屮共有对全等三用形.ZBAD 二40。

人教版数学八年级上册第11章《三角形》和第12章《全等三角形》测试B卷(答案不全)

人教版数学八年级上册第11章《三角形》和第12章《全等三角形》测试B 卷一、填得圆圆满满（每小题4分，共32分）1．木工师傅在做完门框后，为防止门框变形常常需钉两根斜拉的木棒，这样做的数学原理是________．2．ABC DEF △≌△，6cm BC EF ==，ABC △的面积是218cm ，则EF 边上的高是________cm ．3．如图1，AB AE =，AC AD =，只要________（添加一个条件即可），就可得ABC AED △≌△．4．如图2，在ABC △中，AD BC ⊥，BE AC ⊥，CF AB ⊥，三条高相交于H 点，则图中所示ABH △的AH 边上的高是________．5．在一个直角三角形中，如果两个锐角的比为2:3，那么两个锐角中，较大锐角的度数是________．6．如图3，点D 在AB 上，点E 在AC 上，AD 与BE 相交于点O ，且AD AE =，AB AC =，若20B =∠，则C =∠________．7．ABC △中，A B C +=∠∠∠，A ∠的平分线交BC 于点D ，若8cm CD =，则点D 到AB 的距离为________cm ．8．如图4，飞机要从A 地飞往B 地，因受大风影响，一开始就偏离航线18（即18A =∠），飞到了C 地，此时风停了．已知10ABC =∠，现在飞机要到达B 地需以________的角飞行．二、做出正确选择（每小题3分，共21分）9．在下列长度的各组线段中，能组成三角形的是（）Ａ．3，3，6 Ｂ．3，5，9Ｃ．3，4，5 Ｄ．2，3，510．如图6，AD ，BE ，CF 分别是ABC △的高、中线、角平分线，下列表达式中错误的是（）Ａ．AE CE =Ｂ．90ADC =∠ Ｃ．CAD CBE =∠∠Ｄ．2ACB ACF =∠∠11．如图7，ABC CDA △≌△，且4AB =，5BC =，6AC =，则AD 边的长为（）Ａ．4 Ｂ．5 Ｃ．6 Ｄ．不确定12．如图8，12=∠∠，34=∠∠，在下列结论中错误的是（）Ａ．ADC BCD △≌△ Ｂ．ABD BAC △≌△Ｃ．ABO COD △≌△ Ｄ．AOD BOC △≌△13．如图9，已知OA OB =，OC OD =，AC ，BD 相交于点O ，则图中全等三角形有（）Ａ．2对Ｂ．3对Ｃ．4对Ｄ．5对14．下列说法错误的是（）Ａ．两条直角边对应相等的两个直角三角形全等Ｂ．一个锐角和斜边对应相等的两个直角三角形全等Ｃ．有一条边和两个角对在相等的两个三角形全等Ｄ．有两边和其中一边所对的角对应相等的两个三角形全等15．在锐角ABC △中，A B C >>∠∠∠，则下列结论中错误的是（）Ａ．60A >∠ Ｂ．45B >∠ Ｃ．60C <∠ Ｄ．90B C +<∠∠三、用心解答（共67分）16．（10分）如图10，MA OA ⊥，MB OB ⊥，A ，B 为垂足，MA MB =，说明AOM BOM =∠∠的理由．17．（10分）已知，如图11，AB AD =，AC AE =，BAE DAC =∠∠，ABC △与ADE △全等吗？为什么？18．（10分）如图12，一个六边形钢架ABCDEF 由6条钢管连接而成，为使这一钢架稳固，请你用三条钢管连接使它不能活动，至少用三种方法．19．（10分）已知，如图13，AB CD =，AD BC =．则A ∠与C ∠相等吗？为什么？20．（13分）如图14，已知点A ，C 在直线EF 上，AD BC =，AB DC =，AE CF =，试说明E ∠与F ∠相等的理由．21．（14分）如图5，BD ，B D ''分别是ABC △和A B C '''△的高，且BD B D ''=，AB A B ''=，AC A C ''=．那么ABC △与A B C '''△全等吗，为什么？参考答案一、1．运用三角形的稳定性 2．6 3．略．答案不惟一 4．BD 5．546．20 7．8 8．28二、9.Ｃ 10.Ｃ 11.Ｂ 12.Ｃ 13.Ｃ 14.Ｄ 15.Ｄ三、16．由AOM △和BOM △全等可证．17．全等．18．略．答案不惟一．19．相等，理由略．20．略．21．全等．理由略．。

新人教版八年级上11.1全等三角形11.2三角形全等的条件综合测试题

数学: 11.1全等三角形-11.2三角形全等的条件综合测试题(人教新课标八年级上)一、选择题(共10小题，每小题3分，共30分)*1．下列说法:①全等三角形的形状相同；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长、面积分别相等．其中正确的说法为( )A ．①②③④B ．①③④C ．①②④D ．②③④2．(2021年遵义市)．如图，OA OB =，OC OD =，50O ∠=，35D ∠=，则AEC ∠等于( )A ．60B ．50C ．45D ．30*3．如图2，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( )A ．∠1=∠2B ．∠B=∠CC ．∠D=∠ED ．∠BAE=∠CAD4．如图3，有两个长度相同的滑梯(即BC=EF)，左边滑梯的高度AC•与右边滑梯水平方向的长度DF 相等，则下列结论:①AB=DE ；②∠ABC=∠DEF ；•③∠ACB=∠DFE ；④∠ABC+∠DFE=90°，其中成立的有( )A ．①②③④B ．①②③C ．①②D ．②③图35．如图4所示，已知:点D 在AC 上，点B 在AE 上，△ABC ≌△DBE ，且∠BDA ＝∠A ，∠OEA BDCA ∶∠C ＝5∶3，∠DBC 等于( )A ．30°B ．25°C ．20°D ．15°6．如果两个三角形有两边和其中一边上的高对应相等，那么它们第三边所对的角的关系是( )A ．相等B ．互补C ．互余D ．相等或互补7.一扇窗户打开后，用窗钩可将其固定，这里所运用的几何原理是( )A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短8．如图5，在四边形ABCD 中，AD=CB ，DE ⊥AC 于E ，BF ⊥AC 于F ，且DE=•BF ，则图中全等三角形有( )A ．1对B ．2对C ．3对D ．4对9．如图6，在△ABC 中，∠A :∠B :∠C =3:5:10，又△MNC ≌△ABC ，则∠BCM :∠BCN 等于( )A ．1:2B ．1:3C ．2:3D ．1:410.全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC 和△A 1B 1C 1是全等(合同)三角形，点A 与点A 1对应，点B 与点B 1对应，点C 与点C 1对应，当沿周界A→B→C→A ，及A 1→B 1→A 1环绕时，若运动方向相同，则称它们是真正合同三角形(如图7)，若运动方向相反，则称它们是镜面合同三角形(如图8)，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，两个镜面合同三角形要重合，则必须将其中一个翻转180°(如图9)，下列各组合同三角形中，是镜面合同三角形的是()二、填空题11．已知ABC A B C '''△≌△，60A A '==∠∠，70B B '==∠∠，15cm A B ''=，则AB =_____，C =∠_____．_ 图 6#12．用同样粗细，同种材料的金属粗线，构成两个全等三角形，如图2所示，△ABC和△DEF，已知∠B＝∠E，AC的质量为100克，则DF的质量为．13．如图3，在直角三角形ABC中，∠C＝90°，AC＝10cm，BC＝5cm，一条线段PQ＝AB，P、Q两点分别在AC和AC的垂线AX上移动，则当AP＝时，才能使△ABC和△APQ全等．*14．如图4所示，有一块三角形镜子，小明不小心摔破成Ⅰ、Ⅱ两块，现需配制同样大小的镜子．为了方便起见，需带上块即可，其理由是．图4*15. 一个三角形的三边长分别为2，5，m，另一个三角形的三边长分别为n，6，2，若这两个三角形全等，则m+n＝.16.已知如图5，F在正方形ABCD的边BC边上，E在AB的延长线上，FB＝EB，AF交CE于G，则∠AGC的度数是______.*17．如图6，将△ABC沿经过点A的直线AD折叠，使边AC所在的直线与边AB所在的直线重合，点C落在边AB上的点E处，若∠B=450，∠BDE=200，则∠C= ，∠CAD= .#18.如图7，高速公路上有A、B两站(视为线上两点)相距30km，C、D为高速公路同旁的两个村庄(视为两点)，已知DA⊥AB于A点，CB⊥AB于B点，DA＝20km，CB＝10km，现在要在公路AB上建一个土特产收购站E，使C、D两村庄到E站的距离相等，则E站应建在距A站______km处.三、解答题19．(8分)已知△ABC≌△A′B′C′，AD和A′D′分别是BC和B′C′边上的高，AD•和A′D′相等吗？为什么？20.(8分)如图8，AB＝AC，D、E分别为AB、AC的中点，则△ABE≌△ACD，说明理由.图821.(8分)有一块三角形板材，如图所示，根据实际生产的需要，工人师傅要把∠MAN平分开，现在他手边只有一把直尺和一根细绳，你能帮工人师傅想个办法吗？并说明你的根据.22.(10分)如图，已知AB∥DE，AB=DE，AF=DC，请问图中有哪几对全等三角形？请任选一对给予证明.*23. (10分)如图所示，A、B、C、D是四个村庄，B、D、C在一条东西走向公路的沿线上，BD=1千米，DC=1千米，村庄AC、AD间也有公路相连，且AD⊥BC，AC=3千米，只有村庄AB之间由于间隔了一个小湖，所以无直接相连的公路. 现准备在湖面上造一座斜拉桥，测得AE=1.2千米，BF=0.7千米. 试求所建造的斜拉桥长有多少千米？#24.(10分)已知:如图12，AB∥CD，AB=CE，BC=FC，∠DCB+∠ECF=180o，试说明:AC=EF.图1225. (12分)如图7是小明和小刚玩跷跷板的示意图，横板绕它的中点O 上下转动，立柱OC 与地面垂直．当一方着地时，另一方上升到最高点．问:在上下转动横板的过程中，两人上升的最大高度AA '，BB '有何数量关系？为什么？答案一、选择题1.A2. A. 3 .A 4．A 5．C 6．D 7. A 8.C9. D 10. B二、填空题11．15cm ；50 12．100克 13．BC 或AC14．Ⅰ，根据“SAS ”确定三角形全等 15. 1116. 90° 17．65°，35°18. 10提示:将实际问题转化为几何问题以方便求解，关键是利用或构造直角三角形全等来证明线段相等.三、解答题19．相等，证△ABD ≌△A ′B ′D ′20.解:因为AB=AC ，D 、E 分别为AB 、AC 的中点，所以AD=AE.在△ABE 和△ACD 中，()()AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩（已知）公共角已说明，所以△ABE ≌△ACD(SAS)21.根据“边边边”公理构造全等三角形，能把∠MAN 平分开。

八年级数学上册《第十一章三角形》练习题-带答案(人教版)

八年级数学上册《第十一章三角形》练习题-带答案(人教版)姓名班级学号成绩一、选择题：1．三角形中，若一个角等于其他两个角的差，则这个三角形是（）A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等腰三角形2．已知一个多边形的内角和与外角和的比是2∶1，则它的边数为（）A ．9B ．8C ．7D ．63．下列长度的三条线段能首尾相接构成三角形的是（）4．等腰但不等边的三角形的角平分线、高线、中线的总条数是（）A ．3B ．5C ．7D ．95．如图，AB ∥CD ，点P 在AB ，CD 之间，∠ACP=2∠PCD=40°，连结AP ，若∠BAP=α，∠CAP=α+β．下列说法中正确的是( )A ．当∠P=60°时，α=30°B ．当∠P=60°时，β=40°C ．当=20°时，∠P=90°D ．当β=0°时，∠P=90°6．如图，将三角板的直角顶点放在直尺的一边上 1=30∠︒ 2=50∠︒ 3=∠ （）度A ．10B ．20C ．30D ．507．在△ABC 中，D 是BC 上的一点，且△ABD 与△ADC 的面积相等，则线段AD 为△ABC 的（）A ．高B ．角平分线C ．中线D ．不能确定8．如图，D ，E 是△ABC 中BC 边上的点，且BD ＝DE ＝EC ，那么（）A ．S 1＜S 2＜S 3B ．S 1＞S 2＞S 3C ．S 1＝S 2＝S 3D ．S 2＜S 1＜S 3二、填空题：9．已知一个三角形的三条边长为2、7、 x ，则 x 的取值范围是 .10．五边形从一个顶点出发，能引出条对角线，一共有条对角线．11．已知 AD 、AE 分别是△ABC 的高和中线，若 BD ＝2，CD ＝1，则DE 的长为．12．如图AB CD ，AB 与DE 交于点F 40B ︒∠= 70D ︒∠= 则E ∠= .13．过m 边形的一个顶点有7条对角线，n 边形没有对角线，过k 边形一个顶点的对角线条数是边数的12，则m ﹣n+k= ．三、解答题：14．已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数和对角线的条数．15．如图，已知FD ⊥BC 于D ，DE ⊥AB 于E ，∠B=∠C ，∠AFD=140°，求∠EDF 的度数．16．已知：在△ABC 中，AD ⊥BC ，BE 平分∠ABC 交AD 于F ，∠ABE=23°．求∠AFE 的度数．17．如图，在△ABC中、D、E分别是AB，BC上任意一点，连结DE，若BD＝4，DE＝5．（1）BE的取值范围；（2）若DE∥AC，∠A＝85°，∠BED＝35°，求∠B的度数．18．如图①，已知任意三角形ABC，过点C作DE//AB．（1）如图①，求证：三角形ABC的三个内角（即∠A，∠B，∠ACB）之和等于180°；（2）如图②，AB//CD，∠CDE＝110°，GF交∠DEB的平分线EF于点F，且∠AGF＝145°，结合（1）中的结论，求∠F的度数．参考答案：1．B 2．D 3．B 4．C 5．B 6．B 7．C 8．C9．5<x<910．2；511．0.5或1.512．3013．1314．解：设这个多边形的边数为n，则内角和为180°（n﹣2），依题意得：180（n﹣2）=360×3﹣180，解得n=7，对角线条数：(73)72-⨯=14．答：这个多边形的边数是7，对角线有14条15．解：∵FD⊥BC，DE⊥AB∴∠BED=∠FDC=90°∴∠B+∠BDE=90°，∠C+∠CFD=90°∵∠B=∠C∴∠BDE=∠CFD=180°﹣∠AFD=180°﹣140°=40°∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣40°﹣90°=50°．16．解：∵AD⊥BC∴∠ADB=90°∵BE平分∠ABC，∠ABE=23°∴∠FBD=∠ABE=23°∴∠BFD=180°﹣∠ADB﹣∠FBD=67°∴∠AFE=∠BFD=67°17．（1）1＜BE＜9（2）解：∵DE∥AC∴∠BED＝∠C＝35°又∵∠A＝85°∴△ABC中，∠B＝180°﹣∠A﹣∠C＝180°﹣85°﹣35°＝60°18．（1）证明：∵DE∥AB∴∠A＝∠DCE，∠B＝∠ECB∵∠DCE＝180°∴∠DCA+∠ACB+∠ECB＝180°∴∠A+∠ACB+∠B＝180°．（2）解：∵AB∥CD∴∠CDE＝∠BED＝110°∵EF平分∠BED∴∠BEF＝12∠BED＝55°∵∠AGF＝145°∴∠FGE＝35°∵∠BEF＝∠F+∠EGF∴∠F＝55°﹣35°＝20°。

八年级上册第11章全等三角形水平测试题

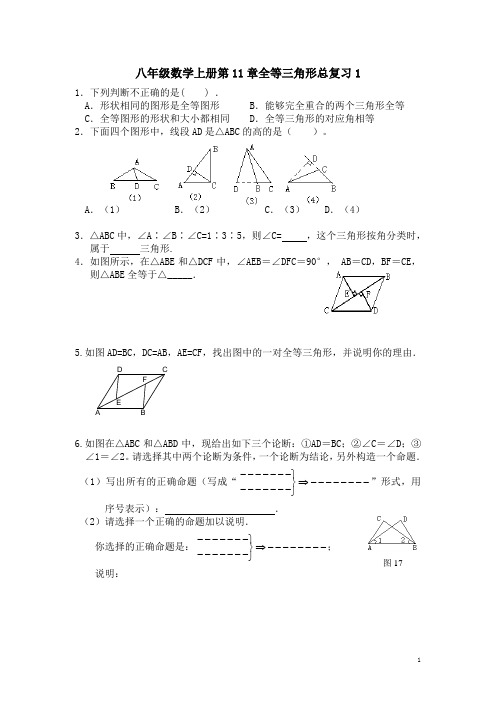
八年级数学上册第11章全等三角形总复习11．下列判断不正确的是( ) ．A ．形状相同的图形是全等图形B ．能够完全重合的两个三角形全等C ．全等图形的形状和大小都相同D ．全等三角形的对应角相等 2．下面四个图形中，线段AD 是△ABC 的高的是（）。

A ．（1）B ．（2）C ．（3）D ．（4）3．△ABC 中，∠A∶∠B∶∠C =1∶3∶5，则∠C= ，这个三角形按角分类时，属于三角形.4．如图所示，在△ABE 和△DCF 中，∠AEB ＝∠DFC ＝90°， AB ＝CD ，BF ＝CE ，则△ABE 全等于△_____．5.如图AD=BC ，DC=AB ，AE=CF ，找出图中的一对全等三角形，并说明你的理由．FEDCBA6.如图在△ABC 和△ABD 中，现给出如下三个论断：①AD ＝BC ；②∠C ＝∠D ；③∠1＝∠2。

请选择其中两个论断为条件，一个论断为结论，另外构造一个命题．（1）写出所有的正确命题（写成“--------⇒⎭⎬⎫--------------”形式，用序号表示）：．（2）请选择一个正确的命题加以说明．你选择的正确命题是：--------⇒⎭⎬⎫--------------；说明：图173．已知一个三角形的周长为15 厘米，且其中两边都等于第三边的2倍，那么这个三角形的最短边为（） A ．1厘米 B ．2厘米 C ．3厘米 D ．4厘米4．在△ABC 中，∠A ＝55°，∠B 比∠C 大25°，则∠B 的度数为（）A ．50°B ．75°C ．100°D ．125° 5．如图，已知CD ⊥AB 于D ，现有四个条件：①AD=ED ②∠A=∠BED③∠C=∠B ④AC=EB ，那么不能得出△ADC ≌△EDB 的条件是（） A ．①③ B ．②④ C ．①④ D ．②③6．有四条线段，长分别是3厘米，5厘米，7厘米，9厘米，如果用这些线段组成三角形，可以组成不同的三角形的个数为（）．A ．2个B ．3个C ．4个D ．5个7．如图2所示，AB ＝CD ，∠ABD ＝∠CDB ，则图中全等三角形共有（）A ．5对B ．4对C ．3对D ．2对图2 8．如图3所示，已知∠1＝∠2，要使△ABC ≌△ADE ，还需条件（）．A ．AB ＝AD ，BC ＝DE B ．BC ＝DE ，AC ＝AE C ．∠B ＝∠D ，∠C ＝∠E D ．AC ＝AE ，AB ＝AD 。

人教版八年级上册数学第十一章全等三角形练习题

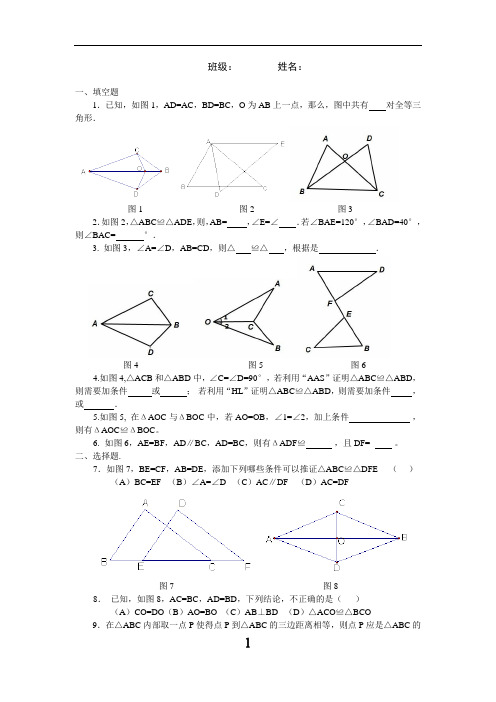
班级：姓名：一、填空题1．已知，如图1，AD=AC，BD=BC，O为AB上一点，那么，图中共有对全等三角形．图1 图2 图32．如图2，△ABC≌△ADE，则，AB= ，∠E=∠．若∠BAE=120°，∠BAD=40°，则∠BAC= °．3.如图3，∠A=∠D，AB=CD，则△≌△，根据是．图4 图5 图64.如图4,△ACB和△ABD中，∠C=∠D=90°，若利用“AAS”证明△ABC≌△ABD，则需要加条件或；若利用“HL”证明△ABC≌△ABD，则需要加条件，或．5.如图5,在ΔAOC与ΔBOC中，若AO=OB，∠1=∠2，加上条件，则有ΔAOC ≌ΔBOC。

6.如图6，AE=BF，AD∥BC，AD=BC，则有ΔADF≌，且DF= 。

二、选择题.7．如图7，BE=CF，AB=DE，添加下列哪些条件可以推证△ABC≌△DFE （）（A）BC=EF （B）∠A=∠D （C）AC∥DF （D）AC=DF图7 图88．已知，如图8，AC=BC，AD=BD，下列结论，不正确的是（）（A）CO=DO（B）AO=BO （C）AB⊥BD （D）△ACO≌△BCO 9．在△ABC内部取一点P使得点P到△ABC的三边距离相等，则点P应是△ABC的哪三条线交点．（）（A ）高（B ）角平分线（C ）中线（D ）垂直平分线已知10．下列结论正确的是（）（A ）有两个锐角相等的两个直角三角形全等；（B ）一条斜边对应相等的两个直角三角形全等；（C ）顶角和底边对应相等的两个等腰三角形全等；（D ）两个等边三角形全等.11．下列条件能判定△ABC ≌△DEF 的一组是（）（A ）∠A=∠D ， ∠C=∠F ， AC=DF （B ）AB=DE ， BC=EF ， ∠A=∠D（C ）∠A=∠D ， ∠B=∠E ， ∠C=∠F （D ）AB=DE ，△ABC 的周长等于△DEF 的周长12．已知，如图9，△ABC 中，AB=AC ，AD 是角平分线，BE=CF ，则下列说法正确的有几个（）图9三、解答题：13．如图10，AB=DF ，AC=DE ，BE=FC ，问：ΔABC 与ΔDEF 全等吗？AB 与DF 平行吗？请说明你的理由。

新人教版八年级数学上册第十一章三角形单元测试题含答案

新人教版八年级数学上册第十一章三角形单元测试题含答案新人教版八年级数学上册第十一章三角形单元测试题（上）一、选择题（30分）1.从五边形的一个顶点出发的对角线，把这个五边形分成（）个三角形。

A.5B.4C.3D.22.以下列各组线段长为边能组成三角形的是（）。

A.1cm，2cm，4cmB.2cm，4cm，6cmC.4cm，6cm，8cmD.5cm，6cm，12cm3.下列图形中一定能说明∠1＞∠2的是（）。

1.211.22.12A。

B.CD4.一个三角形的三条角平分线的交点在（）A.三角形内B.三角形外C.三角形的某边上D.以上三种情形都有可能5.某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板，他购买的瓷砖形状不可以是（）。

A.正三角形B.矩形C.正六边形D.正八边形6.能把一个任意三角形分成面积相等的两部分的是（）。

A.角平分线B.中线C.高D.A、B、C都可以7.一个角的两边与另一个角的两边互相垂直，且这两个角之差为40°，那么这两个角分别为（）。

A.70°和110°B.80°和120°C.40°和140°D.100°和140°8.一个三角形三个内角的度数之比为2:3:7，这个三角形一定是（）。

A．直角三角形 B．等腰三角形 C．锐角三角形 D．钝角三角形9.（n+1）边形的内角和比n边形的内角和大（）。

A.180°B.360°C.n·180°D.n·360°10.如图，把△XXX纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，试着找一找这个规律。

你发现的规律是（）。

BA.∠1+∠2=2∠AB.∠1+∠2=∠AC.∠A=2（∠1+∠2）D.∠1+∠2=∠A/2二、填空题（每题2分，共16分）1.在图1中，∠A+∠B+∠C+∠D+∠E=_____°。

八年级数学上册《第十一章三角形》单元检测卷及答案-人教版

八年级数学上册《第十一章三角形》单元检测卷及答案-人教版学校:___________班级：___________姓名：___________考号：___________一、选择题：（本题共8小题，每小题5分，共40分．）1．若一个多边形的内角和等于720°，则这个多边形的边数是（）A ．5B ．6C ．7D ．82．用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，称为平面图形的镶嵌.在镶嵌图案里若基本图形只有一种，则称为单元镶嵌.下面基本图形不能进行单元镶嵌的是（）A ．等边三角形B ．正方形C ．正五边形D ．正六边形3．如图，已知l 1l 2，∠A ＝45°，∠2＝100°，则∠1的度数为（）A ．50°B ．55°C ．45°D ．60°4．如图，在△ABC 中，∠C ＝70º，沿图中虚线截去∠C ，则∠1＋∠2＝( )A ．360ºB ．250ºC ．180ºD ．140º5．如图，在△ABC 中，AD 、AE 分别是边BC 上的中线与高，AE=4，△ABC 的面积为12，则CD 的长为（）A ．2B ．3C ．4D ．56．如图，在 ABC 中80BAC ∠=︒ ， 60ABC ∠=︒ 若 BF 是 ABC 的高，与角平分线 AE 相交于点 O ，则 EOF ∠ 的度数为（）A．130°B．70°C．110°D．100°7．如图，△ABC的面积为8，AD为BC边上的中线，E为AD上任意一点，连接BE，CE，图中阴影部分的面积为（）A．2 B．3 C．4 D．58．如图，在△ABC中，∠B=46°，∠ADE=40°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠C的大小是（）A．46°B．66°C．54°D．80°二、填空题：（本题共5小题，每小题3分，共15分．）9．△ABC的两条边的长度分别为3和5，若第三条边为偶数，则△ABC的周长为. 10．如图，在△ABC中，AB=AD=DC，∠BAD=32°，则∠C= ．11．如图，已知AD是 ABC的中线，AB＝13cm，AC＝5cm， ABD与 ACD的周长的差是．12．如图，在△ABC中，E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别S、S1、S2，且S=36，则S1-S2= .13．如图，△ABC中，AC=BC，CE为△ABC的中线，BD为AC边上的高，BF平分∠CBD交CE于点G，连接AG交BD于点M，若∠AFG=53°，则∠GAB的度数为．三、解答题：（本题共5题，共45分）14．如图，BO，CO分别是∠ABC，∠ACB的平分线，它们相交于点O，过点O作EF∥BC交AB于E，交AC于F，若∠ABC＝50°，∠ACB＝60°，试求∠BOC度数.15．如图所示，DE⊥AB于E，DF⊥BC于D，∠AFD=155°，∠A=∠C，求∠EDF的度数．16．如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=80°，∠ABC=70°．求∠BAD，∠AOF．17．如图，在△ABC中，∠A＝∠ABC，直线EF分别交AB、AC和CB的延长线于点D、E、F，过点B 作BP//AC交EF于点P.（1）若∠A ＝70°，∠F ＝25°，求∠BPD 的度数.（2）求证：∠F+∠FEC ＝2∠ABP.18．如图，在ABC 中，AE 是ABC 的高．（1）如图1，AD 是BAC ∠的平分线，若38B ∠=︒，62C ∠=︒求DAE ∠的度数．（2）如图2，延长AC 到点F ，CAE ∠和BCF ∠的平分线交于点G ，求G ∠的度数．参考答案:1．B 2．C 3．B 4．B 5．B 6．A 7．C 8．C9．12或1410．37o11．8cm12．613．45°14．解：∵BO 平分∠ABC ，CO 平分∠ACB∠ABC ＝50°，∠ACB ＝60°∴∠EBO ＝∠OBC ＝ 12 ∠ABC ＝25°∠FCO ＝∠OCB ＝ 12 ∠ACB ＝30°在△BOC 中，∠BOC ＝180°﹣∠OBC ﹣∠OCB ＝125°.15．解：∵DE ⊥AB ，DF ⊥BC ∴∠AED=90°，∠FDC=90° ∵∠AFD=∠FDC+∠C=155°∴∠C=155°﹣∠FDC=155°﹣90°=65°∵∠A=∠C∴∠A=65°∵∠A+∠AED+∠EDF+∠AFD=360°∴∠EDF=360°﹣65°﹣90°﹣155°=50°．16．解：∵AD 是高，∠ABC=70°∴∠BAD=90°﹣70°=20° ∵AE 、BF 是角平分线，∠BAC=80°，∠ABC=70°∴∠ABO=35°，∠BAO=40°∴∠AOF=∠ABO+∠BAO=75°17．（1）解：∵∠A ＝∠ABC ＝70°，BP//AC∴∠ABP ＝∠A ＝70°＝∠ABC∴∠PBF ＝180°﹣2×70°＝40°∴∠BPD ＝∠F+∠PBF ＝25°+40°＝65°（2）证明：∵∠F+∠FEC ＝180°﹣∠C ，∠A+∠ABC ＝180°﹣∠C ∴∠F+∠FEC=∠A+∠ABC ＝2∠A ＝2∠ABP.18．（1）解：在ABC 中∵38B ∠=︒ 62C ∠=︒ 180BAC B C ∠+∠+∠=︒ ∴180386280BAC ∠=︒-︒-︒=︒∵AD 是BAC ∠的平分线 ∴1402CAD BAD BAC ∠==∠=︒ ∵AE 是ABC 的高∴90AEC ∠=︒∵62C ∠=︒∴906228CAE ∠=︒-︒=︒∴402812DAE CAD CAE ∠=∠-∠=︒-︒=︒．∴DAE ∠的度数为12︒．（2）解：∵CAE ∠和BCF ∠的平分线交于点G ∴2CAE CAG ∠=∠ 2FCB FCG ∠=∠∵CAE FCB AEC ∠=∠-∠ CAG FCG G ∠=∠-∠ ∴()2222FCG AEC FCG G FCG G ∠-∠=∠-∠=∠-∠ ∴2AEC G ∠=∠∵AE 是ABC 的高∴90AEC ∠=︒∴45G ∠=︒．∴G ∠的度数为45︒。

新人教版八年级上第11章全等三角形单元试卷及参考答案

猪场坪乡中学八年级数学第十一章单元考试试卷班级姓名坐号得分一、选择题（每小题3分，共30分）1．在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是（）A.∠AB.∠BC.∠CD.∠B 或∠C2．如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（） A.线段CD 的中点 B.OA 与OB 的中垂线的交点 C.OA 与CD 的中垂线的交点 D.CD 与∠AOB 的平分线的交点第2题图第3题图第4题图3．如图所示，△ABD ≌△CDB ，下面四个结论中，不正确的是（） A.△ABD 和△CDB 的面积相等 B.△ABD 和△CDB 的周长相等 C.∠A +∠ABD ＝∠C +∠CBD D.AD ∥BC ，且AD ＝BC4．如图，已知AB ＝DC ，AD ＝BC ，E ，F 在DB 上两点且BF ＝DE ，若∠AEB ＝120°，∠ADB ＝30°，则∠BCF ＝（） A.150° B.40° C.80° D.90°5A.6A.ADDACB ODCBA7．如图所示，BE ⊥AC 于点D ，且AD ＝CD ，BD ＝ED ，若∠ABC ＝54°，则∠E ＝（） A.25° B.27° C.30° D.45°8．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（） A. SSS B. SAS C. AAS D. ASA9．如图，在△ABC 中，AD 平分∠BAC ，过B 作BE ⊥AD 于E ，过E 作EF ∥AC 交AB 于F ，则（）A. AF ＝2BFB.AF ＝BFC.AF ＞BFD.AF ＜BF第8题图第9题图第10题图10．将一张长方形纸片按如图所示的方式折叠，B C B D ，为折痕，则C B D ∠的度数为（） A ．60° B ．75° C ．90° D ．95° 二、填空题（每题3分，共15分）11．能够____ 的两个图形叫做全等图形．12．已知，如图，AD =AC ，BD =BC ，O 为AB 上一点，那么，图中共有对全等三角形．13．如图，△ABC ≌△ADE ，则，AB = ，∠E = ∠ ．若∠BAE =120°，∠BAD =40°，则∠BAC = ．14．△ABC ≌△DEF ，且△ABC 的周长为12，若AB =3，EF =4，则AC = ． 15．△ABC 中，∠C =90°，AD 平分∠BAC 交BC 于点D ，且CD =4cm ，则点D 到AB •的距离是________．三、解答题(共55分)16．（7分）如图，已知△ABC 中，AB ＝AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由．DBACBAED第12题图第13题图FEDCBA AECBA ′ E ′D证明： ∵AD 平分∠BAC∴∠________＝∠_________（角平分线的定义）在△ABD 和△ACD 中∵⎪⎪⎩⎪⎪⎨⎧∴△ABD ≌△ACD （）17．（8分）已知：如图，在直线MN 上求作一点P ，使点P 到 ∠AOB 两边的距离相等（要求写出作法，并保留作图痕迹，写出结论）18．（8分）已知： BE ⊥CD ，BE ＝DE ，BC ＝DA ，求证：△BEC ≌△DAE19．（8分）已知：如图，A 、C 、F 、D 在同一直线上，AF ＝D C ，AB ＝DE ，BC ＝EF ，求证：△ABC ≌△DEF ．BCDEF A C EO NMBA20．（8分）已知AB ∥DE ，BC ∥EF ，D ，C 在AF 上，且AD ＝CF ，求证：△ABC ≌△DEF ．21．（8分）已知：如图，AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为D 、E ，BD 、CE 相交于点F ，求证：BE =CD ．22．（8分）如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 面积是282cm ，AB ＝20cm ，AC ＝8cm ，求DE 的长．ACB DEF新人教版八年级数学第十一章单元考试试卷参考答案一、选择题1．A2．D 3．C 4．D 5．D 6．D 7．B 8．D 9．B 10．C二、填空题11．完全重合12．3 13．AD C 80°14．5 15．4cm三、解答题16．BAD CAD AB＝AC ∠BAD＝∠CAD AD＝AD SAS17．作∠BOA的平分线交MN于P点，就是所求做的点。

人教版八年级上第11章三角形单元测试试卷B(含答案)

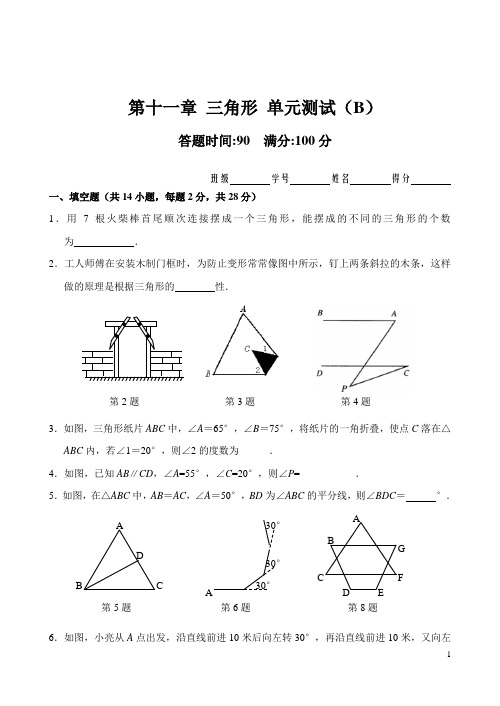
班级学号姓名得分一、填空题（共14小题，每题2分，共28分）1．用7根火柴棒首尾顺次连接摆成一个三角形，能摆成的不同的三角形的个数为．2．工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的性．3．如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数为______．4．如图，已知AB∥CD，∠A=55°，∠C=20°，则∠P=___________．5．如图，在△ABC中，AB＝AC，∠A＝50°，BD为∠ABC的平分线，则∠BDC＝°．6．如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左第十一章三角形单元测试（B）答题时间:90 满分:100分第6题30°30°30°A第8题GFEDCBA第5题DCBA第2题第3题第4题第15题第16题转30°，……照这样走下去，他第一次回到出发地A 点时，一共走了米． 7．如用同一种正多边形地砖镶嵌成平整的地面，那么这种正多边形地砖的形状可以是（写出两种即可）．8．如图所示，∠A +∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G 的度数为．9．如图，△ABC 中，BD 平分∠ABC ，CD 平分∠ACE ，请你写出∠A 与∠D 的关系：． 10．一个多边形，除了一个内角外，其余各角的和为2750°，则这一内角为． 11．在△ABC 中，∠A =55°，高BE 、CF 交于点O ，则∠BOC =______． 12．如图所示，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝______．13．如图所示，已知点D 是AB 上的一点，点E 是AC 上的一点，BE ，CD 相交于点F ，∠A =50°，∠ACD =40°，∠ABE =28°，则∠CFE 的度数为______．14．任何一个凸多边形的内角中，能否有3个以上的锐角？______（填“能”或“不能”）．二、选择题（共4小题，每题3分，共12分）15．如图，AC ⊥BC ，CD ⊥AB ，DE ⊥BC ，分别交BC ，AB ，BC 于点C ，D ，E ，则下列说法中不正确的是（）A ．AC 是△ABC 和△ABE 的高B ．DE ，DC 都是 △BCD 的高 C ．DE 是△DBE 和△ABE 的高 D ．AD ，CD 都是 △ACD 的高 16．如图所示，x 的值为（）A ．45°B ．50°C ．55°D ．70°第9题第12题第13题EDC BA17．边长相等的下列两种正多边形的组合，不能作平面镶嵌的是（）A．正方形与正三角形B．正五边形与正三角形C．正六边形与正三角形D．正八边形与正方形18．如果某多边形的外角分别是10°，20°，30°，…，80°，则这个多边形的边数是（）A．6 B．7 C．8 D．9三、解答题（共60分）19．（4分）△ABC中，∠A＝2∠B＝3∠C，则这个三角形中最小的角是多少度？20．（4分）如图，已知四边形ABCD中，∠A=∠D，∠B=∠C，试判断AD与BC的关系，并说明理由．21．（4分）如图，△ABC的外角∠CBD、∠BCE的平分线相交于点F，若∠A＝68°，求∠F的度数．22．（6分）在△ABC中，AB=AC，AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分，求三角形的三边长．23．（6分）如图所示，某农场有一块三角形土地，准备分成面积相等的4块，分别承包给4位农户，请你设计两种不同的分配方案（在已给的图形中直接画图，保留画图痕迹，不写画法）． 24．（6分）如果一个凸多边形的所有内角从小到大排列起来，恰好依次增加的度数相同，设最小角为100°，最大角为140°，那么这个多边形的边数为多少？ C B A C B A25．（6分）一个大型模板如图所示，设计要求BA与CD相交成30°角，DA与CB相交成20°，怎样通过测量∠A，∠B，∠C，∠D的度数，来检验模板是否合格？26．（8分）如图所示，小明欲从A地去B地，有三条路可走：①A→B；②A→D→B；③A→C→B．（1）在没有其它因素的情况下，我们可以肯定小明是走①，理由是______．（2）小明绝对不会走③，因为③路程最长，即AC+BC＞AD+DB，你能说明其原因吗？DC BA27．（8分）如图1，有一个五角星ABCDE ，你能说明∠A +∠B +∠C +∠D +∠E =180o 吗？如图2、图3，如果点B 向右移到AC 上，或AC 的另一侧时，上述结论仍然成立吗？请分别说明理由．图1 图2 图328．（8分）在日常生活中，观察各种建筑物的地板，你就能发现地板常用各种正多边形地砖铺砌成美丽的图案，也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）如图，请根据下列图形，填写表中空格：（2）如果限于一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？（3）从正三角形、正方形、正六边形中选一种，再在其它正多边形中选一种，请画出用这两种不同的正多边形镶嵌成一个平面图，并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．参考答案:（B卷）一、填空题1．2 2．稳定3．60°4．35°5．82.5 6．120 7．答案不唯一8．540°9．∠A=2∠D10．130°11．55o或125o12．360o13．62o14．否二、选择题15．C 16．C 17．B 18．C三、解答题19．36011⎛⎫⎪⎝⎭o20．AD BC∥21．56o22．三边长为16，16，22或20，20，14 23．略24．六边形25．只要量得∠B＋∠C=150°，∠C＋∠D=160°，则模板即为合格26．（1）两点之间，线段最短；（2）略27．结论都成立，理由略28．（1）60°，90°，108°，120°，(2)180nn-g°；（2）正三角形、正方形、正六边形；（3）答案不唯一，如正方形和正八边形，正三角形和正十二边形．。

人教版八年级上第十一章三角形单元测试题

人教版八年级上第十一章三角形单元测试题第十一章三角形测试题一、选择题（每小题3分，共30分）1.如图，四个图形中，线段BE是△ABC的高的图形是（）。

A。

△ABE。

B。

△BEC。

C。

△BED。

D。

△AED2.下列长度的三条线段中，能组成三角形的是（）。

A。

3cm，5cm，8cm。

B。

8cm，8cm，18cm。

C。

0.1cm，0.1cm，0.1cm。

D。

3cm，40cm，8cm3.若三角形两边长分别是4、5，则周长c的范围是（）。

A。

1 < c < 9.B。

9 < c < 14.C。

10 < c < 18.D。

无法确定4.已知∠A：∠B：∠C=1:2:2，则△ABC三个角度数分别是（）。

A。

40º、80º、80º。

B。

35º、70º、70º。

C。

30º、60º、60º。

D。

36º、72º、72º5.三角形中，有一个外角是79º，则这个三角形的形状是（）。

A。

锐角三角形。

B。

直角三角形。

C。

钝角三角形。

D。

无法确定形状6.一个三角形的三个内角中（）。

A。

至少有一个等于90°。

B。

至少有一个大于90°。

C。

不可能有两个大于89°。

D。

不可能都小于60°7.从n边形的一个顶点作对角线，把这个n边形分成三角形的个数是（）。

A。

n个。

B。

（n-1）个。

C。

(n-2)个。

D。

(n-3)个8.装饰大世界出售下列形状的地砖：○1正方形；○2长方形；○3正五边形；○4正六边形。

若只选购其中某一种地砖镶嵌地面，可供选用的地砖共（）种。

A。

1种。

B。

2种。

C。

3种。

D。

4种9.多边形的边数由n（n>3）增加了3边，其外角和是（）。

A。

增加。

B。

保持不变。

C。

减少。

D。

变成（n-3）×180°10.如图1，点O是△ABC内一点，∠A=80°，∠1=15°，∠2=40°，则∠BOC等于（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十一章全等三角形测试题（B ）
一、选择题（每小题4分，共40分） 1、下列说法正确的是（）
A ：全等三角形是指形状相同的两个三角形 C ：全等三角形的周长和面积分别相等 C ：全等三角形是指面积相等的两个三角形 D ：所有的等边三角形都是全等三角形 2、如图：若△ABE ≌△ACF ，且AB=5，AE=2，则EC 的长为（）
A ：2
B ：3
C ：5
D ：2.5
3、如图：若△ABC ≌△EAC ，则∠EAC 等于（）
A ：∠AC
B B ：∠BAF
C ：∠CAF
D ：∠BAC
4、如图：AB=AD ，AE 平分∠BAD ，则图中有（）对全等三角形。

A ：2
B ：3
C ：4
D ：5
5、如图：△ABC ≌△DEF ，△ABC 的周长等于40㎝， AB=10㎝，BC=16㎝，则DF 的长为（） A ：10㎝ B ：14㎝ C ：16㎝ D ：40㎝
6、能判断△ABC ≌△DEF 的是（）
A ：AB=DE ，BC=EF ，∠A=∠D
B ：∠A=∠E ，∠C=∠F ，AC=EF
C ：∠B=∠E ，∠A=∠F ，AC=EF
D ：∠A=∠D ，∠B=∠
E ，∠C=∠
F 7、如图：EA ∥DF ，AE=DF ，要使△AEC ≌△DBF ，则只要（）
A ：AB=CD
B ：EC=BF
C ：∠A=∠
D D ：AB=BC 8、如图：AD=AC ，AB 平分∠DAC ，下列结论错误的是（）
A ：△AD
B ≌△ACB B ：△ADE ≌△ACE
C ：△EDB ≌△ECB
D ：△AED ≌△CEB 9、如图：直线a ，b ，c 表示三条相互交叉环湖而建的公路，现在建立一个货物中转站，
要求它到三条公路的距离相等，则可供选择的地址有（） A ：1个 B ：2个 C ：3个 D ：4个
10、如图：△ABC 中，∠C=90°，AC=BC ，AD 平分∠CAB 交BC 于D ，DE ⊥AB 于E ， AB=6㎝，则△DEB 的周长是（）
A ：6㎝
B ：4㎝
C ：10㎝
D ：以上都不对二、填空题（每小题4分，共40分）
11、如图：AB=AC ，BD=CD ，若∠B=28°则∠C= ；
（第2题）
F
E
C
B
A
（第3题）F
E
C
B A
（第4题）
E
D
C
B
A （第5题）
F
E D
C B
A
（第7题）
F
E
D
C
B A
（第8题）
E
D
C
B
A
c
b
a
（第9题）
（第10题）E
D
C
B
A
（第11题）
D C
B
A
12、如图：△EDF ≌△BAC ，EC=6㎝，则BF= ； 13、如图：△AEC ≌△ADB ，则∠AEC= ，EC= ；
14、如图5，△ABC 中，∠C ＝90°，AD 平分∠BAC ， AB ＝5，CD ＝2，则△ABD 的面积是______； 15、如图：在△ABC 中，AD=AE ，BD=EC ，
∠ADB=∠AEC=105°，∠B=40°，则∠CAE= ； 16、已知∠MON 的平分线上一点P ，点P 到OM 的距离为3㎝，则点P 到ON 的距离等于㎝；
17、在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E 是 BC 的中点，DE 平分∠ADC，∠CED=35°，如图，则∠EAB = ； 18、如图：BE ，CD 是△ABC 的高，且BD ＝EC ，判定△BCD ≌△CBE 的依据是“ ”； 19、如图：AB ，CD 相交于点O ，AD ＝CB ，请你补充
一个条件，使得△AOD ≌△COB ，你补充的条件是； 20、如图：在△ABC 中，∠B=∠C=50°，D 是BC 的中点，DE ⊥AB ， DF ⊥AC ，则∠BAD= 。

三、解答题（共70分）
21、（8分）如图：AB ∥CD ，AD ∥BC ，求证：AB=CD 。

证明：∵AB ∥CD
∴∠ABD=∠CDB （） ∵AD ∥BC
∴∠ADB=∠CBD （）在△ABD 和△CDB 中 ∠ADB=∠CBD
∵ BD=DB
∠ABD=∠CDB
∴△ABD ≌△CDB （）
∴AB=CD （）
22、（10分）如图：DO=BO ，∠A=∠C 。

求证：△AOD ≌△COB 。

（第12题）
F
E
D
C
B A
（第13题）
E
D
C
B
A
（第14题）D
C
B
A E （第15题）
D C
B
A
E
（第17题）
D
C
B
A
E
（第18题）
D
C
B
A
O
（第19题）
D
C
B
A
F
E
（第20题）
D C B A D
C B A
O
D
C
B
A
23、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

24、（10分）如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

25、（10分）如图：在△ABC 中，BA=BC ，D 是AC 的中点。

求证：BD ⊥AC 。

M
F
E
C
B
A
F
E D
C
B
A D C
B
A
26、（10分）AB=AC ，DB=DC ，F 是AD 的延长线上的一点。

求证：BF=CF
27、（12分）如图：AB=CD ，AE=DF ，CE=FB 。

求证：AF=DE 。

F
D
C
B
A
F
E D
C
B
A。