2018年上海市浦东新区中考数学二模试卷(含答案)
(完整版)2018年上海市中考数学二模试卷

2018年上海市中考数学二模试卷一、选择题(每小题4分,共24分)1.(4分)(2018?上海)计算的结果是()A.B.C.D.32.(4分)(2018?上海)据统计,2013年上海市全社会用于环境保护的资金约为60 800 000 000元,这个数用科学记数法表示为()A.608×108B.60.8×109C.6.08×1010D.6.08×10113.(4分)(2018?上海)如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是()A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2D.y=(x+1)24.(4分)(2018?上海)如图,已知直线a、b被直线c所截,那么∠1的同位角是()A.∠2 B.∠3 C.∠4 D.∠55.(4分)(2018?上海)某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是()A.50和50 B.50和40 C.40和50 D.40和406.(4分)(2018?上海)如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是()A.△ABD与△ABC的周长相等B.△ABD与△ABC的面积相等C.菱形的周长等于两条对角线之和的两倍D.菱形的面积等于两条对角线之积的两倍二、填空题(每小题4分,共48分)7.(4分)(2018?上海)计算:a(a+1)=_________.8.(4分)(2018?上海)函数y=的定义域是_________.9.(4分)(2018?上海)不等式组的解集是_________.10.(4分)(2018?上海)某文具店二月份销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份销售各种水笔_________支.11.(4分)(2018?上海)如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是_________.12.(4分)(2018?上海)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为_________米.13.(4分)(2018?上海)如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是_________.14.(4分)(2018?上海)已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是_________(只需写一个).15.(4分)(2018?上海)如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设=,=,那么=_________(结果用、表示).16.(4分)(2018?上海)甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是_________.17.(4分)(2018?上海)一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y表示的数为_________.18.(4分)(2018?上海)如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为_________(用含t的代数式表示).三、解答题(本题共7题,满分78分)19.(10分)(2018?上海)计算:﹣﹣+||.20.(10分)(2018?上海)解方程:﹣=.21.(10分)(2018?上海)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.水银柱的长度x(cm) 4.2 …8.2 9.8体温计的读数y(℃)35.0 …40.0 42.0(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)用该体温计测体温时,水银柱的长度为 6.2cm,求此时体温计的读数.22.(10分)(2018?上海)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sinB的值;(2)如果CD=,求BE的值.23.(12分)(2018?上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E 是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;(2)连接AE,交BD于点G,求证:=.24.(12分)(2018?上海)在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,﹣2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.25.(14分)(2018?上海)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.2018年上海市中考数学试卷参考答案与试题解析一、选择题(每小题4分,共24分)1.(4分)(2018?上海)计算的结果是()A.B.C.D.3考点:二次根式的乘除法.专题:计算题.分析:根据二次根式的乘法运算法则进行运算即可.解答:解:?=,故选:B.点评:本题主要考查二次根式的乘法运算法则,关键在于熟练正确的运用运算法则,比较简单.2.(4分)(2018?上海)据统计,2013年上海市全社会用于环境保护的资金约为60 800 000 000元,这个数用科学记数法表示为()A.608×108B.60.8×109C.6.08×1010D.6.08×1011考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:60 800 000 000=6.08×1010,故选:C.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(4分)(2018?上海)如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是()A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2D.y=(x+1)2考点:二次函数图象与几何变换.专题:几何变换.分析:先得到抛物线y=x2的顶点坐标为(0,0),再得到点(0,0)向右平移1个单位得到点的坐标为(1,0),然后根据顶点式写出平移后的抛物线解析式.解答:解:抛物线y=x2的顶点坐标为(0,0),把点(0,0)向右平移1个单位得到点的坐标为(1,0),所以所得的抛物线的表达式为y=(x﹣1)2.故选:C.点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.4.(4分)(2018?上海)如图,已知直线a、b被直线c所截,那么∠1的同位角是()A.∠2 B.∠3 C.∠4 D.∠5考点:同位角、内错角、同旁内角.分析:根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角可得答案.解答:解:∠1的同位角是∠5,故选:D.点评:此题主要考查了同位角的概念,关键是掌握同位角的边构成“F“形.5.(4分)(2018?上海)某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是()A.50和50 B.50和40 C.40和50 D.40和40考点:众数;中位数.分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.解答:解:从小到大排列此数据为:37、40、40、50、50、50、75,数据50出现了三次最多,所以50为众数;50处在第4位是中位数.故选:A.点评:本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.6.(4分)(2018?上海)如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是()A.△ABD与△ABC的周长相等B.△ABD与△ABC的面积相等C.菱形的周长等于两条对角线之和的两倍D.菱形的面积等于两条对角线之积的两倍考点:菱形的性质.专题:几何图形问题.分析:分别利用菱形的性质结合各选项进而求出即可.解答:解:A、∵四边形ABCD是菱形,∴AB=BC=AD,∵AC<BD,∴△ABD与△ABC的周长不相等,故此选项错误;B 、∵S △ABD =S 平行四边形ABCD ,S △ABC =S 平行四边形ABCD,∴△ABD 与△ABC 的面积相等,故此选项正确;C 、菱形的周长与两条对角线之和不存在固定的数量关系,故此选项错误;D 、菱形的面积等于两条对角线之积的,故此选项错误;故选:B .点评:此题主要考查了菱形的性质应用,正确把握菱形的性质是解题关键.二、填空题(每小题4分,共48分)7.(4分)(2018?上海)计算:a (a+1)=a 2+a.考点:单项式乘多项式.专题:计算题.分析:原式利用单项式乘以多项式法则计算即可得到结果.解答:解:原式=a 2+a .故答案为:a 2+a点评:此题考查了单项式乘以多项式,熟练掌握运算法则是解本题的关键.8.(4分)(2018?上海)函数y=的定义域是x ≠1.考点:函数自变量的取值范围.分析:根据分母不等于0列式计算即可得解.解答:解:由题意得,x ﹣1≠0,解得x ≠1.故答案为:x ≠1.点评:本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.9.(4分)(2018?上海)不等式组的解集是3<x <4.考点:解一元一次不等式组.专题:计算题.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.解答:解:,解①得:x >3,解②得:x <4.则不等式组的解集是:3<x <4.故答案是:3<x <4点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x 介于两数之间.10.(4分)(2018?上海)某文具店二月份销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份销售各种水笔352支.考点:有理数的混合运算.专题:应用题.分析:三月份销售各种水笔的支数比二月份增长了10%,是把二月份销售的数量看作单位“1”,增加的量是二月份的10%,即三月份生产的是二月份的(1+10%),由此得出答案.解答:解:320×(1+10%)=320×1.1=352(支).答:该文具店三月份销售各种水笔352支.故答案为:352.点评:此题考查有理数的混合运算,理解题意,列出算式解决问题.11.(4分)(2018?上海)如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是k<1.考点:根的判别式.分析:根据一元二次方程ax2+bx+c=0(a≠0)的根的判别式的意义得到△>0,即(﹣2)2﹣4×1×k>0,然后解不等式即可.解答:解:∵关于x的方程x2﹣3x+k=0(k为常数)有两个不相等的实数根,∴△>0,即(﹣2)2﹣4×1×k>0,解得k<1,∴k的取值范围为k<1.故答案为:k<1.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2﹣4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.12.(4分)(2018?上海)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为26米.考点:解直角三角形的应用-坡度坡角问题.专题:应用题.分析:首先根据题意画出图形,根据坡度的定义,由勾股定理即可求得答案.解答:解:如图,由题意得:斜坡AB的坡度:i=1:2.4,AE=10米,AE⊥BD,∵i==,∴BE=24米,∴在Rt△ABE中,AB==26(米).故答案为:26.点评:此题考查了坡度坡角问题.此题比较简单,注意掌握数形结合思想的应用,注意理解坡度的定义.13.(4分)(2018?上海)如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是.考点:概率公式.分析:由从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,直接利用概率公式求解即可求得答案.解答:解:∵从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,∴恰好抽到初三(1)班的概率是:.故答案为:.点评:此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.14.(4分)(2018?上海)已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是y=﹣(只需写一个).考点:反比例函数的性质.专题:开放型.分析:首先根据反比例函数的性质可得k<0,再写一个符合条件的数即可.解答:解:∵反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,∴k<0,∴y=﹣,故答案为:y=﹣.点评:此题主要考查了反比例函数的性质,关键是掌握对于反比例函数y=,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.15.(4分)(2018?上海)如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设=,=,那么=﹣(结果用、表示).考点:*平面向量.分析:由点E在边AB上,且AB=3EB.设=,可求得,又由在平行四边形ABCD中,=,求得,再利用三角形法则求解即可求得答案.解答:解:∵AB=3EB.=,∴==,∵平行四边形ABCD中,=,∴==,∴=﹣=﹣.故答案为:﹣.点评:此题考查了平面向量的知识.此题难度不大,注意掌握三角形法则与平行四边形法则的应用,注意掌握数形结合思想的应用.16.(4分)(2018?上海)甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是乙.考点:方差;折线统计图.专题:图表型.分析:根据方差的意义数据波动越小,数据越稳定即可得出答案.解答:解:根据图形可得:乙的成绩波动最小,数据最稳定,则三人中成绩最稳定的是乙;故答案为:乙.点评:本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.17.(4分)(2018?上海)一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y表示的数为﹣9.考点:规律型:数字的变化类.分析:根据“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,首先建立方程2×3﹣x=7,求得x,进一步利用此规定求得y即可.解答:解:解法一:常规解法∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b∴2×3﹣x=7∴x=﹣1则2×(﹣1)﹣7=y解得y=﹣9.解法二:技巧型∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b∴7×2﹣y=23∴y=﹣9故答案为:﹣9.点评:此题考查数字的变化规律,注意利用定义新运算方法列方程解决问题.18.(4分)(2018?上海)如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F 与BE交于点G.设AB=t,那么△EFG的周长为2t(用含t的代数式表示).考点:翻折变换(折叠问题).专题:几何图形问题.分析:根据翻折的性质可得CE=C′E,再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°,然后求出∠BGD′=60°,根据对顶角相等可得∠FGE=∠∠BGD′=60°,根据两直线平行,内错角相等可得∠AFG=∠FGE,再求出∠EFG=60°,然后判断出△EFG是等边三角形,根据等边三角形的性质表示出EF,即可得解.解答:解:由翻折的性质得,CE=C′E,∵BE=2CE,∴BE=2C′E,又∵∠C′=∠C=90°,∴∠EBC′=30°,∵∠FD′C′=∠D=90°,∴∠BGD′=60°,∴∠FGE=∠BGD′=60°,∵AD∥BC,∴∠AFG=∠FGE=60°,∴∠EFG=(180°﹣∠AFG)=(180°﹣60°)=60°,∴△EFG是等边三角形,∵AB=t,∴EF=t÷=t,∴△EFG的周长=3×t=2t.故答案为:2t.点评:本题考查了翻折变换的性质,直角三角形30°角所对的直角边等于斜边的一半,等边三角形的判定与性质,熟记性质并判断出△EFG是等边三角形是解题的关键.三、解答题(本题共7题,满分78分)19.(10分)(2018?上海)计算:﹣﹣+||.考点:实数的运算;分数指数幂.专题:计算题.分析:本题涉及绝对值、二次根式化简两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=2﹣﹣2+2﹣=.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.20.(10分)(2018?上海)解方程:﹣=.考点:解分式方程.专题:计算题;转化思想.分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解答:解:去分母得:(x+1)2﹣2=x﹣1,整理得:x2+x=0,即x(x+1)=0,解得:x=0或x=﹣1,经检验x=﹣1是增根,分式方程的解为x=0.点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.21.(10分)(2018?上海)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.水银柱的长度x(cm) 4.2 …8.2 9.8体温计的读数y(℃)35.0 …40.0 42.0(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)用该体温计测体温时,水银柱的长度为 6.2cm,求此时体温计的读数.考点:一次函数的应用.专题:应用题;待定系数法.分析:(1)设y关于x的函数关系式为y=kx+b,由统计表的数据建立方程组求出其解即可;(2)当x=6.2时,代入(1)的解析式就可以求出y的值.解答:解:(1)设y关于x的函数关系式为y=kx+b,由题意,得,解得:,∴y=x+29.75.∴y关于x的函数关系式为:y=+29.75;(2)当x=6.2时,y=×6.2+29.75=37.5.答:此时体温计的读数为37.5℃.点评:本题考查了待定系数法求一次函数的解析式的运用,由解析式根据自变量的值求函数值的运用,解答时求出函数的解析式是关键.22.(10分)(2018?上海)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sinB的值;(2)如果CD=,求BE的值.考点:解直角三角形;直角三角形斜边上的中线.专题:几何图形问题.分析:(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:,即可得出sinB的值;(2)根据sinB的值,可得出AC:AB=1:,再由AB=2,得AC=2,则CE=1,从而得出BE.解答:解:(1)∵∠ACB=90°,CD是斜边AB上的中线,∴CD=BD,∴∠B=∠BCD,∵AE⊥CD,∴∠CAH+∠ACH=90°,又∠ACB=90°∴∠BCD+∠ACH=90°∴∠B=∠BCD=∠CAH,即∠B=∠CAH,∵AH=2CH,∴由勾股定理得AC=CH,∴CH:AC=1:,∴sinB=;(2)∵sinB=,∴AC:AB=1:,∴AC=2.∵∠CAH=∠B,∴sin∠CAH=sinB==,设CE=x(x>0),则AE=x,则x2+22=(x)2,∴CE=x=1,AC=2,在Rt△ABC中,AC2+BC2=AB2,∴BC=4,∴BE=BC﹣CE=3.点评:本题考查了解直角三角形,以及直角三角形斜边上的中线,注意性质的应用,难度不大.23.(12分)(2018?上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E 是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;(2)连接AE,交BD于点G,求证:=.考点:相似三角形的判定与性质;全等三角形的判定与性质;平行四边形的判定.专题:证明题.分析:(1)证△△BAD≌△CDA,推出∠ABD=∠ACD=∠CDE,推出AC∥DE即可;(2)根据平行得出比例式,再根据比例式的性质进行变形,即可得出答案.解答:证明:(1)∵梯形ABCD,AD∥BC,AB=CD,∴∠BAD=∠CDA,在△BAD和△CDA中∴△BAD≌△CDA(SAS),∴∠ABD=∠ACD,∵∠CDE=∠ABD,∴∠ACD=∠CDE,∴AC∥DE,∵AD∥CE,∴四边形ACED是平行四边形;(2)∵AD∥BC,∴=,=,∴=,∵平行四边形ACED,AD=CE,∴=,∴=,∴=,∴=.点评:本题考查了比例的性质,平行四边形的判定,平行线的判定的应用,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.24.(12分)(2018?上海)在平面直角坐标系中(如图),已知抛物线y=x 2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,﹣2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.考点:二次函数综合题.专题:代数几何综合题;压轴题.分析:(1)根据待定系数法可求抛物线的表达式,进一步得到对称轴;(2)因为AC与EF不平行,且四边形ACEF为梯形,所以CE∥AF.分别求出直线CE、AF的解析式,进而求出点F的坐标;(3)△BDP和△CDP的面积相等,可得DP∥BC,根据待定系数法得到直线BC的解析式,根据两条平行的直线k值相同可得直线DP的解析式,进一步即可得到t的值.解答:解:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),点C(0,﹣2),∴,解得.故抛物线的表达式为:y=x2﹣x﹣2=(x﹣1)2﹣,对称轴为直线x=1;(2)设直线CE的解析式为:y=kx+b,将E(1,0),C(0,﹣2)坐标代入得:,解得,∴直线CE的解析式为:y=2x﹣2.∵AC与EF不平行,且四边形ACEF为梯形,∴CE∥AF.∴设直线AF的解析式为:y=2x+n.∵点A(﹣1,0)在直线AF上,∴﹣2+n=0,∴n=2.∴设直线AF的解析式为:y=2x+2.当x=1时,y=4,∴点F的坐标为(1,4).(3)点B(3,0),点D(1,﹣),若△BDP和△CDP的面积相等,则DP∥BC,则直线BC的解析式为y=x﹣2,∴直线DP的解析式为y=x﹣,当y=0时,x=5,∴t=5.点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的表达式,待定系数法求直线的解析式,两条平行的直线之间的关系,三角形面积,分类思想的运用,综合性较强,有一定的难度.25.(14分)(2018?上海)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.考点:圆的综合题.专题:压轴题.分析:(1)当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,直接利用勾股定理求出AC进而得出答案;(2)首先得出四边形APCE是菱形,进而得出CM的长,进而利用锐角三角函数关系得出CP以及EF的长;(3)∠GAE≠∠BGC,只能∠AGE=∠AEG,利用AD∥BC,得出△GAE∽△GBC,进而求出即可.解答:解:(1)如图1,设⊙O的半径为r,当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,∴BH=AB?cosB=4,∴AH=3,CH=4,∴AC==5,∴此时CP=r=5;(2)如图2,若AP∥CE,APCE为平行四边形,∵CE=CP,∴四边形APCE是菱形,连接AC、EP,则AC⊥EP,∴AM=CM=,由(1)知,AB=AC,则∠ACB=∠B,∴CP=CE==,∴EF=2=;(3)如图3:过点C作CN⊥AD于点N,∵cosB=,∴∠B<45°,∵∠BCG<90°,∴∠BGC>45°,∴∠BGC>∠B=∠GAE,即∠BGC≠∠GAE,又∠AEG=∠BCG≥∠ACB=∠B=∠GAE,∴当∠AEG=∠GAE时,A、E、G重合,则△AGE不存在.即∠AEG≠∠GAE∴只能∠AGE=∠AEG,∵AD∥BC,∴△GAE∽△GBC,∴=,即=,解得:AE=3,EN=AN﹣AE=1,∴CE===.点评:此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,利用分类讨论得出△AGE是等腰三角形时只能∠AGE=∠AEG进而求出是解题关键.。
上海市各区2018年中考二模数学试题_(2) 推荐

九年级数学试卷参考答案一、选择题:(本大题共6题,每题4分,满分24分)1.A ;2.D ;3.B ;4.D ;5. B ;6.C . 二、填空题:(本大题共12题,每题4分,满分48分)7.x ≠1; 8.1.37×109; 9.x =1; 10.()()2121+---x x ;11. 4;12.m >3; 13. 0.3; 14.6180120+=x x ; 15.)(21b a-; 16.内切; 17.4 ; 18.750或150. 三、解答题:(本大题共7题,满分78分)19.解:原式=333334+-++-…………………………………………………(8分)=133-………………………………………………………………………(2分)AF N第一个观点第一个观点①②③④⑤①②③④⑤①②③④⑤①②③④⑤⑤④③②①20. 解:由①得 x <1. …………………………………………………………………(3分) 由②得 1-≥x .…………………………………………………………………(3分) ∴ 原不等式组的解集为11<≤-x . …………………………………………(2分) 画图略………………………………………………………………………………(2分) 21.解:(1)过点B 作BF ⊥AD 于F 。
…………………………………………………(1分)在Rt ABF △中,∵35==AF BF i ,且10BF m =。
∴6AF m =………………(2分)∴AB = …………………………………………………………(2分)(2)如图,延长EC 至点M ,AD 至点N ,连接MN ,过点E 作EG ⊥AD 于G 。
在Rt △AEG 中,∵65==AG EG i ,且10BF m =, ∴AG =12m ,BE=GF=AG - AF =6 m 。
……………………………………………(2分)∴ABE CMND S S =△梯形 ………………(1()1122BE EG MC ND ∙∙=+。
2018年浦东新区初三数学二模

2018年浦东新区初三数学二模(时间:100分钟,满分:150分)2018.5一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列代数式中,单项式是 (A )x1; (B )0; (C )1+x ; (D )x . 2.下列代数式中,二次根式n m +的有理化因式可以是 (A )n m +; (B )n m -;(C )n m +; (D )n m -.3.已知一元二次方程0122=-+x x ,下列判断正确的是(A )该方程有两个不相等的实数根; (B )该方程有两个相等的实数根; (C )该方程没有实数根; (D )该方程的根的情况不确定.4.某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是 (A )平均数; (B ) 众数; (C ) 方差; (D ) 频率. 5.下列y 关于x 的函数中,当0>x 时,函数值y 随x 的值增大而减小的是(A )2x y = ;(B )22+=x y ; (C )3x y =; (D )xy 1=. 6.已知四边形ABCD 中,AB //CD ,AC=BD ,下列判断中正确..的是 (A )如果BC=AD ,那么四边形ABCD 是等腰梯形;(B )如果AD //BC ,那么四边形ABCD 是菱形; (C )如果AC 平分BD ,那么四边形ABCD 是矩形; (D )如果AC ⊥BD ,那么四边形ABCD 是正方形. 二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:=⋅ba ab 232 ▲ . 8.因式分解:=-224y x ▲ . 9.方程312=-x 的解是 ▲ .10.如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张纸片),那么文字恰好组成“幸福都是奋斗出来的”概率是 ▲ .11. 已知正方形的边长为2cm,那么它的半径长是▲ cm.12.某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植x亩树苗,根据题意可列出关于x的方程▲ .13.近年来,出境旅游成为越来越多中国公民的假期选择.将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图1所示.那么2017年该小区居民出境游中跟团游的人数为▲ .14.如图2,在□ABCD中,E是BC中点,AE交BD于点F,如果=,那么AF= ▲ (用向量表示).15.在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平面观摩点B的俯角为︒60,此时点A、B之间的距离是▲ 米.16.如图3,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'= ▲ .17.如果抛物线C:)0(2≠++=acbxaxy与直线l:)0(≠+=kdkxy都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“点线和谐”关系.如果直线1+=mxy与抛物线nxxy+-=22具有“点线和谐”关系,那么=+nm▲ .18. 已知1l∥2l,1l、2l之间的距离是3cm,圆心O到直线1l的距离是1cm,如果⊙O与直线1l、2l有三个公共点,那么圆O的半径为▲ cm.三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:1-312127-2-18)(++.图2图1图3图 5图420.(本题满分10分)解不等式组⎪⎩⎪⎨⎧+≤-->612163x x x x , ,并把它的解集在数轴(如图4)上表示出来.21.(本题满分10分)如图5,已知AB 是⊙O 的直径,弦CD 交AB 于点E ,30=∠CEA ,OE =4,DE =35.求弦CD 及⊙O 的半径长.22.(本题满分10分,其中第(1)小题5分,第(2)小题5分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y (元)与年用天然气量x (立方米)的关系如图6所示,观察图像并回答下列问题:(1)年用天然气量不超过310立方米时,求y 关于x 的函数解析式(不写定义域); (2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)已知:如图7,在正方形ABCD 中,点E 为边AB 的中点,联结DE .点F 在DE 上,且CF=CD ,过点F 作FG ⊥FC 交AD 于点G . (1)求证:GF=GD ;(2)联结AF ,求证:AF ⊥DE .图6 x 1 2 3 4 5 –1 –2 –3 –4 –5 O 图5图724.(本题满分12分,每小题4分)已知平面直角坐标系xOy(如图8),二次函数y=ax2+bx+4的图像经过A(-2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴...上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图9,已知在△ABC 中,AB=AC ,21tan =B ,BC =4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C 、F (点C 、F 不重合),射线EF 与射线AC 交于点P .(1)求证:AC AP AE ⋅=2;(2)当点F 在线段BC 上,设CF =x ,△PFC 的面积为y ,求y 关于x 的函数解析式及定义域; (3)当21=EF FP 时,求BE 的长.备用图图9一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.A ; 4.C ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分) 7.22ab ;8.()()y x y x 22-+; 9.5=x ;10.21;11.2;12.136060=+-x x ; 13.24; 14.a32; 15.3800;16.9;17.0;18.2或4.三、解答题:(本大题共7题,满分78分)19.解:原式23-1-222++=.…………………………………………………(8分) 2-23=.………………………………………………………………(2分)20. 解:3611.26x x x x >-⎧⎪-+⎨≤⎪⎩,由①得:62->x .…………………………………………………………(2分)解得3->x .…………………………………………………………(1分)由②得:11-3+≤x x )(.……………………………………………………(1分) 133+≤-x x .……………………………………………………(1分)42≤x .解得2≤x .……………………………………………………………(1分) ∴原不等式组的解集为23-≤<x .…………………………………(2分)…………………………………(2分)21. 解:OD M CD OM O ,联结于点作过点⊥.……………………………………(1分) ∵,︒=∠30CEA∴︒=∠=∠30CEA OEM .…………………………………(1分)在Rt △OEM 中,∵OE =4,∴221==OE OM ,3223430cos =⨯=⋅=︒OE EM .(2分) ∵35=DE ,∴33=-=EM DE DM .…………(1分) ∵CD OM OM ⊥过圆心,,∴DM CD 2=.…………(2分) ∴36=CD .……………………………………………(1分) ∵,,332==DM OM∴在Rt △DOM 中,()313322222=+=+=DM OM OD .……(1分)∴ 弦CD 的长为36,⊙O 的半径长为31.……………………………(1分)① ②22.解:(1)设)0(≠=k kx y .…………………………………………………………(1分) ∵)0(≠=k kx y 的图像过点(310,930),……………………………(1分) ∴,k 310930=∴3=k .…………………………………………………(2分)∴ x y 3=.…………………………………………………………… (1分) (2)设)0(≠+=k b kx y .………………………………………………………(1分) ∵ )0(≠+=k b kx y 的图像过点(310,930)和(320,963),∴ ⎩⎨⎧=+=+63.9320930310b k b k , ∴ ⎩⎨⎧-== 3.93.3b k ,……………………………………………………………(1分) ∴933.3-=x y .…………………………………………………………(1分) 当3401029933.31029==-=x x y ,解得时,.……………………(1分) 答:小明家2017年使用天然气量为340立方米.……………………(1分)23.证明:(1)∵是正方形四边形ABCD ,∴︒=∠90ADC .………(1分)∵FG ⊥FC , ∴∠GFC = 90°. …………………………(1分)∵,CD CF = ∴∠CDF =∠CFD .………………………(1分) ∴∠GFC -∠CFD =∠ADC -∠CDE ,即∠GFD =∠GDF .(1分) ∴GF =GD .………………………………………………(1分)(2)联结CG .∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G .……(1分)∴GC ⊥DE ,∴∠CDF +∠DCG = 90°,∵∠CDF +∠ADE = 90°,∴∠DCG =∠ADE .∵是正方形四边形ABCD ,∴AD =DC ,∠DAE =∠CDG = 90°,∴△DAE ≌△CDG .……………………………………………………(1分)∴DG AE =.………………………………………………………… (1分)∵的中点,是边点AB E ∴的中点,是边点AD G∴GF GD AG ==.……………………………………………………(1分) ∴,,GFD GDF AFG DAF ∠=∠∠=∠………………………………(1分)∵,︒=∠+∠+∠+∠180GDF GFD AFG DAF ……………………(1分) ∴,︒=∠+∠18022GFD AFG ∴∠AFD = 90°,即AF ⊥DE .…………………………………………(1分) 证法2:(1)联结CG 交ED 于点H .∵是正方形四边形ABCD ,∴︒=∠90ADC .…………………………(1分)∵FG ⊥FC ,∴∠GFC = 90°.……………………………………………(1分) 在Rt △C FG 与Rt △CDG 中,⎩⎨⎧==.CG CG CD CF ,…………………………………………………………… (1分) ∴Rt △CFG ≌Rt △CDG .………………………………………………(1分)∴GD GF =.…………………………………………………………(1分) (2)∵,,GD GF CD CF ==∴的中垂线上在线段、点FD C G . ……………………………… (1分) ∴FH=HD ,GC ⊥DE ,∴∠EDC +∠DCH = 90°,∵∠ADE +∠EDC= 90°,∴∠ADE =∠DCH .……………………………………………………(1分) ∵是正方形四边形ABCD ,∴AD=DC =AB ,∠DAE =∠CDG= 90°,∵GDC EAD DC AD DCH ADE ∠=∠=∠=∠,,.∴△ADE ≌△DCG .……………………………………………………(1分)∴DG AE =.…………………………………………………………(1分)∵的中点,是边点AB E ∴的中点,是边点AD G∵的中点,是边点FD H ∴GH 是△AFD 的中位线.………………(1分) ∴,AF GH //∴,GHD AFD ∠=∠∵GH ⊥FD ,∴∠GHD = 90°,………………………………………(1分)∴∠AFD = 90°,即AF ⊥DE .………………………………………(1分) 24.解:(1)∵ 抛物线42++=bx ax y 与x 轴交于点A (-2,0),B (4,0),∴ ⎩⎨⎧=++=+.04416042-4b a b a ;…………………………………………………(1分) 解得⎪⎩⎪⎨⎧==.121-b a ;…………………………………………………………(2分)∴ 抛物线的解析式为421-2++=x x y .……………………………(1分) (2)H BC EH E 于点作过点⊥.在Rt △ACO 中, ∵A (-2,0),∴ OA =2, 4421-02=++==x x y x 时,当,∴OC=4,在Rt △C OB 中,∵∠COB=90°,OC=OB=4,∴2445==∠︒BC OCB ,.∵BC EH ⊥,∴CH=EH .∴在Rt △ACO 中,21tan ==∠CO AO ACO …………………………(1分)∵∠CBE=∠ACO ,∴在Rt △EBH 中,1tan 2EH EBH BH ∠==. 设k BH k k EH 2)0(=>=,则,CH=k,CE =. ∴243==+=k HB CH CB . ∴,324=k ……………………………………………………………(1分) ∴,38=CE ………………………………………………………………(1分) ∴,34=EO ∴),(340E .………………………………………………(1分)(3)∵ A (-2,0),B (4,0),∴抛物线的对称轴为直线x =1.………………………………………(1分)①的边时,为菱形当MCNP MC ∴,PN CM //∴∠PNC =∠NCO =45°. ∵点P 在二次函数的对称轴上,∴,的横坐标为点1P 1的横坐标为点N . ∴245sin 1==︒CN . ∵是菱形,四边形MCNP ∴,2==CN CM∴,24+=+=CM OC OM∴)240(+,M .……………………………………………………(1分) ②的边时,不存在为菱形当MCPN MC .……………………(1分)③的对角线时,为菱形当MNCP MC,于点交设Q CM NP ∴互相垂直平分,、NP CM∴1==QP NQ .,QC MQ =∵上,在直线点BC N ∠NCM =∠OCB=45°.PM CEHFBA 在Rt △CQN 中,∴∠NCQ =∠CNQ=45°,∴,1==CQ QN ∴1MQ CQ ==,∴,2=CM ∴,624=+=+=CM OC OM∴ M (0,6).………………………………………………………(1分) ∴综上所述)240(+,M 或 M (0,6).25.证明:(1)∵,AC AB =∴∠B =∠ACB . ∵,EC EF =∴∠EFC =∠ECF .…………………………………(1分)∵,BEF B EFC ∠+∠=∠又∵,ACE ACB ECF ∠+∠=∠ ∴∠BEF =∠ACE .………………………………………………(1分) ∵是公共角,EAC ∠∴△AEP ∽△ACE .……………………………………………(1分) ∴,AEAPAC AE =∴AC AP AE ⋅=2.……………………………(1分) (2)∵∠B =∠ACB ,∠ECF =∠EFC , ∴△ECB ∽△PFC .∴2⎪⎭⎫⎝⎛=∆∆CB FC S S ECB PFC .………………………………………………(1分)E EH CF H ⊥过点做于点,∵,经过圆心,CF EH EH ⊥∴x FC CH 2121==.∴x BH 214-=.…………………………(1分) 在Rt △BEH 中,∵,21tan ==∠BH EH B ∴x EH 41-2=. ∴x x EH BC S ECB 214)412(42121-=-⨯⨯=⋅=∆.…………(1分) ∴24214⎪⎭⎫⎝⎛=-x x y .∴)40(32832<<-=x x x y .………………………………………(2分) (3) ①上时,在线段当点BC F∵,21=EF FPwordA B FE C P ∴,21==EC PE EF PE ∵△AEP ∽△ACE . ∴,EC PE AC AE = ∴12AE AC =.……………………………………………………(1分) M BC AM A ,垂足为点作过点⊥.∵,AC AB =,4=BC ∴,221==BC BM 在Rt △ABM 中,∵,21tan =∠B∴1AM AB AC ==,…(1分) ∴,25=AE ∴253=BE .………………………………………(1分) ②F BC 当点在线段延长线上时,∵∠EFC =∠ECF ,EFC FCP P ∠=∠+∠, ECF B BEC ∠=∠+∠.又∵B ACB ACB FCP ∠=∠∠=∠,,∴∠B =∠FCP .∴∠P =∠BEC .∵是公共角,EAC ∠∴△AEP ∽△ACE ,∴,ECPE AC AE = ∵,21=EF FP ∴32PE PE EF EC ==,∴32AE AC =………(1分) ∴255=BE .………………(1分) 综上所述,253=BE.。
上海市浦东初三数学二模试卷2018年5月

浦东新区2017学年第二学期初三教学质量检测数 学 试 卷(完卷时间:100分钟,满分:150分)2018.5 考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸...规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸...的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列代数式中,单项式是(A )x1; (B )0; (C )1+x ; (D )x . 2.下列代数式中,二次根式n m +的有理化因式可以是(A )n m +; (B )n m -;(C )n m +; (D )n m -. 3.已知一元二次方程0122=-+x x ,下列判断正确的是(A )该方程有两个不相等的实数根; (B )该方程有两个相等的实数根;(C )该方程没有实数根; (D )该方程的根的情况不确定.4.某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是(A )平均数; (B ) 众数; (C ) 方差; (D ) 频率.5.下列y 关于x 的函数中,当0>x 时,函数值y 随x 的值增大而减小的是(A )2x y = ; (B )22+=x y ; (C )3x y = ; (D )xy 1=. 6.已知四边形ABCD 中,AB //CD ,AC=BD ,下列判断中正确..的是 (A )如果BC=AD ,那么四边形ABCD 是等腰梯形;(B )如果AD //BC ,那么四边形ABCD 是菱形;(C )如果AC 平分BD ,那么四边形ABCD 是矩形;(D )如果AC ⊥BD ,那么四边形ABCD 是正方形.二、填空题:(本大题共12题,每题4分,满分48分)7.计算:=⋅ba ab 232 ▲ .8.因式分解:=-224yx▲ .9.方程312=-x的解是▲ .10.如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张纸片),那么文字恰好组成“幸福都是奋斗出来的”概率是▲ .11. 已知正方形的边长为2cm,那么它的半径长是▲ cm.12.某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植x亩树苗,根据题意可列出关于x的方程▲ .13.近年来,出境旅游成为越来越多中国公民的假期选择.将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图1所示.那么2017年该小区居民出境游中跟团游的人数为▲ .14.如图2,在□ABCD中,E是BC中点,AE交BD于点F,如果=,那么= ▲ (用向量表示).15.在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平面观摩点B的俯角为︒60,此时点A、B之间的距离是▲ 米.16.如图3,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'= ▲ .17.如果抛物线C:)0(2≠++=acbxaxy与直线l:)0(≠+=kdkxy都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“点线和谐”关系.如果直线1+=mxy与抛物线nxxy+-=22具有“点线和谐”关系,那么=+nm▲ .18. 已知1l∥2l,1l、2l之间的距离是3cm,圆心O到直线1l的距离是1cm,如果⊙O与直线1l、2l有三个公共点,那么圆O的半径为▲ cm.图2图1图3图 5图4三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:1-312127-2-18)(++. 20.(本题满分10分)解不等式组⎪⎩⎪⎨⎧+≤-->612163x x x x , ,并把它的解集在数轴(如图4)上表示出来.21.(本题满分10分)如图5,已知AB 是⊙O 的直径,弦CD 交AB 于点E ,30=∠CEA ,OE =4,DE =35.求弦CD 及⊙O 的半径长.22.(本题满分10分,其中第(1)小题5分,第(2)小题5分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y (元)与年用天然气量x (立方米)的关系如图6所示,观察图像并回答下列问题:(1)年用天然气量不超过310立方米时,求y 关于x 的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)已知:如图7,在正方形ABCD 中,点E 为边AB 的中点,联结DE .点F 在DE 上,且CF=CD ,过点F 作FG ⊥FC 交AD 于点G .(1)求证:GF=GD ;(2)联结AF ,求证:AF ⊥DE .图6 x 1 2 –1 O 图5 图724.(本题满分12分,每小题4分)已知平面直角坐标系xOy (如图8),二次函数y =ax 2+bx +4的图像经过A (-2,0)、B (4,0)两点,与y 轴交于点C 点.(1)求这个二次函数的解析式;(2)如果点E 在线段OC 上,且∠CBE =∠ACO ,求点E 的坐标;(3)点M 在y 轴上,且位于点C 上方,点N 在直线BC 上,点P 为上述二次函数图像的对称轴...上的点,如果以C 、M 、N 、P 为顶点的四边形是菱形,求点M 的坐标. 25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图9,已知在△ABC 中,AB=AC ,21tan =B ,BC =4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C 、F (点C 、F 不重合),射线EF 与射线AC 交于点P .(1)求证:AC AP AE ⋅=2;(2)当点F 在线段BC 上,设CF =x ,△PFC 的面积为y ,求y 关于x 的函数解析式及定义域;(3)当21=EF FP 时,求BE 的长.备用图图9浦东新区2017学年度第二学期初三教学质量检测数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分)1.B ; 2.C ; 3.A ; 4.C ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.22ab ;8.()()y x y x 22-+; 9.5=x ;10.21;11.2;12.136060=+-x x ; 13.24; 14.a 32; 15.3800;16.9;17.0;18.2或4.三、解答题:(本大题共7题,满分78分) 19.解:原式23-1-222++=.…………………………………………………(8分)2-23=.………………………………………………………………(2分)20. 解:3611.26x x x x >-⎧⎪-+⎨≤⎪⎩, 由①得:62->x .…………………………………………………………(2分)解得3->x .…………………………………………………………(1分)由②得:11-3+≤x x )(.……………………………………………………(1分) 133+≤-x x .……………………………………………………(1分)42≤x .解得2≤x .……………………………………………………………(1分)∴原不等式组的解集为23-≤<x .…………………………………(2分)…………………………………(2分)21. 解:OD M CD OM O ,联结于点作过点⊥.……………………………………(1分)∵,︒=∠30CEA ∴︒=∠=∠30CEA OEM .…………………………………(1分)在Rt △OEM 中,∵OE =4,∴221==OE OM ,3223430cos =⨯=⋅=︒OE EM .(2分) ∵35=DE ,∴33=-=EM DE DM .…………(1分)∵CD OM OM ⊥过圆心,,∴DM CD 2=.…………(2分)∴36=CD .……………………………………………(1分)∵,,332==DM OM∴在Rt △DOM 中,()313322222=+=+=DM OM OD .……(1分)① ②∴ 弦CD 的长为36,⊙O 的半径长为31.……………………………(1分)22.解:(1)设)0(≠=k kx y .…………………………………………………………(1分) ∵)0(≠=k kx y 的图像过点(310,930),……………………………(1分)∴,k 310930=∴3=k .…………………………………………………(2分)∴ x y 3=.…………………………………………………………… (1分)(2)设)0(≠+=k b kx y .………………………………………………………(1分) ∵ )0(≠+=k b kx y 的图像过点(310,930)和(320,963),∴ ⎩⎨⎧=+=+63.9320930310b k b k , ∴ ⎩⎨⎧-== 3.93.3b k ,……………………………………………………………(1分) ∴933.3-=x y .…………………………………………………………(1分)当3401029933.31029==-=x x y ,解得时,.……………………(1分) 答:小明家2017年使用天然气量为340立方米.……………………(1分)23.证明:(1)∵是正方形四边形ABCD ,∴︒=∠90ADC .………(1分)∵FG ⊥FC , ∴∠GFC = 90°. …………………………(1分)∵,CD CF = ∴∠CDF =∠CFD .………………………(1分)∴∠GFC -∠CFD =∠ADC -∠CDE ,即∠GFD =∠GDF .(1分)∴GF =GD .………………………………………………(1分)(2)联结CG .∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G .……(1分)∴GC ⊥DE ,∴∠CDF +∠DCG = 90°,∵∠CDF +∠ADE = 90°,∴∠DCG =∠ADE .∵是正方形四边形ABCD ,∴AD =DC ,∠DAE =∠CDG = 90°,∴△DAE ≌△CDG .……………………………………………………(1分)∴DG AE =.………………………………………………………… (1分)∵的中点,是边点AB E ∴的中点,是边点AD G∴GF GD AG ==.……………………………………………………(1分)∴,,GFD GDF AFG DAF ∠=∠∠=∠………………………………(1分)∵,︒=∠+∠+∠+∠180GDF GFD AFG DAF ……………………(1分)∴,︒=∠+∠18022GFD AFG∴∠AFD = 90°,即AF ⊥DE .…………………………………………(1分) 证法2:(1)联结CG 交ED 于点H .∵是正方形四边形ABCD ,∴︒=∠90ADC .…………………………(1分)∵FG ⊥FC ,∴∠GFC = 90°.……………………………………………(1分)在Rt △C FG 与Rt △CDG 中,⎩⎨⎧==.CG CG CD CF ,…………………………………………………………… (1分) ∴Rt △CFG ≌Rt △CDG .………………………………………………(1分)∴GD GF =.…………………………………………………………(1分)(2)∵,,GD GF CD CF ==∴的中垂线上在线段、点FD C G . ……………………………… (1分)∴FH=HD ,GC ⊥DE ,∴∠EDC +∠DCH = 90°,∵∠ADE +∠EDC= 90°,∴∠ADE =∠DCH .……………………………………………………(1分)∵是正方形四边形ABCD ,∴AD=DC =AB ,∠DAE =∠CDG= 90°,∵GDC EAD DC AD DCH ADE ∠=∠=∠=∠,,.∴△ADE ≌△DCG .……………………………………………………(1分)∴DG AE =.…………………………………………………………(1分)∵的中点,是边点AB E ∴的中点,是边点AD G∵的中点,是边点FD H ∴GH 是△AFD 的中位线.………………(1分)∴,AF GH //∴,GHD AFD ∠=∠∵GH ⊥FD ,∴∠GHD = 90°,………………………………………(1分)∴∠AFD = 90°,即AF ⊥DE .………………………………………(1分)24.解:(1)∵ 抛物线42++=bx ax y 与x 轴交于点A (-2,0),B (4,0),∴ ⎩⎨⎧=++=+.04416042-4b a b a ;…………………………………………………(1分) 解得⎪⎩⎪⎨⎧==.121-b a ;…………………………………………………………(2分)∴ 抛物线的解析式为421-2++=x x y .……………………………(1分)(2)H BC EH E 于点作过点⊥.在Rt △ACO 中, ∵A (-2,0),∴ OA 4421-02=++==x x y x 时,当,∴OC= 在Rt △C OB 中,∵∠COB=90°,∴2445==∠︒BC OCB ,.∵BC EH ⊥,∴CH=EH .∴在Rt △ACO 中,21tan ==∠CO AO ACO …………………………(1分) ∵∠CBE=∠ACO ,∴在Rt △EBH 中,1tan 2EH EBH BH ∠==. 设k BH k k EH 2)0(=>=,则,CH=k,CE =. ∴243==+=k HB CH CB . ∴,324=k ……………………………………………………………(1分) ∴,38=CE ………………………………………………………………(1分) ∴,34=EO ∴),(340E .………………………………………………(1分)(3)∵ A (-2,0),B (4,0),∴抛物线的对称轴为直线x =1.………………………………………(1分)①的边时,为菱形当MCNP MC∴,PN CM //∴∠PNC =∠NCO =45°.∵点P 在二次函数的对称轴上, ∴,的横坐标为点1P 1的横坐标为点N . ∴245sin 1==︒CN . ∵是菱形,四边形MCNP ∴,2==CN CM ∴,24+=+=CM OC OM ∴)240(+,M .……………………………………………………(1分)②的边时,不存在为菱形当MCPN MC .……………………(1分)③的对角线时,为菱形当MNCP MC,于点交设Q CM NP ∴、NP CM ∴1==QP NQ .,QC MQ =∵上,在直线点BC N ∠NCM =∠OCB=45°.PM CEH F B A在Rt △CQN 中,∴∠NCQ =∠CNQ=45°,∴,1==CQ QN ∴1MQ CQ ==,∴,2=CM ∴,624=+=+=CM OC OM∴ M (0,6).………………………………………………………(1分)∴综上所述)240(+,M 或 M (0,6).25.证明:(1)∵,AC AB =∴∠B =∠ACB .∵,EC EF =∴∠EFC =∠ECF .…………………………………(1分)∵,BEF B EFC ∠+∠=∠又∵,ACE ACB ECF ∠+∠=∠∴∠BEF =∠ACE .………………………………………………(1分)∵是公共角,EAC ∠∴△AEP ∽△ACE .……………………………………………(1分) ∴,AEAP AC AE =∴AC AP AE ⋅=2.……………………………(1分) (2)∵∠B =∠ACB ,∠ECF =∠EFC ,∴△ECB ∽△PFC .∴2⎪⎭⎫ ⎝⎛=∆∆CB FC S S ECB PFC .………………………………………………(1分) E EH CF H ⊥过点做于点, ∵,经过圆心,CF EH EH ⊥ ∴x FC CH 2121==.∴x BH 214-=.…………………………(1分) 在Rt △BEH 中,∵,21tan ==∠BH EH B ∴x EH 41-2=. ∴x x EH BC S ECB 214)412(42121-=-⨯⨯=⋅=∆.…………(1分) ∴24214⎪⎭⎫ ⎝⎛=-x x y . ∴)40(32832<<-=x x x y .………………………………………(2分) (3) ①上时,在线段当点BC F∵,21=EF FPA B FE C P ∴,21==EC PE EF PE ∵△AEP ∽△ACE . ∴,EC PE AC AE = ∴12AE AC =.……………………………………………………(1分) M BC AM A ,垂足为点作过点⊥.∵,AC AB =,4=BC ∴,221==BC BM 在Rt △ABM 中,∵,21tan =∠B∴1AM AB AC ===,…(1分) ∴,25=AE ∴253=BE .………………………………………(1分) ②F BC 当点在线段延长线上时,∵∠EFC =∠ECF ,EFC FCP P ∠=∠+∠, ECF B BEC ∠=∠+∠.又∵B ACB ACB FCP ∠=∠∠=∠,,∴∠B =∠FCP .∴∠P =∠BEC .∵是公共角,EAC ∠∴△AEP ∽△ACE ,∴,ECPE AC AE = ∵,21=EF FP ∴32PE PE EF EC ==,∴32AE AC =………(1分) ∴255=BE .………………(1分) 综上所述,253=BE.。
2018年年上海市中考数学二模试卷含答案

2018学年第二学期期中教学质量调研九年级数学试卷(满分150分,100分钟完成)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本调研卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个是正确的,旋转正确项的代号并填涂在答题纸的相应位置上]1.下列实数中,有理数是( )(A )2; (B (C (D 2.下列方程中,有实数根的是( )(Ax =; (B )2(2)10x +-=; (C )210x +=; (D 0. 3.如果a >b ,m <0,那么下列不等式中成立的是( )(A )am >bm ; (B )a b m m>; (C )a +m >b +m ; (D )-a +m >-b +m .4.如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,EG 平分∠BEF ,如果∠EFG =64°,那么∠EGD 的大小是( ) (A )122°;(B )124°;(C )120°;(D )126°.5.已知两组数据:12345a a a a a 、、、、和123451a a a a a --1、-1、-1、-1、,下列判断中错误的是( )(A )平均数不相等,方差相等; (B )中位数不相等,标准差相等; (C )平均数相等,标准差不相等;(D )中位数不相等,方差相等. 6.下列命题中,假命题是( )(A )两组对角分别相等的四边形是平行四边形;(B )有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形; (C )一组邻边互相垂直,两组对边分别平行的四边形是矩形; (D )有一组邻边相等且互相垂直的平行四边形是正方形.二、填空题:(本大题共12题,每题4分,满分48分) [在答题纸相应题号后的空格内直接填写答案] 7.计算:23(2)a a ⋅= ▲ .8.分解因式:2()4x y xy -+= ▲ .9.方程组3,26x y y x +=⎧⎨-=⎩的解是 ▲ .10有意义,那么x 的取值范围是 ▲ .11.如果函数21a y x--=(a 为常数)的图像上有两点1(1,)y ,21(,)3y ,那么函数值1y ▲2y (填“<”,“=”或“>”).12.为了解植物园的某种花卉的生长情况,在一片约为3000株此类花卉的园地内,随机检测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)试估计该园地内此类花卉高度小于55厘米且不小于45厘米的约为 ▲株. 13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数既是奇数又是素数的概率是▲ .14.如图,在△ABC 中,点G 是重心,过点G 作DE ∥BC 分别交AB 、AC 于点D 、E ,已知,AB a CB b == ,那么AE =▲ (用向量表示). 15.如图,已知O 中,直径AB 平分弦CD ,且交CD 于点E ,如果OE =BE ,那么弦CD 所对的圆心角是▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正多边形的边心距是 ▲ .(用含字母a 的代数式表示)17. 在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:(,)(,),(,)(,)f a b a b g a b b a =--=-,那么g [f (1, -2)] ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .三、解答题:(本大题共7题,满分78分)[将下列各题的解答过程,做在答题纸的相应位置上]19.(本题满分10分)201801(cot 45)(3)(sin 30)π--︒++--︒.20.(本题满分10分) 解方程:2456111x xx x x ++=+--.21.(本题满分10分,每小题满分5分)已知:如图,边长为1的正方形ABCD 中,对角线AC 、DB 交于点H ,DE 平分∠ADB ,交AC 于点E ,联结BE 并延长,交边AD 于点F . 求:(1)求证:DC =EC ; (2)求△EAF 的面积.今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价位10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式;(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?(销售利润=销售价-成本价).23.(本题满分12分,第小题满分6分)已知,如图,在平行四边形ABCD中,AC、DB交于点E,点F在BC的延长线上,联结EF、DF,且∠DEF=∠ADC.求证:(1)求证:EF AB=;BF DB(2)如果22=⋅,求证:平行四边形ABCD是矩形.BD AD DF在平面直角坐标系xOy 中,已知点B (8,0)和点C (9,-3)抛物线28y ax ax c =-+(a 、c是常数,a ≠0)经过点B 、C ,且与x 轴的另一个交点为A ,对称轴上有一点M ,满足MA =MC . (1)求这条抛物线的表达式; (2)求四边形ABCM 的面积;(3)如果坐标系内有一点D ,满足三角形ABCD 是等腰梯形,且AD ∥BC ,求点D 的坐标.25.(本题满分14分,第(1)小题满分6分,第(2)小题满分8分)如图,平行四边形ABCD 中,已知AB =6,BC =9,cos ∠ABC =13,对角线AC 、BD 交于点O ,动点P 在边AB 上,P 经过点B ,交线段P A 于点E ,设BP =x ..(1)求AC 的长;(2)设O 的半径为y ,当P 与O 外切时,求y 关于x 的函数关系式,并写出定义域; (3)如果AC 是O 的直径,O 经过点E ,求O 与P 的圆心距OP 的长.九年级数学试卷参考答案及评分标准1、D ,2、B ,3、C ,4、A ,5、C ,6、B7、54a ,8、2()x y +,9、14x y =-⎧⎨=⎩,10、x >4,11、>,12、960,13、13,14、2233a b -,15、120,16,17、(2,1),18111920、x =9,21、(1)略(222、y =-2x +60,(2)15 23、略,24、(1)21833y x x =-+,(2)392,(3)1339(,)55D -,25、(1)9,(2)3)y x <≤,(3)。
上海18年初三数学各区二模23题汇编(含答案)

18年 二模23题汇编求线段比值或者证明线段倍数关系:1. 构造“A ”字形或“8”字形,利用比例线段常见于背景为平行四边形、特殊平行四边形或者梯形等存在隐含平行的几何图形的题目,或者题目已知平行或比值,以及燕尾形中。
2. 利用相似,对应边成比例 3. 利用锐角三角比常见于以直角三角形,矩形、正方形为背景,或者本身已知垂直的题目,遇到等腰梯形或直角梯形也常添加垂直与锐角三角比结合23.(普陀)已知:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =.(1)求证:四边形ABED 是菱形; (2)联结AE ,又知AC ⊥ED ,求证:212AE EF ED =.23.证明: (1)∵AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ·································· (2分) ∵FG ∥AD ,∴FG CFAD CA=. ············································································· (1分) 同理 EF CF AB CA =. ···························································································· (1分) 得FG AD =EF AB∵FG EF =,∴AD AB =. ·············································································· (1分) ∴四边形ABED 是菱形. ····················································································· (1分) (2)联结BD ,与AE 交于点H .∵四边形ABED 是菱形,∴,BD ⊥AE . ········································· (2分)得90DHE ∠= .同理90AFE ∠=. ∴DHE AFE ∠∠=. ························································································ (1分) 又∵AED ∠是公共角,∴△DHE ∽△AFE . ······················································ (1分) ∴EH DE EF AE =. ································································································ (1分) ∴12AE 2=EF i ED . ······················································································· (1分)12EH AE =ABCDEF G图923(崇明)如图,AM 是ABC △的中线,点D 是线段AM 上一点(不与点A 重合).DE AB ∥交BC 于点K ,CE AM ∥,联结AE .(1)求证:AB CMEK CK=; (2)求证:BD AE =.23.(本题满分12分,每小题6分) (1)证明:∵DE AB ∥∴ ABCEKC =∠∠ ……………………………………………………1分 ∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分 ∴AB CMEK CK=………………………………………………………1分 (2)证明:∵CE AM ∥∴DE CMEK CK =………………………………………………………2分 又∵AB CMEK CK=∴DE AB = ………………………………………………………2分 又∵DE AB ∥∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分23.(奉贤)已知:如图7,梯形ABCD ,DC ∥AB ,对角线AC 平分∠BCD ,点E 在边CB 的延长线上,EA ⊥AC ,垂足为点A . (1)求证:B 是EC 的中点;(2)分别延长CD 、EA 相交于点F ,若EC DC AC ⋅=2,求证:FC AC AF AD ::=.(第23题图)ABK MCDEACDE图7B23.(本题满分12分,每小题满分各6分)证明:(1)∵DC ∥AB ,∴∠DCB =∠CAB . ……………………………………………1分 ∵AC 平分∠BCD ,∴∠DCB =∠BCA .∴∠CAB =∠BCA . ………………………………………………………………………1分 ∴BC =BA . ………………………………………………………………………………1分 ∵EA ⊥AC ,∴∠CAB +∠BAE=90°,∠BCA +∠E=90°. ∴∠BAE =∠E . …………1分 ∴BA =BE . …………………………………………………………………………………1分 ∴BC =BE ,即B 是EC 的中点. ………………………………………………………1分 (2)∵EC DC AC ⋅=2,∴AC EC DC AC ::=.∵∠DCA =∠ACE ,∴△DCA ∽△ACE . ………………………………………………2分 ∴EC AC AE AD ::=.……………………………………………………………………1分 ∵∠FCA =∠ECA ,AC=AC ,∠F AC =∠EAC ,∴△FCA ≌△ECA . …………………2分 ∴AE =AF ,EC =FC .∴FC AC AF AD ::=. …………………………………………………………………1分23.(黄浦)如图,点E 、F 分别为菱形ABCD 边AD 、CD 的中点. (1)求证:BE =BF ;(2)当△BEF 为等边三角形时,求证:∠D =2∠A .23. 证:(1)∵四边形ABCD 为菱形,∴AB =BC =AD =CD ,∠A =∠C ,——————————————————(2分) 又E 、F 是边的中点,∴AE =CF ,——————————————————————————(1分)∴△ABE ≌△CBF ———————————————————————(2分) ∴BE =BF . ——————————————————————————(1分)(2)联结AC 、BD ,AC 交BE 、BD 于点G 、O . ——————————(1分) ∵△BEF 是等边三角形, ∴EB =EF ,又∵E 、F 是两边中点, ∴AO =12AC =EF =BE .——————————————————————(1分) 又△ABD 中,BE 、AO 均为中线,则G 为△ABD 的重心, ∴1133OGAO BE GE ===, ∴AG =BG ,——————————————————————————(1分) 又∠AGE =∠BGO ,∴△AGE ≌△BGO ,———— ——————————————————(1分)∴AE =BO ,则AD =BD ,∴△ABD 是等边三角形,—— —————————————————(1分) 所以∠BAD =60°,则∠ADC =120°,即∠ADC =2∠BAD . ——— ——————————————————(1分)FEDCBAE G第23题图C A B DF23.(虹口)如图,四边形ABCD 是矩形,E 是对角线AC 上的一点,EB =ED 且∠ABE =∠ADE . (1)求证:四边形ABCD 是正方形;(2)延长DE 交BC 于点F ,交AB 的延长线于点G ,求证:EF AG BC BE ⋅=⋅.23. 证:(1)证明:联结BD …………………………………………………………………(1分)∵EB =ED ∴∠EBD =∠EDB …………………………………………………(2分)∵∠ABE =∠ADE ∴∠ABD =∠ADB …………………………………………(1分) ∴AB=AD …………………………………………………………………………(1分) ∵四边形ABCD 是矩形 ∴四边形ABCD 是正方形………………………(1分) (2)证明:∵四边形ABCD 是矩形∴AD ∥BC ∴EF ECDE EA =………………………………………………(2分)同理 DC EC AG EA =……………………………………………………………(2分)∵DE=BE∵四边形ABCD 是正方形 ∴BC=DC …………………………………………(1分) ∴EF BC BE AG =∴EF AG BC BE ⋅=⋅ ……………………………………………………………(1分)证明乘积式:1. 化成比例式找相似相似找法,一般为横看或者竖看比例式当中的线段,观察构成两条线段的三个顶点即为要找的三角形顶点2. 找中间量进行转化:1) 找中间比利用等比转化 2) 找中间积利用等积进行转化3. 特殊四边形的特性与判定条件,如对角线相互平分 23.(闵行)如图,已知在△ABC 中,∠BAC =2∠C ,∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ,FG ∥AC ,联结DG .(1)求证:BF BC AB BD ⋅=⋅; (2)求证:四边形ADGF 是菱形.23.证明:(1)∵AE 平分∠BAC ,∴∠BAC =2∠BAF =2∠EAC .∵∠BAC =2∠C ,∴∠BAF =∠C =∠EAC .…………………………(1分) 又∵BD 平分∠ABC ,∴∠ABD =∠DBC .……………………………(1分) ∵∠ABF =∠C ,∠ABD =∠DBC ,∴ABF CBD ∆∆∽.…………………………………………………(1分) ∴AB BF BC BD=.………………………………………………………(1分) ∴BF BC AB BD ⋅=⋅.………………………………………………(1分) (2)∵FG ∥AC ,∴∠C =∠FGB ,∴∠FGB =∠F AB .………………(1分)∵∠BAF =∠BGF ,∠ABD =∠GBD ,BF =BF ,∴ABF GBF ∆∆≌.∴AF =FG ,BA =BG .…………………………(1分) ∵BA =BG ,∠ABD =∠GBD ,BD =BD ,∴ABD GBD ∆∆≌.∴∠BAD =∠BGD .……………………………(1分) ∵∠BAD =2∠C ,∴∠BGD =2∠C ,∴∠GDC =∠C ,∴∠GDC =∠EAC ,∴AF ∥DG .……………………………………(1分) 又∵FG ∥AC ,∴四边形ADGF 是平行四边形.……………………(1分) ∴AF =FG .……………………………………………………………(1分) ∴四边形ADGF 是菱形.……………………………………………(1分)AB E GC F D(第23题图)23.(青浦)如图7,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点M ,点E 在边 BC 上,且DAE DCB ∠=∠,联结AE ,AE 与BD 交于点F .(1)求证:2DM MF MB =⋅; (2)联结DE ,如果3BF FM =,求证:四边形ABED 是平行四边形.23.证明:(1)∵AD //BC ,∴∠=∠DAE AEB , ············································· (1分)∵∠=∠DCB DAE ,∴∠=∠DCB AEB , ································ (1分) ∴AE //DC ,··········································································· (1分)∴=FM AMMD MC. ··································································· (1分) ∵AD //BC ,∴=AM DMMC MB, ··················································· (1分) ∴=FM DM MD MB, ··································································· (1分) 即2=⋅MD MF MB .(2)设=FM a ,则=3BF a ,=4BM a . ··········································· (1分)由2=⋅MD MF MB ,得24=⋅MD a a ,∴2=MD a , ········································································ (1分)∴3==DF BF a . ·································································· (1分) ∵AD //BC ,∴1==AF DFEF BF, ···················································· (1分) ∴=AF EF , ········································································· (1分) ∴四边形ABED 是平行四边形. ··················································· (1分)MFE DCBA图723.(松江)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:(1)四边形BCEF 是菱形;(2).证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE ∴∠AEB =90°∵F 是AB 的中点∴………………………………………………1分∴∠FEB =∠FBE …………………………………………………1分 ∴∠FEB =∠CBE …………………………………………………1分 ∴EF ∥BC …………………………………………………1分 ∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分 ∵∴四边形BCEF 是菱形……………………………………1分 (2) ∵四边形BCEF 是菱形, ∴BC =BF ∵ ∴AB =2BC ………………………………………………1分 ∵ AB ∥CD∴ ∠DEA =∠EAB ∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴ …………………………………………1分∴ BE ·AE =AD ·AB∴ …………………………………1分2BE AE AD BC ⋅=⋅12EF BF AB ==EF BF =12BF AB =AD AEBE AB =2BE AE AD BC ⋅=⋅(第23题图)FA CD EB23. (徐汇)在梯形ABCD 中,AD ∥BC ,AB CD =,BD BC =,点E 在对角线BD 上,且DCE DBC ∠=∠. (1)求证:AD BE =;(2)延长CE 交AB 于点F ,如果CF AB ⊥, 求证:4EF FC DE BD ⋅=⋅.23.(长宁)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =.(1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.证明:(1)∵BC AD // ∴BGDG BE AD = (2分)∵AG GF BE AD = ∴AGGF BG DG = (1分) ∴ CD AB // (2分)(2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分)∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分)∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分) ∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分) 23.(宝山嘉定)如图6,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 边的延长线上,且满足︒=∠90MAN ,联结MN 、AC ,MN 与边AD 交于点E . (1)求证:AN AM =;ACDEF GB第23题图(2)如果NAD CAD ∠=∠2,求证:AE AC AM ⋅=2.证明垂直:1. 所求角所在的三角形与已知直角三角形相似2. 三线合一,勾股定理,证明互余等3. 特殊的四边形特性与判定23.(金山)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F .(1)求证:四边形AEBD 是平行四边形;(2)如果AC =3AF ,求证四边形AEBD 是矩形.23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,…………………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,………………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………………(1分) ∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………………(2分)(2)∵AE //BC,∴AF AEFB BC=.………………………………………………………(1分) ∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分)∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分) 又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.…………………………………………………………(1分)E AF M B D图7C23.(静安)已知:如图,在平行四边形ABCD 中, AC 、DB 交于点E , 点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC . (1)求证:DBABBF EF =; (2)如果DF AD BD ⋅=22,求证:平行四边形ABCD 是矩形.23.(本题满分12分,第(1)小题6分,第(2)小题6分) 证明:(1)∵平行四边形ABCD ,∴AD //BC ,AB //DC∴∠BAD +∠ADC =180°,……………………………………(1分)又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……(1分) ∵∠DEF =∠ADC ∴∠BAD =∠BEF , …………………………(1分) ∵AB //DC , ∴∠EBF =∠ADB …………………………(1分)∴△ADB ∽△EBF ∴DB ABBF EF =………………………(2分) (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………(1分) 在平行四边形ABCD 中,BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………(1分) 又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………(1分) ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………(1分) ∴∠ADC =∠DEF =90° …………………………(1分) ∴平行四边形ABCD 是矩形 …………………………(1分)C第23题图A B DEF11 / 1123. (杨浦)已知:如图7,在平行四边形ABCD 中,点G 为对角线AC 的中点,过点G 的直线EF 分别交边AB 、CD 于点E 、F ,过点G 的直线MN 分别交边AD 、BC 于点M 、N ,且AGE CGN .(1)求证:四边形ENFM 为平行四边形;(2)当四边形ENFM 为矩形时,求证:BE BN .(1)ABCD 是平行四边形∴BC AD CD AB ∥,∥∴ACB DAC ∠=∠在AMG △与CNG △中⎪⎩⎪⎨⎧∠=∠=∠=∠CGNAGM GC AG ACBDACCNG AMG ≌△△∴GN MG =同理CFG AEG ≌△△∴GF EG =∴EMFN 是平行四边形(2)EMFN 是矩形∴GN EG =在AEG △与CNG △中⎪⎩⎪⎨⎧=∠=∠=GNEG CGN AGE GCAGCNG AGE ≌△△∴NC AE GCN GAE =∠=∠,∴AC AB =∴BN EB =。
2018年上海市浦东新区中考数学二模试卷含答案

2018年上海市浦东新区中考数学二模试卷一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4分)下列代数式中,单项式是()A .B .0C .x+1D .2.(4分)下列代数式中,二次根式的有理化因式可以是()A .B .C .D ..3.(4分)已知一元二次方程x 2+2x ﹣1=0,下列判断正确的是()A .该方程有两个不相等的实数根B .该方程有两个相等的实数根C .该方程没有实数根D .该方程的根的情况不确定4.(4分)某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A .平均数B .众数C .方差D .频率5.(4分)下列y 关于x 的函数中,当x >0时,函数值y 随x 的值增大而减小的是()A .y =x2B .yC .yD .y6.(4分)已知四边形ABCD 中,AB ∥CD ,AC =BD ,下列判断中正确的是()A .如果BC =AD ,那么四边形ABCD 是等腰梯形B .如果AD ∥BC ,那么四边形ABCD 是菱形C .如果AC 平分BD ,那么四边形ABCD 是矩形D .如果AC ⊥BD ,那么四边形ABCD 是正方形二.填空题:(本大题共12题,每题4分,满分48分)7.(4分)计算:.8.(4分)因式分解:x 2﹣4y 2=.9.(4分)方程3的解是.10.(4分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.11.(4分)已知正方形的边长为2cm ,那么它的半径长是cm .12.(4分)某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x的方程.13.(4分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为.14.(4分)如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果,那么(用向量表示).15.(4分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.16.(4分)如图,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'=.17.(4分)如果抛物线C:y=ax 2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,那么m+n=.18.(4分)已知l1∥l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为cm.三、解答题:(本大题共7题,满分78分)19.(10分)|1|﹣27()﹣120.(10分)解不等式组:>,并把它的解集在数轴(如图)上表示出来.21.(10分)如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.22.(10分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.23.(12分)已知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF =CD,过点F作FG⊥FC交AD于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.24.(12分)已知平而直角坐标系xOy(如图),二次函数y=ax 2+bx+4的图象经过A(﹣2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图象的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.25.(14分)如图,已知在△ABC中,AB=AC,tanB,BC=4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP?AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当时,求BE的长.2018年上海市浦东新区中考数学二模试卷参考答案与试题解析一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4分)下列代数式中,单项式是()A.B.0C.x+1D.【解答】解:A、不是单项式,不符合题意;B、0是单项式,符合题意;C、x+1是多项式,不符合题意;D、不是单项式,不符合题意;故选:B.2.(4分)下列代数式中,二次根式的有理化因式可以是()A.B.C.D..【解答】解:∵()2=m+n,∴二次根式的有理化因式是,故选:C.3.(4分)已知一元二次方程x 2+2x﹣1=0,下列判断正确的是()A.该方程有两个不相等的实数根B.该方程有两个相等的实数根C.该方程没有实数根D.该方程的根的情况不确定【解答】解:∵a=1,b=2,c=﹣1,∴△=b2﹣4ac=22﹣4×1×(﹣1)=8>0,∴该方程有两个不相等的实数根.故选:A.4.(4分)某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A.平均数B.众数C.方差D.频率【解答】解:在平均数、众数、方差、频率这些统计量中,表示一组数据波动程度的量是方差.故选:C .5.(4分)下列y 关于x 的函数中,当x >0时,函数值y 随x 的值增大而减小的是()A .y =x2B .yC .yD .y【解答】解:A 、二次函数y =x 2的图象,开口向上,并向上无限延伸,在y 轴右侧(x >0时),y 随x 的增大而增大;故本选项错误;B 、一次函数y x+1的图象,y 随x 的增大而增大;故本选项错误;C 、正比例函数y x 的图象在一、三象限内,y 随x 的增大而增大;故本选项错误;D 、反比例函数y中k =1>0,所以当x >0时,y 随x 的增大而减小;故本选项正确;故选:D .6.(4分)已知四边形ABCD 中,AB ∥CD ,AC =BD ,下列判断中正确的是()A .如果BC =AD ,那么四边形ABCD 是等腰梯形B .如果AD ∥BC ,那么四边形ABCD 是菱形C .如果AC 平分BD ,那么四边形ABCD 是矩形D .如果AC ⊥BD ,那么四边形ABCD 是正方形【解答】解:A .如果BC =AD ,那么四边形ABCD 可能是等腰梯形,也可能是矩形,错误;B .如果AD ∥BC ,那么四边形ABCD 是矩形,错误;C .如果AC 平分BD ,那么四边形ABCD 是矩形,正确;D .如果AC ⊥BD ,那么四边形ABCD 不一定是正方形,错误;故选:C .二.填空题:(本大题共12题,每题4分,满分48分)7.(4分)计算:3ab2.【解答】解:原式=3ab 2故答案为:3ab28.(4分)因式分解:x 2﹣4y 2=(x+2y )(x ﹣2y ).【解答】解:x 2﹣4y 2=(x+2y )(x ﹣2y ).9.(4分)方程3的解是x =5.【解答】解:平方,得2x ﹣1=9,解得x =5,故答案为:x=5.10.(4分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.【解答】解:∵将分别写有“幸福”、“奋斗”的2张卡片,随机放入两个框中,只有两种情况,恰好组成“幸福都是奋斗出来的”的情况只有一种,∴其概率是:,故答案为:.11.(4分)已知正方形的边长为2cm,那么它的半径长是cm.【解答】解:如图,∵AB=2,∴OC=1,∴OA,故答案为:12.(4分)某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x的方程.【解答】解:设原计划每天种植x亩,根据题意可得:,故答案为:,13.(4分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为24.【解答】解:∵被调查的总人数为36÷45%=80,∴2017年该小区居民出境游中跟团游的人数为80﹣36﹣20=24(人),故答案为:24.14.(4分)如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果,那么(用向量表示).【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC.∵E是BC的中点,AE交BD于点F,∴2∴AF AE.又,那么.故答案是:.15.(4分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.【解答】解:根据题意得:直升飞机与观摩点B之间的距离是AB米.故答案为:800.16.(4分)如图,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'=9.【解答】解:如图,将△ABD绕着点D逆时针旋转得到△CB′D,作DE∥AB交BC于E,则ABED是平行四边形,BE=AD=3,DE=AB=3,∴EC=BC﹣BE=6﹣3=3,∵DC=3,∴DE=EC=DC=3,∴△DCE是等边三角形,∴∠DCE=60°.∵在梯形ABCD中,AD∥BC,AB=DC,∴∠ABC=∠DCB=60°,∠A=120°,∵将△ABD绕着点D逆时针旋转得到△CB′D,∴△CB′D≌△ABD,∴∠DCB′=∠A=120°,CB′=AB=3,∴∠BCB′=∠BCD+∠DCB′=120°+60°=180°,∴B、C、B′三点共线,∴BB′=BC+CB′=6+3=9.故答案为9.17.(4分)如果抛物线C:y=ax 2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,那么m+n=0.【解答】解:在y=mx+1中,令x=0可求得y=1,在y=x2﹣2x+n中,令x=0可得y=n,∵直线与抛物线都经过y轴上的一点,∴n=1,∴抛物线解析式为y=x2﹣2x+1=(x﹣1)2,∴抛物线顶点坐标为(1,0),∵抛物线顶点在直线上,∴0=m+1,解得m=﹣1,∴m+n=﹣1+1=0,故答案为:0.18.(4分)已知l1∥l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为2或4cm.【解答】解:如下图所示,设圆的半径为r如图一所示,r﹣1=3,得r=4,如图二所示,r+1=3,得r=2,故答案为:2或4.三、解答题:(本大题共7题,满分78分)19.(10分)|1|﹣27()﹣1【解答】解:原式=21﹣3+2=32.20.(10分)解不等式组:>,并把它的解集在数轴(如图)上表示出来.【解答】解:>①由①得:x>﹣3;由得:x≤2;∴原不等式组的解集为﹣3<x≤2,.21.(10分)如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.【解答】解:过点O作OM⊥CD于点M,联结OD,∵∠CEA=30°,∴∠OEM=∠CEA=30°,在Rt△OEM中,∵OE=4,∴,,∵,∴,∵OM过圆心,OM⊥CD,∴CD=2DM,∴,∵,,∴在Rt△DOM中,,∴弦CD的长为,⊙O的半径长为.22.(10分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.【解答】解:(1)设y=kx(k≠0).∵y=kx(k≠0)的图象过点(310,930),∴930=310k,∴k=3.∴y=3x.(2)设y=kx+b(k≠0).∵y=kx+b(k≠0)的图象过点(310,930)和(320,963),∴,∴∴y=3.3x﹣9.3,当y=1029时,3.3x﹣9.3=1029,解得x=340,答:小明家2017年使用天然气量为340立方米.23.(12分)已知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF =CD,过点F作FG⊥FC交AD于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.【解答】证明:(1)∵四边形ABCD是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,∵CF=CD,∴∠CDF=∠CFD,∴∠GFC﹣∠CFD=∠ADC﹣∠CDE,即∠GFD=∠GDF,∴GF=GD.(2)联结CG.∵CF=CD,GF=GD,∴点G、C在线段FD的中垂线上,∴GC⊥DE,∴∠CDF+∠DCG=90°,∵∠CDF+∠ADE=90°,∴∠DCG=∠ADE.∵四边形ABCD是正方形,∴AD=DC,∠DAE=∠CDG=90°,∴△DAE≌△CDG,∴AE=DG,∵点E是边AB的中点,∴点G是边AD的中点,∴AG=GD=GF,∴∠DAF=∠AFG,∠GDF=∠GFD,∵∠DAF+∠AFG+∠GFD+∠GDF=180°,∴2∠AFG+2∠GFD=180°,∴∠AFD=90°,即AF⊥DE.证法2:(1)联结CG交ED于点H.∵四边形ABCD是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,在Rt△CFG与Rt△CDG中,,∴Rt△CFG≌Rt△CDG,∴GF=GD.(2)∵CF=CD,GF=GD,∴点G、C在线段FD的中垂线上,∴FH=HD,GC⊥DE,∴∠EDC+∠DCH=90°,∵∠ADE+∠EDC=90°,∴∠ADE=∠DCH,∵四边形ABCD是正方形,∴AD=DC=AB,∠DAE=∠CDG=90°,∵∠ADE=∠DCH,AD=DC,∠EAD=∠GDC.∴△ADE≌△DCG,∴AE=DG,∵点E是边AB的中点,∴点G是边AD的中点,∵点H是边FD的中点,∴GH是△AFD的中位线,∴GH∥AF,∴∠AFD=∠GHD,∵GH⊥FD,∴∠GHD=90°,∴∠AFD=90°,即AF⊥DE.24.(12分)已知平而直角坐标系xOy(如图),二次函数y=ax 2+bx+4的图象经过A(﹣2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图象的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.【解答】解:(1)∵抛物线y=ax2+bx+4与x轴交于点A(﹣2,0),B(4,0),∴,解得,∴抛物线的解析式为,(2)如图1,过点E作EH⊥BC于点H.在Rt△ACO中,∵A(﹣2,0),∴OA=2,当时,,∴OC=4,在Rt△COB中,∵∠COB=90°,OC=OB=4,∴∠,.∵EH⊥BC,∴CH=EH.∴在Rt△ACO中,∠,∵∠CBE=∠ACO,在Rt△EBH中,∠.设EH=k(k>0),则BH=2k,CH=k,.∴.∴,∴,∴,∴,,(3)∵A(﹣2,0)、B(4,0)∴抛物线的对称轴为直线x=1,①当MC为菱形MCNP的边时,∴CM∥PN,∴∠PNC=∠NCO=45°.∵点P在二次函数的对称轴上,∴点P的横坐标为1,点N的横坐标为1.∴.∵四边形MCNP是菱形,∴,∴,∴,,如图2,当MC为菱形MNCP的对角线时,设NP交CM于点Q,∴CM、NP互相垂直平分,∴NQ=QP=1.MQ=QC,∵点N在直线BC上,∠NCM=∠OCB=45°.在Rt△CQN中,∴∠NCQ=∠CNQ=45°,∴QN=CQ=1,∴MQ=CQ=1,∴CM=2,∴OM=OC+CM=4+2=6,∴M(0,6),∴综上所述,或M(0,6).25.(14分)如图,已知在△ABC中,AB=AC,tanB,BC=4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP?AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当时,求BE的长.【解答】证明:(1)∵AB=AC,∴∠B=∠ACB.∵EF=EC,∴∠EFC=∠ECF,∵∠EFC=∠B+∠BEF,又∵∠ECF=∠ACB+∠ACE,∴∠BEF=∠ACE,∵∠EAC是公共角,∴△AEP∽△ACE,∴,∴AE2=AP?AC,(2)∵∠B=∠ACB,∠ECF=∠EFC,∴△ECB∽△PFC.∴,过点E作EH⊥CF于点H,∵EH经过圆心,EH⊥CF,∴.∴,在Rt△BEH中,∵∠,∴.∴,∴.∴<<,(3)①当点F在线段BC上时,∵,∴,∵△AEP∽△ACE.∴,∴,过点A作AM⊥BC,垂足为点M.∵AB=AC,BC=4,∴,在Rt△ABM中,∵∠,∴,∴,∴,当点F在线段BC延长线上时,∵∠EFC=∠ECF,∠EFC=∠FCP+∠P,∠ECF=∠B+∠BEC.又∵∠B=∠ACB,∠ACB=∠FCP,∴∠B=∠FCP.∴∠P=∠BEC.∵∠EAC是公共角,∴△AEP∽△ACE,∴,∵,∴,∴,∴,综上所述,或.。
2018届中考数学二模-浦东答案(带参考答案)

浦东新区2017学年度第二学期初三教学质量检测数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分)1.B ; 2.C ; 3.A ; 4.C ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.22ab ;8.()()y x y x 22-+; 9.5=x ;10.21;11.2;12.136060=+-x x ; 13.24; 14.a 32; 15.3800;16.9;17.0;18.2或4.三、解答题:(本大题共7题,满分78分)19.解:原式23-1-222++=.…………………………………………………(8分)2-23=.………………………………………………………………(2分)20. 解:3611.26x x x x >-⎧⎪-+⎨≤⎪⎩, 由①得:62->x .…………………………………………………………(2分)解得3->x .…………………………………………………………(1分)由②得:11-3+≤x x )(.……………………………………………………(1分)133+≤-x x .……………………………………………………(1分)42≤x .解得2≤x .……………………………………………………………(1分)∴原不等式组的解集为23-≤<x .…………………………………(2分) -44321-1-2-3x O …………………………………(2分)21. 解:OD M CD OM O ,联结于点作过点⊥.……………………………………(1分)∵,︒=∠30CEA ∴︒=∠=∠30CEA OEM .…………………………………(1分)在Rt △OEM 中,∵OE =4,∴221==OE OM ,3223430cos =⨯=⋅=︒OE EM .(2分) ∵35=DE ,∴33=-=EM DE DM .…………(1分)∵CD OM OM ⊥过圆心,,∴DM CD 2=.…………(2分)∴36=CD .……………………………………………(1分)∵,,332==DM OM∴在Rt △DOM 中,()313322222=+=+=DM OM OD .……(1分)∴ 弦CD 的长为36,⊙O 的半径长为31.……………………………(1分)22.解:(1)设)0(≠=k kx y .…………………………………………………………(1分)∵)0(≠=k kx y 的图像过点(310,930),……………………………(1分)∴,k 310930=∴3=k .…………………………………………………(2分)∴ x y 3=.…………………………………………………………… (1分) ① ②(2)设)0(≠+=k b kx y .………………………………………………………(1分)∵ )0(≠+=k b kx y 的图像过点(310,930)和(320,963),∴ ⎩⎨⎧=+=+63.9320930310b k b k , ∴ ⎩⎨⎧-== 3.93.3b k ,……………………………………………………………(1分) ∴933.3-=x y .…………………………………………………………(1分)当3401029933.31029==-=x x y ,解得时,.……………………(1分)答:小明家2017年使用天然气量为340立方米.……………………(1分)23.证明:(1)∵是正方形四边形ABCD ,∴︒=∠90ADC .………(1分)∵FG ⊥FC , ∴∠GFC = 90°. …………………………(1分)∵,CD CF = ∴∠CDF =∠CFD .………………………(1分)∴∠GFC -∠CFD =∠ADC -∠CDE ,即∠GFD =∠GDF .(1分)∴GF =GD .………………………………………………(1分)(2)联结CG .∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G .……(1分)∴GC ⊥DE ,∴∠CDF +∠DCG = 90°,∵∠CDF +∠ADE = 90°,∴∠DCG =∠ADE .∵是正方形四边形ABCD ,∴AD =DC ,∠DAE =∠CDG = 90°,∴△DAE ≌△CDG .……………………………………………………(1分)∴DG AE =.………………………………………………………… (1分)∵的中点,是边点AB E ∴的中点,是边点AD G∴GF GD AG ==.……………………………………………………(1分)∴,,GFD GDF AFG DAF ∠=∠∠=∠………………………………(1分)∵,︒=∠+∠+∠+∠180GDF GFD AFG DAF ……………………(1分)∴,︒=∠+∠18022GFD AFG∴∠AFD = 90°,即AF ⊥DE .…………………………………………(1分) 证法2:(1)联结CG 交ED 于点H .∵是正方形四边形ABCD ,∴︒=∠90ADC .…………………………(1分)∵FG ⊥FC ,∴∠GFC = 90°.……………………………………………(1分)在Rt △C FG 与Rt △CDG 中,⎩⎨⎧==.CG CG CD CF ,…………………………………………………………… (1分) ∴Rt △CFG ≌Rt △CDG .………………………………………………(1分)∴GD GF =.…………………………………………………………(1分)(2)∵,,GD GF CD CF ==∴的中垂线上在线段、点FD C G . ……………………………… (1分)∴FH=HD ,GC ⊥DE ,∴∠EDC +∠DCH = 90°,∵∠ADE +∠EDC= 90°,∴∠ADE =∠DCH .……………………………………………………(1分)∵是正方形四边形ABCD ,∴AD=DC =AB ,∠DAE =∠CDG= 90°,∵GDC EAD DC AD DCH ADE ∠=∠=∠=∠,,.∴△ADE ≌△DCG .……………………………………………………(1分)∴DG AE =.…………………………………………………………(1分)∵的中点,是边点AB E ∴的中点,是边点AD G∵的中点,是边点FD H ∴GH 是△AFD 的中位线.………………(1分)∴,AF GH //∴,GHD AFD ∠=∠∵GH ⊥FD ,∴∠GHD = 90°,………………………………………(1分)∴∠AFD = 90°,即AF ⊥DE .………………………………………(1分)24.解:(1)∵ 抛物线42++=bx ax y 与x 轴交于点A (-2,0),B (4,0),∴ ⎩⎨⎧=++=+.04416042-4b a b a ;…………………………………………………(1分) 解得⎪⎩⎪⎨⎧==.121-b a ;…………………………………………………………(2分)∴ 抛物线的解析式为421-2++=x x y .……………………………(1分) (2)H BC EH E 于点作过点⊥.在Rt △ACO 中, ∵A (-2,0),∴ OA 4421-02=++==x x y x 时,当,∴OC= 在Rt △C OB 中,∵∠COB=90°,∴2445==∠︒BC OCB ,.∵BC EH ⊥,∴CH=EH .∴在Rt △ACO 中,21tan ==∠CO AO ACO …………………………(1分) ∵∠CBE=∠ACO ,∴在Rt △EBH 中,1tan 2EH EBH BH ∠==. 设k BH k k EH 2)0(=>=,则,CH=k,CE =. ∴243==+=k HB CH CB . ∴,324=k ……………………………………………………………(1分) ∴,38=CE ………………………………………………………………(1分) ∴,34=EO ∴),(340E .………………………………………………(1分)(3)∵ A (-2,0),B (4,0),∴抛物线的对称轴为直线x =1.………………………………………(1分)①的边时,为菱形当MCNP MC∴,PN CM //∴∠PNC =∠NCO =45°.∵点P 在二次函数的对称轴上,∴,的横坐标为点1P 1的横坐标为点N . ∴245sin 1==︒CN . ∵是菱形,四边形MCNP ∴,2==CN CM ∴,24+=+=CM OC OM ∴)240(+,M .……………………………………………………(1分) ②的边时,不存在为菱形当MCPN MC .……………………(1分)③的对角线时,为菱形当MNCP MC,于点交设Q CM NP ∴、NP CM ∴1==QP NQ .,QC MQ =∵上,在直线点BC N ∠NCM =∠OCB=45°.在Rt △CQN 中,∴∠NCQ =∠CNQ=45°,∴,1==CQ QN ∴1MQ CQ ==, ∴,2=CM ∴,624=+=+=CM OC OM∴ M (0,6).………………………………………………………(1分)∴综上所述)240(+,M 或 M (0,6). 25.证明:(1)∵,AC AB =∴∠B =∠ACB .∵,EC EF =∴∠EFC =∠ECF .…………………………………(1分)∵,BEF B EFC ∠+∠=∠又∵,ACE ACB ECF ∠+∠=∠∴∠BEF =∠ACE .………………………………………………(1分)∵是公共角,EAC ∠∴△AEP ∽△ACE .……………………………………………(1分) ∴,AEAP AC AE =∴AC AP AE ⋅=2.……………………………(1分) (2)∵∠B =∠ACB ,∠ECF =∠EFC ,∴△ECB ∽△PFC . ∴2⎪⎭⎫ ⎝⎛=∆∆CB FC S S ECB PFC .………………………………………………(1分) E EH CF H ⊥过点做于点,∵,经过圆心,CF EH EH ⊥P M C E H F B A AB FEC P ∴x FC CH 2121==.∴x BH 214-=.…………………………(1分) 在Rt △BEH 中,∵,21tan ==∠BH EH B ∴x EH 41-2=. ∴x x EH BC S ECB 214)412(42121-=-⨯⨯=⋅=∆.…………(1分) ∴24214⎪⎭⎫ ⎝⎛=-x x y . ∴)40(32832<<-=x x x y .………………………………………(2分)(3) ①上时,在线段当点BC F∵,21=EF FP ∴,21==EC PE EF PE ∵△AEP ∽△ACE .∴,EC PE AC AE = ∴12AE AC =.……………………………………………………(1分)M BC AM A ,垂足为点作过点⊥.∵,AC AB =,4=BC ∴,221==BC BM在Rt △ABM 中,∵,21tan =∠B∴1AM AB AC ===,.…(1分)∴,25=AE ∴253=BE .………………………………………(1分)②F BC 当点在线段延长线上时,∵∠EFC =∠ECF ,EFC FCP P ∠=∠+∠, ECF B BEC ∠=∠+∠. 又∵B ACB ACB FCP ∠=∠∠=∠,,∴∠B =∠FCP . ∴∠P =∠BEC . ∵是公共角,EAC ∠∴△AEP ∽△ACE ,∴,EC PEAC AE= ∵,21=EF FP ∴32PE PE EF EC ==,∴32AE AC ==………(1分) ∴255=BE .………………(1分)综上所述,253=BE。
上海市浦东新区2018学年第二学期初三教学质量检测(二模)数学试题(含答案)

浦东新区2018学年第二学期初三教学质量检测考生注意:1、本试卷共25题2、试卷满分150分,考试时间100分钟3、答题时,考生务必按答题要求在答题纸规定的位置作答,在草稿纸、本试卷上答题一律无效4、除第一、二大题外,其余各题如无特殊说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1、下列各数不是4的因数是( )()A 1; ()B 2; ()C 3; ()D 42、如果分式x y x y+-有意义,则x 与y 必须满足( ) ()A y x -= ()B x y ≠- ()C x y = ()D x y ≠3、直线27y x =-不经过( )()A 第一象限; ()B 第二象限; ()C 第三象限; ()D 第四象限;4、某运动队在一次队内选拔比赛中,甲、乙、丙、丁四位运动员的平均成绩相等,方差分别为85.0、23.1、01.5、46.3,那么这四位运动员中,发挥较稳定的是( ) ()A 甲; ()B 乙; ()C 丙 ()D 丁5、在线段、等边三角形、等腰梯形、平行四边形中,一定是轴对称图形的个数有( ) ()A 1个; ()B 2个; ()C 3个; ()D 4个6、已知在四边形ABCD 中,BC AD //,对角线AC 与BD 相交于点O ,CO AO =,如果添加下列一个条件后,就能判定这个四边形是菱形的是( )()A DO BO = ()B BC AB = ()C CD AB = ()D CD AB //二、填空题:(本大题共12题,每题4分,满分48分)7、25的相反数是 . 8、分解因式:2224m mn n -+-= .9、已知函数()f x =,那么()2f -= .10、如果关于x 的方程220x x m ++=有两个实数根,那么m 的取值范围是 .11、已知一个正多边形的中心角为30度,边长为x 厘米()0x >,周长为y 厘米,那么y 关于x 的函数解析式为 .12、从1、2、3这三个数中任选两个组成两位数,在组成的所有两位数中任意抽取一个数,这个数恰好是偶数的概率是 .13、在四边形ABCD 中,向量、满足4AB CD =-uu u r uu u r ,那么线段AB 与CD 的位置关系是 .14、某校有560名学生,为了解这些学生每天做作业所用的时间,调查人员在这所学校的全体学生中随机抽取了部分学生进行问卷调查,并把结果制成如图1的统计图,根据这个统计图可以估计这个学校全体学生每天做作业时间不少于2小时的人数约为 名.15、已知一个角的度数为50度,那么这个角的补角等于 .16、已知梯形的上底长为5厘米,下底长为9厘米,那么这个梯形的中位线长等于 厘米.17、如图2,已知在ABC ∆中,3=AB ,2=AC ,o 45=∠A ,将这个三角形绕点B 旋转,使点A 落在射线AC 上的点1A 处,点C 落在点1C 处,那么=1AC .18、定义:如果P 是圆O 所在平面内的一点,Q 是射线OP 上一点,且线段OP 、OQ 的比例中项等于圆O 的半径,那么我们称点P 与点Q 为这个圆的一对反演点。
(完整版)2018年上海市中考数学二模试卷

2018年上海市中考数学二模试卷一、选择题(每小题4分,共24分)1.(4分)(2018•上海)计算的结果是()A.B.C.D.32.(4分)(2018•上海)据统计,2013年上海市全社会用于环境保护的资金约为60 800 000 000元,这个数用科学记数法表示为()A.608×108B.60.8×109C.6.08×1010D.6.08×10113.(4分)(2018•上海)如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是()A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2D.y=(x+1)24.(4分)(2018•上海)如图,已知直线a、b被直线c所截,那么∠1的同位角是()A.∠2 B.∠3 C.∠4 D.∠55.(4分)(2018•上海)某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是()A.50和50 B.50和40 C.40和50 D.40和406.(4分)(2018•上海)如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是()A.△ABD与△ABC的周长相等B.△ABD与△ABC的面积相等C.菱形的周长等于两条对角线之和的两倍D.菱形的面积等于两条对角线之积的两倍二、填空题(每小题4分,共48分)7.(4分)(2018•上海)计算:a(a+1)=_________.8.(4分)(2018•上海)函数y=的定义域是_________.9.(4分)(2018•上海)不等式组的解集是_________.10.(4分)(2018•上海)某文具店二月份销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份销售各种水笔_________支.11.(4分)(2018•上海)如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是_________.12.(4分)(2018•上海)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为_________米.13.(4分)(2018•上海)如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是_________.14.(4分)(2018•上海)已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是_________(只需写一个).15.(4分)(2018•上海)如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设=,=,那么=_________(结果用、表示).16.(4分)(2018•上海)甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是_________.17.(4分)(2018•上海)一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y表示的数为_________.18.(4分)(2018•上海)如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为_________(用含t的代数式表示).三、解答题(本题共7题,满分78分)19.(10分)(2018•上海)计算:﹣﹣+||.20.(10分)(2018•上海)解方程:﹣=.21.(10分)(2018•上海)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.水银柱的长度x(cm)4.2 …8.2 9.8体温计的读数y(℃)35.0 …40.0 42.0(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.22.(10分)(2018•上海)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sinB的值;(2)如果CD=,求BE的值.23.(12分)(2018•上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E 是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;(2)连接AE,交BD于点G,求证:=.24.(12分)(2018•上海)在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,﹣2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.25.(14分)(2018•上海)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.2018年上海市中考数学试卷参考答案与试题解析一、选择题(每小题4分,共24分)1.(4分)(2018•上海)计算的结果是()A.B.C.D.3考点:二次根式的乘除法.专题:计算题.分析:根据二次根式的乘法运算法则进行运算即可.解答:解:•=,故选:B.点评:本题主要考查二次根式的乘法运算法则,关键在于熟练正确的运用运算法则,比较简单.2.(4分)(2018•上海)据统计,2013年上海市全社会用于环境保护的资金约为60 800 000 000元,这个数用科学记数法表示为()A.608×108B.60.8×109C.6.08×1010D.6.08×1011考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:60 800 000 000=6.08×1010,故选:C.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(4分)(2018•上海)如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是()A.y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2D.y=(x+1)2考点:二次函数图象与几何变换.专题:几何变换.分析:先得到抛物线y=x2的顶点坐标为(0,0),再得到点(0,0)向右平移1个单位得到点的坐标为(1,0),然后根据顶点式写出平移后的抛物线解析式.解答:解:抛物线y=x2的顶点坐标为(0,0),把点(0,0)向右平移1个单位得到点的坐标为(1,0),所以所得的抛物线的表达式为y=(x﹣1)2.故选:C.点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.4.(4分)(2018•上海)如图,已知直线a、b被直线c所截,那么∠1的同位角是()A.∠2 B.∠3 C.∠4 D.∠5考点:同位角、内错角、同旁内角.分析:根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角可得答案.解答:解:∠1的同位角是∠5,故选:D.点评:此题主要考查了同位角的概念,关键是掌握同位角的边构成“F“形.5.(4分)(2018•上海)某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是()A.50和50 B.50和40 C.40和50 D.40和40考点:众数;中位数.分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.解答:解:从小到大排列此数据为:37、40、40、50、50、50、75,数据50出现了三次最多,所以50为众数;50处在第4位是中位数.故选:A.点评:本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.6.(4分)(2018•上海)如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是()A.△ABD与△ABC的周长相等B.△ABD与△ABC的面积相等C.菱形的周长等于两条对角线之和的两倍D.菱形的面积等于两条对角线之积的两倍考点:菱形的性质.专题:几何图形问题.分析:分别利用菱形的性质结合各选项进而求出即可.解答:解:A、∵四边形ABCD是菱形,∴AB=BC=AD,∵AC<BD,∴△ABD与△ABC的周长不相等,故此选项错误;B、∵S△ABD=S平行四边形ABCD,S△ABC=S平行四边形ABCD,∴△ABD与△ABC的面积相等,故此选项正确;C、菱形的周长与两条对角线之和不存在固定的数量关系,故此选项错误;D、菱形的面积等于两条对角线之积的,故此选项错误;故选:B.点评:此题主要考查了菱形的性质应用,正确把握菱形的性质是解题关键.二、填空题(每小题4分,共48分)7.(4分)(2018•上海)计算:a(a+1)=a2+a.考点:单项式乘多项式.专题:计算题.分析:原式利用单项式乘以多项式法则计算即可得到结果.解答:解:原式=a2+a.故答案为:a2+a点评:此题考查了单项式乘以多项式,熟练掌握运算法则是解本题的关键.8.(4分)(2018•上海)函数y=的定义域是x≠1.考点:函数自变量的取值范围.分析:根据分母不等于0列式计算即可得解.解答:解:由题意得,x﹣1≠0,解得x≠1.故答案为:x≠1.点评:本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.9.(4分)(2018•上海)不等式组的解集是3<x<4.考点:解一元一次不等式组.专题:计算题.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.解答:解:,解①得:x>3,解②得:x<4.则不等式组的解集是:3<x<4.故答案是:3<x<4点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x >较小的数、<较大的数,那么解集为x介于两数之间.10.(4分)(2018•上海)某文具店二月份销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份销售各种水笔352支.考点:有理数的混合运算.专题:应用题.分析:三月份销售各种水笔的支数比二月份增长了10%,是把二月份销售的数量看作单位“1”,增加的量是二月份的10%,即三月份生产的是二月份的(1+10%),由此得出答案.解答:解:320×(1+10%)=320×1.1=352(支).答:该文具店三月份销售各种水笔352支.故答案为:352.点评:此题考查有理数的混合运算,理解题意,列出算式解决问题.11.(4分)(2018•上海)如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是k<1.考点:根的判别式.分析:根据一元二次方程ax2+bx+c=0(a≠0)的根的判别式的意义得到△>0,即(﹣2)2﹣4×1×k>0,然后解不等式即可.解答:解:∵关于x的方程x2﹣3x+k=0(k为常数)有两个不相等的实数根,∴△>0,即(﹣2)2﹣4×1×k>0,解得k<1,∴k的取值范围为k<1.故答案为:k<1.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2﹣4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.12.(4分)(2018•上海)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为26米.考点:解直角三角形的应用-坡度坡角问题.专题:应用题.分析:首先根据题意画出图形,根据坡度的定义,由勾股定理即可求得答案.解答:解:如图,由题意得:斜坡AB的坡度:i=1:2.4,AE=10米,AE⊥BD,∵i==,∴BE=24米,∴在Rt△ABE中,AB==26(米).故答案为:26.点评:此题考查了坡度坡角问题.此题比较简单,注意掌握数形结合思想的应用,注意理解坡度的定义.13.(4分)(2018•上海)如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是.考点:概率公式.分析:由从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,直接利用概率公式求解即可求得答案.解答:解:∵从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,∴恰好抽到初三(1)班的概率是:.故答案为:.点评:此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.14.(4分)(2018•上海)已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是y=﹣(只需写一个).考点:反比例函数的性质.专题:开放型.分析:首先根据反比例函数的性质可得k<0,再写一个符合条件的数即可.解答:解:∵反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,∴k<0,∴y=﹣,故答案为:y=﹣.点评:此题主要考查了反比例函数的性质,关键是掌握对于反比例函数y=,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.15.(4分)(2018•上海)如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设=,=,那么=﹣(结果用、表示).考点:*平面向量.分析:由点E在边AB上,且AB=3EB.设=,可求得,又由在平行四边形ABCD中,=,求得,再利用三角形法则求解即可求得答案.解答:解:∵AB=3EB.=,∴==,∵平行四边形ABCD中,=,∴==,∴=﹣=﹣.故答案为:﹣.点评:此题考查了平面向量的知识.此题难度不大,注意掌握三角形法则与平行四边形法则的应用,注意掌握数形结合思想的应用.16.(4分)(2018•上海)甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是乙.考点:方差;折线统计图.专题:图表型.分析:根据方差的意义数据波动越小,数据越稳定即可得出答案.解答:解:根据图形可得:乙的成绩波动最小,数据最稳定,则三人中成绩最稳定的是乙;故答案为:乙.点评:本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.17.(4分)(2018•上海)一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y表示的数为﹣9.考点:规律型:数字的变化类.分析:根据“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,首先建立方程2×3﹣x=7,求得x,进一步利用此规定求得y即可.解答:解:解法一:常规解法∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b∴2×3﹣x=7∴x=﹣1则2×(﹣1)﹣7=y解得y=﹣9.解法二:技巧型∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b∴7×2﹣y=23∴y=﹣9故答案为:﹣9.点评:此题考查数字的变化规律,注意利用定义新运算方法列方程解决问题.18.(4分)(2018•上海)如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为2t(用含t的代数式表示).考点:翻折变换(折叠问题).专题:几何图形问题.分析:根据翻折的性质可得CE=C′E,再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°,然后求出∠BGD′=60°,根据对顶角相等可得∠FGE=∠∠BGD′=60°,根据两直线平行,内错角相等可得∠AFG=∠FGE,再求出∠EFG=60°,然后判断出△EFG是等边三角形,根据等边三角形的性质表示出EF,即可得解.解答:解:由翻折的性质得,CE=C′E,∵BE=2CE,∴BE=2C′E,又∵∠C′=∠C=90°,∴∠EBC′=30°,∵∠FD′C′=∠D=90°,∴∠BGD′=60°,∴∠FGE=∠BGD′=60°,∵AD∥BC,∴∠AFG=∠FGE=60°,∴∠EFG=(180°﹣∠AFG)=(180°﹣60°)=60°,∴△EFG是等边三角形,∵AB=t,∴EF=t÷=t,∴△EFG的周长=3×t=2t.故答案为:2t.点评:本题考查了翻折变换的性质,直角三角形30°角所对的直角边等于斜边的一半,等边三角形的判定与性质,熟记性质并判断出△EFG是等边三角形是解题的关键.三、解答题(本题共7题,满分78分)19.(10分)(2018•上海)计算:﹣﹣+||.考点:实数的运算;分数指数幂.专题:计算题.分析:本题涉及绝对值、二次根式化简两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=2﹣﹣2+2﹣=.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.20.(10分)(2018•上海)解方程:﹣=.考点:解分式方程.专题:计算题;转化思想.分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解答:解:去分母得:(x+1)2﹣2=x﹣1,整理得:x2+x=0,即x(x+1)=0,解得:x=0或x=﹣1,经检验x=﹣1是增根,分式方程的解为x=0.点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.21.(10分)(2018•上海)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.水银柱的长度x(cm)4.2 …8.2 9.8体温计的读数y(℃)35.0 …40.0 42.0(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.考点:一次函数的应用.专题:应用题;待定系数法.分析:(1)设y关于x的函数关系式为y=kx+b,由统计表的数据建立方程组求出其解即可;(2)当x=6.2时,代入(1)的解析式就可以求出y的值.解答:解:(1)设y关于x的函数关系式为y=kx+b,由题意,得,解得:,∴y=x+29.75.∴y关于x的函数关系式为:y=+29.75;(2)当x=6.2时,y=×6.2+29.75=37.5.答:此时体温计的读数为37.5℃.点评:本题考查了待定系数法求一次函数的解析式的运用,由解析式根据自变量的值求函数值的运用,解答时求出函数的解析式是关键.22.(10分)(2018•上海)如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sinB的值;(2)如果CD=,求BE的值.考点:解直角三角形;直角三角形斜边上的中线.专题:几何图形问题.分析:(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:,即可得出sinB的值;(2)根据sinB的值,可得出AC:AB=1:,再由AB=2,得AC=2,则CE=1,从而得出BE.解答:解:(1)∵∠ACB=90°,CD是斜边AB上的中线,∴CD=BD,∴∠B=∠BCD,∵AE⊥CD,∴∠CAH+∠ACH=90°,又∠ACB=90°∴∠BCD+∠ACH=90°∴∠B=∠BCD=∠CAH,即∠B=∠CAH,∵AH=2CH,∴由勾股定理得AC=CH,∴CH:AC=1:,∴sinB=;(2)∵sinB=,∴AC:AB=1:,∴AC=2.∵∠CAH=∠B,∴sin∠CAH=sinB==,设CE=x(x>0),则AE=x,则x2+22=(x)2,∴CE=x=1,AC=2,在Rt△ABC中,AC2+BC2=AB2,∴BC=4,∴BE=BC﹣CE=3.点评:本题考查了解直角三角形,以及直角三角形斜边上的中线,注意性质的应用,难度不大.23.(12分)(2018•上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E 是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;(2)连接AE,交BD于点G,求证:=.考点:相似三角形的判定与性质;全等三角形的判定与性质;平行四边形的判定.专题:证明题.分析:(1)证△△BAD≌△CDA,推出∠ABD=∠ACD=∠CDE,推出AC∥DE即可;(2)根据平行得出比例式,再根据比例式的性质进行变形,即可得出答案.解答:证明:(1)∵梯形ABCD,AD∥BC,AB=CD,∴∠BAD=∠CDA,在△BAD和△CDA中∴△BAD≌△CDA(SAS),∴∠ABD=∠ACD,∵∠CDE=∠ABD,∴∠ACD=∠CDE,∴AC∥DE,∵AD∥CE,∴四边形ACED是平行四边形;(2)∵AD∥BC,∴=,=,∴=,∵平行四边形ACED,AD=CE,∴=,∴=,∴=,∴=.点评:本题考查了比例的性质,平行四边形的判定,平行线的判定的应用,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.24.(12分)(2018•上海)在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,﹣2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.考点:二次函数综合题.专题:代数几何综合题;压轴题.分析:(1)根据待定系数法可求抛物线的表达式,进一步得到对称轴;(2)因为AC与EF不平行,且四边形ACEF为梯形,所以CE∥AF.分别求出直线CE、AF的解析式,进而求出点F的坐标;(3)△BDP和△CDP的面积相等,可得DP∥BC,根据待定系数法得到直线BC的解析式,根据两条平行的直线k值相同可得直线DP的解析式,进一步即可得到t的值.解答:解:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),点C(0,﹣2),∴,解得.故抛物线的表达式为:y=x2﹣x﹣2=(x﹣1)2﹣,对称轴为直线x=1;(2)设直线CE的解析式为:y=kx+b,将E(1,0),C(0,﹣2)坐标代入得:,解得,∴直线CE的解析式为:y=2x﹣2.∵AC与EF不平行,且四边形ACEF为梯形,∴CE∥AF.∴设直线AF的解析式为:y=2x+n.∵点A(﹣1,0)在直线AF上,∴﹣2+n=0,∴n=2.∴设直线AF的解析式为:y=2x+2.当x=1时,y=4,∴点F的坐标为(1,4).(3)点B(3,0),点D(1,﹣),若△BDP和△CDP的面积相等,则DP∥BC,则直线BC的解析式为y=x﹣2,∴直线DP的解析式为y=x﹣,当y=0时,x=5,∴t=5.点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的表达式,待定系数法求直线的解析式,两条平行的直线之间的关系,三角形面积,分类思想的运用,综合性较强,有一定的难度.25.(14分)(2018•上海)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连接AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.考点:圆的综合题.专题:压轴题.分析:(1)当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,直接利用勾股定理求出AC进而得出答案;(2)首先得出四边形APCE是菱形,进而得出CM的长,进而利用锐角三角函数关系得出CP以及EF的长;(3)∠GAE≠∠BGC,只能∠AGE=∠AEG,利用AD∥BC,得出△GAE∽△GBC,进而求出即可.解答:解:(1)如图1,设⊙O的半径为r,当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,∴BH=AB•cosB=4,∴AH=3,CH=4,∴AC==5,∴此时CP=r=5;(2)如图2,若AP∥CE,APCE为平行四边形,∵CE=CP,∴四边形APCE是菱形,连接AC、EP,则AC⊥EP,∴AM=CM=,由(1)知,AB=AC,则∠ACB=∠B,∴CP=CE==,∴EF=2=;(3)如图3:过点C作CN⊥AD于点N,∵cosB=,∴∠B<45°,∵∠BCG<90°,∴∠BGC>45°,∴∠BGC>∠B=∠GAE,即∠BGC≠∠GAE,又∠AEG=∠BCG≥∠ACB=∠B=∠GAE,∴当∠AEG=∠GAE时,A、E、G重合,则△AGE不存在.即∠AEG≠∠GAE∴只能∠AGE=∠AEG,∵AD∥BC,∴△GAE∽△GBC,∴=,即=,解得:AE=3,EN=AN﹣AE=1,∴CE===.点评:此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,利用分类讨论得出△AGE是等腰三角形时只能∠AGE=∠AEG进而求出是解题关键.。
2018年上海市浦东新区中考数学二模试卷(解析版)

2018年上海市浦东新区中考数学二模试卷一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4分)下列代数式中,单项式是()A.B.0C.x+1D.2.(4分)下列代数式中,二次根式的有理化因式可以是()A.B.C.D..3.(4分)已知一元二次方程x2+2x﹣1=0,下列判断正确的是()A.该方程有两个不相等的实数根B.该方程有两个相等的实数根C.该方程没有实数根D.该方程的根的情况不确定4.(4分)某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A.平均数B.众数C.方差D.频率5.(4分)下列y关于x的函数中,当x>0时,函数值y随x的值增大而减小的是()A.y=x2B.y=C.y=D.y=6.(4分)已知四边形ABCD中,AB∥CD,AC∥BD,下列判断中正确的是()A.如果BC=AD,那么四边形ABCD是等腰梯形B.如果AD∥BC,那么四边形ABCD是菱形C.如果AC平分BD,那么四边形ABCD是矩形D.如果AC⊥BD,那么四边形ABCD是正方形二.填空题:(本大题共12题,每题4分,满分48分)7.(4分)计算:=.8.(4分)因式分解:x2﹣4y2=.9.(4分)方程=3的解是.10.(4分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.11.(4分)已知正方形的边长为2cm,那么它的半径长是cm.12.(4分)某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x 的方程.13.(4分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为.14.(4分)如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果,那么=(用向量表示).15.(4分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.16.(4分)如图,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD 绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'=.17.(4分)如果抛物线C:y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,那么m+n =.18.(4分)已知l1∥l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为cm.三、解答题:(本大题共7题,满分78分)19.(10分)+|1﹣|﹣27+()﹣120.(10分)解不等式组:,并把它的解集在数轴(如图)上表示出来.21.(10分)如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.22.(10分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.23.(12分)已知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE 上CF=CD,过点F作FG⊥FC交AD于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.24.(12分)已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图象经过A(﹣2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图象的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.25.(14分)如图,已知在△ABC中,AB=AC,tan B=,BC=4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP•AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当时,求BE的长.2018年上海市浦东新区中考数学二模试卷参考答案与试题解析一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4分)下列代数式中,单项式是()A.B.0C.x+1D.【解答】解:A、不是单项式,不符合题意;B、0是单项式,符合题意;C、x+1是多项式,不符合题意;D、不是单项式,不符合题意;故选:B.2.(4分)下列代数式中,二次根式的有理化因式可以是()A.B.C.D..【解答】解:∵×=()2=m+n,∴二次根式的有理化因式是,故选:C.3.(4分)已知一元二次方程x2+2x﹣1=0,下列判断正确的是()A.该方程有两个不相等的实数根B.该方程有两个相等的实数根C.该方程没有实数根D.该方程的根的情况不确定【解答】解:∵a=1,b=2,c=﹣1,∴△=b2﹣4ac=22﹣4×1×(﹣1)=8>0,∴该方程有两个不相等的实数根.故选:A.4.(4分)某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A.平均数B.众数C.方差D.频率【解答】解:在平均数、众数、方差、频率这些统计量中,表示一组数据波动程度的量是方差.故选:C.5.(4分)下列y关于x的函数中,当x>0时,函数值y随x的值增大而减小的是()A.y=x2B.y=C.y=D.y=【解答】解:A、二次函数y=x2的图象,开口向上,并向上无限延伸,在y轴右侧(x>0时),y随x的增大而增大;故本选项错误;B、一次函数y=x+1的图象,y随x的增大而增大;故本选项错误;C、正比例函数y=x的图象在一、三象限内,y随x的增大而增大;故本选项错误;D、反比例函数y=中k=1>0,所以当x>0时,y随x的增大而减小;故本选项正确;故选:D.6.(4分)已知四边形ABCD中,AB∥CD,AC∥BD,下列判断中正确的是()A.如果BC=AD,那么四边形ABCD是等腰梯形B.如果AD∥BC,那么四边形ABCD是菱形C.如果AC平分BD,那么四边形ABCD是矩形D.如果AC⊥BD,那么四边形ABCD是正方形【解答】解:四边形ABCD中,AB∥CD,AC∥BD,所以四边形ABCD是平行四边形,A.如果BC=AD,那么四边形ABCD是矩形,错误;B.AD应该与BC相交,不能AD∥BC,错误;C.如果AC平分BD,那么四边形ABCD是矩形,正确;D、如果AC⊥BD,那么四边形ABCD是菱形,错误;故选:C.二.填空题:(本大题共12题,每题4分,满分48分)7.(4分)计算:=3ab2.【解答】解:原式=3ab2故答案为:3ab28.(4分)因式分解:x2﹣4y2=(x+2y)(x﹣2y).【解答】解:x2﹣4y2=(x+2y)(x﹣2y).9.(4分)方程=3的解是x=5.【解答】解:平方,得2x﹣1=9,解得x=5,故答案为:x=5.10.(4分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.【解答】解:∵将分别写有“幸福”、“奋斗”的2张卡片,随机放入两个框中,只有两种情况,恰好组成“幸福都是奋斗出来的”的情况只有一种,∴其概率是:,故答案为:.11.(4分)已知正方形的边长为2cm,那么它的半径长是cm.【解答】解:如图,∵AB=2,∴OC=1,∴OA=,故答案为:12.(4分)某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x的方程.【解答】解:设原计划每天种植x亩,根据题意可得:,故答案为:,13.(4分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为24.【解答】解:∵被调查的总人数为36÷45%=80,∴2017年该小区居民出境游中跟团游的人数为80﹣36﹣20=24(人),故答案为:24.14.(4分)如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果,那么=(用向量表示).【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC.∵E是BC的中点,AE交BD于点F,∴==2∴AF=AE.又,那么=.故答案是:.15.(4分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.【解答】解:根据题意得:直升飞机与观摩点B之间的距离是AB=米.故答案为:800.16.(4分)如图,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD 绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'=9.【解答】解:如图,将△ABD绕着点D逆时针旋转得到△CB′D,作DE∥AB交BC于E,则ABED是平行四边形,BE=AD=3,DE=AB=3,∴EC=BC﹣BE=6﹣3=3,∵DC=3,∴DE=EC=DC=3,∴△DCE是等边三角形,∴∠DCE=60°.∵在梯形ABCD中,AD∥BC,AB=DC,∴∠ABC=∠DCB=60°,∠A=120°,∵将△ABD绕着点D逆时针旋转得到△CB′D,∴△CB′D≌△ABD,∴∠DCB′=∠A=120°,CB′=AB=3,∴∠BCB′=∠BCD+∠DCB′=120°+60°=180°,∴B、C、B′三点共线,∴BB′=BC+CB′=6+3=9.故答案为9.17.(4分)如果抛物线C:y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,那么m+n =0.【解答】解:在y=mx+1中,令x=0可求得y=1,在y=x2﹣2x+n中,令x=0可得y=n,∵直线与抛物线都经过y轴上的一点,∴n=1,∴抛物线解析式为y=x2﹣2x+1=(x﹣1)2,∴抛物线顶点坐标为(1,0),∵抛物线顶点在直线上,∴0=m+1,解得m=﹣1,∴m+n=﹣1+1=0,故答案为:0.18.(4分)已知l1∥l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为2或4cm.【解答】解:如下图所示,设圆的半径为r如图一所示,r﹣1=3,得r=4,如图二所示,r+1=3,得r=2,故答案为:2或4.三、解答题:(本大题共7题,满分78分)19.(10分)+|1﹣|﹣27+()﹣1【解答】解:原式=2+﹣1﹣3+220.(10分)解不等式组:,并把它的解集在数轴(如图)上表示出来.【解答】解:由①得:x>﹣3;由②得:x≤2;∴原不等式组的解集为﹣3<x≤2,.21.(10分)如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.【解答】解:过点O作OM⊥CD于点M,联结OD,∵∠CEA=30°,∴∠OEM=∠CEA=30°,在Rt△OEM中,∵OE=4,∴,,∵,∴,∵OM过圆心,OM⊥CD,∴,∵,∴在Rt△DOM中,,∴弦CD的长为,⊙O的半径长为.22.(10分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.【解答】解:(1)设y=kx(k≠0).∵y=kx(k≠0)的图象过点(310,930),∴930=310k,∴k=3.∴y=3x.(2)设y=kx+b(k≠0).∵y=kx+b(k≠0)的图象过点(310,930)和(320,963),∴,∴∴y=3.3x﹣9.3,当y=1029时,3.3x﹣9.3=1029,解得x=340,答:小明家2017年使用天然气量为340立方米.23.(12分)已知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE 上CF=CD,过点F作FG⊥FC交AD于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.【解答】证明:(1)∵四边形ABCD是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,∵CF=CD,∴∠CDF=∠CFD,∴∠GFC﹣∠CFD=∠ADC﹣∠CDE,即∠GFD=∠GDF,∴GF=GD.(2)联结CG.∵CF=CD,GF=GD,∴点G、C在线段FD的中垂线上,∴GC⊥DE,∴∠CDF+∠DCG=90°,∵∠CDF+∠ADE=90°,∴∠DCG=∠ADE.∵四边形ABCD是正方形,∴AD=DC,∠DAE=∠CDG=90°,∴△DAE≌△CDG,∴AE=DG,∵点E是边AB的中点,∴点G是边AD的中点,∴AG=GD=GF,∴∠DAF=∠AFG,∠GDF=∠GFD,∵∠DAF+∠AFG+∠GFD+∠GDF=180°,∴2∠AFG+2∠GFD=180°,∴∠AFD=90°,即AF⊥DE.证法2:(1)联结CG交ED于点H.∵四边形ABCD是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,在Rt△CFG与Rt△CDG中,,∴Rt△CFG≌Rt△CDG,∴GF=GD.(2)∵CF=CD,GF=GD,∴点G、C在线段FD的中垂线上,∴FH=HD,GC⊥DE,∴∠EDC+∠DCH=90°,∵∠ADE+∠EDC=90°,∴∠ADE=∠DCH,∵四边形ABCD是正方形,∴AD=DC=AB,∠DAE=∠CDG=90°,∵∠ADE=∠DCH,AD=DC,∠EAD=∠GDC.∴△ADE≌△DCG,∴AE=DG,∵点E是边AB的中点,∴点G是边AD的中点,∵点H是边FD的中点,∴GH是△AFD的中位线,∴GH∥AF,∴∠AFD=∠GHD,∵GH⊥FD,∴∠GHD=90°,∴∠AFD=90°,即AF⊥DE.24.(12分)已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图象经过A(﹣2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图象的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.【解答】解:(1)∵抛物线y=ax2+bx+4与x轴交于点A(﹣2,0),B(4,0),∴,解得,∴抛物线的解析式为,(2)如图1,过点E作EH⊥BC于点H.在Rt△ACO中,∵A(﹣2,0),∴OA=2,,∴OC=4,在Rt△COB中,∵∠COB=90°,OC=OB=4,∴.∵EH⊥BC,∴CH=EH.∴在Rt△ACO中,,∵∠CBE=∠ACO,在Rt△EBH中,.设EH=k(k>0),则BH=2k,CH=k,.∴.∴,∴,∴,∴,(3)∵A(1,0),B(5,0),∴抛物线的对称轴为直线x=1,①当MC为菱形MCNP的边时,∴CM∥PN,∴∠PNC=∠NCO=45°.∵点P在二次函数的对称轴上,∴点P的横坐标为1,点N的横坐标为1.∴.∵四边形MCNP是菱形,∴,∴,∴,②当MC为菱形MCPN的边时,不存在,③如图2,当MC为菱形MNCP的对角线时,设NP交CM于点Q,∴CM、NP互相垂直平分,∴NQ=QP=1.MQ=QC,∵点N在直线BC上,∠NCM=∠OCB=45°.在Rt△CQN中,∴∠NCQ=∠CNQ=45°,∴QN=CQ=1,∴MQ=CQ=1,∴CM=2,∴OM=OC+CM=4+2=6,∴M(0,6),∴综上所述或M(0,6).25.(14分)如图,已知在△ABC中,AB=AC,tan B=,BC=4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP•AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当时,求BE的长.【解答】证明:(1)∵AB=AC,∴∠B=∠ACB.∵EF=EC,∴∠EFC=∠ECF,∵∠EFC=∠B+∠BEF,又∵∠ECF=∠ACB+∠ACE,∴∠BEF=∠ACE,∵∠EAC是公共角,∴△AEP∽△ACE,∴,∴AE2=AP•AC,(2)∵∠B=∠ACB,∠ECF=∠EFC,∴△ECB∽△PFC.∴,过点E作EH⊥CF于点H,∵EH经过圆心,EH⊥CF,∴.∴,在Rt△BEH中,∵,∴.∴,∴.∴,(3)①当点F在线段BC上时,∵,∴,∵△AEP∽△ACE.∴,∴,过点A作AM⊥BC,垂足为点M.∵AB=AC,BC=4,∴,在Rt△ABM中,∵,∴∴,∴,②当点F在线段BC延长线上时,∵∠EFC=∠ECF,∠EFC=∠FCP+∠P,∠ECF=∠B+∠BEC.又∵∠B=∠ACB,∠ACB=∠FCP,∴∠B=∠FCP.∴∠P=∠BEC.∵∠EAC是公共角,∴△AEP∽△ACE,∴,∵,∴,∴,∴,综上所述,或.第21页(共21页)。
2018学年浦东二模试卷参考答案

浦东新区2018学年度第二学期初三教学质量检测数学试卷参考答案及评分说明 (2019.5.8)一、选择题:(本大题共6题,每题4分,满分24分)1.C ; 2.D ; 3.B ; 4.A ; 5.C ;6.B . 二、填空题:(本大题共12题,每题4分,满分48分)7.25-; 8.(m -n+2)(m -n -2);9.2; 10.m ≤1; 11.y =12x ; 12.31; 13.平行; 14.160; 15.130; 16.7; 17.22; 18.32. 三、解答题:(本大题共7题,满分78分)19.解:原式=321331-+-+- …………………………………………………(各2分)=-1. ……………………………………………………………………(2分)20.解:由①得 22-≥x . ………………………………………………………………(1分) ∴1-≥x . ………………………………………………………………(2分) 由②得 123<x . ………………………………………………………………(1分) ∴4<x . ………………………………………………………………(2分) ∴原不等式组的解集是41<≤-x . ………………………………………………(2分) ∴原不等式组的自然数解为0、1、2、3. ……………………………………(2分) (注:漏“0”扣1分)21.解:(1)作AD ⊥x 轴,垂足为点D .∵BH ⊥x 轴,AD ⊥x 轴,∴∠BHO =∠ADO =90°.∴AD ∥BH .…………(1分) 又∵BA=2OA ,∴21==AB OA DH OD . …………………………………………(1分) ∵点B 的横坐标为6,∴OH=6.∴OD=2. ………………………………(1分) ∵双曲线xy 6=经过点A ,可得点A 的纵坐标为3. …………………………(1分) ∴点A 的坐标为(2,3). …………………………………………………………(1分) (2)∵双曲线xy 6=上点C 的横坐标为6,∴点C 的坐标为(6,1). ……(1分) 由题意,得 直线AB 的表达式为x y 23=. ……………………………………(1分) ∴设平移后直线的表达式为b x y +=23. ∵平移后的直线b x y +=23经过点C (6,1),∴b +⨯=6231. ………………(1分) 解得8-=b . ……………………………………………………………………(1分) ∴平移后直线的表达式为823-=x y . …………………………………………(1分)22.解:(1)根据题意,得AB=20,∠ABC=70°,CH =BD =2.………………(1分) 在△ACB 中,∵∠ACB =90°,∴sin AC ABC AB∠=. ∵∠ABC=70°,AB=20,∴20sin70200.9418.8AC =⋅≈⨯=o . …………(2分) ∴AH =20.8.答:这辆吊车工作时点A 离地面的最大距离AH 为20.8米. …………(1分)(2)设这次王师傅所开的吊车的速度为每小时x 千米. ……………………(1分) 由题意,得 31402040=--x x . ………………………………………………(1分) 整理,得02400202=--x x .………………………………………………(1分) 解得 x 1=60,x 2=-40. …………………………………………………………(1分) 经检验:x 1=60,x 2=-40都是原方程的解,但x 2=-40不符合题意,舍去.…(1分) 答:这次王师傅所开的吊车的速度为每小时60千米. ……………………(1分)23.证明:(1)∵AB=AD ,∴∠ABD =∠ADB . ……………………………………(1分) ∵AD ∥BC ,∴∠ADB=∠MBC . …………………………………………(1分) ∵AB=AD ,AM ⊥BD ,∴BM =DM . …………………………………………(1分)∵DC ⊥BC ,∴∠BCD =90°.∴BM =DM =CM . ………………………………………………………………(1分) ∴∠MBC =∠BCM . …………………………………………………………(1分) ∴∠ABD=∠BCM . …………………………………………………………(1分)(2)∵∠BNM=∠CNB ,∠NBM=∠NCB ,∴△NBM ∽△NCB . …………(2分) ∴BCBM CN BN =. ………………………………………………………………(2分) ∵BM =DM ,∴BCDM CN BN =. ……………………………………………………(1分) ∴DM CN BN BC ⋅=⋅. ……………………………………………………(1分)24.解:(1)∵抛物线c bx x y ++=231经过点M (3,-4),A (-3,0), ∴⎩⎨⎧+-=++=-.330,33c b c b 4 ………………………………………………………………(1分) 解得⎪⎩⎪⎨⎧-=-=.5,32c b………………………………………………………………(2分)∴这条抛物线的表达式为532312--=x x y . ………………………………(1分) (2)由题意,得 这条抛物线的对称轴为直线1=x . …………………………(1分) 点B 的坐标为(5,0),点C 的坐标为(0,-5). …………………………(1分) 设点P 的坐标为(1,y ).∵PC=BC ,∴PC 2=BC 2. ∴22255)5(1+=++ y . ……………………………………………………(1分)解得y =2或y =-12.∴点P 的坐标为(1,2)或(1,-12).…………………………………………(1分)(3)作PH ⊥BC ,垂足为点H .∵点B (5,0),点C (0,-5),点P (1,2),∴PC =BC =52.…………(1分)∵直线BC 与对称轴相交于点D (1,-4), ∴462116212521⨯⨯+⨯⨯=⨯PH . …………………………………………(1分)解得PH =23. ………………………………………………………………(1分) ∴sin ∠PCB=532523=. ……………………………………………………(1分) 25.解:(1)联结PO 并延长交弦AB 于点H .∵P 是优弧AB ︵ 的中点,PH 经过圆心O ,∴PH ⊥AB ,AH =BH . …………(2分) 在△AOH 中,∵∠AHO =90°,AH=21AB =4,AO=5,∴OH=3. ……(1分) 在△APH 中,∵∠AHP =90°,PH=5+3=8,AH=4,∴AP=54. ……(1分)(2)作OG ⊥AB ,垂足为点G .∵∠OBG =∠ABM ,∠OGB =∠AMB ,∴△OBG ∽△ABM . ………………(1分)∴OB BG AB BM =,即548=BM . ∴532=BM . ……………………………………………………………………(1分) ∴57=OM . ……………………………………………………………………(1分) ∵57<23,∴以点O 为圆心,23为半径的圆与直线AP 相交. …………(1分) (3)作OG ⊥AB ,垂足为点G .∵∠BNO=∠BON ,∴BN=BO . ………………………………………………(1分) ∵BO =AO=5,∴BN=5. ……………………………………………………(1分) (i )当点N 在线段AB 延长线上时,∵BG =21AB =4,∴GN =9. 在△GON 中,∵∠NGO =90°,GN=9,OG=3,∴ON=103.∵圆N 与圆O 相切,∴5103+=r 或5103-=r .∴圆N 的半径为5103-或5103+. …………………………………(各1分) (ii )当点N 在线段AB 上时,同理可得圆N 的半径为105+或105-.……………………………………………………………………………(各1分)。
最新-上海市浦东新区2018年中考二模数学试卷及答案 精
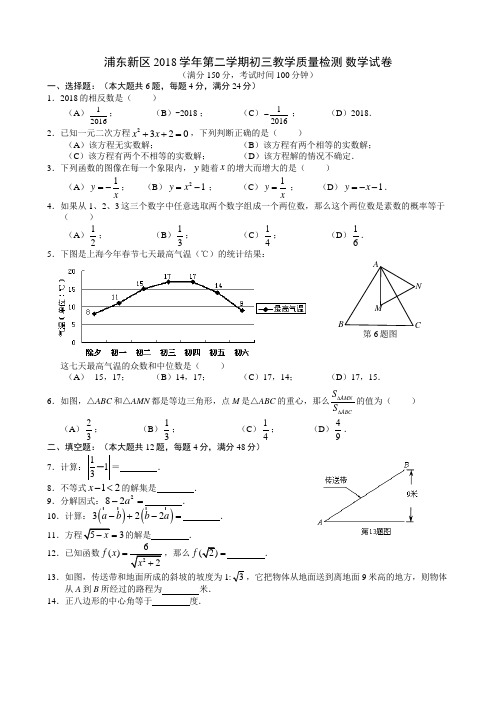
浦东新区2018学年第二学期初三教学质量检测 数学试卷(满分150分,考试时间100分钟)一、选择题:(本大题共6题,每题4分,满分24分) 1.2018的相反数是( )(A )12016; (B )-2018 ; (C )12016- ; (D )2018.2.已知一元二次方程2320x x ++=,下列判断正确的是( )(A )该方程无实数解; (B )该方程有两个相等的实数解; (C )该方程有两个不相等的实数解; (D )该方程解的情况不确定. 3.下列函数的图像在每一个象限内,y 随着x 的增大而增大的是( )(A )1y x=-; (B )21y x =- ; (C )1y x = ; (D )1y x =--.4.如果从1、2、3这三个数字中任意选取两个数字组成一个两位数,那么这个两位数是素数的概率等于( )(A )12; (B )13; (C )14; (D )16. 5.下图是上海今年春节七天最高气温(℃)的统计结果:这七天最高气温的众数和中位数是( ) (A ) 15,17; (B )14,17; (C )17,14;(D )17,15.6.如图,△ABC 和△AMN 都是等边三角形,点M 是△ABC 的重心,那么AMNABCS S ∆∆的值为( ) (A )23;(B )13; (C )14; (D )49.二、填空题:(本大题共12题,每题4分,满分48分)7.计算:1-31= . 8.不等式12x -<的解集是 . 9.分解因式:282a -= .10.计算:()()322a b b a -+-=.11.方程53x -=的解是 . 12.已知函数26()2f x x =+,那么(2)f = .13.如图,传送带和地面所成的斜坡的坡度为1:3,它把物体从地面送到离地面9米高的地方,则物体从A 到B 所经过的路程为 米. 14.正八边形的中心角等于 度.15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的人数是 .16.已知:⊙O 1、⊙O 2的半径长分别为2和R ,如果⊙O 1与⊙O 2相切,且两圆的圆心距d=3,则R 的值为 .17.定义运算“﹡”:规定x ﹡y by ax +=(其中a 、b 为常数),若1﹡1=3,1﹡(1)-=1,则1﹡2= .18.在Rt △ABC 中,∠ACB =90°,BC =15,AC =20.点D 在边AC 上,DE ⊥AB ,垂足为点E ,将△ADE 沿直线DE 翻折,翻折后点A 的对应点为点P ,当∠CPD 为直角时,AD 的长是 . 三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:112sin 4520168+2-⎛⎫︒-+ ⎪⎝⎭.20.(本题满分10分)解方程:228224x x x x x ++=+--.21.(本题满分10分)如图,AB 是⊙O 的弦,C 是AB 上一点,∠AOC =90°,OA =4,OC =3,求弦AB的长.22.(本题满分10分,每小题5分)某工厂生产一种产品,当生产数量不超过40吨时,每吨的成本y (万元/吨)与生产数量x (吨)的函数关系式如图所示:(1)求y 关于x 的函数解析式,并写出它的定义域;(2)当生产这种产品的总成本为210万元时,求该产品的生产数量. (注:总成本=每吨的成本×生产数量)23.(本题满分12分,第(1)、(2)小题各6分)如图,已知:四边形ABCD 是平行四边形, 点E 在边BA 的延长线上,CE 交AD 于点F ,∠ECA = ∠D . (1)求证:∆EAC ∽∆ECB ;(2)若DF = AF ,求AC ︰BC 的值.24.(本题满分12分,每小题4分)如图,二次函数242y ax ax =-+的图像与y 轴交于点A ,且过点(36)B ,. (1)试求二次函数的解析式及点A 的坐标;(2)若点B 关于二次函数对称轴的对称点为点C , 试求CAB ∠的正切值;(3)若在x 轴上有一点P ,使得点B 关于直线AP 的对称点1B 在y 轴上, 试求点P 的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,Rt △ABC 中,90ACB ∠= ,6BC =,点D 为斜边AB 的中点,点E 为边AC 上的一个动点.联结DE ,过点E 作DE 的垂线与边BC 交于点F ,以,DE EF 为邻边作矩形DEFG .(1)如图1,当8AC =,点G 在边AB 上时,求DE 和EF 的长; (2)如图2,若12DE EF =,设AC x =,矩形DEFG 的面积为y ,求y 关于x 的函数解析式; (3)若23DE EF =,且点G 恰好落在Rt △ABC 的边上,求AC 的长.浦东新区2018学年第二学期初三教学质量检测数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分)1.B 2.C 3.A 4.A 5.C 6.B 二、填空题:(本大题共12题,每题4分,满分48分)7.328.3x < 9.2(2)(2)a a +- 10.a b -- 11.4x =- 12. 313. 18 14.4515. 720. 16. 1或5 17.4 18.358三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)解:原式=22122+22⨯-+……………………………………(8分) =1+32……………………………………(2分) 20.(本题满分10分)解方程:228224x x x x x ++=+--解:去分母得:()()2228x x x -++=……………………………………(4分)整理得:220x x +-=……………………………………(2分) 解得:11x =,22x =-……………………………………(2分)经检验11x =是原方程的根,22x =-是原方程的增根………………………(1分) 原方程的根为1x =……………………………………(1分) 21.(本题满分为10分) 解:过点O 作OD ⊥AB 于D在Rt △AOC 中,222OA OC AC +=,AC = 5……………………………………(2分) 在Rt △AOC 中,4COS 5OA OAC AC ∠== ;……………………………………(2分)在Rt △ADO 中,COS DAOAD AO ∠=, ……………………………………(2分)所以AD OA AO AC =,165AD =.……………………………………(1分) 因为在⊙O 中,OD ⊥AB , 所以AB =2AD =5162⨯,……………………………………(2分) 所以AB =325.……………………………………(1分) 22.(本题满分10分,每小题5分)解: ⑴ 设函数解析式为y =kx +b ,将(0,10)、(40,6)分别代入y =kx +b得⎩⎨⎧+==.406,10b k b …………………………(2分)解之得⎪⎩⎪⎨⎧=-=.10,101b k …………………………(1分)所以y =110x -+10(0≤x ≤40)…………………………(1+1分) ⑵ 由(110x -+11)x =210 …………………………(2分)解得x 1=30或x 2=70,…………………………(1分) 由于0≤x ≤40所以x =30…………………………(1分)答:该产品的生产数量是30吨…………………………(1分)23.(本题满分12分,第(1)、(2)小题各6分)(1)证明:因为,四边形ABCD 是平行四边形,所以,∠B = ∠D ,……………(2分) 因为∠ECA = ∠D ,所以∠ECA = ∠B ,………………(2分) 因为∠E = ∠E ,所以△ECA ∽△ECB ………………(2分)(2)解:因为,四边形ABCD 是平行四边形,所以,CD ∥AB ,即:CD ∥AE 所以CD DFAE AF=………………(1分) 因为DF=AF ,所以,CD=AE , ………………(1分)因为四边形ABCD 是平行四边形,所以,AB=CD ,所以AE=AB ,所以,BE =2AE , …(1分) 因为△ECA ∽△EBC 所以AE CE ACCE BE BC==………………(1分) 所以2212CE AE BE BE =⋅=,即:22CE BE =………………(1分) 所以22AC BC =.………………(1分)24.(1) 将点(3,6)B 代入解析式242y ax ax =-+, 可得: 6912 2.a a =-+,解之得.34-=a ………………(2分) 所以二次函数解析式为2416233y x x =-++.………………(1分) 点A 的坐标为(0,2).………………(1分)(2)由题意, (1,6)C , 2BC =, 5AB =, 4tan 3CBA ∠=. ………………(1分) 过点C 作CH AB ⊥于点H .∴85CH =, 65BH =, 195AH =………………(2分)∴8tan 19CAB ∠=.………………(1分)(3) 由题意, 15AB AB ==, 从而点1B 的坐标为(0,3)-或(0,7).………………(2分)① 若点1(0,3)B -, 设(,0)P x , 由1PB PB =, 有2222(3)63x x -+=+, 解得: 6x =, 即(6,0)P ………………(1分)② 若点1(0,7)B , 设(,0)P x , 由1PB PB =, 有2222(3)67x x -+=+, 解得: 23x =-, 即2(,0)3P -………………(1分)综合知, 点P 的坐标为(6,0)或2(,0)3.25.(1) 如图, ∵152AD AB == ∴315544DE FG ==⨯=.………………(2分) 33154544416BG FG ==⨯=∴453551616DG =-=. 即1535,416DE EF ==.………………(2分) (2)过点D 作DH AC ⊥于点H , 从而3DH =. 易得△DHE ∽△ECF , 由12DE EF =, 可得26EC DH ==, 162EH x =-. ………………(3分)所以22223(6)64524x x DE x =+-=-+. ………………(1分)∴22212902x y DE EF DE x =⋅==-+.………………(1分)(3) 由题意,点G 可以在边BC 或者AB 上.①如左图 若点G 在边BC 上, 从而由3DE =,可知92EF =, 于是29AC EF ==;……(2分) ②如右图, 若点G 在边AB 上. 记AD DB a ==, 矩形边长2,3DE b EF b ==, 由△ADE ∽△FGB , 可得AD FGDE GB =, 即223a b b a b=-, 化简可得22340a ab b --=, 因式分解后有:4a b =,即2AD DE =. 而由△ADE ∽△ACB , 所以2AC BC =, 从而12AC =.………………(3分)综上知,AC 的值为9或12.。
【全国区级联考】上海市浦东新区2018届九年级中考二模试卷数学试题(解析版)

浦东新区2017学年度第二学期初三教学质量检测数学试卷一.选择题:(本大题共6题,每题4分,满分24分)1. 下列代数式中,单项式是 ( )A. ;B. 0;C. x+1;D. .【答案】B【解析】分析:根据单项式的概念回答即可.详解:A.分母中有字母,不是单项式.B.0是单项式.C.是多项式.D.不是单项式.故选B.点睛:考查单项式的概念:数与字母的乘积组成的式子叫做单项式,单独的一个数或者一个字母也是单项式.2. 下列代数式中,二次根式的有理化因式可以是 ( )A. B. ; C. D. .【答案】C【解析】分析:找出原式的一个有理化因式即可.详解:二次根式的有理化因式可以是.故选C.点睛:考查二次根式有理化,如果两个二次根式的积是不含根号的式子,那么这两个二次根式就互为有理化因式.3. 已知一元二次方程x2+2x-1=0,下列判断正确的是 ( )A. 该方程有两个不相等的实数根B. 该方程有两个相等的实数根C. 该方程没有实数根D. 该方程的根的情况不确定【答案】A【解析】分析:判断上述方程的根的情况,只要看根的判别式的值的符号就可以了.详解:∵a=1,b=2,c=−1,∴∴方程有两个不相等实数根.故选A.点睛:考查一元二次方程根的判别式,当时,方程有两个不相等的实数根.当时,方程有两个相等的实数根.当时,方程没有实数根.4. 某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是 ( )A. 平均数B. 众数C. 方差D. 频率【答案】C【解析】分析:根据平均数、众数、中位数反映一组数据的集中趋势,而方差、标准差反映一组数据的离散程度或波动大小进行选择.详解:平均数、众数、中位数反映一组数据的集中趋势,而方差、标准差反映一组数据的离散程度或波动大小.故选C.点睛:本题考查了方差的意义,波动越大,标准差越大,数据越不稳定,反之也成立.5. 下列y关于x的函数中,当x>0时,函数值y随x的值增大而减小的是 ( )A. y=x2;B. y=;C. y=;D. y=.【答案】D【解析】分析:A、根据二次函数的图象的性质解答;B、由一次函数的图象的性质解答;C、由正比例函数的图象的性质解答;D、由反比例函数的图象的性质解答.详解:A. 二次函数的图象,开口向上,并向上无限延伸,在y轴右侧(x>0时),y随x的增大而增大;故本选项错误;B. 一次函数的图象,y随x的增大而增大;故本选项错误;C. 正比例函数的图象在一、三象限内,y随x的增大而增大;故本选项错误;D. 反比例函数中的1>0,所以y随x的增大而减小;故本选项正确;故选D.点睛:考查二次函数,一次函数,反比例函数的性质,掌握它们各自的图像与性质是解题的关键.6. 已知四边形ABCD中,AB//CD,AC//BD,下列判断中正确..的是 ( )A. 如果BC=AD,那么四边形ABCD是等腰梯形;B. 如果AD//BC,那么四边形ABCD是菱形;C. 如果AC平分BD,那么四边形ABCD是矩形;D. 如果AC⊥BD,那么四边形ABCD是正方形.【答案】C【解析】分析:根据特殊四边形的判定方法一一判断即可.详解:A.四边形还可能是矩形.故错误.B.两组对边分别平行的四边形是平行四边形,对角线相等的平行四边形是矩形,故错误.C.根据平分,先证明三角形全等,得到根据一组对边平行且相等的四边形是平行四边形可得四边形是平行四边形,根据对角线相等的平行四边形是矩形,则四边形是矩形,故正确.D.对角线相等且互相垂直的四边形不是正方形.故错误.故选C.点睛:考查特殊四边形的判定,熟记和运用它们的判定方法是解题的关键.注意矩形,菱形都可以在平行四边形的基础上判定.二.填空题:(本大题共12题,每题4分,满分48分)7. 计算:______.【答案】【解析】分析:根据分式的乘法法则进行运算即可.详解:故答案为:点睛:考查分式的乘法,比较简单,根据运算法则进行运算即可.8. 因式分解:x2-4y2=________.【答案】【解析】分析:根据平方差公式进行因式分解即可.详解:原式故答案为:点睛:考查因式分解,常见的因式分解的方法有:提取公因式法,公式法,十字相乘法.9. 方程=3的解是________.【答案】【解析】分析:把方程两边平方,去根号后求解.详解:两边同时平方,得:解得:经检验,是原方程的解.故答案为:点睛:考查无理方程的解法,解无理方程通常用的方法是两边平方法或者换元法.10. 如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是_________.【答案】【解析】分析:本题主要分为两种情况,一种是将"幸福"放在第一个括号里,随之"奋斗"在另一个括号里;另一种是"奋斗"在第一个括号里," 幸福"在第二个括号里.详解:依照题意可知,一共有两种情况分别是"幸福都是奋斗出来的","奋斗都是幸福出来的",所以恰巧是"幸福都是奋斗出来的"的概率是故答案为:点睛:本题主要考查的是对于概率的计算问题,概率是指一个随机事件发生可能性的大小,计算随机事件的概率需要先求出事件发生的总数,以及发生这个事件的次数,最后便可以求出随机事件发生的概率.11. 已知正方形的边长为2cm,那么它外接圆的半径长是_______cm.【答案】【解析】分析:运用正方形的性质,以及与外接圆的关系,可求出外接圆半径.详解:∵正方形的边长为2,由中心角只有四个可得出:∴中心角是:正方形的外接圆半径是:sin∠AOC∵∴故答案为:点睛:考查正多边形和圆,涉及垂径定理,解直角三角形,比较简单.12. 某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工树苗亩,根据题意可列出关于x的方程_________.【答案】【解析】分析:设原计划每天种植工树苗亩,实际每天种植树苗亩,根据题目中的等量关系列出方程即可.详解:设原计划每天种植工树苗亩,需要天,实际每天种植树苗亩,需要天,根据提前一天完成任务,可得:故答案为:点睛:考查分式方程的应用,关键是找到题目中的等量关系.13. 近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为_______.【答案】24【解析】分析:根据自由行的人数以及所占百分比求出总人数,再用总人数乘以跟团游的百分比即可求得. 详解:总人数为:人,跟团游的人数为:人.故答案为:24.点睛:考查扇形统计图和条形统计图,找到它们之间的联系是解题的关键.14. 如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果,那么=________(用向量表示).【答案】【解析】分析:根据求出它们的相似比,得到和之间的关系即可.详解:AD∥故答案为:点睛:考查了相似三角形的判定与性质以及向量的线性运算.掌握相似三角形的判定与性质是解题的关键. 15. 在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是________米.【答案】【解析】分析:过A作于C,由题意可知,在直角三角形中,已知角的对边AC求斜边AB,可以用60°正弦函数来计算即可.详解:根据题意得:米,点A、B之间的距离是米.故答案为:.点睛:解直角三角形的应用-仰角俯角问题,熟练运用锐角三角函数是解题的关键.16. 如图,己知在梯形ABCD中,AD//BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'=_______.【答案】9【解析】分析:作出示意图,可知点在同一条直线上,即可求出详解:如图所示:故答案为:9.点睛:考查图形的旋转,作出示意图是解题此题的关键.17. 如果抛物线C: y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,那么m+n=_________.【答案】0【解析】分析:找出直线与y轴的交点坐标,将其代入抛物线解析式中即可求出n的值;再根据抛物线的解析式找出顶点坐标,将其代入直线解析式中即可得出结论;详解:令直线y=mx+1中x=0,则y=1,即直线与y轴的交点为(0,1);将(0,1)代入抛物线中,得n=1.∵抛物线的解析式为∴抛物线的顶点坐标为(1,0).将点(1,0)代入到直线y=mx+1中,得:0=m+1,解得:m=−1.故答案为:点睛:属于新定义题目,考查了一次函数和二次函数的图象与性质,熟练掌握它们的知识点是解题的关键.18. 已知l1//l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为_________cm.【答案】2或4【解析】分析:分两种情况进行讨论即可.详解:圆与直线有三个公共点,则:圆与直线相交,与直线相切,分两种情况进行讨论.如图所示:半径为:半径为:故答案为:2或4.点睛:考查直线与圆的位置关系,根据圆与直线有三个公共点,得出圆与直线相交,与直线相切,是解答此题的关键.三、解答题:(本大题共7题,满分78分)19. 计算:.【答案】【解析】分析:根据实数的运算法则进行运算即可.详解:原式.点睛:本题考查实数的运算,主要考查二次根式,绝对值,负整数指数幂以及立方根,熟练掌握各个知识点是解题的关键.20. 解不等式组:,并把它的解集在数轴(如图)上表示出来.【答案】【解析】分析:分别解不等式,在数轴上表示出解集,找出解集的公共部分即可.详解:由①得:.解得.由②得:...解得.∴原不等式组的解集为................................. ....21. 如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.【答案】弦CD的长为,⊙O的半径长为【解析】分析:过点作于,连接解,得到,根据求得的长,根据垂径定理即可求出弦的长,根据勾股定理即可求出圆的半径.详解:过点作于,连接∵∴.在中,∴,.∵,∴.∵过圆心,∴.∴∵∴在中,∴弦CD的长为,⊙O的半径长为.点睛:属于圆的综合题,考查解直角三角形,勾股定理,垂径定理等,题目比较基础,熟练掌握各个知识点是解题的关键.22. 某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图像并回答下列问题:(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.【答案】(1)y=3x(2)小明家2017年使用天然气量为340立方米【解析】分析:设.把点代入即可求得函数解析式.设函数解析式为.把点和代入求得函数解析式,令,解方程即可.详解:(1)设.∵的图像过点∴∴.∴.(2)设.∵的图像过点和∴∴∴.当时,解得:.答:小明家2017年使用天然气量为340立方米.点睛:考查待定系数法确定函数关系式,熟练掌握待定系数法是解题的关键.23. 己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC 交AD于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.【答案】(1)证明见解析(2)证明见解析【解析】分析:根据等角的余角相等得到即可证明.详解:∵四边形是正方形,∴,∵FG⊥FC,∴∠GFC= 90°,∵∴∠CDF=∠CFD ,∴∠GFC-∠CFD=∠ADC-∠CDE,即∠GFD=∠GDF.∴GF=GD.联结CG.∵∴点在线段的中垂线上,∴GC⊥DE,∴∠CDF+∠DCG= 90°,∵∠CDF+∠ADE= 90°,∴∠DCG=∠ADE.四边形是正方形,∴AD=DC,∠DAE=∠CDG= 90°,∴△DAE≌△CDG,∴.点是边的中点,点是边的中点,∴,∴∵∴∴∠AFD= 90°,即AF⊥DE.点睛:属于四边形的综合题,考查了正方形的性质,全等三角形的判定与性质,等腰三角形的判定与性质等,考查知识点比较多,难度不大,熟练掌握各个知识点是解题的关键.24. 已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、B(4,0)两点,与y轴交于点C点.(1)求这个二次函数的解析式;(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴...上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.【答案】(1)(2)(3)或 M(0,6)【解析】分析:用待定系数法求二次函数解析式即可.过点作于点在Rt△C OB中,得出CH=EH.在Rt△EBH中,. 设则CH=k,.列方程求解即可.分3种情况进行讨论①当为菱形的边时,②当为菱形的边时,③当为菱形的对角线时,分别求解即可.详解:(1)∵抛物线与轴交于点A(-2,0),B(4,0),∴解得∴抛物线的解析式为(2)过点作于点在Rt△ACO中,∵A(-2,0),∴OA=2,当时∴OC=4,在Rt△C OB中,∵∠COB=90°,OC=OB=4,∴.∵,∴CH=EH.∴在Rt△ACO中,,∵∠CBE=∠ACO,∴在Rt△EBH中,.设则CH=k,.∴.∴∴∴∴(3)∵∴抛物线的对称轴为直线①当为菱形的边时,∴∵点P在二次函数的对称轴上,点的横坐标为1,点的横坐标为1,∴.∵四边形是菱形,∴∴∴.②当为菱形的边时,不存在,③当为菱形的对角线时,设交于点∴互相垂直平分,∴.∵点在直线上,在中,∴∴∴∴∴∴综上所述或M(0,6).点睛:属于二次函数综合题,考查待定系数法求二次函数解析式,解三角形,菱形的判定与性质等,综合性比较强,难度比较大.25. 如图,己知在△ABC中,AB=AC,tanB=,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP·AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当时,求BE的长.【答案】(1)证明见解析(2)(3)或【解析】分析:证明根据相似三角形对应边成比例即可证明.证明根据相似三角形的性质得到,..代入即可.分两种情况进行讨论:①当点F在线段BC上时,②当点F在线段BC的延长线上时,分别求解即可.详解:(1)∵∴∵∴∵又∵∴∵是公共角,∴∴∴.(2)∵∴∴.过点作于点∵经过圆心,∴.∴.在中,∵∴.∴.∴.(3)①当点F在线段BC上时,∵∴∵△AEP∽△ACE.∴∴.过点作垂足为点∵∴中,∵∴∴∴.②当点F在线段BC的延长线上时,∵∠EFC=∠ECF,. 又∵∴∴∵是公共角,∴,∴∵∴∴.∴.综上所述,或.点睛:属于圆的综合题,涉及相似三角形的判定与性质,锐角三角函数等知识点,综合性比较强,难度较大.同学们尤其要熟练相似三角形的判定方法.。
2018年上海市浦东新区中考数学二模试卷(可编辑修改word版)

2018 年上海市浦东新区中考数学二模试卷一.选择题:(本大题共6 题,每题4 分,满分24 分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4 分)下列代数式中,单项式是()A.B.0 C.x+1D.2.(4 分)下列代数式中,二次根式的有理化因式可以是()A.B.C.D.3.(4 分)已知一元二次方程x2+2x﹣1=0,下列判断正确的是()A.该方程有两个不相等的实数根B.该方程有两个相等的实数根C.该方程没有实数根D.该方程的根的情况不确定4.(4 分)某运动员进行射击测试,共射靶6 次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A.平均数B.众数C.方差D.频率5.(4 分)下列y 关于x 的函数中,当x>0 时,函数值y 随x 的值增大而减小的是()A.y=x2B.y C.y D.y6.(4 分)已知四边形ABCD 中,AB∥CD,AC=BD,下列判断中正确的是()A.如果BC=AD,那么四边形ABCD 是等腰梯形B.如果AD∥BC,那么四边形ABCD 是菱形C.如果AC 平分BD,那么四边形ABCD 是矩形D.如果AC⊥BD,那么四边形ABCD 是正方形二.填空题:(本大题共12 题,每题4 分,满分48 分)7.(4 分)计算:.8.(4 分)因式分解:x2﹣4y2=.9.(4 分)方程3 的解是.10.(4 分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.11.(4 分)已知正方形的边长为2cm,那么它的半径长是cm.12.(4 分)某市种植60 亩树苗,实际每天比原计划多种植3 亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x 的方程.13.(4 分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017 年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017 年该小区居民出境游中跟团游的人数为.14.(4 分)如图,在平行四边形ABCD 中,E 是BC 的中点,AE 交BD 于点F,如果,那么(用向量表示).15.(4 分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200 米的点A 处,测得其到海平而观摩点B 的俯角为60°,此时点A、B 之间的距离是米.16.(4 分)如图,已知在梯形ABCD 中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD 绕着点D 逆时针旋转,使点A 落在点C 处,点B 落在点B'处,那么BB'=.17.(4 分)如果抛物线C:y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y 轴上一点P,且抛物线C 的顶点Q 在直线l 上,那么称此直线l 与该抛物线C 具有“一带一路”关系.如果直线y=mx+1 与抛物线y=x2﹣2x+n 具有“一带一路”关系,那么m+n =.18.(4 分)已知l1∥l2,l1、l2 之间的距离是3cm,圆心O 到直线l1 的距离是1cm,如果圆O 与直线l1、l2 有三个公共点,那么圆O 的半径为cm.三、解答题:(本大题共7 题,满分78 分)19.(10 分)|1|﹣27()﹣120.(10 分)解不等式组:,并把它的解集在数轴(如图)上表示出来.21.(10 分)如图,已知AB 是圆O 的直径,弦CD 交AB 于点E,∠CEA=30°,OE=4,DE=5,求弦CD 及圆O 的半径长.22.(10 分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310 立方米及以下为第一档;年用天然气量超出310 立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310 立方米时,求y 关于x 的函数解析式(不写定义域);(2)小明家2017 年天然气费为1029 元,求小明家2017 年使用天然气量.23.(12 分)已知:如图,在正方形ABCD 中,点E 为边AB 的中点,联结DE,点F 在DE 上CF=CD,过点F 作FG⊥FC 交AD 于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.24.(12 分)已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4 的图象经过A(﹣2,0)、B(4,0)两点,与y 轴交于点C 点.(1)求这个二次函数的解析式;(2)如果点E 在线段OC 上,且∠CBE=∠ACO,求点E 的坐标;(3)点M 在y 轴上,且位于点C 上方,点N 在直线BC 上,点P 为上述二次函数图象的对称轴上的点,如果以C、M、N、P 为顶点的四边形是菱形,求点M 的坐标.25.(14 分)如图,已知在△ABC 中,AB=AC,tan B,BC=4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C、F(点C、F 不重合),射线EF 与射线AC 交于点P.(1)求证:AE2=AP•AC;(2)当点F 在线段BC 上,设CF=x,△PFC 的面积为y,求y 关于x 的函数解析式及定义域;(3)当时,求BE 的长.2018 年上海市浦东新区中考数学二模试卷参考答案与试题解析一.选择题:(本大题共6 题,每题4 分,满分24 分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.(4 分)下列代数式中,单项式是()A.B.0 C.x+1 D.【解答】解:A、不是单项式,不符合题意;B、0 是单项式,符合题意;C、x+1 是多项式,不符合题意;D、不是单项式,不符合题意;故选:B.2.(4 分)下列代数式中,二次根式的有理化因式可以是()A.B.C.D.【解答】解:∵()2=m+n,∴二次根式的有理化因式是,故选:C.3.(4 分)已知一元二次方程x2+2x﹣1=0,下列判断正确的是()A.该方程有两个不相等的实数根B.该方程有两个相等的实数根C.该方程没有实数根D.该方程的根的情况不确定【解答】解:∵a=1,b=2,c=﹣1,∴△=b2﹣4ac=22﹣4×1×(﹣1)=8>0,∴该方程有两个不相等的实数根.故选:A.4.(4 分)某运动员进行射击测试,共射靶6 次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是()A.平均数B.众数C.方差D.频率【解答】解:在平均数、众数、方差、频率这些统计量中,表示一组数据波动程度的量是方差.故选:C.5.(4 分)下列y 关于x 的函数中,当x>0 时,函数值y 随x 的值增大而减小的是()A.y=x2B.y C.y D.y【解答】解:A、二次函数y=x2的图象,开口向上,并向上无限延伸,在y 轴右侧(x>0 时),y 随x 的增大而增大;故本选项错误;B、一次函数yx+1 的图象,y 随x 的增大而增大;故本选项错误;C、正比例函数yx 的图象在一、三象限内,y 随x 的增大而增大;故本选项错误;D、反比例函数y 中k=1>0,所以当x>0 时,y 随x 的增大而减小;故本选项正确;故选:D.6.(4 分)已知四边形ABCD 中,AB∥CD,AC=BD,下列判断中正确的是()A.如果BC=AD,那么四边形ABCD 是等腰梯形B.如果AD∥BC,那么四边形ABCD 是菱形C.如果AC 平分BD,那么四边形ABCD 是矩形D.如果AC⊥BD,那么四边形ABCD 是正方形【解答】解:A.如果BC=AD,那么四边形ABCD 可能是等腰梯形,也可能是矩形,错误;B.如果AD∥BC,那么四边形ABCD 是矩形,错误;C.如果AC 平分BD,那么四边形ABCD 是矩形,正确;D.如果AC⊥BD,那么四边形ABCD 不一定是正方形,错误;故选:C.二.填空题:(本大题共12 题,每题4 分,满分48 分)7.(4 分)计算:3ab2.【解答】解:原式=3ab2故答案为:3ab28.(4 分)因式分解:x2﹣4y2=(x+2y)(x﹣2y).【解答】解:x2﹣4y2=(x+2y)(x﹣2y).9.(4 分)方程3 的解是 x=5 .【解答】解:平方,得2x﹣1=9,解得x=5,故答案为:x=5.10.(4 分)如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是.【解答】解:∵将分别写有“幸福”、“奋斗”的2 张卡片,随机放入两个框中,只有两种情况,恰好组成“幸福都是奋斗出来的”的情况只有一种,∴其概率是:,故答案为:.11.(4 分)已知正方形的边长为2cm,那么它的半径长是cm.【解答】解:如图,∵AB=2,∴OC=1,∴OA,故答案为:12.(4 分)某市种植60 亩树苗,实际每天比原计划多种植3 亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x 的方程.【解答】解:设原计划每天种植x 亩,根据题意可得:,故答案为:,13.(4 分)近年来,出境旅游成为越来越多中国公民的假期选择,将2017 年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017 年该小区居民出境游中跟团游的人数为 24 .【解答】解:∵被调查的总人数为36÷45%=80,∴2017 年该小区居民出境游中跟团游的人数为80﹣36﹣20=24(人),故答案为:24.14.(4 分)如图,在平行四边形ABCD 中,E 是BC 的中点,AE 交BD 于点F,如果,那么(用向量表示).【解答】解:∵四边形ABCD 是平行四边形,∴AD∥BC.∵E 是BC 的中点,AE 交BD 于点F,∴2∴AFAE.又,那么.故答案是:.15.(4 分)在南海阅兵式上,某架“直﹣8”型直升飞机在海平面上方1200 米的点A 处,测得其到海平而观摩点B 的俯角为60°,此时点A、B 之间的距离是米.【解答】解:根据题意得:直升飞机与观摩点B 之间的距离是AB米.故答案为:800.16.(4 分)如图,已知在梯形ABCD 中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD 绕着点D 逆时针旋转,使点A 落在点C 处,点B 落在点B'处,那么BB'=9 .【解答】解:如图,将△ABD 绕着点D 逆时针旋转得到△CB′D,作DE∥AB 交BC 于E,则ABED 是平行四边形,BE=AD=3,DE=AB=3,∴EC=BC﹣BE=6﹣3=3,∵DC=3,∴DE=EC=DC=3,∴△DCE 是等边三角形,∴∠DCE=60°.∵在梯形ABCD 中,AD∥BC,AB=DC,∴∠ABC=∠DCB=60°,∠A=120°,∵将△ABD 绕着点D 逆时针旋转得到△CB′D,∴△CB′D≌△ABD,∴∠DCB′=∠A=120°,CB′=AB=3,∴∠BCB′=∠BCD+∠DCB′=120°+60°=180°,∴B、C、B′三点共线,∴BB′=BC+CB′=6+3=9.故答案为9.17.(4 分)如果抛物线C:y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y 轴上一点P,且抛物线C 的顶点Q 在直线l 上,那么称此直线l 与该抛物线C 具有“一带一路”关系.如果直线y=mx+1 与抛物线y=x2﹣2x+n 具有“一带一路”关系,那么m+n= 0 .【解答】解:在y=mx+1 中,令x=0 可求得y=1,在y=x2﹣2x+n 中,令x=0 可得y=n,∵直线与抛物线都经过y 轴上的一点,∴n=1,∴抛物线解析式为y=x2﹣2x+1=(x﹣1)2,∴抛物线顶点坐标为(1,0),∵抛物线顶点在直线上,∴0=m+1,解得m=﹣1,∴m+n=﹣1+1=0,故答案为:0.18.(4 分)已知l1∥l2,l1、l2 之间的距离是3cm,圆心O 到直线l1 的距离是1cm,如果圆O 与直线l1、l2 有三个公共点,那么圆O 的半径为 2 或4 cm.【解答】解:如下图所示,设圆的半径为r如图一所示,r﹣1=3,得r=4,如图二所示,r+1=3,得r=2,故答案为:2 或4.三、解答题:(本大题共7 题,满分78 分)19.(10 分)|1|﹣27()﹣1【解答】解:原式=21﹣3+2=32.20.(10 分)解不等式组:,并把它的解集在数轴(如图)上表示出来.【解答】解:由①得:x>﹣3;由②得:x≤2;∴原不等式组的解集为﹣3<x≤2,.21.(10 分)如图,已知AB 是圆O 的直径,弦CD 交AB 于点E,∠CEA=30°,OE=4,DE=5,求弦CD 及圆O 的半径长.【解答】解:过点O 作OM⊥CD 于点M,联结OD,∵∠CEA=30°,∴∠OEM=∠CEA=30°,在Rt△OEM 中,∵OE=4,∴,,∵,∴,∵OM 过圆心,OM⊥CD,∴CD=2DM,∴,∵,∴在Rt△DOM 中,,∴弦CD 的长为,⊙O 的半径长为.22.(10 分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310 立方米及以下为第一档;年用天然气量超出310 立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图象并回答下列问题:(1)年用天然气量不超过310 立方米时,求y 关于x 的函数解析式(不写定义域);(2)小明家2017 年天然气费为1029 元,求小明家2017 年使用天然气量.【解答】解:(1)设y=kx(k≠0).∵y=kx(k≠0)的图象过点(310,930),∴930=310k,∴k=3.∴y=3x.(2)设y=kx+b(k≠0).∵y=kx+b(k≠0)的图象过点(310,930)和(320,963),∴,∴∴y=3.3x﹣9.3,当y=1029 时,3.3x﹣9.3=1029,解得x=340,答:小明家2017 年使用天然气量为340 立方米.23.(12 分)已知:如图,在正方形ABCD 中,点E 为边AB 的中点,联结DE,点F 在DE 上CF=CD,过点F 作FG⊥FC 交AD 于点G.(1)求证:GF=GD;(2)联结AF,求证:AF⊥DE.【解答】证明:(1)∵四边形ABCD 是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,∵CF=CD,∴∠CDF=∠CFD,∴∠GFC﹣∠CFD=∠ADC﹣∠CDE,即∠GFD=∠GDF,∴GF=GD.(2)联结CG.∵CF=CD,GF=GD,∴点G、C 在线段FD 的中垂线上,∴GC⊥DE,∴∠CDF+∠DCG=90°,∵∠CDF+∠ADE=90°,∴∠DCG=∠ADE.∵四边形ABCD 是正方形,∴AD=DC,∠DAE=∠CDG=90°,∴△DAE≌△CDG,∴AE=DG,∵点E 是边AB 的中点,∴点G 是边AD 的中点,∴AG=GD=GF,∴∠DAF=∠AFG,∠GDF=∠GFD,∵∠DAF+∠AFG+∠GFD+∠GDF=180°,∴2∠AFG+2∠GFD=180°,∴∠AFD=90°,即AF⊥DE.证法2:(1)联结CG 交ED 于点H.∵四边形ABCD 是正方形,∴∠ADC=90°,∵FG⊥FC,∴∠GFC=90°,在Rt△CFG 与Rt△CDG 中,,∴Rt△CFG≌Rt△CDG,∴GF=GD.(2)∵CF=CD,GF=GD,∴点G、C 在线段FD 的中垂线上,∴FH=HD,GC⊥DE,∴∠EDC+∠DCH=90°,∵∠ADE+∠EDC=90°,∴∠ADE=∠DCH,∵四边形ABCD 是正方形,∴AD=DC=AB,∠DAE=∠CDG=90°,∵∠ADE=∠DCH,AD=DC,∠EAD=∠GDC.∴△ADE≌△DCG,∴AE=DG,∵点E 是边AB 的中点,∴点G 是边AD 的中点,∵点H 是边FD 的中点,∴GH 是△AFD 的中位线,∴GH∥AF,∴∠AFD=∠GHD,∵GH⊥FD,∴∠GHD=90°,∴∠AFD=90°,即AF⊥DE.24.(12 分)已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4 的图象经过A(﹣2,0)、B(4,0)两点,与y 轴交于点C 点.(1)求这个二次函数的解析式;(2)如果点E 在线段OC 上,且∠CBE=∠ACO,求点E 的坐标;(3)点M 在y 轴上,且位于点C 上方,点N 在直线BC 上,点P 为上述二次函数图象的对称轴上的点,如果以C、M、N、P 为顶点的四边形是菱形,求点M 的坐标.【解答】解:(1)∵抛物线y=ax2+bx+4 与x 轴交于点A(﹣2,0),B(4,0),∴,解得,∴抛物线的解析式为,(2)如图1,过点E 作EH⊥BC 于点H.在Rt△ACO 中,∵A(﹣2,0),∴OA=2,,∴OC=4,在Rt△COB 中,∵∠COB=90°,OC=OB=4,∴.∵EH⊥BC,∴CH=EH.∴在Rt△ACO 中,,∵∠CBE=∠ACO,在Rt△EBH 中,.设EH=k(k>0),则BH=2k,CH=k,.∴.∴,∴,∴,∴,(3)∵A(﹣2,0)、B(4,0)∴抛物线的对称轴为直线x=1,①当MC 为菱形MCNP 的边时,∴CM∥PN,∴∠PNC=∠NCO=45°.∵点P 在二次函数的对称轴上,∴点P 的横坐标为1,点N 的横坐标为1.∴.∵四边形MCNP 是菱形,∴,∴,∴,②如图2,当MC 为菱形MNCP 的对角线时,设NP 交CM 于点Q,∴CM、NP 互相垂直平分,∴NQ=QP=1.MQ=QC,∵点N 在直线BC 上,∠NCM=∠OCB=45°.在Rt△CQN 中,∴∠NCQ=∠CNQ=45°,∴QN=CQ=1,∴MQ=CQ=1,∴CM=2,∴OM=OC+CM=4+2=6,∴M(0,6),∴综上所述或M(0,6).25.(14 分)如图,已知在△ABC 中,AB=AC,tan B,BC=4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C、F(点C、F 不重合),射线EF 与射线AC 交于点P.(1)求证:AE2=AP•AC;(2)当点F 在线段BC 上,设CF=x,△PFC 的面积为y,求y 关于x 的函数解析式及定义域;(3)当时,求BE 的长.【解答】证明:(1)∵AB=AC,∴∠B=∠ACB.∵EF=EC,∴∠EFC=∠ECF,∵∠EFC=∠B+∠BEF,又∵∠ECF=∠ACB+∠ACE,∴∠BEF=∠ACE,∵∠EAC 是公共角,∴△AEP∽△ACE,∴,∴AE2=AP•AC,(2)∵∠B=∠ACB,∠ECF=∠EFC,∴△ECB∽△PFC.∴,过点E 作EH⊥CF 于点H,∵EH 经过圆心,EH⊥CF,∴.∴,在Rt△BEH 中,∵,∴.∴,∴.∴,(3)①当点F 在线段BC 上时,∵,∴,∵△AEP∽△ACE.∴,∴,过点A 作AM⊥BC,垂足为点M.∵AB=AC,BC=4,∴,在Rt△ABM 中,∵,∴∴,∴,②当点F 在线段BC 延长线上时,∵∠EFC=∠ECF,∠EFC=∠FCP+∠P,∠ECF=∠B+∠BEC.又∵∠B=∠ACB,∠ACB=∠FCP,∴∠B=∠FCP.∴∠P=∠BEC.∵∠EAC 是公共角,∴△AEP∽△ACE,∴,∵,∴,∴,∴,综上所述,或.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浦东新区2017学年度第二学期初三教学质量检测数 学 试 卷(完卷时间:100分钟,满分:150分)2018 04考生注意:1.本试卷含三个大题,共25题。
答题时,考生务必按答题要求在答题纸...规定的位置上作答,在草稿纸、本试卷上答题一律无效。
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸...的相应位置上写出证明或计算的主要步骤。
一.选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1.下列代数式中,单项式是 ( ▲ )(A )1x ; (B )0; (C )x +1; (D )√x . 2.下列代数式中,二次根式√m +n 的有理化因式可以是 (▲ )(A )√m +√n ; (B )√m −√n ; (C )√m +n ; (D )√m −n . 3.已知一元二次方程x 2+2x -1=0,下列判断正确的是 (▲ )(A )该方程有两个不相等的实数根 (B )该方程有两个相等的实数根 (C )该方程没有实数根 (D )该方程的根的情况不确定4.某运动员进行射击测试,共射靶6次,成绩记录如下:8.5,9.0,10,8.0,9.5,10,在下列各统计量中,表示这组数据离散程度的量是 (▲ )(A )平均数 (B )众数 (C )方差 (D )频率5.下列y 关于x 的函数中,当x >0时,函数值y 随x 的值增大而减小的是 (▲ ) (A )y =x 2; (B )y =x+22; (C )y =x 3; (D )y =1x .6.已知四边形ABCD 中,AB//CD ,AC//BD ,下列判断中正确..的是 (▲ ) A 如果BC=AD ,那么四边形ABCD 是等腰梯形; B 如果AD//BC ,那么四边形ABCD 是菱形; C 如果AC 平分BD ,那么四边形ABCD 是矩形; D 如果AC ⊥BD ,那么四边形ABCD 是正方形.二.填空题:(本大题共12题,每题4分,满分48分)7.计算:3b3a ·a2b=▲.8.因式分解:x2-4y2= ▲.9.方程√2x−1=3的解是▲.10.如果将分别写着“幸福”、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张卡片),那么文字恰好组成“幸福都是奋斗出来的”概率是▲.11.已知正方形的边长为2cm,那么它的半径长是▲cm.12.某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植工亩树苗,根据题意可列出关于x的方程▲.13.近年来,出境旅游成为越来越多中国公民的假期选择,将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图所示,那么2017年该小区居民出境游中跟团游的人数为▲.14.如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,如果AE⃗⃗⃗⃗⃗ =a,那么AF⃗⃗⃗⃗⃗ = ▲(用向量a表示).15.在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是▲米.16.如图,己知在梯形ABCD中,AD//BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A 落在点C处,点B落在点B'处,那么BB'= ▲.17.如果抛物线C: y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q 在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,那么m+n= ▲.18.已知l1//l2,l1、l2之间的距离是3cm,圆心O到直线l1的距离是1cm,如果圆O与直线l1、l2有三个公共点,那么圆O的半径为▲cm.三、解答题:(本大题共7题,满分78分) 19.(本题共10分)计算:113181227()2-+--+.20.(本题满分10分)解不等式组:{3x >x −6,x−12≤x+16,并把它的解集在数轴(如图4)上表示出来.图4 21.(本题满分10分)如图5,已知AB 是圆O 的直径,弦CD 交AB 于点E ,∠CEA =30°,OE =4,DE =5√3,求弦CD 及圆O 的半径长.22.(本题满分10分,其中第(1)小题5分,第(2)小题5分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y (元)与年用天然气量x (立方米)的关系如图6所示,观察图像并回答下列问题:(1)年用天然气量不超过310立方米时,求y 关于x 的函数解析式(不写定义域); (2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.图5图623.(本题满分12分,其中第(1)小题5分,第(2)小题7分)己知:如图7,在正方形ABCD 中,点E 为边AB 的中点,联结DE ,点F 在DE 上CF =CD ,过点F 作FG ⊥FC 交AD 于点G . (1)求证:GF =GD ; (2)联结AF ,求证:AF ⊥DE .24.(本题满分12分,每小题4分)已知平而直角坐标系xOy (如图8),二次函数y=ax 2+bx +4的图像经过A (-2,0)、 B (4,0)两点,与y 轴交于点C 点. (1)求这个二次函数的解析式;(2)如果点E 在线段OC 上,且∠CBE =∠ACO ,求点E 的坐标;(3)点M 在y 轴上,且位于点C 上方,点N 在直线BC 上,点P 为上述二次函数图像的对称轴...上的点,如果以C 、M 、N 、P 为顶点的四边形是菱形,求点M 的坐标.图7图825.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图9,己知在△ABC中,AB=AC,tanB=12,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.(1)求证:AE2=AP·AC;(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;(3)当FPEF =12时,求BE的长.图9 备用图浦东新区2017学年度第二学期初三教学质量检测数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.A ; 4.C ; 5.D ; 6.C . 二、填空题:(本大题共12题,每题4分,满分48分) 7.22ab ;8.()()y x y x 22-+; 9.5=x ;10.21;11.2;12.136060=+-x x ; 13.24; 14.a 32; 15.3800;16.9;17.0;18.2或4. 三、解答题:(本大题共7题,满分78分)19.解:原式23-1-222++=.……………………………………………(8分)2-23=.…………………………………………………………(2分)20. 解:3611.26x x x x >-⎧⎪-+⎨≤⎪⎩,由①得:62->x .…………………………………………………(2分)解得3->x .…………………………………………………(1分)由②得:11-3+≤x x )(.……………………………………………(1分) 133+≤-x x .……………………………………………(1分)42≤x .解得2≤x .……………………………………………………(1分)∴原不等式组的解集为23-≤<x .…………………………(2分)……………… …………(2分)21. 解:OD M CD OM O ,联结于点作过点⊥.……………………………………(1分) ∵,︒=∠30CEA∴︒=∠=∠30CEA OEM .……………………………(1分)在Rt △OEM 中,∵OE =4,∴221==OE OM ,3223430cos =⨯=⋅=︒OE EM .(2分)-44321-1-2-3xO① ②∵35=DE ,∴33=-=EM DE DM .…………(1分) ∵CD OM OM ⊥过圆心,,∴DM CD 2=.…………(2分) ∴36=CD .……………………………………………(1分) ∵,,332==DM OM∴在Rt △DOM 中,()313322222=+=+=DM OM OD .…(1分)∴ 弦CD 的长为36,⊙O 的半径长为31.……………………(1分)22.解:(1)设)0(≠=k kx y .…………………………………………………(1分) ∵)0(≠=k kx y 的图像过点(310,930),………………………(1分) ∴,k 310930=∴3=k .……………………………………………(2分)∴ x y 3=.……………………………………………………… (1分) (2)设)0(≠+=k b kx y .…………………………………………………(1分) ∵ )0(≠+=k b kx y 的图像过点(310,930)和(320,963),∴ ⎩⎨⎧=+=+63.9320930310b k b k ,∴ ⎩⎨⎧-==.3.93.3b k ,………………………………………………………(1分)∴3.93.3-=x y .……………………………………………………(1分)当34010293.93.31029==-=x x y ,解得时,.…………………(1分) 答:小明家2017年使用天然气量为340立方米. ……………(1分)另解:求出第二档用气单价3.3元,得2分;第二段用气量30立方米,得1分,2017年用气量340立方米,得1分,答句1分.23.证明:(1)∵是正方形四边形ABCD ,∴︒=∠90ADC .……(1分)∵FG ⊥FC , ∴∠GFC = 90°. ………………(1分) ∵,CD CF = ∴∠CDF =∠CF D .……………………(1分)∴∠GFC -∠CFD=∠ADC -∠CDE ,即∠GFD =∠GDF .(1分) ∴GF =GD .……………………………………………(1分)(2)联结CG .∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G .……(1分)∴GC ⊥DE ,∴∠CDF +∠DCG= 90°,∵∠CDF +∠ADE= 90°,∴∠DCG =∠ADE .∵是正方形四边形ABCD ,∴AD=DC ,∠DAE =∠CDG= 90°, ∴△DAE ≌△CDG .……………………………………………(1分)∴DG AE =.…………………………………………………… (1分)∵的中点,是边点AB E ∴的中点,是边点AD G∴GF GD AG ==.………………………………………………(1分) ∴,,GFD GDF AFG DAF ∠=∠∠=∠……………………………(1分) ∵,︒=∠+∠+∠+∠180GDF GFD AFG DAF …………………(1分) ∴,︒=∠+∠18022GFD AFG∴∠AFD= 90°,即AF ⊥DE .…………………………………(1分) 证法2:(1)联结CG 交ED 于点H .∵是正方形四边形ABCD ,∴︒=∠90ADC .………………………(1分)∵FG ⊥FC ,∴∠GFC = 90°.……………………………………(1分) 在Rt △C FG 与Rt △CDG 中,⎩⎨⎧==.CG CG CD CF ,…………………………………………………… (1分)∴Rt △CFG ≌Rt △CDG .…………………………………………(1分) ∴GD GF =.……………………………………………………(1分) (2)∵,,GD GF CD CF ==∴的中垂线上在线段、点FD C G . …………………………… (1分)∴FH=HD ,GC ⊥DE ,∴∠EDC +∠DCH = 90°,∵∠ADE +∠EDC= 90°,∴∠ADE =∠DCH .………………………………………………(1分) ∵是正方形四边形ABCD ,∴AD=DC =AB ,∠DAE =∠CDG= 90°, ∵GDC EAD DC AD DCH ADE ∠=∠=∠=∠,,.∴△ADE ≌△DCG .………………………………………………(1分)∴DG AE =.……………………………………………………(1分)∵的中点,是边点AB E ∴的中点,是边点AD G∵的中点,是边点FD H ∴GH 是△AFD 的中位线.…………(1分)∴,AF GH // ∴,GHD AFD ∠=∠∵GH ⊥FD ,∴∠GHD = 90°,………………………………(1分)∴∠AFD = 90°,即AF ⊥DE .…………………………………(1分) 24.解:(1)∵ 抛物线42++=bx ax y 与x 轴交于点A (-2,0),B (4,0),∴ ⎩⎨⎧=++=+.04416042-4b a b a ;……………………………………………(1分)解得⎪⎩⎪⎨⎧==.121-b a ;…………………………………………………(2分)∴ 抛物线的解析式为421-2++=x x y .………………………(1分) (2)H BC EH E 于点作过点⊥.在Rt △ACO 中, ∵A (-2,0), 4421-02=++==x x y x 时,当,∴OC=4,在Rt △C OB 中,∵∠COB=90°,∴2445==∠︒BC OCB ,.∵BC EH ⊥,∴CH=EH .∴在Rt △ACO 中,21tan ==∠CO AO ACO ……………………(1分) ∵∠CBE=∠ACO ,∴在Rt △EBH 中,1tan 2EH EBH BH ∠==.设k BH k k EH 2)0(=>=,则,CH=k ,CE =. ∴243==+=k HB CH CB . ∴,324=k ………………………………………………………(1分) ∴,38=CE ………………………………………………………(1分)∴,34=EO ∴),(340E .…………………………………………(1分)(3)∵ A (1,0),B (5,0),∴抛物线的对称轴为直线x =1.………………………………(1分) ①的边时,为菱形当MCNP MC ∴,PN CM //∴∠PNC=∠NCO=45°. ∵点P 在二次函数的对称轴上, ∴,的横坐标为点1P 1的横坐标为点N . ∴245sin 1==︒CN . ∵是菱形,四边形MCNP ∴,2==CN CM∴,24+=+=CM OC OM∴)240(+,M .…………………………………………………(1分) ②的边时,不存在为菱形当MCPN MC .……………………(1分)③的对角线时,为菱形当MNCP MC,于点交设Q CM NP 互相垂直平分,、NP CM ∴1==QP NQ .,QC MQ = ∵上,在直线点BC N ∠NCM=∠OCB=45°.在Rt △CQN 中,∴∠NCQ =∠CNQ=45°,∴,1==CQ QN ∴1MQ CQ ==,∴,2=CM ∴,624=+=+=CM OC OM∴ M (0,6).………………………………………………(1分)∴综上所述)240(+,M 或 M (0,6). 25.证明:(1)∵,AC AB =∴∠B=∠ACB .∵,EC EF =∴∠EFC=∠ECF .……………………………(1分)∵,BEF B EFC ∠+∠=∠ 又∵,ACE ACB ECF ∠+∠=∠∴∠BEF=∠ACE .………………………………………(1分)∵是公共角,EAC ∠∴△AEP ∽△ACE .………………………………………(1分) ∴,AEAPAC AE =∴AC AP AE ⋅=2.…………………………(1分) (2)∵∠B=∠ACB ,∠ECF=∠EFC , ∴△ECB ∽△PFC .∴2⎪⎭⎫⎝⎛=∆∆CB FC S S ECB PFC .…………………………………………(1分)PM CEH F B A E EH CF H ⊥过点做于点, ∵,经过圆心,CF EH EH ⊥∴x FC CH 2121==.∴x BH 214-=.………………………(1分)在Rt △BEH 中,∵,21tan ==∠BH EH B ∴x EH 41-2=. ∴x x EH BC S ECB 214)412(42121-=-⨯⨯=⋅=∆.…………(1分) ∴24214⎪⎭⎫⎝⎛=-x x y .∴)40(32832<<-=x x x y .……………………………………(2分)(3) ①上时,在线段当点BC F∵,21=EF FP ∴,21==EC PE EF PE ∵△AEP ∽△ACE .∴,ECPEAC AE = ∴12AE AC =.………………………………………………(1分)M BC AM A ,垂足为点作过点⊥. ∵,AC AB =,4=BC ∴,221==BC BM 在Rt △ABM 中,∵,21tan =∠B∴1AM AB AC ===,(1分)∴,25=AE ∴253=BE .…………………………………(1分) ②F BC 当点在线段延长线上时,AB FECP∵∠EFC=∠ECF ,EFC FCP P ∠=∠+∠, ECF B BEC ∠=∠+∠.又∵B ACB ACB FCP ∠=∠∠=∠,,∴∠B =∠FCP . ∴∠P =∠BEC .∵是公共角,EAC ∠∴△A EP ∽△ACE ,∴,ECPEAC AE = ∵,21=EF FP ∴32PE PE EF EC ==, ∴32AE AC =(1分) ∴255=BE .………………(1分) 综上所述,253=BE 或2.。
