架空线路线长计算
架空线的弧垂线长及应力计算

架空线的弧垂、线长及应力计算1 弧垂、线长计算架空线由于档距很大,材料的刚性影响可忽略不计,架空线的形状就像一条两端悬挂的柔软的索链。
所以,可以按悬链线进行计算其弧垂和线成,其方程为:弧垂 f = σ/g〔ch(gl/2σ)-1〕线长L = 2σ/g〔sh(gl/2σ)〕上二式写成级数形式展开后为:f = σ/g{〔1+(L12g2/8σ2)+(L14g4/38σ4)+……〕-1}= (L12g/8σ)+(L14g3/38σ3)+……L = 2σ/g{(L1g/2σ)+(L13g3/48σ3)+(L15g5/3840σ5)+……}= L1+(L13g2/24σ2)+(L15g4/1920σ4)+……为了简化计算,工程上取f第一项计算弧垂,取L前二项计算线长(即用抛物线方程代替悬链线方程近似计算):f = L12g/8σL = L1+(L13g2/24σ2)= L1+(8 f2/3 L1)式中,L1—档距,m;g —架空线的比载,N/m·mm2g = W/S其中,W —单位长度导线重量,N/m;S —导线截面积,mm2σ—架空线最低点应力(水平应力),N/mm2。
按上式计算的误差:当弧垂不大于档距的5%时,线长误差率小于15×10-4%。
几种情况弧垂计算:①在交叉跨越档距中一般需计算被跨越物上面任一点导线的弧垂f x,以便校验交叉跨越距离。
档距中任一点导线的弧垂按下式计算:f x = x(L1-x)g/2σ= 4 f x(1-x/L1)/L1式中,x—从悬挂点至计算坐标点的水平距离,m。
②在悬挂点具有高差的档距中架空线的计算需用斜抛物线法,即:L =(L1/cosφ)+(L13g2 cosφ/24σ2)f = L12g/8σcosφf x = x(L1-x)g/2σcosφ式中,φ—高差角,φ = arc tg(h/L1)其中,h —高差;L1—档距。
2 应力计算①架空线任一点处的应力架空线各点所受应力的方向是沿架空线切线方向变化的,最低点处的应力称为水平应力,只要知道最低点应力,架空线上任一点的应力都可以用下式计算求得:σX= σ+(f-f x)g式中,σX—架空线任一点处的应力,N/mm2;σ—架空线最低点应力(水平应力),N/mm2;f —架空线弧垂,m;f x—计算点导线的弧垂,m;g —架空线比载,N/m·mm2。
架空线路长度计算系数

架空线路长度计算系数
例如,在电力输电线路设计中,常用的架空线路类型包括单回线、双
回线、三回线和六回线等。
根据架设线路的工程难度和线路导线的安装方
式等因素,可以制定不同的系数来计算架空线路的实际长度。
一般来说,架空线路长度计算系数的制定需要考虑以下几个因素:
1.线路形式:根据架设线路的形式,可分为单回和多回两种情况。
单
回线路只有一根导线,而多回线路则有多根导线并行布置,这会影响架空
线路的实际长度。
2.线路导线安装方式:线路导线可以采用水平悬挂、斜向悬挂和斜拉
等多种方式。
不同的导线安装方式会导致线路的实际长度有所不同,因此
需要考虑这些因素来制定长度计算系数。
3.线路走向:线路所经过的地形和地貌会对线路的长度产生影响。
如
若线路横跨山脉、河流、湖泊等地形,需要施工人员在设计时考虑这些因素,以确定适当的长度系数。
4.线路曲线和折线段:线路中的曲线和折线段数量也会影响线路的实
际长度。
曲线和折线段的安装通常需要较高的技术水平,这也会成为线路
长度计算系数的一部分。
5.其他因素:还有一些其他因素,如电缆的带电距离、导线的伸长率
等等,也会对线路长度产生一定的影响。
总体而言,架空线路长度计算系数的制定需要综合考虑多个因素,并
根据实际情况进行适当的调整和修正。
通过科学合理地确定长度计算系数,
可以准确预估和计算架空线路的实际长度,为架设线路的设计和施工提供科学的依据。
架空线计算公式

类别 参数
悬链线公式
斜抛物线公式 (大高差 0.1<h/l<0.25)
平抛物线公式 (小高差 h/l<0.1)
y
悬 挂 曲 线 方 程
0 ( x a) a [ch ch ] 0 0
y
2 0 x ( x 2a) sh sh 2 0 2 0
l a h sh arcsh 0 Lh 0 2 0 l b h sh arcsh 0 Lh 0 2 0
1 1 a 0 sin ; b 0 sin 2 2
发生在档距中央。
发生在档距中央。
xm a
发生在:
0 h arcsh l
l 0 h h arcsh arcsh 2 l Lh 0
2
L LH 0 h 2
档内 线长
2 l l 2a 0 sh ch 2 0 2 0
yB 0 sh
两点 应力 关系
2 1 y 2 y1
2 1 y 2 y1
2 1 y 2 y1
最低点至 两悬点的 水平距离
a
1 0 h 1 h arcsh ; b 0 arcsh 2 Lh 0 2 Lh 0
注: Lh 0
L
2 0 l sh 2 0
l 2 l 3 cos 2 cos 24 0
Ll L
h2 2l 3 2l 24 0 2
l 2l 3 (修正式) cos 24 0 2
任一 点 应力
架空导线实习长度核算公式

架空导线实习长度核算公式架空导线实习长度核算公式
导线和地线(以下简称导、地线)的方案安全系数不该小于2.5。
地线的方案安全系数,宜大于导线的方案安全系数。
导、地线在弧垂最低点的最大张力,应按式7.0.3核算(7.0.3)式中:Tmax一;一;导、地线在弧垂最低点的最大张力,N;Tp一;一;导、地线的拉断力,N;KC一;一;导、地线的方案安全系数。
悬挂点的方案安全系数不该小于2.25。
架起在滑轮上的导、地线,还应核算悬挂点有些曲折致使的附加张力。
在稀有风速或稀有覆冰气候条件时,弧垂最低点的最大张力,不该逾越拉断力的60%。
悬挂点的最大张力,不该逾越拉断力的66%。
1。
架空线常用计算公式和应用举例

架空线常用计算公式和应用举例前言在基层电力部门从事输电线路专业工作的技术人员,需要掌握导线的基本的计算方法。
这些方法可以从教材或手册中找到。
但是,教材一般从原理开始叙述,用于实际计算的公式夹在大量的文字和推导公式中,手册的计算实例较少,给应用带来一些不便。
本书根据个人在实际工作中的经验,摘取了一些常用公式,并主要应用Excel工作表编制了一些例子,以供相关人员参考。
本书的基本内容主要取材于参考文献,部分取材于网络。
所用参考文献如下:1. GB50545 -2010 《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电力线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线力学计算,中国电力出版社,2003。
5. 刘增良、杨泽江主编,输配电线路设计, 中国水利水电出版社,2004。
6.李瑞祥编,高压输电线路设计基础,水利电力出版社,1994。
7.电机工程手册编辑委员会,电机工程手册,机械工业出版社,1982。
8.张殿生主编,电力工程高压送电线路设计手册,中国电力出版社,2003。
9.浙西电力技工学校主编,输电线路设计基础,水利电力出版社,1988。
10.建筑电气设计手册编写组,建筑电气设计手册,中国建筑工业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国水利水电出版社,2003。
由于个人水平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久 2015-9-16目录第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式二、导线截面选择与校验的方法三、地线的选择第二节架空电力线路的设计气象条件一、设计气象条件的选用二、气象条件的换算第二章导线(地线)张力(应力)弧垂计算第一节导线和地线的机械物理特性与单位荷载一、导线的机械物理特性二、导线的单位荷载第二节导线的最大使用张力和平均运行张力一、导线的最大使用张力二、导线的平均运行张力第三节导线张力弧垂的精确计算一、导线的悬链线解析方程式二、导线的张力、弧垂与线长三、导线的允许档距和允许高差四、导线悬挂点等高时的张力弧垂计算五、架空线的等效张力(平均张力)第四节导线张力弧垂的近似计算一、导线的抛物线解析方程式二、导线的张力、弧垂与线长第五节水平档距和垂直档距一、水平档距和水平荷载二、垂直档距和垂直荷载第六节导线的状态方程式一、孤立档的状态方程式二、连续档的状态方程式和代表档距第七节临界档距一、用斜抛物线状态方程式求临界档二、用临界档距判别控制条件所控制的档距范围第八节导线张力弧垂计算步骤第九节导线应力弧垂分析一、导线和地线的破坏应力与比载二、导线的悬链线公式三、导线应力弧垂的近似计算四、水平档距和垂直档距五、导线的斜抛物线状态方程式六、临界档距第三章特殊情况导线张力弧垂的计算第一节档距中有一个集中荷载时导线张力弧垂的计算一、档距中有一个集中荷载的弧垂和张力二、导线强度及对地或交叉跨越物距离的校验第二节孤立档导线的计算一、耐张绝缘子串的单位荷载二、孤立档导线的张力和弧垂三、孤立档的临界档距第三节导线紧线时的过牵引计算一、紧线施工方法与过牵引长度二、过牵引引起的伸长和变形三、不考虑耐张绝缘子串的导线过牵引计算四、孤立档考虑耐张绝缘子串的导线过牵引计算第四节连续倾斜档的安装计算一、连续倾斜档导线安装时的受力分析二、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘子串倒挂的校验第六节悬垂线夹悬垂角的计算第四章导线和地线的防振计算第一节防振锤和阻尼线一、防振锤的安装二、阻尼线的安装第二节分裂导线的防振第五章架空线的不平衡张力计算第一节刚性杆塔固定横担线路不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时的不平衡张力求解方法三、断线张力求解方法四、导线从悬垂线夹松落时的不平衡张力第二节固定横担线路考虑杆塔挠度时不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张力求解方法三、考虑杆塔挠度时的断线张力求解方法第三节转动型横担线路断线张力的计算一、断线张力的求解方程二、断线张力的计算机试凑求解方法第四节相分裂导线不平衡张力的计算一、计算分裂导线的不平衡张力的公式二、计算公式中几个参数的取值与计算三、不平衡张力的求解方法四、用Excel工作表进行计算的方法第五节地线支持力的计算一、电杆的刚度和刚度系数二、电杆的挠度三、地线支持力的计算四、地线支持力的计算机试凑求解方法第六章架空线弧垂观测计算第一节弧垂观测概述一、观测档的选择二、导线初伸长的处理三、弧垂的观测方法四、弧垂的调整与检查五、观测弧垂时应该注意的问题第二节均布荷载下的弧垂的观测参数计算一、用悬链线法求弧垂观测参数二、弧垂观测角的近似计算公式三、用异长法和等长法观测弧垂时a、b与弧垂f的关系第三节观测档内联有耐张绝缘子串时弧垂的观测参数计算一、观测档弧垂的计算公式二、用等长法和异长法观测弧垂三、用角度法观测弧垂架空线常用计算公式和应用举例 安岳供电公司 李荣久第一章 电力线路的导线和设计气象条件第一节 导线和地线的型式和截面的选择一、导线型式常用导线的型号和名称如表1-1-1。
架空线常用计算公式和应用举例(互联网+)

架空线常用计算公式和应用举例前言在基层电力部门从事输电线路专业工作的技术人员,需要掌握导线的基本的计算方法。
这些方法可以从教材或手册中找到。
但是,教材一般从原理开始叙述,用于实际计算的公式夹在大量的文字和推导公式中,手册的计算实例较少,给应用带来一些不便。
本书根据个人在实际工作中的经验,摘取了一些常用公式,并主要应用Excel工作表编制了一些例子,以供相关人员参考。
本书的基本内容主要取材于参考文献,部分取材于网络。
所用参考文献如下:1. GB50545 -2010 《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电力线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线力学计算,中国电力出版社,2003。
5. 刘增良、杨泽江主编,输配电线路设计, 中国水利水电出版社,2004。
6.李瑞祥编,高压输电线路设计基础,水利电力出版社,1994。
7.电机工程手册编辑委员会,电机工程手册,机械工业出版社,1982。
8.张殿生主编,电力工程高压送电线路设计手册,中国电力出版社,2003。
9.浙西电力技工学校主编,输电线路设计基础,水利电力出版社,1988。
10.建筑电气设计手册编写组,建筑电气设计手册,中国建筑工业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国水利水电出版社,2003。
由于个人水平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久 2015-9-16目录第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式二、导线截面选择与校验的方法三、地线的选择第二节架空电力线路的设计气象条件一、设计气象条件的选用二、气象条件的换算第二章导线(地线)张力(应力)弧垂计算第一节导线和地线的机械物理特性与单位荷载一、导线的机械物理特性二、导线的单位荷载第二节导线的最大使用张力和平均运行张力一、导线的最大使用张力二、导线的平均运行张力第三节导线张力弧垂的精确计算一、导线的悬链线解析方程式二、导线的张力、弧垂与线长三、导线的允许档距和允许高差四、导线悬挂点等高时的张力弧垂计算五、架空线的等效张力(平均张力)第四节导线张力弧垂的近似计算一、导线的抛物线解析方程式二、导线的张力、弧垂与线长第五节水平档距和垂直档距一、水平档距和水平荷载二、垂直档距和垂直荷载第六节导线的状态方程式一、孤立档的状态方程式二、连续档的状态方程式和代表档距第七节临界档距一、用斜抛物线状态方程式求临界档二、用临界档距判别控制条件所控制的档距范围第八节导线张力弧垂计算步骤第九节导线应力弧垂分析一、导线和地线的破坏应力与比载二、导线的悬链线公式三、导线应力弧垂的近似计算四、水平档距和垂直档距五、导线的斜抛物线状态方程式六、临界档距第三章特殊情况导线张力弧垂的计算第一节档距中有一个集中荷载时导线张力弧垂的计算一、档距中有一个集中荷载的弧垂和张力二、导线强度及对地或交叉跨越物距离的校验第二节孤立档导线的计算一、耐张绝缘子串的单位荷载二、孤立档导线的张力和弧垂三、孤立档的临界档距第三节导线紧线时的过牵引计算一、紧线施工方法与过牵引长度二、过牵引引起的伸长和变形三、不考虑耐张绝缘子串的导线过牵引计算四、孤立档考虑耐张绝缘子串的导线过牵引计算第四节连续倾斜档的安装计算一、连续倾斜档导线安装时的受力分析二、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘子串倒挂的校验第六节悬垂线夹悬垂角的计算第四章导线和地线的防振计算第一节防振锤和阻尼线一、防振锤的安装二、阻尼线的安装第二节分裂导线的防振第五章架空线的不平衡张力计算第一节刚性杆塔固定横担线路不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时的不平衡张力求解方法三、断线张力求解方法四、导线从悬垂线夹松落时的不平衡张力第二节固定横担线路考虑杆塔挠度时不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张力求解方法三、考虑杆塔挠度时的断线张力求解方法第三节转动型横担线路断线张力的计算一、断线张力的求解方程二、断线张力的计算机试凑求解方法第四节相分裂导线不平衡张力的计算一、计算分裂导线的不平衡张力的公式二、计算公式中几个参数的取值与计算三、不平衡张力的求解方法四、用Excel工作表进行计算的方法第五节地线支持力的计算一、电杆的刚度和刚度系数二、电杆的挠度三、地线支持力的计算四、地线支持力的计算机试凑求解方法第六章架空线弧垂观测计算第一节弧垂观测概述一、观测档的选择二、导线初伸长的处理三、弧垂的观测方法四、弧垂的调整与检查五、观测弧垂时应该注意的问题第二节均布荷载下的弧垂的观测参数计算一、用悬链线法求弧垂观测参数二、弧垂观测角的近似计算公式三、用异长法和等长法观测弧垂时a、b与弧垂f的关系第三节观测档内联有耐张绝缘子串时弧垂的观测参数计算一、观测档弧垂的计算公式二、用等长法和异长法观测弧垂三、用角度法观测弧垂架空线常用计算公式和应用举例安岳供电公司李荣久第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式常用导线的型号和名称如表1-1-1。
电力架空线路导线长度计算

电力架空线路导线长度计算
电力架空线路导线长度计算是建筑施工中的重要内容,对于上下线路的长度有着重要意义。
电力架空线路导线计算分为几个步骤,以下是按照步骤介绍:
一、检查地形及架线路线:在计算架空线路导线长度时,首先要查看地形,比如地表形状、高程、地势等,以求确定架空线路的最优路线。
二、计算导线有效长度:计算架空线路的导线有效长度,也就是实际长度,包括导线的直线部分和弯曲部分。
在计算导线有效长度时,必须根据地形线形以及架空线路安装形式,准确进行长度计算。
三、根据电缆规格计算所需长度:架空线路导线长度是由已定义的电缆规格决定的,具体电缆规格,包括导线的材质、可承受最大电流、每根导线的重量等等,必须按要求把握,然后根据架空线路的实际长度,计算所需的电缆长度。
四、确定架空线路的总长度:在完成上述步骤后,就可以确定架空线路的最终长度了,根据架空线路的长度,计算出导线的垂直悬挂点的间距,以便确定架空线路的总长度。
电力架空线路导线长度计算一般分为以上几个步骤,在选择架空线路及其导线时,必须充分考虑到实际情况,以减少施工成本和安装难度。
此外,施工单位应加强安全生产意识,全程按照相关规定执行,以确保施工的安全、质量及进度。
架空线路公式

导线截面的选择1、按经济电流密度选择线路的投资总费用Z1式中Z1 =(F0+αΑ)LF0—与导线截面无关的线路单位长费用;α—与导线截面相关的线路单位长度单位截面的费用;Α—导线的截面积;L—线路长度。
线路的年运行费用包括折旧费,检修维护费和管理费等,可用百分比b 表示为线路的年电能损耗费用(不考虑电晕损失):若投资回收年限为n得到导线的经济截面A n经济电流密度J n我国的经济电流密度可以按表查取。
2、按电压损耗校验在不考虑线路电压损耗的横分量时,线路电压、输送功率、功率因数、电压损耗百分数、导线电阻率以及线路长度与导线截面的关系,可用下式表示3、按导线允许电流校验(1)按导线的允许最大工作电流校验导线的允许最大工作电流为其中(2)按短路电流校验根据短路电流的热效应,要求导线的最小截面为4、按电晕条件校验超高压输电线路的导线表面电场强度很高,以至超过周围空气的放电强度,使空气电离形成局部放电,这种现象称为电晕。
电晕可以引起无线电干扰、可听噪声、导线震动等,还会产生有功功率损耗。
导线的电晕随外加电压的升高而出现、加剧。
导线表面开始发生局部放电时的电压,称为起始电晕电压。
导线表面全面发生电晕时的电压,称为临界电晕电压,相应的电场强度称为临界电场强。
倒显得临界电晕电场强,与其直径、表面状况及大气条件等有关。
根据理论分析及试验所的结果,海拔不超过1000m 的地区,如导线直径不小于下表所列数值,一般不必验算电晕。
绝缘子和绝缘子串1、绝缘子的许用荷载绝缘子的许用荷载当绝缘子所受荷载大于其许用荷载时,除可更换大吨位绝缘子外,还可以采取双串和多串联解决。
所需串数N悬垂串片数计算:一般地区单位工作电压所要求的泄露电流(泄露比距):海拔高度1000m~3500m 的地区悬垂串的绝缘子数量按下式计算。
气象参数1、风速的此时换算欲将 4 次定时2 分钟平均风速V2换算成连续自记10 分钟平均风速V10,v需要搜集到两种观测方法的平行观测记录,然后通过相关分析建立二者之间的回归方程式。
第十章10kV以下架空配电线路-说明计算规则

第十章10kV以下架空配电线路说明一、本章定额按平地施工条件考虑,若在其它地形条件下施工,其人工和机械按下表予以调整。
地形系数调整表二、地形划分的特征:1.平地:地形比较平坦、地面比较干燥的地带。
2.丘陵:地形有起伏的矮岗、土丘等地带。
3.一般山地:指一般山岭或沟谷地带、高原台地等。
4.泥沼地带:指经常积水的田地或泥水淤积的地带。
三、预算编制中,全线地形分几种类型时,可近各种类型长度所占百分比求出综合系数进行计算。
四、土质分类如下:1.普通土:指种植土、粘砂土、黄土和盐碱土等,主要利用锹、铲即可挖掘的土质。
2.坚土:指土质坚硬难挖的红土、板状黏土、重块土、高岭土,必须用铁镐、条锄挖松、再用锹、铲挖掘的土质。
3.松砂石:指碎石、卵石和土的混合体。
各种不坚实砾岩、页岩、风化岩,节理和裂缝较多的岩石等(不需用爆破方法开采的),需要镐、撬棍、大锤、楔子等工具配合才能挖掘。
4.岩石:一般指坚实的粗花岗岩、白云岩、片麻岩、玢岩、石英岩、大理岩、石灰岩、石灰质胶结的密实砂岩的石质,不能用一般挖掘工具进行开挖,必须采用打眼、爆破或打凿才能开挖。
5.泥水:指坑的周围经常积水。
坑的土质松散,如淤泥和沼泽地等挖掘时因水渗入和浸润而成泥浆,容易坍塌,而用挡土板和适量排水才能施工。
6.流砂:指坑的土质为砂质或分层砂质,挖掘过程中砂层有上涌现象,容易坍塌,挖掘时需排水和采用挡土板才能施工。
五、线路一次施工工程量按5根以上电杆考虑,如5根以内者,其全部人工、机械乘以系数1.3。
六、如果出现钢管杆的组立,按同高度混凝土杆组立的人工、机械乘以系数1.4,材料不调整。
七、导线跨越架设:1.每个跨越距按50m以内考虑,大于50m而小于100m时按2处计算,依此类推。
2.在同跨越档内,有多种(或多次)跨越物时,应根据跨越物种类分别执行定额。
3.跨越定额仅考虑因跨越而多耗的人工、机械台班和材料,要计算架线工程量时,不扣除跨越档的长度。
八、杆上变压器安装不包括变压器调试、抽芯、干燥工作。
架空线常用计算公式和应用举例

架空线常用计算公式和应用举例前言在基层电力部门从事输电线路专业工作的技术人员,需要掌握导线的基本的计算方法。
这些方法可以从教材或手册中找到。
但是,教材一般从原理开始叙述,用于实际计算的公式夹在大量的文字和推导公式中,手册的计算实例较少,给应用带来一些不便。
本书根据个人在实际工作中的经验,摘取了一些常用公式,并主要应用Excel工作表编制了一些例子,以供相关人员参考。
本书的基本内容主要取材于参考文献,部分取材于网络。
所用参考文献如下:1. GB50545 -2010 《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电力线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线力学计算,中国电力出版社,2003。
5. 刘增良、杨泽江主编,输配电线路设计, 中国水利水电出版社,2004。
6.李瑞祥编,高压输电线路设计基础,水利电力出版社,1994。
7.电机工程手册编辑委员会,电机工程手册,机械工业出版社,1982。
8.张殿生主编,电力工程高压送电线路设计手册,中国电力出版社,2003。
9.浙西电力技工学校主编,输电线路设计基础,水利电力出版社,1988。
10.建筑电气设计手册编写组,建筑电气设计手册,中国建筑工业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国水利水电出版社,2003。
由于个人水平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久 2015-9-16目录第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式二、导线截面选择与校验的方法三、地线的选择第二节架空电力线路的设计气象条件一、设计气象条件的选用二、气象条件的换算第二章导线(地线)张力(应力)弧垂计算第一节导线和地线的机械物理特性与单位荷载一、导线的机械物理特性二、导线的单位荷载第二节导线的最大使用张力和平均运行张力一、导线的最大使用张力二、导线的平均运行张力第三节导线张力弧垂的精确计算一、导线的悬链线解析方程式二、导线的张力、弧垂与线长三、导线的允许档距和允许高差四、导线悬挂点等高时的张力弧垂计算五、架空线的等效张力(平均张力)第四节导线张力弧垂的近似计算一、导线的抛物线解析方程式二、导线的张力、弧垂与线长第五节水平档距和垂直档距一、水平档距和水平荷载二、垂直档距和垂直荷载第六节导线的状态方程式一、孤立档的状态方程式二、连续档的状态方程式和代表档距第七节临界档距一、用斜抛物线状态方程式求临界档二、用临界档距判别控制条件所控制的档距范围第八节导线张力弧垂计算步骤第九节导线应力弧垂分析一、导线和地线的破坏应力与比载二、导线的悬链线公式三、导线应力弧垂的近似计算四、水平档距和垂直档距五、导线的斜抛物线状态方程式六、临界档距第三章特殊情况导线张力弧垂的计算第一节档距中有一个集中荷载时导线张力弧垂的计算一、档距中有一个集中荷载的弧垂和张力二、导线强度及对地或交叉跨越物距离的校验第二节孤立档导线的计算一、耐张绝缘子串的单位荷载二、孤立档导线的张力和弧垂三、孤立档的临界档距第三节导线紧线时的过牵引计算一、紧线施工方法与过牵引长度二、过牵引引起的伸长和变形三、不考虑耐张绝缘子串的导线过牵引计算四、孤立档考虑耐张绝缘子串的导线过牵引计算第四节连续倾斜档的安装计算一、连续倾斜档导线安装时的受力分析二、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘子串倒挂的校验第六节悬垂线夹悬垂角的计算第四章导线和地线的防振计算第一节防振锤和阻尼线一、防振锤的安装二、阻尼线的安装第二节分裂导线的防振第五章架空线的不平衡张力计算第一节刚性杆塔固定横担线路不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时的不平衡张力求解方法三、断线张力求解方法四、导线从悬垂线夹松落时的不平衡张力第二节固定横担线路考虑杆塔挠度时不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张力求解方法三、考虑杆塔挠度时的断线张力求解方法第三节转动型横担线路断线张力的计算一、断线张力的求解方程二、断线张力的计算机试凑求解方法第四节相分裂导线不平衡张力的计算一、计算分裂导线的不平衡张力的公式二、计算公式中几个参数的取值与计算三、不平衡张力的求解方法四、用Excel工作表进行计算的方法第五节地线支持力的计算一、电杆的刚度和刚度系数二、电杆的挠度三、地线支持力的计算四、地线支持力的计算机试凑求解方法第六章架空线弧垂观测计算第一节弧垂观测概述一、观测档的选择二、导线初伸长的处理三、弧垂的观测方法四、弧垂的调整与检查五、观测弧垂时应该注意的问题第二节均布荷载下的弧垂的观测参数计算一、用悬链线法求弧垂观测参数二、弧垂观测角的近似计算公式三、用异长法和等长法观测弧垂时a、b与弧垂f的关系第三节观测档内联有耐张绝缘子串时弧垂的观测参数计算一、观测档弧垂的计算公式二、用等长法和异长法观测弧垂三、用角度法观测弧垂架空线常用计算公式和应用举例 安岳供电公司 李荣久第一章 电力线路的导线和设计气象条件第一节 导线和地线的型式和截面的选择一、导线型式常用导线的型号和名称如表1-1-1。
架空送电线路工程架线施工常用计算公式集锦
6
1
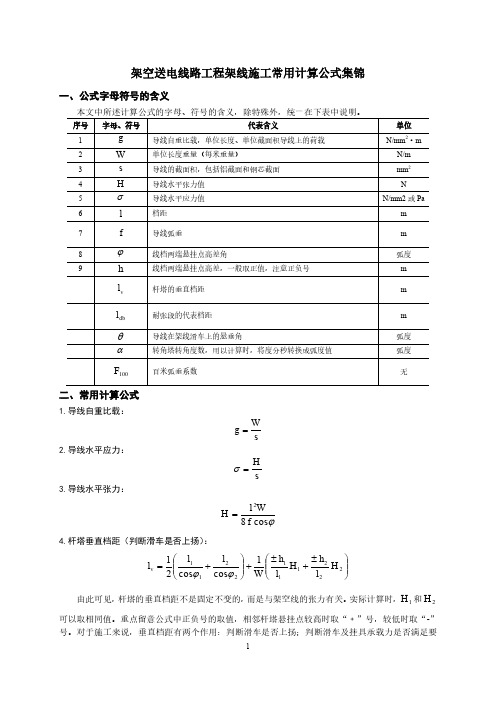
求,是否需要悬挂双滑车或者采取其他补强措施。 5.耐张段代表档距:
l db
l cos l cos
3 i i i 3 i 2 i
i
(李庆林版)
l db
l cos l cos
i
i
(李博之版)
注:地形平坦情况下,两者计算结果相差不大,为了确保精确度,建议采用李博之版。 6.导线在滑车上的悬垂角:
2
当包络角大于 30°时,需要悬挂双滑车,对于光缆来说,可以放大到 60°。 8.相邻导线挂点高差角:
tg 1
9.导线一档线长计算公式
h l
l W 2l 3 L (平抛物线计算公式) cos 24H 2 L
10.弧垂(驰度)计算公式
l W 2 l 3 cos (斜抛物线计算公式) cos 24H 2
lv
l 1 l1 2 2 cos1 cos 2
由此可见, 杆塔的垂直档距不是固定不变的, 而是与架空线的张力有关。 实际计算时,H 1 和 H 2 可以取相同值。重点留意公式中正负号的取值,相邻杆塔悬挂点较高时取“﹢”号,较低时取“-” 号。对于施工来说,垂直档距有两个作用:判断滑车是否上扬;判断滑车及挂具承载力是否满足要
其中: l 为控制档档距,m; x 为障碍物到高悬挂点水平距离,m; y 为高悬挂点到障碍物顶部的垂直净空距离,m。
4
y 0 为导线对正下方障碍物垂直净空距离,即安全距离,m;
为控制档两侧挂点高差角。
16.出口张力计算
T0 1i H i W (h1 1h2 2 h3 1i hi 1i f i )
3
-1 -1
架空线路弧垂应力及线长计算

架空线路弧垂、应力及线长计算1、导线的机械特性和荷载 1.1导线的机械特性导线的特性参数是指导线的瞬时破坏应力σp 、弹性系数E 、温度线膨胀系数α以及密度γ等数据。
这些特性参数是对导线进行机械计算的重要依据,一般可从有关资料或手册中得到。
1.1.1导线的瞬时破坏应力σp 。
对导线做拉伸试验时,将测得的瞬时拉断力除以导线的截面积,即得导线的瞬时破坏应力σp ,计算公式为σp =AT p (N/mm 2) (ZY0400201002-1)式中:T p —导线的瞬时拉断力,N ;A —导线的截面积,mm 2。
对于钢芯铝绞线来说,指的是的综合瞬时破坏应力σp ,可以通过下面的经验公式求得σp =sa sps s ap a a A A σA σA η++η(N/mm 2) (ZY0400201002-2)式中:ηa —铝线绞合引起的强度损失系数,37股以下绞线ηa =0.95,37股以上绞线ηa =0.9; ηs —钢绞线绞合引起的强度损失系数,取ηa =0.85; σap —铝单线的抗拉强度,N /mm 2; σsp —钢线的抗拉强度,N /mm 2; A a —铝部的截面积; A s —钢部的截面积。
1.1.2导线弹性系数E 。
是指在弹性限度内,导线受拉力作用时,其应力σ与应变ε的比例系数E 。
钢芯铝绞线的弹性系数是一个综合弹性系数E ,可按下式计算aaE E E ++=1a s (N/mm 2) (ZY0400201002-3)式中:E s —单股钢线的弹性系数,N /mm 2; E a —单股铝线的弹性系数,N /mm 2;a —导线铝和钢的截面比,LGJ 型a =5.3~6.0,LGJQ 型a =8.0,LGJJ 型a =4.3~4.4。
1.1.3导线温度线膨胀系数α。
是指导线温度升高1℃时长度伸长的相对值,用公式表示为α=tΔε(1/℃) (ZY0400201002-4)式中:ε—温度变化引起的导线相对变形量;∆t —温度变化量,℃。
40m档距架空线路导线实际长度

40m档距架空线路导线实际长度下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!《40m 架空线路导线实际长度计算》1. 引言架空线路作为电力输送的主要形式之一,其导线长度的计算是线路设计中的重要环节。
架空输电线路设计讲座第5章

架空线的线长和弧垂有关计算公式是比载、应力的函 数。当气象条件发生变化时,线长、弧垂、应力发生相应 变化。不同气象条件(状态)下架空线的各参数之间存在 着一定的关系。
状态方程式:揭示架空线从一种气象条件(第一状态) 改变到另一种气象条件(第二状态)下的各参数之间关系 的方程。
第一状态 l1、h1、t1、γ1、σ01、σcp1、L1
气象条件变化
第二状态 l2、h2、t2、γ2、σ02、σcp2、L2 则两种状态下的架空线悬挂曲线长度折算到同一原
始状态下的原始线长相等,所以:
L1
1
cp1
E
(t1
t0 )
L2
1
cp
E
2
(t2
t0 )
(5−2)
结论 不同状态下的架空线悬挂曲线长度,折算到原 始状态下在原始线长相等。
11
2401 cos
1
(t1
t0
)
l2 cos 2
l2 3
22
cos
2
24
2 02
1
1 E
02 cos 2
l2 2
22
2402 cos
2
(t2
t0
)
(5−5)
若档距、高差的大小可认为不变,即l1=l2=l、h1=h2=h (β1=β2=β)时,将上式展开并加以整理后得
(2)当档距很大时:将(5−7)两端除以 l 2,并令档距
l 趋于无限大,状态方程式变为:
02 01 2 1
结论:在档距很大时,架空线的应力变化仅决定于比 载而与温度无关。因此对于大档距架空线,最大比载气象 条件将成为控制条件。
推论:在档距 l 由零逐渐增大至无限大的过程中,必然 存在这样一个档距:气温的作用和比载的作用同等重要, 最低气温和最大比载时架空线的应力相等,即最低气温和 最大比载两个气象条件同时成为控制条件。
架空线路线长计算

第四章 均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此,设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节 架空线悬链线方程的积分普遍形式图4-1 架空线悬挂曲线受力图(a )分离体受力图;(b )整档架空线受力图;图4-1(b )所示为某档架空线,A 、B 均为两悬挂点。
沿架空线线长作用有均布比载γ,方向垂直向下。
在比载γ作用下,架空线呈曲线形状,其最低位置在ο点,在悬挂点A 、B处,架空线的轴向应力分别为A σ和B σ。
选取线路方向(垂直于比载)为坐标系的x 轴,平行于比载方向为y 轴。
在架空线上任选一点C ,取长为OC L 的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有0cos ,0σθσ==∑XX (4- 1)OC XL Y γθσ==∑sin ,0 (4- 2)式(4-1)表明,架空线上任一点C 处的轴向应力X σ的水平分量等于弧垂最低点处的轴向应力0σ,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长OC L 与比载γ之积。
以上两式相除可得tg θ=OCL 0σγdx dy =OC L 0σγ(4- 3)上式为悬链线方程的徽分形式。
从中可以看出,当比值γ/0σ一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
架空输电线路改建线长计算

架空输电线路改建线长计算架空输电线路改建线长计算摘要:介绍了架空输电线路的几种改造情况,提出了对线长变量的计算方法。
关键词:高度、弧垂、应力、线长。
1引言目前,随着社会经济的飞速发展,基础设施建设的全面铺开,运行中的电力线路经常需要进行改造。
在耐张段保持不动的情况下,一般有增加直线杆塔、个别直线杆塔移位升高等改造方式,因架空输电线路建成后,耐张段的导线长度已为一定值,如线路进行改造,该耐张段的线长势必发生变化,如不对线长进行适当调整,导线对地距离、导线安全系数、杆塔受力条件等技术参数将发生较大的变化,甚至可能直接影响到线路安全运行。
为保证导线对地距离、导线安全系数、杆塔受力条件等,都符合线路原来的设计要求,必须对改造后的线长变量进行适当补偿。
因此,在这类改造工程的设计、施工过程中,重点需要研究解决的是线路改造前后的导线线长变量问题。
2改建方法线路要求改建后导线对地距离、架空线应力以及杆塔的受力条件等,都应符合原线路的设计要求,改建施工常用方法是将改建的耐张段按新的情况重新紧线,重新安装线夹。
这种方法施工比较复杂和不经济,安全风险大,施工费用高,而且导线上原来安装线夹的部位串入档内,将降低架空线的使用张力。
另一种方法是不重新紧线,只串动少数几基杆塔上悬垂线夹的位置而完成改建。
已架成的架空输电线路,在运行期间往往会出现新的交叉跨越物,或因地质、水文条件的变化及其它原因,需要将线路中的若干基杆塔进行下列改建工作:a、移动杆塔位置(杆高及数目不变)b、增加杆塔高度(数目不变)c、增设杆塔d、上述项目的组合。
3线长变量计算一般来说,线长变量计算时,改造前后所取的气温条件相同,且导线应力变化非常小,因此气温和导线应力变化引起的线长变化非常小,为简化计算,可忽略不计,线长变化主要是由杆塔高度变化和耐张段代表档距变化后弧垂应力变化。
架空线的弧垂线长及应力计算

架空线的弧垂、线长及应力计算1 弧垂、线长计算架空线由于档距很大,材料的刚性影响可忽略不计,架空线的形状就像一条两端悬挂的柔软的索链。
所以,可以按悬链线进行计算其弧垂和线成,其方程为:弧垂 f = σ/g〔ch(gl/2σ)-1〕线长L = 2σ/g〔sh(gl/2σ)〕上二式写成级数形式展开后为:f = σ/g{〔1+(L12g2/8σ2)+(L14g4/38σ4)+……〕-1}= (L12g/8σ)+(L14g3/38σ3)+……L = 2σ/g{(L1g/2σ)+(L13g3/48σ3)+(L15g5/3840σ5)+……}= L1+(L13g2/24σ2)+(L15g4/1920σ4)+……为了简化计算,工程上取f第一项计算弧垂,取L前二项计算线长(即用抛物线方程代替悬链线方程近似计算):f = L12g/8σL = L1+(L13g2/24σ2)= L1+(8 f2/3 L1)式中,L1—档距,m;g —架空线的比载,N/m·mm2g = W/S其中,W —单位长度导线重量,N/m;S —导线截面积,mm2σ—架空线最低点应力(水平应力),N/mm2。
按上式计算的误差:当弧垂不大于档距的5%时,线长误差率小于15×10-4%。
几种情况弧垂计算:①在交叉跨越档距中一般需计算被跨越物上面任一点导线的弧垂f x,以便校验交叉跨越距离。
档距中任一点导线的弧垂按下式计算:f x = x(L1-x)g/2σ= 4 f x(1-x/L1)/L1式中,x—从悬挂点至计算坐标点的水平距离,m。
②在悬挂点具有高差的档距中架空线的计算需用斜抛物线法,即:L =(L1/cosφ)+(L13g2 cosφ/24σ2)f = L12g/8σcosφf x = x(L1-x)g/2σcosφ式中,φ—高差角,φ = arc tg(h/L1)其中,h —高差;L1—档距。
2 应力计算①架空线任一点处的应力架空线各点所受应力的方向是沿架空线切线方向变化的,最低点处的应力称为水平应力,只要知道最低点应力,架空线上任一点的应力都可以用下式计算求得:σX= σ+(f-f x)g式中,σX—架空线任一点处的应力,N/mm2;σ—架空线最低点应力(水平应力),N/mm2;f —架空线弧垂,m;f x—计算点导线的弧垂,m;g —架空线比载,N/m·mm2。
10kV架空配电线路拉线的长度计算、维护及运行中的作用

浅谈输配电线路拉线的施工、维护及在运行中的作用摘要:目前在输配电线路拉线的施工、维护工作中,存在着施工工艺不规范,运行维护方法不正确,导致线路倾斜及倒杆事故时有发生。
因此拉线是线路安全运行的保障,就此通过多年的运行经验,浅谈一些拉线的施工、维护的工艺及方法,使拉线在线路上应用合理化、科学化、规范化,起到保护线路作用,提高输配电线路运行的可靠性。
关键词:输配电线路;拉线的作用;施工及维护;线路运行安全可靠输配电线路上的拉线时刻都在保护着电网安全稳定运行,一旦拉线受到破坏将会造成电网事故。
提起拉线对于线路维护、检修、施工人员并不陌生,但是在实际工作中我们要知道拉线的作用和在维护、施工时的注意事项。
1、拉线的作用拉线是用于平衡杆塔承受的水平风力和导线、避雷线的张力,根据作用不同,在应力方面分为张力拉线和风力拉线两种。
1.1、张力拉线用于平衡导线、避雷线的张力,其受力情况如图l所示。
由于拉线与地面有一夹角β,所以平衡导线、避雷线张力P的是拉线的水平分力Fx拉线承受的力为:F=P/cosβ式中:F为拉线承受的力(KN);P为导线、避雷线的最大张力(KN);β为拉线与地面的夹角。
1.2、防风拉线用于平衡水平风力。
10kv线路规模较小,钢筋混凝土电杆—般均能承受电杆和导线上的水平风力,通常情况下可以不装设防风(a)人字形:线路两侧拉线与线路方向垂直夹角90°。
(b)十字形:线路两侧拉线与线路方向垂直夹角90°,顺线路方向夹角0°。
(c)X形:线路两侧拉线与线路方向夹角45°。
图2防风拉线示意图拉线,但要根据本地区气候及地理位置的实际情况决定是否装设防风拉线,比如10kv线路经过河套、泥沼地段应适当装设防风拉线,所以10kv线路装设防风拉线时,可根据地势地理情况定夺安装几处。
大多数防风拉线装设在输电线路上,安装在输电线路的两侧,也可采用十字形、x形安装。
(大多是沼泽、河套地段采用)如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此, 设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节架空线悬链线方程的积分普遍形式图4-1架空线悬挂曲线受力图(a)分离体受力图;(b)整档架空线受力图;图4-1(b)所示为某档架空线,A、B均为两悬挂点。
沿架空线线长作用有均布比载,方向垂直向下。
在比载作用下,架空线呈曲线形状,其最低位置在:点,在悬挂点A、B 处,架空线的轴向应力分别为c A和二B。
选取线路方向(垂直于比载)为坐标系的x轴, 平行于比载方向为y轴。
在架空线上任选一点C,取长为L OC的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有7 X =0,二x cos—(4- 1)' 丫 =O,;「X sin v - L OC(4- 2)式(4-1)表明,架空线上任一点C 处的轴向应力匚x 的水平分量等于弧垂最低点处的轴向应力CO ,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长L oc 与比载之积。
以上两式相除可得Vtg 二=——L oc▽0上式为悬链线方程的徽分形式。
从中可以看出,当比值 /匚0 —定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
在弧垂最低点 O 处,曲线的斜率为零,即二=0,将式(4- 3)写成r Vy L OC^0两边微份式(4- 5)是架空线悬链线方程的积分普遍形式。
其中C 1、C 2为积分常数,其值取决于坐dy =2.dx - oL oc(4- 3)dy d(L °c )二 \ dx 2 dy 2二Cy 2dxcr n <r n-0 - 0CT 0分离变量后两端积分dy二dx-0AA + y ,2arcsh( y )= Y(x C 1)-0或写成dy=sh(x C 1)dx- 0(4- 4)上式两端积分,得y=叫 0(xC 1) C 2(4- 5)标系的原点位置。
第二节等高悬点架空线的弧垂、线长和应力一、等高悬点架空线的悬链线方程等高悬点是指架空线的两个悬挂点高度相同。
由于对称性,等高悬点架空线的弧垂最低点位于档距中央,将坐标原为取在该点,如图4-2所示。
图4-2等高悬点架空线的悬链线当x=0时,dy=0,代入式(4- 4)可解得C i = 0;当x=0时,y=0,代入式(4- 5)并利用G = dx0,解得C i = -一°,将C1、C2的值代回式(4- 5),并加以整理即可得到架空线的悬链线方程%y= - (ch x-1) (4-6) 由式(4- 6)可以看出,架空线的悬链线具体形状完全由比值二0/决定,即无论是何种架空线,何种气象条件,只要匚0/相同,架空线的悬挂曲线形状就相同。
在比载一定的情况下,架空线的水平应力二-是决定悬链线形状的唯一因素,所以架线时的水平张力对架空线的空间形状有着决定性的影响。
在导出式(4- 6)的过程中,并没有用到等高悬点的限定条件,因此式(4- 6)同样可用于不等高悬点的情况。
二、等高悬点架空线的弧垂架空线上任一点的弧垂是指该点距两悬挂点连线的垂向距离。
在架空输电线路设计中,(ch」--1)所以利用恒等式c^ -ch : =2sh ■ sh ' 对上式进行变换,可以得到2 22% 2%除非特别说明,架空线的弧垂一般指的是最大弧垂。
最大弧垂在线路的设计、有十分重要的位置。
三、等高悬点架空线的线长弧垂最低点0与任一点C之间的架空线长度L OC(参见图4-1)可由式(4-3)联立求解,并考虑到C^0而得到。
线长L OC计算式为或记为将X =1/2代入上式,可得到半档距架空线的长度L xm/2,整档架空线的线长的2倍,即L = 2L X ±/2 sh rl26 (4- 10)需计算架空线任一点x处的弧垂f x,以验算架空线对地安全距离,参见图4-2 , 显然"ch 1f x-26 — chj-0Fch丄—ch化细]2二0(4- 7)(4- 8)在档距中央,弧垂有最大值f,此时x=0或x1 = -,所以有2f TB -(ch2_-1] =2;「0sh2仁(4-9)施工中占和式(4-4)shrxshrxL是L X耳/226上式表明,在档距I 一定时,架空线的线长随比载和水平应力二0的变化而改变,即架空线的线长是其比载的应力的函数。
应该指出,式(4-10)计算得出的是按架空线的悬挂曲线几何形状的计算长度,与架空线的制造长度不尽相同。
四、等高悬点架空线的应力架空线上任一点C处的应力指的是该点的轴向应力,其方向同该点线轴方向,如图(a)所示。
轴向应力二%可视为水平应力二0和垂向应力二0的合成。
二0是架空线最低点处4-1 的应力,工程上常作为已知条件。
当架空线的比载也已知时,任一点的应力为/ ¥‘ rx + cr osh—I a0丿1 sh2 rX-o根据恒等变换cha =訥+sh% ,可得匚x =Sch2▽o(4-11) 在两等高悬挂点A、B处,有rlA =B = 0Ch2;「o(4-12) 如果用弧垂表示,则为二A *0 rf上式表明,等高悬点处架空线的应力等于其水平应力和作用在其上的比载与中央弧垂的乘积的和。
必须指出,悬挂点处的应力除按式(4- 12)计算的静态应力外,还有线夹的横向挤压应力,考虑刚度时的附加弯曲应力和振动时产生的附加动应力等。
第三节不等高悬点架空线的弧垂、线长和应力地形的起伏不平或杆塔高度的不同,将造成架空线悬挂高度不相等。
同一档距两悬挂点间的高度差简称为高差,两悬挂点连线与水平面的夹角称为高差角。
一、不等高悬点架空线的悬链线方程为应用方便起见,取坐标原点位于左侧悬挂点处,如图4-3所示。
在所选坐标系中,当x=a 时,d y /d x =°,代入式(4-4)求得G - -a ;当x=0时,式(4-5),有a =-arcsh 2 r经sh 」 r 2二0上式中反双曲线函数一项的分母,实际上就是式( 4-10 )表示的等高悬点架空线的档内悬链线长度,记为L h=e ,即相应地,弧垂最低点距右侧高悬挂点的水平距离为y=0,代入式(4-5)并注意到 G = -a ,求得C 2ch^a,将C1、C2之值再代回到-0[ch(X -a)-chra 2"sh -02"sh (x-2a) 2"(4- 13)上式即为不等高悬点架空线的悬链线方程, 但式中架空线最低点至左侧低悬挂点的水平距离a 待求。
将x= |时y= h 的边界条件代入式(4- 13),可以得到所以L h =026sh l26(4- 10/)arcshh Lh:(4- 14)图4-3不等高悬点架空线的悬链线18)= sh[-U arcsh —2;「0Lh z0上式代入式(4-13),便可得到坐标原点位于左悬点时的不等高悬点架空线的悬链线方 程为"6门冒]当h =0时,即得到坐标原点位于左悬挂点时的等高悬点的架空线悬链线方程二、不等高悬点架空线的弧垂根据弧垂的定义,不等高悬点架空线任一点处的弧垂为等高悬点h =0时,有这与式(4-8)是一致的。
由于sh (x —2a )2cr o— arcsh2 r= sh[ x 2 一 32'- 0 '-0(4-15)心(x 」) 2^01 (L h)2丄h z02-‘o L h 卫L h =Q2- o1(, h Ah 导h =02、- 0经sh 丄[上chS2:。
L ”®2:。
1心十(4-16)亠生S ”亠1(L h£2626 :L h 凶h)日说sh 葺]26%026(4- 17)h hx _y 26sh2Ssh (x —2a )26h x -—IL h £J 互込2%△ch4「1 J )2吾込 VL h出 Y 2%2Jh =0 26(4-x(h £)26吃S ”》架空输电线路最常用的是档距中央弧垂,最低点弧垂和最大弧垂(斜切点弧垂)与式(4- 19)比较,最大弧垂公式可表示为对于等高悬点架空线,有4(Ch 斗-1) ,在档距中央x=|/2,代入式(4-18)并化简后得到档距中央弧垂的计算式h 2b 0rl1 (厂—)2」(ch=- -1)L hq 2二0(4-19) 最低点弧垂出现在x=a处,代入任一点弧垂公式(4-18)并注意到式( 4-4),适当整理后得亠1<>h rl2二0 hzQ(4- 20) 同式(4-19)相比较,上式可写成[J harcsh L ,/ h、1(I )L(4- 20/)最大弧垂出现在並=0处,dxdf x dxd ,h(—x - y)dx ld r h 6 _ r(x - a) , ra[x (ch ch )]dx l r解得出现最大弧垂的位置匚0h l - 0h hX m =a arcsh (arcsh arcsh )r l 2 r l L hJ(4- 21) 从上式可以看出,不等高悬点架空线的最大弧垂不在档距中央。
由于L h^>l,所以X m>l / 2,说明最大弧垂位于档距中央稍偏向高悬挂点一侧的位置。
将式(4- 21)代入任点弧垂公式(4- 18),可求得不等高悬点的最大弧垂为fm亠帥诙“心亡)1 (h )2ch rlL h=0 2% 1 (A】(4- 22)二[fghf-arcsh占-C1 (:1h =eh 21 C h )2)]Lh=0/(4- 22 )由于上式两个小括号内的值均为正值且均小,中央,弧垂,但二者非常接近。
前者略大于后者,所以最大弧垂大于档距26上式表明,等高悬点架空线的最大弧垂、档距中央弧垂和最低点弧垂三者重合, 位于档距中央,这是很明显的。
三、不等高悬点架空线的线长不等高悬点架空线的线长可利用弧长微分公式通过积分求得。
根据式(业=sh 丄(x CJ 二 sh 丄(x - a) dx所以dL = J 1 (?)2dx = ,'1 sh 2 r(x 一a)dx = ch r(x-a)dx架空线上任一点至左悬挂点间的线长为当x=l 时,即得到整档线长将x= |代入式(4-13),有将式(4-25 )的平方减去上式的平方所以L =丄気h 2由上式可以看出,高差h 的存在,使得不等高悬点架空线的线长大于等高悬点时的线长。
