图论中几个典型问题的求解.ppt
合集下载
离散数学——图论PPT课件
第19页/共93页
• 完全图：一个（n,m）图G，其n个结点中每个结点均与其它n-1个结点相邻接，记为Kn。 • 无向完全图：m=n(n-1)/2 • 有向完全图：m=n(n-1) • 举例说明以上几种图。
第20页/共93页
定义补图
• 设图G=<V,E> ， G’=<V,E’> ，若G’’=<V,E∪E’> 是完全图，且E∩E’= 空集，则称G’是G的补图。 • 事实上，G与G’互为补图。
正则图
• 所有结点均有相同次数d的图称为d次正则图。 • 如4阶的完全图是3次正则图，是对角线相连的四边形。 • 试画出两个2次正则图。
第27页/共93页
两图同构需满足的条件
• 若两个图同构，必须满足下列条件： （1）结点个数相同 （2）边数相同 （3）次数相同的结点个数相同
• 例子
第28页/共93页
• 图是人们日常生活中常见的一种信息载体，其突出的特点是直观、形象。图论，顾 名思义是运用数学手段研究图的性质的理论，但这里的图不是平面坐标系中的函数， 而是由一些点和连接这些点的线组成的结构 。
第8页/共93页
• 在图形中，只关心点与点之间是否有连线，而不关心点具体代表哪些对象，也不关 心连线的长短曲直，这就是图的概念。
定义图的子图
• 子图：设G=<V,E> ， G’=<V’,E’> ，若V’是V的子集， E’是E的子集，则 G’是G的子图。 • 真子图：若V’是V的子集，E’是E的真子集。 • 生成子图：V’=V，E’是E的子集。 • 举例说明一个图的子图。
第18页/共93页
定义（n,m）图
• (n,m)图：由n个结点，m条边组成的图。 • 零图：m=0。即（n,0）图，有n个孤立点。 • 平凡图：n=1,m=0。即只有一个孤立点。
• 完全图：一个（n,m）图G，其n个结点中每个结点均与其它n-1个结点相邻接，记为Kn。 • 无向完全图：m=n(n-1)/2 • 有向完全图：m=n(n-1) • 举例说明以上几种图。
第20页/共93页
定义补图
• 设图G=<V,E> ， G’=<V,E’> ，若G’’=<V,E∪E’> 是完全图，且E∩E’= 空集，则称G’是G的补图。 • 事实上，G与G’互为补图。
正则图
• 所有结点均有相同次数d的图称为d次正则图。 • 如4阶的完全图是3次正则图，是对角线相连的四边形。 • 试画出两个2次正则图。
第27页/共93页
两图同构需满足的条件
• 若两个图同构，必须满足下列条件： （1）结点个数相同 （2）边数相同 （3）次数相同的结点个数相同
• 例子
第28页/共93页
• 图是人们日常生活中常见的一种信息载体，其突出的特点是直观、形象。图论，顾 名思义是运用数学手段研究图的性质的理论，但这里的图不是平面坐标系中的函数， 而是由一些点和连接这些点的线组成的结构 。
第8页/共93页
• 在图形中，只关心点与点之间是否有连线，而不关心点具体代表哪些对象，也不关 心连线的长短曲直，这就是图的概念。
定义图的子图
• 子图：设G=<V,E> ， G’=<V’,E’> ，若V’是V的子集， E’是E的子集，则 G’是G的子图。 • 真子图：若V’是V的子集，E’是E的真子集。 • 生成子图：V’=V，E’是E的子集。 • 举例说明一个图的子图。
第18页/共93页
定义（n,m）图
• (n,m)图：由n个结点，m条边组成的图。 • 零图：m=0。即（n,0）图，有n个孤立点。 • 平凡图：n=1,m=0。即只有一个孤立点。
迷宫问题求解PPT课件
迷宫问题求解是一个经典的NP完全问题，求解难度较大，需要高效的算法和策略。同时，迷宫问题的规模和复 杂度随着迷宫的增大而急剧增加，对计算资源和算法性能提出了更高的要求。
机遇
随着人工智能和机器学习技术的不断发展，越来越多的算法和模型被应用于迷宫问题求解，如深度学习、强化学 习等。这些算法和模型在处理大规模、复杂迷宫问题方面展现出了强大的潜力和优势，为迷宫问题求解带来了新 的机遇和突破。
并行化搜索适用于具 有良好并行性的迷宫 问题，可以显著提高 求解效率。
通过使用并行计算资 源，可以同时搜索多 个路径，加快求解速 度。
04
迷宫求解的实践案例
简单的迷宫求解
使用深度优先搜索（DFS）
01
从起点开始，探索所有可能的路径，直到找到终点或无路可走。
使用广度优先搜索（BFS）
02
按照从起点到终点的路径长度，逐层搜索，直到找到终点或无
未来研究方向
算法优化
智能化求解
应用拓展
理论分析
针对迷宫问题求解，进一步优 化现有算法和模型，提高求解 效率和质量。研究新的算法和 模型，以更好地处理大规模、 复杂迷宫问题。
结合人工智能和机器学习技术 ，研究智能化求解方法，如基 于深度学习的路径规划、强化 学习算法等。通过智能化技术 提高迷宫问题求解的自动化和 智能化水平。
路可走。
使用回溯法
03
从起点开始，尝试所有可能的路径，如果遇到死胡同或无法到
达终点，则回溯到上一个节点，继续尝试其他路径。优先搜索，在迷宫中寻找 最短路径。
使用遗传算法
模拟生物进化过程，通过交叉、变异等操作，寻 找最优解。
使用模拟退火算法
模拟物理退火过程，通过随机扰动和接受概率， 寻找最优解。
机遇
随着人工智能和机器学习技术的不断发展，越来越多的算法和模型被应用于迷宫问题求解，如深度学习、强化学 习等。这些算法和模型在处理大规模、复杂迷宫问题方面展现出了强大的潜力和优势，为迷宫问题求解带来了新 的机遇和突破。
并行化搜索适用于具 有良好并行性的迷宫 问题，可以显著提高 求解效率。
通过使用并行计算资 源，可以同时搜索多 个路径，加快求解速 度。
04
迷宫求解的实践案例
简单的迷宫求解
使用深度优先搜索（DFS）
01
从起点开始，探索所有可能的路径，直到找到终点或无路可走。
使用广度优先搜索（BFS）
02
按照从起点到终点的路径长度，逐层搜索，直到找到终点或无
未来研究方向
算法优化
智能化求解
应用拓展
理论分析
针对迷宫问题求解，进一步优 化现有算法和模型，提高求解 效率和质量。研究新的算法和 模型，以更好地处理大规模、 复杂迷宫问题。
结合人工智能和机器学习技术 ，研究智能化求解方法，如基 于深度学习的路径规划、强化 学习算法等。通过智能化技术 提高迷宫问题求解的自动化和 智能化水平。
路可走。
使用回溯法
03
从起点开始，尝试所有可能的路径，如果遇到死胡同或无法到
达终点，则回溯到上一个节点，继续尝试其他路径。优先搜索，在迷宫中寻找 最短路径。
使用遗传算法
模拟生物进化过程，通过交叉、变异等操作，寻 找最优解。
使用模拟退火算法
模拟物理退火过程，通过随机扰动和接受概率， 寻找最优解。
图论经典问题
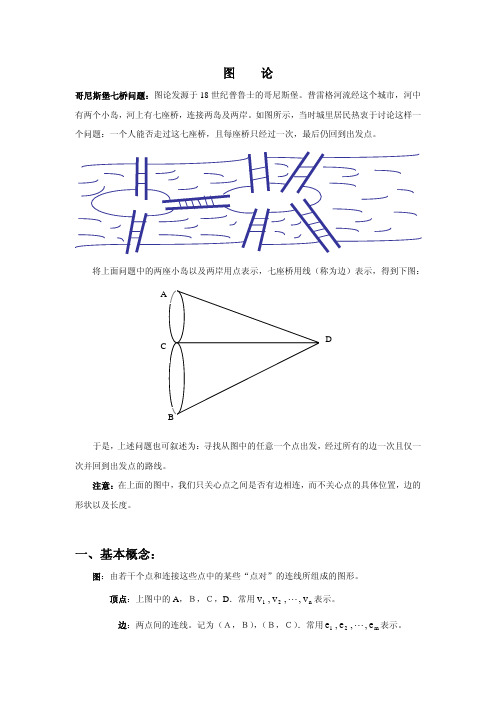
图 论哥尼斯堡七桥问题：图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市，河中有两个小岛，河上有七座桥，连接两岛及两岸。
如图所示，当时城里居民热衷于讨论这样一个问题：一个人能否走过这七座桥，且每座桥只经过一次，最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示，七座桥用线（称为边）表示，得到下图：于是，上述问题也可叙述为：寻找从图中的任意一个点出发，经过所有的边一次且仅一次并回到出发点的路线。
注意：在上面的图中，我们只关心点之间是否有边相连，而不关心点的具体位置，边的形状以及长度。
一、基本概念：图：由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点：上图中的A ，Ｂ，Ｃ，D ．常用表示。
n 21 v , , v , v 边：两点间的连线。
记为（Ａ，Ｂ），（Ｂ，Ｃ）．常用表示。
m 21e , , e , e次：一个点所连的边数。
定点ｖ的次记为d(v)．图的常用记号：Ｇ＝（Ｖ，Ｅ），其中，}{v V i =，}{e E i =子图：图Ｇ的部分点和部分边构成的图，成为其子图。
路：图Ｇ中的点边交错序列，若每条边都是其前后两点的关联边，则称该点边序列为图Ｇ的一条链。
圈（回路）：一条路中所含边点均不相同，且起点和终点是同一点，则称该路为圈（回路）。
有向图：，其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合，A a 称为G 的弧集合。
G {(,)ij i j }n n ==若，则称为的前驱， 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图（网络）：设是一个图，若对G 的每一条边（弧）都赋予一个实数，称为边的权，。
记为。
G (,,)G N E W =两个结论：１、图中所有顶点度数之和等于边数的二倍； ２、图中奇点个数必为偶数。
二、图的计算机存储：1. 关联矩阵简单图：，对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图：，对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图：，对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图：，对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵：简单图：，对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用：例：如图，用点代表7个村庄，边上的权代表村庄之间的路长，现在要在这7个村庄中布电话线，如何布线，使材料最省？分析：需要将图中的边进行删减，使得最终留下的图仍然连通，并且使总的权值最小。
图论中几个典型问题的求解
图论中几个典型问题的求解
具有n个顶点的无向连通图是树的充分必要条 件是它有n-1条边．连通图G的子图T，如果它的 顶点集与G的顶点集相同，且T为树，则称T是图 G的生成树，又称支撑树。如果图的边有权（对 应于边的实数），则生成树上各边权的总和称为 生成树的权，生成树并不唯一，权达到最小的生 成树称为最小生成树(Minimal Spanning Tree， 简称MST)，最小生成树不一定唯一．
end end end end D,R %输出最短路矩阵和最短路的路径矩阵。
图论中几个典型问题的求解
以上程序是通用程序，只需输入初始距离矩 阵，就能输出最短路矩阵以及最短路的路径矩阵， 将程序以文件名floyd.m存盘。
例1 以2007年研究生数学建模竞赛C题为例， 已知16个邮政支局的初始距离矩阵，求任意两个 节点之间的最短路。
§2 最短路问题
图论中几个典型问题的求解
最短路问题是图论应用的基础，很多实际问 题，如线路的布设、运输规划、运输网络最小费 用流等问题，都可以通过建立最短路模型来求解。 有些有深度的图与网络优化问题，如旅行售货商、 中国邮递员等问题，需要在首先求出任意两点之 间最短路的基础上解决。
一、最短路的概念
1．算法原理 设A=[aij]m×n是图的权矩阵（也称带权邻接矩 阵），其中aij是图上连接顶点i和j的边的权，如 果两顶点之间没有直接相连的边（即两顶点不相 邻），则aij=∞。
图论中几个典型问题的求解
令矩阵D(0)=A，作为迭代的初始矩阵，从它出 发按照一定规则求D(1)，又由D(1)按照类似的规则 求D(2)，依此类推进行迭代直至求出D(n)，设矩阵 D(m)的元素为dij(m)，迭代规则为：
输入数据中的inf表示无穷大（两个顶点之间 没有边直接相连）。
具有n个顶点的无向连通图是树的充分必要条 件是它有n-1条边．连通图G的子图T，如果它的 顶点集与G的顶点集相同，且T为树，则称T是图 G的生成树，又称支撑树。如果图的边有权（对 应于边的实数），则生成树上各边权的总和称为 生成树的权，生成树并不唯一，权达到最小的生 成树称为最小生成树(Minimal Spanning Tree， 简称MST)，最小生成树不一定唯一．
end end end end D,R %输出最短路矩阵和最短路的路径矩阵。
图论中几个典型问题的求解
以上程序是通用程序，只需输入初始距离矩 阵，就能输出最短路矩阵以及最短路的路径矩阵， 将程序以文件名floyd.m存盘。
例1 以2007年研究生数学建模竞赛C题为例， 已知16个邮政支局的初始距离矩阵，求任意两个 节点之间的最短路。
§2 最短路问题
图论中几个典型问题的求解
最短路问题是图论应用的基础，很多实际问 题，如线路的布设、运输规划、运输网络最小费 用流等问题，都可以通过建立最短路模型来求解。 有些有深度的图与网络优化问题，如旅行售货商、 中国邮递员等问题，需要在首先求出任意两点之 间最短路的基础上解决。
一、最短路的概念
1．算法原理 设A=[aij]m×n是图的权矩阵（也称带权邻接矩 阵），其中aij是图上连接顶点i和j的边的权，如 果两顶点之间没有直接相连的边（即两顶点不相 邻），则aij=∞。
图论中几个典型问题的求解
令矩阵D(0)=A，作为迭代的初始矩阵，从它出 发按照一定规则求D(1)，又由D(1)按照类似的规则 求D(2)，依此类推进行迭代直至求出D(n)，设矩阵 D(m)的元素为dij(m)，迭代规则为：
输入数据中的inf表示无穷大（两个顶点之间 没有边直接相连）。
图论中的几个典型问题(上) 共76页PPT资料
算 法 的 过 程 就 是 在 每 一 步 改 进 这 两 个 标 记 ， 使 最 终 l ( v ) 为 从 顶 点
u 0 到 v 的 最 短 路 的 权 ． S
输 入 : G 的 带 权 邻 接 矩 阵 w ( u , v )
算法步骤 ：
（ １ ） 赋 初 值 ： 令 S ＝ { u 0 } , l ( u 0 ) = 0 v S V \ S , 令 l ( v ) = W ( u 0 , v ) z , ( v ) = u 0 u u 0
d i ( ) j是 从 v i到 v j的 只 允 许 以 v 1 、 v 2 、 … v 、 作 为 中 间 点 的 路 径 中 最 短 路
u2
u 5 u4 u 5
u2
u5
u1
u4
u6
u8
u3
u7
求赋权图中任意两点的最短路的Floyd算法：
算法的基本思想
直 接 在 图 的 带 权 邻 接 矩 阵 中 用 插 入 顶 点 的 方 法
依 次 构 造 出 个 矩 阵 D ( 1 ) 、 D ( 2 ) 、 … 、 D () ， 使 最 后 得 到 的 矩 阵 D () 成 为 图 的 距 离 矩 阵 ， 同 时 也 求 出 插 入 点 矩 阵 以 便 得 到 两 点 间 的 最 短 路 径 ．
返回
算法原理—— 求距离矩阵的方法
把 带 权 邻 接 矩 阵 W 作 为 距 离 矩 阵 的 初 值 ， 即 D ( 0 ) = ( d i ( 0 ) ) j= W
（ １ ） D ( 1 ) = ( d i ( 1 ) ) j ， 其 中 d i ( 1 ) jm d i ( 0 ) , j d i ( 1 0 ) i d 1 ( 0 j ) } n{
u 0 到 v 的 最 短 路 的 权 ． S
输 入 : G 的 带 权 邻 接 矩 阵 w ( u , v )
算法步骤 ：
（ １ ） 赋 初 值 ： 令 S ＝ { u 0 } , l ( u 0 ) = 0 v S V \ S , 令 l ( v ) = W ( u 0 , v ) z , ( v ) = u 0 u u 0
d i ( ) j是 从 v i到 v j的 只 允 许 以 v 1 、 v 2 、 … v 、 作 为 中 间 点 的 路 径 中 最 短 路
u2
u 5 u4 u 5
u2
u5
u1
u4
u6
u8
u3
u7
求赋权图中任意两点的最短路的Floyd算法：
算法的基本思想
直 接 在 图 的 带 权 邻 接 矩 阵 中 用 插 入 顶 点 的 方 法
依 次 构 造 出 个 矩 阵 D ( 1 ) 、 D ( 2 ) 、 … 、 D () ， 使 最 后 得 到 的 矩 阵 D () 成 为 图 的 距 离 矩 阵 ， 同 时 也 求 出 插 入 点 矩 阵 以 便 得 到 两 点 间 的 最 短 路 径 ．
返回
算法原理—— 求距离矩阵的方法
把 带 权 邻 接 矩 阵 W 作 为 距 离 矩 阵 的 初 值 ， 即 D ( 0 ) = ( d i ( 0 ) ) j= W
（ １ ） D ( 1 ) = ( d i ( 1 ) ) j ， 其 中 d i ( 1 ) jm d i ( 0 ) , j d i ( 1 0 ) i d 1 ( 0 j ) } n{
运筹学--图论 ppt课件
4
5
4 9 8
v1
v3
2
v6
[8,v2]
v8
5 33
1
[2,v1]
v4
v7
[10,v4]
33
Dijkstra算法示例1
3）迭代计算(c)—更新与永久标号节点v2相连的节 (d2+w25=3+7=)10< ∞ (=d5) 点的临时标号。
[3,v1]
v2
[0,-]
7
v5
[10,v2]
2 [+∞,v1] 6
v4
v7
[+∞,v1]
22
Dijkstra算法示例1
2）迭代计算(a)—从临时标号中找到距离上界dk最 小的节点v4，d4=min{dk}，将其变换为永久编号。
[3,v1] [+∞,v1]
v2
[0,-]
7
v5
2 [+∞,v1] 6 1 2 [+∞,v1]
3
5 2 [5,v1]
4
5
4 9 8
v1
v3
最小树问题不一定有唯一解。
10
10
最小支撑树问题的解法
破圈法 算法
初始化 将图G的边按权值从大到小的次序排列，从 原图开始迭代； 迭代
第1步(删边) 从排列中顺序选择一条与图中剩余边构成圈 的边，则将此边从图中删除，进入第2步(结束判断)； 第2步(结束判断) 若图中剩下n-1条边，则已经得到最小支 撑树；否则，进入下一轮迭代，返回第1步(加边)；
柯尼斯堡七桥问题
柯尼斯堡市区横跨普雷格尔河两岸，在河中心有两 个小岛。小岛的两岸共有七座桥将岛与岛、岛与河 岸连接起来。一个人怎样才能一次走遍七座桥，每 座桥只走过一次，并最后回到出发点？
图论相关算法.ppt
w是顶点v在深度优先树上的孩子结点； k是顶点v在深度优先树上由回边联结的祖先结点；
当low[j]<dfn[i](j是i的儿子)时，说明j或者j的子孙 中存在指向i祖先的回边。反之，若对于某个顶点v，存 在孩子结点w，且low[w]>=dfn[v],表明w及其子 孙均无指向v的祖先的回边，则该顶点v必为关节点。 具体算法如下：
0
6
7
8
1
2
3
5
4
10
9
顶点0、4、5、6、
7和11为关节点。
11
12
割点、割边以及连通分量
时间戳：dfn[i]表示结点i是第dfn[i]个被访问到的结点。有的时候我
们
还要记录某个结点被遍历并检查完毕的时间。
void dfs(v)
{
dfn[v]=++times; //记录访问结点的时间戳
visit[v]=1;
if ( adj[curr][i] && !visit[i] )
{
visit[i] = true;
depth[i] = depth[curr] + 1;
time[i] = t++;
queue[++tail] = i;
}
}
}
深度优先搜索
相关概念
递归实现 结点颜色：
白色（开始），灰色（发现），黑色（结束）
到栈中的节点是否为一个强连通分量。
我们仍然定义dfn[i]为节点i搜索的次序编号(时间戳)， low[i]为i或i的子树能够追溯到的最早的栈中节点的次 序号。由定义可以得出: 当dfn(u)=low(u)时，以u为根的搜索子树上的所有 节点构成一个强连通分量。
当low[j]<dfn[i](j是i的儿子)时，说明j或者j的子孙 中存在指向i祖先的回边。反之，若对于某个顶点v，存 在孩子结点w，且low[w]>=dfn[v],表明w及其子 孙均无指向v的祖先的回边，则该顶点v必为关节点。 具体算法如下：
0
6
7
8
1
2
3
5
4
10
9
顶点0、4、5、6、
7和11为关节点。
11
12
割点、割边以及连通分量
时间戳：dfn[i]表示结点i是第dfn[i]个被访问到的结点。有的时候我
们
还要记录某个结点被遍历并检查完毕的时间。
void dfs(v)
{
dfn[v]=++times; //记录访问结点的时间戳
visit[v]=1;
if ( adj[curr][i] && !visit[i] )
{
visit[i] = true;
depth[i] = depth[curr] + 1;
time[i] = t++;
queue[++tail] = i;
}
}
}
深度优先搜索
相关概念
递归实现 结点颜色：
白色（开始），灰色（发现），黑色（结束）
到栈中的节点是否为一个强连通分量。
我们仍然定义dfn[i]为节点i搜索的次序编号(时间戳)， low[i]为i或i的子树能够追溯到的最早的栈中节点的次 序号。由定义可以得出: 当dfn(u)=low(u)时，以u为根的搜索子树上的所有 节点构成一个强连通分量。
第七章图论PPT课件
v V
ห้องสมุดไป่ตู้
deg(v)为偶数，2|E|亦为偶数
vV2
deg(v)为偶数 vV1
|V1|为偶数
定理： 有向图中所有结点的入度之和等于所有结点的出度之和
-
12
7-1 图的基本概念
（5）多重图：含有平行边的图
简单图：不含有平行边和环的图
完全图：每一对结点之间都有边关联的简单图
有向完全图：完全图中每条边任意确定一个方向所得的图
a
e
b
d
f
h
c
g
定理： n个结点的无向（有向）完全图Kn的边数为n(n-1)/2
证明： 在完全图中，每个结点的度数应为n－1，则n个结点的
度数之和为n(n-1)，因此|E|＝n(- n-1)/2
13
7-1 图的基本概念
（6）子图：
G V , E ， 有 G ' V ', E ' ， 且 E ' E ， V ' V ，
a到b的有向边
孤立结点：无邻接点的结点
a
e hi
k
b
df
c
j
l
g
无向边：(a,b), (b,c), (b,d), (c,d), (i,l), (k,l)
有向边：<e,f>, <f,g>, <g,e>, <e,h>, <k,j>, <j,l>
-
5
7-1 图的基本概念
（2）无向图：图中每一边都为无向边
e f
g
deg+(e)=2, deg-(e)=1, deg(e)=3
h deg+(f)=1, deg-(f)=2, deg(f)=3
《管理运筹学》演示(图论)
v3 (v2 ,1)
检查 vs 相邻点 v1 和 v2 。 v2点，fs2 = cs2 =3，不满足标号条件；v1点，fs1 < cs1 , v1点标号为（ vs , l(v1) ）, l(v1) =min[ l(vs) ,( cs1 - fs1 )]= min[+ , 5-1] = 4； 检查 v1 相邻点 v3 和 v2 。 v3点，f13 = c13 =2，不满足标号条件； v2点，f21=1> 0 , v2点标号为（ -v1 , l(v2) ）, l(v2) =min[ l(v1) , f21]= min[4 , 1] = 1； 检查 v2 相邻点 v3 和 v4 。v3点，f32=1> 0 , v3点标号为（ -v2 , l(v3) ）, l(v3) =min[ l(v2) , f32]= min[1 , 1]=1 ； v4点，f24 < c24 =1，v4点标号为（ v2 , 1 ） ；
,
最大流量 v(f ) = 5
最小费用最大流问题
例：求下列网络最小费用最大流。弧旁数字为( bij , cij ) 步骤：
v1
(1,7)
vt
取 f ( 0 ) ＝0为初始可行流； 构造赋权有向图w( f ( 0 ))，
vs
解：
v1
0 0
v2
0
0
v3
vt
0
bij wij bij wij
v8
步 骤：
给 vs点以 P 标号，P(vs) = 0，其余各点给 T 标号，
T(vs) = ＋ ；
若 vs点为刚得到 P 标号的点，考虑这样的点 vj：
( vi , vj )属于A(或[vi , vj ] 属于E )，且vj 为 T 标号。对 vj 的T 标号进行如下的更改：
图论中几个典型问题的求解(精选)163页PPT
谢谢！
163
图论中几个典型问题的求解（精选）
11、不为五斗米折腰。 12、芳菊开林耀，青松冠岩列。怀此 贞秀姿 ，卓为 霜下杰 。
13、归去来兮，田蜀将芜胡不归。 14、酒能祛百虑，菊为制颓龄。 15、春蚕收长丝，秋熟靡王税。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪Байду номын сангаас
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
图论中几个典型问题的求解163页PPT
图论中几个典型问题的求解
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以上程序是通用程序，只需输入初始距离矩 阵，就能输出最短路矩阵以及最短路的路径矩阵， 将程序以文件名floyd.m存盘。
例1 以2007年研究生数学建模竞赛C题为例， 已知16个邮政支局的初始距离矩阵，求任意两个 节点之间的最短路。
解：编写主程序如下：
a=[0, 27, 44, 17, 11, 27, 42, inf, inf, inf, 20, 25, 21, 21, 18, 27, inf;
…………………………………………
inf,inf,inf,inf,30,inf,inf,inf,21,13,20,inf,inf,inf,in f,9,0]; [D,R]=floyd(a);
输入数据中的inf表示无穷大（两个顶点之间 没有边直接相连）。
在图中，两个顶点u和v之间由顶点和边构成 的交错序列（使u和v相通）称为链（通道），没 有重复边的通道称为迹，起点与终点重合的通道 称为闭通道，不重合的称为开通道，没有重复顶 点（必然边也不重复）的开通道称为路，起点与 终点重合的路称为圈（回路）．包含奇数个顶点 （或边）的圈称为奇圈，包含偶数个顶点（或边） 的圈称为偶圈。如果顶点u和v之间存在一条路， 则称u和v是连通的，任意两个顶点都连通的图称 为连通图．无圈的连通图称为树，如果一棵树T 包含了图G的所有顶点，称T为G的生成树．
用 V={v1,v2,…} 表 示 全 体 顶 点 的 集 合 ， 用 E={e1,e2,…} 表示全体边的集合，如果对于E中的 任一条边ek，在V中都有一对顶点(vi,vj)和它对应， 则称由V和E组成的集体为一个图，记为G={V,E}， 简写为G．
二、基本概念
点与边相连接称为关联，与边e关联的顶点称为 该边的端点，与同一条边关联的两个顶点称为相 邻顶点，与同一个顶点关联的边称为相邻边．具 有相同顶点的边称为平行边，两个端点重合的边 称为环．所有线段都没有方向的图称为无向图， 所有线段都有方向的图称为有向图，既称为简单图，任意两个顶点之间都有一条 边相连的简单图称为完全图．任意两个顶点之间 有且只有一条弧相连的有向图称为竞赛图．
for j=1:n R(i,j)=j;
end end
for k=1:n for i=1:n for j=1:n if D(i,k)+D(k,j)<D(i,j) D(i,j)=D(i,k)+D(k,j); %在循环中进
行矩阵迭代 R(i,j)=R(i,k); % R是路径矩阵
end end end end D,R %输出最短路矩阵和最短路的路径矩阵。
d (1) ij
min
{di(j0)
,
d (0) i1
d (0) 1j
}
,
i
j
上式表示dij(1)在dij(0)以及从顶点vi经过顶点v1到 vj的权之和di1(0)+d1j(0)两者之中选择最短长度。依 此规则迭代。
d (2) ij
min
{di(j1)
,
d (1) i2
d (1) 2j
}
,
i
j
上式表示dij(2)在dij(1)以及从顶点vi经过顶点v2到 vj的权之和di2(1)+d2j(1)两者之中选择最短长度。依 此类推，迭代公式为 ：
图论中几个典型 问题的求解
§1 图的基本概念
图是一种直观形象地描述已知信息的方 式，它使事物之间的关系简洁明了，是分 析问题的有用工具，很多实际问题可以用 图来描述。
一、图的定义
图论是以图为研究对象的数学分支，在图论 中，图由一些点和点之间的连线所组成．
称图中的点为顶点（节点），称连接顶点的 没有方向的线段为边，称有方向的线段为弧．
d (m) ij
min
{di(jm1)
,
d (m1) im
d (m11) mj
}
,
i
j
上式表示dij(m)在dij(m-1)以及从顶点vi经过顶点vm 到vj的权之和dim(m-1)+dmj(m-1)两者之中选择最短长 度。当m=n时结束迭代。
2．程序设计 先编写Flody算法的子程序（函数）如下： Function [D,R]=floyd(a) n=size(a,1); D=a; % D是初始矩阵 for i=1:n
1．算法原理
设A=[aij]m×n是图的权矩阵（也称带权邻接矩 阵），其中aij是图上连接顶点i和j的边的权，如 果两顶点之间没有直接相连的边（即两顶点不相 邻），则aij=∞。
令矩阵D(0)=A，作为迭代的初始矩阵，从它出 发按照一定规则求D(1)，又由D(1)按照类似的规则 求D(2)，依此类推进行迭代直至求出D(n)，设矩阵 D(m)的元素为dij(m)，迭代规则为：
一、最短路的概念
给定一个连通的赋权图G={V,E}，设R是连接 节点vi和vj的一条路，该路的权定义为路中所有 各边权之和，如果路R在所有连接节点vi和vj的路 中权最小，则称它为vi和vj间的最短路。
二、任意两点之间的最短路(Floyd算法) Floyd算法利用距离矩阵进行迭代运算，可以 一次性地求出任意两点之间的最短路，该方法的 思路有创意，计算量小，编程较简单，又称矩阵 求解法。
如果图G的每条边e都对应一个实数C(e)，称 C(e)为该边e的权，称图G为赋权图．通常称赋权 的有向图为网络．
v4
e9
e4
v2
e1
e5
v5
e10
v1
e3
e2
e6
e8
e11
v7
v3
e7
v6
图中边e6和e7是平行边，e9是环，顶点v4是悬 挂点，边e4是悬挂边．
§2 最短路问题
最短路问题是图论应用的基础，很多实际问 题，如线路的布设、运输规划、运输网络最小费 用流等问题，都可以通过建立最短路模型来求解。 有些有深度的图与网络优化问题，如旅行售货商、 中国邮递员等问题，需要在首先求出任意两点之 间最短路的基础上解决。
在无向图中与顶点v关联的边的数目（环算两 次）称为该顶点的度（或次数），记为d(v)。度 为奇数的顶点叫做奇点，度为偶数的顶点叫做偶
点。在有向图中，从顶点v引出的边的数目称为 该顶点的出度，记为d+(v)，从顶点v引入的边的 数 目 称为 该 顶点 的 入度 ， 记为 d-(v)， 而 d(v) ＝ d+(v)+d-(v)称为v的次数。