数学中考专题源于课本而活于课本

合集下载

中考数学基础题多数来自课本

中考数学基础题多数来自课本今年中考数学试题难度有所下降。

试题背景学生熟悉，没有陌生和恐惧感，来源于课本的基础题占大多数。

试题亮点之一是弱化圆的知识的考查，加大了数学在实际生活中的运用的考查力度；之二是解答题入口宽，学生易上手，信心足。

此外，试题综合性更强，很好地体现了试题的选拔功能。

注重对数学应用问题的考查，全卷共有9个题共38分考查了学生应用数学知识解决实际问题的能力，题目的背景更加贴近实际生活。

图形的平移、图形的旋转是新课标下新增的内容，中考数学卷第21题中以图形的平移、中心对称、旋转等几何变换知识为载体，着重考查学生的作图能力。

第25题考查了抛物线的平移与几何知识的综合运用，有一定的难度。

A 近三年分析：题型注重基础知识与技能考试的依据不变：从2005年以后的中考试卷都按照课程改革的要求进行命题。

考试内容以《数学课程标准》为依据。

具体的考查内容有：基础知识与基本技能、数学活动过程、数学思考、解决问题能力以及对数学的基本认识等。

试卷的设置不变：近三年来，我市中考数学试卷都一直沿用下面的设置：总题量26题，其中选择题7题，每题3分；填空题10题，每题4分；解答题9题，共89分，大部分的解答题还分两个或三个小题。

试卷难度比为7：2：1。

试卷的题型来源、知识点及难易分布有共性：试题注重基础知识与基本技能、数学思维以及数学思想方法的应用的考查。

试题题型大部分来自课本，基础题较多，基础题主要根据是课本中的练习题、A组习题的题型，个别题加以改造，此外还包含其他一些改编题或自编题。

试题体现学科特点，注重命题的教育价值。

试卷难易程度、题量适中，照顾了中下水平的学生。

力图达到较高的及格率、合格率和平均分。

难度值在0.60-0.65之间，中档题的难度以中等生的难度为参照，中等生可较好发挥，但难题的高度较高，要考高分有一定的困难，满分较难。

难题主要分布在选择题的最后一题或填空题的最后一题或解答题后三题的最后一小题。

源于课本的中考试题例析

(作业本1第22页)已知正△ABC的边长为4 3 cm, 分别以A,B,C为圆心,AB长为半径画弧,所得图形叫弧三角形,求弧三角形ABC的面积。
小权的“发现”：
4
D
作三条角平分线交于点O, 能简化计算。
精读“扇形”的定义：一条弧和经过这条弧两端的两条半径所围成的图形叫扇形。扇形由弧与它所对圆心角的组成。
试题1：（四川）一张报纸对折后的半张报纸与整张报纸相 2 :1 似，则整张报纸的长与宽之比为_____
试题2：（山东潍坊）如图，一般书本的纸张是原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依次类推，若各种开本的矩形都相似，那么 AD 等于（ B ）
AB
A、0.5
B、 2
C、 2 2
D、0.618
试题3：（遂宁）如图一张矩形纸片ABCD，E、F分别为BC、 AD的中点，把纸片沿直线EF对折后，矩形ABEF的长与宽之比等于矩形ABCD的长与宽之比，则AB:AD等于（ B ） A、 2 ：1 B、1： 2 C 、1 ： 3 D、1： 3
九（上）课本中的“探究活动”
浙教版九（上）课本
关注一：探究材料
（课本第100页）取一张长与宽之比为 2 ：1的长方形纸，将它对折，请判断图中两张长方形纸的长与宽这4条线段是否成比例。蕴含的信息
信息1：标准纸的长与宽之比为 2 ：1 (课本第120页) 信息2：长与宽之比为 2 ：1的长方形纸对折，所得小长方形与原长方形相似。
第一章第19页，“用篱笆围菜园子”；第二章第37页，“一座拱桥的解析式”；第三章第62页，“用丁字尺找圆心” ；第70页，“尺规作图”；第四章第97页，“比例线段”；第111页，“等分线段”；第115页，“划分三角形的面积”；第120页，“标准纸”。

课本——中考题的“源头活水”——从中考看一道课本题目的衍变

课本———中考题的“源头活水”———从中考看一道课本题目的衍变256609　山东省滨州市北镇中学初中部　邢成云　于长军课本是《课程标准》的物化,是中考命题的蓝本,同时也是中考命题的天然素材,有了课本这个“源头活水”,一年一度的中考题才会始终给人一种“清如许”的感觉.每年都有大量的中考题目直接出自课本,或撷此作基,繁衍生息1本文兹举一例,探其衍,究其变,力图把握立意,指导教学1题例　(北师大版9年级数学下第二章《二次函数》P 75复习题中的A 组第7题)图1如图1(单位:m),等腰直角三角形ABC 以2米/秒的速度沿直线L 向正方形移动,直到A B 与CD 重合.设x 秒时,三角形与正方形重叠部分的面积为ym 2.(1)写出y 与x 的关系式;(2)当x =2,3.5时,y 分别是多少?(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?答案　(1)y =2x 2(0<x ≤10).(2)8;24.5.(3)此时恰好为AB 与CD 重合的状态,即运动了10米.显然是10÷2=5(秒)点评　本题通过三角形向正方形的平行移动,形成图形的叠合,等腰直角三角形的面积潜藏其中,凸显出“动中有静”、“静中蕴动”的辩证观点,它承载着新课标的理念,富有很强的生命力.我们知道,目前新课程把图形变换摆在了前所未有的高度,因为它是“思维实验”(爱因斯坦语)的引子,是训练思维的优质素材.图形变换是研究几何的重要方法,通过研究其变换,可以得到关于图形的一些新知识,引发新的思考,因此也成了命题的热点,备受命题专家的青睐,2006年烟台市将此题直接照搬成为中考题.本文选取近几年的中考题,探索题例的发展变化1　题型的变化　变为(图象)选择题图形的移动,动出了函数关系,自然和图象结下了不解之缘,故而成了考查数形结合的好素材.例1　(2006滨州市)如图2(单位:m ),直角梯形A BCD 以2m /s 的速度沿直线l 向正方形CEFG 方向移动,直到直线AB 与FE 重合,直角梯形A BCD 与正方形CEFG 重叠部分的面积S 关于移动时间t 的函数图象可能是图2 图3分析　本题将原来的“等腰直角三角形”变为“直角梯形”,把求关系式变成图象选择,其他一概未变.它主要是依托坐标系考查梯形的面积、直角三角形相似等平面几何知识,考查运动变化的思想.在整个运动过程中重叠部分的形状虽然没有变化(始终是梯形),但它并不沿着同一趋势在变,呈现出先增后减的分段态势,因此确定每一段的函数式是问题的关键.作为选择题,从“小题小做”的简化角度而言,可用特例排除法.答案　(一般思路):如图3,设移动t (0≤t ≤5)秒时,直角梯形ABCD 移动到A 1B 1C 1D 1的位置,则DD ==,因为R △MDD ∽R △D,所以MD =DD D ,即MD 5=,则MD =1.1.1.1CC 12t t 1t AH AH 1H 2t10t .故S =12(CM +C 1D 1)CC 1=12(5+t +5)2t=t 2+10t (0≤t ≤5).同理得,当5≤t ≤10时,S =-t 2+10t .综合知应选C .(特殊思路):如取t =2.5时,S <12S 直角梯形ABCD =752,抓住这一信息,结合图象用排除法可得.例2　(2007年赤峰市)如图4所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S (阴影部分),则S 与t的大致图象为图4分析　本题将原来的“等腰直角三角形”替换为“圆”,由直线型过渡到曲线型,看似复杂了,可用会意法.S 由大变小,变到最小时,持续了一段时间,然后再由小变大,并与开始时的由大变小呈对称状态,显然选A.1.2　变为填空题.图5例3　(2007眉山市18)如图5,已知等腰直角△A BC 的直角边长与正方形MN PQ 的边长均为20厘米,AC 与MN 在同一直线上,开始时点A 与点N 重合.让△A BC 以每秒2厘米的速度向左运动,最终点A 与点M 重合,则重叠部分面积y (厘米2)与时间t (秒)之间的函数关系式为1分析　图形没变,只是将平移的方向进行了调整,由于重叠图形是等腰直角三角形,故只需确定A M 的长度即可,而A M =20-2x,则y =12(20-2x)2.2　图形的变化.例　(年丽水市)如图6,在平面直角坐标系中,直角梯形B O 的边O 落在x 轴的正半轴上,且B ∥O ,B ⊥O ,B =,B =6,O =正方形图6-1OD EF 的两边分别落在坐标轴上,且它的面积等于直角梯形A BC O 面积.将正方形ODEF 沿x 轴的正半轴平行移动,设它与直角梯形A BCO 的重叠部分面积为S .(1)分析与计算:求正方形ODEF 的边长;(2)操作与求解:①正方形OD EF 平行移动过程中,通过操作、观察,试判断S (S >0)的变化情况是 ;A.逐渐增大 B .逐渐减少C .先增大后减少 D.先减少后增大②当正方形OD EF 顶点O 移动到点C 时,求S 的值;(3)探究与归纳:设正方形ODEF 的顶点O 向右移动的距离为x,求重叠部分面积S 与x 的函数关系式.分析　本题将原来的“等腰直角三角形”变为“直角梯形”,并置于平面直角坐标系中,摇身一变,细化为由简到繁、步步登高的探索题,问题(1)直接考查梯形与正方形的面积,(2)的①首先让我们通过“思维实验”来体会面积的变化趋势,②是对重叠的终极状态的刻画,问题(3)的变化过程丰富多彩,历经多种重叠图形状态,需要分类讨论思想的支持,汇集了初中阶段很多重要的、核心的知识,是大众化的、富有挑战性的一道压轴题.答案　(1)∵SODE F=S ABCO =12(4+8)×6=36,设正方形边长为x,则x 2=36,∴x =6(-6舍去).(2)①C.②S =12(3+6)×2+6×4=33.(3)①当0≤x <4时,重叠部分为三角形,如图6-2.可得△OMO ′∽△OA N ,∴MO ′6=x 4,MO ′=32x.图6 图634200724-1A C C A C C C A 4C C 8.-2-∴S =12×32x x =34x 2.②当4≤x <6时,重叠部分为直角梯形,如图6-3.S =(x -4+x )×6×12=6x -12.③当6≤x <8时,重叠部分为五边形,如图6-4.可得,MD =32(x -6),AF =x -4.S =12×(x -4+x )×6-12×32(x -6)(x -6)=-34x 2+15x -39.图6-4 图6-5图6-6④当8≤x <10时,重叠部分为五边形,如图6-5.S =S AF O ′D M -S B FO ′C=-34x 2+15x -39-(x -8)×6=-34x 2+9x +9.⑤当10≤x ≤14时,重叠部分为矩形,如图6-6.S =6-(x -8)×6=-6x +84.例5　(2008年辽宁省12市25题)如图7-1,在Rt △ABC 中,∠A =90°,AB =AC,BC =AC,BC =42,另有一等腰梯形D EFG (GF ∥DE )的底边DE 与BC 重合,两腰分别落在AB 、AC 上,且G 、F 分别是AB 、AC 的中点.图7-1 图7-2(1)求等腰梯形D EFG 的面积;(2)操作:固定△A BC,将等腰梯形D EFG 以每秒1个单位的速度沿BC 方向向右运动,直到点D 与点C 重合时停止设运动时间为D F ′G ′(如图)探究　在运动过程中,四边形BDG ′G 能否是菱形?若能,请求出此时x 的值;若不能,请说明理由.探究2　设在运动过程中△A BC 与等腰梯形DEFG 重叠部分的面积为y,求y 与x 的函数关系1分析　本中考题将原来的图形切换为梯形离开三角形进行平行移动而去,形成图形的再次叠合,在相对运动过程中,重叠部分的形状随着图形运动的变化而变化,三角形的中位线、梯形的性质、路程速度时间三量关系、菱形的判定、图形的面积、二次函数等核心知识立体交汇于时间这一主线,同样,分类讨论、方程思想、运动思想加盟其中.解答　如图7-3,(1)过点G 作G M ⊥BC 于M 1A B =AC ,∠BAC =90°,BC =42,G 为A B 中点,∴G M =21又∵G 、F 分别为A B 、AC 的中点,∴GF =12BC =22,∴S 梯形DEFG=12(22+42)×2=6,∴等腰梯形D EFG 的面积为6.图7-3 图7-4(2)探究1:能为菱形如图7-4,由BG ∥DG ′,GG ′∥BC,∴四边形BDG ′G 是平行四边形当BD =BG =12A B =2时,四边形BDG ′G 为菱形,此时可求得x =2,∴当x =2秒时,四边形BD G ′G 为菱形.探究2:分两种情况:①当0≤x <22时,方法1　当0≤x <22时,y 与x 的函数关系式为y =6-2x 1方法2　当0≤x <22时,∵FG ′=x,D =x,G M =,∴重叠部分的面积为.E 7-2.122-C 42-2y =(22-x)+(42-x)2×2=6-2x,∴当0≤x <22时,y 与x 的函数关系式为y =6-2x 1②当22≤x ≤42时,设FC 与DG ′交于点P,则∠PDC =∠PCD =45°,∴∠CPD =90°,PC =PD,作PQ ⊥DC 于Q ,如图7-5,则PQ =DQ =QC =12(42-x )1图7-5∴重叠部分的面积为y =12(42-x)×12(42-x)=14(42-x)2=14x 2-22x +81例6　(2008年益阳市第23题)两个全等的直角三角形ABC 和DEF 重叠在一起,其中∠A =60°,AC =1.固定△A BC 不动,将△DEF 进行如下操作:图8-1(1)如图8-1,△D EF沿线段A B 向右平移(即D 点在线段A B 内移动),连结DC 、CF 、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.图8-2(2)如图8-2,当D 点移到A B 的中点时,请你猜想四边形CDBF 的形状,并说明理由.图3(3)如图8-3,△DEF 的D 点固定在A B 的中点,然后绕D点按顺时针方向旋转△DEF,使D F 落在AB 边上,此时F 点恰好与B 点重合,连结,请你求出α的值分析　本题将图形切换成全等的两个直角三角形,突破了重叠面积以及面积不变的格局,把特殊四边形的理性判断融入其中,并与旋转变换携手,显性考查了三角函数.图8-4解答　(1)如图8-4,过C 点作CG ⊥A B 于G,在Rt △AGC 中,∵sin60°=CGAC,∴CG =321∵A B =2,∴S 梯形C DB F =S △A B C =12×2×32=321(2)菱形.∵CD ∥BF,FC ∥BD,∴四边形CDBF 是平行四边形1∵DF ∥AC,∠ACD =90°,∴CB ⊥D F,∴四边形CDBF 是菱形(3)解法1　如图8-5,过D 点作DH ⊥AE 于H,则S △AD E =12A DEB =12×1×3=321图8-5又S △ADE=12AE DH =32,DH =3AE =37(或217),∴在R t △DHE 中,sinα=DH DE=327(或2114)1解法2　∵△ADH ∽△A BE,∴DH B =AD,即D 3=,∴D =3,8-AE sin .E AEH 17H 7∴sin α=DH DE =327(或2114)1例7　(2008年常德市26题)如图9,在直线l 上摆放有△A BC 和直角梯形DEFG,且CD =6c m;在△A BC 中:∠C =90°,∠A =30°,A B =4c m;在直角梯形D EFG 中:EF ∥DG,∠DGF =90°,DG =6c m,D E =4cm,∠E DG=60°.解答下列问题:图9(1)旋转:将△A BC 绕点C 顺时针方向旋转90°,请你在图中作出旋转后的对应图形△A 1B 1C,并求出A B 1的长度;(2)翻折:将△A 1B 1C 沿过点B 1且与直线l 垂直的直线翻折,得到翻折后的对应图形△A 2B 1C 1,试判定四边形A 2B 1DE 的形状,并说明理由;(3)平移:将△A 2B 1C 1沿直线l 向右平移至△A 3B 2C 2,若设平移的距离为x,△A 3B 2C 2与直角梯形重叠部分的面积为y,当y 等于△ABC 面积的一半时,x 的值是多少?分析　本题将三种图形变换融为一体,进行了一次大盘点,但核心的问题仍然是以平移构建起来的,把原来题例中的图形变化为直角三角形与直角梯形,“守望”的依旧是重叠图形的面积问题.解答　(1)在△ABC 中,由已知得BC =2,AC =AB ×cos30°=23,∴A B 1=AC +CB 1=AC +CB =2+23.(2)四边形A 2B 1D E 为平行四边形.理由如下:∵∠E DG =60°,∠A 2B 1C 1=∠A 1B 1C =∠A BC =60°,∴A 2B 1∥D E 1又A 2B 1=A 1B 1=A B =4,D E =4,∴A 2B 1=D E,故结论成立.(3)由题意可知:S △A B C =12×2×23=23,①当0≤x <2或x ≥10时,y =0,此时重叠部分的面积不会等于△B 的面积的一半1②当≤x <时,直角边B 与等腰梯形的下底边DG 重叠的长度为D =D =(x ),则y =12(x -2)3x -2=32x -22,当y =12S △A B C =3时,即32x -22=3,解得x =2-2(舍)或x =2+ 2.∴当x =2+2时,重叠部分的面积等于△A BC 的面积的一半.③当4≤x <8时,△A 3B 2C 2完全与等腰梯形重叠,即y =231④当8≤x <10时,B 2G =B 2C 2-GC 2=2-(x -8)=10-x,则y =1210-x310-x =3210-x 2,当y =12S △A B C =3时,即3210-x 2=3,解得x =10-2,或x =10+2(舍去).∴当x =10+2时,重叠部分的面积等于△ABC 的面积的一半.由以上讨论知,当x =2+2或x =10+2时,重叠部分的面积等于△A BC 的面积的一半.点评　“动”是题例与拓展题的共性特色,运动思想是新课标十分重视的数学思想,在初中新教材中已经占据了重要的地位,中考中的动态几何问题蓬勃兴起,成为演绎图形变换的优质载体.以上的系列题目充分发挥了相似形、方程、函数等模型的工具性作用,融入了动态几何的变与不变特性,使静态与动态和谐生辉.图形动牵动着学生的思维动,在动感十足的图形“玩耍”中,吊起学生探索的“胃口”.纵观以上,可以发现变化无非是图形的替换,其核心问题———重叠面积统领全军,其中除了显性的各种图形的面积和图形变换外,还蕴藏着相似、一次函数、二次函数等初中的核心知识,同时考查了动静相生的辩证观点、分类讨论思想等.课本为我们命题提供了衍变的素材,如此命题对教学有“仙人指路”之用,重视课本、发掘课本、创造性地用好课本是我们教学不懈的追求、永恒的主旨!(收稿日期3)A C 242C 2C 2C 1C 2-C 1-2c m :2009009。

课本题是中考不竭的源泉

图1FEDCBA 课本题是中考不竭的源泉数学课本上的例题、练习题、习题、探究题的基础性、典型性都非常强，是经过几十年教学实践检验而形成的，是中考命题取之不尽、用之不竭的源泉。

每年都有大量的题目直接或间接源自课本，经过加工、改造、整合而成，体现了中考正确的导向作用。

本文点击不改变课本题的基本特征，而改变题型，再对其延伸拓展，变成开放题、阅读理解题、规律探索题等新题型，希望对同学们有所帮助。

课本题1.如图1，点B ，F ，C ，E 在一条直线上，FB=CE ，AB ∥ED,AC ∥FD ，求证：AB=DE,AC=DF[人教版（下同）八年级上P 16拓广探索11题]。

中考题：（2010南通）如图5，已知：点B,F,C,E 在一条直线上，FB=CE,AC=DF 。

能否由上面的已知条件证明AB ∥ED ？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使AB ∥ED 成立，并给出证明。

供选择的三个条件（请从其中选择一个）： ①AB=ED ； ②BC=EF ；③∠ACB=∠DFE 。

解：由上面两个条件不能证明AB ∥ED 。

有两种添加方法. 第一种：添加①AB=ED证明：∵FB=CE ，∴BC=EF ，又AB=DE,AC=DF ，∴△ABC ≌△DEF, ∴∠ABC=∠DEF ∴AB ∥ED.第二种：添加③∠ACB=∠DFE ，同理有BC=EF ，又∠ACB=∠DFE ，AC=DF ， ∴△ABC ≌△DEF, ∴∠ABC=∠DEF ∴AB ∥ED.点评：将课本题中AB ∥ED 与AC=DF 的位置互换，去掉AC ∥FD ，再改证明为判断，变成了一道条件开放题，题目并不难，但更能考察学生掌握和灵活运用所学知识解题的能力。

课本题2：如图2，小球起始位于（3,0），沿所示的方向击球，小球运动的轨迹如图所示，用坐标描述这个运动，找出小球运动的轨迹上几个关于直线l 对称的点。

例谈源于课本中考题及对教学的启示

测得气球的仰角为４５。．
（１）求气球的高度（结果精确到０．１ｍ）；（２）求气球飘移的平均速度（结果保留３个有效数字）．
蹦８
பைடு நூலகம்
圈９
知每行驶ｌｋｍ的车费求里程）。其实两题也没有多大的区别。３．来源于课本作业题中中考题例３：（２０１０・绍兴）如图５，小敏、小亮从Ａ，Ｂ两地观测空中ｃ处一个气球，分别测得仰角为３０。和６０。，Ａ，Ｂ两地相距１００ｍ．当气球沿与ＢＡ平行地移１Ｏ秒后到达ｃ处时，在Ａ处
２０１４年４
学．ｉ累稚辅导
例谈源于课本中考题及对教学的启示
◎俞欣
课本中例题、习题是教材编写者针对教材内容设置的要点、能力训练点和教学重难点，是学生学习过程中落实基础、提升能力的前沿阵地，也是教师备课时指南针、方向盘。教材的例、习题有着极大的典型性和代表性。纵观近几年绍兴市数学中考卷，不难发现每年至少有３～４题直接源于教材改变题。另外大部分题目的原形还是取自课本，即使是中考的“ 综合题 ” 、 “ 压轴题 ” 等，其基本解题思路和方法也能在课本上找到它的影子。下面就以近几年绍兴市数学中考卷中源于课本中考题为例，浅谈它对我们教学的启示。例谈源于课本的中考题１．来源于课本例题中中考题例１：（２０１１・绍兴）一条排水管的截面如图１所示．已知排水管的截面圆半径ＯＢ：１０，截面圆圆心Ｏ到水面的距离ＯＣ是６，则水面宽ＡＢ是（）

一道源于课本的中考好题

一
运用能力，发了学生的学习兴趣。三问更是激第在一、问的基础上充分挖掘，陈出新，同学二推为们提供了智慧生成与发展的时间与空间，生更学
是情有独钟．
解题过程如下：
２点Ｅ是ＡＢ的中点，Ｄ是高，Ａ上找一，Ａ在Ｄ
（）Ｂ关于ＡＣ３找Ｄ
对称点Ｅ，Ｄ连Ｅ延长
Ｃ
／ ’ ‘ ＼
交Ａ于Ｐ即．／ｃ可尊重
，
’ 毒＼
曰
材开发重组并创造Ａ＝＝＝、、／
性地活用教材，正是新
ｃ
题２（）图６ｃ
题２（）图６ｄ
（）图：２如作点Ｂ关于
好
连
／———＼，４
Ｃ对称点Ｅ则点Ｅ／Ｄ的，正
、ｃ
ｏ．曰ｏｏ￣
ＯＢ题２（）图６ａ题２（）图６ｂ
、连交（ ’ ０接＼ ’ Ｅ＿．，，
ＡＥＣＤ
于一点Ｐ，Ｐ＋ＢＡＰ最短．
（）拓展延伸３
如题２（）图，四边形ＡＤ的对角线６ｄ在ＢＣ
课改新理念对我们一线教师的新的要求，可喜很
２１００年第６期
中学数学教学
‘ ．．
３９
的看到近年中考中还有很多在不同背景下开发利用本习题的创新，现在略举几例补充如下：
因为Ａ的度数为６。点Ｄ０，
＼

数学中考专题——源于课本而活于课本

新人教版数学中考专题——源于课本而活于课本近几年的我市中考数学试题，90%左右的题目均来源于课本，其中绝大部分是课本题目的改编或延伸。

这是因为课本中的例题、习题，具有很强的示范性和典型性，中考命题者，常常以此为蓝本，编拟出综合性强、方法灵活的好题目，这不但有利于培养学生思维的发散性，而且充分体现了源于课本、高于课本的命题原则。

同时这种命题思路既给数学教学以及数学总复习以导向，又引导学生在课本习题上多下功夫，学会灵活的运用所学知识解决问题。

下面我就以几个几何部分四边形方面的题目加以说明：人教版初中数学八年级下册P122的第15题：四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F。

求证：AE=EF.(提示：取AB的中点G，连接EG.)临沂市中考题第25题：数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F。

求证：AE=EF.经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF,所以AE=EF.在此基础上，同学们作了进一步探究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B,C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立。

你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说出理由。

（2）小华提出：如图3，点E是BC延长线上（除C点外）的任意一点，其它条件不变，那么结论“AE=EF”仍然成立。

你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说出理由。

图1 图3图2C类似的还有如：临沂市中考数学试题第25题：如图1，已知矩形ABED ，点C 是边DE 的中点，且AB = 2AD ．（1）判断△ABC 的形状，并说明理由；（2）保持图1中ABC 固定不变，绕点C 旋转DE 所在的直线MN 到图2中（当垂线段AD 、BE 在直线MN 的同侧），试探究线段AD 、BE 、DE 长度之间有什么关系？并给予证明；（3）保持图2中△ABC 固定不变，继续绕点C 旋转DE 所在的直线MN 到图3中的位置（当垂线段AD 、BE 在直线MN 的异侧）．试探究线段AD 、BE 、DE 长度之间有什么关系？并给予证明．临沂市中考数学试题第25题：已知∠MAN ，AC 平分∠MAN 。

源于课本·活于课本·高于课本

多角度、方位考虑问题的能力．样学生在应对各种问题全这
ＤＣ＝５，ＡＤ＝３。ＤＣ＝５，知Ａ √ ｍ，Ａ７。Ｂ０，Ｂ４。又曰＝３ｋ
ＡＢ，，在同一平面内，，ｃＤ试求ｃ，之间的距离．，Ｊ
１ｋ从这三点分别遥望一座电视发射塔ＰＡ见塔在东北ｍ，，方赂，Ｂ见塔在正东方向，ｃ见塔在南偏东６。向，塔到Ｏ方求直路的距离．
［］文．道课本习题的变式教学一文的一点补充２周一
之间的距离，河岸这边选取点ＡＢ，得在，测Ｃ＝４。５，
第一步：系设点；建第二步：出点肘，的坐标；求 Ⅳ 第三步：由距离公式求出ＭＮ．
综上所述，高中数学教学过程中，注重概念的理解在应和基本的运算，足课本，课本中的经典例题、题为基立以习础，进行变化和演习，重挖掘知识的方法和内部逻辑结构，注做到一题多变，一反三，浅入深，层递进．重数学思举由层注想方法，发展求异思维、散思维、向思维，而能培养能发逆从
●
．
．
臻礤
＇■
●
。・
源矛课本 ● 活矛课本 ● 高于课本
◎赵卫国（江省温岭市大溪中学浙３７２）１５５

题虽在书外根却在书内——探究源于课本的中考几何题的设计方法

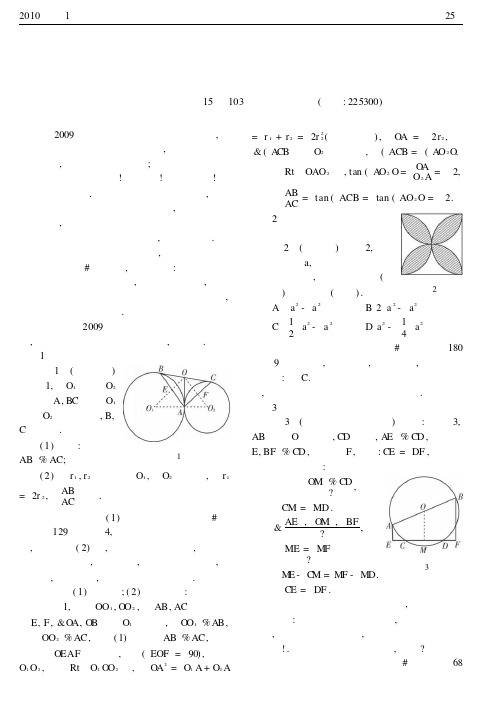
题虽在书外根却在书内探究源于课本的中考几何题的设计方法江苏省泰州市森南新村15栋103室于志洪(邮编:225300)在2009年全国部分省市中考数学试卷中,涌现出一大批源于课本的几何试题,这类试题有的一步到位,直接选用课本原题;有的进行改装、引伸、拓展课本中读一读!想一想!与做一做!的内容成为中考题.这类试题紧扣书本和大纲,体现了基础性和学好课本知识的重要性,有着较好的导向作用,对于引导师生重视基础、重视书本、研究教材、重视教材、用好用活教材,均大有裨益.随着素质教育的不断深化,为进一步体现数学课程标准#的理念,笔者认为:这类紧扣课本的试题将是命题的热点,且会长盛不衰,因此有必要提醒师生注意对课本知识的学习与挖掘,以达到灵活变通的目的.下面就以2009年部分省市中考几何试题为例,谈谈源于课本的试题设计方法,供参考.1直接选用课本例题并增设问题图1例1(承德市)如图1,O 1与O 2外切于A,BC 是O 1和O 2的公切线,B,C 为切点.(1)求证:AB %AC;(2)若r 1,r 2分别为O 1,O 2的半径,且r 1=2r 2,求AB AC的值.点评本题第(1)题选自人教版几何#第三册第129页的例4,并在原题的基础上引伸提高,构思出第(2)题,使问题得到了拓展,对相关知识进行了综合,题目不难,然而它提醒我们,题在书外,根在书内,学好用好课本是关键.简证(1)见课本;(2)简证如下:如图1,连接OO 1,O O 2,与AB,AC 分别交于点E,F,&O A,O B 是O 1的切线,O O 1%A B,同理OO %,根据()的结论B %,可知四边形O F 是矩形,有(OF =),连接O O ,则在R O O O 中,有O =O +O =r 1+r 2=2r 22(射影定理),O A =2r 2,又&(A CB 是O 2的弦切角,(ACB =(A O 2O .在RtOAO 2中,tan (A O 2O =O A O 2A=2,AB AC=tan (ACB =tan (AO 2O =2.图22直接选用课本习题作为中考题例2(广东省)如图2,正方形的边长为a,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为().A a 2-a 2B 2a 2-a 2C 12a 2-a 2D a 2-14a 2点评本题是人教版几何#第三册第180页第9题的原题,解法较多,题目不难,很容易求得结果:选C.这道原题的直接无变化选作中考题,更说明我们学好课本知识的重要性.3直接选用课本习题并进行创新例3(新疆生产建设兵团)已知:如图3,AB 是O 的直径,CD 是弦,A E %CD ,垂足是E,BF %CD ,垂足是F,求证:CE =DF ,小明同学是这样证明的:图3证明O M %CD ?,CM =MD.&AE ,O M ,BF ?,ME =M F?M E -C M =M F -M D.即CE =DF.横线及问号是老师给他的批注,老师还写了如下评语:你的解题思路很清晰,但证明过程欠完整,相信你再思考一下,一定能写出完整的证明过程!请你帮助小明订正此题,好吗?点评本题选自人教版几何#第三册第6252010年第1期中学数学教学2AC 1A AC EA E 9012t 12A 21A 2A.8页第12题,并以订正题创新形式命题,考查了作辅助线、垂径定理及梯形中位线定理的应用,它告诉我们,进行几何证明,必须要有严密的推理过程,对此,应引起重视.简证过O 作OM %CD ,垂足为M,则有CM =MD.&A E %CD ,BF %C D ,A E ,OM ,BF.又易知AB ,\EF ,O A =O B,O M 是梯形AEFB 的中位线,故ME =M F (或运用平行线等分线段定理证),M E -MC =MF -M D ,CE =DF.4根据课本中做一做!改编成中考题图4例4(宁波市)将矩形纸片ABCD 对折,设折痕为MN ,再把点B 叠在折痕MN 上(如图4中点B ),若AB =3,则折痕AE 的长为().A332B 334C 2D 23点评本题由人民教育出版社2001年第1版几何#第二册第126页做一做!改装而成,解题关键在于认识折痕!就是对称轴,从而,借助轴对称的知识和勾股定理简洁明快地求得折痕的长.解如图4,延长EB 交AD 于点F.由题意易知(BAE =30),从而在Rt ABE 中,由AB =3,知AE = 2.故应选C.5根据课本中的想一想!改编成中考题图5例5(天水市)如图5,同一平面内两个相同的正方形ABCD 和A B C D ,点A 与正方形ABCD 的中心重合,且正方形A B C D转动,则它们重叠部分的面积与正方形ABCD 的面积的比是点评本题由人民教育出版社年第版几何#第二册第5页想一想!改装而成,解题关键在于通过两个三角形的全等,推得两个正方形重叠部分的面积等于四分之一正方形ABCD 的面积,本题还可得到CE +CF 等于正方形的边长,为定值!这样一个结论.解联结AC 、BD 交于点A .在A EC 和A FD 中,A C =A D ,(A CE =(A DF =45),(DA F =90)-(CA F =(CA E ,所以,A FD .A E C.则S 四边形A ECF =S A C D =14S 正方形ABCD .故S 四边形A ECF /S 正方形A BCD =1/ 4.6根据课本中的读一读!改编成中考题例6(山东省)2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的(勾股圆方图),它是由四个全等的直角三角形与中间的小正方形拼成一个大正方形(如图6所示),如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b ,那么(a +b )2的值为().图6A 13B 19C 25D 169点评本题是根据人教版几何#第二册第107页读一读!改编而成的试题,题目围绕国际数学家大会会标而命题,构思巧妙新颖,同学们只要运用勾股定理,通过代数式变形,即可迅速求得其解.简解由题设可得(b-a)2=1,0a 2+b 2=1310+1,得2ab =122再将1+2,可得(a +b)2=25,故选C.综上所述可见:我们应重视对课本中的例题、习题、读一读!想一想!和做一做!等内容的研究,这有利于学生系统灵活地掌握学过的知识,提高学习效率,有利于提高学生数学思维的能力和综合运用知识的水平,对于培养学生的探索精神和创新意识,将会起到积极的作用.因此笔者认为:在平时的教学过程中,引导学生适当进行一些专题内容的探索与研究,是很有必要的(收稿日期)26中学数学教学2010年第1期.200119.:20091222。

源于课本的中考题

２０年厦门市中考第２题：０５５已知，Ｏ与ｏＯ相交于点Ａ、过点３６Ｂ，
作ＣＡＢ，Ｄｊ＿分别交６０和ｏ０于点ｃ、３１Ｄ．
（）图３求证：Ｃｏ０的直径；１如，Ａ是（若ＡＣ２）＝ＡＤ，
ＥＡＦ＝９０。．
图２
・
．
。
。．．
由（） △ＡＣ１得Ｄ— ＡＡＦ，Ｅ
。．
．
ＣＤＥＦ９。即Ａ＿ＤＡ＝Ａ＝０．ＣｊＣ．
又。Ａ．Ｄ是６Ｏ的直径， ’ ３
・
．．
ＡＣ６Ｏ的切线．是３
评点：题保留了原题图形的基本特征，是形式不同．这一改看起此只来平常，仔细分析，比原题更具有层次性，注了思考问题的梯度，但它关同时增加了对勾股定理的逆定理和切线的识别等重要知识点的考查．
维普资讯
ＳＨＯＸ
ＸＥＸ｛学学习ＯＩ数
号课本的ｌ考题ｆ，
，，，，
０／罗马
近几年的中考题有不少是由书本的例题、习题改编而成的．这类题
具有典型性，源于教材，于教材，于教材．为此，真研究教材的它高活认例题和习题是一种行之有效的学习方法．下面以华东师大版教材九年级（）７页第１题上第６８为例，分析以此题为背景的２０年的两道中考题．０５教材原题：如图ｌ，已知００与００相交于点Ａ、过点２Ｂ，Ｂ作Ｃ＿ＤＪＡＢ，分别交ＥＯ。３和．，

中考数学热点题型——阅读理解

数学圜学习二二=二：=二=二二二=二=二二二二1I —厶i —口|二=二二二===_■■I=责任编辑：王二喜jQ刘顿阅读理解题是近年来出现的一种新题型．阅读理解题一般由两部分组成．一是阅读材料，二是考查内容．它要求我们根据阅读获取的信息回答问题．阅读的内容丰富，源于课本，高于课本，活于：课本．它考查我们阅读理解的能力和数学知识的综合应用能力，尤其侧重于考查数学思维能力和创新意识．这类题目的结构为：给出一段阅读材料，要求通过阅读，将材料所给的信息加以搜集整理，在此基础上，按照题目的要求进行推理解答．现以2007年的中考题j 为例，归类说明阅读理解题的解法．一、定义新运算定义新运算型阅读理解题，通常是先定义一个运算法则，你只要根据所提供的运算法则，代入相应的数据求出结果即可．例l (梅州市)将4个o ，6，c ，d 排成2行、2列，两边各加一l…一…………………………～………………三而藓函‘忾歹。

中考数学热点题型回谚理饵条竖直线记成I：三l，定义I：三I=甜一6c，上述记号就叫做2阶行腻若E引氓舭=一．解：因为l：引=以一6c，所以l计1铲1l：6可以转化为(石+1)(计1)一(戈一1)(1吨)：6，J l叫z+l即(菇+1)2+(z一1)2=6，所以戈2=2，即龙=±、／丁．评点：只需将新定义的运算转化成一元二次方程，即可求解．二、运用新推导的结论求解例2(德阳市)阅读材料：设一元二次方程僦2+缸+c=0的两根为菇。

，z：，则两根与方程系数之间有如下关系：z。

+石：：一旦，z。

髫：=三．根据该材料填空：已知菇。

，石：是方程戈：+瓯+3：0的两实数根，则丝+卫的值为——．解：通过阅读，因为石l，石：是方程茗2+甑+3=o的两实数根，所以茗l+戈2=一6，名1。

茗2=3．又因为兰+兰：丝：皇生兰兰垫，算l茗2X l髫2石l戈2所以原式：生鱼芝兰卫：1o．评点：解本题的关键是通过阅读材料，掌握一元二次方程∞2+ 6x+c：0的两根为菇．，戈：，则两根的和为一旦，两根的积为三．三、指出解题过程中的错误例3(临安市)阅读下列题目的解题过程：。

不谋而合圆切相辉——多地巧合源于教材的例、习题的中考题

，
的延长线交直线ＣＤ于点Ｅ．（１）求证：ＡＣ平分／＿ＤＡＢ：第１４题如图１，ＡＢ为０ｏ的直径，Ｃ为ｏｏ上一点。ＡＤ和过ｃ点的切线互相垂直垂足为Ｄ。求证：ＡＣ平分（２）若ＡＢ＝４，Ｂ为ＯＥ的中点，ＣＦ上ＡＢ，垂足为点Ｆ，求ＤＡＢＣＦ的长：
课程教育研究
教学管理
不谋而合圆切相辉
— —
多地巧合源于教材的例、习题的中考题
雷敏乾
（湖北省孝感市大悟县四姑镇中学湖北大悟４３２８２７）
ｆ摘要ｌ “ 依据新课标，源于教材 ” 是中考数学命题的一个重要风向标；２０１４年中考，多地命题专家对九年级数学上册《圆的基本性质》的一道习题和一道例题直接引用或进行变式、拓展、提升、综合，又层层推进地设置新的问题情景：这样不仅了达到了源于教材，高于教材，活于教材的作用，又考查了学生的分析问题、解决问题的能力；同时又对我们广大教师今后的教学无疑起了一个导向作用。
一
下吧！
线于Ｅ．
四题开屏：
（１）求证：ＣＤ为ｏＯ的切线：
，
图形基本不变，已知条件基本不变，求证的结论不变，但（２）若３求ｃ。ｓ／＿ＤＡＢ的值．是求证的结论在条件略作增加的情况下进行了提升、综合、推简要思路：题一、二、三的第（１）问的求证与课本第１４题的进．即让学生有似曾相识燕归来的欣喜。又让学生必须经过一是对习题的一个熟练程度的检测。这里只将题一和番苦思冥想．并运用其它的数学知识来分析．从而解决问题。步骤相同．题四的解答作一个简要的分析．题二和题三留给大家思考。让不同的学生有不同的发展可参考金考卷２０１４年全国各省市中考试题汇编（湖北专题一：（２０１４年孝感市）如图３，ＡＢ是ｏｏ的直径，点Ｃ是

一道源于课本中考好题评析论文

一道源于课本的中考好题评析每年，在各省市的数学中考试题里，其实都有不少题目是源于课本，对课本的好题进行变式改编而成的。

2009年中考，四川·绵阳的压轴好题第25题就是源于人教版《义务教育课程标准实验教科书》八年级数学下册133页第15题，以类比思想为中心，以特殊到一般的拓展为载体，主要考查学生的类比思维、探究能力和推理能力的好题。

一、课本原题的解答与评析（八年级数学下册133页）15、如图1：四边形abcd是正方形，点e是边bc的中点，∠aef＝90°，ef交正方形外角的平分线cf 于f。

求证：ae＝ef。

图1 图2〖略证〗：在ab上取中点g，则ag=bg，∵四边形abcd是正方形，且点e是边bc的中点，∴ag＝bg=be＝ec∴∠egb=45°，从而∠age=135°．由bf是外角平分线，得∠ecf=135°，∴∠age=∠ecf．∵∠aef=90°，∴∠fec+∠aeb=90°．在rt△aeb中，∵∠eab+∠aeb=90°，∴∠eab=∠fec，∴△age≌△ecf∴ef=ae．【评析】首先，本题是一道考查学生几何基础知识的好题。

1、从知识、能力看，题目以学生熟悉的正方形为载体，考查了正方形、直角三角形、三角形全等及角平分线等的重要内容，要求学生有具有扎实的数学基本功，较强的探究能力和综合分析问题解决问题的能力；2、从创新、命题技巧看，此题图形富有变化，具有较大的探索空间。

如中点e可以改成是bc上任意一点或在bc上移动的动点，正方形也可以换成矩形等多种变式，2009年四川·绵阳市的中考试卷就体现了这种变式。

二、改编后中考题的解答与评析（2009年四川·绵阳）25．如图，在平面直角坐标系中，矩形aobc在第一象限内，e是边ob上的动点（不包括端点），作∠aef=90°，使ef交矩形的外角平分线bf于点f，设c（m，n）．（1）若m=n时，如图，求证：ef=ae；（2）若m≠n时，如图，试问边ob上是否还存在点e，使得ef =ae？若存在，请求出点e的坐标；若不存在，请说明理由．（3）若m=tn（t＞1）时，试探究点e在边ob的何处时，使得ef=（t+1）ae成立？并求出点e的坐标．〖略解〗（1）由题意得m=n时，aobc是正方形．如图4，在oa上取点g，使ag=be，则og=oe．∴∠ego=45°，从而∠age=135°．由bf是外角平分线，得∠ebf=135°，∴∠age=∠ebf．∵∠aef=90°，∴∠feb+∠aeo=90°．在rt△aeo中，∵∠eao+∠aeo=90°，∴∠eao =∠feb，∴△age≌△ebf，ef=ae．图4图5（2）假设存在点e，使ef=ae．设e（a，0）．作fh⊥x轴于h，如图5．由（1）知∠eao=∠feh，于是rt△aoe≌rt△ehf．∴fh=oe，eh=oa．∴点f的纵坐标为a，即fh=a．由bf是外角平分线，知∠fbh=45°，∴bh=fh=a．又由c（m，n）有ob=m，∴be=ob－oe=m－a，∴eh=m－a+a=m．又eh=oa=n，∴m=n，这与已知m≠n相矛盾．因此在边ob上不存在点e，使ef=ae成立．（3）如（2）图，设e（a，0），fh=h，则eh=oh－oe=h+m－a．由∠aef= 90°，∠eao=∠feh，得△aoe∽△ehf，∴ef=（t+1）ae等价于fh=（t+1）oe，即h=（t+1）a，且，即，整理得nh=ah+am－a2，∴．把h=（t+1）a代入得，即m－a=（t+1）（n－a）．而m=tn，因此tn－a=（t+1）（n－a）．化简得ta=n，解得．∵t＞1，∴＜n＜m，故e在ob边上．∴当e在ob边上且离原点距离为处时满足条件，此时e（，0）．【评析】由上述解题过程可知，此题中的3道小题都是利用一些共同的属性得出∠oae＝∠bef，并进一步构造出与△ebf相似的△age。

源于课本,活于课本的高考题——对高考数学复习的启示

时，道长度最短管
（一］＞ｚ１吼得最、＝－。０，Ｊ
值．ｐ吕矩形ＡＢＤＣ
Ｏ
Ａ
必内接于半圆ｏ，两边长分别为ＡＢ—Ｒｓ０ＤＡ＝且ｉ，ｎ２０Ａ一２ｏ０这个矩形的面积为ＳＲｃｓＤ— ＡＢ・ＤＡ
（）设ＢＡＯ一０（ａ）ｉｒｄ，
７【
百
凼此，行水处理Ｊ罐在矩彤区域肉且到Ａ，两当Ｂ
点距离均为
短．
ｋ时，设的排污管道的总长度最铺
解法二：
将ｙ表示为的函数．（ｉｉ）设Ｐｏ— ｚ（ｍ）将ｋ，表示为ｚ的函数．
—
Ｒｓｎ０・２ｏ０Ｒ。ｉ２０ｉＲｃｓ－ｓｎ．
所以，ｓ２ — １０为锐角）即０４。，形当ｉ０ｎ（， — ５时矩ＡＢＤ的面积取得最大值Ｒ．Ｃ
・
４・０
数学教育研究
２００８年第６期
认真学习《中数学课程标准》《中数学课程标高、高准教学要求》《考考试说明》研读体现新课程改革及高，的新题型、思维、方法，高综合应用的能力，时新新提同关注近几年的高考题和各地模拟试题，里面我们能这体会到高考的相关信息．们曾经在《试高考数学》我考２００８年第１２期看到与本高考题类似的题目：大学、某为了发展需要，准确兴建新校区，校区规划分南北两新

以课本为本,数学中考高效复习的源头

以课本为本，数学中考高效复习的源头作者：邱海冰来源：《中学课程辅导·教学研究》2017年第17期问题的提出：又是一届初三紧张的复习期。

前段时间，市里开了一个中考数学研讨会，专家再三强调：“以本为本，以考纲为纲，把课本看得多重要都不为过。

”去年，笔者也是带初三，复习时一直希望能以课本为主线，却因时间关系，总感觉研究得不透彻。

今年，我真正的研究了，下面谈谈自己的体会。

有人把教材比作小说原著，把教材的优化和开发比作剧本的改编，而教学设计就成了导演手中的创作脚本。

怎样在学生已经学完6本书的基础上，进一步去挖掘教材，让中考数学的复习在有限的时间里最大的提高效率，这真的是需要很大的挑战。

下面我就以课本为本，提高数学中考复习效率谈谈自己的看法。

第一、无论一本复习资料书内容多么丰富多样、齐全都不能满足内容全面的要求。

课本的概念、定理、推论的来龙去脉，知识点的引入，逻辑清晰可见，而资料的知识梳理是无法达到的。

例如，佛山市2014年度第24题第（1）中考题：⑴证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半；要求：根据图1写出定理的已知、求证、证明；在证明过程中，至少有两外写出推理的依据（“已知”除外）这道题，在课本中是整个证明过程都是有的，而在复习资料中是没有这样提到的。

所以在复习的过程中要学生回归课本，理解概念定理和推论的同时，还要适当的掌握它的来龙去脉，要做到这样只有认认真真的再研读课本。

第二、“穿旧鞋，走新路”！中考出题专家都是讲求题目原创的，那么专家每次出题肯定是在认真研究课本的基础上，结合考纲精心的设计题目，题目面目是全新的，但是本质是不变的。

而课本的练习，例题也是难度适中的，教师也可以充分的利用课本的习题结合考纲进行精心的变式或者对比出题，让学生做的复习题针对性更强。

在复习过程中，提问是重要的复习手段，要结合教材内容和学生实际设计问题例如：佛山市2014年的中考题8分题第22题：现有不等式的性质：①在不等式的两边都加上（或减去）同一个整式，不等号的方向不变；②在不等式的两边都乘以同一个数（或整式），乘的数（或整式）为正时不等号的方向不变，乘的数（或整式）为负时不等式的方向改变.请解决以下两个问题：（1）利用性质①比较2a与a的大小（a≠0）；（2）利用性质②比较2a与a的大小（a≠0）.这一道题就是源自于现行课本（北师大版2013年12月第1版）八年级下册第42页数学理解第3题。

中考题的“源头活水”在教材

中考链接\___中考题的“源头活水”在教材固张浩杰纵观各地的中考数学试题，总能发现有些试题直接来源于教材中的习题或例题。

如果我们在平时的数学学习过程中，能够关注到这一点,充分挖掘教材习题、例题的价值，将会让我们的学习过程充满挑战感，也必将为我们的数学学习插上腾飞之翼。

例(2019・黑龙江绥化)如图1,在厶ABC中，AB=AC,点D在AC上，且BD=BC=图1图2【思路解析】从已知条件中，我们发现该图中存在三个等腰三角形，则可以利用等腰三角形的性质及三角形内(外)角和定理打通角与角之间的联系，联合方程思想，进而解决问题。

【解法呈现］.BD=AD,设"=^LABD=x°,■.^DC=2x°o:BD=BC,•.厶C=ABDC=2x。

,.AB^AC,•.AABC=厶C=2x°,/.%+2%+2%=180,艮卩兀=36,.•.Z4=36°o【教材之影】苏科版《数学》八年级上册第2章第5节“等腰三角形的轴对称性”习题第7题。

如图2,厶C=36。

,"=72。

,"40=36。

⑴求厶1和厶2的度数；(2)找出图中的等腰三角形。

【变式探究】(1)如图1,在4ABC,AB=AC,£A= 36°,BD平分"BC。

证明仏DCB为等腰三角形。

(2)如图1,在厶ABC中，如3=4C,"= 36。

,加平分ZMC,BD：DC=m：n。

求509与的面积比。

(3)如图1,在厶ABC中MB=/1C,2S4= 36°,BD平分厶ABC,BD=m,DC=n。

求ZUBD的周长。

（4）如图3,在厶ABC中MB=AC,乙4= 36。

仿照图4,请你再设计两种不同的分法，将AABC分割成3个三角形，使得每个三角形都是等腰三角形。

（注：如果两个图中分割出的3个三角形分别全等而只是分割线的具体位置不同，则视为同一种分割方法。

）图3 图4提示:如图5、图6、图7。

源于课本活于课本的中考题

源于课本活于课本的中考题
刘士勇
【期刊名称】《政治思想史》
【年(卷),期】2005(000)007
【摘要】近几年的天津市中考数学试题，90％左右的题目均来源于课本，其中，绝大部分是课本题目的改编或延伸．这种命题思路，既给数学教学以及数学总复习以导向，又引导学生在课本习题上多下功夫，学会灵活地运用所学知识解决问题．【总页数】3页(P14-16)
【作者】刘士勇
【作者单位】天津市大港油田教研中心,300280
【正文语种】中文
【中图分类】G63
【相关文献】
1.源于课本·活于课本·高于课本 [J], 赵卫国
2.课本——中考题的“源头活水”——从中考看一道课本题目的衍变 [J], 邢成云;于长军
3.源于课本，活于课本的高考题——对高考数学复习的启示 [J], 吴德彬
4.源于课本又高于课本的中考题 [J], 刘克环
5.课本——中考题的“源头活水”——从中考看一道课本题目的衍变 [J], 邢成云; 于长军
因版权原因，仅展示原文概要，查看原文内容请购买。

中考题就是书上的例题

中考题就是书上的例题1、重视数学的基础部分任何学科的学习，都一定要把基础打好，只有把基础打好了，做各种类型的习题才能迎刃而解。

虽然数学是一门理科专业，但书本上的内容同样重要，把书本上的内容消化成自己的知识，数学提分就是非常容易的事情了。

中考数学题就是书上的例题，书本上的概念、公式，学生不仅要滚瓜烂熟，还要对这些知识点理解深刻，如果知识背下来并不理解，还是很难应用到习题中，甚至考察同样的知识点，换一种说法，学生就不知道该怎么做了。

2、有目的有方法地刷题首先也是最重要的，要先把数学书上的所有例题做一遍，因为书上的每一个例题一定是最能代表这一个知识点的题目，只要吃透了书上的例题，在遇到同样知识点的题目时，就很简单了。

其次，我们在刷题的时候一定要准备一个错题本。

错题本可是提分神器，并且每个人的错题本都是独一无二的。

通过错题本，我们可以看出自己没有掌握的知识点是哪些，并且有针对性做训练，那些已经熟练掌握的知识点以后就可以少做，为我们节省很多时间。

当然，错题本并不是把错题和答案抄上去就行了，而是每隔一段时间就要将错题本拿出来回顾之前做错的题目，并且在回顾的时候把答案和过程遮住，重新再做一遍，能够轻松做出来了，就说明你掌握了这道题里的知识点，如果还是不会或者做错，那就再将这道题重点标记，下一次回顾错题时继续做。

如此反复，直到将错题本上的所有错题都吃透。

3、对答案时要带上自己的思考我们在对答案时，一定要带上自己的思考，自己为什么会做错？是粗心了还是知识点没掌握？这道题里面都有哪些知识点？答案上为什么是这样的？如果你只看题目对错，不去研究错在哪，不去研究解题思路，那答案还是答案，你还是你。

而且，并不是说所有市面上的习题册答案都是正确的，要自己去分辨。

当然，遇到不懂的问题，一定要勤问，问老师、问成绩好的同学。

中考的数学考试时间是2小时，因此在考试过程中一定要把握好时间，遇到难题先不要死扣，先把容易做、会做的题做完，把能得到的分都拿到手，再去思考剩下的难题。

中考数学复习最好以课本为主

中考数学复习最好以课本为主数学整体命题难度会降低复习最好以课本为主注意与高中有衔接关系的知识点：回顾一下去年以及前三年的情况，可以发现，2008年广州中考题的编排中，全卷总分150分，容易题目占54分，中档题目占了75分，难题只占了21分，从这个数据可以看清楚，实际上中考的数学难度总体不大。

前三年中考数学市平均分基本上分布在90分左右，2006年93.28分，2007年86.27分。

由于应届生是使用华师大教材的最后一届，下一届现在已经用人教版的了，所以市里给了一个指导方向：“保持稳定，适当调整”。

试题难度和题量都不会有太大的变化。

据纪老师介绍，今年数学的科目难度比去年可能会降低一点，特别是基础题目，填空和选择更平和，难度还会降低。

几次区里面开会都提到“试题会着重考察对高中阶段的学习有基础作用的知识和技能”这样的话。

尤其是会考察对高中知识有积淀作用，涉及到与高一数学存在衔接关系的知识点。

所以，在复习的时候最好以课本为主。

总复习可分三轮进行：从现在到中考，还有最后30多天的时间，我们该如何复习?中考的总复习一般分为三个阶段，第一阶段复习基础，注重系统，第二阶段是注重专题训练，第三阶段是注重模拟试题训练。

其中第一轮系统复习阶段，要过三关，“基础知识关”掌握核心概念和公理公式;“基础技能关”要归纳解题中用了哪些知识;“基本方法关”则要掌握方程式、函数和转化、分类讨论等方面。

目前一模已过，大多数考生正处于第二轮复习中。

第二轮是目前至战前一周，要做的是归纳题型，多题一解;开拓思维，一题多解，并对基础知识点进行查漏补缺。

在这一轮复习中，最有效的不是做题，而是看题，也就是阅读大量的数学考题，近几年的中考题，而且要有详细解答过程。

见识的题目越多越好。

第三轮是考前一周的模拟训练。

通过模拟答题训练找出自己存在的问题，然后加以解决并加强这方面的练习。

距中考3~5天要注意调节时间，不要复习太晚，不要给自己太大的心理压力。