Herglotz函数的转换
python 希尔伯特变换

python 希尔伯特变换Python希尔伯特变换(Hilbert Transform)是一种非常重要的信号处理技术。
它被广泛应用于音频信号、图像处理、雷达信号等领域,其主要作用是通过对信号进行加工处理,使其具有更好的频域特性和时域特性。
本文将详细介绍Python希尔伯特变换的基本概念、算法实现、应用等方面。
一、什么是Python希尔伯特变换?Python希尔伯特变换是指对输入信号进行频域变换,以实现对信号频谱的调整。
它的作用是让信号在频域中的幅度变化与相位变化具有统一的特性。
Python希尔伯特变换常常被用于分析信号的包络特性和相位特性,在数学和物理学中统称为“解析信号”的处理技术。
而Python中,这种技术主要应用于数字信号处理。
二、Python希尔伯特变换的基本算法在Python中,我们可以使用scipy库中的signal模块来实现对信号进行希尔伯特变换的操作。
具体而言,我们可以通过以下代码实现:``` from scipy.signal import hilbertanalytic_signal = hilbert(raw_signal)amplitude_envelope = np.abs(analytic_signal)instantaneous_phase =np.unwrap(np.angle(analytic_signal))instantaneous_frequency =(np.diff(instantaneous_phase) /(2.0*np.pi) * fs) ```需要注意的是,上述代码中涉及到的几个变量参数的含义为:raw_signal表示输入的原始信号;analytic_signal表示经过希尔伯特变换后的解析信号;amplitude_envelope表示解析信号的包络特性;instantaneous_phase表示解析信号的相位特性;instantaneous_frequency表示在信号变化过程中的瞬时频率。
helmholtz函数

helmholtz函数
Helmholtz函数,也称为Helmholtz方程,是一个在物理学和工程学中常用的偏微分方程。
它的一般形式为:
Δu + k^2 u = 0
其中,Δ 是拉普拉斯算子,k 是波数,u 是未知函数。
Helmholtz方程描述了波动在空间中的传播,特别是在声学、电磁学和流体动力学等领域。
它通常用于描述波在给定边界条件下的传播和散射。
Helmholtz方程的解通常需要使用数值方法或解析方法来求解,这取决于问题的具体性质和边界条件。
在某些情况下,可以使用分离变量法或傅里叶分析等数学工具来找到方程的解析解。
然而,对于更复杂的问题,可能需要使用有限元方法、有限差分方法或其他数值方法来求解。
亥姆霍兹方程在极坐标系中的求解过程

亥姆霍兹方程在极坐标系中的求解过程在物理学和工程学中,亥姆霍兹方程是一个非常重要的偏微分方程,它描述了波动现象以及散射和传播等许多自然现象。
在极坐标系中,亥姆霍兹方程的求解过程涉及到复杂的数学理论和方法,需要深入的理论基础和丰富的实际经验。
在本文中,我将从基本概念开始,逐步深入,探讨亥姆霍兹方程在极坐标系中的求解过程,希望能够帮助读者更全面地理解这一重要的数学物理问题。
1. 亥姆霍兹方程简介亥姆霍兹方程是一个描述波动现象的偏微分方程,通常用于描述光、声波、电磁波等在空间中传播的规律。
它的一般形式可以表示为:\[\nabla^2 u + k^2u = 0\]其中,\(\nabla^2\)是拉普拉斯算子,\(u\)表示波函数,\(k\)为波数。
在极坐标系中,亥姆霍兹方程的形式稍有不同,需要进行适当的坐标变换和求解方法。
2. 极坐标系中的亥姆霍兹方程在二维极坐标系中,亥姆霍兹方程可以表示为:\[\frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partialu}{\partial r} \right) + \frac{1}{r^2} \frac{\partial^2u}{\partial\theta^2} + k^2 u = 0\]其中,\(r\)为径向坐标,\(\theta\)为极角,\(u\)为波函数,\(k\)为波数。
在极坐标系中,由于坐标系的特殊性,方程的求解变得更加复杂和有趣。
3. 求解方法在极坐标系中,亥姆霍兹方程的求解通常需要用到分离变量法、复数变换、特殊函数等多种数学方法。
可以尝试对波函数进行分离变量,得到径向方程和角向方程。
根据具体的边界条件和物理问题,选择合适的方法进行求解。
4. 分析与讨论亥姆霍兹方程在极坐标系中的求解过程涉及到大量的数学理论和物理知识,需要深入的理论基础和丰富的实际经验。
在实际应用中,还需要考虑到边界条件、散射问题、波场传播等多种因素,使得求解过程更加复杂和丰富。
希尔伯特曲线值与坐标的转换-概述说明以及解释

希尔伯特曲线值与坐标的转换-概述说明以及解释1.引言1.1 概述引言部分的内容:希尔伯特曲线是一种具有非常有趣数学性质的空间填充曲线。
它由德国数学家大卫·希尔伯特于20世纪初所发现并研究。
希尔伯特曲线具有连续但非常“弯曲”的特征,它能够在单位正方形中填满整个平面。
希尔伯特曲线在计算机图形学、空间分析、数据压缩等领域有着广泛的应用价值。
通过对希尔伯特曲线的分析,我们可以将一维数据转化为二维或多维数据,从而更好地理解和处理数据。
而将坐标转换为希尔伯特曲线值,可以实现空间坐标的编码与压缩,有效地减少存储空间的占用。
本文的目的旨在介绍希尔伯特曲线值与坐标的转换方法,并探讨其应用前景与意义。
通过对希尔伯特曲线的理论与实践研究,我们可以更好地理解曲线的性质与特点,进一步拓展希尔伯特曲线在各个领域的应用范围。
接下来的正文将首先介绍希尔伯特曲线的基本概念与性质,然后详细讨论希尔伯特曲线值的计算方法,最后探究坐标与希尔伯特曲线值的转换方法。
结论部分将总结希尔伯特曲线值与坐标的转换关系,并探讨其应用前景与意义。
同时,我们还将展望未来进一步研究希尔伯特曲线在数据处理与空间分析中的可能方向。
通过本文的阅读,读者将对希尔伯特曲线及其与坐标的转换关系有一个全面的了解,为进一步的研究与实践提供了有力的支持和参考。
相信本文对于相关领域的研究人员和学生都具有一定的参考价值。
1.2 文章结构本文将以希尔伯特曲线值与坐标的转换为主题,分为引言、正文和结论三个部分。
引言部分将首先概述希尔伯特曲线的背景和应用领域,介绍希尔伯特曲线值与坐标之间的关系,并阐明本文的研究目的。
正文部分将详细介绍希尔伯特曲线的概念和特点,解释希尔伯特曲线值的计算方法,并探讨坐标与希尔伯特曲线值之间的转换方法。
我们将逐步介绍计算希尔伯特曲线值的算法,以及如何将坐标点映射到希尔伯特曲线上或从希尔伯特曲线值反推回坐标点的过程。
同时,我们将讨论不同级别的希尔伯特曲线对应的坐标范围和分辨率,以及如何在实际应用中进行坐标与希尔伯特曲线值之间的转换。
变质量力学系统的Herglotz型Lagrange方程

第20卷第6期2022年12月动力学与控制学报JOURNALOFDYNAMICSANDCONTROLVol.20No.6Dec.2022文章编号:1672 6553 2022 20(6) 106 08DOI:10.6052/1672 6553 2022 012 2022 01 04收到第1稿,2022 03 26收到修改稿.国家自然科学基金赞助项目(11972241,11572212),江苏省自然科学基金资助项目(BK20191454) 通信作者E mail:zhy@mail.usts.edu.cn变质量力学系统的Herglotz型Lagrange方程与Noether对称性和守恒量蔡铭俣1 张毅2(1.苏州科技大学数学科学学院,苏州 215009)(2.苏州科技大学土木工程学院,苏州 215011)摘要 Herglotz变分原理提供了非保守耗散问题的变分描述,同时变质量力学在自然界和工程领域有大量的应用,因此将Herglotz变分原理应用于变质量力学系统的Lagrange方程与守恒律研究,为研究变质量力学提供了一个新的途径.文中建立了变质量力学系统的Herglotz型广义变分原理,导出了变质量系统的Her glotz型Lagrange方程.定义了变质量力学系统的Herglotz型Noether对称性,建立并证明了Herglotz型Noether定理及其逆定理.文末给出两个变质量非保守系统的具体例子以说明结果的应用.关键词 变质量力学系统, Herglotz型广义变分原理, Noether定理, 守恒量中图分类号:O316文献标志码:A引言众所周知,对于非保守这样一类自然界广泛存在的现象,人们无法将其纳入哈密顿变分原理的经典框架之中[1].德国数学家Herglotz提出的一类变分问题[2],不仅是对经典变分原理的推广,而且提供非保守和耗散过程的变分描述.Herglotz变分问题与经典变分问题的不同之处在于其微分方程不仅取决于时间、曲线及其导数,还取决于积分泛函本身.Donchev[3]和Lazo等[4,5]对若干重要的非保守经典和量子系统的变分描述进行了研究,如:黏性力下振动弦、非保守电磁理论、非保守薛定谔方程等.Georgieva和Guenther研究了Herglotz型Noether定理[6,7].Santos等[8,9]将Herglotz变分问题推广到高阶微商情形.近年来,张毅等将Herglotz变分问题引入力学系统[10],建立了非保守系统[11,12]、非完整系统[13]和Birkhoff系统[14,15]的Herglotz变分原理和Noether定理.但是,到目前为止关于Herglotz变分原理的研究还仅限于常质量系统.变质量系统力学研究质量变化的物体的运动与作用在其上的力之间的关系.第一个系统地研究变质量力学的是Meshchersky[16],通过引入质量以不为零的相对速度分离或并入物体时所产生的冲击力,他建立了变质量质点的动力学基本方程.1989年,杨来伍和梅凤翔[17]在他们的专著中系统地介绍了变质量系统的牛顿力学和变质量系统的分析力学.变质量系统在自然界和工程技术领域有大量应用实例[18-20],包括复杂系统,如火箭运动、移动机器人拾取或释放物体等,以及简单系统,如喷水系统或漏气的充气气球的运动等.守恒律是变质量系统力学研究的一个重要方面.Cveticanin利用d’Alembert Lagrange原理构建了变质量系统的Noether守恒律[21].梅凤翔在其著作[1,22]中研究了变质量力学系统的对称性与守恒量.最近,姜文安等[23-25]研究了一类变质量系统的Noether守恒律和Mei守恒律.变质量力学系统的问题可分为两类[26]:一类Copyright ©博看网. All Rights Reserved.第6期蔡铭俣等:变质量力学系统的Herglotz型Lagrange方程与Noether对称性和守恒量是质量变化不改变运动学性质;另一类是质量的变化将引起系统运动学性质的改变.本文研究第一类问题.将Herglotz广义变分原理推广到变质量非保守力学系统,导出变质量系统的Herglotz型La grange方程,研究并证明其Noether定理及其逆定理.1 变质量力学系统的Herglotz型Lagrange方程 假设变质量力学系统由N个质点组成.在时刻t,第i个质点的质量为mi(i=1,2,…,N);在时刻t+dt,由质点分离(或并入)的微粒质量为dmi.设系统所受完整约束中不含质点的质量,质点系的位形由n个广义坐标qs(s=1,2,…,n)确定,并假设mi=mi(t,qs,q·s)(1)变质量力学系统的Herglotz变分问题可表述如下:确定函数qs(t)(t∈[t1,t2]),使得泛函z(t2)取得极值,即z(t2)→extr.,其中z(t)由微分方程z·(t)=L(t,qs(t),q·s(t),z(t),mi(t,qs,q·s))(2)定义,且满足端点条件qs(t)|t=t1=qs1,qs(t)|t=t2=qs2(s=1,2,…,n)(3)和初始条件z(t)|t=t1=z1(4)泛函z(t)也称为Herglotz作用量.令ДДt,ДДqs以及ДДq·s分别表示将质量当作常数时对t,qs以及q·s的偏导数,称为凝固偏导数;符号DDt表示将质量当作常数时对时间的导数,称为凝固导数.对方程(2)取等时变分,有δz·=ДLДqsδqs+ДLДq·sδq·s+ L miδmi+ L zδz(5)其中δmi=mi qsδqs+ mi q·sδq·s(6)由交换关系δz·=ddtδz(7)则方程(5)可以表示为ddtδz=A+ Lzδz(8)其中A=ДLДqsδqs+ L mi mi qsδqs+ДLДq·sδq·s+ L mi mi q·sδq·s(9)方程(8)有解δz(t)exp(-∫tt1Lzdθ)-δz(t1)= ∫tt1Aexp(-∫tt1Lzdθ)dτ(10)考虑到初始条件(4),且z(t2)取得极值,因此有δz(t1)=δz(t2)=0(11)所以有∫t2t1Aexp(-∫tt1Lzdθ)dτ=0(12)将式(9)代入方程(12),并对其中含δq·s的项进行分部积分,得∫t2t1exp-∫tt1L zd()θДLДqs+ L mimiqs{-DDtДLДq·s- L miДLДq·sm·i-ddt L mi mi q·()s+ L zДLДq·s+ L z L mimi q·}sδqsdt=0(13)由于δqs的独立性,根据变分学基本引理,可得exp(-∫tt1 L zdθ)-DDtДLДq·s+ДLДqs(+ L zДLДq·s+ψ)s=0(s=1,2,…,n)(14)其中ψs= L mi mi qs+ L z L mi mi q·s- miДLДq·sm·i- ddt( L mimiq·s)(15)方程(14)称为变质量力学系统用凝固导数表示的Herglotz型Lagrange方程.容易证明下述关系:701Copyright ©博看网. All Rights Reserved.动 力 学 与 控 制 学 报2022年第20卷ddtДLДq·s=DDtДLДq·s+ miДLДq·sm·i(16)将式(16)代入式(14)可得:exp(-∫tt1 L zdθ)-ddtДLДq·s+ДLДqs(+ L zДLДq·s+φ)s=0(s=1,2,…,n)(17)其中φs=L mi mi qs+ L z L mi miq·s-ddt L mi miq·()s(18) 方程(17)称为变质量力学系统用半凝固导数表示的Herglotz型Lagrange方程.容易证明下述关系:ddt L q·s=ddtДLДq·s+ddt L mi miq·()s(19) L qs=ДLДqs+ L mi miqs(20)将式(19)和式(20)代入式(17)可得exp-∫tt1 L zd()θ-ddt L q·s+ L qs+ L z L q·()s= 0(s=1,2,…,n)(21)方程(21)称为变质量力学系统用普通导数表示的Herglotz型Lagrange方程.上述三类变质量系统的Herglotz型Lagrange方程是经典变质量完整力学系统广义坐标表示的Lagrange方程[17]的推广.文献[17]指出:当质点质量依赖于广义坐标、广义速度和时间时,应用凝固导数表示的方程最简便,应用普通导数表示的方程最繁杂.2 Herglotz型Noether对称性引入时间t和广义坐标qs的r参数有限变换群Gr的无限小变换t-=t+Δt,q-s(t)=qs(t)+Δqs(s=1,2,…,n)(22)或其展开式t-=t+εαξα0(t,qs,q·s,mi,z),q-s(t)=qs(t)+εαξαs(t,qj,q·j,mi,z),(s,j=1,2,…,n;α=1,2,…,r;i=1,2,…,N)(23)其中,εα为无限小的参数,ξα0和ξαs称为该变换的生成元.在变换式(22)的作用下,Herglotz作用量z变成z-(t-)=z(t)+Δz(t)(24)全变分Δz是Herglotz作用量z在无限小变换中相对于εα的主线性部分的前后之差.对任意函数F(t),有如下关系ΔF=δF+F·Δt(25)对于完整约束系统,有交换关系ddtδF=δddtF=δF·(26)因此得到ΔF·=ddtΔF-F·ddtΔt(27)对式(2)进行非等时变分:Δz·=ДLДtΔt+ДLДqsΔqs+ДLДq·sΔq·s+ L zΔz+ L miΔmi(28)由于Δmi=mi tΔt+ mi qsΔqs+ mi q·sΔq·s(29)将式(29)代入式(28),并利用关系式(27),得ddtΔz=ДLДtΔt+ДLДqsΔqs+ДLДq·sΔq·s+ L zΔz+ L mi mi tΔt+ L mi mi qsΔqs+ L mi mi q·sΔq·s+ LddtΔt(30)方程(30)的解为Δz(t)exp(-∫tt1Lzdθ)-Δz(t1)= ∫tt1exp(-∫τt1L zdθ)(ДLДtΔ{t+ ДLДqsΔqs+ДLДq·sΔq·s+ L mi mi tΔt+ L mi mi qsΔqs+ L mi mi q·sΔq·s+LddtΔt})dτ(31)显然Δz(t1)=0,所以方程(31)还可以写为Δz(t)exp(-∫tt1Lzdθ)=∫tt1ddτLΔt+(ДLДq·s+ L mi miq·s)(Δqs[-q·sΔt{]{)801Copyright ©博看网. All Rights Reserved.第6期蔡铭俣等:变质量力学系统的Herglotz型Lagrange方程与Noether对称性和守恒量 exp(-∫τt L zdθ})+ exp(-∫tt1L zdθ)(-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)(Δqs-q·sΔt})dτ=0(32)由于Δt=εαξα0,Δqs=εαξαs(33)将式(33)代入式(31)可得Δz(t)exp(-∫tt1L zdθ)= ∫tt1exp(-∫τt1L zdθ)(ДLДτ+ L mimiτ)ξα0[{+ (ДLДqs+ L mi mi qs)ξαs+(ДLДq·s+ L mi mi q·s)ξ·αs+ (L-ДLДq·sq·s- L mi miq·sq·s)ξ·α]}0εαdτ(34)将式(33)代入式(32)可得Δz(t)exp(-∫tt1Lzdθ)= ∫tt1ddτLξα0+(ДLДq·s+ L mi mi q·s)ξ-α[]{{s exp(-∫τt1 Lzdθ})+ exp(-∫tt1 L zdθ)(-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)ξ-α}sεαdτ=0(35)其中ξ-αs=ξαs-q·sξα0(36)定义1 对于变质量力学系统(14),如果对于无限小变换(22)的每一个变换,等式Δz(t2)=0(37)成立,则称变换是该系统的Noether对称变换.根据定义1以及方程(34),可以得到如下判据.判据1 在变质量力学系统(14)中,对于无限小变换(23),假设生成元ξα0,ξαs符合下列条件(ДLДt+ L mi mi t)ξα0+(ДLДqs+ L mi mi qs)ξαs+ (ДLДq·s+ L mi mi q·s)ξ·αs+(L-ДLДq·sq·s- L mi miq·sq·s)ξ·α0=0(α=1,2,…,r)(38)则称变换是该系统的Noether对称变换.当r=1时,式(38)给出(ДLДt+ L mi mi t)ξ0+(ДLДqs+ L mi mi qs)ξs+ (ДLДq·s+ L mi mi q·s)ξ·s+(L-ДLДq·sq·s- L mi miq·sq·s)ξ·0=0(39)式(39)为变质量力学系统(14)的Noether等式.3 Herglotz型Noether定理定理1 对于变质量力学系统(14),若给定的有限变换群Gr的无限小变换(23)是Herglotz型Noether对称变换,则系统存在r个线性独立的守恒量IαN=Lξα0+(ДLДq·s+ L mi mi q·s)ξ-α[]sexp (-∫τt1Lzdθ)=cα(40)证明 由于无限小变换(23)是变质量力学系统(14)的Herglotz型Noether对称变换,根据定义1,有Δz(t2)=0.利用公式(35),得到∫t2t1ddτLξα0+(ДLДq·s+ L mi mi q·s)ξ-α[]s{{exp (-∫τt1L zdθ})+exp(-∫tt1Lzdθ) (-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)ξ-α}sεαdτ=0(41)由于区间[t1,t2]是任意的,εα是相互独立的,根据变分法的基本引理,得到ddtLξα0+(ДLДq·s+ L mi mi q·s)ξ-α[]s{exp (-∫tt1L zdθ})+exp(-∫tt1L zdθ) (-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)ξ-αs=0(42)对于变质量力学系统有Herglotz型Lagrange方程(14),因此得ddtLξα0+(ДLДq·s+ L mi mi q·s)ξ-α[]s{exp901Copyright ©博看网. All Rights Reserved.动 力 学 与 控 制 学 报2022年第20卷 (-∫τtLzdθ})=0(43)积分便可得到守恒量(40).4 Herglotz型Noether逆定理已知变质量力学系统(14)有r个线性独立的守恒量Iα=Iα(t,qs,q·s,mi,z)=cα(α=1,2,…,r)(44)求满足Herglotz型Noether对称性的生成函数ξα0和ξαs.将式(14)乘ξ-αs,并对s求和,得到exp(-∫tt1L zdθ)(-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)ξ-αs=0(45)将式(44)对t求导数后与式(45)相加,展开得ДIαДt+ДIαДqsq·s+ДIαДq·sq··s+ Iα mim·s+ IαzL+ exp(-∫tt1 L zdθ)(-DDtДLДq·s+ДLДqs+ L zДLДq·s+ψs)ξ-αs=0(46)令含q··k项的系数为0,可得ДIαДq·s+ Iαmi mi q·s-ξ-αkexp(-∫tt1Lzdθ) Д2LДq·sДq·k+ miДLДq·k mi q·s+ q·s( L mi miq·k[])= 0(s=1,2,…n;α=1,2,…,r)(47)再令式(44)等于式(40),可得ξα0=1Lexp(∫tt1 L zdθ)I[α- (ДLДq·s+ L mi mi q·s)ξ-α]s(α=1,2,…,r)(48)由式(47)和式(48)可以找到无限小生成函数,它们对应变质量力学系统(14)的Noether对称变换.于是有:定理2 对于变质量力学系统(14),如果已知r个线性独立的守恒量(44),那么生成函数由式(47)和式(48)确定的无限小变换相应于系统的Herglotz型Noether对称性.定理2称为变质量力学系统的Herglotz型Noether逆定理.5 算例例1 假设一变质量质点在铅垂平面内运动,其质量为m(t)=m0exp(-αt)(m0=const.;α=const.,α>0)(49)设质点的运动受黏性阻尼的作用,阻尼系数为c=const.,微粒分离的绝对速度为零.试研究该系统的Noether对称性和守恒量.选取广义坐标q1=x,q2=y,则系统的Her glotz型Lagrange函数为L=12m(t)(q·21+q·22)-m(t)gq2- [cm(t)+α]z(50)其中,泛函z满足z·=12m(t)(q·21+q·22)-m(t)gq2- [cm(t)+α]z(51)根据式(14)给出该系统的运动方程为exp[λ(t)][-m(t)q··1-cq·1]=0,exp[λ(t)][-m(t)q··2-m(t)g-cq·2]=0(52)其中,λ(t)=c(eαt-eαt1)αm0+α(t-t1).Noether等式(39)给出[-12αm(t)(q·21+q·22)+αm(t)gq2- αcm(t)z]ξ0-m(t)gξ2+m(t)q·1ξ·1+ m(t)q·2ξ·2-12m(t)(q·21+q·22)+m(t)gq2{+ [cm(t)+α]}zξ·0=0(53)方程(53)有解ξ0=0,ξ1=1,ξ2=0(54)ξ0=0,ξ1=-cαm(t)-lnq·1,ξ2=0(55)由定理1,得到IN=exp[λ(t)]m(t)q·1=const.(56)IN=exp[λ(t)]m(t)q·1[-cαm(t)-lnq·1]=011Copyright ©博看网. All Rights Reserved.第6期蔡铭俣等:变质量力学系统的Herglotz型Lagrange方程与Noether对称性和守恒量 const.(57)式(56)和式(57)分别为生成函数(54)、函数(55)相应的Noether守恒量.根据Herglotz型Noether逆定理,由已知的守恒量求Noether对称性.假设系统有守恒量(56),则由式(47)和式(48),可以得到exp[λ(t)]m(t)(1-ξ-1)=0,-exp[λ(t)]m(t)ξ-2=0(58)以及ξ0=mq·1-mq·1ξ-1-mq·2ξ-2L(59)由方程(58)和方程(59)解得ξ0=0,ξ1=1,ξ2=0(60)例2 球形的雨滴在大气中下落,沿途受到水汽的充实.设雨滴的初始半径为r0,由于凝聚,雨滴的质量以正比于其表面积的速率增加[22],比例系数为α.假设雨滴下落过程中受到与速度成正比的阻力作用,阻力系数为μ.试研究该系统的Noether对称性与守恒量.因为dmdt=4πr2α,r=r0+αt(61)故有m(t)=43πr3(62)系统的Herglotz型Lagrange函数为L=12m(t)(q·21+q·22+q·23)-mgq3-(μm-3αr)z(63)式中的Herglotz作用量z(t)满足方程z·=12m(t)(q·21+q·22+q·23)-mgq3-(μm-3αr)z(64)根据式(14),该系统的运动微分方程为exp[λ(t)](-mq··1-μq·1)=0,exp[λ(t)](-mq··2-μq·2)=0,exp[λ(t)](-mq··3-mg-μq·3)=0(65)其中λ(t)=3ln(r0+αt1r)+3μ8πα(r0+αt1)2- μr2αm(66)Noether等式(39)给出2πr2α(q·21+q·22+q·23)-4πr2αgq3-3αμmr[]zξ0- m(t)gξ3+m(t)q·1ξ·1+m(t)q·2ξ·2+ m(t)q·3ξ·3-12m(t)(q·21+q·22+q·23[)+ m(t)gq3+(μm-3αr)]zξ·0=0(67)方程(67)有解ξ0=0,ξ1=1,ξ2=1,ξ3=0(68)ξ0=0,ξ1=3μ8παr2-lnq·1,ξ2=1,ξ3=0(69)由定理1,得到IN=exp[λ(t)][m(t)q·1+m(t)q·2]=const.(70)IN=exp[λ(t)][mq·2+mq·1(3μ8παr2- lnq·1)]=const.(71)式(70)、式(71)分别为生成函数(68)、函数(69)所导致的Noether守恒量.根据Herglotz型Noether逆定理,由已知守恒量求Noether对称性.假设系统有守恒量(70),则由式(47)和式(48),可以得到exp[λ(t)]m(t)(1-ξ-1)=0,exp[λ(t)]m(t)(1-ξ-2)=0,-exp[λ(t)]m(t)ξ-3=0(72)以及ξ0=m(t)(q·1+q·2-q·1ξ-1-q·2ξ-2-q·3ξ-3)L(73)由方程(72)、方程(73)解得ξ0=0,ξ1=1,ξ2=1,ξ3=0(74)6 结论变质量力学系统研究的是物体质量在不断变化的状态下,物体运动状态与作用在其上力的关系.由于变质量系统在自然界和工程领域普遍存在,因此变质量力学的研究具有重要意义.本文研究了变质量力学系统的Herglotz型Lagrange方程与Noether对称性及其守恒量,主要工作如下:提出了变质量力学系统中的Herglotz型广义变分原理,并基于该原理建立了分别用凝固导数、半凝固导数、普通导数表示的变质量力学系统的Herglotz型111Copyright ©博看网. All Rights Reserved.动 力 学 与 控 制 学 报2022年第20卷Lagrange方程(14)、式(17)和式(21);提出了变质量力学系统Herglotz型Noether对称性的定义及其判据方程(39);建立并证明了变质量力学系统Herglotz型Noether定理(定理1)及其逆定理(定理2).参 考 文 献1梅凤翔.分析力学(下卷).北京:北京理工大学出版社,2013(MeiFX.Analyticalmechanics(VolumeII).Beijing:BeijingInstituteofTechnologyPress,2013(inChinese))2HerglotzG.GesammelteSchriften.G ttingen:Vanden hoeck&Ruprecht,19793DonchevV.Variationalsymmetries,conservedquantitiesandidentitiesforseveralequationsofmathematicalphys ics.JournalofMathematicalPhysics,2014,55(3):0329014LazoMJ,PaivaJ,AmaralJTS,etal.Anactionprin cipleforaction dependentLagrangians:Towardanactionprincipletonon conservativesystems.JournalofMathe maticalPhysics,2018,59(3):0329025LazoMJ,PaivaJ,FredericoGSF.Noethertheoremforaction dependentLagrangianfunctions:conservationlawsfornon conservativesystems.NonlinearDynamics,2019,97(2):1125~11366GeorgievaB,GuentherR.FirstNoether typetheoremforthegeneralizedvariationalprincipleofHerglotz.Topolog icalMethodsinNonlinearAnalysis,2002,20(2):261~2737GeorgievaB.GuentherR.SecondNoether typetheoremforthegeneralizedvariationalprincipleofHerglotz.TopolMethodsNonlinearAnal,2005,26(2):307~3148SantosSPS,MartinsN,TorresDFM.Higher ordervariationalproblemsofHerglotztypewithtimedelay.PureandAppliedFunctionalAnalysis,2016,1(2):291~3079SantosSPS,MartinsN,TorresDFM.Noethercur rentsforhigher ordervariationalproblemsofHerglotztypewithtimedelay.DiscreteandContinuousDynamicalSystems,SeriesS,2018,11(1):91~10210 张毅.相空间中非保守系统Herglotz广义变分原理及其Noether定理.力学学报,2016,48(6):1382~1389(ZhangY.GeneralizedvariationalprincipleofHer glotztypefornonconservativesysteminphasespaceandNoether’stheorem.ChineseJournalofTheoreticalandAppliedMechanics,2016,48(6):1382~1389(inChi nese))11 徐鑫鑫,张毅.分数阶非保守Lagrange系统的一类新型绝热不变量.物理学报,2020,69(22):220401(XuXX,ZhangY.Anewtypeofadiabaticinvariantforfractionalordernon conservativeLagrangiansystems.ActaPhysicaSinica,2020,69(22):220401(inChi nese))12 ZhangY.Herglotz'svariationalproblemfornon conservativesystemwithdelayedargumentsunderLagrangianframeworkanditsNoether’stheorem.Symmetry,2020,12(5):84513 ZhangY,TianX.ConservationlawsofnonholonomicnonconservativesystembasedonHerglotzvariationalproblems.PhysicsLettersA,2019,383:691~69614 ZhangY.VariationalproblemofHerglotztypeforBirkhoffiansystemanditsNoether'stheorem.ActaMechanica,2017,228(4):1481~149215 ZhangY.Noether’stheoremforatime delayedBirkhoffiansystemofHerglotztype.InternationalJournalofNon LinearMechanics,2018,101:36~4316 MeshcherskiiIV.Equationsofmotionofavariablemasspointinthegeneralcase.St.PetersburgPolytechnicUni versityNews,1904,1:77~118(inRussian)17 杨来伍,梅凤翔.变质量系统力学.北京:北京理工大学出版社,1989(YangLW,MeiFX.Variablemasssystemmechanics.Beijing:BeijingInstituteofTechnolo gyPress,1989(inChinese))18 CveticaninL.Areviewondynamicsofmassvariablesystems.JournaloftheSerbianSocietyforComputationalMechanics,2012,6(1):56~7319 HurtadoJE.Analyticaldynamicsofvariable masssystems.JournalofGuidance,Control,andDynamics,2018,41(3):701~70920 JiangWA,HanXJ,ChenLQ,etal.Probabilisticsolutionsofavariable masssystemunderrandomexcitations.ActaMechanica,2020,231(7):2815~282621 CveticaninL.Conservationlawsinsystemswithvariablemass.JournalofAppliedMechanics,1993,60(4):954~95822 梅凤翔.约束力学系统的对称性与守恒量.北京:北京理工大学出版社,2004(MeiFX.Symmetryandcon servedquantitiesofconstrainedmechanicalsystems.Bei jing:BeijingInstituteofTechnologyPress,2004(inChi211Copyright ©博看网. All Rights Reserved.第6期蔡铭俣等:变质量力学系统的Herglotz型Lagrange方程与Noether对称性和守恒量nese))23 JiangWA,LiuK,ZhaoGL,etal.Noethersymmetricalperturbationandadiabaticinvariantsfordisturbednon materialvolumes.ActaMechanica,2018,229(12):4771~477824 JiangWA,LiuK,XiaZW,etal.Meisymmetryandnewconservedquantitiesfornon materialvolumes.ActaMechanica,2018,229(9):3781~378625 LiuK,GaoY,JiangWA,etal.Conformalinvarianceandconservedquantitiesofnonmaterialvolumes.ReportsonMathematicalPhysics,2019,84(3):365~37326 梅凤翔.高等分析力学.北京:北京理工大学出版社,1991(MeiFX.Advancedanalyticalmechanics.Beijing:BeijingInstituteofTechnologyPress,1991(inChi nese))HERGLOTZTYPELAGRANGEEQUATIONSANDNOETHERSYMMETRYANDCONSERVEDQUANTITYFORMECHANICALSYSTEMSWITHVARIABLEMASSCaiMingyu1 ZhangYi2(1.SchoolofMathematicalSciences,SuzhouUniversityofScienceandTechnology,Suzhou 215009,China)(2.CollegeofCivilEngineering,SuzhouUniversityofScienceandTechnology,Suzhou 215011,China)Abstract Herglotz’svariationalprincipleprovidesavariationaldescriptionofnon conservativedissipationprob lems,andvariablemassmechanicsiswidelyusedinnatureandengineering.Therefore,itprovidesanewwaytostudyvariablemassmechanicsbyapplyingHerglotz’svariationalprincipletoLagrangeequationsandconserva tionlawsofvariablemassmechanicssystems.Inthispaper,theHerglotztypegeneralizedvariationalprincipleofmechanicalsystemswithvariablemassisestablishedandtheHerglotztypeLagrangeequationsofmechanicalsys temswithvariablemassarederived.HerglotztypeNoethersymmetryofvariablemassmechanicalsystemsisde fined,andtheHerglotzNoethertheoremanditsinversetheoremareestablishedandproved.Attheendofthispaper,twoconcreteexamplesofnon conservativesystemswithvariablemassaregiventoillustratetheapplicationoftheresults.Keywords variablemassmechanicalsystem,Herglotztypegeneralizedvariationalprinciple,Noethertheorem,conservedquantityReceived4January2022,revised26March2022.TheprojectsupportedbytheNationalNaturalScienceFoundationofChina(11972241,11572212),andtheNaturalScienceFoundationofJiangsuProvinceofChina(BK20191454) CorrespondingauthorE mail:zhy@mail.usts.edu.cn311Copyright ©博看网. All Rights Reserved.。
贝塞尔函数和修正贝塞尔函数

贝塞尔函数和修正贝塞尔函数贝塞尔函数和修正贝塞尔函数,这俩东西听上去就挺复杂的,对吧?它们就像是数学界的小明星,虽然不总是出现在聚光灯下,但一旦登场,真是让人刮目相看。
想象一下,贝塞尔函数就像那位在聚会上总是能引起关注的人,大家都想和他聊聊天。
它们主要用在波动、振动和热传导等领域,感觉有点像那些能在复杂情况下游刃有余的超人,真的是很厉害的存在。
要知道,贝塞尔函数的定义其实是跟圆形、柱面波动有关,听上去是不是有点高大上?不过别担心,我们可以把它简单化想象成,圆圈里发生的一些有趣现象。
比如,你在水面上扔一颗小石子,水面就会荡起涟漪,贝塞尔函数就像是在描述这些涟漪的方式,越是靠近石子的地方,涟漪越明显,越远则越淡。
这就是它的魅力,抓住了变化的本质,又能让我们以一种直观的方式理解。
接着说到修正贝塞尔函数,它就是贝塞尔函数的好朋友,不过有点不同。
想象一下,贝塞尔函数在阳光下舞动,修正贝塞尔函数则是在阴影里优雅地旋转。
修正贝塞尔函数通常出现在更复杂的场合,比如说热传导和电磁波问题。
它们有点像双胞胎,虽然外表相似,但各自都有自己的特点。
修正贝塞尔函数通常用在超出某种范围的情况下,比如高温或者高频的时候,这时候,贝塞尔函数就不太够用了。
再聊聊它们的应用,这可是个大话题。
想想看,贝塞尔函数常常用在工程和物理的方方面面。
无论是振动分析、信号处理,还是图像处理,贝塞尔函数总能找到自己的舞台,像个万能的工具。
而修正贝塞尔函数在控制热流和电磁场中发挥着至关重要的作用。
说到这里,我就不禁感慨,这些数学函数真是日常生活中看不见的英雄啊,默默地支持着我们的科技发展。
要真正理解这些函数,还得下点功夫。
贝塞尔函数和修正贝塞尔函数有很多种不同的形式,各种复杂的方程式可能会让人感到晕头转向。
但是,咱们可以把它们当作一种“秘密武器”,在不同情况下灵活运用。
比如,工程师在设计桥梁或者航天器时,就会用到这些函数,确保每一个细节都尽善尽美。
这就像做一道菜,调料的搭配绝对是关键,缺了什么味道就全糟了。
单位阶跃函数的z变换matlab

单位阶跃函数的z变换matlab{1t>=0u(t)={0t<0其中,u(t)表示单位阶跃函数,t表示时间。
在MATLAB中,我们可以使用z变换来对单位阶跃函数进行分析和处理。
z变换是一种重要的信号处理工具,它将离散时间域信号转换为复数域频率域信号。
首先,我们需要定义单位阶跃函数的离散表达式。
由于单位阶跃函数是连续函数,我们需要将其离散化,即在一定的时间间隔内对其进行采样。
在MATLAB中,我们可以使用以下代码定义单位阶跃函数的离散表达式:t=-10:0.01:10;%定义时间范围和步长u=t>=0;%根据函数定义生成离散值plot(t, u); % 绘制单位阶跃函数图像title('Unit Step Function'); % 设置图像标题```该代码首先定义了时间范围t,然后使用步长0.01对时间范围进行离散化。
接下来,使用比较符号>=对时间序列t进行判断,得到单位阶跃函数u。
接下来,我们可以对单位阶跃函数进行 z 变换。
在 MATLAB 中,可以使用 `ztrans` 函数进行 z 变换计算。
使用以下代码进行单位阶跃函数的z变换:syms z; % 定义符号变量 zU = ztrans(u, t, z); % 进行 z 变换计算pretty(U); % 输出美观的数学表达式```在上述代码中,首先使用 `syms` 函数定义符号变量 z,然后使用`ztrans` 函数对离散序列 u 进行 z 变换计算。
其中,t 表示时间序列,z 表示 z 变换域。
最后,使用 `pretty` 函数可输出美观的数学表达式。
以上就是使用MATLAB进行单位阶跃函数的z变换的方法。
需要注意的是,上述代码仅仅是一个示例,具体的实现方式可能会因具体的场景和要求而有所变化。
如果你有具体的应用场景和要求,可以提供更多细节,我可以提供更加详细和个性化的解答。
matlab极坐标转xyz坐标

标题:探究matlab中极坐标和xyz坐标的转换方法在matlab中,极坐标和xyz坐标的转换是一个常见的需求。
本文将深入探讨这一主题,包括极坐标和xyz坐标的定义、转换方法及实际应用。
希望通过本文的阐述,读者能够全面了解这一主题,提升对matlab编程的技能和应用能力。
一、极坐标和xyz坐标的定义我们来了解一下极坐标和xyz坐标的基本定义。
在笛卡尔坐标系中,xyz坐标是最常见的坐标表示方法,其中x、y、z分别代表空间中的三个轴。
而极坐标则是通过极径和极角来描述平面上的点,其中极径代表点到原点的距离,极角则表示点与x轴正向的夹角。
在matlab中,极坐标通常以[r, theta]的形式表示,其中r为极径,theta为极角。
而xyz坐标则以[x, y, z]的形式表示,分别表示点在三个轴上的坐标值。
二、极坐标转换为xyz坐标接下来,我们将深入探讨如何将极坐标转换为xyz坐标。
在matlab中,可以利用sind()和cosd()函数将极角转换为弧度,并通过简单的三角函数关系得到xyz坐标。
具体而言,可以通过以下公式将极坐标转换为xyz坐标:\[ x = r * cosd(theta) \\y = r * sind(theta) \\z = 0 \]这里,我们需要注意的是,由于极坐标描述的是平面上的点,因此z坐标通常为0。
当需要将极坐标转换为三维空间中的点时,可以将z坐标设为固定值或者根据实际情况进行调整。
三、实际应用与个人观点在实际编程中,极坐标和xyz坐标的转换常常用于图形绘制、运动控制等领域。
通过灵活运用极坐标和xyz坐标的转换方法,可以实现复杂的几何图形绘制和运动路径规划。
个人而言,我认为掌握极坐标和xyz坐标的转换方法对于matlab编程非常重要。
在实际应用中,能够灵活运用这些方法可以提高编程效率,同时也能够更好地理解和把握空间几何关系。
我在编程过程中始终注重学习和实践极坐标和xyz坐标的转换,以提升自己的编程水平和应用能力。
matlabhilbert函数

matlabhilbert函数关于Matlab中的hilbert函数概述:Matlab中的hilbert函数用于生成Hilbert变换的实部和虚部。
Hilbert 变换是一种信号处理技术,可以将一个实函数转换为复函数,常用于信号分析、调制和解调等领域。
本文将介绍hilbert函数的基本用法和详细步骤,帮助读者了解和应用该函数。
1. hilbert函数的基本语法hilbert函数的基本语法如下:y = hilbert(x)其中,x为输入实向量,y为输出复向量。
hilbert函数将实部存储在y的实部,虚部存储在y的虚部。
2. hilbert函数的使用示例为了更好地理解hilbert函数的使用方法,下面将通过一个简单的示例来演示它的功能。
matlab生成一个输入实向量x = [1, 2, 3, 4, 5];使用hilbert函数进行Hilbert变换y = hilbert(x);输出结果disp(y);运行上述代码,可以得到以下输出结果:1.0000 + 0.0000i2.0000 + 1.4142i3.0000 + 0.0000i4.0000 - 1.4142i5.0000 + 0.0000i可以看到,hilbert函数将输入实向量x转换为复向量y,实现了Hilbert 变换的功能。
3. hilbert函数的实现原理hilbert函数的实现原理基于快速傅里叶变换(FFT)。
它将输入信号的FFT 结果的负频率部分置零,然后将其进行逆FFT得到Hilbert变换后的复向量。
该函数的内部实现细节对于大多数用户来说并不重要,但了解其基本原理可以帮助我们更好地理解函数的功能和性能。
4. hilbert函数的参数详解hilbert函数只有一个参数,即输入实向量x。
该向量可以是行向量或列向量,但不能是多维矩阵。
注意,x的长度应为2的幂。
如果长度不是2的幂,则hilbert函数会自动对其进行补零处理。
5. hilbert函数的使用场景hilbert函数可以广泛应用于信号处理和通信系统中。
地震学期末复习整理

复习提纲1、全球地震活动在空间上有什么特点?如何利用现在对地球结构的了解解释这种特点? 呈带状分布。
无论是震源几何位置(地理的、深度的)、震源强度的空间分布、震源机制的空间分布均与板块学说中的大断层十分一致。
断层说是板块学说的组成部分,板块学说中的断层理论很好地解释了地震活动。
板块学说的主要论点:①软流层(热、粘)上驮着岩石层(冷、脆)一起移动;②海岭~张裂、发散;③海沟~腑冲、消没④转换断层~剪切、滑移;⑤各板块绕轴旋转。
2、根据古登堡-里克特的震级频度公式bM a N -=log ,估计某地区所能发生的最大地震震级。
(假定a=6.7,b=0.9)3、评定地震烈度的主要标志有哪些?1)自然景观的变化 2)建筑物的破坏 3)人和动物的反应4、影响地震烈度的主要因素地震本身释放的能量、观测点与震源点之间的距离、地质条件、建筑物的类型、调查人本身的因素、当地人对地震的经验等5、地震烈度和震级的区别?地震烈度:按一定的宏观(野外场地调查)标准,表示地震对地面影响和破坏程度的一种量度,称之为地震烈度。
通常用I 表示。
震级:按一定的微观标准(仪器观测),表示地震波能量大小的量度,常用字母M 表示。
震级和烈度都是衡量地震强度的,根据统计结果,震级M 和震中烈度I0之间有下列关系: 0321I M +=6、全球地震带的分布特征,三个主要地震带?全球的地震带分布:(1)环太平洋地震带位于太平洋边缘地区,即海洋构造和大陆构造的过渡地区。
全球80%的浅震,许多中源地震和差不多的深源地震都发生在这一带,包括大部分灾难性地震。
(2)欧亚地震带沿欧亚大陆南部展布,欧亚地震带内也常发生破坏性地震及少数深源地震,它是最宽的地震带。
我国的大部分地区处于此地震带内。
(3)海岭地震带几乎包括全部海岭构造地区,沿洋中脊展布,又称为洋中脊地震带,它是最长的地震带。
7. 哪个地震带是全球地震活动最强烈的地震带,全球 80%的浅源地震、90%的深源地震均集中在该带上,这是一条对人类危害最大的地震带。
06-谱分析

谱密度与ACVF
定理:
如果平稳序列{X t}的自协方差函数{ k }绝对可和:
| k | .则{X t}有谱密度函数
f
()
ห้องสมุดไป่ตู้
1
2
k eik .
k
由于谱密度函数是实值函数,所以上式还可以写成:
f
()
1
2
k
k
c os (k )
1
2
[ 0
2 k
k 1
c os (k )]
平稳AR(p)模型
定义:设平稳序列{X t}有自协方差{ k }, (1)如果有[ , ]上的单调不减右连续的函数F (),
使得 k
eik dF (),
F ( ) 0,
k ,
就称F ()是{X t}或{ k }的谱分布函数,简称谱函数。
(2)如果有[ , ]上的非负函数f (),
使得 k
eik f ()d,
(1)如果{X t}和{Yt}分别有谱函数FX ()和FY (), 则平稳序列{Zt}有谱函数FZ () FX () FY (). (2)如果{X t}和{Yt}分别有谱密度f X ()和fY (), 则平稳序列{Zt}有谱函数fZ () f X () fY ().
注: 定义:对平稳序列{X t}和{Yt}, (1)如果对任何s,t ,E( X tYs ) 0,则称{X t}和{Yt}是正交的。 (2)如果对任何s,t ,Cov( X t ,Ys ) 0,则称{X t}和{Yt}是不相关的。 对于零均值的平稳序列,正交性和不相关性等价。
考虑平稳AR(p)模型: (B) X t t , t .
改写成如下形式:
X t 1(B)t jt j , j0
希尔伯特黄变换

(5)
图为分解得到的第一个IMF分量c1(t),图中可以 看出极值点数与零点数目满足IMF的要求。
第一个IMF,c1
(4)将c1(t)从s(t)中分离出来,即得到一个去 掉高频分量的差值信号r1(t),即有:
r1(t)=s(t)-c1(t)
(6)
将r1(t)作为原始数据,重复步骤(1)(2)(3),得到第二个IMF分量c2(t) ,重复n次 ,
Yt1P X td
(1)
这里P表示柯西主值,变换对所有 Lp 类成立。根据
这一定义,当X(t)与Y(t)形成一个复共轭时,就可得
到一个解析信号Z(t):Z(t)=X(t)+iY(t)=a(t)ei t (2)
atX 2tY2t,tarc Y X ttta n (3)
这样,Hilben变换提供了一个独特的定义幅度与相位
2.1本征模态函数(IMF)的概念
在物理上,如果瞬时频率有意义,那么函数必须是对 称的,局部均值为零,并且具有相同的过零点和极值 点数目。在此基础上,NordneE.Huang等人提出了本征 模函数(Intrinsic Mode Function,简称IMF)的概念。本 征模函数任意一点的瞬时频率都是有意义的。Hunag等 人认为任何信号都是由若干本征模函数组成,任何时 候,一个信号都可以包含若干个本征模函数,如果本 征模函数之间相互重叠,便形成复合信号。EMD分解 的目的就是为了获取本征模函数,然后再对各本征模 函数进行希尔伯特变换,得到希尔伯特谱。
2.2时间特征尺度
• 现在有三种测量时间尺度的方法:相邻两过零点间隔 的时间尺度,相邻两极值点间隔的时间尺度,相邻两 曲率极值点间隔的时间尺度。三种情况中,时间间隔 都是用来局部测量事物时间变化的。局部极值时间间 隔和曲率时间间隔尺度代表了整个波形,无论波形是 否穿过零线。Huang等人分析认为,时间尺度代表了 信号的局部震荡尺度,并且仅表示一种震荡模式。这 种震荡从一个极值点到另一个相反的极值点,因此时 间尺度是震荡本身所隐含的尺度,称为特征时间尺度。 EMD方法使用的时间尺度是极值点间隔,它当然提供 了一个很好的对时间尺度测量的方法。所谓的局部是 特征尺度是指信号重量邻近极大值点或者极小值点的 时间间隔。HHT分析方法是通过对信号本身的局部特 征进行分析,从局部特征时间尺度入手,获得不同时 间尺度特征的有限个IMF分量。
层析和Herglotz-Wiechert反演公式

层析和Herglotz-Wiechert反演公式RobertL.Nowack;王凯【期刊名称】《地球物理学进展》【年(卷),期】1990(0)3【摘要】本文将线性层析与Herglotz-Wiechert反演公式进行了比较.二维和三维速度结构的层析反演使用了沿射线的线积分,而且可以以Radon交换的形式写出.对球对称介质,Radon变换可简化为Abel交换.因而对于直的射线路径,走时的Abel交换正是一维球对称介质的层析算法.Herglotz-Wiechert,公式应用地震走时资料反演一维地球结构,且通过Abel交换用精确的射线轨进推导.这是有历史意义的,因为它意味若特定的类似于层析的一种方法从本世纪初就应用在地反学中了(Her目心,1907,,八“h口t,1910).用数值例子比较了He叼otz一Wiechert算法和沿宜射线的线性层析.由Her川侧tZ刃犷沮忱h.时算法于特定条件下(无低速层)可应用于非直射线路径,它与层析的联系在评价推广到布曲射线中的层析结果的非唯一性方面非常有用.【总页数】1页(P64-64)【关键词】球对称介质;反演公式;Radon;射线路径;线积分;地震走时;三维速度;地球结构;线轨;低速层【作者】RobertL.Nowack;王凯【作者单位】【正文语种】中文【中图分类】P3【相关文献】1.基于 GPS 层析反演和斜向返回探测反演的电离层二维电子密度重构 [J], 周晨;雷勇;赵正予;张援农2.迭代反投影反演与不分块广义反演的比较:衰减层析成象的研究 [J], Phyl.,HL;梁慧云3.用直接反演公式为精确反演提供初始模型的试验 [J], 阮百尧;朱德兵4.隧道反射波层析成像正反演模拟与TRT反演的对比分析 [J], 彭炎; 方慧; 吕琴音5.全波形反演与断控层析反演联合速度建模——以南海东部A油田为例 [J], 李黎;沈水荣;吴意明;张永江;王要森;董政;刘振;刘南因版权原因,仅展示原文概要,查看原文内容请购买。
阶跃函数的z变换步骤

阶跃函数的z变换步骤引言:阶跃函数是一种常见的信号函数,它在某个时刻突然从0跃升到1,代表了一个信号的启动或触发。
而z变换是一种将离散时间域信号转换为复频率域信号的数学工具。
本文将介绍阶跃函数的z变换步骤,以帮助读者更好地理解和应用这两个概念。
一、阶跃函数的定义和特性阶跃函数常表示为u(t),其中t为时间变量。
在t=0时刻,阶跃函数从0跃升到1,即u(0)=1。
在t<0时刻,阶跃函数为0,即u(t<0)=0。
阶跃函数的图像呈现出一种突变的特点。
二、z变换的定义和基本性质z变换是一种将离散时间序列转换为复频率域序列的方法。
z变换的定义为X(z) = ∑(n=-∞ to ∞) x(n)z^(-n),其中x(n)为离散时间序列,z为复变量。
z变换具有线性性质和时移性质等基本性质。
三、阶跃函数的z变换步骤1. 首先,我们需要将阶跃函数表示为离散时间序列。
对于阶跃函数u(t),我们可以将其表示为u(nT),其中T为采样周期,n为整数。
2. 接下来,我们将阶跃函数的离散时间序列代入z变换的定义中,得到X(z) = ∑(n=-∞ to ∞) u(nT)z^(-n)。
3. 根据阶跃函数的定义,我们可以得到∑(n=-∞ to ∞)u(nT)z^(-n) = ∑(n=0 to ∞) z^(-n)。
4. 对于∑(n=0 to ∞) z^(-n),我们可以使用等比数列求和的公式进行化简,得到X(z) = 1/(1-z^(-1))。
5. 最后,我们可以将X(z)进行进一步的化简,得到X(z) = z/(z-1)。
四、阶跃函数的z变换结果根据上述步骤,我们得到了阶跃函数的z变换结果X(z) = z/(z-1)。
这个结果可以帮助我们在复频率域中分析和处理阶跃函数。
结论:本文介绍了阶跃函数的z变换步骤。
首先,我们需要将阶跃函数表示为离散时间序列,然后将其代入z变换的定义中进行求解。
最后,我们得到了阶跃函数的z变换结果X(z) = z/(z-1)。
补充二、希尔伯特变换及其应用
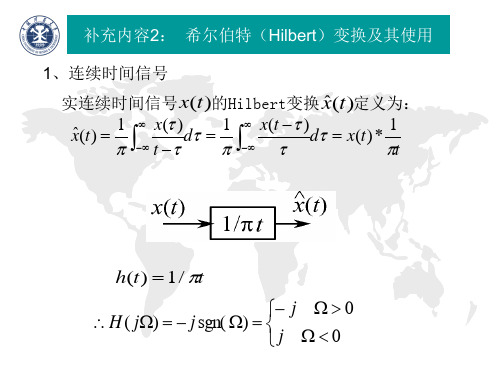
ˆ x(t ) x(t ) 1 1 由时域卷积定理有: , h(t ) t t
ˆ X ( j) X ( j) H ( j) X ( j)[ j sgn( )] jX ( j) sgn( )
ˆ X ( j) j sgn( ) X ( j)
补充内容2: 希尔伯特(Hilbert)变换及其使用 1、连续时间信号
ˆ 实连续时间信号 x(t )的Hilbert变换 x(t )定义为:
x( ) 1 x(t ) 1 ˆ x(t ) d d x(t ) * t t 1
h(t ) 1 / t
1 2 a 2
a 2 2 0 0
a 2 a 2
X
R
Hilbert变换与解析信号
离散时间信号
ˆ x 离散时间信号 x(n)的Hilbert变换记为: ( n) 设Hilbert变换器的单位抽样响应为h(n),与连续信 号Hilbert变换器的频率响应H(jΩ )对应,h(n)的频 率响应H(ejω )为:
0
je jn d
Hilbert变换与解析信号
ˆ ∴ x(n)的Hilbert变换 x( n)为:
2 x(n 2m 1) ˆ x ( n) x ( n) * h( n) m (2m 1) jX (e j ) 0 ˆ X (e j ) X (e j ) H (e j ) j jX (e ) 0
H 因果系统系统函数 ( j )的实部与虚部满足希尔
伯特变换约束关系。
已知h( t ) e
球谐函数

和
现在我们用通常的方法引入极坐标系
即有
通过上面两个式子我们得到一个正交集合
勒让德函数现在通过齐次调和多项式得到,这个齐次调和多项式关于 轴对称,并且在 处等于1.我们有
或者
现在令 是 和 的标量积.由(19)式,我们有
在二维的情形,函数 又被称为切比雪夫多项式.
如果点 和 有坐标 和 ,由下面的式子,我们分别有
为一个 阶的球面调和函数维数为 ,对于每一个阶为 维数都为 的球面调和函数 。定义 称为标准的如果
由于不同度数的球面调和函数是正交的,我们判断它是标准的唯一因素就是当条件 。很容易的得到次数为零的相伴勒让德函数,因为定义4意味着在这种情况下决定了相应的特殊谐波 具有对称性。因此 和 是成比例的,并且我们可以给出这个比例系数
定义2:假设 是均匀的调和的 次多项式具有下列性质:
a)对于所有的离开 不变的向量的正交变换 有 。
b)
那么 就被称之为 次勒让德多项式。
根据这一定义,函数 是唯一确定的,根据表达式(4),由同类多项式 和 ,函数 是唯一确定的。条件(a)说明这类多项式只由表式 确定。
因此我们得到
当 。
和
当 。
除了一系列的常数。函数 是由条件(a)确定的。常数 可以由条件(b)来确定。用参数表示(2)我们得到函数 只由 决定,因为 。
部分积分 次我们可得一个直接且简单的应用.
引理11:设 次连续可微,有
根据引理11的应用,我们可以决定 阶勒让德多项式的首项系数.如果 是 的最高次项的系数,有
(26)
的幂级数的最低次项不可以积分.根据公式(26)左半部分是 .右半部分等同于
因此
由(3)
所以
(27)
完全椭圆积分和Hersch-Pfluger偏差函数

完全椭圆积分和Hersch-Pfluger偏差函数
王根娣;张孝惠;褚玉明;裘松良
【期刊名称】《数学物理学报》
【年(卷),期】2008(028)004
【摘要】该文建立了Hersch-Pfluger偏差函数ψK(r)和第二类完全椭圆积分ε(r)之间的关系.通过对完全椭圆积分及某些初等函数的组合的单调性和凹凸性的研究获得了完全椭圆积分的一些不等式,并且藉此得到Hersch-Pfluger偏差函数ψK(r)的几个渐进精确的上界估计.
【总页数】4页(P731-734)
【作者】王根娣;张孝惠;褚玉明;裘松良
【作者单位】潮州师范学院数学系,湖州,313000;潮州师范学院数学系,湖
州,313000;潮州师范学院数学系,湖州,313000;浙江理工大学理学院,杭州,310018【正文语种】中文
【中图分类】O174.6
【相关文献】
1.关于Hersch-Pfluger偏差函数的一个猜测的证明 [J], 裘松良
2.Cap-cyclide坐标中Jacobi第一种完全椭圆积分和Jacobi椭圆函数的数值计算[J], 单洪森;恰汗·合孜尔
3.完全椭圆积分κ(r)之由三角函数给出的界及其应用 [J], 周丽明;裘松良;王飞
4.关于完全p-椭圆积分的一个函数 [J], 刘钟秦;张孝惠;
5.第二类完全p-椭圆积分关于H(o)lder平均的凹性 [J], 王淼坤;何再银;褚玉明
因版权原因,仅展示原文概要,查看原文内容请购买。
Matlab?Hilbert

Matlab Hilbert这是对几篇参考文章的整理和总结,参考文章在后面会给出链接。
一、Hilbert变换测试参考/s/blog_84024a4a01019opg.html1. hilbert函数matlab中,由hilbert函数得到的信号是合成的复信号,其虚部才是书上定义的Hilbert变换。
这一点在基本概念一文中有说明。
在上面的参考博文中,有这样几句代码:2. hilbert函数可以提取包络和调制信号频率这里主要看第五张图和第七张图调制信号的产生如下(1)包络的提取第五张图中蓝色的线就是通过hilbert变换提取的包络,关键语句如下(y代表的是调制结果信号,也就是我们一般情况下所测得的信号):(2)高频信号的提取这一点主要基于两个信号乘积的hilbert变换取决于高频信号的hilbert变换。
看第七张图,就是调制信号的瞬时频率,主要代码如下:这部分代码主要有两点需要注意(i)unwrap网上有如下解释:对于复数函数,写为指数形式A(t)*exp(j*B(t)),程序中处理的是些离散点,由于用angle求得的相角不是B(t),而是C=rem(B(t),2*Pi)(限制在-Pi到Pi之间),unwrap就是根据C求B(会差一个常数),依据是数据足够密,所以相邻两点之间的相位变化不超过Pi。
(ii)af是归一化的结果,转换到实际频率要乘以fs从结果上看,主要的高频信号为70Hz,与原信号相符(3)有三个信号的情况这个是我后来又增加的200Hz的调制信号,我们只看一下瞬时频率和包络,发现与前面的结论一致。
二、Matlab 官网提供的EMD代码测试参考/s/blog_84024a4a01019opp.html1. IMF代表固有模态函数2. 第四次分解信号的Hilbert分析(1)IMF4是分解出来的第四个固有模式函数(2)IMF4的包络就是前面说的,做hilbert变换后求幅值。
(3)瞬时频率这个在前面也说过(4)调制信号这个也很好理解,信号结果 = 包络 * 调制信号,变换一下就是上面的公式。
GPS数据的坐标变换

3 "4 的推算较复杂 " 我们只写出结果 &
%&’ 房 建 成 ! 万 德 钧 !()* 组 合 导 航 系 统 在 车 辆 导
航中的应用 %+’! 南大学报 !&,,- !".#/
! 上接第 "# 页 $ 能性较大 ! 主要是后靠装置不起征作
用!
&%$ 用万用表检查其相应线路继电器是否能正常
工作 " 触点接触是否可靠 ! 若仍不能排除 " 则应考虑刀 架内部机械配合是否松动 ! 有时会出现由于内齿盘上 有 碎 屑 造 成 夹 紧 不 牢 而 使 定 位 不 准 "此 时 "应 调 整 其 机械装配并清洁内齿盘 !
一个典型公式 !
! 收稿日期 ""##!)#!)#2 !作者简介 " 陈信 !,1/’) &" 男 " 广东茂名人 " 广东省茂名学院技术物理系教师 " 研究方向 ’ 通信工程 $ , ;< ,
七参数坐标变换公 式 " 除布尔莎公式外 " 还 有莫洛琴斯公式和范土 公式 " 这三种公式 " 它们 间的七个参数相差较 大 " 但各自构成完整的 数学模型 " 参数间存在 明确的解析关系 " 可以 相 互 转 换 "分 别 用 它 们 来 换 算 点 的 坐 标 时 " 其 结 果 完 全相同的 ! 因此 " 这三种公式是等价的 " 不再在此一一 详述 ! 是中央子午线的经度 " 其中 " 子午时线弧长 + " 对 于 克 拉索夫斯基椭球按下公式计算 & 式换算精度为 0!00#2 " 式中 "5 为卯圈曲率半径 "
