东莞市2012-2013学年度第二学期教学质量自查七年级数学
人教七年级数学下试题广东省东莞市 第二学期期末考试自查.doc

初中数学试卷桑水出品广东省东莞市2011-2012学年第二学期期末考试自查七年级数学试卷一、选择题(每小题3分,计24分,请把各小题答案填到表格内) 1. 如图所示,下列条件中,不能..判断l 1∥l 2的是 A .∠1=∠3 B .∠2=∠3 C .∠4=∠5 D.∠2+∠4=180°(第1题图)2.为了了解某市5万名初中毕业生的中考数学成绩,从中抽取500名学生的数学成绩进行统计分析,那么样本是A .某市5万名初中毕业生的中考数学成绩B .被抽取500名学生C .被抽取500名学生的数学成绩D .5万名初中毕业生 3. 下列计算中,正确的是A .32x x x ÷=B .623a a a ÷=C . 33x x x =⋅D .336x x x += 4.下列各式中,与2(1)a -相等的是 A .21a -B .221a a -+C .221a a --D .21a +5.有一个两位数,它的十位数数字与个位数字之和为5,则符合条件的数有 A .4个 B .5个 C .6个 D .无数个 6. 下列语句不正确...的是 A .能够完全重合的两个图形全等B .两边和一角对应相等的两个三角形全等C .三角形的外角等于不相邻两个内角的和D .全等三角形对应边相等 7. 下列事件属于不确定事件的是B ′C ′D ′O ′A ′ODC BA(第8题图)A .太阳从东方升起B .2010年世博会在上海举行C .在标准大气压下,温度低于0摄氏度时冰会融化D .某班级里有2人生日相同已知角8.请仔细观察用直尺和圆规.....作一个角∠A ′O ′B ′等于∠AOB 的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A ′O ′B ′=∠AOB 的依据是 A .SASB .ASAC .AASD .SSS二、填空题(每小题3分,计24分)9.生物具有遗传多样性,遗传信息大多储存在DNA 分子上.一个DNA 分子的直径约为0.0000002cm .这个数量用科学记数法可表示为 cm .10.将方程2x+y=25写成用含x 的代数式表示y 的形式,则y= .11.如图,AB∥CD ,∠1=110°,∠ECD=70°,∠E 的大小是 °.12.三角形的三个内角的比是1:2:3,则其中最大一个内角的度数是 °. 13.掷一枚硬币30次,有12次正面朝上,则正面朝上的频率为 .14.不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其它都相同,从中任意摸出一个球,则摸出 球的可能性最小.15.下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据:试验者试验次数n正面朝上的次数m正面朝上的频率nm(第11题图)布丰 4040 2048 0.5069 德·摩根 4092 2048 0.5005 费勤1000049790.4979那么估计抛硬币正面朝上的概率的估计值是 .16.如图,已知点C 是∠AOB 平分线上的点,点P 、P′分别在OA 、OB 上,如果要得到OP =OP′,需要添加以下条件中的某一个即可:①PC=P′C;②∠OPC=∠OP′C;③∠OCP=∠OCP′;④PP′⊥OC.请你写出一个正确结果的序号: . 三、解答题(计72分)17.(本题共8分)如图,方格纸中的△ABC 的三个顶点分别在小正方形的顶点(格点)上,称为格点三角形.请在方格纸上按下列要求画图.在图①中画出与△ABC 全等且有一个公共顶点的格点△C B A '''; 在图②中画出与△ABC 全等且有一条公共边的格点△C B A ''''''.18.计算或化简:(每小题4分,本题共8分) (1)(—3)0+(+0.2)2009×(+5)2010(2)2(x+4) (x-4)19.分解因式:(每小题4分,本题共8分)(1)x x -3 (2)-2x+x 2+1OACP P′B(第16题图)20.解方程组:(每小题5分,本题共10分) (1)⎩⎨⎧=+-=300342150y x y x (2)⎩⎨⎧⨯=+=+300%25%53%5300y x y x21.(本题共8分)已知关于x 、y 的方程组⎩⎨⎧=+=+73ay bx by ax 的解是⎩⎨⎧==12y x ,求a b +的值.22.(本题共9分)如图,AB=EB ,BC=BF ,CBF ABE ∠=∠.EF 和AC 相等吗?为什么?23.(本题9分)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:项目 月功能费基本话费 长途话费短信费 金额/元550(1)请将表格补充完整; (2)请将条形统计图补充完整. (3)扇形统计图中,表示短信费的扇形金额/元FECBA(第22题图)的圆心角是多少度?24.(本题4+8=12分)上海世博会会期为2010年5月1日至2010年10月31日。
东莞市2012-2013学年度第二学期教学质量检查高二理科数学(A卷)含答案

2012-2013学年度第二学期教学质量检查高二理科数学(A 卷)一、选择题:(本大题共10小题,每小题5分,共50分)1. 已知i b ai a +=-,其中i 为虚数单位,b a ,为实数,则b a += ( ) A. -2 B. -1 C. 0 D. 22. 函数)(x f 的定义域为开区间(a ,b ),导函数)(x f '在(a ,b )内的图像如图所示,则函数)(x f在开区间(a ,b )内的极值点是( )A. 1x ,3x ,5xB. 2x ,3x ,4xC. 1x ,5xD. 2x ,4x3. 已知服从正态分布N (μ,2σ)的随机变量在区间(σμ-,σμ+),(σμ2-,σμ2+),和(σμ3-,σμ3+)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm )服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )A. 683套B. 954套C. 972套D. 997套 4. 用数学归纳法证明aa aa a n n --=++++++111322(*,1N n a ∈≠),在验证当n=1时,等式左边应为A. 1B. 1+aC. 1+a+a 2D. 1+a+a 2+a 35. 6)3(y x +的二项展开式中,42y x 项的系数是( )A. 45B. 90C. 135D. 270 6. 曲线y=2sinx 在点P (π,0)处的切线方程为 ( )A. π22+-=x yB. 0=yC. π22--=x yD. π22+=x y 7. 投掷一枚骰子,若事件A={点数小于5},事件B={点数大于2},则P (B|A )= ( ) A.51 B.41 C.31 D.218. 从n(*N n ∈,且n ≥2)人中选两人排A ,B 两个位置,若其中A 位置不排甲的排法数为25,则n=( ) A. 3 B. 4 C. 5 D. 6 9. 已知某一随机变量X ( )A. 5B. 6C. 7D. 810. 函数)(x f 的定义域为R ,2013)2(=-f ,对任意R x ∈,都有)(x f '<x 2成立,则不等式2009)(2+x x f 的解集为 ( )A. (-2,2)B. (-2,+∞)C. (-∞,-2)D. (-∞,+∞) 二、填空题:(本大题共4小题,每小题5分,共20分) 11. 若复数ii z 2131-+=(i 是虚数单位),则z 的模z = .12. 若根据儿童的年龄x (岁)和体重y (kg ),得到利用年龄预报体重的线性回归方程是53ˆ+=x y.现已知5名儿童的年龄分别是3,4,5,6,7,则这5名儿童的平均体重大约是 (kg). 13. 由曲线xy 1=和直线31=x ,3=x 及x 轴所围图形的面积为 .14. 电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则是:一个方块下面有一个雷或没有雷,如果无雷,掀开方块下面就会标有数字(如果数字是0,常省略不标),此数字表明它周围的方块中雷的个数(至多八个),如图甲中的“3”表示它的周围八个方块中有且仅有3个雷.图乙是张三玩的游戏中的局部,根据图乙中信息,上方第一行左起七个方块中(方块上标有字母),能够确定下面一定没有雷的方块有 ,下面一定有雷的方块有 .(请填入所有选定方块上的字母)三、解答题:(本大题共6小题,共80分) 15.(本小题满分12分) 已知复数bi z =(R b ∈),iz +-12是实数,i 是虚数单位.(1)求复数z ;(2)若复数2)(z m +所表示的点在第一象限,求实数m 的取值范围. 图甲 图乙16.(本题满分12分)在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)(1)根据以上数据建立一个2×2的列联表;(2)能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?参考公式及数据:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=.17.(本小题满分14分) 已知函数b x a ax x x f +-+-=)1(31)(223(R b a ∈,),其图像在点(1,)1(f )处的切线方程为03=-+y x . (1)求a ,b 的值;(2)求函数)(x f 的单调区间和极值; (3)求函数)(x f 在区间[-2,5]上的最大值.18. ζ的分布列为(1)若事件A ={购买该平板电脑的3位大学生中,至少有1位采用1期付款},求事件A 的概率P (A ); (2)若签订协议后,在实际付款中,采用1期付款的没有变化,采用2、3期付款的都至多有一次改付款期数的机会,其中采用2期付款的只能改为3期,概率为51;采用3期付款的只能改为2期,概率为31.数码城销售一台该平板电脑,实际付款期数ζ'与利润η(元)的关系为求η的分布列及期望E (η).19.(本小题满分14分)下面四个图案,都是由小正三角形构成,设第n 个图形中所有小正三角形边上黑点的总数为)(n f .图1 图2 图3 图4 (1)求出)2(f ,)3(f ,)4(f ,)5(f ;(2)找出)(n f 与)1(+n f 的关系,并求出)(n f 的表达式; (3)求证:362512)(3117)3(3115)2(3113)1(311+++++++++n n f f f f (*N n ∈).20.(本小题满分14分)已知函数kxe xf =)((k 是不为零的实数,e 为自然对数的底数).(1)若曲线)(x f y =与2x y =有公共点,且在它们的某一公共点处有共同的切线,求k 的值; (2)若函数)22)(()(2--=kx x x f x h 在区间)1,(kk 内单调递减,求此时k 的取值范围.2012—2013学年度第二学期教学质量检查 高二理科数学(A 卷)参考答案及评分标准一、选择题(本大题共10小题,每小题5分,共50分.)二、填空题(本大题共4小题,每小题5分,共20分.)11.2; 12.20; 13.2ln 3; 14.BDEF(3分);AC (2分) 三、解答题(本大题共6小题,共80分.) 15. (本小题满分12分) 解:(1)()z bi b R =∈2211z bi i i --∴=++(2)(1)(1)(1)bi i i i --=+-(2)(2)2b b i-++= ……………2分 2222b b i -+=+. ……………3分 又iz +-12是实数,202b +∴=, ……………5分 2b ∴=-,即i z 2-=. ……………6分 (2) 2z i =-,R ∈m ,∴22222)(2)44(4)4m z m i m mi i m mi +=-=-+=--(, ……………8分又 复数2)(z m +所表示的点在第一象限,240,40,m m ⎧->∴⎨->⎩ ……………10分解得2m <-,即(,2)m ∈-∞-时,复数2)(z m +所表示的点在第一象限. ……………12分16.(本小题满分12分)解: (1)根据题中数据,建立一个2×2的列联表如下:……………6分(2)22160(60552025)30.74580808575K ⨯⨯-⨯=≈⨯⨯⨯ , ……………8分且30.74510.828>,2(10.828)0.001P K ≥≈, ……………10分 所以能在犯错误的概率不超过0.001的情况下认为性别与体育选修项目有关. ……………12分17.(本小题满分14分)解:(1) 由题意,22()21f x x ax a '=-+-. ……………1分又∵函数)(x f 的图象在点))1(,1(f 处的切线方程为03=-+y x ,所以切线的斜率为1-,即(1)1f '=-,∴2210a a -+=,解得1a =. ……………2分又∵点))1(,1(f 在直线03=-+y x 上,∴2)1(=f , ……………3分 同时点))1(,1(f 即点)2,1(在()y f x =上,∴b a a +-+-=)1(3122, ……………4分即b +-+-=)11(13122,解得83b =. ……………5分(2)由(1)有3218()33f x x x =-+,∴2()2f x x x '=-, ……………6分 由()0f x '=可知0x =,或2x =,所以有x 、)(x f '、)(x f 的变化情况表如下:8分由上表可知,)(x f 的单调递增区间是(),0-∞和()2,+∞,单调递减区间是()0,2; ………10分 ∴函数)(x f 的极大值是8(0)3f =,极小值是4(2)3f =. ……………11分(3)由(2),函数)(x f 在区间]5,2[-上的极大值是8(0)3f =. ……………12分又58(2)4,(5)3f f -=-=,……………13分 ∴函数)(x f 在区间]5,2[-上的最大值为583. ……………14分18.(本小题满分14分)解:(1)若事件A={购买该平板电脑的3位大学生中,至少有1位采用1期付款},则事件A={购买该平板电脑的3位大学生中没有1位采用1期付款}.∵216.0)4.01()(3=-=AP, (2)分∴784.0216.01)(1)(=-=-=APAP.……………4分(2)根据题意,实际付款期数'ζ的概率为'2(1)0.45Pξ===,'1119(2)0.25(1)0.355360Pξ==⨯-+⨯=,'1117(3)0.250.35(1)5360Pξ==⨯+⨯-=,……………10分而销售一台该平板电脑的利润η的可能值为200元,250元,300元.……………11分∴2 (200)5Pη==,19 (250)60Pη==,17 (300)60Pη==,∴η的分布列为…………… 12分∴η的期望219171()200250300244560606Eη=⨯+⨯+⨯=(元).……………14分19.(本小题满分14分)解:(1)由题意有3)1(=f,12233)1()2(=⨯++=ff,27433)2()3(=⨯++=ff,48633)3()4(=⨯++=ff,75833)4()5(=⨯++=f f . ……………2分 (2)由题意及(1)知,36)(233)()1(++=⨯++=+n n f n n f n f , …………… 4分 即(1)()63f n f n n +-=+,所以(2)(1)613f f -=⨯+, (3)(2)623f f -=⨯+, (4)(3)633f f -=⨯+, …()(1)6(1)3f n f n n --=-+, …………… 5分 将上面)1(-n 个式子相加,得:()(1)6[123(1)]3(1)f n f n n -=+++⋅⋅⋅+-+- (11)(1)63(1)2n n n +--=⨯+-233n =- …………… 6分 又()13f =,所以2()3f n n =. …………… 7分 (3) 23)(n n f = ∴111)1(1)1(112112)(31122+-=+<+=++=++n n n n n n n n n f . …………… 9分当1n =时,11251436(1)+33f =<,原不等式成立. …………… 10分 当2n =时,3625361391415)2(3113)1(311<=+=+++f f ,原不等式成立. …………… 11分 当3n ≥时,12)(3117)3(3115)2(3113)1(311+++⋅⋅⋅++++++n n f f f f)111()5141()4131(51231133311+-+⋅⋅⋅+-+-++⨯++⨯<n n11114931n =++-+25125=-<, 原不等式成立. …………… 13分综上所述,对于任意*n N ∈,原不等式成立. …………… 14分 20. (本小题满分14分)解:(1)设曲线()y f x =与2y x =有共同切线的公共点为00(,)P x y ,则020kx ex =. …………… 1分又曲线()y f x =与2y x =在点00(,)P x y 处有共同切线,且'()kx f x ke =,2()'2x x =, … 2分 ∴002kx kex =, …………… 3分解得 2k e=±. …………… 4分(2)由()kxf x e =得函数2()(22)kxh x x kx e =--,所以22(())[(22)4]kxh x kx k x k e '=+-- …………… 5分22[(2)4]kx k x k x e k=+--2(2)()kx k x k x e k=-+. …………… 6分又由区间1(,)k k 知,1k k>,解得01k <<,或1k <-. …………… 7分①当01k <<时,由(())h x '=2(2)()0kx k x k x e k -+<,得22x k k-<<,即函数()h x 的单调减区间为2(,2)k k-, …………… 8分要使得函数2()()(22)h x f x x kx =--在区间1(,)k k内单调递减,则有01,2,12,k k k k k⎧⎪<<⎪⎪≥-⎨⎪⎪≤⎪⎩ ……………9分解得12k ≤<. …………… 10分②当1k <-时,由(())h x '=2(2)()0kx k x k x e k-+<,得2x k <,或2x k>-,即函数()h x 的单调减区间为(,2)k -∞和2(,)k-+∞, …………… 11分要使得函数2()()(22)h x f x x kx =--在区间1(,)k k内单调递减,则有112k k k <-⎧⎪⎨≤⎪⎩,或12k k k <-⎧⎪⎨≥-⎪⎩, …………… 12分 这两个不等式组均无解. …………… 13分综上,当12k ≤<时,函数2()()(22)h x f x x kx =--在区间1(,)k k内单调递减. ……… 14分。
2012-2013年第二学期七年级下期末质量调研数学试题及答案

2012-2013年第二学期期末质量调研七年级数学试题一、选择题(本大题共12个小题,每小题4分,计48分) 1、点M (-2,3)所在的象限是( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限 2、16的算术平方根是( )A 、±4B 、±2C 、2D 、-23、.如图所示,直线AB ,CD 相交于O ,所形成的∠1,∠2,∠3,∠4中,∠2的对顶角是( )A 、∠1B 、∠3C 、∠4D 、∠1和∠3 4、在。
1020⋅,722,-2,2π,3.14,2+3,-9 ,0,35,1.2626626662…中,属于无理数的个数是( )A.3个B. 4个C. 5个D.6个 5、下列调查中,适合用全面调查的是( )A 、某厂生产的电灯使用寿命B 、全国初中生的视力情况C 、七年级某班学生的身高情况D 、某种饮料新产品的合格率 6、下列各式中是二元一次方程的是( ) A . 3x-2y=9 B .2x+y=6z C .x1+2=3y D .x-3=4y 27、已知a <b ,下列四个不等式中,不正确的是( )A .2a <2bB .-2a <-2bC .a+2<b+2D .a-2<b-2 8、如图,点C 到直线AB 的距离是指( )A .线段AC 的长度B .线段CD 的长度C .线段BC 的长度D .线段BD 的长度 9、下列四个命题中,正确的是( )A 、相等的角是对顶角B 、互补的角是邻补角C 、两条平行线被第三条直线所截,同位角相等D 不等式两边同时加上一个负数,不等号方向改变10、重庆市某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有x 张成人票,y 张儿童票,根据题意,下列方程组正确的是( ) A 、⎩⎨⎧=+=+1225703520y x y x B 、⎩⎨⎧=+=+1225357020y x y x C 、⎩⎨⎧=+=+2035701225y x y x D 、⎩⎨⎧=+=+2070351225y x y x11、如图,将三角形向右平移2个单位长度,再向上平移3个单位长度, 则平移后三个顶点的坐标是( )A .(1,7),(-2,2),(3,4)B .(1,7),(-2,2),(4,3)C .(1,7),(2,2),(3,4)D .(1,7),(2,-2),(3,3)12、把一些图书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本。
广东省东莞市2013-2014学年高一下学期期末教学质量检查数学(B卷)试题 Word版含答案

东莞2013—2014学年度第二学期教学质量检查高一数学(B 卷)考生注意:本卷共三大题,20小题,满分150分.考试时间120分钟,不能使用计算器.一、选择题:本大题共10小题,每小题5分,共50分. 1.已知(3,1),(,1)a b x ==-,且//a b ,则x 等于 A .13 B .13- C .3 D .3- 2.有下列调查方式:①某学校为了了解高一学生的作业完成情况,从该校20个班中每班抽1人进行座谈;②某班共有50人,在一次期中考试中,15人在120以上,30人在90~120分,5人低于90分.现在从中抽取10人座谈了解情况,120分以上的同学中抽取3人,90~120分的同学中抽取6人,低于90分的同学中抽取1人;③从6名家长志愿者中随机抽取1人协助交警疏导交通.这三种调查方式所采用的抽样方法依次为 A .分层抽样,系统抽样,简单随机抽样 B .简单随机抽样,系统抽样,分层抽样 C .分层抽样,简单随机抽样,系统抽样 D .系统抽样,分层抽样,简单随机抽样3.sin(2014)π=A .1-B .1 CD .04.方程22220x y ax +-+=表示圆心为(2,0)C 的圆,则圆的半径r =AB .2 CD .4 5.右边的程序框图,如果输入三个实数a b c 、、,要求输出这三个数中最大的数,那么在空白的判断框中应该填入A .?c x >B .?x c >C .?c b >D .?b c > 6.如图,平行四边形ABCD 中,(2,0),(3,2)AB AD ==-,则BD AC ⋅= A .6- B .4 C .9 D .13 7.如图所示,半径为3的圆中有一封闭曲线围成的阴影区域,在圆中随(第5题图)(第6题图)机撒一粒豆子,它落在阴影区域内的概率是13,则阴影部分的面积是 A .3πB .πC .2πD .3π 8.把函数()sin()6g x x π=-的图像向右平移6π个单位可以得到函数()f x 的图像,则()6f π=A .12-B .2C .1-D .1 9.由直线1y x =+上的一点向圆22(2)(1)1x y -+-=引切线,则切线长的最小值为A 1B .1C D10.函数()sin 2|sin |([0,2])f x x x x π=+∈的图象与直线y k =有且仅有两个不同的交点,则k 的取值范围是A .[1,1]-B .(1,3)C .(1,0)(0,3)-D .[1,3]二、填空题:本大题共4小题,每小题5分,共20分.11.在空间直角坐标系中,已知(2,3,3),(3,1,3)A B ,则||AB = .12.某射手射击一次击中10环,9环,8环的概率分别为0.3,0.3,0.2,则他射击一次命中8环或9环的概率为 . 13.已知2tan()3πα-=,则cos 2α= . 14.设直线0x y a -+=与圆22(1)(2)4x y -+-=相交于A B 、两点,且弦AB 的长为a = .三、解答题:本大题共6小题,共80分. 15.(本小题满分12分)已知||2,||3,(23)(2)19a b a b a b ==-⋅+=. (1)求a b ⋅的值;(2)若()a a b λ⊥+,求λ的值. 16.(本小题满分12分)已知函数()),02f x x πϕϕ=+<<,且(0)1f =.(1)求()f x 的解析式; (2)已知4(),52f πααπ=<<,求sin cos αα-. 17.(本小题满分14分)某学校对高一800名学生周末在家上网时间进行调查,抽取基中50个样本进行统计,发现上网的时间t (小时)全部介于0至5之间.现将上网时间按如下方式分成五组:第一组[0,1),第二组[1,2),第三组[2,3),第四组[3,4),第五组[4,5],下图是按上述分组方法得到的频率分布直方图.(1)求该样本中上网时间t 在[1,2)范围内的人数;(2)请估计本年级800名学生中上网时间t 在[1,2)范围内的人数;(3)若该样本中第三组只有两名女生,现从第三组中抽两名同学进行座谈,求抽到的两名同学恰好是一名男生和一名女生的概率.18.(本小题满分14分)已知学生的数学成绩与物理成绩具有线性相关关系,某班6名学生的数学和物理成绩如表:(1)求物理成绩y 对数学成绩x 的线性回归方程;(2)当某位学生的数学成绩为70分时,预测他的物理成绩.参考公式:用最小二乘法求线性回归方程ˆˆˆybx a =+的系数公式: 1221ˆˆ,ni ii nii x y n x ybay ax xnx ==-⋅⋅==--∑∑ 参考数据:22222283787368637332224+++++=,83757865737568656360738030810⨯+⨯+⨯+⨯⨯+⨯+⨯=19.(本小题满分14分)已知(sin ,cos ),(sin ,sin )a x x b x x ==,函数()f x a b =⋅. (1)求()f x 的对称轴方程; (2)若对任意实数[,]63x ππ∈,不等式()2f x m -<恒成立,求实数m 的取值范围.20.(本小题满分14分)已知圆22:(2)1M x y -+=,Q 是直线y x =上的动点,QA 、QB 与圆M 相切,切点分别为点A 、B .(1)若点Q 的坐标为(0,0),求切线QA 、QB 的方程; (2)若点Q 的坐标为(,),t t t R ∈,求直线AB 的方程.2013—2014学年度第二学期教学质量检查高一数学(B 卷)参考答案一、选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共4小题,每小题5分,共20分.11 12.0.5 13.51314.-1或3 三、解答题:本大题共6小题,共80分. 15.(本小题满分12分) 解:(1)由()()23219a b a b -⋅+=,可得2244319a a b b -⋅-=.…………2分∵2,3a b ==,∴164919a b -⋅-=,…………4分∴3a b ⋅=-.…………6分(2)由()a a b λ⊥+,可得()=0a a b λ⋅+,…………8分即2=0a ab λ+⋅,…………9分由(1)及2,3a b ==,得43=0λ-, …………11分解得4=3λ. …………12分16.(本小题满分12分)解:(1)∵(0)1f ϕ==,∴sin 2ϕ=, …………2分 又∵02πϕ<<,故4πϕ=, …………4分∴())4f x x π=+.…………5分(2)∵4())sin cos 45f παααα=+=+=,∴216(sin cos )25αα+=,…………8分∴92sin cos 25αα=-,…………10分∴234(sin cos )12sin cos 25αααα-=-=.…………11分又,2παπ<<∴sin cos 5αα-=. …………12分17.(本小题满分14分) 解:(1)由频率分布直方图知,上网时间在第二组)2,1[范围内的频率为:32.01)06.008.016.038.0(12=⨯+++-=f .…3分所以,该样本中上网时间在第二组的人数:1632.0502=⨯=n (人). …………5分(2)由(1),可估计本年级上网时间t 在)2,1[范围内的频率为32.0, …………6分所以,可估计本年级学生上网时间t 在)2,1[范围内的人数为:25632.0800=⨯(人).……8分(3)由频率分布直方图知第三组的频率为0.08,可得第三组共有4人. …………9分将第三组的四人记为a 、b 、c 、d ,其中a 、b 为男生, c 、d 为女生,基本事件列表如下:ab ,ac ,ad ,bc ,bd ,cd ,所以基本事件有6个, …………11分恰为一男一女的事件有ac ,ad ,bc ,bd ,共4个, …………13分所以,抽到的两名同学恰好是一名男生和一名女生的概率为:3264==P . …………14分 18.(本小题满分14分) 解:(1)由题意,837873686373736x +++++==, …………2分756575656080706y +++++==.…………4分53ˆ281281=--=∑∑==xn xy x n yx bi ii ii ,…………7分5131ˆˆ=-=x b y a,…………10分∴313155y x =+. …………11分 (2)由(1)知,当70x =时,68y =, …………13分∴当某位学生的数学成绩为70分时,估计他的物理成绩为68.2.…………14分19.(本小题满分14分)解:(1)由()f x a b =⋅及(sin ,cos )a x x =,(sin ,sin )b x x =,可得x x x x f cos sin sin )(2+= …………2分x x 2sin 2122cos 1+-=…………3分 21)2cos 222sin 22(22+-=x x21)42sin(22+-=πx …………4分令242πππ+=-k x ,Zk ∈,解得832ππ+=k x ,Z k ∈. …………5分所以,()f x 的对称轴方程为832ππ+=k x ,Z k ∈. …………6分(2)∵]3,6[ππ∈x ,∴1254212πππ≤-≤x . …………7分 又∵x y sin =在]2,0[π上是增函数,∴125sin)42sin(12sinπππ≤-≤x . …………8分又∵)432sin(125sinπππ-= 4sin 32cos 4cos 32sin ππππ-=42622212223+=⋅+⋅=, …………9分 ∴()f x 在]3,6[ππ∈x 时的最大值是4332142622)(m a x +=++⨯=x f . …………11分 ∵不等式()2f x m -<恒成立,即m x f <-2)(恒成立, …………12分 ∴m <-+2433,即453->m ,所以,实数m的取值范围是),453(+∞-. …………14分20.(本小题满分14分)解:(1)由题意可知当点Q 的坐标为(0,0)时,切线的斜率存在,可设切线方程为y kx =. ………1分则圆心到切线的距离1d ==,即2241k k =+,=k…………3分∴切线QA 、QB的方程为3y x =±.…………5分(2)设切线QA 、QB 的切点为1122(,),(,)A x y B x y .∵MA QA ⊥,则切线QA 的斜率为1112(0)QA x k y y -=-≠,…………6分则切线QA 的方程为11112()x y y x x y --=--.…………7分化简为211111(2)(2)yy y x x x x -=--+-,即211111(2)(2)yy x x y x x +-=+-∵点11(,)A x y 在圆22:(2)1M x y -+=上,得111(2)23yy x x x +--=-…………8分又∵(,)Q t t 在切线QA 上,∴11(2)23ty t x t +-=-①…………9分同理得22(2)23ty t x t +-=-②…………10分由①②可知直线(2)23t x ty t -+=-过点B A , ∴直线AB 的方程为(2)23t x ty t -+=-…………12分特别当10y =时,11x =或13x =当11x =时切线QA 的方程为1x =,解得1t =,得切点(2,1)B 此时AB 的方程为1x y -=上式也成立 当13x =时得3t =经检验方程也成立综上所述直线AB 的方程为(2)23t x ty t -+=-…………14分。
东莞市2013-2014学年七年级下学期期末考试地理试题

东莞2013~2014学年度第二学期期末教学质量自查七年级地理(考试时间60分钟,满分100分)一、选择题(每小题只有一个选项最符合题意,每小题2分,共60分)读亚洲略图,回答1~4题。
1.图中甲大洋是A.太平洋 B.大西洋C.北冰洋 D.印度洋2.下列注入印度洋的河流是A.鄂毕河 B.黄河C.长江 D.印度河3.图示亚洲地势的叙述,正确的是A.西部高,东部低 B.中部高,四周低C.中部低,四周高 D.北部高,南部低4.几位同学在描述亚洲各地旅游度假的情景时,有一位同学在撒谎,他是A.小明:在印度我乘着雪橇逛街B.小畅:我在去蒙古乌兰巴托的火车上看见了大草原C.小兰:我不会游泳却可以不带游泳圈在死海中畅游D.小华:在沙特阿拉伯,旅店安排我们在屋顶上睡觉据印度农业部发布的最新报告显示,2013/14年度(7月到次年6月)印度粮食产量可能达到创纪录的水平,因为季风降雨良好,种植面积提高。
读“印度资料图”完成5~7题。
5.印度粮食大丰收与季风气候密切相关,给印度带来充沛降雨的季风是A.东北季风 B.西南季风C.西北季风 D.东南季风6.如果图中的风来得早,退得晚,该地区可能会出现严重的A.寒潮 B.飓风C.旱灾 D.水灾7.印度和中国的相似之处有①人口众多,粮食需求量大②都属于发展中国家③高新技术产业已经居世界前列④工业高度发达A.①② B.①③C.③④D.②④读“俄罗斯地形与矿产分布图”,完成下列8~9题。
8.有关俄罗斯的叙述,正确的是A. 地形崎岖,山区面积广大,平原狭小B. 地势东高西低,南高北低C. 东部以平原为主,西部以高原山地为主D. 人口主要集中在东部9.俄罗斯工业发达的有利条件是A.人口众多 B.领土辽阔 C.矿产资源丰富 D.地形平坦2013年世界乒乓球锦标赛于5月13日~20日在法国巴黎举行。
根据图文资料完成10~13题。
10. 下面能集中体现法国特点的是A. 黄种人、红茶绿茶、泰姬陵B. 黑种人、可可咖啡、金字塔C. 白种人、牛奶奶酪、凯旋门D. 混血人、飞饼烤鱼、雪砖冰屋11.综合图中A、B、C三城市的气温曲线和降水量柱状图,对三城市共同的气候特点描述正确的是A.全年高温多雨 B.冬冷夏热 C.全年温和湿润 D.冬季温和湿润,夏季炎热干燥12.由气温曲线和降水量柱状图可知,A—B—C三城市自西向东A.降水量越来越多 B.高温期与多雨期一致C.气温年较差越来越大 D.降水越来越集中在冬季13.外国游客在巴黎可以看到的景点有下图所示区域为长期的热点地区,据此回答14~15题。
[VIP专享]2012-2013学年度东莞市中学三好学生名单
![[VIP专享]2012-2013学年度东莞市中学三好学生名单](https://img.taocdn.com/s3/m/f6b0a09416fc700aba68fc24.png)
附件12012-2013学年度东莞市中学三好学生名单学校东莞市中学三好学生东莞中学邓子锋袁嘉豪叶健安陈奕曈徐晓琴李楚翘周昱均詹凝东莞市第一中学梁秋敏张清源陈宇驰莫梓轩方美斌吴泳霞李嘉敏谢辉贤东莞实验中学马蕴然梁曦陈淑芬连智维周紫妍贺乾清程漪澜梁钧杰东莞高级中学温国明谢嘉慧朱惠珠杜燕婷蔡晓玲吾希洪李国豪梁汉标郑晓靖万江中学洪婉莹张文静陈俊光刘甜甜何嘉伟石龙中学郑曼谭文清叶嘉敏曾清萍刘芷君梁凤婷郑锐举常平中学吴达如周锦原李镇杰曾令林陈国峰刘家因谢淑芬李妮珊覃为虎门中学叶浩超郭志伟朱家豪周詠欣谭焕仪苏佩仪张嘉欣郭巾豪厚街中学潘换弟方巧瑶卢嘉雯陈佩雯陈倩彤王昭祥黄晓锴塘厦中学陆嘉敏李思惠吴凡李旻鸿彭彬吕家俊张枝锦周芬芳长安中学陈雅俐杨晓盈邓杰麻涌中学冼楚业萧晓东莫可莹周清栾东莞市第二高级中学潘文慧王丽娜刘芷莹陈诗伟东莞市第四高级中学梁燕云邓桂莹黄婷婷吴滔陈晓欣黎汝航郭艳红梁瑞英东莞市第五高级中学陈雪枝张佩映宁春燕刘景升张婉君东莞市第六高级中学周添恩叶耀聪李秀娥李淼梁嘉仪东莞市第七高级中学杨婷婷张铸威林楚泽刘锦河东莞市第八高级中学陈嘉坤赖若文杨德琴曾莹东莞市第十高级中学王泳诗梁嘉明陈雅婷东莞中学松山湖学校胡心至邓晓懿何雯婷周梓康陈泳良程思源叶芷呈徐楚敏叶晓圆陈子豪学校东莞市中学三好学生玉兰中学王若舟汪蕊李瑞晶黄东婵林智文陈雪贞东莞中学初中部杨宇通杨忆萱郑起沛尹梓芊傅湘葶罗冠霆温静怡周逸夫可园中学庾倬玮吉冬昱王国谦麦辉煜利曼婷东华初级中学冯淑清陈大慈黄曦欣王欣宇曾焕仁郭嘉欣胡粤杨孙卓睿周钰鹏严瑜然夏瑜刘潇涵周诗琪周桂纯郭立达李可晴东华高级中学刘莹陈粤蔡烨昂王振威徐名琛莫俊荣黄秀峰杨帆李梓澎王子悦光明中学刘影刘紫欣刘湘㼆黄湘嫡王怡君刘奕罗蒙刘诗盈胡凯欣杨嘉豪黄泽宇关铭淇李睿涵廖美霞詹懿琪陈旭麟李东胡婉茜王思远金宇清周湘粤东莞理工学校黎锐辉李思慧卢少恒方建辉陈启安岑伟超钟德坚黎文婷唐家琪东莞市电子商贸学校陈嘉欣林妙容萧锦茵朱永全蔡荣基刘珊珊东莞市家具学校袁嘉敏袁佩君东莞市轻工业学校伍佩珊温文芳廖海鑫郭超越莫锦慧梁雪燕东莞市经济贸易学校蔡婷婷冯桂芬丁婉欣殷芷晴刘嘉韵韩诗婷张颖华陈伟珠邓莉贞黄倩张承志唐影俏东莞市汽车技术学校钟燕君邓敏玲东莞市商业学校林素萍袁宝仪张艺盈叶贝欣蔡敏儿李紫瑶李彩君谢雪映梁瑞菁叶健珊彭永龙东莞市电子科技学校方淑莹巫君英钟金派刘志君黄晓梅黄钊颖石碧岚赖金江李涛东莞市纺织服装学校陈嘉敏陈嘉琪陈永康杜润南李凤英刘泳均吴锐刘洪伸东莞市信息技术学校赖君罗佩琳林凯泳东莞市机电工程学校谭晶张桓溥陆晓敏黎金妹陈安妮江嘉琪东莞体育运动学校李海玲东莞卫生学校李素盈胡慧芬莫锺敏东城朝晖学校李智怡张昊旻东城春晖学校张樱安学校东莞市中学三好学生东城东珠学校李娉婷东城佳华学校钟腾鹏东城岭南学校黄明楷东城旗峰学校马娇妮东城益民学校李梦玲东城初级中学吴璟承王敏瑶杨伟豪万淑桦朱鹏隆刘巧玲东城第一中学刘幽诸蓉谢振扬吴浩贤熊雅婕巫伟康五星职业技术学校邵雪敏李焱黄国飞王永贤蔡培林育才职业技术学校陈思洁林晓彤陆润恩杨日明徐舜梅邹丽婷黄素安彭银银林妙春陈鹏坤南城宏远外国语学校唐瑞黄慧彬南城东晖学校汤高敏南城尚城学校梅玮南城星河学校陈诗惠南城御花苑外国语学校刘恒毅南开实验学校陆芊芊黎凯风巫远枫刘筝羽李牧原香雪锋南城中学方悦胡紫竹胡淼张雪晶李海涛李华锦蒋力南博职业技术学校张丹妮温海霞薛蒂娜陈明赛刘美高谦北师大翰林实验学校邱佳泽周子薇黄泽浩康厚闻庄晓彤谭莉莉曾智李清玲谢淑倩黄冈理想学校付雨帆万江明星学校付亮万江长鸿学校卢泽禧万江第三中学胡嘉欣冯展锋袁丽华万兆聪万江区第二中学罗展锋庾海欣刘韵诗简灿洪谭中宝石碣碣识学校许晓亮陈小漫石碣丽江学校申华丽学校东莞市中学三好学生石碣四海学校潘文妹石碣文晖学校陈奎泼石碣新民学校党扬石碣镇勤径学校赖惠权石碣袁崇焕中学方遒李振潮陈钰栩石碣中学王欣彤江叶青谢立超文志杰华粤职业技术学校关春燕黄秋菊南方舞蹈职业技术学校赵思铭石龙镇龙联学校张诗怡石龙第二中学魏文崟丁璇卓芊芊王滢滢石龙第三中学陈慧怡米国俊何沛珊陈炤君茶山冠华学校于德春茶山华洋学校张杰茶山京华学校曾惠玲江沁茶山品华学校陈莉莉茶山新华学校唐思凌华南师大嘉玛学校付鑫怡杨云浩黄婕吴晓枫茶山中学袁梓豪叶俊杰叶韵琪吕沅玲石排东海学校苏忠松石排燕岭学校庄歆怡石排云岗学校车静文石排中学刘雪晴陈淑媚李泳竹江米倩企石华海学校黄胜兴企石新域学校林倩倩企石中学林宛容李雪婷陈嘉仪姚丽蓉陈晓弋横沥爱华学校陆叶学校东莞市中学三好学生横沥东豪学校黄沛横沥汇星学校郑晓薇横沥中学香立其陈辉邹芷颖北师大石竹附属学校张颖杨景仪吕育星李晓敏颜妙娜林晓婷桥头光辉学校赵慧玲桥头光明学校丁孟欣桥头华立学校陈钰营桥头中学李可鑫诸葛子音徐李鸿谢岗华翔学校钟妍妍谢岗振华学校邓诗净谢岗中学庄钦秀钟璇妍罗婉雅东坑海东学校潘玮璐东坑洪冠学校许金平东坑旭东学校黄佳佳唐瑞彬东坑忠简学校涂先海东坑中学赖妙妃丁淑恒丁金蓉常平常青学校李芳廷常平崇惠学校郑媛妮常平创业学校谭李妍黎振万常平恒正学校何敏华常平嘉华学校邵正阁常平文华学校刘慧娟常平旭升学校欧琳莉常平镇振兴中学萧晓琪殷奕锋袁丽珍严淑娜姜日凡姚可为常平中学初中部李源梁卓莉周燕萍李赏邹晓树宏达职业技术学校陈玲妹学校东莞市中学三好学生寮步东阳学校揭晓梅寮步宏伟初级中学曾小晖谢承豪李伟伦黄炯曾日庆寮步龙光学校蒲海燕寮步信义学校吴泽薇中大附校外国语学校张博昊寮步香市中学黄翕陈建星刘昱君林镇随尹健姗寮步中学龙倬伟叶芷彤韩炜城樟木头鹏程学校袁嘉滢樟木头养贤学校刘玲汛樟木头中学林达生廖泳楠朱惠珊大朗东明学校陈锐萍大朗启东学校陈冰卢观蕊大朗启明星初级中学叶怡蓝陈丹玲莫贵雄黄训权大朗水霖学校张洪亮于小艳大朗洋洋学校骆丹丹大朗第一中学林仁桐陈裕德刘晨傅裕恒张峻彪叶健彬大朗中学刘洁荣黄浩宁王杰鑫叶炜青陈巧怡刘竞光黄江康湖新乐学校郑雨薇黄江育英初级中学陈巧茂黄江中学黎延威刘锐睿袁振岚陈容蔚清溪晨光第一学校孙良众清溪晨光学校黄美云清溪锦程学校蒋荞清溪三中绮丽学校钟宏远清溪银河学校林依静杨兰兰清溪中学黄媛方婉婷郭梦莉张耀文学校东莞市中学三好学生塘厦华辉学校杨良火李德华塘厦华正学校罗日爱罗家鑫陈苏塘厦水霖学校吴迪鲜莉涂若愚陈珊张艳杨梅云塘厦初级中学刘婷婷刘倩楠李阳城李宇豪曾晓华凤岗德恩学校付丽珊凤岗金凤凰学校张靖彤凤岗锦兴学校黄淑芳凤岗明华学校韦小茹凤岗明贤学校郑泽森卢丽珊凤岗侨诚初级中学庄佳庆陈德强凤岗清英学校梁文奇陈仔豪凤岗新世纪英才学校莫锦芳胥雅黄伟平刘正君华侨中学余东玉陈泓机赖熙彤大岭山华强学校朱家莹谢升格大岭山南华学校邱可航大岭山星塘学校蓝家仪大岭山新风中学刘文卓张衍姗蒙陆潘家炜大岭山中学梁楠黎盈君罗扬阳胡燕红长安东安中学孙启泽陈远深长安福海学校陆柳梅郭媚长安培英初级中学李汝锶魏薪光张赵君长安振安中学刘金霞林浩贤严家敏长安镇实验中学巢忠宙曾伟嘉刘戊清曾文键刘诗雅翁雪聪虎门红星学校彭秀玲陈青敏虎门汇英学校曾秋怡王奕徐进军虎门外语学校麦晓琳吴皓陈晓茹李慧曾宇航学校东莞市中学三好学生虎门新英豪学校屈萌虎门智升学校宋浩彬陈平平虎门第三中学詹振伟郑晴丹周颖琪凌伊韵虎门第四中学陈炜坚吴玥霖曹伟楠虎门第五中学彭逸伦农朗刘懿霆李华诗南华职业技术学校刑彩云杨伟侨郑世皇陈嘉宝厚街新园学校郭晓晶厚街镇福民学校陈广玲厚街镇海月学校莫乔熙厚街镇开贤学校陈伟豪厚街镇艺园学校黄哲厚街湖景中学方泽豪刘海聪陈靖娴陈锡伦陈华颖陈肇聪竹溪中学刘芊婷方雪仪王永锋胡淑茵东方明珠学校朱海锐陈冰玲许海城沙田鹏远学校肖丽丽沙田腾辉学校陈军沙田广荣中学陈雨赖婧瑾张悦黎仲恒道滘纪英学校官湘道滘中南学校黎金玲道滘中学王奕深魏晓琪杨嘉华吴嘉敏济川中学叶树芬陈淑莹陈亮帆廖丹丹李月坪卢丽君洪梅中学唐子然麻涌镇第一中学徐汝宝张嘉慧莫俊鹏何楚谦莫尚政望牛墩育林学校何远志望牛墩中学魏文君黄珮文莫映月陈颖仪陈家亮陈沛文陈伟新李商刘靖明叶晓晴叶声豪学校东莞市中学三好学生中堂朝阳学校周春志中堂汇文中学袁优静周涛中堂星晨学校涂泽顺中堂展华学校李忠芬中堂镇实验中学莫凤联李颖康吴雅琪陈少冰中堂中学霍沛贤曾奕阳黎芷君谭纬延高埗宝文学校毛超杰高埗弘正学校莫诗蒽高埗文康学校黎嘉敏高埗英华学校林莹慧低涌中学苏靖慧曾梓威黄瑞婷智通职业技术学校唐炜竣杨瑞林洪丽娟叶国行张淑燕姚云娜松山湖南方外国语学校李晓莹东莞市技师学院钟淦坤赵恩恩叶诗蓝陈效莲林晓峰李远聪合计693人附件2:2012-2013学年度东莞市中学优秀学生干部名单学校东莞市中学优秀学生干部东莞中学张若琳陈俊仪罗淑娴袁境生卢明珊麦素琳张宇晨陈南岳东莞市第一中学马粤周加欣翟浩枫林莞涛苏翠珊温子航张繁玲卫星辰东莞实验中学叶舒棋刘羽轩黎又甄丁卓磊钱嘉欣尹铭嫦龚达强陈仲琨东莞高级中学谢孔航巴克多来提刘丽华谢天欣梁柱佳李泽成林伟烁周欣豪梁泽民万江中学陈柳玎罗绿韵江俊杰云飞钟怡嫣石龙中学舒煜华卢翠钰彭小珍袁乐姚赵莉蔡佳虹袁宇添常平中学刘培壕李文欣罗元漳刘怡兰苏奕茗黄淑仪陈艳芳黄俊贤贺德轩虎门中学何振枫梁锦波邓霭莹曾子芜黄文杰谭靖雯陈秀涓叶秋怡厚街中学万美晴温依雯刘静如李文芬方敏仪王倩雯叶欣仪塘厦中学罗嘉伟曾舒晴黄钰仪叶雪媚林静敏程丽婷林烨文谢丹婷长安中学黄锦圳陈靖雯蒋京锟麻涌中学吴健荣莫颖珊熊燕妹梁美君东莞市第二高级中学黎嘉琪李白云祁晓怡袁敏仪东莞市第四高级中学黎晓惠陈婕玲梁绍豪胡瑞婷罗梓琪黄程冯海深叶瞳瞳东莞市第五高级中学黎淑仪樊可黎梓良黄鑫成李家钰东莞市第六高级中学尹泽江王天遥邓嘉豪汪泳钊钟婉君东莞市第七高级中学莫可琦陈婉莎赖雪珍黄裕威东莞市第八高级中学连伟华赖意军黄舒豪欧阳贝野东莞市第十高级中学郭志荣王志彪黄雅东莞中学松山湖学校张师苑黄婉君彭佩儿林宏耀曾亮学校东莞市中学优秀学生干部玉兰中学李欣静彭莲慧莫慧冰张旭荣东华高级中学杨琳童伊涵王紫萱钟丽莎林己胡颖聪简振雄邓镜良杨健一陈禹聪光明中学邓皓华林燕玲徐浩楠胡轻舟陈泽星林友文温州鹏王鸿展东莞理工学校郭佩仪邹善仪麦智刚郑敦强陈奕鑫梁淑钧姚满怡邓丽华方梓恒东莞市电子商贸学校黄宝宝鲍蓓蔡泽龙周玉琪梁俊杰王嘉辉东莞市家具学校李子权叶伟健东莞市轻工业学校方晓婷方政豪林玉仪欧阳锦顺卢俊杰罗雪雅东莞市经济贸易学校庾競予郑晓香叶晓琳万静文林利镖李可洇何玉莹朱旭东叶润华罗嘉茵钟玉卿陶涛东莞市汽车技术学校钟少芬尹健聪东莞市商业学校谢慧仪吴滔滔张梓和萧伟权袁学辉袁嘉雯李文慧陈培胜李慧贤吴佩如张玉清东莞市电子科技学校杨燕珊徐钦乐李超辉杨家辉蔡志军曾志华邹优慧戴维维黄艺升东莞市纺织服装学校陈倩红黄碧回黎清玲李佳弟马俊钟怀欢张帆帆叶占娣东莞市信息技术学校陈嘉锋李彤李建新东莞市机电工程学校冯耀煌罗艳莫振君钟颖高家杰林燕娜东莞卫生学校陈润弟唐佩瑶李秀凤五星职业技术学校施映祝陈梅娟钟志鹏钟海军杨豌蝶育才职业技术学校王淼张玉燕邹盛吉赖华燕庄景镇林丹微区宁华陈毫林景川肖静南开实验学校莫紫晴叶婧瑶南城中学傅毫毛慧南博职业技术学校伍虹虹温利平黄展程重重钟敏宁孙伟鑫北师大翰林实验学校魏萍贺涛廖春媚姜艳琴石碣中学胡韵诗华粤职业技术学校江蓉张家国学校东莞市中学优秀学生干部南方舞蹈职业技术学校杨泽华华南师大嘉玛学校黄梓莹刘自力茶山中学郑丽丽北师大石竹附属学校刘心怡唐小丁薛洪慧宏达职业技术学校潘锦瑶大朗中学梁伟评陈佩仪张慧英曾君豪塘厦水霖学校冯上耀刘嘉婷凤岗新世纪英才学校肖小粤廖怡欣大岭山中学李佳斐何翠容虎门外语学校樊林川周楚秦南华职业技术学校吴私刘梦瑶余锦开胡景辉东方明珠学校黄荣杜潘婷张美玲济川中学杜嘉慧彭月欣吴淑君智通职业技术学校黄琼萱林海伟蓝振潮粱轩熙潘炎林如情东莞市技师学院邓明瑞刘佳佳黄慈珊魏晓燕陈思杰杨晓波合计295人。
度第二学期东莞市质量自查七年级数学试题及参考答案

2010-2011学年度第二学期教学质量自查七 年 级 数 学(满分100分)一、选择题 (每小题3分,共15分)1. 在平面直角坐标系中,点P (-2,3)位于 ( ) A.第一象限 B.第二象限C.第三象限D.第四象限2. 当mx <my 时,x <y 成立,则m 的取值为 ( ) A .m =0 B. m ≠0 C.m >0 D. m <03.正多边形的一个外角的度数为30°,则这个正多边形的边数为 ( ) A. 12B. 10 C.8 D. 64. 下列调查方式中,适合采用全面调查方式的是 ( ) A.了解一批节能灯的使用寿命B.了解全国中学生的视力和用眼卫生情况 C.检测某城市的空气质量 D. 企业招聘,对应聘人员进行面试5. 如图1,∠1=30°,∠B=60°,AB ⊥AC ,则下列说法正确的是 ( ) A .AB ∥CDB .AD ∥BCC .AC ⊥CDD .∠DAB+∠D=180°二、填空题(每小题3分,共15分) 6.已知3x+y =5,当x =-2时,y 的值是________.7.关于x 的某个不等式组的解集在数轴上表示如图2所示,则该 不等式组的解集为__________.8.已知一个三角形的三边长分别为3,a -1,5,则a 的取值范围是_______________________. 9.已知点P 到x 轴的距离为3,到y 轴的距离为5,则点P 的横坐标为__________________. 10.经调查,某班同学上学所用的交通工具中,自行车占60%,公交车占30%,其他占10%.画扇形图时,“公交车”对应扇形的圆心角度数是. 三、解答题(每小题6分,共30分)1AD图1图211.求不等式组⎪⎩⎪⎨⎧->-++≤+x x x x 213521132的正整数解.12.已知单位长度为1的方格中,△ABC 的位置如图3所示. (1)请在图中建立平面直角坐标系,使点C 的坐标为(-4,-3); (2)在(1)的条件下,将△ABC 向上平移2个单 位长度再向右平移3个单位长度得△A ′B ′C ′,请画出 △A ′B ′C ′,并写出点B 的对应点B ′的坐标.13.如图4,AB ∥CD ,∠DAB =37°,∠AEC=85º,求∠BCD 的度数.图3图414.解方程组⎪⎩⎪⎨⎧=-+=+-=++1232436c b a c b a c b a15.已知△ABC.(1)如图5,若P 为BC 边上的任意一点(与点B 、C 不重合),则图中共有______个三角形; (2)如图6,若P 1、P 2分别为BC 边上的任意两点(与点B 、C 不重合),则图中共有_______个三角形;(3)若在BC 边上任取4点(与点B 、C 不重合),则共有________________个三角形; (4)若在BC 边上任取n 点(与点B 、C 不重合),则共有________________个三角形.四、解答题(每小题8分,共40分)① ②③ 图5 图616.为了解某中学全校学生对排球、乒乓球、篮球、羽毛球、足球五项体育运动的喜爱情况,从中随机调查了若干名学生,并将调查结果绘制成统计表7和统计图8(不完整).请根据图中提供的信息,解答下列问题:(1)补全统计表和统计图.(2)根据以上调查,估计该校1800名学生中,喜欢羽毛球的人数是多少?表7 图817.某养牛场有大牛和小牛共62只,若大牛每天用饲料20千克,小牛每天用饲料5千克,一天共用饲料940千克.求这养牛场有大牛和小牛各是多少?18.某房地产开发商花了1300万元购买了一块地用于建造居民保障性住房,已知住宅楼每平方米的造价约为700元,那么建楼面积必须超过多少平方米,才能将建楼成本控制在每平方米2000元以下?19.如图9,在五边形ABCDE中,AE⊥DE,∠BAE=120°,∠BCD=60°,∠CDE-∠ABC=30°.(1)求∠D的度数;(2)AB∥CD吗?请说明理由.图920.如图10,△ABC中,∠ABC、∠ACB的平分线相交于点O.(1)若∠ABC=32°,∠ACB=58°,则∠BOC的度数是________;(2)若∠A=76°,求∠BOC 的度数;(3)若∠A=α,∠BOC=β,请猜想α与β之间的数量关系,并说明理由.图102010-2011学年度第二学期教学质量自查七年级数学参考答案一.选择题:1.B 2.C 3.A 4.D 5.B二. 填空题:6.11 7.3<x<9 8.x≥1 9.5或-5 10.108°三.解答题:11.解:由①得 x ≤8---------------------------------------------2分由②得 54>x --------------------------------------------------4分∴854≤<x ----------------------------------------------------5分 ∵x 是正整数∴x =1,2,3,4,5,6,7,8-------------------------------------------6分 12.(1)画对平面直角坐标系-------------------------------------2分 (2)画对△A ′B ′C ′------------------------------------------4分B ′(1,-1)---------------------------------------------6分13.解:∵AB ∥CD ,∠DAB =37°,∴∠D=∠DAB=37°---------------------------------------------3分 ∵∠AEC=85º∴∠BCD=∠AEC-∠D=85º-37º=48º--------------------------------6分 14.解:由①+③得,3a +4b =18 ④-------------------------------1分 由②+③得,5a +2b =16 ⑤------------------------------------2分将④、⑤组成方程组,并解得:⎩⎨⎧==32b a ----------------------------4分将⎩⎨⎧==32b a 代入③,得c =1----------------------------------------5分 所以⎪⎩⎪⎨⎧===132c b a ---------------------------------------------------6分15.(1)3-----------------------------------------------------1分(2)6-----------------------------------------------------2分(3)15----------------------------------------------------4分(4)2)1)(2(++n n -------------------------------------------6分四.解答题:16.解:(1)统计表:75;22.5%-----------------------------------2分画对条形图:---------------------------------------------6分 (2)1800×37.5%=675(人)答:喜欢羽毛球的人数是675人-------------------------------------8分17.解:设这养牛场有大牛x 只,小牛y 只,依题意得:-------------------1分⎩⎨⎧=+=+94052062y x y x -------------------------------------------------------------------------4分 解得:⎩⎨⎧==2042y x ---------------------------------------------------------------------------7分答:这养牛场有大牛42只,小牛20只--------------------------------------------8分 18.解:设建楼面积为x 平方米,依题意得:--------------------------1分x x 200070013000000<+------------------------------------------4分解得:10000<x -------------------------------------------------7分 答:建楼面积必须超过10000平方米.-------------------------------8分19.(1)解:∵AE ⊥DE∴∠E=90°------------------------------------------------------1分 ∵五边形的内角和为:(5-2)×180°=540°∴∠A+∠B+∠C+∠D+∠E=540°-------------------------------------2分 ∵∠BAE=120°,∠BCD=60°,∴∠B+∠D=270°-------------------------------------------------3分 又∠D-∠B=30°∴∠D=150°-----------------------------------------------------4分 (2)AB ∥CD------------------------------------------------------5分 ∵∠D=150°,∠D-∠B=30°∴∠B=120°------------------------------------------------------6分 ∵∠B+∠C=180°--------------------------------------------------7分 ∴AB ∥CD---------------------------------------------------------8分 20.(1)135°----------------------------------------------------2分 (2)解:∵∠ABC、∠ACB 的平分线相交于点O∴∠OBC=21∠ABC ,∠OCB=21∠ACB-----------------------------------3分∵∠BOC=180°-(∠OBC +∠OCB )=180°-(21∠ABC +21∠ACB )=180°-21(∠ABC +∠ACB )-----------------------------------------4分又∠ABC +∠ACB=180°-∠A=104°∴∠BOC =180°-21×104°=128°-----------------------------------------------------------5分(3)290αβ+︒=--------------------------------------------------6分证明:由(2)得∠BOC=180°-21(∠ABC +∠ACB )-----------------------------------7分又∠ABC +∠ACB=180°-∠A∴∠BOC=180°-21(180°-∠A )=90°+21∠A即290αβ+︒=-----------------------------------------------------8分。
2012—2013年度第二学期七年级数学期末试题
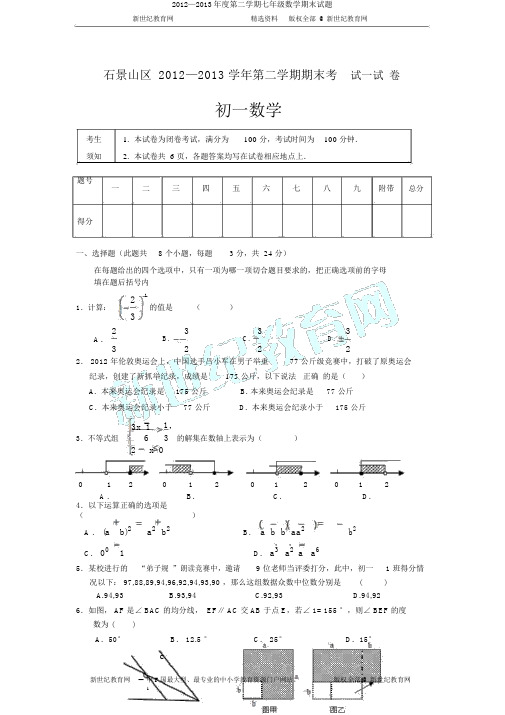
2012—2013年度第二学期七年级数学期末试题新世纪教育网精选资料版权全部@新世纪教育网石景山区 2012—2013 学年第二学期期末考试一试卷初一数学考生 1.本试卷为闭卷考试,满分为100 分,考试时间为100 分钟.须知 2.本试卷共 6 页,各题答案均写在试卷相应地点上.题号一二三四五六七八九附带总分得分一、选择题(此题共8 个小题,每题 3 分,共 24 分)在每题给出的四个选项中,只有一项为哪一项切合题目要求的,把正确选项前的字母填在题后括号内2 1.计算:32A.31的值是()333 B.C.D.2222. 2012 年伦敦奥运会上,中国选手吕小军在男子举重77 公斤级竞赛中,打破了原奥运会纪录,创建了新抓举纪录,成绩是175 公斤,以下说法正确的是()A. 本来奥运会纪录是175 公斤B. 本来奥运会纪录是77 公斤C. 本来奥运会纪录小于77 公斤D. 本来奥运会纪录小于175 公斤3x 11,3.不等式组63的解集在数轴上表示为()2x0012012012012A .B.C.D.4.以下运算正确的选项是()A .(a b)2a2b2B.a b b aa2b2C.001D.a3a2a a65.某校进行的“弟子规”朗读竞赛中,邀请9 位老师当评委打分,此中,初一 1 班得分情况以下: 97,88,89,94,96,92,94,93,90 ,那么这组数据众数中位数分别是()A.94,93B.93,94C.92,93D.94,926.如图, AF 是∠ BAC 的均分线, EF∥ AC 交 AB 于点 E,若∠ 1= 155 °,则∠ BEF 的度数为 ()A.50°B. 12.5 °C. 25°D.15°B E A新世纪教育网精选资料 版权全部 @新世纪教育网第6第77.在a 的正方形中挖去一个b 的小正方形( a >b )(如 甲),把余下的部分拼成一个矩形(如 乙),依据两个 形中暗影部分的面 相等,能够 ( )A . (a b)2 a 22ab b 2B .C . a 2b 2(a b)(a b)D .(a b)2a 2 2ab b 2 (a 2b)( ab)a 2 ab 2b 28.在平面内,假如一个角的两 与另一个角的两 平行, 两个角数目关系是()A. 相等B.互余或互C.相等或互余D.相等或互二、填空 (本 共6 个小 ,每小 3 分,共 18 分.把答案填在 中横 上)9.有 料 示, 2013 年上半年,欧洲 定体制(ESM )拍 19.73 欧元三个月期券,均匀利润率 0.00003,将0.00003用科学 数法表示 ______________.x y 13 的解是 _____________.10.方程 y3x11. 若 p q4, pq2 , p 2 q 2 的 _______________.12. 了估 某市空气 量状况,某同学在30 天里做了以下 : 介入数( w ) 40 60 80 100 120 140天数(天)3510651此中 w <50 空气 量 , 50≤w ≤100 空气 量 良, 100< w ≤150 空气 量度 染, 若 1 年按 365 天 算, 你估 城市在一年中空气 量达到良以上(含良)的天数 ______________天.13. 将一个 方形 条按 所示折叠一下,若∠ 1=140o , ∠ 2=______.12第 1314.下边反应了,按必定 律摆列的方程 和它 解之 的 关系序号1 2 3 ⋯⋯ n2x y 32x y 5 2x y 7 方程x 4 y 16 x 6 y 36 x 2y 4x 2 x 4 x 6 方程 解1y3y5y按此 律,第 n 个方程 ___________,它的解 ___________ ( n 正整数) .三、 算 (本 共4 个小 ,每小5 分,共 20 分)新世纪教育网精选资料 版权全部 @新世纪教育网215.计算:201313.1541.2解 :13 x 7 1 16.解不等式:,并求其非负整数解 .63 66解 :17.计算: 6a 3 2a 222a 2 1 2a .解 :18. 若 m 2m 2,求代数式 (2m1)2m 1 m 2 (2m 3)(3 2m) 的值 .解 :四、分解因式(此题共2 个小题,每题 4分,共 8分)19. 9m 2 n 2 ( a b) n 2 (b a) .20. 12 x 2 y 18xy 22x 3 .解:解:五、简单几何推理(此题共 2 个小题,每题 5 分,共 10 分)21. 如图, AB ⊥ BD ,CD ⊥BD ,∠ A +∠ AEF = 180 °.以下是小贝同学证明 CD ∥ EF 的推理过程或原因,请你在横线上增补完好其推理过程或原因.CB F D新世纪教育网精选资料版权全部@新世纪教育网证明:∵ AB⊥ BD,CD ⊥ BD (已知),∴ ∠ABD =∠ CDB=90°( __________________ ).∴ ∠ABD +∠ CDB=180°.∴AB∥( _____) (____________________________) .∵ ∠A+∠ AEF= 180°(已知),∴AB∥ EF( ___________________________________ ).∴CD∥ EF (___________________________________ ).22.以下图,已知∠ 1= ∠ 2,∠ 3=∠ 4,∠ 5=∠ C,求证: DE//BF 证明:FE1B 45G23 A DC六、列方程(组)解应用题(此题 5 分)23. 北京时间 2013 年 4 月 20 日 8 时 02 分四川省雅安市芦山县发生 7.0 级地震。
广东省东莞市2013-2014学年高二下学期期末教学质量检查数学(理)试题(A卷) 扫描版含答案

2013—2014学年度第二学期教学质量检查高二理科数学(A 卷)参考答案一、选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共4小题,每小题5分,共20分. 11.0.05 12.1- 13.64 14. mk n C + 三、解答题:本大题共6小题,共80分. 15.(本小题满分12分) 解:(1)设(),z x yi x y R =+∈. (1)分由2z i +iy x )2(++=为实数,得2=+y ,即2y =-. …………2分又()()()()12212421z i x i i x x i -=--=--+, (3)分由()12z i -为纯虚数,得()40210x x -=⎧⎪⎨+≠⎪⎩, …………5分 ∴4x =, (6)分∴i z 24-=. (7)分 (2)∵i m m m mi z )2(8)124()(22-+++-=+, …………9分根据条件,可知⎪⎩⎪⎨⎧<->-+,0)2(8,04122m m m …………10分 解得22<<-m , (11)分∴实数m的取值范围是()2,2-.…………12分16.(本小题满分12分) 解:(1)由题意,258)18()10()5(23131520=-+-+-+++++=x , …………1分898)5.3()5.2()5.0(5.05.15.35.35.6=-+-+-+++++=y , …………2分所以41)25(8125689258324ˆ2281281=⨯-⨯⨯-=--=∑∑==xn x yx n yx bi i i ii , …………4分21254189ˆˆ=⨯-=-=x b y a, …………6分 故y 关于x 的线性回归方程:11ˆ42yx =+. …………7分 (2)由题意,设该同学的物理成绩为w ,则物理偏差为:5.91-w . …………8分而数学偏差为128-120=8, …………9分∴218415.91+⨯=-w , …………10分 解得94=w , (11)分所以,可以预测这位同学的物理成绩为94分. …………12分17.(本小题满分14分)解:(1)由题意,每次摸球写有数字“5”的概率为21. …………1分 四次摸球数字之和为30,只能是两次摸到写有数字“5”,另两次写有数字“10”. …………2分设X 为4次摸球中写有数字“5”的次数,则)21,4(~B X , …………3分所以抽奖者四次摸球数字之和为30的概率为:83)211()21()2(24224=-⨯⨯==-C X P .……5分(2)由题意,抽奖者获得的收益ξ可取18元、0元、-2元. …………6分从8个球中任取4个球的结果数为48C ,其中恰好有k 个球写有数字“5”的结果数为kkC C -⋅444,所以从8个球中任取4个球,其中恰好k 个球写有数字“5”的概率为:48444)(C C C k Y P kk -⋅==,4,3,2,1,0=k , …………8分所以351)4()0()18(480440********=⋅+⋅==+===--C C C C C C Y P Y P P ξ, …………9分3516)3()1()0(48344344814414=⋅+⋅==+===--C C C C C C Y P Y P P ξ, …………10分3518)2()2(4824424=⋅===-=-C C C Y P P ξ, …………11分 因此,随机变量ξ的分布列为…………12分35183518)2(3516035118)(-=⨯-+⨯+⨯=ξE . …………13分所以,(1)抽奖者四次摸球数字之和为30的概率为38;(2) 抽奖者收益的期望为18-35元.…14分18.(本小题满分14分)解:(1)由x a x f ln )(=,得x a x f =')(,∴12)2(=='af ,即2=a ,∴x x f ln 2)(=. …………2分∴cxbx x x g ++=2ln 2)(, 从而xcx bx c bx x x g 2222)(2++=++='. …………3分∵)(x g 在21=x 和2=x 处有极值, ∴0221)21(2)21(2=++⨯='xc b g ,02222)2(2=++⨯='xc b g , …………5分解得:1=b ,5-=c , …………7分经检验:1=b ,5-=c 满足题意. …………8分(2)由(1),x x x x g 5ln 2)(2-+=,()2252()0x x g x x x-+'=>.令()0g x '>,得102x <<或2x >;令()0g x '<,得122x <<. ∴()g x 在102⎛⎫ ⎪⎝⎭,,()2+∞,上单调递增,在122⎛⎫ ⎪⎝⎭,上单调递减. …………9分若0,212>≤k k 且,即410≤<k 时,)(x g 在区间)2,(k k 内的单调递增; …………10分若22210<<<<k k ,即2141<<k 时,)(x g 在区间)21,(k 内的单调递增,在区间)2,21(k 内的单调递减; …………11分若2221≤<≤k k ,即121≤≤k 时,)(x g 在区间)2,(k k 内的单调递减; …………12分若k k 2221<<<,即21<<k 时,)(x g 在区间)2,(k 内的单调递减,在区间)2,2(k 内的单调递增; …………13分 若2≥k ,)(x g 在区间)2,(k k 内的单调递增. …………14分19.(本小题满分14分) 解:(1)由121n n a a n +-=-,得:21132322n a a n n n =++++-=-+, …………3分2n b n =. …………4分(2)① 当1n =时,111T S ==,∴()1136T S +=,又3246n n +=,∴1n =时等式成立;……5分② 假设n k =时等式成立,即()3324k k T S k k +=+,则1n k =+时,()()()()()()223111133324311212k k k k k k T S T S b a k k k k k ++++⎡⎤+=+++=+++++-++⎣⎦()()232466161k k k k =++++-+ ()()()2216161k k k k k =-++++ ()()22461k k k =+++()()22141k k ⎡⎤=+++⎣⎦()()32141k k =+++,∴1n k =+时等式也成立. …………8分 根据①②,()()33+24n n T S n n n N +=+∈都成立. …………9分 (3)当3n ≥时,20n b n =>,∴1231211111154n b b b b b b ++++>+=. …………11分 又22212311111111123n b b b b n++++=++++()2111111223341n n <+++++⨯⨯-5111111423341n n ⎛⎫⎛⎫⎛⎫=+-+-++- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭5117424n =+-<. 综上可知:12351111744n b b b b <++++<成立. …………14分 20.(本小题满分14分)可解:(1)假设曲线()y f x =与()y g x =存在“内公切线”,记内公切线与曲线()xg x e =的切点为()00x y ,,则切线l方程为:()000x x y e e x x -=-. …………2分又由()000214x x y e e x x y x ⎧-=-⎪⎨=-⎪⎩可得:()00201104x x x e x x e ++-=. …………3分由于切线l 也和曲线()214f x x =-相切, 所以()()000200110x x x x ex e e e x ∆=--=-+=.000010x x e e x >∴-+=. …………4分当00x >时,0001,10xx e e x >∴-+>; 当00x =时,0001,10xx e e x =∴-+=; 当00x <时,0001,10x x e e x <∴-+<.所以000,1x y ==,故公切线l的方程为:1y x =+. …………5分下面证明1y x =+就是()f x 与()g x 内公切线,即证2114x x x e -≤+≤. ∵2221111110442x x x x x ⎛⎫⎛⎫+--=++=+≥ ⎪ ⎪⎝⎭⎝⎭,∴2114x x -≤+成立. …………7分设()1xh x e x =--,则()/1xh x e =-.令()/0h x =,得0x =.当0x <时,()/0h x <,当0x >时,()/0h x >,∴()h x 在(),0-∞上为减函数,在()0+∞,上为增函数,所以()()00h x h ≥=,即1x x e +≤. …………9分∴2114x x x e -≤+≤,即1y x =+就是曲线()y f x =与()y g x =的内公切线. …………10分(2)∵()/xg x e =,∴21321x x x e e e x x -=-.要证明:132x x x <<,只需证明:2131221x x x x x e e e e e x x -<=<-,只需证明:()()12122121xxxxx x e e e x x e -<-<-,只需证明:()12121xxxx x e e e -<-,及()21221xxxe e x x e -<-,只需证明:()21211x xx x e --+<,及()12121x xx x e --+<. …………13分由(1)知:()1xx e x R +≤∈,所以()21211x x x x e --+<及()12121x xx x e --+<成立,∴132x x x <<. (14)分。
人教版七年级第二学教学质量检测数学试卷和参考答案

七年级数学试卷第1页(共8页)2012-2013学年度第二学期期末综合素质测试七年级数学试卷一、正确选择(每题2分,共16分)1.如图,由下列条件不能得到AB ∥CD 的是( ) A. ∠B +∠BCD =180° B. ∠1=∠2 C. ∠3=∠4D. ∠B =∠52.点P 在第二象限,若该点到x 轴的距离为3,到y 轴的距离为1,则点P 的坐标是 ( )A.(-1,3)B.(-3,1)C.(3,-1)D.(1,3) 3.二元一次方程832=+y x 的正整数解有( ) A .1个 B .2个 C .3个 D .无穷多个4.下面的变形中,不正确的是( ).A.由 a>b ,得 b<aB.由 -a>-b ,得 b>aC.由 -2x>a ,得 x> a 21-D.由 21-x<y ,得 x>-2y5.已知点A(a+2,5)、B(-4,1-2a),若直线AB 平行于x 轴,则a 的值为( ) A.-6 B.2 C.3 D.-26.一个实数的平方根是5a+3和2a-3,则这个实数是( )A.4B.9C.25D.497.下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④1是1的平方根.其中正确的有 ( ).A.0个B.1个C.2个D.3个8. 每个木工一天能装配双人课桌 4张或单人课椅 10把.现有木工9人,怎么分配工作才能使一天能装配的课桌与课椅配套.设 x 个木工装课桌,y 个木工装课椅,则列出的方程组正确的 ( )A ⎩⎨⎧==+y x y x 2049B ⎩⎨⎧==+y x y x 49C ⎩⎨⎧=⨯=+y x y x 10429D ⎩⎨⎧==+y x y x 1049二、准确填空(每题3分,共30分) 9.81的算术平方根是______.七年级数学试卷第2页(共8页)CB A D 10.把命题“平行于同一直线的两直线平行”改写成“如果……,那么……”的形式:_______________________________________________. 11.如图,直线AB 、CD 相交于点O ,作DOE BOD ∠=∠,OF 平分AOE ∠,若28AOC ︒∠=,则EOF ∠=________ 度. 12、如果P (a ,a-1)在X轴上,则P的坐标是 .13、若方程组⎩⎨⎧+=+=+22332k y x k y x 的解x 、y 的和是-12,则k=________.14.在实数32-,0,3,-3.14,4中,无理数有_______个. 15. 如图,AD ∥BC,∠D=100°,CA 平分∠BCD,则∠DAC=_______.16.如果不等式组 ⎩⎨⎧≤≥-m x x 023 有解,则 m 的取值范围是____________.17. 某商品的进价是1000元,售价为1500元,由于销售情况不好,商店决定降价出售,但又要保证利润率不低于5%,那么,此商品最低可以打_______折出售.18、某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%。
2012-2013学年度第一学期教学质量自查七年级数学

2012-2013学年度第一学期教学质量自查七年级数学(满分100分)一、选择题(每小题3分,共15分)1. 用科学记数法表示56 700 000,正确的是 ( )A. 567×105B. 56.7×106C. 5.67×107D. 5.67×1082. 下列算式中,运算结果为负数的是 () A. -(-3) B. 3- C. -32 D. (-3)23. 方程931=-x 的解是 () A. x=3 B. x=-3 C.x=27 D. x=-274. 一本新书按标价的九折出售,仍可获利20%,若该书的进货价为21元,则标价为 () A. 26元 B. 27元 C. 28元 D. 29元5. 下列图形可以作为一个长方体的展开图的是 ( )A. B. C. D.二、填空题(每小题3分,共15分)6. -3的绝对值是 .7. “比x 的2倍小7的数”用式子表示是 .8. 关于x 的方程mx +4=3x +5的解是x =1,则m= .9. 若单项式3x 2y n 与-2x m y 3是同类项,则m+n= .10. 25°31′的角的补角等于 .三、解答题(每小题6分,共30分)11. 计算:2(4x -0.5)-6(1-x 31) .12. 计算:40+(-2)3×5-(-0.28)÷(-2)2 .13. 解方程:3.5x -2=4.5x +0.25 .14. 先化简,再求值:)412()85(22xy x x xy +---,其中x =-21,y =2 .15. 如图1,A 、B 、C 、D 在同一直线上,AB=8,AD=14,C 是BD 的中点,求AC 的长 .图1四、解答题(每小题8分,共40分)16. 解方程:2133210-=--x x x .17. 已知a 为一个有理数,解答下列问题:(1)如果a 的相反数是a ,求a 的值;(2) 10a 一定大于a 吗?说明你的理由.18. 某车间每天能制作甲种零件500只,或者制作乙种零件250只,甲、乙两种零件各一只配成一套产品,现在要在30天内制作最多的成套产品,则甲、乙两种零件各应制作多少天?19. 如图2,O 是直线AC 上一点,OA 是一条射线,OD 平分∠AOB ,OE 在∠BOC 内,∠BOE=31∠EOC ,∠EOC=90°. (1)求∠DOE 的度数;(2)哪些角与∠AOD 互为余角?请说明理由;(3)互为补角的角有几对?20. 一张长方形桌子可坐6人,按图3方式将桌子拼在一起.图3 (1) 2张桌子拼在一起可坐 人,4张桌子拼在一起可坐 人,n 张桌子拼在一起可坐 人.(2) 一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?。
5年东莞市2011-2012-2013-2014-2015-2016学年度第二学期教学质量自查七年级数学期末试卷

东莞市2011-2012学年度第二学期教学质量自查七年级数学期末试卷(满分100分)一、选择题(每小题3分,共15分)1、下列数值中,是不等式32x >50的解的是( )A.60B.73C.75D.792、若点P(x ,y)的坐标满足xy <0,则点P 所在的象限是( ) A.第一象限 B.第二象限C.第一象限或第三象限D.第二象限或者第四象限 3.等边三角形的外角和是( )A.60°B.120°C.180°D.360°4、现有3cm ,5cm ,7cm ,10cm 的四根木条,若选其中三根组成三角形,则其选择方法有( ) A.4种 B.3种 C.2种 D.1种5、如图1所示,是七年级某班学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况所占百分比,则体育对应扇形的圆心角的度数是( ) A.20° B.36° C.60° D.72°二、填空题(每小题3分,共15分)6.为了解一批电视机的使用寿命,从中抽取100台电视机进行试验,这个问题中的样本容量是 。
7.把方程2x -y=3改写成用含x 的式子表示y 的形式是 。
8.若点P(a -2,a+2)在y 轴上,则a= 。
2x -1≥0 9.不等式组 的解集是 。
x + 1<0 10.如图2,已知直线AB ,CD ,EF 相交于点O ,若∠AOC=50°,则∠COB 的度数等于 。
图1娱乐35% 动画 29% 体育 20% 新闻 16%D B F C AE 图2 O三、解答题(每小题6分,共30分)11.解不等式25331--+y y ≥4,并将其解集在数轴上表示出来。
12.如图3,直线a ∥b ,∠1+∠2=128°,求∠3的度数。
13.如图4,将等腰梯形ABCD 向左平移2个单位长度,然后再向上平移3个单位长度,可以得到等腰梯形A'B'C'D',画出平移后的图形,并写出其各个顶点的坐标。
东莞市2012-2013学年度第二学期教学质量自查七年级数学

东莞市2012-2013学年度第二学期教学质量自查一、选择题(每小题2分,共20分)1. 下列实数中,属于无理数的是 ( ) A. 31 B. 3.14159 C. 36 D. 7 2. 已知a 、b 均为实数,且a >b,则下列结论不正确的是 ( )A. a +3>b +3B. a -3>b -3C. 3a >3bD. -3a >-3b3. 下列说法中正确的是 ( )A. 1的平方根是1B. 0没有平方根C. 0.01是0.1的一个平方根D. -1是1的一个平方根4. 方程组⎩⎨⎧=-=+02y x y x 的解是 ( )A. ⎩⎨⎧==20y xB.⎩⎨⎧==02y xC.⎩⎨⎧==11y xD.⎩⎨⎧-=-=11y x 5. 要反映某市一周内每天最高气温的变化情况,宜采用 ( )A. 条形统计图B. 扇形统计图C. 折线统计图D. 频数分布直方图6. 下列调查中,适合采用全面调查方式的是 ( )A. 调查某批次汽车的抗撞击能力B. 调查央视“新闻联播”的收视率C. 检测某城市的空气质量D. 了解某班学生“50米跑”的成绩7. 一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可分成 ( )A. 9组B. 10组C. 11组D. 12组8. 已知点P (4,-3),则点P 到y 轴的距离为 ( )A. 4B. -4C. 3D. -39. 如果点M (3,4-m)在第四象限内,那么m 的取值范围是 ( )A. m ≥4B. m >4C. m ≤4D. m <410. 如图1,下列条件中,可以判断AB//CD 的是 ( )A. ∠1=∠2B. ∠2=∠3C. ∠1=∠4D. ∠3=∠4图1二、填空题(每小题3分,共15分)11. 9的算术平方根是 .12. 若2a+6是非负数,则a 的取值范围是 . 13. 已知⎩⎨⎧=-=31y x 是方程923=-y mx 的解,则m= .14. 如图2,直线AB 与直线CD 相交与点O ,OE ⊥AB ,垂足为O.若∠AOC=65°,则∠DOE 的度数是 .15. 在平面直角坐标系中,已知点O 坐标(0,0),A 点在x 轴上,且OA=5,则A 点坐标为 .三、解答题(每小题5分,共25分)16. 计算: 2252383+--+ 17. 解不等式组⎪⎩⎪⎨⎧-≤--+x x x x 237121)1(325 ,并在数轴上表示出解集.18. 如图3,AD//BC ,∠D=100°,AC 平分∠BCD ,求∠DAC 的度数.图319. 在平面直角坐标系中,已知ABC 三个顶点的坐标分别为A (1,-4),B (5,-4),C (4,-1).(1)画出△ABC ;(2)将△ABC 先向上平移2个单位长度,再向左平移4个单位长度后得到△C B A ''',画出△C B A '''.20. 解方程组⎪⎩⎪⎨⎧-=++=++=-452304z y x z y x y x四、解答题(每小题8分,共40分)21. 某班一次数学测验成绩如下:63,84,91,53,69,81,57,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,88,85,67.(1)补充完整频数分布表:(2)补充完整图4中的频数分布直方图:(3)若80分以上(含80分)的成绩为优秀,那么该班这次数学测验的优秀率是多少?22. 如图5,已知长方形ABCD 四个顶点的坐标分别是A (2,-22),B (5,-22),C (5,-22),D (2,-2).(1)求四边形ABCD 的面积是多少?(2)将四边形ABCD 向上平移22个单位长度,求所得的四边形D C B A ''''的四个顶点的坐标.23.甲、乙两人检修一条长270米的自来水管道,甲每小时比乙多检修10米,两人从管道两端同时开始检修,3小时完成任务.甲、乙两人每小时各检修多少米?24.如图6,点D、E、F分别在AB、BC、AC上,且DE//AC,EF//AB,下面写出了证明“∠A+∠B+∠C=180°的部分过程,请完成填空:∵DE//AC,EF//AB,()∴∠1=∠,∠3=∠.()∵EF//AB,∴∠2=∠.( )∵DE//AC,∴∠4=∠.∴∠2=∠A. ()∵∠1+∠2+∠3=180,∴∠A+∠B+∠C=180.25.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠. 甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场优惠的条件是:每台优惠20%.(1)什么情况下到甲商场购买更优惠?(2)什么情况下到乙商场购买更优惠?(3)什么情况下两家商场的收费相同?东莞市2012-2013学年度第二学期教学质量自查七年级数学参考答案一、选择题三、解答题16. 解:原式=25232+--+ -----------------------------------------------3分=0 -----------------------------------------------------------------------------------5分17. 解:由①得:5.2->x ---------------------------------------------------------2分由②得:4≤x --------------------------------------------------------------------3分所以:45.2≤<-x ------------------------------------------------------------4分其解集在数轴上表示为:------------------------------------------5分18. 解:∵AD ∥BC ,∠D=100°∴∠BCD=180°-∠D=80°-----------------------------------------------------2分∵AC 平分∠BCD∴∠ACB=21∠BCD=40°-------------------------------------------------------4分∴∠DAC=∠ACB=40°----------------------------------------------------------5分19.(1) ------------------------------------------------------3分(2) ------------------------------------------------------5分20. 解:②×5-③得:1934=+y x ④----------------------------------------1分①×4-④得:1919-=-y ------------------------------------------------------2分∴1=y -------------------------------------------------------------------------------3分将1=y 代入①得:4=x --------------------------------------------------------4分将4=x ,1=y 代入②得:2-=z∴⎪⎩⎪⎨⎧-===214z y x -------------------------------------------------------------------------------5分 四、解答题21.(1)6,4-------------------------------------------------------------------------------4分(2)------------------------------------------------------6分(3)%50%10030411=⨯+答:该班这次数学测验的优秀率是50%-------------------------------------------------8分22.解:(1)AB=5-2=3,AD=2222=----------------------------------------2分 ∴四边形ABCD 的面积为:AB ×AD=23-----------------------------------------------4分(2)A ′(2, 0),B ′(5,0,)C ′(5,2),D ′(2,2) ----------------8分23.解:设甲每小时检修x 米,乙每小时检修y 米,根据题意得:--------------1分⎩⎨⎧+==+10270)(3y x y x -----------------------------------------------------------------------4分 解得:⎩⎨⎧==4050y x ------------------------------------------------------------------------------7分答:甲每小时检修50米,乙每小时检修40米. -------------------------------------8分24.已知;------------------------------------------------------------------------------------ 1分C;------------------------------------------------------------------------------------- 2分B;-------------------------------------------------------------------------------------3分两直线平行,同位角相等;-----------------------------------------------------------------4分4;------------------------------------------------------------------------------------5分两直线平行,内错角相等;-------------------------------------------------------------6分A;-------------------------------------------------------------------------------------7分等量代换.-------------------------------------------------------------------------------------8分25.解:设购买电脑x台. -------------------------------------------------------------------- 1分(1)若到甲商场购买更优惠,则:6000+(1-25%)×6000(x-1)<(1-20%)×6000x,-----------------------2分解得:x>5,-----------------------------------------------------------------------------3分∴当购买电脑台数大于5时,甲商场购买更优惠;-----------------------------4分(2)若到乙商场购买更优惠,则:6000+(1-25%)×6000(x-1)>(1-20%)×6000x,解得:x<5,∴当购买电脑台数小于5时,乙商场购买更优惠;-----------------------------6分(3)若两家商场收费相同,则:6000+(1-25%)×6000(x-1)=(1-20%)×6000x,解得:x=5,∴当购买电脑5台时,两家商场收费相同.---------------------------------------8分。
广东省东莞市2013-2014学年高一下学期期末教学质量检查数学试题(A卷) 扫描版含答案

2013—2014学年度第二学期教学质量检查高一数学(A 卷)参考答案一、选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共4小题,每小题5分,共20分.11.)(3,0,0 12.5113. 14.2263()()1055x y -++=三、解答题:本大题共6小题,共80分. 15.(本小题满分12分)解:(1)由()()23219a b a b -⋅+=可得2244319a a b b -⋅-=. …………2分又∵2,3a b ==,∴164919a b -⋅-=, …………3分 即3a b ⋅=-, …………4分∴cos 223a b a bθ⋅===-⨯⋅. …………6分∵πθ≤≤0,…………7分 ∴56πθ=.…………8分 (2)由()a a b λ⊥+可得,()=0a a b λ⋅+,…………10分即2=0a a b λ+⋅,即43=0λ-,解得4=3λ. …………12分16.(本小题满分12分) 解:(1)∵23||T ππω==,且0ω>, ∴23ω=,…………2分∴2()2sin()33f x x π=+.…………4分(2)由3238()2sin[()]2sin()2cos 42342325f ππππαααα+=++=+==,得4cos 5α=. ……6分 ∵02πα>>-,∴3sin 5α=- .…………7分由32310()2sin[()]2sin 22322313f πππβββ-=-+==,得5sin 13β=.…………9分∵02πβ>>,∴12cos 13β=. …………10分∴653313553131254sin sin cos cos )cos(=⨯-⨯=+=-βαβαβα. …………12分17.(本小题满分14分) 解:(1)由频率分布直方图知,上网时间在第二组)2,1[范围内的频率为:32.01)06.008.016.038.0(12=⨯+++-=f .…3分所以,该样本中上网时间在第二组的人数:1632.0502=⨯=n (人). …………4分(2)由(1),可估计本年级上网时间t 在)2,1[范围内的频率为32.0, …………5分所以,可估计本年级学生上网时间t 在)2,1[范围内的人数为:25632.0800=⨯(人).……7分(3)由频率分布直方图知第三组的频率为0.08,可得第三组共有4人; …………8分第五组的频率为0.06,可得第五组共有3人. …………9分其中第三组四人记为a 、b 、c 、d ,其中a 、b 为男生, c 、d 为女生,第五组三人记为1、2、3,其中1、2为男生,3为女生,基本事件列表如下:12个. …………11分其中恰为一男一女的事件有1c ,1d , 2c ,2d ,3a ,3b ,共6个. …………13分所以,抽到的两名同学恰好是一名男生和一名女生的概率为:21126==p . …………14分18.(本小题满分14分) 解:(1)由题意,837873686373736x +++++==, …………2分756575656080706y +++++==.…………4分53ˆ281281=--=∑∑==xn xy x n yx bi ii ii ,…………7分5131ˆˆ=-=x b y a,…………10分∴313155y x =+. …………11分 (2)由(1)知,当70x =时,68y =, …………13分∴当某位学生的数学成绩为70分时,估计他的物理成绩为68.2.…………14分19.(本小题满分14分)解:(1)设),(y x P ,),(11y x A ,),(22y x B .∵P是线段AB的中点,∴1212,2.2x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩ 即⎩⎨⎧=+=+.,2121y y y x x x …………1分 ∵A B 、分别是直线y x =和y x =-上的点, ∴11y x =和22y x =-.∴⎩⎨⎧=-=-.,2121y x x x y y …………3分 又23AB =,∴12)()(221221=-+-y y x x , …………4分即224412y x +=,所以动点P的轨迹C的方程为223x y +=. …………5分(2)依题意,直线l 的斜率存在,故可设直线l 的方程为(1)y k x =-. …………6分设),(33y x M 、),(44y x N 、),0(5y R , 则M N 、两点坐标满足方程组22(1),3.y k x x y =-⎧⎨+=⎩消去y并整理,得2222(1)230k x k x k +-+-=, …………8分∴234221k x x k+=+, ①234231k x x k -=+. ②…………9分∵λ=,∴[]),()0,1(),0(),(33533y x y y x -λ=-, 即⎩⎨⎧λ-=--λ=.,)1(35333y y y x x ∴)1(33x x -λ=.…………10分∵l 与x 轴不垂直,∴13≠x , ∴331x x -=λ.…………11分同理441x x -=μ. (12)分∴443311x xx x -+-=μ+λ34343434()21()x x x x x x x x +-=-++.…………13分将①②代入上式可得3λμ+=-. …………14分20.(本小题满分14分)解:(1)(sin ,cos ),(sin(),sin )6a x xb x x π→→==-,()2f x a b =⋅,2()2sin sin()2sin cos 6sin cos f x x x x xx x xπ∴=⋅-+⋅=+⋅1sin 222sin(2)3x x x π=-+=-+…………2分2x ππ≤≤,252333x πππ∴≤-≤,1sin(2)3x π∴-≤-≤,1()2f x ∴-+≤≤ …………3分3112()1321222,,()332x x f x x x f x ππππππ∴-==--==当时,即时,当时即时…………4分(2)由(1)得,()sin(2)32f x x π=-+()()4xg x f π=,()sin()232g x x ππ∴=-+. …………5分 2()42g x T ππ∴==函数的周期为.…………6分 (1)(2)(3)(4)g g g g ∴+++(5)(6)(7)(8)g g g g =+++ = (2009)(2010)(2011)(2012)g g g g =+++.…………7分(1)(2)(3)(4)g g g g +++=又(1)(2)(3)(4)...(2013)(2014)503(1)(2)g g g g g g g g ∴++++++=⨯+1212=+=+ …………9分(3)由(2)得,()sin()23g x x ππ=-+4T =的周期为, [](),2g x t t ∴+函数在上零点的个数sin()23y x y ππ=-=等价于函数图象与直线.…………10分在同一直角坐标系内作出这两个数的图象.由图象可知, 当444,3k t k k Z <<+∈时,sin()23y x y ππ=-=函数图象与直线, 即()g x 函数无零点;…………12分 当410424444,33k t k k t k k Z +≤<++<≤+∈或时,sin()123y x y ππ=-=函数图象与直线个交点,即()1g x 函数有个零点;………13分 当10244,3k t k k Z +≤≤+∈时,sin()223y x y ππ=-=函数图象与直线个交点,即()g x 函数有个零点.…………14分。
东莞市2013至2018七年级第二学期各年数学期末试卷(共五份)

东莞市2013-2013学年度第二学期教学质量自查七年级数学(满分100分)1、16的算术平方根是( )A 、4B 、4±C 、8D 、8± 2、实数2-,0.3,17π-中,无理数的个数是( ) A 、2 B 、3 C 、4 D 、53、如果座位表上“5列2行”记作(5,2),那么(4,3)表示( ) A 、3列5行 B 、5列3行 C 、4列3行 D 、3列4行4、如果点P (3,y )在第四象限,则y 的取值范围是( )A 、y >0B 、y <0C 、y ≥0D 、y ≤0 5、为了解某市1600多万民众的身体健康状况,从中任意抽取1000人进行调查,在这个问题中,这1000人的身体健康状况是( )A 、总体B 、个体C 、样本D 、样本容量 6、若a >b ,则下列不等式一定成立的是( )A 、b a <1B 、ba>1 C 、a ->b - D 、a b ->07、若21x y =⎧⎨=⎩是关于x ,y 的方程ax-y =3的解,则a 的值是( )A 、1B 、2C 、3D 、48、如图1,实数a 在数轴原点的左边,则实数a ,-a ,1的大小关系表示正确的是( )A 、a <1<-aB 、a <-a <1C 、1<-a <aD 、-a <a <1 图1 9、下列命题中,不正确的是( )A 、邻补角互补B 、内错角相等C 、对顶角相等D 、垂线段最短 10、下列调查中,适合全面调查方式的是( )A 、调查人们的环保意识B 、调查端午节期间市场上粽子的质量C 、调查某班50名同学的体重D 、调查某类烟花爆炸燃放安全质量二、填空题(每小题3分,共15分)11、已知23x=,则x= ;12、当x时,式子3+x的值大于式子112x-的值;13、如图2,直线l与直线AB、CD分别相交于E、F,∠1=105°,当∠2= 度时,AB∥CD;14、方程组23328y xx y=-⎧⎨+=⎩的解是;15、经调查,某校学生上学所用的交通方式中,选择“自行车”、“公交车”、“其他”的比例为7:3:2,若该校学生有3000人,则选择“公交车”的学生人数是;三、解答题(每小题5分,共25分)16)2-17、解不等式组:4111-2x xxx-+⎧⎪⎨⎪⎩≥<18、如图3,直线AB、CD相交于O,OE是∠AOD的角平分线,∠AOC=28°,求∠AOE的度数。
人教版2012-2013学年第二学期七年级期末考试数学试卷分析134

七年级期末考试数学试卷分析期末测试阅卷结束后,我们对数学试卷作了分析。
通过分析,我们看到了我校初中数学教学较好的一面,同时也暴露出一些存在问题。
以下是我们所作的一些分析,并据此提出几点教学想法。
一、基本情况全卷共26道题,满分120分,考试时间120分钟。
我班这次期末考试的考生有38人,其中90分以上的考生有1人,优良率为2.6%,及格人数为4人,及格率10.5%,平均分为35.97分。
由此可见,今年期末数学成绩很不太理想,且低分较多,这一结果表明我校数学教学两极分化的现象严重,不容忽视。
另外也与本次的试卷有关,本次试卷采用的不是本县的期末试卷,是一种难度很大,分数值同2010-2012年河北省中考数学的试卷形式,本人觉得严重偏离了本学期的教学情况。
二、学生学习状况(答题)评价1.选择题考生答题情况分析选择题(1-6)为基础题,主要考查学生数学中的基本概念,计算等(对顶角、平方根、同位角、平行线判定、平移、命题)的理解、计算,以及对基本技能(方根的值)的应用,得分率较高。
7-12小题考查的主要是方程,方程组,不等式(组)数据的容量,扇形图等,难度不小。
2.填空题考生答题情况分析填空题(14)是关于算术平方根的问题,学生需要根据表格提供的数据用绝对值表示,考查的是平方根与算术平方根及应用,有很多学生做错。
填空题(16)主要是借助方程组来解代数式的值。
需要学生理解,有一小部分学生没有注意方程组的特点而做错。
这类试题涉及知识虽然基础,但需要考生具备一定的“学习”能力。
考试结果表明,对于这样的试题,有相当一小部分学生存在能力上的欠缺。
填空题(17)是求不等式组的范围问题,其中一部分学生没有注意值能为负数的问题。
总体而言,填空题的失分主要集中在第14,16,17三题,大约占填空题总失分的一半以上。
3.解答题题考生答题情况分析19大题是一道解方程组和一道解不等式组计算题,考查学生的运算技能,有相当一部分学生基础掌握的还是不错,但是扣分也不少。
广东省东莞市2013届高三上学期期末教学质量检测数学(理)试题

东莞2012-2013学年度第—学期高三调研测试理科数学考生注意:本卷共三大题,满分150分,时问120分钟.不准使用计算器 参考公式:若事件A 与事件B 相互独立,则P (AB )=P (A )P (B ).一、选择题(本大题共8小题,每小题5分,满分40分.每小题各有四个选择支,仅有一 个选择支正确.请用2B 铅笔把答题卡中所选答案的标号涂黑.) 1.若a 实数,1(2)ai i i +=-,则a 等于A .2B .-1C .1D .-2 2.若函数21()cos ()2f x x x R =-∈,则()f x 是 A .最小正周期为2π的奇函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数 D .最小正周期为π的偶函数3.学校为了解学生在课外读物方面的支出情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[10,50) (单 位:元),其中支出在[)30,50(单位:元)的同学 有67人,其频率分布直方图如右图所示,则n 的值为 A .100 B .120 C .130 D .390 4.等差数列{}n a 中,192a =-,352a =-,则该数列前n 项 和n S 取得最小值时n 的值是A .4B .5C .6D .75.设m 、n 是两条不同的直线,α,β是两个不同的平面,则m a ⊥的—个充分条件是A .m//n,n //β, αβ⊥B .,n //β,α//βmC .m//n ,n β⊥,α//β D .m n ⊥,n β⊥,αβ⊥6.甲、乙两位选手进行乒乓球比赛,采取3局2胜制(即3局内谁先赢2局就算胜出,比赛结束,每局比赛没有平局,每局甲获胜的概率为35,则比赛打完3局且甲取胜的概率为 A .18125 B .36125 C .925 D .18257.2012翼装飞行世界锦标赛在张家界举行,某翼人 空中高速飞行,右图反映了他从某时刻开始的15分钟内的速度()v x 与时间x 的关系,若定义“速度差函数”()u x 为时间段[]0,x 内的最大速度与最小速度的差,则()u x 的图像是8.设集合{}012,,S A A A =,在S 上定义运算⊕:i j k A A A ⊕=,其中k 为i j +被3除的余数,{},1,2,3i j ∈,则使关系式0()i j i A A A A ⊕⊕=成立的有序数对(,)i j 总共有 A .1对 B .2对 C .3对 D .4对 9.已知函数1()1f x x=-的定义域为M,()ln g x x =的定义域为N, 则M N = .10.已知变量x,y 满足120x y x y ≥⎧⎪≤⎨⎪-≤⎩则z x y =+的最小值是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东莞市2012-2013学年度第二学期教学质量自查七年级数学(满分100分)一、选择题(每小题2分,共20分)1. 下列实数中,属于无理数的是 ( ) A. 31 B. 3.14159 C. 36 D. 7 2. 已知a 、b 均为实数,且a >b,则下列结论不正确的是 ( )A. a +3>b +3B. a -3>b -3C. 3a >3bD. -3a >-3b3. 下列说法中正确的是 ( )A. 1的平方根是1B. 0没有平方根C. 0.01是0.1的一个平方根D. -1是1的一个平方根4. 方程组⎩⎨⎧=-=+02y x y x 的解是 ( ) A. ⎩⎨⎧==20y x B.⎩⎨⎧==02y x C.⎩⎨⎧==11y x D.⎩⎨⎧-=-=11y x5. 要反映某市一周内每天最高气温的变化情况,宜采用 ( )A. 条形统计图B. 扇形统计图C. 折线统计图D. 频数分布直方图6. 下列调查中,适合采用全面调查方式的是 ( )A. 调查某批次汽车的抗撞击能力B. 调查央视“新闻联播”的收视率C. 检测某城市的空气质量D. 了解某班学生“50米跑”的成绩7. 一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可分成 ( )A. 9组B. 10组C. 11组D. 12组8. 已知点P (4,-3),则点P 到y 轴的距离为 ( )A. 4B. -4C. 3D. -39. 如果点M (3,4-m)在第四象限内,那么m 的取值范围是 ( )A. m ≥4B. m >4C. m ≤4D. m <410. 如图1,下列条件中,可以判断AB//CD 的是 ( )A. ∠1=∠2B. ∠2=∠3C. ∠1=∠4D. ∠3=∠4图1二、填空题(每小题3分,共15分)11. 9的算术平方根是 .12. 若2a+6是非负数,则a 的取值范围是 .13. 已知⎩⎨⎧=-=31y x 是方程923=-y mx 的解,则m= .14. 如图2,直线AB 与直线CD 相交与点O ,OE ⊥AB ,垂足为O.若∠AOC=65°,则∠DOE 的度数是 .15. 在平面直角坐标系中,已知点O 坐标(0,0),A 点在x 轴上,且OA=5,则A 点坐标为 .三、解答题(每小题5分,共25分)16. 计算:2252383+--+17. 解不等式组⎪⎩⎪⎨⎧-≤--+x x x x 237121)1(325 ,并在数轴上表示出解集.18. 如图3,AD//BC ,∠D=100°,AC 平分∠BCD ,求∠DAC 的度数.图319. 在平面直角坐标系中,已知ABC 三个顶点的坐标分别为A (1,-4),B (5,-4),C (4,-1).(1)画出△ABC ;(2)将△ABC 先向上平移2个单位长度,再向左平移4个单位长度后得到△C B A ''',画出△C B A '''.20. 解方程组⎪⎩⎪⎨⎧-=++=++=-452304z y x z y x y x四、解答题(每小题8分,共40分)21. 某班一次数学测验成绩如下:63,84,91,53,69,81,57,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,88,85,67.(1)补充完整频数分布表:(2)补充完整图4中的频数分布直方图:(3)若80分以上(含80分)的成绩为优秀,那么该班这次数学测验的优秀率是多少?22. 如图5,已知长方形ABCD 四个顶点的坐标分别是A (2,-22),B (5,-22),C (5,-22),D (2,-2).(1)求四边形ABCD 的面积是多少?(2)将四边形ABCD 向上平移22个单位长度,求所得的四边形D C B A ''''的四个顶点的坐标.23. 甲、乙两人检修一条长270米的自来水管道,甲每小时比乙多检修10米,两人从管道两端同时开始检修,3小时完成任务.甲、乙两人每小时各检修多少米?24.如图6,点D、E、F分别在AB、BC、AC上,且DE//AC,EF//AB,下面写出了证明“∠A+∠B+∠C=180°的部分过程,请完成填空:∵DE//AC,EF//AB,()∴∠1=∠,∠3=∠.()∵EF//AB,∴∠2=∠.( )∵DE//AC,∴∠4=∠ .∴∠2=∠A. ()∵∠1+∠2+∠3=180,∴∠A+∠B+∠C=180.25.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠. 甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场优惠的条件是:每台优惠20%.(1)什么情况下到甲商场购买更优惠?(2)什么情况下到乙商场购买更优惠?(3)什么情况下两家商场的收费相同?东莞市2012-2013学年度第二学期教学质量自查七年级数学参考答案一、选择题三、解答题16. 解:原式=25232+--+ -----------------------------------------------3分=0 -----------------------------------------------------------------------------------5分17. 解:由①得:5.2->x ---------------------------------------------------------2分由②得:4≤x --------------------------------------------------------------------3分所以:45.2≤<-x ------------------------------------------------------------4分其解集在数轴上表示为:------------------------------------------5分18. 解:∵AD ∥BC ,∠D=100°∴∠BCD=180°-∠D=80°-----------------------------------------------------2分∵AC 平分∠BCD∴∠ACB=21∠BCD=40°-------------------------------------------------------4分∴∠DAC=∠ACB=40°----------------------------------------------------------5分19.(1) ------------------------------------------------------3分(2) ------------------------------------------------------5分20. 解:②×5-③得:1934=+y x ④----------------------------------------1分①×4-④得:1919-=-y ------------------------------------------------------2分 ∴1=y -------------------------------------------------------------------------------3分 将1=y 代入①得:4=x --------------------------------------------------------4分 将4=x ,1=y 代入②得:2-=z∴⎪⎩⎪⎨⎧-===214z y x-------------------------------------------------------------------------------5分 四、解答题21.(1)6,4-------------------------------------------------------------------------------4分(2)------------------------------------------------------6分(3)%50%10030411=⨯+答:该班这次数学测验的优秀率是50%-------------------------------------------------8分22.解:(1)AB=5-2=3,AD=2222=----------------------------------------2分 ∴四边形ABCD 的面积为:AB ×AD=23-----------------------------------------------4分(2)A ′(2, 0),B ′(5,0,)C ′(5,2),D ′(2,2) ----------------8分23.解:设甲每小时检修x 米,乙每小时检修y 米,根据题意得:--------------1分⎩⎨⎧+==+10270)(3y x y x -----------------------------------------------------------------------4分 解得:⎩⎨⎧==4050y x ------------------------------------------------------------------------------7分 答:甲每小时检修50米,乙每小时检修40米. -------------------------------------8分24.已知;------------------------------------------------------------------------------------ 1分C;------------------------------------------------------------------------------------- 2分B;-------------------------------------------------------------------------------------3分两直线平行,同位角相等;-----------------------------------------------------------------4分4;------------------------------------------------------------------------------------5分两直线平行,内错角相等;-------------------------------------------------------------6分A;-------------------------------------------------------------------------------------7分等量代换.-------------------------------------------------------------------------------------8分25.解:设购买电脑x台. -------------------------------------------------------------------- 1分(1)若到甲商场购买更优惠,则:6000+(1-25%)×6000(x-1)<(1-20%)×6000x,-----------------------2分解得:x>5,-----------------------------------------------------------------------------3分∴当购买电脑台数大于5时,甲商场购买更优惠;-----------------------------4分(2)若到乙商场购买更优惠,则:6000+(1-25%)×6000(x-1)>(1-20%)×6000x,解得:x<5,∴当购买电脑台数小于5时,乙商场购买更优惠;-----------------------------6分(3)若两家商场收费相同,则:6000+(1-25%)×6000(x-1)=(1-20%)×6000x,解得:x=5,∴当购买电脑5台时,两家商场收费相同.---------------------------------------8分。
