椭圆offset曲线的多项式逼近算法
常用函数的逼近和曲线拟合

常用函数的逼近和曲线拟合在数学中,函数逼近和曲线拟合都是常见的问题。
函数逼近是指找到一个已知函数,尽可能地接近另一个函数。
而曲线拟合则是给定一组数据点,找到一条曲线来描述这些数据点的分布。
本文将讨论常用的函数逼近和曲线拟合方法。
一、函数逼近1. 插值法插值法是最简单的函数逼近方法之一。
它的基本思想是:给定一组已知点,通过构造一个多项式,使得该多项式在这些点处的函数值与已知函数值相等。
插值法的优点是精度高,缺点是易产生龙格现象。
常用的插值多项式有拉格朗日插值多项式和牛顿插值多项式。
拉格朗日插值多项式的形式为:$f(x)=\sum_{i=0}^{n}y_{i}\prod_{j=i,j\neq i}^{n}\frac{x-x_{j}}{x_{i}-x_{j}}$其中,$x_{i}$是已知点的横坐标,$y_{i}$是已知点的纵坐标,$n$是已知点的数量。
牛顿插值多项式的形式为:$f(x)=\sum_{i=0}^{n}f[x_{0},x_{1},...,x_{i}]\prod_{j=0}^{i-1}(x-x_{j})$其中,$f[x_{0},x_{1},...,x_{i}]$是已知点$(x_{0},y_{0}),(x_{1},y_{1}),...,(x_{i},y_{i})$的差商。
2. 最小二乘法最小二乘法是一种常用的函数逼近方法。
它的基本思想是:给定一组数据点,找到一个函数,在这些数据点上的误差平方和最小。
通常采用线性模型,例如多项式模型、指数模型等。
最小二乘法的优点是适用性广泛,缺点是对于非线性模型要求比较高。
最小二乘法的一般形式为:$F(x)=\sum_{i=0}^{n}a_{i}\varphi_{i}(x)$其中,$a_{i}$是待求的系数,$\varphi_{i}(x)$是一组已知的基函数,$n$是基函数的数量。
最小二乘法的目标是使得$\sum_{i=1}^{m}[f(x_{i})-F(x_{i})]^{2}$最小,其中$m$是数据点的数量。
(整理)数值分析课件 第3章 函数逼近与曲线拟合

第三章 函数逼近与曲线拟合1 函数的逼近与基本概念1.1问题的提出多数计算机的硬件系统只提供加、减、乘、除四种算术运算指令,因此为了计算大多数有解析表达式的函数的值,必须产生可用四则运算进行计算的近似式,一般为多项式和有理分式函数.实际上,我们已经接触到两种逼近多项式,一种是泰乐多项式,一种是插值多项式.泰乐多项式是一种局部方法,误差分布不均匀,满足一定精度要求的泰乐多项式次数太高,不宜在计算机上直接使用.例如,设()f x 是[1,1]-上的光滑函数,它的Taylor 级数0()k k k f x a x ∞==∑,()(0)!k k f a k =在[1,1]-上收敛。
当此级数收敛比较快时,11()()()n n n n e x f x s x a x ++=-≈。
这个误差分布是不均匀的。
当0x =时,(0)0n e =,而x 离开零点增加时,()n e x 单调增加,在1x =±误差最大。
为了使[1,1]-的所有x 满足()()n f x s x ε-<,必须选取足够大的n ,这显然是不经济的。
插值函数出现的龙格现象表明,非节点处函数和它的插值多项式相差太大。
更重要的是,实际中通过观测得到的节点数据往往有各种误差,此时如果要求逼近函数过全部节点,相当于保留全部数据误差,这是不适宜的。
如图1所示,给出五个点上的实验测量数据,理论上的结果应该满足线性关系,即图1中的实线。
由于实验数据的误差太大,不能用过任意两点的直线逼近函数。
如果用过5个点的4次多项式逼近线性函数,显然误差会很大。
实验数据真函数插值多项式逼近精确的线性逼近图11.2范数与逼近一、线性空间及赋范线性空间要深入研究客观事物,不得不研究事物间的内在联系,给集合的元素之间赋予某种“确定关系”也正是这样的道理.数学上常把在各种集合中引入某些不同的确定关系称为赋予集合以某种空间结构,并将这样的集合称为空间.最常用的给集合赋予一种“加法”和“数乘”运算,使其构成线性空间.例如将所有实n 维数对组成的集合,按照“加法”和“数乘”运算构成实数域上的线性空间,记作n R ,称为n 维向量空间.类似地,对次数不超过n 的实系数多项式全体,按通常多项式与多项式加法及数与多项式乘法也构成数域R 上一个线性空间,用n H 表示,称为多项式空间.所有定义在[,]a b 上的连续函数集合,按函数加法和数与函数乘法构成数域R 上的线性空间,记作[,]C a b .类似地,记[,]p C a b 为具有p 阶连续导数的函数空间.在实数的计算问题中,对实数的大小、距离及误差界等是通过绝对值来度量的.实践中,我们常常会遇到对一般线性空间中的向量大小和向量之间的距离进行度量的问题,因此有必要在一般线性空间上,赋予“长度”结构,使线性空间成为赋范线性空间.定义1 设X 是数域K 上一个线性空间,在其上定义一个实值函数,即对于任意,x y X ∈及K α∈,有对应的实数x 和y ,满足下列条件(1) 正定性:0x ≥,而且0x =当且仅当0x =;(2) 齐次性:x x αα=;(3) 三角不等式:x y x y +≤+;称为X 上的范数,定义了范数的线性空间就称为赋范线性空间.以上三个条件刻划了“长度”、“大小”及“距离”的本质,因此称为范数公理.对n X 上的任一种范数,n X ∀∈x,y ,显然有±≥-x y x y .n R 上常用的几种范数有:(1) 向量的∞-范数:1max i i nx ∞≤≤=x(2) 向量的1-范数:11n i i x ==∑x(3) 向量的2-范数:12221()n i i x ==∑x (4) 向量的p -范数:11()n p pi p i x ==∑x其中[1,)p ∈∞,可以证明向量函数()p N x x ≡是nR 上向量的范数. 前三种范数是p -范数的特殊情况(lim p p ∞→∞=x x ).我们只需表明(1).事实上1111111max max max n n p pp p i i i i i n i n i n i i x x x x ≤≤≤≤≤≤==⎛⎫⎛⎫≤≤≤ ⎪ ⎪⎝⎭⎝⎭∑∑及max 1p →∞=,故由数学分析的夹逼定理有1l i m ma x i p p i nx ∞→∞≤≤==x x 。
椭圆曲线中的定点定值问题的四种方法

椭圆曲线中的定点定值问题的四种方法
椭圆曲线密码学是现代密码学领域中的一个重要分支,其核心是解决椭圆曲线上的定点定值问题。
本文将介绍椭圆曲线中的定点定值问题及其四种常用解决方法。
定点定值问题是指给定一个椭圆曲线上的点P和整数k,求kP 的值。
下面将介绍四种方法来解决这个问题:
1. 变形重复平方算法(Double-and-Add Algorithm):这是最简单和直观的方法,通过将k表示为二进制形式,并根据位的值来迭代地进行计算。
当某一位为1时,将点P加到结果上;当某一位为0时,将点P进行加法运算。
该算法的时间复杂度为O(log(k))。
2. NAF (Non-Adjacent Form)方法:在变形重复平方算法的基础上,在k表示为二进制时可以选择使用加1或减1的方式,使得连续1的位数尽可能少。
这样可以减少加法运算的次数,进而提高效率。
3. 有穷域上的运算法则:将椭圆曲线上的点坐标和系数限定在一个有限域中,通过定义该有限域上的加法和乘法运算法则来求解定点定值问题。
这种方法在实际应用中经常使用,可以利用有限域运算的高效性。
4. 同态映射方法:根据椭圆曲线的同态性质,将定点定值问题转化为其他更容易求解的问题,并利用同态映射的特性进行计算。
这种方法具有较高的复杂性和灵活性,适用于特定的情况。
通过掌握这四种方法,我们可以更好地理解和应用椭圆曲线密码学中的定点定值问题。
根据实际情况选择合适的方法可以提高计算效率和保证系统的安全性。
函数逼近的几种算法及其应用汇总

函数逼近的几种算法及其应用汇总函数逼近是数值计算中非常重要的技术之一,它主要用于用已知函数逼近未知函数,从而得到未知函数的一些近似值。
在实际应用中,函数逼近广泛用于数据拟合、插值、信号处理、图像处理等领域。
下面将介绍几种常用的函数逼近算法及其应用。
1. 最小二乘法(Least Square Method)最小二乘法将函数逼近问题转化为最小化离散数据与拟合函数之间的残差平方和的问题。
它在数据拟合和插值中应用广泛。
例如,最小二乘法可以用于拟合数据点,找出最佳拟合曲线;也可以用于信号处理中的滤波器设计。
2. 插值法(Interpolation)插值法旨在通过已知数据点之间的连线或曲线,来逼近未知函数在这些数据点上的取值。
常见的插值方法有拉格朗日插值、牛顿插值和分段线性插值等。
插值法在图像处理中广泛应用,例如可以通过已知的像素点来重构图像,提高图像的质量和分辨率。
3. 最小二乘曲线拟合(Least Square Curve Fitting)最小二乘曲线拟合是一种将渐近函数与离散数据拟合的方法,常见的函数包括多项式、指数函数、对数函数等。
最小二乘曲线拟合可以在一定程度上逼近原始数据,从而得到曲线的一些参数。
这种方法在数据分析和统计学中经常使用,在实际应用中可以拟合出模型参数,从而做出预测。
4. 正交多项式逼近(Orthogonal Polynomial Approximation)正交多项式逼近是一种通过正交多项式来逼近未知函数的方法。
正交多项式具有良好的性质,例如正交性和递推关系,因此可以用于高效地逼近函数。
常见的正交多项式包括勒让德多项式、拉盖尔多项式和切比雪夫多项式等。
正交多项式逼近广泛应用于数值计算和信号处理中,例如用于图像压缩和数据压缩。
5. 插值样条曲线(Interpolating Spline)插值样条曲线是将多个局部的多项式插值片段拼接在一起,从而逼近未知函数的方法。
插值样条曲线在实现光滑拟合的同时,还能逼近离散数据点。
Chebyshev多项式最佳一致逼近-最佳平方逼近
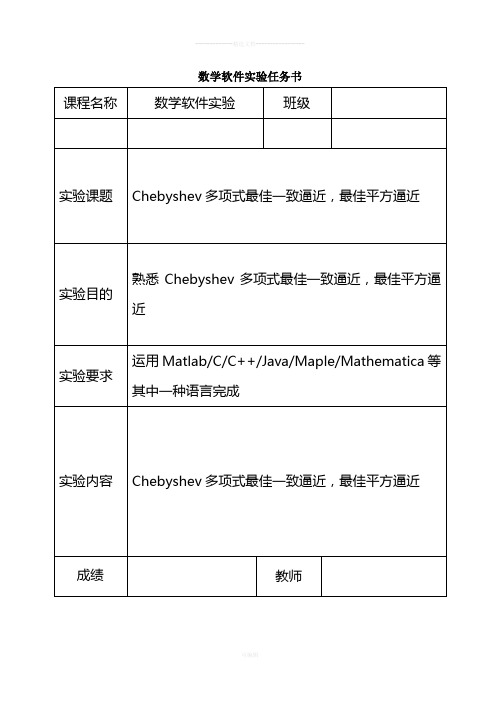
数学软件实验任务书实验1 Chebyshev 多项式最佳一致逼近1 实验原理设()f x 是定义在区间[,]a b 上的函数,寻求另一个构造简单,计算量小的函数()x ϕ来近似的代替()f x 的问题就是函数逼近问题。
通常我们会取一些线性无关的函数系来达到函数逼近的目的:对于给定的函数{()}j x ϕ,寻求函数0()()nj j j x c x ϕϕ==∑ 使()()0max lim n a x bf x x ϕ→∞<<-=的函数称为一致逼近。
使()()()0lim b pa n f x x W x dx ϕ→∞-=⎰ 的函数称为关于权()W x 的p L 逼近。
比较常用的p=2,称为平方逼近。
设()f x 是定义在区间[,]a b 上的函数,则任给定ε,存在一多项式P ε使不等式()f x P εε-<对所有[,]x a b ∈一致成立()()max n a x b f x P x ≤≤-则()n P x 称为()f x 的n 次最佳一致逼近多项式。
求最佳一次逼近多项式的一种方法是可以采用Chebyshev 节点插值,Chebyshev 节点为 1(21)[()cos _],0,1,2,,22(1)j j x b a b a j n n +=-++=+L 2 实验数据求函数()x f x xe =在区间[6,6]上的3,5和12次近似最佳逼近多项式(Chebyshev 插值多项式)3 实验程序function g=cheby(f,n,a,b)for j=0:ntemp1=(j*2+1)*pi/2/(n+1);temp2=(b-a)*cos(temp1)+b+a;temp3(j+1)=temp2/2;endx=temp3;y=f(x);g=lag(x,y);function s=lag(x,y,t)syms p;n=length(x);s=0;for(k=1:n)la=y(k);%构造基函数for(j=1:k-1)la=la*(p-x(j))/(x(k)-x(j)); end;for(j=k+1:n)la=la*(p-x(j))/(x(k)-x(j)); end;s=s+la;simplify(s);endif(nargin==2)s=subs(s,'p','x');s=collect(s);s=vpa(s,4);elsem=length(t);for i=1:mtemp(i)=subs(s,'p',t(i));ends=temp;endf=inline('x.*exp(x)','x');z1=cheby(f,3,-6,6)z2=cheby(f,5,-6,6)z3=cheby(f,12,-6,6)%作出逼近函数图形subplot(2,2,1),ezplot('x*exp(x)'),grid subplot(2,2,2),ezplot(z1),grid subplot(2,2,3),ezplot(z2),grid subplot(2,2,4),ezplot(z3),grid%改变背景为白色set(gcf,'color','white')4 实验结果z1 =-133.0+4.822*x^3+27.38*x^2-20.40*xz2 =.2001*x^5+1.359*x^4-2.020*x^3-18.56*x^2+6.126*x+40.2 5z3 =-.2405e-16+.5187e-7*x^12+.6439e-6*x^11+.1420e-5*x^1 0+.6201e-5*x^9+.2287e-3*x^8+.1813e-2*x^7+.8007e-2*x^6+.3709e-1*x^5+.1682*x^4+.520 9*x^3+.9981*x^2+.9729*x实验2 Chebyshev最佳平方逼近1 实验数据的5 次最佳求函数()arccos,(11)=-≤≤关于权函数f x x x平方逼近。
第三章 参数多项式的插值与逼近

第三章 参数多项式的插值与逼近2009年8月29日10时35分 1本章内容•几何不变性与参数变换•参数多项式插值与逼近的基本概念•参数多项式插值曲线与逼近曲线•张量积曲面•参数双三次曲面片2009年8月29日10时35分 22009年8月29日10时35分 3第一节 几何不变性和参数变换 • 一、几何不变性:1、定义:指曲线曲面不依赖于坐标系的 选择,或者说在旋转与平移变化下不变 的性质。
2、曲线曲面的基表示: 0 n i i i P a j = = å r r 其中: 为矢量系数,修改它可以改变曲线曲面的形状i a r i j 为单参数(表示曲线时)或双参数(表示曲面时) 的基函数,决定曲线曲面的几何性质2009年8月29日10时35分 43、基表示的分类:(1)规范基表示:即满足Cauchy 条件 也称权性。
这种表示下,曲线 (面)上的点是矢量系数的一个重心组 合,重心坐标是基函数。
其中 一、几何不变性:0 1n i i j = º å 我们常见的线性插值就是一种规范基表示。
(2)部分规范基表示:即满足 0 1,0 ki i k n j = º£< å 如: 01 () p u a a u =+ r r r 0 1j =一、几何不变性:(3)非规范基表示:除规范基表示和部分规范基表示以外的其它基表示。
4、基表示与几何不变性的关系:曲线曲面的规范基表示具有仿射不变性, 其余两种只具有几何不变性。
5、几何不变性的意义: (1)方便局部坐标与整体坐标之间的转换;(2)便于平移和旋转变换;(3)节省了计算量。
2009年8月29日10时35分 5• 1、概述• 曲线的参数域总是有界的。
• 曲线的参数可能有某种几何意义,也可能没有。
• 曲线的参数化:即确定曲线上的点与参数域中的参数值之间的一种对应关系。
• 这种对应关系可以是一一对应的,也可以不是一一对应的,后者称为奇点(Singularpoint),如曲线的自交点。
函数逼近的几种算法及其应用

函数逼近的几种算法及其应用函数逼近是数值计算中的一种重要技术,用于在给定的函数空间中找到与目标函数最相近的函数。
函数逼近算法可以在不知道目标函数解析表达式的情况下,通过对给定数据进行处理来逼近目标函数的结果。
这篇文章将介绍几种常见的函数逼近算法及其应用。
1.多项式逼近:多项式逼近是一种利用多项式函数逼近目标函数的方法。
多项式逼近算法有很多种,常见的有最小二乘法、拉格朗日插值法和牛顿插值法等。
多项式逼近广泛应用于数据拟合、信号处理和图像处理等领域。
最小二乘法是一种通过最小化实际观测值与多项式模型之间的差异来确定多项式系数的方法。
最小二乘法可以用于拟合非线性和线性函数。
拉格朗日插值法和牛顿插值法是通过插值多项式来逼近目标函数的方法,可以用于填充缺失数据或者生成曲线过程中的中间点。
2.三角函数逼近:三角函数逼近是一种利用三角函数来逼近目标函数的方法。
三角函数逼近算法有傅里叶级数逼近和小波变换等。
傅里叶级数逼近是一种利用三角函数的线性组合来逼近目标函数的方法。
这种方法广泛应用于信号处理、图像处理和数学建模等领域。
小波变换是一种通过特定的基函数来逼近目标函数的方法。
小波变换可以用于信号去噪、图像压缩和模式识别等应用。
3.插值逼近:插值逼近是一种通过已知数据点在给定区间内的函数值来确定目标函数的方法。
常见的插值逼近方法有拉格朗日插值法、牛顿插值法和差值多项式法等。
插值逼近广泛应用于任何需要通过已知数据点来逼近目标函数的领域。
在实际应用中,函数逼近常用于数据分析和模型构建。
例如,在金融领域,函数逼近可以用于确定股票价格走势的模型和预测。
在工程领域,函数逼近可以用于建立复杂系统的模型和优化控制。
在计算机图形学领域,函数逼近可以用于生成真实感图像和动画。
总结起来,函数逼近是一种重要的数值计算技术,有多种算法可供选择。
多项式逼近、三角函数逼近和插值逼近是常见的函数逼近算法。
函数逼近广泛应用于数据分析、模型构建和优化控制等领域,对于解决实际问题具有重要作用。
多项式逼近和插值

多项式逼近和插值多项式逼近和插值是计算数学中的两个基本概念,它们是求一定准确度下函数近似值所必须采用的数值方法。
多项式逼近是指用低阶多项式逼近原函数,插值是利用已知数据点在插值区间内构造一个多项式函数,使得该函数在已知数据点处等于原函数。
它们的应用范围很广,包括科学工程计算、图像处理、信号处理等领域。
下面介绍它们的原理和应用。
一、多项式逼近当我们需要用低阶多项式逼近原函数时,可以采用最小二乘法。
最小二乘法是一种在数据拟合中广泛使用的方法,通过将误差的平方和最小化来确定函数的系数。
假设给定函数$f(x)$及其在$n+1$个采样点$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$处的值,我们要用一个$m$次多项式$p_m(x)$去逼近$f(x)$。
我们可以将$p_m(x)$表示为$p_m(x)=a_0 + a_1x + a_2x^2 + ... + a_mx^m$,则函数的误差可以表示为$E(a_0,a_1,...,a_m)=\sum_{i=0}^n [f(x_i)-p_m(x_i)]^2$,通过最小化误差函数来确定多项式系数$a_0,a_1,...,a_m$。
最小二乘法可以用线性代数和矩阵计算方法求解。
最小二乘逼近是一种非常有效的数据拟合方法,并且有许多实际应用。
例如,在金融领域中,我们可以用该方法来估计股票期权价格;在图像处理中,我们可以用该方法实现图片的平滑处理和降噪处理。
二、插值插值是利用已知数据点构造一个多项式函数,使得该函数在已知数据点处等于原函数。
插值法可分为以下两种情况:一是利用拉格朗日插值公式,将函数表示为已知节点函数的线性组合;二是利用牛顿插值公式,基于差商的思想构造插值多项式。
两种方法的计算效果是相同的,但在计算机实现过程中,两者有些微小的差别。
在实际应用中,插值方法常常用于图像处理、信号处理、数值微分和数值积分等问题,例如,在金融领域中,也可以利用插值方法对期权的未来价格进行预测。
函数逼近的几种算法及其应用汇总

函数逼近的几种算法及其应用汇总
一、函数逼近的几种算法
1、最小二乘法
最小二乘法是一种基于线性模型的函数逼近算法,它的基本假设是拟合函数的形状可以用线性模型表示,且被拟合数据存在一定的噪声存在,最小二乘法的核心思想就是最小化残差(拟合数据与模型之间的偏差)的平方和来寻找最佳拟合参数。
2、Kriging
Kriging(克里金插值)是一种基于空间相关数据的空间插值算法,它会根据空间相关性分析,通过构建模型,拟合、估计和预测空间数据之间的关系,从而实现函数逼近。
3、K近邻算法
K近邻(K Nearest Neighbors Algorithm)是一种基于实例学习的分类算法,它通过计算测试实例与训练实例之间的距离,来决定其所属的类别。
K近邻算法也可以用于函数逼近,这种方法无需训练阶段,可以快速的拟合不同的函数,而且拟合函数的过程中也不需要优化参数。
4、神经网络
神经网络是一类用于函数逼近的算法,它通过模拟人脑神经网络的连接模式,在一系列训练数据的基础上,得到一些函数的参数,从而实现函数的拟合和预测。
二、函数逼近算法的应用
1、多元线性回归
多元线性回归利用最小二乘法,可以对多元关系进行拟合。
函数逼近方法

函数逼近方法函数逼近方法是一种数学工具,其作用是逼近出一个较为接近于真实情况的函数。
本文将探讨函数逼近方法的定义、原理、应用及优缺点等相关内容。
一、定义函数逼近方法是指用一组建立在确定的样本点上的函数,去逼近一个函数,使得从逼近函数到被逼近函数的误差最小,以达到精确求解的目的。
二、原理函数逼近方法的原理是通过选取一组基函数,利用线性组合的方式来逼近目标函数或函数离散点数据。
其中,基函数的选择对于逼近结果至关重要。
在实际应用中,可以根据问题的性质、数据的分布等因素来选择基函数。
三、应用函数逼近方法在科学研究和工程实践中有着广泛的应用,如图像处理、信号处理、数值计算等领域。
其中,最常见的方法是多项式逼近方法和小波函数逼近方法。
多项式逼近方法是指用高次多项式去近似目标函数的方法,其优点是简单易用、计算速度快,但是缺点是容易产生过拟合现象,且对于一些非线性的函数逼近效果不佳。
小波函数逼近方法是目前应用最广泛的函数逼近方法,其优点是适用于不规则数据、能够有效地处理噪声数据等,并且容易实现。
但是,小波函数逼近方法对于数据的选取和基函数的选择要求较高,且相关算法较为复杂,需要一定的数学基础和算法实现能力。
四、优缺点函数逼近方法的优点是能够处理各种类型的数据,如连续、离散、噪音等,适用性强。
同时,函数逼近方法对于数据分布的要求较低,可以处理不规则数据。
此外,函数逼近方法可以建立模型,进而进行模拟和预测。
函数逼近方法的缺点是容易产生过拟合现象,即模型过于复杂,对训练数据可以完美拟合,但是对测试数据的适应性不强。
此外,函数逼近方法的算法较为复杂,需要一定的数学基础和计算机实现能力。
总之,函数逼近方法在科学研究和工程实践中发挥着重要的作用,对于数据处理和模型建立具有不可或缺的作用。
在应用时,需要根据问题需要选择合适的函数逼近方法,以达到最佳的逼近效果。
f(x)的一次最佳逼近多项式

标题:f(x)的一次最佳逼近多项式:从简到繁,由浅入深的探讨当谈及函数f(x)的一次最佳逼近多项式时,我们首先需要了解什么是一次最佳逼近多项式以及它的应用和意义。
随着人们对数学的深入探索,这一概念在实际问题中的应用日益广泛,对于我们深入理解这一主题,探究其背后的深层含义有着重要的意义。
1. 一次最佳逼近多项式的定义在数学中,一次最佳逼近多项式指的是在一定范围内,通过一次多项式来最佳逼近给定函数f(x)。
这里的“最佳”指的是在这一范围内,该一次多项式与给定函数的误差最小,或者说残差最小。
这一概念的提出源自对函数逼近的需求,通过使用最佳逼近多项式能够更好地对函数进行估计和逼近,具有广泛的理论和实际应用意义。
2. 一次最佳逼近多项式的计算一次最佳逼近多项式的计算是一个经典的数学问题,涉及到最小二乘法、线性代数等多个数学领域的知识。
在实际求解中,可以通过拉格朗日插值法、最小二乘法或者直接求解线性方程组等方法来得到一次最佳逼近多项式。
这些方法各有特点,但都能够有效地逼近给定函数,为实际问题的求解提供了重要的数学工具。
3. 一次最佳逼近多项式的应用一次最佳逼近多项式在实际中有着广泛的应用,尤其在数据处理、信号处理、曲线拟合等领域有着重要的地位。
在经济学中,通过一次最佳逼近多项式能够更好地对经济数据进行趋势预测和分析;在工程中,能够通过一次最佳逼近多项式来对信号进行处理和分析。
这些应用都彰显了一次最佳逼近多项式在实际中的价值和意义。
回顾以上内容,我们对f(x)的一次最佳逼近多项式有了初步的了解,从其定义、计算方法到应用场景我们都有了一定的认识。
然而,我们接下来还需要更深入地探讨这一主题,理解其中的数学原理、背后的逻辑和应用的实际意义。
4. 个人观点和理解作为文章写手,我对f(x)的一次最佳逼近多项式有着自己的理解和观点。
我认为,一次最佳逼近多项式的研究不仅仅是为了得到一个较好的逼近多项式,更重要的是通过对逼近过程中的误差和残差的分析,揭示函数本身的性质和规律。
函数逼近方法

函数逼近方法一、概述函数逼近方法是一种数学工具,用于通过已知数据点的集合来估计或近似出一条连续函数的近似函数。
它在各个领域都有广泛的应用,比如数值计算、统计学、机器学习和信号处理等。
通过函数逼近方法,我们可以在缺少完整数据的情况下对函数的行为进行研究和预测。
二、插值法插值法是函数逼近方法中最常见的一种方法,它基于已知点的函数值,构造出一个多项式函数来逼近原函数。
插值法的基本思想是通过已知点之间的连线或曲线来构造一个连续的函数。
常见的插值方法有拉格朗日插值和牛顿插值等。
2.1 拉格朗日插值拉格朗日插值是一种通过利用拉格朗日基函数构造插值多项式的方法。
给定一个已知函数的离散采样点集合,拉格朗日插值的目标是构造一个多项式函数,该函数在已知点上的函数值等于已知函数在相应点上的函数值。
拉格朗日插值多项式的形式如下:L(x)=∑y ini=0∏x−x jx i−x j nj=0,j≠i其中,y i表示已知点的函数值,x i表示已知点的横坐标。
2.2 牛顿插值牛顿插值是另一种常见的插值方法,它利用差商的概念构造出一个多项式函数。
牛顿插值的优势在于可以递归地计算插值多项式,而不需要重新计算整个多项式。
牛顿插值多项式的形式如下:N(x)=f(x0)+∑[∏(x−x j)i−1j=0]ni=1f[x0,x1,…,x i]其中,f(x0)表示已知点的函数值,f[x0,x1,…,x i]表示差商。
三、最小二乘法最小二乘法是一种通过最小化误差平方和来逼近函数的方法。
最小二乘法的基本思想是找到一个函数的近似函数,使得所有已知数据点到近似函数的距离的平方和最小。
3.1 线性最小二乘法线性最小二乘法是最简单的一种最小二乘逼近方法,它假设要逼近的函数是一个线性函数。
给定一组已知数据点(x i,y i),其中x i为自变量,y i为因变量,线性最小二乘法的目标是找到一个形如y=ax+b的线性函数,使得所有已知数据点到该直线的距离的平方和最小。
函数逼近论方法

函数逼近论方法函数逼近论方法是数学分析中一种重要的方法,其主要应用于函数逼近和函数逼近的误差分析。
它是一种通过一组已知的函数来逼近一个未知的函数,并通过误差分析来确定逼近的精度和可行性的方法。
函数逼近论方法可以分为两种基本类型:插值法和最小二乘法。
插值法是通过已知的数据点去推导出未知函数,而最小二乘法则是通过已知的数据点去求解一个最优的函数逼近问题。
在插值法中,通过已知的数据点去推导出未知函数的形式,通常可以使用拉格朗日插值法或牛顿插值法。
拉格朗日插值法是通过一个多项式去逼近未知函数,这个多项式的系数可以通过已知的数据点来确定;牛顿插值法则是通过多个插值点的差商来构造一个插值多项式。
这两种方法的优缺点不同,适用于不同的情况。
例如,拉格朗日插值法的计算量较小,但插值多项式次数较高;而牛顿插值法的计算量较大,但插值多项式次数较低。
在最小二乘法中,通过已知的数据点去求解一个最优的函数逼近问题,通常可以使用最小二乘多项式逼近法或最小二乘样条逼近法。
最小二乘多项式逼近法是通过一个多项式去逼近未知函数,并使其在已知数据点处的误差平方和最小化;最小二乘样条逼近法则是通过构造一个分段多项式的组合,使其在已知数据点处的误差平方和最小化。
这两种方法的优缺点也各不相同,适用于不同的情况。
例如,最小二乘多项式逼近法适合于数据点较少的情况,而最小二乘样条逼近法则适合于数据点较多的情况。
除了插值法和最小二乘法之外,还有其他的函数逼近方法,例如曲线拟合法和逆问题法等。
曲线拟合法是通过已知的数据点去拟合一个曲线,可以使用多项式拟合、指数拟合、对数拟合等方法;逆问题法则是通过已知的数据点和一个模型,去求解一个逆问题,例如反演地震波形、恢复图像等。
函数逼近论方法在数学分析中是一种非常重要的方法,它可以通过已知的数据点去逼近一个未知的函数,并通过误差分析来确定逼近的精度和可行性。
在实际应用中,我们需要根据具体的问题选择适当的函数逼近方法,以达到最优的逼近效果。
椭圆曲线点乘计算复杂度 多项式

椭圆曲线点乘计算复杂度多项式椭圆曲线点乘是一种在密码学和数论中广泛应用的计算方法。
它涉及到椭圆曲线上的数学运算,通过迭代相加点的方式实现数的倍增运算。
在这篇文章中,我们将详细介绍椭圆曲线点乘的计算复杂度,并从多项式的角度解释其运算过程。
首先,让我们回顾一下椭圆曲线的基本概念。
椭圆曲线是由一组满足特定方程的点构成的集合。
这个方程通常被写为y^2 = x^3 + ax + b,其中a和b是给定的常数。
椭圆曲线不仅具有美丽的几何性质,还具有一些独特的数学特征,这使得它们成为密码学领域中关键的资源。
在椭圆曲线上进行点乘运算时,首先需要选择一个基点(也称为生成点)。
基点是一个已知的椭圆曲线上的点,它的坐标值被事先选定,并且是不变的。
接下来,通过迭代相加点的方式,可以将基点与自身相加多次,从而得到所需的倍增运算结果。
椭圆曲线点乘的计算复杂度可以通过多项式运算的角度来解释。
通常情况下,我们用n来表示点乘的倍数,例如2倍、3倍等。
假设点乘的输入为n个二进制位,那么基于传统的模幂算法,计算一个点乘运算的时间复杂度约为O(n^3)。
这是因为在每一位上都需要进行一次乘法和一次取模运算,总共需要进行n次这样的运算。
但是,通过一些优化技术,可以将椭圆曲线点乘的计算复杂度降低到O(n^2)甚至更低。
其中最常用的优化方法是使用加法链技术。
加法链可以将点乘过程划分为若干个小的步骤,通过预先计算不同的倍数来减少整个运算过程中需要进行的乘法和取模运算次数。
这样一来,点乘运算的复杂度就可以显著降低。
另一种常见的优化方法是使用Montgomery曲线。
Montgomery曲线是一种特殊形式的椭圆曲线,它具有一些特殊的数学属性,能够加速点乘运算。
通过将标准椭圆曲线转化为Montgomery曲线,可以利用其特殊的加法和倍乘运算规则,从而加快点乘运算的速度。
总结起来,椭圆曲线点乘是一种重要的计算方法,在密码学和数论中广泛应用。
它通过迭代相加点的方式实现数的倍增运算,可以通过多项式运算的角度来解释其计算复杂度。
函数逼近使用多项式和三角函数逼近函数

函数逼近使用多项式和三角函数逼近函数函数逼近是数学中一个重要的概念,它允许我们使用简单的数学模型来近似更加复杂的函数。
在函数逼近中,多项式和三角函数是两种常见的逼近方法。
本文将介绍多项式和三角函数逼近函数的相关概念和应用。
一、多项式逼近函数多项式逼近是将给定的函数用多项式函数来近似的过程。
多项式逼近可通过拉格朗日插值法、牛顿插值法以及最小二乘法等方法实现。
这些方法都是通过在给定的区间内找到合适的多项式函数,使其与待逼近函数之间的误差最小化。
在拉格朗日插值法中,我们通过在给定的数据点上构造拉格朗日多项式,来逼近待求函数。
拉格朗日插值法的优点在于其简单易理解,但是在处理大规模数据时,计算量较大。
因此,牛顿插值法应运而生,它通过使用差商来构造逼近多项式,计算效率更高。
另一种常用的多项式逼近方法是最小二乘法。
最小二乘法通过将待逼近函数的残差平方和最小化来找到最佳的逼近多项式。
最小二乘法的优点在于能够处理一些非线性问题,并且具有较好的稳定性和数值精度。
二、三角函数逼近函数三角函数逼近是使用正弦函数和余弦函数来近似给定函数的过程。
正弦函数和余弦函数是周期性函数,具有良好的周期性特征,因此在一定范围内可以较好地逼近一些周期性函数。
在三角函数逼近中,我们通常使用傅里叶级数来表示待逼近函数。
傅里叶级数是将函数表示为一系列正弦函数和余弦函数的线性组合。
通过调整不同频率的正弦函数和余弦函数的系数,可以逐渐逼近待求函数。
三、多项式逼近与三角函数逼近的比较多项式逼近和三角函数逼近都是函数逼近的有效方法,但适用于不同的函数类型和问题。
在选择逼近方法时,需要根据问题的特点和需求做出明智的选择。
多项式逼近适用于大多数常见的函数类型,不受函数的周期性特征限制。
它可以逼近非周期性函数以及周期性函数,对于一些不规则的散点数据,多项式逼近也有很好的表现。
三角函数逼近更适用于一些周期性函数的逼近问题。
正弦函数和余弦函数作为周期性函数,可以很好地逼近一些展现出明显周期性特征的函数。
多项式逼近与莫耳多项式

多项式逼近与莫耳多项式多项式逼近是数学分析中的一种重要方法,它的基本思想是用最简单的多项式函数来逼近复杂的函数,并达到一定的精度要求。
本文将从多项式逼近的基本思想出发,介绍其应用和发展,并着重介绍莫耳多项式及其在多项式逼近中的应用。
一、多项式逼近基本思想在实际问题中,我们常常需要用简单的函数来近似复杂的函数,以便计算机运算。
多项式函数是常用的一种逼近函数,其形式为:$$ f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n $$ 我们的目标是要找到一组多项式系数 $a_0,a_1,\cdots,a_n$,使得多项式函数 $f(x)$ 能够很好地逼近原函数。
为了实现这个目标,我们需要确定一些参考点,然后使用这些参考点构建一个多项式函数,再通过调整系数的方法来逼近原函数。
具体地说,我们可以在 $n+1$ 个点 $\{x_0,x_1,\cdots,x_n\}$ 处采样原函数 $f(x)$,然后在这些采样点处进行多项式逼近。
采样点的数量和位置可以根据受逼近函数的性质和要求来调整。
通常情况下,采样点的数量越多,逼近精度就越高。
在实际应用中,我们常常采用均匀采样或者一些特殊的采样方法(如Chebyshev节点)。
然后,我们需要构造一个度数不超过$n$ 的多项式函数$P(x)$,使得它在采样点处的值和原函数在采样点处的值相等。
一种常见的方式是使用拉格朗日插值多项式,即:$$ P(x)=\sum_{i=0}^nf(x_i)l_i(x) $$ 其中,$l_i(x)=\prod_{j=0,j\neq i}^n\frac{x-x_j}{x_i-x_j}$ 是拉格朗日插值多项式中的基函数。
通过这种方式,我们就能够得到一个最简单的多项式函数 $P(x)$,使得它在采样点处的值和原函数在采样点处的值相等。
最后,我们需要通过调整多项式系数来提高逼近精度。
这可以通过构造误差函数来实现,即:$$ E(x)=f(x)-P(x) $$ 我们的目标是使得误差函数的2-范数尽可能小,即:$$ \|E\|_2=\sqrt{\int_a^bE(x)^2dx} $$ 这可以通过牛顿迭代法或者其他优化方法来实现。
椭圆曲线的Bézier多项式逼近

椭圆曲线的Bézier多项式逼近王珺【期刊名称】《巢湖学院学报》【年(卷),期】2013(000)003【摘要】椭圆曲线是计算机辅助几何设计中基本且重要的曲线。
本文首先利用Tchebyshev多项式去逼近椭圆,再在此基础上得到插值椭圆首、末端点的n次Bézier多项式逼近。
该算法可以逼近整椭圆,而且适合圆的逼近。
% Elliptic curve is a basic and important curve in the computer-aided geometric design. This paper uses Tchebyshev polynomial to approximate the elliptic curve, and a Bézier curve is presented to approximate ellipse, which interpolates first and the end point of ellipse. This algorithm can approximate the whole ellipse and circle.【总页数】4页(P1-4)【作者】王珺【作者单位】巢湖学院数学系,安徽巢湖 238000【正文语种】中文【中图分类】O24【相关文献】1.有理Bézier曲线的多项式逼近新方法 [J], 成敏;王国瑾2.Bézier曲线的等距曲线的同次多项式逼近 [J], 王珺;张江平3.椭圆offset曲线的多项式逼近算法 [J], 刘续征;雍俊海;郑国勤;孙家广4.椭圆曲线的带调节参数的Bézier曲线逼近 [J], 王晶昕;牛鑫5.一类有理Bézier曲线及其求积求导的多项式逼近 [J], 王国瑾; 胡倩倩因版权原因,仅展示原文概要,查看原文内容请购买。
多元连续函数的多项式逼近

多元连续函数的多项式逼近
多项式逼近是一种基于最小二乘拟合的数值分析算法,可用来进行多元连续函
数的拟合和估计。
它能够有效地分析大量样本数据,从而获得函数模型,并得到函数形式表示中的各项系数。
因此,多项式逼近可用于统计分析、曲线拟合,以及机器学习的多元函数建模等场景中。
传统上,多项式逼近主要分为一阶和二阶多项式逼近。
一阶多项式逼近是指将
多元函数逼近为一次函数的过程,其中多元函数只有一阶项,而不包括二阶及以上的项。
而二阶多项式逼近则是将多元函数逼近为二次函数的过程,其中多元函数除一阶项外,还包括二阶以及以上项。
在数据挖掘领域,多项式逼近在多元函数建模中被普遍应用,尤其是用于拟合
具有非线性特性的数据。
这种算法能够从数据中捕捉局部变化,并有效地拟合复杂的数据关系,以获得更加准确的数学模型。
同时,多项式逼近也有利于提升模型的准确性和可靠性,有助于进一步提高模型的预测效率。
此外,多项式逼近还可以用于解决多元非线性函数优化问题,即通过多项式逼
近来求函数的最优解。
通过该方法,可以将极端复杂的函数拆分为相对简单的模型,从而减少优化过程当中的计算复杂性。
总的来说,多项式逼近是一种非常重要的数值分析算法,可用于多元连续函数
的拟合和估计,在数据挖掘领域有着广泛的应用。
未来,随着数据挖掘技术的不断发展,多项式逼近在优化问题中的应用也将受到更多关注,并有望带来更多的发现。
第四章 多项式插值与函数逼近1

问题:
插值类型:
代数插值: 为多项式函数类 有理插值: 为有理分式函数类 三角插值: 为三角函数类
是否存在唯一? 误差估计?
如何构造?
插值节点越多越好?
代数插值存在唯一??
( x) a0 a1 x a2 x2 an xn , ai R 设
满足插值条件: ( xi ) f ( xi ) i 0,1, 2,, n
希望找到li(x),i = 0, …, n 使得 li(xj)=ij;然后令
Pn ( x )
l (x) y
i0 i
i
,则显然有Pn(xi) = yi 。
n
下面构造li(x) : 每个 li(x) 有 n 个根 x0 … xi-1 、 xi+1 … xn
li ( x ) Ci ( x x0 )( x xi 1 )( x xi 1 )( x xn ) C i ( x x j )
i 0 n
多项式,其中 q( x ) 可以是任意多项式。
(3)误差估计
f ( n1) ( ) Rn ( x ) f ( x ) Ln ( x ) n1 ( x ) ( n 1)!
(4)无承袭性,当插值节点增加时,拉氏基函数需要 重新计算。
(5) 给定 xi = i +1, i = 0, 1, 2, 3, 4, 5. 下面哪个是 l2(x)的图像?
g
( n1)
(t )在区间(a,b)上至少有1个零点
故g
( n1)
( ) f
( n1)
( ) (n 1)! k ( x ) 0
f ( n1) ( ) k( x) ( n 1)!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘 要 首 先 对 椭 圆进 行 必 要 的 细 分 , 后 将 每 一 段 椭 圆弧 的 of t 线 用 一 段 B z r 线 逼 近 , 而 得 到 G 然 fe曲 s 6i 曲 e 进 连 续 的分 段 B z r 线 作 为 椭 圆 of t i 曲 e f e 曲线 的近 似 . s 该算 法一 方 面 给 出 了计 算 B z r 线 段 控 制 顶 点 的 表 达 形 式 , 算 简 6i 曲 e 计 单 ; 一 方 面 对 of t 另 f e 曲线 的逼 近误 差 给 出 了 整体 估 计 , 且 利 用 整 体误 差估 计 决 定 细 分 椭 圆 的 段 数 , 造 了 满 足 给 s 并 构
po oe r p s d.Afe o e es r a tto t r s me n c s a y p riin,t e o fe u v f e c l p i r s a pr xi t d by a c b c h fs tc r e o a h el tc a c i p o ma e u i i B6 irs g n .And t n t o eo fe u v t ze e me t he hewh l fs tc r ewih G i b an d.On o e h n so t i e n a d,t l o ihm ssmp e heag rt i i l t ac lt e a s h o r o nt ft eB ̄ irs g n a e e pr se x lcty.On t eot e a d, o c lu a e b c u e t e c ntol i so h ze e me tc n b x e s d e p iil p h h rh n t e g o a ro si to o h l o ih i ie h l b le r r e tma in f r t e ag rt m s gv n.Th r o s i ai n c n b s d t e e mi e t e e r r e tm to a e u e o d tr n he nu e ft e s gme t n t a tton o h lis mb ro h e n si he p r ii ft e el e. p
维普资讯
第 1 卷 第 1 期 8 0
20 0 6年 1 0月
计算 机辅 助设计 与 图形学 学报
J OURNAL OF C OM P UTE AI D S GN & COM P R— DE DE I UTER GRA PHI CS
v 0 . 8.NO. 0 11 1 Oc .,20 t 06
Ke r s o fe u v y wo d fs tc r e;el s li e;B ̄ irc r e;Ha s o f it n e p ze u v u d rfd sa c
圆弧 ) 其 of t , f e 曲线 分别 是 直线 和 圆 弧外 , 他 类 s 其
0 引
Ab t a t s r c
An ag ih t p r xi t fs t f elp e c r e y pic wie u i B6 ir s g n s i lort m o a p o ma e o fe s o l s u v s b e e s c b c i ze e me t s
定容 差 的 近似 曲线 . 关键 词 of t f e 曲线 ; 圆 ; 6i 曲线 ; a s of 距 离 s 椭 Bz r e H ud r f
中 图 法分 类 号 TP 9 31
A l no i lApp o i a i n Al o ih f r Ca c l tn f e s o lp e Cu v s Po y m a r x m to g r t m o l u a i g Of s t fEli s r e
L uXu h n 12 Yo g J n a Z e g Gu qn ) S nJa uห้องสมุดไป่ตู้n ) i z e g , n u h i ) h n o i u ig a g ,
( c o l f& ̄ w r ,T i g u ies y,B i n 1 0 8 ) S h o o f a e s h a Unv ri t n t e ig j 0 04 ( e a t n C mp t in e n eh ooy,T i g u i ri D p rme t f o o ue S e c a d T c n l rc g s h a Unv s y,B i n 1 0 8 ) n e t e ig 3 00 4
言
型 曲线 的 of t f e 曲线 甚至不 能用 有理 曲线来 精 确 表 s 示. 于 of t 对 f e 曲线 可 以 精确 表 示 有 理 曲线 的 一 类 s
曲线 的 of t f e 曲线被 广泛 应 用在 数 据 加工 中的 s
椭 圆 ofe 曲线 的 多项 式 逼 近算 法 fst
刘续征 雍俊海" ’ 郑国勤D 孙家广
”( 清华 大 学 软 件 学 院 北 京 10 8 ) 0 0 4 ( 清华 大 学 计 算 机 科 学 与 技 术 系 北京 10 8 ) 0 0 4
(i x0 @ ma s t n h a e u c ) 1—z2 u i . ig u .d .n l s
