2020-2021学年江苏省盐城市盐城市一中、大丰高级中学等四校高二上学期期终考试数学试题及答案
江苏省盐城市盐城市一中、大丰高级中学等四校2020-2021学年高二上学期期末英语试题 含解析

2020-2021学年第一学期高二年级期终考试英语试题第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分;满分7.5分)听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What's the time now?A. 8:30.B. 7:55.C. 8:35.2.Why does the woman look sad?A. She did badly in the exams.B. She worries about her coming tests.C. She is ill.3.What do we learn about the taxi driver?A. He drove too fast and crashed into a truck.B. He turned suddenly and ran into a tree.C. He was hit by a falling box from a truck.4.What is the man doing?A. He is asking about his letter.B. He is buying plane tickets to Europe.C. He is sending some postcard.5.Where does the conversation mostly take place?A. In a restaurant.B. In the woman's house.C. In the market.第二节(共5小题;每小题1.5分;满分22.5分)听下面5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
江苏省盐城市盐城市一中、大丰高级中学等四校2020-2021学年高二地理上学期期终考试试题(PDF)

第 29、30 题图
(1) 若某日 B 点和 C 点的正午太阳高度相同,此日全球正午太阳高度角的分布规律是
。
(2)从“五一劳动节”到我国的“教师节”,A 点的昼夜长短及变化状况是
、
。
(3)若太阳直射点回归运动的范围在 A、B 之间,则全球的极昼极夜范围将
(扩大或缩
小),北京(40°N)昼夜长短的年变化
22.的的喀喀湖
A.水体参与海陆间循环
B.湖水不冻是受沿岸洋流影响
C.湖面水位 7 月比 1 月高
D.湖水经地表径流注入波波湖
23.乌鲁族人选择生活在漂浮岛上的原因有
①沿岸居住和生产用地有限 ②便于捕鱼 ③建岛原料充足 ④对外联系方便
A.①②③
B.①②④
C.①③④
D.②③④
我国西部某沙漠地区年降水量少于 150mm,年蒸发量超过 l000mm,沙漠东南部散落分布多个
民大会堂举行,中央广播电视总台进行了全程现场直播。据此回答 3~4 题。
3. 仪式开始举行时,下列说法正确的是
A. 旧金山(37°48′N,122°25′W)时间为 17 时 30 分
B. 全球与北京处在同一日的面积约占五分之三
C. 新加坡与哈尔滨相比昼夜长短变化幅度较大
D. 惠灵顿(41°17′S,174°47′E)正值黄昏
该地主管部门将每年的 10 月 3 日定为“卧佛含丹”节。读右
图,回答 5~6 题。
5.“卧佛含丹”节这天,“驴友”小王正在湖畔观赏这一地理奇
观,此时,他的身影朝向
第 5、6 题图
地理试题 第 1 页 共 7 页
A.西北方向
B.东北方向
C.东南方向
D.西南方向
6.小王准备回去后向其他“驴友”推荐这一奇观,并带领他们来观赏。小王应该哪一天带领他们来
江苏省盐城市四校2020-2021学年高二第一学期期末考试化学试题【含答案】

江苏省盐城市四校2020-2021学年高二第一学期期末考试化学试题可能用到的相对原子质量:H 1 C 12 N 14 O 16 B 11 Si 28 P 31 Al 27As 75第Ⅰ卷(选择题共40分)单项选择题:本题包括10小题,每小题2 分,共计20 分。
每小题只有一个选项符合题意。
1.化学与生产、生活、社会密切相关。
下列有关说法不.正确..的是A.预防新型冠状病毒,可用体积分数75%的医用酒精进行消毒B.对“地沟油”进行分馏可以制得汽油、煤油,达到变废为宝的目的C.鉴别织物成分是蚕丝还是“人造丝”可采用灼烧闻气味的方法D.屠呦呦用乙醚从青蒿中提取出对治疗疟疾有特效的青蒿素,该过程包括萃取操作2.下列有关化学用语表示正确的是A. CCl4的电子式: B .Cr的外围电子排布式:3d44s2C. 聚氯乙烯的单体为CH2=CHClD.1,3,4-三甲苯3.根据价层电子对互斥理论,判断下列分子或者离子的空间构型为平面三角形的A. CO32-B. CCl4C. ClO3-D. NH34.乙二酸(HOOC-COOH)受热分解产物为CO、CO2和H2O。
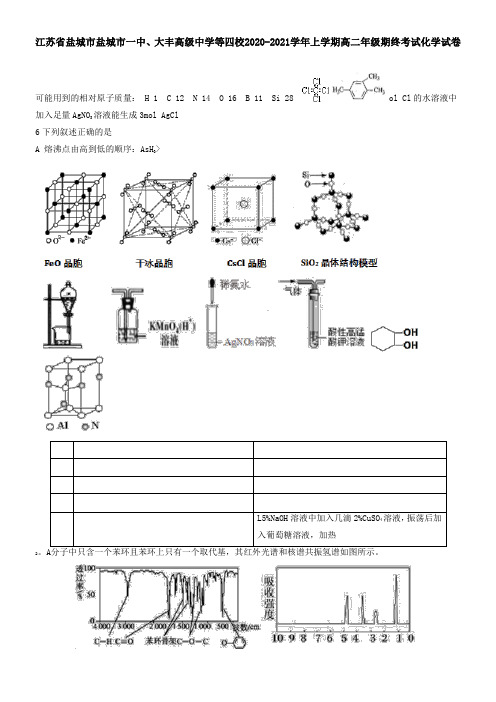
下列有关说法正确的是A. CO的结构式为C=OB. C、H、O元素电负性由大到小的顺序为O>H>CC. HOOC-COOH分子和CO2分子中碳原子轨道杂化类型相同D. HOOC-COOH分子内σ键与π键个数之比为7:25.下列有关说法正确的是A. 新能源可燃冰(CH4•nH2O)中甲烷分子与水分子之间存在氢键B. SO3与HCHO的分子空间构型均为平面三角形,都是非极性分子C. HClO分子中既有“s-p σ键”又有“p-p σ键”D.向含有1 mol [Co(NH3)4Cl2]Cl的水溶液中加入足量AgNO3溶液能生成3mol AgCl6.下列叙述正确的是A. 熔沸点由高到低的顺序:AsH3>PH3>NH3B. 熔沸点由高到低的顺序:硅>金刚石>NaCl>I2C. 某物质熔点1067°C,易溶于水,其水溶液和熔融态均能导电,其晶体一定为离子晶体D. 硫磺与金刚石晶体熔化时,所克服的微粒间相互作用相同7.下图表示一些晶体中的某些结构,下列各项所述的数字不是..4的是A.1个FeO晶胞平均含有O2-个数B.1个干冰晶胞中平均含有CO2分子个数C.氯化铯晶体中,每个Cs+周围距离最近的Cl-个数D.60 g SiO2晶体中含有Si﹣O键的数目FeO晶胞干冰晶胞CsCl晶胞SiO2晶体结构模型8.下列相关说法正确的是A. 淀粉、油脂和蛋白质都属于天然高分子化合物B.用新制Cu(OH)2悬浊液可鉴别麦芽糖和蔗糖C. 要使蛋白质从水溶液中析出而又不改变蛋白质的主要性质,可向蛋白质水溶液中加入CuSO4溶液D. 从溴水中提取溴可用植物油作萃取剂9.下列装置或操作能达到目的的是图1图2图3图4A.图1分离乙醇和乙酸B.图2除去甲烷中的乙烯C.图3配制银氨溶液D.图4检验溴乙烷消去反应产物乙烯10.由苯酚制取时,最简便的流程需要下列哪些反应,其正确的顺序是:①取代;②加成;③氧化;④消去;⑤还原。
专题15 复数的四则运算(解析版)

专题15 复数的四则运算一、单选题1.若复数Z 满足()·1 2z i i -=(i 是虚数部位),则下列说法正确的是 A .z 的虚部是-i B .Z 是实数C .z =D .2z z i +=【试题来源】江苏省盐城市滨海中学2020-2021学年高三上学期迎八省联考考前热身 【答案】C【分析】首先根据题意化简得到1z i =-,再依次判断选项即可.【解析】()()()22122211112i i i i iz i i i i ++====---+-. 对选项A ,z 的虚部是1-,故A 错误. 对选项B ,1z i =-为虚数,故B 错误.对选项C ,z ==C 正确.对选项D ,112z z i i +=-++=,故D 错误.故选C 2.已知复数1z i =+(i 为虚数单位),则1z在复平面内对应的点在 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】安徽省六安市示范高中2020-2021学年高三上学期教学质量检测(文) 【答案】D【分析】由复数的运算化简1z,再判断复平面内对应的点所在象限. 【解析】因为()()11111122i i z i i -==-+-,所以1z 在复平面内对应的点11 ,22⎛⎫- ⎪⎝⎭在第四象限.故选D3.已知复数1z i =+(i 为虚数单位),则1z在复平面内对应的点在 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】安徽省六安市示范高中2020-2021学年高三上学期教学质量检测(理)【答案】D 【分析】化简复数1z,利用复数的几何意义可得出结论. 【解析】因为()()11111112i i z i i i --===++-,所以1z在复平面内对应的点的坐标为11,22⎛⎫- ⎪⎝⎭,在第四象限.故选D . 4.设复数z 满足11zi z+=-,则z = A .i B .i - C .1D .1i +【试题来源】山东省威海市2020-2021学年高三上学期期末 【答案】B【分析】利用除法法则求出z ,再求出其共轭复数即可【解析】11zi z+=-得()11z i z +=-,即()()()()111111i i i z i i i i ---===++-,z i =-,故选B. 5.(1)(4)i i -+= A .35i + B .35i - C .53i +D .53i -【试题来源】安徽省皖西南联盟2020-2021学年高三上学期期末(文) 【答案】D【分析】根据复数的乘法公式,计算结果.【解析】2(1)(4)4453i i i i i i -+=-+-=-.故选D 6.设复数z 满足()11z i i -=+,则z 的虚部为. A .1- B .1 C .iD .i -【试题来源】安徽省芜湖市2020-2021学年高三上学期期末(文) 【答案】B【分析】利用复数的除法化简复数z ,由此可得出复数z 的虚部.【解析】()11z i i -=+,()()()211111i iz i i i i ++∴===--+, 因此,复数z 的虚部为1.故选B . 7.若复数z 满足21zi i=+,则z = A .22i + B .22i - C .22i --D .22i -+【试题来源】安徽省芜湖市2020-2021学年高三上学期期末(理) 【答案】C【分析】求出()2122z i i i =+=-+,再求解z 即可. 【解析】()2122z i i i =+=-+,故22z i =--,故选C. 8.将下列各式的运算结果在复平面中表示,在第四象限的为A .1ii + B .1ii +- C .1i i-D .1i i--【试题来源】河南省湘豫名校2020-2021学年高三上学期1月月考(文) 【答案】A【分析】对A 、B 、C 、D 四个选项分别化简,可得. 【解析】由11ii i+=-在第四象限.故选A . 【名师点睛】(1)复数的代数形式的运算主要有加、减、乘、除及求低次方根; (2)复数除法实际上是分母实数化的过程.9.若复数z 满足()z 1i i +=- (其中i 为虚数单位)则复数z 的虚部为A .12-B .12C .12i -D .12i【试题来源】安徽省马鞍山市2020-2021学年高三上学期第一次教学质量监测(文) 【答案】A【分析】先由已知条件利用复数的除法运算求出复数z ,再求其虚部即可. 【解析】由()z 1i i +=-可得()()()111111222i i i z i i i ----===--+-,所以复数z 的虚部为12-,故选A 10.复数z 满足()212()z i i -⋅+=(i 为虚数单位),则复数z 在复平面内对应的点在 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】宁夏吴忠市2021届高三一轮联考(文) 【答案】D【分析】先计算复数221z i i=++,再求其共轭复数,即可求出共轭复数对应的点,进而可得在复平面内对应的点所在的象限. 【解析】由()()212z i i -⋅+=得()()()()21212211112i i z i i i i i ---====-++-, 所以1z i =+,1z i =-.所以复数z 在复平面内对应的点为()1,1-, 位于第四象限,故选D .11.已知复数z 满足(2)z i i -=(i 为虚数单位),则z = A .125i-+ B .125i-- C .125i- D .125i+ 【试题来源】安徽省名校2020-2021学年高三上学期期末联考(文) 【答案】A【分析】由已知可得2iz i=-,再根据复数的除法运算可得答案. 【解析】因为(2)z i i -=,所以()()()2122225i i i i z i i i +-+===--+.故选A . 12.已知复数3iz i-=,则z =A .4 BCD .2【试题来源】江西省吉安市“省重点中学五校协作体”2021届高三第一次联考(文) 【答案】B【分析】利用复数代数形式的乘除运算化简,再由复数模的计算公式求解. 【解析】因为()()()3331131i i i i z i i i i -⋅----====--⋅-,所以z ==B .【名师点睛】本题考查复数代数形式的乘除运算,考查复数模的求法,属于基础题. 13.复数z 满足:()11i z i -=+,其中i 为虚数单位,则z 的共轭复数在复平面对应的点的坐标为 A .0,1 B .0,1 C .1,0D .()1,0【试题来源】江西宜春市2021届高三上学期数学(理)期末试题 【答案】A【分析】先由()11i z i -=+求出复数z ,从而可求出其共轭复数,进而可得答案【解析】由()11i z i -=+,得21i (1i)2ii 1i (1i)(1+i)2z ++====--, 所以z i =-,所以其在复平面对应的点为0,1,故选A 14.已知复数312iz i+=-,则z =A .1 BCD .2【试题来源】湖南省岳阳市平江县第一中学2020-2021学年高二上学期1月阶段性检测 【答案】B【分析】利用复数的除法法则化简复数z ,利用复数的模长公式可求得z .【解析】()()()()2312337217121212555i i i i i z i i i i +++++====+--+,因此,z ==B . 15.设复1iz i=+(其中i 为虚数单位),则复数z 在复平面内对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限【试题来源】江苏省南通市如皋市2020-2021学年高三上学期期末 【答案】A【分析】利用复数的除法化简复数z ,利用复数的几何意义可得出结论. 【解析】()()()1111111222i i i i z i i i i -+====+++-,因此,复数z 在复平面内对应的点位于第一象限.故选A .16.已知(1)35z i i +=-,则z = A .14i - B .14i -- C .14i -+D .14i +【试题来源】江苏省盐城市一中、大丰高级中学等四校2020-2021学年高二上学期期末联考 【答案】B【分析】由复数的除法求解.【解析】由题意235(35)(1)3355141(1)(1)2i i i i i i z i i i i -----+====--++-.故选B 17.复数(2)i i +的实部为 A .1- B .1 C .2-D .2【试题来源】浙江省绍兴市上虞区2020-2021学年高三上学期期末 【答案】A【分析】将(2)i i +化简即可求解.【解析】(2)12i i i +=-+的实部为1-,故选A .18.已知i 是虚数单位,(1)2z i i +=,则复数z 所对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】山东省德州市2019-2020学年高一下学期期末 【答案】D【分析】利用复数的运算法则求解复数z ,再利用共轭复数的性质求z ,进而确定z 所对应的点的位置.【解析】由(1)2z i i +=,得()()()()2121211112i i i i z i i i i -+====+++-, 所以1z i =-,所以复数z 所对应的点为()1,1-,在第四象限,故选D .【名师点睛】对于复数的乘法,类似于多项式的四则运算,可将含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可;对于复数的除法,关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式. 19.若复数2iz i=+,其中i 为虚数单位,则z =A B C .25D .15【试题来源】重庆市南开中学2020-2021学年高二上学期期末 【答案】B【分析】先利用复数的除法运算法则化简复数2iz i=+,再利用复数模的公式求解即可. 【解析】因为()()()21212222555i i i i z i i i i -+====+++-,所以z ==,故选B . 20.52i i-= A .152i--B .52i-- C .152i- D .152i+ 【试题来源】江西省吉安市2021届高三上学期期末(文) 【答案】A【分析】根据复数的除法的运算法则,准确运算,即可求解. 【解析】由复数的运算法则,可得()5515222i i i ii i i ----==⨯.故选A .21.设复数z 满足()1z i i R +-∈,则z 的虚部为 A .1 B .-1 C .iD .i -【试题来源】湖北省2020-2021学年高三上学期高考模拟演练 【答案】B【分析】根据复数的运算,化简得到()11(1)z i i a b i +-=+++,根据题意,求得1b =-,即可求得z 的虚部,得到答案.【解析】设复数,(,)z a bi a b R =+∈,则()11(1)z i i a b i +-=+++,因为()1z i i R +-∈,可得10b +=,解得1b =-,所以复数z 的虚部为1-.故选B . 22.若复数151iz i-+=+,其中i 为虚数单位,则z 的虚部是 A .3 B .3- C .2D .2-【试题来源】安徽省淮南市2020-2021学年高三上学期第一次模拟(文) 【答案】A【分析】先利用复数的除法运算,化简复数z ,再利用复数的概念求解.【解析】因为复数()()()()1511523111i i i z i i i i -+--+===+++-, 所以z 的虚部是3,故选A. 23.若m n R ∈、且4334im ni i+=+-(其中i 为虚数单位),则m n -= A .125- B .1- C .1D .0【试题来源】湖北省部分重点中学2020-2021学年高三上学期期末联考 【答案】B【分析】对已知进行化简,根据复数相等可得答案.【解析】因为()()()()433443121225343434916i i i ii m ni i i i +++-+====+--++, 根据复数相等,所以0,1m n ==,所以011m n -=-=-.故选B .24.若复数z满足()36z =-(i 是虚数单位),则复数z =A.32-B.32- C.322+D.322-- 【试题来源】湖北省荆州中学2020-2021学年高二上学期期末 【答案】A【分析】由()36z =-,得z =,利用复数除法运算法则即可得到结果.【解析】复数z满足()36z +=-,6332z --=====-∴+,故选A .25.若复数2i()2i+=∈-R a z a 是纯虚数,则z = A .2i - B .2i C .i -D .i【试题来源】河南省驻马店市2020-2021学年高三上学期期末考试(理) 【答案】D【分析】由复数的除法运算和复数的分类可得结果. 【解析】因为2i (2i)(2i)22(4)i2i (2i)(2i)5+++-++===-+-a a a a z 是纯虚数, 所以22040a a -=⎧⎨+≠⎩,则1a =,i =z .故选D .26.复数12z i =+,213z i =-,其中i 为虚数单位,则12z z z =⋅在复平面内的对应点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】江苏省G4(苏州中学、常州中学、盐城中学、扬州中学)2020-2021学年高三上学期期末联考 【答案】D【分析】根据复数的乘法法则,求得55z i =-,即可求得答案. 【解析】由题意得122(2)(13)25355i i i i i z z z =+-=-==--⋅, 所以12z z z =⋅在复平面内的对应点为(5,-5)位于第四象限,故选D27.复数2()2+∈-R a ia i 的虚部为 A .225+aB .45a - C .225a -D .45a +【试题来源】河南省驻马店市2020-2021学年高三上学期期末考试(文) 【答案】D【分析】由得数除法运算化为代数形式后可得. 【解析】因为2i (2i)(2i)22(4)i 2i (2i)(2i)5+++-++==-+-a a a a ,所以其虚部为45a +.故选D . 28.复数z 满足()12z i i ⋅+=,则2z i -=ABCD .2【试题来源】安徽省蚌埠市2020-2021学年高三上学期第二次教学质量检查(文) 【答案】A【分析】先利用除法化简计算z ,然后代入模长公式计算.【解析】()1i 2i z ⋅+=变形得22222221112-+====++-i i i i z i i i ,所以2121-=+-=-==z i i i i A .29.i 是虚数单位,若()17,2ia bi ab R i-=+∈+,则ab 的值是 A .15- B .3- C .3D .15【试题来源】山东省菏泽市2020-2021学年高三上学期期末 【答案】C【分析】根据复数除法法则化简得数后,由复数相等的定义得出,a b ,即可得结论.【解析】17(17)(2)2147132(2)(2)5i i i i i i i i i ------===--++-, 所以1,3a b =-=-,3ab =.故选C . 30.复数3121iz i -=+的虚部为 A .12i -B .12i C .12-D .12【试题来源】江西省赣州市2021届高三上学期期末考试(理) 【答案】C【分析】由复数的乘除法运算法则化简为代数形式,然后可得虚部.【解析】231212(12)(1)1223111(1)(1)222i i i i i i i z i i i i i ---++--=====-+--+, 虚部为12-.故选C . 31.若复数z 满足(1)2i z i -=,i 是虚数单位,则z z ⋅=AB .2C .12D .2【试题来源】内蒙古赤峰市2021届高三模拟考试(理) 【答案】B【分析】由除法法则求出z ,再由乘法法则计算.【解析】由题意222(1)2()11(1)(1)2i i i i i z i i i i ++====-+--+, 所以(1)(1)2z z i i ⋅=-+--=.故选B . 32.若23z z i +=-,则||z =A .1 BCD .2【试题来源】河南省(天一)大联考2020-2021学年高三上学期期末考试(理) 【答案】B【分析】设(,)z a bi a b R =+∈,代入已知等式求得,a b 后再由得数的模的定义计算. 【解析】设(,)z a bi a b R =+∈,则22()33z z a bi a bi a bi i +=++-=-=-,所以以331a b =⎧⎨-=-⎩,解得11a b =⎧⎨=⎩,所以==z B .33.复数z 满足(2)(1)2z i i -⋅+=(i 为虚数单位),则z = A .1 B .2CD 【试题来源】宁夏吴忠市2021届高三一轮联考(理) 【答案】C【分析】先将复数化成z a bi =+形式,再求模. 【解析】由(2)(1)2z i i -⋅+=得2211z i i i-==-+,所以1z i =+,z ==C .34.已知a R ∈,若()()224ai a i i +-=-(i 为虚数单位),则a = A .-1 B .0 C .1D .2【试题来源】浙江省杭州市2020-2021学年高三上学期期末教学质量检测 【答案】B【分析】将()()22ai a i +-展开可得答案.【解析】()()()222444ai a i a a i i +-=+-=-,所以0a =,故选B.35.已知i 为虚数单位,且复数3412ii z+=-,则复数z 的共轭复数为 A .12i -+ B .12i -- C .12i +D .1 2i -【试题来源】湖北省孝感市应城市第一高级中学2020-2021学年高二上学期期末【答案】D【分析】根据复数模的计算公式,以及复数的除法运算,求出z ,即可得出其共轭复数. 【解析】因为3412i i z+=-,所以512z i =-,则()()()512512121212i z i i i i +===+--+, 因此复数z 的共轭复数为1 2i -.故选D . 36.已知复数i()1ia z a +=∈+R 是纯虚数,则z 的值为 A .1 B .2 C .12D .-1【试题来源】江西省赣州市2021届高三上学期期末考试(文) 【答案】A【分析】根据复数除法运算化简z ,根据纯虚数定义求得a ,再求模长. 【解析】()()()()11121122a i i a i a a z i i i i +-++-===+++-是纯虚数,102102a a +⎧=⎪⎪∴⎨-⎪≠⎪⎩,解得1a =-,所以z i ,1z =.故选A . 37.设复数11iz i,那么在复平面内复数31z -对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】陕西省咸阳市2020-2021学年高三上学期高考模拟检测(一)(理) 【答案】C【分析】利用复数的除法法则化简复数z ,再将复数31z -化为一般形式,即可得出结论.【解析】()()()21121112i ii z i i i i ---====-++-,3113z i ∴-=--, 因此,复数31z -在复平面内对应的点位于第三象限.故选C . 38.已知复数13iz i-=+(i 为虚数单位),则z 在复平面内对应的点位于 A .第一象限B .第二象限C .第三象限D .第四象限【试题来源】江西省南昌市新建区第一中学2020-2021学年高二上学期期末考试(理) 【答案】D【分析】将复数化简成z a bi =+形式,则在复平面内对应的点的坐标为(),a b ,从而得到答案.【解析】因为1(1)(3)24123(3)(3)1055i i i i z i i i i ----====-++-, 所以z 在复平面内对应的点12(,)55-位于第四象限,故选D.39.若复数2(1)34i z i+=+,则z =A .45 B .35C .25D 【试题来源】成都市蓉城名校联盟2020-2021学年高三上学期(2018级)第二次联考 【答案】C 【分析】先求出8625iz -=,再求出||z 得解. 【解析】由题得()()()()212342863434343425i i i i iz i i i i +-+====+++-,所以102255z ===.故选C. 40.设复数11iz i,那么在复平面内复数1z -对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【试题来源】陕西省咸阳市2020-2021学年高三上学期高考模拟检测(一)(文) 【答案】C【分析】先求出z i =-,11z i -=--,即得解.【解析】由题得21(1)21(1)(1)2i i iz i i i i ---====-++-, 所以11z i -=--,它对应的点的坐标为(1,1)--, 所以在复平面内复数1z -对应的点位于第三象限.故选C. 二、多选题1.已知m ∈R ,若6()64m mi i +=-,则m =A .B .1-CD .1【试题来源】2021年高考一轮数学(理)单元复习一遍过 【答案】AC【分析】将6()m mi +直接展开运算即可.【解析】因为()()66661864m mi m i im i +=+=-=-,所以68m =,所以m =故选AC . 2.设复数z 满足1z i z+=,则下列说法错误的是 A .z 为纯虚数B .z 的虚部为12i -C .在复平面内,z 对应的点位于第三象限D .2z = 【试题来源】2021年新高考数学一轮复习学与练 【答案】AB【分析】先由复数除法运算可得1122z i =--,再逐一分析选项,即可得答案. 【解析】由题意得1z zi +=,即111122z i i -==---, 所以z 不是纯虚数,故A 错误;复数z 的虚部为12-,故B 错误;在复平面内,z 对应的点为11(,)22--,在第三象限,故C 正确;2z ==,故D 正确.故选AB 【名师点睛】本题考查复数的除法运算,纯虚数、虚部的概念,复平面内点所在象限、复数求模的运算等知识,考查计算求值的能力,属基础题.3.已知复数122z =-,则下列结论正确的有 A .1z z ⋅=B .2z z =C .31z =-D .202012z =-+ 【试题来源】山东新高考质量测评联盟2020-2021学年高三上学期10月联考 【答案】ACD【分析】分别计算各选项的值,然后判断是否正确,计算D 选项的时候注意利用复数乘方的性质.【解析】因为111312244z z ⎛⎫⎛⎫-+=+= ⎪⎪⎪⎪⎝⎭⎭=⎝⋅,所以A 正确;因为221122z ⎛⎫=-⎪⎪⎝⎭=,122z =+,所以2z z ≠,所以B 错误;因为3211122z z z ⎛⎫⎛⎫=⋅=-=- ⎪⎪ ⎪⎪⎝⎭⎝⎭,所以C 正确;因为6331z z z =⋅=,所以()202063364431112222zzz z z ⨯+⎛⎫===⋅=-⋅-=-+ ⎪ ⎪⎝⎭,所以D 正确,故选ACD .【名师点睛】本题考查复数乘法与乘方的计算,其中还涉及到了共轭复数的计算,难度较易. 4.下面是关于复数21iz =-+的四个命题,其中真命题是A .||z =B .22z i =C .z 的共轭复数为1i -+D .z 的虚部为1-【试题来源】福建省龙海市第二中学2019-2020学年高二下学期期末考试 【答案】ABCD【分析】先根据复数的除法运算计算出z ,再依次判断各选项. 【解析】()()()2121111i z i i i i --===---+-+--,z ∴==,故A 正确;()2212z i i =--=,故B 正确;z 的共轭复数为1i -+,故C 正确;z 的虚部为1-,故D 正确;故选ABCD .【名师点睛】本题考查复数的除法运算,以及对复数概念的理解,属于基础题. 5.若复数351iz i-=-,则A .z =B .z 的实部与虚部之差为3C .4z i =+D .z 在复平面内对应的点位于第四象限 【试题来源】2021年新高考数学一轮复习学与练 【答案】AD【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出. 【解析】()()()()351358241112i i i iz i i i i -+--====---+,z ∴==,z 的实部为4,虚部为1-,则相差5,z 对应的坐标为()41-,,故z 在复平面内对应的点位于第四象限,所以AD 正确,故选AD .6.已知复数202011i z i+=-(i 为虚数单位),则下列说法错误的是A .z 的实部为2B .z 的虚部为1C .z i =D .||z =【试题来源】2021年新高考数学一轮复习学与练 【答案】AC【分析】根据复数的运算及复数的概念即可求解.【解析】因为复数2020450511()22(1)11112i i i z i i i i +++=====+---,所以z 的虚部为1,||z =,故AC 错误,BD 正确.故选AC. 7.已知复数cos sin 22z i ππθθθ⎛⎫=+-<< ⎪⎝⎭(其中i 为虚数单位)下列说法正确的是A .复数z 在复平面上对应的点可能落在第二象限B .z 可能为实数C .1z =D .1z的虚部为sin θ 【试题来源】湖北省六校(恩施高中、郧阳中学、沙市中学、十堰一中、随州二中、襄阳三中)2020-2021学年高三上学期11月联考 【答案】BC【分析】分02θπ-<<、0θ=、02πθ<<三种情况讨论,可判断AB 选项的正误;利用复数的模长公式可判断C 选项的正误;化简复数1z,利用复数的概念可判断D 选项的正误.【解析】对于AB 选项,当02θπ-<<时,cos 0θ>,sin 0θ<,此时复数z 在复平面内的点在第四象限;当0θ=时,1z R =-∈; 当02πθ<<时,cos 0θ>,sin 0θ>,此时复数z 在复平面内的点在第一象限.A 选项错误,B 选项正确; 对于C 选项,22cos sin 1z θθ=+=,C 选项正确;对于D 选项,()()11cos sin cos sin cos sin cos sin cos sin i i z i i i θθθθθθθθθθ-===-++⋅-, 所以,复数1z的虚部为sin θ-,D 选项错误.故选BC . 8.已知非零复数1z ,2z 满足12z z R ∈,则下列判断一定正确的是 A .12z z R +∈B .12z z R ∈C .12z R z ∈D .12z R z ∈【试题来源】重庆市南开中学2020-2021学年高二上学期期中 【答案】BD【分析】设12,(,,,)z a bi z c di a b c d R =+=+∈,结合选项逐个计算、判定,即可求解. 【解析】设12,(,,,)z a bi z c di a b c d R =+=+∈,则()()12()()z z a bi c di ac bd ad bc i =++=-++,则0ad bc +=,对于A 中,12()()z z a bi c di a c b d i +=+++=+++,则12z z R +∈不一定成立,所以不正确;对于B 中,12()()ac bd ad bc z R i z =-+∈-一定成立,所以B 正确; 对于C 中,()()()()2122()()a bi c di a bi ac bd ad bc i R c di c di c z di z c d+-++--==∈++-+=不一定成立,所以不正确;对于D 中,()()()()2122()()a bi c di a bi ac bd ad bc iR c di c di c z di z c d ++++++==∈--++=一定成立,所以正确.故选BD .9.已知复数()()()32=-+∈z a i i a R 的实部为1-,则下列说法正确的是 A .复数z 的虚部为5- B .复数z 的共轭复数15=-z i C.z =D .z 在复平面内对应的点位于第三象限【试题来源】辽宁省六校2020-2021学年高三上学期期中联考 【答案】ACD【分析】首先化简复数z ,根据实部为-1,求a ,再根据复数的概念,判断选项. 【解析】()()()()23232323223z a i i a ai i i a a i =-+=+--=++-,因为复数的实部是-1,所以321a +=-,解得1a =-, 所以15z i =--,A .复数z 的虚部是-5,正确;B .复数z 的共轭复数15z i =-+,不正确;C .z ==D .z 在复平面内对应的点是()1,5--,位于第三象限,正确.故选ACD 10.已知复数cos sin 22z i ππθθθ⎛⎫=+-<< ⎪⎝⎭(其中i 为虚数单位),下列说法正确的是() A .复数z 在复平面上对应的点可能落在第二象限 B .cos z θ=C .1z z ⋅=D .1z z+为实数 【试题来源】山东省菏泽市2021届第一学期高三期中考试数学(B )试题 【答案】CD【分析】利用复数对应点,结合三角函数值的范围判断A ;复数的模判断B ;复数的乘法判断C ;复数的解法与除法,判断D . 【解析】复数cos sin ()22z i ππθθθ=+-<<(其中i 为虚数单位),复数z 在复平面上对应的点(cos ,sin )θθ不可能落在第二象限,所以A 不正确;1z ==,所以B 不正确;22·(cos sin )(cos sin )cos sin 1z z i i θθθθθθ=+-=+=.所以C 正确;11cos sin cos sin cos()sin()2cos cos sin z i i i z i θθθθθθθθθ+=++=++-+-=+为实数,所以D 正确;故选CD11.已知i 为虚数单位,下面四个命题中是真命题的是 A .342i i +>+B .24(2)()a a i a R -++∈为纯虚数的充要条件为2a =C .()2(1)12z i i =++的共轭复数对应的点为第三象限内的点D .12i z i +=+的虚部为15i 【试题来源】2020-2021年新高考高中数学一轮复习对点练 【答案】BC【分析】根据复数的相关概念可判断A ,B 是否正确,将()2(1)12z i i =++展开化简可判断C 选项是否正确;利用复数的除法法则化简12iz i+=+,判断D 选项是否正确. 【解析】对于A ,因为虚数不能比较大小,故A 错误;对于B ,若()242a a i ++-为纯虚数,则24020a a ⎧-=⎨+≠⎩,解得2a =,故B 正确;对于C ,()()()211221242z i i i i i =++=+=-+,所以42z i =--对应的点为()4,2--位于第三象限内,故C 正确;对于D ,()()()()12132225i i i i z i i i +-++===++-,虚部为15,故D 错误.故选BC . 12.已知复数(12)5z i i +=,则下列结论正确的是A .|z |B .复数z 在复平面内对应的点在第二象限C .2z i =-+D .234z i =+【试题来源】河北省邯郸市2021届高三上学期期末质量检测【答案】AD【分析】利用复数的四则运算可得2z i =+,再由复数的几何意义以及复数模的运算即可求解.【解析】5512122121212()()()()i i i z i i i i i i -===-=+++-,22,||34z i z z i =-==+ 复数z 在复平面内对应的点在第一象限,故AD 正确.故选AD13.已知i 是虚数单位,复数12i z i -=(z 的共轭复数为z ),则下列说法中正确的是 A .z 的虚部为1B .3z z ⋅=C .z =D .4z z +=【试题来源】山东省山东师大附中2019-2020学年高一下学期5月月考【答案】AC 【分析】利用复数的乘法运算求出122i z i i-==--,再根据复数的概念、复数的运算以及复数模的求法即可求解. 【解析】()()()12122i i i z i i i i ---===---,所以2z i =-+, 对于A ,z 的虚部为1,故A 正确;对于B ,()2225z z i ⋅=--=,故B 不正确;对于C ,z =C 正确;对于D ,4z z +=-,故D 不正确.故选AC14.早在古巴比伦时期,人们就会解一元二次方程.16世纪上半叶,数学家得到了一元三次、一元四次方程的解法.此后数学家发现一元n 次方程有n 个复数根(重根按重数计).下列选项中属于方程310z -=的根的是A.12 B.12-+ C.122-- D .1【试题来源】江苏省苏州市2020-2021学年高二上学期1月学业质量阳光指标调研【答案】BCD【分析】逐项代入验证是否满足310z -=即可.【解析】对A,当122z =+时, 31z -31122i ⎛⎫+- ⎪ ⎪⎭=⎝21112222⎛⎫⎛⎫+⋅+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=21121344i ⎛⎫=++⋅ ⎪⎛⎫+- ⎪ ⎝ ⎭⎭⎪⎪⎝12112⎛⎫=-+⋅⎛⎫+- ⎪ ⎪⎝⎭⎪ ⎪⎝⎭2114⎫=-+-⎪⎪⎝⎭ 13144=--- 2=-,故3120z -=-≠,A 错误; 对B,当12z =-时,31z -3112⎛⎫-+- ⎪ ⎪⎝⎭=211122⎛⎫⎛⎫-⋅-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=2113124242i ⎛⎫=-+⋅ ⎪ ⎪⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭1221122⎛⎫-⎛⎫=--⋅ ⎪+ - ⎪ ⎪⎝⎭⎪⎝⎭21142⎛⎫=-- ⎪ ⎪⎝⎭ 13144=+- 0=,故310z -=,B 正确; 对C,当12z =-时,31z-31122⎛⎫--- ⎪ ⎪⎝⎭=21112222⎛⎫⎛⎫--⋅--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=21131442i ⎛⎫=++⋅ ⎪ ⎪⎛⎫--- ⎪ ⎪⎝⎭⎝⎭12112⎛⎫-⎛⎫=-+⋅ ⎪- - ⎪ ⎪⎝⎭⎪⎝⎭2114⎫=--⎪⎪⎝⎭13144=+-0=,故310z -=,C 正确; 对D ,显然1z =时,满足31z =,故D 正确.故选BCD .15.已知复数()()122z i i =+-,z 为z 的共轭复数,则下列结论正确的是A .z 的虚部为3iB .5z =C .4z -为纯虚数D .z 在复平面上对应的点在第四象限【试题来源】湖南师范大学附属中学2020-2021学年高二上学期期末【答案】BCD【分析】先根据复数的乘法运算计算出z ,然后进行逐项判断即可.【解析】因为()()12243z i i i =+-=+,则z 的虚部为3,5z z ===,43z i -=为纯虚数,z 对应的点()4,3-在第四象限,故选BCD .三、填空题1.已知复数z 满足(1)1z i i ⋅-=+(i 为虚数单位),则z =_________.【试题来源】上海市松江区2021届高三上学期期末(一模)【答案】1【分析】把已知等式变形,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.【解析】由(1)1z i i ⋅-=+,得21(1)1(1)(1)i i z i i i i ++===--+,所以1z =.故答案为1. 2.i 是虚数单位,复数1312i i-+=+_________. 【试题来源】天津市七校2020-2021学年高三上学期期末联考【答案】1i +【分析】分子分母同时乘以分母的共轭复数12i -,再利用乘法运算法则计算即可. 【解析】()()()()22131213156551121212145i i i i i i i i i i i -+--+-+-+====+++--.故答案为1i +. 3.若复数z 满足方程240z +=,则z =_________.【试题来源】上海市复旦大学附属中学2020-2021学年高二上学期期末【答案】2i ±【分析】首先设z a bi =+,再计算2z ,根据实部和虚部的数值,列式求复数..【解析】设z a bi =+,则22224z a b abi =-+=-,则2240a b ab ⎧-=-⎨=⎩,解得02a b =⎧⎨=±⎩,所以2z i =±,故答案为2i ±. 4.复数21i-的虚部为_________. 【试题来源】上海市上海交通大学附属中学2020-2021学年高二上学期期末【答案】1【分析】根据分母实数化,将分子分母同乘以分母的共轭复数1i +,然后即可判断出复数的虚部. 【解析】因为()()()2121111i i i i i +==+--+,所以复数的虚部为1,故答案为1. 5.若复数z 满足(12)1i z i +=-,则复数z 的虚部为_________.【试题来源】山东省山东师大附中2019-2020学年高一下学期5月月考 【答案】35【分析】根据复数的除法运算法则,求出z ,即可得出结果.【解析】因为(12)1i z i +=-,所以()()()()112113213121212555i i i i z i i i i -----====--++-, 因此其虚部为35.故答案为35. 6.复数34i i+=_________. 【试题来源】北京市东城区2021届高三上学期期末考试【答案】43i -【分析】分子和分母同乘以分母的共轭复数,整理后得到最简形式即可. 【解析】由复数除法运算法则可得, ()343434431i i i i i i i i +⋅+-===-⋅-,故答案为43i -. 7.已知复数(1)z i i =⋅+,则||z =_________.【试题来源】北京市西城区2020-2021学年高二上学期期末考试【分析】根据复数的运算法则,化简复数为1z i =-+,进而求得复数的模,得到答案.【解析】由题意,复数(1)1z i i i =⋅+=-+,所以z == 8.i 是虚数单位,复数73i i-=+_________. 【试题来源】宁夏银川一中2020-2021学年高二上学期期末考试(文)【答案】2i -【分析】根据复数除法运算法则直接计算即可. 【解析】()()()()27372110233310i i i i i i i i i ----+===-++-.故答案为2i -. 9.设复数z 的共轭复数是z ,若复数143i z i -+=,2z t i =+,且12z z ⋅为实数,则实数t 的值为_________.【试题来源】宁夏银川一中2020-2021学年高二上学期期末考试(理) 【答案】34【分析】先求出12,z z ,再计算12z z ⋅即得解. 【解析】由题得14334i z i i-+==+,2z t i =-, 所以12(34)()34(43)z z i t i t t i ⋅=+-=++-为实数, 所以3430,4t t -=∴=.故答案为34【名师点睛】复数(,)a bi a b R +∈等价于0b =,不需要限制a .10.函数()n nf x i i -=⋅(n N ∈,i 是虚数单位)的值域可用集合表示为_________. 【试题来源】上海市上海中学2020-2021学年高二上学期期末【答案】{}1【分析】根据复数的运算性质可函数的值域.【解析】()()1111nn n n n n n n f x i i i i i i i i --⎛⎫=⋅⋅⋅⋅= ⎪⎝=⎭==,故答案为{}1. 11.已知()20212i z i +=(i 为虚数单位),则z =_________.【试题来源】河南省豫南九校2021届高三11月联考教学指导卷二(理)【分析】由i n 的周期性,计算出2021i i =,再求出z ,求出z .【解析】因为41i =,所以2021i i =,所以i 12i 2i 55z ==++,所以z z == 【名师点睛】复数的计算常见题型:(1) 复数的四则运算直接利用四则运算法则;(2) 求共轭复数是实部不变,虚部相反;(3) 复数的模的计算直接根据模的定义即可.12.若31z i =-(i 为虚数单位),则z 的虚部为_________. 【试题来源】江西省上饶市2021届高三第一次高考模拟考试(文) 【答案】32-【分析】利用复数的除法化简复数z ,由此可得出复数z 的虚部. 【解析】()()()313333111122i z i i i i i +==-=-=-----+,因此,复数z 的虚部为32-. 故答案为32-. 13.设i 为虚数单位,若复数z 满足()21z i -⋅=,则z =_________. 【试题来源】江西省上饶市2020-2021学年高二上学期期末(文)【答案】2i +【分析】利用复数的四则运算可求得z ,利用共轭复数的定义可求得复数z .【解析】()21z i -⋅=,122z i i ∴=+=-,因此,2z i =+.故答案为2i +. 14.已知i 是虚数单位,则11i i+=-_________. 【试题来源】湖北省宜昌市2020-2021学年高三上学期2月联考【答案】1【分析】利用复数的除法法则化简复数11i i +-,利用复数的模长公式可求得结果. 【解析】()()()21121112i i i i i i i ++===--+,因此,111i i i +==-.故答案为1. 15.i 是虚数单位,复数103i i=+____________. 【试题来源】天津市南开中学2020-2021学年高三上学期第四次月考【答案】13i +【分析】根据复数的除法运算算出答案即可.【解析】()()()()10310313333i i i i i i i i i -==-=+++-,故答案为13i +. 16.在复平面内,复数()z i a i =+对应的点在直线0x y +=上,则实数a =_________.【试题来源】北京市丰台区2021届高三上学期期末练习【答案】1【分析】由复数的运算法则和复数的几何意义直接计算即可得解.【解析】2()1z i a i ai i ai =+=+=-+,其在复平面内对应点的坐标为()1,a -, 由题意有:10a -+=,则1a =.故答案为1.17.已知复数z 满足()1234i z i +=+(i 为虚数单位),则复数z 的模为_________.【试题来源】江苏省苏州市2020-2021学年高二上学期1月学业质量阳光指标调研【分析】求出z 后可得复数z 的模.【解析】()()3412341121255i i i i z i +-+-===+,5z == 18.复数1i i-(i 是虚数单位)的虚部是_________. 【试题来源】北京通州区2021届高三上学期数学摸底(期末)考试【答案】1-【分析】先化简复数得1i 1i i-=--,进而得虚部是1-【解析】因为()()221i i 1i i i 1i i i--==--=--, 所以复数1i i-(i 是虚数单位)的虚部是1-.故答案为1-. 19.已知i 是虚数单位,复数11z i i =+-,则z =_________. 【试题来源】山东省青岛市2020-2021学年高三上学期期末【答案】2【分析】根据复数的除法运算,化简复数为1122z i =-+,再结合复数模的计算公式,即可求解. 【解析】由题意,复数()()111111122i z i i i i i i --=+=+=-+----,所以2z ==.故答案为2. 20.计算12z ==_______. 【试题来源】2021年高考一轮数学(理)单元复习一遍过【答案】-511【分析】利用复数的运算公式,化简求值.【解析】原式1212369100121511()i ==+=-+=--. 【名师点睛】本题考查复数的n次幂的运算,注意31122⎛⎫-+= ⎪ ⎪⎝⎭,()212i i +=, 以及()()612211i i ⎡⎤+=+⎣⎦,等公式化简求值. 四、双空题1.设32i i 1ia b =++(其中i 为虚数单位,a ,b ∈R ),则a =_________,b =_________. 【试题来源】浙江省绍兴市嵊州市2020-2021学年高三上学期期末【答案】1- 1- 【分析】利用复数的除法运算化简32i 1i 1i=--+,利用复数相等的定义得到a ,b 的值,即得解. 【解析】322(1)2211(1)(1)2i i i i i a bi i i i ----===--=+++-,1,1a b ∴=-=-. 故答案为-1;-1.2.已知k ∈Z , i 为虚数单位,复数z 满足:21k i z i =-,则当k 为奇数时,z =_________;当k ∈Z 时,|z +1+i |=_________.【试题来源】2020-2021学年【补习教材寒假作业】高二数学(苏教版)【答案】1i -+ 2【分析】由复数的运算及模的定义即可得解.【解析】当k 为奇数时,()()2211k k k i i ==-=-, 所以1z i -=-即1z i =-+,122z i i ++==; 当k 为偶数时,()()2211k k k i i ==-=,所以1z i =-,122z i ++==;所以12z i ++=.故答案为1i -+;2.3.若复数()211z m m i =-++为纯虚数,则实数m =_________,11z=+_________. 【试题来源】浙江省金华市义乌市2020-2021学年高三上学期第一次模拟考试【答案】1 1255i - 【分析】由题可得21010m m ⎧-=⎨+≠⎩,即可求出m ,再由复数的除法运算即可求出.【解析】复数()211z m m i =-++为纯虚数,21010m m ⎧-=∴⎨+≠⎩,解得1m =,。
2020-2021学年江苏省盐城一中高二上学期期中物理试卷(选修)(含答案解析)

2020-2021学年江苏省盐城一中高二上学期期中物理试卷(选修)一、单选题(本大题共8小题,共24.0分)1.下列叙述中,符合物理史实的是()A. 密立根认为在电荷周围存在着由它产生的电场B. 法国物理学家库仑通过实验测出电子的电量C. 法拉第发现电磁感应现象并独立得出了法拉第电磁感应定律D. 丹麦物理学家奥斯特发现电流可以使周围的小磁针发生偏转,称为电流的磁效应2.下列情况下,电阻仍不变的是()A. 长度均匀伸长为原来的两倍,横截面积增大为原来的两倍B. 长度均匀伸长为原来的两倍,横截面积增大为原来的四倍C. 长度均匀变为原来的一半,半径增大为原来的两倍D. 长度均匀变为原来的一半,半径增大为原来的四倍3.关于通电螺旋线管的磁感线方向的判断,下列示意图中正确的是()A. B.C. D.4.如图所示,为闭合电路中两个不同电源的U−I图象,则两电源的电动势和内阻的关系为()A. E1<E2r1>r2B. E1=E2r1=r2C. E1<E2r1<r2D. E1>E2r1<r25.如图所示,开始时L A、L B两灯均正常发光,突然L B因故障短路,随后调节R2使L A再次正常发光,则在整个过程中,以下有关判断正确的是()A. 调节R2时,P应向a端滑动B. R1的电流先增大后减小C. 电压表示数一直增大D. 电源的输出功率一直减小6.关于如图所示的回旋加速器,下列说法正确的是()A. 带电粒子在D型盒磁场中加速B. 可以加速中子C. 带电粒子的出射最大动能与D型盒半径无关D. 两D型盒间交变电压的周期等于粒子转动的周期7.如图所示,C1=6μF,C2=3μF,R1=3Ω,R2=6Ω电源电动势E=18V,内电阻不计。
下列说法中正确的是()A. 开关S断开时,a、b两点电势相等B. 开关S闭合后,a、b两点间的电流是3AC. 开关S断开时,C1带的电量比开关S闭合后C1带的电量大D. 不论开关S断开还是闭合,C1带的电量总比C2带的电量大8.如图所示,一闭角三线框速度v速穿过匀强磁场区.从BC边进入磁场区开始计时到点离开磁场区止的中,框内感电的情况(以时针方向为电流的正方向)是图中的()A. B. C. D.二、多选题(本大题共4小题,共16.0分)9.如图1所示,质量m A=1kg,m B=2kg的A、B两物块叠放在一起静止于粗糙水平地面上.t=0s时刻,一水平恒力F作用在物体B上,t=1s时刻,撤去F,B物块运动的速度−时间图象如图2所示,若整个过程中A、B始终保持相对静止,则()A. 物体B与地面间的动摩擦因数为0.2B. 1s~3s内物块A不受摩擦力作用C. 0~1s内物块B对A的摩擦力大小为4ND. 水平恒力的大小为12N10.如图所示,一个质量为m、电荷量为q的带负电的粒子(粒子的重力不计),带电粒子从x轴正方向上的P点以速度v沿与x轴成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴正方向射出第一象限。
江苏省盐城市盐城市一中、大丰高级中学等四校2020-2021学年高二上学期期终考试数学试题及答案

考试时间:2021年1月26日14:00-16:002020-2021学年第一学期高二年级期终考试数学试题一、单项选择题:本题共8题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填写在答题卡相应位置上. 1.命题“21,1x x ∀>>”的否定是A. 21,1x x ∀>≤B. 21,1x x ∀≤≤C. 21,1x x ∃≤≤D. 21,1x x ∃>≤2.已知函数()f x 的导函数()f x '的图像如下,若()f x 在0x x =处有极值,则0x 的值为A.3-B.0C.3D.73.已知(1)35z i i +=-,则z =A. 14i -B.14i --C. 14i -+D. 14i +4.平面α的一个法向量是(1,2,3),平面β的一个法向量是(3,0,1)-,则平面α与β的位置关系是A.平行B.相交且不垂直C.相交且垂直D.不确定5.已知x R ∈,则“21x>”是“2x <”的 A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不必要也不充分条件6.在三棱锥O ABC -中,AD DB =,2CE EB =,若DE xOA yOB zOC =++,则 A.111,,263x y z ==-= B.111,,263x y z ===-C. 111,,263x y z =-==D.111,,263x y z ===7.已知2244x y +=,则2211x y +的最小值为A.52B.9C.1D.948.已知函数()sin f x x x =+,若存在[0,]x π∈使不等式(sin )(cos )f x x f m x ≤-成立,则整数m 的最小值为A.1-B.0C.1D.2二、多项选择题:本题共4题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的,请把答案填写在答题卡相应位置上.全部选对得5分,部分选对得3分,不选或有选错的得0分.9.已知双曲线C 的渐近线方程为2y x =±,则该双曲线的离心率为10.在正方体1111ABCD A B C D -中,若点,,E F G 分别为11,,AB BC C D 的中点,则 A.1B D ⊥平面EFG B.1//CD 平面EFG C.1AC ⊥平面EFGD.1//AC 平面EFG11.2018年世界著名的国际科技期刊《Nature 》上有一篇名为《The Universal Decay of Collective Memory and Attention 》的论文,该文以12个不同领域的数据指出双指数型函数1212()x x f x C e C e λλ=+在描绘人类行为时的普适作用.关于该函数下列说法中正确的有A.当120C C >且12λλ≠时函数()f x 有零点B.当120C C <且12λλ≠时函数()f x 有零点C.当12120C C λλ<且12λλ≠时函数()f x 有极值D.当12120C C λλ>且12λλ≠时函数()f x 有极值12.已知无穷数列{}n a 满足121n n n a a a λλ+++=+,其中λ为常数,1λ≠-,则下列说法中正确的有A. 若2λ=-,则{}n a 是等差数列B. 若{}n a 是等差数列,则2λ=-C. 若11a =,22a =-,12λ=-,则{}n a 是等比数列D. 若{}n a 是等比数列,则11a =,22a =-,12λ=-三、填空题:本题共4题,每小题5分,共20分. 请把答案填写在答题卡相应位置上. 13.若点(2021,)P t 在抛物线24y x =上,点F 为该抛物线的焦点,则PF 的值为 ▲ . 14.有一块直角三角形空地ABC ,2A π∠=,250AB =米,160AC =米,现欲建一矩形停车场ADEF ,点,,D E F 分别在边,,AB BC CA 上,则停车场面积的最大值为 ▲ 平方米.15.设函数()ln 1f x ax x =--,若1a =-,则()f x 有 ▲ 个零点;若()f x 有且仅有两个零点,则实数a 的取值范围为 ▲ .(第1空2分,第2空3分) 16.已知数列{}n a 与{}n b 满足11222n n a a a ++++=-,1(1)(1)nn n n a b a a +=--,数列{}n b 的前n 项的和为n S ,若n S M ≤恒成立,则M 的最小值为 ▲ .四、解答题:本题共6题,第17题10分,其余每小题12分,共70分. 请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤. 17. (本小题满分10分)从①125,,a a a 成等比数列,②525S =,③222n nS S n n+-=+,这三个条件中任选一个,补充在下面问题中并作答.已知等差数列{}n a 的前n 项和为n S ,47a =, ,122na n nb a +=+,求数列{}n b 的前n 项和为n T .(注:如果选择多个条件分别解答,那么按照第一个解答计分)18. (本小题满分12分)如图,在直三棱柱111ABC A B C -中,AB AC ⊥,12,3AB AC AA ===. ⑴求异面直线1BC 与1A C 所成角的余弦值; ⑵设13BG BA BC =+,求AG 长.(第18题图)19. (本小题满分12分)已知函数2()ln f x x a x x=--. ⑴已知()f x 在点(1,(1))f 处的切线方程为2y x =-,求实数a 的值; ⑵已知()f x 在定义域上是增函数,求实数a 的取值范围.20. (本小题满分12分)在如图所示的四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,△PAD 是正三角形,平面PAD ⊥平面ABCD .⑴求平面PAB 与平面PCD 所成锐二面角的大小;⑵设E 为PB 上的动点,直线CE 与平面PAB 所成的角为θ,求sin θ的最大值.(第20题图)21. (本小题满分12分)已知椭圆C :22221(0)x y a b a b+=>>的离心率为12,点3(1,)2P 在椭圆C 上.ABCA 1B 1C 1ABCDPE⑴求C 的方程;⑵若椭圆C 的左右焦点分别为12,F F ,过点1F 的直线l 与C 交于A 、B 两点,△12AF F 与△12BF F 的面积分别为12,S S ,122S S =,求直线l 的斜率.22. (本小题满分12分)已知函数22()(31)x f x e x ax a a =-+-+在1x x =和2x x =时取极值,且12x x <.⑴已知12x =-,求2x 的值;⑵已知120x x +<,求12()()f x f x ⋅的取值范围.2020-2021学年第一学期高二年级期终考试数学参考答案1.D2.B3.B4.C5.A6.C7.D8.A9.AD10.AB11.BC12.AC13.2022 14.10000 15.1;(0,1) 16.117. 解:选①,设数列{}n a 的公差为d ,则由47a =可得137a d +=, 由125,,a a a 成等比数列得2111(4)()a a d a d +=+, 联立以上两式可得170a d =⎧⎨=⎩或112a d =⎧⎨=⎩, …………………………6分若17,0a d ==,则7n a =,23n b =,23n T n =; …………………………8分若11,2a d ==,则21n a n =-,212nn b n =-+,21(1)2(12)[12]22212n n n n n T n n +--=⨯+⨯+=+--. …………………………10分选②,设数列{}n a 的公差为d ,则由47a =可得137a d +=, 由525S =得1545252a d ⨯+=, 联立以上两式可得11,2a d ==, …………………………5分则21n a n =-,212nn b n =-+,21(1)2(12)[12]22212n n n n n T n n +--=⨯+⨯+=+--. …………………………10分选③,设数列{}n a 的公差为d ,则由47a =可得137a d +=, ∵1(1)2n n n d S na -=+,∴1(1)2n S n d a n -=+,∴21(1)22n S n da n ++=++, 由222n nS S n n+-=+得2d =,则11a =, …………………………5分 则21n a n =-,212nn b n =-+,21(1)2(12)[12]22212n n n n n T n n +--=⨯+⨯+=+--. …………………………10分18. 解:以1{,,}AB AC AA 为正交基底建立如图所示空间直角坐标系A xyz -,……………2分 则(0,0,0)A ,1(0,0,3)A,B ,(0,2,0)C ,1(0,2,3)C . …………………4分⑴1(2,3)BC =-,1(0,2,3)AC =-,∴111111cos ,||||5BC AC BC AC BC AC ⋅<>===…………………7分则异面直线1BC 与1A C .…………………8分 ⑵∵G 为△1A BC 的重心,1(0,0,3)A ,B ,(0,2,0)C , ∴2(,1)33G , …………………10分 ∴25||(3AG AG ===. …………………12分19. 解:⑴∵2()ln f x x a x x=--,∴22()1a f x x x '=+-,∴(1)3f a '=-,又()f x 在点(1,(1))f 处的切线方程为2y x =-,∴(1)1f '=,∴31a -=,∴2a =. …………………4分 ⑵()f x 的定义域为(0,)+∞,∵()f x 在定义域上为增函数,∴22()10af x x x'=+-≥在(0,)+∞上恒成立, ∴2a x x ≤+在(0,)+∞上恒成立,∴min2a x x ⎛⎫≤+⎪⎝⎭,…………………8分由基本不等式2x x +≥=,当且仅当x =故min2x x ⎛⎫+= ⎪⎝⎭ 故a的取值范围为(,-∞. …………………12分 20.解:取AD 的中点O ,取BC 的中点F ,连接,OP OF , 因为底面ABCD 是正方形,∴OF AD ⊥,∵△PAD 是正三角形,O 为AD 的中点,∴OP AD ⊥, 又因为平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,OP ⊂平面PAD ,∴OP ⊥平面ABCD ,以{,,}OF OD OP 为正交基底建立如图所示空间直角坐标系O xyz -. …………………2分⑴P ,(0,1,0)A -,(2,1,0)B -,则(2,0,0)AB =,AP =, 设(,,)m x y z =为平面PAB 的一个法向量,则200m AB x m AP y ⎧⋅==⎪⎨⋅=+=⎪⎩,则0x =,令1z =,得y =(0,3,1)m =-,…………4分P ,(2,1,0)C ,(0,1,0)D ,则(2,0,0)DC =,(0,DP =-,设(,,)n a b c =为平面PCD 的一个法向量,则200n DC a n DP b ⎧⋅==⎪⎨⋅=-=⎪⎩,则0a =,令1c =,得b =(0,3,1)n =,……………6分 ∴21cos ,222||||m n m n m n ⋅-<>===-⨯,又,[0,]m n π<>∈,∴2,3mn π<>=,∴面PAB 与平面PCD 所成锐二面角的大小为3π. …………………8分 ⑵设BE BP λ=,[0,1]λ∈,则((2,)BE λλλ=-=-,则(0,2,0)(2,)(2,)CE CB BE λλλλ=+=-+-=--, 因为直线CE 与平面PAB 所成的角为θ, ∴||sin |cos ,|||||(CE m CE m CE mθ⋅=<>==-………………10分7==≤=,当且仅当14λ=时取等号, 故求sin θ的最大值为7. …………………12分 21. 解:⑴由22222121914c a ab a bc ⎧=⎪⎪⎪+=⎨⎪⎪=+⎪⎩得2243a b ⎧=⎪⎨=⎪⎩,故C 的方程为22143x y +=. …………………4分⑵1(1,0)F -,显然l 与y 轴不垂直,故可设:1l x ty =-,设11(,)A x y ,22(,)B x y ,由221143x ty x y =-⎧⎪⎨+=⎪⎩消去x 得22(34)690t y ty +--=,则122634t y y t +=+,122934y y t -=+, …………………6分 由122S S =得122y y =-, (8)分 则22634t y t -=+,2229234y t --=+, 消去2y 可得t =:1l x y =-, 得l 的斜率为. …………………12分 22. 解:⑴∵22()(31)x f x e x ax a a =-+-+,∴22()[(2)41]x f x e x a x a a '=+-+-+,∵()f x 在1x x =和2x x =时取极值,∴12()()0f x f x ''==, ∴1x ,2x 是22(2)410x a x a a +-+-+=的两个不等实根,∴12222x x x a +=-+=- ,2122241x x x a a =-=-+,解得21x =,经检验,符合题意. …………………4分⑵由⑴知122x x a +=-,21241x x a a =-+,∴122222121122()()(31)(31)x x f x f x e x ax a a e x ax a a ⋅=-+-+⋅-+-+ ∵1x ,2x 是22(2)410x a x a a +-+-+=的两个不等实根, ∴2211(2)410x a x a a +-+-+=,2222(2)410x a x a a +-+-+=, ∴22111312x ax a a a x -+-+=-,22222312x ax a a a x -+-+=-, ∴1212212121212()()(2)(2)[42()]x x x x f x f x e a x a x e x x a x x a ++⋅=--=-++22222[4(41)2(2)](3124)a a e a a a a a e a a --=-+--+=-+ …………………8分设22()(3124)a g a ea a -=-+,∵120x x +<,∴20a -<,①又1x ,2x 是22(2)410x a x a a +-+-+=的两个不等实根, ∴△=22(2)4(41)0a a a ---+>,得04a <<,②由①②知(0,2)a ∈, …………………10分 而22()(368)a g a ea a -'=--,设2()368h a a a =--,则(0)0h <,(2)0h <,由二次函数的性质可知2()3680h a a a =--<在(0,2)上恒成立, 则()0g a '<在(0,2)上恒成立,则22()(3124)a g a e a a -=-+在(0,2)上单调递减,而24(0)g e =,(2)8g =-,故12()()f x f x ⋅的取值范围为24(8,)e -. …………………12分。
江苏省盐城市盐城市一中、大丰高级中学等四校2021学年上学期高二年级期终考试英语试卷

江苏省盐城市盐城市一中、大丰高级中学等四校2020-2021学年上学期高二年级期终考试英语试卷【考试时间:120分钟分值:150分】第一部分:听力共两节,满分30分第一节(共5小题;每小题1 5分;满分7 5分)听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1 What's the time nowA 8:30B 7:55C 8:352 Why does the woman loo sadA She did badly in the eamsB She worries about her coming testsC She is ill3 What do we learn about the tai driverA He drove too fast and crashed into a trucB He turned suddenly and ran into a treeC He was hit by a falling bo from a truc4 What is the man doingA He is asing about his letterB He is buying mon health conditions21 What is immonly leave their trees to run after a e very aggressive and attac their enemies with their shares from mon waste Better yet, it can run without electricity and requires no farming sills to eee richB get rid of the waste e mon mit suicide and another 10 million atteme infected through contact with it Humans can become infected by changing their infected cats’ litter boes, eating unwashed vegetables, drining water from a mon way which is more liely to be infected with the disease is _____A to eat unwashed vegetables or undercooed meatB to clean a ing bad temmit suicideB Women should eement B informationC nowledgeD feeling42 A failing B continuing C managing D stomon47 A strong B smart C young D local48 A adults B children C scientists D activists49 A wear down B believe in C now about D write off50 A benefits B ing-he never res e with me! I’m looing forward to your ree bac Eric! We would love to be your friend again ” Eric ecitedly re so ha today our friendships will never brea。
江苏省盐城四县2020-2021学年高二上学期期中联考试题 物理(选修)

17.(12 分)如下图所示,固定在同一水平面内的两根平行长直金属导轨的间距为 L,其右端接有 阻值为 R 的电阻,整个装置处在竖直向上磁感应强度大小为 B 的匀强磁场中。一质量为 m(质 量分布均匀)的导体杆 ab 垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦 因数为μ。现杆在水平向左、垂直于杆的恒力 F 作用下从静止开始沿导轨运动距离为 s 时,速 度恰好达到最大值(运动过程中杆始终与导轨保持垂直)。设杆接入电路的电阻为 r,导轨电阻不 计,重力加速度大小为 g.求此过程: (1)速度达到最大值时,通过 R 的电流大小; (2)杆的最大速度 Vm; (3)通过电阻 R 的电量 q;
大
7.矩形导线框 abcd 固定在匀强磁场中,磁感线的方向与导线框所在平面垂直.规定磁场的正方向
1
垂直纸面向里,磁感应强度 B 随时间变化的规律如图所示.若规定顺时针方向为感应电流 i 的 正方向,下列 i-t 图中正确的是( )
8.如图所示,电路中定值电阻阻值 R 大于电源内阻阻值 r,闭合开关 S,
5.如图所示,电源电动势 E=12V,内阻 r=1Ω,限流电阻 R′=3Ω,M 为
直流电动机,其线圈电阻 R=2Ω。当电动机正常工作时,理想电流表示
数为 1A,此时电动机的输出功率是( )
A. 6W
B. 8W
C. 2W
D. 7W
6.如图所示为某回旋加速器示意图,利用回旋加速器对
2 1
H
粒子进行加速,此时 D
16.(11 分)如图所示,在半径为 R m0 的圆形区域内有水平向里的匀强磁场,磁感应强度 B,圆形 Bq
江苏省盐城四县2020-2021学年高二上学期期中联考试题 物理(选修)答案

(4 分)
(3)当 30 时,带电粒子在磁场中运动的轨道半径为 3R
其运动轨迹如图所示,
由图可知 PO2O OO2 R 30
所以带电粒子离开磁场时与水平方向成 30°
d R2 3 R 3
1
d (3 2 3)mv0 3qB (4 分)
17. (1) I F mg (4 分) BL
(2)
y=v0t (1 分)代入数据解得 y=0.3 m (2 分) (2)粒子经过 y 轴时在电场方向的分速度为:
vx=at=2×107 m/s (1 分) 粒子经过 y 轴时速度为
v= vx2+v02=2.5×107m/s (2 分) 与 y 轴正方向夹角大小为θ。
tan θ=vx=4/3 v0
(1 分) θ=53°
(1 分)
(3)要使粒子不进入第Ⅲ象限,如图所示,此时粒子做圆周运动的半径为 R,
则 R+0.8R≤y (1 分)解得:1.8 R≤ y(1 分)
v2 由 qvB=m (1 分)
R
解得 B≥6×10-2T。
(2 分)
2
qB
(2)设带电粒子进入磁场中做匀速圆周运动的轨道半径为 r ,由牛顿第二定律得
Bq0
m 02 r
P
M
●
O1
××
rR
××××
带电粒子在磁场中的运动轨迹为四分之一圆周,轨 × ×O ● × ×
Q
×××
迹对应的圆心角为 ,如图所示,则
2
××
N
t
R 2 0
m 2Bq
2020-2021 学年第一学期高二年级期中考试
物理试卷答案
题号 1
2
3
4
5
江苏省盐城四县2020-2021学年高二上学期期中联考试题 数学 答案

2020-2021学年第一学期高二年级期中考试数学试题答案一、单项选择题:本题共8题,每小题5分,共40分.1—4:B ,C ,B ,A ; 5—8:A ,B ,D ,C二、多项选择题:本题共4题,每小题5分,共20分.全部选对得5分,部分选对得3分,不选或有选错的得0分.9.,B C ;10. ,A C ;11. ,,A B C ;12. ,,A C D三、填空题:本题共4题,每小题5分,共20分.13. x R ∀∈,20x x -≤; 14. 26a -≤≤; 15.10; 16.221412x y -=. 四、解答题:本题共6题,第17题10分,其余每小题12分,共70分.17.⑴26m <<; ⑵23a ≤≤. 每小问5分,不写等号扣1分18.⑴(1,1)-; ⑵ 1x x y +的最小值为3,当且仅当12x y ==时取等号. 每小问6分,不写等号成立条件扣2分19.⑴略; ⑵221n n S n =+-. 每小问6分20. ⑴22184x y +=,m -<< ⑵直线l 的方程为0y =. 第一小问8分(4+4),第二小问4分21.⑴证:由122n n n a a a +=+,且12a =知,0n a >,故有11112n n a a +-=得,所以数列1n a ⎧⎫⎨⎬⎩⎭是等差数列, ……………………3分⑵由1n n n n b b a b +-=得,121n n n b n a b n ++=+=,由累乘法得,(1)n b n n =+,………8分 则不等式22n a n b <可化为2(1)n n n <+,即(1)12n n n +>, 令(1),2n n n n c n N *+=∈,则1n c >. 当1n =时,11c =,不符; 当2n =时,2312c =>,符合;当3n =时,3312c =>,符合;当4n =时,4514c =>,符合; 当5n =时,515116c =<,不符合; 而当5,n n N *≥∈时,()()1111(2)1(2)(1)0222n n n n n n n n n n n c c ++++++-+-=-=<, 故当5,n n N *≥∈不符合;综上所述,{}2,3,4n ∈. ……………………12分(枚举出答案给2分,证明单调性给2分)22. ⑴椭圆2C 的标准方程为22142x y +=;……………………4分 ⑵(i)由22112y x y k x ⎧+=⎪⎨⎪=+⎩,得1212A x k =-+;由2211422,x y y k x ⎧+=⎪⎨⎪=+⎩,得1214212B k x k =-+; 由85PB PA =知,112211422281252k k k k ⎛⎫-=⨯- ⎪ ⎪++⎝⎭,解得212k =, 故21121222202A A k y k x k =+=-+=+; ……………………8分 (ii)同理可得2222B k x =-,由,A C 两点关于坐标原点O 对称知,121222220k k ⎛⎫-+-= ⎪ ⎪⎝⎭,即122k k =-,即212k k -=;……………………10分 而()12211211122122242k k PA PB k k -+==+-, 同理,()()2221212222112121282242222k k k PC PD k k k ⎛⎫-+ ⎪++⎝⎭===⎛⎫++⎛⎫- ⎪+ ⎪ ⎪⎝⎭⎝⎭, 所以()()22112211128542242k k PA PC PB PD k k +++=+=++. ……………………12分。
2020-2021学年江苏省盐城市大丰大桥中学高二数学理上学期期末试题含解析

2020-2021学年江苏省盐城市大丰大桥中学高二数学理上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 计算lg4+lg25=()A.2 B.3 C.4 D.10参考答案:A【考点】对数的运算性质.【分析】利用对数的运算法则即可得出.【解答】解:原式=lg(4×25)=lg102=2.故选:A.【点评】本题考查了对数的运算法则,考查了推理能力与计算能力,属于基础题.2. 某演绎推理的“三段”分解如下:①函数是减函数;②指数函数是减函数;③函数是指数函数,则按照演绎推理的三段论模式,排序正确的是()A.①→②→③ B.③→②→① C.②→①→③ D.②→③→①参考答案:D按照演绎推理的三段论模式可得,已知指数函数是减函数,因为函数是指数函数,所以函数是减函数,即排序正确的是②→③→①,故选D.3. 过双曲线的一个焦点F2作垂直于实轴的直线,交双曲线于P、Q,F1是另一焦点,若∠PF1Q=,则双曲线的离心率e等于()A.B.C.D.参考答案:C 【考点】双曲线的简单性质;双曲线的应用.【分析】根据由题设条件可知,|F1F2|=2c,由此可以求出双曲线的离心率e.【解答】解:由题意可知,|F1F2|=2c,∵∠,∴,∴4a2c2=b4=(c2﹣a2)2=c4﹣2a2c2+a4,整理得e4﹣6e2+1=0,解得或(舍去)故选C.4. 抛物线的准线方程是,则的值为()A.B. C.8 D.参考答案:B5. 已知抛物线的焦点为F,点时抛物线C上的一点,以点M为圆心与直线交于E,G两点,若,则抛物线C的方程是()A. B. C. D.参考答案:C【分析】作,垂足为点,根据在抛物线上可得,再根据得到,结合前者可得,从而得到抛物线的方程.【详解】画出图形如图所示作,垂足为点.由题意得点在抛物线上,则,得.①由抛物线的性质,可知,因为,所以.所以,解得. ②,由①②,解得(舍去)或.故抛物线的方程是.故选C.【点睛】一般地,抛物线上的点到焦点的距离为;抛物线上的点到焦点的距离为.6. 若直线过圆的圆心, 则( )A. 1 B. 1 C. 3 D.3参考答案:B略7. 命题“R,”的否定是()A.R,B.R,C.R,D.R,.参考答案:D8. 从一个含有40个个体的总体中抽取一个容量为7的样本,将个体依次随机编号为01,02,…,40,从随机数表的第6行第8列开始,依次向右,到最后一列转下一行最左一列开始,直到取足样本,则获取的第4个样本编号为()(下面节选了随机数表第6行和第7行)第6行84 42 17 56 31 07 23 55 06 82 77 04 74 43 59 76 30 63 50 25 83 92 12 06第7行63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38.A.06 B.10 C.25 D.35参考答案:A【考点】简单随机抽样.【分析】找到第6行第8列的数开始向右读,依次寻找号码小于500的即可得到结论.【解答】解:找到第6行第8列的数开始向右读,第一个数是63,不成立,第二个数10,成立,第三个数72,不成立,第四个数35,成立,第五个数50,不成立,这样依次读出结果,68,27,70,47,44,35,97,63,06合适的数是27,35,06,其中35前面已经重复舍掉,故第四个数是06.故选:A9. 在△ABC中,bcosA=acosB,则三角形的形状为()A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形参考答案:C考点:正弦定理;余弦定理.专题:三角函数的求值.分析:已知等式利用正弦定理化简,变形后利用两角和与差的正弦函数公式化简,得到A﹣B=0,即A=B,即可确定出三角形形状.解答:解:利用正弦定理化简bcosA=acosB得:sinBcosA=sinAcosB,∴sinAcosB﹣cosAsinB=sin(A﹣B)=0,∴A﹣B=0,即A=B,则三角形形状为等腰三角形.故选:C.点评:此题考查了正弦定理,两角和与差的正弦函数公式,以及等腰三角形的判定,熟练掌握定理及公式是解本题的关键.10. 已知函数集合,则的面积是()A. B. C.D.参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 设p:|4x-3|≤1;q:(x-a)(x-a-1)≤0,若p是q的充分不必要条件,则实数a的取值范围是________.参考答案:[0,]12. 过椭圆的右焦点F作一斜率大于0的直线交椭圆于A、B两点,若点F将线段AB分成2:1两段,则直线AB 的斜率为▲ .参考答案:13. 的内角A,B,C的对边分别为a,b,c.已知b sin A+a cos B=0,则B=___________.参考答案:.【分析】先根据正弦定理把边化为角,结合角的范围可得.【详解】由正弦定理,得.,得,即,故选D.【点睛】本题考查利用正弦定理转化三角恒等式,渗透了逻辑推理和数学运算素养.采取定理法,利用转化与化归思想解题.忽视三角形内角的范围致误,三角形内角均在范围内,化边为角,结合三角函数的恒等变化求角.14. 函数对于总有≥0 成立,则= .参考答案:4略15. 数据5,7,7,8,10,11的标准差是参考答案:216. 已知x,y满足则的取值范围是.参考答案:[﹣1,]【考点】简单线性规划.【专题】数形结合.【分析】本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与(4,1)构成的直线的斜率问题,求出斜率的取值范围,从而求出目标函数的取值范围.【解答】解:由于z==,由x,y满足约束条件所确定的可行域如图所示,考虑到可看成是可行域内的点与(4,1)构成的直线的斜率,结合图形可得,当Q(x,y)=A(3,2)时,z有最小值1+2×=﹣1,当Q(x,y)=B(﹣3,﹣4)时,z有最大值1+2×=,所以﹣1≤z≤.故答案为:[﹣1,]【点评】本题考查线性规划问题,难点在于目标函数几何意义,近年来高考线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.17. 下列四个命题:(1)已知向量是空间的一组基底,则向量也是空间的一组基底;(2)在正方体中,若点在内,且,则的值为1;(3)圆上到直线的距离等于1的点有2个;(4)方程表示的曲线是一条直线.其中正确命题的序号是________.参考答案:(1)(2)(4)(1)已知向量是空间的一组基底,即向量不共面,则也不共面,所以向量是空间的一个基底,正确;(2),,,正确;(3)由圆的方程,得到圆心A坐标为(3,3),半径为3,则圆心(3,3)到直线的距离为,∴圆上的点到直线的距离为1的点有3个,错误;(4)由题意可化为或,不成立,方程表示的曲线是一条直线,正确,故答案为(1)(2)(4).三、解答题:本大题共5小题,共72分。
江苏省盐城市盐城市一中、大丰高级中学等四校2021学年上学期高二年级期终考试化学试卷
江苏省盐城市盐城市一中、大丰高级中学等四校2020-2021学年上学期高二年级期终考试化学试卷可能用到的相对原子质量: H 1 C 12 N 14 O 16 B 11 Si 28 ol Cl的水溶液中加入足量AgNO3溶液能生成3mol AgCl6下列叙述正确的是A 熔沸点由高到低的顺序:AsH3>2。
A的红外光谱 A的核磁共振氢谱下列关于有机化合物A的说法中正确的是mol A与NaOH水溶液反应,最多消耗1 mol NaOHmol A在一定条件下最多可与4molH2发生加成反应的同分异构体中与其属于同类化合物且分子中含有苯环的有5种不含A本身分子能与溴水发生取代反应是合成治疗某心律不齐药物的中间体:下列说法正确的是A.X分子含有羟基和醛基两种官能团B.Y在浓硫酸催化下加热可发生消去反应C.1 mol Z与足量溴水反应,最多消耗1 mol Br2D.1 mol Y与NaOH水溶液反应,最多消耗2 mol NaOH多巴胺是一种有机物,它可用于帕金森综合症的治疗,其结构简式如下:下列关于L-多巴胺的叙述正确的是A该分子中所有碳原子一定处于同一平面B.一定条件下L-多巴胺可发生氧化、取代、加成、缩聚反应C.1mol该有机物跟足量浓溴水反应,最多消耗2molBr2D.它既与HCl反应又与NaOH反应,等物质的量L-多巴胺最多消耗HCl与NaOH的物质的量之比为1:3第Ⅱ卷(非选择题共60分)二、非选择题16(14分)碳、氮元素可形成多种卤化物、含氧酸及其盐和配合物等。
1 常温下NF3是一种无色、无味、无毒的气体,推断NF3分子的空间构型为(用文字描述)。
2 与HNO2互为等电子体的一种阴离子的化学式;推断NaNO2中阴离子的空间构型为(用文字描述)。
(3)配合物Ni(CO)4是无色液体,沸点℃,熔点℃,难溶于水,易溶于CCl4,推测Ni(CO)4是分子(填“极性”或“非极性”)。
(4)写出CN-的电子式;NH4NO3 中氮原子轨道的杂化类型是。
