2013年高考模拟考试文科数学(3)(4.26)
2013高考数学文科模拟试题(带答案)

2013高考数学文科模拟试题(带答案)2013年普通高等学校招生全国统一考试西工大附中第四次适应性训练数学(文科)第Ⅰ卷选择题(共50分)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分)1.设全集集合集合,则=()A.B.C.D.2.设复数(其中为虚数单位),则z的共轭复数等于()A.1+B.C.D.3.已知条件p:,条件q:,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既非充分也非必要条件4.如右图的程序框图所示,若输入,则输出的值是()A.B.1C.D.25.若抛物线上一点到轴的距离为3,则点到抛物线的焦点的距离为()A.3B.4C.5D.76.公差不为零的等差数列第2,3,6项构成等比数列,则这三项的公比为()A.1B.2C.3D.47.已知是单位向量,且夹角为60°,则等于()A.1B.C.3D.8.已知函数对任意,有,且当时,,则函数的大致图象为()9.设函数,则不等式的解集是()A.B.C.D.10.一个三棱锥的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为()A.B.C.1D.第Ⅱ卷非选择题(共100分)二、填空题(本大题共5小题,每小题5分,满分25分,把答案填写在答题卡相应的位置)11.若函数的图象在处的切线方程是,则.12.若椭圆的短轴为,它的一个焦点为,则满足为等边三角形的椭圆的离心率是.13.已知变量满足约束条件,则的最大值为;14.若则;15.选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)A(选修4—4坐标系与参数方程)已知点是曲线上任意一点,则点到直线的距离的最小值是;B(选修4—5不等式选讲)已知则的最大值是.;C(选修4—1几何证明选讲)如图,内接于,,直线切于点C,交于点.若则的长为.三、解答题:解答应写出文字说明,证明过程或演算步骤(本大题共6小题,共75分)16.(本小题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.17.(本小题满分12分)在中,角A,B,C的对边分别为,b,c,且满足,.(Ⅰ)求的面积;(Ⅱ)若,求边与的值.18.(本小题满分12分)各项均为正数的等比数列中,.(Ⅰ)求数列通项公式;(Ⅱ)若等差数列满足,求数列的前项和.19.(本小题满分12分)已知是矩形,,分别是线段的中点,平面.(Ⅰ)求证:平面;(Ⅱ)在棱上找一点,使∥平面,并说明理由.20.(本小题满分13分)已知函数.(Ⅰ)当时,求曲线在点处的切线方程;(Ⅱ)当时,判断方程在区间上有无实根.(Ⅲ)若时,不等式恒成立,求实数的取值范围.21.(本题满分14分)已知椭圆的中心在坐标原点,焦点在轴上,离心率,且点在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)已知、为椭圆上的动点,当时,求证:直线恒过一个定点.并求出该定点的坐标.2013年普通高等学校招生全国统一考试西工大附中第四次适应性训练数学(文科)参考答案与评分标准一、选择题:题号12345678910答案DAADBCCCAD二、填空题:11.312.13.1114.15.A;B.;C.三、解答题16.(本小题满分12分)【解】:在100名电视观众中,收看新闻的观众共有45人,其中20至40岁的观众有18人,大于40岁的观众共有27人。
2013届山东高考模拟数学文

山东省潍坊市2013届高三上学期期末考试数学(文)试题本试卷共4页,分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟。
第I 卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再改涂其它答案标号。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)全集U=R ,集合{}02|2≥+=x x x A ,则[U A= (A )[]0,2-(B )()0,2-(C )(][)+∞⋃-∞-,02,(D )[]2,0(2)已知,54cos ,23,-=⎪⎭⎫ ⎝⎛∈αππα则)4tan(απ-等于 (A )7(B )71(C )71-(D )7-(3)如果等差数列{}n a 中,15765=++a a a ,那么943...a a a +++等于(A )21(B )30(C )35(D )40(4)要得到函数)23sin(-=x y 的图象,只要将函数x y 3sin =的图象 (A )向左平移2个单位 (B )向右平移2个单位(C )向左平移32个单位 (D )向右平移32个单位 (5)“1-=m ”是“直线02)12(=+-+y m mx 与直线033=++my x 垂直”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件(6)下列有关命题的说法正确的是(A )命题“若12=x ,则1=x ”的否命题为“若12=x ,则1≠x ” (B )命题“01,2<-+∈∃x x R x ”的否定是“01,2>-+∈∀x x R x ” (C )命题“若y x =,则y x sin sin =”的逆否命题为假命题 (D )若“p 或q ”为真命题,则p ,q 至少有一个为真命题(7)设m ,n 是两条不同直线,βα,是两个不同的平面,下列命题正确的是(A )βα//,//n m 且,//βα则n m // (B ) βα⊥⊥n m ,且 βα⊥,则 n m ⊥ (C ),,,n m n m ⊥⊂⊥βα 则βα⊥ (D ),//,//,,ββααn m n m ⊂⊂则βα// (8)函数x x y sin =在[]ππ,-上的图象是(9)已知双曲线()0,012222>>=-b a by a x 的一条渐近线的斜率为2,且右焦点与抛物线x y 342=的焦点重合,则该双曲线的离心率等于(A )2(B )3(C )2(D )23(10)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是(A )π12 (B )π24 (C )π32 (D )π48 (11)已知集合{}⎭⎬⎫⎩⎨⎧+-==<--=311|,032|2x x gy x B x x x A ,在区间()3,3-上任取一实数x ,则“B A x ⋂∈”的概率为(A )41 (B )81 (C )31 (D )121 (12)已知函数⎩⎨⎧>≤+=0,10,2)(x nx x kx x f ,若0>k ,则函数1|)(|-=x f y 的零点个数是(A )1(B )2 (C )3(D )4第II 卷(非选择题 共90分)注意事项:1.将第II 卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上。
2013届高中毕业班第一次模拟考文科数学答案

2013届高中毕业班第一次模拟考文科数学答案13. 15 14. {|34}x x x >≠且 15. 250x y -+= 16. 135三. 解答题(共90分)17. 解:由已知得213112203a q a q a q ⎧=⎪⎨+=⎪⎩L L L L ①②………………..4分 ①②得23110q q =+化简得:231030q q -+=…………..5分 133q q ∴==或 (6)分当13q =时,118a =;当3q =时,129a =……………….8分{}n a ∴的通项公式1118()3n n a -=g 或1239n n a -=g ………….10分18. 解:(1)由sin sin A B C +=及正弦定理,得a b c +=,又1a b c ++=……………………….2分 1c + 1c ∴=……………………………6分(2)由1sin 2S ab C =又1sin 6S C = 11sin sin 26ab C C ∴= 13ab ∴=,又a b +=..8分由22222()21cos 222a b c a b ab c C ab ab +-+--===…………11分 60C ∴=o ………………………………………………………12分19. 解:(1)从50名教师随机选出2名的方法数为2501225C =…….2分 选出的2人都来自柳州市的方法数为215105C =……………..4分故2人都来自柳州市的概率为1053122535P ==…………….6分 (2)选出2人来自同一城市的方法数为22222015510350C C C C +++=…….8分 所以选出2人来自不同城市的方法数为250350875C -=……………10分故 2人来自不同城市的概率为875512257P ==………………………..12分20. 解.(1)证明:因为侧面11ABB A ,11ACC A 均为正方形,所以11,AA AC AA AB ⊥⊥,所以1AA ⊥平面ABC ,三棱柱111ABC A B C -是直三棱柱.因为1A D ⊂平面11A B C ,所以11CC A D ⊥, ………………………3分又因为1111A B AC =,D 为11B C 中点, 所以111A D B C ⊥. ……………………5分 因为1111CC B C C = ,所以1A D ⊥平面11BB C C . ……………6分(2)解: 因为侧面11ABB A ,11ACC A 均为正方形, 90BAC ∠= ,所以1,,AB AC AA 两两互相垂直,如图所示建立直角坐标系A xyz -……7分设1AB =,则111(0,10),(1,0,0),(0,0,1),(,,1)22C B AD ,. 1111(,,0),(0,11)22A D AC ==-uuu r uuu r ,, ……………………………8分 设平面1A DC 的法向量为=()x,y,zn ,则有 1100A D A C ⋅=⎧⎨⋅=⎩rrn n ,0x y y z +=⎧⎨-=⎩, x y z =-=-, 取1x =,得(1,1,1)=--n . ……………………9分又因为ABAB⋅==uu u rruu u rrnn,AB⊥平面11ACC A,…………11分所以平面11ACC A的法向量为(1,00)AB=uu u r,,因为二面角1D AC A--是钝角.所以,二面角1D AC A--的余弦值为……………12分21.解:(1)当2a=时,'2()61f x x=-…………………………….1分令'()0f x<,得x<<;…………………………3分令'()0f x>,得x<或x>……………………….5分∴()f x的单调递减区间是(,单调递增区间是(,-∞和()6+∞………………………………………………………6分(2)设过原点所作的切线的切点坐标是2(,)A m am m-,则231k am=-切线方程为32()(31)()y am m am x m--=--,……………….8分把(0,0)代入切线方程,得32()(31)()am m am m--=--m∴=或220am=a≠Q0m∴=………………………………………………11分即只有唯一切点,故过原点作切线只有一条………………….12分22. 解.(1)由已知可得点A(-6,0),F(0,4)设点P(x,y),则APuu u r=(x+6, y),FPuur=(x-4, y),由已知可得22213620(6)(4)0x yx x y⎧+=⎪⎨⎪+-+=⎩…………………………….4分则22x+9x-18=0,x=23或x=-6. 由于y>0,只能x=23,于是y=235.∴点P 的坐标是(23,235)……………………………………..6分(2) 直线AP 的方程是x -3y +6=0. 设点M(m ,0),则M 到直线AP 的距离是26+m . 于是26+m =6-m ,又-6≤m ≤6,解得m =2……………………………………………………8分 椭圆上的点(x ,y )到点M 的距离d 有222222549(2)4420()15992d x y x x x x =-+=-++-=-+,……….10分 由于-6≤X ≤6, ∴当x =29时,d 取得最小值15 ……………….12分。
2013年高考数学文科模拟试卷(含答案详解版)

开始 0k =k =k +131n n =+150?n >输出k ,n结束是 否输入n2013年高考数学模拟试卷(文)第I 卷一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1.1.已知集合{}0 1 2A =,,,集合{}2B xx =>,则A B =A .B .{}0 1 2,,C .{}2x x >D .∅ 2.已知i 为虚数单位,则212ii-++的值等于 ( )A. i -B.12i -C. 1-D.2.定义{|,,}x A B z z x y x A y B y⊗==+∈∈.设集合{0,2}A =,{1,2}B =3.如果奇函数f(x) 是[3,7]上是增函数且最小值为5,那么f(x)在区间[-7,-3]上是( ) A.增函数且最小值为-5 B.减函数且最小值是-5 C.增函数且最大值为-5 D.减函数且最大值是-5 4.如果实数x,y 满足等式(x -2)2+y 2=3,那么xy的最大值是( ) A .21 B .33 C .23 D .35.阅读图1的程序框图. 若输入5n =, 则输出k 的值为. A .2 B .3 C .4 D .56.函数tan()42y x ππ=-的部分图象如图所示,则()O AO BA B +⋅=( )A.6B.4C.4-D.6-7.在纪念中国人民抗日战争胜利六十周年的集会上,两校各派3名代表,校际间轮流发言,对日本侵略者所犯下的滔天罪行进行控诉,对中国人民抗日斗争中的英勇事迹进行赞颂,那么不同的发言顺序共有( ) A.72种 B.36种 C.144种 D.108种O xyAB第6题图图18.已知函数()y f x =的定义域为2(43,32)a a --, 且(23)y f x =-为偶函数,则实数a 的值为( )A .3或-1B .-3或1C .1D .-19.农民收入由工资性收入和其它收入两部分构成。
北京市昌平区2013届高三仿真模拟数学文科试卷3 Word版含答案

北京市昌平区2013届高三仿真模拟数学文科试卷3第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)1.已知集合{}{}3,1,2,3,4A x x B =≥=,则A B =A .{4}B .{3,4}C .{2,3,4}D .{1,2,3,4}2.设条件0:2>+a a p , 条件0:>a q ; 那么q p 是的A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件3. 数列{}n a 对任意*N n ∈ ,满足13n n a a +=+,且38a =,则10S 等于A .155B . 160C .172D .2404. 若b a b a >是任意实数,且、,则下列不等式成立的是 A .22b a > B .1<ab C .0)lg(>-b a D .b a )31()31(<5.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸 (单位:cm ),可得这个几何体的体积是A .πcm 3B .34πcm 3C .35πcm 3 D .2π cm 36. 已知3log ,2321==b a ,则输出的值为A.22B.2C. 212- D. 212+7、已知ABC ∆中,,10,4,3===BC AC AB 则∙等于 A .596- B. 215- C. 215 D. 2968、如图AB 是长度为定值的平面α的斜线段,点A 为斜足,若点P 在平面α内运动,使得ABP ∆的面积为定值,则动点P 的轨迹是A.圆B.椭圆 C 一条直线 D 两条平行线第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分,共30分.)9.i-12= 10.一个正方形的内切圆半径为2,向该正方形内随机投一点P,点P 恰好落在圆内的概率是__________11.《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100mL (不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100mL (含80)以上时,属醉酒驾车。
山东省潍坊市2013年高三三模文科数学试题

2013年高考模拟考试 数学试题(文)2013.5本试卷共5页,分第I 卷(选择题)和第II 卷(非选择题)两部分.共150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设i 是虚数单位,复数2a ii+-是纯虚数,则实数a= A.2-B.2C.12-D.122.已知集合{{},1,,,=A B m A B B m ==⋂=则 A.0或1 B.0或3 C.1或3 D.0或1或33.下列命题中,真命题是A.命题“若p ,则q.”的否命题是“若p ,则.q ⌝”B.命题2:10p x R x ∃∈+<,使得,则:p x R ⌝∀∈,使得210x +≥C.已知命题p 、q ,若“p q ∨”为假命题,则命题p 与q 一真一假D.a+b=0的充要条件是1ab=- 4.某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[)[)50,60,60,70,[)[)[)70,80,80,90,90,100.则成绩在[]90,100内的人数为A.20B.15C.10D.55.函数()()2log 1f x x =+的图象大致是6.一个几何体的三视图如图所示,且其左视图是一个等边三角形,则这个几何体的体积为A.3122π+B.9362π+C.9184π+D.364π+7.已知()(),1,2,4AB k AC ==,若k 为满足4AB ≤的随机整数,则AB BC ⊥的概率为A.17B.27C.13D.238.已知,x y 满足1400x x y x y ≥⎧⎪+-≤⎨⎪-≤⎩,则2z x y =-的最大值是A.5-B.2-C.1-D.19.已知ABC ∆内角A 、B 、C 的对边分别是a 、b 、c ,若1cos ,2,sin 2sin ,4B bC A===则ABC ∆的面积为C.10.已知函数()312,16f x x x a a =-+≥其中,则下列说法正确的是A.()f x 有且只有一个零点B.()f x 至少有两个零点C.()f x 最多有两个零点D.()f x 一定有三个零点11.已知数列()*21n a n n N =-∈,把数列{}n a 的各项排列成如图所示的三角形数阵,记(),M s t 表示该数阵中第s 行从左到右第t 个数,则M (10,9)为A.55B.53C.109D.10712.已知抛物线2:4C y x =的焦点为F ,123P P P 、、是抛物线C 上的不同三点,且1FP 、2FP 、3FP 成等差数列,公差0d ≠,若点2P 的横坐标为3,则线段13PP 的垂直平分线与x 轴交点的横坐标是A.3B.5C.6D.不确定,与d 的值有关第Ⅱ卷(非选择题 共90分)注意事项:1.将第II 卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共4小题,每小题4分,共16分.13.过点(2,3)且以y =为渐近线的双曲线方程是________. 14.设()f x 为定义在()3,3-上的奇函数,当()()230l o g3,xf x x -<<=+时,()1f =_________. 15.运行如图所示的程序框图,输出的S 值为_______.16.如图,两座建筑物AB ,CD 的底部都在同一个水平面上,且AB 、CD 均与水平面垂直,它们的高度分别是9m 和15m ,从建筑物AB 的顶部A 看点D 的仰角为α,看点C 的俯角为β,已知45αβ+=,则BC 的长度是__________m.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知函数()()22sin cos 2f x x x x ππ⎛⎫=-+-⎪⎝⎭. (I )求函数()f x 的单调增区间; (II )若3,2122f απα⎛⎫-=⎪⎝⎭是第二象限角,求cos 23πα⎛⎫+ ⎪⎝⎭的值.18.(本小题满分12分)如图,在几何体ABCDE 中,平面//,ABC BCD AE BD ABC ⊥∆平面,为边长等于2的正三角形,=42,CD BD AE M =,为CD 的中点.(I )证明:平面ECD ⊥平面ABC ; (II )证明:EM 平面ABC .19.(本小题满分12分)已知数列{}n a 是一个公差大于零的等差数列,且362755,16a a a a =+=,数列{}n b 的前n 项和为,22n n n S S b =-且.(I )求数列{}{},n n a b 的通项公式; (II )设,nn na cb =求{}n c 的前n 项和n T .20.(本小题满分12分)某质检机构检测某产品的质量是否合格,在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品,称其质量(单位:克),分别记录抽查数据,获得质量数据茎叶图(如图)。
2013年高三文科数学模拟试题(三)

高三文科数学模拟试题(三)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,U R =且{}{}2|12,|680,A x x B x x x =->=-+<则()U C A B 等于(A )[1,4)- (B )(2,3] (C )(2,3) (D )(1,4)-2.已知i z i 32)33(-=⋅+(i 是虚数单位),那么复数z 对应的点位于复平面内的(A )第一象限(B )第二象限(C )第三象限(D )第四象限3.下列有关命题的说法正确的是(A )命题“若21x =,则1=x ”的否命题为:“若21x =,则1x ≠”. (B )“1x =-”是“2560x x --=”的必要不充分条件.(C )命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈, 均有210x x ++<”. (D )命题“若x y =,则sin sin x y =”的逆否命题为真命题.4.某人骑自行车沿直线匀速旅行,先前进了a 千米,休息了一段时间,又沿原路返回b 千米()a b <,再前进c 千米,则此人离起点的距离s 与时间t 的关系示意图是(A ) (B ) (C ) (D )5.已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数,那么 a 的取值范围是(A )17⎡⎢⎣,⎪⎭⎫31 (B )(0,13) (C )(0,1) (D )⎪⎭⎫⎢⎣⎡1,71 6.如图是一个算法程序框图,当输入的x 值为3时,输出的结果恰好是31,则空白框处的关系式可以是 (A )xy -=3(B )xy 3= (C ) 31-=xy (D )31x y =7.底面边长为2,各侧面均为直角三角形的正三棱锥的四个顶点都在同一球面上,则此球的表面积为(A )π4(B )34π(C )π2 (D ) π38.若]2,0(π∈x ,则使x x x x cot tan sin cos <<<成立的x 取值范围是 (A )(2,4ππ) (B )(ππ,43)(C )(ππ45,)(D )(ππ2,47)9. 设n S 是等差数列{a n }的前n 项和,若3184=S S ,则168S S 等于 (A )103 (B )31 (C )91 (D )8110.已知函数x x f x 2log)31()(-=,正实数a 、b 、c 满足()0()()f c f a f b <<<,若实数d 是函数()f x 的一个零点,那么下列四个判断:①a d <;②b d >;③c d <;④c d >. 其中可能成立的个数为(A )1 (B )2 (C )3 (D )4 11.已知O 是A B C △所在平面内一点,D 为B C 边中点,且02=++OC OB OA ,那么 (A ) AO OD = (B ) 2AO OD = (C ) 3AO OD =(D )2AO OD =12.函数)(x f 、)(x g 都是定义在实数集R 上的函数,且方程-x [])(x g f =0有实根,则函数[])(x f g 的解析式可能是(A )342++x x (B )542+-x x (C ) 322++x x (D )532+-x x二.填空题:本大题共4小题,每小题4分,共16分.13.若在区域34000x y x y +-≤⎧⎪≥⎨⎪≥⎩内任取一点P ,则点P 落在单位圆221x y +=内的概率为 .14. 过圆04622=-++x y x 与028622=-++y y x 的交点,并且圆心在直线04=--y x 上的圆的方程是 .15.设21,F F 是椭圆1162522=+yx的两个焦点,P 是椭圆上的动点(不能重合于长轴的两端点),I 是21F PF ∆的内心,直线PI 交x 轴于点D ,则=IDPI .16.老师给出一个函数=y )(x f ,四个学生甲、乙、丙、丁各指出这个函数的一个性质:甲:对于R x ∈,都有)1()1(x f x f -=+;乙:在(]0,∞-上函数递减;丙:在()+∞,0上函数递增;丁:函数的最小值为0.如果其中恰有三人说得正确,请写出一个这样的函数 . 三.解答题:本大题共6小题,共74分.17.(本小题满分12分)函数πφωφω<>>+=||,0,0),sin()(A x A x f 的图象的一部分如图 (Ⅰ)求函数)(x f 的解析式 ;(Ⅱ)求函数)(x g 的解析式,使得函数)(x f 与)(x g 的图象关于)1,4(π对称.18.(本小题满分12分)如图,在长方体1111D C B A ABCD -中,2==BC AB ,过A 1, C 1 , B 三点的平面截去长方体的一个角后得到几何体111D C A ABCD -,且这个几何体的体积为340.(Ⅰ)证明:直线A 1B // CDD 1C 1; (Ⅱ)求 A 1 A 的长;(Ⅲ)求经过A 1、C 1、B 、D 四点的球的表面积.19.(本小题满分12分)某学校举行“科普与环保知识竞赛”,并从中抽取了部分学生的成绩(均为整数),所得数据的分布直方图如图.已知图中从左至右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分别是0.175和0.075,第2小组的频数为10.(Ⅰ)求所抽取学生的总人数,并估计这次竞赛的优秀率(分数大于80分);(Ⅱ)从成绩落在)5.0.5,650(和)5.100,5.90(的学生中任选两人,求他们的成绩在同一组的概率.20.(本小题满分12分)已知数列{}n a 中,13a =,对于*N n ∈,以1,n n a a +为系数的一元二次方程21210n n a x a x +-+=都有实数根αβ,,且满足(1)(1)2αβ--=.(Ⅰ)求证:数列1{}3n a -是等比数列;(Ⅱ)求数列{}n a 的通项公式; (Ⅲ)求{}n a 的前n 项和n S .21.(本小题满分12分)已知点)0,1(),0,1(C B -,P 是平面上一动点,且满足CB PB BC PC ⋅=⋅||||. (Ⅰ)求动点P 的轨迹方程;(Ⅱ)直线l 过点(-4,43)且与动点P 的轨迹交于不同两点M 、N ,直线OM 、ON (O 是坐标原点)的倾斜角分别为α、β.求βα+的值.22.(本小题满分14分)若存在实常数k 和b ,使函数)(x f 和)(x g 对于其定义域上的任意实数x 分别满足b kx x f +≥)(和b kx x g +≤)(,则称直线b kx y l +=:为曲线)(x f 和)(x g 的“隔离直线”.已知函数2)(x x h =,x e x ln 2)(=ϕ(e 为自然对数的底数).(Ⅰ)求函数)()()(x x h x F ϕ-=的极值;(Ⅱ)函数)(x h 和)(x ϕ是否存在隔离直线?若存在,求出此隔离直线;若不存在,请说明理由.。
数学_2013年山东省济南市高考数学三模试卷(文科)_(含答案)

2013年山东省济南市高考数学三模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.1. 在复平面内,复数z=1+i3−4i 的共轭复数z¯对应的点位于()A 第一象限B 第二象限C 第三象限D 第四象限2. 已知全集U=R,集合A={x||x|≤1, x∈Z},B={x|x2−2x=0},则图中的阴影部分表示的集合为()A {−1}B {2}C {1, 2}D {0, 2}3. 函数f(x)=x−lg1x−2的零点所在区间为()A (0, 1)B (1, 2)C (2, 3)D (3, 4)4. 若△ABC的三个内角满足sinA:sinB:sinC=4:5:7,则△ABC()A 一定是锐角三角形B 一定是直角三角形C 一定是钝角三角形D 可能是锐角三角形,也可能是钝角三角形5. 一个几何体的三视图如图所示,则该几何体的体积为()A 4B 4+π2 C 8+π D 2+π46. 在边长为a的正方形内随机取一个点,则此点落在该正方形的内切圆内部的概率为()A π4 B π6C 2πD 3π7. 函数f(x)=x3−3e x的图象大致是()A B C D8. 将参加夏令营的600名学生编号为:001,002,⋯,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第I营区,从301到495住在第II营区,从496到600在第III营区,三个营区被抽中的人数依次为( )A 26,16,8B 25,17,8C 25,16,9D 24,17,99. 命题p:∃α∈R,cos(π+α)=cosα;命题q:∀m>0,m+1m≥2.则下面结论正确的是( )A p 是假命题B ¬q 是真命题C p ∧q 是假命题D p ∨q 是真命题10. 若A 为不等式组{x ≤0y ≥0y −x ≤2表示的平面区域,则当实数a 从−2连续变化到0时,动直线x +y =a 扫过A 中部分的区域面积为( )A 34B 12C 2D 1 11. 已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)与抛物线y 2=8x 有一个公共的焦点F ,且两曲线的一个交点为P ,若|PF|=5,则双曲线的离心率为( )A 2B 2√2C √5+12D √6 12. 给定两个长度为1的平面向量OA →和OB →,它们的夹角为90∘,如图所示,点C 在以O 为圆心的圆弧AB 上运动,若CO →=xOA →+yOB →,其中x ,y ∈R ,则x +y 的最大值是( )A 1B √2C √3D 2二、填空题:本大题共4个小题,每小题4分,共16分.13. 等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=60,则S 15的值为________.14. 若直线3x +y +a =0过圆x 2+y 2+2x −4y =0的圆心,则a 的值为________.15. 如图所示程序框图若输入x 的值为2011,则输出s 的结果为________.16. 给出定义:若x ∈(m −12, m +12](其中m 为整数),则m 叫做与实数x“亲密的整数”,记作{x}=m ,在此基础上给出下列关于函数f(x)=|x −{x}|的四个命题:①函数y =f(x)在x ∈(0, 1)上是增函数;②函数y=f(x)的图象关于直线x=k2(k∈Z)对称;③函数y=f(x)是周期函数,最小正周期为1;④当x∈(0, 2]时,函数g(x)=f(x)−lnx有两个零点.其中正确命题的序号是________.三、计算题:本大题共6小题,共74分.17. 已知函数f(x)=Asin(ωx+φ)(A>0, ω>0, 0<φ<π)的部分图象如图所示.(1)求f(x)的解析式;(2)求g(x)=f(x)+sin2x的单调递增区间.18. 今年10月在济南举办第十届中国艺术节,届时有很多国际友人参加活动.现有8名“十艺节”志愿者,其中志愿者A1,A2,A3通晓英语,B1,B2,B3通晓俄语,C1,C2通晓韩语.从中选出通晓英语、俄语和韩语的志愿者各1名,组成一个小组.(1)求A1被选中的概率;(2)求B1和C1不全被选中的概率.19. 如图,在四棱锥P−ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC // AD,AB⊥AD.(1)若点E为PD的中点,求证:CE // 平面PAB;(2)在平面PAC内,AF⊥PC.求证:AF⊥平面PCD.20. 某高校有奖励基金本金1000万元,此基金每年购买银行的两种风险和收益不同的理财产品A和B,把每年产生的收益用来奖励品学兼优的大学生,本金继续购买这两种理财产品.第一年购买理财产品A和B各500万元,为了规避风险以后规定:上一年购买产品A的本金,下一年会有20%购买产品B,而上一年购买产品B的本金,下一年会有30%购买产品A.用a n,b n(n∈N∗)分别表示在第n年购买理财产品A和B的本金数(单位:万元).(1)分别求出a2,b2,a3;(2)①证明数列{a n−600}是等比数列,并求a n;②求数列{b n}的前n项和T n.21. 已知函数f(x)=axlnx+b(a, b∈R)的图象过点(1, 0),且在此点处的切线斜率为1.(1)求函数f(x)的单调递减区间;(2)若g(x)=12x2−mx+32,存在x0∈(0, +∞)使得f(x0)≥g(x0)成立,求实数m的取值范围.22. 已知椭圆C:x2a2+y2b2=1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60∘的菱形的四个顶点.(1)求椭圆C的方程;(2)过右焦点F2,斜率为k(k≠0)的直线与椭圆C相交于E,F两点,A为椭圆的右顶点,直线AE,AF分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.求证:k⋅k′为定值.2013年山东省济南市高考数学三模试卷(文科)答案1. C2. B3. B4. C5. B6. A7. C8. B9. D10. D11. A12. B13. 18014. 115. 1216. ②③④17. 解:(1)由图知,A=1,T=π,故2πω=π,解得ω=2;又因为函数f(x)过(π12, 1),代入得sin(π12×2+φ)=1,∴ π6+φ=2kπ+π2(k∈Z).又因为0<φ<π,∴ φ=π3,∴ f(x)=sin(2x+π3);(2)∵ g(x)=f(x)+sin2x=sin(2x+π3)+sin2x=12sin2x+√32cos2x+sin2x=32sin2x +√32cos2x =√3(√32sin2x +12cos2x) =√3sin(2x +π6),由2kπ−π2≤2x +π6≤2kπ+π2,k ∈Z , 解得kπ−π3≤x ≤kπ+π6,k ∈Z .∴ g(x)的单调递增区间为[kπ−π3, kπ+π6](k ∈Z).18. 解:(1)从8人中选出英语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间Ω={(A 1,B 1,C 1),(A 1, B 1, C 2),(A 1, B 2, C 1), (A 1, B 2, C 2),(A 1, B 3, C 1),(A 1, B 3, C 2),(A 2, B 1, C 1),(A 2, B 1, C 2),(A 2, B 2, C 1),(A 2, B 2, C 2),(A 2, B 3, C 1),(A 2, B 3, C 2),(A 3, B 1, C 1),(A 3, B 1, C 2),(A 3, B 2, C 1),(A 3, B 2, C 2),(A 3, B 3, C 1),(A 3, B 3, C 2)}由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.用M 表示“A 1恰被选中”这一事件,则M ={(A 1,B 1,C 1),(A 1, B 1, C 2),(A 1, B 2, C 1), (A 1, B 2, C 2),(A 1, B 3, C 1),(A 1, B 3, C 2)}事件M 由6个基本事件组成,因而P(M)=618=13. (2)用N 表示“B 1,C 1不全被选中”这一事件,则其对立事件N ¯表示“B 1,C 1全被选中”这一事件,由于N ¯={(A 1, B 1, C 1), (A 2, B 1, C 1), (A 3, B 1, C 1)},事件有3个基本事件组成,所以P(N ¯)=318=16,由对立事件的概率公式得P(N)=1−P(N ¯)=1−16=56 19.证明:(1)取PA 的中点为G ,连接BG 、EG ,则EG // 12AD ,EG =12AD ,------------又BC // AD ,BC =12AD ,所以EG // BC ,EG =BC ,四边形BGEC 为平行四边形.-------------所以EC // BG .----------------------------------------又EC ⊄平面PAB ,BG ⊂平面PAB ,故EC // 平面PAB.----------------------------------------(2)因为AB⊥AD,BC // AD,AB=BC,AD=2BC,易证得CD⊥AC.-----------------------因为PA⊥平面ABCD,所以PA⊥CD,因为PA∩AC=A,所以CD⊥平面PAC.----而AF⊂平面PAC,所以CD⊥AF.又已知AF⊥PC又因为CD∩PC=C,所以AF⊥平面PCD.20. (1)解:由已知a n+b n=1000,又a1=500,b1=500,∴ a2=0.8a1+0.3b1=550,∴ b2=450,∴ a3=0.8a2+0.3b2=440+135=575.(2)①证明:由题意得a n+1=0.8a n+0.3b n,∴ a n+1=0.8a n+0.3(1000−a n)=0.5a n+300,∴ a n+1−600=12(a n−600),∴ 数列{a n−600}是首项为−100,公比为12的等比数列,∴ a n−600=−100×(12)n−1,∴ a n=600−100×(12)n−1.②解:由①知,a n+b n=1000,∴ b n=400+100×(12)n−1,∴ T n=400n+100[1−(12)n]1−12=400n+200−200×12n.21.解:(1)由已知可得f(1)=0,f′(1)=1,得b=0,a=1.f(x)=xlnx,f′(x)=1+lnx(x>0),由f′(x)<0得,0<x<1e,所以函数f(x)的单调递减区间为(0, 1e).(2)存在x0∈(0, +∞)使得f(x0)≥g(x0)成立,即f(x)≥g(x)在(0, +∞)上解集不空.即存在x使得m≥12x+32x−lnx成立,即m≥(12x+32x−lnx)min,设ℎ(x)=12x+32x−lnx(x>0),ℎ′(x)=12−32x2−1x=(x+1)(x−3)2x2,当0<x <3时,ℎ′(x)<0,ℎ(x)单调递减, 当x >3时,ℎ′(x)>0,ℎ(x)单调递增, 所以当x =3时,ℎ(x)取到最小值, 即ℎmin (x)=ℎ(3)=2−ln3,所以实数m 的取值范围m ≥2−ln3.22. 解:(1)由题意可得a =2,b =√3,c =1. ∴ 椭圆C 的方程为x 24+y 23=1.(2)设过点F 2(1, 0)的直线l 的方程为:y =k(x −1).设点E(x 1, y 1),F(x 2, y 2),联立{y =k(x −1)x 24+y 23=1,化为(3+4k 2)x 2−8k 2x +4k 2−12=0. 显然△>0,∴ x 1+x 2=8k 23+4k 2,x 1x 2=4k 2−123+4k 2(∗). 直线AE 的方程为y =y 1x 1−2(x −2),直线AF 的方程为y =y 2x 2−2(x −2), 令x =3,得点M(3,y 1x 1−2),N(3,y 2x 2−2).∴ 点P(3,12(y 1x 1−2+y 2x 2−2)).直线PF 2的斜率为k′=12(y 1x 1−2+y 2x 2−2)−03−1 =14(y 1x 1−2+y 2x 2−2) =14y 2x 1+x 2y 1−2(y 1+y 2)x 1x 2−2(x 1+x 2)+4=142kx 1x 2−3k(x 1+x 2)+4kx 1x 2−2(x 1+x 2)+4. 把(∗)代入得k ′=14⋅2k⋅4k 2−123+4k 2−3k⋅8k 23+4k 2+4k 4k 2−123+4k 2−2⋅8k 23+4k 2+4=−34k . ∴ k ⋅k ′=−34为定值.。
2013年高三一模数学(文科)试卷与答案

河北省石家庄市2013届高中毕业班第一次模拟考试数学文科(A 卷)(时间120分钟,满分150分)第I 卷(选择题,共60分)2. 若集合}822|{2≤<∈=+x Z x A ,}02|{2>-∈=x x R x B ,则)(B C A R 所含的元素个数为 A. O B. 1 C. 2 D. 33. 某学校高三年级一班共有60名学生,现采用系统抽样的方法从中抽取6名学生做“早餐 与健康”的调查,为此将学生编号为1、2、…、60,选取的这6名学生的编号可能是A. 1,2,3,4,5,6B. 6,16,26,36,46,56C. 1,2,4,8,16,32 D. 3,9,13 ,27,36,544 已知双曲线的一个焦点与抛物线x 2=20y 的焦点重合,且其渐近线的方程为3x ±4y=0,则 该双曲线的标准方程为5.设l 、m 是两条不同的直线,a,β是两个不同的平面,有下列命题: ①l//m,m ⊂a,则l//a ② l//a,m//a 则 l//m ③a 丄β,l ⊂a ,则l 丄β ④l 丄a ,m 丄a,则l//m 其中正确的命题的个数是 A. 1 B. 2 C. 3 D. 46. 执行右面的程序框图,输出的S 值为 A. 1 B. 9 C. 17 D. 207. 已知等比数列{a n },且a 4+a 8=-2,则a 6(a 2+2a 6+a 10)的值为 A. 4 B. 6 C. 8 D. -98. 现采用随机模拟的方法估计该运动员射击4次,至少击中3次的 概率:先由计算器给出0到9之间取整数值的随机数,指定0、1表 示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数 为一组,代表射击4,次的结果,经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 469812. [x]表示不超过x 的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x ∈R),g(x)=log 4(x-1),则函数h(x)=f(x)-g(x)的零点个数是 A. 1 B. 2 C. 3 D. 4第II 卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题〜第21题为必考题,每个试题考生都必须作 答.第22题~第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分a 13.已知向量 a =(1,2),b=(x,1),u=a+2b,v=2a-b,且u//v,则实数x 的值是______三、解答题:本大题共6小通,共70分.解答应写出文字说明,证明过程或演算步職‘ 17. (本小题满分12分)(I)求角A 的大小;18. (本小题满分12分)如图,在四棱锥P-ABCD 中,PA 丄平面ABCD ,ABC ∠=ADC ∠=90°BAD ∠=1200,AD=AB=1,AC 交 BD 于 O 点. (I)求证:平面PBD 丄平面PAC;(II )求三棱锥D-ABP 和三棱锥P-PCD 的体积之比.19. (本小题满分12分)为了调查某大学学生在周日上网的时间,随机对1OO 名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果: 表1:男生上网时间与频数分布表表2:女生上网时间与频数分布表(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;(II)完成下面的2x2列联表,并回答能否有90%的把握认为“学生周日上网时间与性 别有关”? 表3 :20. (本小題满分12分)重合的直线l 交椭圆于A,B 两点.(I)若ΔABF 2为正三角形,求椭圆的离心率;21(本小题满分12分)已知函数f(x)=e x+ax-1(e 为自然对数的底数).(I)当a=1时,求过点(1,f(1))处的切线与坐标轴围成的三角形的面积;(II)若f(x)≥x 2在(0,1 )上恒成立,求实数a 的取值范围.请考生在22〜24三题中任选一题做答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-l:几何证明选讲如图,过圆O 外一点P 作该圆的两条割线PAB 和PCD,分别交圆 O 于点A,B,C,D 弦AD 和BC 交于Q 点,割线PEF 经过Q 点交圆 O 于点E 、F ,点M 在EF上,且BMF BAD ∠=∠:(I)求证:PA·PB=PM·PQ(II)求证:BOD BMD ∠=∠23. (本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系.x0y 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线 C 的极坐标方程为: θθρcos sin 2=(I)求曲线l的直角坐标方程;点求|AB|的值24. (本小题满分10分)选修4-5:不等式选讲 巳知函数f(x)=|x-2|+2|x-a|(a∈R). (I)当a=1时,解不等式f(x)>3;(II)不等式1)(≥x f 在区间(-∞,+∞)上恒成立,求实数a 的取值范围2013年高中毕业班第一次模拟考试(数学文科答案)一、选择题 A 卷答案1-5 DCBCA 6-10 CACAB 11-12 DB B 卷答案1-5 DBCBA 6-10 BABAC 11-12 DC 二、填空题13.12 14.363515. 2 16 .3724二 解答题17.解:(Ⅰ)法一:由B a A b c cos cos )2(=-及正弦定理得: B A A B C cos sin cos )sin sin 2(=-……………2分 则B A A B A C cos sin cos sin cos sin 2+=sin()B A =+,sin()sin A B C A B C π++=∴+=C A C sin cos sin 2=由于sin 0C ≠,所以,22cos =A ……………… 4分 又0A π<<,故4π=A . …………………… 6分或解:(Ⅰ)由B a A b c cos cos )2(=-及余弦定理得:ac b c a abc a c b b c 22)2(222222-+=-+- ……………………… 2分整理得:bc a c b 2222=-+222cos 222=-+=bc a c b A …………………… 4分又0A π<<,故4π=A . ……………………… 6分(Ⅱ) ABC ∆的面积S =1sin 2bc A=1,故bc =22 ① ………………… 8分根据余弦定理 2222cos a b c bc A =+- 和a, 可得22c b +=6…… ② ………………… 10分 解①②得2b c =⎧⎪⎨=⎪⎩2b c ⎧=⎪⎨=⎪⎩. …………………… 12分 18.解:证明:(Ⅰ)90ABC ADC ∠=∠=,,AD AB =AC 为公共边,Rt ABC Rt ADC ∴∆≅∆ ,………………… 2分则BO=DO,又在ABD ∆中,AB AD =,所以ABD ∆为等腰三角形.AC BD ∴⊥ ,…………………… 4分而⊥PA 面ABCD ,BD PA ⊥, 又⊥∴=BD A AC PA , 面PAC ,又⊂BD 面PBD ,∴平面⊥PAC 平面PBD .…………………… 6分(Ⅱ) 在R t ABC ∆中,1AB =,60BAC ∠=,则BC =,01sin1202ABD S AB AD ∆=⋅111=224=⨯⨯⨯,……………………8分01sin 602BCD S BC CD ∆=⋅1=224=,…………………10分PA BDCO113=133ABD D ABP P ABDABD B PCD P BCDBCD BCD S PAV V S V V S S PA ∆--∆--∆∆⋅===⋅ . …………………12分19.解:(Ⅰ)设估计上网时间不少于60分钟的人数x ,依据题意有30750100x =,…………………4分解得:225x = ,所以估计其中上网时间不少于60分钟的人数是225人.………………… 6分 (Ⅱ)根据题目所给数据得到如下列联表:其中22200(60304070)200 2.198 2.7061001001307091K⨯-⨯==≈<⨯⨯⨯………………10分因此,没有90%的把握认为“学生周日上网时间与性别有关”.…………………12分20. 解:(Ⅰ)由椭圆的定义知12122AF AF BF BF a +=+=,ABC ∴∆周长为4a , 因为2ABF ∆为正三角形,所以22AF BF =,11AF BF =,12F F 为边AB 上的高线,…………………………2分02cos3043ca ∴=,∴椭圆的离心率c e a ==.………………… 4分(Ⅱ)设11(,)A x y ,22(,)B x y 因为0e <<,1c =,所以a >…………6分①当直线AB x 与轴垂直时,22211y a b +=,422b y a =,4121221b OA OB x x y y a ⋅=+=- , 42231a a a -+-=22235()24a a --+, 因为2532+>a ,所以0OA OB ⋅< , AOB ∴∠为钝角.………………………8分②当直线AB 不与x 轴垂直时,设直线AB 的方程为:(1)y k x =+,代入22221x y a b +=,整理得:2222222222()20b a k x k a x a k a b +++-=, 22122222a k x x b a k -+=+,222212222a k a b x x b a k -=+1212OA OB x x y y ⋅=+212121212(1)(1)x x y y x x k x x +=+++2221212(1)()x x k k x x k =++++22222242222222()(1)2()a k ab k a k k b a k b a k -+-++=+2222222222()k a b a b a b b a k +--=+ 24222222(31)k a a a b b a k -+--=+………………10分令42()31m a a a =-+-, 由 ①可知 ()0m a <, AOB ∴∠恒为钝角.………………12分21.解:(Ⅰ)当1a =时,e ()1x f x x =+-,(1)e f =,e ()1x f x '=+,e (1)1f '=+,函数()f x 在点(1,(1))f 处的切线方程为e (e 1)(1)y x -=+- 即(e 1)1yx =+- ……………… 2分设切线与x 、y 轴的交点分别为A ,B .令0x =得1y =-,令0y =得1e 1x =+,∴1(,0)e 1A +,(0,1)B -11112e 12(e 1)S =⨯⨯=++△OAB .在点(1,(1))f 处的切线与坐标轴围成的图形的面积为12(e 1)+ …………………4分(Ⅱ)由2()f x x ≥得2e 1x x a x +-≥, 令2e e 11()x xx h x x x x x +-==+-, 222e e (1)(1)(1)1()1x x x x x h x x x x --+-'=--= 令e ()1xk x x =+-,…………………… 6分 e ()1x k x '=-,∵(0,1)x ∈,∴e ()10xk x '=-<,()k x 在(0,1)x ∈为减函数∴()(0)0k x k <= ,……………………8分又∵10x -<,20x >∴2e (1)(1)()0x x x h x x -+-'=>∴()h x 在(0,1)x ∈为增函数,…………………………10分 e ()(1)2h x h <=-,因此只需2e a -≥. …………………………………12分 22.证明:(Ⅰ)∵∠BAD =∠BMF ,所以A,Q,M,B 四点共圆,……………3分 所以PA PB PM PQ ⋅=⋅.………………5分 (Ⅱ)∵PA PB PC PD ⋅=⋅ , ∴PC PD PM PQ ⋅=⋅ ,又 CPQ MPD ∠=∠ , 所以~CPQ MPD ∆∆,……………7分 ∴PMD PCQ ∠=∠ ,则DCB FMD ∠=∠,………………8分∵BAD BCD ∠=∠,∴2BMD BMF DMF BAD ∠=∠+∠=∠,2BOD BAD ∠=∠,所以BMD BOD ∠=∠.…………………10分23.解:(Ⅰ)依题意22sin cos ρθρθ=………………3分 得:x y =2∴曲线1C 直角坐标方程为:x y =2.…………………5分(Ⅱ)把⎪⎪⎩⎪⎪⎨⎧=-=ty t x 22222代入x y =2整理得: 0422=-+t t ………………7分0>∆总成立,221-=+t t ,421-=t t23)4(4)2(221=-⨯--=-=t t AB ………………10分另解:(Ⅱ)直线l 的直角坐标方程为x y -=2,把x y -=2代入x y =2得: 0452=+-x x ………………7分0>∆总成立,521=+x x ,421=x x23)445(212212=⨯-=-+=x x k AB …………………10分24. 解:(Ⅰ)⎩⎨⎧>-+-≥32222x x x 解得37>x⎩⎨⎧>-+-<<322221x x x 解得φ∈x⎩⎨⎧>-+-≤32221x x x 解得13x <…………………3分 不等式的解集为17(,)(,)33-∞+∞ ………………5分 (Ⅱ)时,2>a ⎪⎩⎪⎨⎧≥--<<-+-≤++-=a x a x ax a x x a x x f ,2232,222,223)(;时,2=a 36,2()36,2x x f x x x -+≤⎧=⎨->⎩; 时,2<a ⎪⎩⎪⎨⎧≥--<<+-≤++-=2,2232,22,223)(x a x x a a x ax a x x f ;∴)(x f 的最小值为)()2(a f f 或;………………8分则⎩⎨⎧≥≥1)2(1)(f a f ,解得1≤a 或3≥a .………………10分。
2013年高考数学模拟题(文)(附详细答案,打印版)
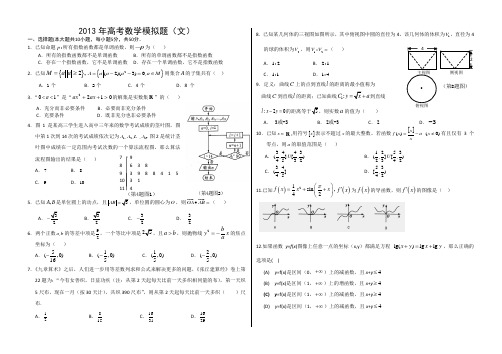
()图27 98 6 3 89 3 9 8 8 4 1 5 10 3 1 11 4侧视图(第4题图1)(第4题图2)(第8题图)≤≥12013年高考数学模拟题(文)一、选择题(本大题共10小题,每小题5分,共50分.1.已知命题:p 所有指数函数都是单调函数,则p ⌝为( )A .所有的指数函数都不是单调函数B .所有的单调函数都不是指数函数C .存在一个指数函数,它不是单调函数D .存在一个单调函数,它不是指数函数 2.已知{}2,M a a =≥{}2(2)(3)0,A a a a a M =--=∈则集合A 的子集共有( ) A .1个B .2个C .4个D .8 个3.“10<<a ”是“0122>++ax ax 的解集是实数集R ”的( ) A .充分而非必要条件 B .必要而非充分条件C .充要条件D .既非充分也非必要条件4.图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为1214,,,.A A A 图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图。
那么算法流程图输出的结果是( ) A .7 B .8C .9D .105.已知,A B 是单位圆上的动点,且AB =O ,则OA AB ∙=( )A.B C .32-D .326.两个正数,a b 的等差中项是92,一个等比中项是a b >,则抛物线2b y x a=-的焦点坐标为( )A .5(,0)16-B .1(,0)5-C .1(,0)5D .2(,0)5-7.《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天起每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则从第2天起每天比前一天多织( )尺布. A .12B .815C .1631D .16298.已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为1V ,直径为4的球的体积为2V ,则12:V V =( ) A .1:2 B .2:1C .1:1D .1:49.定义:曲线C上的点到直线l 的距离的最小值称为 曲线C 到直线l 的距离;已知曲线1:C y a =到直线:20l x y -=a 的值为( )A . 3或-3B .23或-C .2D .-310.已知x ∈R ,用符号[]x 表示不超过x 的最大整数。
2013届普通高考仿真试题(3)数学文

2013年普通高考文科数学仿真试题(三)本试卷分第I 卷和第Ⅱ卷两部分,共4页.满分150分.考试用时120分钟.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4.填空题请直接填写答案,解答题应写出文字说明、演算步骤或推证过程.第I 卷(共60分)一、选择题:本大题共12小题。
每小题5分,共60分.在每小题给出的四个选项中。
只有一项是符合题目要求的. 1.复数121iz i-=-(i 为虚数单位)在复平面上对应的点位于 A.第一象限 B.第二象限C.第三象限D.第四象限2.函数()()2lg 1f x x =+A.)(2,00,2-⋃⎡⎤⎣⎦B.)(1,00,2-⋃⎡⎤⎣⎦C.[]2,2-D.(]1,2-3.已知等比数列{}122373,6n a a a a a +=+==满足,则aA.64B.81C.128D.2434.在给出如下四个命题:①若“p 且q ”为假命题,则p 、q 均为假命题;②命题“若,21a b a b a ->则>”的否命题为“若,21a b a b a ≤≤-则”;③“2,11x R x ∀∈+≥”的否定是“2,11x R x ∃∈+≤”;④在ABC ∆中,“A B >”是“sin sin A B >”的充要条件.其中不正确的命题的个数是A.4B.3C.2D.15.设变量x,y 满足约束条件,236,y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩,则目标函数2z x y=+的最小值为 A.2 B.3 C.4 D.96.执行如图所示的程序框图,若输入x=2,则输出y 的值为A.2B.5C.11D.237.如图,梯形//2ABCD AB CD AB CD =中,,且,对角线AC 、DB 相交于点O.若,,AD a AB b AO ===A.4233a b - B.2133a b + C.2133a b -D.1233a b + 8.已知集合{}21230,lg 3x A x x x B x y x -⎧⎫=--==⎨⎬+⎩⎭<,在区间()3,3-上任取一实数x ,则“x A B ∈⋂”的概率为 A.14B.18C.13D.1129.函数()22cos 0963x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为A.2B.0C.1-D.1-10.函数()()cos lg f x x x =-的部分图象是11.曲线()2120C y px p =:>的焦点F 恰好是曲线()22222:1x y C a a b-=>0,b >0的右焦点,且曲线1C 与曲线2C 交点连线过点F ,则曲线2C 的离心率是1112.已知函数()2,0,0ln ,0,kx x f x k x x +≤⎧=⎨⎩若>>,则函数()1y f x =-的零点个数是A.1B.2C.3D.4第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分. 13.下图是某几何体的三视图,其中主视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是_________.14.为了调查某厂生产某种产品的能力,随机抽查了部分工人某天生产该产品的数量,产品数量的分组区间为[)[)[)[)[)45,55,55,65,65,75,75,85,85,95,由此得到频率分布直方图如图.已知样本中一天生产该产品数量在[)45,65有12人,则样本中一天生产该产品数量在[)75,95的人数为_________.15.已知两点()()222,0,0220A B y x -+-=,,点C 是圆x 上任意一点,则△ABC 面积的最小值是________.16.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3)(3,2),(4,1),(1,5),(2,4)⋅⋅⋅则第57个数对是______.三、解答题:本大题共6小题,共74分,答题时要写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)在△ABC 中,已知445,cos 5A B ==. (I )求sinC 的值;(II )若BC=10,D 为AB 的中点,求CD 的长.18.(本小题满分12分)某公司有男职员45名、女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
2013年高考数学模拟(文科)试题及答案

文科数学本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集R U =,集合}03|{},0)1)(2(|{<≤-=>-+=x x B x x x A ,则)(B C A U 为 (A) }02|{≥-<x x x 或 (B) }12|{>-<x x x 或(C)}03|{≥-<x x x 或 (D) }13|{>-<x x x 或 2. 已知R a ∈,且ii a -+-1为实数,则a 等于(A) 1 (B) 1- (C)2 (D)2-3.如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是(A)(B)(C)(D) 834. 命题:“若12<x ,则11<<-x ”的逆否命题是(A)若12≥x ,则11-≤≥x x ,或 (B)若11<<-x ,则12<x (C)若11-<>x x ,或,则12>x (D)若11-≤≥x x ,或,则12≥x5.当x y 、满足不等式组1101x y y x ⎧-≤⎪≥⎨⎪≤+⎩时,目标函数t x y =+的最大值是(A) 1 (B) 2 (C) 3 (D) 5 6. 将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为(A)π23 (B)π32 (C)6π(D)34π7.对变量,x y 有观测数据(,)(1,2,,10)i i x y i = ,得散点图1;对变量,u v 有观测数据(,)(1,2,,10)i i u v i = ,得散点图2. 由这两个散点图可以判断.(A )变量x 与y 正相关,u 与v 正相关 (B )变量x 与y 正相关,u 与v 负相关 (C )变量x 与y 负相关,u 与v 正相关 (D )变量x 与y 负相关,u 与v 负相关俯视图8. 如图,是一个计算1922221++++ 的程序框图,则其中空白的判断框内,应填入 下列四个选项中的(A)i 19≥ (B) i 20≥ (C)i 19≤ (D)i 20≤9. 已知函数)0)(2cos(3)2sin()(πϕϕϕ<<+++=x x x f 是R 上的偶函数,则ϕ的值为(A)6π(B)3π(C)32π (D)65π10.已知ABC ∆的三边长为c b a 、、,满足直线0=++c by ax 与圆122=+y x 相离,则ABC ∆是 (A )锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 以上情况都有可能 11. 已知集合}),()(|)({R x x f x f x f M ∈=-=,}),()(|)({R x x f x f x f N ∈-=-=,}),1()1(|)({R x x f x f x f P ∈+=-=,}),1()1(|)({R x x f x f x f Q ∈+-=-=,若R x x x f ∈-=,)1()(3,则(A)M x f ∈)( (B) N x f ∈)( (C)P x f ∈)( (D)Q x f ∈)(12. 王先生购买了一步手机,欲使用中国移动“神州行”卡或加入联通的130网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍,若要用联通130应最少打多长时间的长途电话才合算.(A) 300秒 (B) 400秒 (C) 500秒 (D) 600秒 二.填空题:本大题共4小题,每小题4分,共16分.13. 设向量(12)(23)a b == ,,,,若向量a b λ+ 与向量(47)c =--,共线,则=λ .14.ΔABC 中,3=a ,2=b ,45=∠B ,则A ∠= .15.考察下列三个命题,是否需要在“ ”处添加一个条件,才能构成真命题(其中m l ,为直线,βα,为平面)?如需要,请填这个条件,如不需要,请把“ ”划掉. ① αα//_____//l m l m ⇒⎪⎭⎪⎬⎫⊂ ② αα//_____////l m ml ⇒⎪⎭⎪⎬⎫③ αβαβ⊥⇒⎪⎭⎪⎬⎫⊥l l _____// 16. 若从点O 所做的两条射线OM ,ON 上分别有点M 1,M 2,与点N 1,N 2,则面积之比 11221122OM N OM N S O M O N S O M O N ∆∆⋅=⋅.若从点O 所做的不在同一平面内的三条射线OP ,OQ ,OR 上分别有点P 1,P 2,Q 1,Q 2,R 1,R 2,则能推导出的结论是 . 三.解答题:本大题共6小题,共74分. 17. (本小题满分12分)已知函数.cos2)62sin()62sin()(2x x x x f +-++=ππ(Ⅰ)求)(x f 的最小正周期和单调递增区间; (Ⅱ)求使)(x f ≥2的x 的取值范围.18. (本小题满分12分)在四棱锥P - ABCD 中,平面P AD ⊥平面ABCD ,AB // CD ,PAD ∆是等边三角形,已知BD = 2AD =8, AB = 2DC = 54,设M 是PC 上一点, (Ⅰ)证明:平面MBD ⊥平面PAD ; (Ⅱ)求四棱锥P - ABCD 的体积.19. (本小题满分12分)已知关于x 的一元二次函数14)(2+-=bx ax x f .(Ⅰ)设集合}3211{,,,-=P 和}3,2,1,1,2{--=Q 分别从P ,Q 中各取一个数作为a ,b .求函数)(x f y =在区间),1[+∞是增函数的概率;(Ⅱ)设点(a ,b )是区域⎪⎩⎪⎨⎧>>≤-+0008y x y x 内的随机点,求函数)(x f y =在区间),1[+∞是增函数的概率.20. (本小题满分12分)设函数b x x g ax x x f +=+=232)(,)(,已知它们的图象在1=x 处有相同的切线. (Ⅰ)求函数)(x f 和)(x g 的解析式;(Ⅱ)若函数)()()(x g m x f x F ⋅-=在区间]3,21[上是减函数,求实数m 的取值范围.21. (本小题满分12分)已知中心在原点,焦点在x 轴上,离心率为552的椭圆的一个顶点是抛物线241x y =的焦点 .(Ⅰ)求椭圆方程;(Ⅱ)若直线l 过点),(02F 且交椭圆于B A 、两点,交y 轴于点M ,且.,21BF MB AF MA λλ==求21λλ+的值.22. (本小题满分14分)数列}{n a 满足)2,(122*1≥∈++=-n N n a a n n n ,273=a .(Ⅰ)求21,a a 的值; (Ⅱ)已知))((21*N n t a b n nn ∈+=,若数列}{n b 成等差数列,求实数t ;(Ⅲ)求数列}{n a 的前n 项和n S .附:答案及评分标准:一.选择题:AACDD CCBAC DB1. 解析:A.{|12}A x x x =><-或;{|03}U C B x x x =≥<-或,得{|02}U A C B x x x =≥<- 或.2. 解析:A.2()(1)111122a i a i i a a i ii-+-++---==+--,∴1a =.3. 解析:C.该几何体为正四棱锥,底面边长为222=,其体积12233V =⨯⨯⨯=.4. 解析:D.“若p ,则q ”的逆否命题为“若q ⌝,则p ⌝”,易知应选D.5. 解析:D.如图,易求点B 的坐标为(2,3),所以当2,3x y ==时t 取最大值5.6. 解析:C. 最大球为正方体的内切球,则内切球的半径为12,341()326V ππ=⋅=.7. 解析:C.由这两个散点图可以判断,变量x 与y 负相关,u 与v 正相关,选C.8. 解析:B.当1922221++++ 时,19=i ,而1i i =+,此时20i =,输出S 为1922221++++ .9. 解析:A .)0)(2cos(3)2sin()(πϕϕϕ<<+++=x x x f =12(sin(2)))22x x φφ+++=2sin(2)3x πφ++;∵()f x 为偶函数,∴()32k k Z ππφπ+=+∈,又∵0φπ<<,∴6πφ=.10. 解析:C. 根据题意,圆心(0,0)到直线0=++c by ax 的距离1d =>,∴222c a b >+,故选C.11. 解析:D. ()f x M ∈,则函数()f x 关于y 轴对称;()f x N ∈,则函数()f x 关于原点对称;()f x P ∈,则函数()f x 关于直线1x =对称;()f x Q ∈,则函数()f x 关于(1,0)中心对称;3()(1),f x x x R =-∈关于(1,0)中心对称,故选D.12. 解析:B. 设王先生每月拨打长途x 秒,拨打本地电话5x 秒,根据题意应满足50.3650.60120.060.076060x x x x ⋅⋅++≤+,解得400x ≥.二.填空题:13.2;14.3π或32π;15. α⊄l ;α⊄l ;\(划掉);16. 体积之比222111222111OR OQ OP OR OQ OP V V R Q P O R Q P O ⋅⋅⋅⋅=--.13. 解析:2.a b λ+ =(322++λλ,),a b λ+ 与向量(47)c =-- ,共线,则0)4()32()7()2(=-⋅+--⋅+λλ,解得=λ 2.14. 解析:3π或32π.45sin 2sin 3sin sin =⇒=ABb Aa 23sin =⇒A ,A ∠=3π或32π.15. 解析:α⊄l ;α⊄l ;\(划掉).根据线面平行和线面垂直的判定定理,3个位置依次填α⊄l ;α⊄l ;\(划掉).16. 解析:根据结论11221122OM N OM N S O M O N S O M O N ∆∆⋅=⋅可类比得到,在空间中有体积之比222111222111OR OQ OP OR OQ OP V V R Q P O R Q P O ⋅⋅⋅⋅=--.三.解答题17. (本小题满分12分)已知函数.cos2)62sin()62sin()(2x x x x f +-++=ππ(Ⅰ)求)(x f 的最小正周期和单调递增区间; (Ⅱ)求使)(x f ≥2的x 的取值范围. 解:(Ⅰ)x x x x f 2cos2)62sin()62sin()(+-++=ππ12cos 6sin2cos 6cos2sin 6sin2cos 6cos2sin ++-++=x x x x x ππππ--------------1分12cos 2sin 3++=x x 1)62sin(2++=πx --------------------------------------3分ππωπ===22||2T ------------------------------------------------------------5分Z k k x k ∈+≤+≤+-,226222πππππ,Z k k x k ∈+≤≤+-∴,63ππππ,函数)(x f 的递增区间是Z k k k ∈++-∴],6,3[ππππ-----------------------------7分(Ⅱ)由()2f x ≥ 得2sin(2)126x π++≥, 21)62sin(≥+∴πx πππππ6526262+≤+≤+∴k x k )(Z k ∈----------------------------9分)(3Z k k x k ∈+≤≤∴πππ ,2)(≥∴x f 的x 的取值范围是},3|{Z k k x k x ∈+≤≤πππ---------------------------12分18. (本小题满分12分)在四棱锥P - ABCD 中,平面P AD ⊥平面ABCD ,AB // CD ,PAD ∆是等边三角形,已知BD = 2AD =8, AB = 2DC = 54,设M 是PC 上一点, (Ⅰ)证明:平面MBD ⊥平面PAD ; (Ⅱ)求四棱锥P - ABCD 的体积.证明:(Ⅰ)AB =54,BD =8, AD =4,则AB 2 = BD 2+AD 2.∴BD ⊥AD .------------------------------------------2分 设AD 的中点为E ,连接AE ,因为PAD ∆是等边三角形,所以PE ⊥AD ,又平面PAD ⊥平面ABCD ,PE ⊂平面PAD ,所以PE ⊥平面ABCD ,------------------------------------------4分 BD ⊂平面ABCD ,∴PE ⊥BD .E PE AD =⋂,∴BD ⊥平面PADBD ⊂平面BDM ,∴平面MBD ⊥平面P AD .-------------------------------------------------------------------------6分 解(Ⅱ)3223==AD PE ,----------------------------------------------------------------------------------------8分ABCD S 梯形==+∆∆BCD ABD S S ABD ABD ABD S S S ∆∆∆=+2321=2484432123=⋅⋅=⋅⋅⋅DB AD .--------------------------------------------------------------10分 316322431=⋅⋅=-ABCD P V ---------------------------------------------------------------12分19. (本小题满分12分)已知关于x 的一元二次函数14)(2+-=bx axx f(Ⅰ)设集合}3211{,,,-=P 和}3,2,1,1,2{--=Q 分别从P ,Q 中各取一个数作为a ,b .求函数)(x f y =在区间),1[+∞是增函数的概率;(Ⅱ)设点(a ,b )是区域⎪⎩⎪⎨⎧>>≤-+0008y x y x 内的随机点,求函数)(x f y =在区间),1[+∞是增函数的概率. 解:(Ⅰ)分别从P ,Q 中各取一个数作为a ,b 全部可能的基本结果有:(-1,-2),(-1,-1),(-1,1),(-1,2),(-1,3),(1,-2),(1,-1),(1,1),(1,2),(1,3),(2,-2),(2,-1),(2,1),(2,2),(2,3),(3,-2),(3,-1),(3,1),,(3,2),(3,3).共20个基本结果.-------------------------------------------------------------------------------3分函数14)(2+-=bx axx f 的对称轴a bx 2=,要使函数)(x f 在),1[+∞上是增函数,需满足⎪⎩⎪⎨⎧≤>120ab a , ----------------------------------------------------------------------------------------------------------------------------------4分于是满足条件的基本结果为:(1,-2),(1,-1),(2,-2),(2,-1),(2,1),(3,-2),(3,-1),(3,1)共8个.函数)(x f y =在区间),1[+∞是增函数的概率52208==P .----------------------------------------------------------6分(Ⅱ)⎪⎩⎪⎨⎧>>≤-+0008y x y x 所表示的区域如图OAB ∆所示,从区域内取点且函数)(x f y =在),1[+∞上是增函数需满足 的条件⎪⎩⎪⎨⎧≤>>200x y y x 如图阴影部分OAC ∆所示.-----------------------------------------------------------------------------9分解⎪⎩⎪⎨⎧==+28x y y x 得C (38,316).---------------------------------------------------------------------------------------10分 函数)(x f y =在区间),1[+∞是增函数的概率OABOAC S S P ∆∆=31838==----------------------------------------12分20. (本小题满分12分)设函数b x x g ax x x f +=+=232)(,)(,已知它们的图象在1=x 处有相同的切线.(Ⅰ)求函数)(x f 和)(x g 的解析式;(Ⅱ)若函数)()()(x g m x f x F ⋅-=在区间]3,21[上是减函数,求实数m 的取值范围.解:(Ⅰ)根据题意,)1()1(),1()1(''g f g f ==;--------------------------------------------------------------2分4)1(,4)(''==g x x g ,又∵a x x f +=2'3)(,----------------------------------------------------------------------3分∴41(3)1(''==+=)g a f ,∴1=a ;21)1(=+=a f ,∴2)1(2)1(==+=g b g ,得0=b .---5分∴函数)(x f 与)(x g 的解析式为:x x x f +=3)(,22)(x x g =------------------------------------------6分 (Ⅱ)232)()()(mx x x x g m x f x F -+=⋅-=;143)(2'+-=mx x x F ------------------------------7分 ∵函数)(x F 在区间]3,21[上是减函数,∴0143)(2'≤+-=mx x x F 在区间]3,21[上恒成立.-----------8分⎪⎩⎪⎨⎧≤≤0)3(0)21('F F ‘---------------------------------------------------------------------------------------------------------------10分 =⎪⎩⎪⎨⎧≤+⨯-⨯≤+⨯-⨯013433012144132m m 37≥⇒m . 实数m 的取值范围是),37[+∞∈m -------------------------------------------------------------------------------------12分21. (本小题满分12分)已知中心在原点,焦点在x 轴上,离心率为552的椭圆的一个顶点是抛物线241x y =的焦点 .(Ⅰ)求椭圆方程;(Ⅱ)若直线l 过点),(02F 且交椭圆于B A 、两点,交y 轴于点M ,且.,21BF MB AF MA λλ==求21λλ+的值.解:(Ⅰ) 设椭圆的方程为)0(12222>>=+b a by ax ;∵241x y =y x42=⇒的焦点坐标为(0,1),∴1=b . -------------------------------------------------------------------------------------2分⇒==552a c e 5412222=-=a a ac ,得5=a .--------------------------------------------------------------------4分∴所求的椭圆的方程为1522=+yx.-----------------------------------------------------------5分(Ⅱ)因为点),(02F 在椭圆内部,且直线与y 轴相交,所以直线l 不与x 轴垂直,斜率一定存在.设l :)2(-=x k y ------------------------------------------------------------------------------------------------------------6分则052020)51(15)2(222222=-+-+⇒⎪⎩⎪⎨⎧=+-=k x k k x y x x k y --------------- ①设),0(),,(),,(02211y M y x B y x A由①得2221222151520;5120kkx x kkx x +-=+=+,---------------------------------------------------------------8分1M A AF λ= 即 1101111,)(2,)M A x y y AF x y λλ=-==--(得110111,)(2,)x y y x y λ-=--(,111(2)x x λ=-即1112x x λ=-,同理2222x x λ=-------------------------------------------------------------------------------------------------9分12λλ+=112x x -+222x x -=121212122()242()x x x x x x x x +--++=222222222222202052()2()4040101515102020542040542()1515kk k k k k k k k k k k---+++==--+---+++ -----------------------------------------------------------------------------------------------------------------------------------------12分 22. (本小题满分14分)数列}{n a 满足)2,(122*1≥∈++=-n N n a a n n n ,273=a . (Ⅰ)求21,a a 的值; (Ⅱ)已知))((21*N n t a b n nn ∈+=,若数列}{n b 成等差数列,求实数t ;(Ⅲ)求数列}{n a 的前n 项和n S .解法一:(Ⅰ)由)2,(122*1≥∈++=-n N n a a n n n ,得33222127a a =++=29a ⇒=.2212219a a =++=12a ⇒=.--------------------------------------------------------------3分(Ⅱ)*11221(,2)(1)2(1)2n n n n n n a a n N n a a --=++∈≥⇒+=++*(,2)n N n ∈≥1111122n n nn a a --++⇒=+*(,2)n N n ∈≥---------------------------------------------------------6分 1111122n n nn a a --++⇒-=*(,2)n N n ∈≥,令*1(1)()2n n nb a n N =+∈,则数列}{n b 成等差数列,所以1t =.----------------------------------------------------------------------------------------------8分(Ⅲ))}{n b 成等差数列,1(1)n b b n d =+-321(1)22n n +=+-=.121(1)22n n nn b a +=+=;得1(21)21n n a n -=+⋅-*()n N ∈.--------------------------------------------------------------10分n S =21315272(21)2n n n -⋅+⋅+⋅+++⋅- -----------①2n S =23325272(21)22nn n ⋅+⋅+⋅+++⋅- --------------------② ① - ② 得213222222(21)2n nn S n n --=+⋅+⋅++⋅-+⋅+ --------------------------------------------11分11 233222(21)2n n n n =++++-+⋅+ 14(12)3(21)212n nn n --=+-+⋅+- =(21)21n n n -+⋅+-.所以(21)21n n S n n =-⋅-+*()n N ∈-------------------------------------------------------------14分.解法二:(Ⅱ)))((21*N n t a b n n n ∈+=且数列}{n b 成等差数列,所以有1()n n b b +-*()n N ∈为常数. 11111()()22n n n n n n b b a t a t +++-=+-+*()n N ∈ 1111(221)()22n n n n n a t a t ++=+++-+*()n N ∈111112222n n n n n n t t a a ++=++--*()n N ∈ 1112n t+-=+*()n N ∈,要使1()n n b b +-*()n N ∈为常数.需1t =.---------------------------------8分。
2013年高三文科数学模拟试题(附答案)

2013年高三文科数学模拟试题(附答案)骞夸笢鐪佹儬宸炲競2013枃绉戯級?0鍒嗭級ぇ棰樺叡l0椤规槸绗﹀悎棰樼洰瑕佹眰鐨勶紟姣忓皬棰?鍒嗭紝婊″垎50鍒嗭紟 1.鈥?鈥濈殑鍚﹀懡棰樻槸( )锛?A. B. C. D. 2.鍔犲瘑浼犺緭锛屽彂閫佹柟鐢辨槑鏂?瀵嗘枃锛堝姞瀵嗭級锛屾帴鍙楁柟鐢卞瘑鏂?鏄庢枃锛堣В?瀵瑰簲瀵嗘枃锛屼緥濡傦紝鏄庢枃瀵瑰簲瀵嗘枃锛庡綋鎺ュ彈鏂规敹鍒板瘑鏂?鏃讹紝鍒欒В瀵嗗緱鍒扮殑鏄庢枃涓猴紙锛夛紟A锛?4锛?锛?锛? B锛?7锛?锛?锛? C锛?6锛?锛?锛? D锛?1锛?锛?锛? 3.宸茬煡鍚戦噺锛?锛岃嫢锛屽垯瀹炴暟鐨勫€肩瓑浜庯紙锛夛紟 A. B. C. D. 4.?鍊嶏紝鍒欐き鍦嗙殑绂诲績鐜囩瓑浜庯紙锛夛紟A锛?B锛?C锛?D锛?5.鍦ㄤ竴娆″?宸茬煡璇ュ皬缁勭殑骞冲潎鎴愮哗涓??锛夛紟锛?锛?锛?锛?6. ?锛夛紟锛?锛?锛?锛?7.涓や釜瑙嗗浘鐩稿悓鐨勬槸锛?銆€锛夛紟A锛庘憼鈶?B锛庘憼鈶?C锛庘憼鈶?D锛庘憽鈶?8.濡傛灉鎵ц?锛?锛夛紟锛★紟2450 锛?2500 锛o紟2550 锛わ紟2652 9.灏嗗嚱鏁?鐨勫浘璞″厛鍚戝乏骞崇Щ锛岀劧鍚庡皢鎵€寰楀浘璞′笂ョ殑鍊嶏紙绾靛潗鏍囦笉鍙橈級锛屽垯鎵€寰楀埌鐨勫浘璞?瀵瑰簲鐨勫嚱鏁拌В鏋愬紡涓猴紙锛夛紟A锛?B锛?C锛?D锛?10.宸茬煡鍏ㄩ泦R锛岄泦鍚?,>b>0锛?鍒欐湁( )锛?A. B. C. D. ?00鍒嗭級5?4锝?5棰樻槸閫夊仛棰樺緱鍒嗭紟姣忓皬棰?鍒嗭紝婊″垎20鍒嗭紟11锛庡寲绠€锛?锛?12. 宸茬煡R涓婄殑鍑芥暟锛屼笖瀵逛换鎰?锛岄兘鏈夛細锛屽張鍒?锛?13.鑻ュ疄鏁?婊¤冻鏉′欢鐨勬渶澶у€间负_____ 锛?14. (鍧愭爣绯讳笌鍙傛暟鏂圭▼閫夊仛棰??涓婄殑鍔ㄧ偣鍒扮洿绾?鐨勮窛绂荤殑鏈€澶у€兼槸锛?15. (?濡傚彸鍥炬墍绀猴紝鐨勭洿寰勶紝锛?锛?锛屽垯锛?6?0鍒嗭紟瑙g瓟椤诲啓鍑16.12鍒嗭級鍦ㄢ柍ABC鎵€瀵圭殑杈癸紝涓旀弧瓒?锛?(鈪?鐨勫ぇ灏忥紱(鈪?璁?锛屾眰鐨勬渶灏忓€? 17锛??4鍒?逛綋锛?锛孍涓烘1鐨勪腑鐐癸紟(鈪? 姹傝瘉锛?锛?(鈪? 姹傝瘉锛?骞抽潰锛?锛堚參锛夋眰涓夋1閿?18?2鍒嗭級鏈夋湅锛?(鈪?姹備粬涔樼伀杞︽垨椋炴満鏉ョ殑姒傜巼锛?(鈪?姹?锛堚參)19.14鍒嗭級璁惧嚱鏁?鐨勫浘璞″湪鐐?澶勭殑鍒囩嚎鐨勬枩鐜囦负锛屼笖褰?鏃?鏈夋瀬鍊硷紟(鈪?姹?鐨勫€硷紱(鈪?姹?鐨勬墍鏈夋瀬鍊硷紟20. (?4鍒?宸茬煡鍦?锛?鍜屽渾锛岀洿绾?涓庡渾鐩稿垏浜庣偣锛涘渾鐨勫渾蹇冨湪灏勭嚎涓婏紝鍦?杩囧锛?(鈪?姹傜洿绾?鐨勬柟绋?(鈪?姹傚渾鐨勬柟绋嬶紟21?4鍒嗭級宸茬煡鏁板垪锛涙暟鍒?鐨勫墠n椤瑰拰鏄?锛屼笖锛?(鈪? 姹傛暟鍒??(鈪? 姹傝瘉锛氭暟鍒?(鈪? 璁?锛屾眰鐨勫墠n椤瑰拰锛?骞夸笢鐪佹儬宸炲競2013鍙傝€冪瓟妗?1.瑙f瀽锛氬懡棰樷€?鈥濈殑鍚﹀懡棰樻槸锛氣€?鈥濓紝鏁呴€塁锛?2.瑙f瀽锛氱敱宸茬煡锛屽緱锛?锛屾晠閫?锛?3.瑙f瀽锛氳嫢锛屽垯锛岃В寰?锛庢晠閫?锛?4.瑙f瀽锛氱敱棰樻剰寰?锛屽張锛?鏁呴€?锛?5.愮哗涓??锛岀敱骞冲潎鏁扮殑姒傚康锛屽緱锛?锛?鏁呴€?锛?6.瑙f瀽锛???锛?7.ц?锛?8.?锛岄€?锛?9.瑙f瀽锛?鐨勫浘璞″厛鍚戝乏骞崇Щ锛屾í鍧愭爣鍙樹负鍘熸潵鐨?鍊?锛庣瓟妗堬細锛?10.瑙f瀽锛氱壒娈婂€兼硶锛氫护锛屾湁锛庢晠閫?锛?棰樺彿11 12 13 14 1511.瑙f瀽锛?锛?12.瑙f瀽锛氫护锛屽垯锛屼护锛屽垯锛?鍚岀悊寰?鍗冲綋鏃讹紝鐨勫€间互涓哄懆鏈燂紝鎵€浠?锛?13.瑙f瀽锛氱敱鍥捐薄鐭ワ細褰撳嚱鏁?鐨勫浘璞¤繃鐐?鏃讹紝鍙栧緱鏈€澶у€间负2锛?14. (鍧愭爣绯讳笌鍙傛暟鏂圭▼閫夊仛棰?愭爣鏂圭▼锛屽渾涓婄殑鍔ㄧ偣鍒扮洿绾?鐨勮窛绂荤殑鏈€澶у蹇?鍒扮洿绾?鐨勮窛绂?鍐嶅姞涓婂崐寰?锛庢晠濉?锛?15. (閫夊仛棰?瑙f瀽锛氳繛缁?锛?鍒欏湪鍜?锛?涓?锛屾墍浠?锛?鏁?锛?6?0鍒嗭紟瑙g瓟椤诲啓鍑16.殑鏈€鍊硷紟瑙o細(鈪?鈭?锛屸埓锛?鈥︹€︹€︹€︹€︹€?鍒?鍙堚埖锛屸埓锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛堚叀锛?銆€銆€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?锛屸埓锛庛€€銆€鈥︹€︹€︹€︹€?0鍒?鈭村綋鏃讹紝鍙栧緱鏈€灏忓€间负锛?鈥︹€︹€︹€?2鍒?17瑙o細(鈪?璇佹槑锛氳繛缁?锛屽垯// 锛?鈥︹€︹€︹€?鍒?鈭?舰锛屸埓锛庘埖闈?锛屸埓锛?鍙?锛屸埓闈?锛?鈥︹€︹€︹€︹€︹€?鍒?鈭?闈?锛屸埓锛?鈭?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛堚叀锛夎瘉鏄庯細浣?鐨勪腑鐐笷锛岃繛缁?锛?鈭?鏄?鐨勪腑鐐癸紝鈭?锛?鈭村洓杈瑰舰锛?鈥︹€︹€?鍒?鈭?鏄?鐨勪腑鐐癸紝鈭?锛?鍙?锛屸埓锛?鈭村洓杈瑰舰洓杈瑰舰锛?// 锛?鈭?锛?锛?鈭村钩闈?闈?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鍙?骞抽潰锛屸埓闈?锛?鈥︹€︹€︹€︹€︹€?0鍒?锛?锛?锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?1鍒?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?18瑙o細璁欢锛屽垯锛?锛?锛?锛屼笖浜嬩欢?(鈪?鈥︹€︹€?鍒?(鈪??锛??锛?鈥︹€︹€︹€︹€︹€?鍒嗐€€锛堚參)鐢变簬锛?鈥︹€︹€︹€︹€︹€︹€?2鍒嗐€€19.鏋ц?瑙o細(鈪?鐢卞嚱鏁??锛屸€︹€︹€︹€︹€︹€?鍒?鈭?锛屸埓锛庛€€鈥︹€︹€︹€?鍒?鈭?锛屸埓锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?锛屽嵆锛庛€€銆€鈥︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€? 0 + 0锟終鏋佸皬锟絁鏋佸ぇ锟終鈭?锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?20锛庢瀽锛氫富瑕佽€冨療鐩寸嚎锛庡渾鐨勬柟绋嬶紝鐩寸嚎涓庡渾鐨勪綅缃瑙o細(鈪?锛堟硶涓€锛夆埖鐐?鍦ㄥ渾涓婏紝鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭寸洿绾?鐨勬柟绋嬩负锛屽嵆锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛堟硶浜岋級褰撶洿绾?鍨傜洿杞存椂锛屼笉绗﹀悎棰樻剰锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?褰撶洿绾?涓?杞翠笉鍨傜洿鏃讹紝璁剧洿绾?鐨勬柟绋嬩负锛屽嵆锛?鍒欏渾蹇?鍒扮洿绾?鐨勮窛绂?锛屽嵆锛?锛岃В寰?锛屸€︹€?鍒?鈭寸洿绾?鐨勬柟绋嬩负锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒??锛?锛屸埖鍦?杩囧師鐐癸紝鈭?锛?鈭村渾鐨勬柟绋嬩负锛庘€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭靛渾洿绾?锛屸埓鍦嗗績鍒扮洿绾?锛?鐨勮窛绂伙細锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鏁寸悊寰楋細锛岃В寰?鎴?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?0鍒?鈭?锛屸埓锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?鈭村渾锛?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?21锛庢瀽锛氫富瑕佽€冨療绛夊樊銆佺瓑姣旀暟鍒楃殑瀹氫箟銆佸紡锛屾眰鏁板垪鐨勫拰鐨勬柟娉曪紟瑙o細(鈪?璁?锛屽垯锛?锛?锛?鈭?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛堚叀锛夊綋鏃讹紝锛岀敱锛屽緱锛?鈥︹€︹€︹€︹€︹€︹€?鍒?褰?鏃讹紝锛?锛?鈭?锛屽嵆锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?锛庛€€銆€銆€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?癸紝涓哄叕姣旂殑绛夋瘮鏁板垪锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛堚參锛夌敱锛?锛夊彲鐭ワ細锛?銆€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?0鍒?鈭?锛庛€€鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?1鍒?鈭?锛?鈥?4鍒?。
数学_2013年陕西省西安市某校高考数学三模试卷(文科)(含答案)

2013年陕西省西安市某校高考数学三模试卷(文科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分) 1. 复数z =i 1+i在复平面上对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限2. 若a ,b ,c ,d ∈R ,且a >b ,c >d ,则下列结论正确的是( ) A ac 2>bc 2 B ac >bd C 1a <1b D a +c >b +d3. 设函数f(x)=x 2−x −2,x ∈[−5, 5].若从区间[−5, 5]内随机选取一个实数x 0,则所选取的实数x 0满足f(x 0)≤0的概率为( ) A 0.5 B 0.4 C 0.3 D 0.24. 如果等差数列{a n }中,a 3+a 4+a 5=12,那么a 1+a 2+...+a 7=( ) A 14 B 21 C 28 D 355. 已知某几何体的三视图如图所示,则此几何体的体积是( )A 12 B 14 C 16 D 186. 已知m ,n 是两条不同直线,α,β,γ是三个不同平面,下列命题中正确( )A 若m // α,n // α,则m // nB 若α⊥γ,β⊥γ,则α // βC 若m ⊥α,n ⊥α,则m // nD 若m // α,m // β,则α // β7. 过点P(4, 2)作圆x 2+y 2=4的两条切线,切点分别A ,B ,O 是坐标原点,则△AOB 外接圆的方程为( )A (x −4)2+(y −2)2=20B (x −2)2+(y −1)2=5C (x +4)2+(y +2)2=20D (x +2)2+(y +1)2=5 8. 已知F 1、F 2分别为椭圆x 216+y 29=1的左、右焦点,椭圆的弦DE 过焦点F 1,若直线DE 的倾斜角为α(α≠0),则△DEF 2的周长为( ) A 64 B 20 C 16 D 随α变化而变化9. 已知函数y =sin(π4−2x),则其图象的下列结论中,正确的是( )A 关于点(−π8,1)中心对称B 关于直线x =π8轴对称C 向左平移π8后得到奇函数 D 向左平移π8后得到偶函数10. f(x)是定义在R 上的奇函数,当x >0时,(x 2+1)f′(x)+2xf(x)<0,且f(−1)=0,则不等式f(x)>0的解集是( )A (1, +∞)B (−1, 0)∪(1, +∞)C (−∞, −1)D (−∞, −1)∪(0, 1)二、填空题:本大题共5小题,每小题5分,共25分.将答案填写在题中的横线上.11. 集合A={−1, 0, 1},B={x|x=m2+1, m∈R},则A∩B=________.12. 阅读如图的程序框图,若输入m=4,n=6,则输出的a等于________.13. 当x,y满足{|x−1|≤1y≥0y≤x+1时,则t=x−2y的最小值是________.14. 观察下列不等式:1+122<32,1+122+132<53,1+122+132+142<74,…由以上不等式推测到一个一般的结论:对于n∈N∗,1+122+132+⋯+1n2<________.15. (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4−5不等式选讲)若任意实数x使m≥|x+2|−|5−x|恒成立,则实数m的取值范围是________;B.(选修4−1几何证明选讲)如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46∘,∠DCF=32∘,则∠A的度数是________;C.(选修4−4坐标系与参数方程)极坐标系下,直线ρcos(θ−π4)=√2与圆ρ=√2的公共点个数是________.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16. 已知△ABC的角A、B、C所对的边分别是a、b、c,设向量m→=(a,b),n→=(sinB,sinA),p→=(b−2,a−2).(1)若m→ // n→,求证:△ABC为等腰三角形;(2)若m→⊥p→,边长c=2,角C=π,求△ABC的面积.317. 设数列{a n}的前n项和为S n,且S n=2a n−3(n=1, 2,…).(1)证明:数列{a n}是等比数列;(2)若数列{b n}满足b n=a n+2n(n=1, 2,…),求数列{b n}的前n项和为T n.18. 如图,在四棱锥P−ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60∘,Q为AD的中点.(1)求证:AD⊥平面PQB;PC,求四棱锥M−ABCD的体积.(2)若平面PAD⊥平面ABCD,且PM=1219. 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25, 30),第2组[30, 35),第3组[35, 40),第4组[40, 45),第5组[45, 50],得到的频率分布直方图如图所示.(Ⅰ)下表是年龄的频数分布表,求正整数a,b的值;的人数分别是多少?(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.20. 在平面直角坐标系中,已知曲线C上任意一点P到两个定点F1(−√3,0)和F2(√3,0)的距离之和为4.(1)求曲线C的方程;(2)设过(0, −2)的直线l与曲线C交于A、B两点,以线段AB为直径作圆.试问:该圆能否经过坐标原点?若能,请写出此时直线l的方程,并证明你的结论;若不是,请说明理由.21. 设函数f(x)=x2−mlnx,ℎ(x)=x2−x+a.(1)若曲线y=f(x)在x=1处的切线为y=x,求实数m的值;(2)当m=2时,若方程f(x)−ℎ(x)=0在[1, 3]上恰好有两个不同的实数解,求实数a的取值范围;(3)是否存在实数m,使函数f(x)和函数ℎ(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由.2013年陕西省西安市某校高考数学三模试卷(文科)答案1. A2. D3. C4. C5. C6. D7. B8. C9. C10. D11. {1}12. 1213. −414. 2n−1n15. [7, +∞),99∘,116. ∵ m // n∴ asinA=bsinB即a⋅a2R =b⋅b2R.其中R为△ABC外接圆半径.∴ a=b∴ △ABC为等腰三角形.由题意,m⋅p=0∴ a(b−2)+b(a−2)=0∴ a+b=ab由余弦定理4=a2+b2−2ab⋅cosπ3∴ 4=a2+b2−ab=(a+b)2−3ab ∴ (ab)2−3ab−4=0∴ ab=4或ab=−1(舍去)∴ S△ABC=12absinC=12×4×sinπ3=√317. (1)证明:因为S n=2a n−3(n=1, 2,…).,则S n−1=2a n−1−3(n=2, 3,…).…所以当n≥2时,a n=S n−S n−1=2a n−2a n−1,…整理得a n=2a n−1.…由S n=2a n−3,令n=1,得S1=2a1−3,解得a1=3.…所以{a n}是首项为3,公比为2的等比数列.…(2)解:因为a n=3⋅2n−1,…由b n=a n+2n(n=1, 2,…),得b n=3⋅2n−1+2n.所以T n=3(1+21+22+⋯+2n−1)+2(1+2+3+⋯+n)…=31(1−2n)1−2+2⋅n(n+1)2…=3⋅2n+n2+n−3所以T n=3⋅2n+n2+n−3.…18. 解:(1)连接BD∵ PA=PD=AD=2,Q为AD的中点,∴ PQ⊥AD又∵ ∠BAD=60∘,底面ABCD为菱形,∴ △ABD是等边三角形,∵ Q为AD的中点,∴ AD⊥BQ∵ PQ、BQ是平面PQB内的相交直线,∴ AD⊥平面PQB.(2)连接QC,作MH⊥QC于H.∵ 平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD∴ PQ⊥平面ABCD,结合QC⊂平面ABCD,可得PQ⊥QC∵ 平面PQC中,MH⊥QC且PQ⊥QC,∴ PQ // MH,可得MH⊥平面ABCD,即MH就是四棱锥M−ABCD的高线∵ PM=12PC,可得MH=12PQ=12×√32×2=√32,∴ 四棱锥M−ABCD的体积为V M−ABCD=13×12AC×BD×MH=16×2×2√3×√32=1.19. (1)由题设可知,a=0.08×5×500=200,b=0.02×5×500=50.(2)因为第1,2,3组共有50+50+200=300人,利用分层抽样在300名学生中抽取6名学生,每组抽取的人数分别为:第1组的人数为6×50300=1,第2组的人数为6×50300=1,第3组的人数为6×200300=4,所以第1,2,3组分别抽取1人,1人,4人.(Ⅲ)设第1组的1位同学为A,第2组的1位同学为B,第3组的4位同学为C1,C2,C3,C4,则从六位同学中抽两位同学有:(A, B),(A, C1),(A, C2),(A, C3),(A, C4),(B, C1),(B, C2),(B, C3),(B, C4),(C1, C2),(C1, C3),(C1, C4),(C2, C3),(C2, C4),(C3, C4),共15种可能.其中2人年龄都不在第3组的有:(A, B),共1种可能,所以至少有1人年龄在第3组的概率为1−115=1415.20. 解:(1)根据椭圆的定义,可知动点P的轨迹为椭圆,其中a =2,c =√3,则b =√a 2−c 2=1. 所以动点P 的轨迹方程为x 24+y 2=1.(2)当直线l 的斜率不存在时,不满足题意.当直线l 的斜率存在时,设直线l 的方程为y =kx −2,设A(x 1, y 1),B(x 2, y 2), 若OA →⋅OB →=0,则x 1x 2+y 1y 2=0.∵ y 1=kx 1−2,y 2=kx 2−2,∴ y 1y 2=k 2x 1⋅x 2−2k(x 1+x 2)+4. ∴ (1+k 2)x 1x 2−2k(x 1+x 2)+4=0.…①由方程组{x 24+y 2=1y =kx −2得(1+4k 2)x 2−16kx +12=0.∵ △=162k 2−4×12×(1+4k 2)>0,∴ k 2>34…②则x 1+x 2=16k1+4k 2,x 1⋅x 2=121+4k 2,代入①,得(1+k 2)121+4k 2−2k 16k1+4k 2+4=0.即k 2=4,解得k =2或k =−2,满足②式.因此存在直线l ,其方程为y =2x −2或y =−2x −2. 21. 解:(1)∵ 函数f(x)=x 2−mlnx , ∴ 切点为(1, 1),f′(x)=2x −mx ,∵ 曲线y =f(x)在x =1处的切线为y =x , ∴ k =f ′(1)=1,即m =1(2)f(x)−ℎ(x)=0,等价于x 2−2lnx =x 2−x +a ,即a =x −2lnx 令g(x)=x −2lnx ,则g ′(x)=1−2x =x−22∴ x ∈[1, 2]时,g′(x)≤0,函数g(x)=x −2lnx 在[1, 2]内单调递减;x ∈[2, 3]时,g′(x)≥0,函数g(x)=x −2lnx 在[2, 3]内单调递增. 又因为g(1)=1,g(2)=2−2ln2,g(3)=3−2ln3 故2−2ln2<a ≤3−2ln3(3)∵ ℎ(x)=x 2−x +a 在(0,12)单调递减;(12,+∞)单调递增 ∴ f(x)=x 2−mlnx 也应在(0,12)单调递减;(12,+∞)单调递增 ∵ f ′(x)=2x −m x=2x 2−m x,∴ 当m ≤0时,f(x)=x 2−mlnx 在(0, +∞)单调递增,不满足条件;当m >0且√m2=12,即m =12,函数f(x)和函数ℎ(x)在公共定义域上具有相同的单调区间.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年高考文科数学模拟训练(4)
一、选择题:
1.复数()231i
i +-=( )
A .-3-4i
B . -3+4i
C . 3-4i
D . 3+4i
2.命题“2,20x R x x ∃∈-=”的否定是( )
A .2,20x R x x ∀∈-=
B . 2,20x R x x ∃∈-≠
C .2,20x R x x ∀∈-≠
D . 2,20x R x x ∃∈->
3.如图所示,程序框图运行后输出k 的值是 ( )
A .4
B .5
C .6
D .7
4.设双曲线22
21()9
x y a o a -=>的焦点为(5,0),则该双曲线的离心率等于 ( ) A .32 B .43 C .54 D .53
5.已知直线l ⊥平面α,直线m ⊂平面β,下列命题正确的是( )
①l m a ⊥⇒∥β ②l ∥m αβ⇒⊥ ③l αβ⊥⇒∥m ④α∥l m β⇒⊥ A .①② B .③④ C .②④ D .①③
6.直线y x m =+与圆221x y +=在第一象限内有两个不同的交点,则m 取值范围是( )
A . 2m <<
B . 3m <<
C . m <<
D . 1m << 7.函数22x y x =-的图象为( )
8.若正项数列{}n a 满足1111n n ga ga +=+,且a 2001+a 2002+a 2003+…a 2010=2013,则a 2011+a 2012+a 2013+…a 2020 的值为( )
A .2013·1010
B . 2013·1011
C .2014·1010
D . 2014·1011 9.函数2cos ()4y x π=+
的图象沿x 轴向右平移a 个单位(0)a >,所得图象关于y 轴对称,则a 的最小 值为( )
A .π
B .34π
C .2π
D .4
π 10.若a ,b ,c 均为单位向量,且a·b=0,则|a+b -c|的最小值为( )
A
1 B .1 C
1 D
二、填空题:
11
.一空间几何体的三视图如图所示,该几何体的体积为16π+,则图中x 的值为 . 12. 若x ,y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩
,目标函数2z x y =+最大值记为a ,最
小值记为b ,则a -b 的值为 .
13.已知锐角,αβ满足3tan tan()ααβ=+,则tan β的最大值为 .
三、解答题:
17.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知角,sin 3sin .3A B C π=
= (1)求tan C 的值;(2
)若a 求△ABC 的面积。
18.对某校高三年级学生参加社区服务次数进行统计,随机抽取M 名学生作样本,得到这M 名学生参加
社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中M ,p 及图中a 的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区
服务次数在区间[25,30]内的概率。
20.已知四棱锥P -ABCD 中,底面ABCD 是菱形,PA=PD ,∠BAD=60°,E 是AD 的中点,点Q 在侧
棱PC 上。
(1)求证:AD ⊥平面PBE ;
(2)若Q 是PC 的中点,求证PA ∥平面BDQ ;
(3)若3P BCDE Q ABCD V V --=,试求CP CQ 的值。
