1. 试用拉氏方程建立单摆的运动微分方程(已知摆长,摆球质量为m)重点
机械能守恒定律笔记重点

机械能守恒定律笔记重点一、机械能的概念1. 动能- 定义:物体由于运动而具有的能,表达式为E_{k}=(1)/(2)mv^2,其中m是物体的质量,v是物体的速度。
- 动能是标量,且恒为正值。
2. 重力势能- 定义:物体由于被举高而具有的能,表达式为E_{p}=mgh,其中m是物体的质量,g是重力加速度,h是物体相对于参考平面的高度。
- 重力势能是标量,但有正负之分。
参考平面上方的物体重力势能为正,参考平面下方的物体重力势能为负。
3. 弹性势能- 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用而具有的能。
对于弹簧,其弹性势能表达式为E_{p}=(1)/(2)kx^2(k为弹簧的劲度系数,x为弹簧的形变量)。
- 弹性势能也是标量,且恒为正值。
- 机械能:动能和势能(重力势能、弹性势能)统称为机械能,表达式为E = E_{k}+E_{p}(这里E_{p}包括重力势能和弹性势能)。
二、机械能守恒定律1. 内容- 在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
2. 表达式- E_{1}=E_{2},即初状态的机械能等于末状态的机械能。
- Δ E_{k}=-Δ E_{p},动能的增加量等于势能的减少量(或者动能的减少量等于势能的增加量)。
3. 条件- 对单个物体:只有重力做功(如自由落体运动、平抛运动等)。
- 对多个物体组成的系统:- 只有重力或弹力做功。
例如,一个弹簧和一个物体组成的系统,在只有弹簧弹力做功时,系统机械能守恒。
- 其他力不做功或者其他力做功的代数和为零。
如光滑斜面上滑块与弹簧组成的系统,若斜面光滑,滑块下滑过程中,除重力和弹簧弹力外无其他力做功,系统机械能守恒。
三、机械能守恒定律的应用1. 解题步骤- 确定研究对象(单个物体或系统)。
- 分析研究对象的受力情况,判断是否满足机械能守恒定律的条件。
- 选取合适的参考平面(确定重力势能的零点)。
- 确定初状态和末状态的机械能(分别计算动能和势能)。
单摆周期公式及影响单摆周期的因素研究

单摆周期公式及影响单摆周期的因素研究摘要:结合理论知识,基础物理实验,构建线性数学模型。
对单摆运动进行分析。
其中,理论部分主要依据高等数学及数学物理方法的知识,对单摆运动周期公式进行论证;实验部分主要通过改变单摆摆线长度进行实验;观察、分析单摆运动规律。
从而验证单摆周期公式。
并对影响单摆周期的因素展开研究。
最后总结出影响单摆周期的因素。
关键词:数学模型 ; 单摆运动 ; 周期公式单摆运动问题是一个古老的问题,无论是中学物理还是大学物理,我们都在学习研究单摆。
作为一个重要的理想物理模型,单摆的运动周期规律和实验研究在生产生活中意义重大。
单摆问题是物理学中经典问题。
从阅读物理学史并可知道,早在 1583 年,十九岁的伽利略(1564—1642)在比萨教堂祈祷时注意到因被风吹而摆动的大灯,他利用自己的脉搏来测定大灯的摆动周期,发现了摆的等时性。
但现在这个故事的真实性受到怀疑 ,因为比萨大教堂所保留的许多相关历史文献都表明该吊灯是在伽利略二十三岁那年才首次安装的。
专家指出,伽利略是于1602 年注意到单摆运动的等时性,不过伽利略误认为在大摆动条件下等时性也成立,他说:“物体从直立圆环上任一点落到最低位置的时间相同。
”随后吉多彼得做实验发现这个结论与实验不符,伽利略解释说可能是由于摩擦力。
伽利略从实验中得出单摆周期与摆长的平方根成正比。
他还指出周期与摆球质量无关。
他说:“因此我取两个球,一个是铅的而另一个是软木的,前者比后者重 100 多倍,用两根等长细线把它们悬挂起来、把每一个球从铅直位置拉到旁边,我在同一时刻放开它们,它们就沿着以这些等长线为半径的圆周下落,穿过铅垂位置,并且沿同一路径返回。
”最早系统地研究单摆的是惠根斯(ChristiaanH uygens )。
由于当时实验技术条件的落后,重力加速度在惠根斯之前是很难精确测出来的,所以惠更斯不可能从实验中总结出或猜出单摆周期公式的系数π2。
事实上,反过来重力加速度是 1659 年惠更斯根据单摆周期公式首次精确测出来的。
《理论力学》作业

8. 质点系中各质点的惯性力对质心的力矩相互抵消
9.
T
1 2
mrc2
1 2
mi ri 2
10. 主矢和对简化中心的主矩,力偶和合力
11. 1 3 3 6
12. 空间极迹
本体极迹
13. 任意移动,力线平移定理,在平移的同时必须附加一力偶,其力偶矩等于原力对新作用点的力矩。
14. Il I1 2 I 2 2 I3 2 ,刚体对 o 点的三个惯量主轴的转动惯量。
19. a a r ( r) 2 vr
20. F mw2 xi FC 2m v
dv
dm
21.
m dt
F Vr
dt
(或者
d
(e) dm (mv) F u
dm
dt
22. 对力心的动量矩守恒 和 机械能守恒
23. rຫໍສະໝຸດ r r r 2 r 2r24.
H
1 2
mr 2
1 2
L 1 m(r2 r2 2 ) b
24. 已知一运动质点的拉格朗日函数为 2
r ,则哈密顿函数为 H=________(式中b为常
数)。
'
'
1. r r
''
'2
''
''
r r r 2r
2. 质点所在处曲线的切线方向
v ds dt
dv '' az dt S
v2 an
3. d J M dt
O
(3)
T
A
C
x
P
六. 解:由平面运动动力学基本力学方程得
mxc
mg sin
三.试用拉格朗日方程建立弹簧振子的运动微分方程,并求出其振.

三. 试用拉格朗日方程建立弹簧振子的运动微分方程,并求出其振动周期(已知:弹簧的倔强系数为K ,物块的质量为m )。
四. 长l 2,质量为m 的均匀棒,其上端A 靠在光滑的墙上,下端则固联一不能伸长的线BC ,线的上端固结于墙上C 点,C 点与A 点在同一垂直线上,棒与墙所成的角度为α,线与墙所成的角度为β,如果ABC 平面为与墙垂直的铅垂面。
求平衡时αβ与之间的关系。
(用刚体平衡方程求解)。
三. 解:系统自由度1=S ,取q=x,系统的动能2'21x m T = 系统的势能22
1kx V = =-=V T L 2'21x m -22
1kx 代入拉氏方程:0)(=∂∂-∂∂x l x l dt d ,得: 0''=+kx x m 0''=+
∴x m k x 令m
k w =2,则w 为弹簧振子简谐振动的圆频率。
k
m W T ππ22==∴
四. 解:αβ
cos 0(1)
0sin 0(2)0sin 2cos 0(3)()0yi xi
B i
T mg F N T F mgl N l m F ββαα⎧-==⎪-==⎨⎪-==⎩∑∑∑
)
1()2((3)N tg N mg tg mg ββ==得:。
代入式得 sin 2cos 0mgl mg tg l αβα-∙= 即:202tg tg tg tg αβαβ-=∴=。
第三章 两自由度系统振动

d d( tq L j) q L jQ j - q D j (j 1 ,2 , ,n )
式D 中 1 2 C 1 x 1 2 1 2 C 2 (x 1-x 2)2 1 2 C 3 x 2 2
例题: 置于光滑平面的小车质量m1,车上质量为m2的圆柱体可作 无滑动的纯滚动。试建立该系统的运动微分方程。
两自由度与单自由度系统振动特性与分析方法的不同:
①两自由度振动系统具有两阶固有频率; ②两自由度振动系统引入主振型的概念,与系统的固
有频率一样,是系统本身的物理特性与固有特性, 与其初始条件无关。 ③一般情况下系统的振动是两种主振动的叠加,是一 种复杂的非周期运动。当满足一定条件时,系统才 作主振动。
(j1,2, ,n)
或
dd(tqLj)qLj 0 (j1,2, ,n)
(1)
其中,L=T-U称为拉格朗日函数。
2)当作用在系统上的主动力中,部分为有势力,部分 是非有势力,广义力Qj可分为两部分:
Qj Qj Q (j1,2,,n) 其中 Q是对应于非有 义势 力力 Q, j是 的对 广应于有势 广义力。 拉氏方程可写成
1
第三节 两自由度系统振动模型的建立
动力学系统振动模型的建立方法: 牛顿运动定律 定轴转动微分方程 能量法
一、拉氏方程的原理
在理想、完整约束条件下的n个自由度系统,选取广义坐 标为qj(j=1,2, ···,n),其运动可由如下拉格朗日方程来描述:
dT T d( tq j)qj Q j
取静x,平衡位置作为坐标原点,
进行受力分析,建立系统的运 动微分方程:
m1x K1(x r) I0 K1(xr)r K2r2
(必考题)高中物理选修一第二章《机械振动》测试卷(答案解析)(9)
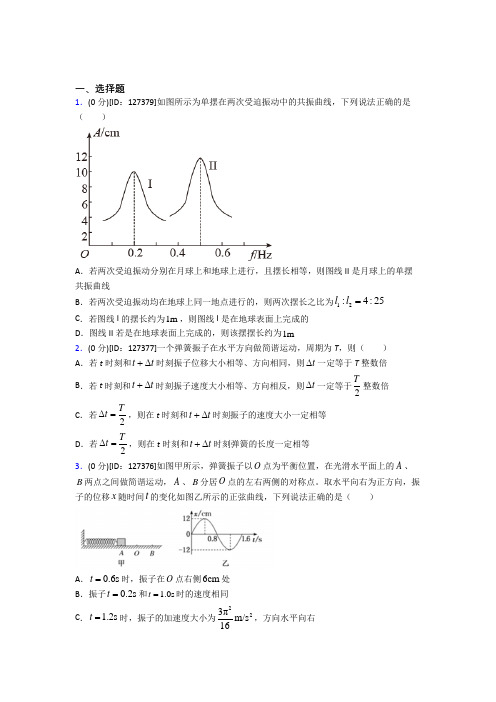
一、选择题1.(0分)[ID :127379]如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是( )A .若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II 是月球上的单摆共振曲线B .若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为12:4:25l l =C .若图线I 的摆长约为1m ,则图线I 是在地球表面上完成的D .图线II 若是在地球表面上完成的,则该摆摆长约为1m2.(0分)[ID :127377]一个弹簧振子在水平方向做简谐运动,周期为T ,则( ) A .若t 时刻和t t +∆时刻振子位移大小相等、方向相同,则t ∆一定等于T 整数倍 B .若t 时刻和t t +∆时刻振子速度大小相等、方向相反,则t ∆一定等于2T整数倍 C .若2Tt ∆=,则在t 时刻和t t +∆时刻振子的速度大小一定相等 D .若2Tt ∆=,则在t 时刻和t t +∆时刻弹簧的长度一定相等 3.(0分)[ID :127376]如图甲所示,弹簧振子以O 点为平衡位置,在光滑水平面上的A 、B 两点之间做简谐运动,A 、B 分居O 点的左右两侧的对称点。
取水平向右为正方向,振子的位移x 随时间t 的变化如图乙所示的正弦曲线,下列说法正确的是( )A .0.6s t =时,振子在O 点右侧6cm 处B .振子0.2s t =和 1.0s t =时的速度相同C . 1.2s t =时,振子的加速度大小为223πm/s 16,方向水平向右D . 1.0s t =到 1.4s t =的时间内,振子的加速度和速度都逐渐增大4.(0分)[ID :127375]把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,如图所示。
不开电动机让这个筛子自由振动时,完成20次全振动用15 s ,在某电压下,电动偏心轮的转速是50 r/min 。
已知增大电动偏心轮电压可使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。
单摆的运动微分方程与解

单摆的运动微分方程与解
单摆是一个基本的物理模型,其运动可以用微分方程来描述。
假设单摆的摆长为L,质量为m,角度为θ,角速度为ω。
根据牛顿第二定律,单摆的运动微分方程可以表示为:
m * d²θ/dt² = -mg * sin(θ)
这里,g 是重力加速度。
这个微分方程描述了单摆在受到重力和阻尼力作用下的运动。
解这个微分方程,可以得到单摆的角速度和角度随时间的变化。
解这个微分方程,可以得到单摆的角速度和角度随时间的变化。
角速度ω 的通解为:
ω = ω₀ * (1 - exp(-t / 2L))
其中,ω₀ 是初始角速度。
角度θ 的通解为:
θ = θ₀ * (1 - exp(-t / 2L)) + θ₁ * exp(-t / 2L)
其中,θ₀ 和θ₁ 是初始角度和最终角度。
这些解描述了单摆在受到重力和阻尼力作用下的运动规律。
高中物理波动的应用题解题思路

高中物理波动的应用题解题思路波动是高中物理课程中的一个重要内容,它广泛应用于生活和科学研究中。
在解决波动应用题时,我们需要掌握一些基本的解题思路和技巧。
本文将通过具体的题目举例,分析解题思路,并给出一些解题技巧,帮助高中学生和他们的父母更好地理解和应用波动知识。
题目一:一根长为L的细绳,一端固定,另一端悬挂一个质量为m的小球。
当小球作简谐振动时,细绳上的波动传播速度为v,频率为f。
求小球的振动周期T。
解题思路:首先,我们需要知道简谐振动的周期与频率之间的关系:T = 1/f。
而频率与波动传播速度之间的关系为:v = λf,其中λ为波长。
细绳上的波动传播速度v可以表示为v = √(T/μ),其中μ为细绳的线密度。
细绳上的波动传播速度v与波长λ之间的关系为:v = λf。
将以上两个关系代入,可以得到:λ = √(Tμ)。
将波长λ代入频率与波长之间的关系,可以得到:T = 1/(f√(μ))。
题目二:一束波长为λ的单色光通过一条宽度为d的狭缝,经过衍射后,观察到第一级主极大的角度为θ。
求狭缝的宽度d。
解题思路:根据衍射的基本原理,我们知道主极大的位置满足sinθ = mλ/d,其中m为主极大的级数。
我们可以通过观察第一级主极大的角度θ,以及波长λ,来求解狭缝的宽度d。
将已知条件代入公式,可以得到:d = mλ/sinθ。
题目三:一根长为L的弦上,由一点源产生的波传播到另一端的时间为t。
现将弦剪短为原来的一半,重新产生波,波传播到另一端的时间为多少?解题思路:首先,我们需要知道波传播速度与弦的线密度和张力之间的关系:v = √(T/μ)。
弦的线密度μ与长度L之间的关系为:μ = m/L,其中m为弦的质量。
弦的张力T与长度L之间的关系为:T = kL,其中k为弦的弹性系数。
将以上两个关系代入波传播速度与弦的线密度和张力之间的关系,可以得到:v = √(k/m)。
根据波传播速度与弦的线密度和张力之间的关系,可以得到:v' = √(k/2m)。
高考物理专题复习二 简谐运动的定义和证明

高考物理专题复习二简谐运动的定义和证明一、简谐运动的定义1.从动力学角度定义:如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。
即回复力F= -kx,这是质点做简谐运动的充要条件。
2.从运动学角度定义:如果质点的位移与时间的关系遵从正弦函数的规律x=A sin(ωt+φ),即它的振动图象(x-t图象)是一条正弦曲线,这样的振动叫做简谐运动,这也是质点做简谐运动的充要条件。
⑴简谐运动的位移x是指偏离平衡位置的位移。
⑵回复力F是一种效果力。
是质点在沿振动方向上所受的合力。
⑶k是回复力系数,有别于弹簧的劲度系数。
二、简谐运动的证明⑴证明过程,凡是题目没出现的物理量,必须说明所设物理量的符号及意义。
⑵根据F= -kx证明简谐运动,步骤是:①建立以平衡位置为原点的坐标系;②在坐标系上任取位移为x的一点(取在正方向即可,位移必须设为x,不能设为d、A等常量;③证明沿振动方向的合力(回复力)F= -kx。
⑶若要求质点振动过程的最大动能,最好选从最远点到平衡位置过程用动能定理,沿振动方向的合外力就是回复力,该过程回复力做的功等于动能变化。
(利用F-x图象或用xW⋅=)F练习题:1.单摆摆长为l,摆球质量为m。
将摆球向左拉动,使其离开平衡位置的距离为A,此时摆线与竖直方向所成角度很小。
无初速释放摆球。
取重力加速度为g。
⑴试证明释放后小球的运动是简谐运动,并求回复力系数k;⑵试求摆球振动过程的最大动能E k。
2.理论研究表明:质量均匀分布的球壳对其内部物体的引力之和为零。
设万有引力常量为G ,地球质量为M ,半径为R ,球心为O ,不考虑地球自转。
求: ⑴在地面以下距地心x 处(x ≤R )的重力加速度大小g x ;⑵设想沿地球直径开通一条隧道,由隧道上端由静止释放一个质量为m 的小球a .试证明小球将做简谐运动;b .已知简谐运动的周期为km T π2=,其中m 为振子质量,k 为回复力系数。
单摆运动微分方程求解

单摆运动微分方程求解## English Response:The equation of motion for a simple pendulum is a second-order nonlinear differential equation. It is given by:$$m l \frac{d^2 \theta}{dt^2} = -m g \sin \theta$$。
where:$m$ is the mass of the pendulum.$l$ is the length of the pendulum.$g$ is the acceleration due to gravity.$\theta$ is the angle of the pendulum from the vertical.This equation can be solved using a variety of methods,including:Analytical methods: These methods involve finding an exact solution to the equation of motion. One common analytical method is to use the separation of variables method.Numerical methods: These methods involve using a computer to approximate the solution to the equation of motion. One common numerical method is to use the Runge-Kutta method.In this example, we will use the separation ofvariables method to find the analytical solution to the equation of motion. The first step is to separate the variables in the equation of motion:$$m l \frac{d^2 \theta}{dt^2} = -m g \sin \theta$$。
单摆周期的一个推论式及其例解

单摆周期的一个推论式及其例解作者:刘维军来源:《中学教学参考·理科版》2010年第01期我们知道,有些单摆受外部因素影响时,单摆的周期不能直接用T=2πLg计算,一般情况下,可以用两种方式解决:一是等效重力加速度的方法;二是等效摆长的方法.下面介绍一种计算单摆周期的通用推论式,供大家参考.一、计算单摆周期的通用推论式单摆模型在平衡位置(最低点)静止时,所受合力为零,所以摆球所受重力与摆线对摆球的拉力平衡,即拉=mg,也就是重力加速度可以用拉m计算,单摆周期公式即可变为T=2πLg=2πL拉m拉.当受外部因素影响,单摆在平衡位置静止时,摆球所受各力的合力仍为零,即摆球所受摆线的拉力与其他各力的合力平衡,如将其余各力的合力等效为“重力”,有拉合=mg′,即可得“等效重力加速度拉m,单摆周期公式即为拉.综合以上情形,可得计算单摆周期的一个通用的推论式:T=2πmLF,其中F为摆球在平衡位置静止时摆线对摆球的拉力.二、应用举例【例1】如图1所示,在一倾角为θ的光滑斜面上固定一长为l的单摆,若使其小角度摆动,它的运动周期为().图1A.T=2πlgB.T=2πlsinθgC.T=2πlgsinθD.T=2πlgcosθ解析:通常情况下,解此题是用等效摆长的方法,如果等效不正确就会得出选项B的错误答案.根据推论式,现只要求出摆球在平衡位置静止时摆线对摆球的拉力,即拉力等于摆球所受重力沿斜面向下的分力:F=mgsinθ,就可运用推论式求出此单摆的运动周期:T=2πmlF=2πlgsinθ,故正确选项为C.【例2】在O点固定一摆长为l细线,另一端固定一个质量为m,带电量为+q的小球(可视为质点),然后沿水平方向加以电场强度为E的匀强电场,小球处于静止状态,如图2所示.若将其拉开一个较小的角度由静止释放,求小球运动的周期.图2 图3解析:摆球在平衡位置静止时的受力如图3所示.摆球所受的拉力为单摆的周期为【例3】在以加速度为a的匀加速上升的电梯的水平地面上固定一光滑圆弧,圆弧半径为R,有一质量为m的小球(可视为质点)静止在圆弧最低点.若将小球拉离一段较小的弧线由静止释放,如图4所示,求小球运动的周期.图4 图5解析:此小球的运动可等效为单摆,圆弧的半径即可视为单摆的摆长,小球在平衡位置所受的支持力即可视为摆球受到的拉力.小球在平衡位置静止时的受力如图5所示.由F-mg=ma,得F=m(g+a).小球运动的周期T=2πmRF=2πRg+a. (责任编辑黄春香)。
单摆运动的分析

单摆的运动规律分析摘要:单摆的理想模型是,假设单摆由不可伸缩的轻绳与一质量为m 的小球组成,不考虑空气阻力。
在此基础上还可以进一步考虑受阻力情况。
关键词:单摆 线性微分方程 非线性微分方程 正文:单摆的理想模型是,假设单摆由不可伸缩的轻绳与一质量为m 的小球组成,不考虑空气阻力。
在此基础上还可以进一步考虑受阻力情况。
单摆在摆动过程中要受到空气阻力的影响,且其在摆动的过程中可能会出现不在同一平面内的情况,若考虑这一系列问题,求解就会变得比较复杂了,首先把问题理想化,假设单摆由不可伸缩的轻绳与一质量为m 的小球组成,不考虑空气阻力。
Ⅰ.由刚体绕定轴转动的微分方程可知:θθsin 222mgl dt d ml -=……⑴当θ很小时:022=+θθl gdtd ……⑵ 令l g w =2则原式化为0222=+θθw dtd ……⑶做任意角度摆动时的情况:0sin 222=+θθw dtd ……⑷ Ⅱ.受大小与速度成正比的阻力作用时:0sin 222=+-θθθw dtd k dt d ……⑸ 做小角度摆动时可近似为:0222=++θθθw dtd k dt d ……⑹ 其中⑵、⑶、⑹式为线性微分方程,⑴、⑷、⑸式为非线性微分方程。
1)小角度震荡时将sin θ近似看作θ i.函数文件:function fc=f0(t,y) global g lfc=[y(2) -g/l*y(1)]' ii.绘图程序:clearclcglobal g lg=9.8;l=1;w0=input('wm0?\n')[t,y]=ode45('f0',[0,100],[0,w0*pi]');plot(t,y(:,1),'r')title('θ-t 图');xlabel('时间/s');ylabel('θ/rad');gridiii.图像:取wm0=0.5.2)振幅增大后,θ将不满足近似条件。
高中物理“单摆”教学中的三个问题
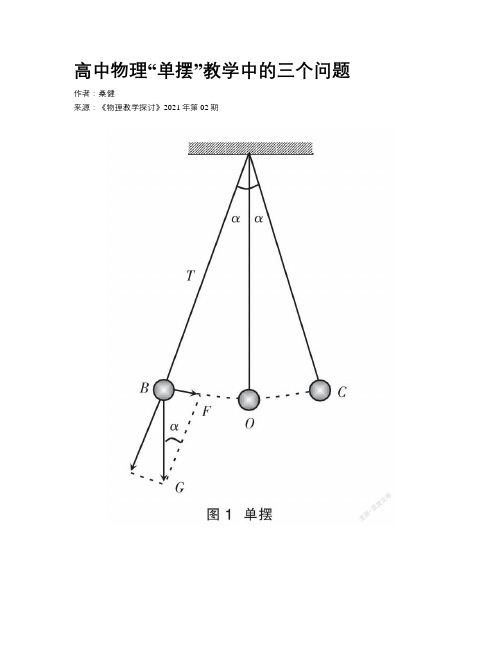
高中物理“单摆”教学中的三个问题作者:***来源:《物理教学探讨》2021年第02期摘要:文章通过单摆在无阻力作用下的运动满足机械能守恒以及圆周运动的知识,推导得出在摆角不超过5°的情况下,单摆在水平方向上的运动近似是简谐运动;通过证明一个做匀速圆周运动的物体在直径上的投影运动是一个简谐运动,该简谐运动的周期等于匀速圆周运动的周期,得到计算简谐运动周期的通式和可操作的方法;最后将这一方法用于圆锥摆周期公式的推导,并且讨论了圆锥摆与单摆等效的条件。
关键词:单摆的运动;单摆的周期;简谐运动;圆锥摆中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2021)2-0061-4在执教高中物理“单摆”与“用单摆测定重力加速度”相关内容的过程中,学生陆续提出三个问题,经过查阅资料、个人研究与备课组研讨,针对这三个问题进行了系统分析,现整理成本文,与大家交流。
问题一:单摆的运动本质是什么?现行上海市高级中学课本《物理·拓展型課程(试用本)》[1]第51至53页有如下表述:“把质量为m的摆球从平衡位置O拉开一小段距离到B点,这时悬线和竖直方向的夹角为α。
放开后,摆球始终受到重力mg和细线拉力T的作用。
重力的一个分力F=mgsinα沿圆弧切线方向,指向平衡位置O,而拉力T在圆弧切线方向没有分力。
正是重力的分力F使摆球回到平衡位置,这个力就是使单摆振动的回复力。
”……“在图1中,当单摆的摆角很小(不超过5°)时,摆球的位移x和圆弧长OB很接近,设摆长为l,则sinα≈α≈■。
于是,回复力F=mgsinα≈mgα≈mg■=■x。
因为式中m、g、l均为常数,可令k=■。
又因为回复力F的方向指向平衡位置,始终与位移x的方向相反,于是有F=-kx。
因此,在单摆摆角α小于5°,摆球所受回复力的大小与位移成正比,方向与位移相反,可知单摆的振动是简谐运动。
”在此,学生提出第一个问题:单摆的平衡位置在O点,如图1所示摆球在B点,摆球的位移是O指向B的一个矢量,当摆角不超过5°的情况下,sinα≈α,弧长OB约等于弦长OB,α=■≈■=■,F=■x,但是回复力的方向是过B点的切线方向,它和位移OB矢量是严格方向相反的吗?摆角不超过5°下的数学运算近似能适用于方向吗?笔者利用单摆在无阻力作用下的运动满足机械能守恒以及圆周运动的知识做了如下推导:如图2所示,设单摆在B与C之间运动,摆长为l,在B点时摆线与竖直方向夹角为α1,在P点时摆线与竖直方向夹角为α2、摆球的速度为v。
常微分方程拉氏变换法求解常微分方程课件

求解得到的代数方程,得到$F(s)$的表达式。
解出常微分方程的解
要点一
反变换求解
通过反拉氏变换将$F(s)$还原为$f(t)$,从而得到常微分方 程的解。
要点二
验证解的正确性
将得到的解代入原常微分方程进行验证,确保解的正确性。
06
总结与展望
总结
拉氏变换法的优势
拉氏变换法在求解常微分方程时 具有明显的优势,它可以将复杂 的微分方程转化为代数方程,大 大简化了求解过程。
通过逐一求解一阶常微分方程,拉氏变换法可以应用于高阶微分方程的求解。
拉氏变换法的缺点
计算量大
在应用拉氏变换法求解常微分方程时,需要进行复 杂的积分和代数运算,计算量较大。
对初值条件敏感
对于某些常微分方程,初值条件的微小变化可能导 致拉氏变换法的失效。
不易理解
拉氏变换法的概念较为抽象,不易被初学者理解。
与其他方法的结合
可以考虑将拉氏变换法与其他数值方法或解析方法结合,以更有效 地求解各种类型的微分方程。
实际应用价值
随着科学技术的不断发展,常微分方程在各个领域的应用越来越广 泛,因此拉氏变换法在实际应用中也将发挥更大的作用。
感谢观 看
THANKS
信号处理中,拉氏变换法可以用于分析信号的滤波、调制 和解调等过程,优化信号处理效果。
04
拉氏变换法的优缺点
拉氏变换法的优点
求解过程简化
拉氏变换法可以将复杂的常微分方程转化为简 单的代数方程,从而简化了求解过程。
适用于多种初值条件
拉氏变换法可以处理多种初值条件,使得该方 法具有更广泛的适用性。
可应用于高阶微分方程
拉氏变换法求解一阶常微分方程
常微分方程拉氏变换法求解常微分方程全文

拉普拉斯变换法用于求解常微分方程的基本思路:
对常微分方程进行拉氏变换法,得代数方程,求解 再反变换获取原方程的解
问题: 1. 什么是拉氏变换 2. 拉氏变换的基本性质 3. 什么是拉氏逆变换 4. 如何用拉氏变换求解微分方程
2
1拉普拉斯变换定义(简称拉氏变换)
对于在 [0, ) 上有定义的函数 f (t)
sx0(n2)
x (n1) 0
16
x(n) a1x(n1) an1x an x f (t)
给(4.32)两端施行Laplace Transform
sn
X
(s)
s n1 x0
sn2 x0
sx0(n2)
x (n1) 0
a1[s n1 X
(s)
sn2 x0
s n3 x0
x (n2) 0
]
an1[sX (s) x0 ] an X (s) F (s)
F (s) test f (t)dt
0
F (n) (s) (1)n t nest f (t)dt
0
F (n) (s) (1)n L[tn f (t)]
10
§3 拉普拉斯逆变换 已知象函数,求原函数
L1[F (s)] f (t)
也具有线性性质
L1[c1F1(s) c2F2 (s)] c1L1[F1(s)] c2L1[F2 (s)]
(sn a1sn1 an1s an ) X (s) F (s) B(s)
X (s) F(s) B(s) A(s)
x(t) L1[ X (s)] L1[ F (s) B(s)] A(s)
17
用拉氏变换求微分方程实例
例5 求 dx x e2t 满足初始条件 x(0) 0的特解
用Lagrange方程求自由质点在球坐标系中运动微分方程

用Lagrange方程求自由质点在球坐标系中运动微分方程1. 引言1.1 研究背景当我们研究物体的运动时,通常会采用拉格朗日方程这一数学工具。
拉格朗日方程是描述多自由度动力学系统的重要工具,它可以方便地推导出物体的运动方程,帮助我们更好地理解物体在运动过程中的行为。
在多种坐标系中,我们可以用拉格朗日方程来描述物体的运动,包括直角坐标系、柱坐标系和球坐标系。
在球坐标系中,物体的运动可以更自然地描述出来,特别是对于涉及到球对称性的运动问题。
通过拉格朗日方程,我们可以推导出物体在球坐标系中的运动微分方程,从而更深入地研究物体的运动规律。
这对于研究天体运动、分子运动等问题都具有重要的意义。
通过对自由质点在球坐标系中的运动微分方程进行研究,可以帮助我们更好地理解物体的运动规律,为解决实际问题提供有力的数学工具。
在本文中,我们将介绍拉格朗日方程的基本概念和推导过程,以及自由质点在球坐标系中的运动微分方程,同时给出一些实际应用的举例,希望能为读者带来一定的启发和帮助。
1.2 研究意义研究自由质点在球坐标系中运动微分方程的意义在于可以帮助我们更好地理解物体在空间中的运动规律。
通过求解这些微分方程,我们可以得到质点在球坐标系中的位置、速度和加速度随时间的变化关系,从而揭示质点在球坐标系内的轨迹和轨迹方程,以及质点受到的力和力矩等信息。
这对于研究空间运动系统的动力学特性、分析系统的稳定性和控制系统的设计等方面都具有重要的意义。
研究自由质点在球坐标系中运动微分方程还可以为实际工程和科学问题的求解提供重要的参考。
在机械工程、航空航天、物理学等领域,往往需要对运动系统进行建模和仿真,以便对系统进行分析和优化。
而球坐标系是描述空间中天体运动和球形机构运动的常用坐标系,因此掌握球坐标系中质点的运动微分方程对于这些领域的研究具有重要的指导意义。
深入研究自由质点在球坐标系中运动微分方程的意义在于提高我们对物体运动规律的理解,为实际问题的数值模拟和分析提供参考,以及指导工程设计和科学研究的开展。
单摆模型

(1)
α ' (0) = 0,α (0) = α 0
这就是理想单摆满足的微分方程。
3.解微分方程
当
α 很小时,有 sin α ≈ α, 为简单起见,(1)式写成:
α
''
+
g α L
= 0
(2)
(2)式的特征方程为:
g λ + =0 L
2
对应的特征根为 其中
λ
=
i
g 故方程(2)的通解为: L
α(t) = c1 sinωt + c2 cosωt
ω =
g L
代入初值条件,可求得满足初值条件的微分方程的解
α (t ) = α 0 cos ωt
当摆球在最低点平衡位置时 , T为周期。即可得出:
α (t ) = 0
=
, 此时
T t = 4
g T L 4
所以得:
π
2
T = 2π
L g
由上图可以看出摆球受到重力和摆线的拉力摆球的质量为m摆线长为l所受合力为mgsin由牛顿第二定律可得
单摆模型
李智
1.单摆模型
• 单摆是一种理想化的模型。 • 在一根不会伸长,忽略质量的悬线下系一质点,质点绕某个位置 来回往复运动。 • 在实验中单摆要满足三个条件: • 1. 线度条件 摆线的长度必须远远大于摆球的直径 2. 质量条件 摆球的质量必须远远大于摆线的质量 3.附加条件 摆线的弹性必须小,摆球形状规则,质量分布均匀,单摆在运动 中受的阻力忽略不计
2.建立理想单摆运动满足的微分方程,由微分方可以看出,摆球受到重力 G
所受合力为mgsin ,
mL α = − mg sin α
单摆--优质获奖精品教案 (11)

11.4单摆教学目标:1.知道什么是单摆,了解单摆运动的特点。
2.通过实验,探究单摆的周期与摆长的关系。
3.知道单摆的周期与摆长、重力加速度的关系。
会用单摆测定重力加速度。
教学重点难点:单摆运动的特点和对单摆周期公式的探究,对单摆的回复力分析及对小角度摆动的近似处理。
教学过程:导入新课:你家有摆钟吗?你知道座钟是谁首先发明的吗?座钟的钟摆摆一个来回需要多少时间?荷兰的惠更斯对摆的研究最为突出。
1.单摆的理想化条件(1)质量关系:细线质量与①小球质量相比可以忽略。
(2)线度关系:小球的②直径与线的长度相比可以忽略。
(3)力的关系:空气等对小球的③阻力与小球重力和线的拉力相比可以忽略。
单摆是实际摆的④理想化模型,实验中为满足上述条件,我们尽量选择⑤质量大、⑥体积小的球和尽量细的线。
2.单摆的回复力(1) 回复力摆球的重力沿⑦圆弧切向的分力是使摆球沿圆弧振动的回复力。
(2) 回复力大小:若摆球质量为m、摆长为l、偏离平衡位置的位移为x,在偏角很小时,单摆的回复力为⑧F=-x。
(3)回复力的特点:在偏角很小时,单摆所受的回复力与它偏离平衡位置的位移成⑨正比,方向总指向⑩平衡位置,即F=-kx。
3.单摆的周期(1)实验表明,单摆振动的周期与摆球质量无关,在振幅较小时与振幅无关,但与摆长有关,摆长越长,周期也越大。
(2)周期公式:荷兰物理学家惠更斯发现单摆的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,他确定了计算单摆周期的公式为T=2π。
4.用单摆测定重力加速度(1)原理:由T=2π得g=,即只要测出单摆的摆长l和周期T,就可以求出当地的重力加速度。
(2)画图法处理实验数据:分别以l和T2为纵坐标和横坐标,画出函数l=T2的图象,它应该是一条直线,由该直线的斜率可求出的值,进而求出重力加速度g。
主题1:单摆的动力学分析甲情景:某同学想研究单摆的运动,他把摆球拉到某一位置然后释放,发现小球总在关于最低点对称的圆弧上振动,并且越靠近最低点运动得越快,如图甲所示。
单摆的振动方程

单摆的振动方程单摆是一种简单而常见的物理现象,它由一个质点和一根不可伸长的轻细线组成。
当质点被偏离平衡位置后,它会受到重力的作用而产生振动。
这种振动可以用振动方程来描述,振动方程是描述物体振动规律的数学表达式。
振动方程可以分为简单单摆和复杂单摆两种情况。
首先,我们先来讨论简单单摆的振动方程。
简单单摆是指摆线无质量,摆球质量可以忽略不计的情况。
对于简单单摆,振动方程可以用以下公式表示:T = 2π√(L/g)其中,T代表单摆的周期,L代表摆线的长度,g代表重力加速度。
这个公式表明,简单单摆的周期与摆线的长度和重力加速度有关。
当摆线长度增加时,周期也相应增加;当重力加速度增大时,周期也会增大。
接下来,我们来讨论复杂单摆的振动方程。
复杂单摆是指摆线有质量,摆球质量不能忽略的情况。
对于复杂单摆,振动方程可以用以下公式表示:T = 2π√(I/mgh)其中,T代表单摆的周期,I代表摆线的转动惯量,m代表摆球的质量,g代表重力加速度,h代表摆球到达的最大高度。
这个公式表明,复杂单摆的周期与转动惯量、摆球质量、重力加速度和摆球到达最大高度有关。
通过振动方程,我们可以计算出单摆的周期。
周期是指单摆从一个极端位置回到同一位置所需的时间。
它是单摆振动规律的重要参数。
根据振动方程,我们可以发现单摆的周期与摆线长度、摆球质量、重力加速度和摆球到达的最大高度有关。
单摆的振动方程不仅可以帮助我们理解单摆的振动规律,还可以用于实际问题的解决。
例如,在工程中,我们可以通过测量单摆的周期来估算重力加速度;在物理实验中,我们可以通过改变摆线长度或摆球质量来研究单摆的振动规律。
单摆的振动方程是描述单摆振动规律的数学表达式。
简单单摆的振动方程与摆线长度和重力加速度有关,而复杂单摆的振动方程与转动惯量、摆球质量、重力加速度和摆球到达的最大高度有关。
通过振动方程,我们可以计算出单摆的周期,并应用于实际问题的解决。
这一方程为我们理解和研究单摆提供了重要的数学工具。
