Quantifiers
关于几个英语语法术语的辨正

关于几个英语语法术语的辨正【摘要】对几个英语语法术语进行辨正,回顾主流术语,比较相关术语,讨论适合bar等词的术语。
【关键词】量词单位名词英语语法术语辨正研究者已达成共识,认为英语中有些名词无论是在功能、语义和修辞效果上,还是在受语义制约方面,都与汉语的量词相当。
它们既能表示物体的数量,也蕴涵事物一定的语义特征,如abarofchocolate,abucketofwater,abunchofcarrots,aloafofbread,aflockofbirds中的bar、bucket、bunch、loaf、flock等名词(以下简称bar等词)。
但是,我国的英语学习者和语言工作者较少针对它们进行深入的学习和探讨,甚至不确定这些词的名称。
哪怕是关注及讨论过它们的研究者或语法学家,也使用不同的术语来指称这些词。
国外出现的术语分别有partitivenouns和quantifiers等,国内更是缺乏统一的名称。
一方面,研究者使用不同的中文术语。
有的接受了前文提到的英语术语,把它们译成相应的中文术语“部分名词”与“量词”;有的使用“英语量词”、“单位词”、“单位名词”的术语。
另一方面,相同的术语出现了不同的中文或英文对应词。
例如,partitivenouns不仅被译为“部分名词”,还被称为“量词”、“单位词”、“表份词”。
相同的中文术语也对应着不同的英语名称,如马丽的“量词”对应partitivenouns,张道真的“量词”对应quantitatives,杨甸虹的“量词”对应unitnouns。
章振邦的“单位词”既对应partitives,又对应unitnouns。
可以说,用来概况bar等词的术语使用情况非常混乱。
因此,针对bar等词的正名研究工作很紧迫,它对进一步的英语学习和研究至关重要。
一、主流术语之回顾综观现代英语语法,可发现国外及国内的主流英语语法著作中都讨论过上述bar等词用以表示事物数量的词。
八年级下册英语整理笔记

八年级下册英语整理笔记1. Unit 1: Things I Like to Do- Vocabulary:- hobbies: 爱好- skateboard: 滑板- video games: 电子游戏- painting: 绘画- camping: 露营- Grammar:- Present Simple Tense: 现在简单时态- Examples:- I play video games every day.- She paints on weekends.2. Unit 2: Around the House- Vocabulary:- furniture: 家具- kitchen: 厨房- bedroom: 卧室- balcony: 阳台- bathroom: 浴室- Grammar:- Prepositions of Place: 位置介词- Examples:- The book is on the table.- The cat is under the bed.3. Unit 3: At the Store- Vocabulary:- grocery shopping: 杂货购物- checkout counter: 收银台- shopping cart: 购物车- cashier: 收银员- discount: 折扣- Grammar:- Quantifiers: 量词- Examples:- I need a bottle of milk.- Give me two bags of chips.4. Unit 4: Vacation Time- Vocabulary:- destination: 目的地- suitcase: 行李箱- ticket: 票- sightseeing: 观光- travel: 旅行- Grammar:- Past Tense: 过去时态- Examples:- Last summer, we visited Beijing. - They went to the beach yesterday.5. Unit 5: Celebrations- Vocabulary:- festival: 节日- decoration: 装饰- fireworks: 烟花- tradition: 传统- parade: 游行- Grammar:- Modal Verbs: 情态动词- Examples:- We should clean the house before the party.- You must wear formal clothes for the ceremony.6. Unit 6: Health and Fitness- Vocabulary:- exercise: 锻炼- diet: 饮食- nutrition: 营养- yoga: 瑜伽- jogging: 慢跑- Grammar:- Adverbs of Frequency: 频率副词- Examples:- They always eat healthy food.- We sometimes go for a run in the morning.以上是八年级下册英语的整理笔记,希望对你有帮助!。
winhex正则-概述说明以及解释

winhex正则-概述说明以及解释1.引言1.1 概述概述部分:正文部分将首先对WinHex进行简介,然后重点介绍其正则表达式功能。
WinHex是一款功能强大的磁盘编辑器和数据恢复工具。
它具有多项功能,可以用于查找和修复文件系统错误、恢复删除的文件、进行磁盘和存储媒体的数据分析等。
同时,WinHex还提供了强大的正则表达式功能,可以在数据中进行查找和替换操作。
正则表达式是一种用于匹配、查找和替换字符串的工具。
它可以通过一系列的字符组合,来定义模式,并且可以利用这些模式在给定的文本中进行搜索和匹配操作。
WinHex的正则表达式功能提供了丰富的语法和选项,使用户可以根据具体需求进行高级的数据操作。
无论是在数据恢复过程中,还是在进行计算机取证或者数据分析时,WinHex的正则表达式功能都能帮助用户快速、准确地搜索和操作数据。
在接下来的正文部分,我们将详细介绍WinHex的正则表达式功能的使用方法和案例。
通过实际的操作演示,读者将能够全面了解和掌握WinHex正则表达式的应用。
同时,我们还将展望WinHex正则表达式的应用前景,探讨其在日常工作中的潜在用途和发展方向。
通过本文的阅读,读者将了解到WinHex作为一款磁盘编辑器和数据恢复工具的强大功能,并且对其正则表达式功能有更深入的了解。
希望读者能够通过本文获得实际操作的指导,提高在数据分析和处理方面的能力,并且能够在工作中充分发挥WinHex正则表达式的优势。
在结论部分,我们将对本文进行总结,并展望WinHex正则表达式在未来的应用前景。
1.2 文章结构文章结构主要分为引言、正文和结论三部分。
引言部分主要是对文章的背景和意义进行说明,概述整篇文章的内容,介绍WinHex正则表达式的重要性以及本文的目的和结构。
正文部分主要是对WinHex及其正则表达式功能进行详细介绍。
首先介绍WinHex的基本信息、用途和应用范围,然后重点阐述WinHex的正则表达式功能,包括其支持的正则表达式语法、常用功能的示例应用等。
离散数学 Predicates and Quantifiers(期望与量词)

2019/8/21
the Foundations:Logic and Proof Guo Jian
2
(3) P(x)--------”x is greater than 3”, propositional function P(4)---------proposition ,true P(2)--------proposition, false
2019/8/21
the Foundations:Logic and Proof Guo Jian
6
(3) Example 8(page 34) P(x)-----”x+1>x” the domain-----all real numbers How about ∀x P(x) ? Answer: ∀x P(x) ------true (4) Example 9 (page 35) Q(x)--------”x<2”
the domain-----all real numbers
How about ∀x Q(x) ? Answer: ∀x Q(x) ------false
2019/8/21
the Foundations:Logic and Proof Guo Jian
7
(5)Example 10 Let P(x) be “x2>0”. the domain ----- integers Show ∀x P(x) is false
logic that deals with predicate and quantifiers.
英语数量词表quantifiers-order
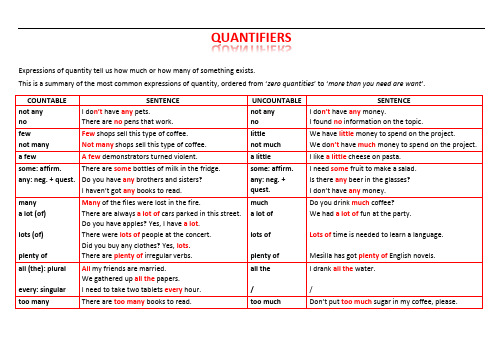
QUANTIFIERSExpressions of quantity tell us how much or how many of something exists.This is a summary of the most common expressions of quantity, ordered from ‘zero quantities’ to ‘more than you need are want’.COUNTABLE SENTENCE UNCOUNTABLE SENTENCEnot any no I do n’t have any pets.There are no pens that work.not anynoI do n’t have any money.I found no information on the topic.fewnot many Few shops sell this type of coffee.Not many shops sell this type of coffee.littlenot muchWe have little money to spend on the project.We do n’t have much money to spend on the project.a few A few demonstrators turned violent. a little I like a little cheese on pasta.some: affirm. any: neg. + quest. There are some bottles of milk in the fridge.Do you have any brothers and sisters?I haven’t got any books to read.some: affirm.any: neg. +quest.I need some fruit to make a salad.Is there any beer in the glasses?I don’t have any money.manya lot (of) lots (of) plenty of Many of the files were lost in the fire.There are always a lot of cars parked in this street.Do you have apples? Yes, I have a lot.There were lots of people at the concert.Did you buy any clothes? Yes, lots.There are plenty of irregular verbs.mucha lot oflots ofplenty ofDo you drink much coffee?We had a lot of fun at the party.Lots of time is needed to learn a language.Mesilla has got plenty of English novels.all (the): plural every: singular All my friends are married.We gathered up all the papers.I need to take two tablets every hour.all the/I drank all the water./too many There are too many books to read. too much Don’t put too much sugar in my coffee, please.。
2015离散数学谓词量词、变元的约束、翻译

(1)
2 是无理数 .
(2) x是有理数. (3) 小王与小李同岁. (4) x 与y具有同学关系.
(1) 凡人都呼吸 . (2) 所有的人都长着黑头发. (3) 兔子比乌龟跑得快. (4) ቤተ መጻሕፍቲ ባይዱ美国留学的学生未必都是亚洲人.
Universal Quantifier
The universal quantification of P(x) is the statement
定义1:约束变元 谓词公式中 , ,后面所跟的 x ,称为相应 量词的指导变元或作用变元或约束变元。 定义2:量词作用域(量词辖域)
给 定 谓 词 公 式 中 , 形 式 为 (x)P(x) , (x) P(x)中的P(x)称为相应量词的作用域(辖域)。
定义3:自由变元 在谓词公式中,除去约束变元以外所出现的 变元,称作自由变元。
with a certain property. Such statements are expressed using existential quantification. With existential quantification, we form a proposition that is true if and only if P(x) is true for at least one value of x in the domain.
Truth value?
We read ∀xP(x) as “for all xP(x)” or “for every xP(x).”An
element for which P(x) is false is called a counterexample of ∀xP(x).
语法术语中英文

语法术语中英文1. Noun (名词)countable uncountable (可数名词、不可数名词)Number of N (名词的数)Irregular plurals (不规那么复数)Genitive case of N (名词的所有格)Double genitive (双重所有格)2.Pronoun (代词)Personal pronoun (人称代词)Possessive pronoun (物主代词)Reflexive pronoun (反身代词)Interrogative pronoun (疑问代词)Indefinite pronoun (不定代词)3.Numeral (数次)Cardinal 、ordinal numbers (基数词、序数词)Percentage (百分数)Fraction (分数)Decimal (小数)Multiple (倍数)4.Determiner (限定词)Definite, indefinite, zero articles (定冠词,不定冠词,零冠词)Quantifiers (数量词)5.Preposition (介词)6.Adjective (形容词)Attributive 定语Predicative 表语Adverb clause equivalent 副词性从句7. Adverb (副词)Modifier of Adj / Adv / Prep-phrase / N-Phrase / Adverb-clause (形容词、副词、介词短语、副词性从句的修饰语)The comparative and superlative degrees of Adj / Adv (形容词和副词的比较级和最高级)9. Verb classes (动词)Transitive and intransitive verbs(及物动词和不及物动词)Auxiliaries and modal auxiliaries(助动词和情态动词)Semi-auxiliaries (半助动词)Phrasal verbs (短语动词)10. Tense (时态)Simple present, past, future and with modals (一样此刻时,一样过去时,一样以后时和情态助动词加动词)Present and past progressive(此刻进行时和过去进行时)Future progressive and with modals(以后进行时和情态动词加进行时)Present and past perfect(此刻完成时和过去完成时)Future perfect and with modals (以后完成时和情态动词加完成时)Present perfect progressive(此刻完成进行时)Past perfect progressive (过去完成进行时)voice (被动语态)Passive voice in simple tense(被动语态的一样时态)Passive voice in perfect and progressive tenses (被动语态的完成和进行时态)Passive voice of phrasal verbs (短语动词的被动语态)12.Subjunctive mood (虚拟语气)13.To V (Infinitive 动词不定式)as subject, object and complement (用作主语,宾语和补足语)Indicating purpose / result (表示目的和结果)Modifying adjective (修饰形容词)as post modifier in a noun phrase (后位修饰名词)to be + V-ed2, to have + V-ed2, to be + V-ing (不定式的被动式,完成式和进行式)14.V-ing (Gerund 动名词)object, subject and predicative (宾语, 主语和表语)N / Pronouns or their possessive + V-ing as subject and object (名词/ 代词或其所有格加动名词作主语和宾语)Prep + N / Pronouns or their possessive + V-ing (介词加名词/代词或其所有格加动名词)being + V-ed2, having + V-ed2, having been + V-ed2 as a noun equivale nt (动名词的被动式,完成式和完成被动式起名词作用)15pre-modifier and post modifier in a noun phrase 此刻分词和过去分词)as complement (补足语)as an adverb clause equivalen t(作状语)When / while, etc. + V-ing / V-ed2 (When / While 等加此刻分词或过去分词)(with) N + V-ing / V-ed2 ( [ with ] 名词加此刻分词或过去分词)Dangling V-ing as adverb clause equivalen t(无归属此刻分词作状语)being + V-ed2, having + V-ed2, having been + V-ed2 as an adverb or adjective clause equivalen t(此刻分词的被动式、完成式和完成被动式作状语或定语)16. Basic sentence patterns and sentence elements (大体句型和句子成份)Pattern 1: S + VPattern 2: S + V + CsPattern 3: S + V + OPattern 4: S + V + Oi + OdPattern 5: S + V + Od + Co17. Interrogative form (疑问形式)Negative form (否定形式)Passive form (被动形式)relative clause (定语从句)Restrictive and non-restrictive (限制Pare nt hesis (插入语)Omission (省略)Omission through coordination (并列结构中的省略)Negation (否定)Total negation (全数否定)Partial negation (部份否定)Double negation (双重否定)Transferred negation (转移否定)性和非限制性定语从句)Appositive clause (同位语从句)Noun phrase appositive to clause(名词短语作句子的同位语)Clause of time and space(时刻从句和地址从句)Clauses of condition, concession and con tras t (条件从句、妥协从句和对照从句)Clauses of cause, result and purpose(缘故从句、结果从句和目的从句)Clauses of manner and comparison(方式从句和比较从句)Clauses of proportion and other types(比例从句和其它从句)3rd person pronouns, and plurals of the 1st and 2nd person pronouns (第三人称代词,第一、二人称代词的复数)indefinite pronouns (不定代词)(+ of + N / Pron)Subjec t-verb inversion(主语与谓语倒装)朗文高级英语语法》第一章动词时态概述(Overview Of Verb Tenses)1- 1 一样时态(The Simple Tenses)1- 2 进行时态(The ProgressiveTenses)31- 3 完成时态(The Perfect Tenses)1- 4 完成进行时态(The PerfectProgressive Tenses)1-5 时态用法总结(Summary Chart ofVerb Tenses)1- 6 -ing 和-ed 形式的拼写(Spelling of -ing and -ed Forms)第二章一样此刻时,一样过去时,此刻进行时和过去进行时(Present And Past,Simple And Progressive)2- 1 一样此刻时(Simple Present) 2- 2 此刻进行时(Present Progressive)2- 3 静态动词( Stative Verbs)2-5 规那么动词和不规那么动词(Regular and Irregular Verbs)2-6 规那么动词:-ed的发音(RegularVerbs: Pronunciation of -ed Endings)2-7 不规那么动词表(Irregular Verbs: an Alphabetical List)2-8 易混淆的动词:raise/rise, set/sit, lay/lie (Troublesome Verbs: raise/rise, set/sit, lay/lie)2-9 一样过去时(Simple Past)2-10 过去进行时(Past Progressive)2-11进行时态与always连用表示抱怨(Using Progressive Verbs with always to Complain)2-12 进行时态中地址状语的用法(Using Expressions of Place with Progressive Verbs) being + Adjective)3- 1 此刻完成时(Present Perfect)2-4 am/is/are being+形容词(am/is/are第三章完成时和完成进行时(Perfect And Perfect Progressive Tenses)3- 2 此刻完成进行时(Present Perfect Progressive) 3- 3 过去完成时(Past Perfect)3- 4 过去完成进行时(Past Perfect Progressive)第四章以后时(Future Time)4- 1 一样以后时:will 和be going to (Simple Future: will and be going to)4- 2 will 与be going to 的比较(will vs. be going to)4- 3 历时刻状语从句表示以后(Expressing the Future in Time Clauses)4-4 用一样此刻时和此刻进行时表示以后(Using the Present Progressive and the Simple Present to Express Future Time)4- 5 以后进行时(Future Progressive)4- 6 以后完成时(Future Perfect)4-7 以后完成进行时(Future Perfect Progressive)第五章时刻状语从句和时态的温习(Adverb Clauses Of Time And Review Of Verb Tenses)5- 1 时刻状语从句:形式(Adverb Clauses of Time: Form)5- 2 历时刻状语从句表示时刻关系(Using Adverb Clauses to Show Time Relationships)第六章主谓一致(Subject-verbAgreement)6-1以-s或-es结尾的词:用法、发音和拼写(Final -s/-es: Use, Pronunciation, and Spelling)6-2 大体的主谓一致问题(BasicSubject-verb Agreement)6-3 主谓一致:表达数量(Subject-verb Agreement: Using Expressions of Quantity)6-4 主谓一致:there be的用法(Subject-verb Agreement: Using there + be)6- 5 主谓一致:不规那么用法(Subject-verb Agreement: Some Irregularities)第七章名词(Nouns)7- 1 名词复数形式的规那么和不规那么转变(Regular and Irregular Plural Nouns)7- 2 所有格(Possessive Nouns)1037- 3 名词作修饰语(Using Nouns as Modifiers)7-4 可数名词和不可数名词(Count andNoncount Nouns)7- 5 不可数名词(Noncount Nouns)7- 6 常见不可数名词(Some Common Noncount Nouns)7-7 冠词的大体用法(Basic ArticleUsage)7-8 冠词用法的大体原那么(General Guidelines for Article Usage)7-9 数量的表达(Expressions of Quantity)7-10 a few 和few, a little 和little 的用法(Using a few and few; a little and little)7-11 带of 的数量表达(Using of in Expressions of Quantity)7-12 all (of)和both (of)〔All (of) and both (of) 7-13 单数的数量表达:one, each, every (Singular Expressions of Quantity: one, each, every)第八章代词(Pronouns)8- 1 人称代词(Personal Pronouns)8- 2 人称代词:与类属名词、不定代词的一致性(Personal Pronouns: Agreement with Generic Nouns and Indefinite Pronouns)8-3 人称代词:与集合名词的一致性(Personal Pronouns: Agreement with Collective Nouns)8- 4 反身代词(Reflexive Pronouns)8-5 you, one 和they 用作非人称代词(Using you, one, and they as Impersonal Pronouns)8- 6 other 的形式(Forms of other)8-7 other 的常见表达(CommonExpressions with other)第九章情态动词(一) (Modals, Part 1)9- 1 概述(Introduction)9-2 I作主语的礼貌请求(PoliteQuestions with I as the Subject)9-3 you 作主语的礼貌请求(PoliteQuestions with you as the Subject)9- 4 would you mind 用作礼貌请求(Polite Requests with would you mind)9- 5 表示必需:must, have to, have got to (Expressing Necessity: must, have to, have got to)9-6 没必要要和禁止:have to和must的否定形式(Lack of Necessity and Prohibition: have to and must in the Negative)9-7 忠告:should, ought to, had better (Advisability: should, ought to, had better)9-8 should 的过去式(The Past Form of should)9-9 期望:be supposed to (Expec tatio ns: be supposed to)9-10 提议:let's, why don't, shall I/we(Making Suggestions: let's, why don't, shall I/we)9-11 提议:could与should的比较(Making Suggestions: could vs. should) 第十章情态动词(二) (Modals, Part 2)10- 1 表示确信程度:此刻时(Degrees of Certainty: Present Time)10-2 表示确信程度:此刻时的否定形式(Degrees of Certainty: Present Time Negative)10-3 表示确信程度:过去时(Degrees of Certainty: Past Time)10-4 表示确信程度:以后时(Degrees of Certainty: Future Time)10-5 情态动词的进行式(Progressive Forms of Modals)10-6 表示能力:can 和could (Ability:can and could)10-7 would 表示过去重复性的动作(Using would to Express a RepeatedAction in the Past)10-8 表示偏向: would rather(Expressing Preference: would rather)10-9 情态动词和短语情态动词的结合(Combining Modals with Phrasal Modals)10-10 情态动词和类似表达的总结表(Summary Chart of Modals and Similar Expressions)第十一章被动语态(The Passive)11-1 被动语态的组成(Forming the Passive)11-2 被动语态的用法(Using thePassive)11-3 间接宾语用作被动语态的主语(Indirect Objects Used as Passive Subjects)11-4 情态动词与短语情态动词的被动语态(The Passive Form of Modals and Phrasal Modals)11-5 静态被动语态(Stative Passive)11-6 常见静态被动语态动词 + 介词(Common Stative Passive Verbs + Prepositions)11-7 get 与被动语态(The Passive with get) 11-8 分词形容词(Participial Adjectives)第十二章名词性从句(Noun Clauses)12-1 概述(Introduction)12-2 以疑问词开头的名词性从句(Noun Clauses Beginning with a Question Word)12-3以whether或if开头的名词性从句(Noun Clauses Beginning with whether or if)12-4疑问词后接不定式(Ques tion Words Followed by Infinitives)12-5 以that 开头的名词性从句(NounClauses Beginning with that)12-6 直接引语(Quoted Speech)12-7 间接引语:名词性从句中动词的形式(Reported Speech: Verb Forms in Noun Clauses)12-8 名词性从句中虚拟语气的用法(Using the Subjunctive in Noun Clauses)12-9 带有-ever的辞汇的用法(Using -ever Words)第十三章定语从句(Adjective Clauses)13- 1 概述(Introduction)13-2 定语从句的关系代词作主语(Adjective Clause Pronouns Used as the Subject)13-3 定语从句的关系代词作动词的宾语(Adjective Clause Pronouns Used as the Object of a Verb)13-4 定语从句的关系代词作介词的宾语(Adjective Clause Pronouns Used as the Object of a Preposition)13-5 定语从句的经常使用句型(UsualPatterns of Adjective Clauses)13-6 whose 的用法(Using whose)13-7定语从句中where的用法(Using where in Adjective Clauses)13-8 定语从句中when的用法(Using when in Adjective Clauses)13-9 定语从句修饰代词的用法(Using Adjective Clauses to Modify Pronouns)13-10 定语从句中标点符号的利用(Punctuating Adjective Clauses) 13-11 定语从句中数量的表示方式(Using Expressions of Quantity in Adjective Clauses)13-12 名词+of which 的用法(U sing Noun + of which)28613-13 which修饰整个句子的用法(Using which to Modify a Whole Sentence)28613-14 将定语从句简化为形容词短语:概述(Reducing Adjective Clauses to Adjective Phrases: Introduction)13-15 将定语从句转变成形容词短语(Changing an Adjective Clause to an Adjective Phrase)第十四章动名词和不定式(一) (GerundsAnd Infinitives, Part 1)14- 1 动名词:概述(Gerunds: Introduction)14-2 动名词作介词的宾语(Using Gerunds as the Objects of Prepositions)14-3 后面接动名词的常见介词短语(Common Preposition CombinationsFollowed by Gerunds)14-4 后面接动名词的常见动词(CommonVerbs Followed by Gerunds)14-5 go+动名词(go + Gerund)14-6后面接动词-ing形式的固定搭配(Special Expressions Followed by -ing)14-7 后面接不定式的常见动词(CommonVerbs Followed by Infinitives)14-8 后面既可接不定式又可接动名词的常见动词(Common Verbs Followed by either Infinitives or Gerunds)14-9 后面接动名词的动词列表(Reference List of Verbs Followed byGerunds) 14-10 后面接不定式的动词列表(Reference List of Verbs Followed by Infinitives)14-11 it +不定式;动名词和不定式作主语(it + Infinitive; Gerunds and Infinitives as Subjects) And Infinitives, Part 2)15-1 表示目的的不定式:in order to (Infinitive of Purpose: in order to)15-2 后面接不定式的形容词(Adjectives Followed by Infinitives)15-3 不定式与too和enough连用(Using Infinitives with too and enough)15-4 不定式和动名词的被动语态和完成式(Passive and Past Forms of Infinitives and Gerunds)15-5 need 后接动名词或不定式的被动语态形式(Using Gerunds or Passive Infinitives Following need)15-6 所有格修饰动名词(Using a Possessive to Modify a Gerund)15-7 感官动词的用法(Using Verbs of Perception)15-8 let和help后接动词原形(Using the Simple Form after let and help)15-9 使役动词的用法:make, have, get(Using Causative Verbs: make, have, get)第十五章动名词和不定式(二) (Gerunds第十六章并列连词(Coordinating16-1 平行结构(Parallel Structure)16-2 成对连词:both・・・and; not only… but also; either … or; neither … nor (Using Paired Conjunctions: both . . . and; not only . . . but also; either . . . or; neither . . . nor)16- 3 用并列连词连接独立分句(Combining Independent Clauses with Coordinating Conjunctions)第十七章状语从句(Adverb Clauses)17- 1 概述(In troduc tion)17-2 缘故状语从句(Using Adverb Clauses to Show Cause and Effect)17-3表达对照(意外的结果):even though 的用法〔Expressing Contrast (Unexpected Result): Using even though〕17-4 表达直接对照:while和whereas (Showing Direct Contrast: while and whereas)17-5条件状语从句:if从句(Expressing Conditions in Adverb Clauses: 17-6 条件状语从句:whether or not和even if 的用法(Adverb Clauses of Condition: Using whether or not and even if)17-7 条件状语从句:in case和in the event that 的用法(Adverb Clauses of Condition: Using in case and in the event that)17-8 条件状语从句:unless的用法(Adverb Clauses of Condition: Using unless)17-9 条件状语从句:only if的用法(Adverb Clauses of Condition: Using only if)第十八章将状语从句简化为修饰性的副词短语(Reduction Of Adverb Clauses To Modifying Adverbial Phrases)18- 1 概述(In troduc tion)18-2 将时刻状语从句简化为修饰性的副词短语(Changing Time Clauses to Modifying Adverbial Phrases)18-3 用修饰性的副词短语表达“与此同时”的概念(Expressing the Idea of “During the Same Time” in Modifying Adverbial Phrases)18-4 用修饰性的副词短语表示因果关系(Expressing Cause and Effect in Modifying Adverbial Phrases)18-5 在修饰性的副词短语中利用“upon + -ing” (Using upon + -ing in Modifying Adverbial Phrases)第十九章表示因果、对照和条件关系的关联词(Connectives That Express Cause And Effect, Contrast, And Condition)19-1 because of 和due to 的用法(Using because of and due to)19-2用过渡词表示因果关系:therefore 和consequently (Using Transitions to Show Cause and Effect: therefore and consequently)19-3 句型和标点符号小结(Summary ofPatterns and Punctuation)19-4其它表示因果关系的方式:such… that 和so …that (Other Ways of Expressing Cause and Effect: such . . . that and so . . . that)19-5 表示目的:so that的用法(Expressing Purpose: Using so that)19-6 表示对照(意料之外的结果) 〔Showing Contrast (Unexpected Result)〕19-7 表示直接对照(Showing Direct Contrast)19-8 表示条件:otherwise 和or (else) 的用法〔Expressing Conditions: Using otherwise and or (else)〕19-9 关联词小结:因果、对照和条件关系(Summary of Connectives: Cause and Effect, Contrast, Condition)第二十章条件句和表达愿望的方式(Conditional Sentences And Wishes)20- 1 条件句中一样动词形式概述(Overview of Basic Verb Forms Used in Conditional Sentences)20-2 此刻和以后的真实条件句(True in the Present or Future)20-3 此刻和以后的非真实条件句(与事实相反)〔Untrue (Contrary to Fact) in the Present or Future〕20-4 过去的非真实条件句 (与事实相反) 〔Untrue (Contrary to Fact) in the Past〕20-5 在条件句中利用动词的进行时形式(Using Progressive Verb Forms in Conditional Sentences)20-6条件句中“混合时刻”的用法(Using“ Mixed Time ” in ConditionalSentences)42420-7 if 的省略(Omitting if)20-8 暗含的条件(Implied Cond it ions)20-9 as if / as though 的用法(Using as if/as though) 20-10 wish后面的动词形式(Verb Forms Following wish)20-11 用would 表达关于以后的希望(Using would to Make Wishes about the Future)434and Objects)A-2 介词和介词短语(Prepositions and Prepositional Phrases) A-3 形容词(Adjectives)A-4 副词(Adverbs)A-5 be 动词(The Verb be)A-6 系动词(Linking Verbs)B单元:疑问句(Questions)B-1 一样疑问句和特殊疑问句的形式(Forms of Yes/No and Information Questions)B-2 疑问词(Ques tion Words)B-3 简化的一样疑问句(Shortened Yes/No Questions)B-4 否定疑问句(Negative Questions) B-5 反意疑问句(Tag Questions)附录增补语法单元(Supplementary Grammar Units)A 单元:大体语法术语(Basic GrammarTerminology)C 单元:缩写(Contractions) D单元:否定句(Negatives)D-1 not与其它否定词的用法(Using not and Other Negative Words)A-1 主语、动词和宾语(Subjects, Verbs,D-2 幸免“重复两次否定” (Avoiding Double Negatives)D-3 以否定词开头的句子(Beginning a Sentence with a Negative Word)E 单元:介词搭配(Preposition Combinations)E 形容词和动词的介词搭配(Preposition Combinations withAdjectives and Verbs)F 单元:用来举例和延续观点的关联词(Connectives To Give Examples And To Continue An Idea)F-1 用来举例的关联词(Connectives to Give Examples)F-2 用来延续观点的关联词(Connectives to Continue the Same Idea)G 单元:动词形式的回忆练习(Verb Form Review Exercises)。
汉语量词与英文用法对照

汉语量词与英文用法对照(Comparison between Chinese Words of Measurement and Their English Equivalents)量词是现代汉语11类词中的一种,运用非常普遍,大约有500多个量词。
除了表“量”以外,它的一个显著特点就是习惯搭配。
即使是华人也有弄错的时候,学中文的外国人更是头疼。
所以正确认识量词,准确翻译汉语量词也是很重要的。
英语中没有像汉语这样的“量词”分类,但有类似的用法和修辞结构,如quantitive determinatives(量词限定词),portative(量词),quantifiers(量词)。
它们之间有相同之处,但更多的是差异。
因而,本节以一定的版面来分析其不同结构和用法,不过,更多的还是靠读者自己潜心收集认识,才能掌握如何翻译。
1、一群一群人a crowd/group/multitude/throng/army/team/class of people;a gang/swarm/horde /pack/band of people(in a derogatory way)troop通常指聚在一起活动的、生气勃勃的一群人。
如:a troop of demonstrators/shoppers/visitorsbevy特指女性的“一群”,有时指鸟类,尤指鹌鹑或云雀。
如:a bevy of actresses/young women/ladies/shop girls/quails表贬义的“一群”有:a mob of angry people/rioters/slaves/liars/blackguardshorde原意为游牧部落,通常含有轻蔑色彩:a horde of lazy-bones/swindlers/locusts/hooligansband;gang常指“帮”:a band of robbers/gangsters/thieves/outlawsa gang of criminals/slaves/prisoners一群牛、象、马、天鹅 a herd of cattle/elephants/horses/swans一群鸟 a flock of birds/geese/hens/goats/swallows/sheep/chickens一群猎狗 a pack of hounds/wolves/grouse一群狐狸 a skulk of foxes一群狮子 a pride of lions一群星星 a cluster of stars一群鱼 a school/shoal of fish/shrimps一群马 a stud/drove of horses一群鹅 a gaggle/flock of geese一群蚊子/蝴蝶 a swarm of mosquitoes/butterflies一群(窝)蚂蚁 a colony of ants/bees一群建筑物 a clump/complex of buildings2、一丝/点/层/片一片草皮 a chunk of turf一丝睡意 a wink of sleep一丝怀疑 a shadow of doubt一点点工作 a stroke of work一线未来之光 a glimpse of future一缕月光 a streak of moonlight/amber(fig)一丝绿意;一片绿色 a tint of green一片心意 a small token of our hearts一丝嫉妒;一阵窘迫 a slight twinge of jealousy/embarrassment一丝恻隐之心 a sign of sympathy for...一丝懊悔 a slight twinge of remorse一层霜/雪/糖霜 a layer of frost/snow/cream一丝失望的眼神 a flicker of disappointment(剩下)一口气/一丝气 a spark/breath of life一丝失望的情绪 a taint/faint of disappointment一片漆黑completely dark;dismal night;pitch dark一片汪洋 a flood of water3、英译“一阵”,颇有学问,且看以下译例(突然爆发出的)一阵哭泣/喝彩/炮击/雷声a burst of tears/cheers/gunfire/thunder(量如洪水的)一阵泪雨/瓢泼大雨/夸夸其谈a flood of tears/rain/boasts少量或稀疏的一阵(小)雨/射击 a spatter of rain/bullets一阵稀疏的掌声/喝彩 a spatter of applause/cheers声响很大的一阵隆隆的炮声/雷声 a peal of artillery/thunder突然而猛烈的一阵暴雨/狂风/烈火 a gust/blast of rain/wind/flame持续短暂的一阵怒气/激情/咳嗽 a fit of anger/passion/coughing一阵呕吐 a vomiting fit持续一段时间的一阵厄运/暑热 a spell of bad luck/summer heat一阵寒潮 a cold spell of weather一阵昏厥 a fainting spell(针捻刀刺般的)一阵内疚/牙痛/风湿痛 a twinge of remorse/toothache/rheumatism一阵尴尬 a twinge of embarrassment(抽搐或颤抖的)一阵痛苦/伤心/咳嗽/激动 a spasm of pain/grief/coughing/excitement 雹打雨淋般的一阵轰炸/打击/咒骂 a hail of bombs/blows/curse一阵弹雨/批评 a shower of bullets/criticism更多的例子一阵欢乐an agony of joy一阵子爱意 a flush of love一点点工作 a stroke of work一阵心脏病发作 a stroke of heart attack一点点满足 a crumb of satisfaction一种混乱的政治局面 a chaos of politics4、“一阵”为何有这么多不同的译法其实原因很简单,汉语“一阵”这个数量词不含修辞色彩,可用于各类描述;而在英语中,“一阵”这个概念则是由许多不同的名词来表述的,而且这些词一般分别具有不同的修辞色彩。
限定词、介词

限定词、介词Classes of Determiners(限定词)1.Articles: Definite, Indefinite and Zero rticles (冠词:定冠词、不定冠词和零冠词)2.Quantifiers (数量词)3.Other Determiners (其他限定词)⼀.Articles: Definite, Indefinite and Zero rticles (冠词:定冠词、不定冠词和零冠词)1. 不定冠词主要表⽰泛指和与one 同源,含"⼀"的意思。
a ⽤在以辅⾳⾳素开头的名词前,an ⽤在以元⾳⾳素开头的名词前,如:a university a man a bookan umbrella an egg an honest child2. 定冠词the 主要表⽰特指的⼈或物及第⼆次提到的⼈或物,或世界上独⼀⽆⼆的东西,如:the sun the moon the world the earth和形容词连⽤,代表⼀类⼈,如:the blind the dead the poor the richhe wounded the young the unemployed3. 在下列情况下不⽤冠词:a. 特殊的专有名词前,如:John Smithb. 物质名词表⽰类别时,如:Gold is a precious metal.c. 抽象名词表⽰泛指时, 如:Knowledge is power.d. 在季节、⽉份、⽇期、节⽇前,如:Februarye. 在餐名、运动、游戏等名词前,如:Sports is good for health.f. 在school, hospital, church, prison等词前,当这些词着重表⽰功⽤⽽不是这些建筑物或物体本⾝时,如:She went to school at seven.(但She went to the school to see her teacher.)g. 在表⽰"种类"的短语,如:a kind (sort) of tree,two kinds (sorts) of books.h. 带有表⽰顺序的基数词前,如:Lesson One (但the First Lesson).i. 表⽰独⼀的职位,头衔等的名词前,如:He was elected president of the society.⼆.Quantifiers (数量词)1.many, much, (a) few, (a) littlea. many, (a) few 只⽤于可数名词前,much, (a) little 只⽤于不可数名词前,如:many (a few, few) booksmuch (a little, little) waterb. many 和much 主要⽤在否定句和疑问句中,但它们前⾯加too 或so时就多⽤在肯定句中,如:We didn't spend much money.How many books do you have?You made too (so) many mistakes.c. a few (= several) 和a little (= some) 含肯定意义;few (= not many) 和little (= not much)含否定意义。
离散数学及其应用重要名词中英对应以及重要概念解释与举例

离散数学及其应用重要名词中英对应以及重要概念解释与举例1 The Foundations: Logic and Proofs(逻辑与证明)1.1 Propositional Logic(命题逻辑)Propositions(命题)——declarative sentence that is either true or false, but not both.判断性语句,正确性唯一。
Truth Table(真值表)Conjunction(合取,“与”,and),Disjunction(析取,or,“相容或”),Exclusive(异或),Negation(非,not),Biconditional(双条件,双向,if and only if)Translating English Sentences1.2 Propositional Equivalences(命题等价)Tautology(永真式、重言式),Contradiction(永假式、矛盾式),Contingency(偶然式)Logical Equivalences(逻辑等价)——Compound propositions that have the same truth values in all possible cases are called logical equivalent.(真值表相同的式子,p<->q是重言式)Logical Equivalences——Page24Disjunctive normal form(DNF,析取范式)Conjunctive normal form(CNF,合取范式) 见Page27~291.3 Predicates and Quantifiers(谓词和量词)Predicates——谓词,说明关系、特征的修饰词Quantifiers——量词Ø Universal Quantifier(全称量词) "全部满足Ø Existential Quantifier(存在量词) $至少有一个Binding Variables(变量绑定,量词作用域与重名的问题)Logical Equivalence Involving QuantifiersNegating Quantified Expressions(量词否定表达:否定全称=存在否定,否定存在=全程否定) Translating from English into Logical Expressions(自然语句转化为逻辑表达)Using Quantifiers in System SpecificationsExamples from Lewis Carrol——全称量词与条件式(p->q)搭配,存在量词与合取式搭配。
第2章逻辑代数(下):谓词演算 (1)

第2章逻辑代数(下):谓词演算2.1 谓词演算基本概念2.1.1 个体谓词演算中把一切讨论对象都称为个体(individuals),它们可以是客观世界中的具体客体,也可以是抽象的客体,诸如数字、符号等。
确定的个体常用a,b,c等小写字母或字母串表示。
a,b,c等小写字母或字母串称为个体常元(constants)。
不确定的个体常用字母x,y,z,u,v,w等来表示。
它们被称为个体变元,或变元(variables)。
谓词演算中把讨论对象——个体的全体称为个体域(domain of individuals),常用字母D表示,并约定个体域都是非空的集合。
当讨论对象未作具体指定,而是泛指一切客体时,个体域特称为全总域(universe),用字母U表示。
当给定个体域时,常元表示该域中的一个确定的成员,而变元则可以取该域中的任何一个成员为其值。
表示D上运算的运算符与常元、变元可组成所谓个体项(terms)。
例如,数学中的代数式a2+b,x2c等。
由于在我们讨论的谓词演算中,其变元只能取值个体对象,不能取值函数、命题或谓词,因此,它又常被叫做一阶谓词演算。
2.1.2 谓词2.1.3 量词谓词演算中的量词(quantifiers)指数学中常用的数量词“所有的”(或“每一个”)和“有”(或“存在”),用符号∀和∃来表示,分别称为全称量词和存在量词。
为了用全称量词∀表示个体域中所有(每一个)个体满足一元谓词P,用存在量词∃表示有(存在)个体满足一元谓词P,还需使用变元:∀xP(x) 读作“所有(任意,每一个)x满足P(x)”,表示个体域中所有的个体满足谓词P(x)。
∃x P(x) 读作“有(存在,至少有一个)x满足P(x)”,表示个体域中至少有一个体满足谓词P(x)。
当量词用于一谓词填式或复合的谓词表达式时,该谓词或复合的谓词表达式称为量词的辖域(domains of quantifiers)。
因此,量词的辖域或者是紧邻其右侧的那个谓词;或者是其右侧第一对括号内的表达式。
离散数学及其应用重要名词中英对应以及重要概念解释与举例

离散数学及其应用重要名词中英对应以及重要概念解释与举例1 The Foundations: Logic and Proofs(逻辑与证明)1.1 Propositional Logic(命题逻辑)Propositions(命题)——declarative sentence that is either true or false, but not both.判断性语句,正确性唯一。
Truth Table(真值表)Conjunction(合取,“与”,and),Disjunction(析取,or,“相容或”),Exclusive(异或),Negation(非,not),Biconditional(双条件,双向,if and only if)Translating English Sentences1.2 Propositional Equivalences(命题等价)Tautology(永真式、重言式),Contradiction(永假式、矛盾式),Contingency(偶然式)Logical Equivalences(逻辑等价)——Compound propositions that have the same truth values in all possible cases are called logical equivalent.(真值表相同的式子,p<->q是重言式)Logical Equivalences——Page24Disjunctive normal form(DNF,析取范式)Conjunctive normal form(CNF,合取范式) 见Page27~291.3 Predicates and Quantifiers(谓词和量词)Predicates——谓词,说明关系、特征的修饰词Quantifiers——量词Ø Universal Quantifier(全称量词) "全部满足Ø Existential Quantifier(存在量词) $至少有一个Binding Variables(变量绑定,量词作用域与重名的问题)Logical Equivalence Involving QuantifiersNegating Quantified Expressions(量词否定表达:否定全称=存在否定,否定存在=全程否定) Translating from English into Logical Expressions(自然语句转化为逻辑表达)Using Quantifiers in System SpecificationsExamples from Lewis Carrol——全称量词与条件式(p->q)搭配,存在量词与合取式搭配。
InterchangeI Unit1~7测试及答案

Interchange 1~7 Test:一,汉译英:1,你从哪里来?2,你的姓氏? 如何拼写你的姓氏?3,这很酷。
4,太棒了【三种】。
/5,事情咋样了?6,你好吗?【三种】7,我真的喜爱化学课。
8,我们在去咖啡店[coffee shops]的路上。
9,你有空吗?10,John 在旅游公司工作。
11,你在哪里工作?12,你在那里做啥?[ 做什么]13,多有趣啊!14,这是一个很棒的工作。
15,我有一个兼职工作。
16,你通常什么时间去上班【工作】?17,你晚上何时回家?18,你不认得我了吗?19,对不起,这件裙子值多少钱?20,它太贵了。
21,让我买给你吧。
他们很适合你。
22,这是你的生日礼物。
23,看,那些夹克真的很不错,你愿意选哪件?24,我比较喜欢皮革的那件,但它没有价格标签。
25,你愿意试穿它一下吗?26,这件皮革的比那件羊毛的更便宜。
27,这件项链比那件更有款【有型】。
28,这件丝绸的比那件羊毛的更漂亮。
29,你喜欢流行音乐吗?不,我喜欢古典音乐。
30,我是莫扎特【Mozart】的大粉丝。
31,他会弹吉他吗?不,他会弹钢琴。
32,我不大喜欢恐怖片。
33,你昨晚做什么,Steven?34,我过的很愉快,我昨晚去卡拉OK厅和几个朋友唱歌。
35,听起来很不错,你们去了Susan的家吗?36,你昨么样?有没有去什么地方?37,不,我整个周末哪都没去,我只是呆在家准备法语考试【French test】。
38,法语考试【French test】是今天吗,我都忘了这事。
39,别担心,你总是【考试】拿A分。
40,嗨,Leo,你的假期过得昨样?41,太棒了,我跟堂哥去了夏威夷。
42,你很幸运。
你们在那住多久。
43,那里天气如何?44,不昨的,多数天总是多云。
但我们每天去冲浪,那波浪让人惊奇。
45,你们整个旅程中最好的事是什么?46,不可思议的事发生了,你不会相信的。
47,Sue,谈谈你的哥哥姐姐。
48,啊,我姐给政府打工。
英语量词知识点总结

英语量词知识点总结Title: A Comprehensive Guide to English Quantifiers.Quantifiers, also known as determiners, are a crucial part of the English language that help us specify the quantity or amount of nouns in a sentence. They play a vital role in conveying precise information and avoiding vagueness. This guide aims to provide a comprehensive overview of English quantifiers, covering various types, their usage, and common mistakes to avoid.Types of Quantifiers.1. Definite Quantifiers.Definite quantifiers specify a specific number or amount of a noun. They include:"The": Used to refer to a unique or specific noun. Example: "The cat is sitting on the mat.""This" and "That": Used to introduce a noun for the first time, indicating proximity or distance. Example: "This book is interesting, while that one is boring.""These" and "Those": Used to introduce plural nouns, indicating proximity or distance. Example: "These apples are ripe, but those oranges are still green."2. Indefinite Quantifiers.Indefinite quantifiers do not specify a specific number or amount of a noun. They include:"A" and "An": Used to introduce a noun for the first time, indicating that it is a general or nonspecific item. Example: "I have a car." "An apple a day keeps the doctor away.""Some": Used to refer to a nonspecific number or amount of a noun, implying a positive existence. Example: "I have some money in my pocket.""Any": Used to refer to a nonspecific number or amount of a noun, implying a choice or possibility. Example: "Do you have any questions?""No": Used to deny the existence of a noun. Example: "I have no time for that.""Every" and "All": Used to refer to all instances of a noun, without exception. Example: "Every student needs to attend the meeting." "All the apples are ripe now."3. Quantifiers of Amount.These quantifiers describe the amount or extent of a noun. They include:"Much": Used to describe an unspecified amount of an uncountable noun. Example: "I have much work to do.""Little": Used to describe a small amount of an uncountable noun. Example: "There is little time left.""A lot of" and "Lots of": Used to describe a significant amount of a noun, whether countable or uncountable. Example: "I have a lot of friends." "There are lots of books on the shelf.""Enough": Used to indicate a sufficient amount of a noun. Example: "There is enough food for everyone."4. Quantifiers of Degree.These quantifiers describe the degree or intensity of a noun or adjective. They include:"Quite": Used to indicate a moderate degree. Example: "She is quite tall.""Very": Used to indicate a high degree. Example: "He is very intelligent.""Fairly": Used to indicate a moderate or somewhat degree. Example: "The weather was fairly warm today.""Rather": Used to indicate a slight or somewhat degree. Example: "I'm rather tired today."Common Mistakes with Quantifiers.1. Using "A" Instead of "An": It is common to make the mistake of using "a" instead of "an" when introducing a noun that starts with a vowel sound. Always remember that "an" is used before nouns that start with a vowel sound (e.g., "an apple," "an hour").2. Using "Some" Instead of "Any": It is common to use "some" when referring to nonspecific quantities in negative sentences or questions, which is incorrect. "Any" should be used in these contexts (e.g., "Do you have any money?" "I don't have some money.").3. Misusing "Every" and "All": It is easy to confuse "every" and "all" when referring to groups of people or things. "Every" refers to each individual item, while "all" refers to the entire group collectively. Therefore, "every"should be used when referring to individuals, and "all" should be used when referring to the group as a whole (e.g., "Every student passed the exam." "All the apples were ripe.").4. Overusing Quantifiers: It is important not tooveruse quantifiers, as they can make sentences clunky and difficult to understand. Use quantifiers sparingly and only when necessary to convey specific information or avoid vagueness.Conclusion.Quantifiers are a crucial part of the English language, allowing us to convey precise information about thequantity or amount of nouns in a sentence. By understanding the different types of quantifiers and their correct usage, we can improve our communication skills and avoid common mistakes. By practicing and applying the knowledge gained from this guide, we can become more proficient in using quantifiers effectively in our daily conversations and written communication.。
英语量词一览表

英语量词一览表:探索语言中的计数与度量The English language is rich in vocabulary, including a diverse array of quantifiers that play a crucial role in counting and measuring. Quantifiers, or measure words, are an integral part of any language, and English is no exception. They help us to express quantities, sizes, and degrees of things, making our communication more precise and detailed.In this article, we will explore the world of English quantifiers, providing a comprehensive list and examples of their usage. We will delve into the different categories of quantifiers, including those used to describe amounts, durations, and degrees. By understanding these quantifiers, we can enhance our language skills and communicate more effectively in English.**Amount Quantifiers**Amount quantifiers are used to describe the quantity or number of things. Some common examples include:* Some: Used to indicate a partial quantity or a few items. Example: "I have some apples." * Many: Used to indicate a large quantity. Example: "There are many booksin the library." * A few: Used to indicate a small numberof items. Example: "I have a few minutes to spare." * A lot of: Used to indicate a significant quantity. Example: "She has a lot of friends." * Few: Used to indicate a small quantity, implying rarity or scarcity. Example: "There are few oranges left."**Duration Quantifiers**Duration quantifiers are used to describe the length of time or duration of an action. Some common examples include: * For a while: Used to indicate a period of time,usually unspecified. Example: "I sat there for a while, thinking about it." * For a long time: Used to indicate a prolonged period of time. Example: "She studied for a long time to prepare for the exam." * For a short time: Used to indicate a brief period of time. Example: "He only stayedfor a short time before leaving." * All day: Used toindicate the entire duration of a day. Example: "She worked all day without taking a break."**Degree Quantifiers**Degree quantifiers are used to describe the intensityor extent of something. Some common examples include:* Quite: Used to indicate a moderate degree. Example: "She is quite tall." * Very: Used to indicate a high degree. Example: "He is very intelligent." * Extremely: Used to indicate an exceptionally high degree. Example: "Theweather was extremely hot that day." * Slightly: Used to indicate a minimal degree. Example: "She smiled slightly when she saw him." * Almost: Used to indicate nearly the entire extent of something. Example: "He almost finishedthe race."Understanding and mastering the use of quantifiers in English can enhance our ability to communicate effectively. They allow us to express ourselves more precisely, whether we are describing the number of apples we have, theduration of a task, or the intensity of a feeling. By familiarizing ourselves with the diverse array ofquantifiers in English, we can expand our vocabulary, improve our language skills, and communicate moreconfidently in this global language.**英语量词一览表:探索语言中的计数与度量**英语作为一门语言,其词汇的丰富性无可比拟,其中量词(或称度量词)在计数和度量方面扮演着至关重要的角色。
英语量词知识点总结大全

英语量词知识点总结大全Types of Quantifiers1. Numbers: Numbers are the most basic type of quantifiers and are used to indicate a specific quantity or amount. They can be cardinal numbers (one, two, three, etc.) or ordinal numbers (first, second, third, etc.). Numbers can be used with both countable and uncountable nouns. For example:- There are three cats in the garden.- She is the first person to arrive at the party.2. Determiners: Determiners are words that come before a noun to give information about quantity, possession, or specificity. There are several types of determiners, including articles (a, an, the), demonstratives (this, that, these, those), possessive pronouns (my, your, his, her, its, our, their), and quantifiers (some, any, much, many, few, several, etc.). Determiners are used with both countable and uncountable nouns. For example:- The cat is sleeping on the couch.- These books are mine.- There are some apples in the fridge.- I don't have much time to finish my homework.3. Pronouns: Pronouns are words that are used instead of a noun and are used to indicate quantity or amount. There are several types of pronouns that can function as quantifiers, including indefinite pronouns (someone, anyone, nobody, everybody, etc.) and interrogative pronouns (how much, how many). Pronouns are used with both countable and uncountable nouns. For example:- Somebody is knocking on the door.- How many students are in the classroom?- Nobody likes to be criticized.Usage of Quantifiers- Countable and Uncountable Nouns: It's important to understand whether a noun is countable or uncountable when using quantifiers. Countable nouns refer to things that can be counted individually, such as books, cats, or cars. Uncountable nouns refer to things that cannot be counted individually, such as water, milk, or happiness. Different quantifiers are used with countable and uncountable nouns. For example:- I have two cats. (countable noun)- There is some milk in the fridge. (uncountable noun)- Specificity: Some quantifiers express a specific or definite quantity, while others express a non-specific or indefinite quantity. For example, "the" is a specific quantifier, while "some" is a non-specific quantifier. This affects the meaning of the sentence. For example:- Please pass me the salt. (specific)- Would you like some water? (non-specific)- Positive and Negative Statements: Quantifiers can be used in both positive and negative statements. For positive statements, quantifiers such as "some" and "many" are used, while for negative statements, quantifiers such as "no" and "few" are used. For example:- She has some free time this afternoon. (positive)- There are few people at the party. (negative)Examples of QuantifiersHere are some examples of how different quantifiers are used in sentences:- Countable Nouns:- I have a few friends in this city.- There are many books on the shelf.- She bought several new dresses for the party.- Uncountable Nouns:- Can you please give me some advice on this matter?- There is not much sugar left in the jar.- I have a little money to lend you.- Specificity:- I need the exact amount of money by the end of the day.- Would you like any help with your homework?- Positive and Negative Statements:- There are no apples left in the basket.- He has some great ideas for the project.Common Mistakes with QuantifiersThere are some common mistakes that English learners make when using quantifiers. Here are a few examples:- Using a plural noun with a non-specific quantifier: Incorrect: There are many informations to consider. Correct: There is much information to consider.- Using a non-specific quantifier with a specific noun: Incorrect: Can you pass me a salt? Correct: Can you pass me the salt?- Forgetting to use a quantifier with an uncountable noun: Incorrect: There is water in the glass. Correct: There is some water in the glass.- Using a singular noun with a plural quantifier: Incorrect: She has many money. Correct: She has much money.ConclusionQuantifiers are an essential part of English grammar and are used to describe the quantity or amount of something. Understanding the different types of quantifiers, their usage, and some examples can help English learners use them correctly in their everyday language. By knowing how to use quantifiers with countable and uncountable nouns, understanding their specificity, and avoiding common mistakes, English learners can enhance their language skills and communicate effectively in English.。
466个英语语法公式

466个英语语法公式English Answer:1. Subject-Verb Agreement: A verb must agree in number and person with its subject.2. Pronoun-Antecedent Agreement: A pronoun must agree in number, gender, and person with its antecedent.3. Verb Tense: The tense of a verb indicates the time of an action or event.4. Modal Verbs: Modal verbs express possibility, necessity, permission, or advice.5. Passive Voice: The passive voice is used when the focus is on the object of a verb.6. Conditional Sentences: Conditional sentences express the relationship between a condition and a result.7. Relative Clauses: Relative clauses provideadditional information about a noun or pronoun.8. Appositives: Appositives provide additional information about a noun or pronoun.9. Coordinating Conjunctions: Coordinating conjunctions connect words, phrases, or clauses of equal importance.10. Subordinating Conjunctions: Subordinating conjunctions introduce subordinate clauses.11. Interrogative Pronouns: Interrogative pronouns are used to ask questions.12. Demonstrative Pronouns: Demonstrative pronouns point out specific people, places, or things.13. Indefinite Pronouns: Indefinite pronouns refer to non-specific people, places, or things.14. Possessive Pronouns: Possessive pronouns indicate ownership or possession.15. Reflexive Pronouns: Reflexive pronouns refer to the subject of a sentence.16. Intensive Pronouns: Intensive pronouns emphasize a noun or pronoun.17. Relative Pronouns: Relative pronouns introduce relative clauses.18. Prepositions: Prepositions show the relationship between a noun or pronoun and another word in the sentence.19. Adverbs: Adverbs modify verbs, adjectives, or other adverbs.20. Conjunctions: Conjunctions connect words, phrases, or clauses.21. Interjections: Interjections express strongemotions or sudden reactions.22. Noun Clauses: Noun clauses function as nouns in a sentence.23. Adjective Clauses: Adjective clauses modify nouns or pronouns.24. Adverb Clauses: Adverb clauses modify verbs, adjectives, or other adverbs.25. Gerunds: Gerunds are verb forms ending in -ing that function as nouns.26. Infinitives: Infinitives are verb forms that function as nouns, adjectives, or adverbs.27. Participles: Participles are verb forms that function as adjectives.28. Phrasal Verbs: Phrasal verbs are idiomatic expressions consisting of a verb and a preposition oradverb.29. Direct Speech: Direct speech reports what someone said or thought.30. Indirect Speech: Indirect speech reports what someone said or thought without using their original words.31. Figure of Speech: Figures of speech are literary devices that create vivid imagery or emphasize a point.32. Idioms: Idioms are expressions that have a figurative meaning different from their literal meaning.33. Phrases: Phrases are groups of words that function as a unit but do not form a complete sentence.34. Clauses: Clauses are groups of words that contain a subject and a verb.35. Sentences: Sentences are groups of words that express a complete thought.36. Paragraphs: Paragraphs are groups of sentences that develop a single topic.37. Essays: Essays are extended pieces of writing that present a thesis and support it with evidence.38. Nouns: Nouns are words that name people, places, things, or concepts.39. Pronouns: Pronouns replace nouns.40. Verbs: Verbs express actions, events, or states of being.41. Adjectives: Adjectives modify nouns or pronouns.42. Adverbs: Adverbs modify verbs, adjectives, or other adverbs.43. Determiners: Determiners specify or limit a noun.44. Quantifiers: Quantifiers indicate the quantity or amount of something.45. Articles: Articles are used to specify whether a noun is definite or indefinite.46. Demonstratives: Demonstratives point out specific nouns or pronouns.47. Possessives: Possessives indicate ownership or possession.48. Interrogatives: Interrogatives are used to ask questions.49. Relative Pronouns: Relative pronouns introduce relative clauses.50. Prepositions: Prepositions show the relationship between a noun or pronoun and another word in the sentence.51. Conjunctions: Conjunctions connect words, phrases,or clauses.52. Interjections: Interjections express strong emotions or sudden reactions.53. Punctuation: Punctuation marks are used to clarify the meaning of a sentence.54. Capitalization: Capitalization is used to indicate the beginning of a sentence, proper nouns, and certain other words.55. Abbreviations: Abbreviations are shortened forms of words or phrases.56. Numbers: Numbers are used to represent quantities.57. Symbols: Symbols are used to represent specific ideas or concepts.58. Acronyms: Acronyms are formed from the firstletters of a series of words.59. Foreign Words and Phrases: Foreign words and phrases are used to express concepts that do not have direct English equivalents.60. Homonyms: Homonyms are words that have the same spelling or pronunciation but different meanings.61. Synonyms: Synonyms are words that have the same or similar meanings.62. Antonyms: Antonyms are words that have opposite meanings.63. Register: Register is the level of formality or informality used in a particular context.64. Tone: Tone is the emotional or attitudinal quality of a piece of writing.65. Syntax: Syntax is the way that words, phrases, and clauses are arranged in a sentence.66. Semantics: Semantics is the study of the meaning of words and sentences.67. Pragmatics: Pragmatics is the study of how language is used in specific contexts.68. Discourse Analysis: Discourse analysis is the study of how language is used in social interaction.69. Sociolinguistics: Sociolinguistics is the study of the relationship between language and society.70. Psycholinguistics: Psycholinguistics is the study of the relationship between language and the human mind.71. Neurolinguistics: Neurolinguistics is the study of the relationship between language and the brain.72. Computational Linguistics: Computationallinguistics is the study of using computers to analyze and generate language.73. Corpus Linguistics: Corpus linguistics is the study of language based on large collections of real-world texts.74. Stylistics: Stylistics is the study of the use of language in literature and other forms of art.75. Historical Linguistics: Historical linguistics is the study of the evolution of languages over time.76. Comparative Linguistics: Comparative linguistics is the study of the similarities and differences between languages.77. Language Acquisition: Language acquisition is the process by which humans learn their native language.78. Second Language Acquisition: Second language acquisition is the process by which learners acquire a language other than their native language.79. Bilingualism: Bilingualism is the ability to speakand understand two or more languages.80. Multilingualism: Multilingualism is the ability to speak and understand three or more languages.81. Dialect: A dialect is a variety of a language thatis spoken by a particular group of people.82. Standard Language: A standard language is a variety of a language that is widely accepted and used by a large group of people.83. Pidgin: A pidgin is a simplified language that is used for communication between people who speak different languages.84. Creole: A creole is a language that develops from a pidgin and becomes the native language of a group of people.85. Esperanto: Esperanto is an international auxiliary language that was created in the late 19th century.86. Interlingua: Interlingua is an international auxiliary language that was created in the mid-20th century.87. Global English: Global English is the English language as it is used in international communication.88. World Englishes: World Englishes are the varietiesof English that are spoken in different parts of the world.89. Anglicisms: Anglicisms are words or phrases from English that are used in other languages.90. Loanwords: Loanwords are words that are borrowed from one language and used in another language.91. Translation: Translation is the process of converting a text from one language to another.92. Interpretation: Interpretation is the process of converting a spoken message from one language to another.93. Transliteration: Transliteration is the process ofconverting a text from one writing system to another.94. Transcription: Transcription is the process of converting a spoken message into a written form.95. Dubbing: Dubbing is the process of replacing the original.。
合量计算英语

合量计算英语In the realm of English language learning, one crucial aspect that students often struggle with is the concept of quantifiers. Quantifiers are words or phrases that provide information about the quantity of a noun in a sentence. Understanding how to use quantifiers correctly is essential for effective communication in English. In this discussion, we will delve into the intricacies of quantifiers, exploring their various types and usage in different contexts.One of the most common types of quantifiers is "some" and "any." These two words are used to indicate an unspecified quantity of something. "Some" is typically used in positive sentences to indicate a non-specific quantity, while "any" is used in negative sentences and questions. For example, "I have some apples" versus "I don't have any apples." Understanding when to use "some" and "any" can be challenging for English learners, but with practice, it becomes easier to grasp.Another important quantifier is "much" and "many." "Much" is used with uncountable nouns to indicate a large quantity, while "many" is used with countable nouns to indicate a large number. For example, "There isn't much sugar left" versus "There are many books on the shelf." Mastering the distinction between "much" and "many" is crucial for accurate and clear communication in English.Additionally, quantifiers such as "a lot of," "lots of," and "plenty of" are used to express a large quantity or number of something. These quantifiers are more informal than "much" and "many" and are commonly used in spoken English. For example, "I have a lot of friends" or "There are plenty of opportunities for growth." Understanding the nuances of these quantifiers can help learners sound more natural and fluent in their English conversations.In contrast, quantifiers like "few" and "little" are used to indicate a small quantity or number of something. "Few" is used with countable nouns, while"little" is used with uncountable nouns. For example, "There are few people at the party" versus "There is little water in the glass." Using these quantifiers effectively can convey a sense of scarcity or limitation in a sentence.Moreover, quantifiers such as "all," "both," and "each" are used to refer to the total quantity or entirety of something. "All" is used with both countable and uncountable nouns, while "both" is used specifically with two items or people. "Each" is used to refer to individual members of a group. For example, "All the students passed the exam" or "Both of my parents are doctors." Understanding how to use these quantifiers accurately can help learners express themselves clearly and effectively in English.In conclusion, mastering the use of quantifiers is essential for English language learners to communicate accurately and effectively. By understanding the nuances of different quantifiers such as "some," "any," "much," "many," "a lot of," "few," "little," "all," "both," and "each," learners can convey the quantity or number of something with precision. Practice and exposure to various contexts will help learners become more confident in using quantifiers in their English conversations. Embracing the challenge of learning quantifiers can lead to improved language proficiency and a deeper understanding of the English language.。
正则匹配原则

正则匹配(Regular Expression Matching)是一种用于查找和匹配文本模式的方法,通常通过使用正则表达式来描述所需的模式。
以下是正则匹配的一些基本原则:1.字符匹配:正则表达式可以用来匹配特定的字符,例如字母、数字、符号等。
使用字符本身可以进行精确匹配,例如字符a匹配字母a。
2.字符类匹配:使用字符类(Character Classes)可以匹配一组字符中的任意一个。
例如,字符类[abc]可以匹配字母a、b或c中的任意一个。
3.通配符匹配:通配符(Wildcard)用于匹配任意字符。
常用的通配符是.,表示匹配任意单个字符。
例如,正则表达式a.可以匹配以字母a开头,后面紧跟任意一个字符的字符串。
4.重复匹配:通过使用重复限定符(Repetition Quantifiers),可以指定某个模式重复出现的次数。
例如,*表示重复零次或更多次,+表示重复一次或更多次,?表示重复零次或一次。
5.边界匹配:边界匹配(Anchors)用于匹配字符串的开头和结尾。
例如,^表示匹配字符串的开头,$表示匹配字符串的结尾。
6.分组匹配:使用圆括号可以将模式分组,从而进行更复杂的匹配操作。
例如,(abc)+表示匹配至少一个由字母abc组成的字符串。
7.转义字符:某些特殊字符在正则表达式中具有特殊的含义,如果要匹配这些字符本身,需要使用转义字符\。
例如,匹配.字符本身需要使用\.。
8.贪婪匹配:默认情况下,正则表达式会尽可能匹配最长的字符串。
如果需要匹配最短的字符串,可以使用非贪婪限定符*?、+?、??等。
总的来说,正则匹配原则是根据需求构建合适的正则表达式,通过匹配文本模式来实现文本搜索、替换等操作。
正则表达式提供了灵活和强大的模式匹配功能,但在使用时需要谨慎处理,确保匹配结果符合预期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
For E. Lepore and B. Smith (eds), Handbook ofPhilosophy of Language, OUP.QuantifiersMichael GlanzbergUniversity of Toronto/UC Davismichael.glanzberg@utoronto.caQuantifiers are terms of generality.They are also among our prime examples of operators which take scope.The distinction between singular and general terms,as well as the ways that general terms enter into scope relations,are certainly fundamental to our understanding of language.Yet when we turn to natural language,we encounter a huge and apparently messy collection of general terms;not just every and some,but most,few,betweenfive and ten,and many others.Natural language sentences also display a complex range of scope phenomena; unlikefirst-order logic,which clearly and simply demarcates scope in its notation.In spite of all this complexity,the study of quantification in natural language has made remarkable progress.Starting with a seminal trio of papers from the early1980s,Barwise and Cooper(1981),Higginbotham and May(1981),and Keenan and Stavi(1986),quantification in natural language has been investigated extensively by philosophers,logicians,and linguists. The result has been an elegant and far-reaching theory.This chapter will present a survey of some of the important components of this theory.Section(I)will present the core of the theory of generalized quantifiers.This theory explores the range of expressions of generality in natural language,and studies some of their logical properties.Section(II)will turn to issues of how quantifiers enter into scope relations.Here there is less unanimity than in the theory of generalized quantifiers.Two basic approaches,representative of the main theories in the literature,will be sketched and compared.Finally,Section(III)will turn briefly to the general question of what a quantifier is.1I Generality in Natural LanguageThefirst of our topics is the notion of quantifiers as expressions of generality.We have already observed that natural languages present us with a wide range of such expressions.We thus confront a number of questions,both foundational and descriptive:what are the semantics of expressions of generality,what sorts of basic semantic properties do they have,and what expressions of generality appear in natural language?One of the accomplishments of research over the last25years is to give interesting answers to these questions.Though many problems remain open,a great deal about the basic semantic properties of natural-language quantifiers is known.This is encapsulated in what is often known as generalized quantifier theory.This section will be devoted to the core of this theory. It should be noted at the outset that generalized quantifier theory is a large and well-developed topic,and there is too much in it to cover in any exhaustive way.There are,fortunately,two very good more specialized surveys to which interested readers may turn for more details and more references:Westerst˚a hl(1989)and Keenan and Westerst˚a hl(1997).I.1Generalizing QuantifiersBefore examining the variety of natural language quantification,we should return to the basic question of what quantifiers are.The basic idea about what quantifiers are comes from Frege(1879,1891,1893).Frege observed that the familiar quantifiers∀and∃can be thought of,in Frege’s terms,as second level concepts.We do not need Frege’s particular idea of a concept,though.Let us suppose, for instance,that the semantic value of a predicate F is its extension:the set of objects that fall under it.Then the universal quantifier takes such an extension as input,and outputs true if that extension is the entire universe,and false if it is not.It is thus a function whose inputs are sets,and outputs are truth values.Likewise,the existential quantifier takes a set as input, and outputs true if that set is non-empty,and false if it is empty.The standard quantifiers offirst-order logic can thus be thought of as functions from sets2to truth values,or equivalently,as sets of sets.This captures Frege’s idea that quantifiers are second-level concepts.1This is a thesis about the semantic values of quantifiers:(1)The semantic values of quantifiers are sets of sets.This thesis,though it will be refined in some ways as we progress,is the core of the theory of quantifiers we will develop.Once we see quantifiers as sets of sets,we can quickly observe that being non-empty and being the entire universe are merely two among many.So,for instance,relative to afixed universe M,we can define:(2) a.(Q R)M={X⊆M||X|>|M\X|}b.(Qα)M={X⊆M||X|≥ℵα}(|X|is the cardinality of a set X.In many cases,where we have some set which is to be thought of as the semantic value of an expression,I will put the set in bold;so(Q R)M interprets Q R relative to a universe M.I shall use‘semantic value’and‘denotation’interchangeably.) These are often called generalized quantifiers or Mostowski quantifiers,in honor of their first extensive study by Mostowski(1957).Mostowski quantifiers can be added to the usual first-order logic.QαxF(x)says that the extension of F has cardinality≥ℵα.(Q R)M is the Rescher quantifier(Rescher,1962).For afinite universe M,(Q R)xF(x)says that the extension of F is more than half the size of M.One fairly technical distinction needs to be made before we close this subsection.We defined Mostowski quantifiers for afixed universe M.These are what are usually called local generalized quantifiers.Global generalized quantifiers are simply functions from sets M to local generalized quantifiers on M.So,for instance,for each M,(Q R)M is the local Rescher quantifier on M.Q R,the global Rescher quantifier,is the function which takes M to(Q R)M.1I am here assuming that semantic values are sets,and that they are extensional.Much of what follows is independent of these assumptions,though there are a number of places at which it will be crucial that predicate semantic values have cardinalities.3I.2Generalized Quantifiers in Natural LanguageThough the kind of generalization of∀and∃given by Mostowski quantifiers is a major step, it is not enough to accurately explain natural language quantifiers.For instance,in a way the Rescher quantifier Q R expresses most,but not the way natural language does.Consider:(3) a.Most students attended the party.b.Most birdsfly.c.Most people have tenfingers.These do not compare the size of a predicate extension with the size of the entire universe. Rather,they compare the size of one subset of the universe with another.Thefirst,for in-stance,says that the set of students who came to the party is larger than the set of students who did not come to the party.Once we see this sort of binary structure,we see that it is quite widespread in natural language.We see,for instance:(4) a.Few students attended the party.b.Most students attended the party.c.Both students attended the party.d.Enough students attended the party.We also see such constructions as:(5) a.Betweenfive and ten students attended the party.b.At least ten students attended the party.c.All butfive students attended the party.d.More male than female students attended the party.e.John’s mother attended the party.f.More of John’s than Mary’s friends attended the party.In fact,the English analogs of∀and∃have the same structure:4(6) a.Every student attended the party.b.Some student attended the party.(These examples are modeled on the much more extensive list in Keenan and Stavi (1986).)The binary pattern in natural-language expressions of generality is no accident.It reflects a fundamental feature of the syntax of natural languages.Simplifying somewhat,we can observe that sentences break down into combinations of noun phrases (NPs)and verb phrases (VPs).Noun phrases also break down,into combinations of determiners (DETs)and common nouns (CNs)(or more complex construction with adjectival modifiers like small brown dog ).Quantifier expressions of the sorts we see in (4–6)occupy the determiner positions in subject noun phrases.The basic structure we see in all those examples follows the pattern:(7)SDET most CN studentsVP attended the party We saw a moment ago that to capture the meaning of most in (3),we need to see the CN position as semantically significant .2To do this,we need a modest extension of the idea of a Mostowskian generalized quantifier.We may retain the basic idea that quantifiers are sets of sets;only now,we need to think of them as relations between sets.They take two inputs,the semantic value of a CN expression like student and a VP expression like attended the party ,and output a truth value.Each of these syntactic constituents gets interpreted as having a set as its semantic value,so quantifier expressions like most should be interpreted as functions from pairs of sets to truth values,i.e.as binary relations between sets.This is our next thesis:2There are a number of syntactic issues I am putting aside here.See any current syntax text,or the hand-book discussions of Bernstein (2001)and Longobardi (2001).For some interesting cross-linguistic work,see Matthewson (2001)and the papers in Bach et al.(1995).5(8)The semantic values of many quantifier expressions(determiners)in natural languagesare functions which take as input two sets,and output truth values,i.e.they are rela-tions between sets.This is often called the relational theory of determiner denotations.It is common to classify quantifiers by their inputs.A Mostowski quantifier,which takes one set input,is classified as type 1 .The quantifiers we have just looked at are classified as type 1,1 ,taking two set(unary relation)inputs.We can now offer a definition:(9) a.A(local)type 1,1 quantifier on M is a function Q M(X,Y)mapping sets X,Y⊆Mto truth values.b.A(global)type 1,1 quantifier is a function from universes M to local quantifiersQ M.This allows us to give definitions for a range of quantifiers.For instance,for each M and X,Y⊆M:(10) a.every M(X,Y)←→X⊆Yb.most M(X,Y)←→|X∩Y|>|X\Y|c.neither M(X,Y)←→|X|=2∧X∩Y=∅d.at least10M(X,Y)←→|X∩Y|≥10Similar definitions can be given for other quantifiers,including those in(4)and(5).We thus see that natural-language determiners can be interpreted as type 1,1 quantifiers. Full NPs can be understood as these quantifiers with one argumentfixed,which are then type 1 quantifiers.3I.3Restricted QuantifiersType 1,1 quantifiers appear to be restricted quantifiers.Whereas∀and∃,and other type 1 quantifiers,range over the entire universe,a quantifier like most ranges over itsfirst input, corresponding to the CN position in a noun phrase.3Terminology varies on whether determiners or full NPs are called‘quantifiers’;for instance,Barwise and Cooper(1981)reserve the term‘quantifier’for NP denotations,i.e.type 1 quantifiers.6It does turn out that natural language quantifiers display important features of restricted quantification,but the reason is more complex,and more interesting,than the mere presence of an extra argument.It is entirely possible to define type 1,1 quantifiers which is not restricted.For instance:(11)more M 1,1 (X,Y)←→|X|>|Y|This does not behave as if its domain is restricted to X,in cases where Y and X do not overlap.The core feature which makes natural language quantifiers behave like restricted quanti-fiers is exhibited by the following pattern:(12) a.i.Every student attended the party.ii.Every student is a student who attended the party.b.i.Few students attended the party.ii.Few students are students who attended the party.c.i.Most students attended the party.ii.Most students are students who attended the party.In each of these,(i)and(ii)are equivalent.The corresponding feature for more M 1,1 would be |X|>|Y|←→|X|>|X∩Y|,which is easily falsified.The pattern we see in(12)but not in(11)is called conservativity:4(13)(CONSERV)Q M(X,Y)is conservative ifffor all X,Y⊆M,Q M(X,Y)←→Q M(X,X∩Y). Conservativity expresses the idea that the interpretation of a sentence with a quantified noun phrase only looks as far as the CN,so the CN restricts the domain of quantification.However, attention to global vs.local notions of quantification suggests that we should strengthen the condition for restricted quantification a little bit.For a restricted global quantifier,we do not want any aspect of the universe M beyond its intersection with X to affect Q M(X,Y).Hence, we want:(14)(UNIV)For each M and X,Y⊆M,Q M(X,Y)←→Q X(X,X∩Y).4This same property was called the‘lives on’property by Barwise and Cooper(1981)and‘intersectivity’by Higginbotham and May(1981).I believe the terminology‘conservativity’is due to Keenan and Stavi(1986).7(‘UNIV’for‘universe-restricting’.Note the subscript on the right-hand side is X.) The difference between CONSERV and UNIV is relatively small,but not entirely trivial.It was observed by van Benthem(1983,1986)that UNIV is equivalent to CONSERV together with the property EXT(for‘extension’):(15)(EXT)For each X,Y⊆M⊆M ,Q M(X,Y)←→Q M (X,Y).As observed by Westerst˚a hl(1985b,1989)EXT,expresses the idea that quantifiers do not change their meanings on different domains.One of the striking facts about natural languages,observed in Barwise and Cooper(1981) and Keenan and Stavi(1986),is that all natural-language determiner denotations satisfy CONS. Once EXT was isolated as a distinct condition,it was observed that determiner denotations satisfy EXT as well.These are proposed linguistic universals:non-trivial empirical restrictions on possible natural languages.We have seen that logic can give us type 1,1 quantifiers which violate these constrains.(11)violates conservativity.A quantifier violating EXT is given by Westerst˚a hl(1985b):(16)many∗M(X,Y)←→|X∩Y|>1/3·|M|The proposed linguistic universals says that all natural language determiner denotations sat-isfy CONS and EXT.There are a number of potential counter-examples to these universals.Some of them re-main controversial,but the consensus in the literature is that the universals hold.Let me give a couple of examples.Why is more M 1,1 not a counter-example?Because the determiner more appears to be a two-place determiner,figuring in constructions like:(17)More students than professors attended the party.More than is conservative.(Quantifiers taking more than two arguments have been investi-gated by Keenan and Moss(1984)and Beghelli(1994)(see Keenan and Westerst˚a hl(1997)for additional discussion).Another much-discussed case is only.It may appear to be an easy example of the failure of conservativity.Consider:8(18)Only dogs bark.A natural reading of this sentence makes it true if and only if the set of barking things is included in the set of dogs.This suggests a highly simplified semantics for only:(19)only M(X,Y)←→Y⊆XThis is simplified in many ways,but it makes the failure of conservativity vivid.Y⊆X←→(Y∩X)⊆X only holds when Y⊆X.Hence,any false sentence suffices to show that conservativityfails.Even so,there is good reason to think that only is not a determiner.It appears outside of noun phrases,in:(20)John only talked to Susan.It also appears in places we do not see determiners in English noun phrases:(21) a.Only the Provost/John talked to Susan.b.Only betweenfive and ten students came to the party.We have good reason to think that only is not a counter-example to conservativity because it is not a determiner.5Finally,what about possible failures of EXT,such as many∗?It is often observed that many is context-dependent,in that what counts as many is heavily influenced by context.Depending on how this sort of context-dependence is handled,it may be possible to interpret many in accord with EXT and CONS.This remains a controversial issue.See Westerst˚a hl(1985b)for extensive discussion.6Conservativity has proved an extremely important property.The space of conservative quantifiers is much more orderly than the full range of type 1,1 quantifiers.This is brought5For more on only,see Rooth(1985,1996).Related to expressions like only are adverbs of quantification, such as always and never.For discussion of these,see Lewis(1975)and von Fintel(1994).6The context-dependence proposed for determiners like many is in the meaning of the determiner,not in the restriction of its domain.For discussions of how context restricts the domains of quantifiers,see Westerst˚a hl (1985a),von Fintel(1994),Stanley and Szab´o(2000)with comments by Bach(2000)and Neale(2000),and Cap-pelen and Lepore(2002).I am skipping over the issue,related to paradoxes,of whether all quantifiers,including such apparently unrestricted ones as everything,wind up with some non-trivial contextual domain restriction. This is discussed in Williamson(2004)and Glanzberg(2005).9out most vividly in the conservativity theorem due initially to Keenan and Stavi(1986),further investigated by van Benthem(1983,1986)and Keenan(1993).The key insight is that the class of conservative quantifiers can be build up inductively,from a base stock of quantifiers and some closure conditions.Let M be afixedfinite universe and let CONS M be the collection of conservative quantifiers on M.We will build up a class of quantifiers D−GEN M on M as follows.D−GEN M contains every and some(as type 1,1 quantifiers).We also assume that each set of members of M is definable by a predicate,and that D−GEN M is closed under Boolean combination and predicate restrictions.The latter assumes that if Q M(X,Y)is in D−GEN M,so is Q M(X∩C,Y)for C⊆M.This amounts to closure under(intersective) adjectival restriction in an NP.The conservativity theorem tells us that for each M:(22)CONS M=D−GEN MThis tells us that the domain of possible natural language determiners is far more orderly than it might have appeared:we can build up all the conservative determiner denotations by the inductive process which builds D−GEN M.The proof of the conservativity theorem also tells us that for a givenfinite universe M,we can build a natural language determiner(possibly quite long)which expresses each conservative quantifier on M.This is the Finite Effability Theorem of Keenan and Stavi(1986):(23)For afinite M,each element of CON M is expressed by a determiner of English.Thus,the conservativity property makes for a much more tractable space of determiner deno-tations,built up in a systematic way which is closely tied to constructions we can carry out in natural language.I.4LogicalityWe began this section with the idea that quantifiers are expressions of generality.Though we have seen a wide range of determiner denotations which fall within CONS and EXT,we have yet to give any statement of what makes them general.One way to articulate the notion10of generality is that it requires the truth of a sentence to be independent of exactly which individuals are involved in interpreting a given quantifier.This can be captured formally by the constraint of permutation invariance:(24)(PERM)Letπbe a permutation of M(i.e.a bijection from M to itself).Then Q M(X,Y)←→Q M(π[X],π[Y]).PERM is a local condition.But a global variant,isomorphism invariance,is quite natural: (25)(ISOM)For any M and M ,ifι:M→M is a bijection,then Q M(X,Y)←→Q M (ι[X],ι[Y]). ISOM is commonly assumed in the mathematical literature,and is built into the definitions of quantifiers in Mostowski(1957)and Lindstr¨o m(1966).7Westerst˚a hl(1985b,1989)observed that if we assume EXT,the domain of quantification ceases to matter,and ISOM and PERM are equivalent.Following van Benthem(1983,1986),one sometimes sees quantifiers satisfying CONS,EXT,and ISOM called logical quantifiers.One of the key features of these logical quantifiers is that they are entirely determined by two cardinal numbers:8(26)For any M and M ,and X,Y⊆M and X ,Y ⊆M ,if|X\Y|=|X \Y |and|X∩Y|=|X ∩Y |,then Q M(X,Y)←→Q M (X ,Y ).There has been a great deal of mathematical work investigating these quantifiers;much of it elegantly discussed in van Benthem(1986)and Westerst˚a hl(1989).ISOM(or PERM)does appear to capture the idea that quantifiers are general,and so not about any objects in particular.It is a further question whether this makes them genuinely log-ical constants,as the label‘logical quantifier’suggests.The idea that some sort of permutation-invariance is a key feature of logical notions has been proposed by Mautner(1946)and Tarski (1986).A vigorous defense of the logicality of ISOM quantifiers is given in Sher(1991).7The condition is called‘ISOM’,asιinduces an isomorphism between the structures M= M,X,Y and M = M ,ι[X],ι[Y] .In essence,as Lindstr¨o m(1966)observed,a type 1,1 generalized quantifier is a class of structures of the form M,X,Y ;if it satisfies ISOM,we have a class of structures closed under isomorphism.8I am not sure who should be credited with this result.As far as I know,it appeared in this formfirst in van Benthem(1984,1986),but related ideas appear in Mostowski(1957)and Higginbotham and May(1981).11I.5Quantifiers and Noun PhrasesWe have seen that,with a few controversial potential exceptions,natural language determiner denotations satisfy CONS and EXT.But there are some clear cases treated by generalized quan-tifier theory which do not satisfy ISOM,and so are not logical quantifiers.Possessive construc-tions like John’s in(5),for instance,often violate ISOM.Another example of a quantifier violating ISOM is provided by proper names.Suppose John denotes an individual j.We can build a type 1 generalized quantifier to interpret the NP John following Montague(1973).Let John M={X⊆M|j∈X}.This is a quantifier violating ISOM.There are two ways to respond to these exceptions.One is to give up on ISOM as a feature of quantifiers in natural language.This leaves the generalization that determiners denote type 1,1 quantifiers satisfying CONS and EXT,but not necessarily ISOM.These determiners build type 1 quantifiers satisfying CONS and EXT when combined with a CN denotation, so we might even make the further generalization that all NPs denote type 1 generalized quantifiers,once we have given up on ISOM.Another response is to attempt to explain away the apparent violations of ISOM.In the type 1 case,we can easily observe that though it is possible to treat John as a generalize quan-tifier,it can also be treated as simply denoting an individual.There are good reasons to take this simpler route(cf.Partee,1986).Thus,an apparently non-ISOM quantifier in natural lan-guage may not be a quantifier at all.Likewise,in the type 1,1 case,we mightfind analyses of possessive constructions which do not treat them as syntactically on par with other determin-ers,or do not treat them as determiners at all.(See Barker(1995)for an extensive discussion of the syntax and semantics of possessives.)This might allow for the stronger hypothesis, that quantifiers in natural language are the denotations of determiners(or a syntactically nat-ural subclass of determiners,perhaps),and they are logical generalized quantifiers satisfying CONS,EXT,and ISOM.The latter hypothesis predicts important differences between quantified noun phrases, build up out of determiners denoting ISOM quantifiers,and other noun phrases like proper names or possessive constructions.And in fact,we do see such differences.One way in which12quantified noun phrases behave differently from other noun phrases is brought out by what are called weak crossover pare:(27) a.*His i mother loves every boy i.b.His i mother loves Mary’s Brother i.c.His i mother loves John i.(The subscripts here are to indicate that the desired reading has his bound by or coreferring with the subsequent expression it is co-indexed with.)A number of authors have noted that we get unacceptability in weak crossover environ-ments with ISOM quantified noun phrases,but not with non-ISOM or non-quantified ones. This is often cited as evidence that there is a genuine subdivision between quantificational noun phrases,built from ISOM determiners,and other noun phrases;just as the strong hy-pothesis predicts(cf.Higginbotham and May,1981;Lasnik and Stowell,1991;Larson and Se-gal,1995).(Readers of the logic literature should be aware that regardless of their status in natural language,most logicians take generalized quantifiers to satisfy ISOM by definition.)I.6Glimpses BeyondWe have now seen the beginnings of generalized quantifier theory,but only the beginnings. The surveys of Westerst˚a hl(1989)and Keenan and Westerst˚a hl(1997)discuss a number of extensions of the theory,and applications of generalized quantifier theory in linguistics.Among the results they discuss is one that shows that the quantifier most defined in(10) cannot be defined by any combination of(ISOM) 1 quantifiers.This shows that we really do need at least type 1,1 quantifiers(cf.V¨a¨a n¨a nen,1997).They also investigate the delicate is-sue of whether we need to go beyond 1,1 .We saw that more should be interpreted as taking three arguments.Whether we will also need to consider what are called polyadic quantifiers, which take relations rather than sets as inputs,remains an active area of research(cf.Higgin-botham and May,1981;van Benthem,1989;May,1989;Keenan,1992;Westerst˚a hl,1994;Hella et al.,1996;Moltmann,1996)13II Quantification and ScopeThe relational theory of determiners which we examined,if all too briefly,in Section(I)explains some of the important properties of the semantic values of determiners.But it does not do very much to explain how determiners interact with the rest of semantics.As an example of where quantifiersfit into semantic theory,I shall present some ideas about how quantifiers take scope in natural language.Perhaps more so than the theory of generalized quantifiers,this area remains controversial. There are a number of good textbook presentations of the basic material,including Larson and Segal(1995)and Heim and Kratzer(1998)(I follow the latter quite closely here).But there is also some significant disagreements in the literature.To illustrate this disagreement,I shall discuss two representative examples of approaches to quantifier scope.I shall need some machinery to do so,which is built up in Sections(II.1–II.4).The actual discussion of scope will be in Section(II.5).II.1Quantifiers and Semantic TypesThe theory of generalized quantifiers as relations between sets pays no attention to the order in which a quantifier’s arguments are‘processed’.For studying the properties of determiners, this has proved a useful idealization,but it is not what we want from a compositional semantic theory in general.A glance at the sentence structure in(7)tells us that the compositional semantics of deter-miners shouldfirst have the determiner’s value combine with the value of the CN,resulting in an NP semantic value.It is the NP value which combines with the VP value to determine the value of the sentence.It is easy enough to re-formulate our account of determiner denotations to keep track of the order of arguments.The official definition(9)made a type 1,1 quantifier Q M a function on two arguments X and Y.We can think of this as a sequence of two functions:Q M(X)is the function from subsets of M to truth values,which is true iffQ M(X,Y)is true.Thus,a14binary relation on subsets of M like Q M can be thought of as a function from subsets of M to functions from subsets of M to truth values.9Q M(X)is a denotation for an NP,and is itself a type 1 quantifier.It will be useful to have some notation to keep track of the inputs and outputs of functions. One way to do this is to use type theory.Type theory is a highly general theory of functions. (In order to try to avoid confusion between types in the sense of quantifier types and this type theory,I shall sometimes call the latter semantic type theory.)Semantic type theory starts with two basic types:t is the type(set)of truth values,which we may take to have two elements and⊥;e is the type(set)of individuals,which we may take to be somefixed universe M.The theory then builds up functions out of these.The type (e,t)is the type of functions from individuals to truth values,i.e.it is a notation for℘(M),the set of subsets of M.We will continue with our assumption that the values of VPs and CNs are sets of individuals,i.e.of type(e,t).We will also continue with the extensional perspective, which gives sentences semantic values of type t(This is of course,an idealization.)We will also assume that non-quantified NPs are of type e.The analysis of determiners which takes their order into account makes them functions whose inputs are sets of individuals,and whose outputs are functions from sets of individuals to truth values.Hence,determiners should denote functions of type((e,t),((e,t),t)).As we are working with afixed universe M,giving type e,all quantifiers are now local.Generally,for any two types a and b,(a,b)is the type of functions from a to b.10II.2Quantifiers in Object PositionOur semantic analysis thus starts with the idea that determiners are of type((e,t),((e,t),t)), CNs are of type(e,t),and VPs are of type(e,t).This makes quantified NPs of type((e,t),t). As a result,in sentences like(7),the VP value is the argument of the NP value,but we still have an appropriate match-up of functions and arguments to produce a type t value for the 9This is what is sometimes called‘Currying’a binary relation,in honor of the logician Haskell B.Curry.10I am writing semantic types with round brackets,such as(a,b).Much of the literature writes semantic types with angle brackets,but these are already being used for quantifier types.15。
