一次函数中的交点坐标问题(2018.09.25)
一次函数交点问题及面积计算问题

一次函数交点问题及面积计算问题一、交点问题(1)与X 轴的交点:令Y=0,解出X ,得出与X 轴的交点坐标为(- bk,0)(2)与Y 轴的交点:令X=0,解出Y ,得出与Y 轴的交点坐标为(0,b ) y=k 1x+b 1(3)两条直线的交点:联立两条直线的解析式 ,解二元一次方程组。
y=k 2x+b 2B (−1,3),直线l 1与l 2交于点C 。
(1)求直线l 2的函数关系式;(2)求点C 、点D 的坐标。
练习1、如图,直线y =2x +3与x 轴交于点A ,与y 轴交于点B 。
求A 、B 两点的坐标。
练习2、已知一次函数y =2x −6与y =−x +3的图象交于点P ,则点P 的坐标为_________。
二、面积计算问题1、线段计算: 横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长 = 纵标之差的绝对值 = -y y 大小=-y y 下上点轴距离:点P (x ,y )到X 轴的距离为y ,到Y 轴的距离为ox 。
练习1、横线段的长度计算:【特点:两端点的y 标相等,长度=-x x 大小】。
(1)若A (2,0),B (10,0),则AB=———————。
(2)若A (-2,0),B (-4,0),则AB=———————。
(3)若M(-3,0),N(10,0),则MN=———————。
(4)若O(0,0),A( t,0),且A在O的右端,则OA=———。
(5)若O(0,0),A( t,0),且A在O的右端,则OA=———。
练习2、纵线段的长度计算:【特点:两端点的x标相等,长度=-y y大小】。
(1)(若A(0,5),B(0,7),则AB=———————。
(2)若A(0,-4),B(0,-8),则AB=——————。
(3)若A(0,2),B(0,-6),则AB=———————。
(4)若O(0,0),A(0,t ),且A在O的上端,则OA=————————。
专题03 一次函数中的交点问题(解析版)

专题03 一次函数中的交点问题知识对接考点一、一次函数y=kx+b(k ≠0)中k,b 的符号对函数性质的影响 1.k 的符号决定函数的增减性: 当k>0时,y 随x 的增大而增大; 当k<0时,y 随x 的增大而减小.2.b 的符号决定函数的图象与y 轴交点的位置: 当b>0时,交点在y 轴的正半轴上; 当b=0时,交点在原点;当b<0时,交点在y 轴的负半轴上.专项训练一、单选题1.若2x =是关于x 的方程()00,0mx n m n +=≠>的解,则一次函数()1y m x n =---的图象与x 轴的交点坐标是( ) A .()2,0 B .()3,0C .()0,2D .()0,3【答案】B 【分析】直线y =mx +n 与x 轴的交点的横坐标就是函数值为0时的方程的解,根据题意得到一次函数y =mx +n 的图象与x 轴的交点为(2,0),进而得到一次函数y =-mx -n 的图象与x 轴的交点为(2,0),由于一次函数y =-mx -n 的图象向右平移一个单位得到y =-m (x -1)-n ,即可求得一次函数y =-m (x -1)-n 的图象与x 轴的交点坐标. 【详解】解:∵方程的解为x =2, ∵当x =2时mx +n =0;∵一次函数y =mx +n 的图象与x 轴的交点为(2,0), ∵一次函数y =-mx -n 的图象与x 轴的交点为(2,0),∵一次函数y =-mx -n 的图象向右平移一个单位得到y =-m (x -1)-n , ∵一次函数y =-m (x -1)-n 的图象与x 轴的交点坐标是(3,0), 故选:B . 【点睛】本题主要考查了一次函数与一元一次方程的关系.任何一元一次方程都可以转化为ax +b =0 (a ,b 为常数,a ≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y =ax +b 确定它与x 轴的交点的横坐标的值.2.如图,一次函数y kx b =+的图象经过点(2,0)-,则下列说法正确的是( )A .0k <B .0b <C .方程0kx b +=的解是2x =-D .y 随x 的增大而减小【答案】C 【分析】利用函数的图象结合一次函数的性质进行解答即可. 【详解】解:∵图象过第一、二、三象限,∵k >0,b >0,y 随x 的增大而而增大,故ABD 错误; 又∵图象与x 轴交于(−2,0), ∵kx +b =0的解为x =−2,故C 正确; 故选:C . 【点睛】此题主要考查了一次函数与一元一次方程,关键是正确从函数图象中获取信息,掌握一次函数的性质.3.如图,经过点()3,0B -的直线y kx b =+与直线42y x =+相交于点()1,2--A ,则420kx b x +<+<的解集为( )A .3x <-B .31x -<<-C .12x >-D .112x -<<-【答案】D 【分析】由图象得到直线y =kx +b 与直线y =4x +2的交点A 的坐标(-1,-2),求出直线y =4x +2与x 轴的交点坐标,观察直线y =kx +b 落在直线y =4x +2的下方且直线y =4x +2落在x 轴下方的部分对应的x 的取值即为所求. 【详解】解:∵经过点B (-2,0)的直线y =kx +b 与直线y =4x +2相交于点A (-1,-2), ∵直线y =kx +b 与直线y =4x +2的交点A 的坐标为(-1,-2), ∵当x >-1时,kx +b <4x +2, 当x <-12时,4x +2<0,∵不等式kx +b <4x +2<0的解集为-1<x <-12. 故选:D . 【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y =ax +b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y =kx +b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合. 4.如图,若一次函数1y k x b =+与反比例函数2k y x=的图象交(,3),(,2)A m B n -两点,过点B 作BC x ⊥轴,垂足为C ,且5ABCS=,则不等式210k k x b x-+<的解集为( )A .2x <-或01x <<B .1x >或20x -<<C .2x >或30x -<<D .3x <-或02x <<【答案】D 【分析】根据题意可得21k k x b x+<,再由图象可得不等式的解集为x n <或0x m <<,根据(,3),(,2)A m B n -,可得CB 长为2,ABC 底边CB 上的高为m n -,然后由5ABCS =,可得5m n -=,根据反比例函数的特征可得32m n =-,可求出2,3m n ==-,即可求解.【详解】 解:由题知,210k k x b x -+<,即为21k k x b x+<, 由图象可知,不等式的解集为x n <或0x m <<, ∵(,3),(,2)A m B n -,∵CB 长为2,ABC 底边CB 上的高为m n -, ∵三角形的面积为12()52m n ⨯⨯-=,∵5m n -=,∵点(,3),(,2)A m B n -的图象在反比例函数2k y y=的图象上, ∵32m n =-,即23m n , ∵5m n -=, ∵2,3m n ==-,∵不等式的解集为3x <-或02x <<. 故选:D . 【点睛】本题主要考查了一次函数与反比例函数的交点问题,函数与不等式解集的关系,求出2,3m n ==-,利用数形结合的思想是解题的关键.5.一次函数2y x m =-+与2y x =+图象的交点位于第二象限,则m 的值可能是( ) A .-4 B .1C .2D .3【答案】B 【分析】根据题意将两个函数联立方程组,再根据交点在第二象限列不等式组,即可求出m 的取值范围. 【详解】解:∵一次函数y =-2x +m 和y =x+2图象相交,∵22y x m y x =-+⎧⎨=+⎩,解得2343m x m y -⎧=⎪⎪⎨+⎪=⎪⎩,∵交点位于第二象限,∵203403m m -⎧<⎪⎪⎨+⎪>⎪⎩①②,解不等式∵得2m <, 解不等式∵得4m >-, ∵不等式的解集为42m -<<, ∵m 的值可能为1, 故选B . 【点睛】本题考查了解不等式及两直线相交:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.6.如图所示,已知函数y ax b =+和y kx =的图象相交于点P ,则关于x ,y 的二元一次方程组y ax b y kx =+⎧⎨=⎩的解是( )A .42x y =⎧⎨=⎩B .42x y =⎧⎨=-⎩C .24x y =-⎧⎨=-⎩D .42x y =-⎧⎨=-⎩【答案】D 【分析】由两个函数的交点坐标同时满足两个函数解析式,从而可得方程组的解. 【详解】解:∵函数y =ax +b 和y =kx 的图象交于点P 的坐标为(-4,-2),∵关于x ,y 的二元一次方程组y ax by kx =+⎧⎨=⎩的解是42x y =-⎧⎨=-⎩.故选D . 【点睛】本题考查的是利用函数的交点坐标确定方程组的解,明确交点坐标的含义与掌握数形结合的方法解题是关键.7.若直线2y kx k =++与x 轴的交点位于x 轴正半轴上,则它与直线21y x =-交点的横坐标a 的取值范围为( )A .32a <B .302a <<C .1342aD .14a >【答案】C 【分析】由直线2y kx k =++与x 轴的交点可得21k<-.分两种情况讨论,即可得20k -<<.联立两条直线解析式即可得交点横坐标32ka k,由k 的范围即可确定出a 的范围. 【详解】解:直线2y kx k =++与x 轴的交点位于x 轴正半轴上,0k ∴≠.令20y kx k ,解得:20k xk,即210k,得21k<-. ∵当0k >时,解得2k <-,与题设矛盾; ∵当0k <时,解得2k >-,所以20k -<<. 当直线2y kx k =++与直线21y x =-相交时,221kx kx ,解得:32kxk, 即32ka k, 又35(2)51222k k ak kk,20k , 02k , 224k,∴111422k , ∴555422k , ∴1531422k. 故选:C . 【点睛】本题主要考查了一次函数的图象性质与不等式的解法,熟练掌握以上知识是解题的关键. 8.一次函数y =kx +b (k ≠0)的图象经过点B (﹣6,0),且与正比例函数y =13x 的图象交于点A (m ,﹣3),若kx ﹣13x >﹣b ,则( )A .x >0B .x >﹣3C .x >﹣6D .x >﹣9【答案】D 【分析】先利用正比例函数解析式,确定A 点坐标;然后利用函数图像,写出一次函数y=kx+b (k≠0)的图像,在正比例函数图像上方所对应的自变量的范围. 【详解】解:把A (m ,﹣3)代入y =13x 得13m =﹣3,解得m =﹣9,所以当x >﹣9时,kx +b >13x ,即kx ﹣13x >﹣b 的解集为x >﹣9.故选D . 【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b 的值大于(或小于)0的自变量x 的取值范围;从函数图像的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.9.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式-kx+b>0的的解集为( )A .x >-2B .x <-2C .2x >D .2x <【答案】D 【详解】由函数y kx b =+和y kx b =-+的图象关于y 轴对称可由y kx b =+的图象得到函数y kx b =-+的图象如图所示,由图可知:函数y kx b =-+的图象位于x 轴之上的部分在点(2,0)的左侧, ∵不等式0kx b -+>的解集为:2x <. 故选D.【点睛】(1)函数y kx b =+和y kx b =-+的图象关于y 轴对称;(2)函数y kx b =+和y kx b =--的图象关于x 轴对称;(3)不等式0kx b +>的解集是函数y kx b =+的图象位于x 轴之上的部分图象所对应的自变量的取值范围;不等式0kx b +<的解集是函数y kx b =+的图象位于x 轴之下的部分图象所对应的自变量的取值范围.10.一次函数y =kx +b 的图象如图所示,当y >0时,x 的取值范围是( )A .x >0B .x <0C .x >﹣2D .x <﹣2【答案】C 【分析】当y >0时,即函数图象在x 轴上方时对应的x 的取值范围,结合图象可求得答案. 【详解】解:由图象可知当x =﹣2时,y =0,且y 随x 的增大而增大, ∵当y >0时,x >﹣2, 故选C . 【点睛】本题主要考查了利用一次函数与x 轴的交点坐标求不等式的解集,解题的关键在于能够熟练掌握相关知识进行求解. 二、填空题11.如果一次函数 y = ax + 4 与 y = bx - 2 的图象的交点在 x 轴上,那么经过点(1,1)的直线y =bax +c 的表达式为__.【答案】1322 y x=-+【分析】根据一次函数y =ax + 4 与y =bx - 2 的图象的交点在x 轴上可求出12ba=-,然后把(1,1)代入求出c即可.【详解】解:当y=0时,ax + 4=0 ,bx - 2=0,∵x=4a-,x=2b.∵y =ax + 4 与y =bx - 2 的图象的交点在x 轴上,∵4a-=2b,∵12ba=-,∵y =12-x +c,把(1,1)代入,得1=12-+c,∵c=32,∵1322y x=-+.故答案为:1322y x=-+.【点睛】本题考查了一次函数图象的交点坐标,以及待定系数法求函数解析式,根据一次函数y =ax+ 4 与y =bx - 2 的图象的交点在x 轴上可求出12ba=-是解答本题的关键.12.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:∵k<0;∵a>0;∵关于x的方程kx﹣x=a﹣b的解是x=3;∵当x<3时,y1<y2中.则正确的序号有____.【答案】∵∵. 【分析】根据一次函数的性质对∵∵进行判断;利用一次函数与一元一次方程的关系对∵进行判断;利用函数图象,当x <3时,一次函数y 1=kx +b 在直线y 2=x +a 的上方,则可对∵进行判断. 【详解】解:∵一次函数y 1=kx +b 经过第一、二、三象限, ∵k <0,b >0,所以∵正确;∵直线y 2=x +a 的图象与y 轴的交点在x 轴,下方, ∵a <0,所以∵错误;∵一次函数y 1=kx +b 与y 2=x +a 的图象的交点的横坐标为3, ∵x =3时,kx +b =x ﹣a ,整理得kx ﹣x =a ﹣b ,所以∵正确; 当x <3时,y 1=kx +b 图像在y 2=x +a 图像的上方, ∵y 1>y 2,所以∵错误. 故答案为∵∵. 【点睛】本题考查一次函数与一元一次方程、一次函数与一元一次不等式、一次函数图象与系数的关系,掌握一次函数与一元一次方程、一次函数与一元一次不等式、一次函数图象与系数的关系是解题关键.13.如图,直线y x m =-+与()40y nx n n =+≠交点的横坐标为2-.则关于x 的不等式40x m nx n -+>+>的解集为______.【答案】42x -<<- 【分析】求出直线4y nx n =+与x 轴的交点,利用图象法即可解决问题; 【详解】解:直线y x m =-+与4(0)y nx n n =+≠的交点的横坐标为2-,∴关于x 的不等式4x m nx n -+>+的解集为2x <-,40ynxn时,4x =-,∴不等式40x m nx n -+>+>的解集为42x -<<-.故答案为:42x -<<-. 【点睛】本题考查了一次函数与一元一次不等式等知识,解题的关键是学会利用图象法解不等式问题. 14.一次函数y kx b =-的图象如图所示,则关于x 的不等式(1)0k x b -->的解集为______.【答案】3x < 【分析】根据题意,先把y kx b =-向右平移1个单位,得到(1)y k x b =--,则结合图象可确定(1)0k x b -->时,图象所在位置,进而可得答案.【详解】 解:根据题意,∵一次函数y kx b =-的图象与x 轴的交点为(2,0), 把y kx b =-向右平移1个单位,得(1)y k x b =--, ∵(1)y k x b =--与x 轴的交点为(3,0), ∵关于x 的不等式(1)0k x b -->的解集为3x <; 故答案为:3x <. 【点睛】本题考查了一次函数的平移,一次函数与一元一次不等式,关键是掌握数形结合思想进行分析.15.如图,点A 是一次函数21y x =+图象上的动点,作AC ∵x 轴与C ,交一次函数4y x =-+的图象于B . 设点A 的横坐标为m ,当m =____________时,AB =1.【答案】43或23【分析】分别用m 表示出点A 和点B 的纵坐标,用点A 的纵坐标减去点B 的纵坐标或用点B 的纵坐标减去点A 的纵坐标得到以m 为未知数的方程,求解即可. 【详解】解:∵点A 是一次函数21y x =+图象上的动点,且点A 的横坐标为m , ∵(,21)A m m + ∵AC ∵x 轴与C , ∵(,0)C m ∵(,4)B m m -+ ∵1AB =∵|21(4)|1m m +--+= 解得,43m =或23故答案为43或23【点睛】本题考查了一次函数图象上点的坐标特征,根据A 点横坐标和点的坐标特征求得A 、B 点纵坐标是解题的关键. 三、解答题16.平面直角坐标系xOy 内,一次函数22y x =-经过点(1,)A m -和(,2)B n . (1)求m ,n 的值;(2)求该直线与x 轴的交点坐标.【答案】(1)42m n =-⎧⎨=⎩;(2)(1,0)【分析】(1)分别将A 、B 两点代入一次函数22y x =-得到关于m ,n 的式子,即可作答; (2)借助依次函数与一元一次方程的关系进行求解,即将y =0代入函数即可作答. 【详解】解:(1)将(1)A m -,和(2)B n ,代入一次函数22y x =-中,得122222m n =-⨯-⎧⎨=-⎩ 解得42m n =-⎧⎨=⎩故答案为:42m n =-⎧⎨=⎩;(2)令0y =,得022x =- 解得1x =该直线与x 轴的交点坐标为(10),; 故答案为:(10),. 【点睛】本题主要考考查了根据一次函数方程计算坐标中的未知量,以及一次函数与一元一次方程的关系,属于基础题.17.已知(),2A n -,()1,4B 是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点.(1)反比例函数的解析式是__________,一次函数的解析式是__________; (2)AOB 的面积是__________; (3)关于x 的不等式0mkx b x+-<的解集是__________. 【答案】(1)4y x=,22y x =+;(2)3;(3)2x <-或01x <<. 【分析】(1)根据题意先求出反比例函数解析式,可得到2n =- ,根据A 、B 两点,即可求出一次函数的解析式;(2)设直线AB 交y 轴于点C ,可得()0,2C ,从而得到AOB AOC BOC S S S =+△△△,即可求解; (3)根据图象可得,当2x <-或01x <<时,mkx b x+<,即可求解. 【详解】解:(1)∵(),2A n -,()1,4B 是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点, ∵4m = ,∵反比例函数解析式为4y x=; 把(),2A n -代入4y x =,得:42n-= ,解得:2n =- , ∵()2,2A --,把()2,2A --,()1,4B 代入y kx b =+,得:224k b k b ⎧-+=-⎨+=⎩,解得:22k b =⎧⎨=⎩ , ∵一次函数的解析式为22y x =+; (2)如图,设直线AB 交y 轴于点C ,当0x = 时,2y = , ∵()0,2C , ∵112212322△=+=⨯⨯+⨯⨯=AOB AOC BOCS SS; (3)根据图象可知:当2x <-或01x <<时,mkx b x+<, ∵不等式0mkx b x+-<的解集是2x <-或01x <<. 【点睛】本题主要考查了求一次函数和反比例函数的解析式,一次函数和反比例函数的图象和性质,利用数形结合的思想是解题的关键.18.已知直线y x b =+和1y ax =-交于点P (−2,1),则关于x 的方程1x b ax +=-的解为___________. 【答案】x =-2 【分析】利用函数图象交点坐标为两函数解析式组成的方程组的解解决问题.【详解】解:∵直线y=x+b和y=ax-1交于点P(−2,1),∵当x=-2时,x+b=ax-1=1,即关于x的方程x+b=ax-1的解为x=-2.故答案为:x=-2.【点睛】本题考查了一次函数与二元一次方程(组):方程组的解就是两个相应的一次函数图象的交点坐标.19.如图,直线l1经过点A(0,4)和C(12,﹣4),点B的坐标为(8,4),点P是线段AB上的动点(点P不与点A重合),直线l2:y=kx+2k(k≠0)经过点P,并与l1交于点M.(1)求直线l1的函数解析式;(2)若点M坐标为(1,103),求APMS;(3)直线l2与x轴的交点坐标为,点P的移动过程中,k的取值范围是.【答案】(1)y=﹣23x+4;(2)815;(3)(﹣2,0),25≤k≤2.【分析】(1)用待定系数法求出解析式即可;(2)根据M点的坐标求出直线l2的解析式,确定P点的坐标,即可求出∵APM的面积;(3)根据直线l2的解析式,求出与x轴的交点即可,根据点P在AB上,分别与点A和点B重合时求出临界值即可确定k的取值范围.【详解】解:(1)∵直线l1经过点A(0,4)和C(12,﹣4),设直线l1的解析式为y=sx+t,代入A点、C点坐标,得4124ts t=⎧⎨+=-⎩,解得234st⎧=-⎪⎨⎪=⎩,∵直线l1的解析式为y=﹣23x+4;(2)∵点M坐标为(1,103),且点M在直线l2:y=kx+2k(k≠0)上,∵k+2k=103,∵k=109,∵直线l2的解析式为y=109x+209,∵点A(0,4),点B (8,4),∵AB//x,当y=4时,109x+209=4,∵x=85,∵P点的坐标为(85,4),∵S∵APM=12×(85﹣0)×(4﹣103)=815;(3)∵直线l2:y=kx+2k(k≠0),∵当y=0时,k=﹣2,∵直线l2与x轴的交点坐标为(﹣2,0),∵点P在线段AB上,∵当点P与A点重合时,2k=4,解得k=2,当点P与B点重合时,8k+2k=4,解得k=25,∵k的取值范围是25≤k≤2,故答案为:(﹣2,0),25≤k≤2.【点睛】本题主要考查了待定系数法求一次函数解析式,一次函数与坐标轴的交点,坐标与图形的性质,以及一次函数的性质,熟练使用待定系数法求解析式及用临界值法求取值范围是解题的关键.20.如图,直线y=kx+b经过点A(﹣5,0),B(﹣1,4).(1)求直线AB的表达式;(2)若直线y=﹣2x﹣4与直线AB相交于点C,求点C的坐标;(3)根据图象,写出关于x的不等式kx+b>﹣2x﹣4的解集.【答案】(1)y=x+5;(2)点C的坐标为(﹣3,2);(3)x>﹣3【分析】(1)利用待定系数法求一次函数解析式解答即可;(2)联立两直线解析式,解方程组即可得到点C的坐标;(3)根据图形,找出点C右边的部分的x的取值范围即可.【详解】解:(1)∵直线y=﹣kx+b经过点A(﹣5,0)、B(﹣1,4),∵504k bk b-+=⎧⎨-+=⎩,解方程组得15kb=⎧⎨=⎩.∵直线AB的解析式为y=x+5;(2)∵直线y=﹣2x﹣4与直线AB相交于点C,∵524y xy x=+⎧⎨=--⎩,解得32xy=-⎧⎨=⎩.∵点C的坐标为(﹣3,2);(3)由图可知,关于x的不等式kx+b>﹣2x﹣4的解集是x>﹣3.【点睛】本题主要考查了一次函数的解析式求解、二元一次方程组的求解和一次函数与一元一次不等式的关系,准确计算是解题的关键.21.如图,直线13y x =+与直线243y mx =+交于点M (﹣1,2),与x 轴分别交于点A ,B ,与y 轴分别交于C ,D .(1)根据图像写出方程组12343y x y mx =+⎧⎪⎨=+⎪⎩的解是__________.(2)根据函数图像写出不等式433x mx +≤+的解集_________.(3)求直线AC ,直线BD 与x 轴围成的∵ABM 的面积.【答案】(1)12x y =-⎧⎨=⎩;(2)1x ≤-;(3)5【分析】(1)二元一次方程组的解根据两条直线交点坐标即可求得; (2)将题干转化为12y y ≤,然后根据图像即可判断;(3)将点M (﹣1,2)代入243y mx =+求得m 的值,然后根据题意求出点A ,B 的坐标.然后根据三角形面积公式即可求解. 【详解】(1)根据题意,两直线交点为点M (﹣1,2),所以方程组的解为12x y =-⎧⎨=⎩;(2)由题意得,433x mx +≤+即为12y y ≤,根据图像可以判断出当1x ≤-时,12y y ≤,故答案为1x ≤-;(3)对于13y x =+,当0y =时,03x =+,解得3x =-,故A 点坐标为A (﹣3,0), 将点M (﹣1,2)代入243y mx =+,得423=-+m ,解得23m =-,∵22433y x =-+,∵对于22433y x =-+,当0y =时,24033x =-+,解得2x =,故B 点坐标为B (2,0),∵5AB =,∵ABM 的高为2M h y ==, ∵1152522ABMSAB h ==⨯⨯=.【点睛】本题考查了一次函数与一元一次方程、一元一次不等式,关键是掌握交点在本类题型中的重要意义,熟悉掌握一次函数的基本性质是解题的关键.22.如图,已知一次函数12y ax =+与21y x =-的图象交于点(2,1)A ,(1)求a 的值;(2)若点C 是直线21y x =-上的点且AC =C 的坐标; (3)直接写出210y y >>时,x 的取值范围.【答案】(1)12a =-;(2)(4,3)C 或(0,1)-;(3)24x <<【分析】(1)把点(2,1)A 代入12y ax =+,即可求解;(2)如图,设(,1)C x x -,作//CM y 轴,//AM x 轴交于M ,则ACM ∆是等腰直角三角形,根据勾股定理列出方程,解方程即可求解;(3)根据图像得出当210y y >>时,需要同时满足两个条件,21y y >和10y >,此时2,x >且,x <4问题得解.【详解】解:(1)∵交点(2,1)A 在直线1y 上 ∵221a += 解得12a =-;(2)如图,设(,1)C x x -作//CM y 轴,//AM x 轴交于M , 则ACM ∆是等腰直角三角形,且2CM AM x ==-,则222(2)(2)x x -+-=, ∵2(2)4x -=,∵22x -=±∵4x =或0, ∵(4,3)C 或(0,1)-;(3)由图像得,当210y y >>时,x 的取值范围为:24x <<. 【点睛】本题考查了一次函数图象点的意义,数形结合思想,勾股定理,函数与不等式等知识点,综合性较强,理解好函数图象上点的意义,函数与不等式关系是解题关键. 23.如图,直线1:1l y x =+与直线22:3l y x a =-+相交于点(1,)p b ;(1)求出a,b 的值;(2)根据图象直接写出不等式2013x x a <+<-+的解集; (3)求出ABP ∆的面积.【答案】(1) a=83,b=2;(2)-1<x <1;(3)5.【分析】(1)把P 点坐标代入y=x+1可得b 的值,继而代入23y x a =-+可求a 的值;(2)根据两函数图象的交点坐标及y=x+1与x 轴的交点可得答案;(3)首先求出点A 、B 的坐标,由此计算AB 的长,再由点P 的坐标,即可计算出ABP ∆的面积. 【详解】解:(1)∵直线l 1:y=x+1过点P (1,b ), ∵b=1+1=2;把点P (1,2)代入23y x a =-+中得a=8 3(2)∵y=x+1与x轴交于点(-1,0),∵在x=-1的左边x=1的右边的图象满足不等式2013x x a <+<-+,∵不等式2013x x a<+<-+的解集是-1<x<1(3)在2833y x=-+中,当y=0时,x=4∵点B的坐标是(4,0)又A(-1,0),∵AB=4+1=5,∵点P(1,2),∵ABP∆的面积为:12×5×2=5.【点睛】此题主要考查了一次函数与二元一次方程组,关键是掌握待定系数法求一次函数解析式,掌握凡是函数图象经过的点必能满足解析式即可.。
一次函数的图像与坐标轴的交点 ppt课件

已知函数y=2x-4
(1)画出它的图象;
(2)写出这条直线与x轴、y轴交点的坐标;
(3)求这条直线与两坐标轴所围成的三角 形的面积。
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
234
-3
-4
三 2 1 24 2
2
1.已知一次函数y=-x+2,求其与两 坐标轴所围成的三角形的面积?
2.已知一次函数y=x+3,求其与两坐
标轴所围成的三角形的面积?
3.已知一次函数y=4x-2,求其与两坐 标轴所围成的三角形的面积?
3.直线 y=4x与-x2轴的交点坐标是 ,与y 轴的交点坐标是______
4.直线 y=-与x-x轴1 的交点坐标是 , 与y轴的交点坐标是_____
思考题
已知一次函数y=2x+4,求其与两 坐标轴所围成的三角形的面积?
y=2x+4 y
分析: (0, 4 ) (-2 ,0)
B▪4
3
24
1
A 2 -4 -3 -▪2 -1 O -1 1 -2
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
例1:画出一次函数y=2x+4的图象
(1)直线y=2x+4与x轴的交点坐标是 ______,与y轴的交点坐标是_______.
1、直线y=-3x+4与x轴的交点坐标是 ______,与y轴的交点坐标是______.
2.直线y=-x+2与x轴的交点坐标是 , 与y轴的交点坐标是_____
一次函数与坐标轴的交点

探索:直线y=kx+b(k≠0)与x轴、y轴交点坐标
求直线y=-2x-4与x轴、y轴的交点坐标,并画出 这条直线
解:当x=0,y=-2×0-4=-4
点(0 ,-4)就是直线与y轴的交点坐标;
当y=0,0=-2x-4,即x=-2
点( -2, 0 )就是直线与x轴的交点坐标。
y
5 4 3 2
1
-4 -3 -2 -1 -O1 1 2 3 4 5 X
-2
-3 -4
y=-2x-4
结论:
• 如何求直线y=kx+b(k≠0)与x轴、y轴交点坐 标?
1、利用函数图象 2、利用函数关系式
与x轴交点:令y=0,求x 与y轴交点:令x=0,求y
试一试
• 求下列直线与x轴、y轴的交点,画出它们 的图象。
(1)y=4x-4
(2) y= 2 x 2 3
课堂达标
• 1、函数y= 1 x 2 的图象与x轴的交点坐 5
标为(_-_1_0_,0_),与y轴的交点坐标为(_0_,_2_)___.
2、直线y=kx+b(k≠0)与x轴交点坐标(__bk___,0, )
与y轴交点坐标(_0_,_b_)
想一想
问题1中,汽车距北京的路程S(千米)与汽车在高 速公路上行驶的时间t(时)之间的函数关系式是 s=570-95t,试画出这个函数的图像。
一次函数的图象与坐标轴的交点
学习目标
• 1、会求直线y=kx+b(k≠0)与x轴y轴的交点坐 标。
• 2、能熟练的选取适当的点画一次函数的图 象
探索:直线y=kx+b(k≠0)与x轴、y轴交点坐标
y=-2x-4
y
5 4 3 2
一次函数图像坐标轴交点

一次函数与坐标轴交点的意义
01
一次函数与x轴交点
该交点是一次函数图像上的一个特殊点,其纵坐标为0。这个点代表着
一次函数在x轴上的截距,即当y=0时,x的取值。通过该点,我们可以
了解一次函数在x轴上的位置以及函数的增减性。
02
一次函数与y轴交点
该交点是一次函数图像上的另一个特殊点,其横坐标为0。这个点代表
着一次函数在y轴上的截距,即当x=0时,y的取值。通过该点,我们可
以了解一次函数在y轴上的位置以及函数的垂直位移。
03
一次函数与坐标轴交点的综合意义
一次函数与坐标轴的交点共同决定了一次函数图像的位置、方向和形状。
这些交点为我们提供了一次函数的基本特征和性质,有助于我们更好地
理解和应用一次函数。
02 一次函数图像与x轴交点
在解决与一次函数相关的实际问 题时,经常需要找到一次函数图
像与x轴的交点。
例如,在解决追及问题、相遇问 题等时,可以通过找到一次函数 图像与x轴的交点,来确定两个
物体的相遇时间或追及时间。
此外,在解决一些与一次函数相 关的最优化问题时,也可以通过 找到一次函数图像与x轴的交点,
来确定最优解的位置。
03 一次函数图像与y轴交点
如果一次函数图像与y轴交点在正半轴,那么函数的截距b>0,函数图像在x轴上方;如果交 点在负半轴,那么b<0,函数图像在x轴下方。
解决与一次函数相关的实际问题
通过分析一次函数图像与坐标轴 的交点,可以解决与一次函数相 关的实际问题,如求解不等式、
方程等。
利用一次函数图像与x轴的交点, 可以求解一元一次方程;利用与 y轴的交点,可以求解一元一次
对未来研究的展望
一次函数与x轴y轴交点公式

一次函数与x轴y轴交点公式一次函数是数学中最基础的函数之一,也是应用最广泛的函数之一。
它的图像是一条直线,具有非常简单的特征。
在学习一次函数时,我们需要掌握一些基本的概念和公式。
其中,与x轴和y轴的交点公式是非常重要的一项。
一、一次函数的定义一次函数是指函数y=kx+b,其中k和b是常数,x和y是变量。
这个函数的图像是一条直线,斜率为k,截距为b。
我们可以通过斜率和截距的值来描述这条直线的特征。
二、斜率的作用斜率是指直线在坐标系中的倾斜程度。
它的计算公式是:k=(y2-y1)/(x2-x1)其中,(x1,y1)和(x2,y2)是直线上的两个点。
斜率的值可以为正、负或零,分别表示直线向上、向下或水平。
斜率的绝对值越大,直线的倾斜程度就越大。
三、截距的作用截距是指直线与y轴的交点。
它的计算公式是:b=y-kx其中,k是直线的斜率,(x,y)是直线上的任意一点。
截距的值可以为正、负或零,分别表示交点在y轴的正半轴、负半轴或原点。
四、一次函数与x轴的交点一次函数与x轴的交点是指函数y=kx+b与x轴的交点。
这个交点的坐标为(x,0),其中x是满足y=kx+b=0时的x值。
我们可以通过以下公式来计算x的值:x=-b/k其中,k是函数的斜率,b是函数的截距。
这个公式的意义是,当y=0时,我们可以通过斜率和截距的值来计算出x的值,从而得到交点的坐标。
五、一次函数与y轴的交点一次函数与y轴的交点是指函数y=kx+b与y轴的交点。
这个交点的坐标为(0,b),其中b是函数的截距。
因为在y轴上,x的值为0,所以我们可以直接得到交点的坐标。
六、实例分析下面我们通过一个实例来说明一次函数与x轴、y轴的交点公式的应用。
例1:已知一次函数y=2x-1,求它与x轴和y轴的交点坐标。
解:首先,我们可以得到这个函数的斜率为2,截距为-1。
然后,根据与x轴的交点公式,我们可以得到:x=-b/k=1/2因此,这个函数与x轴的交点坐标为(1/2,0)。
一次函数x轴交点公式

一次函数x轴交点公式一次函数在数学中可是个相当重要的“角色”,今天咱们就来好好聊聊一次函数与 x 轴交点公式这个事儿。
咱们先来说说啥是一次函数。
简单来讲,一次函数的表达式一般是y = kx + b ,这里的 k 和 b 都是常数,而且 k 不能等于 0 。
那这个一次函数和 x 轴的交点是啥意思呢?其实就是当 y = 0 时,x 的值。
那这个交点的公式是咋来的呢?咱就假设 y = 0 ,代入到一次函数 y = kx + b 中,就得到 0 = kx + b ,然后通过移项,就能算出 x = -b / k ,这就是一次函数与 x 轴交点的公式啦!我还记得之前给学生们讲这个知识点的时候,有个特别有趣的事儿。
当时在课堂上,我讲完这个公式,就出了一道题让大家练习。
题目是这样的:已知一次函数 y = 2x - 4 ,求它与 x 轴的交点。
我在教室里来回走着,观察大家的解题情况。
大部分同学都做得挺认真,可就有个叫小明的同学,抓耳挠腮的,一脸苦相。
我走过去一看,发现他把公式给记错了,算成了 x = b / k 。
我就轻轻地敲了敲他的桌子,问他:“小明,咋啦?是不是思路卡住啦?”小明抬起头,可怜巴巴地看着我,说:“老师,我好像把公式记错了。
”我笑了笑,说:“别着急,咱们再一起来回顾一下这个公式。
你看啊,当 y = 0 时,0 = 2x - 4 ,移项之后是不是 2x = 4 ,那 x 就等于2 ,而按照公式 x = -(-4) / 2 = 2 ,能明白不?”小明听了之后,恍然大悟,赶紧重新做了一遍,还做对了呢,那高兴的样子,我到现在都还记得。
再来说说这个一次函数x 轴交点公式在实际生活中的应用。
比如说,你要计算一辆车的刹车距离。
假设车的速度和刹车时间之间的关系可以用一次函数来表示,当车完全停下时,速度为 0 ,通过这个交点公式,就能算出刹车开始到车完全停下所行驶的距离。
又比如说,在经济领域,如果一个商品的成本和产量之间是一次函数关系,当利润为 0 时,也就是不赚不赔的时候,通过这个交点公式就能算出对应的产量。
一次函数被坐标轴和双曲线所截的线段问题

一次函数被坐标轴和双曲线所截的线段问题在平面几何中,一次函数与坐标轴和双曲线相交的情况是常见的。
这些交点形成的线段长度对于理解函数图像和性质非常重要。
以下是对这个问题的探讨。
首先,考虑一次函数的一般形式 y = kx + b,其中 k 是斜率,b 是 y 轴上的截距。
1.与x轴的交点:当 y = 0 时,从方程 y = kx + b 可得 x = -b/k。
这个解称为一次函数与 x 轴的交点。
2.与y轴的交点:将 x = 0 代入 y = kx + b,得 y = b。
这表示函数与 y 轴的交点是 (0, b)。
对于双曲线,我们通常考虑的是标准形式 y^2 - x^2/a^2 = 1 (a > 0),它表示一个双曲线。
1.与x轴的交点:令 y = 0,从方程 y^2 - x^2/a^2 = 1 可得x = ±a。
这意味着双曲线与 x 轴的交点是 (-a, 0) 和 (a, 0)。
2.与y轴的交点:令 x = 0,从方程 y^2 - x^2/a^2 = 1 可得y = ±1。
这意味着双曲线与 y 轴的交点是 (0, 1) 和 (0, -1)。
当一次函数与双曲线相交时,它们会在某些特定的点相交。
这些交点的性质取决于函数的斜率和截距以及双曲线的参数。
特别地,交点的位置和数量取决于这些参数。
我们可以利用这些信息来进一步分析这些函数的性质和特征。
例如,考虑一个斜率 k 和一个截距 b 的一次函数 y = kx + b 与一个参数为a 的双曲线 y^2 - x^2/a^2 = 1 的交点。
通过解方程组,我们可以找到交点的坐标。
然后,通过观察这些交点的位置和数量,我们可以对一次函数和双曲线的性质有更深入的理解。
此外,这种交点问题在解决实际应用问题中也有广泛的应用,如物理学、工程学、经济学等。
例如,在物理学中,一次函数可以描述物体的运动轨迹,而双曲线可以描述质量分布或能量分布等。
通过找到这些交点,我们可以找到物体运动的关键位置或者资源的分布情况。
反比例函数与一次函数图象交点问题的探讨

反比例函数与一次函数图象交点问题的探讨
相信许多同学都曾接触过反比例函数和一次函数,反比例函数和一次函数的图象也都被大家津津乐道集体讨论,但有一个比较冷门的话题,那就是反比例函数与一次函数图象交点的探讨。
当反比例函数和一次函数图象共线时,会存在一个交点。
这个交点就可以用数学公式表示出来,即:y=-1/ax+b。
解此方程,可以得到一次函数在图像中的横纵坐标,它也正是反比例函数和一次函数的交点坐标。
求解反比例函数和一次函数之间的交点也十分重要,它可以帮助我们了解这两种函数的变化趋势,可以让我们对这两种函数有更深入的理解和分析。
此外,求解反比例函数和一次函数之间的交点也可以提高工作效率,例如在绘制反比例函数时,通过求出反比例函数和一次函数之间的交点,可以准确判断绘图结果,从而更加快捷地完成绘图工作。
综上所述,求解反比例函数和一次函数图象交点十分重要,不仅可以帮助我们了解函数的变化趋势,还可以提高工作效率。
只要能够熟练掌握求交点的公式,就可以有效求解这个问题,从而比了解和分析反比例函数和一次函数的图象变化趋势更加深入。
如何求两个一次函数的交点坐标到原点的距离

如何求两个一次函数的交点坐标到原点的距离要注重对一次函数概念的理解数学来源于生活,我们学习函数的概念,不妨借助生活的经验来理解函数关系,我们生活在运动变化着的世界里,可以说变量无处不在。
让学生自己多思考,多列举一些生活中的实例,归纳出形如y=kx+b(k≠0,b为常数)的式子叫做一次函数。
那我们知道一个x确定后只有唯一的y与之对应,就是说可以一对一如y=2x,也可以多对1如y=x,但不能一对多如y=x,有些时候还以图像的形式考,我们就要看x=a与图像的交点唯一与否,唯一就是函数,不唯一就不是。
必须明晰努力学习一次函数的关键就是图像和性质要了解函数是由数到形,再由形到数,做到数、形的有机结合,这样才能更好地掌握一次函数的性质。
首先要了解一次函数是一条直线,其次要明确如果k﹥0,一次函数过第一、三象限(当b﹥0时,过第一、二、三象限,当b﹤0时,过第一、三、四象限),y随x的增大而增大;如果k﹤0,一次函数过第二、四象限(当b﹥0时,过第一、二、四象限,当b﹤0时过,第二、三、四象限),y随x的增大而减少。
必须认知一次函数和其它科学知识的联系一次函数和代数式以及方程有着密不可分的联系。
如一次函数和正比例函数仍然是函数,同时,等号的两边又都是代数式。
需要注意的是,与一般代数式有很大区别。
首先,一次函数和正比例函数都只能存在两个变量,而代数式可以是多个变量;其次,一次函数中的变量指数只能是1,而代数式中变量指数还可以是1以外的数。
另外,一次函数解析式也可以理解为二元一次方程。
掌控一次函数的解析式的特征1、一次函数解析式的结构特征:kx+b是关于x的一次二项式,其中常数b可以是任意实数,一次项系数k必须是非零数,k≠0,因为当k=0时,y=b(b是常数),由于没有一次项,这样的函数不是一次函数;而当b=0,k≠0,y=kx既是正比例函数,也是一次函数。
基准、以下函数关系中,哪些属一次函数,其中哪些又属正比例函数?(1)面积为10cm2的三角形的底a(cm)与这边上的高h(cm);(2)汽车每小时行40千米,高速行驶的路程s(千米)和时间t(小时).分析:确定函数是否为一次函数或正比例函数,就是看它们的解析式经过整理后与否合乎y=kx+b(k≠0)或y=kx(k≠0)形式,所以此题必须先写下函数解析式后答疑.解:(1)不是一次函数.(4)s=40t,s既是t的一次函数又是正比例函数.2、一次函数与正比例函数的区别与联系:(1)从解析式看看:y=kx+b(k≠0,b就是常数)就是一次函数;而y=kx(k≠0,b=0)就是正比例函数,似乎正比例函数就是一次函数的特例,一次函数就是正比例函数的推展。
一次函数如何求交点坐标

一次函数如何求交点坐标一次函数的交点坐标,听起来是不是有点复杂,其实吧,这个话题就像一碗热腾腾的汤,虽然成分繁杂,但喝上一口,瞬间就觉得舒服。
先说说什么是一条一次函数吧,简单来说,就是那种直线方程,像y = mx + b这种,m是斜率,b是截距。
想象一下,斜率就是斜坡的陡峭程度,截距嘛,就是这条线在y轴上碰到的那个点。
这条线的走势,就像人生,有上有下,有时候陡峭,有时候平缓。
怎么求交点坐标呢?这里就要引入另一条线了,可能是另一条一次函数,也可能是x轴或者y轴,嘿嘿,这时候就像两条河流在交汇,交点就是它们相遇的地方。
一般来说,交点就是把两条方程结合在一起,解出x和y的值。
你可能会问,这怎么做啊?其实挺简单的。
比如说,我们有两条线y = 2x + 1和y = x + 4。
我们只要把这两个方程的y值相等,就可以找到x的值。
简单说,就是2x + 1 = x + 4,这一来一往,化简一下,嘿,x的值就出来了。
得到x之后,别着急,我们还得把它代回去,求出y的值。
就像煮面条,水开了,面放进去,最后得出美味的面条。
这时候,把求得的x代入其中一条方程,算出y,就得到了交点的坐标。
交点坐标就像我们人生中的某个重要时刻,抓住它,就能更清楚地看清前路。
如果咱们遇到的两条线是平行的,怎么办呢?嘿,平行线就像两条永不相交的道路,永远不可能有交点。
这种情况下,交点的坐标就不存在了。
不过,别伤心,人生不就是这样吗,有时候有些路就是不该走嘛,咱们就踏踏实实走自己的路。
再说说特殊情况,如果一条线恰好与x轴或y轴重合,交点的求法就变得简单多了。
比如,y = 0的情况,交点就在x轴上,只需要解出x的值。
y轴上的交点就得看b的值,b就是截距。
记住了,y轴上的交点就是(0,b),简简单单,干脆利落。
说到这里,可能有朋友会问,怎么知道求交点的意义呢?其实吧,求交点不仅仅是数学上的运算,更多的是一种理解和把握。
就像我们生活中的选择,交点就代表着我们做出的决定,有些路的交叉可能是一次美好的相遇,而有些交点则是转折,让我们重新思考前进的方向。
一次函数的交点问题

一次函数的交点问题有时候数学题就像一块难啃的骨头,硬是咬不动,搞得你头大得跟天似的。
可是说实话,今天我们来聊聊一次函数的交点问题,听起来是不是很复杂?其实啊,不那么难,甚至可以说,挺简单的。
咱们就一起来把它搞明白,保证你看了之后,觉得哎,原来这事儿这么轻松!话说回来,数学最吸引人的地方,就是它总能像魔术一样把复杂的事情化繁为简,哪怕是最难懂的公式,背后也藏着不为人知的小秘密。
就像是你走进厨房看见一堆食材,脑袋里可能一片空白,但只要知道了诀窍,做出来的饭菜那叫一个美味可口!说到一次函数,它其实也没那么可怕。
咱们先从简单的开始:一次函数,就是形如( y = ax + b ) 的直线方程,听着是不是有点高大上?别急,咱们一点一点来。
这个公式背后的意思,就是描述了一个斜率为 ( a ),并且截距为 ( b ) 的直线。
就好像你走路,走得越快,斜率就越大,走得慢,斜率就小。
至于截距 ( b ),你可以理解成那条直线穿过的地方,也就是它和 y 轴的交点。
这就像你走进了一个新城市,那个 y 轴,就是你刚到达的地方。
你在这个城市的第一站,正是你遇到的这个交点。
交点问题来啦!你是不是一想交点就会想到两条线相交?没错,一次函数的交点就是两条直线相遇的地方。
比如说,咱们有两条直线,一个是 ( y = 2x + 3 ),另一个是( y = x + 1 ),它们会在哪儿相遇呢?好吧,这就像是两个人走到一起的过程。
你看看他们的走向是不是一样?显然,他们的速度不同,走得方向也不一样。
如果你想知道他们在哪儿相遇,那就得解个方程了。
说白了,就是把这两个公式联立,求出它们的交点坐标。
具体步骤就是:把两个方程的 ( y ) 设成相等。
为什么呢?因为交点就是两条线在同一个 ( x ) 和 ( y ) 坐标上相遇。
所以,咱们把 ( 2x + 3 = x + 1 ),然后解这个方程。
你看,是不是很简单?不过一开始可能有点生疏,但一旦上手了,做起来轻松得很。
一次函数交点知识点引入
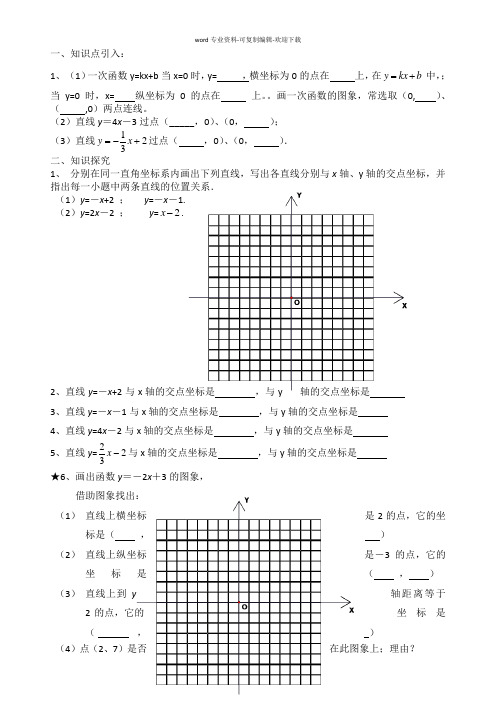
一、知识点引入:1、(1)一次函数y=kx+b 当x=0时,y= ,横坐标为0的点在 上,在y kx b =+中,;当y=0时,x= 纵坐标为0的点在 上。
画一次函数的图象,常选取(0, )、( ,0)两点连线。
(2)直线y =4x -3过点(_____,0)、(0, );(3)直线231+-=x y 过点( ,0)、(0, ). 二、知识探究1、 分别在同一直角坐标系内画出下列直线,写出各直线分别与x 轴、y 轴的交点坐标,并指出每一小题中两条直线的位置关系.(1)y =-x +2 ; y =-x -1.(2)y =2x -2 ; y =2-x .2、直线y =-x +2与x 轴的交点坐标是 ,与y 轴的交点坐标是3、直线y =-x -1与x 轴的交点坐标是 ,与y 轴的交点坐标是4、直线y =4x -2与x 轴的交点坐标是 ,与y 轴的交点坐标是5、直线y =232-x 与x 轴的交点坐标是 ,与y 轴的交点坐标是 ★6、画出函数y =-2x +3的图象,借助图象找出:(1) 直线上横坐标是2的点,它的坐标是( ,) (2) 直线上纵坐标是-3的点,它的坐标是( , )(3) 直线上到y 轴距离等于2的点,它的坐标是( , )(4)点(2、7)是否在此图象上;理由?(5)找出横坐标是-2的点,并标出其坐标;( , )(6)找出到x 轴的距离等于1的点,并标出其坐标;( , )(7)找出图象与x 轴和y 轴的交点,并标出其坐标。
( , )、( , )知识点总结:1、正比例函数的图象(kx y =的图象)是一条过(0,0),(1, k )的直线。
2、一次函数b kx y +=的图象是一条过(k b-,0),(0,b )的直线。
3、小结:函数y kx b =+的图像与坐标轴的两个交点为(b k-,0)和(0,b )函数y kx b =+的图像与坐标轴围成的三角形的面积为22b k。
三、例题讲解例1、直线21y x =-与x 轴的交点坐标是 ;与y 轴的交点坐标是 。
一次函数交点与表达式

一次函数D 交点与表达式【知识要点】1、一次函数与坐标轴的交点y=kx+b 与x 轴交点是(kb,0) y=kx+b 与y 轴交点是(0,b ) 2、求两个一次函数交点的方法:几何意义:直角坐标系中表示两个一次函数的两条直线的交点;求解方法:(1)联立两个一次函数解析式,得到二元一次方程组; (2)解二元一次方程组,求得交点坐标。
3、根据交点确定一次函数的解析式:(1)设出需确定的函数表达式(如y=kx ,y=kx+b );(2)把交点的坐标(有的需要转化)代入所设函数表达式; (3)求出待定系数的值;(4)把求出的待定系数的值代回所设的函数表达式确定的函数表达式。
【典型例题】例1 已知一次函数的图象过点A (2,-1)和点B ,其中点B 是另一条直线y =-21x +3与y 轴的交点,求这个一次函数的表达式.例2 已知直线l 与直线y =2x +1的交点的横坐标为2,与直线y =-x +8的交点的纵坐标为-7,求直线的表达式.例3 求经过原点及两条直线L 1:x-2y+2=0,L 2:2x-y-2=0的交点的直线的方程.例4 当k为何值时,直线y=kx+3,过直线2x-y+1=0与y=x+5的交点? 例5 判断下列各对直线的位置关系,如果相交,求出交点的坐标:(1)l1:x-y=0, l2:3x+3y-10=0;(2)l1:3x-y+4=0, l2:6x-2y=0;(3)l1:3x+4y-5=0, l2:6x+8y-10=0;例6 已知两条直线y1=2x-3和y2=5-x.(1)在同一坐标系内作出它们的图象;(2)求出它们的交点A坐标;(3)求出这两条直线与x轴围成的三角形ABC的面积;(4)k为何值时,直线2k+1=5x+4y与k=2x+3y的交点在每四象限.例7 已知一次函数y=kx+b的图像经过点(-2,5),且与y轴相交于点P,直线132y x=-+与y轴相交于Q点,点Q与点P关于x轴对称,求此一次函数解析式。
一次函数与反比例函数交点问题

一次函数与反比例函数交点问题
“一次函数与反比例函数交点问题”是微积分中常见的问题,也是解决各种应用问题的基础。
因此,对它的理解和掌握具有重要的意义。
一次函数通常表示为 y=ax+b,其中a为斜率,b为截距,x,y为变量;而反比例函数一般表示为 y=k/x,其中k 为一个常数,x和y为变量。
当一次函数与反比例函数在同一坐标系上同时存在时,它们之间必定存在一个交点。
这个交点可以通过对比两个函数的图像来求解,也可以通过利用微积分理论技巧来解决。
首先,设一次函数与反比例函数的方程分别为:
一次函数:y=ax+b
反比例函数:y=k/x
将两式相减,得:
ax+b-k/x=0
可以看出,由此得到的是一个二次方程式,其解的形式为:
x=(2bk±√D)/2a
其中D=4abk-b^2
若D<0,则没有实数根,即表明该一次函数与反比例函数没有交点;若D=0,则有一个实数根,即表明该一次函数与反比例函数只有一个交点;若D>0,则有两个实数根,即表明该一次函数与反比例函数有两个交点。
以上就是“一次函数与反比例函数交点问题”的详细说明。
如果要解决实际问题,应该先确定一次函数与反比例函数的方程,然后利用上述方法求解。
正比例函数与一次函数的交点题目[资料]
![正比例函数与一次函数的交点题目[资料]](https://img.taocdn.com/s3/m/9f479c5cce84b9d528ea81c758f5f61fb7362827.png)
反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.(2)判断正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中的交点个数可总结为:①当k1与k2同号时,正比例函数正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中有2个交点;②当k1与k2异号时,正比例函数正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中有0个交点.反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①二、四象限的角平分线Y=-X;②一、三象限的角平分线Y=X;对称中心是:坐标原点.反比例函数的性质(1)反比例函数y=xk(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.注意:反比例函数的图象与坐标轴没有交点.比例系数k的几何意义在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|2,且保持不变.反比例函数y=xk(k为常数,k≠0)的图象是双曲线,①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.用待定系数法求反比例函数的解析式要注意:(1)设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.(2)判断正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中的交点个数可总结为:①当k1与k2同号时,正比例函数正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中有2个交点;②当k1与k2异号时,正比例函数正比例函数y=k1x和反比例函数y=k2x在同一直角坐标系中有0个交点.(1)利用反比例函数解决实际问题①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.(2)跨学科的反比例函数应用题要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.(3)反比例函数中的图表信息题正确的认识图象,找到关键的点,运用好数形结合的思想.(1)应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能力和从实际问题向数学问题转化的能力.在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识.(2)数形结合类综合题利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.。
