六年级奥数-第5讲 浓度问题
六年级奥数.应用题.浓度问题

一、六年级奥数.应用题.浓度问题(1) 溶质“干货”、“纯货”——被溶解的物质 (2) 溶剂“溶质之外的物质”——用来溶解溶质的物质 (3) 溶液溶液=溶质+溶剂——溶质与溶质的混合体 (4) 浓度——溶质的量占溶液的量的百分比二、 基本方法(1) 寻找不变量,按基本关系或比例求解 (2) 浓度三角(如右图所示) (3) 列方程或方程组求解(1) 重点:浓度问题中的基本关系,不变量的寻找,浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用一、 抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到, 那么这种溶液的食盐浓度为多少?=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-z z-yx-z乙溶液浓度y %甲溶液浓度x %混合浓度z%一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【例2】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水?【例3】买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?1000千克葡萄含水率为96.5%,一周后含水率降为96%,这些葡萄的质量减少了千克.【例4】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克?将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克?【例6】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【例7】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克,混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【例8】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升?甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?【例9】某班有学生48人,女生占全班的37.5%,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生?小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?【例10】有两包糖,第一包糖由奶糖和水果糖组成,其中14为奶糖;第二包糖由酥糖和水果糖组成,其中15为酥糖.将两包糖混合后,水果糖占78%,那么奶糖与酥糖的比例是________.某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?三、综合运用各种方法解决多溶液、多次配比问题【例11】甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
六年级奥数应用题浓度问题

六年级奥数应用题浓度问题Company number:【0089WT-8898YT-W8CCB-BUUT-202108】一、 基本概念与关系 (1) 溶质 “干货”、“纯货”——被溶解的物质(2) 溶剂“溶质之外的物质”——用来溶解溶质的物质(3) 溶液溶液=溶质+溶剂——溶质与溶质的混合体 (4) 浓度——溶质的量占溶液的量的百分比 二、 基本方法(1) 寻找不变量,按基本关系或比例求解(2) 浓度三角(如右图所示)(3) 列方程或方程组求解(1) 重点:浓度问题中的基本关系,不变量的寻找,浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用 重难点 知识框架浓度问题 =100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-z z-y x-z乙溶液浓度y %浓度x %混合浓度z%例题精讲一、抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克【例 2】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖【巩固】浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水【例 3】买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份【巩固】1000千克葡萄含水率为%,一周后含水率降为96%,这些葡萄的质量减少了千克.【例 4】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是________.【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例 5】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克【例 6】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍【例 7】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克,混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克【例 8】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升【巩固】甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样【例 9】某班有学生48人,女生占全班的%,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支【例 10】有两包糖,第一包糖由奶糖和水果糖组成,其中14为奶糖;第二包糖由酥糖和水果糖组成,其中15为酥糖.将两包糖混合后,水果糖占78%,那么奶糖与酥糖的比例是________.【巩固】某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人三、综合运用各种方法解决多溶液、多次配比问题【例 11】 甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
六年级奥数应用题浓度问题

一、 六年级奥数应用题浓度问题(1) 溶质 “干货”、“纯货”——被溶解的物质(2) 溶剂 “溶质之外的物质”——用来溶解溶质的物质(3) 溶液 溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度——溶质的量占溶液的量的百分比二、 基本方法(1) 寻找不变量,按基本关系或比例求解 (2) 浓度三角(如右图所示) (3) 列方程或方程组求解混合浓度z%x-zz-y甲溶液 浓度x%乙溶液 浓度y%z-y : x-z(1) 重点:浓度问题中的基本关系,不变量的寻找,浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与甲方溶程液组质的量综合: 运乙用溶液质量一、 抓住不变量和浓度基本关系解决问题【例 1】某种溶液由 40 克食盐浓度 15%的溶液和 60 克食盐浓度 10%的溶液混合后再蒸发 50 克水1 / 12得到, 那么这种溶液的食盐浓度为多少? 一容器内有浓度为 25%的糖水,若再加入 20 千克水,则糖水的浓度变为 15%,问这个容器内原来含有糖多少千克? 【例 2】 浓度为 20%的糖水 40 克,要把它变成浓度为 40%的糖水,需加多少克糖?浓度为 10%,重量为 80 克的糖水中,加入多少克水就能得到浓度为 8%的糖水? 【例 3】 买来蘑菇 10 千克,含水量为 99%,晾晒一会儿后,含水量为 98%,问蒸发掉多少水份?1000 千克葡萄含水率为 96.5%,一周后含水率降为 96%,这些葡萄的质量减少了 千克. 2 / 12【例 4】 将含农药 的药液,加入一定量的水以后,药液含药 药的百分比是________.,如果再加入同样多的水,药液含一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为 15%;第二次又加入同样多的水,盐水 的含盐百分比变为 12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、 通过浓度三角解决浓度和实际生活中的配比问题【例 5】 有浓度为 20%的盐水 300 克,要配制成 40%的盐水,需加入浓度为 70%的盐水多少克?将 75%的酒精溶液 32 克稀释成浓度为 40%的稀酒精,需加入水多少克?【例 6】 瓶中装有浓度为 的酒精溶液 克,现在又分别倒入 克和 克的 、 两种酒精溶 液,瓶中的浓度变成了 .已知 种酒精溶液浓度是 种酒精溶液浓度的 倍,那么 种 酒精溶液的浓度是百分之几?3 / 12有两种溶液,甲溶液的酒精浓度为 ,盐浓度为 ,乙溶液中的酒精浓度为 ,盐浓度为 .现在有甲溶液 千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的 3 倍?【例 7】 甲瓶中酒精的浓度为 ,乙瓶中酒精的浓度为 瓶酒精各用去 升后再混合,则混合后的浓度是 升?,两瓶酒精混合后的浓度是 .如果两 .问原来甲、乙两瓶酒精分别有多少纯酒精含量分别为 、 的甲、乙两种酒精混合后的纯酒精含量为 .如果每种酒精都多取 克,混合后纯酒精的含量变为 .求甲、乙两种酒精原有多少克?【例 8】 甲种酒精纯酒精含量为 ,乙种酒精纯酒精含量为 ,混合后纯酒精含量为 .如果每种酒精取的数量比原来都多取 升,混合后纯酒精含量为.第一次混合时,甲、乙两种酒精均取了多少升?甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为 的硫酸溶液 600 千克,乙容器中装有浓度为 的硫酸溶液 400 千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶4 / 12液的浓度一样?【例 9】 某班有学生 48 人,女生占全班的 37.5%,后来又转来女生若干人,这时人数恰好是占全班人数 的 40%,问转来几名女生?小明到商店买红、黑两种笔共 66 支.红笔每支定价 5 元,黑笔每支定价 9 元.由于买的数量较多,商 店就给予优惠,红笔按定价 付钱,黑笔按定价 付钱,如果他付的钱比按定价少付了 ,那么他买了红笔多少支?【例 10】 有两包糖,第一包糖由奶糖和水果糖组成,其中 为奶糖;第二包糖由酥糖和水果糖组成,其 中 为酥糖.将两包糖混合后,水果糖占 ,那么奶糖与酥糖的比例是________.某商品 76 件,出售给 33 位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价 ,买 三件降价 ,最后结算,平均每件恰好按原定价的 出售.那么买三件的顾客有多少人? 5 / 12三、 综合运用各种方法解决多溶液、多次配比问题【例 11】 甲容器中有纯酒精 11 升,乙容器中有水 15 升,第一次将甲容器中的一部分纯酒精倒入乙容 器,使酒精与水混合。
【奥数难题】浓度问题-----五分钟学会

【奥数难题】浓度问题-----五分钟学会浓度问题是⼩学六年级⼩升初考试的常见题型,如何理解浓度问题,我们⼀起来看⼀看。
1、常规浓度问题(1)基本知识点:溶质:被溶解的物质溶剂:溶解别的物质的东西溶液:溶质和溶剂的混合物溶液质量(体积)=溶质质量(体积)+溶剂质量(体积)浓度=溶质质量(体积)÷溶液的质量(体积)×100%(2)记忆⽅法:溶质:男⽣(被欺负的同学)溶剂:⼥⽣(欺负男⽣的同学)溶液:班级班级⼈数=男⽣⼈数+⼥⽣⼈数浓度=男⽣⼈数÷全班⼈数×100%注:浓度问题本质上也是分百应⽤题(3)常规解法:抓住不变量①根据不变量列算式求解②若题⽬逻辑较为复杂可根据不变量列⽅程求解2、复杂混合类浓度问题(1)浓度⼗字: 浓度为x%的甲溶液和浓度为y%的⼄溶液要配成浓度为z%的溶液需要甲和⼄的总量之⽐等于对应的浓度差之⽐(假设甲的浓度⾼)如10%的甲溶液与5%的⼄溶液配成8%的溶液需要这两种溶液的总量⽐为________所以甲、⼄的总量之⽐为3%:2%=3:2注:多次混合问题有时候⽤⽅程效果更好【学以致⽤】1、当含盐为30%的60克盐⽔蒸发为含盐40%的盐⽔时,盐⽔重量是_________克。
2、⼀容器内有浓度为25%的糖⽔,若再加⼊20千克⽔,则糖⽔的浓度变为15%,问这个容器内原来含有糖__________千克。
3、⽤浓度为45%和5%的两种盐⽔配制成浓度为30%的盐⽔4千克,需要这两种盐⽔各多少千克?4、5%的盐⽔100克,加上10%和15%的盐⽔100克,变成9%的盐⽔200克,加了____________克10%的盐⽔。
【答案解析】1、当含盐为30%的60克盐⽔蒸发为含盐40%的盐⽔时,盐⽔重量是_________克。
【分析】本题难点在于发现溶质盐的重量不变初学者可以这样理解:男⽣占30%的班级有60⼈,当⾛了部分⼥⽣后男⽣所占⽐例变为40%,问此时班级有多少⼈?盐重量(男⽣⼈数)=60×30%=18克盐⽔重量(全班⼈数)=18÷40%=45克(量率对应)【答案】452、⼀容器内有浓度为25%的糖⽔,若再加⼊20千克⽔,则糖⽔的浓度变为15%,问这个容器内原来含有糖__________千克。
六年级奥数--《浓度问题》-个性化辅导讲义

一、专题简析在百分数应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量/溶液质量×100%=溶质质量/(溶质质量+溶剂质量)×100% 解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。
要根据题目的条件和问题逐一分析,也可以分步解答。
二、例题简析与练习【例题1】有含糖量为7%的糖水600克,要使其含糖量加大到10%,需要再加入多少克糖?【思路导航】根据题意,在7%的糖水中加糖就改变了原来糖水的浓度,糖的质量增加了,糖水的质量也增加了,但水的质量并没有改变。
因此,可以先根据原来糖水中的浓度求出水的质量,再根据后来糖水中的浓度求出现在糖水的质量,用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。
原来糖水中水的质量:600×(1-7%)=558(克)现在糖水的质量:558÷(1-10%)=620(克)加入糖的质量:620-600=20(克)练习一1.现在有浓度为20%的糖水300克,要把它变成浓度为40%的糖水,需要加糖多少克?2.有含盐15%的盐水20千克,要使盐水的浓度为20%,需加盐多少千克?【例题2】一种35%的新农药,如稀释到1.75%时,治虫最有效。
用多少千克浓度为35%的农药加多少千克水,才能配成1.75%的农药800千克?【思路导航】把浓度高的溶液经添加溶剂变为浓度低的溶液的过程称为稀释。
六年级奥数应用题浓度问题

六年级奥数应用题浓度问题TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-一、 基本概念与关系(1) 溶质 “干货”、“纯货”——被溶解的物质(2) 溶剂“溶质之外的物质”——用来溶解溶质的物质(3) 溶液 溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度——溶质的量占溶液的量的百分比二、 基本方法(1) 寻找不变量,按基本关系或比例求解(2) 浓度三角(如右图所示)(3) 列方程或方程组求解(1) 重点:浓度问题中的基本关系,不变量的寻找,浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用例题精讲 重难点 知识框架浓度问题 =100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-z z-y x-z 乙溶液浓度y %浓度x %混合浓度z%一、抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【例 2】【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【例 3】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?【巩固】浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水?【例 4】买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【巩固】1000千克葡萄含水率为%,一周后含水率降为96%,这些葡萄的质量减少了千克.【例 5】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是________.【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例 6】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克?【例 7】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【例 8】【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【巩固】【例 9】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【例 10】【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克,混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【巩固】【例 11】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升?【例 12】【巩固】甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?【巩固】【例 13】某班有学生48人,女生占全班的%,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生?【例 14】【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?【巩固】【例 15】有两包糖,第一包糖由奶糖和水果糖组成,其中14为奶糖;第二包糖由酥糖和水果糖组成,其中15为酥糖.将两包糖混合后,水果糖占78%,那么奶糖与酥糖的比例是________.【巩固】 某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?【巩固】三、 综合运用各种方法解决多溶液、多次配比问题【例 16】 甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
小学生六年级奥数题-浓度问题

小学生六年级奥数题:浓度问题
教案是教师为顺利而有效地开展教学活动,根据课程标准,教学大纲和教科书要求及学生的实际情况,以课时或课题为单位,对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书,包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等,下面是由小编为大家整理的范文模板,仅供参考,欢迎大家阅读.
瓶子里装有浓度为_%的酒精1_0克.现在又分别倒入1_克和4_克的A、B两种酒精,瓶子里的酒精浓度变为_%.已知A种酒精的浓度是B种酒精的2倍,求A 种酒精的浓度.
答案与解析:
依题意,A种酒精浓度是B种酒精的2倍.设B种酒精浓度为_%,则A种酒精浓度为2_%.A种酒精溶液_O克,因此1__2_%为1_克酒精溶液中含纯酒精的克数.B种酒精溶液40O克,因此4___%为4_克酒精溶液中含纯酒精的克数.
解:设B种酒精浓度为_%,则A种酒精的浓度为2_%.
小学生六年级奥数题:浓度问题.到电脑,方便收藏和打印:。
小学六年级奥数系列讲座:浓度问题(含答案解析)

浓度问题一、知识要点在百分数应用题中有一类叫溶液配比问题,即浓度问题。
我们知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值,通常用百分数表示,即,浓度=溶质质量/溶液质量×100%=溶质质量/(溶质质量+溶剂质量)×100%解答浓度问题,首先要弄清什么是浓度。
在解答浓度问题时,根据题意列方程解答比较容易,在列方程时,要注意寻找题目中数量问题的相等关系。
浓度问题变化多,有些题目难度较大,计算也较复杂。
要根据题目的条件和问题逐一分析,也可以分步解答。
二、精讲精练【例题1】有含糖量为7%的糖水600克,要使其含糖量加大到10%,需要再加入多少克糖?【思路导航】根据题意,在7%的糖水中加糖就改变了原来糖水的浓度,糖的质量增加了,糖水的质量也增加了,但水的质量并没有改变。
因此,可以先根据原来糖水中的浓度求出水的质量,再根据后来糖水中的浓度求出现在糖水的质量,用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。
原来糖水中水的质量:600×(1-7%)=558(克)现在糖水的质量:558÷(1-10%)=620(克)加入糖的质量:620-600=20(克)答:需要加入20克糖。
练习1:1.现在有浓度为20%的糖水300克,要把它变成浓度为40%的糖水,需要加糖多少克?2.有含盐15%的盐水20千克,要使盐水的浓度为20%,需加盐多少千克?3.有甲、乙两个瓶子,甲瓶里装了200毫升清水,乙瓶里装了200毫升纯酒精。
第一次把20毫升纯酒精由乙瓶倒入甲瓶,第二次把甲瓶中20毫升溶液倒回乙瓶,此时甲瓶里含纯酒精多,还是乙瓶里含水多?【例题2】一种35%的新农药,如稀释到1.75%时,治虫最有效。
六年级奥数.应用题.浓度问题
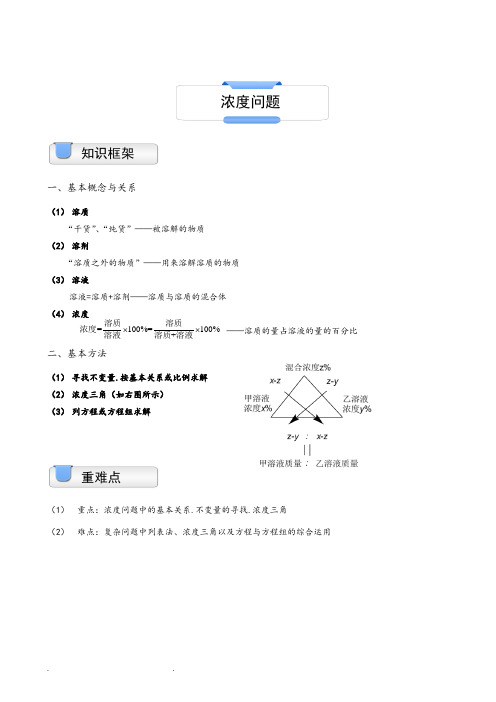
一、基本概念与关系(1) 溶质“干货”、“纯货”——被溶解的物质(2) 溶剂“溶质之外的物质”——用来溶解溶质的物质(3) 溶液溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度——溶质的量占溶液的量的百分比 二、基本方法(1) 寻找不变量.按基本关系或比例求解(2) 浓度三角(如右图所示)(3) 列方程或方程组求解(1) 重点:浓度问题中的基本关系.不变量的寻找.浓度三角(2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用重难点 知识框架浓度问题=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液例题精讲一、抓住不变量和浓度基本关系解决问题【例1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到.那么这种溶液的食盐浓度为多少?【巩固】一容器内有浓度为25%的糖水.若再加入20千克水.则糖水的浓度变为15%.问这个容器内原来含有糖多少千克?【例2】浓度为20%的糖水40克.要把它变成浓度为40%的糖水.需加多少克糖?【巩固】浓度为10%.重量为80克的糖水中.加入多少克水就能得到浓度为8%的糖水?【例3】买来蘑菇10千克.含水量为99%.晾晒一会儿后.含水量为98%.问蒸发掉多少水份?【巩固】1000千克葡萄含水率为96.5%.一周后含水率降为96%.这些葡萄的质量减少了千克.【例4】将含农药30%的药液.加入一定量的水以后.药液含药24%.如果再加入同样多的水.药液含药的百分比是________.【巩固】一杯盐水.第一次加入一定量的水后.盐水的含盐百分比变为15%;第二次又加入同样多的水.盐水的含盐百分比变为12%.第三次再加入同样多的水.盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20%的盐水300克.要配制成40%的盐水.需加入浓度为70%的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精.需加入水多少克?【例6】瓶中装有浓度为15%的酒精溶液1000克.现在又分别倒入100克和400克的A、B两种酒精溶液.瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍.那么A种酒精溶液的浓度是百分之几?【巩固】有两种溶液.甲溶液的酒精浓度为15%.盐浓度为10%.乙溶液中的酒精浓度为45%.盐浓度为5%.现在有甲溶液1千克.那么需要多少千克乙溶液.将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【例7】甲瓶中酒精的浓度为70%.乙瓶中酒精的浓度为60%.两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合.则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克.混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【例8】甲种酒精纯酒精含量为72%.乙种酒精纯酒精含量为58%.混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升.混合后纯酒精含量为63.25%.第一次混合时.甲、乙两种酒精均取了多少升?【巩固】甲、乙两只装满硫酸溶液的容器.甲容器中装有浓度为8%的硫酸溶液600千克.乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中.才能使这两个容器中的硫酸溶液的浓度一样?【例9】某班有学生48人.女生占全班的37.5%.后来又转来女生若干人.这时人数恰好是占全班人数的40%.问转来几名女生?【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元.黑笔每支定价9元.由于买的数量较多.商店就给予优惠.红笔按定价85%付钱.黑笔按定价80%付钱.如果他付的钱比按定价少付了18%.那么他买了红笔多少支?【例10】有两包糖.第一包糖由奶糖和水果糖组成.其中14为奶糖;第二包糖由酥糖和水果糖组成.其中15为酥糖.将两包糖混合后.水果糖占78%.那么奶糖与酥糖的比例是________.【巩固】某商品76件.出售给33位顾客.每位顾客最多买三件.如果买一件按原定价.买两件降价10%.买三件降价20%.最后结算.平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?三、综合运用各种方法解决多溶液、多次配比问题【例11】甲容器中有纯酒精11升.乙容器中有水15升.第一次将甲容器中的一部分纯酒精倒入乙容器.使酒精与水混合。
六年级奥数_浓度问题课件

六年级奥数 浓度问题讲义一、专题引导:什么是浓度呢?(以糖水为例,将糖溶于水中得到糖水,这里糖叫溶质,水叫溶剂,糖水叫溶液。
)三者之间关系:浓度= ×100%=×100% 二、典型例题例1、有浓度为30%的酒精溶液若干,添加了一定数量的水后稀释成浓度为24%的酒精溶液,如果再加入同样的水,那么酒精溶液的浓度变为多少? 思路导航:稀释问题是溶质的重量是不变量。
例2、有浓度为7%的盐水600克,要使盐水的浓度加大到10%,需要加盐多少克?思路导航:溶剂重理不变。
[练习]海水中盐的含量为5%,在40千克海水中,需加多少千克淡水才使海水中盐的含量为2%?例3、在浓度为50%的硫酸溶液100千克中,再加入多少千克浓度为5%的硫酸溶液,就可以配制成浓度为25%的硫酸溶液?思路导航:混合前两种溶液中所含溶质的重量、溶剂的重量、溶液的重量分别等于混合后溶液中所含溶质的重量、溶剂的重量、溶液的重量。
[练习]配制硫酸含量为20%的硫酸溶液1000克,需要用硫酸含量为18%和23%的硫酸溶液各多少克?溶质溶液溶质溶质+溶剂例4、从装满100克浓度为80%的盐水杯中倒出40克盐水,再用清水将杯加满;再倒出40克盐水,然后再用清水将杯加满,如此反复三次后,杯中盐水的浓度是多少?思路导航:反复三次后,杯中又已装满,即最后杯中盐水的重量仍为100克,由此;问题的关键是求出如此反复三次后还剩盐多少克?[练习]①有盐水若干升,加入一定量水后,盐水浓度降到3%,又加入同样多的水后,盐水浓度又降到2%,再加入同样多的水,此时浓度是多少呢?又问未加入水时盐水浓度是多少?②有含糖6%的糖水900克,要使其含糖量加大到10%,需加糖多少克?比和比例应用题例4、乘坐某路汽车成年人票价3元,儿童票价2元,残疾人票价1元,某天乘车的成年人、儿童和残疾人的人数比是5 0:20:1,共收得票款26740元,这天乘车中成年人、儿童和残疾人各有多少人?思路导航:单价比:成年人:儿童:残疾人=3:2:1人数比:50:20:1[练习]甲乙两人走同一段路,甲要20分钟,乙要15分钟,现在甲、乙两人分别同时从相距840米的两地相向而行,相遇时,甲、乙各走了多少米?例5、“希望小学”搞了一次募捐活动,她们用募捐所得的钱购买了甲、乙、丙三种商品,这三种商品的单价分别为30元、15元和10元。
六年级奥数 应用题 浓度问题

一、基本概念与关系 (1) 溶质“干货”、“纯货”——被溶解的物质(2) 溶剂“溶质之外的物质”——用来溶解溶质的物质(3) 溶液 溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度 ——溶质的量占溶液的量的百分比二、基本方法 (1) 寻找不变量,按基本关系或比例求解 (2) 浓度三角(如右图所示)(3) 列方程或方程组求解(1)重点:浓度问题中的基本关系,不变量的寻找,浓度三角 (2) 难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用 重难点知识框架浓度问题 =100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-zz-y x-z乙溶液浓度y %浓度x %混合浓度z%例题精讲一、抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【例 2】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?【巩固】浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水?【例 3】买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【巩固】1000千克葡萄含水率为96.5%,一周后含水率降为96%,这些葡萄的质量减少了千克.【例 4】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是________.【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例 5】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克?【例 6】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【例 7】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克,混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【例 8】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升?【巩固】甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?【例 9】某班有学生48人,女生占全班的37.5%,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生?【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?【例 10】有两包糖,第一包糖由奶糖和水果糖组成,其中14为奶糖;第二包糖由酥糖和水果糖组成,其中15为酥糖.将两包糖混合后,水果糖占78%,那么奶糖与酥糖的比例是________.【巩固】某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?三、综合运用各种方法解决多溶液、多次配比问题【例 11】甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
六年级奥数应用题浓度问题

六年级奥数应用题浓度问题The pony was revised in January 2021一、 基本概念与关系(1) 溶质“干货”、“纯货”——被溶解的物质(2) 溶剂 “溶质之外的物质”——用来溶解溶质的物质(3) 溶液 溶液=溶质+溶剂——溶质与溶质的混合体(4) 浓度 ——溶质的量占溶液的量的百分比二、 基本方法(1) 寻找不变量,按基本关系或比例求解(2) 浓度三角(如右图所示)知识框架 浓度问题 =100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-z z-yx-z 乙溶液浓度y %浓度x %混合浓度z%(3)列方程或方程组求解重难点(1)重点:浓度问题中的基本关系,不变量的寻找,浓度三角(2)难点:复杂问题中列表法、浓度三角以及方程与方程组的综合运用例题精讲一、抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【例 2】【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【例 3】浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?【巩固】浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水?【例 4】买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【巩固】1000千克葡萄含水率为%,一周后含水率降为96%,这些葡萄的质量减少了千克.【例 5】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是________.【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例 6】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克?【巩固】将75%的酒精溶液32克稀释成浓度为40%的稀酒精,需加入水多少克?【例 7】瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【例 8】【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【巩固】【例 9】甲瓶中酒精的浓度为70%,乙瓶中酒精的浓度为60%,两瓶酒精混合后的浓度是66%.如果两瓶酒精各用去5升后再混合,则混合后的浓度是66.25%.问原来甲、乙两瓶酒精分别有多少升?【例 10】【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%.如果每种酒精都多取20克,混合后纯酒精的含量变为45%.求甲、乙两种酒精原有多少克?【巩固】【例 11】甲种酒精纯酒精含量为72%,乙种酒精纯酒精含量为58%,混合后纯酒精含量为62%.如果每种酒精取的数量比原来都多取15升,混合后纯酒精含量为63.25%.第一次混合时,甲、乙两种酒精均取了多少升?【例 12】【巩固】甲、乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.均取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?【巩固】【例 13】某班有学生48人,女生占全班的%,后来又转来女生若干人,这时人数恰好是占全班人数的40%,问转来几名女生?【例 14】【巩固】小明到商店买红、黑两种笔共66支.红笔每支定价5元,黑笔每支定价9元.由于买的数量较多,商店就给予优惠,红笔按定价85%付钱,黑笔按定价80%付钱,如果他付的钱比按定价少付了18%,那么他买了红笔多少支?【巩固】【例 15】有两包糖,第一包糖由奶糖和水果糖组成,其中14为奶糖;第二包糖由酥糖和水果糖组成,其中15为酥糖.将两包糖混合后,水果糖占78%,那么奶糖与酥糖的比例是________.【巩固】某商品76件,出售给33位顾客,每位顾客最多买三件.如果买一件按原定价,买两件降价10%,买三件降价20%,最后结算,平均每件恰好按原定价的85%出售.那么买三件的顾客有多少人?【巩固】三、综合运用各种方法解决多溶液、多次配比问题【例 16】甲容器中有纯酒精11升,乙容器中有水15升,第一次将甲容器中的一部分纯酒精倒入乙容器,使酒精与水混合。
小学六年级奥数题及答案解析:浓度问题

小学六年级奥数题及答案解析:浓度问题1.浓度问题2.浓度应用题乙两只装满硫酸溶液的容器,甲容器中装有浓度为8%的硫酸溶液600千克,乙容器中装有浓度为40%的硫酸溶液400千克.各取多少千克分别放入对方容器中,才能使这两个容器中的硫酸溶液的浓度一样?由题意知,从甲、乙两容器中各取出一定量的溶液放入对方容器中,最终要达到两容器中溶液的浓度相等,在这个变化过程中,两容器中溶液的重量并没有改变。
不妨设从甲、乙两容器中各取出硫酸溶液x千克放入对方容器中,可使甲、乙两容器中硫酸溶液的浓度相等.这时甲容器中硫酸的重量可表示为(600-x)8%+x 40%=48+32%x.甲容器中溶液的浓答:应从两容器中各取出240千克溶液放入对方容器中,才能使两容器中硫酸溶液的浓度相同。
上述问题还可以这样考虑:由于交换前后两容器中溶液的重量均没有改变,而交换一定量的硫酸溶液其目的是将原来两容器中溶液的浓度由不同变为相同,而且交换前后两容器内溶液的重量之和也没有改变,根据这个条件我们可以先计算出两容器中的溶液浓度达到相等时的数值,从而再计算出应交换的溶液的量:甲容器中纯硫酸的重量为600 8%=48(千克);乙容器中纯硫酸的重量为400 40%=160(千克);两容器中纯硫酸的重量和为48+160=208千克,硫酸溶液的重量和为600+400=1000千克。
两容器中溶液混合后浓度为208 1000=20.8%。
所以应交换的硫酸溶液的量为:(600 20.8%-600 8%)(40%-8%)=240(千克)答:应从两容器中各取出240千克放入对方容器中,才能使两容器中硫酸溶液的浓度一样。
3.应用题育红小学四年级学生比三年级学生多25%,五年级学生比四年级学生少10%,六年级学生比五年级学生多10%。
如果六年级学生比三年级学生多38人,那么三至六年级共有多少名学生?分析:以三年级学生人数为标准量,则四年级是三年级的125%,五年级是三年级的125%(1-10%),六年级是三年级的125%(1-10%)(1+10%)。
小学六年级奥数浓度问题习题及解答

小学六年级奥数浓度问题习题及解答糖与糖水重量的比值叫做糖水的浓度;盐与盐水的重量的比值叫做盐水的浓度。
我们习惯上把糖、盐、叫做溶质(被溶解的物质),把溶解这些物质的液体,如水、汽油等叫做溶剂。
把溶质和溶剂混合成的液体,如糖水、盐水等叫做溶液。
一些与浓度的相关的应用题,叫做浓度问题。
浓度问题有下面关系式:浓度=溶质质量÷溶液质量溶质质量=溶液质量×浓度溶液质量=溶质质量÷浓度溶液质量=溶质质量+溶剂质量溶剂质量=溶液重量×(1–浓度)例1、浓度为25%的盐水120千克,要稀释成浓度为10%的盐水,应该怎样做?加水稀释后,含盐量不变。
所以要先求出含盐量,再根据含盐量求得稀释后盐水的重量,进而求得应加水多少克。
120×25%÷10%-120=180克例2、浓度为70%的酒精溶液500克与浓度为50%酒精溶液300克,混合后所得到的酒精溶液的浓度是多少?要求混合后的溶液浓度,需要知道混合后溶液的总重量及所含纯酒精的重量。
(500×70%+300×50%)÷(500+300)=62.5%例3、有含盐8%的盐水40千克,要配制含盐20%的盐水100千克需加水和盐各多少千克?根据“要配制含盐20%的盐水100千克”可求得新的盐水中盐和水的重量。
加盐多少千克:100×20%-40×8%=16.8千克加水多少千克:100-40-16.8=33.2千克【篇二】附自习题1、浓度为25%的盐水60克,要稀释成浓度为6%的盐水,应该怎么做?(提示:浓度变低,说明加了水,盐不变。
)2、现有浓度为20%的糖水350克,要把它变成浓度为30%的糖水,需加糖多少克?(提示:浓度增加,说明加了糖,水不变。
)3、有含盐8%的盐水40千克,要配制含盐20%的盐水100千克,需加入的盐水浓度为百分之几?(提示:其实就是算出水和盐分别加了多少,参考上面例3.)4、浓度为60%的酒精溶液200克,与浓度为30%的酒精溶液300克,混合后所得到的酒精溶液的浓度是多少?(参考例2)5、在100千克浓度为50%的盐水中,再加入多少千克浓度为5%的盐水就能够配制成浓度为25%的盐水?【篇三】在浓度问题的解决中,我们经常能够使用“浓度三角”。
浓度问题六年级应用题奥数

浓度问题六年级应用题奥数
浓度问题是奥数中常见的应用题之一,主要涉及到溶液的配制和浓度计算。
这类问题通常需要学生掌握溶液的基本概念、浓度的计算公式以及一些实际问题的解决技巧。
在解决浓度问题时,首先需要明确题目中所涉及到的溶液种类和数量,以及最终需要配制的溶液的浓度要求。
然后,根据题目中给出的信息,计算出各种溶液的质量和体积,并计算出它们的浓度。
最后,通过比较不同溶液的浓度和体积,确定出最终需要加入的溶液的种类和数量,以达到所需的浓度要求。
例如,假设有100毫升的盐水,其浓度为5%,现在需要将其稀释成2%的盐水。
那么,需要加入多少水呢?
首先,计算出100毫升的盐水中的盐的质量:100毫升 × 5% = 5克。
然后,计算出稀释后的盐水的总质量:5克 / 2% = 250克。
接着,计算出需要加入的水的体积:250克 - 100克 = 150毫升。
因此,需要加入150毫升的水来将100毫升的盐水稀释成2%的盐水。
解决浓度问题需要注意理解题目中的信息,灵活运用浓度计算公式,同时结合实际情况进行分析和计算。
六年级奥数专题-浓度问题

奥数专题-浓度问题
【题型概述】
%100⨯=
溶液质量
溶质质量溶液的浓度 【典型例题】
1、把20克糖放入80克水中进行溶解,溶解后的糖水浓度是多少?
2、小林将50克糖放进250克水中进行溶解,后来又加入了100克水,这时候糖水的浓度是多少?
【拓展提高】
3、将浓度是20%的酒精溶液100克与浓度30%的酒精溶液300克混合,混合后的酒精溶液浓度是多少?
【奥赛训练】
4、将浓度是15%的酒精溶液100克与浓度是24%的酒精溶液200克混合,混合后的酒精溶液浓度是多少?
【典型例题】
1、一种盐水的浓度是20%,加入800克水后,它的浓度变成12%,这种盐水溶液原来有多
少克?
2、一种糖水的浓度是25%,加入30克糖后,它的浓度变为15%,这种糖水溶液原来有多
少克?
3、要配置0.15%的氨水1000千克,需要向多少千克浓度为10%的氨水中加入多少千克的
水才能配成?
【拓展提高】
有一种浓度为8%的酒精溶液400克,要使酒精溶液的浓度变为12%,该怎么办?
【奥赛训练】
有含盐10%的盐水45千克,要变为含盐15%的盐水,需要加盐多少千克?。
六年级奥数浓度问题含答案

浓度问题知识框架一、 基本概念与关系(1) 溶质“干货”、“纯货”——被溶解的物质 (2) 溶剂“溶质之外的物质”——用来溶解溶质的物质 (3) 溶液溶液=溶质+溶剂——溶质与溶质的混合体 (4) 浓度——溶质的量占溶液的量的百分比二、 基本方法(1) 寻找不变量,按基本关系或比例求解 (2) 浓度三角(如右图所示)(3) 列方程或方程组求解重难点(1)(2)例题精讲一、 抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到, 那么这种溶液的食盐浓度为多少?【考点】浓度问题 【难度】2星 【题型】解答【解析】 两种配置溶液共含食盐40×15%+60×10%=12克,而溶液质量为40+60-50=50克,所以这种溶液的浓度为12÷50=24%.=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-z y %浓度x 混合浓度z%【巩固】 一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【考点】浓度问题 【难度】2星 【题型】解答 【解析】 100100207.51525⎛⎫÷-= ⎪⎝⎭. 所以原来含有糖7.5千克.【答案】7.5【例 2】 浓度为20%的糖水40克,要把它变成浓度为40%的糖水,需加多少克糖?【考点】浓度问题 【难度】2星 【题型】解答【解析】 浓度为20%,含糖40×20%=8(克),有水40- 8= 32(克).如果要变成浓度为40%,32克水中,应该含有的糖为:32÷(1-40%)-32=1213(克),需加糖112181333-=(克).【答案】1133【巩固】 浓度为10%,重量为80克的糖水中,加入多少克水就能得到浓度为8%的糖水?【考点】浓度问题 【难度】2星 【题型】解答【解析】 浓度10%,含糖 80×10%= 8(克),有水80-8=72(克).如果要变成浓度为8%,含糖8克,糖和水的总重量是8÷8%=100(克),其中有水100-8=92(克).还要加入水 92- 72= 20(克).【答案】20【例 3】 买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【考点】浓度问题【难度】2星 【题型】解答【解析】 晾晒只是使蘑菇里面的水量减少了,蘑菇里其它物质的量还是不变的,所以本题可以抓住这个不变量来解.原来鲜蘑菇里面其它物质的含量为()10199%0.1⨯-=千克,晾晒后蘑菇里面其它物质的含量还是0.1千克,所以晾晒后的蘑菇有()0.1198%5÷-=千克.【巩固】1000千克葡萄含水率为96.5%,一周后含水率降为96%,这些葡萄的质量减少了千克.【考点】浓度问题【难度】2星【题型】填空【解析】因为减少的是水的质量,其它物质的质量没有变化,设葡萄糖质量减少了x,则有⨯-=-⨯-,解得125x1000(196.5%)(1000)(196%)x=.【答案】125【例 4】将含农药30%的药液,加入一定量的水以后,药液含药24%,如果再加入同样多的水,药液含药的百分比是________.【考点】浓度问题【难度】3星【题型】填空【解析】开始时药与水的比为3:7,加入一定量的水后,药与水的比为24:766:19=,由于在操作开始前后药的重量不变,所以我们把开始时药与水的比化为6:14,即,原来药占6份,水占14份;加入一定量的水后,药还是6份,水变为19份,所以加入了5份的水,若再加入5份的水,则水变为24份,药仍然为6份,所以最后得到的药水中药的百分比为:6(624)100%20%÷+⨯=.【答案】20%【巩固】一杯盐水,第一次加入一定量的水后,盐水的含盐百分比变为15%;第二次又加入同样多的水,盐水的含盐百分比变为12%,第三次再加入同样多的水,盐水的含盐百分比将变为_______%. 【考点】浓度问题【难度】3星【题型】填空【解析】第一次加水后盐水和盐的比为20:3,第二次加水后变为25:3,所以第三次加水后变为30:3,所以盐水的含盐百分比为3÷30×100%=10% .【答案】10%二、通过浓度三角解决浓度和实际生活中的配比问题【例 5】有浓度为20%的盐水300克,要配制成40%的盐水,需加入浓度为70%的盐水多少克?【考点】浓度问题【难度】2星【题型】解答【解析】 将两种溶液的浓度分别放在左右两侧,重量放在旁边,配制后溶液的浓度放在正下方,用直线相连;(见图1)直线两侧标着两个浓度的差,并化成简单的整数比。
小学奥林匹克数学 竞赛数学 六年级上 第5讲浓度问题

我们知道,将糖溶于水得到糖水,将盐溶于水得到盐水,将纯酒精溶于水得到酒精溶液……通常把被溶解的物质叫做溶质,如糖、盐、纯酒精等;把溶解这些溶质的液体称为溶剂,如水;溶质和溶剂的混合液体称为溶液,如糖水、盐水、酒精溶液等.一般地,有下面的关系式:+=溶质的重量溶剂的重量溶液的重量例如:50克纯酒精和150克水混合得到200克酒精溶液.浓度就是溶质重量与溶液重量的比值,通常用百分数表示,即:100%100%=×=×+溶质重量溶质重量浓度溶液重量溶质重量溶剂重量与溶液浓度有关的应用题叫做浓度问题.当溶液混合时,浓度往往会发生变化.那么如何求混合溶液的浓度呢?第一种想法是用浓度的定义来求解.分析 所谓纯果汁,这里是指果汁溶液的浓度为100%.不妨设原来这瓶纯果汁的重量为100克.那么三天后,这瓶果汁的重量是多少克?其中纯果汁的重量又是多少克?练习1. 一个瓶子内最初装有15克水,先倒出5克,再加入10克糖后摇匀,这时溶液的浓度是多少?接着又倒出55克水,那么溶液的浓度变为多少?气喝了五分之一后又放回了冰箱.第二天妈妈拿出来喝了剩下的五分之一,觉得太浓,于是就加水兑满,摇匀之后打算明天再喝.第三天小高拿出这瓶果汁,一口气喝得只剩一半了.他担心妈妈说他喝得太多,于是就加了些水把果汁兑满,那么这时果汁的浓度是多少? 无处不在的百分数有的同学在学习了浓度的计算公式后,可能会有些疑惑:为什么浓度要用百分数来表示呢?在式子的最后还要乘以100%,这不是很麻烦吗?其实,浓度之所以用百分数来表示,是因为百分数的分母都是100,也就是都以1%作单位,便于比较.也正是因为如此,百分数在工农业生产、科学技术、各种实验中有着十分广泛的应用.特别是在进行调查统计、分析比较时,我们经常会遇到和“率”有关的问题,这时百分数便能大显身手了.下面就是一个简单的例子:每天电视台播报天气预报节目时,都会报出当天晚上和明天白天的天气状况、降水概率等,提醒大家提前做好准备.例如今天晚上的降水概率是20%,明天白天有五~六级大风,降水概率是10%,早晚应添加衣服.你们看,20%与10%让人一目了然,既清楚又简练.这就是百分数的便利之处了.其实,这样的例子还有很多.只要同学们留心观察便会发现,百分数在生活中无处不在.分析 浓度的计算公式:100%=×浓糖的重量糖水度糖水重量.第(1)题求混合后的浓度,我们关心的事情是混合后的糖的重量是多少?糖水重量又是多少呢?第(2)题是糖水的加水稀释问题,因为加水前后,糖的重量是一样的,只要紧紧抓住这个“不变量”,便不难求解.练习2.(1)有浓度为30%的糖水400克,浓度为15%的糖水800克,将它们混合之后的浓度是多少?(2)有浓度为10%的糖水500克,加入了一些未知浓度的糖水,配成了浓度为20%的糖水1125克.那么加入了多少克糖水?加入的糖水浓度是多少?625(2 盐水的浓度不能太高小高学习了溶液知识后,就兴冲冲地跑到厨房里,自己做起食盐溶液来.他先在杯子里倒入热水,再一边往里倒食盐一边搅拌.可是小高发现了一件奇怪的事:倒入杯中的食盐达到一定量以后,就再也溶解不了了.于是小高转而又拿了糖,做起糖水溶液.这一回,他放的糖比盐多了许多.可是这些糖没过一会都溶解了.这是怎么回事呢?事实上,在热水中,食盐确实不如糖容易溶解.在一定量的水中,食盐溶解到一定程度就无法再溶解了.这就是浓度问题中从没出现过高浓度的食盐溶液的原因,因为它在现实生活中是不存在的.相反,糖是一种比较容易溶解的溶质,所以在我们遇到的浓度问题中,时不时会出现浓度是百分之六十几甚至七十几的糖水溶液.对于溶液混合的问题,我们有如下重要结论:两种溶液的重量比等于它们的浓度与混合溶液浓度之差的反比.也就是:甲溶液重量∶乙溶液重量=乙溶液与混合溶液浓度差值∶甲溶液与混合溶液浓度差值. 分析 这是一道典型的溶液混合问题,题目已经给出了混合前的两种溶液的浓度,也给出了混合后的溶液的浓度,于是我们便可利用“混合过程中,溶液重量与浓度差值成反比”这一结论来解决问题.练习3. 有浓度为15%的盐水240克,要配制成浓度20%的盐水,需要加入浓度为35%的盐水多少克?溶液,需要加入浓度为分析是两种溶液混合的问题吗练习4. 往浓度为60%原有浓度为60%的糖水多少克?分析 这道题中有几次溶液混合的过程?对于每个混合过程,如何分析呢?练习5. 有甲、乙、丙三瓶糖水,浓度依次为60%、30%、50%,其中丙瓶有24千克.先将乙、丙两瓶中的糖水混和,浓度变为40%;然后把甲瓶中的糖水全部倒入混合液中,得到浓度为45%的糖水.请问原来甲瓶有多少千克糖水?的糖和水后,变成了浓度为其中甲瓶有11把丙瓶中的糖水全部倒入混合液中,得到浓度为瓶有多少千克糖水?例题5分析能像例题5一样,把这道题也转化成一道“两瓶溶液”的题目呢?注意到题中提到了乙瓶和丙瓶的混合溶液,于是我们可以先把乙瓶和丙瓶混合为一瓶新糖水,这时题目的条件就变为:甲瓶有糖水30克,另一瓶糖水有糖水60克.甲瓶的浓度比另一瓶糖水的浓度高9%.如果将这两瓶糖水混合,浓度变为30%.现在你知道怎么做了吗?练习6. 甲、乙、丙三瓶硫酸溶液,重量分别为100克、200克、300克.已知乙瓶溶液的浓度比甲瓶高9%,丙瓶溶液的浓度是13%.现在将三瓶溶液混合,混合后硫酸溶液的浓度是20%.求原来甲瓶硫酸溶液的浓度.如果取40克甲种酒精溶液和为浓度为题糖水混合后,浓度变为度高本讲知识点汇总一、浓度的定义.二、用定义法求解浓度问题.三、用方程法解浓度问题.四、用“两种溶液的重量比等于它们的浓度与混合溶液浓度之差的反比”这一结论求解浓度问题.业1.(1)将浓度为30%的糖水900克和浓度为27%的糖水600克混合,得到的糖水的浓度是多少?(2)要将浓度为10%的盐水900克配制成浓度为19%的盐水,需要加入盐多少克?(3)要将浓度为25%的酒精溶液1020克配制成浓度为17%的酒精溶液,需要加入水多少克?2. 一盆水中放入10克盐,再倒入浓度为5%的盐水200克,配成浓度为2.5%的盐水.问:原来这盆水有多少克?3.两个杯子里分别装有浓度为40%与10%的糖水,倒在一起混合后糖水浓度变为30%.若再加入300克20%的糖水,浓度变为25%,那么原来40%的糖水有多少克?4.(1)现有盐水若干千克,第一次加入一定量的水后,盐水的浓度变为3%;第二次又加入同样多的水后,盐水的浓度变为2%.求原来盐水的浓度;(2)在浓度为10%的盐水中加入一定量的盐后配制成浓度为20%的盐水,如果再加入同样多的盐,盐水浓度将变为多少?5.甲、乙、丙三杯糖水浓度分别为40%、48%、60%,将三杯糖水混合后浓度变为50%.如果乙、丙两杯糖水重量一样,都比甲杯糖水多30千克,那么三杯糖水共有多少千克?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时钟问题
【知识点拔】 浓度=
溶剂
溶质溶质
×100%
溶剂=溶液×(1-浓度) 溶质=溶液×浓度 【典型例题】
【例1】 现在是2点正,什么时刻时针与分针第一次重合?
例2: 晚上到8点之间电视里播出一部动画片,开始时分针与时针正好在成一条直线上,结束时两针正好重合.这部动画片最少播出了多长时间?
例3: 胖胖家有一个闹钟,每小时比标准时间慢1分钟。
有一天晚上8点整时,胖胖对准了闹钟,他想第二天早上5点55分起床,于是他就将闹钟定在了5点55分。
请问;这个闹钟将在标准时间的什么时刻响铃?
【竞赛题选】李老师家有两只挂钟,一只每天快20分,另一只每天慢30分。
现在将这两只挂钟调到标准时间,它们至少再经过多少天才能再次同时显示标准时间?
1、钟面上三时多少分时,分针与时针恰好重合?
2、在7点与8点之间,时针与分针在什么时刻相互垂直?
3、在3点与4点之间,时针与分针在什么时刻位于一条直线上?
4、3点过多少分时,时针与分针离“3”的距离相等并且在“3”的两边?
5、东东家有一个闹钟,每小时比标准时间快2分钟。
星期天上午9点整时,东东对准了闹钟,他想让闹钟在了标准时间的11点30分响起。
请问:他应该将闹钟定在什么时刻?
6、东东的手表每小时比标准时间慢30秒。
早上6点时,东东把手表与标准时间对准。
请问:标准时间中午12点时,东东的手表是几点几分?
7、0点0分时,时针与分针重合。
请问:1---12点之间(不包括12点),时针与分针重合了几次?
8、时针和分针每隔多少时间重合一次?钟面上时针与分针一昼夜重合多少次?
9、钟面上8时20分时,时针与分针之间的夹角是多少度?
10、钟面上12时整时针与分针重合,至少再过多少分钟,时针与分针再一次重合?
1、钟面上5时过多少分时,分针与时针在一条直线上,且指向相反?
2、钟面上6点与7点之间两针夹角为90度时,是六点过多少分?
3、10点过多少分时,时针与分针离数字“10”的距离相等,并且在数字“10”的的两边?
4、明明有一块手表,每分钟比标准时间快2秒。
明明早上8点将手表对准,当这块手表第一次指向12点时,标准时间是几时几分?【竞赛题选】胖胖去看一部电影。
他在电影刚放映时看了一下手表,结束时又看了一下手表,他发现时针和分针刚好交换了一下位置。
已知这场电影不足一小时,请问:这部电影放影时长多少分钟?。
