初一上第二章有理数乘除法练习

合集下载

初一有理数乘除法练习题

初一有理数乘除法练习题有理数的乘除法一、主要知识点1.有理数乘法法则：⑴两个有理数相乘：同号得正，异号得负；并把绝对值相乘；任何数与0相乘都得0.⑵多个有理数相乘：可以从左至右依次相乘，因数有，则积为。

⑶乘积是1的两个数互为倒数，若a，b互为倒数，则ab=1；a=1/b。

2.有理数乘法一般步骤：⑴先观察各因式中有没有0，有则乘积为0；若没有，先确认符号。

⑵确定乘积的符号，若因数是两个数，则同正异负；若因数不止两个数；要全部考虑，因数中负数个数为偶数个时，乘积为正，因数中负数个数为奇数个时，乘积为负。

⑶确定符号后，再把绝对值相乘。

3.有理数乘法运算律：⑴乘法交换律：ab=ba。

⑵乘法结合律：(ab)c=a(bc)。

⑶乘法分配律：a(b+c)=ab+ac。

4.有理数的除法：法则一：除以一个不为0的数，等于乘这个数的倒数a÷b=a×1/b，b≠0.法则二：两数相除，同号得正，异号得负，并把绝对值相除，除以任何一个不为0的数都得。

注：运用法则一，将除法全部转化为乘法，然后运用法则二，进行计算。

除法性质：a÷b÷c=a÷(bc)。

5.有理数乘除混合运算：只有乘除法时从左至右依次计算，有括号的先算括号里面的。

6.有理数乘除混合运算的一般步骤：⑴同一级运算中，要从左到右依次计算。

⑵乘除混合运算时，将除法转换为乘法，算式化成连乘的形式，带分数化成假分数，小数都统一成分数。

二、解题方法与思路1.复杂的因数相乘：⑴分数与小数：算式中既有小数又有分数时，可根据题目将其统一为小数或统一为分数。

⑵带分数的乘法：算式中有带分数，应该把带分数化为假分数后再相乘。

2.有理数乘除混合运算确定符号，看算式中负因数的个数，“奇负偶正”。

3.乘法运算律的推广：⑴乘法交换律和结合律适用于三个或三个以上因数相乘，任意交换位置，积不变。

⑵乘法分配律：不止适用于3个数，可以更多a(b+c+。

+m)=ab+ac+。

七年级数学上册有理数的乘除练习题

七年级数学上册有理数的乘除练习题【例1】下列说法正确的是（）A ．5个有理数相乘，当负因数为3个时，积为负B ．﹣1乘以任何有理数等于这个数的相反数C ．3个有理数的积为负数，则这3个有理数都为负数D ．绝对值大于1的两个数相乘，积比这两个数都大【变式1-1】在下列各题中，结论正确的是（） A ．若a ＞0，b ＜0，则ba ＞0B ．若a ＞b ，则a ﹣b ＞0C ．若 a ＜0，b ＜0，则ab ＜0D ．若a ＞b ，a ＜0，则ba ＜0【变式1-2】已知a +b ＞0且a （b ﹣1）＜0，则下列说法一定错误的是（） A ．a ＞0，b ＞1B ．a ＜﹣1，b ＞1C ．﹣1≤a ＜0，b ＞1D ．a ＜0，b ＞0【变式1-3】下列说法：①若a 、b 互为相反数，则a b=−1；②若b ＜0＜a ，且|a |＜|b |，则|a +b |＝﹣|a |+|b |；③几个有理数相乘，如果负因数的个数为奇数个，则积为负；④当x ＝1时，|x ﹣4|+|x +2|有最小值为5；⑤若ab =c d，则c a=d b；其中错误的有（）【例2】若3a ﹣12没有倒数，则a ＝；已知m ﹣11的倒数为−17，则m +1的相反数是．【变式2-1】（2022•杨浦区校级期中）如果a +3的相反数是﹣513，那么a 的倒数是．【变式2-2】（2022秋•贵港期末）若a 、b 互为相反数，c 、d 互为倒数，m 的绝对值为2．（1）直接写出a +b ，cd ，m 的值；（2）求m +cd +a+b m的值．【变式2-3】已知a 与2互为相反数，x 与3互为倒数，则代数式a +2+|﹣6x |的值为（） A ．0B ．﹣2C ．2D ．无法确定【例3】下列计算正确的是（） A ．﹣30×37−20×（−37）=1507B ．（−23+45）÷（−115）＝﹣2C ．（12−13）÷（13−14）×（14−15）=310D ．−45÷（+45）×（−827）＝0【变式3-1】（1）（−35）×（﹣312）÷（﹣114）÷3 （2）[（+17）﹣（−13）﹣（+15）]÷（−1105）【变式3-2】计算：（1）619÷（﹣112）×1924．（2）﹣125×0.42÷（﹣7）【变式3-3】计算：（1）（−35）×（﹣312）÷（﹣114）÷3；（2）（﹣8）÷23×（﹣112）÷（﹣9）．【例4】写出下列运算中每一步所依据的运算律或法则：（﹣0.4）×（﹣0.8）×（﹣1.25）×2.5 ＝﹣（0.4×0.8×1.25×2.5）（第一步）＝﹣（0.4×2.5×0.8×1.25）（第二步）＝﹣[（0.4×2.5）×（0.8×1.25）]（第三步）＝﹣（1×1）＝﹣1．第一步：；第二步：；第三步：．【变式4-1】计算：（12−34+18）×（﹣24）．【变式4-2】用简便方法计算（1）991718×（﹣9）（2）（﹣5）×（﹣367）+（﹣7）×（﹣367）+12×（﹣367）【变式4-3】用简便方法计算：（1）﹣13×23−0.34×27+13×（﹣13）−57×0.34（2）（−13−14+15−715）×（﹣60）【例5】（2022•利辛县月考）下面是小明同学的运算过程．计算：﹣5÷2×12．解：﹣5÷2×12=−5÷（2×12）...第1步＝﹣5÷1...第2步＝﹣5 (3)请问：（1）小明从第步开始出现错误；（2）请写出正确的解答过程．【变式5-1】计算：（−109）×（−35）．解：（−109）×（−35）=−109×35①=−23．②（1）找错：第步出现错误；（2）纠错：【变式5-2】阅读下面解题过程：计算：5÷（13−212−2）÷6 解：5÷（13−212−2）×6＝5÷（−256）×6…① ＝5÷（﹣25）…② =−15⋯③回答：（1）上面解题过程中有两处错误，第一处是第步，错因是，第二处是，错因是．（2）正确结果应是．【变式5-3】阅读下列材料：计算：124÷（13−14+112）．解法一：原式=124÷13−124÷14+124112=124×3−124×4+124×12=1124．解法二：原式=124÷（412−312+112）=124÷212=124×6=14．解法三：原式的倒数＝（13−14+112）÷124=（13−14+112）×24=13×24−14×24+112×24＝4．所以，原式=14．（1）上述得到的结果不同，你认为解法是错误的；（2）请你选择合适的解法计算：（−142）÷（16−314+23−27）．【例6】（1）三个有理数a ，b ，c 满足abc ＞0，求|a|a +|b|b +|c|c的值．（2）三个有理数a ，b ，c 满足abc ＜0，求|a|a+|b|b+|c|c的值；（3）若a ，b ，c 为三个不为0的有理数，且|a|a +|b|b+|c|c=−1，求abc|abc|的值．【变式6-1】已知非零有理数a ，b ，c 满足ab ＞0，bc ＞0．（1）求|ab|ab +ac|ac|+|bc|bc的值；（2）若a+b+c＜0，求|a|a +b|b|+|c|c+|abc|abc的值．【变式6-2】已知|x|＝3，|y|＝7（1）若x＜y，求x﹣y的值；（2）若xy＞0，求x+y的值；（3）求x2y﹣xy2+21的值．【变式6-3】若a+b+c＜0，abc＞0，则ab|ab|+2•|−bc|bc−3•ac|ac|+4•|abc|abc的最大值为（）A．6B．8C．10D．7【例7】考察下列每一道算式，回答问题：算式：63×67＝4221 72×78＝5616561×569＝3192009 1814×1816＝3294224（1）两个因数个位上的数字之和是多少？其余各位上的数字有何特征？（2）根据四个式子的计算，请你猜想符合上述特征的两个数相乘的运算规律．（3）再举两道符合上述特征的计算题，并用你猜想的规律进行计算．【变式7-1】已知C32=3×21×2=3，C53=5×4×31×2×3=10，C64=6×5×4×31×2×3×4=15，…观察以上规律计算C85=，C10a=45，则a＝．【变式7-2】有一列数a1，a2，a3，…a n，若a1=12，从第二个数开始，每一个数都等于1与它前面那个数的差的倒数．（1）试计算a2，a3，a4；（2）根据以上计算结果，试猜测a2016、a2017的值．【变式7-3】已知一些两位数相乘的算式：62×11，78×69，34×11，63×67，18×22，15×55，12×34，54×11利用这些算式探究两位数乘法中可以简化运算的特殊情形：（1）观察已知算式，选出具有共同特征的3个算式，并用文字描述它们的共同特征；（2）分别计算你选出的算式．观察计算的结果，你能发现不经过乘法运算就可以快速、直接地写出积的规律吗？请用文字描述这个规律；（3）证明你发现的规律；（4）在已知算式中，找出所有可以应用（或经过转化可以应用）上述规律的算式，并将它们写在横线上：．【例8】（2022•江宁区校级月考）天龙顶国家山地公园，位于岑溪市南渡镇吉太附近，距岑溪市35公里，天龙顶是桂东最高峰，史上早已成名，被誉为“土主龙楼”天龙顶形成于远古冰川，由整块红色砂岩劈凿而成，拔地而起，是极限攀岩、野外露营及登山爱好者的天堂．某年寒假，小昌与小勇一起去游天龙顶，他们想知道山的高度．小昌说可以利用温度计测量山峰的高度，小昌在山顶测得温度约是﹣1℃，小勇此时在山脚测得温度约是8.6℃，已知该地区每年增加100米，气温大约下降0.8℃，小昌很快算出了答案，你知道天龙顶的高度约是多少米吗？【变式8-1】妈妈身高多少厘米？【变式8-2】某原料仓库一天的原料进出记录如下表（运进用正数表示，运出用负数表示）：﹣34﹣12﹣5进出数量（单位：吨）进出次数21332（1）这天仓库的原料比原来增加或减少了多少吨？（2）根据实际情况，现有两种方案：方案一：运进每吨原料费用5元，运出每吨原料费用8元；方案二：不管运进还是运出费用都是每吨原料6元；从节约运费的角度考虑，选用哪一种方案较合适？请说明理由．【例9】若定义一种新的运算“*”，规定有理数a*b＝4ab，如2*3＝4×2×3＝24．（1）求3*（﹣4）的值；（2）求（﹣2）*（6*3）的值．【变式9-1】定义：对于一个两位自然数，如果它的个位和十位上的数字均不为零，且它正好等于其个位和十位上的数字的和的n倍（n为正整数），我们就说这个自然数是一个“n 喜数”．例如：24就是一个“4喜数”，因为24＝4×（2+4）；25就不是一个“n喜数”，因为25≠n（2+5）．（1）判断44和72是否是“n喜数”？请说明理由；（2）请求出所有的“7喜数”之和．【变式9-2】“格子乘法”作为两个数相乘的一种计算方法，最早在15世纪由意大利数学家帕乔利提出，在明代数学家程大位著的《算法统宗》一书中被称为“铺地锦”．例如：如图1，计算46×71，将乘数46写在方格上边，乘数71写在方格右边，然后用乘数46的每位数字乘以乘数71的每位数字，将结果计入相应的方格中，最后沿斜线方向相加得3266．（1）如图2，用“格子乘法”计算两个两位数相乘，则x＝，y＝；（2）如图3，用“格子乘法”计算两个两位数相乘，得2176，则m＝，n＝；（3）如图4，用“格子乘法”计算两个两位数相乘，则k＝．【变式9-3】小聪是一个聪明而又富有想象力的孩子．学习了“有理数的乘方”后，他就琢磨着使用“乘方”这一数学知识，脑洞大开地定义出“有理数的除方”概念．于是规定：若干个相同有理数（均不能为0）的除法运算叫做除方，如5÷5÷5，（﹣2）÷（﹣2）÷（﹣2）÷（﹣2）等，类比有理数的乘方．小聪把5÷5÷5记作f（3，5），（﹣2）÷（﹣2）÷（﹣2）÷（﹣2）记作f（4，﹣2）．（1）直接写出计算结果，f（4，1）＝，f（5，3）＝；2（2）关于“有理数的除方”下列说法正确的是．（填序号）①f（6，3）＝f（3，6）；②f（2，a）＝1（a≠0）；③对于任何正整数n，都有f（n，﹣1）＝1；④对于任何正整数n，都有f（2n，a）＜0（a＜0）．（3）小明深入思考后发现：“除方”运算能够转化成乘方运算，且结果可以写成幂的形式，请推导出“除方”的运算公式f（n，a）（n为正整数，a≠0，n≥2），要求写出推导过程将结果写成幂的形式；（结果用含a，n的式子表示）（4）请利用（3）问的推导公式计算：f（5，3）×f（4，13）×f（5，﹣2）×f（6，12）．。

人教版七年级数学上册练习题有理数的乘除法

;
3两数相除，同号得
，异号得
，并把绝对值
于 0 的数都得
.
，0 除以任何一个不等
2.－ 5 ，2.6，|－ 1 |，－（－4），－2.5 的倒数分别为
.
13
7
3.化简下列分数：
（1） 4 ; 12
（2） 36 ; 18
（3）- 24 . 4
拓展提高
1.填空题: （1）-6 的倒数是
，-6 的倒数的倒数是
_，-6 的相反数是
的相反数是
;
2 当两数 3 当两数 4当两数 2.计算:
时，它们的和为 0;
时，它们的积为 0; 时，它们的积为 1.
（1）（+36）÷（－4）;
（2）（－2 1 ）÷（－1 1 ）;
3
6
（3）（－90）÷15;
（4）－1÷（+ 3 ）. 5
3. 计算下列各题：
（1）(-1 700 000)÷(-16)÷(-25)÷25；
（2）(+125)÷(-3)+(-62)÷3+(+187)÷3.
，-6 的相反数
4. 用简便方法计算：
19
(1)(-81)÷÷{(-1 1 )×(-1 5 )-(-3.9)÷［1- 3 +(-0.7)］}.
11
6
4
5.化简下列分数：
2
(1) ;
6
(2)
3 9 ;
（2）（-1 1 ）×3（- 2 ）×（-1 1 ）．
8
3
3
3．下列结论正确的是（）
A．两数之积为正，这两数同为正; B．两数之
积为负，这两数为异号 C．几个数相乘，积的

人教版七上有理数的乘除法(含答案)

1 / 121.4.1有理数乘法（1）随堂检测1、填空：（1）5×（－4）= ＿＿＿；（2）（-6）×4=＿＿＿；（3）（-7）×（-1）=＿＿＿；（4）（-5）×0 =＿＿＿；（5）=-⨯)23(94＿＿＿；（6）=-⨯-)32()61(＿＿＿；（7）（-3）×=-)31(2、填空：（1）-7的倒数是＿＿＿，它的相反数是＿＿＿，它的绝对值是＿＿＿；（2）522-的倒数是＿＿＿，-2.5的倒数是＿＿＿；（3）倒数等于它本身的有理数是＿＿＿。

3、计算：（1）)32()109(45)2(-⨯-⨯⨯-；（2）(-6)×5×72)67(⨯-；（3）（-4）×7×（-1）×（-0.25）；（4）41)23(158)245(⨯-⨯⨯- 4、一个有理数与其相反数的积（）A 、符号必定为正B 、符号必定为负C 、一定不大于零D 、一定不小于零5、下列说法错误的是（）A 、任何有理数都有倒数B 、互为倒数的两个数的积为1C 、互为倒数的两个数同号D 、1和-1互为负倒数典例分析计算)542()413(-⨯-分析：在运算过程中常出现以下两种错误：①确定积得符号时，常常与加法法则中的和的符号规律相互混淆，错误地写成1091)514()413()542()413(-=-⨯-=-⨯-；②把乘法法则和加法法则混淆，错误地写成516)5441()2()3()542()413(-=⨯⨯-⨯-=-⨯-。

为了避免类似的错误，需先把假分数化成带分数，然后再按照乘法法则进行运算。

2 / 12解：1091514413)514()413()542()413(=⨯=-⨯-=-⨯- 课下作业拓展提高1、32-的倒数的相反数是＿＿＿。

2、已知两个有理数a,b ，如果ab ＜0，且a+b ＜0，那么（）A 、a ＞0，b ＞0B 、a ＜0，b ＞0C 、a,b 异号D 、a,b 异号，且负数的绝对值较大 3、计算：（1）)5(252449-⨯；（2）125)5.2()2.7()8(⨯-⨯-⨯-；（3）6.190)1.8(8.7-⨯⨯-⨯-；（4）)251(4)5(25.0-⨯⨯-⨯--。

七年级上册数学同步练习题库：有理数的乘除法(简答题：一般)

有理数的乘除法（简答题：一般）1、用简便方法计算：2、计算（1）简便计算：（2）计算：（3）先化简再求值：，其中x=，y=23、规定一种新的运算：a★b=a×b-a-+1．例如：3★（-4）=3×（-4）-3-+1．请用上述规定计算下面各式：（1）2★5；（2）（-2）★（-5）．4、阅读材料题：式子“1×2×3×4×5×…×100”表示从1开始的100个连续自然数的积，由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“1×2×3×4×5×…×100”表示为n，这里“π”是求积符号．例如：1×3×5×7×9×…×99，即从1开始的100以内的连续奇数的积，可表示为（2n﹣1），又如13×23×33×43×53×63×73×83×93×103可表示为n3，通过对以上材料的阅读，请解答下列问题：（1）2×4×6×8×10×…×100（即从2开始的100以内的连续偶数的积）用求积符号可表示为；（2）1×××…×用求积符号可表示为；（3）计算：（1﹣）．5、在某地区，高度每升高100米，气温下降0.8 ℃.若在该地区的山脚测得气温为15 ℃，在山顶测得气温为－5 ℃，你能求出从山顶到山脚的高度吗？6、探索规律：将连续的偶2，4，6，8，…，排成如下表：（1）十字框中的五个数的和与中间的数和16有什么关系？（2）设中间的数为x，用代数式表示十字框中的五个数的和；（3）若将十字框上下左右移动，可框住另外的五位数，其它五位数的和能等于2010吗？如能，写出这五位数，如不能，说明理由．7、已知：是最小的正整数，是最大的负整数，是的倒数．（1）直接写出：，，；（2）求的值．8、计算（1）（2）（3）（4）9、（1）计算（2）（3）（4）（用简便方法）10、已知，m、n互为相反数，p、q互为倒数，的绝对值为，求的值.11、阅读材料：对于任何数，我们规定符号的意义是.例如：. (1)按照这个规定，请你计算的值.（2）按照这个规定，请你计算当时，值.12、某食品厂从生产的袋装食品中随机抽样检测20袋的质量是否符合标准质量，超过或不足的质量分别用正、负数表示，例如＋2表示该袋食品超过标准质量2g，现记录如下：(2)若标准质量为100g／袋，则这次抽样检测的总质量是多少克？13、小刚在课外书中看到这样一道有理数的混合运算题：计算：她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，他顺利地解答了这道题。

【新】人教版七年级上册数学有理数的乘除法练习题

有理数的乘除法练习题课堂学习检测一、选择题1．下列计算正确的是( )．(A)911)311()311(=-⨯-(B)1172)218(=⨯- (C)766)71()7(-=+⨯-(D)1)31(3-=-⨯2．两个有理数之积是0，那么这两个有理数( )．(A)至少有一个是0 (B)都是0(C)互为倒数 (D)互为相反数3．,04.018)05.041110(54-+-=+-⨯-这个运算应用了( )．(A)加法结合律(B)乘法结合律 (C)乘法交换律 (D)分配律4．比较a 与3a 的大小，正确的是( )．(A)3a ＞a (B)3a ＝a(C)3a ＜a(D)上述情况都可能二、填空题5．式子)66()981()8.3(5.7)6(31-⨯-⨯+⨯⨯-⨯的符号为______．6．若a ＝4，b ＝0，c ＝－3，d ＝－5，则c －ad ＝______，(a －b )(c －d )＝______．三、计算题7．直接将答案写在横线上：(1)=-⨯)54(43______；(2)=-⨯-)4()85(______；(3)=⨯-38)1923(______； (4)=+⨯+)2.1()411(______．8．)720()103()32(-⨯-⨯- 9．)2.0()732()312(-⨯+⨯-10．)721()1179154238312(-⨯+- 11．)194(6)194(13)194(7-⨯--⨯+-⨯-综合、运用、诊断一、填空题12．若a ＜0，b ＜0，c ＞0，则(－a )·b ·(－c )______0． 13．若a ＋b ＜0，且ab ＞0，则a______0，b______0．二、选择题14．已知(－ab )·(－ab )·(－ab )＞0，则( )．(A)ab ＜0(B)ab ＞0(C)a ＞0，b ＜0 (D)a ＜0，b ＜015．｜x －1｜＋｜y ＋2｜＋｜z －3｜＝0，则(x －1)(y －2)(z ＋3)的值为( )．(A)48 (B)－48 (C)0 (D)xyz三、计算题 16．)36()12765321(-⨯-+-17．)95.1(9)772.3()9(228.3⨯--⨯-+-⨯18．)83()154()52()433()322()211(-⨯-⨯+⨯+⨯-⨯-四、解答题 19．巧算下列各题：(1))200411)(120031()151)(411)(131)(211(--⋯----(2)666663333222299999⨯-⨯拓展、探宄、思考20．先观察下图，再解答下题：小李在街上碰到为救助失学儿童募捐的学生，于是将身上一半的钱捐了出来；接着他又碰到第二个募捐的学生，便又捐出了剩下钱的一半；跟着第三个，第四个，他每次都捐出了剩下钱的一半，身上还剩下一元．请你算一算，最初小李身上有多少元钱?21．用计算器计算下列各式，将结果写在横线上：999×21＝______； 999×22＝______； 999×23＝______； 999×24＝______． (1)你发现了什么规律?(2)不用计算器，你能直接写出999×29的结果吗?有理数的除法练习题学习要求理解除法与乘法的逆运算关系，会进行有理数除法运算；巩固倒数的概念，能进行简单有理数的加、减、乘、除混合运算．课堂学习检测一、填空题1．若两数之积为1，则这两数互为________；若两数之商为1，则这两数________；若两数之积为－1，则这两数互为________；若两数之商为－1，则这两数互为________． 2．零乘以________都得零，零除以________都得零．3．若ab ＞0，b ＜0，则a ________0，且ab________0；若ab ＜0，a ＞0，则b ________0，且a b ________0由此可知，ab 与ab的符号________．一、选择题4．下列计算正确的是( )．(A)20)151(5-=-÷- (B)2)81()8(2-=-⨯-÷-(C)40)152()2(38-=-÷-⨯- (D)25)8()116387(-=-÷++-5．已知a 的倒数是它本身，则a 一定是( )．(A)0(B)1(C)－1(D)±16．一个数与－4的乘积等于531，这个数是( )．(A)52(B)52-(C)25 (D)25-7．填空：(1))21()12(-÷-＝_______；(2))2533(2.5-÷＝_______； (3)()=-÷⨯-÷-551)51(5 _______；(4))45(545445-⨯÷⨯-＝_______；三、计算题 8．)3231(32⨯-÷ 9．)2131(15--÷-10．)434()322(+-÷--综合、运用、诊断一、选择题11．若xy ＞0，则(x ＋y )xy 一定( )．(A)小于0(B)等于0(C)大于0(D)不等于012．如果x ＜y ＜0，则化简xyxy x x ||||+的结果为( )． (A)0 (B)－2 (C)2 (D)3二、计算题13．)511()73(25.0--⨯-÷-14．)241()245836121(-÷+-+-15．)911(98999-÷16.)]53()32(1[)]53(32[-⨯-+÷-+-三、解答题17．当a ＝－2，b ＝0，c ＝－5时，求下列式子的值：(1)a ＋bc ；(2)(a －b )(a ＋c )．18．在10.5与它的倒数之间有a 个整数，在10.5与它的相反数之间有b 个整数，求(a ＋b )÷(a －b )＋2的值．拓展、探究、思考19．式子||||||ab abb b a a ++的所有可能的值有( )． (A)2个 (B)3个 (C)4个 (D)无数个20．如果有理数a ，b ，c ，d 都不为0，且它们的积的绝对值等于它们积的相反数，你能确定a ，b ，c ，d 中最少有几个是负数，最多有几个是负数吗?21．一口枯井深64米，井底之蛙想从井底爬上来．第一天白天，它往上爬到井深一半，晚上又滑落了白天所爬路程的一半；第二天白天，它继续往上爬到剩下路程的一半，晚上又滑落了白天所爬路程的一半；每天这样爬，它需要多少天才能爬到井口?做完题后想一想：“一尺之棰，日取其半，万世不竭”这句话的含义．。

人教版七年级数学上册有理数乘除法试题(含答案)

人教版七年级数学上册有理数乘除法试题(含答案)1.有理数乘除法的基本法则如下：1) 乘法交换律：对于有理数a和b，有ab=ba。

2) 乘法结合律：对于有理数a、b和c，有(ab)c=a(bc)。

3) 乘法分配律：对于有理数a、b和c，有a(b+c)=ab+ac。

4) 有理数的乘法法则：对于有理数a和b，同号得正，异号得负，并将绝对值相乘。

5) 倒数的定义：乘积为1的两个数互为倒数。

6) 除以一个数等于乘以这个数的倒数。

2.单选题：1) 答案为C，因为只有①和①互为倒数。

2) 答案为B，因为1的倒数的绝对值是1.3) 答案为C，因为只有选项C是正确的。

4) 答案为B，因为-2×3=-6.5) 答案为C，因为0.24×(1/15)×(-14/61)=-0.016.6) 答案为B，因为a1=-1/2，a2=-3/2，a3=-1/2，a4=-5/2，依此类推，可得a2019=-1008.7) 答案为B，因为12-7×(-4)+8÷(-2)=36.8) 答案为D，因为-2①3=-2+(-2)×3=-8.9) 答案为A，因为取-5和4相乘得到最大积20.10) 答案为丙同学，因为他的计算是正确的。

二、填空题1.272.2019a - 2018b3.(1) 2.(2) -27.(3) -4.(4) -3a4.-145.-1三、解答题16.1) -0.31252) -0.517.1) 6802) -1/5618.1) 正确。

因为(-115)/(-1236) = 115/1236，(-)×(-12) = 12，所以(-115)/(-1236) = 12/1236 = 1/103，1/103 = 0.xxxxxxxx，所以(-)÷(-) = 0.xxxxxxxx。

2) (-1113)/(-) = 1113/，(-)×(-12) = 12，所以(-1113)/(-) = 12/ = 3/6092，3/6092 = 0.xxxxxxxx，所以(-1113)/(-) = 0.xxxxxxxx。

(完整)七年级数学上(有理数乘除法混合运算练习题)

七年级数学上----有理数乘除法练习1、填空：（1）-7的倒数是＿＿＿，它的相反数是＿＿＿，它的绝对值是＿＿＿；（2）522-的倒数是＿＿＿，-2.5的倒数是＿＿；（3）倒数等于它本身的有理数是＿＿。

32-的倒数的相反数是＿＿。

（4）倒数等于它本身的数是＿＿＿＿＿。

（5）绝对值小于2011的所有整数的积为＿＿＿＿＿。

（6）三个数的积为正数，则三个数中负因数的个数是＿个。

－32与52的和的15倍是＿＿，－32与52的15倍的和是＿＿（7）如果一个数的绝对值、倒数都等于它本身，则这个数是＿＿＿＿。

2、下列结论错误的是（）A 、若b a ,异号，则 b a ⋅＜0，ba＜0 B 、若b a ,同号，则b a ⋅＞0，b a＞0 C 、b a b a b a -=-=- D 、b a b a -=--3、一个有理数与其相反数的积（）A 、符号必定为正B 、符号必定为负C 、一定不大于零D 、一定不小于零 4、下列说法错误的是（） A 、任何有理数都有倒数 B 、互为倒数的两个数的积为1 C 、互为倒数的两个数同号 D 、1和-1互为负倒数5、已知两个有理数a,b ，如果ab ＜0，且a+b ＜0，那么（）A 、a ＞0，b ＞0B 、a ＜0，b ＞0C 、a,b 异号D 、a,b 异号，且负数的绝对值较大 6、若ab b a ,2,5-==＞0，则=+b a ＿＿＿。

7、若0≠a ，则aa 的值为。

8、若a,b 互为相反数，c,d 互为倒数，m 的绝对值是1，求m cd b a 2009)(-+的值。

9、化简下列分数：（1）216-＝（2）4812-＝（3）654--＝（4）3.09--＝10、计算：（1）)5(252449-⨯；（2）－141413 ×4 （3）－24×（127－65－1）（4）36×（－191817）（5）（－56）×（－32）＋（－56）×（＋317）（6）)8141121()8(+-⨯-；（7）)24(9441227-÷⨯÷-；（8）)48()6143361121(-⨯-+--。

初一数学有理数乘除法练习题(已整理)

1.4.1有理数乘法（1）随堂检测1、填空：（1）5×（－4）= ＿＿＿；（2）（-6 ）× 4= ＿＿＿；（3）（-7 ）×（-1 ）=4 3 1 2（4）（-5）×0 =＿＿＿；（5）4（3）＿＿＿；（6）（1）（2）＿＿9 2 6 31（7）（-3）× （1）32、填空：（1）-7 的倒数是＿＿＿，它的相反数是＿＿＿，它的绝对值是＿＿＿；2（2） 2 2的倒数是＿＿＿，-2.5 的倒数是＿＿＿；5（3）倒数等于它本身的有理数是＿＿＿。

3、计算：5 9 2 7 2（1）（ 2）（）（）；（2）（-6）×5× （）；4 10 3 6 75 8 3 1（3）（-4 ）× 7×（-1 ）×（-0.25 ）；（4）（）（）24 15 2 44、一个有理数与其相反数的积（）A、符号必定为正 B 、符号必定为负 C 、一定不大于零 D 、一定不小于零5、下列说法错误的是（）A、任何有理数都有倒数B、互为倒数的两个数的积为 1C、互为倒数的两个数同号 D 、1 和-1 互为负倒数拓展提高21、2的倒数的相反数是＿＿＿。

32、已知两个有理数a,b ，如果ab< 0，且a+b<0，那么（a < 0，b >0 C 、a,b 异号 D 、a,b 异号，且负数的7、若 a,b 互为相反数， c,d 互为倒数， m 的绝对值是 1，求 (ab)cd 2009 m 的值。

A 、a >0，b >0B 绝对值较大 3、计算： 1)4925 ( 5)；52) ( 8) ( 7.2) ( 2.5) ；3) 7.8 ( 8.1) 0 19.6 ；14)0.25 ( 5) 4 ( 215) 。

1 1 1 4、计算：( 1)( 8) (12 114 18)； 2) 1 (12 36 3143 16) ( 48) 。

专题有理数的乘除法计算题(八大题型共50题)(解析版) -2024-2025学年七年级数学上册同步

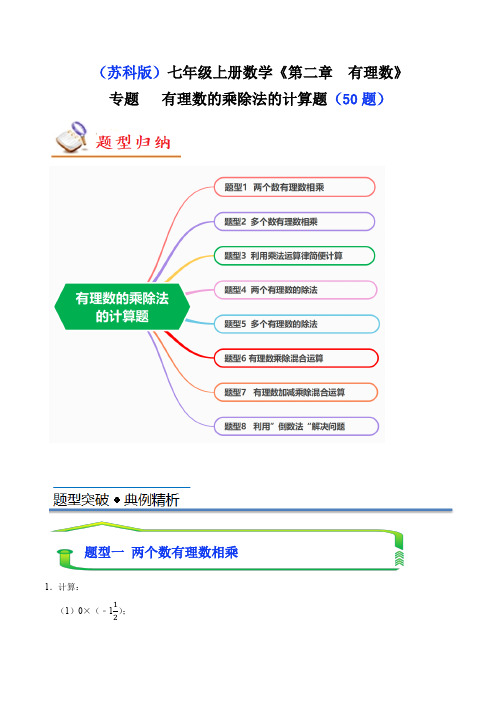
（苏科版）七年级上册数学《第二章有理数》专题有理数的乘除法的计算题（50题）1．计算：（1）0×（﹣112）；题型一两个数有理数相乘（2）（﹣0.25）×（−45）；（3）85×（−154）；（4）（﹣416）×0.2．【分析】根据有理数的乘法运算法则进行计算即可得解．【解答】解：（1）0×（﹣112）＝0；（2）（﹣0.25）×（−45） =14×45 =15；（3）85×（−154）=−85×154 ＝﹣6；（4）（﹣416）×0.2=−256×15 =−56．【点评】本题考查了有理数的乘法运算，熟记运算法则是解题的关键． 2．计算：（1）（﹣3）×（﹣4）；（2）（﹣3.2）×1.5；（3）49×（−32）；（4）134×（﹣8）．【分析】（1）两数相乘，同号得正，再把绝对值相乘即可求解；（2）两数相乘，异号得负，再把绝对值相乘即可求解；（3）两数相乘，异号得负，再把绝对值相乘即可求解；（4）两数相乘，异号得负，再把绝对值相乘即可求解．【解答】解：（1）原式＝3×4＝12；（2）原式＝﹣（3.2×1.5）＝﹣4.8；（3）原式＝﹣（49×32）=−23；（4）原式＝﹣（74×8）＝﹣14．【点评】本题主要考查有理数的乘法，掌握有理数的乘法法则是解题的关键．3．计算：（1）（﹣3）×（﹣4）；（2）（+45）×（﹣114）；（3）（﹣2022）×0；（4）（﹣0.125）×8；（5）25×（﹣1）；（6）（−13）×（﹣3）．【分析】（1）根据有理数乘法法则：两数相乘，同号得正，并把绝对值相乘即可求解；（2）根据有理数乘法法则：两数相乘，异号得负，并把绝对值相乘即可求解；（3）根据有理数乘法法则：任何数与0相乘，都得0即可求解；（4）根据有理数乘法法则：两数相乘，异号得负，并把绝对值相乘即可求解；（5）根据有理数乘法法则：两数相乘，异号得负，并把绝对值相乘即可求解；（6）根据有理数乘法法则：两数相乘，同号得正，并把绝对值相乘即可求解．【解答】解：（1）原式＝3×4＝12；（2）原式＝﹣（45×54）＝﹣1；（3）原式＝0；（4）原式＝﹣（0.125×8）＝﹣1；（5）原式＝﹣（25×1）＝﹣25；（6）原式=13×3=1．【点评】本题主要考查了有理数的乘法，掌握有理数的乘法法则是解题的关键． 4．计算：（1）0×（−5 6）；（2）3×（−1 3）；（3）（﹣7）×（﹣1）；（4）（−16）×（−67）．【分析】根据有理理数的乘法法则进行计算即可．【解答】解：（1）原式＝0；（2）原式＝﹣3×13=−1；（3）原式＝7×1＝7；（4）原式=16×67=17．【点评】本题考查了有理数的乘法．解题的关键是掌握有理数的乘法法则，特别要注意积的符号．5．(−47)×23×(−114)×12．【分析】根据有理数的乘法法则有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘，任何数同零相乘，都得0，进行计算即可得出答案．【解答】解：原式=[(−47)×(−54)]×(23×12)=57×13=521．【点评】本题主要考查了有理数的乘法，熟练掌握有理数的乘法法则进行计算是解决本题的关键．6．计算：（1）（﹣2）×（−12）×（﹣3）；（2）（﹣0.1）×1000×（﹣0.01）．【分析】根据有理数的乘法法则进行计算便可．【解答】解：（1）（﹣2）×（−12）×（﹣3）＝﹣2×12×3＝﹣3；题型二多个有理数相乘（2）（﹣0.1）×1000×（﹣0.01）＝+0.1×1000×0.01 ＝1．【点评】本题主要考查了有理数的乘法，关键是熟记有理数乘法法则． 7．（2022秋•宁远县校级月考）求值：（1）14×（﹣16）×（−45）×（﹣114）；（2）（−511）×（−813）×（﹣215）×（−34）．【分析】根据有理数乘法法则进行计算便可．【解答】解：（1）14×（﹣16）×（−45）×（﹣114）=−14×16×45×54 ＝﹣4；（2）（−511）×（−813）×（﹣215）×（−34）=511×813×115×34 =613．【点评】本题考查了有理数乘法，关键是熟记和应用有理数法则：两数相乘，同号得正，异号得负，并把绝对值相乘，任何数与零相乘积为零；几个不为零的数相乘，积的符号由负因数个数决定，负因数的个数为奇数时，积为负，负因数的个数为偶数时，积为正．8．计算：（1）（﹣8）×154×（−13）；（2）（−37）×（−89）×（﹣6）；（3）23×（−12）×（−45）×（﹣5）．【分析】应用有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘，进行计算即可得出答案．【解答】解：（1）原式＝（﹣30）×（−13）＝10；（2）（−37）×（−89）×（﹣6）原式=821×（﹣6） =−4821；（3）23×（−12）×（−45）×（﹣5）原式＝（−13）×[（−45）×（﹣5）] ＝（−13）×4 =−43．【点评】本题主要考查了有理数的乘法，熟练掌握有理数的乘法法则进行求解是解决本题的关键． 9.计算下列各题：（1）6)2.0()61()30(⨯-⨯-⨯- （2）)98()321(87)53(-⨯-⨯⨯- （3）411)54()16(41-⨯-⨯-⨯ （4）)]751([)91()2.1(45--⨯-⨯-⨯- 【分析】根据有理数的乘法计算即可得出答案．【解答】解：（1）原式=6)62.06130(-=⨯⨯⨯- （2）原式=97)98358753(-=⨯⨯⨯-（3）原式=45)54()16(41⨯-⨯-⨯=4)45541641(=⨯⨯⨯+ （4）原式=72)712915645(751)91()2.1(45-=⨯⨯⨯-=⨯-⨯-⨯-【点评】本题考查多个有理数的乘法，正确掌握运算法则是解题的关键．10．计算：（1）3×（﹣1）×（−13）．（2）﹣1.2×5×（﹣3）×（﹣4）．（3）（−512）×415×（−32）×（﹣6）．（4）54×（﹣1.2）×（−19）．【分析】根据有理数的乘法法则进行计算便可．【解答】解：（1）3×（﹣1）×（−13）＝+3×1×13＝1；（2）﹣1.2×5×（﹣3）×（﹣4）＝﹣1.2×5×3×4 ＝﹣72；（3）（−512）×415×（−32）×（﹣6） =−512×415×32×6 ＝﹣1；（4）54×（﹣1.2）×（−19）=+54×1210×19 =16．【点评】本题主要考查了有理数的乘法，熟记运算法则与是解题的关键．11．计算：（﹣8）×9×（﹣1.25）×（−19）【分析】根据有理数的乘法法则和乘法的交换律进行计算即可．【解答】解：（﹣8）×9×（﹣1.25）×（−19）＝[（﹣8）×（﹣1.25）]×9[×（−19）] ＝10×（﹣1）＝﹣10．【点评】此题考查了有理数的乘法，掌握有理数的乘法法则是解题的关键，是一道基础题．题型三利用乘法运算律简便计算12．用简便方法计算：（﹣8）×（−43）×（﹣1.25）×54．【分析】根据有理数的乘法法则，运用乘法交换律和结合律进行简便计算．【解答】解：原式＝[（﹣8）×（﹣1.25）]×[（−43）×54] ＝10×(−53) =−503．【点评】本题主要考查有理数的乘法，掌握乘法法则，运用乘法交换律和结合律进行简便计算是解题的关键．13．（2022秋•惠城区月考）计算：45×(−25)×78×(−1115)÷14×(−117)．【分析】先确定符号．把除法化为化为乘法，带分数化为假分数，最后计算出结果．【解答】解：45×（﹣25）×78×（−1115）÷14×（﹣117）＝﹣（45×25×78×1115×4×87）＝﹣（78×87×45×1115×25×4）＝﹣3300．【点评】本题考查有理数的混合运算，掌握乘法的交换律和结合律的熟练应用，把除法化为乘法是解题关键．14．计算：（﹣36）×997172【分析】直接利用有理数的乘法运算法则进而得出答案．【解答】解：原式＝（﹣36）×（100−172）＝（﹣36）×100﹣（﹣36）×172 ＝﹣3600+12 ＝﹣359912．【点评】此题主要考查了有理数的乘法运算，正确掌握相关运算法则是解题关键．15．计算：−(−595960)×60；【分析】根据有理数的乘法法则以及乘法运算律则计算即可．【解答】解：原式=595960×60 =(60−160)×60 =60×60−160×60 ＝3600﹣1 ＝3599．【点评】本题主要考查了有理数的乘法，熟练掌握乘法运算律是解答本题的关键．16．用简便方法计算（1）﹣392324×（﹣12）（2）（23−112−115）×（﹣60）【分析】根据乘法分配律，可得答案．【解答】解：（1）原式＝（﹣40+124）×（﹣12）＝﹣40×（﹣12）−124×12＝480−12=47912；（2）原式=23×（﹣60）+112×60+115×60＝﹣40+5+4＝﹣31．【点评】本题考查了有理数的乘法，利用拆项法得出乘法分配律是解题关键． 17．用简便方法计算：（1）﹣13×23−0.34×27+13×（﹣13）−57×0.34 （2）（−13−14+15−715）×（﹣60）【分析】（1）首先应用乘法交换律，把﹣13×23−0.34×27+13×（﹣13）−57×0.34化成 ﹣13×23−13×13−57×0.34﹣0.34×27，然后应用乘法分配律，求出算式的值是多少即可．（2）应用乘法分配律，求出算式（−13−14+15−715）×（﹣60）的值是多少即可．【解答】解：（1）﹣13×23−0.34×27+13×（﹣13）−57×0.34 ＝﹣13×23−13×13−57×0.34﹣0.34×27＝﹣13×（23+13）﹣（57+27）×0.34＝﹣13×1﹣1×0.34 ＝﹣13﹣0.34 ＝﹣13.34（2）（−13−14+15−715）×（﹣60）＝（−13）×（﹣60）−14×（﹣60）+15×（﹣60）−715×（﹣60）＝20+15﹣12+28 ＝51【点评】（1）此题主要考查了有理数的乘法，要熟练掌握，解答此题的关键是要明确有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．（2）此题还考查了乘法运算定律的应用，要熟练掌握．18．用乘法运算律，将下列各式进行简便计算：（1）（﹣112）×（﹣7）×23；（2）)25.1()541(8)5(-⨯-⨯⨯-（3）（﹣48）×（−34+56−712）；（4）0.7×311−6.6×37−1.1×37+0.7×811．（5）﹣392324×（﹣12）（6）4.61×37−5.39×（−37）+3×（−37）．【分析】（1）利用乘法的交换律与结合律计算；（2）利用乘法的交换律与结合律计算；（3）利用乘法的分配律计算即可；（4）逆用乘法的分配律，以简化运算即可．（5）利用乘法的分配律计算即可；（6）逆用乘法的分配律，以简化运算即可．【解答】解：（1）（﹣112）×（﹣7）×23=(−32)×23×(−7) ＝7；（2）)25.1()541(8)5(-⨯-⨯⨯- =)]25.1(8[)]59()5[(-⨯⨯-⨯-=)10(9-⨯=90（3）（﹣48）×（−34+56−712）=−48×(−34)−48×56−48×(−712)＝36﹣40+28＝24；（4）0.7×311−6.6×37−1.1×37+0.7×811=0.7×(311+811)+37×(−6.6−1.1)＝0.7﹣3.3＝﹣2.6．（5）原式＝（﹣40+124）×（﹣12）＝﹣40×（﹣12）−124×12 ＝480−12=47912；（6）原式＝4.61×37+5.39×37−3×37=37×（4.61+5.39﹣3）=37×7＝3．【点评】本题主要考查有理数的运算，关键是使用运算律可使运算简便．19．计算：（1）（﹣6.5）÷（﹣0.5）；（2）4÷（﹣2）；（3）0÷（﹣1 000）；（4）（﹣2.5）÷5 8．【分析】（1）先判断出符号，再绝对值相除即可；（2）先判断出符号，再绝对值相除即可；（3）零除以任何一个不为零的数，商为零，（4）先判断出符号，再绝对值相除，既有分数，又有小数，一般把小数化为分数直接约分即可；【解答】解：（1）（﹣6.5）÷（﹣0.5）＝6.5÷0.5＝13；（2）4÷（﹣2）＝﹣4÷2＝﹣2（3）0÷（﹣1 000）＝0；（4）（﹣2.5）÷58=−2.5÷58=−52×85=−4；【点评】此题是有理数的除法，主要考查了有理数除法的法则，进行计算时，先判断符号，再绝对值相除．20．计算：（1）0÷（﹣2022）；（2）（﹣27）÷9；（3）（−43）÷43；（4）−32÷1.5【分析】（1）0除以任何数都为0；（2）根据九九乘法表计算；（3）根据有理数的除法运算进行计算；（4）换算成小数进行计算；题型四两个有理数的除法【解答】解：（1）0÷（﹣2022）＝0；（2）（﹣27）÷9＝﹣3；（3）（−43）÷43＝﹣1；（4）−32÷1.5＝﹣1；【点评】本题考查了有理数的除法运算，解题关键在于熟知除以一个数等于乘以它的倒数．21．计算：（1）（﹣68）÷（﹣17）；（2）（﹣0.75）÷0.25；（3）（−78）÷（﹣1.75）；（4）312÷（﹣7）【分析】（1）直接利用有理数的除法运算法则计算得出答案；（2）直接利用有理数的除法运算法则计算得出答案；（3）直接利用有理数的除法运算法则计算得出答案；（4）直接利用有理数的除法运算法则计算得出答案．【解答】解：（1）（﹣68）÷（﹣17）＝4；（2）（﹣0.75）÷0.25＝﹣0.75×4＝﹣3；（3）（−78）÷（﹣1.75）=78×47=12；（4）312÷（﹣7） =72×（−17）=−12．【点评】此题主要考查了有理数的乘除运算，正确掌握相关运算法则是解题关键．（1）（+48）÷（+6）；（2）(−323)÷(512)；（3）4÷（﹣2）；（4）0÷（﹣1000）．【分析】原式各项利用除法法则计算即可得到结果．【解答】解：（1）原式＝8；（2）原式=−113×211=−23；（3）原式＝﹣2；（4）原式＝0．【点评】此题考查了有理数的除法，熟练掌握运算法则是解本题的关键．23．计算：（1）（−47）÷（−314）÷（−23）；（2）（﹣0.65）÷（−57）÷（﹣213）÷（+310）．【分析】根据有理数的乘除法则和混合运算顺序进行计算便可．【解答】解：（1）（−47）×（−143）÷（−23）=−47×143×32＝﹣4；（2）（﹣0.65）÷（−57）÷（﹣213）÷（+310）．=−65100×75×37×103＝﹣1.3．【点评】本题主要考查了有理数乘除法，关键是熟记有理数乘除法法则和混合运算顺序．题型五多个有理数的除法（1）（﹣24）÷（﹣2）÷（﹣115）；（2）﹣27÷214÷94÷（﹣24）．【分析】（1）先确定符号再把绝对值相除；（2）先确定符号再把绝对值相除或相乘，最后把除法化为乘法计算．【解答】解：（1）（﹣24）÷（﹣2）÷（﹣115）＝12÷（﹣115）＝﹣10；（2）﹣27÷214÷94÷（﹣24）＝27÷94×49÷24＝27×49×49×124=29．【点评】本题主要考查了有理数除法、乘法，掌握有理数的除法、乘法法则，符号的确定是解题关键．25．计算：（1）（−35）÷（﹣27）÷（﹣114）÷3；（2）（﹣8）÷23÷（﹣23）÷（﹣9）．【分析】各式利用除法法则把除法转化成乘法运算，通过约分即可得到结果．【解答】解：（1）（−35）÷（﹣27）÷（﹣114）÷3=−35×72×45×13=−1425；（2）（﹣8）÷23÷（﹣23）÷（﹣9）＝﹣8×32×32×19=−2．【点评】此题考查了有理数的乘除法，熟练掌握乘除法则是解本题的关键．26．计算：（1）﹣3÷（−34）÷（−34）；（2）（﹣12）÷（﹣4）÷（﹣115）；（3）（−23）÷（−87）÷0.25；（4）（﹣212）÷（﹣5）÷（﹣310）．【分析】（1）直接利用有理数的除法运算法则除法变乘法，再利用有理数的乘法运算法则计算得出答案；（2）直接利用有理数的除法运算法则除法变乘法，再利用有理数的乘法运算法则计算得出答案；（3）直接利用有理数的除法运算法则除法变乘法，再利用有理数的乘法运算法则计算得出答案；（4）直接利用有理数的除法运算法则除法变乘法，再利用有理数的乘法运算法则计算得出答案．【解答】解：（1）原式＝﹣3×（−43）×（−43）=−163；（2）原式＝（﹣12）×（−14）×（−56）=−52；（3）原式＝（−23）×（−78）×4=73；（4）原式＝（−52）×（−15）×（−103）=−53．【点评】此题主要考查了有理数的除法运算，正确掌握相关运算法则是解题关键．27．计算：（1）（−23）÷（−85）÷（﹣0.25）；（2）（﹣81）÷94÷94÷（﹣16）；（3）（﹣6.5）÷（−12）÷（−25）÷（﹣5）．【分析】应用有理数除法法则：有理数除法法则：除以一个不等于0的数，等于乘这个数的倒数，即：a ÷b ＝a •1b （b ≠0），有理数乘法法则：（1）有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．（2）任何数同零相乘，都得0，（3）多个有理数相乘的法则：①几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正．②几个数相乘，有一个因数为0，积就为0．进行计算即可得出答案．【解答】解：（1）原式＝（−23）×（−58）×（﹣4）＝﹣（23×58×4）=−53；（2）原式＝（﹣81）×49×49×（−116）＝（﹣16）×（−116）＝1；（3）（﹣6.5）×（﹣2）÷（−25）÷（﹣5）．原式＝13×（−52）×（−15）＝13×（52×15）＝13×12=132．【点评】本题主要考查了有理数乘法及有理数除法，熟练掌握有理数乘法及有理数除法法则进行求解是解决本题的关键．28．计算：59÷20×185．【分析】根据有理数的除法运算以及乘法运算即可求出答案．【解答】解：原式=59×120×185=110．【点评】本题考查有理数的乘除运算，解题的关键是熟练运用有理数的乘除运算法则，本题属于基础题型．题型六有理数乘除混合运算29．（2022秋•榆树市期中）计算：（﹣54）÷34×43÷（﹣32）．【分析】先确定符号，再把除法化为乘法，根据有理数乘法法则计算．【解答】解：原式＝54×43×43×132＝3．【点评】本题主要考查了有理数的乘法、除法，掌握有理数乘法、除法法则，符号的确定是解题关键．30．（2022秋•丰台区校级期中）计算：(−35)×(−27)÷37．【分析】根据有理数除法法则把有理数除法转化为乘法，再按照有理数乘法法则进行计算便可．【解答】解：(−35)×(−27)÷37=35×27×73=25．【点评】本题考查的是乘除混合运算，掌握“同级运算按照从左往右的顺序进行运算”是解本题的关键．31．计算：（﹣223）×1516÷（﹣1.5）【分析】化有理数除法为乘法，然后计算有理数乘法．【解答】解：（﹣223）×1516÷（﹣1.5），＝（−83）×1516÷（−32），＝（−83）×1516×（−23），=8×15×23×16×3， =53．【点评】本题考查了有理数的乘除法，熟记计算法则即可解题，属于基础题．32．计算：（﹣81）÷214×49÷（﹣16）【分析】原式从左到右依次计算即可得到结果．【解答】解：原式＝81×49×49×116=1．【点评】此题考查了有理数的乘除法，熟练掌握有理数乘除法则是解本题的关键．33．（2022秋•香洲区校级月考）计算：（1）(−5)×6×(−45)×14；（2）−9÷(−0.1)÷(−335 )．【分析】（1）利用有理数的乘法法则原式即可；（2）将有理数的除法转化成乘法后，利用有理数的乘法法则原式即可．【解答】解：（1）原式＝5×6×45×14＝6；（2）原式＝﹣9×（﹣10）×（−5 18）＝﹣9×10×5 18＝﹣25．【点评】本题主要考查了有理数的乘、除法，正确利用有理数的乘除法则运算是解题的关键．34．计算：（1）（﹣32）÷4×（−1 16）；（2）（−23）×（−85）÷（﹣178）．【分析】根据有理数的乘除法则进行计算便可．【解答】解：（1）（﹣32）÷4×（−1 16）＝+32×14×116=12；（2）（−23）×（−85）÷（﹣178）=−23×85×815=−128225．【点评】本题考查了有理数乘除法，熟记有理数乘除法则是解题的关键．35．计算：（1）（﹣134）×（﹣112）÷（﹣118）．（2）（﹣1.25）×54×（﹣8）÷（−34）．【分析】（1）先确定结果的符号，再计算乘除法；（2）先确定结果的符号，再计算乘除法．【解答】解：（1）原式＝﹣134×112÷118 =−74×32×89=−73；（2）原式＝﹣1.25×54×8÷34=−54×54×8×43=−503．【点评】本题考查了有理数乘除法，有理数的除法要分情况灵活选择法则，若是整数与整数相除一般采用“同号得正，异号得负，并把绝对值相除”．如果有了分数，则采用“除以一个不等于0的数，等于乘这个数的倒数”，再约分．乘除混合运算时一定注意两个原则：①变除为乘，②从左到右．36．计算：（1）（−35）×（﹣312）÷（﹣114）÷3；（2）（﹣8）÷23×（﹣112）÷（﹣9）．【分析】各式利用除法法则把除法转化成乘法运算，通过约分即可得到结果．【解答】解：（1）（−35）×（﹣312）÷（﹣114）÷3=−35×72×45×13=−1425；（2）（﹣8）÷23×（﹣112）÷（﹣9）＝﹣8×32×32×19=−2．【点评】此题考查了有理数的乘除法，熟练掌握乘除法则是解本题的关键．37．计算：（1）（−517）×（−34）÷9×（﹣325）；（2）（−72）÷（﹣114）÷3×（−35）；（3）（−320）×246÷910×（−341）．【分析】（1）先将带分数化成假分数，再根据有理数的乘法法则和除法法则求解即可；（2）先将带分数化成假分数，再根据有理数的乘法法则和除法法则求解即可；（3）根据有理数的乘法法则和除法法则求解即可．【解答】解：（1）原式=−517×（−34）×19×（−175）＝[（−517）×（−175）]×[（−34）×19]＝1×（−112）=−112；（2）原式＝（−72）×（−45）×13×（−35）＝﹣（72×45×13×35） =−1425；（3）原式＝（−320）×246×109×(−341) =320×109×341×246=16×341×246=3246×246 ＝3．【点评】本题主要考查了有理数的乘除混合运算，掌握有理数的乘法和除法法则是解题的关键，注意运算顺序．38．(−73)÷(−79)+54×(−85)．【分析】根据除以一个数等于乘以这个数的倒数，可把除法转化成乘法，根据有理数的乘法，可得答案．【解答】解：原式＝（−73）×(−97)+54×(−85)＝3+（﹣2）＝1．【点评】本题考查了有理数的除法，先转化成乘法，再进行乘法运算，注意两数相乘同号得正，异号得负，再把绝对值相乘．39．计算：113×(−212+34)÷(−213)．【分析】直接利用二次根式的乘除运算法则进行计算得出答案．【解答】解：原式=43×(−52+34)÷(−73)=43×(−104+34)×(−37) =43×(−74)×(−37)＝1．40．计算：1.25×(25−215)+125÷6．【分析】把小数化为分数，利用乘法分配律计算，把除法转化为乘法，利用有理数的乘法法则计算，最后算加减即可．【解答】解：原式=54×25−54×215+125×16=12−16+25=1115．【点评】本题考查了有理数的混合运算，掌握乘法分配律a（b+c）＝ab+ac是解题的关键，注意运算顺序．41．计算：（−73）÷（−76）+34×（−83）．题型七有理数加减乘除混合运算【分析】首先将除法转化为乘法，然后按照有理数的乘法法则计算即可．【解答】解；原式=(−73)×(−67)+34×(−83)=2+（﹣2）＝0．【点评】本题主要考查的是有理数的乘除运算，掌握有理数的乘法和除法法则是解题的关键．42．计算：（−72）×（16−12）×314÷（−12）【分析】根据除以一个数等于乘以这个数的倒数，可转化成乘法运算，再根据乘法运算法则，可得答案．【解答】解：原式＝（−72）×(−13)×314×(−2) =−12．【点评】本题考查了有理数的除法运算，除以一个数等于乘以这个数的倒数是解题关键．43．计算：（1）[1124−(38+16−34)×24]×(−15)（2）−5×(−115)+11×(−115)−3×(−225)．【分析】（1）先把括号里面的利用乘法分配律进行计算，然后再次利用乘法分配律进行计算即可得解；（2）先把第三项整理，然后逆运用乘法分配律进行计算即可得解．【解答】解：（1）[1124−（38+16−34）×24]×（−15），＝[1124−（38×24+16×24−34×24）]×（−15），＝[2524−（9+4﹣18）]×（−15），＝（2524+5）×（−15）， =2524×（−15）+5×（−15）， =−524−1，=−2924；（2）﹣5×（−115）+11×（−115）﹣3×（−225），＝﹣5×（−115）+11×（−115）﹣6×（−115），＝（﹣5+11﹣6）×（−11 5），＝0．【点评】本题考查了有理数的乘法，利用运算定律可以使计算更加简便，难点在于（2）的整理．44．计算：（1）−1÷(−18)−3÷(−12)；（2）−81÷13−13÷(−19)．（3）−1+5÷(−16)×(−6)；（4）(13−12)÷114÷110．【分析】（1）（2）（3）根据除以一个数等于乘以这数的倒数把除法转化为乘法运算，然后根据有理数的乘法运算法则和加法运算法则进行计算即可得解；（4）先算小括号里面的，再根据除以一个数等于乘以这数的倒数把除法转化为乘法运算并把带分数化为假分数，然后根据有理数的乘法运算法则进行计算即可得解．【解答】解：（1）﹣1÷（−18）﹣3÷（−12）＝﹣1×（﹣8）﹣3×（﹣2）＝8+6＝14；（2）﹣81÷13−13÷（−19）＝﹣81×3−13×（﹣9）＝﹣243+3＝﹣240；（3）﹣1+5÷（−16）×（﹣6）＝﹣1+5×（﹣6）×（﹣6）＝﹣1+180＝179；（4）（13−12）÷114÷110=−16×45×10=−43．【点评】本题考查了有理数的除法，有理数的乘法，有理数的加减法运算，熟记运算法则和运算顺序是解题的关键，计算时要注意运算符号的处理．45．计算．（1）1.25÷(−0.5)÷(−212)；（2）(−45)÷[(−13)÷(−25)]；（3）(13−56+79)÷(−118)；（4）−32324÷(−112)．【分析】（1）先把小数化为分数，再把除法运算化为乘法运算，然后约分即可；（2）要算中括号内的除法运算；（3）先把除法运算化为乘法运算，然后利用乘法的分配律计算；（4）先确定符合，再把带分数写成整数与真分数的和，然后利用乘法的分配律计算．【解答】解：（1）原式=54×（﹣2）×（−25）＝1；（2）原式＝﹣45÷（13×52）＝﹣45÷56＝﹣45×65＝﹣54；（3）原式＝（13−56+79）×（﹣18） =13×（﹣18）−56×（﹣18）+79×（﹣18）＝﹣6+15﹣14＝﹣5；（4）原式＝（3+2324）×12 ＝3×12+2324×12 ＝36+232 ＝36+1112 ＝4712．【点评】本题考查了有理数除法：除以一个不等于0的数，等于乘这个数的倒数．46．计算：（1）75×(13−12)×37÷54；（2）(56−37+13−914)÷(−142)．【分析】（1）先计算括号中的运算，以及除法化为乘法运算，约分即可得到结果；（2）原式先将除法运算化为乘法运算，再利用乘法分配律计算即可得到结果．【解答】解：（1）原式=75×（−16）×37×45=−225；（2）原式＝（56−37+13−914）×（﹣42）＝﹣35+18﹣14+27＝﹣4．【点评】此题考查了有理数的乘法与除法，熟练掌握运算法则是解本题的关键．题型八利用“倒数法”解决问题47．数学老师布置了一道思考题“计算：（−112）÷(13−56)”，小明仔细思考了一番，用了一种不同的方法解决了这个问题．小明的解法：原式的倒数为（13−56）÷(−112)=（13−56）×（﹣12）＝﹣4+10＝6，所以（−112）÷(13−56)=16．（1）请你判断小明的解答是否正确，并说明理由．（2）请你运用小明的解法解答下面的问题．计算：（−124）÷(13−16+38)．【分析】（1）正确，利用倒数的定义判断即可；（2）求出原式的倒数，即可确定出原式的值．【解答】解：（1）正确，理由为：一个数的倒数的倒数等于原数；（2）原式的倒数为（13−16+38）÷（−124）＝（13−16+38）×（﹣24）＝﹣8+4﹣9＝﹣13，则（−124）÷（13−16+38）=−113．【点评】此题考查了有理数的除法，熟练掌握运算法则是解本题的关键．48．请你认真阅读下列材料计算：（−130）÷（23−110+16−25）解法1：原式＝（−130）÷[23+16−（110+25）]＝（−130）÷（56−12）＝（−130）×3=−110 解法2：将原式的除数与被除数互换（23−110+16−25）÷（−130）＝（23−110+16−25）×（﹣30）＝﹣20+3﹣5+12＝﹣10 故原式=−110根据你对所提供的材料的理解，选择适当的方法计算下面的算式：（−142）÷（−16−314+23−47）【分析】法1：原式先计算括号中的加减运算，再计算除法运算即可得到结果；法2：将原式除数与被除数互换求出值，即可确定出原式的值．【解答】解：法1：原式＝（−142）÷[23−16−（314+47）]＝（−142）÷（12−1114）＝（−142）÷（−27）＝（−142）×（−72）=112；法2：将原式的除数与被除数互换，（−16−314+23−47）÷（−142）＝（−16−314+23−47）×（﹣42）＝7+9﹣28+24＝12，则原式=112．【点评】此题考查了有理数的除法，熟练掌握运算法则是解本题的关键．49．（2022秋•徐州月考）认真阅读材料后，解决问题：计算：130÷（23−110+16−25）．分析：利用通分计算23−110+16−25的结果很麻烦，可以采用以下方法进行计算．解：原式的倒数是（23−110+16−25）÷130 ＝（23−110+16−25）×30 ＝（23×30−110×30+16×30−25×30＝20﹣3+5﹣12＝10，故原式=110．仿照阅读材料计算：（−120）÷（−14−25+910−32）．【分析】仿照所给的求解方式进行运算即可．【解答】解：原式的倒数是：（−14−25+910−32）÷（−120）＝（−14−25+910−32）×（﹣20）=14×20+25×20−910×20+32×20 ＝5+8﹣18+30＝25，故原式=125．【点评】本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．50．阅读材料：计算130÷（23−110+16−25）分析：利用通分计算23−110+16−25的结果很麻烦，可以采用以下方法进行计算解：原式的倒数是：＝（23−110+16−25）×30 ＝（23−110+16−25）×30 =23×30−110×30+16×30−25×30＝10故原式=110请你根据对所提供材料的理解，选择合适的方法计算：148÷（112−316+524+23）【分析】仿照阅读材料中的方法求出原式的值即可．【解答】解：原式的倒数是：（112−316+524+23）÷148 ＝（112−316+524+23）×48＝4﹣9+10+32＝37，故原式=137．【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．。

有理数乘除乘方练习题

一、有理数乘法1. 计算：3 × 42. 计算：5 × (2) × 33. 计算：(2) × (3) × (4)4. 计算：5 × (6) × 75. 计算：(3) × 4 × (2)6. 计算：5 × (2) × (3) × 47. 计算：(3) × (2) × (5) × 48. 计算：6 × (7) × 89. 计算：5 × (3) × 4 × (2)10. 计算：(2) × (3) × (4) × 5二、有理数除法1. 计算：6 ÷ 22. 计算：5 ÷ (3)3. 计算：(2) ÷ (4)4. 计算：6 ÷ (3)5. 计算：5 ÷ (2)6. 计算：(3) ÷ 47. 计算：6 ÷ (2)8. 计算：5 ÷ (3) ÷ 29. 计算：(2) ÷ (4) ÷ (3)10. 计算：6 ÷ (3) ÷ (2)三、有理数乘方1. 计算：（2）^32. 计算：（3）^23. 计算：（4）^34. 计算：（5）^45. 计算：（6）^26. 计算：（7）^37. 计算：（8）^48. 计算：（9）^29. 计算：（10）^310. 计算：（11）^4四、混合运算1. 计算：3 × (2) ÷ 4 + 52. 计算：6 ÷ (3) × (2) 43. 计算：（3）^2 × (2) ÷ 4 + 54. 计算：6 ÷ (3) × (2) ÷ (4) + 75. 计算：（3）^3 ÷ (2) × (4) 56. 计算：6 ÷ (3) × (2) × (4) ÷ (5) + 67. 计算：（3）^2 ÷ (2) × (4) ÷ (5) 78. 计算：6 ÷ (3) × (2) × (4) × (5) + 89. 计算：（3）^3 ÷ (2) × (4) ÷ (5) ÷ (6) + 910. 计算：6 ÷ (3) × (2) × (4) × (5) × (6) + 10一、有理数乘法11. 计算：(7) × 8 × (9)12. 计算：5 × (3) × (2) × 413. 计算：(6) × (5) × 7 × (2)14. 计算：4 × (3) × (2) × 515. 计算：(2) × 7 × (8) × (9)16. 计算：5 × (4) × (3) × 217. 计算：(6) × (7) × 8× (9)18. 计算：3 × 2 × (5) × 419. 计算：(2) × (3) × 6 × (7)20. 计算：5 × (4) × (3) × (2)二、有理数除法21. 计算：12 ÷ (6) ÷ 322. 计算：9 ÷ 3 ÷ (2)23. 计算：(4) ÷ (2) ÷ (3)24. 计算：6 ÷ (3) ÷ (2)25. 计算：5 ÷ 5 ÷ (3)26. 计算：(2) ÷ (4) ÷ (5)27. 计算：8 ÷ (2) ÷ (4)28. 计算：7 ÷ 7 ÷ (3)29. 计算：(3) ÷ (2) ÷ (6)30. 计算：9 ÷ (3) ÷ (2)三、有理数乘方31. 计算：（8）^232. 计算：（5）^333. 计算：（4）^434. 计算：（3）^535. 计算：（2）^636. 计算：（7）^737. 计算：（6）^838. 计算：（5）^939. 计算：（4）^1040. 计算：（3）^11四、混合运算41. 计算：2 × (3) ÷ 4 + 5 × (2)42. 计算：4 ÷ (2) × (3) 6 ÷ 343. 计算：（5）^2 × (3) ÷ 2 + 744. 计算：6 ÷ (3) × (2) ÷ (4) 845. 计算：（3）^3 ÷ (2) × (4) + 546. 计算：6 ÷ (3) × (2) × (4) ÷ (5) 647. 计算：（3）^2 ÷ (2) × (4) ÷ (5) + 748. 计算：6 ÷ (3) × (2) × (4) × (5) + 849. 计算：（3）^3 ÷ (2) × (4) ÷ (5) ÷ (6) 950. 计算：6 ÷ (3) × (2) × (4) × (5) × (6) 10一、有理数乘法51. 计算：(10) × (5) × 652. 计算：7 × (3) × (2) × 453. 计算：(8) × (9) × 7 × (2)54. 计算：4 × 5 × (3) × 255. 计算：(2) × 7 × (8) × 956. 计算：5 × (4) × 3 × (2)57. 计算：(6) × (7) × 8 × (9)58. 计算：3 × 2 × (5) × 459. 计算：(2) × (3) × 6 × 760. 计算：5 × (4) × (3) × (2)二、有理数除法61. 计算：15 ÷ (5) ÷ 362. 计算：9 ÷ 3 ÷ (2)63. 计算：(4) ÷ (2) ÷ (3)64. 计算：6 ÷ (3) ÷ (2)65. 计算：5 ÷ 5 ÷ (3)66. 计算：(2) ÷ (4) ÷ (5)67. 计算：8 ÷ (2) ÷ (4)68. 计算：7 ÷ 7 ÷ (3)69. 计算：(3) ÷ (2) ÷ (6)70. 计算：9 ÷ (3) ÷ (2)三、有理数乘方71. 计算：（9）^272. 计算：（6）^373. 计算：（5）^474. 计算：（4）^575. 计算：（3）^676. 计算：（8）^777. 计算：（7）^878. 计算：（6）^979. 计算：（5）^1080. 计算：（4）^11四、混合运算81. 计算：3 × (2) ÷ 4 + 6 × (2)82. 计算：4 ÷ (2) × (3) 9 ÷ 383. 计算：（5）^2 × (3) ÷ 2 + 1084. 计算：6 ÷ (3) × (2) ÷ (4) 1285. 计算：（3）^3 ÷(2) × (4) + 15. 计算：6 ÷ (3) × (2) × (4) ÷ (5) 1887. 计算：（3）^2 ÷ (2) × (4) ÷ (5) + 2188. 计算：6 ÷ (3) × (2) × (4) × (5) + 2489. 计算：（3）^3 ÷ (2) × (4) ÷ (5) ÷ (6) 2790. 计算：6 ÷ (3) × (2) × (4) × (5) × (6) 30一、有理数乘法91. 计算：(12) × (6) × 592. 计算：8 × (3) × (2) × 493. 计算：(9) × (7) × 8 × (2)94. 计算：5 × 4 × (3) × 295. 计算：(2) × 7 × (8) × 996. 计算：5 × (4) × 3 × (2)97. 计算：(6) × (7) × 8 × (9)98. 计算：3 × 2 × (5) × 499. 计算：(2) × (3) × 6 × 7100. 计算：5 × (4) × (3) × (2)二、有理数除法101. 计算：18 ÷ (9) ÷ 3102. 计算：12 ÷ 3 ÷ (2)103. 计算：(6) ÷ (2) ÷ (3)104. 计算：9 ÷ (3) ÷ (2)105. 计算：10 ÷ 5 ÷ (3)106. 计算：(4) ÷ (2) ÷ (5)107. 计算：16 ÷ (4) ÷ (2)108. 计算：14 ÷ 7 ÷ (3)109. 计算：(5) ÷ (2) ÷ (6)110. 计算：15 ÷ (5) ÷ (2)三、有理数乘方111. 计算：（10）^3112. 计算：（7）^4113. 计算：（6）^5114. 计算：（5）^6115. 计算：（4）^7116. 计算：（3）^8117. 计算：（8）^9118. 计算：（7）^10119. 计算：（6）^11120. 计算：（5）^12四、混合运算121. 计算：4 × (3) ÷ 4 + 7 × (2)122. 计算：5 ÷ (2) × (3) 12 ÷ 3123. 计算：（6）^2 × (3) ÷ 2 + 14124. 计算：9 ÷ (3) × (2) ÷ (4) 18125. 计算：（4）^3 ÷ (2) × (4) + 21126. 计算：8 ÷ (3) × (2) × (4) ÷ (5) 24127. 计算：（3）^2 ÷ (2) × (4) ÷ (5) + 27128. 计算：7 ÷ (3) × (2) × (4) × (5) + 30129. 计算：（3）^3 ÷ (2) × (4) ÷ (5) ÷ (6) 33 130. 计算：8 ÷ (3) × (2) × (4) × (5) × (6) 36答案一、有理数乘法1. 122. 303. 244. 605. 246. 1207. 3608. 969. 12010. 60二、有理数除法1. 32. 5/34. 25. 1/36. 1/57. 3/58. 29. 1/310. 3三、有理数乘方1. 82. 1253. 2564. 2435. 646. 21877. 40968. 5314419. 5904910. 16777216四、混合运算1. 12. 13. 14. 16. 17. 18. 19. 110. 1。

有理数的乘除法(习题及答案)

有理数的乘除法（习题）1. 一个有理数与它的相反数的积一定是（）A ．正数B ．负数C ．非负数D ．非正数 2. 如果两个数的和为正数，积为负数，那么这两个数（）A ．都是正数B ．一个是正数，一个是负数，且负数的绝对值较大C ．都是负数D ．一个是正数，一个是负数，且正数的绝对值较大3. 有5张写着不同数字的卡片-7，-5，0，+4，+10，从中抽取2张卡片，使这2张卡片上的数字相除的商最小，最小的商是________．4. 计算：①9×(-6)=_______；(-7)×(-4) =________；(-0.75)×0=________； ②2934⎛⎫−⨯ ⎪⎝⎭=_______；21513⎛⎫⨯− ⎪⎝⎭=_______； ③1(10)(2)5⎛⎫−⨯−⨯− ⎪⎝⎭=____________； ④521124319152⎛⎫⎛⎫⎛⎫⨯−⨯−⨯− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=____________． 5. （1）(48)16−÷=__________=_____；3(3)128⎛⎫−÷−= ⎪⎝⎭__________=_____； 6255⎛⎫⎛⎫−÷−= ⎪ ⎪⎝⎭⎝⎭__________=_____；155⎛⎫÷− ⎪⎝⎭=__________=_____；（2）324=−__________=_____；548−=−__________=_____；（3）1(2)(5)3⎛⎫−÷−÷−= ⎪⎝⎭_______________=_____； 0.1(0.001)(1)÷−÷−=_______________=_____；5(0.25)(4)4−÷÷−=_______________=_____． 6. 计算：（1）1(0.1)(100)2−÷⨯−；（2）25(2)52⎛⎫−÷−⨯ ⎪⎝⎭；（3）12315574148⎛⎫⎛⎫÷−÷⨯− ⎪ ⎪⎝⎭⎝⎭；（4）11(5)2(0.75)24−÷⨯+−÷；复习巩固（5）55(6)(5)0.25(7)414⎛⎫−⨯−⨯−−÷−⨯ ⎪⎝⎭；（6）21(8)3230.25−−−−÷+−⨯．7. 计算：（1）11112462⎛⎫+−⨯ ⎪⎝⎭；（2）457(36)9612⎛⎫−⨯−+− ⎪⎝⎭；（3）5116312⎛⎫−÷ ⎪⎝⎭；（4）936911⎛⎫−÷ ⎪⎝⎭；（5）111535⎛⎫÷− ⎪⎝⎭；（6）37773711488848⎛⎫⎛⎫⎛⎫⎛⎫−÷−+−÷− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭．8. 若某地区夏季高山上的温度从山脚起每升高100米平均降低0.8℃，已知山脚的温度是28℃，若这座山的高度是5千米，则山顶的温度为____________℃．9. 某冷冻厂的一个冷库，现在的室温是-2℃，现有一批食品，需在-26℃下冷藏，如果每小时能降温4℃，要降到所需温度，需要_______小时．10. 有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：（2）若白菜每千克售价2.1元，则出售这20筐白菜可卖多少元？参考答案1.D 2.D 3. -24. ①-54；28；0；②32−；-25；③-4；④13−． 5. （1）14816−⨯；-3；12833⎛⎫−⨯− ⎪⎝⎭；128；6552⎛⎫−⨯− ⎪⎝⎭；3；5(5)⨯−；-25；（2）1324⎛⎫⨯− ⎪⎝⎭；18−； 1(54)8⎛⎫−⨯− ⎪⎝⎭； 274；（3）12(3)5⎛⎫−⨯−⨯− ⎪⎝⎭；65−；1(1000)(1)10⨯−⨯−；100；141454⎛⎫−⨯⨯− ⎪⎝⎭；120． 6. （1）20；（2）252；（3）43；（4）174−；（5）112；（6）173． 7. （1）-1；（2）7；（3）6；（4）1411−；（5）2252；（6）-2．8. -129. 610. （1）与标准重量比较，20筐白菜总重量不足的千克数为10千克；（2）这20筐白菜可卖1 029元．复习巩固。

人教版七年级上册数学第二章有理数的运算--计算题训练(含解析)

；
（3）解：原式．
4．(1) ；
(2) ；
(3) ；
(4) ；
(5) ；
(6) ．
【分析】本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．
利用有理数的加减运算的法则进行运算即可；
先算除法，乘法，再算加减即可；
先算乘方，绝对值，再算乘法，最后算加减即可；
先算乘方，再算括号里的运算，除法转为乘法，接着算乘法，最后算加减即可；
（1）根据乘法交换律、结合律和有理数的乘法运算法则进行计算即可得解；
（2）把小数化为分数，然后根据有理数的乘法运算法则进行计算即可得解；
（3）逆运用乘法分配律进行计算即可得解；
（4）利用乘法分配律进行计算即可得解．
【详解】（1）解：原式
；
（2）解：原式
；
（3）解：原式
；
（4）解：原式
．
3．(1)
(2)
先算乘方，乘法的分配律，再算加减即可；
先算乘方，除法转为乘法，再算乘法，最后算加减即可．
【详解】（1）解：
；
（2）解：
；
（3）解：
；
（4）解：
；
（5）解：
；
（6）解：
．
5．(1)
(2)1
【分析】本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．
（1）利用有理数的加减运算的法则进行运算即可；
熟练掌握运算法则及性质是解题的关键．
【详解】（1）解：
；
（2）解：
；
（3）解：
；
（4）解：
．
9．(1)
(2)18
(3)
(4)
【分析】本题考查了有理数的加、减、乘法运算，熟练掌握运算法则是解题的关键．

人教版七年级上册数学有理数的乘除专项练习

人教版七年级上册数学有理数的乘除专项练习【例题1】有理数乘法（☆☆）计算：（1）(5)(6)-⨯- （2）11()124-⨯（3）()()825425.1⨯-⨯-⨯ （4）()2431 2.53925⎛⎫⎛⎫⨯-⨯-⨯- ⎪ ⎪⎝⎭⎝⎭（5）(8)(3.76)(0.125)-⨯⨯-【例题2】有理数的巧算（☆☆）计算：（1））（）（24-125836121-⨯+++ （2）36187436597⨯⎪⎭⎫⎝⎛-+-（3）189(15)19⨯- （4）9181799⨯-【练2-1】（☆☆）计算：（1） ()1111202345⎛⎫-+--⨯- ⎪⎝⎭ （2）521220.665⎛⎫⎛⎫-⨯-- ⎪ ⎪⎝⎭⎝⎭（3）24(9)5025-⨯ （4）111112(2111)42612-⨯-+-（5）1111(2345)()2345⨯⨯⨯⨯--- （6）111(5)323(6)3333-⨯+⨯+-⨯【例题3】有理数法则判断（☆☆）（1）已知两个有理数a ，b ，如果ab ＜0，且a ＋b ＜0，那么（）A ．a ＞0，b ＜0B ．a ＜0，b ＞0C ．a 、b 异号D ．a 、b 异号且负数的绝对值较大（2）若a ＋b ＋c ＝0，且b ＜c ＜0，则下列各式中，错误的是（） A ．a ＋b ＞0 B ．b ＋c ＜0 C ．ab ＋ac ＞0 D ．a ＋bc ＞0 （3）已知a ＋b ＞0，a －b ＜0，ab ＜0，则a______0，b_____0，|a|___|b|. 【练3-1】（☆☆）（1）如果a ＋b ＜0，0ba>，则下列结论成立的是（） A ．a ＞0，b ＞0 B ．a ＜0，b ＜0 C ．a ＞0，b ＜0 D ．a ＜0，b ＞0 （2）下列命题正确的是（）A ．若ab ＞0，则a ＞0，b ＞0B ．若ab ＜0，则a ＜0，b ＜0C ．若ab ＝0，则a ＝0或b ＝0D ．若ab ＝0，则a ＝0且b ＝0 【例题4】有理数除法（☆☆）计算：（1）(32)(8)-÷- （2）112(1)36÷-（3）⨯÷）（）（811-71311()(3)(1)3524-⨯-÷-÷【练4-1】（☆☆）计算：（1）12933÷⨯ （2）113()(10.2)(3)245÷-+-÷⨯-（3）530()35÷-⨯【例题5】有理数乘除判断（☆）（1）若实数a 、b 满足0a b a b +=，则ab ab＝___________. （2）若k 是有理数，则(|k|＋k)÷k 的结果是（）A ．正数B ．0C ．负数D ．非负数（3）若A ．b 都是非零有理数，那么aba b a b ab++的值是多少？【例题6】乘法分配律逆用运算（☆☆）计算：（1）()()()56324432+⨯-+-⨯（2）()()()11840.125848487⎛⎫-⨯-+-⨯-⨯- ⎪⎝⎭（3）()4.3657.13.2328.62.3514.3⨯--⨯+⨯-（4）4535525()()()()()(1)51351313513-⨯---⨯++-⨯--【练6-1】（☆☆）计算：（1）5717657119651326513113÷+÷⎪⎭⎫ ⎝⎛-+⨯⎪⎭⎫ ⎝⎛-+⨯⎪⎭⎫ ⎝⎛-（2）554(47.75)2(35.25)(2)12.5(7)999-⨯+-⨯-+⨯-（3）()2215130.34130.343737-⨯-⨯+-⨯-⨯（4）()()()34.07414417334.04314-⨯+-⨯+⨯-⨯-【例题7】可转为分配律的除法（☆☆）计算：2153134121648⎡⎤⎛⎫⎛⎫⎛⎫------÷- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦【练7-1】（☆☆）计算：⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛--+60112715116543【例题8】不可转分配律除法的巧算解：原式的倒数故原式【练8-1】（☆☆）计算：（1）⎪⎭⎫ ⎝⎛--+÷-21526131301 （2）⎪⎭⎫⎝⎛-+-÷⎪⎭⎫ ⎝⎛-526110132301（3））（）（12787431)87()87(12787431--÷-+-÷--【例题9】有理数乘除应用（☆☆）已知|a-1|=3，|b-3|与21）（+c 互为相反数，且a ＞b ，求代数式2a-b+c-abc 的值.【练9-1】（☆☆）已知|a|=5,|b|=2,(1)若a ＜0，b ＞0，求3a-2b 的值；（2）若a ＞0，b ＜0，|c-2|=1，求|c -b |2+c ab .【练9-2】（☆☆）已知ab ＜0，0ca＞，且|c|＞|b|＞|a|,数轴上a 、b 、c 对应的点是A 、B 、C. （1）若|a|=-a 时，请在数轴上标出A ，B ，C 的大致位置；（2）在（1）的条件下，化简|a-b|-|b-c|+|c+a|.【例题10】较难的判断题型（☆☆）下列说法正确的个数有（）①若干个有理数相乘，积的符号由负因数的个数决定；②若a ＞b ，则a 的倒数小于b 的倒数；③若xyz ＜0，则xyz|xyz |z |z |y |y |x |x |+++的值为0或者-4. A.0个 B.1个 C.2个 D.3个【练10-1】（☆☆）下列说法：①两个数互为倒数，则他们乘积为1；②若a ，b 互为相反数，则1-=ba；③几个有理数相乘，若负因数的个数是奇数个，则积为负；④4)2()2()2()2(2-=-⨯-⨯-⨯-；⑤若dc b a =则bda c =.错误的是 . 【练10-2】（☆☆）下列说法：①2020个有理数相乘，其中负数个数是2003个，则所得结果是负数；②若m 满足|m|+m=0,则m ＜0;③有理数ab 的倒数是b a ；④若三个有理数c b a 、、满足1bc|bc |ac |ac |ab |ab |-=++，则1||||||-=++cc b b a a 。

七年级数学上册有理数乘除计算题2试题

富顺县板桥中学七年级数学上册?有理数乘除?计算题〔2〕新人教版1、直接写出结果：〔4×5=20分〕①()()=-⨯-23 ②=⨯⎪⎭⎫ ⎝⎛-43352 ③=⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-21487 ④ =⎪⎭⎫ ⎝⎛-⨯121120 ⑤()⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛-⨯+32802019723= 2、计算：〔4×5=20分〕① 〔-35〕÷〔-7〕②()⎪⎭⎫ ⎝⎛-÷-6118③41432÷⎪⎭⎫⎝⎛-④ ⎪⎭⎫ ⎝⎛-÷91130⑤⎪⎭⎫⎝⎛-÷÷⎪⎭⎫⎝⎛-321143743、计算：〔15×4+10×4=60分〕 ①⎪⎭⎫⎝⎛-⨯⎪⎭⎫⎝⎛-÷⎪⎭⎫⎝⎛-818321 ②9221441254⨯⎪⎭⎫ ⎝⎛-÷⨯-③75.04121391716+⎪⎭⎫⎝⎛-⨯-÷- ④⎪⎭⎫ ⎝⎛-+⨯-21614112⑤⎪⎭⎫⎝⎛+--÷-6521324112 ⑥()331331⨯⎪⎭⎫ ⎝⎛-÷-⨯⑦()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛⨯+-+---2532.0153⑧()511322534125109.01÷----÷÷--+-÷-励志赠言经典语录精选句；挥动**，放飞梦想。

厚积薄发，一鸣惊人。

关于努力学习的语录。

自古以来就有许多文人留下如头悬梁锥刺股的经典的，而近代又有哪些经典的高中励志赠言出现呢?小编筛选了高中励志赠言句经典语录，看看是否有些帮助吧。

好男儿踌躇满志，你将如愿;真巾帼灿烂扬眉，我要成功。

含泪播种的人一定能含笑收获。

贵在坚持、难在坚持、成在坚持。

功崇惟志，业广为勤。

耕耘今天，收获明天。

成功，要靠辛勤与汗水，也要靠技巧与方法。

常说口里顺，常做手不笨。

不要自卑，你不比别人笨。

不要自满，别人不比你笨。

新】人教版七年级上册数学有理数的乘除法练习题

新】人教版七年级上册数学有理数的乘除法练习题有理数的乘除法练题课堂研究检测一、选择题1.下列计算正确的是( )。

A) (-1) × (-1) = 1B) (-8) × (1/2) = 17/3C) (-7) × (+6/77) = -6D) 3 × (-1/2) = -3/22.两个有理数之积是。

那么这两个有理数( )。

A) 至少有一个是B) 都是C) 互为倒数D) 互为相反数3.(-8/5) × (10-1+.05) = -8+1-.04，这个运算应用了( )。

A) 加法结合律B) 乘法结合律C) 乘法交换律D) 分配律4.比较a与3a的大小，正确的是( )。

A) 3a。

aB) 3a = aC) 3a < aD) 上述情况都可能二、填空题5.式子 (3/1) × (-6) × 7.5 × (+3.8) × (-981) × (-66) 的符号为______。

6.若a=4，b=，c=-3，d=-5，则c-ad=______，(a-b)(c-d)=______。

三、计算题7.直接将答案写在横线上：1) (-2/3) × (-3/4) = ______；2) (-8) × (-1/4) = ______；3) (-3)(-3/8) = ______；4) (+1) × (+1.2) = ______。

8.(-1/3) × (-2/3) × (-320/107) = ______。

9.(2-1/3) × (-1/) = ______。

10.(-7/) + (-1) = ______。

综合、运用、诊断一、填空题12.若a0，则(-a) × b × (-c) < 0.13.若a+b0，则a<0，b<0.二、选择题14.已知(-ab) × (-ab) × (-ab)。

七年级数学有理数的乘除法练习题(二)(含答案)

七年级上学期数学《有理数的乘除法》练习题一、选择1.如果两个有理数在数轴上的对应点在原点的同侧,则这两个有理数的积( )A.一定为正B.一定为负C.为零D. 可能为正,也可能为负2.若干个不等于0的有理数相乘,积的符号( )A.由因数的个数决定B.由正因数的个数决定C.由负因数的个数决定D.由负因数和正因数个数的差为决定3.下列运算结果为负值的是( )A.(-7)×(-6)B.(-6)+(-4);C.0×(-2)(-3)D.(-7)-(-15)4.下列运算错误的是( )A.(-2)×(-3)=6B.1(6)32⎛⎫-⨯-=- ⎪⎝⎭C.(-5)×(-2)×(-4)=-40D.(-3)×(-2)×(-4)=-245.若两个有理数的和及它们的积都是正数,则这两个数( )A.都是正数B.是符号相同的非零数C.都是负数D.都是非负数6.下列说法正确的是( )A.负数没有倒数B.正数的倒数比自身小C.任何有理数都有倒数D.-1的倒数是-17.关于0,下列说法不正确的是( )A.0有相反数B.0有绝对值C.0有倒数D.0是绝对值和相反数都相等的数8.下列运算结果不一定为负数的是( )A.异号两数相乘B.异号两数相除C.异号两数相加D.奇数个负因数的乘积9.下列运算有错误的是( )A.13÷(-3)=3×(-3) B.1(5)5(2)2⎛⎫-÷-=-⨯-⎪⎝⎭C.8-(-2)=8+2D.2-7=(+2)+(-7)10.下列运算正确的是( )A.113422⎛⎫⎛⎫---=⎪ ⎪⎝⎭⎝⎭; B.0-2=-2; C.34143⎛⎫⨯-=⎪⎝⎭; D.(-2)÷(-4)=2二、填空1.如果两个有理数的积是正的,则这两个因数的符号一定______.2.如果两个有理数的积是负的,则这两个因数的符号一定_______.3.奇数个负数相乘,结果的符号是_______.4.偶数个负数相乘,结果的符号是_______.5.如果410,0a b>>,则ab_____0.6.如果5a>0,0.3b<0,0.7c<0,则bac____0.7.-0.125的相反数的倒数是________.8.若a>0,则aa=_____;若a<0,则aa=____.三、解答1.计算:(1)384⎛⎫-⨯⎪⎝⎭; (2)12(6)3⎛⎫-⨯-⎪⎝⎭; (3)(-7.6)×0.5; (4)113223⎛⎫⎛⎫-⨯-⎪ ⎪⎝⎭⎝⎭.2.计算.(1)38(4)24⎛⎫⨯-⨯--⎪⎝⎭; (2)38(4)(2)4-⨯-⨯-; (3)38(4)(2)4⎛⎫⨯-⨯-⨯-⎪⎝⎭.3.计算(1)111111111111234567⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯---⨯-⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭;(2)111111 111111 223344⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-⨯+⨯-⨯+⨯-⨯+⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.4.计算(1)(+48)÷(+6); (2)213532⎛⎫⎛⎫-÷⎪ ⎪⎝⎭⎝⎭; (3)4÷(-2); (4)0÷(-1000).5.计算.(1)(-1155)÷[(-11)×(+3)×(-5)]; (2)375÷2332⎛⎫⎛⎫-÷-⎪ ⎪⎝⎭⎝⎭;(3)1213(5)6(5) 33⎛⎫⎛⎫-÷-+-÷-⎪ ⎪⎝⎭⎝⎭.6.计算(1)111382⎛⎫⎛⎫-÷--÷-⎪ ⎪⎝⎭⎝⎭; (2)11181339⎛⎫-÷-÷- ⎪⎝⎭.七年级上学期数学《有理数的乘除法》练习题参考答案一、ACBBA,DCCAB二、1．相同; 2互异; 3负; 4正的; 5.>; 6.>; 7.8; 8.1,-1三、1．（1）-6；（2）14；（3）-3.8；（4）1 8 62．（1）22；（2）2；（3）-48；3．（1）213；（2）584．（1）8；（2）23；（3）-2；（4）05．（1）-7；（2）375；（3）4 6．（1）14；（2）-240。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初一上第二章有理数运算练习
上步中学数学组王望芳
班级______姓名______学号______ 一、填空(每小空2分，共30分)
1、2
11-的相反数是_____，倒数是______，绝对值是_______. 2、绝对值等于5的数是_____。

3、如果a ＜0，b ＞0，那么ab_____0.
4、如果a ＜0，b ＜0，那么b
a _____0. 5、两个有理数的和为负数，且它们的积为正数，则这两个数的符号为_____, _____.
6、若a a =，那么a_____0.
7、三个有理数相乘积为负数，则其中有_____个或_____个负因数.
8、（－1）×（－2）×…×（－99）×0×1×2×…×99=_______. 9、=-⨯⋅⋅⋅⨯-⨯-
2002
)1()1()1(_____. 10、一个数的倒数等于它本身，这个数是________.
11、a 与b 互为相反数，则2ab(a+b)=_________.
二、计算（每小题4分，共80分）
12、（－8）×（－7） 13、2.9×（－0.4）解原式= 解原式=
14、4
1)98(⨯- 15、－91÷13 解原式= 解原式=
16、（－18）÷（－0.6） 17、)12
11(713-÷ 解原式= 解原式=
18、)4
1()59(65)3(-⨯-⨯⨯- 解原式=
19、（－5）×8×（－7）×（＋0.25）
解原式=
20、0.1×（－0.001）×（－1） 21、)511()4()6(÷-÷-
解原式=
解原式=
22、)58
()32(25.0-⨯-÷-
23、)412()211()43(-÷-⨯- 解原式=
解原式=
24、8＋5×（－4）
25、（－3）×（－7）－9×（－6）解原式=
解原式=
26、31
)3()6(⨯---
27、（－1）×（－8）－3×（－2）解原式=
解原式=
28、－8＋4÷（－2）
29、3×（－4）－（－28）÷7 解原式=
解原式=
30、)12()21
61
41
(-⨯-+
31、62524⨯ 解原式=
解原式=。