无向网的构建及其遍历
graph2_

关键活动和关键路径
从源点到汇点可能有多条有向路径,路径上各活动所 需时间之和叫该路径的路径长度 路径长度. 路径长度 具有最大路径长度的路径叫做关键路径 最大路径长度的路径叫做关键路径,上图的关键 最大路径长度的路径叫做关键路径 路径有a1, a4, a7, a10和a1, a4, a8, a11,它们的路径长度均 为18. 关键路径上的所有活动都叫做关键活动 关键活动,对上图的 关键活动 AOE,关键活动是a1,a4, a7, a8, a10 , a11. 关键活动上持续时间的变化可能影响整个工程的工期
MST性质可以用反证法证明如下 性质可以用反证法证明如下: 性质可以用反证法证明如下
由假设图G的任何一棵最小生成树都不包含边(u,v), 显然当把边(u,v)加入到G的一棵最小生成树T中时,由 生成树的定义,将产生一个含有边(u,v)的回路 于T是生成树,T中必存在不同于边(u,v)的另一条边 (u',v'),使得u'∈U,v'∈V-U,且u和u'之间, v和v'之间均有路径相连通 将边(u',v')删除,这样就消除了上述回路,并得到 了另一棵生成树T'.由于W(u,v) ≤W(u',v'),所以 生成树T'的耗费不大于树T的耗费.于是T'是一棵包含 边(u,v)的最小生成树,这与假设矛盾
V V1 设G = 1<V,E>是一个连通网,其中每条边(vi, 6 5 vj)上带有权W(vi,vj).集合U是顶点集V的一 1 1 V2 5 V2 V4 V4 5 个非空真子集.构建生成树时需要一条边连通 V3 V3 3 顶点集合U和V-U.如果(u,v)∈E,其中 4 2 6 u∈U,v∈V-U,且边(u,v)是符合条件的 6 V5 V6 V5 V6 权值W (u,v)最小的,那么一定存在一棵包含 边(u,v)的最小生成树.这条性质也称为MST 性质.
无向网基本操作(最小生成树Prime算法)

无向网基本操作(最小生成树Prime算法)源代码#include"stdio.h"#include"malloc.h"#define MAX_VERTEX_NUM 20typedef struct arc{int adj;int info;}ArcCell,AdjMatrix;typedef struct{char vertex[MAX_VERTEX_NUM];AdjMatrix arc[MAX_VERTEX_NUM][MAX_VERTEX_NUM];int vexnum,arcnum;}UDNGraph;typedef struct{int a[MAX_VERTEX_NUM];int front,rear;}queue;typedef struct MSTE{int v1,v2;int w;}MSTE;queue* initqueue(){queue *q;q=(queue*)malloc(sizeof(queue));q->front=0;q->rear=0;return q;}int queueempty(queue *q){if(q->front==q->rear)return 1;elsereturn 0;}void enqueue(queue *q,int m){q->a[q->rear]=m;q->rear=(q->rear+1)%MAX_VERTEX_NUM;}int dequeue(queue *q){int t;if(q->front==q->rear)return 0;else{t=q->a[q->front];q->front=(q->front+1)%MAX_VERTEX_NUM;return t;}}void BFSTTraverseGraph(UDNGraph *G){int i,j,visited[MAX_VERTEX_NUM];int u;queue *q;q=initqueue();for(i=0;i<G->vexnum;i++)visited[i]=-1;for(i=0;i<G->vexnum;i++)if(visited[i]==-1){visited[i]=1;printf("\t%c",G->vertex[i]);enqueue(q,G->vertex[i]);while(!queueempty){u=dequeue(q);for(j=0;j<G->vexnum;j++)if(visited[j]==-1&&G->arc[u][j].adj!=-1){visited[j]=1;printf("\t%c",G->vertex[j]);enqueue(q,j);}}}}UDNGraph* Create_Graph(){UDNGraph *G;int i,j,w,m,n;G=(UDNGraph*)malloc(sizeof(UDNGraph));printf("Please input the number of the vertex:");scanf("%d",&G->vexnum);printf("Please input the number of the arc:");scanf("%d",&G->arcnum);for(i=0;i<G->vexnum;i++){G->vertex[i]=i+'A';}for(i=0;i<G->vexnum;i++)for(j=0;j<G->vexnum;j++){G->arc[i][j].adj=-1;G->arc[i][j].info=0;}for(i=0;i<G->arcnum;i++){printf("Please input the weight:");scanf("%d%d%d",&m,&n,&w);G->arc[m][n].adj=w;G->arc[n][m].adj=w;}return G;}void PrintGraph(UDNGraph *G){int i,j;for(i=0;i<G->vexnum;i++){for(j=0;j<G->vexnum;j++)printf("\t%d",G->arc[i][j].adj);printf("\n\n");}}void Dfs(UDNGraph *G,int v,int visited[]){int i;visited[v]=1;printf("\t%c",G->vertex[v]);for(i=0;i<G->vexnum;i++)if(visited[i]==-1&&G->arc[v][i].adj !=-1)Dfs(G,i,visited);}void DFSTraverseGraph(UDNGraph *G){int i,v,visited[MAX_VERTEX_NUM];for(i=0;i<G->vexnum;i++)visited[i]=-1;for(v=0;v<G->vexnum;v++)if(visited[v]==-1)Dfs(G,v,visited);printf("\n");}MSTE* Mini_Prime(UDNGraph *G,int u){MSTE *T;int i,j,k,m,min;int v1,v2;int visited[MAX_VERTEX_NUM];T=(MSTE*)malloc((G->vexnum)*sizeof(MSTE));for(i=0;i<G->vexnum;i++)visited[i]=-1;visited[u]=1;for(i=0;i<G->vexnum-1;i++){min=1000;for(j=0;j<G->vexnum;j++)if(visited[j]==1)for(k=0;k<G->vexnum;k++)if(visited[k]==-1&&G->arc[j][k].adj!=-1&&G->arc[j][k].adj<min){min=G->arc[j][k].adj;v1=j;v2=k;}T[i].v1=v1;T[i].v2=v2;T[i].w=G->arc[v1][v2].adj;visited[v2]=1;}return T;}void PrintMin(MSTE T[100],UDNGraph *G){int i;for(i=0;i<G->vexnum-1;i++)printf("Two vertex and weight:%d\t%d\t%d\n",T[i].v1,T[i].v2,T[i].w); }void main(){UDNGraph *G;MSTE *T;int u;G=Create_Graph();printf("The Matrix is:\n");PrintGraph(G);printf("\nThe Depth_First Search is:\n");DFSTraverseGraph(G);printf("\nThe Beradth_fiirst Search is:\n");BFSTTraverseGraph(G);printf("\n");printf("Please input the number of a vertex:");scanf("%d",&u);T=Mini_Prime(G,u);PrintMin(T,G);}。
17年研究生昆明理工计算机818考试题目和答案
昆明理工大学2017年硕士研究生招生入学考试试题(A 卷)
考试科目代码:818 考试科目名称 :计算机学科专业基础综合
考生答题须知
1. 所有题目(包括填空、选择、图表等类型题目)答题答案必须做在考点发给的答题纸上,做在本试题册上无效。
请考生务必在答题纸上写清题号。
2. 评卷时不评阅本试题册,答题如有做在本试题册上而影响成绩的,后果由考生自己负责。
3. 答题时一律使用蓝、黑色墨水笔或圆珠笔作答(画图可用铅笔),用其它笔答题不给分。
4. 答题时不准使用涂改液等具有明显标记的涂改用品。
数据结构部分
一、填空题:(每空1分,共20分)
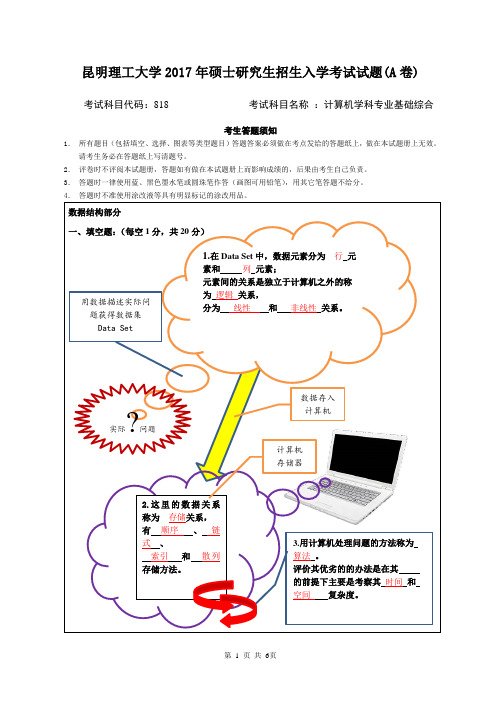
3.用计算机处理问题的方法称为 算法 。
评价其优劣的的办法是在其 的前提下主要是考察其 时间 和 空间 复杂度。
1.在Data Set 中,数据元素分为 行 元素和 列 元素; 元素间的关系是独立于计算机之外的称为 逻辑 关系, 分为 线性 和 非线性 关系。
实际问题
2.这里的数据关系称为 存储关系, 有 顺序 、 链式 、 索引 和 散列 存储方法。
用数据描述实际问题获得数据集 Data Set 计算机 存储器 数据存入计算机
昆明理工大学2017年硕士研究生招生入学考试试题。
人工智能导论知到章节答案智慧树2023年哈尔滨工程大学

人工智能导论知到章节测试答案智慧树2023年最新哈尔滨工程大学第一章测试1.下列关于智能说法错误的是()参考答案:细菌不具有智能2.目前,智能的定义已经明确,其定义为:智能是个体能够主动适应环境或针对问题,获取信息并提炼和运用知识,理解和认识世界事物,采取合理可行的(意向性)策略和行动,解决问题并达到目标的综合能力。
()参考答案:错3.传统人工智能领域将人工智能划分为强人工智能与弱人工智能两大类。
所谓强人工智能指的就是达到人类智能水平的技术或机器,否则都属于弱人工智能技术。
()参考答案:对4.人类历史上第一个人工神经元模型为MP模型,由赫布提出。
()参考答案:错5.下列关于数据说法错误的是()参考答案:我们通常所说的数据即能够直接作为计算机输入的数据是模拟数据6.下列关于大数据的说法中正确的有()参考答案:大数据具有多样、高速的特征;“大数据时代”已经来临;“大数据”是需要新处理模式才能具有更强的决策力、洞察发现力和流程优化能力的海量、高增长率和多样化的信息资产7.大数据在政府公共服务、医疗服务、零售业、制造业、以及涉及个人位置服务等领域都将带来可观的价值。
()参考答案:对8.人工智能在各个方面都有广泛应用,其研究方向也众多,下面属于人工智能研究方向的有()参考答案:语音识别;模式识别;机器学习;知识图谱9.机器人发展经历了程序控制机器人(第一代)、自适应机器人(第二代)、智能机器人(现代)三代发展历程。
()参考答案:对10.下列选项中属于人工智能的应用领域的有()参考答案:智能安防;智能农业;程序设计;智慧城市第二章测试1.生命起源于什么时候?()参考答案:45-35亿年之间2.人工智能使人类改造自然、适应自然的各类技术发展到最高阶段,智能技术使得工具变得有智能,促使技术在以指数级增长速度加速进化(加速回报定律)。
()参考答案:对3.对于人工智能的价值、作用与意义的说法错误的是:()参考答案:生命层面:促进人类社会整体向更高阶段文明加速进化;社会层面:促使人类自身由地球自然智能生命向更高阶的宇宙智能生命进化4.联结主义认为人的思维基元是符号,而不是神经元;人的认知过程是符号操作而不是权值的自组织过程。
一文打尽知识图谱(超级干货,建议收藏!)

⼀⽂打尽知识图谱(超级⼲货,建议收藏!)©原创作者 | 朱林01 序⾔知识是⼈类在实践中认识客观世界的结晶。
知识图谱(Knowledge Graph, KG)是知识⼯程的重要分⽀之⼀,它以符号形式结构化地描述了物理世界中的概念及其相互关系。
知识图谱的基本组成形式为<实体,关系,实体>的三元组,实体间通过关系相互联结,构成了复杂的⽹状知识结构。
图1 知识图谱组成复杂的⽹状知识结构知识图谱从萌芽思想的提出到如今已经发展了六⼗多年,衍⽣出了许多独⽴的研究⽅向,并在众多实际⼯程项⽬和⼤型系统中发挥着不可替代的重要作⽤。
如今,知识图谱已经成为认知和⼈⼯智能⽇益流⾏的研究⽅向,受到学术界和⼯业界的⾼度重视。
本⽂对知识图谱的历史、定义、研究⽅向、未来发展、数据集和开源库进⾏了全⾯的梳理总结,值得收藏。
02 简史图2 知识库简史图2展⽰了知识图谱及其相关概念和系统的历史沿⾰,其在逻辑和⼈⼯智能领域经历了漫长的发展历程。
图形化知识表征(Knowledge Representation)的思想最早可以追溯到1956年,由Richens⾸先提出了语义⽹(Semantic Net)的概念。
逻辑符号的知识表⽰形式可以追溯到1959年的通⽤问题求解器(General Problem Solver, GPS)。
20世纪70年代,专家系统⼀度成为研究热点,基于知识推理和问题求解器的MYCIN系统是当时最著名的基于规则的医学诊断专家系统之⼀,该专家系统知识库拥有约600条医学规则。
此后,20世纪80年代早期,知识表征经历了Frame-based Languages、KL-ONE Frame Language的混合发展时期。
⼤约在这个时期结束时的1984年,Cyc项⽬出现了,该项⽬最开始的⽬标是将上百万条知识编码成机器可⽤的形式,⽤以表⽰⼈类常识,为此专门设计了专⽤的知识表⽰语⾔CycL,这种知识表⽰语⾔是基于⼀阶关系的。
绪论(数据结构教程PPT课件)

在网络传输或文件读写过程中,使 用队列作为缓冲区,暂时存储待处 理的数据,以提高处理效率。
04
串、数组和广义表
串定义及基本操作
串的基本操作包括
赋值操作、连接操作、求串长、比较操作、定位操作等。
串的存储结构包括
顺序存储结构和链式存储结构。
串模式匹配算法
串模式匹配算法是指在一个主串中寻找一个子串(模式串)的位置。
函数调用
在程序执行过程中,使用 栈来保存函数调用的信息, 如函数参数、局部变量和 返回地址等。
队列定义及基本操作
01
队列(Queue)是一种特殊的线性数据结构,其操作在表 的两端进行。一端称为队头(front),另一端称为队尾 (rear)。
02
队列的基本操作包括
03
入队(enqueue):在队尾插入一个元素。
3
线性表的抽象数据类型描述
数据类型名称、数据对象集合、操作集合等
线性表顺序存储结构
01
顺序存储结构的定义
用一段地址连续的存储单元依次存储线性表的数据元素
02
顺序存储结构的基本操作实现
创建、初始化、销毁、判空、清空、求长度、获取元素、修改元素等操
作的实现方法
03
顺序存储结构的优缺点
无需为表示表中元素之间的逻辑关系而增加额外的存储空间;可以快速
线索二叉树
线索二叉树是对二叉树的每个结点增设两个标志位以及一条线索而得到的。根据线索性质的不同,线索二叉树可分为前序线 索二叉树、中序线索二叉树和后序线索二叉树三种。这里以中序线索二叉树为例来说明线索二叉树的构造方法。
中序线索二叉树的构造规则是:若将二叉树的中序遍历序列中的每个结点都看作是相应指针域为空的指针,则称这些指针为 线索,而指向其前驱或后继的指针称为线索指针。加上线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树 (Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种 。
一文读懂社会网络分析(SNA)理论、指标与应用

一文读懂社会网络分析(SNA)理论、指标与应用开新坑!社交网络分析(又称复杂网络、社会网络,Social Network Analysis)是诞生于数学图论、计算机科学、物理学的交叉碰撞中的一门有趣的学科。
缘起:我研究SNA已经有近2年的时光,一路坎坷走来有很多收获、踩过一些坑,也在线上给很多学生讲过SNA的入门知识,最近感觉有必要将心得和基础框架分享出来,抛砖引玉,让各位对SNA感兴趣的同学们一起学习进步。
我的能力有限,如果有不足之处大家一起交流,由于我的专业的影响,本文的SNA知识可能会带有情报学色彩。
面向人群:优先人文社科类的无代码学习,Python、R的SNA 包好用是好用,但是对我们这这些社科的同学来说门槛太高,枯燥的代码首先就会让我们丧失学习兴趣。
特征:类综述文章,主要目的是以通俗的语言和精炼的框架带领各位快速对SNA领域建立起一个全面的认知,每个个关键概念会附上链接供感兴趣的同学深入学习。
开胃菜:SNA经典著作分享《网络科学引论》纽曼 (访问密码 : v9d9g3)2概述:什么是网络?我们从哪些角度研究它?1) 认识网络SNA中所说的网络是由节点(node,图论中称顶点vertex)和边(edge)构成,如下图。
每个节点代表一个实体,可以是人、动物、关键词、神经元;连接各节点的边代表一个关系,如朋友关系、敌对关系、合作关系、互斥关系等。
最小的网络是由两个节点与一条边构成的二元组。
Les Miserables人际关系网络2) 构建网络就是建模马克思说过,“人的本质在其现实性上,它是一切社会关系的总和。
” 事实上,当我们想快速了解一个领域,无论该领域是由人、知识、神经元乃至其他实体集合构成,利用SNA的方法将实体及其相互关系进行抽象和网络构建,我们就完成了对某一领域的“建模”,这个模型就是网络图,拿科学网络计量学家陈超美的观点来说,借助网络图,“一图胜千言,一览无余”。
3) 社会网络类型这里展示了常见和常用的网络类型名词。
数据结构实验报告-无向图的邻接矩阵存储结构

数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码: 6014389 题目: 无向图的邻接矩阵存储结构年级/专业/班: 2010级软件4班学生姓名: 吴超学号: 312010*********开始时间: 2011 年 12 月 9 日完成时间: 2011 年 12 月 30 日课程设计成绩:指导教师签名:年月日数据结构课程设计任务书学院名称:数学与计算机学院课程代码:__6014389______ 专业:软件工程年级:2010一、设计题目无向图的邻接矩阵存储结构二、主要内容图是无向带权图,对下列各题,要求写一算法实现。
1)能从键盘上输入各条边和边上的权值;2)构造图的邻接矩阵和顶点集。
3)输出图的各顶点和邻接矩阵4)插入一条边5)删除一条边6)求出各顶点的度7)判断该图是否是连通图,若是,返回1;否则返回0.8)使用深度遍历算法,输出遍历序列。
三、具体要求及应提交的材料用C/C++语言编程实现上述内容,对每个问题写出一个算法实现,并按数学与计算机学院对课程设计说明书规范化要求,写出课程设计说明书,并提交下列材料:1)课程设计说明书打印稿一份2)课程设计说明书电子稿一份;3)源程序电子文档一份。
四、主要技术路线提示用一维数组存放图的顶点信息,二维数组存放各边信息。
五、进度安排按教学计划规定,数据结构课程设计为2周,其进度及时间大致分配如下:六、推荐参考资料[1] 严蔚敏,吴伟民.数据结构.清华大学出版社出版。
[2] 严蔚敏,吴伟民. 数据结构题集(C语言版) .清华大学出版社.2003年5月。
[3]唐策善,李龙澎.数据结构(作C语言描述) .高等教育出版社.2001年9月[4] 朱战立.数据结构(C++语言描述)(第二版本).高等出版社出版.2004年4月[5]胡学钢.数据结构(C语言版) .高等教育出版社.2004年8月指导教师签名日期年月日系主任审核日期年月日目录引言 (7)1 需求分析 (7)1.1任务与分析 (7)1.2测试数据 (8)2 概要设计 (8)2.1 ADT描述 (8)2.2程序模块结构 (9)2.3各功能模块 (11)3详细设计 (11)3.1类的定义 (11)3.2 初始化 (12)3.3 图的构建操作 (13)3.4 输出操作 (13)3.5 get操作 (14)3.6 插入操作 (14)3.7 删除操作 (15)3.8 求顶点的度操作 (15)3.10 判断连通操作 (17)3.11 主函数 (17)4 调试分析 (17)4.1 测试数据 (20)4.2调试问题 (20)4.3 算法时间复杂度 (20)4.4 经验和心得体会 (21)5用户使用说明 (21)6测试结果 (21)6.1 创建图 (21)6.2插入节点 (22)6.3 深度优先遍历 (22)6.4 求各顶点的度 (22)6.5 输出图 (23)6.6 判断是否连通 (23)6.7 求边的权值 (24)6.8 插入边 (24)6.9 删除边 (25)结论 (26)致谢 (27)摘要随着计算机的普及,涉及计算机相关的科目也越来越普遍,其中数据结构是计算机专业重要的专业基础课程与核心课程之一,为适应我国计算机科学技术的发展和应用,学好数据结构非常必要,然而要掌握数据结构的知识非常难,所以对“数据结构”的课程设计比不可少。
2D-Delaunay 三角网格的数据结构与遍历

2D-Delaunay三角网格的数据结构与遍历高晓沨1,黄懿2(1.清华大学数学系,北京 100080;南开大学数学科学学院,天津 300071) 摘要:本文总结了二维Delaunay三角网格的Bowyer-Watson自动生成算法及其实现步骤,提出了一种类的结构、函数范例(采用Visual C++ 6.0编写程序),并讨论了遍历三角网格各种方法的优劣性,给出实验数据对比;最后得出结论,用广度优先的遍历方法创建网格是生成三角网格一种相对便利有效率的方法;另外,讨论了初始点加入顺序对程序运行时间的影响。
关键词:Delaunay三角网格 类结构 自动生成 广度优先遍历Data Structure and Traverse of 2D-Delaunay TriangulationGao Xiaofeng1, Huang Yi2(Department of Mathematics ,Tsinghua University; Beijing,100080College of Mathematics, Nankai University, Tianjin, 300071) Abstruct: The article summarized the realization of 2D-Delaunay triangulation, thesteps of creating Bowyer-Watson automatic mesh generator, and then constructed a kindof Class structure as well as functions of this algorithm (using Visual C++ 6.0), andfinally discussed the advantage and disadvantage of different methods to traverse thetriangle mesh, using data examination as contrast. Lastly, the author got theconclusion that Width First Traversal method is more effective and convenient. Besides,we discussed the effect between the order of original point set and running time ofthe program.Key Word: Delaunay Triangulation, Class Structure,automatic generation, Width FirstTraversal1.引言近年来,平面任意点集的三角网格化(triangulation)问题一直是人们密切关注的问题。
bfs dfs 的使用场景

bfs dfs 的使用场景BFS和DFS的使用场景BFS(Breadth First Search,广度优先搜索)和DFS(Depth First Search,深度优先搜索)是图遍历算法中常用的两种方法。
它们在不同的场景下有着不同的应用。
本文将分别介绍BFS和DFS的使用场景,并对其特点进行分析。
一、BFS的使用场景1. 最短路径问题:BFS可以求解带权图中的最短路径问题。
通过BFS遍历图的过程中,记录每个顶点到起始顶点的距离,从而得到最短路径。
2. 连通性问题:BFS可以判断无向图或有向图中两个顶点之间是否存在路径。
从起始顶点开始,通过BFS遍历到目标顶点,若能找到路径,则说明两个顶点是连通的。
3. 拓扑排序:BFS可以对有向无环图(DAG)进行拓扑排序,得到图中各个顶点的拓扑序列。
通过BFS遍历图的过程中,记录每个顶点的入度,将入度为0的顶点依次加入拓扑序列中。
4. 游戏寻路:BFS可以用于游戏中的寻路算法。
例如,在迷宫游戏中,可以通过BFS找到从起点到终点的最短路径。
5. 网络爬虫:BFS可以用于网络爬虫的页面抓取。
通过BFS遍历页面链接,从而实现对整个网站的抓取。
二、DFS的使用场景1. 图的连通性:DFS可以判断无向图或有向图中两个顶点之间是否连通。
从起始顶点开始,通过DFS遍历到目标顶点,若能找到路径,则说明两个顶点是连通的。
2. 深度限制搜索:DFS可以用于解决深度限制的搜索问题。
例如在迷宫游戏中,可以通过DFS搜索所有可能的路径,直到找到终点或达到深度限制。
3. 生成树:DFS可以用于生成树的构建。
例如在最小生成树算法中,可以通过DFS遍历图的各个顶点,并按照一定规则选择边加入生成树中。
4. 拓扑排序:DFS也可以对有向无环图(DAG)进行拓扑排序。
通过DFS遍历图的过程中,将已访问的顶点添加到拓扑序列中,最后倒序输出即可得到拓扑排序结果。
5. 回溯算法:DFS可以用于解决回溯问题,如八皇后问题、0-1背包问题等。
830数据结构2021-2021真题答案(有错)

2一、 选择题1 1 1 .B 2.A 3.C 4.A 5.D 6.A 7.B 8.A 9.C 10.C1.B 12.C 13.A 14.C 15.B 16.D 17.D 18.D 19.A 20.A5 解释:线索二叉树中某结点是否有左孩子,不能通过左指针域是否为空来判 断,而要判断左标志是否为 1。
二、 填空题1 2 3 .归并排序。
. 能否将关键字均匀影射到哈希空间上.一端 先进后出有无好的解决冲突的方法4 5 6 7 8 9 . 顺序存储或链式存储 (1+n )/2.从任意节点出发都能访问到整个链表.时间 空间.n-1 n(n-1)/2.2n-1.n n三、 判断题 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 .F.F 非空才成立.F 有向的非强连通图,不成立.T.F 表头没有前驱,表尾没有后序.T.F 先序跟后序不行,中序才行.T.F 不可能0.T1.F2.T3.F4.F5.F四、 应用题1 .逻辑结构是从操作对象抽象出来的数学模型,结构定义中的“关系”描述的 是数据元素之间的逻辑关系;物理结构是数据结构在计算机中的表示(又称 映像),又称存储结构。
物理结构是指数据具体存放在哪个位置,逻辑结构是2 3.由 AOV 网构造拓扑序列的拓扑排序算法主要是循环执行以下两步,直到不存 在入度为 0的顶点为止。
(1) 选择一个入度为 0的顶点并输出之;(2) 从网 中删除此顶点及所有出边。
拓扑序列 1:abcdef 拓扑序列 2:adbcef.二叉树图如下:4 5 .略。
已经不纳入考纲.哈夫曼编码问题编码: 3: 000020: 10 10: 0001 22: 11 18: 001 37: 016.二叉排序树问题比根节点小的往左子树插,大的往右子树插。
图如下:删除50有两种做法:《数据结构》中的解析这里我用第二种做法:五.算法设计题1 & .算法填空(L.elem[i-1]) L.length-1 ++p *p L.length-1;2. 设计算法: 输入 n 个元素的值 创建带头结点的单链线性表 L 。
数据结构与算法综合实验

04
经典问题分析与实现方法论述
最短路径问题——Dijkstra算法和Floyd算法比较
Dijkstra算法
Floyd算法
比较
适用于没有负权边的有向图,通过贪 心策略每次找到距离起点最近的顶点 ,并更新其邻居顶点的距离。时间复 杂度为O(|V|^2),其中|V|为顶点数。
队列是一种特殊的线性 表,其只允许在表的一 端进行插入操作,而在 另一端进行删除操作。 插入元素的一端称为队 尾,删除元素的一端称 为队头。
包括初始化、入队、出 队、判断队列是否为空 等。
包括表达式求值、括号 匹配、迷宫问题、CPU 任务调度等。
树和二叉树基本概念
树定义
树是一种非线性数据结构,由n( n>=0)个有限结点组成一个具有层 次关系的集合。
未来算法的发展将更加注重高效性、 稳定性和可解释性。例如,启发式算 法、近似算法等将在解决NP难问题 中发挥更大作用,通过牺牲部分精度 换取更高的计算效率。同时,随着人 工智能和机器学习的快速发展,智能 算法如神经网络、遗传算法等将在更 多领域得到应用,实现自动化决策和 优化。
要点三
比较
Prim算法适用于稠密图,而Kruskal 算法适用于稀疏图。Prim算法通过不 断扩展已选择顶点的集合来构建最小 生成树,而Kruskal算法通过不断合 并连通分量来构建最小生成树。
拓扑排序问题——Kahn算法和DFS深度优先搜索法比较
Kahn算法
DFS深度优先搜索法
比较
从入度为0的顶点开始,不断删除该 顶点和以该顶点为起点的所有有向边 ,并更新相关顶点的入度。重复此过 程直到所有顶点都被删除或者发现存 在环为止。时间复杂度为O(|V|+|E|) ,其中|V|为顶点数,|E|为边数。
《数据结构》课程标准

《数据结构》课程标准一、概述(一) 课程的性质本课程为计算机专业技术人员提供必要的专业基础知识和技能训练,同时也是计算机应用相关学科所必须掌握的课程。
通过本课程的学习,使学生熟练掌握计算机程序设计中常见的各种数据的逻辑结构、存储结构及相应的运算,初步掌握算法的时间分析和空间分析的技术,并能根据计算机加工的数据特性运用数据结构的知识和技巧设计出更好的算法和程序,并进一步培养基本的良好的程序设计能力。
(二)课程基本理念以培养学生如何合理地组织数据、有效地存储和处理数据,正确地设计算法以及对算法进行的分析和评价的能力,学会数据的组织方法和实现方法,并进一步培养基本的良好的程序设计能力。
(三)课程设计思路本课程标准从计算机软件技术及应用技术专业的视角出发,以满足本专业就业岗位所必须具备的计算机软件技术基础知识为基础,教学内容设计通过岗位工作目标与任务分析,分解完成工作任务所必备的知识和能力,采用并列和流程相结合的教学结构,构建教学内容的任务和达到工作任务要求而组建的各项目,以及教学要求和参考教学课时数。
通过实践操作、案例分析,培养学生的综合职业能力,基本达到程序员级职业技能鉴定标准。
本课程建议课时为64学时,理论课时为20,实训课时为44,在具体教学过程中可进行进行调整。
二、课程目标(一)总目标本课程以培养学生的数据抽象能力和复杂程序设计的能力为总目标。
通过本课程的学习,学生可以学会分析研究计算机加工的数据结构的特性,以便为应用涉及的数据选择适当的逻辑结构、存储结构及其相应的运算,并初步掌握算法的时间分析和空间分析的技术;另一方面,本课程的学习过程也是复杂程序设计的训练过程,要求学生编写的程序结构清楚和正确易读,符合软件工程的规范。
(二)具体目标掌握各种主要数据结构的特点、计算机内的表示方法,以及处理数据的算法实现。
使学生学会分析研究计算机加工的数据结构的特性,以便为应用涉及的数据选择适当的逻辑结构、存储结构及相应的算法,并初步了解对算法的时间分析和空间分析技术。
王道数据结构 第六章 图思维导图
ve(源点)=0
ve(k)
=
Ma
x{ve(j)+Weight(vj
v, k )},vj
v 为
k
的任意前驱
1.求所有事件的最早发生时间ve()
按逆拓扑排序序列,依次求各个顶点的vl(k):
vl(汇点)=ve(汇点)
vl(k)
=
Min{vl(j)-W
eight(vj
v, k )},vj
常见考点:
对于n个顶点的无向图G,
若G是连通图,则最少有n
-1条边,
若G是非连通图,则最多可能有Cn2−
1
条边
对于n个顶点的有向图G,
若G是强连通图,则最少有
n条边
子图/生成子图(子图包括所有顶点)
强连通分量:有向图中的极大强连通子图(必须强连通且保留尽可能多的边)
连通图的生成树是包含图中全部顶点的一个极小连通子图(边尽可能的少但要保 持连通)
n个顶点对应2Cn2
条边
几种特殊的图
稀疏图/稠密图 树:不存在回路,且连通的无向图
n个顶点的树必有n-1条边 常见考点:n个顶点的图,若|E|>n-1,则图中一定存在回路
有向树:一个顶点的入度为0,其余顶点的入度均为1的有向图
有向树不是强连通图
常见考点
邻接矩阵
图的存储
无向图
第i个结点的度 = 第i行(或第i列)的非零元素个数
每一轮时间复杂度:O(2n)
时间复杂度
最短路径问题
Dijkstra算法不适用于有负权值的带权图 算法思想:动态规划
Floyd算法(带权图,无权图)
各顶点间的最短路径
什么是图论及其应用

图论是数学中的一个分支,主要研究图及其相关的问题。
图由若干个节点和连接这些节点的边组成。
节点可以代表现实世界中的对象,而边则代表对象之间的关系。
图论的研究对象包括有向图、无向图、加权图等。
在图论中,节点常常被称为顶点,边则被称为弧或边。
图可以用各种方式表示,如邻接矩阵、邻接表等。
图论的研究内容主要包括图的遍历、最短路径、最小生成树、网络流以及图的染色等。
这些内容构成了图论的核心知识体系。
图论的应用非常广泛,涉及到许多领域。
在计算机科学中,图论被广泛应用于网络路由、图像处理、人工智能等领域。
例如,在网络路由中,图论可以用来寻找最短路径,以确定数据传输的最佳路径。
在图像处理中,图论可以用来进行图像分割,从而提取图像中的目标物体。
在人工智能中,图论可以用来构建知识图谱,从而实现知识的表示和推理。
除了计算机科学,图论还在物理学、生物学等领域中发挥着重要作用。
在物理学中,图论可以用来研究分子结构、粒子物理等问题。
例如,著名的色散关系图就是物理学中的一个重要概念,它描述了声波、电磁波等在介质中的传播特性。
在生物学中,图论可以用来研究蛋白质相互作用网络、基因调控网络等。
这些网络的研究有助于理解生物体内复杂的结构和功能。
此外,图论还在社交网络、交通规划、电路设计等领域中得到了广泛的应用。
在社交网络中,图论可以用来研究用户之间的连接关系,从而推荐好友、发现隐藏关系等。
在交通规划中,图论可以用来优化交通路径,减少拥堵现象。
在电路设计中,图论可以用来优化电路布线,提高电路的性能。
总而言之,图论是数学中一个重要的分支,有着广泛的应用领域。
它不仅在计算机科学中发挥着重要作用,还在物理学、生物学等领域中得到了广泛应用。
图论的发展不仅推动了数学理论的发展,也为各个领域的问题提供了有效的解决方法。
因此,学习和应用图论对于我们来说是非常重要的。
图论中的无向图遍历算法优化

图论中的无向图遍历算法优化在图论中,无向图是一种由节点和节点之间的边组成的数据结构。
无向图遍历是指按照某种规则,从图中的一个节点出发,逐个访问所有其他节点的过程。
无向图遍历算法的目标是能够高效、准确地遍历图中所有节点,并循环检测是否存在环路。
然而,传统的无向图遍历算法在处理大型图时往往效率低下。
本文将介绍一些优化无向图遍历算法的方法,以提高算法的效率。
1. 深度优先搜索(DFS)算法深度优先搜索算法是一种常用的无向图遍历算法。
它通过递归的方式从起始节点开始,一直沿着路径向下直到无法继续,然后回溯到上一个节点,再继续向下搜索。
这种算法的时间复杂度为O(V + E),其中V为节点数,E为边数。
优化方法:- 使用邻接表存储图结构,而不是邻接矩阵。
邻接表只存储节点之间的连接关系,减少了内存开销,并且查询节点的邻居更快。
- 标记已经访问过的节点,避免重复访问。
可以通过布尔数组或者哈希表等方式进行标记,减少遍历过程中的时间开销。
- 选择合适的起始节点。
从度较大的节点开始搜索,可以在整个图上减少搜索的深度,加速遍历过程。
2. 广度优先搜索(BFS)算法广度优先搜索算法是另一种常用的无向图遍历算法。
它以层级的方式遍历图,从起始节点开始,先访问起始节点的所有邻居节点,再依次访问邻居节点的邻居节点,以此类推。
这种算法的时间复杂度也为O(V + E)。
优化方法:- 同样使用邻接表存储图结构。
邻接表的查询和更新操作都比邻接矩阵快速。
- 使用队列来存储待访问节点。
在BFS算法中,待访问的节点总是按照与起始节点的距离逐个访问,队列结构可以方便地实现这一过程。
- 标记已经访问过的节点,避免重复访问。
同样的,可以通过布尔数组或者哈希表等方式进行标记。
3. 迭代加深深度优先搜索(IDDFS)算法迭代加深深度优先搜索算法是对深度优先搜索算法的优化。
它通过控制搜索深度的限制,先从深度1开始搜索,若没有找到目标节点,则增加深度限制再进行搜索。
网络数据建模、分析与应用研究综述

网络数据建模、分析与应用研究综述一、网络数据建模随着互联网的快速发展,网络数据已经成为了研究和应用的重要领域。
网络数据建模是指通过对网络结构和属性进行抽象描述,构建出能够反映网络特征的数据模型。
网络数据建模的目的是为了更好地理解网络的结构、功能和动态变化,为网络分析、管理和决策提供理论依据和技术支持。
图论建模:图论是研究图(Graph)结构及其性质的数学分支。
在网络数据建模中,图论建模主要关注如何用图的形式表示网络结构,以及如何利用图论方法对网络进行分析。
常用的图论建模方法有邻接矩阵法、邻接表法、边权法等。
社会网络建模:社会网络是一种特殊的网络结构,由具有关联关系的人或组织组成。
社会网络建模主要研究如何用图的形式表示社会网络结构,以及如何利用图论方法对社会网络进行分析。
常用的社会网络建模方法有无向图法、有向图法、贝叶斯网络法等。
复杂网络建模:复杂网络是由大量相互连接的节点和边组成的网络结构。
复杂网络建模主要研究如何用图的形式表示复杂网络结构,以及如何利用图论方法对复杂网络进行分析。
常用的复杂网络建模方法有随机游走模型、小世界模型、斑图模型等。
动态网络建模:动态网络是指网络结构和属性随时间发生变化的网络。
动态网络建模主要研究如何用图的形式表示动态网络结构,以及如何利用图论方法对动态网络进行分析。
常用的动态网络建模方法有马尔可夫链模型、随机过程模型等。
多模态网络建模:多模态网络是指具有多种不同类型的信息载体的网络。
多模态网络建模主要研究如何用图的形式表示多模态网络结构,以及如何利用图论方法对多模态网络进行分析。
常用的多模态网络建模方法有多模态图模型、多模态贝叶斯网络模型等。
网络数据建模是一个涉及多个领域的交叉学科,其研究内容和技术方法不断丰富和发展。
随着大数据时代的到来,网络数据建模将继续发挥重要作用,为网络分析、管理和决策提供更多有价值的理论和实践支持。
1. 网络数据的基本概念和特点随着互联网的普及和发展,网络数据已经成为了当今社会中不可或缺的一部分。
ug组的用法 -回复

ug组的用法-回复UG组是一种在计算机科学中常用的数据结构,它被广泛用于解决各种问题和优化算法。
本文将详细介绍UG组的定义、特性、应用及其在算法中的使用方法。
一、UG组的定义UG组,全称为无向图组,是由一个无向图和其上的函数组成的数据结构。
无向图是由一组节点和连接它们的边构成的,每个边都是无向的,没有指向性。
函数可以是节点到节点之间边的关联之一,也可以是节点和另一个数据结构之间的关联。
UG组可以用数学上的G=(V,E)表示,其中V表示节点的有穷非空集合,E 表示边的有穷集合。
每个边都是节点之间相互连接的,可以用一对节点的有序对(u,v)表示。
而函数则可以表示为UG组中节点和其他数据结构之间的映射关系。
二、UG组的特性UG组具有以下几个特性:1. 无向性:UG组中的边是无向的,没有指向性。
即如果节点A连接了节点B,那么节点B也会连接节点A。
2. 连通性:UG组中的任意两个节点之间都存在至少一条路径,可以通过这些路径来进行遍历,找到节点之间的关系。
3. 权值:UG组中的边可以有权值,表示节点之间的距离或者连接强度。
这样可以在算法中根据权重来对边进行排序或者选择路径。
三、UG组的应用UG组可以用于解决各种问题,特别是那些涉及节点之间关系的应用场景。
以下是UG组的几个常见应用:1. 社交网络分析:UG组可以用于表示社交网络中的用户和好友关系,通过分析UG组可以找到用户之间的关系、社区结构等。
2. 网络路由:UG组可以用于表示网络中的路由器和连接关系,通过遍历UG组可以找到最短路径和最优路径,优化网络传输速度。
3. 数据聚类:UG组可以用于表示数据点和距离关系,通过分析UG组可以将相似的数据点聚类在一起,进行数据挖掘和机器学习。
四、UG组在算法中的使用方法UG组在算法中有很多应用,特别是那些需要寻找最优路径、关联关系等的问题。
下面是UG组在算法中的常见使用方法:1. 遍历:可以通过深度优先搜索或者广度优先搜索的方法遍历UG组,找到节点之间的关系和路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
} VNode, AdjList[MAX_VERTEX_NUM];
typedef struct {
AdjList vertices;
int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;
int visited[MAX_VERTEX_NUM];
scanf("%s %s %f", &v1, &v2, &w);
//查询两个顶点在图中存储的位置
i = LocateVex(G, v1);
j = LocateVex(G, v2);
if (i==-1 || j==-1)
{printf("输入的边不正确\n"); exit(0);}
G.arcs[i][j].adj = w;
typedef struct ArcNode{ //表结点
int adjvex; //该弧所指向的顶点的位置
struct ArcNode *nextarc; //指向下一条弧的指针
float info; //网的权值指针
} ArcNode;
typedef struct{ //头结点
VertexType data[100]; //顶点信息
p->info =w;
p->nextarc=G.vertices[j].firstarc; /*将新边表结点p插入到顶点Vj的链表头部*/
G.vertices[j].firstarc=p;
}
return G;
}
VisitFunc(char *ch)//输出顶点的信息
{
printf("%s ",ch);
int LocateVex(MGraph G,char *vert)
{ int i;
for(i=0; i<G.vexnum; i++)
if(strcmp(G.vexs[i],vert)==0)
return i;
return -1;
}
int LocateVex1(ALGraph G,char *vert)
{
j=p->adjvex;
if( !visited[j] ) DFS(G, j);
}
}
void DFSTraverse( ALGraph G){//图的深度优先遍历算法
int v;
for(v=0; v<G.vexnum; v++)
visited[v]=FALSE; //访问标志数组初始化(未被访问)
#define TRUE 1
#define MAXQSIZE100
typedef int QElemType;
typedef float VRType;
typedef float InfoType;
typedef char VertexType;
typedef char VexType;
//=======================================================邻接矩阵的定义
if(!Q.front)
exit(0);
Q.front->next=NULL;
return Q;
}
int EnQueue(LinkQueue* Q, QElemType e){
QueuePtr p;
if( !(p=(QueuePtr)malloc(sizeof(QNode))) )
return ERROR;
QElemType data;
struct QNode1 *next;
}QNode, *QueuePtr;
typedef struct{
QueuePtr front;
QueuePtr rear;
}LinkQueue;
LinkQueue InitQueue(LinkQueue Q){
Q.front=Q.rear=(QueuePtr)malloc(sizeof(QNode));
//=======================================================邻接表的定义
//=======================================================队列定义和基本操作
typedef struct QNode1{//链队列的定义
{ int i;
for(i=0; i<G.vexnum; i++)
if(strcmp(G.vertices[i].data,vert)==0)
return i;
return -1;
}
MGraph CreateMGraph_UDN( MGraph G ){//建立无向图G的邻接矩阵
int i, j,k;
printf("输入顶点数,数边数:");
scanf("%d %d",&(G.vexnum),&(G.arcnum)); /*读入顶点数和边数*/
for(i=0;i<G.vexnum;i++) /*建立有n个顶点的顶点表*/
{
printf("输入第%d个顶点的信息:",i+1);
scanf("%s",&(G.vertices[i].data)) ; /*读入顶点信息*/
p->data = e;
p->next = NULL;
Q->rear->next = p;
Q->rear = p;
return OK;
}
int DeQueue(LinkQueue *Q, QElemType *e) {
QueuePtr p;
if( Q->front == Q->rear )
return ERROR;
for(i=0;i<G.vexnum;i++)
{ for(j=0;j<G.vexnum;j++)
printf("%f ",G.arcs[i][j].adj ); /*邻接矩阵*/
printf("\n");
}
}
Print_ALGraph(ALGraph G) //输出图的邻接表表示Байду номын сангаас
{
int i;
ArcNode *p;
else return 0;
}
int DestroyQueue( LinkQueue *Q ){
while(Q->front) {
Q->rear=Q->front->next;
free(Q->front);
Q->front=Q->rear;
}
return OK;
}
//=======================================================队列定义和基本操作
scanf("%s", &G.vexs[i]);
}
for(i=0; i <G.vexnum; i++)//初始化邻接矩阵
for(j=0; j<G.vexnum; j++)
G.arcs[i][j].adj=0;
for(k=0; k<G.arcnum; k++) {//输入所有的边
printf("输入第%d条边依附的两个顶点和边上的权值:",k+1);
AdjMatrix arcs; //邻接矩阵
int vexnum,arcnum; //图的当前顶点数和弧数
} MGraph ;
//=======================================================邻接矩阵的定义
//=======================================================邻接表的定义
}
void DFS(ALGraph G, int v ) {
int j;
ArcNode *p;//表结点指针
VisitFunc(G.vertices[v].data); //访问第v个顶点
visited[v]=TRUE; //设置访问标志为TRUE(已访问)
for(p=G.vertices[v].firstarc; p;p=p->nextarc)
#include "stdio.h"
#include "malloc.h"
#include "string.h"
#include "stdlib.h"
#define MAX_VERTEX_NUM 20 //最大顶点个数
#define OK 1
#define ERROR 0
#define FALSE 0
typedef struct {
VRType adj;
InfoType info; //该弧相关信息的指针(可无)
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct {
VertexType vexs[MAX_VERTEX_NUM][100]; //顶点向量
p->info =w;
p->nextarc=G.vertices[i].firstarc; /*将新边表结点p插入到顶点Vi的链表头部*/
