大学数学教研中心2013—2014学年第一

浅议大学数学教育如何应对幕课带来的挑战_程池

浅议大学数学教育如何应对幕课带来的挑战程池贺方超商豪李逢高（湖北工业大学理学院，湖北武汉 430068)【摘要】目前，幕课这一全新的在线教育形式得到了国内外各大高校的广泛认可。

针对幕课可能给传统数学带来的挑战，教师应该积极主动，在教学方式上应该更加灵活多变，充分发挥幕课给教学的好处。

同时，在教学内容上应该针对学生的实际情况，努力做到与实际内容相结合。

【关键词】幕课；数学教育；机遇和挑战【中图分类号】G64【文献标识码】A 【文章编号】1008-1151(2013)10-0133-02On how to face the challenges of MOOC in the teaching of colleague mathematicsAbstract: The introduction of Massive 0pen Online Courses (MOOC) has attracted a lot of attention in the teaching of colleague mathematics in and abroad China. Our opinion on how to face the challenges of MOOC in the teaching of colleague mathematics is that, the teachers should be positive and active, and be more flexible in the teaching style to make full use of the benefits that MOOC bring to us. Meanwhile, the content of the teaching should be in accordance with students’ ability, as well as the practical aspects.Keywords: MOOC; teaching of mathematics; opportunity and challenges1引言当今世界，计算机网络的蓬勃发展，已经深刻的影响了生活、工作和学习的各个方面，在线教育就是其中最新的一个实例。

数学教研集体备课中心发言稿（精选5篇）

数学教研集体备课中⼼发⾔稿（精选5篇）数学教研集体备课中⼼发⾔稿（精选5篇）在⽇新⽉异的现代社会中，发⾔稿使⽤的情况越来越多，发⾔稿是在⼀定的场合，⾯对⼀定的听众，发⾔⼈围绕着主题讲话的⽂稿。

那么，怎么去写发⾔稿呢？下⾯是⼩编帮⼤家整理的数学教研集体备课中⼼发⾔稿（精选5篇），供⼤家参考借鉴，希望可以帮助到有需要的朋友。

数学教研集体备课中⼼发⾔稿1各位领导，⽼师：⼤家下午好，很荣幸能在⼤六中、⼤数学组的第⼀次⼤教研会上向各位作汇报交流。

⾃我毕业分配到临沂六中，⾄今已有13个年头了。

有⼈说，教学教副科，别教主课，教主科，别教数学。

⾃第⼀天⾛进数学组，就感受到了，紧张忙碌的⼯作氛围。

上午是很难凑齐⼈的，只能是见到这个，⽽找不到那个。

下午⽼师们基本上没有课，但都埋在作业堆⾥，批改作业，⼀改就将近三节课，就连上厕所都感觉是⼀种奢侈。

作为⼀个⼤教研组，⼈虽然⽐较多，但是在这个⼤家庭⾥，⽼师们亲如兄弟姐妹，⽣活上互相关⼼，⼯作上相互⽀持。

⽼师们⼼胸坦荡，正如我们教的123⼀样简单，这是我们数学组⼀贯的风格，⼀贯的传统，这样才造就了我们组和谐融洽的⼯作氛围。

⽼师们任劳任怨，⼯作上不遗余⼒，务实⾼效。

在这种⼯作氛围⾥，我和同事们⼀样，教学中做到了以下⼏点： 1、认真备课。

反复研究教材，感受编者的意图，明确课程标准中的教学⽬标，把握好重难点。

掌握知识的逻辑，能运⽤⾃如，知道应补充哪些资料，怎样才能较好；根据学⽣实际，估计他们学习新知识可能会有哪些困难，采取相应的预防措施；考虑如何把⾃⼰掌握的教材传授给学⽣。

2、认真上课。

组织好课堂教学，关注全体学⽣，注意信息反馈。

突出体现学⽣的主体地位，激发学⽣的学习兴趣；课堂是学习的主阵地，教育学⽣认真听讲，积极动脑，积极回答问题；注重基础知识的教学，理解好每个定义，定理，所有知识的考察都是源于基础，⾼于基础的。

注重解题⽅法教学，不仅教学⽣怎么做，关键是为什么这样做，引导学⽣探究不同的解题⽅法，并归纳总结。

大学数学教研活动计划方案

一、指导思想为了提高大学数学教学质量，促进教师专业成长，培养学生的数学素养和创新能力，特制定本学期大学数学教研活动计划。

本计划以《高等教育数学课程标准》为指导，以提升教师教学能力和学生数学应用能力为目标，通过多种形式的活动，营造良好的教研氛围，推动数学教育改革与发展。

二、活动目标1. 提高教师的教学水平和科研能力，促进教师的专业成长。

2. 深化数学课程改革，优化教学内容和教学方法。

3. 培养学生的数学素养和创新能力，提高学生的数学应用能力。

4. 加强校际交流与合作，提升我校数学学科的影响力。

三、活动内容1. 教学研讨活动（1）每月组织一次教学研讨会，邀请校内外专家进行专题讲座，分享教学经验和科研成果。

（2）定期开展教学观摩活动，教师之间相互听课、评课，共同探讨教学问题。

（3）组织教师参加教学竞赛，鼓励教师展示教学风采，提高教学水平。

2. 课程建设与改革（1）针对课程设置、教学内容、教学方法等方面进行深入研讨，优化课程体系。

（2）开展课程改革试点，探索新的教学模式，如翻转课堂、混合式教学等。

（3）组织教师编写或修订教材，提升教材质量。

3. 学生活动（1）举办数学竞赛、讲座等活动，激发学生学习数学的兴趣，提高学生的数学素养。

（2）组织学生参加数学建模、数学竞赛等课外活动，培养学生的创新能力和团队协作精神。

（3）建立数学学习互助小组，促进学生之间的交流与合作。

4. 科研活动（1）鼓励教师开展数学教育研究，申请科研项目，提升教师的科研能力。

（2）组织教师参加国内外学术会议，了解数学教育领域的前沿动态。

（3）加强与兄弟院校的交流与合作，共同开展数学教育研究。

四、活动安排1. 时间安排本学期教研活动计划于2023年9月1日开始，至2024年1月31日结束。

2. 具体活动安排- 9月：开展新学期教学工作部署，组织教师学习《高等教育数学课程标准》。

- 10月：举办教学研讨会，邀请校内外专家进行专题讲座。

- 11月：开展教学观摩活动，组织教师参加教学竞赛。

2013全国数学建模

2013全国数学建模
摘要：
一、2013 全国数学建模竞赛概况
1.竞赛时间与地点
2.参赛队伍与规模
3.竞赛奖项设置
二、2013 全国数学建模竞赛获奖情况
1.我校获奖情况
2.获奖学生名单与指导教师
3.全国大学生数学建模竞赛的历史与影响力
正文：
一、2013 全国数学建模竞赛概况
2013 年全国数学建模竞赛于某年某月某日举行，地点分布在全国各地。

该竞赛是面向全国高校的大学生数学建模比赛，旨在培养学生的数学建模能力和解决实际问题的能力。

参赛队伍来自全国各地高校，规模宏大。

竞赛奖项设置包括全国一、二、三等奖。

二、2013 全国数学建模竞赛获奖情况
在2013 年全国数学建模竞赛中，我校共有9 名学生（分3 组）获得3 项全国二等奖，取得了近8 年来最好的成绩。

至此，我校在这项赛事中共获得全国一、二等奖累计达16 项。

获奖学生名单如下：廖然，蔡晨，屠春飞；李约纳，吴晓萍，沈智；刘佳屹，边梦娜，杨文瀚。

指导教师为王福来、罗季、孙洁、郑学东。

全国大学生数学建模竞赛创办于1992 年，每年一届，目前已成为全国高校规模最大的基础性学科竞赛，也是世界上规模最大的数学建模竞赛。

大学数学教研活动模式探讨

中国科教创新导刊中国科教创新导刊I 2008NO .28C hi na Ed uca t i o n I nno va t i o n Her a l d科教动态大学数学作为理工经管类大学生的一门公共基础课程,覆盖范围较广,授课规模较大。

为了进一步提高大学数学教师的教学水平,全面提高大学数学教学质量,认真开展教研活动是一个必不可少的重要环节。

我校是包含理工经管各学科的一所综合性大学,公共基础数学课程实行分层次教学。

如我校的《高等数学》(Ⅱ),每年均有二十多位教师在相同的教学大纲和教学进度的要求下展开这一课程的教学,这为教研活动的顺利开展提供了很好的环境。

一年多来,以信息管理学院自筹教改项目为依托,在借鉴学习了其它学校教研活动先进经验的基础上,进行了有益的探索,每位教师都以教研活动为平台,展现他们各自的优点,相互学习、取长补短,形成了以“反思”为中心的“准备—说课—讲课—评课”的教研活动模式。

1现行教研活动存在的主要问题现行的大学数学教研活动存在的主要问题有:(1)思想上缺乏重视。

大学教师考核的重要指标是科研论文、科研项目的多少,而对于教学,则完成相应的教学任务即可。

这种导向使得教师更重科研,相对忽视教育教学理论的学习,忽视教学技能的提高。

(2)没有具体可行的教研活动模式。

教研活动只是一个空泛的概念,没有具体可操作的实施方案,这使得教研活动很多只停留在形式上,常常是应付检查,缺乏计划性与系统性。

(3)教师之间缺乏相互交流。

大学数学在教学上更多注重个性的发展,在课程学时和内容的规范下,具体实施时在教材的处理、内容的组织上教师之间缺乏交流与协作,忽视了教学应是一种集体智慧的体现。

2“准备—说课—讲课—评课”的教研活动模式2.1准备根据教师以往的教学经验,对教师难上,学生难学难懂的章节特别提出来进行比较筛选,确定此轮教研活动的具体内容。

确定好研究的题目后,则布置全体教研组的教师各自查阅相关资料,专研教材,学习提高后形成自己的教案。

应同学要求,传数学三的一些考纲,这之前的找不到了

2013届钻石卡学员I阶段学习计划（数学三）考研产品部公共课教研中心数学教研室2013届钻石卡学员学习计划---数学三1第一轮复习：基础知识自我复习维杰，我把数三不考的章节也列出来，这样你比较明确一些。

高等数学第九单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第九章多元函数微分法及其应用第9章第1节多元函数的基本概念（P52——P63）第9章第2节偏导数（P63——P69）第9章第3节全微分（P70——P76）第9章第4节多元复合函数的求导法则（P76——P83）第9章第5节隐函数的求导公式（P83——P90）第9章第6节多元函数微分学的几何应用（P90——P101）——本节内容数学三不要求第9章第7节方向导数与梯度（P101——P109）——本节内容数学三不要求第9章第8节多元函数的极值及其求法（P109——P119）第9章第9节二元函数的泰勒公式（P119——P124）——本节内容数学三不要求第9章总复习题（P129——P131）本单元中我们应当学习——1. 二元函数的概念与几何意义；2. 二元函数的极限与连续的概念，有界闭区域上连续函数的性质；3. 多元函数偏导数和全微分的概念，全微分存在的必要条件和充分条件，全微分形式的不变性，会求全微分；4. 多元复合函数一阶、二阶偏导数的求法；5. 隐函数存在定理，计算多元隐函数的偏导数；6.多元函数极值和条件极值的概念，二元函数极值存在的必要条件、充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元函数的最大值和最小值.22013届钻石卡学员学习计划---数学三3第十单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第十章重积分第10章第1节二重积分的概念与性质（P132——P137）第10章第2节二重积分的计算法（P137——P157）本单元中我们应当学习——1. 二重积分的概念和性质，二重积分的中值定理；2. 会利用直角坐标、极坐标计算二重积分；4第十一单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第十二章无穷级数第12章第1节常数项级数的概念和性质（P248——P255）第12章第2节常数项级数的审敛法（P256——P269）第12章第3节幂级数（P269——P278）第12章第4节函数展开成幂级数（P278——P285）本单元中我们应当学习——1. 常数项级数收敛、发散以及收敛级数的和的概念，级数的基本性质及收敛的必要条件；2. 几何级数与p 级数的收敛与发散的条件；3.正项级数收敛性的比较判别法和比值判别法，会用根值判别法； 4.交错级数和莱布尼茨判别法； 5.任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系； 6.函数项级数的收敛域及和函数的概念； 7.幂级数的收敛半径、收敛区间及收敛域的求法； 8.幂级数在其收敛区间内的基本性质（和函数的连续性、逐项求导和逐项积分），会求一些幂级数在收敛区间内的和函数，并会由此求出某些数项级数的和；2013届钻石卡学员学习计划---数学三5第十二单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第十二章无穷级数第12章第7节傅里叶级数（P302——P316）——本节内容数学三不要求第12章第8节一般周期函数的傅里叶级数（P316——P322）——本节内容数学三不要求第12章总复习题（P322——P323）高等数学第八章空间解析几何与向量代数——本章内容数学三不要求高等数学第十章重积分第10章第3节三重积分（P157——P165）——本节内容数学三不要求第10章第4节重积分的应用（P165——P176）——本节内容数学三不要求第10章总复习题（P181——P184）第十三单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第十一章曲线积分与曲面积分——本章内容数学三不要求第十四单元（课前或课后学习内容）计划对应教材：高等数学下册同济大学数学系编高等教育出版社第六版高等数学第十一章曲线积分与曲面积分——本章内容数学三不要求线性代数第十五单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第一章行列式第1章第1节二阶与三阶行列式（P1——P4）第1章第2节全排列及其逆序数（P4——P5）第1章第3节n阶行列式的定义（P5——P8）第1章第4节对换（P8——P9）第1章第5节行列式的性质（P9——P15）第1章第6节行列式按行（列）展开（P16——P21）第1章第7节克拉默法则（P21——P25）62013届钻石卡学员学习计划---数学三7本单元中我们应当学习——1．行列式的概念和性质，行列式按行（列）展开定理．2．用行列式的性质和行列式按行（列）展开定理计算行列式．3．用克莱姆法则解齐次线性方程组．第十六单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第二章矩阵及其运算第2章第1节矩阵（P29——P32）第2章第2节矩阵的运算（P33——P42）第2章第3节逆矩阵（P42——P47）第2章第4节矩阵分块法（P47——P54）线性代数第三章矩阵的初等变换与线性方程组第3章第1节矩阵的初等变换（P57——P65）本单元中我们应当学习——1．矩阵的概念，单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵的概念和性质．2．矩阵的线性运算、乘法运算、转置以及它们的运算规律.3. 方阵的幂与方阵乘积的行列式的性质.4．逆矩阵的概念和性质，矩阵可逆的充分必要条件.5. 伴随矩阵的概念，用伴随矩阵求逆矩阵．6．分块矩阵及其运算．7．矩阵初等变换的概念，初等矩阵的性质，矩阵等价的概念．82013届钻石卡学员学习计划---数学三910。

2013年吉林大学大学生数学建模竞赛获奖名单

高玉洁崔万坤张家旺吴超徐学磊刘铸邹丹丹刘刚陈赟韩生会杨霞高琪刘丹秀吴伯阳吴大庆王鑫阎小俐孙洋明高昊武玲王武迪黄雪宇谢杉杉刘玉福孙研刘野钟安润王也然李宇倩李萧韵王琪刘梦田文博任宇吴龙南闫瑾孔令薇孔文霞叶健松张毅苏宁宁朱言坤黎杭汤莫亚王明
成绩 D D D D D D D D D D
序号 83 84 85 86 87 88 89 90 91 92
队员姓名
殷晨曦王志伟李彤王顺月孙丹潘成龙李秉泽王传进车莹莹翟京坤
关英马帅宁孙菡薇邱硕乔丽萍庄福权杨冠英钟红敏吴迪苏志强
柯润雨徐金景李心胡亚楠王一名刘入源蒋楠江咏甜陈瑶黄天涯
刘洋连士博张明贺鲁杭杭李乐天李通冯佳颖戴铁超白杰丁丁陈咪咪刘林赵瑾吕兆李广喆郑思佳王呵呵高婷婷李卿功李鹏飞
成绩 A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+ A+
隋越贺云昊刘祖飞吕祎涛柴新刚王升超曹琦何林恺秦博佘梦圆李楠陆潇李海涛黄路于英飞蔡周玲冯军杨文娟董树成郑煜圣曹彤彤杨玉洁陈捷元张光攀熊长丽李姣魏万里辛佳棋李泽宇任圣阳乔西宁陈雨薇朱欢欢渠龙高媛任泽龙曾祥雯

数学系简介

数学系简介1．历史沿革数学系的前身数学教研室是我校并校初期建立最早的教研室之一，成立于1956年，隶属于理学院（当时的基础课部）。

分别与1962年、1973年、1977年举办过三届本科“数学师资班”，并于1998年至2004年举办了7届“信息与计算科学”本科专业，于2004年开始招收“数学与应用数学”本科生至今。

根据学校“校、院、系”三级管理体制改革的需要，于2003年成立数学系，数学系还于2000年获准“应用数学”硕士授权点，2003年获准“计算数学”硕士授权授权点，2010年获准“数学”一级硕士授权点，同时于2011年获准增加“基础数学”与“运筹学与控制”两个二级硕士授权点资格。

2．机构设置数学系下设3个教研室：其中高等数学教研室主要负责全校高等数学课程的教学研究和授课任务；工程数学教研室主要负责全校工程数学课程（包括线性代数、概率论与数理统计、复变函数、计算方法、数理方程、运筹学、模糊数学等）的教学研究和授课任务；应用数学教研室主要负责“数学与应用数学”专业的课程设置、教学研究和教学任务。

3．师资队伍数学系现有在职教师62人，其中特聘教授1人，学术学科带头人3人，骨干教师16人；现有教授7人，副教授21人，讲师33人；除承担全校研究生和本科生的全部数学课程的教学任务外，还负责“数学一级硕士点”和“数学与应用数学”本科专业的专业建设和教学任务。

数学系目前有博导1人；硕导16人；教师中具有博士学位的有22人，具有硕士学位的有35人，形成了具有一定后发优势的学科梯队。

4．研究方向数学系从2014年起，确立了8个比较稳定的研究方向：01 半群代数理论02 密码学03 小波分析与数值计算04 泛函分析及其应用05 概率统计与数据分析06 数量经济学与金融数学07 博弈论与函数论的应用08 运筹学与控制论数学系现有导师简介任学明（教授）任学明，校特聘教授，博士生导师，陕西省数学会常务理事。

主要从事半群理论及其在信息科学方面的应用研究。

对大学数学教学创新的思考

科教创新中国科教创新导刊2008N O.33C hi na Educa t i on I nnov at i on H er al d1扬长避短,做好大学数学的素质教育,实现教学理念的创新教学理念是指教师和学生在一定的哲学思想支配下,由现实条件决定的教与学的感性知识和理性知识构成的综合体。

教学理念可以是教学目标的指向和依据,也可以是一定的教学原则,还可以是一种具有指导意义的方法论。

特定的教学理念体现或折射在教学过程中,并且还制约着教学方略及其实现方式。

1.1实施分层教学,实现由部分到全体性的转变教师的基本理念应是选择适应学生的教育而不是选择适合教育的学生。

若按统一的教学计划,统一要求的教学方式,就会出现部分学生感到“吃不消”,而另一部分学生又觉得“吃不饱”的现象。

因此,在实际教学过程,针对学生个体的不同,坚持因材施教,实施分层教学。

对基础知识扎实、接受能力快的学生,在教学时坚持“高起点,快节奏,大容量,精训练”原则,要求学生对有关知识的掌握一步到位;对基础知识薄弱,分析理解问题较慢的学生,教师讲课时低起点,慢节奏,少容量,常反复,允许这些学生对有些知识暂不求甚解”。

1.2注重学生的发展性,实现由片面到全面性的转变社会发展对人的素质要求是全面的而非单一的,从心理学角度看,人的心理活动具有整体性,认知过程与情感过程的产生与发展自始至终是相互交织、相辅相成的。

因而,人的素质发展也具有整体性。

在数学课堂教学中,要着眼于“为人生做准备”,注重数学基本素养和数学基本能力的全面和谐发展。

素质教育理念不仅重视学生知识和技能的掌握,更要重视学生潜能和个性的发展,每个学生身上都有待开发的“金矿脉”,每个学生心灵中都有“沉睡的智力巨人”。

教师要创造各种条件,引发学生的这种无限创造力和潜能,使每个学生都有机会在他天赋所及的一切领域最充分地展示并发展自己的才能。

1.3注重学生的自主意识,实现由主演到主体性的转变教师要着重启发学生在教育教学过程中的自觉性、自主性和创造性,要尊重学生的独立人格即尊重学生人格的价值和独特品质,不仅包括他的优点和长处,也包括他的缺点和短处。

加强直观性和应用性教学提高大学数学教育质量

加强直观性和应用性教学提高大学数学教育质量□肖菲【摘要】20世纪中叶以来，由于计算机技术和现代信息技术的飞速发展，使应用数学和数学应用得到了前所未有的发展，新世纪科技人才对大学生的数学素质要求更高更全面。

目前高等院校的本科大学数学课程教学中存在不少问题，教学模式（思路）较单一，讲授知识点多，讲述数学知识的来源少，讲授知识本身多，讲述知识“身外”之事或关联之事少，缺乏直观性和应用性的教学。

本文首先分析了目前大学数学教学中缺乏直观性和应用性教学的几个普遍现象及其引起的困惑，从几个方面剖析了现象背后的原因，提出了如何加强直观性和应用性教学的方法和建议，以期提高大学数学教育的质量。

【关键词】数学教学；直观性教学；应用性教学；教育质量；教学模式【作者简介】肖菲（1983．4 ），女，齐齐哈尔市建设职工大学基础教研室助教一、目前的现象和困惑由于当前的大学数学教育缺乏直观性和应用性教学，使得在目前的大学数学教学中出现了如下几个较为普遍的现象：（一）“定义+定理（性质、公式）+例题（计算）”现象。

当前教学模式（思路）较单一，讲授的知识点多，讲述数学知识的来源少；讲授知识本身多，讲述知识“身外”之事或者关联之事少，缺乏直观性和应用性的教学。

使得教学内容、教材枯燥无味，缺乏引人入胜的材料，难以激发学生的学习数学的兴趣。

（二）“得意忘形”现象。

“过度”强调数学知识的严密性和数学理论的抽象思维特性，使数学“过度”抽象化、神秘化，淡化了数学的通俗性和实用性。

在数学教学过程中，缺乏或不太重视直观性教学，特别是几何直观性教学，使学生知其然不知其所以然，较大程度上陷入“得意忘形”的境界。

“得”了数学知识的字面定义、性质、定理，“忘”了数学知识的原始来源动机和直观，使学生陷入学习数学的误区。

（三）“数学无实际用处”现象。

使学生认为数学就是“x +y=z”，数学学科的学好学坏对自己以后的发展没关系或者影响不大。

数学知识的来源和应用介绍得少，数学的重要性以及数学对科学技术的发展和其它学科的促进和支撑作用没有充分体现。

2013级高等数学I(1)试卷(A)评分标准

B〖〗考试形式开卷（）、闭卷（√），在选项上打（√）开课教研室大学数学部命题教师命题组命题时间2013-12-12使用学期 2013-2014-1总张数 3 教研室主任审核签字d6()[0,1],(0,1),(0)(1)0,120131.(0,1),().220142013()(),(2)()[0,1],20141120152013(0)0,0,(1)0,(3)2220142014f x f f f f x f x x f x ξξϕϕϕϕ==⎛⎫'== ⎪⎝⎭'=-⎛⎫'==⋅>=-< ⎪⎝⎭七、(本题满分分)设函数在上连续在内可导且本题得分证明：在内至少存在一点使〖证〗设则在上连续且由零点定()1,,1,0.(4)22013()(0,1),()().(5)2014Rolle ,(0,)(0,1),()0,2013().(6)2014f x x f x f ηϕηϕξηϕξξ⎛⎫'∃∈= ⎪⎝⎭'''=-'∃∈⊂=''=理使又在内可导且由定理使即212012201032,[0,1]0.,,,,11,0.(1)(32)d (2)(3)1,1.(4)(32)d y ax bx c x y a b c x x x c ax bx x a b b a V ax bx x π=++∈≥='=''+=+='=-=+⎰⎰六、(本题满分分)设有抛物线当时试确定本题得分的值使该抛物线过原点与直线及轴所围区域的面积为且上述区域绕轴旋转而成的旋转体的体积最小.〖解〗由抛物线过原点得由第二个条件得即从而旋转体体积2222294214(5)3(6),(7)531533d 4159(8)0,,(9)d 15344d 40,(10)d 1559,,0.44a ab b a a V a a b a V V a a bc ππππ⎛⎫⎛⎫'''=++=++ ⎪ ⎪⎝⎭⎝⎭⎛⎫''=+==-= ⎪⎝⎭'=>=-==由得从而此时故旋转体体积最小.所以所求值为。

2012―2013学年第2学期数学学院本科生开课计划

马列中心
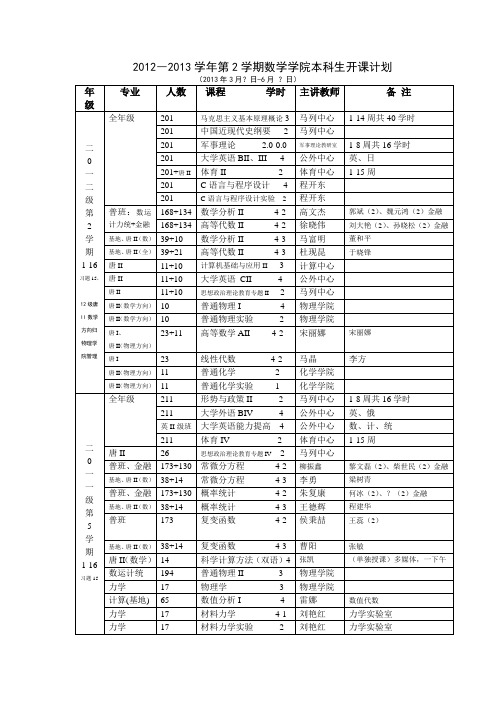
1-8周共16学时
211
大学外语BIV 4
公外中心
英、俄
英II级班
大学英语能力提高4
公外中心
数、计、统
211
体育IV 2
体育中心
1-15周
唐II
26
思想政治理论教育专题IV2
马列中心
普班、金融
173+130
常微分方程4-2
柳振鑫
黎文磊（2）、柴世民（2）金融
基地、唐II（数）
38+14
常微分方程4-3
吕悦
数（选）、运（必）
62
非线性规划（双语）4
黄庆道
数运计统
金融数学(选修) 3
郑文瑞
计算
73
计算实习II 2
李佳民
机房
73
数据结构与算法4
罗宏文
73
数据结构实验2
罗宏文
机房
73
微分方程数值解法4
李永海
数学物理反问题(选) 3
张德悦
力学
17
流体力学II 4
闫广武
17
流体力学实验3
施卫平
力学实验室
17
李勇
梁树青
普班、金融
173+130
概率统计4-2
朱复康
何冰（2）、？（2）金融
基地、唐II（数）
38+14
概率统计4-3
王德辉
程建华
普班
173
复变函数4-2
侯秉喆
王蕊（2）基地、唐Fra bibliotekI（数）38+14
复变函数4-3
曹阳
张敏
唐II（数学）
14

数学建模2013年校赛结果

数学建模2013年校赛结果一等奖10人，数学学院1人陈生运201115020221机械电子工程李盼婷化工学院12级李涛2012 机自廖锋先应数11101班.do林裕鹏2012电信刘博文2011材料11102班刘云帆12材2班唐俊遥自动化12102班王勇自动化12102张芬2011物理专业. 二等奖15人其中数学学院4人陈婷通信12102郭媛，龙丁含，通信11级2班贺红帆2012通信工程专业.李治宏2010级应用化学专业刘莎2011 应数专业孙丹数学11101.do孙清清12102 材料.王春平2012应化王东2010 应化专业肖杰自动化12102.d姚望数计应数11101班张鼎2012级光电专业张加宁机自11101班朱辉应数11101赵青11级应化三等奖27人其中数学学院17人封玉玲物电电信12102冯康2012 机自专业符顺明2011数学与应用数学高新亮2011 信计专业郭勇波信计11101黄兰应用数学12101黄小星2011信计李白英2012应数专业李世林应数11101刘平平2011 应数专业刘晴自动化专业 2刘想大一光电罗含2012 材料陶宝应数12101王熙11级应数专业101班x邬霞初2012通信工程专业吴碧波2011级化学11101班谢胜12级数学与应用数学熊徐应数11101班徐孝林2011 化学许赞波信计11101班杨秀隽2011 数学与应用数学曾芳林2012机自1203班doc张慧2011 应数11101班周久芳通信12102周蜜信计11101班左洋2012级数学与应用数学专业参加校赛各年级情况统计2010级大三学生1人2011级大二学生25人2012级大一学生26人。

华中科技大学数学2013年招生简章

数学与统计学院华中科技大学数学与统计学院始建于1953年，经历了由数学教研室、数学系到数学与统计学院的发展历程。

上世纪50年代初，著名数理统计学家林少宫先生从美国Illinois大学归来与熊庆来先生的弟子戴良谟等数学界老前辈一起主持了本学科的初创工作。

上世纪70年代末，徐利治教授亲任系主任主持了数学系的创建工作，并于1981年获得应用数学硕士点，随后形成了应用数学、计算数学与运筹学协调发展的良好局面，在全国率先举办了数理逻辑、模糊数学等专题讨论班，创建了《数学评论与研究》和《模糊数学》学术期刊，并培养了国际著名数理经济学家田国强、艾春荣，美国Purdue大学教授蔡智强等一批杰出学者。

八十年代中期，陈庆益教授加盟我校进一步推动和加速了本学科的发展，其主持创建了《应用数学》杂志，并培养了长江特聘教授方复全等一大批数学人才。

九十年代初，黄志远教授调来我校创建了随机分析研究中心，其与杰出青年基金获得者、长江特聘教授任佳刚一起推动了我校在概率统计领域的研究，并使我校获得了概率论与数理统计博士点。

经过几十年的艰苦努力，目前数学与统计学院拥有数学博士后流动站、数学一级学科博士点和数学一级学科硕士点、统计学一级学科博士点，以及应用统计专业硕士点。

在学位授权点建设的同时，数学与统计学院也先后建立了数学与应用数学、信息与计算科学、统计学三个本科专业。

学院现有在校学生648人，其中本科生446人、硕士生156人、博士生46人、硕博连读生所占比例为60%左右。

数学与统计学院现有教职工103人，在编教师87人，其中博士生导师13人，教授19人，副教授37人，教师中有博士学位者占61%，有“长江讲座教授”1名、“新世纪百千万人才工程”入选者1名、教育部“(跨)新世纪优秀人才支持计划”入选者5名、“高校青年教师奖”获得者1名、“湖北省有突出贡献的中青年专家”3名、“湖北省楚天学者”1名以及“宝钢优秀教师奖”获得者4名。

近五年来，数学与统计学院的学术团队共获科研经费890万元，其中国家自然科学基金27项，联合获批国家自然科学基金重大、重点项目2项，；发表SCI收录论文260余篇；出版各类专著、教材30余本。

2013年全国大学生数模竞赛广东赛区本科组初评成绩

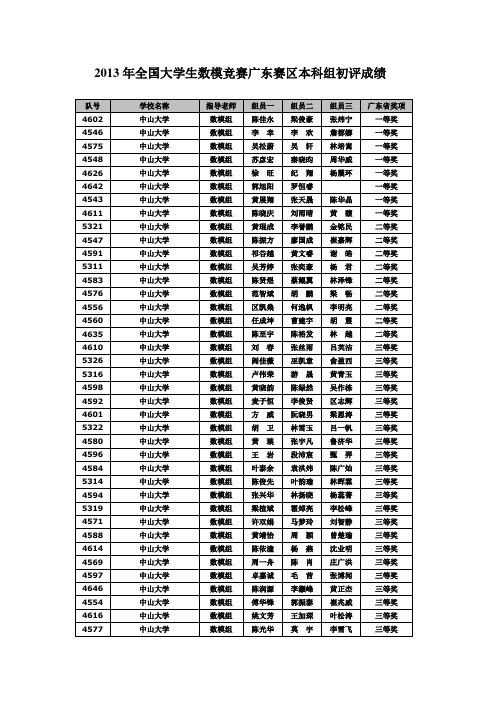
中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学中山大学
刘人翡吴峥
杨东林武晓鸽周欣宇邱晓辉廖子令陈晓洁劳俊逸杨光
吴镕涛王艺儒柯曙昶许宇满廖兴淦王宛
李滋源张翔
王观发常逢娜毛龙霞李侯君李充
赵秋博陈春滔范东杰冯旭
李萌润朱陆蒋畅攀颜
李坷宣
孙汉博
曹家川
4639 4628 4631 4623 4637 4645 4608 4605 4557 4552 4617 4641 4555 4607 4578 4630 4625 4618 4570 4609 4615 5325 4590 5310 4640 4636 4558 4603 4612 5313 4565 4542 5323 4567 4621 4633 5327 4581 4553 5486 5499 5485 5453
贾毅凡王灿杰张博郭梓超陈树波曾嘉豪何冠有苏国鹏陈海鹏陈浩智王汝昕李黎明王行健李浩孙艺芙吴达坤姚尧翔陈宪宇黄伟鹏贾东李崑鹏陈润汝赵海龙高锦黄金洪蒋浩郭备朱敏贤刘伯东刘超斌尹金健王泽众王宇于杰周小波黄梓豪刘晓枫陈俊和闫广雷文康罗如冰潘海明吴亚洲
数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组数模组

高等学校大学数学教学研究与发展中心

高等学校大学数学教学研究与发展中心
张建张蓓周丽娜王静席晋聪解瑞金杨莹王荣李录苹玉强王雅婧吴美华贾子君王敏樊彩虹努恩吉雅曹莉范惠荣高霞袁春红白红梅包图雅河北工业大学河北科技大学河北师范大学河北科技师范学院太原科技大学运城学院运城学院山西财经大学山西大同大学山西师范大学山西大学呼伦贝尔学院内蒙古农业大学内蒙古大学集宁师范学院河套学院内蒙古医科大学内蒙古大学集宁师范学院内蒙古师范大学呼伦贝尔学院内蒙古民族大学概率论与数理统计高等数学线性代数高等数学高等数学线性代数高等数学高等数学高等数学高等数学高等数学概率论与数理统计概率论与数理统计概率论与数理统计线性代数高等数学高等数学高等数学高等数学高等数学高等数学高等数学河北河北河北河北山西山西山西山西山西山西山西内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古内蒙古
6）全国高校数学微课程教学设计竞赛华北赛区获奖名单（排名不分先后次序）
特等奖（16 名）
刘大莲杨晶李亚杰賀慧霞王玉津信秀王秀红邓硕苗文静左会娟武利平王欣洁张新鸿贾荣吴晓红李姝敏北京联合大学清华大学北京邮电大学北京航空航天大学天津商业大学天津理工大学天津商业大学河北地质大学华北科技学院河北师范大学河北大学太原科技大学太原科技大学内蒙古医科大学呼和浩特民族学院内蒙古科技大学包头师范学院北京邮电大学北京信息科技大学北京航空航天大学北京物资学院北京科技大学北京科技大学天津商业大学天津商业大学河北工业大学天津理工大学天津理工大学华北理工大学河北农业大学河北地质大学衡水学院河北地质大学华北理工大学高等数学线性代数概率论与数理统计大学数学应用案例大学数学应用案例高等数学高等数学高等数学高等数学线性代数高等数学高等数学高等数学概率论与数理统计高等数学高等数学北京北京北京北京天津天津天津河北河北河北河北山西山西内蒙古内蒙古内蒙古

数学教研室英文

The Department of Mathematics at [University Name] stands as a beacon of academic excellence and innovation in the field of mathematics. With a rich history of nurturing talent and fostering research, the department has earned a reputation for its rigorous curriculum, distinguished faculty, and vibrant academic community. This article aims to provide an overview of the department's achievements, its curriculum, faculty, research initiatives, and the impact it has on both students and the broader academic community.I. History and BackgroundEstablished in [Year], the Department of Mathematics has grown from a small group of dedicated faculty and students to a vibrant and diverse academic community. Over the years, the department has played a pivotal role in shaping the mathematical landscape of [University Name]. It has produced numerous notable alumni who have gone on to achieve great success in various fields, including academia, industry, and public service.The department's commitment to excellence is evident in its long-standing partnership with leading research institutions and industry partners. This collaboration has not only enriched the department's research portfolio but has also provided students with invaluable opportunities for internships, co-op programs, and real-world problem-solving experiences.II. Curriculum and Academic ProgramsThe Department of Mathematics offers a comprehensive curriculum that spans undergraduate and graduate programs, catering to a diverse range of interests and career aspirations. The curriculum is designed to provide students with a strong foundation in mathematical theory and practical skills, enabling them to excel in their chosen fields.A. Undergraduate ProgramsThe undergraduate program in mathematics provides students with a solid understanding of the fundamental concepts and techniques of mathematics. The curriculum includes a variety of courses, such as calculus, linearalgebra, real analysis, and abstract algebra. Students can also choose from a range of elective courses to specialize in areas such as applied mathematics, statistics, and computational mathematics.The department also offers a dual-degree program in mathematics and another field, such as engineering or computer science, to provide students with a broader skill set and enhance their employability.B. Graduate ProgramsThe graduate program in mathematics is designed to prepare students for careers in research, academia, and industry. The program offers both a Master's and a Ph.D. degree, with concentrations in pure mathematics, applied mathematics, and interdisciplinary fields.The curriculum includes advanced courses in algebra, analysis, geometry, and topology, as well as research seminars and workshops. Graduate students are encouraged to engage in original research under the guidance of experienced faculty members.III. Faculty and Research InitiativesThe Department of Mathematics boasts a distinguished faculty of scholars and educators who are committed to excellence in teaching and research. The faculty members are actively involved in various research initiatives, contributing to the advancement of mathematical knowledge and its applications in various fields.A. Research AreasThe department's research initiatives span a wide range of topics, including:1. Algebra and Number Theory2. Analysis and Differential Equations3. Geometry and Topology4. Probability and Statistics5. Computational Mathematics6. Mathematical PhysicsB. Collaborations and PartnershipsThe faculty members collaborate with researchers from other departments and institutions, both within and outside the country. These partnerships have led to numerous joint publications, research grants, and international conferences.IV. Impact on Students and the Academic CommunityThe Department of Mathematics has a profound impact on its students, preparing them for successful careers and fostering their intellectual growth. The department's commitment to excellence is reflected in the following aspects:A. Student SuccessThe department has a strong track record of student success, with a high percentage of graduates finding employment in their chosen fields. Many alumni have gone on to pursue advanced degrees and achieve notable accomplishments in their respective careers.B. Academic Community EngagementThe department actively engages with the academic community through various events, such as seminars, workshops, and conferences. These events provide a platform for faculty, students, and researchers to share their knowledge, exchange ideas, and foster collaboration.C. Public EngagementThe department is committed to promoting mathematics and itsapplications to the general public. The department organizes outreach programs, workshops, and lectures aimed at inspiring and educating the public about the beauty and importance of mathematics.V. ConclusionThe Department of Mathematics at [University Name] is a premier institution that continues to excel in teaching, research, and publicengagement. With a dedicated faculty, rigorous curriculum, and vibrant academic community, the department has established itself as a leading center for mathematical education and research. As the field of mathematics continues to evolve, the department is poised to play an even more significant role in shaping the future of mathematics and its applications.。

大学高等数学教研活动(3篇)

第1篇一、活动背景高等数学作为大学本科阶段的基础课程，对于培养学生的逻辑思维、抽象思维和创新意识具有重要意义。

为了提高高等数学教学质量，加强教师队伍建设，我校数学与统计学院于2021年11月开展了为期一个月的高等数学教研活动。

本次活动旨在通过研讨、交流和实践，提高教师的教学水平和科研能力。

二、活动内容1. 高等数学教学研讨活动期间，我院组织了多次高等数学教学研讨会。

会议邀请了校内外知名学者和优秀教师进行专题讲座，分享了他们在高等数学教学方面的经验和心得。

此外，我院教师还就教学过程中遇到的问题和困惑进行了深入探讨，共同研究解决方案。

2. 教学观摩与评课为了促进教师之间的交流与合作，我院组织了教学观摩活动。

活动中，优秀教师展示了他们的课堂教学风采，其他教师观摩并提出了宝贵的意见和建议。

同时，我院还开展了评课活动，对教师的教学成果进行评估，以激励教师不断提高教学质量。

3. 教学改革与实践本次活动还关注高等数学教学改革的实践。

教师们结合课程特点和学生需求，积极探索新的教学方法，如翻转课堂、混合式教学等。

通过实践，教师们取得了良好的教学效果，为学生提供了更加优质的学习体验。

4. 科研能力提升为了提高教师的科研能力，我院组织了学术讲座和科研经验交流会。

讲座内容涵盖了高等数学领域的最新研究成果和发展趋势，为教师提供了丰富的学术资源。

此外，教师们还分享了他们在科研过程中的经验和心得，相互学习，共同进步。

三、活动成果1. 提高了教师的教学水平通过本次活动，教师们对高等数学教学有了更深入的认识，教学水平得到了显著提高。

他们在课堂教学中更加注重启发式教学、互动式教学，提高了学生的参与度和学习效果。

2. 促进了教师之间的交流与合作本次活动为教师提供了一个交流的平台，加强了教师之间的联系与合作。

教师们在教学、科研等方面相互学习，共同进步，形成了良好的团队氛围。

3. 推动了教学改革与实践本次活动推动了高等数学教学改革的深入实施。

大学教研室工作计划

大学教研室工作计划大学教研室工作计划1 一、指导思想继续认真学习数学课程标准，进一步确立课程标准的基本理念，围绕教学工作意见，以课程改革为中心，突出有效主题。

以课堂教学与训练的研究与改革为切入口，加大教研、教改力度，转变教研理念，改进教研方法，优化教研模式，积极探索在新课程改革背景下的小学数学教研工作新模式，进一步提高教师的专业水平和课堂教学的效率，努力促进全校数学教学质量的稳步提高。

二、工作目标1、加强新教材教学研究和课题研究，落实新课改的精神，培养学生的创新精神和实践能力。

2、通过组织教师学习新的教育教学理论，彻底改变传统教育思想、教学思路。

3、发挥集体智慧，提高集体备课质量，提高课堂教学效率。

4、积极推进教学质量的提高，有效落实常规管理。

5、改革评价方式，重视过程性评价，促进学生快乐成长。

6、观看名师课堂实录，写看后反思，提高教师的业务水平。

7、本学期数学组学习的专题为：张翼文的《智慧型教师的思与行》。

三、主要措施㈠全面实施素质教育，更新教育观念，树立面向全体学生，因材施教，把知识的学习和能力的发展一并落实到教育实践中去。

1、认真学习新课程理念，深入研究教材，理解和把握新教材的特点和编写意图。

2、充分发挥课堂教学在素质教育中主渠道的作用，在优化学科教学的同时，强化课堂的实践作用。

3、切实减轻学生过重负担，严格控制作业量，严禁以作业为惩罚学生的手段。

㈡强化常规教学1、充分发挥教师的主导作用，树立正确的教育观念，开展说课、讲课和听评课的活动。

帮助教师不断改进教学方法，优化课堂结构，提高自身的业务水平，从而提高课堂效益。

2、定期组织检查备课，作业批改和辅导等。

3、建立和健全学生学习常规制度，对学生学习数学的各个环节，制订具体要求，重视培养学生获取新知识的能力和团结协作能力。

主要活动安排：三月份：1、准确把握教材的特点、编写意图和改革的方向，制订好教学计划。

2、以年级为单位，做好集体备课、单元辅导。

赏析数学中的美

赏析数学中的美发表时间：2013-07-02T09:58:07.483Z 来源：《教育研究·教研版》2012年第10期供稿作者：宁家财[导读] 对称是最能给人以美感的一种形式。

德国数学家魏尔说：“美和对称紧密相关。

”数学中有着各种各样的对称。

宁家财众所周知，数学在我们的基础教育中占有很大的份量，是我们的文化中极为重要的组成部分。

她不但有智育的功能，也有其美育的功能。

数学美深深地感染着人们的心灵，激起人们对她的欣赏。

下面从几个方面来欣赏数学美。

1 展现对称美，增强数学魅力对称是最能给人以美感的一种形式。

德国数学家魏尔说：“美和对称紧密相关。

”数学中有着各种各样的对称。

从几何图形看，有中心对称形、轴对称形、面对称形和转动对称形等。

对称图形虽然千变万化，种类繁多，但他在平面上的种类只有十七种。

例如，行列式就被人们称作“美丽的花园”，它的每一条边都可以扩展。

一个三阶行列式是由九个元素按三行三列所排列成的正方形，即使不懂数学的人也能感受到其排列整齐和处处对称，领略到它的形式之美。

2 体会协同美，知识融会贯通数学思维是人脑和数学对象交互作用并按一般的思维规律认识数学规律的过程。

数学思维的协同美大体上可从以下两个方面表现出来。

归纳和演绎的相互作用。

数学中大量地需要归纳，同时也需要演绎，在许多情况下两者互为作用的。

在数学教学中，总是既用归纳又用演绎。

尽管两者有各自不同的特点，但演绎推理的大前提———表示一般原理的全称判断要靠归纳推理来提供。

为了增强归纳推理的可靠性，不管是以一般原理作指导还是对归纳推理的前提进行分析，都要用演绎推理。

归纳和演绎在思维运行过程中这种辩证统一正体现了两者之间是交互为用的。

形式逻辑与辩证逻辑的并重和统一。

一方面，数学中大量存在相对稳定的状态，我们能用形式逻辑思维的方法进行分析和研究数学对象。

另一方面，也存在显著的运动状态，如有限与无限的相互转化，代数、几何、三角各学科之间的转化以及数学各种相关运算方法的发展与对立统一等，故能用辩证思维的方法认识数学概念的形成和关系的不断发展变化。