二进制微代码
二进制ascii码对照表

二进制ascii码对照表对照表如下:ASCII码(American Standard Code for Information Interchange,美国信息交换标准代码)是一种常见的字符编码系统,用于将字符和数字等信息转换为二进制形式。
ASCII码总共定义了128个字符,并将每个字符用一个7位的二进制数表示(即0-127范围内的值)。
下面是一个二进制ASCII码对照表,列出了每个字符对应的十进制、十六进制和二进制值。
十进制十六进制二进制字符0 00 0000000 NUL (Null)1 01 0000001 SOH (Start of Heading)2 02 0000010 STX (Start of Text)3 03 0000011 ETX (End of Text)4 04 0000100 EOT (End of Transmission)5 05 0000101 ENQ (Enquiry)6 06 0000110 ACK (Acknowledgment)7 07 0000111 BEL (Bell)8 08 0001000 BS (Backspace)9 09 0001001 TAB (Horizontal Tab)10 0A 0001010 LF (Line Feed)11 0B 0001011 VT (Vertical Tab)12 0C 0001100 FF (Form Feed)13 0D 0001101 CR (Carriage Return)14 0E 0001110 SO (Shift Out)15 0F 0001111 SI (Shift In)16 10 0010000 DLE (Data Link Escape)17 11 0010001 DC1 (Device Control 1)18 12 0010010 DC2 (Device Control 2)19 13 0010011 DC3 (Device Control 3)20 14 0010100 DC4 (Device Control 4)21 15 0010101 NAK (Negative Acknowledgment)22 16 0010110 SYN (Synchronous Idle)23 17 0010111 ETB (End of Transmission Block)24 18 0011000 CAN (Cancel)25 19 0011001 EM (End of Medium)26 1A 0011010 SUB (Substitute)27 1B 0011011 ESC (Escape)28 1C 0011100 FS (File Separator)29 1D 0011101 GS (Group Separator)30 1E 0011110 RS (Record Separator)31 1F 0011111 US (Unit Separator)32 20 0100000 Space33 21 0100001 !34 22 0100010 "35 23 0100011 #36 24 0100100 $37 25 0100101 %38 26 0100110 &39 27 0100111 '40 28 0101000 (41 29 0101001 )42 2A 0101010 *43 2B 0101011 +44 2C 0101100 ,45 2D 0101101 -46 2E 0101110 .47 2F 0101111 /48 30 0110000 049 31 0110001 150 32 0110010 251 33 0110011 352 34 0110100 453 35 0110101 554 36 0110110 655 37 0110111 756 38 0111000 857 39 0111001 958 3A 0111010 :59 3B 0111011 ;60 3C 0111100 <61 3D 0111101 =62 3E 0111110 >63 3F 0111111 ?64 40 1000000 @65 41 1000001 A66 42 1000010 B67 43 1000011 C68 44 1000100 D69 45 1000101 E70 46 1000110 F71 47 1000111 G72 48 1001000 H73 49 1001001 I74 4A 1001010 J75 4B 1001011 K76 4C 1001100 L77 4D 1001101 M80 50 1010000 P81 51 1010001 Q82 52 1010010 R83 53 1010011 S84 54 1010100 T85 55 1010101 U86 56 1010110 V87 57 1010111 W88 58 1011000 X89 59 1011001 Y90 5A 1011010 Z91 5B 1011011 [92 5C 1011100 \93 5D 1011101 ]94 5E 1011110 ^95 5F 1011111 _96 60 1100000 `97 61 1100001 a98 62 1100010 b99 63 1100011 c100 64 1100100 d101 65 1100101 e102 66 1100110 f103 67 1100111 g104 68 1101000 h105 69 1101001 i106 6A 1101010 j107 6B 1101011 k110 6E 1101110 n111 6F 1101111 o112 70 1110000 p113 71 1110001 q114 72 1110010 r115 73 1110011 s116 74 1110100 t117 75 1110101 u118 76 1110110 v119 77 1110111 w120 78 1111000 x121 79 1111001 y122 7A 1111010 z123 7B 1111011 {124 7C 1111100 |125 7D 1111101 }126 7E 1111110 ~127 7F 1111111 DEL (Delete)这只是一个基本的ASCII码对照表,其中包含了常见的可打印字符、控制字符和特殊字符。
第四部分 二进制与信息编码

第四部分二进制与信息编码二进制和信息编码是计算机科学中的基础概念。
本文将介绍二进制的基本原理以及常见的信息编码方法。
一、二进制的基本原理二进制是一种由0和1表示的计数系统。
在计算机科学中,所有的数据都被转化成二进制形式进行处理。
二进制的基本原理是利用两个数字0和1来表示所有的数据和信息。
0表示关闭或不存在,1表示开启或存在。
通过不同位置上0和1的组合,可以表示不同的数据。
二进制操作包括加减乘除等基本运算,以及逻辑操作如与、或、非等。
通过这些操作,计算机可以对数据进行处理和运算。
二、信息编码方法信息编码是将信息转换成特定的形式以便在传输和存储中使用的过程。
常见的信息编码方法有以下几种:1. ASCII码ASCII码是美国信息互换标准代码的缩写。
它将字符和符号转化成二进制形式表示。
ASCII码使用7位二进制数来表示不同的字符,共可以表示128个字符。
2. UNICODE码UNICODE码是一种用于表示世界上所有字符的标准编码方案。
它使用16位二进制数来表示字符,可以表示超过65,000个字符。
3. 压缩编码压缩编码是一种将信息进行压缩和编码的方法,以减少存储和传输所需的空间和时间。
常见的压缩编码方法包括哈弗曼编码和算术编码等。
4. 图像和音频编码图像和音频编码是将图像和音频数据转化成二进制形式的方法。
常见的图像和音频编码方法包括JPEG、MP3、AAC等。
总结:二进制和信息编码是计算机科学中非常重要的概念。
理解二进制的基本原理和常见的信息编码方法对于深入理解计算机科学和计算机技术具有重要意义。
特殊符号转二进制

将特殊符号转换为二进制通常涉及使用字符编码表,其中每个字符都映射到一个唯一的二进制表示。
最常用的字符编码是ASCII(美国信息交换标准代码)和Unicode。
下面是一些特殊符号的ASCII 编码和Unicode 编码示例:ASCII 编码:ASCII 编码用于表示美国英语字符和一些常见符号。
以下是一些特殊符号的ASCII 编码:@ 的ASCII 编码是64(二进制表示为01000000)。
$ 的ASCII 编码是36(二进制表示为00100100)。
Unicode 编码:Unicode 是一种更全面的字符编码方案,它包含了几乎所有世界上使用的字符。
以下是一些特殊符号的Unicode 编码:@ 的Unicode 编码是U+0040(二进制表示为00000000 01000000)。
$ 的Unicode 编码是U+0024(二进制表示为00000000 00100100)。
示例:Python 中的编码转换在Python 中,可以使用内置的ord 函数获取字符的Unicode 编码,然后使用bin 函数将其转换为二进制表示。
以下是一个示例:pythonCopy code# ASCII 编码示例ascii_code_at = ord('@')ascii_code_dollar = ord('$')binary_at = bin(ascii_code_at)[2:]binary_dollar = bin(ascii_code_dollar)[2:]print(f'ASCII of @: {ascii_code_at}, Binary: {binary_at}')print(f'ASCII of $: {ascii_code_dollar}, Binary: {binary_dollar}')# Unicode 编码示例unicode_code_at = ord('\u0040')unicode_code_dollar = ord('\u0024')binary_unicode_at = bin(unicode_code_at)[2:]binary_unicode_dollar = bin(unicode_code_dollar)[2:]print(f'Unicode of @: {unicode_code_at}, Binary: {binary_unicode_at}')print(f'Unicode of $: {unicode_code_dollar}, Binary: {binary_unicode_dollar}')这个示例演示了如何使用Python 获取字符的ASCII 编码和Unicode 编码,并将其转换为二进制表示。
二进制数据和二进制编码知识

二进制数据和二进制编码知识二进制编码是计算机内使用最多的码制,它只使用两个基本符号"0"和"1",并且通过由这两个符号组成的符号串来表示各种信息。
二进制的数值数据亦是如此,计算其所代表的数值的运算规则是:m-1N = ∑Di * 2i (2.4)Di 的取值为0或1i = -k例如(1101.0101) 2 = (13.3125) 10 。
等号左右两边括号内的数字为两个不同进制的数字,括号右下脚的2和10分别指明左右两边的数字为二进制和十进制的数。
按公式(2.4),计算二进制的1101.0101的实际值为:1*23+1*22+0*21+1*20+0*2-1+1*2-2+0*2-3+1*2-4=8+4+1+0.25+0.0625 = 13.3125从式中可以进一步看到,由于二进制只用0和1两个符号,在计算二进制位串所代表的实际值时, 只需把符号为1的那些位的位权相加即可, 则上式变为:23 + 22 + 20 + 2-2 + 2-4 = 13.3125熟悉地记清二进制数每位上的位权是有益的。
当位序号为0-12时, 其各位上的位权分别为1、2、4、8、16、32、64、128、256、512、1024、2048和4096。
数制与进位计数法基础在采用进位记数的数字系统中, 如果只用r个基本符号(例如0,1,2,…r-1) 、通过排列起来的符号串表示数值,则称其为基r数制(Radix-r Number System),r称为该数制的基(Radix)。
假定用m+k个自左向右排列的符号Di(-k≤i≤m-1)表示数值N,即N = Dm-1 Dm-2 …D1 D0 D-1 D-2 …D-k (2.1)式中的Di(-k≤i≤m-1)为该数制采用的基本符号,可取值0、1、2、…、r-1,小数点位置隐含在D0与D-1位之间, 则Dm-1 …D0 为N的整数部分,D-1 …D-n 为N的小数部分。
基本模型机的设计与实现

基本模型机的设计与实现1.设计目的1、在掌握部件单元电路实验的基础上,进一步将其组成系统构造一台基本模型计算机。
2、为其定义五条机器指令,并编写相应的微程序,具体上机调试,掌握整机软硬件组成概念。
2.设计内容2.1设计原理部件实验过程中,各部件单元的控制信号是人为模拟产生的,而本次实验将能在微程序控制下自动产生各部件单元控制信号,实现特定指令的功能。
这里,计算机数据通路的控制将由微程序控制器来完成,CPU从内存中取出一条机器指令到指令执行结束的一个指令周期全部由微指令组成的序列来完成,即一条机器指令对应一个微程序。
2.1.1有关微控制器部分的介绍微程序控制电路:微程序控制器的组成见图10,其中控制存储器采用3片2816的E2PROM,具有掉电保护功能,微命令寄存器18位,用两片8D触发器(74273)和一片4D(74175)触发器组成。
微地址寄存器6位,用三片正沿触发的双D触发器(7474)组成,它们带有清“0”端和预置端。
在不判别测试的情况下,T2时刻打入微地址寄存器的内容即为下一条微指令地址。
当T4时刻进行测试判别时,转移逻辑满足条件后输出的负脉冲通过强置端将某一触发器置为“1”状态,完成地址修改。
在该实验电路中设有一个编程开关(位于实验板右上方),它具有三种状态:PROM (编程)、READ(校验)、RUN(运行)。
当处于“编程状态”时,实验者可根据微地址和微指令格式将微指令二进制代码写入到控制存储器2816中。
当处于“校验状态”时,可以对写入控制存储器中的二进制代码进行验证,从而可以判断写入的二进制代码是否正确。
当处于“运行状态”时,只要给出微程序的入口微地址,则可根据微程序流程图自动执行微程序。
图中微地址寄存器输出端增加了一组三态门,目的是隔离触发器的输出,增加抗干扰能力,并用来驱动微地址显示灯。
微指令格式:上图为地址转移逻辑电其中UA5--UA0为6位的后续微地址,A,B,C为三个译码字段,分别由三个控制位译码出多个微命令。
《二进制与编码》PPT课件

a
17
从小比特到大数字
• 你一定遇到过这些术语
– 24位色彩 – 100兆连接速度 – 32位计算机 – 128位SSL加密
a
18
从小比特到大数字
• 计算机如何表示二进制
– 利用晶体管或电容表示二进制(如内存)
– 利用磁盘表面的磁介质状态表示(硬盘、磁带) – 利用碟片表面反光特性表示(CD或DVD等)
– 这样浪费更大的空间和更多的时间
– 于是人们发明了许多不同的方法来减少储存或 发送图片需要占用的体积,减小文件体积的过 程被称为压缩
a
53
从比特到图像
• 游程压缩
– 因为在图片中会有大块连续的白色像素以及连 续的黑色像素的特点
– 因此只须记录下每个白色或黑色像素连续区块 的长度,就可以表示整张图像
a
45
从比特到字母
• 传音游戏
– 那么怎么用蜂鸣声来传送二进制0111? – 十进制9用怎样传送呢? – 如何用字母传送字母“q”?
a
46
从比特到字母
• 莫尔斯电码
– 莫尔斯电码的原理也是类似的 – 它有两种“符号”用来表示字符点(.)和划(-)或
称为“滴”(Dit)和“答”(Dah)
a
47
从比特到字母
a
30
从小比特到大数字
a
31
从小比特到大数字
a
32
从小比特到大数字
• 读心术
a
33
从小比特到大数字
• 读心术
– 将包含某个数字的卡片标上1,其他为0
17 = 0 1 63 = 1 1 23 = 0 1
0
001
1
111
0
111
北方工业大学《数字逻辑与计算机组成原理》课程运算器实验报告总结

计算机组成原理实验系统实验指导书北方工业大学计算机系《数字逻辑与计算机组成原理》课程实验报告实验名称实验一运算器实验姓名专业计算机科学与技术学号实验日期班级成绩一、实验目的和要求实验目的:1.掌握运算器的组成及工作原理;2.了解4 位函数发生器74LS181 的组合功能,熟悉运算器执行算术操作和逻辑操作的具体实现过程;3.验证带进位控制的74LS181 的功能。
实验要求:1.复习本次实验所用的各种数字集成电路的性能及工作原理;2.预习实验步骤,了解实验中要求的注意之处。
二、实验内容(包括实验原理,必要实验原理图、连接图等)1.实验原理及原理图:运算器的结构框图见图1-5:算术逻辑单元ALU是运算器的核心。
集成电路74LS181是4位运算器,四片74LS181以并/串形式构成16位运算器。
它可以对两个16位二进制数进行多种算术或逻辑运算,74LS181 有高电平和低电平两种工作方式,高电平方式采用原码输入输出,低电平方式采用反码输入输出,这里采用高电平方式。
三态门74LS244 作为输出缓冲器由ALU-G 信号控制,ALU-G 为“0”时,三态门开通,此时其输出等于其输入;ALU-G 为“1”时,三态门关闭,此时其输出呈高阻。
四片74LS273作为两个16数据暂存器,其控制信号分别为LDR1和LDR2,当LDR1和LDR2 为高电平有效时,在T4脉冲的前沿,总线上的数据被送入暂存器保存。
2.电路组成:本模块由算术逻辑单元ALU 74LS181(U7、U8、U9、U10)、暂存器74LS273(U3、U4、U5、U6)、三态门74LS244(U11、U12)和控制电路(集成于EP1K10 内部)等组成。
电路图见图1-1(a)、1-1(b)。
算术逻辑单元ALU 是由四片74LS181 构成。
74LS181 的功能控制条件由S3、S2、S1、S0、M、Cn 决定。
高电平方式的74LS181 的功能、管脚分配和引出端功能符号详见表1-1、图1-2和表1-2。
二进制与编码原理

二进制与编码原理二进制是一种计数系统,它仅由两个数字0和1组成。
在计算机科学领域,二进制是最常用的计数系统,用于表示和处理数字、文本、图像和音频等各种数据。
本文将深入探讨二进制的原理以及与之相关的编码原理。
二进制的原理很简单,它利用了数字电路中的两个基本状态:高电平和低电平,用1表示高电平,用0表示低电平。
通过组合0和1,可以表示任何数字。
例如,二进制数1101可以表示十进制数13,因为1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13。
二进制的简单原理使得计算机能够高效地存储和处理数据。
计算机中的所有数据都是以二进制形式存储和表示的。
例如,计算机内存中的每个存储单元都可以存储一个二进制位,而计算机的中央处理器(CPU)可以执行各种二进制操作,如加法、减法和逻辑运算等。
除了表示数字之外,二进制还可以用于编码。
编码是将某种信息转化为特定符号的过程。
在计算机科学中,常用的编码方式有ASCII码和Unicode。
ASCII码(American Standard Code for Information Interchange)是一种使用7位二进制数表示字符的编码系统。
它将常见的英文字母、数字和标点符号都转换成二进制形式,使计算机可以直接处理和存储这些字符。
随着计算机技术的发展,ASCII码变得不够用,因为它无法表示其他语言的字符。
于是,Unicode编码应运而生。
Unicode采用了更多的二进制位来表示字符,它可以表示超过100,000个字符,包括各种语言的字符、符号和表情符号等。
Unicode编码使得计算机可以更好地支持全球化和多语言处理。
除了数字和字符编码,二进制还可以用于表示图像和音频等多媒体数据。
在计算机中,图像和音频被转换为二进制数据,然后存储和处理。
图像可以通过像素阵列来表示,每个像素都有一个对应的二进制值来表示其颜色。
音频可以通过采样和量化来表示,通过将声音信号转换为一系列二进制值来表示其振幅。
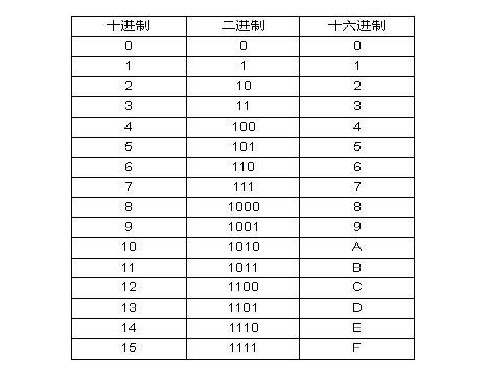
一、二进制代码
四、声音、图像和视频信息的数字化
1、声音数字化 声音是振动产生的波,它是一种模拟信息,话筒 以及相关电路可以把声波转换成电压的波形,但这 仍然是一种连续平滑变化的模拟信号。只有通过采 样和量化,模拟信号才能转换成数字信号。例如, 在录制声音的过程中, 声源的声音是一种模拟量, 话筒是传感器,声卡则对采样和量化所得的声音信 号进行编码,最后形成数字化的声音文件。
三、模数转换
现实世界中各种各样的信息,通常是连续 变化的“模拟量”,计算机如果要存储、处理它 们,首先要将它们数字化,即将它们变成一系列 二进制数据形式的“数字量”。 基本的方法是以很小的时间间隔不断测得 模拟量在这些瞬间的样品(幅度)值(采样), 并以某种数值(量化)形式加以保存,通过“采 样”和“量化”就可以实现模拟量的数字化,这 个过程称为“模数转换(A/D转换)”。而反之, 将数字信号转换成模拟信号的过程称为“数模转 换(D/A转换)”。
ASCII码是一种通用的字符编码,包 含了大小写英文字母、数字等128个字 符。可见ASCII码解决了西文字符的编 码问题。汉字与西文字符一样,在计 算机内也是以二进制代码的形式表示 的。那么汉字又是如何编码的呢?
二、汉字编码 汉字在计算机内部也是以二进制 代码形式表示的,这些代码,称为汉 字编码。 1981年制定国家标准GB2312-80。 国标码规定用2个字节表示1个汉字, 每个字节只用低7位,最高位为0。
• 究竟怎样区分数值和字符呢?例如, 内存中有一个字节的内容是01000001, 它究竟表示的是A这个字母,还是65这 个数值,或是其他?
如果面对一个孤立的字节,确实无法区分, 但存放和使用这个数据的软件,会以其他方 式保存这些数码所属的数码类型的信息,指 明这个数据是数值类型,或是字符类型,或 是其他类型。
二到十进制码的编码方式

二到十进制码的编码方式二进制码是一种只使用0和1两个数字来表示数值的编码方式。
每一位二进制码称为一个位(bit),是计算机中最基本的数据存储和传输单位。
而十进制码则是我们平常生活中最常用的数字表示方式。
本文将详细介绍从二进制码到十进制码的编码过程,帮助读者更好地理解编码方式的转换。
一、什么是二进制码二进制码是由0和1两个数字组成的编码方式。
它是计算机理解和处理信息的基础,因为计算机中的数据和指令都是以二进制码的形式存储和传输的。
每一位二进制码都代表一个权重,权重从右向左依次为1、2、4、8、16、32……。
二、二进制码转换为十进制码二进制码转换为十进制码的方法很简单,只需将每一位二进制位数与对应的权重相乘,然后将结果相加即可。
步骤一:准备待转换的二进制码。
例如,我们有一个八位的二进制码10101100。
步骤二:确定二进制位数的权重。
根据权重规律,我们可以得到如下权重值:1 0 4 8 0 32 64 128步骤三:将二进制码的每一位与对应权重相乘。
根据二进制码的每一位与权重的对应关系,可以得到如下结果:1*128 + 0*64 + 1*32 + 0*16 + 1*8 + 1*4 + 0*2 + 0*1步骤四:将结果相加得到十进制码。
计算得到的结果为:128 + 0 + 32 + 0 + 8 + 4 + 0 + 0 = 172因此,二进制码10101100转换为十进制码为172。
三、十进制码转换为二进制码十进制码转换为二进制码的方法需要用到除法和取余的运算。
步骤一:准备待转换的十进制码。
例如,我们有一个十进制码248。
步骤二:确定二进制位数的权重。
由于二进制码每一位的权重依次为1、2、4、8、16、32……,我们需要找到最大的权重,使得它小于或等于待转换的十进制码。
在本例中,最大的权重小于248的二进制位数为128。
步骤三:进行除法运算,直到商为0为止。
以本例为例,我们用248除以128,商为1,余数为120。
二进制代码

463.5 10
不能省略!
863.2 10
01400 11810
0110
6
1100
6
0011 .
3
0011 .
3
01501 00210
8421BCD 不能省略!
2421BCD
1.4.2 格 雷 码
• 格雷码是一种无权码。 • 编码特点是:任何两个相邻代码 之间仅有一位不同。
1.4 二进制代码
1.4.1 二-十进制码 1.4.2 格雷码 1.4.3 ASCII码
1.4 二进制代码
码制:编制代码所要遵循的规则 二进制代码的位数(n),与需要编码的事件(或信息)的个 数(N)之间应满足以下关系: 2n-1≤N≤2n 1. 二—十进制码进制码(数值编码) (BCD码----- Binary Code Decimal) 用4位二进制数来表示一位十进制数中的0~9十个数码。 从4 位二进制数16种代码中,选择10种来表示0~9个数码的 方案有很多种。每种方案产生一种BCD码。
• 该特点常用于模拟量的转换。当 模拟量发生微小变化,格雷码仅仅 改变一位,这与其它码同时改变2 位或更多的情况相比,3b2b1b0
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
0100
0100
0111
0100
5
0101
1011
1000
1000
1100
6
0110
1100
1001
1001
1101
7
0111
1101
1010
2进制的符号

二进制是一种基数为2的记数系统,通常使用两个符号来表示数字,即0和1。
二
进制是计算机中常用的数据表示方式之一,因为计算机中的信息都是以二进制形式存储和处理的。
在二进制中,每一位数字表示一个特定的权值,例如在十进制中,个位表示1,十位表示10,百位表示100等等。
而在二进制中,第一位表示2的0次方,第二位表示2的1次方,第三位表示2的2次方等等。
因此,二进制中的每一位数字都有其特定的权值。
在二进制中,通常使用小写的字母b来表示二进制数,例如b0001表示二进制的1,b1000表示二进制的8。
另外,在计算机科学中,也常常使用大写的字母B来表示二进制数,例如B0001和B1000。
需要注意的是,在计算机中表示二进制数时,通常使用补码形式来表示正数和负数。
补码表示法是一种二进制编码方式,其中最高位为符号位,正数的符号位为
0,负数的符号位为1。
其余位表示数值本身。
使用补码表示法可以方便地进行数值运算和比较操作。
keil 支持2进制

KEIL C51二进制数输入宏2008年11月09日星期日 13:33KEIL C51二进制数输入宏在C语言中有十进制,十六进制,八进制;没有二进制的定义,在C51中使用十六进制表示有时不太直观,下面介绍几种方法表示二进制[均来自网络]方法一#define _BIN(a,b,c,d,e,f,g,h) ((a<<7)+(b<<6)+(c<<5)+(d<<4)+(e<<3)+(f<<2)+(g<<1)+(h<<0))#define _bin _BIN // _bin,_BIN均可Example:i = _bin(1,1,1,1, 0,0,0,0); // i=0xF0i = _bin(1,0,1,0, 1,0,0,1); // i=0xA9方法二#define LongToBin(n) (((n>>21)&0x80)|((n>>18)&0x40)|((n>>15)&0x20)|((n>>12)&0x10)|((n>>9)\ & 0x08)|((n>>6)&0x04)|((n>>3)&0x02)|((n)&0x01))#define bin(n) LongToBin(0x##n##l)在实际应用中:比如要用置P1为0x0f 可以这样写:P1=bin(00001111);//then P1=0X0f方法三/*------------binary.h----------------*/#define B00000000 0x00#define B00000001 0x01#define B00000010 0x02#define B00000011 0x03#define B00000100 0x04#define B00000101 0x05#define B00000110 0x06#define B00000111 0x07#define B00001000 0x08#define B00001001 0x09#define B00001010 0x0A#define B00001011 0x0B#define B00001100 0x0C#define B00001101 0x0D#define B00001110 0x0E#define B00001111 0x0F#define B00010000 0x10#define B00010001 0x11#define B00010010 0x12#define B00010011 0x13#define B00010100 0x14#define B00010101 0x15#define B00010111 0x17 #define B00011000 0x18 #define B00011001 0x19 #define B00011010 0x1A #define B00011011 0x1B #define B00011100 0x1C #define B00011101 0x1D #define B00011110 0x1E #define B00011111 0x1F#define B00100000 0x20 #define B00100001 0x21 #define B00100010 0x22 #define B00100011 0x23 #define B00100100 0x24 #define B00100101 0x25 #define B00100110 0x26 #define B00100111 0x27 #define B00101000 0x28 #define B00101001 0x29 #define B00101010 0x2A #define B00101011 0x2B #define B00101100 0x2C #define B00101101 0x2D #define B00101110 0x2E #define B00101111 0x2F#define B00110000 0x30 #define B00110001 0x31 #define B00110010 0x32 #define B00110011 0x33 #define B00110100 0x34 #define B00110101 0x35 #define B00110110 0x36 #define B00110111 0x37 #define B00111000 0x38 #define B00111001 0x39 #define B00111010 0x3A #define B00111011 0x3B #define B00111100 0x3C #define B00111101 0x3D #define B00111110 0x3E#define B01000000 0x40 #define B01000001 0x41 #define B01000010 0x42 #define B01000011 0x43 #define B01000100 0x44 #define B01000101 0x45 #define B01000110 0x46 #define B01000111 0x47 #define B01001000 0x48 #define B01001001 0x49 #define B01001010 0x4A #define B01001011 0x4B #define B01001100 0x4C #define B01001101 0x4D #define B01001110 0x4E #define B01001111 0x4F#define B01010000 0x50 #define B01010001 0x51 #define B01010010 0x52 #define B01010011 0x53 #define B01010100 0x54 #define B01010101 0x55 #define B01010110 0x56 #define B01010111 0x57 #define B01011000 0x58 #define B01011001 0x59 #define B01011010 0x5A #define B01011011 0x5B #define B01011100 0x5C #define B01011101 0x5D #define B01011110 0x5E #define B01011111 0x5F#define B01100000 0x60 #define B01100001 0x61 #define B01100010 0x62 #define B01100011 0x63 #define B01100100 0x64 #define B01100101 0x65 #define B01100110 0x66 #define B01100111 0x67#define B01101001 0x69 #define B01101010 0x6A #define B01101011 0x6B #define B01101100 0x6C #define B01101101 0x6D #define B01101110 0x6E #define B01101111 0x6F#define B01110000 0x70 #define B01110001 0x71 #define B01110010 0x72 #define B01110011 0x73 #define B01110100 0x74 #define B01110101 0x75 #define B01110110 0x76 #define B01110111 0x77 #define B01111000 0x78 #define B01111001 0x79 #define B01111010 0x7A #define B01111011 0x7B #define B01111100 0x7C #define B01111101 0x7D #define B01111110 0x7E #define B01111111 0x7F#define B10000000 0x80 #define B10000001 0x81 #define B10000010 0x82 #define B10000011 0x83 #define B10000100 0x84 #define B10000101 0x85 #define B10000110 0x86 #define B10000111 0x87 #define B10001000 0x88 #define B10001001 0x89 #define B10001010 0x8A #define B10001011 0x8B #define B10001100 0x8C #define B10001101 0x8D #define B10001110 0x8E #define B10001111 0x8F#define B10010000 0x90#define B10010010 0x92 #define B10010011 0x93 #define B10010100 0x94 #define B10010101 0x95 #define B10010110 0x96 #define B10010111 0x97 #define B10011000 0x98 #define B10011001 0x99 #define B10011010 0x9A #define B10011011 0x9B #define B10011100 0x9C #define B10011101 0x9D #define B10011110 0x9E #define B10011111 0x9F#define B10100000 0xA0 #define B10100001 0xA1 #define B10100010 0xA2 #define B10100011 0xA3 #define B10100100 0xA4 #define B10100101 0xA5 #define B10100110 0xA6 #define B10100111 0xA7 #define B10101000 0xA8 #define B10101001 0xA9 #define B10101010 0xAA #define B10101011 0xAB #define B10101100 0xAC #define B10101101 0xAD #define B10101110 0xAE #define B10101111 0xAF#define B10110000 0xB0 #define B10110001 0xB1 #define B10110010 0xB2 #define B10110011 0xB3 #define B10110100 0xB4 #define B10110101 0xB5 #define B10110110 0xB6 #define B10110111 0xB7 #define B10111000 0xB8 #define B10111001 0xB9 #define B10111010 0xBA#define B10111100 0xBC #define B10111101 0xBD #define B10111110 0xBE #define B10111111 0xBF#define B11000000 0xC0 #define B11000001 0xC1 #define B11000010 0xC2 #define B11000011 0xC3 #define B11000100 0xC4 #define B11000101 0xC5 #define B11000110 0xC6 #define B11000111 0xC7 #define B11001000 0xC8 #define B11001001 0xC9 #define B11001010 0xCA #define B11001011 0xCB #define B11001100 0xCC #define B11001101 0xCD #define B11001110 0xCE #define B11001111 0xCF#define B11010000 0xD0 #define B11010001 0xD1 #define B11010010 0xD2 #define B11010011 0xD3 #define B11010100 0xD4 #define B11010101 0xD5 #define B11010110 0xD6 #define B11010111 0xD7 #define B11011000 0xD8 #define B11011001 0xD9 #define B11011010 0xDA #define B11011011 0xDB #define B11011100 0xDC #define B11011101 0xDD #define B11011110 0xDE #define B11011111 0xDF#define B11100000 0xE0 #define B11100001 0xE1 #define B11100010 0xE2 #define B11100011 0xE3#define B11100101 0xE5 #define B11100110 0xE6 #define B11100111 0xE7 #define B11101000 0xE8 #define B11101001 0xE9 #define B11101010 0xEA #define B11101011 0xEB #define B11101100 0xEC #define B11101101 0xED #define B11101110 0xEE #define B11101111 0xEF#define B11110000 0xF0 #define B11110001 0xF1 #define B11110010 0xF2 #define B11110011 0xF3 #define B11110100 0xF4 #define B11110101 0xF5 #define B11110110 0xF6 #define B11110111 0xF7 #define B11111000 0xF8 #define B11111001 0xF9 #define B11111010 0xFA #define B11111011 0xFB #define B11111100 0xFC #define B11111101 0xFD #define B11111110 0xFE #define B11111111 0xFF。
二进制ascii码表

二进制ascii码表
ASCII码是计算机中用得最广泛的字符集及其编码。
二进制数可以表示2种状态:0、1;而2位二进制数可以表示(2=)4种状态:00、01、10、11;依次类推,7位二进制数可以表示(2=)128种状态,每种状态都唯一地编为一个7位的二进制码,对应一个字符(或控制码),这些码可以排列成一个十进制序号0~127。
所以,7位ASCII码是用七位二进制数进行编码的,可以表示128个字符。
以下是部分二进制ASCII码的表示:
*001000103422"
*0010001135230
*001001013725%
*001001103826&
*001001113927
*001010014129)
*00101010422A*
*00101011432B+
*00101100442C,
*00101101452D-
*00101110462E.
*00101111472F/
*0011000048300
*0011000149311
*0011001050322
*以此类推,直到:
*0011100157399
这些是二进制ASCII码的示例,可以通过将字符或数字与相应的二进制编码相对应来理解和使用它们。
灰色二进制代码

灰色二进制代码【原创实用版】目录1.灰色二进制代码的概述2.灰色二进制代码的用途3.灰色二进制代码的实现方法4.灰色二进制代码的优缺点5.灰色二进制代码的发展前景正文1.灰色二进制代码的概述灰色二进制代码,是一种基于灰色系统理论的编码方式。
灰色系统理论是我国学者邓聚龙教授于 1989 年提出的一种新的系统科学理论。
灰色二进制代码,顾名思义,是由两种颜色组成的,即黑色和白色。
在计算机领域,通常用 0 表示黑色,1 表示白色。
灰色二进制代码是一种介于 0 和 1 之间的编码方式,它可以更好地描述现实世界中的不确定性和模糊性。
2.灰色二进制代码的用途灰色二进制代码在许多领域都有广泛的应用,包括计算机科学、通信技术、信号处理、控制系统等。
它可以用来解决一些复杂的问题,如数据压缩、模式识别、图像处理等。
3.灰色二进制代码的实现方法灰色二进制代码的实现方法主要包括两种:一种是基于数学模型的实现,另一种是基于计算机程序的实现。
基于数学模型的实现,主要是通过建立灰色系统模型,然后求解模型得到灰色二进制代码。
基于计算机程序的实现,主要是通过编写计算机程序,对输入的数据进行处理,得到灰色二进制代码。
4.灰色二进制代码的优缺点灰色二进制代码的优点主要有:适应性强,可以描述现实世界中的不确定性和模糊性;计算简单,易于实现。
缺点主要有:理论基础较弱,尚未得到广泛的认可;应用范围有限,主要应用于一些特定的领域。
5.灰色二进制代码的发展前景随着灰色系统理论的研究深入,灰色二进制代码的应用范围将会越来越广,其在各个领域的作用也将越来越大。
同时,随着计算机技术的发展,灰色二进制代码的实现方法也将越来越便捷。
第1页共1页。
二进制向量编码方式

二进制向量编码方式是一种将向量数据转换为二进制编码的方法。
在机器学习和数据压缩等领域,二进制向量编码被广泛使用。
二进制向量编码的基本思想是将一个高维的向量空间映射到一个低维的二进制空间。
具体来说,给定一个高维向量,我们可以将其转换为一系列的二进制位,其中每一位都表示向量的一个维度。
例如,假设我们有一个长度为10的向量,其值为[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]。
我们可以将其转换为一系列的二进制位,例如[1, 0, 1, 0, 1, 1, 1, 1, 1, 1]。
这种编码方式的主要优点是压缩了数据,减少了存储空间的需求。
同时,由于二进制编码的简单性,它也提高了处理速度。
然而,这种编码方式可能会丢失一些原始数据的细节和信息,因此在使用时需要权衡其优缺点。
此外,还有一些其他的向量编码方式,如稀疏编码、哈希编码等,它们都有各自的特点和适用场景。
