(完整版)哈工大选修课LINEARALGEBRA试卷及答案,推荐文档
哈工大选修课 LINEAR ALGEBRA 试卷及答案

LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix; (2) Echelon Form; (3) Elementary operations;(4) Onto mapping and one-to-one mapping; (5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the 33⨯ matrix that corresponds to the composite transformation of a scaling by 0.3, a rotation of 90︒, and finally a translation that adds (-0.5, 2) to each point of a figure.4. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col A of the matrix1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let a and b be positive numbers. Find the area of the region bounded by the ellipse whose equation is22221x y ab+=7. Provide twenty statements for the invertible matrix theorem. 8. Show and prove the Gram-Schmidt process. 9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1.All nonzero rows are above any rows of all zeros.2.Each leading entry of a row is in a column to the right of the leading entry of the row above it.3.All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4.The leading entry in each nonzero row is 1.5.Each leading 1 is the only nonzero entry in its column.(3)Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1.(Replacement) Replace one row by the sum of itself anda multiple of another row.2.(Interchange) Interchange two rows.3.(scaling) Multiply all entries in a row by a nonzero constant.(4)Onto mapping and one-to-one mapping:A mapping T : n →m is said to be onto m if each b in m is the image of at least one x in n.A mapping T : n →m is said to be one-to-one if each b in m is the image of at most one x in n.(5)Linearly independence:An indexed set of vectors {V1, . . . ,V p} in n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such that c 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form. Solution: Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top. Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position. Step 3:Use row replacement operations to create zeros in all positions below the pivot. Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify. Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the 33⨯ matrix that corresponds to the composite transformation of a scaling by 0.3, a rotation of 90︒, and finally a translation that adds (-0.5, 2) to each point of a figure. Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.0100001010y x R o t a t e⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x T r a n s l a t eThe matrix for the composite transformation is ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix 361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form: A ~ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---00002302101000201, x 1-2x 2 -x 4+3x 5=0 x 3+2x 4-2x 5=0 0=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free. ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w . That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weights x 2, x 4, and x 5 are all zero.So {u, v , w} is a basis for Nul A.5. Find a basis for Col A of the matrix 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution: A ~ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001, so the rank of A is 3. Then we have a basis for Col A of the matrix: U = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001, v = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let a and b be positive numbers. Find the area of the region bounded by the ellipse whose equation is22221x y ab+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=⎥⎦⎤⎢⎣⎡b a 00, because if u= ⎥⎦⎤⎢⎣⎡21u u , x=⎥⎦⎤⎢⎣⎡21x x , and x = Au, then u 1 =ax 1 and u 2 =bx 2It follows that u is in the unit disk, with 12221≤+u u , if and only if x is in E , with1)()(2221≤+b x a x . Then we have{area of ellipse} = {area of T (D )} = |det A| {area of D} = ab π(1)2= πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square n n ⨯ matrix. Then the following statements are equivalent. That is, for a given A, the statements are either all true or false. a. A is an invertible matrix.b. A is row equivalent to the n n ⨯ identity matrix.c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x → Ax is one-to-one.g. The equation Ax = b has at least one solution for each b in n.h. The columns of A spann.i. The linear transformation x → Ax maps nonton.j. There is an n n ⨯ matrix C such that CA = I. k. There is an n n ⨯ matrix D such that AD = I. l. A T is an invertible matrix. m. If 0A ≠, then ()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If 0A ≠, then ()()*11*A A --=q. ()*1n *A 1)(A --=-r. If 0A ≠, then ()()L11L A A --= ( L is a natural number )s. ()*1n *A K)(KA --=-t. If 0A ≠, then *1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of n, define11x v = 1112222v v v v x x v ⋅⋅-=222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for p k ≤≤1 PROOFFor p k ≤≤1, let W k = Span {v 1, . . . , v p }. Set 11x v =, so that Span {v 1} = Span {x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w1k 1k x p r o j x v k+++-= By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, 0v 1k ≠+ because x k+1 is not in W k = Span {x 1, . . . , x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem. Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal. PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say, 1λand 2λ. T o show that 0v v 21=⋅, compute2T 12T 11211v )(A v v )v (λv v λ==⋅ Since v 1 is an eigenvector ()()2T12T T1Avv v A v ==)(221v v Tλ=2122T12v v λv v λ⋅==Hence ()0v v λλ2121=⋅-, but ()0λλ21≠-, so 0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent. Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯ matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that 1p p p 11v v c v c +=+⋅⋅⋅+ (1) Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain 111+=+⋅⋅⋅+p p p Av Av c Av c11111++=+⋅⋅⋅+p p p p p v v c v c λλλ (2) Multiplying both sides of (1) by 1+p λ and subtracting the result from (2), we have0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλ (3) Since {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of the factors 1+-p i λλ are zero, because the eigenvalues are distinct. Hence 0=i c for i = 1, . . . ,p. But when (1) says that 01=+p v , which is impossible. Hence {v 1, . . . , v r } cannot be linearly dependent and therefore must be linearly independent.。
(北师大版)哈尔滨市高中数学选修4-4第一章《坐标系》检测题(含答案解析)

一、选择题1.在同一平面直角坐标系中,经过伸缩变换22x xy y ''=⎧⎨=⎩后,曲线C 变为曲线()()22561x y -++=,则曲线C 的对称中心是( )A .()5,6-B .5,32⎛⎫-⎪⎝⎭C .()10,12-D .5,62⎛⎫-⎪⎝⎭2.已知点P 的极坐标是1,2π⎛⎫⎪⎝⎭,则过点P 且垂直极轴的直线方程是( ) A .12ρ=B .1cos 2ρθ=C .12cos ρθ=-D .2cos ρθ=-3.极坐标方程2cos22cos 1ρθρθ-=表示的曲线是( ) A .圆B .椭圆C .抛物线D .双曲线4.圆5cos ρθθ=-的圆心极坐标是( )A .45,3π⎛⎫ ⎪⎝⎭B .5,3π⎛⎫ ⎪⎝⎭C .25,3π⎛⎫ ⎪⎝⎭D .55,3π⎛⎫ ⎪⎝⎭5.在同一平面直角坐标系中,经过伸缩变换53x xy y''=⎧⎨=⎩后,曲线C 变为曲线2241x y ''+=,则曲线C 的方程为( )A .2225361x y +=B .2291001x y +=C .10241x y +=D .22281259x y +=6.在极坐标系中,已知圆C 经过点6P π⎛⎫⎪⎝⎭,,圆心为直线sin 4πρθ⎛⎫+= ⎪⎝⎭轴的交点,则圆C 的极坐标方程为 A .4cos ρθ=B .4sin ρθ=C .2cos ρθ=D .2sin ρθ=7.在球坐标系中,点3,,46P ππ⎛⎫ ⎪⎝⎭和点33,,46Q ππ⎛⎫⎪⎝⎭之间的距离为( )A B .C .D8.在直角坐标系xOy 中,直线l 的方程为0x =,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,则l 的极坐标方程为( )A .sin 32πρθ⎛⎫+= ⎪⎝⎭ B .sin 32πρθ⎛⎫-= ⎪⎝⎭C .sin 62πρθ⎛⎫+= ⎪⎝⎭ D .sin 62πρθ⎛⎫-= ⎪⎝⎭9.已知曲线C 与曲线5ρ=5sin?θθ-关于极轴对称,则曲线C 的方程为( )A .10cos ρ=-π-6θ⎛⎫ ⎪⎝⎭ B .10cos ρ=π-6θ⎛⎫ ⎪⎝⎭ C .10cos ρ=-π6θ⎛⎫+⎪⎝⎭D .10cos ρ=π6θ⎛⎫+⎪⎝⎭10.在极坐标系中,曲线1:2cos C ρθ=,曲线2:4C πθ=,若曲线1C 与2C 交于,A B 两点,则线段AB 的长度为( ) A .2BC.D .111.在极坐标系中,直线cos()4ρθπ-=ρ的公共点的个数为A .1B .2C .0D .无法确定12.若曲线2 1x ty t=-⎧⎨=-+⎩(t为参数)与曲线ρ=B , C 两点,则BC 的值为( ) ABCD二、填空题13.已知直线l的极坐标方程为2sin()4πρθ-=A的极坐标为7)4π,则点A 到直线l 的距离为____.14.在平面直角坐标系xOy 中,圆22:(1)(1)1C x y -+-=,以坐标原点O 为极点,x 轴正半轴为极轴,直线l 的极坐标方程为(0)2πθαα=<<,直线l 交圆C 于,A B 两点,P 为,A B 中点.若||||AB OP ⋅,则α=________.15.求圆心为(3,)6C π,半径为3的圆的极坐标方程为 ___________________.16.在极坐标系中,直线sin cos 1ρθρθ-=被曲线1ρ=截得的线段长为_____________. 17.在极坐标系中,已知(2,)6A π,5(4,)6B π,则A ,B 两点之间的距离AB 为__________.18.在极坐标系中,O 是极点,设点(1,)6A π,(2,)2B π,则OAB ∆的面积是__________.19.在直角坐标系xOy 中,曲线C 1的参数方程为2x cosay =⎧⎪⎨=⎪⎩(α为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线C 2的方程为ρ(cos θ-sin θ)+1=0,则C 1与C 2的交点个数为________. 20.过点P (2,4π)并且与极轴垂直的直线的方程是___________________________. 三、解答题21.在极坐标系中,已知直线l 过点1,0A ,且其向上的方向与极轴的正方向所成的最小正角为3π,求:(1)直线的极坐标方程; (2)极点到该直线的距离. 22.在平面直角坐标系xOy 中,圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),以点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求圆C 的极坐标方程;(2)过极点O 作直线与圆C 交于点A ,求OA 的中点所在曲线的极坐标方程.23.以平面直角坐标系的坐标原点O 为极点,以x 轴的非负半轴为极轴,以平面直角坐标系的长度为长度单位建立极坐标系. 已知直线l 的参数方程为23{12x ty t=-=-+ (为参数),曲线的极坐标方程为2sin 4cos ρθθ= . (1)求曲线C 的直角坐标方程;(2)设直线与曲线C 相交于A B 、两点,求AB .24.在直角坐标系xOy 中,已知曲线221:(1)1C x y -+=以坐标原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2cos()336πρθ-=(1)求曲线1C 的极坐标方程;(2)已知点(4,0)M ,直线l 的极坐标方程为3πθ=,它与曲线1C 的交点为O ,P ,与曲线2C 的交点为Q ,求MPQ 的面积.25.在平面直角坐标系xOy 中,圆C 的参数方程为3cos ,3sin x m a y α=+⎧⎨=⎩(α为参数,m 为常数).在以原点O 为极点、以x 轴的非负半轴为极轴的极坐标系中,直线l 的极坐标方程为cos 24πρθ⎛⎫-= ⎪⎝⎭若直线l 与圆C 有两个公共点,求实数m 的取值范围. 26.已知平面直角坐标系xOy ,直线l 过点3)P ,且倾斜角为α,以O 为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为24cos()103πρρθ---=.(1)求直线l 的参数方程和圆C 的标准方程;(2)设直线l 与圆C 交于M 、N 两点,若||||PM PN -=,求直线l 的倾斜角α的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据题意,点(,)x y ''在曲线()()22561x y -++=上,由伸缩变换公式22x xy y ''=⎧⎨=⎩,将其代入()()22561x y -++=中化简,将其变形为标准方程即可求解. 【详解】解:由题意,点(,)x y ''在曲线()()22561x y -++=上,()()22561x y ''∴-++=,又22x x y y '==⎩'⎧⎨,()()()22225125261324x y x y ⎛⎫∴-++=⇒-++= ⎪⎝⎭,所以曲线C 的对称中心是5,32⎛⎫- ⎪⎝⎭.故选:B 【点睛】本题考查伸缩变换公式的应用, 关键是将变换后的量代入方程进行化简,考查理解辨析能力及运算求解能力,属于基础题.2.C解析:C 【分析】把极坐标化为直角坐标,求出直线的直角坐标方程,再化为极坐标方程. 【详解】1,2P π⎛⎫⎪⎝⎭的直角坐标是1,02⎛⎫- ⎪⎝⎭,∴过P 且与极轴垂直的直线的直角坐标方程为12x =-,其极坐标方程为1cos 2ρθ=-,即12cos ρθ=-.故选:C . 【点睛】本题考查求直线的极坐标方程,解题时利用极坐标与直角坐标的互化求解.3.D解析:D 【分析】将极坐标方程化为直角坐标方程,就可以得出结论; 【详解】解:极坐标方程2cos22cos 1ρθρθ-=可化为:()222cos sin 2cos 1ρθθρθ--=,2221x y x ∴--=,即22(1)2x y --=,它表示中心在()1,0的双曲线. ∴极坐标方程2cos22cos 1ρθρθ-=表示的曲线是双曲线.故选:D . 【点睛】本题研究极坐标问题,我们的解法是将极坐标方程化为直角坐标方程,再进行研究,属于中档题.4.D解析:D 【分析】先把圆的极坐标方程化成直角坐标方程求出圆心的直角坐标为5(,22-,再把直角坐标化成极坐标得解. 【详解】由题得25cos sin ρρθθ=-,所以22225,50x y x x y x +=-∴+-+=,所以圆心的坐标为5(,2--,即5(,2.所以该点的极径5ρ==,极角θ在第四象限,且5tan 3θθπ==. 所以圆心极坐标是5(5,)3π. 故选:D 【点睛】本题主要考查极坐标和直角坐标的互化,考查圆的一般方程,意在考查学生对这些知识的理解掌握水平.5.A解析:A 【分析】将伸缩变换53x xy y''=⎧⎨=⎩代入曲线2241x y ''+=中即可解.【详解】解:把53x x y y ''=⎧⎨=⎩代入曲线2241x y ''+=,可得:()()225431x y +=,即2225361x y +=,即为曲线C 的方程. 故选:A . 【点睛】考查平面直角坐标系的伸缩变换,题目较为简单. 伸缩变换:设点(,)P x y 是平面直角坐标系中的任意一点,在变换,(0):,(0)x x y y λλϕμμ'=⋅>⎧⎨'=⋅>⎩的作用下,点(,)P x y 对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 6.A解析:A 【分析】求出圆C 的圆心坐标为(2,0),由圆C 经过点6P π⎛⎫⎪⎝⎭,得到圆C 过极点,由此能求出圆C 的极坐标方程. 【详解】在sin 4πρθ⎛⎫+= ⎪⎝⎭0θ=,得2ρ=, 所以圆C 的圆心坐标为(2,0). 因为圆C 经过点6P π⎛⎫⎪⎝⎭,,所以圆C 的半径2r =,于是圆C 过极点,所以圆C 的极坐标方程为4cos ρθ=. 故选A 【点睛】本题考查圆的极坐标方程的求法,考查直角坐标方程、参数方程、极坐标方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,属于中档题.7.C解析:C 【解析】 【分析】先化,P Q 两点的球坐标化为直角坐标,再利用两点间距离公式求解 【详解】将,P Q 两点的球坐标化为直角坐标,得,4242P Q -⎝⎭⎝⎭,所以||PQ ==故选:C 【点睛】本题考查球坐标与直角坐标的转化,考查距离公式,是基础题8.C解析:C 【解析】 【分析】利用cos ,sin x y ρθρθ==,将直线的直角坐标方程转化为极坐标方程,并利用辅助角公式进行化简,由此得出正确选项. 【详解】因为cos sin 2 sin 06x πρθθρθ⎛⎫=+= ⎪⎝⎭,所以l 的极坐标方程为 sin 62πρθ⎛⎫+= ⎪⎝⎭.故选C. 【点睛】本小题主要考查直角坐标方程化为极坐标方程,考查三角函数辅助角公式,属于基础题.9.B解析:B 【解析】 【分析】将方程5sin ρθθ=-化为直角坐标方程,然后求出该方程关于极轴对称的方程,再转化为极坐标方程即可. 【详解】 ∵5sin ρθθ=-,∴2cos 5sin ρθρθ=-,将222,?,?x y cos x sin y ρρθρθ=+==代入上式,得225x y y +=-,∴曲线关于极轴对称的曲线C 的直角坐标方程为225x y y +=+,化为极坐标方程为5sin ρθθ=+,即ρ=θ+5sin θ=10co πs 6θ⎛⎫- ⎪⎝⎭. 故选B . 【点睛】(1)进行极坐标方程与直角坐标方程互化的关键是抓住互化公式:x =ρcos θ,y =ρsin θ,ρ2=x 2+y 2,ytan xθ=(x ≠0). (2)进行极坐标方程与直角坐标方程互化时,要注意ρ,θ的取值范围及其影响;要善于对方程进行合理变形,并重视公式的逆向与变形使用;要灵活运用代入法和平方法等技巧.10.B解析:B 【解析】 【分析】分别将曲线1C ,2C 的极坐标方程化为普通方程,根据直线与圆相交,利用点到直线的距离公式结合垂径定理,可得结果 【详解】 根据题意, 曲线()222221:22cos 211C cos x y xx y ρθρρθ==+=-+=曲线2:4C y x πθ==,则直线与圆相交,圆的半径为1,圆心到直线y x =的距离为d ==设AB 长为m ,则有22212m d r ⎛⎫+= ⎪⎝⎭,即211142m +=解得m =(舍负)故线段AB 故选B 【点睛】本题主要考查的是极坐标与直角坐标方程的互化,圆的方程以及直线与圆的位置关系,是一道基础题11.A解析:A 【解析】将直线cos 4πρθ⎛⎫-= ⎪⎝⎭22x y +=20x y +-=;将圆ρ=化为直角坐标方程为222x y +=,其圆心坐标为()0,0又圆心()0,0到直线20x y +-=的距离为d ==所以直线20x y +-=与圆222x y +=相切,所以直线cos 4πρθ⎛⎫-= ⎪⎝⎭ρ只有一个公共点.故选A .12.C解析:C 【分析】分析:把参数方程化为普通方程,把极坐标方程化为直角坐标方程,利用直线与圆相交的弦长处理方法计算.详解:曲线21x ty t =-⎧⎨=-+⎩的普通方程为10x y +-=,曲线ρ=228x y +=,圆心O 到直线的距离为d ==r =∴BC ==C . 点睛:直线与圆相交的弦长有两种方法:一是代数方法,一是几何方法,代数法就是由直线与圆方程联立方程组解得交点坐标,再由两点间距离公式求得弦长,常用的是几何方法:用垂径定理,即求出圆心到直线的距离d ,则弦长l =二、填空题13.【解析】直线的直角坐标方程为点的直角坐标为所以点到直线的距离为解析:2【解析】直线l 的直角坐标方程为1y x -= ,点A 的直角坐标为(2,2)- ,所以点A 到直线l 的距离522. 14.或【分析】把圆方程化为极坐标方程设对应的极径是用表示出则由此计算可得结论【详解】由题意圆的一般方程为化为极坐标方程将代入得成立设对应的极径是则∴∴∴(舍去)又∴或∴或故答案为:或【点睛】本题考查直角解析:12π或512π【分析】把圆方程化为极坐标方程,设,,A B P 对应的极径是120,,ρρρ,用α表示出12,ρρ,则12AB ρρ=-,122OP ρρ+=,由此计算可得结论.【详解】由题意圆的一般方程为222210x y x y +--+=,化为极坐标方程22(cos sin )10ρρθθ-++=,将θα=代入得22(cos sin )10ρραα-++=,24(cos sin )40αα∆=+->成立, 设,,A B P 对应的极径是120,,ρρρ,则122(cos sin )ρραα+=+,121ρρ=,∴120cos sin 2ρρραα+==+,∴AB 12ρρ=-===0cos )AB OP ραα==+=4sin 2(1sin 2)3αα+=,(2sin 21)(2sin 23)0αα-+=,∴1sin 22α=(32-舍去), 又(0,)2πα∈,∴26πα=或526πα=.∴12πα=或512πα=. 故答案为:12π或512π. 【点睛】本题考查直角坐标方程与直角坐标方程的互化,考查极坐标的应用,以极点为顶点的射线上两点,A B 对应的极径是12,ρρ,则12AB ρρ=-,线段AB 中点对应的极径为122ρρ+.15.【分析】求出圆心的直角坐标写出圆的直角坐标方程再利用转化成极坐标方程【详解】由题:圆心为直角坐标为所以圆的标准方程:化简得:所以其极坐标方程为:故答案为:【点睛】此题考查曲线直角坐标方程与极坐标方程解析:3sin ρθθ=+【分析】求出圆心的直角坐标,写出圆的直角坐标方程,再利用cos ,sin x y ρθρθ==转化成极坐标方程. 【详解】由题:圆心为(3,)6C π,直角坐标为0033cos 3sin 662x y ππ====,所以圆C 的标准方程:223(()92x y +-=,化简得:2230x y y +--=,cos ,sin x y ρθρθ==,2cos 3sin ρθρθ=+,所以其极坐标方程为:3sin ρθθ=+.故答案为:3sin ρθθ=+【点睛】此题考查曲线直角坐标方程与极坐标方程之间的互相转化,通过几何关系转化固然轻松,当几何关系寻找比较困难时,考虑直角坐标与极坐标的直接代换,虽计算量稍大,但通式通法一定能求解.16.【解析】【分析】首先将极坐标化为直角坐标然后利用弦长公式求弦长即可【详解】直线的极坐标方程化为直角坐标方程即:曲线的极坐标方程化为直角坐标方程即:则圆心到直线的距离:由弦长公式可得弦长为:【点睛】本【解析】【分析】首先将极坐标化为直角坐标,然后利用弦长公式求弦长即可.【详解】直线sin cos 1ρθρθ-=的极坐标方程化为直角坐标方程即:10x y -+=,曲线1ρ=的极坐标方程化为直角坐标方程即:221x y +=,则圆心到直线的距离:d ==== 【点睛】 本题主要考查极坐标与直角坐标的互化,圆想弦长公式及其应用等知识,意在考查学生的转化能力和计算求解能力.17.【分析】先利用直角坐标与极坐标间的关系即利用ρcosθ=xρsinθ=y 进行代换将极坐标化成直角坐标再在直角坐标系中算出两点间的距离即可【详解】根据x=ρcosθy=ρsinθ点的直角坐标为:故答案解析:【分析】先利用直角坐标与极坐标间的关系,即利用ρcosθ=x ,ρsinθ=y ,进行代换将极坐标化成直角坐标,再在直角坐标系中算出两点间的距离即可.【详解】根据x=ρcosθ,y=ρsinθ,点52,,4,66A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,的直角坐标为:A B AB -∴==),(), ,故答案为【点睛】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,本题解题的关键是能进行极坐标和直角坐标的互化.18.【解析】分析:由题意结合三角形面积公式整理计算即可求得三角形的面积详解:的面积点睛:本题主要考查三角形面积公式的应用极坐标的几何意义等知识意在考查学生的转化能力和计算求解能力【解析】分析:由题意结合三角形面积公式整理计算即可求得三角形的面积.详解:OAB 的面积11sin 12232OAB S OA OB π=⨯⨯⨯=⨯⨯= 点睛:本题主要考查三角形面积公式的应用,极坐标的几何意义等知识,意在考查学生的转化能力和计算求解能力.19.2【解析】由曲线C2的方程为p (cosθ﹣sinθ)+1=0∴x ﹣y+1=0即y=x+1;将曲线C1的参数方程化为普通方程为∴消去y 整理得:7x2+8x ﹣8=0△>0∴此方程有两个不同的实根故C1与解析:2【解析】由曲线C 2的方程为p (cosθ﹣sinθ)+1=0,∴x ﹣y+1=0.即y=x+1;将曲线C 1的参数方程化为普通方程为22143x y +=. ∴消去y 整理得:7x 2+8x ﹣8=0.△>0,∴此方程有两个不同的实根,故C 1与C 2的交点个数为2.故答案为2.点睛:这个题目考查的是直线和曲线的交点个数的判断问题;一般直线和椭圆,直接联立判△>0则由两个交点,△<0无交点,△=0,只有一个交点.直线和双曲线则数形结合的情况较多,比较直线和双曲线的渐近线的斜率,从而得到交点个数.20.【解析】设是直线上任意一点如图由于所以应填答案解析:cos ρθ【解析】设(,)M ρθ是直线上任意一点,如图,由于2222OH =⨯=,所以cos 2OH ρθ==,应填答案cos 2ρθ=。
(完整版)哈工大选修课LINEARALGEBRA试卷及答案,推荐文档

LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix;(2) Echelon Form;(3) Elementary operations;(4) Onto mapping and one-to-one mapping;(5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒4. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b +=7. Provide twenty statements for the invertible matrix theorem.8. Show and prove the Gram-Schmidt process.9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1. All nonzero rows are above any rows of all zeros.2. Each leading entry of a row is in a column to the right of the leading entry of the row above it.3. All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4. The leading entry in each nonzero row is 1.5. Each leading 1 is the only nonzero entry in its column.(3) Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1. (Replacement) Replace one row by the sum of itself anda multiple of another row.2. (Interchange) Interchange two rows.3. (scaling) Multiply all entries in a row by a nonzero constant.(4) Onto mapping and one-to-one mapping:A mapping T : R n → R m is said to be onto R m if each b in R m is the image of at least one x in R n.A mapping T : R n → R m is said to be one-to-one if each b in R m is the image of at most one x in R n.(5) Linearly independence:An indexed set of vectors {V1, . . . ,V p} in R n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such thatc 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form.Solution:Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top.Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position.Step 3:Use row replacement operations to create zeros in all positions below the pivot.Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify.Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.010*******y x Rotate⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x Translate The matrix for the composite transformation is⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form:A ~ , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---000023021010002001x 1-2x 2 -x 4+3x 5=0x 3+2x 4-2x 5=00=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free.⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w. That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weights x 2, x 4, and x 5 are all zero.So {u, v, w} is a basis for Nul A.5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution:A ~ , so the rank of A is 3.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001Then we have a basis for Col of the matrix:A U = , v = and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=, because if u= , x=, and x = Au, then ⎥⎦⎤⎢⎣⎡b a 00⎥⎦⎤⎢⎣⎡21u u ⎥⎦⎤⎢⎣⎡21x x u 1 = and u 2 = a x 1bx 2It follows that u is in the unit disk, with , if and only if x is in E , with12221≤+u u1)()(2221≤+x a x . Then we have{area of ellipse} = {area of T (D )}= |det A| {area of D} = ab π(1)2 = πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square matrix. Then the following statements are equivalent. That is, for a n n ⨯given A, the statements are either all true or false.a. A is an invertible matrix.b. A is row equivalent to the identity matrix.n n ⨯c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x Ax is one-to-one.→g. The equation Ax = b has at least one solution for each b in R n .h. The columns of A span R n .i. The linear transformation x Ax maps R n onto R n .→j. There is an matrix C such that CA = I.n n ⨯k. There is an matrix D such that AD = I.n n ⨯l. A T is an invertible matrix.m. If , then 0A ≠()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If , then 0A ≠()()*11*A A--=q. ()*1n *A 1)(A --=-r. If , then ( L is a natural number )0A ≠()()L 11L A A--=s. ()*1n *A K)(KA --=-t. If , then 0A ≠*1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of R n , define11x v = 1112222v v v v x x v ⋅⋅-= 222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for pk ≤≤1PROOFFor , let W k = Span {v 1, . . . , v p }. Set , so that Span {v 1} = Span p k ≤≤111x v ={x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w 1k 1k x proj x v k +++-=By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, because x k+1 is not in W k = Span {x 1, . . . , 0v 1k ≠+x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem.Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say,and . To 1λ2λshow that , compute0v v 21=⋅ Since v 1 is an eigenvector2T 12T 11211v )(Av v )v (λv v λ==⋅()()2T 12T T 1Av v v A v ==)(221v v Tλ= 2122T 12v v λv v λ⋅==Hence , but , so ()0v v λλ2121=⋅-()0λλ21≠-0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that (1)1p p p 11v v c v c +=+⋅⋅⋅+Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain111+=+⋅⋅⋅+p p p Av Av c Av c (2)11111++=+⋅⋅⋅+p p p p p v v c v c λλλMultiplying both sides of (1) by and subtracting the result from (2), we have1+p λ (3)0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλSince {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of the factors are zero, because the eigenvalues are distinct. Hence for i = 1, . . . , p.1+-p i λλ0=i cBut when (1) says that , which is impossible. Hence {v 1, . . . , v r } cannot be linearly 01=+p v dependent and therefore must be linearly independent.。
大学数学实验智慧树知到答案章节测试2023年黑龙江工程学院

绪论单元测试1.MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室)。
()A:错B:对答案:B2.MATLAB和、c语音并称为三大数学软件。
()A:对B:错答案:B3.MATLAB的基本数据单位是矩阵.( )A:对B:错答案:A4.matlab的优点有以下哪些?( )A:高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来;B:具有完备的图形处理功能,实现计算结果和编程的可视化;C:友好的用户界面及接近数学的自然化语言,使学者易于学习和掌握;D:功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
答案:ABCD5.MATLAB只能做高数、线代、概率的计算题,不能做其他的。
()A:对B:错答案:B6.matlab主要应用于以下哪些领域()A:工程计算、控制设计B:信号处理与通讯C:金融建模设计与分析等领域D:图像处理、信号检测答案:ABCD7.本课程仅仅学习了matlab的冰山一角。
()A:对B:错答案:A8.matlab也加入了对C,FORTRAN,C++,JAVA的支持。
()A:对B:错答案:A9.本课程只研究在matlab在高等数学、概率论、线性代数三大学科中的简单应用,姑且把matlab当做一个大型的计算器。
()A:对B:错答案:A10.“mathematica 可能是数学界最好的狙击枪,但MATLAB能给你一座军火库。
“这句话形容了矩阵运算、数据可视化、GUI(用户界面)设计、甚至是连接其他编程语言,MATLAB都能轻松实现。
()A:错B:对答案:B第一章测试1.定义变量的命令为syms ()A:错B:对答案:B2.正弦函数的函数命令为sinx ()A:错B:对答案:A3.余弦函数的函数命令为cos(x) ()A:对B:错答案:A4.matlab不区分输入法的半角和全角()A:对B:错答案:B5.matlab不区分函数命令的大小写()A:对B:错答案:B6.指数函数的函数命令为e^x ()A:对B:错答案:B7.floor(x)是指对x朝-∞方向取整()A:错B:对答案:B8.plot命令可以画离散数据的函数曲线图()A:错B:对答案:B9.ezplot命令可以画连续函数的曲线图()A:对B:错答案:A10.正切函数tanx 可以直接用plot命令画0到pi之间的图形()A:错B:对答案:A第二章测试1.计算极限:()A:-1/exp(1/3)B:1/exp(1/3)C:1D:0答案:B2.计算极限:()A:2B:-1C:1D:0答案:A3.计算极限:()A:INFB:-3/5C:0D:3/5答案:D4.计算极限:()A:-1/3B:0C:1/3D:1答案:C5.计算极限:()A:1B:0C:INFD:-1答案:B6.计算极限:()A:1B:0C:INFD:-1答案:D7.计算极限:()A:INFB:0C:1D:-1答案:B8.计算极限:()A:1/exp(1/3)B:-1/2C:0D:1/2答案:D9.计算极限:( )A:0B:2C:-1D:1答案:A10.计算极限:( )A:1B:-1C:0D:2答案:A第三章测试1.求由参数方程确定的函数的导数。
最新数学理科选修4-4《极坐标》完整版-经典习题及详细答案

数学理科选修4-4第一讲《极坐标》习题一.选择题1.已知⎪⎭⎫ ⎝⎛-3,5πM ,下列所给出的不能表示点的坐标的是( ) A .⎪⎭⎫ ⎝⎛-3,5π B .⎪⎭⎫ ⎝⎛34,5π C .⎪⎭⎫ ⎝⎛-32,5π D .⎪⎭⎫ ⎝⎛--35,5π2.点()3,1-P ,则它的极坐标是( ) A .⎪⎭⎫ ⎝⎛3,2π B .⎪⎭⎫ ⎝⎛34,2π C .⎪⎭⎫ ⎝⎛-3,2π D .⎪⎭⎫ ⎝⎛-34,2π3.极坐标方程⎪⎭⎫⎝⎛-=θπρ4cos 表示的曲线是( ) A .双曲线 B .椭圆 C .抛物线 D .圆4.圆)sin (cos 2θθρ+=的圆心坐标是( )A .⎪⎭⎫ ⎝⎛4,1π B .⎪⎭⎫ ⎝⎛4,21π C .⎪⎭⎫ ⎝⎛4,2π D .⎪⎭⎫⎝⎛4,2π5.在极坐标系中,与圆θρsin 4=相切的一条直线方程为( ) A .2sin =θρ B .2cos =θρ C .4cos =θρ D .4cos -=θρ6、 已知点()0,0,43,2,2,2O B A ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--ππ则ABO ∆为( ) A 、正三角形 B 、直角三角形 C 、锐角等腰三角形 D 、直角等腰三角形 7、)0(4≤=ρπθ表示的图形是( )A .一条射线B .一条直线C .一条线段D .圆8、直线αθ=与1)cos(=-αθρ的位置关系是( )A 、平行B 、垂直C 、相交不垂直D 、与有关,不确定9.两圆θρcos 2=,θρsin 2=的公共部分面积是( ) A.214-πB.2-πC.12-πD.2π10.已知点1P 的球坐标是)4,,32(1πϕP ,2P 的柱坐标是)1,,5(2θP ,求21P P .A .2B .3C .22D .22二.填空题11.极坐标方程52sin 42=θρ化为直角坐标方程是12.圆心为⎪⎭⎫⎝⎛6,3πC ,半径为3的圆的极坐标方程为 13.已知直线的极坐标方程为22)4sin(=+πθρ,则极点到直线的距离是 14、在极坐标系中,点P ⎪⎭⎫⎝⎛611,2π到直线1)6sin(=-πθρ的距离等于____________。
黑龙江省哈尔滨工业大学附中2024-2025学年八年级上学期9月月考物理试题

黑龙江省哈尔滨工业大学附中2024-2025学年八年级上学期9月月考物理试题一、单选题1.刻度尺是实验室中常用的一种测量工具,它用来测量()A.时间B.温度C.长度D.质量2.如图所示,小明正跑着下电扶梯。
旁边有人提醒道:“这样很危险,乘电扶梯时应该站着不动。
”这里“站着不动”是相对于()A.商场里的地面B.人所站的阶梯C.展柜里的商品D.迎面而上的乘客3.如图所示声波的波形图,下列说法正确的是A.乙、丁的响度和音色相同B.甲、丁的音调和响度相同C.甲、乙的音调和响度相同D.丙、丁的音色和响度相同4.小李同学在校园运动会上,参加了初中男子组50m短跑比赛。
他正常完成比赛所用的时间可能为()A.0.8s B.8s C.8min D.8h5.对于匀速直线运动,下列说法中正确的是()A.物体运动的速度越大,通过的路程越长B.物体运动的速度越大,所用的时间越少C.物体运动的速度与路程成正比,与时间成反比D.速度的大小不变,与路程和时间无关6.“复兴号”高速列车正在平直的轨道上匀速行驶,下图中的四个图像能反映列车在做匀速直线运动的是()A.B.C.D.7.对于声音的产生,下列说法正确的是A.只有固体的振动才能发声B.声音是由物体的振动产生的C.物体不振动也能发声D.振动停止后,发声体仍能发声8.北宋沈括在他的著作《梦溪笔谈》中提到:行军宿营,士兵枕着皮制的箭筒睡在地上,可尽早听到来袭敌人的马蹄声。
这样做能尽早听到马蹄声的主要原因是()A.声音在土地中传播的速度比在空气中快B.使马蹄声的音调变高了C.改变了马蹄声的音色D.提高了士兵的听力9.目前,全球的气候均在变暖,近150年来,全球平均气温升高了1℃,这个数字在气象学上是个不可忽视的大数字。
对这种现象,有些科学家认为:可能是由于大量排放二氧化碳而造成的温室效应。
科学家提出这种观点是属于科学探究中的()A.猜想与假设B.提出问题C.进行实验与收集证据D.得出结论、作出解释10.甲、乙两列火车在平直铁轨上匀速前进,它们行驶的路程比是3℃1,所用的时间比是2℃3,则两列车行驶的速度比是()A.9℃8B.8℃9C.9℃2D.2℃111.下列几种估测最符合实际情况的是()A.人步行的速度约为5m/s B.全新的2B铅笔长约18cmC.人心脏跳动一次的时间大约1min D.一张试卷的厚度大约1cm12.琵琶演奏者通过按住琴弦的不同位置来改变声音的()A.响度B.音调C.音色D.速度二、多选题13.声音在某些介质中的传播速度如表所示,分析表格信息,关于声速推断正确的是()A.声速大小与介质有关B.声速大小与温度有关C.声音在固体中的传播速度一定比在液体中快D.声音从空气传到水中,它的传播速度将变慢14.如图所示,图甲是小车甲运动的s t-图象,图乙是小车乙运动的v t-图象。
自动控制原理课件(哈工大)自测题答案
一、单项选择题(共18分)【注:易丢分题,个别拔高题】1-5:AACBD 【第5题提示:据频率特性定义】; 6-9:D C B B 二、填空题(共16分)【注:易丢分题,个别拔高题】1.被控对象;2.0,0;3.0.1;4.10(1)()(0.11)s G s s s +=+5.1【提示:令分母=0用劳斯判据】;6.0=e ;7.1221()()()1()RG z G z C z G HG z =+(其中,21G HG 之间、1RG 之间顺序可交换)三、计算题(共16分)22123()()C s N s122()()L G s H s =, 2123()()()L G s G s H s =-221231()()()()()G s H s G s G s H s ∆=-+,11∆=, 21∆=212122123()()()()()()1()()()()()G s G s G s H s C s N s G s H s G s G s H s -=-+ 2.解:原系统的闭环传递函数为()(1)(21)Ks s s s KΦτ=+⋅++因误差)()()(t c t r t e -=,将原系统等效成单位负反馈系统【注:拔高题---考的是误差定义】,则等效后的单位负反馈系统的误差传递函数为22(1)()1()(21)e s K ss s s s KτΦΦ+-=-=++22002(1)1lim ()()lim 0(21)ss e s s s K s e s s R s s s s K s τ→→+-=Φ=⋅⋅=++10K K τ-=,则1Kτ= 四、计算题(共15分) 解:1.系统根轨迹方程()()()514.8K s G s s s +==--,故绘制180°根轨迹【注:不可缺】。
1) 120, 4.8p p ==,2n =;15z =-,1m =; 2)实轴上的根轨迹为~5-∞-以及0~4.8;3)根轨迹与实轴的分离点:()4.8[]05s s dK dds ds s -=-=+则210240s s +-=,实轴上的分离点122,12x x s s ==-。
2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)

一、单选题二、多选题1. 已知抛物线的焦点为,准线为,为上一点,过作的垂线,垂足为. 若,则( )A.B.C.D.2. 已知数列是递减的等比数列,的前项和为,若,,则=( )A .54B .36C .27D .183. 互相垂直且有公共原点的两条数轴构成平面直角坐标系,但如果平面坐标系中两条坐标轴不垂直,则这样的坐标系称为“斜坐标系”.如图,在斜坐标系中,过点作两坐标轴的平行线,其在轴和轴上的截距,分别作为点的坐标和坐标,记.若斜坐标系中,轴正方向和轴正方向的夹角为,则该坐标系中和两点间的距离为()A .2B .1C.D.4.已知函数,则的一个充分不必要条件是( ).A.B.C .3D.5. 如图甲(左),圣索菲亚教堂是哈尔滨的标志性建筑,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美.为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高约为40,如图乙(右),在它们之间的地面上的点(三点共线)处测得楼顶、教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则估算索菲亚教堂的高度约为()A .50B .55C .60D .706. 下列函数中,既是偶函数又在上单调递增的函数是A.B.C.D.7. 已知定义在上的函数,满足,函数的图象关于点中心对称,对于任意、,,都有成立.则的解集为( )A.B.C.D.8. 从一批含有13件正品,2件次品的产品中不放回地抽3次,每次抽取1件,设抽取的次品数为ξ,则E (5ξ+1)=( )A .2B .1C .3D .49. 某城市为吸引和留住人才,推出“共有产权房”政策,由政府出资30%(1~4级人才)或20%(5~7级人才)垫付首付,支持高层次人才到本区购房落户.以下是某小区5套共有产权房成交价格y (单位:万元)与住房面积x (单位:m 2)之间的统计数据(成交价格受面积、楼层、位置等因素影响)2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)三、填空题四、解答题面积x /m 28095105110125价格y /万元120142161171186若y 与x 之间具有线性相关关系,根据表中数据可求得y 关于x 的回归方程为,则下列说法正确的是( )A.B .变量x 与y 具有负相关关系C .当住房面积增加1m 2时,其价格增加约0.98万元D .根据回归方程估计,若住房面积为150m 2,则成交价格约为202万元10. 已知,,,四点在球心为,半径为5的球面上,且满足,,设,的中点分别为,,则( )A .点有可能在上B.线段的长有可能为7C.四面体的体积的最大值为20D.四面体的体积的最大值为5611.质点和同时出发,在以原点为圆心,半径为的上逆时针作匀速圆周运动.的角速度大小为,起点为与轴正半轴的交点;的角速度大小为,起点为射线与的交点.则当与重合时,的坐标可以为( )A.B.C.D.12.已知函数,则( )A.函数的图象关于点对称B .函数在区间上单调递增C.函数的图象向左平移个单位长度所得到的图象所对应的函数为偶函数D .函数在区间上恰有3个零点13. 已知,则______.14. 已知椭圆与双曲线有公共的焦点,为右焦点,为坐标原点,双曲线的一条渐近线交椭圆于点,且点在第一象限,若,则椭圆的离心率等于_________.15. 袋中有6个大小相同的球,其中1个红球,m 个白球,n 个黑球,现依次取球,每次取出一个,取出不放回,直到取出的球中有两种不同颜色的球时结束,已知取到1个红球1个白球的概率为,则__________,用表示终止时取球的次数,则随机变量的数学期望__________.16. 已知函数满足,且函数与函数互为反函数.(1)求函数、解析式;(2)函数在上有零点,求实数的取值范围.17. 随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.成绩优秀成绩不够优秀总计选修生涯规划课151025不选修生涯规划课61925总计212950(Ⅰ)根据列联表运用独立性检验的思想方法分析:能否有的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数的分布列和数学期望(将频率当作概率计算).参考附表:0.1000.0500.0100.0012.7063.841 6.63510.828参考公式,其中.18. 已知中的三个内角A,B,C所对的边分别为a,b,c,角B为钝角,且.(1)求角B的大小;(2)若点D在AC边上,满足,且,,求BC边的长.19. 某乡镇在实施乡村振兴的进程中,大力推广科学种田,引导广大农户种植优良品种,进一步推动当地农业发展,不断促进农业增产农民增收.为了解某新品种水稻品种的产量情况,现从种植该新品种水稻的不同自然条件的田地中随机抽取400亩,统计其亩产量x(单位:吨(t)).并以此为样本绘制了如图所示的频率分布直方图.(1)求这400亩水稻平均亩产量的估计值(同一组中的数据用该组区间的中点值代表,精确到小数点后两位);(2)若这400亩水稻的灌溉水源为河水和井水,现统计了两种水源灌溉的水稻的亩产量,并得到下表:亩产量超过0.7t 亩产量不超过0.7t合计河水灌溉18090270井水灌溉7060130合计250150400能否有95%的把握认为亩产量与所用灌溉水源相关?0.1000.0500.0100.001k0 2.706 3.841 6.63510.828附:.20. 某省农科院为支持省政府改善民生,保证冬季蔬菜的市场供应举措,深入开展了反季节蔬菜的相关研究,其中一项是冬季大棚内的昼夜温差x(℃)与反季节蔬菜种子发芽数y(个)之间的关系,经过一段时间观测,获得了下列一组数据(y值为观察值):温差x(℃)89101112发芽数y(个)2324262730(1)在所给坐标系中,根据表中数据绘制散点图,并判断y与x是否具有明显的线性相关关系(不需要说明理由);(2)用直线l的方程来拟合这组数据的相关关系,若直线l过散点图中的中间点(即点(10,26)),且使发芽数的每一个观察值与直线l上对应点的纵坐标的差的平方之和最小,求出直线l的方程;(3)用(2)中求出的直线方程预测当温度差为15℃时,蔬菜种子发芽的个数.21. 某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:方式实施地点大雨中雨小雨模拟实验总次数A甲4次6次2次12次B乙3次6次3次12次C丙2次2次8次12次假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:(1)求甲、乙、丙三地都恰为中雨的概率;(2)考虑到旱情和水土流失,如果甲地恰需中雨或小雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是大雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量X,求随机变量X的分布列和均值E(X).。
(完整版)哈工大matlab期末考试题试题及答案(95分)分解,推荐文档

春季学期MATLAB 期末作业学院:机电工程学院专业:机械制造设计及其自动化学号:班号:姓名:姓名:学号:学院:机电学院专业:机械制造2013 年春季学期MATLAB 课程考查题一、必答题:1.matlab 常见的数据类型有哪些?各有什么特点?常量:具体不变的数字变量:会根据已知条件变化的数字字符串:由单引号括起来的简单文本复数:含有复数的数据2.MATLAB 中有几种帮助的途径?(1)帮助浏览器:选择 view 菜单中的 Help 菜单项或选择 Help 菜单中的MATLAB Help 菜单项可以打开帮助浏览器;(2)help 命令:在命令窗口键入“help”命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor 命令:在命令窗口键入“lookfor关键词”可以搜索出一系列与给定关键词相关的命令和函数(4)模糊查询:输入命令的前几个字母,然后按 Tab 键,就可以列出所有以这几个字母开始的命令和函数。
注意:lookfor 和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用 help 命令显示详细信息。
3.Matlab 常见的哪三种程序控制结构及包括的相应的语句?1.顺序结构:数据输入A=input(提示信息,选项)数据输出disp(X)数据输出fprintf(fid,format,variables)暂停pause 或pause(n)2.选择结构:If 语句:if expression (条件)statements1(语句组1)elsestatements2(语句组2)EndSwitch 语句:switch expression (表达式)case value1 (表达式1)statement1(语句组1)case value2 (表达式2)statement2(语句组2)... ...case valuem (表达式m)statementm(语句组m)otherwisestatement (语句组)end3.循环结构:For 循环:for variable=expression(循环变量)statement(循环体)endWhile 循环:while expression (条件<循环判断语句>)statement(循环体)end4.命令文件与函数文件的主要区别是什么?命令文件:不接受输入参数,没有返回值,基于工作空间中的数据进行操作,自动完成需要花费很多时间的多步操作时使用。
哈工大物理试题及答案

哈工大物理试题及答案一、选择题(每题5分,共20分)1. 光在真空中的传播速度是:A. 300,000 km/sB. 1,000 km/sC. 3,000 km/sD. 3×10^8 m/s答案:D2. 根据牛顿第二定律,以下说法正确的是:A. 物体的质量越大,加速度越大B. 物体的质量越大,加速度越小C. 物体的质量越大,加速度不变D. 物体的质量越大,加速度越难改变答案:D3. 电磁波的波长与频率的关系是:A. 波长与频率成正比B. 波长与频率成反比C. 波长与频率无关D. 波长与频率成正比,但需要考虑介质的影响答案:B4. 根据热力学第一定律,以下说法正确的是:A. 能量可以被创造B. 能量可以被消灭C. 能量既不能被创造也不能被消灭D. 能量可以在不同形式间转换答案:D二、填空题(每题5分,共20分)1. 根据欧姆定律,电阻R、电压V和电流I之间的关系是:V =________。
答案:IR2. 光的折射定律,也称为斯涅尔定律,其公式为:n1 * sin(θ1) = ________。
答案:n2 * sin(θ2)3. 根据库仑定律,两个点电荷之间的力F与它们的电荷量q1和q2以及它们之间的距离r的关系是:F = ________。
答案:k * q1 * q2 / r^24. 根据牛顿第三定律,作用力和反作用力的关系是:它们大小相等、方向相反、作用在_______。
答案:不同的物体上三、简答题(每题10分,共20分)1. 简述麦克斯韦方程组的四个方程及其物理意义。
答案:麦克斯韦方程组包括高斯定律、高斯磁定律、法拉第电磁感应定律和安培环路定律。
高斯定律描述了电场线不闭合的性质,高斯磁定律表明磁场线也是闭合的,法拉第电磁感应定律说明了变化的磁场可以产生电场,安培环路定律描述了电流和磁场之间的关系。
2. 解释什么是波粒二象性,并举例说明。
答案:波粒二象性是指微观粒子如电子、光子等既表现出波动性,又表现出粒子性。
线性代数智慧树知到期末考试章节课后题库2024年新疆理工学院

线性代数智慧树知到期末考试答案章节题库2024年新疆理工学院1.任意两个矩阵都可以做加法运算。
()答案:错2.两个单位矩阵可能不相等。
()答案:错3.答案:对4.将行列式转置,行列式的值改变。
()答案:错5.答案:对6.答案:对7.答案:错8.答案:对9.设A,B,C为同阶方阵,A可逆,则下列命题错误的是()答案:10.答案:11.答案:12.下列方阵中一定可对角化的是()。
答案:对称矩阵13.答案:14.答案:15.答案:16.若矩阵A是n阶矩阵,下列命题一定正确的是().答案:17.答案:1,1 18.答案:19.答案:020.答案:21.答案:22.答案:负定的23.设A,B为同阶可逆矩阵,则下列运算正确的是()答案:A+B可逆24.设A,B,C为n阶方阵,且ABC=E,则()。
答案:BCA=E25.答案:26.答案:27.答案:对28.向量A的任意两个最大无关组所含向量的个数相同。
()答案:对29.答案:对30.n阶方阵A与B合同,若 A 为对称阵,则 B 不一定为对称阵。
()答案:错31.任一矩阵都可通过初等行变换化为行阶梯形矩阵和行最简形矩阵。
()答案:对32.若矩阵A和B相似,则矩阵A和B具有相同的特征值、特征向量。
()答案:错33.答案:错34.答案:35.答案:36.已知3阶方阵A的特征值是0,1,-1,则下列命题中不正确的是()。
答案:1和-1所对应的特征向量正交37.答案:38.答案:39.答案:340.答案:-1241.答案:142.任何阶方阵都是可以对角化的。
()答案:错43.将行列式的某一行(列)的所有元素同乘以数k后加于另一行(列)对应位置的元素上,行列式的值改变。
()答案:错44.答案:对45.含有零向量的向量组一定线性相关。
()答案:对46.矩阵的某一行中所有的元素都乘同一个数,等于用数乘以此矩阵。
()答案:错47.可逆线性变换可能改变二次型的秩。
()答案:错48.设A,B是两个n阶可逆矩阵,则下列各式错误的是()答案:49.答案:A-E可逆50.答案:451.答案:52.设A,B均为n阶矩阵,下列关系一定成立的是()答案:53.答案:54.答案:55.向量组的秩是惟一的。
高等数学(下)知识点汇总与典型题解析(黑龙江联盟)智慧树知到答案章节测试2023年哈尔滨工程大学

第一章测试1.函数的所有间断点是()。
A:,其中B:,其中C:,其中D:,其中答案:B2.极限的值是()。
A:0B:eC:1D:答案:D3.极限的值是()。
A:不存在B:1C:∞D:0答案:A4.设函数,则()。
A:极限不存在B:极限不存在C:极限存在,但在点(0,0)处不连续D:在点(0,0)处连续答案:B5.函数在点偏导数存在是在该点连续的()。
A:必要条件,但不是充分条件B:充分条件,但不是必要条件C:充分必要条件D:既不是充分条件,也不是必要条件答案:D6.设函数则()。
A:1B:0C:不存在D:2答案:A7.设,则()。
A:2B:C:0答案:B8.设,则()。
A:不存在B:1C:-1D:0答案:D9.设是由方程所确定的函数,其中是变量u,v的任意可微函数,a,b为常数,则必有()。
A:B:C:D:答案:B10.已知函数,其中,并且这些函数均有一阶连续偏导数,那么()。
A:B:C:D:答案:D11.A:1B:-1C:aD:b答案:A12.设函数u=xyz在点(1,1,2)的某邻域内可微分,则函数u在点(1,1,1)处的梯度为()。
A:3B:C:5D:答案:D13.曲线在点的切线一定平行于()。
A:平面B:平面C:平面D:平面答案:C14.曲面在点处的切平面方程为()。
A:B:C:答案:B15.空间曲线,在点处的法平面必()。
A:垂直于平面B:平行于轴C:平行于轴D:垂直于平面答案:C16.A:B:C:D:答案:A17.函数在点的全微分就是曲面在点的切平面上的点的坐标的改变量。
()A:错B:对答案:B18.设具有连续偏导数,则曲面的切平面平行于一定直线,其中为常数。
()A:错B:对答案:B19.函数在某点的方向导数存在, 则函数在此点的偏导数存在。
()A:错B:对答案:A20.函数沿其梯度方向的方向导数达到最大值, 且最大值为梯度的模。
()A:错B:对答案:B21.若函数及都在点可导, 函数在对应点具有连续偏导数, 则复合函数在点可导,且其导数为。
哈尔滨市选修一第一单元《空间向量与立体几何》检测卷(包含答案解析)
一、选择题1.如图所示,在直三棱柱111ABC A B C -中,AC BC ⊥,且3BC =,4AC =,13CC =,点P 在棱1AA 上,且三棱锥A PBC -的体积为4,则直线1BC 与平面PBC 所成角的正弦值等于( )A .10 B .6 C .10 D .15 2.正方体1111ABCD A B C D -中,动点M 在线段1A C 上,E ,F 分别为1DD ,AD 的中点.若异面直线EF 与BM 所成的角为θ,则θ的取值范围为( ) A .[,]63ππB .[,]43ππC .[,]62ππD .[,]42ππ3.如图,三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,则异面直线1AB 与1BC 所成角的余弦值为( )A .306B .63C 3D .664.如图,正方体1111ABCD A B C D -的棱长为a ,E 是DD 1的中点,则( )A .直线B 1E //平面A 1BD B .11B E BD ⊥C .三棱锥C 1-B 1CE 的体积为313aD .直线B 1E 与平面CDD 1C 1所成的角正切值为255.已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为( ) A .[]0,4B .[]0,2C .[]1,4D .[]1,26.在底面为锐角三角形的直三棱柱111ABC A B C -中,D 是棱BC 的中点,记直线1B D 与直线AC 所成角为1θ,直线1B D 与平面111A B C 所成角为2θ,二面角111C A B D --的平面角为3θ,则( ) A .2123,θθθθ<<B .2123 ,θθθθ><C .2123 ,θθθθD .2123 ,θθθθ>>7.在如图所示的几何体ABCDEF 中,四边形EDCF 是正方形,ABCD 是等腰梯形,AD DE =,90ADE ∠=,//AB CD ,120ADC ∠=.给出下列三个命题:1:p 平面ABCD ⊥平面EDCF ;2:p 异面直线AF 与BD 所成角的余弦值为34;3:p 直线AF 与平面BDF 5那么,下列命题为真命题的是( ) A .12p p ∧B .13p p ⌝∧C .23p p ∧D .13p p ∧8.棱长为1的正四面体ABCD 中,点E ,F 分别是线段BC ,AD 上的点,且满足13BE BC =,14AF AD =,则AE CF ⋅=( )A .1324-B .12-C .12D .13249.我国古代数学名著《九章算术》中记载的“刍甍”(chumeng )是底面为矩形,顶部只有一条棱的五面体.如下图五面体ABCDEF 是一个刍甍,其中四边形ABCD 为矩形,其中8AB =,23AD =,ADE 与BCF △都是等边三角形,且二面角E AD B --与F BC A --相等,则EF 长度的取值范围为( )A .(2,14)B .(2,8)C .(0,12)D .(2,12)10.正方形ABCD 沿对角线BD 折成直二面角,下列结论:①AD 与BC 所成的角为60︒:②AC 与BD 所成的角为90︒:③BC 与面ACD 所成角的正弦值为63:④二面角A BC D --2:其中正确结论的个数为( ) A .4B .3C .2D .111.在棱长为1的正方体1111ABCD A B C D -中,M ,N ,H 分别在棱1BB ,BC ,BA 上,且满足134BM BB =,12BN BC =,12BH BA =,O 是平面1B HN ,平面ACM 与平面11B BDD 的一个公共点,设BO xBH yBN zBM =++,则3x y z ++=( ) A .105B .125C .145D .16512.已知空间四边形ABCD 的每条边和对角线的长都等于1,点E ,F 分别是AB 、AD 的中点,则EF DC ⋅=( ) A .14B .14-C 3D .3-13.以下四个命题中正确的是( )A .空间的任何一个向量都可用其他三个向量表示B .若{},,a b c 为空间向量的一组基底,则{},,a b b c c a +++构成空间向量的另一组基底C .ABC ∆为直角三角形的充要条件是0AB AC ⋅=D .任何三个不共线的向量都可构成空间向量的一个基底二、填空题14.三棱锥O ABC -中,OA 、OB 、OC 两两垂直,且OA OB OC ==.给出下列四个命题:①()()223OA OB OCOA ++=;②()0BC CA CO ⋅-=;③()OA OB +和CA 的夹角为60;④三棱锥O ABC -的体积为()16AB AC BC ⋅. 其中所有正确命题的序号为______________.15.已知空间向量(0,1,1),(1,0,1)a b ==,则向量a 与b 的夹角为_____________. 16.如图所示,在棱长为2的正方体1111ABCD A B C D -中,O 是底面ABCD 的中心,E 、F 分别是1CC 、AD 的中点,那么异面直线OE 和1FD 所成角的余弦值等于______.17.设空间任意一点O 和不共线三点A B C ,,,且点P 满足向量关系OP xOA yOB zOC =++,若,,,P A B C 四点共面,则x y z ++=______.18.如图,点P 在正方形ABCD 所在的平面外,PD ABCD PD AD 底面,⊥=,则PA 与BD 所成角的度数为____________.19.在空间直角坐标系中, ()()()2,1,1,3,4,,2,7,1,A B C AB CB 若λ-⊥,则λ=____ 20.如图,已知正方体1111ABCD A B C D -的棱长为1,E ,F ,G 分别是棱111,,AA BC C D 的中点,设M 是该正方体表面上的一点,若(,)EM xEF yEG x y =+∈R ,则点M 的轨迹所形成的长度是________.21.如图,在三棱柱111ABC A B C -中,1AC CC ⊥,AC BC ⊥,2AC BC ==,160C CB ∠=︒,13CC =,点D ,E 分别在棱1AA 和棱1CC 上,且1AD =,2CE =,则二面角1B B E D --的正切值_______22.如图,在四棱锥P ABCD -中,底面ABCD 是底边为1的菱形,60BAD ∠=,2PB =,PA PD =,当直线PB 与底面ABCD 所成角为30时,二面角P CD A --的正弦值为______.23.已知(2,1,3),(1,4,2),(3,5,)a b c λ=-=-=-,若,,a b c 三向量共面,则实数λ=_____.24.如图,在空间四边形OABC 中,M ,N 分别为OA 、BC 的中点,点G 在线段MN 上,且3MG GN =,用向量OA 、OB 、OC 表示向量OG ,设OG x OA y OB z OC =⋅+⋅+⋅,则x 、y 、z 的和为______.25.在正方体1111ABCD A B C D -中,M ,N 分别为1B B ,CD 的中点,有以下命题: ①//MN 平面1A BD ;②1MN CD ⊥;③平面1A MN ⊥平面1A AC , 则正确命题的序号为______.26.在平行六面体1111ABCD A B C D -中,已知1160BAD A AB A AD ∠=∠=∠=︒,14,3,5AD AB AA ===,1AC =__.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】利用锥体的体积公式可求得2PA =,然后以点C 为坐标原点,CB 、CA 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可求得直线1BC 与平面PBC 所成角的正弦值. 【详解】由已知得1AA ⊥底面ABC ,且AC BC ⊥,所以111344332A PBC P ABC ABC V V S PA PA --==⨯⨯=⨯⨯⨯⨯=△,解得2PA =. 如图所示,以点C 为坐标原点,CB 、CA 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则()0,0,0C 、()0,4,2P 、()3,0,0B 、()10,0,3C , 则()3,0,0CB =,()0,4,2CP =,()13,0,3BC =-. 设平面BCP 的法向量为(),,n x y z =, 则由00n CB n CP ⎧⋅=⎨⋅=⎩可得30420x y z =⎧⎨+=⎩,即020x y z =⎧⎨+=⎩,得0x =,令1y =,得2z =-,所以()0,1,2n =-为平面BCP 的一个法向量. 设直线1BC 与平面PBC 所成的角为θ, 则()()1122221610sin cos ,3312n BC n BC n BC θ⋅-=<>===⋅-+⨯+-【点睛】方法点睛:求直线与平面所成角的方法:(1)定义法,①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键; ②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;③求,利用解三角形的知识求角; (2)向量法,sin cos ,AB n AB n AB nθ⋅=<>=⋅(其中AB 为平面α的斜线,n 为平面α的法向量,θ为斜线AB 与平面α所成的角).2.A解析:A 【详解】以D 点为原点,1,,DA DC DD 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系, 如图设DA 2=,易得()1,0,1EF=-,设()()()12,2,20122,2,2CM CA BM λλλλλλλλ==-≤≤=--,, 则cos θcos ,?BM EF =, 即())222201122321222823()33cos θλλλλλλ===≤≤-+-+-+.当13λ=时,cos θ取到最大值32,当1λ=时,cos θ取到最小值12,所以θ的取值范围为,63ππ⎡⎤⎢⎥⎣⎦.点睛:本题主要考查异面直线所成的角,属于难题.求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.3.D解析:D 【分析】根据三棱柱的边长和角度关系,设棱长为1,分别求得AB AC ⋅、1AB AA ⋅、1AC AA ⋅的数量积,并用1,,AA AC AB 表示出1AB 和1BC ,结合空间向量数量积的定义求得11AB BC ⋅,再求得1AB 和1BC ,即可由向量的夹角公式求得异面直线1AB 与1BC 所成角的余弦值. 【详解】三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,设棱长为1,则111cos602AB AC ⋅=⨯⨯︒=,1111cos602AB AA ⋅=⨯⨯︒=,1111cos602AC AA ⋅=⨯⨯︒=. 11AB AB AA =+,11BC AA AC AB =+-,所以()()1111AB BC AB AA AA AC AB ⋅=+⋅+-221111AB AA AB AC AB AA AA AC AA AB =⋅+⋅-++⋅-⋅11111112222=+-++-= 而()222111123AB AB AA AB AB AA AA =+=+⋅+=,()2111BC AA AC AB =+-==,所以111111cos 62AB BC AB BC AB BC ⋅<⋅>===⋅, 故选:D. 【点睛】本题考查了空间向量的线性运算,空间向量数量积的定义与运算,异面直线夹角的向量求法,属于中档题.4.D解析:D建立空间直角坐标系,利用空间向量一一验证即可; 【详解】解:如图建立空间直角坐标系,则()1,0,A a a ,()1,,Ba a a ,0,0,2a E ⎛⎫⎪⎝⎭,(),,0B a a ,()0,0,0D ,()10,0,D a ,则1,,2a B E a a ⎛⎫=-- ⎪⎝⎭,(),,0DB a a =,()1,0,DA a a =,()1,,BD a a a =--,设面1A BD 的法向量为(),,n x y z =,所以00ax az ax ay +=⎧⎨+=⎩,取1x =,则1y z ==-,所以()1,1,1n =--,所以()()()()11111122a aB E n a =⨯-+-⨯-+-⨯=-,当2a ≠时10B E n ≠,故1B E 不一定平行面1A BD ,故A 错误;因为()()()()2115022a B E BD a a a a a a =-⨯-+-⨯-+⨯=≠,所以1B E 与1BD 不垂直,故B 错误; 111113111136C B CE B C EC C ECV V SB C a --===,故C 错误;面11CDD C 的法向量为()1,0,0m =,设直线B 1E 与平面CDD 1C 1所成的角为θ,则121222sin 312m B E m B Ea a a θ===⎛⎫⨯++ ⎪⎝⎭,所以25cos 1sin 3θθ=-= 所以2sin 253tan cos 553θθθ===,故D 正确; 故选:D【点睛】本题考查了立体几何中的线面平行的判定和线面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.5.B解析:B 【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围. 【详解】设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选:B . 【点睛】本题考查向量数量积的取值范围的求解问题,关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.6.A解析:A 【分析】以A 为坐标原点,建立空间直角坐标系,写出点的坐标,分别求出直线的方向向量以及平面的法向量,通过向量法即可求得各个角度的余弦值,再结合余弦函数的单调性即可判断. 【详解】由题可知,直三棱柱111ABC A B C -的底面为锐角三角形,D 是棱BC 的中点, 设三棱柱111ABC A B C -是棱长为2的正三棱柱,以A 为原点,在平面ABC 中,过A 作AC 的垂线为x 轴,AC 为y 轴,1AA 为z 轴,建立空间直角坐标系,则1(0,0,2)A ,1(3,1,2)B ,(0,2,0)C ,33,022D ⎛⎫⎪ ⎪⎝⎭,(0,0,0)A , (0,2,0)AC =,131,22B D ⎛⎫=- ⎪ ⎪⎝⎭,11(3,1,0)A B =,因为直线1B D 与直线AC 所成的角为1θ,10,2πθ⎛⎤∈ ⎥⎝⎦,111||cos ||||25θ⋅∴==⋅B D AC B D AC ,因为直线1B D 与平面111A B C 所成的角为2θ,20,2πθ⎡⎤∈⎢⎥⎣⎦, 平面111A B C 的法向量()0,0,1n =,121||sin ||5∣θ⋅∴==⋅B D n B D n ,222cos 155θ⎛⎫∴=-= ⎪⎝⎭, 设平面11A B D 的法向量(,,)m a b c =,则1113031202m A B a b m B D b c ⎧⋅=+=⎪⎨⋅=-+-=⎪⎩, 取3a =33,3,2m ⎛⎫=-- ⎪⎝⎭, 因为二面角111C A B D --的平面角为3θ, 由图可知,其为锐角,33||2cos ||575749m n m n θ⋅∴===⋅∣,231cos cos cos θθθ>>, 由于cos y θ=在区间(0,)π上单调递减,故231θθθ<<,则2123,θθθθ<<. 故选:A . 【点睛】本题考查利用向量法研究空间中的线面角以及二面角,属综合基础题.7.D解析:D 【分析】利用面面垂直的判定定理可判断命题1p 的真假,利用空间向量法可得判断命题2p 、3p 的真假,再利用复合命题的真假可得出结论. 【详解】90ADE ∠=,AD DE ∴⊥,四边形EDCF 是正方形,则DC DE ⊥,AD DC D ⋂=,DE ∴⊥平面ABCD ,又DE ⊂平面EDCF ,故平面ABCD ⊥平面EDCF ,故1p 为真命题;由已知//DC EF ,DC ⊄平面ABFE ,EF ⊂平面ABFE ,所以//DC 平面ABFE .又DC ⊂平面ABCD ,平面ABCD 平面ABFE AB =,故//AB CD ,又AD DE =,所以AD CD =,令1AD =,则2AB =,60BAD ∠=, 由余弦定理可得2222cos 3BD AB AD AB AD BAD =+-⋅∠=,222AD BD AB ∴+=,AD BD ∴⊥,如图,以D 为原点,以DA 的方向为x 轴正方向,建立空间直角坐标系D xyz -,则()0,0,0D ,()1,0,0A ,13,22F ⎛⎫- ⎪ ⎪⎝⎭,()3,0B , 所以33,12FA ⎛⎫=- ⎪ ⎪⎝⎭,()3,0=DB ,132DF ⎛⎫=- ⎪ ⎪⎝⎭,所以异面直线AF 与BD 所成角的余弦值为332cos ,423FA DB FA DB FA DB-⋅<>===⨯⋅2p 为假命题;设平面BDF 的法向量为(),,n x y z =,由00n DB n DF ⎧⋅=⎨⋅=⎩,所以0102x y z =⎨-+=⎪⎩, 取2x =,则0y =,1z =,得()2,0,1n =,cos ,2F FA n FA A n n⋅<>===⨯⋅ 设直线AF 与平面BDF 所成的角为θ,则sin θ=. 所以直线AF 与平面BDF ,故3p 为真命题. 所以13p p ∧为真命题,12p p ∧、13p p ⌝∧、23p p ∧均为假命题. 故选:D. 【点睛】本题考查复合命题的真假的判断,涉及面面垂直的判断、异面直线所成角以及线面角的计算,涉及空间向量法的应用,考查推理能力与计算能力,属于中等题.8.A解析:A 【分析】设AB a =,AC b =,AD c =,以这3个向量为空间中的基底,将AE CF ⋅转化为基底的数量积运算,即可得答案. 【详解】设AB a =,AC b =,AD c =, 由题意可得121()333AE AB BE a b a a b =+=+-=+,14CF c b =-, 则211334AE CF a b c b ⎛⎫⎛⎫⋅=+⋅-⎪ ⎪⎝⎭⎝⎭2121163123a c a b b c b =⋅-⋅+⋅- 11211111316232122324=⨯-⨯+⨯-⨯=-. 故选:A. 【点睛】本题考查空间向量基本定理的运用、数量积运算,考查空间想象能力和运算求解能力,求解时注意基底思想的运用.9.A解析:A 【分析】求得EF 长度的两个临界位置的长度,由此求得EF 的取值范围. 【详解】由于ADE ∆与BCF ∆都是等边三角形,且边长为3.当E AD B --和F BC A --趋向于0时,8332EF →--=,如下图所示.当E AD B --和F BC A --趋向于π时,83314EF →++=,如下图所示.所以EF 的取值范围是()2,14. 故选:A 【点睛】本小题主要考查空间线段长度范围的判断,考查空间想象能力,属于基础题.10.A解析:A 【分析】取BD 中点O ,连结AO ,CO ,以O 为原点,OC 为x 轴,OD 为y 轴,OA 为z 轴,建立空间直角坐标系,利用向量法和空间中线线、线面、面面间的位置关系逐一判断四个命题得结论. 【详解】解:取BD 中点O ,连结AO ,CO , ∵正方形ABCD 沿对角线BD 折成直二面角,∴以O 为原点,OC 为x 轴,OD 为y 轴,OA 为z 轴,建立空间直角坐标系, 设1OC =,则()0,0,1A ,()0,1,0B -,()1,0,0C ,()0,1,0D ,()0,1,1AD =-,()1,1,0BC =,1cos 222AD BC AD BC AD BC⋅⋅===⋅⋅, ∴异面直线AB 与CD 所成的角为60︒,故①正确:()1,0,1AC =-,()0,2,0BD =,∵0AC BD ⋅=,∴AC BD ⊥,故②正确:设平面ACD 的一个法向量为(),,t x y z =,由00t AC x z t AD y z ⎧⋅=-=⎨⋅=-=⎩,取1z =,得()1,1,1t =,()1,1,0BC =, 设BC 与面ACD 所成角为θ,则6sin cos ,332BC t BC t BC tθ⋅====⋅⋅,故③正确:平面BCD 的法向量()0,0,1n =,()0,1,1BA =,()1,1,0BC =, 设平面ABC 的法向量(),,m x y z =,则00m BA y z m BC x y ⎧⋅=+=⎨⋅=+=⎩,取1x =,得()1,1,1m =-,cos ,3m n m n m n ⋅<>==⋅, ∴6sin ,3m n <>=. ∴二面角A BC D --的平面角正切值是:2,故④正确. 故选:A.【点睛】本题考查利用空间向量法解决立体几何中的问题,属于综合题.11.C解析:C 【分析】根据条件确定O 点位置,再根据向量表示确定,,x y z 的值,即得结果. 【详解】如图,Q 为AC 与BD 交点,P 为BQ 中点,O 为MQ 与1B P 的交点.过P 作PT 平行MQ 交1BB 于T .如图,则T 为BM 中点,所以1111131334224242MT BM BB MB MB ==⨯=⨯⨯=. 所以123B O OP =, 因此1323421411()555352555BO BB BP BM BH BN BM BH BN =+=⋅+⋅+=++, 因为BO xBH yBN zBM =++,所以411,,555z x y ===,1435x y z ∴++=. 故选:C 【点睛】本题考查平面向量基底表示,考查综合分析求解能力,属中档题.12.B解析:B 【分析】由题意作图,可得所求数量积为12BD DC ,由已知易得其模长和夹角,由数量积的定义可得答案. 【详解】解:如图连接空间四边形ABCD 的对角线AC ,BD , 由空间四边形ABCD 的每条边和对角线的长都等于1,可知底面BCD 为等边三角形,故60BDC ∠=︒, 又点E 、F 分别是AB 、AD 的中点,所以12EF BD =, 故11||||cos()22EF DC BD DC BD DC BDC π==-∠ 11111224⎛⎫=⨯⨯⨯-=- ⎪⎝⎭, 故选:B .【点睛】本题考查向量的数量积的运算,涉及向量的基本运算,属于基础题.13.B解析:B 【分析】根据空间向量基底的定义:任何三个不共面的向量都可构成空间向量的一组基底,逐一分析A ,B ,D 可判断这三个结论的正误;根据向量垂直的充要条件,及直角三角形的几何特征,可判断C 的真假. 【详解】对A ,空间的任何一个向量都可用其他三个不共面的向量表示,A 中忽略三个基底不共面的限制,故A 错误;对B ,若{},,a b c 为空间向量的一组基底,则,,a b c 三个向量互不共面;则,,a b b c c a +++,也互不共面,故{,,}a b b c c a +++可又构成空间向量的一组基底,故B 正确;对C ,0AB AC ABC ⋅=⇔∆的A ∠为直角ABC ⇒∆为直角三角形,但ABC ∆为直角三角形时,A ∠可能为锐角,此时0AB AC ⋅>,故C 错误;对D ,任何三个不共面的向量都可构成空间向量的一组基底,三个向量不共线时可能共面,故D 错误; 故选:B . 【点睛】本题以命题的真假判断为载体考查空间向量的基底概念、向量垂直的充要条件,考查对概念的理解与应用,属基础题.二、填空题14.①②③【分析】设以点为坐标原点所在直线分别为轴建立空间直角坐标系利用空间向量数量积的坐标运算可判断①②③④的正误【详解】设由于两两垂直以点为坐标原点所在直线分别为轴建立空间直角坐标系如下图所示:则对解析:①②③ 【分析】设OA OB OC a ===,以点O 为坐标原点,OA 、OB 、OC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量数量积的坐标运算可判断①②③④的正误.【详解】设OA OB OC a ===,由于OA 、OB 、OC 两两垂直,以点O 为坐标原点,OA 、OB 、OC 所在直线分别为x 、y 、z 轴建立空间直角坐标系, 如下图所示:则()0,0,0O、(),0,0A a 、()0,,0B a 、()0,0,C a .对于①,(),,OA OB OC a a a ++=,所以,()()22233OA OB OC a OA ++==,①正确;对于②,(),0,0CA CO OA a -==,()0,,BC a a =-,则()0BC CA CO ⋅-=,②正确;对于③,(),,0OA OB a a +=,(),0,CA a a =-,()()221cos ,2OA OB CA a OA OB CA OA OB CA+⋅<+>===+⋅, 0,180OA OB CA ≤<+>≤,所以,()OA OB +和CA 的夹角为60,③正确;对于④,(),,0AB a a =-,(),0,AC a a =-,()0,,BC a a =-,则2AB AC a ⋅=,所以,()22316666a a AB AC BC BC a ⋅===,而三棱锥O ABC -的体积为3111326V OA OB OC a =⨯⋅⋅=,④错误. 故答案为:①②③. 【点睛】关键点点睛:在立体几何中计算空间向量的相关问题,可以选择合适的点与直线建立空间直角坐标系,利用空间向量的坐标运算即可.15.【分析】根据两向量的夹角余弦公式即可求出两向量的夹角【详解】解:10向量与的夹角为故答案为:【点睛】本题考查空间两向量的夹角大小的应用问题是基础题目 解析:3π【分析】根据两向量的夹角余弦公式,即可求出两向量的夹角. 【详解】 解:(0a =,1,1),(1b =,0,1),∴·1a b =,||2a =,||2b =,cos a ∴<,12||||2a b b a b >===⨯⨯,向量a 与b 的夹角为3π. 故答案为:3π. 【点睛】本题考查空间两向量的夹角大小的应用问题,是基础题目.16.【分析】建立空间直角坐标系写出的坐标写出向量的坐标用两向量的夹角公式求出余弦值【详解】建立空间直角坐标系如图所示则所以异面直线和所成角的余弦值等于故答案为:【点睛】本题考查异面直线所成的角属于基础题 解析:5【分析】建立空间直角坐标系,写出1,,,D F O E 的坐标,写出向量1,FD OE 的坐标,用两向量的夹角公式求出余弦值.【详解】建立空间直角坐标系,如图所示则()()()()10,0,2,1,0,0,1,1,0,0,2,1D F O E ,()()111,0,2,1,1,1,5,3FD OE FD OE ∴=-=-==, 11115cos ,535OE FD OE FD OE FD ∴〈〉===⨯, 所以异面直线OE 和1FD 所成角的余弦值等于155. 15. 【点睛】本题考查异面直线所成的角,属于基础题. 17.【分析】先根据不共线三点用平面向量基底表示;再根据平面向量基本定理表示求和即得结果【详解】因为四点共面三点不共线所以因为因为是任意一点故可不共面所以故故答案为:1【点睛】本题考查用基底表示向量以及平 解析:1【分析】先根据不共线三点A B C ,,,用平面向量基底AB AC ,表示PA ;再根据平面向量基本定理表示,,x y z ,求和即得结果.【详解】因为,,,P A B C 四点共面,三点A B C ,,不共线,所以,,,m n R PA mAB nAC ∃∈=+()(),(1)OA OP m OB OA n OC OA OP m n OA mOB nOC -=-+-∴=++--因为OP xOA yOB zOC =++,因为O 是任意一点,故,,OA OB OC 可不共面,所以1,,x m n y m z n =++=-=-, 故1x y z ++=.故答案为:1【点睛】本题考查用基底表示向量以及平面向量基本定理应用,考查基本分析求解能力,属基础题. 18.【分析】以D 为坐标原点DA 所在的直线为轴DC 所在的直线为轴DP 所在的直线为轴建立空间直角坐标系令求得利用向量的夹角公式即可求解【详解】如图所示以D 为坐标原点DA 所在的直线为轴DC 所在的直线为轴DP 所 解析:60【分析】以D 为坐标原点,DA 所在的直线为x 轴,DC 所在的直线为y 轴,DP 所在的直线为z 轴,建立空间直角坐标系,令1PD AD ==,求得()()1,0,1,1,1,0PA BD =-=--,利用向量的夹角公式,即可求解.【详解】如图所示,以D 为坐标原点,DA 所在的直线为x 轴,DC 所在的直线为y 轴,DP 所在的直线为z 轴,建立空间直角坐标系,因为点P 在正方形ABCD 所在平面外,PD ⊥平面,ABCD PD AD =,令1PD AD ==,所以()()()()1,0,0,0,0,1,1,1,0,0,0,0A P B D ,所以()()1,0,1,1,1,0PA BD =-=--, 所以1cos 222PA BDPA BD θ⋅===⨯⋅,所以060θ=, 即异面直线PA 与BD 所成的角为060【点睛】本题主要考查了异面直线所成的角的求解,其中解答中根据几何体的结构特征建立适当的空间直角坐标系,利用空间向量的夹角公式求解是解答的关键,着重考查了推理与运算能力,属于基础题.19.【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题然后利用向量的数量积坐标运算计算的值即可【详解】又即解得故答案为【点睛】本题主要考查空间向量的应用向量垂直的充分必要条件等知识意在考 解析:3±【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题,然后利用向量的数量积坐标运算计算λ的值即可.【详解】()()()2,1,1,3,4,,2,7,1A B C λ-, ∴AB ()1,3,1,λ=+CB ()1,3,1λ=--, 又,AB CB ⊥0AB CB ∴⋅=,即()()()1133110λλ⨯+⨯-++-=,解得3λ=±,故答案为3±.【点睛】本题主要考查空间向量的应用,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.20.【分析】首先确定点的轨迹再求长度【详解】在平面上取的中点则点的轨迹是正六边形轨迹长度是正六边形的周长故答案为:【点睛】关键点点睛:本题的关键是确定在平面上并能作出平面与正方体的交线 解析:32【分析】首先确定点M 的轨迹,再求长度.【详解】(,)EM xEF yEG x y =+∈R ,M ∴在平面EFG 上,取11A D ,AB ,1CC 的中点,,N H P ,则点M 的轨迹是正六边形EHFPGN ,轨迹长度是正六边形的周长,632l EN ==.故答案为:32【点睛】关键点点睛:本题的关键是确定M 在平面EFG 上,并能作出平面EFG 与正方体的交线.21.【分析】根据题意先得到平面所以向量为平面的一个法向量;分别以为轴轴以垂直于平面过点的直线为轴建立空间直角坐标系根据题意求出平面的一个法向量根据向量夹角公式求出二面角的夹角余弦值进而可求出结果【详解】解析:3【分析】根据题意,先得到AC ⊥平面11BCC B ,所以向量AC 为平面11BCC B 的一个法向量;分别以CA ,CB 为x 轴,y 轴,以垂直于平面ABC 过点C 的直线为z 轴,建立空间直角坐标系C xyz -,根据题意求出平面1B ED 的一个法向量,根据向量夹角公式求出二面角的夹角余弦值,进而可求出结果.【详解】因为AC BC ⊥,1AC CC ⊥,1BC CC C =,且1,BC CC ⊂平面11BCC B , 所以AC ⊥平面11BCC B ,所以向量AC 为平面11BCC B 的一个法向量;分别以CA ,CB 为x 轴,y 轴,以垂直于平面ABC 过点C 的直线为z 轴,建立空间直角坐标系C xyz -,因为2AC BC ==,160C CB ∠=︒,13CC =,所以()2,0,0A ,()0,0,0C ,()2,0,0B ,则12,2D ⎛ ⎝⎭,(E,170,2B ⎛ ⎝⎭,所以12,,22ED ⎛⎫=-- ⎪ ⎪⎝⎭,150,22EB ⎛⎫= ⎪ ⎪⎝⎭,()2,0,0AC =-设平面1B ED 的一个法向量为(),,m x y z =,则 1m ED m EB ⎧⊥⎪⎨⊥⎪⎩,即11202502m ED x y z m EB y z ⎧⋅=-=⎪⎪⎨⎪⋅=+=⎪⎩,解35x z y z ⎧=⎪⎪⎨⎪=⎪⎩,令5z =,则()3,m =, 所以cos ,4AC mAC m AC m ⋅<>===, 由图像可得,二面角1B B E D --为锐角,记为θ,所以co 3cos 1s ,3AC m θ>=<=, 因此328sin 13131θ=-=, 所以sin 28221tan cos 33θθθ===.221. 【点睛】 本题主要考查求二面角的正切值,根据向量的方法求解即可,属于常考题型.22.1【分析】取中点过作于点;由等腰三角形三线合一和线面垂直的判定定理可证得平面从而得到;再根据线面垂直判定定理得到面由线面角定义可知通过勾股定理可求得由此可知在直线上从而得到面面垂直关系可知二面角为从 解析:1【分析】取AD 中点E ,过P 作PF BE ⊥于F 点;由等腰三角形三线合一和线面垂直的判定定理可证得AD ⊥平面PBE ,从而得到AD PF ⊥;再根据线面垂直判定定理得到PF ⊥面ABCD ,由线面角定义可知30PBF ∠=,通过勾股定理可求得EF BE =,由此可知F 在直线CD 上,从而得到面面垂直关系,可知二面角为90,从而得到正弦值.【详解】取AD 中点E ,连接BE 并延长,过P 作PF BE ⊥于F 点PA PD =,E 为AD 中点 PE AD ⊥∴四边形ABCD 为菱形,60BAD ∠= ABD ∴∆为等边三角形 BE AD ∴⊥ ,PE BE ⊂平面PBE ,PE BE E ⋂= AD ∴⊥平面PBEPF ⊂平面PBE AD PF ∴⊥又PF BF ⊥,,BF AD ⊂平面ABCD ,BFAD E = PF ∴⊥面ABCD ∴直线PB 与底面ABCD 所成角为PBF ∠ sin 2sin301PF PB PBF ∴=⋅∠=⨯=在PBE ∆中,由余弦定理得:22233372cos 444222PE PB BE PB BE PBE =+-⋅∠=+-⨯= 223EF PE PF ∴=-=,又3BE = F ∴在CD 延长线上 PF ∴⊂平面PCD ∴平面PCF ⊥平面ABCD∴二面角P CD A --的大小为90,正弦值为1故答案为:1【点睛】本题考查立体几何中二面角的求解问题,涉及到线面垂直的判定与性质、面面垂直的判定定理、直线与平面所成角、勾股定理等知识的应用;关键是能够通过线面垂直关系确定直线与平面所成角的位置.23.【分析】由题意结合向量基本定理得到方程组求解方程组即可确定的值【详解】由题意可知存在实数满足:据此可得方程组:求解方程组可得:故答案为【点睛】本题主要考查空间向量基本定理方程的数学思想等知识意在考查解析:1-【分析】由题意结合向量基本定理得到方程组,求解方程组即可确定λ的值.【详解】由题意可知,存在实数,m n 满足:c ma nb =+,据此可得方程组:325432m n m n m n λ-=-⎧⎪=-+⎨⎪=+⎩,求解方程组可得:111m n λ=-⎧⎪=⎨⎪=-⎩. 故答案为1-.【点睛】本题主要考查空间向量基本定理,方程的数学思想等知识,意在考查学生的转化能力和计算求解能力.24.【分析】利用向量的加法公式得出再由得出的值即可得出的和【详解】即故答案为:【点睛】本题主要考查了用空间基底表示向量属于中档题 解析:78【分析】 利用向量的加法公式得出111222MN OA OB OC =-++,再由1324OG OM MG OA MN =+=+,得出,,x y z 的值,即可得出,,x y z 的和. 【详解】MN MA AB BN =++11111()22222OA OB OA OC OB OA OB OC =+-+-=-++ 13131112424222OG OM MG OA MN OA OA OB OC ⎛⎫∴=+=+=+-++ ⎪⎝⎭813388OA OB OC =++ 133,,888x y z ∴=== 即78x y z ++=故答案为:78【点睛】本题主要考查了用空间基底表示向量,属于中档题. 25.①②【分析】建立如图所示的空间直角坐标系把空间中的平行垂直关系归结为方向向量法向量之间的关系后可得正确的选项【详解】建立如图所示的空间直角坐标系设正方体的棱长为2则故所以故所以故②正确又设平面的法向 解析:①②【分析】建立如图所示的空间直角坐标系,把空间中的平行、垂直关系归结为方向向量、法向量之间的关系后可得正确的选项.【详解】建立如图所示的空间直角坐标系,设正方体的棱长为2,则()()()()2,0,0,0,0,0,0,2,0,2,2,0A D C B ,()()()()11112,0,2,0,0,2,0,2,2,2,2,2A D C B ,故()()2,2,1,0,1,0M N ,所以()2,1,1MN =---,()10,2,2CD =-,故10MN CD ⋅=,所以1MN CD ⊥,故②正确.又()2,2,0DB =,()12,0,2DA =,设平面1A BD 的法向量为(),,n x y z =, 由100n DB n DA ⎧⋅=⎪⎨⋅=⎪⎩得00x y x z +=⎧⎨+=⎩,取1z =-,则()1,1,1n =--, 因为0MN n ⋅=且MN ⊄平面1A BD ,故//MN 平面1A BD ,故①正确.又()10,2,1A M =-,设平面1A MN 的法向量为(),,m x y z =, 由100m MN m A M ⎧⋅=⎪⎨⋅=⎪⎩得2020x y z y z ---=⎧⎨-=⎩,取1y =,则3,1,22m ⎛⎫=- ⎪⎝⎭, 平面1A AC 的法向量为()2,2,0a =,则0m a ⋅≠故平面1A MN ⊥平面1A AC 不成立,故③错,故答案为:①②.【点睛】本题考查空间中平行关系、垂直关系的判断,注意根据几何体的特征建立合适的空间直角坐标系后再利用空间向量来处理,本题属于中档题.26.【分析】先由空间向量的基本定理将向量用一组基底表示再利用向量数量积的性质计算即可【详解】∵六面体ABCD ﹣A1B1C1D1是平行六面体∵=++∴=(++)2=+++2+2+2又∵∠BAD=∠A1AB【分析】先由空间向量的基本定理,将向量1AC 用一组基底1AA AD AB ,,表示,再利用向量数量积的性质22a a =,计算1AC 即可【详解】∵六面体ABCD ﹣A 1B 1C 1D 1是平行六面体,∵1AC =1AA +AD +AB ∴21AC =(1AA +AD +AB )2=21AA +2AB +2AD +21AA AD ⋅+21AA AB ⋅+2AB AD ⋅ 又∵∠BAD=∠A 1AB=∠A 1AD=60°,AD=4,AB=3,AA 1=5, ∴21AC =16+9+25+2×5×4×cos60°+2×5×3×cos60°+2×3×4×cos60°=97 ∴197AC =【点睛】本题考察了空间向量的基本定理,向量数量积运算的意义即运算性质,解题时要特别注意空间向量与平面向量的异同。
(必考题)高中数学高中数学选修4-4第一章《坐标系》测试题(有答案解析)(4)

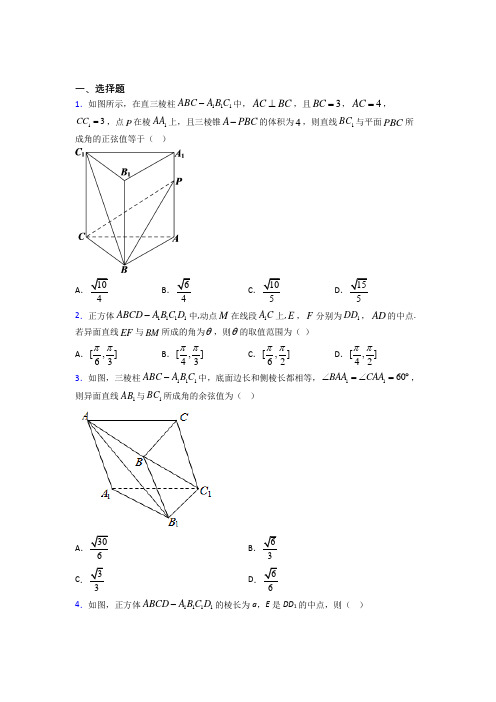
一、选择题1.在极坐标系中,与点8,6π⎛⎫- ⎪⎝⎭关于极点对称的点的一个坐标是( ) A .8,6π⎛⎫⎪⎝⎭B .58,6π⎛⎫-⎪⎝⎭C .58,6π⎛⎫- ⎪⎝⎭D .8,6π⎛⎫--⎪⎝⎭2.在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2sin 42a πρθ⎛⎫+= ⎪⎝⎭,曲线2C 的参数方程为cos sin x y θθ=⎧⎨=⎩(θ为参数,0θπ).若1C 与2C 有且只有一个公共点,则实数a 的取值范围是( )A .2±B .(2,2)-C .[1,1)-D .[1,1)-或23.如图,点A 、B 是函数1y x=在第I 象限的图像上两点且满足OAB 90∠=且AO AB =,则OAB ∆的面积等于( )A .12B .22C .32D 5 4.在极坐标系中,已知圆C 经过点236P π⎛⎫⎪⎝⎭,,圆心为直线sin 24πρθ⎛⎫+= ⎪⎝⎭轴的交点,则圆C 的极坐标方程为 A .4cos ρθ=B .4sin ρθ=C .2cos ρθ=D .2sin ρθ=5.在极坐标系中,曲线1:2cos C ρθ=,曲线2:4C πθ=,若曲线1C 与2C 交于,A B 两点,则线段AB 的长度为( ) A .2 B 2C .22D .16.以π-2,4⎛⎫⎪⎝⎭2 ) A .ρ=-(sin θ+cosθ) B .ρ=sin θ+cosθ C .ρ=-2(sin θ+cosθ)D .ρ=2(sin θ+cosθ)7.已知()()()12cos ,cos 0f x x f x x ωω==>,()2f x 的图象可以看做是把()1f x 的图象在其所在的坐标系中的横坐标压缩到原来的13倍(纵坐标不变)而得到的,则ω为( ) A .12B .2C .3D .138.已知点P 的极坐标是π2,6⎛⎫⎪⎝⎭,则过点P 且平行极轴的直线方程是( ) A .ρ1= B .ρsin θ=C .1ρsin θ=-D .1ρsin θ=9.()04πθρ=≥表示的图形是( )A .一条线段B .一条直线C .一条射线D .圆10.曲线cos 104πρθθ+==关于对称的曲线的极坐标方程是( )A .sin 10ρθ+=B .sin 10ρθ-=C .cos 10ρθ-=D .cos 10ρθ+= 11.在同一坐标系中,将直线1x y +=变换为直线236x y +=的一个伸缩变换是( )A .32x x y y ''=⎧⎨=⎩B .23x xy y ''=⎧⎨=⎩C .1312x x y y ⎧=⎪⎪⎨=''⎪⎪⎩D .1213x x y y ⎧=⎪⎪⎨=''⎪⎪⎩12.在极坐标系中,直线cos()4ρθπ-=ρ的公共点的个数为A .1B .2C .0D .无法确定二、填空题13.在极坐标系中,曲线C 的方程为28cos 10sin 320ρρθρθ--+=,直线l 的方程为0()R θθρ=∈,0tan 2θ=,若l 与C 交于A ,B 两点,O 为极点,则||||OA OB +=________.14.在极坐标系中,直线sin 4πρθ⎛⎫-= ⎪⎝⎭4ρ=截得的弦长为______. 15.在平面直角坐标系xOy 中,圆C 的参数方程为cos x a y sin θθ=+⎧⎨=⎩(θ为参数),以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为sin 4πρθ⎛⎫-= ⎪⎝⎭若直线l 与圆C 相切,则实数a =______.16.已知直线l 和曲线Γ的极坐标方程分别为()sin cos 1ρθθ-=和1ρ=,若l 和Γ相交于两点,A B ,则AB =_______.17.在直角坐标系xoy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 1的极坐标方程为sin()104πρθ++=,曲线C 2的参数方程为(为参数,),则C 1与C 2有______个不同公共点.18.(坐标系与参数方程选做题)已知圆C 的圆心为(6,)2π,半径为5,直线(,)2r πθαθπρ=≤<∈被圆截得的弦长为8,则α=_____.19.将曲线221x y +=按伸缩变换公式'2'3x xy y =⎧⎨=⎩变换后得到曲线C ,则曲线C 上的点(,)P m n 到直线:260l x y +-=的距离最小值为_____________.20.在极坐标系中,以点1,22π⎛⎫⎪⎝⎭为圆心,12为半径的圆的极坐标方程是____________ 三、解答题21.在平面直角坐标系xOy 中,圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),以点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求圆C 的极坐标方程;(2)过极点O 作直线与圆C 交于点A ,求OA 的中点所在曲线的极坐标方程.22.在平面直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知曲线1C 的极坐标方程为:2222cos 3sin 3+=ρθρθ,曲线2C 的参数方程是31x ty t⎧=⎪⎨=+⎪⎩(t 为参数).(1)求曲线1C 和2C 的直角坐标方程.(2)设曲线1C 和2C 交于两点A ,B ,求以线段AB 为直径的圆的直角坐标方程. 23.在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 22sin x ty t =⎧⎨=+⎩(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos ρθ=. (1)说明1C 是哪种曲线,并将1C 的方程化为极坐标方程; (2)设点M 的极坐标为()4,0,射线θα=(02πα<<)与1C 的异于极点的交点为A ,与2C 的异于极点的交点为B ,若4AMB π∠=,求tan α的值.24.在平面直角坐标系xOy 中,直线l 的参数方程为cos 1sin x t y t αα=⎧⎨=+⎩(其中t 为参数02πα≤≤),以原点为极点,x 轴非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为2432cos ρθ=+.(1)求曲线C 的焦点的极坐标;(2)若曲线C 的上焦点为F ,直线l 与曲线C 交于A ,B 两点,34FA FB ⋅=,求直线l 的斜率.25.在平面直角坐标系xOy 中,动点P (x ,y )的坐标满足2x ty t =⎧⎨=⎩(t 为参数),以原点O 为极点,x 正半轴为极轴建立极坐标系,曲线l 的极坐标方程为ρsin (θ+φ)=cosφ(其中φ为常数,且φ2k k Z ππ≠+∈,)(1)求动点P 的轨迹C 的极坐标方程;(2)设直线l 与轨迹C 的交点为A ,B ,两点,求证:当φ变化时,∠AOB 的大小恒为定值.26.已知在平面直角坐标系xOy 中,直线l的参数方程为4x ty =-⎧⎪⎨=+⎪⎩(t 为参数),曲线1C 的方程为22(1)1y x +-=以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求直线l 和曲线1C 的极坐标系方程; (2)曲线2C :0,02πθαρα⎛⎫=><<⎪⎝⎭分别交直线l 和曲线1C 交于A 、B ,求22OB OA +的最大值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】由点(),ρθ关于极点对称的点为()(),2k k Z ρππθ++∈,结合极径为负数的点的定义,即可得答案; 【详解】点(),ρθ关于极点对称的点为()(),2k k Z ρππθ++∈,故点8,6π⎛⎫- ⎪⎝⎭关于极点对称的点的一个坐标为78,6π⎛⎫- ⎪⎝⎭,即8,6π⎛⎫ ⎪⎝⎭.故选:A. 【点睛】本题考查极径为负数的极坐标的定义,考查对概念的理解,属于基础题.2.D解析:D 【解析】 【分析】先把曲线1C ,2C 的极坐标方程和参数方程转化为直角坐标方程和一般方程,若1C 与2C 有且只有一个公共点可转化为直线和半圆有一个公共点,数形结合讨论a 的范围即得解. 【详解】因为曲线1C 的极坐标方程为2sin ,42a πρθ⎛⎫+= ⎪⎝⎭即222(sin cos )222a ρθθ+= 故曲线1C 的直角坐标方程为:0x y a +-=.消去参数θ可得曲线2C 的一般方程为:221x y +=,由于0θπ,故0y ≥如图所示,若1C 与2C 有且只有一个公共点,直线与半圆相切,或者截距11a -≤< 当直线与半圆相切时122O l d a -==∴=由于为上半圆,故02a a >∴= 综上:实数a 的取值范围是[1,1)-2故选:D 【点睛】本题考查了极坐标、参数方程与直角坐标方程、一般方程的互化,以及直线和圆的位置关系,考查了学生数形结合,数学运算的能力,属于中档题.3.D解析:D 【分析】设点B 的极坐标为(),ρθ,则04πθ<<,由OAB ∆为等腰直角三角形可得出点A 的极坐标,24πρθ⎛⎫+ ⎪ ⎪⎝⎭,将函数1y x =的解析式表示为极坐标方程,将A 、B 两点的极坐标代入曲线的极坐标方程,可计算出2ρ的值,再利用三角形的面积公式可计算出OAB ∆的面积. 【详解】设点B 的极坐标为(),ρθ,则04πθ<<,由题意知,OAB ∆为等腰直角三角形,且OAB 90∠=,则点A 的极坐标,24πρθ⎛⎫+ ⎪ ⎪⎝⎭,将函数1y x =的解析式化为极坐标方程得1sin cos ρθρθ=,即2sin cos 1ρθθ=,化简得2sin 22ρθ=,将点B 的极坐标代入曲线的极坐标方程得2sin 22ρθ=,将点A 的极坐标代入曲线的极坐标方程得2sin 224πρθ⎫⎡⎤⎛⎫+=⎪ ⎪⎢⎥⎪⎝⎭⎣⎦⎝⎭, 化简得2cos24ρθ=,于是有22sin 22cos 24ρθρθ⎧=⎨=⎩,()()242222sin 2cos 22420ρρθρθ∴=+=+=,得2ρ=,因此,OAB ∆的面积为111sin 2424OAB S OA OB πρ∆=⋅=⨯=⨯ 故选D.【点睛】本题考查三角形面积的计算,解题的关键就是将问题转化为极坐标方程求解,将代数问题转化为几何问题求解,考查转化与化归数学思想,属于中等题.4.A解析:A 【分析】求出圆C 的圆心坐标为(2,0),由圆C 经过点6P π⎛⎫⎪⎝⎭,得到圆C 过极点,由此能求出圆C 的极坐标方程. 【详解】在sin 4πρθ⎛⎫+= ⎪⎝⎭0θ=,得2ρ=,所以圆C 的圆心坐标为(2,0). 因为圆C 经过点6P π⎛⎫⎪⎝⎭,,所以圆C 的半径2r =,于是圆C 过极点,所以圆C 的极坐标方程为4cos ρθ=. 故选A 【点睛】本题考查圆的极坐标方程的求法,考查直角坐标方程、参数方程、极坐标方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,属于中档题.5.B解析:B 【解析】 【分析】分别将曲线1C ,2C 的极坐标方程化为普通方程,根据直线与圆相交,利用点到直线的距离公式结合垂径定理,可得结果 【详解】 根据题意, 曲线()222221:22cos 211C cos x y xx y ρθρρθ==+=-+=曲线2:4C y x πθ==,则直线与圆相交,圆的半径为1,圆心到直线y x =的距离为2d ==设AB 长为m ,则有22212m d r ⎛⎫+= ⎪⎝⎭,即211142m +=解得m =(舍负)故线段AB 故选B 【点睛】本题主要考查的是极坐标与直角坐标方程的互化,圆的方程以及直线与圆的位置关系,是一道基础题6.C解析:C 【解析】分析:先求出圆心的直角坐标,再写出圆的直角坐标方程,最后把直角坐标方程化为极坐标方程得解.详解:由题得cos 1,sin1,44x y ππ==-==-所以点的直角坐标为(-1,-1),所以圆的方程为22(1)(1)2x y +++=,所以222220,2cos 2sin 0x y x y ρρθρθ+++=∴++=, 所以2cos 2sin ρθθ=--,故答案为C.点睛:(1)本题主要考查极坐标和直角坐标的互化,考查极坐标方程的求法,意在考查学生对这些知识的掌握水平和分析转化能力.(2)求极坐标方程,一般先求出直角坐标方程,再化成极坐标方程.7.C解析:C 【解析】分析:根据变换规律得113ω=,解得结果. 详解:函数y =cos ωx ,x ∈R (其中ω>0,ω≠1)的图像,可以看做把余弦曲线上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1ω倍(纵坐标不变)而得到.因此11,3,3ωω==应选C. 点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.8.D解析:D 【解析】分析:把点P 的极坐标化为直角坐标,求出过点P 且平行极轴的直线直角坐标方程,再把它化为极坐标方程.详解:把点P 的极坐标π2,6⎛⎫⎪⎝⎭化为直角坐标为), 故过点P 且平行极轴的直线方程是1y = , 化为极坐标方程为1sin ρθ=, 故选D .点睛:本题主要考查把点的极坐标化为直角坐标,把直角坐标方程化为即坐标方程的方法,属于基础题.9.C解析:C 【解析】 【分析】利用极坐标方差化为直角坐标方程即可得出. 【详解】()04πθρ=≥表表示的图形是一条射线:y=x (x≥0).故选C . 【点睛】本题考查了射线的极坐标方程,考查了推理能力与计算能力,属于基础题.10.A解析:A 【解析】 【分析】先把两曲线极坐标方程化为普通方程,求得对称曲线,再转化为极坐标方程。
哈工大强基计划校测笔试试题

选择题(每题有一个正确答案)下列关于哈工大特色的学科领域,哪一项是正确的?A. 航空航天B. 医学C. 艺术设计D. 农林科学在线性代数中,若矩阵A和B满足AB=BA,则称A和B为:A. 相似矩阵B. 逆矩阵C. 可交换矩阵D. 正交矩阵在计算机科学中,以下哪个概念与数据存储和检索有关?A. 算法B. 数据结构C. 操作系统D. 编程语言物理学中,牛顿第二定律的数学表达式是:A. F = maB. F = mvC. F = 1/2mv^2D. F = mv/r在化学中,下列哪种元素是金属元素?A. 氢B. 氧C. 铁D. 氯在地理学中,哪个概念与地球的自转和公转相关?A. 气候B. 海拔C. 季节变化D. 板块运动简答题描述哈工大在航空航天领域的主要贡献和特色。
解释什么是线性方程组,并给出求解线性方程组的一般方法。
简述计算机编程中函数的作用和重要性。
牛顿第三定律的内容是什么?请举例说明其在日常生活中的应用。
描述化学元素周期表中元素排列的规律及其重要性。
简述地球自转和公转对气候和季节变化的影响。
填空题哈工大以________和________等学科著称于世。
在线性代数中,矩阵的行列式用于描述矩阵的________和________。
计算机程序的基本结构包括________、________和________。
牛顿第一定律的内容是:一个物体将保持________状态或________状态,除非受到外力作用。
元素周期表中的元素按照________和________进行排列。
哈工大MATLAB选修课最终大作业

2014年春季学期MATLAB 课程考查题姓名:学号:11208学院:机电工程学院专业:机械设计制造及其自动化一.必答题(80分)1. 如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有何区别?答:设置当前目录和搜索路径:在File菜单中选择SetPath选项,之后选择AddFolder增加目录。
当前工作目录是指MATLAB运行文件时的目录,只有在当前工作目录或搜索路径下的文件、函数可以被运行或调用。
2. 创建符号变量和符号表达式有哪几种方法?答:(1)符号变量:x = sym(‘x’) 创建x为符号变量,默认复数区域x = sym(‘x’, ‘real’) 创建实数的符号变量xx = (‘x’, ‘positive’) 创建正数的符号变量xx = sym('x', 'clear')创建一个没有额外属性的纯形式上的符号变量xs=sym(‘ab’,’flag’) 创建flag数域(复数,实数,正数)符号变量名s,内容ab(2)符号表达式:①直接法:>> x=sym('x');>> a=sym('a');>> b=sym('b');>> f=sin(b*x)+exp(-a*x)②整体定义法:f=sym(‘expression’)③字符串符号表达式:f=‘expression’3. GUIDE提供哪些常用的控件工具,各有什么功能?(5分)答:按钮(Push Buttons) :通过鼠标单击按钮可以执行某种预定的功能或操作;静态文本框(Static Texts):仅用于显示单行的说明文字.文本编辑器(Editable Texts):用来使用键盘输入字符串的值,可以对编辑框中的内容进行编辑、删除和替换等操作;单选按钮(Radio Button):单个的单选框用来在两种状态之间切换,多个单选框组成一个单选框组时,用户只能在一组状态中选择单一的状态,或称为单选项;滚动条(Slider):可输入指定范围的数量值,通过移动滚动条来改变指定范围内的数值输入,滚动条的位置代表输入数值。
国家精品课程哈工大05年线代期末试题

05秋05级《代数与几何》期末试卷(此卷满分50分)() n A A R A A E n '(本试卷中表示 的转置矩阵; 表示矩阵的秩,表示阶单位矩阵)一、填空题(每小题2分,共10分) 1. 在空间直角坐标系中,点)3,4,2(A 到直线123x y z -=-=-的距离为 .2. 若n 阶方阵,, A B C 满足AB CB =,||0A C -≠,则=B .3. 101100 01120, ()=103A b R A a a c ⎛⎫⎛⎫⎧⎪ ⎪⎪=-⎨ ⎪⎪⎪ ⎪⎪-⎝⎭⎝⎭⎩已知则. 101 011,33123 0 PA P X AX -⎛⎫ ⎪=-⨯= ⎪ ⎪-⎝⎭= 4. 已知其中是可逆矩阵,则 是齐次线性方程组 的通解.5. 若(1,1)ξ'=是方阵110A a -⎛⎫= ⎪⎝⎭的一个特征向量,则 , 是A 的全部特征值.二、选择题(每小题2分,共10分)1. 设A 是n m ⨯矩阵,对于线性方程组β=AX ,下列结论正确的是(A) 若()R A n <,该方程组有无穷多解. (B) 若()R A m =,该方程组有解.(C) 若()R A n =,该方程组有唯一解. (D) 若n m >,该方程组无解.【 】2. 设有n 阶矩阵A ,n 维列向量组 (I) 12,,,s ααα; (II) 12,,,s A A A ααα,则(A) 若(I )相关,则(II )相关. (B) 若(II )相关,则(I )相关.(C) 若A 可逆,则(II )无关. (D) 若(II )无关,则A 可逆.【 】 3. xoy 坐标面上的双曲线222930x y z ⎧-=⎨=⎩绕x 轴旋转一周,所生成的旋转曲面的方程为.(A) 222()93x z y +-=. (B) 2229()3x y z -+=.(C) 2222293x z y +-= (D) 2222993x y z --=.【 】4. 1, 1 2 A 已知 是 阶矩阵的特征值,则必有(A) 11 01A ⎛⎫ ⎪⎝⎭与相似. (B) 01 10A ⎛⎫ ⎪⎝⎭与相似.(C) 2, A E A ≠若则不能相似对角化. (D) A 可以相似对角化.【 】33222123111122133211222233311322333,(,,)()()()ij B b f x x x b x b x b x b x b x b x b x b x b x ⨯==++++++++ 5. 已知实矩阵()实二次型 (A)123 (,,)0f x x x B ≠正定的充要条件是 (B) 123(,,)f x x x 不正定(C)123 (,,)f x x x B 正定的充要条件是正定 (D) 123 (,,)f x x x 正定【 】三、(本题5分)当a等于何值时,方程组123123123,1,.x x ax ax ax xax x x a++=⎧⎪++=⎨⎪++=⎩无解,有唯一解,有无穷多解?当有无穷多解时,写出通解.四、(本题5分)求直线10390x y zx y z-++=⎧⎨-++-=⎩在平面1x y z++=上的投影直线的方程.五、(本题5分)已知A 与B 相似,其中, 11719020091B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦. (1) 求A A ';(2)求一个与A 相似的对角阵D ;(3)求3E A - 的特征多项式.222 (,,)222 1 ;2 (,,) 1 f x y z x y z xy xz yz f A f f x y z =---+++=六、(本题5分)已知实二次型.给出 的矩阵. 试用正交变换化 为标准形, 并求出所用的正交变换矩阵; 3. 方程 表示空间直角坐标系中何种二次曲面.七、(本题5分)设n 阶行列式1A =, β是1⨯n 矩阵,b 是常数,110A b ββ-'-+= 0, .A A P Q A A b βββ*⎡⎤⎡⎤==⎢⎥⎢⎥''-⎣⎦⎣⎦(1)求PQ . (2)求1Q -的表达式.12312123, ,,,{1,2,3} ,,,,i i ααααβββααββββ∈1212八.(本题5分)已知列向量组线性无关,且可由列向量组线性 表示,试证:存在 使得向量组 与向量组 等价.。
黑龙江省哈工大附中2020-2021学年高二下学期期末考试 物理 试题(含答案)

哈工大附中2020-2021学年度第二学期期末试题高二物理时间:90分钟 分值 100一、选择题(本题共12小题,每小题4分,共计48分。
1~8题有1项符合题目要求,9~12题有多项符合题目要求。
全部选对的得4分,选对但不全的得2分,有选错的得0分。
) 1.下列说法正确的是( ) A .运动的物体也可以作为参考系B .只要是体积小的物体,都能看成质点C .时刻表示很短的时间,时间表示较长的时间D .质点是一种理想化模型,无实际意义2.如图所示为直升飞机由地面垂直起飞过程速度—时间图象,则关于飞机的运动,下面说法正确的是( )A .0~5s 内飞机做匀速直线运动B .5~15s 内飞机在空中处于悬停状态C .15~20s 内飞机匀减速下降D .25s 时飞机离地面高度为250m3.物体做匀加速直线运动,相继经过两段距离为16 m 的路程,第一段用时4 s ,第二段用时2 s ,则物体的加速度是( )A.23 m/s 2B.43 m/s 2C.89 m/s 2D.169 m/s 24.一小球竖直向上抛出,先后经过抛出点的上方h =5m 处的时间间隔Δt =2s ,不计阻力。
则下列说法正确的是( )A .小球的初速度v 0为5m/sB .小球的初速度v 0为102m/sC .小球从抛出到返回原处所经历的时间是2sD .小球从抛出到返回原处所经历的时间是2s5.物体静止于水平桌面上,则( )A .物体对桌面的压力和桌面对物体的支持力是一对相互平衡的力B .物体的重力和桌面对它的支持力是一对作用力与反作用力C .物体对桌面的压力就是物体的重力,这两个力是同性质的力D .桌面对物体的支持力大小等于物体的重力大小,这两个力是一对平衡力6.如图所示,重力为G 的物体静止在倾角为α的斜面上,将重力为G 分解为垂直斜面向下的力F 1和平行斜面向下的力F 2,那么( ) A .F 1就是物体对斜面的压力B .物体对斜面的压力方向与F 1的方向相同,大小为cos GC .F 2就是物体受到的静摩擦力D .物体受到重力、斜面对物体的支持力、静摩擦力、F 1、F 2五个力的作用7.如图所示,甲物体在沿斜面的推力F 的作用下静止于乙物体上,乙物体静止在水平面上,现增大外力F ,两物体仍然静止,则下列说法正确的是( ) A .乙对甲的摩擦力一定增大 B .乙对甲的摩擦力一定减小C.乙对地面的摩擦力一定增大D.乙对地面的摩擦力可能减小8.如图所示,光滑的轻滑轮用细绳OO'悬挂于O点,另一细绳跨过滑轮,其一端悬挂货物A,人拉绳的另一端缓慢向右移动,使货物缓慢提升,在此过程中()A.细绳对人的拉力逐渐变大B.细绳OO'的张力逐渐变小C.水平面对人的支持力逐渐变小D.水平面对人的摩擦力逐渐变小9.如图所示,两上下底面平行的滑块重叠在一起,置于固定的、倾角为θ的斜面上,滑块A、B的质量分别为M、m,A与斜面间的动摩擦因数为μ1,B与A之间的动摩擦因数为μ2.已知两滑块都从静止开始以相同的加速度从斜面滑下,滑块上B受到的摩擦力( )A、等于零B、方向沿斜面向上C、大小等于μ1mgcosθD、大小等于μ2mgcosθ10.如图所示,物体A放在物体B上,物体B放在光滑的水平面上,已知m A=6kg,m B=2kg.A、B间动摩擦因数μ=0.2.A物上系一细线,细线能承受的最大拉力是20N,水平向右拉细线,下述中正确的是(g=10m/s2)()A.当拉力F<12N时,A静止不动B.当拉力F>12N时,A相对B滑动C.当拉力F=16N时,B受A摩擦力等于4ND.无论拉力F多大,A相对B始终静止11.如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心.已知在同一时刻,甲、乙两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点,丙球由C点自由下落到M点,有关下列说法正确的是( )A.甲球下滑的加速度小于乙球下滑的加速度B.丙球最先到达M点C.甲、乙、丙球同时到达M点D.甲、丙两球到达M点时的速率相等12.质量分别为M和m的两物块A、B大小相同,将它们用轻绳跨过光滑定滑轮连接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix;(2) Echelon Form;(3) Elementary operations;(4) Onto mapping and one-to-one mapping;(5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒4. Find a basis for the null space of the matrix 361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b +=7. Provide twenty statements for the invertible matrix theorem.8. Show and prove the Gram-Schmidt process.9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1. All nonzero rows are above any rows of all zeros.2. Each leading entry of a row is in a column to the right of the leading entry of the row above it.3. All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4. The leading entry in each nonzero row is 1.5. Each leading 1 is the only nonzero entry in its column.(3) Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1. (Replacement) Replace one row by the sum of itself anda multiple of another row.2. (Interchange) Interchange two rows.3. (scaling) Multiply all entries in a row by a nonzero constant.(4) Onto mapping and one-to-one mapping:A mapping T : R n → R m is said to be onto R m if each b in R m is the image of at least one x in R n.A mapping T : R n → R m is said to be one-to-one if each b in R m is the image of at most one x in R n.(5) Linearly independence:An indexed set of vectors {V1, . . . ,V p} in R n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such thatc 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form.Solution:Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top.Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position.Step 3:Use row replacement operations to create zeros in all positions below the pivot.Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify.Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.010*******y x Rotate⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x Translate The matrix for the composite transformation is⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form:A ~ , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---000023021010002001x 1-2x 2 -x 4+3x 5=0x 3+2x 4-2x 5=00=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free.⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w. That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weightsx 2, x 4, and x 5 are all zero.So {u, v, w} is a basis for Nul A.5. Find a basis for Col of the matrix A 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution:A ~ , so the rank of A is 3.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001Then we have a basis for Col of the matrix:A U = , v = and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=, because if u= , x=, and x = Au, then ⎥⎦⎤⎢⎣⎡b a 00⎥⎦⎤⎢⎣⎡21u u ⎥⎦⎤⎢⎣⎡21x x u 1 =and u 2 = a x 1bx 2It follows that u is in the unit disk, with , if and only if x is in E , with 12221≤+u u1)()(2221≤+x a x . Then we have{area of ellipse} = {area of T (D )}= |det A| {area of D} = ab π(1)2 = πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square matrix. Then the following statements are equivalent. That is, for a n n ⨯given A, the statements are either all true or false.a. A is an invertible matrix.b. A is row equivalent to the identity matrix.n n ⨯c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x Ax is one-to-one.→g. The equation Ax = b has at least one solution for each b in R n .h. The columns of A span R n .i. The linear transformation x Ax maps R n onto R n .→j. There is an matrix C such that CA = I.n n ⨯k. There is an matrix D such that AD = I.n n ⨯l. A T is an invertible matrix.m. If , then 0A ≠()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If , then 0A ≠()()*11*A A--=q. ()*1n *A 1)(A --=-r. If , then ( L is a natural number )0A ≠()()L 11L A A--=s. ()*1n *A K)(KA --=-t. If , then 0A ≠*1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of R n , define11x v = 1112222v v v v x x v ⋅⋅-= 222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for pk ≤≤1PROOFFor , let W k = Span {v 1, . . . , v p }. Set , so that Span {v 1} = Span p k ≤≤111x v ={x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w 1k 1k x proj x v k +++-=By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, because x k+1 is not in W k = Span {x 1, . . . , 0v 1k ≠+x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem.Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say, and . To 1λ2λshow that , compute0v v 21=⋅ Since v 1 is an eigenvector2T 12T 11211v )(Av v )v (λv v λ==⋅()()2T 12T T 1Av v v A v ==)(221v v Tλ= 2122T 12v v λv v λ⋅==Hence , but , so ()0v v λλ2121=⋅-()0λλ21≠-0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that (1)1p p p 11v v c v c +=+⋅⋅⋅+Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain111+=+⋅⋅⋅+p p p Av Av c Av c (2)11111++=+⋅⋅⋅+p p p p p v v c v c λλλMultiplying both sides of (1) by and subtracting the result from (2), we have1+p λ (3)0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλSince {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of thefactors are zero, because the eigenvalues are distinct. Hence for i = 1, . . . , p. 1+-p i λλ0=icBut when (1) says that , which is impossible. Hence {v 1, . . . , v r } cannot be linearly 01=+p v dependent and therefore must be linearly independent.。
