七年级数学复习资料一第一章《三角形的初步认识》测试卷(含答案)
三角形全章测试题(含答案)

七年级(一)三角形全章测试题班级姓名成绩说明:本试题满分100分,时间100分钟。
一、选择题(每题3分,共计24分)1.如果在一个顶点周围用两个正方形和n 个正三角形恰好可以进行平面镶嵌,则n 的值是( ).A .3 B .4 C .5 D .62.下面四个图形中,线段BE 是⊿ABC 的高的图是( )3.已知三角形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作为第三边的是( ) A .13cmB .6cmC .5cmD .4cm4.三角形一个外角小于与它相邻的内角,这个三角形是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .属于哪一类不能确定 5.如图,在直角三角形ABC 中,AC ≠AB ,AD 是斜边上的高, DE ⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (∠C 除外)相等的角的个数是( ) A 、3个 B 、4个 C 、5个 D 、6个6.如图,将一副三角板叠放在一起,使直角的顶点重合于O , 则∠AOC+∠DOB=( )A 、900B 、1200C 、1600D 、1807.以长为13cm 、10cm 、5cm 、7cm 的四条线段中的三条线段为边,可以画出三角形的个数是( )(A)1个 (B)2个 (C)3个 (D)4个8.给出下列命题:①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外 ⑤任何一个三角形都有三条高、三条中线、三条角平分线 ⑥三角形的三条角平分线交于一点,且这点在三角形内。
正确的命题有( )A.1个B.2个C.3个D.4个 二、填空题(每题3分,共计24分)9.如图,一面小红旗其中∠A=60°, ∠B=30°,则∠BCD=。
第5题图第6题图10.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是___________________.11.把一副常用的三角板如图所示拼在一起,那么图中∠ADE 是度。
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.下列选项中的三角形全等的是()A.两角及其夹边对应相等的两个三角形B.有两个角对应相等的两个三角形C.面积相等的两个三角形D.都是锐角三角形的两个三角形答案:A2.下列说法错误的是()A.有一个外角是锐角的三角形是钝角三角形B.有两个角互余的三角形是直角三角形C.直角三角形只有一条高D.任何一个三角形中,最大角不小于60度答案:C3.如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC的长为()A.4cm B.4.5cm C.1.5cm D.不能确定答案:C4.如图,△ABC≌△DCB,AB=5cm,AC=7 cm,BC=8 cm,那么DC的长是()A.8 cm B.7 cm C.6cm D.5 cm答案:D5.如图,已知0A=OC,OB=OD,那么根据“SAS”能直接判定三角形全等的对数为()A.1对B.2对C.3对D.4对答案:B6.如图,△ABD≌△CDB,∠ABD=40°,∠C=110°,则∠CBD等于()A.20°B.30°C.40°D.50°答案:B7.如图所示,△ABC≌△BAD.A与B,C与D是对应顶点,若AB=4cm,BD=4.5 cm,AD=1.5 cm,则BC的长为()A 4.5 cm B.4 cm C.1.5 cm D.不能确定答案:C8.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B9.如图所示,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE内部时,则∠A 与∠l+∠2之间有一种数量关系始终保持不变,你认为该规律是()A.∠A=∠l+∠2 B.2∠A=∠l+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)答案:B二、填空题10.三角形两个外于第三个内角的 4倍,则第三个内角等于 .解析:60°11.如图,在△ABC中,AB=AC=10cm,DE是AB的中垂线,△BDC 的周长为 16 cm,则 BC 的长为 .解析:6cm12.Rt△ABC中,∠C=Rt∠,∠A=30°,AB的中垂线交AB于D,交AC于E,若△ADE的面积是8,EC=3,BC=4,则△ABC的面积为.解析:2213.如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º解析:14.如图所示,已知AB=DC,AD=BC,E,F是BD上两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= .解析:70°15.如图所示:(1)若△ABD≌△ACE,AB=AC,则对应边还有,对应角有.(2)若△BOE≌△COD,则0E的对应边是,∠EB0的对应角是;(3)若△BEC≌△CDB,则相等的边有.解析: (3)BE=CD,CE=BD,BC=CB (1)AD与AE,BD与CE;∠A与∠A,∠ABD与∠ACE,∠ADB与∠AEC;(2)OD,∠DCO;16.如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.解析:48cm217.已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.解析:2,8三、解答题18.如图,已知 AB=DC,AD=BC,说出下列判断成立的理由:(1)△ABC≌△ACD; (2)∠B=∠D.解析:略19.如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.解析:△ABD≌△ACD(SAS),则BD=CD.20.如图所示,已知∠α,线段a,b,求作一个三角形,使其两边长分别为a,a+b,两边的夹角等于∠α.解析:略21.画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.解析:略22.如图①所示,长方形通过剪切可以拼成直角三角形,方法如下:仿照上图,用图示的方法,解答下列问题:(1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面积的长方形;(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等面积的长方形.解析:(1)(2)23.如图所示,已知∠BAC=∠DAE,∠B=∠C,BD=CE.证明:AB=AC,AD=AE.解析:略24.如图所示,A,D,F,B在同一直线上,AD=BF,AE=BC,且∠A=∠B,说明下列各式成立的理由.(1)△AEF≌△BCD;(2)∠BFE=∠ADC.解析:略25.三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.解析:高线的交点可以在三角形的外部、内部及其顶点上26.如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.解析:略27.一个三角形有两条边相等,它的最长的边比最短的边多2,已知这个三角形的周长为8,求它的三条边长.解析:103,103,4328.如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置关系,并说明理由.解析:CD⊥AB,理由略29.已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.解析:∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°30.(1)为了求出四边形的内角和,你能根据图中的两种添线方法,分别求出四边形的内角和吗?(2)请你用类似的方法求出五边形、六边形的内角和,比较一下,你发现了什么规律?(3)利用你发现的规律,可以求得20边形的内角和为度.解析:(1)360°;(2)规律:n边形的内角和为(n-2)·180°;(3)3240。
精选2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含标准答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.在△ABC 和△A ′B ′C ′中,已知 AB=A ′B ′,∠B=∠B ′,要保证△ABC ≌△A ′B ′C ′,可补充的条件是( )A .∠B+∠A=90°B . AC=A ′C ′ C .BC=B ′C ′D .∠A+∠A ′=90° 答案:C2.下列长度的三条线段,能组成三角形的是( )A .224,,B .225,,C .236,,D .245,,答案:D3..如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是( )A .甲和乙B .乙和丙C .只有乙D .只有丙答案:C4.下面三种说法:①两个能够重合的三角形是全等三角形;②全等三角形的形状和大小相同;③全等三角形的面积相等.其中正确的个数有 ( )A .3个B .2个C .1个D .0个答案:A5.如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A .34OB B .1()2OB OA - C .1()2OA OB + D .以上都不对答案:C6.如图所示,0P 平分∠AOB ,PE ⊥OB ,PF ⊥OA ,则下列结论中正确的个数有( ) ①OE=0F ;②FP=PE ;③OP ⊥EF ;④∠PEF=∠PFE ;⑤0P 平分∠FPE ;⑥PQ=0QA .6个B .5个C .4个D .2个7.如图,△ABD≌△DCA,B和C是对应顶点,则∠ADB和∠DAC所对的边是() A.A0和DO B.AB和DC C.A0和BD D.D0和AC答案:B8.如图所示,△ADF≌△CBE,则结论:①AF=CE;②∠1=∠2;③BE=CF,④AE=CF.其中正确的个数为()A.1个B.2个C.3个D.4个答案:C9.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B10.如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个答案:D11.如果三角形的两边长分别为7和2,且它的周长为偶数,那么,第三边的长为() A.5 B.6 C.7 D.8C B A12.在△ABC 和△A ′B ′C ′中,①AB=A ′B ′;②BC=B ′C ′;③AC=A ′C ′;④∠A=∠A ′;⑤∠B=∠8′;⑥∠C=∠C ′,则下列条件中不能使△ABC ≌△A ′B ′C ′的是( )A .②④⑤B .①②③C .①③⑤D .①②⑤答案:C二、填空题13.如图,AC 、BD 相交于点O ,∠A=∠D ,,请你再补充一个条件,使得△AOB ≌△DOC ,你补充的条件是 .解析:AO = DO 或AB = DC 或BO=CO14.如图,在△ABC 中,已知∠BAC=80°,∠B=40°,AD 是△ABC 的角平分线,那么∠ADB= .解析:100°15.如图,在ABC ∆中,AD 是BC 边上的高线,︒=∠60B ,︒=∠30C ,则图中有 个直角三角形. 解析:316.如图所示,已知在Rt △ABC 中,∠C=90°,AD 是△ABC 的角平分线,BC=5,CD :BD=2:3,则点D 到AB 的距离为 .解析:217.如图所示,已知△ABD ≌△ACE ,∠B=∠C ,那么AB= ,AD= , BD= ,∠A= ,∠ADB= .解析:AC,AE,CE,∠A,∠AEC18.如图所示,在△ABC中,∠B=35°,∠C=60°,AE是∠BAC的平分线,AD⊥BC于D,则∠DAE的度数为.解析:12.5°19.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE,ACD20.如图所示.(1)图中共有个三角形,分别是;(2)∠CDB是的内角,是的外角;(3)在AACD中,∠A是边和的夹角,边AC是的对边.解析:(1)3;△ACD,△BCD,△ABC;(2)△BDC,△ACD;(3)AD,AC,∠ADC 21.四条长度分别是2,3,4,5的线段,任选3条可以组成个三角形.解析:322.在Rt△ABC中,∠C=90°,其中∠A,∠B的平分线的交点为E,则∠AEB的度数为.解析:135°三、解答题23.如图,已知BD=CD,∠1=∠2,请说明△ABD≌△ACD的理由.解析:略24.如图所示,已知线段a,c,求作Rt△ABC,使BC=a,AB=c.解析:提示:两种情况25.如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整.①∠1=∠2;②BE=CF;③CD=FN;④△AEM≌△AFN.成立的有:.我选,理由如下:解析:①②④,以下略26.如图所示,已知∠BAC=∠DAE,∠B=∠C,BD=CE.证明:AB=AC,AD=AE.解析:略27.如图所示,已知AB=CD,BE=CF,E、F在直线AD上,并且AF=DE,说明△ABE≌△DCF的理由.解析:略28.如图所示,在△ABC中,∠ABC=∠ACB,且∠ACB=2∠A,BD⊥AC于D,求∠DBC的度数.解析:18°29.A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?解析:(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)30.如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.解析:∠P=70°。
最新2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如果一个三角形有一个角是99°,那么这个三角形是( )A .锐角三角形B .钝角三角形C .直角三角形D .钝角三角形或直角三角形答案:B2.下列长度的三条线段,能组成三角形的是( )A .224,,B .225,,C .236,,D .245,,答案:D3.如图所示,△ABD ≌△CDB ,∠ABD=40°,∠CBD=30°,则∠C 等于 ()A .20°B .100°C .110°D .115°答案:C4.△ABC 中,∠A :∠B :∠C=1:2:3,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角或钝角三角形答案:B5.关于三角形的高的位置,下列判断中正确的是( )A .必在三角形内B .必在三角形外C .不在三角形内,就在三角形外D .以上都不对答案:D6.以下列各组线段的长为边,能构成三角形的是( )A .4 cm ,5 cm ,6 cmB .2 cm ,3 cm ,5 cmC .4 cm ,4 cm 。
9 cmD .12 cm ,5 cm ,6 cm答案:A7.下列说法中:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的是()A.①和②B.②和③C.①和③D.①②③答案:C二、填空题8.如图,∠A=80°,∠2=130°,则∠l= .解析:130°9.如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠+∠=.AOC DOB解析:180°10.在ΔABC中, ∠C=90°,BD平分∠ABC,交AC于D,若AB=5,CD=2, 则ΔABD的面积是 .解析:511.如图所示,已知AB=DC,AD=BC,E,F是BD上两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= .解析:70°12.如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE与△DEC的面积之比为.解析:1:213.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE,ACD14.如图所示.(1)AD是△ABC的角平分线,则∠BAC=2 =2 ;(2)AE是△ABC的中线,则 = 2BE=2 .解析:(1)∠BAD,∠CAD;(2)BC,CE15.如图所示.(1)图中共有个三角形,分别是;(2)∠CDB是的内角,是的外角;(3)在AACD中,∠A是边和的夹角,边AC是的对边.解析:(1)3;△ACD,△BCD,△ABC;(2)△BDC,△ACD;(3)AD,AC,∠ADC 16.四条长度分别是2,3,4,5的线段,任选3条可以组成个三角形.解析:317.(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.解析:(1)三角形的稳定性;(2)5三、解答题18.如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.解析:19.如图,在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB 上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.解析:∠ABE=30°,∠ACF=30°,∠BHC=120°.20.如图,AB⊥BD于B,DE⊥BD于D,已知AB=CD,BC=ED,求∠ACE的度数.解析:△ABC≌△CDE(SAS),则∠ACB=∠E,由于∠ACB+∠ACE =∠E+∠D, 则∠ACE=∠D=90°.21.如图,已知线段AC=8,BD=6.(1)已知线段AC⊥BD于0.设图①,图②,图③中的四边形ABCD的面积分别为S1,S2,S3,则 S1= ,S2= ,S3= ;(2)如图④,对于线段AC与线段BD垂直相交(垂足O不与A,B,C,D重合)的任意情况,请你猜想四边形ABCD的面积,并说明你的猜想是正确的;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连结点A,B,C,D,A所围成的封闭图形的面积是多少;请画出图形,并说明你的猜想是正确的.解析:(1)S1=24,S2=24,S3=24;(2)面积为24,411111()8624 22222S BD AO BD CO BD AO CO BD AC=⋅+⋅=+=⋅=⨯⨯=;(3)图略,原理类似于(2),面积为2422.如图所示,已知线段a,c,求作Rt△ABC,使BC=a,AB=c.解析:提示:两种情况23.如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.解析:略24.如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.解析:略25.如图所示,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点,说出AF是CD的中垂线的理由.解:连结AC,AD,在△ABC和△AED中,AB=AE(已知),∠B=∠E(已知),BC=ED(已知),∴△ABC≌△AED(SAS).∴AC=AD(全等三角形的对应边相等).请把后面的过程补充完整:解析:略26.如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?解析:略27.如图所示,已知AB=AC,D是BC的中点,说明AD⊥BC的理由.解:∵D是BC的中点( ),∴ (中点的定义).在△和△中,= ( ),= (已证),= ( ),∴△≌△ ( ),∴∠l=∠2( )∴∠+∠2= ,∴∠l=∠2= ,即AD⊥BC.解析:已知,BD=CD,ABD,ACD,AB,AC,已知,BD,CD,AD,AD,公共边,ABD,ACD,SSS,全等三角形对应角相等,l80°,90°28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略29.如图所示,已知△ABD≌△ACE,AD=6 cm,AC=4 cm,∠ABD=50°,∠E=30°.求BE的长和∠COD的度数.解析:BE=2 cm,∠COD=20°30.如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.解析:略。
七年级下册第一章《认识三角形》单元检测(含答案)

bCa aAB70°31°D123ADO CBA1 35100第一章《认识三角形》单元检测题一、选择题1、在ABC △中,4080B C ∠=∠= ,,则A ∠的度数为( ) A .30B .40C .50D .602、已知三角形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作为第三边的是( ) A .13cmB .6cmC .5cmD .4cm3、如果三角形的两边分别为3和5,那么这个三角形的周长可能是( ) A .15B .16C .8D .74、如图1,直线a ∥b ,则∠A 的度数是A .28°B .31°C .39°D .42°图1 图2 图35、如图2,AB CD ∥,AD 和BC 相交于点O ,35A ∠=,75AOB ∠=,则C ∠等于( ) A .35B .75C .70D .806、已知一个三角形三个内角度数的比是1:5:6,则其最大内角的度数为( ) A .60B .75C .90D .1207、如图3,11002145∠=∠=,,那么3∠=( ) A .55°B .65°C .75°D .85°8、如图4,ABC △中,50A =∠,点D E ,分别在AB AC ,上,则12+∠∠的大小为( )A .130B .230C .180D .310图4 图5 图69、如图5,在ABC ∆中,AD 平分BAC ∠且与BC 相交于点D ,∠B = 40°,∠BAD = 30°,则C ∠的度数是( )A .70°B .80°C .100°D .110°10、将一副直角三角尺如图6放置,已知AE BC ∥,则AFD ∠的度数是( ) A .45B .50C .60D .75二、填空题11、如图7,图中的1∠= ;图7 图8 图9 12、等腰三角形的两边长分别是3和7,则其周长为______.13、如图8,是一块三角形木板的残余部分,量得100A ∠= ,40B ∠=,这块三角形木板另外一个角是 度.14、已知在△ABC 和△A 1B 1C 1中,AB =A 1B 1,∠A =∠A 1,要使△ABC ≌△A 1B 1C 1,还需添加一个..条 件,这个条件可以是 .15、如图9,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只添一个即可)ACEB D AB F EDOABCDE16、如图10,点D B C 、、在同一直线上,605025A C D ∠=∠=∠= ,,,则BED ∠= 度.图10 图11 图1217、如图11,DE ∥BC 交AB 、AC 于D 、E 两点,CF 为BC 的延长线,若∠ADE =50°,∠ACF =110°,则∠A = 度.18、已知:如图12,△OAD ≌△OBC ,且∠O =70°,∠C =25°,则∠AEB = 度. 19、一副三角板如图13所示叠放在一起,则图中α∠的度数是_________.图13 图1420、用直尺和圆规作一个角等于已知角的示意图如图14所示,则说明A O B AOB '''∠=∠的依据是 . 三、证明题21、如图,在△ABC 中,D 是∠ABC 与∠ACB 的平分线的交点,BD 的延长线交AC 于E ,且∠EDC =50°. 求∠A 的度数.22、已知:如图,C 为BE 上一点,点A D ,分别在BE 两侧.AB ED ∥,AB CE =,BC ED =. 求证:AC CD =.23、已知:如图,B C E ,,三点在同一条直线上,AC DE ∥,AC CE =, ACD B ∠=∠. 求证:ABC CDE △≌△.24、如图,点B F C E 、、、在一条直线上,FB CE AB DE AC DF =,∥,∥.求证:AB DE =.ACE DFBADBC EA CEDB3045α25、如图,四边形ABCD 的对角线AC 与BD 相交于O 点,12∠=∠,34∠=∠. 求证:BO DO =.26、如图,某同学给出一种作角平分线的方法:分别在OA 、OB 上截取OM=OE 、ON=•OF ,连结MF 、NE ,交于点P ,作射线OP ,则OP 平分∠AOB ,你认为他的作法对吗?若对,•请你加以说明.DCBAO1 23 4DCBA O123 4 参考答案一、选择题1、D2、B3、A4、C5、C6、C7、B8、B9、B 10、D 二、填空题11、65,35 12、1713、40 14、答案不唯一(如:∠B =∠B 1,∠C =∠C 1,AC =A 1C 1) 15、C D ∠=∠或ABC BAD ∠=∠或AC BD =或OAD OBC ∠=∠ 16、45 17、60 18、120 19、7520、全等三角形的对应角相等 三、证明题21、∵∠A+∠ABC+∠ACB =180°,∴∠ABC+∠ACB =180°-∠A .∵BD ,CD 分别是∠ABC 与∠ACB 的平分线, ∴∠BDC =12∠ABC ,∠BCD=12∠ACB .∴∠BDC+∠BCD =12∠ABC +12∠ACB=50°, ∴∠ABC+∠ACB =100°,即∠A =80°. 22、证明:AB ED ∥,B E ∴∠=∠.在ABC △和CED △中,AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩,,, ABC CED ∴△≌△. AC CD ∴=.23、证明:AC DE ∥,ACD D ∴∠=∠,BCA E ∠=∠.又ACD B ∠=∠ ,B D ∴∠=∠.又AC CE = ,ABC CDE ∴△≌△.24、证明:AB DE B E ∴∠=∠ ∥,.AC DF ACB DFE ∴∠=∠ ∥,. FB CE FB FC CE FC =∴+=+ ,,即BC EF =.ABC DEF ∴△≌△.AB DE ∴=.25、证明:在ABC △和ADC △中1234AC AC ∠=∠⎧⎪=⎨⎪∠=∠⎩ABC ADC ∴△≌△.AB AD ∴=.又12∠=∠ ,BO DO ∴=.26、对,∵△ONE ≌△OFM (SAS )∴∠ONE=∠MFO ,•再证△MPN ≌△EPF (AAS ) ∴PM=PE ,再证△OMP ≌△OEP (SSS ) ∴∠AOP=∠BOP.ACEDFB。
最新精选2019年七年级下册数学单元测试题-三角形的初步认识完整考题(含标准答案)
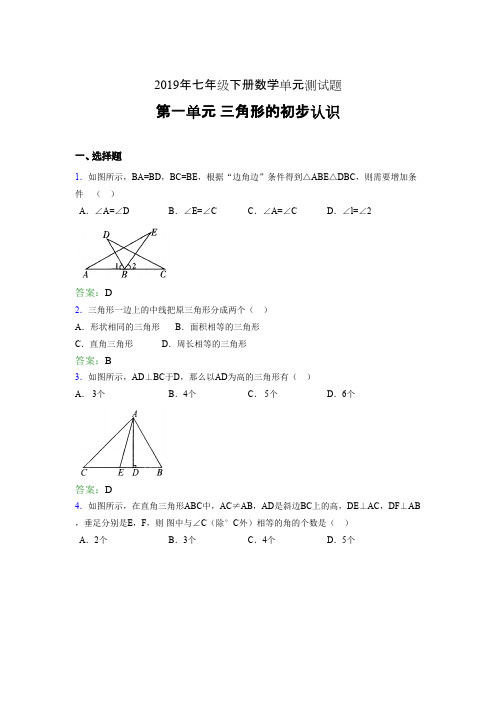
仿照上图,用图示的方法,解答下列问题: (1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面 积的长方形;
(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等 面积的长方形.
解析:(1) (2) 27.已知,如图所示,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断 ∠B与∠DEC是否相等,并说明理由.
A.2个
B.3个
C.4个
D.5个
答案:B
5.如图所示是跷跷板的示意图,支柱0C与地面垂直,点0是横板AB的中点,AB可以绕着
点0上下转动,当A端落地时,∠0AC=20°.跷跷板上下可转动的最大角度(即∠A′OA
)是( )
A.800
B.60°
C.40°
D.20°
答案:C
6.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是( ) A 10° B.20° C.30° D.40°
(1)经过线段中点的直线是线段的中垂线. ( )
(2)以AB为直径可以作一个圆. ( )
(3)已知两条边和一个角可以作唯一的三角形. ( )
(4)已知两角一边可以作唯一的三角形. ( )
解析:(1)× (2)√ (3)× (4)×
19.如图所示,∠1=∠2,∠ABC=∠DCB,AC,BD相交于O,请将下列说明AB=DC的理 由的过程补充完整.
解析:CD⊥AB,理由略
解析:∠B=∠DEC,理由略 28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.
解析:略 29.怎样作一条线,就能使如图所示的正五角星成为两个全等的图形?这样的线共有几条?
解析:5 30.如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置 关系,并说明理由.
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》考核题完整版(含参考答案)
2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图,已知直线L是线段PQ的垂直平分线,垂足为O,M、N是直线L上两点,下列结论中,错误的是()A.△MPN≌△MQN B.MO=NO C.OP=OQ D.∠MPN=∠MQN答案:B2.下列图形中,能说明∠1>∠2的是()答案:D3.如图所示,已知AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,还需要() A.∠B=∠B′B.∠C=∠C′C.AC=A′C′D.以上均可答案:D4.如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对答案:C5.如图所示,△ADF≌△CBE,则结论:①AF=CE;②∠1=∠2;③BE=CF,④AE=CF.其中正确的个数为()A.1个B.2个C.3个D.4个答案:C6.△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.锐角或钝角三角形答案:B7.关于三角形的高的位置,下列判断中正确的是()A.必在三角形内B.必在三角形外C.不在三角形内,就在三角形外D.以上都不对答案:D8.下列叙述中正确的个数是()①三角形的中线、角平分线都是射线;②三角形的中线、角平分线都在三角形内部;③三角形的中线就是过一边中点的线段;④三角形三条角平分线交于一点.A.0个B.1个C.2个D.3个答案:C9.在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠8′;⑥∠C=∠C′,则下列条件中不能使△ABC≌△A′B′C′的是()A.②④⑤B.①②③C.①③⑤D.①②⑤答案:C10.如图,已知BC=BD,∠ABE=∠CBD,∠ADB=∠BCE.要说明BA=BE,则只要先说明()A.△ABE≌△DBC B.△ABD≌△EBC C.△BDG≌△BEH D.△ABG≌△BCH答案:B11.下列长度的三条线段,能够组成三角形的是()A.2.5,2.5,5 B. l,6,6 C.2,8,4 D.10,7,2答案:B二、填空题12.如图,AD=AE,DB=EC,则图中一共有对全等三角形.解析:413.如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º解析:14.判断正误,对的打“√”,错的打“×”.(1)经过线段中点的直线是线段的中垂线. ( )(2)以AB为直径可以作一个圆. ( )(3)已知两条边和一个角可以作唯一的三角形. ( )(4)已知两角一边可以作唯一的三角形. ( )解析:(1)× (2)√ (3)× (4)×15.要使△ABC≌△A′B′C′,已知AB=A′B′,∠B=∠B′,如果利用“ASA”,要补充条件,如果利用“AAS”,要补充条件.解析:∠A=∠A′,∠=∠C′16.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃.最省事的办法是带去,理由是.解析:③,可根据③中的两角及夹边画出一个与之全等的三角形17.如图所示,直线AD交△ABC的BC边于D点,且AB=AC.(1)若已知D为BC中点,则可根据,说明△ABD≌△ACD;(2)若已知AD平分∠BAC,可以根据说明△ABD≌△ACD;(3)若AD是BC的中垂线,则可以根据,说明△ABD≌△ACD,还可以根据说明△ABD≌△ACD.解析:(1)SSS;(2)SAS;(3)SAS,SSS18.如图所示:(1)若△ABD≌△ACE,AB=AC,则对应边还有,对应角有.(2)若△BOE≌△COD,则0E的对应边是,∠EB0的对应角是;(3)若△BEC≌△CDB,则相等的边有.解析: (3)BE=CD,CE=BD,BC=CB (1)AD与AE,BD与CE;∠A与∠A,∠ABD与∠ACE,∠ADB与∠AEC;(2)OD,∠DCO;19.木材加工厂堆放木料的方式如图所示:依此规律可以得出第六堆木料的根数是根.解析:2820.如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△ABD= ,S△AOF= .解析:6,221.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE ,ACD22.如图所示,∠1=135°,∠2=75°,则∠3的度数是 .解析:30°23.四条长度分别是2,3,4,5的线段,任选3条可以组成 个三角形. 解析:3三、解答题24.如图 ,AB=AD ,∠BAD=∠CAE ,AC=AE ,试说明CB=ED.解析:可证△ABC ≌△ADB ,然后说明CB =ED25.如图,DF ⊥AB ,∠A=430,∠D=42°,求∠ACB 的度数.E B DF C AF E DC B A ∠ACB=89 º.解析:26.如图,BD =CD ,∠ABD =∠ACD ,DE 、DF 分别垂直于AB 及AC 交延长线于E 、F .求证:DE =DF .解析:∠ABD=∠ACD ,则∠E+∠BDE =∠F+∠CDF, 由于 ∠E=∠F ,∴∠BDE =∠CDF ,∴△BED ≌△CFD(AAS),∴DE=DF .27.根据条件作图:(1)任意画一个Rt △ABC ,使∠C=90°;(2)画∠CAB 的平分线交对边于D ;(3)画出点D 到Rt △ABC 的斜边的垂线段DE .解析:略28.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略29.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.解析:18°30.已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.解析:∠C=90°。
最新精选2019年七年级下册数学单元测试题-三角形的初步认识完整考试题(含参考答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图,从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA =∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确结论的个数是()A. 1 B.2 C.3 D.4答案:B2.如图,已知 AE=CF,BE =DF.要证△ABE≌△CDF,还需添加的一个条件是()A.∠BAC=∠ACD B.∠ABE=∠CDF C.∠DAC=∠BCA D.∠AEB=∠CFD答案:D3.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且AP平分∠BAC,则△APD与△APE 全等的理由是()A.AAS B.ASA C.SSS D.AAS答案:D4.一个三角形的三个内角中,至少有()A.一个锐角B.两个锐角C.一个钝角D.一个直角答案:B5.下面三种说法:①两个能够重合的三角形是全等三角形;②全等三角形的形状和大小相同;③全等三角形的面积相等.其中正确的个数有()A.3个B.2个C.1个D.0个6.下列6组长度的线段中,可以首尾相接组成三角形的是( )①3,4,5;②1,1,3;③1,2,3;④5,5,5;⑤2,2,5;⑥3,7,4A .①②③④⑤⑥B .①④⑤C .①③④D .①②③④ 答案:D7.如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A .34OB B .1()2OB OA - C .1()2OA OB + D .以上都不对答案:C8.如图所示,由∠ABC=∠DCB ,∠ACB=∠DBC ,直接能判定全等的三角形是 ( )A .△AB0≌△DODB .△ABC ≌△DCB C .△ABD ≌△DCA D .△OAD ≌△0BC答案:B9.如图所示,已知CD=CE ,AE=BD ,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD 的度数是 ( )A .72°B .54°C . 46°D .20°答案:C10.如图所示,△ADF ≌△CBE ,则结论:①AF=CE ;②∠1=∠2;③BE=CF , ④AE=CF .其中正确的个数为( )A .1个B .2个C .3个D .4个11.如图所示,△ABC≌△BAD.A与B,C与D是对应顶点,若AB=4cm,BD=4.5 cm,AD=1.5 cm,则BC的长为()A 4.5 cm B.4 cm C.1.5 cm D.不能确定答案:C12.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B13.如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个答案:D二、填空题14.如果一个三角形的两个角都是80°,那么第三个角的度数是 .解析:20°15.如图所示,点B在AE上,且∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是(写一个即可):.解析:AC=AD或∠C=∠D等16.如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.解析:ABE,ACD17.如图所示,在△ABC中,AD是角平分线,已知∠B=66°,∠C=38°,那么∠ADB= ,∠ADC= .解析:76°,l04°18.如图所示,∠1=135°,∠2=75°,则∠3的度数是.解析:30°19.已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.解析:2,8三、解答题20.如图,已知BD=CD,∠1=∠2,请说明△ABD≌△ACD的理由.解析:略21.如图,DF ⊥AB ,∠A=430,∠D=42°,求∠ACB 的度数.∠ACB=89 º.解析:22.如图,四边形ABCD 是一防洪堤坝的横截面,AE ⊥CD ,BF ⊥CD ,且AE=BF ,∠D=∠C ,问:AD 与BC 是否相等?说明你的理由.解: AE ⊥CD∴∠AED=BF ⊥CD∴∠BFC=∴ =在△ADE 和△BCF 中,()()()⎪⎩⎪⎨⎧=∠=∠=∠_____________________________________________________________________AE AED D ∴△ADE ≌△BCF( )∴AD=BC( )90 º ,90 º,∠AED ,∠BFC ,∠C ,已知,BFC ,已证,BF , 已知,AAS ,全等三角形E B DF CA的对应边相等.解析:23.如图所示,已知∠α,线段a,b,求作一个三角形,使其两边长分别为a,a+b,两边的夹角等于∠α.解析:略24.如图所示,△ABC中,AB=AC,BE,CD分别是AC,AB的中线,说明下列各式成立的理由.(1)BE=CD;(2)∠1=∠2.解析:略25.如图所示,已知AB=CD,BE=CF,E、F在直线AD上,并且AF=DE,说明△ABE≌△DCF的理由.解析:略26.怎样作一条线,就能使如图所示的正五角星成为两个全等的图形?这样的线共有几条?解析:527.如图所示,在△ABC中,AD是高,CE是角平分线,它们相交于点P.已知∠APE=55°,∠AEP=80°,求△ACB各个内角的度数.解析:∠B=45°,∠ACB=70°,∠BAC=6528.如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.解析:略29.A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?解析:(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)30.已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.解析:∠C=90°。
七年级第一章三角形的初步认识练习及答案

第一章 三角形一、细心选一选1.下列说法正确的是……………………………………………………………( ) A.周长相等的两个三角形全等 B.面积相等的两个三角形全等 C.三个角对应相等的两个三角形全等 D.三条边对应相等的两个三角形全等2.下列各组线段能组成三角形的是……………………………………………( ) A.3cm ,3cm ,6cm B.7cm,4cm,5cm C.3cm,4cm,8cm D.4.2cm,2.8cm,7cm3.下列图形中,与已知图形全等的是………………………………………………( )4.如图,已知△ABC ≌△CDE,其中AB=CD,那么下列结论中, 不正确的是……………………… ( )A.AC=CEB.∠BAC=∠CDE C.∠ACB=∠ECD D.∠B=∠D5.下列条件中,不能判定三角形全等的是……………………………………( ) A.三条边对应相等 B.两边和一角对应相等 C.两角和其中一角的对边对应相等 D.两角和它们的夹边对应相等6. 如图,把图形沿BC 对折,点A 和点D 重合,那么图中共有 全等三角形…………………………………………( ) A.1对 B.2对 C.3对 D.4对7.在△ABC 和△A ′B ′C ′中,已知AB= A ′B ′,∠B=∠B ′要保证△ABC ≌△A ′B ′C ′,可补充的条件是…………………………………………………………………………( )A.∠B+∠A=900B.AC= A ′C ′C.BC=B ′C ′D. ∠A+∠A ′=9008.已知在△ABC 和△A ′B ′C ′中,AB= A ′B ′,∠B=∠B ′,补充下面一个条件,不能说明△ABC ≌△A ′B ′C ′的是………………………………………………………………( )A. BC=B ′C ′B. AC= A ′C ′C. ∠C=∠C ′D. ∠A=∠A ′(A) (B) (C)(D)第3题图ABCDE第4题ABDCE9.如图,已知AE=CF,BE=DF.要证△ABE ≌△CDF,还需添加的一个条件是………( ) A.∠BAC=∠ACD B.∠ABE=∠CDF C.∠DAC=∠BCA D.∠AEB=∠CFD10.如图AD 是△ABC 的角平分线,DE 是△ABD 的高,EF 是△ACD 的高,则…( ) A.∠B=∠C B.∠EDB=∠FDC C.∠ADE=∠ADF D. ∠ADB=∠ADC 11.如图AC 与BD 相交于点O ,已知AB=CD,AD=BC,则图中全等三角形有………( ) A.1对 B.2对 C.3对 D.4对 12.如图,D 、E 分别是AB,AC 上一点,若∠B=∠C ,则在下列条件中,无法判定△ABE ≌△ACD 是………………………………( ) A.AD=AE B.AB=ACC.BE=CDD.∠AEB=∠ADC 二、专心填一填:13.如图,△ABC ≌△DEF,点B 和点E, 点A 和点D 是对应顶点, 则AB= ,CB= , ∠C= ,∠CAB= . 14.若已知两个三角形有两条边对应,则要视这两个三角形全等, 还需增加的条件可以是 或 .17.在△ABC 和△DEF 中,AB=4, ∠A=350, ∠B=700,DE=4, ∠D= , ∠E=700,根据 判定△ABC ≌△DEF.18.如图,在△ABC 和△DEF 中AB=DC(BC=DA(=⎧⎪⎨⎪⎩已知)已知)()∴△ABC ≌△DEF( )19.如图∠B=∠DEF,AB=DE,要证明△ABC ≌△DEF ,(1)若以“ASA ”为依据,需添加的条件是 ; (2)若以“SAS ”为依据,需添加的条件是 . 20.如图,△ABC 中,AB=AC=13cm ,AB 的垂直平分线交AB 于D, 交AC 于E,若△EBC 的周长为21cm,则BC= cm.A B C DF E第9题AA AAA 第10题A BCDO第11题ABCE第12题D第13题ABC DEF第19题B CAE CD第18题ABC DA BCE D第20题三、耐心答一答:23.(本题6分)如图,已知BD=CD ,∠1=∠2.说出△ABD ≌△ACD 的理由.轴对称单元试题一、填空题:1、轴对称是指____个图形的位置关系;轴对称图形是指____个具有特殊形状的图形。
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》完整考题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图,在△ABC中,DE是边AB的垂直平分线,BC=8cm,AC=5cm 则△ADC的周长为()A.14 cm B.13 cm C.11 cm D.9 cm答案:B2.下列6组长度的线段中,可以首尾相接组成三角形的是()①3,4,5;②1,1,3;③1,2,3;④5,5,5;⑤2,2,5;⑥3,7,4A.①②③④⑤⑥B.①④⑤C.①③④D.①②③④答案:D3.下列条件中,不能作出唯一..三角形的是()A.已知两边和夹角B.已知两边和其中一边的对角C.已知两角和夹边D.已知两角和其中一角的对边答案:B4.如图所示,已知∠1=∠2,AD=CB,AC,BD相交于点0,MN经过点O,则图中全等三角形的对数为()A.4对B.5对C.6对D.7对答案:C5.如图所示,若根据“SAS”来说明△ABC≌△DBC,已知BC是公共边,需要补充的条件是()A.AB=DB,∠l=∠2 B.AB=DB,∠3=∠4C.AB=DB,∠A=∠D D.∠l=∠2,∠3=∠4答案:B6.如图所示,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是()A 10° B.20° C.30° D.40°答案:B7.如图所示是跷跷板的示意图,支柱0C与地面垂直,点0是横板AB的中点,AB可以绕着点0上下转动,当A端落地时,∠0AC=20°.跷跷板上下可转动的最大角度(即∠A′OA)是()A.800 B.60°C.40°D.20°答案:C8.三角形的三边长都是整数,并且唯一的最长边是5,则这样的三角形共有()A 1个 B.2个 C.3个 D.4个答案:D二、填空题9.如图,AF、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAF = .解析:20010.若一个三角形的两条高在这个三角形的外部,那么这个三角形的形状是___________三角形.解析:钝角11.已知:△ABC 中,∠A=100°,∠B -∠C =60°,则∠C=__________.解析:10°12.如图,在△ABC 中,AD 是BC 边上的中线,若△ABC 的周长为20,BC=11,且△ABD 的周长比△ACD 的周长大3,则AB= ,AC= . 6,313.,AC=CD ,∠ACD=60°, 则∠ACB= .解析:30°14.已知△ABC ≌△A ′B ′C ′,AB+AC=18 cm ,BC=7 cm ,则△A ′B ′C ′的周长是 .解析:25 cm15.如图所示,将两块相同的直角三角板的直角顶点重合放在一起,若∠AOD=110°,则∠BOC= .请你用符号表示图中的全等三角形: .解析:70°,△AOB ≌△COD16.如图所示,△ABC 中,∠B=∠C ,FD ⊥BC 于D ,DE ⊥AB 于E ,∠AFD=155°,则∠EDF= .解析:65°17.直角三角形的两个锐角的平分线AD ,BE 交于点0,则∠AOB= .解析:135°三、解答题18. 如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四 D B种不同的分法,把4×4的正方形分割成两个全等图形.解析:19.如图,AB⊥BD于B,DE⊥BD于D,已知AB=CD,BC=ED,求∠ACE的度数.解析:△ABC≌△CDE(SAS),则∠ACB=∠E,由于∠ACB+∠ACE =∠E+∠D, 则∠ACE=∠D=90°.20.如图,在△ABC和△DEF中,AC=DF,AE=BD,BC=EF,则∠C=∠F,请说明理由(填空).解:∵ AE=BD(已知)∴ =∴ =在△ABC和△DEF中===∴△ABC≌△DEF ( )∴∠C=∠F ( )解析:AE-BE,BD-BE,AB,DE,AC,DF,AB,DE,BC,EF,SSS,全等三角形的角相等.21.画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.解析:略22.如图所示,已知AB=CD,BE=CF,E、F在直线AD上,并且AF=DE,说明△ABE≌△DCF的理由.解析:略23.如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?解析:略24.把大小为4×4的正方形方格图形分割成两个全等图形,如右图所示,请在下图中,沿着虚线再画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形解析:略25.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.解析:18°26.如图所示,在△ABC中,∠ABC=∠ACB,且∠ACB=2∠A,BD⊥AC于D,求∠DBC的度数.解析:18°27.如下表,“谢氏三角”是波兰著名数学家谢尔宾斯基在1915年~l916年期间提出的,它的作法是:第一步:取一个等边三角形(记为P 1),连结各边的中点,得到完全相同的小正三角形,挖掉中间的一个;第二步:将剩下的三个小正三角形(记为P 2),按上述办法各自取中点,各自分成4个小三角形,去掉各自中间的一个小正三角形;依次类推,不断划分出小的正三角形,同时去掉中间的一个小正三角形.试求P 4的“黑”三角形的个数,“黑”三角形的总边数,边长,周长和面积,并将结果填入下表中.解析:27,81,118a ,1818a ,12764S 28.如图所示,已知△ABC 的边AB 和BC 边上的中线AD ,请把△ABC 补画完整.解析:连结BD,并延长BD到C,使DC=BD,连结AC29.在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.解析:∠A=70°,∠B=60°,∠C=50°30.如图,从建筑物顶端A处拉一条宣传标语条幅到地面C处,为了测量条幅AC的长,在地面另一处选一点D,使D、C、B(B为建筑物的底部)三点在同一直线上,并测得∠D=40°,∠ACB=80°,求∠DAC的度数.解析:40°AB CD。
第1章 三角形的初步认识单元测试(A卷基础篇)(浙教版)(解析版)

第1章三角形的初步认识单元测试(A卷基础篇)【浙教版】参考答案与试题解析一.选择题(共10小题,每小题3分,共30分)1.(3分)(2019秋•余杭区期末)下列各组线段中(单位:cm),能组成三角形的是()A.5,15,20 B.6,8,15 C.2,2.5,3 D.3,8,15【思路点拨】根据三角形两边之和大于第三边进行判断即可.【答案】解:A、5+15=20,不符合三角形的三边关系,故A不合题意;B、8+6<15,不符合三角形的三边关系,故B不合题意;C、2+2.5>3,符合三角形的三边关系,故C符合题意;D、8+3<15,不符合三角形的三边关系,故D不合题意;故选:C.【点睛】本题主要考查三角形的三边关系,掌握三角形的两边之和大于第三边,两边之差小于第三边是解题的关键.2.(3分)(2019秋•下城区期末)已知△ABC中,∠A=20°,∠B=70°,那么△ABC是()A.直角三角形B.锐角三角形C.钝角三角形D.正三角形【思路点拨】先求出∠C的度数,进而可得出结论.【答案】解:∵△ABC中,∠A=20°,∠B=70°,∴∠C=180°﹣20°﹣70°=90°,∴△ABC是直角三角形.故选:A.【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.3.(3分)(2020•越城区模拟)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是()A.B.C.D.【思路点拨】根据高线的定义即可得出结论.【答案】解:B,C,D都不是△ABC的边BC上的高,故选:A.【点睛】本题考查的是作图﹣基本作图,熟知三角形高线的定义是解答此题的关键.4.(3分)(2020春•椒江区期末)下列命题中,是假命题的为()A.两直线平行,同旁内角相等B.两直线平行,内错角相等C.同位角相等,两直线平行D.同旁内角互补,两直线平行【思路点拨】根据平行线的性质对A、B进行判断;根据平行线的判定方法对C、D进行判断.【答案】解:A、两直线平行,同旁内角互补,所以A选项为假命题;B、两直线平行,内错角相等,所以B选项为真命题;C、同位角相等,两直线平行,所以C选项为真命题;D、同旁内角互补,两直线平行,所以D选项为真命题.故选:A.【点睛】本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.5.(3分)(2019秋•海曙区期末)如图,△ABC≌△AEF且点F在BC上,若AB=AE,∠B=∠E,则下列结论错误的是()A.AC=AF B.∠AFE=∠BFE C.EF=BC D.∠EAB=∠F AC【思路点拨】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可.【答案】解:∵△ABC≌△AEF,∴AC=AF,EF=BC,故A,C正确;∠EAF=∠BAC,∴∠F AC=∠EAB,故D正确;∠AFE=∠C,故B错误;故选:B.【点睛】本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.6.(3分)(2019秋•桐梓县期末)如图,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且△ABC的面积为16,则△BEF的面积是()A.2 B.4 C.6 D.8【思路点拨】因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,△EBC与△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等积变换可解答.【答案】解:解:如图,点F是CE的中点,∴△BEF的底是EF,△BEC的底是EC,即EF=EC,高相等;∴S△BEF=S△BEC,同理得,S△EBC=S△ABC,∴S△BEF=S△ABC,且S△ABC=16,∴S△BEF=4,即阴影部分的面积为4.故选:B.【点睛】本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.7.(3分)(2020•温州模拟)如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是()A.∠ABC=∠DCB B.∠ABD=∠DCA C.AC=DB D.AB=DC【思路点拨】根据全等三角形的判定定理逐个判断即可.【答案】解:A、∵在△ABC和△DCB中∴△ABC≌△DCB(ASA),故本选项不符合题意;B、∵∠ABD=∠DCA,∠DBC=∠ACB,∴∠ABD+∠DBC=∠ACD+∠ACB,即∠ABC=∠DCB,∵在△ABC和△DCB中∴△ABC≌△DCB(ASA),故本选项不符合题意;C、∵在△ABC和△DCB中∴△ABC≌△DCB(SAS),故本选项不符合题意;D、根据∠ACB=∠DBC,BC=BC,AB=DC不能推出△ABC≌△DCB,故本选项符合题意;故选:D.【点睛】本题考查了全等三角形的判定定理,能灵活运用全等三角形的判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.8.(3分)(2019秋•余杭区期末)如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①CE=BF;②△ACE和△CDE面积相等;③BF∥CE;④△BDF ≌△CDE.其中正确的有()A.1个B.2个C.3个D.4个【思路点拨】根据“SAS”可证明△CDE≌△BDF,则可对④进行判断;利用全等三角形的性质可对①进行判断;由于AE与DE不能确定相等,则根据三角形面积公式可对②进行判断;根据全等三角形的性质得到∠ECD=∠FBD,则利用平行线的判定方法可对③进行判断.【答案】解:∵AD是△ABC的中线,∴CD=BD,∵DE=DF,∠CDE=∠BDF,∴△CDE≌△BDF(SAS),所以④正确;∴CE=BF,所以①正确;∵AE与DE不能确定相等,∴△ACE和△CDE面积不一定相等,所以②错误;∵△CDE≌△BDF,∴∠ECD=∠FBD,∴BF∥CE,所以③正确;故选:C.【点睛】本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.9.(3分)(2019秋•慈溪市期末)如图,已知,AB=AD,∠ACB=∠AED,∠DAB=∠EAC,则下列结论错误的是()A.∠B=∠ADE B.BC=AE C.∠ACE=∠AEC D.∠CDE=∠BAD【思路点拨】由“AAS”可得△ABC≌△ADE,可得∠B=∠ADE,AC=AE,BC=DE,可得∠ACE=∠AEC,由等腰三角形的性质和外角性质可得∠CDE=∠BAD,即可求解.【答案】解:∵∠DAB=∠EAC,∴∠BAC=∠DAE,且∠ACB=∠AED,AB=AD,∴△ABC≌△ADE(AAS)∴∠B=∠ADE,AC=AE,BC=DE,∴∠ACE=∠AEC,故选项A,C不符合题意,∵AB=AD,∴∠B=∠ADB=∠ADE,∵∠ADC=∠B+∠BAD=∠CDE+∠ADE,∴∠CDE=∠BAD,故选项D不符合题意,故选:B.【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明△ABC≌△ADE是本题的关键.10.(3分)(2019秋•临海市期末)有甲、乙、丙三人,甲说乙在说谎,乙说丙在说谎,丙说甲和乙都在说谎,则()A.甲说实话,乙和丙说谎B.乙说实话,甲和丙说谎C.丙说实话,甲和乙说谎D.甲、乙、丙都说谎【思路点拨】分情况,依次推理可得.【答案】解:A、若甲说的是实话,即乙说的是谎话,则丙没有说谎,即甲、乙都说谎是对的,与甲说的是实话相矛盾,故A不合题意;B、若乙说的是实话,即丙说的谎话,即甲、乙都说谎是错了,即甲,乙至少有一个说了实话,与乙说的是实话不矛盾,故B符合题意;C、若丙说的是实话,甲、乙都说谎是对的,那甲说的乙在说谎是对的,与丙说的是实话相矛盾,故C不合题意;D、若甲、乙、丙都说谎,与丙说的甲和乙都在说谎,相矛盾,故D不合题意;故选:B.【点睛】本题考查的是推理与论证,通过假设找出条件矛盾之处是本题的关键.二.填空题(共6小题,每小题4分,共24分)11.(4分)(2019秋•唐河县期末)把命题“三条边对应相等的两个三角形全等”改写成“如果…那么…”的形式,可写为如果两个三角形的三条边对应相等,那么这两个三角形全等.【思路点拨】命题改写成“如果…那么…”的形式,其中如果后面的部分是题设,那么后面的部分是结论.【答案】解:如果两个三角形的三条边对应相等,那么这两个三角形全等.【点睛】命题由题设和结论两部分组成,命题可写成“如果…那么…”的形式,其中如果后面的部分是题设,那么后面的部分是结论.12.(4分)(2019秋•嘉兴期末)如图,已知AC=DC,BC=EC,要使△ABC≌△DEC,需添加的一个条件是AB=DE.【思路点拨】此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.【答案】解:添加的条件是AB=DE,理由是:∵在△ABC和△DEC中∴△ABC≌△DEC(SSS),故答案为:AB=DE.【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键.13.(4分)(2019秋•正阳县期末)已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是2b﹣2c.【思路点拨】先根据三角形三边关系判断出a+b﹣c与b﹣a﹣c的符号,再把要求的式子进行化简,即可得出答案.【答案】解:∵△ABC的三边长分别是a、b、c,∴a+b>c,b﹣a<c,∴a+b﹣c>0,b﹣a﹣c<0,∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣(﹣b+a+c)=a+b﹣c+b﹣a﹣c=2b﹣2c;故答案为:2b﹣2c【点睛】此题考查了三角形三边关系,用到的知识点是三角形的三边关系、绝对值、整式的加减,关键是根据三角形的三边关系判断出a+b﹣c与,b﹣a﹣c的符号.14.(4分)(2019秋•温州期中)如图,△ABC三边的中线AD,BE,CF的公共点为G,若S△ABC=16,则图中阴影部分的面积是.【思路点拨】根据三角形的中线把三角形的面积分成相等的两部分,知△ABC的面积即为阴影部分的面积的3倍.【答案】解:∵△ABC的三条中线AD、BE,CF交于点G,∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,∵S△ACF=S△BCF=S△ABC=×16=8,∴S△CGE=S△ACF=×8=,S△BGF=S△BCF=×8=,∴S阴影=S△CGE+S△BGF=,故答案为:.【点睛】本题考查了三角形的面积,正确的识别图形是解题的关键.15.(4分)(2019秋•三台县期末)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=55°.【思路点拨】求出∠BAD=∠EAC,证△BAD≌△CAE,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.【答案】解:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,在△BAD和△CAE中,∴△BAD≌△CAE(SAS),∴∠2=∠ABD=30°,∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°,故答案为:55°.【点睛】本题考查了全等三角形的性质和判定,三角形的外角性质的应用,解此题的关键是推出△BAD ≌△CAE.16.(4分)(2019秋•宁都县期末)如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于点E,交AC 于点F,∠CDE=∠ACB=30°,BC=DE,则∠ADF=45°.【思路点拨】证明△ABC≌△CED(ASA),得出AC=CD,由等腰三角形的性质得出求出∠CDA=∠CAD =75°,即可得出答案.【答案】解:∵DE∥AB,∴∠DEC=∠B=90°,∵∠CDE=∠ACB=30°,∴∠CDE=30°,在△ABC和△CED中,,∴△ABC≌△CED(ASA),∴AC=CD,∴∠CDA=∠CAD=(180°﹣30°)=75°,∴∠ADF=∠CDA﹣∠CDE=45°;故答案为:45°.【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质、直角三角形的性质以及三角形内角和定理;熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.三.解答题(共7小题,共66分)17.(6分)(2019秋•乌鲁木齐期末)如图,已知AB∥DC,AD∥BC,求证:AB=CD.【思路点拨】根据平行线的性质得出∠BAC=∠DCA,∠DAC=∠BCA,根据ASA推出△BAC≌△DCA,根据全等三角形的性质得出即可.【答案】证明:∵AB∥DC,AD∥BC,∴∠BAC=∠DCA,∠DAC=∠BCA,在△BAC和△DCA中∴△BAC≌△DCA,∴AB=CD.【点睛】本题考查了全等三角形的性质和判定,平行线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.18.(8分)(2019秋•商河县期末)如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°,求∠DAE的度数.【思路点拨】根据三角形的内角和定理求出∠BAC的度数,根据角平分线的定义求出∠BAE的度数,根据三角形的外角性质得到∠AEC的度数,再根据三角形的内角和定理即可求出答案.【答案】解:∵∠B=40°,∠C=60°,∴∠BAC=180°﹣∠B﹣∠C=80°,∵AE平分∠BAC,∴∠BAE=∠BAC=40°,∴∠AEC=∠B+∠BAE=80°,∵AD⊥BC,∴∠ADE=90°,∴∠DAE=180°﹣∠ADE﹣∠AED=10°.答:∠DAE的度数是10°.【点睛】本题主要考查了三角形的内角和定理,三角形的外角性质,三角形的角平分线,垂直的定义等知识点,能熟练地运用这些性质进行计算是解此题的关键.19.(8分)(2019秋•南浔区期末)如图,已知点B,F,E,C在同一条直线上,AB∥CD,且AB=CD,∠A=∠D.求证:BE=CF.【思路点拨】先由平行线的性质得∠B=∠C,从而利用ASA判定△ABF≌△DCE,再根据全等三角形的性质得BF=CE,然后利用等量加等量和相等,可得结论.【答案】证明:∵AB∥CD,∴∠B=∠C,在△ABF和△DCE中∴△ABF≌△DCE(ASA)∴BF=CE,∴BF+EF=CE+EF,即BE=CF.【点睛】本题考查了全等三角形的判定与性质,这属于几何基础知识的考查,难度不大.20.(10分)(2020•温州三模)如图,在△ABC中,∠C=90°,在边AB上取一点D,使得BD=AC,过B 作AC的平行线BE,过D作AB的垂线与BE交于点E,连结AE.(1)求证:△ABC≌△BED.(2)若∠BAC=34°,求∠AED的度数.【思路点拨】(1)由平行线的性质得出∠BAC=∠EBD,可证明△ABC≌△BED(ASA);(2)由(1)可知AB=BE,则∠EAB=∠AEB,求出∠EAB的度数,则可求出答案.【答案】(1)证明:∵BE∥AC,∴∠BAC=∠EBD,∵DE⊥AB,∴∠EDB=90°,∴∠EDB=∠C,又∵BD=AC,∴△ABC≌△BED(ASA).(2)解:∵△ABC≌△BED,∴AB=BE,∴∠EAB=∠AEB,∵∠BAC=34°,∴∠EBD=34°,∴∠EAB===73°,∴∠AED=90°﹣∠EAB=90°﹣73°=17°.【点睛】本题考查了等腰三角形的性质,平行线的性质,全等三角形的判定与性质,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.21.(10分)(2019秋•苍南县期末)已知:如图,∠ACB=∠DCE,AC=BC,CD=CE,AD交BC于点F,连结BE.(1)求证:△ACD≌△BCE.(2)延长AD交BE于点H,若∠ACB=30°,求∠BHF的度数.【思路点拨】(1)根据∠ACB=∠DCE,可以得到∠ACD=∠BCE,再根据题目中的条件,利用SAS可以证明结论成立;(2)根据题意作出合适的辅助线,然后根据(1)中的结论和三角形内角和可以得到∠BHF的度数.【答案】证明:(1)∵∠ACB=∠DCE,∴∠ACB+∠DCB=∠DCE+∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,∴△ACD≌△BCE(SAS);(2)∵△ACD≌△BCE,∴∠A=∠B,∵∠BFH=∠AFC,∴∠BHF=∠ACB,∵∠ACB=30°,∴∠BHF=30°.【点睛】本题考查全等三角形的判定与性质,解答本题的关键是明确题意,利用全等三角形的判定与性质、数形结合的思想解答.22.(12分)(2020•玉山县一模)如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.你添加的条件是:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC.证明:AC=BD.【思路点拨】要使AC=BD,可以证明△ACB≌△BDA或者△ACO≌△BDO从而得到结论.【答案】解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.证明:(1)如果添加条件是AD=BC时,∵BC=AD,∠2=∠1,AB=BA,在△ABC与△BAD中,,∴△ABC≌△BAD,∴AC=BD;(2)如果添加条件是OC=OD时,∵∠1=∠2∴OA=OB∴OA+OD=OB+OD∴BC=AD又∵∠2=∠1,AB=BA在△ABC与△BAD中,,∴△ABC≌△BAD,∴AC=BD;(3)如果添加条件是∠C=∠D时,∵∠2=∠1,AB=BA,在△ABC与△BAD中,,∴△ABC≌△BAD,∴AC=BD;(4)如果添加条件是∠CAO=∠DBC时,∵∠1=∠2,∴∠CAO+∠1=∠DBC+∠2,∴∠CAB=∠DBA,又∵AB=BA,∠2=∠1,在△ABC与△BAD中,,∴△ABC≌△BAD,∴AC=BD.故答案为:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC.【点睛】本题考查了全等三角形的判定及性质;判定两个三角形全等的方法有:SSS,SAS,ASA,AAS,本题已知一边一角,所以可以寻找夹这个角的另外一边或者是另外两个角.23.(12分)(2019秋•新昌县期中)如图,△ABC中,∠A=40°,(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)【思路点拨】(1)根据三角形内角和定理和角平分线定义得出∠PBC+∠PCB=(∠ABC+∠ACB)=65°,根据三角形的内角和定理得出∠P的度数;(2)由三角形内角和定理和邻补角关系得出∠CBD+∠BCE=360°﹣130°=230°,由角平分线得出∠PBC+∠PCB=(∠CBD+∠BCE)=115°,再由三角形内角和定理即可求出结果;(3)由三角形的外角性质和角平分线的定义证出∠P=∠A,即可得出结果;(4)由(1)(2)(3),容易得出结果.【答案】解:(1)∵∠A=40°,∴∠ABC+∠ACB=140°,∴∠PBC+∠PCB=(∠ABC+∠ACB)=×140°=70°,∴∠BPC=180°﹣70°=110°;(2)∵∠DBC=∠A+∠ACB,∵P为△ABC两外角平分线的交点,∴∠DBC=∠A+∠ACB,同理可得:∴∠BCE=∠A+∠ABC,∵∠A+∠ACB+∠ABC=180°,∴(∠ACB+∠ABC)=90°﹣∠A,∵180°﹣∠BPC=∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC,∴180°﹣∠BPC=∠A+∠ACB+∠ABC,180°﹣∠BPC=∠A+90°﹣∠A,∴∠BPC=90°﹣∠A=70°;(3)∵点P是∠ABC与∠ACF平分线的交点,∴∠PBC=∠ABC,∠PCF=∠ACF,∵∠PCF=∠P+∠PBC,∠ACF=∠A+∠ABC,∴2(∠P+∠PBC)=∠A+∠ABC,∴∠P=∠A=20°;(4)若∠A=β,在(1)中,∠P=180°﹣(180°﹣β)=90°+β;在(2)中,同理得:∠P=90°﹣β;在(3)中同理得:∠P=∠A=β.【点睛】本题考查了三角形的内角和定理、三角形的角平分线、三角形的外角性质、邻补角关系等知识点;熟练掌握三角形内角和定理,弄清各个角之间的数量关系是解决问题的关键.。
数学七年级上册第一章第1节--《认识三角形》专题训练及答案解析
第一节《认识三角形》专题训练一.选择题(共17小题)1.如图所示,图中三角形的个数共有()A.1个B.2个C.3个D.4个(1)(3)(5)2.已知△ABC的一个外角为50°,则△ABC一定是()A.锐角三角形B.钝角三角形C.直角三角形D.锐角三角形或钝角三角形3.图中的三角形被木板遮住了一部分,这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能4.(2012•德州)不一定在三角形内部的线段是()A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线5.如图,AD是△ABC的中线,已知△ABD比△ACD的周长大6 cm,则AB与AC的差为()A.2cm B.3cm C.6cm D.12cm6.下面四个图形中,线段BE是△ABC的高的图是()A.B.C.D.7.下列说法正确的是()①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.A.①②③B.①②C.②③D.①③8.已知三角形两边长分别为3和8,则该三角形第三边的长可能是()A. 5 B.10 C.11 D.129.下列线段能构成三角形的是()A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,610.(2014•包头)长为9,6,5,4的四根木条,选其中三根组成三角形,选法有()A.1种B.2种C.3种D.4种11.已知不等边三角形的两边长分别是2cm和9cm,如果第三边的长为整数,那么第三边的长为()A.8cm B.10cm C.8cm或10cm D.8cm或9cm12.已知三角形的三边长分别为3、8、x,若x的值为偶数,则x的值有()A.6个B.5个C.4个D.3个13.已知三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是()A.1 B.3C.5D.914.已知在△ABC中,∠C=∠A+∠B,则△ABC的形状是()A.等边三角形B.锐角三角形C.直角三角形D.钝角三角形15.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°(15)(16)(17)(19)16.如图,在△ABC中,∠A=70°,∠C=60°,D、E分别是AB、AC上的点,且DE∥BC,则∠ADE 的度数为()A.60°B.70°C.50°D.80°17.如图,DE∥BC,∠A=60°,∠ADE=40°,则∠C为()A.60°B.7O°C.80°D.100°二.填空题(共5小题)18.(2014•淮安)若一个三角形三边长分别为2,3,x,则x的值可以为_________(只需填一个整数)19.如图所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是_________ cm.(20)(21)(22)20.(2014•威海)直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2=_________.21.(2014•随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_________度.2·1·c·n·j·y22.(2013•大连一模)如图,AB∥CD,CE与AB交于点A,BE⊥CE,垂足为E.若∠C=37°,则∠B= _________°.三.解答题(共3小题)23.如图:(1)在△ABC中,BC边上的高是_________.(2)在△AEC中,AE边上的高是_________.(3)在△FEC中,EC边上的高是_________.(4)若AB=CD=2cm,AE=3cm,则S△AEC=_________cm2,CE=_________cm.24.已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.25.如图,在△ABC中,∠A=80°,∠C=75°,求∠B的度数.第一节《认识三角形》专题训练参考答案一.选择题(共17小题)1.C.2.B.3.D.4.C.5.C.6.D.7.B.8.B.9.B.10.C.11.C.12.D.13.C.14.C.15.C.16.C.17.C.二.填空题(共5小题)18.419.620.40°21.7522.53°三.解答题(共3小题)23.如图:(1)在△ABC中,BC边上的高是AB.(2)在△AEC中,AE边上的高是CD.(3)在△FEC中,EC边上的高是FE.(4)若AB=CD=2cm,AE=3cm,则S△AEC=3cm2,CE=3cm.24.解:∵EF∥BC,∠CEF=55°,∴∠ECD=∠CEF=55°,∵CE是△ABC的一个外角平分线,∴∠ACD=2∠ECD=2×55°=110°,∵∠A=60°,∴∠B=∠ACD﹣∠A=110°﹣60°=50°,∵EF∥BC,∴∠EFB=180°﹣∠B=180°﹣50°=130°.25.解:∵∠A=80°,∠C=75°,∴∠B=180°﹣∠A﹣∠C=180°﹣80°﹣75°=25°.。
精选最新2019年七年级下册数学单元测试题《三角形的初步认识》完整版考核题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.在下列条件中,不能说明△ABC≌△A′B′C′的是()A.∠A=∠A′,∠B=∠B′,AC=A′C′B.∠A=∠A′,AB=A′B′,BC=B′C′C.∠B=∠B′,BC=B′C′、AB=A′B′D.AB=A′B′,BC=B′C′,AC=A′C ′答案:B△),管理员从BC边上的一点D出发,沿2.一块试验田的形状是三角形(设其为ABC→→→的方向走了一圈回到D处,则管理员从出发到回到原处在途中身DC CA AB BD体()A.转过90B.转过180C.转过270D.转过360答案:D3.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm答案:B4.如图,AC=AD,BC=BD,则图中全等三角形的对数是()A.6对 B.3对 C.2对D.1对答案:B5.如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是()A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE答案:B6.如图所示,△ABC中,AB=AC,BE=CE,则由“SSS”可直接判定()A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.以上答案都不对答案:B7.下列说法中正确的个数有( )①全等i 角形对应角所对的边是对应边,对应边所夹的角是对应角②全等三角形对应边所对的角是对应角,对应边所夹的角是对应角③全等三角形中的公共边是对应边,公共角是对应角,对顶角是对应角④两个全等三角形中,相等的边是对应边,相等的角是对应角A .1个B 2个C .3个D .4个答案:D8.如图所示,在直角三角形ABC 中,AC ≠AB ,AD 是斜边BC 上的高,DE ⊥AC ,DF ⊥AB ,垂足分别是E ,F ,则 图中与∠C (除°C 外)相等的角的个数是( )A .2个B .3个C .4个D .5个答案:B9.如果三角形的两边长分别为7和2,且它的周长为偶数,那么,第三边的长为( )A .5B .6C .7D .8答案:C10.下列条件中不能判定两个直角三角形全等的是 ( )A .两条直角边对应相等B .直角边和斜边对应相等C .两个锐角对应相等D .斜边和锐角对应相等答案:C二、填空题11.在ABC △中,BC 边不动,点A 竖直向上运动,A ∠越来越小,BC ∠∠,越来越大.若A ∠减少α度,B ∠增加β度,C ∠增加γ度,则αβγ,,三者之间的等量关系是 .解析:αβγ=+12.如图所示,AB=BD ,AC=CD ,∠ACD=60°, 则∠ACB= .解析:30°13.只要三角形三边的长度固定,这个三角形的和就完全确定,三角形的这个性质叫做三角形的.解析:形状,大小,稳定性14.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,则△ABC斜边上的高是,AB边上的高是,△ADB的BD边上的高是.解析:BD,BC,AD15.直角三角形的两个锐角的平分线AD,BE交于点0,则∠AOB= .解析:135°16.一个三角形最多有个钝角,最多有个直角.解析:1,117.在△ABC中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C,则∠A= ;(4)∠A=∠B,∠C=80°,则∠B= .解析:(1)70°;(2)90°;(3)60°;(4)50°三、解答题18.如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.解析:19.如图,已知BD=CD ,∠1=∠2,请说明△ABD ≌△ACD 的理由.解析:略20.2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB 的长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.解析:利用全等三角形的判定(AAS ,SAS ,ASA)来设计完成21.如图所示,有1l ,2l ,3l 三条公路交于A ,B ,C ,现要在△ABC 内建一加油站,使它到三 条公路的距离相等,问应如何建?作出加油站的位置,并说明理由.解析:分别作∠ABC与∠BCA的角平分线,两条角平分线的交点即为加油站的位置,根据角平分线上的点到角两边的距离相等即可说明22.如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.解析:略23.如图所示,已知AB=AE,∠BAE=∠CAD,AC=AD,说出下列结论成立的理由.(1)△ABC≌△AED;(2)BC=ED.解析:略24.如图所示,已知点A,B,C,D在一条直线上,AB=CD.AE=DF,EC=FB,说明∠ACE=∠DBF的理由.解析:略25.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略26.如图所示,△ABC≌△ADE,试说明BE=CD的理由.解析:略27.如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.解析:(1)48°;(2)42°;(3)132°28.如图所示,已知△ABC.画出AC边上的中线BM和∠BAC的平分线AD.解析:略29.如图所示,一张三个内角都相等的三角形纸片ABC,∠CBP=20°(图①).现将纸片沿射线BP折叠成图②的形状,BP交AC于点E,BC′交AC于点D.求图②中∠ADC′,∠AEC′的度数.解析:∠ADC′=80°,∠AEC′=20°30.在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.解析:∠A=70°,∠B=60°,∠C=50°。
精选新版2019年七年级下册数学单元测试题《三角形的初步认识》测试题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图所示,若根据“SAS”来说明△ABC≌△DBC,已知BC是公共边,需要补充的条件是()A.AB=DB,∠l=∠2 B.AB=DB,∠3=∠4C.AB=DB,∠A=∠D D.∠l=∠2,∠3=∠4答案:B2.以下列各组线段的长为边,能构成三角形的是()A.4 cm,5 cm,6 cm B.2 cm,3 cm,5 cmC.4 cm,4 cm。
9 cm D.12 cm,5 cm,6 cm答案:A3.如果三条线段的比是:(1)1:4:6;(2)1:2:3;(3)3:4:5;(4)7:7:11;(5)3 : 3:6,那么其中可构成三角形的比有()A.1种B.2种C.3种D.4种答案:B4.如图所示,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别是E,F,则图中与∠C(除°C外)相等的角的个数是()A.2个B.3个C.4个D.5个答案:B5.如图所示,在4×4的正方形网格中,∠l,∠2,∠3的大小关系是()A.∠l>∠2>∠3 B.∠1=∠2>∠3C.∠l<∠2=∠3 D.∠l=∠2=∠3答案:B6.如图所示,∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()A.120°B. ll5°C.110°D.105°答案:B7.如果三角形的一个外角是锐角,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.以上三种都可能答案:B8.如图①,在△ABC中,D,E分别是AB,AC的中点,把△ADE沿线段DE向下折叠.使点A落在BC上,记作点A′,得到图②,下列四个结论中,不一定成立的是()A.DB=DA B.∠B+∠C+∠l=180° C.BA=CA D.△ADE≌△A′DE答案:C9.如图,△ABD≌△CDB,∠ABD=40°,∠C=110°,则∠CBD等于()A.20°B.30°C.40°D.50°答案:B10.在下列长度的四根木棒中,能与4 cm ,9 cm 长的两根木棒钉成一个三角形的是( )A .4 cmB .5 cmC .9cmD .13 cm答案:C11.如图所示,BA=BD ,BC=BE ,根据“边角边”条件得到△ABE △DBC ,则需要增加条件 ( )A .∠A=∠DB .∠E=∠C C .∠A=∠CD .∠l=∠2答案:D12. 如图,已知∠C =∠D ,AC=AE ,要得到△ABC ≌△AED 还应给出的条件中错误的是( )A .∠BAD =∠EACB .∠B=∠EC .ED=BC AB =AE答案:D13.如图,在ABC ∆中,AB=AC=10,AB 的垂直平分线交AC 于G ,BC=7,则GBC ∆的周长是( )A .10B .20C .17D .13答案:C14..如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是( )A .甲和乙B .乙和丙C .只有乙D .只有丙答案:C15.如图△ABC 中,AB 的中垂线交AC 于D ,AB =10,AC =8,△DBC 的周长是a ,则BC 等于 ( )A . a -6B .a -8C .a -10D .10-a答案:B16. 一个三角形的三个内角中,至少有( )A . 一个锐角B . 两个锐角C . 一个钝角D .一个直角 答案:B17.如图所示,已知△ABC ≌△DCB ,那么下列结论中正确的是( )A .∠ABC=∠CDB ,∠BAC=∠DCB ,∠ACB=∠DBCB .∠ABC=∠DCB ,∠BAC=∠CDB ,∠ACB=∠ABDC.∠ABC=∠DCB,∠BAC=∠CDB,∠ACB=∠DBCD.∠ABC=∠DBC,∠BAC=∠CDB,∠ACB=∠ACD答案:C二、填空题18.如图,AC、BD相交于点O,∠A=∠D,,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .解析:AO = DO或AB = DC或BO=CO19.在Rt△ABC中,∠C=90°,CE是△ABC的中线,若AC=2.4 cm,BC=1.5 cm,则△AE的面积为.解答题解析:0.9cm220.判断正误,对的打“√”,错的打“×”.(1)经过线段中点的直线是线段的中垂线. ( )(2)以AB为直径可以作一个圆. ( )(3)已知两条边和一个角可以作唯一的三角形. ( )(4)已知两角一边可以作唯一的三角形. ( )解析:(1)× (2)√ (3)× (4)×21.如图所示,直线AD交△ABC的BC边于D点,且AB=AC.(1)若已知D为BC中点,则可根据,说明△ABD≌△ACD;(2)若已知AD平分∠BAC,可以根据说明△ABD≌△ACD;(3)若AD是BC的中垂线,则可以根据,说明△ABD≌△ACD,还可以根据说明△ABD≌△ACD.解析:(1)SSS;(2)SAS;(3)SAS,SSS22.如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△ABD= ,S△AOF= .解析:6,2三、解答题23.如图,已知D、E分别在AC、AB上,BD、CE相交于点O,且AB = AC,∠1=∠2. (1)写出图中所有的全等三角形.(2)要说明以上各对三角形全等,应先说明哪一对?并说明这一对三角形全等的理由.解析:(1)△AEO≌△ADO,△EOB≌△DOC,△ABO≌△ACO,△ABD≌△ACE;(2)△AOB≌△AOC,理由: △AOB≌△AOC(SAS) .24.如图所示,已知∠β=30°,a=3 cm.用直尺和圆规完成下列尺规作图(不写作法,保留痕迹),求作△ABC,使∠B=∠β,BC=a,AC=1.5 cm.AB CE DO12解析:略25.如图所示,已知AB=AE,∠BAE=∠CAD,AC=AD,说出下列结论成立的理由.(1)△ABC≌△AED;(2)BC=ED.解析:略26.如图所示,在四边形ABCD中,已知AB=AD,CB=CD,则在不添加其他线时,图中的哪两个角必定相等?请说明理由.解析:∠D=∠B,理由略27.如图所示,把△ACB沿着AB翻转,点C与点D重合,请用符号表示图中所有的全等三角形.解析:△ACE≌△ADE,△BCE≌△BDE,△ACB≌△ADB28.如图所示,CD是△ABC的高,∠BAE=25°,∠BCD=35°.求∠AEC的度数.解析:80°29.如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.解析:∠P=70°30.如图所示,已知△ABC的边AB和BC边上的中线AD,请把△ABC补画完整.解析:连结BD,并延长BD到C,使DC=BD,连结AC。
精选新版2019年七年级下册数学单元测试题-三角形的初步认识完整题(含参考答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如图,CD 是△ABC 的中线,DE 是△ACD 的中线,BF 是△ADE 的中线,若△AEF 的面积是 1cm 2,则△ABC 的面积是( )A . 4cm 2B .5 cm 2C . 6 cm 2D .8 cm 2答案:D2.下列各组长度的三条线段能组成三角形的是( )A .3cm,3cm , 6cmB .7 cm,4cm , 5cmC .3cm,4cm , 8cmD .4.2 cm, 2.8cm , 7cm答案:B3.下列说法错误的是( )A .有一个外角是锐角的三角形是钝角三角形B .有两个角互余的三角形是直角三角形C .直角三角形只有一条高D .任何一个三角形中,最大角不小于60度答案:C4. 一个三角形的三个内角中,至少有( )A . 一个锐角B . 两个锐角C . 一个钝角D .一个直角 答案:B5.如图,直线123,,l l l 表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处答案:D6.下列各条件中,不能作出惟一三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边答案:C7.如图,123,,∠∠∠的大小关系为( )A .213>>∠∠∠B .132>>∠∠∠C .321>>∠∠∠D .123>>∠∠∠ 答案:D8.下列条件中,不能作出唯一..三角形的是( ) A .已知两边和夹角B .已知两边和其中一边的对角C .已知两角和夹边D .已知两角和其中一角的对边答案:B9.如图所示,0P 平分∠AOB ,PE ⊥OB ,PF ⊥OA ,则下列结论中正确的个数有( ) ①OE=0F ;②FP=PE ;③OP ⊥EF ;④∠PEF=∠PFE ;⑤0P 平分∠FPE ;⑥PQ=0QA .6个B .5个C .4个D .2个答案:B10.如图所示,已知∠1=∠2,AD=CB ,AC ,BD 相交于点0,MN 经过点O ,则图中全等三角形的对数为( )A .4对B .5对C .6对D .7对答案:C11.如图,△ABD ≌△CDB ,∠ABD=40°,∠C=110°,则∠CBD 等于 ( )A .20°B .30°C .40°D .50°答案:B12.如图所示,△ADF ≌△CBE ,则结论:①AF=CE ;②∠1=∠2;③BE=CF , ④AE=CF .其中正确的个数为( )A.1个B.2个C.3个D.4个答案:C13.三角形的三边长都是整数,并且唯一的最长边是5,则这样的三角形共有()A 1个 B.2个 C.3个 D.4个答案:D二、填空题14.如图,在Rt△ABC中,AD是BC边上的高,若∠C=36°,则∠B= ,∠DAB= .解析:54°, 36°15.如图,AB=AC ,要使ACD∆≌,应添加的条件是____________ (添加一个条ABE∆件即可)解析:B C∠=∠(答案不唯一)16.如图所示,点B在AE上,且∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是(写一个即可):.解析:AC=AD或∠C=∠D等17.如图所示,已知点C是∠AOB角平分线上的一点,点P,P′分别在边0A,OB上,如果要得到OP=OP′,需添加以下条件中的某一个即可,请你写出所有可能结果的序号:.①∠0CP=∠OCP′;②∠0PC=∠OP′C;③PC=P′C;④PP′⊥0C;⑤PC⊥OA,P′C ⊥OB.解析:①②④⑤18.判断正误,在括号内打“√”或“×”.(1)三角形的一条角平分线把三角形分成面积相等的两部分. ( )(2)若一个三角形的两条高在这个三角形外部,则这个三角形是钝角三角形. ( )(3)直角三角形的三条高的交点恰为直角顶点. ( )(4)三角形的中线可能在三角形的外部. ( )解析:(1)× (2)√ (3)√ (4)×19.如图所示,△ABC中,∠B=∠C,FD⊥BC于D,DE⊥AB于E,∠AFD=155°,则∠EDF= .解析:65°20.(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.解析:(1)三角形的稳定性;(2)521.等腰三角形两边长分别是7cm和3 cm,则第三边长是.解析:7 cm22.已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.解析:2,8三、解答题23..(1)已知△ABC,求作:①BC边上的中线;②BC边上的高;③∠B的平分线;(2)已知线段a,c,∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α(不必写出作法).解析:略24.如图所示,已知∠α,线段a,b,求作一个三角形,使其两边长分别为a,a+b,两边的夹角等于∠α.解析:略25.如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整.①∠1=∠2;②BE=CF;③CD=FN;④△AEM≌△AFN.成立的有:.我选,理由如下:解析:①②④,以下略26.如图所示,把△ACB沿着AB翻转,点C与点D重合,请用符号表示图中所有的全等三角形.解析:△ACE≌△ADE,△BCE≌△BDE,△ACB≌△ADB27.在下列图形中,分别画出△ABC的三条高.解析:略28.如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.解析:∠P=70°29.如图所示,点E在△ABC的边AB上,点D在CA的延长线上,点F在BC的延长线上.试问:∠ACF与∠AED的关系如何?请说明理由.解析:∠ACF>∠AED,理由略30.已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.解析:∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°。
最新精选2019年七年级下册数学单元测试题《三角形的初步认识》完整考试题(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.下列长度的三条线段能首尾相接构成三角形的是()A.4,2,2 B.1,2,3,C.2,3,6 D.3,6,6答案:D2.如图,O是直线AB上的一点,过O点作射线OC,已知OD、OE分别平分∠AOC、∠COB.则△ODE是()A.钝角三角形B.锐角三角形C.直角三角形D.无法判断答案:C3.下列6组长度的线段中,可以首尾相接组成三角形的是()①3,4,5;②1,1,3;③1,2,3;④5,5,5;⑤2,2,5;⑥3,7,4A.①②③④⑤⑥B.①④⑤C.①③④D.①②③④答案:D4.下列条件中,不能作出唯一..三角形的是()A.已知两边和夹角B.已知两边和其中一边的对角C.已知两角和夹边D.已知两角和其中一角的对边答案:B5.如图所示,已知AD⊥BC,BD=CD,则①△ABD≌△ACD,②△ABD和△ACD不全等,③AB=AC,④∠BAD=∠CAD,以上判断正确的是()A.①B.②C.①③④D.①②③答案:C6.如图所示,若根据“SAS”来说明△ABC≌△DBC,已知BC是公共边,需要补充的条件是()A.AB=DB,∠l=∠2 B.AB=DB,∠3=∠4C.AB=DB,∠A=∠D D.∠l=∠2,∠3=∠4答案:B7.如图所示,△ABD≌△CDB,∠ABD=40°,∠CBD=30°,则∠C等于()A.20°B.100°C.110°D.115°答案:C8.△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.锐角或钝角三角形答案:B9.如图所示,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别是E,F,则图中与∠C(除°C外)相等的角的个数是()A.2个B.3个C.4个D.5个答案:B10.如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个答案:D11.下列说法中正确的是()A.从三角形一个顶点向它对边所在直线画垂线,此垂线就是三角形的高B.三角形的角平分线是一条射线C.直角三角形只有一条高D.钝角三角形的三条高所在的直线的交点在此三角形的外部答案:D12.将矩形ABCD沿AE折叠.得到如图所示的图形,已知∠CED′=60°.那么∠AED 的大小是()A.50°B.55°C.60°D.75°答案:C二、填空题13.如图,在Rt△ABC中,AD是BC边上的高,若∠C=36°,则∠B= ,∠DAB= .解析:54°, 36°14.如图,△ABC≌△CDA,A与C对应,D与B对应,则∠1与是对应角.解析:∠315.如图,BE,CD是△ABC的高,且AD=AE,判定△ACD≌△ABE的依据是“______”.解析:ASA(或AAS)16.如图所示,点B在AE上,且∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是(写一个即可):.解析:AC=AD或∠C=∠D等17.如图所示,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是.解析:三角形的稳定性18.△ABC与△DEF全等,AB=DE,若∠A=50°,∠B=60°,则∠D= .解析:50°或60°19.如图所示,点E,F在△ABC的BC边上,点D在BA的延长线上,则∠DAC=+ ,∠AFC=∠B+ =∠AEF+ .解析:∠B,∠C,∠BAF,∠EAF20.如图所示,∠1=135°,∠2=75°,则∠3的度数是.解析:30°21.(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.解析:(1)三角形的稳定性;(2)522.在Rt△ABC中,∠C=90°,其中∠A,∠B的平分线的交点为E,则∠AEB的度数为.解析:135°三、解答题23..(1)已知△ABC,求作:①BC边上的中线;②BC边上的高;③∠B的平分线;(2)已知线段a,c,∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α(不必写出作法).解析:略24.如图,AC=AE,AB=AD,∠1=∠2.请说明下列结论成立的理由:(1) △ABC≌△ADE;(2)BC=DE.解析:(1)∠1=∠2,则∠CAB=∠EAD,ΔABC≌ΔADE(SAS);(2)ΔABC≌ΔADE,则BC=DE25.根据条件作图:(1)任意画一个Rt△ABC,使∠C=90°;(2)画∠CAB的平分线交对边于D;(3)画出点D到Rt△ABC的斜边的垂线段DE.解析:略26.如图所示,已知AB=AC,D是BC的中点,说明AD⊥BC的理由.解:∵D是BC的中点( ),∴ (中点的定义).在△和△中,= ( ),= (已证),= ( ),∴△≌△ ( ),∴∠l=∠2( )∴∠+∠2= ,∴∠l=∠2= ,即AD⊥BC.解析:已知,BD=CD,ABD,ACD,AB,AC,已知,BD,CD,AD,AD,公共边,ABD,ACD,SSS,全等三角形对应角相等,l80°,90°27.如图所示,已知△ABC≌△DCB,其中AB=DC,试说明∠ABD=∠ACD的理由.解析:略28.如图所示,在△ABC中,∠B=35°,∠C=75°,AD是△ABC的角平分线.(1)∠BAC等于多少度?(2)∠ADC等于多少度?解析:(1)70°;(2)70°29.在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.解析:∠A=70°,∠B=60°,∠C=50°30.如图,已知∠A=∠D,AB=DE.AF=DC,图中有哪几对全等三角形?并选取其中一对说明理由.解析:△ABF≌△DEC,△FCB≌△CFE,△ABC≌△DEF,证明略。
浙教版七年级数学第一章三角形的初步认识测试(含答案)

第一章三角形的初步认识测试班级学号姓名一、细心选一选(每小题3分,共36分)1.下列长度的线段能首尾相接构成三角形的是………………………………( )A.4,2,2B.6,3,2C.2,3,6D.3,6,62.下列给出的每组线段,不能组成三角形的是………………………………( )A.5,12,13B.5,7,7C.5,7,12D.101,102,1033.三角形的三条角平分线是三条………………………………………………( )A.直线B.射线C.线段D.都可以4.在△ABC中,∠A=360,∠B=470.则△ABC是………………………………… ( )A.锐角三角形B.直角三角形C.钝角三角形D.锐角三角形或钝角三角形5. 在三角形中,最大的内角不能小于…………………………………………( )A.300B.450C.600D.9006. 三角形的三条高是……………………………………………………………( )A.直线B.射线C.线段D.都可以7.若AD是△ABC的中线则下列结论不正确的是……………………………… ( )A.AD平分∠BACB.BD=DCC.AD平分BCD.BC=2DC8.一个三角形的周长为15cm,其中两边都等于第三边的两倍,那么这个三角形最短的边为……………………………………………………………………………( )A.1cmB.2cmC.3cmD.4cm9.在△ABC中,已知∠A=∠B+∠C,则△ABC是…………………………………( )A.锐角三角形B.直角三角形C.钝角三角形D.无法确定10.在下列长度的四根木棒中能与4cm ,9cm 长的两根木棒首尾相接,钉成一个三角形的是……………………………………………………………………………( ) A.4cm B.5cm C.9cm D.13cm11.锐角三角形中,任意两角之和一定大于……………………………………( ) A.900B.1000C.1100D.120012.如图,△ABC 中,BO,CO 分别是∠BAC,∠ACB 的平分线,∠A=700,则∠BOC 的度数是…………………………………( ) A.1400B.1250C.1100D.700二、专心填一填:(每小题3分,共24分)13.三角形的内角和等于 ,三角形的外角和等于 .14.已知直角三角形的两锐角之比为1∶2,则这两个锐角的度数分别为 . 15.在△ABC 中,∠C=900, ∠A=370.则∠B= .16.在△ABC 中,∠B=∠C, ∠A=720.则∠C= . 17.a 、b 、c 是△ABC 的三边长,已知a=3cm ,b=7cm ,则第三边c 的取值范围是 .18.图中共有 个三角形,分别是 . 19.a 、b 、c 是△ABC 的三边长,已知△ABC 的周长为12cm ,a+b=2c, c+a=15cm,则a= cm,b= cm,c= cm. 20.如图,△ABC 中,∠B=∠C ,E 是AC 上一点,ED ⊥BC,DF ⊥AB,垂足分别是D 、F,若∠AED=1400,则∠C= .三、耐心答一答:(本题有6小题,共40分)21.(本题6分)已知△ABC 的周长为22cm ,三边的长度之比为2∶4∶5,求这个三角形的三边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3题图
第4
题图
第5题图
第6题图
七年级数学复习资料一:第一章三角形的初步认识复习(1)2011-7-10
一、填空题:
1、在Rt △ABC 中,一个锐角为250
, 则另一个锐角为________;
2、 在△ABC 中,AB =3,BC =7,则AC 的长x 的取值范围是___ _____;
3、如图,AD 是△ABC 的中线, △ABC 的面积为100cm 2,则△ABD 的面积是___ ___cm 2;
4、如图, △ABC 中, ∠ABC=740
,AD 为△ABC 的高,则∠BAD=_______;
5、如图, △ABC 中,AB=12,EF 为AC 的垂直平分线,若EC=8,则BE 的长为_______;
6、如图, △ABC 中,∠ABC 和∠ACB 的平分线交于点O,若∠A=700
,则∠BOC=_______; 7、如图, △ABC 中,高BD 、CE 相交于点H,若∠A=600
,则∠BHC=_____;
8、 如右图,∠1∶∠2∶∠3=1∶2∶3,则∠4=________; 9、已知△ABC 中, ∠A=
12∠B=1
3
∠C,则△ABC 为_____ ______ 三角形; 10、 如图,四边形ABCD 是一防洪堤坝的横截面,AE ⊥CD ,BF ⊥CD ,且AE=BF ,∠D=∠C ,问AD 与BC 是否相等?说明你的理由。
解:在△ADE 和△BCF 中, ∠D=∠C ( ) ∠AED=∠
(垂直的意义) AE=BF ( )
∴△ADE ≌△BCF (_______ ) ∴AD=BC (______________________)
二、选择题:
C
b
1、以下列各组线段为边,能组成三角形的是( );
A .2cm 、2cm 、4cm
B .2cm 、6cm 、3cm
C .8cm 、6cm 、3cm
D .11cm 、4cm 、6cm
2、 有下列关于两个三角形全等的说法: ㈠三个角对应相等的两个三角形全等;㈡三条边对应相等的两个三角形全等;㈢两角与一边对应相等的两个三角形全等;㈣两边和一角对应相等的两个三角形全等.其中正确的个数是( ); A.1 B.2 C.3 D.4
3、如图,可以作为三角形的外角是( ); A. ∠1 B.∠2 C.∠3 D.∠4
4、若三角形的一个外角小于和它相邻的内角,A.锐角三角形 B.钝角三角形 C. 直角三角形 D 无法确定
5、对于三角形的内角,下列判断中不正确的是( ); A.至少有两个锐角; B.最多有一个直角; C.必有一个角大于600
; D.至少有一个角不小于600
6、下列四组中一定是全等三角形的是( );
A .两条边对应相等的两个锐角三角形;
B .面积相等的两个钝角三角形;
C .斜边相等的两个直角三角形;
D .周长相等的两个等边三角形 7、若AD 是△ABC 的中线,则下列结论错误的是( ); A.AD 平分∠BAC B.BD=DC C.AD 平分BC D.BC=2DC
8.如果三角形的一个内角等于其他两个内角的差,那么这个三角形是 ( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定 9. 如图,在ΔABC 中,BC 边上的垂直平分线交AC 于点D,
已知AB=3,AC=7,BC=8,则ΔABD 的周长为: ( ) A.10 B.11 C.15 D.12
10.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 ( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定 三、解答题:
1、如图,在⊿ABC 中, ∠BAC 是钝角,按要求完成下列画图,并用适当的符号在图中表示(必须写出结论): ①∠BAC 的角平分线 ②AC 边上的高 ③AB
边上的中线
2、尺规作图:已知线段a,b 和∠α. 求作:ΔABC,使BC=a , AC=b , ∠C=∠α
(画出图形,保留作图痕迹,不写作法,写出结论)
3、如图:已知△ABC 中,AD ⊥BC 于D ,AE 为∠BAC 的平分线,且∠B=35°,
∠C=65°求∠DAE 的度数。
4、如图,已在AB=AC,AD=AE, ∠1=∠2,试说明ΔABD ≌ΔACE 的理由. 解:∵∠1=∠2( ) ∴∠1+∠ =∠2+∠
即:∠BAD=∠CAE 在△BAD 和△CAE 中 AB=AC ( ) ∠BAD=∠CAE
AD=AE ( ) ∴△BAD ≌△CAE( )
5、如图.在△ABC 和△DEF 中,B 、E 、C
、F 在同一直线上,下面有四个条件.请你在其中选三个作为已知条件,余下的一个作为结论,写出—个正确的结沦,并说明理由。
①AB =DE ; ②AC =DF ;
A
B
E D
C
③∠ABC =∠DEF ; ④BE =CF .(填写序号即可) 已知: ; 结沦: ; 理由:
6、设计三种不同方案,把ΔABC 的面积三等分
7、如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O,已知∠CAE=∠DBF,AC=BD. 说出∠CAD=∠
DBC 的理由. .
第一章《三角形的初步认识》复习1参考答案:
一、填空题:
1、650
2、4<x<10
3、50
4、160
5、4
6、1250
7、1200
8、720 9、直角 10、已知,BFC,已知,AAS,全等三角形的对应边相等。
二、选择题:
三、解答题:
1、(略).
2、(略).
3、150.
4、已知,BAE,BAE,已知,已知,SAS.
5、答案不唯一.
四、附加题:
1、(略);
2、解:∵∠CAE=∠DBF(已知)
∴∠CAB=∠DBA(等角的补角相等)
在△ABC和△DBA中
AC=BD(已知)
∠CAB=∠DBA
AB=BA(公共边)
∴△ABC≌△DBA(SAS)
∴∠ABC=∠BAD(全等三角形的对应角相等)
∴∠CAB-∠BAD=∠DBA-∠ABC
即:∠CAD=∠DBC.。
