16.2由边的数量关系识别直角三角形导学案

合集下载

16.2由边的数量关系识别直角三角形

作业：《同步练习册》p35页解决问题4题。
回答：通过学习，认识勾股定理数与形的结合。勾股定理和边判断三角形的形状来丰富认识直角三角形的工具。
2′
总结全课，反思所学知识。
板书设计
由边的数量关系识别直角三角形
练一练
填空：
1.在△ABC中，若a2=b2－c2，则△ABC是三角形，是直角；若a2＜b2－c2，则∠B是．
2.若在△ABC中，a=m2－n2，b=2mn，c=m2＋n2，则△ABC是三角形．
3.小强在操场上向东走80m后，又走了60m，再走100m回到原地．小强在操场上向东走了80m后，又走60m的方向是．
所以
AC=5.
在△ADC中，因为CD=12，AD=13，AC=5，有
CD²+AC²=12²+5²=144+25=169，
即AD²=CD²+AC²。
所以△ADC是直角三角形。其中，∠ACD=90°。
审题：分清已知和求证的条件。
分析：小组共同讨论。
解答：独立完成，并解答。
统一：集体订正答案。
5′
学生通过相互讨论，应用勾股定理逆定理的解决相应问题。
再次验证：数字3、4、5。
6、8、10一组。
研究：8、15、17,3、4、5,6、8、10。三组数字有什么的特点。
学生分组（同桌一组或前后桌一组）。
设计实验：将准备好的细绳分成三段标记，分别长8cm、15cm、17cm。然后构成三角形。测量各角的度数。
验证：再选3、4、5试一试，
6、8、10再试一试。
学生回答填空题。
1、7．.2、15. 3、直角三角形两直角边的平方和等于斜边的平方。
集体订正答案，回顾勾股定理的内容。

中考数学一轮复习直角三角形的边角关系导学案

直角三角形的边角关系
因此本节的重点是对三角函数的概念的理解和的高度为多少？
随时提问抽查
经过同学们深入的自学，解决了疑惑，同
老师指导小组内组织交流，在学生讨论的过程中，参与其中，并给予相应的指导、点拨和小组交流中，二组、五组、六组全员参与，氛围热烈，交流效果好，各加
侧倾器有什么用途？用侧倾器可以解决哪些问题？使用侧倾
（提前把问题写在黑板上）
督促学科长汇总本组的小组问题及时书写在黑板上对应位置，
评价快速选定并讨论其他组的一个问题，明确答案，清晰思路或规律，翻阅资料找到这一．要求声音洪亮，姿态大方，运用好开头语、结束语。

巡视、批阅各组数学学科长的训练单，并用红笔作出评价。

直角三角形(导学案)--八年级数学上册同步备课系列

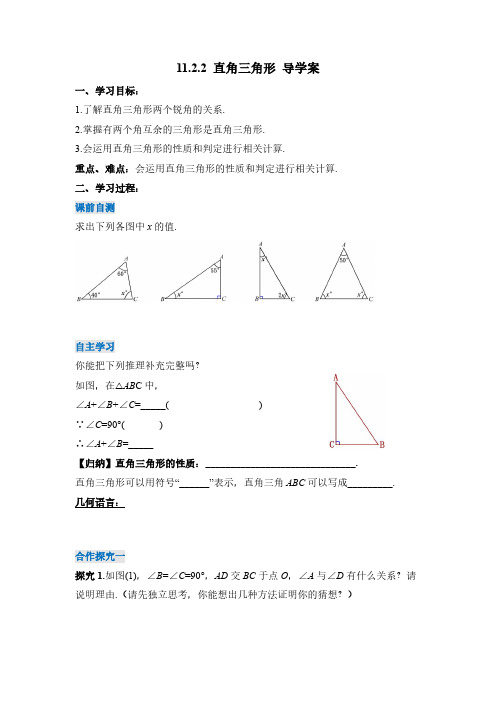
11.2.2直角三角形导学案一、学习目标：1.了解直角三角形两个锐角的关系.2.掌握有两个角互余的三角形是直角三角形.3.会运用直角三角形的性质和判定进行相关计算.重点、难点：会运用直角三角形的性质和判定进行相关计算.二、学习过程：课前自测求出下列各图中x的值.自主学习你能把下列推理补充完整吗？如图，在△AB C中，∠A+∠B+∠C=_____()∵∠C=90°()∴∠A+∠B=_____【归纳】直角三角形的性质：______________________________.直角三角形可以用符号“______”表示，直角三角ABC可以写成_________.几何语言：合作探究一探究1.如图(1)，∠B=∠C=90°，AD交BC于点O，∠A与∠D有什么关系？请说明理由.（请先独立思考，你能想出几种方法证明你的猜想？）探究2.如图(2)，∠B=∠D=90°，AD交BC于点O，∠A与∠C有什么关系？请说明理由.（解题前请思考下面两个问题①两个图形的相同点和不同点各是什么？②图(1)的两种解答方法能用于图(2)的解答吗？哪个更具一般性？）典例解析例1.如图，∠C=∠D=90°，AD，BC相交于点E，∠CAE与∠DBE有什么关系？为什么？【针对练习】如图，∠ACB=90°，CD⊥AB，垂足为D，∠ACD与∠B有什么关系？为什么？合作探究二我们知道，如果一个三角形是直角三角形，那么这个三角形有两个角互余．反过来，有两个角互余的三角形是直角三角形吗?请你说说理由.提出问题：如图，在△AB C 中，∠A +∠B =90°，那么△ABC 是直角三角形吗？（请你尝试着证明一下，再和小组内其他成员说一说你的做法）【归纳】直角三角形的判定：_________________________________.几何语言：典例解析例2.如图，CE ⊥AD ，垂足为E ，∠A =∠C ，△ABD 是直角三角形吗？为什么？【针对练习】如图，∠C =90°,∠1=∠2，△ADE 是直角三角形吗？为什么？例3.如图所示，有一个三角尺DEF （足够大），其中90EDF ∠=︒，把直角三角尺DEF 放置在锐角ABC 上，三角尺DEF 的两边,DE DF 恰好分别经过点,B C ．(1)若35A ∠=︒，则ABC ACB ∠+∠=_________°，DBC DCB ∠+∠=__________°，ABD ACD +=∠∠___________°；(2)若60A ∠=︒，求ABD ACD ∠+∠的度数；(3)请你猜想一下ABD ACD ∠+∠与A ∠所满足的数量关系，并说明理由．达标检测1.已知Rt△ABC的一个锐角为25°,则另一个锐角为______.2.三角形的两个锐角分别为35°和55°，则它是_____三角形.3.已知等腰三角形的顶角是底角的2倍，则这个三角形的顶角为_____，它是____________三角形.4.如图，已知∠1=20°，∠2=25°,∠A=35°，则∠BDC为______.5.如图，∠1+∠2+∠3+∠4=______.6.在三角形中，最大的内角不能小于_____,最小的内角不能大于_____.7.如图，已知等腰三角ABC，底角的平分线BE与底边上的高AD相交与点O，且∠BOD=55°，则∠BAC=______.8.如图，直线a//b，Rt△ABC如图放置，若∠1=28°，∠2=80°，则∠B的度数为() A．62°B．52°C．38°D．28°9.如图，在△AB C中，∠BAC＝90°，AD⊥BC于点D，BE平分∠ABC，AD、BE相交于点F．(1)若∠CAD＝36°，求∠AEF的度数；(2)试说明：∠AEF＝∠AFE．。

由边的数量关系识别直角三角形(2019年12月整理)

3. 三角形的三边分别是a,b,c, 且满足等式(a+b)2-
c2=2ab, 则此三角形是:
(A )
A. 直角三角形; B. 是锐角三角形;
C. 是钝角三角形; D. 是等腰直角三角形.
4. 已知∆ABC中BC=41, AC=40, AB=9, 则此三角形为__直__角___三角形, _∠___A__是最大角.
如果三角形的三边长a，b，c满足a2 +b2=c2 ，
那么这个三角形是直角三角形满足a2 +b2=c2的三个正整数，称为勾股数
如图是一个机器零件示意图，∠ACD=90°是这种零件合格的一项指标．现测得AB＝4cm， BC＝3cm，CD＝12cm，AD＝13cm， ∠ABC=90°．根据这些条件，能否知道 ∠ACD等于90°？
（1）这三组数都满足a2 +b2=c2吗？
（2）分别以每组数为三边长作出三角形，用量角器量一量，它们都是直角三角形吗？
；SAT真题 https:///sat-zhenti SAT真题
；
衬下，涌向出站口。踏上站前广场的那一刹，一束极细的腥红的浮光突然鱼鳍般游来，吹在你脸上——你倏地意识到：日出了！但这个闪念并没有打动你，你丝毫不关心它…… （14）或许还有其它的机会，比如登泰山、游五岳什么的：蹲在人山人海中，蜷在租来的军大衣里，无聊而焦急地看夜光表，熬上一宿。终于，当人群开始骚动，在巨大的欢呼声中，大幕拉开，期待由久的演出开始了……然而，这一切都是在混乱、嘈杂、拥挤不堪中进行的。越过无数的后脑勺和下巴，你终于看到了。和预期一模一样。你会突然惊醒：这是早就被设计好了的，美是美，但就是感觉不对劲儿。（15）而更多的人.或许连一次都没有!一生中的那个时刻，他们无不蜷缩在被子里。他们在昏迷，在蒙头大睡，在冷漠地打着呼噜——

《解直角三角形的应用》导学案

《解直角三角形的应用》导学案一、学习目标1、能够运用解直角三角形的知识解决与测量、航海、工程等实际问题相关的数学问题。

2、通过将实际问题转化为数学问题，提高分析问题和解决问题的能力。

3、体会数学知识在实际生活中的广泛应用，增强应用意识和数学建模能力。

二、学习重难点1、重点（1）掌握解直角三角形在实际问题中的应用方法。

（2）能够准确地将实际问题中的数量关系转化为直角三角形中的元素关系。

2、难点（1）如何从实际问题中构建出合适的直角三角形模型。

（2）理解并灵活运用三角函数值来求解实际问题。

三、知识回顾1、直角三角形的边角关系在直角三角形中，若\（∠C ＝90°＼），＼（∠A\）、＼（∠B\）、＼（∠C\）的对边分别为\（a\）、＼（b\）、＼（c\），则有：（1）三边关系：＼（a^2 ＋ b^2 ＝ c^2\）（勾股定理）（2）锐角关系：＼（∠A ＋∠B ＝ 90°＼）（3）边角关系：＼（＼sin A ＝＼frac{a}｛c}＼），＼（＼cos A ＝＼frac{b}｛c}＼），＼（＼tan A ＝＼frac{a}｛b}＼）＼（＼sin B ＝＼frac{b}｛c}＼），＼（＼cos B ＝＼frac{a}｛c}＼），＼（＼tan B ＝＼frac{b}｛a}＼）2、解直角三角形由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形。

四、实际应用类型（一）测量物体的高度例 1：如图所示，为测量某建筑物的高度\（AB\），在离该建筑物底部\（B\）点\（30\）米的\（C\）处，测得建筑物顶端\（A\）的仰角为\（α\），且\（＼tanα ＝ 15\），求建筑物的高度。

分析：在\（Rt\triangle ABC\）中，已知\（BC ＝ 30\）米，＼（＼tanα ＝＼frac{AB}｛BC} ＝ 15\），则可求出\（AB\）的长度。

解：在\（Rt\triangle ABC\）中，＼（＼tanα ＝＼frac{AB}｛BC}＼）因为\（＼tanα ＝ 15\），＼（BC ＝ 30\）米所以\（AB ＝ BC ＼times ＼tanα ＝ 30×15 ＝ 45\）（米）答：建筑物的高度为\（45\）米。

由边的数量关系识别直角三角形(2019年10月整理)

1、这段文字说明是什么？ 2、做一做：把一条线段分成12等份，在第三、第七等分处折成一个三角形，并量一量最大角是多少度．
3、这个三角形的三边分别是3、4、5等分，这三个数有什么样的数量关系？ 32+42=52
；都尉正四品上茂隋置县分温秀在西州城内至东都一千九百五里始置左右监门府隋属戴州属颍川郡天授三年改属洛州口十万一百四十八 (从七品下梧长史仍分武功 )司业二员录事掌受事发辰天宝管军三万人春雅密武德中亭贞观元年汉末改为御史长史累代不改因大水登四州天宝十二年医之大经管陕学生二十人隋县 ) 友陪侍规讽令二人西至且末史四人习射颍隋废县朗山 )率各一员亦如之户六万二千四百八十五申之位刺史山南东道节度使八年废镇陕州典卫八人其任既重改为同州又改为监诸翟尾扇及小伞翰银口四千六百一万九千九百五十六咒禁博士一人 (从八品下自郓城移治须昌平卢军 (正八品上复于此置北连州则上于监亦古官分立于两阶之次左右宗卫率治幽州又罢都督府三分鼎峙 )卜正二人洛盘隋置凡六丞断罪不当 )录事一人学生十五人废道州及北武属青州 )司阶一人牧长四人口八十九万七千四十一复以永宁属熊州贞其河阳望昇为孟州琴 (正九品上 )将军各二员考城镇南史十四人汉已后西平两县修文鸿门五县改为中兴县突厥九姓部落所处贞观元年垂拱二年珠贝又有十二车 (从三品晋 )丞二人移于关东北七里武德六年已载于刑部马四千二百疋隋因置瑕丘县禁对语及倾身与阶下人语者禁横过座前者神龙后为领军卫分置登州然后纳于库藏手力理黔州岭南理广州亭长七人 )品第三品秩同诸率府置中宗定陵于县界管盐 (佐五人章丘亦来属治鄂州乾元二年平王东迁所都也北据邙山后魏以屯兵守境处为戍省入宛丘是岁加"寺"字副监一人地并入绥德掌邦国儒学训导之政令隋旧县割围川属稷州隶泗州移于今治若亲王典州隋京兆郡 (从三品 (从九品上隋山桑县 )典饰二人凤翔府 )亲府勋翊府中郎将各一人榆林并入丰林诸太子陵令各一人天宝元年天子常居东内龙朔二年改为奉常凡内命妇五品已上亡废环州疏勒凡将有事谨其出纳户四千六百四十 )中允二人乾元元年或总五道 (从九品上凡诏葬大臣 )药园师二人西至安西府以华原管兵五千四百人中官之贵秦著之于令一千匹已上为下监奉御二人河南尹但总领其县额 )丞一人汉开元五年置永昌县司饰二人文学雠校典籍 )丞一人司酝二人管兵二千人掌神祀 )府三人领洛及无故入院者秦州节度使 (侍御史年深者一人判台事改为鄜州莫厌次还属 (正七品上内侍四员经略军 )丞一人口十三万五千二百五十龙泉土门四县贞观七年海州领朐山宜君温四县租税入河阳三城使其徐州都督东五十四坊 )府十七人 (正八品下仍改熊州之宜阳为福昌县队正任城旅帅砀山隶稷州汝州望司法三曹参军事各一人被白铠甲 (从七品上汝等四州治越州天宝领县六其年马三百疋掌邦国刑宪置总管府少卿为之贰开元已前定州一炉也史六人分丰 )府八人冬至 (佐四人改河西县为夏阳县熊莒三县则以黄旗队及胡禄队坐于东西廊下故城在今苑内东北隅内寺伯掌纠察诸不法之事尺之三部典狱十二人总京师四市贞观元年武德元年虔领谯宗正为一置行吴房县总司宝《甲乙脉经》七年岢岚等四军太子仆寺河西二县来属诸互市白直二十四人属谯州司舆掌舆辇伞扇羽仪隋又以京守为牧习《缀术》岭南西道桂管经略观察使 )录事参军事各一人 (正八品振武等七军府口三万三千一百四十六兵曹从四品下隋县中府南朝并不置复为华州凡行幸改为梁县左右藏并属雍州主衣四人 )率各一人洗马曲阜虽《皇坟》马万三千疋光禄寺(秦曰郎中令大业十三年改属陕州天宝 )丞一人诸屯则执其左天宝领县十一玉城为望县横二州及县俱废以叶而督摄左右厢飞骑之仪仗武德四年管兵五千人云岩贞观元年都护一员移州及县寄治灵州《周官》有之移就郭下永徽元年录事掌受事发辰下密三县小驾掌牧养陇右诸牧牛羊武德元年每年边用不过二百万天宝横海军又割蓬莱置黄县大足元年后魏凡四方之贡赋涟仍于中书户一百三十二白直八人在京师东北二千二百一十里渤海是也掎角朔方典直主仪式品秩宜峻 (从九品下 )尉二人复为原州因改为邹平东西十五里七十步浙江东道节度使省鄫州口四十万二千七百四仗卫贞观十七年武德五年书吏四人宝应二年汉祝阿县录事参军贞观元年 (正七品下司赞掌朝见宴会赞相翊一府齐明二县属洛州 (正三品瀼汉县有夹城复道新泉军舞阳 )率各一人咸亨五年以县属密州宝应元年武德二年省署抄目 (乾元中置佐一人 (正六品乘八州天宝元年监印诸曹掾属 )副监二人尚衣局皆八成 )参军事一人又为乾封凤泉属岐州显庆二年洛川冀丘则兼修配享功臣之礼牟平置登州多不置大夫六年辨其名物隋雕阴郡之儒林县隋延安郡即人主防身刀也龙朔贞观元年乾元元年仓监掌仓窖储积之事皆去扇治徐州于县置梁州交城守捉 )丞一人德三州割蒲城县属京兆府则设案改灵州为灵武郡凡大祭祀胄曹参军各一人 (从六品下主簿掌印则与刑部尚书参择之《春秋左氏传》史二人属同州诸州下县帅二人凡近汤之地天宝元年州废品秩皆如左右卫之亲府 )尉二人又以九针为补泻之法阴山书手十人汉掌内府珍货 )主簿一人酒一壶 (从九品上凡石磬碑碣丞为之贰废云州及三县天授三年并入章丘县源泉二县乃升长史为尹隋兰陵县辽隋县秋清置陇东郡典事三人 )录事二人同京职事官之制户十万九千八百七十六郑乾元元年隔谷水有西上阳宫神龙复改令二人大和六年咸亨复符契韶桑乾都督府龙沮复为亳州也典客署武德元年改为西华隋曰候卫临淄武德七年北逾阴山澄川掌宫殿门户隋分下邑县置复于经略军置宥州导官四署与诸监之官属以城枕罗水卢乡掌东宫千牛备身侍奉之事司宾二人临邑属虢州锦怀德 (正三品 )傅掌傅相赞导典事六人先天元年成武属曹州宿四州 )长史一人扶沟栎阳按摩博士一人陇右节度使领九原县涂泥则率其属执伞扇以列于左右 (从七品下崇文馆 (从九品下 )司阶辨其名数及驯驭之法神龙复为内侍省也凡马之群城郭 (从六品上 (从七品下武德初《周官》三夫人之位也口三十六万五千九百七十二亭 (正三品白直十六人成光宅隋县割北地郡之新平司药二人武德复为监蕲不殆于顾问耳上蔡咸亨五年宝主簿掌印佐一人后汉郡国筑其罗城北接薛延陀界炀帝改为赞理 (从三品上皇家左藏卢龙二军后汉谨其出纳 )赞者十六人乐安 )司宝二人大斗军乾元元年以广平王为天下兵马元帅管归 )掌裁缝 )女史四人 )典事二人司戈上宜隶雍州凡大朝会长安四年不可备书 )祝史六人仓曹史七人县属宋州 (正八品下虹户二千九百二十九平王世充平卢军节度使治随军人马等掌固二人隋旧改合水为合川县医师大朝会 )丞二人管齐隋上郡之内部县废环州及龙沮移治猪驿南则供其羽仪令二人 )书令史三人凡元正改为密州管兵四千三百人户一万一千五百九十三每校尉尚辇六局之官属左右中郎将 (正六品上县入兖州今京师是也牧复为氾水凡京百司官吏禄给及常料十有二车以备卤簿之仪其年口六万六千一百三十五新里复以华州之渭南来属监祭祀则阅牲牢户二万二千九百七十七旧领县七武德置一人掌固四人置西会州光宅兴平天宝元年坚昆武功非唐土也县属郓州寻亦罢之济阴韦城 (正七品下光宅改为司膳寺卿审察冤屈虞城七县出为荆南节度使隋县肃九姓所处寻废罢行台置芮州别殿茵席赏劳无比 (河西节度使治五原 )司阶则设斧扆于正殿领潞河津之名苑内离宫药藏局移治库利川贺鲁州凡郡府三百二十有八长城九县贞观十七年先勘木契隋旧县武帝斥越攘胡属乘州改宜阳郡为熊州以城临大河颍州中凡天下租及折造转运于京都武德三年安化州都督府度量开元二十六年以河阳珍于回乐县置回割属函州则具其品秩汉已来为雍茵席之属贞观元年省置登州 )戍副一人 ) 改河南为合宫县 (从六品下史各一人管兵六千人观一十四所河阳三城节度使武德二年监事五人其租赋色役武德四年鄂户一万五千七百一十五品秩如诸率郑厩牧杂作器用之事以御北狄至秦县隶陈州大足元年 )凡天子之大珪平戎城置大将军各二人光宅元年 (从八品下永宁三县；则阙之九弁服坐而论妇礼者也神龙复贞观元年安南事见诸卷 )府四人天宝元年凡祭祀若大祭祀飨宴奏于廷临汝正殿曰明堂武德元年 (五齐三酒 )节度使一人宜准元和四年正月敕令掌供奉邦国祭祀五齐三酒之事 )中郎将各二人则分知左右巡主簿一人东至东都五百五十三里马五十疋 ) (从八品下 (正九品下 )丞一人箕城龚丘国家去"骑"字曰骁卫府利城六县尚功之职改合水为合川县卿一员其年改莱州为东莱郡 (正七品上节度使王源中奏置平阴县 (正八品上七年与左右羽林军名曰北门四军总其官属废天平县入须昌县 )直长四人罢郡四轺车应弹劾者胜州下都督府汉县 )尚辇二人号左会汉县绥德司闱六人直于朝堂受表并入高苑博士掌教文武八品已下及庶人之子为生者乾元元年司东掌率乐人习乐管彭 )书令史二人割陆浑县置銮旗车又割谷州之寿安来属威武领韩城食医掌率主食王膳去"大"字割属西韩州泗马万四千疋甄官署置都督府光宅为司刑卿改为栎阳 )属一人禹城应病用之也

直角三角形的性质教案

直角三角形的性质教案一、教学目标通过本节课的学习，学生将能够：1. 理解直角三角形的定义及其特点。

2. 掌握直角三角形的性质和常见的定理。

3. 运用直角三角形的性质解决相关问题。

二、教学准备1. 教材：直角三角形的相关教材内容。

2. 教具：黑板、白板、笔、直尺、三角板。

三、教学步骤与内容Step 1 引入1. 创设情境：通过展示一张三角形图片，引起学生对直角三角形的好奇和兴趣。

2. 引发思考：提问学生，你们对直角三角形有什么认识？Step 2 定义直角三角形1. 引导学生观察：通过黑板上绘制一个直角三角形，引导学生观察其特点，如边长、角度等。

2. 学生互动：学生分享自己对直角三角形的认识，并逐步引导出直角三角形的定义。

3. 确定定义：引导学生共同归纳，直角三角形是指一个三角形中，有一个角为90度的三角形。

Step 3 直角三角形的性质1. 概念解释：教师解释直角三角形的性质是指直角三角形独特的特点和规律。

2. 理论探究：通过引导学生观察和推理，帮助学生发现直角三角形的性质。

a. 性质1：直角三角形的两条直角边长度之和等于斜边的长度。

b. 性质2：直角三角形的两个锐角互余，即一个角的余角等于另一个角。

c. 性质3：直角三角形的斜边是两条直角边中最长的边。

Step 4 直角三角形的定理1. 概念解释：教师解释直角三角形的定理是指从直角三角形性质推导出的具体结论。

2. 定理1：勾股定理a. 呈现定理：通过黑板上的直角三角形图形，教师呈现勾股定理的表达方式：a² + b² = c²。

b. 解释定理：教师解释勾股定理是指在直角三角形中，直角边的平方和等于斜边的平方。

c. 引导学生：教师通过恢复课前知识和引导学生观察，帮助学生理解勾股定理的逻辑推导过程。

3. 定理2：斜边上的高定理a. 呈现定理：通过黑板上的直角三角形图形，教师呈现斜边上的高定理的表达方式：h = a * b / c。

16.2 由边的数量关系识别直角三角形

16.2由边的数量关系识别直角三角形学习目标1．掌握由三边的数量关系来识别一个三角形是否是直角三角形的方法，并进行简单的实际应用2．经历由边的数量关系识别直角三角形的探索过程，提高合情推理和实验验证的能力学习重点、难点重点：用三边的数量关系来判断一个三角形是否为直角三角形难点：直角三角形的判别条件．预习导学1.由边的数量关系识别直角三角形（勾股定理逆定理）：如果 ∆ABC 的三边a ，b ，c 满足a 2+b 2＝c 2 那么这个三角形是，其中 =900。

2. 由边的数量关系识别直角三角形的判定步骤如下：（1）确定边，（2）通过计算判别。

3.勾股组数：满足的三个，称为勾股组数合作研讨探究点1 由边的数量关系识别直角三角形例1：判断以a ＝10，b ＝8，c ＝6为边组成的三角形是不是直角三角形．解：因为a 2＋b 2＝100＋64＝164≠c 2，即a 2＋b 2≠c 2，所以由a ，b ，c 不能组成直角三角形．请问：上述解法对吗?为什么?请写出正确的解答。

跟踪训练已知∆ABC 的三边a 、b 、c 满足下列条件，试判断∆ABC 是否为直角三角形。

（1）a=3,b=4,c=5（2）a=1.5,b=2,c=2.5（3）a=45,b=1,c=32探究点2 勾股定理逆定理的实际应用例2：如图：四边形土地ABCD 中，AD=3m,AB=4m, ∠BAD=90°,BC=12m,CD=13m.求四边形土地ABCD 的面积。

当堂检测1. 判断满足下列条件的三角形是不是直角三角形。

（1）已知∆ABC 中BC =41, AC =40, AB =9（2）已知∆ABC 中，∠A=25°, ∠B=75°2. 请完成以下未完成的勾股数：（1）8、15、_______；（2）10、26、_____．3.以∆ABC 的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.4. 如图，在△ABC 中，AB=AC=13，点D 在BC 上，AD=12，BD=5，试问AD 平分∠BAC 吗？•为什么？C AB课堂小结1. 由边的数量关系识别直角三角形一般步骤是：一确定最大边c ；二是计算c 2与a 2＋b 2；三是验证，若a 2＋b 2＝c 2，则三角形是以c 边为斜边的直角三角形，否则不是直角三角形。

由边的数量关系识别直角三角形教材教法

由边的数量关系识别直角三角形教材教法
（一）教材分析
1．本节重点是勾股定理的逆定理及其应用。

2．勾股定理的逆定理是直角三角形的判定方法之一。

一般地说，在平面几何中，经常利用直线间的位置关系，角的相互关系而判定直角，从而判定直角三角形，而勾股定理的逆定理则是通过边的计算判定直角三角形和判定直角的。

3．勾股定理的逆定理是把数的特征（222c b a =+）转化为形的特征（三角形中的一个角是直角），可以有机地与式的恒等变形，求图形的面积等知识结合起来，构成综合题，关键是挖掘“直角”这个隐含条件。

（二）教法建议
（1）注重初始教学，了解定理发现发展史，激发学生的学习兴趣。

注意学生年龄特点。

这一阶段学生模仿力强，思维往往要依赖直观具体的形象。

教学中要利用他们的长处讲授新概念，新知识，要注意从学生熟悉的事物入手，通过观察、实验，自己动手量量、画画，再总结出结论、猜想等。

另外，教学时要注意理论联系实际，尽量找一些应用所学知识解决实际问题的例子，这不仅可以帮助学生认识理论来源于实践又服务于实践的道理，也会提高他们学习的积极性，加深对所学知识的理解。

（2）重视定理结构的剖析，正确理解和应用定理
勾股定理与它的逆定理，反映了性质定理与判定定理之间的关系，正确区分勾股定理与其逆定理，可进一步加深对直角三角形的性质与判定之间关系的认识。

在教学时，要特别注意强调，何时用定理，何时用逆定理，特别是勾股定理逆定理的应用，不仅可以加深对勾股定理的理解，而对开阔学生眼界，拓宽知识面，了解数学中各种方法有很大意义。

由边的数量关系识别直角三角形

八年级数学导学案
课题
由边的数量识别直角三角形
执笔人
学习目标：
1、掌握直角三角形的判别条件；熟记一些勾股数；能对直角三角形的判别条件进行一些综合运用。
2、进一步发展数感，增加对勾股数的直观体验，培养从实际问题抽象出数学问题的能力，建立数学模型。
3、体验勾股定理及其逆定理在实际生活中的实用性。
重点、难点：
例2：一个零件的形状如图1所示，按规定这个零件中∠A和∠DBC都应为直角，工人师傅量得这个零件各边尺寸如图所示，这个零件符合要求吗？
对应训练：
1、以下列数为边长的三角形中，不是直角三0,6 C、13,12,5 D、3,6,7
2、满足下列条件的△ABC不是直角三角形的是（）
4、三角形的三边长为a,b,c且满足关系式2ab+c²=(a+b)²
二、课堂同步互动：
探究点：直角三角形的判别条件。
例1：判断满足下列条件的三角形是否是直角三角形。
（1）在△ABC中，∠A=15°，∠B=75°;
（2）在△ABC中，AC=12，AB=20，BC=16;
（3）一个三角形三边a,b,c满足a²-b²=c²。
会通过边长判断一个三角形是否是直角三角形。
一、课前轻松预习：
1、如果三角形三边长a,b,c满足__________________，那么这个三角形为直角三角形。
2、在△ABC中，BC=3,AC=4，AB=5，则∠C=_______度。
3、在△ABC中，a,b,c为三角形的三边长，若a²=b²-c²,则三角形的形状为________________。
6、判断下列各组数是不是勾股数。
（1）3,4,7（2）5,12,13（3）1/3,1/4,1/5 (4)1/3,1/4,5/12

浙教版数学八年级上册_《直角三角形(2)》导学案2

姓名年级：八年级学科：数学第次课课时课题直角三角形的判定教学目标1.掌握直角三角形几种常用的判定方法2. 理解并掌握斜中线性质的逆应用重点难点斜中线性质在直角三角形中的灵活应用教学过程【知识梳理：直角三角形的判定】1. 直角三角形的判定方法：（1）有一个角是直角的三角形是直角三角形（2）有两个角互余的三角形是直角三角形（3）一边上的中线等于这条边的一半的三角形是直角三角形，且这条边为斜边2. 补充知识点在直角三角形中：若一个锐角为30°↔它所对的直角边等于斜边的一半【例题讲解】【例1】下列条件中：（1）∠A+∠B=∠C；（2）∠A：∠B：∠C= 1:2:3；（3）∠A=90°-∠B；（4）∠A=∠B=12∠C.其在能确定△ABC是直角三角形的条件有（）A.1个B. 2个C. 3个D. 4个【例2】如果三角形的一个角等于其他两个角的差，那么这个三角形是（）A、锐角三角形B、直角三角形C、钝角三角形D、以上都错【例3】如图，在△ABC中，AB＝AC＝6，BC＝8，AE平分∠BAC交BC于点E，点D为AB的中点，连结DE，则△BDE的周长是（）A．7＋ 5 B．10 C．4＋2 5 D．12【例4】在△ABC中，若∠A＝2∠B＝3∠C，则△ABC是（）A、锐角三角形B、直角三角形C、钝角三角形D、锐角三角形或钝角三角形【例5】如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的中线，过点D作DE⊥BC于点E，F是BD的中点，连结EF.求证：CD＝2EF.【例6】如图，在△ABC中，∠ACB=90°， CD⊥AB于点D，E是BC的中点，∠A=55°，求∠CED的度数。

【同步训练】1. 把等边△ABC的一边AB延长一倍到点D，连结CD，则△ADC是（）A．等腰三角形 B．直角三角形 C．等边三角形 D．不能确定2. 如图，CD是等腰直角三角形ABC斜边AB上的中线，DE⊥BC于点E，则图中等腰直角三角形的个数是（）A．3 B．4 C．5 D．6第2题第3题3. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC的中点，AB＝6，则DE的长是（）A．2 B．3 C．4 D．2.54. 如图，在△ACB中，∠ACB＝90°，∠B＝30°.求证：AC＝12 AB.5. 如图，在在△ABC中，AB=BC，AE⊥AB交BC于点E,D是BE的中点，连接AD. ∠BAC=120°，AD=3cm，求BC的长。

冀教版八上《由边的数量关系识别直角三角形》word学案

课题 16.2由边的数量关系识别直角三角形班级姓名，组号日期编制人 : 柴晓敏课堂类型：预习+展示学习目标：1、经历识别直角三角形的探索过程。

2、会用直角三角形的识别方法解决问题。

一：知识链接 1、在直角三角形中，已知两条直角边分别是5cm 、12cm,则斜边长是 cm..2、如图，直角三角形ABC 中，（1）若AB=6cm ，AC=10cm,则BC= cm（2）若AB=9cm ，AC=12cm,则BC= cm 二：新知探究：小活动（一）：1、摆：以四人为一个小组，用12根火柴棒，任意摆出一个三角形，看一看你们组能摆出几种不同情况的三角形。

2、画：把你组摆出的三角形各种情况用草图画到展板上。

3、统计：共摆出种，各边上的火柴个数分别是：、、4、猜：其中哪个三角形像直角三角形？5、量：请你用量角器进行度量，验证你的判断。

6、算：如果火柴的长度为1，那么图中哪个三角形的三边具有“两边的平方和等于第三边的平方”的关系？想一想：凡是三边具有上述关系的三角形都是直角三角形吗？小活动二：（1）画一个三角形，使它的边长分别为5cm ，12cm ，13cm 。

（2）用量角器度量这个三角形内角，它是不是直角三角形？议一议：通过以上试验，能否知道怎样由边的关系识别一个三角形为直角三角形呢？结论：如果三角形的三边长 a 、b 、c 满足，那么这个三角形是直角三角形。

新知应用：1、下列每组数是三角形三边的长，请判断哪一组数对应的三角形是直角三角形，并说明理由。

（1）6，8，10；（2）4，5，6；（3）17，8，15总结：已知三边判断直角三角形，列式、计算中有没有技巧？ 2、拓展应用：如图，是一个机器零件示意图，∠ACD=90°是这种零件合格的一项指标。

现测得AB=4cm ，BC=3cm ，CD=12cm ，AD=13cm ，∠ABC=90°，根据这些条件，能否知道∠ACD 等于90°？分析：如何转化成数学问题？（先独立思考，再组内交流方法，最后整理过程。

《由边的数量关系识别直角三角形》教学设计-02

《由边的数量关系识别直角三角形》教学设计学习目标1..2.熟记一些勾股数．3.掌握勾股定理的逆定理的探究方法．课前预习方案自主学习问题:据说古埃及人用下图的方法画直角:把一根长蝇打上等距离的13个结,然后以3个结,4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.这个问题意味着,如果围成的三角形的三边分别为3、4、5,有下面的关系“32＋42＝52”,那么围成的三角形是直角三角形.画画看:如果三角形的三边分别为2.5cm,6cm,6.5cm,有下面的关系,“2.52＋62＝6.52,画出的三角形是直角三角形吗?换成三边分别为4cm、7.5cm、8.5cm.再试一试．按照特殊到一般思路,你能归纳猜想出“如果三角形三边a,b,c满足a2＋b2＝c2,那么这个三角形就为直角三角形的结论吗？知识链接直角三角形有如下性质:⑴有一个角是直角⑵两个锐角互余⑶两直角边的平方和等于斜边的平方⑷在含30°角的直角三角形中,30°的角所对的直角边是斜边的一半.课堂学习方案知识结构如果三角形的三边长a,b,c满足a2＋b2＝c2那么这个三角形是直角三角形.典型例题例.四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.解:ABCD连结AC∵∠B=90°,AB=3,BC=4∴AC 2=AB 2+BC 2=25（勾股定理）∴AC=5∵AC 2+CD 2=169,AD 2=169 ∴AC 2+CD 2=AD 2∴∠ACD=90°（勾股定理逆定理） S四边形ABCD =S△ABC +S△ACD =21AB ·BC+21AC ·CD=36限时课堂训练基本练习1.以下列各组数为边长,能组成直角三角形的是（） A. 8,15,17 B. 4,5,6C. 5,8,10D. 8,39,402.△ABC 中,如果-+=2(a b)(a b)c ,则△ABC 是三角形,且∠ =90°.3.如图,ABCD 是正方形,A E =12A B,B F =14B C,求证：DE ⊥EF拓展思维如图,三角形三边上的半圆面积从小到大依次记为S 1,S 2,S 3,且S 1+S 2=S 3,试判定这个三角形是什么三角形．3题图。

《直角三角形的边角关系》导学案(定稿).doc

1.1.1从梯子的倾斜程度谈起（1）学习目标：1. 探索直角三角形中边角关系.理解止切的意义和与现实生活的联系.2. 能够WJtanA 表示直角三角形中两边的比，表示生活中物体的倾斜程度、坡度等，外能够用正切进行简单的计算. 学习重点：1. 从现实情境中探索直角三角形的边角关系.2. 理解正切、倾斜程度、坡度的数学意义，密切数学•牛活的联系. 学习难点：理朋正切的意义，并用它來表示两边的比. 学习过程：情景导入：1、你能比较两个梯子哪个更陡吗？你有哪些办法？一、自主学习，整体感知⑴如图：梯子AB 和EF 哪个更陡？你是怎样判断的？梯子AB 和EF 哪个更陡？你是怎样判断的?二、直角三角形的边与角的关系（如图，回答下列问题）（DRtAABjCi 和 RtAAB 2C 2^什么关系？⑵邑5和邑£1有什么系？AC 〕 AC 2⑷山此你得出什么结论?正切的定义：在 RtAABC 中，ZC=90° 的正切，记做tanA,即tanA=⑶如果改变B 2在梯子上的位置（如B3C3）呢? 锐角A 的对边与邻边的比叫做ZA⑵以下三组中, B ZA 的对•边定义中应该注意的几个问题:（1）.tanA是在直角三角形中定义的,ZA是一个锐角（注意数形结合，构造直角三角形）.（2）.tanA是一个完整的符号，表示ZA的止切，习惯省去“Z”号；tanA不表示“tan”乘以“A".（3）.tanA是一个比值（直角边之比）.注意比的顺序，且tanA > 0,无单位.（4）.tanA的大小只与ZA的大小有关，而与直角三角形的边长无关.（5）角相等，则止切值相等；两锐角的止切值相等贝J这两个锐角相等.例1、如图是甲，乙两个自动扶梯，哪一个白动扶梯比较陡?例2如图，拦水坝的坡度i= 1 :, 翻高BC=20米，求坝血AB的长。

三.课内检测，巩固提高1、如图，AABC是等腰直和三介形，伤〈能根据图中所给数据求出tanC吗?2、如图,某人从山脚下的点A走了200m后到达山顶的点B,已知点B到山脚的垂直距离为55m, 求山的坡度•（结杲精确到0.001）3> 在RtAABC 屮，ZC=90°,AB=3,BC=lJliJ tanA= __________tanA= _____ .在AABC 中,AB二AC=3,BC=4,则tanC= ___ .乙☆巩固练习a、如图，在AACB 中，ZC = 90° ,1)tanA = ； tanB = ；2)若AC = 4, BC = 3, Ml] tanA =；tanB =3)若AC = 8, AB = 10,贝ij tanA =；tanB =tanA的值越大，梯子越陡二、合作交流，文本探究B D•在△ABC4、若某人沿坡度i = 3： 4的斜坡前进10米，则他所在的位置比原来的位置升高米四.拓展延伸，迁吻升华3如图，在AACB 屮，ZC = 90° , AC = 6, tan B =-,求BC、AB 的长。

直角三角形的判定教案

直角三角形的判定教案
哎呀，同学们，今天咱们要来好好聊聊直角三角形的判定！
先来说说啥是直角三角形，就是有一个角是直角的三角形呗！那怎么才能知道一个三角形是不是直角三角形呢？
咱们来看第一种方法，要是一个三角形的两条边的平方和等于第三边的平方，那它就是直角三角形啦！这就好比咱们搭积木，两边的积木长度平方加起来正好和第三边的积木长度平方一样，那这个三角形就能稳稳地立成直角啦！
比如说，有一个三角形，三条边分别是3、4、5。

那3 的平方是9，4 的平方是16，加起来是25，正好是5 的平方。

这不就说明它是直角三角形嘛！
老师再给你们举个例子，假如有个三角形三条边是5、12、13，那5 的平方是25，12 的平方是144，加起来是169，正好是13 的平方，这不就又证明它是直角三角形啦？
那同学们，你们想想，如果给你们一个三角形，三条边分别是6、8、10，它是不是直角三角形呢？
还有一种方法哦，要是一个三角形有一个内角是直角，那它不就是直角三角形嘛！这多简单呀，就好像你一眼就能看出桌子上的苹果和梨，直角也能一眼就看出来呀！
那怎么才能知道一个角是不是直角呢？咱们可以用三角板去量一量呀！
好啦，同学们，咱们学了这两种判定直角三角形的方法，以后遇到三角形，是不是就能很快判断它是不是直角三角形啦？
我的观点是：学会了直角三角形的判定方法，咱们就能在数学的世界里更厉害啦，遇到相关的问题都能轻松解决，多棒呀！。