高考数学专题知识点系列复习训练题及答案解析(珍藏版):04三角函数与解三角形真题汇编与预赛典型例题
高三数学三角函数与解三角形多选题知识点-+典型题附解析

高三数学三角函数与解三角形多选题知识点-+典型题附解析一、三角函数与解三角形多选题1.在ABC 中,角,,A B C 所对的边分别为,,a b c ,下列命题正确的是( )A .若::4:5:6a b c =,ABC 的最大内角是最小内角的2倍B .若cos cos a B b A c -=,则ABC 一定为直角三角形 C .若4,5,6a b c ===,则ABCD .若()()()cos cos cos 1A B B C C A ---=,则ABC 一定是等边三角形 【答案】ABD 【分析】对于A 选项,求得2A C =,由此确定选项正确.对于B 选项,求得2A π=,由此确定选项正确.对于C 选项,利用正弦定理求得ABC 外接圆半径,由此确定选项错误.对于D 选项,证得()()()cos cos cos 1A B B C C A -=-=-=,得到A B C ==,确定选项正确. 【详解】对于A 选项,A 角最小,C 角最大.由余弦定理得253616453cos 0256604A +-===>⨯⨯,16253651cos 0245408C +-===>⨯⨯,2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭,cos2cos A C =.0,022A C ππ<<<<,则02A π<<,所以2A C =,所以A 选项正确.对于B 选项,cos cos a B b A c -=,由正弦定理得sin cos sin cos sin A B B A C -=,()sin cos cos sin sin sin cos cos sin A B A B A B A B A B -=+=+,cos sin 0=A B ,由于0,0A B ππ<<<<,所以2A π=,故B 选项正确.对于C 选项,16253651cos 245408C +-===⨯⨯,0C π<<,sin C ==, 设三角形ABC 外接圆半径为R,则2sin 2sin c cR R C C=⇒===,故C 选项错误.对于D 选项,0,0,A B A B ππππ<<-<-<-<-<,故()1cos 1A B -<-≤,同理可得()()1cos 1,1cos 1B C C A -<-≤-<-≤, 要使()()()cos cos cos 1A B B C C A ---=, 则需()()()cos cos cos 1A B B C C A -=-=-=,所以0,0,0A B B C C A -=-=-=,所以A B C ==,所以D 选项正确. 故选:ABD 【点睛】利用正弦定理可求得三角形外接圆的半径R ,要注意公式是2sin aR A=,而不是sin aR A =.2.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,有以下四个命题中正确的是( ) A .22S a bc +的最大值为12B .当2a =,sin 2sin BC =时,ABC 不可能是直角三角形 C .当2a =,sin 2sin B C =,2A C =时,ABC的周长为2+D .当2a =,sin 2sin B C =,2A C =时,若O 为ABC 的内心,则AOB的面积为13- 【答案】ACD 【分析】利用三角形面积公式,余弦定理基本不等式,以及三角换元,数形结合等即可判断选项A ;利用勾股定理的逆定理即可判断选项B ;利用正弦定理和三角恒等变换公式即可判断选项C ;由已知条件可得ABC 是直角三角形,从而可以求出其内切圆的半径,即可得AOB 的面积即可判断选项D. 【详解】 对于选项A :2221sin 1sin 222cos 2222cos bc AS A b c a bc b c bc A bc Ac b==⨯++-+++- 1sin 4cos 2A A ≤-⨯-(当且仅当b c =时取等号).令sin A y =,cos A x =,故21242S ya bc x ≤-⨯+-, 因为221x y +=,且0y >,故可得点(),x y 表示的平面区域是半圆弧上的点,如下图所示:目标函数2yz x =-上,表示圆弧上一点到点()2,0A 点的斜率, 数形结合可知,当且仅当目标函数过点13,22H ⎛⎫ ⎪ ⎪⎝⎭,即60A =时,取得最小值3- 故可得32yz x ⎡⎫=∈⎪⎢⎪-⎣⎭, 又21242S yx bc x ≤-⨯+-,故可得213324312S a bc ⎛≤-⨯-= +⎝⎭, 当且仅当60A =,b c =,即三角形为等边三角形时,取得最大值,故选项A 正确; 对于选项B :因为sin 2sin B C =,所以由正弦定理得2b c =,若b 是直角三角形的斜边,则有222a c b +=,即2244c c +=,得33c =,故选项B 错误; 对于选项C ,由2A C =,可得π3B C =-,由sin 2sin B C =得2b c =,由正弦定理得,sin sin b c B C=,即()2sin π3sin c c C C =-, 所以sin32sin C C =,化简得2sin cos 22cos sin 2sin C C C C C +=, 因为sin 0C ≠,所以化简得23cos 4C =, 因为2b c =,所以B C >,所以3cos 2C =,则1sin 2C =,所以sin 2sin 1B C ==,所以π2B =,π6C =,π3A =,因为2a =,所以23c =,33b =,所以ABC 的周长为223+,故选项C 正确; 对于选项D ,由C 可知,ABC 为直角三角形,且π2B =,π6C =,π3A =,33c =,33b =,所以ABC 的内切圆半径为123433212r ⎛=+= ⎝⎭,所以ABC的面积为11122cr ⎛== ⎝⎭所以选项D 正确, 故选:ACD 【点睛】关键点点睛:本题的关键点是正余弦定理以及面积公式,对于A 利用面积公式和余弦定理,结合不等式得21sin 1sin 224cos 222cos S A Ab c a bc A A c b=⨯≤-⨯+-++-,再利用三角换元、数形结合即可得证,综合性较强,属于难题.3.设函数()2sin sin 2cos2f x x x =++,给出下列四个结论:则正确结论的序号为( ) A .()20f >B .()f x 在53,2ππ⎛⎫--⎪⎝⎭上单调递增 C .()f x 的值域为[]12cos2,32cos2-++ D .()f x 在[]0,2π上的所有零点之和为4π 【答案】ABD 【分析】由()23sin 22cos2f =+,结合3224ππ<<,可判定A 正确;作出函数2sin sin y x x =+的图象,可得函数()f x 的值域及单调性,可判定B 正确,C 不正确;结合函数的图象,可得()f x 在[]0,2π上的所有零点之和,可判定D 正确. 【详解】由题意,函数()2sin sin 2cos2f x x x =++, 可得()22sin 2sin 22cos23sin 22cos2f =++=+ 因为3224ππ<<,所以sin 2cos20>->,所以()20f >,所以A 正确; 由3sin ,222sin sin ,sin ,222x k x k y x x k Z x k x k πππππππ≤≤+⎧=+=∈⎨-+≤≤+⎩,作出函数2sin sin y x x =+的图象,如图所示, 可得函数()f x 是以2π为周期的周期函数,由函数2sin sin y x x =+的图象可知,函数()f x 在3(,)2ππ上单调递增, 又由()f x 是以2π为周期的周期函数,可得函数()f x 在5(3,)2ππ--上单调递增, 所以B 是正确的;由由函数2sin sin y x x =+的图象可知,函数()f x 的值域为[2cos 2,32cos 2]+, 所以C 不正确; 又由2223ππ<<,所以1cos 202-<<,则02cos21<-<, 令()0f x =,可得2sin sin 2cos2x x +=-,由图象可知,函数()f x 在[]0,2π上的所有零点之和为4π,所以D 正确. 故选:ABD.【点睛】本题主要考查了三角函数的图象与性质的综合应用,其中解答中熟记三角函数的图象与性质是解答的关键,着重考查转化思想,以及数形结合思想的应用,以及推理与运算能力,属于中档试题.4.ABC 中,2BC =,BC 边上的中线2AD =,则下列说法正确的有( ) A .AB AC →→⋅为定值B .2210AC AB += C .co 415s A << D .BAD ∠的最大值为30【答案】ABD 【分析】A 利用向量的加减法及向量的数量积公式运算即可,B 根据余弦定理及角的互补运算即可求值,C 利用余弦定理及基本不等式求出cos A 范围即可,D 根据余弦定理及基本不等式求出cos BAD ∠的最小值即可. 【详解】 对于A ,22413AB AC AD DB AD DB AD DB →→→→→→→→⎛⎫⎛⎫⋅=+-=-=-= ⎪⎪⎝⎭⎝⎭,AB AC →→∴⋅为定值,A 正确; 对于B ,cos cos ADC ADB∠=-∠2222222cos 2cos AC AB AD DC AD DC ADC AD DB AD DB ADB ∴+=+-⋅⋅∠++-⋅⋅∠2222AD DB DC =++2221110=⨯++=,故B 正确;对于C ,由余弦定理及基本不等式得224242122b c bc cosA bc bc bc+--=≥=-(当且仅当b c =时,等号成立),由A 选项知cos 3bc A =,22cos cos 1133cos AA A∴≥-=-, 解得3cos 5A ≥,故C 错误; 对于D,2222213cos 44c c BAD c c +-+∠==≥=(当且仅当c =立),因为BAD ABD ∠<∠, 所以(0,)2BAD π∠∈,又cos BAD ∠≥BAD ∠的最大值30,D 选项正确. 故选:ABD 【点睛】本题主要考查了向量的数量积运算,余弦定理,基本不等式,考查了推理能力,属于难题.5.(多选题)已知22tan 2tan 10x y --=,则下列式子成立的是( ) A .22sin 2sin 1y x =+ B .22sin 2sin 1y x =-- C .22sin 2sin 1y x =-D .22sin 12cos y x =-【答案】CD 【分析】对原式进行切化弦,整理可得:222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,结合因式分解代数式变形可得选项. 【详解】∵22tan 2tan 10x y --=,2222sin sin 210cos cos x yx y-⋅-=, 整理得222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,∴()()()22222221cos 1sin sin cos cos sin cos x x y x y y x ---⋅=+, 即22222221cos sin sin cos sin cos cos x y y x y x x --+⋅-⋅=, 即222sin 12cos 2sin 1y x x =-=-,∴C 、D 正确. 故选:CD 【点睛】此题考查三角函数的化简变形,根据弦切关系因式分解,结合平方关系变形.6.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,下列说法正确的是( )A .函数()y f x =的周期为πB .函数()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦单调递减 C .函数()y f x =的图象关于直线512x π=-对称 D .该图象向右平移6π个单位可得2sin 2y x =的图象 【答案】ACD 【分析】先根据图像求出()y f x =的解析式,再分别验证A 、B 、C 、D 是否正确. 对于A :利用周期公式求周期;对于B :利用复合函数“同增异减”求单调区间; 对于C :计算512f π⎛-⎫⎪⎝⎭,看512x π=-是否经过顶点; 对于D :利用“左加右减”判断. 【详解】由图像可知:A =2,周期24,2312T T ππππω⎛⎫=-=∴==⎪⎝⎭; 由=2sin 2212122f ππϕπϕ⎧⎛⎫⎛⎫⨯+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪<⎪⎩解得:3πϕ=故函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭对于A :4312T πππ⎛⎫=-= ⎪⎝⎭,故A 正确; 对于B :当236x ππ-≤≤- 时203x ππ-≤+≤,所以()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦上不单调.故B 错误;对于C :当512x π=-时255s 2121232in f πππ⎛⎫⎛⎫=-=- ⎪ ⎭⎝-⎪⎭+⎝⨯,即直线512x π=-是()y f x =的一条对称轴.故C 正确;对于D :()y f x =向右平移6π个单位得到2sin 222sin 263y x x ππ⎛⎫=-⨯+= ⎪⎝⎭,故D 正确. 故选:ACD 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.7.已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<的部分图象如图所示,则下列说法正确的是( )A .23ϕπ=B .()f x 的最小正周期为πC .()f x 的图象关于直线12x π=对称D .()f x 的图象关于点5,06π⎛⎫⎪⎝⎭对称 【答案】BCD 【分析】利用图象,把(3代入求ϕ,利用周期求出2ω=,从而2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,研究对称轴和对称中心.【详解】由图可知2sin ϕ=sin ϕ=,根据图象可知0x =在()f x 的单调递增区间上,又0ϕπ<<,所以3πϕ=,A 项错误;因为()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭,所以结合图像,由五点法得33ωπππ+=,解得2ω=,则()f x 的最小正周期2T ππω==,B 项正确;将12x π=代入2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,得2sin 21263f πππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,所以()f x 的图象关于直线12x π=对称,C 项正确﹔将56x π=代入可得552sin 0633f πππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,所以点5,06π⎛⎫⎪⎝⎭是()f x 图象的一个对称中心,D 项正确. 故选:BCD. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.8.在ABC 中,下列说法正确的是( ) A .若A B >,则sin sin A B > B .存在ABC 满足cos cos 0A B +≤ C .若sin cos A B <,则ABC 为钝角三角形 D .若2C π>,则22sin sin sin C A B >+【答案】ACD 【分析】A 项,根据大角对大边定理和正弦定理可判断;B 项,由A B π+<和余弦函数在()0,π递减可判断;C 项,显然2A π≠,分02A π<<和2A π>两种情况讨论,结合余弦函数的单调性可判断;D 项,根据2A B π+<和正弦函数的单调性得出0sin cos A B <<和0sin cos B A <<,再由放缩法可判断. 【详解】解:对于A 选项,若A B >,则a b >,则2sin 2sin R A R B >,即sin sin A B >,故A 选项正确;对于B 选项,由A B π+<,则A B π<-,且(),0,A B ππ-∈,cos y x =在()0,π上递减,于是cos cos A B >-,即cos cos 0A B +>,故B 选项错误﹔ 对于C 选项,由sin cos A B <,得cos cos 2A B π⎛⎫-< ⎪⎝⎭,cos y x =在()0,π上递减, 此时:若02A π<<,则2A B π->,则2A B π+<,于是2C π>; 若2A π>,则cos cos 2A B π⎛⎫-< ⎪⎝⎭,则2A B π->,于是2A B π>+,故C 选项正确;对于D 选项,由2C π>,则2A B π+<,则022A B ππ<<-<,sin y x =在0,2π⎛⎫⎪⎝⎭递增,于是sin sin 2A B π⎛⎫<- ⎪⎝⎭, 即0sin cos A B <<,同理0sin cos B A <<, 此时,22sin sin()sin cos cos sin sin sin sin sin sin sin C A B A B A B A A B B A B=+=+>⋅+⋅=+所以D 选项正确. 故选:ACD 【点睛】关键点点睛:正余弦函数的单调性,正弦定理的边角互化,大边对大角定理以及大角对大边定理,不等式的放缩等等,综合使用以上知识点是解决此类题的关键.二、数列多选题9.数列{}n a 满足11a =,且对任意的*n ∈N 都有11n n a a a n +=++,则下列说法中正确的是( ) A .(1)2n n n a +=B .数列1n a ⎧⎫⎨⎬⎩⎭的前2020项的和为20202021C .数列1n a ⎧⎫⎨⎬⎩⎭的前2020项的和为40402021D .数列{}n a 的第50项为2550 【答案】AC 【分析】用累加法求得通项公式,然后由裂项相消法求1n a ⎧⎫⎨⎬⎩⎭的和即可得. 【详解】因为11n n a a a n +=++,11a =, 所以11n n a a n +-=+, 所以2n ≥时,121321(1)()()()1232n n n n n a a a a a a a a n -+=+-+-++-=++++=, 11a =也适合此式,所以(1)2n n n a +=, 501275a =,A 正确,D 错误, 12112()(1)1n a n n n n ==-++, 数列1n a ⎧⎫⎨⎬⎩⎭的前2020项和为202011111404021223202020212021S ⎛⎫=-+-++-=⎪⎝⎭,B 错,C 正确. 故选:AC . 【点睛】本题考查用累加法数列的通项公式,裂项相消法求和.数列求和的常用方法: 设数列{}n a 是等差数列,{}n b 是等比数列,(1)公式法:等差数列或等比数列的求和直接应用公式求和; (2)错位相减法:数列{}n n a b 的前n 项和应用错位相减法; (3)裂项相消法;数列1{}n n ka a +(k 为常数,0n a ≠)的前n 项和用裂项相消法; (4)分组(并项)求和法:数列{}n n pa qb +用分组求和法,如果数列中的项出现正负相间等特征时可能用并项求和法;(5)倒序相加法:满足m n m a a A -+=(A 为常数)的数列,需用倒序相加法求和.10.在n n n A B C (1,2,3,n =)中,内角,,n n n A B C 的对边分别为,,n n n a b c ,n n nA B C 的面积为n S ,若5n a =,14b =,13c =,且222124n n n a c b ++=,222124n n n a b c ++=,则( )A .n n n ABC 一定是直角三角形B .{}n S 为递增数列C .{}n S 有最大值D .{}n S 有最小值【答案】ABD 【分析】先结合已知条件得到()222211125=252n n n n b c b c +++-+-,进而得到22225=n n n b c a +=,得A 正确,再利用面积公式得到递推关系1221875=644n n S S ++,通过作差法判定数列单调性和最值即可. 【详解】 由222124n n n a c b ++=,222124n n n a b c ++=得,222222112244n n n n n n a c a b bc+++++=+()2221122n n n a b c =++()2225122n n b c =++,故()222211125=252n n n n b c b c +++-+-, 又221125=0b c +-,22250n n b c ∴+-=,22225=n n n b c a ∴+=,故n n n A B C 一定是直角三角形,A 正确;n n n A B C 的面积为12n n n S b c =,而()4222222222221124224416n n n n n n n n n n n n a b c a b c a c a b b c +++++++=⨯=, 故()42222222222111241875161875==1616641n n n n n n n n n n n a b c a b bS S c c S +++++++==+,故22212218751875==6446434n n n n n S S SS S +-+--,又22125=244n n n n n b c b c S +=≤(当且仅当=n n b c 22121875=06344n n n S SS +∴--≥,又由14b =,13c =知n n b c ≠不是恒成立,即212n n S S +>,故1n n S S +>,故{}n S 为递增数列,{}n S 有最小值16=S ,无最大值,故BD 正确,C 错误. 故选:ABD. 【点睛】本题解题关键是利用递推关系得到()222211125=252n n n n b c b c +++-+-,进而得到22225=n n n b c a +=,再逐步突破.数列单调性常用作差法判定,也可以借助于函数单调性判断.。
高三数学三角函数与解三角形多选题知识点及练习题附解析

高三数学三角函数与解三角形多选题知识点及练习题附解析一、三角函数与解三角形多选题1.已知函数()(|sin |cos )(sin cos )f x x x x x =-+,x ∈R ,则( )A .()f x 在0,3π⎛⎫⎪⎝⎭上单调递减B .()f x 是周期为2π的函数C .()f x 有对称轴D .函数()f x 在(0,2)π上有3个零点【答案】BD 【分析】先判断出()f x 是周期为2π的函数,再在给定的范围上研究()f x 的单调性和零点,从而可判断BCD 的正误,再利用反证法可判断C 不正确. 【详解】因为[][]()(2)|sin(2)|cos(2)(sin(2)cos(2))f x x x x x f x πππππ+=+-+⋅+++=, 故()f x 是周期为2π的函数,故B 正确. 当0,3x π⎛⎫∈ ⎪⎝⎭时,22()sin cos cos 2f x x x x =-=-, 因为220,3x π⎛⎫∈ ⎪⎝⎭,而cos y u =-在20,3π⎛⎫ ⎪⎝⎭为增函数, 故()cos2f x x =-在0,3π⎛⎫⎪⎝⎭为增函数,故A 错误.由(sin cos )(sin cos )002x x x x x π⎧-+=⎨<<⎩可得4x π=或34x π=或74x π=,故D 正确.若()f x 的图象有对称轴x a =,因为()f x 的周期为2π,故可设[)0,2a π∈, 则()()2f x f a x =-对任意的x ∈R 恒成立,所以()()02f f a =即1(|sin 2|cos 2)(sin 2cos 2)a a a a -=-+①, 也有222f f a ππ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭即1(|cos 2|sin 2)(cos 2sin 2)a a a a =--+②, 也有222f f a ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭即1(|cos 2|sin 2)(cos 2sin 2)a a a a -=+-③, 由②③可得cos 2sin 20cos 2sin 2cos 2sin 2a a a a a a -≠⎧⎨+=-⎩, 故sin 20a =,由①②可得cos21a =-,故π2a或32a π=.若π2a,则21116222f π⎛⎛⎛⎫-=-+=- ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭,而2711162226f f ππ⎛⎛⎛⎫⎛⎫=-=-+≠- ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,若32a π=,则21911162226f f ππ⎛⎛⎛⎫⎛⎫=+-=-+≠-⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭这与()()2f x f a x =-对任意的x ∈R 恒成立矛盾, 故D 不成立. 故选:BD. 【点睛】方法点睛:与三角函数相关的函数性质的研究,应该依据一定次序,比如先研究函数的奇偶性或周期性,再根据前者把函数的研究限制在一定的范围内进行讨论.2.已知函数()()()sin 0,0,0πf x A x B A ωϕωϕ=++>><<的部分自变量、函数值如下表所示,下列结论正确的是( ).A .函数解析式为()5π3sin 226f x x ⎛⎫ ⎝=⎪⎭++ B .函数()f x 图象的一条对称轴为2π3x =- C .5π,012⎛⎫-⎪⎝⎭是函数()f x 图象的一个对称中心 D .函数()f x 的图象左平移π12个单位,再向下移2个单位所得的函数为奇函数 【答案】ABD 【分析】首先根据表格,利用最值求A 和B ,再根据周期求ω,以及根据最小值点求ϕ,求得函数的解析式,再分别代入23x π=-和512x π=-,判断BC 选项,最后根据平移规律求平移后的解析式. 【详解】由表格可知,2B =, 函数的最大值是5,所以25A B A +=+=,即3A =,当3x π=时,函数取得最小值,最小值点和相邻的零点间的距离是71234πππ-=,所以12244ππωω⨯=⇒=, 当3x π=时,322,32k k Z ππϕπ⨯+=+∈,解得:526k πϕπ=+,0ϕπ<<, 56πϕ∴=,所以函数()53sin 226f x x π⎛⎫=++ ⎪⎝⎭,故A 正确; B.当23x π=-时,252362πππ⎛⎫⨯-+=- ⎪⎝⎭,能使函数取得最小值,所以23x π=-是函数的一条对称轴,故B 正确; C.当512x π=-时,5520126ππ⎛⎫⨯-+= ⎪⎝⎭,此时2y =,所以5,212π⎛⎫- ⎪⎝⎭是函数的一个对称中心,故C 不正确; D.函数向左平移12π个单位后,再向下平移2个单位后,得()53sin 2223sin 23sin 2126y x x x πππ⎡⎤⎛⎫=+++-=+=- ⎪⎢⎥⎝⎭⎣⎦,函数是奇函数,故D 正确.故选:ABD 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证次区间是否是函数sin y x =的增或减区间.3.函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图象如图所示,则下列结论正确的是( )A .1()2sin 36f x x π⎛⎫=-⎪⎝⎭ B .若把()f x 的横坐标缩短为原来的23倍,纵坐标不变,得到的函数在[],ππ-上是增函数C .若把函数()f x 的图像向左平移2π个单位,则所得函数是奇函数 D .函数()y f x =的图象关于直线4x π=-对称【答案】ACD 【分析】根据函数的图象求出函数的解析式,得选项A 正确; 求出213263x πππ--得到函数在[],ππ-上不是增函数,得选项B 错误;求出图象变换后的解析式得到选项C 正确; 求出函数的对称轴方程,得到选项D 正确. 【详解】 A, 如图所示:1732422T πππ=-=, 6T π∴=,∴2163πωπ==,(2)2f π=,∴2(2)2sin()23f ππϕ=+=,即2sin()13πϕ+=, ∴22()32k k Z ππϕπ+=+∈, ∴2()6k k Z πϕπ=-∈,||ϕπ<,∴6πϕ=-,∴1()2sin()36f x x π=-,故选项A 正确;B, 把()y f x =的横坐标缩短为原来的23倍,纵坐标不变,得到的函数12sin()26y x π=-,[x π∈-,]π,∴213263x πππ--,∴12sin()26y x π=-在[π-,]π上不单调递增,故选项B 错误;C, 把()y f x =的图象向左平移2π个单位,则所得函数12sin[()]2sin 3223xy x ππ=-+=,是奇函数,故选项C 正确; D, 设1,,32,362x k k Z x k πππππ-=+∈∴=+当24k x π=-⇒=-,所以函数()y f x =的图象关于直线4x π=-对称,故选项D 正确.故选:ACD 【点睛】方法点睛:求三角函数的解析式,一般利用待定系数法,一般先设出三角函数的解析式sin()y A wx k ,再求待定系数,,,A w k ,最值确定函数的,A k ,周期确定函数的w ,非平衡位置的点确定函数的φ.4.已知函数()2sin 26f x x π⎛⎫=+⎪⎝⎭,则( ) A .函数()f x 的最小正周期为π B .()f x 的图像关于直线6x π=对称C .()f x 的图象关于点,03π⎛⎫⎪⎝⎭对称 D .()f x 在区间(0,)π上有两个零点【答案】ABD 【分析】借助于()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图像及y =sin x 的性质,对ABCD 四个选项一一验证: 对于A :利用2T πω=求周期;对于B :利用图像观察,也可以根据()26f π=判断;对于C :利用图像观察,也可以根据()13f π=否定结论;对于D :利用图像观察,可以得到()f x 在区间(0,)π上有两个零点. 【详解】对于A :函数()y f x =的周期222T πππω===故A 正确; 对于B :∵ ()2sin 22666f πππ⎛⎫=⨯+= ⎪⎝⎭,∴()f x 的图像关于直线6x π=对称,故B 正确;对于C :∵ 5()2sin 22sin 13366f ππππ⎛⎫⎛⎫=⨯+== ⎪ ⎪⎝⎭⎝⎭,故()f x 的图像不经过点,03π⎛⎫ ⎪⎝⎭,,03π⎛⎫⎪⎝⎭也不是其对称中心,故C 错误; 对于C :由图像显然可以观察出,()f x 在区间(0,)π上有两个零点.也可以令()()00f x x π=<<,即2sin 206x π⎛⎫+= ⎪⎝⎭,解得:512x π=或1112π,故()f x 在区间(0,)π上有两个零点,故D 正确.故选:ABD 【点睛】三角函数问题通常需要把它化为“一角一名一次”的结构,即()sin y A x B ωϕ=++的结构:(1)画出图像,利用图像分析性质;(2)用t x ωϕ=+借助于sin y x =或cos y x =的性质解题.5.已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<的部分图象如图所示,则下列说法正确的是( )A .23ϕπ=B .()f x 的最小正周期为πC .()f x 的图象关于直线12x π=对称D .()f x 的图象关于点5,06π⎛⎫⎪⎝⎭对称 【答案】BCD 【分析】利用图象,把(3代入求ϕ,利用周期求出2ω=,从而2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,研究对称轴和对称中心. 【详解】由图可知2sin 3ϕ=3sin ϕ=,根据图象可知0x =在()f x 的单调递增区间上,又0ϕπ<<,所以3πϕ=,A 项错误;因为()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭,所以结合图像,由五点法得33ωπππ+=,解得2ω=,则()f x 的最小正周期2T ππω==,B 项正确;将12x π=代入2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,得2sin 21263f πππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,所以()f x 的图象关于直线12x π=对称,C 项正确﹔将56x π=代入可得552sin 0633f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以点5,06π⎛⎫⎪⎝⎭是()f x 图象的一个对称中心,D 项正确. 故选:BCD. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值;(2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.6.已知函数)()lg1( 2.7)x x f x x e e e -=+-+≈⋯,若不等式(sin cos )2(sin 2)f f t θθθ+<--对任意R θ∈恒成立,则实数t 的可能取值为( )A .1BC .3D .4【答案】CD 【分析】令)()lgx x g x x e e -=+-,则()()1f x g x =+,可判断()g x 是奇函数且单调递增,不等式可变形可得(sin cos )(sin 2)g g t θθθ+<-,所以sin cos sin 2t θθθ>++,令()sin cos sin 2h θθθθ=++,换元法求出()h θ的最大值,()max t h θ>即可. 【详解】令)()lgx x g x x e e -=+-,则()()1f x g x =+,()g x 的定义域为R ,))()()lglgx x x x g x g x x e e x e e ---+=+-++-0=,所以()()g x g x -=-,所以()g x 是奇函数, 不等式(sin cos )2(sin 2)f f t θθθ+<--等价于[](sin cos )1(sin 2)1f f t θθθ+-<---,即(sin cos )(sin 2)(sin 2)g g t g t θθθθ+<--=-,当0x >时y x =单调递增,可得)lgy x =单调递增,x y e =单调递增,x y e -=单调递减,所以)()lgx x g x x e e -=+-在()0,∞+单调递增,又因为)()lg x x g x x e e -=+-为奇函数,所以)()lgx x g x x e e -=+-在R 上单调递增,所以sin cos sin 2t θθθ+<-,即sin cos sin 2t θθθ>++, 令()sin cos sin 2h θθθθ=++,只需()max t h θ>,令sin cos m θθ⎡+=∈⎣,则21sin 2m θ=+,2sin 21m θ=-,所以()21h m m m =+-,对称轴为12m =-,所以m =()max 211h m ==,所以1t >可得实数t 的可能取值为3或4,故选:CD 【点睛】关键点点睛:本题解题的关键点是构造函数()g x 奇函数且是增函数,将原不等式脱掉f 转化为函数恒成立问题.7.在ABC 中,下列说法正确的是( ) A .若A B >,则sin sin A B > B .若2C π>,则222sin sin sin C A B >+C .若sin cos A B <,则ABC 为钝角三角形D .存在ABC 满足cos cos 0A B +≤ 【答案】ABC 【分析】根据大角对大边,以及正弦定理,判断选项A ;利用余弦定理和正弦定理边角互化,判断选项B ;结合诱导公式,以及三角函数的单调性判断CD. 【详解】 A.A B >,a b ∴>,根据正弦定理sin sin a bA B=,可知sin sin A B >,故A 正确; B.2C π>,222cos 02a b c C ab +-∴=<,即222a b c +<,由正弦定理边角互化可知222sin sin sin C A B >+,故B 正确;C.当02A π<<时,sin cos cos cos 2A B A B π⎛⎫<⇔-<⎪⎝⎭,即22A B A B ππ->⇒+<,即2C π>,则ABC 为钝角三角形,若2A π>,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒>+成立,A 是钝角,当2A π=是,sin cos A B >,所以综上可知:若sin cos A B <,则ABC 为钝角三角形,故C 正确;D.A B A B ππ+<⇒<-,0,0A B πππ<<<-<,()cos cos cos A B B π∴>-=-,即cos cos 0A B +>,故D 不正确. 故选:ABC 【点睛】关键点点睛:本题考查判断三角形的形状,关键知识点是正弦定理和余弦定理,判断三角形形状,以及诱导公式和三角函数的单调性.8.已知函数()()tan (0)6ωωπ=->f x x ,则下列说法正确的是( ) A .若()f x 的最小正周期是2π,则12ω=B .当1ω=时,()f x 的对称中心的坐标为()π0()6π+∈Z k k , C .当2ω=时,π2π()()125-<f f D .若()f x 在区间()π3π,上单调递增,则203ω<≤ 【答案】AD 【分析】根据正切函数的性质,采用整体换元法依次讨论各选项即可得答案. 【详解】解:对于A 选项,当()f x 的最小正周期是2π,即:2T ππω==,则12ω=,故A 选项正确;对于B 选项,当1ω=时,()()tan 6f x x π=-,所以令,62k x k Z ππ-=∈,解得:,62k x k Z ππ=+∈,所以函数的对称中心的坐标为()0()62k k ππ+∈Z ,,故B 选项错误; 对于C 选项,当2ω=时,()()tan 26f x x π=-,()()()()ππ10tan 2tan tan 12126330f πππ⎡⎤-=⨯--=-=-⎢⎥⎣⎦,()()()2π2π1911tan 2tan tan 5563030f πππ=⨯-==-,由于tan y x =在,02π⎛⎫- ⎪⎝⎭单调递增,故()()π2π125f f ->,故C 选项错误; 对于D 选项,令,262k x k k Z ππππωπ-+<-<+∈,解得:233k k x ππππωωωω-+<<+ 所以函数的单调递增区间为:2,,33k k k Z ππππωωωω⎛⎫-++∈ ⎪⎝⎭,因为()f x 在区间()π3π,上单调递增,所以33,23k k Z k πππωωπππωω⎧-+≤⎪⎪∈⎨⎪+≥⎪⎩,解得:213,3k k k Z ω-+≤≤+∈,另一方面,233T ππππω=≥-=,32ω≤,所以2332k +≤,即56k ≤,又因为0>ω,所以0k =,故203ω<≤,故D 选项正确. 故选:AD【点睛】 本题考查正切函数的性质,解题的关键在于整体换元法的灵活应用,考查运算求解能力,是中档题.其中D 选项的解决先需根据正切函数单调性得213,3k k k Z ω-+≤≤+∈,再结合233T ππππω=≥-=和0>ω得0k =,进而得答案.二、数列多选题9.已知数列{}n a 的首项1a m =且满足()()14751221n n a a n n a a +⎡⎤=-⋅-⋅+-⋅-⎣⎦,其中n *∈N ,则下列说法中正确的是( )A .当1m =时,有3n n a a +=恒成立B .当21m =时,有47n n a a ++=恒成立C .当27m =时,有108111n n a a ++=恒成立D .当()2k m k N *=∈时,有2n k n k a a +++=恒成立【答案】AC【分析】 题设中的递推关系等价为1,231,n n n n n a a a a a +⎧⎪=⎨⎪+⎩为偶数为奇数,根据首项可找到{}n a 的局部周期性,从而可得正确的选项.【详解】因为()()14751221n n a a n n a a +⎡⎤=-⋅-⋅+-⋅-⎣⎦,故1,231,n n n n n a a a a a +⎧⎪=⎨⎪+⎩为偶数为奇数, 当1m =即11a =时,24a =,32a =,41a =,故{}n a 为周期数列且3n n a a +=,故A 正确.当21m =即121a =时,264a =,同理416a =,58a =,64a =,72a =,81a =,故58a a ≠,故B 错误.当2k m =即12k a =时,根据等比数列的通项公式可有11222k k k a -⎛⎫= ⎪⎝⎭=,+1+21,4k k a a ==,+32k a =, +1+3k k a a ≠,故D 错误.对于C ,当27m =时,数列{}n a 的前108项依次为:27,82,42,124,62,31,94,47,142,71,214,107,322,161,484242,121,364,182,91,274,, 137,412,206,103,310,155,466,233,700,350,175,526,263,790,395,1186,593,1780, 890,445,1336,668,334,167,502,251,754,377,1132,566,283,850,425,1276,638,319,958,479,1438,719,2158,1079,3238,1619,4858,2429,7288,3644,1822,911,2734, 1367,4102,2051,6154,3077,9232,4616,2308,1154,577,1732,866,433,1300,650, 325,976,488,244,122,61,184,92,46,23,70,35,106,53,160,80,40,20,10,5,16, 故1098a =,1104a =,1112a =,1121a =,1134a =,所以109112n n a a ++=对任意1n ≥总成立.(备注:因为本题为多选题,因此根据A 正确,BD 错误可判断出C 必定正确,可无需罗列出前108项)故选:AC.【点睛】方法点睛:对于复杂的递推关系,我们应该将其化简为相对简单的递推关系,对于数列局部周期性的研究,应该从特殊情况中总结出一般规律,另外,对于多选题,可以用排除法来确定可选项.10.设首项为1的数列{}n a 的前n 项和为n S ,已知121n n S S n +=+-,则下列结论正确的是( )A .数列{}n a 为等比数列B .数列{}n S n +为等比数列C .数列{}n a 中10511a =D .数列{}2n S 的前n 项和为2224n n n +---【答案】BCD【分析】 由已知可得11222n n n n S n S n S n S n++++==++,结合等比数列的定义可判断B ;可得2n n S n =-,结合n a 和n S 的关系可求出{}n a 的通项公式,即可判断A ;由{}n a 的通项公式,可判断C ;由分组求和法结合等比数列和等差数列的前n 项和公式即可判断D.【详解】因为121n n S S n +=+-,所以11222n n n n S n S n S n S n++++==++. 又112S +=,所以数列{}n S n +是首项为2,公比为2的等比数列,故B 正确;所以2n n S n +=,则2n n S n =-.当2n ≥时,1121n n n n a S S --=-=-,但11121a -≠-,故A 错误;由当2n ≥时,121n n a -=-可得91021511a =-=,故C 正确;因为1222n n S n +=-,所以2311222...2221222...22n n S S S n ++++=-⨯+-⨯++- ()()()23122412122...2212...224122n n n n n n n n n ++--⎡⎤=+++-+++=-+=---⎢⎥-⎣⎦ 所以数列{}2n S 的前n 项和为2224n n n +---,故D 正确.故选:BCD .【点睛】关键点点睛:在数列中,根据所给递推关系,得到等差等比数列是重难点,本题由121n n S S n +=+-可有目的性的构造为1122n n S S n n +++=+,进而得到11222n n n n S n S n S n S n++++==++,说明数列{}n S n +是等比数列,这是解决本题的关键所在,考查了推理运算能力,属于中档题,。
高考数学压轴专题新备战高考《三角函数与解三角形》难题汇编含答案

高考数学《三角函数与解三角形》课后练习一、选择题1.在ABC ∆中,若2sin sin cos 2CA B =,则ABC ∆是( ) A .等边三角形 B .等腰三角形C .不等边三角形D .直角三角形【答案】B 【解析】试题分析:因为2sin sin cos2CA B =,所以,1cos sin sin 2C A B +=,即2sin sin 1cos[()],cos()1A B A B A B π=+-+-=,故A=B ,三角形为等腰三角形,选B 。
考点:本题主要考查和差倍半的三角函数,三角形内角和定理,诱导公式。
点评:简单题,判断三角形的形状,一般有两种思路,一种是从角入手,一种是从边入手。
2.已知函数()sin f x a x x =的一条对称轴为56x π=,函数()f x 在区间()12,x x 上具有单调性,且()()12f x f x =-,则下述四个结论:①实数a 的值为1;②()()1,x f x 和()()22,x f x 两点关于函数()f x 图象的一条对称轴对称; ③21x x -的最大值为π, ④12x x +的最小值为23π. 其中所有正确结论的编号是( ) A .①②③ B .①③④C .①④D .③④【答案】B 【解析】 【分析】 根据56x π=是函数()f x 的一条对称轴,确定函数()f x ,再根据函数()f x 在区间()12,x x 上具有单调性,得到21x x -的最大值为2Tπ=,然后由()()12f x f x =-,得到()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称求解验证.【详解】 ∵56x π=是函数()f x 的一条对称轴,∴()53f x f x π⎛⎫=-⎪⎝⎭,令0x =,得()503f f π⎛⎫=⎪⎝⎭,即-1a =,①正确;∴()sin 3cos 2sin 3π⎛⎫=-=- ⎪⎝⎭f x x x x .又因为函数()f x 在区间()12,x x 上具有单调性, ∴21x x -的最大值为2Tπ=,且()()12f x f x =-, ∴()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称,∴121233223x x x x k ππ⎛⎫⎛⎫-+- ⎪ ⎪+π⎝⎭⎝⎭=-=π,k Z ∈, ∴12223x x k ππ+=+,k Z ∈,当0k =时,12x x +取最小值23π,所以①③④正确,②错误. 故选:B 【点睛】本题主要考查三角函数的图象和性质,还考查了推理论证,运算求解的能力,属于中档题.3.小赵开车从A 处出发,以每小时40千米的速度沿南偏东40︒的方向直线行驶,30分钟后到达B 处,此时,小王发来微信定位,显示他自己在A 的南偏东70︒方向的C 处,且A 与C 的距离为153千米,若此时,小赵以每小时52千米的速度开车直线到达C 处接小王,则小赵到达C 处所用的时间大约为( )()7 2.6≈A .10分钟B .15分钟C .20分钟D .25分钟【答案】B 【解析】 【分析】首先根据题中所给的条件,得到30BAC ∠=︒,20AB =,153AC =,两边和夹角,之后应用余弦定理求得5713BC =≈(千米),根据题中所给的速度,进而求得时间,得到结果. 【详解】根据条件可得30BAC ∠=︒,20AB =,153AC =,由余弦定理可得2222cos30175BC AB AC AB AC ︒=+-⋅⋅=,则13BC =≈(千米), 由B 到达C 所需时间约为130.2552=(时)15=分钟. 故选:B . 【点睛】该题是一道关于解三角形的实际应用题,解题的关键是掌握余弦定理的应用,属于简单题目.4.若函数()sin 2f x x =向右平移6π个单位后,得到()y g x =,则关于()y g x =的说法正确的是( ) A .图象关于点,06π⎛⎫- ⎪⎝⎭中心对称 B .图象关于6x π=-轴对称C .在区间5,126ππ⎡⎤--⎢⎥⎣⎦单调递增 D .在5,1212ππ⎡⎤-⎢⎥⎣⎦单调递增 【答案】D 【解析】 【分析】利用左加右减的平移原则,求得()g x 的函数解析式,再根据选项,对函数性质进行逐一判断即可. 【详解】函数()sin 2f x x =向右平移6π个单位,得()sin 2()sin(2)63g x x x ππ=-=-. 由23x π-=k π,得26k x ππ=+()k ∈Z ,所以,06π⎛⎫- ⎪⎝⎭不是()g x 的对称中心,故A 错; 由23x π-=2k ππ+, 得212k x π5π=+()k ∈Z ,所以()g x 的图象不关于6x π=-轴对称,故B 错;由222232k x k πππππ-≤-≤+,得1212k x k π5ππ-≤≤π+()k ∈Z , 所以在区间5,126ππ⎡⎤--⎢⎥⎣⎦上()g x 不单调递增,在5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增, 故C 错,D 对; 故选:D . 【点睛】解答三角函数问题时一般需将解析式化简为sin()y A x B ωϕ=++或cos()y A x B ωϕ=++,从而可利用正(余)弦型周期计算公式2||T πω=周期,对正弦型函数,其函数图象的对称中心为,k B πϕω-⎛⎫⎪⎝⎭,且对称中心在函数图象上,而对称轴必经过图象的最高点或最低点,此时函数取得最大值或最小值.5.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表: 黄赤交角 2341︒'2357︒'2413︒'2428︒'2444︒'正切值 0.439 0.444 0.450 0.455 0.461 年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ) A .公元前2000年到公元元年 B .公元前4000年到公元前2000年 C .公元前6000年到公元前4000年 D .早于公元前6000年【答案】D 【解析】 【分析】先理解题意,然后根据题意建立平面几何图形,在利用三角函数的知识计算出冬至日光与春秋分日光的夹角,即黄赤交角,即可得到正确选项. 【详解】解:由题意,可设冬至日光与垂直线夹角为α,春秋分日光与垂直线夹角为β, 则αβ-即为冬至日光与春秋分日光的夹角,即黄赤交角, 将图3近似画出如下平面几何图形:则16tan 1.610α==,169.4tan 0.6610β-==, tan tan 1.60.66tan()0.4571tan tan 1 1.60.66αβαβαβ---==≈++⨯g .0.4550.4570.461<<Q ,∴估计该骨笛的大致年代早于公元前6000年.故选:D . 【点睛】本题考查利用三角函数解决实际问题的能力,运用了两角和与差的正切公式,考查了转化思想,数学建模思想,以及数学运算能力,属中档题.6.{}n a 为等差数列,公差为d ,且01d <<,5()2k a k Z π≠∈,223557sin 2sin cos sin a a a a +⋅=,函数()sin(4)(0)f x d wx d w =+>在20,3π⎛⎫⎪⎝⎭上单调且存在020,3x π⎛⎫∈ ⎪⎝⎭,使得()f x 关于0(,0)x 对称,则w 的取值范围是( ) A .20,3⎛⎤ ⎥⎝⎦ B .30,2⎛⎤ ⎥⎝⎦C .24,33⎛⎤⎥⎝⎦D .33,42⎛⎤⎥⎝⎦【答案】D 【解析】 【分析】推导出sin4d =1,由此能求出d ,可得函数解析式,利用在203x π⎛⎫∈ ⎪⎝⎭,上单调且存在()()0020203x f x f x x π⎛⎫∈+-= ⎪⎝⎭,,,即可得出结论. 【详解】∵{a n }为等差数列,公差为d ,且0<d <1,a 52k π≠(k ∈Z ), sin 2a 3+2sin a 5•cos a 5=sin 2a 7, ∴2sin a 5cos a 5=sin 2a 7﹣sin 2a 3=2sin372a a +cos 732a a -•2cos 372a a +sin 732a a -=2sin a 5cos2d •2cos a 5sin2d , ∴sin4d =1,∴d 8π=.∴f (x )8π=cosωx ,∵在203x π⎛⎫∈ ⎪⎝⎭,上单调 ∴23ππω≥, ∴ω32≤; 又存在()()0020203x f x f x x π⎛⎫∈+-= ⎪⎝⎭,,, 所以f (x )在(0,23π)上存在零点, 即223ππω<,得到ω34>. 故答案为 33,42⎛⎤⎥⎝⎦故选D 【点睛】本题考查等差数列的公差的求法,考查三角函数的图象与性质,准确求解数列的公差是本题关键,考查推理能力,是中档题.7.已知函数()()πsin 06f x x ωω⎛⎫=-> ⎪⎝⎭,若()π02f f ⎛⎫=- ⎪⎝⎭在π0,2⎛⎫⎪⎝⎭上有且仅有三个零点,则ω= ( ) A .23B .2C .143D .263【答案】C 【解析】∵函数()()sin 06f x x πωω⎛⎫=-> ⎪⎝⎭,()02f fπ⎛⎫=- ⎪⎝⎭∴1sin()sin()6262πππω-=--=- ∴2266k πππωπ-=+或52,266k k Z πππωπ-=+∈ ∴243k ω=+或42,k k ω=+∈Z∵函数()f x 在0,2π⎛⎫⎪⎝⎭上有且仅有三个零点 ∴(,)6626x ππωππω-∈-- ∴2326ωππππ<-≤∴131933ω<≤ ∴143ω=或6ω= 故选C.8.设函数())cos(2)f x x x ϕϕ=+++(||)2πϕ<,且其图像关于直线0x =对称,则( )A .()y f x =的最小正周期为π,且在(0,)2π上为增函数B .()y f x =的最小正周期为2π,且在(0,)4π上为增函数 C .()y f x =的最小正周期为π,且在(0,)2π上为减函数D .()y f x =的最小正周期为2π,且在(0,)4π上为减函数【答案】C 【解析】试题分析:())cos(2)f x x x ϕϕ=+++2sin(2)6x πϕ=++,∵函数图像关于直线0x =对称,∴函数()f x 为偶函数,∴3πϕ=,∴()2cos 2f x x =,∴22T ππ==, ∵02x π<<,∴02x π<<,∴函数()f x 在(0,)2π上为减函数.考点:1.三角函数式的化简;2.三角函数的奇偶性;3.三角函数的周期;4.三角函数的单调性.9.若函数()sin()f x A x ωϕ=+(其中0A >,||)2πϕ<图象的一个对称中心为(3π,0),其相邻一条对称轴方程为712x π=,该对称轴处所对应的函数值为1-,为了得到()cos2g x x =的图象,则只要将()f x 的图象( )A .向右平移6π个单位长度 B .向左平移12π个单位长度 C .向左平移6π个单位长度 D .向右平移12π个单位长度【答案】B 【解析】 【分析】由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数()sin y A x ωϕ=+的图象变换规律,诱导公式,得出结论. 【详解】根据已知函数()()sin f x A x ωϕ=+(其中0A >,)2πϕ<的图象过点,03π⎛⎫ ⎪⎝⎭,7,112π⎛⎫-⎪⎝⎭, 可得1A =,1274123πππω⋅=-, 解得:2ω=. 再根据五点法作图可得23πϕπ⋅+=,可得:3πϕ=,可得函数解析式为:()sin 2.3f x x π⎛⎫=+ ⎪⎝⎭ 故把()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度, 可得sin 2cos236y x x ππ⎛⎫=++= ⎪⎝⎭的图象, 故选B . 【点睛】本题主要考查由函数()sin y A x ωϕ=+的部分图象求解析式,由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,函数()sin y A x ωϕ=+的图象变换规律,诱导公式的应用,属于中档题.10.若函数tan 23y x k π⎛⎫=-+ ⎪⎝⎭,0,6x π⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方,则实数k 的取值范围为( )A .)+∞ B .)+∞C .()+∞D .()【答案】A 【解析】 【分析】计算tan 203x π⎛⎫<-< ⎪⎝⎭,tan 23x k π⎛⎫->- ⎪⎝⎭恒成立,得到答案.【详解】∵0,6x π⎛⎫∈ ⎪⎝⎭,∴2033x ππ-<-<,∴tan 203x π⎛⎫-< ⎪⎝⎭,函数tan 23y x k π⎛⎫=-+ ⎪⎝⎭,0,6x π⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方, 即对任意的0,6x π⎛⎫∈ ⎪⎝⎭,都有tan 203x k π⎛⎫-+> ⎪⎝⎭,即tan 23x k π⎛⎫->- ⎪⎝⎭,∵tan 23x π⎛⎫-> ⎪⎝⎭k -≤,k ≥ 故选:A . 【点睛】本题考查了三角函数恒成立问题,转化为三角函数值域是解题的关键.11.函数()22sin 3cos 2f x x x =+-,2,36x ππ⎡⎤∈-⎢⎥⎣⎦的值域为( ) A .40,3⎡⎤⎢⎥⎣⎦B .41,3⎡⎤⎢⎥⎣⎦C .51,4⎡⎤⎢⎥⎣⎦D .50,4⎡⎤⎢⎥⎣⎦【答案】A 【解析】 【分析】化简得到()23sin 2sin 1f x x x =-++,设sin t x =,利用二次函数性质得到答案. 【详解】根据22sin cos 1x x +=,得()23sin 2sin 1f x x x =-++,2,36x ππ⎡⎤∈-⎢⎥⎣⎦, 令sin t x =,由2,36x ππ⎡⎤∈-⎢⎥⎣⎦,得1sin 1,2x ⎡⎤∈-⎢⎥⎣⎦, 故[]0,1t ∈,有2321y t t =-++,[]0,1t ∈,二次函数对称轴为13t =, 当13t =时,最大值43y =;当1t =时,最小值0y =,综上,函数()f x 的值域为40,3⎡⎤⎢⎥⎣⎦.故选:A . 【点睛】本题考查了三角函数值域,换元可以简化运算,是解题的关键.12.在三角形ABC 中,给出命题:p “2ab c >”,命题:q “3C π<”,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】 【分析】由余弦定理将2c 化为222cos a b ab C +-,整理后利用基本不等式求得12cos 2C +>,求出C 范围,即可判断充分性,取4a =,7b =,6c =,则可判断必要性不成立,两者结合可得正确的选项. 【详解】充分性:由余弦定理,2222cos c a b ab C =+-, 所以2ab c >,即222cos ab a b ab C >+-,整理得,2212cos a b C ab++>,由基本不等式,222a b ab +≥=,当且仅当a b =时等号成立, 此时,12cos 2C +>,即1cos 2C >,解得3C π<, 充分性得证;必要性:取4a =,7b =,6c =,则164936291cos 247562C +-==>⨯⨯,故3C π<,但228ab c =<,故3C π<推不出2ab c >.故必要性不成立; 故p 是q 的充分不必要条件. 故选:A 【点睛】本题主要考查充分必要条件的判断、余弦定理的应用和基本不等式的应用,考查学生分析转化能力,属于中档题.13.若θ是第二象限角,则下列选项中能确定为正值的是( )A .sinB .cosC .tanD .cos2θ【答案】C 【解析】 【分析】直接利用三角函数象限角的三角函数的符号判断即可. 【详解】由θ是第二象限角可得为第一或第三象限角,所以tan >0.故选C 【点睛】本题考查三角函数值的符号的判断,是基础题.14.在ABC ∆中,60B ∠=︒,AD 是BAC ∠的平分线交BC 于D ,2BD =,1cos 4BAC ∠=,则AD =( ) A .2 B 2C 3D .62【答案】A 【解析】 【分析】先求出6sin 4BAD ∠=,再利用正弦定理求AD. 【详解】∵21cos 12sin 4BAC BAD ∠=-∠=, ∴6sin BAD ∠=.在ABD ∆中,sin sin AD BD B BAD =∠, ∴3sin 222sin 6BAD BD BAD =⋅==∠. 【点睛】本题主要考查二倍角的余弦和正弦定理解三角形,意在考查学生对这些知识的理解掌握水平和分析推理能力.15.已知函数()()sin x f x x R ωφ+=∈,,其中0ωπφπ>-<,≤.若函数()f x 的最小正周期为4π,且当23x π=时,()f x 取最大值,是( ) A .()f x 在区间[]2ππ--,上是减函数 B .()f x 在区间[]0π-,上是增函数C .()f x 在区间[]0π,上是减函数 D .()f x 在区间[]02π,上是增函数 【答案】B 【解析】 【分析】先根据题目所给已知条件求得()f x 的解析式,然后求函数的单调区间,由此得出正确选项. 【详解】由于函数()f x 的最小正周期为4π,故2π14π2ω==,即()1sin 2f x x φ⎛⎫=+ ⎪⎝⎭,2ππsin 1,33π6f φφ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭=⎭⎝.所以()1πsin 26f x x ⎛⎫=+ ⎪⎝⎭.由π1ππ2π2π2262k x k -≤+≤+,解得4π2π4π4π33k x k -≤≤+,故函数的递增区间是4π2π4π,4π33k k ⎡⎤-+⎢⎥⎣⎦,令0k =,则递增区间为4π2π,33⎡⎤-⎢⎥⎣⎦,故B 选项正确.所以本小题选B. 【点睛】本小题主要考查三角函数解析式的求法,考查三角函数单调区间的求法,属于基础题.16.函数()sin())f x x x ωϕωϕ=+++(ω>0)的图像过点(1,2),若f (x )相邻的两个零点x 1,x 2满足|x 1-x 2|=6,则f (x )的单调增区间为( ) A .[-2+12k ,4+12k](k ∈Z ) B .[-5+12k ,1+12k](k ∈Z ) C .[1+12k ,7+12k](k ∈Z ) D .[-2+6k ,1+6k](k ∈Z )【答案】B 【解析】 【分析】由题意得()23f x sin x πωϕ⎛⎫=++⎪⎝⎭,根据相邻两个零点满足126x x -=得到周期为12T =,于是可得6π=ω.再根据函数图象过点()1,2求出2()k k Z ϕπ=∈,于是可得函数的解析式,然后可求出单调增区间. 【详解】由题意得()()()23f x sin x x sin x πωϕωϕωϕ⎛⎫=++=++ ⎪⎝⎭, ∵()f x 相邻的两个零点1x ,2x 满足126x x -=, ∴函数()f x 的周期为12T =,∴6π=ω, ∴()263f x sin x ππϕ⎛⎫=++⎪⎝⎭.又函数图象过点()1,2,∴2222632sin sin cos πππϕϕϕ⎛⎫⎛⎫++=+== ⎪ ⎪⎝⎭⎝⎭, ∴cos 1ϕ=, ∴2()k k Z ϕπ=∈, ∴()263f x sin x ππ⎛⎫=+ ⎪⎝⎭.由22,2632k x k k Z ππππππ-+≤+≤+∈,得512112,k x k k Z -+≤≤+∈,∴()f x 的单调增区间为[]()512,112k k k Z -++∈. 故选B . 【点睛】解答本题的关键是从题中所给的信息中得到相关数据,进而得到函数的解析式,然后再求出函数的单调递增区间,解体时注意整体代换思想的运用,考查三角函数的性质和应用,属于基础题.17.已知函数())(0f x x ωϕω=+>,)22ππ-<ϕ<,1(3A ,0)为()f x 图象的对称中心,B ,C 是该图象上相邻的最高点和最低点,若4BC =,则()f x 的单调递增区间是()A .2(23k -,42)3k +,k Z ∈ B .2(23k ππ-,42)3k ππ+,k Z ∈C .2(43k -,44)3k +,k Z ∈ D .2(43k ππ-,44)3k ππ+,k Z ∈【答案】C 【解析】 【分析】由三角函数图像的性质可求得:2πω=,6πϕ=-,即()sin()26f x x ππ=-,再令222262k x k ππππππ--+剟,求出函数的单调增区间即可.【详解】解:函数())(0f x x ωϕω=+>,)22ππ-<ϕ<, 因为1(3A ,0)为()f x 图象的对称中心,B ,C 是该图象上相邻的最高点和最低点,又4BC =,∴222()42T +=,即221216πω+=,求得2πω=.再根据123k πϕπ+=g ,k Z ∈,可得6πϕ=-,()3sin()26f x x ππ∴=-,令222262k x k ππππππ--+剟,求得244433k x k -+剟, 故()f x 的单调递增区间为2(43k -,44)3k +,k Z ∈, 故选:C . 【点睛】本题考查了三角函数图像的性质及单调性,属中档题.18.已知向量m =r (1,cosθ),(sin ,2)n θ=-r ,且m r ⊥n r,则sin 2θ+6cos 2θ的值为( ) A .12B .2C .D .﹣2【答案】B 【解析】 【分析】根据m r ⊥n r 可得tanθ,而sin 2θ+6cos 2θ22226sin cos cos sin cos θθθθθ+=+,分子分母同除以cos 2θ,代入tanθ可得答案. 【详解】因为向量m =r (1,cosθ),n =r(sinθ,﹣2),所以sin 2cos m n θθ⋅=-u r r因为m r ⊥n r ,所以sin 2cos 0θθ-=,即tanθ=2,所以sin 2θ+6cos 2θ22222626226141sin cos cos tan sin cos tan θθθθθθθ++⨯+====+++ 2. 故选:B. 【点睛】本题主要考查平面向量的数量积与三角恒等变换,还考查运算求解的能力,属于中档题.19.化简21sin 352sin 20︒︒-=( )A .12B .12-C .1-D .1【答案】B 【解析】 【分析】利用降次公式和诱导公式化简所求表达式,由此求得正确结论. 【详解】依题意,原式1cos7011cos701sin 20122sin 202sin 202sin 202--==-⨯=-⨯=-o o o o o o ,故选B. 【点睛】本小题主要考查三角函数降次公式,考查三角函数诱导公式,属于基础题.20.在极坐标系中,曲线4sin 6πρθ⎛⎫=+ ⎪⎝⎭关于( ) A .直线3πθ=对称B .直线6πθ=对称C .点2,6π⎛⎫⎪⎝⎭对称 D .极点对称【答案】A 【解析】 【分析】 由4sin 6πρθ⎛⎫=+ ⎪⎝⎭,得直角坐标方程:2220x x y -+-=,圆心为( ,又因为直线3πθ=即:y =过点(,由此便可得出答案.【详解】由曲线4sin 6πρθ⎛⎫=+⎪⎝⎭,即:24sin 6πρρθ⎛⎫=+ ⎪⎝⎭,又因为cos sin x y ρθρθ=⎧⎨=⎩,化简得曲线的直角坐标方程:2220x x y -+-=,故圆心为( . 又因为直线3πθ=,直角坐标方程为:y =,直线y =过点(,故曲线关于直线3πθ=对称故选:A. 【点睛】本题主要考查曲线及直线的极坐标方程与直角坐标方程的转化,以及圆关于过圆心的直线对称的知识,属于中等难度题目.。
高考数学——三角函数和解三角形经典试题练习及解析

1 / 14高考数学 三角函数和解三角形试题及解析1、在①ac =sin 3c A =,③=c 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由、问题:是否存在ABC ,它的内角,,A B C 的对边分别为,,a b c ,且sin 3sin AB ,6C π=,________?【解析】由sin 3sin A B可得:ab=不妨设(),0a b m m ==>,则:2222222cos 32c a b ab C m m m m =+-=+-⨯=,即c m =. 选择条件①的解析:据此可得:2ac m =⨯==,1m ∴=,此时1c m ==. 选择条件②的解析:据此可得:222222231cos 222b c a m m m A bc m +-+-===-,则:sin A ==sin 3c A m ==,则:c m ==选择条件③的解析: 可得1c mb m==,c b =,与条件=c 矛盾,则问题中的三角形不存在.2、在ABC 中,角,,A B C 所对的边分别为,,a b c、已知5,a b c ===2 / 14(Ⅰ)求角C 的大小; (Ⅱ)求sin A 的值;(Ⅲ)求sin 24A π⎛⎫+⎪⎝⎭的值。
【解析】(Ⅰ)在ABC中,由5,a b c ===222cos 22a b c C ab +-===, 又因为(0,)C π∈,所以4Cπ;(Ⅰ)在ABC 中,由4Cπ,a c ==可得sin sin a CA c===13; (Ⅰ)由a c <知角A为锐角,由sin A =cos A ==进而2125sin 22sin cos ,cos22cos 11313A A A A A ===-=,所以125sin(2)sin 2coscos2sin4441313A A A πππ+=+=+=. 【答案】(Ⅰ)4Cπ;(Ⅰ)sin 13A =;(Ⅰ)sin 2426A π⎛⎫+=⎪⎝⎭.3、在ABC 中,11a b +=,再从条件①、条件②这两个条件中选择一个作为己知,求: (Ⅰ)a 的值:(Ⅱ)sin C 和ABC 的面积、3 / 14条件①:17,cos 7c A ==-; 条件②:19cos ,cos 816A B ==、 注:如果选择条件①和条件②分别解答,按第一个解答计分、【答案】选择条件①(Ⅰ)8(Ⅱ)sin C =, S = 选择条件②(Ⅰ)6(Ⅱ)sin 4C =, 4S =. 【解析】选择条件①(Ⅰ)17,cos 7c A ==-,11a b +=22222212cos (11)72(11)7()7a b c bc A a a a =+-∴=-+--⋅⋅-8a ∴=(Ⅱ)1cos (0,)sin 7A A A π=-∈∴==,由正弦定理得:7sin sin sin sin 2a c C A C C ==∴=11sin (118)822S ba C ==-⨯=选择条件②(Ⅰ)19cos ,cos ,(0,)816A B A B π==∈,sin A B ∴====4 / 14由正弦定理得:6sin sin a b a A B ===(Ⅱ)91sin sin()sin cos sin cos 8161684C A B A B B A =+=+=+=11sin (116)622S ba C ==-⨯=4、在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且222b a c ac =+-, (Ⅰ)求角B 的大小;(Ⅱ)若a =c =2,求△ABC 的面积; (Ⅲ)求sinA +sinC 的取值范围.【答案】(1)60°; (2; (3)⎝. 【解析】(Ⅰ)由.2222a c b cosB ac+-=,得12cosB =,所以3B π=;(Ⅱ)由(Ⅰ)得1602ABCSacsin =︒=(Ⅲ)由题意得23sinA sinC sinA sin A π⎛⎫+=+-⎪⎝⎭32sinA =+6A π⎛⎫=+ ⎪⎝⎭.因为0<A <23π,所以26A π⎛⎫<+≤ ⎪⎝⎭.5 / 14故所求的取值范围是⎝.模拟试题1、△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A π++=、 (1)求A ;(2)若b c -=,证明:△ABC 是直角三角形、 【答案】(1)3A π=;(2)证明见解析【解析】(1)因为25cos cos 24A A π⎛⎫++=⎪⎝⎭,所以25sin cos 4A A +=,即251cos cos 4A A -+=, 解得1cos 2A =,又0A π<<, 所以3A π=;(2)因为3A π=,所以2221cos 22b c a A bc +-==, 即222b c a bc +-=①,又b c -=②, 将②代入①得,()2223b c b c bc +--=, 即222250b c bc +-=,而b c >,解得2b c =,6 / 14所以a =, 故222b a c =+, 即ABC 是直角三角形、2、在ABC 中,角,,A B C 的对边分别为,,a b c ,且满足πsin sin 3c A a C ⎛⎫=+⎪⎝⎭. (Ⅰ)求角C 的大小; (Ⅱ)若ABC的面积为1a b -=,求c 和()cos 2A C -的值.【答案】(Ⅰ)3π;(Ⅱ)c =,()6os 22c 1A C -=. 【解析】(Ⅰ)由正弦定理可知:sin sin a c A C =,已知πsin sin 3c A a C ⎛⎫=+ ⎪⎝⎭,所以sin sin sin (sin coscos sin )33C A A C C ππ⋅=⋅⋅+⋅,(0,)sin 0A A π∈∴≠,所以有sin tan 3C C C C π=⇒==.(Ⅱ)41sin 12,132a S ab C ab a b b =⎧=⋅=⇒=-=⇒⎨=⎩,由余弦定理可知:2222cos 13c a b ab C c =+-⋅=⇒=222cos sin 2b c a A A bc +-==⇒==,211sin 22sin cos 22cos 11313A A A A A =⋅==-=-, ()cos 2cos 2cos sin 2s 1111132i 6n 2A C A C A C -⨯=+⋅=-⋅=.7 / 143、ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知sin sin 2A Ca b A +=、 (1)求B ;(2)若ABC ∆为锐角三角形,且1c =,求ABC ∆面积的取值范围、【答案】(1) 3B π=;(2)(82. 【解析】(1)根据题意sin sin 2A C a b A +=,由正弦定理得sin sin sin sin 2A CA B A +=,因为0A π<<,故sin 0A >,消去sin A 得sin sin 2A CB +=、 0<B π<,02AC π+<<因为故2A C B +=或者2A CB π++=,而根据题意A BC π++=,故2A C B π++=不成立,所以2A CB +=,又因为A BC π++=,代入得3B π=,所以3B π=. (2)因为ABC 是锐角三角形,由(1)知3B π=,A B C π++=得到23A C π+=, 故022032C C πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得62C ππ<<.又应用正弦定理sin sin a cA C=,1c =, 由三角形面积公式有:222sin()111sin 3sin sin sin 222sin sin ABCC a A Sac B c B c B c C Cπ-=⋅=⋅=⋅=22sin cos cos sin 2123133(sin cos )4sin 43tan 38tan 8C C C C C ππππ-=⋅=-=+.又因,tan 62C C ππ<<>318tan C <+<8 / 14ABCS <<. 故ABCS的取值范围是,)824、在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c,且sin a b C +=、 (1)求角A 的大小;(2)若等差数列{}n a 的公差不为零,1sin 1a A =,且2a 、4a 、8a 成等比数列,求14n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n S 、【答案】(1)6π;(2)1n n + 【解析】Ⅰ1)由得,所以又(2)设的公差为,由(1)得,且,Ⅰ、又ⅠⅠⅠⅠ、ⅠⅠ5、在△ABC中,a=c=,________.(补充条件)(1)求△ABC的面积;(2)求sin(A+B).从①b=4,②cosB=,③sinA=这三个条件中任选一个,补充在上面问题中并作答.【答案】详见解析【解析】选择①(1)在△ABC中,因为a=c=,b=4,由余弦定理得22222a b ccosCab+-===,因为C∈(0,π),所以2sinC==,所以1142222S absinC==⨯=.(2)在△ABC中,A+B=π﹣C.所以()2sin A B sinC+==.选择②(1)因为cosB=,B∈(0,π),所以sinB==,因为a=c=11222S acsinB===.9/ 1410 / 14(2)因为a =c =,cosB =, 由b 2=a 2+c 2﹣2accosB,得222216b ⎛=+-= ⎝⎭,解得b =4,由sin sin bc BC ,解得2sinC =, 在△ABC 中,A +B =π﹣C ,()sin A B sinC +==. 选择③依题意,A为锐角,由sinA =cosA ==,在△ABC中,因为a=c =cosA =, 由余弦定理a 2=b 2+c 2﹣2bccosA,得222210b =+-, 解得b =2或b =4,(1)当b =2时,112122S bcsinA ==⨯=. 当b =4时,114222S bcsinA ==⨯=. (2)由a=c=,10sinA =,a c sinA sinC=,得2sinC =,11 / 14在△ABC 中,A +B =π﹣C ,()sin A B sinC +==. 7、在ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,并且222b c a bc +-=.(1)已知_______________,计算ABC 的面积;请①a =2b =,③sin 2sin C B =这三个条件中任选两个,将问题(1)补充完整,并作答.注意,只需选择其中的一种情况作答即可,如果选择多种情况作答,以第一种情况的解答计分.(2)求cos cos B C +的最大值.【答案】(1)见解析(2)1【解析】(1)若选②2b =,③sin 2sin C B =、sin 2sin C B =,24c b ∴==,222b c a bc +=+,2221cos 22b c a A bc +-∴==, 又(0,)A π∈,3A π∴=、ABC ∆∴的面积11sin 24222S bc A ==⨯⨯⨯= 若选①a =②2b =、由222b c a bc +=+可得3c =,222b c a bc +=+,2221cos 22b c a A bc +-∴==, 又(0,)A π∈,12 / 14 3A π∴=、ABC ∆∴的面积11sin 2322S bc A ==⨯⨯=、 若选①a =③sin 2sin C B =sin 2sin C B =,2c b ∴=,又222b c a bc +=+,222472b b b ∴+=+,可得b =,c =ABC ∆∴的面积11sin 22MBC S bc A ===、 (2)3A π=1cos cos cos cos[()]cos cos()cos cos 332B C B B B B B B B πππ∴+=+-+=-+=-1cos sin()26B B B π==+ 203B π<<, 5366B πππ∴<+< ∴当3B π=时,sin()cos cos 6B B C π+=+有最大值1、 8、已知ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,5a b +=,3c =,________.是否存在以a ,b ,c 为边的三角形?如果存在,求出ABC 的面积;若不存在,说明理由.从①1cos 3C =;②1cos 3=-C;③sin 3C =这三个条件中任选一个,补充在上面问题中并作答.13 / 14【答案】详见解析【解析】若选取条件①1cos 3C =,此时sin 3C ==, 因为5a b +=,所以()2222252a b a b ab ab +=+-=-, 由余弦定理,22225291cos 223a b c ab C ab ab +---===,解得6ab =, 则22252613a b +=-⨯=,所以()222213121a b a b ab -=+-=-=, 所以1a b -=±,又5a b +=,解得32a b =⎧⎨=⎩或者23a b =⎧⎨=⎩, 所以存在以a ,b ,c为边的三角形,其面积为12323ABCS =⨯⨯⨯=若选取条件②1cos 3=-C , 因为5a b +=,所以()2222252a b a b ab ab +=+-=-, 由余弦定理,22225291cos 223a b c ab C ab ab +---===-,解得12ab =, 则22252121a b +=-⨯=,所以()22221240a b a b ab -=+-=-<,显然不成立,所以不存在以a ,b ,c 为边的三角形.若选取条件③sin C =,得1cos 3C =±, 由选取条件①可知,当1cos 3C =时,存在以a ,b ,c为边的三角形,其面积为ABC S =14 / 14由选取条件②可知,当1cos 3=-C 时,不存在以a ,b ,c 为边的三角形. 9、在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12 n mile 的水面上,有蓝方一艘小艇正以每小时10 n mile 的速度沿南偏东75°方向前进,若侦察艇以每小时14 n mile 的速度,沿北偏东45°+α方向拦截蓝方的小艇、若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值、【解析】如图,设红方侦察艇经过x 小时后在C 处追上蓝方的小艇,则AC Ⅰ14x ⅠBC Ⅰ10x ⅠⅠABC Ⅰ120°.根据余弦定理得(14x )2Ⅰ122Ⅰ(10x )2Ⅰ240x cos 120°Ⅰ解得x Ⅰ2.故AC Ⅰ28ⅠBC Ⅰ20.根据正弦定理得ⅠⅠ解得sin αⅠⅠ.所以红方侦察艇所需要的时间为2小时,角α的正弦值为.。
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》难题汇编附答案解析
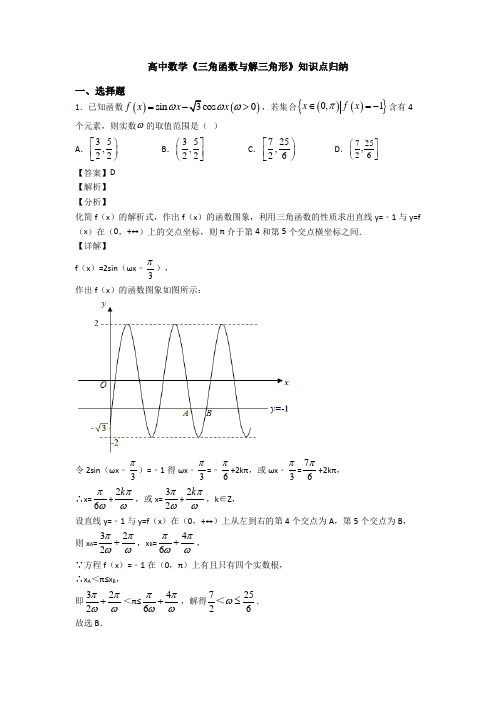
高中数学《三角函数与解三角形》知识点归纳一、选择题1.已知函数()()sin 3cos 0x f x x ωωω=->,若集合()(){}0,1x f x π∈=-含有4个元素,则实数ω的取值范围是( ) A .35,22⎡⎫⎪⎢⎣⎭B .35,22⎛⎤⎥⎝⎦C .725,26⎡⎫⎪⎢⎣⎭D .725,26⎛⎤⎥⎝⎦【答案】D 【解析】 【分析】化简f (x )的解析式,作出f (x )的函数图象,利用三角函数的性质求出直线y=﹣1与y=f (x )在(0,+∞)上的交点坐标,则π介于第4和第5个交点横坐标之间. 【详解】 f (x )=2sin (ωx ﹣3π), 作出f (x )的函数图象如图所示:令2sin (ωx ﹣3π)=﹣1得ωx ﹣3π=﹣6π+2kπ,或ωx ﹣3π=76π+2kπ, ∴x=6πω+2k πω,或x=32πω+2k πω,k ∈Z , 设直线y=﹣1与y=f (x )在(0,+∞)上从左到右的第4个交点为A ,第5个交点为B , 则x A =322ππωω+,x B =46ππωω+, ∵方程f (x )=﹣1在(0,π)上有且只有四个实数根, ∴x A <π≤x B ,即322ππωω+<π≤46ππωω+,解得72526ω≤<. 故选B .【点睛】本题考查了三角函数的恒等变换,三角函数的图象与性质,属于中档题.2.要得到函数y =sin (2x +9π)的图象,只需将函数y =cos (2x ﹣9π)的图象上所有点( ) A .向左平移518π个单位长度 B .向右平移518π个单位长度 C .向左平移536π个单位长度 D .向右平移536π个单位长度 【答案】D 【解析】 【分析】先将函数cos 29y x π⎛⎫=- ⎪⎝⎭转化为7sin 218y x π⎛⎫=+⎪⎝⎭,再结合两函数解析式进行对比,得出结论. 【详解】 函数75cos 2sin 2sin 2sin 299218369y x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=+=++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ∴要得到函数sin 29y x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数cos 29y x π⎛⎫=- ⎪⎝⎭的图象上所有点向右平移536π个单位长度,故选D . 【点睛】本题考查函数()sin y A x b ωϕ=++的图象变化规律,关键在于能利用诱导公式将异名函数化为同名函数,再根据左右平移规律得出结论.3.已知ABC V 的三条边的边长分别为2米、3米、4米,将三边都增加x 米后,仍组成一个钝角三角形,则x 的取值范围是( ) A .102x << B .112x << C .12x << D .01x <<【答案】D 【解析】 【分析】根据余弦定理和三角形三边关系可求得x 的取值范围. 【详解】将ABC V 的三条边的边长均增加x 米形成A B C '''V ,设A B C '''V 的最大角为A '∠,则A '∠所对的边的长为()4x +米,且A '∠为钝角,则cos 0A '∠<,所以()()()()()2222342340x x x x x x x ⎧+++<+⎪+++>+⎨⎪>⎩,解得01x <<.故选:D. 【点睛】本题考查利用余弦定理和三角形三边关系求参数的取值范围,灵活利用余弦定理是解本题的关键,考查计算能力,属于中等题.4.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形 C .等腰三角形 D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=, 变形可得:sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.5.已知在锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos b C c B =,则111tan tan tan A B C++的最小值为( ) ABCD.【答案】A 【解析】 【分析】先根据已知条件,把边化成角得到B,C 关系式,结合均值定理可求. 【详解】∵2cos cos b C c B =,∴2sin cos sinCcos B C B =, ∴tan 2tan C B =.又A B C π++=, ∴()()tan tan tan A B C B C π=-+=-+⎡⎤⎣⎦22tan tan 3tan 3tan 1tan tan 12tan 2tan 1B C B BB C B B +=-=-=---, ∴21112tan 111tan tan tan 3tan tan 2tan B A B C B B B -++=++27tan 36tan B B =+. 又∵在锐角ABC ∆中, tan 0B >,∴27tan 36tan B B +≥=,当且仅当tan 2B =时取等号,∴min111tan tan tan 3A B C ⎛⎫++=⎪⎝⎭,故选A. 【点睛】本题主要考查正弦定理和均值定理,解三角形时边角互化是求解的主要策略,侧重考查数学运算的核心素养.6.已知函数sin(),0()cos(),0x a x f x x b x +≤⎧=⎨+>⎩的图像关于y 轴对称,则sin y x =的图像向左平移( )个单位,可以得到cos()y x a b =++的图像( ). A .4π B .3π C .2π D .π【答案】D 【解析】 【分析】根据条件确定,a b 关系,再化简()cos y x a b =++,最后根据诱导公式确定选项. 【详解】 因为函数()()(),0,0sin x a x f x cos x b x ⎧+≤⎪=⎨+>⎪⎩的图像关于y 轴对称,所以sin cos 22a b ππ⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭,()()sin cos a b ππ-+=+,即sin cos sin cos b a a b ,==,因此π2π()2a b k k Z +=+∈, 从而()()cos sin y x a b sinx x π=++=-=+,选D. 【点睛】本题考查偶函数性质、诱导公式、三角函数图象变换,考查基本分析识别能力,属中档题.7.已知函数()sin()R,0,0,||2f x A x x A πωϕωϕ⎛⎫=+∈>>< ⎪⎝⎭的图象(部分)如图所示,则ω,ϕ分别为( )A .,3πωπϕ==B .2,3πωπϕ==C .,6πωπϕ==D .2,6πωπϕ==【答案】C 【解析】 【分析】由最大值可确定振幅A ,由周期确定ω,由1()23f =确定ϕ. 【详解】 由图可得,2A =,5114632T =-=,所以22T πω==,ωπ=,又1()23f =,所以12sin()23πϕ⨯+=,2,32k k Z ππϕπ+=+∈,即2,6k k Z πϕπ=+∈, 又2πϕ<,故6π=ϕ. 故选:C 【点睛】本题考查由图象确定正弦型函数解析式中的参数问题,考查学生逻辑推理能力,是一道中档题.8.锐角ABC ∆中,角A 、B 、C 所对的边分别为,,a b c ,若()sin 303A B C π⎛⎫+++= ⎪⎝⎭,2b =26c +=,则角B =( )A .6π B .4π C .3π D .512π 【答案】B 【解析】 【分析】先由()sin 03A B C π⎛⎫+++= ⎪⎝⎭求出3A π=,然后用余弦定理算出a =再用余弦定理算出cos B 即可. 【详解】因为()sin 03A B C π⎛⎫+++= ⎪⎝⎭所以11sin sin 022A A A A A +==所以tan A =0,2A π⎛⎫∈ ⎪⎝⎭,所以3A π=所以由余弦定理得:22222co 12322s a b c bc A -=+-=+=⎝⎭所以a =所以222232cos 22a c b B ac +-+-===因为0,2B π⎛⎫∈ ⎪⎝⎭,所以4B π=故选:B 【点睛】本题考查的是利用余弦定理解三角形,数据不特殊,计算能力是解题的关键.9.将函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭的图象向右平移6π个单位长度后,所得图象关于y 轴对称,且1π2f ω⎛⎫=- ⎪⎝⎭,则当ω取最小值时,函数()f x 的解析式为( )A .()sin 26f x x π⎛⎫=+⎪⎝⎭B .()sin 2π6f x x ⎛⎫=- ⎪⎝⎭C .()sin 4π6f x x ⎛⎫=+ ⎪⎝⎭D .()sin 4π6f x x ⎛⎫=- ⎪⎝⎭【答案】C 【解析】 【分析】由题意利用函数()sin y A x ωφ=+的图象变换规律,可得所得函数的解析式,由12f πω⎛⎫=- ⎪⎝⎭,求出φ,再根据所得图象关于y 轴对称求出ω,可得()f x 的解析式.【详解】解:将函数()()sin (0,)2f x x πωφωφ=+><的图象向右平移6π个单位长度后,可得sin 6y x ωπωφ⎛⎫=-+ ⎪⎝⎭的图象;∵所得图象关于y 轴对称,∴62k ωππφπ-+=+,k Z ∈.∵()1sin sin 2f ππφφω⎛⎫=-=+=- ⎪⎝⎭,即1sin 2φ=,26ππφφ<=,. ∴63k ωπππ-=+,620k ω=-->,则当ω取最小值时,取1k =-,可得4ω=, ∴函数()f x 的解析式为()sin 46f x x π⎛⎫=+ ⎪⎝⎭. 故选C . 【点睛】本题主要考查函数()sin y A x ωφ=+的图象变换规律,正弦函数的性质,属于中档题.10.在三角形ABC 中,给出命题:p “2ab c >”,命题:q “3C π<”,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】 【分析】由余弦定理将2c 化为222cos a b ab C +-,整理后利用基本不等式求得12cos 2C +>,求出C 范围,即可判断充分性,取4a =,7b =,6c =,则可判断必要性不成立,两者结合可得正确的选项. 【详解】充分性:由余弦定理,2222cos c a b ab C =+-, 所以2ab c >,即222cos ab a b ab C >+-,整理得,2212cos a b C ab++>,由基本不等式,222a b ab ab+≥=,当且仅当a b =时等号成立, 此时,12cos 2C +>,即1cos 2C >,解得3C π<, 充分性得证;必要性:取4a =,7b =,6c =,则164936291cos 247562C +-==>⨯⨯,故3C π<,但228ab c =<,故3C π<推不出2ab c >.故必要性不成立; 故p 是q 的充分不必要条件. 故选:A 【点睛】本题主要考查充分必要条件的判断、余弦定理的应用和基本不等式的应用,考查学生分析转化能力,属于中档题.11.在ABC ∆中,060,A BC D ∠==是边AB 上的一点,CD CBD =∆的面积为1,则BD 的长为( ) A .32B .4C .2D .1【答案】C 【解析】1sin 1sin2BCD BCD ∠=∴∠=2242BD BD ∴=-=∴=,选C12.若函数()sin()f x A x ωϕ=+(其中0A >,||)2πϕ<图象的一个对称中心为(3π,0),其相邻一条对称轴方程为712x π=,该对称轴处所对应的函数值为1-,为了得到()cos2g x x =的图象,则只要将()f x 的图象( )A .向右平移6π个单位长度 B .向左平移12π个单位长度C .向左平移6π个单位长度 D .向右平移12π个单位长度【答案】B 【解析】 【分析】由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数()sin y A x ωϕ=+的图象变换规律,诱导公式,得出结论. 【详解】根据已知函数()()sin f x A x ωϕ=+(其中0A >,)2πϕ<的图象过点,03π⎛⎫ ⎪⎝⎭,7,112π⎛⎫-⎪⎝⎭, 可得1A =,1274123πππω⋅=-, 解得:2ω=. 再根据五点法作图可得23πϕπ⋅+=,可得:3πϕ=,可得函数解析式为:()sin 2.3f x x π⎛⎫=+⎪⎝⎭故把()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度, 可得sin 2cos236y x x ππ⎛⎫=++= ⎪⎝⎭的图象, 故选B . 【点睛】本题主要考查由函数()sin y A x ωϕ=+的部分图象求解析式,由函数的图象的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,函数()sin y A x ωϕ=+的图象变换规律,诱导公式的应用,属于中档题.13.若,2παπ⎛⎫∈ ⎪⎝⎭,2cos2sin 4παα⎛⎫=- ⎪⎝⎭,则sin 2α的值为( )A .78-B .78C .18-D .18【答案】A 【解析】 【分析】利用二倍角公式及两角差的正弦公式化简得到cos sin 4αα+=,再将两边平方利用二倍角正弦公式计算可得; 【详解】解:因为2cos2sin 4παα⎛⎫=-⎪⎝⎭所以()222cos sin sincos cossin 44ππαααα-=-所以()())2cos sin cos sin cos sin αααααα-+=- ,cos sin 02παπαα⎛⎫∈-≠ ⎪⎝⎭Q ,所以cos sin 4αα+=所以()21cos sin 8αα+=,即221cos 2cos sin sin 8αααα++=,11sin 28α+= 所以7sin 28α=- 故选:A 【点睛】本题考查两角和差的正弦公式、二倍角公式的应用,属于中档题;14.已知sin α,sin()10αβ-=-,,αβ均为锐角,则β=( ) A .512πB .3π C .4π D .6π 【答案】C 【解析】 【分析】 由题意,可得22ππαβ-<-<,利用三角函数的基本关系式,分别求得cos ,cos()ααβ-的值,利用sin[(]sin )ααββ=--,化简运算,即可求解.【详解】由题意,可得α,β均为锐角,∴-2π <α-β<2π.又sin(α-β),∴cos(α-β).又sin α=5,∴cos α=5, ∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=-×10⎛⎫- ⎪ ⎪⎝⎭.∴β=4π. 【点睛】本题主要考查了三角函数的化简、求值问题,其中熟记三角函数的基本关系式和三角恒等变换的公式,合理构造sin[(]sin )ααββ=--,及化简与运算是解答的关键,着重考查了推理与运算能力,属于基础题.15.在OAB ∆中,已知OB =u u u v 1AB u u u v=,45AOB ∠=︒,点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ,其中λ,μ满足23λμ+=,则OP u u u v的最小值为( )ABCD【答案】A 【解析】 【分析】根据OB =u u u r,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r.再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP u u u r的最小值.【详解】在OAB ∆中,已知OB =u u u r,1AB =uu u r ,45AOB ∠=︒由正弦定理可得sin sin AB OBAOB OAB=∠∠u u u r u u u rsin OAB =∠,解得sin 1OAB ∠=即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22,22⎛ ⎝⎭所以2222OA ⎛= ⎝⎭u u u r ,)2,0OB =u u ur因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫⎪ ⎪⎝⎭= 则2222222OP λμλ⎛⎫=++⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r 2222λλμμ=++因为23λμ+=,则32μλ=- 代入上式可得()()22322232λλλλ+-+-218518λλ-=+299555λ⎛⎫=-+ ⎪⎝⎭所以当95λ=时, min 9355OP ==u u u r 故选:A 【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.16.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC ∆的面积S =根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为( )AB.CD.【答案】A 【解析】 【分析】根据()cos 3cos 0a B b c A ++=,利用正弦定理边化为角得sin cos cos sin 3sin cos 0A B A B C A ++=,整理为()sin 13cos 0C A +=,根据sin 0C ≠,得1cos 3A =-,再由余弦定理得3bc =,又2222a b c --=,代入公式=S . 【详解】由()cos 3cos 0a B b c A ++=得sin cos cos sin 3sin cos 0A B A B C A ++=, 即()sin 3sin cos 0A B C A ++=,即()sin 13cos 0C A +=, 因为sin 0C ≠,所以1cos 3A =-, 由余弦定理22222cos 23a b c bc A bc --=-==,所以3bc =, 由ABC ∆的面积公式得S ===故选:A 【点睛】本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于中档题.17.将函数cos y x =的图象先左移4π,再纵坐标不变,横坐标缩为原来的12,所得图象的解析式为( ) A .sin 24y x π⎛⎫=+⎪⎝⎭B .13sin 24y x π⎛⎫=+⎪⎝⎭C .1sin 24y x π⎛⎫=+ ⎪⎝⎭D .3sin 24y x π⎛⎫=+ ⎪⎝⎭ 【答案】D【分析】根据三角函数的平移伸缩变换法则得到答案. 【详解】cos sin 2y x x π⎛⎫==+ ⎪⎝⎭向左平移4π个单位,故变为3sin 4y x π⎛⎫=+ ⎪⎝⎭,纵坐标不变,横坐标缩为原来的12,变为3sin 24y x π⎛⎫=+ ⎪⎝⎭. 故选:D . 【点睛】本题考查了三角函数的平移伸缩变换,意在考查学生对于平移伸缩变换的理解和掌握.18.函数()22sin 3cos 2f x x x =+-,2,36x ππ⎡⎤∈-⎢⎥⎣⎦的值域为( ) A .40,3⎡⎤⎢⎥⎣⎦B .41,3⎡⎤⎢⎥⎣⎦C .51,4⎡⎤⎢⎥⎣⎦D .50,4⎡⎤⎢⎥⎣⎦【答案】A 【解析】 【分析】化简得到()23sin 2sin 1f x x x =-++,设sin t x =,利用二次函数性质得到答案. 【详解】根据22sin cos 1x x +=,得()23sin 2sin 1f x x x =-++,2,36x ππ⎡⎤∈-⎢⎥⎣⎦, 令sin t x =,由2,36x ππ⎡⎤∈-⎢⎥⎣⎦,得1sin 1,2x ⎡⎤∈-⎢⎥⎣⎦, 故[]0,1t ∈,有2321y t t =-++,[]0,1t ∈,二次函数对称轴为13t =, 当13t =时,最大值43y =;当1t =时,最小值0y =, 综上,函数()f x 的值域为40,3⎡⎤⎢⎥⎣⎦. 故选:A . 【点睛】本题考查了三角函数值域,换元可以简化运算,是解题的关键.19.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且222b c a bc +=+若2sin sin sin B C A ⋅=,则ABC ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形【解析】 【分析】直接利用余弦定理的应用求出A 的值,进一步利用正弦定理得到:b =c ,最后判断出三角形的形状. 【详解】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c , 且b 2+c 2=a 2+bc .则:2221222b c a bc cosA bc bc +-===,由于:0<A <π,故:A 3π=.由于:sin B sin C =sin 2A , 利用正弦定理得:bc =a 2, 所以:b 2+c 2﹣2bc =0, 故:b =c ,所以:△ABC 为等边三角形. 故选C . 【点睛】本题考查了正弦定理和余弦定理及三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.20.已知曲线1:sin C y x =,21:cos 23C y x π⎛⎫=- ⎪⎝⎭,则下面结论正确的是( )A .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2CD .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2C 【答案】D【分析】根据三角函数的周期变换和左右平移变换依次得到各选项中所得的函数解析式,从而得到正确选项. 【详解】A 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向右平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=-- ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 错误;B 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向右平移3π个单位长度后得:11121sin sin cos cos 232622632y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,B 错误;C 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向左平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+=++=+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,C 错误;D 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向左平移3π个单位长度后得:1111sin sin cos cos 232622623y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+=-+=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,D 正确. 故选:D 【点睛】本题考查三角函数的周期变换和平移变换的问题,关键是能够准确掌握变换原则,得到变换后的函数解析式.。
专题04 三角函数与解三角形A辑(解析版)-2021年高考数学压轴必刷题(第一辑)

2021年高考数学压轴必刷题(第一辑)专题04三角函数与解三角形A辑1.【2020年全国3卷文科12】已知函数f(x)=sin x+1sinx,则()A.f(x)的最小值为2B.f(x)的图像关于y轴对称C.f(x)的图像关于直线x=π对称D.f(x)的图像关于直线x=π2对称【答案】D【解析】∵sinx可以为负,所以A错;∵sinx≠0∴x≠kπ(k∈Z)∵f(−x)=−sinx−1sinx=−f(x)∴f(x)关于原点对称;∵f(2π−x)=−sinx−1sinx ≠f(x),f(π−x)=sinx+1sinx=f(x),故B错;∴f(x)关于直线x=π2对称,故C错,D对故选:D2.【2020年北京卷10】2020年3月14日是全球首个国际圆周率日(πDay).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值.按照阿尔·卡西的方法,π的近似值的表达式是().A.3n(sin30°n +tan30°n)B.6n(sin30°n+tan30°n)C.3n(sin60°n +tan60°n)D.6n(sin60°n+tan60°n)【答案】A 【解析】单位圆内接正6n边形的每条边所对应的圆周角为360°n×6=60°n,每条边长为2sin30°n,所以,单位圆的内接正6n边形的周长为12nsin30°n,单位圆的外切正6n边形的每条边长为2tan30°n ,其周长为12ntan30°n,∴2π=12nsin30°n +12ntan 30°n2=6n (sin 30°n+tan30°n),则π=3n (sin 30°n+tan30°n).故选:A.3.【2019年天津文科07】已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,且f (x )的最小正周期为π,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .2【答案】解:∵f (x )是奇函数,∴φ=0, ∵f (x )的最小正周期为π, ∴2πω=π,得ω=2,则f (x )=A sin2x ,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ). 则g (x )=A sin x ,若g (π4)=√2,则g (π4)=A sinπ4=√22A =√2,即A =2,则f (x )=A sin2x ,则f (3π8)=2sin (2×3π8=2sin 3π4=2×√22=√2,故选:C .4.【2019年天津理科07】已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .2【答案】解:∵f (x )是奇函数,∴φ=0, 则f (x )=A sin (ωx )将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ). 即g (x )=A sin (12ωx )∵g (x )的最小正周期为2π, ∴2π12ω=2π,得ω=2,则g (x )=A sin x ,f (x )=A sin2x ,若g (π4)=√2,则g (π4)=A sinπ4=√22A =√2,即A =2,则f (x )=2sin2x ,则f (3π8)=2sin (2×3π8=2sin 3π4=2×√22=√2,故选:C .5.【2019年新课标2文科11】已知α∈(0,π2),2sin2α=cos2α+1,则sin α=( )A .15B .√55 C .√33 D .2√55【答案】解:∵2sin2α=cos2α+1, ∴可得:4sin αcos α=2cos 2α, ∵α∈(0,π2),sin α>0,cos α>0,∴cos α=2sin α,∵sin 2α+cos 2α=sin 2α+(2sin α)2=5sin 2α=1, ∴解得:sin α=√55. 故选:B .6.【2019年新课标1文科11】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a sin A ﹣b sin B =4c sin C ,cos A =−14,则bc =( )A .6B .5C .4D .3【答案】解:∵△ABC 的内角A ,B ,C 的对边分别为a ,b ,c , a sin A ﹣b sin B =4c sin C ,cos A =−14, ∴{a 2−b 2=4c 2cosA =b 2+c 2−a 22bc =−14,解得3c 2=12bc , ∴bc =6.故选:A .7.【2019年新课标3理科12】设函数f (x )=sin (ωx +π5)(ω>0),已知f (x )在[0,2π]有且仅有5个零点.下述四个结论:①f (x )在(0,2π)有且仅有3个极大值点 ②f (x )在(0,2π)有且仅有2个极小值点③f (x )在(0,π10)单调递增④ω的取值范围是[125,2910)其中所有正确结论的编号是( ) A .①④B .②③C .①②③D .①③④【答案】解:当x ∈[0,2π]时,ωx +π5∈[π5,2πω+π5], ∵f (x )在[0,2π]有且仅有5个零点, ∴5π≤2πω+π5<6π, ∴125≤ω<2910,故④正确,因此由选项可知只需判断③是否正确即可得到答案, 下面判断③是否正确, 当x ∈(0,π10)时,ωx +π5∈[π5,(ω+2)π10],若f (x )在(0,π10)单调递增,则(ω+2)π10<π2,即ω<3,∵125≤ω<2910,故③正确.故选:D .8.【2019年新课标1理科11】关于函数f (x )=sin|x |+|sin x |有下述四个结论: ①f (x )是偶函数②f (x )在区间(π2,π)单调递增③f (x )在[﹣π,π]有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是( ) A .①②④ B .②④C .①④D .①③【答案】解:f (﹣x )=sin|﹣x |+|sin (﹣x )|=sin|x |+|sin x |=f (x )则函数f (x )是偶函数,故①正确, 当x ∈(π2,π)时,sin|x |=sin x ,|sin x |=sin x ,则f (x )=sin x +sin x =2sin x 为减函数,故②错误, 当0≤x ≤π时,f (x )=sin|x |+|sin x |=sin x +sin x =2sin x ,由f (x )=0得2sin x =0得x =0或x =π,由f (x )是偶函数,得在[﹣π,)上还有一个零点x =﹣π,即函数f (x )在[﹣π,π]有3个零点,故③错误, 当sin|x |=1,|sin x |=1时,f (x )取得最大值2,故④正确, 故正确是①④, 故选:C .9.【2019年北京文科08】如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,∠APB 是锐角,大小为β,图中阴影区域的面积的最大值为( )A .4β+4cos βB .4β+4sin βC .2β+2cos βD .2β+2sin β 【答案】解:由题意可得∠AOB =2∠APB =2β, 要求阴影区域的面积的最大值,即为直线QO ⊥AB , 即有QO =2,Q 到线段AB 的距离为2+2cos β, AB =2•2sin β=4sin β,扇形AOB 的面积为12•2β•4=4β,△ABQ 的面积为12(2+2cos β)•4sin β=4sin β+4sin βcos β=4sin β+2sin2β,S △AOQ +S △BOQ =4sin β+2sin2β−12•2•2sin2β=4sin β, 即有阴影区域的面积的最大值为4β+4sin β. 故选:B .10.【2018年新课标1文科11】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A(1,a ),B (2,b ),且cos2α=23,则|a ﹣b |=( ) A .15B .√55 C .2√55D .1 【答案】解:∵角α的顶点为坐标原点,始边与x 轴的非负半轴重合, 终边上有两点A (1,a ),B (2,b ),且cos2α=23, ∴cos2α=2cos 2α﹣1=23,解得cos 2α=56, ∴|cos α|=√306,∴|sin α|=√1−3036=√66,|tan α|=|b−a2−1|=|a ﹣b |=|sinα||cosα|=√66√306=√55. 故选:B .11.【2018年新课标2文科10】若f (x )=cos x ﹣sin x 在[0,a ]是减函数,则a 的最大值是( ) A .π4B .π2C .3π4D .π【答案】解:f (x )=cos x ﹣sin x =﹣(sin x ﹣cos x )=−√2sin (x −π4), 由−π2+2k π≤x −π4≤π2+2k π,k ∈Z , 得−π4+2k π≤x ≤34π+2k π,k ∈Z , 取k =0,得f (x )的一个减区间为[−π4,3π4],由f (x )在[0,a ]是减函数, 得a ≤3π4. 则a 的最大值是3π4.故选:C .12.【2018年新课标3文科11】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为a 2+b 2−c 24,则C =( ) A .π2B .π3C .π4D .π6【答案】解:∵△ABC 的内角A ,B ,C 的对边分别为a ,b ,c . △ABC 的面积为a 2+b 2−c 24,∴S△ABC=12absinC=a2+b2−c24,∴sin C=a2+b2−c22ab=cos C,∵0<C<π,∴C=π4.故选:C.13.【2018年北京理科07】在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为()A.1B.2C.3D.4【答案】解:由题意d=√1+m2=|√m2+1sin(θ+α)−2|√m+1,tanα=1m=y x,∴当sin(θ+α)=﹣1时,d max=1√m+1≤3.∴d的最大值为3.故选:C.14.【2018年北京文科07】在平面直角坐标系中,AB̂,CD̂,EF̂,GĤ是圆x2+y2=1上的四段弧(如图),点P其中一段上,角α以Ox为始边,OP为终边.若tanα<cosα<sinα,则P所在的圆弧是()A.AB̂B.CD̂C.EF̂D.GĤ【答案】解:A.在AB段,正弦线小于余弦线,即cosα<sinα不成立,故A不满足条件.B.在CD段正切线最大,则cosα<sinα<tanα,故B不满足条件.C.在EF段,正切线,余弦线为负值,正弦线为正,满足tanα<cosα<sinα,D.在GH段,正切线为正值,正弦线和余弦线为负值,满足cosα<sinα<tanα不满足tanα<cosα<sinα.故选:C.15.【2017年新课标1文科11】△ABC的内角A,B,C的对边分别为a,b,c,已知sin B+sin A(sin C﹣cos C)=0,a=2,c=√2,则C=()A.π12B.π6C.π4D.π3【答案】解:sin B=sin(A+C)=sin A cos C+cos A sin C,∵sin B+sin A(sin C﹣cos C)=0,∴sin A cos C+cos A sin C+sin A sin C﹣sin A cos C=0,∴cos A sin C+sin A sin C=0,∵sin C≠0,∴cos A=﹣sin A,∴tan A=﹣1,∵π2<A<π,∴A=3π4,由正弦定理可得csinC =asinA,∴sin C=csinA a,∵a=2,c=√2,∴sin C=csinAa=√2×√222=12,∵a>c,∴C =π6, 故选:B .16.【2017年天津理科07】设函数f (x )=2sin (ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f (5π8)=2,f (11π8)=0,且f (x )的最小正周期大于2π,则( ) A .ω=23,φ=π12 B .ω=23,φ=−11π12 C .ω=13,φ=−11π24 D .ω=13,φ=7π24【答案】解:由f (x )的最小正周期大于2π,得T4>π2,又f (5π8)=2,f (11π8)=0,得T 4=11π8−5π8=3π4,∴T =3π,则2πω=3π,即ω=23.∴f (x )=2sin (ωx +φ)=2sin (23x +φ), 由f (5π8)=2sin(23×5π8+φ)=2,得sin (φ+5π12)=1.∴φ+5π12=π2+2kπ,k ∈Z . 取k =0,得φ=π12<π. ∴ω=23,φ=π12. 故选:A .17.【2017年天津文科07】设函数f (x )=2sin (ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f (5π8)=2,f (11π8)=0,且f (x )的最小正周期大于2π,则( ) A .ω=23,φ=π12 B .ω=23,φ=−11π12 C .ω=13,φ=−11π24 D .ω=13,φ=7π24【答案】解:由f (x )的最小正周期大于2π,得T4>π2, 又f (5π8)=2,f (11π8)=0,得T 4=11π8−5π8=3π4,∴T =3π,则2πω=3π,即ω=23.∴f (x )=2sin (ωx +φ)=2sin (23x +φ),由f (5π8)=2sin(23×5π8+φ)=2,得sin (φ+5π12)=1. ∴φ+5π12=π2+2kπ,k ∈Z . 取k =0,得φ=π12<π. ∴ω=23,φ=π12. 故选:A .18.【2016年新课标1理科12】已知函数f (x )=sin (ωx +φ)(ω>0,|φ|≤π2),x =−π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在(π18,5π36)上单调,则ω的最大值为( )A .11B .9C .7D .5【答案】解:∵x =−π4为f (x )的零点,x =π4为y =f (x )图象的对称轴, ∴2n+14⋅T =π2,即2n+14⋅2πω=π2,(n ∈N )即ω=2n +1,(n ∈N ) 即ω为正奇数, ∵f (x )在(π18,5π36)上单调,则5π36−π18=π12≤T2,即T =2πω≥π6,解得:ω≤12, 当ω=11时,−11π4+φ=k π,k ∈Z , ∵|φ|≤π2, ∴φ=−π4, 此时f (x )在(π18,5π36)不单调,不满足题意;当ω=9时,−9π4+φ=k π,k ∈Z , ∵|φ|≤π2, ∴φ=π4, 此时f (x )在(π18,5π36)单调,满足题意;故ω的最大值为9, 故选:B .19.【2016年新课标2文科11】函数f (x )=cos2x +6cos (π2−x )的最大值为( )A .4B .5C .6D .7【答案】解:函数f (x )=cos2x +6cos (π2−x ) =1﹣2sin 2x +6sin x , 令t =sin x (﹣1≤t ≤1), 可得函数y =﹣2t 2+6t +1 =﹣2(t −32)2+112,由32∉[﹣1,1],可得函数在[﹣1,1]递增,即有t =1即x =2k π+π2,k ∈Z 时,函数取得最大值5. 故选:B .20.【2016年天津文科08】已知函数f (x )=sin 2ωx 2+12sin ωx −12(ω>0),x ∈R ,若f (x )在区间(π,2π)内没有零点,则ω的取值范围是( ) A .(0,18]B .(0,14]∪[58,1)C .(0,58]D .(0,18]∪[14,58]【答案】解:函数f (x )=sin 2ωx 2+12sin ωx −12=1−cosωx 2+12sin ωx −12=√22sin(ωx −π4), 由f (x )=0,可得sin(ωx −π4)=0,解得x =kπ+π4ω∉(π,2π),∴ω∉(18,14)∪(58,54)∪(98,94)∪⋯=(18,14)∪(58,+∞), ∵f (x )在区间(π,2π)内没有零点, ∴ω∈(0,18]∪[14,58]. 故选:D .21.【2014年天津文科08】已知函数f (x )=√3sin ωx +cos ωx (ω>0),x ∈R ,在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,则f (x )的最小正周期为( )A .π2B .2π3C .πD .2π【答案】解:∵已知函数f (x )=√3sin ωx +cos ωx =2sin (ωx +π6)(ω>0),x ∈R ,在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,正好等于f (x )的周期的13倍,设函数f (x )的最小正周期为T ,则13⋅T =π3,∴T =π,故选:C .22.【2013年新课标2理科12】已知点A (﹣1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( ) A .(0,1) B .(1−√22,12) C .(1−√22,13] D .[13,12) 【答案】解:解法一:由题意可得,三角形ABC 的面积为 12⋅AB ⋅OC =1,由于直线y =ax +b (a >0)与x 轴的交点为M (−ba ,0),由直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,可得b >0, 故−ba≤0,故点M 在射线OA 上.设直线y =ax +b 和BC 的交点为N ,则由{y =ax +b x +y =1可得点N 的坐标为(1−b a+1,a+b a+1).①若点M 和点A 重合,则点N 为线段BC 的中点,故N (12,12),把A 、N 两点的坐标代入直线y =ax +b ,求得a =b =13.②若点M 在点O 和点A 之间,此时b >13,点N 在点B 和点C 之间, 由题意可得三角形NMB 的面积等于12,即12⋅MB ⋅y N =12,即 12×(1+ba )⋅a+ba+1=12,可得a =b 21−2b >0,求得 b <12, 故有13<b <12.③若点M 在点A 的左侧,则b <13,由点M 的横坐标−b a<−1,求得b >a .设直线y =ax +b 和AC 的交点为P ,则由 {y =ax +by =x +1求得点P 的坐标为(1−b a−1,a−b a−1),此时,由题意可得,三角形CPN 的面积等于12,即 12•(1﹣b )•|x N ﹣x P |=12,即12(1﹣b )•|1−ba+1−1−ba−1|=12,化简可得2(1﹣b )2=|a 2﹣1|.由于此时 b >a >0,0<a <1,∴2(1﹣b )2=|a 2﹣1|=1﹣a 2 .两边开方可得 √2(1﹣b )=√1−a 2<1,∴1﹣b 2,化简可得 b >1−√22, 故有1−√22<b <13. 再把以上得到的三个b 的范围取并集,可得b 的取值范围应是 (1−√22,12), 故选:B .解法二:当a =0时,直线y =ax +b (a >0)平行于AB 边,由题意根据三角形相似且面积比等于相似比的平方可得(1−b 1)2=12,b =1−√22,趋于最小. 由于a >0,∴b >1−√22. 当a 逐渐变大时,b 也逐渐变大,当b =12时,直线经过点(0,12),再根据直线平分△ABC 的面积,故a 不存在,故b <12.综上可得,1−√22<b <12,故选:B .23.【2012年天津文科07】将函数y =sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点(3π4,0),则ω的最小值是( ) A .13B .1C .53D .2【答案】解:将函数y =sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象对应的函数为y =sin ω(x −π4).再由所得图象经过点(3π4,0)可得sin ω(3π4−π4)=sin (ωπ2)=0,∴ω•π2=k π,k ∈z .故ω的最小值是2, 故选:D .24.【2011年新课标1理科11】设函数f (x )=sin (ωx +φ)+cos (ωx +φ)(ω>0,|φ|<π2)的最小正周期为π,且f (﹣x )=f (x ),则( ) A .f (x )在(0,π2)单调递减B .f (x )在(π4,3π4)单调递减C .f (x )在(0,π2)单调递增D .f (x )在(π4,3π4)单调递增【答案】解:由于f (x )=sin (ωx +ϕ)+cos (ωx +ϕ)=√2sin(ωx +ϕ+π4), 由于该函数的最小正周期为T =2πω,得出ω=2, 又根据f (﹣x )=f (x ),得φ+π4=π2+k π(k ∈Z ),以及|φ|<π2,得出φ=π4. 因此,f (x )=√2sin(2x +π2)=√2cos2x ,若x ∈(0,π2),则2x ∈(0,π),从而f (x )在(0,π2)单调递减, 若x ∈(π4,3π4),则2x ∈(π2,3π2),该区间不为余弦函数的单调区间,故B ,C ,D 都错,A 正确. 故选:A .25.【2010年浙江理科09】设函数f (x )=4sin (2x +1)﹣x ,则在下列区间中函数f (x )不存在零点的是( ) A .[﹣4,﹣2]B .[﹣2,0]C .[0,2]D .[2,4]【答案】解:在同一坐标系中画出g (x )=4sin (2x +1)与h (x )=x 的图象 如下图示:由图可知g (x )=4sin (2x +1)与h (x )=x 的图象在区间[﹣4,﹣2]上无交点,由图可知函数f(x)=4sin(2x+1)﹣x在区间[﹣4,﹣2]上没有零点故选:A.26.【2010年上海理科18】某人要制作一个三角形,要求它的三条高的长度分别为113,111,15,则此人将()A.不能作出这样的三角形B.作出一个锐角三角形C.作出一个直角三角形D.作出一个钝角三角形【答案】解:设三边分别为a,b,c,利用面积相等可知1 13a=111b=15c,∴a:b:c=13:11:5令a=13,b=11,c=5由余弦定理得cos A=52+112−1322×5×11<0,所以角A为钝角,故选:D.27.【2010年北京文科07】某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为()A.2sinα﹣2cosα+2B.sinα−√3cosα+3C.3sinα−√3cosα+1D.2sinα﹣cosα+1【答案】解:由正弦定理可得4个等腰三角形的面积和为:4×12×1×1×sinα=2sinα由余弦定理可得正方形边长为:√12+12−2×1×1×cosα=√2−2cosα故正方形面积为:2﹣2cosα所以所求八边形的面积为:2sinα﹣2cosα+2故选:A.。
高考数学专题复习《解三角形》知识梳理及典型例题讲解课件(含答案)

(2)三角函数关系: </m> ; <m></m> ; <m></m> ; <m></m> .
(3)等差关系:若三角形三内角 <m></m> , <m></m> , <m></m> 成等差数列,则 <m></m> , <m></m> ;若三角形三边 <m></m> , <m></m> , <m></m> 成等差数列,则 <m></m> .
A. B. C. D.
解:依题意,由余弦定理得, ,即 ,所以 .故选A.
(2)在 中,若 , 则 ( )
A. B. C. D.
解:因为 ,由正弦定理得, ,即 ,由余弦定理得, ,因为 ,所以 .故选B.
√
变式2.(1)(2021年全国乙卷)记 的内角 , , 的对边分别为 , , ,面积为 , , ,则 _.
两倍
4.6 解三角形2023.11.2
正弦定理
余弦定理
公式
_ _______________
_ _______________
常见变形
________, ________, _________ , , ______ , , .
_ ________, _ ________, _ ________.
×
考点一 正弦定理的应用
例1【多选题】 的内角 , , 的对边分别为 , , ,则下列命题正确的是( )
高考数学复习专题训练—三角函数与解三角形解答题(含解析)

高考数学复习专题训练—三角函数与解三角形解答题1.(2021·山东滨州期中)已知向量a=(cos x,sin x),b=(4√3sin x,4sin x),若f(x)=a·(a+b).(1)求f(x)的单调递减区间;]上的最值.(2)求f(x)在区间[0,π22.(2021·北京丰台区模拟)如图,△ABC中,∠B=45°,N是AC边的中点,点M在AB边上,且MN⊥AC,BC=√6,MN=√3.(1)求∠A;(2)求BM.3.(2021·山东潍坊二模)如图,D为△ABC中BC边上一点,∠B=60°,AB=4,AC=4√3.给出如下三种数值方案:①AD=√5;②AD=√15;③AD=2√7.判断上述三种方案所对应的△ABD的个数,并求△ABD唯一时,BD的长.4.(2021·海南海口月考)在△ABC中,已知a,b,c分别是角A,B,C的对边,b cos C+c cos B=4,B=π.请再在下4列三个条件:①(a+b+c)(sin A+sin B-sin C)=3a sin B;②b=4√2;③√3c sin B=b cos C中,任意选择一个,添加到题目的条件中,求△ABC的面积.5.(2021·辽宁大连一模)如图,有一底部不可到达的建筑物,A为建筑物的最高点.某学习小组准备了三种工具:测角仪(可测量仰角与俯角)、米尺(可测量长度)、量角器(可测量平面角度).(1)请你利用准备好的工具(可不全使用),设计一种测量建筑物高度AB的方法,并给出测量报告;注:测量报告中包括你使用的工具,测量方法的文字说明与图形说明,所使用的字母和符号均需要解释说明,并给出你最后的计算公式.(2)该学习小组利用你的测量方案进行了实地测量,并将计算结果汇报给老师,发现计算结果与该建筑物实际的高度有误差,请你针对误差情况进行说明.6.(2021·湖北武汉3月质检)在△ABC中,它的内角A,B,C的对边分别为a,b,c,且B=2π3,b=√6.(1)若cos A cos C=23,求△ABC的面积;(2)试问1a +1c=1能否成立?若能成立,求此时△ABC的周长;若不能成立,请说明理由.7.(2021·湖南长沙模拟)在△ABC中,内角A,B,C所对的边分别为a,b,c,且(b-c)sinCb+a=sin B-sin A.(1)求角A;(2)若a=2,求1tanB +1tanC的最小值.8.(2021·江苏南京期中)如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=2π3.计划在BC⏜上再建一座观赏亭P,记∠POB=θ(0<θ<π2).(1)当θ=π3时,求∠OPQ的大小;(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,当游客在观赏亭P处的观赏效果最佳时,求sin θ的值.答案与解析1.解由于f(x)=a·(a+b)=|a|2+a·b=1+4√3sin x cos x+4sin2x=1+2√3sin 2x+4·1-cos2x2=2√3sin 2x-2cos 2x+3=4sin(2x-π6)+3.(1)由π2+2kπ≤2x-π6≤3π2+2kπ(k∈Z),解得π3+kπ≤x≤5π6+kπ(k∈Z),所以f(x)的单调递减区间是[π3+kπ,5π6+kπ](k∈Z).(2)由于x∈[0,π2],所以2x-π6∈[-π6,5π6],故当2x-π6=π2即x=π3时,函数f(x)取最大值7;当2x-π6=-π6即x=0时,函数f(x)取最小值1.2.解(1)如图,连接MC,因为N是AC边的中点,且MN⊥AC, 所以MC=MA.在Rt△AMN中,MA=MNsinA=√3sinA,所以MC=√3sinA.在△MBC中,由正弦定理可得MCsinB=BCsin∠BMC,而∠BMC=2∠A,所以√3sinA·sin45°=√6sin2A,即√3sinA·√22=√62sinAcosA,所以cos A=12,故∠A=60°.(2)由(1)知MC=MA=√3sin60°=2,∠BMC=2∠A=120°.在△BCM中,由余弦定理得BC2=BM2+MC2-2BM·MC·cos∠BMC,所以(√6)2=BM2+22-2BM·2·cos 120°,解得BM=√3-1(负值舍去).3.解过点A作AE⊥BC,垂足为点E(图略),则AE=4·sin 60°=2√3,当AD=√5时,AD<AE,所以方案①对应△ABD无解,当AD=√15时,AE<AD<AB<AC ,所以方案②对应△ABD 有两解, 当AD=2√7时,AB<AD<AC ,所以方案③对应△ABD 只有一解. 由方案③知AD=2√7,设BD=x (x>0),所以在△ABD 中由余弦定理得(2√7)2=42+x 2-2×4×x×cos 60°,即x 2-4x-12=0,解得x=6或x=-2(舍去).又因为在△ABC 中易得BC=8,BD=6<BC ,符合题意, 所以BD 的长为6.4.解 若选择条件①,则(a+b+c )(sin A+sin B-sin C )=3a sin B ,由正弦定理可得(a+b+c )(a+b-c )=3ab ,所以(a+b )2-c 2=3ab ,整理得a 2+b 2-c 2=ab ,所以cos C=12,故C=π3.又B=π4,所以A=π-π3−π4=5π12. 又因为b cos C+c cos B=4,所以b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac=4,即a=4.由正弦定理可得asinA =bsinB , 所以b=asinB sinA=4sin π4sin 5π12=4(√3-1), 故△ABC 的面积S=12ab sin C=12×4×4(√3-1)×sin π3=4(3-√3). 若选择条件②,则b=4√2. 又因为b cos C+c cos B=4,所以b ·a 2+b 2-c 22ab +c ·a 2+c 2-b22ac =4,即a=4.又B=π4,所以由正弦定理可得asinA =bsinB , 所以sin A=asinBb=4sin π44√2=12,所以A=π6或A=5π6.由于b>a ,所以B>A ,因此A=5π6不合题意舍去,故A=π6,从而C=π-π6−π4=7π12. 故△ABC 的面积S=12ab sin C=12×4×4√2×sin 7π12=4(√3+1). 若选择条件③,因为b cos C+c cos B=4, 所以b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac=4,所以a=4.因为√3c sin B=b cos C ,所以√3sin C sin B=sin B cos C ,所以tan C=√33,于是C=π6,从而A=π-π6−π4=7π12,所以由正弦定理可得a sinA =bsinB , 所以b=asinB sinA=4sin π4sin 7π12=4(√3-1), 故△ABC 的面积S=12ab sin C=12×4×4(√3-1)×sin π6=4(√3-1). 5.解 (1)选用测角仪和米尺,如图所示.①选择一条水平基线HG ,使H ,G ,B 三点在同一条直线上;②在H ,G 两点用测角仪测得A 的仰角分别为α,β,HG=a ,即CD=a.测得测角仪器的高是h ;③(方法一)在△ACD 中,由正弦定理,得ACsinα=CDsin (β-α), 所以AC=CDsinαsin (β-α)=asinαsin (β-α),在Rt △ACE 中,有AE=AC sin β=asinαsinβsin (β-α), 所以建筑物的高度AB=AE+h=asinαsinβsin (β-α)+h. (方法二)在Rt △ADE 中,DE=AEtanα, 在Rt △ACE 中,CE=AEtanβ, 所以CD=DE-CE=AEtanα−AEtanβ=AE (tanβ-tanα)tanαtanβ,所以AE=atanαtanβtanβ-tanα,所以建筑物的高度AB=AE+h=atanαtanβtanβ-tanα+h. (2)①测量工具问题;②两次测量时位置的间距差; ③用身高代替测角仪的高度.6.解 (1)由B=2π3,得A+C=π3,cos(A+C )=cos A cos C-sin A sin C ,即12=cos A cos C-sin A sin C.因为cos A cos C=23,所以sin A sin C=16.因为a sinA =c sinC =√6√32=2√2,所以a=2√2sin A ,c=2√2sin C.所以S △ABC =12·2√2sin A·2√2sin C·sin B=4sin A·sin B sin C=4×16×√32=√33. (2)假设1a +1c =1能成立,所以a+c=ac.由余弦定理,得b 2=a 2+c 2-2ac cos B ,所以6=a 2+c 2+ac.所以(a+c )2-ac=6,所以(ac )2-ac-6=0,所以ac=3或ac=-2(舍去),此时a+c=ac=3. 不满足a+c ≥2√ac ,所以1a +1c =1不成立.7.解 (1)由(b -c )sinCb+a =sin B-sin A ,可得(b-c )sin C=(sin B-sin A )(b+a ),由正弦定理得(b-c )c=(b-a )(b+a ),即b 2+c 2-a 2=bc , 由余弦定理,得cos A=b 2+c 2-a 22bc=12,因为0<A<π,可得A=π3.(2)由(1)知A=π3,设△ABC 的外接圆的半径为R (R>0),可得2R=asinA =4√33, 由余弦定理得a 2=b 2+c 2-2bc cos A=b 2+c 2-bc ≥bc , 即bc ≤a 2=4,当且仅当b=c=2时取等号, 又1tanB +1tanC =cosBsinB +cosCsinC =cosBsinC+sinBcosCsinBsinC =sin (B+C )sinBsinC =sinAsinBsinC =2R ·2RsinA 2RsinB ·2RsinC=2R ·abc =8√33bc ≥8√33×4=2√33,所以1tanB +1tanC 的最小值为2√33.8.解 (1)在△POQ 中,因为∠AQC=2π3,所以∠AQO=π3.又OA=OB=3,所以OQ=√3. 设∠OPQ=α,则∠PQO=π2-α+θ. 由正弦定理,得3sin (π2-α+θ)=√3sinα,即√3sin α=cos(α-θ), 整理得tan α=√3-sinθ,其中θ∈(0,π2).当θ=π3时,tan α=√33.因为α∈(0,π2),所以α=π6. 故当θ=π3时,∠OPQ=π6.(2)设f(θ)=√3-sinθ,θ∈(0,π2),则f'(θ)=-sinθ(√3-sinθ)+cos 2θ(√3-sinθ)2=1-√3sinθ(√3-sinθ)2.令f'(θ)=0,得sin θ=√33,记锐角θ0满足sin θ0=√33,当0<θ<θ0时,f'(θ)>0;当θ0<θ<π2时,f'(θ)<0, 所以f(θ)在θ=θ0处取得极大值亦即最大值.由(1)可知tan α=f(θ)>0,则α∈(0,π2),又y=tan α单调递增,则当tan α取最大值时,α也取得最大值.故游客在观赏亭P处的观赏效果最佳时,sin θ=√33 .。
高考数学复习专题过关测评—三角函数与解三角形(含答案及解析)

高考数学复习专题过关测评—三角函数与解三角形一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2021·江西临川期中)已知角θ的终边经过点P(√2,a),若θ=-π3,则a=()A.√6B.√63C.-√6 D.-√632.(2021·北京房山区一模)将函数f(x)=sin 2x的图象向左平移π6个单位长度得到函数y=g(x)的图象,则函数g(x)的图象的一条对称轴方程为()A.x=-π6B.x=-π12C.x=π12D.x=π63.(2021·北京西城区一模)在△ABC中,内角A,B,C所对的边分别为a,b,c,且C=60°,a+2b=8,sin A=6sin B,则c=()A.√35B.√31C.6D.54.(2021·山西吕梁一模)已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<π2)部分图象如图所示,则f(π3)=()A.√32B.12C.-√3D.√35.(2021·北京海淀区模拟)已知sin(π6-α)=13+cos α,则sin(2α+5π6)=()A.-79B.-4√39C.4√39D.796.(2021·福建福州期末)疫情期间,为保障市民安全,要对所有街道进行消毒处理,某消毒装备的设计如图所示,PQ为路面,AB为消毒设备的高,BC为喷杆,AB⊥PQ,∠ABC=2π3,C处是喷洒消毒水的喷头,且喷射角∠DCE=π3,已知AB=2,BC=1,则消毒水喷洒在路面上的宽度DE的最小值为()A.5√2-5B.5√2C.5√33D.5√37.(2021·浙江宁波模拟)在△ABC中,“tan A tan B>1”是“△ABC为钝角三角形”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.(2021·安徽淮北一模)函数f(x)=2sin x+π4+cos 2x的最大值为()A.1+√2B.3√32C.2√2D.3二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.在△ABC中,角A,B,C所对的边分别为a,b,c,且(a+b)∶(a+c)∶(b+c)=9∶10∶11,则下列结论正确的是()A.sin A∶sin B∶sin C=4∶5∶6B.△ABC是钝角三角形C.△ABC的最大内角是最小内角的2倍D.若c=6,则△ABC的外接圆半径R为8√7710.(2021·江苏苏州月考)已知函数f(x)=(sin x+√3cos x)2,则()A.f(x)在区间[0,π6]上单调递增B.f(x)的图象关于点(-π3,0)对称C.f(x)的最小正周期为πD.f(x)的值域为[0,4]11.(2021·辽宁沈阳二模)关于f(x)=sin x·cos 2x的说法正确的为()A.∀x∈R,f(-x)-f(x)=0B.∃T≠0,使得f(x+T)=f(x)C.f(x)在定义域内有偶数个零点D.∀x∈R,f(π-x)-f(x)=012.(2021·山东潍坊统考)在△ABC中,内角A,B,C所对的边分别为a,b,c,若1tanA ,1tanB,1tanC依次成等差数列,则下列结论不一定成立的是()A.a,b,c依次成等差数列B.√a,√b,√c依次成等差数列C.a2,b2,c2依次成等差数列D.a3,b3,c3依次成等差数列三、填空题:本题共4小题,每小题5分,共20分.13.(2021·安徽合肥期中)已知cos(α+5π4)=-√63,则sin 2α=.14.(2021·北京东城区一模)已知函数f(x)=A sin(2x+φ)(A>0,|φ|<π2),其中x和f(x)部分对应值如下表所示:则A=.15.(2021·广东茂名二模)在矩形ABCD内(包括边界)有E,F两点,其中AB=120 cm,AE=100√3cm,EF=80√3 cm,FC=60√3 cm,∠AEF=∠CFE=60°,则该矩形ABCD的面积为cm2.(答案如有根号可保留)16.(2021·湖南长郡中学二模)如图,某湖有一半径为100 m的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 m的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足AB=AC,∠BAC=90°.四边形OACB及其内部区域为“直接监测覆盖区域”.设∠AOB=θ,则“直接监测覆盖区域”面积的最大值为m2.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)(2021·江西上饶一模)已知f(x)=2cos x·sin x+π3-√3sin2x+sin x cos x.(1)求函数f(x)的单调递增区间;(2)若x∈(-π4,π6),求y=f(x)的值域.18.(12分)(2021·河北石家庄一模)在△ABC中,内角A,B,C的对边分别为a,b,c,已知2a-b=2c cos B.(1)求角C;(2)若a=2,D是AC的中点,BD=√3,求边c.19.(12分)(2021·广东韶关一模)在①cos C+(cos A-√3sin A)cos B=0;②cos 2B-3cos(A+C)=1;③b cosC+√33c sin B=a这三个条件中任选一个,补充在下面的问题中并解答.问题:在△ABC中,角A,B,C所对的边分别为a,b,c,若a+c=1,,求角B和b的最小值. 20.(12分)(2021·山东枣庄二模)已知函数f (x )=sin(ωx+φ)ω>0,0<φ<π2的部分图象如图所示,f (0)=12,f (5π12)=0. (1)求f (x )的解析式;(2)在锐角△ABC 中,若A>B ,f (A -B 2-π12)=35,求cosA -B2,并证明sin A>2√55.21.(12分)(2021·福建宁德期末)在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:若建立平面直角坐标系Oxy 如图所示,则股价y (单位:元)和时间x (单位:天)的关系在ABC 段可近似地用函数y=a sin(ωx+φ)+b (0<φ<π)来描述,从C 点走到今天的D 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D 点和C 点正好关于直线l :x=34对称.老张预计这只股票未来的走势可用曲线DE 描述,这里DE 段与ABC 段关于直线l 对称,EF 段是股价延续DE 段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A (0,22),点B (12,19),点D (44,16)来确定函数解析式中的常数a ,b ,ω,φ,并且求得ω=π72.(1)请你帮老张算出a ,b ,φ,并回答股价什么时候见顶(即求点F 的横坐标);(2)老张如能在今天以点D 处的价格买入该股票3 000股,到见顶处点F 的价格全部卖出,不计其他费用,这次操作他能赚多少元?22.(12分)(2021·深圳实验学校月考)已知函数f (x )=√3sin(ωx+φ)+2sin 2(ωx+φ2)-1(ω>0,0<φ<π)为奇函数,且f (x )图象的相邻两对称轴间的距离为π2. (1)当x ∈[-π2,π4]时,求f (x )的单调递减区间;(2)将函数f (x )的图象向右平移π6个单位长度,再把横坐标缩小为原来的12(纵坐标不变),得到函数y=g (x )的图象,当x ∈[-π12,π6]时,求函数g (x )的值域;(3)对于第(2)问中的函数g (x ),记方程g (x )=43在区间[π6,4π3]上的根从小到大依次为x 1,x 2,…,x n ,试确定n 的值,并求x 1+2x 2+2x 3+…+2x n-1+x n 的值.答案及解析1.C解析由题意,角θ的终边经过点P(√2,a),可得|OP|=√2+a2(O为坐标原点),又由θ=-π3,根据三角函数的定义,可得cos(-π3)=√2√2+a2=12,且a<0,解得a=-√6.2.C解析将函数f(x)=sin 2x的图象向左平移π6个单位长度,得到y=g(x)=sin[2(x+π6)]=sin(2x+π3),令2x+π3=kπ+π2,k∈Z,解得x=kπ2+π12,k∈Z,结合四个选项可知,函数g(x)的图象的一条对称轴方程为x=π12 .3.B解析因为sin A=6sin B,所以a=6b,又a+2b=8,所以a=6,b=1,因为C=60°,所以c2=a2+b2-2ab cos C,即c2=62+12-2×6×1×12,解得c=√31.4.D解析由题中函数f(x)=A sin(ωx+φ)A>0,ω>0,|φ|<π2的部分图象知,A=2,34T=11π3−2π3=3π,所以T=4π=2πω,所以ω=12.又f(2π3)=2sin(12×2π3+φ)=2,可得12×2π3+φ=2kπ+π2,k∈Z,解得φ=2kπ+π6,k∈Z.∵|φ|<π2,∴φ=π6,∴f(x)=2sin(12x+π6).故f(π3)=2sin(12×π3+π6)=2sinπ3=√3.5.D解析由sin(π6-α)=13+cos α可得sinπ6·cos α-cosπ6·sin α=13+cos α,∴12cos α-√32sinα=13+cos α,∴√32sin α+12cos α=-13,∴sin(α+π6)=-13,∴sin(2α+5π6)=sin[π2+(2α+π3)]=cos(2α+π3)=1-2sin2(α+π6)=79.6.C解析在△CDE中,设定点C到底边DE的距离为h,则h=2+1·sin(2π3-π2)=52,又S△CDE=12DE·h=12CD·CE sinπ3,即5DE=√3CD·CE,利用余弦定理得DE2=CD2+CE2-2CD·CE cosπ3=CD2+CE2-CD·CE≥2CD·CE-CD·CE=CD·CE,当且仅当CD=CE时,等号成立,故DE 2≥CD·CE ,而5DE=√3CD·CE ,所以DE 2≥5√33DE ,则DE ≥5√33,故DE 的最小值为5√33. 7.D 解析 因为tan A tan B>1,所以sinAsinBcosAcosB >1,因为0<A<π,0<B<π,所以sin A sin B>0,cos A cos B>0,故A ,B 同为锐角,因为sin A sin B>cos A cos B ,所以cos A cos B-sin A sin B<0,即cos(A+B )<0,所以π2<A+B<π,因此0<C<π2,所以△ABC 是锐角三角形,不是钝角三角形,所以充分性不满足.反之,若△ABC 是钝角三角形,也推不出“tan A tan B>1”,故必要性不成立,所以为既不充分也不必要条件.8.B 解析 因为f (x )=2sin (x +π4)+cos 2x ,所以f (x )=2sin (x +π4)+sin [2(x +π4)]=2sin x+π4+2sin (x +π4)cos (x +π4). 令θ=x+π4,g (θ)=2sin θ+2sin θcos θ=2sin θ+sin 2θ,则g'(θ)=2cos θ+2cos 2θ=2(2cos 2θ-1)+2cos θ=4cos 2θ+2cos θ-2,令g'(θ)=0,得cos θ=-1或cos θ=12,当-1≤cos θ≤12时,g'(θ)≤0;当12≤cos θ≤1时,g'(θ)≥0,所以当θ∈[-5π3+2kπ,-π3+2kπ](k ∈Z )时,g (θ)单调递减;当θ∈[-π3+2kπ,π3+2kπ](k ∈Z )时,g (θ)单调递增,所以当θ=π3+2k π(k ∈Z )时,g (θ)取得最大值,此时sin θ=√32,所以f (x )max =2×√32+2×√32×12=3√32.9.ACD 解析 因为(a+b )∶(a+c )∶(b+c )=9∶10∶11,所以可设a+b=9x ,a+c=10x ,b+c=11x (其中x>0),解得a=4x ,b=5x ,c=6x ,所以sin A ∶sin B ∶sin C=a ∶b ∶c=4∶5∶6,所以A 中结论正确;由以上解答可知c 边最大,所以三角形中角C 最大,又cos C=a 2+b 2-c 22ab=(4x )2+(5x )2-(6x )22×4x×5x=18>0,所以C 为锐角,所以B 中结论错误;由以上解答可知a 边最小,所以三角形中角A 最小, 又cos A=c 2+b 2-a 22cb=(6x )2+(5x )2-(4x )22×6x×5x=34,所以cos 2A=2cos2A-1=18,所以cos 2A=cos C.由三角形中角C最大且角C为锐角可得2A∈(0,π),C∈(0,π2),所以2A=C,所以C中结论正确;由正弦定理,得2R=csinC(R为△ABC外接圆半径),又sin C=√1-cos2C=3√78,所以2R=3√78,解得R=8√77,所以D中结论正确.10.ACD解析f(x)=(sinx+√3cosx)2=sin2x+3cos2x+2√3sin x cos x=2+cos 2x+√3sin2x=2sin2x+π6+2;对于A选项:∵x∈[0,π6],∴2x+π6∈[π6,π2],∴f(x)=2sin(2x+π6)+2在区间[0,π6]上单调递增,故A正确;对于B选项:f(-π3)=2sin[2×(-π3)+π6]+2=0,由函数f(x)的图象(图略)可知-π3是f(x)的一个极小值点,故B错误;对于C选项:由f(x)=2sin(2x+π6)+2可知,函数的最小正周期T=2π2=π,故C正确;对于D选项,∵sin(2x+π6)∈[-1,1],∴f(x)=2sin(2x+π6)+2∈[0,4],故D正确.11.BD解析对于A,当x=π3时,f(-π3)-f(π3)=sin(-π3)cos2π3-sinπ3cos2π3=-√32×(-12)−√32×(-1 2)=√32≠0,故A错误.对于B,因为f(x+2π)=sin(2π+x)cos[2(x+2π)]=sin x cos 2x,所以∃T=2π≠0,使得f(x+T)=f(x),故B正确.对于C,因为f(-x)=sin(-x)cos(-2x)=-sin x cos 2x=-f(x),所以f(x)为奇函数,因为x=0在定义域内,所以f(0)=0,故f(x)有奇数个零点,故C错误.对于D,f(π-x)-f(x)=sin(π-x)cos[2(π-x)]-sin x cos 2x=sin x cos 2x-sin x cos 2x=0,故D正确.12.ABD 解析 因为1tanA ,1tanB ,1tanC 依次成等差数列,所以2tanB =1tanA +1tanC ,整理得2cosB sinB=cosC sinC +cosAsinA ,所以2·a 2+c 2-b 22abc=a 2+b 2-c 22abc+b 2+c 2-a 22abc ,整理得2b 2=a 2+c 2,即a 2,b 2,c 2依次成等差数列.但数列a ,b ,c 或√a,√b,√c 或a 3,b 3,c 3不一定是等差数列,除非a=b=c ,但题目没有说△ABC 是等边三角形.13.-13 解析 由cos (α+5π4)=-√63可得cos (α+π4)=√63,所以√22(cos α-sin α)=√63,即cos α-sin α=2√33,两边平方可得1-sin 2α=43,故sin 2α=-13.14.4 解析 由题意可得{f (0)=-2√3,f (π4)=2,即{Asinφ=-2√3,Asin (π2+φ)=2,所以{Asinφ=-2√3,Acosφ=2,所以tan φ=-√3,又因为|φ|<π2, 所以φ=-π3,所以A=√3-√32=4. 15.14 400√3 解析 连接AC 交EF 于点O (图略),由∠AEF=∠CFE=60°,得AE ∥FC ,所以△AEO 与△CFO 相似,所以OEOF =AECF =53,所以EO=50√3 cm,FO=30√3 cm,在△AEO 中,由余弦定理得,AO 2=AE 2+EO 2-2AE·EO·cos ∠AEO=(100√3)2+(50√3)2-2×100√3×50√3cos 60°=22 500,所以AO=150 cm,同理CO=90 cm,所以AC=240 cm,从而BC=√AC 2-AB 2=120√3 cm,所以矩形ABCD 的面积为14 400√3 cm 2.16.(10 000√5+25 000) 解析 在△OAB 中,∵∠AOB=θ,OB=100 m,OA=200 m,∴AB 2=OB 2+OA 2-2OB·OA·cos ∠AOB ,即AB=100√5-4cosθ,∴S 四边形OACB =S △OAB +S △ABC =12·OA·OB·sin θ+12AB 2,于是S 四边形OACB =1002(sinθ-2cosθ+52)=1002√5sin(θ-φ)+52(其中tan φ=2),所以当sin(θ-φ)=1时,S 四边形OACB 取最大值10 000(√5+52)=10 000√5+25 000,即“直接监测覆盖区域”面积的最大值为(10 000√5+25 000)m 2.17.解 (1)f (x )=2cos x sin (x +π3)−√32(1-cos 2x )+12sin 2x=2cos x (12sinx +√32cosx)−√32+√32cos 2x+12sin 2x=12sin 2x+√32(2cos 2x-1)+√32cos 2x+12sin 2x=sin 2x+√3cos 2x=2sin (2x +π3), 令2k π-π2≤2x+π3≤π2+2k π,k ∈Z , 解得k π-5π12≤x ≤k π+π12,k ∈Z ,因此,函数f (x )的单调递增区间为[kπ-5π12,kπ+π12],k ∈Z .(2)∵x ∈(-π4,π6),∴-π6<2x+π3<2π3,∴-12<sin (2x +π3)≤1,∴-1<f (x )≤2, 因此当x ∈(-π4,π6)时,y=f (x )的值域为(-1,2].18.解 (1)因为2a-b=2c cos B ,由正弦定理得2sin A-sin B=2sin C cos B ,因为sin A=sin(B+C )=sin B cos C+cos B sin C ,代入上式得,2sin B cos C+2cos B sin C-sin B=2sin C cos B ,即2sin B cos C-sin B=0,即sin B (2cos C-1)=0.因为B ∈(0,π),所以sin B ≠0,所以2cos C=1,即cos C=12,又0<C<π,所以C=π3. (2)依题意,在△CBD 中,CB=2,CD=12b ,BD=√3,C=π3, 利用余弦定理的推论可得,cos C=cos π3=12=4+(12b )2-32×2×12b,即b 2-4b+4=0,解得b=2.在△ABC 中,b=a=2,C=π3,故△ABC 是等边三角形,故c=2.19.解 若选择①:在△ABC 中,有A+B+C=π,则由题意可得cos[π-(A+B )]+(cos A-√3sinA )cos B=0,即-cos(A+B )+cos A cos B-√3sin A cos B=0, sin A sin B-cos A cos B+cos A cos B-√3sin A cos B=0, sin A sin B=√3sin A cos B ,又sin A ≠0,所以sin B=√3cos B ,则tan B=√3. 又B ∈(0,π),所以B=π3.因为a+c=1,所以c=1-a ,a ∈(0,1).所以b 2=a 2+c 2-2ac cos B=a 2+c 2-ac=a 2+(1-a )2-a (1-a )=3a2-3a+1=3(a -12)2+14,因为a ∈(0,1),所以当a=12时,b 2取得最小值,且(b 2)min =14,即b 的最小值为12. 若选择②:在△ABC 中,有A+B+C=π,则由题意可得2cos 2B-1-3cos(π-B )=2cos 2B+3cos B-1=1,解得cos B=12或cos B=-2(舍去),又B ∈(0,π),所以B=π3.因为a+c=1,所以c=1-a ,a ∈(0,1).所以b 2=a 2+c 2-2ac cos B=a 2+c 2-ac=a 2+(1-a )2-a (1-a )=3a2-3a+1=3(a -12)2+14,因为a ∈(0,1),所以当a=12时,b 2取得最小值,且(b 2)min =14,即b 的最小值为12. 若选择③:由正弦定理可将已知条件转化为sin B cos C+√33sin C sin B=sin A , 又sin A=sin[π-(B+C )]=sin(B+C )=sin B cos C+sin C cos B ,所以√33sin C sin B=sin C cos B ,又sin C ≠0,所以sin B=√3cos B ,所以tan B=√3. 又B ∈(0,π),所以B=π3.因为a+c=1,所以c=1-a ,a ∈(0,1).所以b 2=a 2+c 2-2ac cos B=a 2+c 2-ac=a 2+(1-a )2-a (1-a )=3a2-3a+1=3(a -12)2+14,因为a ∈(0,1),所以当a=12时,b 2取得最小值,且(b 2)min =14,即b 的最小值为12. 20.解 (1)由f (0)=12,得sin φ=12,又0<φ<π2,所以φ=π6.由f (5π12)=0,得sin (ω·5π12+π6)=0,所以ω·5π12+π6=k π,k ∈Z ,即ω=25(6k-1),k ∈Z . 由ω>0,结合题中函数f (x )的图象可知12·2πω>5π12, 所以0<ω<125,所以有0<25(6k-1)<125,即16<k<76, 又k ∈Z ,所以k=1,从而ω=25×(6×1-1)=2,因此,f (x )=sin (2x +π6). (2)由f (A -B2-π12)=35,得sin(A-B )=35,又由题意可知0<A-B<π2,故cos(A-B )=45,于是cos A -B2=√1+cos (A -B )2=√10,sin A -B2=√10, 又A+B>π2,所以A=A+B 2+A -B 2>π4+A -B2,又因为函数y=sin x 在区间(0,π2)上单调递增,A ∈(0,π2),π4+A -B 2∈(0,π2),所以sin A>sin π4+A -B2=√22×(3√10+1√10)=2√55.21.解 (1)∵点C ,D 关于直线l 对称,∴点C 坐标为(2×34-44,16),即(24,16). 把点A ,B ,C 的坐标分别代入函数解析式,得{22=asinφ+b , ①19=asin (π6+φ)+b ,②16=asin (π3+φ)+b ,③②-①,得a [sin (π6+φ)-sinφ]=-3, ③-①,得a [sin (π3+φ)-sinφ]=-6,∴2sin (π6+φ)-2sin φ=sin (π3+φ)-sin φ, ∴cos φ+√3sin φ=√32cos φ+32sin φ,∴(1-√32)cos φ=(32-√3)sin φ=√3(√32-1)sin φ,∴tan φ=-√33.∵0<φ<π,∴φ=5π6,代入②,得b=19. 将φ=5π6,b=19代入①得,a=6.于是ABC 段对应的函数解析式为y=6sin (π72x +5π6)+19,由对称性得DEF 段对应的函数解析式为y=6sin π72(68-x )+5π6+19.设点F 的坐标为(x F ,y F ),则由π72(68-x F )+5π6=π2,解得x F =92. 因此可知,当x=92时,股价见顶.(2)由(1)可知,y F =6sin [π72×(68-92)+5π6]+19=6sin π2+19=25,故这次操作老张能赚3 000×(25-16)=27 000(元).22.解 (1)由题意,函数f (x )=√3sin(ωx+φ)+2sin 2(ωx+φ2)-1=√3sin(ωx+φ)-cos(ωx+φ)=2sin (ωx +φ-π6),因为函数f (x )图象的相邻两对称轴间的距离为π2, 所以T=π,可得ω=2.又f (x )为奇函数,且f (x )在x=0处有定义,可得f (0)=2sin (φ-π6)=0, 所以φ-π6=k π,k ∈Z ,因为0<φ<π,所以φ=π6, 因此f (x )=2sin 2x.令π2+2k π≤2x ≤3π2+2k π,k ∈Z ,解得π4+k π≤x ≤3π4+k π,k ∈Z , 所以f (x )的单调递减区间为[π4+kπ,3π4+kπ],k ∈Z , 又因为x ∈[-π2,π4],故函数f (x )的单调递减区间为[-π2,-π4].(2)将函数f (x )的图象向右平移π6个单位长度,可得y=2sin (2x -π3)的图象,再把横坐标缩小为原来的12,得到函数y=g (x )=2sin 4x-π3的图象,当x ∈[-π12,π6]时,4x-π3∈[-2π3,π3],当4x-π3=-π2时,函数g (x )取得最小值,且最小值为-2,当4x-π3=π3时,函数g (x )取得最大值,且最大值为√3,故函数g (x )的值域为[-2,√3].(3)由方程g (x )=43,即2sin (4x -π3)=43,即sin 4x-π3=23.(*)因为x ∈[π6,4π3],可得4x-π3∈[π3,5π],设θ=4x-π3,其中θ∈[π3,5π],则方程(*)可转化为sin θ=23,结合正弦函数y=sin θ的图象,如图,可得方程sin θ=23在区间[π3,5π]上有5个解,设这5个解分别为θ1,θ2,θ3,θ4,θ5,所以n=5,其中θ1+θ2=3π,θ2+θ3=5π,θ3+θ4=7π,θ4+θ5=9π,即4x 1-π3+4x 2-π3=3π,4x 2-π3+4x 3-π3=5π,4x 3-π3+4x 4-π3=7π,4x 4-π3+4x 5-π3=9π, 解得x 1+x 2=11π12,x 2+x 3=17π12,x 3+x 4=23π12,x 4+x 5=29π12,所以x 1+2x 2+2x 3+2x 4+x 5=(x 1+x 2)+(x 2+x 3)+(x 3+x 4)+(x 4+x 5)=20π3.。
三角函数与解三角形高考专题大题练习(含答案)

【详解】
解法一:(1)因为 且 ,
所以 ,
根据正弦定理,得 ,
因为 ,所以 ,所以 ,
因为 ,所以 ;
(2)由(1)知, ,
因为 , ,
所以 的面积 ,
因为 是 上的点, 平分 ,
所以 ,
因为 ,
所以 .
【详解】
(Ⅰ)由正弦定理得 ,
所以 ,因 ,故 .
,故 .
(Ⅱ) ,由正弦定理 ,及 得 ,∴ ,
∴ 周长
∵ ∴当 即 时
所以 周长 的最大值为6.
【点睛】
在解三角形中,如果题设条件是边角的混合关系,那么我们可以利用正弦定理或余弦定理把这种混合关系式转化为边的关系式或角的关系式.三角形中的关于边的最值问题,可以利用正弦定理化为关于某角的三角函数式的最值问题(多元问题转化为一元函数问题).
三角函数与解三角形专题练习
1. 的内角 的对边分别为 ,且
(Ⅰ)求 ;
(Ⅱ)若 ,设 , 的周长为 ,求 的解析式并求 的最大值.
2. 的内角 的对边分别为 , 且 .
(1)求 ;
(2)若 , 是 上的点, 平分 ,求 的面积.
3.已知 的内角A,B,C的对边分别为a,b,c,若
(1)证明: 是直角三角形:
若①③成立,则 ;若②③成立,则 ,不成立,所以①②成立.
(2) , ,故 ,
所以在 中,由余弦定理
,
故 ,当且仅当 时取等.
.
【点睛】
本题考查了三角恒等变换,正余弦定理,向量平行求参数,面积公式,意在考查学生的计算能力和综合应用能力.
高考数学专项知识点:三角函数及解三角形(含真题)精选全文完整版

专题六三角函数及解三角形知识必备一、任意角、弧度制及任意角的三角函数1.角的概念的推广(1)定义:角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S ={β|β=α+k ·360°,k ∈Z}.2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad.(2)公式角α的弧度数公式|α|=lr (弧长用l 表示)角度与弧度的换算1°=180 rad ;1rad =180°弧长公式弧长l =|α|r 扇形面积公式S =12lr =12|α|r 23.任意角的三角函数(1)定义:设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么sin α=y ,cos α=x ,tan α=yx(x ≠0).(2)几何表示:三角函数线可以看作是三角函数的几何表示,正弦线的起点都在x 轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP ,OM ,AT 分别叫做角α的正弦线,余弦线和正切线.1.三角函数值在各象限的符号规律:一全正,二正弦,三正切,四余弦.2.若α∈2,0(,则tan α>α>sin α.3.角度制与弧度制可利用180°=πrad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.4.象限角的集合二、同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin cos=tan__α.2.三角函数的诱导公式公式一二三四五六角2k π+α(k ∈Z)π+α-απ-α2-α2+α正弦sin α-sin__α-sin__αsin__αcos__αcos__α余弦cos α-cos__αcos__α-cos__αsin__α-sin__α正切tan αtan__α-tan__α-tan__α口诀函数名不变,符号看象限函数名改变,符号看象限3.常用结论(1)同角三角函数关系式的常用变形(sin α±cos α)2=1±2sin αcos α;sin α=tan α·cos α.(2)诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指2的奇数倍和偶数倍,变与不变指函数名称的变化.(3)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.三、三角函数的图象及性质1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),)1,2( ,(π,0),)1,23(,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),)0,2( ,(π,-1),)0,23(,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z)函数y =sin xy =cos xy =tan x图象定义域R R {x |x R x ≠k π+2}值域[-1,1][-1,1]R 周期性2π2ππ奇偶性奇函数偶函数奇函数四、正弦定理余弦定理1.正弦定理:a sin A =b sin B =csin C=2R ,其中R 是三角形外接圆的半径.由正弦定理可以变形:(1)a ∶b ∶c =sin_A ∶sin_B ∶sin_C ;(2)a=2R sin_A ,b =2R sin_B ,c =2R sin_C ;(3)sin A =a 2R ,sin B =b 2R ,sin C =c2R等形式,以解决不同的三角形问题.2.余弦定理:a 2=b 2+c 2-2bc cos_A ,b 2=a 2+c 2-2ac cos_B ,c 2=a 2+b 2-2ab cos_C .余弦定理可以变形:cos A =b 2+c 2-a 22bc,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab3.S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R 、r .4.在△ABC 中,已知a 、b 和A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式a =b sin A b sin A <a <b a ≥b a >b 解的个数一解两解一解一解5.实际问题中的常用角(1)仰角和俯角与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方叫仰角,目标视线在水平视线下方叫俯角(如图①).(2)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°等.(3)方位角指从正北方向顺时针转到目标方向线的水平角,如B 点的方位角为α(如图②).(4)坡度:坡面与水平面所成的二面角的正切值.[难点正本疑点清源]1.在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .2.根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.真题再现1.【2020年高考全国Ⅲ卷文数】已知πsin sin =3 ()1,则πsin =6()A .12B C .23D 【答案】B【解析】由题意可得:13sin sin cos 122,则:3sin cos 122 ,1sin cos 223,从而有:sin coscos sin 663,即sin 63.故选:B.【点睛】本题主要考查两角和与差的正余弦公式及其应用,属于中等题.2.【2020年高考全国Ⅰ卷文数】设函数π()cos()6f x x 在[−π,π]的图像大致如下图,则f (x )的最小正周期为A .10π9B .7π6C .4π3D .3π2【答案】C【解析】由图可得:函数图象过点4,09,将它代入函数 f x 可得:4cos 096,又4,09是函数 f x 图象与x 轴负半轴的第一个交点,所以4962,解得32 .所以函数 f x 的最小正周期为224332T故选C.【点睛】本题主要考查了三角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.3.【2020年高考全国Ⅲ卷文数】在△ABC 中,cos C =23,AC =4,BC =3,则tan B =AB .C .D .【答案】C【解析】设,,AB c BC a CA b22222cos 916234933c a b ab C c2221cos sin tan 4299a cb B B B ac 故选:C【点睛】本题考查余弦定理以及同角三角函数关系,考查基本分析求解能力,属基础题.4.【2020年高考全国Ⅲ卷文数】已知函数f (x )=sin x +1sin x,则A .f (x )的最小值为2B .f (x )的图像关于y 轴对称C .f (x )的图像关于直线x 对称D .f (x )的图像关于直线2x对称【答案】D【解析】sin x ∵可以为负,所以A 错;1sin 0()()sin ()sin x x k k Z f x x f x xQ Q ()f x 关于原点对称;11(2)sin (),()sin (),sin sin f x x f x f x x f x x x Q 故B 错;()f x 关于直线2x对称,故C 错,D 对故选:D【点睛】本题考查函数定义域与最值、奇偶性、对称性,考查基本分析判断能力,属中档题.5.【2020年高考天津】已知函数π()sin(3f x x .给出下列结论:①()f x 的最小正周期为2π;②π(2f 是()f x 的最大值;③把函数sin y x 的图象上所有点向左平移π3个单位长度,可得到函数()y f x 的图象.其中所有正确结论的序号是A .①B .①③C .②③D .①②③【答案】B【解析】因为()sin()3f x x,所以周期22T,故①正确;51()sin(sin 122362f ,故②不正确;将函数sin y x 的图象上所有点向左平移3个单位长度,得到sin(3y x 的图象,故③正确.故选:B.【点晴】本题主要考查正弦型函数的性质及图象的平移,考查学生的数学运算能力,逻辑分析那能力,是一道容易题.6.【2020年高考北京】2020年3月14日是全球首个国际圆周率日( Day ).历史上,求圆周率 的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n 充分大时,计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长,将它们的算术平均数作为2 的近似值.按照阿尔·卡西的方法, 的近似值的表达式是A.30303sin tan n n nB.30306sin tan n n nC.60603sin tan n n nD.60606sin tan n n n【答案】A【解析】单位圆内接正6n 边形的每条边所对应的圆周角为360606n n,每条边长为302sin n,所以,单位圆的内接正6n 边形的周长为3012sin n n,单位圆的外切正6n 边形的每条边长为302tann ,其周长为3012tan n n,303012sin12tan 303026sin tan 2n n n n n n n,则30303sin tan n n n.故选:A.【点睛】本题考查圆周率 的近似值的计算,根据题意计算出单位圆内接正6n 边形和外切正6n 边形的周长是解答的关键,考查计算能力,属于中等题.7.【2020年新高考全国Ⅰ卷】下图是函数y =sin(ωx +φ)的部分图像,则sin(ωx +φ)=A .πsin(3x )B .πsin(2)3x C .πcos(26x D .5πcos(2)6x 【答案】BC【解析】由函数图像可知:22362T ,则222T,所以不选A,当2536212x时,1y 5322122k k Z ,解得: 223k k Z ,即函数的解析式为:2sin 22sin 2cos 2sin 236263y x k x x x.而5cos 2cos(2)66x x故选:BC.【点睛】已知f (x )=Asin (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)由ω=2T即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0,则令ωx 0+φ=0(或ωx 0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A ,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.8.【2020年高考全国Ⅱ卷文数】若2sin 3x ,则cos 2x __________.【答案】19【解析】22281cos 212sin 12()1399x x.故答案为19.【点睛】本题考查了余弦的二倍角公式的应用,属于基础题.9.【2020年高考江苏】已知2sin ()4 =23,则sin 2 的值是▲.【答案】13【解析】221sin ()cos )sin 2)4222Q 121(1sin 2)sin 2233故答案为:13【点睛】本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.10.【2020年高考北京】若函数()sin()cos f x x x 的最大值为2,则常数 的一个取值为________.【答案】2(2,2k k Z均可)【解析】因为 cos sin sin 1cos f x x x x,2 ,解得sin 1 ,故可取2.故答案为:2(2,2k k Z均可).【点睛】本题主要考查两角和的正弦公式,辅助角公式的应用,以及平方关系的应用,考查学生的数学运算能力,属于基础题.11.【2020年高考浙江】已知tan 2 ,则cos 2 _______,πtan(4_______.【答案】35-;13【解析】2222222222cos sin 1tan 123cos 2cos sin cos sin 1tan 125,tan 1211tan(41tan 123,故答案为:31,53【点睛】本题考查二倍角余弦公式以及弦化切、两角差正切公式,考查基本分析求解能力,属基础题.12.【2020年高考江苏】将函数πsin(32)4y x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是▲.【答案】524x【解析】3sin[2(]3sin(2)6412y x x72()()122242k x k k Z x k Z 当1k 时524x.故答案为:524x【点睛】本题考查三角函数图象变换、正弦函数对称轴,考查基本分析求解能力,属基础题.13.【2020年新高考全国Ⅰ卷】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O 为圆孔及轮廓圆弧AB 所在圆的圆心,A 是圆弧AB 与直线AG 的切点,B 是圆弧AB 与直线BC 的切点,四边形DEFG 为矩形,BC ⊥DG ,垂足为C ,tan ∠ODC =35,BH DG ∥,EF =12cm ,DE=2cm ,A 到直线DE 和EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为________cm 2.【答案】542【解析】设 OB OA r ,由题意7AM AN ,12EF ,所以5NF ,因为5AP ,所以45AGP ,因为//BH DG ,所以45AHO ,因为AG 与圆弧AB 相切于A 点,所以OA AG ,即OAH △为等腰直角三角形;在直角OQD △中,52OQ r,72DQ r ,因为3tan 5OQ ODC DQ ,所以212522r r ,解得r等腰直角OAH △的面积为1142S;扇形AOB 的面积 2213324S,所以阴影部分的面积为1215422S S.故答案为:542.【点睛】本题主要考查三角函数在实际中应用,把阴影部分合理分割是求解的关键,以劳动实习为背景,体现了五育并举的育人方针.14.【2020年高考全国Ⅰ卷文数】ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a ,b ,求ABC △的面积;(2)若sin A C =2,求C .【解析】(1)由题设及余弦定理得2222832cos150c c ,解得2c (舍去),2c ,从而a .ABC △的面积为12sin1502.(2)在ABC △中,18030A B C C ,所以sin sin(30)sin(30)A C C C C ,故sin(30)2C.而030C ,所以3045C ,故15C .【点睛】本题考查余弦定理、三角恒等变换解三角形,熟记公式是解题的关键,考查计算求解能力,属于基础题.15.【2020年高考全国Ⅱ卷文数】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A .(1)求A ;(2)若3b c a ,证明:△ABC 是直角三角形.【解析】(1)由已知得25sin cos 4A A ,即21cos cos 04A A .所以21(cos 02A ,1cos 2A .由于0A ,故3A .(2)由正弦定理及已知条件可得sin sin B C A.由(1)知23B C ,所以2sin sin()33B B .即11sin 222B B ,1sin()32B .由于03B ,故2B .从而ABC △是直角三角形.【点睛】本题主要考查诱导公式和平方关系的应用,利用勾股定理或正弦定理,余弦定理判断三角形的形状,属于基础题.16.【2020年高考江苏】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B .(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ,求tan DAC ∠的值.【解析】(1)在ABC △中,因为3,45a c B ,由余弦定理2222cos b a c ac B ,得29223455b ,所以b 在ABC △中,由正弦定理sin sin b c B C ,得=sin 45sin C,所以sin C(2)在ADC △中,因为4cos 5ADC ,所以ADC 为钝角,而180ADC C CAD ,所以C 为锐角.故cos C 则sin 1tan cos 2C C C .因为4cos 5ADC,所以3sin 5ADC ,sin 3tan cos 4ADC ADC ADC .从而31tan()242tan tan(180)tan()===311tan tan 111()42ADC C ADC ADC C ADC C ADC C .【点睛】本小题主要考查正弦定理、余弦定理解三角形,考查三角恒等变换,属于中档题.17.【2020年高考天津】在ABC △中,角,,A B C 所对的边分别为,,a b c.已知5,a b c .(Ⅰ)求角C 的大小;(Ⅱ)求sin A 的值;(Ⅲ)求πsin(24A 的值.【解析】(Ⅰ)在ABC △中,由余弦定理及5,a b c222cos 22a b c C ab .又因为(0,π)C ,所以π4C .(Ⅱ)在ABC △中,由正弦定理及π,4C a c sin 213sin 13a C A c .(Ⅲ)由a c 及213sin 13A,可得313cos 13A ,进而2125sin 22sin cos ,cos 22cos 11313A A A A A.所以,πππ125sin(2)sin 2cos cos 2sin 44413213226A A A .【点晴】本题主要考查正、余弦定理解三角形,以及三角恒等变换在解三角形中的应用,考查学生的数学运算能力,是一道容易题.18.【2020年高考北京】在ABC 中,11a b ,再从条件①、条件②这两个条件中选择一个作为己知,求:(Ⅰ)a 的值:(Ⅱ)sin C 和ABC 的面积.条件①:17,cos 7c A;条件②:19cos ,cos 816A B .注:如果选择条件①和条件②分别解答,按第一个解答计分.【解析】选择条件①(Ⅰ)17,cos 7c A ∵,11a b 22222212cos (11)72(11)7()7a b c bc A a a a ∵8a(Ⅱ)1cos(0,)sin77A A A∵,由正弦定理得:7sinsin sin sin2437a c CA C C11sin(118)8222S ba C选择条件②(Ⅰ)19cos,cos,(0,)816A B A B∵sin816A B由正弦定理得:6sin sin816a b aA B(Ⅱ)91sin sin()sin cos sin cos8161684C A B A B B A11sin(116)62244S ba C【点睛】本题考查正弦定理、余弦定理,三角形面积公式,考查基本分析求解能力,属中档题.19.【2020年高考浙江】在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知2sin0b A .(Ⅰ)求角B的大小;(Ⅱ)求cos A+cos B+cos C的取值范围.【解析】(Ⅰ)由正弦定理得2sin sinB A A,故sin2B ,由题意得π3B .(Ⅱ)由πA B C得2π3C A,由ABC△是锐角三角形得ππ(,62A .由2π1cos cos()sin322C A A A得11π113cos cos cos sin()(,]2226222A B C A A A.故cos cos cosA B C的取值范围是13(,]22.【点睛】解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求最值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是转化为关于某个角的函数,利用函数思想求最值.20.【2020年新高考全国Ⅰ卷】在①ac ,②sin 3c A ,③c 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在ABC △,它的内角,,A B C 的对边分别为,,a b c ,且sin A B ,6C,________?注:如果选择多个条件分别解答,按第一个解答计分.【解析】方案一:选条件①.由6C 和余弦定理得22222a b c ab .由sin A B 及正弦定理得a .222b c .由①ac ,解得1a b c .因此,选条件①时问题中的三角形存在,此时1c .方案二:选条件②.由6C 和余弦定理得2222a b c ab .由sin A B 及正弦定理得a .22232 ,由此可得b c ,6B C ,23A .由②sin 3c A ,所以6c b a .因此,选条件②时问题中的三角形存在,此时c 方案三:选条件③.由6C 和余弦定理得22222a b c ab .由sin A B 及正弦定理得a .2222 ,由此可得b c .由③c ,与b c 矛盾.因此,选条件③时问题中的三角形不存在.【点睛】在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.。
新高考数学(理)之三角函数与解三角形 专题04 三角恒等变换(解析版)

新高考数学(理)三角函数与平面向量04 三角恒等变换一、具本目标:1.两角和与差的三角函数公式 (1)会用向量的数量积推导出两角差的余弦公式;(2)能利用两角差的余弦公式导出两角差的正弦、正切公式;(3)能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系;2.简单的三角恒等变换:能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆)3.(1) 已知两角的正余弦,会求和差角的正弦、余弦、正切值. (2) 会求类似于15°,75°,105°等特殊角的正、余弦、正切值. (3) 用和差角的正弦、余弦、正切公式化简求值. (4)逆用和差角的正弦、余弦、正切公式化简求值. (5) 会配凑、变形、拆角等方法进行化简与求值. 二、知识概述:知识点一 两角和与差的正弦、余弦、正切公式两角和与差的正弦公式: ()sin sin cos cos sin α+β=αβ+αβ,()sin sin cos cos sin α-β=αβ-αβ.两角和与差的余弦公式:()cos cos cos sin sin α+β=αβ-αβ, ()cos cos cos sin sin α-β=αβ+αβ. 两角和与差的正切公式:()tan tan tan 1tan tan α+βα+β=-αβ,【考点讲解】()tan tan tan 1tan tan α-βα-β=+αβ.【特别提醒】公式的条件:1. 两角和与差的正弦、余弦公式中的两个角α、β为任意角.2.两角和与差的正切公式中两个角有如下的条件:(),,,.2222k k k k k z ππππα+β≠π+α-β≠π+α≠π+β≠π+∈知识点二 公式的变用1. 两角和与差的正弦公式的逆用与辅助角公式:()22sin cos sin a x b x a b x +=++ϕ(其中φ角所在的象限由a,b 的符号确定,φ的值由tan baϕ=确定),在求最值、化简时起着重要的作用. 2. ()tan tan tan 1tan tan α+βα+β=-αβ变形为()()tan tan tan 1tan tan α+β=α+β-αβ,()tan tan tan 1tan tan α+βα+β=-αβ变形为()tan tan tan tan 1tan α+βαβ=-α+β.()tan tan tan 1tan tan α-βα-β=+αβ变形为()()tan tan tan 1tan tan α-β=α-β+αβ,()tan tan tan 1tan tan α-βα-β=+αβ变形为()tan tan tan tan 1tan α-βαβ=-α-β来使用. 条件为:(),,,.2222k k k k k z ππππα+β≠π+α-β≠π+α≠π+β≠π+∈ 知识点三 二倍角公式: 1.22tan sin 22sin cos 1tan ααααα==+ 2222221tan cos 2cos sin 2cos 112sin 1tan ααααααα-=-=-=-=+ 22tan tan 21tan ααα=-2. 常见变形:(1)22cos 1sin 2αα-=,22cos 1cos 2αα+=(2)()2cos sin 2sin 1ααα+=+,()2cos sin 2sin 1ααα-=-;(3)αα2cos 22cos 1=+,αα2sin 22cos 1=-.3.半角公式:2cos 12sin αα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan+-±=,αααααsin cos 1cos 1sin 2tan-=+=.1.【2019年高考全国Ⅱ卷文理】已知a ∈(0,π2),2sin2α=cos2α+1,则sin α=( ) A .15B .55 C .33D .255【解析】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查.2sin 2cos21αα=+Q ,24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭Q ,sin 0,α>2sin cos αα∴=,又22sin cos 1αα+=,2215sin 1,sin 5αα∴==,又sin 0α>,5sin 5α∴=,故选B . 【答案】B2.【2019年高考全国Ⅲ卷文数】函数()2sin sin2f x x x =-在[0,2π]的零点个数为( ) A .2B .3C .4D .5【解析】由()2sin sin 22sin 2sin cos 2sin (1cos )0f x x x x x x x x =-=-=-=,得sin 0x =或cos 1x =,[]0,2πx ∈Q ,0π2πx ∴=、或.()f x ∴在[]0,2π的零点个数是3,故选B .【答案】B3.【2018年高考全国Ⅰ卷文数】已知函数()222cos sin 2f x x x =-+,则( )A .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为 4【真题分析】【解析】本题考查的是二倍角公式及余弦型函数的周期及最值问题.根据题意有()135cos 21(1cos 2)2cos 2222f x x x x =+--+=+,所以函数()f x 的最小正周期为2ππ2T ==,且最大值为()max 35422f x =+=,故选B. 【答案】B4.【2018年高考全国Ⅰ卷】若1sin 3α=,则cos2α=( ) A .89 B .79 C .79- D .89-【解析】本题主要考查二倍角公式及求三角函数的值.2217cos 212sin 12()39αα=-=-⨯=.故选B. 【答案】B5.【2018年高考全国Ⅰ卷文数】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos 23α=,则a b -=( )A .15 B .55 C .255D .1 【解析】本题主要考查任意角的三角函数和三角恒等变換根据条件,可知,,O A B 三点共线,从而得到2b a =,因为22212cos22cos 12131a ⎛⎫=-=⋅-= ⎪+⎝⎭αα,解得215a =,即55a =,所以525a b a a -=-=. 【答案】B6.【2017年高考全国Ⅰ卷文数】已知4sin cos 3αα-=,则sin 2α=( ) A .79-B .29-C .29D .79【解析】()2sin cos 17sin 22sin cos 19ααααα--===--.所以选A. 【答案】A7.【2019年高考全国Ⅰ卷文数】函数3π()sin(2)3cos 2f x x x =+-的最小值为___________. 【解析】23π()sin(2)3cos cos 23cos 2cos 3cos 12f x x x x x x x =+-=--=--+23172(cos )48x =-++, 1cos 1x -≤≤Q ,∴当cos 1x =时,min ()4f x =-,故函数()f x 的最小值为4-.【答案】4-8.【2019年高考北京卷理数】函数f (x )=sin 22x 的最小正周期是__________.【解析】本题主要考查二倍角的三角函数公式、三角函数的最小正周期公式,函数()2sin 2f x x ==1cos 42x -,周期为π2. 【答案】π29.【2019年高考江苏卷】已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭,则πsin 24α⎛⎫+ ⎪⎝⎭的值是 . 【解析】由()tan 1tan tan tan 2tan 1πtan 13tan 1tan 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭,得23tan 5tan 20αα--=, 解得tan 2α=,或1tan 3α=-.πππsin 2sin 2cos cos 2sin 444ααα⎛⎫+=+ ⎪⎝⎭()2222222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎛⎫+-=+ ⎪+⎝⎭2222tan 1tan =2tan 1ααα⎛⎫+- ⎪+⎝⎭, 当tan 2α=时,上式22222122==22110⎛⎫⨯+-⨯ ⎪+⎝⎭; 当1tan 3α=-时,上式=22112()1()2233[]=1210()13⨯-+--⨯-+. 综上,π2sin 2.410α⎛⎫+= ⎪⎝⎭ 【答案】21010.【2018年高考全国Ⅰ卷文数】已知5π1tan()45-=α,则tan =α__________. 【解析】本题主要考查三角恒等变换,考查考生的运算求解能力.5πtan tan5πtan 114tan 5π41tan 51tan tan 4ααααα--⎛⎫-=== ⎪+⎝⎭+⋅,解方程得3tan 2=α.故答案为32. 【答案】3211.【2018年高考全国Ⅱ理数】已知sin cos 1αβ+=,cos sin 0αβ+=,则sin()αβ+=__________. 【解析】本题主要考查三角恒等变换.因为sin cos 1+=αβ,cos sin 0+=αβ,所以()()221sin cos 1,-+-=αα所以11sin ,cos 22==αβ, 因此()22111111sin sin cos cos sin cos 1sin 1.224442+=+=⨯-=-+=-+=-αβαβαβαα【答案】12-12.【2017年高考江苏卷】若π1tan(),46-=α则tan =α .【解析】11tan()tan7644tan tan[()]14451tan()tan 1446ααααππ+-+ππ=-+===ππ---.故答案为75. 【答案】7513.【2018年高考全国Ⅰ理数】已知函数()2sin sin2f x x x =+,则()f x 的最小值是_____________.【解析】()()212cos 2cos 24cos 2cos 24cos 1cos 2f x x x x x x x ⎛⎫'=+=+-=+-⎪⎝⎭, 所以当1cos 2x <时函数单调递减,当1cos 2x >时函数单调递增,从而得到函数的递减区间为()5ππ2π,2π33k k k ⎡⎤--∈⎢⎥⎣⎦Z ,函数的递增区间为()ππ2π,2π33k k k ⎡⎤-+∈⎢⎥⎣⎦Z , 所以当π2π,3x k k =-∈Z 时,函数()f x 取得最小值,此时33sin ,sin222x x =-=-, 所以()min 33332222f x ⎛⎫=⨯--=- ⎪ ⎪⎝⎭,故答案是332-.【答案】332-14.【2017年高考全国Ⅱ理数】函数()23sin 3cos 4f x x x =+-(π0,2x ⎡⎤∈⎢⎥⎣⎦)的最大值是 . 【解析】本题主要考查的是三角函数式的化简及三角函数的问题转化为二次函数的问题,二次函数、二次方程与二次不等式统称“三个二次”化简三角函数的解析式的综合考查.()2223131cos 3cos cos 3cos cos 1442f x x x x x x ⎛⎫=-+-=-++=--+ ⎪ ⎪⎝⎭,由自变量的范围:π0,2x ⎡⎤∈⎢⎥⎣⎦可得:[]cos 0,1x ∈,当3cos 2x =时,函数()f x 取得最大值1.【答案】115.【2019年高考浙江卷】设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124y f x f x ππ=+++的值域. 【解析】本题主要考查三角函数及其恒等变换等基础知识.(1)因为()sin()f x x θθ+=+是偶函数,所以,对任意实数x 都有sin()sin()x x θθ+=-+, 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+,故2sin cos 0x θ=,所以cos 0θ=. 又[0,2π)θ∈,因此π2θ=或3π2. (2)2222ππππsin sin 124124y fx f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 2133621cos 2sin 222222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭=+=-- ⎪ ⎪⎝⎭3π1cos 223x ⎛⎫=-+ ⎪⎝⎭. 因此,函数的值域是33[1,1]22-+. 【答案】(1)π2θ=或3π2;(2)33[1,1]22-+. 16.【2018年高考北京卷文数】已知函数2()sin 3sin cos f x x x x =+.(1)求()f x 的最小正周期; (2)若()f x 在区间[,]3m π-上的最大值为32,求m 的最小值. 【解析】本题主要考查二倍角公式、辅助角公式、正弦函数的性质. (1)1cos 23311π1()sin 2sin 2cos 2sin(2)2222262x f x x x x x -=+=-+=-+, 所以()f x 的最小正周期为2ππ2T ==. (2)由(1)知π1()sin(2)62f x x =-+.因为π[,]3x m ∈-,所以π5ππ2[,2]666x m -∈--.要使得()f x 在π[,]3m -上的最大值为32,即πsin(2)6x -在π[,]3m -上的最大值为1. 所以ππ262m -≥,即π3m ≥.所以m 的最小值为π3.【答案】(1)π;(2)π3.1. sin15°sin105°的值是( ) A .14 B .14-C .34D .34-【解析】本题的考点二倍角的正弦和诱导公式:sin15°sin105°=sin15°cos15°=12sin30°=14,故选A . 【答案】A2.已知sin2α=13,则cos 2(π4α-)=( ) A .34 B .23 C .45 D .56【解析】本题考点二倍角的余弦,三角函数的化简求值.∵sin2α=13,∴cos 2(π4α-)=π11cos 211sin 22232223αα⎛⎫+-+⎪+⎝⎭===.故选B . 【答案】B3.已知sin α=45-,α∈(π,3π2),则tan 2α等于( ) A .-2 B .12 C .12-或2 D .-2或12【解析】∵sin α=45-,α∈(π,3π2),∴cos α=35-,∴tan α=43.∵α∈(π,3π2),∴2α∈(π2,3π4),∴tan 2α<0. tan α=22tan21tan 2αα- =43,即2tan 22α+ 3tan2α-2=0,解得tan2α=-2,或tan2α=12(舍去),故选A .【答案】A【模拟考场】4.设π0,2α⎛⎫∈ ⎪⎝⎭,π0,4β⎛⎫∈ ⎪⎝⎭,且tan α=1sin 2cos 2ββ+,则下列结论中正确的是( ) A .2π4αβ-=B .π24αβ+=C .π4αβ-=D .π4αβ+= 【解析】本题的考点二倍角的余弦,二倍角的正弦..tan α=()222sin cos 1sin 2sin cos 1tan cos 2cos sin cos sin 1tan ββββββββββββ++++===---πtan 4β⎛⎫=+ ⎪⎝⎭ 因为π0,2α⎛⎫∈ ⎪⎝⎭,πππ,442β⎛⎫+∈ ⎪⎝⎭,所以π4αβ-=.故选C . 【答案】C5.已知角αβ,均为锐角,且cos α=35,tan (α−β)=−13,tan β=( ) A .13 B .913 C .139D .3【解析】∵角α,β均为锐角,且cos α=35,∴sin α=21cos α- =45,tan α=43,又tan (α−β)=tan tan 1+tan tan αβαβ-=4tan 341+tan 3ββ-=−13, ∴tan β=3,故选D .【答案】D6.设α为锐角,若π3cos()65α+=,则πsin()12α-=( ) A .210 B .210- C .45 D .45- 【解析】因为α为锐角,所以ππ2π,663α⎛⎫+∈ ⎪⎝⎭,因为π3cos()65α+=,所以π4sin()65α+=,故πππππsin()sin sin cos 126464ααα⎡⎤⎛⎫⎛⎫-=+-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ππ2432cos sin 6425510α⎛⎫⎛⎫+=-= ⎪ ⎪⎝⎭⎝⎭.故选A.【答案】A7.设函数2()sin sin f x x b x c =++,则()f x 的最小正周期( )A .与b 有关,且与c 有关B .与b 有关,但与c 无关C .与b 无关,且与c 无关D .与b 无关,但与c 有关【解析】本题考查的是二倍角的降幂公式与三角函数的最小正周期,先利用三角恒等变换(降幂公式)化简函数()f x ,再判断b 和c 的取值是否影响函数()f x 的最小正周期.21cos 2cos 21()sin sin sin sin 222-=++=++=-+++x x f x x b x c b x c b x c ,其中当0=b 时,cos 21()22=-++x f x c ,此时周期是π;当0≠b 时,周期为2π,而c 不影响周期.故选B . 【答案】B8.已知34cos sin =-αα,则=α2sin ( ) A .97- B .92- C .92 D .97【解析】本题的考点是二倍角的正弦正逆用,将34cos sin =-αα两边平方()2234cos sin ⎪⎭⎫ ⎝⎛=-αα, 化简后可得916cos sin 2cos sin 22=-+αααα即=α2sin 97-.【答案】A 9.函数()⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=6cos 3sin 51ππx x x f 的最大值为( ) A .56B .1C .53D .51【解析】将()⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=6cos 3sin 51ππx x x f 化简,利用两角和、差的正余弦公式及辅助角公式,三角函数 最值的性质可以求得函数最大值.由()6sin sin 6cos cos 3sin cos 3cos sin 51ππππx x x x x f ++⎪⎭⎫ ⎝⎛+= x x x x sin 21cos 23cos 103sin 101+++=⎪⎪⎭⎫ ⎝⎛+=+=x x x x cos 23sin 2156cos 533sin 53⎪⎭⎫ ⎝⎛+=3sin 56πx , 因为13sin 1≤⎪⎭⎫ ⎝⎛+≤-πx ,所以函数的最大值为56.【答案】A10.若tan 2tan 5πα=,则3cos()10sin()5παπα-=-( ) A.1 B.2 C.3 D.4【解析】本题考点是两角和与差的正弦(余弦)公式,同角间的三角函数关系,三角函数的恒等变换. 三角恒等变换的主要是求值,在求值时只要根据求解目标的需要,结合已知条件选用合适的公式计算.本例应用两角和与差的正弦(余弦)公式化简所求式子,利用同角关系式求出使已知条件可代入的值,然后再化简,求解过程中注意公式的顺用和逆用.3cos()10sin()5παπα-=-33cos cos sin sin 1010sin cos cos sin 55ππααππαα+-33cos tan sin 1010tan cos sin 55ππαππα+=-33cos 2tan sin 105102tan cos sin 555ππππππ+=- 33cos cos 2sin sin 510510sin cos 55ππππππ+==333cos cos sin sin sin sin 510510510sin cos 55ππππππππ++ =333cos cos sin 5101010sin cos 55ππππππ⎛⎫-+ ⎪⎝⎭=13cos sin 1025sin cos 55ππππ+1cos cos 10210sin cos 55ππππ+=1cos cos 1021014sin 210πππ+= 3cos103cos 10ππ==.【答案】C11.已知向量a r =(sin θ,2-),b r =(1,cos θ),且a r ⊥b r ,则sin 2θ+cos 2θ的值为( )A .1B .2C .12D .3 【解析】本题考点是三角函数的恒等变换及化简求值,数量积判断两个平面向量的垂直关系.由题意可得a r ·b r =sin θ-2cos θ=0,即tan θ=2.∴sin 2θ+cos 2θ=2222sin cos +cos cos +sin θθθθθ=22tan +11+tan θθ=1,故选A . 【答案】A12.已知cos θ=-725,θ∈(-π,0),则sin 2θ+cos 2θ=( )A .125B .15±C .15D .15- 【解析】∵cos θ=-725,θ∈(-π,0), ∴cos 22θ-sin 22θ=(cos 2θ+sin 2θ)(cos 2θ-sin 2θ)<0,2θ∈(π2-,0), ∴sin 2θ+cos 2θ<0,cos 2θ-sin 2θ>0,∵(sin 2θ+cos 2θ)2=1+sin θ=1-491625-=125,∴sin 2θ+cos 2θ=15-.故选D .【答案】D13. =+οο75sin 15sin .【解析】本题考查的是三角恒等变换及特殊角的三角函数值的求解. 法一、6sin15sin 75sin15cos152sin(1545)2+=+=+=o o o o o o . 法二、6sin15sin 75sin(4530)sin(4530)2sin 45cos302+=-++==o o o o o o o o . 法三、62626sin15sin 75442-++=+=o o . 【答案】62. 14.在锐角三角形ABC 中,若sin 2sin sin A B C =,则tan tan tan A B C 的最小值是 .【解析】本题考查的是三角恒等变换及正切的性质,本题要求会利用三角形中隐含的边角关系作为消元依据,同时要记住斜三角形ABC 中恒有tan tan tan tan tan tan A B C A B C =++,sin sin(B C)2sin sin tan tan 2tan tan A B C B C B C =+=⇒+=,因此tan tan tan tan tan tan tan 2tan tan 22tan tan tan tan tan tan 8A B C A B C A B C A B C A B C =++=+≥⇒≥,即最小值为8.【答案】8.15.【2018江苏卷16】已知,αβ为锐角,4tan 3α=,5cos()5αβ+=-. (1)求cos2α的值;(2)求tan()αβ-的值.【解析】(1)因为,,所以. 4tan 3α=sin tan cos ααα=4sin cos 3αα=因为,所以, 因此,. (2)因为为锐角,所以.又因为,所以, 因此.因为,所以, 因此,. 16.【2016高考山东理数】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知tan tan 2(tan tan ).cos cos A B A B B A +=+ (Ⅰ)证明:a +b =2c ;(Ⅱ)求cos C 的最小值.【解析】试题分析:(Ⅰ)根据两角和的正弦公式、正切公式、正弦定理即可证明;(Ⅱ)根据余弦定理公式表示出cosC ,由基本不等式求cos C 的最小值.试题解析:()I 由题意知sin sin sin sin 2cos cos cos cos cos cos A B A B A B A B A B ⎛⎫+=+ ⎪⎝⎭, 化简得()2sin cos sin cos sin sin A B B A A B +=+,即()2sin sin sin A B A B +=+.因为A B C π++=,所以()()sin sin sin A B C C π+=-=.从而sin sin =2sin A B C +.由正弦定理得2a b c +=.()∏由()I 知2a b c +=, 所以 2222222cos 22a b a b a b c C ab ab +⎛⎫+- ⎪+-⎝⎭==311842b a a b ⎛⎫=+-≥ ⎪⎝⎭, 当且仅当a b =时,等号成立.故 cos C 的最小值为12. 17.已知函数()22sin sin 6f x x x π⎛⎫=-- ⎪⎝⎭,R x ∈ 22sin cos 1αα+=29cos 25α=27cos22cos 125αα=-=-,αβ(0,π)αβ+∈5cos()5αβ+=-225sin()1cos ()5αβαβ+=-+=tan()2αβ+=-4tan 3α=22tan 24tan 21tan 7ααα==--tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+(I)求()f x 最小正周期;(II)求()f x 在区间[,]34p p -上的最大值和最小值. 【解析】本题考点两角和与差的正余弦公式、二倍角的正余弦公式、三角函数的图象与性质.综合运用三角 知识,从正确求函数解析式出发,考查最小正周期的求法与函数单调性的应用,从而求出函数的最大值与最小值,体现数学思想与方法的应用.(I) 由已知,有1cos 21cos211313()cos2sin 2cos2222222x x f x x x x π⎛⎫-- ⎪⎛⎫-⎝⎭=-=+- ⎪⎝⎭ 311sin 2cos2sin 24426x x x π⎛⎫--=- ⎪⎝⎭. 所以()f x 的最小正周期22T ππ==. (II)因为()f x 在区间[,]36p p --上是减函数,在区间[,]64p p -上是增函数, 113(),(),()346244f f f πππ-=--=-=,所以()f x 在区间[,]34p p -上的最大值为34,最小值为12-. 【答案】(I)π; (II) max 3()4f x =,min 1()2f x =-.。
高考数学压轴专题最新备战高考《三角函数与解三角形》知识点总复习有答案解析

【高中数学】数学高考《三角函数与解三角形》试题含答案一、选择题1.已知函数()()πsin 06f x x ωω⎛⎫=-> ⎪⎝⎭,若()π02f f ⎛⎫=- ⎪⎝⎭在π0,2⎛⎫⎪⎝⎭上有且仅有三个零点,则ω= ( ) A .23B .2C .143D .263【答案】C 【解析】∵函数()()sin 06f x x πωω⎛⎫=-> ⎪⎝⎭,()02f f π⎛⎫=-⎪⎝⎭∴1sin()sin()6262πππω-=--=- ∴2266k πππωπ-=+或52,266k k Z πππωπ-=+∈ ∴243k ω=+或42,k k ω=+∈Z ∵函数()f x 在0,2π⎛⎫⎪⎝⎭上有且仅有三个零点 ∴(,)6626x ππωππω-∈-- ∴2326ωππππ<-≤∴131933ω<≤ ∴143ω=或6ω= 故选C.2.在ABC ∆中,角,,A B C 所对应的边分别为,,a b c ,已知cos cos 2b C c B b +=,则ab=( )A .B .2CD .1【答案】B 【解析】 【分析】由正弦定理及题设可知,sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=,又A B C π++=,可得sin 2sin A B =,再由正弦定理,可得解【详解】由正弦定理:2sin sin b cR B C==,又cos cos 2b C c B b += 得到sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=在ABC ∆中,A B C π++=故sin()2sin A B π-=,即sin 2sin A B =故sin 2sin a A b B == 故选:B 【点睛】本题考查了正弦定理在边角互化中的应用,考查了学生综合分析,转化划归,数学运算能力,属于中档题3.已知在锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos b C c B =,则111tan tan tan A B C++的最小值为( ) ABCD.【答案】A 【解析】 【分析】先根据已知条件,把边化成角得到B,C 关系式,结合均值定理可求. 【详解】∵2cos cos b C c B =,∴2sin cos sinCcos B C B =, ∴tan 2tan C B =.又A B C π++=, ∴()()tan tan tan A B C B C π=-+=-+⎡⎤⎣⎦22tan tan 3tan 3tan 1tan tan 12tan 2tan 1B C B BB C B B +=-=-=---, ∴21112tan 111tan tan tan 3tan tan 2tan B A B C B B B -++=++27tan 36tan B B =+. 又∵在锐角ABC ∆中, tan 0B >,∴27tan 36tan B B +≥=,当且仅当tan 2B =时取等号,∴min111tan tan tan 3A B C ⎛⎫++=⎪⎝⎭,故选A. 【点睛】本题主要考查正弦定理和均值定理,解三角形时边角互化是求解的主要策略,侧重考查数学运算的核心素养.4.如图,边长为1正方形ABCD ,射线BP 从BA 出发,绕着点B 顺时针方向旋转至BC ,在旋转的过程中,记([0,])2ABP x x π∠=∈,BP 所经过的在正方形ABCD 内的区域(阴影部分)的面积为()y f x =,则函数()f x 的图像是( )A .B .C .D .【答案】D 【解析】 【分析】根据条件列()y f x =,再根据函数图象作判断. 【详解】 当0,4x π⎡⎤∈⎢⎥⎣⎦时,()112y f x tanx ==⨯⨯; 当,42x ππ⎛⎤∈⎥⎝⎦时,()11112y f x tanx ==-⨯⨯; 根据正切函数图象可知选D. 【点睛】本题考查函数解析式以及函数图象,考查基本分析识别能力,属基本题.5.已知函数f (x )=2x -1,()2cos 2,0?2,0a x x g x x a x +≥⎧=⎨+<⎩(a ∈R ),若对任意x 1∈[1,+∞),总存在x 2∈R ,使f (x 1)=g (x 2),则实数a 的取值范围是()A .1,2⎛⎫-∞ ⎪⎝⎭B .2,3⎛⎫+∞⎪⎝⎭C .[]1,1,22⎛⎫-∞ ⎪⎝⎭U D .371,,224⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦U 【答案】C 【解析】 【分析】对a 分a=0,a <0和a >0讨论,a >0时分两种情况讨论,比较两个函数的值域的关系,即得实数a 的取值范围. 【详解】当a =0时,函数f (x )=2x -1的值域为[1,+∞),函数()g x 的值域为[0,++∞),满足题意. 当a <0时,y =22(0)x a x +<的值域为(2a ,+∞), y =()cos 20a x x +≥的值域为[a +2,-a +2],因为a +2-2a =2-a >0,所以a +2>2a , 所以此时函数g (x )的值域为(2a ,+∞), 由题得2a <1,即a <12,即a <0. 当a >0时,y =22(0)x a x +<的值域为(2a ,+∞),y =()cos 20a x x +≥的值域为[-a +2,a +2], 当a ≥23时,-a +2≤2a ,由题得21,1222a a a a -+≤⎧∴≤≤⎨+≥⎩. 当0<a <23时,-a +2>2a ,由题得2a <1,所以a <12.所以0<a <12. 综合得a 的范围为a <12或1≤a ≤2, 故选C . 【点睛】本题主要考查函数的图象和性质,考查指数函数和三角函数的图象和性质,意在考查学生对这些知识的理解掌握水平和分析推理能力.6.已知函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象如图所示,其中()01f =,5||2MN =,则点M 的横坐标为( )A .12B .25-C .1-D .23-【答案】C 【解析】 【分析】 由(0)1f =求出56πϕ=,由5||23MN πω=⇒=,再根据()2f x =可得答案.【详解】由函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象, 可得(0)2sin 1f ϕ==,56πϕ∴=, 22512||2243MN ππωω⎛⎫==+⋅= ⎪⎝⎭, ∴函数5()2sin 36f x x ππ⎛⎫=+ ⎪⎝⎭,令52sin 236x ππ⎛⎫+= ⎪⎝⎭, 得52,0362x k k ππππ+=+=得1x =-. 故选:C. 【点睛】本题主要考查三角函数的图象与性质,考查了数形结合思想的应用,解题的关键是利用勾股定理列方程求出3πω=,属于中档题.7.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表: 黄赤交角 2341︒'2357︒'2413︒'2428︒'2444︒'正切值 0.439 0.444 0.450 0.455 0.461 年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ) A .公元前2000年到公元元年 B .公元前4000年到公元前2000年 C .公元前6000年到公元前4000年 D .早于公元前6000年【答案】D 【解析】 【分析】先理解题意,然后根据题意建立平面几何图形,在利用三角函数的知识计算出冬至日光与春秋分日光的夹角,即黄赤交角,即可得到正确选项. 【详解】解:由题意,可设冬至日光与垂直线夹角为α,春秋分日光与垂直线夹角为β, 则αβ-即为冬至日光与春秋分日光的夹角,即黄赤交角, 将图3近似画出如下平面几何图形:则16tan 1.610α==,169.4tan 0.6610β-==, tan tan 1.60.66tan()0.4571tan tan 1 1.60.66αβαβαβ---==≈++⨯g .0.4550.4570.461<<Q ,∴估计该骨笛的大致年代早于公元前6000年.故选:D .【点睛】本题考查利用三角函数解决实际问题的能力,运用了两角和与差的正切公式,考查了转化思想,数学建模思想,以及数学运算能力,属中档题.8.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()23f x =的解为12,x x (120x x π<<<),则()21sin x x -=( )A .23B .49C D 【答案】C 【解析】 【分析】 由已知可得2123x x π=-,结合x 1<x 2求出x 1的范围,再由()121122236sin x x sin x cos x ππ⎛⎫⎛⎫-=-=-- ⎪ ⎪⎝⎭⎝⎭求解即可. 【详解】因为0<x π<,∴112666x πππ⎛⎫-∈- ⎪⎝⎭,, 又因为方程()23f x =的解为x 1,x 2(0<x 1<x 2<π), ∴1223x x π+=,∴2123x x π=-, ∴()121122236sin x x sin x cos x ππ⎛⎫⎛⎫-=-=-- ⎪ ⎪⎝⎭⎝⎭, 因为122123x x x x π=-<,,∴0<x 13π<,∴12662x πππ⎛⎫-∈- ⎪⎝⎭,,∴由()112263f x sin x π⎛⎫=-= ⎪⎝⎭,得126cos x π⎛⎫-= ⎪⎝⎭,∴()12sin x x -=,故()21sin x x -故选C . 【点睛】本题考查了三角函数的恒等变换及化简求值和三角函数的图象与性质,属中档题.9.如图,直三棱柱ABC A B C '''-的侧棱长为3,AB BC ⊥,3AB BC ==,点E ,F分别是棱AB ,BC 上的动点,且AE BF =,当三棱锥B EBF '-的体积取得最大值时,则异面直线A F '与AC 所成的角为( )A .2π B .3π C .4π D .6π 【答案】C 【解析】 【分析】设AE BF a ==,13B EBF EBF V S B B '-'=⨯⨯V ,利用基本不等式,确定点 E ,F 的位置,然后根据//EF AC ,得到A FE '∠即为异面直线A F '与AC 所成的角,再利用余弦定理求解. 【详解】设AE BF a ==,则()()23119333288B EBFa a V a a '-+-⎡⎤=⨯⨯⨯-⨯≤=⎢⎥⎣⎦,当且仅当3a a =-,即32a =时等号成立, 即当三棱锥B EBF '-的体积取得最大值时,点E ,F 分别是棱AB ,BC 的中点, 方法一:连接A E ',AF ,则352A E '=352AF =2292A F AA AF ''=+=,13222EF AC ==, 因为//EF AC ,所以A FE '∠即为异面直线A F '与AC 所成的角,由余弦定理得222819452424cos 93222222A F EF A E A FE A F EF +-''+-'∠==='⋅⋅⨯,∴4A FE π'∠=.方法二:以B 为坐标原点,以BC 、BA 、BB '分别为x 轴、y 轴、z 轴建立空间直角坐标系,则()0,3,0A ,()3,0,0C ,()0,3,3A ',3,0,02F ⎛⎫⎪⎝⎭,∴3,3,32A F ⎛⎫'=-- ⎪⎝⎭u u u u r ,()3,3,0AC =-u u u r ,所以9922cos ,92322A F AC A F AC A F AC +'⋅'==='⋅⨯u u u u r u u u r u u u u r u u u r u u u u r u u u r ,所以异面直线A F '与AC 所成的角为4π. 故选:C 【点睛】本题主要考查异面直线所成的角,余弦定理,基本不等式以及向量法求角,还考查了推理论证运算求解的能力,属于中档题.10.已知函数()sin()R,0,0,||2f x A x x A πωϕωϕ⎛⎫=+∈>>< ⎪⎝⎭的图象(部分)如图所示,则ω,ϕ分别为( )A .,3πωπϕ==B .2,3πωπϕ==C .,6πωπϕ==D .2,6πωπϕ==【答案】C 【解析】 【分析】由最大值可确定振幅A ,由周期确定ω,由1()23f =确定ϕ. 【详解】由图可得,2A =,5114632T =-=,所以22T πω==,ωπ=,又1()23f =,所以12sin()23πϕ⨯+=,2,32k k Z ππϕπ+=+∈,即2,6k k Z πϕπ=+∈, 又2πϕ<,故6π=ϕ. 故选:C 【点睛】本题考查由图象确定正弦型函数解析式中的参数问题,考查学生逻辑推理能力,是一道中档题.11.在△ABC 中,7b =,5c =,3B π∠=,则a 的值为 A .3 B .4C .7D .8【答案】D 【解析】 【分析】根据题中所给的条件两边一角,由余弦定理可得2222cos b a c ac B =+-,代入计算即可得到所求的值. 【详解】因为7,5,3b c B π==∠=,由余弦定理可得2222cos b a c ac B =+-,即214925252a a =+-⨯⨯,整理得25240a a --=, 解得8a =或5a =-(舍去),故选D. 【点睛】该题考查的是有关解三角形的问题,在解题的过程中,涉及到的知识点有余弦定理,解三角形所用的就是正弦定理和余弦定理,结合题中的条件,选择适当的方法求得结果.12.已知ABC V 的内角,,A B C 的对边分别为,,a b c ,且cos cos a B b A +=,1a =,b =c =( )A B .1CD 【答案】B 【解析】 【分析】先由正弦定理将cos cos a B b A +=中的边转化为角,可得sin()A B +=可求出角6C π=,再利用余弦定理可求得结果.【详解】解:因为cos cos 2cos a B b A C+=,所以正弦定理得,sin cos sin cos A B B A +=所以sin()A B +=sin 2cos C C C=,因为sin 0C ≠,所以cos C =, 又因为(0,)C π∈,所以6C π=,因为1a =,b =所以由余弦定理得,2222cos 13211c a b ab C =+-=+-⨯=, 所以1c =故选:B【点睛】此题考查的是利用正、余弦定理解三角形,属于中档题.13.已知1F 、2F 分别为双曲线22146x y -=的左、右焦点,M 为双曲线右支上一点且满足120MF MF ⋅=u u u u v u u u u v ,若直线2MF 与双曲线的另一个交点为N ,则1MF N ∆的面积为( )A .12B .C .24D .【答案】C【解析】【分析】 设1MF m =,2MF n =,根据双曲线的定义和12MF MF ⊥,可求出6m =,2n =,再设2NF t =,则14NF t =+根据勾股定理求出6t =即可求出三角形的面积.【详解】 解:设1MF m =,2MF n =,∵1F 、2F 分别为双曲线22146x y -=的左、右焦点,∴24m n a -==,122F F c ==∵120MF MF ⋅=u u u u v u u u u v ,∴12MF MF ⊥,∴222440m n c +==,∴()2222m n m n mn -=+-,即2401624mn =-=,∴12mn =,解得6m =,2n =, 设2NF t =,则124NF a t t =+=+,在1Rt NMF ∆中可得()()222426t t +=++,解得6t =,∴628MN =+=,∴1MF N ∆的面积111862422S MN MF =⋅=⨯⨯=. 故选C .【点睛】本题考查了双曲线的定义和向量的数量积和三角形的面积,考查了运算能力和转化能力,属于中档题.14.若,2παπ⎛⎫∈⎪⎝⎭,2cos2sin 4παα⎛⎫=- ⎪⎝⎭,则sin 2α的值为( ) A .78- B .78 C .18- D .18【答案】A【解析】【分析】利用二倍角公式及两角差的正弦公式化简得到2cos sin αα+=,再将两边平方利用二倍角正弦公式计算可得;【详解】解:因为2cos2sin 4παα⎛⎫=- ⎪⎝⎭所以()222cos sin sin cos cos sin 44ππαααα-=-所以()())2cos sin cos sin cos sin 2αααααα-+=- ,cos sin 02παπαα⎛⎫∈-≠ ⎪⎝⎭Q ,所以cos sin αα+=所以()21cos sin 8αα+=,即221cos 2cos sin sin 8αααα++=,11sin 28α+= 所以7sin 28α=-故选:A【点睛】 本题考查两角和差的正弦公式、二倍角公式的应用,属于中档题;15.已知双曲线()222210,0x y a b a b-=>>的左右焦点分别为1F ,2F ,M 为双曲线上一点,若121cos 4F MF ∠=,122MF MF =,则此双曲线渐近线方程为( ) A.y =B.3y x =± C .y x =± D .2y x =±【答案】A【解析】【分析】 因为M 为双曲线上一点,可得122MF MF a -=,在12F MF ∆使用余弦定理,结合已知条件即可求得答案.【详解】Q 双曲线()222210,0x y a b a b-=>>的左右焦点分别为1F ,2F ,M 为双曲线上一点 ∴ 121222MF MF a MF MF ⎧-=⎪⎨=⎪⎩,解得:14MF a =,22MF a = 在12F MF ∆中,根据余弦定理可得:∴ 12121222122c 2os F F MF MF M MF MF F F ∠=+-⋅⋅可得:2221(2)(4)(2)2424c a a a a =+-⋅⋅⋅化简可得:2c a = 由双曲线性质可得:22222243b c a a a a =-=-=可得:b =Q 双曲线渐近线方程为:b y x a=±则双曲线渐近线方程为: y =故选:A.【点睛】本题考查了求双曲线渐近线方程问题,解题关键是掌握双曲线的基本知识,数形结合,考查分析能力和计算能力,属于中档题.16.在ABC ∆中,角A ,B ,C 所对的边分别为,,,3,sin a b c a c b A ===cos ,6a B b π⎛⎫+= ⎪⎝⎭则( )A .1B C D 【答案】C【解析】【分析】将sin b A = cos 6a B π⎛⎫+⎪⎝⎭结合正弦定理化简,求得B ,再由余弦定理即可求得b . 【详解】 因为sin b A = cos 6a B π⎛⎫+ ⎪⎝⎭,展开得sin b A = 1?cos sin 22a B a B -,由正弦定理化简得sin sinB A =1?cos sin 2B sinA B -= cos B即tanB =,而三角形中0<B<π,所以π 6B = 由余弦定理可得2222cos b a c ac B =+- ,代入(2223236b π=+-⨯⨯解得b =所以选C【点睛】本题考查了三角函数式的化简,正弦定理与余弦定理的应用,属于基础题.17.在∆ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .则“sin >sin A B ”是“a b >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 【答案】C【解析】 由正弦定理得sin sin 22a b A B a b R R>⇔>⇔> ,所以“sin sin A B >”是“a b >”的充要条件,选C. 18.已知函数()sin()f x x πϕ=+某个周期的图象如图所示,A ,B 分别是()f x 图象的最高点与最低点,C 是()f x 图象与x 轴的交点,则tan ∠BAC =( )A .12B .47C 255D 76565【答案】B【解析】【分析】过A 作AD 垂直于x 轴于点D ,AB 与x 轴交于E ,设C (a ,0),可得32CD =,11,2AD DE ==,3tan 2CD CAD AD ∠==,1tan 2ED EAD AD ∠==,再利用tan tan()BAC CAD EAD ∠=∠-∠计算即可. 【详解】过A 作AD 垂直于x 轴于点D ,AB 与x 轴交于E ,由题可得周期为2,设(,0)C a ,则1(,1)2B a +-,3(,1)2A a +, 所以32CD =,11,2AD DE ==, 3tan 2CD CAD AD ∠==,1tan 2ED EAD AD ∠==所以tan tan tan tan()1tan tanCAD EADBAC CAD EADCAD EAD∠-∠∠=∠-∠=+∠⋅∠31422317122-==+⨯.故选:B【点睛】本题主要考查两角差的正切公式,涉及到正弦型函数图象等知识,考查学生数学运算能力,是一道中档题.19.设函数f(x)=cos(x+3π),则下列结论错误的是A.f(x)的一个周期为−2πB.y=f(x)的图像关于直线x=83π对称C.f(x+π)的一个零点为x=6πD.f(x)在(2π,π)单调递减【答案】D【解析】f(x)的最小正周期为2π,易知A正确;f8π3⎛⎫⎪⎝⎭=cos8ππ33⎛⎫+⎪⎝⎭=cos3π=-1,为f(x)的最小值,故B正确;∵f(x+π)=cosππ3x⎛⎫++⎪⎝⎭=-cosπ3x⎛⎫+⎪⎝⎭,∴fππ6⎛⎫+⎪⎝⎭=-cosππ63⎛⎫+⎪⎝⎭=-cos2π=0,故C正确;由于f2π3⎛⎫⎪⎝⎭=cos2ππ33⎛⎫+⎪⎝⎭=cosπ=-1,为f(x)的最小值,故f(x)在,2ππ⎛⎫⎪⎝⎭上不单调,故D错误.故选D.20.在ABC△中,若a=3,c=7,∠C=60°,则边长b为A .5B .8C .5或-8D .-5或8【答案】B【解析】 由余弦定理c 2=a 2+b 2-2ab cos C ,得24993b b =+-,即()()850b b -+=, 因为b >0,所以b =8.故选B .。
高考数学三角函数与解三角形多选题之知识梳理与训练含答案

高考数学三角函数与解三角形多选题之知识梳理与训练含答案一、三角函数与解三角形多选题1.在ABC 中,下列说法正确的是( )A .若AB >,则sin sin A B > B .存在ABC 满足cos cos 0A B +≤ C .若sin cos A B <,则ABC 为钝角三角形D .若2C π>,则22sin sin sin C A B >+【答案】ACD 【分析】A 项,根据大角对大边定理和正弦定理可判断;B 项,由A B π+<和余弦函数在()0,π递减可判断;C 项,显然2A π≠,分02A π<<和2A π>两种情况讨论,结合余弦函数的单调性可判断;D 项,根据2A B π+<和正弦函数的单调性得出0sin cos A B <<和0sin cos B A <<,再由放缩法可判断. 【详解】解:对于A 选项,若A B >,则a b >,则2sin 2sin R A R B >,即sin sin A B >,故A 选项正确;对于B 选项,由A B π+<,则A B π<-,且(),0,A B ππ-∈,cos y x =在()0,π上递减,于是cos cos A B >-,即cos cos 0A B +>,故B 选项错误﹔ 对于C 选项,由sin cos A B <,得cos cos 2A B π⎛⎫-< ⎪⎝⎭,cos y x =在()0,π上递减, 此时:若02A π<<,则2A B π->,则2A B π+<,于是2C π>; 若2A π>,则cos cos 2A B π⎛⎫-< ⎪⎝⎭,则2A B π->, 于是2A B π>+,故C 选项正确;对于D 选项,由2C π>,则2A B π+<,则022A B ππ<<-<,sin y x =在0,2π⎛⎫⎪⎝⎭递增,于是sin sin 2A B π⎛⎫<- ⎪⎝⎭, 即0sin cos A B <<,同理0sin cos B A <<, 此时,22sin sin()sin cos cos sin sin sin sin sin sin sin C A B A B A B A A B B A B=+=+>⋅+⋅=+所以D 选项正确. 故选:ACD 【点睛】关键点点睛:正余弦函数的单调性,正弦定理的边角互化,大边对大角定理以及大角对大边定理,不等式的放缩等等,综合使用以上知识点是解决此类题的关键.2.设函数()2sin 1xf x x x π=-+,则( )A .()43f x ≤B .()5f x x ≤C .曲线()y f x =存在对称轴D .曲线()y f x =存在对称中心【答案】ABC 【分析】 通过()22sin sin 11324x xf x x x x ππ==-+⎛⎫-+⎪⎝⎭可发现函数()y f x =具有对称轴及最大值,再利用函数对称中心的特点去分析()y f x =是否具有对称中心,再将()5f x x ≤化为32sin 555x x x x π≤-+,通过数形结合判断是否成立.【详解】函数解析式可化为:()22sin sin 11324x xf x x x x ππ==-+⎛⎫-+⎪⎝⎭,因为函数sin y x =π的图象关于直线12x =对称,且函数21324y x ⎛⎫=-+ ⎪⎝⎭的图象也关于直线12x =对称,故曲线()y f x =也关于直线12x =对称,选项C 正确; 当12x =时,函数sin y x =π取得最大值1,此时21324y x ⎛⎫=-+ ⎪⎝⎭取得最小值34,故()14334f x ≤=,选项A 正确; 若()5f x x ≤,则32sin 555x x x x π≤-+,令()32555g x x x x =-+,则()()221510553210g x x x x x '=-+=-+>恒成立,则()g x 在R 上递增,又()00g =,所以当0x <时,()00g <;当0x >时,()0g x >; 作出sin x π和32555x x x -+的图象如图所示:由图象可知32sin 555x x x x π≤-+成立,即()5f x x ≤,选项B 正确;对于D 选项,若存在一点(),a b 使得()f x 关于点(),a b 对称,则()()2f a x f a x b -++=,通过分析发现()()f a x f a x -++不可能为常数,故选项D 错误. 故选:ABC. 【点睛】本题考查函数的综合应用,涉及函数的单调性与最值、对称轴于对称中心、函数与不等式等知识点,难度较大. 对于复杂函数问题一定要化繁为简,利用熟悉的函数模型去分析,再综合考虑,注意数形结合、合理变形转化.3.设函数g (x )=sinωx (ω>0)向左平移5πω个单位长度得到函数f (x ),已知f (x )在[0,2π]上有且只有5个零点,则下列结论正确的是( )A .f (x )的图象关于直线2x π=对称B .f (x )在(0,2π)上有且只有3个极大值点,f (x )在(0,2π)上有且只有2个极小值点C .f (x )在(0,)10π上单调递增 D .ω的取值范围是[1229,510) 【答案】CD 【分析】利用正弦函数的对称轴可知,A 不正确;由图可知()f x 在(0,2)π上还可能有3个极小值点,B 不正确;由2A B x x π≤<解得的结果可知,D 正确;根据()f x 在3(0,)10πω上递增,且31010ππω<,可知C 正确. 【详解】依题意得()()5f x g x πω=+sin[()]5x πωω=+sin()5x πω=+, 2T πω=,如图:对于A ,令52x k ππωπ+=+,k Z ∈,得310k x ππωω=+,k Z ∈,所以()f x 的图象关于直线310k x ππωω=+(k Z ∈)对称,故A 不正确; 对于B ,根据图象可知,2A B x x π≤<,()f x 在(0,2)π有3个极大值点,()f x 在(0,2)π有2个或3个极小值点,故B 不正确, 对于D ,因为5522452525A x T ππππωωωω=-+=-+⨯=,22933555B x T ππππωωωω=-+=-+⨯=,所以2429255πππωω≤<,解得1229510ω≤<,所以D 正确;对于C ,因为1123545410T ππππωωωω-+=-+⨯=,由图可知()f x 在3(0,)10πω上递增,因为29310ω<<,所以33(1)0101010πππωω-=-<,所以()f x 在(0,)10π上单调递增,故C 正确;故选:CD. 【点睛】本题考查了三角函数的相位变换,考查了正弦函数的对称轴和单调性和周期性,考查了极值点的概念,考查了函数的零点,考查了数形结合思想,属于中档题.4.设函数()sin 6f x M x πω⎛⎫=+ ⎪⎝⎭(0,0)M ω>>的周期是π,则下列叙述正确的有( )A .()f x 的图象过点10,2⎛⎫ ⎪⎝⎭B .()f x 的最大值为MC .()f x 在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递减 D .5,012π⎛⎫⎪⎝⎭是()f x 的一个对称中心 【答案】BCD 【分析】已知只有周期的条件,只能求出ω,其中M 未知;A 选项代值判定;B 选项由解析式可知;C 选项由()f x 的单调递减区间在32,2,22k k k Z ππππ⎛⎫++∈⎪⎝⎭上化简可得;D 选项由()f x 的对称中心为(),0,k k Z π∈化简可得. 【详解】 由题可知2T ππω==,解得2ω=,即()sin 26f x M x π⎛⎫=+ ⎪⎝⎭当0x =时,()0sin 20sin 662Mf M M ππ⎛⎫=⨯+== ⎪⎝⎭,故选项A 错误; 因为()sin 26f x M x π⎛⎫=+⎪⎝⎭,所以最大值为M ,故选项B 正确; 由解析式可知()f x 在3222,262k x k k Z πππππ+≤+≤+∈ 即2,63x k k ππππ⎡⎤∈++⎢⎥⎣⎦上单调递减,当0k =时,选项C 正确; 由解析式可知()f x 的对称中心的横坐标满足26x k ππ+=,即212k x ππ=- 当1k =时,512x π=,对称中心为5,012π⎛⎫⎪⎝⎭,故选项D 正确. 故选:BCD 【点睛】本题考查()()sin f x A x =+ωϕ型三角函数的性质,其中涉及最值、对称轴、对称中心,属于较难题.5.已知函数()()cos 2f x A x b ϕ=++(0A >,0ϕπ<<)的部分图像如图所示,则( )A .2A =B .点7,112π⎛⎫⎪⎝⎭是()f x 图像的一个对称中心C .6π=ϕ D .直线3x π=是()f x 图像的一条对称轴【答案】ABD 【分析】由图知函数最大值为3,最小值为1-,且函数图像与y 轴的交点为()0,2,进而待定系数得()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,再整体换元讨论B,D 选项即可.【详解】 因为0A >,所以31A b A b +=⎧⎨-+=-⎩,解得21A b =⎧⎨=⎩,故A 正确;()02cos 12f ϕ=+=,则1cos 2ϕ=.又0ϕπ<<,所以3πϕ=,故C 错误;()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,令23x k ππ+=,k ∈Z ,解得62πk πx =-+,k ∈Z , 所以()f x 图像的对称轴方程为62πk πx =-+, 令1k =,则3x π=,D 正确;令232x k πππ+=+,k ∈Z ,解得122k x ππ=+,k ∈Z , 令1k =,则712x π=且7112f π⎛⎫= ⎪⎝⎭,故B 正确. 故选:ABD 【点睛】本题考查三角函数图像求解析式,三角函数的对称轴,对称中心等,考查运算求解能力,是中档题.解题的过程中,需要注意形如()()sin 0y A x B A ωϕ=++>,()()cos 0y A x B A ωϕ=++>,max min ,y A B y A B =+=-+,ϕ的求解通常采用待定系数法求解.6.函数()sin 24f x x π⎛⎫=+⎪⎝⎭,则( ) A .函数()y f x =的图象可由函数sin 2y x =的图象向右平移4π个单位得到 B .函数()y f x =的图象关于直线8x π=轴对称C .函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称D .函数2()y x f x =+在08π⎛⎫ ⎪⎝⎭,上为增函数 【答案】BCD 【分析】对四个选项,一一验证:对于选项A ,利用三角函数相位变化即可;对于选项B ,利用正弦函数的对称轴经过最高(低)点判断; 对于选项C ,利用正弦函数的对称中心直接判断; 对于选项D ,利用复合函数的单调性“同增异减”判断; 【详解】由题意,对于选项A ,函数sin 2y x =的图象向右平移4π个单位可得到()sin 2sin 2cos 242f x x x x ππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以选项A 错误;对于选项B ,sin 21884f πππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,取到了最大值,所以函数()y f x =的图象关于直线8x π=轴对称,所以选项B 正确;对于选项C ,08f π⎛⎫-= ⎪⎝⎭,所以函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称,所以选项C 正确;对于选项D ,函数2yx 在08π⎛⎫ ⎪⎝⎭,上为增函数,08x π⎛⎫∈ ⎪⎝⎭,时,2442x πππ⎛⎫+∈ ⎪⎝⎭,,单调递增,所以函数2()y x f x =+在08π⎛⎫⎪⎝⎭,上为增函数,所以选项D 正确. 故选:BCD. 【点睛】(1)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题;(2)求单调区间,最后的结论务必写成区间形式,不能写成集合或不等式.7.将函数()2πsin 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π6个单位长度后得到函数()g x 的图象,则下列说法正确的是( )A .π4g ⎛⎫= ⎪⎝⎭B .π,06⎛⎫⎪⎝⎭是函数()g x 图象的一个对称中心 C .函数()g x 在π0,4⎡⎤⎢⎥⎣⎦上单调递增D .函数()g x 在ππ,63⎡⎤-⎢⎥⎣⎦上的值域是⎡⎢⎣⎦【答案】BC 【分析】首先求得函数()sin 23g x x π=-⎛⎫⎪⎝⎭,再根据选项,整体代入,判断函数的性质. 【详解】()2sin 2sin 2633g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,1sin 462g ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,故A 错误;sin 0633g πππ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,故B 正确;0,4x π⎡⎤∈⎢⎥⎣⎦时,2,,33622x πππππ⎡⎤⎡⎤-∈-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,所以函数()g x 在0,4⎡⎤⎢⎥⎣⎦π上单调递增,故C 正确;,63x ππ⎡⎤∈-⎢⎥⎣⎦时,22,333x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,函数取得最小值-1,当233x ππ-=1,2⎡-⎢⎣⎦.故选:BC 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.8.已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<的部分图象如图所示,则下列说法正确的是( )A .23ϕπ=B .()f x 的最小正周期为πC .()f x 的图象关于直线12x π=对称D .()f x 的图象关于点5,06π⎛⎫⎪⎝⎭对称 【答案】BCD 【分析】利用图象,把(3代入求ϕ,利用周期求出2ω=,从而2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,研究对称轴和对称中心. 【详解】由图可知2sin 3ϕ=3sin 2ϕ=,根据图象可知0x =在()f x 的单调递增区间上,又0ϕπ<<,所以3πϕ=,A 项错误;因为()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭,所以结合图像,由五点法得33ωπππ+=,解得2ω=,则()f x 的最小正周期2T ππω==,B 项正确;将12x π=代入2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,得2sin 21263f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以()f x 的图象关于直线12x π=对称,C 项正确﹔将56x π=代入可得552sin 0633f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以点5,06π⎛⎫ ⎪⎝⎭是()f x 图象的一个对称中心,D 项正确. 故选:BCD. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.9.已知函数)()lg1( 2.7)x x f x x e e e -=+-+≈⋯,若不等式(sin cos )2(sin 2)f f t θθθ+<--对任意R θ∈恒成立,则实数t 的可能取值为( )A .1BC .3D .4【答案】CD 【分析】令)()lgx x g x x e e -=+-,则()()1f x g x =+,可判断()g x 是奇函数且单调递增,不等式可变形可得(sin cos )(sin 2)g g t θθθ+<-,所以sin cos sin 2t θθθ>++,令()sin cos sin 2h θθθθ=++,换元法求出()h θ的最大值,()max t h θ>即可. 【详解】令)()lgx x g x x e e -=+-,则()()1f x g x =+,()g x 的定义域为R ,))()()lglgx x x x g x g x x e e x e e ---+=+-++-0=,所以()()g x g x -=-,所以()g x 是奇函数, 不等式(sin cos )2(sin 2)f f t θθθ+<--等价于[](sin cos )1(sin 2)1f f t θθθ+-<---,即(sin cos )(sin 2)(sin 2)g g t g t θθθθ+<--=-,当0x >时y x =单调递增,可得)lgy x =单调递增,x y e =单调递增,x y e -=单调递减,所以)()lgx x g x x e e -=+-在()0,∞+单调递增,又因为)()lg x x g x x e e -=+-为奇函数,所以)()lgx x g x x e e -=+-在R 上单调递增,所以sin cos sin 2t θθθ+<-,即sin cos sin 2t θθθ>++, 令()sin cos sin 2h θθθθ=++,只需()max t h θ>,令sin cos m θθ⎡+=∈⎣,则21sin 2m θ=+,2sin 21m θ=-,所以()21h m m m =+-,对称轴为12m =-,所以m =()max 211h m ==,所以1t >可得实数t 的可能取值为3或4,故选:CD【点睛】关键点点睛:本题解题的关键点是构造函数()g x 奇函数且是增函数,将原不等式脱掉f 转化为函数恒成立问题.10.设函数()()sin f x A x =+ωϕ,x ∈R (其中0A >,0>ω,2πϕ<),在,62ππ⎛⎫ ⎪⎝⎭上既无最大值,也无最小值,且()026f f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,则下列结论错误的是( ) A .若()()()12f x f x f x ≤≤对任意x ∈R ,则21min x x π-=B .()y f x =的图象关于点,03π⎛-⎫ ⎪⎝⎭中心对称 C .函数()f x 的单调减区间为()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D .函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是2π 【答案】ABD【分析】根据条件先求函数的解析式,对于A:判断出()1f x 为最小值,()2f x 为最大值,即可;对于B:根据函数的对称性进行判断;对于C:求出角的范围,结合三角函数的单调性进行判断;对于D:根据函数的对称性即对称轴之间的关系进行判断.【详解】因为函数()f x 在,62ππ⎛⎫⎪⎝⎭上既无最大值,也无最小值, 所以,62ππ⎛⎫ ⎪⎝⎭是函数的一个单调区间,区间长度为263πππ-=, 即函数的周期2233T ππ≥⨯=,即223ππω≥,则03ω<≤ 因为()06f f π⎛⎫= ⎪⎝⎭,所以06212ππ+=为函数的一条对称轴;则1223πππωϕωϕπ+=+=①②由①②解得:=2=3πωϕ,,即()sin 23f x A x π⎛⎫=+ ⎪⎝⎭,函数的周期=T π. 对于A: 若()()()12f x f x f x ≤≤对任意x ∈R 恒成立,则()1f x 为最小值,()2f x 为最大值,所以12||22T k x x k π-==,则21x x -必为2π的整数倍,故A 错误,可选A; 对于B:3x π=-时,()sin 03f x A π⎛⎫=-≠ ⎪⎝⎭,故,03π⎛-⎫ ⎪⎝⎭不是()y f x =的对称中心,B 错误,可选B;对于C:当7,1212x k k ππππ⎡⎤∈++⎢⎥⎣⎦时,322,2322x k k πππππ⎡⎤+∈++⎢⎥⎣⎦,此时()y f x =单调递减,C 正确,不选C;对于D: 函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是44T π=,故D 错误,可选D故选:ABD【点睛】(1)求三角函数解析式的方法:①求A 通常用最大值或最小值;②(2)求ω通常用周期;③求φ通常利用函数上的点带入即可求解;(2)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题.。
高考数学压轴专题最新备战高考《三角函数与解三角形》全集汇编及答案解析

数学《三角函数与解三角形》复习知识点(1)一、选择题1.函数y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦在一个周期内的图象是( )A .B .C .D .【答案】B 【解析】 【分析】首先根据二倍角余弦公式化简得到函数的解析式,再由函数表达式得到函数的单调性和周期,进而得到选项. 【详解】根据两角和差公式展开得到: y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 22πππcos sin cos 2424x x x ⎛⎫⎛⎫⎛⎫+-+=+ ⎪ ⎪ ⎪⎝⎭⎝=⎝⎭⎭=-sin2x ,函数在0的右侧是单调递减的,且周期为π,故选B. 故答案选B . 【点睛】这个题目考查了三角函数的恒等变换,题型为已知函数表达式选择函数的图像,这种题目,一般是先根据函数的表达式得到函数的定义域,或者值域,进行排除;也可以根据函数的表达式判断函数的单调性,周期性等,之后结合选项选择.2.△ABC 中,已知tanA =13,tanB =12,则∠C 等于( )A .30°B .45°C .60°D .135°【答案】D 【解析】 【分析】利用三角形内角和为180o ,可得:tan tan()tan(+)C A B A B π=--=-,利用两角和公式和已知条件,即可得解. 【详解】在△ABC 中,11tan tan 32tan tan()tan(+)=-1111tan tan 132A BC A B A B A B π++=--=-=-=---⋅,所以135C ?o .故选:D. 【点睛】本题考查了正切的两角和公式,考查了三角形内角和,考查了转化思想和计算能力,属于中档题.3.小赵开车从A 处出发,以每小时40千米的速度沿南偏东40︒的方向直线行驶,30分钟后到达B 处,此时,小王发来微信定位,显示他自己在A 的南偏东70︒方向的C 处,且A 与C 的距离为153千米,若此时,小赵以每小时52千米的速度开车直线到达C 处接小王,则小赵到达C 处所用的时间大约为( )()7 2.6≈A .10分钟B .15分钟C .20分钟D .25分钟【答案】B 【解析】 【分析】首先根据题中所给的条件,得到30BAC ∠=︒,20AB =,153AC =,两边和夹角,之后应用余弦定理求得5713BC =≈(千米),根据题中所给的速度,进而求得时间,得到结果. 【详解】根据条件可得30BAC ∠=︒,20AB =,153AC =, 由余弦定理可得2222cos30175BC AB AC AB AC ︒=+-⋅⋅=, 则5713BC =≈(千米), 由B 到达C 所需时间约为130.2552=(时)15=分钟. 故选:B . 【点睛】该题是一道关于解三角形的实际应用题,解题的关键是掌握余弦定理的应用,属于简单题目.4.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形 C .等腰三角形 D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=, 变形可得:sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.5.在ABC ∆中,角,,A B C 所对的边分别为,,a b c 满足,222b c a bc +-=,0AB BC ⋅>u ur u u r u u ,a =b c +的取值范围是( )A .31,2⎛⎫ ⎪⎝⎭B .322⎛⎫⎪⎪⎝⎭C .13,22⎛⎫⎪⎝⎭D .31,2⎛⎤ ⎥⎝⎦【答案】B 【解析】 【分析】利用余弦定理222cos 2b c a A bc+-=,可得3A π=,由|||cos()|0AB BC AB BC B π⋅=⋅->u u u u u u u u r u ur u r u r,可得B 为钝角,由正弦定理可得sin sin(120)30)o o b c B B B ∴+=+-=+,结合B 的范围,可得解【详解】由余弦定理有:222cos 2b c a A bc+-=,又222b c a bc +-=故2221cos 222b c a bc A bc bc +-===又A 为三角形的内角,故3A π=又2a=sin sin sin(120)ob c c B C B ==- 又|||cos()|0AB BC AB BC B π⋅=⋅->u u u u u u u u r u ur u r u r故cos 0B B <∴为钝角3sin sin(120)sin 30)22o o b c B B B B B ∴+=+-=+=+(90,120)o o B ∈Q ,可得130(120150)sin(30)(2o o o o B B +∈∴+∈,330))2o b c B ∴+=+∈ 故选:B 【点睛】本题考查了正弦定理、余弦定理和向量的综合应用,考查了学生综合分析,转化划归,数学运算能力,属于中档题6.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2πC .76π D .π【答案】B 【解析】 【分析】根据两个函数相等,求出所有交点的横坐标,然后求和即可. 【详解】令sin cos2x x =,有2sin 12sin x x =-,所以sin 1x =-或1sin 2x =.又[],2x ππ∈-,所以2x π=-或32x π=或6x π=或56x π=,所以函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象交点的横坐标的和3522266s πππππ=-+++=,故选B. 【点睛】本题主要考查三角函数的图象及给值求角,侧重考查数学建模和数学运算的核心素养.7.如图,边长为1正方形ABCD ,射线BP 从BA 出发,绕着点B 顺时针方向旋转至BC ,在旋转的过程中,记([0,])2ABP x x π∠=∈,BP 所经过的在正方形ABCD 内的区域(阴影部分)的面积为()y f x =,则函数()f x 的图像是( )A .B .C .D .【答案】D 【解析】 【分析】根据条件列()y f x =,再根据函数图象作判断. 【详解】 当0,4x π⎡⎤∈⎢⎥⎣⎦时,()112y f x tanx ==⨯⨯; 当,42x ππ⎛⎤∈⎥⎝⎦时,()11112y f x tanx ==-⨯⨯; 根据正切函数图象可知选D. 【点睛】本题考查函数解析式以及函数图象,考查基本分析识别能力,属基本题.8.已知函数f (x )=2x -1,()2cos 2,0?2,0a x x g x x a x +≥⎧=⎨+<⎩(a ∈R ),若对任意x 1∈[1,+∞),总存在x 2∈R ,使f (x 1)=g (x 2),则实数a 的取值范围是() A .1,2⎛⎫-∞ ⎪⎝⎭B .2,3⎛⎫+∞⎪⎝⎭C .[]1,1,22⎛⎫-∞ ⎪⎝⎭U D .371,,224⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦U 【答案】C 【解析】 【分析】对a 分a=0,a <0和a >0讨论,a >0时分两种情况讨论,比较两个函数的值域的关系,即得实数a 的取值范围. 【详解】当a =0时,函数f (x )=2x -1的值域为[1,+∞),函数()g x 的值域为[0,++∞),满足题意.当a <0时,y =22(0)x a x +<的值域为(2a ,+∞), y =()cos 20a x x +≥的值域为[a +2,-a +2],因为a +2-2a =2-a >0,所以a +2>2a , 所以此时函数g (x )的值域为(2a ,+∞), 由题得2a <1,即a <12,即a <0. 当a >0时,y =22(0)x a x +<的值域为(2a ,+∞),y =()cos 20a x x +≥的值域为[-a +2,a +2], 当a ≥23时,-a +2≤2a ,由题得21,1222a a a a -+≤⎧∴≤≤⎨+≥⎩. 当0<a <23时,-a +2>2a ,由题得2a <1,所以a <12.所以0<a <12. 综合得a 的范围为a <12或1≤a ≤2, 故选C . 【点睛】本题主要考查函数的图象和性质,考查指数函数和三角函数的图象和性质,意在考查学生对这些知识的理解掌握水平和分析推理能力.9.要得到函数y =sin (2x +9π)的图象,只需将函数y =cos (2x ﹣9π)的图象上所有点( ) A .向左平移518π个单位长度 B .向右平移518π个单位长度 C .向左平移536π个单位长度 D .向右平移536π个单位长度 【答案】D 【解析】 【分析】先将函数cos 29y x π⎛⎫=- ⎪⎝⎭转化为7sin 218y x π⎛⎫=+⎪⎝⎭,再结合两函数解析式进行对比,得出结论. 【详解】 函数75cos 2sin 2sin 2sin 299218369y x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=+=++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ∴要得到函数sin 29y x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数cos 29y x π⎛⎫=- ⎪⎝⎭的图象上所有点向右平移536π个单位长度,故选D . 【点睛】本题考查函数()sin y A x b ωϕ=++的图象变化规律,关键在于能利用诱导公式将异名函数化为同名函数,再根据左右平移规律得出结论.10.在ABC ∆中,060,10,A BC D ∠==是边AB 上的一点,2,CD CBD =∆的面积为1,则BD 的长为( ) A .32B .4C .2D .1【答案】C 【解析】1210sin 1sin 25BCD BCD ⨯⨯⨯∠=∴∠= 2222102210425BD BD ∴=+-⨯⨯⨯=∴=,选C11.已知函数()sin()f x x πϕ=+某个周期的图象如图所示,A ,B 分别是()f x 图象的最高点与最低点,C 是()f x 图象与x 轴的交点,则tan ∠BAC =( )A .12B .47C 255D 76565【解析】 【分析】过A 作AD 垂直于x 轴于点D ,AB 与x 轴交于E ,设C (a ,0),可得32CD =,11,2AD DE ==,3tan 2CD CADAD ∠==,1tan 2ED EAD AD ∠==,再利用tan tan()BAC CAD EAD ∠=∠-∠计算即可.【详解】过A 作AD 垂直于x 轴于点D ,AB 与x 轴交于E , 由题可得周期为2,设(,0)C a ,则1(,1)2B a +-,3(,1)2A a +, 所以32CD =,11,2AD DE ==,3tan 2CD CAD AD ∠==,1tan 2ED EAD AD ∠== 所以tan tan tan tan()1tan tan CAD EADBAC CAD EAD CAD EAD∠-∠∠=∠-∠=+∠⋅∠31422317122-==+⨯. 故选:B【点睛】本题主要考查两角差的正切公式,涉及到正弦型函数图象等知识,考查学生数学运算能力,是一道中档题.12.已知角α的终边与单位圆交于点34(,)55P -,则cos α的值为( ) A .35B .35-C .45D .45-【解析】 【分析】根据已知角α的终边与单位圆交于点34(,)55P -,结合三角函数的定义即可得到cos α的值. 【详解】因为角α的终边与单位圆交于点34(,)55P -, 所以34,,155x y r =-==, 所以3cos 5α=-, 故选B. 【点睛】该题考查的是有关已知角终边上一点求其三角函数值的问题,涉及到的知识点有三角函数的定义,属于简单题目.13.函数()2sin sin cos y x x x =+的最大值为( )A .1B 1CD .2【答案】A 【解析】由题意,得()22sin sin cos 2sin 2sin cos sin2cos21y x x x x x x x x =+=+=-+π2114x ⎛⎫=-+≤ ⎪⎝⎭;故选A.14.在OAB ∆中,已知OB =u u u v 1AB u u u v=,45AOB ∠=︒,点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ,其中λ,μ满足23λμ+=,则OP u u u v的最小值为( )A B C D .2【答案】A 【解析】 【分析】根据OB =u u u r,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r.再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP uu u r的最小值.【详解】在OAB ∆中,已知2OB =u u u r,1AB =uu u r ,45AOB ∠=︒由正弦定理可得sin sin AB OBAOB OAB=∠∠u u u r u u u r 代入2sin 2OAB =∠,解得sin 1OAB ∠=即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22,22⎛ ⎝⎭所以2222OA ⎛= ⎝⎭u u u r ,)2,0OB =u u ur因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫⎪ ⎪⎝⎭=则2222222OP λμλ⎛⎫=++⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r 2222λλμμ=++因为23λμ+=,则32μλ=- 代入上式可得()()22322232λλλλ+-+-218518λλ-=+=所以当95λ=时, min OP ==u u u r 故选:A【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.15.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c ,若1b =,c =,且2sin()cos 12cos sin B C C A C +=-,则ABC V 的面积是( )A .4B .12C .4或2D .14或12【答案】C【解析】【分析】 根据已知关系求出1sin 2B =,根据余弦定理求出边a ,根据面积公式即可得解. 【详解】因为2sin()cos 12cos sin B C C A C +=-,所以2sin cos 12cos sin A C A C =-, 所以2sin cos 2cos sin 1A C A C +=,所以2sin()1A C +=,所以2sin 1B =,即1sin 2B =,因为b c <,所以B C <,所以角B 为锐角,所以cos 2B ==,由余弦定理2222cos b a c ac B =+-得2132a a =+-⨯, 整理可得2320a a -+=,解得1a =或2a =.当1a =时,ABC V 的面积是111sin 1222S ac B ==⨯=当2a =时,ABC V 的面积是111sin 2222S ac B ==⨯=. 故选:C.【点睛】 此题考查根据余弦定理解三角形,关键在于熟练掌握定理公式,结合边角关系解方程,根据面积公式求解.16.在ABC ∆中,角A ,B ,C 所对的边分别为,,,3,sin a b c a c b A ===cos ,6a B b π⎛⎫+= ⎪⎝⎭则( )A .1B C D 【答案】C【解析】【分析】将sin b A = cos 6a B π⎛⎫+⎪⎝⎭结合正弦定理化简,求得B ,再由余弦定理即可求得b . 【详解】 因为sin b A = cos 6a B π⎛⎫+ ⎪⎝⎭,展开得sin b A =1?cos sin 2B a B -,由正弦定理化简得sin sinB A =1?cos sin 22sinA B sinA B -= cos B即tanB =,而三角形中0<B<π,所以π 6B = 由余弦定理可得2222cos b a c ac B =+- ,代入(2223236b π=+-⨯⨯解得b =所以选C【点睛】 本题考查了三角函数式的化简,正弦定理与余弦定理的应用,属于基础题.17.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且222b c a bc +=+若2sin sin sin B C A ⋅=,则ABC ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形【答案】C【解析】【分析】直接利用余弦定理的应用求出A 的值,进一步利用正弦定理得到:b =c ,最后判断出三角形的形状.【详解】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且b 2+c 2=a 2+bc . 则:2221222b c a bc cosA bc bc +-===, 由于:0<A <π, 故:A 3π=.由于:sin B sin C =sin 2A ,利用正弦定理得:bc =a 2,所以:b 2+c 2﹣2bc =0,故:b =c ,所以:△ABC 为等边三角形.故选C .【点睛】本题考查了正弦定理和余弦定理及三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.18.在ABC V 中,角A 的平分线交边BC 于D ,4AB =,8AC =,2BD =,则ABD △的面积是( )A .15B .315C .1D .3【答案】A【解析】【分析】先根据正弦定理求得DC ,再结合余弦定理求得cos B ,进而求出ABD S V ,即可求得结论.【详解】如图:()sin sin sin ADC ADB ADB π∠=-∠=∠,在ABD △中,由正弦定理得sin sin BD AB BAD ADB=∠∠,同理可得sin sin CD AC CAD ADC=∠∠, 因为ABC V 中,角A 的平分线交边BC 于D ,上述两个等式相除得BD AB CD AC=,4AB =Q ,8AC =,2BD =,8244AC BD CD AB ⋅⨯∴===,6BC ∴=.2222224681cos 22464AB BC AC B AB BC +-+-∴===-⋅⨯⨯,sin B == 1sin 2ABD S AB BD B ∴=⋅⋅=V 故选:A .【点睛】本题考查三角形面积的求法以及角平分线的性质应用,是中档题,解题时要注意余弦定理的合理运用,考查计算能力,属于中等题.19.设2α是第一象限角,且cos cos αα=-,则α是第( )象限角 A .一B .二C .三D .四【答案】B【解析】【分析】计算得到720180720k k α︒<<︒+︒,k Z ∈,再根据cos 0α<得到答案.【详解】 ∵2α是第一象限角,∴360903602k k α︒<<︒+︒,k Z ∈, ∴720180720k k α︒<<︒+︒,k Z ∈,∴α为第一象限角或第二象限角或终边在y 轴正半轴上的轴线角, ∵cos cos αα=-,∴cos 0α<,∴α是第二象限角.故选:B .【点睛】本题考查了角度所在象限,意在考查学生的计算能力和转化能力.20.在三棱锥P ABC -中,PA ⊥平面ABC ,2π,43BAC AP ∠==,AB AC ==P ABC -的外接球的表面积为( ) A .32πB .48πC .64πD .72π 【答案】C【解析】【分析】先求出ABC V 的外接圆的半径,然后取ABC V 的外接圆的圆心G ,过G 作//GO AP ,且122GO AP ==,由于PA ⊥平面ABC ,故点O 为三棱锥P ABC -的外接球的球心,OA 为外接球半径,求解即可.【详解】在ABC V 中,23AB AC ==,23BAC π∠=,可得6ACB π∠=, 则ABC V 的外接圆的半径2323π2sin 2sin 6AB r ACB ===,取ABC V 的外接圆的圆心G ,过G 作//GO AP ,且122GO AP ==, 因为PA ⊥平面ABC ,所以点O 为三棱锥P ABC -的外接球的球心,则222OA OG AG =+,即外接球半径()222234R =+=,则三棱锥P ABC -的外接球的表面积为24π4π1664πR =⨯=.故选C.【点睛】本题考查了三棱锥的外接球表面积的求法,考查了学生的空间想象能力,属于中档题.。
高考数学压轴专题最新备战高考《三角函数与解三角形》专项训练解析含答案

数学《三角函数与解三角形》期末复习知识要点一、选择题1.设函数())cos(2)f x x x ϕϕ=+++(||)2πϕ<,且其图像关于直线0x =对称,则( )A .()y f x =的最小正周期为π,且在(0,)2π上为增函数B .()y f x =的最小正周期为2π,且在(0,)4π上为增函数 C .()y f x =的最小正周期为π,且在(0,)2π上为减函数D .()y f x =的最小正周期为2π,且在(0,)4π上为减函数【答案】C 【解析】试题分析:())cos(2)f x x x ϕϕ=+++2sin(2)6x πϕ=++,∵函数图像关于直线0x =对称,∴函数()f x 为偶函数,∴3πϕ=,∴()2cos 2f x x =,∴22T ππ==, ∵02x π<<,∴02x π<<,∴函数()f x 在(0,)2π上为减函数.考点:1.三角函数式的化简;2.三角函数的奇偶性;3.三角函数的周期;4.三角函数的单调性.2.已知在锐角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos b C c B =,则111tan tan tan A B C++的最小值为( )A B C D .【答案】A 【解析】 【分析】先根据已知条件,把边化成角得到B,C 关系式,结合均值定理可求. 【详解】∵2cos cos b C c B =,∴2sin cos sinCcos B C B =, ∴tan 2tan C B =.又A B C π++=, ∴()()tan tan tan A B C B C π=-+=-+⎡⎤⎣⎦22tan tan 3tan 3tan 1tan tan 12tan 2tan 1B C B BB C B B +=-=-=---,∴21112tan 111tan tan tan 3tan tan 2tan B A B C B B B -++=++27tan 36tan B B =+. 又∵在锐角ABC ∆中, tan 0B >,∴27tan 36tan 3B B +≥=,当且仅当tan B =时取等号,∴min111tan tan tan A B C ⎛⎫++=⎪⎝⎭ A. 【点睛】本题主要考查正弦定理和均值定理,解三角形时边角互化是求解的主要策略,侧重考查数学运算的核心素养.3.在ABC ∆中,若sin :sin :sin 2:3:4A B C =,则ABC ∆是( ) A .直角三角形 B .钝角三角形C .锐角三角形D .等腰直角三角形【答案】B 【解析】 【分析】由题意利用正弦定理,推出a ,b ,c 的关系,然后利用余弦定理求出cosC 的值,即可得解. 【详解】∵sinA :sinB :sinC=2:3:4∴由正弦定理可得:a :b :c=2:3:4, ∴不妨令a=2x ,b=3x ,c=4x ,∴由余弦定理:c 2=a 2+b 2﹣2abcosC ,所以cosC=2222a b c ab+-=2224916223x x x x x +-⨯⨯=﹣14, ∵0<C <π, ∴C 为钝角. 故选B . 【点睛】本题是基础题,考查正弦定理,余弦定理的应用,考查计算能力,常考题型.4.若函数()sin 2f x x =向右平移6π个单位后,得到()y g x =,则关于()y g x =的说法正确的是( )A .图象关于点,06π⎛⎫-⎪⎝⎭中心对称 B .图象关于6x π=-轴对称C .在区间5,126ππ⎡⎤--⎢⎥⎣⎦单调递增 D .在5,1212ππ⎡⎤-⎢⎥⎣⎦单调递增【答案】D 【解析】 【分析】利用左加右减的平移原则,求得()g x 的函数解析式,再根据选项,对函数性质进行逐一判断即可. 【详解】函数()sin 2f x x =向右平移6π个单位,得()sin 2()sin(2)63g x x x ππ=-=-. 由23x π-=k π,得26k x ππ=+()k ∈Z ,所以,06π⎛⎫- ⎪⎝⎭不是()g x 的对称中心,故A 错; 由23x π-=2k ππ+, 得212k x π5π=+()k ∈Z ,所以()g x 的图象不关于6x π=-轴对称,故B 错;由222232k x k πππππ-≤-≤+,得1212k x k π5ππ-≤≤π+()k ∈Z , 所以在区间5,126ππ⎡⎤--⎢⎥⎣⎦上()g x 不单调递增,在5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增, 故C 错,D 对; 故选:D . 【点睛】解答三角函数问题时一般需将解析式化简为sin()y A x B ωϕ=++或cos()y A x B ωϕ=++,从而可利用正(余)弦型周期计算公式2||T πω=周期,对正弦型函数,其函数图象的对称中心为,k B πϕω-⎛⎫⎪⎝⎭,且对称中心在函数图象上,而对称轴必经过图象的最高点或最低点,此时函数取得最大值或最小值.5.如图,边长为1正方形ABCD ,射线BP 从BA 出发,绕着点B 顺时针方向旋转至BC ,在旋转的过程中,记([0,])2ABP x x π∠=∈,BP 所经过的在正方形ABCD 内的区域(阴影部分)的面积为()y f x =,则函数()f x 的图像是( )A .B .C .D .【答案】D 【解析】 【分析】根据条件列()y f x =,再根据函数图象作判断. 【详解】当0,4x π⎡⎤∈⎢⎥⎣⎦时,()112y f x tanx ==⨯⨯; 当,42x ππ⎛⎤∈ ⎥⎝⎦时,()11112y f x tanx ==-⨯⨯; 根据正切函数图象可知选D. 【点睛】本题考查函数解析式以及函数图象,考查基本分析识别能力,属基本题.6.已知函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象如图所示,其中()01f =,5||2MN =,则点M 的横坐标为( )A .12B .25-C .1-D .23-【答案】C 【解析】 【分析】 由(0)1f =求出56πϕ=,由5||23MN πω=⇒=,再根据()2f x =可得答案.【详解】由函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象, 可得(0)2sin 1f ϕ==,56πϕ∴=, 22512||2243MN ππωω⎛⎫==+⋅= ⎪⎝⎭, ∴函数5()2sin 36f x x ππ⎛⎫=+ ⎪⎝⎭,令52sin 236x ππ⎛⎫+= ⎪⎝⎭, 得52,0362x k k ππππ+=+=得1x =-. 故选:C. 【点睛】本题主要考查三角函数的图象与性质,考查了数形结合思想的应用,解题的关键是利用勾股定理列方程求出3πω=,属于中档题.7.要得到函数y =sin (2x +9π)的图象,只需将函数y =cos (2x ﹣9π)的图象上所有点( ) A .向左平移518π个单位长度 B .向右平移518π个单位长度 C .向左平移536π个单位长度 D .向右平移536π个单位长度【答案】D 【解析】 【分析】先将函数cos 29y x π⎛⎫=- ⎪⎝⎭转化为7sin 218y x π⎛⎫=+⎪⎝⎭,再结合两函数解析式进行对比,得出结论. 【详解】 函数75cos 2sin 2sin 2sin 299218369y x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=+=++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ∴要得到函数sin 29y x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数cos 29y x π⎛⎫=- ⎪⎝⎭的图象上所有点向右平移536π个单位长度,故选D . 【点睛】本题考查函数()sin y A x b ωϕ=++的图象变化规律,关键在于能利用诱导公式将异名函数化为同名函数,再根据左右平移规律得出结论.8.在△ABC 中,7b =,5c =,3B π∠=,则a 的值为 A .3 B .4C .7D .8【答案】D 【解析】 【分析】根据题中所给的条件两边一角,由余弦定理可得2222cos b a c ac B =+-,代入计算即可得到所求的值. 【详解】因为7,5,3b c B π==∠=,由余弦定理可得2222cos b a c ac B =+-,即214925252a a =+-⨯⨯,整理得25240a a --=, 解得8a =或5a =-(舍去),故选D. 【点睛】该题考查的是有关解三角形的问题,在解题的过程中,涉及到的知识点有余弦定理,解三角形所用的就是正弦定理和余弦定理,结合题中的条件,选择适当的方法求得结果.9.函数y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦在一个周期内的图象是( )A .B .C .D .【答案】B 【解析】 【分析】首先根据二倍角余弦公式化简得到函数的解析式,再由函数表达式得到函数的单调性和周期,进而得到选项. 【详解】根据两角和差公式展开得到: y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 22πππcos sin cos 2424x x x ⎛⎫⎛⎫⎛⎫+-+=+ ⎪ ⎪ ⎪⎝⎭⎝=⎝⎭⎭=-sin2x ,函数在0的右侧是单调递减的,且周期为π,故选B. 故答案选B . 【点睛】这个题目考查了三角函数的恒等变换,题型为已知函数表达式选择函数的图像,这种题目,一般是先根据函数的表达式得到函数的定义域,或者值域,进行排除;也可以根据函数的表达式判断函数的单调性,周期性等,之后结合选项选择.10.如图,在等腰直角ABC ∆中,D ,E 分别为斜边BC 的三等分点(D 靠近点B ),过E 作AD 的垂线,垂足为F ,则AF =u u u v( )A .3155AB AC +u u uv u u u vB .2155AB AC +u u uv u u u vC .481515AB AC +u u uv u u u v D .841515AB AC +u u uv u u u v 【答案】D 【解析】 【分析】设出等腰直角三角形ABC 的斜边长,由此结合余弦定理求得各边长,并求得cos DAE ∠,由此得到45AF AD =u u u r u u u r,进而利用平面向量加法和减法的线性运算,将45AF AD =u u u r u u u r 表示为以,AB AC u u u r u u u r为基底来表示的形式.【详解】设6BC =,则2AB AC BD DE EC =====,AD AE ===,101044cos 2105DAE +-∠==⨯, 所以45AF AF AD AE ==,所以45AF AD =u u u r u u u r . 因为()1133AD AB BC AB AC AB =+=+-u u u r u u u r u u u r u u u r u u u r u u u r 2133AB AC =+u u ur u u u r , 所以421845331515AF AB AC AB AC ⎛⎫=⨯+=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r. 故选:D 【点睛】本小题主要考查余弦定理解三角形,考查利用基底表示向量,属于中档题.11.已知sin α,sin()10αβ-=-,,αβ均为锐角,则β=( ) A .512πB .3π C .4π D .6π 【答案】C 【解析】 【分析】 由题意,可得22ππαβ-<-<,利用三角函数的基本关系式,分别求得cos ,cos()ααβ-的值,利用sin[(]sin )ααββ=--,化简运算,即可求解.【详解】由题意,可得α,β均为锐角,∴-2π <α-β<2π. 又sin(α-β)=-10,∴cos(α-β)=10. 又sin αcos α∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=-×10⎛⎫-⎪ ⎪⎝⎭.∴β=4π.【点睛】本题主要考查了三角函数的化简、求值问题,其中熟记三角函数的基本关系式和三角恒等变换的公式,合理构造sin[(]sin )ααββ=--,及化简与运算是解答的关键,着重考查了推理与运算能力,属于基础题.12.将函数cos y x =的图象先左移4π,再纵坐标不变,横坐标缩为原来的12,所得图象的解析式为( ) A .sin 24y x π⎛⎫=+ ⎪⎝⎭B .13sin 24y x π⎛⎫=+⎪⎝⎭C .1sin 24y x π⎛⎫=+ ⎪⎝⎭D .3sin 24y x π⎛⎫=+ ⎪⎝⎭ 【答案】D 【解析】 【分析】根据三角函数的平移伸缩变换法则得到答案. 【详解】cos sin 2y x x π⎛⎫==+ ⎪⎝⎭向左平移4π个单位,故变为3sin 4y x π⎛⎫=+ ⎪⎝⎭,纵坐标不变,横坐标缩为原来的12,变为3sin 24y x π⎛⎫=+ ⎪⎝⎭. 故选:D . 【点睛】本题考查了三角函数的平移伸缩变换,意在考查学生对于平移伸缩变换的理解和掌握.13.函数2()sin cos 2cos f x a x a x x =+-的图象关于直线4πx =-对称,则()f x 的最大值为( )A .2BC .D 或【答案】D 【解析】 【分析】根据函数2()sin cos 2cos f x a x a x x =+-的图象关于直线4πx =-对称,则有()(0)2f f π-=,解得a ,得到函数再求最值.【详解】因为函数2()sin cos 2cos f x a x a x x =+-的图象关于直线4πx =-对称,所以()(0)2f f π-=,即220a a +-=, 解得2a =-或1a =,当2a =-时,()sin 2cos 2cos 44f x x x x x π⎛⎫=--=- ⎪⎝⎭,此时()f x的最大值为;当1a =时,()sin cos 2cos 4f x x x x x π⎛⎫=+-=- ⎪⎝⎭,此时()f x;综上()f x或. 故选:D 【点睛】本题主要考查三角函数的性质,还考查了分类讨论的思想和运算求解的能力,属于中档题.14.已知1tan 4,tan θθ+=则2sin ()4πθ+=( )A .15B .14C .12D .34【答案】D 【解析】 【分析】根据同角三角函数的关系化简1tan 4tan θθ+=成关于正余弦的关系式,再利用降幂公式与诱导公式化简2sin ()4πθ+求解即可.【详解】由题, 1tan 4,tan θθ+=则22sin cos sin cos 444sin cos 1cos sin sin cos θθθθθθθθθθ++=⇒=⇒=, 故1sin 22θ=.所以2sin ()4πθ+=1cos 222πθ⎛⎫-+ ⎪⎝⎭1sin 2324θ+==. 故选:D 【点睛】本题主要考查了三角函数的公式运用,在有正切函数时可考虑转化为正余弦的关系进行化简,属于基础题.15.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表: 黄赤交角 2341︒'2357︒'2413︒'2428︒'2444︒'正切值 0.439 0.444 0.450 0.455 0.461 年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ) A .公元前2000年到公元元年 B .公元前4000年到公元前2000年 C .公元前6000年到公元前4000年 D .早于公元前6000年【答案】D 【解析】 【分析】先理解题意,然后根据题意建立平面几何图形,在利用三角函数的知识计算出冬至日光与春秋分日光的夹角,即黄赤交角,即可得到正确选项. 【详解】解:由题意,可设冬至日光与垂直线夹角为α,春秋分日光与垂直线夹角为β, 则αβ-即为冬至日光与春秋分日光的夹角,即黄赤交角, 将图3近似画出如下平面几何图形:则16tan 1.610α==,169.4tan 0.6610β-==,tan tan 1.60.66tan()0.4571tan tan 1 1.60.66αβαβαβ---==≈++⨯g .0.4550.4570.461<<Q ,∴估计该骨笛的大致年代早于公元前6000年.故选:D . 【点睛】本题考查利用三角函数解决实际问题的能力,运用了两角和与差的正切公式,考查了转化思想,数学建模思想,以及数学运算能力,属中档题.16.ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =c =( )A .B .2CD .1【答案】B 【解析】1sin A ===cos A =,所以22212c c =+-2320,c c -+=求得1c =或 2.c = 若1c =,则三角形为等腰三角形,030,60A C B ===不满足内角和定理,排除. 【考点定位】本题考查正弦定理和余弦定理的应用,考查运算能力和分类讨论思想.当求出cos 2A =后,要及时判断出0030,60A B ==,便于三角形的初步定型,也为排除1c =提供了依据.如果选择支中同时给出了1或2,会增大出错率.17.已知向量m =r (1,cosθ),(sin ,2)n θ=-r ,且m r ⊥n r,则sin 2θ+6cos 2θ的值为( )A .12B .2C .D .﹣2【答案】B 【解析】 【分析】根据m r ⊥n r 可得tanθ,而sin 2θ+6cos 2θ22226sin cos cos sin cos θθθθθ+=+,分子分母同除以cos 2θ,代入tanθ可得答案. 【详解】因为向量m =r (1,cosθ),n =r(sinθ,﹣2),所以sin 2cos m n θθ⋅=-u r r因为m r ⊥n r ,所以sin 2cos 0θθ-=,即tanθ=2,所以sin 2θ+6cos 2θ22222626226141sin cos cos tan sin cos tan θθθθθθθ++⨯+====+++ 2. 故选:B. 【点睛】本题主要考查平面向量的数量积与三角恒等变换,还考查运算求解的能力,属于中档题.18.设2α是第一象限角,且cos cos αα=-,则α是第( )象限角 A .一 B .二C .三D .四【答案】B 【解析】 【分析】计算得到720180720k k α︒<<︒+︒,k Z ∈,再根据cos 0α<得到答案. 【详解】∵2α是第一象限角,∴360903602k k α︒<<︒+︒,k Z ∈,∴720180720k k α︒<<︒+︒,k Z ∈,∴α为第一象限角或第二象限角或终边在y 轴正半轴上的轴线角,∵cos cos αα=-,∴cos 0α<,∴α是第二象限角. 故选:B . 【点睛】本题考查了角度所在象限,意在考查学生的计算能力和转化能力.19.在函数:①cos |2|y x =;②|cos |y x =;③cos 26y x π⎛⎫=+ ⎪⎝⎭;④tan 24y x π⎛⎫=- ⎪⎝⎭中,最小正周期为π的所有函数为( ) A .①②③ B .①③④C .②④D .①③【答案】A 【解析】逐一考查所给的函数:cos 2cos2y x x == ,该函数为偶函数,周期22T ππ== ; 将函数cos y x = 图象x 轴下方的图象向上翻折即可得到cos y x = 的图象,该函数的周期为122ππ⨯= ; 函数cos 26y x π⎛⎫=+⎪⎝⎭的最小正周期为22T ππ== ;函数tan 24y x π⎛⎫=-⎪⎝⎭的最小正周期为22T ππ==;综上可得最小正周期为π的所有函数为①②③. 本题选择A 选项.点睛:求三角函数式的最小正周期时,要尽可能地化为只含一个三角函数的式子,否则很容易出现错误.一般地,经过恒等变形成“y =A sin(ωx +φ),y =A cos(ωx +φ),y =A tan(ωx +φ)”的形式,再利用周期公式即可.20.在极坐标系中,曲线4sin 6πρθ⎛⎫=+ ⎪⎝⎭关于( ) A .直线3πθ=对称B .直线6πθ=对称C .点2,6π⎛⎫⎪⎝⎭对称 D .极点对称【答案】A 【解析】 【分析】由4sin 6πρθ⎛⎫=+ ⎪⎝⎭,得直角坐标方程:2220x x y -+-= ,圆心为( ,又因为直线3πθ=即:y = 过点(,由此便可得出答案.【详解】由曲线4sin 6πρθ⎛⎫=+⎪⎝⎭,即:24sin 6πρρθ⎛⎫=+⎪⎝⎭,又因为cos sin x y ρθρθ=⎧⎨=⎩,化简得曲线的直角坐标方程:2220x x y -+-= ,故圆心为( .又因为直线3πθ=,直角坐标方程为:y = ,直线y =过点(,故曲线关于直线3πθ=对称故选:A. 【点睛】本题主要考查曲线及直线的极坐标方程与直角坐标方程的转化,以及圆关于过圆心的直线对称的知识,属于中等难度题目.。
高三数学三角函数与解三角形多选题知识点-+典型题及答案

高三数学三角函数与解三角形多选题知识点-+典型题及答案一、三角函数与解三角形多选题1.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且2a =,sin 2sin B C =,有以下四个命题中正确的是( )A .满足条件的ABC 不可能是直角三角形B .ABC 面积的最大值为43C .当A =2C 时,ABC 的周长为2+D .当A =2C 时,若O 为ABC 的内心,则AOB 【答案】BCD 【分析】对于A ,利用勾股定理的逆定理判断;对于B ,利用圆的方程和三角形的面积公式可得答案; 对于C ,利用正弦定理和三角函数恒等变形公式可得答案对于D ,由已知条件可得ABC 为直角三角形,从而可求出三角形的内切圆半径,从而可得AOB 的面积 【详解】对于A ,因为sin 2sin B C =,所以由正弦定理得,2b c =,若b 是直角三角形的斜边,则有222a c b +=,即2244c c +=,得3c =,所以A 错误; 对于B ,以BC 的中点为坐标原点,BC 所在的直线为x 轴,建立平面直角坐标系,则(1,),(1,0)B C -,设(,)A m n ,因为2b c ==, 化简得22516()39m n ++=,所以点A 在以5,03⎛⎫- ⎪⎝⎭为圆心,43为半径的圆上运动, 所以ABC 面积的最大值为1442233⨯⨯=,所以B 正确; 对于C ,由A =2C ,可得3B C π=-,由sin 2sin B C =得2b c =,由正弦定理得,sin sin b cB C=,即2sin(3)sin c c C C π=-,所以sin32sin C C =,化简得2sin cos 22cos sin 2sin C C C C C +=, 因为sin 0C ≠,所以化简得23cos 4C =,因为2b c =,所以B C >,所以cos C =,则1sin 2C =,所以sin 2sin 1B C ==,所以2B π=,6C π=,3A π=,因为2a =,所以c b ==,所以ABC 的周长为2+,所以C 正确; 对于D ,由C 可知,ABC 为直角三角形,且2B π=,6C π=,3A π=,c b ==,所以ABC 的内切圆半径为1212r ⎛=+= ⎝⎭,所以AOB 的面积为111122333cr ⎛=⨯-= ⎝⎭所以D 正确, 故选:BCD 【点睛】此题考查三角形的正弦定理和面积公式的运用,考查三角函数的恒等变换,考查转化能力和计算能力,属于难题.2.在单位圆O :221x y +=上任取一点()P x y ,,圆O 与x 轴正向的交点是A ,将OA 绕原点O 旋转到OP 所成的角记为θ,若x ,y 关于θ的表达式分别为()x fθ=,()y g θ=,则下列说法正确的是( )A .()x f θ=是偶函数,()y g θ=是奇函数;B .()x f θ=在()0,π上为减函数,()y g θ=在()0,π上为增函数;C .()()1fg θθ+≥在02πθ⎛⎤∈⎥⎝⎦,上恒成立;D .函数()()22t f g θθ=+.【答案】ACD 【分析】依据三角函数的基本概念可知cos x θ=,sin y θ=,根据三角函数的奇偶性和单调性可判断A 、B ;根据辅助角公式知()()4f g πθθθ⎛⎫+=+ ⎪⎝⎭,再利用三角函数求值域可判断C ;对于D ,2cos sin2t θθ=+,先对函数t 求导,从而可知函数t 的单调性,进而可得当1sin 2θ=,cos θ=时,函数t 取得最大值,结合正弦的二倍角公式,代入进行运算即可得解. 【详解】由题意,根据三角函数的定义可知,x cos θ=,y sin θ=, 对于A ,函数()cos fθθ=是偶函数,()sin g θθ=是奇函数,故A 正确;对于B ,由正弦,余弦函数的基本性质可知,函数()cos f θθ=在()0,π上为减函数,函数()sin g θθ=在0,2π⎛⎫⎪⎝⎭为增函数,在,2ππ⎛⎫⎪⎝⎭为减函数,故B 错误; 对于C ,当0θπ⎛⎤∈ ⎥2⎝⎦,时,3,444πππθ⎛⎤+∈ ⎥⎝⎦()()cos sin 4f g πθθθθθ⎛⎫+=+=+∈ ⎪⎝⎭,故C 正确;对于D ,函数()()222cos sin2t fg θθθθ=+=+,求导22sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)t θθθθθθ'=-+=-+-=--+, 令0t '>,则11sin 2θ-<<;令0t '<,则1sin 12θ<<, ∴函数t 在06,π⎡⎤⎢⎥⎣⎦和5,26ππ⎡⎤⎢⎥⎣⎦上单调递增,在5,66ππ⎛⎫⎪⎝⎭上单调递减,当6πθ=即1sin 2θ=,cos 2θ=时,函数取得极大值1222t =⨯=又当2θπ=即sin 0θ=,cos 1θ=时,212012t =⨯+⨯⨯=,所以函数()()22t f g θθ=+,故D 正确.故选:ACD. 【点睛】方法点睛:考查三角函数的值域时,常用的方法:(1)将函数化简整理为()()sin f x A x ωϕ=+,再利用三角函数性质求值域; (2)利用导数研究三角函数的单调区间,从而求出函数的最值.3.设函数()2sin sin 2cos2f x x x =++,给出下列四个结论:则正确结论的序号为( ) A .()20f >B .()f x 在53,2ππ⎛⎫--⎪⎝⎭上单调递增 C .()f x 的值域为[]12cos2,32cos2-++ D .()f x 在[]0,2π上的所有零点之和为4π 【答案】ABD【分析】由()23sin 22cos2f =+,结合3224ππ<<,可判定A 正确;作出函数2sin sin y x x =+的图象,可得函数()f x 的值域及单调性,可判定B 正确,C 不正确;结合函数的图象,可得()f x 在[]0,2π上的所有零点之和,可判定D 正确. 【详解】由题意,函数()2sin sin 2cos2f x x x =++, 可得()22sin 2sin 22cos23sin 22cos2f =++=+ 因为3224ππ<<,所以sin 2cos20>->,所以()20f >,所以A 正确; 由3sin ,222sin sin ,sin ,222x k x k y x x k Z x k x k πππππππ≤≤+⎧=+=∈⎨-+≤≤+⎩,作出函数2sin sin y x x =+的图象,如图所示, 可得函数()f x 是以2π为周期的周期函数,由函数2sin sin y x x =+的图象可知,函数()f x 在3(,)2ππ上单调递增, 又由()f x 是以2π为周期的周期函数,可得函数()f x 在5(3,)2ππ--上单调递增, 所以B 是正确的;由由函数2sin sin y x x =+的图象可知,函数()f x 的值域为[2cos 2,32cos 2]+, 所以C 不正确; 又由2223ππ<<,所以1cos 202-<<,则02cos21<-<, 令()0f x =,可得2sin sin 2cos2x x +=-,由图象可知,函数()f x 在[]0,2π上的所有零点之和为4π,所以D 正确. 故选:ABD.【点睛】本题主要考查了三角函数的图象与性质的综合应用,其中解答中熟记三角函数的图象与性质是解答的关键,着重考查转化思想,以及数形结合思想的应用,以及推理与运算能力,属于中档试题.4.设函数()2sin 1xf x x x π=-+,则( )A .()43f x ≤B .()5f x x ≤C .曲线()y f x =存在对称轴D .曲线()y f x =存在对称中心【答案】ABC 【分析】 通过()22sin sin 11324x xf x x x x ππ==-+⎛⎫-+⎪⎝⎭可发现函数()y f x =具有对称轴及最大值,再利用函数对称中心的特点去分析()y f x =是否具有对称中心,再将()5f x x ≤化为32sin 555x x x x π≤-+,通过数形结合判断是否成立.【详解】函数解析式可化为:()22sin sin 11324x xf x x x x ππ==-+⎛⎫-+⎪⎝⎭,因为函数sin y x =π的图象关于直线12x =对称,且函数21324y x ⎛⎫=-+ ⎪⎝⎭的图象也关于直线12x =对称,故曲线()y f x =也关于直线12x =对称,选项C 正确; 当12x =时,函数sin y x =π取得最大值1,此时21324y x ⎛⎫=-+ ⎪⎝⎭取得最小值34,故()14334f x ≤=,选项A 正确; 若()5f x x ≤,则32sin 555x x x x π≤-+,令()32555g x x x x =-+,则()()221510553210g x x x x x '=-+=-+>恒成立,则()g x 在R 上递增,又()00g =,所以当0x <时,()00g <;当0x >时,()0g x >; 作出sin x π和32555x x x -+的图象如图所示:由图象可知32sin 555x x x x π≤-+成立,即()5f x x ≤,选项B 正确;对于D 选项,若存在一点(),a b 使得()f x 关于点(),a b 对称,则()()2f a x f a x b -++=,通过分析发现()()f a x f a x -++不可能为常数,故选项D 错误. 故选:ABC. 【点睛】本题考查函数的综合应用,涉及函数的单调性与最值、对称轴于对称中心、函数与不等式等知识点,难度较大. 对于复杂函数问题一定要化繁为简,利用熟悉的函数模型去分析,再综合考虑,注意数形结合、合理变形转化.5.(多选题)已知22tan 2tan 10x y --=,则下列式子成立的是( ) A .22sin 2sin 1y x =+ B .22sin 2sin 1y x =-- C .22sin 2sin 1y x =-D .22sin 12cos y x =-【答案】CD 【分析】对原式进行切化弦,整理可得:222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,结合因式分解代数式变形可得选项. 【详解】∵22tan 2tan 10x y --=,2222sin sin 210cos cos x yx y-⋅-=, 整理得222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,∴()()()22222221cos 1sin sin cos cos sin cos x x y x y y x ---⋅=+, 即22222221cos sin sin cos sin cos cos x y y x y x x --+⋅-⋅=, 即222sin 12cos 2sin 1y x x =-=-,∴C 、D 正确. 故选:CD 【点睛】此题考查三角函数的化简变形,根据弦切关系因式分解,结合平方关系变形.6.下列结论正确的是( )A .在三角形ABC 中,若AB >,则sin sin A B > B .在锐角三角形ABC 中,不等式2220b c a +->恒成立 C .若sin 2sin 2A B =,则三角形ABC 为等腰三角形D .在锐角三角形ABC 中,sin sin cos cos A B A B +>+ 【答案】ABD 【分析】由正弦定理及三角形性质判断A ,由余弦定理判断B ,由正弦函数性质判断C ,利用锐角△ABC 这个条件,可得2A B π+>,结合三角函数的单调性比较sin A 与cos B 大小即可判断D . 【详解】ABC 中,A B a b >⇔>,由sin sin a bA B=,得sin sin A B >,A 正确; 在锐角三角形ABC 中,222222cos 0,02b c a A b c a bc+-=>∴+->,B 正确;ABC 中,若sin 2sin 2A B =,则22A B =或22180A B ︒+=,即A B =或90A B ︒+=,ABC 为等腰三角形或直角三角形,C 错误;在锐角三角形ABC 中,2A B π+>,022A B ππ∴>>->,sin sin 2A B π⎛⎫∴>- ⎪⎝⎭,即sin cos A B >,同理:sin cos B A >sin sin cos cos A B A B ∴+>+,D 正确.故选:ABD. 【点睛】关键点睛:本题考查正弦定理,余弦定理,正弦函数的性质,诱导公式等,学会公式的灵活应用是解答本题的关键.7.函数()cos |cos |f x x x =+,x ∈R 是( ) A .最小正周期是π B .区间[0,1]上的减函数 C .图象关于点(k π,0)()k Z ∈对称 D .周期函数且图象有无数条对称轴 【答案】BD 【分析】根据绝对值的意义先求出分段函数的解析式,作出函数图象,利用函数性质与图象关系分别对函数的周期、单调区间、对称中心和对称轴进行判断求解. 【详解】2cos (22)22()30(22)22x k x k f x k x k ππππππππ⎧-+⎪⎪=⎨⎪+<≤+⎪⎩,则对应的图象如图:A 中由图象知函数的最小正周期为2π,故A 错误,B 中函数在[0,]2π上为减函数,故B 正确,C 中函数关于x k π=对称,故C 错误,D 中函数由无数条对称轴,且周期是2π,故D 正确 故正确的是B D 故选:BD【点睛】本题考查由有解析式的函数图象的性质. 有关函数图象识别问题的思路:①由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置; ②由函数的单调性,判断图象的变化趋势; ③由函数的奇偶性,判断图象的对称性; ④由函数的周期性,判断图象的循环往复.8.已知函数()()sin 22sin cos 644f x x x x x πππ⎛⎫⎛⎫⎛⎫=--++∈ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭R ,现给出下列四个命题,其中正确的是( ) A .函数()f x 的最小正周期为2π B .函数()f x 3C .函数()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上单调递增 D .将函数()f x 的图象向左平移512π个单位长度,得到的函数解析式为()()2g x x =【答案】BD 【分析】首先利用三角恒等变形化简函数()23f x x π⎛⎫=-⎪⎝⎭,再根据函数的性质依次判断选项,AB 选项根据解析式直接判断,C 选项可以先求23x π-的范围,再判断函数的单调性,D 选项根据平移规律直接求解平移后的解析式. 【详解】()12cos 2sin 2222f x x x x π⎛⎫=--+ ⎪⎝⎭132cos 2cos 22cos 222x x x x x =--=-23x π⎫⎛=- ⎪⎝⎭,函数()f x 的周期22T ππ==,故A 不正确;B.B 正确; C.,44x ππ⎡⎤∈-⎢⎥⎣⎦时,52,366x πππ⎡⎤-∈-⎢⎥⎣⎦,当52,362x πππ⎡⎤-∈--⎢⎥⎣⎦时函数单调递减,即,412x ππ⎡⎤∈--⎢⎥⎣⎦时函数单调递减,,124x ππ⎡⎤∈-⎢⎥⎣⎦时,函数单调递增,故C 不正确;D. ()23f x x π⎛⎫=-⎪⎝⎭向左平移512π个单位长度,得到()52221232g x x x x πππ⎡⎤⎛⎫⎛⎫=+-=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故D 正确. 故选:BD 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.二、数列多选题9.斐波那契数列{}n a :1,1,2,3,5,8,13,21,34,…,又称黄金分割数列,是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,其通项公式1122n nn a ⎡⎤⎛⎛-⎢⎥=- ⎢⎥⎝⎭⎝⎭⎣⎦,是用无理数表示有理数的一个范例,该数列从第三项开始,每项等于其前相邻两项之和,即21n n n a a a ++=+,记该数列{}n a 的前n 项和为n S ,则下列结论正确的是( )A .10711S a =B .2021201920182a a a =+C .202120202019S S S =+D .201920201S a =-【答案】AB 【分析】选项A 分别求出710S a ,可判断,选项B 由21n n n a a a ++=+,得()112n n n a a a n +-=+≥,相加得2n a +12n n a a -=+可判断,选项C ,由202112342021S a a a a a =+++++,202012S a a =+++2020a ,两式错位相减可判断.选项D.由()()()()()324354652122n n n n S a a a a a a a a a a a a +++=-+-+-+-++-=-可判断.【详解】因为10143S =,711143a =,所以10711S a =,则A 正确;由21n n n a a a ++=+,得()112n n n a a a n +-=+≥,相加得2n a +12n n a a -=+, 所以2021201920182a a a =+,所以B 正确; 因为202112342021S a a a a a =+++++,202012S a a =+++2020a ,两式错位相减可得202120201220192019101S S a a a S -=+++++=+,所以2021202020191S S S =++,所以C 错误; 因为()()()()()123324354652122n n n n n S a a a a a a a a a a a a a a a a +++=++++=-+-+-+-++-=-21n a +=-,所以201920211S a =-,所以D 错误.故选:AB. 【点睛】关键点睛:本题考查数列的递推关系的应用,解答本题的关键是由202112342021S a a a a a =+++++,202012S a a =+++2020a ,两式错位相减可得202120201220192019101S S a a a S -=+++++=+,以及由递推关系可得()()()()()324354652122n n n n S a a a a a a a a a a a a +++=-+-+-+-++-=-,属于中档题.10.已知等差数列{}n a 的前n 项和为n S ,218a =,512a =,则下列选项正确的是( ) A .2d =-B .122a =C .3430a a +=D .当且仅当11n =时,n S 取得最大值 【答案】AC【分析】先根据题意得等差数列{}n a 的公差2d =-,进而计算即可得答案.【详解】解:设等差数列{}n a 的公差为d , 则52318312a a d d =+=+=,解得2d =-. 所以120a =,342530a a a a +=+=,11110201020a a d =+=-⨯=, 所以当且仅当10n =或11时,n S 取得最大值. 故选:AC【点睛】本题考查等差数列的基本计算,前n 项和n S 的最值问题,是中档题. 等差数列前n 项和n S 的最值得求解常见一下两种情况: (1)当10,0a d ><时,n S 有最大值,可以通过n S 的二次函数性质求解,也可以通过求满足10n a +<且0n a >的n 的取值范围确定; (2)当10,0a d <>时,n S 有最小值,可以通过n S 的二次函数性质求解,也可以通过求满足10n a +>且0n a <的n 的取值范围确定;。
高考数学三角函数与解三角形多选题(讲义及答案)及解析

高考数学三角函数与解三角形多选题(讲义及答案)及解析一、三角函数与解三角形多选题1.已知函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭且对于R x ∀∈都有144f x f x ππ⎛⎫-=- ⎪⎛⎫⎝⎭+ ⎪⎝⎭成立.现将函数()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位长度,再把所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是( ) A .函数066g x g x ππ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭B .函数()g x 相邻的对称轴距离为πC .函数23g x π⎛⎫+ ⎪⎝⎭是偶函数 D .函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增 【答案】ABCD 【分析】先利用已知条件求出()f x 的周期T π=,即可得2ω=,再利三角函数图象的平移伸缩变换得()g x 的解析式,在逐一判断四个选项的正误即可得正确选项. 【详解】因为对于R x ∀∈都有144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭成立 所以()12f x f x π=-⎛⎫+ ⎪⎝⎭,()12f x f x ππ⎛⎫+=- ⎪+⎝⎭, 所以()()()11f x f x f x ππ=-=+-+对于R x ∀∈都成立, 可得()f x 的周期T π=,所以22Tπω==, 所以()2sin 26f x x π⎛⎫=+⎪⎝⎭, 将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向右平移6π个单位长度,可得 2sin 22sin 2666y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦再把所有点的横坐标伸长到原来的2倍可得()2sin 6g x x π⎛⎫=- ⎪⎝⎭,()2sin 2sin 2sin 2sin 0666666g x g x x x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫-++=--++-=-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故选项A 正确;对于选项B :函数()g x 周期为221T ππ==,所以相邻的对称轴距离为2Tπ=,故选项B正确;对于选项C :222sin 2sin 2cos 3362g x x x x ππππ⎛⎫⎛⎫⎛⎫+=+-=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是偶函数,故选项C 正确; 对于选项D :当63x ππ≤≤,066x ππ≤-≤,所以函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增,故选项D 正确, 故选:ABCD 【点睛】关键点点睛:本题解题的关键点是由144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭恒成立得出 ()()f x f x π=+可得ω的值,求出()f x 的解析式.2.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,有以下四个命题中正确的是( ) A .22S a bc +B .当2a =,sin 2sin BC =时,ABC 不可能是直角三角形 C .当2a =,sin 2sin B C =,2A C =时,ABC的周长为2+D .当2a =,sin 2sin B C =,2A C =时,若O 为ABC 的内心,则AOB的面积为【答案】ACD 【分析】利用三角形面积公式,余弦定理基本不等式,以及三角换元,数形结合等即可判断选项A ;利用勾股定理的逆定理即可判断选项B ;利用正弦定理和三角恒等变换公式即可判断选项C ;由已知条件可得ABC 是直角三角形,从而可以求出其内切圆的半径,即可得AOB 的面积即可判断选项D.对于选项A :2221sin 1sin 222cos2222cos bc AS A b c a bc b c bc A bc Ac b==⨯++-+++- 1sin 4cos 2A A ≤-⨯-(当且仅当b c =时取等号).令sin A y =,cos A x =,故21242S ya bc x ≤-⨯+-,因为221x y +=,且0y >,故可得点(),x y 表示的平面区域是半圆弧上的点,如下图所示:目标函数2yz x =-上,表示圆弧上一点到点()2,0A 点的斜率, 数形结合可知,当且仅当目标函数过点13,22H ⎛⎫ ⎪ ⎪⎝⎭,即60A =时,取得最小值33-, 故可得32yz x ⎡⎫=∈⎪⎢⎪-⎣⎭, 又21242S yx bc x ≤-⨯+-,故可得213324312S a bc ⎛≤-⨯-= +⎝⎭, 当且仅当60A =,b c =,即三角形为等边三角形时,取得最大值,故选项A 正确; 对于选项B :因为sin 2sin B C =,所以由正弦定理得2b c =,若b 是直角三角形的斜边,则有222a c b +=,即2244c c +=,得33c =,故选项B 错误; 对于选项C ,由2A C =,可得π3B C =-,由sin 2sin B C =得2b c =,由正弦定理得,sin sin b c B C=,即()2sin π3sin c c C C =-, 所以sin32sin C C =,化简得2sin cos 22cos sin 2sin C C C C C +=, 因为sin 0C ≠,所以化简得23cos 4C =,因为2b c =,所以B C >,所以3cos C =,则1sin 2C =,所以sin 2sin 1B C ==,所以π2B =,π6C =,π3A =,因为2a =,所以233c =,433b =,所以ABC 的周长为223+,故选项C 正确; 对于选项D ,由C 可知,ABC 为直角三角形,且π2B =,π6C =,π3A =,233c =,433b =,所以ABC 的内切圆半径为123433212r ⎛⎫=+-=- ⎪ ⎪⎝⎭, 所以ABC 的面积为1123331122333cr ⎛⎫-=⨯⨯-= ⎪ ⎪⎝⎭所以选项D 正确, 故选:ACD 【点睛】关键点点睛:本题的关键点是正余弦定理以及面积公式,对于A 利用面积公式和余弦定理,结合不等式得21sin 1sin 224cos 222cos S A Ab c a bc A A c b=⨯≤-⨯+-++-,再利用三角换元、数形结合即可得证,综合性较强,属于难题.3.如图,ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若a b =,且()3cos cos 2sin a C c A b B +=,D 是ABC 外一点,1DC =,3DA =,则下列说法正确的是( )A .ABC 是等边三角形B .若23AC =A ,B ,C ,D 四点共圆 C .四边形ABCD 533 D .四边形ABCD 面积最小值为5332- 【答案】AC【分析】利用三角函数恒等变换化简已知等式可求sin B ,再利用a b =,可知ABC 为等边三角形,从而判断A ;利用四点A ,B ,C ,D 共圆,四边形对角互补,从而判断B ;设AC x =,0x >,在ADC 中,由余弦定理可得2106cos x D =-,利用三角形的面积公式,三角函数恒等变换的,可求ABCD S 四边形,利用正弦函数的性质,求出最值,判断CD .【详解】由正弦定理2sin ,2sin ,2sin a R A b R B c R C ===,(sin cos sin cos )2sin sin A C C A B B +=⋅,2sin ,sin B B =∴=, a b =,B 是等腰ABC 的底角,(0,)2B π∴∈,,3B ABC π∴=∴△是等边三角形,A 正确;B 不正确:若,,,A BCD 四点共圆,则四边形对角互补, 由A 正确知21,cos 32D D π∠==-,但由于1,3,DC DA AC ===22211cos 232DC DA AC D DA DC +-===-≠-⋅⋅,∴B 不正确. C 正确,D 不正确:设D θ∠=,则2222cos 106cos AC DC DA DC DA θθ=+-⋅⋅=-,(106cos )ABC S θθ∴=-=△, 3sin 2ADC S θ=△,3sin 2ABCADCABCD S S Sθθ∴=+=-+四边形13(sin cos 2θθ=⋅-+,3sin()3πθ=-+(0,),sin()(3πθπθ∈∴-∈,5333ABCD S ∴-<≤+四边形,∴C 正确,D 不正确; 故选:AC.. 【点睛】本题主要考查正弦定理,余弦定理,三角函数恒等变换,正弦函数的图象和性质在解三角形中的综合应用,考查计算能力和转化思想,属于中档题.4.(多选题)如图,设ABC 的内角、、A B C 所对的边分别为a b c 、、,若a b c 、、成等比数列,、、A B C 成等差数列,D 是ABC 外一点,1,3DC DA ==,下列说法中,正确的是( )A .3B π=B .ABC 是等边三角形C .若A B CD 、、、四点共圆,则13AC =D .四边形ABCD 面积无最大值 【答案】ABC 【分析】根据等差数列的性质和三角形内角和可得3B π=,根据等比中项和余弦定理可得a c =,即ABC 是等边三角形,若A B C D 、、、四点共圆,根据圆内接四边形的性质可得23D π=,再利用余弦定理可求13AC =211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+和2222cos AC AD CD AD CD D 可得3335353sin 3sin()23S D D D π=-+=-+. 【详解】由、、A B C 成等差数列可得,2A+C =B ,又A B C π++=, 则3B π=,故A 正确;由a b c 、、成等比数列可得,2b ac =,根据余弦定理,2222cos b a c ac B =+-,两式相减整理得,2()0a c -=,即a c =,又3B π=,所以,ABC 是等边三角形,故B 正确;若A B C D 、、、四点共圆,则B D π+=,所以,23D π=, ADC 中,根据余弦定理,2222cos AC AD CD AD CD D ,解得AC =C 正确; 四边形ABCD 面积为:211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+23sin 24D AC =+ 又2222cos 106cos AC AD CD AD CD D D =+-⋅=-,所以,3sin 3sin()23S D D D π==-+因为(0,)D π∈,当四边形面积最大时,sin()13D π-=,此时max 3S =,故D 错误. 故选:ABC 【点睛】本题考查解三角形和平面几何的一些性质,同时考查了等差等比数列的基本知识,综合性强,尤其是求面积的最大值需要一定的运算,属难题.5.已知函数()()sin f x x ωϕ=+(其中,0>ω,||2ϕπ<),08f π⎛⎫-= ⎪⎝⎭,3()8f x f π⎛⎫≤ ⎪⎝⎭恒成立,且()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调,则下列说法正确的是( )A .存在ϕ,使得()f x 是偶函数B .3(0)4f f π⎛⎫=⎪⎝⎭C .ω是奇数D .ω的最大值为3【答案】BCD 【分析】 根据3()8f x f π⎛⎫≤⎪⎝⎭得到21k ω=+,根据单调区间得到3ω≤,得到1ω=或3ω=,故CD 正确,代入验证知()f x 不可能为偶函数,A 错误,计算得到B 正确,得到答案. 【详解】08f π⎛⎫-= ⎪⎝⎭,3()8f x f π⎛⎫≤ ⎪⎝⎭,则3188242k T πππ⎛⎫⎛⎫--==+ ⎪ ⎪⎝⎭⎝⎭,k ∈N , 故221T k π=+,21k ω=+,k ∈N ,08f π⎛⎫-= ⎪⎝⎭,则()s n 08i f x πωϕ⎛⎫=+= ⎪⎭-⎝,故8k πωϕπ+=-,8k ϕπωπ=+,k Z ∈,当,1224x ππ⎛⎫∈-⎪⎝⎭时,,246x k k ωπωπωϕππ⎛⎫+∈++ ⎪⎝⎭,k Z ∈,()f x 在区间,1224ππ⎛⎫-⎪⎝⎭上单调,故241282T πππ⎛⎫--=≤ ⎪⎝⎭,故4T π≥,即8ω≤,0243ωππ<≤,故62ωππ≤,故3ω≤,综上所述:1ω=或3ω=,故CD 正确;1ω=或3ω=,故8k ϕππ=+或38k ϕππ=+,k Z ∈,()f x 不可能为偶函数,A 错误;当1ω=时,(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭,33sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故3(0)4f f π⎛⎫= ⎪⎝⎭; 当3ω=时,3(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭, 393sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故3(0)4f f π⎛⎫= ⎪⎝⎭, 综上所述:3(0)4f f π⎛⎫= ⎪⎝⎭,B 正确; 故选:BCD. 【点睛】本题考查了三角函数的性质和参数的计算,难度较大,意在考查学生的计算能力和综合应用能力.6.已知函数()f x 的定义域为D ,若对于任意()()()a b c D f a f b f c ∈,,,,,分别为某个三角形的边长,则称()f x 为“三角形函数”,其中为“三角形函数”的函数是( ) A .()4sin f x x =-B .()22sin 10cos 13f x x x =-++C .()tan 2xf x =D .()sin 20,34f x x x ππ⎛⎫⎡⎤=++∈ ⎪⎢⎥⎝⎭⎣⎦【答案】AD 【分析】结合三角形的性质有:两边之差小于第三边,得若()f x 为 “三角形函数”则()()()max min min f x f x f x <-恒成立,即()()max min 2f x f x <恒成立即可,根据条件求出函数的最大值和最小值,进行判断即可. 【详解】解:①()4sin f x x =-,则()max 415f x =+=,()min 413f x =-= 则()()max min 2f x f x <恒成立,则A 满足条件②()22532cos 10cos 112cos 22f x x x x ⎛⎫=++=+= ⎪⎝⎭ 当0,2x π⎡⎤∈⎢⎥⎣⎦时,0cos 1x ≤≤∴当cos 0x =时,函数()f x 取得最小值()min 11f x =,当cos 1x =时,函数()f x 取得最大值,()max 23f x =则()()max min 2f x f x <不恒成立,则B 不满足条件 ③()()()tan ,00,2xf x =∈-∞⋃+∞,则不满足条件()()max min 2f x f x <恒成立,故C 不是④()sin 23f x x π⎛⎫=++ ⎪⎝⎭0,4x π⎡⎤∈⎢⎥⎣⎦,52,336x πππ⎡⎤∴+∈⎢⎥⎣⎦,则()max sin12f x π=+=+()min 51sin62f x π=+=+则()min 21f x =+,则()()max min 2f x f x <恒成立,故D 满足条件 故选AD 【点睛】本题考查了三角形的性质及“三角形函数”的概念,根据条件转化为()()max min 2f x f x <恒成立是解决本题的关键,综合性较强,有一定的难度.7.将函数()2πsin 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π6个单位长度后得到函数()g x 的图象,则下列说法正确的是( )A .π4g ⎛⎫= ⎪⎝⎭B .π,06⎛⎫⎪⎝⎭是函数()g x 图象的一个对称中心 C .函数()g x 在π0,4⎡⎤⎢⎥⎣⎦上单调递增D .函数()g x 在ππ,63⎡⎤-⎢⎥⎣⎦上的值域是⎡⎢⎣⎦【答案】BC 【分析】首先求得函数()sin 23g x x π=-⎛⎫⎪⎝⎭,再根据选项,整体代入,判断函数的性质. 【详解】()2sin 2sin 2633g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,1sin 462g ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,故A 错误;sin 0633g πππ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,故B 正确;0,4x π⎡⎤∈⎢⎥⎣⎦时,2,,33622x πππππ⎡⎤⎡⎤-∈-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,所以函数()g x 在0,4⎡⎤⎢⎥⎣⎦π上单调递增,故C 正确;,63x ππ⎡⎤∈-⎢⎥⎣⎦时,22,333x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,函数取得最小值-1,当233x ππ-=时,函数取得最大值2,所以函数的值域是1,2⎡-⎢⎣⎦.故选:BC 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.8.在ABC 中,下列说法正确的是( ) A .若A B >,则sin sin A B > B .若2C π>,则222sin sin sin C A B >+C .若sin cos A B <,则ABC 为钝角三角形D .存在ABC 满足cos cos 0A B +≤ 【答案】ABC 【分析】根据大角对大边,以及正弦定理,判断选项A ;利用余弦定理和正弦定理边角互化,判断选项B ;结合诱导公式,以及三角函数的单调性判断CD. 【详解】A.A B >,a b ∴>,根据正弦定理sin sin a bA B=,可知sin sin A B >,故A 正确; B.2C π>,222cos 02a b c C ab +-∴=<,即222a b c +<,由正弦定理边角互化可知222sin sin sin C A B >+,故B 正确;C.当02A π<<时,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒+<,即2C π>,则ABC 为钝角三角形,若2A π>,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒>+成立,A 是钝角,当2A π=是,sin cos A B >,所以综上可知:若sin cos A B <,则ABC 为钝角三角形,故C 正确;D.A B A B ππ+<⇒<-,0,0A B πππ<<<-<,()cos cos cos A B B π∴>-=-,即cos cos 0A B +>,故D 不正确. 故选:ABC 【点睛】关键点点睛:本题考查判断三角形的形状,关键知识点是正弦定理和余弦定理,判断三角形形状,以及诱导公式和三角函数的单调性.二、数列多选题9.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,0n a ≠,且202021111212a a ++≤+( )A .若数列{}n a 为等差数列,则20210S ≥B .若数列{}n a 为等差数列,则10110a ≤C .若数列{}n a 为等比数列,则20200T >D .若数列{}n a 为等比数列,则20200a <【答案】AC 【分析】由不等关系式,构造11()212xf x =-+,易得()f x 在R 上单调递减且为奇函数,即有220200a a +≥,讨论{}n a 为等差数列、等比数列,结合等差、等比的性质判断项、前n 项和或积的符号即可. 【详解】 由202021111212a a ++≤+,得2020211110212212a a +-+-≤+,令11()212x f x =-+,则()f x 在R 上单调递减,而1121()212212xx x f x --=-=-++, ∴12()()102121xx x f x f x -+=+-=++,即()f x 为奇函数,∴220200a a +≥,当{}n a 为等差数列,22020101120a a a +=≥,即10110a ≥,且2202020212021()02a a S +=≥,故A 正确,B 错误;当{}n a 为等比数列,201820202a a q=,显然22020,a a 同号,若20200a <,则220200a a +<与上述结论矛盾且0n a ≠,所以前2020项都为正项,则202012020...0T a a =⋅⋅>,故C 正确,D 错误. 故选:AC. 【点睛】关键点点睛:利用已知构造函数,并确定其单调性和奇偶性,进而得到220200a a +≥,基于该不等关系,讨论{}n a 为等差、等比数列时项、前n 项和、前n 项积的符号.10.已知数列{}n a 的前n 项和为n S ,则下列说法正确的是( ) A .若21,n S n =-则{}n a 是等差数列B .若21,nn S =-则{}n a 是等比数列C .若{}n a 是等差数列,则995099S a =D .若{}n a 是等比数列,且10,0,a q >>则221212n n n S S S -+⋅>【答案】BC 【分析】由n S 求n a ,根据通项公式可判断AB 是否正确,由等差数列的性质可判断C ,取1n =时,结合等比数列求和公式作差比较13S S ⋅与22S 大小即可判断D. 【详解】对于A 选项,若21n S n =-,当2n ≥时,21n a n =-,10a =不满足21n a n =-,故A错误;对于B 选项,若21nn S =-,则1112,21,1n n n n S S n a S n --⎧-=≥=⎨==⎩,由于11a =满足12n n a -=,所以{}n a 是等比数列,故B 正确;对于C 选项,若{}n a 是等差数列,则()199995099992a a S a +==,故C 正确.对于D 选项,当1n =时,()()222222132111110S S S a q qa q a q ⋅-=++-+=-<,故当1n =时不等式不等式,故221212n n n S S S -+⋅>不成立,所以D 错误.故选:BC 【点睛】本题考查数列的前n 项和为n S 与n a 之间的关系,等差数列的性质,等比数列的前n 项和为n S 的公式等,考查运算求解能力.本题D 选项解题的关键将问题特殊化,讨论1n =时,13S S ⋅与22S 大小情况.此外还需注意一下公式:11,2,1n n n S S n a S n --≥⎧=⎨=⎩;若{}n a 是等差数列,则()2121n n S n a -=-.。
高考数学三角函数与解三角形多选题复习题含答案

高考数学三角函数与解三角形多选题复习题含答案一、三角函数与解三角形多选题1.设函数()2sin sin 2cos2f x x x =++,给出下列四个结论:则正确结论的序号为( ) A .()20f >B .()f x 在53,2ππ⎛⎫--⎪⎝⎭上单调递增 C .()f x 的值域为[]12cos2,32cos2-++ D .()f x 在[]0,2π上的所有零点之和为4π 【答案】ABD 【分析】由()23sin 22cos2f =+,结合3224ππ<<,可判定A 正确;作出函数2sin sin y x x =+的图象,可得函数()f x 的值域及单调性,可判定B 正确,C 不正确;结合函数的图象,可得()f x 在[]0,2π上的所有零点之和,可判定D 正确. 【详解】由题意,函数()2sin sin 2cos2f x x x =++, 可得()22sin 2sin 22cos23sin 22cos2f =++=+ 因为3224ππ<<,所以sin 2cos20>->,所以()20f >,所以A 正确; 由3sin ,222sin sin ,sin ,222x k x k y x x k Z x k x k πππππππ≤≤+⎧=+=∈⎨-+≤≤+⎩,作出函数2sin sin y x x =+的图象,如图所示, 可得函数()f x 是以2π为周期的周期函数,由函数2sin sin y x x =+的图象可知,函数()f x 在3(,)2ππ上单调递增, 又由()f x 是以2π为周期的周期函数,可得函数()f x 在5(3,)2ππ--上单调递增, 所以B 是正确的;由由函数2sin sin y x x =+的图象可知,函数()f x 的值域为[2cos 2,32cos 2]+, 所以C 不正确; 又由2223ππ<<,所以1cos 202-<<,则02cos21<-<, 令()0f x =,可得2sin sin 2cos2x x +=-,由图象可知,函数()f x 在[]0,2π上的所有零点之和为4π,所以D 正确. 故选:ABD.【点睛】本题主要考查了三角函数的图象与性质的综合应用,其中解答中熟记三角函数的图象与性质是解答的关键,着重考查转化思想,以及数形结合思想的应用,以及推理与运算能力,属于中档试题.2.函数()sin()f x x ωϕ=+的部分图像如图中实线所示,图中的M 、N 是圆C 与()f x 图像的两个交点,其中M 在y 轴上,C 是()f x 图像与x 轴的交点,则下列说法中正确的是( )A .函数()y f x =的一个周期为56B .函数()f x 的图像关于点4,03成中心对称C .函数()f x 在11,26⎛⎫-- ⎪⎝⎭上单调递增 D .圆C 的面积为3136π【答案】BD 【分析】根据图象,结合三角函数的对称性、周期性、值域以及圆的中心对称性,可得,,C M N 的坐标,进而可得()f x 的最小正周期、对称中心、单调减区间,及圆的半径,故可判断选项的正误. 【详解】由图知:1(,0)3C ,3)M ,23()3N , ∴()f x 中111()2362T =--=,即1T =;对称中心为1,0,23k k Z ⎛⎫+∈ ⎪⎝⎭;单调减区间为17,,1212k k k Z ⎡⎤++∈⎢⎥⎣⎦;圆的半径r ==,则圆的面积为3136π; 综上,知:AC 错误,而BD 正确. 故选:BD. 【点睛】本题考查了三角函数的性质,结合了圆的中心对称性质判断三角函数的周期、对称中心、单调区间及求圆的面积,属于难题.3.函数()sin 24f x x π⎛⎫=+⎪⎝⎭,则( ) A .函数()y f x =的图象可由函数sin 2y x =的图象向右平移4π个单位得到 B .函数()y f x =的图象关于直线8x π=轴对称C .函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称D .函数2()y x f x =+在08π⎛⎫⎪⎝⎭,上为增函数【答案】BCD 【分析】对四个选项,一一验证:对于选项A ,利用三角函数相位变化即可;对于选项B ,利用正弦函数的对称轴经过最高(低)点判断; 对于选项C ,利用正弦函数的对称中心直接判断; 对于选项D ,利用复合函数的单调性“同增异减”判断; 【详解】由题意,对于选项A ,函数sin 2y x =的图象向右平移4π个单位可得到()sin 2sin 2cos 242f x x x x ππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以选项A 错误;对于选项B ,sin 21884f πππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,取到了最大值,所以函数()y f x =的图象关于直线8x π=轴对称,所以选项B 正确;对于选项C ,08f π⎛⎫-= ⎪⎝⎭,所以函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称,所以选项C 正确;对于选项D ,函数2yx 在08π⎛⎫ ⎪⎝⎭,上为增函数,08x π⎛⎫∈ ⎪⎝⎭,时,2442x πππ⎛⎫+∈ ⎪⎝⎭,,单调递增,所以函数2()y x f x =+在08π⎛⎫⎪⎝⎭,上为增函数,所以选项D 正确.故选:BCD. 【点睛】(1)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题;(2)求单调区间,最后的结论务必写成区间形式,不能写成集合或不等式.4.已知函数()2sin()05,||2f x x πωϕωϕ⎛⎫=+<<< ⎪⎝⎭,且对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,3y f x π⎛⎫=+⎪⎝⎭为奇函数,则下列说法正确的是( ) A .函数()f x 的图象关于原点对称 B .函数()f x 的最小正周期为π C .函数()f x 的图象关于直线2x π=对称D .函数()f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z 【答案】BD 【分析】由()12f x f π⎛⎫≤ ⎪⎝⎭恒成立可得212f π⎛⎫=± ⎪⎝⎭,即()122k k ωππϕπ+=+∈Z ,由3y f x π⎛⎫=+ ⎪⎝⎭为奇函数可得()3k k ωπϕπ''+=∈Z ,即可求出2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,再根据正弦函数的性质分别判断即可. 【详解】因为对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,所以2sin 21212f πωπϕ⎛⎫⎛⎫=+=± ⎪⎪⎝⎭⎝⎭, 即sin 112ωπϕ⎛⎫+=±⎪⎝⎭,得()122k k ωππϕπ+=+∈Z ①. 2sin 2sin 333f x x x ππωπωϕωϕ⎡⎤⎛⎫⎛⎫⎛⎫+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,因为3y f x π⎛⎫=+ ⎪⎝⎭为奇函数,所以()3k k ωπϕπ''+=∈Z ②.由①②可得()(),3122k k k k ωπωπππ''-=--∈Z ,即()(42,)k k k k ω''=--∈Z .又05ω<<,所以1k k '-=,2ω=, 则(2,)33k k k k ππϕππ=+=-'∈'Z ,得3πϕ=,所以2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,由于(0)30f =≠,故()f x 的图象不关于原点对称,所以A 不正确; ()f x 的最小正周期22T ππ==,所以B 正确; 2sin 22sin 2sin 3222333f ππππππ⎛⎫⎛⎫⎛⎫=⨯+=+=-=-≠± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以C 不正确;令222232k x k πππππ-≤+≤+,k ∈Z ,得51212k x k ππππ-≤≤+,k ∈Z , 故函数() f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ,所以D 正确. 故选:BD. 【点睛】关键点睛:本题考查正弦型函数的性质,解题的关键是:(1)根据“对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立”得到“212f π⎛⎫=± ⎪⎝⎭”;(2)得到“2sin 33f x x πωπωϕ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭”后,能根据“3y f x π⎛⎫=+⎪⎝⎭为奇函数”得到“()3k k ωπϕπ''+=∈Z ”.5.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,下列说法正确的是( )A .函数()y f x =的周期为πB .函数()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦单调递减C .函数()y f x =的图象关于直线512x π=-对称 D .该图象向右平移6π个单位可得2sin 2y x =的图象 【答案】ACD 【分析】先根据图像求出()y f x =的解析式,再分别验证A 、B 、C 、D 是否正确. 对于A :利用周期公式求周期;对于B :利用复合函数“同增异减”求单调区间; 对于C :计算512f π⎛-⎫⎪⎝⎭,看512x π=-是否经过顶点; 对于D :利用“左加右减”判断. 【详解】由图像可知:A =2,周期24,2312T T ππππω⎛⎫=-=∴==⎪⎝⎭; 由=2sin 2212122f ππϕπϕ⎧⎛⎫⎛⎫⨯+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪<⎪⎩解得:3πϕ=故函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭对于A :4312T πππ⎛⎫=-= ⎪⎝⎭,故A 正确; 对于B :当236x ππ-≤≤- 时203x ππ-≤+≤,所以()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦上不单调.故B 错误; 对于C :当512x π=-时255s 2121232in f πππ⎛⎫⎛⎫=-=- ⎪ ⎭⎝-⎪⎭+⎝⨯,即直线512x π=-是()y f x =的一条对称轴.故C 正确;对于D :()y f x =向右平移6π个单位得到2sin 222sin 263y x x ππ⎛⎫=-⨯+= ⎪⎝⎭,故D 正确. 故选:ACD 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.6.在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知()()(::5:)4:6b c c a a b +++=,下列结论正确的是( )A .::7:5:3sinA sinB sinC = B .0AB AC ⋅>C .若6c =,则ABC 的面积是D .若8+=b c ,则ABC 的外接圆半径是3【答案】ACD 【分析】先利用已知条件设4,5,6b c k c a k a b k +=+=+=,进而得到3.5, 2.5, 1.5a k b c k ===,利用正弦定理可判定选项A ;利用向量的数量积公式可判断选项B ;利用余弦定理和三角形的面积公式可判定选项C ;利用余弦定理和正弦定理可判断选项D. 【详解】依题意,设4,5,6b c k c a k a b k +=+=+=, 所以 3.5, 2.5, 1.5a k b c k ===,由正弦定理得:::::7:5:3sinA sinB sinC a b c ==, 故选项A 正确;222222cos 22b c a b c a AB AC bc A bc bc +-+-⋅==⨯=222222.5 1.5 3.515028k k +-==-<,故选项B 不正确;若6c =,则4k =, 所以14,10a b ==,所以222106141cos 21062A +-==-⨯⨯,所以sin A =,故ABC 的面积是:11sin 61022bc A =⨯⨯= 故选项C 正确;若8+=b c ,则2k =, 所以7,5,3a b c ===,所以2225371cos 2532A +-==-⨯⨯,所以sin A =, 则利用正弦定理得:ABC 的外接圆半径是:12sin a A ⨯=, 故选项D 正确; 故选:ACD. 【点睛】关键点睛:本题主要考查正余弦定理以及三角形面积公式. 利用已知条件设4,5,6b c k c a k a b k +=+=+=,再利用正余弦定理以及三角形面积公式求解是解决本题的关键.7.已知函数22()(sin cos )2cos f x x x x =++,则( ) A .()f x 的最小正周期是πB .()f x 的图像可由函数()22g x x =+的图像向左平移8π个单位而得到 C .4x π=是()f x 的一条对称轴D .()f x 的一个对称中心是,08π⎛⎫- ⎪⎝⎭【答案】AB 【分析】首先化简函数()224f x x π⎛⎫=++ ⎪⎝⎭,再根据三角函数形式的公式,以及代入的方法判断选项. 【详解】()1sin 2cos 21224f x x x x π⎛⎫=+++=++ ⎪⎝⎭,A.函数的最小正周期22T ππ==,故A 正确;B.根据图象的平移变换规律,可知函数()22g x x =+的图像向左平移8π个单位而得到()222284f x x x ππ⎛⎫⎛⎫=++=++ ⎪ ⎪⎝⎭⎝⎭,故B 正确;C.当4x π=时,32444πππ⨯+=,不是函数的对称轴,故C 不正确;D.当8x π=-时,2084ππ⎛⎫⨯-+= ⎪⎝⎭,此时函数值是2,故函数的一个对称中心应是,28π⎛⎫- ⎪⎝⎭,故D 不正确. 故选:AB 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.8.已知4παπ≤≤,32ππβ≤≤,4sin 25α=,cos()10αβ+=-,则( )A .cos 10α=- B .sin cos 5αα-=C .34πβα-= D .cos cos 5αβ=-【答案】BC 【分析】先根据4sin 25α=,判断角α的范围,再根据cos2α求cos α; 根据平方关系,判断sin cos αα-的值;利用公式cos()cos[()2]βααβα-=+-求值,并根据角的范围判断角βα-的值;利用公式()cos βα+和()cos βα-,联合求cos cos αβ.【详解】 ①因为4παπ≤≤,所以222παπ≤≤,又4sin 205α=>,故有22παπ≤≤,42ππα≤≤,解出2231cos 22cos 1cos cos 55αααα=-=-⇒=⇒=,故A 错误; ②()21sin cos 1sin 25ααα-=-=, 由①知:42ππα≤≤,所以sin cos αα>,所以sin cos 5αα-=,故B 正确; ③由①知:42ππα≤≤,而32ππβ≤≤,所以524παβπ≤+≤,又cos()010αβ+=-<,所以5342ππαβ≤+≤,解得sin()αβ+=所以34cos()cos[()2]1051052βααβα⎛⎫⎛⎫-=+-=--+-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭又因为5342ππαβ≤+≤,22ππα-≤-≤-, 所以4πβαπ≤-≤,有34πβα-=,故C 正确;④由cos()cos cos sin sin 1010αβαβαβ+=-⇒-=-,由③知,cos()cos cos sin sin 2βααβαβ-=+=-,两式联立得:cos cos 10αβ=-,故D 错误. 故选:BC 【点睛】关键点点睛:本题的关键是三角函数恒等变形的灵活应用,尤其是确定角的范围,根据三角函数值4sin 25α=,确定22παπ≤≤,且cos()010αβ+=-<,进一步确定5342ππαβ≤+≤,这些都是确定函数值的正负,以及角的大小的依据.9.设函数()()1sin 022f x x x πωωω⎛⎫=++> ⎪⎝⎭,已知()f x 在[]0,π有且仅有3个零点,则( )A .在()0,π上存在1x 、2x ,满足()()122f x f x -=B .()f x 在()0,π有且仅有1个最小值点C .()f x 在0,2π⎛⎫⎪⎝⎭上单调递增 D .ω的取值范围是1723,66⎡⎫⎪⎢⎣⎭【答案】AD【分析】化简函数()f x 的解析式为()sin 6f x x πω⎛⎫=+ ⎪⎝⎭,令6t x πω=+,由[]0,x π∈可求得,66t ππωπ⎡⎤∈+⎢⎥⎣⎦,作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象,可判断AB 选项的正误;由图象得出346ππωππ≤+<可判断D 选项的正误;取3ω=,利用正弦型函数的单调性可判断C 选项的正误.【详解】 ()3131sin sin sin cos sin 222226f x x x x x x ππωωωωω⎛⎫⎛⎫=++=+=+ ⎪ ⎪⎝⎭⎝⎭, 当[]0,x π∈时,,666x πππωωπ⎡⎤+∈+⎢⎥⎣⎦,令6t x πω=+,则,66t ππωπ⎡⎤∈+⎢⎥⎣⎦, 作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象如下图所示:对于A 选项,由图象可知,max 1y =,min 1y =-,所以,在()0,π上存在1x 、2x ,满足()()122f x f x -=,A 选项正确;对于B 选项,()f x 在()0,π上有1个或2个最小值点,B 选项错误;对于D 选项,由于函数()f x 在[]0,π有且仅有3个零点,则346ππωππ≤+<,解得172366ω≤<,D 选项正确; 对于C 选项,由于172366ω≤<,取3ω=,当0,2x π⎛⎫∈ ⎪⎝⎭时,53663x πππ<+<, 此时,函数()f x 在区间0,2π⎛⎫ ⎪⎝⎭上不单调,C 选项错误. 故选:AD.【点睛】关键点点睛:本题考查利用正弦型函数在区间上的零点个数判断正弦型函数的基本性质,解本题的关键在于换元6t x πω=+,将问题转化为函数sin y t =在区间,66ππωπ⎡⎤+⎢⎥⎣⎦上的零点个数问题,数形结合来求解.10.在ABC 中,下列说法正确的是( )A .若AB >,则sin sin A B >B .若2C π>,则222sin sin sin C A B >+C .若sin cos A B <,则ABC 为钝角三角形D .存在ABC 满足cos cos 0A B +≤【答案】ABC【分析】根据大角对大边,以及正弦定理,判断选项A ;利用余弦定理和正弦定理边角互化,判断选项B ;结合诱导公式,以及三角函数的单调性判断CD.【详解】A.A B >,a b ∴>,根据正弦定理sin sin a b A B =,可知sin sin A B >,故A 正确; B.2C π>,222cos 02a b c C ab +-∴=<,即222a b c +<,由正弦定理边角互化可知222sin sin sin C A B >+,故B 正确;C.当02A π<<时,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒+<,即2C π>,则ABC 为钝角三角形,若2A π>,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒>+成立,A 是钝角,当2A π=是,sin cos A B >,所以综上可知:若sin cos A B <,则ABC 为钝角三角形,故C 正确;D.A B A B ππ+<⇒<-,0,0A B πππ<<<-<,()cos cos cos A B B π∴>-=-,即cos cos 0A B +>,故D 不正确.故选:ABC【点睛】关键点点睛:本题考查判断三角形的形状,关键知识点是正弦定理和余弦定理,判断三角形形状,以及诱导公式和三角函数的单调性.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题04 三角函数与解三角形真题汇编与预赛典型例题1.【2019年全国联赛】对任意闭区间I ,用表示函数y =sinx 在I 上的最大值.若正数a 满足,则a的值为.2.【2017年全国联赛】已知x 、y 满足.则的取值范围是___________。
3.【2016年全国联赛】设函数.若对任意实数a ,均有,则k 的最小值为________.4.【2015年全国联赛】若,则__________. 5.【2015年全国联赛】设为正实数.若存在,使得,则的取值范围是______.6.【2013年全国联赛】在中,已知,则______.7.【2012年全国联赛】设的内角的对边分别为,且满足.则______.8.【2012年全国联赛】满足的所有正整数的和是______.9.【2011年全国联赛】若,则的取值范围为______. 10.【2010年全国联赛】已知函数的最小值为.则实数的取值范围是________.11.【2019年全国联赛】在△ABC 中,BC =a ,CA =b ,AB =c .若b 是a 与c 的等比中项,且sinA 是sin (B -A )与sinC 的等差中项,求cosB 的值. 12.【2012年全国联赛】已知函数,其中,,且.(1)若对任意,都有,求的取值范围.tan cos αα=41cos sin αα+=(2)若,且存在,使,求的取值范围.1.【2018年浙江预赛】已知,得,所以_____2.【2018年浙江预赛】在△ABC中,AB+AC=7,且三角形的面积为4,则sin∠A的最小值为________. 3.【2018年浙江预赛】设满足,则x的取值范围为________. 4.【2018年山西预赛】计算的值为________.5.【2018年江苏预赛】函数的值域是________.6.【2018年贵州预赛】如图,在△ABD中,点C在AD上,,AB=CD=1.则AC=__ __.7.【2018年贵州预赛】若边长为6的正△ABC的三个顶点到平面α的距离分别为1,2,3,则△ABC的重心G到平面α的距离为_______.8.【2018年贵州预赛】函数的所有零点之和等于________.9.【2018年重庆预赛】在△ABC中,,则________.10.【2018年陕西预赛】设的内角所对的边分别为,且成等差数列,则________.11.【2018年陕西预赛】设的内角所对的边分别为,且成等差数列,则________.12.【2018年陕西预赛】设的内角所对的边分别为,且成等差数列,则________.13.【2018年贵州预赛】函数的所有零点之和等于__________. 14.【2018年广西预赛】设.则________.15.【2018年安徽预赛】函数的最小正周期=_________.16.【2018年湖南预赛】函数的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是_____.17.【2018年广东预赛】已知△ABC的三个角A、B、C成等差数列,对应的三边为a、b、c,且a、c、成等比数列,则___________.18.【2018年贵州预赛】如图,在△ABD中,点C在AD上,,AB=CD=1.则AC=_ ___.19.【2018年湖北预赛】若对任意的,不等式恒成立,则实数的最小值为______. 20.【2018年湖北预赛】设的重心,若,则的最大值为______.21.【2016年四川预赛】在△ABC 中,∠A 、∠B 、∠C 的对边长分别为a 、b 、c.命题,且b+c=2a ;命题为正三角形.则命题P 是命题q 的()条件.A .充分必要B .充分但不必要C .必要但不充分D .既不充分又不必要22.【2016年辽宁预赛】设A 、B 、C 为抛物线上不同的点,R 为△ABC 外接圆的半径.求R 的取值范围.23.【2016年甘肃预赛】在非等腰中,的对边分别为a 、b 、c ,且满足.(1)求的大小; (2)若,求面积的取值范围.24.【2016年陕西预赛】设均为非零实数,且满足.(Ⅰ)求的值; (Ⅰ)在中,若,求的最大值. 25.【2016年吉林预赛】在中,a 、b 、c 分别为的对边,,且.求(1);x y 、sincos955tan 20cos sin 55x y x y πππππ+=-yxABC ∆tan yC x=sin 22cos A B +(2)的最大值.专题04 三角函数与解三角形真题汇编与预赛典型例题1.【2019年全国联赛】对任意闭区间I,用表示函数y=sinx在I上的最大值.若正数a满足,则a的值为.【答案】或【解析】由图像分析得或.2.【2017年全国联赛】已知x、y满足.则的取值范围是___________。
【答案】【解析】由于.由,知因此,当时, 有最小值-1,此吋,y可以取;当时, 有最大值此时,y可以取由的值域为,知的取值范围是。
故答案为:3.【2016年全国联赛】设函数.若对任意实数a,均有,则k的最小值为________.【答案】16【解析】由条件知,当且仅当时,取到最大值.根据条件,知任意一个长为1的开区间至少包含一个最大值点.从而,.反之,当时,任意一个开区间均包含的一个完整周期,此时,.综上,k 的最小值为,其中,表示不超过实数x 的最大整数.4.【2015年全国联赛】若,则__________. 【答案】2【解析】由有,而,求出值舍去),所以。
5.【2015年全国联赛】设为正实数.若存在,使得,则的取值范围是______. 【答案】【解析】 由.而,故已知条件等价于:存在整数,使得. ①当时,区间的长度不小于,故必存在满足式①.当时,注意到,.tan cos αα=41cos sin αα+=tan cos αα=2sin cos ,sin cos cos ααααα==22sin cos 1αα+=cos α=2442111cos cos 2sin cos 2αααα⎛-+=+=+= ⎝⎭故只要考虑如下几种情形:(1),此时,,且,无解;(2),此时,;(3),此时,.综上,并注意到也满足条件,知.故答案为:6.【2013年全国联赛】在中,已知,则______.【答案】11【解析】由.7.【2012年全国联赛】设的内角的对边分别为,且满足.则______.【答案】4【解析】解法1 有题设及余弦定理得.故.解法2 如图4,过点,垂足为.则.由题设得.又,联立解得.故.解法3 由射影定理得.又,与上式联立解得.故.8.【2012年全国联赛】满足的所有正整数的和是______.【答案】33.【解析】由正弦函数的凸性,知当时,.故,.因此,满足的正整数的所有值分别为10、11、12,其和为33.9.【2011年全国联赛】若,则的取值范围为______.【答案】【解析】题设不等式等价于.设,所以,所以上的增函数,所以,.故.由,知的取值范围是.故答案为:10.【2010年全国联赛】已知函数的最小值为.则实数的取值范围是________.【答案】【解析】令.于是,原函数化为.由内的最小值为,即.故. ①当,时,式①总成立;当时,;当时,.从而,.11.【2019年全国联赛】在△ABC中,BC=a,CA=b,AB=c.若b是a与c的等比中项,且sinA是sin(B-A)与sinC的等差中项,求cosB的值.【答案】【解析】由题意ac=b2,,整理即sin B=tan A.对ac=b2利用正弦定理并结合三项的等差数列得.即.于是.即..令,则,解得.12.【2012年全国联赛】已知函数,其中,,且.(1)若对任意,都有,求的取值范围.(2)若,且存在,使,求的取值范围.【答案】(1)(2)【解析】(1).令.则.由题设知解得的取值范围为.(2)因为,所以,.故.从而,.由题设知.解得.故的取值范围是.1.【2018年浙江预赛】已知,得,所以_____【答案】【解析】.2.【2018年浙江预赛】在△ABC中,AB+AC=7,且三角形的面积为4,则sin∠A的最小值为________.【答案】【解析】由,又时取等号.3.【2018年浙江预赛】设满足,则x的取值范围为________.【答案】【解析】由.令,,所以.4.【2018年山西预赛】计算的值为________.【答案】【解析】记,则,所以,. 5.【2018年江苏预赛】函数的值域是________.【答案】【解析】,因为,所以.故答案为:6.【2018年贵州预赛】如图,在△ABD中,点C在AD上,,AB=CD=1.则AC=____.【答案】【解析】在△ABD中,(其中AD=x)①在△BCD中,②由①②得,因为x+2>0,∴x3=2.即.故答案为:7.【2018年贵州预赛】若边长为6的正△ABC的三个顶点到平面α的距离分别为1,2,3,则△ABC的重心G到平面α的距离为_______.【答案】【解析】(1)当△ABC的三个顶点在平面α的同侧时,由公式求得重心G到平面α的距离为2.(2)当△ABC的三个顶点中,其中一点与另两点分别在平面α的异侧时,求得重心G到平面α的距离分别为0,.故答案为:8.【2018年贵州预赛】函数的所有零点之和等于________.【答案】60【解析】函数的零点即为方程2(5-x)sinπx在区间[0,10]上的解函数y=2sinπx 的图像与函数的图像在区间[0,10]上的交点的横坐标.因为函数y=2sinπx的图像与函数的图像均关于点(5,0)对称,且在区间[0,10]上共有12个交点(6组对称点).每组对称点的横坐标之和为10,即这12个点横坐标之和为60.所以函数y=2(5-x)sinπ-1(0≤x≤10)的所有零点之和等于60.故答案为:609.【2018年重庆预赛】在△ABC中,,则________.【答案】【解析】因为所以注意到:故.故答案为:10.【2018年陕西预赛】设的内角所对的边分别为,且成等差数列,则【答案】【解析】分析:根据三角形内角和定理及其关系,用∠C表示∠A与∠B;根据成等差,得到,利用正弦定理实现边角转化。
得到关于∠C的等式;由即可得到最后的值。
详解:;所以,同取正弦值,得因为成等差,所以,由正弦定理,边化角,根据倍角公式展开所以,等式两边同时平方得,化简,即而点睛:本题考查了三角函数正弦定理的应用,三角函数求值中各个边角转化和角的形式变化,需要熟练掌握各个式子的相互转化,属于难题。
11.【2018年陕西预赛】设的内角所对的边分别为,且成等差数列,则【答案】【解析】分析:根据三角形内角和定理及其关系,用∠C表示∠A与∠B;根据成等差,得到,利用正弦定理实现边角转化。
