多组分物系的泡点和露点计算
合集下载
2-3泡露点计算
几点说明： （1）内、外循环的安排： 当压力不大时（2MPa以下）， Ki对yi不敏感， 而对温度较为敏感，因此将yi放在内层循环。 （2）圆整yi：
old
yi
new
yi old y i
（3）判断收敛的准则或者是温度的调节方案直接
关系到收敛速度和稳定性。
二、泡点压力的计算
组分 xDi 甲烷(1) 0.0132 乙烯(2) 0.8108 乙烷(3) 0.1721 丙烯(3) 0.0039
试计算塔顶产品的饱和温度（泡点温度）。
① 假设T=-18℃，查P-T-K图得： K1=5.06，K2=1.06，K3=0.72，K4=0.20 则：S y
y K x
i i i 1
VmL,i p pis i pisis K i V exp i p RT
活度法计算平衡常数公式
圆整yi，计算iV
Y
yi有无变化
N N
Y
( n) y i 1
Ln yi
Y
输出T，y
y
( n) i
结束
y
y
( n 1) i ( n 1) i
Bi K i xi (t C ) 2 k i ，则认为迭代结束。
K x
i
i
1
[例题2-2]
某厂氯化法合成甘油车间，氯丙烯精馏二塔的釜液组成为： 3- 氯丙烯 0.0145， 1,2-二 氯丙烷 0.3090，1,3-二氯丙烯 0.6765（摩尔分数）。塔釜压力为常压，试求塔釜温度。各组 分的饱和蒸汽压关系为：（ P s ： kPa ； t ： ℃）： (1) 3- 氯丙烯
Ki Ki
Ki ij K j
四 多组分物系的泡点和露点计算
二阶导数 T k1 T k
2
2 f (T k ) f (T k )
f (T k ) f (T k )
T k1 T k 0.0001
收敛快！
Chongqing university of technology
❖ 对与汽相满足理想气体，液相满足理想溶液的体系，
❖ 其平衡常数可以表示为：
迭代3次！ 已达到牛顿法 t5的精度，故t3为所求。
Chongqing university of technology
(2) Ki与组成有关
对于非理想性较强的物系：
Ki = f (T, P, xi , yi )
Ki
i Pisis
ˆ Vi P
expiL
(P R
T
Pi
s
)
例1
计算机计算——按牛顿迭代求解
❖ 牛顿迭代计算结果为：
迭代5次！ 达到迭代精度要求，故泡点温度为99.812℃。
Chongqing university of technology
例1
计算机计算——按牛顿迭代求解
❖ 若用Richmond算法，还需求二阶导数
f ''(t)
Ki
xi
{
2.303Bi
当P不太高时，P的影响不太大，收敛较快。
i ——T, P，xi 一般受压力的影响较小
Chongqing university of technology
泡点温度计算框图
因为
v i
f (T , P, yi ) ，
其中
开始
Ki
i
Pi
泡点和露点计算
正丁烷 （1）
2.1
0.315
正戊烷 （2） 0.71
0.284
正己烷 （3） 0.25
0.1125
∑ 0.7115
传质分离过程
设温度为60℃，查P-T-K 图得K，将K值列于下表
组分 正丁烷 正戊烷 正己烷
∑
Ki
2.8
0.93
0.36
Kixi
0.42
0.372 0.162 0.954
yi
0.42
Ki f T, P, xi , yi
计算步骤：
L i
Pi S
iS
ˆ Vi P
exp ViL
P PiS RT
已知p,假设T 求出（或查出）各组分的相应参数
由已知的 x按i 理想状态求出Ki，初步算出 yi
求出 Ki，由已知的xi yi Ki xi
Ki xi 1 (通常取为0.005) 泡点T
如果 Ki xi 1 ; 升高T,重新计算。 Ki xi 1 ; 降低T,重新计算。
传质分离过程
开始 Y
输入P、y及有关参数
设T并令 1 作第一次迭代
计算PiS ,ViL ,iS ,ˆiV
调整T
计算 K i和xi 计算 xi
是否第一次迭代
圆整 xi
计算 i
Y
N
xi有无变化
N
xi 1 N
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义：泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法：根据相律 f=c-π+2=c。
类型 泡点温度
泡点压力 露点温度 露点压力
规定变量
P, x1 , x2 L L xc
泡点和露点计算课件
1. Ki与组成无关：if Ki f(T,P)
泡点方程：
C
fTKixi 10
i1
计算过程：
已知p 设T
计算或查图 得Ki
计算
C
f (T ) Ki xi 1 i 1
调整T
f (T )
是
结束 输出T，y
否
例题2-3
• 例2-3
• 三种组分含量 相差不大，取 分子量居中的 正戊烷在该压 力下的沸点为 初值
？定义哪些变量
称为设计变量
一、气液平衡系统设计 变量
多组分泡点、露点 计算的类型
二、泡露点计算重点、难点
相平衡常数Ki
• 与系统T、p有关
• 对非理想体系，还与气液相组成x,y
有关
• 计算的重点、难点：Ki的计算
(1)列线图 法求K值
p12
部分轻烃 忽略组成变化 对K值的影响
T升高，K如何变化？ P增加，K如何变化？
计算中，如何适当的调整试差的温度（或压力）？
本节内容
• 气液平衡系统的设计变量 • 泡露点计算的重点、难点 • 泡点温度计算 • 露点温度计算
2.2 多组分物系的泡点和露点计算 Bubble-point and Dew-point Calculation for Multicomponent Systems
Kx yii iˆpV iis pisexV piL(R pT pis)
（2）活度系数、逸度系数法计算K值
Liquid
Gas
Ideal solution Real solution
Ideal gas
Ki
Pi s P
Ki
i Pi s
P
Ideal solution Real gas
泡露点计算
γ 的计算 wilson方程
T T
x1 x1
x2 x2
g12-g11 x3
g21-g22 V1
V1 V2
V2 V3
VanLaar方程 若A12、A21已知 A12 若A12、A21未知 x1 p2-s
A21
x1
x2
lnγ1 γ1 lnγ2 #DIV/0! #DIV/0! #DIV/0! p γ1 #D^Φ2 #DIV/0!
^Φ1 #DIV/0!
x3 p3-s φ3s γ3 φ3v y3 y3 φ 3v y3
Σy #DIV/0! #DIV/0! Σy #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
迭代φ v，直到前后两次Σ y的值相等。必须用选择性粘贴！
已知汽液平衡数据 x2 y2 p p1-s 1 1 γ1 γ2 A12 A21 #DIV/0! #DIV/0! #DIV/0! #DIV/0! y1
已知恒沸点数据
Margules方程 若A12、A21已知 A12
A21
x1
x2
lnγ1 0
γ1 1
lnγ2 0
φv计算：（低压时为1） 如果不知道Bij值：
lnγ2 γ2 #DIV/0! #DIV/0! g23-g22 g32-g33 Λ23 Λ32 γ1 γ2 γ3 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! Λ23 Λ32 γ1 γ2 γ3 #NUM! #NUM! #NUM!
γ2 #DIV/0! 已知恒沸点数据 p1-s p2-s γ2 A12 A21 #DIV/0! #DIV/0! #DIV/0!
^Φ2 #DIV/0!
B(1) #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! δ23 #DIV/0! ln^Φ2 #DIV/0!
化工分离过程第二章
(2) 逸度与组成的关系 气相逸度与气相组成yi的关系为：
fˆiV
fi0V
V i
yi
Pi0V
V i
yi
PˆiV yi
式中：fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下，纯组分i的气相逸度系数 φiV 在系统温度和压力下，组分i的气相分逸度系数且
ˆiL
i0L
L i
平衡时，汽液两相逸度相等，通过平衡常数Ki的定义式可求 出相平衡常数。
10
1. 汽液平衡关系（Vapor-liquid phase equilibrium）
fˆiV fˆi L
(2-4)
引入逸度系数 ：
ˆ i
，汽相中组分i的逸度系数 ˆ Vi 定义为
ˆ iV fˆiV / yiP
ZM
PVt RT
RT (Vt b
a Vt2
)Vt
RT
Vt Vt
b
a RTVt
2
④计算汽相逸度系数
将（2—15）积分后代入以上结果：
ln
) i
bi Vt b
ln[ZM
(1
b Vt
)]
2 aai RTVt
3
25
⑤用xi代替yi，按照②～④步骤求各组分的液相逸度 系数
⑥由式（2-14）求Ki值。
fi L
Pi S iS
exp[ViL (P PiS )] RT
（2-21）
33
由式（2—21）可知，纯液体i在T、P下的逸度等于饱和 蒸汽压乘以两个校正系数。
S i
为校正处于饱和蒸汽压下的蒸汽对理想气体的偏离，
而指数校正项也称普瓦廷（Poynting）因子，是校正压
2.2 多组分物系的泡点和露点计算2007.9.10
解：
常压
气相—— 气相 为理想气体 液相—— 液相 为理想溶液
•参考解法： 参考解法： 参考解法
Pi Ki = P
s
（1）试差法（手算） 试差法（手算） （2）相对挥发度法 （3）计算机求解
结构相似
例2-4
（1）试差法-计算（见下表） 试差法-计算（见下表）
塔釜温度应为100℃。 ℃ 塔釜温度应为
ˆ υiL ( P − Pi s ) Φ iL γ i Pi Φ Ki = exp = ˆV V ˆ RT Φi P Φi
s s i
1、泡点温度计算 、
严格计算法 ——计算过程 计算过程
xi , P → yi , T
Ki
s i
Pi Φ υ
s
s i
——T, P
(一般受 的影响较小 一般受P的影响较小 一般受 的影响较小)
Ki = f (P, T, xi, yi)
2.2.1 泡点温度和泡点压力计算
总变量：C-xi，C-yi，C-Ki，T，P。共3C+2 总变量： 个 已知C个变量：（ 已知C个变量：（C-1）个组分和T或P ：（C 个组分和T 未知变量为2C+2个 未知变量为2C+2个 由上述2C+2个方程求解 唯一解） 由上述2C+2个方程求解（唯一解） 个方程求解（ 需试差计算
2.2 多组分物系的泡点和露点计算
泡点计算： 泡点计算： 泡点温度计算：已知x 泡点温度计算：已知xi，p，求解T，yi 温度计算 求解T 泡点压力计算：已知x 泡点压力计算：已知xi，T，求解P，yi 压力计算 求解P 露点计算： 露点计算： 露点温度计算：已知y 露点温度计算：已知yi，P， 求解T，xi 温度计算 求解T 露点压力计算：已知y 露点压力计算：已知yi，T， 求解P，xi 压力计算 求解P
分离工程04多组分单级分离计算
Ci -34.42 -39.94 -48.78
解法1：用试差法计算
Ki
Pi0 P
Kixi 1
T（设） 50 ℃ 60 ℃ 55 ℃ 57.5℃
Kixi 0.799 1.062 0.924 0.991
∴ T=57.5℃
解法2：电算〔Newtow迭代法〕
t ( K 1)
t (K )
F (t K F (t K
当迭代到达收敛时，应满足以下方程：
f iV f iL
C
在该模型中i 1规y定i 的 收1 敛精度要求为：
(f iV / f iL ) 1 10 3
C
yi 1 10 5
i 1
或收：敛精度T 可k 根T据k1计算1精02度要〔求k为予迭以代选次择数。〕 在进展较复杂的迭代计算时，通常将一些需要反复 执行的运算内容变成子程序，以便主程序随时调用，应 用SHBWR模型计算泡点(或露点)时需编制以下子程序：
4-2-1、理想物系泡点及泡点压力的计算 1). 用图解法计算泡点温度
理想物系其组成对K的影响较小，因而在简 化计算中可将K近似视为T和P的函数，即K=f(T， P)。该式的函数关系通常用诺谟图 (简称T-P-K 图 ) 表示。
应用简化K进展泡点计算时，可采用以下形 式的泡点方程
C
当指定Pi、1 Kxi求i x i解T1、yi时，因Ki=f(T,P)，(4上-3式) 需
T0
Kixi 1
i1
C i1
[(CxiiKiTB)i 2
]
T0
yi 1
i 1
C
yiBi
i1 (C i T ) 2
T0
C i 1
xi
p
0 i
泡点和露点计算-PPT
1. Ki与组成无关：if Ki f(T,P)
泡点方程：
C
fT Kixi 10
i1
计算过程：
已知p 设T
计算或查图 得Ki
计算
C
f (T ) Ki xi 1 i 1
调整T
f (T )
是
结束 输出T，y
否
12
例题2-3
• 例2-3 • 三种组分含量
相差不大，取 分子量居中的 正戊烷在该压 力下的沸点为 初值 • 从p-T-K图上 查得T0=62’C
当汽相为理想气体，液相为非理想溶液时：
c
pb i pis xi i1
当Ki=f(T,p,x,y)时，用活度系数法（压力不太高）或 状态方程法（压力较高）计算泡点压力。
28
开始
输入T，x及有关参数 估计p,并令iV＝1，作第一次迭代
计算pis、ViL、is、i
调整p
N
计算Ki和yi
计算 yi
是否第一次迭代
RCoalucnudlateyiˆ Vi
Whether first Y iteration or not
N
yi Change Y
or not N
n yi
Output p, y
活 度 系 数 法 计 算 泡 点 压 力 的 框 图
End
29
输入T, x及有关参数， p和y估计值
求iV和iL
计算Ki
N
Ln yi
Y
输出T，y
圆整yi，计算iV
Y
Y
结束
Adjust T
Start Input p, x
Set T and ˆ Vi 1 as first iteration
精馏
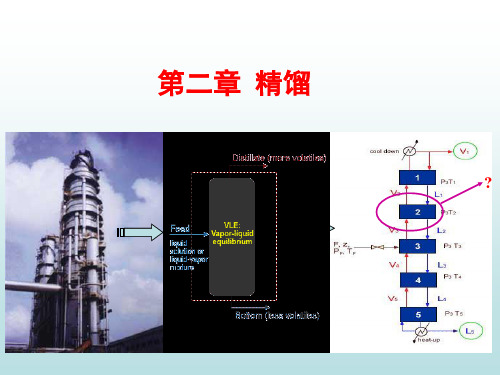
三、活度系数法计算汽液平衡常数的简化形式：
（1）汽相为理想气体，液相为理想溶液：
1 1 1
viL ( P Pi s ) yi i Pi sis Ki V exp ˆ P xi RT i
1
化简得：
Pi s Ki P
（2）汽相为理想气体，液相为非理想溶液
？求取基准态逸度、液相活度系数和汽相逸度系数。
1、基准态逸度 fiOL：
活度系数等于1的状态
（1）可凝组分基准态逸度：
基准态：xi 1时，i 1。
ˆ 代入 f i L i xi f i OL
fiOL ——在系统T、P下液相中纯组分i的逸度。 即基准态是与系统具有相同T、P和同一相态的纯i组分。
1、需用其他的方法获得液体的 偏摩尔体积（在计算高压汽液 平衡时需要此数据）； 2、对含有超临界组分的系统应 用不够方便，必须引入亨利定 律； 3、难以在临界区内应用。
2.2 多组分物系的泡点和露点计算
2.2.1 泡点温度和压力的计算 2.2.2 露点温度和压力的计算
2.2.1 泡点温度和压力的计算
方法 状态 方程法 优点
1、不需要基准态； 2、只需要P-V-T数据，原则 上不需有相平衡数据； 3、可以应用对比状态理论； 4、可以用在临界区 。
缺点
1、没有一个状态方程能完全适 用于所有的密度范围； 2、受混合规则的影响很大； 3、对于极性物质、大分子化合 物和电解质系统很难应用。
活度 系数法
1、简单的液体混合物的模型 已能满足要求； 2、温度的影响主要表现在fiL 上而不在i上； 3、对许多类型的混合物，包 括聚合物、电解质系统都能 应用。
汽液相平衡关系： 汽相：
ˆ ˆ f iV f i L
《分离工程》复习摘要解析
分析精馏塔内的温度、流率和浓度分布。
一、关键组分（Key Components） 二、多组分精馏特性
19
一、关键组分（Key Components）
Na=串级数(2)＋分配器(1) ＋侧线采出(0)＋传热单元 (2)
（不论有多少个组分）
F
已被指定的可调变量： （1）进料位置 feed stage location ； （2）回流比 reflux ratio ； （3）全凝器饱和液体回流或冷凝器的传热面积或馏 出液温度。heat transfer area of the condenser or condensate temperature( i.e., saturated liquid) (4)余下的2个可调设 计变量一般用来指定 某个组分在馏出液和 另一个组分在釜液中 的浓度。
c
（4）判断 f T （一般为0.01 ）否； （4）若 f T ，输出T，yi 结束； （5）若 f T 不成立，令K
k 1 i
y k 1 k 1 K ~ （5） i K ，由K i 得T 重复（2） i i 1
k i
注意：同一组分，规定 了一端的回收率，另一 端的量已确定。不能重 复！
3. 关键组分的指定原则 由工艺要求决定 例：ABCD（按挥发度依次减少排列）混合物 分离 ◆工艺要求按AB与CD分开： 则：B为LK；C为HK ◆工艺要求先分出A： 则：A为LK；B为HK
二、多组分精馏特性
二元精馏 vs 多元精馏 计算方法上：
分离媒介分为能量媒介（ ESA ）和物质媒 介（MSA）。 速率分离过程 —— 借助某种推动力 ( 如浓度 差、压力差、温度差、电位差等 ) 的作用，某些 情况下在选择性透过膜的配合下，利用各组分扩 散速度的差异而实现混合物的分离操作。
一、关键组分（Key Components） 二、多组分精馏特性
19
一、关键组分（Key Components）
Na=串级数(2)＋分配器(1) ＋侧线采出(0)＋传热单元 (2)
（不论有多少个组分）
F
已被指定的可调变量： （1）进料位置 feed stage location ； （2）回流比 reflux ratio ； （3）全凝器饱和液体回流或冷凝器的传热面积或馏 出液温度。heat transfer area of the condenser or condensate temperature( i.e., saturated liquid) (4)余下的2个可调设 计变量一般用来指定 某个组分在馏出液和 另一个组分在釜液中 的浓度。
c
（4）判断 f T （一般为0.01 ）否； （4）若 f T ，输出T，yi 结束； （5）若 f T 不成立，令K
k 1 i
y k 1 k 1 K ~ （5） i K ，由K i 得T 重复（2） i i 1
k i
注意：同一组分，规定 了一端的回收率，另一 端的量已确定。不能重 复！
3. 关键组分的指定原则 由工艺要求决定 例：ABCD（按挥发度依次减少排列）混合物 分离 ◆工艺要求按AB与CD分开： 则：B为LK；C为HK ◆工艺要求先分出A： 则：A为LK；B为HK
二、多组分精馏特性
二元精馏 vs 多元精馏 计算方法上：
分离媒介分为能量媒介（ ESA ）和物质媒 介（MSA）。 速率分离过程 —— 借助某种推动力 ( 如浓度 差、压力差、温度差、电位差等 ) 的作用，某些 情况下在选择性透过膜的配合下，利用各组分扩 散速度的差异而实现混合物的分离操作。
第二章 2.2泡点和露点计算概要
• 取正己烷纯物质的沸点为初始温度 • 查p-T-K图，可得T0=86’C
练习2
• 求含乙烷(1)0.1、丙烯(2)0.35、丙烷(3)0.4、 异丁烷(4)0.15（摩尔百分比）的烃类混合 物在400kPa时的泡点温度
五、泡点、露点压力计算
• 与泡点、露点温度计算类似，只是矫正的 是压力 • 注意：用p-T-K图计算时，如果p增加，Ki值 减少，因此在试差计算过程中要注意p的调 整方向
Output p, y
输出p，y
结束
活 度 系 数 法 计 算 泡 点 压 力 的 框 图
End
输入T, x及有关参数， p和y估计值
输出 p 和 y
Y
求iV和iL
调整p
N
Kixi=1
N
计算Ki
归一化yi
Y
Y
Kixi是否变化
计算 Kixi
第一次迭代
N
状 态 方 程 法 计 算 泡 点 压 力 的 框 图
f (T ) yi / K i 1
i 1
C
f (T )
是
结束 输出T，x
调整T
否
参见例［2－6］
（二）露点压力计算
• 类似泡点压力计算，仅泡点压力方程不同
本章总结
• 泡点方程 • 泡点温度计算过程
已知p 设T 计算或查图 得Ki 计算
f (T ) K i xi 1
i 1
C
f (T )
是
结束 输出T，y
调整T
否
• 露点方程 • 露点温度计算
已知p 设T 计算或查图 得Ki 计算
Round yi ˆV Calculate i
计算 yi
练习2
• 求含乙烷(1)0.1、丙烯(2)0.35、丙烷(3)0.4、 异丁烷(4)0.15（摩尔百分比）的烃类混合 物在400kPa时的泡点温度
五、泡点、露点压力计算
• 与泡点、露点温度计算类似，只是矫正的 是压力 • 注意：用p-T-K图计算时，如果p增加，Ki值 减少，因此在试差计算过程中要注意p的调 整方向
Output p, y
输出p，y
结束
活 度 系 数 法 计 算 泡 点 压 力 的 框 图
End
输入T, x及有关参数， p和y估计值
输出 p 和 y
Y
求iV和iL
调整p
N
Kixi=1
N
计算Ki
归一化yi
Y
Y
Kixi是否变化
计算 Kixi
第一次迭代
N
状 态 方 程 法 计 算 泡 点 压 力 的 框 图
f (T ) yi / K i 1
i 1
C
f (T )
是
结束 输出T，x
调整T
否
参见例［2－6］
（二）露点压力计算
• 类似泡点压力计算，仅泡点压力方程不同
本章总结
• 泡点方程 • 泡点温度计算过程
已知p 设T 计算或查图 得Ki 计算
f (T ) K i xi 1
i 1
C
f (T )
是
结束 输出T，y
调整T
否
• 露点方程 • 露点温度计算
已知p 设T 计算或查图 得Ki 计算
Round yi ˆV Calculate i
计算 yi
[工学]22多组分物系的泡点和露点计算
![[工学]22多组分物系的泡点和露点计算](https://img.taocdn.com/s3/m/e61653e9710abb68a98271fe910ef12d2af9a97b.png)
2.ln Pi、S = Ai − Bi (t + Ci )
3. 常压操作
解法1：用相平衡常数法计算
Ki
=
PiS P
∑ Ki xi = 1
T（设） 70 ℃ 110 ℃ 98 ℃
100℃
∑ K i xi 0.379 1.344 0.9513 1.00
∴ T=100℃
解法2：用相对挥发度法计算（适用于完全理想系）
8
泡露点计算是分离过程设计中最基 本的汽液平衡计算。例如在精馏过程的 严格计算中 ,为确定各塔板的温度，要 多次反复进行泡点温度的运算。为了确 定适宜的精馏塔操作压力，就要进行泡 露点压力的计算。在给定温度下作闪蒸 计算时，也是从泡露点温度计算开始， 以估计闪蒸过程是否可行。
9
泡露点计算
分离过程设计中最基本的气液平衡计算。 例如：
泡点压力计算
若系统包含C个组分，则未知变量数为C+1个，需 要寻找C+1个独立关系式。
（1）相平衡关系：
C个
yi = Ki xi i = 1,2,..., C
（2）摩尔分率加和方程：
1个
∑ yi = 1
C＋1
i
泡点方程
∑ 即
Ki xi −1 = 0 Bubble point equation
i
关键在于求Ki
= T设 = Ki
xi
→
结束
NO
缺点是收敛速度较慢
计算中：若 ∑ K i xi > 1, 说明T偏高； 若∑ K i xi < 1, 说明T偏低。
相平衡常数法－低压下理想混合物
该情形下：
Ki
=
pi s P
相平衡关系式：
yi
3. 常压操作
解法1：用相平衡常数法计算
Ki
=
PiS P
∑ Ki xi = 1
T（设） 70 ℃ 110 ℃ 98 ℃
100℃
∑ K i xi 0.379 1.344 0.9513 1.00
∴ T=100℃
解法2：用相对挥发度法计算（适用于完全理想系）
8
泡露点计算是分离过程设计中最基 本的汽液平衡计算。例如在精馏过程的 严格计算中 ,为确定各塔板的温度，要 多次反复进行泡点温度的运算。为了确 定适宜的精馏塔操作压力，就要进行泡 露点压力的计算。在给定温度下作闪蒸 计算时，也是从泡露点温度计算开始， 以估计闪蒸过程是否可行。
9
泡露点计算
分离过程设计中最基本的气液平衡计算。 例如：
泡点压力计算
若系统包含C个组分，则未知变量数为C+1个，需 要寻找C+1个独立关系式。
（1）相平衡关系：
C个
yi = Ki xi i = 1,2,..., C
（2）摩尔分率加和方程：
1个
∑ yi = 1
C＋1
i
泡点方程
∑ 即
Ki xi −1 = 0 Bubble point equation
i
关键在于求Ki
= T设 = Ki
xi
→
结束
NO
缺点是收敛速度较慢
计算中：若 ∑ K i xi > 1, 说明T偏高； 若∑ K i xi < 1, 说明T偏低。
相平衡常数法－低压下理想混合物
该情形下：
Ki
=
pi s P
相平衡关系式：
yi
多组分物系的泡点和露点计算
lg P1s
6.05543 1115.5 t 231
lg
P2s
6.09036 1296.4 t 221
lg P3s
6.98530
1879.8 t 273.2
例2-4
已知：3-氯丙烯x1=0.0145, 1,2-二氯丙烷x2=0.3090, 1,3二氯丙烯x3=0.6765，P—常压。求：Tb, yi（i=1,2,3）
ik xi ik xi
ik xi
yi
i=1,2,…k…c
ik xi
N
?
yi 1
Y
Tb
Pks
Pks f (T ) Pks Kk P
Kk
1
K k ik xi
1、泡点温度计算
（2）严格计算法（计算机计算）
对于非理想性较强的物系：
Ki = f (T, P, xi , yi )
1、泡点温度计算
计算方法
1. 简化计算（手算）（Ki与组成无关) (1) 试差法 (2) 相对挥发度法
2. 严格计算法（计算机计算） （Ki与组成有关) Ki = f (T, P, xi, yi )
1、泡点温度计算
(1)简化计算
已知 xi, p
气相—理想气体或理想溶液
Ki与组成无关 Ki = f (T, P)
—wilson(T,P,xｉ)
G （ 1／ T） 线 性 ,P<20ａ ｔｍ，用牛顿－拉普森 （Neuton-Raphson）迭代
法（线性）切线法。
第一次迭代时
v i
1
调整T
计算Ki和yi 计算Σ yi
圆整ｙｉ
计算
2.2多组分物系的泡点和露点计算
2.2 多组分物系的泡点和露点计算
2.2.1 泡点温度和压力的计算 2.2.2 露点温度和压力的计算
2.2.1 泡点温度和压力的计算
规定液相组成 x 和压力p（或温度T），计算汽相组成 y 和温度T（或压力p）。
已知： x 、p 计算： y 、T
泡点温度计算
已知： x 、T 计算： y 、p
泡点压力计算
K i = Pis/ P
（3）温度T的调整
T设高了，降低T。 T设低了，提高T。 T的调整幅度可采用牛顿－拉普森法：
参见例［2－3］，例［2－4］
2. Ki与组成有关：
由状态方程法或活度系数法求取Ki：
活 度 系 数 法 计 算
泡 点 温 调整T 度 的 框 图
开始
输入p，x及有关参数 设T并令iV＝1，作第一次迭代
计
算
计算Ki和yi
泡
调整p
点
计算 yi
圆整yi，计算iV
压
是否第一次迭代
Y
N
yi有无变化
Y
N
力 的 框 图
N
Ln yi
Y
输出p，y
结束
输入T, x及有关参数， p和y估计值
求iV和iL
N
调整p
状
态
输出p和y
方 程
Y
法
Kixi=1
计 算
泡
计算Ki
计算 Kixi
N
点
归一化yi Y Kixi是否
计算pis、ViL、is、i
计算Ki和yi
计算yi
是否第一次迭代
N
yi有无变化
N
圆整yi，计算iV
Y
Y
N
2.2.1 泡点温度和压力的计算 2.2.2 露点温度和压力的计算
2.2.1 泡点温度和压力的计算
规定液相组成 x 和压力p（或温度T），计算汽相组成 y 和温度T（或压力p）。
已知： x 、p 计算： y 、T
泡点温度计算
已知： x 、T 计算： y 、p
泡点压力计算
K i = Pis/ P
（3）温度T的调整
T设高了，降低T。 T设低了，提高T。 T的调整幅度可采用牛顿－拉普森法：
参见例［2－3］，例［2－4］
2. Ki与组成有关：
由状态方程法或活度系数法求取Ki：
活 度 系 数 法 计 算
泡 点 温 调整T 度 的 框 图
开始
输入p，x及有关参数 设T并令iV＝1，作第一次迭代
计
算
计算Ki和yi
泡
调整p
点
计算 yi
圆整yi，计算iV
压
是否第一次迭代
Y
N
yi有无变化
Y
N
力 的 框 图
N
Ln yi
Y
输出p，y
结束
输入T, x及有关参数， p和y估计值
求iV和iL
N
调整p
状
态
输出p和y
方 程
Y
法
Kixi=1
计 算
泡
计算Ki
计算 Kixi
N
点
归一化yi Y Kixi是否
计算pis、ViL、is、i
计算Ki和yi
计算yi
是否第一次迭代
N
yi有无变化
N
圆整yi，计算iV
Y
Y
N
第二章-3 泡露点计算
• 两相区 ：物系处于泡点露点之间
(1)泡点、露点计算的目的
• 确定气体和液体的饱和条件，及判别平衡位置
(2) 计算类别 • 已知Pv 求 Tv ---求泡、露点温度 • 已知Tv 求Pv ---求泡、露点压力 一类：已知液相组成 xi（或气相组成yi ）和系 统的平衡压力P，求泡点温度T（或露点温度） 和平衡的气相组成yi（液相组成xi ）。 另一类：已知液相组成 xi（或气相组成yi ）和 系统的平衡温度T，求泡点压力P（或露点压力） 和平衡的气相组成yi（液相组成xi ）
泡点方程泡点判别式露点方程露点判别式物系处于露点之上过热蒸汽物系处于泡点之下过冷液体判别是否存在两相区框图小结泡点计算若已知操作压力p液相组成x用试差法求泡点温度的步骤如下
2.5 泡点、露点计算 • • • • 泡点： 形成第一个气泡的温度和压力 露点： 形成第一个液滴的温度和压力: 物系处于露点以上，所有Ki＞1
ri p ki = p
s i
2.6 绝热闪蒸计算 Q=0, 求ϕ ， T 基本闪蒸方程既是ϕ的函数 ，又是 T的函数， 必须建立另外迭代方程 一般做法是：由基本闪蒸方程迭代ϕ，由热平 衡方程迭代T
求解思路： 对宽沸程物系，先假设T，迭代ϕ，再迭代T 对窄沸程物系，先假设ϕ ，迭代T，再迭代ϕ 对ϕ和T均敏感的物系，采用联立方程求解
i i i i
=0
∑z k
i
i
=1
露点时： ϕ=1
z i (1 − k ) z i (1 − k i ) zi zi ∑ 1 + ϕ (k − 1) = ∑ k = ∑ ( k − z i ) = ∑ k − 1 = 0 i i i i
∑
zi = 1 ki
∑z k
4-2020泡点和露点
A T-P-K列线图—适用于烃类体系(p40-41)
B
ki
Pi o P
1 P exp( Ai
Bi ) Ci T
适用于体系为理想气体和 理想溶液的系统
Ai , Bi , Ci
f (物性，T )
可在物性手册中查 取
安托因方程：
log P0 = A - B / T +C
手算方法：
注意：
ε一般取10-3即可 第一次试差温度可取混合物中含量最多的那个组分 在系统压力下的沸点温度左右为第一个试差温度，
比较不变 No
P47，图2-6
露点温度和压力的计算（对汽相而言）：
C
f (T ) xi 1.0 i1
计算机计算泡点和露点：
平衡常数可表示为温度T的函数时，Newton-Raphson,Richmond迭代法 P49 例2-7
3) 四元溶液：三个塔，五种方案 当挥发度：A>B>C>D
A,B,C,D
A B
B,C,D C,D
(Ⅰ)
A,B,C,D
A
B
B,C
C
B,C,D
C
D D
(Ⅱ)
• 总结：若 C---组分数，n---所需塔数 z---可供选择的流程方案数
则有：
C2
3
4
5
6
7
8
n
1
2
3
4
5
6
7
Z
1
2
5
14 42 132 429
(2C+2) ,Xc,,Ki ,Xc,,Ki ,Xc,,Ki ,Xc, ,Ki
泡点温度和压力的计算（对液相而言）：
Ki
泡点.露点计算简便法举例
1、一液体混合物的组成为：苯0.50；甲苯0.25；对二甲苯0.25(摩尔分率)。
分别用平衡常数法和相对挥发度法计算该物系在100kPa 时的平衡温度和汽相组成。
假设为完全理想系。
解1：(1)平衡常数法： 设T=368K 用安托尼公式得：kPa P s 24.1561= ；k P a P s28.632= ；k P a P s 88.263=由式(2-36)得：562.11=K ；633.02=K ；269.03=K 781.01=y ；158.02=y ；067.03=y；006.1=∑i y 由于∑i y >1.001，表明所设温度偏高。
由题意知液相中含量最大的是苯，由式(2-62)得：可得K T 78.367'=重复上述步骤：553.1'1=K ；6284.0'2=K ；2667.0'3=K 7765.0'1=y ；1511.0'2=y ；066675.0'3=y ；0003.1=∑i y所以在温度为367.78K 时，存在与之平衡的汽相， 组成为：苯0.7765、甲苯0.1511、对二甲苯0.066675。
2、含有80%(mol)醋酸乙酯(A)和20%乙醇(E)的二元物系，液相活度系数用V an Laar 方程计算，AE A =0.144，EA A =0.170。
试计算在101.3kPa压力下的泡点温度和露点温度。
安托尼方程为： 醋酸乙酯：()15.5750.27900444.21ln --=T P SA乙醇：()68.4198.38038047.23ln --=T P SE (PS ：Pa ；T ：K)解2：(1)计算活度系数：0075.0)2.017.08.0144.01(144.0}1(ln 22=⨯⨯+=+=EEA A AE AE A x A x A A rA r =1.0075 10137.0}8.0144.02.017.01(17.0}1(ln 22=⨯⨯+=+=AAE E EA EA E x A x A A rE r =1.107(2)计算泡点温度 设T=353.15K(80℃)617.1115.5715.35350.27900444.21ln =--=s A P∴Pa P s A 5101097.1⨯=5917.1168.4115.35398.38088047.23ln =--=s E P∴Pa P s E 510082.1⨯=∴1037.110013.1101097.10075.155=⨯⨯⨯==P P r K S A A A1821.110013.110082.1107.155=⨯⨯⨯==P P r K S E E E∴1194.12.01821.18.01037.1=⨯+⨯=∑i i x K调整98597.01194.11037.12==A K)15.575.27900444.21exp(0075.110013.198597.0522--=⨯⨯==T r P K P A A SA解得T2=349.65，即T2=76.50℃∴s A P ln =11.504 Pa P sA 41091.9⨯=s E P ln =11.453Pa P s E 4104175.9⨯=∴A K =0.9857E K =1.028819943.02.00288.18.09857.0≈=⨯+⨯=∑ii xK故泡点温度为76.5℃ (3)计算露点温度 设T=353.15K(80℃) 由k 'c =k c ⨯i i /k y ∑∴9867.0894.01037.12=⨯=A K)15.575.27900444.21exp(0075.110013.19867.0522--=⨯⨯==T r P K P A A SA解得T2=349.67K(76.52℃)∴sA P ln =11.505Pa P s A 41092.9⨯=s E P ln =11.454Pa P s E 410425.9⨯=9866.0013.1992.00075.1=⨯=A K 03.1013.19425.0107.1=⨯=E K1005.103.12.09866.08.0≈=+=∑ix故露点温度为76.52℃3、某汽相混合物的组成及平衡常数如下：求P=1atm 时，混合物的露点温度，误差判据可取0.001。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.2.1 泡点温度和泡点压力计算
已知 xi (i=1,2,…c),P 或 T
yi ,T或P
计算方程有：
①相平衡关系
yi = Ki xi (i=1,2, …c)
C个 1个
y
②浓度和式
c
x
i 1
i 1 c
i
1 1
2C+2个
1个 C个
i
③汽液平衡常数关系式
Ki = f (P, T, xi, yi)
yi ik K k xi
1、泡点温度计算
—相对挥发度法
c c i 1 i 1
•公式推导： yi ik K k xi 1
yi ik K k xi
ik xi
K k ik xi 1
i 1
c
Kk
1
i 1
c
yi
ik
xi
i 1
c
ik
L s L ˆ i Pi i ( P Pi ) i Ki exp V V ˆiP ˆi RT s s i
1、泡点温度计算
严格计算法 ——计算过程
xi , P yi , T
Ki
s i
Pi
sቤተ መጻሕፍቲ ባይዱ
s i
——T, P
(一般受P的影响较小)
一阶导数
T k 1
k f ( T ) k T f (T k )
k 1 Tk 二阶导数 T
2 2 f (T k ) f (T k ) k f (T ) f (T k )
T k 1 T k
0.001
收敛快！
泡点温度计算框图（P50图2-5）
开 始
v 因为 i f (T , P, yi ) ， 其中
Ki
ˆV i
——T, P，yi
计算 ˆ V 或 yi时 需迭代（因T未知）。
i
当P不太高时，P的影响不太大，收敛较快。 一般受压力的影响较小
i
——T, P，xi
1、泡点温度计算
严格计算法 ——计算方法
•牛顿迭代法：
f (T ) K i xi 1
i 1
c
T——初值可由相对挥发度求得 ,也 可取某组分i的沸点为初值。
i→Ki
K x
i 1
c
i i
f (T )
Y
设 yi
T， yi
1、泡点温度计算
2）相对挥发度法
方法依据：相对挥发度随温度变化比Ki小得多，在一定温 度范围内可视为常数.
•相对挥发度定义：
Ki ik Kk
•计算式推导：
k—i组分中任选的一个基准组分
K i ik K k
后计算 iv f (T , P, yi )
当T,P一定时，
i -yｉ成对应。
v
外循环： 迭代计算泡点温度Tb
内循环：
在一定温度下，试差计算逸度系数 ，迭代计算ｙｉ
结 束
例2-3
例2-4 确定含正丁烷（1）1.15、正戊烷（2）0.4和正 己烷（ 3 ） 0.45 （均为摩尔分率 ）之烃类混合物 在 0.2MPa压力下的泡点温度。
(1)简化计算
已知 xi, p Ki与组成无关 Ki = f (T, P) P已知，Ki=f(T)
c
气相—理想气体或理想溶液 —常压或中压下烃类混合物
液相—理想溶液
—各组分分子结构相似
f (T ) Ki xi 1
i 1
1、泡点温度计算
1）试差法
N
已知 xi, P
设T
P-T-K图
K i Ki=f (T，P，xi，yi )
2.2.1 泡点温度和泡点压力计算
总变量：C-xi，C-yi，C-Ki，T，P。共3C+2 个 已知C个变量：（C-1）个组分和T或P 未知变量为2C+2个 由上述2C+2个方程求解（唯一解）
需试差计算
2.2.1 泡点温度和泡点压力计算
1、泡点温度计算
泡点方程：
K x
i 1 i
yi
未知，
Ki
i Pi
S
ˆVP i
S i
V ( P Pi ) exp i RT
L S
故初次令 iv 1
输入P、ｘ及有关参数
yi K i xi
G（1／T）非线性,高压下 的烃类（非理想） T 的调 整 采 用 抛 物 线 法 （Muller）； G （ 1 ／ T ）线性 ,P<20 ａ ｔｍ，用牛顿－拉普森 （ Neuton-Raphson）迭代 法（线性）切线法。
0.45
0.76
0.28
0.304
0.126
说明所设温度偏低。 重设T=58.7℃
解： •因各组分都是烷烃，所以汽、液相均可看成理想 溶液，平衡常数只取决于温度和压力。 •如计算要求不甚高，可使用烃类的P-T-K图（见 图2-1）。
例2-3
假设T=50℃,因P=0.2MPa,查图求平衡常数：
组分 正丁烷 xi 0.15 Ki 2.5 yi=Kixi 0.375
正戊烷
正己烷
0.40
s
已知 xi, P
设T
Pis
,
Pks , ...
i=1,2,…k…c
Tb
P f (T )
s k
ik xi
ik xi yi ik xi
N
ik i
x
yi
s k
y 1
i
?
Y
P
s k
Kk
Kk
P Kk P
1
ik
xi
1、泡点温度计算
（2）严格计算法（计算机计算） 对于非理想性较强的物系： Ki = f (T, P, xi , yi )
调整T
ˆ iv＝1作第一次迭代 设定T并令
设T 计算Pis、ViL、Ф is、 i
纯组分i
is —维里方程， i —wilson(T,P,xｉ)
第一次迭代时
iv 1
计算Ki和yi
圆整ｙｉ 计算 ˆv
i
计算Σ yi
先圆整
Y 是否第一次迭代 N Y Σ yi 有 无 变 化 N N lnΣ yi≤ε Y 输出T、ｙ
xi
1、泡点温度计算
—相对挥发度法
yi
由
ik xi
i 1
c
ik i
x
可计算
i 1
c
c
ik
xi
Pks Kk P
Kk
1
i 1
ik
xi
通常不需要试差！
Pks f (T )
T
1、泡点温度计算
—相对挥发度法——计算步骤
K P ik i i s K k Pk
c
i
1
c
已知 xi, P
或
f (T ) Ki xi 1 0
i 1
1、泡点温度计算
计算方法
1. 简化计算（手算）（Ki与组成无关) (1) 试差法 (2) 相对挥发度法 2. 严格计算法（计算机计算） （Ki与组成有关) Ki = f (T, P, xi, yi )
1、泡点温度计算
已知 xi (i=1,2,…c),P 或 T
yi ,T或P
计算方程有：
①相平衡关系
yi = Ki xi (i=1,2, …c)
C个 1个
y
②浓度和式
c
x
i 1
i 1 c
i
1 1
2C+2个
1个 C个
i
③汽液平衡常数关系式
Ki = f (P, T, xi, yi)
yi ik K k xi
1、泡点温度计算
—相对挥发度法
c c i 1 i 1
•公式推导： yi ik K k xi 1
yi ik K k xi
ik xi
K k ik xi 1
i 1
c
Kk
1
i 1
c
yi
ik
xi
i 1
c
ik
L s L ˆ i Pi i ( P Pi ) i Ki exp V V ˆiP ˆi RT s s i
1、泡点温度计算
严格计算法 ——计算过程
xi , P yi , T
Ki
s i
Pi
sቤተ መጻሕፍቲ ባይዱ
s i
——T, P
(一般受P的影响较小)
一阶导数
T k 1
k f ( T ) k T f (T k )
k 1 Tk 二阶导数 T
2 2 f (T k ) f (T k ) k f (T ) f (T k )
T k 1 T k
0.001
收敛快！
泡点温度计算框图（P50图2-5）
开 始
v 因为 i f (T , P, yi ) ， 其中
Ki
ˆV i
——T, P，yi
计算 ˆ V 或 yi时 需迭代（因T未知）。
i
当P不太高时，P的影响不太大，收敛较快。 一般受压力的影响较小
i
——T, P，xi
1、泡点温度计算
严格计算法 ——计算方法
•牛顿迭代法：
f (T ) K i xi 1
i 1
c
T——初值可由相对挥发度求得 ,也 可取某组分i的沸点为初值。
i→Ki
K x
i 1
c
i i
f (T )
Y
设 yi
T， yi
1、泡点温度计算
2）相对挥发度法
方法依据：相对挥发度随温度变化比Ki小得多，在一定温 度范围内可视为常数.
•相对挥发度定义：
Ki ik Kk
•计算式推导：
k—i组分中任选的一个基准组分
K i ik K k
后计算 iv f (T , P, yi )
当T,P一定时，
i -yｉ成对应。
v
外循环： 迭代计算泡点温度Tb
内循环：
在一定温度下，试差计算逸度系数 ，迭代计算ｙｉ
结 束
例2-3
例2-4 确定含正丁烷（1）1.15、正戊烷（2）0.4和正 己烷（ 3 ） 0.45 （均为摩尔分率 ）之烃类混合物 在 0.2MPa压力下的泡点温度。
(1)简化计算
已知 xi, p Ki与组成无关 Ki = f (T, P) P已知，Ki=f(T)
c
气相—理想气体或理想溶液 —常压或中压下烃类混合物
液相—理想溶液
—各组分分子结构相似
f (T ) Ki xi 1
i 1
1、泡点温度计算
1）试差法
N
已知 xi, P
设T
P-T-K图
K i Ki=f (T，P，xi，yi )
2.2.1 泡点温度和泡点压力计算
总变量：C-xi，C-yi，C-Ki，T，P。共3C+2 个 已知C个变量：（C-1）个组分和T或P 未知变量为2C+2个 由上述2C+2个方程求解（唯一解）
需试差计算
2.2.1 泡点温度和泡点压力计算
1、泡点温度计算
泡点方程：
K x
i 1 i
yi
未知，
Ki
i Pi
S
ˆVP i
S i
V ( P Pi ) exp i RT
L S
故初次令 iv 1
输入P、ｘ及有关参数
yi K i xi
G（1／T）非线性,高压下 的烃类（非理想） T 的调 整 采 用 抛 物 线 法 （Muller）； G （ 1 ／ T ）线性 ,P<20 ａ ｔｍ，用牛顿－拉普森 （ Neuton-Raphson）迭代 法（线性）切线法。
0.45
0.76
0.28
0.304
0.126
说明所设温度偏低。 重设T=58.7℃
解： •因各组分都是烷烃，所以汽、液相均可看成理想 溶液，平衡常数只取决于温度和压力。 •如计算要求不甚高，可使用烃类的P-T-K图（见 图2-1）。
例2-3
假设T=50℃,因P=0.2MPa,查图求平衡常数：
组分 正丁烷 xi 0.15 Ki 2.5 yi=Kixi 0.375
正戊烷
正己烷
0.40
s
已知 xi, P
设T
Pis
,
Pks , ...
i=1,2,…k…c
Tb
P f (T )
s k
ik xi
ik xi yi ik xi
N
ik i
x
yi
s k
y 1
i
?
Y
P
s k
Kk
Kk
P Kk P
1
ik
xi
1、泡点温度计算
（2）严格计算法（计算机计算） 对于非理想性较强的物系： Ki = f (T, P, xi , yi )
调整T
ˆ iv＝1作第一次迭代 设定T并令
设T 计算Pis、ViL、Ф is、 i
纯组分i
is —维里方程， i —wilson(T,P,xｉ)
第一次迭代时
iv 1
计算Ki和yi
圆整ｙｉ 计算 ˆv
i
计算Σ yi
先圆整
Y 是否第一次迭代 N Y Σ yi 有 无 变 化 N N lnΣ yi≤ε Y 输出T、ｙ
xi
1、泡点温度计算
—相对挥发度法
yi
由
ik xi
i 1
c
ik i
x
可计算
i 1
c
c
ik
xi
Pks Kk P
Kk
1
i 1
ik
xi
通常不需要试差！
Pks f (T )
T
1、泡点温度计算
—相对挥发度法——计算步骤
K P ik i i s K k Pk
c
i
1
c
已知 xi, P
或
f (T ) Ki xi 1 0
i 1
1、泡点温度计算
计算方法
1. 简化计算（手算）（Ki与组成无关) (1) 试差法 (2) 相对挥发度法 2. 严格计算法（计算机计算） （Ki与组成有关) Ki = f (T, P, xi, yi )
1、泡点温度计算