有理数乘方和混合运算强化练习
有理数的乘、除、乘方、混合运算习题

有理数的乘法、除法、乘方练习一、有理数的乘法运算法则:(一)没有0因数相乘的情况下:1、由负因数的个数确定符号----------+⎧⎨⎩奇数(如1,3,5,)个负因数,积为“—”偶数(如2,4,6,)个负因数,积为“”,可省略,再把绝对值相乘---------- (二)有一个以上的0因数相乘,积为0(三)适用的运算律: 1.2.()3.()a b b a a b c a b c a b c d a b a c a d ⨯=⨯⎧⎪ ⨯⨯=⨯⨯⎨⎪ ⨯+-=⨯+⨯-⨯⎩(四)策略:在有理数的乘、除中,碰到小数就 ,碰到带分数就 练习:1、(–4)×(–9)= 2、(–52)×81 = 3、(–253)×135= 4、(–12)×2.45×0×9×100 5、10.12512(16)(2)2-⨯⨯-⨯- 6、(-6)×(-4)-(-5)×107、(0.7-103-254+ 0.03)×(-100) 8、(–11)×52+(–11)×953二、有理数的倒数:(一)定义:如 ,则称a 与b 互为倒数;其中一个是另一个的倒数。
(二)几种情况下的倒数:1、整数:2的倒数是 ;12-的倒数是 ;0没有倒数发现:①互为倒数的两数必然 ;②把整数的分母看成 ,然后分子与分母2、分数:12的倒数是 ;23-的倒数是 ; 112的倒数是 ;223-的倒数是 ; 发现:求倒数时,碰到带分数,必须化为3、小数:0.25的倒数是 ; 1.125-的倒数是 ;发现:求倒数时,碰到小数,必须化为 ,练习:求下列各数的倒数: 4.25-是 235是 1.14-是 三、有理数的除法法则:(a b a b ÷=⨯的 )即看到除法,就转化为练习:1、(-18)÷(-9)2、-3÷(-31) 3、0÷(–105) 4、(-2)÷(-1.5)×(-3)5、 -0.2÷(-151)×(-261) 6、[65÷(-21-31)+281]÷(-181)四、乘方:(一)在n a 中,a 称为 ;n 称为 ;n a 称为 。
有理数的加减乘除乘方混合运算专题训练(带答案)

有理数的加减乘除乘方混合运算专题训练(带答案)1.先进行乘方运算,然后进行乘除运算,最后进行加减运算。
2.同级运算从左到右进行。
3.如果有括号,先进行括号内的运算,按照小括号、中括号、大括号的顺序进行。
1.18 - 6 ÷ 352.-81 ÷ (-2.25) × (-) ÷ 163.11 + (-22) - 3 × (-11)4.(+12) × (-) - 15 × (-1)5.- × [-32 × (-)2 - 2]6.-23 ÷ (-4)3 -7.12 ÷ [(-)2 - ]8.[(-2)2 × (-3)] ×9.[(-0.5) - ] × (-6)10.| - | × (-) ÷11.-22 - (-2)2 - 23 + (-2)312.-62 × (-1)2 - (-3)2 ÷ (-1)3 × (-3)13.-(-1)1997 - (1 - 0.5) × ÷ (-)14.(-1)3 - (-8) × + (-3)3 ÷ [(-2)5 + 5]15.-10 + 8 ÷ (-2)2 - (-4) × (-3)16.-49 + 2 × (-3)2 + (-6) ÷ (-)17.-14 + (1 - 0.5) × × [2 × (-3)2]18.(-2)2 - 2 × [(-)2 - 3 × ] ÷19.5 × (-6) - (-4)2 ÷ (-8)20.(-)2 + (- + 1) ×21.(- + ) × (-12) ÷ 622.(-) × (-4)2 - 0.25 × (-5) × (-4)223.(-)2 + × (- -2)24.-42 × [(-7) ÷ 6] + (-5)3 - 3 ÷ (-2)325.6 - (-12) ÷ (-2)26.(-48) ÷ 8 - (-5) ÷ (-)227.42 × (-) + (-) ÷ 0.2528.-81 ÷ (-3)229.-2 × (-3) - (-3) ÷ 330.(-5) × 6 + (-125) ÷ (-5)31.-(-0.25) × (-5) × 4 × (-1)1、-2×(-2)×1×8 + (-2)/(-2)/3 = 33/42、-12 + (-3)²/2 = -9.53、3/3 = 14、36/2 - 4×(-4)×(-3) = 1045、(3×4)×(-3) + 6 = -66、(-23)/(-2) - 13/(-4) = 5.57、23/2 × [(-2)×0.5 - (-1.6)] - 2 = -9.58、[(-2) - (-4)]/3 = 2/39、无法计算,方括号内为010、16/(-3) - (-5)×(-2)×(-2) - (-4) = -31/311、1、-44、-12、-112、无法计算,分母为013、-15 - [(-0.4)×(-2.5)] = -1414、(-8)×5 - 40 = -8015、(-1.2)/(-2) - (-2) = 1.416、-20/5×(5-3×(-3))/15 = 2/317、-3[-5+(1-0.2)/(-2)] = 1218、-23/1×(-1)²/(1)² - (2-(-4))×(-2.4) = -15/71.答案:(1) 17.(2) 删除。
有理数乘方经典练习题

有理数乘方经典练习题一、基础题1. 计算:(−3)^22. 计算:(1/2)^33. 计算:2^54. 计算:(−4)^35. 计算:(3/4)^2二、进阶题1. 计算:(−2)^4 ÷ (−2)^22. 计算:(1/3)^3 × (1/3)^23. 计算:(−5)^2 × (−5)^34. 计算:(2/5)^4 ÷ (2/5)^25. 计算:(−3/4)^3 × (−3/4)^2三、应用题1. 一个正方形的边长为2,求其面积。
2. 一个立方体的边长为3,求其体积。
3. 一个长方体的长、宽、高分别为2、3、4,求其体积。
4. 一个正方形的边长为1/2,求其面积。
5. 一个立方体的边长为1/3,求其体积。
四、挑战题1. 计算:(−1)^{100}2. 计算:(3/4)^{2}3. 计算:(−2)^{3} × (−2)^{4}4. 计算:(1/2)^{5} ÷ (1/2)^{3}5. 计算:(−4)^{5} × (−4)^{5}五、混合运算题1. 计算:(2^3) × (1/2)^22. 计算:(−3)^4 ÷ (3^2)3. 计算:(4^2) ÷ (2^3) × (1/2)^44. 计算:(−5)^3 + (5^2) × (−5)^15. 计算:(3/5)^3 (2/5)^3六、比较大小题1. 比较:(−2)^4 和 (−3)^4 的大小。
2. 比较:(1/2)^5 和 (1/3)^5 的大小。
3. 比较:(−4)^3 和 (−4)^2 的大小。
4. 比较:(3/4)^2 和 (2/3)^2 的大小。
5. 比较:(5^2) 和 (6^2) 的大小。
七、填空题1. 若 (−1/2)^n = 1/4,则 n = _______。
2. 若 2^m = 1/8,则 m = _______。
有理数的乘方及混合运算(基础)巩固练习

【巩固练习】-、选择题1. 下列说法中,正确的个数为 ()① 对于任何有理数 m,都有m > 0; ② 对于任何有理数 m 都有mi = ( — m)2;③ 对于任何有理数 m n(m ^ n),都有(m — n) > 0;33④ 对于任何有理数 m 都有m = ( — m).44.式子的意义是 ( )5A. 4与5商的立方的相反数B.4 的立方与5的商的相反数C.4 的立方的相反数除54D. 的立方55. (2010 •浙江杭州)计算(-1)2+(- 1)3=()A . -2B . - 1C . 0D . 2 6.观察下列等式: 71=7, 72= 49 , 73= 343, 74= 2401, 75= 16807, 76=117649…由此可判 断7100的个位数字是().A . 7B . 9C . 3D . 1;一个数的立方等于它本身的数是1 3 22 — = . -----------------------_________ ? ______352 一个数的平方等于它本身的数是,在—中底数是5,指数是A. 1 B . 2C2. 下列说法中,正确的是( ) A. —个数的平方一定大于这个数; C. 一个数的平方一定小于这个数; 3•下列各组数中,计算结果相等的是3D. 0B •一个数的平方一定是正数; D •一个数的平方不可能是负数 ( ).A . -23与(-2) 3B . -22 与(-2)2C .(2)2与手D .( 2)与 | 27. 一根1米长的绳子,第 次剪去 「半,第二次剪去剩下「半,如此下去,下的绳子的长度为()1A .米B . 215 米2C .16 米 2D .1 121米2二、填空题6次后剩2,13 5 71 2 6. ( 23)------------------三、解答题 1. 计算下列各式:(1) - 22+(3-6)2-8X (- 1)4;2. 已知x 的倒数和绝对值都是它本身,2y 、z 是有理数,并且|y 3| (2x 3z)5X 22yZ 的值. x y 53.探索规律:观察下面三行数,2, -4, 8, -16, 32, -64,… ① -2,-8,4, -20,28,-68,…② -1, 2, -4, 8, -16, 32,… ③(1) 第①行第10个数是多少?2 取每行第10个数,计算这三个数的和4.[ ( 3)]2 3 32 ( 2)3______从而猜想:1 3 52005(2) ( 3)32122(3)( 5)127 0.8 (2.25)(4)--9 6 1818 1.45 6 3.95 6 .5. 1 3249 9【答案与解析】 一、选择题1.【答案】B 【解析]①错:当 m 为0时,不满足;②③对;④错:次数为 奇数次方的结果也互为相反数 .2.【答案]D 3,互为相反数的两个数的2 ;而(】)21 1;020 ,2 4 2A C 均错; 一个数的平方是正数或 0, 即非负数, 3. 【答案] A 【解析] -23=-8, (-2) 3= -8.4. 【答案]B【解析] 43,一 ,,、、,表示4的立方与 5的商的相反数 55. 【答案] C【解析] (-1)2= 1, (- 1)3=- 16. 【答案] D【解析]个位上的数字每 4个一循环,100是 7. 【答案] C_ 二填空题1. 【答案] 4 , -2 , 3 , 2, 2, 2 【解析] 依据乘方的定义解答2.【答案] 0,1 ; 0,1,-1; 3. 【答案] …c143, -32,,27 54.【答案] -27, 725.【答案] 21003【解析] 21 3 22 , 1 35 3 2, 1 3从而 从而猜想: 所以 B 错, 【解析]一个数的平方与这个数的大小不定, 例如:224 只有D 对. 4的倍数,所以7100的个位数字应为1.6. 所以1 3【答案]【解析] 三、解答题 1•【解析]5 7 42,每组数中,右边的幕的底数a 与左边的最后一个数 n 的关系是:a 2005 (1 2005)210032.4 59 1 2 1 27 2(23)2 (2 3)2(3)25 9(1) - 23+(3-6)2-8X (- 1)4= - 8+9- 8 = -7;94 9 1 (5)— -( -) —754 77 4 9 151 ;9 5 4 7“752(4)18 1.45 6 3.95 69 6187 18 5 18 2 18 6 ( 1.45 3.95) 961814 15 2 6 2.5 1 15 16.2.【解析】 因为 X 的倒数和绝对值都是它本身,所以 x = 1,又因为 |y+3| +(2X +3Z )2= 0,所以 y+3 = 0 且 2x+3z = 0.所以 y = -3.当 X = 1 时,2X +3Z = 0, Z -33. 【解析】(1) 2, -4, 8, -16 , 32, -64 ,(2) ( 3)32144 22(3) ( 5)444 - 94 - 92716120.8 ( 2.25) 7把 X = 1, y =-3, Z彳代入得:5X 2yzX 3 y 255 2(3) 13 ( 3)2 5由-2 的指数规律,可以知道n=10 时,即=-1024为第①行第10个数.(2) 第②行数是第①行相应的数减4;第③行数是第①行相应的数的-0.5倍;由-2 的指数规律,可以知道n=10 时,即(3) 第②行第10个数为-1024-4=-1028第③行第10 个数为( -0.5) -1024) =512(2) 第②③行数与第①行数分别有什么关系?所以第①行、第②行、第③行第10个数字之和为-1024+ (-1028) +512=-1540.。
有理数的加减乘除乘方混合运算专题训练带答案

1. 先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号的运算,按小括号、中括号、大括号依次进行。
1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷22231113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、-10 + 8÷(-2 )2 -(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ].(1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32;(3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯.(1)36×23121)-(; (2)12.7÷)(-1980⨯;(3)6342+)(-⨯; (4))(-43×)-+(-31328;(5)1323-)(-÷)(-21; (6)320-÷34)(-81-;(7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[ 2322-)(- ];(9)[ 2253)-(-)(- ]÷)(-2; (10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-;(3)2332-)(-; (4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯.(1))-(-258÷)(-5; (2)-33121)(--⨯;(3)223232)-(-)(-⨯⨯; (4)0132432⨯⨯)+(-)(-;(5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 (1)17; (2)511; (3)31; (4)-11 2、【答案】 (1)-10; (2)22; (3)-16; (4)-25 3、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64; (8)37; (9)8; (10)-25. 4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71; (6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20; (7)-2; (8)-67. 6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516; (6)-2.9复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________.4.23×(-41)3=________;(-91)÷(+34)2=________. 5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国省的面积约为3600平方公里,用科学记数法表示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22 ②(21)2________(21)3 ③32________22 ④(-2)3________(-2)2二、判断题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( ) 15.(-3)5表示5个-3相乘( )三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中结果大于0的是 A .1-910×3 B .(1-910)×3C .1-(9×3)10D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不可能为负数22.用科学记数法表示的数2.89×104,原来是 A .2890 B .2890000 C .28900 D .289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16)27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-200230.(3分)-)45()45(5222-÷-⨯⨯31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3)33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a 2+a 3+……+a 2000(1)若a =1,求A 的值.(2)若a =-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91 913 -32 4.-81 -161 5.-23 23 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -141 10.> > > < 二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C四、23.-90 24.1 25.-3 26.41 27.15 28.1 29.-2002 30.1 31.30 32.-49 33.-4 五、34.(1)2000 (2)0。
有理数的乘方及混合运算(基础)巩固练习

【巩固练习】一、选择题1.(2015•郴州)计算(﹣3)2的结果是( )A .﹣6B . 6C . ﹣9D . 92.下列说法中,正确的是( )A .一个数的平方一定大于这个数;B .一个数的平方一定是正数;C .一个数的平方一定小于这个数;D .一个数的平方不可能是负数.3.下列各组数中,计算结果相等的是 ( ). A .-23与(-2)3 B .-22与(-2)2C .22()5与225 D .(2)--与2-- 4.式子345-的意义是( ) A. 4与5商的立方的相反数 B.4的立方与5的商的相反数C.4的立方的相反数除5D.45-的立方 5.(2016•宝应县一模)(﹣1)2016的值是( )A .1B .﹣1C .2016D .﹣20166.观察下列等式:71=7,72=49,73=343,74=2401,75=16807,76=117649…由此可判断7100的个位数字是( ) .A .7B .9C .3D .17.一根1米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此下去,第6次后剩下的绳子的长度为( ) .A .312⎛⎫ ⎪⎝⎭米B .512⎛⎫ ⎪⎝⎭米C .612⎛⎫ ⎪⎝⎭米D .1212⎛⎫ ⎪⎝⎭米 二、填空题8.在(-2)4中,指数是________,底数是________,在-23中,指数是________,底数是________,在225中底数是________,指数是________. 9.(2015•湖州)计算:23×()2= . 10.()3--= ;52-= ;313⎛⎫-- ⎪⎝⎭= ;225= . 11. 3[(3)]_______---=,233(2)_______-⨯-=12.213____+= , 2135_____++=,21357_____+++= ,……,从而猜想:135+++……22005_____+=. 13. 21(2)________3-=三、解答题14.(2016春•浦东新区期中)(﹣3)2﹣(1)3×﹣6÷|﹣|3.15. 已知x 的倒数和绝对值都是它本身,y 、z 是有理数,并且2|3|(23)0y x z +++=,求32525x yz x y --+-的值. 16. 探索规律:观察下面三行数,2, -4, 8, -16, 32, -64,… ①-2, -8, 4, -20, 28, -68,… ②-1, 2, -4, 8, -16, 32,… ③(1) 第①行第10个数是多少?(2) 第②③行数与第①行数分别有什么关系?(3) 取每行第10个数,计算这三个数的和.【答案与解析】一、选择题1.【答案】D2.【答案】D【解析】一个数的平方与这个数的大小不定,例如:2242=>;而2111()242=<;200=,从而A ,C 均错;一个数的平方是正数或0,即非负数,所以B 错,只有D 对.3.【答案】A【解析】-23=-8, (-2)3= -8.4.【答案】B 【解析】345-表示4的立方与5的商的相反数 5. 【答案】A【解析】解:∵(﹣1)2016=1,∴(﹣1)2016的值是1,故选A .6.【答案】D【解析】个位上的数字每4个一循环,100是4的倍数,所以1007的个位数字应为1. 7.【答案】C二、填空题8.【答案】4 , -2 , 3 , 2, 2, 2【解析】依据乘方的定义解答9.【答案】2.【解析】23×()2=8×=2.10.【答案】3, -32, 14,27511.【答案】-27,7212.【答案】21003【解析】2132+= , 21353++=,213574+++=, ……从而猜想:每组数中,右边的幂的底数a 与左边的最后一个数n 的关系是:12n a +=. 所以135+++……22120052005()10032++==. 13.【答案】459【解析】222117494(2)(2)()533399-=+=== 三、解答题14. 【解析】解:原式=9﹣×﹣6÷=9﹣﹣6×=9﹣﹣=9﹣21=﹣12.15.【解析】因为x 的倒数和绝对值都是它本身,所以x =1,又因为|y+3|+(2x+3z)2=0,所以y+3=0且2x+3z =0.所以y =-3.当x =1时,2x+3z =0,23z =-. 把x =1,y =-3,23z =-代入得:3232252(3)52541351(3)51953x yz x y ⎛⎫-⨯-⨯- ⎪--⎝⎭===-+--+---+-. 16.【解析】(1)2, -4, 8, -16, 32, -64,… ①第①行可以改写为:2,,,,……,,…… 由-2的指数规律,可以知道n=10时,即=-1024为第 ①行第10个数.(2)第②行数是第①行相应的数减4;第③行数是第①行相应的数的-0.5倍;(3)第②行第10个数为-1024-4=-1028第③行第10个数为(-0.5)(-1024)=512所以第①行、第②行、第③行第10个数字之和为-1024+(-1028)+512=-1540.。
有理数乘方及混合运算(习题及答案)

有理数乘方及混合运算(习题及答案)1. 计算下列各式的值:a) (3/4)^2解:将3/4写成分数形式为3/4,所以(3/4)^2 = (3/4) × (3/4) = 9/16。
b) (-2/3)^3解:将-2/3写成分数形式为-2/3,所以(-2/3)^3 = (-2/3) × (-2/3) × (-2/3) = -8/27。
c) (5/6)^0解:任何非零实数的0次方都等于1,所以(5/6)^0 = 1。
2. 计算下列各式的值:a) 2/3 + 1/4解:将2/3和1/4的分母都改为12,得到8/12 + 3/12 = 11/12。
b) 5/6 - 2/9解:将5/6和2/9的分母都改为18,得到15/18 - 4/18 = 11/18。
c) (1/2)^2 + (2/3)^3解:将(1/2)^2和(2/3)^3分别计算得到1/4和8/27,所以(1/2)^2 +(2/3)^3 = 1/4 + 8/27 = 27/108 + 32/108 = 59/108。
3. 计算下列各式的值:a) 2/3 × 5/7解:将2/3和5/7相乘得到10/21。
b) 3/4 ÷ 2/5解:将3/4除以2/5转化为乘法,即3/4 × 5/2 = 15/8。
c) (3/5)^2 × (5/7)^3解:将(3/5)^2和(5/7)^3分别计算得到9/25和125/343,所以(3/5)^2 × (5/7)^3 = 9/25 × 125/343 = 1125/8575。
4. 混合运算:a) 2/3 + 1/4 × 3/5解:先计算1/4 × 3/5 = 3/20,然后将2/3和3/20相加得到40/60 + 3/20 = 43/60。
b) 1/2 - 3/4 ÷ 2/3解:先计算3/4 ÷ 2/3 = 9/8,然后将1/2和9/8相减得到4/8 - 9/8 = -5/8。
有理数的加减乘除乘方混合运算专题训练(带答案)
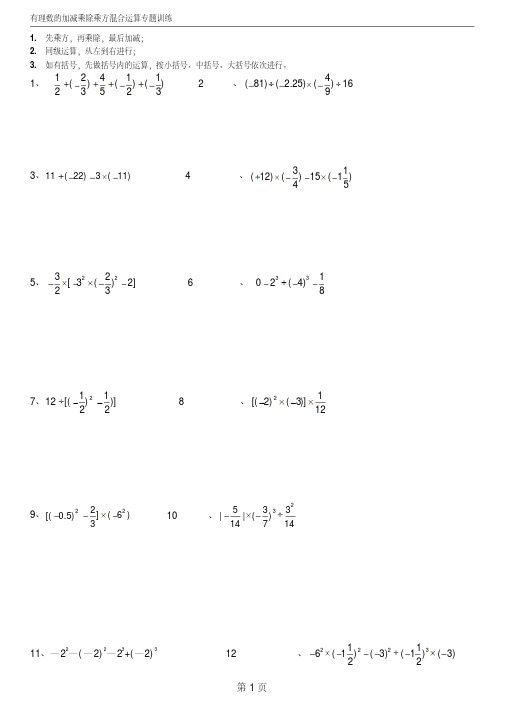
1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、12411()()()23523 2、4(81)( 2.25)()1693、11(22)3(11) 4、31(12)()15(1)455、2232[3()2]236、33102(4)87、)]21)21[(1228、121)]3()2[(29、)6(]32)5.0[(2210、23533||()14714223 322231113、199711(1)(10.5)()31214、33514(1)(8)(3)[(2)5]21715、-10 + 8÷(-2 )2-(-4 )×(-3 ) 16、-49 + 2×(-3 )2+ (-6 )÷(-91)17、-14+ ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(5220、0)132()43(235722523、)23232(21)21(224、332)2(3)5(6)7(425、6-(-12)÷2)2( 26、(-48)÷ 8-(-5)÷2)21(27、42×)43()32(÷ 0.25 28、23)9181(29、33323230、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0 32、22)3(61)2132(11、【基础题】计算:(1)618-÷)(-)(-312;(2))(-+51232;(3))(-)(-49+)(-60÷12;(4)23)(-×[ )+(--9532 ]. (1))(-)+(-2382;(2)100÷22)(--)(-2÷)(-32;(3))(-4÷)(-)(-343;(4))(-31÷231)(--3214)(-.(1)36×23121)-(;(2)12.7÷)(-1980;(3)6342+)(-;(4))(-43×)-+(-31328;(5)1323-)(-÷)(-21;(6)320-÷34)(-81-;(7)236.15.02)-(-)(-÷22)(-;(8))(-23×[ 2322-)(- ];(9)[ 2253)-(-)(- ]÷)(-2;(10)16÷)(-)-(-)(-48123.(1)11+(-22)-3×(-11);(2)0313243)-(-)(-;(3)2332-)(-;(4)23÷[ )-(-)(-423];(5))-(8743÷)(-87;(6))+()(-654360;(7)-27+2×23+(-6)÷231;(8))(-)-+-(-4151275420361.(1))-(-258÷)(-5;(2)-33121)(--;(3)223232)-(-)(-;(4)0132432)+(-)(-;(5))(-+51262;(6)-10+8÷22-4×3;(7)-51-55.24.0;(8)251-(1-0.5)×31;(1)(-8)×5-40;(2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15;(4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2;(6)-52+(1276185)×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/343 11、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、9 1、【答案】(1)17;(2)511;(3)31;(4)-112、【答案】(1)-10;(2)22;(3)-16;(4)-253、【答案】(1)1;(2)0;(3)42;(4)423;(5)18;(6)0;(7)-4.64;(8)37;(9)8;(10)-25.4、【答案】(1)22;(2)0;(3)-17;(4)-423;(5)71;(6)-95;(7)-85;(8)6 .5、【答案】(1)3;(2)1;(3)-54;(4)0;(5)526;(6)-20;(7)-2;(8)-67.6、【答案】(1)-80;(2)5.6;(3)-2;(4)16;(5)-516;(6)-2.9复习有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分)1.3×(-2)=________,(-6)×(-31)=________.2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________.4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用科学记数法表示为________.9.+121的倒数是________;________的倒数是-54.10.用“>”“<”填空:①23________22②(21)2________(21)3③32________22④(-2)3________(-2)2二、判断题(每小题1分,共5分)11.零除以任何数都得零()12.互为相反数的两个数的积为负数()13.如果ab >0,则a >0且b >0()14.1除以一个非零数的商叫做这个数的倒数()15.(-3)5表示5个-3相乘()三、选择题(每小题3分,共21分)16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与-22D .|-2|与-|-2|19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .120.下列各式中结果大于0的是A .1-910×3 B .(1-910)×3C .1-(9×3)10D .(1-9)10×321.下列说法中正确的是A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不可能为负数22.用科学记数法表示的数2.89×104,原来是A .2890B .2890000C .28900D .289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21)24.(3分)-6÷(+3)÷(-4)×(+2)25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16)27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-200230.(3分)-)45()45(522231.(3分)(-5)2÷5×6 32.(3分)(-2.5)÷(-310)×(-3)33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a 2+a 3+……+a 2000(1)若a=1,求A 的值.(2)若a=-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91913-32 4.-81-1615.-23236.-1.2 7.1800 8.3.6×103平方公里9.32-14110.>>><二、11.×12.×13.×14.√15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C 四、23.-90 24.1 25.-3 26.4127.15 28.1 29.-2002 30.1 31.30 32.-4933.-4五、34.(1)2000 (2)0。
有理数地加减乘除乘方混合运算专题训练(带答案)

有理数的加减乘除乘方混合运算专题训练1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、 1 ( 2 ) 4 ( 1 ) ( 1) 2 、 ( 81) ( 2.25) ( 4) 162 3 5 2 3 93、11 ( 22) 3 ( 11) 4 、( 12) ( 3) 15 ( 11)4 55、3[ 323(4)31( 2)2 2] 6 、022 3 87、12 [( 1) 21 )] 8 、[( 2)2 ( 3)] 12 2 129、[( 0.5)22]( 62 ) 10 、 | 5 | ( 32) 3 33 14 7 1411、— 22— ( — 2) 2— 23+( —2) 312 、 62 ( 11)2 ( 3)2( 11)3 ( 3)第 1 页13、 ( 1)1997(1 0.5) 1( 1 )14 、( 1)3 ( 81) 4 ( 3)3 [( 2)55]3 12 2 1715、-10 + 8 ÷(-2 ) 2-(-4 ) ×(-3 ) 16 、-49+2×(-3)2+( -6)÷(-1)917、-14 + ( 1 -0.5 ) ×1×[2 ×( -3) 2] 18 、( -2) 2-2×[( -1 ) 2-3×3]÷1.3 24 519、5 ( 6) ( 4)2( 8) 20 、( 3)2( 21) 04 321、( 7 5 3)(12)6 22 、( 5) ( 4)20.25 ( 5) ( 4)212 6 4 823、 ( 1)2 1 ( 2 2 2 ) 24 、 42(7) 6 (5)3 3 (2)32 23 325、6-(- 12)÷ ( 2) 226 、( -48 )÷ 8-(-5)÷ ( 1)2227、42× ( 2 ) ( 3) ÷ 0.25 28 、( 811)3 23 4 929、 2 3 2 3 3 3 30 、( -5) ×6+( -125) ÷( -5) 331、0.25 (5) 4( 1 )32 、 12( 21) 1 ( 3)225 3 2 61、【基础题】计算:(- )(- 1) + 2 (- 1 ) (1)18-6 ÷ 2 ;(2)3 2 5 ; 3(3)(-9)(-4)+(- 60)÷12 ; 2 2 5(4)(-3)×[ - +(- ) ].3 9(1) 22 28+(- 3) (- 2) (- 2) (- ); ;(2)100÷ -(-2)÷ 3(- 3 )(- 3)1 (- 12 1 3( )(- ) - (- ) (3)(-4)÷ ; )÷ 4 .4 43 3 2(1) 36 ×(1 - 1 2( ) 12.7÷(- 8 )0 ;);2 3 2 19第 4 页有理数的加减乘除乘方混合运算专题训练(3)2(-3)(-+2-1)4 (- 3)+6;(4)4×83 3;3(-1)3 3-1(- 2)-13(6) 0-2 ÷(- 4);(5)÷2 ;83 2 2 3(-2 2(7)(- 2)0.5-(- 1.6)÷(-2);()(-)×[ )-2 ] ;82 32 2÷(-);163 1(9)[ (- 3)-(- 5)] (10)÷(-)-(-)(-)2 2 4 .8(1)11+(- 22)- 3×(- 11);( 2)(-3)(-2-1) 0;4 3 3第 5 页有理数的加减乘除乘方混合运算专题训练3 2;( )÷3( 3)(- 2)-323 (- 2)-(-4)] ;4 [( 3- 7) (-7)(- )(3+ 5) ( 5)÷ ; (6)60;4884 6( 7)- 7 2 × 2 (- )÷ 1 2 ; (8)(- 1 - 3 + 4 - 7)(-15 4) +2 3 +63 6 20 5 12 .(1) 8-(- 25)÷(-5);(2)-1 3 3-2 (-1);( 3)(- ) 2 -(- 23 2 2; ) ; (4)(- ) (- +1) 0 2 3 2 34 3第 6 页有理数的加减乘除乘方混合运算专题训练( 5) + 2(- 1) ()-+÷ 2 - × ; 6 2; 25 6 10 8 4 3(7)- 5 - 0.4 2.5 5 25 -( - )× 1 ; 1;( ) 1 0.58 13(1)(- 8)× 5- 40; (2)(-1.2 )÷( - 1)- (-2 );3(3)-20 ÷5× 1+5×( -3 )÷ 15; (4)-3[-5+ (1-0.2 ÷ 3)÷( -2 )] ;45(5)-23÷1 3 ×( -1 1)2÷(1 2)2;(6)- 2 +( 5 1 7) ×( -2.4)53 35 86 12第7 页有理数的加减乘除乘方混合运算专题训练参考答案1、 -1/5 2 、 -1 3 、 22 4、9 5 、9 6 、 07、-488 、-1 9、-15 10 、-15/34311、-24 12 、-89 13 、 314 、2 15 、-20 16、23 17 、 2 18 、24 19 、-28 20 、9/16 21、1 22 、10 23 、-1/12 24 、104/3 25 、926、14 27 、 -31 28 、-81 又 1/81 29 、-9 30 、 -2931、-1/5 32 、91、【答案】( 1) 17;(2)11;(3)31;(4)- 1152、【答案】( 1)- 10;(2)22;(3)- 16;(4)-5(2)0;(3)42;(4)23;23、【答案】(1)1;(5)18;( 6) 0;(7)- 4.64 ;(8)7;(9)8;(10)-5 .43 2(4)-23;(5)1;4、【答案】(1)22;( 2)0;(3)- 17;(6)- 95;( 7)4 7-85;(8)6 .5、【答案】( 1)3;(2)1;(3)-54;(4)0;( 5)26;(6)-20;(7)- 2;(8)5-7 .66、【答案】( 1)- 80;(2)5.6 ;(3)- 2;(4)16;(5)-16;(6)- 2.95第8 页有理数的加减乘除乘方混合运算专题训练复习有理数的乘除、乘方运算测试题一、填空题(每小题3 分,共30 分)1. 3×(- 2) =________,(- 6)×(-1) =________.32.(- 3)2的底数是 ________,结果是 ________ ;- 32的底数是 ________ ,结果是________.3.(-1)÷( + 3)=________;-3÷(- 1 6)=________;( +8)÷(-1)=________.6 2 497 4 4. 23×(-1)3=________ ;(-1)÷( + 4)2=________.4 9 35.(-2)× ________=1;(-2)× ________=- 13 36.-5×(- 2.4)×(-3) =________.6 57.- 32×(- 5)2÷(-1)3=________.28.我国台湾省的面积约为3600 平方公里,用科学记数法表示为________.9. +1 1的倒数是 ________; ________的倒数是-4.2 510.用“>”“<”填空:① 23________22②(1)2 ________(1)32 2③ 32________22④(- 2)3________(- 2)2二、判断题(每小题1 分,共5分)11.零除以任何数都得零()12.互为相反数的两个数的积为负数()13.如果 ab> 0,则 a>0 且 b> 0()14. 1 除以一个非零数的商叫做这个数的倒数()15.(- 3)5表示 5 个- 3 相乘()三、选择题(每小题3 分,共21 分)16.下列说法,其中错误的有①一个数与 1 相乘得原数;②一个数乘以-1 得原数的相反数;③0 乘以任何数得 0;④同号两数相乘,符号不变.A.1 个B.2 个C.3 个D.4 个17.下列各对数:① 1 与 1;②- 1 与 1;③ a- b 与 b- a;④- 1 与- 1;⑤,- 5 与 |6|其中互为倒数的是A.①②③B.①③⑤C.①③④D.①④18.下列各题中两个式子的值相等的是A.- 23与(- 2)3B.32与 231有理数的加减乘除乘方混合运算专题训练C.(- 2)2与-22D. | -2| 与- | -2| 19.下列结论中,其中正确的个数为① 0 的倒数是 0;②一个不等于0 的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若 a, b 互为倒数,则- ab=- 1.A. 4 B. 3C. 2 D. 120.下列各式中结果大于0 的是10 10A. 1-9 ×3 B.(1-9 )× 3 C. 1-( 9× 3)10D.( 1- 9)10× 3 21.下列说法中正确的是A.一个数的平方必为正数B.一个数的平方必小于这个数的绝对值C.一个数的平方必大于这个数D.一个数的平方不可能为负数22.用科学记数法表示的数2. 89×104,原来是A. 2890 B. 2890000C. 28900 D. 289000四、计算题(共35 分)23.(3 分)(- 3)×(- 5)×( +12)×(- 1 )224.(3 分)- 6÷( +3)÷(- 4)×( +2)25.(3 分)- 5- 6÷(- 3)26.(3 分)(- 81)÷ 2 1×1÷(- 16)4 927.(3 分)- 22×(- 3)÷452有理数的加减乘除乘方混合运算专题训练28.(3 分)(- 1)2000×(- 1)2001×(- 1)2002÷(- 1)200329.(3 分)(- 2)×(- 2001 )×[- 1 -(-1)]× 1- 20022 230.(3 分)- 2 2( 5)2( 5)5 4 431.(3 分)(- 5)2÷ 5× 632.(3 分)(- 2.5 )÷(-10)×(- 3)333.(5分)30×(1-1+3-9)2 3 5 103有理数的加减乘除乘方混合运算专题训练五、解答题(9 分)34.已知 A=a+a2+a 3+⋯⋯ +a2000( 1)若 a=1,求 A 的值.( 2)若 a=- 1,求 A 的值.参考答案一、 1.- 6 2 2.-3 9 3 -9 3.-13- 324.-1 1 5.-3 3 9 91-6.- 1.2 7. 1800 8.3.6 × 103平方公里8 16 2 29.2- 1 110.>>><3 4二、 11.×12.×13.×14.√ 15.√三、 16. A17. D 18.A 19.B 20. D 21. D 22. C四、 23.-90 24. 1 25.-3 26.127. 15 28. 1 29.-200232.-9430. 1 31. 3033.- 44五、34.( 1)2000 (2)04。
有理数的乘方及混合运算(基础)知识讲解及巩固练习

【答案与解析】 (1)44222222555555⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+⨯+⨯+⨯+=+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭; (2)(-3.7)×(-3.7)×(-3.7)×(-3.7)×5×5=(-3.7)4×52;(3) 62xxxxxxyy x y =【总结升华】乘方时,当底数是分数、负数时,应加上括号.2.计算:(1)3(4)- (2)34- (3)4(3)-(4)43- (5)⎛⎫⎪⎝⎭335 (6)335 (7)22×3()(8)22×3 【答案与解析】(1)3(4)-(4)(4)(4)64=-⨯-⨯-=-;(2)34-44464=-⨯⨯=-;(3)4(3)-(3)(3)(3)(3)81=-⨯-⨯-⨯-=;(4)43-333381=-⨯⨯⨯=-;(5)⎛⎫⎪⎝⎭33533327555125=⨯⨯=;(6)3353332755⨯⨯==;(7)3⨯(2)22636==;(8)22×32918=⨯=【总结升华】()n a -与n a -不同,()()()()-=--⋅⋅⋅-n n a a a a 个,而n n a a a a -=-⋅⋅⋅个表示a 的n 次幂的相反数.举一反三:【变式1】计算:(1)(-4)4 (2)23 (3)225⎛⎫⎪⎝⎭ (4)(-1.5)2【答案】 (1)(-4)4=(-4)×(-4)×(-4)×(-4)=256;(2)23=2×2×2=8; (3)2222455525⎛⎫=⨯= ⎪⎝⎭ (4) (-1.5)2=(-1.5)×(-1.5)=2.25【变式2】(2015•长沙模拟)比较(﹣4)3和﹣43,下列说法正确的是( )A . 它们底数相同,指数也相同B . 它们底数相同,但指数不相同C . 它们所表示的意义相同,但运算结果不相同D . 虽然它们底数不同,但运算结果相同【答案】D .解:比较(﹣4)3=(﹣4)×(﹣4)×(﹣4)=﹣64,﹣43=﹣4×4×4=﹣64,底数不相同,表示的意义不同,但是结果相同.类型二、乘方的符号法则3.不做运算,判断下列各运算结果的符号.(-2)7,(-3)24,(-1.0009)2009,553⎛⎫ ⎪⎝⎭,-(-2)2010 【答案与解析】根据乘方的符号法则直接判断,可得:(-2)7运算的结果是负;(-3)24运算的结果为正;(-1.0009)2009运算的结果是负;553⎛⎫ ⎪⎝⎭运算的结果是正;-(-2)2010运算的结果是负.【总结升华】“一看底数,二看指数”,当底数是正数时,结果为正;当底数是0时,结果是0;当底数是负数时,再看指数,若指数为偶数,结果为正;若指数是奇数,结果为负. 举一反三:【变式】计算:(-1)2009的结果是( ).A .-lB .1C .-2009D .2009【答案】A类型三、有理数的混合运算4.计算: (1)()⎡⎤⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭⎣⎦211-1-0.5××2--33(2)()⎡⎤⎣⎦341-1-×2--36 (3)3201111(1+-2.75)×(-24)+(-1)--238(4)33211-+|-2-3|(-0.1)(-0.2)【答案与解析】(1)法一:原式=517(1)(7)(7)666-⨯-=⨯-=-; 法二:原式=1117(11)(29)(7)2366-+⨯⨯-=⨯-=- (2)原式()=⎡⎤⎣⎦1-1-×2--276=1-1-×296=35-6(3) 原式=4111(+-)×(-24)-1-8384=-32-3+66-9=22 (4) 原式=11-+|-8-3|-0.0010.04=-1000-25+11=-1014 【总结升华】有理数的混合运算,确定运算顺序是关键,细心计算是运算正确的前提. 举一反三:【变式1】计算:4211(10.5)[2(3)]3---⨯---【答案】原式111151(29)1(7)17523666⎛⎫=--⨯--=----=--+= ⎪⎝⎭ 【变式2】计算:2421(2)(4)12⎛⎫-÷-⨯- ⎪⎝⎭【答案】原式11116(4)11612444=÷-⨯-=-⨯⨯-=- 5. 20032004(2)(2)-+-= ( )(A )2- (B )4007(2)- (C )20032 (D )20032- 【答案】C【解析】逆用分配律可得:20032004200320032003(2)(2)(2)[1(2)](2)2-+-=-+-=--=,所以答案为:C 【总结升华】当几项均为幂的形式,逆用分配律提出共同的因数时,要提指数较小的幂的形式.举一反三:【变式】计算:7734()()43-⨯- 【答案】7773434()()[()()]14343-⨯-=-⨯-= 类型四、探索规律 6. (2014秋•埇桥区校级期中)你见过拉面馆的师傅拉面吗?他们用一根粗的面条,第1次把两头捏在一起抻拉得到两根面条,再把两头捏在一起抻拉,反复数次,就能拉出许多根细面条,如下图,第3次捏合抻拉得到 根面条,第5次捏合抻拉得到 根面条,第n 次捏合抻拉得到 根面条,要想得到64根细面条,需 次捏合抻拉.第1次 第2次 第3次【答案】8; 32; 2n ; 6【解析】由题意可知,每次捏合后所得面条数是捏合前面条数的2倍,所以可得到: 第1次:122=;第2次:224=;第3次:328=;…;第n 次:2n . 第3次捏合抻拉得到面条根数:32,即8根;第5次得到:52,即32根;第n 次捏合抻拉得到2n ;因为6264=,所以要想得到64根面条,需要6次捏合抻拉.【总结升华】解答此类问题的方法一般是:从所给的特殊情形入手,再经过猜想归纳,从看似杂乱的问题中找出内在的规律,使问题变得有章可循.举一反三:【变式】已知21=2,22=4,23=8,24=16,25=32,…,观察上面的规律,试猜想22008的末位数字是________.【答案】6 【巩固练习】一、选择题1.(2015•郴州)计算(﹣3)2的结果是( )A .﹣6B . 6C . ﹣9D .92.下列说法中,正确的是( )A .一个数的平方一定大于这个数;B .一个数的平方一定是正数;C .一个数的平方一定小于这个数;D .一个数的平方不可能是负数.3.下列各组数中,计算结果相等的是 ( ).A .-23与(-2)3B .-22与(-2)2C .22()5与225 D .(2)--与2-- 4.式子345-的意义是 ( ) A. 4与5商的立方的相反数 B.4的立方与5的商的相反数 C.4的立方的相反数除5D.45-的立方5.计算(-1)2+(-1)3=( )A .-2B .- 1C .0D .26.观察下列等式:71=7,72=49,73=343,74=2401,75=16807,76=117649…由此可判断7100的个位数字是( ) .A .7B .9C .3D .17.一根1米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此下去,第6次后剩下的绳子的长度为( ) .A .312⎛⎫ ⎪⎝⎭米B .512⎛⎫ ⎪⎝⎭米C .612⎛⎫ ⎪⎝⎭米D .1212⎛⎫ ⎪⎝⎭米 二、填空题8.在(-2)4中,指数是________,底数是________,在-23中,指数是________,底数是________,在225中底数是________,指数是________. 9.(2015•湖州)计算:23×()2= . 10.()3--= ;52-= ;313⎛⎫-- ⎪⎝⎭= ;225= . 11. 3[(3)]_______---=,233(2)_______-⨯-=12.213____+= , 2135_____++=,21357_____+++= ,……,从而猜想:135+++……22005_____+=.13. 21(2)________3-=三、解答题14.(2014秋•渭城区校级期末)﹣23+(﹣3)2﹣32×(﹣2)2.15. 已知x 的倒数和绝对值都是它本身,y 、z 是有理数,并且2|3|(23)0y x z +++=,求32525x yz x y --+-的值. 16. 探索规律:观察下面三行数,2, -4, 8, -16, 32, -64,… ①-2, -8, 4, -20, 28, -68,… ②-1, 2, -4, 8, -16, 32,… ③(1) 第①行第10个数是多少?(2) 第②③行数与第①行数分别有什么关系?(3) 取每行第10个数,计算这三个数的和. 【答案与解析】 一、选择题 1.【答案】D2.【答案】D【解析】一个数的平方与这个数的大小不定,例如:2242=>;而2111()242=<;200=,从而A ,C 均错;一个数的平方是正数或0,即非负数,所以B 错,只有D 对.3.【答案】A【解析】-23=-8, (-2)3= -8. 4.【答案】B【解析】345-表示4的立方与5的商的相反数 5.【答案】C【解析】 (-1)2=1,(-1)3=-16.【答案】D【解析】个位上的数字每4个一循环,100是4的倍数,所以1007的个位数字应为1. 7.【答案】C二、填空题8.【答案】4 , -2 , 3 , 2, 2, 2【解析】依据乘方的定义解答9.【答案】2.【解析】23×()2=8×=2.10.【答案】3, -32,14,275 11.【答案】-27,7212.【答案】21003【解析】2132+= , 21353++=,213574+++=, ……从而猜想:每组数中,右边的幂的底数a 与左边的最后一个数n 的关系是:12n a +=. 所以135+++……22120052005()10032++==. 13.【答案】459【解析】222117494(2)(2)()533399-=+=== 三、解答题14.【解析】解:﹣23+(﹣3)2﹣32×(﹣2)2=﹣8+9﹣9×4=﹣8+9﹣36=﹣44+9=﹣35.15.【解析】因为x的倒数和绝对值都是它本身,所以x=1,又因为|y+3|+(2x+3z)2=0,所以y+3=0且2x+3z=0.所以y=-3.当x=1时,2x+3z=0,23 z=-.把x =1,y=-3,23z=-代入得:3232252(3)52541351(3)51953x yzx y⎛⎫-⨯-⨯-⎪--⎝⎭===-+--+---+-.16.【解析】(1)2, -4,8,-16,32,-64,…①第①行可以改写为:2,,,,……,,……由-2的指数规律,可以知道n=10时,即=-1024为第①行第10个数. (2)第②行数是第①行相应的数减4;第③行数是第①行相应的数的-0.5倍;(3)第②行第10个数为-1024-4=-1028第③行第10个数为(-0.5)(-1024)=512所以第①行、第②行、第③行第10个数字之和为-1024+(-1028)+512=-1540.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、有理数的乘方
【知识点一】乘方的意义
1 求几个_____________的______的运算,叫乘方. 2、______数的任何次方都是_______数.
______数的_____次方是_____数,_____数的______次方是______数.
在进行有理数的乘方运算时,第一步也应先确定结果的 .
知识过关 1、2
3 读作_____________;底数为______;指数为_____;结果等于_______;
2
3-)( 读作__________;底数为______;指数为_____;结果等于_______;
2
3-读作_____________;底数为______;指数为_____;结果等于_______.
2、平方得16的数是_______,立方得-27的数是_______.
3、有理数乘方
180= ; =25 ; =-3)2( ; =-4
)10( ; =-2
)2.0( ; =-2)2
1
1( ;
=-3)3
2
1( ; =-1)2009(
=-8888)1( ; =-5555)1( .
4、有理数的混合运算
5、 有理数的混合运算
=-+-1110)1()1( ; =-+-33)2(2 =---3
3)2(2 ; =---11
10
)1()1(
=-⨯-33)21
(2 ; =-⨯-22)4
1(4
=-÷-)10()10(33 ; =-÷-)5()5(22 222)4(5)2
1
(-⨯⨯-= 6、以下各题请打好草稿,认真完成.
(1) 一个数的平方等于它本身,则这个数是______. (2)一个数的平方等于它的相反数,则这个数是______. (3)一个数的平方等于它的绝对值,则这个数是______. (4)一个数的平方等于它的倒数,这个数是________. (5)一个数的平方等于它的立方,则这个数是_______.
7、0)2(52=++-y x ,则______=-y x 8、混合计算
(1)2)5(95
59)81(-÷⨯÷-
(2)99)1()4(2
1
1683-÷-⨯-⨯-
(3)[]
224
)3(27
1
1--⨯--
(4)3
2692)2
11()3(3
2-÷-⨯--
(5)])3()2[()8
1
1(]812)3123(65[23-+---÷+--
÷
有理数的混合运算练习
(1))5.1()9()21(4-÷---⨯
(2)52)1()4(3992----+-
(3))2()3()3
2
()32(22
-⨯---÷-⨯-
(4)⎥⎦
⎤⎢⎣⎡-⨯---+-)3(2
)32(243)5(
(5)2232)64()2
1
()2()2(4---⨯---÷-
(6)224
5.04
1
])3(2[61)32
5.0()1(-----⨯÷---
有理数的混合预算强化练习
33514
(1)(8)(3)[(2)5]217
---⨯+-÷-+
32)1(}20)3
5
(])25()4.0()41(433{[-⨯--÷-⨯++-÷
)12
787431()87()87()12787431(--÷-+-÷--。
