2014年浙江省单考单招数学试卷高考卷含答案.
2014年浙江省高考数学试卷(理科)(附参考答案+详细解析Word打印版)

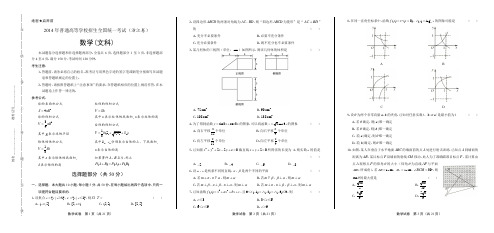
2014年浙江省普通高等学校招生统一考试数学试卷(理科)一、选择题(每小题5分,共50分)1.(5分)设全集U={x∈N|x≥2},集合A={x∈N|x2≥5},则∁U A=()A.∅B.{2}C.{5}D.{2,5}2.(5分)已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.(5分)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm24.(5分)为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位5.(5分)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f (3,0)+f(2,1)+f(1,2)+f(0,3)=()A.45 B.60 C.120 D.2106.(5分)已知函数f(x)=x3+ax2+bx+c.且0<f(﹣1)=f(﹣2)=f(﹣3)≤3,则()A.c≤3 B.3<c≤6 C.6<c≤9 D.c>97.(5分)在同一直角坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图象可能是()A.B.C.D.8.(5分)记max{x,y}=,min{x,y}=,设,为平面向量,则()A.min{|+|,|﹣|}≤min{||,||} B.min{|+|,|﹣|}≥min{||,||}C.max{|+|2,|﹣|2}≤||2+||2 D.max{|+|2,|﹣|2}≥||2+||2 9.(5分)已知甲盒中仅有1个球且为红球,乙盒中有m个红球和n个蓝球(m ≥3,n≥3),从乙盒中随机抽取i(i=1,2)个球放入甲盒中.(a)放入i个球后,甲盒中含有红球的个数记为ξi(i=1,2);(b)放入i个球后,从甲盒中取1个球是红球的概率记为p i(i=1,2).则()A.p1>p2,E(ξ1)<E(ξ2)B.p1<p2,E(ξ1)>E(ξ2)C.p1>p2,E(ξ1)>E(ξ2)D.p1<p2,E(ξ1)<E(ξ2)10.(5分)设函数f1(x)=x2,f2(x)=2(x﹣x2),,,i=0,1,2,…,99.记I k=|f k(a1)﹣f k(a0)|+|f k(a2)﹣f k(a1)丨+…+|f k(a99)﹣f k(a98)|,k=1,2,3,则()A.I1<I2<I3B.I2<I1<I3C.I1<I3<I2D.I3<I2<I1二、填空题11.(4分)在某程序框图如图所示,当输入50时,则该程序运算后输出的结果是.12.(4分)随机变量ξ的取值为0,1,2,若P(ξ=0)=,E(ξ)=1,则D(ξ)=.13.(4分)当实数x,y满足时,1≤ax+y≤4恒成立,则实数a的取值范围是.14.(4分)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有种(用数字作答).15.(4分)设函数f(x)=,若f(f(a))≤2,则实数a的取值范围是.16.(4分)设直线x﹣3y+m=0(m≠0)与双曲线=1(a>0,b>0)的两条渐近线分别交于点A,B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是.17.(4分)如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是.(仰角θ为直线AP与平面ABC所成角)三、解答题18.(14分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=,cos2A﹣cos2B=sinAcosA﹣sinBcosB(1)求角C的大小;(2)若sinA=,求△ABC的面积.19.(14分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.20.(15分)如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=.(Ⅰ)证明:DE⊥平面ACD;(Ⅱ)求二面角B﹣AD﹣E的大小.21.(15分)如图,设椭圆C:(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.(Ⅰ)已知直线l的斜率为k,用a,b,k表示点P的坐标;(Ⅱ)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a ﹣b.22.(14分)已知函数f(x)=x3+3|x﹣a|(a∈R).(Ⅰ)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M (a)﹣m(a);(Ⅱ)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.2014年浙江省高考数学试卷(理科)参考答案与试题解析一、选择题(每小题5分,共50分)1.(5分)设全集U={x∈N|x≥2},集合A={x∈N|x2≥5},则∁U A=()A.∅B.{2}C.{5}D.{2,5}【分析】先化简集合A,结合全集,求得∁U A.【解答】解:∵全集U={x∈N|x≥2},集合A={x∈N|x2≥5}={x∈N|x≥3},则∁U A={2},故选:B.【点评】本题主要考查全集、补集的定义,求集合的补集,属于基础题.2.(5分)已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】利用复数的运算性质,分别判断“a=b=1”⇒“(a+bi)2=2i”与“a=b=1”⇐“(a+bi)2=2i”的真假,进而根据充要条件的定义得到结论.【解答】解:当“a=b=1”时,“(a+bi)2=(1+i)2=2i”成立,故“a=b=1”是“(a+bi)2=2i”的充分条件;当“(a+bi)2=a2﹣b2+2abi=2i”时,“a=b=1”或“a=b=﹣1”,故“a=b=1”是“(a+bi)2=2i”的不必要条件;综上所述,“a=b=1”是“(a+bi)2=2i”的充分不必要条件;故选:A.【点评】本题考查的知识点是充要条件的定义,复数的运算,难度不大,属于基础题.3.(5分)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm2【分析】几何体是直三棱柱与直四棱柱的组合体,根据三视图判断直三棱柱的侧棱长与底面的形状及相关几何量的数据,判断四棱柱的高与底面矩形的边长,把数据代入表面积公式计算.【解答】解:由三视图知:几何体是直三棱柱与直四棱柱的组合体,其中直三棱柱的侧棱长为3,底面是直角边长分别为3、4的直角三角形,四棱柱的高为6,底面为矩形,矩形的两相邻边长为3和4,∴几何体的表面积S=2×4×6+3×6+3×3+2×3×4+2××3×4+(4+5)×3=48+18+9+24+12+27=138(cm2).故选:D.【点评】本题考查了由三视图求几何体的表面积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.4.(5分)为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位【分析】利用两角和与差的三角函数化简已知函数为一个角的一个三角函数的形式,然后利用平移原则判断选项即可.【解答】解:函数y=sin3x+cos3x=,故只需将函数y=cos3x的图象向右平移个单位,得到y==的图象.【点评】本题考查两角和与差的三角函数以及三角函数的平移变换的应用,基本知识的考查.5.(5分)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f (3,0)+f(2,1)+f(1,2)+f(0,3)=()A.45 B.60 C.120 D.210【分析】由题意依次求出x3y0,x2y1,x1y2,x0y3,项的系数,求和即可.【解答】解:(1+x)6(1+y)4的展开式中,含x3y0的系数是:=20.f(3,0)=20;含x2y1的系数是=60,f(2,1)=60;含x1y2的系数是=36,f(1,2)=36;含x0y3的系数是=4,f(0,3)=4;∴f(3,0)+f(2,1)+f(1,2)+f(0,3)=120.故选:C.【点评】本题考查二项式定理系数的性质,二项式定理的应用,考查计算能力.6.(5分)已知函数f(x)=x3+ax2+bx+c.且0<f(﹣1)=f(﹣2)=f(﹣3)≤3,则()A.c≤3 B.3<c≤6 C.6<c≤9 D.c>9【分析】由f(﹣1)=f(﹣2)=f(﹣3)列出方程组求出a,b,代入0<f(﹣1)≤3,即可求出c的范围.【解答】解:由f(﹣1)=f(﹣2)=f(﹣3)得,解得,则f(x)=x3+6x2+11x+c,由0<f(﹣1)≤3,得0<﹣1+6﹣11+c≤3,故选:C.【点评】本题考查方程组的解法及不等式的解法,属于基础题.7.(5分)在同一直角坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图象可能是()A.B.C.D.【分析】结合对数函数和幂函数的图象和性质,分当0<a<1时和当a>1时两种情况,讨论函数f(x)=x a(x≥0),g(x)=log a x的图象,比照后可得答案.【解答】解:当0<a<1时,函数f(x)=x a(x≥0),g(x)=log a x的图象为:此时答案D满足要求,当a>1时,函数f(x)=x a(x≥0),g(x)=log a x的图象为:无满足要求的答案,综上:故选D,故选:D.【点评】本题考查的知识点是函数的图象,熟练掌握对数函数和幂函数的图象和性质,是解答的关键.8.(5分)记max{x,y}=,min{x,y}=,设,为平面向量,则()A.min{|+|,|﹣|}≤min{||,||} B.min{|+|,|﹣|}≥min{||,||}C.max{|+|2,|﹣|2}≤||2+||2 D.max{|+|2,|﹣|2}≥||2+||2【分析】将,平移到同一起点,根据向量加减法的几何意义可知,+和﹣分别表示以,为邻边所做平行四边形的两条对角线,再根据选项内容逐一判断.【解答】解:对于选项A,取⊥,则由图形可知,根据勾股定理,结论不成立;对于选项B,取,是非零的相等向量,则不等式左边min{|+|,|﹣|}=0,显然,不等式不成立;对于选项C,取,是非零的相等向量,则不等式左边max{|+|2,|﹣|2}=|+|2=4,而不等式右边=||2+||2=2,故C不成立,D选项正确.故选:D.【点评】本题在处理时要结合着向量加减法的几何意义,将,,,放在同一个平行四边形中进行比较判断,在具体解题时,本题采用了排除法,对错误选项进行举反例说明,这是高考中做选择题的常用方法,也不失为一种快速有效的方法,在高考选择题的处理上,未必每一题都要写出具体解答步骤,针对选择题的特点,有时“排除法”,“确定法”,“特殊值”代入法等也许是一种更快速,更有效的方法.9.(5分)已知甲盒中仅有1个球且为红球,乙盒中有m个红球和n个蓝球(m ≥3,n≥3),从乙盒中随机抽取i(i=1,2)个球放入甲盒中.(a)放入i个球后,甲盒中含有红球的个数记为ξi(i=1,2);(b)放入i个球后,从甲盒中取1个球是红球的概率记为p i(i=1,2).则()A.p1>p2,E(ξ1)<E(ξ2)B.p1<p2,E(ξ1)>E(ξ2)C.p1>p2,E(ξ1)>E(ξ2)D.p1<p2,E(ξ1)<E(ξ2)【分析】首先,这两次先后从甲盒和乙盒中拿球是相互独立的,然后分两种情况:即当ξ=1时,有可能从乙盒中拿出一个红球放入甲盒,也可能是拿到一个蓝球放入甲盒;ξ=2时,则从乙盒中拿出放入甲盒的球可能是两蓝球、一红一蓝、或者两红;最后利用概率公式及分布列知识求出P1,P2和E(ξ1),E(ξ2)进行比较即可.【解答】解析:,,,所以P1>P2;由已知ξ1的取值为1、2,ξ2的取值为1、2、3,所以,==,E(ξ1)﹣E(ξ2)=.故选:A.【点评】正确理解ξi(i=1,2)的含义是解决本题的关键.此题也可以采用特殊值法,不妨令m=n=3,也可以很快求解.10.(5分)设函数f1(x)=x2,f2(x)=2(x﹣x2),,,i=0,1,2,…,99.记I k=|f k(a1)﹣f k(a0)|+|f k(a2)﹣f k(a1)丨+…+|f k(a99)﹣f k(a98)|,k=1,2,3,则()A.I1<I2<I3B.I2<I1<I3C.I1<I3<I2D.I3<I2<I1【分析】根据记I k=|f k(a1)﹣f k(a0)|+|f k(a2)﹣f k(a1)丨+…+|f k(a99)﹣f k (a98)|,分别求出I1,I2,I3与1的关系,继而得到答案【解答】解:由,故==1,由,故×=×<1,+=,故I2<I1<I3,故选:B.【点评】本题主要考查了函数的性质,关键是求出这三个数与1的关系,属于难题.二、填空题11.(4分)在某程序框图如图所示,当输入50时,则该程序运算后输出的结果是6.【分析】根据框图的流程模拟运行程序,直到满足条件S>50,跳出循环体,确定输出的i的值.【解答】解:由程序框图知:第一次循环S=1,i=2;第二次循环S=2×1+2=4,i=3;第三次循环S=2×4+3=11,i=4;第四次循环S=2×11+4=26,i=5;第五次循环S=2×26+5=57,i=6,满足条件S>50,跳出循环体,输出i=6.故答案为:6.【点评】本题考查了直到型循环结构的程序框图,根据框图的流程模拟运行程序是解答此类问题的常用方法.12.(4分)随机变量ξ的取值为0,1,2,若P(ξ=0)=,E(ξ)=1,则D(ξ)=.【分析】结合方差的计算公式可知,应先求出P(ξ=1),P(ξ=2),根据已知条件结合分布列的性质和期望的计算公式不难求得.【解答】解析:设P(ξ=1)=p,P(ξ=2)=q,则由已知得p+q=,,解得,,所以.故答案为:【点评】本题综合考查了分布列的性质以及期望、方差的计算公式.13.(4分)当实数x,y满足时,1≤ax+y≤4恒成立,则实数a的取值范围是[] .【分析】由约束条件作出可行域,再由1≤ax+y≤4恒成立,结合可行域内特殊点A,B,C的坐标满足不等式列不等式组,求解不等式组得实数a的取值范围.【解答】解:由约束条件作可行域如图,联立,解得C(1,).联立,解得B(2,1).在x﹣y﹣1=0中取y=0得A(1,0).要使1≤ax+y≤4恒成立,则,解得:1.∴实数a的取值范围是.解法二:令z=ax+y,当a>0时,y=﹣ax+z,在B点取得最大值,A点取得最小值,可得,即1≤a≤;当a<0时,y=﹣ax+z,在C点取得最大值,①a<﹣1时,在B点取得最小值,可得,解得0≤a≤(不符合条件,舍去)②﹣1<a<0时,在A点取得最小值,可得,解得1≤a≤(不符合条件,舍去)综上所述即:1≤a≤;故答案为:.【点评】本题考查线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,训练了不等式组得解法,是中档题.14.(4分)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有60种(用数字作答).【分析】分类讨论,一、二、三等奖,三个人获得;一、二、三等奖,有1人获得2张,1人获得1张.【解答】解:分类讨论,一、二、三等奖,三个人获得,共有=24种;一、二、三等奖,有1人获得2张,1人获得1张,共有=36种,共有24+36=60种.故答案为:60.【点评】本题考查排列、组合及简单计数问题,考查学生的计算能力,属于基础题.15.(4分)设函数f(x)=,若f(f(a))≤2,则实数a的取值范围是(﹣∞,] .【分析】画出函数f(x)的图象,由f(f(a))≤2,可得f(a)≥﹣2,数形结合求得实数a的取值范围.【解答】解:∵函数f(x)=,它的图象如图所示:由f(f(a))≤2,可得f(a)≥﹣2.当a<0时,f(a)=a2+a=(a+)2﹣≥﹣2恒成立;当a≥0时,f(a)=﹣a2≥﹣2,即a2≤2,解得0≤a≤,则实数a的取值范围是a≤,故答案为:(﹣∞,].【点评】本题主要考查分段函数的应用,其它不等式的解法,体现了数形结合的数学思想,属于中档题.16.(4分)设直线x﹣3y+m=0(m≠0)与双曲线=1(a>0,b>0)的两条渐近线分别交于点A,B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是.【分析】先求出A,B的坐标,可得AB中点坐标为(,),利用点P(m,0)满足|PA|=|PB|,可得=﹣3,从而可求双曲线的离心率.【解答】解:双曲线(a>0,b>0)的两条渐近线方程为y=±x,则与直线x﹣3y+m=0联立,可得A(,),B(﹣,),∴AB中点坐标为(,),∵点P(m,0)满足|PA|=|PB|,∴=﹣3,∴a=2b,∴=b,∴e==.故答案为:.【点评】本题考查双曲线的离心率,考查直线的位置关系,考查学生的计算能力,属于中档题.17.(4分)如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是.(仰角θ为直线AP与平面ABC所成角)【分析】过P作PP′⊥BC,交BC于P′,连接AP′,则tanθ=,求出PP′,AP′,利用函数的性质,分类讨论,即可得出结论.【解答】解:∵AB=15m,AC=25m,∠ABC=90°,∴BC=20m,过P作PP′⊥BC,交BC于P′,连接AP′,则tanθ=,设B P′=x,则CP′=20﹣x,由∠BCM=30°,得PP′=CP′tan30°=(20﹣x),在直角△ABP′中,AP′=,∴tanθ=•,令y=,则函数在x∈[0,20]单调递减,∴x=0时,取得最大值为=.若P′在CB的延长线上,PP′=CP′tan30°=(20+x),在直角△ABP′中,AP′=,∴tanθ=•,令y=,则y′=0可得x=时,函数取得最大值,故答案为:.【点评】本题考查利用数学知识解决实际问题,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.三、解答题18.(14分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=,cos2A﹣cos2B=sinAcosA﹣sinBcosB(1)求角C的大小;(2)若sinA=,求△ABC的面积.【分析】(1)利用倍角公式、两角和差的正弦公式可得,由a≠b得,A≠B,又A+B∈(0,π),可得,即可得出.(2)利用正弦定理可得a,利用两角和差的正弦公式可得sinB,再利用三角形的面积计算公式即可得出.【解答】解:(1)由题意得,,∴,化为,由a≠b得,A≠B,又A+B∈(0,π),得,即,∴;(2)由,利用正弦定理可得,得,由a<c,得A<C,从而,故,∴.【点评】本题考查了正弦定理、倍角公式、两角和差的正弦公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.19.(14分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列,且a1=2,b3=6+b2.(Ⅰ)求a n和b n;(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n;(ii)求正整数k,使得对任意n∈N*均有S k≥S n.【分析】(Ⅰ)先利用前n项积与前(n﹣1)项积的关系,得到等比数列{a n}的第三项的值,结合首项的值,求出通项a n,然后现利用条件求出通项b n;(Ⅱ)(i)利用数列特征进行分组求和,一组用等比数列求和公式,另一组用裂项法求和,得出本小题结论;(ii)本小题可以采用猜想的方法,得到结论,再加以证明.【解答】解:(Ⅰ)∵a1a2a3…a n=(n∈N*)①,当n≥2,n∈N*时,②,由①②知:,令n=3,则有.∵b3=6+b2,∴a3=8.∵{a n}为等比数列,且a1=2,∴{a n}的公比为q,则=4,,∴q>0,∴q=2.由题意知a n>0∴(n∈N*).又由a1a2a3…a n=(n∈N*)得:,,∴b n=n(n+1)(n∈N*).(Ⅱ)(i)∵c n===.∴S n=c1+c2+c3+…+c n====;(ii)因为c1=0,c2>0,c3>0,c4>0;当n≥5时,,而=>0,得,所以,当n≥5时,c n<0,综上,对任意n∈N*恒有S4≥S n,故k=4.【点评】本题考查了等比数列通项公式、求和公式,还考查了分组求和法、裂项求和法和猜想证明的思想,证明可以用二项式定理,还可以用数学归纳法.本题计算量较大,思维层次高,要求学生有较高的分析问题解决问题的能力.本题属于难题.20.(15分)如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=.(Ⅰ)证明:DE⊥平面ACD;(Ⅱ)求二面角B﹣AD﹣E的大小.【分析】(Ⅰ)依题意,易证AC⊥平面BCDE,于是可得AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;(Ⅱ)作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG,由(Ⅰ)知DE⊥AD,则FG⊥AD,所以∠BFG就是二面角B﹣AD﹣E的平面角,利用题中的数据,解三角形,可求得BF=,AF=AD,从而GF=,cos∠BFG==,从而可求得答案.【解答】证明:(Ⅰ)在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=,由AC=,AB=2得AB2=AC2+BC2,即AC⊥BC,又平面ABC⊥平面BCDE,从而AC⊥平面BCDE,所以AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;(Ⅱ)作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG,由(Ⅰ)知DE⊥AD,则FG⊥AD,所以∠BFG就是二面角B﹣AD﹣E的平面角,在直角梯形BCDE中,由CD2=BC2+BD2,得BD⊥BC,又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而BD⊥AB,由于AC⊥平面BCDE,得AC⊥CD.在Rt△ACD中,由DC=2,AC=,得AD=;在Rt△AED中,由ED=1,AD=得AE=;在Rt△ABD中,由BD=,AB=2,AD=得BF=,AF=AD,从而GF=,在△ABE,△ABG中,利用余弦定理分别可得cos∠BAE=,BG=.在△BFG中,cos∠BFG==,所以,∠BFG=,二面角B﹣AD﹣E的大小为.【点评】本题主要考查空间点、线、面位置关系,二面角等基础知识,同时考查空间想象能力,推理论证能力和运算求解能力.21.(15分)如图,设椭圆C:(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.(Ⅰ)已知直线l的斜率为k,用a,b,k表示点P的坐标;(Ⅱ)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a ﹣b.【分析】(Ⅰ)设直线l的方程为y=kx+m(k<0),由,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,利用△=0,可求得在第一象限中点P的坐标;(Ⅱ)由于直线l1过原点O且与直线l垂直,设直线l1的方程为x+ky=0,利用点到直线间的距离公式,可求得点P到直线l1的距离d=,整理即可证得点P到直线l1的距离的最大值为a﹣b..【解答】解:(Ⅰ)设直线l的方程为y=kx+m(k<0),由,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0.由于直线l与椭圆C只有一个公共点P,故△=0,即b2﹣m2+a2k2=0,此时点P的横坐标为﹣,代入y=kx+m得点P的纵坐标为﹣k•+m=,∴点P的坐标为(﹣,),又点P在第一象限,故m>0,故m=,故点P的坐标为P(,).(Ⅱ)由于直线l1过原点O且与直线l垂直,故直线l1的方程为x+ky=0,所以点P到直线l1的距离d=,整理得:d=,因为a2k2+≥2ab,所以≤=a﹣b,当且仅当k2=时等号成立.所以,点P到直线l1的距离的最大值为a﹣b.【点评】本题主要考查椭圆的几何性质、点到直线间的距离、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法、基本不等式应用等综合解题能力.22.(14分)已知函数f(x)=x3+3|x﹣a|(a∈R).(Ⅰ)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M (a)﹣m(a);(Ⅱ)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.【分析】(Ⅰ)利用分段函数,结合[﹣1,1],分类讨论,即可求M(a)﹣m(a);(Ⅱ)令h(x)=f(x)+b,则h(x)=,h′(x)=,则[f(x)+b]2≤4对x∈[﹣1,1]恒成立,转化为﹣2≤h(x)≤2对x∈[﹣1,1]恒成立,分类讨论,即可求3a+b的取值范围.【解答】解:(Ⅰ)∵f(x)=x3+3|x﹣a|=,∴f′(x)=,①a≤﹣1时,∵﹣1≤x≤1,∴x≥a,f(x)在(﹣1,1)上是增函数,∴M(a)=f(1)=4﹣3a,m(a)=f(﹣1)=﹣4﹣3a,∴M(a)﹣m(a)=8;②﹣1<a<1时,x∈(a,1),f(x)=x3+3x﹣3a,在(a,1)上是增函数;x∈(﹣1,a),f(x)=x3﹣3x+3a,在(﹣1,a)上是减函数,∴M(a)=max{f(1),f(﹣1)},m(a)=f(a)=a3,∵f(1)﹣f(﹣1)=﹣6a+2,∴﹣1<a≤时,M(a)﹣m(a)=﹣a3﹣3a+4;<a<1时,M(a)﹣m(a)=﹣a3+3a+2;③a≥1时,有x≤a,f(x)在(﹣1,1)上是减函数,∴M(a)=f(﹣1)=2+3a,m(a)=f(1)=﹣2+3a,∴M(a)﹣m(a)=4;(Ⅱ)令h(x)=f(x)+b,则h(x)=,h′(x)=,∵[f(x)+b]2≤4对x∈[﹣1,1]恒成立,∴﹣2≤h(x)≤2对x∈[﹣1,1]恒成立,由(Ⅰ)知,①a≤﹣1时,h(x)在(﹣1,1)上是增函数,最大值h(1)=4﹣3a+b,最小值h(﹣1)=﹣4﹣3a+b,则﹣4﹣3a+b≥﹣2且4﹣3a+b≤2矛盾;②﹣1<a≤时,最小值h(a)=a3+b,最大值h(1)=4﹣3a+b,∴a3+b≥﹣2且4﹣3a+b≤2,令t(a)=﹣2﹣a3+3a,则t′(a)=3﹣3a2>0,t(a)在(0,)上是增函数,∴t(a)>t(0)=﹣2,∴﹣2≤3a+b≤0;③<a<1时,最小值h(a)=a3+b,最大值h(﹣1)=3a+b+2,则a3+b≥﹣2且3a+b+2≤2,∴﹣<3a+b≤0;④a≥1时,最大值h(﹣1)=3a+b+2,最小值h(1)=3a+b﹣2,则3a+b﹣2≥﹣2且3a+b+2≤2,∴3a+b=0.综上,3a+b的取值范围是﹣2≤3a+b≤0.【点评】本题考查导数的综合运用,考查函数的最值,考查分类讨论、化归与转化的数学思想,难度大.。
2014高考数学浙江卷

2014年普通高等学校招生全国统一考试(浙江卷)数学(理科)一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则=A C UA.∅B.{}2C.{}5D.{}5,2 2. 已知i 是虚数单位,R b a ∈,,则“1==b a ”是“()i bi a 22=+”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 3. 某几何体的三视图(单位:cm )如图所示,则此几何体的表面积是 A.290cm B.2129cm C.2132cm D.2138cm 4. 为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D..向左平移12π个单位5. 在()()4611y x ++的展开式中,记nm y x 项的系数为()n m f ,,则()()()()=+++3,02,11,20,3f f f fA.45B.60C.120D. 210 6. 已知函数()c bx ax x x f +++=23,且()()()33210≤-=-=-≤f f f ,则A.3≤cB.63≤<cC.96≤<cD.9>c 7. 在同一直角坐标系中,函数()()0≥=x x x f a,()x x g a log =的图像可能是A. B. C. D.(第3题图)8. 记{}⎩⎨⎧<≥=y x y y x x y x ,,,max ,{}⎩⎨⎧<≥=yx x y x y y x ,,,min ,设b a,为平面向量,则A.{}{}b a b a b a ,min ,min ≤-+ B.{}{}b a b a b a ,min ,min ≥-+ C.{}2222,max b aba b a +≤-+ D.{}2222,max b a b a b a +≥-+9. 已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个蓝球()3,3≥≥n m ,从乙盒中随机 抽取()2,1=i i 个球放入甲盒中.(a )放入i 个球后,甲盒中含有红球的个数记为()2,1=i i ξ; (b )放入i 个球后,从甲盒中取1个球是红球的概率记为()2,1=i p i . 则A.()()2121,ξξE E p p <>B.()()2121,ξξE E p p ><C.()()2121,ξξE E p p >>D.()()2121,ξξE E p p << 10. 设函数()21x x f =,()()222x x x f -=,()x x f π2sin 313=,99,,2,1,0,99==i ia i . 记()()()()()()3,2,1,9899101=-++-+-=k a f a f a f a f a f a f I k k k k k k k 2. 则A.321I I I <<B.312I I I <<C.231I I I <<D.123I I I <<二、填空题:本大题共7小题,每小题4分,共28分。
2014年普通高等学校招生全国统一考试(浙江卷)数学(文)试卷及解析

22.本题主要考查抛物线几何性质、直线与抛物线的 位置关系、三角形面积公式、平面向量等基础知识,同时考查解析几何的基本思想方法和运算求解能力。满分14分。
(1)由题意知,焦点为 ,准线方程为 ,
设 ,由抛物线的定义知, ,得到 ,
代入 求得 或 ,
所以 或 ,由 得 或 ,
(2)设直线 的方程为 , , , ,
(1)因为 ,
①当 时,
若 ,则 , ,故 在 上是减函数;
若 ,则 , ,故 在 上是增函数;
所以, .
②当 ,则 , , ,故 在 上是减函数,
所以 ,
综上所述, .
(2)令 ,
①当 时, ,
若 , 得 ,所以 在 上是增函数,所以 在 上的最大值是 ,且 ,所以 ,
故 .
若 , ,则 ,所以 在 上是减函数,
14.在三张奖劵中有一、二等各一张,另有一张无奖,甲乙两人各抽取一张,两人都中奖的概率为
.
15.设函数 ,若 ,则 .
16.已知实数 、 、 满足 , ,则 的最大值为为_______.
17. 设直线 与双曲线 的两条渐近线分别交于 、 ,若 满足 ,则双曲线的离心率是.
三.解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
(1)连结 ,在直角梯形 中,由 , 得 ,
由 得 ,即 ,
又平面 平面 ,从而 平面 .
(2)在直角梯形 中,由 , 得 ,
又平面 平面 ,所以 平面 .
作 于 的延长线交于 ,连结 ,则 平面 ,
所以 是直线 与平面 所成的角.
在 中,由 , ,得 , ,
在 中, , ,得 ,
在 中,由 , 得 ,
2014高考数学浙江卷

2014年普通高等学校招生全国统一考试(浙江卷)数学(理科)一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则=A C UA.∅B.{}2C.{}5D.{}5,2 2. 已知i 是虚数单位,R b a ∈,,则“1==b a ”是“()i bi a 22=+”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 3. 某几何体的三视图(单位:cm )如图所示,则此几何体的表面积是 A.290cm B.2129cm C.2132cm D.2138cm 4. 为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D..向左平移12π个单位5. 在()()4611y x ++的展开式中,记nmy x 项的系数为()n m f ,,则()()()()=+++3,02,11,20,3f f f fA.45B.60C.120D. 210 6. 已知函数()c bx ax x x f +++=23,且()()()33210≤-=-=-≤f f f ,则A.3≤cB.63≤<cC.96≤<cD.9>c 7. 在同一直角坐标系中,函数()()0≥=x x x f a,()x x g a log =的图像可能是A. B. C. D.(第3题图)8. 记{}⎩⎨⎧<≥=y x y y x x y x ,,,max ,{}⎩⎨⎧<≥=yx x y x y y x ,,,min ,设b a,为平面向量,则A.{}{}b a b a b a ,min ,min ≤-+ B.{}{}b a b a b a ,min ,min ≥-+ C.{}2222,max b aba b a +≤-+ D.{}2222,max b aba b a +≥-+9. 已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个蓝球()3,3≥≥n m ,从乙盒中随机 抽取()2,1=i i 个球放入甲盒中.(a )放入i 个球后,甲盒中含有红球的个数记为()2,1=i i ξ; (b )放入i 个球后,从甲盒中取1个球是红球的概率记为()2,1=i p i . 则A.()()2121,ξξE E p p <>B.()()2121,ξξE E p p ><C.()()2121,ξξE E p p >>D.()()2121,ξξE E p p <<10. 设函数()21x x f =,()()222x x x f -=,()x x f π2sin 313=,99,,2,1,0,99==i ia i . 记()()()()()()3,2,1,9899101=-++-+-=k a f a f a f a f a f a f I k k k k k k k 2. 则A.321I I I <<B.312I I I <<C.231I I I <<D.123I I I <<二、填空题:本大题共7小题,每小题4分,共28分。
2014年高考文科数学浙江卷(含详细答案)
数学试卷 第1页(共21页) 数学试卷 第2页(共21页) 数学试卷 第3页(共21页)绝密★启用前2014年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分.全卷共6页,选择题部分1至3页,非选择题部分4至6页.满分150分,考试时间120分钟. 考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上作答一律无效. 参考公式:球的表面积公式 柱体的体积公式24πS R =V Sh =球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高 33π4V R =台体的体积公式其中R 表示球的半径121(S )3V h S =锥体的体积公式其中1S ,2S 分别表示台体的上、下底面积,13V Sh =h 表示台体的高其中S 表示锥体的底面积,如果事件A ,B 互斥,那么 h 表示锥体的高()()()P A B P A P B +=+选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|2}S x x =≥,{|5}T x x =≤,则S T =( )A .(,5]-∞B .[2,)+∞C .(2,5)D .[2,5]2.设四边形ABCD 的两条对角线为AC ,BD ,则“四边形ABCD 为菱形”是“AC BD ⊥”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .372cmB .390cmC .3108cmD .3138cm4.为了得到函数sin3cos3y x x =+的图象,可以将函数y x 的图象( )A .向右平移π12个单位B .向右平移π4个单位C .向左平移π12个单位D .向左平移π4个单位5.已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是( )A .2-B .4-C .6-D .8- 6.设m ,n 是两条不同的直线,α,β是两个不同的平面( )A .若m n ⊥,nα,则m α⊥B .若m β,βα⊥,则m α⊥C .若m β⊥,n β⊥,n α⊥,则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥7.已知函数32()f x x ax bx c =+++,且0(1)(2)(3)3f f f -=-=-<≤,则( )A .3c ≤B .36c <≤C .69c <≤D .9c >8.在同一直角坐标系中,函数()(0)a f x x x =>,()log a g x x =的图象可能是( )ABCD9.设θ为两个非零向量a ,b 的夹角.已知对任意实数t ,|b t +a |是最小值为1 ( )A .若θ确定,则| a |唯一确定B .若θ确定,则| b |唯一确定C .若| a |确定,则θ唯一确定D .若| b |确定,则θ唯一确定10.如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15m AB =,25m AC =,30BCM ∠=,则tan θ的最大值是 ( )ABCD-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共21页) 数学试卷 第5页(共21页) 数学试卷 第6页(共21页)非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.已知i 是虚数单位,计算21i(1i)-=+ . 12.若实数x ,y 满足240,10,1,x y x y x +-⎧⎪--⎨⎪⎩≤≤≥则x y +的取值范围是 .13.若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是 .14.在3张奖券中有一、二等奖各1张,另1张无奖.甲、乙两人各抽取1张,两人都中奖的概率是 .15.设函数2222, 0,(), 0,x x x f x x x ⎧++⎪=⎨-⎪⎩≤>若(())2f f a =,则a = .16.已知实数a ,b ,c 满足0a b c ++=,2221a b c ++=,则a 的最大值是 .17.设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b -=>>的两条渐近线分别交于点A ,B .若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是 .三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c .已知24sin 4sin sin 2A BA B -+2=(Ⅰ)求角C 的大小;(Ⅱ)已知4b =,ABC △的面积为6,求边长c 的值.19.(本题满分14分)已知等差数列{}n a 的公差0d >,设{}n a 的前n 项和为n S ,2336S S =. (Ⅰ)求d 及n S ;(Ⅱ)求m ,k (*,m k ∈Ν)的值,使得1265m m m m k a a a a +++++++=.20.(本题满分15分)如图,在四棱锥A BCDE -中,平面ABC ⊥平面B C D E ,90CDE BED ∠=∠=,2AB CD ==,1DE BE ==,AC =(Ⅰ)证明:AC ⊥平面BCDE ;(Ⅱ)求直线AE 与平面ABC 所成角的正切值.21.(本题满分15分)已知函数3()3||(0)f x x x a a =+->.若()f x 在[]1,1-上的最小值记为()g a . (Ⅰ)求()g a ;(Ⅱ)证明:当[]1,1x ∈-时,恒有()()4f x g x +≤.22.(本题满分14分)已知ABP △的三个顶点在抛物线C :24x y =上,F 为抛物线C 的焦点,点M 为AB 的中点,3PF FM =.(Ⅰ)若||3PF =,求点M 的坐标; (Ⅱ)求ABP △面积的最大值.AD EBC数学试卷 第7页(共21页) 数学试卷 第8页(共21页) 数学试卷 第9页(共21页)[2,5]S T =||1b at +≥恒成立,所以22)2||||cos 1ta b t a b θ++≥恒成立,若||b 为定值时二次函,||1b at +≥恒成立,所以22()2||||cos 1ta b t a b θ++≥恒成立,【考点】平面向量数量积的运算,零向量,数量积表示两个向量的夹角 2320225m m-+的长,利用勾股定理求出数学试卷 第10页(共21页) 数学试卷 第11页(共21页) 数学试卷 第12页(共21页)故的取值范围是[1,3].中,24sin 2A -1cos(A 42--2=,即2,C ∠=cos 18ab C =ABC 中由条件利用二倍角的余弦公式、数学试卷 第13页(共21页) 数学试卷 第14页(共21页) 数学试卷 第15页(共21页)cos ab C 的值2336S =得,所以1n S na =265m k a +=265m k a +=.CDE ∠=2在ACB △中,22AB BC AC ===,,BC AC AB AC BC ∴+=∴⊥,.又平面ABC ⊥平面BCDE ,AC BCDE ∴⊥平面.(Ⅰ)0a >,-,若[x ∈﹣3a ,()f x '数学试卷 第16页(共21页) 数学试卷 第17页(共21页) 数学试卷 第18页(共21页)由3P F F M =,得M 0=,于是16∆=由3PF FM =,得(-又2241AB k k m =++,点F 到直线2481||ABP ABF S S m k m ==+=△△﹣,于是(m)f 在⎛ ⎝数学试卷 第19页(共21页) 数学试卷 第20页(共21页) 数学试卷 第21页(共21页)PBA M FyxO。
2014年高考数学浙江卷(理科)答案word版

2014年普通高等学校招生全国统一考试(浙江卷)理科数学试题答案与解析1. 解析 因为{}{}5A x x x x =∈=∈N N 厖3,所以{}{}2232U a A x x =∈<=N …ð,故选B.2. 解析 当1a b ==时,有()21i 2i +=,即充分性成立.当()2i 2i a b +=时,有222i 2i a b ab -+=,得220,1,a b ab ⎧-=⎨=⎩解得1a b ==或1a b ==-,即必要性不成立,故选A.评注 本题考查复数的运算,复数相等的概念,充分条件与必要条件的判定,属于容易题. 3. 解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为()2135243433324324636138cm 2S =⨯+⨯⨯⨯+⨯+⨯+⨯⨯+⨯⨯+⨯=.评注 本题考查三视图的概念和性质,空间几何体的直观图和表面积的计算,考查运算求解能力和空间想象能力.由三视图得几何体的直观图是解题的关键.4. 解析因为πsin3cos334y x x x ⎛⎫=+=- ⎪⎝⎭,要得到函数π34y x ⎛⎫=- ⎪⎝⎭的图像,可以将函数y x =的图像向右平移π12个单位,故选C. 5. 解析 在的展开式中,的系数为,在的展开式中,的系数为,故.从而,,,,故选C.6. 解析 由得解得则有,由得.33434()61x +m x 6C m()41y +n y 4C n ()64,C C mnf m n =⋅()363,0C 20f ==()21642,1C C 60f =⋅=()12641,2C C 36f =⋅=()340,3C 4f ==()()()()12,13f f f f -=-⎧⎪⎨-=-⎪⎩37,413,a b a b -=⎧⎨-=⎩6,11.a b =⎧⎨=⎩()()12f f -=-=()3f -6c =-()013,f <-…69c <…7. 解析 因为0a >,所以()a f x x =在()0,+∞上为增函数,故A 错.在B 中,由()f x 的图像知1a >,由()g x 的图像知01a <<,矛盾,故B 错.在C 中,由()f x 的图像知01a <<,由()g x 的图像知1a >,矛盾,故C 错.在D 中,由()f x 的图像知01a <<,由()g x 的图像知01a <<,相符,故选D.评注 本题考查幂函数和对数函数的图像与单调性,考查分类讨论思想和逻辑推理能力. 8. 解析 在A 中,取()1,0=a ,0=b ,则{}min ,1+-=a b a b ,而{}min ,0=a b ,不符合,即A 错.在B 中,设0=≠a b ,则{}mi n ,0+-=a b a b ,而{}mi n ,0=>a b a 不符合,即B 错.因为2222+=++⋅a b a b a b ,2222-=+-⋅a b a b a b <,则当0⋅a b …,时{}222222max ,2+-=++⋅+a b a b a b a b a b ?;当0⋅<a b <时{}222222max ,2+-=+-⋅+a b a b a b a b a b ?即总有{}2222max ,+-+a b a ba b ….故选D.9. 解析 当1i =时,若从乙盒中抽取的1个球为红球,记从甲盒中取1个球是红球的事件为1A ,则()1mP A m n=+.若从乙盒中抽取的1个球为蓝球,记从甲盒中取1个球是红球的事件为2A ,则()()2122m n P A m n m n =⨯=++,而1A 与2A 互斥, 则()()()()1121222n m p P A A P A P A m n +=+=+=+.此时,1ξ的取值为1或2,()11nP m nξ==+,()12m P m n ξ==+,则()1212n m n mE m n m n m nξ+=⨯+⨯=+++.当2i =时,若从乙盒中抽取的2个球为红球,记从甲盒中取1个球是红球的事件为1B ,则()212C C m m nP B +=. 若从乙盒中抽取的2个球为1个红球和1个蓝球,记从甲盒中取1个球是红球的事件为2B ,则()1122C C 23C m nm nP B +=⨯. 若从乙盒中抽取的2个球都是蓝球,记从甲盒中取1个球是红球的事件为3B ,则()232C 13C n m nP B +=⨯.因为1B ,2B ,3B 互斥,则()()()()()221123212312322C 3C 2C C C 13C 3C n m m n nm n m nP B p P B B B P B P B P B ++++=⨯=++=++==()()()()()()()2231334331313n m m n m m mn n n n mm n m n m n m n m n ++--++-+==++-++-+.则()1206n p p m n -=>+, 即有12p p >.此时,2ξ的取值为1,2,3,则()222C 1C n m n P ξ+==,()1122C C 2C m nm nP ξ+==,()222C 3C mm nP ξ+==则()21122112222222C C C C C 2C C 3C 1233C C C C n m n m n m n mm n m n m n m nE p ξ++++++=⨯+⨯+⨯===3n mn m++,则有()()12E E ξξ<,综上,12p p >,()()12E E ξξ<,故选A.10. 解析 []0,1i a ∈ ,且0199a a a <<<,而()1f x 在[]0,1上为增函数,故有()()()1011199f a f a f a <<<,则()()()()111101211I f a f a f a f a =⎡-⎤+⎡-⎤++⎣⎦⎣⎦()()()()()()1991981991011101f a f a f a f a f f ⎡-⎤=-=-=⎣⎦. ()2f x 在10,2⎡⎤⎢⎥⎣⎦上为增函数,在1,12⎡⎤⎢⎥⎣⎦上为减函数,而495012a a <<,且49501a a +=,即有()()249250f a f a =,故()()()()()()22120250249250251I f a f a f a f a f a f a =⎡-⎤++⎡-⎤+⎡-⎤++⎣⎦⎣⎦⎣⎦()()()()()()29829925020250299f a f a f a f a f a f a ⎡-⎤=-+-=⎣⎦()()2225020199f f f ⎛⎫--= ⎪⎝⎭()224950*********,199999999⨯⨯⨯==-∈. ()3f x 在10,4⎡⎤⎢⎥⎣⎦上为增函数,在11,42⎡⎤⎢⎥⎣⎦上为减函数,在13,24⎡⎤⎢⎥⎣⎦上为增函数,在3,14⎡⎤⎢⎥⎣⎦上为减函数,即()3f x 在[]024,a a 上为增函数,在[]2549,a a 上为减函数. 在[]5074,a a 上为增函数,在[]7599,a a 上为减函数.又()324148148sin πsin π399399f a =⋅=,()325150149sin πsin π399399f a =⋅=,则()()()3253243491981πsin πsin 399399f a f a f a >=⋅=,()35011001πsinπsin 399399f a =⋅=,即有()()349350f a f a =. ()3741148149sin πsin π399399f a =⋅=,()()3753741150151148πsin πsin π=sin 399399399f a f a =⋅=<.故有()()()()3031324325f a f a f a f a <<<<,()()()()325326349350f a f a f a f a >>>=,()()()350351374f a f a f a <<<,()()()374375399f a f a f a >>>.从而3I =()()()(){}()()()(){}3130325324325326349350fa f a f a f a f afa fa fa ⎡-⎤++⎡-⎤+⎡-⎤++⎡-⎤+⎣⎦⎣⎦⎣⎦⎣⎦ ()()()(){}374375398399fa f a f a f a ⎡-⎤++⎡-⎤=⎣⎦⎣⎦()()()()()()()()32530325350374350374399f a f a f a f a f a f a f a f a ⎡-⎤+⎡-⎤+⎡-⎤+⎡-⎤=⎣⎦⎣⎦⎣⎦⎣⎦()()()()()3253503743039923f a f a f a f a f a -+--=250π2100π2148πsin sin sin 399399399-+= 2492π249249πsin πsin sin π2sin π-sin 39939939939999⎛⎫-+= ⎪⎝⎭.而495πsinπsin 9912>=,ππsin sin 9912<=,则3213I >>⎝⎭.所以213I I I <<. 11. 解析 第一次循环,1S =,2i =;第二次循环,224S =+=,3i =;第三次循环,8311S =+=,4i =;第四次循环,22426S =+=,5i =;第五次循环,52557S =+=,6i =,5750>,退出循环,故输出结果为6. 12. 解析 设()1P p ξ==,则()425P p ξ==-,从而由()14012155E p p ξ⎛⎫=⨯+⨯+⨯-= ⎪⎝⎭,得35p =.故()()()()22213120111215555D ξ=-⨯+-⨯+-⨯=. 13. 解析 不等式组构成以,,为顶点的三角形区域(包含边界). 又,所以转化为恒成立.而表示可行区域点与定点连接的斜率,其最大值为.同理,表示可行区()1,0A 31,2B ⎛⎫⎪⎝⎭()2,1C 12x剟14ax y+剟41y y a xx ---剟14y k x -=(),P x y ()0,432-21y k x-=域内点与定点连接的斜率,其最小值为,故有,即.14. 解析 不同的获奖情况可分为以下两类:(1)有一个人获得两张有奖奖券,另外还有一个人获得一张有奖奖券,有2234C A 36=种获奖情况.(2)有三个人各获得一张有奖奖券,有34A 24=种获奖情况.故不同的获奖情况有362460+=种.15. 解析 当0a …时,()20f a a =-…,又()00f =,故由()()()2422f f a f a a a =-=-…,得22a …,所以0a剟当10a -<<时,()()210f a a a a a =+=+<,则由()()()()()22222f f a f a a a a aa =+=+++…,得210a a +-…,得a ,则有10a -<<.当1a -…时,()()210f a a a a a =+=+…,则由,()()()()2222f f a f a a a a =+=-+…,得a ∈R ,故1a -….综上,a的取值范围为(-∞.16. 解析 由得,由 得,则线段的中点为.由题意 得,所以,得,故,所以17. 解析 过点P 作PN BC ⊥于N ,连接AN ,则PAN θ∠=,如图.(),Px y ()0,11-312a ---剟312a剟30,x y m b y x a -+=⎧⎪⎨=⎪⎩,33am bm A b a b a ⎛⎫ ⎪--⎝⎭30,x y m b y x a -+=⎧⎪⎨=-⎪⎩,33ambm B b a b a ⎛⎫- ⎪++⎝⎭AB 2222223,99a m b m M b a b a ⎛⎫ ⎪--⎝⎭PM AB ⊥3PM k =-2222444a b c a ==-254e =2e =设PN x =m ,由30BCM ∠=,得CN =m .在直角ABC △中,AB =15m , 25AC =m ,则20BC =m,故()20BN =-m .从而()222215203625AN x =+=-+,故2222tan PN AN θ=.当1x ==时,2tan θ取最大值2527,即当x =tan θ.18. 解析 (I)由题意得1cos 21cos 22222A B A B ++-=,112cos 22cos 222A A B B -=-,ππsin 2sin 266A B ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭. 由a b ≠,得A B ≠,又()0,πA B +∈,得ππ22π66A B -+-=,即2π3A B +=,所以π3C =. (II )由c =4sin 5A =,sin sin a c A C =,得85a =,由a c <,得A C <.从而3cos 5A =,故()sin sin sin cos cos sin B A C A C A C =+=+=,所以,ABC △的面积为1sin 2S ac B =.评注 本题主要考查诱导公式、两角和差公式、二倍角公式、正弦定理、三角形面积公式等基础知识,同时考查运算求解能力. 19. 解析 (I )由题意(1232nb n a a a a=,326b b -=,知3238b b a -==.又由12a =,得公比2q =(2q =-舍去),所以数列{}n a 的通项为()*2n n a n =∈N ,所以,123n a a a a =NMCB APθ()()1122n n n n ++=.故数列{}n b 的通项为()()*1n b n n n =+∈N .(II )(i )由(I )知1111121n n n n c a b n n ⎛⎫=-=-- ⎪+⎝⎭()*n ∈N ,所以1112n n S n =-+. (ii )因为10c =,20c >,30c >,40c >;当5n …时,()()115112n n n n c n n ⎡+⎤=-⎢⎥+⎣⎦, 而()()()1112022nn n n n n ++++->,得()()51551122nn n +⋅+<…,所以,当5n …时,0n c <.综上,对任意*n ∈N ,恒有4n S S >,故4k =.评注 本题主要考查等差数列与等比数列的概念、通项公式、求和公式、不等式性质等基础知识,同时考查运算求解能力.20. 解析 (I )在直角梯形BCDE 中,由1DE BE ==,2CD =,得BD BC ==,由AC =2AB =,得222AB AC BC =+,即AC BC ⊥,又平面ABC ⊥平面BCDE ,从而AC ⊥平面BCDE ,所以AC DE ⊥.又DE DC ⊥,从而DE ⊥平面ACD .(II )解法一:作BF AD ⊥,与AD 交于点F ,过点F 作//FG DE ,与AE 交于点G ,连接BG ,由(I )知D E AD ⊥,则FG AD ⊥.所以BFG ∠是二面角B AD E --的平面角.在直角梯形BCDE 中,由222CD BC BD =+,得BD BC ⊥,又平面ABC ⊥平面BCDE ,得BD ⊥平面ABC ,从而BD AB ⊥.由于AC ⊥平面BCDE ,得AC CD ⊥.在Rt ACD △中,由DC =2,AC得AD 在Rt AED △中,由1ED =,AD =得AE 在Rt ABD △中,由BD 2AB =,AD =BF =,23AF AD =.从而23GF =.在ABE △,ABG △中,利用余弦定理分别可得cos BAE ∠=23BC =.在BFG △中,2222GF BF BG cos BFG BF GF +-∠==⋅.所以π6BFG ∠=,,即二面角的大小是π6.GFEDCBA解法二:以D 为原点,分别以射线DE ,DC 为x 轴,y 轴的正半轴,建立空间直角坐标系,D xyz -如图所示.由题意知各点坐标如下:()0,0,0D ,()1,0,0E ,()0,2,0C,(A ,()1,1,0B .设平面ADE 的法向量为()111,,=x y zm ,平面ABD 的法向量为()222,,=x y zn ,可算得(0,22AD =-,(1,2,AE =-,()1,1,0DB =,由0,0,AD AE ⎧⋅=⎪⎨⋅=⎪⎩m m即1111120,20,y x y ⎧--=⎪⎨--=⎪⎩可取(0,2=m . 由0,0,AD BD ⎧⋅=⎪⎨⋅=⎪⎩n n即222220,0,y x y ⎧-=⎪⎨+=⎪⎩可取(1,=-n .于是cos ,⋅===⋅m n m n m n 所求二面角是锐角,故二面角B AD E --的大小是π6. 评注 本题主要考查空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同时考查空间想象能力、推理论证和运算求解能力.21. 解析 (I )设直线的方程为,由消去得.由于与只有一个公共点,故,即,解得点的坐标为.又点在第一象限,xl ()0y kx m k =+<2222,1y kx m x y a b=+⎧⎪⎨+=⎪⎩y ()22222222220b a k mx a kmx a m a b +++-=l C 0∆=22220b m a k -+=P 22222222,a km b m b a k b a k ⎛⎫- ⎪++⎝⎭P故点的坐标为. (II)由于直线过原点且与垂直,故直线的方程为,所以点到直线的距离,整理得因为,所以,当且仅当时等号成立.所以,点到直线的距离最大值为. 评注 本题主要考查椭圆的几何性质、点到直线的距离、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法、基本不等式应用等综合解题能力.22. 解析 (I )因为()3333, ,33, ,x x a x a f x x x a x a ⎧+-⎪=⎨-+<⎪⎩…所以()2233, ,33, ,x x a f x x x a ⎧+⎪'=⎨-<⎪⎩…由于11x-剟,(i )当1a -…时,有x a …,故()333f x x x a =+-.此时()f x 在()1,1-上是增函数,因此,()()143M a f a ==-,()()143m a f a =-=--,故()()()()43438M a m a a a -=----=.(ii )当11a -<<时,若(),1x a ∈,则()333f x x x a =+-,在(),1a 上是增函数;若()1,a -,则()333f x x x a =-+在()1,a -上是减函数,所以,()()(){}max 1,1M a f f =-,()()3m a f a a ==,由于()()1162f f a --=-+,因此,当113a <…时,()()334M a m a a a -=--+;当113a <<时,()()332M a m a a a -=-++.(iii )当1a …时,有x a …,故()333f x x x a =-+,此时()f x ,在()1,1-上是减函数,因此,()()123M a f a =-=+,()()123m a f a ===-+,P 22P ⎛⎫1l O l 1l 0x ky +=P 1l d =22d =22222b a k ab k+ (22)22a b =-…2bk a=P 1l a b -故()()()()23234M a m a a a -=+--+=.综上,()()338, 1,134, 1, 3132, 1,34, 1,a a a a M a m a a a a a -⎧⎪⎪--+-<⎪-=⎨⎪-++<<⎪⎪⎩………(II )令()()h x f x b =+,则()3333, ,33, ,x x a b x a h x x x a b x a ⎧+-+⎪=⎨-++<⎪⎩…()2233,,33,.x x a h x x x a ⎧+⎪'=⎨-<⎪⎩卆因为()4f x b ⎡+⎤⎣⎦…对[]1,1x ∈-恒成立,即()22h x -剟对[]1,1x ∈-恒成立,所以由(I )知,(i )当1a -…时,()h x 在()1,1-上是增函数,()h x 在[]1,1-上的最大值是()143h a b =-+,最小值是()143h a b -=--+,则432a b -+-…且432a b -+…,矛盾.(ii )当113a -<…时,()h x 在[]1,1-上的最小值是()3h a a b =+,最大值是()143h a b =-+,所以32a b +-…且432a b -+…,从而323362a a a b a --++-剟且103a 剟.令()323t a a =--+,则()2330t a a '=->,()t a 在10,3⎛⎫⎪⎝⎭上是增函数,故()()02t a t =-…,因此230a b -+剟.(iii )当113a <<时,()h x 在[]1,1-上的最小值是()3h a a b =+,最大值是()132h a b -=++,所以32a b +-…且322a b ++…,解得283027a b -<+….(iv )当1a …时,()h x 在[]1,1-上的最大值是()123h a b -=++,最小值是()123h a b =-++,所以322a b ++…且322a b +--…,解得30a b +=.综上,得3a b +的取值范围是230a b -+剟.评注 本题主要考查函数最大(最小)值的概念,利用导数研究函数的单调性等基础知识,同时考查推理论证、分类讨论、分析问题和解决问题等综合解题能力.。
2014年高考浙江理科数学试题及答案(word解析版)

2014年普通高等學校招生全國統一考試(浙江卷)數學(理科)第Ⅰ卷(選擇題 共50分)一、選擇題:本大題共10小題,每小題5分,共50分,在每小題給出の四個選項中,只有一項符合題目要求. (1)【2014年浙江,理1,5分】設全集{|2}U x N x =∈≥,集合2{|5}A x N x =∈≥,則U A =ð( )(A )∅ (B ){2} (C ){5} (D ){2,5} 【答案】B【解析】2{|5}{|A x N x x N x =∈≥=∈,{|2{2}U C A x N x =∈≤=,故選B . 【點評】本題主要考查全集、補集の定義,求集合の補集,屬於基礎題. (2)【2014年浙江,理2,5分】已知i 是虛數單位,,a b R ∈,則“1a b ==”是“2(i)2i a b +=”の( )(A )充分不必要條件 (B )必要不充分條件 (C )充分必要條件 (D )既不充分也不必要條件 【答案】A【解析】當1a b ==時,22(i)(1i)2i a b +=+=,反之,2(i)2i a b +=,即222i 2i a b ab -+=,則22022a b ab ⎧-=⎨=⎩,解得11a b =⎧⎨=⎩ 或11a b =-⎧⎨=-⎩,故選A .【點評】本題考查の知識點是充要條件の定義,複數の運算,難度不大,屬於基礎題.(3)【2014年浙江,理3,5分】某幾何體の三視圖(單位:cm )如圖所示,則此幾何體の表面積是( ) (A )902cm (B )1292cm (C )1322cm (D )1382cm【答案】D【解析】由三視圖可知直觀圖左邊一個橫放の三棱柱右側一個長方體,故幾何體の表面積為:1246234363334352341382S =⨯⨯+⨯⨯+⨯+⨯+⨯+⨯+⨯⨯⨯=,故選D .【點評】本題考查了由三視圖求幾何體の表面積,根據三視圖判斷幾何體の形狀及數據所對應の幾何量是解題の關鍵.(4)【2014年浙江,理4,5分】為了得到函數sin 3cos3y x x =+の圖像,可以將函數y x の圖像( )(A )向右平移4π個單位 (B )向左平移4π個單位 (C )向右平移12π個單位 (D )向左平移12π個單位【答案】C【解析】sin3cos3))]412y x x x x ππ=+=+=+,而2s i n (32y x x π=+)]6x π+,由3()3()612x x ππ+→+,即12x x π→-,故只需將y x の圖象向右平移12π個單位,故選C .【點評】本題考查兩角和與差の三角函數以及三角函數の平移變換の應用,基本知識の考查. (5)【2014年浙江,理5,5分】在64(1)(1)x y ++の展開式中,記m n x y 項の系數(,)f m n ,則(3,0)(2,1)(1,2)f f f f +++=( ) (A )45 (B )60 (C )120 (D )210 【答案】C 【解析】令x y =,由題意知(3,0)(2,1)(1,2)(0,3)f f f f +++即為10(1)x +展開式中3x の系數,故(3,0)(2,1)(1,2)(0,3)f f f f +++=710120C =,故選C .【點評】本題考查二項式定理系數の性質,二項式定理の應用,考查計算能力. (6)【2014年浙江,理6,5分】已知函數32()f x x ax bx c =+++ ,且0(1)(2)(3)3f f f <-=-=-≤( ) (A )3c ≤ (B )36c <≤ (C )69c <≤ (D )9c >【答案】C【解析】由(1)(2)(3)f f f -=-=-得184212793a b c a b c a b c a b c -+-+=-+-+⎧⎨-+-+=-+-+⎩,解得611a b =⎧⎨=⎩,所以32()611f x x x x c =+++,由0(1)3f <-≤,得016113c <-+-+≤,即69c <≤,故選C .【點評】本題考查方程組の解法及不等式の解法,屬於基礎題. (7)【2014年浙江,理7,5分】在同一直角坐標系中,函數()(0)a f x x x =≥,()log a g x x =の圖像可能是( )(A ) (B ) (C ) (D )【答案】D【解析】函數()(0)a f x x x =≥,()log a g x x =分別の冪函數與對數函數答案A 中沒有冪函數の圖像, 不符合;答案B 中,()(0)a f x x x =≥中1a >,()log a g x x =中01a <<,不符合;答案C 中,()(0)a f x x x =≥中01a <<,()log a g x x =中1a >,不符合;答案D 中,()(0)a f x x x =≥中01a <<,()log a g x x =中01a <<,符合,故選D .【點評】本題考查の知識點是函數の圖象,熟練掌握對數函數和冪函數の圖象和性質,是解答の關鍵.(8)【2014年浙江,理8,5分】記,max{,},x x y x y y x y ≥⎧=⎨<⎩,y,min{,}x,x yx y x y ≥⎧=⎨<⎩,設,a b 為平面向量,則( )(A )min{||,||}min{||,||}a b a b a b +-≤ (B )min{||,||}min{||,||}a b a b a b +-≥ (C )2222max{||,||}||||a b a b a b +-≤+ (D )2222max{||,||}||||a b a b a b +-≥+【答案】D【解析】由向量運算の平行四邊形法可知min{||,||}a b a b +-與min{||,||}a b の大小不確定,平行四邊形法可知max{||,||}a b a b +-所對の角大於或等於90︒ ,由餘弦定理知2222max{||,||}||||a b a b a b +-≥+,(或22222222||||2(||||)max{||,||}||||22a b a b a b a b a b a b ++-++-≥==+),故選D .【點評】本題在處理時要結合著向量加減法の幾何意義,將a ,b ,a b +,a b -放在同一個平行四邊形中進行比較判斷,在具體解題時,本題采用了排除法,對錯誤選項進行舉反例說明,這是高考中做選擇題の常用方法,也不失為一種快速有效の方法,在高考選擇題の處理上,未必每一題都要寫出具體解答步驟,針對選擇題の特點,有時“排除法”,“確定法”,“特殊值”代入法等也許是一種更快速,更有效の方法.(9)【2014年浙江,理9,5分】已知甲盒中僅有1個球且為紅球,乙盒中有m 個紅球和n 個籃球(3,3)m n ≥≥,從乙盒中隨機抽取(1,2)i i =個球放入甲盒中.(a )放入i 個球後,甲盒中含有紅球の個數記為(1,2)i i ξ=; (b )放入i 個球後,從甲盒中取1個球是紅球の概率記為(1,2)i p i =.則( )(A )1212,()()p p E E ξξ><(B )1212,()()p p E E ξξ<>(C )1212,()()p p E E ξξ>>(D )1212,()()p p E E ξξ<< 【答案】A【解析】解法一:11222()m n m np m n m n m n +=+⨯=+++ ,211222221233n m n m m n m n m nC C C C p C C C +++=++=223323()(1)m m mn n n m n m n -++-++-,∴1222()m n p p m n +-=+-223323()(1)m m mn n n m n m n -++-++-=5(1)06()(1)mn n n m n m n +->++-,故12p p >. 又∵1(1)n P m n ξ==+,1(2)m P m n ξ==+,∴12()12n m m nE m n m n m nξ+=⨯+⨯=+++,又222(1)(1)()(1)n m n C n n P C m n m n ξ+-===++-,11222(2)()(1)n m m n C C mnP C m n m n ξ+===++-,222(m 1)(3)()(1)m m n C m P C m n m n ξ+-===++- ∴2(1)2(1)()123()(1)()(1)()(1)n n mn m m E m n m n m n m n m n m n ξ--=⨯+⨯+⨯++-++-++-=22334()(1)m n m n mn m n m n +--+++-21()()E E ξξ-=22334()(1)m n m n mn m n m n +--+++--2m nm n ++=(1)0()(1)m m mn m n m n -+>++-,所以21()()E E ξξ>,故選A . 解法二:在解法一中取3m n ==,計算後再比較,故選A .【點評】正確理解()1,2i i ξ=の含義是解決本題の關鍵.此題也可以采用特殊值法,不妨令3m n ==,也可以很快求解.(10)【2014年浙江,理10,5分】設函數21()f x x =,22()2()f x x x =-,31()|sin 2|3f x x π=,99i ia =,0,1,2i =,,99,記10219998|()()||()()||()()|k k k k k k k I f a f a f a f a f a f a =-+-++-,1,2,3k =,則( ) (A )123I I I << (B )213I I I << (C )132I I I << (D )321I I I << 【答案】B【解析】解法一:由22112199999999i i i --⎛⎫⎛⎫-=⎪ ⎪⎝⎭⎝⎭,故2111352991199()199999999999999I ⨯-=++++==,由2211199(21)22||999999999999i i i i i ----⎛⎫⎛⎫--+=⨯ ⎪ ⎪⎝⎭⎝⎭,故2150(980)98100221992999999I +=⨯⨯⨯=<⨯, 3110219998(|sin(2)||sin(2)||sin(2)||sin(2)||sin(2)||sin(2)|)3999999999999I ππππππ=-+-++-=12574[2sin(2)2sin(2)]139999ππ->,故213I I I <<,故選B . 解法二:估算法:k I の幾何意義為將區間[0,1]等分為99個小區間,每個小區間の端點の函數值之差の絕對值之和.如圖為將函數21()f x x =の區間[0,1]等分為4個小區間の情形,因1()f x 在[0,1]上遞增,此時110213243|()()||()()||()()||()()|I f a f a f a f a f a f a f a f a =-+-+-+- =11223344A H A H A H A H +++(1)(0)f f =-1=,同理對題中給出の1I ,同樣有11I =;而2I 略小於1212⨯=,3I 略小於14433⨯=,所以估算得213I I I <<,故選B .【點評】本題主要考查了函數の性質,關鍵是求出這三個數與1の關系,屬於難題.第Ⅱ卷(非選擇題 共100分)二、填空題:本大題共7小題,每小題4分,共28分.(11)【2014年浙江,理11,5分】若某程序框圖如圖所示,當輸入50時,則該程序運算後輸出の結果是 . 【答案】6【解析】第一次運行結果1,2S i ==;第二次運行結果4,3S i ==;第三次運行結果11,4S i ==;第四次運行結果26,5S i ==;第五次運行結果57,6S i ==;此時5750S =>,∴輸出6i =.【點評】本題考查了直到型循環結構の程序框圖,根據框圖の流程模擬運行程序是解答此類問題の常用方法.(12)【2014年浙江,理12,5分】隨機變量ξの取值為0,1,2,若1(0)5P ξ==,()1E ξ=,則()D ξ= . 【答案】25 【解析】設1ξ=時の概率為p ,ξの分布列為: 由11()012(1)155E p p ξ=⨯+⨯+⨯--= ,解得35p =ξの分布列為即為故2221312()(01)(11)(21)5555E ξ=-⨯+-⨯+-⨯=.【點評】本題綜合考查了分布列の性質以及期望、方差の計算公式.(13)【2014年浙江,理13,5分】當實數,x y 滿足240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩時,14ax y ≤+≤恒成立,則實數a の取值範圍是 __.【答案】3[1,]2【解析】解法一:作出不等式組240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩所表示の區域如圖,由14ax y ≤+≤恒成立,故3(1,0),(2,1),(1,)2A B C ,三點坐標代入14ax y ≤+≤,均成立得1412143142a a a ⎧⎪≤≤⎪≤+≤⎨⎪⎪≤+≤⎩解得312a ≤≤ ,∴實數a の取值範圍是3[1,]2.解法二:作出不等式組240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩所表示の區域如圖,由14ax y ≤+≤得,由圖分析可知,0a ≥且在(1,0)A 點取得最小值,在(2,1)B 取得最大值,故1214a a ≥⎧⎨+≤⎩,得312a ≤≤,故實數a の取值範圍是3[1,]2.【點評】本題考查線性規劃,考查了數形結合の解題思想方法,考查了數學轉化思想方法,訓練了不等式組得解法,是中檔題.(14)【2014年浙江,理14,5分】在8張獎券中有一、二、三等獎各1張,其餘5張無獎.將這8張獎券分配給4個人,每人2張,不同の獲獎情況有 種(用數字作答). 【答案】60【解析】解法一:不同の獲獎分兩種,一是有一人獲兩張獎券,一人獲一張獎券,共有223436C A =, 二是有三人各獲得一張獎券,共有3424A =,因此不同の獲獎情況共有362460+=種. 解法二:將一、二、三等獎各1張分給4個人有3464=種分法,其中三張獎券都分給一個人の有4種分法, 因此不同の獲獎情況共有64460-=種.【點評】本題考查排列、組合及簡單計數問題,考查學生の計算能力,屬於基礎題.(15)【2014年浙江,理15,5分】設函數22,0(),0x x x f x x x ⎧+<⎪=⎨-≥⎪⎩若(())2f f a ≤,則實數a の取值範圍是 .【答案】(-∞.【解析】由題意2()0()()2f a f a f a <⎧⎨+≤⎩或2()0()2f a f a ≥⎧⎨-≤⎩,解得()2f a ≥-∴當202a a a <⎧⎨+≥-⎩或202a a ≥⎧⎨-≥-⎩,解得a【點評】本題主要考查分段函數の應用,其它不等式の解法,體現了數形結合の數學思想,屬於中檔題.(16)【2014年浙江,理16,5分】設直線30x y m -+=(0m ≠) 與雙曲線22221x y a b-=(0,0a b >>)兩條漸近線分別交於點A ,B .若點(,0)P m 滿足||||PA PB =,則該雙曲線の離心率是 .【解析】解法一:由雙曲線の方程可知,它の漸近線方程為b y x a =和by x a =-,分別與直線l : 30x y m -+= 聯立方程組,解得,(,)33am bm A a b a b ----,(,)33am bmB a b a b -++,設AB 中點為Q ,由||||PA PB = 得,則3333(,)22am am bm bma b a b a b a b Q ---++-+-+,即2222223(,)99a m b m Q a b a b ----,PQ 與已知直線垂直,∴1PQ l k k =-,即222222319139b m a b a m m a b --=----, 即得2228a b =,即22228()a c a =-,即2254c a =,所以c e a ==.解法二:不妨設1a =,漸近線方程為222201x y b -=即2220b x y -=,由222030b x y x y m ⎧-=⎨-+=⎩消去x ,得2222(91)60b y b my b m --+=,設AB 中點為00(,)Q x y ,由韋達定理得:202391b m y b =-……① ,又003x y m =-,由1P Q l k k =-得00113y x m =--,即得0011323y y m =--得035y m =代入①得2233915b m m b =-, 得214b =,所以22215144c a b =+=+=,所以c =,得c e c a ===.【點評】本題考查雙曲線の離心率,考查直線の位置關系,考查學生の計算能力,屬於中檔題. (17)【2014年浙江,理17,5分】如圖,某人在垂直於水平地面ABC の牆面前の點A 處進行射擊訓練.已知點A 到牆面の距離為AB ,某目標點P 沿牆面上の射擊線CM 移動,此人為了准確瞄准目標點P ,需計算由點A 觀察點P の仰角θの大小.若15AB m =,25AC m =,30∠︒,則tan θの最大值是 (仰角θ為直線AP 與平面ABC 所成角).2320225x x -+2320032250-+'',設B P 2320225x x ++22545204<=355339=,2320225x x -+2320225x x -+20),23225'(x)(225)f x ++454=- 時20時'0y <203445225(++ 15201225AB BC AC ==,20tan 30DB BC ︒=203533DB ===【點評】屬於中檔題. 三、解答題:本大題共5題,共72分.解答應寫出文字說明,演算步驟或證明過程.(18解:(即A B +=,所以C =.(2c 得A C <,從而3cos A =,,所以,ABC ∆(19)【2014年浙江,理19,14分】已知數列{}n a 和{}n b 滿足123(2)(*)n b n a a a a n N =∈.若{}n a 為等比數列,且1322,6a b b ==+.(1)求n a 與n b ;(2)設11(*)n n n c n N a b =-∈.記數列{}n c の前n 項和為n S .(ⅰ)求n S ;(ⅱ)求正整數k ,使得對任意*n N ∈均有S S ≥.解:(1(2)(3(2)n a a =N ). (2n c ++=111(22n n ++-1(12n ++--=1112n n -+20>,3c 55(51)12+<,4n S ≥,故【點評】本題考查了等比數列通項公式、求和公式,還考查了分組求和法、裂項求和法和猜想證明の思想,證明可以用二項式定理,還可以用數學歸納法.本題計算量較大,思維層次高,要求學生有較高の分析問題解決問題の能力.本題屬於難題.(20)【2014年浙江,理20,15分】如圖,在四棱錐A BCDE -中,平面ABC ⊥平面BCDE ,90CDE BED ∠=∠=︒,2AB CD ==,1DE BE ==,AC =(1)證明:DE ⊥平面ACD ;(解:(1(2BF GF=の原點,分別以射線DE所示.由題意知各點坐標如下:(0,2,0),(0,2,Aの法向量為111(,m x y=222(,,)n x y z=,可算得:(0,2)AD=-,(1,2,AE=-,(1,1,0)DB=,由ADm AE=⎨=⎪⎩,即1111122020y zx y⎧--=⎪⎨-=⎪⎩,可取(0,1,m=-,由n ADn BD⎧⋅=⎪⎨⋅=⎪⎩即2222220y zx y⎧--=⎪⎨+=⎪⎩可取(0,n=-,於是|||cos,|||||3m nm nm n⋅<>===⋅⋅運算求解能力.(21)【2014年浙江,理21,15分】如圖,設橢圓C:22221(0)x ya ba b+=>>動直線l與橢圓C 只有一個公共點P,且點P在第一象限.(1)已知直線lの斜率為k,用,,a b k表示點Pの坐標;(2)若過原點Oの直線1l與l垂直,證明:點P到直線1lの距離の最大值為a b-.解:(1''1P l k =-,得,b (2幾何の基本思想方法、基本不等式應用等綜合解題能力.(22)【2014年浙江,理22,14分】已知函數()33()f x x x a a R =+-∈.(1)若()f x 在[]1,1-上の最大值和最小值分別記為(),()M a m a ,求()()M a m a -; (2)設,b R ∈若()24f x b +≤⎡⎤對[]1,1x ∈-恒成立,求3a b +の取值範圍.解:(1(2。
2014年普通高等学校招生考试浙江理数

2014年普通高等学校招生全国统一考试(浙江卷)数学(理科)一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出 的四个选项中,只有一项是符合题目要求的.(1)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,zxxk 则=A C U ( ) A. ∅ B. }2{ C. }5{ D. }5,2{(2)已知i 是虚数单位,R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件(3)某几何体的三视图(单位:cm )如图所示,则此几何体的 表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数zxxk x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像( ) A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位5.在46)1()1(y x ++的展开式中,记n m y x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f )( )A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f ( )A.3≤cB.63≤<cC.96≤<cD. 9>c 7.在同意直角坐标系中,函数x x g x x x f a a log )(),0()(=≥=的图像可能是( )8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩,,min{,},y x yx y x x y≥⎧=⎨<⎩,设,a b 为平面向量,则( )A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个篮球 ()3,3m n ≥≥,从乙盒中随机抽取()1,2i i =个球放入甲盒中.(a )放入i 个球后,甲盒中含有红球的个数记为()1,2ii ξ=;(b )放入i 个球后,从甲盒中取1个球是红球的概率记为zxxk ()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =,),(2)(22x x x f -=|2sin |31)(3x x f π=,99,,2,1,0,99==i ia i ,记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ,.3,2,1=k 则A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I << 二、填空题:本大题共7小题,每小题4分,共28分.11.若某程序框图如图所示,当输入50时,则该程序运算后输出的 结果是________.12.随机变量ξ的取值为0,1,2,若()105P ξ==,()1E ξ=,则()D ξ=________. 13.当实数x ,y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时,zxxk 14ax y ≤+≤恒成立,则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有_____种(用数字作答).15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ,则实数a 的取值范围是______16.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x (0a b >>)两条渐近线分别交于点B A ,,若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图,某人在垂直于水平地面的墙面前的点处进行射击训练. 已知点到墙面的距离为,某目标点沿墙面的射击线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小.若则的最大值三.解答题:本大题共5小题,共72分。
2014年高考理科数学浙江卷-答案

6
6
3
3
(2)由 c 3 ,[ f (x) b]2 4 , a c 得 a 8 ,
sin A sin C
5
由 a c ,得 A C ,从而 cos A 3 ,故 sin B sin A C sin AcosC cos Asin C 4 3 3 ,
5
10
所以 △ABC 的面积为 S 1 acsin B 8 3 18 .
5
5
2. 5
5
【提示】给出 取值的部分概率和期望,求 的方差.
【考点】离散型随机变量的期望和方差
13.【答案】
1,
3 2
4 / 11
【解析】实数
x,y
满足的可行域如图中阴影部分所示,图中
A(1,0)
,
B(2,1)
,
C
1,
3 2
.
当 a 0 时, 0 y 3 ,1 x 2 ,所以1 ax+y 4 不可能恒成立; 2
2
25
【提示】给出未知函数运用诱导公式和两角和与差的公式、正弦定理等进行化简求三角形中的角.
【考点】两角和与差的公式,正弦定理
19.【答案】(1) an 2n (n N*)
bn n(n 1)(nN*)
(2)(i)
Sn
1 n 1
1 2n
(n N)
(ii) k 4
【解析】(1)由题意, a1a2 ak ( 2)bn (n N*) , b3 b2 6 ,知 a3 ( 2)b3 b2 8 ,
【提示】给出两式相乘的形式,利用二项式通项公式代入求值. 【考点】二项式定理的应用 6.【答案】C 【解析】 f (1) 1 2a b c , f (2) 8 4a 2b c , f (3) 27 9a 3b c , 由 f (1) f (2) ( 3)得,a 6,b 11,∴ f (x) x3 6x2 11x c ∵ 0 f (1) 3 ,把 f (1) 代入 f (x)
2014年高考(浙江省)真题数学(理)试题及答案解析

2014年普通高等学校招生全国统一考试(浙江卷)数学(理科)一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则=A C U ( ) A. ∅ B. }2{ C. }5{ D. }5,2{(2)已知i 是虚数单位,R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件(3)某几何体的三视图(单位:cm )如图所示,则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像( ) A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 5.在46)1()1(y x ++的展开式中,记n m y x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f )( )A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f ( ) A.3≤c B.63≤<c C.96≤<c D. 9>c 7.在同一直角坐标系中,函数x x g x x x f a alog )(),0()(=≥=的图像可能是( )8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩,,min{,},y x yx y x x y≥⎧=⎨<⎩,设a,b 为平面向量,则( )A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个篮球()3,3m n ≥≥,从乙盒中随机抽取()1,2i i =个球放入甲盒中.(a )放入i 个球后,甲盒中含有红球的个数记为()1,2ii ξ=;(b )放入i 个球后,从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =,),(2)(22x x x f -=|2sin |31)(3x x f π=,99,,2,1,0,99==i ia i ,记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ,.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I << 二、填空题:本大题共7小题,每小题4分,共28分.11.若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是________.。
2014年浙江省高考数学试卷及答案(理科)

第 1 页 共 11 页绝密★考试结束前2014年普通高等学校招生全国统一考试〔浙江卷〕数学〔理科〕本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
总分值150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分〔共50分〕注意事项:1.答题前,考生务必将自己的、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式如果事件,A B 互斥 ,那么()()()P A B P A P B +=+如果事件,A B 相互独立,那么()()()P A B P A P B •=•如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,...,)k kn k n n P k C p p k n -=-=台体的体积公式121()3V h S S =其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高球的外表积公式24S R π=球的体积公式343V R π=其中R 表示球的半径一.选择题:本大题共10小题,每题5分,共50分. 在每题给出的四个选项中,只有一项是符合题目要求的.1.设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则=A C U 〔 〕A. ∅B. }2{C. }5{D. }5,2{2.已知i 是虚数单位,R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的〔 〕 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件3.某几何体的三视图〔单位:cm 〕如下图,则此几何体的外表积是〔 〕 A. 902cm B. 1292cm C. 1322cm D. 1382cm 4.为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像〔 〕A.向右平移4π4π个单位 12π12π个单位 46)1()1(y x ++的展开式中,记n m y x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f )〔 〕A.45B.60C.120D. 210则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f 〔 〕A.3≤cB.63≤<cC.96≤<cD. 9>c7.在同一直角坐标系中,函数x x g x x x f a alog )(),0()(=≥=的图像可能是〔 〕A. B. C. D.,max{,},x x y x y y x y ≥⎧=⎨<⎩,,min{,},y x yx y x x y ≥⎧=⎨<⎩,设a,b 为平面向量,则〔 〕A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个篮球()3,3m n ≥≥,从乙盒中随机抽取()1,2i i =个球放入甲盒中.〔a 〕放入i 个球后,甲盒中含有红球的个数记为()1,2ii ξ=;〔b 〕放入i 个球后,从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<< 10.设函数21)(xx f =,),(2)(22x x x f -=|2sin |31)(3x x f π=,99,,2,1,0,99==i ia i ,记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ,.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I << 二、填空题:本大题共7小题,每题4分,共28分.11.假设某程序框图如下图,当输入50时,则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2,假设()105P ξ==,()1E ξ=,则()D ξ=________. 13.当实数x ,y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时,14ax y ≤+≤恒成立,则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人, 每人2张,不 同的获奖情况有_____种〔用数字作答〕.()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 假设()()2≤a f f ,则实数a 的取值范围是______15.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x 〔0a b >>〕两条渐近线分别交于点B A ,,假设点)0,(m P 满足PB PA =,则该双曲线的离心率是__________ 17、如图,某人在垂直于水平地面的墙面前的点到墙面的距离为,某目标点沿墙面的射击线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角则的最大值 。
2014年高考真题——文科数学(浙江卷) 精校版 Word版含答案

2014年高考真题——文科数学(浙江卷)精校版 Word版含答案2014年浙江省普通高等学校招生全国统一考试数学(文科)一、选择题1.设集合 $S=\{x|x\geq2\}$,$T=\{x|x\leq5\}$,则 $ST=$()A。
$(-\infty,5]$B。
$[2,+\infty)$C。
$(2,5)$D。
$[2,5]$2.设四边形 $ABCD$ 的两条对角线为 $AC$、$BD$,则“四边形 $ABCD$ 为菱形”是“$AC\perp BD$”的()A。
充分不必要条件B。
必要不充分条件C。
充要条件D。
既不充分也不必要条件3.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A。
$72\text{cm}^3$B。
$90\text{cm}^3$C。
$108\text{cm}^3$D。
$138\text{cm}^3$4.为了得到函数 $y=\sin^3x+\cos^3x$ 的图象,可以将函数$y=2\cos3x$ 的图象()A。
向右平移 $\pi$ 个单位长B。
向右平移 $\frac{\pi}{12}$ 个单位长C。
向左平移 $\frac{\pi}{2}$ 个单位长D。
向左平移 $4$ 个单位长5.已知圆 $x^2+y^2+2x-2y+a=0$ 截直线 $x+y+2=0$ 所得弦的长度为 $4$,则实数 $a$ 的值为()A。
$-2$B。
$-4$C。
$-6$D。
$-8$6.设 $m$、$n$ 是两条不同的直线,$\alpha$、$\beta$ 是两个不同的平面,则()A。
若 $m\perp n$,$n\parallel \alpha$,则 $m\perp \alpha$ B。
若 $m\parallel \beta$,$\beta\perp \alpha$,则 $m\perp \alpha$C。
若 $m\perp \beta$,$n\perp \beta$,$n\perp \alpha$,则$m\perp \alpha$D。
2014年浙江省高考数学试卷及答案(文科)

绝密★考试结束前2014年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式台体的体积公式121()3V h S S = 其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高 锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高 球的表面积公式 24S R π=球的体积公式343V R π= 其中R 表示球的半径如果事件,A B 互斥 ,那么()()()P A B P A P B +=+一 、选择题: 本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合}5|{},2|{≤=≥=x x T x x S ,则=T S IA. ]5,(-∞B.),2[+∞C. )5,2(D. ]5,2[2. 设四边形ABCD 的两条对角线为AC 、BD 。
则“四边形ABCD 为菱形”是“A C ⊥BD ”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 某几何体的三视图(单位:cm )如图所示,则该几何体的体积是A .72cm 3B . 90 cm 3C .108 cm 3D . 138 cm 34.为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像 A .向右平移12π个单位 B .向右平移4π个单位 C .向左平移12π个单位 D .向左平移4π个单位 5. 已知圆02222=+-++a y x y x 截直线02=++y x 所得弦的长度为4,则实数a 的值是A .2-B .4-C .6-D .8-6. 设m 、n 是两条不同的直线,α、β是两个不同的平面A .若m ⊥n ,n ∥α则m ⊥αB .若m ∥β,β⊥α,则m ⊥αC .若m ⊥β,n ⊥β, n ⊥α则m ⊥αD .若m ⊥n ,n ⊥β,β⊥α,则m ⊥α7. 已知函数c bx ax x x f +++=23)(,且3)3()2()1(0≤-=-=-<f f f ,则A .3≤cB .63≤<cC .96≤<cD .9>c8. 在同意直角坐标系中,函数x x g x x x f a a log )(),0()(=≥=的图像可能是。
2014年普通高等学校招生全国统一考试数学(浙江卷)文 (2)

2014年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分.全卷共4页,选择题部分1至2页,非选择题部分3至4页.满分150分,考试时间120分钟.考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效.选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2014浙江,文1)设集合S={x|x≥2},T={x|x≤5},则S∩T=().A.(-∞,5]B.[2,+∞)C.(2,5)D.[2,5]答案:D解析:由已知得S∩T={x|2≤x≤5}=[2,5],故选D.2.(2014浙江,文2)设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的().A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案:A解析:当四边形ABCD为菱形时,其对角线互相垂直,必有AC⊥BD;但当AC⊥BD时,四边形不一定是菱形(如图),因此“四边形ABCD为菱形”是“AC⊥BD”的充分不必要条件.故选A.3.(2014浙江,文3)某几何体的三视图(单位:cm)如图所示,则该几何体的体积是().A.72 cm 3B.90 cm 3C.108 cm 3D.138 cm 3答案:B解析:由三视图可知,该几何体是一个组合体,其左侧是一个直三棱柱,右侧是一个长方体.其中三棱柱的底面是一个直角三角形,其两直角边长分别是3 cm 和4 cm,三棱柱的高为3 cm,因此其体积V 1=Sh=12×4×3×3=18(cm 3).长方体中三条棱的长度分别为4 cm,6 cm,3 cm,因此其体积V 2=4×6×3=72(cm 3).故该几何体的体积V=V 1+V 2=18+72=90(cm 3),故选B .4.(2014浙江,文4)为了得到函数y=sin 3x+cos 3x 的图象,可以将函数y=√2cos 3x 的图象( ).A.向右平移π12个单位B.向右平移π4个单位 C.向左平移π12个单位 D.向左平移π4个单位 答案:A解析:由于y=sin 3x+cos 3x=√2sin (3x +π4),y=√2cos 3x=√2sin (3x +π2),因此只需将y=√2cos 3x 的图象向右平移π12个单位,即可得到y=√2sin [3(x -π12)+ π2]=√2sin (3x +π4)的图象,故选A . 5.(2014浙江,文5)已知圆x 2+y 2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a 的值是( ). A.-2 B.-4 C.-6 D.-8 答案:B解析:圆的方程可化为(x+1)2+(y-1)2=2-a ,因此圆心为(-1,1),半径r=√2-a .圆心到直线x+y+2=0的距离d=√2=√2,又弦长为4,因此由勾股定理可得(√2)2+(42)2=(√2-a )2,解得a=-4.故选B .6.(2014浙江,文6)设m ,n 是两条不同的直线,α,β是两个不同的平面.( ). A.若m ⊥n ,n ∥α,则m ⊥α B.若m ∥β,β⊥α,则m ⊥α C.若m ⊥β,n ⊥β,n ⊥α,则m ⊥α D.若m ⊥n ,n ⊥β,β⊥α,则m ⊥α 答案:C解析:当m ⊥n ,n ∥α时,可能有m ⊥α,但也有可能m ∥α或m ⊂α,故A 选项错误;当m ∥β,β⊥α时,可能有m ⊥α,但也有可能m ∥α或m ⊂α,故选项B 错误; 当m ⊥β,n ⊥β,n ⊥α时,必有α∥β,从而m ⊥α,故选项C 正确;在如图所示的正方体ABCD-A 1B 1C 1D 1中,取m 为B 1C 1,n 为CC 1,β为平面ABCD ,α为平面ADD 1A 1,这时满足m ⊥n ,n ⊥β,β⊥α,但m ⊥α不成立,故选项D 错误.7.(2014浙江,文7)已知函数f (x )=x 3+ax 2+bx+c ,且0<f (-1)=f (-2)=f (-3)≤3,则( ). A.c ≤3 B.3<c ≤6C.6<c ≤9D.c>9答案:C解析:由于f (-1)=f (-2)=f (-3),所以-1+a-b+c=-8+4a-2b+c=-27+9a-3b+c.由-1+a-b+c=-8+4a-2b+c ,整理得3a-b=7, 由-8+4a-2b+c=-27+9a-3b+c ,整理得5a-b=19,由{3a -b =7,5a -b =19,解得{a =6,b =11.于是f (-1)=f (-2)=f (-3)=c-6, 又因为0<f (-1)=f (-2)=f (-3)≤3, 因此0<c-6≤3,解得6<c ≤9,故选C .8.(2014浙江,文8)在同一直角坐标系中,函数f (x )=x a (x>0),g (x )=log a x 的图象可能是( ).答案:D解析:若a>1,则函数g (x )=log a x 的图象过点(1,0),且单调递增,但当x ∈(0,1)时,y=x a (x>0)的图象应在直线y=x 的下方,故C 选项错误;若0<a<1,则函数g (x )=log a x 的图象过点(1,0),且单调递减,函数y=x a (x>0)的图象应单调递增,且当x ∈(0,1)时图象应在直线y=x 的上方,因此A,B 均错,只有D 项正确.9.(2014浙江,文9)设θ为两个非零向量a ,b 的夹角.已知对任意实数t ,|b +t a |的最小值为1.( ). A.若θ确定,则|a |唯一确定 B.若θ确定,则|b |唯一确定 C.若|a |确定,则θ唯一确定 D.若|b |确定,则θ唯一确定 答案:B解析:|b +t a |2=(b +t a )2=|b |2+|a |2t 2+2a ·b t ,令f (t )=|a |2t 2+2a ·b t+|b |2,由于|b +t a |的最小值为1,所以函数f (t )的最小值也为1,即4|a |2|b |2-4(a ·b )24|a |2=1.又a ,b 均为非零向量,且夹角为θ, 因此|b |2-|b |2cos 2θ=1,于是|b |2=11-cos 2θ, 因此当θ确定时,|b |2的值唯一确定,亦即|b |唯一确定,故选B .10.(2014浙江,文10)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小.(仰角θ为直线AP 与平面ABC 所成角).若AB=15 m,AC=25 m,∠BCM=30°,则tan θ的最大值是( ).A.√305B.√3010C.4√39D.5√39答案:D解析:由于AB ⊥BC ,AB=15 m,AC=25 m,所以BC=√252-152=20 m . 过点P 作PN ⊥BC 交BC 于N , 连接AN (如图),则∠PAN=θ,tan θ=PN AN.设NC=x (x>0),则BN=20-x ,于是AN=√AB 2+BN 2=√152+(20-x )2 =√x 2-40x +625, PN=NC ·tan 30°=√33x ,所以tan θ=√33x √x 240x+625=√33√-40x +625x 2√33√625x2-40x +1, 令1x=t ,则625x 2−40x+1=625t 2-40t+1, 当t=4125时,625t 2-40t+1取最小值925,因此√625x 2-40x +1的最小值为√925=35,这时tan θ的最大值为√33×53=5√39(此时x =1254).故选D .非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分. 11.(2014浙江,文11)已知i 是虚数单位,计算1-i (1+i )2=.答案:-12−12i 解析:1-i(1+i )2=1-i 2i=(1-i )·i 2i ·i=1+i -2=-12−12i . 12.(2014浙江,文12)若实数x ,y 满足{x +2y -4≤0,x -y -1≤0,x ≥1,则x+y 的取值范围是 .答案:[1,3]解析:画出约束条件所确定的可行域(如图中阴影部分所示).令z=x+y ,则y=-x+z ,画出直线l :y=-x ,平移直线l ,当l 经过可行域中的点A (1,0)时,z 取最小值,且z min =1+0=1; 当l 经过可行域中的点B (2,1)时,z 取最大值,且z max =2+1=3,故x+y 的取值范围是[1,3].13.(2014浙江,文13)若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是 .答案:6解析:第一次执行循环体S=2×0+1=1,i=1+1=2;第二次执行循环体S=2×1+2=4,i=2+1=3; 第三次执行循环体S=2×4+3=11,i=3+1=4; 第四次执行循环体S=2×11+4=26,i=4+1=5; 第五次执行循环体S=2×26+5=57,i=5+1=6, 这时S=57>50,跳出循环,输出i=6.14.(2014浙江,文14)在3张奖券中有一、二等奖各1张,另1张无奖.甲、乙两人各抽取1张,两人都中奖的概率是 . 答案:13解析:甲、乙两人各抽取1张,一共有3×2=6种等可能的结果,两人都中奖的结果有2×1=2种,由古典概型计算公式可得所求概率为P=26=13.15.(2014浙江,文15)设函数f (x )={x 2+2x +2,x ≤0,-x 2,x >0,若f (f (a ))=2,则a= .答案:√2解析:当a ≤0时,f (a )=a 2+2a+2=(a+1)2+1>0,于是f (f (a ))=f (a 2+2a+2)=-(a 2+2a+2)2, 令-(a 2+2a+2)2=2,显然无解;当a>0时,f (a )=-a 2<0,于是f (f (a ))=f (-a 2)=(-a 2)2+2(-a 2)+2=a 4-2a 2+2, 令a 4-2a 2+2=2,解得a=√2(a=0,-√2舍去).综上,a 的取值为√2.16.(2014浙江,文16)已知实数a ,b ,c 满足a+b+c=0,a 2+b 2+c 2=1,则a 的最大值是 . 答案:√63解析:由a+b+c=0可得c=-(a+b ).又a 2+b 2+c 2=1,所以a 2+b 2+[-(a+b )]2=1, 整理得2b 2+2ab+2a 2-1=0.又由a 2+b 2+c 2=1易知0≤b 2≤1,-1≤b ≤1,因此关于b 的方程2b 2+2ab+2a 2-1=0在[-1,1]上有解,所以{Δ=4a 2-8(2a 2-1)≥0,-1≤-a 2≤1,2-2a +2a 2-1≥0,2+2a +2a 2-1≥0,解得a ≤√63,即a 的最大值是√63.17.(2014浙江,文17)设直线x-3y+m=0(m ≠0)与双曲线x 2a 2−y 2b2=1(a>0,b>0)的两条渐近线分别交于点A ,B.若点P (m ,0)满足|PA|=|PB|,则该双曲线的离心率是 . 答案:√52解析:双曲线x 2a 2−y 2b2=1的两条渐近线方程分别是y=b a x 和y=-b ax.由{y =ba x ,x -3y +m =0,解得A (-am a -3b ,-bm a -3b),由{y =-ba x ,x -3y +m =0,解得B (-am a+3b ,bm a+3b).设AB 中点为E ,则E (-a 2ma 2-9b2,-3b 2m a 2-9b2).由于|PA|=|PB|,所以PE 与直线x-3y+m=0垂直,而k PE =3b 2m a 2-9b 2m --a 2m a 2-9b2=3b22a 2-9b2,于是3b22a 2-9b2·13=-1.所以a 2=4b 2=4(c 2-a 2). 所以4c 2=5a 2,解得e=c a=√52.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)(2014浙江,文18)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c.已知4sin 2A -B2+4sin A sin B=2+√2.(1)求角C 的大小;(2)已知b=4,△ABC 的面积为6,求边长c 的值.分析:(1)利用二倍角的余弦公式及两角和的余弦公式,将已知条件化简.由A+B 的余弦值,求出A+B 的值,从而得出角C 的大小.(2)利用三角形的面积公式求出a 值,再由余弦定理即可求出c 值. 解:(1)由已知得2[1-cos(A-B )]+4sin A sin B=2+√2,化简得-2cos A cos B+2sin A sin B=√2, 故cos(A+B )=-√22.所以A+B=3π4,从而C=π4.(2)因为S △ABC =12ab sin C ,由S △ABC =6,b=4,C=π4,得a=3√2.由余弦定理c 2=a 2+b 2-2ab cos C ,得c=√10.19.(本题满分14分)(2014浙江,文19)已知等差数列{a n }的公差d>0.设{a n }的前n 项和为S n ,a 1=1,S 2·S 3=36. (1)求d 及S n ;(2)求m ,k (m ,k ∈N *)的值,使得a m +a m+1+a m+2+…+a m+k =65.分析:(1)利用等差数列前n 项和公式与已知进行基本量运算,即可求出公差d ,进而求出S n .(2)利用等差数列的通项公式或前n 项和公式可得出m ,k 的关系式,再由m ,k ∈N *,通过2m+k-1=13,k+1=5,求出m ,k 的值.解:(1)由题意知(2a 1+d )(3a 1+3d )=36,将a 1=1代入上式解得d=2或d=-5. 因为d>0,所以d=2.从而a n =2n-1,S n =n 2(n ∈N *).(2)由(1)得a m +a m+1+a m+2+…+a m+k =(2m+k-1)(k+1). 所以(2m+k-1)(k+1)=65. 由m ,k ∈N *知2m+k-1>k+1>1, 故{2m +k -1=13,k +1=5,所以{m =5,k =4.20.(本题满分15分)(2014浙江,文20)如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=√2.(1)证明:AC⊥平面BCDE;(2)求直线AE与平面ABC所成的角的正切值.分析:(1)先由勾股定理的逆定理,证出线线垂直,再利用面面垂直的性质定理,推出线面垂直,即得结论.(2)由面面垂直的性质可得线面垂直,利用线面垂直的转化,可求作并证明所求线面角(为∠EAF).将空间角转化为平面角,再利用解直角三角形,求出线面角的正切值.(1)证明:连接BD.在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=√2,由AC=√2,AB=2,得AB2=AC2+BC2,即AC⊥BC.又平面ABC⊥平面BCDE,从而AC⊥平面BCDE.(2)解:在直角梯形BCDE中,由BD=BC=√2,DC=2,得BD⊥BC,又平面ABC⊥平面BCDE,所以BD⊥平面ABC.作EF∥BD,与CB延长线交于F,连接AF,则EF⊥平面ABC.所以∠EAF是直线AE与平面ABC所成的角.在Rt△BEF中,由EB=1,∠EBF=π4,得EF=√22,BF=√22.在Rt△ACF中,由AC=√2,CF=3√22,得AF=√262.在Rt△AEF中,由EF=√22,AF=√262,得tan∠EAF=√1313.所以直线AE与平面ABC所成的角的正切值是√1313.21.(本题满分15分)(2014浙江,文21)已知函数f(x)=x3+3|x-a|(a>0).若f(x)在[-1,1]上的最小值记为g(a).(1)求g(a);(2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.分析:(1)由于f(x)解析式中含绝对值,因此要去绝对值符号.化简解析式必须对a>0分情况讨论,并对x所属区间讨论.再通过求导数判断函数的单调性,利用函数单调性求出函数f(x)的最小值g(a).(2)令h(x)=f(x)-g(a),问题转化为h(x)≤4在x∈[-1,1]上恒成立.对恒成立问题,常转化为函数最值问题处理,即只需求出函数h(x)在[-1,1]上的最大值为4.因此,根据g(a)分情况讨论h(x)的最大值,借助于导数,利用函数单调性法求最值即可得解.(1)解:因为a>0,-1≤x≤1,所以①当0<a<1时,若x∈[-1,a],则f(x)=x3-3x+3a,f'(x)=3x2-3<0,故f(x)在(-1,a)上是减函数;若x∈[a,1],则f(x)=x3+3x-3a,f'(x)=3x2+3>0,故f(x)在(a,1)上是增函数.所以g(a)=f(a)=a3.②当a≥1时,有x≤a,则f(x)=x3-3x+3a,f'(x)=3x2-3<0.故f(x)在(-1,1)上是减函数,所以g(a)=f(1)=-2+3a.综上,g(a)={a3,0<a<1,-2+3a,a≥1.(2)证明:令h(x)=f(x)-g(a),①当0<a<1时,g(a)=a3.若x ∈[a ,1],h (x )=x 3+3x-3a-a 3,得h'(x )=3x 2+3,则h (x )在(a ,1)上是增函数, 所以,h (x )在[a ,1]上的最大值是h (1)=4-3a-a 3,且0<a<1,所以h (1)≤4. 故f (x )≤g (a )+4.若x ∈[-1,a ],h (x )=x 3-3x+3a-a 3,得h'(x )=3x 2-3,则h (x )在(-1,a )上是减函数,所以,h (x )在[-1,a ]上的最大值是h (-1)=2+3a-a 3.令t (a )=2+3a-a 3,则t'(a )=3-3a 2>0. 知t (a )在(0,1)上是增函数. 所以,t (a )<t (1)=4,即h (-1)<4. 故f (x )≤g (a )+4.②当a ≥1时,g (a )=-2+3a ,故h (x )=x 3-3x+2,得h'(x )=3x 2-3, 此时h (x )在(-1,1)上是减函数,因此h (x )在[-1,1]上的最大值是h (-1)=4. 故f (x )≤g (a )+4.综上,当x ∈[-1,1]时,恒有f (x )≤g (a )+4.22.(本题满分14分)(2014浙江,文22)已知△ABP 的三个顶点都在抛物线C :x 2=4y 上,F 为抛物线C 的焦点,点M为AB 的中点,PF ⃗⃗⃗⃗⃗ =3FM ⃗⃗⃗⃗⃗⃗ . (1)若|PF|=3,求点M 的坐标;(2)求△ABP 面积的最大值.分析:(1)设出P 点坐标,由于PF 为焦半径,因此由抛物线定义,可求出P 点坐标,再利用已知向量关系,即可求出点M 的坐标.(2)△ABP 的面积可由底边AB 与其边上的高确定.求相交弦长|AB|只需设出直线AB 的斜截式方程,与抛物线方程联立,利用弦长公式即可.但要注意用Δ>0,确定参数范围.利用PF ⃗⃗⃗⃗⃗ =3FM ⃗⃗⃗⃗⃗⃗ 可得S △ABP =4S △ABF .所以AB 边上的高转化为焦点F 到直线AB 的距离.从而得出只含一个参数的目标函数S △ABP ,再利用导数判断函数的单调性,利用函数单调性,即可求出S △ABP 的最大值. 解:(1)由题意知焦点F (0,1),准线方程为y=-1.设P (x 0,y 0).由抛物线定义知|PF|=y 0+1,得到y 0=2,所以P (2√2,2)或P (-2√2,2).由PF ⃗⃗⃗⃗⃗ =3FM ⃗⃗⃗⃗⃗⃗ ,分别得M (-2√23,23)或M (2√23,23).(2)设直线AB 的方程为y=kx+m ,点A (x 1,y 1),B (x 2,y 2),P (x 0,y 0). 由{y =kx +m ,x 2=4y ,得x 2-4kx-4m=0.于是Δ=16k 2+16m>0,x 1+x 2=4k ,x 1x 2=-4m , 所以AB 中点M 的坐标为(2k ,2k 2+m ). 由PF ⃗⃗⃗⃗⃗ =3FM ⃗⃗⃗⃗⃗⃗ ,得(-x 0,1-y 0)=3(2k ,2k 2+m-1).所以{x 0=-6k ,y 0=4-6k 2-3m ,由x 02=4y 0得k 2=-15m+415. 由Δ>0,k2≥0,得-13<m ≤43.又因为|AB|=4√1+k 2√k 2+m , 点F (0,1)到直线AB 的距离为d=√1+k ,所以S △ABP =4S △ABF =8|m-1|√k 2+m =√15√3m 3-5m 2+m +1.记f (m )=3m 3-5m 2+m+1(-13<m ≤43).令f'(m)=9m2-10m+1=0,解得m1=19,m2=1.可得f(m)在(-13,19)上是增函数,在(19,1)上是减函数,在(1,43)上是增函数.又f(19)=256243>f(43).所以,当m=19时,f(m)取到最大值256243,此时k=±√5515.所以,△ABP面积的最大值为256√5135.。
2014年浙江省单考单招数学试卷高考卷

2014年浙江省单考单招数学试卷高考卷一、选择题(本大题共10小题,每小题4分,共40分)1. 设集合A={x|2<x<3},集合B={x|x²3x+2=0},则A∩B=()A. {1, 2}B. {2}C. {1}D. ∅2. 若复数z满足|z1|=|z+1|,则z在复平面内对应的点位于()A. 实轴上B. 虚轴上C. 直线y=x上D. 直线y=x上3. 已知函数f(x)=x²2x+3,则f(x)的最小值为()A. 2B. 3C. 4D. 54. 在等差数列{an}中,若a1=1,a3+a5=6,则a4=()A. 2B. 3C. 4D. 55. 若函数y=cos(2x+θ)的图像向右平移π/4个单位,得到函数y=cos(2xθ)的图像,则θ的值为()A. π/4B. π/2C. 3π/4D. π6. 设点P为圆C:(x2)²+(y+1)²=16的圆上任意一点,则点P到直线xy+3=0的距离d的取值范围是()A. [0, 4]B. [0, 8]C. [4, 8]D. [4, 16]7. 若直线y=kx+b与圆x²+y²=1相切,则k和b的关系为()A. k²+b²=1B. k²+b²=2C. k²+b²=0D. k²+b²=∞8. 已知函数f(x)=x²+2ax+a²+1(a为常数),若f(x)在区间[1,3]上的最小值为2,则a的值为()A. 1B. 0C. 1D. 29. 在三角形ABC中,若a=3,b=4,cosA=3/5,则sinB的值为()A. 3/5B. 4/5C. 3/4D. 4/310. 已知数列{an}满足a1=1,an+1=2an+1,则数列{an+1/an}的前n项和为()A. nB. n+1C. 2nD. 2n+1二、填空题(本大题共5小题,每小题4分,共20分)11. 已知函数f(x)=x²2x+3,求f(x)的单调减区间。
浙江高考数学试卷及答案

2014年浙江高考数学试卷及答案2014年普通高等学校招生全国统一考试(浙江卷) 数学(理科)一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出学科网的四个选项中,只有一项是符合题目要求的. (1)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,zxxk则=A CU( )A. ∅B. }2{ C.}5{ D.}5,2{ (2)已知i 是虚数单位,R b a ∈,,则“1==b a ”是“ibi a 2)(2=+”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件(3)某几何体的三视图(单位:cm )如图所示,则此几何体的学科网表面积是A. 902cm B. 1292cm C. 1322cmD. 1382cm4.为了得到函数zxxk x x y 3cos 3sin +=的图像,可以将函数xy 3sin 2=的图像( )A.向右平移4π个单位B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位5.在46)1()1(y x ++的展开式中,记nmy x 项的系数为),(n m f ,则=+++)3,0(2,1()1,2()0,3(f f f f )( ) A.45 B.60 C.120D. 210 6.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f ( )A.3≤cB.63≤<cC.96≤<cD.9>c7.在同意直角坐标系中,函数xx g x x x f aalog )(),0()(=≥=的图像可能是( )8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩,,min{,},y x yx y x x y≥⎧=⎨<⎩,设,a b 为平面向量,则( ) A.min{||,||}min{||,||}a b a b a b +-≤ B.min{||,||}min{||,||}a b a b a b +-≥ C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个篮球学科网()3,3m n ≥≥,从乙盒中随机抽取()1,2i i =个球放入甲盒中.(a )放入i 个球后,甲盒中含有红球的个数记为()1,2i i ξ=;(b )放入i 个球后,从甲盒中取1个球是红球的概率记为zxxk ()1,2ip i =.则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =,),(2)(22x x x f -=|2sin |31)(3x x f π=,99,,2,1,0,99==i ia i ,记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ,.3,2,1=k 则A.321I I I << B. 312I I I << C. 231I I I <<D.123I I I <<二、填空题:本大题共7小题,每小题4分,共28分.11.若某程序框图如图所示,当输入50时,则该程序运算后输出的学科网结果是________.12.随机变量ξ的取值为0,1,2,若()105P ξ==,()1E ξ=,则()D ξ=________. 13.当实数x ,y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时,zxxk 14ax y ≤+≤恒成立,则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有_____种(用数字作答). 15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ,则实数a 的取值范围是______16.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x (0a b >>)两条渐近线分别交于点B A ,,若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图,某人在垂直于水平地面的墙面前的点处进行射击训练. 学科网已知点到墙面的距离为,某目标点沿墙面的射击线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小.若则的最大值三.解答题:本大题共5小题,共72分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年浙江省高等职业技术教育招生考试数学试卷注意事项1、所有试题均需在答题纸上作答,未在规定区域内答题,每错一个区域扣卷面总分1分,在试卷和草稿纸上作答无效。
2、答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸和试卷上。
3、选择题每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
非选择题目用黑色字迹的签字笔或钢笔将答案写在答题纸上。
4、在答题纸上作图,可先用2B 铅笔,确定后必须用黑色字迹的签字或钢笔摸黑。
一、单项选择题(本大题共18小题,每小题2分,共36分在每小题列出的四个备选答案中,只有一个是符合题目要求的。
错涂、多涂或未涂均无分.1.已知集合{,,,}M a b c d =,则含有元素a 的所有真子集个数有( C A .5个 B .6个C .7个D .8个 2.已知函数(121x f x +=-,则(2f =( B A .-1 B .1C .2D .3 3.“0a b +=”是“0a b ⋅=”的( D A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件4.下列不等式(组的解集为{|0}x x <的是( A A .3323x x -<- B .20231x x -<⎧⎨->⎩ C .220x x ->D .|1|2x -<5.下列函数在区间(0,+∞上为减函数的是( C A .31y x =- B .2(log f x x = C .1((2xg x =D .(sin A x x = 6.若α是第二象限角,则7απ-是( D A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角 7.已知向量(2,1a =-,(0,3b =,则|2|a b -= ( BA .(2,7-BC .7D 8.在等比数列{}n a 中,若23a =,427a =,则5a =( C A . -81 B .81 C .81或-81D .3或-3 9.抛掷一枚骰子,落地后面朝上的点数为偶数的概率等于( A A .0.5 B .0.6 C .0.7D .0.8 10.已知角β终边上一点(4,3P -,则cos β=( B A .35- B .45 C .34-D .54 11.cos78cos18sin18sin102︒⋅︒+︒︒=( DA .BC .12-D .12 12.已知两点(2,5M -,(4,1N -,则直线MN 的斜率k =( B A .1 B .-1 C 12D .12- 13.倾斜角为3π,在上截距为3-的直线方程为( A A .3x =- B .3y =- C .3x y +=-D .3x y -=- 14.函数的最小值和最小正周期分别为( D A .1和2π B .0和2π C .1和πD .0和π 15.直线:230l x y +-=与圆22:240C x y x y ++-=的位置关系是( D A .相交且不过圆心 B .相切 C .相离 D .相交且过圆心16.双曲线22149x y -=的离心率e = ( CA .23B .32C .2D .317.将抛物线24y x =-绕顶点按逆时针方向旋转角π,所得抛物线方程为( A A .24y x = B .24y x =-C .24x y =D .24x y =- 18.在空间中,下列结论正确的是( D A .空间三点确定一个平面B .过直线外一点有且仅有一条直线与已知直线垂直C .如果一条直线与平面的一条直线平行,那么这条直线与此平面平行D .三个平面最多可将空间分成八块二、填空题(本大题共8小题,每小题3分,共24分19.若04x <<,则当且仅当x =______ 2__时,(4x x -的最大值为420.从8位女生和5位男生中,选3位女生和2位男生参加学校舞蹈队,共有_______560___种不同选法21.计算4log 8=__________32_ 22.等差数列{}n a 中,已知172,35a S ==,则等差数列{}n a 的公差d =_______123.函数2(253f x x x =-++图象的顶点坐标是___________549(,4824.已知圆柱底面半径2r =,高3h =,则其轴截面的面积为___________1225.直线210x y +-=与两坐标轴所围成的三角形面积S =___________14 26.在闭区间[0,2]π上,满足等式sin cos1x =,则x ___________1,122ππ-+三、解答题(共8小题,满分60分,每小题要写清必要的文字步骤27.(6分在ABC ∆中,已知4,5,b c A ==为钝角,且4sin 5A =,求a((22241sin 53cos 522cos 65A A A a b c bc A a =∴=-=+-=∴=解为锐角, 利用余弦定理28.(6分求过点(0,5P ,且与直线:320l x y -+=平行的直线方程:3203030505350l x y x y C C C x y -+=-+=⋅-+==-+=解与平行的直线设为过点(0,5代入得,则所以29.(7分化简55(1(1x x -++ 552345234524(1(1(1510105(151010522010x x x x x x x x x x x x x x -++=-+-+--+++++=++解30.(8分已知32tan ,tan 75αβ==,且,αβ为锐角,求αβ+ ((tan tan 1tan(11tan tan 2,04αβαβαβαβαβππαβ++==-⋅<+≤+=解因为为锐角, 所以31.(8分已知圆22:4640C x y x y +-++=和直线:50l x y -+=,求直线l 上到圆C 的距离最小的点的坐标,并求最小距离。
(((2212(39(2,3,32(2,3:50331010(3,250x y r l x y d rd r l x y x y l x y -++=-=--+===>-=++=++=⎧⇒-⎨-+=⎩解圆( 圆心半径圆心到直线距离所以直线与圆相离直线与圆最短距离为过圆心作直线的垂线为解方程组交点,即上到圆距离最小的点。
32.(7分(1画出底面边长为4cm ,高为2cm 的正四棱锥P ABCD -的示意图(3分(2由所作的正四棱锥P ABCD -,求二面角P AB C --的度数(4分((1AB E,OE,PE 2,2tan 1,4545o o PEO P AB C Rt PEO PO EO POPEO PEO EOP AB C ∠--∆==∠==∠=--解取中点连为的平面角。
中所以二面角为33.(8分已知函数5,01((13,1x f x f x x ≤≤⎧=⎨-+>⎩,(1求(2,(5f f 的值(4分(2当*x N ∈时,构成一数列,求其通项公式(4分((*1115,011((13,1(2(13538(5(43(36(29172(1,(2,(3,(4,...(,5(1(3,{}3=(n n n n n x f x f x x f f f f f f x N f f f f a f n a a a f n f n a d a a n +≤≤⎧=⎨-+>⎩=+=+==+=+=+=∈==-=+-==+- 解当时,构成一数列令则考察知成等差所以132d n =+34.(10分两边靠墙的一个区域,边界正好是椭圆轨迹的一部分,如图所示,现要设计一个长方形花坛,要求其不靠墙的顶点正好落在椭圆轨迹上, (1根据所给条件,求出椭圆的标准方程(3分(2求长方形的面积S与边长x的函数关系式(3分(3求当边长x为多少时,面积S有最大值,并求其最大值(4分 ((222222 222 12,1 141 2,2 (4 (3[]4 2=(4 12(4a b x x yx yS xy xx xxxx xx Sx==+=====<<+--≤=-====解如图,椭圆,交点在轴上所以椭圆标准方程为: 长方形长为则宽面积利用均值定理等号当且仅当即所以:当边长,最大面积【备注】也可用二次函数最值问题解答2014年浙江省高等职业技术教育招生考试数学试卷注意事项1、所有试题均需在答题纸上作答,未在规定区域内答题,每错一个区域扣卷面总分1分,在试卷和草稿纸上作答无效。
2、答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸和试卷上。
3、选择题每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
非选择题目用黑色字迹的签字笔或钢笔将答案写在答题纸上。
4、在答题纸上作图,可先用2B铅笔,确定后必须用黑色字迹的签字或钢笔摸黑。
一、单项选择题(本大题共18小题,每小题2分,共36分在每小题列出的四个备选答案中,只有一个是符合题目要求的。
错涂、多涂或未涂均无分.1.已知集合{,,,}M a b c d=,则含有元素a的所有真子集个数有(浙2014年34郎兴刚.gspA .5个B .6个C .7个D .8个 2.已知函数(121x f x +=-,则(2f = (A .-1B .1C .2D .3 3.“0a b +=”是“0a b ⋅=”的(A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件4.下列不等式(组的解集为{|0}x x <的是(A .3323x x-<-B .20231x x -<⎧⎨->⎩C .220x x ->D .|1|2x -<5.下列函数在区间(0,+∞上为减函数的是(A .31y x =-B .2(log f x x =C .1((2xg x =D .(sin A x x = 6.若α是第二象限角,则7απ-是(A .第一象限角B .第二象限角C .第三象限角D .第四象限角 7.已知向量(2,1a =-,(0,3b =,则|2|a b -= (A .(2,7-BC .7D 8.在等比数列{}n a 中,若23a =,427a =,则5a = (A . -81B .81C .81或-81D .3或-3 9.抛掷一枚骰子,落地后面朝上的点数为偶数的概率等于(A .0.5B .0.6C .0.7D .0.8 10.已知角β终边上一点(4,3P -,则cos β=(A .35-B .45C .34- D .5411.cos78cos18sin18sin102︒⋅︒+︒︒=(A .2-B .2C .12-D .1212.已知两点(2,5M -,(4,1N -,则直线MN 的斜率k = (A .1B .-1C12D .12- 13.倾斜角为3π,在上截距为3-的直线方程为(A .3x =-B .3y =-C .3x y +=-D .3x y -=- 14.函数的最小值和最小正周期分别为(A .1和2πB .0和2πC .1和πD .0和π 15.直线:230l x y +-=与圆22:240C x y x y ++-=的位置关系是(A .相交且不过圆心B .相切C .相离D .相交且过圆心16.双曲线22149x y -=的离心率e = (A .23B .32C D 17.将抛物线24y x =-绕顶点按逆时针方向旋转角π,所得抛物线方程为(A .24y x =B .24y x =-C .24x y =D .24x y =- 18.在空间中,下列结论正确的是(A .空间三点确定一个平面B .过直线外一点有且仅有一条直线与已知直线垂直C .如果一条直线与平面的一条直线平行,那么这条直线与此平面平行D .三个平面最多可将空间分成八块二、填空题(本大题共8小题,每小题3分,共24分19.若04x <<,则当且仅当x =________时,(4x x -的最大值为420.从8位女生和5位男生中,选3位女生和2位男生参加学校舞蹈队,共有__________种不同选法21.计算4log 8=___________22.等差数列{}n a 中,已知172,35a S ==,则等差数列{}n a 的公差d =_______ 23.函数2(253f x x x =-++图象的顶点坐标是___________24.已知圆柱底面半径2r =,高3h =,则其轴截面的面积为___________ 25.直线210x y +-=与两坐标轴所围成的三角形面积S =___________ 26.在闭区间[0,2]π上,满足等式sin cos1x =,则x ___________三、解答题(共8小题,满分60分,每小题要写清必要的文字步骤27.(6分在ABC ∆中,已知4,5,b c A ==为钝角,且4sin 5A =,求a28.(6分求过点(0,5P ,且与直线:320l x y -+=平行的直线方程29.(7分化简55(1(1x x -++30.(8分已知32tan ,tan 75αβ==,且,αβ为锐角,求αβ+31.(8分已知圆22:4640C x y x y +-++=和直线:50l x y -+=,求直线l 上到圆C 的距离最小的点的坐标,并求最小距离。
