奈奎斯特 ppt课件
合集下载
最新奈奎斯特稳定判据演示教学

G 1
0.5 0
E D
F
H
C
-0.5
B
-1
A
-1.5
-2 -1 -0.5 0 0.5 1 1.5 2 2.5 3
2. 围线CS只包围零点不包围极点
如图所示围线CS包围一个零点z=-2,先考察因子(s+2)辐角a,当 变点s沿CS顺时针绕行一周时,a的变化为-360°。映射到F(S)平 面上对应变点F(S)沿CF绕行一周后的辐角变化也应等于-360°。
F(s) F(s2)F(s1)
im1(s2
zi
)
n
(s2
j1
pj
)im1(s1
zi
)
n
(s1
j1
pj
)
im1(s2
zi
m
)(s1 i1
zi
)
jn1(s2
pj
)
n
(s1
j1
pj
)
m
n
(szi)(s pj)
i1
j1
例
F(s) F(s2) F(s1)
F(s) s2 s
(s22) (s20) (s12) (s10)
⒋ 围线CS包围Z个零点和P个极点 由上述讨论显然可知,当变点s沿CS顺时针绕行一周时,CF应顺 时针包围原点Z-P次。亦即CF顺时针包围原点次数N=Z-P。
2
A BC
s平面
H
2
a
D
1
1.5
1
0.5
0
D
-0.5
E G A
G F E CS顺时针
-1 -1.5
C
-2 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
控制工程基础 (第12讲) 第五章 乃魁斯特(Nyquist)稳定性判据 PPT课件

如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…),
即包围的零点数与极点数相同,则在 F(s) 平面上,
相应的封闭曲线不包围 F(s) 平面上的原点。
上述讨论是映射定理的图解说明,奈奎斯特稳 定判据正是建立在映射定理的基础上。
相角(幅角)定理:
如果闭合曲线 s 以顺时针方向为正方向,在 s 平
在右半s平面内的零点数和极点数联系起来的判据。这 种方法无须求出闭环极点,得到广泛应用。
奈奎斯特稳定判据是建立在复变函数理论中的图形映 射基础上的 。
相角(幅角)定理:
如果闭合曲线 S 以顺时针方向为正方向,在[S]平
面上包围了Fs 的 Z 个零点和 P 个极点,但不经过
任何一个零点和极点,那么,对应的映射曲线 F 也以
奈魁斯特稳定判据是利用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性,而且可根据相对稳定的 概念,讨论闭环系统的瞬态性能,指出改善系统性能的途径。 它从代数判据脱颖而出,故可以说是一种几何判据。
06-7-20
控制系统系统的稳定性分析
2
奈魁斯特稳定判据无需求取闭环系统的特征根,而是利用
F(s) 的轨迹将逆时针方向包围 F(s)平面上原点两次
06-7-20
控制系统系统的稳定性分析
9
s平面
B3
2
1
A0
-1
-2
F -3 -3
-2
-1
j
Im
C
2
1.5
F (s)平面
1 B1
0.5
D
E1
0 C1
F1 -0.5
-1
A
-1.5
D1
奈奎斯特稳定判据

闭环系统稳定的充分必要条件为:在 Gk(s)平面上的开环频率特
性曲线及其镜象当w从-∞变化到+∞时,将以逆时针的方向围绕
(-1,j0)点P圈。 对于开环系统稳定的情况,P=0,则闭环系统稳定的充分必
要条件是开环频率特性曲线及其镜象不包围(-1,j0)点。 不稳定的闭环系统在s右半平面的极点数为:Z = N + P。
F (s) F (s2 ) F (s1) 00 1800 (450 1350 ) 900
F (s)平面
df (0, j1)
8
1. 围线CS既不包围零点也不包围极点
如图所示,在S平面上当变点s沿围线 CS按顺时针方向运动一周时,我们 来考察F(S)中各因子项的辐角的变化 规律。 现以图中未被包围的零点-2为例。当 变点s沿CS绕行一周后,因子(s+2)的 辐角a的变化为0°。
F(S)平面上,围线CF应逆时针包围原点一次。
2 F
1.5
s平面 A B C
1
G
E
0.5
2
H
1
b
D
0H -0.5
D
GF E
CS顺时针
-1 A
C
-1.5
B -2
-1 -0.5 0 0.5 1 1.5 2 2.5 3
同理,当围线CS的内域只包含P个极点时, CF应逆时针包围原点 13 P次,或者说, CF顺时针包围原点-P次。
F(s)的零点为 闭环传递函数的极点;
17
奈奎斯特为了应用柯西辐角原理研究闭环系统的稳定性, 因此设想:
如果有一个s平面的封闭曲线能包围整个s右半平面,则根据 柯西辐角原理知:该封闭曲线在F(s)平面上的映射包围原点的次 数应为:
N=F(s)的右半零点数-F(s)的右半极点数 =闭环系统右半极点数-开环系统右半极点数
性曲线及其镜象当w从-∞变化到+∞时,将以逆时针的方向围绕
(-1,j0)点P圈。 对于开环系统稳定的情况,P=0,则闭环系统稳定的充分必
要条件是开环频率特性曲线及其镜象不包围(-1,j0)点。 不稳定的闭环系统在s右半平面的极点数为:Z = N + P。
F (s) F (s2 ) F (s1) 00 1800 (450 1350 ) 900
F (s)平面
df (0, j1)
8
1. 围线CS既不包围零点也不包围极点
如图所示,在S平面上当变点s沿围线 CS按顺时针方向运动一周时,我们 来考察F(S)中各因子项的辐角的变化 规律。 现以图中未被包围的零点-2为例。当 变点s沿CS绕行一周后,因子(s+2)的 辐角a的变化为0°。
F(S)平面上,围线CF应逆时针包围原点一次。
2 F
1.5
s平面 A B C
1
G
E
0.5
2
H
1
b
D
0H -0.5
D
GF E
CS顺时针
-1 A
C
-1.5
B -2
-1 -0.5 0 0.5 1 1.5 2 2.5 3
同理,当围线CS的内域只包含P个极点时, CF应逆时针包围原点 13 P次,或者说, CF顺时针包围原点-P次。
F(s)的零点为 闭环传递函数的极点;
17
奈奎斯特为了应用柯西辐角原理研究闭环系统的稳定性, 因此设想:
如果有一个s平面的封闭曲线能包围整个s右半平面,则根据 柯西辐角原理知:该封闭曲线在F(s)平面上的映射包围原点的次 数应为:
N=F(s)的右半零点数-F(s)的右半极点数 =闭环系统右半极点数-开环系统右半极点数
自动控制原理5.4 奈奎斯特判据

二、奈氏判据
设Gk s在s右半平面的极点数为p,则闭环系 统稳定的充要条件是:在 Gk s 平面上的
11
★奈氏判据
§5—4 奈奎斯特判据
Gk j 曲线及其镜像当从 时,将逆时
针绕(- 1,j0)点转p周。
(1) 若开环本身稳定,则p 0, 故稳定的充要条件是:
系统稳定,否则系统不稳定。 但Gk F s 1 所以F(s)的Γ曲线绕原点运动相当于 Gk j 的封闭 曲线绕(-1,j0)点运动, 因为F( s)与Gk s只差常数1。
9
★幅角定理(续)
§5—4 奈奎斯特判据
Gk GH的封闭曲线即为 时Gk j 的
1
Mk Nk
Nk Mk Nk
Nb Nk
1
★幅角定理(续)
§5—4 奈奎斯特判据
其中Nk s为开环特征式,Nb s为闭环特征式。
F s的特点:
1、Fs的极点 开环极点, Fs的零点 闭环极点;
2、Fs的零极点个数相等n m;
3、F s与G( s)只差常数1。
§5—4 奈奎斯特判据
[F(s)] 0
5
★幅角定理(续)
§5—4 奈奎斯特判据
★幅角定理:设s平面上不通过F(s)任何奇点的封 闭曲线Γ包围s平面上F(s)的z个零点和p个极点。 当s以顺时针方向沿着封闭曲线Γ移动一周时, 则在F(s)平面上相对应于封闭曲线Γ的映射函数
j
1'
s
j 2'
F s
曲线。
因为对应于奈氏回线中:
1) 0 ; 3) 0;
只有2)半径R , Fs 1 Gk s,
而Gk
设Gk s在s右半平面的极点数为p,则闭环系 统稳定的充要条件是:在 Gk s 平面上的
11
★奈氏判据
§5—4 奈奎斯特判据
Gk j 曲线及其镜像当从 时,将逆时
针绕(- 1,j0)点转p周。
(1) 若开环本身稳定,则p 0, 故稳定的充要条件是:
系统稳定,否则系统不稳定。 但Gk F s 1 所以F(s)的Γ曲线绕原点运动相当于 Gk j 的封闭 曲线绕(-1,j0)点运动, 因为F( s)与Gk s只差常数1。
9
★幅角定理(续)
§5—4 奈奎斯特判据
Gk GH的封闭曲线即为 时Gk j 的
1
Mk Nk
Nk Mk Nk
Nb Nk
1
★幅角定理(续)
§5—4 奈奎斯特判据
其中Nk s为开环特征式,Nb s为闭环特征式。
F s的特点:
1、Fs的极点 开环极点, Fs的零点 闭环极点;
2、Fs的零极点个数相等n m;
3、F s与G( s)只差常数1。
§5—4 奈奎斯特判据
[F(s)] 0
5
★幅角定理(续)
§5—4 奈奎斯特判据
★幅角定理:设s平面上不通过F(s)任何奇点的封 闭曲线Γ包围s平面上F(s)的z个零点和p个极点。 当s以顺时针方向沿着封闭曲线Γ移动一周时, 则在F(s)平面上相对应于封闭曲线Γ的映射函数
j
1'
s
j 2'
F s
曲线。
因为对应于奈氏回线中:
1) 0 ; 3) 0;
只有2)半径R , Fs 1 Gk s,
而Gk
奈奎斯特稳定判据

二、控制系统的频域稳定性判据
3. n阶系统 n阶系统稳定的充要条件是当ω由0→∞时, 特征矢量D(jω)的相角变化量为 Δ Arg[D(jω)]= n² 90 °
奈奎斯特稳定判据
三、奈奎斯特判据(奈氏判据) 1. 0型系统(开环没有串联积分的系统)
⑴开环是稳定的系统
如果已知开环系统是稳定的,那么当ω由0→∞时, 若矢量F(j ω)的相角变化量为0,也就是F(j ω)的轨迹不包 围原点,那么闭环系统的特征方程式DB(s)的根全部在s 左半平面,系统是稳定的。否则,系统是不稳定的。 这样,系统稳定问题转化为找出ω由0→∞时,矢量 F(j ω)的相角变化量问题。
奈奎斯特稳定判据
四、伯德图上的稳定性判据 奈氏判据除了可以表示在极坐标图上, 还可以表示在伯德图上。
w + w=+ w=0 -1 P=0 w
0
180
-
+
四、伯德图上的稳定性判据
由图可知,幅相曲线不包围(-1,j0)点。 此结果也可以根据ω增加时,幅相曲线自下 向上(幅角减小)和自上向下(幅角增加) 穿越实轴区间(-∞,-1)的次数决定。
如果把自上向下的穿越称为正穿越,正穿越次 数用N+表示。把自下向上的穿越称为负穿越,负 穿越次数用N-表示,则R可以用N+和N-之差确定, 即 R= N+- N-
由图可知, N+=1, N-=1,故R=0。
四、伯德图上的稳定性判据
1.Bode图与Nyquist图的对应关系 a. Nyquist图的单位圆 | G(j )H(j ) | 1 对应 Bode图的横轴 20lg | G(j )H(j ) | 0 b. | G(j )H(j ) | 1 单位圆外 对应 20lg| G(j )H(j ) | 0 横轴以上区域
奈奎斯特曲线

第五章 频域分析法
幅相频率特性G(j) : G(j) 的幅值和相位均随输入正弦信 号角频率的变化而变化。
A() 1/ R , T L / R 1 (T)2
幅频特性A(): 稳态输出信号的幅值与输入信号的幅值之比 。
arctan L arctanT
• 频域分析法
➢动态性能 频带宽度, 频率特性曲线的形状 ➢稳定性分析 奈奎斯特稳定判据
第五章 频域分析法
一、频率特性的基本概念
[例]: R-L串联回路
u U sin t
U U e jt
Z R j L
G j
UI&&
R
1
jL
1/ R
1 T j
1/ R e j A()e j 1 (T)2
1
0.5
0
-0.5
-1
-1.5
-2
0
0.5
1
1.5
2
2.5
3
线性系统
5
4
3
2
1
0
-1
-2
-3
-4
-5
0
0.5
1
1.5
2
2.5
3
输出的振幅和相位一般均不同于输入量,
且随着输入信号频率的变化而变化 。
第五章 频域分析法
G(s) 1 1 RCs
G( j) 1 1 1 RCj 1 Tj
(1)不必求解系统的特征根,采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析,因而具有形象直观和计算量少的特 点。
Байду номын сангаас
奈奎斯特准则

8
h(t)的主波峰跨越了3个Tb ;而拖尾每Tb过零一次。
h(t)
h(t)并不满足
h(t)满足
的条件
9
以“111100”的响应波形为 例:
若用h(t)作为传送波形,码元间隔为Tb,显然每个Tb 并非都是过零点。在每个Tb时刻抽样,确有串扰。 然而,在(n+1/2)Tb时刻抽样,串扰只发生在相邻两码 元之间。每个抽样值等于该时刻本码元的值加上前一 码元的值。������ 相邻码元极性相反时贡献相抵消,相邻码元极性相同 时贡献相迭加。 10
复习
1
奈奎斯特准则:
实际系统的传输函数很难具有理想低通的形式。 有没有其它形式的传输函数也能满足:
t = nTb处过 零,此即抽 样位置
把上式的积分区间(-∞,∞)用分段积分代替,每 段长为2π/Tb,则上式可写成:
2
令ω′=ω-2mπ/Tb,变量代换后又可用ω代替 ω′,则有
引入等效系统传输函数:
27
对双极性不归零码(信源等概) :
“1”码电平A1 =A / 2 ,平均功率为A2 / 4 。 “0”码电平A0 = -A / 2 ,平均功率为A2 / 4 。
信号平均功率为 S = P(1)· 1 + P(0) · 0=A2/ 4 S S 噪声平均功率为 N = σn2 信噪比为γ= S / N =A2 / 4σn2, 则双极性不归零码误码率为
5
判断一个系统有无码间干扰,不仅要看它的传输 函数经分段、平移、叠加后的等效传输函数是否 具有理想低通形式,还要看等效传输函数的带宽 是否与所设定的码率匹配。
定义等效传输函数的带宽BN叫做奈奎斯特 带宽。它与所设定的码率的关系为: BN = 1/2Tb= RB/2 或RB = 2BN
h(t)的主波峰跨越了3个Tb ;而拖尾每Tb过零一次。
h(t)
h(t)并不满足
h(t)满足
的条件
9
以“111100”的响应波形为 例:
若用h(t)作为传送波形,码元间隔为Tb,显然每个Tb 并非都是过零点。在每个Tb时刻抽样,确有串扰。 然而,在(n+1/2)Tb时刻抽样,串扰只发生在相邻两码 元之间。每个抽样值等于该时刻本码元的值加上前一 码元的值。������ 相邻码元极性相反时贡献相抵消,相邻码元极性相同 时贡献相迭加。 10
复习
1
奈奎斯特准则:
实际系统的传输函数很难具有理想低通的形式。 有没有其它形式的传输函数也能满足:
t = nTb处过 零,此即抽 样位置
把上式的积分区间(-∞,∞)用分段积分代替,每 段长为2π/Tb,则上式可写成:
2
令ω′=ω-2mπ/Tb,变量代换后又可用ω代替 ω′,则有
引入等效系统传输函数:
27
对双极性不归零码(信源等概) :
“1”码电平A1 =A / 2 ,平均功率为A2 / 4 。 “0”码电平A0 = -A / 2 ,平均功率为A2 / 4 。
信号平均功率为 S = P(1)· 1 + P(0) · 0=A2/ 4 S S 噪声平均功率为 N = σn2 信噪比为γ= S / N =A2 / 4σn2, 则双极性不归零码误码率为
5
判断一个系统有无码间干扰,不仅要看它的传输 函数经分段、平移、叠加后的等效传输函数是否 具有理想低通形式,还要看等效传输函数的带宽 是否与所设定的码率匹配。
定义等效传输函数的带宽BN叫做奈奎斯特 带宽。它与所设定的码率的关系为: BN = 1/2Tb= RB/2 或RB = 2BN
奈奎斯特稳定判据

幅角原理:如果封闭曲线内有Z个F(s)的零点, P个
F(s)的极点 ,则s 沿封闭曲线s 顺时针方向转一圈时,在
F(s)平面上,曲线F(s)绕其原点逆时针转过的圈数。
+
5. 4 . 3 奈氏判据
(1)0型系统
0
s为包围虚轴和整个右半平面。
s平面s 映射 F(s)
解:① 由开环传递函数知 P = 1 。 ② 作系统的开环对数频率特性曲线。
() = 90 + arctanT2 (180 arctanT1 )
270
arctan
(T1 1
T2 ) 2T1 T2
当() = 180时,g =(1/T1T2)1/2 ,A(g)=kT2
③ 稳定性判别。 G(s)H(s)有一个积分环节N =1 ,故
开环极坐标图如图
j
01
19
k(0.1s 1) Gk (s) s(s 1)
=0
Im
增补线
1 0.1k
Re 0
(3) 稳定性判别: 因为是1型系统,需作增补线如图
当 0.1k < 1 ,k > 10时, R =1/2,z = p 2R = 0
闭环系统是稳定的。
20
5.4.4 伯德图上的稳定性判据
Im
() 1
(+)
0
由图可知,幅相曲线 不 包 围 (1 , j0) 点 。 此 结
Re 果也可以根据 增加时幅
相曲线自下向上(幅角减 小)和自上向下(幅角增加) 穿越实轴区间(,1)的 次数决定。
R = N N
自实轴区间(,1)开始向下的穿越称为半次正穿越,自实轴
区间(,1)开始向上的穿越为半次负穿越。
奈奎斯特稳定判据09

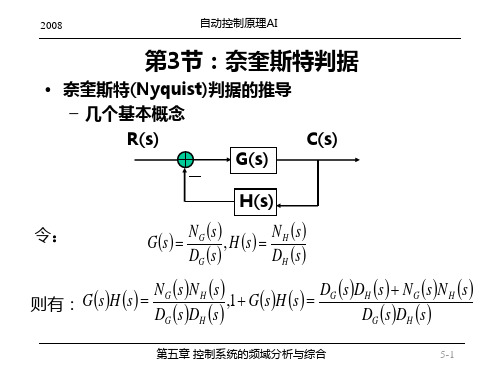
R(s)
一、控制系统的辅助函数
开环传递函数为: Gk ( s ) G ( s ) H ( s ) M ( s )
G (s )
C (s )
H (s )
N (s) G (s) 闭环传递函数为: ( s ) 1 G ( s) H ( s)
M ( s) M (s) N (s) 特征多项式为: 1 G ( s ) H ( s ) 1 N (s) N (s)
对于一个控制系统,若其特征根处于s右半平面,则系统是不稳定的。 对于上面讨论的辅助函数 F(s)=1+Gk(s),其零点恰好是闭环系统的极点, 因此,只要搞清F(s)的零点在s右半平面的个数,就可以给出稳定性结论。如 果F(s)的右半零点个数为零,则闭环系统是稳定的。 奈奎斯特为了应用柯西幅角原理研究闭环系统的稳定性,因此设想: 如果有一个s平面的封闭曲线能包围整个s右半平面,则根据柯西幅角原 理知:该封闭曲线在F(s)平面上的映射包围原点的次数应为: N = F(s)的右半零点数-F(s)的右半极点数 = 闭环系统右半极点数-开环系统右半极点数 当已知开环右半极点数时,便可由N判断闭环右极点数。
C
-2 -1 -0.5
2.5
3
同理,当围线CS的内域只包含P个极点时, CF应逆时针包围原点P次, 或者说, CF顺时针包围原点-P次。
⒋ 围线CS包围Z个零点和P个极点
由上述讨论显然可知,当变点s沿CS顺时针绕行一周时,CF应顺时针包围 原点Z-P次。亦即CF顺时针包围原点次数N=Z-P。
这就是所谓幅角原理。
1. 围线CS既不包围零点也不包围极点
如图所示,在s平面上当变点s沿围线CS按 顺时针方向运动一周时,我们来考察F(s)中 各因子项的幅角的变化规律。 现以图中未被包围的零点-2为例。当变点s 沿CS绕行一周后,因子(s+2)的幅角a的变化 为0°。
一、控制系统的辅助函数
开环传递函数为: Gk ( s ) G ( s ) H ( s ) M ( s )
G (s )
C (s )
H (s )
N (s) G (s) 闭环传递函数为: ( s ) 1 G ( s) H ( s)
M ( s) M (s) N (s) 特征多项式为: 1 G ( s ) H ( s ) 1 N (s) N (s)
对于一个控制系统,若其特征根处于s右半平面,则系统是不稳定的。 对于上面讨论的辅助函数 F(s)=1+Gk(s),其零点恰好是闭环系统的极点, 因此,只要搞清F(s)的零点在s右半平面的个数,就可以给出稳定性结论。如 果F(s)的右半零点个数为零,则闭环系统是稳定的。 奈奎斯特为了应用柯西幅角原理研究闭环系统的稳定性,因此设想: 如果有一个s平面的封闭曲线能包围整个s右半平面,则根据柯西幅角原 理知:该封闭曲线在F(s)平面上的映射包围原点的次数应为: N = F(s)的右半零点数-F(s)的右半极点数 = 闭环系统右半极点数-开环系统右半极点数 当已知开环右半极点数时,便可由N判断闭环右极点数。
C
-2 -1 -0.5
2.5
3
同理,当围线CS的内域只包含P个极点时, CF应逆时针包围原点P次, 或者说, CF顺时针包围原点-P次。
⒋ 围线CS包围Z个零点和P个极点
由上述讨论显然可知,当变点s沿CS顺时针绕行一周时,CF应顺时针包围 原点Z-P次。亦即CF顺时针包围原点次数N=Z-P。
这就是所谓幅角原理。
1. 围线CS既不包围零点也不包围极点
如图所示,在s平面上当变点s沿围线CS按 顺时针方向运动一周时,我们来考察F(s)中 各因子项的幅角的变化规律。 现以图中未被包围的零点-2为例。当变点s 沿CS绕行一周后,因子(s+2)的幅角a的变化 为0°。
Nquist稳定判据.ppt

例1 已知系统开环传递函数为
G(s)H(s)
K
(s 0.5)(s 1)(s 2)
试绘制(1) K=5,(2)K=10时的奈氏图, 并判断系统的
稳定性。
解 (1) 当K=5时, 开环幅频特性和相频特性分别为
A()
5
1 0.252 1 2 1 42
() arctan0.5 arctan arctan2
解 开环幅频特性和相频特性分别为
A()
10
2 12 2 4
() 180 arctan arctan0.5
从而有ω=0+时, A(ω)=∞, φ(ω)= -180°-Δ,Δ为一个正的 很 小 角 度 , 故 奈 氏 图 起 点 在 第 Ⅱ 象 限 ;ω=+∞ 时 , A(ω)=0, φ(ω)= -360°+Δ, 故奈氏图在第Ⅰ象限趋向终 点(0, j0)。
j0)点的运动情况, 如图4所示。
jV F (s)平面
jV G (s)H (s)平面
(-1,j0)
0
U
(-1, j0) 0
U
CF C GH
图 4 奈氏回线映射在F(s)平面和G(s)H(s)平面上
绘制映射曲线CGH的方法是: 令s=jω代入G(s)H(s), 得到开环频率特性G(jω)H(jω), 然后绘制ω从-∞变
)
z2
)(s
zm
)
(s s1)(s (s p1)(s
s2 )(s sn ) p2 )(s pn )
由上式可见,复变函数F(s)的零点为系统特征方程 的根(系统闭环极点)s1、s2、…、sn, F(s)的极点则为 系统的开环传函极点p1、p2、…、 pn。
GB(S)
奈奎斯特稳定性判据课件

在多变量系统和非线性系统的 分析中,奈奎斯特稳定性判据 具有重要的应用价值。
03
判据的数学模型
模型建立
01
02
03
确定系统传递函数
首先需要确定控制系统的 传递函数,包括开环和闭 环传递函数。
绘制极坐标图
将传递函数转换为极坐标 形式,以便于分析系统的 频率响应特性。
确定临界频率
根据系统的开环和闭环传 递函数,确定系统的临界 频率。
。
在生物医学工程、环境 工程等领域,利用奈奎 斯特稳定性判据研究复 杂系统的动态行为和稳
定性问题。
TH 据的未来发展
研究方向
深入研究奈奎斯特稳定性判据 的数学原理,探索其在控制系
统中的更广泛应用。
结合现代控制理论和算法, 发展新的稳定性分析方法。
研究奈奎斯特稳定性判据与其 他稳定性判据的关系,完善稳
定性理论体系。
技术发展
1
利用计算机技术和数值计算方法,提高奈奎斯特 稳定性判据的运算效率和精度。
它提供了一种有效的数学方法来分析系统的动态行为,帮助工程师预测系 统的性能和行为。
判据的应用场景
控制系统设计
在控制系统设计中,奈奎斯特稳 定性判据用于分析控制系统的稳 定性和性能。
通信系统分析
在通信系统中,奈奎斯特稳定性 判据用于分析信号传输的稳定性 和可靠性。
信号处理
在信号处理中,奈奎斯特稳定性 判据用于分析信号的频域特征和 系统的稳定性。
2
开发适用于不同控制系统的奈奎斯特稳定性判据 分析工具。
3
探索将奈奎斯特稳定性判据应用于非线性控制系 统的方法。
应用前景
01
02
03
在航空航天、电力、化 工等领域,利用奈奎斯 特稳定性判据优化控制 系统的设计和性能。
03
判据的数学模型
模型建立
01
02
03
确定系统传递函数
首先需要确定控制系统的 传递函数,包括开环和闭 环传递函数。
绘制极坐标图
将传递函数转换为极坐标 形式,以便于分析系统的 频率响应特性。
确定临界频率
根据系统的开环和闭环传 递函数,确定系统的临界 频率。
。
在生物医学工程、环境 工程等领域,利用奈奎 斯特稳定性判据研究复 杂系统的动态行为和稳
定性问题。
TH 据的未来发展
研究方向
深入研究奈奎斯特稳定性判据 的数学原理,探索其在控制系
统中的更广泛应用。
结合现代控制理论和算法, 发展新的稳定性分析方法。
研究奈奎斯特稳定性判据与其 他稳定性判据的关系,完善稳
定性理论体系。
技术发展
1
利用计算机技术和数值计算方法,提高奈奎斯特 稳定性判据的运算效率和精度。
它提供了一种有效的数学方法来分析系统的动态行为,帮助工程师预测系 统的性能和行为。
判据的应用场景
控制系统设计
在控制系统设计中,奈奎斯特稳 定性判据用于分析控制系统的稳 定性和性能。
通信系统分析
在通信系统中,奈奎斯特稳定性 判据用于分析信号传输的稳定性 和可靠性。
信号处理
在信号处理中,奈奎斯特稳定性 判据用于分析信号的频域特征和 系统的稳定性。
2
开发适用于不同控制系统的奈奎斯特稳定性判据 分析工具。
3
探索将奈奎斯特稳定性判据应用于非线性控制系 统的方法。
应用前景
01
02
03
在航空航天、电力、化 工等领域,利用奈奎斯 特稳定性判据优化控制 系统的设计和性能。
第4讲_5.5奈奎斯特稳定判据

2014-12-22 第五章 频率响应 16
GH
K 1 (T2 ) 2
() 180 arctanT2 arctanT1
K (1 T2T1 2 ) j (T2 T1 ) G ( j ) 2 (1 (T1 ) 2 ) 2 (1 (T1 ) 2 )
2014-12-22
第五章 频率响应
13
例4
K
K GH 2 ,K 0,T 0 S (1 TS )
解 : G ( j )
2 1 T 2 2
() 180 arctanT
因为 p 0, N 2 P Z, 所以 z 2 闭环系统不稳定。
Z = P -2( N’+ - N’- )
由以上分析可知,开环系统型别过高会影响稳定性,而串联 比例微分调节器可以改善系统的稳定性,起到校正的作用,但要 选择合适的参数。
2014-12-22 第五章 频率响应 20
三、奈氏判据在对数坐标图上的应用
由于系统开环对数频率特性曲线的绘制较奈 奎斯特曲线更为简单、方便,自然使用伯德图来 进行系统稳定性判别就更适用。该判据不但可以 回答系统稳定与否的问题,还可以研究系统的稳 定裕量(相对稳定性),以及研究系统结构和参 数对系统稳定性的影响。
2.能够确定系统的稳定程度(相对稳定性); 3.可用于分析系统的瞬态性能,利于对系统的分析与设计; 4.基于系统的开环奈氏图,是一种图解法。
2014-12-22
第五章 频率响应
2
一、幅角原理
令F (S )
K ( s z1 )(s z2 ) (s zn ) ( s p1 )( s p2 ) ( s pn )
设开环传递函数在右半s平面上的极点数为P,则
GH
K 1 (T2 ) 2
() 180 arctanT2 arctanT1
K (1 T2T1 2 ) j (T2 T1 ) G ( j ) 2 (1 (T1 ) 2 ) 2 (1 (T1 ) 2 )
2014-12-22
第五章 频率响应
13
例4
K
K GH 2 ,K 0,T 0 S (1 TS )
解 : G ( j )
2 1 T 2 2
() 180 arctanT
因为 p 0, N 2 P Z, 所以 z 2 闭环系统不稳定。
Z = P -2( N’+ - N’- )
由以上分析可知,开环系统型别过高会影响稳定性,而串联 比例微分调节器可以改善系统的稳定性,起到校正的作用,但要 选择合适的参数。
2014-12-22 第五章 频率响应 20
三、奈氏判据在对数坐标图上的应用
由于系统开环对数频率特性曲线的绘制较奈 奎斯特曲线更为简单、方便,自然使用伯德图来 进行系统稳定性判别就更适用。该判据不但可以 回答系统稳定与否的问题,还可以研究系统的稳 定裕量(相对稳定性),以及研究系统结构和参 数对系统稳定性的影响。
2.能够确定系统的稳定程度(相对稳定性); 3.可用于分析系统的瞬态性能,利于对系统的分析与设计; 4.基于系统的开环奈氏图,是一种图解法。
2014-12-22
第五章 频率响应
2
一、幅角原理
令F (S )
K ( s z1 )(s z2 ) (s zn ) ( s p1 )( s p2 ) ( s pn )
设开环传递函数在右半s平面上的极点数为P,则
自动控制原理--奈奎斯特稳定判据及应用

Ⅱ
F( j)
Ⅲ Ⅰ
F(s)与Gk (s) 的关系图。
11
若奈氏曲线G( jω )H( jω )逆时针包围(−1, j0)点的次数R等于位于右半平面上开环极 点数P。则闭环系统稳定,否则闭环系统不
稳定。
约束条件:在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论:当奈氏曲线通过(−1,j0)点,则表示闭环系 统
。式中, zi , p j
(s pj)
为F(s)的零、极点。
j 1
结论:F(s)的极点为开环传递函数的极点;
F(s)的零点为闭环传递函数的极点;
F(S)平面的坐标原点就是G(S)H(S)平面的
点(-1,0j)
3
F(s)是复变量s的单值有理函数。如果函数F(s)在s平面上指
定的区域内是解析的,则对于此区域内的任何一点 d s都可以在 F(s)平面上找到一个相应的点d f ,d f 称为 ds 在F(s)平面上的映射。
若考虑平面G( jω )H( jω ),则相当于曲线F( jω )左
移一个单位的奈氏图,即开环幅相频率特性,原F平面
原点对应于GH平面(−1, j0)点
G( jω )H( jω ) = F( jω ) −1
∴若要系统稳定,则Z=P−R=0,R为GH 映射曲线绕
(−1,j0)点次数
10
Gk ( j )
P:s平面上被封闭曲线 s 包围的F(S)的极点 Z: s平面上被封闭曲线 s 包围的F(S)的零点 R: F平面上被封闭曲线 f 包围的原点的次数
若R为正,表示 f 逆时针运动,包围原点圈数; 若R为0,表示 f 逆时针运动,不包围原点圈数; 若R为负,表示 f 顺时针运动,包围原点圈数。
6
F( j)
Ⅲ Ⅰ
F(s)与Gk (s) 的关系图。
11
若奈氏曲线G( jω )H( jω )逆时针包围(−1, j0)点的次数R等于位于右半平面上开环极 点数P。则闭环系统稳定,否则闭环系统不
稳定。
约束条件:在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论:当奈氏曲线通过(−1,j0)点,则表示闭环系 统
。式中, zi , p j
(s pj)
为F(s)的零、极点。
j 1
结论:F(s)的极点为开环传递函数的极点;
F(s)的零点为闭环传递函数的极点;
F(S)平面的坐标原点就是G(S)H(S)平面的
点(-1,0j)
3
F(s)是复变量s的单值有理函数。如果函数F(s)在s平面上指
定的区域内是解析的,则对于此区域内的任何一点 d s都可以在 F(s)平面上找到一个相应的点d f ,d f 称为 ds 在F(s)平面上的映射。
若考虑平面G( jω )H( jω ),则相当于曲线F( jω )左
移一个单位的奈氏图,即开环幅相频率特性,原F平面
原点对应于GH平面(−1, j0)点
G( jω )H( jω ) = F( jω ) −1
∴若要系统稳定,则Z=P−R=0,R为GH 映射曲线绕
(−1,j0)点次数
10
Gk ( j )
P:s平面上被封闭曲线 s 包围的F(S)的极点 Z: s平面上被封闭曲线 s 包围的F(S)的零点 R: F平面上被封闭曲线 f 包围的原点的次数
若R为正,表示 f 逆时针运动,包围原点圈数; 若R为0,表示 f 逆时针运动,不包围原点圈数; 若R为负,表示 f 顺时针运动,包围原点圈数。
6
04奈奎斯特三准则

P P 11 12 P P 转移概率用转移矩阵表示 22 P = 21 ... ... P ≥0 ij N 11 P 1 P ... PN 1 ... P N 2 ... ... ... P NN
马尔可夫信源
转移矩阵中每一行元素之和等于1
∑P
j =1
N
ij
S(t) =
∑a g(t − nT ) 是基带
∞
自相关函数
数字基带信号的自相关函数为
Rs (t +τ , t ) =
n=−∞ m=−∞
∑ ∑R(m− n)g(t +τ − mT )g(t − nT ) = R (t ,t ) = R (t,τ )
s s s 1 2 s
∞
∞
对于 Rs (t1, t2 ) 这种自相关函数是以 Ts 为周 期的周期函数。它满足:
5.1.2 一般情况下随机序列功率谱
上面讨论的数字基带信号中各码元波形相同而 取值不同的情况,对于有些情况,数字基带信 号各码元所取的波形不同。 数字信号:S(t) = ∑Sn (t − nTs )
n=∞ ∞
而对于 Sn (t − nTs ) 有n种不同的信号元(波 形)。 , 也就是说 Sn (t) ∈{gi (t); i =1 2,…, n}
数字信号的传输
通信的任务是准确迅速地传递信息。 信源信号经过信源编码之后成为离散的 二进制数字信号。我们用一些离散的波 形来代替这些数字信号。这些离散的信 号可以直接进行传输,或者调制到载波 上进行传输。这样就形成了两种最基本 的数字信号的传输方式:基带传输和频 带传输。
数字信号传输的基本方式
基带传输
离散谱分量
– 除了上面讲到的连续谱分量,还存在着离散
马尔可夫信源
转移矩阵中每一行元素之和等于1
∑P
j =1
N
ij
S(t) =
∑a g(t − nT ) 是基带
∞
自相关函数
数字基带信号的自相关函数为
Rs (t +τ , t ) =
n=−∞ m=−∞
∑ ∑R(m− n)g(t +τ − mT )g(t − nT ) = R (t ,t ) = R (t,τ )
s s s 1 2 s
∞
∞
对于 Rs (t1, t2 ) 这种自相关函数是以 Ts 为周 期的周期函数。它满足:
5.1.2 一般情况下随机序列功率谱
上面讨论的数字基带信号中各码元波形相同而 取值不同的情况,对于有些情况,数字基带信 号各码元所取的波形不同。 数字信号:S(t) = ∑Sn (t − nTs )
n=∞ ∞
而对于 Sn (t − nTs ) 有n种不同的信号元(波 形)。 , 也就是说 Sn (t) ∈{gi (t); i =1 2,…, n}
数字信号的传输
通信的任务是准确迅速地传递信息。 信源信号经过信源编码之后成为离散的 二进制数字信号。我们用一些离散的波 形来代替这些数字信号。这些离散的信 号可以直接进行传输,或者调制到载波 上进行传输。这样就形成了两种最基本 的数字信号的传输方式:基带传输和频 带传输。
数字信号传输的基本方式
基带传输
离散谱分量
– 除了上面讲到的连续谱分量,还存在着离散
5-4 奈奎斯特

G( j ) H ( j ) 与复变函数 F ( s) 1 G( s) H ( s) 位于S平面右半部的零、 极点数目联系起来的一种判据。奈氏判据是一种图解法,它依 据的是系统的开环频率特性。由于系统的开环特性可用解析法 或实验法获得,因此,应用奈氏判据分析系统的稳定性兼有方 便和实用的优点。奈氏判据还有助于建立相对稳定性的概念。
bm s m bm 1 s m 1 b1 s b0 G( s) H ( s) ( s p1 )( s p 2 ) ( s p n )
k ( s z1 )( s z 2 ) ( s z n ) ( s p1 )( s p 2 ) ( s p n )
6
前面我们已经指出, (s ) 的极点数等于开环传递函数 G(s) H (s) 的极点数,因 F 此当我们从 F (s ) 平面上确定了封闭曲线F 的旋转周数N以后,则在 S 平面上 封闭曲线s 包含的零点数Z(即系统的闭环极点数)便可简单地由下式计算出 来
Z=P-N
(5-109)
封闭曲线s和F 的形状是无关紧要的,因为它不影响上述结论。 关于幅角定理的数学证明请读者参考有关书籍,这里仅从几何图形上简单 说明。 设有辅助函数为
前面已经指出,辅助函数 F (s) 的极点等于系统的 开环极点, (s)的零点等于系统的闭环极点。因此,如 F 果奈氏轨迹中包围F (s)的零点数Z=0,系统是稳定的,
此时由F (s)映射到 F (s)平面上的封闭曲线F 逆时针绕 平面坐标原点的周数应为 N=P (5-114)( s) 2 ( P Z ) 2N N=P-Z
(5-112) (5-113)
Im
j
p1
0
F s
F (s1 )
bm s m bm 1 s m 1 b1 s b0 G( s) H ( s) ( s p1 )( s p 2 ) ( s p n )
k ( s z1 )( s z 2 ) ( s z n ) ( s p1 )( s p 2 ) ( s p n )
6
前面我们已经指出, (s ) 的极点数等于开环传递函数 G(s) H (s) 的极点数,因 F 此当我们从 F (s ) 平面上确定了封闭曲线F 的旋转周数N以后,则在 S 平面上 封闭曲线s 包含的零点数Z(即系统的闭环极点数)便可简单地由下式计算出 来
Z=P-N
(5-109)
封闭曲线s和F 的形状是无关紧要的,因为它不影响上述结论。 关于幅角定理的数学证明请读者参考有关书籍,这里仅从几何图形上简单 说明。 设有辅助函数为
前面已经指出,辅助函数 F (s) 的极点等于系统的 开环极点, (s)的零点等于系统的闭环极点。因此,如 F 果奈氏轨迹中包围F (s)的零点数Z=0,系统是稳定的,
此时由F (s)映射到 F (s)平面上的封闭曲线F 逆时针绕 平面坐标原点的周数应为 N=P (5-114)( s) 2 ( P Z ) 2N N=P-Z
(5-112) (5-113)
Im
j
p1
0
F s
F (s1 )
奈奎斯特判据
具体度量的指标:增益裕量、相位裕量
第五章 控制系统的频域分析与综合 5-19
G(j)H(j) =
2008
k(1+jT1)... (1+jTm) 自动控制原理AI (j) (1+jTa)... (1+jTn) [GH]
n m, 所有T>0 Im
1/a
–1 •
Im a
[GH]
=g =+ 0
第五章 控制系统的频域分析与综合
5-26
自动控制原理AI 2008 在Bode图上确定相位裕 量的步骤:
1. 确定增益剪切频率c; 2.过c点作轴的垂线与 对数相频特性曲线相交,
查出交点处的纵坐标值 (c);
3. 代入计算公式
M = 180º+(c)
(c)
设计时,经验值:>30°, 一般选40 º ° 第五章 控制系统的频域分析与综合 ~60
5-10
2008
自动控制原理AI
Nyquist稳定判据举例(续2)
• 例5.5:
s2 G K s 2 s
广义D型围线
第五章 控制系统的频域分析与综合
5-11
2008
自动控制原理AI
Nyquist稳定判据举例(续3) • 例5.6
K G K s ss 3s 5
5< <50, 积分环节、比例环节、1/0.2S+1惯性环节决定
>50, 积分环节、比例环节、2个一阶惯性环节决定 5-28 第五章 控制系统的频域分析与综合
10 自动控制原理AI G(S)H(S)= S(0.2S+1)(0.02S+1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/12/2
5
奈氏准则在数据通信中的意义
奈氏准则是在理想条件下推导出的。在实际条 件下,最高码元传输速率要比理想条件下得出 的数值还要小些。电信技术人员的任务就是要 在实际条件下,寻找出较好的传输码元波形, 将比特转换为较为合适的传输信号。
2020/12/2
6
需要注意的是,奈氏准则并没有对信息传输速 率(b/s)给出限制。要提高信息传输速率就 必须使每一个传输的码元能够代表许多个比特 的信息。(增加一个波特率跟比特率的关系)
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
2020/12/2
4
根据奈奎斯特准则我们可以推断出: 给定了信道的带宽,则该信道的极限波特率就
确定了,不可能超过这个极限波特率传输码元, 除非改善该信道的带宽;
要想增加信道的比特传送率有两条途径,一方 面可以增加该信道的带宽,另一方面可以选择 更高的编码方式。(增加一下波特率与比特率 的关系)
fs(t)为采样后的样值序列,则
fs(t)=f (t)δT(t)
如果存在以下傅立叶变换: f(t)
f (t) F(ω)
×
fS( t)
fs(t) Fs(ω) δT(t) δT(ω)
2020/12/2
p(t) T (t) (t nTs )
图1
11
下面我们从频域角度来证明这个定理。
因为抽样脉冲序列是一个周期性冲激序列,它可以表示为
2020/12/2
7
对于频带宽度已确定的信道,如果信噪比不能 再提高了,并且码元传输速率也达到了上限值, 那么根据奈氏准则还有办法提高信息的传输速 率。这就是用编码的方法让每一个码元携带更 多比特的信息量。
2020/12/2
8
对于频带宽度已确定的信道,如果信噪比不能 再提高了,并且码元传输速率也达到了上限值, 那么根据奈氏准则还有办法提高信息的传输速 率。这就是用编码的方法让每一个码元携带更 多比特的信息量。
14
采样定理图解分析
f(t)
F(ω )
o
t
(a)
p(t)
-2Ts
-T
o
s(c)
Ts 2Ts
t
fs(t)
-ωmo ωm
ω
(b)
δ T(ω)
ωs =2π/TS
-ω s o
ωs ω
(d)
Fs(ω)
o
(e)
2020/12/2
t
- ω s-ωm o ωm ω s
ω
图7-2
(f)
15
采样定理图解分析(续)
Fs(ω)
2020/12/2
9
采样定理(Nyquist定理)
定理:
若 f (t)是一个频带受限于 f m 的连续信号,则当采样间隔 TS≤1/(2 fm) 时,f (t)就可以由采样序列{f(nTs)}无失真地恢复 重建
f (t)
× fS(t)=f(nTS )
p (t) =δT (t) = ∑δ(t- nTS )
奈奎斯特简介
奈奎斯特(1889-1976),美 国物理学家。1917AT&T公司与 贝尔实验室任职。奈奎斯特为 近代信息理论做出了突出贡献。 他总结的奈奎斯特采样定理是 信息论、特别是通讯与信号处 理学科中的一个重要基本结论。
2020/12/2
1
奈奎斯特准则
• 1924年,奈奎斯特(Nyquist)就推导出在理 想低通信道下的最高码元传输速率的公式:
ωs >=<222ωωωmmm
-ωs
-ωm
ωm
ωs ω
F(ω )
可以看出:
-ω m o ωm ω
只要 f s ≥ 2 f m,就不会发生重叠和失真
若通过一截止频率为fm的理想低通滤波器,则可以恢复信号f(t)
2020/12/2
16
fs(t) f(nTs)(tnTs)( 4)
根据频率卷积定理,式 (3) fs(t)f(t)T(t)所表述的抽
样后信号的频谱为
Fs()21[F()T()]
( 5)
式中F(ω)是低通信号f(t)的频谱,其最高角频率为ωm。将式 ( 2)代入上式有
Fs()T 1s[F() T(ns)]
2020/12/2
•
• C = 2Blog2N
• 其中B是理想低通信道的带宽,单位为赫兹; N是多相调制的相数
2020/12/2
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
说明: 在采样定理中,最大允许的采样间隔TS 称为Nyquist间隔; 最低允许的采样频率2 f m称为Nyquist频率。 一个最高频率限制在f m 的连续信号,无须知道其所有瞬间 值就可了解其全部内容。
2020/12/2
10
用理想采样对采样定理进行证明
设:
p(t)是周期为TS的单位冲激序列,即 p (t ) T (t ) (t nTs )
T(t) (t nTs)
(1)
由于δT(t)是周期性函数,它的频谱δT(ω)必然是离散的,可求
得
T()2Ts n(ns)
s
2
fsቤተ መጻሕፍቲ ባይዱ
2
Ts
( 2)
抽样过程可看成是f(t)与δT(t)相乘,即抽样后的信号可表示为
( 3)
fs(t)f(t)T(t)
2020/12/2
12
根据冲激函数性质, f(t)与δT(t)相乘的结果也是一个冲激 序列,其冲击的强度等于f(t)在相应时刻的取值,即样值f(nTs)。 因此抽样后信号fs(t)又可表示为
13
由冲激卷积关系, 上式可写成
Fs()T1s
F(ns)
( 6)
结论:
抽样后信号的频谱Fs(ω)由无限多个间隔为ωs的F(ω)相叠加而 成,这意味着抽样后的信号fs(t)包含了信号f(t)的全部信息。 如果ωs≥2ωm,
即
也即 fs 2 fH
Ts
1 2 fH
(7)
定理证毕。
2020/12/2
