物化食5-4-18相变热力学
物理化学第一章热力学第一定律

第二节 热力学基本概念
一、系统与环境(system and surroundings)
系统:人为划定的研究对象。 环境:与体系密切相关的部分。
空气、水蒸气
杯子 水
加热器
系统分类: ① 敞开系统(或开放系统) ② 封闭系统 ③孤立系统(或隔离系统)
Zn(s) + 2HCl(aq) = ZnCl2(aq) + H2(g)
二、系统的性质(properties)
描述系统状态的物理量(体积、压力、温度等)。
① 广度性质:与系统物质的量有关,具有加和性。 (质量、体积、内能)
② 强度性质:取决于自身特性,与系统物质的量无 关,不具有加和性。(温度、压力、密度)
2、化学动力学——化学反应的速率和机理问题。
3、物质结构——物质性质与其结构之间的关系。
化 学
化学热力学基础
第一章 第二章
热力学定律
热 力 学
第三章 化学热力学应用 第四章
化学平衡、 相平衡
第五章 电化学
第七章 表面现象
化学能与热能转 化规律
化学能与电能转 化规律
表面现象知识
第八章 胶体分散系统
胶体知识
物理化学
物理化学
——是研究有关物质化学变化和物理变化之间联系规律的一门学科。 ——是药学专业的基础课。掌握物理化学基本理论、实验方法、基 本技能,初步具有分析、解决与药学实践有关问题的能力,为学习 药剂学、药物分析等后续课程奠定基础。
一、物理化学的研究对象和内容
——从研究物质的物理现象和化学现象的联系入 手,探求化学变化的基本规律,又称理论化学。 1、化学热力学——能量转化及化学变化的方向和限度问题。
物理化学 第5章_相变热力学-3

=114.52 J· -1 K
18
4 相变过程自发性判据
(1):熵判据:把系统和环境看成是一个孤立系统, 用孤立系统的熵变作为判据来判断过程的自发性。
例5-1-5 求1.00mol过冷水在101325Pa及-10℃ 时凝固过程的△S。已知冰的质量熔化焓为334.7 J·-1,水和冰的质量热容分别为Cp(H2O,1) =4.184 g J·-1· -1,Cp(H2O,s) = 2.092J·-1· -1。 g K g K 解: H2O(1,263K)→H2O(s,263K) 这是一个不可逆相变过程。
= -1.00×8.314×630kJ= -5.24 kJ
Qp=ΔH = 58.5kJ58.5kJ
ΔU = Qp+W = (58.5-5.24)kJ = 53.3kJ53.26kJ
6
例:习题5-1:
解:
pV 50.663 103 100 103 n水 1.6377( mol) RT 8.314 373
解:根据相变热与温度的关系:
vap Hm (142.9 C ) vap Hm (100 C )
416.1 373.2
C
p,m
( g ) C p,m (1)dT
vap Hm (100 C ) Cp,m ( g) Cp,m (1)(T2 T1 )
vap Hm (142.9 C ) 40.63 (34.56 76.56 103 (416.1 373.2) )
38.83kJ mol1
12
三、相变化过程熵变的计算 (1)可逆相变过程相变熵 可逆相变:是指在无限接近相平衡条件下进 行的相变化。 当相变发生在两相平衡共存的温度和压力下 时,称为可逆相变。 任何纯物质的可逆相变均具有恒温、恒压的 特点,根据熵变的定义式,对于恒温恒压的 可逆相变,相变熵为:
物化各种公式概念总结

第一章热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律 热力学第一定律:ΔU =Q +W 。
三、基本关系式1、体积功的计算 δW = -p 外d V恒外压过程:W = -p 外ΔV定温可逆过程(理想气体):W =nRT 1221ln ln p p nRT V V = 2、热效应、焓:等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; ΔH =ΔU +Δ(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容:热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂= 定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p ,m =a +bT +cT 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p 外d V等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d pC V (㏑T 2-㏑T 1)=nR(㏑V 1-㏑V 2)(T 与V 的关系)C p (㏑T 2-㏑T 1)=nR(㏑P 2-㏑P 1) (T 与P 的关系)不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p 外(V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化 可逆相变化:ΔH =Q =n ΔH ; W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、实际气体节流膨胀:焦耳-汤姆逊系数:μJ-T (理想气体在定焓过程中温度不变,故其值为0;其为正值,则随p 降低气体T 降低;反之亦然)4、热化学标准摩尔生成焓:在标准压力和指定温度下,由最稳定的单质生成单位物质的量某物质的定压反应热(各种稳定单质在任意温度下的生成焓值为0) 标准摩尔燃烧焓:…………,单位物质的量的某物质被氧完全氧化时的反应焓第二章 热力学第二定律一、基本概念 自发过程与非自发过程二、热力学第二定律热力学第二定律的数学表达式(克劳修斯不等式)T Q dS δ≥ “=”可逆;“>”不可逆三、熵(0k 时任何纯物质的完美结晶丧子为0)1、熵的导出:卡若循环与卡诺定理(页522、熵的定义:T Q dS r δ=3、熵的物理意义:系统混乱度的量度。
化学十八物质的相变与热力学分析

化学十八物质的相变与热力学分析相变是物质在一定条件下由一种状态转变为另一种状态的过程。
化学中,我们常见的相变有固态到液态的熔化、液态到气态的汽化、气态到液态的凝华、液态到固态的凝固等。
这些相变背后的热力学性质对于我们理解物质行为以及应用研究具有重要意义。
本文将对18种常见物质的相变进行热力学分析。
1. 水(H2O)水的相变表现出了许多特殊性质。
在常压下,0℃处水从液态转变为固态,称为结冰;100℃处水由液态转变为气态,称为沸腾。
水的相变分别对应着凝固潜热和汽化潜热,其数值分别为334焦耳/克和2260焦耳/克。
2. 铁(Fe)铁的相变点位于1535℃,称为铁的熔点。
在熔点以下,铁属于固态;在熔点以上,铁转变为液态,即熔化。
铁的固态到液态的相变所吸收的能量称为熔化潜热。
3. 氧气(O2)在常温常压下,氧气处于气态。
氧气的凝固点为-218.79℃,在该温度下由气态转变为固态。
氧气的凝固潜热为222焦耳/克。
4. 硫酸(H2SO4)为固态。
硫酸的凝固潜热为512焦耳/克。
5. 汞(Hg)汞是唯一一个常温常压下为液态的金属元素。
其固态到液态的相变称为熔化,熔点为-38.83℃。
汞的熔化潜热为11.26焦耳/克。
6. 氨(NH3)氨在常温常压下为气态。
其临界温度为132.4℃,当温度超过该值时,氨转变为液态。
氨的气态到液态的相变称为凝结,其凝结潜热为582焦耳/克。
7. 氯气(Cl2)氯气在常温常压下为气态。
其凝结点为-101.5℃,即氯气由气态转变为固态。
氯气的凝结潜热为188焦耳/克。
8. 二氧化碳(CO2)二氧化碳在常温常压下为气态。
其凝结点为-78.5℃,当温度低于该值时,二氧化碳由气态转变为固态。
二氧化碳的凝结潜热为25.2焦耳/克。
9. 苯(C6H6)苯在常温常压下为液态。
其熔点为 5.5℃,即苯从液态转变为固态。
苯的凝固潜热为34.7焦耳/克。
10. 乙醇(C2H5OH)为固态。
乙醇的凝固潜热为110焦耳/克。
物化公式
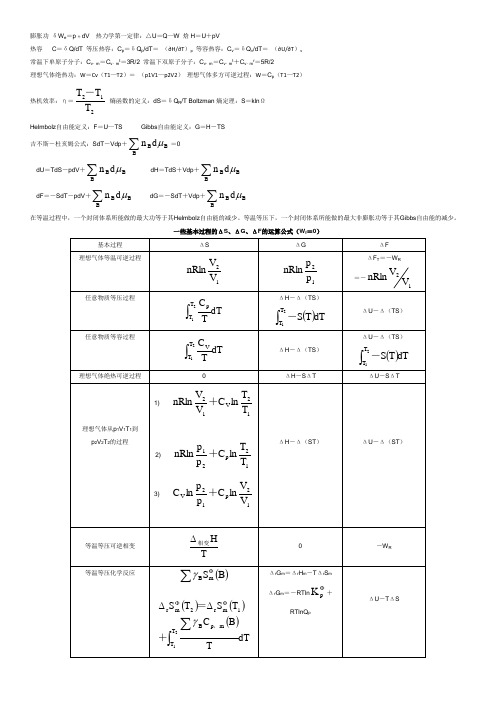
膨胀功 δW e =p 外dV 热力学第一定律:△U =Q —W 焓H =U +pV热容 C =δQ/dT 等压热容:C p =δQ p /dT = (∂H/∂T )p 等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2 常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2理想气体绝热功:W =Cv (T1—T2)= (p1V1—p2V2) 理想气体多方可逆过程:W =C p (T1—T2)热机效率:η=212T T T - 熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln ΩHelmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 吉不斯-杜亥姆公式:SdT -Vdp +∑BBBd nμ=0dU =TdS -pdV +∑B BBd nμ dH =TdS +Vdp +∑B BBd nμdF =-SdT -pdV +∑BBBd nμ dG =-SdT +Vdp +∑BBBd nμ在等温过程中,一个封闭体系所能做的最大功等于其Helmbolz 自由能的减少。
等温等压下,一个封闭体系所能做的最大非膨胀功等于其Gibbs 自由能的减少。
一些基本过程的ΔS 、ΔG 、ΔF 的运算公式(W f =0)基本过程ΔSΔGΔF 理想气体等温可逆过程12V V nRln12p p nRlnΔF T =-W R=-12V V nRln任意物质等压过程dTTC 21T T p ⎰ΔH -Δ(TS )()dTT S 21T T ⎰-ΔU -Δ(TS )任意物质等容过程dTTC 21T T V ⎰ΔH -Δ(TS )ΔU -Δ(TS )()dTT S 21T T ⎰-理想气体绝热可逆过程ΔH -S ΔT ΔU -S ΔT理想气体从p 1V 1T 1到p 2V 2T 2的过程1)12V 12T T lnC V V nRln+ 2)12p 21T T lnC p p nRln+3)12p 12V V V lnC p p ln C +ΔH -Δ(ST )ΔU -Δ(ST )等温等压可逆相变TH 相变∆-W R等温等压化学反应()B S m B∑Φγ()()()dTTB C T S T S 21T T m p B 1mr 2mr ⎰∑ΦΦ∆∆,+=γΔr G m =Δr H m -T Δr S m Δr G m =-RTln Φp K +RTlnQ pΔU -T ΔS溶液组成的表示法:(1)物质的量分数:B B n x n=(2)质量摩尔浓度:B B An m W =(3)物质的量浓度:B B n c V=(4)质量浓度B ω拉乌尔定律A A A p p x *= 亨利定律:x m B c Bp k x k m k c ===化学势的各种表示式和某些符号的物理意义: 气体:(1)纯理想气体的化学势()()T,p T RT ln ppμμΦΦ=+ 标准态:任意温度,p =p φ=101325Pa 。
湖南大学《无机材料物理化学》课件-第五章 热力学应用

将经典热力学理论与方法用于如硅酸盐这样 凝聚系统,须注意其理论与方法在凝聚态体系中 应用的特点和局限性。
一、化学反应过程的方向性
化学反应是凝聚态系统常见的物化过程。恒 温、恒压条件下只做膨胀功的开放体系,化学反 应过程沿吉布斯自由能减少的方向自发进行。过 程自发进行的判据为:
GT·P ≤ 0
(5-1)
故不能认为在所有情况下对一过程的热 力学估计就将决定这一过程的实际状况。
特别在硅酸盐系统出现的物化过程中, 动力学因素对热力学分析所得结果有不同程 度的制约。
第二节 热力学应用计算方法
用热力学原理分析硅酸盐系统在等温等压条件 下过程发生的方向或判断产物的稳定性,归结到
是系统自由能变化G的计算。
基于热力学函数不同,计算方法有:
第五章 热力学应用
应用热力学的理论和不多的参数,可 以解决和描述体系过程(如化学反应、相 变等)发生的方向性、平衡条件、体系能 量等问题,避免一些艰巨的、甚至不可能 实现的实验研究。
第一节 热力学在凝聚态体系中应用的特点
凝聚态体系中发生的物化过程与气相体系、 理想溶液体系不同。
凝聚态系统:多相性、质点扩散速度很小, 凝聚态体系中进行的物化过程往往难以达到热 力学真正意义上的平衡,过程的产物常处于亚 稳状态(如玻璃体或胶体)。
CP为一常数(CP=c)以简化G
0 R
计算过程。
此时G0R 与T的函数关系为:
G
0 R
=
H
0R298-
TS
0 R298
+
CPT(ln
298 T
+
1-
298 )
T
(5-11)
当反应前后物质等压热容不变,CP=0。反应源自G 与T关系简化为:G
物化知识点

1.1热力学基本概念1. 系统和环境系统(system),是热力学研究的对象。
包括指定的物质和空间。
可分为:(1)敞开系统(2)封闭系统(3)隔离系统环境是指系统以外的物质和空间。
2. 广度性质(n, V, U, H, A, G)和强度性质(T, p, H m等)3. 热和功热Q, 系统得到热量时,Q>0,Q sy =-Q su体积功W V,系统得到体积功(被压缩)时,W V>04. 相和相变只要物质的存在形式有任何一种物理或化学性质不同,它们便属于不同的相。
相变,是指物质从一种聚集形态转变为另一种聚集形态,包括液体的气化(vaporization),气体的液化(liquefaction),液体的凝固(freezing),固体的熔化(fusion),固体的升华(sublimation),气体的凝华,固体不同晶型间的转化(crystal form transition)等。
5. 液体的正常沸点和标准沸点液体在正常压力(101.325 kPa)下的沸点称为该液体的正常沸点;在标准压力(100 kPa)下的沸点称为该液体的标准沸点。
6. 状态函数和过程函数状态函数的特点是,其改变量只取决于系统的始态和终态,而与系统变化的途径无关。
过程函数的特点是,其正负和大小是和过程直接相关的。
7. 系统的典型变化过程:(1)定温过程:T1=T2=T su。
(2)定压过程:p1=p2=p su。
(3)定容过程:d V= 0。
系统体积始终保持恒定。
(4)绝热过程:Q = 0。
(5)对抗恒外压过程:p su=常数。
气体向真空的膨胀过程属于对抗恒外压过程. (6)循环过程:系统经多次变化后又回到原来的始态,即系统的终态和始态是同一状态。
对于循环过程,所有状态函数的改变值一定为0。
1.2体积功的计算几种典型过程的体积功:(1)定容过程:(2)对抗恒定外压膨胀过程:3)气体自由膨胀过程:(4)定温准静态膨胀过程(p=p su):给出了体积功计算实例两个:(1)有状态方程的(2)化学反应的1.4可逆途径与可逆过程多个相继的过程称为途径。
化工热力学第五章4

200.5kJ kg
锅炉吸热量 qH 为
1
qH h2 h1 3390 .9 200 .5 31904kJ kg 1 .
朗肯循环提供的净功 wN 为透平产功与水泵耗功之代数和,即
化工热力学
第五章
热力学第二定律及其应用
第四节
wN 12736 8.676 12649kJ kg 1 . .
另外,根据式(5—22)我们也可求得 wN , 即
wN qH qL 3190 .4 1925 .5 12649kJ kg 1 .
朗肯循环的热效率为
(b)已知透平的 s 0.75 ,则透平产功
wN 1264 .9 T 0.3965 q H 3190 .4
ws 为
负号表示工质放热。水泵的可逆轴功 ws R , Pump 为
1
ws R , Pump v4 P P4 1
由已知的 P 8600 kPa 和 P4 10kPa 查饱和水蒸汽表得 1
v4 1.010103 m3 kg 1将上述已知数据代入式(4—27),得
透平等熵膨胀产生的轴功 ws R 为
ws R hs h2 h3 3390 .9 2117 .3
化工热力学
第五章
热力学第二定律及其应用
第四节
12736kJ kg 1 .
冷凝过程传热量 qL 为
. qL h4 h3/ 191 .83 2117 .3 19255kJ kg
值,可以从附表3(饱和水蒸汽表)中查到对应的饱和蒸汽压
P 747.64kPa, h3 27663kJ kg 1 . 。再从附表3(过热蒸汽 3
表)查到点4(747.64kPa、 500℃ )的焓和熵值,即
物化材料5-1-15相变热力学

长春工业大学 化学教研室
第五章
相变热力学
5.1相变焓和相变熵
1.相变焓 摩尔相变焓:是指1mol纯物质于恒定温度及 该温度的平衡压力下发生相变时相应的焓 变。 相变 H m (T ) 单位:kJ.mol-1 符号:
vap H m
fus H m
sub H m
trs H m
其中:vap、fus、sub、trs分别指蒸发、熔化、 升华和晶型转变
2.相变焓与温度的关系
H 2 (T2 ) H1 C p,m dT
T1 T2
例:已知水在100℃、101.325kPa下,其摩 尔蒸发焓为20.63kJ.mol-1,水与水蒸气的平 均摩尔定压热容分别为76.56J.mol-1.K-1和 34.56J.mol-1.K-1。设水蒸气为理想气体,试 求水在142.9 ℃及其平衡压力下的摩尔蒸发 焓。
F CPn
练习 6.1指出下列平衡体系中的组分数C,相数P及 自由度F。 (1)I2(s)与其蒸气成平衡 (2)CaCO3(s)与其分解产物CaO(s)、CO2(g) 成平衡 (3)NH4HS(s)放入一抽空的容器中,并与其 分解产物NH3(g)和H2S(g)成平衡 (4)取任意量的NH3(g)和H2S(g)与NH4HS(s) 成平衡 (5)I2作为溶质在两不互溶液体H2O和CCl4中 达到分配平衡(凝聚系统)。
S 2 (T2 ) S1
T2 T1
C p ,m T
dT
例:计算101.325kPa、50 ℃的1molH2O(l) 变成101.325kPa、50 ℃的1molH2O(g) 的相变熵。 -1 -1 C ( H O , g )= 33 . 6 J.mol . K 已知 , p,m 2
物化第二章

CV,m
δQV dT
Um T V
f(T)
C p,m
δQ p dT
H m T
p
f(T)
35
1. 摩尔定容热容
(1) 定义 在某温度T 时,物质的量为n 的物质在恒
容且非体积功为零的条件下,若温度升高无限小
量dT 所需要的热量为Q,1则δQV
就定义为该
物质在该温度下的摩尔定容n 热dT容,以
δW pambdV
p
注意:1. 加“-”号,因为气体膨胀(dV>0)而系统输
出功(W<0) 。上式对气体压缩过程同样适用。 19
2. 计算功时用的是环境的压力pamb。
注意:功是能量传递的一种形式,且是与途径有关的量, 而不是状态函数,而是途径函数。
例:
1 mol
Wa pa,环(V2-V1)=0
例如,理想气体的状态方程可表示为:
pV=nRT 11
(2)状态函数的分类-广度量和强度量
描述热力学系统的性质分为:
广度量:在均相系统中,它们的数值与系统所含
物质的数量成正比(如V、H、U、G、 A等)。
强度量:在确定的状态下,它们的数值与系统所
含物质的多少无关(如 P、T、ρ、x等)
广度性质具有加和性,强度性质则无; 将广度性质除以描述数量的广度性质,可得 到一强度性质(如Vm=V/n, Cm=C/n 等等)。 12
恒压过程:
变化过程中始终p(系) = p(环) = 常数。 仅仅是p(终) = p(环) = 常数,为恒外压过程
恒容过程:过程中系统的体积始终保持不变。
绝热过程:系统与环境间无热交换的过程。
循环过程:经历一系列变化后又回到始态的过程。 循
物化第三章

恒温恒压 H2O(s), 1 kg
S = ?
263.15 K 100 kPa
可逆相变 0℃、100kPa下的凝固或熔化过程; 可逆判断 不可逆相变过程; 过程设计
H2O(l), 1 kg 263.15 K 100 kPa S1 H2O(l), 1 kg 273.15 K 100 kPa
T2 1 T 1 源自 Q2 > 1 Q 1
T2 Q 2 > T1 Q1
Q1 Q2 > T1 T2
δ Q2 δ Q1 0 (2)无限小循环: T2 T1
<0 不可逆循环 =0 可逆循环
(3)任意循环:
δQ T 0
3.3 熵、熵增原理
Siso S sys Samb 0
> 0 ir =0 r
※iso——隔离系统 ※sys——封闭系统 ※amb——环境
三、应用
封闭 1.应用:判断隔离系统过程的可逆性; 2.说明:一般认为环境内部无不可逆变化; →→封闭系统+环境=隔离系统
※隔离系统可逆→→封闭系统可逆;
※隔离系统不可逆→→封闭系统不可逆。
→→ΔSiso>0即封闭系统过程不可逆;
ΔSiso=0即封闭系统过程可逆;
熵增原理例题
0。 1.一隔离系统可逆变化中,ΔSsys> 0,ΔSamb < 0。 0,ΔU = 2.实际气体经历不可逆循环,ΔSsys =
0。 0,ΔU < 3.实际气体绝热可逆膨胀,ΔSsys = 0。 0, ΔSamb > 4.理想气体经不可逆循环,ΔSsys = 0。 0, ΔSamb > 5.过冷水结成同温度的冰,ΔSsys <
;
S
2
Qr
T
1
物理化学主要公式及使用条件

式中 , b, c及d对指定气体皆为常数。 (6)平均摩尔定压热容
7. 摩尔蒸发焓与温度 —
(l),上式适用于恒压蒸发过程。
8. 体积功 (1)定义式
或
(2)
适用于理想气体恒压过程。 (3)
(4)
适用于恒外压过程。
适用于理想气体恒温可逆过程。 (5)
例:H = U + PV HB = UB + PVB ; A = U - TS AB = UB - TSB ;
G = H – TS GB = HB - TSB ;… 4. 化学势
定义
5. 单相多组分系统的热力学公式
但按定义,只有 才是偏摩尔量,其余3个均不是偏摩尔量。 6. 化学势判据
在dT = 0 , dp = 0 δW’= 0 的条件下, 其中, 指有多相共存, 指 相内的B 物质。 7. 纯理想气体B在温度T﹑压力p时的化学势 pg 表示理想气体,* 表示纯态, 为气体的标准化学势。真实气体标准态与理想气体标准态均规定为纯理
式不能用,而需根据平衡系统中有多少个压力数值改写“2”这一 项;(c)要正确应用相律必须正确判断平衡系统的组分数C和相数P。 而C值正确与否又取决与R与R‘的正确判断;(d)自由度数F只能取0以 上的正值。如果出现F<0,则说明系统处于非平衡态。
2. 杠杆规则 杠杆规则在相平衡中是用来计算系统分成平衡两相(或两部分) 时,两相(或两部分)的相对量,如图6-1所示,设在温度为T下,系 统中共存的两相分别为α相与β相。
第四章 多组分系统热力学 主要公式及其适用条件
1. 偏摩尔量: 定义:
(1)
其中X为广延量,如V﹑U﹑S...... 全微分式:
化工物化知识点归纳总结

化工物化知识点归纳总结一、化工物化基础知识1. 化学元素和化合物化学元素是由一种原子型轨道结构组成的基本物质,化合物是由两种或两种以上元素以一定的质量比结合成的物质。
元素的分类:金属元素、非金属元素、半金属元素和稀有元素。
元素的性质:电负性、价态、化学活性和金属性等。
化合物的分类:无机化合物和有机化合物。
2. 化学反应化学反应是化学物质之间发生的一种转化过程。
根据反应机理和反应类型,化学反应分为酸碱中和反应、氧化还原反应、置换反应、复分解反应、合成反应等。
3. 化学平衡化学平衡是指反应物浓度和生成物浓度的比例达到一个固定的数值。
根据化学平衡定律,当反应物比例达到平衡之后,逆反应速度和正反应速度相等。
4. 溶液和溶解度溶液是由溶质和溶剂混合形成的均匀的混合物。
溶解度是指在一定温度下,最多可以溶解多少溶质的量。
5. 酸碱性酸碱性是指物质所具有的酸性或碱性特性。
酸碱中和是指酸和碱反应形成盐和水的过程。
二、化工物化分析技术1. 质谱技术质谱技术是一种通过对射入质谱质子化后分子碎片质谱进行检测和分析的方法。
可以用于分子结构解析、各种样品的成分分析和污染物检测等。
2. 红外光谱分析红外光谱分析是一种通过物质对红外辐射的吸收特性进行分析的方法。
可以用于物质的成分鉴定、结构分析和化合物含量的定量分析。
3. 色谱法色谱法是一种利用物质在固定相和流动相之间进行分配的方法,通过分离和检测物质成分的技术。
4. 核磁共振技术核磁共振技术是一种通过物质对外加磁场和射频辐射的响应来分析物质结构和成分的方法。
5. 色度法色度法是一种通过检测物质对可见光的吸收或透射特性来进行定性和定量分析的方法。
三、化工物化热力学1. 热力学基本概念热力学是研究能量转化和能量转移规律的科学。
包括能量、功、热、焓、熵等概念。
2. 热力学定律热力学第一定律:能量守恒定律,能量不能自行消失,也不能新生。
热力学第二定律:热量自然流向热量低的物体,不可能自行流向高温物体。
化工热力学第五章

化学反应 相变化 体系状态变化, 体系状态变化,如 温度变化
∆H
3)对化工机器的绝热过程 3)对化工机器的绝热过程
当体系在绝热情况下,与环境进行功的交换时, 当体系在绝热情况下 , 与环境进行功的交换时 , 1 ∆C 2 = 0 g∆Z = 0 Q=0 ∵ 2
∴
Ws = ∆H
此式说明了在绝热情况下, 此式说明了在绝热情况下,当动能和位能的 变化相对很小时, 变化相对很小时,体系与环境交换的功量等 于体系焓的减少
第五章
化工过程的能量分析
5.1 能量平衡方程
• 一. 热力学第一定律的实质
热力学第一定律的实质就是能量在数量上是守恒的 基本形式为: 基本形式为: Δ(体系的能量)+Δ(环境的能量)=0 体系的能量) 环境的能量) 体系的能量)=-Δ 环境的能量) 或 Δ(体系的能量)=-Δ(环境的能量) 体系的能量的增加等于环境的能量的减少。 体系的能量的增加等于环境的能量的减少。
正卡诺循环的结果是热部分地转化为功, 正卡诺循环的结果是热部分地转化为功,用热效率来评价循环的经济性
热效率: 热效率:
− WS 移走净功 η= = QH 热量输入
热效率的物理意义: 热效率的物理意义: 工质从高温热源吸收的热量转化为净功的比率。 工质从高温热源吸收的热量转化为净功的比率。
26
据热力学第一定律: 据热力学第一定律: ∵ ∴ 又∵ ∴
20
自发、非自发和可逆、非可逆之间的区别? 自发、非自发和可逆、非可逆之间的区别?
• 自发与非自发过程决定物系的始、终态与 自发与非自发过程决定物系的始、 环境状态; 环境状态;
• 可逆与非可逆过程是(考虑)过程完成的 可逆与非可逆过程是(考虑) 方式,与状态没有关系。 方式,与状态没有关系。
物化上热力学第一定律知识点总结

1 热力学第一定律1.1 重点与难点严格区分状态函数与非状态函数(Q 、W ),并熟练掌握状态函数的数学特征 状态的定义,状态函数性质及数学特征。
体系始终态一旦确定,其状态函数改变量可通过设计途经而求算。
体系状态发生变化,其状态函数值可能发生变化,但并不一定全部状态函数都一定发生变化。
求算过程的热与功,不能随意设计途径。
唯有在特定条件下 Q,W 能与状态函数改变量相关联(如等压无其他功 Q p =ΔH ),才与途径无关。
体系状态函数具备五个数学特征。
1.1.1 热力学第一定律数学表达式及其在理想气体中的应用表达式()'V UQ W Q W W ∆=-=-+,只适用于封闭体系,随着条件变化,存在 ΔU 与 Q 、W 之间的转换关系。
一定量理想气体 U 和 H ,均决定于温度(但若有相变发生,或并非自始至终为理想气体,则不属此列)。
故它无论发生 p,V 怎样变化,只要有 T 变化,可直接引用2211T T vm pm T T U nC dTH nC dT∆=∆=⎰⎰或 。
弄清节流过程与绝热过程的区别。
明确理想气体绝热可逆过程方程与状态方程的实质;前者指某过程进行中各参量间的关系,后者指体系达平衡状态时各参量间的关系。
在 p ~V 图上绝热线的陡度比等温线的大,两线只能相交一点。
自同一始态出发,经绝热可逆与绝热不可逆过程是不能达到相同的终态,但计算绝热体积功时可用同一式:,1122,(1p m a V mC p V p V W C γγγ-==-为热容商,即)1.1.2 掌握比较热力学可逆过程与不可逆过程的定义,特点。
热力学第一定律在热化学中的应用热总值不变定律,意味着固定始终且指定同一条件(全部恒压,或全部恒容,决非恒压恒容混相)下,ΔH 或 ΔU 可自设计各步途径热值之加和而求算。
基尔霍夫(Kirchhoff)定律:()()2121T r m r m Tr pm H T H T C dT θθ∆=∆+⎰∆ 有积分号"∫"意指可逆,故中间若有相变,则另添加焓变值。
物化第一章 热力学第一定律

21
证明:系统状态一定时,内能值就为定值。 (反证法)系统状态从A经1或2到B ΔU1=UB–UA=ΔU2 p A 1 2 B
若假设ΔU1>ΔU2 1 2 系统状态 A B A
一次循环ΔU=ΔU1 –ΔU2>0 如此每经过一次循环,就有多余的能量产生
16
1. 热平衡:thermal equilibrium 无阻碍下,系统中各部分温度相同。 2. 机 械 平 衡 ( 或 力 平 衡 ) : mechanical equilibrium 系统中无刚壁存在时,系统中压力相同。 3. 化学平衡:chemical equilibrium 系统中无化学变化阻力存在时,无宏观化 学反应发生 4. 相平衡:phase equilibrium 系统中各相的数量和组成不随时间变化, 无宏观相变
20
(1)热力学能(内能)的概念
1、热力学能:除整体动能、整体势能以外的系统 中一切形式的能量(如分子的平动能、转动能、 振动能、电子运动能及原子核内的能等等)。
2、热力学能是系统的状态函数。(证明见下页) 3、热力学能是容量性质。 4、热力学能的绝对值现在无法测量,但对热力学 来说,重要的是ΔU。 ΔU = W绝热 5、dU在数学上是全微分。
不断循环进行,就构成了第一类永动机
V
所以原假设不成立,即ΔU1=ΔU2 。
推论:系统状态发生变化时,系统的内能变化只决 定于始终态,而与变化途径无关。
22
定义:功和热是系统和环境之间交换能量的仅有 两种形式 功的种类:体积功WV, 非体积功W’。 功和热不是系统的状态性质,但与系统的状态变
化有关,其数值大小与变化途径有关。
相变材料的物理化学性质分析

相变材料的物理化学性质分析相变材料是一种能够在温度或压力变化下发生物理或化学相变的材料。
它们具有独特的物化性质,因此在许多领域中得到广泛应用。
本文将着重分析相变材料的物理化学性质,并探讨其在实际应用中的潜力。
1. 相变材料的基本概念相变材料是一种能够在经过一定的外部刺激下从一个状态转变至另一个状态的物质。
这种物质不同于普通的单一状态物质,具有两种或多种不同的物理化学状态,可以在外部环境的影响下自由转换。
相变材料通常分为两种类型:热致形变材料和相变储存材料。
热致形变材料是一种在温度变化下变形的材料,它们通过收缩或膨胀来实现形状的改变。
相变储存材料则是一种能够通过吸收或释放热量来储存能量的材料,这种材料广泛应用于能源存储和利用领域。
2. 相变材料的物理化学性质相变材料的物理化学性质取决于其结构、成分、热力学参数等多种因素。
下面将分别从热力学、结构和电学性质三个方面详细探讨相变材料的物理化学性质。
(1)热力学性质相变材料的热力学性质是指其在相变过程中发生的能量变化。
相变材料特有的热力学性质是其在相变过程中吸收或释放的潜热。
实际应用中,相变储存材料通常是基于这种热力学性质来设计和制造的。
潜热是指相变材料在相变过程中吸收或释放的热量,这个潜热通常是很大的。
对于相变储存材料来说,他们通常被设计成可以吸收或释放大量热量的材料,以实现能量储存和利用。
(2)结构性质相变材料的结构性质是指其物质结构和形态等因素对其性质的影响。
相变材料常见的结构形态包括晶体、非晶体、气相、液相等。
材料的结构形态直接决定了其物理或化学性质,所以研究相变材料的结构性质对于深入分析其性质非常重要。
(3)电学性质相变材料的电学性质是指其在外加电场或磁场的作用下的电学响应。
相变材料具有较好的电学性质,可以应用于电子器件和存储器件等领域。
大量研究表明,相变材料对电流和电压响应都非常敏感。
3. 相变材料的应用前景相变材料具有独特的物理化学性质,这些特性使其在许多实际应用中都能发挥非常重要的作用。
物化公式归纳

物化公式归纳 第一章 化学热力学基础 公式总结1.体积功 We = -Pe △V2.热力学第一定律的数学表达式 △U = Q + W 3.n mol 理想气体的定温膨胀过程.定温可逆时:Wmax=-Wmin=4.焓定义式 H = U + PV 在封闭体系中,W ′= 0,体系发生一定容过程 Qv = △U在封闭体系中,W ′= 0,体系发生一定压过程 Qp = H2 – H1 = △H5.摩尔热容 Cm ( J·K -1·mol -1 ):定容热容 CV(适用条件 :封闭体系、无相变、无化学变化、 W ′=0 定容过程适用对象 : 任意的气体、液体、固体物质 )定压热容 Cp⎰=∆21,T T m p dTnC H (适用条件 :封闭体系、无相变、无化学变化、 W ′=0 的定压过程适用对象 : 任意的气体、液体、固体物质 )单原子理想气体: Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体: Cv,m = 2.5R , Cp,m = 3.5R 多原子理想气体: Cv,m = 3R , Cp,m = 4RCp,m = Cv,m + R6.理想气体热力学过程ΔU 、ΔH 、Q 、W 和ΔS 的总结7.定义:△fHm θ(kJ·mol -1)-- 标准摩尔生成焓△H —焓变; △rHm —反应的摩尔焓变 △rHm θ—298K 时反应的标准摩尔焓变;△fHm θ(B)—298K 时物质B 的标准摩尔生成焓; △cHm θ(B) —298K 时物质B 的标准摩尔燃烧焓。
1221ln ln P PnRT V V nRT =⎰=∆21,T T m V dTnC U8.热效应的计算由物质的标准摩尔生成焓计算反应的标准摩尔焓变 △rH θm = ∑νB △fH θm ,B 由物质的标准摩尔燃烧焓计算反应的标准摩尔焓变 △rH θm = -∑νB △cH θm ,B 9.Kirchhoff (基尔霍夫) 方程 △rHm (T2) = △rHm (T1) + 如果 ΔCp 为常数,则△rHm (T2) = △rHm (T1) + △Cp ( T2 - T1) 10.热机的效率为 对于卡诺热机= 可逆循环过程 < 不可逆循环过程 11.熵变定义式 (体系经历一可逆过程的热温商之和等于该过程的熵变.) 12.热力学第二定律的数学表达式(不等式中, “ > ”号表示不可逆过程 , “ = ” 号表示可逆过程“ T ”—环境温度 , 对可逆过程也是体系温度. )13.熵增原理 (孤立体系的熵永不减少) △S 孤立 ≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡 .对于封闭体系△S 孤立 = △S 封闭 + △S 环境 ≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡 14.定温定压的可逆相变15.化学反应熵变的计算 △rS θm = ∑νBS θm ,B16.△rH θm 和△rS θm 与温度的关系:△rH θ m (T2) = △rH θ m (T1) +△rS θ m (T2) = △rS θ m (T1) +第二章 自由能、化学势和溶液 公式1.第一和第二定律的联合公式为 2.吉布斯自由能定义式 G = U + PV – TS = H – TS △G = △H -T △S(G----体系的状态函数, ( J ) , 绝对值无法测量 ) 3.在定温定压下,有如下关系: ΔG=W’最大2211≤+T Q T Q ∑≥∆ii i T Q S )(δ环体环环环境T Q T Q S -==∆dTC p T T ⎰∆21d TTC pT T ∆⎰214.吉布斯自由能判据< 不可逆过程, 自发过程 = 可逆过程, 平衡态> 反方向为自发过程5.判断过程方向及平衡条件的总结6定压下.对任意相变或化学变化7.定温物理变化?G的计算(W’=0的封闭体系). 理想气体定温过程. 纯液体或纯固体的定温过程. 定温定压可逆相变 dG = -SdT + VdP dT =0 dP =0 ?G T , P, W' = 0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长春工业大学Leabharlann 化学教研室5.5二组分凝聚态系统平衡相图
二组分不互溶相图绘制 基本原理:二组分体系 C=2,指定压力不变,
F C P 1=3 - P
P 1 P2
P3
F 2 F 1
F 0
双变量体系 单变量体系 无变量体系
首先将二组分体系加热熔化,记录冷却过程 中温度随时间的变化曲线,即步冷曲线。 当体系有新相凝聚,放出相变热,步冷曲 线的斜率改变。F=1,出现转折点;F=0, 出现水平线段。据此在T-x图上标出对应的 位置,得到低共熔T-x图。
生化合物的二组分凝聚态系统相图
(1)稳定化合物
形成不稳定化合物的相图
还有一些常见的二元相图
祝同学们学习、生活快乐!
谢谢各位同学!
Cd-Bi二元相图的绘制 1.首先标出纯Bi和纯Cd的熔点
2 .作含20Cd,80Bi的步冷曲线。
3.作含40Cd的步冷曲线
4.完成Bi-Cd T-x相图
图上有4个相区(讨论) 有三条多相平衡曲线
有三个特殊点: A点,纯Bi(s)的熔点 H点,纯Cd(s)的熔点 E点,Bi(s)+Cd(s)+ l 三相共存点。 因为E点温度均低于A点和H点的温度,称为 低共熔点。在该点析出的混合物称为低共 熔混合物(eutectic mixture)。它不是化 合物,由两组分组成,只是混合得非常均 匀。E点的温度会随外压的改变而改变,在 这T-x图上,E点仅是某一压力下的一个截 点。
二组分固态互溶系统液-固平衡相图
完全互溶固溶体的相图
完全互溶固溶体出现最低点或最高点
固相部分互溶的固液相图 两个组分在液态可无限混溶,而在固态只能 部分互溶,形成类似于部分互溶双液系的 帽形区。在帽形区外,是固溶体单相,在 帽形区内,是两种固溶体两相共存。
(1) 有一低共熔点者
(2) 有一转熔温度者
