3.-4函数单调性与曲线的凹凸性
3-4函数单调性与曲线的凹凸性

1:确定函数的定义域D,判断函数f (x)在D上连续,可导; 2:求出f (x) 0的点及 f (x)不存在的点; 3:用f (x) 0的点及 f (x)不存在的点来划分函数 f (x)的 定义区间; 4:判断各个区间内导数的符号,得出它的单调性.
例2 解
确定函数 f ( x) 2x3 9x2 12x 3的单调区间.
在[2 a, a]上单调减少; 3
3、在[k , k ]上单调增加, 22 3
在[k , k ]上单调减少,(k 0,1,2,) . 2 32 2
四、(1)a 1 时没有实根; e
(2)0 a 1 时有两个实根; e
(3)a 1时只有 x e一个实根. e
3、函数 y x 2 ln x 2 的单调区间为____________,
单减区间为_____________.
二、 确定下列函数的单调区间:
1、 y
10
;
4x3 9x2 6x
2、 y 3 (2 x a)(a x)2 (a 0);
3、 y x sin 2x .
三、证明下列不等式: 1、当 x 0时,1 x ln( x 1 x 2 ) 2、当 x 4时,2 x x 2 ; 3、若 x 0,则sin x x 1 x 3. 6
f ( x) 6x2 18x 12 6( x 1)(x 2) 解方程f ( x) 0 得, x1 1, x2 2. 当 x 1时, f ( x) 0, 在(,1]上单调增加; 当1 x 2时, f ( x) 0, 在[1,2]上单调减少; 当2 x 时, f ( x) 0, 在[2,)上单调增加; 单调区间为 (,1], [1,2],[2,).
充分小的邻域内单调递增?
思考题解答
函数的单调性与凹凸性判别

定理1(函数单调性的判定法) 设函数f(x)在[a b]上连续 在(a, b)内可导 (1)如果在(a b)内f (x)>0 则f(x)在[a b]上单调增加 (2)如果在(a b)内f (x)<0 则f(x)在[a b]上单调减少 例 解 判定函数 yxsin x 在[0 2p]上的单调性 因为在(0, 2p)内 y1cos x >0 所以, 函数 yxsin x 在[0 2p]上的单调增加
3
证
x , x ( a , b ), 且 x x ,应用拉氏定理,得 1 2 1 2
f ( x ) f ( x ) f ( )( x x ) ( x x ) 2 1 2 1 1 2
x x 0 , 2 1
若 ( a , b ) 在 内 f ( x ) , 0 , 则 f ( ) 0 ,
9
说明: • 单调区间的分界点除驻点外,也可是导数不存在的点.
3 2 例如, y x,x ( , )
33 x y x0
2) 如果函数在某驻点两边导数同号, 则不改变函数的单调性 .
3 y x ,x ( , ) 例如,
y
2
y y 3 x2
利用单调性证明不等式的步骤:
①将要证的不等式作 恒等变形(通常是移项)使 一端为0, 另一端即为所作的辅助函数f(x). ②求 f (x) 验证f(x)在指定区间上的单调性. ③与区间端点处的函数值或极限值作比较即得证.
6
二、单调区间求法
问题 如上例, 函数在定义区间上不是单调的, 但在各个部分区间上单调. 定义 若函数在其定义域的某个区间内是单调的, 则该区间称为函数的单调区间.
高等数学方明亮34函数的单调性与曲线的凹凸性

y f (x) B
A
yA y f (x) B
oa
bx
f ( x) 0
oa
bx
f ( x) 0
定理 1 (函数单调性的判定法) 设函数 y f (x) 在 [a,b] 上 连 续 , 在 (a,b) 内 可 导 .( 1 ) 如 果 在 (a,b) 内 , f (x) 0 ,则 y f (x) 在 [a,b] 上单调增加;(2)如果在 (a,b) 内, f (x) 0 ,则 y f (x) 在[a,b] 上单调减少.
2019年9月14日星期六
9
目录
上页
下页
返回
定义 设函数 f (x) 在区间 I 上连续,如果对 I 上任意
两点 x1, x2 (不妨设 x1 x2 )及任意正数 (0 1) ,恒
有
f [x1 (1 ))x2 ] f (x1) (1 ) f (x2 ),
解:已知 f (x0 ) 0 ,不妨设 f (x0 ) 0 , 由于 f (x0 ) 在 x x0 的某邻域内连续,
因此必存在 0 ,当 x (x0 , x0 ) 时 f (x) 0
又已知 f (x0 ) 0
从而当 x (x0 , x0 ) 时 f (x) f (x0 ) 0 ,函数凸
则称曲线 y f (x) 在 I 上是凹的.
类似地,可给出曲线是凸的定义,若上式中不等 号反向,则称曲线 y f (x) 在 I 上是凸的.
直接利用定义来判别曲线的凹凸性是比较困难的,
下面利用二阶导数来判别曲线的凹凸性.
2019年9月14日星期六
10
目录
上页
下页
返回
3-4函数单调性与凹凸性(09)

二、函数单调性的应用
——证明不等式和判断方程根的个数. ——证明不等式和判断方程根的个数. 证明不等式和判断方程根的个数 1. 证明不等式 关键是根据所证不等式及所给区间构造辅助函数 关键是根据所证不等式及所给区间构造辅助函数, 并讨论 构造辅助函数 它在指定区间内的单调性. 它在指定区间内的单调性. 例4 证明不等式 e x ≥ x + 1 证
令 f 2 ( x ) = ln(1 + x ) − x
因 为 f2 (0) = 0, 而 f2′( x) =
−x < 0 ( x > 0) 1+ x
则 f ( x )单减 即 f 2 ( x ) < f 2 (0)( x > 0) 故 单减.
ln(1 + x ) < x
证
x3 令 f ( x ) = tan x − x − 3
f ′(x) ≤ 0 A y = f (x)
B
o
a
b
x
o a
b x
各点处切线的斜率为正
各点处切线的斜率为负
在区间(a, 上单调递增 若 y = f (x)在区间 b)上单调递增 在区间 在区间(a, 上单调递减 若y = f (x)在区间 b)上单调递减 在区间
f ′( x) ≥ 0
f ′( x) ≤ 0
研究函数的单调性, 就是判断它在哪些区间内递增, 注1 研究函数的单调性 就是判断它在哪些区间内递增 哪些 区间内递减. 对可导函数的单调性, 区间内递减 由定理 1 对可导函数的单调性 可根据导数的正 负情况予以确定. 负情况予以确定 注2 包括无穷区间) 定理 1 的结论对其他各种区间 (包括无穷区间 也成立 包括无穷区间 也成立.
函数的单调性与曲线的凹凸性ppt课件

第四节 函数的单调性与曲线的凹凸性
在区间 I 上连续 ,
(1) 若恒有 图形是凹的;
则称
(2) 若恒有
则称
图形是凸的 .
设 是区间 I 内的点,如果曲 yyy 拐点
线
在经过点
时,
曲线的凹凸性改变了, 那么就称点 OOO
为这曲线的 拐点.
x x1x1x1x21x22x2x2x2 x x
高等数学(上)
类似地可以证明 f (x) 0 的情形.
高等数学(上)
第三章 微分中值定理与导数的应用
第四节 函数的单调性与曲线的凹凸性
例1 判定函数y x sin x 在 [0, 2 ] 上的单调性 解 因为在 (0, 2 )内
y 1 cos x 0,
所以函数 y x sin x在 [0, 2 ] 上的单调增加.
2)若函数在其定义域的某个区间内是单调的, 则该区间称为函数的单调区间.
3)导数等于零的称为驻点(或称稳定点、临界
点),驻点可能是单调区间的分界点. 4)如果函数在某驻点两边导数同号,
y
y x3
则不改变函数的单调性 . 例如,
O
x
高等数学(上)
第三章 微分中值定理与导数的应用
第四节 函数的单调性与曲线的凹凸性
第三章 微分中值定理与导数的应用
第四节 函数的单调性与曲线的凹凸性
求函数单调区间的步骤: 1)确定函数 的定义域;
2)在定义域内求出使 存在的点;
的点与 不
3)用上述这些点把定义域分成若干个互不重叠 的子区间;
4)考察 在这些子区间内的符号,并由定
理1得出单调区间. 注意上述这些点中若有某些点两 侧的单调性一致, 则应将两侧合在一起构成一个单 调区间.
函数的单调性与曲线的凹凸性

§3。
4 函数的单调性与曲线的凹凸性一、函数单调性的判别法 定理1 设)(x f 在区间I 上可导,则)(x f 在I 上递增(减)的充要条件是)()('00≤≥x f .证 若f为增函数,则对每一I x ∈0,当0x x ≠时,有()()000≥--x x x f x f 。
令0x x →,即得00≥)('x f 。
反之,若)(x f 在区间I 上恒有0≥)('x f ,则对任意I x x ∈21,(设21x x <),应用拉格朗日定理,存在,使得()()()01212≥-=-x x f x f x f ξ')(。
由此证得f 在I 上为增函数。
定理2 若函数f 在),(b a 内可导,则f 在),(b a 内严格递增(递减)的充要条件是:(1)),(b a x ∈∀有)()('00≤≥x f ;(2) 在),(b a 内的任何子区间上0≠)('x f .推论 设函数在区间I 上可微,若))('()('00<>x f x f , 则f 在I 上(严格)递增(递减).注1 若函数f 在),(b a 内(严格)递增(递减),且在点a 右连续,则f在),[b a 上亦为(严格)递增(递减), 对右端点b 可类似讨论。
注2 如果函数)(x f 在定义区间上连续,除去有限个导数不存在的点外,导数存在且连续,那么只要用方程0=)('x f 的根及)('x f 不存在的点来划分函数)(x f 的定义区间就能保证)('x f 在各个部分区间保持固定符号,因而函数)(x f 在每个部分区间上单调。
注意:如果函数)(x f 在区间],[b a 上连续,在),(b a 内除个别点处一阶导数为零或不存在外,在其余点上都有0>)('x f (或0<)('x f ),那么由于连续性,)(x f 在区间],[b a 上仍然是单调增加(或单调减少)的。
函数的单调性与曲线的凹凸性

例8、求曲线 的拐点
3、课堂小结、布置作业
课后
作业
P161/4,5,8
教学
后记
周次
日期
课时安排
课题
函数的极值与最值
教材的重点、难点
分析
1、一元函数的极值
2、一元函数的最值
教
学
目
标
1、理解一元函数极值的定义以及可能的极值点;
2、会求各种形式的一元函数的极值。
3、理解一元函数最值的定义以及可能的最值点
学
目
标
1、理解原函数的定义及其性质;
2、掌握原函数的存在性及应用
3、理解不定积分的概念并掌握其基本性质
4、掌握基本积分公式(一)
教学方法
和
教学手段
教
学
过
程
教
学
过
程
1、原函数
1、原函数的概念
定义:如果在区间 上,可导函数 的导函数为 ,即对 ,都有 或者 ,那末函数 就称为 (在区间 上的原函数。
2、原函数的性质
例、求解下列不定积分
四、课堂总结与布置作业
课后
作业
教学
后记
2、解题思路
例1、设 ,求下列不定积分
例2、求下列不定积分
例3、求下列不定积分
2、第三类换元积分法
1、数学原理
定理:设 是单调的、可导的函数,并且 .又设 具有原函数 ,,则f(x)具有原函数 则有换元公式:
其中 是 的反函数.
2、例题选讲
例3、求下列不定积分
3、课堂总结与布置作业
课后
作业
教学
后记
周次
1)设 在区间 上有原函数,则它的原函数有无穷多个,且任意两个原函数相差一个常数。
3.4函数的单调性与凹凸性

1. 单调性判别法
2. 单调性的判别是拉格朗日中值定理的重要应用 3. 曲线凹凸性与拐点的概念 4. 曲线凹凸性与拐点的判别法
一、单调性的判别法
f ( x ) 定理 设函数 y 在 [a, b]上连续, 在 (a,b)
内可导
' ( x ) 0 ,则函数 y (1) 若在 (a,b)内 f f ( x ) 在
5 1 ,0 ) 综上所述可知, 方程 x 在区间 ( x 1 0
内有且只有一个实根.
二、曲线凹凸的概念 问题 如何研究曲线的弯曲方向?
x x f ( x ) f ( x ) 1 2 1 2 两点 x ( ) , 1, x 2,恒有 f 2 2 则称 f (x)在 I上的图形是凹的. 若对 I 上任意 x x f ( x ) f ( x ) 1 2 1 2 两点 x ( ) , 1, x 2,恒有 f 2 2 则称 f (x)在 I上的图形是凸的.
[a, b]上单调增加;
' ( x ) 0 , f ( x ) 在 则函数 y (2) 若在 (a,b) 内 f
[a, b] 上单调减少;
证 x , x ( a , b ), x ,应用拉氏定理得 且 x 1 2 1 2
( x x ), f ( x ) f ( x ) f ' ( )( x x ) 1 2 2 1 2 1
函数单调减少; 函数单调增加.
注:函数的单调性是一个区间上的性质,要用导
数在这一区间上的符号来判定,而不能用一点处 的导数符号来判别一个区间上的单调性.
完
单调区间的求法 问题: 如何确定函数在定义域内各部分区间上函 数的单调性. 定义: 若函数在其定义域的某个区间内是单调的, 则该区间称为函数的单调区间. 注意: 导数等于零的点和不可导点, 均可能是单调
第四节函数的单调性与曲线的凹凸性描述

2 36 x( x ) 3
y y
2018/12/9
凹
0 拐点 凸 (0,1)
2 3 0
(2 , ) 3
拐点
( 2 , 11 ) 3 27
凹
22
3-4 单调性和凹凸性
2 2 故该曲线在( , 0) 及( , ) 上向上凹, 在 (0 , ) 上 3 2 11 3 向上凸 , 点 ( 0 , 1 ) 及 ( , ) 均为拐点. 3 27
3-4 单调性和凹凸性
12
例4 当x 0时, 试证x ln(1 x )成立.
证 : 设f ( x ) x ln(1 x ), 则 1 x f ( x ) 1 . 1 x 1 x f ( x )在[0,)上连续, 且(0,)可导, f ( x ) 0,
第四节 函数的单调性与 曲线的凹凸性
一、函数单调性的判定法
二、曲线的凹凸与拐点
2018/12/9
3-4 单调性和凹凸性
1
y
y f ( x)
A
B
பைடு நூலகம்
y
A y f ( x)
B
o a
b
x
o a
b x
f ( x ) 0
f ( x ) 0
2018/12/9
3-4 单调性和凹凸性
2
一、函数单调性的判定法
3 7 在[0,2]内曲线有拐点为 ( ,0), ( ,0). 4 4
2018/12/9
3-4 单调性和凹凸性
25
• 用一阶导数符号判别单调性;用二阶导数符 号判别凹凸性。 • 一阶导数为0或不存在的点为单调性发生变 化的可疑点;二阶导数为0或不存在的点为 凹凸性发生变化的可疑点。
高等数学-曲线的凹凸性及拐点

曲线的凹凸性和拐点的判别
例3 求曲线 =
解
3
的凹凸区间和拐点.
定义域为(−∞, +∞).
′
=
1
3
3 2
,
″
=−
2
39Leabharlann 2. = 0时, ′ ,′′都不存在.
+
凹
0
凸
由表可知,曲线的凹区间为(−∞, 0) ,凸区间为(0, + ∞),
曲线的拐点为 (0,0).
9
″ () = 12 2 − 30 + 12 = 6(2 − 1)( − 2),
令 ″ ()
= 0,得1 =
+
凹
1
,2
2
0
= 2.
凸
0
+
凹
1
由表可知,曲线的凹区间为(−∞, )和(2, +∞),凸区间为
2
1
1 7
( , 2),曲线的拐点为( , )和(2, −5).
2
2 16
8
02
微分中值定理及导数的应用
第6讲
曲线的凹凸性及拐点
本节内容
01 曲线的凹凸性和拐点的定义
02 曲线的凹凸性和拐点的判别
2
01 曲线的凹凸性和拐点的定义
定义3.2
设函数 = ()在开区间(, )内可导,在该
区间内如果曲线位于其任何一点切线的上方,
那么称此曲线在区间(, )内是凹的,区间
区间(, )内具有二阶导数.
(1)在(, )内,若 ″ () > 0,那么曲线 = ()在
[, ]上是凹的.
(2)在(, )内,若 ″ () < 0,那么曲线 = ()在
高考数学冲刺曲线的凹凸性考点精讲

高考数学冲刺曲线的凹凸性考点精讲在高考数学中,曲线的凹凸性是一个重要的考点,它不仅是函数性质的重要组成部分,也是解决许多数学问题的关键工具。
对于即将参加高考的同学们来说,深入理解和掌握这一考点至关重要。
一、曲线凹凸性的定义曲线的凹凸性是描述曲线弯曲方向的一种性质。
直观地说,如果一条曲线在某一段上看起来像是向上凸起的,那么就称这段曲线是凸的;如果看起来像是向下凹陷的,那么就称这段曲线是凹的。
从数学定义上讲,设函数 f(x) 在区间 I 上连续,如果对 I 上任意两点 x₁,x₂,恒有 f(x₁+ x₂)/2 > f(x₁) + f(x₂)/2,则称 f(x) 在区间 I 上的图形是凸的;如果恒有 f(x₁+ x₂)/2 < f(x₁) + f(x₂)/2,则称 f(x) 在区间 I 上的图形是凹的。
二、曲线凹凸性的判断方法1、二阶导数法这是判断曲线凹凸性最常用的方法。
设函数 f(x) 在区间 I 上具有二阶导数 f''(x)。
如果在区间 I 上 f''(x) > 0,则 f(x) 的图形在区间 I 上是凹的;如果 f''(x) < 0,则 f(x) 的图形在区间 I 上是凸的。
例如,对于函数 f(x) = x²,其一阶导数 f'(x) = 2x,二阶导数 f''(x) = 2 > 0,所以函数 f(x) = x²的图像在其定义域内是凹的。
2、切线法在曲线的某一点处,如果曲线位于切线的上方,则曲线在该点附近是凸的;如果曲线位于切线的下方,则曲线在该点附近是凹的。
三、曲线凹凸性的性质1、若曲线是凹的,则曲线的切线位于曲线的下方;若曲线是凸的,则曲线的切线位于曲线的上方。
2、若函数在某区间上是凹的(凸的),则函数在该区间上单调递增(递减)。
四、曲线凹凸性的应用1、证明不等式利用曲线的凹凸性可以证明一些不等式。
例如,要证明对于任意的x₁,x₂∈ 0, +∞),有 x₁+ x₂ ≥ 2√(x₁x₂) 。
第四节函数的单调性与曲线的凹凸性

y
拐点的判别法:
( x0 , f ( x0 ))
o
x
若 f ( x) 在 x0 两侧异号, 则点 ( x0 , f ( x0 ))是拐点.
求凹凸区间及拐点的方法:
(1) 求函数 f (x) 的定义域 D; (2) 求 f ( x); (3) 求 方 程 f ( x) 0 的 实 根,
证: x1, x2 [a, b], 且 x1 x2, 应用拉氏定理,得
f ( x2 ) f ( x1) f ( )( x2 x1 ) ( ( x1, x2 ))
(1) 若 在(a, b)内, f ( x) 0, 则 f ( ) 0, 又 x2 x1 0,
( A) f (1) f (0) f (1) f (0) (B) f (1) f (1) f (0) f (0) (C) f (1) f (0) f (1) f (0) (D) f (1) f (0) f (1) f (0) 提示: 利用 f ( x)单调增加 , 及
且点( x0 , f ( x0 ))是拐点,则
f ( x0 ) 0.
例14. 已知(2,4)是曲线y x3 ax2 bx c 的拐点,
且曲线在点x 3 处有极值,求常数a, b, c.
解:
(2,4) 是拐点
4
8 4a 2b c
(1)
y 12 2a 0 (2)
( x 0)
x (, 0) 0 (0 , )
f ( x) 不存在
f (x)
该函数在(,0]上单调减少; 在[0,) 上单调增加.
说明:导数不存在的点划分函数的定义区间为两 个具有单调性的区间.
函数单调性和凹凸性省公开课获奖课件说课比赛一等奖课件
证 (1). 设 x1 , x2 (a, b), ( x1 x2 ) , 应用拉格朗日中值定理
11
x3
2 5x 1
33
9
9
9 3 x4
令 y 0 得 x1 1/ 5, 当 x2 0 时, y不存在.
列表: x (,1/ 5 ) 1/ 5 (1/ 5,0) 0
(0, )
y
0
不存在
y
有拐点 无拐 点
综上,曲线在(,1/ 5 ) 为上凸旳
点
1 5,Biblioteka 6 53 25是拐点.
在 (-1/5, )上为下凸旳.
上凸旳。
问题:拟定函数在那些区间上图形上凸旳,那些区间上图 形是下凸旳,即求函数旳凸向区间。
8
例1.判断曲线 y x3 旳凸向
解 y 3x2 y 6x
x 0 时, y 0, 曲线 在 (, 0)内是上凸旳. x 0 时, y 0, 曲线 在 (0,)内时是下凸旳.
定义 曲线上上凸弧与下凸弧旳分界点,称为拐点.
如例1中,点(0,0) 是曲线 y x3 旳拐点.
y y x3
0
•
x
注意 1.若点 (x0, f (x0)) 是拐点,则 f ( x0 ) 0.或f ( x0 )不存在
2.由f ( x0 ) 0. 或不存在 所拟定旳点(x0, f (x0 )) 未必是拐点.
如 f ( x) x4 , f (0) 0, 但点 (0,0) 不是拐点.
2
例1. 鉴定函数 y x sin x 在 [0,2 ] 上旳单调性.
§3.4 函数的单调性与凹凸性

为铅直渐近线
导数的应用
又因
即
为斜渐近线.
( x 3) 2 y 4( x 1)
5) 求特殊点
( x 3)( x 1) y 4( x 1) 2 2 y ( x 1)3
导数的应用
6)绘图
(极大)
无 定 义
(极小)
铅直渐近线 斜渐近线 特殊点
1
( x 3) 2 y 4( x 1)
的单调区间.
导数的应用
2.函数的极值
定义:
在其中当 (1) 时,
则称
称
为
的极大点 ,
为函数的极大值 ;
(2)
则称 称
为
的极小点 , 为函数的极小值 .
极大点与极小点统称为极值点 .
导数的应用
3. 函数极值的判定 定理3.4.2 (极值第一充分条件) 设 f (x) 在 x0 处连续, 在 x0 的某去心 δ 邻域内可导, (1) 如果当 如果当 (2) 如果当 如果当 (3) 如果 在
导数的应用
§3.4 函数的单调性与凹凸性
3.4.1 函数的单调性与极值 3.4.2 函数凹凸性及其判定 内容小结与作业
导数的应用
3.4.1 函数的单调性与极值
1. 函数的单调性判定
y B D
A
O
C
x
对曲线段
、
,其各点处的切线斜率为正,曲
线是上升的;对曲线段 为负,曲线是下降的.
,其各点处的切线斜率
f ( x) 0.
导数的应用 \\5.4.2 函数凹凸性及其判定
例9
求曲线
的凹凸区间和拐点.
例10 求曲线
的凹凸区间和拐点.
导数的应用
同济大学的高等数学讲义 (9)

4Байду номын сангаас − 1 x
2 3
,
1 当 x = 时,f ′( x) = 0 ,当x=0时,导数不存在,用 4
1 x=0, 即 x = 4
将定义域区间划分成三个部分小区间:
1 1 (−∞,0), (0, ), ( , +∞), 4 4
现将每个部分区间上导数的符号与函数单调性列表如
x + ( 1( 1)⎞ 0′ x 1 ⎛f−∞,0) ⎞ ⎜ 0, ,+∞ ⎟ ⎟ 4 ⎝4 4⎠ ⎠
y
y y= f (x) y= f (x)
θ
o a
θ
b x o a b x
单调上升
单调下降
上述关于函数单调性的图象性质,可以得到一般的结 论,即有 定理(可导函数单调的必要条件) 设函数f ∈C[a ,b],并且 f ∈D(a, b),若在区间[a ,b]上单调增加(减少),则对任意 的x∈(a , b) ,有 f ′( x) ≥ 0 ( ≤ 0 ). 反之,可以通过导数的符号来判定函数的单调性,即 有下面的判定定理:
2.函数图形凹凸性及其判别法 ⑴定义 设I 是一个区间,若对任意的x1,x2∈I (x1≠x2)成
立不等式
⎛ x1 + x2 ⎞ f ( x1) + f ( x2 ) ⎛ ⎛ x1 + x2 ⎞ f ( x1) + f ( x2 ) ⎞ f⎜ ⎜f⎜ ⎟, ⎟< ⎟> 2 2 ⎝ 2 ⎠ ⎝ ⎝ 2 ⎠ ⎠
ADB 是向上凹的弧.
定义
设I 是一个区间,若对任意的x1,x2∈I (x1≠x2)成立
不等式
⎛ x1 + x2 ⎞ f ( x1) + f ( x2 ) , f⎜ ⎟< 2 ⎝ 2 ⎠
高数3-4

例3 确定函数 f ( x ) = 2 x 3 − 9 x 2
+ 12 x − 3的单调区间.
解 ∵ D : ( −∞ ,+∞ ).
f ′( x ) = 6 x 2 − 18 x + 12 = 6( x − 1)( x − 2)
解方程 f ′( x ) = 0 得, x1 = 1, x2 = 2.
3 2
∵ D : ( −∞ ,+∞ )
( 2 ,+∞ ) 3
f ′′( x )
f ( x)
+
凹的
0
拐点
−
凸的
0
拐点 ( 2 , 11 ) 3 27
+
凹的
(0,1)
凹凸区间为 ( −∞ ,0],
[0, 2 ], 3
[ 2 ,+∞ ). 3
方法2:
设函数 f ( x ) 在 x 0 的邻域内三阶可导 , 且 f ′′( x 0 ) = 0, 而 f ′′′( x 0 ) ≠ 0 , 那末 ( x 0 , f ( x 0 )) 是曲
二式两边相加,得
f ( x1 ) + f ( x2 ) =
1 2 f ( x0 ) + [ f ′′(ξ1 )( x1 − x0 )2 + f ′′(ξ 2 )( x2 − x0 )2 ] 2
由 f ′′( x) > 0 ⇒ f ( x1 ) + f ( x2 ) > 2 f ( x0 ),
x1 + x2 1 即 f( ) < [ f ( x1 ) + f ( x2 )] 2 2
又f ′(0) = 0
∴ f ′( x ) > f ′(0) = 0,
曲线凹凸性的判断方法

曲线凹凸性的判断方法
曲线凹凸性判断是识别函数曲线处处向量切线方向的重要方法,用于求解微积分、动力学等重要问题,也是检测函数曲线任意点处变化状态的依据。
曲线凹凸性的判断方法有以下几种:
1、利用积分法:将曲线上的每一片分段折线积分,由积分结果得出曲线的凹
凸性,即根据积分结果的符号大小来确定曲线的凹凸性:若积分结果为正,则曲线向上凸出,上升趋势明显;若积分结果为负,则曲线向下凹陷,下降趋势明显。
2、利用微分法:以曲线上任一点为中心,考察它及其附近的某点处方向与曲
线段的夹角大小及趋势,从而判断曲线凹凸性:若夹角大于零,则曲线向上凸出,上升趋势明显;若夹角小于零,则曲线向下凹陷,下降趋势明显。
3、利用数值分析法:画出曲线的网格折线,采用直接数值法求出曲线的凹凸性,即根据曲线上点之间的数值大小比较结果来判断曲线的凹凸性:若曲线点值持续上升,则曲线向上凸出,上升趋势明显;若曲线点值持续下降,则曲线向下凹陷,下降趋势明显。
4、利用图象识别法:观察曲线的图象,根据曲线的连续变化特点来确定曲线
的凹凸性,即观察曲线的拐点位置及方向确定曲线的凹凸性:若拐点持续向上,则曲线向上凸出,上升趋势明显;若拐点持续向下,则曲线向下凹陷,下降趋势明显。
以上便是曲线凹凸性判断的主要方法,各种方法有各种优缺点,在实际应用中,以上四种方法相互之间可以结合使用,以达到合理判断曲线凹凸性的效果,使曲线凹凸性判断得以正确与准确地实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3 4 函数单调性与曲线的凹凸性
一.教学目的
(一)知识目的
(1)了解函数单调性与曲线的凹凸性的有关概念;
(2)会利用导数判断函数图形的凹凸性和拐点;
(二)能力目标
(1)培养学生将实际问题转化为数学问题的能力;
(2)培养学生观察、比较、抽象、概括的能力;
(3)训练学生思维的灵活性。
(三)德育目标
~
(1)激发学生的内在动机;
(2)养成良好的学习习惯。
二.教学的重、难点及教学设计
(一)教学重点:应用导数判断函数单调性与曲线的凹凸性
(二)教学难点:用导数判断函数单调性与曲线的凹凸性方法的推导
(三)教学设计要点:1.用导数判断函数的单调性;
2.用导数判断函数图形的凹凸性和拐点;
3.单调性及凹凸性的应用;
三.教学过程
1、函数单调性的判定法
—
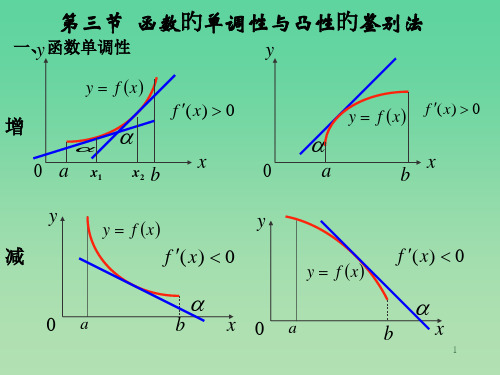
如果函数y f(x)在[a b]上单调增加(单调减少)那么它的图形是一条沿x轴正向上升(下降)的曲线这时曲线的各点处的切线斜率是非负的(是非正的)即y f(x)0(y f(x)0)由此可见函数的单调性与导数的符号有着密切的关系
反过来能否用导数的符号来判定函数的单调性呢
定理1(函数单调性的判定法) 设函数y f(x)在[a b]上连续在(a b)内可导
(1)如果在(a b)内f(x)0那么函数y f(x)在[a b]上单调增加
(2)如果在(a b)内f(x)0那么函数y f(x)在[a b]上单调减少
证明只证(1)在[a b]上任取两点x1x2(x1x2)应用拉格朗日中值定理得到
f(x2)f(x1)f()(x2x1) (x1x2)
由于在上式中x2x10因此如果在(a b)内导数f(x)保持正号即f (x)0那么也有f()0于是f(x2)f(x1)f()(x2x1)0即f(x1)f(x2)
这函数y f(x) 在[a b]上单调增加
注判定法中的闭区间可换成其他各种区间
】
例1 判定函数y x sin x在[0 2]上的单调性
解因为在(0 2)内,,y1cos x0
所以由判定法可知函数y x cos x在[0 2]上的单调增加
例2 讨论函数y e x x1的单调性(没指明在什么区间怎么办)
解 y e x 1
函数y e x x 1的定义域为( ) 因为在( 0)内y 0 所以函数
y e x x 1在( 0] 上单调减少 因为在(0 )内y 0 所以函数y e
x
x 1在[0 )上单调增加
例3 讨论函数32x y =的单调性
解 函数的定义域为(
) 函数的导数为 332x
y ='(x 0) 函数在
x 0处不可导 当x 0时 函数的导数不存在 因为x 0时 y 0 所以函数在(, 0] 上单调减少 因为x 0时 y 0 所以函数在[0, )上单调增加 &
如果函数在定义区间上连续 除去有限个导数不存在的点外导数存在且连续 那么只要用方程f (x )0的根及导数不存在的点来划分函数f (x )的定义区间 就能保证f (x )在各个部分区间内保持固定的符号 因而函数f (x )在每个部分区间上单调 例4 确定函数f (x )2x 39x 212x 3的单调区间 解 这个函数的定义域为:( )
函数的导数为:f (x )6x 2 18x 12 6(x 1)(x 2) 导数为零的点有两个 x 1 1、x 2 2
列表分析
(
1] [1 2]
[2
)
f
(x ) )
f (x )
↗
↘
↗
函数f (x )在区间( 1]和[2 )内单调增加 在区间[1 2]上单调减少
例5 讨论函数y x 3的单调性 解 函数的定义域为 ( ) ?
函数的导数为 y 3x 2 除当x 0时 y 0外 在其余各点处均有y 0 因此函数
y x 3在区间( 0]及[0 )内都是单调增加的 从而在整个定义域 ( )内是单调增加的 在x 0处曲线有一水平切线
一般地 如果f (x )在某区间内的有限个点处为零 在其余各点处均为正(或负)时 那么f (x )在该区间上仍旧是单调增加(或单调减少)的 例6 证明 当x 1时 x
x 1
32-
>
证明
令)
1
3(2)(x x x f --= 则 )
1(111)(22-=-='x x x x
x x f
因为当x 1时 f
(x )0 因此f (x )在[1, )上f (x )单调增加 从而当x 1时
f (x )f (1)
由于f (1)0 故f (x )f (1)0 即 0
)1
3(2>--x
x 也就是x
x 1
32->(x 1)
二、曲线的凹凸与拐点
定义 (凹凸性)设f (x )在区间I 上连续 如果对I 上任意两点x 1 x 2 恒有
;
2)
()()2(
2121x f x f x x f +<+
那么称f (x )在I 上的图形是(向上)凹的(或凹弧) 如果恒有
2
)
()()2(
2121x f x f x x f +>+
那么称f (x )在I 上的图形是(向上)凸的(或凸弧)
定义 设函数y f (x )在区间I 上连续 如果函数的曲线位于其上任意一点的切线的上方,则称该曲线在区间I 上是凹的;如果函数的曲线位于其上任意一点的切线的下方,则称该曲线在区间I 上是凸的 凹凸性的判定
定理 设f (x )在[a b ]上连续 在(a b )内具有一阶和二阶导数 那么 (1)若在(a b )内f (x )>0 则f (x )在[a b ]上的图形是凹的 (2)若在(a b )内f (x )<0 则f (x )在[a b ]上的图形是凸的 》
简要证明 只证(1)
设21 ,x x x 1 x 2[a b ] 且x 1x 2 记2
210x x x +=
由拉格朗日中值公式 得
2)
())(()()(21101101x x f x x f x f x f -'=-'=-ξξ 011x x <<ξ 2)
())(()()(12202202x x f x x f x f x f -'=-'=-ξξ 2
20x x <<ξ
两式相加并应用拉格朗日中值公式得
2
)]()([)(2)()(1
212021x x f f x f x f x f -'-'=-+ξξ 02
)
)((1
212>--''=x x f ξξξ 2
1ξξξ<<
即
)2
(2)()(2121x
x f x f x f +>+ 所以f (x )在[a b ]上的图形是凹的
拐点 连续曲线y f (x )上凹弧与凸弧的分界点称为这曲线的拐点
<
确定曲线y f (x )的凹凸区间和拐点的步骤
(1)确定函数y f (x )的定义域 (2)求出在二阶导数f` (x )
(3)求使二阶导数为零的点和使二阶导数不存在的点 (4)判断或列表判断 确定出曲线凹凸区间和拐点 注 根据具体情况(1)(3)步有时省略 例1 判断曲线y ln x 的凹凸性 解 x
y 1
=
' 2
1
x
y -=''
因为在函数y ln x 的定义域(0 )内 y <0 所以曲线y ln x 是凸的
例2 判断曲线y x 3的凹凸性
解 y 3x 2 y 6x 由y 0 得x 0
'
因为当x <0时 y <0 所以曲线在( 0]内为凸的
因为当x >0时 y >0 所以曲线在[0 )内为凹的
例3 求曲线y 2x 33x 22x 14的拐点 解 y 6x 26x 12 )
2
1
(12612+=+=''x x y 令y 0 得2
1-=x
因为当2
1
-<x 时
y
0 当2
1
->x 时
y
所以点(2
1-
2
1
20)是曲
线的拐点
例4 求曲线y 3x 44x 31的拐点及凹、凸的区间 解 (1)函数y 3x 44x 31的定义域为( ) (2)231212x x y -=')
3
2(3624362-=-=''x x x x y
(3)解方程y
0 得0
1=x 3
22=
x
:
(4)列表判断
;
在区间( 0]和[2/3 )上曲线是凹的 在区间[0 2/3]上曲线是凸的 点(0
1)和(2/3 11/27)是曲线的拐点 例5 问曲线y x 4是否有拐点
解 y 4x 3 y 12x 2 当x 0时 y >0 在区间( )内曲线是凹的 因此曲线无拐点 例6 求曲线3x y =的拐点 解 (1)函数的定义域为( ) (2) 3
2
31
x y =
' 3
2
92x x y -
=''
(3)无二阶导数为零的点 二阶导数不存在的点为x 0
(4)判断 当x <0当 y >0 当x >0时 y <0 因此 点(0 0)曲线的拐点
四. 布置作业
做练习册第19大页
有能力的同学可以附加做课后习题
( 0) 0 (0 2/3) 2/3 (2/3 ) f (x ) 0 0。
