基桩动力检测高应变检测技术基本原理
高应变检测

高应变简介用重锤冲击桩顶,实测桩顶部的速度和力时程曲线,通过波动理论分析,对单桩竖向抗压承载力和桩身完整性进行判断的检测方法。
高应变检测的基本原理高应变榆测的基本原理就是往桩顶滞轴向施加一个冲击力,使桩产生足够的贯入度,实测由此产生的桩身质点应力和加速度的响应,通过波动理论分析,判定单桩竖向抗承载力及桩身完整性的榆测方法。
用重锤冲击桩顶,使桩~土之间产生足够的相对位移,以充分激发桩周土阻力和桩端支承力.从桩身运动方向来说,有产生向下运动和向上运动之分。
习惯把桩身受压(小沦是内力、应力还是应变)看作正的,把桩身受拉看作是负的;把向下运动(不论是位移、速度还是加速度)看作正的,而把向上的运动看作负的。
南于应力波在其沿着桩身的传播过程中将产生十分复杂的透射和反射,因此,有必要把桩身内运动的各种应力波划分为上行波和下行波。
由于下行波的行进方向和规定的正向运动方向一致,在下行波的作用下正的作用力(即压力)将产生正向的运动,而负的作用力(拉力)则产生负向的运动。
上行波则正好相反,上行的压力波(其力的符号为正)将使桩产生负向的运动,而上行波的拉力(力的符号为负)则产生正向的运动。
由于锤击所产生的压力波向下传播,在有桩侧摩阻力或桩载而突然增大处会产生一个压力同波,这一压力回到桩顶时,将使桩顶处的力增加,速度减少。
同时,下行的压力波在桩载面突然减小处或有负摩阻力处,将产生一个拉力回波。
拉力波返回桩顶时,将使桩顶处的力值减小,速度增加。
掌握这一基本概念就可以在实测的力波曲线和速度曲线中根据两者变化关系来判断桩身的各种情况。
●测试系统示意图●应用要点1 检测桩数由于工程桩是不允许不合格桩存在的,因此在进行检测时,不应简单地采用随机抽样的方式,而应根据打桩记录,经过综合分析,抽检那些估计质量可能较差的桩。
以提高检测结果的可靠度,减少工程隐患。
基桩的高应变动力检测有两种情况:一种是根据《建筑桩基技术规范》中的有关规定进行的例行检测,其检测桩数不宜少于总桩数的5%,并不得少于5根;另一种是发现桩基工程有质量问题,必须对桩基施工质量、承载能力作出总体评价时,应由有关方面协商,适当增加抽检桩数,一般不应少于总桩数的10%。
6 高应变检测

基桩高应变检测高应变检测实际上是用重锤锤击桩顶,使桩产生一个位移,同时测出桩身中锤击应力随时间的变化及桩身质点振动速度随时间的变化,再经过数值拟合计算,确定单桩承载力。
基桩高应变检测 基桩高应变检测 新闻打桩公式修正新闻打桩公式式中 ——单桩极限承载力 ——锤重 ——桩重c ——桩土体系总的弹性变形 e ——最终贯入度 ——机械折减系数 n ——撞击时恢复系数 1.凯斯法(Case ) 基本原理和计算公式一次锤击时,沿桩身各处所受到的实际土反力值的总和为:r u W hP e cξ=+2r p r u r pW n W W hP e cW W ξ+=⨯++u P r W p W ξ()()()()()()1212111112221222T Z V t V t R F t F t L Z V t V t C L F t F t C -⎡⎤⎣⎦=++⎡⎤⎣⎦⎡⎤⎛⎫-+⎪⎢⎥⎡⎤⎛⎫⎝⎭⎣⎦=+++ ⎪⎢⎥⎝⎭⎣⎦由于⊿L/t 表示单位时间内变形大小,即质点振动速度V=⊿L/t ,而L/t 表示波在整个桩长传播的波速C=L/t ,所以可表示为F=VAE/C=VZ 。
它的物理意义是外力消耗是与内部阻抗和质点的振动速度乘积相关。
再分析RT 公式中右侧第二项: 可以清楚看到,此式是桩质量与实测加速度平均值的成积,即为桩的惯性力。
如果与质量——弹簧——阻尼系统的振动方程相比较,惯性力+阻尼力+弹簧力=外力 基桩高应变检测 凯司法作如下假定:①桩身质量均匀,且无明显缺陷,所以桩身阻抗恒定; ②动阻尼只存在桩端,忽略桩侧阻尼的影响;③应力波在桩身中传播时,除土阻力影响外,没有其他因素造成能量扩散;④土体对桩的阻力只与其相对位移有关,与其位移大小无关,也即一有位移,土阻力即达极限状态。
L F AE AE Lε∆=⨯=⨯⨯t t ()()()()2112212V t V t Z V t V t mt t --=-⎡⎤⎣⎦-0i tm x C xkx p e ω++=桩端动阻力:=因为土的总阻力 ,代入上式所以即为凯司法中用阻尼系数求单桩承载力公式,适用于中小型桩。
《基桩高应变法检测》课件

基桩高应变法检测的重要性
提高工程质量
通过基桩高应变法检测,可以及时发现基桩的缺陷和问题,采取相应措施进行加固或修复 ,提高工程质量。
保障安全
基桩是各类工程的基础结构,其承载力和完整性直接关系到整个工程的安全性。通过基桩 高应变法检测,可以确保基桩的安全性和稳定性,防止因基桩问题导致的工程事故。
节约成本
常用的信号处理技术包括快速傅 里叶变换(FFT)、小波变换、 时频分析等,这些技术能够提供 对信号更深入的理解和分析。
Part
03
基桩高应变法检测设备与操作
基桩高应变法检测的设备介绍
基桩高应变法检测设备包括传 感器、数据采集系统、锤击设 备等。
传感器用于采集桩身的应变和 加速度信号,数据采集系统负 责信号的放大、滤波和模数转 换。
基桩高应变法检测的物理原理基于波动理论和动力学理论,通过建立数学模型来描 述基桩的振动响应。
基桩高应变法检测的数学模型
基桩高应变法检测的数学模型基 于波动方程和动力学方程,通过 求解这些方程来预测基桩的振动
响应。
波动方程描述了波动在基桩中的 传播和衰减,而动力学方程描述 了基桩在冲击荷载下的动态响应
THANKS
感谢您的观看
基桩高应变法检测的未来展望
广泛应用
随着基础设施建设的不断发展和 人们对工程质量要求的提高,基 桩高应变法检测将得到更广泛的
应用。
技术创新
未来将不断涌现新的技术创新,推 动基桩高应变法检测技术的持续发 展和进步。
国际化发展
随着国际交流和合作的加强,基桩 高应变法检测技术将得到更广泛的 认可和应用,推动其国际化发展。
智能化技术应用
随着人工智能和机器学习的发展,基 桩高应变法检测将更加智能化,能够 自动识别和判断桩基的完整性。
基桩高应变法检测

《规范》JGJ106-2003以强制性条文做出 如下规定: 当出现下列情况之一时,高应变锤击信号 不得作为承载力分析计算的依据: 1 传感器安装处混凝土开裂或出现严重塑 性变形使力曲线最终未归零。 2 严重锤击偏心,两侧力信号幅值相差超 过1倍。 3 触变效应的影响,预制桩在多次锤击下 承载力下降。 4 四通道测试数据不全。
.土阻力 在低应变检测中,土阻力的作用被忽略,视弹性波 的传播局限在桩身内部。但是土阻力对弹性波传播 过程的影响是确实存在的。高应变检测中无法忽视 土阻力的存在,因为检测桩承载力的过程主要就是 分析研究桩周围土静阻力发挥作用的过程。土阻力 对弹性波传播过程的影响是非线性的(详细可见有 关专著)。这里,强调应力波在传播时,土阻力的 变化同样会产生反射与透射,会产生类似杆件的阻 抗(E、A、)中任一项或几项的变化的反射与透射。 高应变检测技术的难点不仅要识别阻抗(E、A、) 的变化,还要识别和计算土阻力的变化;还有一个 难点是把土体振动时动态的土阻力(阻尼)如何等 效为土的静阻力。
vR 与vI符号相反
波之间关系。 在实际桩的动力检测时,施加于桩顶的荷 载为压力,按习惯定义位移u,质点运动速 度V和加速度a以向下为正(即x轴正向), 桩身轴力F,应力σ和应变ε以受压为正。 (1) 当初始入射波FI沿x正向(向下)传播 尚未到达阻抗变化界面前,下行波就是入 射波,无上行波; (2) 入射波到达阻抗变化界面将产生反射 和透射,反射力波FR沿阻抗为Z1的杆x轴负 向(向上)传播,称为上行波;透射力波 FT沿阻抗为Z2的杆x轴正向(向下)传播, 此时下行波就是透射波。
.振动速度V 和 力F 的关联。根据虎克定律,应力与应
变之比等于弹性模量E.
.下式中等号右边第一项称为下行力波Fd(也简称为下
高应变检测基本知识讲解

第二步 仪器设备的安装与连接
1.放置重锤
2.放置固定架
3.传感器与应变环的安装
4.仪器连接
第三步 测试参数设定 开机,选择RS模式 设置高应变相关参数
设置桩土参数
第四步 检查和确认仪器、设备的工作状态
1.检查仪器设备是否正常连接 2.调试应力环的应变值
监视
应变值范围±1000
第五步 重锤锤击(重锤低击)
粗砂--0.05,砂土--0.1~0.15,粉质砂土0.15~0.25,粉土0.25~0.4,粉质 黏土0.4~0.7,黏土0.7~1.0,固定端为0,自由端为1 case法主要定3点:行波起跳点,行波峰值点,桩底反射点 2.在case法分析的基础上再用武汉岩海拟合分析程序进行拟合。 按地勘资料输入桩侧土的摩阻力和端阻力→按f键人工计算,这是第一次拟 合→拟合不满意→继续修改“土单元参数”或“整体参数”→再按f键人工 计算→想要电脑自动拟合→按u键“卸载优化”→拟合效果仍有待改进→按r 键“阻力优化”→反复使用这两种优化直到拟合满意为止。 卸载优化对曲线的整段综合优化即大方向的拟合较好 阻力优化对曲线的2L/c即桩底反射前的信号段拟合较好 辐射阻尼优化对曲线的尾部拟合较好 土塞优化对曲线的2L/c附近拟合较好
2.检测频率
抽检数量不宜少于总桩数的5%,且不得少于5根。
第二节 适用范围及检测方法
适用范围
1、可检测预制桩、预应力管桩和钢管桩的单桩竖向抗压承载力 和完整性; 2、监测打入桩的桩身应力和锤击能量传递比,为沉桩工艺参数 及桩端持力层选择提供依据; 3、对于灌注桩检测,应具备现场实测经验和本地区相似条件条 件下的可靠对比试验资料。 4、对于Q-s曲线为缓变形的大直径桩、扩底桩、嵌岩桩等,其桩 端阻力发挥所需的位移很大,难于把桩打动,一般不采用高应 变法。
工程检测与评估3高应变基桩动力检测

h
6
第一章 基本概念及检测原理 四个基本假定:
基本假定
(1)桩是一个时不变的系统,即桩的基本特性在测试所涉及的 时间内可以看作是固定不变的。
(2)桩是一个线性系统,即桩在总体上是弹性的,所有的输入 和输出都可以简单叠加,这个假定并不妨碍我们在桩身的局部 环节上采用某些办法来考虑其非弹性性状。
(3)桩是一个一维的杆件,即桩身每个截面上的应力应变都是
高应变基桩动力检测
h
1
高应变基桩承载力检测
目录
第一章 基本概念及检测原理 第二章 检测系统 第三章 现场检测技术 第四章 实测波形汇编
h
2
第一章 基本概念及检测原理
目录
第一节 概述 第二节 基本假设 第三节 基本理论 第四节 CASE法的检测原理
h
3
第一章 基本概念及检测原理
概述
所谓高应变动力试桩法,广义上讲,是指所有能使桩土间产 生永久变形(或较大动位移)的动力检测桩基承载力的方法, 无庸置言,这类方法要求给桩土系统施加较大能量的瞬时荷载, 以保证桩土间产生一定的相对位移。自19世纪人们开始采用打 桩公式计算桩基承载力以来,这种方法包括:
在上述假定下,我们的问题在原理上被简化为 一维的线性波动力学问题。
h
8
1、高、低应变法动力试桩的区分
(1)
动力试桩是在桩顶作用一动态力(动荷载),在桩顶量测桩土 系统的动力响应,如位移,速度或加速度信号,对信号的时域和频域 进行分析,可以对单桩承载力和桩身完整性进行评价。
(2)
高应变法,用重锤(重量为预估单桩极限承载力的1%~1.5%) 自由下落锤击桩顶,使其应力和应变水平接近静力试桩的水平,使桩 土之间的土产生塑性变形,即使桩产生贯入度,一般贯入度≮2mm, 但≯6mm.桩对外有抗力(承载力)是通过位移产生,有了位移,桩 侧土强度得到充分发挥,桩端土强度也得到一定程度的发挥,此时,量 测的信号含有承载力的因素。但对于嵌岩桩和超长的摩擦桩,要使桩 端土强度发挥几乎是不可能的。
浅谈高应变检测在工程基桩检测上应用以及注意的事项

T :5. B I 明
T1=8.
 ̄ : i. r l/ ∞ z
T]- ̄1.z且 g-
2
=10
图 2 拟 合结 果图
最近该 站在江门市江海区某工地的检测中 ,再次有效地 印 证 了这一观点 :本站使用 高应 变和静载相结合 的方法对江 门市 江海区某工 地的全盘桩基 进行 检测。在高应 变检测其 中一座建
rn f c ne e e A tr es
2 1 年0 月 00 6
浅谈 高应变检 测在 工程基桩 检测上应用 以及 注意的事项
粱如 福
( 江门市 江海 区建设工程质量检测站 ,广东 江门 5 9 0 2 00)
摘 要: 高应 变检测的原理是在桩顶作用一个高能量 冲击 , 使得桩土体 系产生相 对位移 , 激发 出桩侧 土的摩 阻力,根据加速度传感器和应力传感 器测得的数据获得桩 身的动应力 响应曲线,在 一些基本假定的基础上 ,来预估基桩 承载 力。在 实际操作 中,锤击能量选 择、原始材料 收集、检测 时间选择、传感器安装 以及桩 头处理好坏都会影响 高应 变检测 法的准确性和 可靠性 ,因此在使 用时应 当对这 些方 面给予足够的重视 。 关键 词 :高应 变检测 ;基桩 ;注意事项 中图分类号 :T 4 3 文献标 识码 : U 7 A 文章编号 :1 0 0 0—83 2 1 1 —0 5 —0 16( 0 0) 8 0 2 3
1 前言
高应变动力法测试技术于 2 世纪 8 0 O年代随美 国 P I 司 D公 的 P A仪器引入我国 , 0 D 2 世纪 9 年代初国内类似 的仪器 和计 0 算软件业相继面世。近几年 ,随着 国内高层建筑数量 的增 多, 该技术得到 了广泛的应用和发展 。 高应 变检测的理论和方法 … 很多 ,但其基本原 理都类似 :即在桩顶作用一个高能量 冲击 , 使得桩土体系产生相对位移 ,激发 出桩侧 土的摩 阻力 ,根据加 速度传感器 和应力传感器测得 的数据获得桩身 的动应力响应 曲 线 ,在一些基本假定 的基础上 ,来预估基桩承载力和完整性 。 与低应变检测方法相 比,不 同点在于 :高应变测试 中,利用高 能量锤 的冲击会使 土体产生永久变形 , 激发出桩侧土 的摩 阻力 。
桩基检测中高应变动力检测原理及方法

【施测鉴工】住宅与房地产2019年9月桩基检测中高应变动力检测原理及方法车言飞(烟台市建工检测服务中心,山东 烟台 264001)摘要:高应变动力检测技术是一种专用于桩基检测的检测技术,其具有诸多其他桩基检测技术难以比拟的优点,是如今桩基检测过程中应用前景比较良好的一种检测技术。
文章着重对高应变动力检测的相关原理及方法进行深入的研究分析,并总结出一些可能会影响高应变动力检测技术准确性的影响因素,以期能够提升高应变动力检测技术的应用范围。
关键词:高应变动力检测技术;桩基检测;原理中图分类号:U443.15 文献标志码:A 文章编号:1006-6012(2019)09-0190-01在桩基工程的实际作业过程中,一般都需要对桩基进行实际的质量检查,而质量检查过程中的主要检查项目便是对单桩垂直承载力进行相关检测,以此来确定其承载力是否能够符合标准。
而高应变动力测试技术相比较传统的静载荷实验技术而言,不仅对于人力物力的耗费比较小,还能对大吨位的桩基进行承载力检测,因此对于高应变动力测试技术进行相关的研究,对于如今的桩基质量检查有着极为重要的现实意义。
1 高应变动力检查技术的原理及方法1.1 凯斯法理论凯斯法理论是一种建立在应力波理论之上的检测理论。
在实际桩基承载力检测过程中,凯斯法理论会将桩体假设成为一根等截面的单桩,并将桩体当作是一种连续的弹性杆件,然后根据行波理论,将桩体上实际测量到的数据进行相应的计算,最终计算并确认该桩基的极限承载力,然后将桩基的承载力与项目的需求进行对比,确认该桩基是否符合项目工程的实际需求。
另外,凯斯法理论在对桩基实施承载力计算的过程中,因为其是使用对土助力来进行钢塑法而得出的相关数据数据,所以其所计算得出的数据一般而言都是对该桩体的承载力计算估值,虽然比较近似于桩体的极限承载力,但也有着一定的差距。
因此在实际凯斯法理论应用过程中,往往都需要通过多次计算来得出最终的结果,以此来确保桩体极限承载力计算的准确性。
6第六章 高应变基桩检测

纵波波速C :应力波在桩身中的传播速度,高应
变检测时混凝土桩的正常波速一般为3000—4000m/s。
质点运动速度V:其质点的振动速度V取决于应
力的大小和介质的特性。 弹性杆中的应力波引起的质点运动速度与应变
成正比。例:对于低碳钢,c=5120m/s,屈服限对应
的变形约为1‰即ε=1000με,则质点运动速度
V=5.12m/s。
应变1
应变2
F1=E.A.应变1
F2=E.A.应变2
(F1+F2)/2
平均力
a1
a2
积分得V1
积分得V2
(V1+V2)/2
平均速度V
平均力F
平均速度V
与波阻抗Z乘积
F
ZV
与时间的函数
Fபைடு நூலகம்ZV波形
分析方法 1)采用Case法 2)实测曲线拟合法
1)case法
2)曲线拟合 法
紧贴桩身表面
应变计不能有变形
程序设置
在开始检测之前必须根据不同桩的情况
对程序进行设置,功能及程序中出现的参数
见操作说明书。
信号采集注意事项 重锤角架放置牢固
桩头处理到位
采集前对正个系统的调试
波形存盘
1. 上、下行波
第 4 节 性
判断桩身完整
2u 2 2u c 2 t x 2 桩身中任意点的力和速度,都是上行波和下行波的叠 加。
实测曲线拟合法采用了较复杂的桩—土 力学模型,选择实测力或速度或上行波作为 边界条件进行拟合,拟合完成时计算曲线应 与实测曲线基本吻合,桩侧土摩阻力应与地 质资料基本相符,贯入度的计算值应与实测 值基本吻合,从而获得桩的竖向承载力和桩
身完整性。
高应变动力检测的基本原理

高应变动力检测的基本原理高应变动力试桩法作为基桩检测确定单桩承载力的最有前途的新技术,以其快速、经济、可靠等特点得到广泛应用。
尤其是在大直径大吨位的桩基工程检测中发挥了巨大作用。
克服了静载试验的周期长、费用高、检测项目少、静载荷不可能太大等缺点,已部分取代了传统的静载试验。
而作为现场把握采集数据可靠性和基桩承载力的高应变(CASE法),自30年代产生以来,已成为高应变动力试桩的主导方法之一,地位与作用极其重要。
随着建设部《基桩高应变动力试验规程》JGJ106-97的颁布实施,高应变动力试桩的地位将更加巩固和提高。
CASE法是通过一维波动方程计算,而获得岩土对桩的支承阻力的最常用的高应变动力试桩方法。
1、基本模型(1)、基桩模型Case法将桩视为一维均质连续的弹性体,基本上不考虑桩身缺陷影响,应变与质点速度之间满足协调方程。
(2)、桩周土动力模型为排除动力试桩过程中土体的动力效应,Case法假定土的动阻力全部集中于桩尖,且与桩尖速度和广义波阻抗成正比。
(3)、桩周土动力模型为排除动力试桩过程中土体的动力效应,Case法假定土的动阻力全部集中于桩尖,且与桩尖速度和广义波阻抗成正比。
2、基本原理高应变动力试桩的基本原理:用重锤冲击桩顶,使桩-土产生足够的相对位移,以充分激发桩周土阻力和桩端支承力;通过安装在桩顶以下桩身两侧的力和加速度传感器接收桩的应力波信号;应用应力波理论分析处理力和速度时程曲线来判定桩的承载力和评价桩身质量完整性。
CASE 法承载力计算:桩身受一向下的锤击力后,桩身向下运动,桩身产生压应力波P (T ),在桩身的每一载面Xi 处作用有土的摩阻力R (I,t ),应力波到达该处后产生生一新的压力波向上和向下传播。
上行波为幅值等于1/2R (I,t )的压应力波,在桩顶附近安装一组传感器,可接收到锤击力产生的应力波P (T )和每一载面Xi 处传来的上行波。
同样,下行波是幅值为1/2R (I ,t )的拉力波,到达桩尖后反射成压力波向桩顶传播,到达传感器位置后被传感器接收,这些波在桩身中反复传播,每到传感器位置时均被传感器接收,在公式的推导过程中不考虑应力波的传播过程中能量的耗散,可得桩的静极限承载力。
桩基高应变检测方案

桩基高应变检测方案检测中心二00年月日目录一、前言工程桩基检测位于;二、高应变检测检测目的高应变检测目的是检测工程桩的竖向抗压承载力和桩身结构完整性,并对基桩的质量进行评价;检测标准及数量规定本次试验按照中华人民共和国行业标准建筑基桩检测技术规范JGJ106-2003,根据规范规定,高应变检测数量不少于总桩数的5%,且不少于5根; 仪器设备及基本原理本次检测仪器采用美国桩基动力学公司生产的PDA打桩分析仪PAL型,检测示意图如图3;位移,以充分激发桩周土阻力和桩端支承力,通过安装在桩顶以下桩身两侧的力和加速度传感器接收桩的应力波信号,应用应力波理论分析处理力和速度时程曲线,从而判定桩的承载力和评价桩身质量完整性;设桩为一维线弹性杆,测点下桩长为L,桩身横截有效面积为A,桩材弹性模量为E,桩材质量密度为ρ,桩身内弹性波速为CC2=E/ρ,广义波阻抗为Z=AρC;其桩身应力应变关系可写为:假设土阻力是由静阻力和动阻力两部分组成:R=Rs+Rd推导可得桩的一维波动方程:分析方法采用Case法和实测曲线拟合法:记冲击速度峰值对应时间为t1,t2=t1+2L/C为桩底反射对应时间,根据实测的力曲线Ft,速度曲线Vt推导可得Case法判定桩的承载力的计算公式为:对于等截面桩,桩顶下第一个缺陷对应的完整性系数由下式计算:其中:Rx—缺陷点X以上的桩周土阻力;桩身缺陷位置可根据缺陷反射波的对应时间tx由下式确定:Lx=C·tx-t1/2实测曲线拟合法采用了较复杂的桩—土力学模型,选择实测力或速度或上行波作为边界条件进行拟合,拟合完成时计算曲线应与实测曲线基本吻合,桩侧土摩阻力应与地质资料基本相符,贯入度的计算值应与实测值基本吻合,从而获得桩的竖向承载力和桩身完整性;检测的工作面要求1为确保试验时锤击力的正常传递和提高工作效率,应先凿掉桩顶部的破碎层和软弱混凝土,对灌注桩、桩头严重破损的混凝土预制桩和桩头已出现屈服变形的钢桩,试验前应对桩头进行修复或加固处理;2 桩头顶面应水平、平整,桩头中轴线与桩身中轴线应重合,桩头截面积应与原桩身截面积相同,桩头主筋应全部直通至桩顶混凝土保护层之下,各主筋应在同一高度上;3 距桩顶上1倍桩径范围内,宜用3~5mm钢板围裹或距桩顶倍桩径范围内设箍筋,间距不宜大于150mm;桩顶应设置钢筋网片2~3层,间距60~100mm,桩头混凝土强度等级宜比桩身混凝土提高1~2级,且不得低于C30;4桩头应高出桩周土2~3倍桩径,桩周以内应平整夯实;5从成桩到开始试验的休止时间:在桩身强度达到设计要求的前提下,一般对于砂类土不应少于7d;粉土不应少于10d;非饱和粘性土不应少于15d;饱和粘性土,不应少于25d,预制桩承载力的时间效应可通过复打试验确定;对于泥浆护壁灌注桩,宜适当延长休止时间;检测中心二OO年月日。
工程检测与评估3高应变基桩动力检测

第一章 基本概念及检测原理
基本理论
桩身阻抗变化在F-v图上的表现
(1)阻抗减少将产生上行的拉力波,在达到检测截面时,将引 起力值的减少和速度值的增加,即力曲线下移而速度曲线上移。
(2)阻抗增大将产生上行的压力波,在到达检测载面时,将引 起力值的增大和速度值的减少,即力曲线上移而速度曲线下移。
(3)上述反射信号到达检测截面的时间和变阻抗截面所在深度 成正比,可以根据反射信号在时间轴上的位置和已知的总体平均 波速大体确定其所在深度。
高应变基桩承载力检测
目录
第一章 基本概念及检测原理 第二章 检测系统 第三章 现场检测技术 第四章 实测波形汇编
第一章 基本概念及检测原理
目录
第一节 概述 第二节 基本假设 第三节 基本理论 第四节 CASE法的检测原理
第一章 基本概力试桩法,广义上讲,是指所有能使桩土间产 生永久变形(或较大动位移)的动力检测桩基承载力的方法, 无庸置言,这类方法要求给桩土系统施加较大能量的瞬时荷载, 以保证桩土间产生一定的相对位移。自19世纪人们开始采用打 桩公式计算桩基承载力以来,这种方法包括:
(1)打桩公式法,用于预制桩施工时的同步测试,采用刚体碰 撞过程中的动量与能量守恒原理,打桩公式法以工程新闻公式 和海利打桩公式最为流行。
(2)锤击贯入法,简称锤贯法,曾在我国许多地方得到应用, 仿照静载荷试验法获得动态打击力与相应沉降之间的曲线。通 过动静对比系数计算静承载力,也有人采用波动方程法和经验 公式法计算承载力 。
(5)波动方程拟合法,即CAPWAP法,是目前广泛应用的一 种较合理的方法。
(6)静动法(Statnamic),其意义在于延长冲击力作用时间 (~100ms),使之更接近一静载试验状态。
高应变动测操作介绍
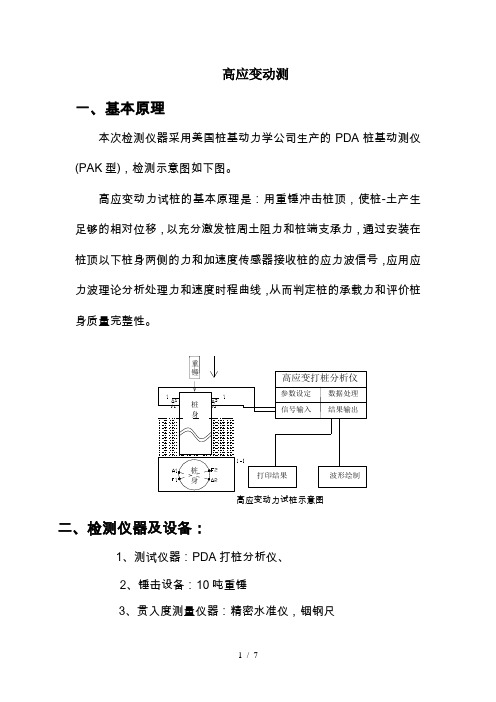
高应变动测一、基本原理本次检测仪器采用美国桩基动力学公司生产的PDA桩基动测仪(PAK型),检测示意图如下图。
高应变动力试桩的基本原理是:用重锤冲击桩顶,使桩-土产生足够的相对位移,以充分激发桩周土阻力和桩端支承力,通过安装在桩顶以下桩身两侧的力和加速度传感器接收桩的应力波信号,应用应力波理论分析处理力和速度时程曲线,从而判定桩的承载力和评价桩身质量完整性。
二、检测仪器及设备:1、测试仪器:PDA打桩分析仪、2、锤击设备:10吨重锤3、贯入度测量仪器:精密水准仪,铟钢尺4、分析设备及分析软件:笔记本电脑、CAPWAP软件三、检测时间:高应变测试在静载试验前检测。
四、现场检测:1、桩头加固处理具体见抗压静载试验试桩桩顶加固方案。
2、锤击装置安装为了减小锤击偏心和避免击碎桩头,我们将保证锤击装置与桩身对中且平稳地冲击桩顶。
3、传感器安装为了减小锤击在桩顶产生的应力集中和对锤击偏心进行补偿,传感器会安装在距桩顶一定的距离以下,一般取1.5倍桩径。
检测时将对称安装冲击力F和桩身质点速度v传感器各两个,传感器安装见下4、桩垫或锤垫本项目将采用自由落锤装置,桩头顶部设置桩(锤)垫,可采用10~30mm厚的木板或胶合板等材料。
a)检查和确认仪器的工作状态b)高应变检测时,一般情况下桩头不宜重复多次锤击,因此检测工程师会在锤击前检查和识别仪器的工作状态。
主要是:利用仪器内置标准的模拟信号触发所有测试通道进行自检,以确认包括传感器、连接电缆在内的仪器系统是否处于正常工作状态。
c)重锤低击采用自由落锤,确保重锤低击,最大锤击落距不宜大于1.5m。
8、检查采集数据质量检测时应及时检查采集数据的质量;每根受检桩记录的有效锤击信号应根据桩顶最大动位移﹑贯入度以及桩身最大拉、压应力和缺陷程度及其发展情况综合确定。
发现测试波形紊乱,应分析原因;桩身有明显缺陷或缺陷程度加剧,应停止检测。
四、数据分析1、实测曲线拟合法判定单桩承载力实测曲线拟合法是通过波动问题数值计算,反演确定桩和土的力学模型及其参数值。
桩基高应变法检测

桩基高应变法检测桩基高应变法检测是一种常用的地基工程质量检测方法,通过测量桩基在施工和使用过程中的应变情况,来评估桩基的稳定性和承载能力。
本文将介绍桩基高应变法检测的原理、步骤和应用。
一、原理桩基高应变法检测是基于桩身应变与桩身受力之间的关系进行分析的。
当桩基受到外力作用时,桩身会发生应变,通过测量桩身上的应变变化,可以推断桩基的受力情况。
桩基高应变法检测主要依赖于高精度应变计和数据采集系统,通过对桩身上的应变进行实时监测和记录,来获取桩基的受力信息。
二、步骤桩基高应变法检测通常包括以下几个步骤:1. 安装应变计:在桩身上选择一定数量的应变计点位,将应变计粘贴或固定在桩身表面,并连接到数据采集系统。
2. 数据采集:启动数据采集系统,实时监测桩身上的应变变化,并将数据记录下来。
数据采集系统可以通过有线或无线方式与应变计进行连接,以便实时传输数据。
3. 外力施加:在进行检测时,需要施加一定的外力于桩基上,常用的方法包括静载试验、动载试验等。
外力的施加应符合设计要求,并在监测过程中逐渐增加,以获取不同荷载下的应变数据。
4. 数据分析:通过对采集到的应变数据进行分析,可以得到桩基在不同荷载下的应变变化曲线。
根据应变曲线的特征,可以评估桩基的稳定性和承载能力。
三、应用桩基高应变法检测在地基工程中具有广泛的应用价值。
主要应用于以下几个方面:1. 桩基质量评估:通过对桩基的应变变化进行监测和分析,可以评估桩基的质量状况,判断桩身是否存在缺陷或损伤。
2. 承载能力评估:桩基高应变法检测可以提供桩基在不同荷载下的应变数据,通过分析这些数据,可以评估桩基的承载能力,为工程设计提供依据。
3. 施工质量控制:在桩基施工过程中,通过实时监测桩身上的应变变化,可以及时发现施工质量问题,并采取相应的措施进行调整和修正。
4. 桩基安全监测:对于已经使用的桩基,通过定期进行高应变法检测,可以监测桩基的变形和应变情况,及时发现潜在的安全隐患。
高应变检测基本知识讲解

2021/10/10
5
第三节 检测系统及仪器设备
检测示意图
2021/10/10
6
试验仪器及配件
重锤
重锤应材质均匀、 形状对称、锤底平 整,高径(宽)比 应在1.0~1.5范围 内,且不得小于1, 重量应大于预估单 桩极限承载力的 1.0%~1.5%
2021/10/10
架 子
7
应力环
2021/10/10
2.检测频率
抽检数量不宜少于总桩数的5%,且不得少于5根。
2021/10/10
3
第二节 适用范围及检测方法
适用范围
1、可检测预制桩、预应力管桩和钢管桩的单桩竖向抗压承载力 和完整性; 2、监测打入桩的桩身应力和锤击能量传递比,为沉桩工艺参数 及桩端持力层选择提供依据; 3、对于灌注桩检测,应具备现场实测经验和本地区相似条件条 件下的可靠对比试验资料。 4、对于Q-s曲线为缓变形的大直径桩、扩底桩、嵌岩桩等,其桩 端阻力发挥所需的位移很大,难于把桩打动,一般不采用高应 变法。
2021/10/10
10
第二步 仪器设备的安装与连接
1.放置重锤
2.放置固定架
2021/10/10
11
3.传感器与应变环的安装
4.仪器连接
2021/10/10
12
第三步 测试参数设定 开机,选择RS模式 设置高应变相关参数
设置桩土参数
2021/10/10
13
第四步 检查和确认仪器、设备的工作状态
基桩高应变法检测知识培训
2021/10/10
2014.2.28
1
基桩高应变法检测技术
第一节 第二节 第三节 第四节 第五节
基本原理和检测频率 适用范围和检测方法 检测系统及仪器设备 现场检测技术 波形分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多年来,我国不少应用单位对Case法进行了有益的探索,提出了适用本地区情况的Jc值,修改了PDI公司的给定值,这里给出了几组有代表性的Jc值。
(4-5)
由质点速度的连续条件可得
(4-6)
最终可得出:
(4-7)
(六) 行波理论
(七) 土的总阻力
六、七部分详见《桩的动测新技术》(基础结构动态诊断)中的相关内容。
二、凯斯(Case)法
波动方程法一般指完全使用波动方程解的计算机程序在给定的锤、垫、桩、土的参数变化范围内通过程序的参数分析功能迅速绘制出多组理论承载,即以纵坐标为不同的设定桩周土总静阻力值,横坐标为假定参数计算所得的打入阻力(每击贯入度的倒数)。每组曲线的某些参数(视要求而定)为设定值,其余变量相应便形成一组曲线。确定承载力时桩的最终贯入度及锤的落高为实测,其余参数参照取用。因此从各组曲线中选出相应的承载曲线便可由打入阻力反查总静阻力。如还有动静载对比试验数据则更可作相应修正。显然这种方法对某一地区的固定施工场地有一定的适用性也极方便,因为对土质、锤的效率、垫层耗能状况等都是熟悉而稳定的,易于掌握。波动方程法更多的用途是对大型打桩工程的沉桩能力分析与预测。在纯粹的工程桩承载力事后控测中很少应用。
经过力学与数学的推导,可将上过杆的纵向振动用二阶编微分方程来描述:
整理得杆纵向振的微分方程为 (4-1)
考虑桩周土作用的完整桩纵向振动(或波动)方程
(4-2)
(二)纵波波速C
上式中的C为杆的纵向振动波沿杆的传播速度,可以理解为应力波在桩身中的传播速度,即桩基测试界道常所说的波速,它的单位为m/s,混凝土桩的正常波速约3000—4000m/s之间
桩基测试技术中所称的Case法是美国桩基动力学公司提出的一种测定桩的静极限承载力的一种简便方法。该法只在引用应力波行波理论及激发土阻力所产生的上、下行波概念方面与波动方程法一致。
Case法理论要点
(一)Case法的基本假定
为了简化问题,Case采用了下述假定:
(1)桩看作一维杆体,桩身等阻抗,即截面不变、桩身材质均匀且无明显缺陷;
(三)质点运动速度V
传递波动的物质称为介质,介质的运动随时间的变化称为振动;整个介质随空间、时间的运动变化情况,则称为波动。在应力波作用下,桩身产生运动。其质点的振动速度V取决于应力的大小和介质的特性。
(4-3)
(四)桩的阻抗Z
由一维波动理论可知,桩阻抗是其横截面积、材料密度和弹性模量的函数。
(4-4)
Z——桩身阻抗,为P(密度)、c(波速)、A(截面积)的乘积。
表4.1 PDI公司推荐的Jc值
土质
纯砂
粉砂
粉土
亚粘土
粘土
Jc
0.1~0.4~0.7
0.7~1.0
(三) 关于Case法的几点说明
(1)Case法公式确实很简单,(4-9)式中未知数仅为Jc,其它为实测值,在现场只要输入Jc值,即可得预测承载力值;
(4)Case法有一定适用范围,对短桩(桩长与桩径之比较小),对扩底桩、对桩身截面变化较复杂或桩身存在较严重缺陷的桩,因基本不符合Case法假设前提,一般来说不适宜用Case法,而应该用Capwapc(曲线拟合法)或静载法解决。
经过以上的讨论,我们可以看出,对大部分桩,动静对比求取Jc值除反映桩尖土的颗粒粗细程度外,还包括了试桩与Case法假设前提背离程度的影响。换句话说,Jc值除和桩尖土有关外,还与桩周土、不同桩类型有关。所以说Jc值 具地区性,不同地区均需要作动静对比,求取不同桩型、不同桩径大小、不同地质条件下桩的凯斯系数,其道理就在这。上述第(4)点所提到的各种桩,因试桩条件与假设前提背离程度太大,Jc值的求取当然就很困难了,所以,就不适宜用Case法。
(4-9)
式中:
Rt——桩对土的实际总阻力;
Rsp——阻尼系数法所确定的桩的静阻力(即桩的极限垂直承载力);
Jc——桩尖土层的凯斯系数,其取值与桩尖岩土颗粒粗细有关,高勃尔建议如表4.1取值;
P1、V1——t1时刻(或应力波初始峰值时刻)实测的力值、速度值;
P2、V2——t2时刻(t2=t1+2L/c即来自桩底反射波时刻)实测的力值、速度值;
也可表达为F=ZV
Z为桩的阻抗(单位为N·S/m)
E为桩的弹性摸量(单位为N/m2)
A为桩的横截面积(单位为m2)
为桩的质量密度(单位为Kg/m3)
(五)应力波的反射与透射
当应力波在杆件内传播时,如果杆件的阻抗有变化时,即杆件的E、A、 中任一项或几项有变化而使阻抗产生改变的,应力波即产生反射与透射。如分别以 表示入射波, 表示反射波, 表示透射波,且遵照压力为(+)拉力为(-),速度以朝向X轴正向为(+),朝向X轴负向为(-)的符号规则,根据力的平衡条件可得:
基桩动力检测高应变检测技术基本原理
一、若干基本概念
高应变动力试桩的基本理论是一维波动方程,为方便分析,将桩看作一根截面积,材料均相同的“无限长弹性杆”。设杆的单位体积的质量为р,杆长为l,截面积为A,材料弹性模为E。在外加轴向力的作用下,杆的纵向振动位移ц(x、t)是纵向坐标和时间两个变量的函数。
(一)一维波动方程
(2)根据基本假定,符合条件的桩为初打阶段的打入桩,这时Jc值为桩尖土层的Case阻尼系数。实际上,Jc值正是高勃尔根据120根打入桩动静对比结果总结出来的。
(3)应该说,对复打阶段的预制桩、对静压桩、对桩侧动阻力比较明显的灌注桩、对挖孔桩,均无法和假设条件完全一致,这时Jc值变成了一个没有明确物理意义的经验系数,综合反映试桩各个方面的特定条件。
(2)只考虑桩底的动阻尼,忽略桩身周围的动阻尼;
(3)应力波在传播过程中没有能量耗散和信号畸变;
(4)在(tl~tl+4L/C)时段内桩侧各点的摩阻力不变。
(二)Case法基本公式——阻尼系数法
基于上述假定,Case法导出,在锤的冲击下,岩土对桩的实际总阻力Rt为:
(4-8)
我们的希望的是岩土对桩的静阻力,所以必须从总阻力Rt中扣除由于桩身在土中运动而受到的附加阻力Rd,根据第二点假设,桩侧动阻力可不予考虑,Case法假定桩尖动阻力与桩尖的运动速度Vb成正比,令Jc为比例常数,经推导得:
