全国大联考

合集下载

化学丨青桐鸣大联考河南省2025届高三10月大联考化学试卷及答案

2025届普通高等学校招生全国统一考试大联考（高三）化学注意事项：1．答卷前，考生务必将自己的姓名、班级、考场号、座位号、考生号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．可能用到的相对原子质量：H-1 C-12 N-14 O-16 S-32 Fe-56 Co-59 Ni-59一、选择题：本题共14小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．中华文化源远流长，化学与文化传承密不可分．下列叙述正确的是（）A．“金以刚折，水以柔全”，高碳钢比低碳钢硬且脆B．“凡火药，硫为纯阳，硝为纯阴”中的“硫”指的是硫酸C．“浮梁巧烧瓷，颜色比琼玖”中的“瓷”不能被任何物质腐蚀D．“客从南溟来，遗我泉客珠”，珍珠的主要成分为轻质合金2．下列化学用语错误的是（）SA．中子数为17的硫原子：3316Fe OB．磁性氧化铁的化学式：34COC．分子的空间填充模型：2NClD．用电子式表示的形成过程：33．化学实验中，具有安全和规范意识是重要的学科素养．下列叙述或做法合理的是（）A．实验后未用完的钠不能放回原试剂瓶B．做“钾与水的反应”实验时佩戴护目镜C．不慎将金属汞撒落桌面，必须尽可能收集，并深埋处理D．浓NaOH溶液不慎沾到皮肤上，立即用大量水冲洗，然后涂上小苏打溶液4．下列实验装置和操作能达到相应实验目的的是（）A．制备并收集少量氨气B．除去中的HCl2Cl C．探究盐酸与溶液反应的热3NaHCO效应D．探究浓度对反应速率的影响5．氯碱车间用浓氨水检验氯气管道是否泄漏，相关反应为．表示阿伏32428NH3Cl6NH Cl N+=+AN加德罗常数的值，下列说法正确的是（）A．溶液中数目小于11mol L-⋅4NH Cl4NH+ANB．标准状况下，消耗3.36 L 时转移的电子数为2ClA0.3NC．当有0.8 mol 被氧化时，消耗的分子数为3NH2ClA0.3ND．将17 g 通入水中充分溶解，溶液中的分子数为3NH32NH H O⋅AN6．下列离子组因发生氧化还原反应而不能大量共存的有（）①、、、②、、、H+K+Cl-ClO-2Fe+H+3NO-I-③、、、④、、、3Fe+4NH+I-24SO-2Ba+K+24SO-4ClO-A．1组B．2组C．3组D．4组阅读下列材料，完成7～8题．硫的化合物在生产、生活、科研等方面应用广泛．常用作染料的助染剂；主要用于净水2Na S()243Al SO和造纸；制铵明矾[]的主要原料之一是；可用作消化系统X()4422NH Al SO12H O⋅()442NH SO4BaSO射线检查的内服药剂；（连二亚硫酸钠，俗称保险粉）用于食品防腐剂、抗氧化剂；224Na S O228Na S O （过二硫酸钠）在酸性条件下能将氧化为．2Mn+4MnO-7．下列物质性质与用途具有对应关系的是（）选项用途性质A用除去废水中的2Na S2Hg+具有还原性2Na SB 用作净水剂()243Al SO铝盐水解生成氢氧化铝胶体C用制铵明矾 ()442NH SO 易分解 ()442NH SO D 用作胃肠道造影剂4BaSO 不溶于水 4BaSO 8．下列离子方程式正确的是（） A ．向溶液中滴加稀硝酸：2Na S 22S 2H H S -++=↑B ．向溶液中滴加足量的氨水： ()243Al SO ()33244Al 4NH H O Al OH 4NH -++⎡⎤+⋅=+⎣⎦C ．溶液与酸性溶液混合：228Na S O 4MnSO 222282442Mn 5S O 8H O 2MnO 10SO 16H +---+++=++D ．溶液和碱性溶液混合，制纳米级银粉：3AgNO 224Na S O2224422Ag S O 4OH 2Ag 2SO 2H O +---++=↓++9．工业上以软锰矿（含和少量的、、）为原料制备硫酸锰晶体的流程如图所2MnO 23Fe O 23Al O 2SiO 示：下列说法错误的是（）A ．“酸浸”时作还原剂4FeSO B ．“氧化”阶段实际消耗的大于理论值22H O C ．“滤渣1”和“滤渣2”均为软锰矿中所含少量的氧化物的水化物D ．实验室进行“系列操作”所需要的玻璃仪器有玻璃棒、漏斗、烧杯、酒精灯等10．短周期主族元素A 、B 、C 、D 、E 的原子序数依次增大，这些元素组成的常见化合物、22A C 、、均能使酸性高锰酸钾溶液褪色．下列叙述正确的是（）224A B C 2DC 24B A A ．“褪色”现象，说明上述物质均具有漂白性 B ．简单离子半径：E>D>CC ．A 、C 、D 三种元素组成的化合物含有离子键D ．B 的氢化物的沸点可能高于C 的氢化物的沸点 11．南京大学某实验室开发了一种由MPT 溶解的DMSO 基电极液和TOOS 基电极液组成的新型2Li O -电池双相电解液，使高性能电池日用化成为可能，该电池放电时的工作原理如图所示：2Li O -放电时，下列说法错误的是（）A ．电子流向：N 电极→灯泡→M 电极B ．TOOS 基电极液可用溶液代替 24Li SOC ．M 极电势高于N 极电势D ．M 极电极反应式为 222O 2e 2Li Li O -+++=12．硝酸钠在玻璃业、染料业、农业等领域应用广泛．工业上以含氮氧化物废气为原料生产硝酸钠的流程如图所示：已知：①；2233222NO Na CO NaNO NaNO CO +=++②．22322NO NO Na CO 2NaNO CO ++=+下列叙述正确的是（）A ．属于酸性氧化物2NO B ．同时发生反应①和②时，被氧化的氮元素与被还原的氮元素的质量之比可能为2：1C ．“转化器”中生成的既是氧化产物，又是还原产物3NaNO D ．不考虑流程中钠、氮元素的损失，则 42e d a c ++=13．Y 形试管是一种特殊的实验仪器，与其他仪器组合可以进行某些探究实验．某学生按如图装置进行实验，观察到以下实验现象（尾气处理装置未画出）：①将甲中Y 形试管向左倾斜使反应发生，一段时间后，乙中无明显现象；②将丙中Y 形试管向左倾斜使反应发生，一段时间后，乙中有沉淀产生．下列叙述正确的是（）A ．实验前可用稀盐酸和溶液检验是否变质()32Ba NO 23Na SO B ．为了提高甲中生成的速率，可选用质量分数为98.3%的浓硫酸2SO C ．若将甲中换成，也可能发生①和②类似的现象23Na SO 23Na CO D ．丙中的试剂a 和b 可以分别是和浓盐酸2MnO 14．向某恒容密闭容器中通入一定量的，发生反应，平衡时各物质的2H S ()()()2222H S g S g 2H g + 物质的量随温度的变化如图所示：下列叙述正确的是（） A ．曲线Ⅱ代表B ．的分解速率：a 点大于b 点 ()2S g 2H SC ．a 点的体积百分数为50%D ． 2H S 163x =二、非选择题：本题共4小题，共58分．15．（14分）有机物可用作金属矿物的浮选剂，其结构式如图甲所示．已知X 、Y 、Z 、W 、()22ZX YP P 、M 为原子序数依次增大的短周期主族元素，其中W 、P 为同主族元素．a 是Z 元素对应的最高价氧化物的水化物．回答下列问题：（1）由X 元素与Z 元素组成的18电子分子的结构式为____________．（2）已知对应单质的氧化性：M 大于P ．从原子结构角度解释其原因：________________________，导致M 得电子能力大于P ．（3）X 、Z 、M 三种元素能组成一种常见的离子化合物，在实验室检验该化合物中阳离子的反应原理为____________________________________（用离子方程式表示）．（4）元素Y 、P 、M 对应的最高价氧化物的水化物的酸性由强到弱的顺序为__________________（用化学式表示）（5）查阅资料：室温下，a 的稀溶液和铜丝反应速率较慢．为解决反应速率慢的问题，某同学设计如图乙装置制取并收集ZW ．①实验时，试管A 中可观察到反应剧烈进行，铜丝逐渐变细，溶液变绿，________________________．反应过程中，a 表现出的性质有________________________．②装置B 中发生反应的化学方程式为______________________________．③实验结束后，对于A 中的溶液呈绿色，而不显蓝色，甲同学认为是该溶液中硝酸铜的质量分数较高所致，而乙同学认为是该溶液中溶解了生成的气体．同学们设计了以下3种实验方案来判断两种看法是否正确．这些方案中可行的是______（填选项字母）．a ．加热该绿色溶液，观察颜色变化b ．加水稀释该绿色溶液，观察颜色变化c ．向该绿色溶液中通入氮气，观察颜色变化16．（14分）金属及其化合物在生活、生产和科技中有着广泛的应用．回答下列问题：（1）因能与反应可作潜水艇的供氧剂，涉及反应的化学方程式为22Na O 2CO ________________________；的电子式为__________________．22Na O （2）铝粉和氧化铁组成的铝热剂能用于焊接钢轨，文献中有关“铝热反应”实验现象有这样的描述：“反应放出大量的热，并发出耀眼的光芒”“纸漏斗的下部被烧穿，有熔融物落入沙中”．甲同学取冷却后的熔融物适量，加入NaOH 溶液中，发现部分固体溶解并有气泡产生，用离子方程式解释产生气泡的原因：______________________________；乙同学另取一块冷却后的熔融物投入少量稀硫酸中，向反应后的混合液中滴加KSCN 溶液，观察到溶液颜色未变红，从而得出熔融物中不含有这一结论，丙同学认23Fe O 为该结论不合理，理由是__________________________________________．（3）利用铁及其氧化物能循环制氢，原理如图所示．向反应器Ⅰ充入2x mol CO 和x mol ，通过该方2H 法制氢，理论上反应器Ⅱ中可获得______mol （用含x 的代数式表示）2H（4）钴的氧化物常用作磁性材料，通过热分解可获得钴的氧化物（钴的常见化合价有+2、+3）． 3CoCO ①取47.6 g 样品在空气中加热，充分反应冷却后，获得31.28 g 固体氧化物X ，通过计算可知X 3CoCO 的化学式为______．②以钴的氧化物（）为电极、KOH 溶液为电解液，通电时钴的氧化物转化为CoO （OH ），写出生Co O x y 成CoO （OH ）的电极反应式：____________________________________（用含x 、y 的反应式表示）．17．（15分）某小组在实验室制备α-NiS 的装置如图所示（加热及夹持装置略）．已知α-NiS 在潮湿空气中易被氧化．实验步骤如下：①按图连接好装置，检查气密性后，加入药品，打开，通入．1K 2N ②装置内空气排尽后，打开仪器a 开关，滴入盐酸，装置C 中有沉淀产生．③反应完成后，关闭，打开，用抽气筒吸出装置C 中溶液，再用b 中的溶液洗涤沉淀，洗涤液也用1K 2K 抽气筒吸出，如此反复2～3次，最后干燥．回答下列问题：（1）仪器a 的名称为______，该仪器的优点是______________________________．（2）装置E 的作用为__________________________________________．（3）步骤③用b 中的溶液洗涤沉淀的好处为__________________________________________．（4）去掉装置D ，实验中可能带来的后果是__________________________________________．（5）将步骤③得到的α-NiS 固体加入足量的稀硝酸中，固体全部溶解，得到溶液，向其中加入氨4NiSO 水—氯化铵缓冲溶液掩蔽干扰离子，再加入铬黑T 作为指示剂，用 EDTA 二钠（）标1mol L c -⋅22Na H Y 准溶液滴定，消耗标准溶液V mL ．22Na H Y 已知：．2222Ni H Y NiY 2H +--++=+①写出NiS 溶入稀硝酸发生反应的离子方程式：____________________________________．②根据上述实验步骤及FeS 固体的质量可计算出α-NiS 的产率为______（用含m 、c 、V 的代数式表示），有同学指出由此计算出的α-NiS 的实际产量要比理论产量高，其原因可能是________________________．18．（15分）由废钼催化剂（主要成分为、，含少量CoO 、CoS 、NiO 、等）回收有3MoO 2MoS 23Fe O 价金属的一种工艺流程如图所示：已知：①溶液中金属离子形成氢氧化物沉淀时，开始沉淀和刚好完全沉淀的pH 如表所示．②“沉钴”后的滤液中镍元素全部以形式存在．()236Ni NH +⎡⎤⎣⎦回答下列问题：（1）若在实验室检验“焙烧”生成的气体A ，可选用的试剂是____________；工业上常用______（填物质名称）吸收该气体．（2）“沉钼”前钼元素主要以形式存在．写出“沉钼”时发生反应的离子方程式：24MoO -________________________________________________．（3）“除铁”时，若控制pH 的范围为，则______、______；在该过程中一般需要将pH x y ≤<x =y =其加热3~5 min ，其目的除使充分水解外，还能________________________．3Fe +（4）若“沉镍”时生成的和的物质的量浓度比约为5：1． 32NH H O ⋅4NH +①写出生成的离子方程式：____________________________________．3NiCO ②倘若“沉镍”前溶液中含镍微粒的浓度为，加入相同体积相同浓度的溶液，0~4 10.32mol L -⋅3NaHCO min 时间段内“沉镍”率为80%，则0~4 min 含镍微粒的“沉镍”平均速率为__________________．（5）高温下用还原得到金属钼，则该反应中氧化剂与还原剂的物质的量之2H ()4322NH O 4MoO 2H O ⋅⋅比为____________．。

2023届全国乙卷高三5月大联考语文试题

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1~3题。

礼乐之“结盟”，肇端于夏商，而大成于西周的礼乐制度，其一体性之论述则在春秋战国的儒家那里获得定型。

在传统儒家经史子集或“六经”“六艺”的人文知识体系中，礼乐在理论和精神上的一体性远大于差异性。

历朝历代在国家层面的演礼典乐之实践，更加深了这种礼乐论述的一体性，而那些俗乐，亦多渗透着礼义的精神而具有“礼乐”的性质。

要而言之，传统礼乐在国家制度层面有其一体之实践，在文化思想层面有其一体之论述。

自20世纪以来，近现代学人开始以西方的学科观念和方法重新阐释中国传统礼乐文化，礼与乐逐渐分离。

其中，乐因为符合现代艺术和美学观念而被纳入美学和艺术研究领域。

而礼则因为其内涵过于丰富、外延过于宽泛，且在新文化运动时期被一部分启蒙思想者指认为“吃人”的礼教，与现代美学所定位的自由价值相违背，而被美和艺术排除在外。

自此以后，近现代学人对传统礼乐的研究，或者特别强调其形式上的审美价值，或者只是将礼分解为宗教、政治范畴等，儒家礼乐的一体性论述被彻底切割。

中国传统的乐其实包含现代所谓诗歌乐舞，在现代学术视野中被看作审美和艺术的对象，已被“理所当然”地纳入美和艺术的研究范围。

而对于礼，从美学和艺术学视野所做的接引却没有那么顺畅。

但近现代一些具有西方学术眼光和观念自觉的学人，却在这方面做了巨大努力。

这些学人大致可以分成两种类型：一种侧重于礼仪与主体的情感关系，即礼作为情感的表现和对情感的教育；另一种侧重于艺术客体，侧重于礼作为一种“有意味的形式”。

当然二者之间又总是交合在一起的，很多学人在两个方面兼而有之。

中国传统的礼具有多侧面、多层次的含义。

其中，礼容、礼数、礼节等，是礼的最基本含义。

从美学观之，这是一套感性的符号体系，即于周旋揖让、俯仰进退中呈现的优美言行，这就是美。

以此为背景，礼还有礼义、礼制、礼秩的含义。

这个含义的礼，就是所谓抽象理念和秩序，它更倾向于善。

2024届高三12月大联考(全国乙卷)理综答案(全解全析及评分标准)

2024届高三12月大联考（全国乙卷）理综生物·全解全析及评分标准1．B 【解析】胃蛋白酶、抗体、胰岛素都是分泌蛋白，呼吸作用发生在细胞内，所以呼吸酶是在细胞内发挥作用的，不是分泌蛋白，A错误；分泌蛋白都是蛋白质，单体是氨基酸，每个氨基酸都有氨基，含有氮元素，B正确；分泌蛋白合成和运输过程中内质网膜面积减小，高尔基体膜面积基本不变，细胞膜面积增大，C错误；蛋白质结构不同的根本原因是控制它们合成的基因不同，D错误。

2．B 【解析】前20 min内，甲组原生质体体积相对值逐渐变小，说明细胞在失水，水分子从渗透压低的一侧向高的一侧扩散，所以细胞液渗透压小于细胞质基质渗透压，A错误；实验开始20 min时，甲、乙两组原生质体体积相对值相等，说明细胞失水量相同，甲组蔗糖分子没有进入细胞，而乙组KNO3溶液中有离子进入细胞，使细胞液渗透压升高，B正确；实验开始30 min后，乙组细胞可能因为吸收了K+、NO3-，细胞液浓度升高，引起细胞吸水，原生质体体积增大，C错误；实验开始40 min后，乙组细胞吸水和失水达到平衡，由于植物细胞壁的限制，细胞液的渗透压可能大于或等于外界溶液的渗透压，因此不能得出40 min后细胞液中KNO3的浓度与外界溶液浓度相等的结论，D错误。

3．A 【解析】植物各个部位都能产生乙烯，乙烯的作用是促进果实成熟，A正确；用一定浓度的生长素类似物处理可以促进子房发育成果实，得到无子番茄，不能诱导染色体数目加倍，B错误；植物打顶通过解除顶芽产生的生长素对侧芽的抑制作用，进而促进侧芽生长，C错误；植物的生长发育是基因组在一定的时间和空间上程序性表达的结果，而不是基因组改变的结果，D错误。

4．D 【解析】在性状分离比的模拟实验中，两个小桶模拟了生物的雌、雄生殖器官，小球代表生殖细胞，雌性生殖细胞数量一般少于雄性生殖细胞数量，所以两个小桶中的彩球总数可以不相等，A错误；用32P、35S标记的噬菌体侵染未被标记的细菌，可证明DNA分子是噬菌体的遗传物质，B错误；探究酵母菌细胞呼吸的方式实验中，有氧和无氧组都是实验组，形成对比实验，C错误；在绿叶中色素的提取和分离实验中，先用无水乙醇提取再用层析液分离色素，D正确。

2023年高三5月大联考(全国乙卷)文科数学试题及参考答案

2023届高三5月大联考（全国乙卷）文理科数学试题及参考答案一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在复平面内，设复数21,z z 对应的点分别为()()1,12021-Z Z ，，，则=21z z （）A .2B .3C .2D .12.已知集合()(){}012<+-=x x x M ，{}30≤≤=x x N ，则=N M （）A .[)20，B .[]30，C .(]31，-D .(]32，3.《“健康中国2030”规划纲要》提出，将康时促进人的全面发展的必然要求，是经济社会发展的基础条件.实现国民健康长寿，是国家富强、民族振兴的重要标志.也是全国各族人民的共同愿望.为普及健康知识，某公益组织为某社区居民组织了一场健康知识公益讲座，讲座后居民要填写健康知识问卷（百分制），为了解讲座效果，随机抽取了10为居民的问卷，并统计得分情况如下表所示：则下列说法错误的是（）A .该10位居民的问卷得分的极差为30B .该10位居民的问卷得分的中位数为94C .该10位居民的问卷得分的中位数小于平均数D .该社区居民的问卷得分不低于90分的概率估计值大于0.24.已知2.0log 1.0=a ，a b lg =，ac 2=，则c b a ,,的大小关系为（）A .c b a <<B .b c a <<C .a c b <<D .ca b <<5.从装有若干个红球和白球（除颜色外其余均相同）的黑色布袋中，随机不放回地摸球两次，每次摸出一个球.若事件“两个球都是红球”的概率为152，“两个球都是白球”的概率为31，则“两个球颜色不同”的概率为（）A .154B .157C .158D .1511答题居民序号12345678910得分728365768890659095766.若执行如图所示的程序框图，则输出S 的值为（）A.94B .98C .115D .11107.若函数()()⎩⎨⎧≥++<++=0,1ln 0,122x a x x ax ax x f 恰有2个零点，则实数a 的取值范围是（）A .()()∞+∞-，，10 B .()1,0C .()1，∞-D .()∞+，08.若平面向量b a ,满足b a 2=，且b a22+与b 垂直，则b a ,的夹角为（）A .43πB .32πC .3πD .4π9.已知椭圆E ：()012222>>=+b a b y a x 的左顶点为A ，上顶点为B ，左、右焦点分别为21,F F ，延长2BF 交椭圆E 于点P .若点A 到直线2BF 的距离为3216，21F PF ∆的周长为16，则椭圆E 的标准方程为（）A .1162522=+y xB .1323622=+y xC .1484922=+y x D .16410022=+y x 10.已知数列{}n a 的前n 项和为n S ，且n n n n a S S S -=+++1232，7264=-a a ，344=S ，则2023是数列{}n a 的（）A .第566项B .第574项C .第666项D .第674项11.已知函数()()ϕω+=x x f cos 2()00<<->ϕπω，，()30=f ，且()x f 在[]π,0上有且只有三个极值点，则下列说法错误的个数是（）①存在ω值，使得函数()x f 在[]π,0上有两个极小值点；②ω的取值范围为⎥⎦⎤⎝⎛619613，；③函数()x f 在⎪⎭⎫ ⎝⎛50π，上单调递增；④若Z ∈ω，则函数()x f 图象的一个对称中心为⎪⎭⎫⎝⎛092π.A .4B .3C .2D .112.在正三棱锥ABC P -中，E D ,分别为侧棱PC PB ,的中点，若BE AD ⊥，且7=AD ，则正三棱锥ABC P -外接球的表面积为（）A .π435B .π572C .π7108D .π9152二、填空题：本题共4小题，每小题5分，共20分.13.曲线xxy ln =在1=x 处的切线方程为.14.已知公比小于0的等比数列{}n a 的前n 项和为n S ，12232+==S a a ，，=1a .15.在直四棱柱1111D C B A ABCD -中，底面四边形ABCD 是菱形，︒=∠120ADC ，121AA AD =，E 是棱1AA 的中点，O 为底面菱形ABCD 的中心，则异面直线EO 和AD 所成角的余弦值为.16.已知双曲线C ：()0,012222>>=-b a by a x 的左、右焦点分别为21,F F ，M 是双曲线C右支上一点，记21F MF ∆的垂心为G ，内心为I .若GI F F 1221=，则双曲线C 的离心率为.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分17.（12分）2023年，某地为了帮助中小微企业渡过难关，给予企业一定的专项贷款资金支持.如图是该地120家中小微企业的专项贷款金额（万元）的频率分布直方图：（1）确定a 的值，并估计这120家中小微企业的专项贷款金额的中位数（结果保留整数）；（2）按专项贷款金额进行分层抽样，从这120家中小微企业中随机抽取20甲.记专项贷款金额在[200,300]内应抽取的中小微企业数为m .①求m 的值.②从这m 家中小微企业中随机抽取3家，这3家中小微企业的专项贷款金额都在[200,250）内的概率.18.（12分）在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，且ABC ∆的面积为3，12222=-+c b a .（1)求C ；（2）若33cos cos -=B A ,求c .19.（12分）如图，在直三棱柱111C B A ABC -中，︒=∠90BAC ，2211===AA AC AB ，141AA AE =，D 为棱1CC 的中点，F 为棱BC 的中点.（1）求证：⊥BE 平面C AB 1；（2）求三棱锥DEF B -的体积.20.（12分）已知函数()()01ln >+=a ax xx f .（1）当21e a =时，求()x f 的单调区间；（2）若函数()axx f y 1+=有两个不同的零点，求a 的取值范围.21.（12分）已知抛物线C ：()022>=p px y ，M 是其准线与x 轴的交点，过点M 的直线l 与抛物线C 交于B A ,两点，当点A 的坐标为()0,4y 时，有BA MB =.（1）求抛物线C 的方程；（2）设点A 关于x 轴的对称点为点P ，证明：直线BP 过定点，并求出该定点坐标.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22.（10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，直线l 的参数方程为⎪⎩⎪⎨⎧+==ααsin 21cos t y t x （t 为参数）.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为⎪⎭⎫ ⎝⎛+=4sin 22πθρ.（1）写出曲线C 的直角坐标方程；（2）已知点P 的直角坐标为⎪⎭⎫ ⎝⎛210，，若直线l 与曲线C 交于N M ,两点，求PN PM -的最大值.23.（10分）【选修4-5：不等式选讲】已知c b a ,,都是正实数..（1）若1=ac ，求证：()()b c b b a 4≥++；（2）若1112121=++++cb a ，求c b a ++的最小值.参考答案一、选择题1.C解析：由题意，知i z 21=，i z -=12，∴i i i z z +-=-=11221，∴221=z z .2.A 解析：∵集合{}21<<-=x x M ，{}30≤≤=x x N ，∴[)20，=N M .3.B解析：将这10为居民的问卷得分按照从小到大的顺序排列为65,65,72,76,76,83,88,90,90,95，∴极差为95-65=30，故A 正确；中位数为5.7928376=+，故B 错误；平均数为()5.798095909088837676726565101>=+++++++++⨯，故C 正确；由题表及样本估计总体，知该社区居民问卷得分不低于90分的概率估计值为2.03.0103>=，故D 正确.4.D解析：∵x y 1.0log =在()∞+，0上单调递减，∴1.0log 2.0log 1log 1.01.01.0<<，即10<<a .∵x y lg =在()∞+，0上单调递增，∴1lg lg <a ，即0<b .∵xy 2=在R 上单调递增，∴022>a，即1>c .综上，得c a b <<.5.C解析：设“两个球都是红球”为事件A，“两个球都是白球”为事件B，“两个球颜色不同”为事件C，则()()31152==B P A P ，且B A C =.∵C B A ,,两两互斥，∴()()()()()[]158311521111=--=+-=-=-=B P A P B A P C P C P .6.A解析：初始值20==n S ，.第一次执行循环体：43113111212=⨯=⨯=-=n S a ，，，否；第二次执行循环体：6531311531=⨯+⨯=⨯=n S a ，，，否；第三次执行循环体：8751531311751=⨯+⨯+⨯=⨯=n S a ，，，否；第四次执行循环体：10971751531311971=⨯+⨯+⨯+⨯=⨯=n S a ，，，是，输出S .∵9491717151513131121971751531311=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=⨯+⨯+⨯+⨯=S ，∴输出S 的值为94.7.A 解析：①当0=a 时，()()⎩⎨⎧≥+<=0,1ln 0,1x x x x f ，则()x f 只有一个零点0，不符合题意；②当0<a 时，作出函数()x f 的大致图象，如图1，()x f 在()0，∞-和[)∞+，0上各有一个零点，符合题意；③当0>a 时，作出函数()x f 的大致图象，如图2，()x f 在[)∞+，0上没有零点.若()x f 在()0，∞-上有两个零点，则符合题意，此时必须满足()011<-=-a f ，解得1>a .综上，得0<a 或1>a ，故选A.8.B 解析：∵b a 22+与b 垂直，∴()022=⋅+b b a ，化简得222b b a -=⋅.设b a ,的夹角为θ，则21cos -=⋅⋅=ba b a θ.∵[]πθ，0∈，∴32πθ=.9.B解析：由题意，得()()()0,,00,2c F b B a A ，，-，则直线2BF 的方程为0=-+bc cy bx ，∴点A 到直线2BF 的距离()321622=+=+--=c a a bc b bc abd ①.由21F PF ∆的周长为16，得16222121=+=++c a F F PF PF ，即8=+c a ②联立①②解得a b 322=③∵222c a b -=，∴a c 31=④.联立②④，解得26==c a ，，∴24=b ，故椭圆E 额标准方程为1323622=+y x .10.D 解析：由n n n n a S S S -=+++1232，得()n n n n n a S S S S --=-+++1122，即122++=+n n n a a a ，∴数列{}n a 是等差数列，设公差为d ，则由7264=-a a 和344=S 得⎩⎨⎧=+=+1732711d a d a ，解得⎩⎨⎧==341d a ，∴()13314+=⨯-+=n n a n .由202313=+n ，得674=n .11.B 解析：∵()30=f ，∴23cos =ϕ.∵0<<-ϕπ，∴6πϕ-=.当[]π,0∈x 时，⎥⎦⎤⎢⎣⎡--∈-6,66πωπππωx ，∵()x f 在[]π,0上有且只有三个极值点，∴ππωππ362<-≤得619613<≤ω，∴根据图象可以判断，()x f 在[]π,0上有两个极大值点，一个极小值点，∴①错误，②错误；当⎪⎭⎫⎝⎛∈5,0πx 时，6566ππωπωππ-<-≤-，显然065>-ππω，不符合题意∴③错误；由Z ∈ω得3=ω，∴()⎪⎭⎫ ⎝⎛-=63cos 2πx x f ，令Z k k x ∈+=-，263πππ，得Z k k x ∈+=，923ππ，当0=k 时，92π=x ，∴④正确.故选B.12.C 解析：如图，∵ABC P -为正三棱锥，P AC PBC P AB ∆≅∆≅∆，7==BE AD .取线段PE 的中点F ，连接AF DF ,，∵D 为PB 的中点，∴BE DF ∥，BE DF 21=.∵BE AD ⊥，∴DF AD ⊥.在ADF Rt ∆中，72==DF AD ，由勾股定理，得235=AF .设x P A APB ==∠，θ.在P AD ∆中，由余弦定理的推论，得222745212741cos x xx x x -=⋅-+=θ①同理，在P AF ∆中，由余弦定理的推论，得222235817412435161cos x xx x x -=⋅-+=θ②.联立①②，解得32=x ，32cos =θ.在P AB ∆中，由余弦定理，得()()832323223232cos 222222=⨯⨯⨯-+=∠⋅⋅-+=APB PB P A PB P A AB ，∴22=AB .取ABC ∆的中心1O ，连接11AO PO ，，则⊥1PO 平面ABC ，三棱锥ABC P -的外接球球心O 在1PO 上，连接OA ，设外接球半径为R .在1P AO Rt ∆中，R OA =，36232231=⨯=AB AO ，∴()321236232222121=⎪⎪⎭⎫ ⎝⎛-=-=AO P A PO ，∴R R PO OO -=-=321211，∴21212AO OO AO +=，即2223623212⎪⎪⎭⎫ ⎝⎛+-=R R ，解得7213=R ，∴所求外接球的表面积为ππ710842=R .二、填空题13.01=--y x 解析：2ln 1xxy -='，当1=x 时，1='y .又当1=x 时，0=y ，∴曲线xxy ln =在1=x 处的切线方程为1-=x y ，即01=--y x .14.4-解析：设等比数列{}n a 的公比为()0<q q ，将22=a 代入123+=S a ，得1222++=qq ，∴02322=--q q ，解得21-=q 或2=q （舍去），∴41-=a .15.1473解析：如图，连接C D C A AC 11，，，∵O 为AC 的中点，E 是棱1AA 的中点，∴C A OE 1∥.∵11D A AD ∥，∴C A D 11∠或其补角为异面直线EO 与AD 所成的角.不妨设1=AD ，则211111=====DD AA CD AD D A ，.在ADC ∆中，由余弦定理得：32111211120cos 22222=⎪⎭⎫⎝⎛-⨯⨯⨯-+=︒⋅-+=DC AD DC AD AC .∵1111D C B A ABCD -为直四棱柱，∴⊥1AA 平面ABCD .又⊂DC AC ,平面ABCD ，∴DC AA AC AA ⊥⊥11，.∵11AA DD ∥，∴DC DD ⊥1，∴()732222211=+=+=AC AA C A ，512222211=+=+=DC DD C D 在C D A 11∆中，由余弦定理的推论得：14737125712cos 111212121111=⨯⨯-+=⋅-+=∠C A D A C D C A D A C A D .16.2解析：如图，连接MI GM ，并延长，与21F F 分别交于点D O ,.设双曲线C 的焦距为c 2.由题意得c GI 61=.∵21F F GI ∥，且G 为重心，则32=ODGI ，∴4c OD =.∵I 为21F MF ∆的内心，∴MD 为21MF F ∠的平分线，∴35212121===∆∆DF D F S S MF MF MDF D MF ，∴2135MF MF =.又a MF MF 221=-，∴a MF a MF 3521==，.设21F MF ∆的内切圆半径为r ，则M 到x 轴的距离为r 3，∵r F F S F MF 3212121⋅⋅=∆，()r F F MF MF S F MF ⋅++⋅=∆21212121，∴2121213F F MF MF F F ++=，∴a c 2=，∴双曲线C 的离心率2==ace .三、解答题（一）必考题17.解：（1）由频率分布直方图，得()150001.0006.02003.0002.0=⨯++++a ，解得004.0=a .设中位数为t ，专项贷款金额在[0,150)内的频率为0.45，在[150,200)内的频率为0.3，∴中位数t 在[150,200)内，∴()05.0006.0150=⨯-t ，解得158≈t ，∴估计这120家中小微企业的专项贷款金额的中位数为158万元.（2）①由题意，得抽取比例为6112020=，专项贷款金额在[200,300]内的中小微企业有()30001.0004.050120=+⨯⨯家，∴应抽取56130=⨯家，∴5=m .②在抽取5家中小微企业中，专项贷款金额在[200,250)内的有4545=⨯家，记为D C B A ，，，，专项贷款金额在[250,300]内的有1515=⨯家，记为E .从这5家中小微企业中随机抽取3家的可能情况为CDE BDE BCE BCD ADE ACE ACD ABE ABD ABC ,,,,,,,,,，共10种，其中这3家中小微企业的专项贷款金额都在[200,250)内的情况为BCD ACD ABD ABC ,,,，共4种，∴所求概率52104==P .18.解：（1）∵ABC ∆的面积为3，∴3sin 21=C ab ，即32sin =C ab ①由余弦定理的推论，得abc b a C 2cos 222-+=.∵12222=-+c b a ，∴6cos =C ab ②.易知2π≠C ，①÷②，得33tan =C .∵()π，0∈C ，∴6π=C .（2）∵6π=C ，∴23cos =C ，即()23cos =+-B A ，∴23sin sin cos cos -=-B A B A .又33cos cos -=B A ，∴63sin sin =B A .由正弦定理得c CcB b A a 2sin sin sin ===，∴B c b A c a sin 2sin 2==，.由（1），知32sin =C ab ，∴34=ab ，∴34sin sin 42=B A c ，即23sin sin cB A =，∴6332=c ，解得6=c .19.解：（1）∵11112141BB AA AA AC AB AA AE ====，，，∴12121BB AB AB AE ==，，∴1BB ABAB AE =.∵111C B A ABC -为直三棱柱，∴侧面11A ABB 为矩形，∴︒=∠=∠9011ABB AB A ，∴1~BAB AEB ∆∆，∴AEB BAB ∠=∠1.又︒=∠+∠90AEB EBA ，∴︒=+∠901BAB EBA ，∴1AB BE ⊥.∵⊥1AA 平面ABC ，⊂AC 平面ABC ，∴AC AA ⊥1.又⊂=⊥11AA A AB AA AB AC ，，平面11A ABB ，∴⊥AC 平面11A ABB ，∵⊂BE 平面11A ABB ，∴BE AC ⊥.∵⊂=11AB A AC AB ，平面C AB 1，⊂AC 平面C AB 1，∴⊥BE 平面C AB 1.（2）连接AF ，∵⊄111AA BB AA ，∥平面11B BCC ，⊂1BB 平面11B BCC ，∴∥1AA 平面11B BCC ，∴三棱锥DEF B -的体积CD S V V V V ABF ABF D BDF A BDF E DEF B ⋅====∆----31.∵︒=∠==902BAC AC AB ，，F 为BC 的中点，∴BC AF BC ⊥=，22，∴2==BF AF ，∴1222121=⨯⨯=⋅⋅=∆AF BF S ABF ，∴三棱锥DEF B -的体积32213131=⨯⨯=⋅=∆-CD S V ABF DEF B .20.解：（1）由题意，知()x f 的定义域为()∞+，0，当21e a =时，()()()222222ln 1ln e x x e x e x f e x x e x f +⎪⎪⎭⎫⎝⎛+-='+=，.令()x e x x g 2ln 1+-=，则()0122<--='xe x x g ，∴()x g 在()∞+，0上单调递减.∵()02=eg ，∴当()2,0e x ∈时，()0>x g ，从而()0>'x f ；当()+∞∈,2e x 时，()0<x g ，从而()0<'xf ，∴()x f 的单调递增区间为()2,0e ，单调递减区间为()+∞,2e.（2）函数()ax x f y 1+=有两个不同的零点等价于()01=+axx f 有两个不同的解，等价于()011ln =++x ax 有两个不同的解.令()()11ln ++=x ax x h ，()+∞∈,0x ，则()()2ln +='x a x h .由()0='x h ，得21ex =.又0>a ，∴当⎪⎭⎫ ⎝⎛∈21,0e x 时，()0<'x h ；当⎪⎭⎫⎝⎛+∞∈,12e x 时，()0>'x h ，∴()x h 在⎪⎭⎫ ⎝⎛21,0e 上单调递减，在⎪⎭⎫⎝⎛+∞,12e 上单调递增，∴()22min 11e a e h x h -=⎪⎭⎫⎝⎛=.①当012≥-ea 即20e a ≤<时，()x h 至多有一个零点，不符合题意；②当012<-e a 即2e a >时，012<⎪⎭⎫ ⎝⎛e h ，()011>+=a h .由单调性和函数零点存在定理，知()x h 在⎪⎭⎫⎝⎛+∞,12e 上有且只有一个零点.∵2e a >，∴22111e a a <<，且a aa a h ln 2112-+=⎪⎭⎫ ⎝⎛.令()x x x ln 21-+=ϕ，则()xx x 2-='ϕ，∴当()+∞∈,2x 时，()0>'x ϕ，∴()x ϕ在()∞+，2上单调递增.∵22>>e a ，∴()()04ln 32>-=>ϕϕa ，∴012>⎪⎭⎫⎝⎛a h .由单调性和函数零点存在定理，知()x h 在⎪⎭⎫⎝⎛21,0e 上有且只有一个零点.∴当2e a >时，()x h 有两个不同的零点，即()axx f y 1+=有两个不同的零点，符合题意.综上，a 的取值范围是()+∞,2e .21.解：（1）设()B B y x B ,，由BA MB =得B 诶线段MA 的中点.∵⎪⎭⎫ ⎝⎛-0,2p M ，∴⎪⎩⎪⎨⎧=-=02242y y p x B B ，∴⎪⎪⎩⎪⎪⎨⎧=-=2420y y p x B B ，即⎪⎭⎫ ⎝⎛-2,420y p B ，把⎪⎭⎫ ⎝⎛-2,420y p B 代入px y 22=中，得⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛422220p p y ，把()0,4y A 代入px y 22=中，得p y 820=，∴p p p 2422=⎪⎭⎫⎝⎛-.又0>p ，∴4=p ，∴抛物线C 的方程为x y 82=.（2）由题意，知直线l 的斜率存在且不为0，∵()02，-M ，∴可设直线l 的方程为2-=my x .设()()2211,,y x B y x A ，，则点()11,y x P -.由⎩⎨⎧=-=xy my x 822消去x 得01682=+-my y ，∴0>∆，根据根与系数的关系得1682121==+y y m y y ，.直线BP 的斜率12212212121288y y y y y y x x y y k -=-+=-+=，直线BP 的方程为()21228x x y y y y --=-，∴()()()221222122122128181********y y y y y y y x y y y y y y x ++--=+---=()28112+-=y y y ，即直线BP 的方程可表示为()28112+-=y y y x .∴直线BP 过定点，且定点坐标为()02，.（二）选考题22.解：（1）∵⎪⎭⎫ ⎝⎛+=4sin 22πθρ，∴θθρcos 2sin 2+=，即θρθρρcos 2sin 22+=.又θρcos =x ，θρsin =y ，222ρ=+y x ，∴曲线C 的直角坐标方程为02222=--+y x y x .（2）依题意，将直线l 的参数方程代入曲线C 的直角坐标方程得：()043cos 2sin 2=-+-t t αα.设点N M ,所对应的参数分别为21,t t ，则43cos 2sin 2121-=+=+t t t t ，αα.∵点P 的直角坐标为⎪⎭⎫ ⎝⎛210，，∴1t PM =，2t PN =.∵021<t t ，∴2121t t t t PN PM +=-=-()ϕααα+=+=sin 5cos 2sin ，其中552sin 55cos ==ϕϕ，.由()03cos 2sin 2>++=∆αα，得R ∈α，∴当()1sin ±=+ϕα时，PN PM -最大，且最大值为5.23.解：（1）∵c b a ,,都是正实数，∴02>≥+ab b a ，02>≥+bc c b ，∴()()bc ab c b b a 22⋅≥++，当且仅当1===c b a 时，等号成立，即()()ac b c b b a 4≥++.又∵1=ac ，∴()()b c b b a 4≥++.（2）∵1112121=++++c b a ，∴12212422=++++cb a .由柯西不等式，得()()[]()22122212142221242++≥⎪⎭⎫⎝⎛++++++++c b a c b a ，即()22215222+≥+++c b a ，即222+≥++c b a ，当且仅当()c b a 21222=+=+，即222222+===c b a ，，时等号成立，∴c b a ++的最小值为222+.。

全国第一次大联考试卷语文

一、选择题1. 下列词语中，字形、字音、字义完全正确的一项是（）A. 装腔作势（qiang）水滴石穿（dian）B. 风驰电掣（che）比比皆是（ji）C. 美轮美奂（huan）饮鸩止渴（zhen）D. 悲天悯人（men）翻箱倒柜（tang）2. 下列句子中，没有语病的一项是（）A. 城市的夜晚，霓虹灯五光十色，犹如一座不夜城。

B. 为了迎接国庆节，学校举行了一场盛大的文艺晚会。

C. 随着科技的进步，人们的生活水平不断提高。

D. 他在比赛中勇夺金牌，受到了大家的热烈欢迎。

3. 下列各句中，修辞手法运用不恰当的一项是（）A. 红日初升，其道大光。

B. 时光荏苒，日月如梭。

C. 春风又绿江南岸，明月何时照我还？D. 两岸猿声啼不住，轻舟已过万重山。

4. 下列各句中，表达效果最生动形象的一项是（）A. 小明站在讲台上，口若悬河，滔滔不绝。

B. 她的笑声清脆悦耳，如同夜莺在歌唱。

C. 那里的风景美不胜收，令人陶醉。

D. 老师走进教室，目光如炬，扫视全班。

5. 下列各句中，语序不当的一项是（）A. 他虽然学习努力，但成绩一直不理想。

B. 会议室里，大家热烈讨论，气氛十分活跃。

C. 她一边唱歌，一边跳舞，赢得了观众的掌声。

D. 母亲为了照顾我们，付出了很多心血。

二、非选择题6. 阅读下面的文言文，完成下列小题。

范百禄字子功，是范镇兄长范锴的儿子，成都华阳人。

进士及第后，又被举荐为才识兼茂科。

熙宁年间，邓绾举荐他担任御史，他推辞不就任。

后来担任提点江东、利、梓路刑狱一职，又在直集贤院。

熊本处理泸州蛮人造反一事，有一位蛮人首领招架不住，请求投降，裨将贾昌言想杀了对方作为功劳，范百禄吩咐他别这样做，对方不听。

范百禄就过去对熊本说：“杀降将不祥，使千人存活才能福及子孙。

何必纵容骄兵悍将横行境内呢？”熊本惊惧，立刻下令阻止手下。

与徐禧处理李士宁的案件，上奏朝廷说李士宁使童妇迷惑，以致生出不轨之心，罪该万死不可赦免。

徐禧偏袒李士宁，认为他无罪。

2024全国名校大联考高三上学期第一联考(月考)语文试题及答案

2024全国名校大联考高三上学期第一联考（月考）语文试题试卷满分150分，考试时间150分钟一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1-5题。

材料一：从人类文明形态的角度看，人类历史的发展与变迁，表现为不同文明形态不断演进更替的过程，这一过程主要取决于生产力和生产关系的发展及其相互作用。

一种新的人类文明形态的产生，一般需要满足以下条件：一是旧的文明形态已经难以驾驭并容纳愈益发展的生产力和文明成果；二是新的文明形态已经发育起来，并达到一定成熟程度。

旧的文明形态走向衰落，新的文明形态繁荣兴盛，是不以人的主观意志为转移的历史性变迁。

长期以来，凭借西方现代化的先发优势和话语权强势，一些西方学者极力宣扬资本主义文明是普世的文明形态。

事实上，这种观点并不符合人类文明发展演进规律。

资本主义生产方式所固有的矛盾带来其无法克服的弊病，诸如经济危机频发、物质主义膨胀、贫富两极分化、对自然资源竭泽而渔、对外掠夺扩张等，这些弊病不仅越来越成为人类社会发展的阻碍，而且越来越成为人类文明进步的桎梏。

当今世界，人类面临着多重挑战和危机。

世界经济复苏艰难，发展鸿沟不断拉大，生态环境持续恶化，冷战思维阴魂不散，人类社会现代化进程又一次来到历史的十字路口。

两极分化还是共同富裕？物质至上还是物质精神协调发展？竭泽而渔还是人与自然和谐共生？零和博弈还是合作共赢？照抄照搬别国模式还是立足自身国情自主发展？我们究竟需要什么样的现代化？怎样才能实现现代化？面对这一系列的现代化之问，西方现代化模式没有也不可能给出科学回答，更难以满足人类社会现代化发展的普遍诉求，世界迫切需要新的人类文明形态引领和推动人类社会现代化进程。

中国式现代化及其所创造的人类文明新形态，探索出人口规模巨大、全体人民共同富裕、物质文明和精神文明相协调、人与自然和谐共生、走和平发展道路的现代化之路，极大推动经济社会发展和人类文明进步。

2024届高三12月大联考(全国乙卷)语文答案

2024届高三12月大联考（全国乙卷）语文·全解全析及评分标准1．D【解析】D项，“成为了传统文学在新时代创作的标准”曲解文意。

原文第3段说的是“尽管当下的网络文学存在这样那样的问题……但它想象的不羁、对各种领域和题材的勇敢开掘，以及表达方式上前所未有的奔放自由，都给铠甲重重的传统文学提供了新的参照和启发”。

2．B【解析】B项，曲解文意，且论据和论点不匹配。

“渐趋完善”错，从唐诗到宋词再到元曲的发展并非“渐趋完善”；同时，宋词对唐诗的突破、元曲对宋词的突破，说明在饱和期文学能自我协调与发展。

3．B【解析】A项，“到了宋代，人们不再认同这些美”曲解文意，原文中说“三美兼具的文体形式，成了宋词必须打破的桎梏”，只是说宋代的文学在寻求文学形式的突破，并非是宋代人不再认同唐诗的这些审美特点。

C项，“所以作家对文学发展的作用很小”于文无据，文中并没有提及作家对文学发展的作用。

D项，“传统文学和网络文学相交与融合的现状”曲解文意，原文说的是“也许在眼下，两者的生产机制和接受群体都有所差异，但假以时日，相交与融合必是大势所趋”。

4．C【解析】C项，“这说明多信使天文学时代已经到来”变未然为已然，原文说的是“预示着多信使天文学时代的到来”。

5．C【解析】A项，“直接探测到引力波信号以来”错，原文说的是“20世纪70—80年代，引力波的存在通过观测脉冲双星系统的轨道变化得以间接证实”，20世纪70—80年代只是间接证实引力波存在。

B项，或然和确然的错位，“李柯伽认为纳赫兹引力波包括宇宙早期原初引力波残存至今的部分”错，原文说的是“还可能有宇宙早期原初引力波残存至今的部分和宇宙弦等奇异对象产生的引力波”。

D项，论点和论据错位，“这说明纳赫兹引力波的探测极具挑战性，并且困难重重”错，原文中举中国、印度等加入纳赫兹引力波探测领域，是为了说明“发现纳赫兹引力波是国际物理和天文领域竞赛的焦点之一”。

6．优势：中国天眼灵敏度高、可监测脉冲星数目多、测量精度更高，并且自主开发的独立数据分析软件有算法优势。

2024届高三5月大联考(全国乙卷)语文试题()

绝密★启用前2024届高三5月大联考（全国乙卷）语文本卷满分150分，考试时间150分钟。

注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

意象美学是中国当代美学的一个重要流派，其理论价值和研究成果愈来愈引起人们的关注。

相比中国当代诸多美学派别，意象美学有一个特点，那就是它不像其他理论派别那样倚重西方美学的理论资源，而是将重点放在中国传统美学与艺术实践方面，重视中国传统意象美学理论的研究。

首先，中国当代美学家之所以重视传统意象美学理论研究，一个重要原因就在于，深入研究和梳理意象理论的思想资源，对于把握中国古代美学的文化基因和美学思维特点有着重要意义。

中国文化是重象尚象的文化，中国古代的思维方式包含着丰富的“象”的文化基因，这从远古时期的神话和器具意识的起源、以“象形”为基础的汉字构造、《易经》的卦象符号创造中就充分体现出来。

先秦哲学家和思想家正是在此基础上对“象”进行哲学阐释和理论超越，提出一系列重要命题与观点，如老子将“道”“气”“象”联结起来的哲学观念，庄子的“象罔”命题和关于“言意关系”的理解，《周易》的“立象以尽意”“观物取象”哲学命题，等等，对于中国古代意象理论和思维方式的形成产生重要影响，并成为中国美学理论体系建构的活水源头。

其次，以“意象”为中心的中国传统美学理论研究，可以使人们意识到中国古代艺术创造对于美学理论建构的重要性，将中国美学理论观念的研究与中国古代艺术审美实践紧密结合起来。

宗白华提出，中国美学史的研究，不仅要注意理论形态的著作，而且尤其要重视几千年的艺术创造。

全国名校大联考2023-2024学年高三上学期第一联考(月考)物理试题及答案

2023~2024学年高三第一次联考（月考）试卷物理考生注意：1．本试卷分选择题和非选择题两部分.满分100分，考试时间75分钟.2．答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3．考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．．．．．．．．．．．．．．．．．．．．．．．．．．．.．4．本卷命题范围：必修第一册.一、选择题：本题共6小题，每小题4分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．2023年5月30日，我国“神舟十六号”飞船发射并和空间站组合体成功对接，实现“神舟十六号”和“神舟十五号”号乘组太空会师，对接后的组合体绕地球运行速度约为7.68km/s，绕地球一周约90min，则下列说法正确的是（）A．“90min”指的是时刻B．“7.68km/s”为平均速率C．为了实现对接，应将空间站组合体看作质点D．对接成功后，空间站中的宇航员相对地球是静止的2．如图所示为我国著名举重运动员抓举比赛时的情景，运动员从图示状态由静止向上站起直至站立的过程中，下列说法正确的是（）A．杠铃先失重后超重B．手对杠的作用力大于杠对手的作用力C．运动员对地面的压力先大于地面对人的支持力后小于地面对人的支持力D．运动员对地面的压力先大于人和杠铃的总重力后小于人和杠铃的总重力3．如图所示，质量为1kg的物块静止在水平地面上A点，现加3NF=的水平拉力，当物块运动到B点撤去F，之后物块继续运动到C 点停止，测得2BC AB =，重力加速度取210m/s g =，则物块与水平地面间的动摩擦因数为（）A ．0.25B ．0.2C ．0.15D ．0.14．将小球A 在地面上方某一高度的P 点由静止释放，当A 运动t 时间时，在P 点正下方的地面上竖直向上抛出一个初速度大小等于gt 的小球B ，g 为重力加速度，B 抛出后运动t 时间A 、B 两球刚好相遇，不计空气阻力，则P 点离地面的高度为（）A ．252gtB ．232gtC ．22gtD ．2gt5．如图所示，质量为M 、倾角为θ的斜面体静止在水平面上，质量为m 的物块以一定的初速度从斜面底端沿斜面上滑，物块与斜面间的动摩擦因数tan µθ<，斜面足够长，斜面体始终保持静止，不计物块的大小，则下列说法正确的是（）A ．物块沿斜面向上运动的时间大于沿斜面向下运动的时间B ．物块沿斜面运动过程中，地面对斜面体的摩擦力先向左后向右C ．物块沿斜面上滑时地面对斜面体摩擦力大于物块沿斜面下滑时地面对斜面体摩擦力D ．物块沿斜面上滑时地面对斜面体支持力大于物块沿斜面下滑时地面对斜面体支持力6．如图所示，半径为R 的四分之一光滑圆弧和半径为0.6R 的四分之一光滑圆弧固定在竖直面内，两圆弧的最低点相接，接点切线水平，质量为1m 的A 球和质量为2m 的B 球用轻杆连接在圆弧面内处于平衡状态，杆刚好水平，大圆弧圆心1O 到杆的距离为0.6R ，不计小球的大小，则A 、B 两球的质量之比12m m 为（）ABCD二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，选对但不全的得3分，有选错的得0分.7．如图所示，小球A 和大球B 都与竖直墙面接触，在水平推力F 作用下整体静止，现使B球缓慢沿水平面向右移动直至两个球心等高，在此过程中，水平推力F 作用线始终通过B 球心O ，不计一切摩擦，则下列说法正确的是（）A ．水平推力F 不断增大B ．B 对地面的压力不断减小C ．A 对B 的作用力不断增大D ．墙对A 的作用力不断减小8．如图所示，小球甲、乙的质量相等，两小球按如图的方式连接，其中a 、b 为两弹性绳（满足胡克定律），c 为不可伸长的轻绳，系统静止时，轻绳c 与竖直方向的夹角为45α=°，弹性绳a 沿水平方向，且两弹性绳的伸长量相等.已知重力加速度为g ，则下列说法正确的是（）A ．两弹性绳的弹力大小相等B ．弹性绳a 、b 的劲度系数之比为2:1C ．将轻绳c 剪断的瞬间，小球乙的加速度大小为gD ．将轻绳c 剪断的瞬间，小球甲的加速度大小为9．A 、B 两个质点同时同地沿同向从静止开始做匀加速直线运动，两质点的t υ−图像如图所示，当A 的速度为0υ时，B 的速度为034υ，此时A 、B 运动的时间为0t ，此时A 立即做匀减速直线运动，当A 的速度减为零时，A 、B 刚好相遇，则从A 、B 开始运动到A 、B 相遇过程中，下列说法正确的是（）A ．A 、B 相遇时，B 的速度为0υB ．A 、B 相遇时，A 运动的路程为0023t υC ．A 、B 运动过程中相距的最大距离为0018t υD ．A 做加速运动和做减速运动的时间之比为4:110．测试人员对某型号无人机做性能测试实验，质量为m 的无人机其最大升力为其自身重力的2倍，在地面从静止开始以最大升力竖直上升，上升t 时间关闭发动机，上升到最高点后沿原路返回，当到离地面某一高度时，开启发动机，保持最大升力下降，到地面时速度刚好为零，无人机运动过程中受到的阻力为其重力的0.2倍，重力加速度为g ，则下列说法正确的是（）A ．上升过程中，加速与减速的时间之比为2:3B ．上升过程中，加速与减速的位移之比为3:2C ．上升过程的总时间等于下降过程的总时间D ．上升过程的最大速度大于下降过程的最大速度三、非选择题：本题共5小题，共56分.11．（6分）某同学用如图所示装置做“探究弹力和弹簧伸长的关系”实验，先测出不挂钩码时弹簧的自然长度，再将钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度l ，记录对应的悬挂钩码的质量m ．（实验中弹簧始终未超过弹性限度，取29.8m/s g =）（1）实验时可以用钩码所受重力的大小来代替弹簧弹力的大小，这样做依据的物理规律是_______．（2）将实验测得的数据在图乙上标出.请作出m l −的关系图线，由图像可知，该弹簧的劲度系数为_______N/m ．（结果保留3位有效数字）（3）另一个同学用A 、B 两个弹簧分别做了实验，根据测得的数据绘出如图丙所示的图像，从图像上看，A 和B 的原长_______（填“相等”或“不等”），A 、B 两根弹簧的劲度系数A k _______（选填“>”“=”或“<”）B k ．由于该组同学没能完全按实验要求做，使图像上端成为曲线，图像上端成为曲线的原因是_______．12．（9分）某实验小组用如图甲所示装置探究加速度与合外力的关系，小车的质量为M ，打点计时器使用的交流电频率为50Hz.．（1）按装置图甲安装好装置，平衡摩擦力后进行实验，小车靠近打点计时器，需要调节定滑轮A ，使_______，调节定滑轮B ，使_______．（2）接通电源，释放钩码，多次改变钩码质量，记录弹簧秤的读数F ，某次弹簧秤的示数如图乙所示，则小车受到细线的拉力大小为_______N ，实验打出的一条纸带如图丙所示，相邻记数点间还有4个点没有画出来，则小车运动的加速度a =_______m/s （结果保留三位有效数字）．（3）多次改变钩码的质量进行实验，测得多组弹簧测力计的示数F 及小车的加速度，作a F −图像，如果图像是过原点的一条倾斜直线，且图像的斜率等于_______，表明物体质量一定时，加速度与合外力成正比. 13．（10分）如图所示，倾角为37θ=°的斜面体静止在水平面上，质量为1kg 的物块放在斜面上，橡皮条（满足胡克定律）一端固定在竖直墙上的O 点，另一端连接在物块上，橡皮条与斜面平行，物块刚好不滑动，物块与斜面间的动摩擦因数为0.5，最大静摩擦力等于滑动摩擦力，橡皮条的劲度系数为1N/cm ，橡皮条的形变在弹性限度内，重力加速度取210m/s g =，sin 370.6°=，cos370.8°=，求：（1）橡皮条的伸长量；（2）地面对斜面体的摩擦力大小；14．（14分）如图所示，A 、C 两个物块用绕过光滑定滑轮的足够长细线连接，B 、C 用较短的细线连接，A 、B 的质量均为m ，用外力使物块A 处于静止，此时A 、B 离地面的高度相等，若撤去作用在A 上的外力，使连接体由静止开始运动，B 下落t 时间刚好落地；若先剪断B 、C 间的细线再撤去外力，使连接体由静止开始运动，则A 的时间刚好落地，重力加速度为g ，求：（1）物块C 的质量；（2）若在B 下落到初始离地高度的一半时剪断B 、C 间的细线，求A 上升的最高点离地面的高度15．（17分）如图所示为某传送装置，由倾角为37θ=°的倾斜传送带和放在水平面上的质量为1kg 的长木板组成，传送带长1 1.45m L =，长木板长20.9m L =，长木板的左端靠近传送带的下端，传送带以02m/s υ=的速度沿顺时针方向匀速运行，将质量为1kg 的物块轻放在传送带的上端，物块与传送带间的动摩擦因数为0.5，与长木板间的动摩擦因数为0.4，长木板与水平面间的动摩擦因数为0.1，不计物块从传送带滑上长木板时机械能损失，重力加速度取210m/s g =，sin 370.6°=，cos370.8°=，求：（1）物块滑离传送带时的速度大小；（2）物块滑上长木板后，物块与长木板运动的位移分别为多少；（3）若在长木板的右侧地面上立一个高度略小于板厚度的固定挡板，物块滑上长木板后，在运动过程中，长木板与挡板碰撞后速度立即减为零，此后物块恰好能滑离长木板，求开始时长木板的右端离挡板的距离．物理一参考答案、提示及评分细则1．B “90min ”指的是一段时间，A 错误；“7.68km/s ”为平均速率，B 正确；为了实现对接，不能将空间站组合体看作质点，C 错误；对接成功后，空间站中的宇航员相对地球是运动的，D 错误。

2024届高三10月大联考(全国乙卷)文科数学含答案解析

2024届高三10月大联考（全国乙卷）文科数学一、单选题(共36 分)1已知集合A={x∈Z∣x2+1<5},B={−1,1,3}则A∪B中元素的个数为（）A3B4C5D6【答案】B【分析】化简集合A即可求出A∪B中元素的个数【详解】由题意因为A={x∈Z∣x2+1<5}={x∈Z∣x2<4}={−1,0,1},B={−1,1,3}所以A∪B={−1,0,1,3}有4个元素故选：B2已知命题p:∃x0≥0,√x0>x02则命题p的否定为（）A∃x0<0,√x0≤x02B∀x≥0,√x<x2C∀x<0,√x>x2D∀x≥0,√x≤x2【答案】D【分析】利用含有一个量词的命题的否定的定义求解【详解】解：因为命题p:∃x0≥0,√x0>x02是特称命题所以其否定为全称命题即“∀x≥0,√x≤x2”故选：D3若不等式x2−5ax+1<0的解集为(1a,a)则a=（）A−12B12C−14D14【答案】A 【分析】根据给定的解集结合一元二次方程根与系数的关系求解即得【详解】由不等式x 2−5ax +1<0的解集为(1a ,a)得1a ,a 是方程x 2−5ax +1=0的两个根且1a <a 于是a +1a =5a 解得a =±12由a >1a 得−1<a <0或a >1因此a =−12且当a =−12时(−5a)2−4>0所以a =−12 故选：A4若函数f (x )={e x −x,x ≤3lnx −2,x >3则f(f (e 2))=（）A −1B −2 C1 D ln2−2【答案】C 【分析】先计算出f (e 2)=0进而求出f(f (e 2))=f (0)=1 【详解】因为e 2>3所以f (e 2)=lne 2−2=0所以f(f (e 2))=f (0)=e 0−0=1 故选：C5已知p:1<a <53,q:log a 43>2(a >0且a ≠1)则p 是q 的（） A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件【答案】B 【分析】对于q ：利用对数函数单调性解得1<a <2√33再根据包含关系结合充分、必要条件分析判断【详解】对于q ：因为log a 43>2=log a a 2（a >0且a ≠1）当0<a <1时y =log a x 在定义域内单调递减则a 2>43无解；当a >1时y =log a x 在定义域内单调递增则a 2<43可得1<a <2√33；综上所述：不等式log a 43>2的解集为(1,2√33) 又因为(1,2√33)是(1,53)的真子集所以p 是q 的必要不充分条件故选：B6函数f (x )=x 2log 42+x2−x 的大致图象是（）A B C D【答案】D 【分析】方法一：根据函数的奇偶性及函数值的符号排除即可判断；方法二：根据函数的奇偶性及某个函数值的符号排除即可判断【详解】方法一：因为2+x2−x >0即(x +2)⋅(x −2)<0所以−2<x <2 所以函数f (x )=x 2log 42+x2−x 的定义域为(−2,2)关于原点对称又f (−x )=(−x)2log 42−x 2+x =−f (x )所以函数f (x )是奇函数其图象关于原点对称故排除B,C ；当x ∈(0,2)时2+x2−x >1即log 42+x2−x >0因此f (x )>0故排除A 故选D方法二：由方法一知函数f (x )是奇函数其图象关于原点对称故排除B,C ；又f (1)=12log 23>0所以排除A 故选：D7白色污染是人们对难降解的塑料垃圾（多指塑料袋）污染环境现象的一种形象称谓经过长期研究一种全生物可降解塑料（简称PBAT ）逐渐被应用于超市购物袋､外卖包装盒等产品研究表明在微生物的作用下PBAT 最终可被完全分解为二氧化碳和水进入大自然当其分解率（分解率=已分解质量总质量×100%）超过60%时就会成为对环境无害的物质为研究总质量为100g 的PBAT 的已分解质量y （单位：g ）与时间x （单位：月）之间的关系某研究所人员每隔1个月测量1次PBAT 的已分解质量对通过实验获取的数据做计算处理研究得出已分解质量y 与时间x 的函数关系式为y =100−e 4.6−0.1x 据此研究结果可以推测总质量为100g 的PBAT 被分解为对环境无害的物质的时间至少为（）（参考数据：ln40≈3.7） A8个月 B9个月 C10个月 D11个月【答案】C 【分析】根据题意令y =100−e 4.6−0.1x >60求解即可【详解】令y =100−e 4.6−0.1x >60得0.1x >4.6−ln40≈0.9解得x >9故至少需要10个月总质量为100g 的PBAT 才会被分解为对环境无害的物质故选：C8已知α,β∈(0,π2),α>β且cosα(cosα−cosβ)+sinα(sinα−sinβ)=15,sinαcosβ=710则sin (α+β)=（） A 45 B 35C 25D 310【答案】A 【分析】利用两角和与差的正弦公式和余弦公式化简即可【详解】因为cosα(cosα−cosβ)+sinα(sinα−sinβ)=15cos 2α−cosαcosβ+sin 2α−sinαsinβ=15即1−cos (α−β)=15所以cos (α−β)=45因为α,β∈(0,π2),α>β所以0<α−β<π2所以sin (α−β)=35即sinαcosβ−cosαsinβ=35又sinαcosβ=710所以cosαsinβ=110所以sin (α+β)=sinαcosβ+cosαsinβ=710+110=45 故选：A9已知O 是△ABC 所在平面内一点若OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0⃗ ,AM ⃗⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ ,AN ⃗⃗⃗⃗⃗⃗ =yAC ⃗⃗⃗⃗⃗ ,MO ⃗⃗⃗⃗⃗⃗ =λON ⃗⃗⃗⃗⃗⃗ ,x,y 均为正数则xy 的最小值为（） A 12 B 49C1D 43【答案】B 【分析】由题设O 是△ABC 的重心应用向量加法、数乘几何意义可得AO ⃗⃗⃗⃗⃗ =13x AM ⃗⃗⃗⃗⃗⃗ +13y AN ⃗⃗⃗⃗⃗⃗ 根据MO ⃗⃗⃗⃗⃗⃗ =λON ⃗⃗⃗⃗⃗⃗ 得13x +13y =1最后应用基本不等式求xy 最小值注意等号成立条件【详解】因为OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0⃗ 所以点O 是△ABC 的重心所以AO ⃗⃗⃗⃗⃗ =23×12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=13(AB ⃗⃗⃗⃗⃗ +AC⃗⃗⃗⃗⃗ ) 因为AM ⃗⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ ,AN ⃗⃗⃗⃗⃗⃗ =yAC ⃗⃗⃗⃗⃗ 所以AB ⃗⃗⃗⃗⃗ =1x AM ⃗⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ =1yAN⃗⃗⃗⃗⃗⃗ 综上AO ⃗⃗⃗⃗⃗ =13x AM ⃗⃗⃗⃗⃗⃗ +13y AN⃗⃗⃗⃗⃗⃗ 因为MO ⃗⃗⃗⃗⃗⃗ =λON⃗⃗⃗⃗⃗⃗ 所以M,O,N 三点共线则13x +13y =1即1x +1y =3 因为x,y 均为正数所以1x +1y ≥2√1xy 则√1xy ≤32所以xy ≥49（当且仅当1x =1y =32即x =y =23时取等号）所以xy 的最小值为49 故选：B10若函数f (x )=Asin (ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示则下列说法正确的个数为（）①ω=2；②φ=−π6；③f (x )在(π2,5π6)上单调递减；④f (−π2)=√3 A1B2C3D4【答案】C 【分析】由图像经过的特殊点(5π12,2)和(π6,0)逐项判断即可【详解】由题图得A =2最小正周期T =4×(5π12−π6)=π 又T =2πω=π所以ω=2故①正确；f (x )=2sin (2x +φ)又f (x )的图象过点(5π12,2) 所以2×5π12+φ=2kπ+π2,k ∈Z 所以φ=2kπ−π3,k ∈Z又|φ|<π2所以φ=−π3故②错误； f (x )=2sin (2x −π3)令t =2x −π3当π2<x <5π6时2π3<t <4π3函数y =sint 在(2π3,4π3)上单调递减故③正确；f (−π2)=2sin (−π−π3)=√3故④正确故选：C11已知函数f (x )是偶函数当x >0时f (x )=|log 2x |−1则不等式x−1f (−x )−2f (x )≥0的解集是（） A (−12,0)∪(0,12) B (−2,−1]∪[1,2)C (−2,−12)∪(0,12) D (−∞,−2)∪(−12,0)∪(0,12)∪[1,2)【答案】D 【分析】根据已知画出y =f (x )的图象并将不等式化为{f(x)(x −1)≤0f(x)≠0数形结合求不等式解集【详解】根据题意作偶函数y =f (x )的图象如下图示由f(−x)=f(x)不等式可化为x−1−f(x)≥0则{f(x)(x−1)≤0f(x)≠0所以{x−1≥0f(x)<0或{x−1≤0f(x)>0由图知：1≤x<2或0<x<12或−12<x<0或x<−2所以不等式解集为(−∞,−2)∪(−12,0)∪(0,12)∪[1,2)故选：D12已知函数f(x)=a x+a−x+cosx+x2(a>1)则f(√2),f(−e1e),f(π1π)的大小关系为（）A f(π1π)<f(−e 1e)<f(√2)B f(√2)<f(π1π)<f(−e1e)C f(π1π)<f(√2)<f(−e1e)D f(−e1e)<f(π1π)<f(√2)【答案】B【分析】根据函数的奇偶性只需要考虑x>0时的情况利用导数求解函数单调性构造函数φ(x)=2x−sinx,g(x)=lnxx即可由导数求解单调性利用函数单调性即可比较大小【详解】易知f(x)=a x+a−x+cosx+x2(a>1)是偶函数f′(x)=(a x−a−x)lna+2x−sinx当x>0时因为a>1所以lna>0,a x−a−x>0令φ(x)=2x−sinx,x>0则φ′(x)=2−cosx>0所以φ(x)单调递增所以φ(x)>φ(0)=0所以f′(x)>0,f(x)在(0,+∞)上单调递增构造函数g(x)=lnxx 则g′(x)=1−lnxx2令g′(x)>0得0<x<e令g′(x)<0得x>e所以g(x)在区间(0,e)上单调递增在区间(e,+∞)上单调递减又ln22=ln44所以g(4)<g(π)<g(e)所以ln22=ln44<lnππ<lnee所以212<π1π<e1e所以f(√2)<f(π1π)<f(e 1e)=f(−e1e)即f(√2)<f(π1π)<f(−e1e)故选:B【点睛】方法点睛：利用导数比较大小的基本步骤:(1)作差或变形；(2)构造新的函数ℎ(x)；(3)利用导数研究ℎ(x)的单调性或最值；(4)根据单调性及最值得到所证不等式．二、填空题(共12 分)13已知向量a=(1,−2)b⃗=(2,λ)若a⊥b⃗则实数λ的值为___________【答案】1【分析】根据向量垂直的坐标表示由题中条件列出方程即可求出结果【详解】因为向量a=(1,−2)b⃗=(2,λ)若a⊥b⃗则a⋅b⃗=2−2λ=0解得λ=1故答案为：114请写出一个满足对任意的x1,x2∈(0,+∞)；都有f(x1x2)=f(x1)f(x2)的函数__________【答案】f(x)=x−12（答案不唯一）【分析】取幂函数f(x)=x−12验证得到答案【详解】任意定义域为(0,+∞)的幂函数均可例如f(x)=x−12f(x1x2)=(x1x2)−12,f(x1)f(x2)=x1−12⋅x2−12=(x1x2)−12即f(x1x2)=f(x1)f(x2)成立故答案为：f(x)=x−12（答案不唯一）15《海岛算经》是魏晋时期数学家刘徽所著的测量学著作书中有一道测量山上松树高度的题目受此题启发小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度如图把塔底与塔顶分别看作点CDCD 与地面垂直小李先在地面上选取点AB （点A,B 在建筑物的同一侧且点A,B,C,D 位于同一个平面内）测得AB =20√3m 在点A 处测得点C,D 的仰角分别为30∘,67∘在点B 处测得点D 的仰角为33.5∘则塔高CD 为__________m （参考数据：sin37∘≈35）【答案】24 【分析】在△ACD 中求出AD =20√3∠CAD =37∘,∠ACD =120∘利用正弦定理求解即可【详解】如图延长DC 与BA 的延长线交于点E 则∠DAE =67∘,∠CAE =30∘,∠DBA =33.5∘所以∠ADB =67∘−33.5∘=33.5∘,∠CAE =90∘−30∘=60∘ 所以AD =AB =20√3在△ACD 中∠CAD =67∘−30∘=37∘,∠ACD =180∘−60∘=120∘ 由正弦定理得CD =ADsin37∘sin120∘≈20√3×35√32=24（m ）故答案为：2416已知函数f (x )=(x +a )lnx −2x 在定义域上单调递增则实数a 的取值范围为______ 【答案】[1,+∞) 【分析】把原函数在区间上单调递增问题转化为a ≥x −xlnx 在(0,+∞)上恒成立构造函数g (x )=x −xlnx(x>0)利用导数求解函数的最值即可求解【详解】f(x)=(x+a)lnx−2x的定义域为(0,+∞)由f(x)=(x+a)lnx−2x在定义域上单调递增得f′(x)=lnx+ax−1≥0在(0,+∞)上恒成立即a≥x−xlnx在(0,+∞)上恒成立设g(x)=x−xlnx(x>0)所以只需a≥g(x)max又g′(x)=−lnx当0<x<1时g′(x)>0当x>1时g′(x)<0所以g(x)在(0,1)上单调递增在(1,+∞)上单调递减所以g(x)max=g(1)=1所以a≥1所以实数a的取值范围为[1,+∞)故答案为：[1,+∞)【点睛】方法点睛：已知函数在区间上单调递增（递减）求参数范围解决这类问题的一般方法是：利用导数转化为不等式恒成立问题然后参变分离根据分离后的式子结构构造函数利用导数求解函数最值即可解决三、问答题(共12 分)已知向量a=(sinx+cosx,1),b⃗=(2cosx,−1)函数f(x)=a⋅b⃗将函数f(x)的图象向右平移π6个单位长度得到函数g(x)的图象17 求函数f(x)的最小正周期和单调递增区间；18 解方程g(x)=0【答案】17 T=π单调递增区间为[kπ−3π8,kπ+π8],k∈Z18 {x|x=kπ2+π24,k∈Z}【分析】（1）利用向量数量积求出f(x)利用正弦函数的周期性与单调性即可求得f(x)的最小正周期和单调递增区间（2）先求出g(x)表达式根据正弦函数零点取值得到g(x)=0的解集【17题详解】由已知得f(x)=a⋅b⃗=2cosx(sinx+cosx)−1=sin2x +cos2x=√2sin (2x +π4)所以函数f (x )的最小正周期T =2πω=2π2=π由2kπ−π2≤2x +π4≤2kπ+π2,k ∈Z 解得kπ−3π8≤x ≤kπ+π8,k ∈Z所以函数f (x )的单调递增区间为[kπ−3π8,kπ+π8],k ∈Z【18题详解】将函数f (x )的图象向右平移π6个单位长度得到函数g (x )=√2sin [2(x −π6)+π4]=√2sin (2x −π12)的图象令g (x )=√2sin (2x −π12)=0得2x −π12=kπ,k ∈Z 解得x =kπ2+π24,k ∈Z所以方程g (x )=0的解集为{x |x =kπ2+π24,k ∈Z }如图在平行四边形ABCD 中AM ⃗⃗⃗⃗⃗⃗ =13AD ⃗⃗⃗⃗⃗ 令AB ⃗⃗⃗⃗⃗ =a AC⃗⃗⃗⃗⃗ =b ⃗19用a ,b ⃗ 表示AM ⃗⃗⃗⃗⃗⃗ BM ⃗⃗⃗⃗⃗⃗ CM⃗⃗⃗⃗⃗⃗ ； 20若AB =AM =2且AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10求cos⟨a ,b⃗ ⟩ 【答案】19 AM ⃗⃗⃗⃗⃗⃗ =13(b ⃗ −a )BM ⃗⃗⃗⃗⃗⃗ =13b ⃗ −43a CM ⃗⃗⃗⃗⃗⃗ =−13a −23b⃗ 20√3468【分析】（1）利用平面向量的四则运算法则求解即可；（2）利用平面向量数量积的公式和运算律求解即可【19题详解】因为AB ⃗⃗⃗⃗⃗ =a AC ⃗⃗⃗⃗⃗ =b ⃗ 且ABCD 是平行四边形所以BC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =b ⃗ −a所以AM ⃗⃗⃗⃗⃗⃗ =13BC ⃗⃗⃗⃗⃗ =13(b ⃗ −a ) 所以BM ⃗⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =13(b ⃗ −a )−a =13b ⃗ −43a所以CM ⃗⃗⃗⃗⃗⃗ =BM ⃗⃗⃗⃗⃗⃗ −BC ⃗⃗⃗⃗⃗ =13b ⃗ −43a −(b ⃗ −a )=−13a −23b ⃗ 【20题详解】方法一：由（1）知AM ⃗⃗⃗⃗⃗⃗ =13(b ⃗ −a ),BM ⃗⃗⃗⃗⃗⃗ =13b ⃗ −43a又AC ⃗⃗⃗⃗⃗ =b ⃗ ,AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10,AB =AM =2所以b ⃗ ⋅(13b ⃗ −43a )=10,|13(b ⃗ −a )|=2,|a |=2即b ⃗ 2−4a ⋅b ⃗ =30,b ⃗ 2+a 2−2a ⋅b ⃗ =36 解得a ⋅b⃗ =1,|b ⃗ |=√34 所以cos⟨a ,b ⃗ ⟩=a ⃗ ⋅b ⃗ |a ⃗ ||b ⃗ |=√3468方法二：因为AM ⃗⃗⃗⃗⃗⃗ =13AD ⃗⃗⃗⃗⃗ ,AM =2所以AD =BC =6因为AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )⋅(BA ⃗⃗⃗⃗⃗ +13BC ⃗⃗⃗⃗⃗ )=−BA ⃗⃗⃗⃗⃗ 2+23BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ +13BC ⃗⃗⃗⃗⃗ 2且AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10所以−22+23×6×2×cos∠ABC +13×62=10 解得cos∠ABC =14所以a ⋅b ⃗ =(−BA ⃗⃗⃗⃗⃗ )⋅(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )=−BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ 2=−2×6×14+22=1又|a |=2,|b ⃗ |=√(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )2=√BC ⃗⃗⃗⃗⃗ 2−2BC ⃗⃗⃗⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ 2=√34所以cos⟨a ,b ⃗ ⟩=a ⃗ ⋅b ⃗ |a ⃗ ||b ⃗ |=√3468四、应用题(共 6 分)某公园池塘里浮萍的面积y （单位：m 2）与时间t （单位：月）的关系如下表所示：现有以下三种函数模型可供选择：①y =kt +b ②y =p ⋅a t +q ③y =m ⋅log a t +n 其中k,b,p,q,m,n,a 均为常数a >0且a ≠121 直接选出你认为最符合题意的函数模型并求出y 关于t 的函数解析式；22 若该公园池塘里浮萍的面积蔓延到15m 2,31m 2,211m 2所经过的时间分别为t 1,t 2,t 3写出一种t 1,t 2,t 3满足的等量关系式并说明理由【答案】21 模型②y=2t+122 t1+t2=t3+1理由见解析【分析】（1）根据表格数据选择函数模型然后求解析式；（2）根据指数幂运算公式计算【21题详解】应选择函数模型②y=p⋅a t+q依题意得{p×a1+q=3p×a2+q=5 p×a3+q=9解得{p=1 a=2 q=1所以y关于t的函数解析式为y=2t+1【22题详解】t1+t2=t3+1理由：依题意得2t1+1=152t2+1=312t3+1=211所以2t1=142t2=302t3=210所以2t1⋅2t2=420所以2t1⋅2t2=2t1+t2=420=2×2t3=2t3+1所以t1+t2=t3+1五、问答题(共12 分)在△ABC中内角A,B,C所对的边分别为a,b,c且__________在①√3a =1−cosCsinA；②sinAbc−sinCab=sinA−sinBac两个条件中任选一个填入上面横线处并解决下列问题注：若选择不同的条件分别解答则按第一个解答计分23 求C；24 若△ABC外接圆的半径为2√3,△ABC的面积为√3求△ABC的周长【答案】23 C=π324 4√3+6【分析】(1)选①先利用正弦定理化边为角再利用和差角公式结合角的取值范围即得选②先用正弦定理化边为角再有余弦定理和角的范围即得(2)由正弦定理和外接圆半径求出c再利用余弦定理即可求出答案【23题详解】若选①：由√3a =1−cosCsinA及正弦定理得sinCsinA=√3sinA(1−cosC)∵sinA≠0,∴sinC+√3cosC=√3∴sin(C+π3)=√32又0<C<π,∴π3<C+π3<4π3∴C+π3=2π3,∴C=π3若选②：由sinAbc −sinCab=sinA−sinBac得asinA−csinC=bsinA−bsinB由正弦定理得a2+b2−c2=ab由余弦定理得cosC=a 2+b2−c22ab=ab2ab=12因为C∈(0,π)所以C=π3【24题详解】设△ABC外接圆的半径为R由正弦定理得c=2RsinC=2×2√3×sinπ3=6又S△ABC=12absinC=12ab×√32=√3所以ab=4由c2=a2+b2−2abcosC=(a+b)2−2ab−2ab×12可得36=(a+b)2−12解得a+b=4√3所以△ABC的周长为a+b+c=4√3+6已知函数f(x)=e x−ax2+x−125 当a=1时求曲线y=f(x)在x=1处的切线方程；26 若f(x)=0有两个不等的实根求实数a的取值范围【答案】25 (e−1)x−y=026 (−∞,0)∪{e2+14}【分析】（1）求导得到f(1)=e−1,f′(1)=e−1,进而求出切线方程；（2）f(0)=0故只需当x≠0时f(x)=0有且仅有一个实根参变分离转化为两函数只有1个交点求导得到g(x)=e x+x−1x2(x≠0)的单调性画出其图象数形结合得到参数的取值范围【25题详解】当a=1时f(x)=e x−x2+x−1,f′(x)=e x−2x+1f(1)=e−1,f′(1)=e−1,所以曲线y=f(x)在x=1处的切线方程为y−(e−1)=(e−1)(x−1)即(e−1)x−y=0【26题详解】显然f(0)=0要使方程f(x)=0有两个不等的实根只需当x≠0时f(x)=0有且仅有一个实根当x≠0时由方程f(x)=0得a=e x+x−1 x2令g(x)=e x+x−1x2(x≠0)则直线y=a与g(x)=e x+x−1x2(x≠0)的图象有且仅有一个交点g′(x)=(e x+1)x2−2x(e x+x−1)x4=(x−2)(e x−1)x3又当x<0时g′(x)<0,g(x)单调递减当0<x<2时g′(x)<0,g(x)单调递减当x>2时g′(x)>0,g(x)单调递增所以当x=2时g(x)取得极小值g(2)=e 2+1 4又当x<0时e x<1所以e x+x−1<0即g(x)<0当x>0时e x>1,e x+x−1>0即g(x)>0所以作出g(x)的大致图象如图所示由图象知要使直线y=a与g(x)=e x+x−1x2(x≠0)的图象有且仅有一个交点只需a<0或a=e 2+1 4综上若f(x)=0有两个不等的实根则a的取值范围为(−∞,0)∪{e 2+1 4}六、其它(共6 分)已知函数f(x)=x−alnx−4,a∈R27 讨论函数f(x)的单调性；28 当a=1时令F(x)=(x−2)e x−f(x)若x=x0为F(x)的极大值点证明：0<F(x0)<1【答案】27 答案见解析；28 证明见解析【分析】（1）对参数a分类讨论根据不同情况下导函数函数值的正负即可判断单调性；（2）利用导数判断F(x)的单调性求得x0的范围满足的条件以及F(x0)根据x0的范围夹逼F(x0)的范围即可【27题详解】函数f(x)的定义域为(0,+∞),f′(x)=1−ax =x−ax①当a≤0时f′(x)>0函数f(x)在(0,+∞)上单调递增；②当a>0时由f′(x)>0得x>a由f′(x)<0得0<x<a所以函数f(x)在(a,+∞)上单调递增在(0,a)上单调递减综上当a≤0时函数f(x)在(0,+∞)上单调递增；当a>0时函数f(x)在(a,+∞)上单调递增在(0,a)上单调递减【28题详解】当a=1时F(x)=(x−2)e x−x+lnx+4,F′(x)=(x−1)e x−1+1x =(x−1)(e x−1x)设g(x)=e x−1x 则g′(x)=e x+1x2当x>0时g′(x)>0所以g(x)在(0,+∞)上单调递增又g(12)=√e−2<0,g(1)=e−1>0所以存在x1∈(12,1)使得g(x1)=0且当x∈(0,x1),g(x)<0,x∈(x1,+∞),g(x)>0；又当x∈(0,1),y=x−1<0;x∈(1,+∞),y=x−1>0；故当x∈(0,x1)F′(x)>0；当x∈(x1,1)F′(x)<0；当x∈(1,+∞)F′(x)>0所以F(x)在(0,x1)上单调递增在(x1,1)上单调递减在(1,+∞)上单调递增所以当x=x1时F(x)取得极大值故x0=x1且e x0−1x0=0所以e x0=1x0,lnx0=−x0F(x0)=(x0−2)e x0−x0+lnx0+4=x0−2x0−x0−x0+4=5−2(x0+1x0)又y=x+1x 在(12,1)单调递减所以0<F(x0)<1【点睛】关键点点睛：本题考察含参函数单调性的讨论以及导数中的隐零点问题；处理问题的关键是能够准确分析F(x)的单调性以及求得隐零点的范围以及满足的条件属综合中档题。

普通高等学校招生全国统一考试2024届高三上学期青桐鸣大联考试题语文含解析

2024届普通高等学校招生全国统一考试语文（答案在最后）全卷满分150分，考试时间150分钟。

注意事项：1.答卷前，考生务必将自己的姓名、班级、考场号、座位号、考生号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1~5题。

材料一：为何中华文明五千多年来一脉相承、从未中断，一直延续到今天？这涉及许多方面的原因。

古往今来，中国人民为维护中华文明的连续发展付出了艰辛努力，其中蕴含的中国智慧对于人类文明发展有着重要借鉴意义。

比如，中国古代政治人物关于创与守、得与失、安与危、兴与亡等关系的讨论，大多蕴含着辩证的思想，反映出对于国家治理的谨慎态度，虽然其根本目的在于维护自身统治，但其中包含着一些不可违背的历史法则。

对这些历史法则的遵循，是中华文明连续发展的一个重要原因。

中国古代的许多政治人物都十分重视总结历史经验并提出一些理念，形成独有的政治文化和政治哲学，这种政治文化和政治哲学反过来又推动政治发展和文明发展，这对于中华文明的连续发展有着十分重要的意义。

西周统治者从商朝衰亡中汲取经验教训，强调“我不可不监于有夏，亦不可不监于有殷”，把“天命”搁在一边，倡导以“德”治国，这是中华文明发展史上较早的对历史经验的总结和借鉴。

汉高祖要求陆贾“试为我著秦所以失天下，吾所以得之者何，及古成败之国”。

唐太宗君臣经常以短祚的秦、隋两朝为例，讨论历史借鉴问题。

中国古代政治人物注重总结和借鉴历史经验，这对于维护中华文明突出的连续性具有重要意义。

与汲取历史经验教训紧密联系的，是一些政治人物对国家治理所面临的艰难常怀深深的忧虑，所以都十分重视思考“创业”难还是“守成”难的问题。

2024届高三上学期10月大联考(全国乙卷)文科地理试题(含全解全析)

2024届高三10月大联考（全国乙卷）地理本卷满分100分，考试时间90分钟。

注意事项：1.答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共22小题，每小题2分，共44分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

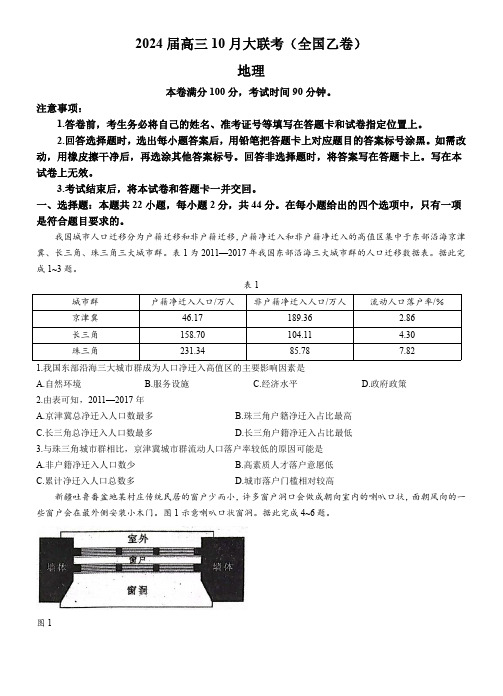
我国城市人口迁移分为户籍迁移和非户籍迁移，户籍净迁入和非户籍净迁入的高值区集中于东部沿海京津冀、长三角、珠三角三大城市群。

表1为2011—2017年我国东部沿海三大城市群的人口迁移数据表。

据此完成1~3题。

表1城市群户籍净迁入人口/万人非户籍净迁入人口/万人流动人口落户率/％京津冀46.17189.36 2.86长三角158.70104.11 4.30珠三角231.3485.787.821.我国东部沿海三大城市群成为人口净迁入高值区的主要影响因素是A.自然环境B.服务设施C.经济水平D.政府政策2.由表可知，2011—2017年A.京津冀总净迁入人口数最多B.珠三角户籍净迁入占比最高C.长三角总净迁入人口数最多D.长三角户籍净迁入占比最低3.与珠三角城市群相比，京津冀城市群流动人口落户率较低的原因可能是A.非户籍净迁入人口数少B.高素质人才落户意愿低C.累计净迁入人口总数多D.城市落户门槛相对较高新疆吐鲁番盆地某村庄传统民居的窗户少而小，许多窗户洞口会做成朝向室内的喇叭口状，面朝风向的一些窗户会在最外侧安装小木门。

图1示意喇叭口状窗洞。

据此完成4~6题。

图14.该地传统民居窗户少而小的主要原因是①夏季减少室内太阳辐射②夏季增强室内通风③冬季减少室内太阳辐射④冬季增强室内保暖A.①③B.①④C.②③D.②④5.当地窗户设计成喇叭口状的主要目的是A.增加室内采光B.减少风沙进入C.节省建筑材料D.提高美观效果6.当地安装小木门的窗户，主要朝向A.东北方B.东南方C.西南方D.西北方2003年成立于湖南长沙的甲公司，主要从事高端乳品生产、研发及销售。

2024届高三12月大联考(全国乙卷)文科数学及答案

绝密★启用前2024届高三12月大联考（全国乙卷）文科数学本卷满分150分，考试时间120分钟.注意事项：1.答卷前，考生务必将自己的姓名､考生号等填写在答题卡和试卷指定位置上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集{}0,1,2,3,4U =，集合{}{}0,1,4,0,3,4M N ==，则()U M N ⋂=ð（）A.{}3B.{}0,2,3,4C.{}0,1,2,4D.{}0,1,2,3,42.若复数z 满足216i z z =+-（i 为虚数单位），则z =（）3.已知实数,x y 满足不等式组202406120x y x y x y -≥⎧⎪+-≥⎨⎪--≥⎩，则3z x y =-的最小值是（）A.1B.2C.3D.64.已知α为第二象限角，且终边与单位圆的交点的横坐标为45-，则5cos 4πα⎛⎫-= ⎪⎝⎭（）A.C.5.已知P 是抛物线2:2(0)C y px p =>上一点，它在抛物线C 的准线l 上的射影为点,Q F 是抛物线C 的焦点，若FPQ 是边长为2的等边三角形，则抛物线C 的准线l 的方程为（）A.14x =-B.12x =-C.1x =- D.2x =-6.某班举办趣味数学活动，规则是：某同学从分别写有1至9这9个整数的9张卡片中随机抽取两张，将卡片上较大的数作为十位数字，较小的数作为个位数字组成一个两位数.若这个两位数与将它的个位数字与十位数字调换后得到的两位数的差为45，就视为该同学获奖.若该班同学A 参加这项活动，则他获奖的概率为（）A.172 B.136C.118D.197.已知函数()()cos (0,0)f x x ωϕωϕπ=+><<在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减，且63f f ππ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭2，则ϕ=（）A.6πB.3πC.4πD.23π8.某校为庆祝建校60周年，有奖征集同学们设计的文创作品.王同学设计的一款文创水杯获奖，其上部分是圆台（多功能盖），下部分是正六棱台（水杯），圆台与棱台的高之比为0.382：0.618，寓意建校60周年，学校发展步入黄金期.这款水杯下部分的三视图如图所示，则这款水杯下部分的容（体）积约为（）A.B.C.D.9.已知函数()()[)2log ,43,4,3x x f x x x ∞⎧∈⎪=⎨∈+⎪-⎩，则满足()13f x ≤≤的x 的取值范围为（）A.][0,24,6⎡⎤⋃⎣⎦B.[]11,4,682⎡⎤⋃⎢⎥⎣⎦C.[]11,2,482⎡⎤⋃⎢⎥⎣⎦D.[]11,2,682⎡⎤⋃⎢⎥⎣⎦10.在ABC 中，内角,,A B C 的对边分别为,,a b c ，已知()sin cos2A Cb B C a ++=，且ABC的面积为，则22a c b+的最小值为（）A.2C.4D.11.已知双曲线2222:1(0,0)y x E a b a b-=>>，过点(),0M b -的两条直线12,l l 分别与双曲线E 的上支､下支相切于点,A B .若MAB 为锐角三角形，则双曲线E 的离心率的取值范围为（）A.⎛ ⎝B.⎛ ⎝C.∞⎫+⎪⎪⎭ D.∞⎫+⎪⎪⎭12.已知323sin ,,ln 232a b c ===，则,,a b c 的大小关系是（）A.b a c >> B.a b c>>C.a c b>> D.b c a>>二､填空题：本题共4小题，每小题5分，共20分.13.已知向量()()1,,2,1a m b ==-.若()2a b + ∥()2a b - ，则实数m 的值为__________.14.在三棱锥P ABC -中，PA ⊥平面,2,ABC AB AC BC PA ====，则三棱锥P ABC -的内切球的表面积等于__________.15.已知数列{}n a 的前n 项和为n S ，且3220,21n n S na n S -+==-，则数列{}n a 的通项公式为n a =__________.16.设函数()f x 是定义域为R 的奇函数，且x ∀∈R ，都有()()20f x f x --=.当(]0,1x ∈时，()ln 21f x x x =+-，则函数()f x 在区间19,22⎡⎤⎢⎥⎣⎦上有__________个零点.三､解答题：共70分.解答应写出文字说明､证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.（一）必考题：共60分.17.（12分）某社区为了解居民生活垃圾分类的投放情况，对本社区10000户居民进行问卷调查（满分：100分），并从这10000份居民的调查问卷中，随机抽取100份进行统计，绘制成如图所示的频率分布直方图.（1）估计该社区10000份调查问卷得分的平均数（同一组中的数据用该组区间的中点值为代表）和这10000户居民中调查问卷得分不低于85分的居民户数；（2）该社区从调查问卷得分为满分的居民中随机挑选了6户，其中两户为,A B ，并将这6户居民随机分配到社区两个宣传点，每个宣传点3户，且每户居民只能去一个宣传点，帮助社区工作人员开展宣传活动，求,A B 两户居民分在不同宣传点的概率.18.（12分）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，4,2,,PA PD AD AB M N ====分别为,PD AB 的中点.（1）求证：AM ⊥平面PCD ；（2）求证：MN ∥平面PBC ；（3）求三棱锥A CMN -的体积.19.（12分）已知数列{}n a 是各项均为正数的等比数列，n S 为数列{}n a 的前n 项和，且1328,327a a ==，213n n nn b a -=.（1）求数列{}n a 的通项公式；（2）求数列{}n b 的前n 项和n T .20.（12分）已知椭圆2222:1(0)x y E a b a b+=>>的左､右焦点分别为())12,F F ，点P 在椭圆E 上，且满足2PF x ⊥轴，12tan PF F ∠=.（1）求椭圆E 的标准方程；（2）设椭圆E 的右顶点为A ，左顶点为B ，是否存在异于点A 的定点(),0(0)Q m m >，使过定点(),0Q m 的任一条直线l 均与椭圆E 交于()()1122,,,M x y N x y （异于,A B 两点）两点，且使得直线AN 的斜率为直线BM 的斜率的2倍？若存在，求出m 的值；若不存在，请说明理由.21.（12分）已知函数()eexax f x x +=+，其中a ∈R ，e 为自然对数的底数.（1）当1a =-时，求函数()f x 的最值；（2）当(]0,e a ∈时，讨论函数()f x 的极值点个数.（二）选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.22.[选修4-4：坐标系与参数方程]（10分）已知直线l 的参数方程为4334x ty t =+⎧⎨=+⎩（t 为参数），以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线M 的极坐标方程为8cos 6sin ρθθ=+.（1）求直线l 的极坐标方程；（2）设直线l 与曲线M 交于,A B 两点，求AOB 的面积.23.[选修4-5：不等式选讲]（10分）已知函数()|1|||f x x x m =--+.（1）当1m =时，求不等式()1f x ≥的解集；（2）若()3f x ≤恒成立，求实数m 的取值范围.2024届高三12月大联考（全国乙卷）文科数学·全解全析及评分标准一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.A 【解析】因为全集{}0,1,2,3,4U =，集合{}0,1,4M =，所以{}U 2,3M =ð.又{}0,3,4N =，所以(){}U3M N ⋂=ð.故选A.2.A 【解析】设()i ,z a b a b =+∈R ，则()i 2i 16i a b a b +=-+-，所以21,26a a b b =+=--，解得1,2a b =-=-，所以z ==，故选A.3.C 【解析】作出不等式组202406120x y x y x y -≥⎧⎪+-≥⎨⎪--≥⎩所表示的可行域，如图中阴影部分所示.3z x y =-，即3y x z =-.当直线3y x =自左上向右下平移时，z -逐渐减小，z 逐渐增大，所以当直线3y x z =-经过直线20x y -=与直线6120x y --=的交点()3,6C 时，z 取得最小值，最小值为3363⨯-=.故选C .4.D 【解析】由题意，得43cos ,sin 55αα=-=，所以5333cos cos cos cos sin sin 4444ππππαααα⎛⎫⎛⎫-=+=- ⎪⎪⎝⎭⎝⎭，故选D.5.B 【解析】不妨设点P 的坐标为()()1111,0,0x y x y >>，依题意，得FQ PQ =，即12p x =+①.又2112y px =②，联立①②，解得113,2p x y ==.22p ==，得1p =，所以抛物线C 的准线l 的方程为122p x =-=-，故选B .6.D 【解析】设同学A 随机抽取得到的两位数的十位数字为x ，个位数字为()y x y >.依题意，若2x =，则1y =，有1种情况；若3x =，则1,2y =，有2种情况⋅ 若9x =，则1,2,,8y = ，有8种情况，共计有12836+++= 种情况，其中满足获奖的情况是()()101045x y y x +-+=，即5x y -=，也即获奖情况只有6,1;7,2;8,3;9,4x y x y x y x y ========，这4种情况，所以该班同学A 参加这项活动获奖的概率为41369=.故选D.7.B 【解析】因为()()cos (0)f x x ωϕω=+>在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减，且263f f ππ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，所以()f x 的最小正周期2,1366T f ππππ⎡⎤⎛⎫⎛⎫=--=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以2,cos 13πωϕ⎛⎫=-+= ⎪⎝⎭，所以()23k k πϕπ=+∈Z .又0ϕπ<<，所以3πϕ=，故选B.8.A 【解析】由三视图，知这款水杯的下部分是上底边长为4，下底边长为3，高为6的正六棱台，226364S S ====下底上底，所以这款水杯下部分的容（体）积约为(11633V S S h =++⨯=⨯⨯=下底上底.故选A.9.D 【解析】令()1f x =，则()()2log 10,4xx =∈∣或[)()314,3x x ∞=∈+-，解得12x =或2x =或6x =.令()3f x =，则()()2log 30,4xx =∈∣或[)()334,3x x ∞=∈-，解得18x =或4x =.画出函数()f x 图象的草图（如图），得满足()13f x ≤≤的x 的取值范围为[]11,2,682⎡⎤⋃⎢⎥⎣⎦.故选D.10.B 【解析】由正弦定理和()sin cos 2A Cb B C a ++=，得sin sin sin sin 2B B A A ⋅=⋅.因为sin 0,sin02B A >>，所以1cos 22B =.因为0,22B π⎛⎫∈ ⎪⎝⎭，所以23B π=.又ABC1sin 2ac B =，所以4ac =.由余弦定理，得222222cos 312b a c ac B a c ac ac =+-=++≥=，当且仅当a c =时取等号，所以b ≥，所以22244a cb b b b b+-==-.因为函数4y b b =-在)∞⎡+⎣上单调递增，所以当b =时，22a c b +故选B.11.D 【解析】如图，设过点(),0M b -的直线()1:(0)l y k x b k =+>，联立()22221y k x b y x ab ⎧=+⎪⎨-=⎪⎩，整理，得()()222232222220b k axb k x b b k a -++-=，依题意，得()2642222Δ440b k bb ka=--=，所以2222a k b=.由双曲线的对称性，得201k <=<，所以()2222a c a <-，整理，得双曲线E的离心率c e a =>故选D.12.B 【解析】方法一：因为sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增，所以32sin sin 233a b π=>=>=.设()1ln g x x x =--，则()111x g x x x -=-='，当[)1,x ∞∈+时，()10x g x x-=≥'，所以()3111ln102g g ⎛⎫>=--= ⎪⎝⎭，所以331ln 22->，即13ln 22>，所以213ln 322b c =>>=.综上，得a b c >>，故选B .方法二：因为sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增，所以32sin sin 233a b π=>=>=.又213ln 322b c =>=>==.综上，得a b c >>，故选B.二､填空题：本题共4小题，每小题5分，共20分.13.12-【解析】因为()()1,,2,1a m b ==- ，所以()()24,21,23,2a b m a b m +=--=-+ .又()2a b + ∥()2a b - ，所以()()423210m m ++-=，解得12m =-.故填12-.14.1225π【解析】如图，由已知，得ABC 的面积为112⨯=三棱锥P ABC -在底面ABC 上的高为PA =，等腰三角形PBC 底边BC 上的高为2，所以三棱锥P ABC -的表面积1122222S =⨯⨯+⨯⨯=，体积113V ==.又三棱锥P ABC -的体积13V Sr =（其中r 为三棱锥P ABC -内切球的半径），所以r =，所以三棱锥P ABC -的内切球的表面积为212425r ππ=.故填1225π.15.53n -+ 【解析】方法一：当1n =时，11220S a -+=，解得12a =-.又220n n S na n -+=，所以()()1222n n n n a n a a S -+==，所以数列{}n a 为等差数列.又321S =-，所以()313212a a +=-，解得312a =-，所以数列{}n a 的公差3152a a d -==-，所以数列{}n a 的通项公式为53n a n =-+.故填53n -+.方法二：*,220n n n S na n ∀∈-+=N 恒成立，当1n =时，11220S a -+=，解得12a =-.当3n =时，332360S a -+=，且321S =-，解得312a =-.当2n ≥时，()()1121210n n S n a n ----+-=①，又220n n S na n -+=②，①-②，得()()12120n n n a n a -----=③，所以()1120n n n a na +---=④.④-③，得()()11120n n n n a a a +---+=.因为2n ≥，所以1120n n n a a a +--+=，即11n n n n a a a a +--=-.又132,12a a =-=-，所以数列{}n a 是首项为-2，公差为-5的等差数列，所以数列{}n a 的通项公式为53n a n =-+.故填53n -+.16.6 【解析】如图，因为函数()f x 是定义域为R 的奇函数，所以()()f x f x -=-，且()00f =.又()()20f x f x --=，即()()2f x f x =-，所以函数()f x 的图象关于直线1x =对称，且()()()2f x f x f x +=-=-，所以()()()42f x f x f x +=-+=，所以4是函数()f x 的一个周期，所以()()()0240f f f ===.易知函数()ln 21f x x x =+-在(]0,1上单调递增，且()11ln 11ln20,1ln1211022f f ⎛⎫=+-=-<=+-=>⎪⎝⎭，所以函数()f x 在区间()0,1上仅有1个零点，且零点在区间1,12⎛⎫⎪⎝⎭上.由对称性，知函数()f x 在区间()1,2上有且仅有1个零点.因为()f x 是定义域为R 的奇函数且是4是它的一个周期，所以()()40f x f x -+=，所以函数()f x 的图象关于点()2,0中心对称，所以函数()f x 在区间()2,4上有且仅有2个零点.因为函数()f x 在区间10,2⎛⎫ ⎪⎝⎭上没有零点，所以函数()f x 在区间94,2⎛⎫⎪⎝⎭上没有零点.结合()()240f f ==，得函数()f x 在区间19,22⎡⎤⎢⎥⎣⎦上有6个零点.故填6.三､解答题：共70分.解答应写出文字说明､证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.（一）必考题：共60分.17.（12分）【解析】（1）由频率分布直方图，得样本平均数为()550.008650.012750.024850.040950.01610x =⨯+⨯+⨯+⨯+⨯⨯79.4=，所以估计该社区10000份调查问卷得分的平均数为79.4.因为这10000户居民中调查问卷得分不低于85分的频率为()90850.0400.016100.36-⨯+⨯=，所以估计该社区这10000户居民中调查问卷得分不低于85分的居民户数为100000.363600⨯=.（2）将6户居民分别记为,,,,,A B c d e f ，依题意，6户居民被随机分到两个宣传点的所有情况有(),ABc def ，()()()()()()()(),,,,,,,,,,,,,,,ABd cef ABe cdf ABf cde Acd Bef Ace Bdf Acf Bde Ade Bcf Adf Bce ，()()()()()()()(),,,,,,,,,,,,,,,Aef Bcd Bcd Aef Bce Adf Bcf Ade Bde Acf Bdf Ace Bef Acd cde ABf ，()()(),,,,,cdf ABe cef ABd def ABc ，共20种，其中,A B 两户居民分在不同宣传点的情况有()()()()(),,,,,,,,,Acd Bef Ace Bdf Acf Bde Ade Bcf Adf Bce ，()()()()()()(),,,,,,,,,,,,,Aef Bcd Bcd Aef Bce Adf Bcf Ade Bde Acf Bdf Ace Bef Acd ，共12种，所以,A B 两户居民分在不同宣传点的概率123205P ==.另解：若采用排列组合解答酌情给分：6户居民均分到两个宣传点共有36C 种情况，其中,A B 两户居民分在相同宣传点有142C 种情况，所以,A B 两户居民分在不同宣传点的概率14362C 31C 5P =-=.18.（12分）【解析】（1）因为底面ABCD 为矩形，所以AD CD ⊥.又平面PAD ⊥平面ABCD ，平面PAD ⋂平面,ABCD AD CD =⊂平面ABCD ，所以CD ⊥平面PAD .又AM ⊂平面PAD ，所以CD AM ⊥.因为在PAD 中，,PA PD AD M ==为PD 的中点，所以AM PD ⊥.又,CD PD D CD ⋂=⊂平面,PCD PD ⊂平面PCD ，所以AM ⊥平面PCD .（2）如图，取PC 的中点E ，连接,ME BE .因为M 为PD 的中点，所以ME ∥CD ，且12ME CD =.又N 为AB 的中点，底面ABCD 为矩形，所以BN∥CD ，且12BN CD =，所以BN ∥EM ，且BN EM =，所以四边形NBEM 为平行四边形，所以BE ∥NM .又BE ⊂平面,PBC MN ⊄平面PBC ，所以MN∥平面PBC .（3）如图，因为,4,2A CMN M ACN V V PA PD AD AB --=====，平面PAD ⊥平面ABCD ，所以点P 到平面ABCD 的距离即为等边三角形PAD 的高，所以点P 到平面ABCD 的距离为4=.又M 为PD 的中点，所以点M 到平面ANC 又11422ANC S =⨯⨯= ，所以123M ACN V -=⨯=A CMN -.19.（12分）【解析】（1）设等比数列{}n a 的公比为(0)q q >.由1328,327a a ==，得228327q =，解得249q =.因为{}n a 的各项均为正数，所以23q =，所以数列{}n a 是以23为首项，23为公比的等比数列，所以数列{}n a 的通项公式为1222333n nn a -⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭.（2）由（1）得21212132233n nn n n n n n n b a ---===⎛⎫⋅ ⎪⎝⎭，所以1221321222n n n n T b b b -=+++=+++ ，231113212222n n n T +-=+++ ，两式相减，得23111111212222222n n n n T +-⎛⎫=++++- ⎪⎝⎭ 1111112142212212n n n -+⎛⎫- ⎪-⎝⎭=+⨯--1323,22n n ++=-所以2332n nn T +=-.20.（12分）【解析】（1）因为2PF x ⊥12tan PF F ∠，解得21,2PF =所以172PF ==.根据椭圆的定义，得12712422a PF PF =+=+=，解得2a =.又c =，所以2221b a c =-=，所以椭圆E 的标准方程为2214x y +=.（2）假设存在满足题意的定点(),0Q m .依题意，设直线l 的方程为,0x ty m m =+>，联立2214x ty m x y =+⎧⎪⎨+=⎪⎩，消去x 并整理，得()2224240t y tmy m +++-=，由()()()22222Δ(2)4441640tm t mt m =-+-=-+>，得224m t <+.由根与系数的关系，得212122224,44tm m y y y y t t -+=-=++.由()()2,2,0,2,0ANBM k k A B =-，得2121222y y x x =⋅-+，所以2121222y y ty m ty m =⋅+-++，即()()1212222m y m y ty y --++=，所以()()()212242224t m m y m y t ---++=+，所以()()()21221224222424t m m y m y t tm y y t ⎧-⎪--++=⎪+⎨⎪+=-⎪+⎩，所以()()()()()21212222222224m y m y tm m m y m y t ⎧⎪--++=⎪⎨+⎪+++=-⎪+⎩②，②-①，得()()()12232324t m m m y t -+--=+，当320m -≠时，解得()()12222424t m y t t m y t ⎧-+=⎪⎪+⎨--⎪=⎪+⎩，所以()()22122244t m y y t-=+.又212244m y y t -=+，所以()()2222224444t m mt t --=++.因为上式在t 变化时恒成立，所以240m -=.又0m >，所以2m =.此时点Q 与点A 重合，不合题意，舍去；所以320m -=，即23m =，此时点2,03Q ⎛⎫⎪⎝⎭在椭圆E 的内部，满足直线l 均与椭圆E 交于,M N 两点，所以存在定点2,03Q ⎛⎫⎪⎝⎭满足题意，23m =.21.（12分）【解析】（1）当1a =-时，()e e x x f x x -+=+，则()e 1e e 11e ex x xx x f x '--+--=+=.令()e e 1xx x ϕ=+--，则()x ϕ在R 上单调递增，且()1e 1e 10ϕ=+--=，所以当(),1x ∞∈-时，()0x ϕ<，即()0f x '<；当()1,x ∞∈+时，()0x ϕ>，即()0f x '>，所以()f x 在(),1∞-上单调递减，在()1,∞+上单调递增，所以函数()f x 在1x =处取得极小值()112ef =-，即()f x 有最小值12e-，没有最大值.（2）因为()e e x ax f x x +=+，其中(]0,e a ∈，所以()()()2e e e e e 1e ex x x x x a ax ax a f x -+⋅'-+-=+=.令()e e xg x ax a =-+-，则()e xg x a '=-.因为0a >，令()e 0xg x a =-='，则ln x a =，所以当(),ln x a ∞∈-时，()0g x '<；当()ln ,x a ∞∈+时，()0g x '>，所以()g x 在(),ln a ∞-上单调递减，在()ln ,a ∞+上单调递增，所以()min ()ln 2ln e g x g a a a a ==--.设()2ln e h a a a a =--，其中(]0,e a ∈，则()1ln h a a =-'.令()1ln 0h a a =-='，解得e a =.当(]0,e a ∈时，()0h a '≥，所以()h a 在(]0,e 上单调递增，所以()max ()e 2e elne e 0h a h ==--=.所以当()0,e a ∈时，min ()2ln e 0g x a a a =--<；当e a =时，min ()0g x =.①当e a =时，min ()0g x =，即()0g x ≥，也即()0f x '≥，所以()f x 在R 上单调递增，所以()f x 没有极值点.②当()0,e a ∈时，()ln 1,a g x <在(),ln a ∞-上单调递减.设()e e ln ln t a a a a a ⎛⎫=--=+ ⎪⎝⎭，则当()0,e a ∈时，()221e e 0a t a a a a '-=-=<，所以()()e 20t a t >=>，即当()0,e a ∈时，eln a a-<.又()g x 在(),ln a ∞-上单调递减，所以()g x 在e ,a ∞⎛⎫--⎪⎝⎭上单调递减，且在e ,ln a a ⎡⎫-⎪⎢⎣⎭上单调递减，所以当e ,x a ∞⎛⎫∈-- ⎪⎝⎭时，()e ee e e e e 0aa g x g a a a --⎛⎫>-=++-=+> ⎪⎝⎭，所以()g x 在e ,a ∞⎛⎫--⎪⎝⎭上没有零点，且()e ln 0g g a a ⎛⎫-⋅< ⎪⎝⎭.又()g x 在e ,ln a a ⎡⎫-⎪⎢⎣⎭上单调递减，所以在e ,ln a a ⎡⎫-⎪⎢⎣⎭内存在唯一0x ，使()00g x =，所以当()0,x x ∞∈-时，()0g x >；当()0,ln x x a ∈时，()0g x <，也即当()0,x x ∞∈-时，()0f x '>；当()0,ln x x a ∈时，()0f x '<，所以0x 为()f x 的一个极大值点.又()()10,g g x =在()ln ,a ∞+上单调递增，ln 1a <，所以当()ln ,1x a ∈时，()0g x <；当()1,x ∞∈+时，()0g x >，即当()ln ,1x a ∈时，()0f x '<；当()1,x ∞∈+时，()0f x '>，所以1为()f x 的一个极小值点，所以当()0,e a ∈时，()f x 有2个极值点.综合①②，当()0,e a ∈时，()f x 有2个极值点；当e a =时，()f x 没有极值点.（二）选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.22.[选修4-4：坐标系与参数方程]（10分）【解析】（1）直线l 的参数方程为4334x ty t=+⎧⎨=+⎩（t 为参数），消去参数t 并整理，得4370x y --=.因为cos ,sin x y ρθρθ==，所以直线l 的极坐标方程为4cos 3sin 70ρθρθ--=.（2）由（1）知直线l 的普通方程为4370x y --=.曲线M 的极坐标方程为8cos 6sin ρθθ=+，化为直角坐标方程为22(4)(3)25x y -+-=，所以曲线M 是圆心为()4,3，半径为5的圆.又直线l 过圆心()4,3，所以10AB =，所以原点O 到直线l的距离75d ，所以AOB 的面积1710725AOB S =⨯⨯= .23.[选修4-5：不等式选讲]（10分）【解析】（1）当1m =时，()2,1112,11,2,1x f x x x x x x -≥⎧⎪=--+=--<<⎨⎪≤-⎩所以()1f x ≥可化为211x ≥⎧⎨≤-⎩，或2111x x -≥⎧⎨-<<⎩，或211x -≥⎧⎨≥⎩，解得1,2x ≤-所以不等式()1f x ≥的解集为1,2∞⎛⎤-- ⎥⎝⎦.（2）()3f x ≤恒成立，即13x x m --+≤恒成立.因为||1|||||1|x x m m --+≤+恒成立，所以13m +≤，解得42m -≤≤，所以实数m 的取值范围是[]4,2-.。

2024届高三上学期10月大联考(全国乙卷)生物数学试题全解全析

2024届高三10月大联考（全国乙卷）生物学·全解全析及评分标准1．【答案】C【解析】细胞的命名者是英国科学家虎克，A错误；细胞学说揭示了动植物的统一性，没有揭示其多样性，B错误；细胞学说提出细胞是一个相对独立的单位，C正确；细胞学说使人们对生命的认识由个体水平进入细胞水平，D错误。

2．【答案】B【解析】肺炎支原体中有由DNA和蛋白质组成的复合物，如DNA复制时由酶和DNA组成的复合物，A正确；支原体、衣原体、立克次氏体虽然主要营活细胞寄生生活，但它们有细胞结构，故能用培养基培养，B错误；支原体、衣原体、立克次氏体都是原核生物，没有核膜和核仁，C正确；三者均属于单细胞生物，因此其属于生命系统的细胞层次和个体层次，D正确。

3．【答案】D【解析】氰化物能与线粒体内膜的某种蛋白质结合，抑制A TP的合成，因此氰化物会阻断人体细胞内有氧呼吸的第三阶段，A错误；氰化物影响的是有氧呼吸的第三阶段，并不需要光照，即抗氰呼吸不需要光照，B错误；人体细胞中A TP合成可在细胞质基质、线粒体内膜和线粒体基质中进行，三处均有ATP 合成酶，C错误；细胞在消耗等量相同呼吸底物的情况下，抗氰呼吸与正常呼吸释放的能量是相同的，其中一部分用来合成A TP，其余部分以热能形式散失，抗氰呼吸比正常呼吸产生的热量多，则合成的ATP 就少，D正确。

4．【答案】C【解析】蛋白质种类繁多的原因是组成蛋白质的氨基酸种类、数目和排列顺序不同以及肽链的盘曲、折叠方式及其形成的空间结构千差万别，不同种类氨基酸的连接方式相同，都是脱水缩合，A错误；细胞中的无机盐并不都是以离子形式存在的，也有的以化合物形式存在，如有些钙在骨骼、牙齿中以碳酸钙的形式存在，B错误；胆固醇既是动物细胞膜的重要成分，又参与人体血液中脂质的运输，C正确；细胞中的水包括自由水和结合水，晾晒使种子失去的是自由水，结合水并未丢失，D错误。

5．【答案】B【解析】人工淀粉是多糖，组成元素只有C、H、O，A正确；人工淀粉彻底水解的产物是葡萄糖，B错误；ASAP过程与光合作用类似，都要进行能量的转化与储存，C正确；植物利用CO2合成淀粉的过程发生在叶绿体基质中，D正确。

2024届普通高等学校招生全国统一考试青桐鸣4月大联考语文试题及答案

2024 届普通高等学校招生全国统一考试青桐鸣大联考(高三)语文全卷满分150分，考试时间150分钟。

注意事项：1.答卷前，考生务必将自己的姓名、班级、考场号、座位号、考生号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，18分）阅读下面的文字，完成1~5题。

在微粒说与波动说的第一次交锋中，以牛顿为首的微粒说战胜了波动说，取得了在物理学界被普遍公认的地位。

近一个世纪过去了，英国米尔沃顿的一个教徒的家庭里诞生了一个男孩，他被取名为托马斯·杨。

经过学习和探究，他最终形成了光具有波动性质的想法，这个认识源于波动中所谓的“干涉”现象，波的干涉现象是各种波所独有的基本特征。

我们都知道，普通的物质是具有累加性的，一滴水加上一滴水一定是两滴水，而不会一起消失。

但是波动就不同了，一列普通的波，有着波的高峰和波的谷底，如果两列振幅相同的波相遇，当它们正好都处在高峰时，那么叠加起来的这个波就会达到两倍的峰值，如果都处在低谷时，叠加的结果就会?答案是它们会互相抵消。

如果两列波在这样的情况下相遇——物理上叫作“反相”——那么在它们重叠的地方将会波平如镜，既没有高峰，也没有谷底。

这就像一个人把你往左边拉，另一个人用相同的力气把你往右边拉，结果是你会站在原地不动。

托马斯·杨在研究牛顿环的明暗条纹的时候，被这个关于波动的想法给深深打动了。

为什么会形成一明一暗的条纹呢?一个想法渐渐地在杨的脑海里成形：用波来解释不是很简单吗?明亮的地方，那是因为两道光正好是“同相”的，就好像有两个人同时在左边或者右边拉你，它们的波峰和波谷都得到增强，结果造成了两倍光亮的效果；而黑暗的那些条纹，则一定是两道光处于“反相”，它们的波峰、波谷相对时，就好像两个人同时往两边拉你，正好互相抵消了。

2024届高三上学期10月大联考(全国乙卷)文科数学试题及答案

绝密★启用前2024届高三10月大联考（全国乙卷）文科数学本卷满分150分，考试时间120分钟.注意事项：1.答卷前，考生务必将自己的姓名､考生号等填写在答题卡和试卷指定位置上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}215,1,1,3A x x B =∈+<=-Z∣，则A B ⋃中元素的个数为（）A.3B.4C.5D.62.已知命题200:p x x ∃≥>，则命题p 的否定为（）A.200x x ∃<≤ B.2x x ∀≥<C.2x x ∀<> D.2x x ∀≥≤3.若不等式2510x ax -+<的解集为1,a a ⎛⎫⎪⎝⎭，则a =（）A.12-B.12C.14-D.144.若函数()e ,3ln 2,3x x x f x x x ⎧-≤=⎨->⎩，则()()2ef f =（）A.-1B.-2C.1D.ln22-5.已知54:1,:log 2(033a p a q a <<>>且1)a ≠，则p 是q 的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.函数()242log 2xf x x x+=-的大致图象是（）A. B.C. D.7.白色污染是人们对难降解的塑料垃圾（多指塑料袋）污染环境现象的一种形象称谓，经过长期研究，一种全生物可降解塑料（简称PBAT ）逐渐被应用于超市购物袋､外卖包装盒等产品.研究表明，在微生物的作用下，PBAT 最终可被完全分解为二氧化碳和水进入大自然，当其分解率（100%=⨯已分解质量分解率总质量）超过60%时，就会成为对环境无害的物质.为研究总质量为100g 的PBAT 的已分解质量y （单位：g ）与时间x （单位：月）之间的关系，某研究所人员每隔1个月测量1次PBAT 的已分解质量，对通过实验获取的数据做计算处理，研究得出已分解质量y 与时间x 的函数关系式为 4.60.1100e x y -=-.据此研究结果可以推测，总质量为100g 的PBAT 被分解为对环境无害的物质的时间至少为（）（参考数据：ln40 3.7≈）A.8个月B.9个月C.10个月D.11个月8.已知,0,,2παβαβ⎛⎫∈> ⎪⎝⎭，且()()17cos cos cos sin sin sin ,sin cos 510ααβααβαβ-+-==，则()sin αβ+=（）A.45B.35 C.25D.3109.已知O 是ABC 所在平面内一点，若0,,,,,OA OB OC AM xAB AN y AC MO ON x y λ++====均为正数，则xy 的最小值为（）A.12B.49C.1D.4310.若函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭∣的部分图象如图所示，则下列说法正确的个数为（）①2ω=；②6πϕ=-；③()f x 在5,26ππ⎛⎫⎪⎝⎭上单调递减；④32f π⎛⎫-= ⎪⎝⎭.A.1B.2C.3D.411.已知函数()f x 是偶函数，当0x >时，()2log 1f x x =-，则不等式()()102x f x f x -≥--的解集是（）A.11,00,22⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭B.][()2,11,2--⋃C.112,0,22⎛⎫⎛⎫--⋃ ⎪ ⎪⎝⎭⎝⎭D.()[)11,2,00,1,222∞⎛⎫⎛⎫--⋃-⋃⋃ ⎪ ⎪⎝⎭⎝⎭12.已知函数()2cos (1)xxf x a ax x a -=+++>，则11e 2,e ,ff fππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭的大小关系为（）A.11e e 2f f f ππ⎛⎫⎛⎫<-< ⎪ ⎪⎝⎭⎝⎭.B.11e 2e ff f ππ⎛⎫⎛⎫<<- ⎪ ⎪⎝⎭⎝⎭C.11e2e f ff ππ⎛⎫⎛⎫<<- ⎪ ⎪⎝⎭⎝⎭D.11e e 2f f f ππ⎛⎫⎛⎫-<< ⎪ ⎪⎝⎭⎝⎭二､填空题：本题共4小题，每小题5分，共20分.13.已知向量()()1,2,2,a b x =-= ，若a b ⊥ ，则实数x =__________.14.请写出一个满足对任意的()12,0,x x ∞∈+；都有()()()1212f x x f x f x =的函数__________.15.《海岛算经》是魏晋时期数学家刘徽所著的测量学著作，书中有一道测量山上松树高度的题目，受此题启发，小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度.如图，把塔底与塔顶分别看作点C ，D ，CD 与地面垂直，小李先在地面上选取点A ，B （点,A B 在建筑物的同一侧，且点,,,A B C D 位于同一个平面内），测得AB =，在点A 处测得点,C D 的仰角分别为30,67 ，在点B 处测得点D 的仰角为33.5 ，则塔高CD 为__________m .（参考数据：3sin375≈）16.已知函数()()ln 2f x x a x x =+-在定义域上单调递增，则实数a 的取值范围为__________.三､解答题：共70分.解答应写出文字说明､证明过程或演算步骤.17.（10分）已知向量()()sin cos ,1,2cos ,1a x x b x =+=- ，函数()f x a b =⋅，将函数()f x 的图象向右平移6π个单位长度，得到函数()g x 的图象.（1）求函数()f x 的最小正周期和单调递增区间；（2）解方程()0g x =.18.（12分）如图，在平行四边形ABCD 中，13AM AD = ，令,AB a AC b ==.（1）用,a b表示,,AM BM CM ；（2）若2AB AM ==，且10AC BM ⋅= ，求cos ,a b.19.（12分）某公园池塘里浮萍的面积y （单位：2m ）与时间t （单位：月）的关系如下表所示：时间/t 月1234浮萍的面积2/m y 35917现有以下三种函数模型可供选择：①y kt b =+，②t y p a q =⋅+，③log a y m t n =⋅+，其中,,,,,,k b p q m n a 均为常数，0a >且1a ≠.（1）直接选出你认为最符合题意的函数模型，并求出y 关于t 的函数解析式；（2）若该公园池塘里浮萍的面积蔓延到22215m ,31m ,211m 所经过的时间分别为123,,t t t ，写出一种123,,t t t 满足的等量关系式，并说明理由.20.（12分）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，且__________.1cossin C A -=；②sin sin sin sin A C A Bbc ab ac --=两个条件中任选一个，填入上面横线处，并解决下列问题.（1）求C ；（2）若ABC 外接圆的半径为ABC 的面积为ABC 的周长.注：若选择不同的条件分别解答，则按第一个解答计分.21.（12分）已知函数()2e 1xf x ax x =-+-.（1）当1a =时，求曲线()y f x =在1x =处的切线方程；（2）若()0f x =有两个不等的实根，求实数a 的取值范围.22.（12分）已知函数()ln 4,f x x a x a =--∈R .（1）讨论函数()f x 的单调性；（2）当1a =时，令()()()2e xF x x f x =--，若0x x =为()F x 的极大值点，证明：()001F x <<.2024届高三10月大联考（全国乙卷）文科数学•全解全析及评分标准一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.B 【解析】因为{}{}221541,0,1,1,1,3A x x x x B =∈+<=∈<=-=-ZZ ∣∣，所以{}1,0,1,3A B ⋃=-，有4个元素，故选B.2.D 【解析】根据特称命题的否定为全称命题，知命题“200x x ∃≥>”的否定是“2x x ∀≥”，故选D.3.A 【解析】因为不等式2510x ax -+<的解集为1,a a ⎛⎫⎪⎝⎭，所以15a a a +=，解得12a =±.又1a a >，所以1a >或0a <，所以12a =-（12a =不满足题意，舍去），当12a =-时，2(5)40a -->，故选A.4.C 【解析】因为2e 3>，所以()22e lne20f =-=，所以()()()2e 0e01f f f ==-=，故选C.5.B 【解析】对于q ，若4log 23a>，则24log log 3a a a >.当01a <<时，243a >，无解.当1a >时，243a <，得2313a <<，即不等式4log 23a >的解集为1,3⎛⎫ ⎪ ⎪⎝⎭.因为1,3⎛⎫ ⎪ ⎪⎝⎭⫋51,3⎛⎫⎪⎝⎭，所以p 是q 的必要不充分条件，故选B.6.D【解析】方法一：由题意，知函数()242log 2xf x x x+=-的定义域为()2,2-，关于原点对称，且()()242()log 2xf x x f x x --=-=-+，所以函数()f x 是奇函数，其图象关于原点对称，故排除B,C ；当()0,2x ∈时，212x x +>-，即42log 02xx +>-，因此()0f x >，故排除A.故选D.方法二：由方法一，知函数()f x 是奇函数，其图象关于原点对称，故排除B,C ；又()211log 302f =>，所以排除A.故选D.7.C 【解析】令 4.60.1100e 60x y -=->，得0.1 4.6ln400.9x >-≈，解得9x >，故至少需要10个月，总质量为100g 的PBAT 才会被分解为对环境无害的物质.故选C.8.A【解析】因为()()1cos cos cos sin sin sin 5ααβααβ-+-=，所以()11cos 5αβ--=，所以()4cos 5αβ-=.因为,0,,2παβαβ⎛⎫∈> ⎪⎝⎭，所以02παβ<-<，所以()3sin 5αβ-=，所以3sin cos cos sin 5αβαβ-=.又7sin cos 10αβ=，所以1cos sin 10αβ=，所以()714sin sin cos cos sin 10105αβαβαβ+=+=+=.故选A.9.B 【解析】因为0OA OB OC ++=，所以点O 是ABC 的重心，所以()()211323AO AB AC AB AC =⨯+=+ .因为,AM xAB AN y AC ==，所以11,AB AM AC AN x y == ，所以1133AO AM AN x y=+ .因为MO ON λ=，所以,,M O N 三点共线，所以11133x y +=，即113x y+=.因为,x y 均为正数，所以11x y +≥32≤，所以49xy ≥1132x y ==，即23x y ==时取等号），所以xy 的最小值为49.故选B.10.C 【解析】由题图，得2A =，最小正周期54126T πππ⎛⎫=⨯-= ⎪⎝⎭.又2T ππω==，所以2ω=，故①正确；()()2sin 2f x x ϕ=+，又()f x 的图象过点5,212π⎛⎫⎪⎝⎭，所以522122k k ππϕπ⨯+=+∈Z ，所以2,3k k πϕπ=-∈Z .又2πϕ<，所以3πϕ=-，故②错误；()2sin 23f x x π⎛⎫=- ⎪⎝⎭，令23t x π=-，当526x ππ<<时，2433t ππ<<，函数sin y t =在24,33ππ⎛⎫⎪⎝⎭上单调递减，故③正确；2sin23f πππ⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭.故选C.11.D【解析】根据题意，作出函数()y f x =的图象，如图所示.因为函数()y f x =是偶函数，所以()()f x f x -=.由()()102x f x f x -≥--，得()10x f x -≥-，所以()10x f x -≤，所以()()()100f x x f x ⎧-≤⎪⎨≠⎪⎩，所以()100x f x -≥⎧⎨<⎩或()100x f x -≤⎧⎨>⎩，观察图象，得12x ≤<或102x <<或102x -<<或2x <-，故选D.12.B 【解析】易知()2cos (1)xxf x a ax x a -=+++>是偶函数，()()ln 2sin x x f x a a a x x -=-+-'，当0x >时，因为1a >，所以ln 0,0x x a a a ->->.令()2sin ,0x x x x ϕ=->，则()2cos 0x x ϕ=->'，所以()x ϕ单调递增，所以()()00x ϕϕ>=，所以()()0,f x f x '>在()0,∞+上单调递增.构造函数()ln xg x x=，则()21ln xg x x-='.令()0g x '>，得0e x <<，令()0g x '<，得e x >，所以()g x 在区间()0,e 上单调递增，在区间()e,∞+上单调递减.又ln2ln424=，所以()()()4e g g g π<<，所以ln2ln4ln lne24e ππ=<<，所以111e22e ππ<<，所以111e ee e ff f f ππ⎛⎫⎛⎫⎛⎫<<=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即11ee f f f ππ⎛⎫⎛⎫<<- ⎪ ⎪⎝⎭⎝⎭.故选B .二､填空题：本题共4小题，每小题5分，共20分.13.1【解析】因为a b ⊥ ，所以()1220x ⨯+-=，解得1x =.故填1.14.()12f x x-=（答案不唯一）【解析】任意定义域为()0,∞+的幂函数均可，例如()12f x x-=，()()()()()111122221212121212,f x x x x f x f x x x x x ----==⋅=，即()()()1212f x x f x f x =成立.故可填()12f x x-=.15.24【解析】如图，延长DC 与BA 的延长线交于点E ，则67,30,33.5DAE CAE DBA ∠∠∠=== ，所以33.5ADB ∠= ，所以AD AB ==在ACD 中，37,120CAD ACD ∠∠==，由正弦定理，得3sin37524sin120AD CD =≈=.故填24.16.[)1,∞+【解析】()()ln 2f x x a x x =+-的定义域为()0,∞+，由()()ln 2f x x a x x =+-在定义域上单调递增，得()ln 10af x x x=+-≥'在()0,∞+上恒成立，即ln a x x x ≥-在()0,∞+上恒成立.设()ln (0)g x x x x x =->，所以只需()max (),ln a g x g x x -'≥=，当01x <<时，()0g x '>，当1x >时，()0g x '<，所以()g x 在()0,1上单调递增，在()1,∞+上单调递减，所以()max ()11g x g ==，所以1a ≥，所以实数a 的取值范围为[)1,∞+.故填[)1,∞+.三､解答题：共70分.解答应写出文字说明､证明过程或演算步骤.17.（10分）【解析】（1）由已知，得()f x a b =⋅()2cos sin cos 1x x x =+-sin 2cos 2x x=+24x π⎛⎫=+ ⎪⎝⎭所以函数()f x 的最小正周期222T πππω===.由222242k x k k πππππ-≤+≤+∈Z ，解得3,88k x k k ππππ-≤≤+∈Z ，所以函数()f x 的单调递增区间为3,,88k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z .（2）将函数()f x 的图象向右平移6π个单位长度，得到函数()226412g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象.令()2012g x x π⎛⎫=-= ⎪⎝⎭，得2,12x k k ππ-=∈Z ，解得,224k x k ππ=+∈Z ，所以方程()0g x =的解集为,224k x x k ππ⎧⎫=+∈⎨⎬⎩⎭Z ∣.18.（12分）【解析】（1）因为,AB a AC b ==，所以BC AC AB b a =-=-，所以()11,33AM BC b a ==-所以()114333BM AM AB b a a b a =-=--=- ，所以()14123333CM BM BC b b a a b =-=---=-- .（2）方法一：由（1）知()114,333AM b a BM =-=-.又,10,2AC b AC BM AB AM =⋅===，所以()14110,2,2333b b a b a a ⎛⎫⋅-=-== ⎪⎝⎭，即222430,236b a b b a a b -⋅=+-⋅=，解得1,a b b ⋅==所以34cos ,68a b a b a b⋅〈〉==.方法二：因为1,23AM AD AM ==，所以6AD =，所以6BC =.因为()22121333AC BM BC BA BA BC BA BA BC BC ⎛⎫⋅=-⋅+=-+⋅+ ⎪⎝⎭，且10AC BM ⋅= ，所以2221262cos 61033ABC ∠-+⨯⨯⨯+=，解得1cos 4ABC ∠=，所以()()22126214a b BA BC BA BA BC BA ⋅=-⋅-=-⋅+=-⨯⨯= .又2,a b ===，所以cos ,68a b a b a b⋅〈〉==.19.（12分）【解析】（1）应选择函数模型②t y p a q =⋅+.依题意，得12335,9p a q p a q p a q ⎧⨯+=⎪⨯+=⎨⎪⨯+=⎩解得12,1p a q =⎧⎪=⎨⎪=⎩所以y 关于t 的函数解析式为21t y =+.（2）1231t t t +=+.理由：依题意，得3122115,2131,21211t t t +=+=+=，所以312214,230,2210t t t ===，所以1222420,t t ⋅=所以3312121222420222t t t t t t ++⋅===⨯=，所以1231t t t +=+.20.（12分）【解析】（11cossin C A -=及正弦定理，得()sin sin 1cos C A A C =-.sin 0,sin A C C ≠∴+= ，sin 32C π⎛⎫∴+= ⎪⎝⎭.又40,333C C ππππ<<∴<+<，2,333C C πππ∴+=∴=.若选②：由sin sin sin sin A C A B bc ab ac --=，得sin sin sin sin a A c C b A b B -=-.由正弦定理，得222a b c ab +-=.由余弦定理，得2221cos 222a b c ab C ab ab +-===.因为()0,C π∈，所以3C π=.（2）设ABC 外接圆的半径为R ，由正弦定理，得2sin 2sin63c R C π==⨯=.又113sin 222ABC S ab C ab ==⨯= ，所以4ab =.由222212cos ()222c a b ab C a b ab ab =+-=+--⨯，可得236()12a b =+-，解得a b +=，所以ABC 的周长为6a b c ++=.21.（12分）【解析】（1）当1a =时，()()2e 1,e 21x xf x x x f x x =-+-'=-+，()()1e 1,1e 1,f f =-=-'所以曲线()y f x =在1x =处的切线方程为()()()e 1e 11y x --=--，即()e 10x y --=.（2）显然()00f =，要使方程()0f x =有两个不等的实根，只需当0x ≠时，()0f x =有且仅有一个实根，当0x ≠时，由方程()0f x =，得2e 1x x a x+-=.令()()2e 10x x g x x x +-=≠，则直线y a =与()()2e 10x x g x x x +-=≠的图象有且仅有一个交点.()()()()()243e 12e 12e1x x x x x x x g x x x +-+---=='.又当0x <时，()()0,g x g x '<单调递减，当02x <<时，()()0,g x g x '<单调递减，当2x >时，()()0,g x g x '>单调递增，所以当2x =时，()g x 取得极小值()2e 124g +=，又当0x <时，e 1x <，所以e 10x x +-<，即()0g x <，当0x >时，e 1,e 10x x x >+->，即()0g x >，所以作出()g x 的大致图象如图所示.由图象，知要使直线y a =与()()2e 10x x g x x x +-=≠的图象有且仅有一个交点，只需0a <或2e 14a +=.综上，若()0f x =有两个不等的实根，则a 的取值范围为()2e 1,04∞⎧⎫+-⋃⎨⎬⎩⎭.22.（12分）【解析】（1）函数()f x 的定义域为()()0,,1a x a f x x x∞-+=-='，①当0a ≤时，()0f x '>，函数()f x 在()0,∞+上单调递增；②当0a >时，由()0f x '>，得x a >，由()0f x '<，得0x a <<，所以，函数()f x 在(),a ∞+上单调递增，在()0,a 上单调递减.综上，当0a ≤时，函数()f x 在()0,∞+上单调递增；当0a >时，函数()f x 在(),a ∞+上单调递增，在()0,a 上单调递减.（2）当1a =时，()()()()()112e ln 4,1e 11e x x x F x x x x F x x x x x ⎛⎫=--++=--+=-- ⎪⎝⎭'，设()1e x g x x =-，则()21e x g x x =+'，当0x >时，()0g x '>，所以()g x 在()0,∞+上单调递增，又()120,1e 102g g ⎛⎫=-<=-> ⎪⎝⎭，所以存在01,12x ⎛⎫∈ ⎪⎝⎭，使得()00g x =，所以当00x x <<时，()0F x '>，当01x x <<时，()0F x '<，当1x >时，()0F x '>，所以()F x 在()00,x 上单调递增，在()0,1x 上单调递减，在()1,∞+上单调递增，所以当0x x =时，()F x 取得极大值，且001e 0xx -=，所以00001e ,ln x x x x ==-，()()00000000000212e ln 4452x x F x x x x x x x x x ⎛⎫-=--++=--+=-+ ⎪⎝⎭.因为01,12x ⎛⎫∈ ⎪⎝⎭，所以()001F x <<.。

全国大联考

化学丨青桐鸣大联考河南省2025届高三10月大联考化学试卷及答案

2023届全国乙卷高三5月大联考语文试题

2024届高三12月大联考(全国乙卷)理综答案(全解全析及评分标准)

2023年高三5月大联考(全国乙卷)文科数学试题及参考答案

全国第一次大联考试卷语文

2024全国名校大联考高三上学期第一联考(月考)语文试题及答案

2024届高三12月大联考(全国乙卷)语文答案

2024届高三5月大联考(全国乙卷)语文试题()

全国名校大联考2023-2024学年高三上学期第一联考(月考)物理试题及答案

2024届高三10月大联考(全国乙卷)文科数学含答案解析

普通高等学校招生全国统一考试2024届高三上学期青桐鸣大联考试题 语文含解析

2024届高三上学期10月大联考(全国乙卷)文科地理试题(含全解全析)

2024届高三12月大联考(全国乙卷)文科数学及答案

2024届高三上学期10月大联考(全国乙卷)生物数学试题全解全析

2024届普通高等学校招生全国统一考试青桐鸣4月大联考语文试题及答案

2024届高三上学期10月大联考(全国乙卷)文科数学试题及答案

普通高等学校招生全国统一考试2024届高三上学期青桐鸣大联考试题语文含解析