电力阻塞回归预测

合集下载

电力系统中的电力需求预测方法

电力系统中的电力需求预测方法电力需求预测是电力系统规划和运营的关键环节之一。

准确预测电力需求可以有效指导发电计划、调度和节能措施，提高电力系统的可靠性和经济性。

本文将介绍几种常见的电力需求预测方法，并探讨其优缺点及适用场景。

一、统计分析法统计分析法是一种常用的电力需求预测方法。

它基于历史数据，通过对电力需求的趋势进行分析和预测。

其中，最常用的方法是时间序列分析法。

时间序列分析法假设未来的电力需求与过去的需求存在一定的关联，因此可以根据过去的数据来预测未来的需求。

时间序列分析法主要包括以下几个步骤：首先，对历史数据进行平稳性检验，以确保数据的稳定性；然后，通过自相关和偏自相关函数的分析，确定合适的模型阶数；接下来，根据确定的模型，进行参数估计和模型检验；最后，利用确定的模型来进行未来的需求预测。

统计分析法的优点是简单易用，只需要依靠历史数据即可进行预测。

但是，该方法假设未来的需求与过去的需求完全一致，无法考虑到外部因素的影响。

此外，该方法对数据的平稳性有一定要求，如果数据存在趋势或季节性，需要进行预处理。

二、回归分析法回归分析法是一种通过寻找自变量与因变量之间的关系，来进行预测的方法。

在电力需求预测中，通常将天气等外部因素作为自变量，电力需求作为因变量，建立回归关系，进而进行需求预测。

回归分析法的关键是选择合适的自变量。

在电力需求预测中，常用的自变量包括温度、湿度、季节等因素。

通过建立多元回归模型，可以较准确地预测电力需求。

回归分析法的优点是可以考虑到外部因素的影响，可以提高预测的准确性。

然而，该方法需要收集大量的外部数据，并且需要对不同自变量进行分析和筛选，这增加了分析的复杂性和计算的难度。

三、人工神经网络人工神经网络是一种模仿人脑神经网络结构和功能的数学模型。

它通过模拟神经元之间的相互作用来进行信息处理和预测。

在电力需求预测中，可以利用人工神经网络来建立电力需求与各种因素之间的复杂非线性关系，从而进行预测。

用线性回归分析法进行电力负荷预测

用线性回归分析法进行电力负荷预测摘要：电力负荷预测是电网规划的基础，论文介绍了电力负荷线性回归模型预测基本原理，通过对变量数据统计分析，确定其之间的相关关系。

以福建建阳地区为例分析历史数据，采用EXCEL回归模型的求解方法，证明拟合曲线方程具有较高的预测精确度、实用性。

能够作为福建建阳电力公司进行负荷预测的科学依据。

关键词：电力负荷预测；线性回归分析；最小二乘法1、概述电力负荷预测是供电公司或电力调度部门制定购电计划的依据，是电网规划决策的基础，一个高准确性的负荷预测为电力系统经济、安全运行提供了有力保证。

电力负荷预测从预测内容分类，可分为电量预测和电力预测两大类，其中电量预测主要包含的数据为全社会用电量、网供电量、各产业电量等，电力预测主要包含的数据为最大负荷、最小负荷、负荷曲线等；从预测时间长短分类，可分为超短期、短期、中期和长期预测。

中长期预测受到经济，社会发展、环境等诸多因素的影响，在地区电网规划中应用最多。

2、电力负荷原始数据资料收集电力系统负荷预测，是从已知的社会经济、发展数据以及电力需求为出发点，通过对历史数据统计分析，得出电力需求高度相关的社会经济、发展数据变量拟合曲线方程。

以此作为科学依据，用未来年份社会经济、发展数据预测结果，对电力需求做出预测。

在电力负荷预测之前,需要调研和收集包括电力企业资料、国民经济部门相关资料及数据，选择可靠的和有用的数据作为预测依据。

负荷预测收集的资料一般应包括以下内容：该地区国民经济及社会发展规划、社会经济基本情况、电力系统发展规划、电网现状及存在问题、历年来该地区用电负荷及用电量等。

3、电力负荷线性回归模型预测基本原理电力负荷线性回归模型预测，是根据历史负荷数据建立数学模型，用数理统计中的回归分析法对未来的负荷进行预测。

即采用最小二乘法对已知变量进行统计分析，观测每组变量数据，确定其之间的相关性，拟合出关系曲线，从而实现预测的目的。

在实际预测中，对自变量x 和因变量y 作n 次试验观察，其n 对观察值记为：(x1,y1)，(x2,y2)，…，(xn,yn)是相互独立的样本观测值。

电力负荷预测模型的建立与精度评估方法

电力负荷预测模型的建立与精度评估方法随着电力系统的快速发展和电力需求的不断增长，准确预测电力负荷成为了电力行业和能源规划的关键问题。

电力负荷预测模型的建立和精度评估方法成为了研究热点，对于电力系统的稳定运行、经济调度和资源配置具有重要意义。

一、电力负荷预测模型的建立电力负荷预测模型是基于历史负荷数据和相关影响因素的统计学方法，通过建立合适的数学模型来预测未来一段时间内的电力负荷。

常用的电力负荷预测模型包括回归分析模型、时间序列模型和人工神经网络模型等。

1. 回归分析模型回归分析模型是一种常用的电力负荷预测方法，它基于历史负荷数据和相关影响因素之间的线性关系建立预测模型。

常见的回归分析模型包括线性回归模型和多元回归模型。

首先，根据历史负荷数据和影响因素数据进行数据预处理，包括数据清洗和特征提取等。

然后，建立回归方程，通过最小二乘法估计模型参数。

最后，利用建立的回归模型对未来一段时间的电力负荷进行预测。

2. 时间序列模型时间序列模型是一种基于时间趋势的电力负荷预测方法，它假设未来的负荷与过去的负荷存在某种规律和关系。

常用的时间序列模型包括移动平均模型、指数平滑模型和自回归移动平均模型等。

首先，对历史负荷数据进行平稳性检验，确保数据满足模型的基本假设。

然后，选择适当的时间序列模型，比如ARIMA模型。

最后，利用选定的模型对未来一段时间的电力负荷进行预测。

3. 人工神经网络模型人工神经网络模型是一种基于机器学习的电力负荷预测方法，它通过构建多层神经网络模型来模拟人脑的神经元网络，实现非线性模型的建立和预测。

常用的人工神经网络模型包括前馈神经网络、循环神经网络和长短期记忆网络等。

首先，根据历史负荷数据和相关影响因素构建神经网络结构，包括输入层、隐藏层和输出层。

然后，通过反向传播算法训练神经网络模型，不断调整权值和阈值以提高模型的预测性能。

最后，利用训练好的神经网络模型对未来一段时间的电力负荷进行预测。

二、精度评估方法电力负荷预测模型的精度评估是衡量模型预测性能的重要指标，常用的评估方法包括均方根误差（RMSE）、平均绝对百分比误差（MAPE）和相关系数等。

基于逐步回归-灰色预测的中长期电力需求预测

ＤＯＩ：１０．１９３９２／ｊ．ｃｎｋｉ．１６７１７３４１．２０２０１９１３０基于逐步回归灰色预测的中长期电力需求预测张明慧　李存斌华北电力大学经济与管理学院　北京　１０２２０６摘　要：随着电力市场的发展，中长期电力需求预测的重要性日益显现，准确的电力需求预测不仅可以保证电网安全稳定运行，而且是社会经济高效发展的基础。

在本文中应用逐步回归法对历史数据进行分析计算，得出社会用电量的线性回归方程，进而灰色预测法对线性回归方程中的自变量进行预测，进而带入线性回归方程得到预测结果。

最后对某地２０２０２０２５年的电力需求做预测，总体趋势显示我国的电力需求在未来几年将会稳步增长。

关键词：电力需求预测；逐步回归；灰色预测电力工业是国民经济的支柱行业，电力工业的快速发展不仅为全社会的用电需求提供了保障，而且有力地支撑了经济社会的快速发展，各行各业的发展都离不开电力行业的支持。

通过科学的电力需求预测来科学地规划电力系统、适时调整电力供应，不仅是保障电力工业健康、稳定发展的重要条件，而且是电力生产调度和市场营销的重要依据。

近年来，国内外学者对电力需求预测的模型进行了研究，预测理论技术不断地进行改进，其中电力需求预测的经典方法有适用于大区域中长期预测的电力弹性系数预测法、适用于中短期宏观预测的单耗法、适用于中长期宏观预测的转导法与类比法和适用于城市电网规划方面预测的负荷密度法。

随着科学技术的不断发展，新的预测技术不断出现，如时间序列预测方法、回归预测方法、投入产出预测方法、神经网络、遗传算法（ＧＡ）和系统动力学（ＳＤ）等。

汲国强等选用（对数平均迪氏指数）ＬＭＤＩ分解模型对用电增长量进行分解，根据影响因素分解为生产效应、结构效应和强度效应，然后选用布谷鸟搜索优化的最小二乘支持向量机对各效应进行拟合及预测在加总得到预测用电需求量［１］。

程鹏等将人工神经网络和灰色预测方法相结合提出了一种并联灰色神经网络预测方法［２］。

电力负荷预测模型与分析

电力负荷预测模型与分析电力负荷预测是电力系统中的重要环节，它对于电力生产和调度具有重要意义。

通过准确预测电力负荷，可以合理安排电力资源，提高供电可靠性，并有效降低成本。

本文将介绍电力负荷预测模型与分析的相关内容，探讨其中的方法与应用。

一、电力负荷预测模型的分类电力负荷预测模型可以分为经典模型和基于机器学习的模型两类。

1. 经典模型经典的电力负荷预测模型主要包括回归模型、时间序列模型和神经网络模型。

回归模型是一种基于统计方法的预测模型，它通过建立负荷与影响因素的数学关系，如温度、湿度、日期等，来预测未来的电力负荷。

常见的回归模型包括线性回归、多项式回归和岭回归等。

时间序列模型是一种基于时间序列数据进行预测的模型。

常见的时间序列模型包括ARIMA模型、VAR模型和GARCH模型等。

这些模型可以考虑历史数据的趋势、周期性和随机性，并根据这些规律进行负荷预测。

神经网络模型是一种基于人工神经网络的预测模型，它通过构建复杂的网络结构，使用反向传播算法进行训练，以实现对电力负荷的预测。

常见的神经网络模型包括BP神经网络、RNN神经网络和LSTM神经网络等。

2. 基于机器学习的模型近年来，随着机器学习算法的发展，基于机器学习的电力负荷预测模型越来越受到关注。

支持向量机是一种常用的机器学习方法，它通过构建高维特征空间，并寻找最优超平面，来实现对电力负荷的预测。

随机森林是一种集成学习方法，它通过构建多个决策树，并结合这些决策树的结果进行预测。

随机森林可以有效地处理高维特征和大规模数据，并具有较好的预测效果。

深度学习是一种基于神经网络的机器学习方法，它通过构建多层的神经网络，使用反向传播算法进行训练，以实现对复杂问题的预测。

深度学习在电力负荷预测中取得了显著的成果，尤其是基于卷积神经网络和循环神经网络的模型。

二、电力负荷预测模型的应用电力负荷预测模型在电力系统运行和调度中具有广泛应用。

1. 电力供需平衡电力负荷预测模型可以帮助电力公司合理安排电力资源，以满足用户的电力需求。

浅谈电力学之输电阻塞管理模型

浅谈电力学之输电阻塞管理模型摘要：本文在现有市场条件下，研究电网的输电阻塞管理问题，文中假设局部线性化，采用多维线性回归求得阻塞费用和机组出力分配预案，并根据交易规范，考虑到时间效率，采用Huffman决策树和递归策略来进行分配预案，进而求得计算公式，进行阻塞优化调整，得到输电阻塞管理模型。

关键词：多元线性回归模型；递归策略；Huffman决策树0 引言我国电力市场一直在进行整改，电力市场的输电阻塞管理愈发重要，因为电能传输时有输电线路传输容量的限制，所以必须调整机组出力分配方案，消除阻塞，以免发生危险。

本文在遵循电网“安全第一”的原则下，查阅了2013年的电网统计年鉴[1]，并对当前市场现状进行调查，得出分配预方案，调整计算公式，从而制定出电网市场管理模型。

1 输电阻塞管理模型的建立首先应研究线路潮流与机组出力的关系，根据2013年的统计年鉴，发现两者即使在给定的输电系统下也很难有明确的函数关系，只有统计数据的规律性。

其次考虑到阻塞费用问题，其涉及到机组利益损失，必须合理分摊。

然后进行预案计算，阻塞检查，对其进行调整并利用安全裕度输电等规划出力分配。

1.1 引进潮流分布公式以2013年的电网统计年鉴为样本，利用两种多维回归模型求出潮流分布近似公式，首先进行回归模型的建立[2]Pj=ijbi +ej（1）或Pj=ijbi +cj+ ej（2）其中Pj+表示第j条线路上的有功潮流值（单位MW）、aij表示第j条线路有功潮流值在第i台机组出力值上的线性系数、bi 表示第i台发电机的出力调整值、cj表示第j条线路有功潮流在各机组出力近似公式上的常数项、ej～N（0，δ）为误差项，j=1，2，3……采用最小二乘法估计aij和bj得方程[3]KTKAj=KTLJ解得Aj的最小二乘估计值，并且可知方程为Aj的无偏估计。

1.2 回归结果的检验与求解首先运用假设检验方法验算样本值：假设条件[4]1：a1j= a2j= a3j= a4j= ...= anj= 0假设条件2：对于i = 1，2，. . . ，n至少存在一个aij 不等于0.然后利用MATLAB统计工具箱进行检验，发现公式（2）与实际情况更加吻合，所以应该用公式（2）进行计算，从而得出结论，即对于给定电网，功率应按需分配。

线性回归短期负荷预测

摘要短期电力负荷预测是电力系统运行调度中非常重要的内容，它既是保证电力系统安全经济运行和实现电网科学管理及调度的重要方面，又是能量管理系统的组成部分，也是今后进行电网商业化运营所必需的基本内容。

本文系统的介绍了配电网负荷预测的意义和研究现状，对现行的负荷预测方法进行了简单的总结，在综合介绍了负荷预测的分类、特点及其基本原理等的基础上，详细研究了线性回归模型在负荷预测中的应用，并对吉林白城地区进行了算例分析。

关键字：电力系统、短期负荷预测、线性回归ABSTRACTShort-term load forecasting is very an important element in the scheduling of power system operation, it is both the important aspects to ensure safe and economic operation of power system and scientific management and scheduling of power grid, and an integral part of the energy management system, also the basic content of the future power grid commercial operation.This paper introduces the significance of load forecasting and summarizes the existing load forecasting method, then introduces its classification, characteristics and the basic principles. In the paper, I studies linear regression model in the load forecasting, and list a numerical example in an area of jilin baicheng.KEY WORDS: power system, short-term forecasting, linear regression目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1 选题背景与意义 (1)1.1.1 选题的背景 (1)1.1.2 选题的意义 (1)1.2 国内外研究负荷预测的现状 (1)1.2.1 传统预测方法 (2)1.2.2 人工智能预测方法 (2)1.3 本文的主要研究工作 (4)第2章电力负荷预测的概论 (5)2.1 电力负荷预测的分类 (5)2.1.1 按预测周期分类 (5)2.1.2 按行业分类 (5)2.1.3 按负荷预测特性分类 (5)2.2负荷预测的特点 (5)2.3 电力系统负荷预测的基本原理 (6)2.4 负荷预测的基本步骤 (7)第3章线性回归模型在短期负荷预测中的应用 (9)3.1短期负荷预测的基本模型 (9)3.1.1 影响负荷变化的因素 (9)3.1.2 负荷预测模型的要求 (10)3.1.3 短期负荷预测基本模型 (11)3.2 线性回归模型的概念与特点 (11)3.2.1 线性回归模型的概念 (11)3.2.2 线性回归的特点 (12)3.3 一元线性回归模型 (13)3.4 多元线性回归模型 (14)3.4.1 多元线性回归的定义 (14)3.4.2 多元线性回归模型的数学表达 (14)3.5 线性回归模型的建立 (15)3.6 算例分析 (15)3.6.1 确定预测内容 (15)3.6.2 资料搜集 (15)3.6.3 基础资料分析 (25)3.6.4 建立负荷预测模型 (25)3.6.5 进行负荷预测 (25)第4章总结 (28)参考文献 (29)致谢 (30)第1章绪论1.1 选题背景与意义1.1.1 选题的背景近些年来，随着电力市场改革的深入开展，用电用户的负荷对电力系统输送的电能质量的要求也越来越高。

电力负荷预测第七章回归分析预测法

主要内容
1.模型描述 2.参数估计 3.相关系数 4.显著性检验 5.预测及预测区间的确定 6.算例
1.模型描述
因变量
自变量
y a bx
i
i
i
——一元线性回归模型
i 1, n
xi: 影响因素（可以控制或预先给定）；
ε：各种随机因素对y的影响的总和，服从正态分布，即
ε~N(0, σ2)；
教学重点
●相关分析与回归分析的基本概念； ●一元线性回归模型的建立与参数检验；
教学难点
●相关系数的含义 ●参数检验的作用
一.概述
回归分析预测法——
从各种现象的相互关系出发，通过对与预测对象有联系的现象的变动趋势分析，推算预测对象未来状态数量表现的一种方法。
负荷y
x1
xj
影响因素
时间
y=f(t)—时间序列模型 y=f(x) —关联序列模型
②需区分自变量与因变量。
●相互联系——先相关分析，后回归分析。
相
回
关
归
分
分
析
析
判断关联关系初级
可建模推算预测高级
●相关分析是回归分析的基础； ●序列相关并不一定能建立回归模型；
4.相关分析与回归分析的作用
●对数量关系的研究分析，深入认识现象之间的相互依存关系。
●通过对回归模型，进行预测和预报。
i
(y i
yi
)2
(y y)2 i
Q Q
1
2
Q1
(
y i
yi
)2
剩余离差（或残差平方和）
Q ( y y)2 回归离差（或回归平方和）
2
i
离差项的物理含义：

电力负荷预测中回归方法的运用

量回归算法具有更好的适应性和预测精度。．
［关键词］负荷预测支持向量机
１引言．
序列最小优化灰色关联分析度阈值为０７，．６则预测点前１～４时刻负荷值、空气温度、气湿度等６空个参数与预测负荷的灰关联度满足要求，本文选取这些参数作为辅助变量，结合序列最小优化算法形成了基于灰色理论的序列最小优化算法。
的适应性。２多元线性回归．
本文根据某省电网公司提供的某年９６点负荷数据，分别用以上四种方法进行实验。８１日９３的工作日４天数据中前３天用月至月Ｏ３０的数据预测后１的１：０时刻的负荷值。３天２０图１中黑色折线代表原始负荷数据；蓝色折线代表线性回归预测结果；色折线代表ＳＲ预测结果；色折线代表Ｓ绿Ｖ黄ＭＯ预测结果；红色折线代表基于灰色理论的序列最小优化算法预测结果。由图Ｉ和表１可知，基于灰色理论的序列最小优化算法比ＳＯ算Ｍ法、ＶＳＲ算法和多元线性回归算法具有更为精确的预测误差，同时说明
科技信息
高校理科研究
电力负荷预测【回归方法的运用ｌ】
大唐保定热电厂解森
［摘
哈尔滨工程大学王亚丹
要］电力负荷预测作为电力市场的一个重要研究领域，直接关系到市场计划或调度部门制定购电计划、安排机组启停的工作
效益和效率，有着重要的实际意义。本文分别将多元线性回归、支持向量回归、列最小优化、序基于灰色理论的序列最小优化四种方法应用到负荷预测中，对某省负荷数据算例进行了实验对比分析，结果表明基于灰色理论的序列最小优化算法比线性回归、支持向

多元线性回归模型在电力负荷预测中的应用

多元线性回归模型在电力负荷预测中的应用学院：电气工程学院专业：电力系统*名：***学号：***********指导老师：***成绩：重庆大学电气工程学院2012年5月20日多元线性回归模型在电力负荷预测中的应用摘要：电力负荷预测是电力系统规划和运行的重要依据，是电力系统调度的重要组成部分，科学、准确地电力需求预测对电力工业的健康发展，乃至对整个国民经济的发展均有着十分重要的意义。

本文介绍了多元线性回归模型的原理，针对我国1994年至2009年人口、GDP和全社会用电量的历史数据，建立多元线性回归数学模型进行中、长期电力负荷预测，多元线性回归模型通过变量GDP和人口实现对全社会用电量的电力负荷定量预测。

结果表明该模型具有有效性，有良好的应用前景，为电力负荷预测的滚动修正，实现电力负荷控制和预测提供了科学依据。

关键词：负荷预测；多元线性；回归模型1引言1.1电力负荷预测的重要作用电力负荷预测是供电部门的重要工作之一，准确的负荷预测可以经济合理地安排电网内部发电机组的启停，保持电网运行的安全稳定性，减少不必要的旋转储备容量，合理安排机组检修计划，保证社会的正常生产和生活，有效降低发电成本，提高经济效益和社会效益[1]。

负荷预测的结果还有利于决定未来新的发电机组的安装，装机容量的大小、地点和时间，电网的增容和改建，电网的建设和发展等。

因此，电力负荷预测工作的水平已成为衡量一个电力企业的管理是否走向现代化的显著标志之一，尤其在我国电力事业空前发展的今天，用电管理走向市场，电力负荷预测问题的解决已经成为我们面临的重要而艰巨的任务。

1.2电力负荷预测电力负荷预测是指在满足一定精度的条件下，在充分考虑电力负荷特性、经济、社会、气象等的历史数据的基础上，探索电力负荷历史数据的变化规律，寻求电力负荷与各种相关因素之间的内在联系，从而预测出电力负荷在未来时期的变化趋势及状态[2]。

由于电力负荷具有周期性（年、月、天）、趋势性和随机性（受温度、气候、产业结构、政治等因素的影响）等特征，故电力负荷预测可分为超短期（15分钟或1个小时）、短期（1年以内的天或月）和中、长期（5~10年）负荷预测。

某地区电力负荷数据分析与预测

某地区电力负荷数据分析与预测一、引言电力负荷数据分析与预测是在某地区电力供需平衡和能源规划中至关重要的一环。

通过对电力负荷数据的分析与预测，可以匡助电力公司和相关部门做出合理的调度安排，提高电力供应的可靠性和效率。

本文将详细介绍某地区电力负荷数据的分析与预测方法，以及在实际应用中的一些案例和效果。

二、电力负荷数据分析1. 数据采集与处理首先，我们需要采集某地区一段时间内的电力负荷数据。

这些数据可以通过电力公司的监测系统获取，也可以通过其他途径获得。

采集到的数据需要进行清洗和预处理，包括去除异常值、填补缺失值等。

2. 数据可视化与描述统计接下来，我们可以利用数据可视化技术对电力负荷数据进行分析。

通过绘制折线图、柱状图等图表，可以直观地展示电力负荷的变化趋势、周期性和季节性特征。

同时，还可以计算电力负荷的均值、方差、峰值等描述统计量，以进一步了解数据的特征。

3. 时间序列分析电力负荷数据通常具有一定的时间相关性，因此可以应用时间序列分析方法进行进一步的分析。

常用的时间序列分析方法包括平稳性检验、自相关函数（ACF）和偏自相关函数（PACF）的分析、ARIMA模型等。

通过这些方法，可以揭示电力负荷数据的内在规律和趋势。

三、电力负荷数据预测1. 基于时间序列的预测方法基于时间序列的预测方法是最常用的电力负荷预测方法之一。

其中，ARIMA模型是一种经典的时间序列预测模型，通过对历史数据的拟合，可以预测未来一段时间内的电力负荷。

此外，还可以考虑引入季节性因素，使用SARIMA模型进行预测。

2. 基于回归分析的预测方法除了时间序列方法，还可以考虑利用回归分析方法进行电力负荷的预测。

回归分析可以通过建立电力负荷与其他因素（如气温、人口数量等）之间的关系模型，来预测未来的电力负荷。

可以使用线性回归、多项式回归、岭回归等方法进行建模。

3. 机器学习方法近年来，随着机器学习技术的发展，越来越多的研究者开始尝试将机器学习方法应用于电力负荷预测中。

对江苏省电力负荷进行回归预测

摘要：本丈主要根据２００１ — ２０１１年江苏省用电量样本数据，建立了江苏省电力负荷与人均ＧＤＰ、工业化以及人口数之间的多元回归预测方程，并预测了江苏省２０１４ — ２０２０年总用电量数据，在此基础上提出了相应的建议。
文采用了多元回归预测的方法，并将经济增长和工业化，
２００６２００７２００８２００９２０１０
２５８４＿３２２９５２．０２３１１８＿３２３３１３．９９３８６４＿３７
１．４３６９
１．６７４３２．００３１２．４６１６
４６
４８．３５Ｏ．１５０．８
７４０５．５
７４５７．７７５２２．９５７５８８．２４
越发展，未来城镇的用电量会不断增加，因此很有必要对
・６４・
价值工程
对江苏省电力负荷进行回归预测
ＲｅｇｒｅｓｓｉｏｎＦｏｒｅｃａｓｔｉｎｇｏｆｔｈｅＰｏｗｅｒＬｏａｄｉｎＪｉａｎｇｓｕＰｒｏｖｉｎｃｅ
ｄａｔａｆｒｏｍ２０１４ｔｏ２０２０ｉｎＪｉａｎｇｓｕｉｓｐｒｅｄｉｃｔｅｄ，ａｎｄｃｏｒｒｅｓｐｏｎｄｉｎｇｒｅｃｏｍｍｅｎｄａｔｉｏｎｓａｒｅｐｒｏｐｏｓｅｄ．

电力预测原理+python

电力预测原理与python实现一、引言1. 电力预测在能源行业中扮演着重要的角色，它可以帮助电力公司合理安排发电计划，降低能源浪费，提高能源利用率。

2. 本文将介绍电力预测的基本原理，并利用Python语言实现电力预测模型，帮助读者更好地理解和应用电力预测技术。

二、电力预测的原理1. 电力预测是一种利用历史数据和相关变量来预测未来电力需求的技术。

2. 电力预测的基本原理是利用时间序列分析、回归分析或者机器学习等方法，根据历史用电数据和相关的影响因素，建立数学模型来预测未来一定时期内的电力使用情况。

3. 在电力预测中，我们通常需要考虑的因素包括季节变化、天气因素、经济因素以及用电习惯等，这些因素都可能会对电力需求产生影响，需要在预测模型中进行合理的考虑和处理。

三、基于Python的电力预测模型实现1. 数据准备a. 我们需要准备历史用电数据和相关的影响因素数据，可以从电力公司的数据库中获取。

b. 对于天气因素和经济因素等数据，可以从气象局、统计局等机构获取，并进行数据清洗和整合。

2. 建立预测模型a. 在Python中，我们可以利用pandas、numpy等库对数据进行处理和分析，通过matplotlib、seaborn等库对数据进行可视化。

b. 我们可以利用statsmodels、scikit-learn等库建立时间序列模型、回归模型或者机器学习模型，通过模型拟合和评估来选择最合适的预测模型。

3. 模型评估与优化a. 在建立预测模型之后，我们需要对模型进行评估和优化，可以利用交叉验证、网格搜索等技术来选择最佳模型参数，提高预测的准确性和稳定性。

b. 通过误差分析、预测结果可视化等方法，对模型进行进一步的优化和改进，确保预测结果的可靠性和有效性。

4. 预测应用与部署a. 我们可以利用建立好的电力预测模型，对未来的电力需求进行预测，为电力公司的运营决策提供参考，例如发电计划的安排、电力市场的交易等。

第07章-电力需求预测

电量还可按电力客户的用电性质进行分类，包括农、
林、牧场、渔、水利业用电；工业用电；地质、勘探业
用电；建筑业用电；交通运输、邮电通信业用电；商业、
公共饮食业、物资供销和仓储业用电；城乡居民生活用
电；其他用电。
1-16
（2）电力预测。电力需求预测的另一个内容就是电力预测，也称负荷预测。负荷是指发电、供电地区或电网在某一瞬间所消耗的功率之和。
（4）电力需求预测中的长期预测非常重要。由于电力
建设周期长、耗资大，使电力需求预测中的长期预测更
为重要。
1-10
5.电量负荷预测主要分析的因素
1)能源变化的情况 2)国民生产总值增长率 3)工业生产发展速度 4)设备投资、人口增长 5) 时间发展 6) 其他因素
与电量负荷增长的关系
1-11
❖ 其他因素指：
电力需求预测必须按照一定的预测程序进行，用科学的预测技术将资料进行分析、加工和整理，从而得出规律性的结论。电力需求预测一般可依据以下程序：
1. 确定预测目标
预测必须要有明确的目标，明确目标是有效地进行预测的前提。要充分认识到明确目标在预测中的重要性。
2. 收集、分析、整理有关资料
明确预测目标之后，要广泛收集、分析和整理预测
1-28
一、经验预测技术
经验预测技术一般用于没有历史数据，不能采用模型进行预测的情况，此时采用经验预测方法，对事物今后的发展趋势进行描述。在电力需求预测中，常采用经验预测技术对电力需求的发展趋势进行描述，从而对电力需求给出一个方向性的结论。常用的经验预测技术有专家意见法、类比法和主观概率法等。
1-20
其它的规定：
（1）长期负荷预测的预测周期为数年至数十年；中期负荷预测的预测周期为1月至1年，用于水库调度、机组检修、交换计划、燃料计划的长期运行计划的编制；短期负荷预测的预测周期为i EI~I_周，用于编制调度计划；超短期负荷预测的预测周期为未来1小时以内，用于质量控制时为5~10 s，用于安全监视时为1-5 min，用于预防控制和紧急状态处理时为10~60 min。

基于SPSS回归分析对中长期居民用电负荷预测

基于SPSS回归分析对中长期居民用电负荷预测中长期居民用电负荷预测对于电力系统的规划和调度具有重要意义。

利用回归分析方法对中长期居民用电负荷进行预测，可以有效地为电力系统提供合理的资源调配和供电策略。

回归分析是指根据变量之间的统计关系，建立预测模型，从而预测一个或多个自变量对因变量的影响程度。

在中长期居民用电负荷预测中，自变量可以包括时间、室温、自然光照、人口数量等因素，而因变量则是居民用电负荷。

通过分析这些自变量和因变量之间的统计关系，可以建立回归模型，并利用该模型进行负荷预测。

在进行回归分析之前，需要先进行数据收集和预处理。

首先，需要收集历史用电负荷数据，包括电力系统的总体用电负荷数据和居民用电负荷数据。

其次，需要收集自变量的数据，如时间段（年、季度、月份、星期、小时）、室温、自然光照、人口数量等数据。

然后，对收集到的数据进行预处理，包括数据清洗、数据预处理、数据标准化等步骤，以确保数据的准确性和可靠性。

在回归分析中，可以选择多种回归模型进行预测。

最常用的回归模型是线性回归模型，其公式为：y = β0 + β1x1 + β2x2 + β3x3 + ... + βnxn + ε其中，y是居民用电负荷，x1、x2、x3等为自变量，β0、β1、β2、β3等为回归系数，表示自变量对因变量的影响程度，ε为误差项。

回归系数的估计可以通过最小二乘法进行求解。

在进行回归分析时，需要先进行模型的选择和检验。

可以利用SPSS 等统计软件进行模型的拟合和检验，判断模型的拟合情况和显著性。

常用的模型选择和检验方法包括F检验、t检验、R2等指标的判断。

在模型的拟合和检验完成后，可以利用回归模型进行中长期居民用电负荷的预测。

可以根据自变量的变化情况，输入到回归模型中，从而得到预测的居民用电负荷。

预测结果可以用于电力系统的规划和调度，以合理安排供电计划和资源分配。

在实际应用中，需要注意回归分析的局限性和假设。

回归分析假设了自变量和因变量之间是线性关系，且不存在多重共线性等问题。

电力系统的电力负荷预测方法

电力系统的电力负荷预测方法电力负荷预测是电力系统运行管理中至关重要的一环。

准确的负荷预测可以帮助电力公司优化发电计划、调度设备、调整能源需求和节约成本。

因此，研究和应用有效的电力负荷预测方法是电力行业的一个重要课题。

目前，电力负荷预测方法主要可以分为传统的统计方法和基于机器学习的方法。

传统的统计方法包括时间序列分析、回归分析和指数平滑等。

其中，时间序列分析主要关注历史负荷数据的模式和趋势，通过建立适当的模型来预测未来的负荷。

回归分析则是建立负荷与其他影响因素（如天气、社会经济因素等）之间的数学关系，并利用这些关系进行负荷预测。

指数平滑方法则是基于历史负荷数据的平滑处理，通过对历史负荷数据赋予权重来进行负荷预测。

这些方法简单易行，适用于一些负荷变化规律较为明显、受因素较少的场景。

然而，随着电力系统的复杂性不断增加，传统的统计方法的局限性也逐渐显现出来。

例如，统计方法通常假设历史数据与未来数据之间存在着稳定的关系，但在电力系统中，受到天气、经济、政策等诸多因素的影响，历史数据与未来数据之间的关系可能会发生变化。

此外，在处理大规模的历史负荷数据时，传统的统计方法也面临着计算效率低下的问题。

为了克服传统方法的局限性，基于机器学习的电力负荷预测方法逐渐被引入。

机器学习方法通过从大量历史负荷数据中学习和总结规律，来进行未来负荷的预测。

其中，常用的机器学习算法包括支持向量机、人工神经网络、决策树和随机森林等。

支持向量机是一种通过寻找最佳超平面来进行分类和回归分析的机器学习方法。

在电力负荷预测中，支持向量机可以根据历史负荷数据以及其他相关因素（如节假日、天气等）之间的关系，建立起一个适合负荷预测的模型。

人工神经网络则是模仿人脑神经元之间的连接和传递信息的机制，通过训练神经网络来进行负荷预测。

决策树方法则是通过对一系列问题进行决策，最终得出预测结果。

随机森林方法则是基于多个决策树的集成方法，通过多个决策树的投票来得出最终的预测结果。

电力阻塞

电力市场的输电阻塞管理摘要本文研究了电力市场的输电阻塞管理问题。

电网公司在组织交易、调度和配送时，遵循的是电网“安全第一，兼顾经济”的原则，制订的电力市场交易规则，是按照购电费用最小的经济目标来运作的。

问题一，我们利用给出的数据，采用多元线性回归来求取有功潮流与各机组出力之间的关系。

而且用题中所给的数据进行了其进行相应的误差分析与灵敏度分析，残差很小，并且分析了所得线性函数中的常数项存在的物理背景。

问题二，网方对发电商的供电取舍有着宏观调控的能力，在竞价中可能会造成发电商的一定损失。

网方必须对这部分损失给与发电商一定补偿，即阻塞费用。

阻塞补偿=)(清p q z -+()清p x x j ij ij i ∑∑==-81'101 问题三，其目标是总费用最小。

又因为各机组均受爬坡速率的限制，因此我们可以建立一线性规划模型，运用Matlab 工具箱计算得到各机组的出力。

问题四，根据给出各线路的潮流值，检验是否会产生输电阻塞。

若产生，则按照输电阻塞管理原则，依次采取调整预案、裕度输电、拉闸限电来保证输电线路安全运行。

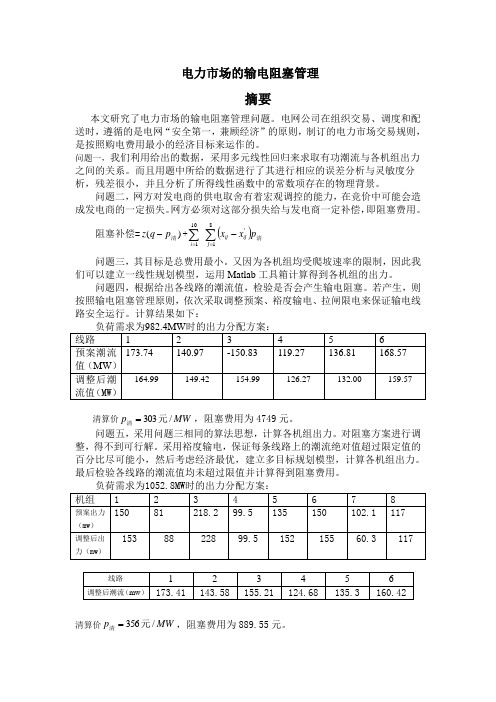
计算结果如下：清算价MW p /303元清=，阻塞费用为4749元。

问题五，采用问题三相同的算法思想，计算各机组出力。

对阻塞方案进行调整，得不到可行解。

采用裕度输电，保证每条线路上的潮流绝对值超过限定值的百分比尽可能小，然后考虑经济最优，建立多目标规划模型，计算各机组出力。

最后检验各线路的潮流值均未超过限值并计算得到阻塞费用。

清算价MW p /356元清=，阻塞费用为889.55元。

一、问题重述电力从生产到使用的四大环节发电、输电、配电和用电是瞬间完成的。

我国电力市场初期是发电侧电力市场，采取交易与调度一体化的模式。

电网公司在组织交易、调度和配送时，必须遵循电网“安全第一”的原则，同时要制订一个电力市场交易规则，按照购电费用最小的经济目标来运作。

市场交易-调度中心根据负荷预报和交易规则制订满足电网安全运行的调度计划，即各发电机组的出力（发电功率）分配方案。

研究电力市场的输电阻塞问题(

电力市场输电阻塞管理模型探究摘要我们探究了电力市场的输电阻塞管理，建立了较完善的模型，计算并解决了电力市场存在的一些问题.针对问题一，我们先对所给数据进行分析，得知发电机组出力对条线路有功潮流为线性影响，从而建立多元线性回归模型，求出了近似表达式，最后还进行统计检验，确定模型准确可行.求得表达式如线路一：112110.47750.08260.0478y x x =+++ 3456780.05280.11990.02570.12160.1220.0015x x x x x x +-++-.针对问题二，我们建立了一个规划模型，且定义了每小时的阻塞费用，考虑到过载，看是否可以消除，不能消除的转入到安全裕度内考虑，根据报价曲线得出了调整过后的对应报价的清算价，若过载不能消除，甚至超出了安全裕度，这时应当拉闸限电.针对问题三，我们根据附录2的出力分配方案0，得到下一个时段各组的出力限额，判断出问题三的负荷电价是在当前出力分配总和和下一时段出力限额总数之间，通过机组出力分配预算的N-S 图进行数据处理，求得下时段各机组处理的分配方案和清算价303元/MWh.针对问题四，我们结合问题一、三，计算出各条线路的有功潮流，得到1，5，6线路都超出了限值，但未超出安全裕度，然后建立单目标线性规划函数，化简即为公式4.21.最后通过lingo 得到该线性规划的最优方案.得出优化后的输电潮流值都在限制内了，同时计算出阻塞费用为21177.63元.针对问题五，当m=1052.8MW ，根据问题三、四的过程得到相应的出力分配方案和相应的清算价356元/MWh ，以及1，5线路超出了限值.按照问题四的单目标线性规划函数和lingo 进行求解，发现函数无可行解.然后需要考虑安全裕度，我们重新建立了多目标规划模型，得到2，3，4未超出限制，1，5，6都在安全裕度内并计算出最低阻塞费用40801元.关键词输电阻塞；多元线性回归；模型关键词；规划模型；单目标线性规划模型；多目标规划模；1问题重述1.1 问题背景我国电力系统的市场化改革正在积极、稳步地进行．2003年3月国家电力监管委员会成立，2003年6月该委员会发文列出了组建东北区域电力市场和进行华东区域电力市场试点的时间表，标志着电力市场化改革已经进入实质性阶段．可以预计，随着我国用电紧张的缓解，电力市场化将进入新一轮的发展，这给有关产业和研究部门带来了可预期的机遇和挑战．电力市场交易规则：1、以15分钟为一个时段组织交易，每台机组在当前时段开始时刻前给出下一个时段的报价．各机组将可用出力由低到高分成至多10段报价，每个段的长度称为段容量，每个段容量报一个价（称为段价），段价按段序数单调不减．在最低技术出力以下的报价一般为负值，表示愿意付费维持发电以避免停机带来更大的损失．2、在当前时段内，市场交易-调度中心根据下一个时段的负荷预报，每台机组的报价、当前出力和出力改变速率，按段价从低到高选取各机组的段容量或其部分（见下面注释），直到它们之和等于预报的负荷，这时每个机组被选入的段容量或其部分之和形成该时段该机组的出力分配预案（初始交易结果）．最后一个被选入的段价（最高段价）称为该时段的清算价，该时段全部机组的所有出力均按清算价结算．注释：（a）每个时段的负荷预报和机组出力分配计划的参照时刻均为该时段结束时刻．（b）机组当前出力是对机组在当前时段结束时刻实际出力的预测值．（c）假设每台机组单位时间内能增加或减少的出力相同，该出力值称为该机组的爬坡速率．由于机组爬坡速率的约束，可能导致选取它的某个段容量的部分．（d）为了使得各机组计划出力之和等于预报的负荷需求，清算价对应的段容量可能只选取部分．市场交易-调度中心在当前时段内要完成的具体操作过程如下：1、监控当前时段各机组出力分配方案的执行，调度AGC（自动发电控制）辅助服务，在此基础上给出各机组的当前出力值．2、作出下一个时段的负荷需求预报．3、根据电力市场交易规则得到下一个时段各机组出力分配预案．4、计算当执行各机组出力分配预案时电网各主要线路上的有功潮流，判断是否会出现输电阻塞．如果不出现，接受各机组出力分配预案；否则，按照如下原则实施阻塞管理：（1）调整各机组出力分配方案使得输电阻塞消除．（2）如果（1）做不到，还可以使用线路的安全裕度输电，以避免拉闸限电（强制减少负荷需求），但要使每条线路上潮流的绝对值超过限值的百分比尽量小．（3）如果无论怎样分配机组出力都无法使每条线路上的潮流绝对值超过限值的百分比小于相对安全裕度，则必须在用电侧拉闸限电．（4）当改变根据电力市场交易规则得到的各机组出力分配预案时，一些通过竞价取得发电权的发电容量（称序内容量）不能出力；而一些在竞价中未取得发电权的发电容量（称序外容量）要在低于对应报价的清算价上出力．因此，发电商和网方将产生经济利益冲突．网方应该为因输电阻塞而不能执行初始交易结果付出代价，网方在结算时应该适当地给发电商以经济补偿，由此引起的费用称之为阻塞费用．网方在电网安全运行的保证下应当同时考虑尽量减少阻塞费用．1.2问题提出1、根据题目中的数据，试用这些数据确定6条线路上有功潮流关于8台发电机组出力的近似表达式．2、设计一种简明、合理的阻塞费用计算规则，不仅要考虑市场规则，还要注意输电阻塞发生时公平地对待序内容量不能出力的部分和报价高于清算价的序外容量出力的部分．3、假设下一个时段预报的负荷需求是982．4MW，结合各机组的段容量、段价和爬坡速率，按照电力市场规则给出下一个时段各机组的出力分配预案．4、按照给出的潮流限值，检查问题三得到的出力分配预案是否会引起输电阻塞，并在发生输电阻塞时，根据安全原则，调整各机组出力分配方案，给出与该方案相应的阻塞费用．5、假设下一个时段预报的负荷需求是1052．8MW，重复回答问题三和问题四．2问题分析2.1 问题一分析对于每条线路而言，他都可能受到每台发电机组的影响，因此可以猜测其近似表达式是多元的，然后利用所给数据研究每个发电机组对每条线路的影响，从而确定每个表达式是几元的以及是否为线性，最后再利用所给数据求6条线路上有功潮流关于8台发电机组出力的近似表达式．2.2 问题二分析在出现线路阻塞的情况下我们要先给出一个计算阻塞费用的计算规则，根据问题要求，我们必须考虑到计算规则的合理性、对待对序内容量不能出力部分的违约费和对序外容量出力部分的补偿费，然后按照安全和阻塞费用最小的原则来消除阻塞，这样就可以建立一个规划模型，可以通过迭代来求解．对于不能消除阻塞的情况下，必须考虑其安全裕度．使每条线路上的绝对值超过限制的百分比尽量小的原则下避免拉闸限电．2.3 问题三分析在每一个给定的段容量上必定有其相应的段价，根据电力市场交易规则，段价按段序数单调不减，所以可以根据段价从低到高取得相应的段容量，直到段容量累计总和等于下一时段的负荷需求，最后的取得的段价便作为下一时段符合需求的清算价．每个机组段容量的总和便是该机组的出力方案．所有机组的段容量便构成了处理分配方案．2.4 问题四分析在给定下一时段的出力分配方案的基础上，在结合问题一所得出的输电潮流与出力的近似关系式和问题二输电阻塞费用计算公式，得到6条线路各自的输电潮流值，在未超出限值的情况下，根据多个约束条件求得符合目标函数条件的最优解，再根据最优输电潮流得出最少的阻塞费用．2.5 问题五分析问题五是在解决了问题三和问题四的基础上换个值再重新解决一次，但与前一次解决的问题四有所不同，此次得到的最优输电潮流解有部分超出限值，这需要建立多目标线性规划模型求解，顾名思义，即是存在多个目标函数同时要满足多个目标的解作为该模型的最优解．3 基本问题假设及符号说明3.1 基本问题假设● 假设在输电线路上的损耗为零● 假设各发电机组相互独立，不会互相影响● 假设各线路有功潮流仅与各发电机组有关● 假设负荷需求是各个发电机组出力之和● 假设当前出力是对发电机组在当前时段结束时刻实际出力的预测值3.2 符号说明ij x发电机组i 方案j 的出力 ij y线路i 方案j 的有功潮流值 16y y ,, 6个线路有功潮流值18x x ,,8个发电机组出力08ββ ,,回归系数 e随机误差 T总离差平方和 U回归平方和 Q残差平方和 1ˆy将ij x 代入回归方程所求得的回归值 1y1j y 的平均值 2R 回归平方和占总离差平方和的比重0H 原假设1H 备择假设α 显著水平M 总体分布值t 变量分布值()0i i C x 机组i 的报价曲线m 下一时段预报的负荷需求F 阻塞管理费用om C 清算价'om C 调整后对应报价的清算价1i x 、2i x 分别为调整前后的出力'21-om i om i C x C x付给其费用 B()16,,b b ij b第i 台机组对线路j 的贡献度 ()''18,,x x 调整后的方案出力 ()''18,,y y 调整后的方案有功潮流值'y∆调整后过载量jy第l条线路超载最严重lx新的出力分配方案y新的出力分配方案对应的有向潮流值C功率增长限额nv爬坡速率nn机组编号T当前分配方案的各出力值nP下一时段出力限额n(),a i j各机组的段容量(),b i j各机组的段价()d i下一时段的出力限额()c i下一时段各机组分配方案m下一个时段预报的负荷需求Y i线路有功潮流的限值iβ各线路潮流超过限值的百分比4 模型建立、求解4.1 问题一求解图 4-1问题一解题流程图4.1.1 数据分析根据表1、表2数据，设ij x 为机组i ()1,2,i = ,8方案j ()1,2,32j = ,的出力，ij y 为线路i ()1,2,6i = ,方案j ()1,2,32j = ,的有功潮流值．根据1j x 与1j y 的数值，利用matlab 作出散点图，如下图：图 4-21j x 与1j y 散点图同理画出ij x ()2,3,8i = ,与1j y 的散点图，分析8个散点图，得知ij x 对1j y 的影响都是线性的．进一步分析其他数据，得知ij x ()1,2,8i = ,对ij y ()1,2,6i = ,的影响都是线性的，因此我们可以建立多元线性回归模型求解问题一．4.1.2 多元线性回归模型以下，我们以线路1为例，求解有功潮流关于发电机组出力的近似表达式． 101188y x x e βββ=++++ (4.1) 式中1y 为线路1有功潮流值，128,x x x ,,分为机组1-8出力，018,βββ ,,为回归系数，e 是随机误差．根据ij x ()1,2,8i = ,与1j y 的数值，利用matlab 求得回归系数估计值及回归系数置信区间，结果如下表：回归系数回归系数估计值回归系数置信区间0β 110.4775 [109.5421，111.4129]1β0.0826 [0.0808，0.0844]2β0.0478 [0.0437，0.0518] 3β0.0528 [0.0514，0.0542] 4β 0.1199[0.1166，0.1231] 5β -0.0257[-0.0277，-0.0237] 6β 0.1216[0.1190，0.1243] 7β 0.122[0.1189，0.1251] 8β-0.0015 [-0.0037，0.0007]表 4-1回归系数估计值及回归系数置信区间则112345110.47750.08260.04780.05280.11990.0257y x x x x x =++++- 6780.12160.1220.0015x x x ++-利用matlab 画出杠杆残差图，如下图：图 4-3杠杆残差图从杠杆残差图可以看出，各数据的残差离零点均较近，且残差的置信区间均包含零点，这说明多元线性回归模型能较好的符合原始数据．4.1.3 多元线性回归模型统计检验 4.1.3.1 拟合优度检验在多元线性回归模型中，可用判定系数2R 来衡量样本回归线对样本观测值的拟合程度．记()322111jj T yy ==-∑为总离差平方和，()211ˆU yy =-∑为回归平方和，()322111ˆj j Q y y==-∑为残差平方和，则()()322211111ˆˆj j T U Q yy y y ==+=-+-∑∑ (4.2)60.87890.034060.9128=+=式中向量1ˆy为将ij x 代入回归方程所求得的回归值，1y 为1j y 的平均值．回归平方和反映了总离差平方和中可由样本回归线解释的部分，它越大，残差平方和越小，表明样本回归线与样本观测值的拟合程度越高．因此，可由回归平方和占总离差平方和的比重2R 衡量样本回归线对样本观测值的拟合程度．2UR T=(4.3)经计算20.9994R =很接近1，因此拟合度很高． 4.1.3.2 方程总体线性的显著性检验对于公式(4.1)，我们设原假设与备择假设为：01280,0,0H βββ=== ：,()11,2,8i H i β= ：,不全为零根据数理统计学中的知识，在原假设成立的条件下，统计量()88233281UU M QQ==-- (4.4)服从自由度为()8,23的M 分部．因此，给定一个显著水平0.5α=，由matlab 得到临界值()0.58,230.9442M =．经计算得5376.8M =，则0.5M M >，所以拒绝原假设0H ，原方程总体上的线性关系显著成立． 4.1.3.3 变量的显著性检验在变量显著性检验中，针对某变量()1,2,8i x i = ,设计的原假设与备择假设为：0i :0H β= 1i :0H β≠给定一个显著水平=0.5α，由matlab 得到临界值()2230.6848t α=．由matlab计算得||t 均大于()223t α，则拒绝0H ，所以对应的变量均包含在模型中．4.1.4 小结对数据分析后得知ij x ()1,2,8i = ,对ij y ()1,2,6i = ,都是线性影响，因此建立多元线性回归模型，以线路1为例得有功潮流关于各发电机组出力的近似表达式：112345110.47750.0826.0.04780.05280.11990.0257y x x x x x =++++-+6780.12160.1220.0015x x x +-．(4.5)之后进行了残差分析、拟合优度检验、方程总体线性的显著性检验和变量的显著性检验，得出模型准确可行．同理计算分析得其他线路近似表达式：2123456131.35210.05470.12750.00010.03320.08670.1127y x x x x x x =-+-++-780.01860.0985x x -+；(4.6)3123456108.99280.06940.0620.15650.00990.12470.0024y x x x x x x =--+--++780.00280.2012x x --；(4.7)412345677.61160.03460.10280.2050.02090.0120.0057y x x x x x x =--+--+780.14520.0763x x ++；(4.8)5123456133.13340.00030.24280.06470.04120.06550.07y x x x x x x =++---+780.00390.0092x x --；(4.9)6123456120.84810.23760.06070.07810.09290.04660.0003y x x x x x x =+--++-780.16640.0004x x ++．(4.10)4.2 问题二求解设()0i i C x 为机组i 的报价曲线，om C 为清算价，m 为下一时段预报的负荷需求，则()(){}011088max ,,om C C x C x = ，那么，目标函数为：()8811min om i om i om i i F C x C x C m=====∑∑ (4.11)()()().1i i i s t P t P t U t --≤：其中()()=i i U t v t ．要使F 达到最小，就是要在约束条件下找到最小的清算价om C ．这是一个线性规划模型．可以按照段价从低到高的顺序来选择可能的清算价． 4.2.1 电力阻塞模型按购电费用增量来定义每小时阻塞费用：()()()8''211min *om i om i om om i F C x C x C C m==-=-∑ (4.12)式中F 为阻塞管理费用，'om C 为调整后对应报价的清算价，1i x 、2i x 分别为调整前后的出力，'21-om i om i C x C x 为付给其费用． 4.2.1.1 模型建立为了调整预案使各线路阻塞消失，引进贡献度来表示机组对i y 的影响程度，记()16,,B b b = ，其中j b 为列向量．则第i 台机组对线路j 的贡献度就可以理解为ij b ，以下给出一个简单的事实：输电产生阻塞的充分必要条件为j ∃，使得=->0j j j y y a ∆．记调整后的方案为()''18,,x x ，对应的潮流值为()''18,,y y ，过载量为'j y ∆，建立如下的调整模型：()'min *om om F C C m=- (4.13)().:1,2,60j s t j j ∀=∆< ,，y如果在上面的模型中无法做到对于所有的'<0j y ∆无可行解，那么就需要考虑在安全裕度内输电．记=-j j j y y a ∆，如上面分析，可建立安全裕度内的调整模型：()'min *om om F C C m=- (4.14)().:1,2,60j s t j j ∀=∆< ,，y()''16,,a a a = =(165，150，160，155，132，162)为各线路的潮流限制矩阵，()'''16,,a a a = =(186.45，177，174.4，172.05，151.6，184.68)为各线路的潮流安全裕度矩阵．如果在上面的模型中依然无可行解，则必须在用电侧拉闸限电． 4.2.1.2 算法及结果首先尽可能的去消除过载，直至消除过载．否则转入到安全裕度内考虑，然后根据报价曲线给出调整过后的'om C ．记()16,,y y y = ，j j j y a η=-()1,2,,6j = ．{}1,2,max l j j ηη==…,6表示第l 条线路超载最严重，其对应的潮流值为：1188l l l y b x b x =++(4.15)令{}max 1,2,8max l il pl j b b b ===…,、{}min 1,2,8max l il ml j b b b ===…,则可以分三种情况讨论： 1) ()01,,8il b i >=…：由于pl b 为第p 个机组出力p x 的系数，所以p x 的变化对l y 的影响最大，故p x 应减小出力，按照给出的原则对其进行调整． 2) ()01,,8il b i <=…：与一同理．3) il b 有正有负：由于ml b 为最小，则肯定小于0，所以应使m x 增加出力；同理，由于il b 为最大，则肯定大于0，所以应使j x 减小出力．按照给定的原则对其进行调整．经过上述3种情形的不断调节，如果最终能使<0j η，则记()18,,x x x = 为新的出力分配方案，()16,,y y y = 为新的出力分配方案对应的有向潮流值（可通过模型求出来）．令j j j y a η=-，对k η重复以上过程．如果最终0j η>则认为不能消除阻塞，所以考虑在安全裕度内输电．记()'''16,,a a a = ，其中()1,2,k k a a k =+∆= ,6，j j j y a η=-()1,2,,6j = ．对j η重复以上过程，直到所有的j η都小于0，则可在裕度范围内输电．否则，应当拉闸限电． 4.3 问题三求解当前时段的出力分配方案(即附录2方案0)为(120，73，180，80，125，125，81. 1，90 )MW ．由于以15分钟为一个时段组织交易，所以我们可以得到：*15n n C v =(4.16)式中n C 为功率增长限额，n v 为爬坡速率，n 为机组编号．可以得到下一个时段各机组的出力限额：n n n d T C =+(4.17)式中n T 为当前分配方案的各出力值．根据有关数据们可以得到下表：表 4-2机组出力限额表机组 123456 7 8 爬坡速率 2.2 1 3.2 1.3 1.8 2 1.4 1.8 功率增长限额33 15 48 19.5 27302127 当前出力分配方案120 73 18080125 125 81.190下一时段出力限额153 88 228 99.5 152 155 102.1 117有当前出力的分配方案总和：81874.10nn TMW ==∑而下一时段出力限额：811094.60n n P MW ==∑显然问题三下一个时段预报的负荷需求是982. 4MW 在当前出力分配方案总和和下一时段出力配案限额总数之间，符合条件.我们根据下一个时段的负荷预报，每台机组的报价、当前出力和出力改变速率，按段价从低到高选取各机组的段容量或其部分，直到它们之和等于预报的负荷，这时每个机组被选入的段容量或其部分之和形成该时段该机组的出力分配预案作出筛选数据及计算的N-S 图如下：图 4-4机组出力分配预案计算的N-S 图其中(),a i j 表示各机组的段容量，(),b i j 表示各机组的段价，()d i 下一时段的出力限额，()c i 表示下一时段各机组分配方案，m 表示下一个时段预报的负荷需求，n 表示机组数.数据处理后得到的分配方案，如下表：表 4-3 下时段各机组处理分配方案机组 12345678分配方案(MW)150.00 79.00 180.00 99.50 125.00 140.00 95.00 113.90同时得到最后的清算价为303元/MWh. 4.4 问题四求解由问题一已知了各线路上有功潮流关于各发电机组出力的近似表达式：公式（4.5）、（4.6）、（4.7）、（4.8）、（4.9）、（4.10）.根据上述表达式和问题三所得到的下时段出力分配方案计算得到下表的各条路线的有功潮流：表 4-4 有功潮流线路 1 2 3 4 5 6 限值 165 150 160 155 132 162 安全裕度 13% 18% 9% 11% 15% 14% 安全裕度处理后的限值 186.45177174.4172.05151.8184.68有功潮流173.3084 140.8917 -150.919 120.9034 136.8083 162.1768由表4-4可以看出1，5，6线路都超出了限值，但未超出安全裕度，即1，5，6线路出现输电阻塞，现在需要解决的是按照输电阻塞原则消除阻塞.由于该阻塞问题解决需要根据安全且经济的原则，调整各机组出力分配方案，并给出与该方案相应的阻塞费用，涉及到线性规划，所以这里我们建立了模型进行解决.我们将所需阻塞费用记为F ，则*om F m C =，om C 为清算价；最小费用记为()min F .得到目标函数：()()min min *om F m C =(4.18)由问题一所给的有功潮流关于各发电机组出力的近似表达式可以将其写成：01122334455667788i i i i i i i i i i y a a x a x a x a x a x a x a x a x =++++++++801i ij jj a a x ==+∑()1,2,3,4,5,6i =即有功潮流：()8011,2,3,4,5,6i i ij j j y a a x i ==+=∑，i i y Y ≤(4.19)i Y 表示i 线路有功潮流的限值.下一时段的负荷需求：8'1i i m c ==∑(4.20)出力分配方案的约束条件为：()'1,2,3,4,5,6,7,8i i i i i T C c T C i -≤≤+=这里的i c 相当于上面有功潮流公式中的j x ，所以我们将j x 用i c 代替. 综上所诉得到一个单目标线性规划模型：()()()()()8'1'8'011,2,...,6..1,2,...,61,2,...,6min min *i i i i i i i i i ij j j i i om m c T C c T C i s t y a a c i y Y i F m C ==⎧=⎪⎪-≤≤+=⎪⎪⎨=+=⎪⎪≤=⎪⎪=⎩∑∑ 由问题二我们已经得到：()()()8'''21001min *()om i om i om om i F C x C x C C m m ==-=--∑(4.21)通过lingo 得到该线性规划的最优方案(代码见附录4)见下图：表 4-5 出力最优方案机组x1x2x3x4x5x6x7x8优化前 150.000 79.000 180.000 99.500 125.000 140.000 95.000 113.900 优化后 150.160 88.000 228.000 80.000 152.000 97.258 69.982 117.000表 4-6各线路潮流最优方案线路 1 2 3 4 5 6 限值165150160155132162优化前 173.308 140.892 -150.919 120.903 136.808 162.177 优化后 165.000 149.432 -154.980 126.257 132.000 159.556可以看出优化后的方案的输电潮流值都在限值内了，同时得到最优解()min 21177.63F =元，所以相应的阻塞费用为21177.63元4.5 问题五求解当m=1052.8MW 时，按照问题三中的方法得到下表数据表 4-7 m 为1052.8MW 时的出力分配方案机组12345678下时段出力分配方案(MW) 150 81 218.2 99.5 135 150 102.1 117得到最后的清算价为356元/MWh.同样根据此方案结合问题一中得到的近似函数得到相应的输电潮流如下表：表 4-8 m 为1052.8MW 时的输电潮流方案线路 1 2 3 4 5 6 限值 165 150 160 155 132 162 安全裕度13%18%9%11%15%14%安全裕度处理后的限值 186.45 177 174.4 172.05 151.8 184.68有功潮流177.2415 141.0461 -156.1459 129.7333 134.8112 160.7176从上表中我们可以得到1，5路线超出了限值，但在安全裕度内，所以出现输电堵塞，解决方法同问题四把一个多目标规划问题转化为了以机组出力为决策变量的单目标非线性规划问题.通过lingo 继续求解，发现此时lingo 出现无可行解，这时我们要考虑安全裕度，并使其百分比达到最小.结合问题四可以得到一个多目标规划模型：()()()()()()()8'1'8'011,2,...,61,2,...,6..1,2,...,6min min *min min i i i i i i i ii ij j j i i om i m c T C c T C i y a a c i s t y Y i F m C B β==⎧=⎪⎪-≤≤+=⎪⎪⎪=+=⎨⎪≤=⎪⎪=⎪⎪=⎩∑∑ 其中这里β表示各线路潮流超过限值的百分比表 4-9出力方案最优解机组x1 x2x3 x4x5x6 x7x8优化前 150 81 218.2 99.5 135 150102.1 117优化后 150 8122899.5 135 140.2 102.1 117表 4-10输电潮流最优解及其安全百分比线路 1 2 3 4 5 6 限值 165 150 160 155 132 162 安全裕度 13% 18% 9% 11% 15% 14% 安全裕度处理后的限值 186.45177174.4172.05151.8184.68有功潮流 177.2415 141.0461 -156.1459 129.7333 134.8112 160.7176 最优解潮流 176.5673 142.2846 157.7031 131.6864 133.4911 166.2933 超出限度百分比7.01%-5.14%-1.44%-15.04%1.13%2.65%由此可见2，3，4线路潮流值未超过限值，1，5，6 线路潮流值在安全裕度内.最低阻塞费用40801元.5模型评价、改进及推广5.1 模型评价●模型优点：采用多元线性回归模型，简单明了；实用性强，对现实具有指导意义．●模型不足：模型建立过程中做了一些简化可能会造成部分偏差；使用的数据部分为实验值，存在误差，没有用实际数据检验．5.2 模型改进本文在求解6条线路上有功潮流关于8台发电机组出力的近似表达式时，忽略了一些偏差，采用一次多元线性回归模型，如果进一步作细致处理，采用多次处理，可能求得的近似表达式会更加准确．5.3 模型推广本文的模型可以推广到客运管理中．6参考文献[1]陈家鼎，数理统计学讲义[M]，北京：高等教育出版社，1992.[2]姜启源、谢金星、叶俊，数学模型(第二版)[M]，北京：高等教育出版社，2003.[3]赵明珠、张俊英、亢晓龙，多元线性回归模型分析的应用---以汉中市中学教师薪金影响因素分析为例，绵阳师范学院学报，29(11)：15，2010.[4]郭金、谭忠富，金融输电权和输电期权在输电阻塞管理中的应用[J]. 电力自动化设备， 24(6)：62，2004.[5]柯进、管霖，电力市场下的输电阻塞管理技术[J]，电力系统自动化，26(14) ：22，2002.[6]李海奎、唐守正，非线性回归组件的设计与实现[J]，计算机应用研究，2004(2)，141.[7]百度文库，matlab建立多元线性回归模型并进行显著性检验及预测问题，http：///view/053f1d7c31b765ce05081436.html###，2012-8-10.[8]张其亮，电力市场的输电阻塞管理模型研究，http：//d.g.wanfangdata.c/Periodical_cqgxyxb200602033.Aspx，2012-8-11.7附录附录1：问题一代码C=inv(X'*X);% 最小二乘回归分析beta_hat=C*X'*Y % 回归系数β% 离差和参数计算Q=(Y-Y_hat)'*(Y-Y_hat) % 残差平方和U=(Y_hat-Y_mean)'*(Y_hat-Y_mean) % 回归离差平方和T=(Y-Y_mean)'*(Y-Y_mean) % 总离差平方和，且满足T=Q+UR=sqrt(U/T) % 复相关系数，表征回归离差占总离差的百分比，越大越好[n，p]=size(X) % p变量个数，n样本个数% 回归显著性检验fV=(U/(p-1))/(Q/(n-p)) % 服从F分布，F的值越大越好fH=fV>finv(alpha，p-1，n-p) % H=1，线性回归方程显著(好)；H=0，回归不显著% 回归系数的显著性检验chi2=sqrt(diag(C)*Q/(n-p)) % 服从χ2(n-p)分布tV=beta_hat./chi2 % 服从T分布，绝对值越大线性关系显著tInv=tinv(0.5+alpha/2，n-p)tH=abs(tV)>tInv % H(i)=1，表示Xi对Y显著的线性作用；H(i)=0，Xi对Y的线性作用不明显% 回归系数区间估计tW=[-chi2，chi2]*tInv % 接受H0，也就是说如果在beta_hat(i)对应区间中，那么Xi与Y线性作用不明显stats=struct('fTest'，[fH，fV]，'tTest'，[tH，tV，tW]，'TUQR'，[T，U，Q，R])附录2：问题二表格各机组出力方案（单位：兆瓦，记作MW）方案1 2 3 4 5 6 7 8机组0 120 73 180 80 125 125 81. 1 901 133. 02 73 180 80 125 125 81. 1 902 129. 63 73 180 80 125 125 81. 1 903 158. 77 73 180 80 125 125 81. 1 904 145. 32 73 180 80 125 125 81. 1 905 120 78. 596 180 80 125 125 81. 1 906 120 75. 45 180 80 125 125 81. 1 907 120 90. 487 180 80 125 125 81. 1 908 120 83. 848 180 80 125 125 81. 1 909 120 73 231. 39 80 125 125 81. 1 9010 120 73 198. 48 80 125 125 81. 1 9011 120 73 212. 64 80 125 125 81. 1 9012 120 73 190. 55 80 125 125 81. 1 9013 120 73 180 75. 857 125 125 81. 1 9014 120 73 180 65. 958 125 125 81. 1 9015 120 73 180 87. 258 125 125 81. 1 9016 120 73 180 97. 824 125 125 81. 1 9017 120 73 180 80 150. 71 125 81. 1 9018 120 73 180 80 141. 58 125 81. 1 9019 120 73 180 80 132. 37 125 81. 1 9020 120 73 180 80 156. 93 125 81. 1 9021 120 73 180 80 125 138. 88 81. 1 9022 120 73 180 80 125 131. 21 81. 1 9023 120 73 180 80 125 141. 71 81. 1 9024 120 73 180 80 125 149. 29 81. 1 9025 120 73 180 80 125 125 60. 582 9026 120 73 180 80 125 125 70. 962 9027 120 73 180 80 125 125 64. 854 9028 120 73 180 80 125 125 75. 529 9029 120 73 180 80 125 125 81. 1 104. 8430 120 73 180 80 125 125 81. 1 111. 2231 120 73 180 80 125 125 81. 1 98. 09232 120 73 180 80 125 125 81. 1 120. 44 附录3：问题三代码#include <stdio．h>#include <string．h>int a[8][10]={70,0,50,0,0,30,0,0,0,40,30,0,20,8,15,6,2,0,0,8,110,0,40,0,30,0,20,40,0,40,55,5,10,10,10,10,15,0,0,1,75,5,15,0,15,15,0,10,10,10,95,0,10,20,0,15,10,20,0,10,50, 15,5,15,10,10,5,10,3,2,70, 0,20,0,20,0,20,10,15,5},b[8][10]={-505,0,124,168,210,252,312,330,363,489,-560,0,182,203,245,300,320,360,410,495,-610,0,152,189,233,258,308,356,415,500,-500,150,170,200,255,302,325,380,435,800,-590,0,116,146,188,215,250,310,396,510,-607,0,159,173,205,252,305,380,405,520,-500,120,180,251,260,306,315,335,348,548,-800,153,183,233,253,283,303,318,400,800};double c[8],d[8]={153,88,228,99．5,152,155,102．1,117}; int main(){int i,min=1000,t,j,k,s;double sum=0,n;scanf("%lf",&n);memset(c,0,sizeof(c));while(sum<n){for(i=0;i<8;i++){for(k=0;k<10;k++){if(min>b[i][k]){min=b[i][k];t=i,s=k;}}}sum+=a[t][s];b[t][s]=1000;j=min;min=1000;if(sum<n){c[t]+=a[t][s];if(c[t]>d[t]){sum-=(c[t]-d[t]);c[t]=d[t];}}else{c[t]+=(n-(sum-a[t][s]));if(c[t]>d[t]){sum-=(c[t]-d[t]);c[t]=d[t];}}}printf("%d\n",j);for(i=0;i<8;i++){printf("%．2lf ",c[i]);}printf("\n");return 0;}附录4：问题四代码lingo code1：min=(70-X11)*(303+505)+(50-X13)*(303-124)+(30-X16)*(303-252)+X110*(489-303)+ (30-X21)*(303+560)+(20-X23)*(303-182)+(8-X24)*(303-203)+(15-X25)*(303-245)+(6-X 26)*(303-300)+X27*(320-303)+X210*(495-303)+(110-X31)*(303+610)+(40-X33)*(303-152)+(30-X35)*(303-233)+X37*(308-303)+X38*(35 6-303)+X310*(500-303)+(55-X41)*(303+500)+(5-X42)*(303-150)+(10-X43)*(303-170)+(10-X44)*(303-200)+(10-X45)*(303-255)+(10-X46)*(303-302)+X47*(325-303)+X410*(800-303)+(75-X51)*(590+303)+(5-X52)*(303-0)+(15-X53)*(303-116)+(15-X55)*(303-188)+(15-X5 6)*(303-215)+X58*(310-303)+X59*(396-303)+X510*(510-303)+(95-X61)*(303+607)+(10-X3)*(303-159)+(20-X64)*(303-173)+(15-X66)*(303-252)+X67* (305-303)+X68*(380-303)+X610*(520-303)+(50-X71)*(303+500)+(15-X72)*(303-120)+(5-X73)*(303-180)+(15-X74)*(303-251)+(10-X75)*(303-260)+X76*(306-303)+X77*(315-303)+X78*(335-303)+X79*(348-303)+X710*(54 8-303)+(70-X81)*(303+800)+(20-X83)*(303-183)+(20-X85)*(303-253)+X88*(318-303)+X89*(400 -303)+X810*(800-303);x11<70;x13<50;x16<30;x110<40;x1=x11+x13+x16+x110;x1>87;x1<153;x21<30;x23<20;x24<8;x25<15;x26<6;x27<2;x210<8;x2=x21+x23+x24+x25+x26+x27+x210;x2>58;x2<88;x31<110;x33<40;x35<30;x37<20;x38<40;x310<40;x3=x31+x33+x35+x37+x38+x310;x3>132;x3<228;x41<55;x42<5;x43<10;x44<10;x45<10;x46<10;x47<15;x410<1;x4=x41+x42+x43+x44+x45+x46+x47+x410;x4>60．5;x4<99．5;x51<75;x52<5;x53<15;x55<15;x56<15;x58<10;x59<10;x510<10;x5=x51+x52+x53+x55+x56+x58+x59+x510;x5>98;x5<152;x61<95;x63<10;x64<20;x66<15;x67<10;x68<20;x610<10;x6=x61+x63+x64+x66+x67+x68+x610;x6>95;x6<155;x71<50;x72<15;x73<5;x74<15;x75<10;x76<10;x77<5;x78<10;x79<3;x710<2;x7=x71+x72+x73+x74+x75+x76+x77+x78+x79+x710;x7>60．1;x7<102．1;x81<70;x83<20;x85<20;x87<20;x88<10;x89<15;x810<5;x8=x81+x83+x85+x87+x88+x89+x810;x8>63;x8<117;x1+x2+x3+x4+x5+x6+x7+x8=982．4;0．0826*x1+0．0478*x2+0．0528*x3+0．1199*x4-0．0257*x5+0．1216*x6+0．122*x7-0．0015*x8-y1=-110．4775;-0．0547*x1+0．1275*x2-0．0001*x3+0．0332*x4+0．0867*x5-0．1127*x6-0．0186*x7+0．0985*x8-y2=-131．3521;-0．0694*x1+0．062*x2-0．1565*x3-0．0099*x4+0．1247*x5+0．0024*x6-0．0028*x7-0．2012*x8+y3=108．9928;-0．0346*x1-0．1028*x2+0．2050*x3-0．0209*x4-0．012*x5+0．0057*x6+0．1452*x7+0．0763*x8-y4=-77．6116;0．0003*x1+0．2428*x2-0．0647*x3-0．0412*x4-0．0655*x5+0．07*x6-0．0039*x7-0．0 092*x8-y5=-133．1334;0．2376*x1-0．0607*x2-0．0781*x3+0．0929*x4+0．0466*x5-0．0003*x6+0．1664*x7+0．0004*x8-y6=-120．8481;y1<165;y2<150;y3<160;y4<155;y5<132;y6<162;end;lingo code2：(55-X41)*(356+500)+(5-X42)*(356-150)+(10-X43)*(356-170)+(10-X44)*(356-200)+(10-X45)*(356-255)+(10-X46)*(356-302)+(15-X47)*(356-325)+X410*(800-356)+(75-X51)*(590+356)+(5-X52)*(356-0)+(15-X53)*(356-116)+(15-X55)*(356-188)+(15-X5 6)*(356-215)+(10-X58)*(356-310)+X59*(396-356)+X510*(510-356)+(95-X61)*(356+607)+(10-X3)*(356-159)+(20-X64)*(356-173)+(15-X66)*(356-252)+(10-X67)*(356-305)+X68*(380-356)+X610*(520-356)+(50-X71)*(356+500)+(15-X72)*(356-120)+(5-X73)*(356-180)+(15-X74)*(356-251)+(10-X75)*(356-260)+(10-X76)*(356-306)+(5-X77)*(356-315)+(10-X78)*(356-335)+(3-X79)* (356-348)+X710*(548-356)+(70-X81)*(356+800)+(20-X83)*(356-183)+(20-X85)*(356-253)+(20-X87)*(356-303)+(10 -X88)*(356-318)+X89*(400-356)+X810*(800-356);x11<70;x13<50;x16<30;x110<40;x1=x11+x13+x16+x110;x1>87;x1<153;x21<30;x23<20;x24<8;x25<15;x26<6;x27<2;x210<8;x2=x21+x23+x24+x25+x26+x27+x210;x2>58;x2<88;x31<110;x33<40;x35<30;x37<20;x38<40;x310<40;x3=x31+x33+x35+x37+x38+x310;x3>132;x3<228;x41<55;x42<5;x43<10;x44<10;x45<10;x46<10;x47<15;x410<1;x4=x41+x42+x43+x44+x45+x46+x47+x410;x4>60．5;x4<99．5;x51<75;x52<5;x53<15;x55<15;x56<15;x58<10;x59<10;x510<10;x5=x51+x52+x53+x55+x56+x58+x59+x510;x5>98;x5<152;x61<95;x63<10;x64<20;x66<15;x67<10;x68<20;x610<10;x6=x61+x63+x64+x66+x67+x68+x610;x6>95;x6<155;x71<50;x72<15;x73<5;x74<15;x75<10;x76<10;x77<5;x78<10;x79<3;x710<2;x7=x71+x72+x73+x74+x75+x76+x77+x78+x79+x710;x7>60．1;x7<102．1;x81<70;x83<20;x85<20;x87<20;x88<10;x89<15;x810<5;x8=x81+x83+x85+x87+x88+x89+x810;x8>63;x8<117;x1+x2+x3+x4+x5+x6+x7+x8=1052．8;0．0826*x1+0．0478*x2+0．0528*x3+0．1199*x4-0．0257*x5+0．1216*x6+0．122*x7-0．0015*x8-y1=-110．4775;-0．0547*x1+0．1275*x2-0．0001*x3+0．0332*x4+0．0867*x5-0．1127*x6-0．0186*x7+0．0985*x8-y2=-131．3521;-0．0694*x1+0．062*x2-0．1565*x3-0．0099*x4+0．1247*x5+0．0024*x6-0．0028*x7-0．2012*x8+y3=108．9928;-0．0346*x1-0．1028*x2+0．2050*x3-0．0209*x4-0．012*x5+0．0057*x6+0．1452*x7+0．0763*x8-y4=-77．6116;0．0003*x1+0．2428*x2-0．0647*x3-0．0412*x4-0．0655*x5+0．07*x6-0．0039*x7-0．0 092*x8-y5=-133．1334;0．2376*x1-0．0607*x2-0．0781*x3+0．0929*x4+0．0466*x5-0．0003*x6+0．1664*x7+0．0004*x8-y6=-120．8481;y1<186．45;y2<177;y3<174．4;y4<172．05;y5<151．8;y6<184．68;end;。