Dynamics of Scalar Fields in the Background of Rotating Black Holes
时变跨尺度结构动力学行为与机理研究

时变跨尺度结构动力学行为与机理研究The research topic I seek to explore is the dynamicbehavior and mechanisms of spatio-temporal structural changes across multiple scales.我想要探索的研究主题是关于不同尺度上时空结构变化的动态行为及其机理。
At the core of this study is the investigation into how structures evolve, adapt, and interact across various scales, from the atomic level to macroscopic dimensions. By studying these dynamic behaviors, we aim to gain a deep understanding of how different spatial and temporal factors influence structural dynamics.该研究的核心是探究在不同尺度上结构如何演变、适应和相互作用,从原子级到宏观维度。
通过研究这些动态行为,我们旨在深入了解不同的时空因素如何影响结构动力学。
The first aspect we will focus on is understanding how individual components within a structure respond andinteract at the microscopic scale. This involves investigating the behavior of atoms, molecules, or even smaller subunits that make up a larger structure. By studying these fundamental interactions, we can uncover the forces and patterns that govern their collective behavior and ultimately shape the overall structural dynamics.我们将重点关注微观尺度下结构内各个组成部分的响应和相互作用方式。
汽车侧向动力学
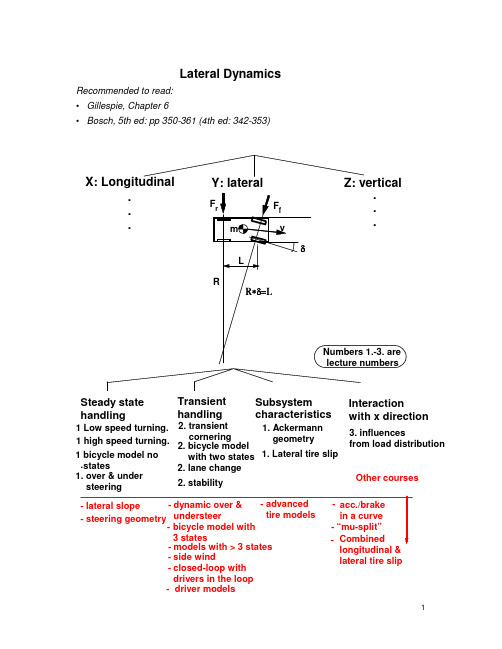
Lateral DynamicsRecommended to read:• Gillespie, Chapter 6• Bosch, 5th ed: pp 350-361 (4th ed: 342-353)Z: verticalInteractionwith x directionOther coursesX: Longitudinal Y: lateralSubsystem characteristicsSteady state handlingTransient handling1. over & under steering2. stability2. lane change1. Lateral tire slip 1 bicycle model no stateslateral tire slip2. bicycle modelwith two states 1. Ackermanngeometry- side wind2. transient cornering 1 Low speed turning. 1 high speed turning. - driver models- closed-loop with drivers in the loop3. influences from load distribution.General questionsSketch your view of the open- and closed-loop system, i.e. without and with the driver. Use a control system block diagram or similarOpen-loop vs closed loop studies of lateral dynamics. Closed-loop studies involve the driver response to feedback in the system. See text in Gillespie, p195, Bosch 5th ed p 354 (4th ed p 346).This course will only treat open-loop vehicle dynamics. How can we upgrade to closed-loop? For example: driver models, simulators or experimentsQuestions on low speed turningDraw a top view of a 4 wheeled vehicle during a turning manoeuvre. How should the wheel steering angles be related to each other for perfect rolling at low speeds?Ackermann steering geometry Array Deviations from Ackerman geometry affect tire wear and steering system forcessignificantly but less influence on directional response.Consider a rigid truck with 1 steered front axle and 2 non-steered rear axles. How do we predict the turning centre?Assume: low speed, small steering angles, low traction.We still cannot assume that each wheel is moving as it is directed. A lateral slip iscreated at all axles. The turning centre is then not only dependent of geometry, but also forces. The difference in the 3 axle vehicle compared to the two axle vehicle is that we now have 3 unknown forces but only 2 relevant equilibrium equations. In other words, the system is not statically determinateApprox. for small angles:Equilibrium: Fyf+Fyr1=Fyr2 and Fyf*lf+Fyr2*lr=0 Compatibility: (αr1+αr2)*lf/lr+αr1=δf -αf Constitutive relations: F yf =C αf *αfF yr1=C αr1*αr1F yr2=C αr2*αr2C α = cornering stiffness [N/rad]Together,3 eqs and 3 unknowns (the three slip angles) can be obtained for the figure below. Note that we assume a lateral force vector at each axle by choosing a slip angle:C αf *αf - C αr1*αr1 + C αr2*αr2 = 0 (Sum of forces in Y direction) C αf *αf *lf - C αr2*αr2*lr= 0 (sum of moments about r1) (αr1+αr2)*lf/lr + αr1 = δf - αf (compatibility)Steady state cornering at high speedIn a steady state curve at high speed, centripetal forces are needed to keep the vehicle on the curved track. Where do we find them? How large must these be? How are they developed in practice?Same C α at all axlesTest, e.g. prescribe steering angle. Calculate slip angles:VfThe centripetal force = F c=m*R*Ω2= m*Vx2/R. It has to be balanced by the wheel/road lateral contact forces:Equilibrium: Fyf+Fyr = F c = m*Vx2/R and Fyf*b-Fyr*c=0(Why not Fyf*b-Fyr*c=I*dΩ/dt ??? )Constitutive equations: F yf=Cαf*αf and F yr=Cαr*αrCompatibility: tan(δ−αf)=(b*Ω+Vy)/Vx and tan(αr)=(c*Ω-Vy)/Vxeliminating Vy for small angles and using Vx=R*Ω: δ−αf+αr=L/RTogether, eliminate slip angles:Fyf=(lr/L)*m*Vx2/R and Fyr=(lf/L)*m*Vx2/Rδ−F yf/Cαf+F yr/Cαr=L/REliminate lateral forces:d = L/R +[(lr/L)/Caf - (lf/L)/Car] * m*Vx2/Rwhich also can be expressed as: δ = L/R + [Wf/Cαf - Wr/Cαr] *Vx2/(g*R)(Wf and Wr are vertical weight load at each axle, respectively.)Wf/Cαf - Wr/Cαr is called understeer gradient or coefficient, denoted K or K us and simplifies to: d = L/R + K *Vx2/(g*R)A more general definition of understeer gradient:Note that this relation between δ , R and Vx is only first order theory. (Why?) Study a 2 axle vehicle in a low speed turn. How do we find the steering angle needed to negotiate a turn at a given constant radius? How do the following quantities vary with steering angle and longitudinal speed:•yaw velocity or yaw rate, i.e. time derivative of heading angle•lateral accelerationFor a low speed turn:Needed steering angle: δ = L / R (not dependent of speed)Yaw rate: Ω = Vx / R = Vx * δ / L (prop. to speed and steering angle)Lateral acceleration: ay = Vx2 / R = Vx2 * δ / L (prop. to speed and steering angle) Since steering angle is the control input, it is natural to define “gains”, i.e. division by δ:Yaw rate gain = Ω/δ =Vx/LLateral acceleration gain: ay/δ = Vx2/LFor a high speed turn:δ = L/R + K *Vx2/(g*R)Yaw rate gain = Ω/δ =(Vx/R) / δ=Vx/(L + K *Vx2/g)Lateral acceleration gain: ay/δ = (Vx2/R) / δ= Vx2/(L + K *Vx2/g)These can be plotted vs Vx:What happens at Critical speed? Vehicle turns in an unstable way, even with steering angle=0.What happens at Characteristic speed? Nothing special, except that twice the steeringangle is needed, compared to low speed or neutral steering..How is the velocity of the centre of gravity directed for low and high speeds?See the differences and similarities between side slip angle for a vehicle and for a single wheel. Bosch calls side slip angle “floating angle”.Some (e.g., motor sport journalists) use the word under/oversteer for positive/negative vehicle side slip angle.Transient corneringNOTE: Transient cornering is not included in Gillespie. This part in the course is defined by the answer in this part of lecture notes. For more details than given on lectures, please see e.g. Wong.To find the equations for a vehicle in transient cornering, we have to start from 3 scalar equations of motion or dynamic equilibrium. Sketch these equations.vm*dV I*d NOTE: It will m*dv/dt (2D vector equation)We like to express them without introducing the heading angle, since we thenwould need an extra integration when solving (to keep track of heading angle). In conclusion, we would like to use “vehicle fixed coordinates”.But the torque equation is straight forward:m*dV y /dt=Fyr+Fxf*sin(δ)+Fyf*cos(δ)x /dt=Fxr+Fxf*cos(δ)-Fyf*sin(δ)Ω/dt= -Fyr*c+Fxf*sin(δ)*b+Fyf*cos(δ)*bv is a vector. Let F also be vectors.NOT be correct if we only consider each component of v (Vx and Vy)separately, like this:=ΣF equation )I*d Ω/dt = ΣMz (1D scalar would like to express all equations as scalarequations . We would alsoMotion of a body on a plane surface:If we consider a rigid body (like a car) travelling on the road, we can analyse the motion of a reference frame attached to the vehicle.The body fixed to the x,y axes start with an orientation θ relative to the Global (earth fixed)system. The body has velocities V x and V y in the x,y system. Relative to the x,y system the point P has velocities:Ω−=y Vx vxΩ+=x Vy vyat time t t δ+, the velocities for P are:)()(Ω+Ω−+=′δδy Vx Vx x v )()(Ω+Ω++=′δδx Vy Vy y vSince the velocities have rotated by the angle δθ, the transformation of the velocities for P at time t t δ+to the original orientation:Time t+YTime tδ t)cos()sin()sin()cos(δθδθδθδθy v x v y v y v x v x v t t ′+′=′′−′=′where subscript “t” refers to coordinate system at time tThe difference of velocities for P in the time interval will then bevyy v vy vx x v vx −′=−′=δδSubstituting the values above:[][]()[][]()Ω+−Ω+Ω+++Ω+Ω−+=Ω−−Ω+Ω++−Ω+Ω−+=x Vy x Vy Vy y Vx Vx vy y Vx x Vy Vy y Vx Vx vx )cos()()()sin()()()sin()()()cos()()(δθδδδθδδδδθδδδθδδδIf consider that t δis very small, then )cos(δθ=1 and )sin(δθ=δθ and divide by t δtVy t x t y t y t Vx t Vx t vy t x t x t Vy t Vy t y t Vx t vx δδδδδδθδδδδδθδδδδδδδθδδδθδδθδδδθδδδδδδ+Ω+Ω−ΩΩ−+Ω=Ω−Ω−−−Ω−=()()()(if we let t=0 and let the global and local coordinate systems align at t=0 we can write dtd t ()()=δδ. We can also defineΩ=tδδθand ignore the second order terms ()()δδ⋅:22Ω−Ω+Ω+=Ω−Ω−Ω−=y dtd x Vx dt dVy ay x dtd y Vy dt dVx axAnd at the center of x,y system x=0, y=0:Ω+=Ω−=Vx dtdVyay Vy dtdVxaxNow, it will be correct if:m*a x = m*(dVx/dt - Vy*Ω) = Fxr + Fxf*cos(δ) - Fyf*sin(δ) m*a y = m*(dVy/dt + Vx*Ω)=Fyr + Fxf*sin(δ) + Fyf*cos(δ) I*d Ω/dt = - Fyr*c + Fxf*sin(δ)*b + Fyf*cos(δ)*bTry to understand the difference between (ax,ay) and (dVx/dt,dVy/dt).[The quantities (ax,ay) are accelerations, while (dVx/dt,dVy/dt) are “changes in velocities”. The driver will have the instantaneous feel of mass forces according to (ax,ay) but he will get the visual input over time according to (dVx/dt,dVy/dt).][Example: If going in a curve with constant longitudinal speed with driver in vehicle centre of gravity: The driver feel only “ax=0 and ay=centrifugal force=radius*Ω*Ω“ in his contact with the seat. However, he sees no changes in the velocity with which outside objects move, i.e. “dVx/dt=0 and dVy/dt=ay-Vx*Ω=radius*Ω*Ω-radius*Ω*Ω=0“.]Constitutive equations: F yf=Cαf*αf and F yr=Cαr*αrCompatibility: tan(δ−αf)=(b*Ω+V y)/V x and tan(αr)=(c*Ω-V y)/V xEliminate lateral forces yields:m*(dV x/dt - V y*Ω) = F xr + F xf*cos(δ) - Cαf*αf*sin(δ)m*(dV y/dt + V x*Ω) = Cαr*αr + F xf x*sin(δ) + Cαf*αf*cos(δ)I*dΩ/dt = -Cαr*αr*c + Fxf*sin(δ)*b + Cαf*αf*cos(δ)*bEliminate slip angles yields (a 3 state non linear dynamic model):m*(dV x/dt - V y*Ω) = Fxr + Fxf*cos(δ) - Cαf*[δ−atan((b*Ω+V y)/V x)]*sin(δ)m*(dV y/dt + V x*Ω) = Cαr*atan((c*Ω-V y)/V x) + Fxf*sin(δ) + Cαf*[δ−atan((b*Ω+V y)/V x)]*cos(δ) I*dΩ/dt = -Cαr*atan((c*Ω-V y)/V x)*c + Fxf*sin(δ)*b + Cαf*[δ−atan((b*Ω+V y)/V x)]*cos(δ)*b For small angles and dV x/dt=0 (V x=constant) and small longitudinal forces at steered axle (here Fxf =0), we get the 2 state linear dynamic model:m*dV y/dt +[(Cαf+Cαr)/V x]*V y + [m*V x+(Cαf*b-Cαr*c)/V x]*Ω=Cαf*δI*dΩ/dt +[(Cαf*b-Cαr*c)/V x]*V y + [(Cαf*b2+Cαr*c2)/V x]*Ω =Cαf*b*δThis can be expressed as:What can we use this for?- transient response (analytic solutions)- eigenvalue analysis (stability conditions)If we are using numerical simulation, there is no reason to assume small angles. Response on ramp in steering angle:• True transients (step or ramp in steering angle, one sinusoidal, etc.) (analysed in time domain) • Oscillating stationary conditions (analysed i frequency domain, transfer functions etc., cf. methods in the vertical art of the course).Examples of variants? Trailer (problem #2), articulated, 6x2/2-truck, all-axle-steering, ...ExampleShow that critical speed for a vehicle is sqrt(-L*g/K), using the differentialequation system valid for transient response. Assume some numerical vehicle parameters. Which is the mode for instability (eigenvector, expressed in lateral speed and yaw speed)?How to find global coordinates? dX/dt=Vx*cos ψ - Vy*sin dY/dt=Vy*cos ψ + Vx*sin X (global,Y (global,earth fixed) earth fixed)heading angle, Vx VyΩSolution sketch (using Matlab notation):» [m I g L l Cf/1000 Cr/1000] = 1000 1000 9.8 3 1.5 100000 80000(These are the assume vehicle parameters in SI units)» K=m*g/2*(1/Cf-1/Cr) = -0.0122 (understeer coefficient)» A=[m 0;0 I] =1000 00 1000 (mass matrix)» Vx=sqrt(-L*g/K)= 48.9898 (critical speed according to formula)» B=-[(Cf+Cr)/Vx m*Vx+(Cf*l-Cr*l)/Vx ;(Cf*l-Cr*l)/Vx (Cf*l*l+Cr*l*l)/Vx];» C=inv(A)*B; [V,D]=eig(C)0.9973 0.9864-0.0739 0.1644D = (diagonal elements are eigenvalues)0.0000 00 -11.9413Note that the first eigenvalue is zero, which means border between stability and instability. This is the proof!The eigenvector is first column of V, i.e. Vy=0.9973 and Ωz=-0.0739 (amplitudes):ExampleVehicles that have lost their balance might sometimes be stabilized through one-sided brake interventions on individual wheels (ESP systems). Which wheels and how much does one have to brake in the following situation?Vx=30 m/s, cornering radius=100 m.Before time=0: Cf=Cr=100000 /radAt time=0, the vehicle loses its road grip on the front axle, which can be modelled as a sudden reduction of cornering stiffness to 50000 N/rad.Assume realistic (and rather simplifying!) vehicle parameters.Solution (very brief and principal):Assume turning to the right, i.e. right side is inner side. Use the differential equation system for transient vehicle response, but add a term for braking m*dV y /dt + [(C αf +C αr )/V x ]*V y + [m*V x +(C αf *b-C αr *c)/V x ]*Ω=C αf *δ I*d Ω/dt + [(C αf *b-C αr *c)/V x ]*V y + [(C αf *b 2+C αr *c 2)/V x ]*Ω =C αf *b*δ ++ Mzwhere Mz=Fr*B/2, Fr=brake forces at the two right wheels, B=track width For t<0: Solve the eqs with dV y /dt = d Ω/dt = Mz=0 and Cf=Cr=100000 and Ω=Vx/radius=30/100 rad/s. This gives values of δ and Vy.For t=0: Insert the resulting values for δ and Vy into the same equation system but with Cf=50000 and do not constrain Mz to zero. Instead calculate Mz, which gives a certain brake force on the two right wheels, Fr.Check whether Fr is possible or not (compare with available friction, µ*normal force). If possible, put most of Fr on the rear wheel since front axle probably has the largest risk to drift outwards in the curve.Longitudinal & lateral load distribution during corneringWhen accelerating, the rear axle will have more vertical load. Explore what happens with the cornering characteristics for each axle. Look at Gillespie, fig 6.3. ...C Part of: Gillespie, fig 6.3o r n e r i n g s t i f f n e s sVertical loadSo, the cornering stiffness will increase at the rear axle and decrease at front axle, due to the longitudinal vertical load distribution during acceleration. This means lesstendency for the rear to drift outwards in a curve (and increased tendency for front axle) when accelerating.The opposite reasoning applies for braking (negative acceleration.)So, longitudinal distribution of vertical loads influence handling properties.NOTE: A larger influence is often found from the combined longitudinal and lateral slip which occurs due to the traction force needed to accelerate.In a curve, the outer wheels will have more vertical load. Explore what happens with the lateral force on an axle, for a given slip angle, if vertical load is distributed differently toSo, lateral distribution of vertical loads influence handling properties.How to calculate the vertical load on inner and outer side wheels, respectively, when the vehicle goes in a curve?First consider the loads on the vehicle body and axle:Force in Springs)(x x Ks Fi ∆+=, )(x x Ks Fo ∆−= where x is the static displacement of the springand Dx is the change in spring length due to body rollSum moments about chassis CGM sx x Ks s x x Ks =∆−−∆+2)(2)(2φs x =∆M K sKs ==φφ2where K φ is the roll stiffness for the axleMoment applied from body to axle=K φ φIf we take the sum of the moments about point A:ΣM A =00222=++−φφK hr RV m t Fzi t FzoThis simplifies to:02)(2=+=−φφK hr RV m t Fzi Fzo022)(2=+=−tK t hr R V m Fzi Fzo φφwe can define the term ∆Fz as∆Fz= (Fzo-Fzi)/2where ∆Fz is where the change of vertical load for each tire on the axleHow can we account for the whole vehicle? If we assume that the chassis is rigid, we can assume that it rotates around the roll centers for each axle. This is shown in the figure below:Roll moment about x axis M φ = {mV 2/R h 1 cos(φ) + mg h 1 sin(φ)} cos(ε)for small angles• M φ = mV 2/R h 1 + mg h 1 φ– Let W=mg• M φ = W h 1 (V 2/Rg+ φ)• If we know M φ = M φf+ M φr• M φ = (K φf +K φr )φthen:(K φf +K φr )φ= W h 1 (V 2/Rg+ φ)(K φf +K φr - W h 1 ) φ= W h 1 V 2/Rg)(121Wh K K Rg VWh r f −+=φφφThis is the roll angle based on the forward speed and curve radius.From previous expression for one axle2∆Fz= 2mV 2/R hr/t + 2K φ φ/twhere hr is the roll axis height. For front axle, Substitute the value the following into the previous equation.For front axle: mV 2/R=Wf/gV 2/RThis results in the relationship: )(11212Wh K K Rg V Wh t K t h Rg V W F r f f f f Zf −+⋅+⋅=∆φφφSimilarly for rear axle:)(11212Wh K K Rg V Wh t K t h Rg V W F r f r r r Zr −+⋅+⋅=∆φφφThese equations allow the exact load on each tire to be calculated. Then the cornering stiffness can be calculated if a functional relationship is known between the cornering stiffness C α and Fz.How is vertical load distributed between front/rear, if we know distribution inner/outer?It depends on roll stiffness at front and rear. Using an extreme example, without any roll stiffness at rear, all lateral distribution is taken by the front axle. .In a more general case:Mxf=kf*φ Mxr=kr*φ , where kf and kr are roll stiffness and φ=roll angle.Eliminating roll angle tells us that Mxf=kf/(kf+kr)*Mx and Mxr=kr/(kf+kr)*Mx, i.e. the roll moment is distributed proportional to the roll stiffness between front and rear axle. We can express each Fz in m*g, ay, geometry and kf/kr. This is treated in Gillespie, page 211-213.How would the diagrams in Gillespie, fig 6.5-6.6 change if we include lateral load distribution in the theory?It results in a new function =func(Vx), (eq 6-48 combined with 6-33 and 6-34). It could be used to plot new diagrams like Gillespie, fig 6.5-6.6:Equations to plot these curves are found in Gillespie, pp 214-217. Gillespie uses the non linear constitutive equation: Fy=Cα*α where Cα=a*Fz-b*Fz2 .What more effects can change the steady state cornering characteristics for a vehicle at high speeds?See Gillespie, pp 209-226: E.g. Roll steer and tractive (or braking!) forces. Braking in a curve is a crucial situation. Here one analyses both road grip, but also combined dive and roll (so called warp motion).Try to think of some empirical ways to measure the curves in diagrams in Gillespie, fig 6.5-6.6.See Gillespie, pp 27-230:Constant radius• Constant speed• Constant steer angle (not mentioned in Gillespie)How to calculate the vertical load on front and rear axles, respectively, when the vehicle accelerates?In general: ΣFz=mg and ΣFz,rear=mg/2+(h/L)*m*ax, where L=wheel base and h=centre of gravity height. ax=longitudinal acceleration. Still valid for braking because ax is then negative.Component CharacteristicsPlot a curve for constant side slip angle, e.g. 4 degrees, in the plane of longitudinal force and lateral force. Do the same for a constant slip, e.g. 4%. Use Gillespie, fig 10.22 as input.See Gillespie Fig 10.23Summary•low speed turning: slip only if non-Ackermann geometry•steady state cornering at high speeds: always slip, due to centrifugal acceleration of the mass, m*v2/R•transient handling at constant speed: always slip, due to all inertia forces, both translational mass and rotational moment of inertia•transient handling with traction/braking: not really treated, except that the system of differential equations was derived (before linearization, when Fx anddVx/dt was still included)•load distribution, left/right, front/rea r: We treated influences by steady state cornering at high speeds. Especially effects from roll moment distribution.Recommended exercise on your own: Gillespie, example problem 1, p 231. (If you try todetermine “static margin”, you would have to study Gillespie, pp 208-209 by yourself.)。
Reservoir Computing Approaches toRecurrent Neural Network Training

1. Introduction Artificial recurrent neural networks (RNNs) represent a large and varied class of computational models that are designed by more or less detailed analogy with biological brain modules. In an RNN numerous abstract neurons (also called units or processing elements ) are interconnected by likewise abstracted synaptic connections (or links ), which enable activations to propagate through the network. The characteristic feature of RNNs that distinguishes them from the more widely used feedforward neural networks is that the connection topology possesses cycles. The existence of cycles has a profound impact: • An RNN may develop a self-sustained temporal activation dynamics along its recurrent connection pathways, even in the absence of input. Mathematically, this renders an RNN to be a dynamical system, while feedforward networks are functions. • If driven by an input signal, an RNN preserves in its internal state a nonlinear transformation of the input history — in other words, it has a dynamical memory, and is able to process temporal context information. This review article concerns a particular subset of RNN-based research in two aspects: • RNNs are used for a variety of scientific purposes, and at least two major classes of RNN models exist: they can be used for purposes of modeling biological brains, or as engineering tools for technical applications. The first usage belongs to the field of computational neuroscience, while the second
Dynamic Field Theory (DFT

Dynamic Field Theory (DFT):Applications in Cognitive Science and RoboticsWolfram Erlhagen1 and Estela Bicho21Dep. of Mathematics for S&T, 2Dep. of Industrial ElectronicsUniversity of Minho, Portugal(wolfram.erlhagen@mct.uminho.pt, estela.bicho@dei.uminho.pt)IntroductionIn recent years, there has been an increasing interest in the dynamical systems approach to cognitive science that challenges the more traditional, computational view on cognition ([1], [2], [3]). The heart of the dynamic approach is the hypothesis that natural cognition embedded in a nervous system and in an environment unfolds continuously in time as the result of the complex interplay between a variety of internal and external forces. Proponents of this new direction argue that cognitive processes can be conceptualized in terms of position, distance and trajectories in the space of possible states of the system. Consequently, the primary focus of their theoretical and empirical research program is on understanding the nature of change in time. The dynamic hypothesis strongly contrasts with the computational approach that explains cognitive behaviour as a rule-based manipulation of static internal representations.The theory of nonlinear dynamical systems is the mathematical framework that offers essential concepts and tools such as attractor, repeller, stability, bifurcation, trajectory in state space and the like. However, these concepts are certainly necessary but not sufficient for a dynamical systems approach to higher cognitive capacities. The problem is that flexible and intelligent behaviour very often depends on past and future events of the environment that are not represented in the immediate stream of sensory signals. The forces that are supposed to shape the unfolding trajectories are thus not available all time. What is needed is the notion of complex persisting inner states that allow the cognitive agent, for instance, to compensate for temporally missing sensory input, or to anticipate future environmental inputs that may inform the decision about a specific goal-directed behaviour [1].Dynamic Field Theory or DFT provides a theoretical framework that bridges the representational gap in the dynamic system approach ([4], [5]). Dynamic fields formalized by differential equations have been originally introduced by Wilson and Cowan [6] and Amari [7] in the 1970’s as simplified mathematical models for pattern formation in neural tissue. The architecture of this model family reflects the hypothesis that strong recurrent interactions in local populations of neurons form a basic mechanism for cortical information processing. This hypothesis is supported by anatomical and psychological findings showing that a cortical neuron gets its largest input from neighbouring cells. The recurrent interactions cause non-trivial dynamic behaviour in neural populations. Most importantly, population activity which is initiated by time-dependent external signals may become self-sustained in the absence of any external input. Such attractor states of the population dynamics may be used by the nervous systems to guide complex behaviour that goes beyond a simple input-output mapping. On this view, DFT complements the dynamic approach by adding the notion of sub-symbolic dynamic representations that are consistent with fundamental principles of cortical information processing.In the following we briefly discuss representative examples that shall illustrate the basic concepts of DFT and its application in different cognitive domains (for a recent survey of the mathematical treatment see [5]). As embodied validations of the approach, we include studies in which autonomous robots were endowed with some cognitive capacities such as decision making, memory, action understanding or anticipation. The reader is encouraged to visit the original publications for proper treatment.Basic conceptsDynamic fields are defined over metric dimensions that in most applications reflect parameters of the experimental setup such as for instance visual space, object features or movement parameters. A localized peak of activation within the field represents metric information about the underlying dimension. In analogy to the concept of neural population coding, the localized peak may be interpreted as the activation pattern of a pool of neighbouring neurons with similar tuning properties in an otherwise inactive population [8]. The peak evolves under the influence of time-dependent external input but is mainly shaped by the recurrent interactions within the population. Due to the interactions the peak is self-sustained and may thus serve to memorize information. However, in order to perform a working memory the field dynamics has to be bi-stable. The attractor state of a persistent firing pattern coexists with a stable homogenous activation distribution that represents the absence of information. A sufficiently strong transient input specifying a particular instance of the metric dimension is able to “switch on” the memory function by destabilizing the uniform rest state. A suitable inhibitory signal, on the other hand, may destabilize the excited state, resulting in a decay of activation back to resting state. The critical parameter that decides whether or not the uniform state becomes unstable is input strength. Below a certain threshold, inhomogeneous solutions of the field dynamics exist that are mainly input driven. In many applications this regime is exploited to represent for instance ambiguous prior information about the dimension spanned by the field. Much like prior distributions in the Bayesian sense, multi-modal patterns of subthreshold activation may encode the probability of choices [9].Within the DFT framework, the existence of a memory function is closely linked to decision making. A self-sustained activation peak is the result of the interplay between excitatory and inhibitory forces within the field. Excitatory interactions between neighbouring neurons are counterbalance by lateral inhibition. Since inhibitory interactions dominate at larger distances, a competition process takes place whenever two or more suprathreshold inputs are simultaneously applied. At the field site that integrates the highest level of sensory or other evidence a single activation peak will emerge. It suppresses the activation elsewhere in the field below resting level. Once the stable attractor state has been reached, the decision represented by the peak location is protected against noise and fluctuations in the input stream. This does not mean, however, that the peak is completely immune against change. Localized input that spatially overlaps with the peak position causes the peak to drift in the direction of this input. Mathematically, the attractor can be described as being continuous along the dimension spanned by the field. This property of the field dynamics has been exploited for instance to explain and apply the capacity of tracking time-varying input in real time ([10], [11]).Although the formation of spatially localized peaks is certainly the backbone of most DFT-based models thus fare, it is important to note that the field dynamics - if properly tuned - may exhibit other types of self-organizing patterns (e.g., .travellingpulse and wave, active transient etc., see [12] for a recent overview) that play an important role in some applications of the dynamic field approach to cognition (see the examples below).Applications in Cognitive Science: Action, Perception and Reasoning The dynamic field approach has been first developed and applied in the context of simple sensorimotor decisions ([13], [14], [15]). Timed-movement initiation paradigms reveal that plans for goal-directed arm or eye movements evolve continuously in time. Early during action preparation an externally forced decision to move reflects the prior knowledge about the task (e.g., number and probability of possible targets) whereas later in time the decision is dominated by the visual information specifying the target. In the DFT model [14], a localised activation peak in the movement parameter field evolves in time under the influence of the two inputs sources represented by activation patterns in two connected fields. Due to the constant input from the task field, the build up starts from a pre-activated initial state reflecting prior task knowledge. Since the level of pre-activation affects the rate at which the activation peak rises, all classical effects of task environment on reaction time can be modelled. Moreover, the field model also accounts for experimental findings showing that not only the informational content (e.g., number and probability of choices) but also the metric of the movement parameter space matters. A simple example is a two choice task in which the relative distance between the possible directions of the movement is systematically varied. A general experimental finding is that reaction time decreases with decreasing distance. In the model, the two-choice setting lead to a bimodal preshape. For metrically close directions, however, the two preshape inputs start to overlap, resulting in a higher level of pre-activation. As a consequence, the buildup of the peak in response to a specific input is faster compared to the case of two movement directions metrically fare from each other.It is worth mentioning that the dynamic field concepts can be generalized to the case of multiple movement parameters by introducing multidimensional activation fields. A two-dimensional field spanned over movement direction and movement amplitude has been used for instance to explain differences in the process of specification of the two parameters as revealed in precuing paradigms [14].The DFT approach to sensorimotor decisions has been extended to address fundamental questions in developmental cognitive science. An excellent example is the DFT model of Piaget’s classic ‘A-not-B’ error [16]. In this task, an infant is faced with two similar opaque containers with lids. The experimenter hides a toy under the lid at location A and the infant is trained to reach for the toy. If after several A trials the object is hidden for the first time at location B and a short delay is imposed, younger infants nevertheless reach toward container A. This typical ‘A-not-B’ error is absent in older infants. The DFT model explains this change in behaviour as a shift from an input-driven regime of decision making in younger infants to an interaction-dominated regime in older children (but see [17] for a recent refinement of the model). The motor decision field is spanned over the space of reachable directions. It evolves under the influence of the specific input representing the location of the toy, input from the task field representing the perceptual layout of the work space, and input from the preshape field representing the memory trace of previous A-reaches. If the decision field is input-driven, that is, the transient input representing the toy at B does not reach the threshold for triggering the cooperative forces within the population, the activation pattern at therespective field site will decay during the delay towards resting level. As a result, movement history represented by the preshape field will start to dominate movement selection, leading to the ‘A-not-B’ error. If, by contrast, the field is able to self-stabilize activation patterns, the evolving peak at the B location will suppress the conflicting input from the preshape field.During the delay period between the presentation of the cue at a certain location and movement onset, the peak serves as spatial working memory. However, since the peak attractor is continuous, spatially overlapping preshape input will cause a continuous drift of the localized activity pattern whenever there exists no additional input that may ‘fix’ the peak at the cued position. The predicted distortion over time of spatial memory has been indeed observed in experiments with goal-directed actions to remembered locations with no salient location cues [18].Cognitive vision is another attractive area for DFT research [19]. The basic concept of self-stabilized internal representations provide the means to cope with some of the fundamental problems any cognitive agents has to solve in order to organize goal-directed behaviour in a continuously changing world. Very importantly, the system has to compensate for long and unreliable delays involved in the processing of visual information about moving objects. As revealed in psychophysical experiments, the position percept very often does not agree with the physical measurements. Furthermore, a continuous stream of sensory signals that may guide behaviour is not guaranteed in cluttered environments. There is thus a need for mechanisms that allow the system to extrapolate past trajectory information into the future.The DFT-based model of object location in visual space has been originally developed to explain nonlinear interaction effects found in neuronal population activity of primary visual cortex [20]. It has been later extended to bridge the gap to the perceptual level. The model accounts for various systematic localization errors observed with moving and stationary targets ([21], [22], [23], [24]). In response to an object in real or apparent motion, the field develops a self-stabilized travelling pulse of activation that locks to the stimulus. Its peak position is taken as a neural correlate for the location percept. Due to the lateral interactions within the population, neurons encoding future stimulus positions become pre-activated, leading to a path-dependent facilitation of processing. In the model, the latency of the suprathreshold population response to the external input may be further reduced by integrating additional preshape input from other information sources such as for instance actions plans directed toward the moving object. Moreover, like a physical object in motion, the internal representation of target position cannot be halted instantaneously upon stimulus offset but continues to travel for some time. In line with experimental findings in position judgement tasks, the model predicts a perceptual overshooting at the end of the motion trajectory whenever the cooperative forces within the population are sufficiently strong. The extent to which the internal representation extrapolates past trajectory information depends on a single model parameter that controls the interplay between excitation and inhibition within the field. If properly tuned, the self-organizing wave may fill in missing trajectory information whenever the sensory input is temporally disrupted due to occluding surfaces for instance [25].Decision making, memory and object permanence are all examples of basic cognitive functionalities. Recently, attempts have been made to extend the DFT approach to higher cognitive capacities such as off-line reasoning and prediction that are often crucially involved in the control and coordination of real action in real time. Togive a concrete example from the domain of social cognition, a fluent and efficient coordination of actions and decisions among partners in a joint action task requires that each individual is able to understand others’ action goals. The DFT model of goal inference [26] implements the idea that action simulation supports action understanding. Without the need to rely on any explicit symbolic communication, we understand the purpose of observed actions by internally replicating action effects using our own motor repertoire. The model has been validated in tasks which involve goal-directed reaching-grasping-placing sequences. The model architecture consists of various reciprocally coupled dynamic fields that represent in their firing patterns action means, action goals and contextual cues. In the action simulation layer (ASL) learned action chains composed of populations encoding different motor acts exist that are linked to specific placing goals or end states. Individual chains may be preshaped by connected populations representing contextual cues and prior task information. Through mappings between populations encoding congruent motor acts in the action observation (AOL) and the action simulation layer, the chain is triggered whenever input from AOL indicates the observation of a specific motor act. The self-stabilizing properties of the neural populations forming the chain ensure that the associated goal representation reaches a suprathreshold activation level even in cases where only partial visual information about the action performed by another person is available (e.g., only the reaching toward the object is observed). In a joint action context, the information about the inferred goal may then be used by the observer to select an appropriate complementary action sequence.It is worth stressing that the dynamic field model within which the high-level reasoning capacity is realized represents a distributed but fully integrated dynamical system that emerges from sensorimotor origins. The same action chains that support overt motor behaviour are covertly used during action observation to make sense of the behaviours of others. The populations forming the chains encode entire goal-directed motor primitives such as grasping and placing that abstract from the fine details of the hand movements. For such a high-level motor vocabulary the metric structure of the underlying space, which is a core concept of DFT, is not directly observable. However, the metric may still be defined operationally by the degree of overlap of neuronal representations. In the present implementations, a motor acts such as grasping is represented by a localized activation pattern in an otherwise inactive population. The pool of grasping neurons that becomes activated above threshold gets input from connected populations. In a modelling attempt to explain the development of goal-directed chains, it has been recently shown that the interplay of the field dynamics and a Hebbian learning dynamics may result in the emergence of distinct, non-overlapping subpopulations of grasping neurons that become linked during learning to specific goal representations [27]. In other words, depending on the ultimate goal of the action sequence in which the grasping behaviour is embedded, the localized activity pattern in the grasping field will evolve at different locations of the field. On this view, the similarity on the goal level defines the metric of the field, that is, the extent to which subpopulations will overlap. The development of such goal-directed representations has important implications for cognitive behaviour since it allows individuals to act at the time of the grasping in anticipation of others’ motor intentions.Applications in RoboticsAn active area of research is the validation of the neuro-plausible mechanisms and concepts of the DFT approach to cognition in autonomous artificial agents. Implementations on robots controlled in closed-loop by sensory information provide feedback about hidden assumptions and missing links to the sensory and motor surfaces.A major challenge is to demonstrate that inner persistent states and internal simulations are not a costly information processing bottleneck [28] but actually support fluent real-world behaviour.DFT has been first introduced into the domain of robotics in navigation tasks with the goal to modify the behaviour of an autonomous vehicle through memorized sensory information ([29], see [30], [11], [31] for follow up studies). In the DFT-based control architectures, the fields are spanned over the heading direction of the robot relative to an arbitrary but fixed frame of reference. The path planning field integrates on-line information about the target location and the location of obstacles coming form on-board sensors. In addition, it receives input from an object memory field that contains self-stabilized activation peaks. They represent the location of previously detected obstacles that are currently invisible to the sensors. This memorized information is coupled into the movement planning field in the form of inhibitory input, defining undesirable heading directions. Since the field dynamics supports the existence of a single localized activation peak, decision can be made and stabilized even in navigation tasks with several potential targets. The demonstrations on vehicles equipped with low-level sensors and controlled by non-linear attractor dynamics demonstrate that the navigation behaviour in cluttered environments is quite smooth and robust [11]. The robustness is a direct consequence of the strong recurrent interactions within the fields that amplify and stabilize noisy and corrupted sensory inputs.Smooth real-time tracking of a moving target (e.g., another agent) is possible by exploiting that the self-stabilized activation peak in the target layer of the control architecture follows the continuously moving sensory input. This sensor-dependent tracking process will be disrupted, however, if the target disappears behind an occluding surface. The solution of this problem offered by DFT is a self-stabilized wave which travels in the direction of the moving target with a speed that can be controlled depending on the task. For instance, to anticipate future locations of the moving target the speed of the travelling wave may be chosen slightly faster than the actual velocity of the target. This predictive mechanism has been applied in a joint action task in which two agents (robot-robot or robot-human teams) have to search objects in a common workspace with the goal to transport them to a predefined area ([5], [32]). To guarantee an efficient division of the search space without the help of direct communication, each teammate has to infer from the partner’s motion future positions and possible action goals. The self-stabilized wave representing the predicted motion trajectory couples into the decision field of the observing robot as inhibitory input. As a consequence, the decision about the object toward which the robot will move appears to be biased by sensed or memorized targets in other locations of the workspace.The neuro-cognitive mechanisms implemented by the dynamic field approach to cognition represent a promising research direction for the domain of human-robot interaction (HRI). The basic idea followed by a number of studies ([33],[34],[35],[38]) is that in order to advance towards socially aware robots able to cooperate with humans in a natural and efficient manner, the robot design should reflect similar processing principles.An example on the perceptual level is the interactive learning of labels for different objects that are manipulated in joint action tasks [36]. The dynamic field architecture consists of various coupled two-dimensional feature label fields that get input from the camera system. Object features like colour, shape and size represent one dimension of a field whereas the object label is represented along the second dimension. The output of all label feature fields is integrated in a decision layer that contains one node for each label. There exist lateral connections between the feature label fields that ensure that during the recognition process the same labels belonging to different features fields excite each other. Feedback connections from the output field, on the other hand, guarantee that activation peaks in the feature label fields that do not match the decision in the output field are extinguished. During the supervised training phase, a correct label is given to the robot if recognition fails. Learning within the distributed network takes place in form of a buildup of preshape (or memory trace) at positions where a peak has emerged during successful recognition trials.The DFT model of action understanding has been integrated in control architectures to endow robots with the capacity of goal-directed imitation ([5], [37]). It has been validated in the context of grasping-placing sequences. The defining feature of the three-layer field architecture is a learned mapping from motor primitives in the action observation layer onto motor primitives in the action execution layer. It implements a matching on the goal and not on the movement level. The architecture can thus cope with differences in embodiment, task constraints and motor skills between teacher and robot. A self-stabilized activation peak representing a certain goal biases the decision process in the action execution layer toward the selection of motor primitives that can be used by the robot to achieve that goal. Moreover, the existence of goal-directed action chains in the middle layer of the field architecture allows the robot to act on a goal that it has to infer since the end state of the sequence was hidden from view or the user accidently failed to place the object at the desired location. If the meaning of an action is understood, further knowledge may be transferred from an experienced teacher to the robot in imitation paradigms. For instance, knowledge where o place a certain class of objects (e.g., defined by colour or shape) may be acquired and will be represented in learned synaptic links between neural populations encoding the goal and specific object features.For cooperative joint tasks, imitating the human behaviour is normally not beneficial for the robot and the team. The interpretation of observed actions in terms of goals should lead to the selection of an appropriate complementary behaviour. Both processes, goal inference and the action selection, depend on the situational context. A dynamic field architecture that establishes a context dependent mapping from observed actions onto complementary actions has been recently developed and tested in a task in which a robot and a human jointly construct a toy robot [38]. The state of the construction that defines which sub-goals are currently available for the team is represented by neural populations in the common sub-goal layer (CSGL) of the field architecture. If the input from this layer and from the intention layer (IL) representing the inferred goal of the partner converge on the representation of a particular action sequence in the action execution layer (AEL), this action sequence will normally win the competition process between all possible actions. If a mismatch between the inferred goal and the possible sub-goals exist, the robot is able to detect this error since an activation peak in the error monitoring layer (EML) will automatically appear. A selection of communicative gestures like pointing to ‘explain’ the error to the human partner may then constitute an appropriate complementary behaviour. Interestingly, how social the robot behaves can be controlled by a simple adaptation of the synapticweights form the intention layer to the action selection layer. If the weights are relatively weak, the action selection process of the robot will be dominated by information sources other than the behaviour of the partner.References[1] A. Clark, The dynamical challenge, Cognitive Science: A Multidisciplinary Journal 21: 461-481, 1997[2] T. van Gelder, The dynamical hypothesis in cognitive science, Behav. Brain Sci. 21: 615-665, 1998[3] S. Schöner, Dynamical Systems Approaches to Cognition, In: The Cambridge Handbook of Computational Psychology, R. Sun (ed.), pp. 101-125, Cambrige University Press, 2008[4] J. P. Spencer, G. Schöner, Bridging the representational gap in the dynamic systems approach to development, Developmental Science, 6, 392-412, 2003.[5] W, Erlhagen and E. Bicho, The dynamic neural field approach to cognitive robotics, Journal of Neural Engineering 3:R36-R54, 2006[6] H.R. Wilson, J. D. Cowan, A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue Kybernetik (Biol. Cybern.) 13 55–80, 1973[7] S. Amari, Dynamics of pattern formation in lateral-inhibitory type neural fields. Biological Cybernetics 27: 77–87, 1977.[8] W. Erlhagen, A. Bastian, D. Jancke, A. Riehle and G. Schöner, The distribution of population activation (DPA) as a tool to study interaction and integration in cortical representations, Journal of Neuroscience Methods, 94:53-66, 1999.[9] R. H. Cuijpers, W. Erlhagen, Implementing Bayes’ Rules with Neural Fields, In: ICANN 2008, Part II, LNCS 5164, V. Kurková et al. (eds.), pp 228-237, Springer-Verlag, 2008[10] S. Wu, S. Amari, Computing with Continuous Attractors: Stability and Online Aspects, Neural Computation, 17:2215-2239, 2005[11] E. Bicho, P. Mallet, and G. Schöner, Target representation on an autonomous vehicle with low-level sensors, The International Journal of Robotics Research, 19: 424–447, 2000.[12] S. Coombes, Waves, bumps, and patterns in neural field theories, Biological Cybernetics, 93: 91-108, 2005[13] G. Schöner, K. Kopecz, W. Erlhagen, The dynamic neural field theory of motor programming: Arm and eye movement”. In P. Morasso, V. Sanguineti, (eds.), Self-Organization, Computational Maps and Motor Control, Elsevier Science, pp. 271—310, 1997.[14] W. Erlhagen, G. Schöner, Dynamic field theory of motor preparation, Psychological Review, 109:545-572, 2002.[15] C. Wilimzig, S. Schneider, G. Schöner, The time course of saccadic decision making; Dynamic field theory, Neural Networks, 19:1059-1074, 2006。
On the ground state of a free massless (pseudo)scalar field in two dimensions

a r X i v :h e p -t h /0212226v 2 29 J u n 2003On the ground state of a free massless (pseudo)scalarfield in two dimensionsM.Faber ∗and A.N.Ivanov †‡February 1,2008Atominstitut der ¨Osterreichischen Universit¨a ten,Arbeitsbereich Kernphysik und Nukleare Astrophysik,Technische Universit¨a t Wien,Wiedner Hauptstr.8-10,A-1040Wien,¨OsterreichAbstractWe investigate the ground state of a free massless (pseudo)scalar field in 1+1–dimensional space–time.We argue that in the quantum field theory of a free massless (pseudo)scalar field without infrared divergences (Eur.Phys.J.C 24,653(2002))the ground state can be represented by a tensor product of wave functions of the fiducial vacuum and of the collective zero–mode,describing the motion of the “cen-ter of mass”of a free massless (pseudo)scalar field.We show that the bosonized version of the BCS wave function of the ground state of the massless Thirring model obtained in (Phys.Lett.B 563,231(2003))describes the ground state of the free massless (pseudo)scalar field.1IntroductionThe problem which we study in this paper is related to our investigations of the massless Thirring model[1],where we have found a new phase with a wave function of the BCS–type and massive quasiparticles.The(pseudo)scalar collective excitationsϑ(x)of these massive quasiparticles are bound by a Mexican hat potential and described by the LagrangianL(x)=1= +∞−∞dx1Π(x0,x1),(1.3)∂x0where j0(x)is the time–component of the conserved current jµ(x)=∂µϑ(x)andΠ(x)= j0(x)is the conjugate momentum of theϑ–field obeying the canonical commutation rela-tion[Π(x0,x1),ϑ(x0,y1)]=−iδ(x1−y1).(1.4) From this canonical commutation relation followsϑ′(x)=e+iαQ(x0)ϑ(x)e−iαQ(x0)=ϑ(x)+α.(1.5) Acting with the operator e−iαQ(0)on the vacuum wave function|Ψ0 we get the wave function|α =e−iαQ(0)|Ψ0 .(1.6) This wave function is normalized to unity and possesses all properties of the vacuum state [5].The average value of theϑ–field calculated for the wave functions|α is equal toα|ϑ(x)|α =α.(1.7) The same result can be obtained for the vacuum expectation value of theϑ′–field(1.2)Ψ0|ϑ′(x)|Ψ0 = Ψ0|ϑ(x)|Ψ0 +α=α.(1.8) This testifies that the parameterαdescribes the position of the“center of mass”.Hence, it is related to the collective zero–mode of the free massless(pseudo)scalarfieldϑ(x) [2]–[4].The quantumfield theory of the free massless(pseudo)scalarfieldϑ(x)with the La-grangian(1.1)is well–defined if the collective zero–mode,describing the motion of the “center of mass”of thefieldϑ(x),is removed from the states which can be excited by an external source J(x)in the generating functional of Green functions[2]–[4]Z[J]= Ψ0 T e i d2xϑ(x)J(x) Ψ0 =1= Dϑe i d2x12πwhere a (k 1)and a †(k 1)are annihilation and creation operators and obey the standard commutation relation [1,2,3,4][a (k1),a †(q 1)]=(2π)2k 0δ(k 1−q 1).(1.12)For the free massless (pseudo)scalar field (1.11)one can define the Wightman functionD (+)(x ;µ)= Ψ0|ϑ(x )ϑ(0)|Ψ0 ==12k 0e −i k ·x =−12π+∞−∞dk 12π +∞dk 12πlimµ→0+∞µdk 12π|˜h(0,0)|2lim µ→0ℓn µ−1dk1|˜h (k 1,k 1)|2=−12π+∞−∞dk 1dxdx =−lim δ→0+ℓn δϕ(0)−∞ℓnxdϕ(x )dx[θ(x )ℓn x ]ϕ(x )dx(see Ref.[25]of Carg`e se Lectures [9]).Since the Fourier transform ˜h(k 0,k 1)of the test function h (x )from the Schwartz class S (R 2)has a support at k 0=k 1=0,i.e ˜h(0,0)=0,the momentum integralis logarithmically divergent in the infrared region atµ→0.The convergence of themomentum integral in the infrared region can be provided only for the test functions from the Schwartz class S0(R2)={h(x)∈S(R2);˜h(0,0)=0}[9].Recently[3,4]we have analysed the physical meaning of the test functions h(x)in Wightman’s observables(1.14).We have shown that the test functions can be interpreted as apparatus functions characterizing the device used by the observer for detecting quantaof the free massless(pseudo)scalarfield.This interpretation of test functions agrees with our results obtained in Ref.[2],where we have shown that a quantumfield theory of a freemassless(pseudo)scalarfieldϑ(x)can be constructed without infrared divergences if one removes from theϑ–field the collective zero–mode,describing the motion of the“center of mass”.We have shown that the collective zero–mode does not affect the evolutionof the other modes of the free massless(pseudo)scalarfieldϑ(x).The removal of the collective zero–mode has been carried out within the path–integral approach in terms of the generating functional of Green functions defined by(1.9).As has been shown in[2]the generating functional of Green functions(1.9)with˜J(0)=0vanishes identically, Z[J]=0.This agrees well with Wightman’s statement[9]about the non–existence of aquantumfield theory of a free massless(pseudo)scalarfield defined on test functions h(x) from S(R2)with˜h(0,0)=0.Hence,the removal of the collective zero–mode of theϑ(x)-field implies the immeasur-ability of this state in terms of Wightman’s observables.The insensitivity of the detectors to the collective zero–mode can be obtained by the constraint˜h(0,0)=0[3,4].Math-ematically this means that the test functions h(x)should belong to the Schwartz classS0(R2)={h(x)∈S(R2);˜h(0,0)=0}[2,3,4].As has been shown in[3,4]the quan-tumfield theory of a free massless(pseudo)scalarfieldϑ(x)defined on the test functionsfrom S0(R2)is unstable under spontaneous breaking of the continuous symmetry(1.2). Quantitatively the symmetry broken phase is characterized by a non–vanishing sponta-neous magnetization M=1[2,3,4].Goldstone bosons are the quanta of a free massless (pseudo)scalarfield[2,3,4].Coleman’s theorem reformulated for the test functions from S0(R2)={h(x)∈S(R2);˜h(0,0)=0}does not refute this statement.The paper is organized as follows.In Section2we describe the collective zero–mode by a rigid rotor.In Section3we calculate the generating functional of Green functions and show that the infrared divergences of the free massless(pseudo)scalarfield are due to the classical evolution of the collective zero–mode from infinite past to infinite future. In Section4we construct the wave function of the ground state of the free massless (pseudo)scalarfield for the bosonized version of the massless Thirring model which is of the BCS–type.In the Conclusion we discuss the obtained results.2Collective zero–modeThe collective zero–mode of the free massless(pseudo)scalarfieldϑ(x)=ϑ(x0,x1), describing the“center of mass”motion,is a mode orthogonal to all vibrational modes. Due to this we can treat thefieldϑ(x)in the form of the following decompositionϑ(x)=ϑ0(x0)+ϑv(x),(2.1) whereϑv(x)is thefield of all vibrational modes.This decomposition can be very well justified for the free massless(pseudo)scalarfield in thefinite volume L(see Eq.(2.7)).The Lagrangian of theϑv(x)–field is given byL v(x)=1∂x0 2−1∂x1 2.(2.2)Unlike the oscillator modes of a free massless(pseudo)scalarfield the collective zero–modeϑ0(x0)is defined by the LagrangianL0(x0)=12Ni=1˙q2i(x0)+12˙Q2(x0)+12˙ϑ2(x0)+12˙ϑ2(x0)+1The creation and annihilation operators a†n and a n obey the commutation relations[a n,a†n′]=δnn′,[a†n,a†n′]=[a n,a n′]=0,(2.8) where k n=(k0n,k1n)is the2–dimensional momentum defined by k n=(2π|n|/L,2πn/L) for n∈Z and0≤x1≤L.The annihilation operators act on the vacuum state as a n|Ψ0 =0.The Lagrange function of the collective zero–modeϑ0(x0)is equal toL0(ϑ0,˙ϑ0)= L/2−L/2dx1L0(x)=L∂˙ϑ0=L˙ϑ0(2.11) and the Hamilton function is defined byh0(ϑ0,π0)=π20(x0)2L =−1dϑ20.(2.13)The wave functionψ(ϑ0)of the collective zero–mode in theϑ0–representation is the solu-tion of the Schr¨o dinger equation−1dϑ2=E0ψ(ϑ0).(2.14)Imposing periodic boundary conditionsψ(ϑ0)=ψ(ϑ0+2π)the normalized solutions of this equation readψm(ϑ0)= ϑ0|m =12πe+i mϑ0,m=0,±1,±2,...,(2.15)where m is the“magnetic”quantum number,m∈Z.The wave functionsψm(ϑ0)are also eigenfunctions of the conjugate momentumˆπ0and the total charge operatorˆQ=ˆπ0=−id/dϑ0with the eigenvalues m∈ZQψm(ϑ0)=mψm(ϑ0)⇐⇒ˆQ|m =m|m .(2.16) The energy spectrum is defined byE(m) 0=m22L +2πL n∈Z n a†n a n.(2.19)It is well–known that the wave function of the ground state should be eigenfunction of the total Hamilton and momentum operators with eigenvalue zero.Forfinite L this requirement is fulfilled only for the wave function|Ω0 =|0 0⊗|Ψ0 ,|Ψ0 =|0 1···⊗|0 k⊗···(2.20) where|0 is the eigenfunction of the operator(2.13)with eigenvalue m=0.In the ϑ0–representation the wave function|0 is equal to ϑ0|0 =ψ0(ϑ0)=1/√The factor Z[J]in this product concerns the vibrational modes and coincides with(1.9). The other factorZ0[J0;L,T]=e iW0[J0;L,T]==N−1(L,T) Dϑ0exp i T−T dx0 L2 +T−T dx0˙ϑ20(x0) (3.3)Let us perform a Fourier transformationϑ0(x0)= +∞−∞dω2π +∞−∞dω′(ω+ω′)× −ωω′˜ϑ0(ω)˜ϑ0(ω′)+2L +∞−∞dω2πsin((ω+ω′)T)ωω′ .(3.6)Atfinite T the functional W0[J0;L,T]has a superficial infrared divergence(1.1).It seems that due to the infrared divergence W[J0;L,T]becomes infinite and Z0[J0;L,T]vanishes. This should agree with Wightman’s assertion concerning the non–existence of a well–defined quantumfield theory of a free massless(pseudo)scalarfield in1+1–dimensional space–time which we discussed above.In our treatment of the collective zero–mode of the free massless(pseudo)scalarfield the infrared divergence appears at the quantum mechanical level and admits a simple physical interpretation,as we will discuss below. The divergence does not appear due to unbounded quantumfluctuations.It is just the opposite,there is only one contribution to the generating functional Z0[J0;L,T],the classical trajectory which is defined by the initial conditions.The correlation functions gets unbounded due to the laws of classical mechanics.In order to show that the functional W0[J0;L,T]tends to infinity at T→∞and that this is related to a classical motion we suggest to determine the path–integral(3.2), decomposingϑ0(x0)into a classical part¯ϑ0(x0)and afluctuating partϕ(x0),ϑ0(x0)=¯ϑ(x0)+ϕ(x0).With the standard conditionsϕ(−T)=ϕ(+T)=0and choosing the classicalfield¯ϑ0(x0)as a special solution of the“2nd axiom of Newton”¨¯ϑ0(x0)=12˙¯ϑ2(x0)+¯ϑ0(x0)J0(x0)) .(3.8)It is important to emphasize that due to this decoupling of quantum and classical degrees of freedom the external source J0(x0)can excite the classical degrees of freedomϑ0only.Integrating by parts in the exponent of(3.8)and using(3.7)we get for the action integralW0[J0;L,T]=12 ¯ϑ0(x0)˙¯ϑ0(x0)+T−T.(3.9)Obviously,this integral and therefore the generating functional(3.2)depends on the initial condition.This is the usual situation for classical systems.Now we insert in Eq.(3.9)a solution of Eq.(3.7).The general solution of(3.7)reads¯ϑ0(x0)=12L +T−T dy0J0(y0), C2=−12L +T−T dy0(|x0−y0|+(x0−y0))J0(y0)=14L +T−T dx0 +T−Tdy0J0(x0)|x0−y0|J0(y0)+1limit T→∞.This occurs even if the external source generates an arbitrary small fluctuation of the collective zero–mode.This can also be seen defining the classicalfield ϑ0(x0) in terms of the generating functional Z0[J0;L,T].According to the standard definition the classicalfield ϑ0(x0) is given byϑ0(x0) =1δJ0(x0)=δW0[J0;L,T]2L +T−T dy0[|x0−y0|+(T−x0)+(T−y0)]J0(y0),(3.15) but the response is quadraticW0[J0;L,T]=1δJ0(x0)δJ0(y0)=12L|x0−y0|(3.18)Since at˜J0(0)=0ϑ0(x0) =1it evolves along the classical trajectory only,see Eq.(3.8).This explainsalso whythecorrelation does not vanish for large time intervals.In the Schwinger formulation of the quantumfield theory[15]the generating functional Z0[J0;L,T=∞]defines the amplitude for the transition from the ground state of the center of mass motion at x0=−∞to the ground state at x0=+∞caused by the external force J0(x0).For vanishing perturbation this amplitude does not converge to unity and gives the impression that the evolution of the system is ill defined.But this is not the case.Let the state of the center of mass at x0=0be described byϑ0=αand˙ϑ0=0. Then the classical evolution of the system guarantees that the system will remain in this state for anyfinite time and the corresponding transition amplitude is unity.Due to the quadratic extension of the exponentϑ0(x0)=¯ϑ0(x0)+ϕ(x0)in the gen-erating functional of Green functions Z0[J0;L,T]and the condition(3.7),the vibrational degrees of freedom do not couple to the external source J0(x0)which excites the collec-tive zero–mode.As a result,the generating functional of Green functions Z0[J0;L,T] is defined by one classical trajectory(3.8)and for J0(x0)=0depends on the temporal boundary conditions onlyW0[J0;L,T]=LL4T[∆+2πm]2 == 4πiT exp i L∆22T,πLiπt θ3 z t (3.23)we transcribe the functional Z0[0;L,T]into the formZ0[0;L,T]=12,−T2π m∈Z expi m∆−i T2π m∈Z e i m[ϑ0(+T)−ϑ0(−T)]−i E m2T.(3.24)The r.h.s.contains a sum over the stationary quantum states of the rigid rotor[16] Z0[0;L,T]= m∈Z ϑ0(+T)|m m|ϑ0(−T) = ϑ0(+T)|ϑ0(−T) (3.25)describing the amplitude for the transitionϑ0(−T)→ϑ0(+T).For the reduction of the r.h.s.of(3.25)we have used the notationsϑ0(+T)|m =12πe+i mϑ0(+T)−i E m T,m|ϑ0(−T) =12πe−i mϑ0(−T)+i E m(−T)(3.26)with E m=m2/2L and|ϑ0(x0) as eigenstate of the Heisenberg operatorˆϑ0(x0)and the completeness conditionm∈Z|m m|=1.(3.27)In the limit T→∞the excited stated with m=0in the sum(3.24)are dying out and only the ground state with m=0survives.This yields Z0[0;L,∞]=1.4Wave function of the ground state of the free mass-less(pseudo)scalarfieldAs has been shown in[17]the wave function of the ground state of the free massless (pseudo)scalarfield,describing the bosonized version of the massless Thirring model, quantized in the chirally broken phase with the BCS wave function of the ground state, takes the form|Ω(0) BCS=exp iπg +∞−∞dx1sin(βˆϑ(0,x1)) |Ψ0 .(4.1)where M is the dynamical mass of the massless Thirring fermionfield quantized in the chiral broken phase,and g is the Thirring coupling constant[1].The parameterβin the definition of the wave function(4.1),used in[17],sinβϑ(0,x1),can be removed rescaling theϑ–field.Indeed,the Lagrangian(2.8)can be transcribed as followsLL0(ϑ0,˙ϑ0)=d22Lm2.(4.4)2LFor the ϑ0–field with the moment of inertia L/β2the total Hamilton and momentum operators are defined byˆh [ϑ]=β2L n ∈Z |n |a †n a n ,ˆπ[ϑ]=ˆπ0+2π√2 =δα′α,(4.11)where we used the formula[20]∞m=−∞J2m(λ)e−im(α′−α)=J0 2λsin α′−αdϑ0−λcosϑ0ϑ0|Ω(0) BCS=0.(4.13)The operator in the l.h.s.of(4.13)is the conjugate momentum operatorˆΠ0in theϑ0–representation related to the conjugate momentumˆπ0=−id/dϑ0by the unitary trans-formation[21]ˆΠ=Uˆπ0U†,(4.14) where U is defined byU=e+iλsin ˆϑ0.(4.15)The unitary operator U relates the wave functions|Ω0 and|Ω(0) BCS|Ω(0) BCS=U|Ω0 .(4.16) The operatorˆΠ0is equal toˆΠ=ˆπ0+iλ[sinˆϑ0,ˆπ0]=ˆπ0−λcosˆϑ0,(4.17) where we have used the canonical commutation relation[ˆϑ0,ˆπ0]=i.The operatorˆΠ0, given by(4.17),coincides with the differential operator in the l.h.s.of(4.13)in theϑ0–representation.The unitary transformation(4.16)is canonical,since it retains the canonical commu-tation relations[ˆϑ0,ˆΠ0]= Uˆϑ0U†,Uˆπ0U† =[ˆϑ0,ˆπ0]=i,[ˆΠ0,ˆΠ0]= Uˆπ0U†,Uˆπ0U† =[ˆπ0,ˆπ0]=0.(4.18)According to Anderson[21]the transformations(4.15)can be called similarity(gauge) transformations.Due to the canonical transformation(4.14)thefield operatorˆϑ0does not change but the Hamilton operator transforms as followsˆh 0(ˆϑ0,ˆπ0)→ˆH0(ˆϑ0,ˆΠ0)=Uˆh0(ˆϑ0,ˆπ0)U†=β22L ˆπ20+2πL n∈Z n a†n a n|Ω0 =0.(4.21)By the canonical transformation(4.16)we transcribe(4.21)as follows Uˆh[ϑ]U†|Ω(0) BCS= β2L n∈Z|n|a†n a n |Ω(0) BCS=0,Uˆπ[ϑ]U†|Ω(0) BCS= ˆΠ0+2π2L ˆΠ2+2πL n∈Z n a†n a n|Ω(α) BCS=0.(4.23)Finally,we would like to show that the“magnetic”quantum number m defines the chi-rality of the fermionic state.In order to prove this we suggest to use the results obtained by Nambu and Jona–Lasinio[22].This concerns the analysis of the BCS wave function in terms of the wave functions with a certain chirality X,the eigenvalue of theγ5operator, X=0,±1,±2,....The BCS wave function of the ground state of the massless Thirring model is defined by[1,17]|Ω(0) BCS= k1[u k1+v k1a†(k1)b†(−k1)]|Ψ0 ,(4.24)where the coefficients u k1and v k1have the properties:(i)u2k1+v2k1=1and(ii)u−k1=u k1and v−k1=−v k1[1,17],a†(k1)and b†(k1)are creation operators of fermions and an-tifermions with momentum k1.According to Nambu and Jona–Lasinio[22]the wave function(4.24)should be a linear superposition of the eigenfunctions|Ω2n with eigenval-ues X n=2n,n∈Z,i.e.|Ω(0) BCS= n∈Z C2n|Ω2n .(4.25)For chiral rotations of fermionfields with a chiral phaseαA the wave function(4.24) changes as follows[1]|Ω(αA) BCS= k1[u k1+v k1e−2iε(k1)αA a†(k1)b†(−k1)]|Ψ0 ,(4.26) whereε(k1)is a sign function.In terms of|Ω(αA) the products C2n|Ω2n are defined by C2n|Ω2n = 2π0dαA2πe+2inαA e iλsin(ˆϑ0−2αA)|Ω0 == m∈Z J m(λ)|m ⊗|Ψ0 2π0dαAindependent on the exact value of the total chirality of all fermion–antifermion pairs,we need spontaneous breaking of chiral symmetry similar to the the spontaneous breaking ofZ(3)symmetry in QCD.Such a spontaneous breaking of chiral symmetry is realized by the BCS wave function.5ConclusionWe have shown that the ground state of the free massless(pseudo)scalarfield,the bosonized version of the massless Thirring model in the non–trivial phase,can be definedby a direct product of thefiducial vacuum|Ψ0 and a BCS–type wave function(4.1). We have demonstrated that the BCS wave function is related to the collective zero–modedescribed by a rigid rotor(4.8).BCS wave functions differing in the values of thefield–shifts(1.2)are orthogonal BCS Ω(α′)|Ω(α) BCS=δαα.We have analysed the generating functional of Green functions Z[J].We have shownthat for˜J(0)=0the infrared divergences have a simple physical interpretation in terms ofa classically moving rigid rotor acquiring an infinite angle for an infinite interim even if its motion has been initiated by an infinitesimal external perturbation.These divergences can be removed by the constraint on the external source˜J(0)=0.As a result the collective zero–mode cannot be excited and the correlation functions are determined by the contribution of the vibrational modesϑv(x)only.These modes are quantized relative to thefiducial vacuum|Ψ0 .According to[3,4]this testifies that the quantumfield theory of the free massless(pseudo)scalarfieldϑv(x),in the Wightman sense[9],deals with Wightman’s observables defined on the test functions from S0(R2).The BCS type wave function(4.8)of the ground state is not invariant under the con-tinuous symmetry(1.2)and behaves as(4.10).Hence,according to the Goldstone theorem[10]the continuous symmetry(1.2)is spontaneously broken.As has been shown in[2,3,4] the phase of spontaneously broken continuous symmetry(1.2)is characterized quantita-tively by the non–vanishing spontaneous magnetization M= Ψ0|cosβϑv(x)|Ψ0 =1. This confirms the non–vanishing value of the fermion condensate in the massless Thirring model with fermionfields quantized in the chirally broken phase[1].Hence,the massless Thirring model possesses a chirally broken phase as has been pointed out in[1]–[4,17,23].In the rigid rotor treatment of the collective zero–mode the variationδϑ(x)of thefree massless(pseudo)scalarfieldϑ(x),caused by thefield–shift transformation(1.2),isdefined by a canonical quantum mechanical commutatorδϑ(x)=αi[Q(x0),ϑ(x)]=αi[π0,ϑ0]=α,which can never be equal to zero[8].This result does not depend on whether the ground state of the free massless(pseudo)scalarfield is invariant or non–invariant under symmetry transformations(1.2).Since the removal of the collective zero–mode from the observable modes of the freemassless(pseudo)scalarfieldϑ(x)agrees with the definition of Wightman’s observable onthe test functions from S0(R2)the obtained non–vanishing of the variationδϑ(x)does not contradict Coleman’s theorem valid only for Wightman’s observables defined on the test functions from S(R2)[3,4].References[1]M.Faber and A.N.Ivanov,Eur.Phys.J.C20,723(2001),hep-th/0105057.[2]M.Faber and A.N.Ivanov,Eur.Phys.J.C24,653(2002),hep–th/0112184.[3]M.Faber and A.N.Ivanov,On spontaneous breaking of continuous symmetry in1+1–dimensional space–time,hep–th/0204237.[4]M.Faber and A.N.Ivanov,Quantumfield theory of a free massless(pseudo)scalarfield in1+1–dimensional space–time as a test for the massless Thirring model, hep–th/0206244.[5]K.Yoshida,Nucl.Phys.B105,272(1976).[6]M.Faber and A.N.Ivanov,On the solution of the massless Thirring model withfermionfields quantized in the chiral symmetric phase,hep–th/0112183.[7]N.D.Mermin and H.Wagner,Phys.Rev.Lett.17,1133(1966);P.C.Hohenberg,Phys.Rev.158,383(1967);N.D.Mermin,J.Math.Phys.8,1061(1967).[8]S.Coleman,Comm.Math.Phys.31,259(1973).[9]A.S.Wightman,Introduction to Some Aspects of the Relativistic Dynamics of Quan-tized Fields,in HIGH ENERGY ELECTROMAGNETIC INTERACTIONS AND FIELD THEORY,Carg`e se Lectures in Theoretical Physics,edited by M.Levy,1964, Gordon and Breach,1967,pp.171–291;R.F.Streater and A.S.Wightman,in PCT, SPIN AND STATISTICS,AND ALL THAT,Princeton University Press,Princeton and Oxford,Third Edition,1980.[10]J.Goldstone,Nuovo Cimento19,154(1961);J.Goldstone,A.Salam,and S.Wein-berg,Phys.Rev.127,965(1962).[11]S.Coleman,Phys.Rev.D11,2088(1975).[12]I.M.Gel’fand and G.E.Shilov,in GENERALIZED FUNCTIONS,Properties andOperations,Vol.1,Academic Press,New York,1964.[13]A.L.Fetter and J.D.Walecka,in THEORETICAL MECHANICS OF PARTICLESAND CONTINUA,McGraw–Hill Publishing Co.,New York,1980,pp.86–130;K.Huang,in QUANTUM FIELD THEORY,From Operators to Path Integrals,John Willey&Sons,Inc.,New York,1998,pp.1–7.[14]J.Kogut and L.Susskind,Phys.Rev.D11,3594(1975).[15]J.Schwinger in PARTICLES AND SOURCES,Gordon and Breach,New York1969and PARTICLES,SOURCES AND FIELDS,Addison–Wesley Publishing Co.,Mas-sachusetts1970[16]L.S.Schulman,Phys.Rev.176,1558(1968);Phys.Rev.188,1139(1969);J.Math.Phys.12,304(1971);L.S.Schulman,in TECHNIQUES AND APPLICATIONS OF PATH INTEGRATION,John&Sons,New York,1981,pp.190–213.[17]M.Faber and A.N.Ivanov,Phys.Lett.B563,231(2003).[18]HANDBOOK OF MATHEMATICAL FUNCTIONS,with Formulas,Graphs,andMathematical Tables,ed.by M.Abramowitz and I.E.Stegun,U.S.Department of Commerce,National Bureau of Standards,Applied Mathematics Series•55,1972, p.361formula(9.1.41).[19]I.S.Gradshtein and I.M.Ryzhik,in TABLE OF INTEGRALS,SERIES ANDPRODUCTS,Academic Press,New York and London,1965,p.980formula(8.536.3).[20](see[18]p.979formula(8.531.3)).[21]A.Anderson,Ann.of Phys.232,292(1994).[22]Y.Nambu and G.Jona–Lasinio,Phys.Rev.122,345(1960).[23]M.Faber and A.N.Ivanov,J.of Phys.A36,issue28(2003),hep–th/0205249;Massless Thirring model in the bosonfield representation.hep–th/0206034.。
宇宙学概述

E>0 E=0
E<0
-9+9来自■宇宙学原理revisit 视界疑难 暴胀模型
光速和宇宙年龄有限 可观测宇宙有限 宇宙对观测者的视界。 宇宙中可能有因果联系的区域有限 如果两个时空点之间的固有距离> 视界,则二者之间不可能有因果联系 视界疑难:物理上没有任何机
为不变量,称为点xa与点xa+dxa之间的时空间隔。方程中采用了Einstein求和约
定,其附标“均衡”。hab生成间隔的机制称为度规。从dxa可以生成各种矢量, 例如4-速度矢量:ua ≡dxa/dt,和各种张量,例如能量张量Tab ≡ mua ub..
微商:
协变微商: ua;b ≡ ua,b - Gmabum
四、宇宙学
I. 几何宇宙学
■ geometrodynamics over/re-view: ★事件、时空与 Riemann几何 ★局域 Lorentz几何 ★几何单位制与符号系 统 ★时空间隔、 度规与曲率 ★ Einstein引力定律(场方程) ★ ( Schwarzschild)黑洞∣引力红移 ■宇宙学原理(假设) Robertson-Walker度规 ■几何宇宙学:宇宙学假设下Einstein引力场方程的解 ■宇宙学原理revisit 视界疑难 暴胀模型 平坦性疑难
宇宙学、引力与Doppler红移。
宇宙学红移
光子的传播
波的开始 波的结束
■几何宇宙学: 宇宙学假设下Einstein引力场方程的解
封闭宇宙 开放宇宙 平直宇宙
Possible Fates of the Universe
Accelerating universe Requires dark energy.
★ Einstein引力定律(场方程)
Two-Dimensional Gas of Massless Dirac Fermions in Graphene

Two-Dimensional Gas of Massless Dirac Fermions in Graphene K.S. Novoselov1, A.K. Geim1, S.V. Morozov2, D. Jiang1, M.I. Katsnelson3, I.V. Grigorieva1, S.V. Dubonos2, A.A. Firsov21Manchester Centre for Mesoscience and Nanotechnology, University of Manchester, Manchester, M13 9PL, UK2Institute for Microelectronics Technology, 142432, Chernogolovka, Russia3Institute for Molecules and Materials, Radboud University of Nijmegen, Toernooiveld 1, 6525 ED Nijmegen, the NetherlandsElectronic properties of materials are commonly described by quasiparticles that behave as nonrelativistic electrons with a finite mass and obey the Schrödinger equation. Here we report a condensed matter system where electron transport is essentially governed by the Dirac equation and charge carriers mimic relativistic particles with zero mass and an effective “speed of light” c∗ ≈106m/s. Our studies of graphene – a single atomic layer of carbon – have revealed a variety of unusual phenomena characteristic of two-dimensional (2D) Dirac fermions. In particular, we have observed that a) the integer quantum Hall effect in graphene is anomalous in that it occurs at halfinteger filling factors; b) graphene’s conductivity never falls below a minimum value corresponding to the conductance quantum e2/h, even when carrier concentrations tend to zero; c) the cyclotron mass mc of massless carriers with energy E in graphene is described by equation E =mcc∗2; and d) Shubnikov-de Haas oscillations in graphene exhibit a phase shift of π due to Berry’s phase.Graphene is a monolayer of carbon atoms packed into a dense honeycomb crystal structure that can be viewed as either an individual atomic plane extracted from graphite or unrolled single-wall carbon nanotubes or as a giant flat fullerene molecule. This material was not studied experimentally before and, until recently [1,2], presumed not to exist. To obtain graphene samples, we used the original procedures described in [1], which involve micromechanical cleavage of graphite followed by identification and selection of monolayers using a combination of optical, scanning-electron and atomic-force microscopies. The selected graphene films were further processed into multi-terminal devices such as the one shown in Fig. 1, following standard microfabrication procedures [2]. Despite being only one atom thick and unprotected from the environment, our graphene devices remain stable under ambient conditions and exhibit high mobility of charge carriers. Below we focus on the physics of “ideal” (single-layer) graphene which has a different electronic structure and exhibits properties qualitatively different from those characteristic of either ultra-thin graphite films (which are semimetals and whose material properties were studied recently [2-5]) or even of our other devices consisting of just two layers of graphene (see further). Figure 1 shows the electric field effect [2-4] in graphene. Its conductivity σ increases linearly with increasing gate voltage Vg for both polarities and the Hall effect changes its sign at Vg ≈0. This behaviour shows that substantial concentrations of electrons (holes) are induced by positive (negative) gate voltages. Away from the transition region Vg ≈0, Hall coefficient RH = 1/ne varies as 1/Vg where n is the concentration of electrons or holes and e the electron charge. The linear dependence 1/RH ∝Vg yields n =α·Vg with α ≈7.3·1010cm-2/V, in agreement with the theoretical estimate n/Vg ≈7.2·1010cm-2/V for the surface charge density induced by the field effect (see Fig. 1’s caption). The agreement indicates that all the induced carriers are mobile and there are no trapped charges in graphene. From the linear dependence σ(Vg) we found carrier mobilities µ =σ/ne, whichreached up to 5,000 cm2/Vs for both electrons and holes, were independent of temperature T between 10 and 100K and probably still limited by defects in parent graphite. To characterise graphene further, we studied Shubnikov-de Haas oscillations (SdHO). Figure 2 shows examples of these oscillations for different magnetic fields B, gate voltages and temperatures. Unlike ultra-thin graphite [2], graphene exhibits only one set of SdHO for both electrons and holes. By using standard fan diagrams [2,3], we have determined the fundamental SdHO frequency BF for various Vg. The resulting dependence of BF as a function of n is plotted in Fig. 3a. Both carriers exhibit the same linear dependence BF = β·n with β ≈1.04·10-15 T·m2 (±2%). Theoretically, for any 2D system β is defined only by its degeneracy f so that BF =φ0n/f, where φ0 =4.14·10-15 T·m2 is the flux quantum. Comparison with the experiment yields f =4, in agreement with the double-spin and double-valley degeneracy expected for graphene [6,7] (cf. caption of Fig. 2). Note however an anomalous feature of SdHO in graphene, which is their phase. In contrast to conventional metals, graphene’s longitudinal resistance ρxx(B) exhibits maxima rather than minima at integer values of the Landau filling factor ν (Fig. 2a). Fig. 3b emphasizes this fact by comparing the phase of SdHO in graphene with that in a thin graphite film [2]. The origin of the “odd” phase is explained below. Another unusual feature of 2D transport in graphene clearly reveals itself in the T-dependence of SdHO (Fig. 2b). Indeed, with increasing T the oscillations at high Vg (high n) decay more rapidly. One can see that the last oscillation (Vg ≈100V) becomes practically invisible already at 80K whereas the first one (Vg <10V) clearly survives at 140K and, in fact, remains notable even at room temperature. To quantify this behaviour we measured the T-dependence of SdHO’s amplitude at various gate voltages and magnetic fields. The results could be fitted accurately (Fig. 3c) by the standard expression T/sinh(2π2kBTmc/heB), which yielded mc varying between ≈ 0.02 and 0.07m0 (m0 is the free electron mass). Changes in mc are well described by a square-root dependence mc ∝n1/2 (Fig. 3d). To explain the observed behaviour of mc, we refer to the semiclassical expressions BF = (h/2πe)S(E) and mc =(h2/2π)∂S(E)/∂E where S(E) =πk2 is the area in k-space of the orbits at the Fermi energy E(k) [8]. Combining these expressions with the experimentally-found dependences mc ∝n1/2 and BF =(h/4e)n it is straightforward to show that S must be proportional to E2 which yields E ∝k. Hence, the data in Fig. 3 unambiguously prove the linear dispersion E =hkc∗ for both electrons and holes with a common origin at E =0 [6,7]. Furthermore, the above equations also imply mc =E/c∗2 =(h2n/4πc∗2)1/2 and the best fit to our data yields c∗ ≈1⋅106 m/s, in agreement with band structure calculations [6,7]. The employed semiclassical model is fully justified by a recent theory for graphene [9], which shows that SdHO’s amplitude can indeed be described by the above expression T/sinh(2π2kBTmc/heB) with mc =E/c∗2. Note that, even though the linear spectrum of fermions in graphene (Fig. 3e) implies zero rest mass, their cyclotron mass is not zero. The unusual response of massless fermions to magnetic field is highlighted further by their behaviour in the high-field limit where SdHO evolve into the quantum Hall effect (QHE). Figure 4 shows Hall conductivity σxy of graphene plotted as a function of electron and hole concentrations in a constant field B. Pronounced QHE plateaux are clearly seen but, surprisingly, they do not occur in the expected sequence σxy =(4e2/h)N where N is integer. On the contrary, the plateaux correspond to half-integer ν so that the first plateau occurs at 2e2/h and the sequence is (4e2/h)(N + ½). Note that the transition from the lowest hole (ν =–½) to lowest electron (ν =+½) Landau level (LL) in graphene requires the same number of carriers (∆n =4B/φ0 ≈1.2·1012cm-2) as the transition between other nearest levels (cf. distances between minima in ρxx). This results in a ladder of equidistant steps in σxy which are not interrupted when passing through zero. To emphasize this highly unusual behaviour, Fig. 4 also shows σxy for a graphite film consisting of only two graphene layers where the sequence of plateaux returns to normal and the first plateau is at 4e2/h, as in the conventional QHE. We attribute this qualitative transition between graphene and its two-layer counterpart to the fact that fermions in the latter exhibit a finite mass near n ≈0 (as found experimentally; to be published elsewhere) and can no longer be described as massless Dirac particles. 2The half-integer QHE in graphene has recently been suggested by two theory groups [10,11], stimulated by our work on thin graphite films [2] but unaware of the present experiment. The effect is single-particle and intimately related to subtle properties of massless Dirac fermions, in particular, to the existence of both electron- and hole-like Landau states at exactly zero energy [912]. The latter can be viewed as a direct consequence of the Atiyah-Singer index theorem that plays an important role in quantum field theory and the theory of superstrings [13,14]. For the case of 2D massless Dirac fermions, the theorem guarantees the existence of Landau states at E=0 by relating the difference in the number of such states with opposite chiralities to the total flux through the system (note that magnetic field can also be inhomogeneous). To explain the half-integer QHE qualitatively, we invoke the formal expression [9-12] for the energy of massless relativistic fermions in quantized fields, EN =[2ehc∗2B(N +½ ±½)]1/2. In QED, sign ± describes two spins whereas in the case of graphene it refers to “pseudospins”. The latter have nothing to do with the real spin but are “built in” the Dirac-like spectrum of graphene, and their origin can be traced to the presence of two carbon sublattices. The above formula shows that the lowest LL (N =0) appears at E =0 (in agreement with the index theorem) and accommodates fermions with only one (minus) projection of the pseudospin. All other levels N ≥1 are occupied by fermions with both (±) pseudospins. This implies that for N =0 the degeneracy is half of that for any other N. Alternatively, one can say that all LL have the same “compound” degeneracy but zeroenergy LL is shared equally by electrons and holes. As a result the first Hall plateau occurs at half the normal filling and, oddly, both ν = –½ and +½ correspond to the same LL (N =0). All other levels have normal degeneracy 4B/φ0 and, therefore, remain shifted by the same ½ from the standard sequence. This explains the QHE at ν =N + ½ and, at the same time, the “odd” phase of SdHO (minima in ρxx correspond to plateaux in ρxy and, hence, occur at half-integer ν; see Figs. 2&3), in agreement with theory [9-12]. Note however that from another perspective the phase shift can be viewed as the direct manifestation of Berry’s phase acquired by Dirac fermions moving in magnetic field [15,16]. Finally, we return to zero-field behaviour and discuss another feature related to graphene’s relativistic-like spectrum. The spectrum implies vanishing concentrations of both carriers near the Dirac point E =0 (Fig. 3e), which suggests that low-T resistivity of the zero-gap semiconductor should diverge at Vg ≈0. However, neither of our devices showed such behaviour. On the contrary, in the transition region between holes and electrons graphene’s conductivity never falls below a well-defined value, practically independent of T between 4 and 100K. Fig. 1c plots values of the maximum resistivity ρmax(B =0) found in 15 different devices, which within an experimental error of ≈15% all exhibit ρmax ≈6.5kΩ, independent of their mobility that varies by a factor of 10. Given the quadruple degeneracy f, it is obvious to associate ρmax with h/fe2 =6.45kΩ where h/e2 is the resistance quantum. We emphasize that it is the resistivity (or conductivity) rather than resistance (or conductance), which is quantized in graphene (i.e., resistance R measured experimentally was not quantized but scaled in the usual manner as R =ρL/w with changing length L and width w of our devices). Thus, the effect is completely different from the conductance quantization observed previously in quantum transport experiments. However surprising, the minimum conductivity is an intrinsic property of electronic systems described by the Dirac equation [17-20]. It is due to the fact that, in the presence of disorder, localization effects in such systems are strongly suppressed and emerge only at exponentially large length scales. Assuming the absence of localization, the observed minimum conductivity can be explained qualitatively by invoking Mott’s argument [21] that mean-free-path l of charge carriers in a metal can never be shorter that their wavelength λF. Then, σ =neµ can be re-written as σ = (e2/h)kFl and, hence, σ cannot be smaller than ≈e2/h per each type of carriers. This argument is known to have failed for 2D systems with a parabolic spectrum where disorder leads to localization and eventually to insulating behaviour [17,18]. For the case of 2D Dirac fermions, no localization is expected [17-20] and, accordingly, Mott’s argument can be used. Although there is a broad theoretical consensus [18-23,10,11] that a 2D gas of Dirac fermions should exhibit a minimum 3conductivity of about e2/h, this quantization was not expected to be accurate and most theories suggest a value of ≈e2/πh, in disagreement with the experiment. In conclusion, graphene exhibits electronic properties distinctive for a 2D gas of particles described by the Dirac rather than Schrödinger equation. This 2D system is not only interesting in itself but also allows one to access – in a condensed matter experiment – the subtle and rich physics of quantum electrodynamics [24-27] and provides a bench-top setting for studies of phenomena relevant to cosmology and astrophysics [27,28].1. Novoselov, K.S. et al. PNAS 102, 10451 (2005). 2. Novoselov, K.S. et al. Science 306, 666 (2004); cond-mat/0505319. 3. Zhang, Y., Small, J.P., Amori, M.E.S. & Kim, P. Phys. Rev. Lett. 94, 176803 (2005). 4. Berger, C. et al. J. Phys. Chem. B, 108, 19912 (2004). 5. Bunch, J.S., Yaish, Y., Brink, M., Bolotin, K. & McEuen, P.L. Nanoletters 5, 287 (2005). 6. Dresselhaus, M.S. & Dresselhaus, G. Adv. Phys. 51, 1 (2002). 7. Brandt, N.B., Chudinov, S.M. & Ponomarev, Y.G. Semimetals 1: Graphite and Its Compounds (North-Holland, Amsterdam, 1988). 8. Vonsovsky, S.V. and Katsnelson, M.I. Quantum Solid State Physics (Springer, New York, 1989). 9. Gusynin, V.P. & Sharapov, S.G. Phys. Rev. B 71, 125124 (2005). 10. Gusynin, V.P. & Sharapov, S.G. cond-mat/0506575. 11. Peres, N.M.R., Guinea, F. & Castro Neto, A.H. cond-mat/0506709. 12. Zheng, Y. & Ando, T. Phys. Rev. B 65, 245420 (2002). 13. Kaku, M. Introduction to Superstrings (Springer, New York, 1988). 14. Nakahara, M. Geometry, Topology and Physics (IOP Publishing, Bristol, 1990). 15. Mikitik, G. P. & Sharlai, Yu.V. Phys. Rev. Lett. 82, 2147 (1999). 16. Luk’yanchuk, I.A. & Kopelevich, Y. Phys. Rev. Lett. 93, 166402 (2004). 17. Abrahams, E., Anderson, P.W., Licciardello, D.C. & Ramakrishnan, T.V. Phys. Rev. Lett. 42, 673 (1979). 18. Fradkin, E. Phys. Rev. B 33, 3263 (1986). 19. Lee, P.A. Phys. Rev. Lett. 71, 1887 (1993). 20. Ziegler, K. Phys. Rev. Lett. 80, 3113 (1998). 21. Mott, N.F. & Davis, E.A. Electron Processes in Non-Crystalline Materials (Clarendon Press, Oxford, 1979). 22. Morita, Y. & Hatsugai, Y. Phys. Rev. Lett. 79, 3728 (1997). 23. Nersesyan, A.A., Tsvelik, A.M. & Wenger, F. Phys. Rev. Lett. 72, 2628 (1997). 24. Rose, M.E. Relativistic Electron Theory (John Wiley, New York, 1961). 25. Berestetskii, V.B., Lifshitz, E.M. & Pitaevskii, L.P. Relativistic Quantum Theory (Pergamon Press, Oxford, 1971). 26. Lai, D. Rev. Mod. Phys. 73, 629 (2001). 27. Fradkin, E. Field Theories of Condensed Matter Systems (Westview Press, Oxford, 1997). 28. Volovik, G.E. The Universe in a Helium Droplet (Clarendon Press, Oxford, 2003).Acknowledgements This research was supported by the EPSRC (UK). We are most grateful to L. Glazman, V. Falko, S. Sharapov and A. Castro Netto for helpful discussions. K.S.N. was supported by Leverhulme Trust. S.V.M., S.V.D. and A.A.F. acknowledge support from the Russian Academy of Science and INTAS.43µ (m2/Vs)0.8c4P0.4 22 σ (1/kΩ)10K0 0 1/RH(T/kΩ) 1 2ρmax (h/4e2)1-5010 Vg (V) 50 -10ab 0 -100-500 Vg (V)50100Figure 1. Electric field effect in graphene. a, Scanning electron microscope image of one of our experimental devices (width of the central wire is 0.2µm). False colours are chosen to match real colours as seen in an optical microscope for larger areas of the same materials. Changes in graphene’s conductivity σ (main panel) and Hall coefficient RH (b) as a function of gate voltage Vg. σ and RH were measured in magnetic fields B =0 and 2T, respectively. The induced carrier concentrations n are described by [2] n/Vg =ε0ε/te where ε0 and ε are permittivities of free space and SiO2, respectively, and t ≈300 nm is the thickness of SiO2 on top of the Si wafer used as a substrate. RH = 1/ne is inverted to emphasize the linear dependence n ∝Vg. 1/RH diverges at small n because the Hall effect changes its sign around Vg =0 indicating a transition between electrons and holes. Note that the transition region (RH ≈ 0) was often shifted from zero Vg due to chemical doping [2] but annealing of our devices in vacuum normally allowed us to eliminate the shift. The extrapolation of the linear slopes σ(Vg) for electrons and holes results in their intersection at a value of σ indistinguishable from zero. c, Maximum values of resistivity ρ =1/σ (circles) exhibited by devices with different mobilites µ (left y-axis). The histogram (orange background) shows the number P of devices exhibiting ρmax within 10% intervals around the average value of ≈h/4e2. Several of the devices shown were made from 2 or 3 layers of graphene indicating that the quantized minimum conductivity is a robust effect and does not require “ideal” graphene.ρxx (kΩ)0.60 aVg = -60V4B (T)810K12∆σxx (1/kΩ)0.4 1ν=4 140K 80K B =12T0 b 0 25 50 Vg (V) 7520K100Figure 2. Quantum oscillations in graphene. SdHO at constant gate voltage Vg as a function of magnetic field B (a) and at constant B as a function of Vg (b). Because µ does not change much with Vg, the constant-B measurements (at a constant ωcτ =µB) were found more informative. Panel b illustrates that SdHO in graphene are more sensitive to T at high carrier concentrations. The ∆σxx-curves were obtained by subtracting a smooth (nearly linear) increase in σ with increasing Vg and are shifted for clarity. SdHO periodicity ∆Vg in a constant B is determined by the density of states at each Landau level (α∆Vg = fB/φ0) which for the observed periodicity of ≈15.8V at B =12T yields a quadruple degeneracy. Arrows in a indicate integer ν (e.g., ν =4 corresponds to 10.9T) as found from SdHO frequency BF ≈43.5T. Note the absence of any significant contribution of universal conductance fluctuations (see also Fig. 1) and weak localization magnetoresistance, which are normally intrinsic for 2D materials with so high resistivity.75 BF (T) 500.2 0.11/B (1/T)b5 10 N 1/2025 a 0 0.061dmc /m00.04∆0.02 0c0 0 T (K) 150n =0e-6-3036Figure 3. Dirac fermions of graphene. a, Dependence of BF on carrier concentration n (positive n correspond to electrons; negative to holes). b, Examples of fan diagrams used in our analysis [2] to find BF. N is the number associated with different minima of oscillations. Lower and upper curves are for graphene (sample of Fig. 2a) and a 5-nm-thick film of graphite with a similar value of BF, respectively. Note that the curves extrapolate to different origins; namely, to N = ½ and 0. In graphene, curves for all n extrapolate to N = ½ (cf. [2]). This indicates a phase shift of π with respect to the conventional Landau quantization in metals. The shift is due to Berry’s phase [9,15]. c, Examples of the behaviour of SdHO amplitude ∆ (symbols) as a function of T for mc ≈0.069 and 0.023m0; solid curves are best fits. d, Cyclotron mass mc of electrons and holes as a function of their concentration. Symbols are experimental data, solid curves the best fit to theory. e, Electronic spectrum of graphene, as inferred experimentally and in agreement with theory. This is the spectrum of a zero-gap 2D semiconductor that describes massless Dirac fermions with c∗ 300 times less than the speed of light.n (1012 cm-2)σxy (4e2/h)4 3 2 -2 1 -1 -2 -3 2 44Kn7/ 5/ 3/ 1/2 2 2 210 ρxx (kΩ)-4σxy (4e2/h)0-1/2 -3/2 -5/2514T0-7/2 -4 -2 0 2 4 n (1012 cm-2)Figure 4. Quantum Hall effect for massless Dirac fermions. Hall conductivity σxy and longitudinal resistivity ρxx of graphene as a function of their concentration at B =14T. σxy =(4e2/h)ν is calculated from the measured dependences of ρxy(Vg) and ρxx(Vg) as σxy = ρxy/(ρxy + ρxx)2. The behaviour of 1/ρxy is similar but exhibits a discontinuity at Vg ≈0, which is avoided by plotting σxy. Inset: σxy in “two-layer graphene” where the quantization sequence is normal and occurs at integer ν. The latter shows that the half-integer QHE is exclusive to “ideal” graphene.。
School of Mathematical and Physical Sciences, University of Sussex,

We investigate the range of in ationary universe models driven by scalar elds possessing a general interaction potential of the form V ( ) = V0 n exp(? m ). Power-law, de Sitter and intermediate in ationary universes emerge as special cases together with several new varieties of in ation. Analysing the behaviour of these models at the extrema of we derive su cient constraints on the m - n parameter space such that in ation may occur as both an early and late-time phenomenon. We also compute the scalar and tensor perturbations produced in the model and compare these results with recent observations.
SUSSEX-AST 95/1-1 astro-ph/9501086 (January 1995)
Generalised Scalar Field Potentials and In ation
Paul Parsons and John D. Barrow
Astronomy Centre, School of Mathematical and Physical Sciences, University of Sussex, Brighton BN1 9QH, U. K.
AdsCft在凝聚态中应用简介

Why AdS/CMT ?
• Understand strongly coupled quantum many body systems is difficult.
(Non-fermion liquid, High T SC, interplay between disorder and interaction, metal/insulator phase transition)
The Duality Dictionary
Finite Temperature
Gauge/Gravity Duality as a LAB
Black hole full of answers (Nature 448, 1000-1001 (30 August 2007))
Some Applications
Another example: Area laws for the entanglement entropy - a review,J. Eisert, M. Cramer, M.B. Plenio, arXiv:0808.3773
Ancient thoughts源自• 天地万物莫大于秋毫。《庄子》 • 一花一世界。 •
• What is AdS/CFT?
Applied AdS/CFT
• How it works? • Two typical examples of AdS/CMT • Conclusion and future
What is Gauge/Gravity duality and the position of it
The Conclusion Of Gauge/Gravity (AdS/CFT) Duality Maldacena 1997
Autodesk CFD软件使用教程:建筑火灾和烟雾模拟说明书

BLD 195948Autodesk CFD for Fire and Smoke Simulation in BuildingsDr. Munirajulu. ML&T Construction, Larsen & Toubro LimitedDescriptionThis class will cover the use of Autodesk CFD software as a design analysis tool for fire and smoke simulation in buildings. We will examine how fire contaminant and smoke generation is modeled, and take you through the procedures and techniques necessary to obtain an efficient solution. You will learn how to identify design risk from the results visualization of smoke and temperature from the simulation. We will show you how to evaluate smoke-free height, tenable temperature, and smoke visibility to meet life-safety goals. Based on the Autodesk CFD results, you will understand how you can gain insight into behavior of smoke from fire, and make good design decisions to minimize smoke hazards. We will also highlight benefits and limitations of smoke simulation in relation to real-world fire scenarios. Finally, you will be able to relate the procedures and techniques described here for large spaces such as atria, convention centers, shopping malls, exhibition halls, airport terminals, and sports arenas.SpeakerDr. Munirajulu. M, B.Tech and Ph.D. from IIT, Kharagpur, India, has more than 22 years of direct and indirect involvement with CFD technology as a design analysis tool in areas such as HVAC, Automotive, Fluid Handling Equipment, Steam turbines and boilers. He has been with Larsen & Toubro Limited since 2005 and prior to this, he has worked with ABB Limited and Alstom Projects India Limited for about 9 years. His professional interests include state of the art CAE technologies (CAD, CFD and FEA). Currently he is responsible for CFD analysis in MEP design related to commercial buildings and airports in L&T Construction, Larsen & Toubro Limited, Chennai. He has been using Autodesk CFD Simulation software for HVAC and MEP applications in areas such as thermal comfort, data center cooling, basement car park ventilation, DG room ventilation effectiveness, rain water free surface flow for roof design, and smoke simulation in buildings in design stage as well as for trouble shooting. He has published 4 nos. of technical papers in international journals of repute and has been a speaker at technical conferences including AU 2017.Learning Objectives• Learn how fire and smoke is modeled • Visualize and Highlight key results• Gain insight into making good design decisions • Understand Benefits and limitationsContentsAutodesk CFD for Fire and Smoke Simulation in Buildings (1)Key word– Life Safety. (4)Back to basics (4)Fire Triangle/ Tetrahedron (4)Stages of fire (5)How fire spreads (6)Effects of uncontrolled fire (7)Hot smoke and life safety—what does temperature do? (7)Smoke contaminant and life safety – what does smoke do? (8)Loss due to fire (8)Objective 1: Fire and smoke modeling using Autodesk CFD (9)Fire safety strategy (9)Codes / standards used (9)General practice of smoke simulation (10)Building geometry: Retail shopping mall (11)Material properties (12)Boundary conditions (13)Mesh details (14)Initial conditions (15)Solver settings (15)Objective 2: Key results for final design (16)What do we look for in CFD analysis? (16)Smoke development (17)Key result 1: Smoke visibility (18)Temperature development (19)Key Result 2: Smoke temperature (20)Air flow field development (20)Key result 3: Air flow field (21)Outcome for final design (22)Objective 3: Insights from CFD analysis for good design decisions (22)Challenges in design..... . (22)Comparison of smoke control zones (23)Comparison of smoke visibility (24)Comparison of smoke temperature (25)Comparison of air/smoke flow field (25)Optimize smoke exhaust system design... summary . (26)More examples: (27)Objective 4: Benefits and limitations (27)Benefits: (27)Limitations: (27)Key word– Life Safety.We are going to look at what would ensure safety of people in a Retail shopping mallbuilding based on CFD analysis to understand smoke and temperature development in the event of fire.Back to basicsBefore we jump into the fire modeling using CFD, let us look at some basics •Fire triangle/ tetrahedron•Stages of fire•What is fire dynamics? How does fire spread?Fire Triangle/ Tetrahedron•The fire triangle identifies thethree needed components offire:•fuel (something that will burn)•heat (enough to make the fuelburn)•and air (oxygen)• a fourth component – theuninhibited chain reaction/news-and-research/news-and-media/press-room/reporters-guide-to-fire-and-nfpa/all-about-fireFire Triangle – Controlled firehttps:///wiki/Fire_triangleFire Tetrahedron – Uncontrolled fireStages of fire•Ignition: Fuel, oxygen andheat join together in asustained chemical reaction.•Growth: With the initial flameas a heat source, additionalfuel ignites. The size of the fireincreases and the plumereaches the ceiling.•Fully developed: Fire hasspread over much of fuel;temperatures reach their peak•Decay (burnout): The fireconsumes available fuel,temperatures decrease, firegets less intense.How fire spreadsFire spreads by transferring the heat energy from the flames in three different ways: - •Conduction: The passage of heat energy through or within a material because of direct contact, such as a burning wastebasket heating a nearby couch, which ignites and heats the drapes hanging behind, until they too burst into flames.•Convection: The flow of fluid or gas from hot areas to cooler areas.•Radiation: Heat traveling via electromagnetic waves, without objects or gases carrying it along. Radiated heat goes out in all directions, unnoticed until it strikes an object.ConductionConvectionhttps:///%3Cfront%3E/fire-dynamicsRadiationEffects of uncontrolled fire•Human loss•Structural damage•Material damage•Disruption of work•Financial lossesHot smoke and life safety—what does temperature do?https:///%3Cfront%3E/fire-dynamicsSmoke contaminant and life safety – what does smoke do?/news-and-research/news-and-media/press-room/reporters-guide-to-fire-and-nfpa/consequences-of-fire#fumesLoss due to fireHaving gone through certain relevant information about fire and facts about consequences of fire in terms of personal and economic loss, we will now get into details about how Autodesk CFD simulation can be useful in evaluating smoke spread and temperature distribution in a Retail mall building with a view to validate smoke exhaust system design for life safety. Objective 1: Fire and smoke modelling using Autodesk CFDFire safety strategyEngineering based approach to fire safe design:•Automatic fire detection (Smoke & heat detectors) - beam detectors in atrium/skylight areas and point type detectors in occupied areas•Automatic alarm system•Automatic fire sprinkler system for fire suppression•Exit signage•Smoke control – make up air and smoke extract fans•Egress – available safe egress time based on NFPA 101•Smoke zones - designed to restrict smoke from spreading from one smoke zone to another•Fire detection system - zoned identical to the smoke zones, including all visual and audible fire alarms.•Fire sprinkler system - zoned similar to the smoke zones and vice versa throughout the building.Codes / standards used•National Building Code (NBC 2005) of India•NFPA 101 Life Safety Code (2006)•NFPA 92 B - Standard for Smoke-control systems (2012 )•BS PD 7974-6:2004General practice of smoke simulation Flow only enters andleaves through thebottom and top surfaces.The main flow directionshould be to the vertical.Gap underneath the firefor cool air to be drawn inBuilding geometry: Retail shopping mallSectional details of the Retail mallMaterial propertiesAir : Variable quantity, to account for density variation with temperature and buoyancy Fire PartUse free arearatio =0.85 andconductivity of200 W/m-K tospread the heatwithin the flameFire modelled as a short cylinder and assigned as resistance material.Steel ring around the fire part (~1/2 flame height) and suppressed fromthe meshFast t- squared fire growth up to 2500 kW and steady state thereafter is considered, Firediameter = 3.35 m (NFPA 92B, A.5.2.1, based on HRRPUA 568 kW/m 2 and fire size of 5 MW). Variation of fire size with respect to time. Fire size reaches 1.75 MW (convective portion of 2.5 MW) at 210 seconds. Convective portion is taken as 70% of the total fire HRR.Boundary conditionsInlet boundary conditions – air domain inlet ambient temperature, scalar and pressureOutlet boundary conditions --smoke exhaust fan capacitiesMesh detailsThe fire and the air above and below - good uniform mesh- to capture the flow accurately by CFDFire sourceSolid ring suppressed from the mesh and ensures that flow only enters and leaves through the bottom and top surfacesInitial conditionsAir domain set at initial conditions as scalar = 0, temperature = 35.20 CSolver settingsObjective 2: Key results for final designWhat do we look for in CFD analysis?For designers and regulators, information about• Smoke movement• Temperature distribution• Airflow fieldSmoke transport is tracked w.r.t rise of smoke in atrium, along corridors and interconnected spacesKey results to look for :• Smoke free space• Tenable smoke temperatureBased on BS PD 7974-6:2004, Annex G•Smoke tenability limit - 10m visibility, Table G.1•Temperature tenability limit - 600C, Table G.3•Toxicity is deemed acceptable if visibility >10mSmoke developmentSmoke visibility (Smoke free space) – X PlaneSmoke visibility (Smoke free space) – Y PlaneSmokevisibility(Smokefreespace)****************+2floor(Z-plane)Key result 1: Smoke visibilitySmoke visibility-10m (smoke free space)Most of walking corridor space is smoke free (smoke free clear height of 1.8m above the corridor floor)Temperature development X PlaneY PlaneKey Result 2: Smoke temperatureTenable smoke temperatureIn G+2 floor below 1.8m FFL,smoke temperature is below600C and hence tenabilitylimits for smoke temperatureis not breached up to 20minutes from start of fireAir flow field development(at UG level above fire location)Y PlaneKey result 3: Air flow fieldAir flow field•Fresh air velocity contacting smoke plume has notexceeded 1.02 m/s. Hencesmoke plume does not getdispersed and rises as plumeabove required smoke freeclear height.•Replacement air velocity atentrance to the shopping malldoes not exceed 1.6 m/s andhence does not hinder peopleescape through the entrance.Outcome for final design•Well defined plume development and smoke rising towards smoke exhaust fans•Make up air does not disturb the smoke plume –no smoke dispersion and visibility problems•Hot smoke temperature is within acceptable limits for human safety.•Smoke visibility is within acceptable limits for safe evacuationBottom line: Smoke exhaust fan capacity and layout is adequate to provide smoke free space for about 20 minutes for the final designObjective 3: Insights from CFD analysis for good design decisionsChallenges in design…..•building geometry is large and complex• a prior distribution of smoke/ air velocities is not known•prescriptive code provides only guidance• a number of scenarios for ventilation fan layout and capacities are possibleSo to arrive at the final design, we had to analyze few design variants and results for the initial design and final design are compared leading to an adequate and good design….Comparison of smoke control zonesOptimize smoke exhaust system design... helpful tool •Estimate smoke exhaust volume flow rate based on:•fire size•outdoor ambient temperature•distance from base of fire to smoke layer interfaceAlso we can estimate:•minimum edge-to-edge separation•maximum number of fans•maximum flow through each fan to avoid plug holingComparison of smoke visibilitySmoke development w.r.t time during fire event- Y planeSmoke development w.r.t time during fire event- z planeComparison of smoke temperatureComparison of air/smoke flow fieldOptimize smoke exhaust system design... SummaryBased on a given smoke exhaust fan layout and fire zoning logic, Autodesk CFD analysis can accurately predict:• smoke development•smoke movement•Visibility levels and temperature distribution.Hence this approach can be used to make good design decisions to minimize smoke hazards.More examples:Objective 4: Benefits and limitationsBenefits:•Easy to use•Quick validation of smoke control strategy•Engineering based approach to fire safety measures (performance based)•Interface with Revit so CAD model to CFD model is easy•More insight leads to better design decisionsLimitations:•Transient solution requires small time step so run time is long –many hours •Scalar for smoke generation (=1) instead of generation rate (Kg/s) as input •Uncertainty in smoke particulate yield values•Tenability for fire brigade –radiation from the smoke layer simulation- challenge •Limited verification of smoke modelThank you for listening…. I hope you enjoyed the class and have met the objectives of the AU class and now will be able to:•Learn how fire and smoke is modeled•Visualize and Highlight key results•Gain insight into making good design decisions•Understand benefits and limitationsMy Contact details are given below:*******************Twitter: @m_munirajuluLinkedIn: https: ///in/ dr-munirajulu-m-3901a219For info on who we are and what we do…。
dynamic kinetic resolution

dynamic kinetic resolutionDynamic kinetic resolution (DKR) is an innovative process developed to achieve asymmetric synthesis in complex molecules. It is a type of chemical reaction which helps to obtain a target product with enhanced asymmetric selectivity by using a dynamic kinetic process. It is an environmentally friendly process which is cost-effective and offers shorter reaction timelines as compared to conventional methods.Dynamic kinetic resolution (DKR) consists of two parts, i.e., a kinetic resolution part and a dynamic resolution part. During the kinetic resolution part, a catalyst is used to promote a reaction between two similar molecules. The dynamicresolution part, on the other hand, involves a complex set of reactions in which two different components of a mixture are separated into two different fractions. The reaction is carried out at a temperature and pressure over a certain period of time such that the components are rearranged in accordance with the desired target product.The main advantage of dynamic kinetic resolution (DKR) is that it allows for the production of a target product with high chiral selectivity. This feature is essential for the production of enhanced enantioselective products. It also offers other advantages such as shorter reaction times, cost savings, and reduction of the use of hazardous chemicals. Moreover, it is a selective and targeted process which avoids the use of toxic and hazardous solvents and catalysts. Moreover, itis capable of producing chiral compounds in yields that exceed 50%.Dynamic kinetic resolution (DKR) is most commonly employed in the synthesis of chiral compounds such as natural products, pharmaceuticals, fine chemicals, and agrochemicals. This process is also used in the development of new drugs, fragrances, and optical brighteners. It is also used for the production of complex compounds and the separation of optically active compounds from racemic mixtures. DKR is a versatile and powerful method which provides high yields of the desired product with excellent selectivity.In conclusion, dynamic kinetic resolution (DKR) is a powerful and selective process which offers a number of advantages. It has many applications in the production of chiral compounds and the separation of optically active compoundsfrom racemic mixtures. It is also cost-effective, environmentally friendly and offers shorter reaction times as compared to conventional methods. Thus, DKR is an important tool for the production of complex molecules in organic chemistry.。
Laser Ranging to the Moon, Mars and Beyond

a r X i v :g r -q c /0411082v 1 16 N o v 2004Laser Ranging to the Moon,Mars and BeyondSlava G.Turyshev,James G.Williams,Michael Shao,John D.AndersonJet Propulsion Laboratory,California Institute of Technology,4800Oak Grove Drive,Pasadena,CA 91109,USAKenneth L.Nordtvedt,Jr.Northwest Analysis,118Sourdough Ridge Road,Bozeman,MT 59715USA Thomas W.Murphy,Jr.Physics Department,University of California,San Diego 9500Gilman Dr.,La Jolla,CA 92093USA Abstract Current and future optical technologies will aid exploration of the Moon and Mars while advancing fundamental physics research in the solar system.Technologies and possible improvements in the laser-enabled tests of various physical phenomena are considered along with a space architecture that could be the cornerstone for robotic and human exploration of the solar system.In particular,accurate ranging to the Moon and Mars would not only lead to construction of a new space communication infrastructure enabling an improved navigational accuracy,but will also provide a significant improvement in several tests of gravitational theory:the equivalence principle,geodetic precession,PPN parameters βand γ,and possible variation of the gravitational constant G .Other tests would become possible with an optical architecture that would allow proceeding from meter to centimeter to millimeter range accuracies on interplanetary distances.This paper discusses the current state and the future improvements in the tests of relativistic gravity with Lunar Laser Ranging (LLR).We also consider precision gravitational tests with the future laser rangingto Mars and discuss optical design of the proposed Laser Astrometric Test of Relativity (LATOR)mission.We emphasize that already existing capabilities can offer significant improvements not only in the tests of fundamental physics,but may also establish the infrastructure for space exploration in the near future.Looking to future exploration,what characteristics are desired for the next generation of ranging devices,what is the optimal architecture that would benefit both space exploration and fundamental physics,and what fundamental questions can be investigated?We try to answer these questions.1IntroductionThe recent progress in fundamental physics research was enabled by significant advancements in many technological areas with one of the examples being the continuing development of the NASA Deep Space Network –critical infrastructure for precision navigation and communication in space.A demonstration of such a progress is the recent Cassini solar conjunction experiment[8,6]that was possible only because of the use of Ka-band(∼33.4GHz)spacecraft radio-tracking capabilities.The experiment was part of the ancillary science program–a by-product of this new radio-tracking technology.Becasue of a much higher data rate transmission and, thus,larger data volume delivered from large distances the higher communication frequency was a very important mission capability.The higher frequencies are also less affected by the dispersion in the solar plasma,thus allowing a more extensive coverage,when depp space navigation is concerned.There is still a possibility of moving to even higher radio-frequencies, say to∼60GHz,however,this would put us closer to the limit that the Earth’s atmosphere imposes on signal transmission.Beyond these frequencies radio communication with distant spacecraft will be inefficient.The next step is switching to optical communication.Lasers—with their spatial coherence,narrow spectral emission,high power,and well-defined spatial modes—are highly useful for many space applications.While in free-space,optical laser communication(lasercomm)would have an advantage as opposed to the conventional radio-communication sercomm would provide not only significantly higher data rates(on the order of a few Gbps),it would also allow a more precise navigation and attitude control.The latter is of great importance for manned missions in accord the“Moon,Mars and Beyond”Space Exploration Initiative.In fact,precision navigation,attitude control,landing,resource location, 3-dimensional imaging,surface scanning,formationflying and many other areas are thought only in terms of laser-enabled technologies.Here we investigate how a near-future free-space optical communication architecture might benefit progress in gravitational and fundamental physics experiments performed in the solar system.This paper focuses on current and future optical technologies and methods that will advance fundamental physics research in the context of solar system exploration.There are many activities that focused on the design on an optical transceiver system which will work at the distance comparable to that between the Earth and Mars,and test it on the Moon.This paper summarizes required capabilities for such a system.In particular,we discuss how accurate laser ranging to the neighboring celestial bodies,the Moon and Mars,would not only lead to construction of a new space communication infrastructure with much improved navigational accuracy,it will also provide a significant improvement in several tests of gravitational theory. Looking to future exploration,we address the characteristics that are desired for the next generation of ranging devices;we will focus on optimal architecture that would benefit both space exploration and fundamental physics,and discuss the questions of critical importance that can be investigated.This paper is organized as follows:Section2discusses the current state and future per-formance expected with the LLR technology.Section3addresses the possibility of improving tests of gravitational theories with laser ranging to Mars.Section4addresses the next logical step—interplanetary laser ranging.We discuss the mission proposal for the Laser Astrometric Test of Relativity(LATOR).We present a design for its optical receiver system.Section5 addresses a proposal for new multi-purpose space architecture based on optical communica-tion.We present a preliminary design and discuss implications of this new proposal for tests of fundamental physics.We close with a summary and recommendations.2LLR Contribution to Fundamental PhysicsDuring more than35years of its existence lunar laser ranging has become a critical technique available for precision tests of gravitational theory.The20th century progress in three seem-ingly unrelated areas of human exploration–quantum optics,astronomy,and human spaceexploration,led to the construction of this unique interplanetary instrument to conduct very precise tests of fundamental physics.In this section we will discuss the current state in LLR tests of relativistic gravity and explore what could be possible in the near future.2.1Motivation for Precision Tests of GravityThe nature of gravity is fundamental to our understanding of the structure and evolution of the universe.This importance motivates various precision tests of gravity both in laboratories and in space.Most of the experimental underpinning for theoretical gravitation has come from experiments conducted in the solar system.Einstein’s general theory of relativity(GR)began its empirical success in1915by explaining the anomalous perihelion precession of Mercury’s orbit,using no adjustable theoretical parameters.Eddington’s observations of the gravitational deflection of light during a solar eclipse in1919confirmed the doubling of the deflection angles predicted by GR as compared to Newtonian and Equivalence Principle(EP)arguments.Follow-ing these beginnings,the general theory of relativity has been verified at ever-higher accuracy. Thus,microwave ranging to the Viking landers on Mars yielded an accuracy of∼0.2%from the gravitational time-delay tests of GR[48,44,49,50].Recent spacecraft and planetary mi-crowave radar observations reached an accuracy of∼0.15%[4,5].The astrometric observations of the deflection of quasar positions with respect to the Sun performed with Very-Long Base-line Interferometry(VLBI)improved the accuracy of the tests of gravity to∼0.045%[45,51]. Lunar Laser Ranging(LLR),the continuing legacy of the Apollo program,has provided ver-ification of GR improving an accuracy to∼0.011%via precision measurements of the lunar orbit[62,63,30,31,32,35,24,36,4,68].The recent time-delay experiments with the Cassini spacecraft at a solar conjunction have tested gravity to a remarkable accuracy of0.0023%[8] in measuring deflection of microwaves by solar gravity.Thus,almost ninety years after general relativity was born,Einstein’s theory has survived every test.This rare longevity and the absence of any adjustable parameters,does not mean that this theory is absolutely correct,but it serves to motivate more sensitive tests searching for its expected violation.The solar conjunction experiments with the Cassini spacecraft have dramatically improved the accuracy in the solar system tests of GR[8].The reported accuracy of2.3×10−5in measuring the Eddington parameterγ,opens a new realm for gravitational tests,especially those motivated by the on-going progress in scalar-tensor theories of gravity.1 In particular,scalar-tensor extensions of gravity that are consistent with present cosmological models[15,16,17,18,19,20,39]predict deviations of this parameter from its GR value of unity at levels of10−5to10−7.Furthermore,the continuing inability to unify gravity with the other forces indicates that GR should be violated at some level.The Cassini result together with these theoretical predictions motivate new searches for possible GR violations;they also provide a robust theoretical paradigm and constructive guidance for experiments that would push beyond the present experimental accuracy for parameterized post-Newtonian(PPN)parameters(for details on the PPN formalism see[60]).Thus,in addition to experiments that probe the GR prediction for the curvature of the gravityfield(given by parameterγ),any experiment pushingthe accuracy in measuring the degree of non-linearity of gravity superposition(given by anotherEddington parameterβ)will also be of great interest.This is a powerful motive for tests ofgravitational physics phenomena at improved accuracies.Analyses of laser ranges to the Moon have provided increasingly stringent limits on anyviolation of the Equivalence Principle(EP);they also enabled very accurate measurements fora number of relativistic gravity parameters.2.2LLR History and Scientific BackgroundLLR has a distinguished history[24,9]dating back to the placement of a retroreflector array onthe lunar surface by the Apollo11astronauts.Additional reflectors were left by the Apollo14and Apollo15astronauts,and two French-built reflector arrays were placed on the Moon by theSoviet Luna17and Luna21missions.Figure1shows the weighted RMS residual for each year.Early accuracies using the McDonald Observatory’s2.7m telescope hovered around25cm. Equipment improvements decreased the ranging uncertainty to∼15cm later in the1970s.In1985the2.7m ranging system was replaced with the McDonald Laser Ranging System(MLRS).In the1980s ranges were also received from Haleakala Observatory on the island of Maui in theHawaiian chain and the Observatoire de la Cote d’Azur(OCA)in France.Haleakala ceasedoperations in1990.A sequence of technical improvements decreased the range uncertainty tothe current∼2cm.The2.7m telescope had a greater light gathering capability than thenewer smaller aperture systems,but the newer systemsfired more frequently and had a muchimproved range accuracy.The new systems do not distinguish returning photons against thebright background near full Moon,which the2.7m telescope could do,though there are somemodern eclipse observations.The lasers currently used in the ranging operate at10Hz,with a pulse width of about200 psec;each pulse contains∼1018photons.Under favorable observing conditions a single reflectedphoton is detected once every few seconds.For data processing,the ranges represented by thereturned photons are statistically combined into normal points,each normal point comprisingup to∼100photons.There are15553normal points are collected until March2004.Themeasured round-trip travel times∆t are two way,but in this paper equivalent ranges in lengthunits are c∆t/2.The conversion between time and length(for distance,residuals,and dataaccuracy)uses1nsec=15cm.The ranges of the early1970s had accuracies of approximately25cm.By1976the accuracies of the ranges had improved to about15cm.Accuracies improvedfurther in the mid-1980s;by1987they were4cm,and the present accuracies are∼2cm.One immediate result of lunar ranging was the great improvement in the accuracy of the lunarephemeris[62]and lunar science[67].LLR measures the range from an observatory on the Earth to a retroreflector on the Moon. For the Earth and Moon orbiting the Sun,the scale of relativistic effects is set by the ratio(GM/rc2)≃v2/c2∼10−8.The center-to-center distance of the Moon from the Earth,with mean value385,000km,is variable due to such things as eccentricity,the attraction of the Sun,planets,and the Earth’s bulge,and relativistic corrections.In addition to the lunar orbit,therange from an observatory on the Earth to a retroreflector on the Moon depends on the positionin space of the ranging observatory and the targeted lunar retroreflector.Thus,orientation ofthe rotation axes and the rotation angles of both bodies are important with tidal distortions,plate motion,and relativistic transformations also coming into play.To extract the gravitationalphysics information of interest it is necessary to accurately model a variety of effects[68].For a general review of LLR see[24].A comprehensive paper on tests of gravitationalphysics is[62].A recent test of the EP is in[4]and other GR tests are in[64].An overviewFigure1:Historical accuracy of LLR data from1970to2004.of the LLR gravitational physics tests is given by Nordtvedt[37].Reviews of various tests of relativity,including the contribution by LLR,are given in[58,60].Our recent paper describes the model improvements needed to achieve mm-level accuracy for LLR[66].The most recent LLR results are given in[68].2.3Tests of Relativistic Gravity with LLRLLR offers very accurate laser ranging(weighted rms currently∼2cm or∼5×10−11in frac-tional accuracy)to retroreflectors on the Moon.Analysis of these very precise data contributes to many areas of fundamental and gravitational physics.Thus,these high-precision studies of the Earth-Moon-Sun system provide the most sensitive tests of several key properties of weak-field gravity,including Einstein’s Strong Equivalence Principle(SEP)on which general relativity rests(in fact,LLR is the only current test of the SEP).LLR data yielded the strongest limits to date on variability of the gravitational constant(the way gravity is affected by the expansion of the universe),and the best measurement of the de Sitter precession rate.In this Section we discuss these tests in more details.2.3.1Tests of the Equivalence PrincipleThe Equivalence Principle,the exact correspondence of gravitational and inertial masses,is a central assumption of general relativity and a unique feature of gravitation.EP tests can therefore be viewed in two contexts:tests of the foundations of general relativity,or as searches for new physics.As emphasized by Damour[12,13],almost all extensions to the standard modelof particle physics(with best known extension offered by string theory)generically predict newforces that would show up as apparent violations of the EP.The weak form the EP(the WEP)states that the gravitational properties of strong and electro-weak interactions obey the EP.In this case the relevant test-body differences are their fractional nuclear-binding differences,their neutron-to-proton ratios,their atomic charges,etc. General relativity,as well as other metric theories of gravity,predict that the WEP is exact. However,extensions of the Standard Model of Particle Physics that contain new macroscopic-range quantumfields predict quantum exchange forces that will generically violate the WEP because they couple to generalized‘charges’rather than to mass/energy as does gravity[17,18]. WEP tests can be conducted with laboratory or astronomical bodies,because the relevant differences are in the test-body compositions.Easily the most precise tests of the EP are made by simply comparing the free fall accelerations,a1and a2,of different test bodies.For the case when the self-gravity of the test bodies is negligible and for a uniform external gravityfield, with the bodies at the same distance from the source of the gravity,the expression for the Equivalence Principle takes the most elegant form:∆a= M G M I 2(1)(a1+a2)where M G and M I represent gravitational and inertial masses of each body.The sensitivity of the EP test is determined by the precision of the differential acceleration measurement divided by the degree to which the test bodies differ(position).The strong form of the EP(the SEP)extends the principle to cover the gravitational properties of gravitational energy itself.In other words it is an assumption about the way that gravity begets gravity,i.e.about the non-linear property of gravitation.Although general relativity assumes that the SEP is exact,alternate metric theories of gravity such as those involving scalarfields,and other extensions of gravity theory,typically violate the SEP[30,31, 32,35].For the SEP case,the relevant test body differences are the fractional contributions to their masses by gravitational self-energy.Because of the extreme weakness of gravity,SEP test bodies that differ significantly must have astronomical sizes.Currently the Earth-Moon-Sun system provides the best arena for testing the SEP.The development of the parameterized post-Newtonian formalism[31,56,57],allows one to describe within the common framework the motion of celestial bodies in external gravitational fields within a wide class of metric theories of gravity.Over the last35years,the PPN formalism has become a useful framework for testing the SEP for extended bodies.In that formalism,the ratio of passive gravitational to inertial mass to thefirst order is given by[30,31]:M GMc2 ,(2) whereηis the SEP violation parameter(discussed below),M is the mass of a body and E is its gravitational binding or self-energy:E2Mc2 V B d3x d3yρB(x)ρB(y)EMc2 E=−4.64×10−10andwhere the subscripts E and m denote the Earth and Moon,respectively.The relatively small size bodies used in the laboratory experiments possess a negligible amount of gravitational self-energy and therefore such experiments indicate nothing about the equality of gravitational self-energy contributions to the inertial and passive gravitational masses of the bodies [30].TotesttheSEP onemustutilize planet-sizedextendedbodiesinwhichcase theratioEq.(3)is considerably higher.Dynamics of the three-body Sun-Earth-Moon system in the solar system barycentric inertial frame was used to search for the effect of a possible violation of the Equivalence Principle.In this frame,the quasi-Newtonian acceleration of the Moon (m )with respect to the Earth (E ),a =a m −a E ,is calculated to be:a =−µ∗rM I m µS r SEr 3Sm + M G M I m µS r SEr 3+µS r SEr 3Sm +η E Mc 2 m µS r SEMc 2 E − E n 2−(n −n ′)2n ′2a ′cos[(n −n ′)t +D 0].(8)Here,n denotes the sidereal mean motion of the Moon around the Earth,n ′the sidereal mean motion of the Earth around the Sun,and a ′denotes the radius of the orbit of the Earth around the Sun (assumed circular).The argument D =(n −n ′)t +D 0with near synodic period is the mean longitude of the Moon minus the mean longitude of the Sun and is zero at new Moon.(For a more precise derivation of the lunar range perturbation due to the SEP violation acceleration term in Eq.(6)consult [62].)Any anomalous radial perturbation will be proportional to cos D .Expressed in terms ofη,the radial perturbation in Eq.(8)isδr∼13ηcos D meters [38,21,22].This effect,generalized to all similar three body situations,the“SEP-polarization effect.”LLR investigates the SEP by looking for a displacement of the lunar orbit along the direction to the Sun.The equivalence principle can be split into two parts:the weak equivalence principle tests the sensitivity to composition and the strong equivalence principle checks the dependence on mass.There are laboratory investigations of the weak equivalence principle(at University of Washington)which are about as accurate as LLR[7,1].LLR is the dominant test of the strong equivalence principle.The most accurate test of the SEP violation effect is presently provided by LLR[61,48,23],and also in[24,62,63,4].Recent analysis of LLR data test the EP of∆(M G/M I)EP=(−1.0±1.4)×10−13[68].This result corresponds to a test of the SEP of∆(M G/M I)SEP=(−2.0±2.0)×10−13with the SEP violation parameter η=4β−γ−3found to beη=(4.4±4.5)×10−ing the recent Cassini result for the PPN parameterγ,PPN parameterβis determined at the level ofβ−1=(1.2±1.1)×10−4.2.3.2Other Tests of Gravity with LLRLLR data yielded the strongest limits to date on variability of the gravitational constant(the way gravity is affected by the expansion of the universe),the best measurement of the de Sitter precession rate,and is relied upon to generate accurate astronomical ephemerides.The possibility of a time variation of the gravitational constant,G,wasfirst considered by Dirac in1938on the basis of his large number hypothesis,and later developed by Brans and Dicke in their theory of gravitation(for more details consult[59,60]).Variation might be related to the expansion of the Universe,in which case˙G/G=σH0,where H0is the Hubble constant, andσis a dimensionless parameter whose value depends on both the gravitational constant and the cosmological model considered.Revival of interest in Brans-Dicke-like theories,with a variable G,was partially motivated by the appearance of superstring theories where G is considered to be a dynamical quantity[26].Two limits on a change of G come from LLR and planetary ranging.This is the second most important gravitational physics result that LLR provides.GR does not predict a changing G,but some other theories do,thus testing for this effect is important.The current LLR ˙G/G=(4±9)×10−13yr−1is the most accurate limit published[68].The˙G/G uncertaintyis83times smaller than the inverse age of the universe,t0=13.4Gyr with the value for Hubble constant H0=72km/sec/Mpc from the WMAP data[52].The uncertainty for˙G/G is improving rapidly because its sensitivity depends on the square of the data span.This fact puts LLR,with its more then35years of history,in a clear advantage as opposed to other experiments.LLR has also provided the only accurate determination of the geodetic precession.Ref.[68]reports a test of geodetic precession,which expressed as a relative deviation from GR,is K gp=−0.0019±0.0064.The GP-B satellite should provide improved accuracy over this value, if that mission is successfully completed.LLR also has the capability of determining PPNβandγdirectly from the point-mass orbit perturbations.A future possibility is detection of the solar J2from LLR data combined with the planetary ranging data.Also possible are dark matter tests,looking for any departure from the inverse square law of gravity,and checking for a variation of the speed of light.The accurate LLR data has been able to quickly eliminate several suggested alterations of physical laws.The precisely measured lunar motion is a reality that any proposed laws of attraction and motion must satisfy.The above investigations are important to gravitational physics.The future LLR data will improve the above investigations.Thus,future LLR data of current accuracy would con-tinue to shrink the uncertainty of˙G because of the quadratic dependence on data span.The equivalence principle results would improve more slowly.To make a big improvement in the equivalence principle uncertainty requires improved range accuracy,and that is the motivation for constructing the APOLLO ranging facility in New Mexico.2.4Future LLR Data and APOLLO facilityIt is essential that acquisition of the new LLR data will continue in the future.Accuracies∼2cm are now achieved,and further very useful improvement is expected.Inclusion of improved data into LLR analyses would allow a correspondingly more precise determination of the gravitational physics parameters under study.LLR has remained a viable experiment with fresh results over35years because the data accuracies have improved by an order of magnitude(see Figure1).There are prospects for future LLR station that would provide another order of magnitude improvement.The Apache Point Observatory Lunar Laser-ranging Operation(APOLLO)is a new LLR effort designed to achieve mm range precision and corresponding order-of-magnitude gains in measurements of fundamental physics parameters.For thefirst time in the LLR history,using a3.5m telescope the APOLLO facility will push LLR into a new regime of multiple photon returns with each pulse,enabling millimeter range precision to be achieved[29,66].The anticipated mm-level range accuracy,expected from APOLLO,has a potential to test the EP with a sensitivity approaching10−14.This accuracy would yield sensitivity for parameterβat the level of∼5×10−5and measurements of the relative change in the gravitational constant,˙G/G, would be∼0.1%the inverse age of the universe.The overwhelming advantage APOLLO has over current LLR operations is a3.5m astro-nomical quality telescope at a good site.The site in southern New Mexico offers high altitude (2780m)and very good atmospheric“seeing”and image quality,with a median image resolu-tion of1.1arcseconds.Both the image sharpness and large aperture conspire to deliver more photons onto the lunar retroreflector and receive more of the photons returning from the re-flectors,pared to current operations that receive,on average,fewer than0.01 photons per pulse,APOLLO should be well into the multi-photon regime,with perhaps5–10 return photons per pulse.With this signal rate,APOLLO will be efficient atfinding and track-ing the lunar return,yielding hundreds of times more photons in an observation than current√operations deliver.In addition to the significant reduction in statistical error(useful).These new reflectors on the Moon(and later on Mars)can offer significant navigational accuracy for many space vehicles on their approach to the lunar surface or during theirflight around the Moon,but they also will contribute significantly to fundamental physics research.The future of lunar ranging might take two forms,namely passive retroreflectors and active transponders.The advantages of new installations of passive retroreflector arrays are their long life and simplicity.The disadvantages are the weak returned signal and the spread of the reflected pulse arising from lunar librations(apparent changes in orientation of up to10 degrees).Insofar as the photon timing error budget is dominated by the libration-induced pulse spread—as is the case in modern lunar ranging—the laser and timing system parameters do√not influence the net measurement uncertainty,which simply scales as1/3Laser Ranging to MarsThere are three different experiments that can be done with accurate ranges to Mars:a test of the SEP(similar to LLR),a solar conjunction experiment measuring the deflection of light in the solar gravity,similar to the Cassini experiment,and a search for temporal variation in the gravitational constant G.The Earth-Mars-Sun-Jupiter system allows for a sensitive test of the SEP which is qualitatively different from that provided by LLR[3].Furthermore,the outcome of these ranging experiments has the potential to improve the values of the two relativistic parameters—a combination of PPN parametersη(via test of SEP)and a direct observation of the PPN parameterγ(via Shapiro time delay or solar conjunction experiments).(This is quite different compared to LLR,as the small variation of Shapiro time delay prohibits very accurate independent determination of the parameterγ).The Earth-Mars range would also provide for a very accurate test of˙G/G.This section qualitatively addresses the near-term possibility of laser ranging to Mars and addresses the above three effects.3.1Planetary Test of the SEP with Ranging to MarsEarth-Mars ranging data can provide a useful estimate of the SEP parameterηgiven by Eq.(7). It was demonstrated in[3]that if future Mars missions provide ranging measurements with an accuracy ofσcentimeters,after ten years of ranging the expected accuracy for the SEP parameterηmay be of orderσ×10−6.These ranging measurements will also provide the most accurate determination of the mass of Jupiter,independent of the SEP effect test.It has been observed previously that a measurement of the Sun’s gravitational to inertial mass ratio can be performed using the Sun-Jupiter-Mars or Sun-Jupiter-Earth system[33,47,3]. The question we would like to answer here is how accurately can we do the SEP test given the accurate ranging to Mars?We emphasize that the Sun-Mars-Earth-Jupiter system,though governed basically by the same equations of motion as Sun-Earth-Moon system,is significantly different physically.For a given value of SEP parameterηthe polarization effects on the Earth and Mars orbits are almost two orders of magnitude larger than on the lunar orbit.Below we examine the SEP effect on the Earth-Mars range,which has been measured as part of the Mariner9and Viking missions with ranging accuracy∼7m[48,44,41,43].The main motivation for our analysis is the near-future Mars missions that should yield ranging data, accurate to∼1cm.This accuracy would bring additional capabilities for the precision tests of fundamental and gravitational physics.3.1.1Analytical Background for a Planetary SEP TestThe dynamics of the four-body Sun-Mars-Earth-Jupiter system in the Solar system barycentric inertial frame were considered.The quasi-Newtonian acceleration of the Earth(E)with respect to the Sun(S),a SE=a E−a S,is straightforwardly calculated to be:a SE=−µ∗SE·r SE MI Eb=M,Jµb r bS r3bE + M G M I E b=M,Jµb r bS。
State Space Reconstruction for Multivariate Time Series Prediction

a r X i v :0809.2220v 1 [n l i n .C D ] 12 S e p 2008APS/123-QEDState Space Reconstruction for Multivariate Time Series PredictionI.Vlachos ∗and D.Kugiumtzis †Department of Mathematical,Physical and Computational Sciences,Faculty of Technology,Aristotle University of Thessaloniki,Greece(Dated:September 12,2008)In the nonlinear prediction of scalar time series,the common practice is to reconstruct the state space using time-delay embedding and apply a local model on neighborhoods of the reconstructed space.The method of false nearest neighbors is often used to estimate the embedding dimension.For prediction purposes,the optimal embedding dimension can also be estimated by some prediction error minimization criterion.We investigate the proper state space reconstruction for multivariate time series and modify the two abovementioned criteria to search for optimal embedding in the set of the variables and their delays.We pinpoint the problems that can arise in each case and compare the state space reconstructions (suggested by each of the two methods)on the predictive ability of the local model that uses each of them.Results obtained from Monte Carlo simulations on known chaotic maps revealed the non-uniqueness of optimum reconstruction in the multivariate case and showed that prediction criteria perform better when the task is prediction.PACS numbers:05.45.Tp,02.50.Sk,05.45.aKeywords:nonlinear analysis,multivariate analysis,time series,local prediction,state space reconstructionI.INTRODUCTIONSince its publication Takens’Embedding Theorem [1](and its extension,the Fractal Delay Embedding Preva-lence Theorem by Sauer et al.[2])has been used in time series analysis in many different settings ranging from system characterization and approximation of invariant quantities,such as correlation dimension and Lyapunov exponents,to prediction and noise-filtering [3].The Em-bedding Theorem implies that although the true dynam-ics of a system may not be known,equivalent dynamics can be obtained under suitable conditions using time de-lays of a single time series,treated as an one-dimensional projection of the system trajectory.Most applications of the Embedding Theorem deal with univariate time series,but often measurements of more than one quantities related to the same dynamical system are available.One of the first uses of multivari-ate embedding was in the context of spatially extended systems where embedding vectors were constructed from data representing the same quantity measured simulta-neously at different locations [4,5].Multivariate em-bedding was used for noise reduction [6]and for surro-gate data generation with equal individual delay times and equal embedding dimensions for each time series [7].In nonlinear multivariate prediction,the prediction with local models on a space reconstructed from a different time series of the same system was studied in [8].This study was extended in [9]by having the reconstruction utilize all of the observed time series.Multivariate em-bedding with the use of independent components analysis was considered in [10]and more recently multivariate em-2as x n=h(y n).Despite the apparent loss of information of the system dynamics by the projection,the system dynamics may be recovered through suitable state space reconstruction from the scalar time series.A.Reconstruction of the state space According to Taken’s embedding theorem a trajectory formed by the points x n of time-delayed components from the time series{x n}N n=1asx n=(x n−(m−1)τ,x n−(m−2)τ,...,x n),(1)under certain genericity assumptions,is an one-to-one mapping of the original trajectory of y n provided that m is large enough.Given that the dynamical system“lives”on an attrac-tor A⊂Γ,the reconstructed attractor˜A through the use of the time-delay vectors is topologically equivalent to A.A sufficient condition for an appropriate unfolding of the attractor is m≥2d+1where d is the box-counting dimension of A.The embedding process is visualized in the following graphy n∈A⊂ΓF→y n+1∈A⊂Γ↓h↓hx n∈R x n+1∈R↓e↓ex n∈˜A⊂R m G→x n+1∈˜A⊂R mwhere e is the embedding procedure creating the delay vectors from the time series and G is the reconstructed dynamical system on˜A.G preserves properties of the unknown F on the unknown attractor A that do not change under smooth coordinate transformations.B.Univariate local predictionFor a given state space reconstruction,the local predic-tion at a target point x n is made with a model estimated on the K nearest neighboring points to x n.The local model can have a simple form,such as the zeroth order model(the average of the images of the nearest neigh-bors),but here we consider the linear modelˆx n+1=a(n)x n+b(n),where the superscript(n)denotes the dependence of the model parameters(a(n)and b(n))on the neighborhood of x n.The neighborhood at each target point is defined either by afixed number K of nearest neighbors or by a distance determining the borders of the neighborhood giving a varying K with x n.C.Selection of embedding parametersThe two parameters of the delay embedding in(1)are the embedding dimension m,i.e.the number of compo-nents in x n and the delay timeτ.We skip the discussion on the selection ofτas it is typically set to1in the case of discrete systems that we focus on.Among the ap-proaches for the selection of m we choose the most popu-lar method of false nearest neighbors(FNN)and present it briefly below[13].The measurement function h projects distant points {y n}of the original attractor to close values of{x n}.A small m may still give badly projected points and we seek the reconstructed state space of the smallest embed-ding dimension m that unfolds the attractor.This idea is implemented as follows.For each point x m n in the m-dimensional reconstructed state space,the distance from its nearest neighbor x mn(1)is calculated,d(x m n,x mn(1))=x m n−x mn(1).The dimension of the reconstructed state space is augmented by1and the new distance of thesevectors is calculated,d(x m+1n,x m+1n(1))= x m+1n−x m+1n(1). If the ratio of the two distances exceeds a predefined tol-erance threshold r the two neighbors are classified as false neighbors,i.e.r n(m)=d(x m+1n,x m+1n(1))3 III.MULTIV ARIATE EMBEDDINGIn Section II we gave a summary of the reconstructiontechnique for a deterministic dynamical system from ascalar time series generated by the system.However,it ispossible that more than one time series are observed thatare possibly related to the system under investigation.For p time series measured simultaneously from the samedynamical system,a measurement function H:Γ→R pis decomposed to h i,i=1,...,p,defined as in Section II,giving each a time series{x i,n}N n=1.According to the dis-cussion on univariate embedding any of the p time seriescan be used for reconstruction of the system dynamics,or better,the most suitable time series could be selectedafter proper investigation.In a different approach all theavailable time series are considered and the analysis ofthe univariate time series is adjusted to the multivariatetime series.A.From univariate to multivariate embeddingGiven that there are p time series{x i,n}N n=1,i=1,...,p,the equivalent to the reconstructed state vec-tor in(1)for the case of multivariate embedding is of theformx n=(x1,n−(m1−1)τ1,x1,n−(m1−2)τ1,...,x1,n,x2,n−(m2−1)τ2,...,x2,n,...,x p,n)(3)and are defined by an embedding dimension vector m= (m1,...,m p)that indicates the number of components used from each time series and a time delay vector τ=(τ1,...,τp)that gives the delays for each time series. The corresponding graph for the multivariate embedding process is shown below.y n∈A⊂ΓF→y n+1∈A⊂Γւh1↓h2...ցhpւh1↓h2...ցhpx1,n x2,n...x p,n x1,n+1x2,n+1...x p,n+1ցe↓e...ւeցe↓e...ւex n∈˜A⊂R M G→x n+1∈˜A⊂R MThe total embedding dimension M is the sum of the individual embedding dimensions for each time seriesM= p i=1m i.Note that if redundant or irrelevant information is present in the p time series,only a sub-set of them may be represented in the optimal recon-structed points x n.The selection of m andτfollows the same principles as for the univariate case:the attrac-tor should be fully unfolded and the components of the embedding vectors should be uncorrelated.A simple se-lection rule suggests that all individual delay times and embedding dimensions are the same,i.e.m=m1and τ=τ1with1a p-vector of ones[6,7].Here,we set againτi=1,i=1,...,p,but we consider bothfixed and varying m i in the implementation of the FNN method (see Section III D).B.Multivariate local predictionThe prediction for each time series x i,n,i=1,...,p,is performed separately by p local models,estimated as in the case of univariate time series,but for reconstructed points formed potentially from all p time series as given in(3)(e.g.see[9]).We propose an extension of the NRMSE for the pre-diction of one time series to account for the error vec-tors comprised of the individual prediction errors for each of the predicted time series.If we have one step ahead predictions for the p available time series,i.e.ˆx i,n, i=1,...,p(for a range of current times n−1),we define the multivariate NRMSENRMSE=n (x1,n−¯x1,...,x p,n−¯x p) 2(4)where¯x i is the mean of the actual values of x i,n over all target times n.C.Problems and restrictions of multivariatereconstructionsA major problem in the multivariate case is the prob-lem of identification.There are often not unique m and τembedding parameters that unfold fully the attractor.A trivial example is the Henon map[17]x n+1=1.4−x2n+y ny n+1=0.3x n(5) It is known that for the state space reconstruction from the observable x n the appropriate embedding parame-ters are m=2andτ=1.Due to the fact that y n is a lagged multiple of x n the attractor can obviously be reconstructed from the bivariate time series{x n,y n} equally well with any of the following two-dimensional embedding schemesx n=(x n,x n−1)x n=(x n,y n)x n=(y n,y n−1) since they are essentially the same.This example shows also the problem of redundant information,e.g.the state space reconstruction would not improve by augmenting the delay vector x n=(x n,x n−1)with the component y n that actually duplicates x n−1.Redundancy is inevitable in multivariate time series as synchronous observations of the different time series are generally correlated and the fact that these observations are used as components in the same embedding vector adds redundant information in them.We note here that in the case of continuous dynamical systems,the delay parameterτi may be se-lected so that the components of the i time series are not correlated with each other,but this does not imply that they are not correlated to components from another time series.4 A different problem is that of irrelevance,whenseries that are not generated by the same dynamicaltem are included in the reconstruction procedure.may be the case even when a time series is connectedtime series generated by the system underAn issue of concern is also the fact thatdata don’t always have the same data ranges andtances calculated on delay vectors withdifferent ranges may depend highly on only some ofcomponents.So it is often preferred to scale all theto have either the same variance or be in the samerange.For our study we choose to scale the data torange[0,1].D.Selection of the embedding dimension vector Taking into account the problems in the state space reconstruction from multivariate time series,we present three methods for determining m,two based on the false nearest neighbor algorithm,which we name FNN1and FNN2,and one based on local models which we call pre-diction error minimization criterion(PEM).The main idea of the FNN algorithms is as for the univariate case.Starting from a small value the embed-ding dimension is increased by including delay compo-nents from the p time series and the percentage of the false nearest neighbors is calculated until it falls to the zero level.The difference of the two FNN methods is on the way that m is increased.For FNN1we restrict the state space reconstruction to use the same embedding dimension for each of the p time series,i.e.m=(m,m,...,m)for a given m.To assess whether m is sufficient,we consider all delay embeddings derived by augmenting the state vector of embedding di-mension vector(m,m,...,m)with a single delayed vari-able from any of the p time series.Thus the check for false nearest neighbors in(2)yields the increase from the embedding dimension vector(m,m,...,m)to each of the embedding dimension vectors(m+1,m,...,m), (m,m+1,...,m),...,(m,m,...,m+1).Then the algo-rithm stops at the optimal m=(m,m,...,m)if the zero level percentage of false nearest neighbors is obtained for all p cases.A sketch of thefirst two steps for a bivariate time series is shown in Figure1(a).This method has been commonly used in multivariate reconstruction and is more appropriate for spatiotem-porally distributed data(e.g.see the software package TISEAN[18]).A potential drawback of FNN1is that the selected total embedding dimension M is always a multiple of p,possibly introducing redundant informa-tion in the embedding vectors.We modify the algorithm of FNN1to account for any form of the embedding dimension vector m and the total embedding dimension M is increased by one at each step of the algorithm.Let us suppose that the algorithm has reached at some step the total embedding dimension M. For this M all the combinations of the components of the embedding dimension vector m=(m1,m2,...,m p)are considered under the condition M= p i=1m i.Then for each such m=(m1,m2,...,m p)all the possible augmen-tations with one dimension are checked for false nearest neighbors,i.e.(m1+1,m2,...,m p),(m1,m2+1,...,m p), ...,(m1,m2,...,m p+1).A sketch of thefirst two steps of the extended FNN algorithm,denoted as FNN2,for a bivariate time series is shown in Figure1(b).The termination criterion is the drop of the percent-age of false nearest neighbors to the zero level at every increase of M by one for at least one embedding dimen-sion vector(m1,m2,...,m p).If more than one embedding dimension vectors fulfill this criterion,the one with the smallest cumulative FNN percentage is selected,where the cumulative FNN percentage is the sum of the p FNN percentages for the increase by one of the respective com-ponent of the embedding dimension vector.The PEM criterion for the selection of m= (m1,m2,...,m p)is simply the extension of the goodness-of-fit or prediction criterion in the univariate case to account for the multiple ways the delay vector can be formed from the multivariate time series.Thus for all possible p-plets of(m1,m2,...,m p)from(1,0,...,0), (0,1,...,0),etc up to some vector of maximum embed-ding dimensions(m max,m max,...,m max),the respective reconstructed state spaces are created,local linear mod-els are applied and out-of-sample prediction errors are computed.So,totally p m max−1embedding dimension vectors are compared and the optimal is the one that gives the smallest multivariate NRMSE as defined in(4).IV.MONTE CARLO SIMULATIONS ANDRESULTSA.Monte Carlo setupWe test the three methods by performing Monte Carlo simulations on a variety of known nonlinear dynamical systems.The embedding dimension vectors are selected using the three methods on100different realizations of each system and the most frequently selected embedding dimension vectors for each method are tracked.Also,for each realization and selected embedding dimension vec-5ate NRMSE over the100realizations for each method is then used as an indicator of the performance of each method in prediction.The selection of the embedding dimension vector by FNN1,FNN2and PEM is done on thefirst three quarters of the data,N1=3N/4,and the multivariate NRMSE is computed on the last quarter of the data(N−N1).For PEM,the same split is used on the N1data,so that N2= 3N1/4data are used tofind the neighbors(training set) and the rest N1−N2are used to compute the multivariate NRMSE(test set)and decide for the optimal embedding dimension vector.A sketch of the split of the data is shown in Figure2.The number of neighbors for the local models in PEM varies with N and we set K N=10,25,50 for time series lengths N=512,2048,8192,respectively. The parameters of the local linear model are estimated by ordinary least squares.For all methods the investigation is restricted to m max=5.The multivariate time series are derived from nonlin-ear maps of varying dimension and complexity as well as spatially extended maps.The results are given below for each system.B.One and two Ikeda mapsThe Ikeda map is an example of a discrete low-dimensional chaotic system in two variables(x n,y n)de-fined by the equations[19]z n+1=1+0.9exp(0.4i−6i/(1+|z n|2)),x n=Re(z n),y n=Im(z n),where Re and Im denote the real and imaginary part,re-spectively,of the complex variable z n.Given the bivari-ate time series of(x n,y n),both FNN methods identify the original vector x n=(x n,y n)andfind m=(1,1)as optimal at all realizations,as shown in Table I.On the other hand,the PEM criterionfinds over-embedding as optimal,but this improves slightly the pre-diction,which as expected improves with the increase of N.Next we consider the sum of two Ikeda maps as a more complex and higher dimensional system.The bivariateI:Dimension vectors and NRMSE for the Ikeda map.2,3and4contain the embedding dimension vectorsby their respective frequency of occurrenceNRMSEFNN1PEM FNN2 512(1,1)1000.0510.032 (1,1)100(2,2)1000.028 8192(1,1)1000.0130.003II:Dimension vectors and NRMSE for the sum ofmapsNRMSEFNN1PEM FNN2 512(2,2)650.4560.447(1,3)26(3,3)95(2,3)540.365(2,2)3(2,2)448192(2,3)430.2600.251(1,4)37time series are generated asx n=Re(z1,n+z2,n),y n=Im(z1,n+z2,n).The results of the Monte Carlo simulations shown in Ta-ble II suggest that the prediction worsens dramatically from that in Table I and the total embedding dimension M increases with N.The FNN2criterion generally gives multiple optimal m structures across realizations and PEM does the same but only for small N.This indicates that high complex-ity degrades the performance of the algorithms for small sample sizes.PEM is again best for predictions but over-all we do not observe large differences in the three meth-ods.An interesting observation is that although FNN2finds two optimal m with high frequencies they both give the same M.This reflects the problem of identification, where different m unfold the attractor equally well.This feature cannot be observed in FNN1because the FNN1 algorithm inspects fewer possible vectors and only one for each M,where M can only be multiple of p(in this case(1,1)for M=2,(2,2)for M=4,etc).On the other hand,PEM criterion seems to converge to a single m for large N,which means that for the sum of the two Ikeda maps this particular structure gives best prediction re-sults.Note that there is no reason that the embedding dimension vectors derived from FNN2and PEM should match as they are selected under different conditions. Moreover,it is expected that the m selected by PEM gives always the lowest average of multivariate NRMSE as it is selected to optimize prediction.TABLE III:Dimension vectors and NRMSE for the KDR mapNRMSE FNN1PEM FNN2512(0,0,2,2)30(1,1,1,1)160.7760.629 (1,1,1,1)55(2,2,2,2)39(0,2,1,1)79(0,1,0,1)130.6598192(2,1,1,1)40(1,1,1,1)140.5580.373TABLE IV:Dimension vectors and NRMSE for system of Driver-Response Henon systemEmbedding dimensionsN FNN1PEM FNN2512(2,2)100(2,2)75(2,1)100.196(2,2)100(3,2)33(2,2)250.127(2,2)100(3,0)31(0,3)270.0122048(2,2)100(2,2)1000.093(2,2)100(3,3)45(4,3)450.084(2,2)100(0,3)20(3,0)190.0068192(2,2)100(2,2)1000.051(2,2)100(3,3)72(4,3)250.027(2,2)100(0,4)31(4,0)300.002TABLE V:Dimension vectors and NRMSE for Lattice of3coupled Henon mapsEmbedding dimensionsN FNN1PEM FNN2512(2,2,2)94(1,1,1)6(1,2,1)29(1,1,2)230.298(2,2,2)98(1,1,1)2(2,0,2)44(2,1,1)220.2282048(2,2,2)100(1,2,2)34(2,2,1)300.203(2,2,2)100(2,1,2)48(2,0,2)410.1318192(2,2,2)100(2,2,2)97(3,2,3)30.174(2,2,2)100(2,1,2)79(3,2,3)190.084NRMSEC FNN2FNN1PEM0.4(1,1,1,1)42(1,0,2,1)170.2850.2880.8(1,1,1,1)40(1,0,1,2)170.3140.2910.4(1,1,1,1)88(1,1,1,2)70.2290.1900.8(1,1,1,1)36(1,0,2,1)330.2250.1630.4(1,1,1,1)85(1,2,1,1)80.1970.1370.8(1,2,0,1)31(1,0,2,1)220.1310.072 PEM cannot distinguish the two time series and selectswith almost equal frequencies vectors of the form(m,0)and(0,m)giving again over-embedding as N increases.Thus PEM does not reveal the coupling structure of theunderlying system and picks any embedding dimensionstructure among a range of structures that give essen-tially equivalent predictions.Here FNN2seems to de-tect sufficiently the underlying coupling structure in thesystem resulting in a smaller total embedding dimensionthat gives however the same level of prediction as thelarger M suggested by FNN1and slightly smaller thanthe even larger M found by PEM.ttices of coupled Henon mapsThe last system is an example of spatiotemporal chaosand is defined as a lattice of k coupled Henon maps{x i,n,y i,n}k i=1[22]specified by the equationsx i,n+1=1.4−((1−C)x i,n+C(x i−1,n+x i+1,n)ple size,at least for the sizes we used in the simulations. Such a feature shows lack of consistency of the PEM cri-terion and suggests that the selection is led from factors inherent in the prediction process rather than the quality of the reconstructed attractor.For example the increase of embedding dimension with the sample size can be ex-plained by the fact that more data lead to abundance of close neighbors used in local prediction models and this in turn suggests that augmenting the embedding vectors would allow to locate the K neighbors used in the model. On the other hand,the two schemes used here that ex-tend the method of false nearest neighbors(FNN)to mul-tivariate time series aim atfinding minimum embedding that unfolds the attractor,but often a higher embedding gives better prediction results.In particular,the sec-ond scheme(FNN2)that explores all possible embedding structures gives consistent selection of an embedding of smaller dimension than that selected by PEM.Moreover, this embedding could be justified by the underlying dy-namics of the known systems we tested.However,lack of consistency of the selected embedding was observed with all methods for small sample sizes(somehow expected due to large variance of any estimate)and for the cou-pled maps(probably due to the presence of more than one optimal embeddings).In this work,we used only a prediction performance criterion to assess the quality of state space reconstruc-tion,mainly because it has the most practical relevance. There is no reason to expect that PEM would be found best if the assessment was done using another criterion not based on prediction.However,the reference(true)value of other measures,such as the correlation dimen-sion,are not known for all systems used in this study.An-other constraint of this work is that only noise-free multi-variate time series from discrete systems are encountered, so that the delay parameter is not involved in the state space reconstruction and the effect of noise is not studied. It is expected that the addition of noise would perplex further the process of selecting optimal embedding di-mension and degrade the performance of the algorithms. For example,we found that in the case of the Henon map the addition of noise of equal magnitude to the two time series of the system makes the criteria to select any of the three equivalent embeddings((2,0),(0,2),(1,1))at random.It is in the purpose of the authors to extent this work and include noisy multivariate time series,also fromflows,and search for other measures to assess the performance of the embedding selection methods.AcknowledgmentsThis paper is part of the03ED748research project,im-plemented within the framework of the”Reinforcement Programme of Human Research Manpower”(PENED) and co-financed at90%by National and Community Funds(25%from the Greek Ministry of Development-General Secretariat of Research and Technology and75% from E.U.-European Social Fund)and at10%by Rik-shospitalet,Norway.[1]F.Takens,Lecture Notes in Mathematics898,365(1981).[2]T.Sauer,J.A.Yorke,and M.Casdagli,Journal of Sta-tistical Physics65,579(1991).[3]H.Kantz and T.Schreiber,Nonlinear Time Series Anal-ysis(Cambridge University Press,1997).[4]J.Guckenheimer and G.Buzyna,Physical Review Let-ters51,1438(1983).[5]M.Paluˇs,I.Dvoˇr ak,and I.David,Physica A StatisticalMechanics and its Applications185,433(1992).[6]R.Hegger and T.Schreiber,Physics Letters A170,305(1992).[7]D.Prichard and J.Theiler,Physical Review Letters73,951(1994).[8]H.D.I.Abarbanel,T.A.Carroll,,L.M.Pecora,J.J.Sidorowich,and L.S.Tsimring,Physical Review E49, 1840(1994).[9]L.Cao,A.Mees,and K.Judd,Physica D121,75(1998),ISSN0167-2789.[10]J.P.Barnard,C.Aldrich,and M.Gerber,Physical Re-view E64,046201(2001).[11]S.P.Garcia and J.S.Almeida,Physical Review E(Sta-tistical,Nonlinear,and Soft Matter Physics)72,027205 (2005).[12]Y.Hirata,H.Suzuki,and K.Aihara,Physical ReviewE(Statistical,Nonlinear,and Soft Matter Physics)74, 026202(2006).[13]M.B.Kennel,R.Brown,and H.D.I.Abarbanel,Phys-ical Review A45,3403(1992).[14]D.T.Kaplan,in Chaos in Communications,edited byL.M.Pecora(SPIE-The International Society for Optical Engineering,Bellingham,Washington,98227-0010,USA, 1993),pp.236–240.[15]B.Chun-Hua and N.Xin-Bao,Chinese Physics13,633(2004).[16]R.Hegger and H.Kantz,Physical Review E60,4970(1999).[17]M.H´e non,Communications in Mathematical Physics50,69(1976).[18]R.Hegger,H.Kantz,and T.Schreiber,Chaos:An Inter-disciplinary Journal of Nonlinear Science9,413(1999).[19]K.Ikeda,Optics Communications30,257(1979).[20]C.Grebogi,E.Kostelich,E.O.Ott,and J.A.Yorke,Physica D25(1987).[21]S.J.Schiff,P.So,T.Chang,R.E.Burke,and T.Sauer,Physical Review E54,6708(1996).[22]A.Politi and A.Torcini,Chaos:An InterdisciplinaryJournal of Nonlinear Science2,293(1992).。
Dark Matter and Dark Energy

Now is the time to be a cosmologist. We have obtained through remarkable technological advances and heroic and ingenious experimental efforts a direct and extraordinarily detailed picture of the early Universe and maps of the distribution of matter on the largest scales in the Universe today. We have, moreover, an elegant and precisely quantitative physical model for the origin and evolution of the Universe. However, the model invokes new physics, beyond the standard model plus general relativity, not just once, but at least thrice: (1) Inflation, the physical mechanism for making the early Universe look precisely as it does, posits some new ultra-high-energy physics; we don’t know, however, what it is. (2) The growth of large-scale-structure and the dynamics of galaxies and galaxy clusters requires that we invoke the existence of collisionless particles or objects; we don’t know what this stuff is. (3) The accelerated expansion of the Universe requires the introduction of a new term, of embarrassingly small value, in Einstein’s equation, a modification of general relativity, and/or the introduction of some negative-pressure “dark energy,” again, the nature of which remains a mystery.
Incremental dynamic analysis

EARTHQUAKE ENGINEERING AND STRUCTURAL DYNAMICSEarthquake Engng Struct.Dyn.2002;31:491–514(DOI:10.1002/eqe.141)Incremental dynamic analysisDimitrios Vamvatsikos and C.Allin Cornell∗;†Department of Civil and Environmental Engineering;Stanford University;CA94305-4020;U.S.A.SUMMARYIncremental dynamic analysis(IDA)is a parametric analysis method that has recently emerged in several di erent forms to estimate more thoroughly structural performance under seismic loads.It involves subjecting a structural model to one(or more)ground motion record(s),each scaled to multiple levels of intensity,thus producing one(or more)curve(s)of response parameterized versus intensity level.To establish a common frame of reference,the fundamental concepts are analysed,a uniÿed terminology is proposed,suitable algorithms are presented,and properties of the IDA curve are looked into for both single-degree-of-freedom and multi-degree-of-freedom structures.In addition,summarization techniques for multi-record IDA studies and the association of the IDA study with the conventional static pushover analysis and the yield reduction R-factor are discussed.Finally,in the framework of performance-based earthquake engineering,the assessment of demand and capacity is viewed through the lens of an IDA study.Copyright?2001John Wiley&Sons,Ltd.KEY WORDS:performance-based earthquake engineering;incremental dynamic analysis;demand;collapse capacity;limit-state;non-linear dynamic analysis1.INTRODUCTIONThe growth in computer processing power has made possible a continuous drive towards increasingly accurate but at the same time more complex analysis methods.Thus,the state of the art has progressively moved from elastic static analysis to dynamic elastic,non-linear static andÿnally non-linear dynamic analysis.In the last case,the convention has been to run one to several di erent records,each once,producing one to several‘single-point’analyses, mostly used for checking the designed structure.On the other hand,methods like the non-linear static pushover(SPO)[1]or the capacity spectrum method[1]o er,by suitable scaling of the static force pattern,a‘continuous’picture as the complete range of structural behaviour∗Correspondence to:C.Allin Cornell,Department of Civil and Environmental Engineering,Stanford University, CA94305-4020,U.S.A.†E-mail:cornell@Contract=grant sponsor:Reliability of Marine Structures A liates Program of Stanford University.Received15January2001Revised31August2001 Copyright?2001John Wiley&Sons,Ltd.Accepted31August2001492 D.VAMVATSIKOS AND C.A.CORNELLis investigated,from elasticity to yielding andÿnally collapse,thus greatly facilitating our understanding.By analogy with passing from a single static analysis to the incremental SPO,one arrives at the extension of a single time-history analysis into an incremental one,where the seismic ‘loading’is scaled.The concept has been mentioned as early as1977by Bertero[2],and has been cast in several forms in the work of many researchers,including Luco and Cornell[3;4], Bazurro and Cornell[5;6],Yun and Foutch[7],Mehanny and Deierlein[8],Dubina et al.[9], De Matteis et al.[10],Nassar and Krawinkler[11,pp62–155]and Psycharis et al.[12]. Recently,it has also been adopted by the U.S.Federal Emergency Management Agency (FEMA)guidelines[13;14]as the incremental dynamic analysis(IDA)and established as the state-of-the art method to determine the global collapse capacity.The IDA study is now a multi-purpose and widely applicable method and its objectives,only some of which are evident in Figure1(a)and1(b),include:1.thorough understanding of the range of response or‘demands’versus the range of po-tential levels of a ground motion record,2.better understanding of the structural implications of rarer=more severe ground motionlevels,3.better understanding of the changes in the nature of the structural response as the intensityof ground motion increases(e.g.changes in peak deformation patterns with height,onset of sti ness and strength degradation and their patterns and magnitudes),4.producing estimates of the dynamic capacity of the global structural system and5.ÿnally,given a multi-record IDA study,understanding how stable(or variable)all theseitems are from one ground motion record to another.Our goal is to provide a basis and terminology to unify the existing formats of the IDA study and set up the essential background to achieve the above-mentioned objectives.2.FUNDAMENTALS OF SINGLE-RECORD IDAsAs aÿrst step,let us clearly deÿne all the terms that we need,and start building our method-ology using as a fundamental block the concept of scaling an acceleration time-history. Assume we are given a single acceleration time-history,selected from a ground motion database,which will be referred to as the base,‘as-recorded’(although it may have been pre-processed by seismologists,e.g.baseline corrected,ÿltered and rotated),unscaled accelerogram a1,a vector with elements a1(t i),t i=0;t1;:::;t n−1.To account for more severe or milder ground motions,a simple transformation is introduced by uniformly scaling up or down the amplitudes by a scalar ∈[0;+∞):a[= ·a1.Such an operation can also be conveniently thought of as scaling the elastic acceleration spectrum by or equivalently,in the Fourier domain,as scaling by the amplitudes across all frequencies while keeping phase information intact.Deÿnition1The Scale Factor(SF)of a scaled accelerogram,a[,is the non-negative scalar ∈[0;+∞) tat produces a[when multiplicatively applied to the unscaled(natural)acceleration time-history a1.Copyright?2001John Wiley&Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514INCREMENTAL DYNAMIC ANALYSIS493Maximum interstorey drift ratio, θmax"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1,5%) (g )Peak interstorey drift ratio θiS t o r e y l e v e l Figure 1.An example of information extracted from a single-record IDA study of a T 1=4s,20-storey steel moment-resisting frame with ductile members and connections,including global geometric nonlinearities (P – )subjected to the El Centro,1940record (fault parallel component).Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514494 D.VAMVATSIKOS AND C.A.CORNELLNote how the SF constitutes a one-to-one mapping from the original accelerogram to all its scaled images.A value of =1signiÿes the natural accelerogram, ¡1is a scaled-down accelerogram,while ¿1corresponds to a scaled-up one.Although the SF is the simplest way to characterize the scaled images of an accelero-gram,it is by no means convenient for engineering purposes as it o ers no information of the real ‘power’of the scaled record and its e ect on a given structure.Of more practical use would be a measure that would map to the SF one-to-one,yet would be more informative,in the sense of better relating to its damaging potential.Deÿnition 2A Monotonic Scalable Ground Motion Intensity Measure (or simply intensity measure,IM)of a scaled accelerogram,a [,is a non-negative scalar IM ∈[0;+∞)that constitutes a function,IM=f a 1( ),that depends on the unscaled accelerogram,a 1,and is monotonically increasing with the scale factor, .While many quantities have been proposed to characterize the ‘intensity’of a ground mo-tion record,it may not always be apparent how to scale them,e.g.Moment Magnitude,Duration,or Modiÿed Mercalli Intensity;they must be designated as mon examples of scalable IMs are the Peak Ground Acceleration (PGA),Peak Ground Velocity,the =5%damped Spectral Acceleration at the structure’s ÿrst-mode period (S a (T 1;5%)),and the normalized factor R = = yield (where yield signiÿes,for a given record and struc-tural model,the lowest scaling needed to cause yielding)which is numerically equiva-lent to the yield reduction R -factor (e.g.Reference [15])for,for example,bilinear single-degree-of-freedom (SDOF)systems (see later section).These IMs also have the property of being proportional to the SF as they satisfy the relation IM prop = ·f a 1.On the other hand,the quantity S am (T 1; ;a ;b;c )=[S a (T 1; )]a [S a (cT 1; )]b proposed by Shome and Cornell [16]and Mehanny [8]is scalable and monotonic but non-proportional,unless a +b =1.Some non-monotonic IMs have been proposed,such as the inelastic displacement of a non-linear oscillator by Luco and Cornell [17],but will not be focused upon,so IM will implicitly mean monotonic and scalable hereafter unless otherwise stated.Now that we have the desired input to subject a structure to,we also need some way to monitor its state ,its response to the seismic load.Deÿnition 3Damage Measure (DM)or Structural State Variable is a non-negative scalar DM ∈[0;+∞]that characterizes the additional response of the structural model due to a prescribed seismic loading.In other words,a DM is an observable quantity that is part of,or can be deduced from,the output of the corresponding non-linear dynamic analysis.Possible choices could be max-imum base shear,node rotations,peak storey ductilities,various proposed damage indices (e.g.a global cumulative hysteretic energy,a global Park–Ang index [18]or the stability index proposed by Mehanny [8]),peak roof drift,the oor peak interstorey drift angles Â1;:::;Ân of an n -storey structure,or their maximum,the maximum peak interstorey drift angle Âmax =max(Â1;:::;Ân ).Selecting a suitable DM depends on the application and the structure Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514INCREMENTAL DYNAMIC ANALYSIS495itself;it may be desirable to use two or more DMs(all resulting from the same non-linear analyses)to assess di erent response characteristics,limit-states or modes of failure of inter-est in a performance-based earthquake engineering(PBEE)assessment.If the damage to non-structural contents in a multi-storey frame needs to be assessed,the peak oor accelerations are the obvious choice.On the other hand,for structural damage of frameÂmax relates well to joint rotations and both global and local storey collapse,thus becoming a DM candidate.The latter,expressed in terms of the total drift,instead of the e ective drift which would take into account the building tilt,(see Reference[19,p88])will be our choice of DM for most illustrative cases here,where foundation rotation and column shortening are not severe.The structural response is often a signed scalar;usually,either the absolute value is used or the magnitudes of the negative and the positive parts are separately considered.Now we are able to deÿne the IDA.Deÿnition4A Single-Record IDA Study is a dynamic analysis study of a given structural model param-eterized by the scale factor of the given ground motion time-history.Also known simply as IDA or dynamic pushover(DPO),it involves a series of dynamic non-linear runs performed under scaled images of an accelerogram,whose IMs are,ideally, selected to cover the whole range from elastic to non-linear andÿnally to collapse of the structure.The purpose is to record DMs of the structural model at each level IM of the scaled ground motion,the resulting response values often being plotted versus the intensity level as continuous curves.Deÿnition5An IDA Curve is a plot of a state variable(DM)recorded in an IDA study versus one or more IMs that characterize the applied scaled accelerogram.An IDA curve can be realized in two or more dimensions depending on the number of the IMs.Obviously,at least one must be scalable and it is such an IM that is used in the conventional two-dimensional(2D)plots that we will focus on hereafter.As per standard engineering practice,such plots often appear‘upside-down’as the independent variable is the IM which is considered analogous to‘force’and plotted on the vertical axis(Figure1(a))as in stress–strain,force–deformation or SPO graphs.As is evident,the results of an IDA study can be presented in a multitude of di erent IDA curves,depending on the choices of IMs and DM.To illustrate the IDA concept,we will use several multi-degree-of-freedom(MDOF)and SDOF models as examples in the following sections.In particular,the MDOFs used are a T1=4s20-storey steel-moment resisting frame[3]with ductile members and connec-tions,including aÿrst-order treatment of global geometric non-linearities(P– e ects),a T1=2:2s9-storey and a T1=1:3s3-storey steel-moment resisting frame[3]with ductile mem-bers,fracturing connections and P– e ects,and a T1=1:8s5-storey steel chevron-braced frame with ductile members and connections and realistically buckling braces including P– e ects[6].Copyright?2001John Wiley&Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514496 D.VAMVATSIKOS AND C.A.CORNELL(a) A softening case(b) A bit of hardeningMaximum interstorey drift ratio, θmax"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g )Weaving behavio r Figure 2.IDA curves of a T 1=1:8s,5-storey steel braced frame subjected to four di erent records.3.LOOKING AT AN IDA CURVE:SOME GENERAL PROPERTIESThe IDA study is accelerogram and structural model speciÿc;when subjected to di erent ground motions a model will often produce quite dissimilar responses that are di cult to pre-dict a priori .Notice,for example,Figure 2(a)–2(d)where a 5-storey braced frame exhibits responses ranging from a gradual degradation towards collapse to a rapid,non-monotonic,back-and-forth twisting behaviour.Each graph illustrates the demands imposed upon the struc-ture by each ground motion record at di erent intensities,and they are quite intriguing in both their similarities and All curves exhibit a distinct elastic linear region that ends at S yield a (T 1;5%)≈0:2g and Âyield max ≈0:2%when the ÿrst brace-buckling occurs.Actually,any structural model with ini-tially linearly elastic elements will display such a behaviour,which terminates when the ÿrst non-linearity comes into play,i.e.when any element reaches the end of its elasticity.The slope IM =DM of this segment on each IDA curve will be called its elastic ‘sti ness’for the given DM,IM.It typically varies to some degree from record to record but it will be the same across records for SDOF systems and even for MDOF systems if the IM takes into account the higher mode e ects [17].Focusing on the other end of the curves in Figure 2,notice how they terminate at di erent levels of IM.Curve (a)sharply ‘softens’after the initial buckling and accelerates towards large drifts and eventual collapse.On the other hand,curves (c)and (d)seem to weave around the elastic slope;they follow closely the familiar equal displacement rule,i.e.the Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514INCREMENTAL DYNAMIC ANALYSIS 497Maximum interstorey drift ratio, θmax"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g )Figure 3.IDA curves of peak interstorey drifts for each oor of a T 1=1:8s,5-storey steel braced frame.Notice the complex ‘weaving’interaction where extreme softening of oor 2acts as a fuse to relieve those above (3,4,5).empirical observation that for moderate period structures,inelastic global displacements are generally approximately equal to the displacements of the corresponding elastic model [20].The twisting patterns that curves (c)and (d)display in doing so are successive segments of ‘softening’and ‘hardening’,regions where the local slope or ‘sti ness’decreases with higher IM and others where it increases.In engineering terms,this means that at times the structure experiences acceleration of the rate of DM accumulation and at other times a de-celeration occurs that can be powerful enough to momentarily stop the DM accumulation or even reverse it,thus locally pulling the IDA curve to relatively lower DMs and making it a non-monotonic function of the IM (Figure 2(d)).Eventually,assuming the model for some collapse mechanism and the DM used can track it,a softening segment oc-curs when the structure accumulates DM at increasingly higher rates,signaling the of dynamic instability .This is deÿned analogously to static instability,as the point where de-formations increase in an unlimited manner for vanishingly small increments in the IM.The curve then attens out in a plateau of the maximum value in IM as it reaches the atline and DM moves towards ‘inÿnity’(Figure 2(a)and 2(b)).Although the examples shown are based on S a (T 1;5%)and Âmax ,these modes of behaviour are observable for a wide choice of DMs and IMs.Hardening in IDA curves is not a novel observation,having been reported before even for simple bilinear elastic–perfectly plastic systems,e.g.by Chopra [15,pp 257–259].Still,it remains counter-intuitive that a system that showed high response at a given intensity level,may exhibit the same or even lower response when subjected to higher seismic intensities Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514498 D.VAMVATSIKOS AND C.A.CORNELL"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g ) (a) IDA curveDuctility, µ A c c e l e r a t i o n (g) (b) Loma Prieta, Halls Valley (090 component)0510152025303540(c) Response at S = 2.2gD u c t i l i t y , µ= 2.8gD u c t i l i t y , µTime (sec)____Figure 4.Ductility response of a T =1s,elasto-plastic oscillator at multiple levels of shaking.Earlier yielding in the stronger ground motion leads to a lower absolute peak response.Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514INCREMENTAL DYNAMIC ANALYSIS 499Maximum interstorey drift ratio, θ m ax"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g )Structural resurrectionFigure 5.Structural resurrection on the IDA curve of a T 1=1:3s,3-storey steel moment-resisting frame with fracturing connections.due to excessive hardening.But it is the pattern and the timing rather than just the inten-sity that make the di erence.As the accelerogram is scaled up,weak response cycles in the early part of the response time-history become strong enough to in ict damage (yield-ing)thus altering the properties of the structure for the subsequent,stronger cycles.For multi-storey buildings,a stronger ground motion may lead to earlier yielding of one oor which in turn acts as a fuse to relieve another (usually higher)one,as in Figure 3.Even simple oscillators when caused to yield in an earlier cycle,may be proven less responsive in later cycles that had previously caused higher DM values (Figure 4),perhaps due to ‘pe-riod elongation’.The same phenomena account for the structural resurrection ,an extreme case of hardening,where a system is pushed all the way to global collapse (i.e.the analy-sis code cannot converge,producing ‘numerically inÿnite’DMs)at some IM,only to reap-pear as non-collapsing at a higher intensity level,displaying high response but still standing (e.g.Figure 5).As the complexity of even the 2D IDA curve becomes apparent,it is only natural to examine the properties of the curve as a mathematical entity.Assuming a monotonic IM,the IDA curve becomes a function ([0;+∞)→[0;+∞]),i.e.any value of IM produces a single value DM,while for any given DM value there is at least one or more (in non-monotonic IDA curves)IMs that generate it,since the mapping is not necessarily one-to-one.Also,the IDA curve is not necessarily smooth as the DM is often deÿned as a maximum or contains absolute values of responses,making it non-di erentiable by deÿnition.Even more,it may contain a (hopefully ÿnite)number of discontinuities,due to multiple excursions to collapse and subsequent resurrections.Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514500 D.VAMVATSIKOS AND C.A.CORNELL4.CAPACITY AND LIMIT-STATES ON SINGLE IDA CURVES Performance levels or limit-states are important ingredients of PBEE,and the IDA curve contains the necessary information to assess them.But we need to deÿne them in a less abstract way that makes sense on an IDA curve,i.e.by a statement or a rule that when satisÿed,signals reaching a limit-state.For example,Immediate Occupancy[13;14]is a structural performance level that has been associated with reaching a given DM value,usually inÂmax terms,while(in FEMA350[13],at least)Global Collapse is related to the IM or DM value where dynamic instability is observed.A relevant issue that appears then is what to do when multiple points (Figure6(a)and6(b))satisfy such a rule?Which one is to be selected?The cause of multiple points that can satisfy a limit-state rule is mainly the hardening issue and,in its extreme form,structural resurrection.In general,one would want to be conservative and consider the lowest,in IM terms,point that will signal the limit-state.Generalizing this concept to the whole IDA curve means that we will discard its portion‘above’theÿrst(in IM) atline and just consider only points up to thisÿrst sign of dynamic instability.Note also that for most of the discussion we will be equating dynamic instability to numeri-cal instability in the prediction of collapse.Clearly the non-convergence of the time-integration scheme is perhaps the safest and may be the only numerical equivalent of the actual phe-nomenon of dynamic collapse.But,as in all models,this one can su er from the quality of the numerical code,the stepping of the integration and even the round-o error.Therefore, we will assume that such matters are taken care of as well as possible to allow for accurate enough predictions.That being said,let us set forth the most basic rules used to deÿne a limit-state.First comes DM-based rule which is generated from a statement of the format:‘If DM¿C DM then limit-state is exceeded’(Figure6(a)).The underlying concept is usu-ally that DM is a damage indicator,hence,when it increases beyond a certain value the structural model is assumed to be in the limit-state.Such values of C DM can be obtained through experiments,theory or engineering experience,and they may not be deterministic but have a probability distribution.An example is theÂmax=2%limit that signiÿes the Im-mediate Occupancy structural performance level for steel moment-resisting frames(SMRFs) with type-1connections in the FEMA guidelines[14].Also the approach used by Mehanny and Deierlein[8]is another case where a structure-speciÿc damage index is used as DM and when its reciprocal is greater than unity,collapse is presumed to have occurred.Such limits may have randomness incorporated,for example,FEMA350[13]deÿnes a local col-lapse limit-state by the value ofÂmax that induces a connection rotation su cient to destroy the gravity load carrying capacity of the connection.This is deÿned as a random variable based on tests,analysis and judgment for each connection type.Even a unique C DM value may imply multiple limit-state points on an IDA curve(e.g.Figure6(a)).This ambiguity can be handled by an ad hoc,speciÿed procedure(e.g.by conservatively deÿning the limit-state point as the lowest IM),or by explicitly recognizing the multiple regions conforming and non-conforming with the performance level.The DM-based rules have the advantage of simplicity and ease of implementation,especially for performance levels other than collapse. In the case of collapse capacity though,they may actually be a sign of model deÿciency. If the model is realistic enough it ought to explicitly contain such information,i.e.show a collapse by non-convergence instead of by aÿnite DM output.Still,one has to recognize that such models can be quite complicated and resource-intensive,while numerics can oftenCopyright?2001John Wiley&Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514Maximum interstorey drift ratio, θ max"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g )DM-based ruleMaximum interstorey drift ratio, θ max"f i r s t -m o d e " s p e c t r a l a c c e l e r a t i o n S a (T 1, 5%) (g )Figure 6.Two di erent rules producing multiple capacity points for a T 1=1:3s,3-storey steel moment-resisting frame with fracturing connections.The DM rule,where the DM is Âmax ,is setat C DM =0:08and the IM rule uses the 20%slope criterion.Copyright ?2001John Wiley &Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514be unstable.Hence,DM-based collapse limit-state rules can be quite useful.They also have the advantage of being consistent with other less severe limit-states which are more naturally identiÿed in DM terms,e.g.Âmax.The IM-based rule,is primarily generated from the need to better assess collapse capacity,by a single point on the IDA curve that clearly divides it to two regions, of non-collapse(lower IM)and one of collapse(higher IM).For monotonic IMs,such a rule is generated by a statement of the form:‘If IM¿C IM then the limit-state is exceeded’(Figure6(b)).A major di erence with the previous category is the di culty in prescribing a C IM value that signals collapse for all IDA curves,so it has to be done individually,curve by curve.Still,the advantage is that it clearly generates a single collapse region,and the disadvantage is the di culty of deÿning such a point for each curve in a consistent fashion. In general,such a rule results in both IM and DM descriptions of capacity.A special(extreme) case is taking the‘ÿnal’point of the curve as the capacity,by using the(lowest) atline to deÿne capacity(in IM terms),where all of the IDA curve up to theÿrst appearance of dynamic instability is considered as non-collapse.The FEMA[13]20%tangent slope approach is,in e ect,an IM-based rule;the last point on the curve with a tangent slope equal to20%of the elastic slope is deÿned to be the capacity point.The idea is that the attening of the curve is an indicator of dynamic insta-bility(i.e.the DM increasing at ever higher rates and accelerating towards‘inÿnity’).Since ‘inÿnity’is not a possible numerical result,we content ourselves with pulling back to a rate ofÂmax increase equal toÿve times the initial or elastic rate,as the place where we mark the capacity point.Care needs to be exercised,as the‘weaving’behaviour of an IDA curve can provide several such points where the structure seems to head towards col-lapse,only to recover at a somewhat higher IM level,as in Figure6(b);in principle,these lower points should thus be discarded as capacity candidates.Also the non-smoothness of the actual curve may prove to be a problem.As mentioned above,the IDA curve is at best piecewise smooth,but even so,approximate tangent slopes can be assigned to every point along it by employing a smooth interpolation.For sceptics this may also be thought of as a discrete derivative on a grid of points that is a good‘engineering’approximation to the ‘rate-of-change’.The above-mentioned simple rules are the building blocks to construct composite rules, posite logical clauses of the above types,most often joined by logical OR operators. For example,when a structure has several collapse modes,not detectable by a single DM, it is advantageous to detect global collapse with an OR clause for each individual mode.An example is o shore platforms where pile or soil failure modes are evident in deck drift while failures of braces are more evident in maximum peak intertier drift.Theÿrst—in IM terms—event that occurs is the one that governs collapse capacity.Another case is Global Collapse capacity,which as deÿned by FEMA in References[13;14]is in fact an OR conjunction of the20%slope IM-based rule and a C DM=10%DM-based rule,where S a(T1;5%)andÂmax are the IM and DM of choice.If either of the two rules obtains,it deÿnes capacity.This means that the20%sti ness detects impending collapse,while the10%cap guards against excessive values ofÂmax,indicative of regions where the model may not be trustworthy.As a DM description of capacity is proposed,this deÿnition may su er from inaccuracies,since close to the atline a wide range of DM values may correspond to only a small range of IMs, thus making the actual value of DM selected sensitive to the quality of IDA curve tracing and to the(ad hoc)20%value.If,on the other hand,an IM description is used,the ruleCopyright?2001John Wiley&Sons,Ltd.Earthquake Engng Struct.Dyn.2002;31:491–514。
Analysis of experimental uncertainties in the R-correlation measurement in the decay of fre

The work presented in this thesis would not have been possible without the involvement of a number of people. I would like to thank the following persons in particular: • Prof. Kazimierz Bodek, my supervisor, for his preciuos advice and suggestions concerning my work, for great knowledge and experience he shares with his students. I would also like to thank for involving me in physics of cold neutrons and for giving me the possibility to work with the nTRV group; • dr Stanislaw Kistryn for being my tutor during two first years of my studies, for his help and sense of humour; • Prof. Reinhard Kulessa for allowing me to prepare this thesis in the Nuclear Physics Department of the Jagellonian University; • Prof. Boguslaw Kamys for interesting lectures and a lot of help; • dr El˙ zbieta Stephan for help and ideas concerning the Monte Carlo simulation; • dr Adam Kozela, dr Jacek Zejma, Aleksandra Bialek, Pierre Gorel and Jacek Pulut, other members of our group, for constant assistance and lots of fruitful discussions; • all residents, guests and numerous friends of the famous students’ flat on Zamkowa Street for lots of discussions; • my colleagues Malgorzata Kasprzak, Joanna Przerwa, Michal Janusz and Tytus Smoli´ nski for the great atmosphere of daily work; • my dear Parents for their love, enormous patience and permanent support during the five years of my studies.
The Andante Regime of Scalar Field Dynamics

arXiv:astro-ph/9408016v1 4 Aug 1994
Federal do Rio de Janeiro, Instituto de F´ isica, Rio de Janeiro - RJ - Brasil -21943
2 where g ≡ detgµν , κ2 ≡ 8πm− P and mP is the Planck mass. We choose units such that c = h ¯ = 1. If the Universe is spatially isotropic, closed and flat with a world-interval ds2 = −N 2 (t)dt2 + e2α(t) [dx2 + dy 2 + dz 2 ] and lapse function N (t), the Arnowitt-DeserMisner (ADM) action is
1
Introduction
A study of the evolution of self-interacting scalar fields in the early Universe is important for a number of reasons. Firstly, in addition to offering a possible resolution to some of the fundamental problems of the hot big bang model, the inflationary scenario provides a causal mechanism for generating adiabatic density perturbations [1]. These may produce anisotropies in the cosmic microwave background and act as a seed for galaxy formation via gravitational instability. During inflation the Universe is dominated by the potential energy V (φ) associated with the self-interactions of a quantum scalar field φ. If the field is initially displaced from the global minimum of the potential and the potential is sufficiently flat, the scalar field will evolve very slowly towards the true vacuum state. The potential therefore behaves as an effective cosmological constant and introduces a negative pressure into the Universe that drives the accelerated expansion. Secondly, many natural extensions to General Relativity may be expressed in terms of Einstein gravity minimally coupled to a self-interacting scalar field after a suitable conformal transformation on the metric tensor. Two classes of theory that have received much attention in recent years are scalartensor theories of gravity and higher-order theories, where the gravitational lagrangian is an analytic function of the Ricci scalar R. However, only a limited number of exact solutions to the isotropic Einstein-scalar field equations have been found to date. These have recently been classified by Barrow in terms of the potential V = V0 φN exp(AφM ), where {V0 , A, M, N } are constants [2]. Special cases include V = constant corresponding to exponential expansion, power-law inflation from an exponential potential (N = 0, M = 1) [3, 5, 6, 7] and intermediate inflation from a combination of power-law potentials (N < 0, M = 0) [4, 8]. Solutions corresponding to potentials leading to hybrid inflation [9] have been presented in Refs. [10, 11] and exact solutions have also been found for hyperbolic and trigonometric potentials [12, 13]. Consequently, it is common practice to invoke the slow-roll approximation. This assumes that the kinetic energy of the scalar field is negligible relative to its potential energy and that the dominant term in the scalar field equation is due to friction arising from the expansion of the Universe. The system is therefore reduced to a set of coupled, first-order differential equations. The slow-roll approximation is usually valid during the initial stages of the inflationary expansion, but as the field rolls towards the minimum, the approximation inevitably breaks down at some point. Moreover, inflation arises whenever the strong energy condition is violated and this does not necessarily require the slow-roll approximation to be valid. Therefore, it is important to develop analytical techniques that allow deviations from the slow-roll regime to be accounted for and in this paper we discuss how this may be achieved. After summarizing the general features of scalar field dynamics in Sec. II, we illustrate how corrections to the slow-roll approximation may be included in Sec. III and we derive the corresponding field equations. In Sec. IV these equations are solved in parametric form for the class of power law potentials V (φ) ∝ φ2n in terms of the inverse error function. The rapid increase in the scale factor during inflation is naturally explained by using the properties of this function.
Furthermore

?c
u+ t p div u
?
r =
u
?c +r ? t div
in = 0 in ( on ?c = g on ?d ; = ?DG(u) f g in = 0 in = 0 on ?:
R
obs
(5)
With the gradient of J available the following gradient algorithm can be applied to reduce the value of the cost functional J . 1. Set k = 0 and choose 0 2. = argmin 0 H ( ) := J ( k ? rJ ( k )) 3. k+1 = k ? rJ ( k ) 4. k = k + 1, goto 2. In this algorithm the expensive part is step 2. Every evaluation H ( ) involves the solution of system (5) with = k ? rJ ( k ), so that an e cient inexact line-search should be utilized. At this stage the structure of problem (P) must be exploited. The optimal step-size in the minimum problem of step 2. can again be characterized by a Lagrangian approach. For the problems under consideration a suitable estimate of the step-size is given by H0 (6) = ? H 00(0) ; (0) where Z Z 0 (0) = ? jrJ ( )j2 dS; H 00 (0) = H (lrJ ( ) ? c@ ~ + ~ )rJ ( ) dS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Typeset using REVTEX 1
I. INTRODUCTION
Perhaps the simplest wave phenomenon in relativity is the propagation of linearized waves on a fixed, curved background. When observed at a fixed spatial point, the dynamics of a wave propagating on spherically symmetric, time-independent, asymptotically flat, background geometries consists of three stages: During the first stage, the observed wave depends on the structure of the initial pulse and its reflection from the origin (Burst phase). This phase is followed by an exponentially decaying quasi-normal ringing of the black hole (Quasi-normal phase). In the last stage, the wave slowly dies off as a power-law tail (Tail phase). The last two phases are dictated by the interference of the part of the wave backscattered at the tail of the potential and the part reflected by the potential barrier. The tail phenomenon can be understood as due to the scattering of the wave off the effective curvature potential of the background geometry [1,2]. Tails have been mostly investigated on Schwarzschild backgrounds [3–5], Reissner-Nordstrom black-holes [5], and for collapsing scalar fields [6,7]. The study of tails has also implications in connection with the gravitational radiation emerging from inspiraling binary systems [8]. For spherically symmetric systems, after separation of variables, the three-dimensional wave equation ∇µ ∇µ Φ = 0 reduces, in a suitable radial coordinate x, to the one-dimensional wave equation:
(1)
Abstract
A numerical study of the evolution of a massless scalar field in the background of rotating black holes is presented. First, solutions to the wave equation are obtained for slowly rotating black holes. In this approximation, the background geometry is treated as a perturbed Schwarzschild spacetime with the angular momentum per unit mass playing the role of a perturbative parameter. To first order in the angular momentum of the black hole, the scalar wave equation yields two coupled one-dimensional evolution equations for a function representing the scalar field in the Schwarzschild background and a second field that accounts for the rotation. Solutions to the wave equation are also obtained for rapidly rotating black holes. In this case, the wave equation does not admit complete separation of variables and yields a two-dimensional evolution equation. The study shows that, for rotating black holes, the late time dynamics of a massless scalar field exhibit the same power-law behavior as in the cround independently of the angular momentum of the black hole. 04.30.Nk
Dynamics of Scalar Fields in the Background of Rotating Black Holes
William Krivan,(1,2) Pablo Laguna(2) and Philippos Papadopoulos(2)
Institut f¨ ur Astronomie und Astrophysik Universit¨ at T¨ ubingen, D-72076 T¨ ubingen, Germany (2) Department of Astronomy & Astrophysics and Center for Gravitational Physics & Geometry Penn State University, University Park, PA 16802 (June 6, 1996)
2 [−∂t2 + ∂x − V (x)]Φ(x, t) = 0 ,
(1)
where V (x) denotes the effective curvature potential. Recently, the late-time behavior of equation (1) has been the subject of detailed numerical and analytic investigations by Gundlach et al. [5] and Ching et al. [3,4]. Gundlach et al. [5,7] studied both, the late-time behavior of massless fields around a fixed Schwarzschild geometry and the full nonlinear evolution of a minimally coupled scalar field. Their study shows a remarkable agreement between the numerically computed quasi-normal frequencies and power-law tails and their corresponding theoretical predictions. Using a null characteristic approach, they found tails not only at timelike infinity, but also at future null infinity and at the future horizon of the black hole. The time behavior of the tails is shown to be Φ ∼ (t − x) (t + x)−(2l+P +1)
existence of power-law tails [9]. When the point of view that tails arise from backscattering off an effective potential is adopted, it is not clear whether the tail behavior would remain unchanged, or be present at all, for intrinsically two or three dimensional systems [10]. A natural multi-dimensional generalization of the dynamics of scalar fields is obtained by considering the family of Kerr spacetimes. In contrast to the Schwarzschild background geometry, the wave equation ∇µ∇µ Φ = 0 in the background of a rotating black hole only admits separation of the azimuthal coordinate, so in principle a two-dimensional evolution problem has to be solved. It has been suggested [3], that tails similar to those present in Schwarzschild spacetimes should exist on Kerr backgrounds, a detailed analysis, however, has not been undertaken. This study considers the dynamics of scalar fields on the background of rotating black holes in two regimes: slowly and rapidly rotating holes. A considerable mathematical simplification of the problem is achieved in the case of slowly rotating black holes since the angular momentum can be treated as a perturbative parameter. Thus, to first order in the angular momentum, the scalar wave equation yields two one-dimensional evolution equations. This formalism is described in Section II. Results of the numerical calculations are presented in Section III, where power-law tails are discussed. The case of rapidly rotating black holes is discussed in Section IV.
