2007-2008-2线性代数期末试卷(B)

合集下载

2007-2008-2线性代数试卷(肖)解答

2007-2008-2线性代数期考试卷B 参考答案和评分标准一、单项选择题（每题3分，共30分）1．D 2．C 3．A 4．C 5．B 6．D 7．B 8．C 9．D 10. A 。

二、填空题（每题4分，共20分）1. 0； 2. 3 ； 3. n+a ，()1,1, (1)n R ∈； 4. 2221232y y y -++，222123z z z -++； 5. n 。

三、解答题（每题10分，共40分）1．解：系数矩阵初等变换过程如下：121323(1)(1)(1)11111111110110121121000E E E λλλμλμλμμλμμ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ ， ——-（4分）当0μ≠而且1λ≠时，齐次线性方程组只有零解。

——-（7分）当0μ=或者1λ=时，齐次线性方程组有非零解。

——-（10分）2．解：()()()322001112442113λλλλλλλ----=--+=---， ——-（3分） 2λ=是3重特征值。

——-（4分） 000000111111111000⎛⎫⎛⎫ ⎪ ⎪-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，得两个线性无关的特征向量 ()11,1,0T x =，()20,1,1Tx =。

——-（8分）矩阵A 的属于特征值2的特征向量为 1122x k x k x =+，其中12,k k 不全为零。

——————————-（10分）3．解：（1）()123123100101,,,,,110012111110αααβββ⎛⎫ ⎪= ⎪ ⎪-⎝⎭—————（2分） 1β在基{}123,,ααα的坐标是()1,1,1T -；2β在基{}123,,ααα的坐标是()0,1,2T -；3β在基{}123,,ααα的坐标是()1,1,2T -。

基{}123,,ααα到基{}123,,βββ的过渡矩阵为101111122⎛⎫ ⎪- ⎪ ⎪--⎝⎭———————————-（7分）（2）()()123123231231232222223ααααβββββββββββ=-+=-+--++-=-+ 所求的坐标为()2,2,3T -。

(完整版)线性代数期末测试题及其答案.doc

线性代数期末考试题一、填空题（将正确答案填在题中横线上。

每小题 5 分，共 25 分）1 3 1 1.若0 5 x 0，则__________。

1 2 2x1 x2 x3 02．若齐次线性方程组x1 x2 x3 0 只有零解，则应满足。

x1x2x303．已知矩阵A，B，C (c ij )s n，满足 AC CB ，则 A 与 B 分别是阶矩阵。

4．已知矩阵A为 3 3的矩阵，且| A| 3，则| 2A|。

5．n阶方阵A满足A23A E 0 ，则A1。

二、选择题（每小题 5 分，共 25 分）6．已知二次型 f x12 x22 5x32 2tx1x2 2x1 x3 4x2 x3,当t取何值时，该二次型为正定？（）A. 40 B.4 4C. 0 t4 4 1t5t D. t2 5 5 5 51 42 1 2 37．已知矩阵A 0 3 4 , B 0 x 6 ,且 A ~ B ，求x的值（）0 4 3 0 0 5A.3B.-2C.5D.-58 ．设 A 为 n 阶可逆矩阵，则下述说法不正确的是（）A. A0B. A 1 0C.r (A) nD.A 的行向量组线性相关9 ．过点（ 0， 2， 4）且与两平面x 2z 1和 y 3z 2 的交线平行的直线方程为（）1xy 2 z 4A.312xy 2 z 4C.31 2x y2 z 4B.32 2x y2 z 4D.322103 1 ．已知矩阵 A, 其特征值为（）51A. 12, 2 4 B. C.12,24D.三、解答题（每小题 10 分，共 50 分）1 12,2, 22441 1 00 2 1 3 40 2 1 30 1 1 011.设B, C 0 2 1 且矩阵满足关系式0 0 1 1 00 10 0 0 2T X(C B)E，求。

a1 12212. 问 a 取何值时，下列向量组线性相关？111, 2a ,3。

2 1 21 a22x 1 x 2x 3 313.为何值时，线性方程组x 1 x 2x 3 2有唯一解，无解和有无穷多解？当方x 1 x 2x 32程组有无穷多解时求其通解。

线性代数期末考试试卷+答案.

×××大学线性代数期末考试题一、填空题（将正确答案填在题中横线上。

每小题分，共分）若022150131=---x ，则=χ 。

．若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解，则λ应满足。

．已知矩阵n s ij c C B A ⨯=)(，，，满足CB AC =，则A 与B 分别是阶矩阵。

．矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性。

．n 阶方阵A 满足032=--E A A ，则=-1A 。

二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。

每小题分，共分）若行列式D 中每个元素都大于零，则0〉D 。

（）零向量一定可以表示成任意一组向量的线性组合。

（）向量组m a a a ，，， 21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，， 21线性相关。

（）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ，则A A =-1。

（）若λ为可逆矩阵A 的特征值，则1-A 的特征值为λ。

三、单项选择题每小题仅有一个正确答案，将正确答案题号填入括号内。

每小题分，共分设A 为n 阶矩阵，且2=A ，则=T A A （）。

① n 2② 12-n③ 12+n④n 维向量组 s ααα，，， 21（）线性无关的充要条件是（）。

① s ααα，，， 21中任意两个向量都线性无关 ② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示 ④ s ααα，，， 21中不含零向量下列命题中正确的是。

① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关设A ，B 均为阶方阵，下面结论正确的是。

07-08线代BA卷答案

2007-2008学年第二学期期末试卷-A 卷线性代数B课程号： 11020063B 课序号： 01-13 开课系：数学与数量经济学院一、填空题（每小题3分，共15分）1．6427811694143211111= 12 。

2．设 A 为3阶可逆矩阵，1=A ，则=-*1)(A 1 。

3. 设321,,ααα线性无关,则321211,,αααααα+++线性____无 ___关。

4. 设A 为4阶方阵，且()3=A r ，则齐次线性方程组*0A X =（*A 是A 的伴随矩阵）的基础解系所包含的线性无关向量的个数为 3 。

5．设T T T ===),3,1(,)3,2,1(,)1,1,1(321t ααα，若向量组321,,ααα线性相关，则=t 5 。

二、单项选择题(每小题2分，共10分)1．非齐次线性方程组AX B =中未知量的个数为n ，方程个数为m ，系数矩阵A 的秩为r ，则 B 。

（A ）r = m 时，方程组AX B =有解（B ）r = n 时，方程组AX B =有唯一解（C ）m = n 时，方程组AX B =有唯一解（D ）r 〈 n 时，方程组AX B =有无穷多解2．设A 为n 阶矩阵，且0A =，则A 的列向量中C 。

（A ）必有两个向量对应分量成比例（B ）必有一个向量为零向量（C ）必有一个向量是其余向量的线性组合（D ）任一向量是其余向量的线性组合3．设A 为n 阶单位矩阵，则矩阵A 的特征值为 B。

（A ）0λ= （B ）1λ= （C ）2λ= （D ）3λ=4．下面结论不正确的是C 。

（A ）相似矩阵有相同的特征值（B ）相似矩阵有相同的行列式（C ）相似矩阵的秩一定不相同（D ）实对称矩阵的属于不同特征值的特征向量是正交的5．123(2,1,3),(3,1,1),(1,1,2)ααα==-=-，则向量组1α，2α，3α是A。

（A ）线性无关（B ）线性相关（C ）1α可以由2α，3α线性表示（D ）3α可以由1α，2α线性表示三（10分）计算下列n 阶行列式 ab b b a b bb a D n==1[(1)]()n a n b a b -+-- 四（10分）解矩阵方程 A 2X AX =+，其中A = 3 0 1 1 1 00 1 4⎛⎫ ⎪ ⎪ ⎪⎝⎭ 5 -2 -2 4 -3 -2 -2 2 3X ⎛⎫ ⎪= ⎪ ⎪⎝⎭五（10分）已知向量组()5,4,3,11-=α，()9,7,2,22-=α，()12,9,3,33=α试求这个向量组的一个极大无关组，并把其余向量用此极大无关组线性表示。

线性代数期末考试(B卷)及答案

北京师范大学XX 分校2007-2008学年第一学期期末考试（B 卷）开课单位：应用数学系课程名称：线性代数任课教师：__ __ 考试类型：_ 闭卷_ 考试时间：__120 __分钟学院___________ 姓名___________ 学号______________ 班级____________试卷说明：（本试卷共4页，满分100分）------------------------------------------------------------------------------------------------------一、填空（每空3分，共30分）1、行列式123345__0____567= 2、行列式sin cos cos sin _______+-=-1313113xxxx 3、设行列式 -5 11 1 31 0 2D =1，则______-+=21222350A A A4、设A ，B 均为三阶方阵且||,||A B ==45，则||______=20A B5、设A 为3阶方阵，且A =2，则A-=12 46、设矩阵A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭12311102103，则A 的秩()R A = 37、已知3阶矩阵A 的伴随矩阵的行列式A *=9，则=A 38、向量组,,,αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1234111322023001线性相关还是无关线性相关试卷装订线9、设向量()(),,,,,x αα==1232963线性相关，则___1____=x10、设5元方程组=0A x 的系数矩阵A 的秩为3，则其解向量的秩应为 2二、选择题（每小题3分，共15分）1、行列式13632196233418第2行第2列元素的代数余子式A =22（ D ）（A ）6；（B ）9；（C ）12；（D ）15。

线性代数期末考试试题及答案

线性代数期末考试试题及答案一、选择题（每题2分，共10分）1. 下列矩阵中，哪个是可逆矩阵？A. [1, 2; 3, 4]B. [2, 0; 0, 1]C. [1, 1; 1, 1]D. [0, 0; 0, 0]2. 如果向量v = (3, -2)，那么其对应的单位向量是什么？A. (1, -2/3)B. (3/√13, -2/√13)C. (3/√29, -2/√29)D. (3/√10, -2/√10)3. 对于矩阵A，|A|表示其行列式，那么|A| = 0表示：A. A是单位矩阵B. A是零矩阵C. A不是满秩矩阵D. A是可逆矩阵4. 矩阵的特征值是什么？A. 矩阵的对角元素B. 矩阵的迹C. 满足Av = λv的非零向量v对应的λD. 矩阵的行列式5. 下列哪个矩阵是对称矩阵？A. [1, 2; 3, 4]B. [2, 0; 0, 2]C. [1, -1; 1, 1]D. [1, 0; 0, 1]二、填空题（每题3分，共15分）6. 如果矩阵A的秩为1，那么A的零空间的维数是_________。

7. 对于任意非零向量α和β，如果α + β和α - β都是零向量，那么向量α和β_________。

8. 一个向量空间的一组基的向量数量至少是_________。

9. 如果矩阵A是n阶方阵，且A^2 = I（单位矩阵），那么矩阵A是_________矩阵。

10. 对于实数域上的向量空间，任意两个非零向量的标量积是_________的。

三、简答题（每题10分，共20分）11. 解释什么是线性变换，并给出一个线性变换的例子。

12. 证明如果矩阵A和B是可交换的，即AB = BA，那么它们的行列式之积等于各自行列式的乘积，即|AB| = |A||B|。

四、计算题（每题15分，共30分）13. 给定矩阵A = [4, 1; 3, 2]，求A的逆矩阵A^-1。

14. 设向量空间V是所有2x2实对称矩阵的集合，证明V是一个向量空间，并找出一组基。

2007线性代数考试试题B

,考试作弊将带来严重后果！华南理工大学期末考试《线性代数－2007》试卷B1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：开（闭）卷；本试卷共五大题，满分100分，考试时间120分钟单项选择题（每小题2分，共40分）。

．设矩阵22, B 23, C 32A ⨯⨯⨯为矩阵为矩阵为矩阵，则下列矩阵运算无意义的是【】A . BAC B. ABC C . BCA D. CAB设n 阶方阵A 满足A 2 ＋E =0，其中E 是n 阶单位矩阵，则必有【】A. 矩阵A 不是实矩阵B. A=-EC. A=ED. det(A)=1设A 为n 阶方阵，且行列式det(A)=1 ,则det(-2A)= 【】A. 2－B. ()n2－ C. n 2－ D. 1设A 为3阶方阵，且行列式det(A)=0，则在A 的行向量组中【】A.必存在一个行向量为零向量B.必存在两个行向量，其对应分量成比例C. 存在一个行向量，它是其它两个行向量的线性组合D. 任意一个行向量都是其它两个行向量的线性组合．设向量组321,,a a a 线性无关，则下列向量组中线性无关的是【】A ．133221,,a a a a a a --- B. 212132,,a a a a - C. 32322,2,a a a a + D. 1321,,a a a a －6.向量组(I): )3(,,1≥m a a m 线性无关的充分必要条件是【】A.(I)中任意一个向量都不能由其余m-1个向量线性表出B.(I)中存在一个向量,它不能由其余m-1个向量线性表出C.(I)中任意两个向量线性无关D.存在不全为零的常数0,,,111≠++m m m a k a k k k 使7．设a 为n m ⨯矩阵，则n 元齐次线性方程组0=Ax 存在非零解的充分必要条件是【】A ．A 的行向量组线性相关B . A 的列向量组线性相关 C. A 的行向量组线性无关 D. A 的列向量组线性无关8.设i a 、i b 均为非零常数（i =1，2，3），且齐次线性方程组⎩⎨⎧=++=++00332211332211x b x b x b x a x a x a的基础解系含2个解向量，则必有【】 A.03221= b b a a B.02121≠ b b a a C.332211b a b a b a == D.02131= b b a a9.方程组12312312321 21 3 321x x x x x x x x x a ++=⎧⎪++=⎨⎪++=+⎩有解的充分必要的条件是【】A. a=-3B. a=-2C. a=3D. a=110. 设η1，η2，η3是齐次线性方程组Ax = 0的一个基础解系，则下列向量组中也为该方程组的一个基础解系的是【】A. 可由η1，η2，η3线性表示的向量组B. 与η1，η2，η3等秩的向量组C.η1－η2，η2－η3，η3－η1D. η1，η1-η3，η1-η2-η3 11. 已知非齐次线性方程组的系数行列式为0，则【】A. 方程组有无穷多解B. 方程组可能无解，也可能有无穷多解C. 方程组有唯一解或无穷多解D. 方程组无解12.n 阶方阵A 相似于对角矩阵的充分必要条件是A 有n 个【】A.互不相同的特征值B.互不相同的特征向量C.线性无关的特征向量D.两两正交的特征向量13. 下列子集能作成向量空间R n 的子空间的是【】A. }0|),,,{(2121=a a a a a nB. }0|),,,{(121∑==ni i n a a a aC. },,2,1,|),,,{(21n i z a a a a i n =∈D. }1|),,,{(121∑==n i i n a a a a 14.若2阶方阵A 相似于矩阵⎥⎦⎤⎢⎣⎡=3- 20 1B ,E 为2阶单位矩阵,则方阵E –A 必相似于矩阵【】A. ⎥⎦⎤⎢⎣⎡4 10 1B. ⎥⎦⎤⎢⎣⎡4- 1 0 1-C. ⎥⎦⎤⎢⎣⎡4 2-0 0 D. ⎥⎦⎤⎢⎣⎡4- 2-0 1-15.若矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8020001 a a A 正定,则实数a 的取值范围是【】A ．a < 8 B. a ＞4 C ．a ＜-4 D ．-4 ＜a ＜4二、填空题（每小题2分，共20分）。

《线性代数》期末考试题及详细答案(本科A、B试卷)

XXX 学年期末考试试卷《线性代数》期末考试题及详细答案（本科A 、B 试卷）A 卷一、填空题（将正确答案填在题中横线上。

每小题2分，共10分）。

1、设1D =3512， 2D =345510200，则D =12DD OO=_____________。

2、四阶方阵A B 、，已知A =116，且=B ()1-12A 2A --，则B =_____________。

3、三阶方阵A 的特征值为1，-1，2，且32B=A -5A ，则B 的特征值为_____________。

4、若n 阶方阵A 满足关系式2A -3A-2E O =，若其中E 是单位阵，那么1A -=_____________。

5、设()11,1,1α=，()21,2,3α=，()31,3,t α=线性相关，则t=_____________。

二、单项选择题（每小题仅有一个正确答案，将正确答案的番号填入下表内，每小题2分，共20分）。

1、若方程13213602214x x xx -+-=---成立，则x 是：课程代码：适用班级：命题教师：任课教师：（A ）-2或3；（B ）-3或2；（C ）-2或-3；（D ）3或2； 2、设A 、B 均为n 阶方阵，则下列正确的公式为：（A ）()332233A B+3AB +B A B A +=+； B ）()()22A B A+B =A B --；（C ）()()2A E=A E A+E --；（D ）()222AB =A B ； 3、设A 为可逆n 阶方阵，则()**A=？（A ）A E ；（B ）A ；（C ）nA A ；（D ）2n A A -；4、下列矩阵中哪一个是初等矩阵：（A ）100002⎛⎫ ⎪⎝⎭；（B ）100010011⎛⎫⎪⎪ ⎪⎝⎭；（C ）011101001-⎛⎫ ⎪- ⎪ ⎪⎝⎭；（D ）010002100⎛⎫⎪- ⎪ ⎪⎝⎭；5、下列命题正确的是：（A ）如果有全为零的数1,k 2k 3,,,m k k 使1122m m k k k αααθ+++=，则1,α2α，，m α 线性无关；（B ）向量组1,α2α，，m α 若其中有一个向量可由向量组线性表示，则1,α2α，，m α线性相关；（C ）向量组1,α2α，，m α 的一个部分组线性相关，则原向量组本身线性相关；（D ）向量组1,α2α，，m α线性相关，则每一个向量都可由其余向量线性表示。

2007-2008第二学期线代试卷B及答案

武汉理工大学教务处试题标准答案及评分标准用纸课程名称:线性代数（ B 卷）一、选择题（每小题3分，共12分）1、 B2、 A3、 A4、 C 二、填空题（每小题3分，共12分）1、 6006⎛⎫⎪⎝⎭； 2、. 1201113002A --⎛⎫ ⎪= ⎪ ⎪⎝⎭； 3、（1，1，-1）； 4、 6；三、1、121000121000(1)2121000121121n n n x x n xn x n n D x x n n x xn nn n-+-++⎡⎤==+⎢⎥⎣⎦+-+--………………………（6分） (1)12(1)(1)2n n n n n x x --+⎡⎤=-+⎢⎥⎣⎦…………………………………………………………………………………（9分） 2、记1200A A A ⎛⎫=⎪⎝⎭，则1111200A A A ---⎛⎫= ⎪⎝⎭， ……………………………………………………………（2分）又*11211,10A A ⎛⎫==⎪-⎝⎭，故112110A -⎛⎫=⎪-⎝⎭…………………………………………………………（4分）*21211,31A A -⎛⎫=-=⎪-⎝⎭，故122131A --⎛⎫=⎪-⎝⎭………………………………………………………（6分）所以1210010000021031A-⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭。

…………………………………………………………………（9分） 3、记()1234,,,A αααα=，对A 进行行初等变换，将其化为行最简形：1211241012213631A -⎛⎫ ⎪- ⎪=⎪--- ⎪-⎝⎭～121100320032064-⎛⎫ ⎪- ⎪ ⎪- ⎪-⎝⎭～12110032000000-⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭～11203200130000000⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪⎪ ⎪⎝⎭…………………（5分）()2R A =，又显然13,αα线性无关，所以13,αα即为原向量组的一个最大无关组；………………………（7分）且212αα=，4131233ααα=--。

线性代数B期末试卷及答案

2008 -2009学年第二学期《线性代数 B 》试卷量组1，2，，m ，的秩为5. 设A 为实对称阵，且AI M 0,则二次型f =x T A x 化为f =y T A -1 y 的线性变换是x= __________ .T6. 设 R 3 的两组基为 a 11,1,1 ，a 2 1,0, 1 ，a 3 1,0,1 ；2,3,4 , 3 3,4,3 ，则由基 a !,a 2,a 3到基 1, 2, 3的过渡矩阵为、单项选择题（共6小题，每小题3分，满分18 分）一一一-二二 -三四五六总分(共 0 0 12. A 为n 阶方阵,AA T = E 且A 0,则A E |.3•设方阵A1 2 24 t 3 , B 为三阶非零矩阵，且AB=O,则t 3114.设向量组m线性无关，向量不能由它们线性表示，贝U 向1(1,2,1,)T ，22009年6月22日6小题，每小题3分，满分18分）、填空题 1 0 0 10 01.设D n 为n 阶行列式，则D n = 0的必要条件是[]. (A) D n 中有两行元素对应成比例； (B) D n 中各行元素之和为零； (C) D n 中有一行元素全为零；(D)以D n 为系数行列式的齐次线性方程组有非零解.2.若向量组，，线性无关，，，线性相关，则[](A)必可由，，线性表示； (B)必可由，，线性表示； (C)必可由，，线性表示； (D)必可由，，线性表示.3.设3阶方阵A 有特征值0,— 1,1，其对应的特征向量为P i , P 2,P 3, 令1 亠( P 1, P 2, P 3)，则 P —1AP =[ ].1 0 00 0 0(A) 01 0 ；(B) 01 0 ；0 0 0 0 0 10 01 0(C) 0 10 ；(D) 0 00 .0 0 —10 0—14. 设 a 1, a, a 线性无关，则下列向量组线性相关的是[](A) a, a, a - a ；(B) a 1,a + a, a 1+ a ；(C) a +( 也， a + a, a + a ； (D) a 1- a, a - a, a - a .5. 若矩阵A a x 4有一个3阶子式不为0,则A 的秩R ( A )=[]. (A) 1； (B) 2; (C) 3；(D) 4.6. 实二次型f 二X T A X 为正定的充分必要条件是[].(A) A 的特征值全大于零； (B) A 的负惯性指数为零；(C)AI > 0 ；(D) R(A) = n .、解答题(共5小题，每道题8分，满分40分)。

线性代数B期末试卷及答案

线性代数B期末试卷及答案2008 – 2009学年第⼆学期《线性代数B 》试卷⼀⼆三四五六总分⼀、填空题(共6⼩题，每⼩题 3 分，满分18分）1。

设??-=*8030010000100001A ,则A ＝。

2。

A 为n 阶⽅阵，T AA =E 且=+3．设⽅阵12243,311t -??=-A B 为三阶⾮零矩阵，且AB=O ，则=t . 4。

设向量组m ααα,,,21 线性⽆关，向量不能由它们线性表⽰，则向量组,,,,21m ααα的秩为。

5．设A 为实对称阵，且｜A |≠0,则⼆次型f =x T A x 化为f =y T A —1 y 的线性变换是x = ．６．设3R 的两组基为()T11,1,1a =，()21,0,1a T=-，()31,0,1a T=；),1,2,1(1=βT ，()()232,3,4,3,4,3ββ==T T，则由基123,,a a a 到基123,,βββ的过渡矩阵为 .得分6⼩题，每⼩题3分，满分18分）1.设D n为n阶⾏列式，则D n＝0的必要条件是[ ].（A）D n中有两⾏元素对应成⽐例；(B) D n中各⾏元素之和为零;(C） D n中有⼀⾏元素全为零；（D）以D n为系数⾏列式的齐次线性⽅程组有⾮零解．2．若向量组，，线性⽆关，，，线性相关，则[ ].(A)必可由，,线性表⽰；（B) 必可由，,线性表⽰;(C）必可由,,线性表⽰；(D）必可由，，线性表⽰.３．设3阶⽅阵A有特征值0，－1，1,其对应的特征向量为P1，P2，P3,令P＝（P1，P2，P3），则P－1AP＝[ ]。

（A)100010000-；（B)000010001-；（C)000010001－； (D）100000001－．４．设α1，α2，α3线性⽆关，则下列向量组线性相关的是[ ］.（A）α1，α2，α3 - α1；（B)α1，α1+α2，α1+α3；(C)α1+α2，α2+α3，α3+α1； (D)α1-α2，α2—α3，α3—α1.５．若矩阵A3×4有⼀个3阶⼦式不为0，则A的秩Ｒ（A） =[ ].（A) 1； (B）2；（C）3； (D）4．６．实⼆次型f＝x T Ax为正定的充分必要条件是［］.（A) A的特征值全⼤于零；（B） A的负惯性指数为零；（C）｜A| > 0 ; （D) R(A) = n .得分三、解答题（共5⼩题，每道题8分，满分40分）1。

2007年-2008年-自考-线性代数-经管类-真题详细答案

全国2007年4月高等教育自学考试线性代数（经管类）参考答案课程代码：04184一、单项选择题（本大题共10小题，每小题2分，共20分） 1．设A 为3阶方阵,且2||=A ，则=-|2|1A （ D ） A ．—4 B ．—1 C ．1D ．44218||2|2|131=⨯==--A A ． 2．设矩阵A =(1，2），B =⎪⎪⎭⎫⎝⎛4321，C =⎪⎪⎭⎫ ⎝⎛654321，则下列矩阵运算中有意义的是（ B ) A ．ACBB ．ABCC ．BACD ．CBA3．设A 为任意n 阶矩阵,下列矩阵中为反对称矩阵的是（ B ） A ．A ＋A TB ．A －A TC ．AA TD ．A T A)()()(T T T T T T T A A A A A A A A --=-=-=-，所以A －A T 为反对称矩阵．4．设2阶矩阵A =⎪⎪⎭⎫ ⎝⎛d cb a,则A ＊=( A ） A ．⎪⎪⎭⎫ ⎝⎛--a cb dB ．⎪⎪⎭⎫ ⎝⎛--a bc d C ．⎪⎪⎭⎫ ⎝⎛--a cb dD ．⎪⎪⎭⎫ ⎝⎛--a bc d5．矩阵⎪⎪⎭⎫⎝⎛-0133的逆矩阵是（ C ）A ．⎪⎪⎭⎫⎝⎛-3310B ．⎪⎪⎭⎫⎝⎛-3130C ．⎪⎪⎭⎫ ⎝⎛-13110D ．⎪⎪⎪⎭⎫ ⎝⎛-01311 6．设矩阵A =⎪⎪⎪⎭⎫⎝⎛--500043200101，则A 中（ D ）A ．所有2阶子式都不为零B ．所有2阶子式都为零C ．所有3阶子式都不为零D ．存在一个3阶子式不为零7．设A 为m×n 矩阵,齐次线性方程组Ax =0有非零解的充分必要条件是（ A ） A ．A 的列向量组线性相关 B ．A 的列向量组线性无关 C ．A 的行向量组线性相关D ．A 的行向量组线性无关Ax =0有非零解⇔n A r <)(⇔ A 的列向量组线性相关．8．设3元非齐次线性方程组Ax=b 的两个解为T )2,0,1(=α，T )3,1,1(-=β，且系数矩阵A 的秩r （A ）=2，则对于任意常数k , k 1, k 2，方程组的通解可表为（ C ） A ．k 1（1，0，2)T +k 2（1,-1，3)T B ．(1,0，2)T +k (1,—1，3)T C ．(1,0,2）T +k （0,1,-1）TD ．(1，0，2）T +k （2，-1,5）TT )2,0,1(=α是Ax=b 的特解，T )1,1,0(-=-βα是Ax =0的基础解系，所以Ax=b 的通解可表为=-+)(βααk (1，0,2)T +k （0,1,—1)T ．9．矩阵A =⎪⎪⎪⎭⎫ ⎝⎛111111111的非零特征值为（ B )A ．4B ．3C ．2D ．1111111111)3(111111333111111111||-------=---------=---------=-λλλλλλλλλλλλA E )3(0000111)3(2-=-=λλλλλ,非零特征值为3=λ．10．4元二次型413121214321222),,,(x x x x x x x x x x x f +++=的秩为（ C ) A ．4 B ．3 C ．2 D ．1⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛=000000001110000100000000000111100001000100011111A ，秩为2．二、填空题（本大题共10小题，每小题2分，共20分）11．若,3,2,1,0=≠i b a i i 则行列式332313322212312111b a b a b a b a b a b a b a b a b a =__0__．行成比例值为零．12．设矩阵A =⎪⎪⎭⎫ ⎝⎛4321，则行列式｜A TA |=__4__．4)2(4321||||||||222=-====A A A A A TT．13．若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000333232131323222121313212111x a x a x a x a x a x a x a x a x a 有非零解,则其系数行列式的值为__0__．14．设矩阵A =⎪⎪⎪⎭⎫⎝⎛100020101，矩阵E A B -=,则矩阵B 的秩r(B ）= __2__．E A B -==⎪⎪⎪⎭⎫ ⎝⎛000010100，r(B )=2．15．向量空间V=｛x =（x 1，x 2,0)｜x 1，x 2为实数｝的维数为__2__．16．设向量)3,2,1(=α，)1,2,3(=β，则向量α，β的内积),(βα=__10__．17．设A 是4×3矩阵，若齐次线性方程组Ax =0只有零解，则矩阵A 的秩r(A )= __3__．18．已知某个3元非齐次线性方程组Ax =b 的增广矩阵A 经初等行变换化为:⎪⎪⎪⎭⎫ ⎝⎛-----→1)1(0021201321a a a A ，若方程组无解,则a 的取值为__0__．0=a 时，2)(=A r ，3)(=A r ．19．设3元实二次型),,(321x x x f 的秩为3，正惯性指数为2，则此二次型的规范形是232221y y y -+．秩3=r ，正惯性指数2=k ，则负惯性指数123=-=-k r ．规范形是232221y y y -+．20．设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛-300021011a 为正定矩阵，则a 的取值范围是1<a ．011>=∆，0121112>-=-=∆a a,0)1(33000210113>-=-=∆a a ⇒1<a ．三、计算题（本大题共6小题，每小题9分,共54分)21．计算3阶行列式767367949249323123．解：0760300940200320100767367949249323123==．22．设A =　⎪⎪⎪⎭⎫⎝⎛--523012101，求1-A ．解：　⎪⎪⎪⎭⎫ ⎝⎛--100010001523012101→　⎪⎪⎪⎭⎫⎝⎛---103012001220210101→　⎪⎪⎪⎭⎫⎝⎛---127012001200210101 →　⎪⎪⎪⎭⎫ ⎝⎛---127012002200210202→　⎪⎪⎪⎭⎫ ⎝⎛----127115125200010002→　⎪⎪⎪⎭⎫⎝⎛----2/112/71152/112/5100010001， =-1A ⎪⎪⎪⎭⎫⎝⎛----2/112/71152/112/5． 23．设向量组T )1,2,1,1(1-α,T )2,4,2,2(2--α,T )1,6,0,3(3-α，T )4,0,3,0(4-α．（1）求向量组的一个极大线性无关组；(2）将其余向量表为该极大线性无关组的线性组合．解：=),,,(4321αααα⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----4121064230210321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---4440000033000321 →⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---0000330044400321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0000110011100321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-0000110000103021→⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000110000103001．（1）321,,ααα是一个极大线性无关组；（2）=4α32103ααα++-．24．求齐次线性方程组 ⎪⎩⎪⎨⎧=++=-+=++000543321521x x x x x x x x x 的基础解系及通解．解:⎪⎪⎪⎭⎫ ⎝⎛-=111000*********A →⎪⎪⎪⎭⎫ ⎝⎛--111001010010011→⎪⎪⎪⎭⎫⎝⎛--010001010010011→⎪⎪⎪⎭⎫ ⎝⎛010001010010011，⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==--=55453225210x x x x x x x x x x , 基础解系为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00011，⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--10101，通解为T T k k )1,0,1,0,1()0,0,0,1,1(21--+-=η．25．设矩阵A =⎪⎪⎭⎫ ⎝⎛1221，求正交矩阵P ,使AP P 1-为对角矩阵．解：)3)(1(324)1(1221||22-+=--=--=----=-λλλλλλλλA E ，特征值11-=λ，32=λ．对于11-=λ,解齐次线性方程组0)(=-x A E λ:⎪⎪⎭⎫⎝⎛→⎪⎪⎭⎫⎝⎛----=-00112222A E λ，⎩⎨⎧=-=2221x x x x ，基础解系为⎪⎪⎭⎫⎝⎛-=111α，单位化为⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==21211121||1111ααβ；对于32=λ，解齐次线性方程组0)(=-x A E λ：⎪⎪⎭⎫⎝⎛-→⎪⎪⎭⎫⎝⎛--=-00112222A E λ，⎩⎨⎧==2221x x x x ，基础解系为⎪⎪⎭⎫⎝⎛=112α，单位化为⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛==21211121||1222ααβ．令⎪⎪⎪⎪⎭⎫ ⎝⎛-=21212121P ，则P 是正交矩阵，使⎪⎪⎭⎫ ⎝⎛-=-30011AP P ． 26．利用施密特正交化方法,将下列向量组化为正交的单位向量组：⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00111α， ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=01012α．解：正交化，得正交的向量组:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==001111αβ，⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-=012/12/10011210101||),(1211222βββααβ；单位化，得正交的单位向量组：⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==002/12/1001121||1111ββp ，⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-==06/26/16/1012/12/162||1222ββp ．四、证明题（本大题6分）27．证明:若A 为3阶可逆的上三角矩阵,则1-A 也是上三角矩阵．证：设⎪⎪⎪⎭⎫⎝⎛=33232213121100a a a a a a A ，则⎪⎪⎪⎭⎫⎝⎛==*-3323133222123121111||1||1A A A A A A A A A A A A A ，其中000332312=-=a a A ，00002213=-=a A ，00121123=-=a aA ，所以⎪⎪⎪⎭⎫⎝⎛=-3332223121111||1A A A A A A A A 是上三角矩阵．全国2007年7月高等教育自学考试线性代数（经管类）试题答案课程代码：04184一、单项选择题（本大题共10小题，每小题2分，共20分） 1．设A 是3阶方阵，且|A ｜=21-,则|A -1｜=（ A ） A ．—2B ．21- C ．21D ．22．设A 为n 阶方阵,λ为实数，则=||A λ（ C ） A ．||A λB ．||||A λC ．||A n λD ．||||A n λ3．设A 为n 阶方阵，令方阵B =A +A T ，则必有（ A ) A ．B T =BB ．B =2AC ．B B T -=D ．B =0B A A A A A A A A B T T T T T T T T =+=+=+=+=)()(．4．矩阵A =⎪⎪⎭⎫ ⎝⎛--1111的伴随矩阵A ＊=（ D ) A ．⎪⎪⎭⎫ ⎝⎛--1111 B ．⎪⎪⎭⎫ ⎝⎛--1111 C ．⎪⎪⎭⎫⎝⎛--1111D ．⎪⎪⎭⎫ ⎝⎛--11115．下列矩阵中，是初等矩阵的为（ C ）A ．⎪⎪⎭⎫⎝⎛0001 B ．⎪⎪⎪⎭⎫ ⎝⎛--100101110 C ．⎪⎪⎪⎭⎫ ⎝⎛101010001D ．⎪⎪⎪⎭⎫ ⎝⎛0013000106．若向量组)0,1,1(1+=t α，)0,2,1(2=α，)1,0,0(23+=t α线性相关，则实数t =（ B ）A ．0B ．1C ．2D ．30)1)(1(2111)1(100021011222=-+=++=++t t t t t t ⇒1=t ．7．设A 是4×5矩阵，秩(A )=3,则（ D ) A ．A 中的4阶子式都不为0 B ．A 中存在不为0的4阶子式 C ．A 中的3阶子式都不为0D ．A 中存在不为0的3阶子式8．设3阶实对称矩阵A 的特征值为021==λλ，23=λ,则秩(A )=（ B ） A ．0 B ．1 C ．2 D ．3A 相似于⎪⎪⎪⎭⎫⎝⎛=200000000D ，秩(A ）= 秩（D ）=1．9．设A 为n 阶正交矩阵，则行列式=||2A （ C )A ．-2B ．-1C ．1D ．2A 为正交矩阵，则E A A T =，==22||||A A 1||||||==A A A A T T ． 10．二次型2.2),,(y x z y x f -=的正惯性指数p 为（B ）A ．0B ．1C ．2D ．3二、填空题（本大题共10小题，每小题2分，共20分）11．设矩阵A =⎪⎪⎭⎫ ⎝⎛1121，则行列式=||TAA __1__． 1)1(1121||||||||22=-====A A A AA T T ．12．行列式1694432111中)2,3(元素的代数余子式=32A __—2__．2421132-=-=A ． 13．设矩阵A =⎪⎪⎭⎫ ⎝⎛21,B =⎪⎪⎭⎫ ⎝⎛21，则=B A T__5__． 521)2,1(=⎪⎪⎭⎫⎝⎛=B A T ．14．已知βααα=+-32125，其中)1,4,3(1-=α，)3,0,1(2=α，)5,2,0(-=β，则=3α⎪⎭⎫ ⎝⎛-211,1,1．⎪⎭⎫ ⎝⎛-=-=+---=211,1,1)11,2,2(21)]3,0,1(5)1,4,3()5,2,0[(213α 15．矩阵A =⎪⎪⎪⎭⎫⎝⎛-613101的行向量组的秩=__2__．⎪⎪⎪⎭⎫ ⎝⎛-613101→⎪⎪⎪⎭⎫ ⎝⎛-603001→⎪⎪⎪⎭⎫⎝⎛-003001,秩=2． 16．已知向量组)1,1,1(1=α，)0,2,1(2=α，)0,0,3(3=α是3R 的一组基，则向量)3,7,8(=β在这组基下的坐标是)1,2,3(．设332211αααβx x x ++=，即)0,0,3()0,2,1()1,1,1()3,7,8(321x x x ++=，得⎪⎩⎪⎨⎧==+=++37283121321x x x x x x ,解得⎪⎩⎪⎨⎧===123321x x x ． 17．已知方程组⎩⎨⎧=+-=-0202121tx x x x 存在非零解，则常数t =__2__．02211=-=--t t，2=t ．18．已知3维向量T )1,3,1(-=α，T )4,2,1(-=β,则内积=),(βα__1__．19．已知矩阵A =⎪⎪⎪⎭⎫ ⎝⎛x 01010101的一个特征值为0，则x =__1__．0|0|=-A E ，所以0||=A ,即0111101010101=-==x xx，1=x ．20．二次型323121232221321822532),,(x x x x x x x x x x x x f +-+++=的矩阵是⎪⎪⎪⎭⎫ ⎝⎛--541431112．三、计算题（本大题共6小题，每小题9分，共54分）21．计算行列式D=210121012的值．解：4)26(2123210121230210121012=+--=---=--=．22．设矩阵A =⎪⎪⎭⎫ ⎝⎛3512，B =⎪⎪⎭⎫⎝⎛0231，求矩阵方程XA =B 的解X ．解：⎪⎪⎭⎫⎝⎛--→⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛=252610022501101220016101210013512),(E A⎪⎪⎭⎫ ⎝⎛--→25131001，⎪⎪⎭⎫ ⎝⎛--=-25131A ，⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛==-26512251302311BA X ． 23．设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛---a 363124843121，问a 为何值时，（1）秩(A ）=1；（2）秩(A ）=2．解:⎪⎪⎪⎭⎫ ⎝⎛---a 363124843121→⎪⎪⎪⎭⎫ ⎝⎛--900000003121a →⎪⎪⎪⎭⎫ ⎝⎛--000090003121a ． (1）9=a 时,秩（A )=1；（2)9≠a 时，秩(A ）=2．24．求向量组1α=⎪⎪⎪⎭⎫ ⎝⎛-111，2α=⎪⎪⎪⎭⎫ ⎝⎛531，3α=⎪⎪⎪⎭⎫ ⎝⎛626，4α=⎪⎪⎪⎭⎫⎝⎛-542的秩与一个极大线性无关组．解:⎪⎪⎪⎭⎫ ⎝⎛--565142312611→⎪⎪⎪⎭⎫ ⎝⎛--3126028402611→⎪⎪⎪⎭⎫ ⎝⎛--142014202611→⎪⎪⎪⎭⎫⎝⎛--000014202611，秩为2，1α,2α是一个极大线性无关组．25．求线性方程组⎪⎩⎪⎨⎧=++=+=++362232234232132321x x x x x x x x 的通解．解：⎪⎪⎪⎭⎫ ⎝⎛=362232203421A →⎪⎪⎪⎭⎫ ⎝⎛---322032203421→⎪⎪⎪⎭⎫ ⎝⎛000032203421→⎪⎪⎪⎭⎫⎝⎛000032200201→⎪⎪⎪⎭⎫ ⎝⎛00002/31100201，⎪⎪⎩⎪⎪⎨⎧=-=-=333231232x x x x x x ，通解为⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎭⎫ ⎝⎛11202/30k ．26．设矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1630310104A ，求可逆矩阵P 及对角矩阵D ，使得D AP P =-1．解:2)1)(2(31104)1(1630310104||-+=--+-=-----+=-λλλλλλλλλA E ，特征值21-=λ，132==λλ．对于21-=λ,解齐次线性方程组0)(=-x A E λ：⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛-----=-00013050300013001531300000511210510513630510102A E λ⎪⎪⎪⎭⎫ ⎝⎛-→0003/1103/501，⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=3332313135x x x x x x ,基础解系为 ⎪⎪⎪⎭⎫⎝⎛-=13/13/51α；对于132==λλ，解齐次线性方程组0)(=-x A E λ：⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛----=-0000000210210210210630210105A E λ,⎪⎩⎪⎨⎧==-=3322212x x x x x x ，基础解系为⎪⎪⎪⎭⎫ ⎝⎛-=0122α,⎪⎪⎪⎭⎫⎝⎛=1003α．令⎪⎪⎪⎭⎫ ⎝⎛--=101013/1023/5P ，⎪⎪⎪⎭⎫⎝⎛-=100010002D ，则P 是可逆矩阵，使D AP P =-1．四、证明题（本大题6分)27．设向量组1α,2α线性无关，证明向量组211ααβ+=,212ααβ-=也线性无关．证:设02211=+ββk k ，即0)()(212211=-++ααααk k ，0)()(221121=-++ααk k k k ．由1α，2α线性无关,得⎩⎨⎧=-=+002121k k k k ，因为021111≠-=-，方程组只有零解，所以1β,2β线性无关．全国2007年10月高等教育自学考试线性代数（经管类)试题答案课程代码:04184一、单项选择题（本大题共10小题，每小题2分，共20分） 1．设行列式2211b a b a =1，2211c a c a =2，则222111c b a c b a ++=（ D ） A ．—3B ．-1C ．1D ．3222111c b a c b a ++=2211b a b a +2211c a c a =1+2=3．2．设A 为3阶方阵，且已知2|2|=-A ，则=||A （ B ) A ．-1B ．41-C ．41 D ．12|2|=-A ，2||)2(3=-A ，41||-=A ．3．设矩阵A ,B ，C 为同阶方阵，则=T ABC )(（ B ） A ．A T B T C TB ．C T B T A TC ．C T A T B TD ．A T C T B T4．设A 为2阶可逆矩阵,且已知⎪⎪⎭⎫⎝⎛=-4321)2(1A ，则A =( D ）A ．2⎪⎪⎭⎫⎝⎛4321B ．⎪⎪⎭⎫⎝⎛432121C ．214321-⎪⎪⎭⎫⎝⎛D ．1432121-⎪⎪⎭⎫⎝⎛ ⎪⎪⎭⎫ ⎝⎛=-4321)2(1A ，143212-⎪⎪⎭⎫ ⎝⎛=A ，1432121-⎪⎪⎭⎫⎝⎛=A ． 5．设向量组s ααα,,,21 线性相关,则必可推出（ C ） A ．s ααα,,,21 中至少有一个向量为零向量 B ．s ααα,,,21 中至少有两个向量成比例C ．s ααα,,,21 中至少有一个向量可以表示为其余向量的线性组合D ．s ααα,,,21 中每一个向量都可以表示为其余向量的线性组合6．设A 为m×n 矩阵，则齐次线性方程组Ax=0仅有零解的充分必要条件是（ A ） A ．A 的列向量组线性无关 B ．A 的列向量组线性相关 C ．A 的行向量组线性无关D ．A 的行向量组线性相关Ax=0仅有零解⇔n A r =)(⇔ A 的列向量组线性无关．7．已知21,ββ是非齐次线性方程组Ax =b 的两个不同的解,21,αα是其导出组Ax =0的一个基础解系，21,C C 为任意常数，则方程组Ax =b 的通解可以表为（ A ） A ．)()(212121121ααC αC ββ++++ B ．)()(212121121ααC αC ββ+++-C ．)()(212121121ββC αC ββ-+++ D ．)()(212121121ββC αC ββ+++- )(2121ββ+是Ax =b 的特解，211,ααα+是Ax =0的基础解系． 8．设3阶矩阵A 与B 相似，且已知A 的特征值为2，2，3,则=-||1B （ A )A ．121 B ．71 C ．7 D ．12B 相似于⎪⎪⎪⎭⎫⎝⎛300020002，12300020002||==B ，121||||11==--B B ．9．设A 为3阶矩阵，且已知0|23|=+E A ，则A 必有一个特征值为( B ）A ．23-B ．32-C ．32 D ．23 0|23|=+E A ⇒032=--A E ⇒A 必有一个特征值为32-． 10．二次型312123222132142),,(x x x x x x x x x x f ++++=的矩阵为( C ） A ．⎪⎪⎪⎭⎫⎝⎛104012421B ．⎪⎪⎪⎭⎫⎝⎛100010421C ．⎪⎪⎪⎭⎫⎝⎛102011211D ．⎪⎪⎪⎭⎫⎝⎛120211011二、填空题（本大题共10小题,每小题2分，共20分）11．设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛100012021，B =⎪⎪⎪⎭⎫ ⎝⎛310120001，则A+2B =⎪⎪⎪⎭⎫⎝⎛720252023．12．设3阶矩阵A =⎪⎪⎪⎭⎫ ⎝⎛002520310,则=-1)(T A ⎪⎪⎪⎭⎫⎝⎛--002/1130250．→),(E A T⎪⎪⎪⎭⎫⎝⎛100010001053021200→⎪⎪⎪⎭⎫⎝⎛001100010200053021→⎪⎪⎪⎭⎫⎝⎛--001130010200010021 →⎪⎪⎪⎭⎫⎝⎛---001130250200010001→⎪⎪⎪⎭⎫ ⎝⎛--002/1130250100010001，=-1)(T A ⎪⎪⎪⎭⎫⎝⎛--002/1130250．13．设3阶矩阵A =⎪⎪⎪⎭⎫ ⎝⎛333022001,则A *A =⎪⎪⎪⎭⎫⎝⎛600060006．==*E A A A ||⎪⎪⎪⎭⎫⎝⎛==6000600066333022001E E ．14．设A 为m ×n 矩阵，C 是n 阶可逆矩阵，矩阵A 的秩为r ，则矩阵B =AC 的秩为__r__． B =AC ，其中C 可逆，则A 经过有限次初等变换得到B ,它们的秩相等．15．设向量)1,1,1(=α，则它的单位化向量为⎪⎪⎭⎫⎝⎛31,31,31．16．设向量T )1,1,1(1=α，T )0,1,1(2=α，T )0,0,1(3=α,T )1,1,0(=β,则β由321,,ααα线性表出的表示式为3210αααβ-+=．设332211αααβk k k ++=，即⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001011111110321k k k ,⎪⎩⎪⎨⎧==+=++110121321k k k k k k ，⎪⎩⎪⎨⎧-===101321k k k ．17．已知3元齐次线性方程组⎪⎩⎪⎨⎧=++=++=-+0320320321321321x x x ax x x x x x 有非零解，则a =__2__．02412141121200132132111=-=+=+=-a a a a ，2=a ．18．设A 为n 阶可逆矩阵，已知A 有一个特征值为2，则1)2(-A 必有一个特征值为41． 2=λ是A 的特征值，则41)2(1=-λ是1)2(-A 的特征值．19．若实对称矩阵A =⎪⎪⎪⎭⎫ ⎝⎛a a a 000103为正定矩阵，则a 的取值应满足30<<a ．031>=∆,031322>-==∆a a a，0)3(00010323>-==∆a a aa a ⇒30<<a ． 20．二次型2221212122),(x x x x x x f -+=的秩为__2__．⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫ ⎝⎛-=301112111112A ，秩为2．三、计算题（本大题共6小题，每小题9分，共54分）21．求4阶行列式1111112113114111的值．解：6300102010011000100010011020130011111112113114111===．22．设向量)4,3,2,1(=α，)0,2,1,1(-=β，求(1）矩阵βαT ；（2)向量α与β的内积),(βα．解：(1)()⎪⎪⎪⎪⎪⎭⎫⎝⎛----=-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=08440633042202110,2,1,14321βαT ；(2）50621),(=++-=βα． 23．设2阶矩阵A 可逆，且⎪⎪⎭⎫ ⎝⎛=-21211b ba a A ，对于矩阵⎪⎪⎭⎫ ⎝⎛=10211P ，⎪⎪⎭⎫ ⎝⎛=01102P ,令21AP P B =,求1-B ．解:⎪⎪⎭⎫ ⎝⎛-=-102111P ，⎪⎪⎭⎫ ⎝⎛=-011012P ，111121----=P A P B=⎪⎪⎭⎫⎝⎛0110⎪⎪⎭⎫ ⎝⎛2121b b a a ⎪⎪⎭⎫ ⎝⎛-1021=⎪⎪⎭⎫⎝⎛2121a ab b ⎪⎪⎭⎫ ⎝⎛-1021=⎪⎪⎭⎫⎝⎛--12112122a a a b b b ．24．求向量组T )3,1,1,1(1=α，T )1,5,3,1(2--=α，T )4,1,2,3(3-=α，T )2,10,6,2(4--=α的秩和一个极大线性无关组．解：⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----24131015162312311→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------85401246041202311→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------0700070041202311→⎪⎪⎪⎪⎪⎭⎫⎝⎛------0000070041202311，秩为3，321,,ααα是一个极大线性无关组．25．给定线性方程组⎪⎩⎪⎨⎧-=++-=++-=++223321321321ax x x x ax x a x x x ．(1)问a 为何值时，方程组有无穷多个解;（2）当方程组有无穷多个解时，求出其通解（用一个特解和导出组的基础解系表示)．解:（1)⎪⎪⎪⎭⎫ ⎝⎛---=2112113111a a a A →⎪⎪⎪⎭⎫ ⎝⎛-----a a a a a 110010103111，1=a 时，方程组有无穷多解;(2）1=a 时，A →⎪⎪⎪⎭⎫ ⎝⎛-000000002111,⎪⎩⎪⎨⎧==---=33223212x x x x x x x ，通解为⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-10101100221k k ． 26．求矩阵A =⎪⎪⎪⎭⎫ ⎝⎛------011101110的全部特征值及对应的全部特征向量．解:100010111)2(1111111)2(1212112111111||--+=+=+++==-λλλλλλλλλλλλλλλA E)2()1(2+-=λλ，特征值21-=λ，132==λλ．对于21-=λ，解齐次线性方程组0)(=-x A E λ:⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---=-000330211330330211112121211211121112A E λ⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--→000110101000110211，⎪⎩⎪⎨⎧===333231x x x x x x ，基础解系为⎪⎪⎪⎭⎫⎝⎛=111α,对应的全部特征向量为αk （k 是任意非零常数）；对于132==λλ,解齐次线性方程组0)(=-x A E λ：⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛=-000000111111111111A E λ，⎪⎩⎪⎨⎧==--=3322321x x x x x x x ，基础解系为⎪⎪⎪⎭⎫ ⎝⎛-=0111α，⎪⎪⎪⎭⎫⎝⎛-=1012α，对应的全部特征向量为2211ααk k +(21,k k 是不全为零的任意常数）．四、证明题（本大题6分)27．设A 是n 阶方阵，且0)(2=+E A ，证明A 可逆．证：由0)(2=+E A ,得022=++E A A ，E A A =+-)2(2，E A E A =+-)2(．所以A 可逆，且)2(1E A A +-=-．16全国2008年1月高等教育自学考试线性代数（经管类）试题答案课程代码：04184一、单项选择题（本大题共10小题，每小题2分，共20分） 1．设A 为三阶方阵且2||-=A 则=|3|A A T （ D ） A ．—108B ．—12C ．12D ．108108)2(27||3|3|223=-⨯==A A A T ．2．如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解,则k =（ B )A ．-2B ．—1C ．1D ．20)1(1241434014013=+=-=--k kkk ，1-=k ．3．设A 、B 为同阶方阵,下列等式中恒正确的是（ D ） A ．BA AB =B ．111)(---+=+B A B AC ．||||||B A B A +=+D ．T T T B A B A +=+)(4．设A 为四阶矩阵，且2||=A ，则=*||A （ C ) A ．2B ．4C ．8D ．12=*||A 82||||331===-A A n ．5．设β可由向量)0,0,1(1=α，)1,0,0(2=α线性表示,则下列向量中β只能是( B )A ．)1,1,2(B ．)2,0,3(-C ．)0,1,1(D ．)0,1,0(-),0,(212211k k k k =+=ααβ．6．向量组s ααα,,,21 的秩不为s (2≥s )的充分必要条件是（ C ） A ．s ααα,,,21 全是非零向量 B ．s ααα,,,21 全是零向量C ．s ααα,,,21 中至少有一个向量可由其它向量线性表出D ．s ααα,,,21 中至少有一个零向量s ααα,,,21 的秩不为s ⇔s ααα,,,21 线性相关．177．设A 为m n ⨯矩阵，方程AX =0仅有零解的充分必要条件是( C ) A ．A 的行向量组线性无关 B ．A 的行向量组线性相关 C ．A 的列向量组线性无关D ．A 的列向量组线性相关AX =0仅有零解⇔n A r =)(⇔A 的列向量组线性无关．8．设A 与B 是两个相似n 阶矩阵，则下列说法错误．．的是（ D ） A ．||||B A =B ．秩(A )=秩（B)C ．存在可逆阵P ，使B AP P =-1D ．BE A E -=-λλ9．与矩阵A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200010001相似的是（ A ）A ．⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100020001B ．⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200010011C ．⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200011001D ．⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100020101有相同特征值的同阶对称矩阵一定(正交）相似．10．设有二次型232221321),,(x x x x x x f +-=，则),,(321x x x f （ C )A ．正定B ．负定C ．不定D ．半正定当0,0,1321===x x x 时，0>f ；当0,1,0321===x x x 时0<f ．总之，f 有正有负．二、填空题（本大题共10小题，每小题2分,共20分） 11．若0211=k ，则k =21． 012211=-=k k ，21=k ． 12．设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤411023，B =⎢⎣⎡⎥⎦⎤010201，则AB =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡241010623． AB =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤411023⎢⎣⎡⎥⎦⎤010201=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡241010623．1813．设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤220010002，则=-1A ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-2/110010002/1． ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100010001220010002→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-120010001200010002→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-2/110010002/1100010001． 14．设A 为33⨯矩阵,且方程组Ax =0的基础解系含有两个解向量,则秩（A ）= __1__．秩（A )=123=-=-r n ．15．已知A 有一个特征值2-，则E A B 22+=必有一个特征值__6__．2-=λ是A 的特征值,则62)2(222=+-=+λ是E A B 22+=的特征值．16．方程组0321=-+x x x 的通解是T T k k )1,0,1()0,1,1(21+-．⎪⎩⎪⎨⎧==+-=3322321x x x x x x x ，通解是⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-10101121k k ． 17．向量组)0,0,1(1=α，)0,1,1(2=α,)0,2,5(3-=α的秩是__2__．⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛-000010001025011001,秩是2． 18．矩阵A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200020002的全部特征向量是T T T k k k )1,0,0()0,1,0()0,0,1(321++不全为零）（321,,k k k ．2321===λλλ，⎪⎪⎪⎭⎫ ⎝⎛=-000000000A E λ，⎪⎩⎪⎨⎧===332211x x x x x x ，基础解系为⎪⎪⎪⎭⎫ ⎝⎛001,⎪⎪⎪⎭⎫ ⎝⎛010，⎪⎪⎪⎭⎫⎝⎛100． 19．设三阶方阵A 的特征值分别为1,1,2-，且B 与A 相似，则=|2|B __—16__． =|2|B 16)2(810001000223-=-⨯=-．1920．矩阵A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-301012121所对应的二次型是3121232221321243),,(x x x x x x x x x x f +++-=．三、计算题(本大题共6小题,每小题9分，共54分）21．计算四阶行列式1002210002100021的值．解：151500021000210002118002100021000211040210021000211002210002100021-=-==-=．22．设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤101111123，求1-A ．解：⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100010001101111123→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤001010100123111101→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤---301110100220010101 →⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤----121110100200010101→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤----121110200200010202→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-----121110121200010002→⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤---2/112/11102/112/1100010001，1-A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤---2/112/11102/112/1．23．设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-200200011,B =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤300220011，且A ，B ，X 满足E X B A B E T T =--)(1，求X ，1-X ．解：由E X B A B E T T =--)(1，得E X A B E B T =--)]([1，即E X A BB BE T =--)(1,20E X A B T =-)(，=-1X ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-100020002100020002)(TT A B ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=10002/10002/1X ． 24．求向量组)4,2,1,1(1-=α，)2,1,3,0(2=α，)14,7,0,3(3=α，)6,5,1,2(4=α，)0,2,1,1(5-=α 的一个极大线性无关组．解：⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--021165121470321304211→⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---4002130213021304211→⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---4004000000021304211→⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--0004000000021304211， 421,,ααα是一个极大线性无关组．25．求非齐次方程组⎪⎪⎩⎪⎪⎨⎧=-+-+=+++-=-+++=++++12334523622232375432154325432154321x x x x x x x x x x x x x x x x x x x 的通解．解：=A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----12133452362210231123711111→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----------236281023622102362210711111 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------0006000000002362210711111→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------0000000006002362210711111 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000001002362210711111→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000001002362010711011→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---00000000010023620101651001， ⎪⎪⎪⎩⎪⎪⎪⎨⎧===--=++-=5544354254106223516x x x x x x x x x x x ，通解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1006501021000231621k k ．2126．设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤----020212022，求P 使AP P 1-为对角矩阵．解：λλλλλλλλλ4)2(4)2)(1(2021222||-----=--=-A E 86323+--=λλλ )2(3)42)(2()2(3)8(23+-+-+=+-+=λλλλλλλλ)4)(1)(2()45)(2(2--+=+-+=λλλλλλ，特征值21-=λ,12=λ，43=λ．对于21-=λ，解齐次线性方程组0)(=-x A E λ：⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---=-220220012220232012220232024A E λ→⎪⎪⎪⎭⎫⎝⎛--000220012 →⎪⎪⎪⎭⎫ ⎝⎛--000110012→⎪⎪⎪⎭⎫ ⎝⎛--000110102→⎪⎪⎪⎭⎫ ⎝⎛--0001102/101,⎪⎪⎩⎪⎪⎨⎧===33323121x x x x xx ，基础解系为⎪⎪⎪⎭⎫ ⎝⎛=112/11α；对于12=λ，解齐次线性方程组0)(=-x A E λ:⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛-=-120120021120101021120202021A E λ→⎪⎪⎪⎭⎫ ⎝⎛-000120021→⎪⎪⎪⎭⎫⎝⎛--000120101→⎪⎪⎪⎭⎫ ⎝⎛0002/110101，⎪⎪⎩⎪⎪⎨⎧=-=-=33323121x x x x x x ，基础解系为⎪⎪⎪⎭⎫ ⎝⎛--=12/112α；对于43=λ,解齐次线性方程组0)(=-x A E λ：⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛=-000210022420210022420232022A E λ→⎪⎪⎪⎭⎫ ⎝⎛000210011→⎪⎪⎪⎭⎫ ⎝⎛-000210201，22⎪⎩⎪⎨⎧=-==33323122xx x x x x ,基础解系为⎪⎪⎪⎭⎫⎝⎛-=1223α．令⎪⎪⎪⎭⎫ ⎝⎛---=11122/11212/1P ，则P 是可逆矩阵，使=-AP P 1⎪⎪⎪⎭⎫ ⎝⎛-400010002．四、证明题（本大题6分）27．设321,,ααα是齐次方程组Ax =0的基础解系，证明1α,21αα+，321ααα++也是Ax =0的基础解系．证：(1）Ax =0的基础解系由3个线性无关的解向量组成．（2）321,,ααα是Ax =0的解向量,则1α,21αα+,321ααα++也是Ax =0的解向量．（3）设0)()(321321211=+++++ααααααk k k ，则0)()(332321321=+++++αααk k k k k k ，由321,,ααα线性无关，得⎪⎩⎪⎨⎧==+=++000332321k k k k k k ，系数行列式01100110111≠=,只有零解0321===k k k ,所以1α，21αα+，321ααα++线性无关．由（1）（2）（3）可知,1α,21αα+，321ααα++也是Ax =0的基础解系．23全国2008年4月高等教育自学考试线性代数(经管类）试题答案课程代码:04184一、单项选择题（本大题共10小题，每小题2分，共20分）1．设行列式D =333231232221131211a a a a a a a a a =3，D 1=333231312322212113121111252525a a a a a a a a a a a a +++，则D 1的值为（ C ） A ．—15B ．-6C ．6D ．15D 1=620222555333231232221131211333131232121131111=+=+D a a a a a a a a a a a a a a a a a a ． 2．设矩阵⎪⎪⎭⎫ ⎝⎛+d b a 04=⎪⎪⎭⎫⎝⎛-32c b a ，则( C ) A ．3,1,1,3==-==d c b a B ．3,1,3,1===-=d c b a C ．3,0,1,3==-==d c b aD ．3,0,3,1===-=d c b a3,0,4,2===-=+d c b a b a ⇒3,0,1,3==-==d c b a ．3．设3阶方阵A 的秩为2,则与A 等价的矩阵为( B ）A ．⎪⎪⎪⎭⎫⎝⎛000000111B ．⎪⎪⎪⎭⎫⎝⎛000110111C ．⎪⎪⎪⎭⎫⎝⎛000222111D ．⎪⎪⎪⎭⎫⎝⎛3332221114．设A 为n 阶方阵，2≥n ，则=-|5|A （ A ） A ．||)5(A n -B ．||5A -C ．||5AD ．||5A n5．设A =⎪⎪⎭⎫ ⎝⎛4321，则=*||A （ B ）A ．-4B ．—2C ．2D ．424321||||||121-====--*A A A n ． 6．向量组s ααα,,,21 (2>s ）线性无关的充分必要条件是（ D ) A ．s ααα,,,21 均不为零向量B ．s ααα,,,21 中任意两个向量不成比例C ．s ααα,,,21 中任意1-s 个向量线性无关D ．s ααα,,,21 中任意一个向量均不能由其余1-s 个向量线性表示247．设3元线性方程组b Ax =，A 的秩为2,1η，2η,3η为方程组的解，T )4,0,2(21=+ηη，T )1,2,1(31-=+ηη，则对任意常数k ，方程组b Ax =的通解为（ D ）A ．T T k )1,2,1()2,0,1(-+B ．T T k )4,0,2()1,2,1(+-C ．T T k )1,2,1()4,0,2(-+D ．T T k )3,2,1()2,0,1(+取b Ax =的特解：T )2,0,1()(2121=+=ηηη； 0=Ax 的基础解系含一个解向量：T )3,2,1()()(312132=+-+=-=ηηηηηηα．8．设3阶方阵A 的特征值为2,1,1-，则下列矩阵中为可逆矩阵的是（ D ） A ．A E -B ．A E --C ．A E -2D ．AE --22-不是A 的特征值，所以0|2|≠--A E ,A E --2可逆．9．设λ=2是可逆矩阵A 的一个特征值，则矩阵12)(-A 必有一个特征值等于（ A ） A ．41 B ．21 C ．2 D ．42=λ是A 的特征值，则41)(12=-λ是12)(-A 的特征值．10．二次型432423222143212),,,(x x x x x x x x x x f ++++=的秩为( C ） A ．1 B ．2 C ．3 D ．4⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00001100001000011100110000100001A ，秩为3．二、填空题（本大题共10小题，每小题2分,共20分)11．行列式332313322212312111b a b a b a b a b a b a b a b a b a =__0__．行成比例值为零．12．设矩阵A =⎪⎪⎭⎫ ⎝⎛4321,P =⎪⎪⎭⎫ ⎝⎛1011，则=T AP ⎪⎪⎭⎫ ⎝⎛4723． =TAP ⎪⎪⎭⎫ ⎝⎛4321⎪⎪⎭⎫ ⎝⎛1101=⎪⎪⎭⎫⎝⎛4723．2513．设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛111110100，则=-1A ⎪⎪⎪⎭⎫ ⎝⎛--001011110．⎪⎪⎪⎭⎫⎝⎛100010001111110100→⎪⎪⎪⎭⎫ ⎝⎛001010100100110111→⎪⎪⎪⎭⎫ ⎝⎛--001011101100010011→⎪⎪⎪⎭⎫ ⎝⎛--001011110100010001． 14．设矩阵A =⎪⎪⎪⎭⎫⎝⎛54332221t ,若齐次线性方程组Ax =0有非零解，则数t =__2__． 02121412014022154332221||=-=----=----==t t t t A ,2=t ．15．已知向量组⎪⎪⎪⎭⎫ ⎝⎛-=2111α，⎪⎪⎪⎭⎫ ⎝⎛-=1212α,⎪⎪⎪⎭⎫⎝⎛=113t α的秩为2，则数t =__-2__．⎪⎪⎪⎭⎫ ⎝⎛--11212111t →⎪⎪⎪⎭⎫ ⎝⎛+--123013011t t t →⎪⎪⎪⎭⎫ ⎝⎛+--20013011t t t ，秩为2，则2-=t ． 16．已知向量T )3,0,1,2(=α，T k ),1,2,1(-=β，α与β的内积为2,则数k =32．2),(=βα，即23022=++-k ，3/2=k ．17．设向量Tb ⎪⎪⎭⎫⎝⎛=21,21,α为单位向量,则数b =__0__． 112121||22=+=++=b b α，0=b ． 18．已知λ=0为矩阵A =⎪⎪⎪⎭⎫ ⎝⎛-----222222220的2重特征值,则A 的另一特征值为__4__．021==λλ,220321++=++λλλ，所以43=λ．19．二次型32212322213212452),,(x x x x x x x x x x f +--+=的矩阵为⎪⎪⎪⎭⎫⎝⎛---510122021．2620．已知二次型232221321)2()1()1(),,(x k x k x k x x x f -+-++=正定，则数k 的取值范围为2>k ．⎪⎩⎪⎨⎧>->->+020101k k k ，⎪⎩⎪⎨⎧>>->211k k k ,2>k ．三、计算题（本大题共6小题，每小题9分，共54分）21．计算行列式D =4001030100211111的值．解：2202100111011112200210111011113110121011111114001030100211111-=----=----=------=．22．已知矩阵A =⎪⎪⎪⎭⎫ ⎝⎛-210011101,B =⎪⎪⎪⎭⎫⎝⎛410011103，(1）求A 的逆矩阵1-A ；(2）解矩阵方程B AX =．解：（1）⎪⎪⎪⎭⎫ ⎝⎛-100010001210011101→⎪⎪⎪⎭⎫ ⎝⎛---100011001210110101→⎪⎪⎪⎭⎫ ⎝⎛----111011001100110101→⎪⎪⎪⎭⎫ ⎝⎛-----111122112100010001→⎪⎪⎪⎭⎫ ⎝⎛-----111122112100010001,1-A =⎪⎪⎪⎭⎫ ⎝⎛-----111122112；（2）==-B A X 1⎪⎪⎪⎭⎫ ⎝⎛-----111122112⎪⎪⎪⎭⎫ ⎝⎛410011103=⎪⎪⎪⎭⎫⎝⎛-----322234225．23．设向量)1,1,1,1(--=α,)1,1,1,1(--=β,求(1)矩阵βαT A =；（2）2A ．27解：（1）βαT A ===--⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--)1,1,1,1(1111⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------111111*********1; （2)2A =⎪⎪⎪⎪⎪⎭⎫⎝⎛--------111111*********1⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------111111*********1=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------4444444444444444． 24．设向量组T )4,2,1,1(1-=α,T )2,1,3,0(2=α,T )14,7,0,3(3=α，T )0,2,1,1(4-=α,求向量组的秩和一个极大线性无关组，并将其余向量用该极大线性无关组线性表示．解：⎪⎪⎪⎪⎪⎭⎫⎝⎛--=01424271210311301),,,(4321αααα→⎪⎪⎪⎪⎪⎭⎫⎝⎛-4220011003301301→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2110011001101301→⎪⎪⎪⎪⎪⎭⎫⎝⎛-2000000001101301→⎪⎪⎪⎪⎪⎭⎫⎝⎛1000000001101301→⎪⎪⎪⎪⎪⎭⎫⎝⎛0000100001101301，向量组的秩为3，421,,ααα是一个极大线性无关组，=3α42103ααα++．25．已知线性方程组⎪⎩⎪⎨⎧=+-=-+--=+ax x x x x x x x 32132131522312 ，（1)求当a 为何值时,方程组无解、有解；（2）当方程组有解时，求出其全部解（要求用其一个特解和导出组的基础解系表示)．解:=),(b A ⎪⎪⎪⎭⎫ ⎝⎛----a 51223111201→⎪⎪⎪⎭⎫ ⎝⎛+---211011101201a →⎪⎪⎪⎭⎫ ⎝⎛+--300011101201a ．（1)3-≠a 时，方程组无解，3-=a 时,方程组有解;(2)3-=a 时，),(b A →⎪⎪⎪⎭⎫ ⎝⎛--000011101201，⎪⎩⎪⎨⎧=+=--=333231121x x x x x x ，全部解为⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-112011k ．2826．设矩阵A =⎪⎪⎭⎫⎝⎛2178，(1）求矩阵A 的特征值与对应的全部特征向量；（2）判定A 是否可以与对角阵相似,若可以，求可逆阵P 和对角阵Λ，使得Λ=-AP P 1．解：)9)(1(9102178||2--=+-=----=-λλλλλλλA E ，特征值11=λ，92=λ．对于11=λ，解齐次线性方程组0)(=-x A E λ：⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫⎝⎛----=-00111177A E λ，⎩⎨⎧=-=2221x x x x ，基础解系为 ⎪⎪⎭⎫⎝⎛-=111α，对应的全部特征向量为11αk （1k 是任意非零常数）；对于92=λ，解齐次线性方程组0)(=-x A E λ:⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎭⎫⎝⎛--=-00717171A E λ，⎩⎨⎧==22217x x x x ,基础解系为 ⎪⎪⎭⎫ ⎝⎛=172α，对应的全部特征向量为22αk （2k 是任意非零常数）．令⎪⎪⎭⎫ ⎝⎛-=1171P ,⎪⎪⎭⎫ ⎝⎛=Λ9001，则P 是可逆矩阵，使得Λ=-AP P 1．四、证明题(本题6分）27．设n 阶矩阵A 满足A A =2，证明A E 2-可逆,且A E A E 2)2(1-=--．证：由A A =2,得E A A E A A E A E A E =+-=+-=--4444)2)(2(2，所以A E 2-可逆，且A E A E 2)2(1-=--．29全国2008年7月高等教育自学考试线性代数（经管类）试题答案课程代码：04184一、单项选择题（本大题共10小题，每小题2分，共20分）1．设3阶方阵],,[321ααα=A ，其中i α（3,2,1=i )为A 的列向量，且2||=A ，则=+=|],,3[|||3221ααααB （ C ）A ．-2B ．0C ．2D ．6333231232221131211||a a a a a a a a a A =，2||333||333232312322222113121211==+++=A a a a a a a a a a a a a B ． 2．若方程组⎩⎨⎧=-=+002121x kx x x 有非零解,则k =（ A )A ．—1B ．0C ．1D ．201111||=--=-=k k A ，1-=k ．3．设A ,B 为同阶可逆方阵，则下列等式中错误的是（ C ) A ．||||||B A AB =B ．111)(---=A B ABC ．111)(---+=+B A B AD ．T T T A B AB =)(反例：⎪⎪⎭⎫ ⎝⎛=1001A ，⎪⎪⎭⎫⎝⎛--=1001B ． 4．设A 为三阶矩阵，且2||=A ,则=-*|)(|1A （ A ) A ．41 B ．1 C ．2 D ．441||1||1||1|)(|211====-*-*A A A A n ． 5．已知向量组A :4321,,,αααα中432,,ααα线性相关，那么( B ) A ．4321,,,αααα线性无关B ．4321,,,αααα线性相关C ．1α可由432,,ααα线性表示D ．43,αα线性无关部分相关⇒全体相关．。

经济数学《线性代数》期末试卷二(含答案解析)

《线性代数》试卷二一．选择题（每题3分，共30分）1.若行列式1023145xx 中，代数余子式121A =-，则21A =（） A.2 B.2- C.3 D.3- 【解答】由于31211(1)4545x A x =-=-=-，可解得1x =，进而有32102(1)215A =-=，故选A.2.已知A ，B 均为n 阶方阵，则必有（）A.222()2A B A AB B +=++ B.TTT()AB A B = C.n n AB O ⨯=时，A ，B 中至少有一个为零矩阵 D.以上都不对【解答】本题考察矩阵的乘法运算的性质.在A ，B 相乘可换时，选项A 才成立；()T T T AB B A =，故选项B 是错误的；n n AB O ⨯=说明B 的列向量组均为齐次方程组0Ax =的解向量，故选项C 亦不成立.故选D.3.设A 是m n ⨯矩阵，B 是n m ⨯矩阵，且AB E =，其中E 为m 阶单位矩阵，则（）. A. ()()r A r B m == B.()()，r A m r B n == C. ()()，r A n r B m == D. ()()r A r B n ==【解答】显然有()min{(),()}max{(),()}r AB r A r B r A r B m ≤≤≤，于是由AB E =可知()()r A r B m ==.故选A.4.向量组12,,,m ααα（3≥m ）线性无关的充要条件是（）A. 存在不全为零的数12,,,s k k k ，使11220s s k k k ααα+++=；B. 所给向量组中任意两个向量都线性无关；C. 所给向量组中存在一个向量，它不能用其余向量线性表示；D. 所给向量组中任意一个向量都不能用其余向量线性表示.【解答】本题考察线性无关的定义.选项A 为线性相关的定义；选项B.选项C 为必要条件；故选D.5.设向量⎪⎪⎪⎭⎫ ⎝⎛=001α，⎪⎪⎪⎭⎫ ⎝⎛=100β，下列选项中（）为βα,的线性组合.A.1B.⎪⎪⎪⎭⎫ ⎝⎛-=403ηC.⎪⎪⎪⎭⎫ ⎝⎛=022ηD.⎪⎪⎪⎭⎫⎝⎛-=010η【解答】由βα,的第二个分量均为零易知其线性组合亦必满足第二个分量为零，因此选B.6.当λ取（）时,方程组12323232132(3)(4)(2)x x x x x x x +-=-⎧⎪-=-⎨⎪-=--+-⎩λλλλλλ有无穷多解.A.1B.2C.3D.4【解答】思路同上题，欲使该方程组有无穷多解，系数行列式12131301λλ--=--必为零.故选C.7.设A 为n 阶实矩阵，T A 是A 的转置矩阵，则对于线性方程组（Ⅰ）0Ax =和（Ⅱ）T 0A Ax =必有（）.A.（Ⅱ）的解是（Ⅰ）的解，（Ⅰ）的解也是（Ⅱ）的解 B ．（Ⅱ）的解是（Ⅰ）的解，但（Ⅰ）的解不是（Ⅱ）的解 C ．（Ⅱ）的解不是（Ⅰ）的解，（Ⅰ）的解不是（Ⅱ）的解 D ．（Ⅰ）的解是（Ⅱ）的解，但（Ⅱ）的解不是（Ⅰ）的解【解答】事实上，齐次方程组（Ⅰ）0Ax =和（Ⅱ）T 0A Ax =为同解方程组.证明如下：一方面，显然（Ⅰ）的解是（Ⅱ）的解；另一方面，设β是（Ⅱ）的解，则T0A A β=，进而()()TT T 0A A A A ββββ==，由此可知0A β=，即β亦是（Ⅰ）的解.命题得证. 由此可知选A.8.设1λ与2λ是A 的两个互异特征值，ξ与η分别为其特征向量，则下列说法正确的是（） A ．对任意非零常数12,k k ，12k k ξη+均为A 的特征向量 B ．存在非零常数12,k k ，使得12k k ξη+均为A 的特征向量C ．对任意非零常数12,k k ，12k k ξη+均不是A 的特征向量D ．存在唯一的一组非零常数12,k k ，使得12k k ξη+均为A 的特征向量【解答】首先易知，ξ与η线性无关.又知对于任意非零常数12,k k ，若12k k ξη+为属于特征值3λ的特征向量，则有()123132A k k k k ξηλξλη+=+，()12121122A k k k A k A k k ξηξηλξλη+=+=+同时成立，于是()()1132230k k λλξλλη-+-=进而可知123λλλ==，与题设矛盾.故12k k ξη+不是A 的特征向量.选C.9.设矩阵1111400011110000,1111000011110000A B ⎛⎫⎛⎫⎪⎪⎪⎪== ⎪ ⎪⎪⎪⎝⎭⎝⎭,则A 与B （）.A.合同且相似B.合同但不相似C.不合同但相似D.不合同且不相似【解答】易知A 为对称矩阵且其特征值为4,0,0,0，故A 必可正交对角化为矩阵B .进而A 与B 合同且相似.故选A.10.二次型()2221231231223,,244f x x x x x ax x x x x =++--经正交变换化为标准形22212325f y y by =++，则（）A.3,1a b ==B.3,1a b ==-C.3,1a b =-= Ｄ.3,1a b =-=-【解答】由题意知，矩阵12022202A a -⎛⎫⎪=-- ⎪ ⎪-⎝⎭的特征值为2,5,b ，直接计算可知3,1a b ==-，故选B.二．填空题（每题3分，共18分）1．设A 为4阶方阵，且A 的行列式13A =，则12A -= . 【解答】易知13A -=，故1412216348A A --==⨯=.2.已知1231100011000100000101n n na a a D a a ---=-,若12--=+n n n n D a D kD ,则k = .【解答】按最后一行展开，得()()121312100011000100110000011n n n n n n a a a D a D a +-----=+---()()1121211n n n n n n n n a D D a D D +-----=+--=+,所以1k =.3.若非齐次方程组123412341234 242 217411x x x x x x x x x x x x λ+-+=⎧⎪-++=⎨⎪+-+=⎩ 有解，则λ=【解答】非齐次方程组有解当且仅当增广矩阵化为行阶梯阵时，最后一个非零行不具有“有且只有最后一个元素非零”的形式，于是直接计算可知5λ=。

武汉大学线代试题2007-2008B(工54A卷)

武汉大学数学与统计学院2007－2008第二学期《线性代数B 》（A 卷，工54）学院专业学号姓名注：所有答题均须有详细过程，内容必须写在答题纸上，凡写在其它地方一律无效。

一、（10分）计算下列行列式；1. 123123123123n n n n nx a a a a a x a a a a a x a a D a a a xa +++=+;2. 若12312,,,,αααββ都是四维列向量，且四阶行列式12311223,,m n αααβααβα==求四阶行列式()32112αααββ+.二、（10分）若有不全为零的数12,,,,m λλλ使1111m m m m O λαλαλβλβ+++++=成立，则12,,,m ααα线性相关，12,,,m βββ也线性相关.试讨论该结论是否正确？三、（12分）设3阶方阵200121101⎛⎫⎪=- ⎪ ⎪⎝⎭A ，试求：1、A 的特征值和特征向量；2、kA （k 为正整数）及其特征值和特征向量。

四、（15分）当λ为何值时，方程组123123123322,x x x x x x x x x λλλλ++=-⎧⎪++=-⎨⎪++=-⎩有唯一解、无解、有无穷多解？在有解时，求出方程组的解.五、（15分）设二次型()22212312313,,222T f x x x X AX ax x x bx x ==+-+()0,b >其中二次型的矩阵A 的特征值之和为1，特征值之积为12.-1、,a b 的值；2、用正交变换将二次型f 化为标准形，并写出所用的正交变换与正交矩阵.六（18分）在四维实向量构成的线性空间4R 中,已知：12341111011100110001,,,αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭；1234111111102001100,,,a a ββββ--⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭。

线性代数期末考试试卷+答案

大学线性代数期末考试题一、填空题（将正确答案填在题中横线上。

每小题2分，共10分）1. 若022150131=---x ，则=χ__________。

2．若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解，则λ应满足。

3．已知矩阵n s ij c C B A ⨯=)(，，，满足CB AC =，则A 与B 分别是阶矩阵。

4．矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性。

5．n 阶方阵A 满足032=--E A A ，则=-1A 。

二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。

每小题2分，共10分）1. 若行列式D 中每个元素都大于零，则0〉D 。

（）2. 零向量一定可以表示成任意一组向量的线性组合。

（）3. 向量组m a a a ，，， 21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，， 21线性相关。

（）4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ，则A A =-1。

（）5. 若λ为可逆矩阵A 的特征值，则1-A 的特征值为λ。

( )三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。

每小题2分，共10分)1. 设A 为n 阶矩阵，且2=A ，则=T A A （）。

① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα，，， 21（3 ≤ s ≤ n ）线性无关的充要条件是（）。

① s ααα，，， 21中任意两个向量都线性无关 ② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示④ s ααα，，， 21中不含零向量 3. 下列命题中正确的是( )。

① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ，B 均为n 阶方阵，下面结论正确的是( )。

线代期末考试B卷及答案

2011－2012学年第一学期期末考试《线性代数》试卷（B ）评阅人:_____________ 总分人：______________一、单项选择题。

(本大题共10小题，每小题3分,共30分) 1．下列等式中正确的是（） A ．()222A B A AB BA B +=+++ B ．()TT T AB A B = C ．()()A B A B A B -+=-22　D ．()33A A A A -=-22.设⎪⎪⎪⎭⎫ ⎝⎛=311132213A 则21a 的代数余子式21A 的值为（）A. 1.B. 1-C. 2.D. 2-3．设12,ββ是非齐次线性方程组AX b =的两个解，则下列向量中仍为方程组解的是（） A ．ββ12+B ．12ββ-C ．1222ββ+ D ．12325ββ+ 4．设0λ是可逆矩阵A 的一个特征值，则21A -必有一个特征值是（）A ．210λ B ．021λ C ．20λD ．2λ 5．设向量组(I)：1α，2α，…r α，向量组(II)：1α，2α，…r α，1r +α，…，s α则必有（）。

A ．若(I)线性无关，则(II)线性无关B ．若(II)线性无关，则(I)线性无关C ．若(I)线性无关，则(II)线性相关D ．若(II)线性相关，则(I)线性相关6.设⎪⎪⎪⎭⎫ ⎝⎛-=211121113A 的三个特征值分别是321,,λλλ，则321λλλ++的值等于（） A. 0. B. 1. C. 2. D. 3.7.已知A 是一个43⨯阶矩阵，则下列命题正确的是( )__________________系__________专业___________班级姓名_______________ 学号_______________………………………………（密）………………………………（封）………………………………（线）………………………………2 A. 若A 中所有三阶子式都为零，则 2.R AB. 若 2.R A则A 中所有三阶子式都为零C. 若A 中所有二阶子式都不为零，则 2.R AD. 若 2.R A则A 中所有二阶子式都不为零8.．设n 阶方阵A 的0=A 则A 的列向量（）A ．0)(=A RB ． 0)(≠A RC ．线性相关D ．线性无关 9.设向量组A 可由向量组B 线性表示，则有（）A. )()(B R A R ≤B. )()(B R A R ≥C. )()(B R A R =D. 不能确定)(A R 和)(B R 的大小. 10．设n 元线性方程组Ax =b 且为()()n b A R A R ==,，则该方程组（）A.有唯一解；B.有无穷多解；C.无解；D.不确定。

2007-2008线性代数

2007-2008第二学期考试课程：线性代数班级：学号：一、选择题(每题3分,共15分)1．设行列式D =333231232221131211a a a a a a a a a =3，D 1=333231312322212113121111252525a a a a a a a a a a a a +++，则D 1的值为（） (A) -15 (B) –6 (C) 6 (D) 152．设A 为n 阶方阵，2n ≥，则5A -=（）(A) (5)n A - (B) (5)A - (C) 5A (D) 5n A 3. 向量组12,,S ααα (2s >) 线性无关的充分必要条件是（）(A) 12,,S ααα 均不为零向量(B) 12,,S ααα 中任意两个向量不成比例 (C) 12,,S ααα 中任意1s -个向量线性无关(D)12,,S ααα 中任意一个向量均不能由其余的1s -个向量线性表示4．设λ=2是可逆矩阵A 的一个特征值，则矩阵21()A -必有一个特征值等于（）(A)14(B)12(C) 2 (D) 45. 设n n j i a A ⨯=)(, 则二次型∑=+++=ni n n i i i n x a x a x ax x x f 12221121)(),,,( 的矩阵为（）(A) A (B) 2A (C) A A T(D) TAA二．填空题(每题3分,共15分)1. 设矩阵1234A ⎛⎫= ⎪⎝⎭，1101p ⎛⎫= ⎪⎝⎭，则TAP =2. 方阵 1 2 32 2 13 4 3A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则1A -=3. 已知向量组⎪⎪⎪⎭⎫ ⎝⎛-=α2111，⎪⎪⎪⎭⎫ ⎝⎛-=α1212，⎪⎪⎪⎭⎫ ⎝⎛=α113t 的秩为2，则数t =__________4. 设矩阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=18121321841812132b a A 为正交矩阵，则=a ,=b 5．已知二次型222123123(,,)(1)(1)(3)f x x x k x k x k x =++-+-正定，则数k 的取值范围为________三.解答题（10分）计算n 阶行列式12121233 3n n n x x x x x x x x x +++四.解答题（14分）当λ为何值时，非齐次线性方程组12312321231x x x x x x x x x λλλλλ⎧++=⎪++=⎨⎪++=⎩有唯一解，无解，无穷多解，并求出无穷多解时的通解。

2007线性代数期末试卷(B)

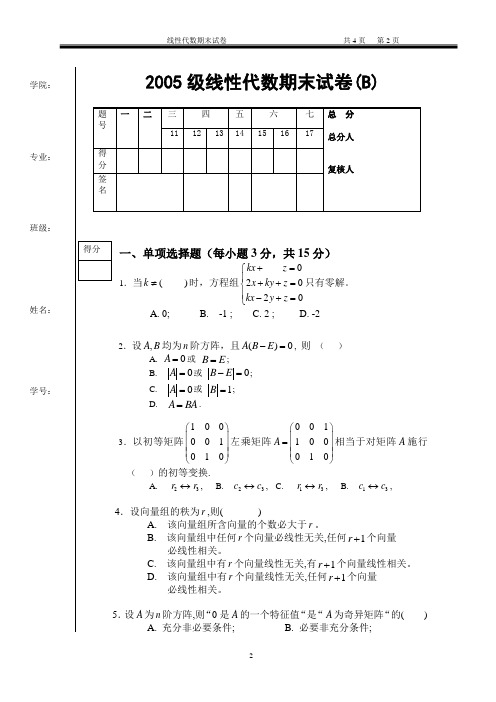
学院：专业：班级：装姓名：线学号：2005级线性代数期末试卷(B)一、单项选择题（每小题3分，共15分）1．当()k ≠时，方程组02020kx z x ky z kx y z +=⎧⎪++=⎨⎪-+=⎩只有零解。

A. 0;B. -1 ;C. 2 ;D. -22．设,A B 均为n 阶方阵，且()0A B E -=, 则（） A. 0A =或 B E =;B. 0A =或 0B E -=;C. 0A =或 1B =;D. A BA =.3．以初等矩阵100001010⎛⎫ ⎪ ⎪ ⎪⎝⎭左乘矩阵001100010A ⎛⎫ ⎪= ⎪⎪⎝⎭相当于对矩阵A 施行（）的初等变换.A. 23r r ↔,B. 23c c ↔,C. 13r r ↔, B. 13c c ↔,4．设向量组的秩为r ,则( )A. 该向量组所含向量的个数必大于r 。

B. 该向量组中任何r 个向量必线性无关,任何1r +个向量必线性相关。

C. 该向量组中有r 个向量线性无关,有1r +个向量线性相关。

D. 该向量组中有r 个向量线性无关,任何1r +个向量必线性相关。

5．设A 为n 阶方阵,则“0是A 的一个特征值“是“A 为奇异矩阵“的( )A. 充分非必要条件;B. 必要非充分条件;C. 既非充分也非必要条件;D. 充分必要条件。

二、填空题（每小题3分，共15分） 6．设()2201x x e f x =，则()'0f =7．设A,B 均为n 阶方阵，2,3A B ==-，则*12A B -= 。

8．设A 是43⨯矩阵，且()2R A =，而102020103B ⎛⎫ ⎪= ⎪ ⎪-⎝⎭，则()R AB = 。

9．设()()()1231,1,1,,0,,1,3,2a b ααα===，若1,23,ααα线性相关，则,a b 满足关系式。

10．设n 阶方阵A 有n 个特征值0,1,2,,1n -,且方阵B 与A 相似，则B E += 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学院：
专业：
班级：
装
姓名：
线
学号： 2008年春线性代数期末试卷(B)
一、单项选择题（每小题3分，共15分） 1.行列式2222111a ab b a a b b +=（） A. ()3a b -; B. ()3b a -; C. ()3a b +; D. ()2a b -.
2. 设n 阶方阵,,A B C 满足关系式ABC E =，其中E 是n 阶单位阵，则必有（） A. ACB E =； B. CBA E =； C. BAC E =； D. B C A E =.
3. 对于齐次线性方程组，以下说法正确的是（）
A. 若0AX =有解，则必有0A ≠；
B. 若0AX =无解，则必有0A =；
C. 若0AX =有非零解，则必有0A ≠；
D. 若0AX =唯有零解，则必有0A ≠。

4. 已知()()()1232,6,12,4,2,1,2,1,1,3,6,2,T
T T
ααα==-=-
()43,5,10,2,T α=()52,1,2,10T
α=-，则该向量组得秩为（）
A. 2；
B. 1；
C. 4；
D. 3。

5. 实二次型()2
322212
13214,,x x x x tx x x x f +++=秩为2，则=t （）.
A. 1;
B. 4;
C. 3;
D. 2.
二、填空题（每小题3分，共15分） 6．设A 为33⨯矩阵，且A ＝2，则=*A A ；
7．设矩阵020003400A ⎛⎫ ⎪= ⎪ ⎪⎝⎭
，则1A -=
8．设矩阵110211301A -⎛⎫ ⎪= ⎪ ⎪⎝⎭
，则齐次线性方程组0AX =的自由向量的个数为个；
9．矩阵1234234534564567A ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭
，则A 的秩为
10．实二次型()222121212,tx x x x x x f ++=正定，则t 应满足不等式
三、计算题（每小题10分，共50分）
11. 计算行列式11111111
1111
1111x x D y y
+-=+-
12．解矩阵方程100301120121023X ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭
13.
求线性方程组⎪⎪⎩⎪⎪⎨⎧=--+=--+=+-+=+-13413212302432143214321421x x x x x x x x x x x x x x x 的通解。

14．已知向量组()()()()12341,2,2,3,6,6,1,,0,3,
0,4,2T T T T
αααα====-，
求出它的一个最大无关组。

15.
利用施密特正交化向量组121121,1102αα⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭。

16.已知方阵
100
212
312
A
-⎛⎫
⎪
= ⎪
⎪
⎝⎭
，求m
A
17. 设方阵A 有一个特征值为2=λ，证明：方阵E A A B 22+-=有一个特征值为4。