西安交通大学计算方法(C)讲义
西南交通大学计算机程序设计基础(C++)

西南交通大学C++实验报告计算机程序设计基础(C++)实验1一、实验目的1.熟悉C++程序的集成开发环境;2.学习新建和打开控制台应用程序的方法;3.掌握简单数据运算,以及输入与输出方法。
二、实验任务1.输入一摄氏温度,输出显示所转换的华氏温度。
(提示:摄氏温度=(华氏温度-32)×5/9)2.画出一头威武雄壮的雄狮。
,%%%%%%,%%/\%%%%/\%,%%%\c "" J/%%%%. %%%%/ o o \%%%`%%. %%%% _ |%%`%% `%%%%(__Y__)%// ;%%%%`\-/%%%'(( / `%%%%%%%'\\ .' |\\ / \ | |\\/ ) | |\ /_ | |__(___________)))))))三、实验结果(源程序+ 注释)1.源程序#include<iostream>using namespace std;void main(){double a,b;cout<<"请输入一摄氏温度:"<<endl;cin>>a;b=a*9/5+32;cout<<"转换的华氏温度为:"<<b<<endl;}2.源程序#include<iostream>using namespace std;void main(){cout<<" ,%%%%%% "<<endl;cout<<" ,%%/\%%%%/\% "<<endl;cout<<" ,%%%\c "" J/%%% "<<endl;cout<<"%. %%%%/ o o \%%% "<<endl;cout<<"`%%. %%%% _ |%% "<<endl;cout<<" `%% `%%%%(__Y__)% "<<endl;cout<<" // ;%%%%`\-/%%%' "<<endl;cout<<"(( / `%%%%%%%' "<<endl;cout<<" \\ .' | "<<endl;cout<<" \\ / \ | | "<<endl;cout<<" \\/ ) | | "<<endl;cout<<" \ /_ | |__ "<<endl;cout<<" (___________))))))) "<<endl;}实验2一、实验目的1.掌握对一般数据的输入和输出格式控制方法;2.掌握对实型数据输出形式的设置和小数位数的控制方法;3.了解数据输入的相关注意事项。
西安交通大学《计算方法》课程课件-第五章

特点
(1)速度快:Newton迭代法比简单迭代法收敛快
(2)由于要计算导数,因此计算量稍大
可以使用一点Newton迭代法
x ( k 1)
(k ) (k ) f ( x ) f ( x ) (k ) x( k ) x , k 0,1, 2... (k ) (0) f ( x ) f ( x )
因此,由连续函数的介值定理知, , 必有x* [a, b], 使 ( x* ) 0
即有x* ( x* ), 因此, ( x)在[a, b]中存在不动点x* (2)证明根唯一 __ __ __ 若 ( x)在[a, b]还有一个不动点 x ,使 x = ( x ),则
x x (x ) ( x) q x x x x
第5章 非线性方程求解 5.2 收敛性问题 5.2.1 简单迭代---不动点
证明: (1)证明有根 由条件(2)知,函数 ( x)连续 ,构造辅助函数 ( x) x ( x)
则 ( x)在[a, b]上也连续 ,由条件(1)知 ( a ) a (a) 0 同理 (b) b (b) 0
否则令x
(k )
x ,取I
( k 1)
(k )
=[ x , x( k 1) ]
( k 1)
__
(4)计算区间长度,若 x
x
x( k ) x( k 1) < , 则停止,令x , 输出 2
*
否则,令k k 1, 转(2)
第5章 非线性方程求解 5.2 收敛性问题 5.2.1 简单迭代---不动点
x( k 1) ( x( k ) ), k 0,1, 2,...
(5-3)
C语言解决多元多次方程

一 理论背景我们先考虑线性方程,线性方程组的解便不难得出了。
与线性方程相比,非线性方程问题无论是从理论上还是从计算公式上,都要复杂得多。
对于一般的非线性方程()0f x =,计算方程的根既无一定章程可寻也无直接法可言。
例如,求解高次方程组637 1.50x x x -+-=的根,求解含有指数和正弦函数的超越方程cos()0xe x π-=的零点。
解非线性方程或方程组也是计算方法中的一个主题。
在解方程方面,牛顿(I . Newton )提出了方程求根的一种迭代方法,被后人称为牛顿算法。
三百年来,人们一直用牛顿算法,改善牛顿算法,不断推广算法的应用范围。
牛顿算法,可以说是数值计算方面的最有影响的计算方法。
对于言程式()0f x =,如果()f x 是线性函数,则它的求根是容易的。
牛顿法实质上是一种线性化方法,其基本思想是将非线性方程式()f x 逐步归结为某种线性方程来求解。
解非线性方程组只是非线性方程的一种延伸和扩展。
二 主要理论 考虑方程组111(,...)0,.................(, 0n n n f x x f x x =⎧⎪⎨⎪=⎩ ()1 其中1,...,n f f 均为1(,...)n x x 多元函数。
若用向量记号记11(,...),(,...,)T n T n n x x x R F f f =∈=,()1 就可写成()0.F x = (2)当2,n ≥,且(1,...,)i f i n =中至少有一个是自变量(1,...,)i x i n = 的非线性函数时,则称方程组(1)为非线性方程组。
非线性方程组求根问题是前面介绍的方程即(1)n =求根的直接推广,实际上只要把单变量函数()f x 看成向量函数()F x 则可将单变量方程求根方法推广到方程组(2)。
若已给出方程组(2)的一个近似根 ()1(,...,),k k k Tnx x x = 将函数()F x 的分量()(1,...,)i f x i n =在()k x 用多元函数泰勒展开,并取其线性部分,则可表示为 ()()()()()()().k k k F x F xF x x x '≈+-令上式右端为零,得到线性方程组()()()()()(),k k k F x x x F x '-=- (3) 其中111122221212()()()()()()()()()()n n n n n n f x f x f x x x x f x f x f x x x x F x f x f x f x x x x ∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎢⎥'=⎢⎥⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥∂∂∂⎣⎦L L MM M L(4) 称为()F x 为雅可比(Jacobi )矩阵。
大学C 程序设计教程 - 西安交通大学共25页文档

语句序列可以是一个语句,也可以是复合语句结构(分程序)
6
分程序
{ <局部数据变量说明部分> <执行语句段>
}
▪ 分程序在语法上是一个整体,相当于一个语句。 ▪ 分程序中也可以再嵌套新的分程序,用以构成更加复杂
的控制结构。
7
选择结构(之二)
▪ 多路(开关)选择语句 :
switch(整数表达式)
{ case 数值1: 语句序列1; …... case 数值n: 语句序列n; [default : 语句序列n+1;]
条件?
不成立
9
循环结构(之二)
▪ for语句用来实现计数循环: for (<表达式1>; <表达式2>; <表达式3>)
<循环体>
10
C++数据类型的分类
11
类型不同的数据之间的混合算术运算
▪ 不同类型的数据在参加运算之前会自动转换成 相同的类型, 然后再进行运算。
▪ 转换规则
• 转换的原则是由低级向高级转换 char -> int -> float -> double
化)处理,最后到求解域中只是比较简单的编程问题。
20
基本思想和方法
▪ 基本思想
• 从问题本身开始,经过逐步求精,将解决问题的步骤分解为由 基本程序结构模块组成的结构化程序框图,据此编写程序。
▪ 基本方法
• 从题目本身开始, 找出解决问题的基本思路, 将其用结构化框 图(可能是非常粗糙)表示。
• 对框图中的比较抽象的、用文字描述的模块进一步分析细化, 结果仍用结构化框图表示。
23
结束语
西安交通大学计算方法C讲义--资料

计算方法(C)目录第1章绪论1.1 数值计算1.2 数值方法的分析1.2.1计算机上数的运算1.2.2算法分析第2章线性代数方程组2.1 Gauss消去法2.1.1消去法2.1.2主元消去法2.2 矩阵分解2.2.1Gauss消去法的矩阵意义2.2.2矩阵的LU分解及其应用2.2.3其他类型矩阵的分解2.2.4解三对角矩阵的追赶法2.3线性方程组解的可靠性2.3.1向量和矩阵范数2.3.2残向量与误差的代数表征2.4解线性方程组解的迭代法2.4.1基本迭代法2.4.2迭代法的矩阵表示2.4.3收敛性第3章数据近似3.1 多项式插值3.1.1插值多项式3.1.2Lagrange插值多项式3.1.3Newton插值多项式3.1.4带导数条件的插值多项式3.1.5插值公式的余项3. 2 最小二乘近似3.2.1 最小二乘问题的法方程3.2.2 正交化算法第4章数值微积分4.1 内插求积,Newton-Cotes公式4.1.1Newton-Cotes公式4.1.2复化求积公式4.1.3步长的选取4.1.4Romberg方法4.1.5待定系数法4.2数值微分4.2.1插值公式方法4.2.2Taylor公式方法(待定系数法)4.2.3外推法第5章非线性方程求解5.1 解一元方程的迭代法5.1.1简单迭代法5.1.2Newton法5.1.3割线法5.1.4区间方法5.2 收敛性问题5.2.1简单迭代——不动点5.2.2收敛性的改善5.2.3Newton法的收敛性5.2.4收敛速度第1章绪论1.1数值计算现代科学的发展,已导致科学与技术的研究从定性前进到定量,尤其是现代数字计算机的出现及迅速发展,为复杂数学问题的定量研究与解决,提供了强有力的基础。
通常我们面对的理论与技术问题,绝大多数都可以从其物理模型中抽象出数学模型,因此,求解这些数学模型已成为我们面临的重要任务。
一、本课程的任务:寻求解决各种数学问题的数值方法——如何将高等数学的问题回归到初等数学(算术)的方法求解——了解计算的基础方法,基本结构(否则只须知道数值软件)——并研究其性质。
西安交通大学复数与复变函数教学PPT

解得 a x, 所以
b x2 1
1 2ix x 2 1 ( x i x 2 1)
西安交通大学
例3.证明 | z1 z2 |2 | z1 z2 |2 2(| z1 |2 | z2 |2 ), 并说明几何意义 证:| z1 z2 |2 ( z1 z2 )( z1 z2 )
y Im( z )
所以,2)的方程为
Im( z ) 5
z z 10i 0
zz zz ,y 方程较复杂时,一般用: x 2 2i
西安交通大学
例6 说明下列方程所表示的平面图形.
1. z 2i z 2 2. z 1, Im z 0
解:
1. z 2i z 2
再将模变到原来的r2倍
y
r1r2
z1 z2
r2
2
z2 1 2
r1 z1
1 2
o
1
x
西安交通大学
类似得
z1 r1 i (1 2 ) e . z2 r2
从而
两个复数商的模等于它们模的商; 两个复数商的辐角等于它们辐角的差.
西安交通大学
2)复数的乘幂与方根 n次幂
z r e z .z ...z
西安交通大学
例1.计算 3 8 ,并说明几何意义。 解:3 8 3 8e i 2e
k 0,1,2 2k 2k 2 cos( ) i sin( ) , k 0,1,2 3 3 1 i 3 k0 y 2 k 1 w1 k2 1 i 3 ,
18世纪: 1. 欧拉(L.Euler)建立复数理论,
西安交通大学《计算方法》课件-第六章
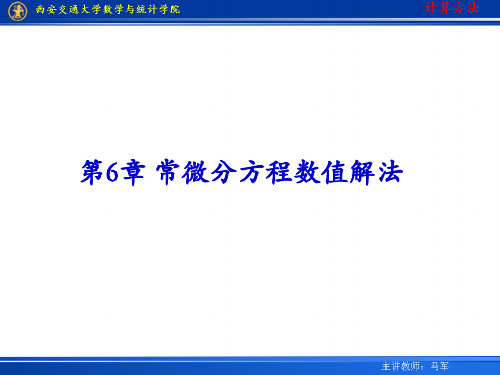
当f (t , y)在区域a t b c y d 中连续 ,且对变量y
满足Lipschitz条件 :对t [a, b] , y1 , y2 [c, d ] , 都有
f (t , y1 ) f (t , y2 ) L y1 y2 (6-2)
其中L为常数 则初值问题(6-1)的解存在且唯一
y(t ) f (t , y (t ))确定了函数y (t )在平面 上的方向场
yi 1 yi hf (ti , yi )是y(ti 1 )的一个近似,即由(ti , yi )到(ti 1 , yi 1 )的 直线段局部近似代替了由(ti , y(ti ))到(ti 1 , y(ti 1 ))的曲线
( 3)可以看出后退Euler方法比Euler方法的结果更好一些
显式方法:由yi直接计算yi 1的算法 隐式方法:不能直接由yi直接计算yi 1,而需要从方程中求解yi 1的算法
第6章 常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.2 多步法
对于微分方程 y f ( t , y( t ))
条件下是
h h2 (b a) y( ) O(h), a b y (i ) 2 i 1 2
N
若初值问题(6-1)通过某一种数值方法得到yN ,则最终误差 E ( y(b), h) y(b) - yN
称为总体截断误差 简记为 EN
第6章 常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.1 Euler方法及其变形
令t0 0, y0 1 yi 1 yi h( yi 2sin ti )进行计算,得到数值解.
程序演示
第6章 常微分方程数值解法
例.用Euler法求解初值问题
计算方法课件适合打印版

在F (2,3, -1, 2)中
2
(0.100 2 ) (0.110 2 ) 0.110 2
在F (2,3, -1, 2)中
(0.100 20 ) (0.111 20 ) 0.1101 21
(0.100 20 ) (0.110 21 ) 0.110 22
第1章 绪论
1.2 数值方法的分析
1.2 数值方法的分析
1.2.1 计算机上数的运算 浮点数运算结果产生误差的情况 (3)在浮点数系中数据的尾数字长t是有限
1.2.1 计算机上数的运算
浮点运算应注意
(4)在相同的指数条件下,两个数量相差较大的数字相 加(减)时,较小数的有效数字会被丧失
(1)避免产生大结果的运算,尤其是避免小数作为除数 参加运算; (2)避免“大”“小”数相加减; (3)避免相近数相减,防止大量有效数字损失; (4)尽可能简化运算步骤,减少运算次数。
算法SUM4(A,n,S) 将数组A中的数按其符号分成两组,分别按算法 SUM3求和,最后计算和S 1. 0->n1;0->n2; 2. For i=1,2,…,n 2.1 if a[i]>=0 then n1+1->n1; a[i]->b[n1]; else n2+1->n2; a[i]->c[n2]; 3. 调用SUM3(B,n1,S1); 4. 调用SUM3(C,n2,S2); 5. S1+S2->S
定义 通常以计算机完成操作 a+b*c ,即一次浮点加法 一次浮点乘法,所需的时间作为一个时间单位,称为 浮点运算,记为flop.
例1.3 设A1 , A2 , A3 , A4分别为10 20, 20 50,50 1,1100的矩阵,则按 结合律,有
西安交通大学《计算方法》课件-第一章
浮点运算原则
(1)避免产生大结果的运算,尤其是避免小数作为除数 参加运算 (2)避免“大”“小”数相加减 (3)避免相近数相减,防止大量有效数字损失 (4)尽可能简化运算步骤,减少运算次数
第1章 绪论
定义 数据相对小的变化引起解的相对大的变化的问题 称为病态问题,否则称为良态问题。
问题的性态就是指问题的解对原始数据扰动的敏感性
第1章 绪论
浮点数系运算误差
(2)计算结果的尾数多于t位数字
在F (2,3,1,2)中
(0.100 20 ) (0.111 20 ) 0.1101 21 (0.100 22 ) (0.111 21 ) 0.1000111 22
需要对结果进行舍入处理,产生的差称为舍入误差
记为F ( , t , L,U )
l
将计算机中所能表示的全体数的集合称为计算机的浮点数系
浮点数系中的数的个数是有限的,其个数为
2( 1) t 1 (U L 1) 1
第1章 绪论
浮点数系的误差
在计算机的浮点数系中,四则运算是非封闭的 为使经过算术运算产生的结果仍然要用浮点数系中的数 表示,因此必须用一个比较接近的数来代替 因此产生误差 称此误差称为舍入误差
第1章 绪论
第1章 绪论
什么是计算方法
《计算方法》介绍基本的数学问题中的主要数值方法, 介绍方法的思想、结构、条件、对输入数据的要求、生成 数据的意义、应注意的事项等 介绍数值计算中的一些最基本的概念 设计常见应用问题的数值处理方法 对数值方法的数值特性进行研究 分析方法的可靠性 分析方法的效率
第1章 绪论
问题的性态
已知问题f ( x)的输入数据只有一个 ,用x来表示 若有两个输入数据x和~ x , 则可以得到两个不同的结果f ( x)和f ( ~ x)
第1章C语言程序设计概述-西安交大.

利用循环实现,算法简练。
例2 将50个学生中成绩在80分以上者打印出来。
i变量记录人数,g 变量存放成绩
S1:1→ i
S2:输入学生成绩 → g
S3:如果g≥80,打印g;否则,不打印;
S4: i +1 → i
S5:如果i≤50,重新执行S2及后面;否则,算法 结束
算法特性
• • • • • 有穷性 确定性 有零个或多个输入 有一个或多个输出 有效性
}
通过以上例子可以看出: 1.C程序是由函数构成的。每个C源程序由一个或多个 函数组成,其中必须有且仅有一个主函数main( )。 2. 一个函数由两部分组成:函数说明部分+函数体。 (1)函数说明部分:包括函数名、函数类型、函数参 数(形参)名、形式参数类型。 如:int max(int x,int y ,int z),其中: int max (int x, int y ,int z) 函数类型 函数名 形式参数(类型+名) (2)函数体部分:包括声明部分和执行部分
N–S流程图 1.顺序结构
2.选择结构
Y
S1 S2 3.循环结构 当满足件时
循环体
S1
条件 N
S2
循环体
直到条件满足时 直到型循环
当型循环
传统流程图与N-S流程图的比较
开始 0t,1i t+it i+1i
0t,1i
t+it
i+1i 直到 t100
不成立
输出 t 的值
t100 成立 输出 t 的值 结束
美国国家标准学会在以前C版本的基础上制定了 一个C语言标准,通常称之为ANSI C。 微机上常用的C:Microsoft C,Turbo C,, Borland C 等
西安交通大学C++复习课件

2012.8
0
2.温度转换。输入华氏温度,用下列公式将其转 换为摄氏温度并输出。
5 C ( F 32) 9
样例输clude <iostream> using namespace std; int main() { double c,f; cin>>f; c=5.0/9*(f-32); cout<<c<<endl; return 0; }
23
13.求a+aa+aaa+aaaa+...+aa...a(第n项,n个a),其 中a是1~9的整数。例如,a=1,n=3时,式子为 1+11+111;当a=5,n=4时,式子为5+55+555+5555。 样例输入输出: 输入: 25 输出: 24690
2015-3-6
24
int main(){ int a,n,u=0,sum=0; int i; cin>>a>>n; for(i=1;i<=n;i++) { u=u*10+a; sum=sum+u; } cout<<sum<<endl; return 0; }
int main() { int a,b,c,x,z; cin>>a>>b>>c; x=a+b+c; y=x/3.0; z=(int)(y+0.5); cout<<x<<endl; cout<<y<<endl; cout<<z<<endl; return 0; }
2015-3-6
一种快速求取空间任意两条曲线交点的算法

! 戴葵等译 R(美)/5FA01 SR 85251" 86T5F> PR +CUBA=" /5FV 8R PC5WC 著 R
X 焦李成 R 神经网络的应用与实现 R 西安:西安电子科技大学出版社, !**YR
’ 孙靖民 R 机械优化设计 R 北京:机械工业出版社,!**%R % 许崎,李永生,威学成 R 梯度法与 PQ 神经网络的结合在机械优化设
2在两条曲线存在交点的区间内计算两条曲线的最短距离在两条曲线存在交点可能的参数区间内利用控制顶点正算出所对应的曲线段求两条曲线的最短距离
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!"
《机械设计与制造》 ,GAR #&&’ -6R % /5G=01CFM +C@021 _ /51BD5GABFC
所对应的两条曲线没有交点,如图 0 + ; , 和图 0 + < , 所示。
上述判断原理的算法步骤为:
%=*&06 分别选取两条曲线控制多边形的其中一条边。
%=*&"6 计算 !0 和 !",如果 !0 与 !" 方向相反,计算 !! 与 !5,如果 !! 与 !5 方向相反,则所对应的两条曲线存在相交的可 能性,分别记录所对应的控制顶点 + !" $ 0/ !"/ !" 7 0/ !" 7 " , 、+ -$ $ 0/ -$/ -$ 7 0/ -$ 7 " , 及参数区间,以备下一步处理。如果 !! 与 !5 方向相 同,则所对应的两条曲线没有交点。如果 !0 与 !" 方向相同,则 所对应的两条曲线也没有交点。
西安交通大学热传学课件:传热学9-2

d qm1c1 dห้องสมุดไป่ตู้1
d qm2c2 dt 2
《传热学》讲义
14
《传热学》讲义
d qm1c1 dt1 d qm2c2 dt 2
dt1
1 qm1c1
d
dt 2
1 qm2c2
d
dt dt1 dt2
dt
1 qmhch
1 qmccc
d
d
d k dA t 15
《传热学》讲义
dt d k dA t
5
《传热学》讲义
壳管式换热器(1-2型)
6
《传热学》讲义
壳管式换热器(2-4型)
7
《传热学》讲义
壳式换热器(螺旋折流板)
8
《传热学》讲义
板式换热器
9
《传热学》讲义
螺旋板式换热器
10
《传热学》讲义
交叉流换热器
11
《传热学》讲义
二 简单顺流与逆流的平均温差计算
传热方程的一般形式
kAtm
dt kdA
t
tx dt k Ax dA
t t
0
ln
tx t
k Ax
16
《传热学》讲义
tx t e(kAx )
tm
1 A
A 0
t xdAx
tm
1 A
A 0
tekAx dAx
t ' A
1
k
e k Ax
A
0
t ' ekA 1
k A
17
tm
t '
k A
e k A
tm (tm )ctf
• (tm )ctf 是给定的冷热流体的进出口温度布
西南交大数值计算

西南交⼤数值计算1.秦九韶算法利⽤秦九韶算法简化求多项式1110n n n n x a x a y x a a --=++++ 的值的运算式,并写程序计算多项式42352x y x x =--+在1x =-点处的值。
1.2秦九韶算法简化多项式计算多项式1110n n n n x a x a y x a a --=++++ 的值:1.直接计算i i x a ,逐项相加,共需要加法和乘法的次数为n 次、2)1(+n n 次; 2.⽤秦九韶算法简化,则y=(…0121)...))(a x a x a x a x a n n n +++++--,从内到外逐步计算⼀次多项式的值,共需要加法和乘法的次数各为n 次。
2.⽜顿法及基于⽜顿算法下的Steffensen 加速法分别⽤⽜顿法,及基于⽜顿算法下的Steffensen 加速法(1) 求ln(x +sin x )=0的根。
初值x0分别取0.1, 1,1.5, 2, 4进⾏计算。
(2) 求sin x =0的根。
初值x0分别取1,1.4,1.6, 1.8,3进⾏计算。
分析其中遇到的现象与问题。
2.1 问题分析⽜顿法是⼀种迭代法,是求⽅程根的重要⽅法之⼀,通过使⽤函数f(x)在近似根0x 附近的⼀阶泰勒多项式近似表⽰来寻找⽅程的根,在⽅程f(x) = 0的单根附近具有平⽅收敛。
其迭代公式为:)()(1k k k k x f x f x x '-=+ Steffensen 加速法公式:)()()(x f x f x x '-=? )(n n x y ?= )(n n y z ?=nn n n n n n x y z x y x x +---=+2)(212.2求ln(x+sinx)=0的根 2.2.1⽜顿法kk k k k k k x x x x x x x sin cos 1)sin ln(1+++-=+2.2.2 Steffensen 加速法 2.2.3 结果及分析初值⽜顿法结果(循环次数) Steffensen 加速法结果(循环次数)0.1 0.5109734294(7) -2.118746196 0.2 0.5109734294(6) 0.5109734294(5) 0.5 0.5109734294(4)0.5109734294(3) 1 0.5109734294(6)0.5109734294(5)1.5 溢出 1.5 2 溢出 2 4溢出4(误差限为20-e )2.3求sinx=0的根 2.3.1 ⽜顿法kkk k x x x x cos sin 1-=+ 2.3.2 Steffensen 加速法 2.3.3 结果及分析初值⽜顿法结果(循环次数) Steffensen 加速法结果(循环次数)1 溢出 01.43.1415926535898(7) -3.141592651(4)1.6 31.4159265358965(8) 25.13274123(6) 1.8 6.28318530141765(4) 6.283185307(3) 33.14159265330048(3) 3.141592654(3)3.数值积分(1)实际验证梯形求积公式、Simpson 求积公式、Newton-Cotes 求积公式的代数精度。
西安交通大学计算方法C讲义

计算方法(C)目录第1章绪论1。
1 数值计算1。
2 数值方法的分析1.2.1计算机上数的运算1.2.2算法分析第2章线性代数方程组2。
1 Gauss消去法2.1.1消去法2.1.2主元消去法2.2 矩阵分解2.2.1Gauss消去法的矩阵意义2.2.2矩阵的LU分解及其应用2.2.3其他类型矩阵的分解2.2.4解三对角矩阵的追赶法2.3线性方程组解的可靠性2.3.1向量和矩阵范数2.3.2残向量与误差的代数表征2.4解线性方程组解的迭代法2.4.1基本迭代法2.4.2迭代法的矩阵表示2.4.3收敛性第3章数据近似3。
1 多项式插值3.1.1插值多项式3.1.2Lagrange插值多项式3.1.3Newton插值多项式3.1.4带导数条件的插值多项式3.1.5插值公式的余项3. 2 最小二乘近似3.2.1 最小二乘问题的法方程3.2.2 正交化算法第4章数值微积分4.1 内插求积,Newton-Cotes公式4.1.1Newton—Cotes公式4.1.2复化求积公式4.1.3步长的选取4.1.4Romberg方法4.1.5待定系数法4.2数值微分4.2.1插值公式方法4.2.2Taylor公式方法 (待定系数法)4.2.3外推法第5章非线性方程求解5。
1 解一元方程的迭代法5.1.1简单迭代法5.1.2Newton法5.1.3割线法5.1.4区间方法5。
2 收敛性问题5.2.1简单迭代—-不动点5.2.2收敛性的改善5.2.3Newton法的收敛性5.2.4收敛速度第1章绪论1。
1数值计算现代科学的发展,已导致科学与技术的研究从定性前进到定量,尤其是现代数字计算机的出现及迅速发展,为复杂数学问题的定量研究与解决,提供了强有力的基础.通常我们面对的理论与技术问题,绝大多数都可以从其物理模型中抽象出数学模型,因此,求解这些数学模型已成为我们面临的重要任务.一、本课程的任务:寻求解决各种数学问题的数值方法—-如何将高等数学的问题回归到初等数学(算术)的方法求解—-了解计算的基础方法,基本结构(否则只须知道数值软件)——并研究其性质.立足点:面向数学——解决数学问题面向计算机—-利用计算机作为工具充分发挥计算机的功能,设计算法,解决数学问题例如:迭代法、并行算法二、问题的类型1、离散问题:例如,求解线性方程组bAx= -—从离散数据:矩阵A和向量b,求解离散数据x;2、连续问题的离散化处理:例如,数值积分、数值微分、微分方程数值解;3、离散问题的连续化处理:例如,数据近似,统计分析计算;1.2数值方法的分析在本章中我们不具体讨论算法,首先讨论算法分析的基础--误差.一般来讲,误差主要有两类、三种(对科学计算):1)公式误差-—“截断误差”,数学↔计算,算法形成——主观(人为):数学问题-数值方法的转换,用离散公式近似连续的数学函数进行计算时,一般都会发生误差,通常称之为“截断误差”;——以后讨论2)舍入误差及输出入误差——计算机,算法执行—-客观(机器):由于计算机的存储器、运算器的字长有限,在运算和存储中必然会发生最末若干位数字的舍入,形成舍入误差;在人机数据交换过程中,十进制数和二进制数的转换也会导致误差发生,这就是输入误差.这两种误差主要是由于计算机的字长有限,采用浮点数系所致。
第4章-管内气液两相流的阻力计算-讲义版

内容概要
4.1
Chapter 4. 管内气液两相流的阻力计算 (Gas-liquid flow resistance calculation) 4.2 4.3
王树众 教授 西安交通大学能源与动力工程学院
引言 摩擦压降计算 加速压降 重位压力降
4.4 4.5
局部阻力
2
4.1 引言
压力降计算是气液两相流研究中最重要的课题之一 只有正确地进行压力降计算,才能使系统具有安全可靠和足够的 压头,才能为动力设备的选型以及安全经济运行提供必要的依据。 气液两相流的压力降包括四部分,即重位压力降、摩擦阻力压力降、 加速压力降和局部阻力压力降,亦即: △PT= △ Pg+ △ Pf+ △ Pa+ △ Pb 式中 △ PT -总压力降
2 L
2 L
假设汽水两相分开流动时都呈紊流状态,同时利用常压下的 空气—水混合物试验数据和高压汽—水混合物的试验数据建
2 立了 L0
PF f ( x, p )的关系曲线。 P0
该方法适用于双组分的气液两相流在低压时摩擦阻力计算,因其计算数据是建 立在低压的气液流动基础之上的(双组分低压下的流动更趋于气液流动的流型) 为了适用于汽—水混合物的摩擦阻力压力降的计算,mastinelli-nelson对此方 法进行了改进。
x
G
(1 x )
L
(4-9) 按此法计算,当干度x=1时,不能正确反映全部为气体流过 时的数值,因为在此计算法中 f (ReL )的函数不能转化为气体 雷诺数的函数。为了避免这一不足,有些作者采用一个平均 的两相动力黏度 值来表明 和 的关系。这一 值和干度x 的关系应能满足当x=0时, ,当 x=1时, 的条件 L G ( L及G分别为液体及气体的动力黏度)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算方法(C)目录第1章绪论1.1 数值计算1.2 数值方法的分析1.2.1计算机上数的运算1.2.2算法分析第2章线性代数方程组2.1 Gauss消去法2.1.1消去法2.1.2主元消去法2.2 矩阵分解2.2.1Gauss消去法的矩阵意义2.2.2矩阵的LU分解及其应用2.2.3其他类型矩阵的分解2.2.4解三对角矩阵的追赶法2.3线性方程组解的可靠性2.3.1向量和矩阵范数2.3.2残向量与误差的代数表征2.4解线性方程组解的迭代法2.4.1基本迭代法2.4.2迭代法的矩阵表示2.4.3收敛性第3章数据近似3.1 多项式插值3.1.1插值多项式3.1.2Lagrange插值多项式3.1.3Newton插值多项式3.1.4带导数条件的插值多项式3.1.5插值公式的余项3. 2 最小二乘近似3.2.1 最小二乘问题的法方程3.2.2 正交化算法第4章数值微积分4.1 内插求积,Newton-Cotes公式4.1.1Newton-Cotes公式4.1.2复化求积公式4.1.3步长的选取4.1.4Romberg方法4.1.5待定系数法4.2数值微分4.2.1插值公式方法4.2.2Taylor公式方法(待定系数法)4.2.3外推法第5章非线性方程求解5.1 解一元方程的迭代法5.1.1简单迭代法5.1.2Newton法5.1.3割线法5.1.4区间方法5.2 收敛性问题5.2.1简单迭代——不动点5.2.2收敛性的改善5.2.3Newton法的收敛性5.2.4收敛速度第1章绪论1.1数值计算现代科学的发展,已导致科学与技术的研究从定性前进到定量,尤其是现代数字计算机的出现及迅速发展,为复杂数学问题的定量研究与解决,提供了强有力的基础。
通常我们面对的理论与技术问题,绝大多数都可以从其物理模型中抽象出数学模型,因此,求解这些数学模型已成为我们面临的重要任务。
一、本课程的任务:寻求解决各种数学问题的数值方法——如何将高等数学的问题回归到初等数学(算术)的方法求解——了解计算的基础方法,基本结构(否则只须知道数值软件)——并研究其性质。
立足点:面向数学——解决数学问题面向计算机——利用计算机作为工具充分发挥计算机的功能,设计算法,解决数学问题例如:迭代法、并行算法二、问题的类型1、离散问题:例如,求解线性方程组bAx=——从离散数据:矩阵A和向量b,求解离散数据x;2、连续问题的离散化处理:例如,数值积分、数值微分、微分方程数值解;3、离散问题的连续化处理:例如,数据近似,统计分析计算;1.2数值方法的分析在本章中我们不具体讨论算法,首先讨论算法分析的基础——误差。
一般来讲,误差主要有两类、三种(对科学计算):1)公式误差——“截断误差”,数学↔计算,算法形成——主观(人为):数学问题-数值方法的转换,用离散公式近似连续的数学函数进行计算时,一般都会发生误差,通常称之为“截断误差”;——以后讨论2)舍入误差及输出入误差——计算机,算法执行——客观(机器):由于计算机的存储器、运算器的字长有限,在运算和存储中必然会发生最末若干位数字的舍入,形成舍入误差;在人机数据交换过程中,十进制数和二进制数的转换也会导致误差发生,这就是输入误差。
这两种误差主要是由于计算机的字长有限,采用浮点数系所致。
首先介绍浮点数系1.2.1 计算机上的运算——浮点运算面向计算机设计的算法,则先要讨论在计算机上数的表示。
科学记数法——浮点数:约定尾数中小数点之前的数全为零,小数点后第一个数不能为零。
目前,一般计算机都采用浮点数系,一个存储单元分成首数和尾数:首数 尾数(位)其中首数存放数的指数(或“阶”)部分,尾数存放有效数字。
对于β进制,尾数字长为t 位的浮点数系),,,(U L t F β中的(浮点)数,可以用以下形式表示:t j jd d l tt d dd x fl ,,3,2,011)221()( =<≤<≤⨯++±=ββββββ此处,指数l (称为阶)限制在U l L ≤≤范围内。
以下记实数系中的实数为R x ∈,它在浮点数系),,,(U L t F β中对应的浮点数记为),,,()(U L t F x fl β∈——β进制,t 尾数位数,U L ,阶的范围。
几乎所有近代计算机都采用“二进制”(即2=β):位、字节和字分别是指位数不同的二进制数。
例如位是一个二进制数(即0或1);字节是8个二进制数字;上表的最后一列是字节。
单精度浮点数(single precision )按32位存储,双精度浮点数(double precision )按64位存储。
精度用于指明每个浮点数保留多少位以及尾数和阶数各分配多少位。
单精度浮点数的尾数为23位、阶数为8位;双精度浮点数的尾数为53位(包含符号位)、阶数为11位(包含符号位)。
双精度浮点数的等价二进制数如下所示:位位尾数符号位位指数(含符号位)645211ddddd ddd f bb bbbb 浮点数的特点:1、 实数转换到浮点数——浮点化,〈缺点:〉总会产生误差(除极个别的情况: ,2,1,0,2±±==l x l )按 四舍五入,绝对误差:t l x fl x -≤-β21)((举例),〈优点:〉浮点化产生的相对误差有界(与数字本身的数量级无关)t x x fl x x -≤-=121)()(βδ 注:设实数R x ∈,则按β进制可表达为:1,,,3,2,011)11221(+=<≤<≤⨯+++++++±=t t j j d d l t t d t t d d d x βββββββ按四舍五入的原则,当它进入浮点数系),,,(U L t F β时,若β211<+t d ,则 l tt d dd x fl ββββ⨯+++±=)221()(若β211≥+t d ,则 ltt d d d x fl ββββ⨯++++±=)1221()(对第一种情况:t l lt l t t d x fl x -++=⨯≤⨯+=-βββββ21)21(1)()(11对第二种情况:t l lt l t t d x fl x -++=⨯≤⨯--=-ββββββ21)21(1)(11就是说总有: tl x fl x -≤-β21)( 另一方面,由浮点数要求的 β<≤11d , 有lx ββ1≥,将此两者相除,便得t x x fl x -≤-121)(β2、每一个浮点数系的数字有限: 1)1()1(21++---L U t ββ3、浮点数系中的运算非自封闭,(因为数字有限、尾数字长有限、指数数字有限等)例:在)5,5,4,10(-F 中,32102001.,105420.⨯=⨯=-y x ,运算y x *和y x /,的结果显然已不在此浮点数系内,而y x +或y x -也不在此浮点数系内,需)(y x fl 结果才在此浮点数系内。
浮点运算应注意:1)避免产生大结果的运算,尤其是避免小数作为除数参加运算; 2)避免“大”“小”数相加减;3)避免相近数相减,防止大量有效数字损失; 4)尽可能简化运算步骤,减少运算次数。
原因:记tx x fl x x -=-==121)(max)(max βδ∆,由x x fl x ∆≤-)(,可得: y x y x fl y x ∆≤-)()( (“。
”表示任意一种四则运算)此处 ∆ 是由机器字长(实质上是尾数字长t 的大小)确定的常数(它反映了实际运算的精度)。
显然,若要求运算的舍入误差小,应使运算结果(如:yx y x y x ,,⋅±)较小。
尤其是小分母运算:yy x y x δδ=-+,小y ⇒大误差。
其次,当浮点数系中两个数量级相差较大的数相加(或减),注意到由于浮点数系中数字字长的有限性,可能导致“大数吃小数”。
例如,)5,5,4,10(-F 中13102317.,108231.-⨯=⨯=y x ,则x y x =⨯±⨯=⨯±⨯=±-3313100000.108231.102317.108231.似乎)(x y y <<没有参加运算。
第三,同样,由于浮点数系中数字字长的有限性,当两个相近数相减时:例如,在)5,5,8,10(-F 中,331082317832.,1082317844.⨯=⨯=y x ,两数相减:31012000000.-⨯=-y x ,计算结果仅剩2位有效数字,而原来参加运算的数字有8位有效数字,这将严重影响最终计算结果的精度。
1.2.2 算法分析作为一个可用的算法,必须考虑其效率和可靠性,定义:计算机完成一个乘法和一个加法,称为一个浮点运算(记为flop ); 注:由于计算机在运算时,加(减)法所耗时间远少于乘(除)法,所以通常只须计算乘法的次数,因此也有“一个算法需要多少个‘乘法’”这一提法。
1、计算效率——可计算性(计算复杂性——空间、时间)例:解线性方程组b Ax =的Grammar 方法:AA ii x =,其中A 是方程组系数矩阵A 对应的行列式,而i A 则是以右端向量b 替代A 的第i 列所得矩阵对应的行列式。
由线性代数知识可知,若)(ij α=A ,则∑-=n nni ii i i i J ααα 212121),()1(A ,其中),,,(21n i i i J 是由{n ,,2,1 }变换到{n i i i ,,21}所需的置换次数。
可见每计算一个行列式,需要!)1(n n ⋅-个浮点运算;因此,按Grammar 方法解方程组约需!)1(2n n N ⋅-= 个浮点运算。
当20=n 时 201070728.9⨯≈N ,用一个运算速度为秒/108的计算机进行求解,约需510078.3⨯年(日前报道我国计算机已达到/1038408⨯秒,这仍需近10年)。
而n=20的方程组应该说是一个小型的方程组。
因此Grammar 方法是一个不能接受的算法,它缺乏可计算性。
第二章将介绍的Gauss 消去法和迭代法就有较高的效率,具有很好的可计算性。
2、计算可靠性作为算法,除了考虑其效率外,必须重视可靠性,它包括两方面: 问题的性态 和 方法的稳定性 问题的性态所计算的问题当原始数据发生小扰动时,问题的解一般也发生扰动。
问题的性态——问题的解对原始数据发生变化的敏感性。
原始数据小扰动⇒问题解 ⎩⎨⎧—问题是病态的—大变化—问题是良态的—小扰动例:线性方程组:⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++604751413112134131216113121321321321x x x x x x x x x 的解是:⎪⎪⎪⎭⎫ ⎝⎛=111X若将方程组的系数改写成具有2位有效数字的小数:⎪⎩⎪⎨⎧=++=++=++78.020.025.033.01.125.033.050.08.133.050.000.132132121x x x x x x x x x 的解则变成:⎪⎪⎭⎫ ⎝⎛--=65.3325.3822.6~X ;这是一个典型的病态方程组。
