第六章玻耳兹曼统计ppt演示文稿
合集下载
玻尔兹曼分布律重力场中粒子按高度分布

玻尔兹曼分布律在物理学中的应用
气体分子运动论
01
玻尔兹曼分布律是气体分子运动论的基础,可以用来描述气体
分子在平衡态下的速度分布和能量分布。
热力学
02
玻尔兹曼分布律在热力学中也有广泛应用,如热力学第二定律、
熵的概念等都涉及到玻尔兹曼分布律。
固体物理
03
在固体物理中,玻尔兹曼分布律可以用来描述电子在金属中的
05 结论与展望
研究结论
玻尔兹曼分布律在重力场中粒 子按高度分布的研究表明,在 一定条件下,粒子分布符合玻
尔兹曼分布。
随着高度的增加,粒子分布 逐渐稀疏,但仍保持玻尔兹
曼分布特征。
重力场对粒子分布的影响表现 为在低处粒子聚集,高处粒子 较少,这与玻尔兹曼分布的特
性相符合。
研究限制与不足
01
本研究仅限于理论分析和模拟,未能进行实际实验验证。
能量状态
根据能量守恒,可以得出 粒子在重力场中的能量状 态由动能和势能共同决定。
能量变化
在重力场中,粒子的能量 会发生变化,主要表现在 动能和势能之间的转换。
03 玻尔兹曼分布律与重力场 的结合
玻尔兹曼分布律在重力场中的适用性
玻尔兹曼分布律适用于粒子在平衡态 下的分布情况,当粒子受到重力作用 时,其分布情况同样适用玻尔兹曼分 布律。
玻尔兹曼分布律重力 场中粒子按高度分布
目录
CONTENTS
• 玻尔兹曼分布律的概述 • 重力场中粒子的运动规律 • 玻尔兹曼分布律与重力场的结合 • 实验验证与结果分析 • 结论与展望
01 玻尔兹曼分布律的概述
定义与特性
定义
玻尔兹曼分布律是描述粒子在平衡态下按能量分布的规律,其数学表达式为f(E) = exp(-E/kT),其中E为粒子能量,k为玻尔兹曼常数,T为绝对温度。
《物理化学第4版》第六章6.4 玻尔兹曼分布ppt课件

即 q0 = qt·qr qv0qe0qn0
能量零点的选择对玻尔 兹曼分布有无影响 ?
ni
N
gq0 qe0 kT
形式完全相同!
ni
N q
g i e i
kT
N q0 eε 0
kT
g e
ε
0 i
ε
0
kT
i
N q0
g eε
0 i
i
kT
结论:对玻尔兹曼分布中任一能级上粒子的分布
4. 能量零点的选择对配分函数的影响
设粒子的能级为ε0,ε1,ε2,…,则
q
g i e i
kT
g 0 e 0
kT
g e1 / kT 1
i
通常选择粒子的基态能级作为能量的零点(任何能级的
能量不为负),各能级的能量为 i0 i 0
q0
g ei0 i
kT
g eε
0 0
0
kT
g1eε
0 1
/ kT
数 ni 没有影响。
结论:选择不同的能量零点会影响配分函数的
值,但对计算玻尔兹曼分布中任一能级上粒子 的分布数 ni 没有影响。
注意:
由基态能级的能位为零的粒子 配分函数q0,计算所得系统系
U
nii
ni
(
0 i
0)
统的热力学函数U、H、A、G
i
i
,与由绝对能量对应的粒子配
ni
0 i
N 0
kT
i
振动配分函数
qv
g e v,i v ,i
kT
i
电子配分函数
qe
g ee ,i e ,i
kT
i
能量零点的选择对玻尔 兹曼分布有无影响 ?
ni
N
gq0 qe0 kT
形式完全相同!
ni
N q
g i e i
kT
N q0 eε 0
kT
g e
ε
0 i
ε
0
kT
i
N q0
g eε
0 i
i
kT
结论:对玻尔兹曼分布中任一能级上粒子的分布
4. 能量零点的选择对配分函数的影响
设粒子的能级为ε0,ε1,ε2,…,则
q
g i e i
kT
g 0 e 0
kT
g e1 / kT 1
i
通常选择粒子的基态能级作为能量的零点(任何能级的
能量不为负),各能级的能量为 i0 i 0
q0
g ei0 i
kT
g eε
0 0
0
kT
g1eε
0 1
/ kT
数 ni 没有影响。
结论:选择不同的能量零点会影响配分函数的
值,但对计算玻尔兹曼分布中任一能级上粒子 的分布数 ni 没有影响。
注意:
由基态能级的能位为零的粒子 配分函数q0,计算所得系统系
U
nii
ni
(
0 i
0)
统的热力学函数U、H、A、G
i
i
,与由绝对能量对应的粒子配
ni
0 i
N 0
kT
i
振动配分函数
qv
g e v,i v ,i
kT
i
电子配分函数
qe
g ee ,i e ,i
kT
i
热力学统计 第六章 课件

系统的微观运动状态就是它的力学运动状态。
全同粒子组成的系统就是由具有完全相同的内禀属性 (相同的质量、电荷、自旋等)的同类粒子组成的系统。
近独立粒子组成的系统,是指系统中粒子之间相互作 用很弱,相互作用的平均能量远小于单个粒子的平均能量,因而 可以忽略粒子间的相互作用,将整个系统的能量表达为单 个粒子能量之和
3
不确定关系指出,粒子坐标的不确定值Δq和与之共
轭的动量的不确定值Δp满足ΔqΔp≈h。
如果用坐标q和动量p来描述粒子的运动状态,一个状 态必然对应于μ空间的一个体积,称之为一个相格。
对于自由度为1的粒子,相格大小为h。如果粒子自由 度为r,各自由度的坐标和动量的不确定值Δqi和Δpi分别 满足ΔqiΔpi≈h,相格的大小为 Δq1…Δqr Δp1 … Δpr≈hr
由此,前一式可理解为,将μ空间的体积Vdpxdpydpz除以 相格大小h3而得到的三维自由粒子在Vdpxdpydpz内的量子
态数。
对于自由粒子的动量,若采用球极坐标p、θ、φ来描 写,则有 px p sin cos , py p sin sin , pz p cos 动量空间体积元为p2sinθdpdθdφ。
§6.2 粒子运动状态的量子描述
微观粒子普遍具有波粒二象性。
德布罗意提出,能量为ε、动量为 p 的自由粒子联系 着圆频率为ω、波矢为 k 的平面波(德布罗意波)。
能量ε与圆频率ω,动量 p 与波矢 k 的关系为
, p k
此式称为德布罗意关系,适用于一切微观粒子。常量h和
ħ=h/2π都称为普朗克常量,数值为
经典描述 设粒子的自由度为r。 经典力学指出,粒子在任一时刻的力学运动状态由粒
子的r个广义坐标
q1,q2 ,…,qr 和与之共轭的r个广义动量 p1,p2,…,pr
全同粒子组成的系统就是由具有完全相同的内禀属性 (相同的质量、电荷、自旋等)的同类粒子组成的系统。
近独立粒子组成的系统,是指系统中粒子之间相互作 用很弱,相互作用的平均能量远小于单个粒子的平均能量,因而 可以忽略粒子间的相互作用,将整个系统的能量表达为单 个粒子能量之和
3
不确定关系指出,粒子坐标的不确定值Δq和与之共
轭的动量的不确定值Δp满足ΔqΔp≈h。
如果用坐标q和动量p来描述粒子的运动状态,一个状 态必然对应于μ空间的一个体积,称之为一个相格。
对于自由度为1的粒子,相格大小为h。如果粒子自由 度为r,各自由度的坐标和动量的不确定值Δqi和Δpi分别 满足ΔqiΔpi≈h,相格的大小为 Δq1…Δqr Δp1 … Δpr≈hr
由此,前一式可理解为,将μ空间的体积Vdpxdpydpz除以 相格大小h3而得到的三维自由粒子在Vdpxdpydpz内的量子
态数。
对于自由粒子的动量,若采用球极坐标p、θ、φ来描 写,则有 px p sin cos , py p sin sin , pz p cos 动量空间体积元为p2sinθdpdθdφ。
§6.2 粒子运动状态的量子描述
微观粒子普遍具有波粒二象性。
德布罗意提出,能量为ε、动量为 p 的自由粒子联系 着圆频率为ω、波矢为 k 的平面波(德布罗意波)。
能量ε与圆频率ω,动量 p 与波矢 k 的关系为
, p k
此式称为德布罗意关系,适用于一切微观粒子。常量h和
ħ=h/2π都称为普朗克常量,数值为
经典描述 设粒子的自由度为r。 经典力学指出,粒子在任一时刻的力学运动状态由粒
子的r个广义坐标
q1,q2 ,…,qr 和与之共轭的r个广义动量 p1,p2,…,pr
玻尔兹曼统计

V2
)(V
b)
RT
范德瓦尔斯方程
V (T, P) V0(T0,0)[1(T T0) P]
简单固体和液 体的状态方程
f (T, H , M ) 0
如:
C M
T Tc
居里 - 外斯定律, 顺 磁系统的状态方程.
当磁介质内部出现自发磁化时, 系统的一种可能的状态方程.
② 根据热力学的理论: 只要了解了系统的状态方程, 就利用
§1 热力学量的统计表达式 §2 理想气体的物态方程 §3 能量均分定理 §4 理想气体的内能与热容量 §5 理想气体的熵
§1 热力学量的统计表达式
一、系统的内能:
内能是系统中粒子无规则运动总能量的统计平均值.
对近独立子系有: U
all
e l ll
其配分函数:
l
l
Z
el l
N
lA
A
lA )alA
l
( ln
alB
lB
B
lB )alB
0
由此可知联合系统的最概然分布应满足:
ln
alA
lA
A
lA
0
ln
alB
lB
B
lB
0
alA
NA ZA
e
A l
A
l
alB
NB ZB
e
B l
B
l
这就是两个互为热平衡的系统达到平衡态时的分布情况.
可见: 处于热平衡的两个系统, 它们中的值是相同的.
2)的应用。
§4 理想气体的内能与热容量
一、 初步分析:
1、单粒子的能量: 平动能量t, 转动能量r, 振动能量v.
t r v
)(V
b)
RT
范德瓦尔斯方程
V (T, P) V0(T0,0)[1(T T0) P]
简单固体和液 体的状态方程
f (T, H , M ) 0
如:
C M
T Tc
居里 - 外斯定律, 顺 磁系统的状态方程.
当磁介质内部出现自发磁化时, 系统的一种可能的状态方程.
② 根据热力学的理论: 只要了解了系统的状态方程, 就利用
§1 热力学量的统计表达式 §2 理想气体的物态方程 §3 能量均分定理 §4 理想气体的内能与热容量 §5 理想气体的熵
§1 热力学量的统计表达式
一、系统的内能:
内能是系统中粒子无规则运动总能量的统计平均值.
对近独立子系有: U
all
e l ll
其配分函数:
l
l
Z
el l
N
lA
A
lA )alA
l
( ln
alB
lB
B
lB )alB
0
由此可知联合系统的最概然分布应满足:
ln
alA
lA
A
lA
0
ln
alB
lB
B
lB
0
alA
NA ZA
e
A l
A
l
alB
NB ZB
e
B l
B
l
这就是两个互为热平衡的系统达到平衡态时的分布情况.
可见: 处于热平衡的两个系统, 它们中的值是相同的.
2)的应用。
§4 理想气体的内能与热容量
一、 初步分析:
1、单粒子的能量: 平动能量t, 转动能量r, 振动能量v.
t r v
热力学统计物理第六章

l
l
l
N al 0 l
E lal 0 l
[lnlnBB.E.E
lNal[lEn(]l
精l 品a课la)件llnlnalla]l
al
l
0
33
…… ……
即:能级1上有a1个粒子, 能级2上有a2个粒
子,……。
精品课件
l
al
2
a2
1
a17 1
1、玻耳兹曼系统εl 上的ωl 个量子态时,第一个粒
子可以占据ω 个量子态中的任何一个态,有ωl 种可能的
占据方式。由于每个量子态能够容纳的粒子数不受限制,在第 一个粒子占据了某一个量子态以后,第二个粒子仍然有ωl种
的占据方式,这样al 个编了号的粒子占据ωl个la量l 子态共有
种可能的占据方式,
精品课件
18
(2) 各个能级都考虑在内,系统总的占据方式数:
al l
l
(3) 现在考虑将N个粒子互相交换,不管是否在同一能级上,交换
数是N!,在这个交换中应该除去在同一能级上al 个粒子的交换al !
因此得因子
N!/ al!
A
A AA
⑤⑥ A
A
AA
两个玻色子占据3个量子态有6种方式
精品课件
10
(2)费米系统:即自旋量子数为半整数的粒子组成的系统
粒子不可分辨,每个个体量子态上最多能容纳一个 粒子(费米子遵从泡利原理)。
系统由两个粒子组成(定域子)。粒子的个体量子 态有3个, 讨论系统有那些可能的微观状态
量子态1 量子态2 量子态3
❖ 微观粒子的状态杂乱无章,一个系统的力学状态也是 杂乱无章的,有很多个可能的状态,那么,每个状态 出现的概率为多少呢,与什么因素有关
玻尔兹曼统计

d
ln Z N d (ln Z ) d N ln Z d ln Z
d
dQ与什么微观量对应, 所以不能象计算U和Y那 样直接从系统的分布函 数得到dQ,但是根据热 量学第一定律,对于准 静态过程,我们仍然可 以得到微热量dQ与系统 的配分函数Z之间的关系 式。 那么,如何得到系统的 熵S与配分函数Z之间的 关系呢? 14
-
e e e e Z
l
l
l
Z N e Z ln N
上面给出了、N、Z 之间的关系。可以利 U== e-- 用这种关系消去内能 N= e-- 计算式中的 。 6
U N lnZ N Y ln Z y
热量Q是热现象中特有的宏观量,与内能和广义 力不同,没有与热量相对应的微观量;熵S本身 是一个宏观统计的结果,也没有与之对应的微观 量。因此,不可能根据分布直接计算得出。一个 可行的办法是从热力学第一、二定律出发,将内 能和广义功的统计表达式进行比较得到。
4
玻尔兹曼统计
1、热力学量的统计表达式 定域系统或者满足经典极限条件的玻色、费米系统都 服从玻尔兹曼分布。本章根据玻尔兹曼分布讨论这两类系 统的热力学性质(内能、熵、自由能等)。首先推导热力 学量的统计表达式。 根据玻尔兹曼分布,系 统的内能和粒子数可以 由右边的两式计算。式 中,和是两个常数。
Y y
对于服从玻尔兹曼分布的系统,知道 其配分函数Z,就可以求得广义力Y!
9
对于定域(玻尔兹曼)系 统,或者遵从经典极限条 件下的非定域(玻色和费 米)系统,如果知道了系 统的配分函数Z,就可以直 接利用分布公式计算系统 的内能U和外界对系统的广 义力Y。
热力学统计物理玻耳兹曼统计
义
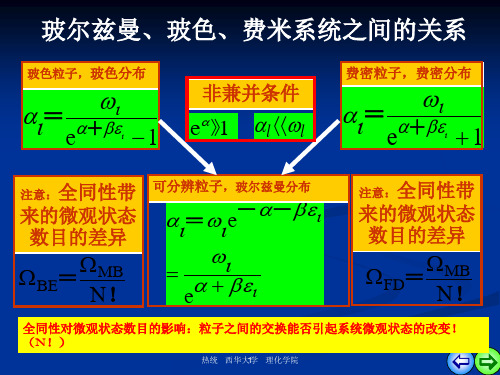
粒子处在该
能级的几率
有效状 态数
al
N Z1
l
e
l
al
el l
N
Z1
el l el l
玻耳兹
曼因子 粒子总是优先占据较低能级;温度升高,占 据该能级的几率增大。
Z1——有效状态和 一个粒子所有可能达到的有效状态的总和。
热统 西华大学 理化学院
6
f e s
l 能量为εl的一个量子态s上的平均粒子数
p
3.粒子配分函数的经典表达式
处元于内能层的l 粒l内子,数运为动:状态处于相体积
al
l
h0r
fs
l h0r
e l
N Z1
l
h0r
el
l x
Z1
l
el l
h0r
al
N Z1
l
h0r
el
取 l 足够小,求和可化为积分:
Z1
el d
h0r
e ( p,q) dq1dq2 dqr dp1dp2 dpr h0r
l l
FD l l! BE
l
l
l
e l
ln
l l
l
对于满足非兼并条件的处
于平衡态(最可几分布) lnFD lnBE l ln l lnl !
的非定域(玻色、费米) 系统,通过对所对应的系 统微观状态数目取对数, 得到了微观状态数目的对 数ln与系统包含的粒子数
l
l
l ln l l ln l 1
玻尔兹曼、玻色、费米系统之间的关系
玻色粒子,玻色分布
=
e+
1
非兼并条件
e》1 l l
费密粒子,费密分布
热力学统计物理第六章

4Vp2 dp h3
sind d 4
0 0
2
在体积 V 内,在 p ~ p dp 的动量大小范围内 自由粒子可能的量子态(非相对论情况下)
p2 2m
代入上式,则有
2V 2m 3 h
3 2 1 2d
D d
统计物理学
统计物理学是从宏观物质系统是由大量微观粒子组 成这一事实出发,认为物质的宏观性质是大量微观粒子 行为的集体表现,宏观物理量是相应微观物理量的统计 平均值。因此,对于统计物理学来说,首要的问题是怎 样去描述组成热力学系统的微观粒子的运动状态。
运动状态是指粒子的力学运动状态,根据它遵从的是
经典的还是量子的运动规律,分为经典描述和量子描述。
三、系统微观运动状态的量子描述 量子的全同粒子一般来说是不可分辨的,在含有多个全同 粒子的系统中,将任何两个全同粒子加以对换,不改变整个系 统的微观状态,此为微观粒子的全同性原理。
但如果系统的微观粒子受到空间的限制(定域系统),那
么可用粒子的位置来分辨粒子。这时描述系统的微观运动状态 需要确定每一个粒子的量子态。 如果系统的微观粒子不受空间的限制(非定域统系统), 必须考虑微观粒子的全同性原理。 如果全同粒子是不可以分辨,确定由全同近独立粒子组 成的系统的微观状态归结为确定每一个体量子态上的粒子数。
p
h
2
一维自由粒子的能量
nx
2 2 p x 2 2 2 n x 2m m L2
nx 0,1,2,
(2)三维自由粒子
2 px nx L
边长为 L 的正方形空间
nx 0,1,2,
nx
2 n y 0,1,2, py ny L nz 0,1,2, 2 pz nz L n y nz 是表征三维自由粒子运动状态的量子数
sind d 4
0 0
2
在体积 V 内,在 p ~ p dp 的动量大小范围内 自由粒子可能的量子态(非相对论情况下)
p2 2m
代入上式,则有
2V 2m 3 h
3 2 1 2d
D d
统计物理学
统计物理学是从宏观物质系统是由大量微观粒子组 成这一事实出发,认为物质的宏观性质是大量微观粒子 行为的集体表现,宏观物理量是相应微观物理量的统计 平均值。因此,对于统计物理学来说,首要的问题是怎 样去描述组成热力学系统的微观粒子的运动状态。
运动状态是指粒子的力学运动状态,根据它遵从的是
经典的还是量子的运动规律,分为经典描述和量子描述。
三、系统微观运动状态的量子描述 量子的全同粒子一般来说是不可分辨的,在含有多个全同 粒子的系统中,将任何两个全同粒子加以对换,不改变整个系 统的微观状态,此为微观粒子的全同性原理。
但如果系统的微观粒子受到空间的限制(定域系统),那
么可用粒子的位置来分辨粒子。这时描述系统的微观运动状态 需要确定每一个粒子的量子态。 如果系统的微观粒子不受空间的限制(非定域统系统), 必须考虑微观粒子的全同性原理。 如果全同粒子是不可以分辨,确定由全同近独立粒子组 成的系统的微观状态归结为确定每一个体量子态上的粒子数。
p
h
2
一维自由粒子的能量
nx
2 2 p x 2 2 2 n x 2m m L2
nx 0,1,2,
(2)三维自由粒子
2 px nx L
边长为 L 的正方形空间
nx 0,1,2,
nx
2 n y 0,1,2, py ny L nz 0,1,2, 2 pz nz L n y nz 是表征三维自由粒子运动状态的量子数
玻耳兹曼统计热力学统计物理

02
出发点:
03
思路
04
气体分子质心的平移运动
05
*
二、速度分布率
*
,求动量在 中粒子数目,对空间积分 利用式 是能量在体积元 粒子数目 l w D
在速度区间
的粒子数 单位体积内在速度区间 的粒子数 即 麦克斯韦速度分布率 为单位体积内粒子数
*
三、速率分布
*
特征速率 最概然速率:使速率分布函数取极大值的速率; 把速率分为相等的间隔,vm所在间隔分子数最多。
*
低温下,氢的热容与实验结果不符 不能得到 低温下的氢, 即不满足条件
wenfalu的个人博客 王竹溪先生错了吗?
结论:在玻尔兹曼分布适用的条件下,如果任意两个相邻能级的能量差Δε远小于热运动能量kT,粒子的能量就可以看作准连续的变量,由量子统计和有经典统计得到的内能和热容量是相同的。
电子:原子内电子的激发态与基态能量差1~10eV,相应的特征温度104~105K,远大于 ,常温下,电子只能处在基态而不改变内能,即常温下电子对气体的热容没有贡献。 O, Fe,NO 在与特征温度可以比拟的温度范围内,电子运动对热容是有 贡献的。
三、振动能量
两个原子的相对运动可以看作圆频率 ω 线性振动,能量 的量子表达式
式
简并度
*
振动配分函数
*
内能
与温度无关,N个振子的零点能量
热容量
温度为T时的热激发能量
01
03
02
04
振动特征温度
A
B
C
或
高温极限
高温极限和低温极限
*
高温极限和低温极限
01
02
03
04
*
热力学与统计物理第六章

L dnx dpx 2 L dpy dny 2 dn L dp z z 2
3
考虑到自由粒子的量子态由三个量子数的数值表征,这样在体 p 积V L3 内, 在 p x 到 px dp x , y 到 p y dp y ,p z 到 pz dp z的动 量范围内,三维自由粒子可能的量子数(或状态数)为:
微观状态的描述
(ii) 线性谐振子 :线性谐振子的自由度为1。任一时刻离开原点的位 移为x,相应得动量为 p mx,其能量是动能和势能之和,为
2 2 E= p + A x2 = p + 1 mω2x2 2m 2 2m 2
上式可化成标准形式:
p2 + x2 =1 2mE 2E mω2
以x和p为直角坐标构成二维µ空间, 由标准式可以看出振子的运动状态 轨迹为一个椭圆,E不同,对应的 椭圆就不同,如,qr; p1, p2, …, pr共2r个参量为直角坐标,构 成一个2r维空间称为µ空间 。粒子在任一时刻的力学运动状态可用该 空间内的一个点表示。
微观状态的描述
µ 空间的特点:
(i) µ 空间是人为想象出来的超越空间,是个相空间。µ 空间中的一个 代表点就表示一个粒子的微观运动状态而不是一个粒子。 (ii) 在经典力学范围,对于无相互作用的粒子系统,任何粒子总可以 找到和它相应的µ 空间来形象地描述它的运动状态,但不是所有的 粒子的运动状态可以在同一个µ 空间中描述。如一个3维自由度的 粒子,其µ空间为6维;而一个5维自由度的粒子,其µ空间为10维。
1 1 mV x2 mx 2 ) 2 2
对于一位自由粒子的运动,如图所示 : x和Px组成的二维µ空间。L表示一维容器的 长度,所以x可以取0到L中的任何数值,Px可以 取-∞到+∞中的任何数值,这样粒子的任何一个 运动状态(x , Px),可由µ空间在上述范围中 的一个点表示。 同样对于n维的自由粒子,它的µ 空间为2n维,可以把它2n维的µ 空间分成 n个2维的子空间进行描述。
3
考虑到自由粒子的量子态由三个量子数的数值表征,这样在体 p 积V L3 内, 在 p x 到 px dp x , y 到 p y dp y ,p z 到 pz dp z的动 量范围内,三维自由粒子可能的量子数(或状态数)为:
微观状态的描述
(ii) 线性谐振子 :线性谐振子的自由度为1。任一时刻离开原点的位 移为x,相应得动量为 p mx,其能量是动能和势能之和,为
2 2 E= p + A x2 = p + 1 mω2x2 2m 2 2m 2
上式可化成标准形式:
p2 + x2 =1 2mE 2E mω2
以x和p为直角坐标构成二维µ空间, 由标准式可以看出振子的运动状态 轨迹为一个椭圆,E不同,对应的 椭圆就不同,如,qr; p1, p2, …, pr共2r个参量为直角坐标,构 成一个2r维空间称为µ空间 。粒子在任一时刻的力学运动状态可用该 空间内的一个点表示。
微观状态的描述
µ 空间的特点:
(i) µ 空间是人为想象出来的超越空间,是个相空间。µ 空间中的一个 代表点就表示一个粒子的微观运动状态而不是一个粒子。 (ii) 在经典力学范围,对于无相互作用的粒子系统,任何粒子总可以 找到和它相应的µ 空间来形象地描述它的运动状态,但不是所有的 粒子的运动状态可以在同一个µ 空间中描述。如一个3维自由度的 粒子,其µ空间为6维;而一个5维自由度的粒子,其µ空间为10维。
1 1 mV x2 mx 2 ) 2 2
对于一位自由粒子的运动,如图所示 : x和Px组成的二维µ空间。L表示一维容器的 长度,所以x可以取0到L中的任何数值,Px可以 取-∞到+∞中的任何数值,这样粒子的任何一个 运动状态(x , Px),可由µ空间在上述范围中 的一个点表示。 同样对于n维的自由粒子,它的µ 空间为2n维,可以把它2n维的µ 空间分成 n个2维的子空间进行描述。
第六章玻耳兹曼统计ppt

§6.2 理想气体的物态方程
三、讨论:气体一般满足 e 1 经典极限条件是 e 1 考虑单原子分子气体 N 利用求出的单原子分子配分函数,代入 e Z
V 2 mkT e N h2
32
1
1
对一般气体来说,如果(1)N/V愈小,即气体愈稀 薄;(2)温度愈高;(3)分子质量愈大。经典极 (1)、(2)是理想气体条 限条件愈易得到满足。 件。所以理想气体一般满足 e 1 V 1 h 经典极限条件也往往采用右式表示 N 2 mkT h h 分子的德布罗意波长为 p 2m 若将ε理解为分子热运动的平均能量,并估 3 n 1 计为πkT ,经典极限条件又可表示为
§6.1 热力学量的统计表达式
例如:求以T、V为变量的特性函数的统计表达式 对定域系统
F NkT ln Z1
对满足经典极限条件的玻色(费米)系统
F NkT ln Z1 kT ln N !
玻耳兹曼理论求热力学函数的一般方法是:先 求配分函数,再利用热力学量的统计公式求出 热力学函数。求配分函数的关键是确定出粒子 的能级和能级简并度,利用配分函数的定义式 写出配分函数。
13 12
§6.3 麦克斯韦速度分布律
一、无外场条件下理想气体分子速度分布 分子速度分布情况用在单位体积内,分布在微小速 度区间的分子数反映。表示为 f (v x , v y , v z )dv x dv y dv z
1. 麦克斯韦速度分布律 对满足经典极限条件的气体系统,在温度为T的平衡 态,在单位体积内,速度在vx —vx +dvx 、 vy—vy +dvy 、 vz —vz +dvz内的分子数为
第六章玻耳兹曼统计pptppt文档

第六章玻耳兹曼统计ppt
第五章指出:定域系统和满足经典极限条件的玻 色(费米)系统都遵从玻耳兹曼分布。按照统计 思想,宏观量是对应微观量的统计平均值,根据 等概率原理,这两类系统玻耳兹曼分布出现的概 率最大,其他分布实际上不出现,所以对这两类 系统,宏观量是玻耳兹曼分布下微观量的统计平 均值。本章根据玻耳兹曼分布讨论这两类系统的 热力学性质。
kT
上考式虑中到k两应个是互熵为S热的平函衡数的。系下统面合说起明来其总实能k与量熵守S恒无,关
这两个系统必有一个共同的β因子(习题6.5), 正好与互为热平衡的系统温度相同一致。所以,β
只能是温度的函数,不可能与熵有关 。
上式中k应是常数。称为玻耳兹曼常数,在将理论 用于实际问题(例如理想气体)时得到k值为
本章主要内容
玻耳兹曼统计的热力学量表达式 玻耳兹曼统计的统计公式的应用 理想气体的物态方程,理想气体的内能和热容量, 固体热容量的爱因斯坦理论
玻耳兹曼统计的分布公式的应用 麦克斯韦速度分布律,能量均分定律, 两者的应用
§6.1 热力学量的统计表达式
本节根据玻耳兹曼分布推导热力学量的统计表 达式。要解决的问题:宏观量(如:热力学基 本函数)与玻耳兹曼分布的联系。我们根据宏 观量是微观量的统计平均值去寻找联系。
§6.1 热力学量的统计表达式
五、经典统计理论中热力学函数的表达式
配分函数的经典表达式
§6.1 热力学量的统计表达式
由于熵与系统的微观状态数有关,所以对于即使满
足经典极限条件的玻色(费米)系统,若 S k ln 仍然成立,则系统的微观状态数应换为 M.B. N!
S
Nk ln
Z1
ln
Z1
k
ln
N!
第五章指出:定域系统和满足经典极限条件的玻 色(费米)系统都遵从玻耳兹曼分布。按照统计 思想,宏观量是对应微观量的统计平均值,根据 等概率原理,这两类系统玻耳兹曼分布出现的概 率最大,其他分布实际上不出现,所以对这两类 系统,宏观量是玻耳兹曼分布下微观量的统计平 均值。本章根据玻耳兹曼分布讨论这两类系统的 热力学性质。
kT
上考式虑中到k两应个是互熵为S热的平函衡数的。系下统面合说起明来其总实能k与量熵守S恒无,关
这两个系统必有一个共同的β因子(习题6.5), 正好与互为热平衡的系统温度相同一致。所以,β
只能是温度的函数,不可能与熵有关 。
上式中k应是常数。称为玻耳兹曼常数,在将理论 用于实际问题(例如理想气体)时得到k值为
本章主要内容
玻耳兹曼统计的热力学量表达式 玻耳兹曼统计的统计公式的应用 理想气体的物态方程,理想气体的内能和热容量, 固体热容量的爱因斯坦理论
玻耳兹曼统计的分布公式的应用 麦克斯韦速度分布律,能量均分定律, 两者的应用
§6.1 热力学量的统计表达式
本节根据玻耳兹曼分布推导热力学量的统计表 达式。要解决的问题:宏观量(如:热力学基 本函数)与玻耳兹曼分布的联系。我们根据宏 观量是微观量的统计平均值去寻找联系。
§6.1 热力学量的统计表达式
五、经典统计理论中热力学函数的表达式
配分函数的经典表达式
§6.1 热力学量的统计表达式
由于熵与系统的微观状态数有关,所以对于即使满
足经典极限条件的玻色(费米)系统,若 S k ln 仍然成立,则系统的微观状态数应换为 M.B. N!
S
Nk ln
Z1
ln
Z1
k
ln
N!
中小学优质课件Boltzmann统计课件.ppt

t
h2 8mV 2/3
(nx2
n
2 y
nz2 )
nx、ny、nz—
分别是x、y、z轴向的平动量子数 取值为1,2,3…正整数
能级
t
h2 8mV
2/3
6
nx ,ny,nz 可以取值: (1,2,1)、(1,1,2)、(2,1,1)
能量相同的三种取值,有三种不同的微观状态,
则简并度
g 3
当能级有简并时定位体系的Bolzmann最概然分 布的分布数:
g
N k
k
N! N1!N2! Nk!
t N!
g Ni i
i Ni!
(12)
———定位体系能级有简并度时, 某分布的微态数
则体系的总微态数 Ω(U ,V , N ) ti
N!
g Ni i
i Ni!
求和的限制条件仍为:
Ni N , Ni i U
i
i
仍采用最概然分布处理方法:
lnΩ ln tm
由①式
ln t N ln N N Ni ln Ni Ni 对N1 求偏导:
( ln t
/ N1)
ln
Ni
Ni
1 Ni
1
ln
Ni
代入第一个方程 ( ln t / N1) β 1 0
得到 1 ln N1
∴
N1* e 1
类推得通式: Ni* e i
(7)
∵
Ni* N ei e ei
∴ e N / ei
∴
Ni*
Nei ei
i
(8)
用数学方法可证明:
1
kT
k—Boltzmann常数
∴
Ni*
麦克斯韦-玻耳兹曼分布PPT课件

解: v ( 1 / 2)h
gv 1
N j
Ng je j /(kT ) g ei /(kT )
ii
Ng je j /(kT ) q
N e
(v 0 ) kT
N0
0, 1, 2,
h
e kT
例:一维简谐振子的振动能 v
1 2
h 。一定温
度下已知处于振动第二激发能级的分子数与基态分
Nj / N
粒子处于j 能级的概率
gj越大,Nj /N越大
j越大,Nj /N越小
N j
N g je j /(kT ) g e i /(kT )
ii
N g je j /(kT ) 或 q
Nj N
g e j /(kT ) j q
上述系统中 麦玻分布 = 最概然分布 = 平衡分布
g je j /kT 玻耳兹曼因子 与平衡时系统中能量为j 的分子数成正比
求取未定乘数 和
ln
gj Nj
j
0
N j g jee j
N
j N j e
j g je j
e N
j g je j
玻耳兹曼常数
kR L
E
j N j j N
g e j
j jj
j g je j
1 / (kT )
麦克斯韦–玻尔兹曼分布
e N
j g je j
N j gie e j
N!
(
gNj j
)
j N j!
ln = lnN! j N jlng j j lnN j!
斯特林近似式 N 1时,ln N ! N ln N N
N!
2 N N N
exp(
玻耳兹曼统计

可以从正则分布导出玻耳兹曼分布,反之,也可以从玻耳兹曼分布导出正则分布。’
两者都基于等几率假设,即假定处于统计平衡的孤立系统所有微观状态出现的几率相等。
玻耳兹曼分布与正则分布的函数形式相似,由它们导出的热力学公式的形式也相似。
当讨论由近独立粒子所组成的孤立系统时,两种统计法所得结果相同,两者是等价的。前面已提及最可儿分 布井不穷尽全部可能的微观状态,但对于由很大数量的粒子组成的系统来说,由于热力学几率分布曲线在极大值 附近非常陡,以致共他分布所对应的微观态数与最可几分布对应的微观态数相比非常少,可以忽略它们对宏观量 的贡献。
激活介质是指在一定的外界条件下,它的某两个能级实现了粒子数反转并对特定频率的光基有放大作用的介 质.制造激光器一定要有激活介质。因为不是任何物质的任意两个能级间都能实现粒子数反转的,因此必须寻找建 立某两个能级间粒子数反转的条件。根据热平衡态下粒子数分布满足玻耳兹曼分布律而建立起的速率方程,可用 来判断满足粒子数反转的条件。在原子体系中每个能级的粒子数变化可分成与外界辐射场有关的部分(受激项)和 与外界作用无关的部分(弛豫项)。用体表示光对介质的激励概率,用P表示弛豫概率,它等于自发辐射概率与无 辐射概率之和。
玻尔兹曼的贡献主要在热力学和统计物理方面。1869年,他将麦克斯韦速度分布律推广到保守力场作用下的 情况,得到了玻尔兹曼分布律。1872年,玻尔兹曼建立了玻尔兹曼方程(又称输运方程),用来描述气体从非平 衡态到平衡态过渡的过程。1877年他又提出了著名的玻尔兹曼熵公式。
原理表述
全同粒子的经典统计法。又称麦克斯韦-玻耳兹曼统计或经典统计。考虑由同一种分子组成的气体。把每个 分子看成近独立的子系统,它可能有Ki个能量为εi的状态。设有Ni个分子处于这组状态中。经典统计中对于状态 的占有方式没有限制,而且每个分子都是可以识别的。把Ni个分子放到Ki个状态中的方式共有种,于是气体的熵 满足:
两者都基于等几率假设,即假定处于统计平衡的孤立系统所有微观状态出现的几率相等。
玻耳兹曼分布与正则分布的函数形式相似,由它们导出的热力学公式的形式也相似。
当讨论由近独立粒子所组成的孤立系统时,两种统计法所得结果相同,两者是等价的。前面已提及最可儿分 布井不穷尽全部可能的微观状态,但对于由很大数量的粒子组成的系统来说,由于热力学几率分布曲线在极大值 附近非常陡,以致共他分布所对应的微观态数与最可几分布对应的微观态数相比非常少,可以忽略它们对宏观量 的贡献。
激活介质是指在一定的外界条件下,它的某两个能级实现了粒子数反转并对特定频率的光基有放大作用的介 质.制造激光器一定要有激活介质。因为不是任何物质的任意两个能级间都能实现粒子数反转的,因此必须寻找建 立某两个能级间粒子数反转的条件。根据热平衡态下粒子数分布满足玻耳兹曼分布律而建立起的速率方程,可用 来判断满足粒子数反转的条件。在原子体系中每个能级的粒子数变化可分成与外界辐射场有关的部分(受激项)和 与外界作用无关的部分(弛豫项)。用体表示光对介质的激励概率,用P表示弛豫概率,它等于自发辐射概率与无 辐射概率之和。
玻尔兹曼的贡献主要在热力学和统计物理方面。1869年,他将麦克斯韦速度分布律推广到保守力场作用下的 情况,得到了玻尔兹曼分布律。1872年,玻尔兹曼建立了玻尔兹曼方程(又称输运方程),用来描述气体从非平 衡态到平衡态过渡的过程。1877年他又提出了著名的玻尔兹曼熵公式。
原理表述
全同粒子的经典统计法。又称麦克斯韦-玻耳兹曼统计或经典统计。考虑由同一种分子组成的气体。把每个 分子看成近独立的子系统,它可能有Ki个能量为εi的状态。设有Ni个分子处于这组状态中。经典统计中对于状态 的占有方式没有限制,而且每个分子都是可以识别的。把Ni个分子放到Ki个状态中的方式共有种,于是气体的熵 满足:
玻尔兹曼方程PPT课件

5.4.4 (k)的物理意义
如果在上式中忽略掉(1-cos)因子,积分将表示在 k 状态
的电子被散射的总的概率,因而,上式说明弛豫时间就是电子
的自由碰撞时间。
式中(1-cos )因子的作用可作如下分析:
' ' 1 1 ( k , k )1 cos dk 3 ( 2 π)
e ( k ) k m
将上面式子比较得
如果 沿x轴方向,则
' ' ( k ) ' 1 1 dk ( k , k )1 3 ( 2π) (k )
' k 'x ' 1 ( k , k )1 dk 3 ( 2π) kx 1
, B
温度梯度
k
变化
f变化 f变化
r 变化
电子分布函数f是波矢 k 、空间坐标
r 和时间t的函数。
1.相空间
以波矢 k 坐标 r 为变量组成的空间称为相空间。 在相空间中讨论非平衡条件下电子的分布函数。
f (r , k , t ) 描述t时刻电子在晶体内 r 处波矢为 k 的概率。
1 r k E
f r f rT T
e k ( v B )
玻尔兹曼方程为:
f f0 1 f e ( k E T ) ( v B ) k f T (k )
§5.4-2 弛豫时间的统计理论
碰撞项:由于晶格原子的振动或杂质的存在等具体的原
' 因,电子不断发生从 k k态的跃迁,电子态的这种变化常称
为散射。 只考虑相同自旋态之间的跃迁。
高二物理竞赛玻尔兹曼分布函数PPT(课件)
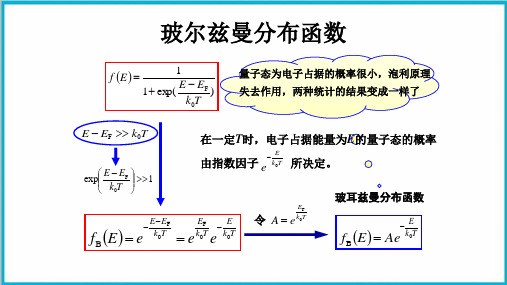
Why? 思考:导带中绝大多数电子分布在导带底附近 价带中绝大多数空穴分布在价带顶附近
总电子数微分: dN fB (E)gc (E)dE
玻尔兹曼分布:
fB
(E)
exp(
E EF k0T
)
态密度:
gc (E)
V
2 2
(2mn* )3/2
3
(E EC )1/2
dN
V
2 2
(2mn* )3/ 2
3
E E k T 热平衡状态下的非简并半导体
半 故导其体空中 穴, 分E布F可常用位玻于耳禁兹带曼内分,布且函与数导描带F写底或价带0顶的距离远大于k0T
在一定T时,电子占据能量为E的量子态的概率
由指数因子 e 与掺杂无关,与费米能级无关
与掺杂无关,与费米能级无关
故其空穴分布可用玻耳兹曼分布函数描写
对导带中的所有量子态来说
被电子占据的概率,一般都满足 f(E)<<1 故其电子分布可用玻耳兹曼分布函数描写
对价带中的所有量子态来说
被空穴占据的概率,一般都满足 1 f E 1
故其空穴分布可用玻耳兹曼分布函数描写
有何区 别?
非简并性系统:服从玻耳兹曼统计律的电子系统
简并性系统:服从费米统计律的电子系统
热温有 半平度兴导衡 、 趣体状半的 中态导最 ,下体高 EF的材温常非料度位简的为于并导5禁0半电0带K导类内体型,e、且x杂p与质导E的带k含底0T量E或以F价及带能顶量的1零距点离的远选大取于有k0关T。
E k0T
所决定。 玻耳兹曼分布函数
EEF
EF E
fB E e k0T ek0T e k0T
也就是量子态被空穴占据的概率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
kT
上考式虑中到k两应个是互熵为S热的平函衡数的。系下统面合说起明来其总实能k与量熵守S恒无,关
这两个系统必有一个共同的β因子(习题6.5), 正好与互为热平衡的系统温度相同一致。所以,β
只能是温度的函数,不可能与熵有关 。
上式中k应是常数。称为玻耳兹曼常数,在将理论 用于实际问题(例如理想气体)时得到k值为
§6.1 热力学量的统计表达式
由于熵与系统的微观状态数有关,所以对于即使满
足经典极限条件的玻色(费米)系统,若 S k ln 仍然成立,则系统的微观状态数应换为 M.B. N!
S
Nk ln
Z1
ln
Z1
k
ln
N!
S k ln k ln M .B
N!
四、玻耳兹曼统计统计公式的使用方法 如果求得配分函数Z1,可以求得基本热力学函数内能、 物态方程和熵,从而确定系统的全部平衡性质。
外界对系统作功是粒子分布不变时由于能级改变而
增加的内能,准静态过程中系统从外界吸收的热量
等于粒子在各能级重新分布所增加的内能。
§6.1 热力学量的统计表达式
三、熵的统计表达式
考虑到熵与系统在可逆过程中吸收 的热量有关,微小可逆过程有
dS 1 dQ T
由热力学第一定律 dS 1 dQ 1 (dU Ydy)
讨论:准静态过程元功和系统微小吸热的物理本质
外界对系统所作的元功
Ydy dy
l
l
y
al
l
ald l
对内能 U al l 求全微分,有 dU ald l ldal
l
l
l
内与能热的力改 学变 第可 一以定分律为和两元项功,的第表一达项式是对粒 照子 知分布不变 时由于能级改变而引起的内能变化,第二项是粒子 能第级一不项变 是时 在由 准于静粒态子过分程布中改外变界所对系引统起所的做内的能功变,化第。 二项是准静态过程中系统从外界吸收的热量。可见,
一、内能的统计表达式
内能是系统中粒子无规则运动总能量的统计平 均值
遵从玻耳兹曼分布的系统的内能为
U
all
el ll
l
l
e
l
el l
本式求和在粒子的能级和简并度知道后就能计算
§6.1 热力学量的统计表达式
为了方便,引入粒子配分函数Z1
Z1
el l
l
由约束的另一条件知,粒子配分函数满足的
§6.1 热力学量的统计表达式
五、经典统计理论中热力学函数的表达式
条N件为e
el l
e Z1
l
即 N e Z1 本式给出N和Z1的关系
U e ( )
l
lel
N ( Z1 )
Z1
N
ln Z1
即
U N ln Z1
此式即内能的统计表达式
§6.1 热力学量的统计表达式
二、广义力的统计表达式
1. 外界对系统的广义力
系统在准静态元过程中,当外参量y变化dy时,外
因此,lnZ1是以β、y(对于简单系统即T、V)为变量的
特性函数。
§6.1 热力学量的统计表达式
例如:求以T、V为变量的特性函数的统计表达式
对定域系统 F NkT ln Z1 对满足经典极限条件的玻色(费米)系统
F NkT ln Z1 kT ln N!
玻耳兹曼理论求热力学函数的一般方法是:先 求配分函数,再利用热力学量的统计公式求出 热力学函数。求配分函数的关键是确定出粒子 的能级和能级简并度,利用配分函数的定义式 写出配分函数。
广义力是系统中粒子的广义微观力 l 之和的统
y
计平均值
Y
l
l y
al
l
l y
e l l
e ( 1
) y
l
el l
N 1 Z1 ( y )Z1
N y ln Z1
即
N Y y ln Z1
这是广义力的统计表达式
一个重要特例:pVT系统压强的统计表达式为
p
N
V
ln
Z1
§6.1 热力学量的统计表达式
界对系统的功为
dW Ydy
Y是与外参量y对应的外界对系统的广义作用力 例如:系统在准静态元过程中体积变化dV时,外 界的功为–pdV。广义力是压强。
2.广义微观力
粒子能量是外参量的函数,能级εl上一个粒子在
外参量y变化时受到的广义微观力为 l y
§6.1 热力学量的统计表达式
3. 外界对系统的广义力的统计表达式
k 1.381023J K1
dS
Nkd ln
Z1
ln
Z1
S
式是熵的统计表达式,积分时已将积分常数选为零。
§6.1 热力学量的统计表达式
讨论:熵的统计意义---玻耳兹曼关系
根据熵的统计表达式、玻耳兹曼统计中Z1与α的
关系和玻耳兹曼分布公式,可以证明
S k ln
本章主要内容
玻耳兹曼统计的热力学量表达式 玻耳兹曼统计的统计公式的应用 理想气体的物态方程,理想气体的内能和热容量, 固体热容量的爱因斯坦理论
玻耳兹曼统计的分布公式的应用 麦克斯韦速度分布律,能量均分定律, 两者的应用
§6.1 热力学量的统计表达式
本节根据玻耳兹曼分布推导热力学量的统计表 达式。要解决的问题:宏观量(如:热力学基 本函数)与玻耳兹曼分布的联系。我们根据宏 观量是微观量的统计平均值去寻找联系。
TT
上式说明1/T是đQ的一个积分因子,可以证明β
也是đQ的一个积分因子。即 dQ (dU Ydy) 能写成一个完整微分式。写出该完整微分与上式 比较可得到熵。
可以证明
(dU
Ydy)
Nd ln
Z1
ln
Z1
上式是完整微分式,说明β也是đQ的积分因子
§6.1 热力学量的统计表达式
根据微分方程关于积分因子的理论,取 1
第六章玻耳兹曼统计ppt演示文稿
第五章指出:定域系统和满足经典极限条件的玻 色(费米)系统都遵从玻耳兹曼分布。按照统计 思想,宏观量是对应微观量的统计平均值,根据 等概率原理,这两类系统玻耳兹曼分布出现的概 率最大,其他分布实际上不出现,所以对这两类 系统,宏观量是玻耳兹曼分布下微观量的统计平 均值。本章根据玻耳兹曼分布讨论这两类系统的 热力学性质。
上式称为玻耳兹曼关系,熵是用系统宏观态上出现 的微观状态数来量度的。某个宏观态对应的微观状 态数越多,系统微观上运动的变化就越多端,它的 混乱程度就越大,熵也越大。玻耳兹曼关系给出了 熵的统计意义:熵是系统混乱程度的量度。
注 意
S k ln 中的Ω应是ΩM.B.。上面熵的统计表达式和
统计解释只适用于粒子可分辨的系统(定域系统)
上考式虑中到k两应个是互熵为S热的平函衡数的。系下统面合说起明来其总实能k与量熵守S恒无,关
这两个系统必有一个共同的β因子(习题6.5), 正好与互为热平衡的系统温度相同一致。所以,β
只能是温度的函数,不可能与熵有关 。
上式中k应是常数。称为玻耳兹曼常数,在将理论 用于实际问题(例如理想气体)时得到k值为
§6.1 热力学量的统计表达式
由于熵与系统的微观状态数有关,所以对于即使满
足经典极限条件的玻色(费米)系统,若 S k ln 仍然成立,则系统的微观状态数应换为 M.B. N!
S
Nk ln
Z1
ln
Z1
k
ln
N!
S k ln k ln M .B
N!
四、玻耳兹曼统计统计公式的使用方法 如果求得配分函数Z1,可以求得基本热力学函数内能、 物态方程和熵,从而确定系统的全部平衡性质。
外界对系统作功是粒子分布不变时由于能级改变而
增加的内能,准静态过程中系统从外界吸收的热量
等于粒子在各能级重新分布所增加的内能。
§6.1 热力学量的统计表达式
三、熵的统计表达式
考虑到熵与系统在可逆过程中吸收 的热量有关,微小可逆过程有
dS 1 dQ T
由热力学第一定律 dS 1 dQ 1 (dU Ydy)
讨论:准静态过程元功和系统微小吸热的物理本质
外界对系统所作的元功
Ydy dy
l
l
y
al
l
ald l
对内能 U al l 求全微分,有 dU ald l ldal
l
l
l
内与能热的力改 学变 第可 一以定分律为和两元项功,的第表一达项式是对粒 照子 知分布不变 时由于能级改变而引起的内能变化,第二项是粒子 能第级一不项变 是时 在由 准于静粒态子过分程布中改外变界所对系引统起所的做内的能功变,化第。 二项是准静态过程中系统从外界吸收的热量。可见,
一、内能的统计表达式
内能是系统中粒子无规则运动总能量的统计平 均值
遵从玻耳兹曼分布的系统的内能为
U
all
el ll
l
l
e
l
el l
本式求和在粒子的能级和简并度知道后就能计算
§6.1 热力学量的统计表达式
为了方便,引入粒子配分函数Z1
Z1
el l
l
由约束的另一条件知,粒子配分函数满足的
§6.1 热力学量的统计表达式
五、经典统计理论中热力学函数的表达式
条N件为e
el l
e Z1
l
即 N e Z1 本式给出N和Z1的关系
U e ( )
l
lel
N ( Z1 )
Z1
N
ln Z1
即
U N ln Z1
此式即内能的统计表达式
§6.1 热力学量的统计表达式
二、广义力的统计表达式
1. 外界对系统的广义力
系统在准静态元过程中,当外参量y变化dy时,外
因此,lnZ1是以β、y(对于简单系统即T、V)为变量的
特性函数。
§6.1 热力学量的统计表达式
例如:求以T、V为变量的特性函数的统计表达式
对定域系统 F NkT ln Z1 对满足经典极限条件的玻色(费米)系统
F NkT ln Z1 kT ln N!
玻耳兹曼理论求热力学函数的一般方法是:先 求配分函数,再利用热力学量的统计公式求出 热力学函数。求配分函数的关键是确定出粒子 的能级和能级简并度,利用配分函数的定义式 写出配分函数。
广义力是系统中粒子的广义微观力 l 之和的统
y
计平均值
Y
l
l y
al
l
l y
e l l
e ( 1
) y
l
el l
N 1 Z1 ( y )Z1
N y ln Z1
即
N Y y ln Z1
这是广义力的统计表达式
一个重要特例:pVT系统压强的统计表达式为
p
N
V
ln
Z1
§6.1 热力学量的统计表达式
界对系统的功为
dW Ydy
Y是与外参量y对应的外界对系统的广义作用力 例如:系统在准静态元过程中体积变化dV时,外 界的功为–pdV。广义力是压强。
2.广义微观力
粒子能量是外参量的函数,能级εl上一个粒子在
外参量y变化时受到的广义微观力为 l y
§6.1 热力学量的统计表达式
3. 外界对系统的广义力的统计表达式
k 1.381023J K1
dS
Nkd ln
Z1
ln
Z1
S
式是熵的统计表达式,积分时已将积分常数选为零。
§6.1 热力学量的统计表达式
讨论:熵的统计意义---玻耳兹曼关系
根据熵的统计表达式、玻耳兹曼统计中Z1与α的
关系和玻耳兹曼分布公式,可以证明
S k ln
本章主要内容
玻耳兹曼统计的热力学量表达式 玻耳兹曼统计的统计公式的应用 理想气体的物态方程,理想气体的内能和热容量, 固体热容量的爱因斯坦理论
玻耳兹曼统计的分布公式的应用 麦克斯韦速度分布律,能量均分定律, 两者的应用
§6.1 热力学量的统计表达式
本节根据玻耳兹曼分布推导热力学量的统计表 达式。要解决的问题:宏观量(如:热力学基 本函数)与玻耳兹曼分布的联系。我们根据宏 观量是微观量的统计平均值去寻找联系。
TT
上式说明1/T是đQ的一个积分因子,可以证明β
也是đQ的一个积分因子。即 dQ (dU Ydy) 能写成一个完整微分式。写出该完整微分与上式 比较可得到熵。
可以证明
(dU
Ydy)
Nd ln
Z1
ln
Z1
上式是完整微分式,说明β也是đQ的积分因子
§6.1 热力学量的统计表达式
根据微分方程关于积分因子的理论,取 1
第六章玻耳兹曼统计ppt演示文稿
第五章指出:定域系统和满足经典极限条件的玻 色(费米)系统都遵从玻耳兹曼分布。按照统计 思想,宏观量是对应微观量的统计平均值,根据 等概率原理,这两类系统玻耳兹曼分布出现的概 率最大,其他分布实际上不出现,所以对这两类 系统,宏观量是玻耳兹曼分布下微观量的统计平 均值。本章根据玻耳兹曼分布讨论这两类系统的 热力学性质。
上式称为玻耳兹曼关系,熵是用系统宏观态上出现 的微观状态数来量度的。某个宏观态对应的微观状 态数越多,系统微观上运动的变化就越多端,它的 混乱程度就越大,熵也越大。玻耳兹曼关系给出了 熵的统计意义:熵是系统混乱程度的量度。
注 意
S k ln 中的Ω应是ΩM.B.。上面熵的统计表达式和
统计解释只适用于粒子可分辨的系统(定域系统)
