=series公式 - 360文档中心

excel平滑曲线的秘密

在 Excel 中使用指定的区域创建动态图表2008-11-19 09:30如果您选择一个图表系列并查看 Excel 的公式行，则会看到系列是由使用 SERIES 函数的公式生成的。

SERIES 是一种用于定义图表系列的特殊函数，它只能在此类环境中使用。

您不能将它用于工作表，也不能在它的参数中包含工作表的函数或公式。

关于 SERIES 函数的参数在除气泡图以外的所有图表类型中，SERIES 函数都具有下表中列出的参数。

在气泡图中，SERIES 函数还要用一个额外的参数来指定气泡的大小。

参数必选/可选指定名称可选显示在图例中的名称分类标志可选显示在分类轴上的标志（如果忽略，Excel 将使用连续的整数作为标志）值必选 Excel 所绘制的值顺序必选系列的绘制顺序比如公式 =SERIES(Sheet1!$B$1,Sheet1!$A$2:$A$1624,Sheet1!$B$2:$B$1624,1)该公式中的参数与“源数据”对话框中各项的关系如下所示：名称参数参数 Sheet1!$B$1 显示在“名称”框中。

由于 Sheet1!$B$1 包含“价格”标志，因此该系列在“系列”框中以“价格”作为标识。

分类标志参数参数 Sheet1!$A$2:$A$1624 显示在“分类(X)轴标志”框中。

值参数参数 Sheet1!$B$2:$B$1624 显示在“值”框中。

顺序参数由于此图表只有一个系列，因此顺序参数为 1。

这种默认的绘制顺序由“价格”系列在“系列”列表框中的位置反映。

SERIES 函数的作用：创建动态图表。

例如，最新输入的 30 个点。

您可能已经知道，Excel 中的所有名称都是公式名称而不是区域名称。

公式通常解析为区域引用。

例如，如果选择 Sheet1 上的 A1:A10，并使用“定义”命令（“插入”菜单，“名称”命令）为区域选择创建名称，Excel 会将该名称定义为：=Sheet1!$A$1:$A$10 如果将某些函数添加到定义名称的公式中，该名称就可以根据工作表的情况而引用不同的工作表区域。

EXCEL图表笔记

18.添加次坐标轴(即第二个数值轴)需要先选定一个数据系列,然后在"数据系列格式"对话框里的"坐标轴"中选择"次坐标轴".
19.第18项后访问"图表选项"中的"坐标轴"选项卡,可以添加第二个分类轴.
20.对于图表工作表,"图表区"通常就是整个工作表,但可以利用"页面设置"中"图表"选项卡,指定"打印图表大小"项下的"自定义"选项来调整它.
21.绘图区格式中"区域"如果选择为"无",则"绘图区"将是透明的.
22.创建了一个迷人的图表并花了许多的时间定制它.现在,必须再创建一个一样的图表,有三种办法:
A.用选择性粘贴
B.复制图表,更改数据来源
C.创建自定义图表
23.三维曲面图的系列无法选择,要更改系列格式可以通过"图例标识格式"设置.
xlusrgal.xls:保存用户定义的自定义图表类型
7.由数字组成的分类标志(比如年份)经常被EXCEL误认为是一数据系列,最简单的处理方法就是删除分类标志列标题.
8.给已有的图表添加新系列,EXCEL提供下面几种方法:
A.为新系列选择数据区域,然后将其拖进图表.
B.复制此区域,然后使用"编辑->选择性粘贴"命令将此数据粘贴进图表.
SERIES公式的区域引用总是包含有工作表名称,且总是绝对引用.不相邻的区域引用也是有效的(区域地址由逗号分开并加上圆括号).此变量还可以由加了花括号的值数组组成.
11.数值次序反转选项实际上没有更改SERIES公式的绘图次序.SERIES公式保持原样,但EXCEL以相反次序在系列轴上显示它们.(在书中82页)

series函数举例

series函数举例【篇一：series函数举例】此函数不需要特意主动使用。

只要在表格中正确选择数据源即可。

插入图表，在图表中右键选择“选择数据”，圈选数据区域，点选“切换行列”，编辑图例项，编辑、圈选水平分类轴标签。

调整好图表后，点图表上的一组图形，在编辑栏就会看到这个函数。

但是如果直接在编辑栏里调整此函数的话，因为不够直观，所以容易出错。

【篇二：series函数举例】将x值放在a列,y值放在b列选中数据区后启动图表向导,图表类型选xy散点图根据实际做必要的修改.【篇三：series函数举例】如果您选择一个图表系列并查看 excel 的公式行，则会看到系列是由使用 series 函数的公式生成的。

series 是一种用于定义图表系列的，它只能在此类环境中使用。

您不能将它用于工作表，也不能在它的参数中包含工作表的函数或公式。

关于 series 函数的参数在除气泡图以外的所有图表类型中，series 函数都具有下表中列出的参数。

在气泡图中，series 函数还要用一个额外的参数来指定气泡的大小。

参数必选/可选指定名称可选显示在图例中的名称分类标志可选显示在分类轴上的标志（如果忽略，excel 将使用连续的整数作为标志）值必选 excel 所绘制的值顺序必选系列的绘制顺序比如公式=series(sheet1!$b$1,sheet1!$a$2:$a$1624,sheet1!$b$2:$b$162 4,1)该公式中的参数与“源数据”对话框中各项的关系如下所示：名称参数参数 sheet1!$b$1 显示在“名称”框中。

由于 sheet1!$b$1 包含“价格”标志，因此该系列在“系列”框中以“价格”作为标识。

分类标志参数参数 sheet1!$a$2:$a$1624 显示在“分类(x)轴标志”框中。

值参数参数 sheet1!$b$2:$b$1624 显示在“值”框中。

顺序参数由于此图表只有一个系列，因此顺序参数为 1。

第二讲 Excel应用技巧(4、图表图形)

二、图表通用技巧
22.图表背景—四象限图表
• • 含有负数的数据创建的散点图，X和Y轴会将绘图区分成4个象限，如何把每个象限设成不同的背景色？在“绘图”工具栏选“矩形”自选图形，在工作表中画一个矩形，双击该矩形，设置高度和宽度均为 4cm（视图表大小而定），将该矩形再复制3个，并设置这4个矩形的填充色各不相同，最后将它们组合成一个大正方形→将该正方形复制到“画图”程序中，另存为jpg格式文件→在Excel中双击图表绘图区，单击“填充效果”钮，“图片”中单击“选择图片”，选取刚才保存的文件，确定. （例子23）
二、图表通用技巧
15.在图表中使用对数刻度
• 如果数值轴中各个数据点的值相差悬殊，则需用对数刻度
• 双击数值轴，“坐标轴格式”，“刻度”中勾选 “对数刻度”，确定。（例子16）
二、图表通用技巧
16.制作瀑布图
• 能反映数据的多少，又能反映出数据的增减变化
• 为源数据增加辅助数据列，用以计算数据之间的差额。如B 列为辅助列，B2单元格为空，B3单元格的公式为=C2， B4单元格的公式为=B3+C3，然后填充B列，完成B列公式的输入→选取数据源，制作一张堆积柱形图→双击图表中任一柱体的白色部分，“数据系列格式”，“图案”中选 “边框”为无，“内部”为无，确定→双击图表中任一柱体的红色部分，“数据系列格式”，“选项”中设置“分类间距”为0；“数据标志”中勾选“值”。另外还可以在“图案”中设置更漂亮的填充效果，确定。（例子17）
二、图表通用技巧
6. 快速添加图表数据系列
• 一般是在“源数据”对话框中逐个添加数据系列的，其实有2 种快速添加的方法：
• • 复制粘贴法：选择需添加的数据系列，复制→选中图表，粘贴直接拖放法：选择需添加的数据系列，鼠标拖到图表中。（例子7）

全错位排列公式

全错位排列公式什么是错位全排列问题？其实很简单，在生活中可能都会遇到：“装错信封问题”是由当时最有名的数学家约翰·伯努利(Johann Bernoulli，1667－1748)的儿子丹尼尔·伯努利(Danid Bernoulli，1700－1782)提出来的，大意如下：一个人写了 n 封不同的信及相应的n 个不同的信封，他把这 n 封信都装错了信封，问都装错信封的装法有多少种？为了解决这个看似简单的问题，我们从数学的角度出发，尝试几个常用的方法。

记装错 n 封信的种类为 D_n ，并且有 n 封信a_1,a_2,...,a_n（1）枚举法（Enumeration method）计算种数当 n 的值较小时，可以利用枚举法：n=1 时，不可能装错信，则 D_1=0 ；n=2 时，显然装错信时，只可能为两者调换位置，则D_2=1 ；n=3 时，有 (a_2,a_3,a_1) ， (a_3,a_1,a_2) 两种装法，则D_3=2 ；n=4 时，装法如下：(a_2,a_1,a_4,a_3) ， (a_2,a_3,a_4,a_1) ，(a_2,a_4,a_1,a_3) ，(a_3,a_1,a_4,a_2) ，(a_3,a_4,a_1,a_2) ， (a_3,a_4,a_2,a_1) ，(a_4,a_1,a_2,a_3) ， (a_4,a_3,a_2,a_1) ，(a_4,a_3,a_1,a_2) ，则 D_4=9 。

当 n 的值越来越大时，枚举会变得异常复杂。

可以考虑用排列数（Permutation）和组合数（Combination），来得到错位全排列的计算公式。

（2）排列组合计算种数显然， n 封信的组合方式共有 A_n^n=n! 种装法，接下来我们要做的就是扣掉其中重复的种类，保证计数“不重不漏”。

假设第一封信装对，即为剩下的 n-1 个元素的一个全排列（All permutation），则有 A_{n-1}^{n-1}=(n-1)! 种装法；并且当第二封信装对时，也有 A_{n-1}^{n-1}=(n-1)! ，以此类推，每一封信装对时，都有 (n-1)! 种装法。

excel序列公式series

excel序列公式seriesExcel序列公式系列：序列综述序列是数学中的一个重要概念，它在Excel中也有着广泛的应用。

在Excel中，序列公式是一种强大的工具，可以帮助我们快速生成各种序列，提高工作效率。

本文将介绍一些常见的序列公式，并探讨它们的应用场景。

一、基本序列公式1. 顺序序列顺序序列是最基本的序列，它由一列连续的数字组成。

在Excel中，可以使用SERIES函数来生成顺序序列。

例如，要生成1到10的顺序序列，可以使用以下公式：=SERIES(1, , 1, 10, 1)2. 偶数序列偶数序列是由一列连续的偶数组成的序列。

要生成偶数序列，可以使用以下公式：=SERIES(2, , 2, 10, 2)3. 奇数序列奇数序列是由一列连续的奇数组成的序列。

要生成奇数序列，可以使用以下公式：=SERIES(3, , 1, 9, 2)4. 自定义序列除了基本的顺序、偶数和奇数序列外，我们还可以根据需要生成自定义的序列。

例如，要生成斐波那契数列，可以使用以下公式：=SERIES(4, , 1, 10, 1, {1,1,2,3,5,8,13,21,34,55})二、应用场景1. 数据填充序列公式在数据填充方面有着广泛的应用。

我们可以使用序列公式快速填充日期、时间、月份等数据。

例如，要生成2019年1月1日到2019年12月31日的日期序列，可以使用以下公式：=SERIES(1, , DATE(2019,1,1), DATE(2019,12,31), 1)2. 数据分析序列公式还可以在数据分析中发挥重要作用。

我们可以使用序列公式生成等差数列或等比数列，进行数据分析和预测。

例如，要生成首项为1，公差为2的等差数列，可以使用以下公式：=SERIES(1, , 1, 10, 2)3. 图表绘制序列公式在图表绘制中也有着重要的应用。

我们可以使用序列公式生成图表的数据源，从而实现动态更新图表数据的功能。

例如，要生成一个随机数的序列，可以使用以下公式：=SERIES(1, , RAND(), RAND(), 1)三、总结序列公式是Excel中非常实用的功能之一，它可以帮助我们快速生成各种序列，并应用于数据填充、数据分析和图表绘制等场景。

eviews e的公式

eviews e的公式
EViews是一种经济统计和金融数据分析软件。

它具有许多功能，并使用了各种数学和统计公式。

以下是一些常见的公式：
1. 序列求和：SUM(series)。

这个公式用于计算序列中所有观测值的总和。

2. 序列均值：MEAN(series)。

它用于计算序列所有观测值的平均值。

3. 序列标准差：STD(series)。

这个公式用于计算序列的标准差，反映了观测值偏离平均值的程度。

4. 线性回归：OLS(y, x)。

这个公式用于进行简单的线性回归分析，其中y是因变量，x是自变量。

5. 时间序列平滑：SMOOTH(series, alpha)。

它将时间序列通过指数加权平均方法进行平滑处理，其中alpha是平滑因子。

6. 时序差分：DIFF(series, d)。

这个公式用于对时间序列进行差分运算，其中d表示差分次数。

7. 协整分析：VECM(y, x, lags)。

它用于检验和建模两个或多个时间序列之间的长期关系。

这些公式可以在EViews软件中使用，帮助经济学家、金融分析师和其他使用者进行数据分析、建模和预测。

运用EXCEL图表进行海森格纸绘制

【关键词】Excel 函数工程水文频率曲线Microsoft Excel （简称Excel）是Microsoft Office中的一个重要组件，具有强大的计算功能，为工程水文及水利计算中的有关计算提供广阔的平台。

利用Excel可以有效提高工程水文及水利计算的速度和精度，具有快速、简便、灵活的特点。

特别是使用Excel的“拖动充填”、“排序”、“插入函数ƒx”、“图表”等功能，充分体现其优越性，可以充分解决工程水文及水力计算的有关问题。

本文可以通过其内置功能介绍如何比较轻松准确的绘制水文频率曲线。

其具体绘制步骤如下：1.制作海森机率格纸主要运用EXCEL电子表格中的NORMSINV函数进行计算。

（详见图1）在表中B2单元格中输入公式：=NORMSINV(A2%) （1.1）拖动单元格右下角的填充柄，将公式复制到本列其他单元格中。

在表中C6单元格中输入公式：=-$B$4-(-B6) （1.2）拖动单元格右下角的填充柄，将公式复制到本列其他单元格中。

在表中D2单元格中输入最小值，如“0”；在D3单元格中输入最大值，如“1600”；在D4单元格输入“=D2”；在D5单元格输入“=D3”。

拖动单元格右下角的填充柄，将公式复制到本列其他单元格中。

在表中E2单元格中输入公式：=1/A2*100 （1.3）拖动单元格右下角的填充柄，将公式复制至本列E25单元格止。

在表中E26单元格中输入公式：=1/(1-A26/100) （5）拖动单元格右下角的填充柄，将公式复制到本列其他单元格中。

图1 海森机率格纸2.绘制海森机率格纸在图1表格中点击“插入”菜单中的“图表”命令，在“标准类型”的“图表类型”表框中选择“XY散点图”，在“子图表类型”表框中选择“散点图”。

单击“下一步”按钮。

（详见图2）图2单击“系列”标签，在“系列”栏下点击“添加”按钮，在“X值”文本框内选取数据区域“海森机率格纸！$C$2:$C49”，在“Y值”文本框内选取数据区域“海森机率格纸！$D$2:$D49”。

泰勒级数——精选推荐

泰勒级数泰勒公式（Taylor Series）能把⼤多数的函数展开成幂级数，即f(x)=∞∑n=0A n x n式⼦当中只有加法与乘法，容易求导，便于理解与计算。

这种特性使得泰勒公式在数学推导（如：微分⽅程以幂级数作为解），数值逼近（如：求e、开⽅），函数逼近（在计算机某些计算优化时，可以把某些繁琐的式⼦进⾏泰勒展开，仅保留加法与乘法运算），复分析等多种应⽤中有⼴泛应⽤。

条件：有实函数f，f在闭区间[a,b]是连续的，f在开区间(a,b)是n+1阶可微。

则可以对函数f进⾏泰勒展开：f(x)=10!f(x0)+11!(x−x0)f′(x0)+12!(x−x0)2f″其中x_0为区间(a,b)中的某⼀点，x_0 \in (a,b)，变量x也在区间(a,b)内。

泰勒展开得到的是⼀个多项式，可以写成f(x) = \displaystyle{ \sum_{k=0}^{n}\frac{(x-x_0)^k}{k!}f^{(k)}(x) + R_n }其中R_n为泰勒公式的余项（Remainder）。

该余项可以写成以下形式R_n = \displaystyle{ \int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt }余项R_n还可以进⼀步表⽰成：存在⼀点x_0<\xi<x使得下⾯的式⼦成⽴R_n = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}泰勒公式推导的起点为微积分基本定理（Fundamental Theorem of Calculus）：\displaystyle{ \int_{x_0}^x f'(t)dt } = f(x) – f(x_0)因此有：\displaystyle{ f(x) = f(x_0) + \int_{x_0}^x f'(t)dt }然后⽤分部积分法(Integration by parts)对积分部分进⾏分解:\begin{align*} f(x) &=\color{red}{f(x_0) + \int_{x_0}^x f'(t)dt} \\ &=f(x_0) + \left. tf'(t)\right|_{x_0}^x - \int_{x_0}^x tf''(t)dt \qquad udv = uv -vdu \\ &=f(x_0) + xf'(x) – x_0f'(x_0) - \int_{x_0}^x tf''(t)dt \\ &=f(x_0) + x\left( f'(x_0) + \int_{x_0}^x f''(t)dt \right ) – x_0f'(x_0) - \int_{x_0}^x tf''(t)dt \\ &\qquad Fundamental \ Theorem \ of \ Calculus\\ &=\color{red}{f(x_0) + (x-x_0)f'(x_0) + \int_{x_0}^x (x-t)f''(t)dt} \\ &=f(x_0) + (x-x_0)f'(x_0) + \left.(xt - \frac{1}{2}t^2)f''(t)\right|_{x_0}^x - \int_{x_0}^x(xt - \frac{1}{2}t^2) f'''(t)dt \qquad udv = uv - vdu \\ &=f(x_0) + (x-x_0)f'(x_0) + \frac{x^2} {2}f''(x) + \frac{-2x_0x + {x_0}^2}{2}f''(x_0) - \int_{x_0}^x\frac{2xt-t^2}{2} f'''(t)dt \\ &=f(x_0) + (x-x_0)f'(x_0) + \frac{x^2}{2}\left( f''(x_0) +\int_{x_0}^x f'''(t)dt \right ) + \frac{-2x_0x + {x_0}^2}{2}f''(x_0) \\ &\quad+ \int_{x_0}^x\frac{-2xt+t^2}{2} f'''(t)dt \quad Fundamental \ Theorem \ of \ Calculus\\ &=\color{red}{f(x_0) + (x-x_0)f'(x_0) + \frac{(x-x_0)^2}{2}f''(x_0) + \int_{x_0}^x\frac{(x-t)^2}{2} f'''(t)dt} \end{align*}运⽤微积分基本定理以及分部积分法继续推导下去可以得到：\begin{align*} f(x) &= \frac{1}{0!}f(x_0) \\ &+\frac{1}{1!}(x-x_0)f'(x_0) \\ &+\frac{1}{2!}(x-x_0)^2f''(x_0) \\ &+\cdot \cdot \cdot \\ &+\frac{1}{n!} (x-x_0)^nf^{(n)}(x_0) \\ &+\int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt \qquad * \end{align*}由此得到余项R_n = \int_{x_0}^x \frac{f^{(n+1)}(t)}{n!}(x-t)^ndt泰勒公式的余项能写成多种形式，我们这⾥只对它的拉格朗⽇（Lagrange）形式进⾏推导拉格朗⽇余项为：存在⼀点x_0<\xi<x使得下⾯的式⼦成⽴R_n = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}推导过程如下：令\begin{align*} F(x) &= \frac{1}{0!}f(x_0) \\ &+ \frac{1}{1!}(x-x_0)f'(x_0) \\ &+ \frac{1}{2!}(x-x_0)^2f''(x_0) \\ &+ \cdot\cdot\cdot \\ &+ \frac{1}{n!}(x-x_0)^nf^n(x_0) \end{align*}那么就有R_n(x) = f(x) – F(x)由于f(x)与F(x)在区间(a,b)上都有n+1阶导，因此R_n(x)在此区间上也有n+1阶导。

泰勒级数展开公式

泰勒级数（Taylor series）是将一个光滑的函数展开为一个无限级数，每一项都包括函数在某一点的导数。

泰勒级数展开公式允许我们将一个复杂的函数近似为一个多项式，从而便于以下计算：在数值分析、微积分、微分方程等领域具有广泛应用。

泰勒级数的一般形式如下：
f(x) ≈ f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ... + f^n(a)(x-a)^n/n! + ... 其中，f(x) 是我们要展开的函数，a 是泰勒级数的展开点，n 是级数项数，f^n 表示函数的 n 次导数。

如果展开点是 0 (a=0)，则泰勒级数被称为麦克劳林级数（Maclaurin series）：f(x) ≈ f(0) + f'(0)x + f''(0)x^2/2! + f'''(0)x^3/3! + ... + f^n(0)x^n/n! + ...
泰勒公式并不是所有函数的近似，也不是所有情况下都能使用。

有些函数在某些点无法展开，有些函数展开后的级数可能发散而无法收敛到原函数。

因此，在实际应用泰勒级数时，需要根据具体问题分析近似误差和级数的收敛性。

excel表格递减公式

excel表格递减公式
Excel表格中，递减公式是一个常用的函数，用于按照一定的规则递减序列的值。

以下是关于递减公式的详细介绍：
1.定义递减公式
递减公式是一种函数，它接受一个初始值，然后按照一定的步长递减这个值。

在Excel中，这个函数通常被表示为“序列”函数。

2.创建递减公式
要创建一个递减公式，首先需要在Excel表格中输入初始值，然后输入“=SERIES(初始值,递减步长,次数)”。

其中，“初始值”是序列的起始值，“递减步长”是每次递减的数值，“次数”是序列中元素的数量。

例如，如果要在表格中创建一个从10开始，每次递减2，共有5个元素的递减序列，可以使用公式“=SERIES(10,2,5)”。

3.调整递减公式
如果需要调整递减公式，可以在“递减步长”和“次数”参数中修改数值。

例如，如果要将上述递减序列的步长改为3，数量改为8，可以在公式中修改为“=SERIES(10,3,8)”。

4.注意点
在使用递减公式时，需要注意以下几点：
•递减公式的初始值、递减步长和数量都必须为正数。

•如果递减步长大于初始值，那么递减序列将出现负数。

•如果递减次数为偶数，那么递减序列的最后一个值将等于初始值加上递减步长。

•如果递减次数为奇数，那么递减序列的最后一个值将等于初始值减去递减步长。

泰勒公式解决平方根编程

泰勒公式是一种数学方法，用于近似计算平方根或其他复杂函数的值。

它通过将函数展开为无穷级数的方式来表达函数，并将这些级数用于求解。

泰勒公式的基本思想是将一个复杂函数f(x)表示为一系列项的无穷和，其中每个项都是函数f(x)在某一点的导数的乘积加上一个常数。

平方根函数的泰勒展开式为：√x = x^(1/2) = x^(-1/2) = (1 + 1/2x)^(-1/2) = 1 - 1/2x + 1/4x^2 - 1/8x^3 + ...以下是使用泰勒公式解决平方根编程的示例代码（以Python为例）：```pythonimport mathdef taylor_sqrt(x):# 将平方根展开为无穷级数series = 1 / (math.sqrt(2 * math.pi) * x ** 0.5)series += 1 / (2 * x ** 0.5)series += 1 / (4 * x ** 0.5 * (x - 1))series += 1 / (8 * x ** 0.5 * (x - 1) * (x - 2))series += 1 / (32 * x ** 0.5 * (x - 1) * (x - 2) * (x - 3))return series# 测试代码x = 15print("The square root of", x, "approximated by Taylor series is", taylor_sqrt(x))```在这个示例代码中，我们定义了一个名为`taylor_sqrt`的函数，它接受一个参数`x`，并返回一个无穷级数的和，该级数可以近似表示为平方根。

该函数首先将平方根展开为无穷级数，然后将每一项加到结果中。

注意，这里我们使用了Python的内置库`math`来计算平方根和数学常数。

最后，我们使用测试代码来验证我们的结果是否正确。

常见麦克劳林公式大全_wrapper_wrapper

常见麦克劳林公式大全_wrapper_wrapper常见麦克劳林公式大全麦克劳林公式（Maclaurin series）是一种将函数表示为无穷级数的方法，通过将函数展开成泰勒级数的特殊情况，以麦克劳林级数（Maclaurin series）的形式呈现。

麦克劳林公式在数学、物理和工程等领域中被广泛应用，具有重要的理论和实际价值。

本文将介绍常见麦克劳林公式的推导和应用。

一、麦克劳林公式的推导要将一个函数表示为麦克劳林级数，首先需要找到函数在某一点的各阶导数。

然后，可以使用泰勒公式来表示这个函数：f(x) = f(a) + f'(a)(x - a) + f''(a)(x - a)^2/2! + f'''(a)(x - a)^3/3! + ...其中，f'(x)表示函数f(x)的一阶导数，f''(x)表示函数f(x)的二阶导数，以此类推。

当将此公式应用到麦克劳林级数时，公式可简化为：f(x) = f(0) + f'(0)x + f''(0)x^2/2! + f'''(0)x^3/3! + ...这就是麦克劳林公式的一般形式。

二、常见麦克劳林公式1. 正弦函数（sinx）的麦克劳林公式：sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...2. 余弦函数（cosx）的麦克劳林公式：cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...3. 指数函数（ex）的麦克劳林公式：e^x = 1 + x + x^2/2! + x^3/3! + ...4. 自然对数函数（ln(1+x)）的麦克劳林公式：ln(1+x) = x - x^2/2 + x^3/3 - x^4/4 + ...5. 正切函数（tanx）的麦克劳林公式：tan(x) = x + x^3/3 + 2x^5/15 + 17x^7/315 + ...三、麦克劳林公式的应用1. 近似计算：麦克劳林公式可以将函数用一个无穷级数表示，通过截取级数的前几项来近似计算函数的值。

泰勒公式里的o(x)

泰勒公式里的o(x)摘要：一、泰勒公式简介1.泰勒公式定义2.泰勒公式的应用领域二、泰勒公式中的o(x)1.o(x)的含义2.o(x)与泰勒公式的关系3.o(x)的作用三、泰勒公式中o(x)的性质1.o(x)的加法和乘法性质2.o(x)的极限性质四、o(x)在泰勒公式求解中的应用1.泰勒公式展开2.泰勒级数3.泰勒公式在实际问题中的应用正文：一、泰勒公式简介泰勒公式（Taylor formula），又称泰勒展开式，是由英国数学家布鲁克·泰勒（Brook Taylor）在18世纪初提出的一种数学公式。

它用来表示一个可微函数在某一点附近的值，可以通过该点的函数值、导数值和高阶导数值的有限和来近似计算。

泰勒公式广泛应用于数值分析、工程计算等领域。

二、泰勒公式中的o(x)1.o(x)的含义在泰勒公式中，o(x)表示当x趋近于0时，比x^n更高阶的无穷小量。

换句话说，o(x)表示当x无限接近0时，它的影响可以忽略不计。

o(x)通常用来表示函数在x=0附近的高阶无穷小量。

2.o(x)与泰勒公式的关系泰勒公式可以写成以下形式：f(x) = f(0) + f"(0)x + (f""(0)/2!)x^2 + ...+ (f^n(0)/n!)x^n + o(x^n)其中，o(x^n)表示当x趋近于0时，比x^n更高阶的无穷小量。

3.o(x)的作用o(x)在泰勒公式中起到一个“误差”的作用，表示函数在x=0附近的精度。

当n趋近于无穷大时，泰勒级数的前n项和越来越接近真实的函数值，而o(x^n)的影响则越来越小。

三、泰勒公式中o(x)的性质1.o(x)的加法和乘法性质当两个o(x)项相加或相乘时，它们仍然是o(x)。

即，如果a_n = o(x^n)且b_m = o(x^m)，那么a_n + b_m = o(x^n)且a_n * b_m = o(x^(n+m))。

2.o(x)的极限性质当n趋近于无穷大时，o(x^n)的极限为0。

excel使用series（）函数

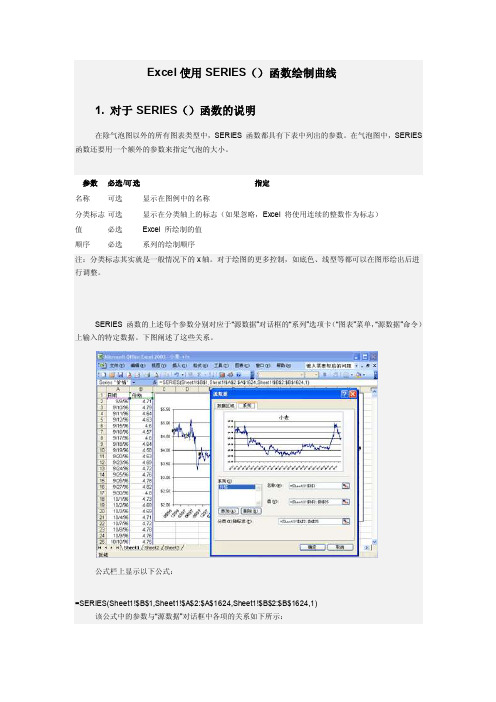
Excel使用SERIES（）函数绘制曲线1. 对于SERIES（）函数的说明在除气泡图以外的所有图表类型中，SERIES 函数都具有下表中列出的参数。

在气泡图中，SERIES 函数还要用一个额外的参数来指定气泡的大小。

参数必选/可选指定名称可选显示在图例中的名称分类标志可选显示在分类轴上的标志（如果忽略，Excel 将使用连续的整数作为标志）值必选Excel 所绘制的值顺序必选系列的绘制顺序注：分类标志其实就是一般情况下的x轴。

对于绘图的更多控制，如底色、线型等都可以在图形绘出后进行调整。

SERIES 函数的上述每个参数分别对应于“源数据”对话框的“系列”选项卡（“图表”菜单，“源数据”命令）上输入的特定数据。

下图阐述了这些关系。

公式栏上显示以下公式：=SERIES(Sheet1!$B$1,Sheet1!$A$2:$A$1624,Sheet1!$B$2:$B$1624,1)该公式中的参数与“源数据”对话框中各项的关系如下所示：名称参数参数Sheet1!$B$1 显示在“名称”框中。

由于Sheet1!$B$1 包含“价格”标志，因此该系列在“系列”框中以“价格”作为标识。

分类标志参数参数Sheet1!$A$2:$A$1624 显示在“分类(X)轴标志”框中。

值参数参数Sheet1!$B$2:$B$1624 显示在“值”框中。

顺序参数由于此图表只有一个系列，因此顺序参数为1。

这种默认的绘制顺序由“价格”系列在“系列”列表框中的位置反映。

文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

现在指的是公司或企业中从事文字工作的职位，就是以文字来表现已经制定的创意策略。

文案它不同于设计师用画面或其他手段的表现手法，它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程，多存在于广告公司，企业宣传，新闻策划等。

基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代，文案的称呼主要用在商业领域，其意义与中国古代所说的文案是有区别的。

常用的8个麦克劳林公式

常用的8个麦克劳林公式麦克劳林公式（Maclaurin series）是数学中的一种级数展开方法，它可以将一个函数用一系列无限求和的项表示出来。

麦克劳林公式是泰勒级数的一种特殊情况，在函数值为零的点附近进行展开，并且只考虑了函数在展开点处的导数。

下面介绍常见的八个麦克劳林公式。

1.以指数函数展开指数函数e^x在x=0附近的麦克劳林展开式为：e^x=1+x+(x^2/2!)+(x^3/3!)+(x^4/4!)+...=Σ(x^n/n!)2.以正弦函数展开正弦函数sin(x)在x = 0附近的麦克劳林展开式为：sin(x) = x - (x^3 / 3!) + (x^5 / 5!) - (x^7 / 7!) + (x^9 / 9!) - ... = Σ((-1)^n * (x^(2n+1)) / (2n+1)!)3.以余弦函数展开余弦函数cos(x)在x = 0附近的麦克劳林展开式为：cos(x) = 1 - (x^2 / 2!) + (x^4 / 4!) - (x^6 / 6!) + (x^8 / 8!) - ... = Σ((-1)^n * (x^(2n)) / (2n)!)4.以正切函数展开正切函数tan(x)在x = 0附近的麦克劳林展开式为：tan(x) = x + (x^3 / 3) + (2x^5 / 15) + (17x^7 / 315) +(62x^9 / 2835) + ... = Σ(B_(2n) * x^(2n-1) / (2n)!)其中B_(2n)为贝尔数（Bell number）。

5.以对数函数展开自然对数函数ln(1 + x)在x = 0附近的麦克劳林展开式为：ln(1 + x) = x - (x^2 / 2) + (x^3 / 3) - (x^4 / 4) + (x^5 / 5) - ... = Σ((-1)^(n-1) * (x^n) / n)6.以正弦反函数展开正弦反函数arcsin(x)在x = 0附近的麦克劳林展开式为：arcsin(x) = x + (x^3 / 6) + (3x^5 / 40) + (5x^7 / 112) + ... = Σ(((2n-1)!) * (x^(2n+1)) / ((2n+1)!))其中(2n-1)!表示双阶乘（double factorial）。

反双曲三角函数麦克劳林展开式

反双曲三角函数麦克劳林展开式是
f(x)=f(x0)+f'(x0)*(x-x0)+f"(x0)/2!*(x-x0)^2+...+f(n)(x0)/n!*(x-x0)^n。

麦克劳林公式(Maclaurin's series) 是泰勒公式的一种特殊形式，公式适用于数学学科，1719年由麦克劳林提出。

麦克劳林公式
运用：
一般情况下遇到的极限有两种情况：
(1)分子是两个或者以上的函数相加减，这种情况比较简单，只要将两个函数展开到与分母同阶即可
(2)分子是两个或以上的函数相乘，这种情况比较复杂，主要考虑的是分子相乘会出现的所有与分母同阶的项。

举个例子，比如分母是三阶，那么两个多项式必须都展开到三阶，因为一个函数的常数项与另一个函数的三次项，一个函数的一次项与另一个函数的二次项相乘都是三次，也就说，必须要保证展开的阶数相乘会得到所有与分母同阶的三次项。

常见麦克劳林公式

常见麦克劳林公式麦克劳林公式（MacLaurin series）是数学中常用的一种级数展开方法。

它由苏格兰数学家柯林·麦克劳林（Colin Maclaurin）于18世纪提出，适用于将任意函数表示为一个无穷级数的形式。

麦克劳林公式在微积分、物理学、工程学以及其他学科的数学应用中都有重要的作用。

麦克劳林公式表达了一个函数f(x)在一些点a的附近可以通过级数展开近似表示的情况。

假设函数f(x)在点a及其一些邻域内的所有阶导数都存在，那么该函数在点a的麦克劳林展开式为：f(x)=f(a)+f'(a)(x-a)/1!+f''(a)(x-a)^2/2!+f'''(a)(x-a)^3/3!+...这个级数中每一项都是函数f在点a的导数值的其中一种组合，其中包括了所有的导数值。

这样，通过截取级数中的有限项，我们可以近似地表示函数f(x)在点a附近的取值。

特别地，如果我们截取级数的前n项，那么这个近似值的误差为函数在点a的一个高阶导数在截取区间内的最大值与(x-a)^n/n!的乘积。

麦克劳林展开式的使用有很多好处。

首先，通过其级数展开形式，我们可以用更简单的函数来逼近更复杂的函数，从而简化计算。

其次，级数展开也可以提供我们对函数行为的重要信息，比如函数在一些点的极限值。

最后，麦克劳林公式也可以帮助我们更好地理解函数的性质和特征。

下面将介绍一些常见的麦克劳林公式及其应用：1.指数函数的麦克劳林展开式：exp(x) = 1 + x + x^2/2! + x^3/3! + ... + x^n/n! + ...这个麦克劳林展开式表达了自然对数的指数函数，该级数展开是无限项的。

通过截取其中的有限项，我们可以方便地计算指数函数在不同点的近似值。

同时，该展开式有助于我们理解指数函数的增长速度，并在一定程度上替代复杂的指数运算。

2.三角函数的麦克劳林展开式：sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ... + (-1)^n *x^(2n+1) / (2n+1)! + ...cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ... + (-1)^n * x^(2n) / (2n)! + ...这两个麦克劳林展开式分别是正弦函数和余弦函数的级数展开形式。

常见麦克劳林公式大全

常见麦克劳林公式大全麦克劳林公式（Maclaurin series）是泰勒级数（Taylor series）的一种特殊形式。

它是一种将一个函数展开成无穷级数的表达方式，通过将函数在其中一点处的导数插入泰勒级数中，可以得到一个关于这个点附近的近似函数的级数表示。

在数学和物理学中，麦克劳林公式经常被用来求解复杂函数的近似值。

下面是一些常见的麦克劳林公式的展开形式。

1.指数函数的麦克劳林展开：e^x=1+x+(x^2)/2!+(x^3)/3!+(x^4)/4!+...=Σ(x^n)/n!2.正弦函数的麦克劳林展开：sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ... = Σ(-1)^n * (x^(2n+1))/(2n+1)!3.余弦函数的麦克劳林展开：cos(x) = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ... = Σ(-1)^n * (x^(2n))/(2n)!4.自然对数函数的麦克劳林展开：ln(1+x) = x - (x^2)/2 + (x^3)/3 - (x^4)/4 + ... = Σ(-1)^(n-1) * (x^n)/n5.正切函数的麦克劳林展开：tan(x) = x + (x^3)/3 + (2x^5)/15 + (17x^7)/315 + ... = ΣB2n * (x^(2n-1))/(2n)!6.反正切函数的麦克劳林展开：arctan(x) = x - (x^3)/3 + (x^5)/5 - (x^7)/7 + ... = Σ(-1)^(n-1) * (x^(2n-1))/(2n-1)7.开方函数的麦克劳林展开：sqrt(1+x) = 1 + (x^2)/2 - (x^4)/8 + (x^6)/16 - ... = Σ(-1)^(n+1) * (x^(2n))/(2n)!8.指数函数的麦克劳林展开：(1+x)^p = 1 + px + (p(p-1)x^2)/2! + (p(p-1)(p-2)x^3)/3! + ... = Σ(p(p-1)...(p-k+1)x^k)/k!以上是一些常见的麦克劳林公式的展开形式。