2018年浙江高考数学试卷
(完整版)2018年浙江省数学高考真题试卷(含答案解析)

2018年普通高等学校招生全国统一考试(浙江卷)数 学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:若事件A ,B 互斥,则 ()()()P A B P A P B +=+若事件A ,B 相互独立,则()()()P AB P A P B =若事件A 在一次试验中发生的概率是p ,则n 次独立重复试验中事件A 恰好发生k 次的概率()C (1)(0,1,2,,)k kn k n n P k p p k n -=-= 台体的体积公式121()3V S S h=++其中分别表示台体的上、下底面积,12,S S 表示台体的高h 柱体的体积公式V Sh=其中表示柱体的底面积,表示柱体的高S h 锥体的体积公式13V Sh=其中表示锥体的底面积,表示锥体的高S h 球的表面积公式24S R =π球的体积公式343V R =π其中表示球的半径R 一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
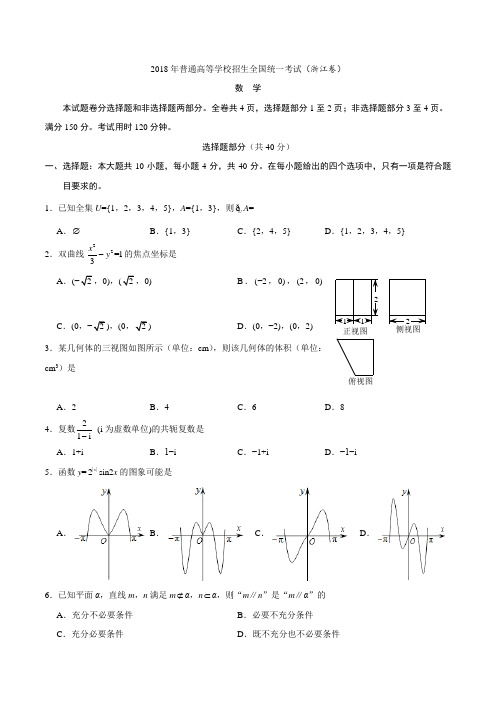
1.已知全集U ={1,2,3,4,5},A ={1,3},则C A=U A .B .{1,3}C .{2,4,5}D .{1,2,3,4,5}∅2.双曲线的焦点坐标是221 3=x y -A .,0),,0)B .(−2,0),(2,0)C .(0,),(0)D .(0,−2),(0,2)3.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是侧侧侧侧侧侧A .2B .4C .6D .84.复数(i 为虚数单位)的共轭复数是21i-A .1+iB .1−i C .−1+iD .−1−i5.函数y =sin2x 的图象可能是||2xA B C D6.已知平面α,直线m ,n 满足m α,n α,则“m ∥n ”是“m ∥α”的⊄⊂A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.设0<p <1,随机变量ξ的分布列是ξ012P12p -122p 则当p 在(0,1)内增大时,A .D (ξ)减小B .D (ξ)增大C .D (ξ)先减小后增大D .D (ξ)先增大后减小8.已知四棱锥S −ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为θ1,SE 与平面ABCD 所成的角为θ2,二面角S −AB −C 的平面角为θ3,则A .θ1≤θ2≤θ3B .θ3≤θ2≤θ1C .θ1≤θ3≤θ2D .θ2≤θ3≤θ19.已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为,向量b 满足b 2−4e ·bπ3+3=0,则|a −b |的最小值是( )A B C .2D .10.已知成等比数列,且.若,则( )1234,,,a a a a 1234123ln()a a a a a a a +++=++11a >A .B .C .D .1324,a a a a <<1324,a a a a ><1324,a a a a <>1324,a a a a >>非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分11.我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。
2018年高考数学浙江卷(精校版)

2018年高考数学浙江卷(精校版)一、选择题:1.[2018浙江1]已知全集{}1,2,3,4,5U =,{}1,3A =,则=U A ð( )A.∅B.{}1,3C.{}2,4,5D.{}1,2,3,4,5【答案:C 】2.[2018浙江2]双曲线221 3=x y -的焦点坐标是( )A.()),B.()()2,0,2,0-C.((0,,D.()()0,2,0,2-【答案:B 】3.[2018浙江3]某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A.2B.4C.6D.8【答案:C 】4.[2018浙江4]复数21i- (i 为虚数单位)的共轭复数是( ) A.1i +B.1i -C.1i -+D.1i --【答案:B 】5.[2018浙江5]函数2sin 2xy x =的图象可能是( )俯视图正视图A. B. C. D.【答案:D 】6.[2018浙江6]已知平面α,直线,m n 满足m α⊄,n α⊂,则“//m n ”是“//m α”的( )A.充分不必要条件B.必不充分条件C.充分必要条件D.既不充分也不必要条件【答案:A 】7.[2018浙江7]设01p <<,随机变量ξ的分布列是222则当P 在()0,1内增大时,A.()D ξ减小B.()D ξ增大C.()D ξ先减小后增大D.()D ξ先增大后减小【答案:D 】8.[2018浙江8]已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则( )A.123θθθ≤≤B.321θθθ≤≤ C .132θθθ≤≤ D .231θθθ≤≤【答案:D 】9.[2018浙江9] 已知,,a b e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为3π,向量b 满足2430b e b -⋅+=,则a b -的最小值是( )1 1 C.2 D.2【答案:A 】10.[2018浙江10]已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则( )A.1324,a a a a <<B.1324,a a a a ><C.1324,a a a a <>D.1324,a a a a >> 【答案:B 】二、填空题:11.[2018浙江11]我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一.凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为,,x y z ,则1001531003x y z x y z ++=⎧⎪⎨++=⎪⎩,当81z =时,x = , y =________.【答案:8;11】12.[2018浙江12]若,x y 满足约束条件0262x y x y x y -≥⎧⎪+≤⎨⎪+≥⎩,则3z x y =+的最小值是 ,最大值是 . 【答案:28-,】 13.[2018浙江13]在ABC ∆中,角,,A B C 所对的边分别为,,a b c .若a 2b =,60A =,则sin B =___________,c = .】 14.[2018浙江14]二项式81)2x的展开式的常数项是 . 【答案:7】15.[2018浙江15]已知R λ∈,函数()24,43,x x f x x x x λλ-≥⎧=⎨-+<⎩,当2λ=时,不等式()0f x <的解集是 .若函数()f x 恰有2个零点,则λ的取值范围是 . 【答案:()(]()1,4;1,34,+∞】16.[2018浙江16]从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成 个没有重复数字的四位数.(用数字作答) 【答案:1260】17.[2018浙江17]已知点()0,1P ,椭圆()2214x y m m +=>上两点,A B 满足2AP PB =,则当m = 时,点B 横坐标的绝对值最大. 【答案:5】三、解答题:18.[2018浙江18]已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点34,54P ⎛⎫-- ⎪⎝⎭.(1)求()sin απ+的值; (2)若角β满足()5sin 13αβ+=,求cos β的值. 【答案】:(1)45. (2)5665-或1665-.19.[2018浙江19]如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=,14A A =,11C C =,12AB BC B B ===.(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.【答案】:(1)略,(2.20.[2018浙江20]已知等比数列{}n a 的公比1q >,且34528a a a ++=,42a +是3a ,5a 的等差中项.数列{}n b 满足11b =,数列(){}1n n n b b a +-的前n 项和为22n n +. (1)求q 的值;(2)求数列{}n b 的通项公式.【答案】:(1)2q =;(2)()2115432n n b n -⎛⎫=-+⋅ ⎪⎝⎭.21.[2018浙江21]如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线2:4C y x =上存在不同的两点,A B 满足,PA PB 的中点均在C 上. (1)设AB 中点为M ,证明:PM 垂直于y 轴;(2)若P 是半椭圆()22104x y x +=<上的动点,求PAB ∆面积的取值范围.【答案】:(1)略;(2)⎡⎢⎣⎦.22.[2018浙江22]已知函数()ln f x x =.(1)若()f x 在()1212,x x x x x =≠处导数相等,证明:()()1288ln 2f x f x +>-; (2)若34ln 2a ≤-,证明:对于任意0k >,直线y kx a =+与曲线()y f x =有唯一公共点.【答案】:(1)略; (2)略.。
2018年度浙江数学高考试题(整理汇编含标准答案)

绝密★启用前2018年普通高等学校招生全国统一考试 (浙江卷)数学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分 3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题 纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求, 在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
其中R 表示球的半径选择题部分(共40分)一、选择题:本大题共 10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是 符合题目要求的。
1.已知全集 U={1 , 2, 3, 4, 5}, A={1 , 3},则 e u A=A .B . {1 , 3} C. {2 , 4, 5} D . {1 , 2, 3, 4, 5}22 .双曲线—y 2 = 1的焦点坐标是参考公式:若事件A, B 互斥,贝U P(A B) P(A) P(B) 若事件A, B 相互独立,贝U P(AB) P(A) P(B) 若事件A 在一次试验中发生的概率是p,则n次独立重复试验中事件 A 恰好发生k 次的概率_ k kn kP n (k) C n P (1 p) (k 0,1,2,L ,n)台体的体积公式V 1(Si - S1S 2 S 2)h其中Si,&分别表示台体的上、下底面积,h 表柱体的体积公式V Sh其中S 表示柱体的底面积, h 表示柱体的高 锥体的体积公式V - Sh3其中S 表示锥体的底面积, h 表示锥体的高 球的表面积公式―_2S 4 R球的体积公式R 33A . (- y/2 , 0),(握,0)D.既不充分也不必要条件7 .设0<p<1,随机变量E 的分布列是3.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位: cm 3)是A . 2B . 44 .复数—(i 为虚数单位)的共轴复数是1 iC.充分必要条件A .充分不必要条件B.必要不充分条件则|a- b|的最小值是则当 p 在(0, 1)内增大时,B. D ( &增大C. D ( &先减小后增大D. D ( &先增大后减小8 .已知四棱锥S-ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设 SE与BC 所成的角为SE 与平面ABCD 所成的角为也,二面角S- AB- C 的平面角为 饱 则C.9 .已知a, b, e 是平面向量, e 是单位向量. 若非零向量 a 与e 的夹角为,向量 b 满足 b 2-4e b+3=0,A . 73-1B . ^3+1 C. D . 2-4310.已知 ai,a 2,a 3,a 4成等比数列,且 a i a? & a 4 ln(a i a ? a 3).若 A. a 〔 a 3,a 2a 4B. a 1 a 3,a 2 a 4C. a a 3,a 2 a 4非选择题部分(共110分)二、填空题:本大题共 7小题,多空题每题 6分,单空题每题4分,共36分。
2018年普通高等学校招生全国统一考试数学试题(浙江卷,含解析)

2018年普通高等学校招生全国统一考试数学试题(浙江卷)本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:互斥,则相互独立,则分别表示台体的上、下底面积,台体的高柱体的体积公式其中表示柱体的底面积,表示柱体的高锥体的体积公式其中表示锥体的底面积,表示锥体的高球的体积公式其中表示球的半径选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知全集U={1,2,3,4,5},A={1,3},则A. B. {1,3} C. {2,4,5} D. {1,2,3,4,5}【答案】C【解析】分析:根据补集的定义可得结果.详解:因为全集,,所以根据补集的定义得,点睛:若集合的元素已知,则求集合的交集、并集、补集时,可根据交集、并集、补集的定义求解. 2. 双曲线的焦点坐标是A. (−,0),(,0)B. (−2,0),(2,0)C. (0,−),(0,)D. (0,−2),(0,2) 【答案】B【解析】分析:根据双曲线方程确定焦点位置,再根据求焦点坐标. 详解:因为双曲线方程为,所以焦点坐标可设为,因为,所以焦点坐标为,选B.点睛:由双曲线方程可得焦点坐标为,顶点坐标为,渐近线方程为.3. 某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是俯视图正视图A. 2B. 4C. 6D. 8 【答案】C【解析】分析:先还原几何体为一直四棱柱,再根据柱体体积公式求结果.详解:根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1,2,梯形的高为2,因此几何体的体积为选C.点睛:先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等. 4. 复数(i 为虚数单位)的共轭复数是A. 1+iB. 1−iC. −1+iD. −1−i【解析】分析:先分母实数化化简复数,再根据共轭复数的定义确定结果.详解:,∴共轭复数为,选B.点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数的相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭复数为.5. 函数y=sin2x的图象可能是A. B.C. D.【答案】D【解析】分析:先研究函数的奇偶性,再研究函数在上的符号,即可判断选择.详解:令,因为,所以为奇函数,排除选项A,B;因为时,,所以排除选项C,选D.点睛:有关函数图象的识别问题的常见题型及解题思路:(1)由函数的定义域,判断图象的左、右位置,由函数的值域,判断图象的上、下位置;(2)由函数的单调性,判断图象的变化趋势;(3)由函数的奇偶性,判断图象的对称性;(4)由函数的周期性,判断图象的循环往复.6. 已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】分析:根据线面平行的判定定理得充分性成立,而必要性显然不成立.详解:因为,所以根据线面平行的判定定理得.由不能得出与内任一直线平行,所以是的充分不必要条件,故选A.点睛:充分、必要条件的三种判断方法:(1)定义法:直接判断“若则”、“若则”的真假.并注意和图示相结合,例如“⇒”为真,则是的充分条件.(2)等价法:利用⇒与非⇒非,⇒与非⇒非,⇔与非⇔非的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)集合法:若⊆,则是的充分条件或是的必要条件;若=,则是的充要条件.7. 设0<p<1,随机变量ξ的分布列是则当p在(0,1)内增大时,A. D(ξ)减小B. D(ξ)增大C. D(ξ)先减小后增大D. D(ξ)先增大后减小【答案】D【解析】分析:先求数学期望,再求方差,最后根据方差函数确定单调性.详解:,,,∴先增后减,因此选D.点睛:8. 已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】D【解析】分析:分别作出线线角、线面角以及二面角,再构造直角三角形,根据边的大小关系确定角的大小关系.详解:设O为正方形ABCD的中心,M为AB中点,过E作BC的平行线EF,交CD于F,过O作ON垂直EF于N,连接SO,SN,OM,则SO垂直于底面ABCD,OM垂直于AB,因此从而因为,所以即,选D.点睛:线线角找平行,线面角找垂直,面面角找垂面.9. 已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2−4e·b+3=0,则|a−b|的最小值是A. −1B. +1C. 2D. 2−【答案】A【解析】分析:先确定向量所表示的点的轨迹,一个为直线,一个为圆,再根据直线与圆的位置关系求最小值.详解:设,则由得,由得因此的最小值为圆心到直线的距离减去半径1,为选A.点睛:以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算,将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系,是解决这类问题的一般方法.10. 已知成等比数列,且.若,则A. B. C. D.【答案】B【解析】分析:先证不等式,再确定公比的取值范围,进而作出判断.详解:令则,令得,所以当时,,当时,,因此,若公比,则,不合题意;若公比,则但,即,不合题意;因此,,选B.点睛:构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2018年浙江数学高考试题及答案解析
2018年普通高等学校招生全国统一考试(浙江卷)数 学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分3至4页。
满分150分。
考试用时120分钟。
选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U ={1,2,3,4,5},A ={1,3},则=U A ð A .∅B .{1,3}C .{2,4,5}D .{1,2,3,4,5}2.双曲线221 3=x y -的焦点坐标是A .(−2,0),(2,0)B .(−2,0),(2,0)C .(0,−2),(0,2)D .(0,−2),(0,2)3.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .2B .4C .6D .84.复数21i- (i 为虚数单位)的共轭复数是 A .1+iB .1−iC .−1+iD .−1−i5.函数y =||2x sin2x 的图象可能是A .B .C .D .6.已知平面α,直线m ,n 满足m ⊄α,n ⊂α,则“m ∥n ”是“m ∥α”的 A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件侧视图俯视图正视图22117.设0<p <1,随机变量ξ的分布列是ξ 012P12p- 12 2p 则当p 在(0,1)内增大时, A .D (ξ)减小B .D (ξ)增大C .D (ξ)先减小后增大D .D (ξ)先增大后减小 8.已知四棱锥S −ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为θ1,SE 与平面ABCD 所成的角为θ2,二面角S −AB −C 的平面角为θ3,则 A .θ1≤θ2≤θ3B .θ3≤θ2≤θ1C .θ1≤θ3≤θ2D .θ2≤θ3≤θ19.已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为π3,向量b 满足b 2−4e ·b +3=0,则|a −b |的最小值是 A .3−1B .3+1C .2D .2−310.已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则 A .1324,a a a a <<B .1324,a a a a ><C .1324,a a a a <>D .1324,a a a a >>非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2018年浙江省高考数学试卷(含详细解析)

2018年浙江省高考数学试卷一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(4分)已知全集U={1,2,3,4,5},A={1,3},则∁U A=()A.∅B.{1,3}C.{2,4,5}D.{1,2,3,4,5}2.(4分)双曲线﹣y2=1的焦点坐标是()A.(﹣,0),(,0)B.(﹣2,0),(2,0)C.(0,﹣),(0,)D.(0,﹣2),(0,2)3.(4分)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.2 B.4 C.6 D.84.(4分)复数(i为虚数单位)的共轭复数是()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i5.(4分)函数y=2|x|sin2x的图象可能是()A.B.C.D.6.(4分)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.(4分)设0<p<1,随机变量ξ的分布列是ξ012P则当p在(0,1)内增大时,()A.D(ξ)减小B.D(ξ)增大C.D(ξ)先减小后增大D.D(ξ)先增大后减小8.(4分)已知四棱锥S﹣ABCD的底面是正方形,侧棱长均相等,E是线段AB 上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S﹣AB﹣C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ19.(4分)已知,,是平面向量,是单位向量.若非零向量与的夹角为,向量满足﹣4•+3=0,则|﹣|的最小值是()A.﹣1 B.+1 C.2 D.2﹣10.(4分)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则()A.a1<a3,a2<a4B.a1>a3,a2<a4C.a1<a3,a2>a4D.a1>a3,a2>a4二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2018年高考真题浙江卷数学试题及答案解析

绝密★启用前2018年普通高等学校招生全国统一考试(浙江卷)数学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:若事件A,B互斥,则若事件A,B相互独立,则若事件A在一次试验中发生的概率是p,则n次独立重复试验中事件A恰好发生k次的概率台体的体积公式其中分别表示台体的上、下底面积,表示台体的高柱体的体积公式其中表示柱体的底面积,表示柱体的高锥体的体积公式其中表示锥体的底面积,表示锥体的高球的表面积公式球的体积公式其中表示球的半径选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知全集U={1,2,3,4,5},A={1,3},则A. B. {1,3} C. {2,4,5} D. {1,2,3,4,5}【答案】C【解析】分析:根据补集的定义可得结果.详解:因为全集,,所以根据补集的定义得,故选C.点睛:若集合的元素已知,则求集合的交集、并集、补集时,可根据交集、并集、补集的定义求解.2. 双曲线的焦点坐标是A. (−,0),(,0)B. (−2,0),(2,0)C. (0,−),(0,)D. (0,−2),(0,2)【答案】B【解析】分析:根据双曲线方程确定焦点位置,再根据求焦点坐标.详解:因为双曲线方程为,所以焦点坐标可设为,因为,所以焦点坐标为,选B.点睛:由双曲线方程可得焦点坐标为,顶点坐标为,渐近线方程为.3. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是A. 2B. 4C. 6D. 8【答案】C【解析】分析:先还原几何体为一直四棱柱,再根据柱体体积公式求结果.详解:根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1,2,梯形的高为2,因此几何体的体积为选C.点睛:先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.4. 复数(i为虚数单位)的共轭复数是A. 1+iB. 1−iC. −1+iD. −1−i【答案】B【解析】分析:先分母实数化化简复数,再根据共轭复数的定义确定结果.详解:,∴共轭复数为,选B.点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数的相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭复数为.5. 函数y=sin2x的图象可能是A. B.C. D.【答案】D【解析】分析:先研究函数的奇偶性,再研究函数在上的符号,即可判断选择.详解:令,因为,所以为奇函数,排除选项A,B; 因为时,,所以排除选项C,选D.点睛:有关函数图象的识别问题的常见题型及解题思路:(1)由函数的定义域,判断图象的左、右位置,由函数的值域,判断图象的上、下位置;(2)由函数的单调性,判断图象的变化趋势;(3)由函数的奇偶性,判断图象的对称性;(4)由函数的周期性,判断图象的循环往复.6. 已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】分析:根据线面平行的判定定理得充分性成立,而必要性显然不成立.详解:因为,所以根据线面平行的判定定理得.由不能得出与内任一直线平行,所以是的充分不必要条件,故选A.点睛:充分、必要条件的三种判断方法:(1)定义法:直接判断“若则”、“若则”的真假.并注意和图示相结合,例如“⇒”为真,则是的充分条件.(2)等价法:利用⇒与非⇒非,⇒与非⇒非,⇔与非⇔非的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)集合法:若⊆,则是的充分条件或是的必要条件;若=,则是的充要条件.7. 设0<p<1,随机变量ξ的分布列是ξ0 1 2P则当p在(0,1)内增大时,A. D(ξ)减小B. D(ξ)增大C. D(ξ)先减小后增大D. D(ξ)先增大后减小【答案】D【解析】分析:先求数学期望,再求方差,最后根据方差函数确定单调性.详解:,,,∴先增后减,因此选D.点睛:8. 已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】D【解析】分析:分别作出线线角、线面角以及二面角,再构造直角三角形,根据边的大小关系确定角的大小关系.详解:设O为正方形ABCD的中心,M为AB中点,过E作BC的平行线EF,交CD于F,过O作ON垂直EF于N,连接SO,SN,OM,则SO垂直于底面ABCD,OM垂直于AB,因此从而因为,所以即,选D.点睛:线线角找平行,线面角找垂直,面面角找垂面.9. 已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2−4e·b+3=0,则|a−b|的最小值是A. −1B. +1C. 2D. 2−【答案】A【解析】分析:先确定向量所表示的点的轨迹,一个为直线,一个为圆,再根据直线与圆的位置关系求最小值.详解:设,则由得,由得因此的最小值为圆心到直线的距离减去半径1,为选A.点睛:以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算,将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系,是解决这类问题的一般方法.10. 已知成等比数列,且.若,则A. B. C. D.【答案】B【解析】分析:先证不等式,再确定公比的取值范围,进而作出判断.详解:令则,令得,所以当时,,当时,,因此,若公比,则,不合题意;若公比,则但,即,不合题意;因此,,选B.点睛:构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2018年浙江省高考数学试卷及答案解析(名师精校版)

台体的体积公式 其中 分别表示台体的上、下底面积, 表示 台体的高
球的体积公式 其中 表示球的半径
选择题部分(共 40 分)
一、选择题:本大题共 10 小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符
合题目要求的。
1. 已知全集 U={1,2,3,4,5},A={1,3},则
A.
B. {1,3} C. {2,4,5} D. {1,2,3,4,5}
【答案】C
第 2 页 共 25 页
【解析】分析:根据补集的定义可得结果.
详解:因为全集
,
,所以根据补集的定义得
,
故选 C.
点睛:若集合的元素已知,则求集合的交集、并集、补集时,可根据交集、并集、补集的定义求解.
2. 双曲线
的焦点坐标是
【解析】分析:先研究函数的奇偶性,再研究函数在 上的符号,即可判断选择.
详解:令
,
因为
,所以
为奇函数,排除选项 A,B;
因为
时,
,所以排除选项 C,选 D.
点睛:有关函数图象的识别问题的常见题型及解题思路:(1)由函数的定义域,判断图象的左、右位置, 由函数的值域,判断图象的上、下位置;(2)由函数的单调性,判断图象的变化趋势;(3)由函数的奇偶 性,判断图象的对称性;(4)由函数的周期性,判断图象的循环往复. 6. 已知平面α,直线 m,n 满足 m α,n α,则“m∥n”是“m∥α”的 A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据线面平行的判定定理得充分性成立,而必要性显然不成立.
详解:因为Байду номын сангаас
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年普通高等学校招生全国统一考试 (浙江卷) 数学
一、选择题(本大题共10小题,每小题4分,共40分)
1. 已知全集U ={1,2,3,4,5},A ={1,3},则C U A =( )
A . φ
B . {1,3}
C . {2,4,5}
D . {1,2,3,4,5}
2. 双曲线
−y 2=1的焦点坐标是( )
A . (−,0),(,0)
B . (−2,0),(2,0)
C . (0,−),(0,)
D . (0,−2),(0,2)
3. 某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:
cm 3)是( )
A . 2
B . 4
C . 6
D . 8 4. 复数
(i 为虚数单位)的共轭复数是( )
A . 1+I
B . 1−I
C . −1+I
D . −1−i 5. 函数y =
sin 2x 的图象可能是(
)
D
C
6. 已知平面α,直线m ,n 满足m ⊄α,n ⊂α,则“m ∥n ”是“m ∥α”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
7. 设0<p <1
则当p 在(0,1)A . D (ξ)减小 B . D (ξ)增大 C . D (ξ)先减小后增大 D . D (ξ)先增大后减小 8. 已知四棱锥S −ABCD 的底面是正方形,侧棱长均相等,E
是线段AB 上的点(不含端点
),
设SE 与BC 所成的角为θ1,SE 与平面ABCD 所成的角为θ2,二面角S −AB −C 的平面角
俯视图
正视图
为θ3,则( )
A. θ1≤θ2≤θ3
B. θ3≤θ2≤θ1
C. θ1≤θ3≤θ2
D. θ2≤θ3≤θ1
9.已知a,b,e是平面向量,e是单位向量,若非零向量a与e的夹角为,向量b满足
b2−4e•b+3=0,则|a−b|的最小值是( )
A. −1
B. +1
C. 2
D. 2−
10.已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则( )
A. a1<a3,a2<a4
B. a1>a3,a2<a4
C. a1<a3,a2>a4
D. a1>a3,a2>a4
二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)
11.我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,
值钱三;鸡雏三,值钱一,凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁、鸡母,鸡雏个数分别为x,y,z,则,当z=81时,x=_______,y=_______ 12.若x,y满足约束条件,则z=x+3y的最小值是___________,最大值是___________
13.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=,b=2,A=60°,则
sinB=_________________,c=___________________
14.二项式(+)8的展开式的常数项是_________________________
15.已知λ∈R,函数f(x)=,当λ=2时,不等式f(x)<0的解集是
___________________,若函数f(x)恰有2个零点,则λ的取值范围是__________________ 16.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成
______________________个没有重复数字的四位数(用数字作答)
17.已知点P(0,1),椭圆+y2=m(m>1)上两点A,B满足=2,则当
m=____________________时,点B横坐标的绝对值最大
三、解答题(本大题共5小题,共74分)
18.(14分)已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点
34
P--,(1)求sin(α+π)的值;(2)若角β满足sin(α+β)=,求c osβ的值
(,)
55
19.(15分)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,
A1A=4,C1C=1,AB=BC=B1B=2
(1)证明:AB1⊥平面A1B1C1
(2)求直线AC1与平面ABB1所成的角的正弦值
20.(15分)已知等比数列{a n}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项,数列
{b n}满足b1=1,数列{(b n+1−b n)a n}的前n项和为2n2+n
(1)求q的值
(2)求数列{b n}的通项公式C1
B1
A1
C A
21.(15分)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点
A,B满足PA,PB的中点均在C上
(1)设AB中点为M,证明:PM垂直于y轴
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取
值范围Array
22.(15分)已知函数f(x )=−lnx
(1)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8−8ln2
(2)若a≤3−4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点。
