现代信号处理Matlab仿真——例611
信号与系统(第5版)MATLAB仿真举例

MATLAB仿真举例一、MATLAB应用概要1. MATLAB的知识与特点MATLAB是由美国Mathworks公司于1984年推出的一种功能强大的科学计算软件,主要适用于矩阵运算、信息处理和控制等领域的分析与设计。
MA TLAB是“矩阵实验室”(MA Trix LABoratoy)的缩写。
它以矩阵运算为基础,以简洁便用的“科学便笺式”编程语言,可交互的集成环境,强大的图形可视化功能,广泛应用于科学、工程和绘图的各种领域,受到科学界和教育界的高度好评。
其特点是:(1) 数值计算功能强,每个数值元素都视为复数,用双精度(64位)一种格式,编程简化;(2) 具有符号计算功能;(3) 简单而强大的作图功能;(4) 人机界面适合科技人员;(5) 功能多,可扩展性强,有多种工具箱作专门处理。
2.MATLAB的窗口与应用常识(1) 命令窗口以MA TLAB6.x为例,其集成环境有桌面平台及8个组成部分:指令窗口、历史指令窗口、工作台及工具箱窗口、工作目录窗口、工作空间窗口、矩阵编辑器、程序编辑器和帮助浏览器。
点击桌面上的MA TLAB图标进入MATLAB后,即可看到命令窗口(Command Window),它是主窗口,当显示“〉〉”时,表示系统处于准备接受命令的状态。
(2) 图形窗口一般,只要执行任一种绘图命令,就会自动产生图形窗口,以后的绘图都在这一个图形窗口中进行。
(3) 文本编辑窗口用MA TLAB计算有两种方式,一种是简单计算,可在命令窗口一行一行地输入各命令,另一种是对复杂计算时,把多行命令组成一个M文件,让MA TLAB自动执行。
(4) M文件采用MATLAB所规定的一套语言及语法编写的源文件记作.m文件。
其文件名不能以数字开头,也不能包含文字,但可以用下划线“_”。
(5) Help命令Help命令是查询函数相关信息的最基本方式,信息会直接显示在命令窗口中。
(6) 应用常识①MA TLAB使用双精度数据,所有系统命令都是小写形式。
利用Matlab进行模拟和实时系统仿真的指南

利用Matlab进行模拟和实时系统仿真的指南引言Matlab是一种强大的数学计算和仿真软件,广泛应用于科学研究、工程设计、数据分析等领域。
本文将为大家介绍如何使用Matlab进行模拟和实时系统仿真,帮助读者快速上手并取得良好的仿真效果。
一、Matlab的基本介绍1. Matlab的特点和优势Matlab具有易学易用、功能强大、成熟稳定的特点,可以进行高效的数值计算、绘图和数据处理。
通过Matlab,用户可以快速实现各类算法和模型,并进行可视化演示。
2. Matlab的基本操作和界面介绍Matlab的界面分为命令窗口、编辑器窗口、变量窗口和绘图窗口等区域,用户可以在不同窗口之间切换,并通过命令行输入相关指令进行计算和操作。
Matlab的操作类似于一种交互式的编程语言,用户可以通过函数和脚本来实现相应的功能。
二、Matlab的模拟仿真工具1. Matlab的Simulink工具Simulink是Matlab中的一个重要模块,用于图形化建模和仿真系统。
通过Simulink,用户可以使用图形化界面拖拽各类模块,建立复杂的系统模型,并进行仿真分析。
2. Simulink的使用方法用户可以通过拖拽不同的模块进行系统的建模,如信号源、控制器、传感器等,并通过参数设置实现相应功能。
Simulink还提供了丰富的仿真工具,例如时域仿真、频域分析等,帮助用户更好地理解系统性能。
三、Matlab的实时仿真工具1. Matlab的Real-Time Workshop工具Real-Time Workshop是Matlab中用于生成实时代码的工具,这使得用户可以将建立的仿真模型直接部署到硬件平台上进行实时控制。
2. Real-Time Workshop的使用方法用户可以通过将Simulink中的模型进行编译和配置,生成适用于不同硬件平台的实时代码。
通过这种方式,用户可以在硬件平台上实现实时控制,进行闭环仿真等应用。
四、案例分析1. 汽车倒车雷达系统仿真以汽车倒车雷达系统为例,介绍如何使用Matlab进行仿真。
基于MATLAB的常用信号调制仿真

1 前言1.1 信号调制仿真的概念仿真是衡量系统性能的工具,它通过仿真模型的仿真结果来判断原系统的性能从而为新系统的建立或原系统的改造提供可靠的参考。
通过仿真,可以降低新系统失败的可能性,消除系统中潜在的瓶颈,防止对系统中某些功能部件造成过量的负载,优化系统的整体性能,因此,仿真是科学研究和工程建设中不可缺少的方法[1-2]。
实际的信号调制是一个功能结构相当复杂的系统,对这个系统做出的任何改变(如改变某个参数的设置、改变系统的结构等)都可能影响到整个系统的性能和稳定。
因此,在对原有的系统作出改进或建立一个新系统之前,通常需要对这个系统进行建模和仿真。
通过仿真结果衡量方案的可行性,从中选择最合理的系统配置和参数设置,然后再应用于实际系统中,这个过程就是信号调制仿真[3]。
与一般的仿真过程类似,在对信号调制实施仿真之前,首先需要研究信号调制的特性,通过归纳和抽象建立信号调制的仿真模型。
图1-1是关于信号调制仿图1-1 仿真流程示意图从图中可以看到,信号调制仿真是一个循环往复的过程,它从当前系统出发,通过分析建立起一个能够在一定程度上描述原信号调制的仿真模型,然后通过仿真实验得到相关的数据。
通过对仿真数据的分析可以得到相应的结论,然后把这个结论应用到对当前信号调制系统的改造中。
值得注意的是,信号调制仿真并不是一个机械的过程,它实际上是人的思维活动在计算机协助下的一种延伸。
1.2 信号调制仿真问题的提出、研究价值及研究现状1.2.1 信号调制仿真问题的提出信号调制的性能可以用基于公式的计算方法、波形级仿真或通过硬件样机研究和测量来估计得到。
以简化模型为基础的公式法只能应用于一些理想化和过于简单的例子,要想估计出复杂信号调制的性能是非常困难的。
基于测量的性能估计方法通常代价很高,并且很不灵活。
用基于仿真的方法来估计性能时,系统可以用任何所期待的细节(主观的,当然有一定局限)来模拟。
与公式法或测量法相比较。
Matlab在工程设计与仿真中的应用案例

Matlab在工程设计与仿真中的应用案例近年来,Matlab(全称Matrix Laboratory)在工程设计与仿真中的应用越来越广泛。
Matlab是一款功能强大的计算软件,具有矩阵计算、数据处理和可视化等多种功能。
本文将通过几个实际案例,展示Matlab在工程设计与仿真中的应用。
一、电路设计与仿真电路设计是工程领域中重要的一环,而Matlab提供了强大的电路设计与仿真工具。
以滤波器设计为例,Matlab配备了丰富的滤波器设计函数,可以根据特定的滤波系数和频响要求,快速设计出满足需求的滤波器。
同时,Matlab还支持频域仿真,可以对信号进行傅里叶变换和滤波操作,以实现不同的信号处理需求。
二、机械系统建模与控制在机械系统建模与控制方面,Matlab也发挥了重要的作用。
例如,在机械结构设计中,Matlab可以通过有限元分析建立结构的数值模型,对结构的强度、刚度等进行分析与求解。
同时,Matlab还支持控制系统建模与仿真,可以通过控制系统的设计,提高机械系统的性能和稳定性。
三、通信系统设计与仿真通信系统设计与仿真是Matlab应用的另一个重要领域。
例如,在无线通信系统设计中,Matlab提供了丰富的信号处理工具,可以对传输信号进行调制、解调和通道编码等操作,实现数据的可靠传输。
此外,Matlab还支持多输入多输出系统的建模与仿真,可以分析和优化系统的传输性能。
四、图像处理与计算机视觉近年来,图像处理和计算机视觉成为热门的研究领域。
而Matlab提供了一系列的图像处理函数与工具箱,可以进行图像的滤波、分割、特征提取和目标识别等操作。
通过Matlab的强大功能,研究人员可以开展多样化的图像处理与计算机视觉应用,如人脸识别、车牌识别等。
五、仿真与优化算法Matlab凭借其强大的数值计算能力和优化算法,成为工程设计中的重要辅助工具。
例如,在电力系统中,Matlab可以应用潮流计算和稳定性分析等算法,发现潮流分布、电压质量等问题,优化电力系统的稳定性和效率。
信号与系统课程的Matlab仿真应用_苏宁馨

科技经济市场对周围小区的干扰,以及周围小区对本小区的干扰存在。
扫频仪自身携带GPS天线,接收GPS卫星信号,通过内置GPS接收机输出的时钟信号,以及扫频仪与基站同步时钟之间的差值就可以得到从基站到扫频仪的测量时延。
基站GPS时钟正常情况下:测量时延=传输时延基站GPS时钟异常情况下:测量时延=传输时延+GPS偏移在不消除传播时延的情况下,由于GPS导致的基站的偏移范围应该在0-6400chip内。
因此在考虑了多径效应的影响后,我们可以设定一个门限,比如250chip作为怀疑存在失步问题的门限。
在路测时,发现某小区的测量时延(帧头偏移)超过了1000chip(单位:1/4chip),就认为是失步。
通过以上主要定位方法和辅助定位方法来综合分析,判断具体是由于哪些基站的GPS跑偏导致TD-SCDMA系统干扰。
通过解决基站的GPS故障,进而消除系统干扰。
参考文献:[1]李世鹤,杨运年.TD-SCDMA第三代移动通信系统[M].北京:人民邮电出版社,2009.[2]朱东照,汪丁鼎.TD-SCDMA无线网络规划设计与优化.人民邮电出版社,2008.信号与系统课程历来是一门难学难教的课程,由于该课程理论性较强,而且数学能力要求比较高,同时该门课程还与物理、电路分析、复变函数等多门课程有相关联系,知识面要求较广,综合分析能力要求强,同时在电子信息和通信专业开设的后续课程(如通信原理、数字信号处理等)都需要借助信号与系统中的知识,这门课程对于理论和实践两个体系都有很高的要求。
由此可见,信号与系统课程的教学质量对电子信息类专业人才培养的重要性。
在传统教学中由于学生缺乏对知识的总结应用且又无法对实际系统进行感性认识,所以学生感到难学。
为此,在信号与系统课程的教学理念、教学内容、实验教学、教学方法与手段、评价体系等诸多方面都必须进行全面改革与创新。
1新型教学形式的提出教学理念的升华:淡化理论教学与实验教学的界限,将理论教学与实验教学有机的结合,融知识传授、能力培养、素质教育于一体,实现原理、方法、应用的有机结合。
MATLAB仿真实例

MATLAB仿真实例通信原理是指传输信息的原理和方法。
MATLAB可以用于实现各种通信原理的仿真,包括信号的调制、发送、接收、解调等过程。
下面我将介绍一个基于MATLAB的通信原理仿真实例。
本实例以频率调制通信原理为基础,以调频调制(FM)为例进行仿真。
1.首先定义模拟信号源,生成一个基带信号。
例如,我们可以选择一个正弦波信号作为基带信号,其频率为$f_m$。
2.接下来,我们需要将基带信号进行调频调制。
在调频调制过程中,我们将基带信号的频率进行调制,生成载频为$f_c$的调制信号。
3. 在MATLAB中,我们可以使用freqmod函数来进行调频调制。
该函数接受基带信号、载频和调制指数作为输入参数,并返回调制信号。
4.在得到调制信号后,我们可以进行发送模拟。
发送模拟是指将调制信号通过信道传输,可以简单地将信号存储为一个信道矩阵。
5. 在接收端,我们需要对接收到的信号进行解调,以恢复基带信号。
在调频调制中,我们可以使用freqdemod函数进行解调。
该函数接受解调信号、载频和调制指数作为输入参数,并返回解调后的信号。
6.最后,我们可以将解调信号与原始信号进行比较,计算它们之间的误差。
可以使用均方根误差(RMSE)作为误差度量指标。
通过以上过程,我们可以完成一个简单的基于MATLAB的调频调制仿真。
为了使仿真更贴近实际通信场景,我们还可以添加信道噪声等因素。
例如,我们可以在发送模拟过程中,向信道矩阵中添加高斯白噪声。
这样可以更真实地模拟信号在传输过程中受到干扰和噪声的情况。
通过以上步骤,我们可以利用MATLAB进行通信原理的仿真实践。
这个实例不仅可以帮助我们加深理解通信原理的基本概念和过程,还可以通过实际操作和仿真结果进行验证和验证。
总之,MATLAB是一个非常强大的工具,可以用于各种通信原理的仿真。
通过利用MATLAB进行仿真实践,我们可以更深入地理解通信原理的基本原理和过程,提高我们的理论水平和实践能力。
MATLAB控制系统各种仿真例题(包括simulink解法)

一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ,T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5));GTransfer function:s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]);H=tf(num,den,'Ts',0.1)Transfer function:z^2 + 0.56-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.992. 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点,并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ,T=0.05s>>z=[-1-j -1+j];p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain:8 (s^2 + 2s + 2)--------------------------s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6];p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846)-------------------------(z-0.122)Sampling time: 0.05>>pzmap (H )num=[0,7.1570,-6.4875 ];den=[1,-2.2326,1.7641,-0.4966];sysd=tf(num,den,0.05,'variable','z^-1')Transfer function:7.157 z^-1 - 6.487 z^-2-----------------------------------------1 - 2.233 z^-1 + 1.764 z^-2 - 0.4966 z^-3Sampling time: 0.05二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
matlab通信仿真实例

matlab通信仿真实例在Matlab中进行通信系统的仿真,可以涉及到多种不同的通信技术和协议,包括调制解调、信道编码、多址接入等。
以下以OFDM系统为例,介绍Matlab 中通信仿真的实例。
OFDM(正交频分复用)是一种常用于现代通信系统中的技术,它将高速数据流分割成多个较低速的子流,并将每个子流分配到不同的子载波上。
优点是能够抵抗多径效应和频率选择性衰落,并提供高数据速率。
首先,我们需要创建一个包含OFDM系统参数的结构体。
例如:ofdmParam.M = 16; % 子载波数量ofdmParam.K = 4; % 用于混合多路复用的用户数量ofdmParam.N = ofdmParam.M * ofdmParam.K; % 总子载波数量ofdmParam.CP = 16; % 循环前缀长度接下来,我们可以生成用于OFDM仿真的数据流。
例如,我们可以使用随机整数生成器生成一系列整数,并将其转换为复数形式的调制符号:data = randi([0, ofdmParam.M-1], 1, ofdmParam.N);dataMod = qammod(data, ofdmParam.M);然后,我们可以创建一个包含OFDM信号的函数。
在OFDM系统中,生成的数据符号将分配到不同的子载波上,然后在时域中通过插入循环前缀进行叠加:function[ofdmSignal] = createOFDMSignal(dataMod, ofdmParam) ofdmSignal = [];for k = 0:ofdmParam.K-1% 提取相应的数据符号,并进行IFFTofdmData =ifft(dataMod(k*ofdmParam.M+1:(k+1)*ofdmParam.M));% 添加循环前缀ofdmDataWithCP = [ofdmData(end-ofdmParam.CP+1:end), ofdmData];% 将OFDM符号添加到OFDM信号中ofdmSignal = [ofdmSignal, ofdmDataWithCP];endend将OFDM信号传输到信道中,我们可以使用加性高斯白噪声(AWGN)信道模型来模拟实际通信环境:EbNo = 10; % 信噪比snr =10*log10(ofdmParam.N*ofdmParam.M/(ofdmParam.N*ofdmParam.M+1 )*(10^(EbNo/10)));ofdmSignalNoisy = awgn(ofdmSignal, snr, 'measured');最后,我们可以对接收到的OFDM信号进行解调和信号恢复。
信号与系统MATLAB仿真——信号及其运算

信号与系统MATLAB仿真——信号及其运算1. 知识回顾(1)信号的分类:确定信号与随机信号;周期信号与⾮周期信号;周期信号在时间上必须是⽆始⽆终的f(t)=f(t+T)f[k]=f[k+N]连续时间信号和离散时间信号;连续信号是指在信号的定义域内,除若⼲个第⼀类间断点外,对于任意时刻都由确定的函数值的信号离散信号是指在信号的定义域内,只在某些不连续规定的时刻给出函数值,⽽在其他时刻没有给出函数的信号能量信号、功率信号与⾮功率⾮能量信号;时限与频限信号;物理可实现信号。
(2)信号能量:E=limT→∞∫T−T f2(t)dtP=limT→∞12T∫T−Tf2(t)dtE=limN→∞N∑k=−N|f[k]|2P=limN→∞12N+1N∑k=−N|f[k]|2能量信号:0<E<∞,P=0;功率信号:0<P<∞,E=∞。
(3)冲激函数的性质加权特性(筛选特性):f(t)δ(t−t0)=f(t0)δ(t−t0)取样特性:∫+∞−∞f(t)δ(t−t0)=f(t0)偶函数:f(t)=f(−t)展缩特性:δ(at)=1|a|δ(t)δ(at−t0)=1|a|δ(t−t0a)导数及其特性。
(4)正弦两个频率相同的正弦信号相加,即使其振幅和相位各不相同,但相加后结果仍是原频率的正弦信号;若⼀个正弦信号的频率是另⼀个正弦信号频率的整数倍时,则合成信号是⼀个⾮正弦周期信号,其周期等于基波的周期。
正弦型序列:f[k]=A sin(Ω0k+φ)2π/Ω0是正整数:周期序列,周期为N;2π/Ω0为有理数,2π/Ω0=N/m:周期序列,周期N=m(2π/Ω0);2π/Ω0为⽆理数:⾮周期序列,但包络仍为正弦函数。
(5)抽样信号Sa(t)=sin t t偶函数;Sa(0)=1;t=kπ为其零点;∫+∞−∞Sa(t)dt=π;limt→±∞Sa(t)=0。
(6)信号的分解分解为直流分量与交流分量;奇偶分解;分解为实部和虚部;分解为基本信号的有限项之和;因⼦分解;连续信号分解为矩形脉冲序列;正交分解。
MATLAB在仿真与模拟方面的应用实例

MATLAB在仿真与模拟方面的应用实例一、简介MATLAB是一款强大且广泛应用于科学计算和工程设计领域的软件工具。
它提供了丰富的函数库和工具箱,方便用户进行数据分析、数值计算、信号处理以及模拟仿真等工作。
本文将介绍MATLAB在仿真与模拟方面的应用实例,分别从电子电路设计、通信系统仿真以及控制系统设计等方面展开。
二、电子电路设计电子电路设计是电子工程领域中一项重要的工作。
MATLAB提供了一系列丰富的工具箱,例如Simulink和Simscape等,可以用于电子电路的建模和仿真。
以放大器设计为例,我们可以使用MATLAB进行仿真。
首先,我们可以使用Simulink建立电路模型,包括信号源、滤波器、放大器等组件,并设置相应的参数。
然后,通过添加信号源以及观察输出信号的方式,可以对放大器的性能进行评估,并通过实时仿真结果进行调整和优化。
此外,MATLAB还提供了各种仿真工具和函数,如电路分析工具箱和电路设计工具箱等,可以用于分析电路参数以及进行设计和优化。
通过MATLAB的电子电路设计工具,工程师们能够更加高效地进行电子电路的仿真和设计工作。
三、通信系统仿真通信系统是一种用于传输和接收信息的系统。
MATLAB提供了用于建模和仿真通信系统的工具箱,例如通信工具箱和信号处理工具箱等。
通过使用MATLAB的通信工具箱,我们可以建立和仿真各种通信系统,如数字调制解调、信道编码解码以及误码率分析等。
我们可以设置发送端和接收端的参数,并使用各种信号处理算法进行仿真。
通过调整参数和算法,可以评估和优化通信系统的性能。
此外,MATLAB还提供了用于处理和分析信号的函数和工具箱,如滤波器设计、频谱分析和信号重构等。
这些工具有助于工程师们更好地理解信号特性,并进行通信系统的仿真和设计。
四、控制系统设计控制系统是一种用于控制和调节系统行为的系统。
MATLAB提供了用于建模和仿真控制系统的工具箱,例如控制系统工具箱和优化工具箱等。
MATLAB仿真技术

4. 系统建模 4.1 连续系统建模
线性系统建模举例
例3:复位积分器的功用示例。 在仿真启动时,积分器从零开始对 0.5 t 进行积分。当复位口 信号 t-5=0 瞬间,积分器被重置为零。此后,再对0.5 ( t-5 ) 进行积分。
例3_4_2:积分模块直接构造微分方程求解模型。
假设从实际自然界(力学、电学、生态等)或社会中,抽象 出有初始状态为0的二阶微分程 x 0.2x 0.4x 0.2u,(t) u(t)是单位阶跃函数。本例演示如何用积分器直接构搭求解该微 分方程的模型。
符号矩阵的基本运算:加、减、乘、除、微积分等。 符号代数方程的求解。 符号微分方程的求解。 符号积分变换。
目录 主页
MATLAB的可视化功能
(1)二维曲线图形和三维曲面图形
二维符号函数曲线。
二维曲线图形。
三维符号函数曲线。 三维曲面图形。
三维线性图形。
目录 主页
(2)句柄图形 句柄图形(Handle Graphics)是一种面向对象的绘图系统。 图形对象、对象句柄和句柄图形树。 • MATLAB把用于数据可视和界面制作的基本绘图要素称 为句柄图形对象。 • 构成MATLAB句柄图形体系有12个图形对象(见句柄图形 树) 。
例:直接利用传递函数模块求解方程。
对二阶微分程进行拉氏变换:s2 X (s) 0.2sX (s) 0.4X (s) 0.2U (s)
可以得到: G(s) X (s)
0.2
U (s) s 2 0.2s 0.4
目录 主页
4.1 连续系统建模(续)
非线性系统建模举例
例3:求非线性系统
目录 主页
MATLAB的数值计算功能
MATLAB仿真实例

MATLAB仿真实例通信原理是研究信息在传输中的传递、编码、解码、调制、解调、信道等各个方面的原理和技术。
MATLAB是一种基于数值计算和可视化的高级计算语言和交互式环境,常用于科学计算、算法开发、数据分析和可视化等领域。
下面将介绍一个基于MATLAB的通信原理仿真实例。
实例描述:假设有一个发送端和一个接收端,通过一个信道进行通信。
发送端生成了一个数字信号序列,将其通过一种调制技术转换为模拟信号,经过信道传输到接收端后,接收端需要对接收到的模拟信号进行解调,得到原始的数字信号序列,并与发送端生成的数字信号序列进行比较,评估通信系统的性能。
实例步骤:1.生成数字信号序列:使用MATLAB生成一个随机的二进制数字信号序列。
例如,一个200个比特的数字信号序列可以使用以下代码生成:```MATLABbits = randi([0 1], 1, 200);```2. 调制:在本例中,我们使用二进制相移键控(Binary Phase Shift Keying,BPSK)调制方式将数字信号序列转换为模拟信号。
将1映射为1,将0映射为-1、以下是BPSK调制的MATLAB代码实现:```MATLABmodulated_signal = 2*bits - 1;```3. 添加通道噪声:在信道传输过程中,由于各种原因(如传输损耗、多径效应等),信号可能会受到一定的噪声干扰。
在本例中,我们假设信道噪声为高斯白噪声。
可以使用MATLAB的awgn函数在模拟信号中添加高斯白噪声。
以下是添加高斯白噪声的MATLAB代码实现:```MATLABSNR_dB=10;%信噪比(信号功率与噪声功率之比)received_signal = awgn(modulated_signal, SNR_dB, 'measured');```4.解调:接收端需要对接收到的带有噪声的模拟信号进行解调,以恢复原始的数字信号序列。
对于BPSK调制,可以通过判断接收信号的正负性来解调。
matlab仿真教程

前言MA TLAB的简介MATLAB是一种适用于工程应用的各领域分析设计与复杂计算的科学计算软件,由美国Mathworks公司于1984年正式推出,1988年退出3.X(DOS)版本,19992年推出4.X(Windows)版本;19997年腿5.1(Windows)版本,2000年下半年,Mathworks公司推出了他们的最新产品MATLAB6.0(R12)试用版,并于2001年初推出了正式版。
随着版本的升级,内容不断扩充,功能更加强大。
近几年来,Mathworks公司将推出MATLAB语言运用于系统仿真和实时运行等方面,取得了很多成绩,更扩大了它的应用前景。
MATLAB已成为美国和其他发达国家大学教学和科学研究中最常见而且必不可少的工具。
MATLAB是“矩阵实验室”(Matrix Laboratory)的缩写,它是一种以矩阵运算为基础的交互式程序语言,着重针对科学计算、工程计算和绘图的需要。
在MATLAB中,每个变量代表一个矩阵,可以有n*m个元素,每个元素都被看做复数摸索有的运算都对矩阵和复数有效,输入算式立即可得结果,无需编译。
MATLAB强大而简易的做图功能,能根据输入数据自动确定坐标绘图,能自定义多种坐标系(极坐标系、对数坐标系等),讷讷感绘制三维坐标中的曲线和曲面,可设置不同的颜色、线形、视角等。
如果数据齐全,MATLAB通常只需要一条命令即可做图,功能丰富,可扩展性强。
MATLAB软件包括基本部分和专业扩展部分,基本部分包括矩阵的运算和各种变换、代数和超越方程的求解、数据处理和傅立叶变换及数值积分风,可以满足大学理工科学生的计算需要,扩展部分称为工具箱,它实际上使用MATLAB的基本语句编成的各种子程序集,用于解决某一方面的问题,或实现某一类的新算法。
现在已经有控制系统、信号处理、图象处理、系统辨识、模糊集合、神经元网络及小波分析等多种工具箱,并且向公式推倒、系统仿真和实时运行等领域发展。
matlab 通信仿真案例

matlab 通信仿真案例MATLAB是一种常用的科学计算软件,被广泛应用于各个领域的仿真和模拟中。
在通信领域,MATLAB也是一个非常强大的工具,可以用来进行通信系统的仿真和设计。
下面我将通过一个简单的通信仿真案例来展示MATLAB在通信领域的应用。
假设我们要设计一个基本的数字通信系统,包括信号的生成、调制、传输、解调和接收等过程。
首先,我们需要生成一个信号源,这里我们选择一个简单的正弦波信号作为输入信号。
利用MATLAB的信号处理工具箱,我们可以很方便地生成一个正弦波信号,并对其进行调制。
接下来,我们将对信号进行调制,这里我们选择将信号调制为一种常见的调制方式——正交振幅调制(QAM)。
在MATLAB中,可以很容易地实现QAM调制,同时也可以设置调制阶数和载波频率等参数。
然后,我们需要模拟信号在传输过程中的传输情况,包括信道的噪声和衰落等影响。
在MATLAB中,可以通过添加高斯噪声或其他类型的信道噪声来模拟传输过程。
同时,可以通过调整信号的功率和信道的信噪比等参数来观察信号在传输过程中的性能表现。
接收端的解调也是通信系统中非常重要的一个环节。
在MATLAB中,可以很方便地实现QAM的解调过程,并对接收到的信号进行解调和解码。
通过观察解调后的信号和原始信号的误码率等性能指标,可以评估通信系统的性能。
除了基本的信号处理和调制解调,MATLAB还提供了丰富的工具箱和函数,可以用来实现各种通信系统中常见的功能和算法。
比如信道编码、调制解调、信号检测、自适应调制等。
可以根据具体的需求和应用场景,选择合适的工具箱和函数来实现通信系统的仿真和设计。
总的来说,MATLAB是一个非常强大的工具,在通信系统的仿真和设计中有着广泛的应用。
通过上面的简单案例,我们可以看到MATLAB在通信领域的强大功能和灵活性,为工程师和研究人员提供了一个方便快捷的平台,用来实现各种通信系统的仿真和设计。
希望通过这个案例的介绍,读者对MATLAB在通信领域的应用有所了解,也能够在实际工作中运用MATLAB来进行通信系统的仿真和设计。
matlab信号处理——算法、仿真与实现

matlab信号处理——算法、仿真与实现MATLAB信号处理是一种广泛应用于各种工程领域的计算机语言和软件环境,其核心理念是用数字信号来处理实际的物理信号,使其在控制、通信、生物医学、天文学等应用中得到应用。
本文将简要介绍MATLAB信号处理的算法、仿真和实现。
算法:MATLAB信号处理的算法通常由两个主要部分组成:滤波和谱分析。
滤波是一种数字信号处理技术,可以从信号中过滤出所需的频率范围内的成分。
同时,还可以去除噪声和干扰信号,让信号更加清晰。
谱分析是一种用于检测信号频率组成的技术,可以将信号中不同频率的成分分解出来,并显示其功率谱和频率谱等分析结果。
MATLAB的信号处理工具箱中,有着很多种滤波和谱分析算法,比如数字滤波器设计、窗函数处理、FFT、STFT等等。
具体使用哪种算法,取决于所要处理的信号的特殊需要和噪声干扰的情况。
仿真:MATLAB信号处理提供了一种方便快捷的方式,将设计的算法模拟成一个完整的信号处理系统,以有效的验证其功能和正确性。
MATLAB的仿真工具包括仿真模型设计、数据可视化、参数调整等等,并可以集成其他MATLAB工具箱中的算法,如图像处理、统计分析等。
钟形图、波形图、频谱图等类型的可视化功能,让仿真数据的输出更加直观明了,以及可以快速检验算法和调整参数。
实现:MATLAB信号处理是通过在计算机中实现信号处理算法来实现的。
实现的具体方式,即设计一个MATLAB程序,将处理算法编写成代码并运行。
程序可以接受实时或离线信号,并对其进行处理和分析。
MATLAB的实现方式具有非常高的灵活性和可定制性,可以满足各种不同应用场景的需要。
总之,MATLAB信号处理可以通过对算法的选择、仿真的建模和实现的编写来完成,进而用于控制、通信、生物医学、天文学等各种应用中。
Matlab的信号处理仿真应用

Matlab的信号处理仿真应⽤上海电⼒学院课程报告课程名称:Matlab的信号处理仿真应⽤班级:2014071姓名:郭茂学号:20140898⼀:MATLAB概述与⼊门1.MATLAB强⼤的计算功能及命令窗⼝的简单使⽤简单计算:例1.计算sin(45° )>>sin(45*pi/180)运⾏窗⼝如图⼀;图⼀:例2.计算半径为5.2m的圆的周长和⾯积。
>>radius=5.2; %圆的半径>>area=pi*radius^2, circle_len=2*pi*radius运⾏窗⼝如图⼆;图⼆:2.MATLAB的演⽰功能例3:绘制复杂的3d图形t = linspace(0, 2*pi, 512);[u,v] = meshgrid(t);a = -0.4;b = .5;c = .1;n = 3;x = (a*(1 - v/(2*pi)) .* (1+cos(u)) + c) .* cos(n*v);y = (a*(1 - v/(2*pi)) .* (1+cos(u)) + c) .* sin(n*v);z = b*v/(2*pi) + a*(1 - v/(2*pi)) .* sin(u);surf(x,y,z,y)axis offaxis equalcolormap(hsv(1024))shading interpmaterial shinylighting phongcamlight('left', 'infinite')view([-160 25]) 图三:复杂3D图形的绘制结果如图三;例4.求解线性⽅程组a = [2,3,-1;8,2,3;45,3,9];%建⽴系数矩阵ab = [2;4;23];%建⽴列向量b x = inv(a)*b 图四:运⾏结果所得结果如图四:运⽤MATLAB 中的INV 函数(如图五,MALAB 中的help 指令)求得系数的逆矩阵,进⽽所得线性⽅程组的解;图五:INV 函数的说明例5.多项式曲线拟合x=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 原函数: y=[1.2, 3, 4, 4, 5, 4.7, 5, 5.2, 6, 7.2] ⼀次多项式拟合: p1 = polyfit(x,y,1) 三次多项式拟合: p3 = polyfit(x,y,3)plot 原始数据、⼀次拟合曲线和三次拟合曲线 x2=1:0.1:10; y1=polyval(p1,x2) y3=polyval(p3,x2)plot( x, y, ’*’, x2, y1, ‘:’, x2, y3) 拟合图形如图六:图六:拟合结果由图可见,三次拟合结果较好。
MATLAB与现代信号处理

8.1 时间域建模 (3)8.1.1 线性预报法(AR模型) (3)8.1.2 Prony 法(ARMA模型) (4)8.1.3 Steiglity-McBride法(ARMA模型) (4)8.2 频率域建模 (5)8.2.1 模拟滤波器的s域建模 (6)8.2.2 数字滤波器的z域内建模 (6)第9章随机信号分析 (8)9.1 随机信号的数字特征 (8)9.1.1 均值、均方值、方差 (8)9.1.2 离散随机信号 (9)9.1.3 估计 (9)9.2 相关函数和协方差 (10)9.2.1 相关函数和自协方差 (10)9.2.2 互相关函数和互协方差 (11)9.2.3 计算相关函数和协方差的MATLAB函数 (11)9.3 功率谱估计 (16)9.3.1 功率谱密度 (16)9.3.2 周期图法 (16)9.3.3 多窗口法 (26)9.3.4 最大熵法(Maxmum entropy method, MEM法) (28)9.3.5 多信号分类法 (30)9.4 传递函数估计 (31)9.5 相干函数 (33)9.6运用功率谱提取地球自由振荡信息 (35)9.6.1 资料 (35)9.6.2方法 (36)9.6.3结果 (37)第10章数字信号处理的几个前沿课题 (42)10.1 时谱(倒谱)分析 (42)10.2 地震观测系统的仿真和地面运动的恢复 (44)10.3小波分析举例 (56)10.3.1 小波变换与突变 (57)10.3.2 资料 (61)10.3.3 本尼奥夫应变资料的小波分析 (62)1 1900~2001年中国大陆地震资料的小波分析 (62)2 1500~2001年华北地区地震资料的小波分析 (63)第8章 参数化建模由前几章的讨论可见,无论是模拟滤波器还是数字滤波器,均是根据输入信号和系统的传递函数求得系统的输出信号。
反过来,能否通过系统的输入信号和输出信号,或滤波器的频率响应或脉冲响应求得系统的传递函数呢?这在一定的假设下是可以得到的。
MATLAB实现通信系统仿真实例
补充内容:模拟调制系统的MATLAB 仿真1.抽样定理为了用实验的手段对连续信号分析,需要先对信号进行抽样(时间上的离散化),把连续数据转变为离散数据分析。
抽样(时间离散化)是模拟信号数字化的第一步。
Nyquist 抽样定律:要无失真地恢复出抽样前的信号,要求抽样频率要大于等于两倍基带信号带宽。
抽样定理建立了模拟信号和离散信号之间的关系,在Matlab 中对模拟信号的实验仿真都是通过先抽样,转变成离散信号,然后用该离散信号近似替代原来的模拟信号进行分析的。
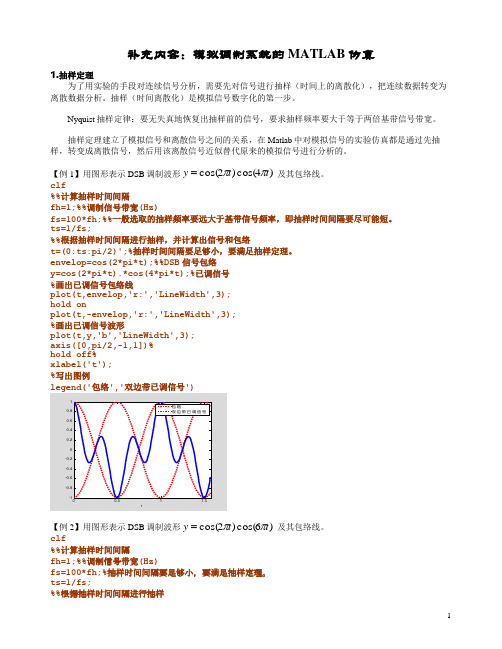
【例1】用图形表示DSB 调制波形)4cos()2cos(t t y ππ= 及其包络线。
clf%%计算抽样时间间隔fh=1;%%调制信号带宽(Hz)fs=100*fh;%%一般选取的抽样频率要远大于基带信号频率,即抽样时间间隔要尽可能短。
ts=1/fs;%%根据抽样时间间隔进行抽样,并计算出信号和包络t=(0:ts:pi/2)';%抽样时间间隔要足够小,要满足抽样定理。
envelop=cos(2*pi*t);%%DSB 信号包络y=cos(2*pi*t).*cos(4*pi*t);%已调信号%画出已调信号包络线plot(t,envelop,'r:','LineWidth',3);hold onplot(t,-envelop,'r:','LineWidth',3);%画出已调信号波形plot(t,y,'b','LineWidth',3);axis([0,pi/2,-1,1])%hold off%xlabel('t');%写出图例【例2】用图形表示DSB 调制波形)6cos()2cos(t t y ππ= 及其包络线。
clf%%计算抽样时间间隔fh=1;%%调制信号带宽(Hz)fs=100*fh;%抽样时间间隔要足够小,要满足抽样定理。
数字信号处理MATLAB仿真(DOC)

实验一 数字信号处理的Matlab 仿真一、实验目的1、掌握连续信号及其MATLAB 实现方法;2、掌握离散信号及其MA TLAB 实现方法3、掌握离散信号的基本运算方法,以及MATLAB 实现4、了解离散傅里叶变换的MA TLAB 实现5、了解IIR 数字滤波器设计6、了解FIR 数字滤波器设计1二、实验设备计算机,Matlab 软件三、实验内容(一)、 连续信号及其MATLAB 实现1、 单位冲击信号()0,0()1,0t t t dt εεδδε-⎧=≠⎪⎨=∀>⎪⎩⎰例1.1:t=1/A=50时,单位脉冲序列的MATLAB 实现程序如下:clear all;t1=-0.5:0.001:0;A=50;A1=1/A;n1=length(t1);u1=zeros(1,n1);t2=0:0.001:A1;t0=0;u2=A*stepfun(t2,t0);t3=A1:0.001:1;n3=length(t3);u3=zeros(1,n3);t=[t1 t2 t3];u=[u1 u2 u3];plot(t,u)axis([-0.5 1 0 A+2])2、 任意函数()()()f t f t d τδττ+∞-∞=-⎰例1.2:用MA TLAB 画出如下表达式的脉冲序列()0.4(2)0.8(1) 1.2() 1.5(1) 1.0(2)0.7(3)f n n n n n n n δδδδδδ=-+-+++++++clear all;t=-2:1:3;N=length(t);x=zeros(1,N);x(1)=0.4;x(2)=0.8x(3)=1.2;x(4)=1.5;x(5)=1.0;x(6)=0.7;stem(t,x);axis([-2.2 3.2 0 1.7])3、 单位阶跃函数1,0()0,0t u t t ⎧≥⎪=⎨<⎪⎩例1.3:用MA TLAB 实现单位阶跃函数clear all;t=-0.5:0.001:1;t0=0;u=stepfun(t,t0);plot(t,u)axis([-0.5 1 -0.2 1.2])4、 斜坡函数0()()g t B t t =-例1.4:用MA TLAB 实现g(t)=3(t-1)clear all;t=0:0.01:3;B=3;t0=1;u=stepfun(t,t0);n=length(t);for i=1:nu(i)=B*u(i)*(t(i)-t0);endplot(t,u)axis([-0.2 3.1 -0.2 6.2])5、 实指数函数()at f t Ae =例1.5:用MA TLAB 实现0.5()3t f t e=clear all;t=0:0.001:3;A=3;a=0.5;u=A*exp(a*t);plot(t,u)axis([-0.2 3.1 -0.2 14])6、 正弦函数 02()cos()t f t A T πϕ=+ 例1.6:用MA TLAB 实现正弦函数f(t)=3cos(10πt+1)clear all;t=-0.5:0.001:1;A=3;f=5;fai=1;u=A*sin(2*pi*f*t+fai);plot(t,u)axis([-0.5 1 -3.2 3.2])(二)、离散信号及其MATLAB 实现1、 单位冲激序列1,0()0,0n n n δ⎧=⎪=⎨≠⎪⎩例2.1:用MA TLAB 产生64点的单位冲激序列clear all;N=64;x=zeros(1,N);x(1)=1;xn=0:N-1;stem(xn,x)axis([-1 65 0 1.1])2、 任意序列()()()m f n f m n m δ∞=-∞=-∑例2.2:用MA TLAB 画出如下表达式的脉冲序列()8.0() 3.4(1) 1.8() 5.6(3) 2.9(4)0.7(5)f n n n n n n n δδδδδδ=+-++-+-+-clear all;N=8;x=zeros(1,N);x(1)=8.0;x(2)=3.4x(3)=1.8;x(4)=5.6;x(5)=2.9;x(6)=0.7;xn=0:N-1;stem(xn,x)axis([-1 8 0 8.2])3、 单位阶跃序列1,0()0,0n u n n ⎧≥⎪=⎨<⎪⎩例2.3:用MA TLAB 实现单位阶跃函数clear all;N=32;x=ones(1,N);xn=0:N-1;stem(xn,x)axis([-1 32 0 1.1])4、 斜坡序列0()()g n B n n =-例2.4:用MA TLAB 实现g(n)=3(n-4)点数为32的斜坡序列clear all;N=32;k=4B=3;t0=1;x=[zeros(1,k) ones(1,N-k)];for i=1:Nx(i)=B*x(i)*(i-k);endxn=0:N-1;stem(xn,x)axis([-1 32 0 90])5、 正弦序列()sin(2)x n A fn πϕ=+例2.5:用MA TLAB 实现幅度A=3,频率f=100,初始相位Φ=1.2,点数为32的正弦信号 clear all;N=32;A=3;f=100;fai=1.2;xn=0:N-1;x=A*sin(2*pi*f*(xn/N)+fai);stem(xn,x)axis([-1 32 -3.2 3.2])6、 实指数序列()n x n Aa =例2.6:用MA TLAB 实现0.7()3x n e=,点数为32的实指数序列clear all;N=32;A=3;a=0.7;xn=0:N-1;x=A*a.^xn;stem(xn,x)7、 复指数序列 ()(),a j n x n Ae n ω+=∀例2.7:用MA TLAB 实现幅度A=3,a=0.7,角频率ω=314,点数为32的实指数序列 clear all;N=32;A=3;a=0.7;w=314;xn=0:N-1;x=A*exp((a+j*w)*xn);stem(xn,x)8、 随机序列利用MATLAB 产生两种随机信号:rand(1,N)在区间上产生N 点均匀分布的随机序列randn(1,N)产生均值为0,方差为1的高斯随机序列,即白噪声序列例2.8:用MA TLAB 产生点数为32的均匀分布的随机序列与高斯随机序列clear all;N=32;x_rand=rand(1,N);x_randn=randn(1,N);xn=0:N-1;figure(1);stem(xn,x_rand)figure(2);stem(xn,x_randn)(三)、离散信号的基本运算1、 信号的延迟给定离散信号x(n),若信号y(n)定义为:y(n)=x(n-k),那么y(n)是信号x(n)在时间轴上右移k 个抽样周期得到的新序列。
matlab数字信号处理仿真

matlab数字信号处理仿真第一实验室:基础实验篇第Ⅰ部分基本训练题目第Ⅱ部分简介各题目的原理、程序、效果第Ⅲ部分基研训练程序软件压缩文件第Ⅰ部分基本训练题目1-1-1 序列的图示方法 DSP11011-1-2 连续信号及采样信号的图示方法 DSP 11021-1-3单位冲激序列函数impseq单位冲激序列图示 DSP 11031-1-4 单位阶跃序列函数stepseq单位阶跃序列图示 DSP11041-1-5 矩形序列)(n R N 及图示 DSP11051-1-6 实指数序列)(n a n ε及图示 DSP11061-1-7 正弦序列)sin(n *ω及图示 DSP11071-1-8 复指数序列n jm e *+)(σ及图示 DSP11081-1-9 周期序列)()(N n x n x +=及图示 DSP 11091-1-10 常用5种连续信号及图示 DSP11101-1-11 离散序列的运算 DSP11111-1-12 输入序列)(n x 与系统冲激响应)(n h 的卷积),(h x conv DSP11121-1-13 非零起点时两信号的卷积),(h x convm DSP11131-2-1 指数序列)(8.0)(n n x n ε=的离散时间傅立叶变换DSP 12011-2-2 矩形序列)(n R N 的离散时间傅立叶变换 DSP12021-2-3 离散时间傅立叶变换的性质 DSP12031-2-4 正弦序列输入,输出为正弦序列,幅度相位因)(ωj e H 变化DSP1204 1-2-5 模拟信号t a e t x 1000)(-=付氏变换与采样信号的离散时间傅立叶变换DSP 12051-3-1 N 点离散傅立叶变换 dft(xn,N)1-3-2 N 点离散傅立叶反变换 idft(xn,N)1-3-3 DFT 与)(n x 的Z 变换关系 DSP13031-3-4 DFT 与)(n x 的离散时间傅立叶变换的关系 DSP 13041-3-5 有限长序列添零填充,得高密度DFT ,离散时间付氏频谱不变DSP1305 1-3-6 采样点增多的高分辨率DFT ,采样点数少仅添零的高密度DFT DSP1306 1-3-7 DFT 的圆周移位函数cirshftt 1-3-8 DFT 圆周移位实例 DSP13081-3-9 圆周卷积 DSP13091-3-10 复共轭序列的DFT DSP13101-3-11 DFT 的共轭对称性 DSP 13111-3-12 补零填充实现线性卷积 DSP13121-3-13 重迭保留法实现线性卷积 DSP13131-3-14 重迭保留实现函数 ovrlpsav1-3-15 DET 对连续信号作近似谱分析:滤高频,避免混迭频谱;截高时;变有限长序列,避免泄漏频谱 DSP13151-3-16 采样点为100,进行200点DFT ,对)(t e t ε-进行谱分析DSP 1316 1-3-17 实序列的奇偶分解及DFT 的虚实分量 DSP1317 1-3-18 实序列的奇偶分解函数 DSP13181-3-19 用FFT 分析信号频率成分 DSP13191-3-20 用FFT 分析语言信号的频谱 DSP13201-3-21 DCT 变换 DSP13211-3-22 用DCT 变换进行语言压缩 DSP13221-3-23 线性调频Z 变换 DSP13231-3-24 利用CZT 计算滤波器100—150HZ 频率特性的细节DSP13242-1-1 直接型实现系统函数H (Z )的IIR 数字滤波器 DSP 2101 2-1-2 级联型实现系统H (Z )的IIR 数字滤波器 DSP21022-1-3 级联型实现H (Z )的IIR 数字滤波器 DSP21032-1-4 直接型实现H (Z )的IIR 数字滤波器 DSP21042-1-5 并联型实现H (Z )的IIR 数字滤波器 DSP 21052-1-6 并联型 DSP 21062-1-7 直接型 DSP21072-1-8 最终的级联,并联 DSP21082-1-9 直接型?级联型 dir2cas(b,a)2-1-10 级联型→直接型 cas2par(b0,B,A)2-1-11 直接型→并联型 dir2par2-1-12 并联型→直接型 par2dire2-1-13 并联型→级联型 casfilter2-1-14 级联型→并联型 parfilter2-2-1 FIR 直接型滤波器 DSP 22012-2-2 FIR 级联型滤波器 DSP22022-2-3 FIR 的频率取样形式结构 DSP 22032-2-4 (原例11)由频率样本{2,1,0315,......5,415.00)(====k k k k H求频率采样形式,及单位冲激响应)(n h DSP22042-2-5 窄带滤波器中的频率采取滤波器是由直接型转换为频率采样型 dir2fs(n)3-1-1 偶对称奇序列的⒈型FIR 滤波器的振幅响应 hr_type13-1-2 偶对称奇序列的)(ωH 及零极点分布 DSP31023-1-3 偶对称偶序列的Ⅱ型FIR 滤波器的振幅响应 hr_type23-1-4 偶对称偶序列的)(ωH 及零极点分布 DSP31043-1-5 奇对称奇序列的Ⅲ型FIR 滤波器的振幅响应 hr_type33-1-6 奇对称奇序列的)(ωH 及零极点分布 DSP31063-1-7 奇对称偶序列的Ⅳ型FIR 滤波器的振幅响应 hr_type43-1-8 奇对称偶序列的)(ωH 及零极点分布 DSP31083-1-9 线性相位FIR 滤波器的零点位置有4种可能 DSP31093-1-10 常用加窗函数 DSP32103-1-11 对信号用加窗函数的DFT 分析频谱 DSP32113-2-1 计算理想低通滤波器的)(n h a DSP32013-2-2 计算FIR 滤波器的绝对和相对的幅度响应 DSP32023-2-3 提取大于50dB 衰减的汉明窗FIR 低通滤波器 DSP3203 3-2-4 理想高通,偶对称因果序列,N 为奇的窗函数,滤波器的单位冲激响应)(n h d DSP32043-2-5 汉宁窗,44dB 最小阻带衰减,过度带N π2.6 DSP3205 3-2-6 理想高通,奇对称因果序列,N 为偶的窗函数,滤波器的单位冲激响应)(n h d DSP32063-2-7 汉宁窗,44dB 最小阻带衰减,过度带N π2.6 DSP3207 3-2-8 理想高通,偶对称因果序列,N 为奇的窗函数,滤波器的单位冲激响应)(n h d DSP32083-2-9 设计一个数字FIR 带通滤波器 DSP32093-2-10 理想带通数字滤波器的频率响应)(e H jw d DSP3210 3-2-11 设计一个具有2π相移的数字FIR 带通滤波器 DSP3211 3-2-12 理想带阻,偶对称因果序列,N 为奇的窗函数,滤波器的单位冲激响应)(n h d ideal-be()3-2-13 设计一个数字FIR带阻滤波器DSP32133-3-1 采样点ω=0处的频率采样法DSP33013-3-2 在过渡带上加两个T1和T2 DSP33023-3-3 设计2型FIR低通滤波器 DSP33033-3-4 设计1型FIR高通滤波器 DSP33043-3-5 设计4型FIR高通滤波器 DSP33053-3-6 设计2型FIR带通滤波器 DSP33063-3-7 设计1型FIR带阻滤波器 DSP33073-3-8 设计1型FIR低通滤波器 DSP33083-3-9 设计1型FIR高通滤波器 DSP33093-3-10 设计4型FIR高通滤波器 DSP33103-3-11 设计3型FIR带通滤波器 DSP33113-4-1 用频率响应采样法1设计具有线性相位 DSP34013-4-2 用窗函数法设计具有线性相位 DSP34023-4-3 用频率采样法1设计低通滤波器对其进行除噪 DSP3403 4-1-1 在MATLAB中用afd_butt(Omegap,Omegar,Ap,Ar)函数来设计巴特沃斯模拟低通滤波器 DSP41014-1-2 若设计非归一化(Ωc≠1)巴特沃斯模拟低通滤波器原型DSP4102 4-1-3 freqs_m(b,a,Omega_max)函数 DSP4103 4-1-4 sdir2cas函数 DSP41044-1-5 设计一个巴特沃斯模拟滤波器 DSP41054-2-1 用来实现N阶、通带波动为δ的归一化切比学夫1型模拟低通滤波器DSP42014-2-2 根据技术指标设计切比学夫1型模拟滤波器 DSP42024-2-3 设计一个低通切比学夫1型滤波器 DSP42034-2-4 设计归一化切比学夫2型模拟滤波器 DSP42044-2-5 根据给定指标设计切比学夫2型模拟滤波器 DSP42054-2-6 设计一个切比学夫2型低通滤波器 DSP42064-3-1 用imp_invr函数实现脉冲响应不变法DSP 43014-3-2 设计一个巴特沃斯模拟滤波器 DSP43024-3-3 设计低通数字滤波器 DSP43034-3-4 设计低通数字滤波器 DSP43044-4-1 双线性变换法设计低通数字滤波器 DSP44014-4-2 切比雪夫滤波器原型用双线性变换法设计低通数字滤波器DSP44024-5-14-5-24-5-34-5-4 分别设计一个巴特沃斯滤波器和切比雪夫高通滤波器DSP45044-5-5 分别设计一个巴特沃斯滤波器和切比雪夫高通滤波器DSP45054-5-6 设计一个巴特沃斯带通滤波器 DSP45064-5-7 设计一个切比雪夫带通滤波器 DSP45074-5-8 设计一个滤波器 DSP45084-5-9 设计一个滤波器 DSP45094-5-10 设计一个滤波器 DSP45104-6-1 zampping DSP46014-6-2用zmapping函数实现例11中的高通滤波器 DSP4602 4-6-3切比雪夫1型高通数字滤波器,上述过程由chebhpf函数实现 DSP4603 4-6-4用数字频域变换法,设计一个切比雪夫1型高通数字滤波器 DSP46044-6-5 用双线性变换法设计低通滤波器 DSP46054-6-6 用脉冲响应不变法设计的低通滤波器对其除噪 DSP4606 4-6-7 模拟信号DSP46075-1-1下采样DSP 51015-1-2 例题DSP51025-1-3上采样DSP51035-1-4 程序DSP51045-1-5 采样率的非整数倍转换DSP51055-1-6 程序DSP51065-1-7 例题DSP51075-1-8 用傅立叶变换对信号进行消噪声处理DSP51085-1-9 信号特定频率的提取DSP51095-1-10例题DSP51105-1-11信号特定频率区间的抑制DSP5111第Ⅱ部分简介各题目的原理、程序、效果1-1-1 序列的图示方法DSP1101原理:数字信号处理中,所有信号都是离散时间信号——序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6.11
利用卡尔曼滤波估计一个未知常数
题目:
设已知一个未知常数x 的噪声观测集合,已知噪声v(n)的均值为零,
方差为
,v(n)与x 不相关,试用卡尔曼滤波估计该常数
题目分析:
回忆Kalman 递推估计公式
由于已知x 为一常数,即不随时间n 变化,因此可以得到: 状态方程: x(n)=x(n-1)
观测方程: y(n)=x(n)+v(n)
得到A(n)=1,C(n)=1, , 将A(n)=1,代入迭代公式
得到:P(n|n-1)=P(n-1|n-1)
用P(n-1)来表示P(n|n-1)和P(n-1|n-1),这是卡尔曼增益表达式变为
从而 2v σ1ˆˆ(|1)(1)(1|1)(|1)(1)(1|1)(1)()()(|1)()[()(|1)()()]ˆˆˆ(|)(|1)()[()()(|1)](|)[()()](|1)H w H H v x n n A n x n n P n n A n P n n A n Q n K n P n n C n C n P n n C n Q n x
n n x n n K n y n C n x n n P n n I K n C n P n n --=----=----+=--+=-+--=--2()v v
Q n σ=()0w Q n =(|1)(1)(1|1)(1)()H w P n n A n P n n A n Q n -=----+21
()(|1)[(|1)]v K n P n n P n n σ-=--+22(1)()[1()](1)(1)v
v P n P n K n P n P n σσ-=--=-+
利用递归的方法
...
得到一般的P(n)计算式
将上式代入卡尔曼增益K(n)计算式得:
最后得到离散卡尔曼滤波器计算式:
22(0)(1)(0)v v P P P σσ=+2222(1)(0)(2)(1)2(0)v v v v P P P P P σσσσ==++2222(2)(0)(3)(2)3(0)v v v v
P P P P P σσσσ==++22(0)()(0)v v P P n nP σσ=+22(1)(0)()(1)(0)v v P n P K n P n nP σσ-==-++2(0)ˆˆˆ()(1)[()(1)](0)v P x n x n y n x n nP σ=-+--+
Matlab实现
clear
N=200;
%w(n)=0
A=1;
x(1)=50;%initial state
for k=2:N;
x(k)=A*x(k-1);
end
V=randn(1,N);
rv_sd=std(V);
Rvv=rv_sd.^2;
%Rxx no use,Rww is 0
C=1;
Y=C*x+V;
%Kalman filter to estimate
p(1)=10;%initial MSE value
s(1)=100;%initial estimated value
for t=2:N;
p(t)=p(1).*Rvv/(t*p(1)+Rvv);
k(t)=p(1)/(t*p(1)+Rvv);
s(t)=A*s(t-1)+k(t)*(Y(t)-A*C*s(t-1)); end
t=1:N;
figure(1)
plot(t,k); title('Kalman Gain');
figure(2)
plot(t,s,'r',t,Y,'g',t,x,'b');
legend('estimated','measured','state'); figure(3)
plot(t,p); title('Mean Square of Error');
仿真结果。
