2014数学初一完全平方法练习题
初一数学专题练习完全平方公式汇编

a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2的变化应用一有关配方问题(一)对于a2+2ab+b2=(a+b)2、a2-2ab+b2=(a-b)2的配方问题是,对于a2,2ab,b2这三项,认准特点,式子中缺哪项就补哪项,但要保证式子相等。
具体操作:先确定第一项,再确定第三项,最后确定中间项,并且要检验中间项与原式中的中间项相等。
(二)练习: 1.若x2+mx+9是完全平方式,则m=_____.2. 若x2+12x+m2是完全平方式,则m=_____.3. 若x2-mx+9=(x+3)2,则m=_____.4. 若4x2-mx+9是完全平方式,则m=_____.5.若4x2+12x+m2是完全平方式,则m=_____.6.若(mx)2+12x+9是完全平方式,则m=_____.7.若mx2+12x+9是完全平方式,则m=_____.8.已知x2-2(m+1)xy+16y2是一个完全平方式,那么m的值是_____.9.(1)化简(a-b)2+(b-c)2+(a-c).(2)利用上题的结论,且a-b=10,b-c=5,求a2+b2+c2-ab-bc-ac的值.(3)已知a=2x-12,b=2x-10,c=2x+4,求a2+b2+c2-ab-bc-ac的值(4)已知a,b,c是三角形的三边且满足a2+b2+c2-ab-bc-ac=0,判断三角形的形状.10.已知x2-2x+y2+6y+10=0,求x=_____,y=_____,x+y=_____.11. 已知x2-4x+y2+6y+13=0,求x=_____,y=_____,xy=_____.12.试说明N=x2-4x+y2+6y+15永远为正值.二、整体计算方面(一)在a2+2ab+b2=(a+b)2, a2-2ab+b2=(a-b)2中,利用加法的交换律与结合律,可以得到(a+b)2 =( a2+ b2)+ 2ab,(a-b)2=( a2+ b2)- 2ab,共三部分,其中知道两部分的值,就可以求得第三部分的值.另外两个式子结合还能变成:( a2+ b2)= (a+b)2-2ab, ( a2+ b2)= (a-b)2+2ab, (a+b)2+(a-b)2=2(a2+b2),(a+b)2-(a-b)2=4ab,要理解并且会应用.(二)练习:1.x2+y2=(x+y)2-_____=(x+y)2+_____.2.将多项式x2+4加一个整式,使其成为完全平方式,试写出满足上述条件的两个整式:_____,_____.3. 将多项式x2+4加一个整式,使其成为完全平方式,试写出满足上述条件的整式:_____,_____,_____.4. 将多项式x2+4加一个代数式,使其成为完全平方式,试写出满足上述条件的所有代数式.5.已知x+(1/x)=4,求x2+(1/x)2,(x-1/x)2,x4+( 1/x)4的值.6.已知x-(1/x)=4,求x2+(1/x)2,(x-1/x)2,x4+ (1/x)4的值.7.若a+b=5,ab=-14,求a2+b2和(a+b)2的值.8.已知a-b=1, a+b=25,求ab的值.9. 已知(x+y)2=25, (x-y)2=25,求xy的值.10. 若a-b=5,ab=4,求3a2+3b2和(a+b)2的值.11. 若a2+ b2=9,ab=4,求3(a+b)2和(a-b)2的值.12.已知(x+y-5)2+(xy-8)2=0,则x2+y2 =_____.。
七年级数学下---平方差、完全平方公式专项练习题

A .(a+b )(b+a )B .(-a+b )(a -bC .( a+b )(b - a )D .(a 2-b )(b 2+a ) ×21 . 10.计算:(a+2)(a 2+4)(a 4+16)(a -2).(2)(3+1)(32+1)(34+1)…(32008+1)-. 七年级数学下---平方差、完全平方公式专项练习题平方差:一、选择题1.平方差公式(a+b )(a -b )=a 2-b 2 中字母 a ,b 表示()A .只能是数B .只能是单项式C .只能是多项式D .以上都可以2.下列多项式的乘法中,可以用平方差公式计算的是()1 13 33.下列计算中,错误的有( ) A .1 个B .2 个C .3 个D .4 个①(3a+4)(3a -4)=9a 2-4; ②(2a 2-b )(2a 2+b )=4a 2-b 2;③(3-x )(x+3)=x 2-9;④(-x+y )·(x+y )=-(x -y )(x+y )=-x 2-y 2.4.若 x 2-y 2=30,且 x -y=-5,则 x+y 的值是( )A .5B .6C .-6D .-5二、填空题:5、(a+b -1)(a -b+1)=(_____)2-(_____)2.6.(-2x+y )(-2x -y )=______.7.(-3x 2+2y 2)(______)=9x 4-4y 4.8.两个正方形的边长之和为 5,边长之差为 2,那么用较大的正方形的面积减去较小的正方形的面积,差是_____.三、计算题 9.利用平方差公式计算:20 2 13 3B 卷:提高题1.计算:(1)(2+1)(22+1)(24+1)…(22n +1)+1(n 是正整数);340162(1)计算: .(2)计算: .C .(-2a 2b )·4a=-24a 6b3D .(- a -4b )( a -4b )=16b 2- a 22 2.式计算:2009×2007-20082.3.解方程:x (x+2)+(2x+1)(2x -1)=5(x 2+3).2007200722007 2 - 2008 ⨯ 20062008 ⨯ 2006 + 14.广场内有一块边长为 2a 米的正方形草坪,经统一规划后,南北方向要缩短 3 米,东西方向要加长 3 米,则改造后的长方形草坪的面积是多少?5.下列运算正确的是( ) A .a 3+a 3=3a 6B .(-a )3·(-a )5=-a 81 1 1 3 3 96.计算:(a+1)(a -1)=______.C 卷:课标新型题1.(规律探究题)已知 x≠1,计算(1+x )(1-x )=1-x 2,(1-x )(1+x+x 2)=1-x 3,(1-x )(•1+x+x +x 3)=1-x 4.(1)观察以上各式并猜想:(1-x )(1+x+x 2+…+x n )=_____ _.(n 为正整数)(2)根据你的猜想计算:①(1-2)(1+2+22+23+24+25)=______. ②2+22+23+…+2n =______(n 为正整数).③(x -1)(x 99+x 98+x 97+…+x 2+x+1)=_______.(3)通过以上规律请你进行下面的探索:2 3、已知 (a + b )2 = 16, a b = 4, 求 与 (a - b )2 的值。
初中数学完全平方公式专项练习题

完全平方公式专项练习60题(有答案)1.(1)(x+y﹣z)(x+y+z);(2)(x+y)2﹣(x﹣y)2.2.已知a﹣b=3,ab=2,求:(1)(a+b)2 (2)a2﹣6ab+b2的值.3.已知(a+b)2=6,(a﹣b)2=2,试比较a2+b2与ab的大小.4.已知(x+y)2=7,(x﹣y)2=3.求:(1)x2+y2的值;(2)x4+y4的值;(3)x6+y6的值.5.已知a2+b2=13,ab=6,求a+b的值.6.已知x+y=3,x2+y2﹣3xy=4.求下列各式的值:(1)xy;(2)x3y+xy3.7.阅读理解:求代数式y2+4y+8的最小值.解:∵y2+4y+8=(y2+4y+4)+4=(y+2)2+4≥4∴当y=﹣2时,代数式y2+4y+8的最小值是4.仿照应用(1):求代数式m2+2m+3的最小值.仿照应用(2):求代数式﹣m2+3m+的最大值.8.已知a2+b2=1,a﹣b=,求a2b2与(a+b)4的值.9.已知实数a,b满足a(a+2)﹣(a2+b)=6,求4a2﹣4ab+b2﹣8a+4b﹣15的值.10.99.82.11.用乘法公式计算:.12.利用公式求2×20092﹣20102﹣20082的值.13.已知:x2+3x+1=0,求的值.14.已知,试求的值.15.已知a2+3a+1=0,求:①,②,③.16.已知x﹣y=6,xy=﹣8,(1)求x2+y2的值;(2)求代数式的值.17.已知(2012﹣a)•(2010﹣a)=2011,求(2012﹣a)2+(2010﹣a)2的值.18.已知x+y=1,求x2+xy+y2的值.19.如果a+b+c=0,,求(a+1)2+(b+2)2+(c+3)2的值.20.已知a+b=3,ab=﹣10,求下列各式的值.(1)a2+b2(2)a2﹣ab+b2(3)(a﹣b)2.21.若(x﹣z)2﹣4(x﹣y)(y﹣z)=0,试求x+z与y的关系.22.证明:(a+b+c)2+a2+b2+c2=(a+b)2+(b+c)2+(a+c)2.23.已知a+b+c=1,a2+b2+c2=2,求ab+bc+ca的值.24.运用完全平方公式计算(1)(x+y)2 (2)(2a+3b)2 (3)(4)(5)(a﹣1)2 (6).25.运用完全平方公式计算(1)100.22 (2)98×98 (3)372(4)(5)20082 (6).26.已知(a+b)2=3,(a﹣b)2=23,求代数式a2+b2﹣3ab的值.27.已知a+b+c=1,a2+b2+c2=2,a3+b3+c3=3,求(1)abc的值:(2)a4+b4+c4的值.28.已知m=4x2﹣12xy+10y2+4y+9,当x、y各取何值时,m的值最小?29.计算:5062+1012×505+5052﹣10102.30.先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.解:∵m2+2mn+2n2﹣6n+9=0∴m2+2mn+n2+n2﹣6n+9=0∴(m+n)2+(n﹣3)2=0∴m+n=0,n﹣3=0∴m=﹣3,n=3问题(1)若x2+2y2﹣2xy+4y+4=0,求x y的值.(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.31.如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.32.已知多项式4x2+1,添上一项,使它成为一个完全平方式,你有哪几种方法?33.如果x2+2(m﹣2)x+9是完全平方式,那么m的值等于_________ .34.已知a2﹣4a+4+9b2+6b+1=0,求a、b的值.35.试说明:(a2+3a)(a2+3a+2)+1是一个完全平方式.36.已知a=2002,b=2003,c=2004,求a2+b2+c2﹣ab﹣ac﹣bc的值.37.代数式(a+1)(a+2)(a+3)(a+4)+1是一个完全平方式吗?请说明你的理由.38.已知(a+1)(a+2)(a+3)(a+4)+m是一个完全平方式,求常数m的值.39.x,y都是自然数,求证:x2+y+1和y2+4x+3的值不能同时是完全平方.40.试求出所有整数n,使得代数式2n2+n﹣29的值是某两个连续自然数的平方和.41.若x2+2xy+y2﹣a(x+y)+25是完全平方式,求a的值.42.已知二次三项式9x2﹣(m+6)x+m﹣2是一个完全平方式,试求m的值.43.观察下列等式:1×32×5+4=72=(12+4×1+2)22×42×6+4=142=(22+4×2+2)23×52×7+4=232=(32+4×3+2)24×62×8+4=342=(42+4×4+2)2…(1)根据你发现的规律,12×142×16+4是哪一个正整数的平方;(2)请把n(n+2)2(n+4)+4写成一个整数的平方的形式.44.(1)当a=﹣2,b=1时,求两个代数式(a+b)2与a2+2ab+b2的值;(2)当a=﹣2,b=﹣3时,再求以上两个代数式的值;(3)你能从上面的计算结果中,发现上面有什么结论.结论是:_________ ;(4)利用你发现的结论,求:19652+1965×70+352的值.45.当a=﹣3,b=1,时,分别求代数式(a﹣b)2与a2﹣2ab+b2的值,并比较计算结果;你有什么发现?利用你发现的结果计算:20122﹣2×2012×2011+20112.46.一个正整数a恰好等于另一个正整数b的平方,则称正整数a为完全平方数.如64=82,64就是一个完全平方数;若a=29922+29922×29932+29932.求证:a是一个完全平方数.47.用图说明公式:(a+b+c+d)2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd.48.观察如图图形由左到右的变化,计算阴影部分的面积,并用面积的不同表达形式写出相应的代数恒等式.49.如图所示:(1)指出图中有多少个边长为a的正方形?有多少个边长为b的正方形?有多少个两边长分别为a和b的矩形?(2)请在图中指出面积为(a+2b)2的图形,利用乘法公式计算结果,并利用图形的关系验证相应的结果.50.计算:(1)(x3n+1)(x3n﹣1)﹣(x3n﹣1)2;(2)(2x n+1)2(﹣2x n+1)2﹣16(x n+1)2(x n﹣1)2.51.阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式,例如由图(a)可以得到a2+3ab+2b2=(a+2b)(a+b).请解答下列问题:(1)写出图(b)中所表示的数学等式_________ ;(2)试画出一个长方形,使得计算它的面积能得到2a2+3ab+b2=(2a+b)(a+b).52.如图是用四个长、宽分别为a、b(a>b)的相同长方形和一个小正方形镶嵌而成的正方形图案.(1)用含有a、b的代数式表示小正方形的面积.(用两种不同的形式来表示)(2)如果已知大正方形图案的面积为28,小正方形的面积是6,求a2+b2+ab的值.53.图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开,可分成四块小长方形.(1)你认为图1的长方形面积等于_________ ;(2)将四块小长方形拼成一个图2的正方形.请用两种不同的方法求图2中阴影部分的面积.方法1:_________ ;方法2:_________ ;(3)观察图2直接写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系_________ ;(4)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含m、n的代数式表示).54.已知x1,x2,x3,…,x n中每一个数值只能取﹣2,0,1中的一个,且满足x1+x2+…+x n=﹣17,x12+x22+…+x n2=37,求x13+x23+…+x n3的值.55.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8;…根据以上规律,解答下列问题:(1)(a+b)4展开式共有_________ 项,系数分别为_________ ;(2)(a+b)n展开式共有_________ 项,系数和为_________ .56.阅读下列材料并解答后面的问题:利用完全平方公式(a±b)2=a2±2ab+b2,通过配方可对a2+b2进行适当的变形,如a2+b2=(a+b)2﹣2ab或a2+b2=(a﹣b)2+2ab.从而使某些问题得到解决.例:已知a+b=5,ab=3,求a2+b2的值.解:a2+b2=(a+b)2﹣2ab=52﹣2×3=19.问题:(1)已知a+=6,则a2+= _________ ;(2)已知a﹣b=2,ab=3,求a4+b4的值.57.阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.例如:(x﹣1)2+3、(x﹣2)2+2x、(x﹣2)2+x2是x2﹣2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项﹣﹣见横线上的部分).请根据阅读材料解决下列问题:(1)比照上面的例子,写出x2﹣4x+2三种不同形式的配方;(2)将a2+ab+b2配方(至少两种形式);(3)已知a2+b2+c2﹣ab﹣3b﹣2c+4=0,求a+b+c的值.58.1261年,我国宋代数学家杨辉写了一本书《详解九章算术》.书中记载了一个用数字排成的三角形我们叫作杨辉三角形(a+b)0=1 (1)(a+b)1=a+b…1 1(a+b)2=a2+2ab+b2…1 2 1(a+b)3=a3+3a2b+3ab2+b3…1 3 3 1(a+b)4=a4+4a3b+6a2b2+4ab3+b4…••1 4 6 4 1(1)请写出第五行的数字_________ ;(2)第n行杨辉三角形数字与(a+b)n的展开结果关系如上图所示,请写出(a+b)5的展开结果;(3)已知(a﹣b)1=a﹣b,(a﹣b)2=a2﹣2ab+b2,(a﹣b)3=a3﹣3a2b+3ab2﹣b3(a﹣b)4=a4﹣4a3b+6a2b2﹣4ab3+b4.请写出(a﹣b)5的展开结果.59.先阅读下面一段文字,然后猜想,解答问题:由32=9=4+5,发现有32+42=52成立;又52=25=12+13,仍然有52+122=132;而72=49=24+25,还是有72+242=252…(1)猜想92=81=x+y(x、y均为正整数,且x<y),并且92+x2=y2,则x= _________ ,y= _________ .(2)是否大于1的奇数都有上面这样的规律?证明你的猜想.60.操作与探究(1)比较下列两个算式结果的大小(在横线上填“>”“=”“<”(每空1分)①32+42_________ 2×3×4;②()2+()2_________ 2××;③(﹣2)2+(﹣3)2_________ 2×(﹣2)×(﹣3);④(﹣)2+(﹣)2_________ 2×(﹣)×(﹣)⑤(﹣4)2+(﹣4)2_________ 2×(﹣4)×(﹣4)…(2)观察并归纳(1)中的规律,用含a,b的一个关系式把你的发现表示出来.(3)若已知mn=8,且m,n都是正数,试求2m2+2n2的最小值.参考答案:1.解:(1)原式=(x+y)2﹣z2=x2+2xy+y2﹣z2;(2)原式=(x+y+x﹣y)(x+y﹣x+y)=4xy.2.解:(1)将a﹣b=3两边平方得:(a﹣b)2=a2+b2﹣2ab=9,把ab=2代入得:a2+b2=13,则(a+b)2=a2+b2+2ab=13+4=17;(2)a2﹣6ab+b2=a2+b2﹣6ab=13﹣12=13.解:∵(a+b)2=a2+b2+2ab=6①,(a﹣b)2=a2+b2﹣2ab=2②,∴①+②得:2(a2+b2)=8,即a2+b2=4;①﹣②得:4ab=4,即ab=14.解:(1)∵(x+y)2=7,(x﹣y)2=3,x2+2xy+y2=7,x2﹣2xy+y2=3,∴x2+y2=5,xy=1;(2)x4+y4=(x2+y2)2﹣2x2y2=25﹣2=23;(3)x6+y6=(x2+y2)(x4﹣x2y2+y4)=5×(23﹣1)=1105.解:∵a2+b2=13,ab=6,(a+b)2=a2+2ab+b2=a2+b2+2ab=13+2×6=25,∴a+b==±5.6.解:(1)∵x+y=3,∴(x+y)2=9,∴x2+y2+2xy=9,∴x2+y2=9﹣2xy,代入x2+y2﹣3xy=4,∴9﹣2xy﹣3xy=4,解得:xy=1.(2)∵x2+y2﹣3xy=4,xy=1,∴x2+y2=7,又∵x3y+xy3=xy(x2+y2),∴x3y+xy3=1×7=77.解:应用(1)m2+2m+3=(m2+2m+1)+2=(m+1)2+2≥2,∴当m=﹣1时,m2+2m+3的最小值是2,应用(2)﹣m2+3m+=﹣(m2﹣3m+)++=﹣(m﹣)2+3≤3,∴当m=时,﹣m2+3m+的最大值是38.解:a2+b2=1,a﹣b=,∴(a﹣b)2=a2+b2﹣2ab,∴ab=﹣[(a﹣b)2﹣(a2+b2)]=﹣×(﹣1)=,∴a2b2=(ab)2=()2=;∵(a+b)2=(a﹣b)2+4ab=+4×=,∴(a+b)4=[(a+b)2]2=9.解:∵a(a+2)﹣(a2+b)=6,∴a2+2a﹣a2﹣b=6,∴2a﹣b=6,原式=(2a﹣b)2﹣4(2a﹣b)﹣15,当2a﹣b=6时,原式=62﹣4×6﹣15=﹣3 10.解:99.82=(100﹣0.2)2,=1002﹣2×100×0.2+0.22,=10000﹣40+0.04,=9960.0411.解:===164012.解:设a=2009,原式=2a2﹣(a+1)2﹣(a﹣1)2=2a2﹣a2﹣2a﹣1﹣a2+2a﹣1=﹣213.解:∵x≠0,∴已知方程变形得:x+3+=0,即x+=﹣3,则x2+=(x+)2﹣2=9﹣2=714.解:对式子两边平方得,a2+﹣2=,∴a2+=,∴()2=a2++2,=+2,=,∴=±15.解:①∵a2+3a+1=0,∴a≠0,∴在等式的两边同时除以a,得a+3+=0,∴a+=﹣3;②由①知,a+=﹣3,则(a+)2=+2=9,解得,=7;③由②知,=7,则()2=+2=49,解得,=4716.解:(1)∵x﹣y=6,xy=﹣8,∴(x﹣y)2=x2+y2﹣2xy,∴x2+y2=(x﹣y)2+2xy=36﹣16=20;(2)∵(x+y+z)2+(x﹣y﹣z)(x﹣y+z)﹣z(x+y),=(x2+y2+z2+2xy+2xz+2yz)+[(x﹣y)2﹣z2]﹣xz﹣yz,=x2+y2+z2+xy+xz+yz+x2+y2﹣xy﹣z2﹣xz﹣yz,=x2+y2,又∵x2+y2=20,∴原式=2017.解:∵(2012﹣a)•(2010﹣a)=2011,∴(2012﹣a)2+(2010﹣a)2=[(2012﹣a)﹣(2010﹣a)]2+2(2012﹣a)(2010﹣a)=4+2×2011=402618.解:x2+xy+y2=(x+y)2=×1=.19.解:由,去分母,得(b+2)(c+3)+(a+1)(c+3)+(a+1)(b+2)=0,而(a+1)2+(b+2)2+(c+3)2=[(a+1)+(b+2)+(c+3)]2﹣2[(b+2)(c+3)+(a+1)(c+3)+(a+1)(b+2)] =(a+b+c+6)2=(0+6)2=3620.解:(1)a2+b2=(a+b)2﹣2ab=9+20=29;(2)a2﹣ab+b2=(a+b)2﹣3ab=9+30=39;(3)原式=(a+b)2﹣4ab=9+49=5821.解:∵x﹣z=x﹣y+y﹣z,∴原式可化为[(x﹣y)+(y﹣z)]2﹣4(x﹣y)(y﹣z)=0,(x﹣y)2﹣2(x﹣y)(y﹣z)+(y﹣z)2=0,(x﹣y﹣y+z)2=0,∴x+z=2y22.证明:(a+b+c)2+a2+b2+c2=[(a+b)+c]2+a2+b2+c2,=(a+b)2+2(a+b)c+c2+a2+b2+c2,=(a+b)2+2ac+2bc+c2+a2+b2+c2,=(a+b)2+(a2+2ac+c2)+(b2+2bc+c2),=(a+b)2+(a+c)2+(b+c)223.解:∵a+b+c=1,∴(a+b+c)2=a2+b2+c2+2ab+2bc+2ac=1,∵a2+b2+c2=2,∴2+2ab+2bc+2ac=1,解得ab+bc+ac=﹣24.解:(1)原式=x2+2xy+y2;(2)原式=4a2+12ab+9b2;(3)原式=m2+4m+16;(4)原式=x2+x+;(5)原式=a2﹣2a+1;(6)原式=﹣2ab+9b225.(1)原式=(100+0.2)2=10000+40+0.04=10040.04;(2)原式=(100﹣2)2=10000﹣400+4=9604;(3)原式=(40﹣3)2=1600﹣240+9=1351;(4)原式=(20+)2=400+20+=420;(5)原式=(2000+8)2=4000000+32000+64=4032064;(6)原式=(14+)2=196++=217.26.解:∵(a+b)2=a2+2ab+b2=3①,(a﹣b)2=a2﹣2ab+b2=23②,∴①+②得:2(a2+b2)=26,即a2+b2=13,①﹣②得:4ab=﹣20,即ab=﹣5,则原式=13+15=2827.解:(1)(a+b+c)2=a2+b2+c2+2(ab+bc+ac),即1=2+2(ab+bc+ac),∴ab+bc+ac=﹣,a3+b3+c3﹣3abc=(a+b+c)(a2+b2+c2﹣ab﹣ac﹣bc),即3﹣3abc=2+,∴abc=;(2)(a+b+c)(a3+b3+c3)=a4+b4+c4+7(ab+bc+ac)﹣abc(a+b+c),即:3=a4+b4+c4+7×(﹣)﹣×1,a4+b4+c4=28.解:m=4x2﹣12xy+10y2+4y+9=(2x﹣3y)2+(y+2)2+5,由于m等于两个非负数的和加上5,所以最小值是0+5=5,即m=5,即2x﹣3y=0,y+2=0,∴x=﹣3,y=﹣2.故m=5,x=﹣3,y=﹣229.解:原式=5062+2×506×505+5052﹣10102=(506+505)2﹣10102=10112﹣10102=(1011+1010)(1011﹣1010)=202130.解:(1)x2+2y2﹣2xy+4y+4=x2﹣2xy+y2+y2+4y+4=(x﹣y)2+(y+2)2=0,∴x﹣y=0,y+2=0,解得x=﹣2,y=﹣2,∴x y=(﹣2)﹣2=;(2)∵a2+b2=10a+8b﹣41,∴a2﹣10a+25+b2﹣8b+16=0,即(a﹣5)2+(b﹣4)2=0,a﹣5=0,b﹣4=0,解得a=5,b=4,∵c是△ABC中最长的边,∴5≤c<931.解:∵36x2+(m+1)xy+25y2=(6x)2+(m+1)xy+(5y)2,∴(m+1)xy=±2•6x•5y,∴m+1=±60,∴m=59或﹣6132.解:4x,﹣4x,4x4设所求的一项是y,则①当y是中间项时,∵4x2+1±y是完全平方式,∴4x2+y+1=(2x+1)2,∴4x2±y+1=4x2+4x+1,∴y=±4x;②当y是尾项时,1=2×2x•,则y=.不合题意,舍去33.解:∵x2+2(m﹣2)x+9是一个完全平方式,∴这两个数是x和3,∴2(m﹣2)=±6,解得m=5或﹣1,故答案为m1=5,m2=﹣134.解:∵a2﹣4a+4+9b2+6b+1=(a﹣2)2+(3b+1)2=0,而(a﹣2)2≥0,(3b+1)2≥0,∴a﹣2=0,3b+1=0,解得a=2,b=﹣35.证明:(a2+3a)(a2+3a+2)+1,=(a2+3a)2+2(a2+3a)+1,=(a2+3a+1)2,∴(a2+3a)(a2+3a+2)+1是一个完全平方式36.解:∵2(a2+b2+c2﹣ab﹣ac﹣bc),=a2+b2﹣2ab+a2+c2﹣2ac+b2+c2﹣2bc,=(a﹣b)2+(a﹣c)2+(b﹣c)2,=(2002﹣2003)2+(2002﹣2004)2+(2003﹣2004)2=1+4+1,=6,∴a2+b2+c2﹣ab﹣ac﹣bc=337.解:原式=(a+1)(a+4)(a+2)(a+3)+1=(a2+5a+4)(a2+5a+6)+1=(a2+5a)2+10(a2+5a)+25=(a2+5a+5)2.则代数式是完全平方式38.解:(a+1)(a+2)(a+3)(a+4)+m,=(a+1)(a+4)(a+2)(a+3)+m,=(a2+5a+4)(a2+5a+6)+m,=(a2+5a)2+10(a2+5a)+24+m,∵多项式是一个完全平方式,∴24+m=25,∴m=139.解:设x2+y+1和y2+4x+3的值能同时是完全平方,那么有x2+y+1=(x+1)2,y2+4x+3=(y+)2,∴y=2x,4x=2y,即y=2x,x=y,又∵x、y是自然数,∴y必是无理数,∴与已知矛盾,故x2+y+1和y2+4x+3的值不能同时是完全平方40.解:设两个连续自然数是x、x+1,则根据题意知2n2+n﹣29=x2+(x+1)2,化简为2x2+2x+30﹣2n2﹣n=0 ①∴x==②因为x是自然数,所以4n2+2n﹣59必为某个整数的平方(完全平方数),因此设4n2+2n﹣59=k2③∴n==④因为n是整数,所以4k2+237必为某个整数的平方(完全平方数),设4k2+237=a2⑤则有a2﹣4k2=237,即(a+2k)(a﹣2k)=237,所以有或,解之得或由⑤式得4k2+237=1192或412,代入④式得n1=10,n2=﹣30,∴符合条件的整数n是10或﹣3041.解:原式=(x+y)2﹣a(x+y)+52,∵原式为完全平方式,∴﹣a(x+y)=±2×5•(x+y),解得a=±1042.解:∵9x2﹣(m+6)x+m﹣2=(3x)2﹣(m+6)x+()2,∴±(m+6)=2•3•,两边平方并整理得,m2﹣24m+108=0,解得m1=6,m2=18,所以m的值为6或1843.解:(1)由题意,可得12×142×16+4=(122+4×12+2)2=1942;(2)n(n+2)2(n+4)+4=(n2+4n+2)244.解:(1)当a=﹣2,b=1时,(a+b)2=1,a2+2ab+b2=1(2)当a=﹣2,b=﹣3时,(a+b)2=25,a2+2ab+b2=25(3)(a+b)2=a2+2ab+b2(4)原式=19652+2×1965×35+352=(1965+35)2=400000045.解:当a=﹣3,b=1时,(a﹣b)2=(﹣3﹣1)2=16,a2﹣2ab+b2=(﹣3)2﹣2×(﹣3)×1+12=9+6+1=16,∴(a﹣b)2=a2﹣2ab+b2;根据结果,20122﹣2×2012×2011+20112=(2012﹣2011)2=1 46.证明:令2992=m,则2993=m+1,于是a=m2+m2•(m+1)2+(m+1)2,=m4+2m3+3m2+2m+1,=m4+2m3+2m2+m2+2m+1,=(m2)2+2•m2•(m+1)+(m+1)2,=(m2+m+1)2,所以是a一个完全平方数47.解:依题意,画一个边长是a+b+c+d的正方形,则(a+b+c+d)2=a2+ab+ac+ad+ab+b2+bc+bd+ac+bc+c2+cd+ad+bd+cd+d2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd48.解:左边图形的阴影部分面积为:(a+b)2﹣(a﹣b)2,右边图形的阴影部分面积为:a×4b=4ab,根据两图形的阴影部分面积相等可得,(a+b)2﹣(a﹣b)2=4ab.故答案为:(a+b)2﹣(a﹣b)2=4ab49.解:(1)图中有1个边长为a的正方形;有4个边长为b的正方形;有4个两边长分别为a和b的矩形;(2)图形中最大正方形的面积为(a+2b)2=a2+4ab+4b2;最大正方形的边长为a+2b,故面积为(a+2b)2;最大正方形的面积S=a2+4ab+4b2,故(a+2b)2=a2+4ab+4b250.解:(1)原式=x6n﹣1﹣x6n+2x3n﹣1=2x3n﹣2.(2)原式=[(1+2x n)(1﹣2x n)]2﹣16[(x n+1)(x n﹣1)]2=(1﹣4x2n)2﹣16(x2n﹣1)2=1﹣8x2n+16x4n﹣16x4n+32x2n﹣16=24x2n﹣1551.解:(1)由图形可知:2a2+5ab+2b2=(a+2b)(2a+b);(2)52.解:(1)∵如图是用四个长、宽分别为a、b(a>b)的相同长方形和一个小正方形镶嵌而成的正方形图案,∴小正方形的面积为:(a﹣b)2或(a+b)2﹣4ab;(2)∵大正方形图案的面积为28,小正方形的面积是6,∴(a+b)2﹣4ab=6,∴28﹣4ab=6,∴ab=,∴a2+b2+ab=(a+b)2﹣ab=28﹣=22.553.解:(1)长方形面积=2a•2b=4ab;(2)方法1:S阴影部分=(a+b)2﹣4ab;方法2:S阴影部分=(a﹣b)2;(3)根阴影部分的面相等得到(a+b)2﹣4ab=(a﹣b)2;(4)两块阴影部分的周长和=2a+2(n﹣2b)+2×2b+2(n﹣a)=4n.故答案为4ab;(a+b)2﹣4ab;S阴影部分=(a﹣b)254.解:设有p个x取1,q个x取﹣2,有,(5分)解得,(5分)所以原式=1×13+9×(﹣2)3=﹣71.55.解:(1)根据题意知,(a+b)4的展开后,共有5项,各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1;(2)当a=b=1时,(a+b)n=2n.故答案为:(1)5,1,4,6,4,1;(2)n+1,2n56.解:(1)∵=a2+2∴a2+=﹣2=34;(2)∵a﹣b=2,ab=3,∴a2+b2=(a﹣b)2+2ab,=4+2×3,=10,a2b2=9,∴a4+b4=(a2+b2)2﹣2a2b2,=100﹣2×9,=8257.解:(1)x2﹣4x+2的三种配方分别为:x2﹣4x+2=(x﹣2)2﹣2,x2﹣4x+2=(x+)2﹣(2+4)x,x2﹣4x+2=(x ﹣)2﹣x2;(2)a2+ab+b2=(a+b)2﹣ab,a2+ab+b2=(a+b)2+b2;(3)a2+b2+c2﹣ab﹣3b﹣2c+4,=(a2﹣ab+b2)+(b2﹣3b+3)+(c2﹣2c+1),=(a2﹣ab+b2)+(b2﹣4b+4)+(c2﹣2c+1),=(a ﹣b)2+(b﹣2)2+(c﹣1)2=0,从而有a ﹣b=0,b﹣2=0,c﹣1=0,即a=1,b=2,c=1,∴a+b+c=458.解:(1)根据题意可推出第五行的数字为:1、5、10、10、5、1,(2)(a+b)5=(a+b)3(a+b)2=a5+5a4b+10a3b2+10a2b3+5ab4+b5,(3)(a﹣b)5=(a﹣b)3(a﹣b)2=(a3﹣3a2b+3ab2﹣b3)(a2﹣2ab+b2)=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5.故答案为1、5、10、10、5、159.解:(1)92=81=40+41,且92+402=412,第21 页共22 页故答案为:40,41.(2)(2n﹣1)2+(2n2﹣2n)2=(2n2﹣2n+1)2,证明:(2n﹣1)2+(2n2﹣2n)2=4n2﹣4n+1+4n4﹣8n3+8n2﹣4n+1,(2n2﹣2n+1)2=4n4﹣8n3+8n2﹣4n+1,即(2n﹣1)2+(2n2﹣2n)2=(2n2﹣2n+1)2,故答案为:40,4160.解:(1)32+42>2×3×4;②()2+()2>2××;③(﹣2)2+(﹣3)2>2×(﹣2)×(﹣3);④(﹣)2+(﹣)2>2×(﹣)×(﹣)⑤(﹣4)2+(﹣4)2=2×(﹣4)×(﹣4)…故答案为>、>、>、>、=;(2)a2+b2≥2ab;(3)∵m2+n2≥2mn,而mn=8,∴m2+n2≥16,∴2m2+2n2的最小值为32第22 页共22 页。
初一数学完全平方公式题40道和平方差公式20道

初一数学完全平方公式题40道和平方差公式20道完全平方公式题40道:1. 已知a=3,b=4,则(a+b)² = (3+4)² = 492. 计算(5-2)² = 93. 已知x=2,y=5,则(x+y)² = (2+5)² = 494. 计算(10+3)² = 1695. 已知a=7,b=9,则(a+b)² = (7+9)² = 2566. 计算(8-3)² = 257. 已知x=3,y=4,则(x+y)² = (3+4)² = 498. 计算(6+2)² = 649. 已知a=5,b=6,则(a+b)² = (5+6)² = 12110. 计算(12-5)² = 4911. 已知x=6,y=7,则(x+y)² = (6+7)² = 16912. 计算(9+1)² = 10013. 已知a=4,b=8,则(a+b)² = (4+8)² = 14414. 计算(7-4)² = 915. 已知x=1,y=9,则(x+y)² = (1+9)² = 10016. 计算(8-6)² = 417. 已知a=2,b=5,则(a+b)² = (2+5)² = 4918. 计算(11+7)² = 32419. 已知x=8,y=9,则(x+y)² = (8+9)² = 28920. 计算(6-1)² = 2521. 已知a=6,b=10,则(a+b)² = (6+10)² = 25622. 计算(9+4)² = 16923. 已知x=5,y=6,则(x+y)² = (5+6)² = 12124. 计算(7-2)² = 2525. 已知a=3,b=7,则(a+b)² = (3+7)² = 10026. 计算(5+3)² = 6427. 已知x=4,y=8,则(x+y)² = (4+8)² = 14428. 计算(9-6)² = 929. 已知a=8,b=10,则(a+b)² = (8+10)² = 32430. 计算(12+3)² = 22531. 已知x=2,y=8,则(x+y)² = (2+8)² = 10032. 计算(6-2)² = 1633. 已知a=5,b=9,则(a+b)² = (5+9)² = 19634. 计算(7+3)² = 10035. 已知x=7,y=10,则(x+y)² = (7+10)² = 28936. 计算(5-3)² = 437. 已知a=4,b=8,则(a+b)² = (4+8)² = 14438. 计算(10-6)² = 1639. 已知x=3,y=7,则(x+y)² = (3+7)² = 10040. 计算(9+5)² = 196平方差公式20道:1. 计算16²-9² = 1752. 已知a=3,b=4,则a²-b² = 3²-4² = -73. 计算25²-16² = 3694. 已知x=2,y=5,则x²-y² = 2²-5² = -215. 计算9²-4² = 656. 已知a=7,b=9,则a²-b² = 7²-9² = -327. 计算15²-9² = 1448. 已知x=3,y=4,则x²-y² = 3²-4² = -79. 计算12²-5² = 11910. 已知a=5,b=6,则a²-b² = 5²-6² = -1111. 计算11²-7² = 4812. 已知x=6,y=7,则x²-y² = 6²-7² = -1313. 计算14²-12² = 4014. 已知a=4,b=8,则a²-b² = 4²-8² = -4815. 计算10²-3² = 9116. 已知x=1,y=9,则x²-y² = 1²-9² = -8017. 计算8²-5² = 3918. 已知a=6,b=10,则a²-b² = 6²-10² = -6419. 计算17²-15² = 6420. 已知x=8,y=9,则x²-y² = 8²-9² = -17。
完全平方公式展开练习题

完全平方公式展开练习题完全平方公式是数学中常见的一个公式,用于展开一个二次多项式。
它的形式为:(a + b)^2 = a^2 + 2ab + b^2在这个公式中,a和b可以是任意实数。
通过应用这个公式,我们可以将一个二次多项式展开为一系列项的和。
接下来,我将给出一些完全平方公式展开的练习题,帮助大家更好地理解和应用这个公式。
1. 将 (x + 3)^2 展开。
解答:根据完全平方公式,展开后的结果为 x^2 + 6x + 9。
2. 将 (2y - 5)^2 展开。
解答:根据完全平方公式,展开后的结果为 4y^2 - 20y + 25。
3. 将 (3a + 2b)^2 展开。
解答:根据完全平方公式,展开后的结果为 9a^2 + 12ab + 4b^2。
4. 将 (m - n)^2 展开。
解答:根据完全平方公式,展开后的结果为 m^2 - 2mn + n^2。
通过这些练习题,我们可以看到完全平方公式的应用非常简单。
只需要将括号中的两个项分别平方,然后将结果相加即可。
这个公式在解决二次多项式的展开问题中非常有用。
除了展开二次多项式,完全平方公式还可以用于因式分解。
通过将一个二次多项式展开为完全平方的形式,我们可以更容易地找到它的因式。
下面是一个例子:将 x^2 + 6x + 9 因式分解。
解答:观察到这个多项式是一个完全平方,可以写成 (x + 3)^2 的形式。
因此,x^2 + 6x + 9 = (x + 3)^2。
通过这个例子,我们可以看到完全平方公式在因式分解中的应用。
通过将一个多项式转化为完全平方的形式,我们可以更容易地找到它的因式,从而简化问题的解决过程。
完全平方公式不仅在数学中有广泛的应用,还在其他学科中发挥着重要的作用。
在物理学中,完全平方公式可以用于解决运动学问题。
在经济学中,完全平方公式可以用于解决成本和收益的关系。
在计算机科学中,完全平方公式可以用于优化算法的设计。
总之,完全平方公式是数学中一个重要且常用的公式。
完全平方公式专项练习50题(有答案)

完全平方公式专项练习知识点:完全平方公式:(a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
1、完全平方公式也可以逆用,即a 2+2ab+b 2=(a+b)2 a 2-2ab+b 2=(a-b)22、能否运用完全平方式的判定①有两数和(或差)的平方即:(a+b)2或 (a-b)2或 (-a-b)2或 (-a+b)2②有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同。
即:a 2+2ab+b 2或a 2-2ab+b 2-a 2-2ab-b 2或 -a 2+2ab-b 2专项练习:1.(a +2b )22.(3a -5)23..(-2m -3n )24. (a 2-1)2-(a 2+1)25.(-2a +5b )26.(-21ab 2-32c )2 7.(x -2y )(x 2-4y 2)(x +2y )8.(2a +3)2+(3a -2)29.(a -2b +3c -1)(a +2b -3c -1);10.(s -2t )(-s -2t )-(s -2t )2;11.(t -3)2(t +3)2(t 2+9)2.12. 972;13. 20022;14. 992-98×100;15. 49×51-2499.16.(x -2y )(x +2y )-(x +2y )217.(a +b +c )(a +b -c )18.(2a +1)2-(1-2a )219.(3x -y )2-(2x +y )2+5x (y -x )20.先化简。
再求值:(x +2y )(x -2y )(x 2-4y 2),其中x =2,y =-1.21.解关于x 的方程:(x +41)2-(x -41)(x +41)=41. 22.已知x -y =9,x ·y =5,求x 2+y 2的值.23.已知a (a -1)+(b -a 2)=-7,求222b a +-ab 的值. 24.已知a +b =7,ab =10,求a 2+b 2,(a -b )2的值. 25.已知2a -b =5,ab =23,求4a 2+b 2-1的值. 26.已知(a +b )2=9,(a -b )2=5,求a 2+b 2,ab 的值.27.已知 2()16,4,a b ab +==求223a b +与2()a b -的值。
七年级数学下---平方差、完全平方公式专项练习题

七年级数学下-—-平方差、完全平方公式专项练习题平方差:一、选择题1.平方差公式(a+b)(a-b)=a2-b2中字母a,b表示()A.只能是数 B.只能是单项式 C.只能是多项式 D.以上都可以2.下列多项式的乘法中,可以用平方差公式计算的是()A.(a+b)(b+a) B.(-a+b)(a-b C.(13a+b)(b-13a) D.(a2-b)(b2+a)3.下列计算中,错误的有() A.1个 B.2个 C.3个 D.4个①(3a+4)(3a-4)=9a2-4;②(2a2-b)(2a2+b)=4a2-b2;③(3-x)(x+3)=x2-9;④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.4.若x2-y2=30,且x-y=-5,则x+y的值是( )A.5 B.6 C.-6 D.-5二、填空题: 5、(a+b-1)(a-b+1)=(_____)2-(_____)2.6.(-2x+y)(-2x-y)=______.7.(-3x2+2y2)(______)=9x4-4y4.8.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是_____.三、计算题9.利用平方差公式计算:2023×2113. 10.计算:(a+2)(a2+4)(a4+16)(a-2).B卷:提高题1.计算:(1)(2+1)(22+1)(24+1)…(22n+1)+1(n是正整数);(2)(3+1)(32+1)(34+1)…(32008+1)-401632.2.式计算:2009×2007-20082. 3.解方程:x(x+2)+(2x+1)(2x-1)=5(x2+3).(1)计算:22007200720082006-⨯.(2)计算:22007200820061⨯+.4.广场内有一块边长为2a米的正方形草坪,经统一规划后,南北方向要缩短3米,东西方向要加长3米,则改造后的长方形草坪的面积是多少?5.下列运算正确的是( ) A.a3+a3=3a6 B.(-a)3·(-a)5=-a8C.(-2a2b)·4a=-24a6b3 D.(-13a-4b)(13a-4b)=16b2-19a26.计算:(a+1)(a-1)=______.C卷:课标新型题1.(规律探究题)已知x≠1,计算(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(•1+x+x2+x3)=1-x4.(1)观察以上各式并猜想:(1-x)(1+x+x2+…+x n)=_____ _.(n为正整数)(2)根据你的猜想计算:①(1-2)(1+2+22+23+24+25)=______.②2+22+23+…+2n=______(n为正整数).③(x-1)(x99+x98+x97+…+x2+x+1)=_______.①(a -b )(a+b )=_______ . ②(a -b )(a 2+ab+b 2)=_____ _. ③(a -b)(a 3+a 2b+ab 2+b 3)=____ __.2.(结论开放题)请写出一个平方差公式,使其中含有字母m,n 和数字4.完全平方公式变形的应用完全平方式常见的变形有:ab b a b a 2)(222-+=+;ab b a b a 2)(222+-=+ab b a b a 4)(22=--+)(; bc ac ab c b a c b a 222)(2222---++=++1、已知m 2+n 2—6m+10n+34=0,求m+n 的值2、已知0136422=+-++y x y x ,y x 、都是有理数,求y x 的值。
初中七年级 完全平方公式练习题(含答案)

初中七年级 完全平方公式练习题(含答案)一、选择题1.运用乘法公式计算(x +3)2的结果是( )A .x 2+9B .x 2-6x +9C .x 2+6x +9D .x 2+3x +92.下列计算正确的有( )①(a +b )2=a 2+b 2; ②(a -b )2=a 2-b 2;③(a +2b )2=a 2+2ab +2b 2; ④(-2m -3n )2=(2m +3n )2.A .1个B .2个C .3个D .4个3.若用简便方法计算19992,应当用下列哪个式子 ( )A .(2000-1)2B .(2000-1)×(2000+1)C .(1999-1)×(1999+1)D .(1999+1)24.如果多项式x 2+kx +64是某个整式的平方,那么k 的值是( )A .8B .-8C .±8D .±165.若|x +y -5|+(xy -3)2=0,则x 2+y 2的值为( )A .19B .31C .27D .236.如图K -25-1,从边长为(a +4)cm 的正方形纸片中剪去一个边长为(a +1)cm 的小正方形(a >0),剩余部分沿虚线剪拼成一个长方形(不重叠且无缝隙),则长方形的面积为( )图K -25-1A .(2a 2+5a )cm 2B .(3a +15)cm 2C .(6a +9)cm 2D .(6a +15)cm 2二、填空题7.计算:(1)⎝⎛⎭⎫12x -2y 2=______________;(2)(2x +5y )2=______________;(3)(-2x +3y )2=______________; (4)(-2m -5n )2=______________.8.计算:(1)100.12=________;(2)3012=__________.9.已知(x -3y )2=x 2-6xy +ky 2,则k =________.10.(________+y )2=________+xy +y 2.11.整式A 与m 2-2mn +n 2的和是(m +n )2,则A =________.12.已知a +b =3,ab =2,则(a -b )2=________.13.多项式x 2+1添加一个单项式后可变为完全平方式,则添加的单项式可以是________.(任写一个符合条件的单项式即可)三、解答题14.计算:(1)2018·无锡 (x +1)2-(x 2-x );(2)2018·江西 计算:(a +1)(a -1)-(a -2)2;(3)(x +y -3)2.15.先化简,再求值:(1)2018·宁波 (x -1)2+x (3-x ),其中x =-12;(2)(x +y )(x -y )+(x -y )2-(x 2-3xy ),其中x =2,y =12.16.解方程:(2x -3)2-4(x -2)(x +2)=1.17.已知a 2+2ab +b 2=0,求代数式a (a +4b )-(a +2b )(a -2b )的值.18.如图K -25-2,某市区有一块长为(3a +b )米,宽为(2a +b )米的长方形地块,现准备进行绿化,中间有一边长为(a+b)米的正方形区域将修建一座雕像,则绿化的面积是多少平方米?并求出当a=5,b=3时的绿化面积.图K-25-219 已知图K-25-3①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图②的形状拼成一个正方形.(1)你认为图②中阴影部分的正方形的边长是多少?(2)请用两种不同的方法求图②中阴影部分的面积.方法一:________;方法二:________.(3)观察图②,你能写出下列三个代数式之间的等量关系吗?(m+n)2;(m-n)2;mn.(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,求(a-b)2的值.图K-25-31.C 2.A3.A [解析] A 项,(2000-1)2=19992,故本选项正确;B 项,(2000-1)×(2000+1)=20002-1,故本选项错误;C 项,(1999-1)×(1999+1)=19992-1,故本选项错误;D 项,(1999+1)2=20002,故本选项错误.故选A .4.D [解析] 由完全平方公式的特点可知,当k =±16时,多项式x 2+kx +64是某个整式的平方.故选D .5.A [解析] 因为||x +y -5≥0,(xy -3)2≥0,||x +y -5+(xy -3)2=0,所以x +y =5,xy =3,则x 2+y 2=(x +y)2-2xy =52-2×3=19.6.D7.(1)14x 2-2xy +4y 2 (2)4x 2+20xy +25y 2(3)4x 2-12xy +9y 2 (4)4m 2+20mn +25n 2 8.(1)10020.01 (2)90601[解析] 100.12=(100+0.1)2=1002+2×100×0.1+0.01=10020.01;3012=(300+1)2=3002+2×300+1=90601.9.9 10.12x 14x 2 11.4mn 12.1 [解析] (a -b)2=(a +b)2-4ab =32-4×2=1,故答案为1.13.答案不唯一,如14x 4,2x ,-2x 14.解:(1)原式=x 2+2x +1-x 2+x =3x +1.(2)原式=a 2-1-(a 2-4a +4)=a 2-1-a 2+4a -4=4a -5.(3)原式=(x +y)2-2(x +y)×3+32=x 2+2xy +y 2-6x -6y +9.15.解:(1)原式=x 2-2x +1+3x -x 2=x +1.当x =-12时,原式=-12+1=12. (2)原式=x 2-y 2+x 2-2xy +y 2-x 2+3xy =x 2+xy.当x =2,y =12时,原式= 22+2×12= 4+1=5.16.解:4x 2-12x +9-4(x 2-4)=1,4x 2-12x +9-4x 2+16=1,-12x +25=1,-12x =-24,x =2.17.解:因为a 2+2ab +b 2=0,所以(a +b)2=0,所以a +b =0,所以a(a +4b)-(a +2b)(a -2b)=4ab +4b 2=4b(a +b)=0.18.解:由题意可知绿化面积为(3a +b)(2a +b)-(a +b)(a +b)=6a 2+5ab +b 2-a 2-2ab -b 2=5a 2+3ab.当a =5,b =3时,原式=125+45=170.所以当a =5,b =3时的绿化面积为170平方米.19 解:(1)m -n.(2)(m +n)2-4mn (m -n)2(3)(m +n)2-4mn =(m -n)2.(4)(a -b)2=(a +b)2-4ab.因为a +b =8,ab =5,所以(a-b)2=64-20=44.。
完全平方公式专项练习50题(有答案)ok

完全平方公式专项练习50题(有答案)ok完全平方公式是数学中的一个重要概念。
它可以用来计算两数和(或差)的平方。
具体公式为(a+b)²=a²+2ab+b²,(a-b)²=a²-2ab+b²。
这个公式可以逆用,即a²+2ab+b²=(a+b)²,a²-2ab+b²=(a-b)²。
运用完全平方式的判定有两种情况,一是有两数和(或差)的平方,即(a+b)、(a-b)、(-a-b)、(-a+b);二是有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同,即a²+2ab+b²、a²-2ab+b²、-a²-2ab-b²、-a²+2ab-b²。
以下是50道完全平方公式的专项练题,带有答案:1.(a+2b)²答案:a²+4ab+4b²2.(3a-5)²答案:9a²-30a+253.(-2m-3n)²答案:4m²+12mn+9n²4.(a²-1)²-(a²+1)²答案:-4a²5.(-2a+5b)²答案:4a²-20ab+25b²6.(-ab²-c)²答案:a²b⁴+2abc²+ c²7.(x-2y)(x²-4y²)(x+2y)答案:-12xy(x²-4y²)8.(2a+3)²+(3a-2)²答案:13a²+139.(a-2b+3c-1)(a+2b-3c-1)答案:a²-6bc+4b²+4c²+2ac-2a-2b+6c+1 10.(s-2t)(-s-2t)-(s-2t)²答案:-4st11.(t-3)²(t+3)²(t²+9)²答案:(t⁴-9t²+81)³12.972答案:(6³)²13.200²-2²答案:14.99²-101²答案:-40415.49×51-50²答案:116.(x-2y)(x+2y)-(x+2y)²答案:-4y²17.(a+b+c)(a+b-c)答案:a²+b²+c²-ab-ac-bc18.2a+1-1+2a答案:4a19.3x-y-2x-y+5xy-5x²答案:-2x²+4xy-y20.(x+2y)(x-2y)(x-4y),其中x=2,y=-1 答案:12021.(x+1/x)-(x-1/x)((x+1/x)+1)答案:222.x-y=9,xy=5,求x+y答案:1423.a(a-1)+(b-a)-(ab)= -7,求-ab答案:-524.a+b=7,ab=10,求a²+b²,(a-b)²答案:a²+b²=33,(a-b)²=925.2a-b=5,ab=3/2,求4a²+b²-1答案:47/226.(a+b)²=9,(a-b)²=5,求a²+b²,ab 答案:a²+b²=7,ab=127.已知(a+b)²=25,求(a-b)²答案:928.已知(a+b)²=16,求(a-b)²答案:429.已知(a-b)²=9,求(a+b)²答案:2530.已知(a+b)²=36,求(a-b)²答案:031.已知(a+b)²=49,求ab答案:1232.已知(a-b)²=16,求ab答案:-1233.已知ab=3,a²+b²=13,求a-b答案:234.证明对于任意的x,y,代数式a=x²+2xy+y²+3x+2y+1的值总是正数。
七年级数学下册习题 《完全平方公式》(详细答案)

《完全平方公式》习题一、选择题1.下列等式成立的是( )A.(-1)3=-3B.(-2)2×(-2)3=(-2)6C.2a-a=2D.(x-2)2=x2-4x+42.若(2x-5y)2=(2x+5y)2+m,则代数式m为( )A.-20xyB.20xyC.40xyD.-40xy3.下列计算中,正确的是( )A.x2•x5=x10B.3a+5b=8abC.(a+b)2=a2+b2D.(-x)6÷(-x)4=x24.下面各运算中,结果正确的是( )A.2a3+3a3=5a6B.-a2•a3=a5C.(a+b)(-a-b)=a2-b2D.(-a-b)2=a2+2ab+b25.若m+n=3,则2m2+4mn+2n2-6的值为( )A.12B.6C.3D.06.不论x,y为何有理数,x2+y2-10x+8y+45的值均为( )A.正数B.零C.负数D.非负数二、填空题7.已知:a-b=3,ab=1,则a2-3ab+b2=_____.8.若a+b=4,则a2+2ab+b2的值为_____.9.若a2b2+a2+b2+1-2ab=2ab,则a+b的值为_____.10.填上适当的整式,使等式成立:(x-y)2+_____=(x+y)2.三、解答题11.已知实数x、y都大于2,试比较这两个数的积与这两个数的和的大小,并说明理由.12.已知(a+b)2=24,(a-b)2=20,求:(1)ab的值是多少?(2)a2+b2的值是多少?13.已知2(x+y)=-6,xy=1,求代数式(x+2)-(3xy-y)的值.14.计算:①29.8×30.2;②46×512;③2052.15.计算:(a-2b+3c)(a+2b-3c).参考答案一、选择题1.答案:D解析:【解答】A:(-1)3=(-1)×(-1)×(-1)=-1,故选项A错误;B:(-2)2×(-2)3=(-2)2+3=(-2)5,故选项B错误;C:2a-a=(2-1)a=a,故选项C错误;D:(x-2)2=x2-2•x•2+22=x2-4x+4,故选项D正确.故选:D【分析】根据同底数幂的乘法运算,底数不变指数相加,以及有理数的乘方,完全平方公式算出即可.2.答案:D解析:【解答】(2x-5y)2=(2x+5y)2+m,整理得:4x2-20xy+25y2=4x2+20xy+25y2+m,∴-20xy=20xy+m,则m=-40xy.故选:D【分析】利用完全平方公式化简已知等式,根据多项式相等的条件即可求出m.3.答案:D解析:【解答】A、因为x2•x5=x2+5=x7,故本选项错误;B、3a和5b不是同类项的不能合并,故本选项错误;C、应为(a+b)2=a2+2ab+b2,故本选项错误;D、(-x)6÷(-x)4=(-x)6-4=(-x)2=x2.正确.故选D.【分析】利用同底数幂相乘,底数不变,指数相加;完全平方公式;同底数幂相除,底数不变指数相减,对各选项计算后利用排除法求解.4.答案:D解析:【解答】A、原式=5a3,故选项错误;B、原式=-a5,故选项错误;C、原式=-(a+b)2=-a2-2ab-b2,故选项错误;D、原式=(a+b)2=a2+2ab+b2,故选项正确.故选D.【分析】A、原式合并同类项得到结果,即可做出判断;B、原式利用同底数幂的乘法法则计算得到结果,即可做出判断;C、原式变形后,利用完全平方公式展开得到结果,即可做出判断;D、原式利用完全平方公式展开得到结果,即可做出判断.5.答案:A解析:【解答】原式=2(m2+2mn+n2)-6,=2(m+n)2-6,=2×9-6,=12.故选A.【分析】根据完全平方公式的逆用,先整理出完全平方公式的形式,再代入数据计算即可.6.答案:A解析:【解答】x2+y2-10x+8y+45,=x2-10x+25+y2+8y+16+4,=(x-5)2+(y+4)2+4,∵(x-5)2≥0,(y+4)2≥0,∴(x-5)2+(y+4)2+4>0,故选A.【分析】根据完全平方公式对代数式整理,然后再根据平方数非负数的性质进行判断.二、填空题7.答案:8解析:【解答】∵(a-b)2=32=9,∴a2-3ab+b2=(a-b)2-ab=9-1=8【分析】应把所给式子整理为含(a-b)2和ab的式子,然后把值代入即可.8.答案:16解析:【解答】∵a+b=4,∴a2+2ab+b2=(a+b)2=16.【分析】原式利用完全平方公式化简,将a+b的值代入计算即可求出值.9.答案:2或-2解析:【解答】∵a2b2+a2+b2+1-2ab=2ab,∴a2b2+a2+b2+1-2ab-2ab=0,∴a2b2-2ab+1+a2+b2-2ab=0,∴(ab-1)2+(a-b)2=0,∴ab=1,a-b=0,∴a=b=1或-1,∴a+b=2或-2.【分析】首先把2ab移到等式的左边,然后变为a2b2+a2+b2+1-2ab-2ab=0,接着利用完全平方公式分解因式,最后利用非负数的性质即可求解.10.答案:4xy解析:【解答】(x+y)2-(x-y)2=(x2+2xy+y2)-(x2-2xy+y2)=4xy.【分析】所填的式子是:(x+y)2-(x-y)2,化简即可求解.三、解答题11.答案:见解答过程解析:【解答】xy>x+y,理由是:∵x>2,y>2,∴xy>2y,xy>2x,∴相加得:xy+xy>2y+2x,∴2xy>2(x+y),∴xy>x+y.【分析】根据已知得出xy>2y,xy>2x,相加得出xy+xy>2y+2x,即可求出答案.12.答案:(1)ab=1;(2)a2+b2=22.解析:【解答】∵(a+b)2=24,(a-b)2=20,∴a2+b2+2ab=24…①,a2+b2-2ab=20…②,(1)①-②得:4ab=4,则ab=1;(2)①+②得:2(a2+b2)=44,则a2+b2=22.【分析】由(a+b)2=24,(a-b)2=20,可以得到:a2+b2+2ab=24…①,a2+b2-2ab=20…②,通过两式的加减即可求解.13.答案:-4.解析:【解答】∵2(x+y)=-6,即x+y=-3,xy=1,∴(x+2)-(3xy-y)=x+2-3xy+y=(x+y)-3xy+2=-3-3+2=-4.【分析】将所求式子去括号整理变形后,把x+y与xy的值代入计算,即可求出值.14.答案:①899.96;②1012;③42025.解析:【解答】①29.8×30.2=(30+0.2)(30-0.2)=302-0.22=900-0.04=899.96;②46×512=212×512=(2×5)12=1012;③2052=(200+5)2=40000+2000+25=42025.【分析】①首先将原式变为:(30+0.2)(30-0.2),然后利用平方差公式求解即可求得答案;②利用幂的乘方,可得46=212,然后由积的乘方,可得原式=(2×5)12=1012;③首先将205化为:200+5,然后利用完全平方公式求解即可求得答案.15.答案:a2-4b2+12bc-9c2解析:【解答】(a-2b+3c)(a+2b-3c)=[a-(2b-3c)][a+(2b-3c)]=a2-(2b-3c)2=a2-(4b2-12bc+9c2)=a2-4b2+12bc-9c2.【分析】首先将原式变为:[a-(2b-3c)][a+(2b-3c)],然后利用平方差公式,即可得到a2-(2b-3c)2,求出结果.。
初一数学下册《完全平方公式》分类专题训练
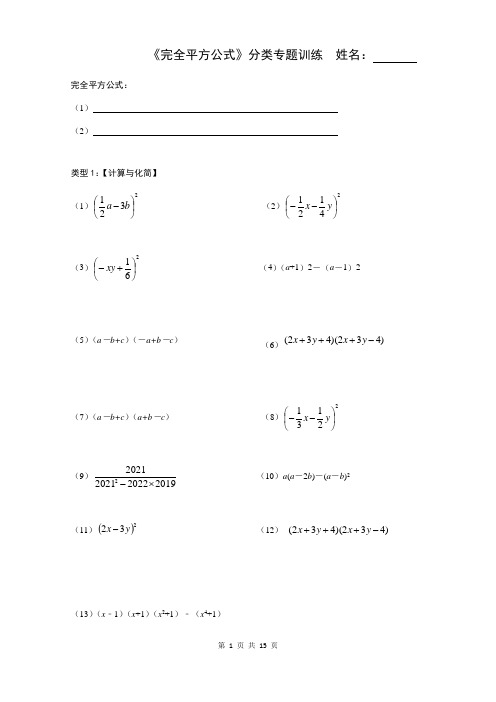
《完全平方公式》分类专题训练 姓名:完全平方公式:(1) (2)类型1:【计算与化简】(1)2321⎪⎭⎫ ⎝⎛-b a (2)24121⎪⎭⎫ ⎝⎛--y x(3)261⎪⎭⎫ ⎝⎛+-xy (4)(a +1)2-(a -1)2(5)(a -b+c )(-a+b -c ) (6))432)(432(-+++y x y x(7)(a -b+c )(a+b -c ) (8)22131⎪⎭⎫ ⎝⎛--y x(9)20192022202120212⨯-(10)a (a -2b )-(a -b )2(11)()232y x - (12) )432)(432(-+++y x y x(13)(x ﹣1)(x +1)(x 2+1)﹣(x 4+1)(14)2213⎪⎭⎫ ⎝⎛+x (15)()493 22+-=x x x(16)()()c b a c b a ++-+ (17)22)(b a - (18)()()()2112+--+x x x (19)22)331()331(b a b a --+(20)))((z y x z y x -+++ (21)()21x +(22)221⎪⎭⎫⎝⎛-b a (23)210151⎪⎭⎫ ⎝⎛--y x(24)221⎪⎭⎫ ⎝⎛+-cd (25))12)(12(-+++y x y x(26))2)((4)2(2y x y x y x +--- (27)4992(28)9982 (29)(2m +5)(2m -5)2(30)[(x+y )2-(x -y )2]÷(2xy ) (31)(x + y )(x -y )-(x -y )2(32)(2a+b -c )2-(2a -b+c )2 (33)(a + 2)(a -2)(a 2 + 4)(a 4 +16)(34)(2a +3)2-(2a -3)2 (35)(-21ab 2-32c )2(36)(x -3y -2)(x +3y -2) (37)(x -2y )(x 2-4y 2)(x +2y );类型2:【配方法】 1、=++9131412x x ( )2 2、=++9131412x x (答案不唯一) 3、配方:=++4131912x x ( )2 4、a 2 + 9b 2 +_______ =(a+3b )2 4a 2 + 25b 2 + _______ =(2a -5b )25、若a =2019,b =2020,c =2021, 求ac bc ab c b a ---++222的值6、若a =2020,b =2021,c =2022,求ac bc ab c b a ---++222的值。
七年级数学下::平方差、完全平方公式专项练习题

七年级数学下---平方差、完全平方公式专项练习题平方差:一、选择题1.平方差公式(a+b)(a-b)=a2-b2中字母a,b表示()A.只能是数 B.只能是单项式 C.只能是多项式 D.以上都可以2.下列多项式的乘法中,可以用平方差公式计算的是()A.(a+b)(b+a) B.(-a+b)(a-b C.(13a+b)(b-13a) D.(a2-b)(b2+a)3.下列计算中,错误的有() A.1个 B.2个 C.3个 D.4个①(3a+4)(3a-4)=9a2-4;②(2a2-b)(2a2+b)=4a2-b2;③(3-x)(x+3)=x2-9;④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.4.若x2-y2=30,且x-y=-5,则x+y的值是()A.5 B.6 C.-6 D.-5二、填空题: 5、(a+b-1)(a-b+1)=(_____)2-(_____)2.6.(-2x+y)(-2x-y)=______.7.(-3x2+2y2)(______)=9x4-4y4.8.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是_____.三、计算题9.利用平方差公式计算:2023×2113. 10.计算:(a+2)(a2+4)(a4+16)(a-2).B卷:提高题1.计算:(1)(2+1)(22+1)(24+1)…(22n+1)+1(n是正整数);(2)(3+1)(32+1)(34+1)…(32008+1)-401632.2.式计算:2009×2007-20082. 3.解方程:x(x+2)+(2x+1)(2x-1)=5(x2+3).(1)计算:22007200720082006-⨯.(2)计算:22007200820061⨯+.4.广场内有一块边长为2a米的正方形草坪,经统一规划后,南北方向要缩短3米,东西方向要加长3米,则改造后的长方形草坪的面积是多少?5.下列运算正确的是( ) A .a 3+a 3=3a 6 B .(-a )3·(-a )5=-a 8C .(-2a 2b )·4a=-24a 6b 3D .(-13a -4b )(13a -4b )=16b 2-19a 26.计算:(a+1)(a -1)=______. C 卷:课标新型题1.(规律探究题)已知x ≠1,计算(1+x )(1-x )=1-x 2,(1-x )(1+x+x 2)=1-x 3,(1-x )(•1+x+x 2+x 3)=1-x 4.(1)观察以上各式并猜想:(1-x )(1+x+x 2+…+x n)=_____ _.(n 为正整数)(2)根据你的猜想计算:①(1-2)(1+2+22+23+24+25)=______. ②2+22+23+ (2)=______(n 为正整数).③(x -1)(x 99+x 98+x 97+…+x 2+x+1)=_______. (3)通过以上规律请你进行下面的探索:①(a -b )(a+b )=_______ . ②(a -b )(a 2+ab+b 2)=_____ _. ③(a -b )(a 3+a 2b+ab 2+b 3)=____ __.2.(结论开放题)请写出一个平方差公式,使其中含有字母m ,n 和数字4.完全平方公式变形的应用完全平方式常见的变形有:ab b a b a 2)(222-+=+;ab b a b a 2)(222+-=+ab b a b a 4)(22=--+)(; bc ac ab c b a c b a 222)(2222---++=++1、已知m 2+n 2-6m+10n+34=0,求m+n 的值2、已知0136422=+-++y x y x ,y x 、都是有理数,求y x 的值。
初一完全平方公式的变形题

初一完全平方公式的变形题1. 引言同学们,今天我们来聊聊一个数学中的“小明星”——完全平方公式。
你可能会觉得这话题有点干巴巴的,但别急,咱们用轻松的方式来搞定它,保准你学得明明白白的。
完全平方公式其实就是初一数学里的一个重要工具,它可以帮我们化繁为简,变复杂为简单。
2. 完全平方公式的基础知识2.1 什么是完全平方公式?完全平方公式就是一种帮我们处理二次方程的公式。
简单来说,它是这样两个公式的结合:1. ((a + b)^2 = a^2 + 2ab + b^2)。
2. ((a b)^2 = a^2 2ab + b^2)。
这两个公式,看起来是不是像魔法一样?有了它们,很多数学题都会变得简单起来。
2.2 为什么要学习完全平方公式?完全平方公式的妙处在于它能让我们很快地展开平方数,简化表达式。
举个例子,如果你遇到一个式子像 ((x + 3)^2),直接用公式展开就是 (x^2 + 6x + 9)。
是不是很方便?3. 完全平方公式的变形3.1 变形的意义学会了完全平方公式,你就能在解题时更加得心应手。
变形的意思就是把问题转换成我们能用公式解决的形式。
这就像你有了一个万能钥匙,无论什么问题,都能轻松打开。
3.2 变形题示例比如,我们遇到一个题目:(x^2 + 8x + 16)。
乍一看,它可能让你觉得有点头疼,但别担心,我们可以用完全平方公式来解。
1. 首先,注意到这个式子可以表示成 ((x + 4)^2),因为 (8x) 是 (2 cdot 4 cdot x),16 刚好是 (4^2)。
所以 (x^2 + 8x + 16 = (x + 4)^2)。
2. 再比如,(a^2 10a + 25) 这个式子,我们可以用 ((a 5)^2) 来表示它,因为 (10a) 是 (2 cdot 5 cdot a),25 刚好是 (5^2)。
4. 变形题的实用技巧4.1 找出平方项变形题的核心就是找到平方项。
先看看你的式子是否可以转换成 ((a pm b)^2) 的形式。
(完整)七年级数学下---平方差、完全平方公式专项练习题

七年级数学下---平方差、完全平方公式专项练习题平方差:一、选择题1.平方差公式(a+b)(a-b)=a2-b2中字母a,b表示()A.只能是数 B.只能是单项式 C.只能是多项式 D.以上都可以2.下列多项式的乘法中,可以用平方差公式计算的是()A.(a+b)(b+a) B.(-a+b)(a-b C.(13a+b)(b-13a) D.(a2-b)(b2+a)3.下列计算中,错误的有() A.1个 B.2个 C.3个 D.4个①(3a+4)(3a-4)=9a2-4;②(2a2-b)(2a2+b)=4a2-b2;③(3-x)(x+3)=x2-9;④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.4.若x2-y2=30,且x-y=-5,则x+y的值是()A.5 B.6 C.-6 D.-5二、填空题: 5、(a+b-1)(a-b+1)=(_____)2-(_____)2.6.(-2x+y)(-2x-y)=______.7.(-3x2+2y2)(______)=9x4-4y4.8.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是_____.三、计算题9.利用平方差公式计算:2023×2113. 10.计算:(a+2)(a2+4)(a4+16)(a-2).B卷:提高题1.计算:(1)(2+1)(22+1)(24+1)…(22n+1)+1(n是正整数);(2)(3+1)(32+1)(34+1)…(32008+1)-401632.2.式计算:2009×2007-20082. 3.解方程:x(x+2)+(2x+1)(2x-1)=5(x2+3).(1)计算:22007200720082006-⨯.(2)计算:22007200820061⨯+.4.广场内有一块边长为2a米的正方形草坪,经统一规划后,南北方向要缩短3米,东西方向要加长3米,则改造后的长方形草坪的面积是多少?5.下列运算正确的是() A.a3+a3=3a6 B.(-a)3·(-a)5=-a8C.(-2a2b)·4a=-24a6b3 D.(-13a-4b)(13a-4b)=16b2-19a26.计算:(a+1)(a-1)=______.C卷:课标新型题1.(规律探究题)已知x≠1,计算(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(•1+x+x2+x3)=1-x4.(1)观察以上各式并猜想:(1-x)(1+x+x2+…+x n)=_____ _.(n为正整数)(2)根据你的猜想计算:①(1-2)(1+2+22+23+24+25)=______.②2+22+23+…+2n=______(n为正整数).③(x-1)(x99+x98+x97+…+x2+x+1)=_______.(3)通过以上规律请你进行下面的探索:①(a -b )(a+b )=_______ . ②(a -b )(a 2+ab+b 2)=_____ _. ③(a -b )(a 3+a 2b+ab 2+b 3)=____ __.2.(结论开放题)请写出一个平方差公式,使其中含有字母m ,n 和数字4.完全平方公式变形的应用完全平方式常见的变形有:ab b a b a 2)(222-+=+;ab b a b a 2)(222+-=+ab b a b a 4)(22=--+)(; bc ac ab c b a c b a 222)(2222---++=++1、已知m 2+n 2-6m+10n+34=0,求m+n 的值2、已知0136422=+-++y x y x ,y x 、都是有理数,求y x 的值。
完全平方公式题50道

完全平方公式题50道1.求以下各式的完全平方公式:a)(x+2)^2b)(x-3)^2c)(2x+5)^2d)(3x-4)^2e)(4x+8)^22.计算并化简以下各式:a)(x+3)^2-(x+2)^2b)(4x-5)^2-(x-2)^2c)(2x+3)^2-(3x+4)^2d)(x+4)^2-(x-4)^2e)(x+1)^2-(x-1)^23.解下列完全平方公式:a)x^2+6x+9=0b)x^2-4x+4=0c)4x^2+20x+25=0d)9x^2-24x+16=0e)16x^2+64x+64=04.求解下列完全平方公式:a)9x^2+12x+4=0b)16x^2-24x+9=0c)25x^2+20x+4=0d)4x^2-12x+9=0e)36x^2+24x+4=05.解以下完全平方公式并判断方程有几个解:a)x^2-10x+25=0b)x^2+8x+16=0c)x^2-14x+49=0d)x^2-6x+9=0e)x^2+4x+4=06.解下列完全平方公式,并判断方程的解是否为实数:a)x^2+3x+2=0b)x^2-9x+20=0c)x^2+5x+6=0d)x^2-2x+3=0e)x^2+2x+1=07.给定下列完全平方公式的解集合,请将其转化为方程形式:a){-4,1}b){2,2}c){-3,2}d){0,3}e){4,4}8.化简并求解以下完全平方公式:a)(x+2)(x+2)-4(x+2)+4b)(2x-3)(2x-3)-4(2x-3)+4c)(3x+4)(3x+4)-4(3x+4)+4d)(x-4)(x-4)-4(x-4)+4e)(x+1)(x+1)-4(x+1)+4以上是50道完全平方公式题目,请注意这些题目都是基于完全平方公式进行求解的。
你可以根据需要进行分组、删减或添加额外题目来适应你的学习需求。
完全平方题目及答案50道题

完全平方题目及答案50道题完全平方是数学中最常用的概念之一,它是一种表示数字的乘幂操作,它可以将一个数学表达式乘以自己得到另一个数字,下面是50道完全平方题目及答案:Q1:若 (x+y)=25,则x+y=?A1:x+y=16Q2:若 x-2x+5x-6=0,则x(x-3)(x+2)的值为多少?A2:x(x-3)(x+2)的值为-36Q3:若 x+11x+30=0,则x的值为多少?A3:x的值为-5和6Q4:若 (x+3)=25,则x的值是多少?A4:x的值是4Q5:若 x+11x+30=0,则x+14x+49的值是多少?A5:x+14x+49的值是0Q6:若 (x-3)=25,则x的值是多少?A6:x的值是8Q7:若 x+7x+12=0,则x的值是多少?A7:x的值是-4和3Q8:若 (x+4)=36,则x的值是多少?A8:x的值是-4Q9:若 4x-9x+5=0,x-2x+1的值是多少?A9:x-2x+1的值是0A10: x的值是7Q11:若 x-3x+7=0,则x的值是多少? A11:x的值是2和7Q12:若 (x-1)=64,则x的值是多少? A12:x的值是2Q13:若 x+9x+20=0,则x的值是多少? A13:x的值是-5和4Q14:若 (x+1)=49,则x的值是多少? A14:x的值是-6Q15:若 3x+5x+2=0,则x的值是多少? A15:x的值是-2和1/3Q16:若 (x+6)=64,则x的值是多少? A16:x的值是-8Q17:若 x+4x+3=0,则x的值是多少? A17:x的值是-3和1Q18:若 (x-5)=81,则x的值是多少? A18:x的值是10Q19:若 x+5x+6=0,则x的值是多少? A19:x的值是-3和2Q20:若 (x+3)=121,则x的值是多少? A20:x的值是-9A21:x的值是-8Q22:若 (x-4)=81,则x的值是多少? A22:x的值是9Q23:若 5x-7x+3=0,则x的值是多少? A23:x的值是3/5和7/5Q24:若 (x-1)=16,则x的值是多少? A24:x的值是2Q25:若 x+7x+10=0,则x的值是多少? A25:x的值是-5和2Q26:若 (x+5)=169,则x的值是多少? A26:x的值是-10Q27:若 x-5x+6=0,则x的值是多少? A27:x的值是3和2Q28:若 (x-4)=64,则x的值是多少? A28:x的值是6Q29:若 x+2x+1=0,则x的值是多少? A29:x的值是-1和-1Q30:若 (x+2)=81,则x的值是多少? A30:x的值是-9Q31:若 x-2x+1=0,则x的值是多少? A31:x的值是1和1A32:x的值是6Q33:若 x+4x+4=0,则x的值是多少? A33:x的值是-2和-2Q34:若 (x+4)=81,则x的值是多少? A34:x的值是-9Q35:若 9x-2x+1=0,则x的值是多少? A35:x的值是1/9和2Q36:若 (x-5)=49,则x的值是多少? A36:x的值是10Q37:若 (x+2)=25,则x的值是多少? A37:x的值是-4Q38:若 x-3x+2=0,则x的值是多少? A38:x的值是2和1Q39:若 (x-1)=169,则x的值是多少? A39:x的值是2Q40:若 x+9x+20=0,则x的值是多少? A40:x的值是-5和4Q41:若 (x+5)=64,则x的值是多少? A41:x的值是-10Q42:若 x-4x+3=0,则x的值是多少? A42:x的值是3和1A43:x的值是11Q44:若 (x+1)=36,则x的值是多少?A44:x的值是-5Q45:若 x+3x+2=0,则x的值是多少?A45:x的值是-2和-1Q46:若 (x+7)=169,则x的值是多少?A46:x的值是-10Q47:若 (x-3)=9,则x的值是多少?A47:x的值是3Q48:若 x-5x+6=0,则x的值是多少?A48:x的值是3和2Q49:若 (x+4)=64,则x的值是多少?A49:x的值是-8Q50:若 (x-2)=9,则x的值是多少?A50:x的值是4以上是50道完全平方题目及答案,完全平方是数学中最常用的概念之一,它可以帮助我们轻松解决一些复杂的数学问题,它也是为更复杂的几何问题提供基础和依据的思考方式。
