OpenGL计算机图形学梁友栋裁剪算法实验代码及运行结果
OpenGL计算机图形学梁友栋裁剪算法实验代码及运行结果

《计算机图形学实验》报告任课教师:钱文华2016年春季学期实验:梁友栋裁剪实验时间:2016年11月17日实验地点:信息学院2204实验目的:掌握梁友栋裁剪程序代码:#include <stdio.h>#include <glut.h>#include <stdlib.h>#include <math.h>class wcPt2D{public:GLfloat x,y;void setCoords(GLfloat xCoord,GLfloat yCoord){x=xCoord;y=yCoord;}GLfloat getx() const{return x;}GLfloat gety() const{return y;}};inline GLint round(const GLfloat a){return GLint(a+0.5);}void setPixel(int x,int y){glBegin(GL_POINTS);glVertex2i(x,y);glEnd();}void init(){glClearColor(1.0,1.0,1.0,0.0);glMatrixMode (GL_PROJECTION);gluOrtho2D(-200.0,200.0,-200.0,200.0);}void lineBres(GLfloat x0,GLfloat y0,GLfloat xEnd,GLfloat yEnd){ int dx = fabs(xEnd - x0),dy = fabs(yEnd - y0);int p = 2*dy - dx;int twoDy = 2*dy,twoDyMinusDx = 2*(dy - dx);int x,y;if(x0>xEnd){x = xEnd;y = yEnd;xEnd = x0;}else{x = x0;y = y0;}setPixel(x,y);while(x<xEnd){x++;if(p<0)p+=twoDy;else{y++;p+=twoDyMinusDx;}setPixel(x,y);}}GLint clipTest(GLfloat p,GLfloat q,GLfloat *u1,GLfloat *u2){ GLfloat r;GLint returnValue = true;if(p<0.0){r = q/p;if(r>*u2)returnValue = false;elseif(r>*u1)*u1 = r;}elseif(p>0.0){r = q/p;if(r<*u1)returnValue = false;else if(r<*u2)*u2 = r;}elseif(q<0.0)returnValue = false;return(returnValue);}void lineClipLiangBarsk(wcPt2D winMin,wcPt2D winMax,wcPt2D p1,wcPt2D p2){GLfloat u1 = 0.0,u2 = 1.0,dx = p2.getx()-p1.getx(),dy;GLfloat x1 = p1.getx(),y1 = p1.gety();GLfloat x2 = p2.getx(),y2 = p2.gety();if(clipTest(-dx,p1.getx()-winMin.getx(),&u1,&u2))if(clipTest(dx,winMax.getx()-p1.getx(),&u1,&u2)){dy = p2.gety()-p1.gety();if(clipTest(-dy,p1.gety()-winMin.gety(),&u1,&u2)){if(clipTest(dy,winMax.gety()-p1.gety(),&u1,&u2)){if(u2<1.0){p2.setCoords(p1.getx()+u2*dx,p1.gety()+u2*dy);}if(u1>0.0){p1.setCoords(p1.getx()+u1*dx,p1.gety()+u1*dy);}glColor3f(0.0,0.0,0.0);lineBres(x1,y1,p1.getx(),p1.gety());lineBres(p2.getx(),p2.gety(),x2,y2);glColor3f(1.0,0.0,0.0);lineBres(p1.getx(),p1.gety(),p2.getx(),p2.gety());}}else{glColor3f(0.0,0.0,0.0);lineBres(x1,y1,x2,y2);}}}void displayliangyoudongcaijian(){glClear(GL_COLOR_BUFFER_BIT);glLineWidth(5.0);glColor3f(0.0,0.0,0.0);glBegin(GL_LINE_LOOP);glVertex2i(100,100);glVertex2i(100,-100);glVertex2i(-100,-100);glVertex2i(-100,100);glEnd();glPointSize(4);wcPt2D test1[4] = {{-100.0,-100.0},{100.0,100.0},{-150.0,-200.0},{200.0,120.0}};wcPt2D test2[4] = {{-100.0,-100.0},{100.0,100.0},{-150.0,-120.0},{0.0,0.0}};wcPt2D test3[4] = {{-100.0,-100.0},{100.0,100.0},{-50.0,50.0},{150.0,150.0}};wcPt2D test4[4] = {{-100.0,-100.0},{100.0,100.0},{-50.0,0.0},{60.0,50.0}};wcPt2D test5[4] = {{-100.0,-100.0},{100.0,100.0},{-170.0,-200.0},{200.0,-120.0}};lineClipLiangBarsk(test1[0],test1[1],test1[2],test1[3]);lineClipLiangBarsk(test2[0],test2[1],test2[2],test2[3]);lineClipLiangBarsk(test3[0],test3[1],test3[2],test3[3]);lineClipLiangBarsk(test4[0],test4[1],test4[2],test4[3]);lineClipLiangBarsk(test5[0],test5[1],test5[2],test5[3]);glFlush();}void main(int argc, char* argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowPosition(50,100);glutInitWindowSize(400,300);glutCreateWindow("梁友栋裁剪算法");init();glutDisplayFunc(displayliangyoudongcaijian);glutMainLoop();}实验结果:。
计算机图形学——梁友栋-Barsky算法

计算机图形学——梁友栋-Barsky算法梁算法是计算机图形学上最经典的⼏个算法,也是⽬前唯⼀⼀个以中国⼈命名的出现在国内外计算机图形学课本的算法,我之前在介绍裁剪算法的时候介绍过这个算法这⼏天复习图形学,发现当时那篇博客写的很空洞,⼀些关键性的推理式⼦讲的不是很清楚,于是在这⾥仔细介绍⼀下。
最近发现中国⼤学MOOC上中国农业⼤学的赵明教授讲的很不错,课程短⼩精悍,感兴趣的同学可以去看⼀下⼀、直线的参数⽅程梁算法表⽰直线是通过直线的参数⽅程来确定的,也就是说给出两个点,利⽤参数表⽰直线。
这⾥对U的理解就是(x,y)点在所给两点之间线段上的位置。
⼆、出边和⼊边把被裁剪的红⾊直线段看 成是⼀条有⽅向的线段,把窗⼝ 的四条边分成两类:⼊边和出边⼊边:直线由窗⼝外向窗⼝内移动时和窗⼝边界相交的边(左边界和下边界)。
出边:直线由窗⼝内向窗⼝外移动时和窗⼝边界相交的边(右边界和上边界)。
裁剪结果的线段起点是直线和两条⼊边的交点以及始端点三 个点⾥最前⾯的⼀个点,即参数u最⼤的那个点;裁剪线段的终点是和两条出边的交点以及端点最后⾯的⼀个 点,取参数u最⼩的那个点。
值得注意的是,当u从-∞到+∞遍历直线时,⾸先对裁剪窗⼝的两条边界直线(下边和左边)从外⾯向⾥⾯移动,再对裁剪窗⼝两条边界直线(上边和右边)从⾥⾯向外⾯移动。
如果⽤u1,u2分别表⽰ 线段(u1≤u2)可见部分的开始和结束上⾯就是梁友栋先⽣的发现,但⼜有了新的问题:如何判断出边和⼊边?四个U值是如何求出来的?判断线段某⼀部分是否在窗⼝内,可以简化为判断直线上⼀个点是否在窗⼝内的问题。
我们知道梁友栋算法的基本出发点是直线的参数⽅程,那么对于那些不会被裁剪掉的点⼀定会满⾜下⾯的不等式:三、运算所⽤的量将上⾯的不等式移项得:在这⾥可以确定那些直线与裁剪窗⼝的交点中P K<0的点输⼊⼊边,P K>0的点属于出边1)分析P k=0的情况如果还满⾜q k<0则线段完全在边界外,应舍弃该线段如果q k≥0则进⼀步判断(2)当p k≠0时:当p k<0时线段从裁剪边界延长线的外部 延伸到内部,是⼊边交点当p k> 0时线段从裁剪边界延长线的内部 延伸到外部,是出边交点线段和窗⼝边界⼀共有四个交点,根据p k的符号,就知道 哪两个是⼊交点,哪两个是出交点当p k< 0时:对应⼊边交点当p k> 0时:对应出边交点⼀共四个u值,再加上u=0、u=1两个端点值,总共六个值把pk<0的两个u值和0⽐较去找最⼤的,把pk>0的两个u值 和1⽐较去找最⼩的,这样就得到两个端点的参数值四、⼩结直线参数化直线段看成是有⽅向的把窗⼝的四条边分为⼊边和出边。
opengl算法学习---直线裁剪算法

opengl 算法学习---直线裁剪算法裁剪是从数据集合提取信息的过程,它是计算机图形学许多重要问题的基础。
裁剪典型的⽤途就是从⼀个⼤的场景中提取所需的信息,以显⽰某⼀局部场景或视图。
⽐如浏览地图时,对感兴趣的区域放⼤显⽰,此时窗⼝内显⽰的内容会相应减少。
确定图形的哪些部分在窗⼝内,哪些部分在窗⼝外(不可见区域),只显⽰窗⼝内的那部分图形,这个选择处理过程就是裁剪。
这⾥详细讲述两种算法Cohen-Sutherland 编码裁剪算法Cohen-Sutherland 编码裁剪算法算法思想1)若线段完全在窗⼝之内则显⽰该线段称为“取”,2)若线段明显在窗⼝之外则丢弃该线段称为“弃”3)若线段既不满⾜“取”的条件也不满⾜“弃”的条件则把线段分割为两段,对于完全在窗⼝之外的部分可弃之。
具体实现为快速判断⼀条直线段与矩形窗⼝的位置关系采⽤如图所⽰的空间划分和编码⽅案(四位⼆进制编码上下右左)裁剪⼀条线段时先求出两端点所在的区号,若皆为零保留。
若端点编码按位取与运算的结果不为零,意味着线段位于窗⼝之外,应舍弃。
否则求出线段与窗⼝某边的交点并将该线段⼀分为⼆后,舍弃完全在窗⼝外的线段并对另⼀段重复上述处理。
代码实现Liang-Barsky 算法概念Liang-Barsky 算法的基本思想是,从 A 、B 和 P1中找出最靠近 P2的点,如图所⽰为 P1;从C 、D 和 P2中找出最靠近P1的点,显然为C 点;也即 PC1即为裁剪后部分。
具体实现稍后再补对于区域内存在的线段P1P2,根据两点坐标构造⽅程x=x_{1}+u(x_{2}-x_{1})y=y_{1}+u(y_{2}-y_{1})令\Delta x=x_{2}-x_{1} \Delta y=y_{2}-y_{1}即可推出x=x_{1}+u\Delta xy=y_{1}+u\Delta yLiang-Barsky算法通过计算两端点截取后的u值,绘制截取后的线段,设截取后线段的两端点u为u_{1}、u_{2} u_{1}初始值=0,即线段初始点,u_{2}初始值=1,即线段终点对于x⽽⾔x_{l} \leqslant x \leqslant x_{r}同理y_{b} \leqslant y \leqslant y_{t}\Rightarrow \left\{\begin{matrix} x_{l} \leqslant x_{1}+u\Delta x \leqslant x_{r} \\ y_{b} \leqslant y_{1}+u\Delta y \leqslant y_{t} \end{matrix}\right.即可推得\Rightarrow \left\{\begin{matrix} u\Delta x \leqslant x_{r}-x_{1} \\ -u\Delta x \leqslant x_{1}-x_{l} \\ u\Delta y \leqslant y_{t}-y_{1} \\ -u\Delta y \leqslant y_{1}-y_{b} \end{matrix}\right.构造p_{k} \leqslant q_{k} ,k={1,2,3,4}每个k对应上式每种情况\Rightarrow \left\{\begin{matrix} p_{1}=\Delta x & q_{1}=x_{r}-x_{1} \\ p_{2}=-\Delta x & q_{2}=x_{1}-x_{l} \\ p_{3}=\Delta y & q_{3}=y_{t}-y_{1} \\ p_{4}=-\Delta y & q_{4}=y_{1}-y_{b} \end{matrix}\right.当p_{k}=0时,该线段平⾏于轮廓线如果q_{k}<0当k=1时,x_{r}<x_{1}当k=2时,x_{1}<x_{l}当k=3时,y_{t}<y_{1}当k=4时,y_{1}<y_{b}可推出若q_{k}<0时,该线段位于裁剪区域外如果q_{k}\geqslant 0则该线段位于区域内当p_{k} \neq 0时,此时线段延长线与轮廓线交点在上式中u值=\frac{q_{k}}{p_{k}}若p_{k}<0则该线段部分为由边界外到边界内,u_{1}=max(u_{1},u)若p_{k}>0则该线段部分为由边界内到边界外,u_{2}=min(u_{2},u)通过以上过程,可推出截取后线段两端点的u_{1}与u_{2},若u_{1}>u_{2},则该线段不为于裁剪区域内代码实现void LiangBarsky(Point p1,Point p2,Rectan rec){float u1=0,u2=1,p[4],q[4];p[0]=p1.x-p2.x;p[1]=p2.x-p1.x;p[2]=p1.y-p2.y;p[3]=p2.y-p1.y;q[0]=p1.x-rec.xl;q[1]=rec.xr-p1.x;q[2]=p1.y-rec.yb;q[3]=rec.yt-p1.x;for(int i=0;i<4;i++){if(!p[i] && q[i]<0) return ;else if(p[i]){float u=q[i]/p[i];if(p[i]<0) u1=max(u1,u);else u2=min(u2,u);}}if(u1>u2) return ;drawline(Point(p1.x+u1*(p2.x-p1.x),p1.y+u1*(p2.y-p1.y)),Point(p1.x+u2*(p2.x-p1.x),p1.y+u2*(p2.y-p1.y)),BLUE);}Processing math: 0%。
梁友栋-Barsky直线裁剪算法计算机图形学课程设计

河南理工大学万方科技学院课程设计报告2011 — 2012学年第二学期课程名称计算机图形学设计题目计算机图形学基本算法演示系统设计学生姓名学号专业班级网络11升—1班指导教师徐文鹏2012 年5 月28 日目录第1章设计内容与要求 (1)1.1 总体目标和要求 (1)1.2内容与要求 (1)1.2.1 直线的生成 (1)1.2.2 圆弧的生成 (1)1.2.3 线段裁剪 (2)1.2.4 多边形裁剪 (2)1.2.5 综合 (2)第2章总体设计 (3)2.1 Bresenham算法画直线 (3)2.1.1 Bresenham算法画直线理论基础 (3)2.1.2 Bresenham算法画直线原理 (3)2.2 Bresenham算法画圆 (4)2.2.1 Bresenham算法画圆理论基础 (4)2.2.2 Bresenham算法画圆原理 (5)2.3 梁友栋-Barsky算法进行线段裁剪 (6)2.3.1梁友栋-Barsky算法进行线段裁剪基本原理 (6)2.4 Sutherland-Hodgman算法进行多边形裁剪 (8)2.4.1 Sutherland—Hodgman多边形裁剪算法思想 (8)2.4.2 点在边界内侧的判断方法 (8)2.4.4 Sutherland-Hodgeman多边形裁剪算法特点 (8)第3章详细设计 (9)3.1 Bresenham算法画直线 (9)3.1.1 Bresenham 算法画线算法具体实现过程 (9)3.2 Bresenham算法画圆 (9)3.2.1 Bresenham 算法画圆核心代码 (9)3.3 梁友栋-Barsky算法进行线段裁剪 (10)3.3.1梁友栋-Barsky算法推导过程 (10)3.3.2梁友栋-Barsky算法进行线段裁剪的步骤 (11)3.4 Sutherland-Hodgman算法进行多边形裁剪 (11)3.4.1 Sutherland—Hodgman多边形裁剪算法步骤 (11)3.5将画线、画圆、线段裁剪和多边形裁剪综合 (12)第4章功能实现 (14)4.1用Bresenham算法画线测试结果 (14)4.2用Bresenham算法画圆测试结果 (14)4.3梁友栋-Barsky算法进行线段裁剪测试结果 (15)4.4 Sutherland-Hodgman算法进行多边形裁剪测试结果 (16)4.5将四种算法综合测试结果 (16)第5章总结 (17)参考文献 (18)第1章设计内容与要求1.1 总体目标和要求目标:以图形学算法为目标,深入研究。
计算机图形学直线裁剪代码

using System;using ;using ponentModel;using System.Data;using System.Drawing;using System.Text;using ;namespace LineCut_Cohen{public partial class Form1 : Form{public Form1(){InitializeComponent();}//定义钻石参数int x0 = 100;int y0 = 100;int n = 13;int r = 50;int[] x;int[] y;////计算钻石顶点 by tiantian//public void ZuanShi(){float t = (float)3.14159 * 2 / n;x = new int[n];y = new int[n];for (int i = 0; i < n; i++){x[i] = (int)(r * Math.Cos(i * t) + x0);y[i] = (int)(r * Math.Sin(i * t) + y0);}}////计算点(x,y)的编码//void CompOutCode(int x, int y, Rectangle rect, OutCode outCode){outCode.all = 0;outCode.top = outCode.bottom = 0;if (y < rect.Top) //rect类的top相当于我们惯常用的坐标系的bottomby:tiantian{outCode.bottom = 1;outCode.all += 1;}else if (y > rect.Bottom)//rect类的bottom相当于我们惯常用的坐标系的top by:tiantian{outCode.top = 1;outCode.all += 1;}outCode.right = outCode.left = 0;if (x > rect.Right){outCode.right = 1;outCode.all += 1;}else if (x < rect.Left){outCode.left = 1;outCode.all += 1;}}////线段裁剪,p0(x0,y0),p1(x1,y1)为待裁剪线断,rect为裁剪窗口//bool ChoenSutherlandLineClip(ref int x0, ref int y0, ref int x1, ref int y1, Rectangle rect) //这里必须是引用传递!by:tiantian{Boolean accept, done;OutCode outCode0 = new OutCode();OutCode outCode1 = new OutCode();OutCode outCodeOut = new OutCode();int x = 0;int y = 0;accept = false;done = false;CompOutCode(x0, y0, rect, outCode0);CompOutCode(x1, y1, rect, outCode1);do{int code0 = outCode0.Code();int code1 = outCode1.Code();if ((outCode0.all == 0) && (outCode1.all == 0)) //完全可见{accept = true;done = true;}else if ((code0 & code1) != 0) //显然不可见 by ttdone = true;else //进行求交测试{if (outCode0.all != 0) //判断哪一点位于窗口之外outCodeOut = outCode0;else outCodeOut = outCode1;if (outCodeOut.left == 1)//线段与窗口的左边相交{x = rect.Left;y = y0 + (y1 - y0) * (x - x0) / (x1 - x0);}else if (outCodeOut.right == 1)//线段与窗口的右边相交{x = rect.Right;y = y0 + (y1 - y0) * (x - x0) / (x1 - x0);}else if (outCodeOut.top == 1)//线段与窗口的上边相交{y = rect.Bottom;x = x0 + (x1 - x0) * (y - y0) / (y1 - y0);}else if (outCodeOut.bottom == 1)//线段与窗口的下边相交{y = rect.Top;x = x0 + (x1 - x0) * (y - y0) / (y1 - y0);}//以交点为界,将线段位于窗口边所在的直线的外侧的部分丢弃。
计算机图形学裁剪

《计算机图形学》实验报告学院:理学院专业:信息与计算科学班级:structRectangle{floatxmin,xmax,ymin,ymax;};Rectanglerect;intx0,y0,x1,y1;intCompCode(intx,inty,Rectanglerect){intcode=0x00;if(y<rect.ymin)code=code|4;if(y>rect.ymax)code=code|8;if(x>rect.xmax)code=code|2;if(x<rect.xmin)code=code|1;returncode;}intcohensutherlandlineclip(Rectanglerect,int&x0,int&y0,int&x1,int&y1){ intaccept,done;floatx,y;accept=0;done=0;intcode0,code1,codeout;code0=CompCode(x0,y0,rect);code1=CompCode(x1,y1,rect);do{if(!(code0|code1)){accept=1;done=1;}elseif(code0&code1)done=1;else{if(code0!=0)codeout=code0;elsecodeout=code1;if(codeout&LEFT_EDGE){y=y0+(y1-y0)*(rect.xmin-x0)/(x1-x0);x=(float)rect.xmin;}elseif(codeout&RIGHT_EDGE){y=y0+(y1-y0)*(rect.xmax)/(x1-x0);x=(float)rect.xmax;}elseif(codeout&BOTTOM_EDGE){x=x0+(x1-x0)*(rect.ymin-y0)/(y1-yO);y=(float)rect.ymin;}elseif(codeout&TOP_EDGE){x=x0+(x1-x0)*(rect.ymax-y0)/(y1-y0);y=(float)rect.ymax;if(codeout==code0){x0=x;y0=y;code0=CompCode(x0,y0,rect);}else{x1=x;y1=y;code1=CompCode(x1,y1,rect);}}while(!done);if(accept)LineGL(x0,y0,x1,y1);returnaccept;}voidmyDisplay(){glClear(GL_COLOR_BUFFER_BIT);glColor3f(1.0f,0.0f,0.0f);glRectf(rect.xmin,rect.ymin,rect.xmax,rect.ymax);LineGL(x0,y0,x1,y1);glFlush();voidInit(){glClearColor(0.0,0.0,0.0,0.0);glShadeModel(GL_FLAT);rect.xmin=100;rect.xmax=300;rect.ymin=100;rect.ymax=300;x0=450,y0=0,x1=0,y1=450;printf("Presskey'c'toClip!\nPresskey'r'toRrstore!\n");}voidReshape(intw,inth){glViewport(0,0,(GLsizei)w,(GLsizei)h);glMatrixMode(GL_PROJECTION);glLoadldentityO;gluOrtho2D(0.0,(GLdouble)w,0.0,(GLdouble)h);}voidkeyboard(unsignedcharkey,intx,inty){switch(key){case'c':cohensutherlandlineclip(rect,x0,y0,x1,y1);glutPostRedisplay();break;case'r':Init();glutPostRedisplay();break;case'x':exit(0);break;default:break;}}voidmain(intargc,char**argv){glutInit(&argc,argv);glutInitDisplayMode(GLUT_RGBIGLUT_SINGLE);glutInitWindowPosition(100,100);glutInitWindowSize(640,480);glutCreateWindow("helloworld");Init();glutDisplayFunc(myDisplay);glutReshapeFunc(Reshape);glutMainLoop();}Mhellovorld实验结。
计算机图形学实验报告-OpenGL基本使用

学生实验实习报告册学年学期:2016-2017学年 春□√秋学期课程名称:大学计算机基础学生学院:通信与信息工程学院专业班级:学生学号:学生姓名:联系电话:重庆邮电大学教务处印制实验实习名OpenGL基本使用指导教师秦红星考核成绩课程名称计算机图形学A 课程编号实验实习地点信息科技大厦S306 完成日期学生姓名学生学号学院专业广电与数字媒体类所在班级教师评语教师签名:年月日一、实验实习目的及要求目的:认识了解OpenGL的性质、功能要求:1.利用OpenGL绘制一个简单的场景:比如球体、正方体2.加入灯光3.实现交互操作:平移、缩放、旋转二、实验实习设备(环境)及要求(软硬件条件)采用Microsoft Visual C 2010生成环境并用C++编写程序三、实验实习内容与步骤内容:背景为黑色,在点光源下,能够实现平移、缩放、旋转的球。
步骤:建立立体-->添加光照-->添加变换1.先写“主函数”,在主函数中将窗口生成好。
2.在“自定义函数1”中对窗口进行清除、填色等操作。
3.在“自定义函数1”中设置点光源,设置光照的各种参数。
4.在“自定义函数1”中设置平移、缩放、旋转及各参数。
5.在“自定义函数2”中设置平移和缩放的循环。
6.在主函数中调用这两个自定义函数,并且在主函数里面用“自定义函数1”为参数调用glutDisplayFunc()来注册一个绘图函数。
其次用空闲回调函数glutIdleFunc()来使球体不停地循环有缩放、平移功能的函数。
实现动画。
四、实验实习过程或算法(源程序、代码)#include<GL/glut.h>GLfloat angle = 0.0f;GLfloat multiply = 0.0f;void display(void){glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);glClearColor(0.0f, 0.0f, 0.0f, 0.0f); //设置窗口里面的背景颜色glMatrixMode(GL_PROJECTION);glLoadIdentity();gluPerspective(90.0f, 1.0f, 1.0f, 20.0f);glLoadIdentity();gluLookAt(0.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);{//设置一个点光源GLfloat light_position[] = { 0.5f,0.0f,0.0f,1.0f };//(xyzw)w为1时代表点光源,0时代表方向光源GLfloat light_ambient[] = { 0.5f,0.5f,0.5f,1.0f };//(0001)GLfloat light_diffuse[] = { 1.0f,1.0f,1.0f,1.0f };//(1111)GLfloat light_specular[] = { 1.0f, 1.0f, 1.0f, 1.0f };//(1111)glLightfv(GL_LIGHT0, GL_POSITION, light_position);glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);//光源环境光强值glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);//光源漫反射强值glLightfv(GL_LIGHT0, GL_SPECULAR, light_specular);//光源镜面反射强值glEnable(GL_LIGHT0);//打开该光源glEnable(GL_LIGHTING);//打开光照}{glRotatef(angle, 0.0f, 1.0f, 0.0f);glTranslatef(0.0f, 0.0f, 0.6f); //平移glScaled(multiply, multiply, multiply); //缩放glutSolidSphere(0.2, 50, 50);}glutSwapBuffers();}void rotateAndzoom(void) //旋转和缩放{angle += 1.0f;if (angle >= 360.0f)angle = 0.0f;display();//设置旋转multiply += 0.01f;if (multiply >= 2.0f)// multiply -= 0.01f;//if (multiply <= 1.0f)multiply = 1.0f;display();//设置缩放}int main(int argc, char* argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);glutInitWindowPosition(400, 50);glutInitWindowSize(800, 800);glutCreateWindow("立体");glutDisplayFunc(&display);glutIdleFunc(&rotateAndzoom);//旋转glutMainLoop();//调用该函数启动程序,所有以创建的窗口将会显示return 0;}五、实验实习结果分析和(或)源程序调试过程实验实习名直线扫面和区域填充实现指导教师考核成绩课程名称课程编号实验实习地点完成日期学生姓名学生学号学院专业通信与信息工程学院广电与数字媒体类所在班级教师评语教师签名:年月日一、实验实习目的及要求项目目的:熟悉光栅图形学中的相关算法项目要求:1.应用OpenGL点绘制函数直线与区域2.采用直线扫面算法绘制一条线段,直线有离散点组成3.利用区域填充算法绘制多边形区域,区域由离散点组成二、实验实习设备(环境)及要求(软硬件条件)采用Microsoft Visual C 2010生成环境并用C++编写程序三、实验实习内容与步骤内容:1.用DDA算法实现点绘制直线。
裁剪III(计算机图形学)

2009-2010-2:CG:SCUEC
14
多边形裁剪-凸多边形的二维裁剪
多边形是由一组线段围成的封闭区域,线段裁剪是多边形 裁剪的基础。下图(b)是多边形的线段被裁剪后的结果,但 已不再是封闭的区域。正确的剪裁结果应是一个有边界的区 域,即裁剪后的结果仍是一个(或多个)多边形 ,这就要求
x t x R x 0 y t y0 yB y t y T y 0
令
QR x QB y QT y
则有 t Q i D i i L , R , B , T
2009-2010-2:CG:SCUEC
3
梁友栋-Barsky算法
凸多边形裁剪区域
3) N (P(t)-A) < 0,则P(t)在L外侧。
性质1表明,P(t)在凸多边形内的充要条件是,对于凸多边形边界上 任意一点A和该处内法向量N,都有N (P(t)-A) 0 。
2009-2010-2:CG:SCUEC
9
Cyrus-Beck算法
现假设多边形有k条边,在每条边界Li上取1个点 Ai ,该点处的内法 向量Ni(i=1,2,…,k),则可见线段的参数区间为下列不等式组的解
由
t Q i D i i L , R , B , T
i , j { L , R }i j
Dj Di (Q i 0 ) t (Q j 0 ) Q Qj i D Dj i (Q i 0 ) t (Q j 0 ) Qj Qi 0 t 1
i , j { B , T }i j
2009-2010-2:CG:SCUEC
4
梁友栋-Barsky算法
图形学实验报告裁剪

#ifdef _AFXDLL
Enable3dControls();// Call this when using MFC in a shared DLL
#else
Enable3dControlsStatic();// Call this when linking to MFC statically
// CMyApp
BEGIN_MESSAGE_MAP(CMyApp, CWinApp)
//{{AFX_MSG_MAP(CMyApp)
// NOTE - the ClassWizard will add and remove mapping macros here.
// DO NOT EDIT what you see in these blocks of generated code!
//}}AFX_MSG
ON_COMMAND(ID_HELP, CWinApp::OnHelp)
END_MESSAGE_MAP()
/////////////////////////////////////////////////////////////////////////////
// CMyApp construction
#endif
CMyDlg dlg;
m_pMainWnd = &dlg;
int nResponse = dlg.DoModal();
if (nResponse == IDOK)
{
// TODO: Place code here to handle when the dialog is
计算机图形学OpenGL版实验1-4

实验1 OpenGL初识一、实验目的:熟悉编程环境;了解光栅图形显示器的特点;了解计算机绘图的特点;利用VC+OpenGL作为开发平台设计程序,以能够在屏幕上生成任意一个像素点为本实验的结束。
二、实验内容:(1)了解和使用VC的开发环境,理解简单的OpenGL程序结构。
(2)掌握OpenGL提供的基本图形函数,尤其是生成点的函数。
三、该程序的作用是在一个黑色的窗口中央画一个矩形、三角形和三个点,如图所示。
下面对各行语句进行说明:首先,需要包含头文件#include <GL/glut.h>,这是GLUT的头文件。
然后看main函数。
int main(int argc, char *argv[]),这个是带命令行参数的main函数。
这种以glut开头的函数都是GLUT工具包所提供的函数,下面对用到的几个函数进行介绍;1)glutInit,对GLUT进行初始化,这个函数必须在其它的GLUT使用之前调用一次。
其格式比较固定,一般都是glutInit(&argc, argv)就行;2) glutInitDisplayMode,设置显示方式,其中GLUT_RGB表示使用RGB颜色,与之对应的还有GLUT_INDEX(表示使用索引颜色)。
GLUT_SINGLE表示使用单缓冲,与之对应的还有GLUT_DOUBLE(使用双缓冲)。
更多信息,以后的实验教程会有讲解介绍;3) glutInitWindowPosition,设置窗口在屏幕中的位置;4) glutInitWindowSize,设置窗口的大小;5) glutCreateWindow,根据前述设置的信息创建窗口。
参数将被作为窗口的标题。
注意:窗口被创建后,并不立即显示到屏幕上。
需要调用glutMainLoop才能看到窗口;6) glutDisplayFunc,设置一个函数,当需要进行画图时,这个函数就会被调用。
(暂且这样理解);7) glutMainLoop,进行一个消息循环。
CohenSutherland裁剪算法并使用OpenGL实践

CohenSutherland裁剪算法并使⽤OpenGL实践 还是其⼏天写的,这是最简单的⼀个直线裁剪算法了吧,它针对的是⼀个矩形和⼀条线段。
并且还是边与坐标轴平⾏的矩形。
在实际应⽤上应该会经常⽤于屏幕对各种线段的裁剪吧。
算法很简单效率也很⾼。
⾸先是算法的两种特例:平凡接受和平凡拒绝。
(图⽚来⾃《计算机图形学(OpenGL)》第三版) 当线段的两个端点都在矩形内部,则平凡接受,不需要裁剪。
如图中的AB。
⽽当线段的两个端点都在某条边的外边时,平凡拒绝,也不需要裁剪。
如图中的CD。
检测这两种情况的⽅法可以先形成两个端点的码字,如下:那么可以得到如下的⼏种码字: 如果两个点都在矩形内部,那么码字应该都是FFFF,则平凡接受,返回当前线段就好。
⽽如果两个点的某⼀位都是T,则说明他们都在矩形某条边的外⾯,则平凡拒绝。
如图3.17中的CD,对应的码字分别应是FTTF和FFTF,在第三位上都是T,他们都在矩形的右边,则平凡拒绝。
我们运⾏这样的算法来裁剪⼀条线段: 最后,代码如下:1 #include <GL/gl.h>2 #include <GL/glu.h>3 #include <GL/glut.h>4 #include <cmath>5 #include <iostream>6using namespace std;78struct Point2D9 {10float _x, _y;11 Point2D()12 {13 _x = 0.0f;14 _y = 0.0f;15 }16 Point2D(const Point2D& p)17 {18 _x = p._x;19 _y = p._y;20 }21 Point2D(float xx, float yy)22 {23 _x = xx;24 _y = yy;25 }26 Point2D& operator=(const Point2D& p)27 {28 _x = p._x;29 _y = p._y;30return *this;31 }32 Point2D& operator+(const Point2D& p)33 {34 Point2D temp;35 temp._x = _x + p._x;36 temp._y = _y + p._y;37return temp;38 }39 Point2D& operator-(const Point2D& p)40 {41 Point2D temp(_x - p._x, _y - p._y);42return temp;43 }44float operator*(const Point2D& p)45 {46return _x * p._x + _y * p._y;47 }4849float length()50 {51return sqrtf(_x * _x + _y * _y);52 }53 };5455struct Line2D56 {57 Point2D _start;58 Point2D _end;59float _length;6061 Line2D() : _start(), _end()62 {63 _length = 0.0f;64 }65 Line2D(const Point2D& start, const Point2D& end) : _start(start), _end(end)66 {67 }68 Line2D(const Line2D& line) : _start(line._start), _end(line._end)69 {}7071float length()72 {73 _length = (_end - _start).length();74 }7576 Line2D& operator = (const Line2D& line)77 {78 _start = line._start;79 _end = line._end;80 }81 };8283struct Rect84 {85float _left;86float _right;87float _up;88float _down;8990float width()91 {92return _right - _left;93 }94float height()95 {96return _down - _up;97 }98 };99100enum CutRes101 {102 CR_ACCEPTED = 0,103 CR_REFUSED = 1,104 };105106enum CSBIT107 {108 CB_BELOW = 0x01,//0001109 CB_RIGHT = 0x02,//0010110 CB_ABOVE = 0x04,//0100111 CB_LEFT = 0x08,//1000112113 CB_BELOW_INV = 0xfe,//1111 1110114 CB_RIGHT_INV = 0xfd,//1111 1101115 CB_ABOVE_INV = 0xfb,//1111 1011116 CB_LEFT_INV = 0xf7,//1111 0111117 };118119 typedef unsigned char KEY;120121/*Global Varibles*/122const int SCREEN_WIDTH = 800;123const int SCREEN_HEIGHT = 600;124 Point2D g_Start;125 Point2D g_End;126 Line2D src;127 Line2D dest;128bool acc;129 Rect g_Rect;130int g_Count;131132 KEY GenKey(const Point2D& p, const Rect& r) 133 {134 KEY key = 0;135136if(p._y > r._down)137 {138 key |= CB_BELOW;139 }140if(p._y < r._up)141 {142 key |= CB_ABOVE;143 }144if(p._x < r._left)145 {146 key |= CB_LEFT;147 }148if(p._x > r._right)149 {150 key |= CB_RIGHT;151 }152153return key;154 }155156void ShowKey(KEY key)157 {158if(key & CB_LEFT)159 cout << "T";160else161 cout << "F";162163if(key & CB_ABOVE)164 cout << "T";165else166 cout << "F";167168if(key & CB_RIGHT)169 cout << "T";170else171 cout << "F";172173if(key & CB_BELOW)174 cout << "T";175else176 cout << "F";177 }178179/*180key: TTFF181left above right below182*/183int Cohen_Sutherland(const Line2D& src, Line2D& dest, const Rect& rect)184 {185 cout << "===============In Cohen_Sutherland===============\n";186 Point2D start = src._start;187 Point2D end = src._end;188 KEY s, e;189 dest = src;190191for(unsigned int i = 0; i < 4; ++i)192 {193 cout << "\nNow Line: start(" << start._x << ", " << start._y <<") end(" << end._x << ", " << end._y << ")\n"; 194195 s = GenKey(start, rect);196 e = GenKey(end, rect);197 cout << "Key of Line: start ";ShowKey(s);cout << " end: ";ShowKey(e); cout << endl;198199if((s == e) && (s == 0))200 {201//accept, all point inside the rect202 dest._start = start;203 dest._end = end;204return CR_ACCEPTED;205 }206int _b = 1 << i;207if((s & _b) && (e & _b))208 {209//all point at same side210return CR_REFUSED;211 }212213switch(i)214 {215case0:216 {217//below218if(s & _b)219 {220float scale = (rect._down - end._y) / (start._y - end._y);221 start._x = (start._x - end._x) * scale + end._x;222 start._y = rect._down;223 cout << "Start Below Rect. Cutted: " << start._x << ", " << start._y << endl;224 }225if(e & _b)226 {227float scale = (rect._down - start._y) / (end._y - start._y);228 end._x = (end._x - start._x) * scale + start._x;229 end._y = rect._down;230 cout << "end Below Rect. Cutted: " << end._x << ", " << end._y << endl;231 }232 }break;233case1:234 {235//right236if(s & _b)237 {238float scale = (rect._right - end._x) / (start._x - end._x);239 start._x = rect._right;240 start._y = (start._y - end._y) * scale + end._y;241 cout << "start right Rect. Cutted: " << start._x << ", " << start._y << endl;242 }243if(e & _b)244 {245float scale = (rect._right - start._x) / (end._x - start._x);246 end._x = rect._right;247 end._y = (end._y - start._y) * scale + start._y;248 cout << "end right Rect. Cutted: " << end._x << ", " << end._y << endl;250 }break;251case2:252 {253//above254if(s & _b)255 {256float scale = (rect._up - end._y) / (start._y - end._y);257 start._x = (start._x - end._x) * scale + end._x;258 start._y = rect._up;259 cout << "start above Rect. Cutted: " << start._x << ", " << start._y << endl;260 }261if(e & _b)262 {263float scale = (rect._up - start._y) / (end._y - start._y);264 end._x = (end._x - start._x) * scale + start._x;265 end._y = rect._up;266 cout << "end above Rect. Cutted: " << end._x << ", " << end._y << endl;267 }268 }break;269case3:270 {271//left272if(s & _b)273 {274float scale = (rect._left - end._x) / (start._x - end._x);275 start._x = rect._left;276 start._y = (start._y - end._y) * scale + end._y;277 cout << "start left Rect. Cutted: " << start._x << ", " << start._y << endl;278 }279if(e & _b)280 {281float scale = (rect._left - start._x) / (end._x - start._x);282 end._x = rect._left;283 end._y = (end._y - start._y) * scale + start._y;284 cout << "end left Rect. Cutted: " << end._x << ", " << end._y << endl;285 }286 }break;287 }288 }289 s = GenKey(start, rect);290 e = GenKey(end, rect);291292 cout << "At Last, Key of Line: start ";ShowKey(s);cout << " end: ";ShowKey(e); cout << endl;293if((s == e) && (s == 0))294 {295//accept, all point inside the rect296 dest._start = start;297 dest._end = end;298return CR_ACCEPTED;299 }300else301 {302return CR_REFUSED;303 }304 }305306void myInit()307 {308/*309 Output Info310*/311312 g_Rect._up = 100;313 g_Rect._down = 500;314 g_Rect._left = 100;315 g_Rect._right = 700;316 g_Count = 0;317 acc = false;318 cout << "Rect: {" << g_Rect._left << ", " << g_Rect._up << ", " << g_Rect._right << ", "<< g_Rect._down << "}\n"; 319320 glClearColor((float)0x66 / 0x100, (float)0xcc / 0x100, 1.0, 0.0);321 glColor3f(0.0f, 0.0f, 0.0f);//Map Color Black322 glPointSize(1.0);323 glMatrixMode(GL_PROJECTION);324325 glLoadIdentity();326 gluOrtho2D(0.0, (GLdouble)SCREEN_WIDTH, (GLdouble)SCREEN_HEIGHT, 0.0);327 glViewport(0.0, SCREEN_WIDTH, 0.0, SCREEN_HEIGHT);328 }329330void myMouse(int button, int state, int x, int y)331 {332if(button != GLUT_LEFT_BUTTON || state != GLUT_DOWN)334335 cout << "MyMouse Called with " << x << ", " << y << endl; 336switch(g_Count)337 {338case0:339 {340 ++g_Count;341 g_Start._x = x;342 g_Start._y = y;343 src._start = g_Start;344 }break;345case1:346 {347 ++g_Count;348 g_End._x = x;349 g_End._y = y;350 src._end = g_End;351 acc = Cohen_Sutherland(src, dest, g_Rect);352if(acc)353 {354 cout << "Refused.\n";355 }356else357 cout << "Accept.\n";358359 glutPostRedisplay();360 }break;361case2:362 {363 g_Start._x = x;364 g_Start._y = y;365 src._start = g_Start;366 g_Count = 1;367 }break;368 }369 }370371void myDisplay()372 {373 glClear(GL_COLOR_BUFFER_BIT);374375//Draw Rect376377 glColor3f(0.0f, 0.0f, 0.0f);//Rect378 glPointSize(2.0);379 glBegin(GL_LINE_STRIP);380 glVertex2d(g_Rect._left, g_Rect._up);381 glVertex2d(g_Rect._right, g_Rect._up);382 glVertex2d(g_Rect._right, g_Rect._down);383 glVertex2d(g_Rect._left, g_Rect._down);384 glVertex2d(g_Rect._left, g_Rect._up);385 glEnd();386387if(g_Count == 2)388 {389//Draw Line390 glColor3f(1.0f, 0.0f, 0.0f);//Normal Line, Red391 glPointSize(2.0);392 glBegin(GL_LINES);393 glVertex2d(src._start._x, src._start._y);394 glVertex2d(src._end._x, src._end._y);395 cout << "\nDraw Line\n";396if(acc == CR_ACCEPTED)397 {398//Draw Cutted Line399 glColor3f(0.0f, 1.0f, 0.0f);//Normal Line, Green400 glPointSize(2.0);401 glVertex2d(dest._start._x, dest._start._y);402 glVertex2d(dest._end._x, dest._end._y);403 cout << "\nDraw CutLine\n";404 }405 glEnd();406 }407408//glutSwapBuffers();409 glFlush();410//cout << "Render Over\n";411 }412413int main(int argc, char* argv[])414 {415 glutInit(&argc, argv);416//glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);417 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);418 glutInitWindowSize(SCREEN_WIDTH, SCREEN_HEIGHT);419 glutInitWindowPosition(0, 0);420 glutCreateWindow("Cohen Sutherland");421 glutDisplayFunc(myDisplay);422 glutMouseFunc(myMouse);423424 myInit();425 glutMainLoop();426427return0;428 }Cohen_Sutherland_with_GL 程序最上⾯是⼀些数据结构的定义,包括Point2D、Line2D、Rect等。
梁友栋裁剪算法

梁友栋裁剪算法梁友栋裁剪算法是计算机图形学中的一种裁剪算法,主要用于将一个多边形或直线段与一个矩形框进行裁剪。
该算法由梁友栋提出,因此得名。
该算法的基本思想是:将线段或多边形的端点表示为参数方程式,并通过求解参数方程式与裁剪边界的交点来确定裁剪后的线段或多边形。
具体来说,对于一条线段(或多边形的一条边),假设其起点为P1(x1,y1),终点为P2(x2,y2),则可以将其表示为以下参数方程式:x = x1 + t * (x2 - x1)y = y1 + t * (y2 - y1)其中t取值范围为[0,1]。
这个参数方程式描述了从P1到P2之间所有可能的点。
现在需要判断这条线段是否与矩形框相交,如果相交,则需要找到相交部分并输出。
对于矩形框上下左右四条边,可以分别用以下参数方程式表示:左:x = xmin右:x = xmax上:y = ymax下:y = ymin接下来需要求解线段和每条矩形边界的交点。
以左侧矩形边界为例,将其参数方程式代入线段参数方程式中,得到以下两个方程:x1 + t * (x2 - x1) = xminy1 + t * (y2 - y1) = y解这个方程组可以得到t的值,进而可以求出相交点的坐标。
对于其他边界也是类似的求解过程。
求解出所有相交点后,需要判断哪些部分需要被保留。
对于线段而言,如果起点和终点都在矩形框内,则整条线段需要被保留;如果起点和终点都在矩形框外,则整条线段需要被裁剪掉;如果只有一端在矩形框内,则需要根据相交点位置判断哪一部分需要被保留。
对于多边形而言,可以将每条边看作一个线段,然后分别进行裁剪操作。
裁剪后的所有线段再组合成新的多边形。
梁友栋裁剪算法的优势在于其简单易懂、高效快速、适用范围广泛。
它不仅可以用于二维图形的裁剪,还可以扩展到三维图形中去。
此外,在实际应用中,该算法还常常和其他算法结合使用,如多边形填充算法、图像变换算法等。
总之,梁友栋裁剪算法是计算机图形学中一种重要的裁剪算法,具有广泛的应用前景和研究价值。
计算机图形学实验报告实验2裁剪算法实验

一、实验目的:直线段的裁剪:编码裁剪算法,中点分割裁剪算法。
二、实验内容://BasicGraph.cpp//请将下列裁剪程序补充完整,并用注释说明是何种裁剪算法void Encode (int x,int y,int *code,int XL,int XR,int YB,int YT) {//请将此程序补充完整int c=0;if(x<XL) c=c|LEFT;else if(x>XR) c=c|RIGHT;if(y<YB) c=c|BOTTOM;else if(y>YT) c=c|TOP;(*code)=c;}//编码裁剪算法:void C_S_Line(POINT &p1,POINT &p2,int XL,int XR,int YB,int YT) {//请将此程序补充完整int x1,x2,y1,y2,x,y,code1,code2,code;x1=p1.x; x2=p2.x; y1=p1.y; y2=p2.y;Encode(x1,y1,&code1,XL,XR,YB,YT);Encode(x2,y2,&code2,XL,XR,YB,YT);while(code1!=0||code2!=0){if((code1&code2)!=0) return;code=code1;if(code1==0) code=code2;if((LEFT&code)!=0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if((RIGHT&code)!=0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}if((BOTTOM&code)!=0){y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1);}else if((TOP&code)!=0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if(code==code1){x1=x;y1=y;Encode(x,y,&code1,XL,XR,YB,YT);}else{x2=x;y2=y;Encode(x,y,&code2,XL,XR,YB,YT);}}p1.x=x1;p1.y=y1;p2.x=x2;p2.y=y2;}int IsInArea(POINT point,int XL,int XR,int YB,int YT){//请将此程序补充完整if(point.x>=XL && point.x<=XR && point.y>YB && point.y<YT) return 1;else return 0;}int NotIntersect(POINT begin,POINT end,int XL,int XR,int YB,int YT) {//请将此程序补充完整int maxx,maxy,minx,miny;maxx=(begin.x>end.x)?begin.x:end.x;minx=(begin.x<end.x)?begin.x:end.x;maxy=(begin.y>end.y)?begin.y:end.y;miny=(begin.y<end.y)?begin.y:end.y;if(maxx<XL|| minx>XR||maxy<YB||miny>YT) return 1;else return 0;}//中点裁剪算法:POINT ClipMid(POINT begin,POINT end,int XL,int XR,int YB,int YT){//请将此程序补充完整POINT mid,temp;if(IsInArea(begin,XL,XR,YB,YT)) temp=begin;else if(NotIntersect(begin,end,XL,XR,YB,YT)) temp=begin;else{mid.x=(begin.x+end.x)/2;mid.y=(begin.y+end.y)/2;if(abs(mid.x-end.x)<=1&& abs(mid.y-end.y)<=1) temp=mid;else{if(NotIntersect(begin,mid,XL,XR,YB,YT))temp=ClipMid(mid,end,XL,XR,YB,YT);elsetemp=ClipMid(begin,mid,XL,XR,YB,YT);}}return temp;}//Liang-Barsky直线裁剪算法:void ClipParameter(POINT &p1,POINT &p2,int XL,int XR,int YB,int YT) {float u1=0.0,u2=1.0;float dx=p2.x-p1.x,dy=p2.y-p1.y;if(clipTest(-dx,p1.x-XL,&u1,&u2))if(clipTest(dx,XR-p1.x,&u1,&u2))if(clipTest(-dy,p1.y-YB,&u1,&u2))if(clipTest(dy,YT-p1.y,&u1,&u2)){if(u2<1.0){p2.x=p1.x+u2*dx;p2.y=p1.y+u2*dy;}if(u1>0.0){p1.x=p1.x+u1*dx;p1.y=p1.y+u1*dy;}}}int clipTest(float p,float q,float *u1,float *u2){float r;int remainFlag=1;if(p<0.0){r=q/p;if(r>*u2) remainFlag=0;else if(r>*u1) *u1=r;}else if(p>0.0){r=q/p;if(r<*u1) remainFlag=0;else if(r<*u2) *u2=r;}else //*p=0if(q<0.0) remainFlag=0;return remainFlag;}//逐边裁剪算法://typedef struct tRes { int yes,isIn; POINT pout;} Res;Res TestIntersect(int edge,int type,POINT p1,POINT p2){//判断p2是否在所裁剪的窗边edge的内侧,是否与p1点分别在窗边edge的异侧float dx,dy,m;Res res;int isIn=0,yes=0;POINT pout;dy=p2.y-p1.y;dx=p2.x-p1.x;m=dy/dx;switch(type){case 1: /*right*/if(p2.x<=edge){isIn=1;if(p1.x>edge)yes=1;}else if(p1.x<=edge)yes=1;break;case 2: /*bottom*/if(p2.y>=edge){isIn=1;if(p1.y<edge)yes=1;}else if(p1.y>=edge)yes=1;break;case 3: /*left*/if(p2.x>=edge){isIn=1;if(p1.x<edge)yes=1;}else if(p1.x>=edge)yes=1;break;case 4: /*top*/if(p2.y<=edge){isIn=1;if(p1.y>edge)yes=1;}else if(p1.y<=edge)yes=1;default: break;}if(yes){if((type==1) || (type==3)){ pout.x=edge;pout.y=p1.y+m*(pout.x-p1.x);}if((type==2) || (type==4)){ pout.y=edge;pout.x=p1.x+(pout.y-p1.y)/m;}}res.isIn=isIn;res.yes=yes;res.pout=pout;return res;}int clipSingleEdge(int edge,int type,int nin,POINT pin[50],POINT pout[50])/*对多边形pin与窗边edge进行裁剪,返回裁剪后的多边形pout及点数*/ {int i,k=0;POINT p;Res res;p.x=pin[nin-1].x;p.y=pin[nin-1].y;for(i=0;i<nin;i++){res=TestIntersect(edge,type,p,pin[i]);if(res.yes){ pout[k].x=res.pout.x;pout[k].y=res.pout.y;k++;} if(res.isIn){ pout[k].x=pin[i].x;pout[k].y=pin[i].y;k++;}p.x=pin[i].x;p.y=pin[i].y;}return k;}void ClipEdgePolygon(POINT ps[50],int &n,int XL,int XR,int YB,int YT) { /*对多边形ps进行逐边裁剪*/int n1=0,n2=0;POINT pt[50];n1=clipSingleEdge(XR,1,n,ps,pt);n2=clipSingleEdge(YB,2,n1,pt,ps);n1=clipSingleEdge(XL,3,n2,ps,pt);n2=clipSingleEdge(YT,4,n1,pt,ps);n=n2;}//多边形编码裁剪算法:void ClipEncodePolygon(POINT ps[50],int &n,int XL,int XR,int YB,int YT) {POINT tp[50];int k=0,m;int code1,code2,code;int x,y;for(int i=0;i<n-1;i++){Encode(ps[i].x,ps[i].y,&code1,XL,XR,YB,YT);Encode(ps[i+1].x,ps[i+1].y,&code2,XL,XR,YB,YT);code=code1;m=i;for(int j=0;j<2;j++){if((code1 & code2)!=0) //线段两端都在窗口外的同一侧{switch(code){case 1:x=XL;y=ps[m].y;break;case 2:x=XR;y=ps[m].y;break;case 4:x=ps[m].x;y=YB;break;case 5:x=XL;y=YB;break;case 6:x=XR;y=YB;break;case 8:x=ps[m].x;y=YT;break;case 9:x=XL;y=YT;break;case 10:x=XR;y=YT;break;}tp[k].x=x;tp[k].y=y;k++;}else if((code1 & code2)==0) //线段两端不在窗口的同一侧{if(code==0){tp[k]=ps[m];k++;}else if ((LEFT & code) !=0) //线段与左边界相交 {x=XL;y=ps[i].y+(ps[i+1].y-ps[i].y)*(XL-ps[i].x)/(ps[i+1].x-ps[i].x);if(y>YB && y<YT){tp[k].x=x;tp[k].y=y;k++;}}else if((TOP & code)!=0) //线段与上边界相交{y=YT;x=ps[i].x+(ps[i+1].x-ps[i].x)*(YT-ps[i].y)/(ps[i+1].y-ps[i].y);if(x>XL && x<XR){tp[k].x=x;tp[k].y=y;k++;}}else if((RIGHT & code)!=0) //线段与右边界相交 {x=XR;y=ps[i].y+(ps[i+1].y-ps[i].y)*(XR-ps[i].x)/(ps[i+1].x-ps[i].x);if(y>YB && y<YT){tp[k].x=x;tp[k].y=y;k++;}}else if((BOTTOM & code) != 0) //线段与下边界相交 {y=YB;x=ps[i].x+(ps[i+1].x-ps[i].x)*(YB-ps[i].y)/(ps[i+1].y-ps[i].y);if(x>XL && x<XR){tp[k].x=x;tp[k].y=y;k++;}}}code=code2;m++;}//for(j)}//for(i)for(i=0;i<k;i++)ps[i]=tp[i];n=k;}//函数的调用,裁剪窗口的调整//DrawView.cpp文件//裁剪窗口的调整CDrawView::CDrawView(){/************请在此函数中将裁剪窗口大小调整为长度100单位像素,宽度50单位像素的矩形********/// TODO: add construction code here//m_pWidth=1;m_pStyle=PEN_STYLE_SOLID;m_pColor=RGB(0,0,0);m_FFlag=0;m_FColor=RGB(0,0,0);m_HFlag=0;CurrentDraw=DRAW_VCLINE;m_Num=0;m_Drag=0;m_HCursor=AfxGetApp()->LoadStandardCursor(IDC_CROSS);//DrawType=0;ClipFlag=0;ClipType=-1;XL=200;XR=300;YB=150;YT=200;//XL=200;XR=500;YB=150;YT=400;ClipWindowColor=RGB(192,192,50);}void CDrawView::OnDraw(CDC* pDC){CDrawDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereif(ClipFlag){CPen NewPen,*pOldPen;NewPen.CreatePen(PS_DASH,1,ClipWindowColor);pOldPen=pDC->SelectObject(&NewPen);pDC->MoveTo(XL,YB);pDC->LineTo(XR,YB);pDC->LineTo(XR,YT);pDC->LineTo(XL,YT);pDC->LineTo(XL,YB);}int index;index=pDoc->GetShapeNumber();for(int i=0;i<index;i++)pDoc->GetShape(i)->Drawing(pDC);}void CDrawView::OnInitialUpdate(){CSize sizeTotal;sizeTotal.cx = 640; sizeTotal.cy = 480;SetScrollSizes(MM_TEXT, sizeTotal);// TODO: Add your specialized code here and/or call the base class }void CDrawView::OnLButtonDown(UINT nFlags, CPoint point){// TODO: Add your message handler code here and/or call defaultCClientDC dc(this);OnPrepareDC(&dc);dc.DPtoLP(&point);m_pPrev=point;m_pOrigin=point; //点击鼠标左键作为拖动绘图的第一点m_Drag=1;SetCapture();RECT rect;GetClientRect(&rect);ClientToScreen(&rect);ClipCursor(&rect);CScrollView::OnLButtonDown(nFlags, point);}//函数调用处void CDrawView::OnLButtonUp(UINT nFlags, CPoint point){// TODO: Add your message handler code here and/or call defaultif(m_Drag){m_Drag=0;ReleaseCapture();ClipCursor(NULL);CDrawDoc *pDoc=GetDocument();CShape *pShape;POINT p1,p2;if(CurrentDraw==DRAW_VCLINE || CurrentDraw==DRAW_DDALINE ||CurrentDraw==DRAW_MIDLINE || CurrentDraw==DRAW_BSHLINE){if(ClipFlag){switch(ClipType){/****************编码裁剪函数调用处*************/case CLIP_ENCODE:C_S_Line(m_pOrigin,m_pPrev,XL,XR,YB,YT); break; /****************中点分割裁剪函数调用处************/case CLIP_MIDPOINT: ClipMid(m_pPrev,m_pOrigin,XL,XR,YB,YT);p1=ClipMid(m_pPrev,m_pOrigin,XL,XR,YB,YT);p2=ClipMid(m_pOrigin,m_pPrev,XL,XR,YB,YT);m_pOrigin=p1;m_pPrev=p2;break;case CLIP_PARAMETER:ClipParameter(m_pOrigin,m_pPrev,XL,XR,YB,YT);break;}}pShape=newCLine(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,DrawType);pDoc->AddShape(pShape);}if(CurrentDraw==DRAW_RECTANGLE){if(ClipType==CLIP_WINDOW){XL=m_pOrigin.x;XR=m_pPrev.x;YB=m_pOrigin.y;YT=m_pPrev.y;}else{pShape=newCRectangle(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch);pDoc->AddShape(pShape);}}if( CurrentDraw==DRAW_VCCIRCLE || CurrentDraw==DRAW_MIDCIRCLE || CurrentDraw==DRAW_BSHCIRCLE){pShape=newCCircle(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch,DrawType);pDoc->AddShape(pShape);}if(CurrentDraw==DRAW_VCELLIPSE || CurrentDraw==DRAW_MIDELLIPSE) {pShape=newCEllipse(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch,DrawType);pDoc->AddShape(pShape);}pDoc->UpdateAllViews(NULL);}CScrollView::OnLButtonUp(nFlags, point);}三实验结果:四、实验总结通过这次试验使我了解到如何运用计算机程序对窗口进行剪裁,了解到编码剪裁算法直观方便,速度较快,中点分割剪裁算法不用进行乘除运算,剪裁效率高,Liang-Barsky直线裁剪算法更快。
实验报告
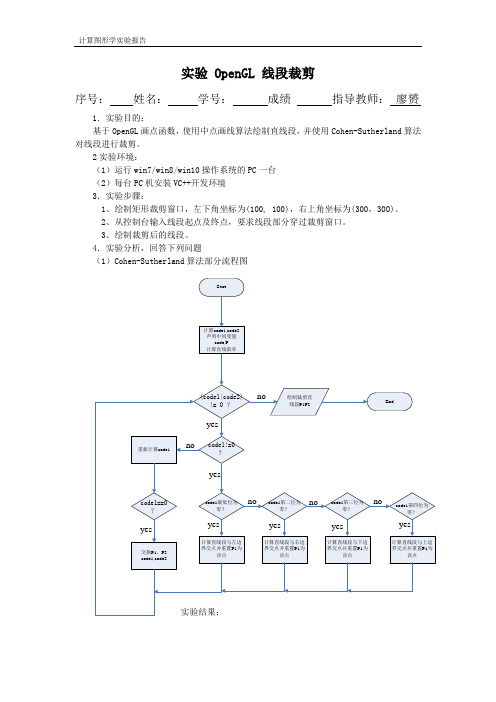
实验 OpenGL 线段裁剪序号:姓名:学号:成绩指导教师:廖赟1.实验目的:基于OpenGL画点函数,使用中点画线算法绘制直线段,并使用Cohen-Sutherland算法对线段进行裁剪。
2实验环境:(1)运行win7/win8/win10操作系统的PC一台(2)每台PC机安装VC++开发环境3.实验步骤:1、绘制矩形裁剪窗口,左下角坐标为(100, 100),右上角坐标为(300,300)。
2、从控制台输入线段起点及终点,要求线段部分穿过裁剪窗口。
3、绘制裁剪后的线段。
4.实验分析,回答下列问题(1)Cohen-Sutherland算法部分流程图(2)Cohen-Sutherland算法代码(包含完整注释)答:void Cohen_Sutherland(){int code1 = EnCode(P1);int code2 = EnCode(P2);int code;ALPoint P;int dx = P2.x - P1.x, dy = P2.y - P1.y;double k = (double)dy/(double)dx; //设置斜率while((code1 | code2) != 0){if(code1!= 0){ //P1在窗口外,计算直线段与窗口边界交点,替换P1 if((code1 & LEFT)== 1){ //c0==1, 计算线段与左边界交点P = P1;P1.x = XWMIN;P1.y = P.y + (P1.x - P.x)*k;}if((code1 & RIGHT)== 2){ //c1==1,计算线段与右边界交点P = P1;P1.x = XWMAX;P1.y = P.y + (P1.x - P.x)*k;}if((code1 & BOTTOM)== 4){ //c2==1,计算线段与下边界交点P = P1;P1.y = YWMIN;P1.x = P.x + (P1.y - P.y)*(1/k);}if((code1 & TOP)== 8){ //c3==1,计算线段与上边界交点P = P1;P1.y = YWMAX;P1.x = P.x + (P1.y - P.y)*(1/k);}}code1 = EnCode(P1);if (code1 == 0){ //code1=0,P1在窗口内,交换P1,P2的坐标值和编码P = P1;P1 = P2;P2 = P;code2 = code1;code1 = EnCode(P1);}}glColor3f(0.0,0.0,1.0); //设置点颜色蓝色lineBres(P1,P2);}(3)简述Cohen-Sutherland算法?答:Cohen-Sutherland算法是一种对线段端点进行编码的线段裁剪算法。
梁友栋-barsky算法

/** clip.cpp* This program clips the line with the given window.*/#include <windows.h>#include <GL/glut.h>#include <math.h>void myinit(void){glShadeModel (GL_FLA T);glClearColor (0.0, 0.0, 0.0, 0.0);}void myReshape(int w, int h){glViewport(0, 0, w, h);glMatrixMode(GL_PROJECTION);glLoadIdentity();if (w <= h)gluOrtho2D (0.0, 1.0, 0.0, 1.0*(GLfloat)h/(GLfloat)w);elsegluOrtho2D (0.0, 1.0*(GLfloat)w/(GLfloat)h, 0.0, 1.0);glMatrixMode(GL_MODELVIEW);}//-------------------------------// your task//-------------------------------int Clip(float p,float q,float *m,float *n){int flag=1;/*flag为标志变量,0表示舍弃,1表示可见*/ float r;if (p<0.0){r=q/p;if (r>*n)flag=0;else if (r>*m){*m=r;/*m取进入点最大参数值*/flag=1;}}else if (p>0.0){r=q/p;if (r<*m)flag=0;else if (r<*n){*n=r;/*n取离开点的最小值*/flag=1;}}else if (q<0 && p==0) //平行于边界,而且在界外的线flag=0;return flag;}void myclip()// line clipping algorithm{float dx,dy,m,n,x1,x2,y2,y3,xmin,xmax,ymin,ymax;m=0.0,n=1.0;glBegin(GL_LINES);glColor4f (0.5, 0.0, 1.0, 0.0);glV ertex2f(0.1f, 0.5f); // line startpointglV ertex2f(0.9f, 0.2f); // line endpointglEnd();x1=0.1,x2=0.9,y2=0.5,y3=0.2;dx=x2-x1;xmin=0.2,xmax=0.8,ymin=0.3,ymax=0.7;if (Clip(-dx,x1-xmin,&m,&n))if(Clip(dx,xmax-x1,&m,&n)){dy=y3-y2;if (Clip(-dy,y2-ymin,&m,&n))if (Clip(dy,ymax-y2,&m,&n)){if (n<1.0){x2=x1+n*dx;//通过n求得裁剪后的p2端点y3=y2+n*dy;}if (m>0.0){x1=x1+m*dx;//通过m求得裁剪后的p1端点y2=y2+m*dy;}glBegin(GL_LINES);glColor4f (0.0, 0.5, 0.0, 1.0);glV ertex2f( x1, y2); // clipped line startpointglV ertex2f( x2, y3); // clipped line endpointglEnd();}}}void display(void){glClear(GL_COLOR_BUFFER_BIT);// The window// ------------------------------------// you can change the window definition on yourself.// ------------------------------------//x1=0.1f,y2=0.5f,x2=0.9f,y3=0.2f;glColor4f (0.0, 1.0, 1.0, 0.75);glBegin(GL_POLYGON);glV ertex2f( 0.2f, 0.3f); // Bottom LeftglV ertex2f( 0.8f, 0.3f); // Bottom LeftglV ertex2f( 0.8f, 0.7f); // Bottom RightglV ertex2f( 0.2f, 0.7f); // Bottom RightglEnd();// ------------------------------------// please define your own line segment and draw// it here with different color and line width// ------------------------------------//-------------------------------//do the clipping in myclip() funtion//-------------------------------myclip();//min=0.2f;//max=0.8f;//min=0.3f;//max=0.7f;// ------------------------------------// please draw clipped line here with another// color and line width// ------------------------------------glFlush();}/* Main Loop* Open window with initial window size, title bar,* RGBA display mode, and handle input events.*/int main(int argc, char** argv){glutInit(&argc, argv);glutInitDisplayMode (GLUT_SINGLE | GLUT_RGBA);//define size and the relative positon of the applicaiton window on the display glutInitWindowSize (500, 500);glutInitWindowPosition (100, 100);//init the defined window with "argv[1]" as topic showed on the top the window glutCreateWindow (argv[0]);// opengl setupmyinit ();//define callbacksglutDisplayFunc(display);glutReshapeFunc(myReshape);//enter the loop for displayglutMainLoop();return 1; }。
计算机图形学实验报告代码

计算机图形学OpenGL实验指导书目录实验一:OpenGL基础知识 (1)实验二OpenGL中的建模与变换 (2)实验三OpenGL中的光照 (6)实验四OpenGL中的拾取 (9)实验五OpenGL中的纹理映射 (12)实验一:OpenGL基础知识一、实验目的1、建立Windows系统下的OpenGL实验框架。
2、学习理解OpenGL工作流程。
二、实验环境⒈硬件:每个学生需配备计算机一台。
⒉软件:Visual C++;三、实验内容1、建立非控制台的Windows程序框架。
2、建立OpenGL框架。
3、建立OpenGL框架的类文件。
4、完善Windows框架。
5、理解程序间的相互关系。
四、实验要求1、学习教材第2章的内容。
2、理解教材中相关实例的代码,按要求添加到适当的地方,调试并通过运行。
3、运行结果应该与教材中的相关实例相符。
4、编译第2章的框架代码,修改背景色、窗口标题。
五、程序设计提示(略)六、报告要求1.认真书写实验报告,字迹清晰,格式规范。
报告中应写清姓名、学号、实验日期、实验题目、实验目的、实验原理。
2.报告中应书写主要源程序,且源程序中要有注释。
3.报告中应包含运行结果及结果分析。
如调试通过并得到预期的效果,请注明…通过‟并粘贴运行效果图;如未调试通过或结果不正确,试分析原因。
4.报告最后包含实验总结和体会。
实验二OpenGL中的建模与变换一、实验目的1.学习配置OpenGL环境。
2.掌握在OpenGL中指定几何模型的方法。
3. 掌握OpenGL中的透视投影和正投影的设置方法,学会诊断投影问题导致的显示异常。
二、实验环境⒈硬件:每个学生需配备计算机一台。
⒉软件:Visual C++;三、实验内容1.建立OpenGL编程环境(注:Windows自带gl和glu,还需要安装glut库文件。
)(a)查看Windows自带的OpenGL文件。
在文件夹c:\windows\system32下查看是否存在文件opengl32.dll和glu32.dll;在Visual Studio的安装目录Vc7\PlatformSDK\Include\gl下查看是否存在gl.h和glu.h;在Vc7\PlatformSDK\Lib下是否存在opengl32.lib和glu32.lib。
实验四4梁友栋

计算机图形学实验报告实验[四]:梁友栋-Barsky直线裁剪算法学生:杨双涛学号: 201206090130班级:网络121班实验时间: 2014.11.27学院:电气与信息工程学院梁友栋-Barsky直线裁剪算法1.实验目的1、深入理解Liang-Barsky裁剪算法的原理;2、学会使用Liang-Barsky裁剪算法实现对直线段以及多边形的裁剪函数;3、比较Liang-Barsky裁剪算法与Cohen-Sutherland裁剪算法的区别,并动手实现两种算法,体会Liang-Barsky裁剪算法的优势;4、掌握Liang-Barsky裁剪算法的裁剪原理,在理解的基础上动手完成实验任务。
2、实验环境Visual C++6.03、实验原理梁友栋与Barsky提出了比Cohen-Sutherland裁剪算法速度更快的直线段裁剪算法。
该算法是以直线的参数方程为基础设计的,把判断直线段与窗口边界求交的二维裁剪问题转化为求解一组不等式,确定直线段参数的一维裁剪问题。
Liang-Barsky裁剪算法把直线段与窗口的相互位置关系划分为两种情况进行讨论:平行于窗口边界的直线段与不平行与窗口边界的直线段。
设起点为P0(x0,y0),终点坐标为P1(x1,y1)的直线段参数方程为:P=P0+t(P1-P0)展开形式为:X=x0+t(x1-x0)Y=y0+t(y1-y0)式中,0 ≤ t ≤ 1。
对于对角点(Wxl,Wyt)、(Wxr,Wyb)的矩形裁剪窗口,直线段裁剪条件如下:Wxl≤x0+t(x1-x0)≤WxrWyt≤y0+t(y1-y0)≤Wyb分解后有:t(x0-x1)≤x0-Wxlt(x1-x0)≤Wxr-x0t(y0-y1)≤y0-Wybt(y1-y0)≤Wyt-y0将△x=x1-x0,△y=y1-y0代入上式得到:t*(-△x)≤x0-Wxlt*△x≤Wxr-x0t*(-△y)≤y0-Wybt*△y≤Wyt-y0令:u1=-△x,v1=x0-Wxlu2=△x,v2=Wxr-x0u3=-△y,v3=y0-Wybu4=△y,v4=Wyt-y0则统一表示为:t*Un≤Vn,n=1,2,3,4N代表直线段裁剪时,窗口的边界顺序,n=1表示左边界;n=2表示右边界;n=3表示下边界;n=4表示上边界。
裁剪II(计算机图形学)

5. AP2的中点为P3,AP3简弃,再处理P3P2, 其中点为P4, 得到与A最近的点P4 6. P1P2的中点为P5, P5P2可简取,处理P1P5 7. P1P5的中点P6,简弃P6P1,得到与B最近的点P6 8. 处理完毕,得到裁剪结果 P4P6
B
中点分割裁剪算法演示例子
12
2009-2010-2:CG:SCUEC
XL
0000 A
0010
YB
0101
0100
XR
0110
2009-2010-2:CG:SCUEC
2
端点(x,y)编码流程
初值flag =0 y>YT Y flag首位为1 N N y<YB Y Flag第二位为1 N N
x>XR Y flag第三位为1
x<XL Y flag第四位为1
返回
2009-2010-2:CG:SCUEC
2009-2010-2:CG:SCUEC
10
中点分割裁剪算法框图
P0可见否? N P0P1显然不可见 N Pm= (P0+P1)/2 Y Y A= P0 exit 原线完全不可见 exit
|Pm – P0|<ε? N
Y A= Pm exit
P0Pm显然不可见?
Y P0 = Pm N P1= Pm
2009-2010-2:CG:SCUEC
3
Sutherland-Cohen裁剪算法-判断
对要被裁剪的线段的两个端点, 如果其所在的区域的编码均是 0000,则这条线段完全可见; 比如线段AB,两端点的编 码都为0000
1001 G 0001 A 1000 B 0000 1010
E
0010 F L 0110 K
计算机图形学实验四 :裁剪
贵州大学实验报告学院:计算机科学与技术专业:计算机科学与技术班级:计科131glColor3f(0.0f, 1.0f, 0.0f);glVertex2f(x1, y1);glEnd();}//矩形的结构体typedef struct Rectangle{float xmin;float xmax;float ymin;float ymax;} Rectan;Rectan rect;int x0, y0, x1, y1;//求出坐标点的Cohen-Sutherland编码int CompCode(int x, int y, Rectan rect) {int code = 0x00;if (y < rect.ymin){code = code | 4;}if (y>rect.ymax){code = code | 8;}if (x>rect.xmax){code = code | 2;}if (x<rect.xmin){code = code | 1;}return code;}//裁剪直线int cohensutherlandlineclip(Rectan rect, int& x0, int& y0, int& x1, int& y1) {int accept = 0, done = 0;float x, y;int code0, code1, codeout;int x00 = x0, y00 = y0, x11 = x1, y11 = y1;code0 = CompCode(x0, y0, rect);code1 = CompCode(x1, y1, rect);//直线全部在矩形框内部,应保留if (!(code0 | code1)){accept = 1;done = 1;}//直线和矩形不相交,并且划直线的两点在矩形同侧(上、下、右。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
glMatrixMode (GL_PROJECTION); gluOrtho2D(-200.0,200.0,-200.0,200.0); } void lineBres(GLfloat x0,GLfloat y0,GLfloat xEnd,GLfloat yEnd){ int dx = fabs(xEnd - x0),dy = fabs(yEnd - y0); int p = 2*dy - dx; int twoDy = 2*dy,twoDyMinusDx = 2*(dy - dx); int x,y; if(x0>xEnd){ x = xEnd; y = yEnd; xEnd = x0; } else{ x = x0; y = y0; } setPixel(x,y);
inline GLint round(const GLfloat a){return GLint(a+0.5);} void setPixel(int x,int y){ glBegin(GL_POINTS); glVertex2i(x,y); glEnd(); }
void init(){ glClearColor(1.0,1.0,1.0,0.0);
if(clipTest(-dy,p1.gety()-winMin.gety(),&u1,&u2)){ if(clipTest(dy,winMax.gety()-p1.gety(),&u1,&u2)){ if(u2<1.0){ p2.setCoords(p1.getx()+u2*dx,p1.gety()+u2*dy); } if(u1>0.0){ p1.setCoords(p1.getx()+u1*dx,p1.gety()+u1*dy); } glColor3f(0.0,0.0,0.0); lineBres(x1,y1,p1.getx(),p1.gety()); lineBres(p2.getx(),p2.gety(),x2,y2); glColor3f(1.0,0.0,0.0); lineBres(p1.getx(),p1.gety(),p2.getx(),p2.gety()); } } else{ glColor3f(0.0,0.0,0.0); lineBres(x1,y1,x2,y2); } } } void displayliangyoudongcaijian(){
class wcPt2D{ public: GLfloat x,yoord,GLfloat
yCoord){x=xCoord;y=yCoord;} GLfloat getx() const{return x;} GLfloat gety() const{return y;} };
glClear(GL_COLOR_BUFFER_BIT); glLineWidth(5.0); glColor3f(0.0,0.0,0.0); glBegin(GL_LINE_LOOP); glVertex2i(100,100); glVertex2i(100,-100); glVertex2i(-100,-100); glVertex2i(-100,100); glEnd(); glPointSize(4); wcPt2D test1[4] =
{{-100.0,-100.0},{100.0,100.0},{-170.0,-200.0},{200.0,-120.0}}; lineClipLiangBarsk(test1[0],test1[1],test1[2],test1[3]); lineClipLiangBarsk(test2[0],test2[1],test2[2],test2[3]);
lineClipLiangBarsk(test3[0],test3[1],test3[2],test3[3]); lineClipLiangBarsk(test4[0],test4[1],test4[2],test4[3]); lineClipLiangBarsk(test5[0],test5[1],test5[2],test5[3]); glFlush(); }
while(x<xEnd){ x++; if(p<0) p+=twoDy; else{ y++; p+=twoDyMinusDx; } setPixel(x,y); } } GLint clipTest(GLfloat p,GLfloat q,GLfloat *u1,GLfloat *u2){ GLfloat r; GLint returnValue = true;
init(); glutDisplayFunc(displayliangyoudongcaijian); glutMainLoop(); }
实
验
结
果
:
p1,wcPt2D p2){ GLfloat u1 = 0.0,u2 = 1.0,dx = p2.getx()-p1.getx(),dy; GLfloat x1 = p1.getx(),y1 = p1.gety(); GLfloat x2 = p2.getx(),y2 = p2.gety(); if(clipTest(-dx,p1.getx()-winMin.getx(),&u1,&u2)) if(clipTest(dx,winMax.getx()-p1.getx(),&u1,&u2)){ dy = p2.gety()-p1.gety();
void main(int argc, char* argv[]){ glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); glutInitWindowPosition(50,100); glutInitWindowSize(400,300); glutCreateWindow("梁友栋裁剪算法");
{{-100.0,-100.0},{100.0,100.0},{-50.0,50.0},{150.0,150.0}}; wcPt2D test4[4] =
{{-100.0,-100.0},{100.0,100.0},{-50.0,0.0},{60.0,50.0}}; wcPt2D test5[4] =
《计算机图形学实验》报告
任课教师:钱文华
2016 年春季学期
实验:梁友栋裁剪
实验时间:2016 年 11 月 17 日 实验地点:信息学院 2204 实验目的:掌握梁友栋裁剪
程序代码:#include <stdio.h> #include <glut.h> #include <stdlib.h> #include <math.h>
if(p<0.0){ r = q/p; if(r>*u2) returnValue = false; else if(r>*u1) *u1 = r;
} else if(p>0.0){ r = q/p; if(r<*u1) returnValue = false; else if(r<*u2) *u2 = r; } else if(q<0.0) returnValue = false; return(returnValue); } void lineClipLiangBarsk(wcPt2D winMin,wcPt2D winMax,wcPt2D
{{-100.0,-100.0},{100.0,100.0},{-150.0,-200.0},{200.0,120.0}}; wcPt2D test2[4] =
{{-100.0,-100.0},{100.0,100.0},{-150.0,-120.0},{0.0,0.0}}; wcPt2D test3[4] =
