7年级奥数第6讲
七年级奥数题(有理数的巧算)

七年级奥数题(有理数的巧算)有理数的巧算1.计算题1.计算(1)2002的值。
答案:B。
12.a为有理数,则a+2000的值不能是什么?答案:C。
03.计算2007{2006[2007(20062007)]}的值。
答案:B。
20094.计算(-1)+(-1)-(-1)×(-1)÷(-1)的结果。
答案:A。
-15.计算(-1)2006+(-1)2007÷(-1)2008的结果。
答案:A。
06.计算-2÷(-2)+(-2)的结果。
答案:D。
07.计算:3.825×(-1.825)+0.25×3.825+3.825×0.的结果。
答案:无8.计算:2002-2001+2000-1999+。
+2-1的结果。
答案:无9.计算:(-1)3÷2.5×(-0.75)×(-1)÷(-1)的结果。
答案:无10.计算:-5×+6×的结果。
答案:无11.练:计算2-2+2-3+2-4+。
+2-29+2-10的结果。
答案:2n(2-1)=2n-112.计算:(1/3)1+(1/3)2+(1/3)3+。
+(1/3)10的结果。
答案:(1-1/3^10)/(1-1/3)=2.13.计算:(1/2)+(2/3)+(3/4)+。
+(98/99)+(99/100)的结果。
答案:无14.求x+1+x-2的最小值及取最小值时x的取值范围。
答案:最小值为-1/2,x的取值范围为[1/2,2]15.练:已知实数a,b,c满足-1c>a,求c-1+a-c-a-b的值。
答案:-2b7年级奥数教案——有理数的巧算1.计算 $(-1)^{1998}+(-1)^{1999}+\cdots+(-1)^{2007}$ 的值为(C)A。
1B。
$-1$C。
0D。
102.若 $m$ 为正整数,那么 $1-\dfrac{(-1)^{m^2-1}}{4}$ 的值为(B)A。
716.奇数和偶数-奥数精讲和测试7年级1116

例1.在1、2、3、⋯、2007中的每个数前面任意添上一个正号或负号,试判断它们的代数和是奇数还是偶数。
例2.1、2、3、⋯98共98个自然数中,能够表示成两整数的和与这两整数的差的积的数的个数有多少个?例3.将图中的圆圈任意涂上红色或蓝色,问有无可能使得在同一条直线上的红圈数都是奇数?说明理由。
例4.在6张纸片的正面分别写上整数1、2、3、4、5、6。
打乱次序后将纸片翻过来,在它们的反面也随意分别写上1~6这六个整数。
然后计算每张纸片正面与反面所写数字之差的绝对值,得出6个数,证明:所得的六个数中至少有两个是相同的。
例5.设1、2、3、…、9的任一排列的a1、a2、…、a9,求证:(a l−1)(a2−2)…(a9−9)是一个偶数。
例6.有n个数x1、x2、…、x n,它们中的每一个数或者为1,或者为−1。
如果x1x2+x2x3+⋯+x n−1x n+x n x1=0,求证:n是4的倍数。
例7.设a、b是正整数,且满足关系式(11111+a)(11111−b)=123456789,求证:a−b是4的倍数。
A卷一、填空题01.三个质数之和为86,三个质数是______________。
02.已知三个整数a、b、c的和为奇数,(a+b+c)(a+b−c)一定是_______数(填奇或偶)。
03.三个不同的质数m、n、p满足m+n=p,mnp的最小值是_________。
04.摆渡船往返于江的两岸,若最初从北岸开始,若干次后又回到北岸,那么船过江的次数是_________(奇数或偶数)。
若从北岸出发过江2003次后停在_______ (南或北)岸。
05.五个连续奇数的和是85,其中最大的数是_______,最小的数是_______。
06.如图1是一张靶纸,靶纸上的1、3、5、7、9表示射中该靶区的分数。
甲说:“我打了六枪,每枪都中靶得分,共得了27分”;乙说:“我打了3枪,每枪都中靶得分,共得了27分。
七年级奥数题训练十篇

七年级奥数题训练十篇1.七年级奥数题训练篇一1、姐妹两人骑车从相距10千米的甲地去乙地,妹妹比姐姐早出发10分钟,结果两人同时到达,姐妹两人骑车速度比是5:4,求姐姐甲地去乙地用了多少时间?2、小张爬山,下山按原路返回,往返共用了1.5小时。
上山时间是下山时间的1.5倍,上山速度比下山速度每分钟慢50米。
小张上下山共行了多少米?3、一辆汽车往返于甲、乙两地。
去时的速度是返回速度的3/4,去时比返回时多用了1小时,已知返回速度是每小时60千米,求甲、乙两地相距多少千米?4、一个快钟每时比标准时间快1分,一个慢钟每时比标准时间慢2分.若将两个钟同时调到标准时间,结果在24时内,快钟显示9点整时,慢钟恰好显示8点整.此时的标准时间是多少?何时将两个钟同时调准的?5、某科学家设计了一只怪钟,这只怪钟每昼夜10时,每小时100分钟.当这只钟显示5点整时,实际上是中午12点整.当这只钟显示3点75分时,实际上是什么时间?实际时间下午5点24分时,这只钟显示什么时间?2.七年级奥数题训练篇二1、学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?2、有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?3、甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米?4、学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?5、一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?3.七年级奥数题训练篇三1.两袋玻璃球,每袋个数相等。
面积问题-奥数精讲与测试7年级
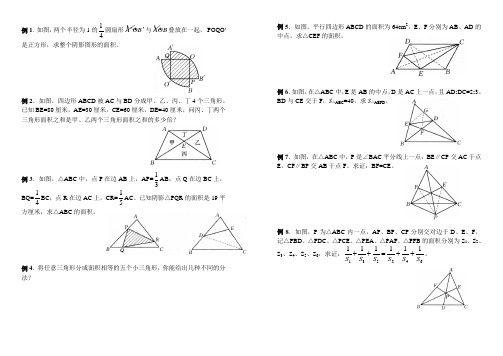
例1.如图,两个半径为1的14圆扇形¼''A OB 与¼AOB叠放在一起,POQO'是正方形,求整个阴影图形的面积。
例2.如图,四边形ABCD被AC与BD分成甲、乙、丙、丁4个三角形。
已知BE=80厘米,AE=30厘米,CE=60厘米,DE=40厘米,问丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?例3.如图,△ABC中,点P在边AB上,AP=13AB;点Q在边BC上,BQ=14BC;点R在边AC上,CR=15AC。
已知阴影△PQR的面积是19平方厘米,求△ABC的面积。
例4.将任意三角形分成面积相等的五个小三角形,你能给出几种不同的分法?例5.如图,平行四边形ABCD的面积为64cm2,E、F分别为AB、AD的中点,求△CEF的面积。
例6.如图,在△ABC中,E是AB的中点,D是AC上一点,且AD:DC=2:3。
BD与CE交于F,S△ABC=40,求S△AEFD。
例7.如图,在△ABC中,P是∠BAC平分线上一点,BE∥CP交AC于点E,CF∥BP交AB于点F。
求证:BF=CE。
例8.如图,P为△ABC内一点,AP、BP、CP分别交对边于D、E、F。
记△PBD、△PDC、△PCE、△PEA、△PAF、△PFB的面积分别为S1、S2、S3、S4、S5、S6,求证:135246111111S S S S S S++=++。
A卷一、填空题01.若长方形的长增加了a%以后,为了使长方形的面积保持不变,则这个长方形的宽应该减少________。
02.已知凸四边形ABC D的面积是a,E、F、G、H分别是AB、BC、CD、DA的中点,且EG,HF交于点O,四边形AEOH与OFCG面积和是________。
03.如图1,一个矩形被分成A、B、C、D四个矩形。
已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,原来矩形的面积是________平方厘米。
小学四年级奥数第6讲 算式迷(二)(含答案分析)

第6讲算式谜(二)一、知识要点解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
二、精讲精练【例题1】在下面的方框中填上合适的数字。
练习1:在□里填上适当的数。
【例题2】在下面方框中填上适合的数字。
练习2:在□内填入适当的数字,使下列除法竖式成立。
【例题3】下面算式中的a、b、c、d这四个字母各代表什么数字?练习3:求下列各题中每个汉字所代表的数字。
1 华罗庚金杯× 3华罗庚金杯 1花红柳绿× 9柳绿花红盼望祖国早日统一×一盼盼盼盼盼盼盼盼盼【例题4】在1、2、3、4、5、6、7、8、9这九个数字中间加上“+、-”两种运算符号,使其结果等于100(数字的顺序不能改变)。
1 2 3 4 5 6 7 8 9 = 100练习4:(1)在下面等号左边的数字之间添上一些加号,使其结果等于99(数字的顺序不能改变)。
9 8 7 6 5 4 3 2 1 = 99(2)一个乘号和七个加号添在下面的算式中合适的地方,使其结果等于100(数字的顺序不能改变)。
1 2 3 4 5 6 7 8 9 = 100(3)添上适当的运算符号和括号,使下列等式成立。
1 2 3 4 5 = 100【例题5】在下面的式子里添上括号,使等式成立。
7×9+12÷3-2 = 23练习5:1.在下面的式子里添上括号,使等式成立。
(1)7×9+12÷3-2 = 75(2)7×9+12÷3-2 = 47(3)88+33-11÷11×2 = 52.在1、2、3、4、5、6、7、8、9这九个数字中间加上“+、-”两种运算符号,使其结果等于100(数字的顺序不能改变)。
最新小学五年级奥数全册讲义(1-30讲)(含详解)【值得拥有】

小学五年级奥数全册讲义第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性(一)第8讲奇偶性(二)第9讲奇偶性(三)第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数(一)第13讲最大公约数与最小公倍数(二)第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题(一)第25讲行程问题(二)第26讲行程问题(三)第27讲逻辑问题(一)第28讲逻辑问题(二)第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
三年级奥数详解答案-第六讲-简单数列的规律

第六讲找简单数列的规律日常生活中,我们经常接触到许多按一定顺序排列的数,如:自然数:1,2,3,4,5,6,7, (1)年份:1990,1991,1992,1993,1994,1995,1996 (2)某年级各班的学生人数(按班级顺序一、二、三、四、五班排列)45,45,44,46,45 (3)像上面的这些例子,按一定次序排列的一列数就叫做数列.数列中的每一个数都叫做这个数列的项,其中第1个数称为这个数列的第1项,第2个数称为第2项,…,第n个数就称为第n项。
如数列(3)中,第1项是45,第2项也是45,第3项是44,第4项是46,第5项45.根据数列中项的个数分类,我们把项数有限的数列(即有有穷多个项的数列)称为有穷数列,把项数无限的数列(即有无穷多个项的数列)称为无穷数列,上面的几个例子中,(2)(3)是有穷数列,(1)是无穷数列。
研究数列的目的是为了发现其中的内在规律性,以作为解决问题的依据,本讲将从简单数列出发,来找出数列的规律.例1观察下面的数列,找出其中的规律,并根据规律,在括号中填上合适的数.①2,5,8,11,(),17,20。
②19,17,15,13,(),9,7。
③1,3,9,27,(),243。
④64,32,16,8,(),2。
⑤1,1,2,3,5,8,(),21,34…⑥1,3,4,7,11,18,(),47…⑦1,3,6,10,(),21,28,36,()。
⑧1,2,6,24,120,(),5040。
⑨1,1,3,7,13,(),31。
⑩1,3,7,15,31,(),127,255。
(11)1,4,9,16,25,(),49,64。
(12)0,3,8,15,24,(),48,63。
(13)1,2,2,4,3,8,4,16,5,().(14)2,1,4,3,6,9,8,27,10,()。
分析与解答①不难发现,从第2项开始,每一项减去它前面一项所得的差都等于3.因此,括号中应填的数是14,即:11+3=14.②同①考虑,可以看出,每相邻两项的差是一定值2。
小学三年级奥数第6讲 植树问题(含答案分析)

第6讲植树问题一、知识要点1、基本概念:总长:植树路线的全长。
棵距:两棵数之间的距离。
段数:总长中共有几个棵距棵数:植树的总棵树2、基本类型以及关系式:(1)路的两端都要植树棵树=线路总长÷棵距+1线路总长=棵距×(棵树-1)棵距=线路总长÷(棵数-1)(2)路的两端都没有植树棵树=线路总长÷棵距-1棵数=段数-1(3)路的一端植树,另一端不植树棵树=线路总长÷棵距棵数=段数另外,生活中还有一些问题,可以用植树问题的方法来解答。
比如锯木头、爬楼梯问题等等,这时解题的关键是要将题目中的条件和问题与植树问题中的“总距离”、“间隔长”、“棵数”对应起来。
二、精讲精练【例题1】小朋友们在路的一边植树,先植一棵树,以后每隔3米植一棵,已经植了9棵,问第一棵和第九棵树相距多少米?练习1:(1)在路的一侧插彩旗,每隔5米插一面,从起点到终点共插了20面,这条道路有多长?(2)在学校的走廊两边,每隔4米放一盆菊花,从起点到终点一共放了20盆,这条走廊长多少米?【例题2】在一条长42米的大路两侧栽树,从起点到终点一共栽了14棵,已知相邻两棵树之间的距离都相等,问相邻两棵树之间的距离是多少米?练习2:在公园一条长30米的路的两侧放椅子,从起点到终点共放了12把椅子,相邻两把椅子的距离相等,相邻两把椅子之间相距多少米?【例题3】把一根钢管锯成小段,一共花了28分钟,已知每锯开一段需要4分钟,这根钢管被锯成了多少段?练习3:一根圆木锯成2米长的小段,一共花了12分钟。
已知每锯下一段要3分钟,这根圆木长多少米?【例题4】甲、乙两人比赛爬楼梯,甲跑到4楼时,乙恰好跑到3楼,照这样计算,甲跑到16楼时,乙跑到了多少楼?练习4:小明和小红两人爬楼梯比赛,小明跑到第4层时,小红跑到第5层,照这样计算,当小明跑到第16层时,小红跑到了第几层?【例题5】一个圆形跑道长300米,沿跑道周围每隔6米插一面红旗,每两面红旗中间插一面黄旗,跑道周围各插了多少面红旗和黄旗?练习5:(1)有一个正方形水池,周长是200米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【学习目标】
1、单项式与多项式的概念考查。
2、理解单项式与多项式的系数与次数,明确它们之间的关系。
3、能够进行整式的运算。
【经典例题】
1.下列说法正确的是( ).
A .a 的系数是0
B .1y
是一次单项式 C .-5x 的系数是5 D .0是单项式
2.下列单项式书写不正确的有( ).
①312a 2b ; ②2x 1y 2; ③-32
x 2; ④-1a 2b . A .1个 B .2个 C .3个 D .4个
3、为了做一个试管架,在长为a (cm )(a>6)的木板上钻3个小孔(如图),每
个小孔的直径为2cm ,则x 等于( ).
A .3366 (4444)
a a a a cm B cm C cm D -+-+cm 4、某班a 名同学参加植树活动,其中男生
b 名(b<a ),若只由男生完成,•每人
需植树15株;若只由女生完成,则每人需植树________棵.
5、某种商品进价m 元/件.在销售旺季,该商品售价较进价高30%;销售旺季过后,又以7折(70%)的价格开展促销活动,这时一件商品的售价是 元。
6、多项式2x 4-3x 5-5是 次 项式,最高次项的系数是 ,四次项的系数是 ,常数项是 .
7、多项式a 3-3ab 2+3a 2b-b 3是 次 项式,它的各项的次数都是 .
8、-254143
a b ab -+是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
【课堂练习】姓名: 成绩:
1、如果一个多项式是五次多项式,那么( )
A .这个多项式最多有六项;
B .这个多项式只能有一项的次数是六;
C .这个多项式一定是五次六项式
D .这个多项式最少有二项,并且最高次项的次数是五.
2、下列说法正确的是( )
A 、222,3;3
x y --的系数是次数是 B 、0,0a 单项式的系数是次数是 C 2
341,1x y x -+-是三次三项式常数项是; D 、2392,22ab --单项式的次数是系数为. 3、下列说法正确的是( ).
A .21不是单项式;
B .a b 是单项式
C .x 的系数是0;
D .3x 2y 2
-是整式. 4、某音像公司对外出租光盘的收费方法是:每张光盘出租后的前2•天每天收费0.8元,以后每天收费0.5元,那么一张光盘在出租后第n 天(n>•2,•且为整数)•应收费_______元.
5.多项式2-3x 2y+2y 2-7x 的项数与次数分别为( )
A.4 ,7
B.4,3
C.3,4
D.3,3
6、父亲年龄比儿子年龄的3倍少5岁,设儿子的年龄为x 岁,则父亲的年龄为 岁。
7、多项式25(2)3m x y m xy x +-+.(1)如果多项式的次数为4次,则m 为多少?(2)如果多项式只有二项,则m 为多少?
8、若关于x 的多项式1)32()12(523--+---x n x m x 不含二次项和一次项,求m ,n 的值。
9.当x=2,y=-2时,求多项式2-3x 2y+2y 2-7x 的值。
10、.已知n 是自然数,多项式1332n y x x ++-是三次三项式,那么n 可以是哪些数?
【课后作业】姓 名 成 绩 家长签名
1.下列说法正确的是( ).
A .整式就是多项式
B .π是单项式
C .x 4+2x 3是七次二项次
D .
315
x -是单项式 2.下列说法错误的是( ).
A .3a+7b 表示3a 与7b 的和
B .7x 2-5表示x 2的7倍与5的差
C .1a -1b 表示a 与b 的倒数差
D .x 2-y 2表示x ,y 两数的平方差
3.m ,n 都是正整数,多项式x m +y n +3m+n 的次数是( ).
A .2m+2n
B .m 或n
C .m+n
D .m ,n 中的较大数
4.随着通讯市场竞争日益激烈,•某通讯公司的手机市话收费标准按原标准每分
钟降低a 元后,再次下调25%,现在的收费标准是每分钟b 元,则原收费标准是每分钟为( )元.
A .(54b -a )
B .(54b+a )
C .(34
b+a ) D .(43b+a ) 5.张老板以每颗a 元的单价买进水蜜桃100颗.现以每颗比单价多两成的价格
卖出70颗后,再以每颗比单价低b 元的价格将剩下的30颗卖出,•求全部水蜜桃共卖多少元?( ).
A .70a+30(a -b )
B .70×(1+20%)×a+30b
C .100×(1+20%)×a-30(a -b )
D .70×(1+20%)×a+30(a -b )
6.按图程序计算,
若开始输入的值为
x=3,则最后输出的
结果是( ).
A.6 B.21 C.156 D.231
7.多项式-m2n2+m3-2n-3是_____次_____项式,最高次项的系数为_______,•常数项是_______.
8.多项式x m+(m+n)x2-3x+5是关于x的三次四项式,且二次项系数是-2,则m=_____,n=_______.
9.a平方的2倍与3的差,用代数式表示为________;当a=-1•时,•此代数式的值为_________.
10.某电影院的第一排有m个座位,后面每排比前一排多2个座位,则第k排的座位数是_______.
11.已知x2-2y=1,那么2x2-4y+3=_______.
13.已知多项式x-3x2y m+1+x3y-3x4-1是五次四项式,单项式3x3n y4-m z与多项式的次数相同,求m,n的值.。
