第四章角度计量和测量技术
20
线角度工作计量器具
线角度工作计量器具包括由光栅等作为圆分度标准的 圆分度仪器和圆分度器具。 线角度的传递方法有比对、排列互比，直接测量等三种 国家基准和副基准之间用比对，同等标准之间用排列互比法检定， 即标准圆分度检验仪可与同等的标准圆分度器具以排列互比法检定； 上级基准、标准对下级标准或工作计量器具的检定具有排列互比和 直接测量两种方法。这两种方法按检定系统框图选用。
17
五等标准为1级角度块，量限范围为100°，测量不确定度为3″， 以及标准测角仪或NJ角装置，量限范围为360°，测量不确定度为5″ 六等标准为2级角度块，量限范围为100°，测量不确定度为10″
属于面角度的工作计量器具有 ：
角度规、J07，J1，J2，J6，J30经纬仪、倾斜仪(允许误差： 5″，10″)、整度或非整度多面棱体(允许误差：5″、10″)、 分度头或分度台(允许误差：2″，10″，30″)、测角仪或测角 装置(允许误差：10″，30″)、测角比较仪等
21
小角度是指量限范围在土1°以内的角度，光栅、感应同步器等器具 小于刻划角栅距的误差，即细分误差(感应同步器常称为“函数误差”)； 各种用于对准并测量微小偏差的自准直仪、各种水平仪都属于小角度 的范畴。
小角度国家基准和副基准为激光小角度测量仪，其量限范围为土l°， 以零为起点分度的总不确定度为0.03″，其置信因子为3，激光小角 度测量仪基准由激光小角度测量仪和与副基准比对用的专用角度块 以及光学角规组成。
密位的写法如下： 6000密位写作60—00； 600密位写作06—00； 60密位写作00—60； 6密位写作00—06； 0.6密位写作00—006； 3254密位写作32—54
11
5.角度单位制的换算
12
13
14
15
二、平面角计量器具国家计量检定系统
国家技术监督局批准JJG 2057—2006：平面角计量器具检定系统； 它规定了平面角单位国家基准由面角度、线角度和小角度等三部分 组成。
线角度的计量标准器具共分为四等， 一等计量标准为标准圆分度检验仪和标准圆分度器具，其量限范围
均为360°，测量不确定度均为0.05″； 二等标准的标准圆分度检验仪和标准圆分度器具的量限范围均为360°， 测量不确定度均为0.2″； 三等标准的标准圆分度检验仪和标准圆分度器具的量限范围均为360°， 测量不确定度均为0.5″；
1g分成100等份，每份记为c，1c又分成100等份，每份记为c，
即一圆周角＝400g=40 000c＝4 000 000cc。
10
4.密位
密位是军用光学仪器的一种角度计量单位。目前世界各国定义密位的方法有
两种，一是将圆周分为6000等分，每一分即为1密位，相当于六十进制的
3ˊ36“；另外一种将圆周分为6400等分，每一分即为1密位，相当于六十进 制的3ˊ22.5“
第四章 角度计量和测量
1
角度计量的奠基
古代中国只有角度测量，不存在角度计量。 古人一般情况下是用子、丑、寅、卯、辰、巳、午、未、申、酉、戌、 亥这十二个地支来表示12个地平方位 ，如图1。 在要求更细致一些的情况下，古人采用的是在十二地支之外又加上了十 干中的甲、乙、丙、丁、庚、辛、壬、癸和八卦中的乾、坤、艮[gèn] 、 巽[xùn]，组成二十四个特定名称，用以表示方位 ，图2。
19
“线角度”是指由刻线或类似刻线组成的角度，光学度盘、光栅编码器 (码盘）、感应同步器是由刻线组成的角度，而磁栅尽管没有可见的 刻线，但是所录的磁信号相当于刻线的作用，因此也属于线角度。 线角度国家基准和副基准是“精密圆分度测量仪”基准和副准，精密 圆分度测量仪基准由精密圆分度测量仪及与副基准比耐用的光栅盘 组成，基准和副基准的量限范围为360°，分度间隔测量不确定度 (消除分度的系统不确定度，置信因子为3)为0.03"。
秒是六十分制的最小单位，小于一秒时，习惯按十进制计算。例如十分之 五秒，写作0.5′。对于不满一度的分度值，也可按十进制计算，例如30′可写 作0.5°。
9
1g
3.百进制
在18世纪末，法国数学家和力学家拉格朗日提出了“百进位制”的系 统，又称新度，百进位制的基本单元是直角，直角因其特殊优点及自 检方便，在任何系统中，都占有重要地位。百分制角度单位是将整圆 分成四个直角，每个直角又分成100等 份，每份记为g，
2.六十进制
六十进制又称秒角度制。将整个圆周分成360等份时，每一等份弧长所对 应的圆心角，叫一“度”，记作1°，再将一度的弧长分为60等份，每一等份 弧 所对应的圆心角称为 l“分”，记作1′。同样1分弧长分成60等份，每一等份 称作1“秒”，记作1″。因此，一圆周所对应的圆心角等于 360°＝21 600′＝129 600″。
8
一、 角度计量单位
1.弧度制
在一个圆内，两条半径间的夹角，在圆周上所截取的弧长恰好等于半径的长 度时，它所对应的角称为一弧度，一弧度过去也称一弪。用弧长作单位来量 角的单位制度，叫弧度制。
在长度测量中对垂直度位置的偏差和水平位置的偏差等通常以线值单位表示 角度偏差，例如，垂直度在100mm偏差为5μm，可用5 μm／100mm 表示。
基准、标准和工作汁量器具之间的传递方法有比对、排列互比、 常角组合、直接测量和多位置测量等五种
18
国家基准和副基准采用相互“比对”的方法，排列互比用于计量基准、 标准之间的检定，可以是高一级对下级标准的传递，也可用于同 级标准之间的检定，
例如：副基准对一等计量标准的传递需采用排列互比．以减小传 递误差；二、三等计量标准中，同等的标准多面棱体和标准测角仪 或测角装置可以采用排列互比法检定；直接测量法、常角组合法、 多位置测量法用于上级计量标准对下级计量标准或工作计量器具的 检定。这五种方法的选用应按“平面角计量器具检定系统框图”的 规定执行。
三等标准包括：标准经纬仪检定装置、标准测角仪或测角装置、 标准整度多面棱体和标准非整度多面陵体，其量限范围为360°
测量不确定度为 0.5
四等标准包括；0级角度块。其量限范围为100°，测量不确定度为1″， 以及标准整度多面棱体、标准非整度多面棱体、标准倾斜仪、标准测 角仪或测角装置、标准经纬仪检定装置等，其量限范围均为360°， 测量不确定度均为2″；
3
在一些工程制作所需的技术规范中，古人则采用规定特定的角 的办法。
例如《考工记·车人之事》中就规定了这样一套特定的角度： 车人之事，半矩谓之宣，一宣有半谓之欘[zhú] ，一欘有半谓之 柯，一柯有半谓之磬折。 矩是直角，因此这套角度如果用现行360°分度体系表示，则 一矩 ＝ 90° 一宣 ＝ 90°× 1／2 ＝ 45° 一欘 ＝ 45°＋ 45°× 1／2 ＝ 67°30′ 一柯 ＝ 67°30′＋ 67°30′×1／2＝ 101°15′ 一磬折 ＝ 101°15′＋ 101°15′× 1／2 ＝ 151°52′30″
16
面角度计量标准器具共分为六等
一等标准为标准测角仪或测角装置，以及标准整度或非整度多面棱体。 其量限范围为360°。分度间隔测量不确定度(消除分度的系统不确定 度，置信因子为3，以下同）为 0.05 二等标准包括：标准非整度多面棱体，标准整度多面棱体， 标准测角仪或测角装置，量限范围为360°，测量不确定度为0.2″
22
角度的实物基准
1、角度块规：
形状：三角形（1个角度） 长方形（4个角度）
材料：与量块相同（稳定、耐磨） 基准：工作面的夹角 应用：测量零件角度，相对测量基准
精度：0级±3"，1级±10"，2级±30"，
超出这套体系之外的角度，古人也不得不另做规定
4
在古代中国，与现行360°分度体系最为接近的是古人在进行天文 观测时，所采用的分天体圆周为365 1/4度的分度体系。这种分度体系 的产生，是由于古人在进行天文观测时发现，太阳每365 1/4日在恒星 背景上绕天球一周，这启发他们想到，若分天周为365 1/4度，则太阳 每天在天球背景上运行一度，据此可以很方便地确定一年四季太阳的 空间方位。古人把这种分度方法应用到天文仪器上，运用比例对应测 量思想测定天体的空间方位，从而为我们留下了大量定量化了的天文 观测资料。
图1 十二支方位表示法
图2 二十四支方位表示法
2
不管是十二地支方位表示法，还是二十四支方位表示法，它 们的每一个特定名称表示的都是一个特定的区域，区域之内没有 进一步的细分。所以，用这种方法表示的角度是不连续的。更重 要的是，它们都是只具有特定用途的角度体系，只能用于表示地 平方位，不能任意用到其他需要进行角度测量的场合。因此，由 这种体系不能发展出角度计量来。
我们在讨论古人的天文观测结果时，尽管可以直接把他们的记录视 同角度，但由这种分度体系本身，却是不可能演变出角度计量来的。
5
传教士带来的角度概念，打破了这种局面，为角度计量在中国的 诞产生奠定了基础。这其中，利玛窦（Matthieu Ricci，1552－1610） 发挥了很大作用。
利玛窦为了能够顺利地在华进行传教活动，采取了一套以科技开路 的办法，通过向中国知识分子展示自己所掌握的科技知识，博取中国人 的好感。他在展示这些知识的同时，还和一些中国士大夫合作翻译了一 批科学书籍，传播了令当时的中国人耳目一新的西方古典科学。在这些 书籍中，最为重要的是他和徐光启合作翻译的《几何原本》一书。《几 何原本》是西方数学经典，其作者是古希腊著名数学家欧几里德。该书 是公认的公理化著作的代表，它从一些必要的定义、公设、公理出发， 以演绎推理的方法，把已有的古希腊几何知识组合成了一个严密的数学 体系。《几何原本》所运用的证明方法，一直到17世纪末，都被人们奉 为科学证明的典范。利玛窦来华时，将这样一部科学名著携带到了中国， 并由他口述，徐光启笔译，将该书的前六卷介绍给了中国的知识界。 。就计量史而言，《几何原本》对中国角度计量的建立起到了奠基的作 用。它给出了角的一般定义，描述了角的分类及各种情况、角的表示方 法，以及如何对角与角进行比较。这对于角度概念的建立是非常重要的。 因为如果没有普适的角度概念，角度计量就无从谈起。
角度测量技术的基本原理和应用
角度测量技术的基本原理和应用角度测量技术是应用于工程、导航、地理测量等领域的一种重要的测量方法。
它通过测量物体或地点之间的角度来确定其位置关系，从而帮助我们更好地理解和掌握所研究领域的特性和性质。
本文将介绍角度测量技术的基本原理和一些常见的应用。
一、基本原理角度测量技术的基本原理依赖于测量物体或地点之间的角度差异。
在测量过程中，通常使用角度计量仪器（如经纬仪、陀螺仪）来测量目标物体或地点相对于参考方向的角度。
角度计量仪器的精度和测量范围是影响角度测量精度和可行性的关键因素。
例如，经纬仪常用于测量地理位置，利用水平仪和径向刻度来测量目标位置相对于地球表面和参考方向之间的角度。
而陀螺仪则是一种精密的角度计量仪器，主要用于导航和航空领域，利用陀螺仪的旋转和惯性原理来测量目标物体或地点的角度。
在角度测量中，还常常使用三角法来计算和测量角度。
三角法是一种基于三角关系的几何学方法，用于测量和计算未知角度。
通过测量已知角度和物体间的边长关系，三角法可以推导出目标角度的大小。
二、应用领域1. 工程测量角度测量技术在工程测量中有着广泛的应用。
例如，在建筑工程中，我们需要测量建筑物之间的夹角以确保建筑物的位置和方向准确无误。
另外，在制造业中，角度测量常用于测量零件和工件之间的相对位置和角度，以确保生产过程的正确性和质量。
2. 导航定位角度测量技术对于导航和定位具有重要意义。
航海、航空和航天等领域都依赖于角度测量来确定目标物体的位置和方向。
例如，罗盘是一种常用的导航仪器，利用地球的磁场来测量船只和飞行器的方向。
另外，一些现代导航系统如全球定位系统（GPS），则利用卫星信号和三角测量原理来测量目标物体的位置和方向。
3. 地理测量角度测量技术在地理测量中也有着重要的应用。
地理测量主要研究地球表面的形状、地理位置和地形特征。
通过测量目标物体或地点之间的角度，地理学家可以绘制地图、测量地形和研究地球的变化。
例如，地球测量学使用角度测量技术来测量地球的大小、形状和旋转轴的倾斜度。
测量学课件角度测量
视线水平、指标铅垂时，竖盘读数为常数：
盘左时一般 L0=90 ，盘右时一般 R0=270 。
（2）竖直角的观测与计算
盘左 270
盘右 90
180
0
0
180
90
270
• 竖直角观测
仪器对中整平后，盘左位置，十字丝横丝精确切准目标顶部。
转动竖盘水准管微动螺旋，使竖盘水准管气泡居中。
读取盘左读数 L，得上半测回竖角：L 90 L
741924 741915
741906
第2方向
K
B 测站
起始方向第一个读数应调成0或180/N(N为测回数)；
分、秒数写足二位； 一测回过程中，不得再调整水准管气泡或改变度盘
位置。
三、水平角测量
1.测回法
(1)上半测回(盘左又称正镜) 左 b1 a1
(2)下半测回(盘右又称倒镜)右 b2 a2
C
A
对中、整平、瞄准、 读数
1.对中——将仪器中心安置在过测
站点的铅垂线上。对中
误差3mm。
B
垂球对中步骤：
粗略对中：移动三脚架，使垂球尖离测
站中心12cm内；
精确对中：稍微松开中心螺丝，在脚架
头上移动(不能旋转)仪器，使垂球尖精
确对中测站标志中心，旋紧中心螺丝。
光学对中步骤：对准、调平、整平、对中
(3)照准部
ＤJ6光学经纬仪 ＤJ6光学经纬仪外观图
3.2.1 DJ6光学经纬 仪 1.DJ6光学经纬
仪外观图
2. 主要轴线和几何条件
• 主要轴线 (1)望远镜视准轴CC (2)仪器横轴HH (3)照准部水准管轴LL (4)仪器竖轴VV • 几何条件 (1)LL垂直于VV (2)VV垂直于HH (3)HH垂直于CC (4)十字丝竖丝垂直于HH
角度测量原理及方法ppt课件
4、记录与计算
水平角的观测和记录
观测方向 盘左读数 盘右读数
半测回 方向值
一测回 方向值
方向中数
第一测回
33
36
马头山
0 00 00 0 02 36 180 02 36
0 00 00 0 00 00
垂直指标读数与垂直角关系：
α＝90－δ
a
水平面
P
P´
铅垂面
p
§4.2 光学经纬仪
一、J6级光学经纬仪
1、基本结构
（1）脚架
（2）基座 竖 轴
（3）照准部
横 轴 三轴
照准轴 水平度盘
垂直度盘
水准器
照 垂直度盘
准 轴 支 架 水平度盘
竖 轴
读数显微镜
横轴
照
支
准
架
部
基 座
三 脚 架
J6 经纬仪
垂直度盘
时间：下周三下午 下周五上午
J6光学经纬仪
经纬仪三轴
横轴
望远镜赖以俯仰的轴 与水平度盘平行 通过垂直度盘中心并与其正交
竖轴
照准部赖以水平旋转的轴 测角时与地面标志点在同一铅 垂线上
照准轴 望远镜物镜中心与十字丝交 点的连线，照准方向线
三轴关系 横轴与竖轴正交 照准轴与横轴正交
J6经纬仪度盘
例：
水平角读数
213°01′24″
垂直角读数
95°55′30 ″
V
§4.2光学经纬仪
4、J6经纬仪的安平装置 （1）水准器 有管水准器和圆水准器两种。
管水准器：
H
《角度 测量》课件
常用工具
量角器
量角器是一种常用的工具，用 于测量角度的大小。
直角器
直角器用于测量和绘制直角， 是建筑设计中的常用工具。
三角板
三角板可以在测量角度和长度 时提供更准确的结果。
角度测量的步骤
确定测量角度的位置
在测量之前，需要确定要测量的角度所在的位置。
选择合适的工具
根据角度的大小和要求，选择合适的工具进行测量。
通过选择合适的工具和 遵循正确的测量步骤， 可以获得准确的角度测 量结果。
3 角度测量的应用场
景
角度测量广泛应用于地 图绘制、建筑设计和工 程项目中。
放置测量工具
将选定的工具放置在角度上，并将其与其他参考线对齐。
读取测量结果
使用工具上的刻度或标记，读取测量结果并记录。
角度测量的误差
坐标系的误差
不正确对齐坐标系可能导致角度误差。
物体形状的误差
不规则的物体形状可能导致角度测量的不准确。
测量工具本身的误差
精度不高或磨损的测量工具可能产生误差。
角度测量的应用
《角度 测量》PPT课件
角度测量是一种重要的技能，它在许多领域中起着关键作用。通过本课件， 我们将详细了解角度的定义、测量方法以及常用工具。
什么是角度测量
1 角度定义
角度是两条射线之间的夹角，用于衡量方向和位置的变化。
2 角度单位
角度可以度数、弧度或百分比表示。
3 角度测量的方法
常用的测量方法包括使用量角器、直角器和三角板等工具。
地图绘制
角度测量在地图设计和导航 中起着重要作用，帮助确定 方向和位置。
架桥
在架桥工程中，准确的角度 测量是确保结构稳定性和安 全性的关键。
培训教材-角度计量
第一章角度单位与国家检定系统角度是一种重要的物理量。
角度计量是几何量计量的重要组成局部。
角度量的范围广，平面角按平面所在的空间位置可分为：在水平面内的水平角(或称方位角)，在垂直面内的垂直角(或倾歪角)，空间角是水平角和垂直角的合成；按量程可分为圆周分度角和小角度；按标称值可分为定角和任意角；按组成单元可分为线角度和面角度；按形成方式可分为固定角和动态角，固定角是指加工或装配成的零组件角度，仪器转动后恢复至静态时的角位置等，动态角是指物体或系统在运动过程中的角度，如卫星轨道对地球赤道面的夹角，周密设备主轴转动时的轴线角漂移，测角设备在一定角速度和角加速度运动时，输出的实时角度信号等。
对一些特定角，往往给予专门名称，如基面、轴线或准线相互间夹角为0°或180°时称为平行度，90°或270°时称为垂直度；角度量在应用时还往往引进特定的参考基准，所指的角度是对参考基准的夹角，如：水平度是以大地水平面或铅垂线为参考的倾歪角；天文方位角是以天文北为参考的水平角；经、纬度是以通过格林尼治天文台的子午线和赤道面为参考的水平角和垂直角。
第一节角度单位人类的生产、生活、战争等活动都离不开计量单位。
国际单位制了七个全然单位和两个辅助单位，这两个辅助单位确实是根基“平面角〞和“立体角〞。
平面角是在平面内的夹角，其单位是“弧度〞(rad)，“弧度〞是一圆内两条半径之间的平面角，这两条半径在圆周上截取的弧长与半径相等，它所对应的角称为一弧度，一圆周所对应的圆心角等于2π弧度，π＝3．1415926…。
立体角的单位为“球面度〞(sr)，“球面度〞是顶点位于球心的一立体角，它在球面上所截取的面积等于以球半径为边长的正方形面积。
弧度和球面度都纯属几何单位，其定义根基上无量纲的量，但应用时，能够作为无量纲的数，也能够作为有独立量纲的量，作为有独立量纲的量时，能够作为全然单位，如角速度单位为弧度每秒(rad/s)，角加速度单位为弧度每二次方秒(rad/s2)等，弧度是全然单位；当作为无量纲的数时，可作为导出单位，如：电动机的机械功率(牛顿米每秒(N·m/s)等于转矩牛顿米(N·m)和转速弧度每秒(rad/s)之积，转速的弧度在运算中自动消逝，否那么等号两边就不平衡，这确实是根基辅助单位的两重性。
(光学测量技术)第4章光学零件的测量
第4章 光学零件的测量 (1)光圈不圆，呈椭圆形。此时用椭圆的长轴和短轴方 向上干涉条纹之差(或在互相垂直的方向上干涉条纹的最大 代数差值)Δ 1 N 来表示，并称为像散偏差。
其中， N x 、 N y 分别为椭圆长、短轴方向的光圈数，它们 都为代数量。 (2 )光圈局部变形。变形量用光圈数表示为 Δ 2 N ，称 为局部偏差。 一般情况下，半径偏差和面形偏差总是同时存在，因此， 有的光圈在样板孔径之内可能看不到其全部，而只能看到其 一分。在 GB2831-81 中，将上述偏差都称为面形偏差。
第4章 光学零件的测量 检验面形偏差时，应使由标准面上反射得到的标准波面 与被测面上反射得到的测试波面两者球心重合，或稍有横向 偏离，并观测其干涉图，当上述两波面之间没有差别时，干 涉图为均匀一片或很少的几条平行直条纹，并且不管条纹方 向如何(它对应两波面球心沿不同方向横向偏离)都为直线， 间距也相等。如果存在面形偏差，则条纹呈现椭圆形或发生 局部弯曲(分别对应 Δ1 N 和 Δ 2 N )，这时可按前述光圈识别 方法判读。
第4章 光学零件的测量 下面先讨论面形偏差的表示方法和光圈的识别方法。 1 )球面零件面形偏差的表示方法 半径偏差:即使零件的表面是标准球面，它还可能与样 板有不同的曲率半径，此时产生规则的牛顿环(光圈)，这种 半径偏差就可以用有效孔径内的光圈数 N 表示。为表示偏 差的性质，光圈数 N 用代数量表示。高光圈 N 取正值;反之， N 取负值。样板的孔径一般要大于被测零件的孔径。 面形偏差:指被检面对球面的偏离。这种偏差一般可分 为两种情况。
第4章 光学零件的测量 测量曲率半径时，只需移动被测件，使被测面的球面的 顶点及球心分别瞄准标准球面球心，并测出被测件移动的距 离，即可得到被测球面的曲率半径。被测件移动的距离可由 精密测长机构(如光学测长、计量光栅测长或激光测长)测出。 在这里，瞄准是通过干涉的方法进行的，即以瞄准时干涉场 上干涉图的特征作为判别准则来进行瞄准，由第 2 章干涉仪 的介绍可知，这个位置的干涉条纹最疏，甚至看不到条纹 (干涉场上具有均匀的亮度)。
测量学四. 角度测量和经纬仪
四. 角度测量和经纬仪思考题1.什么是水平角？试绘图说明用经纬仪测量水平角的原理。
2.什么是竖直角？为什么测竖直角时可只瞄准一个目标？3.经纬仪测角时，若照准同一竖直面内不同高度的两目标点，其水平度盘读数是否相同？若经纬仪架设高度不同，照准同一目标点，则该点的竖直角是否相同？4.何谓视差？产生视差的原因是什么？观测时如何消除视差？5.简述电子经纬仪的主要特点。
它与光学经纬仪的根本区别是什么？6.简述编码度盘测角系统的测角原理。
7.简述光栅度盘测角系统的测角原理。
8.安置经纬仪时，对中和整平的目的是什么?若用光学对中器应如何进行？9.试述用方向观测法观测水平角的步骤。
如何进行记录、计算？有哪些限差规定？10.水平角方向观测法中的2c有何含义？为什么要计算2c并检核其互差？11.何谓竖盘指标差？如何计算和检验竖盘指标差？12.试述水平角观测中的照准误差与目标偏心误差有什么区别。
13.根据水平角观测的原理，试说明经纬仪轴系之间的关系应有哪些基本要求部分习题答案15.16. 8.3″;18. 3.4″;19. 3′26.3″22. x c=+15.1″;23. x i=-1.06″;24. –10.7″25. A. 12″; B. 12.2″; C. 13.9″26. A. 24″; B. 24.4″; C. 27.8″27. C=-8″; i=-9.7″28. 2.6″29. (1)υ=40″, (2)τ=20″, (3) c=0, (4) i=10″31. ±8.0″32. ±9.8″33. ±6.1″34. ±8.5″,±8.5″。
角度测量—认识角度测量原理(工程测量)
角度测量原理
角度测量原理
➢ 角度测量是确定地面点位的基本测量工作之一，分为水平角测量和竖
直角测量。
➢ 水平角测量用于测定点的平面位置。
➢ 竖直角测量用于测定高程或将倾斜距离转化为水平距离。
角度测量原理
➢ 水平角测量原理
铅
垂
线
地面上一点到两目标方向线在水平
面上的垂直投影所构成的夹角称为
′
水平角，通常以 表示。
水平角变化范围为 ° ~°
水平投影面
′
铅
垂
线
角度测量原理
➢ 水平角测量原理
在点的铅垂线方向上安置一水平
度盘，其中心′ 在通过点的铅垂
线上，设、方向线在水平度
盘上的投影读数为和。
则水平角为两读数之差，即：
=−
（当 > 时） 或
= − + ° （当 < 时）
铅
垂
线
线
铅
垂
线
角度测量原理
➢ 竖直角测量原理
在同一铅垂面内，观测方向线与水
（+）
平线之间的夹角称为竖直角（又称
垂直角或高度角），通常以 表示。
（-）
水平线
竖直角变化范围为 ° ~±° 。
视线在水平线之上称为仰角，角值
为正；反之称为俯角，角值为负。
角度测量原理
➢ 竖直角测量原理
在视线与水平线相交处的铅垂面内
设置一度盘，则竖直角可通过水
平视线读数与目标视线读数之差求
得。
竖
直
度
盘
水平线
铅
垂
线
水准、角度、测距测量的原理、公式、图解都给你汇总好了
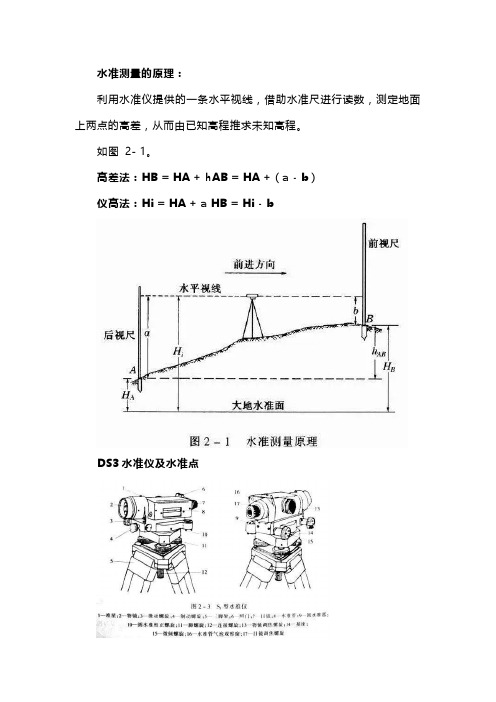
水准测量的原理：利用水准仪提供的一条水平视线，借助水准尺进行读数，测定地面上两点的高差，从而由已知高程推求未知高程。
如图2- 1。
高差法：HB = HA + hAB = HA + ( a - b )仪高法：Hi = HA + a HB = Hi - bDS3水准仪及水准点水平角测量原理（一）定义：水平角就是地面上某点到两目标的方向线铅垂投影到水平面上所成的角度，其取值范围为0 ~ 360。
（二）测角原理：如图3-1测回法测回法是测水平角的基本方法，用于两个目标方向之间的水平角的观测。
如图，设O为测站点，A、B为观测目标，用测回法观测OA与OB两方向之间的水平角β。
竖直角测量原理：（一）定义地面某点至目标的方向线与水平面之间的夹角，取值范围为–90~90。
仰角为正，俯角为负。
（二）测角原理：如图距离：两标志点之间的水平直线长度。
直线定线：把多根标杆标定在已知直线的工作。
方法有目估定线和经纬仪定线。
钢尺量距：精密钢尺量距时必须对所量距离施加尺长改正、温度改正，倾斜，即用钢尺的实际长度。
其实际长度用尺长方程式表示，它的一般形式为：l t = l + Δl + a ×l（t - t0 ）视距测量：利用望远镜的视距丝装置，根据几何光学原理同时测定距离和高差的方法。
视线水平时：距离：D = k·l 高差：h = i –v斜距情况下：距离：D = kl cos2α高差：h = ( 1 / 2 ) kl sin2α+ i –v式中：l为上下丝读数之差；α为竖直角；i为仪器高；v为目标高（中丝读数）；k = 100光电测距：原理：通过测定光波在两点间传播的时间计算距离的方法。
公式：D′= ( 1 / 2 )* c* t式中：c为空气中的光速；t为光波在两点间往返的时间。
第四章角度计量和测量技术
传教士带来的角度概念，打破了这种局面， 传教士带来的角度概念，打破了这种局面，为角度计量在中国的 诞产生奠定了基础。这其中，利玛窦（ 诞产生奠定了基础。这其中，利玛窦（Matthieu Ricci，1552－1610） ， － ） 发挥了很大作用。 发挥了很大作用。 利玛窦为了能够顺利地在华进行传教活动， 利玛窦为了能够顺利地在华进行传教活动，采取了一套以科技开路 的办法，通过向中国知识分子展示自己所掌握的科技知识， 的办法，通过向中国知识分子展示自己所掌握的科技知识，博取中国人 的好感。他在展示这些知识的同时， 的好感。他在展示这些知识的同时，还和一些中国士大夫合作翻译了一 批科学书籍，传播了令当时的中国人耳目一新的西方古典科学。 批科学书籍，传播了令当时的中国人耳目一新的西方古典科学。在这些 书籍中，最为重要的是他和徐光启合作翻译的《几何原本》一书。 书籍中，最为重要的是他和徐光启合作翻译的《几何原本》一书。《几 何原本》是西方数学经典，其作者是古希腊著名数学家欧几里德。 何原本》是西方数学经典，其作者是古希腊著名数学家欧几里德。该书 是公认的公理化著作的代表，它从一些必要的定义、公设、公理出发， 是公认的公理化著作的代表，它从一些必要的定义、公设、公理出发， 以演绎推理的方法， 以演绎推理的方法，把已有的古希腊几何知识组合成了一个严密的数学 体系。 几何原本》所运用的证明方法，一直到17世纪末 世纪末， 体系。《几何原本》所运用的证明方法，一直到 世纪末，都被人们奉 为科学证明的典范。利玛窦来华时，将这样一部科学名著携带到了中国， 为科学证明的典范。利玛窦来华时，将这样一部科学名著携带到了中国， 并由他口述，徐光启笔译，将该书的前六卷介绍给了中国的知识界。 并由他口述，徐光启笔译，将该书的前六卷介绍给了中国的知识界。 就计量史而言， 几何原本》 。就计量史而言，《几何原本》对中国角度计量的建立起到了奠基的作 它给出了角的一般定义，描述了角的分类及各种情况、 用。它给出了角的一般定义，描述了角的分类及各种情况、角的表示方 以及如何对角与角进行比较。这对于角度概念的建立是非常重要的。 法，以及如何对角与角进行比较。这对于角度概念的建立是非常重要的。 因为如果没有普适的角度概念，角度计量就无从谈起。 因为如果没有普适的角度概念，角度计量就无从谈起。