福建省晋江市养正中学2013届高三5月月考数学(文)试题

合集下载

福建省安溪一中、养正中学2013届高三上学期期中联考数学(文)试题

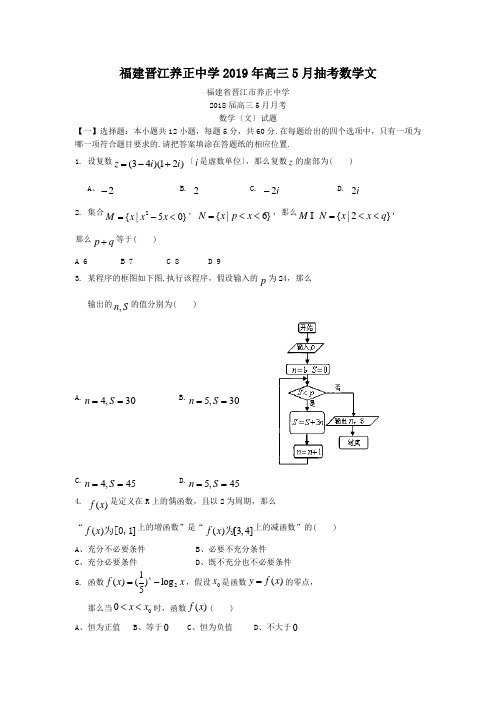
侧视图正视图一、选择题（共12小题，每小题5分，共60分，四个选项中，只有一项是符合题目要求的） 1．已知全集U=N ，{}2|7100,U A x N x x C A =∈-+≥=则（） A ．{}2,3,4,5B ．{}3,4,5C ．{}2,3,4D ．{}3,42．命题“R x ∈∃0，使20log 0x ≤成立”的否定为（）A ．R x ∈∃0，使20log 0x >成立B ．R x ∈∃0，使20log 0x ≥成立C ．R x ∈∀0，均有20log 0x ≥成立D ．R x ∈∀0，均有20log 0x >成立 3．设()f x ，()g x 是定义在R 上的函数，()()()h x f x g x =+，则“()f x ，()g x 均为偶函数”是“()h x 为偶函数”的（）A ．充分而不必要的条件B ．必要而不充分的条件C ．充分必要条件D ．既不充分也不必要的条件4．已知m 、n 是两条不同的直线，α、β是两个不同的平面，则下面命题中正确的是（）A m n m ,,αα⊂⊂∥β，n ∥βα⇒∥βB α∥β，βα⊂⊂n m ,m ⇒∥nC m n l m l n αα⊂⊂⊥⊥⇒，，，α⊥lD m ∥n ，⊥n αm ⇒α⊥ 5．如果实数x 、y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩，那么2x y -的最大值为（）A ．2B ． 1C ．2-D ．3-6．在各项均为正数的等比数列{}n a中，351,1,a a ==+则2326372a a a a a ++=（） A ．4 B ．6C ．8 D．8-8．平面上有一个△ABC 和一点O ，设OA a = ，OB b = ,OC c =，又OA 、BC 的中点分别为D 、E ，则向量DE等于（）A. ()12a b c ++B. ()12a b c -++C. ()12a b c -+D. ()12a b c +-9．如图，为了得到这个函数的图象，只要将sin ()y x x R =∈的图象上所有的点（） A ．向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变B ．向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 C ．向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变D ．向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变10．在ABC ∆中，5=a ，7=c ，︒=120C , 则三角形的面积为（）A.215 B.415 C.4315 D.231512．在实数集R 中，我们定义的大小关系“>”为全体实数排了一个“序”，类似地，我们在复数集C 上也可以定义一个称为“序”的关系，记为“ ”。

福建省晋江市养正中学高三5月月考语文试题.pdf

（一）默写常见的名句名篇(6分) 1．补写出下列名句名篇中空缺的部分。

(6分) （1）进不入以离尤兮，。

（屈原《离骚》）（2），钟鸣鼎食之家。

（王勃《滕王阁序》））（3）元嘉草草，封狼居胥，。

（辛弃疾《京口北固亭怀古》）（4），衣冠简朴古风存。

（陆游《游山西村》）（5）猥以微贱，当侍东宫，李密陈情表 6．阅读下面这首诗歌，回答问题。

（6分）荻港早行〔元〕许有壬水国宜秋晚，羁愁感岁华。

清霜醉枫叶，淡月隐芦花。

涨落高低路，川平远近沙。

炊烟青不断，山崦有人家。

（1）诗歌描写了一幅什么样的景色，抒发什么样的情感？（2分）答：（2）这首诗颔联的“醉”字和“隐”字有何好处？请结合诗句简要分析。

（4分）答：二、文学名著、文化经典阅读(16分) （一）文学名著阅读(10分) 7.下列各项中，对作品故事情节的叙述不正确的两项是（）（）(5分) A.晚饭过后，拿侬到葛朗台先生的房里去拿一瓶果子酒，下楼时几乎摔一跤。

葛朗台看到拿侬面色刷白，就让拿侬喝一小杯果子酒压压惊，然后他到烤面包的小间里去找木板、钉子和木工工具，亲自修补虫蚀的楼梯。

（《欧也妮·葛朗台》） B.高老太爷的病给高家带来了很大的骚动，在药没有多大效力的情况下，高家全家人开始去求神的帮助，先后请来了道士、巫师来捉鬼，虔诚地企盼高老太爷康复。

但是这个做法并没能留住高老太爷的生命，他最终还是离开了人世。

（《家》）C.紫鹃为宝、黛的爱情操心、担心，谎说“林妹妹要回自己家里去了”，以此来试探宝玉是否真心，结果宝玉信以为真，急得几乎疯狂。

深夜，黛玉、紫鹃都睡不着，好心的紫鹃劝黛玉对自己的终身大事要早拿主意。

（《红楼梦》D.卡秋莎连夜冒雨赶往火车站到达车站时，火车快要开了她看见车厢内的聂赫柳朵夫，，但对方没火车开动后，她追着火车跑个不停她想自杀，但胎儿的颤动使她打消了这个念头，从此她的思想发生了巨变。

E.范博文说老太爷在乡下已经是“古老的僵尸”，是因为吴老太爷自从二十五年前习武骑马跌伤了腿，又不幸而渐渐成为半身不遂的毛病后，二十五年来，他就不曾跨出他的书斋半步，也不曾读过《太上感应篇》之外的任何书报。

福建省晋江市养正中学2013届高三第一次月考数学(文)试题

考试时间120分钟试卷分值：150分一、选择题：本小题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把答案填涂在答题纸的相应位置.1．已知i 为虚数单位，则复数()1z i i =⋅+在复平面内对应的点位于（） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限 2、记等差数列}{n a 的前n 项和为n S ，已知2211=S ，则6a 的值为（）A 、1B 、2C 、3D 、43．已知向量()1,1a =，()2,0b =，则向量,a b 的夹角为（） A 、B 、C 、D 、4．设等差数列}{n a 的前n 项和为n s ，若369,36s s ==，则789a a a ++=（） A 、63 B 、45 C 、36 D 、275．已知数列}{n a 满足121-=-n n a a ，21=a ，则n a 的通项公式为（）A 、12-n B 、121--n C 、121-+n D 、n 21+6、已知ABC ∆和点M 满足=++，若存在实数m ，使m =+成立，则m =（）A 、6B 、32C 、2D 、37．在ABC ∆中，2AB =，D 是AC 的中点，若4AB AC ⋅=,则AB BD ⋅=（）A 、2-B 、2C 、4D 、218．下列结论错误的是（）A 、命题“若p ，则q”与命题“若¬q，则¬p”互为逆否命题B 、命题p ：1],1,0[≥∈∀xex ，命题q ：01,2<++∈∃x x R x ，则p ∨q 为真C 、若am 2＜bm 2，则a ＜b”的逆命题为真命题 D 、若p ∨q 为假命题，则p 、q 均为假命题9．已知双曲线22221y x a b-=的一个焦点与抛物线24x y =的焦点重合，且双曲线的实轴长是虚轴长的一半，则该双曲线的方程为（）A 、225514x y -= B 、22154x y -= C 、22154y x -=D 、225514y x -= 10、设函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭，则下列结论正确的是（）A 、f （x ）的图象关于直线3x π=对称B 、f （x ）的图象关于点（4π，0）对称C 、把f （x ）的图象向左平移12π个单位，得到一个偶函数的图象 D 、f （x ）的最小正周期为π，且在[0，6π]上为增函数11．某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若最初生产出的溶液含杂质2%，需要进行过滤，且每过滤一次可使杂质含量减少，则要使产品达到市场要求至少应过滤（）A 、3次B 、4次C 、5次D 、6次12．平面向量也叫二维向量，二维向量的坐标表示及其运算可以推广到n （n≥3）维向量， n 维向量可用（x 1，x 2，x 3，x 4，…，x n ）表示．设a =（a 1，a 2，a 3，a 4，…，a n ），b =（b 1，b 2，b 3，b 4，…，b n ），规定向量a 与b 夹角θ的余弦为cos θ=．已知n 维向量a ，b ，当a =（1，1，1，1，…，1），b =（﹣1，﹣1，1，1，1，…，1）时，cos θ等于（） A 、B 、C 、D 、二、填空题(本大题共4小题，每小题4分，共16分)13．若角α的终边经过点)2,1(-P 则αsin 的值为14．已知函数()()2sin f x x ωϕ=+（ω＞0）的部分图象如图所示，则函数()f x 的解析式为15、已知函数()f x 是以1为周期的偶函数，且当x ∈（0，1）时，f （x ）=x2，则f （3log 2-）的值为16．在四边形ABCD 中，==（3，4），，则四边形ABCD 的面积是三、解答题：本大题共6个小题，共74分，解答时应写出文字说明证明、过程或推演步骤. 17．(本小题满分12分）已知函数()22sin 24f x x x π⎛⎫=+-⎪⎝⎭（Ⅰ）求()f x 的最小正周期；（Ⅱ）若不等式()2f x m -<在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立，求实数m 的取值范围． 18．（本小题满分12分）已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量()()(),,sin ,sin ,2,2m a b n B A p b a ===--．（1）若//m n ，求证：△ABC 为等腰三角形；（2）若m p ⊥=2，向量和的夹角为π32，求△ABC 的面积．19．(本小题满分12分)设数列}{n a 的前n 项和为n s ，点()*,n s n n N n ⎛⎫∈ ⎪⎝⎭均在函数1y x =+的图象上．（1）求数列}{n a 的通项公式；（2）若}{n b 为正项等比数列，且11=b ，8321=b b b ，求}{n b 的通项公式和前n 项和n G ；（3）求}{n n b a ⋅的前n 项和n T 。

泉州市2013届高三5月质量检查数学文试题 Word版含答案

准考证号________________ 姓名________________（在此卷上答题无效）保密★启用前泉州市2013届普通中学高中毕业班质量检测文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）．本试卷共6页，满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0．5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据1x 、2x 、…、n x 的标准差：s =，其中x 为样本平均数；柱体体积公式：V Sh =，其中S 为底面面积，h 为高；锥体体积公式：13V Sh =，其中S 为底面面积，h 为高；球的表面积、体积公式：24S R π=，343V R π=，其中R 为球的半径．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若i 是虚数单位，则复数i (2i)⋅+在复平面内所对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设全集U =R ，{(3)0}A x x x =+<，{1}B x x =<-，则图中阴影部分表示的集合为A ．(3,1)--B ．(1,0)-C ．[1,0)-D ．(,1)-∞-3．某校组织班班有歌声比赛，8个评委为某个班级打出的分数如茎叶图所示，则这些数据的中位数是A ．84B ．85C ．86D ．87.54．执行如图所示程序框图所表达的算法，若输出的x 值为48，则输入的x 值为A ．3B ．6C ．8D ．125．若0a >，0b >，且1,,,4a b 构成等比数列，则ks5uA ．22a b +有最小值4 B ．a b +有最小值4C ．22a b +无最小值D ．a b +有最小值26．圆0422=-+x y x 在点)3,1(P 处的切线方程为A ．023=-+y xB ．043=-+y xC ．043=+-y xD ．023=+-y x 7．下列函数中，既是奇函数又是减函数的是A ．13y x =B ．x x f tan )(-=C ．2()1x f x x =- D ．x x x f 22)(-=- 8．设,a b ∈R ，那么“>1a b”是“>>0a b ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件9．若双曲线()222210,0x y a b a b-=>>的一个焦点在直线20x y a --=上，则其渐近线方程为A ．y =B ．3y x =±C ．13y x =±D ．3y x =±10．已知()21()cos cos 02f x x x x ωωωω=⋅->的图象与1y =的图象的两相邻交点间的距离为π，要得到()y f x =的图象，只须把cos 2y x =的图象A ．向左平移3π个单位 B ．向右平移3π个单位 C ．向左平移6π个单位 D ．向右平移6π个单位 11．已知周期函数()f x 的定义域为R ，周期为2，且当11x -<≤时，2()1f x x =-．若直线y x a =-+与曲线()y f x =恰有2个交点，则实数a 的所有可能取值构成的集合为A ．3{|24a a k =+或524k +,k ∈Z }B ．1{|24a a k =-或324k +,k ∈Z } C ．{|21a a k =+或524k +,k ∈Z } D ．{|21a a k =+,k ∈Z } 12．如图，在棱长为1的正方体1111ABCD A BC D -的对角线1AC 上任取一点P ，以A 为球心，AP 为半径作一个球.设AP x =，记该球面与正方体表面的交线的长度和为()f x ，则函数()f x 的图象最有可能的是ks5uA ．B ．C ．D ．第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分．将答案填在答题卡的相应位置．13．已知向量(4,)m =a ，(1,2)=-b ，若+=-a b a b ，则实数m 等于．14．根据2012年初我国发布的《环境空气质量指数AQI 技术规定（试行）》，AQI 共分为六级：(0,50]为优，(50,100]为良，(100,150]为轻度污染，(150,200]为中度污染，(200,300]为重度污染，300以上为严重污染．2013年5月1日出版的《A 市早报》报道了A 市2013年4月份中30天的AQI统计数据，右图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A 市该月环境空气质量优良的总天数为．15．一水平放置的平面图形OABC ，用斜二测画法画出它的直观图''''O A B C 如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形OABC 的面积为．16．对于30个互异的实数，可以排成m 行n 列的矩形数阵，右图所示的5行6列的矩形数阵就是其中之一．将30个互异的实数排成m 行n 列的矩形数阵后，把每行中最大的数选出，记为12,,m a a a ⋅⋅⋅，并设其中最小的数为a ；把每列中最小的数选出，记为12,,n b b b ⋅⋅⋅，并设其中最大的数为b .两位同学通过各自的探究，分别得出两个结论如下：①a 和b 必相等； ②a 和b 可能相等；③a 可能大于b ； ④b 可能大于a ．以上四个结论中，正确结论的序号是__________________（请写出所有正确结论的序号）．126126126x x x y y y z z z三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．在某次模块水平测试中，某同学对于政治、历史、地理这三个学科每个学科是否能达到优秀水平的概率都为12，记政治、历史、地理达到优秀水平的事件分别为1A 、2A 、3A ，未达到优秀水平的事件分别为1A 、2A 、3A ．（Ⅰ）若将事件 “该同学这三科中恰有两科达到优秀水平” 记为M ，试求事件M 发生的概率；（Ⅱ）请依据题干信息，仿照（Ⅰ）的叙述，设计一个关于该同学测试成绩情况的事件N ，使得事件N 发生的概率大于%85，并说明理由．18．已知ABC ∆外接圆O 的半径为1，且12OA OB ⋅=- ．（Ⅰ）求AB 边的长及角C 的大小；（Ⅱ）从圆O 内随机取一个点M ，若点M 取自ABC ∆ABC ∆的形状．19．在数列}{n a 和等比数列}{n b 中，01=a ，23=a ，1*2()n a n b n N +=∈．（Ⅰ）求数列{}n b 及}{n a 的通项公式；（Ⅱ）若n n n b a c ⋅=，求数列{}n c 的前n 项和n S ．20．已知长方体1111ABCD A BC D -中，底面ABCD 为正方形，1D D ⊥面ABCD ，4AB =，12AA =，点E 在棱11C D 上，且13D E =．（Ⅰ）试在棱CD 上确定一点1E ，使得直线1//EE 平面1D DB ，并证明；（Ⅱ）若动点F 在底面ABCD 内，且2AF =，请说明点F 的轨迹，并探求EF 长度的最小值．21．已知(0,1)F 是中心在坐标原点O 的椭圆C 的一个焦点，且椭圆C 的离心率e 为12．（Ⅰ）求椭圆C 的方程；（Ⅱ）设：11(,)M x y 、22(,)N x y 为椭圆C 上不同的点，直线MN 的斜率为1k ；A 是满足OM ON OA λ+= （0λ≠）的点，且直线OA 的斜率为2k ．①求12k k ⋅的值；②若A 的坐标为3(,1)2，求实数λ的取值范围．22．定义域为D 的函数()f x ，其导函数为'()f x ．若对x D ∀∈，均有()'()f x f x <，则称函数()f x 为D 上的梦想函数．（Ⅰ）已知函数()sin f x x =，试判断()f x 是否为其定义域上的梦想函数，并说明理由；（Ⅱ）已知函数()1g x ax a =+-（a ∈R ，(0,)x π∈）为其定义域上的梦想函数，求a 的取值范围；（Ⅲ）已知函数()sin 1h x x ax a =++-（a ∈R ，[0,]x π∈）为其定义域上的梦想函数，求a 的最大整数值．泉州市2013届普通中学高中毕业班质量检测文科数学试题参考解答及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分．1．B 2．A 3．C 4．B 5．B 6．D7．D 8．B 9．A 10．C 11．C 12．B二、填空题：本大题考查基础知识和基本运算．每小题4分，满分16分.13．2 14．12 15． 16．②③三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．本小题主要考查古典概型等基础知识，考查运算求解能力以及应用意识，考查必然与或然思想等．满分12分．解：（Ⅰ）依题意，总的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共8种，………………2分事件M 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共3种，…4分由于每个基本事件发生的可能性都相等，故事件M 发生的概率83)( M P ．……6分（Ⅱ）方案一：记“该同学这三科中至少有一科达到优秀水平”的事件为N ，则事件N 发生的概率大于%85.…………8分理由：事件N 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共7种，……10分由于每个基本事件发生的可能性都相等，所以%8587)(>=N P ．……12分方案二：记 “该同学参加这次水平测试成绩不全达到优秀水平”的事件为N ，则事件N 发生的概率大于%85.…………8分理由：事件N 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共7种，……10分由于每个基本事件发生的可能性都相等，故%8587)(>=N P ．………12分 18．本小题主要考查向量的数量积、几何概型、解三角形等基础知识，考查运算求解能力，考查函数与方程思想等. 满分12分.解：（Ⅰ）依题意1cos 2OA OB OA OB AOB ⋅=⋅⋅∠=- ，………………2分得1cos 2AOB ∠=-，又0AOB π<∠<，故23AOB π∠=，…4分又AOB ∆为等腰三角形，故AB = …………5分而123C AOB π∠=∠=或12(2)23C AOB ππ∠=-∠=．………………6分（Ⅱ）依题意，从圆O 内随机取一个点，取自ABC ∆内的概率OABC S S P 圆∆=，可得S ABC ∆=．………………8分设BC a =，AC b =.设23C π∠=，由1sin 24ABC S ab C ∆=⋅⋅=，得3ab =， ……① 由2222cos 3AB a b ab C =+-=，得223a b ab ++=， ……②联立①②得220a b +=,这是不可能的. 所以必有3C π∠=. …………9分由1sin 24ABC S ab C ∆=⋅⋅=，得3ab =， ……① 由2222cos 3AB a b ab C =+-=，得223a b ab +-=，226a b += …②………11分联立①② 解得a b ==所以ABC ∆为等边三角形．………………12分19．本小题主要考查等比数列、数列通项公式、数列求和等基础知识，考查运算求解能力，考查函数与方程思想等. 满分12分.解法一：（Ⅰ）依题意21=b ，8233==b ，………………2分设数列}{n b 的公比为q ，由120n a n b +=>，可知0q >，………3分由822213=⋅=⋅=q q b b ，得42=q ，又0>q ，则2=q ，………4分故n n n n q b b 222111=⋅==--，………5分又由n a n 221=+，得1-=n a n ．………………6分（Ⅱ）依题意n n n c 2)1(⋅-=．………………7分n n n n n S 2)1(2)2(2221201321⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=- ， ①则14322)1(2)2(2221202+⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=n n n n n S ②……9分①-②得21231122222(1)2(1)212n n n n n S n n +++--=++⋅⋅⋅+--⋅=--⋅-， …………11分即12)2(4+⋅-+-=-n n n S ，故12)2(4+⋅-+=n n n S ．………………12分解法二：（Ⅰ）依题意}{n b 为等比数列，则q b b n n =+1（常数），由120n a n b +=>，可知0q >，………………2分由q n n nn a a a ==-+++112221，得q a a n n 21log =-+（常数），故}{n a 为等差数列，…………4分设}{n a 的公差为d ，由01=a ，220213=+=+=d d a a ，得1=d ，故1-=n a n ．…………6分（Ⅱ）同解法一．20．本小题主要考查直线与直线、直线与平面的位置关系等基础知识，考查空间想象能力、推理论证能力及运算求解能力，考查化归与转化思想等.满分12分.解：（Ⅰ）取CD 的四等分点1E ，使得13DE =，则有1//EE 平面1D DB . 证明如下：………1分因为11//D E DE 且11D E DE =，所以四边形11D EE D 为平行四边形，则11//D D EE ，………2分因为1DD ⊂平面1D DB ，1EE ⊄平面1D DB ，所以1//EE 平面1D DB ．………4分（Ⅱ）因为2AF =,所以点F 在平面ABCD 内的轨迹是以A 为圆心，半径等于2的四分之一圆弧．………………6分因为11//EE DD ，1D D ⊥面ABCD ，所以1E E ⊥面ABCD ， ………………7分故EF ==8分所以当1E F 的长度取最小值时，EF 的长度最小，此时点F为线段1AE 和四分之一圆弧的交点，………………10分即11523E F E A AF =-=-=，所以EF ==．即EF 12分21．本小题主要考查椭圆的标准方程、直线与椭圆等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想、数形结合思想等．满分12分．解：（Ⅰ）依题意，可设椭圆C 的方程为22221y x a b+=（0a b >>），………………1分由1c =，12c e a ==，得2a =，由222b ac =-，可得23b =，………………3分故椭圆C 的方程为22143y x +=．………………4分（Ⅱ）解法一：①由11(,)M x y 、22(,)N x y 且1k 存在，得21121y y k x x -=-，………………5分由OM ON OA λ+= ，0λ≠且2k 存在，得21221y y k x x +=+，则222121211222212121y y y y y y k k x x x x x x +--⋅=⋅=+--.………………6分 ∵11(,)M x y ，22(,)N x y 在椭圆上，∴2211143y x +=，2222143y x +=，………7分两式相减得22222121043y y x x --+=，2221222143y y x x -=--， ∴1243k k ⋅=-．………………8分 ②若A 的坐标为3(,1)2，则223k =，由①可得12k =-.设直线:2MN y x m =-+（m ∈R ），由222,1,43y x m y x =-+⎧⎪⎨+=⎪⎩得2216123120x mx m -+-=，……ks5u ……9分所以1234mx x +=. ∵OM ON OA λ+= ，∴1232x x λ+=，2m λ=. …………10分又由()()22124163120m m ∆=--⋅⋅->，解得44m -<<，………………11分∴22λ-<<且0λ≠．………………12分解法二：①设直线1:MN y k x m =+（m ∈R ），若0m =，则120,x x +=由A 满足OM ON OA λ+=（λ∈R ，0λ≠），得0A x =，∵直线OA 的斜率2k 存在，∴0m ≠. ………5分由122,1,43y k x m y x =+⎧⎪⎨+=⎪⎩得22211(43)63120k x k mx m +++-=……(*).……………6分 ∵11(,)M x y 、22(,)N x y ，∴11221643k mx x k +=-+. ……7分 ∵12112()2y y k x x m +=++，A 满足OM ON OA λ+=，∴直线OA 的斜率2121211121214323y y k mk k k x x x x k ++==+=-++，经化简得1243k k ⋅=-. ………9分 ②若A 的坐标为3(,1)2，则223k =，由①可得12k =-. ………10分∴方程(*)可化为2216123120x mx m -+-=，下同解法一.22．本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等．满分14分. 解：（Ⅰ）函数()sin f x x =不是其定义域上的梦想函数．………………1分理由如下：()sin f x x =定义域D R =，()'cos f x x =，………………2分存在3x π=，使()'()33f f ππ>，故函数()sin h x x =不是其定义域R D =上的梦想函数．……4分ks5u（Ⅱ）()1g x ax a =+-，()'g x a =，若函数()1g x ax a =+-在(0,)x π∈上为梦想函数，则1ax a a +-<在(0,)x π∈上恒成立，………………5分即1a x <在(0,)x π∈上恒成立，因为1y x =在(0,)x π∈内的值域为1(,)π+∞，………………7分所以1a π≤．………………8分（Ⅲ）a x x h +=cos )('，由题意)()('x h x h >在[0,]x π∈恒成立，故cos sin 1x a x ax a +>++-，即cos sin 1ax x x <-+在[0,]x π∈上恒成立． ①当0x =时，0cos 0sin 012a ⋅<-+=显然成立；……………9分 ②当0x π<≤时，由cos sin 1ax x x <-+可得cos sin 1x x a x-+<对任意(]0,x π∈恒成立. 令cos sin 1()x x F x x -+=，则2(s i n c o s )(c o ss i n 1)'()x x x x x F x x --⋅--+=，…10分令)1sin (cos )cos sin ()(+--⋅--=x x x x x x k ，则'()(sin cos )sin()4k x x x x x π=-⋅=⋅-．当(0,]4x π∈时，因为0)('≤x k ，所以)(x k 在(0,]4π单调递减；当(,]4x ππ∈时，因为0)('≥x k ，所以)(x k 在(,]4ππ单调递增．∵(0)20k =-<，()104k π=-<， ∴当(0,]4x π∈时，()k x 的值均为负数.∵()104k π=-<，()0k ππ=>， ∴当(,]4x ππ∈时，()k x 有且只有一个零点0x ，且0(,)4x ππ∈. ……………11分∴当0(0,)x x ∈时，0)(<x k ，所以'()0F x <，可得()F x 在0(0,)x 单调递减；当0(,)x x π∈时，0)(>x k ，所以'()0F x >，可得()F x 在0(,)x π单调递增．则00min 00cos sin 1()()x x F x F x x -+==．…………12分因为0)(0=x k ，所以00000cos sin 1(sin cos )x x x x x -+=--⋅，min 0000()()sin cos )4F x F x x x x π==--=+．…………13分∵)(x k 在(,]4ππ单调递增，02)2(<-=ππk ，012)43(>-=πk ，∴0324x ππ<<，所以01)04x π-<+<，即01()0F x -<<．ks5u又因为0()a F x <，所以a 的最大整数值为1-．…………14分。

福建省安溪一中、晋江养正中学高三数学上学期期中联考试题文新人教A版

安溪一中、晋江养正中学2013-2014学年度第一学期期中考考试高三数学试卷（文科）考试时间120分钟试卷分值：150分第Ⅰ卷 (选择题共60分)一、选择题：本小题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把答案填涂在答题纸的相应位置. 1．已知集合{}0,M x x =≥{}0,1,2N =，则（） A ．M N ⊆ B ．N M ⊆ C ．M N N = D ．MN =∅2.函数()321()2x f x x -=-的零点所在区间为（）A ．)1,0(B ．)2,1(C ．)3,2(D ．)4,3(3．完成一项装修工程，木工和瓦工的比例为2∶3，请木工需付日工资每人50元，请瓦工需付日工资每人40元，现有日工资预算2 000元，设每天请木工x 人、瓦工y 人，则每天请木、瓦工人数的约束条件（）⎩⎨⎧∈≤+*N y x y x A ,532.⎪⎩⎪⎨⎧=≤+3220004050.y x y x B⎪⎪⎩⎪⎪⎨⎧∈=≤+*N y x y x y x C ,3220045. ⎪⎩⎪⎨⎧=≤+3210065.y x y x D 4.给出下列三个结论： ①命题“若0m >，则函数mx x x f -+=2)(有零点”的逆否命题为：“函数m x x x f -+=2)(无零点，则m ≤0”；②”“q p ∧为真是”“q p ∨为真的充分不必要条件； ③若命题:,()P x R f x m ∀∈<，则命题的否定P ⌝： ,x R ∃∈使得()f x m ≥. 其中正确结论的个数为（） A.0B.1C.2D.35.已知数列{}n a 满足)(221*∈+=++N n a a a n n n ，且π8951=++a a a ，则)co s (73a a +的值为（）A B ． C ．12D ．12-6．若函数c cx x x x f 22)(23-+-=在2=x 处有极值，则函数)(x f 的图象在1=x 处的切线的斜率为（）A.5-B.8-C.10-D.1-7．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．9πB ．10πC ．11πD ．12π 8.“21≤<a ”是“函数21f(x =9ln 2x x -）在区间[]1,1a a -+上单调递减”的（）既不充分也不必要条件充要条件必要不充分条件充分不必要条件....D C B A9.下列命题中①若实数d c b a ,,,满足0,0>>>>d c b a ，则c b d a ->-22；②若实数b a ,满足b a >，则ba )31()31(<；③若实数b a ,满足2,0,022=+>>b a b a 且，则b a +的最小值为2； ④若实数b a ,满足ab b a b a =+>>且,0,0，则ab 的最大值为4；假命题的是（）A. ①②B. ②③C. ①④D. ③④ 10．已知函数x x x f cos )(2-=，则)5.0(),0(),6.0(-f f f 的大小关系是（）A.)6.0()5.0()0(f f f <-<B.)5.0()6.0()0(-<<f f f .C.)0()5.0()6.0(f f f <-<D.)6.0()0()5.0(f f f <<-11.如下面左图所示，半径为2的圆M 切直线AB 于O ，射线OC 从OA 出发绕着O 点顺时针旋转到OB 。

晋江市养正中学高三数学周练(4)2013.4(教师版)

晋江市养正中学周练(4)2013.4(教师版)数学试题（理科）（命卷:郑明铿审卷:高三备课组考试时间：120分钟；满分：150分）第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题,每小题5分，共50分.在每小题给出的四个选项中，只有一项是满足题目要求的.1. 下列命题中的假命题是( D )A. 0,2≥∈∀x R xB. 1log ,2=∈∃x R xC. 0)21(,>∈∀xR x D. 25sin ,=∈∃x R x2. 已知直线α平面⊥l ，直线β平面⊂m ，则“βα//”是“m l ⊥”的( A ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3. 已知某三棱锥的三视图（单位:C m)如图所示，则该三棱锥的体积是( A )A. 1cm 3B. 2cm 3C. 3 cm 3D. 6cm 34. 已知向量a ,b ，满足|a|=3,|b|=23且a 丄(a +b ),则a 与b 的夹角为( D ) A. 2πB.32π C.43π D.65π5. 某物体在变力F(x)=5-x 2 （x 的单位：m ，F 的单位：N)的作用下，沿着与F (x)成30°方向做直线运动，则从x=1处运动到x = 2处时变力F (x)所做的功为( C )A. J 23 B. J 3 C.J 334 D. 2J 36. 设复数iix -=12（i 是虚数单位），则20132013201333201322201312013xC x C x C x C +⋯+++=( C )A.iB. -iC. -1 +iD.1+i7.ΔABC 的内角A,B,C 的对边分别为a ，b,c ，已知c o s (A -C )+ cosB = 1,a =2c ，则C =( B )A.656ππ或B.6πC.323ππ或D.3π8. 某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1千克3原料2千克；生产乙产品1桶需耗A 原料2千克,B 原料1千克.每桶甲产品的利润是300元，每桶乙产品的利润是400元.公司在生产这两种产品的计划中，要求每天消耗A ，B 原料都不超过12千克.通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是( C )A. 1800 元B. 2400 元C. 2800 元D. 3100 元9. 已知F 1、F 2分别是双曲线12222=-by ax 的左、右焦点,P 为双曲线右支上的任意一点.若a PF PF 8||||221=，则双曲线离心率的取值范围是( C )A. (1,2]B. [2 +∞)C. (1,3]D. [3，+∞)10. 已知方程(1)(||2)4y x ++=,若对任意[,](,)x a b a b Z ∈∈，都存在唯一的[0,1]y ∈使方程成立；且对任意[0,1]y ∈，都有[,](,)x a b a b Z ∈∈使方程成立，则a b +的最大值等于（ D ） A ．-2B ． 0C ．1D ． 2第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共20分.11.右图是一个算法流程图，则输出的k 的值是________612.将甲、乙、丙3名志愿者安排在周一至周五的5天中参加某项志愿者活动，要求每人参加一天且每天至多安排一人，并要求甲安排在乙、丙的前面，则不同的安排方法共有______种.2013.在等比数列{a n }中，若r,s,t 是互不相等的正整数，则有等式成立.类比上述性质，相应地，在等差数列{b n }中,若r ，s ，t 是互不相等的正整数，则有等式____________________成立. (r-s)b t +(s-t)b r +(t-r)b s =014. 一袋中有红、黄、蓝三种颜色的小球各一个，每次从中取出一个，记下颜色后放回，当三种颜色的球全部取出时停止取球，则恰好取5次球时停止取球的概率为_______811415. 函数()f x 的导函数为()f x '，若对于定义域内任意1x 、2x 12()x x ≠，有121212()()()2f x f x x x f x x -+'=-恒成立，则称()f x 为恒均变函数．给出下列函数：①()=23f x x +；②2()23f x x x =-+；③1()=f x x；④()=x f x e ；⑤()=ln f x x ．其中为恒均变函数的序号是 .（写出所有满足条件的函数的序号）①②三、解答题：解答应写出文字说明、证明过程或演算步骤.16.(本小题满分13分）已知x 0, x 0+2π是函数f(x)=cos 2(ωx-6π)-sin 2ωx(ω>0)的两个相邻的零点.(I )求)12(πf 的值；(II)若对]0,127[π-∈∀x ，都有1|)(|≤-m x f ，求实数m 的取值范围.17. （本小题满分13分）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为12.（Ⅰ）求该校报考飞行员的总人数; （Ⅱ）以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X 表示体重超过60公斤的学生人数，求X 的分布列和数学期望.18.(本小题满分13分）如图,在ΔAOB 中，已知,6,2ππ=∠=∠BAO AOB AB ＝4，D 为线段贴的中点. ΔAOC 是由绕直线AO 旋转而成，记二面角B-AO-C 的大小为θ 6.(I )当平面COD 丄平面AOB 时，求θ的值；（II ）当θ＝32π 求二面角B －OD －C 的余弦值19 (本小题满分13分）.如图,长为m +1(m>0)的线段A B 的两个端点A 和B 分别在x轴和y 轴上滑动,点M 是线段AB上一点,且MB m AM =(I)求点M 的轨迹Γ的方程,并判断轨迹Γ为何种圆锥曲线； (II)设过点Q(21,0)且斜率不为0的直线交轨迹Γ于C 、D 两点.试问在x轴上是否存在定点P ，使PQ 平分乙CPD ∠?若存在,求点P 的坐标；若不存在,请说明理由20. (本小题满分14分） (I)已知函数)1,0,0()()(2)(1>>+-+=-p a x a x a xx f pp pp ，求f(x)的最小值；(I I )证明：2)2(pppb a b a +≤+，其中a >0,b > O,P > 1；(III)证明na a a na a a pnp p pn+⋯++≤+⋯++21121)(其中a 1, a 2,…a n >0,p>1,*N n ∈21. 本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题做答，满分14分，如果多做，则按所做的前两题计分. 作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中.（1）（本小题满分7分）选修4—2；矩阵与变换已知在一个二阶矩阵M 的变换作用下，点A(1,2)变成了点A′(4, 5)，点B(3，－1)变成了点B′(5,1)．（Ⅰ）求矩阵M ；（Ⅱ）若在矩阵M 的逆矩阵的变换作用下，点C(x,0)变成了点C′(4，y)，求x+y 的值. （2）（本小题满分7分）选修4—4：坐标系与参数方程在直角坐标系xOy 中，圆O 的参数方程为2cos 22sin 2x r y r θθ⎧=-+⎪⎨⎪=-+⎩，(θ为参数，0r >).以O 为极点，x 轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l 的极坐标方程为()2s i n 42πρθ+=. （Ⅰ）写出圆心的极坐标，（Ⅱ）求当r 为何值时，圆O 上的点到直线l 的最大距离为3.（3）（本小题满分7分）选修4—5：不等式选讲（Ⅰ）设2a a ∈≠-R 且，试比较222a a-+与的大小．（Ⅱ）求函数142y x x =-++的最大值．参考答案17解：（Ⅰ）设报考飞行员的人数为n ,前三小组的频率分别为321,,p p p ,则由条件可得:⎪⎩⎪⎨⎧=⨯++++==15)013.0037.0(323211312p p p p p p p解得375.0,25.0,125.0321===p p p ………………………………………………4分又因为np 1225.02==，故48=n ……………………………………………………6分（Ⅱ）由（Ⅰ）可得,一个报考学生体重超过60公斤的概率为855)013.0037.0(3=⨯++=p p ………………………………………………………8分所以x 服从二项分布,k k k C k x p -==33)83()85()(∴随机变量x 的分布列为：x 0123p51227512135512225512125…………………………………………………………………12分则815512125351222525121351512270=⨯+⨯+⨯+⨯=Ex ………………………………13分(或: 815853=⨯=Ex )18.21. 本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题做答，满分14分，如果多做，则按所做的前两题计分. 作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中.（1）（本小题满分7分）选修4—2；矩阵与变换已知在一个二阶矩阵M 的变换作用下，点A(1,2)变成了点A′(4, 5)，点B(3，－1)变成了点B′(5,1)．（Ⅰ）求矩阵M ；（Ⅱ）若在矩阵M 的逆矩阵的变换作用下，点C(x,0)变成了点C′(4，y)，求x+y 的值.解：（Ⅰ）设该二阶矩阵为ab M cd ⎛⎫⎪⎝⎭＝，由题意得1425a b c d ⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,3511a b cd ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭,所以24253531a b c da bc d+=⎧⎪+=⎪⎨-=⎪⎪-=⎩解得2,1,1,2a b c d ====,故2112M ⎛⎫⎪⎝⎭＝…………………3分（Ⅱ）因为1212133det 30,121233M M-⎛⎫-⎪==≠=⎪- ⎪⎝⎭， 212044333,,6,2,12010333x x x y y x y ⎛⎫⎧-+=⎛⎫⎛⎫ ⎪⎪===-⎨⎪ ⎪ ⎪⎝⎭⎝⎭⎪--+= ⎪⎝⎭⎩解得4x y ∴+=.…………7分（2）（本小题满分7分）选修4—4：坐标系与参数方程在直角坐标系xOy 中，圆O 的参数方程为2cos 22sin 2x r y r θθ⎧=-+⎪⎨⎪=-+⎩，(θ为参数，0r >).以O为极点，x 轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l 的极坐标方程为()2sin 42πρθ+=. （Ⅰ）写出圆心的极坐标，（Ⅱ）求当r 为何值时，圆O 上的点到直线l 的最大距离为3.解：（Ⅰ）圆心的极坐标()51,4π.…………………………………………………………3分（Ⅱ）直线为10x y +-=，圆心22,22O ⎛⎫-- ⎪⎝⎭到直线的距离212d --=.圆O 上的点到直线的最大距离为2132r --+=，解得222r =-.……………7分（3）（本小题满分7分）选修4—5：不等式选讲（Ⅰ）设2a a ∈≠-R 且，试比较222a a -+与的大小．（Ⅱ）求函数142y x x =-++的最大值．解: （Ⅰ）()22222a a a a --=++, 20=22a a a=-+当时,； 22<22a a a <--+当时,；220>22a a a a >-≠-+当且时,.…………………………3分[]-2,1(II)函数定义域为， []()2(12)1x x x x +≥-+由柯西不等式得（1-）+（2+）4+2, 即()219,13x x x x -+≤-+≤4+2即4+2()m ax =013x x x -+=当且仅当时，等号成立，4+2.……………………7分。

福建省晋江市养正中学高三上学期期中考试数学(理)试题(有答案)

养正中学、惠安一中、安溪一中2017届高三上学期期中联合考试数学（理）科试卷满分：150分，考试时间：120分钟第Ⅰ卷 (选择题共60分)一、选择题：本大题共2小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把答案涂在答题卡的相应位置.1、若集合{}{}1,0,1,|cos ,M N x x k k Z π=-==∈，则M C N =（） A ．∅ B ．0 C ．{}0 D ．{}1,1-2、已知命题12:1,log 0p x x ∀>>，命题3:,3xq x R x ∃∈≥，则下列命题为真命题的是（）A ．p q ∧B ．()p q ∨⌝C ．()p q ∧⌝D ．()p q ⌝∧ 3、设函数()2,12,1xx b x f x x -<⎧=⎨≥⎩，若142f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，则b =（） A ．-1 B ．23-C ．-1或23- D ．2 4、角α的终边过函数log (3)2a y x =-+的定点P ，则sin 2cos2αα+=（） A ．75 B.65C.4D.5 5、函数2()sin()f x x x =的图象大致为（）A B C D6、已知m ，n 表示两条不同直线，α表示平面．下列说法正确的是( ) A ．若//,//m n σσ，则//m n B ．若,m n σσ⊥⊂则m ⊥n C ．若,m m n σ⊥⊥，则//n σ D ．若//,m m n σ⊥，则n σ⊥ 7，直线2-=x y 及y 轴所围成的封闭图形的面积为（）A B C ．4 D ．6 8、使sin (0)y x ωω=>在区间]1,0[至少出现2次最大值，则ω的最小值为（） A ．π25 B ．π45 C ．π D ．π239、已知三棱锥ABCD 的棱长都相等，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为( )A.16B.36C.13D.33 10、2sin 473sin17cos17-的值为A ．B ． 1-CD ．111.设函数()21ln 2f x x ax bx =--，若1x =是()f x 的极大值点，则a 的取值范围为（）A ．()1,0-B ．()1,-+∞C ．()0,+∞D ．()(),10,-∞-+∞12.若函数()f x 在区间A 上，对a b c A ∀∈，，，()f a ，()f b ，()f c 为一个三角形的三边长，则称函数()f x 为“三角形函数”.已知函数()ln f x x x m =+在区间21[,]e e上是“三角形函数”，则实数m 的取值范围为（）A ．212(,)e e e + B ．2(,)e +∞ C. 1(,)e+∞ D ．22(,)e e ++∞ 第Ⅱ卷（非选择题共90分）二、填空题本大题共4小题，每小题5分，满分20分.请把答案填在答题纸的相应位置.13、若幂函数()()21m f x m m x =--在()0,+∞上为增函数，则实数m 的值是．14、多面体的三视图如图所示，则该多面体的体积为 3cm ．15、已知,a b 为正实数，函数3()2xf x ax bx =++在[0,1]的最大值为4，则()f x 在[1,0]-的最小值为16、已知函数x x x f -=sin )(，若0)22()s i n 2(co s 2>--++m f m f θθ对任意的(0,)2πθ∈恒成立，则实数m 的取值范围为三、解答题本大题共6小题，共70分.解答应写出文字说明,证明过程或演算步骤. 17．（本小题满分12分）设集合{|12}A x x =-≤≤，22{|()0}B x x x m m =-+-<．(1)当12m <时，化简集合B ； (2) :p x A ∈，命题:q x B ∈，且命题p 是命题q 的必要不充分条件，求实数m 的取值范围．18、（本小题满分12分）已知函数()()22sincos cos 0,f x x x x x ωωωωω=+->()f x 的图象相邻两条对称轴的距离为4π。

【语文】福建省晋江市养正中学2013届高三上期末考试题

养正中学2013届高三上期末考试语文试题一、古代诗文阅读（29分）（一）默写常见的名句名篇（8分）1．补写出下列名句名篇中的空缺部分。

（8分）（1）渔舟唱晚，___________________。

（王勃《滕王阁序》）（2）苔痕上阶绿，。

（刘禹锡《陋室铭》）（3）__________________________，铁骑突出刀枪鸣。

（白居易《琵琶行》）（4）__________________________，报养刘之日短也。

（李密《陈情表》）（5）_________________________，处江湖之远则忧其君。

（范仲淹《岳阳楼记》）（6）此情可待成追忆，_________________________。

（李商隐《锦瑟》）（7）地崩山摧壮士死，_________________________。

（李白《蜀道难》）.（8）驾一叶之扁舟，_________________________。

（苏轼《赤壁赋》）（二）文言文阅读（15分）廉耻[清]顾炎武《五代史·冯道传·论》曰：礼义廉耻，国之四维，四维不张，国乃灭亡。

善乎，管生之能言也!礼义，治人之大法；廉耻，立人之大节；盖不廉则无所不取，不耻则无所不为。

人而如此，则祸败乱亡，亦无所不至；况为大臣而无所不取，无所不为，则天下其有不乱，国家其有不亡者乎?然而四者之中，耻尤为要。

故夫子之论士，曰：“行己有耻。

”孟子曰：“耻之于人大矣，为机变之巧者，无所用耻焉。

”所以然者，人之不廉，而至于悖礼犯义，其原皆生于无耻也。

故士大夫之无耻，是谓国耻。

吾观三代以下，世衰道微，弃礼义，捐廉耻，非一朝一夕之故。

然而松柏后凋于岁寒，鸡鸣不已于风雨，彼昏之日，固未尝无独醒之人也!顷读《颜氏家训》有云：“齐朝一士夫尝谓吾曰：‘我有一儿，年已十七，颇晓书疏，教其鲜卑语，及弹琵琶，稍欲通解，以此伏事公卿，无不宠爱。

’吾时俯而不答。

异哉，此人之教子也!若由此业自致卿相，亦不愿汝曹为之。

福建省泉州市2013届高三5月质量检查数学文试题Word版附答案

准考证号________________ 姓名________________（在此卷上答题无效）保密★启用前泉州市2013届普通中学高中毕业班质量检测文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）．本试卷共6页，满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0．5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据1x 、2x 、…、n x 的标准差：s =，其中x 为样本平均数；柱体体积公式：V Sh =，其中S 为底面面积，h 为高；锥体体积公式：13V Sh =，其中S 为底面面积，h 为高；球的表面积、体积公式：24S R π=，343V R π=，其中R 为球的半径．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若i 是虚数单位，则复数i (2i)⋅+在复平面内所对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设全集U =R ，{(3)0}A x x x =+<，{1}B x x =<-，则图中阴影部分表示的集合为A ．(3,1)--B ．(1,0)-C ．[1,0)-D ．(,1)-∞-3．某校组织班班有歌声比赛，8个评委为某个班级打出的分数如茎叶图所示，则这些数据的中位数是A ．84B ．85C ．86D ．87.54．执行如图所示程序框图所表达的算法，若输出的x 值为48，则输入的x 值为A ．3B ．6C ．8D ．125．若0a >，0b >，且1,,,4a b 构成等比数列，则ks5uA ．22a b +有最小值4 B ．a b +有最小值4C ．22a b +无最小值D ．a b +有最小值26．圆0422=-+x y x 在点)3,1(P 处的切线方程为 A ．023=-+y x B ．043=-+y xC ．043=+-y xD ．023=+-y x 7．下列函数中，既是奇函数又是减函数的是A ．13y x =B ．x x f tan )(-=C ．2()1x f x x =- D ．x x x f 22)(-=- 8．设,a b ∈R ，那么“>1a b”是“>>0a b ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件9．若双曲线()222210,0x y a b a b-=>>的一个焦点在直线20x y a --=上，则其渐近线方程为A ．y =B ．3y x =±C ．13y x =±D ．3y x =±10．已知()21()cos cos 02f x x x x ωωωω=⋅->的图象与1y =的图象的两相邻交点间的距离为π，要得到()y f x =的图象，只须把cos 2y x =的图象A ．向左平移3π个单位 B ．向右平移3π个单位 C ．向左平移6π个单位 D ．向右平移6π个单位 11．已知周期函数()f x 的定义域为R ，周期为2，且当11x -<≤时，2()1f x x =-．若直线y x a =-+与曲线()y f x =恰有2个交点，则实数a 的所有可能取值构成的集合为A ．3{|24a a k =+或524k +,k ∈Z }B ．1{|24a a k =-或324k +,k ∈Z } C ．{|21a a k =+或524k +,k ∈Z } D ．{|21a a k =+,k ∈Z } 12．如图，在棱长为1的正方体1111ABCD A B C D -的对角线1AC 上任取一点P ，以A 为球心，AP为半径作一个球.设AP x =，记该球面与正方体表面的交线的长度和为()f x ，则函数()f x 的图象最有可能的是ks5uA ．B ．C ．D ．第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分．将答案填在答题卡的相应位置．13．已知向量(4,)m =a ，(1,2)=-b ，若+=-a b a b ，则实数m 等于．14．根据2012年初我国发布的《环境空气质量指数AQI 技术规定（试行）》，AQI 共分为六级：(0,50]为优，(50,100]为良，(100,150]为轻度污染，(150,200]为中度污染，(200,300]为重度污染，300以上为严重污染．2013年5月1日出版的《A 市早报》报道了A 市2013年4月份中30天的AQI统计数据，右图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A 市该月环境空气质量优良的总天数为．15．一水平放置的平面图形OABC ，用斜二测画法画出它的直观图''''O A B C 如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形OABC 的面积为．16．对于30个互异的实数，可以排成m 行n 列的矩形数阵，右图所示的5行6列的矩形数阵就是其中之一．将30个互异的实数排成m 行n 列的矩形数阵后，把每行中最大的数选出，记为12,,m a a a ⋅⋅⋅，并设其中最小的数为a ；把每列中最小的数选出，记为12,,n b b b ⋅⋅⋅，并设其中最大的数为b .两位同学通过各自的探究，分别得出两个结论如下：①a 和b 必相等； ②a 和b 可能相等；③a 可能大于b ； ④b 可能大于a ．以上四个结论中，正确结论的序号是__________________（请写出所有正确结论的序号）．126126126x x x y y y z zz三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．在某次模块水平测试中，某同学对于政治、历史、地理这三个学科每个学科是否能达到优秀水平的概率都为12，记政治、历史、地理达到优秀水平的事件分别为1A 、2A 、3A ，未达到优秀水平的事件分别为1A 、2A 、3A ．（Ⅰ）若将事件 “该同学这三科中恰有两科达到优秀水平” 记为M ，试求事件M 发生的概率；（Ⅱ）请依据题干信息，仿照（Ⅰ）的叙述，设计一个关于该同学测试成绩情况的事件N ，使得事件N 发生的概率大于%85，并说明理由．18．已知ABC ∆外接圆O 的半径为1，且12OA OB ⋅=-．（Ⅰ）求AB 边的长及角C 的大小；（Ⅱ）从圆O 内随机取一个点M ，若点M 取自ABC ∆内的概率恰为4π，试判断ABC ∆的形状．19．在数列}{n a 和等比数列}{n b 中，01=a ，23=a ，1*2()n a n b n N +=∈．（Ⅰ）求数列{}n b 及}{n a 的通项公式；（Ⅱ）若n n n b a c ⋅=，求数列{}n c 的前n 项和n S ．20．已知长方体1111ABCD A B C D -中，底面ABCD 为正方形，1D D ⊥面ABCD ，4AB =，12AA =，点E 在棱11C D 上，且13D E =．（Ⅰ）试在棱CD 上确定一点1E ，使得直线1//EE 平面1D DB ，并证明；（Ⅱ）若动点F 在底面ABCD 内，且2AF =，请说明点F 的轨迹，并探求EF 长度的最小值．21．已知(0,1)F 是中心在坐标原点O 的椭圆C 的一个焦点，且椭圆C 的离心率e 为12．（Ⅰ）求椭圆C 的方程；（Ⅱ）设：11(,)M x y 、22(,)N x y 为椭圆C 上不同的点，直线MN 的斜率为1k ；A 是满足OM ON OA λ+=（0λ≠）的点，且直线OA 的斜率为2k ．①求12k k ⋅的值；②若A 的坐标为3(,1)2，求实数λ的取值范围．22．定义域为D 的函数()f x ，其导函数为'()f x ．若对x D ∀∈，均有()'()f x f x <，则称函数()f x 为D 上的梦想函数．（Ⅰ）已知函数()sin f x x =，试判断()f x 是否为其定义域上的梦想函数，并说明理由；（Ⅱ）已知函数()1g x ax a =+-（a ∈R ，(0,)x π∈）为其定义域上的梦想函数，求a 的取值范围；（Ⅲ）已知函数()sin 1h x x ax a =++-（a ∈R ，[0,]x π∈）为其定义域上的梦想函数，求a 的最大整数值．泉州市2013届普通中学高中毕业班质量检测文科数学试题参考解答及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分．1．B 2．A 3．C 4．B 5．B 6．D7．D 8．B 9．A 10．C 11．C 12．B二、填空题：本大题考查基础知识和基本运算．每小题4分，满分16分.13．2 14．12 15． 16．②③三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．本小题主要考查古典概型等基础知识，考查运算求解能力以及应用意识，考查必然与或然思想等．满分12分．解：（Ⅰ）依题意，总的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共8种，………………2分事件M 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共3种，…4分由于每个基本事件发生的可能性都相等，故事件M 发生的概率83)( M P ．……6分（Ⅱ）方案一：记“该同学这三科中至少有一科达到优秀水平”的事件为N ，则事件N 发生的概率大于%85.…………8分理由：事件N 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共7种，……10分由于每个基本事件发生的可能性都相等，所以%8587)(>=N P ．……12分方案二：记 “该同学参加这次水平测试成绩不全达到优秀水平”的事件为N ，则事件N 发生的概率大于%85.…………8分理由：事件N 包含的基本事件有“123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ，123(,,)A A A ”，共7种，……10分由于每个基本事件发生的可能性都相等，故%8587)(>=N P ．………12分 18．本小题主要考查向量的数量积、几何概型、解三角形等基础知识，考查运算求解能力，考查函数与方程思想等. 满分12分.解：（Ⅰ）依题意1cos 2OA OB OA OB AOB ⋅=⋅⋅∠=-，………………2分得1cos 2AOB ∠=-，又0AOB π<∠<，故23AOB π∠=，…4分又AOB ∆为等腰三角形，故AB = …………5分而123C AOB π∠=∠=或12(2)23C AOB ππ∠=-∠=．………………6分（Ⅱ）依题意，从圆O 内随机取一个点，取自ABC ∆内的概率O ABC S S P 圆∆=，可得S ABC ∆=．………………8分设BC a =，AC b =.设23C π∠=，由1sin 2ABC S ab C ∆=⋅⋅=，得3ab =， ……① 由2222cos 3AB a b ab C =+-=，得223a b ab ++=， ……② 联立①②得220a b +=,这是不可能的. 所以必有3C π∠=. …………9分由1sin 2ABC S ab C ∆=⋅⋅=，得3ab =， ……① 由2222cos 3AB a b ab C =+-=，得223a b ab +-=，226a b += …②………11分联立①② 解得a b ==所以ABC ∆为等边三角形．………………12分19．本小题主要考查等比数列、数列通项公式、数列求和等基础知识，考查运算求解能力，考查函数与方程思想等. 满分12分.解法一：（Ⅰ）依题意21=b ，8233==b ，………………2分设数列}{n b 的公比为q ，由120n a n b +=>，可知0q >，………3分由822213=⋅=⋅=q q b b ，得42=q ，又0>q ，则2=q ，………4分故n n n n q b b 222111=⋅==--，………5分又由n a n 221=+，得1-=n a n ．………………6分（Ⅱ）依题意n n n c 2)1(⋅-=．………………7分n n n n n S 2)1(2)2(2221201321⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=- ， ①则14322)1(2)2(2221202+⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=n n n n n S ②……9分①-②得21231122222(1)2(1)212n n n n n S n n +++--=++⋅⋅⋅+--⋅=--⋅-， …………11分即12)2(4+⋅-+-=-n n n S ，故12)2(4+⋅-+=n n n S ．………………12分解法二：（Ⅰ）依题意}{n b 为等比数列，则q b b n n =+1（常数），由120n a n b +=>，可知0q >，………………2分由q n n n n a a a a ==-++++1122211，得q a a n n 21log =-+（常数），故}{n a 为等差数列，…………4分设}{n a 的公差为d ，由01=a ，220213=+=+=d d a a ，得1=d ，故1-=n a n ．…………6分（Ⅱ）同解法一．20．本小题主要考查直线与直线、直线与平面的位置关系等基础知识，考查空间想象能力、推理论证能力及运算求解能力，考查化归与转化思想等.满分12分.解：（Ⅰ）取CD 的四等分点1E ，使得13DE =，则有1//EE平面1D DB . 证明如下：………1分因为11//D E DE 且11D E DE =，所以四边形11D EE D 为平行四边形，则11//D D EE ，………2分因为1DD ⊂平面1D DB ，1EE ⊄平面1D DB ，所以1//EE 平面1D DB ．………4分（Ⅱ）因为2AF =,所以点F 在平面ABCD 内的轨迹是以A 为圆心，半径等于2的四分之一圆弧．………………6分因为11//EE DD ，1D D ⊥面ABCD ，所以1E E ⊥面ABCD ， ………………7分故EF ==．………………8分所以当1E F 的长度取最小值时，EF 的长度最小，此时点F为线段1AE 和四分之一圆弧的交点，………………10分即11523E F E A AF =-=-=，所以EF ==．即EF 12分21．本小题主要考查椭圆的标准方程、直线与椭圆等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想、数形结合思想等．满分12分．解：（Ⅰ）依题意，可设椭圆C 的方程为22221y x a b+=（0a b >>），………………1分由1c =，12c e a ==，得2a =，由222b ac =-，可得23b =，………………3分故椭圆C 的方程为22143y x +=．………………4分（Ⅱ）解法一：①由11(,)M x y 、22(,)N x y 且1k 存在，得21121y y k x x -=-，………………5分由OM ON OA λ+=，0λ≠且2k 存在，得21221y y k x x +=+，则222121211222212121y y y y y y k k x x x x x x +--⋅=⋅=+--.………………6分 ∵11(,)M x y ，22(,)N x y 在椭圆上，∴2211143y x +=，2222143y x +=，………7分两式相减得22222121043y y x x --+=，2221222143y y x x -=--， ∴1243k k ⋅=-．………………8分 ②若A 的坐标为3(,1)2，则223k =，由①可得12k =-.设直线:2MN y x m =-+（m ∈R ），由222,1,43y x m y x =-+⎧⎪⎨+=⎪⎩得2216123120x mx m -+-=，……ks5u ……9分所以1234mx x +=. ∵OM ON OA λ+=，∴1232x x λ+=，2m λ=. …………10分又由()()22124163120m m ∆=--⋅⋅->，解得44m -<<，………………11分∴22λ-<<且0λ≠．………………12分解法二：①设直线1:MN y k x m =+（m ∈R ），若0m =，则120,x x +=由A 满足OM ON OA λ+=（λ∈R ，0λ≠），得0A x =， ∵直线OA 的斜率2k 存在，∴0m ≠. ………5分由122,1,43y k x m y x =+⎧⎪⎨+=⎪⎩得22211(43)63120k x k mx m +++-=……(*).……………6分 ∵11(,)M x y 、22(,)N x y ，∴11221643k mx x k +=-+. ………7分∵12112()2y y k x x m +=++，A 满足OM ON OA λ+=，∴直线OA 的斜率2121211121214323y y k mk k k x x x x k ++==+=-++，经化简得1243k k ⋅=-. ………9分 ②若A 的坐标为3(,1)2，则223k =，由①可得12k =-. ………10分∴方程(*)可化为2216123120x mx m -+-=，下同解法一.22．本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等．满分14分. 解：（Ⅰ）函数()sin f x x =不是其定义域上的梦想函数．………………1分理由如下：()sin f x x =定义域D R =，()'cos f x x =，………………2分存在3x π=，使()'()33f f ππ>，故函数()sin h x x =不是其定义域R D =上的梦想函数．……4分ks5u（Ⅱ）()1g x ax a =+-，()'g x a =，若函数()1g x ax a =+-在(0,)x π∈上为梦想函数，则1ax a a +-<在(0,)x π∈上恒成立，………………5分即1a x <在(0,)x π∈上恒成立，因为1y x =在(0,)x π∈内的值域为1(,)π+∞，………………7分所以1a π≤．………………8分（Ⅲ）a x x h +=cos )('，由题意)()('x h x h >在[0,]x π∈恒成立，故cos sin 1x a x ax a +>++-，即cos sin 1ax x x <-+在[0,]x π∈上恒成立． ①当0x =时，0cos0sin012a ⋅<-+=显然成立；……………9分 ②当0x π<≤时，由cos sin 1ax x x <-+可得cos sin 1x x a x-+<对任意(]0,x π∈恒成立. 令cos sin 1()x x F x x -+=，则2(s i n c o s )(c o ss i n 1)'()x x x x x F x x --⋅--+=，…10分令)1sin (cos )cos sin ()(+--⋅--=x x x x x x k ，则'()(sin cos )sin()4k x x x x x π=-⋅=⋅-．当(0,]4x π∈时，因为0)('≤x k ，所以)(x k 在(0,]4π单调递减；当(,]4x ππ∈时，因为0)('≥x k ，所以)(x k 在(,]4ππ单调递增．∵(0)20k =-<，()1044k π=--<， ∴当(0,]4x π∈时，()k x 的值均为负数.∵()1044k π=--<，()0k ππ=>，∴当(,]4x ππ∈时，()k x 有且只有一个零点0x ，且0(,)4x ππ∈. ……………11分∴当0(0,)x x ∈时，0)(<x k ，所以'()0F x <，可得()F x 在0(0,)x 单调递减；当0(,)x x π∈时，0)(>x k ，所以'()0F x >，可得()F x 在0(,)x π单调递增．则00min 00cos sin 1()()x x F x F x x -+==．…………12分因为0)(0=x k ，所以00000cos sin 1(sin cos )x x x x x -+=--⋅，min 0000()()sin cos )4F x F x x x x π==--=+．…………13分∵)(x k 在(,]4ππ单调递增，02)2(<-=ππk ，012)43(>-=πk ，∴0324x ππ<<，所以01)04x π-<+<，即01()0F x -<<．ks5u又因为0()a F x <，所以a 的最大整数值为1-．…………14分。

福建省2013届高三毕业班质量检测数学文试题 Word版含答案

2013年福建省普通高中毕业班质量检查文科数学本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)．本试卷共5页．满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据x 1，x 2， …，x n 的标准差锥体体积公式V =31Sh 其中x 为样本平均数其中S 为底面面积，h 为高柱体体积公式球的表面积、体积公式 V =Sh24S R =π，343V R =π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题共60分）一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数1i z =-，z 为z 的共轭复数，则下列结论正确的是A ．1i z =--B ．1+i z =-C ．2z =D ．z =2．已知,0a b c >≠，则下列不等式一定成立的是 A ．22a b >B ．ac bc >C ．a c b c +>+D ．a b c c> 3．执行如图所示的程序框图，若输入的x 值为2，则输出的x 值为 A ．3 B ．8 C ．9 D ．63 4．“1x =”是“210x -=”的Ａ．充分而不必要条件Ｂ．必要而充分不条件Ｃ．充要条件Ｄ．既不充分也不必要条件5．函数2cos 22y x x x ππ⎛⎫=-≤≤ ⎪⎝⎭的图象是6．已知集合{}|28M x x =-≤≤，{}2|320N x x x =-+≤，在集合M 中任取一个元素x ，则 “x M N ∈ ”的概率是A ．110B ．16C ．310D ．127．已知1F ，2F 是椭圆C 的两个焦点，焦距为4.若P 为椭圆C 上一点，且12PF F ∆的周长为14，则椭圆C 的离心率e 为 A ．15 B ．25 C ．45D ．5A CD8．若变量,x y 满足约束条件310,3110,2,x y x y y --≥⎧⎪+-≤⎨⎪≥⎩则2z x y =-的最小值为A ．4B ．1C ．0D ．1- 9．设,m n 为两条不同的直线，βα,是两个不同的平面，下列命题正确的是 A ．若β//,//m n m ，则β//n B ．若αα//,//n m ，则n m // C ．若β⊥m n m ,//，则β⊥n D ．若n m n m //,,βα⊂⊂，则βα// 10．已知点()0,0O ，()1,2A ,()3,2B ，以线段AB 为直径作圆C ，则直线:30l x y +-=与圆C 的位置关系是A ．相交且过圆心B ．相交但不过圆心C ．相切D ．相离11．已知点()()()0000167n O ,,A ,,A ,,点()1212n A ,A ,,A n ,n -∈≥N 是线段0n A A 的n 等分点，则011+n n OA OA OA OA -+++等于A ．5nB ．10nC ．()51n +D ．()101n +12．定义两个实数间的一种新运算“*”：()lg 1010,x yx y *=+,x y ∈R .对任意实数,,a b c ，给出如下结论：①()()c b a c b a ****=； ②a b b a **=； ③()()()**a b c a c b c +=++；其中正确的个数是A ． 0B ．1C ．2D ．3第Ⅱ卷（非选择题共90分）二、填空题:本大题共4小题，每小题4分，共16分．把答案填在答题卡相应位置． 13．一支田径队有男运动员28人，女运动员21人，现按性别用分层抽样的方法，从中抽取14位运动员进行健康检查，则男运动员应抽取________人． 14．在ABC ∆中，角,,A B C 所对的边分别为,,a b c ．已知3a =，8b =，C=3π，则c = ．15．若函数2,0,()ln ,0x a x f x x x ⎧-≤=⎨>⎩有两个不同的零点，则实数a 的取值范围是．16．观察下列等式：12133+=； 781011123333+++=； 16171920222339333333+++++=； …则当m n <且,m n ∈N 表示最后结果.313232313333n n m m ++--++++= （最后结果用,m n 表示最后结果）．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分12分)某工厂生产,A B 两种元件，其质量按测试指标划分为：大于或等于7．5为正品，小于7．5为次品．现从一批产品中随机抽取这两种元件各5件进行检测，检测结果记录如下：由于表格被污损，数据y x ,看不清，统计员只记得x y <，且,A B 两种元件的检测数据的平均值相等，方差也相等．（Ⅰ）求表格中x 与y 的值；（Ⅱ）若从被检测的5件B 种元件中任取2件，求2件都为正品的概率． 18．(本小题满分12分)已知函数()sin cos f x x x =+，x ∈R ．（Ⅰ）求12f π⎛⎫⎪⎝⎭的值；（Ⅱ）试写出一个函数()g x ，使得()()cos 2g x f x x =，并求()g x 的单调区间． 19．(本小题满分12分)某几何体111C B A ABC -的三视图和直观图如图所示．（Ⅰ）求证：平面11AB C ⊥平面11AA C C ；（Ⅱ）若E 是线段1AB 上的一点，且满足1111191C B A ABC C AA E V V --=，求AE 的长．20．(本小题满分12分)某工业城市按照“十二五”（2011年至2015年）期间本地区主要污染物排放总量控制要求，进行减排治污．现以降低SO 2的年排放量为例，原计划“十二五”期间每年的排放量都比上一年减少0.3万吨，已知该城市2011年SO 2的年排放量约为9.3万吨，（Ⅰ）按原计划，“十二五”期间该城市共排放SO 2约多少万吨？（Ⅱ）该城市为响应“十八大”提出的建设“美丽中国”的号召，决定加大减排力度．在2012年刚好按原计划完成减排任务的条件下，自2013年起，SO 2的年排放量每年比上一年减少的百分率为p ，为使2020年这一年的SO 2年排放量控制在6万吨以内，求p 的取值范围. （参考数据9505.0328≈，9559.0329≈）． 21．(本小题满分12分)已知函数()2e xf x ax bx =++．（Ⅰ）当0,1a b ==-时，求()f x 的单调区间；（Ⅱ）设函数()f x 在点()(),P t f t ()01t <<处的切线为l ，直线l 与y 轴相交于点Q .若点Q 的纵坐标恒小于1，求实数a 的取值范围． 22．(本小题满分14分)某同学用《几何画板》研究抛物线的性质：打开《几何画板》软件，绘俯视图侧(左)视图正(主)视图1A制某抛物线2:2E y px =，在抛物线上任意画一个点S ，度量点S 的坐标(),S S x y ，如图．（Ⅰ）拖动点S ，发现当4S x =时，4S y =，试求抛物线E 的方程；（Ⅱ）设抛物线E 的顶点为A ，焦点为F ，构造直线SF 交抛物线E 于不同两点S 、T ，构造直线AS 、AT 分别交准线于M 、N 两点，构造直线MT 、NS ．经观察得：沿着抛物线E ，无论怎样拖动点S ，恒有MT //NS .请你证明这一结论．（Ⅲ）为进一步研究该抛物线E 的性质，某同学进行了下面的尝试：在（Ⅱ）中，把“焦点F ”改变为其它“定点(),0G g ()0g ≠”，其余条件不变，发现“MT 与NS 不再平行”．是否可以适当更改（Ⅱ）中的其它条件，使得仍有“MT //NS ”成立？如果可以，请写出相应的正确命题；否则，说明理由．2013年福建省普通高中毕业班质量检查文科数学试题参考解答及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数．选择题和填空题不给中间分．一、选择题：本大题考查基础知识和基本运算．每小题5分，满分60分． 1．D 2．C 3．B 4．A 5．B 6．A 7．B 8．A 9．C 10．B 11．C 12．D二、填空题：本大题考查基础知识和基本运算．每小题4分，满分16分． 13．8； 14．7； 15．01a <≤； 16．22n m -．三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．本小题主要考查古典概型、统计等基础知识，考查数据处理能力、运算求解能力以及应用意识，考查必然与或然思想等．满分12分．解：(Ⅰ)因为11=+7+75+9+95=8=858555x x x y ⋅⋅+⋅+⋅+A B （7），（6+），由=x x A B，得17x y +=． ① ………………………………………2分因为222211=1+1+0.25+1+2.25=1.1=4+8+0.25+0.25+855x y ⎡⎤--⎣⎦A B ，s （）s （）（），由22=A Bs s ，得228+8=1x y --（）（）． ② …………………………………………4分由①②解得89x y =⎧⎨=⎩，，或98.x y =⎧⎨=⎩，因为x y <，所以8x y ==． ………………………………………6分(Ⅱ) 记被检测的5件B 种元件分别为12345,,,,B B B B B ，其中2345,,,B B B B 为正品，从中任取2件,共有10个基本事件，列举如下:()12,B B ，()13,B B ，()14,B B ，()15,B B ，()23,B B ， ()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B ， ………………………………………8分记“2件都为正品”为事件C ，则事件C 包含以下6个基本事件：()23,B B ，()24,B B ，()25,B B ，()34,B B ，()35,B B ，()45,B B .……………………………10分所以63()105P C ==，即2件都为正品的概率为35. ………………………………………12分 18．本小题主要考查三角函数的图象与性质、两角和与差三角公式、二倍角公式、三角函数的恒等变换等基础知识，考查运算求解能力，考查化归与转化思想等．满分12分．解法一：(Ⅰ)因为())4f x x π=+，………………………………………3分所以1212432f ππππ⎛⎫⎛⎫=+==⎪ ⎪⎝⎭⎝⎭……………………………6分 (Ⅱ)()cos sin g x x x =-. …………………………………………………………7分下面给出证明：因为()()22(cos sin )(sin cos )cos sin cos 2,g x f x x x x x x x x =-+=-=所以()cos sin g x x x =-符合要求．……………………………………………………9分又因为()cos sin 4g x x x x π⎛⎫=-=+ ⎪⎝⎭，…………………………………………10分由222,4k x k πππππ+<+<+得3722,44k x k ππππ+<<+ 所以()g x 的单调递增区间为372244k k ππππ⎛⎫++ ⎪⎝⎭，k ∈Z .………………………………11分又由224k x k ππππ<+<+,得32244k x k ππππ-<<+,所以()g x 的单调递减区间为32244k k ππππ⎛⎫-+⎪⎝⎭，，k ∈Z .………………………………12分解法二：(Ⅰ)因为()21s i n 2,fxx =+⎡⎤⎣⎦所以231s i n 1262f ππ⎡⎤⎛⎫=+=⎪⎢⎥⎝⎭⎣⎦，………………………………3分又因为0,12f π⎛⎫>⎪⎝⎭所以12f π⎛⎫= ⎪⎝⎭．………………………………6分 (Ⅱ)同解法一．解法三：(Ⅰ)sin cos sin cos 1212123434f πππππππ⎛⎫⎛⎫⎛⎫=+=-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭sincoscossincoscossinsin34343434ππππππππ=-++…………………3分1122222222=-++2=………………………………6分 (Ⅱ)同解法一．注：若通过()()cos 2xg x f x =得到()g x 或由()()(cos sin )(cos sin )g x f x x x x x =+-两边同时约去()f x 得到()g x 不扣分．19．本小题主要考查三视图、直线与直线、直线与平面、平面与平面的位置关系，几何体的体积等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查函数与方程思想、数形结合思想、化归与转化思想．满分12分．解法一：（Ⅰ）由三视图可知，几何体111C B A ABC -为三棱柱，侧棱1111C B A AA 底面⊥，1111C A C B ⊥,且41==AC AA ，2=BC ．………………………………………2分 1111C B A AA 平面⊥ ，11111111,C B AA C B A C B ⊥∴⊂平面， …………………3分 11111111,A C A AA C A C B =⊥ ，1111ACC A C B 平面⊥∴．……………………5分又1111C AB C B 平面⊂ ， C C AA C AB 1111平面平面⊥∴．………………………6分（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分1111191C B A ABC C AA E V V --= ，,9131111AA S EF S ABC C AA ⋅=⋅∴∆∆ ……………………8分1111442443292EF ⎛⎫⎛⎫∴⨯⨯⨯⨯=⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭，解得32=EF .……………………9分在Rt ABC ∆中，AB ===，在1Rt ABB ∆中，16AB ===，……………………10分由111C B EFAB AE =， ……………………11分得22326C B EFAB AE 111=⨯=⋅=. ……………………12分解法二：（Ⅰ）同解法一.（Ⅱ）过点E 作11//C B EF 交1AC 于F ，由（Ⅰ）知，11ACC A EF 平面⊥，即EF 为C AA E 1-三棱锥的高. ………7分11111111133C AA B C B A A C B A ABC V V V ---== ，111111113191C AA B C B A ABC C AA E V V V ---==∴ ………8分,313131111111C B S EF S C AA C AA ⋅⨯=⋅∴∆∆,3111C B EF =∴ ………9分在ABC Rt ∆中，5224AB 2222=+=+=BC AC ，在1ABB Rt ∆中，()6452AB 222121=+=+=BB AB ，……………………10分由111C B EFAB AE =， ……………………11分得2AB 31AE 1==. ……………………12分 20．本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力和应用意识，考查函数与方程思想.满分12分.解：（Ⅰ）设“十二五”期间，该城市共排放SO 2约y 万吨，依题意，2011年至2015年SO 2的年排放量构成首项为9.3，公差为0.3-的等差数列，……………3分所以()55159.3(0.3)=43.52y ⨯-=⨯+⨯-（万吨）．所以按计划“十二五”期间该城市共排放SO 2约43．5万吨．……………………6分（2）由已知得， 2012年的SO 2年排放量9.60.32=9-⨯（万吨），…………………7分所以2012年至2020年SO 2的年排放量构成首项为9，公比为1p -的等比数列，…………………9分由题意得891p ⨯-（）＜6，即1p -＜832，所以10.9505p -<，解得 4.95%p >.所以SO 2的年排放量每年减少的百分率p 的取值范围4.95%1p <<<……………………12分21．本小题主要考查函数、导数等基础知识，考查推理论证能力、运算求解能力，考查分类与整合思想、数形结合思想、化归与转化思想．满分12分．解：（Ⅰ）当0,1a b ==-时，()e xf x x =-，()e 1xf x '=-，……………………1分所以，当(,0x ∈-∞时，()0f x '<；当(0,x ∈+∞时，()0f x '>；……………………3分所以函数()f x 的单调递减区间为(),0-∞，单调递增区间为(0,)+∞．……………………4分（Ⅱ）因为()2xf x e ax b '=++，所以()(),P t f t 处切线的斜率()2tk f t e at b '==++，所以切线l 的方程为()()()22t ty e at bt e at bx t -++=++-，令0x =，得()21ty t e at =-- ()01t <<.…………………………………………5分当01t <<时，要使得点Q 的纵坐标恒小于1，只需()211tt e at --<，即()2110tt e at -++>()01t <<.……………… 6分令()()211tg t t e at =-++，则()()2tg t t e a '=+，………………………………………………………… 7分因为01t <<，所以1t e e <<， ①若21a ≥-即12a ≥-时，20t e a +>，所以，当()0,1t ∈时，()0g t '>，即()g t 在()0,1上单调递增，所以()(0)0g t g >=恒成立，所以12a ≥-满足题意.………………………………8分 ②若2a e ≤-即2ea ≤-时，20t e a +<，所以，当()0,1t ∈时，()0g t '<，即()g t 在()0,1上单调递减，所以()(0)0g t g <=，所以2ea ≤-不满足题意.………………………………………9分 ③若21e a -<<-即122e a -<<-时，0ln(2)1a <-<.则t 、()g t '、()g t 的关系如下表：所以()()ln(2)00g a g -<=，所以22a -<<-不满足题意.……………………11分综合①②③，可得，当12a ≥-时，()0g t >()01t <<时，此时点Q 的纵坐标恒小于1.…………12分22．本小题主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想、数形结合思想等．满分14分．解法一：（Ⅰ）把4S x =，4S y =代入22y px =，得248p =，……………………2分所以2p =，………………………………………………………………………3分因此，抛物线E 的方程24y x =．…………………………………………………4分（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意可设直线:1l my x =-，由241y x my x ⎧=⎨=-⎩，得2440y my --=，则121244.y y m y y +=⎧⎨⋅=-⎩， ①……………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，所以12211,y MT x y x ⎛⎫=++ ⎪⎝⎭ ，21121,y NS x y x ⎛⎫=++ ⎪⎝⎭ ， ……………………7分又因为()()1221121211y y y x y x x x ⎛⎫⎛⎫++-++ ⎪ ⎪⎝⎭⎝⎭……………………………………8分 2221121241411144y y y y y y ⎛⎫⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22122112*********4y y y y y y y y y y ⎛⎫⎛⎫=+++-+++ ⎪ ⎪⎝⎭⎝⎭()21121212144y y y y y y y y -=-+()22121212164y y y y y y ⎛⎫-=- ⎪⎝⎭， ②把①代入②，得()221212121604y y y y y y ⎛⎫--= ⎪⎝⎭，………………………………………………10分即()()12211212110y y y x y x x x ⎛⎫⎛⎫++-++= ⎪ ⎪⎝⎭⎝⎭，所以//MT NS，又因为M 、T 、N 、S 四点不共线，所以MT //NS ．………………………………11分（Ⅲ）设抛物线2:4E y x =的顶点为A ，定点()(),00G g g ≠，过点G 的直线l 与抛物线E 相交于S 、T 两点，直线AS 、AT 分别交直线x g =-于M 、N 两点，则MT //NS ．……………………14分解法二：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()221122,2,,2S t t T t t ，……………………5分依题意,可设直线:1ST l my x =-，由241y x my x ⎧=⎨=-⎩得2440y my --=，则1212224,224,t t m t t +=⎧⎨⋅=-⎩所以12124,1.t t m t t +=⎧⎨⋅=-⎩…………………………………………………………………………7分又因为2:2AS l y t x =-，1:2AT l y t x =-，所以()21,2M t -，()11,2N t -，………………………………………………………10分所以0MT k =，0NS k =，…………………………………………………………………10分又因为M 、T 、N 、S 四点不共线，所以MT //NS .…………………………………11分（Ⅲ）同解法一. 解法三：（Ⅰ）同解法一.（Ⅱ）因为抛物线E 的焦点为()1,0F ，设()()1122,,,S x y T x y ，依题意，设直线:1l my x =-，由241y x my x ⎧=⎨=-⎩得2440y my --=，则121244y y m y y +=⎧⎨⋅=-⎩，……………………………6分又因为11:AS y l y x x =，22:AT yl y x x =，所以111,y M x ⎛⎫-- ⎪⎝⎭，221,y N x ⎛⎫-- ⎪⎝⎭，又因为212y y x ⎛⎫--⎪⎝⎭2212111222224404y y y y y y y y x y y +=+=+=+==，……………………9分所以212y y x =-，所以NS 平行于x 轴；同理可证MT 平行于x 轴；又因为M 、T 、N 、S 四点不共线，所以MT //NS .………………………………11分（Ⅲ）同解法一. …………………………………………………14分。

福建晋江养正中学2019年高三5月抽考数学文

福建晋江养正中学2019年高三5月抽考数学文福建省晋江市养正中学 2018届高三5月月考数学〔文〕试题【一】选择题：本小题共12小题，每题5分，共60分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的.请把答案填涂在答题纸的相应位置.1. 设复数)21)(43(i i z +-=〔i 是虚数单位〕，那么复数z 的虚部为( )A 、2- B. 2 C. i 2- D. i 22. 集合}05|{2<-=x x x M ，}6|{<<=x p x N ，那么}2|{q x x N M <<= ，那么q p +等于( )A 6B 7C 8D 93. 某程序的框图如下图,执行该程序，假设输入的p 为24，那么输出的S n ,的值分别为( )A.30,4==S nB.30,5==S nC.45,4==S nD.45,5==S n4.()f x 是定义在R 上的偶函数，且以2为周期，那么“()]f x 为[0,1上的增函数”是“()[3,4]f x 为上的减函数”的( ) A 、充分不必要条件 B 、必要不充分条件 C 、充分必要条件 D 、既不充分也不必要条件那么当00x x <<时，函数()f x ( )A 、恒为正值B 、等于0C 、恒为负值D 、不大于06. 假设当4x π=时，函数()sin()(0)f x A x A ϕ=+>取得最小值，那么函数3()4y f x π=-是( )A 、奇函数且图象关于点(,0)2π对称 B 、偶函数且图象关于点(,0)π对称C 、奇函数且图象关于直线2x π=对称 D 、偶函数且图象关于点(,0)2π对称7. 一个几何体的三视图如右图所示，那么它的体积为( )A. 203B. 403C. 20D. 408. m 、n 、l 是三条不同的直线，α、β、γ是三个不同的平面， ① 假设,//m n αα⊂，那么//m n ； ② 假设l m l n m ⊥=⋂⊥⊂⊂,,,,βαβαβα，那么n m ⊥；③ 假设//n m ，m α⊂，那么//n α； ④ 假设//αγ，//βγ，那么//αβ、其中正确命题的序号是() A.②④ B.②③C.③④D.①③9.函数13y x x=-的图象大致为()10.两旅客坐火车外出旅游，盼望座位连在一起，且仅有一个靠窗，火车上的座位的排法如表格所示，那么以下座位号码符合要求的是()A 、48，49B 、62，63C 、84，85D 、75，7611.过双曲线22221(0,0)x y a b a b -=>>的左焦点(,0)(0)F c c ->，作圆2224a x y +=的切线，切点为E ，延长FE 交双曲线右支于点P ，假设2OP OE OF=-uur uu u r uu u r ，那么双曲线的离心率为() ABCD12.为提高信息在传输中的抗干扰能力，通常在原信息中按一定规那么加入相关数据组成传输信息、设定原信息为012i a a a a ，{01}∈，〔012i =，，〕，传输信息为00121h a a a h ，其中00110h a a h h a =⊕=⊕，，⊕运算规那么为：000⊕=，011⊕=，101⊕=，110⊕=，例如原信息为111，那么传输信息为01111、传输信息在传输过程中受到干扰可能导致接收信息出错，那么以下接收信息一定有误的是〔〕 A 、11010B 、01100C 、 00011D 、10111【二】填空题(本大题共4小题，每题4分，共16分)13、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.依照收集到的数据(如下表〕，由最小二乘法求得回归方程9.5467.0+=x y现发明表中有一个数据模糊看不清，请你推断出该数据的值为______ 14、实数x ，y 满足⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ，那么y x z 3-=的最小值是.15、向量),1(x =，),1(x -=，假设b a -2与b 垂直，那么b =16、ABC ∆的顶点,A B 分别是离心率为e 的圆锥曲线221x y m n+=的焦点，顶点C 在该曲线上；一同学已正确地推得：当0m n >>时，有C B A e sin )sin (sin =+，类似地，当0,0m n ><时，有.【三】解答题：本大题共6个小题，共74分，解答时应写出文字说明证明、过程或推演步骤. 17、(本小题总分值12分〕等差数列{}n a 的前n 项和为n S ，且满足24a =，3417a a +=、(1)求{}n a 的通项公式；(2)设22n a n b +=，证明数列{}n b 是等比数列并求其前n 项和n T 。

中学高三数学5月月考试题文新人教A版

养正中学高三5月月考数学（文）试题一、选择题：本小题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把答案填涂在答题纸的相应位置.1. 设复数)21)(43(i i z +-=（i 是虚数单位），则复数z 的虚部为( ) A ．2- B. 2C. i 2-D. i 22. 已知集合}05|{2<-=x x x M ，}6|{<<=x p x N ，则}2|{q x x N M <<=I ，则q p +等于( )A 6B 7C 8D 93. 某程序的框图如图所示,执行该程序，若输入的p 为24，则输出的S n ,的值分别为( )A.30,4==S nB.30,5==S nC.45,4==S nD.45,5==S n4. 已知()f x 是定义在R 上的偶函数，且以2为周期，则“()]f x 为[0,1上的增函数”是“()[3,4]f x 为上的减函数”的( ) A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5. 已知函数21()()log 5x f x x =-，若0x 是函数()y f x =的零点，则当0x x <<时，函数()f x ( )A ．恒为正值B ．等于0C ．恒为负值D ．不大于06. 若当4x π=时，函数()sin()(0)f x A x A ϕ=+>取得最小值，则函数3()4y f x π=-是( )A ．奇函数且图象关于点(,0)2π对称 B ．偶函数且图象关于点(,0)π对称C ．奇函数且图象关于直线2x π=对称 D ．偶函数且图象关于点(,0)2π对称7. 一个几何体的三视图如右图所示，则它的体积为( )A. 203 B. 403 C. 20 D. 408. 已知m 、n 、l 是三条不同的直线，α、β、γ是三个不同的平面，给出以下命题：若,//m n αα⊂，则//m n ；若l m l n m ⊥=⋂⊥⊂⊂,,,,βαβαβα，则n m ⊥；若//n m ，m α⊂，则//n α；若//αγ，//βγ，则//αβ．其中正确命题的序号是( )A. ②④B. ②③C. ③④D. ①③ 9. 函数13y x x =-的图象大致为( )10. 两旅客坐火车外出旅游，希望座位连在一起，且仅有一个靠窗，已知火车上的座位的排法如表格所示，则下列座位号码符合要求的是()A．48，49 B．62，63 C．84，85 D．75，7611. 过双曲线22221(0,0) x ya ba b-=>>的左焦点(,0)(0)F c c->，作圆2224ax y+=的切线，切点为E，延长FE交双曲线右支于点P，若2OP OE OF=-uur uu u r uu u r，则双曲线的离心率为( )A．10B．10C．10D．212. 为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息．设定原信息为012ia a a a，{01}∈，（012i=，，），传输信息为00121h a a a h，其中001102h a a h h a=⊕=⊕，，⊕运算规则为：000⊕=，011⊕=，101⊕=，110⊕=，例如原信息为111，则传输信息为01111．传输信息在传输过程中受到干扰可能导致接收信息出错，则下列接收信息一定有误的是（）A．11010 B．01100 C．00011 D．10111二、填空题(本大题共4小题，每小题4分，共16分)13．某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表），由最小二乘法求得回归方程9.5467.0+=xy)现发现表中有一个数据模糊看不清，请你推断出该数据的值为______14．已知实数x，y满足⎪⎩⎪⎨⎧≤≥+≥+-35xyxyx，则yxz3-=的最小值是.15、已知向量),1(x a =，),1(x b -=，若b a ρ-2与b ρ垂直，则b =r16．已知ABC ∆的顶点,A B 分别是离心率为e 的圆锥曲线221x y m n +=的焦点，顶点C 在该曲线上；一同学已正确地推得：当0m n >>时，有C B A e sin )sin (sin =+，类似地，当0,0m n ><时，有 .三、解答题：本大题共6个小题，共74分，解答时应写出文字说明证明、过程或推演步骤.17．(本小题满分12分）已知等差数列{}n a 的前n 项和为nS ，且满足24a =，3417a a +=．(1)求{}n a 的通项公式； (2)设22n a n b +=，证明数列{}n b 是等比数列并求其前n 项和nT 。

福建省晋江市养正中学2013届高三上学期第一次月考语文试题(无答案)

养正中学2013届高三第一次月考语文试题本试卷分五大题。

满分150分，考试时间150分钟。

一、古代诗文阅读(46分)（一）默写常见的名句名篇（10分）1．补写下列名句名篇中的空缺部分。

（10分）（1）夙兴夜寐，。

（《诗经•氓》）（2），非能水也，而绝江河。

（《荀子•劝学》）（3）高余冠之岌岌兮，。

（屈原《离骚》）（4）此中有真意，。

（陶潜《饮酒》）（5）气息奄奄，，朝不虑夕。

（李密《陈情表》）（6）黄鹤之飞尚不得过，。

（李白《蜀道难》）（7）寄蜉蝣于天地，。

（苏轼《赤壁赋》）（8），山岳潜形。

(范仲淹《岳阳楼记》)（9）无丝竹之乱耳，___________________ 。

（刘禹锡《陋室铭》）（10）浩荡离愁白日斜，。

（龚自珍《己亥杂诗》）（二）文言文阅读（30分）阅读下面的文言文，完成2—6题。

（18分）专诸者，吴堂邑人也。

伍子胥之亡楚而如吴也，知专诸之能。

伍子胥既见．吴王僚，说以伐楚之利。

吴公子光曰：‚彼伍员父兄皆死于楚而员言伐楚，欲自为报私仇也，非能为吴。

‛吴王乃止。

伍子胥知公子光之．欲杀吴王僚，乃曰：‚彼光将有内．志，未可说以外事。

‛乃．进专诸于公子光。

……（节选自《史记•刺客列传》）2．下列各组句子中，加点词的意义相同的一组是（）（3分）A．伍子胥既见．吴王僚图穷而匕首见．B．彼光将有内．志距关，毋内．诸侯C．将兵．围楚之灊项羽兵．四十万D．而具．酒请王僚私见张良，具．告以事3．下列各组句子中，加点词的意义和用法相同的一组是（）（3分）A．伍子胥知公子光之．欲杀吴王僚非蛇鳝之．穴无可寄托者B．乃．进专诸于公子光度我至军中，公乃．入C．光既．得专诸始皇既．没，余威震于殊俗D．使专诸置匕首鱼炙之腹中而．进之因人之力而．敝之4．下列各组句子中，分别与例句①加点字活用类型相同、与例句②句式相同的一组是（）（3分）例句①：善客．待之例句②：季子虽来，不吾废也A．天下云．集响应大王来何操B．吾从而师．之所以兴怀，其致一也C．吾得兄．事之客有吹洞箫者D．以其乃华山之阳名．之也然而不王者，未之有也5．下列对原文有关内容的理解和分析，不正确的一项是（）（3分）A．公子光认为伍子胥所说得攻打楚国是为了报私仇，因此不采纳他的建议。

高三语文月考试题带答案-晋江市养正中学届高三5月月考试题

养正中学2013届高三5月月考语文试题一、古代诗文阅读(27分)（一）默写常见的名句名篇(6分)1．补写出下列名句名篇中空缺的部分。

(6分)（1）进不入以离尤兮，。

（屈原《离骚》）（2），钟鸣鼎食之家。

（王勃《滕王阁序》））（3）元嘉草草，封狼居胥，。

（辛弃疾《京口北固亭怀古》）（4），衣冠简朴古风存。

（陆游《游山西村》）（5）猥以微贱，当侍东宫，。

（李密《陈情表》）（6），色愈恭，礼愈至。

（宋濂《送东阳马生序》）（二）文言文阅读（15分）阅读下面的文言文，完成2～5小题。

传是楼记〔清〕汪琬昆山徐健庵先生，筑楼于所居之后，凡七楹。

间命工木为橱，贮书若干万卷，区为经史子集四种，经则传注义疏之书附焉，史则日录家乘山经野史之书附焉，子则附以卜筮医药之书，集则附以乐府诗余之书，凡为橱者七十有二，部居类汇，各以其次．，素标缃帙①，启钥灿然。

于是先生召诸子登斯楼而诏之曰：“吾何以传女曹哉？吾徐先世，故以清白起家，吾耳目濡染旧．矣。

盖尝慨夫为人之父祖者，每欲传其土田货财，而子孙未必能世富也；欲传其金玉珍玩、鼎彝尊斝②之物，而又未必能世宝．也；欲传其园池台榭、舞歌舆马之具，而又未必能世享其娱乐也。

吾方以此为鉴。

然则吾何以传女曹哉？”因指书而欣然笑曰：“所传者惟是矣！”遂名其楼为“传是”，而问记于琬。

琬衰病不及为，则先生屡书督之，最后复于先生曰：甚矣，书之多厄也！由汉氏以来，人主往往重官赏以购之，其下名公贵卿，又往往厚金帛以易之，或亲操翰墨，及分命笔吏以缮录之。

然且裒聚未几，而辄至于散佚，以是知藏书之难也。

琬顾．谓藏之之难不若守之之难，守之之难不若读之之难，尤不若躬体而心得之之难。

是故藏而勿守，犹勿藏也；守而弗读，犹勿守也。

夫既已读之矣，而或口与躬违，心与迹忤，采其华而忘其实，是则呻佔③记诵之学所为哗众而窃名者也，与弗读奚以异哉！古之善读书者，始乎博，终乎约，博之而非夸多斗靡也，约之而非保残安陋也。

善读书者根柢于性命而究极于事功：沿流以溯源，无不探也；明体以适用，无不达也。

福建省晋江市养正中学2012-2013学年高二数学下学期第一次月考试题文新人教A版

养正中学2012-2013学年高二下学期第一次月考数学文试题参考公式：线性回归方程ˆˆˆy bx a =+的系数公式：1122211()()ˆ()nniii ii i nniii i x x y y x y nxybx x xnx ====---==--∑∑∑∑，ˆˆa y bx =-。

2×2列联表2K 公式：22()()()()()n ad bc K a b c d a c b d -=++++（其中d c b a n +++=为样本容量），2K 的临界值表：2()P K k ≥ 0.500.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.828一、选择题（本题共12个小题，每小题只有一个正确答案，每小题5分，共60分）1.复数2)1(i -的值是（） A. i 2 B. i 2- C. 2 D. 2-2．某质点按规律()23s t t =+（s 单位：m ，t 单位：s ）作变速直线运动，则该质点在1t =时的瞬时速度为（）A ．2 /m sB ．3 /m sC ．4 /m sD ．5/m s 3．如图所示，图中有5组数据，去掉组数据后（填字母代号），剩下的4组数据的线性相关性最强（）A. EB. CC. DD. A4．复数i z a b =+),(R b a ∈的虚部记作()Im z b =，则1Im 2i ⎛⎫= ⎪+⎝⎭（） A ．13 B ．25 C ．13- D ．15-5．用反证法证明命题：“三角形的内角中至少有一个不大于60”时，反设正确的是（）A.假设三内角都不大于60 B.假设三内角都大于60 C.假设三内角至多有一个大于60 D.假设三内角至多有两个大于606．函数e e xy x =-的单调递增区间（） A ．(),0-∞B ．(),1-∞ C ．()0,+∞D ．()1,+∞7.在两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的2R 如下，其中拟合效果最好的模型是（）A. 模型1的2R 为0.975 B.模型2的2R 为0.79 C. 模型3的2R 为0.55 D.模型4的2R 为0.25 8．下面几种推理过程是演绎推理的是（）A. 由平面三角形的性质，推测空间四面体性质.B ．两条直线平行，同旁内角互补，如果A ∠和B ∠是两条平行直线的同旁内角，则180A B ∠+∠=︒.C.某校高三共有10个班，1班51人，2班53人，3班52人，由此推测各班都超过50人.D.在数列{}n a 中，()111111,22n n n a a a n a --⎛⎫==+≥ ⎪⎝⎭，由此归纳出{}n a 的通项公式.9.方程3269100x x x -+-=的实根个数是（） A.3B.2C.1D.010.已知()f x 为R 上的可导函数，且x R ∀∈，均有()()f x f x '>，则有（）A ．2013(2013)(0)e f f -<，2013(2013)(0)f e f > B ．2013(2013)(0)ef f -<，2013(2013)(0)f e f <C ．2013(2013)(0)e f f ->，2013(2013)(0)f e f >D ．2013(2013)(0)e f f ->，2013(2013)(0)f e f < 11、复数i i+-11与复数i 31-在复平面上所对应的向量分别是OB OA ,，O 为原点，则这两个向量的夹角AOB ∠等于（）A. 6π B ．4π C. 3π D.2π12．己知函数)(x f 是定义域为R 的奇函数，且1)5(-=-f ，)(x f 的导函数)(x f y '=的图象如图所示。

福建省晋江养正中学2013届高三上学期第一次月考数学理试题

晋江养正中学2012-2013学年度高三第一次月考数学试题 (理科)（完卷时间120分钟满分150分命卷：郑明铿审核：高三数学备课组）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一个是符合题目要求的.1.已知集合{}0≥=x x A ，{}2,1,0=B ，则（）（A ）B A ⊆ （B ）A B ⊆ （C ）B B A = （D ）∅=B AA. ),1(+∞B. ),1()1,0(+∞⋃C.)0,1()1,(-⋃--∞D. )1,0()0,(⋃-∞3. 若x R ∈，则“12x -≤≤”是“1x <”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4. 的切线方程是上的点过曲线)21(13，xx y +=( ) A ．x y 2= B ．32+=x y C ．24-=x y D ．32-=x y5．已知函数()f x 是定义在R 上的奇函数，当0x >时，()2,(3)xf x f =-则的值是（） A ．18 B ．18-C ．8D ．-86. 已知幂函数()f x 图象过点)2,2(P ，则)5(f 等于（）A ．10B ．16C ．25D ．327. 已知函数K x A y ++=)sin(ϕω的一部分图象如右图所示，如果2||,0,0πϕω<>>A ，则( )A ．A=4B ．K=48. 将函数x y 2sin =的图象向右平移4π个单位，所得函数图象对应的解析式为( ) A ．sin(2)4y x π=-B ．sin 2y x =-C ．cos 2y x =-D ．cos 2y x =9．函数13)(||+-=x x f 的图象大致是( )10. 对于非空集合A 、B,定义运算}.,|{B A x B A x x B A ⋂∉⋃∈=⊕且已知两个开区间),(b a M =,),(d c N =，其中d c b a ,,,满足0,<=+<+cd ab d c b a ，则N M ⊕=（）A ．),(),(d c b a ⋃ B. ),(),(d b c a ⋃ C. ),(),(c b d a ⋃ D. ),(),(b d a c ⋃ 二、填空题（每小题4分，共20分）11. 已知sin 2cos =αα，那么tan 2α的值为．12．如图，角θ的始边OA 落在ox 轴上，其始边、终边与单位圆分别交于点C A ,， θ∈(0,2π), 且△AOB 为等边三角形.若点C 的坐标为(532,513)，则BOC ∠cos 的值为____． 13．设a =⎰+π)cos (sin dx x x ，则二项式6)1(xx a -展开式中2x 的系数为 .（用数字作答）14. 若x ∆趋近于0时，xx ∆-∆+--332)2(趋近于定数M ，则M 的值为 .15. 已知定义域为),0(+∞的单调函数)(x f ,若对任意),0(+∞∈x ，都有三、解答题（解答请写出详细的过程和步骤，共80分）： 16. 已知函数()=x f .cos sin sin 32x x x +（Ⅰ）求函数)(x f 在区间],2[ππ上的零点；（Ⅱ）设x x f x g 2sin 3)()(-=，求函数)(x g 的图象的对称轴方程.17. 甲、乙两班参加数学知识竞赛，每班出3人组成代表队，每人一道必答题，答对为本队得1分，答错或不答得0分，假如甲队每人答对的概率均为32，乙队3人答对的概率分别为32、32、21，且每人回答正确与否相互之间没有影响，用ξ表示甲队总得分数. （Ⅰ）求随机变量ξ的分布列与均值)(ξE ；（Ⅱ）用A 表示事件“甲、乙两队得分和为3”，B 表示事件“甲队得分大于乙队得分”，求P(AB) ．18. 已知函数()=x f 1cos 5sin cos 352++x x x .（Ⅰ）求函数()x f 的周期及()x f 的最大值和最小值；（Ⅱ）求()x f 在[]π,0上的单调递增区间.19．某工厂生产某种产品，每日的成本C (单位：元）与日产里x (单位:吨）满足函数关系式x C 2010000+=，每日的销售额R (单位:元）与日产量x 满足函数关系式⎪⎩⎪⎨⎧≥<<++-=.120,20400,1200,29030123x x x ax x R已知每日的利润C R y -=，且当30=x 时100-=y .(I)求a 的值；(II)当日产量为多少吨时，毎日的利润可以达到最大,并求出最大值.20. 已知函数32()23f x ax x =-，其中0>a ．（Ⅰ）求证：函数)(x f 在区间(,0)-∞上是增函数；（Ⅱ）若函数[]()()()(0,1)g x f x f x x '=+∈在0x =处取得最大值，求a 的取值范围．21. 已知函数ax x a a x x f 2ln )2143(21)(22-++=，R a ∈. (Ⅰ)当21-=a 时，求函数)(x f 的极值点； (Ⅱ)若函数)(x f 在导函数)(x f '的单调区间上也是单调的，求a 的取值范围； (Ⅲ) 当810<<a 时，设x a x a x a a x f x g )12()21(ln )12143()()(22+++-++-=，且21,x x 是函数)(x g 的极值点，证明：2ln 23)()(21->+x g x g .高三第一次月考数学试题 (理科) 答案一、选择题：BDBAD CDCAB 二、填空题 11. 34-12． 10613- 13．－192 14. 163- 15. 2 三、解答题16.解：（Ⅰ）法一：令0)(=x f ，得0)cos sin 3(sin =+x x x ………………2分所以,0sin =x 或33tan -=x . ……………………4分由].,2[,0sin ππ∈=x x 得π=x ……………………6分由33tan -=x ，].,2[ππ∈x 得65π=x …………8分综上，)(x f 的零点为π=x 或65π=x .法二：23)32sin(2sin 21)2cos 1(23)(+-=+-=πx x x x f …………3分令0)(=x f ，得23)32sin(-=-πx ………5分因为],,2[ππ∈x 所以]35,32[32πππ∈-x ……7分所以，当3432ππ=-x ，或3532ππ=-x 时，0)(=x f ……8分综上，)(x f 的零点为π=x 或65π=x .（Ⅱ）x x x x g 2sin 21cos sin )(==，……9分由2()2x k k Z ππ=+∈得：,()24k x k Z ππ=+∈……12分即函数()g x 的图象的对称轴方程为： ,()24k x k Z ππ=+∈……13分17.解：（Ⅰ）ξ的可能取值为0，1，2，3；…………… 1分而P(ξ=0)=271，P(ξ=1)=92，P(ξ=2)=94，P(ξ=3)=278 …………… 5分因而ξ的分布列为…………… 6分)(ξE =2…………… 8分（Ⅱ）P(AB)=24334………… 13分 18.解：（Ⅰ）()=x f 122cos 152sin 235cos 6sin sin cos 3522++⋅+=++xx x x x x …2分2762sin 5272cos 52sin 35+⎪⎭⎫ ⎝⎛+=++=πx x x ………………………4分ππ==∴22T …………………5分()23,217-为的最大值和最小值分别x f ………………7分（Ⅱ）()x f 的单调递增区间为226222πππππ+≤+≤-k x k ……………9分63ππππ+≤≤-∴k x k ……………10分60,63,0πππ≤≤∴≤≤-∴=x x k 令……11分ππππ≤≤∴≤≤=x x k 32,6732,1……12分所以，[]π,0上的单调递增区间为⎥⎤⎢⎡⎥⎤⎢⎡πππ,2,,0……………13分20.（Ⅰ）证明：)1(666)(2-=-='ax x x ax x f ．因为0>a 且0<x ，所以0)(>'x f ．所以函数)(x f 在区间()0,∞-上是增函数． ………6分（Ⅱ）由题意[]32()2(63)6,0,1g x ax a x x x =+--∈.则22()62(63)66(21)1g x ax a x ax a x '⎡⎤=+--=+--⎣⎦. …………8分令0)(='x g ，即2(21)10ax a x +--=. ①由于0142>+=∆a ，可设方程①的两个根为1x ，2x ，由①得ax x 121-=，由于，0>a 所以021<x x ，不妨设210x x <<， 12()6()()g x a x x x x '=--．当102<<x 时，)(2x g 为极小值，所以在区间[]1,0上，()g x 在0=x 或1=x 处取得最大值；当2x ≥1时，由于)(x g 在区间[]1,0上是单调递减函数，所以最大值为)0(g ，综上，函数)(x g 只能在0=x 或1=x 处取得最大值． …………11分又已知)(x g 在0=x 处取得最大值，所以)0(g ≥)1(g ，即0≥98-a ，解得a ≤89，又因为0>a ，所以∈a （89,0］． ………14分21. 解: (Ⅰ)f(x)= 12 x 2- 116 lnx+x （0>x ）f’(x)=x - 116x + 1=16x 2+16x-116x=0∴x 1=-2- 5 4 ，x 2=-2+ 5 4 ………1分∵(0，-2+ 54]单调减 [-2+ 54，+∞)单调增……… 2分 ∴f(x)在x= -2+ 54时取极小值………3分(Ⅱ)解法一：f’(x)=x 2-2ax+ 34 a 2+ 12ax)0(>x ………4分令g(x)=x 2-2ax+ 34 a 2+ 12a ， △=4a 2-3a 2-2a=a 2-2a ，设g(x)=0的两根)(,2121x x x x <10当△≤0时即0≤a ≤2，f’(x)≥0∴f(x)单调递增，满足题意………5分20当△>0时即a<0或a>2时(1)若210x x <<，则 34 a 2 + 12 a<0 即- 23<a<0时,)(x f 在),0(2x 上减，),(2+∞x 上增f’(x)=x+ 34 a 2 + 12 a x -2a ,f’’(x)=1- 34 a 2 + 12a x2≥0 ∴f ’(x) 在(0，+∞)单调增，不合题意………6分(2)若021<<x x 则⎪⎩⎪⎨⎧<≥+021432a a a ,即a ≤- 23时f(x)在(0，+∞)上单调增，满足题意。

福建省泉州五中高三数学5月月考试题文新人教A版

2013届高三文科数学模拟考试卷一选择题：（每小题5分，共60分）1.若复数z 满足12ii z+=（i 为虚数单位），则z 的虚部为（）A.2iB.2C.1D.1-2．根据右边程序框图，若输出y 的值是4，则输入的实数x 的值为（）A ．1B ．2-C ．1或2D ．1或2-3．用单位立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值与最大值分别为（）A ．9与13B ．7与10C ．10与16D ．10与154．从点(P 向圆221x y +=作两条切线PA 、PB ，切点为A 、B 。

则弦AB 所在的直线的倾斜角的大小为（）A ．6πB ．3πC ．23π D ．56π 5.若数列{}n a 的通项公式是(1)(32)n n a n =--，则1210a a a ++⋯+等于( )A.12-B.15-C.12D.156.在面积为S 的矩形ABCD 内随机取一点P ，则PBC ∆的面积小于4S的概率是（） A.61 B.41 C.31D.21 7.已知函数()cos(2)f x x ϕ=+满足()(1)f x f ≤对R x ∈恒成立，则( )A.函数(1)f x +一定是偶函数B.函数(1)f x -一定是偶函数C.函数(1)f x +一定是奇函数D.函数(1)f x -一定是奇函数8．若椭圆2215x y m+=的离心率e =，则m 的值为（）A ．1 BCD ． 3或2539.甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，1x，2x 分别表示甲乙两名运动员这项测试成绩的平均数，1s ，2s 分别表示甲乙两名运动员这项测试成绩的标准差，则有( )A. 1212,x x s s ><B. 1212,x x s s =<C. 1212,x x s s ==D 1212,x x s s <>.10．在棱长为2的正方体ABCD －A 1B 1C 1D 1中，点E ，F 分别是棱AB ，BC 的中点，则点C 1到平面B 1EF 的距离是（）ABC ．83D ．4311．若01a <<，且函数()|log |a f x x =，则下列各式中成立的是（）A ．11(2)34f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭B ．11(2)43f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C ．11(2)34f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D ．11(2)43f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭12.给定集合A ，若对于任意,a b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合，给出如下四个结论:①集合{}4,2,0,2,4A =--为闭集合; ②集合{}3,1,0,1,3A =--为闭集合; ③集合{}|3,Z A n n k k ==∈为闭集合; ④若集合A 1，A 2为闭集合，则12A A 为闭集合;其中正确．．结论的序号．．是( ) A. ①B. ②C. ③D. ④二、填空题（每题4分，共16分）13．从长度分别为2，3，4，5的线段中任取三条，则以这三条线段为边可以构成三角形的概率是。

福建省晋江市养正中学2013届高三第一次月考化学试题.pdf

可能用到的相对原子质量H -1 C-12 N-14 O-16 Al- 27 S-32 Fe -56 Cu -64 一、选择题，每小题只有一个选项。

（每小题2分，共20分） 1．化学与工农业生产和人类生活密切相关。

下列说法错误的是 ?A．医院用BaCO3代替BaSO4作“钡餐”?B．生石灰、硅胶是食品包装中常用的干燥剂?C．“雨后彩虹”是与胶体、光学等知识有关的自然现象?D．为防止月饼等富脂食品氧化变质，常在包装袋中放入硫酸亚铁 .下列有关物质分类或归纳的说法中，正确的数目有 ①氨水、冰醋酸、水都是电解质 ②漂白粉、水玻璃都是混合物 ③干馏、裂化、盐析都是化学变化 A．1 B．2 C．3 D．0 3.下列表述正确的是 ①人造刚玉的熔点很高，可用作高级耐火材料，主要成分是二氧化硅　②化学家采用玛瑙研钵摩擦固体反应物进行无溶剂合成，玛瑙的主要成分是硅酸盐　③提前建成的三峡大坝使用了大量水泥，水泥是硅酸盐材料　④夏天到了，游客佩戴由添加氧化亚铜的二氧化硅玻璃制作的变色眼镜来保护眼睛　⑤太阳能电池可采用硅材料制作，其应用有利于环保、节能A.①②③B.②④C.③④⑤D.③⑤ 4．若NA表示阿伏加德罗常数，下列说法正确的是 A．标况下，8g SO3分子的体积为2.24L B．1molFeCl3与沸水反应生成胶体后，含有NA个Fe(OH)3胶粒NA个氧原子 5．下列离子方程式正确的是 A、向Na2S2O3溶液中通入足量氯气：S2O32－＋2Cl2＋3H2O＝2SO32－＋4Cl－＋6H＋C. Na投入水中：Na+2H2O=Na++2OH-+H2↑ D、过量铁粉与氯化铁溶液反应： Fe3+ + Fe=2Fe2+ 6．钡和钠相似，也能形成O的过氧化物，则下列叙述错误的是A．过氧化钡的化学式是Ba2O2 B．1 mol过氧化钠或过氧化钡跟足量水反应都生成0.5 mol氧气 C．过氧化钡是离子化合物 D．过氧化钠和过氧化钡都是强氧化剂．下列对焰色反应实验操作注意事项的说明，正确的是①钾的火焰颜色，要透过蓝色钴玻璃观察　②先把铂丝灼烧到与原来火焰颜色相同，再蘸取被检验的物质　③每次实验后，要用盐酸把铂丝洗净　④实验时最好选择本身颜色较微弱的火焰　A．仅有③不正确 B．仅有④不正确 C．仅有不正确 D．全对 . 下列反应中，浓硝酸既表现氧化性，又表现出酸性的是①浓硝酸中滴入石蕊试液并微热②氧化亚铁与浓硝酸反应③氢氧化铝与浓硝酸反应④碳与浓硝酸A.①② B.③④ C.①④ D.②③ 9．用类推的方法可能会得出错误结论，因此推出的结论要经过实践的检验才能确定其正确与否．下列类推结论中正确的是A．Na失火不能用CO2灭火，K失火不能用CO2灭火 B．工业上电解熔融MgCl2制取金属镁，也用电解熔融AlCl3的方法制取金属铝 C．Al与S直接化合可以得到Al2S3，Fe与S直接化合也可以得到Fe2S3 D．Fe3O4可以写成FeO·Fe2O3，Pb3O4也可写成PbO·Pb2O3 离子要求AK+、A1O2-、Cl-、MnO4－c（K+）＜c（Cl-） BFe3+、NO3-、I-、HCO3- 逐滴滴加盐酸立即有气体产生CNa+、Al3+、Cl-、SO42-逐滴滴加NaOH溶液先有沉淀产生，后沉淀消失DNH4+、Al3+、SO42-、CH3COOH滴加NaOH浓溶液立刻有气体产生二、选择题，每小题只有一个选项。