《相交线与平行线》证明题专项训练B

合集下载

(B卷)湘教版七年级下册数学第4章相交线与平行线含答案

湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题，共计45分)1、已知∠α的两边分别与∠β的两边垂直，且∠α=20°，则∠β的度数为（）A.20°B.160°C.20°或160°D.70°2、如图，已知，那么（）.A. B. C. D.3、如图，在△ABC中，∠C＝90°，AC＝2，∠B＝30°，点P是BC边上一动点，连接AP，则AP的长度不可能是（）A.2B.3C.4D.54、如果两个角的两边分别平行，而其中一个角比另一个角的3倍少20°，那么这两个角是（）A.50°、130°B.都是10°C.50°、130°或10°、10°D.以上都不对5、如图，把长方形纸片ABCD沿EF对折，若∠1 = 50°，则∠AEF等于（）A.50°B.65°C.80°D.115°6、如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠DCE；④AD∥BC且∠B=∠D．其中，能推出AB∥DC的是（）A.①④B.②③C.①③D.①③④7、如图，属于内错角的是（）A.∠1和∠2B.∠2和∠3C.∠1和∠4D.∠3和∠48、下列图形中，不能由平移得到的是（）A. B. C.D.9、如图，在Rt△ABC中，AB=3cm，BC=4cm，沿直角边BC所在的直线向右平移3cm，得到△DEF，DE交AC于G，则所得到的△GEC的面积是（）cm2．A. B.１ C. D.10、如图，直线AB，CD相交于O点，若∠1=30°，则∠2，∠3的度数分别为（）A.120°，60°B.130°，50°C.140°，40°D.150°，30°11、同桌读了：“子非鱼焉知鱼之乐乎？”后，兴高采烈地利用电脑画出了几幅鱼的图案，请问：由图中所示的图案通过平移后得到的图案是（）A. B. C. D.12、将一块三角板按如图所示位置放置，AB∥CD，∠1=55°，则∠2的度数为（）A.20°B.22°C.25°D.34°13、下列结论中，不正确的是（）A.两点确定一条直线B.两点之间的所有连线中，线段最短C.对顶角相等D.过一点有且只有一条直线与已知直线平行14、直角三角板和直尺如图放置，若∠1=20°，则∠2的度数为（）A.60°B.50°C.40°D.30°15、已知点M(-4，2)，若点N是y轴上一动点，则M，N两点之间的距离最小值为（）A.-4B.2C.4D.-2二、填空题(共10题，共计30分)16、如图所示的网格式正方形网格，A、B、P是网格线交点，则∠PAB+∠PBA＝________ °．17、如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是________18、如图，若使，需要添加一个条件，则这个条件是________（填一个即可）。

2023年七年级下册数学第五章相交线与平行线证明题阅读理解填理由专项训练(14道)

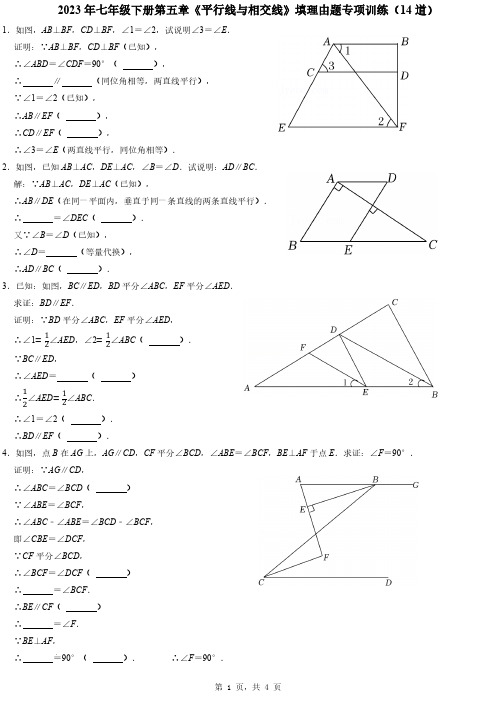
2023年七年级下册第五章《平行线与相交线》填理由题专项训练（14道）1．如图，AB⊥BF，CD⊥BF，∠1＝∠2，试说明∠3＝∠E．证明：∵AB⊥BF，CD⊥BF（已知），∴∠ABD＝∠CDF＝90°（），∴∥（同位角相等，两直线平行），∵∠1＝∠2（已知），∴AB∥EF（），∴CD∥EF（），∴∠3＝∠E（两直线平行，同位角相等）．2．如图，已知AB⊥AC，DE⊥AC，∠B＝∠D．试说明：AD∥BC．解：∵AB⊥AC，DE⊥AC（已知），∴AB∥DE（在同一平面内，垂直于同一条直线的两条直线平行）．∴＝∠DEC（）．又∵∠B＝∠D（已知），∴∠D＝（等量代换），∴AD∥BC（）．3．已知：如图，BC∥ED，BD平分∠ABC，EF平分∠AED．求证：BD∥EF．证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=12∠AED，∠2=12∠ABC（）．∵BC∥ED，∴∠AED＝（）∴12∠AED=12∠ABC．∴∠1＝∠2（）．∴BD∥EF（）．4．如图，点B在AG上，AG∥CD，CF平分∠BCD，∠ABE＝∠BCF，BE⊥AF于点E．求证：∠F＝90°．证明：∵AG∥CD，∴∠ABC＝∠BCD（）∵∠ABE＝∠BCF，∴∠ABC﹣∠ABE＝∠BCD﹣∠BCF，即∠CBE＝∠DCF，∵CF平分∠BCD，∴∠BCF＝∠DCF（）∴＝∠BCF．∴BE∥CF（）∴＝∠F．∵BE⊥AF，5．（2023秋•海口期末）如图，AB∥CD，∠1＝∠A．（1）试说明：AC∥ED；（2）若∠2＝∠3，FC与BD的位置关系如何？为什么？解：（1）∵AB∥CD，（已知）∴∠1＝∠BED，（）又∵∠1＝∠A，（已知）∴∠BED＝∠，（等量代换）∴∥．（）（2）FC与BD的位置关系是：．理由如下：∵AC∥ED，（已知）∴∠2＝∠．（）又∵∠2＝∠3，（已知）∴∠＝∠．（等量代换）∴∥．（）6．已知：如图，在△ABC中，FG∥CD，∠1＝∠3．求证：∠B+∠BDC＝180°．解：因为FG∥CD（已知），所以∠1＝．又因为∠1＝∠3（已知），所以∠2＝（等量代换）．所以BC∥（），所以∠B+∠BDE＝180°（）．7．如图，已知∠D＝108°，∠BAD＝72°，AC⊥BC于C，EF⊥BC于F．求证：∠1＝∠2．证明：∵∠D＝108°，∠BAD＝72°（已知）∴∠D+∠BAD＝180°∴AB∥CD（）∴∠1＝（）又∵AC⊥BC于C，EF⊥BC于F（已知）∴EF∥（）∴∠2＝（）∴∠1＝∠2（）8．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°．试说明：∠GDC＝∠B．解：∵AD⊥BC，EF⊥BC（已知）∴∠ADB＝∠EFB＝90°（）∴EF∥AD（）∴+∠2＝180°（）又∵∠2+∠3＝180°（已知）∴∠1＝（）∴∥（）9．（2023秋•丹江口市期末）如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G，求证：AB∥CD．证明：∵AF⊥CE（已知），∴∠CGF＝90°（垂直的定义），∵∠1＝∠D（已知），∴AF∥（），∴∠4＝＝90°（），又∵∠2+∠3+∠4＝180°，∴∠2+∠3＝90°，∵∠2与∠C互余（已知），∴∠2+∠C＝90°，∴∠C＝，∴AB∥．（）10．（2023秋•青神县期末）如图，AB与EF交于点B，CD与EF交于点D，根据图形，请补全下面这道题的解答过程．（1）∵∠1＝∠2（已知）∴∥CD（）∴∠ABD+∠CDB＝（）（2）∵∠BAC＝65°，∠ACD＝115°，（已知）∴∠BAC+∠ACD＝180°（等式性质）∴AB∥CD（）（3）∵CD⊥AB于D，EF⊥AB于F，∠BAC＝55°，（已知）∴∠ABD＝∠CDF＝90°（垂直的定义）∴∥（同位角相等，两直线平行）又∵∠BAC＝55°，（已知）∴∠ACD＝．（）11．如图所示，已知∠1+∠2＝180°，∠3＝∠B，试判断∠AED与∠C的大小关系，并说明理由．证明：∵∠1+∠2＝180°（）∠1＝∠DFH（）∴（）∴EH∥AB（）∴∠3＝∠ADE（）∵∠3＝∠B∴∠B＝∠ADE（）∴DE∥BC∴∠AED＝∠C（）12．如图，已知AB∥CD，BE平分∠ABC，DB平分∠CDF，且∠ABC+∠CDF＝180°．求证：BE⊥DB．证明：∵AB∥CD∴∠ABC＝∠BCD（）∵∠ABC+∠CDF＝180°（）∴∠BCD+∠CDF＝180°（）∴BC∥DF（）于是∠DBC＝∠BDF（）∵BE平分∠ABC，DB平分∠CDF∴∠EBC=12∠ABC，∠BDF＝（）∵∠EBC+∠DBC＝∠EBC+∠BDF=12（∠ABC+∠CDF）即∠EBD＝∴BE⊥DB（）13．如图，EF⊥BC，∠1＝∠C，∠2+∠3＝180°，试说明∠ADC＝90°．请完善解答过程，并在括号内填写相应的理论依据．解：∵∠1＝∠C，（已知）∴GD∥．（）∴∠2＝∠DAC．（）∵∠2+∠3＝180°，（已知）∴∠DAC+∠3＝180°．（等量代换）∴AD∥EF．（）∴∠ADC＝∠．（）∵EF⊥BC，（已知）∴∠EFC＝90°．（）∴∠ADC＝90°．（等量代换）14．（2023秋•南关区期末）如图，已知AB∥DC，AC⊥BC，AC平分∠DAB，∠B＝50°，求∠D的大小．阅读下面的解答过程，并填括号里的空白（理由或数学式）．解：∵AB∥DC（），∴∠B+∠DCB＝180°（）．∵∠B＝（已知），∴∠DCB＝180°﹣∠B＝180°﹣50°＝130°．∵AC⊥BC（已知），∴∠ACB＝（垂直的定义）．∴∠2＝．∵AB∥DC（已知），∴∠1＝（）．∵AC平分∠DAB（已知），∴∠DAB＝2∠1＝（角平分线的定义）．∵AB∥DC（已知），∴+∠DAB＝180°（两条直线平行，同旁内角互补）．。

人教版七年级数学相交线与平行线证明题专项训练

C A B O F E 证明题专1如图，已知AB ∥CD, ∠1=∠3, 试说明AC ∥BD.2、如图，已知CD ⊥AD ，DA ⊥AB ，∠1＝∠2。

则DF 与AE 平行吗？为什么？3、如图，AB ∥CD,AD ∥BC,∠A=3∠B.求∠A 、∠B 、∠C 、∠D 的度数.4、如图，AB ∥CD,直线EF 交AB 、CD 于点G 、H.如果GM 平分∠BGF,HN 平分∠CHE ，那么GM 与HN 平行吗？为什么？5、已知，如图15，∠ACB ＝600，∠ABC ＝500，BO 、CO 分别平分∠ABC 、∠ACB ，EF 是经点O 且平行于BC 的直线，求∠BOC 的度数。

6、已知：如图ＡＢ∥ＣＤ，ＥＦ交ＡB 于G ，交CD 于F ，FH 平分∠EFD ，交AB 于H ，∠AGE=500 求：∠BHF 的度数。

7、如图，直线AB 、CD 相交于点O ，OA 平分∠COE ，∠COE ：∠EOD=4：5求∠BOD 的度数。

8、已知一个角的余角的补角比这个角的补角的一半大90°，则这个角的度数等于多少度9、如图：已知AD ∥BE, ∠1=∠2, 请说明∠A=∠E 的理由. 10、已知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。

求证：AD ∥ 11、已知如图，直线AB 、CD 相交于O ，OE 平分∠BOD ，OF 平分∠COB ，∠2∶∠1＝4∶求∠AOF 的度数。

12、已知：如图∠1=∠2，∠C=∠D ，∠A=∠F 相等吗？试说明由13、已知：如图,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB. 21O E D C B A F H GF E D C B A A DC B A B CD EF G HM N F O EC B A图15E C A BDO AD B CEF 123 4。

(典型题)初中数学专项练习《相交线与平行线》100道解答题包含答案(专项练习)

初中数学专项练习《相交线与平行线》100道解答题包含答案（专项练习）一、解答题(共100题)1、如图，五边形 ABCDE中，AE∥CD，∠A=107°，∠B=121°，求∠C的度数。

2、如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．3、补全解答过程：已知：如图，直线，直线与直线，分别交于点G，H；平分，．求的度数．解：与交于点H，（已知）．（▲），（已知）．（▲），与，交于点G，H，（已知）（▲）▲平分，（已知）▲．（角平分线的定义）4、如图所示，直线AB∥CD，∠1＝75°，求∠2的度数。

5、如图，AB与CD相交于O，OE平分∠AOC，OF⊥AB于O，OG⊥OE于O，若∠BOD=40°，求∠AOE和∠FOG的度数．6、如图，已知点B，E，C，F在同一条直线上，BE=CF，AB∥DE，∠A=∠D．求证：AB=DE．7、如图，已知，，，.AB 与DE平行吗？为什么？8、已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE⊥AC于E，BE与CD 相交于点F．求证：BF=AC．9、把下面的说理过程补充完整：已知：如图，BC//EF，BC＝EF，AF＝DC线段AB和线段DE平行吗？请说明理由．答：AB//DE理由：∵AF＝DC（已知）∴AF+FC＝DC+ ▲∴AC＝DF（▲）（填推理的依据）∵BC//EF（已知）∴∠BCA＝∠▲（两直线平行，内错角相等）又∵BC＝EF（已知）∴ （▲）（填推理的依据）∴∠A＝∠▲（全等三角形的对应角相等）∴AB//▲（内错角相等，两直线平行）10、小明在踢足球时把一块梯形ABCD的玻璃的下半部分打碎了，若量得上半部分∠A=123 ，∠D=105 ，你能知道下半部分的两个角∠B和∠C的度数吗？请说明理由.11、如图，BE∥CG，∠1＝∠2，求证：BD∥CF12、如图，EF∥BC，AC平分∠BAF，∠B=80°．求∠C的度数．13、如图，已知AB∥CD，∠B=40°，CN是∠BCE的平分线，CM⊥CN，求∠BCM 的度数．14、如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？15、已知：如图，∠1=∠2，∠3=∠E，求证：∠A=∠CBE．16、如图，在直角△ABC 中，∠ACB=90°，CD 是高，∠1=35°，求∠2，∠B 与∠A 的度数．17、在平行四边形ABCD中, ∠A＋∠C＝160°，求∠A，∠C，∠B，∠D的度数．18、已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠EFD=72°，则∠EGC等于多少度？19、如图，AF=BE，AC∥BD，CE∥DF，则(1)AC=_____，CE=______，(2)证明(1)中的结论。

相交线与平行线专项训练及解析答案

相交线与平行线专项训练及解析答案一、选择题1．下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是( )A．1个B．2个C．3个D．4个【答案】B【解析】解：①符合对顶角的性质，故本小题正确；②两直线平行，内错角相等，故本小题错误；③符合平行线的判定定理，故本小题正确；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故本小题错误．故选B．2．如图，若AB∥CD，则∠α、∠β、∠γ之间关系是（）A．∠α+∠β+∠γ=180°B．∠α+∠β﹣∠γ=360°C．∠α﹣∠β+∠γ=180°D．∠α+∠β﹣∠γ=180°【答案】D【解析】试题解析：如图，作EF∥AB，∵AB∥CD，∴EF∥CD，∵EF∥AB，∴∠α+∠AEF=180°，∵EF∥CD，∴∠γ=∠DEF，而∠AEF+∠DEF=∠β，∴∠α+∠β=180°+∠γ，即∠α+∠β-∠γ=180°．故选：D ．3．如图，已知ABC ∆，若AC BC ⊥，CD AB ⊥，12∠=∠，下列结论：①//AC DE ；②3A ∠=∠；③3EDB ∠=∠；④2∠与3∠互补；⑤1B ∠=∠，其中正确的有（）A ．2个B ．3个C ．4个D ．5个【答案】C【解析】【分析】根据平行线的判定得出AC ∥DE ，根据垂直定义得出∠ACB=∠CDB=∠CDA=90°，再根据三角形内角和定理求出即可．【详解】∵∠1=∠2，∴AC ∥DE ，故①正确；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDB=90°，∴∠A+∠B=90°，∠3+∠B=90°，∴∠A=∠3，故②正确；∵AC ∥DE ，AC ⊥BC ，∴DE ⊥BC ，∴∠DEC=∠CDB=90°，∴∠3+∠2=90°（∠2和∠3互余），∠2+∠EDB=90°，∴∠3=∠EDB ，故③正确，④错误；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDA=90°，∴∠A+∠B=90°，∠1+∠A=90°，∴∠1=∠B ，故⑤正确；即正确的个数是4个，故选：C ．【点睛】此题考查平行线的判定和性质，三角形内角和定理，垂直定义，能综合运用知识点进行推理是解题的关键．4．如图，已知正五边形ABCDE ，AF ∥CD ，交DB 的延长线于点F ，则∠DFA 的度数是（）A ．28°B ．30°C ．38°D ．36°【答案】D【解析】【分析】根据两直线平行，内错角相等，得到∠DFA=∠CDB ，根据三角形的内角和求出∠CDB 的度数从而得到∠DFA 的度数.【详解】解：∠C=(52)1801085︒-⨯=，且CD=CB ， ∴∠CDB=∠CBD ∵由三角形的内角和∠C+∠CDB+∠CBD=180°∴∠CDB+∠CBD=180°-∠C =180°-108°=72°∴∠CDB==∠CBD=72362︒︒= 又∵AF ∥CD∴∠DFA=∠CDB=36°（两直线平行，内错角相等）故选D【点睛】本题主要考查多边形的基本概念和三角形的基本概念，正n 边形的内角读数为(2)180n n-⨯.5．下列结论中：①若a=b a b ；②在同一平面内，若a ⊥b ，b//c ，则a ⊥c ；③直线外一点到直线的垂线段叫点到直线的距离；33( ) A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】【详解】解：①若a=b 0≥a b②在同一平面内，若a ⊥b,b//c ，则a ⊥c ，正确③直线外一点到直线的垂线段的长度叫点到直线的距离 33正确的个数有②④两个6．如图，下列推理错误的是( )A．因为∠1＝∠2，所以c∥d B．因为∠3＝∠4，所以c∥dC．因为∠1＝∠3，所以a∥b D．因为∠1＝∠4，所以a∥b【答案】C【解析】分析：由平行线的判定方法得出A、B、C正确，D错误；即可得出结论．详解：根据内错角相等，两直线平行，可知因为∠1＝∠2，所以c∥d，故正确；根据同位角相等，两直线平行，可知因为∠3＝∠4，所以c∥d，故正确；因为∠1和∠3的位置不符合平行线的判定，故不正确；根据内错角相等，两直线平行，可知因为∠1＝∠4，所以a∥b，故正确.故选：C.点睛：本题考查了平行线的判定方法；熟练掌握平行线的判定方法，并能进行推理论证是解决问题的关键．7．如图所示，b∥c，a⊥b，∠1=130°，则∠2=（）．A．30°B．40°C．50°D．60°【答案】B【解析】【分析】证明∠3=90°，利用三角形的外角的性质求出∠4即可解决问题．【详解】如图，反向延长射线a交c于点M，∵b∥c，a⊥b，∴∠3=90°，∵∠1=90°+∠4，∴130°=90°+∠4，∴∠4=40°，∴∠2=∠4=40°，故选B．【点睛】本题考查平行线的性质，垂线的性质，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识8．下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的．其中真命题的个数是（）A．2个B．3个C．4个D．5个【答案】B【解析】【分析】根据平面直角坐标系的概念，在两直线平行的条件下，内错角相等，两个无理数的和可以是无理数也可以是有理数，进行判断即可.【详解】①正确；②在两直线平行的条件下，内错角相等，②错误；③正确；④反例：两个无理数π和-π，和是0，④错误；⑤坐标平面内的点与有序数对是一一对应的，正确；故选：B．【点睛】本题考查实数，平面内直线的位置；牢记概念和性质，能够灵活理解概念性质是解题的关键．9．下列命题是真命题的是（）A．同位角相等B．对顶角互补C．如果两个角的两边互相平行，那么这两个角相等D ．如果点P 的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上．【答案】D【解析】【分析】根据平行线的性质定理对A 、C 进行判断；利用对顶角的性质对B 进行判断；根据直角坐标系下点坐标特点对D 进行判断．【详解】A ．两直线平行，同位角相等，故A 是假命题；B ．对顶角相等，故B 是假命题；C ．如果两个角的两边互相平行，那么这两个角相等或互补，故C 是假命题；D ．如果点的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上，故D 是真命题故选：D【点睛】本题考查了真命题与假命题，正确的命题称为真命题，错误的命题称为假命题．利用了平行线性质、对顶角性质、直角坐标系中点坐标特点等知识点．10．如图，11,,33AB EF ABP ABC EFP EFC ∠=∠∠=∠∥，已知60FCD ∠=︒，则P ∠的度数为（）A ．60︒B ．80︒C ．90︒D ．100︒【答案】B【解析】【分析】延长BC 、EF 交于点G ，根据平行线的性质得180ABG BGE +=︒∠∠，再根据三角形外角的性质和平角的性质得60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠，最后根据四边形内角和定理求解即可．【详解】延长BC 、EF 交于点G∵//AB EF∴180ABG BGE +=︒∠∠∵60FCD ∠=︒∴60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠∵11,33ABP ABC EFP EFC ∠=∠∠=∠ ∴360P PBC BCF PFC =︒---∠∠∠∠2236012033ABG EFC =︒---︒∠∠ ()223606012033ABG BGE =︒--︒+-︒∠∠ 223604012033ABG BGE =︒--︒--︒∠∠ ()22003ABG BGE =︒-+∠∠ 22001803=︒-⨯︒ 80=︒故答案为：B ．【点睛】本题考查了平行线的角度问题，掌握平行线的性质、三角形外角的性质、平角的性质、四边形内角和定理是解题的关键．11．下列图形中线段PQ 的长度表示点P 到直线a 的距离的是（）A ．B ．C ．D ．【答案】C【解析】【分析】根据点到直线的距离的定义，可得答案．【详解】由题意得PQ ⊥a ，P 到a 的距离是PQ 垂线段的长，故选C ．【点睛】本题考查了点到直线的距离，点到直线的距离是解题关键．12．如图，在△ABC中，AB＝AC，∠A＝36°，D、E两点分别在边AC、BC上，BD平分∠ABC，DE∥AB．图中的等腰三角形共有（）A．3个B．4个C．5个D．6个【答案】C【解析】【分析】已知条件，根据三角形内角和等于180，角的平分线的性质求得各个角的度数，然后利用等腰三角形的判定进行判断即可．【详解】解：∵AB＝AC，∠A＝36°，∴∠ABC＝∠C＝72°，∵BD平分∠ABC，∴∠ABD＝∠DBC＝36°，∴∠BDC＝180°﹣36°﹣72°＝72°，∵DE∥AB，∴∠EDB＝∠ABD＝36°，∴∠EDC＝72°﹣36°＝36°，∴∠DEC＝180°﹣72°﹣36°＝72°，∴∠A＝∠ABD，∠DBE＝∠BDE，∠DEC＝∠C，∠BDC＝∠C，∠ABC＝∠C，∴△ABC、△ABD、△DEB、△BDC、△DEC都是等腰三角形，共5个，故选C．【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质，由已知条件利用相关的性质求得各个角相等是解题的关键．13．如图，∠BCD ＝95°，AB ∥DE ，则∠α与∠β满足（）A ．∠α+∠β＝95°B ．∠β﹣∠α＝95°C ．∠α+∠β＝85°D ．∠β﹣∠α＝85°【答案】D【解析】【分析】过点C 作CF ∥AB ，然后利用两直线平行，内错角相等；两直线平行，同旁内角互补进行推理证明即可.【详解】解：过点C 作CF ∥AB∵AB ∥DE ，CF ∥AB∴AB ∥DE ∥CF∴∠BCF=∠α∠DCF+∠β=180°∴∠BCD ＝∠BCF +∠DCF∴∠α+180°-∠β=95°∴∠β﹣∠α＝85°故选：D【点睛】本题考查平行线的性质，熟练掌握平行线的性质进行推理证明是本题的解题关键.14．如图，直线//a b ，将一块含45︒角的直角三角尺（90︒∠=C ）按所示摆放．若180︒∠=，则2∠的大小是（）A ．80︒B ．75︒C ．55︒D ．35︒【答案】C【解析】【分析】先根据//a b 得到31∠=∠，再通过对顶角的性质得到34,25∠=∠∠=∠，最后利用三角形的内角和即可求出答案.【详解】解：给图中各角标上序号，如图所示：∵//a b∴3180︒∠=∠=（两直线平行，同位角相等），又∵34,25∠=∠∠=∠（对顶角相等），∴251804180804555A ∠=∠=︒-∠-∠=︒-︒-︒=︒.故C 为答案.【点睛】本题主要考查了直线平行的性质（两直线平行，同位角相等）、对顶角的性质（对顶角相等），熟练掌握直线平行的性质是解题的关键.15．如图，1B ∠=∠，2C ∠=∠，则下列结论正确的个数有（）①//AD BC ；②B D ∠=∠；③//AB CD ；④2180B ∠+∠=︒A ．4个B ．3个C ．2个D ．1个【答案】A【解析】【分析】根据∠1=∠B可判断AD∥BC，再结合∠2=∠C可判断AB∥CD，其余选项也可判断.【详解】∵∠1=∠B∴AD∥BC，①正确；∴∠2+∠B=180°，④正确；∵∠2=∠C∴∠C+∠B=180°∴AB∥CD，③正确∴∠1=∠D，∴∠D=∠B，②正确故选：A【点睛】本题考查平行的证明和性质，解题关键是利用AD∥BC推导出∠B+∠2=180°，为证AB∥DC 作准备.16．如图，DE∥BC，BE平分∠ABC，若∠1=70°，则∠CBE的度数为（）A．20°B．35°C．55°D．70°【答案】B【解析】【分析】根据平行线的性质可得∠1=∠ABC=70°，再根据角平分线的定义可得答案．【详解】∵DE∥BC，∴∠1=∠ABC=70°，∵BE平分∠ABC，∴1352CBE ABC∠=∠=︒，故选：B．【点睛】此题主要考查了平行线的性质，以及角平分线的定义，解题的关键是掌握两直线平行，内错角相等．17．下列说法中错误的个数是( )(1)过一点有且只有一条直线与已知直线平行；(2)过一点有且只有一条直线与已知直线垂直；(3)不相交的两条直线叫做平行线；(4)有公共顶点且有一条公共边的两个互补的角互为邻补角．A．1个B．2个C．3个D．4个【答案】C【解析】（1）应强调过直线外一点，故错误；（2）正确；（3）不相交的两条直线叫做平行线，没有说明是否是在同一平面内，所以错误；（4）有公共顶点且有一条公共边的两个角不一定互为邻补角，角平分线的两个角也满足，但可以不是,故错误.错误的有3个，故选C.18．如图，小慧从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C 处，此时需要将方向调整到与出发时一致，则方向的调整应为（）A．左转80°B．右转80°C．左转100°D．右转100°【答案】B【解析】【分析】如图，延长AB到D，过C作CE//AD，由题意可得∠A=60°，∠1=20°，根据平行线的性质可得∠A=∠2，∠3=∠1+∠2，进而可得答案.【详解】如图，延长AB到D，过C作CE//AD，∵此时需要将方向调整到与出发时一致，∴此时沿CE方向行走，∵从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，∴∠A=60°，∠1=20°，AM∥BN，CE∥AB，∴∠A=∠2=60°，∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°，∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质，解答时要注意以北方为参照方向，进行角度调整.19．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（）A ．110°B ．120°C ．140°D ．150° 【答案】B【解析】【详解】解：∵AD ∥BC ，∴∠DEF=∠EFB=20°，图b 中∠GFC=180°-2∠EFG=140°，在图c 中∠CFE=∠GFC-∠EFG=120°，故选B ．20．如图，在矩形ABCD 中，6AB =，8BC =，若P 是BD 上的一个动点，则PB PC PD ++的最小值是（）A ．16B ．15.2C ．15D ．14.8【答案】D【解析】【分析】根据题意，当PC ⊥BD 时，PB PC PD ++有最小值，由勾股定理求出BD 的长度，由三角形的面积公式求出PC 的长度，即可求出最小值.【详解】解：如图，当PC ⊥BD 时，PB PC PD BD PC ++=+有最小值，在矩形ABCD 中，∠A=∠BCD=90°，AB=CD=6，AD=BC=8，由勾股定理，得226810BD +=，∴=10PB PD BD +=，在△BCD 中，由三角形的面积公式，得11=22BD PC BC CD ••，即1110=8622PC ⨯⨯⨯⨯，解得： 4.8PC =， ∴PB PC PD ++的最小值是：10 4.814.8PB PC PD BD PC ++=+=+=；故选：D.【点睛】本题考查了勾股定理解直角三角形，最短路径问题，垂线段最短，以及三角形的面积公式，解题的关键是熟练掌握勾股定理，正确确定点P 的位置，得到PC 最短.。

平行线与相交线证明题专项（最终五篇）

平行线与相交线证明题专项（最终五篇）第一篇：平行线与相交线证明题专项证明题专练二、两组平行线的证明题【找出连接两组平行线的角】1.已知：如图，CD平分∠ACB，AC∥DE，∠DCE=∠FEB，求证：EF平分∠DEB．1、如图已知，AB∥CD.AF,CF分别是∠EAB、∠ECD的角平分线，F是两条角平分线的一、平行线之间的基本图交点；求证：∠F= 1B2∠AEC.E FCDB2、已知AB//CD，此时∠A、∠AEF、∠EFC和∠C的关系又如何？你能找出其中的规律吗？ ED3、将题变为如下图：AB//CD此时∠A、∠AEF、∠EFD和∠D的关系又如何？你能找出其中的规律吗？CD4、如图，AB//CD，那么∠A、∠C与∠AEC有什么关系？ ECDEC E B3、已知：如图2-96,DE⊥AO于E,BO⊥AO,FC⊥AB于C，∠1=∠2,求证：DO⊥AB.三、两组平行线构造平行四边形1．已知：如图，AB是一条直线，∠C = ∠1，∠2和∠D互余，BE⊥FD于G．求证：AB∥CD ．2、如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证DF∥AC．DF42A(第22B 题)C五、寻找角之间的关系1、如图2-97,已知：∠1=∠2，∠3=∠4，∠5=∠6.求证:AD∥BC.2、已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。

求证：AD∥BE。

D3．如图12，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1 +∠2 = 90°．求证：（1）AB∥CD；（2）∠2 +∠3 = 90°．六、翻折图103、如图，M、N、T和A、B、C分别在同一直线上，且∠1=∠3，∠P=∠T，求证：∠M=∠R。

四、证特殊角1、AB∥CD，∠BAC的平分线和∠ACD的平分线交于点E，则∠AEC的度数是．图7 图82、AB∥CD，直线EF与AB、CD分别相交于E、F两点，EP平分∠AEF，过点F作PF⊥EP垂足为P，若∠PEF＝30，则∠PFC＝_____．3、如图，已知：DE∥AC，CD平分∠ACB，EF平分∠DEC，∠1与∠2互余，求证：DG∥EF.A1、如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为．2、如图（1），已知矩形ABCD，将△BCD沿对角线BD折叠，记点C的对应点为C′，若D5.如图已知直线a∥b，AB平分∠MAD，AC平分∠NAD，DE⊥AC 于E，求证：∠1=∠2．∠ADC′=20°，则∠DBC=的度数为。

(完整版)相交线与平行线的综合证明题训练

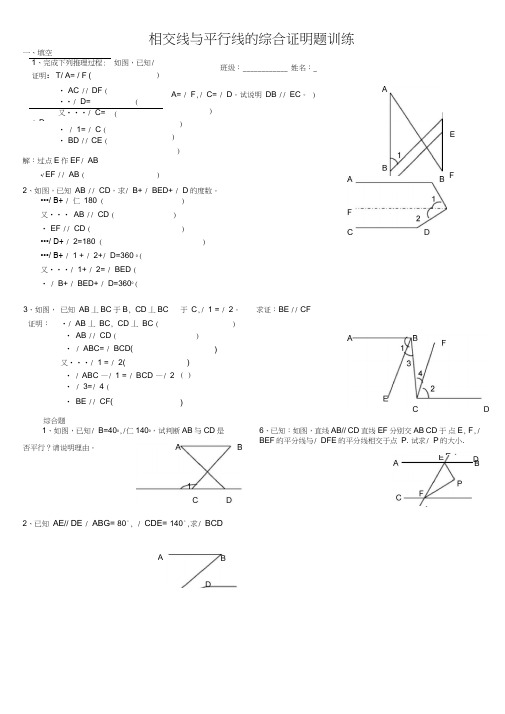
相交线与平行线的综合证明题训练一、填空1、完成下列推理过程: 如图，已知/ 证明：T/ A= / F ()• AC // DF (••/ D= (又•••/ C= / D(• / 1= / C (• BD // CE (班级： ____________ 姓名：_A= / F ,/ C= / D 。

试说明 DB // EC 。

))) ) )解：过点E 作EF / AB•/ EF // AB ()•••/ B+ / 仁 180° ( )又••• AB // CD ( ) • EF // CD ()•••/ D+ / 2=180° ()•••/ B+ / 1 + / 2+/ D=360 0 (又•••/ 1+ / 2= / BED ( • / B+ / BED+ / D=3600 (综合题1、如图，已知/ B=400,/仁1400，试判断AB 与CD 是2、已知 AE // DE / ABG= 80°, / CDE= 140°,求/ BCD6、已知：如图，直线 AB// CD 直线EF 分别交 AB CD 于点E , F ,/ BEF 的平分线与/ DFE 的平分线相交于点 P. 试求/ P 的大小.3、如图，已知 AB 丄BC 于B , CD 丄BC 于 C ,/ 1 = / 2。

求证：BE // CF证明： •/ AB 丄 BC , CD 丄 BC ( )• AB // CD ( )• / ABC= / BCD( )又•••/ 1 = / 2( )• / ABC —/ 1 = / BCD —/ 2 ( )• / 3=/ 4 (• BE // CF()A2、如图，已知 AB // CD ，求/ B+ / BED+ / D 的度数。

否平行？请说明理由。

BD EF3、如图，AD丄BC于D点，EF± BC于点F,且EF交于点G,交CA延长线于点E,Z仁/ 2•求证：AD平分 / BAC。

相交线与平行线证明题专项练习

相交线与平行线证明题（一）一、已知：如图，COD 是直线，∠=∠13。

求证：A 、O 、B 三点在同一条直线上。

证明： COD 是一条直线（） ∴∠+∠=12___________（） ∠=∠13（） ∴__________+∠=3__________ ∴_______________（）二、如图7，∠B=∠C ，AB ∥EF 试说明：∠BGF=∠C解：∵∠B=∠C∴AB ∥CD （）又∵AB ∥EF∴EF ∥CD （）∴∠BGF=∠C （三、已知：如图，AO BO ⊥∠=∠，12。

求证：CO DO ⊥。

证明： AO BO ⊥（） ∴∠=︒AOB 90（）∴∠+∠=︒1390 ∠=∠12（） ∴∠+∠=︒2390 ∴⊥CO DO （）四、如图，已知AB BC ⊥，BC CD ⊥，12=∠∠．试判断BE 与CF 的关系，并说明你的理由．解:BE ∥CF.理由：∵AB BC ⊥,BC CD ⊥ ( )∴________ = ________=o90 ( ) ∵12=∠∠ ( ) ∴∠ABC －∠1=∠BCD －∠2即∠EBC=∠BCF∴________∥________ ( )五、如图，已知AB ∥CD ，∠1＝∠2，试说明EP ∥FQ ．证明：∵AB ∥CD ，∴∠MEB ＝∠MFD （）又∵∠1＝∠2，∴∠MEB －∠1＝∠MFD －∠2，即 ∠MEP ＝∠______∴EP ∥_____．（）六、如图，EF ∥AD ，∠1 =∠2，∠BAC = 70°。

将求∠AGD 的过程填写完整。

解∵EF ∥AD ，∴ ∠2 = ( ) 又∵ ∠1 = ∠2， ∴ ∠1 = ∠3。

图7GAB CD EFAC12 O3DBBC D2 3 1O AAB CD EF1423第19题)∴AB ∥ ( ) ∴∠BAC + = 180°。

又∵∠BAC = 70°， ∴∠AGD = 。

北师大版七年级下册相交线与平行线证明训练题

相交线与平行线的证明练习1、如图：∵∠2=∠3∴ ____∥_____ ( ) 又∵EF ∥GH∴____=______ ( ) ∴ ∠1=∠32、如图，已知∠A=∠F ，∠C=∠D ，试说明BD ∥CE. 解：∵∠A=∠F(已知)∴AC ∥DF ( )∴∠D=∠ ( ) 又∵∠C=∠D(已知) ∴∠1=∠C(等量代换)∴BD ∥CE( ) 3、如图，已知∠B+∠BCD=180°，∠B=∠D.求证：∠E=∠DFE.证明：∵∠B+∠BCD=180°(已知 ), ∴AB ∥CD( ). ∴∠B=∠DCE （）. 又∵∠B=∠D （已知）,∴∠DCE=∠D ( ). ∴AD ∥BE( ).∴∠E=∠DFE （）. 4、如图，已知：∠1=∠2，当DE ∥FH 时，（1）证明：∠EDA=∠HFB （2）CD 与FG 有何关系?证明：（1）∵DE ∥FH (已知),∴∠EDF=∠DFH ( ),∴∠EDA=∠HFB ( ). (2) ∵∠EDF=∠DFH ( ), 且∠CDF=∠EDF-∠1 ,∠DFG=∠DFH-∠2 ,又∵∠1=∠2（已知）,∴CD ∥FG( ). 5、如右图,已知AD ⊥BC,EF ⊥BC,∠1=∠2. 求证:DG ∥BA.证明：∵AD ⊥BC,EF ⊥BC ( ) ∴∠EFB=∠ADB=90° ( ) ∴EF ∥AD( ) ∴∠1=∠BAD( )A B ECGHF12DG H KFEDC B A 又∵∠1=∠2 ( ) ∴ （等量代换）∴DG ∥BA.( )6、如图：已知：AD ⊥BC 于D ，EF ⊥BC 于F ，∠1=∠3，求证：AD 平分∠BAC 。

证明：∵AD ⊥BC EG ⊥BC 于F （已知） ∴AD ∥EF （） ∴∠1＝∠E （） ∠2＝∠3（）又∵∠3＝∠E （已知） ∴∠1＝∠2（） ∴AD 平分∠BAC （）7、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=30°,试说明AB ∥CD. 证明：∵EG ⊥AB （已知）∴∠EGK=90°( ),∴ 在ΔEGK 中∠E+∠EKG=90°（），又∵∠E=30°（） ∴∠EKG=600 又∵∠CHF=600 ∴∠EKG=∠CHF∴AB ∥CD.（）。