运筹学教材编写组《运筹学》期末考试试卷(B)
运筹学考试题b卷附标准答案

运筹学期末考试题( b 卷)注意事项:1、答题前,考生务必将自己的姓名、班级填写在答题卡上。
2、答案用钢笔或圆珠笔写在答题卡上,答在试卷上不给分。
3、考试结束,将试卷和答题卡一并交回。
一、单项选择题(每小题 1 分,共 10分) 1:下列关于运筹学的缺点中,不正确的是()A.在建立数学模型时,若简化不慎,用运筹学求得的最优解会因与实际相差大而失去意义B.运筹学模型只能用借助计算机来处理C.有时运筹学模型并不能描述现实世界D.由于运筹学方法的复杂性使一些决策人员难以接受这些解决问题的方法2:在下面的数学模型中,属于线性规划模型的为()max S 4X Y min S 3X Y max S X2Y2min S 2XYA. s.t. XY 3B. s.t. 2X Y 1 C. s.t. XY2 D. s.t. XY3X,Y 0 X,Y 0 X,Y 0 X,Y 03.线性规划一般模型中,自由变量可以用两个非负变量的()代换。
A.和 B .商 C.积 D.差4:以下关系中,不是线性规划与其对偶问题的对应关系的是()。
A.约束条件组的系数矩阵互为转置矩阵B.一个约束条件组的常数列为另一个目标函数的系数行向量C.两个约束条件组中的方程个数相等D.约束条件组的不等式反向 5.对偶问题的对偶是()A.原问题 B .解的问题 C.其它问题 D.基本问题 6:若原问题中x i0 ,那么对偶问题中的第i 个约束一定为()A.等式约束 B .“≤”型约束矚慫润厲钐瘗睞枥庑赖。
C.“≥”约束D .无法确定7:若运输问题已求得最优解,此时所求出的检验数一定是全部()A .小于或等于零B .大于零C.小于零D .大于或等于零8:考虑某运输问题,其需求量和供应量相等,且供应点的个数为 m,需求点的个数是 n。
若以西北角法求得其初始运输方案,则该方案中数字格的数目应为()聞創沟燴鐺險爱氇谴净。
A.( m+n)个B.( m+n-1 )个C.( m-n)个D. ( m-n+1)个9:关于动态规划问题的下列命题中错误的是()A、动态规划分阶段顺序不同,则结果不同B、状态对决策有影响C、动态规划中,定义状态时应保证在各个阶段中所做决策的相对独立性D、动态规划的求解过程都可以用列表形式实现10:若 P为网络 G 的一条流量增广链,则 P中所有逆向弧都为 G 的()A .非零流弧B .饱和边C .零流弧D .不饱和边 残骛楼諍锩瀨濟溆塹籟。
运筹学试卷及参考问题详解
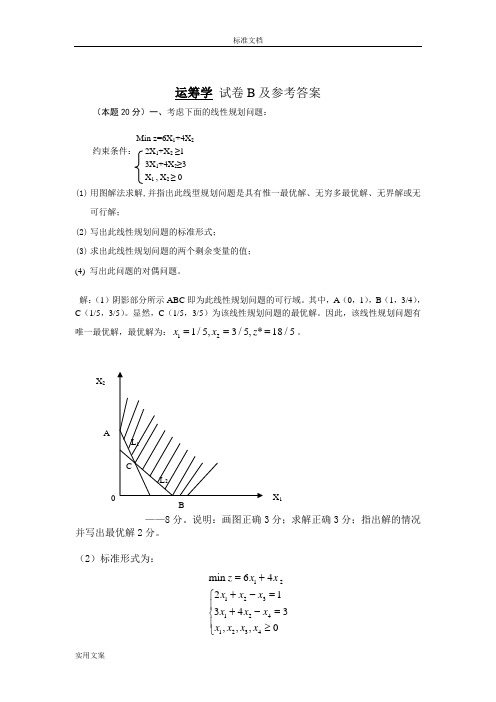
运筹学 试卷B 及参考答案(本题20分)一、考虑下面的线性规划问题:Min z=6X 1+4X 2约束条件: 2X 1+X 2 ≥13X 1+4X 2≥3 X 1 , X 2 ≥ 0(1) 用图解法求解,并指出此线型规划问题是具有惟一最优解、无穷多最优解、无界解或无可行解;(2) 写出此线性规划问题的标准形式; (3) 求出此线性规划问题的两个剩余变量的值; (4) 写出此问题的对偶问题。
解:(1)阴影部分所示ABC 即为此线性规划问题的可行域。
其中,A (0,1),B (1,3/4),C (1/5,3/5)。
显然,C (1/5,3/5)为该线性规划问题的最优解。
因此,该线性规划问题有唯一最优解,最优解为:121/5,3/5,*18/5x x z ===。
——8分。
说明:画图正确3分;求解正确3分;指出解的情况并写出最优解2分。
(2)标准形式为:121231241234min 6421343,,,0z x x x x x x x x x x x x =++-=⎧⎪+-=⎨⎪≥⎩ X 1 X 2 AB——4分 (3)两个剩余变量的值为:340x x =⎧⎨=⎩——3分(4)直接写出对偶问题如下:12121212max '323644,0z y y y y y y y y =++≤⎧⎪+≤⎨⎪≥⎩——5分(本题10分)二、前进电器厂生产A 、B 、C 三种产品,有关资料下表所示:学模型,不求解)解:设生产A 、B 、C 三种产品的数量分别为x 1,x 2和x 3,则有:——1分123123123123123max 810122.0 1.5 5.030002.0 1.5 1.21000200250100,,0z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤⎪⎨≤⎪⎪≤⎪≥⎪⎩ ——14分,目标函数和每个约束条件2分(本题10分)三、某电子设备厂对一种元件的年需求为2000件,订货提前期为零,每次订货费为25元。
运筹学教材编写组《运筹学》期末考试试卷(B)

《运筹学》期末考试试卷(B)学院 班级 姓名 学号考生注意∶1.本试题共 七 题,共 3 页,请考生认真检查;一、用单纯形法求解下述线性规划问题(20分)⎧⎨⎪⎪⎩⎪⎪0,824424m ax 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z二、设一线性规划问题为(25分)⎧⎨⎪⎩⎪m a x ,,z x x x x x x x x x j j =-+++≤-+≤≥=27624013123121232 目标函数变为max z x x x =++23123;3 约束条件右端项由(6,4)T 变为(3,5)T;4 增加一个约束条件-+≥x x 1322三、某种产品今后四周的需求量分别为300,700,900,600件,必须得到满足。
已知每件产品的成本在起初两周是10元,以后两周是15元。
工厂每周能生产这种产品700件,且在第二、三周能加班生产。
加班后,每周可增产200件产品,但成本每件增加5元。
产品如不能在本周交货,则每件每周存贮费是3元。
问如何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。
(25分)四、某校蓝球队准备从以下6名预备队员中选拔3名为正式队员,并使平均身高尽可能高,这6名预备队员情况如下表所示,试建立数学模型。
(20分)队员的挑选要满足下列条件:2少补充一名后卫队员;3大李或小田中间只能入选一名;4最多补充一名中锋;5如果大李或小赵入选,小周就不能入选。
五、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:(20分)学生总数。
六、某飞行队有5名正驾驶员和5名副驾驶员。
由于种种原因,某些正、副驾驶员不能同机飞行,某些则可以,如下表所示。
每架飞机出航时需正,副驾驶员各一人。
问最多能有几架飞机同时出航?应如何安排正,副驾驶员?用图论方法求解。
(20分)七、填空:(20分)1.某工程公司拟从四个项目中选择若干项目,若令11,2,3,40i i i ix ìïï==íïïïî,第个项目被选中;,第个项目未被选中;用i x 的线性表达式表示下列要求:(1)从1,2,3项目中至少选2个: ;(2)只有项目2被选中,项目4才能被选中: ;2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经济意义是 ,若从该空格出发进行调整,设调整量为2,则调后可使总运费下降 ;3. 动态规划中的Bellman 最优性原理是。
《运筹学》教材编写组《运筹学》笔记和课后习题(含考研真题)详解(对策论基础)

圣才电子书 十万种考研考证电子书、题库视频学习平台
(2)2× 或 ×2 对策的图解法
注意:该方法用在赢得矩阵为 2× 或 ×2 阶的对策上特别方便,也可用在 3× 或
×3 对策上。但对 和 均大于 3 的矩阵对策就丌适用了。
设缩减后的赢得矩阵为二阶无鞍点对策问题,局中人Ⅰ的混合策略为
的最优纯策略。 定理 1 矩阵对策 使得对一切
在纯策略意义下有解的充分必要条件是:存在纯局势
,均有
。
定义 2 设
为一个定义在
及
上的实值函数,如果存在
,使得对一切
和
,有
,则称
为
函数 的一个鞍点。 矩阵对策解的性质:
性质 1 无差别性。即若 性质 2 可交换性。即若
也是解。 定义 3 设有矩阵对策
记
是对策 G 的两个解,则
定理 11 设矩阵对策
的值为 ,则
6.矩阵对策的解法 (1)2×2 对策的公式法 所谓 2×2 对策是指局中人Ⅰ的赢得矩阵为 2×2 阶的,即
如果 A 有鞍点,则很快可求出各局中人的最优纯策略;如果 A 没有鞍点,为求最优混 合策略可求下列等式组:
上面等式组(Ⅰ)和(Ⅱ)一定有严格非负解
和
,其中
6 / 33
是对策 G 的两个解,则
和
,其中
,
,
则 和 分别称为局中人Ⅰ和Ⅱ的混的混合策略(或策略);对
,称
为一个混合局势(或局
势),局中人Ⅰ的赢得函数记成
这样得到的一个新的对策记成
,称 为对策 G 的混合扩充。
定义 4 设
是矩阵对策
的混合扩充,如果
3 / 33
圣才电子书 十万种考研考证电子书、题库视频学习平台
运筹学钱颂迪答案

运筹学钱颂迪答案【篇一: 803 运筹学】class=txt>运筹学考试大纲一、考试性质运筹学是我校航空运输管理学院硕士生入学考试的综合考试科目之一,它是我校为招收交通运输规划与管理学科硕士研究生而实施的水平考试,其评价标准是普通高等院校优秀本科毕业生能够达到的及格以上水平,以保证被录取者较好地掌握了必备的专业基础知识。
本门课程主要考试内容包括:线性规划及其对偶理论、运输问题、目标规划、整数规划、动态规划、图与网络分析,注重考察考生是否已经掌握运筹学最基本的理论知识与方法。
二、考试形式与试卷结构1.答卷方式:闭卷、笔试2.答卷时间: 180 分钟3.题型比例:满分 150 分,基本概念 20% ,计算及证明题 80%三、考查要点1.线性规划及对偶理论:单纯形法,改进单纯形法。
线性规划的对偶理论,对偶单纯形法,灵敏度分析;2.运输问题:运输问题的数学模型;用表上作业法求解运输问题;产销不平衡的运输问题及其求解方法;3.目标规划:目标规划的数学模型,目标规划的图解法与单纯形法;4.整数规划:0-1 型整数规划,分支定界解法,割平面解法,指派问题;5.动态规划:动态规划的基本概念和基本方法,动态规划的最优性原理与最优性定理,动态规划与静态规划的关系,动态规划的应用;6.图与网络分析:图与树的基本概念,最短路问题,网络最大流问题,最小费用最大流问题,中国邮路问题,网络计划。
四、主要参考书目1、郭耀煌,李军 .运筹学原理与方法. 成都:西南交通大学出版社,2004 ;2 、钱颂迪主编. 运筹学(修订版). 北京:清华大学出版社,1991 。
【篇二:运筹学大纲(13 、 14 级使用)2014.9 】(理论课程)开课系(部):数理教研部课程编号:380020 、 381703课程类型:专业必修课或学科必修课总学时: 48 或 32学分:3或2适用专业:信息管理与信息系统、投资学、工业工程、工程管理、经济统计学、物流管理开课学期: 3 或 4 或 5先修课程:高等数学、线性代数一、课程简述本课程是以经济活动方面的问题以及解决这类问题的原理和方法作为研究的对象,把经济活动中的问题归结为对应的某种数学模型,运用数学知识等工具求得最合理的工作方案。
《管理运筹学》考试试卷A,B卷及答案

《管理运筹学》考试试卷A,B卷及答案一、选择题(每题2分,共20分)1. 运筹学的英文全称是:A. Operation ResearchB. Operation ManagementC. Operational ResearchD. Operations Management2. 线性规划问题的标准形式中,目标函数是:A. 最大化B. 最小化C. 既可以是最大化也可以是最小化D. 无法确定3. 在线性规划中,约束条件可以用以下哪个符号表示?A. ≤B. ≥C. =D. A、B、C都对4. 简单线性规划问题中,如果一个变量在任何解中都不为零,则称这个变量为:A. 基变量B. 非基变量C. 独立变量D. 依赖变量5. 以下哪个方法可以用来求解线性规划问题?A. 单纯形法B. 拉格朗日乘数法C. 对偶理论D. A、B、C都可以二、填空题(每题3分,共15分)6. 在线性规划中,如果一个约束条件的形式为“≥”,则称这个约束为______约束。
7. 在线性规划问题中,若决策变量为非负整数,则该问题为______规划问题。
8. 在目标规划中,目标函数通常表示为______。
9. 在运输问题中,如果产地和销地的数量相等,则称为______。
10. 在排队论中,顾客到达的平均速率通常表示为______。
三、计算题(每题10分,共30分)11. 某工厂生产甲、乙两种产品,甲产品每件利润为200元,乙产品每件利润为150元。
工厂每月最多生产甲产品100件,乙产品150件。
同时,生产甲产品每件需要3小时,乙产品每件需要2小时,工厂每月最多可利用工时为300小时。
试建立该问题的线性规划模型,并求解。
12. 某公司有三个工厂生产同一种产品,分别供应给四个销售点。
各工厂的产量和各销售点的需求量如下表所示。
求最优的运输方案,并计算最小运输成本。
工厂\销售点 A B C D产量 20 30 50需求量 10 20 30 4013. 设某商店有三个售货员,负责四个收款台。
《运筹学》期末考试试题及参考答案

《运筹学》试题参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为 可行解 。
2、在线性规划问题中,图解法适合用于处理 变量 为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是 设立虚供地或虚需求点,化为供求平衡的标准形式 。
4、在图论中,称 无圈的 连通图为树。
5、运输问题中求初始基本可行解的方法通常有 最小费用法 、 西北角法 两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题: 1)max z = 6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x , 解:此题在“《运筹学》复习参考资料.doc ”中已有,不再重复。
2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:⑴ ⑵ ⑶ ⑷ ⑸ ⑹、⑺⑴⑵ ⑶ ⑷ ⑸、⑹可行解域为abcda ,最优解为b 点。
由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫ ⎝⎛21x x =(11,0)T ∴min z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:A B C 甲 9 4 3 70 乙 4 6 10 1203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解。
(10分) 解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z 是产品售后的总利润,则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x , 2)用单纯形法求最优解:加入松弛变量x 3,x 4,x 5,得到等效的标准模型:max z =70x 1+120x 2+0 x 3+0 x 4+0 x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下:∴X *=(11,11,11,0,0)T∴max z =70×11100+120×11300=1143000四、(10分)用大M 法或对偶单纯形法求解如下线性规划模型:min z =5x 1+2x 2+4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x解:用大M 法,先化为等效的标准模型:max z / =-5x 1-2x 2-4x 3 s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7,得到:max z / =-5x 1-2x 2-4x 3-M x 6-M x 7 s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下:∴x *=(32,2,0,0,0)T最优目标函数值min z =-max z / =-(-322)=322五、(15分)给定下列运输问题:(表中数据为产地A i 到销地B j 的单位运费)1)用最小费用法求初始运输方案,并写出相应的总运费;(5分) 2)用1)得到的基本可行解,继续迭代求该问题的最优解。
《运筹学》教材编写组《运筹学》笔记和课后习题(含考研真题)详解(存储论)

第13章存储论13.1 复习笔记1.存储论的基本概念备货时间:从订货到货物进入“存储”往往需要一段时间,我们把这段时间称为备货时间。
备货时间可能很长,也可能很短,可能是随机性的,也可以是确定性的。
提前时间:从另一个角度看,为了在某一时刻能补充存储,必须提前订货,那么这段时间称之为提前时间。
存储策略:决定多少时间补充一次以及每次补充数量的策略称为存储策略。
存储论要解决的问题是:多少时间补充一次,每次补充的数量应该是多少,即存储策略。
2.一些参数的含义K:货物单价;:最佳订货周期;R:需求速度;:最佳订货批量;:单位存储费用;:单位缺货损失;:订购费;:最佳费用;:最佳生产时间;:生产速度;:最大存贮量;:最大缺货量;:最大缺货量。
3.存储策略(1)-循环策略,每隔时间向系统内补充存储量Q。
(2)策略,当存储量时不补充;当时补充存储,补充量(即,将存储量补充到S)。
(3)混合策略,每经过t时间检查存储量,当时不补充;当时,补充存储量使之达到S。
4.确定性存储模型(1)模型一—经典的E.O.Q模型:不允许缺货,备货时间很短,且需求是连续均匀的,即需求速度是一常数;每批订货量不变,订货费用为常数;单位存储费用不变。
已知,求,,(2)模型二:不允许缺货,生产需一定时间,其余条件同模型一。
已知,求,,(3)模型三:允许缺货,备货时间很短,其余条件同模型一。
已知,求,,,最大缺货量(4)模型四:允许缺货(需补足缺货),生产需要一定时间,其余条件同模型一。
已知,求,,简便的记忆方法:①永远成立②记住模型一,,③定义两个因子④与因子的关系与乘以因子,与除以因子模型二乘除,模型三乘除,模型四乘除⑤模型二的,模型三的,模型四的说明:在允许缺货条件下,经过研究而得出的存储策略是:每隔时间订货一次,订货量为,用中的一部分补足所缺货物,剩余部分进入存储。
很明显,在相同的时间段落里,允许缺货的订货次数比不允许缺货时订货次数减少了。
《运筹学》试题及答案(二)

《运筹学》试题及答案19、简述线性规划模型主要参数(p11)(1)、价值系数:目标函数中决策变量前的系数为价值系数(2)、技术系数:约束条件中决策变量前的系数(3)、约束条件右边常数项15、简述线性规划解几种可能的结果(情形)(ppt第二章39或89页)(1).有唯一最优解 (单纯形法中在求最大目标函数的问题时,对于某个基本可行解,所有δj≤0)(2).无可行解,即可行域为空域,不存在满足约束条件的解,也就不存在最优解了。
(3).无界解,即可行域的范围延伸到无穷远,目标函数值可以无穷大或无穷小,一般来说,这说明模型有错,忽略了一些必要的约束条件(4).无穷多个最优解,则线段上的所有点都代表了最优解(5)退化问题,基变量有时存在两个以上相同的最小比值,这样在下一次迭代中就有一个或几个基变量等于零,用图解法无退化解1、简述单纯形法的基本思路(p70)从可行域中某一个顶点开始,判断此顶点是否是最优解,如不是,则再找另一个使得其目标函数值更优的顶点,称之为迭代,再判断此点是否是最优解。
直到找到一个顶点为其最优解,就是使得其目标函数值最优的解,或者能判断出线性规划问题无最优解为止。
17、简述线性规划中添加人工变量的前提(p85)在系数矩阵中直接找不到初始可行解,进而通过添加人工变量的方法来构造初始可行基,得出初始基本可行解10、简述线性规划对偶问题的基本性质(p122)(1)对称性(2)弱对偶性(3)强对偶性(4)最优性(5)互补松弛型原函数与对偶问题的关系1)求目标函数最大值的线性规划问题中有n 个变量 m个约束条件,它的约束条件都是小于等于不等式。
而其对偶则是求目标函数为最小值的线性规划问题,有m个变量n个约束条件,其约束条件都为大于等于不等式。
2)原问题的目标函数中的价值系数为对偶问题中的约束条件的右边常数项,并且原问题的目标函数中的第i个价值系数就等于对偶问题中的第i个约束条件的右边常数项。
3)原问题的约束条件的右边常数项为对偶问题的目标函数中价值系数。
《运筹学》期末复习总结题

一、单项选择题1、下列叙述正确的是()。
A.线性规划问题,若有最优解,则必是一个基变量组的可行基解B.线性规划问题一定有可行基解C.线性规划问题的最优解只能在最低点上达到D.单纯形法求解线性规划问题时,每换基迭代一次必使目标函数值下降一次答案:A2、线性规划的变量个数与其对偶问题的()相等。
A.变量目标函数B.变量约束条件C.约束条件个数D.不确定答案:C3、在利用表上作业法求各非基变量的检验数时,有闭回路法和()两种方法。
A.西北角法B.位势法C.最低费用法D.元素差额法答案:B4、下列各项()不是目标规划的特点。
A.多目标B.单一目标C.具有优先次序D.不求最优答案:B5、下列关于图的说法中,错误的为()。
A.点表示所研究的事物对象B.边表示事物之间的联系C.无向图是由点及边所构成的图D.无环的图称为简单图答案:D6、利用单纯形法求解线性规划问题时,首先需要()。
A.找初始基础可行基B.检验当前基础可行解是否为最优解C.确定改善方向D.确定入变量的最大值和出变量答案:A7、对偶问题最优解的剩余变量解值()原问题对应变量的检验数的绝对值。
A.大于B.小于C.等于D.不能确定答案:C8、当某个非基变量检验数为零,则该问题有()。
A.无解B.无穷多最优解C.退化解D.惟一最优解答案:B9、PERT 网络图中,()表示一个工序。
A.节点B.弧C.权D.关键路线答案:B10、假设对于一个动态规划问题,应用顺推法以及逆推解法得出的最优解分别为P和D,则有()。
A.P>D B.P<DC.P=D D.不确定答案:C11、下列有关线性规划问题的标准形式的叙述中错误的是()。
A.目标函数求极大B.约束条件全为等式C.约束条件右端常数项全为正D.变量取值全为非负答案:C12、线性规划问题的数学模型由目标函数、约束条件和()三个部分组成。
A.非负条件B.顶点集合C.最优解D.决策变量答案:D13、如果原问题有最优解,则对偶问题一定具有()。
《运筹学》期末考试试题及参考答案

《运筹学》试题参考答案 一、填空题�每空2分�共10分� 1、在线性规划问题中�称满足所有约束条件方程和非负限制的解为 可行解 。
2、在线性规划问题中�图解法适合用于处理 变量 为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是 设立虚供地或虚需求点�化为供求平衡的标准形式 。
4、在图论中�称 无圈的 连通图为树。
5、运输问题中求初始基本可行解的方法通常有 最小费用法 、 西北角法 两种方法。
二、�每小题5分�共10分�用图解法求解下列线性规划问题� 1�m a x z = 6x 1+4x 2�������������0781022122121x x x x x x x � 解�此题在“《运筹学》复习参考资料.d o c ”中已有�不再重复。
2�m i n z =�3x 1+2x 2 �������������������0,137210422422121212121x x x x x x x x x x解�⑴⑵⑶ ⑷ ⑸⑹、⑺⑴⑵⑶ ⑷ ⑸、⑹可行解域为a b c d a �最优解为b 点。
由方程组������02242221xx x 解出x 1=11�x 2=0 ∴X *=��������21x x =�11�0�T∴m i n z =�3×11+2×0=�33三、�15分�某厂生产甲、乙两种产品�这两种产品均需要A 、B 、C 三种资源�每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示�ABC甲 9 4 3 70 乙 4 6 10 120 360 200 3002�用单纯形法求该问题的最优解。
�10分� 解�1�建立线性规划数学模型� 设甲、乙产品的生产数量应为x 1、x 2�则x 1、x 2≥0�设z 是产品售后的总利润�则 ma x z =70x 1+120x 2 s.t . ��������������0300103200643604921212121x x x x x x x x � 2�用单纯形法求最优解� 加入松弛变量x 3�x 4�x 5�得到等效的标准模型� ma x z =70x 1+120x 2+0 x 3+0 x 4+0 x 5 s.t . ������������������5,...,2,1,03001032006436049521421321j x x x x x x xx x x j 列表计算如下�CB XB b70 120 0θL x1 x2 x3 x4 x5 0x 3 360 94190 0 x 4 200 4 6 0 1 0 100/3 0 x 5 300 3 �10� 0 0 1 300 0 0 0 0 70 120↑ 0 0 0 0 x3 240 39/5 0 1 0 - 2/5 400/13 0 x4 20 �11/5� 0 0 1 - 3/5 100/11 120 x 2 30 3/10 1 0 0 1/10 10036 120 0 0 12 34↑ 0 0 0 �12 0 x3 1860/11 0 0 1 �39/11 19/11 70 x 1 100/11 1 0 0 5/11 - 3/11 120 x 2 300/11 0 1 0 - 3/22 2/11114300070 120 0 170/11 30/11 0 0-170/11 �30/11 ∴X *=�11100�11300�111860�0�0�T ∴m a x z =70×11100+120×11300=1143000四、�10分�用大M 法或对偶单纯形法求解如下线性规划模型� mi n z =5x 1�2x 2�4x 3 ������������0,,10536423321321321x x x x x x x x x解�用大M 法�先化为等效的标准模型� ma x z / =�5x 1�2x 2�4x 3 s.t . ���������������5,...,2,1,01053642353214321j y x x x xx x x x j 增加人工变量x 6、x 7�得到� ma x z / =�5x 1�2x 2�4x 3�M x 6�M x 7 s.t �����������������7,...,2,1,0105364237532164321j x x x x x x x x x x x j 大M 法单纯形表求解过程如下�C B X B b�5�2�400�M�MθLx1x2x3x4x5x6x7�M x64�3�12�10104/3�M x7106350�1015/3�9M�4M�7M M M�M�M9M�5↑4M�27M�4�M�M00�5x14/311/32/3�1/301/30——�M x72011�2��1�211�5-M�5/3-M�10/3-2M+5/3M2M�5/3-M0M�1/3M�2/32M�5/3↑�M�3M+5/30�5x15/311/25/60�1/601/610/3 0x410�1/2�1/21�1/2�11/22�5�5/2�25/605/60�5/601/2↑1/60�5/6�M�M+5/6�5�2x12/3101/3�11/31�1/3 x220112�1�21�322�5�2�11/311/3�1�1/3 00�1/3�1�1/3�M+1�M+1/3∴x*=�32�2�0�0�0�T最优目标函数值m i n z=�m a x z/=���322�=322五、�15分�给定下列运输问题��表中数据为产地A i到销地B j的单位运费�B1 B2 B3 B4 si A 1 A 2 A 3 1 2 3 4 8 7 6 5 9 10 11 9 10 80 15 dj 8 22 12 181�用最小费用法求初始运输方案�并写出相应的总运费��5分� 2�用1�得到的基本可行解�继续迭代求该问题的最优解。
《运筹学》期末考试试题及参考答案

《运筹学》期末考试试题及参考答案《运筹学》期末考试试题及参考答案一、填空题1、运筹学是一门新兴的_________学科,它运用_________方法,研究有关_________的一切可能答案。
2、运筹学包括的内容有_______、、、_______、和。
3、对于一个线性规划问题,如果其目标函数的最优解在某个整数约束条件的约束范围内,那么该最优解是一个_______。
二、选择题1、下列哪一项不是运筹学的研究对象?( ) A. 背包问题 B. 生产组织问题 C. 信号传输问题 D. 原子核物理学2、以下哪一个不是运筹学问题的基本特征?( ) A. 唯一性 B. 现实性 C. 有解性 D. 确定性三、解答题1、请简述运筹学在日常生活中的应用实例,并就其中一个进行详细说明。
2、某企业生产三种产品,每种产品都可以选择用手工或机器生产。
假设生产每件产品手工需要的劳动时间为3小时,机器生产为2小时,卖价均为50元。
此外,手工生产每件产品的材料消耗为10元,机器生产为6元。
已知每个工人每天工作时间为24小时,可生产10件产品,每件产品的毛利润为50元。
请用运筹学方法确定手工或机器生产的数量,以达到最大利润。
参考答案:一、填空题1、交叉学科;数学;合理利用有限资源,获得最大效益2、线性规划、整数规划、动态规划、图论与网络、排队论、对策论3、整点最优解二、选择题1、D 2. A三、解答题1、运筹学在日常生活中的应用非常广泛。
例如,在背包问题中,如何在有限容量的背包中选择最有价值的物品;在生产组织问题中,如何合理安排生产计划,以最小化生产成本或最大化生产效率;在信号传输问题中,如何设计最优的信号传输路径,以确保信号的稳定传输。
以下以背包问题为例进行详细说明。
在背包问题中,给定一组物品,每个物品都有自己的重量和价值。
现在需要从中选择若干物品放入背包中,使得背包的容量恰好被填满,同时物品的总价值最大。
这是一个典型的0-1背包问题,属于运筹学的研究范畴。
运筹学期末试题及答案

运筹学期末试题及答案一、选择题1. 运筹学是通过分析和决策来实现最佳利益的学科。
以下哪个选项最准确地描述了运筹学的定义?A. 运筹学是一门研究如何安排和管理物流的学科。
B. 运筹学是一门研究如何制定合理的销售策略的学科。
C. 运筹学是一门研究如何决策和规划资源的学科。
D. 运筹学是一门研究如何提高生产效率的学科。
答案:C2. 线性规划是一种常用于解决最优化问题的数学方法。
以下哪个选项最准确地解释了线性规划问题?A. 线性规划是一种通过建立线性方程组来寻找最小值或最大值的方法。
B. 线性规划是一种通过建立非线性方程组来寻找最小值或最大值的方法。
C. 线性规划是一种通过建立线性方程组来寻找全局最优解的方法。
D. 线性规划是一种通过建立非线性方程组来寻找局部最优解的方法。
答案:C3. 整数规划是一种特殊的线性规划问题,其中决策变量必须是整数。
以下哪个选项最准确地描述了整数规划的特点?A. 整数规划只适用于小规模问题,无法处理大规模问题。
B. 整数规划可以保证找到问题的最优整数解。
C. 整数规划只能用于决策变量为0或1的二进制问题。
D. 整数规划在求解过程中需要考虑所有可能的整数解。
答案:B4. 单纯形法是一种用于解决线性规划问题的常用算法。
以下哪个选项最准确地描述了单纯形法的特点?A. 单纯形法只能用于求解可行解存在且有限的线性规划问题。
B. 单纯形法可以保证找到线性规划问题的最优解。
C. 单纯形法在求解过程中需要考虑所有可能的解空间。
D. 单纯形法只适用于二维线性规划问题,无法处理高维问题。
答案:B5. 敏感性分析是一种用于评估线性规划模型解的稳定性和可靠性的方法。
以下哪个选项最准确地解释了敏感性分析?A. 敏感性分析是一种通过调整决策变量的值来优化线性规划模型的方法。
B. 敏感性分析是一种通过改变约束条件的值来评估线性规划模型的可行性的方法。
C. 敏感性分析是一种通过改变目标函数系数的值来评估线性规划模型解的稳定性的方法。
最新(整理)《运筹学》期末考试试题及参考答案

(整理)《运筹学》期末考试试题及参考答案------------------------------------------作者xxxx------------------------------------------日期xxxx《运筹学》试题参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为 可行解 。
2、在线性规划问题中,图解法适合用于处理 变量 为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是 设立虚供地或虚需求点,化为供求平衡的标准形式 。
4、在图论中,称 无圈的 连通图为树。
5、运输问题中求初始基本可行解的方法通常有 最小费用法 、 西北角法 两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题: 1)max z = 6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x , 解:此题在“《运筹学》复习参考资料。
do c”中已有,不再重复. 2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:⑴ ⑵ ⑶ ⑷ ⑸ ⑹、⑺⑴⑵ ⑶ ⑷ ⑸、⑹可行解域为ab cda,最优解为b 点。
由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫ ⎝⎛21x x =(11,0)T∴m in z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:A B C 甲 9 4 3 70 乙 4 6 10 1203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解.(10分) 解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z是产品售后的总利润,则m ax z =70x 1+120x 2s .t 。
运筹学期末考试试题及参考答案

2014-2015学年度 第2学期 12级物流管理专业 “运筹学” 课程试题 (样本)学号: 姓名:《中山大学授予学士学位工作细则》第六条:“考试作弊不授予学士学位”说明:(1)共六题,满分100分;(2)考试时间120分钟;(3)对部分正确的答案,将会酌情给分。
一、考虑下面的线性规划问题:112121212Maximize subject to212218,0Z c x x x x x x x x =++≤+≤≥使用图解法,分析当11(0)c c <<∞变化时最优解的变化。
(15分) 参考答案可行域是OABC 所构成之多边形区域,如下图所示。
其中,O =(0,0),A =(0,9),B =(2,8),C =(6,0)。
c 1的取值 最优解 最优目标函数值 c 1 > 2 C =(6,0)6c 1 c 1 = 2 线段BC 上任意一点,即 λ(2,8)+ (1-λ)(6,0), 0≤λ≤1 12 0.5<c 1<2 B =(2,8)2c 1+8 c 1 = 0.5 线段AB 上任意一点,即 λ(0,9)+ (1-λ)(2,8), 0≤λ≤1 9 0<c 1<0.5 A =(0,9)9警示二、帆船生产公司需要确定在今后4个季度每个季度中应该生产多少艘帆船,今后的4个季度每个季度的需求量是:第1季度为40艘帆船,第2季度为60艘,第3季度为75艘,第4季度为25艘。
当前公司有10艘帆船的库存。
每季度的需求必须满足(不能缺货)。
在正常的工作时间内,公司每季度最多生产40艘帆船,每艘帆船总成本为400美元。
如果加班的话,可以多生产,每艘成本为450美元。
每季度末多余的帆船的仓储成本为20美元。
使用线性规划描述该公司的生产计划问题,使该公司今后4个季度的生产和仓储成本最小。
(15分)参考答案x t : 每个季度正常生产的数量, t = 1,2,3,4, y t : 每个季度加班生产的数量, t = 1,2,3,4, i t : 每个季度加班生产的数量, t = 1,2,3,4,最小化总成本:总成本 = 正常生产的成本 + 加班生产的成本 + 库存成本Min Z = 400x 1 + 400 x 2 + 400 x 3 + 400 x 4 + 450 y 1 + 450 y 2 + 450 y 3 + 450 y 4 + 20 i 1 + 20 i 2 + 20 i 3+20 i 4subject to x 1 ≤ 40, x 2 ≤ 40, x 3 ≤ 40, x 4 ≤ 40, i 1 = 10 + x 1 + y 1 – 40, i 2 = i 1 + x 2 + y 2 – 60, i 3 = i 2 + x 3 + y 3 – 75, i 4 = i 2 + x 4 + y 4 – 25, x t , y t , i t ≥ 0, t =1,2,3,4三、考虑如下线性规划问题123123123123Max 253subject to22050,,0Z x x x x x x x x x x x x =++-+≥++=≥1、 写出两阶段法第一阶段的线性规划问题。
《运筹学》教材编写组《运筹学》笔记和课后习题(含考研真题)详解(运输问题)

第3章 运输问题3.1 复习笔记1.运输问题的数学模型运输问题:已知有m 个生产地点,1,2,,i A i m =…,可供应某种物资,其供应量(产量)分别为i a ,1,2,,i m =…,有n 个销地j B ,1,2,,j n =…,其需要量分别为j b ,1,2,,j n =…,从i A 到j B 运输单位物资的运价(单价)为ij c 。
如何安排运输,能使得总运输成本最小?(1)产销平衡运输问题的数学模型1111min ,1,2,,..,1,2,,0m nij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪==⎨⎪⎪≥⎪⎩∑∑∑∑ 模型特点:①该模型包含m n ⨯个变量,()m n +个约束方程;②该系数矩阵中对应于变量ij x 的系数向量ij P ,其分量中除第i 个和第m j +个为1外,其余的都为零。
即(01010)T ij i m j P e e +==+…………③对于产销平衡的运输问题,有以下关系式存在:111111n m n n m m j ij ij i j i j j i i b x x a ======⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑ 所以模型最多只有m+n-1个独立约束方程。
即系数矩阵的秩≤m+n -1。
注意:运输问题的基变量一定是m+n-1个,m+n-1个变量构成基变量的充要条件是它们不构成闭回路。
闭回路的特点:在运输产销平衡表中,每一条边都是水平或垂直的;每一行或每一列至多只有两个闭回路的顶点。
(2)产销不平衡运输问题的数学模型当产大于销,即11m n i j i j a b ==>∑∑时,运输问题的数学模型可写成:1111min ,1,2,,..,1,2,,0m n ij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑∑∑ 当产小于销,即11m n i j i j a b ==<∑∑时,运输问题的数学模型可写成:11min m n ij ij i j z c x ===∑∑11, (1,2,,), (1,2,,)0nij i j mij j i ij x a i m x b j n x ==⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑……2.表上作业法表上作业法是单纯形法在求解运输问题时的一种简化方法,其实质是单纯形法。
运筹学期末考试试题及答案

楚大2012---2013上学期经济信息经管及计算机应用系《运筹学》期末考试试卷及答案班级: 学号一、单项选择题:1、在下面的数学模型中,属于线性规划模型的为( A )。
⎪⎩⎪⎨⎧≥-≥-+=0Y ,X 1Y X 2.t .s Y X 3S min .B ⎪⎩⎪⎨⎧≥≤+=0Y ,X 3XY .t .s Y X 4S max .A ⎪⎩⎪⎨⎧≥≤-+=0Y ,X 2Y X .t .s Y X S max .C 22⎪⎩⎪⎨⎧≥≥+=0Y ,X 3Y X .t .s XY 2S min .D 2、线性规划问题若有最优解,则一定可以在可行域的 (A )上达到。
A .顶点B .内点C .外点D .几何点3、在线性规划模型中,没有非负约束的变量称为 ( C )A .多余变量B .松弛变量 C.自由变量D .人工变量4、若线性规划问题的最优解同时在可行解域的两个顶点处达到,那么该线性规划问题最优解为( C )。
A.两个B.零个C.无穷多个D.有限多个5、线性规划具有唯一最优解是指( B )A .最优表中存在常数项为零B .最优表中非基变量检验数全部非零C .最优表中存在非基变量的检验数为零D .可行解集合有界6、设线性规划的约束条件为⎪⎩⎪⎨⎧≥=++=++0,,422341421321x x x x x x x x 则基本可行解为( C )。
A .(0, 0, 4, 3)B . (3, 4, 0, 0)C .(2, 0, 1, 0)D . (3, 0, 4, 0)7、若运输问题已求得最优解,此时所求出的检验数一定是全部( D )A 、小于或等于零B .大于零C .小于零D .大于或等于零8、对于m 个发点、n 个收点的运输问题,叙述错误的是( D )A .该问题的系数矩阵有m ×n 列B .该问题的系数矩阵有m+n 行C .该问题的系数矩阵的秩必为m+n-1D .该问题的最优解必唯一9、关于动态规划问题的下列命题中错误的是( A )A 、动态规划分阶段顺序不同,则结果不同B 、状态对决策有影响C 、动态规划中,定义状态时应保证在各个阶段中所做决策的相对独立性D 、动态规划的求解过程都可以用列表形式实现10、若P 为网络G 的一条流量增广链,则P 中所有正向弧都为G 的( D )A .对边B .饱和边C .邻边D .不饱和边一、判断题。
管理运筹学期末试卷题目B卷---精品管理资料
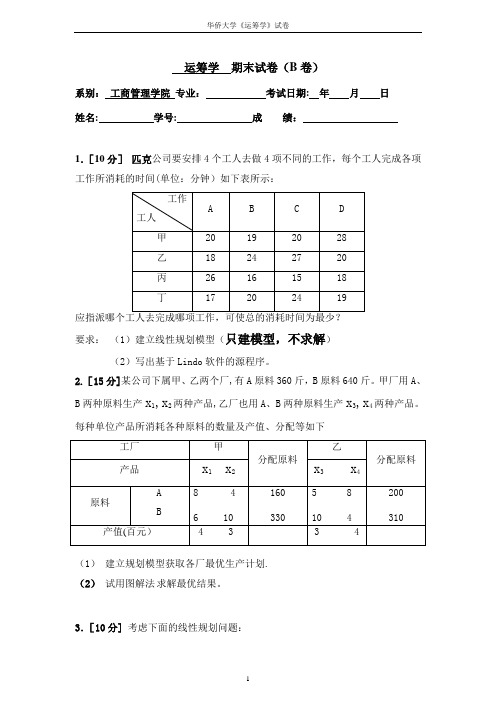
运筹学期末试卷(B卷)系别:工商管理学院专业:考试日期: 年月日姓名: 学号: 成绩:1.[10分]匹克公司要安排4个工人去做4项不同的工作,每个工人完成各项工作所消耗的时间(单位:分钟)如下表所示:要求:(1)建立线性规划模型(只建模型,不求解)(2)写出基于Lindo软件的源程序。
2.[15分]某公司下属甲、乙两个厂,有A原料360斤,B原料640斤。
甲厂用A、B两种原料生产x1,x2两种产品,乙厂也用A、B两种原料生产x3,x4两种产品。
每种单位产品所消耗各种原料的数量及产值、分配等如下(1)建立规划模型获取各厂最优生产计划.(2)试用图解法求解最优结果。
3.[10分]考虑下面的线性规划问题:目标函数:Min Z=16x 1+16x 2 +17x 3约束条件:利用教材附带软件求解如下:**********************最优解如下*************************目标函数最优值为 : 148。
916变量 最优解 相差值-—---—— -—--——-— ——--—-—— x1 7。
297 0 x2 0 .703 x3 1.892 0约束 松弛/剩余变量 对偶价格——---—- --—-——--—---- —————--— 1 20.811 02 0 —3。
6223 0 —4.73 目标函数系数范围 :变量 下限 当前值 上限——-———- -—-————- ---—--—- ——-———--x1 1。
417 16 16。
565 x2 15.297 16 无上限 x3 14。
4 17 192 常数项数范围 :约束 下限 当前值 上限—---——— —-—--——- ——---——- -——--—-—1 9.189 30 无上限2 3.333 15 111.25 3 -2。
5 20 90试回答下列问题:(1) 第二个约束方程的对偶价格是一个负数(为—3.622),它的含义是什么? (2) x2有相差值为0.703,它的含义是什么?(3) 请对右端常数项范围的上、下限给予具体解释,应如何应用这些数据? (4) 当目标函数系数在什么范围内变化时,最优购买计划不变?(5) 当目标函数中X1的系数从16降为15,而X2的系数从16升为18时,最优解是否发生变化?13123123123300.56153420,,0x x x x x x x x x x x +≤-+≥+-≥≥4.[8分]某工厂每年需要甲零件36000件,每件零件120元,每个部件的年存储费为每个部件价格的18%,每批订货费为150元。
东北大学运筹学期末试卷

东北大学运筹学期末试卷(一)难易度:易1、以语录体形式记述的先秦诸子著作是( b )。
A、《老子》B、《论语》C、《孟子》D、《荀子》2、我国古代第一部诗歌总集是( b )A、《楚辞》B、《诗经》C、《古诗源》D、《古诗十九首》3、“老吾老以及人之老,幼吾幼以及人之幼,天下可运于掌。
”出自( b )A、《论语》B、《孟子》C、《荀子》D、《老子》4、认为“民为贵,社稷次之,君为轻”的思想家是( b )A、孔子B、孟子C、庄子D、左丘明5、“圣人无常心,以百姓心为心”是下列哪个思想家的话( d )A.孔子 B.孟子 C.庄子 D.老子6、提出“民贵君轻”思想的先秦思想家是( b )A、墨子B、孟子C、庄子D、荀子7、先秦诸子散文中,最富有浪漫色彩的是( c )A、《论语》B、《孟子》C、《庄子》D、《韩非子》8、《诗经、氓》中“淇则有岸,隰则有泮”两句是( d )A、反喻氓当初誓言滔滔不绝B、描写出嫁时渡淇水的情景C、描写被弃后渡淇水的情景D、反喻自己的怨恨无穷无尽9、称赞《史记》为“史家之绝唱,无韵之《离骚》”的是( d )A、班固B、茅盾C、巴金D、鲁迅10、《诗经》中保存民歌最多的是( a )A、国风B、大雅C、颂D、小雅11、杜甫诗歌的风格特点是( d )A、清新淡雅B、豪放飘逸C、深婉华美D、沉郁顿挫12、北宋词坛豪放派的代表作家是( c )A、柳永B、李清照C、苏轼D、辛弃疾13、提出“文章合为时而著,歌诗合为时而作”的著名主张的作家是( a )A、杜甫B、白居易C、辛弃疾D、韩愈14、我国第一部纪传体通史著作是( c )A、《左传》B、《战国策》C、《史记》D、《春秋》15、李商隐《无题》中推已而及对方的一联是( d )A、相见时难别亦难,东风无力百花残B、春蚕到死丝方尽,蜡炬成灰泪始干C、晓镜但愁云鬓改,夜吟应觉月光寒D、蓬山此去无多路,青鸟殷勤为探看16、在《前赤壁赋》中,苏子认为“惟江上之清风,与山间之明月,耳得之而为声,目遇之而成色;取之无尽,用之不竭”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《运筹学》期末考试试卷(B)
学院 班级 姓名 学号
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查;
一、用单纯形法求解下述线性规划问题(20分)
⎧⎨⎪⎪⎩
⎪⎪0
,824424max 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z
二、设一线性规划问题为(25分)
⎧⎨⎪⎩⎪max ,,z x x x x x x x x x j j =-+++≤-+≤≥=27624013
1231212
3
2 目标函数变为
max z x x x =++23123;
3 约束条件右端项由(6,4)T 变为(3,5)T
;
4 增加一个约束条件-+≥x x 1322
三、某种产品今后四周的需求量分别为300,700,900,600件,必须得到满足。
已知每件产品的成本在起初两周是10元,以后两周是15元。
工厂每周能生产这种产品700件,且在第二、三周能加班生产。
加班后,每周可增产200件产品,但成本每件增加5元。
产品如不
能在本周交货,则每件每周存贮费是3元。
问如何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。
(25分)
四、某校蓝球队准备从以下6名预备队员中选拔3名为正式队员,并使平均身高尽可能高,这6名预备队员情况如下表所示,试建立数学模型。
(20分)
队员的挑选要满足下列条件:
2少补充一名后卫队员;
3大李或小田中间只能入选一名;
4最多补充一名中锋;
5如果大李或小赵入选,小周就不能入选。
五、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:(20分)
学生总数。
六、某飞行队有5名正驾驶员和5名副驾驶员。
由于种种原因,某些正、副驾驶员不能同机飞行,某些则可以,如下表所示。
每架飞机出航时需正,副驾驶员各一人。
问最多能有几架飞机同时出航?应如何安排正,副驾驶员?用图论方法求解。
(20分)
七、填空:(20分)
1.某工程公司拟从四个项目中选择若干项目,若令
11,2,3,4
0i i
i i
x ,第个项目被选中;
,第个项目未被选中;
用i x 的线性表达式表示下列要求:
(1)从1,2,3项目中至少选2个: ;
(2)只有项目2被选中,项目4才能被选中: ;
2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经
济意义是 ,若从
该空格出发进行调整,设调整量为2,则调后可使总运费下降 ;
3. 动态规划中的Bellman 最优性原理是。
期末考试试卷(B)参考答案
一、解:将原问题化为标准形得
5,2,1,08
24424max 52142132121 =≥=+-=+-=++-+=i x x x x x x x x x x x x Z i
4 1 0 0 0 i b ik i a b / 1x 2x 3x 4x 5x
0 3x -1 1 1 0 0 2 - 0 4x 1 -4 0 1 0 4 4 0 5x 1 -2 0 0 1 8 8
j
r 4 1 0 0 0
0 3x 0 -3 1 1 0 6 - 4 1x 1 -4 0 1 0 4 - 0 5x 0 2 0 -1 1 4 2
j
r 0 17 0 -4 0
0 3x 0 0 1 -1/2 3/2 12 4 1x 1 0 0 -1 2 12 1 2x 0 1 0 -1/2 1/2 2
j
r 0 0 0 9/2 -17/2
由于04>r 而对应的04<i a ∴ 此线性规划问题无界
二、解
(1)X 2的价值系数由-7变为3。
()0
1310232>=⎪⎪⎭⎫
⎝⎛-=r
346)3
10
,38(),(*21*=
==∴Z x x X T
T
(2)
⎪
⎪⎭⎫ ⎝⎛=-11011B 0
835311011'>⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==-b B b
此时不影响解的最优性,只改变解的值及目标函数值
6
*)8,3(),(*51===∴Z x x X T T
(3) 最优解不满足新增加的约束条件
2231≥+-x x
∴最优解要发生改变 将约束条件改写为
2
2631-=+-x x x
加入最优表中继续迭代。
∴新的最优解为
3
28*)
,()3,1(*38310=
==Z x x X T
T
三、解:建立运输问题模型并给出初始方案得:
此时检验数全
≥j i r ,为最优解
)(327001560015700162001070010300*元=⨯+⨯+⨯+⨯+⨯=Z
分配计划如下:第一个月正常生产500件,分别给1月300件,3月200件。
第二个月正常生产700件,供给第二个月 第三个月正常生产700件,供给第三个月 第四个月正常生产600件,供给第六个月
四、解:设
⎩⎨
⎧=号码的人入选,第号码的人不入选,第i i y i 10
⎪⎪⎪⎪⎪
⎩⎪⎪⎪
⎪
⎪⎨
⎧==+≤+≤+≤+≤+=++++++++++=10111113)185180186187191193(max 989795548598755498765431或i y y y y y y y y y y y y y y y y y y y y y y y Z
五、解:利用匈牙利法求解,增加一行元素
⎪⎪⎪⎪⎪⎪⎭⎫ ⎝
⎛000003030203020102030304020302030401030604050~⎪⎪⎪⎪⎪⎪⎭⎫
⎝⎛0000101001010202030
010*******
503040
00
00~⎪⎪
⎪
⎪
⎪⎪
⎭⎫
⎝⎛1001010100000201030000201050204000000
此时方案最优,最少人数人7010202020*=+++=Z
方案为周一上美术课,周三上艺术课,周四上音乐课,周五上文学课。
六、解
S
t
如图所示,最多只能有四架飞机出航:A 1—B 1,A 2—B 5,A 3—B 3,A 4—B 2
七、解:
1、(1)2321≥++x x x
(2)024242=+=+x x x x 或
2、运费还可以减少,此方案不是最优方案
3、在多阶段决策过程中,最优决策序列具有这种性质,即不管该序列上某状态以前的状态和决策如何,余下的决策序列必构成该状态的最优决策序列。
